前の30件 | -
No.369 - 高校数学で理解する素数判定の数理 [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
今まで「高校数学で理解する・・・」という記事を何回か書きましたが、その中に暗号についての一連の記事があります。
No.310「高校数学で理解するRSA暗号の数理(1)」
No.311「高校数学で理解するRSA暗号の数理(2)」
No.313「高校数学で理解する公開鍵暗号の数理」
No.315「高校数学で理解する楕円曲線暗号の数理(1)」
No.316「高校数学で理解する楕円曲線暗号の数理(2)」
の5つです。これらは公開鍵暗号と、その中でも代表的な RSA暗号、楕円曲線暗号の数学的背景を書いたものです。情報通信をインフラとする現代社会は、この公開鍵暗号がなくては成り立ちません。"数学の社会応用" の典型的な例と言えるでしょう。
これらの暗号では、10進数で数10桁~数100桁の素数が必要です。ないしは、数10桁~数100桁の数が素数かどうかを判定する必要があります。
たとえば、マイナンバー・カードの認証に使われている RSA暗号の公開鍵は 2048ビットで、1024ビットの素数2つを掛け合わせて個人ごとに作られます。1024ビットということは \(2^{1023}\) ~ \(2^{1024}-1\) の数であり、10進では約300桁の巨大数です。素数を生成する式はないので、作るためには1024ビットの数をランダムに選び、それが素数かどうかを実用的な時間で判定する必要があります。
ビットコインのデジタル署名で使われているのは、256ビットの楕円曲線暗号です。この暗号の公開鍵は一般に公開されていますが(暗号の仕組みから個人ごとに作る必要はない)、この公開鍵を設計するときに必要なのは、256ビット=約80桁(10進)の数が素数かどうかを判定することです。
つまり、公開鍵暗号の基礎となっている技術が「素数判定」なのです。そこで今回は、素数判定の方法で一般的な「Miller-Rabin テスト」の数学的背景を書きます。Miller、Rabin は、このテストを考案した数学者2人の名前です。
前提知識
本論に入る前に前提知識について整理します。「高校数学で理解する・・・」というタイトルは「高校までで習う数学の知識だけを前提とする」という意味です。従って、その前提からはずれるものはすべて証明するのが基本方針です。
今回は、以前の「高校数学で理解する・・・」で証明した事項を前提知識とします。
・合同式
・フェルマの小定理
・中国剰余定理
・オイラー関数
・群
です。また、暗号の記事ではありませんが、No.355「高校数学で理解するガロア理論(2)」の次の事項も前提とします。
・剰余群
・既約剰余類群
・巡回群
・群の直積
・群の同型
以下、剰余群以下の事項について、素数判定に関わるところを簡単に復習します。
剰余群
整数の集合を \(Z\) で表し、整数 \(n\) の倍数の集合を \(nZ\) とします。また、
\(\ol{j_n}\)
は、\(\bs{n}\) で割った余りが \(\bs{j}\) である整数の集合とします(剰余類と呼ばれる)。たとえば、\(n=9,\:j=2\) とすると、\(\ol{2_9}\) は「\(9\) で割ったら \(2\) 余る整数の集合」で、
\(\ol{2_9}=\{\:\cd,\:-16,\:-7,\:2,\:11,\:20,\:29,\:\cd\:\}\)
です。剰余群 \(Z/nZ\) とは、
\(Z/nZ=\{\ol{0_n},\:\ol{1_n},\:\cd\:,\:\ol{(n-1)_n}\}\)
で示される「無限集合を元とする有限集合」です。\(n=9\) だと、
\(Z/9Z=\{\ol{0_9},\:\ol{1_9},\:\ol{2_9},\:\ol{3_9},\:\ol{4_9},\:\ol{5_9},\:\ol{6_9},\:\ol{7_9},\:\ol{8_9}\}\)
です。この集合の元の加算 \(+\) を、
\(\ol{i_n}+\ol{j_n}=\ol{(i+j)_n}\)
と定義すると(右辺は整数のたし算)、\(Z/nZ\) はこの演算について群の定義を満たし(=加法群)、この群を剰余群と呼びます。一般に有限群 \(G\) の元の数=群位数を \(|G|\) で表しますが、剰余群の群位数は、
\(|Z/nZ|=n\)
です。以降、剰余類と整数を同一視して、
\(Z/9Z=\{0,\:1,\:2,\:3,\:4,\:5,\:6,\:7,\:8\}\)
というように書きます。従って、\(1\) は 整数の \(1\) を表すことも、また、\(Z/nZ\) の元(= \(n\) で割ると \(1\) 余る数の集合= \(\ol{1_n}\))を表すこともあります。どちらかは文脈で決まります。
既約剰余類群
\(Z/nZ\) の元 \(\{0,\:1,\:\cd\:,\:j,\:\cd\:,\:n-1\}\) から \(\mr{gcd}(j,\:n)=1\) となる元(= \(n\) と素な元)だけを取り出した集合を既約剰余類群といい、\((Z/nZ)^{*}\) で表します。例をあげると、
\(\begin{eqnarray}
&&\:\:(Z/9Z)^{*}&=\{\ol{1_9},\:\ol{2_9},\:\ol{4_9},\:\ol{5_9},\:\ol{7_9},\:\ol{8_9}\}\\
&&&=\{\:1,\:2,\:4,\:5,\:7,\:8\:\}\\
\end{eqnarray}\)
です。この集合の、元と元との乗算 \(\cdot\) を、
\(\ol{i_n}\cdot\ol{j_n}=\ol{(ij)_n}\)
で定義すると(右辺の \(ij\) は整数の乗算)、\((Z/nZ)^{*}\) は乗算を演算とする群になります(=乗法群)。従って、任意の元 \(a\in(Z/nZ)^{*}\) の逆元 \(a^{-1}\) が存在して、
\(a\cdot a^{-1}=1\)
が成り立ちます。つまり乗算と除算が自由にできます。\((Z/9Z)^{*}\) の例では、
\(\begin{eqnarray}
&&\:\:1^{-1}&=1&&\\
&&\:\:2^{-1}&=5, &5^{-1}&=2\\
&&\:\:4^{-1}&=7, &7^{-1}&=4\\
&&\:\:8^{-1}&=8&&\\
\end{eqnarray}\)
です。\((Z/nZ)^{*}\) の群位数は、オイラー関数 \(\varphi\) を使って、
\((Z/nZ)^{*}=\varphi(n)\)
で表されます。\(\varphi(n)\) は「\(n\) 以下で \(n\) とは互いに素な数の個数」です。\(p,\:q\) を異なる素数とすると、
\(\begin{eqnarray}
&&\:\:\varphi(p)&=p-1\\
&&\:\:\varphi(pq)&=(p-1)(q-1)\\
&&\:\:\varphi(p^2)&=p(p-1)\\
\end{eqnarray}\)
などが成り立ちます。
巡回群
\(p\) を奇素数(\(p\neq2\))とすると、既約剰余類群 \((Z/pZ)^{*}\) は生成元 \(g\) をもちます。つまり、
\((Z/pZ)^{*}=\{\:g,\:g^2,\:g^,\:\cd\:,\:g^{p-1}=1\:\}\)
と表され、群位数は \(\varphi(p)=p-1\) です。このように、一つの生成元の累乗で全ての元が表せる群を巡回群と言います(\(1\) の次は再び \(g\) になって巡回する)。また、\(n\) が \(p\) の累乗、\(n=p^{\al}\:(\al\geq2)\) のときも \((Z/p^{\al}Z)^{*}\) は生成元をもつ巡回群です。\(\al=2\) のときの群位数は、
\(|(Z/p^2Z)^{*}|=\varphi(p^2)=p(p-1)\)
です。\((Z/9Z)^{*}\) の場合、群位数は \(\varphi(9)=6\) で、\(g=2\) と \(g=5\) が生成元になり、
\(\begin{eqnarray}
&&\:\:(Z/9Z)^{*}&=\{2,\:2^2=4,\:2^3=8,\:2^4=7,\:2^5=5,\:2^6=1\}\\
&&&=\{5,\:5^2=7,\:5^3=8,\:5^4=4,\:5^5=2,\:5^6=1\}\\
\end{eqnarray}\)
などと表せます。\(1,\:4,\:7,\:8\) は生成元ではありません。
群の直積、群の同型
\(G\) と \(H\) を有限群とし、その元を \(g_i\in G,\:h_j\in H\) として、2つの元のペア、
\((g_i,\:h_j)\) \((1\leq i\leq|G|,\:1\leq j\leq|H|)\)
を作るとき、すべてのペアを元とする集合を「群の直積」と言い、\(G\times H\) で表します。元と元の演算を \(g_i\) と \(h_i\) で個別に行うことで、直積も群になります。その群位数は、
\(|G\times H|=|G|\cdot|H|\)
です。
中国剰余定理によると、\(m,\:n\) が互いに素のとき、
\(x\equiv a\:\:(\mr{mod}\:m)\)
\(x\equiv b\:\:(\mr{mod}\:n)\)
の連立合同方程式は、\(mn\) を法として唯一の解を持ちます。\(x\) を \(m\) で割った余りを \(x_m\)、\(n\) で割った余りを \(x_n\) とし、
\(f\::\:x\:\longrightarrow\:(x_m,\:x_n)\)
の写像 \(f\) を定義すると、中国剰余定理によって \(f\) は1対1写像であり、かつ、
\(\begin{eqnarray}
&&\:\:f(xy)&=((xy)_m,\:\:(xy)_n)\\
&&&=((x_m\cdot y_m)_m,\:\:(x_n\cdot y_n)_n)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(x)f(y)&=(x_m,\:x_n)\:(y_m,\:y_n)\\
&&&=((x_m\cdot y_m)_m,\:\:(x_n\cdot y_n)_n)\\
\end{eqnarray}\)
なので、
\(f(xy)=f(x)f(y)\)
が成り立ちます。また同様に \(f(x+y)=f(x)+f(y)\) であり、\(f\) は演算を保存する同型写像です。従って、剰余群 \(Z/mnZ\) は、2つの群の直積との間で "群の同型" が成り立ち、
\(Z/mnZ\cong Z/mZ\times Z/nZ\)
です(=中国剰余定理の群による表現)。また 既約剰余類群 \((Z/mnZ)^{*}\) は、
\((Z/mnZ)^{*}\cong(Z/mZ)^{*}\times(Z/nZ)^{*}\)
と直積で表現できます。\(m,\:n\) がともに奇素数で \(m=p,\:n=q\:(\neq p)\)だと、
\((Z/pqZ)^{*}\cong(Z/pZ)^{*}\times(Z/qZ)^{*}\)
です。\((Z/pqZ)^{*}\) は巡回群でありませんが、2つの巡回群の直積で表現できることになります。
以上を前提として「Miller-Rabin テスト」のことを書きますが、これは「確率的素数判定アルゴリズム」の一種です。
「Miller-Rabin テスト」は「フェルマ・テスト」の発展形と言えるものです。そこでまず、「フェルマ・テスト」の原理になっている「フェルマの小定理」から始めます。
フェルマの小定理
素数がもつ重要な性質を示したのが、フェルマの小定理です。
この定理の \(a\) を、指数関数の「底(base)」と呼びます。偶数の素数は \(2\) しかないので、以降、\(\bs{n}\) は \(\bs{3}\) 以上の奇数として素数判定を考えます。フェルマの小定理を素数判定用に少々言い換えると、次のように表現できます。
このフェルマの小定理の対偶は次のようになります。
\(n\) が \(3\) 以上の奇数の合成数のとき、\(1\leq a\leq n-1\) について、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
\(a^{n-1}\not\equiv1\:\:(\mr{mod}\:n)\)
のどちらになるのか、\(a\) ごとに検討してみます。もちろん \(a=1\) なら \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) です。また、\(a=n-1\:(=-1)\) でも、\(n-1\) が偶数なので、 \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) です。
また、\(a\) が \(n\) と互いに素でないとき、つまり \(\mr{gcd}(n,\:a)\neq1\) ときは \(a^{n-1}\not\equiv1\:\:(\mr{mod}\:n)\) です。なぜなら、\(a\) と \(n\) の最大公約数を \(d\:(\neq1)\) として、もし \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) だとすると、
\(a^{n-1}=k\cdot n+1\:\:(k\) は整数\()\)
と表わせますが、
左辺について \(d\mid a^{n-1}\)
右辺について \(d\nmid(k\cdot n+1)\)
となってしまい、矛盾するからです。
\(a\neq1,\:n-1\)、 \(\mr{gcd}(n,\:a)=1\) のときにどうなるかは、\(a\) によって両方がありえます。ためにしに、\(n=21\) で計算してみると、
となります。色を塗った10個が \(a\neq1,\:n-1\)、 \(\mr{gcd}(n,\:a)=1\) のところですが、\(\equiv1\) \((a=8,\:13)\) と \(\not\equiv1\)(それ以外の8個)があることがわかります。とにかく、上の表で一つでも \(\bs{\not\equiv1}\) があれば、\(n\) は合成数だと判断できます。
このフェルマの小定理の対偶を利用して、巨大整数(数10桁~数100桁) \(n\) が素数かどうかを確率的に判定できます。つまり、\(1\leq a\leq n-1\) である数をランダムに、順々に選び、ある \(a\) がフェルマの条件に反すれば、その時点で \(n\) は合成数と判定します。何回か試行してすべての \(a\) がフェルマの条件に合致するなら(=合成数だと判定できなければ)、\(n\) は素数の可能性が高い。
しかし困ったことに「合成数でありながら、多数の \(\bs{a}\) でフェルマの条件を満たしてしまう \(\bs{n}\)」が存在します。"カーマイケル数" です。最小のカーマイケル数は \(561=3\cdot11\cdot17\) ですが、\(\mr{gcd}(561,\:a)=1\) であるすべての \(a\:\:(1\leq a\leq560)\) で、
\(a^{560}\equiv1\:\:(\mr{mod}\:561)\)
が成り立ちます。その理由ですが、\(a\) を \(3,\:11,\:17\) のすべてと素な任意の数(= \(561\) と素な任意の数)とすると、フェルマの小定理より、
\(\begin{eqnarray}
&&\:\:a^{2}&\equiv1\:\:(\mr{mod}\:3)\\
&&\:\:a^{10}&\equiv1\:\:(\mr{mod}\:11)\\
&&\:\:a^{16}&\equiv1\:\:(\mr{mod}\:17)\\
\end{eqnarray}\)
が成り立ちます。\(560\) は、\(2,\:10,\:16\) 全部の倍数なので、それぞれの合同式の両辺を適切に累乗すると、
\(a^{560}\equiv1\:\:(\mr{mod}\:3)\)
\(a^{560}\equiv1\:\:(\mr{mod}\:11)\)
\(a^{560}\equiv1\:\:(\mr{mod}\:17)\)
が成り立つ。そうすると、中国剰余定理により、
\(a^{560}\equiv1\:\:(\mr{mod}\:3\cdot11\cdot17)\)
が成り立ちます。\(560\) 以下で \(561\) と素な数の個数は、オイラー関数 \(\varphi(n)\)(= \(n\) 以下で \(n\) と素な数の個数)を使うと、
\(\begin{eqnarray}
&&\:\:\varphi(561)&=\varphi(3)\varphi(11)\varphi(17)\\
&&&=2\cdot10\cdot16=320\\
\end{eqnarray}\)
なので、\(\dfrac{320}{560}=\dfrac{4}{7}\)、つまり半数以上の \(a\) でフェルマの条件が満たされることになります。これを一般的に言うと、カーマイケル数 \(c\) が3個の素数 \(p,\:q,\:r\) の積の場合、
\(\begin{eqnarray}
&&\:\:c&=pqr\\
&&\:\:\varphi(c)&=(p-1)(q-1)(r-1)\\
\end{eqnarray}\)
なので、この2つの比は、\(p,\:q,\:r\) が大きくなると \(1\) に近づきます。それは、ほとんど全ての \(a\:\:(1\leq a\leq c-1)\) がフェルマの条件を満たすことを意味します。
カーマイケル数は、特に \(n\) が巨大だと極めて希です。Wikipedia によると、「\(1\) から \(10^{21}\) の間には \(20,138,200\) 個のカーマイケル数があり、これはおよそ \(5\cdot10^{13}\) 個にひとつの割合」だそうです。しかし、カーマイケル数が無限個あることも証明されています。\(n\) が "運悪く" カーマイケル数だと、フェルマ\(\cdot\)テストでは素数と判定されてしまう。つまり、フェルマの条件を使って素数を確率的に判定するアルゴリズムには問題があるわけです。
Miller-Rabin の条件
そこで、素数の条件として、フェルマの条件とは別のものを考えます。フェルマの条件、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
において、\(n\) が素数とすると、\(n-1\) は偶数です。そこで、
\(n-1=2^ek\) (\(e\geq1,\:k\) は奇数)
と表します。この表記を用いて、\(a^{n-1}-1\) という式を因数分解すると、
\(\begin{eqnarray}
&&\:\:a^{n-1}-1&=a^{2^ek}-1\\
&&&=(a^{2^{e-1}k})^2-1\\
&&&=(a^{2^{e-1}k}+1)(a^{2^{e-1}k}-1)\\
&&&=(a^{2^{e-1}k}+1)((a^{2^{e-2}k})^2-1)\\
&&&=(a^{2^{e-1}k}+1)(a^{2^{e-2}k}+1)(a^{2^{e-2}k}-1)\\
&&& \vdots\\
\end{eqnarray}\)
と続きます。結局、因数分解は、
となります。これを \((\br{A})\) 式とします。\(n\) が素数のときは、フェルマの条件を変形すると、
\(a^{n-1}-1\equiv0\:\:(\mr{mod}\:n)\)
なので、フェルマの条件と等価な式は、
\((\br{A})\) 式の右辺 \(\equiv0\:\:(\mr{mod}\:n)\)
であり、ということは、
が成立します。\(\bs{n}\) が素数であるのがポイントです。\(n\) が合成数ならこんなことは言えません。このことより、\(n\) が素数であるための新たな条件が導けます。次項です。
素数の条件(Miller-Rabin)
\(a^{2^ik}\:\:(0\leq i\leq e-1)\) の \(e\) 個の数列を Miller-Rabin 系列と呼ぶことにします。
\(a^k,\:a^{2k},\:a^{4k},\:\cd\:,\:a^{2^{e-1}k}\)
です。この系列は、ある項の2乗が次の項になっています。従って \(\mr{mod}\:n\) でみて \(a^{2^rk}\equiv-1\) になれば、以降の項はすべて \(\equiv1\:(\mr{mod}\:n)\) になります。ということは、系列の中で \(\equiv-1\) となる項は「全く無い」か「一つだけある」のどちらかです。
ちなみに、Miller-Rabin による素数の条件の対偶は次の通りです。これを利用して合成数の判定ができます。
\(\bs{n}\) が素数であれば、フェルマーの条件と Miller-Rabin の条件は等価です。しかし、\(n\) が合成数のときは、フェルマの条件と Miller-Rabin の条件の意味が違ってきます。それが次です。
\(n\) が合成数のとき
\(n\) が合成数のときは、フェルマの条件から Miller-Rabin の条件を導くことはできません。なぜなら「\(n\)が素数」が導出のキーだからです。つまり、
とすると、\(a\in F\) であっても \(a\in M\) とは限らない。しかし、\((\br{A})\) 式でわかるように \(a\in M\) なら必ず \(a\in F\) です。従って、
\(M\:\subset\:F\)
です。ということは、数 \(a\) についてのフェルマーの条件によって \(n\) が合成数だと判定できなくても(つまり \(a\in F\))、Miller-Rabin の条件で合成数と判定できる(つまり \(a\notin M\))可能性があることになります。つまり合成数の判定においては、Miller-Rabin の条件はフェルマーの条件より厳格です。
しかも Miller-Rabin の条件は、合成数を合成数だと判定できる確率(ないしは判定できない確率)が、\(\bs{n}\) の値にかかわらず示せるのです。それが次の定理です。
Miller-Rabin の定理
\(\bs{n}\) がいかなる数であっても成り立つのがポイントです。実際に計算をしてみます。\(n\) を \(9\leq n < 10000\) である奇数の合成数とします。調べてみると、その総数は \(3771\)個です。そして、
とし、\(3771\)個の \(n\) のうち \(P\geq0.2\) のものをリストアップすると、次の5つだけです。
\(n=9\) のとき、\(P\) は最大値の \(0.25\) です。それ以降、\(n=1891\) のときに \(P\fallingdotseq0.24\) となりますが、\(0.25\) を越える \(n\) は( \(9\leq n < 10000\) では)無いことがわかります。そしてこの定理は、\(\bs{n}\) がいかなる奇数の合成数であっても \(\bs{P\leq0.25}\) と主張しているわけです。
これでまず言えることは、Miller-Rabin の条件にとっての「カーマイケル数のような数」はあり得ないことです。
さらにこの定理によって、素数判定の信頼度を示すことができます。比喩で言うと次のとおりです。
以上の考え方で \(n\) の素数判定をするアルゴリズムが次です。
\(r=40\) だとすると、Miller-Rabin の素数判定アルゴリズムで「素数と判定したにもかかわらず実は合成数」の確率は、
\(\dfrac{1}{4^{40}}\) 以下
であることが保証されます。\(4^{40}\) は、\(\fallingdotseq\:1.2\times10^{24}\) で、\(10\)進数で\(25\)桁の数です。あまりに巨大すぎて想像するのは難しいのですが、たとえば、1秒の \(100\)万分の \(1\) の時間は \(1\) マイクロ秒で、\(1\) 秒間に地球を \(7.5\)周する光が \(300\)メートルしか進まない時間です。一方、宇宙の年齢は \(138\)億年程度と言われています。この宇宙の年齢をマイクロ秒で表すと、\(4.4\times10^{23}\) マイクロ秒です。ということは、\(4^{40}\) はその3倍近い数字です。
\(\dfrac{1}{4^{40}}\) は、数学的には \(0\) ではありませんが、確率としては実用的に \(0\) です。以上が Miller-Rabin の素数判定の原理です。
以降、 なぜ \(\dfrac{1}{4}\) 以下であると言えるのか、その証明をします。
定理を再度述べると次の通りです。
3つのケースにわけて証明します。以降の証明は、後藤・鈴木(首都大学東京)「Miller-Rabin素数判定法における誤り確率の上限」を参考にしました。
② ③ のケースは \(n\) が平方因子を持たないので ① と排他的であり、また ② と ③ も排他的です。いずれの場合も \(n\) が奇数なので、素因数に \(2\) は現れません。以降の3つのケースに分けた証明では、\(p\) を素数としたとき既約剰余類群 \((Z/pZ)^{*}\) 、\((Z/p^2Z)^{*}\) が巡回群であることを利用します。
1. \(n=p^2t\:\:(\:p\)は奇素数。\(t\geq1\) は奇数\()\)
Miller-Rabin の条件を満たす \(a\:(0\leq a\leq n-1)\) の集合を \(M\) とします。上で説明したように、\(n\) が合成数であったとしても Miller-Rabin の条件が成立すればフェルマの条件も成立します(\(n\) が合成数だとその逆は成り立たない)。従って、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
が成り立ちます。このフェルマの条件を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(F\) とすると、\(M\:\subset\:F\) なので元の数は、
\(|M|\leq|F|\)
です。さらに、\(p^2\mid n\)(= \(p^2\) が \(n\) を割り切る)なので、
も同時に成り立ちます。\((\br{B})\) 式を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(R_1\) とすると、\(a\in F\) なら \(a\in R_1\) なので、
\(\begin{eqnarray}
&&\:\:F&\subset R_1\\
&&\:\:|F|&\leq|R_1|\\
\end{eqnarray}\)
が成り立ちます。\(|M|\leq|F|\) とあわせると、
\(|M|\leq|R_1|\)
です。次に、剰余群 \(Z/p^2Z\) の元 で \((\br{B})\) 式を満たす \(a\:(0\leq a\leq p^2-1)\) の集合を \(R_2\) とします。\(x\in R_2\) だとすると、\(\mr{mod}\:p^2\) では、
\(\begin{eqnarray}
&&\:\:x&=x+p^2\\
&&&=x+2p^2\\
&&& \vdots\\
&&&=x+(t-1)p^2\leq p^2t-1\\
\end{eqnarray}\)
です。つまり、\((\br{B})\) 式を満たす \(Z/p^2Z\) の元1個に対して、\((\br{B})\) 式を満たす、\(0\leq a\leq n-1\:(p^2t-1)\) の \(t\)個の数が対応します。従って、
\(t|R_2|=|R_1|\)
です。\(|M|\leq|R_1|\) とあわせると、
\(|M|\leq t|R_2|\)
です。
剰余群 \(Z/p^2Z\) の元で \((\br{B})\) 式を満たすのは、\(p^2\) と互いに素な元だけです。つまり、既約剰余類群 \((Z/p^2Z)^{*}\) の元で \((\br{B})\) 式を満たすものの集合が \(R_2\) であるとも言えます。以降、 \((Z/p^2Z)^{*}\) を使って \(R_2\) の元の数、\(|R_2|\) を見積もります。それには \((Z/p^2Z)^{*}\) が巡回群であることを利用します。
一般に、巡回群においては次が成り立ちます。この定理を \((\br{C})\) とします。
【証明】
\(h=\mr{gcd}(m,\:d)\) とおく。位数 \(d\) の巡回群 \(G\) は、生成元 \(g\) を用いて、
\(G=\{g,\:g^2,\:g^3,\:\cd\:,\:g^{d-1},\:g^d=1\}\)
と表現できる。そこで \(x=g^i\:\:(1\leq i\leq d)\) と表すと、
\(\begin{eqnarray}
&&\:\:(g^i)^m&=1\\
&&\:\:g^{im}&=1\\
\end{eqnarray}\)
なので、\(im\) は群位数 \(d\) の整数倍である。つまり、
\(d\mid im\)
である。\(h=\mr{gcd}(m,\:d)\) として \(d\,'=\dfrac{d}{h}\) \(m\,'=\dfrac{m}{h}\) とおくと、
\(d\,'\mid im\,'\)
になるが、\(d\,'\) と \(m\,'\) は互いに素なので、
\(d\,'\mid i\)
である。つまり \(i\) は \(d\,'=\dfrac{d}{h}\) の倍数である。従って、\(1\leq i\leq d\) であることを考慮すると、
\(i=\dfrac{d}{h}\cdot j\:\:(1\leq j\leq h)\)
と表せる。つまり、\(x^m=1\) を満たす \(x\) の個数は \(h=\mr{gcd}(m,\:d)\) 個である。【証明終】
既約剰余類群 \((Z/p^2Z)^{*}\) は巡回群であり、群位数は\(\varphi(p^2)=p(p-1)\) です。従って、\((Z/p^2Z)^{*}\) の元で \(a^{n-1}=1\) を満たす元の数(\(=|R_2|\))は定理 \((\br{C})\) により、
\(\begin{eqnarray}
&&\:\:|R_2|&=\mr{gcd}(p(p-1),\:n-1)\\
&&&=\mr{gcd}(p(p-1),\:p^2t-1)\\
\end{eqnarray}\)
となります。ここで、\(p^2t-1\) は \(p\) で割り切れないので、
\(\mr{gcd}(p(p-1),\:p^2t-1)=\mr{gcd}(p-1,\:p^2t-1)\)
ですが、この式の右辺は \(p-1\) 以下です。従って、
\(|R_2|\leq p-1\)
です。\(|M|\leq t|R_2|\) とあわせると、
\(|M|\leq t(p-1)\)
が得られました。従って、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&\leq\dfrac{t(p-1)}{tp^2-1}\\
&&&=\dfrac{p-1}{p^2-\dfrac{1}{t}}\\
\end{eqnarray}\)
となります。定義によって \(t\geq1,\:p\geq3\) ですが、上式の右辺は \(t\) についても \(p\) についても単調減少です。従って右辺の最大値は \(t=1,\:p=3\) のときで、
\(\dfrac{t(p-1)}{tp^2-1}\leq\dfrac{1}{4}\)
です。結論として、
\(\dfrac{|M|}{n-1}\leq\dfrac{1}{4}\)
となり、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(\dfrac{1}{4}\) 未満であることが証明されました。
ちなみに、この証明はフェルマの条件しか使っていません。つまり、
と言えます。ということは、平方因子をもつ数はカーマイケル数にはなりえないことが分かります。
2. \(n=p_1\cdot p_2\:(\:p_1,\:p_2\) は奇素数で \(p_1\neq p_2\:)\)
Miller-Rabin の定理を再掲します。
証明のポイントは2つあります。(2) の条件に関する Miller-Rabin 系列、
\(a^k,\:a^{2k},\:\:a^{4k},\:\cd\:,\:a^{(e-1)k}\)
を考えると、ある項の2乗が次の項なので、\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) となる項があれば、それ以降の項は全て \(\equiv1\) となります。つまり、\(a^{2^rk}\equiv-1\) となる項は1つしかありません。従って、\(r\) を一つ決めたときに \(a^{2^rk}\equiv-1\) を満たす \(a\) の集合を \(A_2(r)\) とし、(2) を満たすすべての \(a\) の集合を \(A_2\) とすると、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
が成り立ちます。さらに (1) の条件を満たす \(a\) の集合を \(A_1\) とすると、(1) と (2) は排他的です。従って、Miller-Rabin の条件を満たす \(a\) の集合を \(M\) とすると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&=|A_1|+\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\\
\end{eqnarray}\)
です。このことを以下の証明で利用します。もう一つの証明のポイントは、「1.\(\bs{n=p^2t\:\:(\:p}\) は奇素数。\(\bs{t\geq1}\) は奇数\(\bs{)}\)」での証明と同じように、巡回群の性質を利用することです。
まず前提として、Miller-Rabin の条件を満たす \(a\:(0\leq a\leq n-1)\) は、フェルマの条件、\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) も満たしますが、これが成り立つ \(a\) は \(n\) とは素です。従って、既約剰余類群 \((Z/nZ)^{*}\:=\:(Z/p_1p_2Z)^{*}\) の範囲で \(a\) の個数を検討します。
もちろん、\(p_1\neq p_2\) なので、既約剰余類群 \((Z/p_1p_2Z)^{*}\) は巡回群ではありません。しかし \(p_1,\:p_2\) が互いに素なので、\((Z/p_1p_2Z)^{*}\) は2つの既約剰余類群の直積と同型であり、
\((Z/p_1p_2Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
と表せます。つまり、\(a\in(Z/p_1p_2Z)^{*}\) とし、
\(a\) を \(p_1\) で割った余りを \(a_{p_1}\)
\(a\) を \(p_2\) で割った余りを \(a_{p_2}\)
と書くと、\(a_{p_1}\in(Z/p_1Z)^{*},\:\:a_{p_2}\in(Z/p_2Z)^{*}\) ですが、ここで、
\(f\::\:a\:\longrightarrow\:(a_{p_1},\:a_{p_2})\)
の写像を定義すると、この写像は1対1(全単射)で、同型写像であり、上の「直積と同型」の式が成り立ちます。同型写像は \(f(xy)=f(x)f(y)\) というように演算を保存するので、演算してから写像した結果と写像してから演算した結果は同じです。
また、この \((Z/p_1Z)^{*}\) と \((Z/p_2Z)^{*}\) は、\(p_1\) と \(p_2\) が素数なので、生成元をもつ巡回群です。それぞれの群位数は、
\(\begin{eqnarray}
&&\:\:|(Z/p_1p_2Z)^{*}|&=\varphi(p_1p_2)\\
&&&=(p_1-1)(p_2-1)\\
\end{eqnarray}\)
\(|(Z/p_1Z)^{*}|=\varphi(p_1)=p_1-1\)
\(|(Z/p_2Z)^{*}|=\varphi(p_2)=p_2-1\)
であり、
\(|(Z/p_1p_2Z)^{*}|=|(Z/p_1Z)^{*}|\cdot|(Z/p_2Z)^{*}|\)
が成り立ちます。ここで \((Z/p_1Z)^{*}\) の任意の部分集合を \(H_1\)、\((Z/p_2Z)^{*}\) の任意の部分集合を \(H_2\) とします。
\(H_1\subset(Z/p_1Z)^{*}\)
\(H_2\subset(Z/p_2Z)^{*}\)
です。\((Z/p_1p_2Z)^{*}\) の元 \(a\) で、
\(a_{p_1}\in H_1\)
\(a_{p_2}\in H_2\)
となる \(a\) を考え、このような \(a\) の集合を \(H\) と書くと、
\(f\::\:a\:\longrightarrow\:(a_{p_1},\:\:a_{p_2})\)
の写像は1対1対応であり(=中国剰余定理)、集合の元の数については、
\(|H|=|H_1|\cdot|H_2|\)
が成り立ちます。
以上を踏まえて証明に進みます。一般に、
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\) なら
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\)
が言えます。また、\(p_1\) と \(p_2\) は互いに素なので、
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\) なら
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\)
も言えます。なぜなら、\(p_1\mid(x-y)\) かつ \(p_2\mid(x-y)\) なら、\(p_1p_2\mid(x-y)\) だからです。つまり、
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\)
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\)
の2つは、\(p_1,\:p_2\) が素数という前提では等価です。従って、Miller-Rabin の条件は次のように言い換えることができます。
このように言い換えて、\((Z/p_1p_2Z)^{*}\) での問題を、\((Z/p_1Z)^{*}\) と \((Z/p_2Z)^{*}\) の問題に置き換えます。Miller-Rabin の条件を満たす、
とすると、元の数については、
\(|M|=|M_1|\cdot|M_2|\)
が成り立ちます。以降、(1)\(,\) (2) の条件ごとに \(|M_1|\) と \(|M_2|\) を見積もることで、条件ごとの \(|M|\) を見積もり、そこから目的である \(|M|\) の数を評価します。(1)\(,\) (2) の条件ごとの \(M\) については、既に上で使ったように、
(1)を満たす \(M\) の部分集合を \(A_1\)
(2)を満たす \(M\) の部分集合を \(A_2\)
とします。
\(n-1=2^ek\) とおいたのと同じように、
\(p_1-1=2^{e_1}k_1\) (\(e_1\geq1,\:k_1\):奇数)
\(p_2-1=2^{e_2}k_2\) (\(e_2\geq1,\:k_2\):奇数)
とします。ここで、
\(e_1\leq e_2\)
とします。\(p_1\) と \(p_2\) は入れ替えてもよいので、こうすることで一般性は失われません。まず初めに、\(e,\:e_1,\:e_2\) の関係を整理しておきます。\(n-1=2^ek\) の式ですが、
\(\begin{eqnarray}
&&\:\:n-1&=p_1\cdot p_2-1\\
&&&=(2^{e_1}k_1+1)\cdot(2^{e_2}k_2+1)-1\\
&&&=2^{e_1+e_2}k_1k_2+2^{e_1}k_1+2^{e_2}k_2\\
&&&=2^{e_1}(2^{e_2}k_1k_2+k_1+2^{e_2-e_1}k_2)\\
\end{eqnarray}\)
と計算されます。この式を、
\(n-1=2^{e_1}\cdot K\)
\(K=2^{e_2}k_1k_2+k_1+2^{e_2-e_1}k_2\)
と表わすと、
\(e_1 < e_2\) のときは、\(K\) は奇数なので \(e=e_1\)
\(e_1=e_2\) のときは、\(K\) は偶数なので \(e > e_1\)
となり、いずれにせよ、
\(e_1\leq e\)
です。
以降、
\(e_1 < e_2\)
\(e_1=e_2\)
の2つに分けて証明します。
2.1 \(e_1 < e_2\) の場合
(1)が成立するとき
(1) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_1\) とします。巡回群に関する定理 \((\br{C})\) により、\((Z/pZ)^{*}\) の群位数は \(p-1\) なので、
\(a^k=1\) となる \((Z/p_1Z)^{*}\) の元は \(\mr{gcd}(k,\:p_1-1)\) 個
\(a^k=1\) となる \((Z/p_2Z)^{*}\) の元は \(\mr{gcd}(k,\:p_2-1)\) 個
です。また、\(n=p_1p_2\) のとき、
\((Z/nZ)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
の同型が成り立つので、
\(\begin{eqnarray}
&&\:\:|A_1|&=\mr{gcd}(k,\:p_1-1)\cdot\mr{gcd}(k,\:p_2-1)\\
&&&=\mr{gcd}(k,\:2^{e_1}k_1)\cdot\mr{gcd}(k,\:2^{e_2}k_2)\\
\end{eqnarray}\)
です。ここで、\(k,\:k_1,\:k_2\) は全て奇数です。従って、
\(\mr{gcd}(k,\:2^{e_1}k_1)=\mr{gcd}(k,\:k_1)\)
\(\mr{gcd}(k,\:2^{e_2}k_2)=\mr{gcd}(k,\:k_2)\)
が成り立ち、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
となります。ここで \(|A_1|\) の上限値を評価すると、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
であり、
\(|A_1|\leq k_1k_2\)
が結論づけられます。
(2)が成立するとき
(2) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_2\) とします。まず、\(0\leq r\leq e-1\) である \(r\) を一つ固定して考え、
\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_1)\) かつ
\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_2)\)
であるような集合を \(A_2(r)\) とします。そうすると、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
が成り立ちます。まず、次を証明します。
【証明】
\((Z/p_1Z)^{*}\) は群位数 \(p_1-1\) の巡回群なので、その生成元を \(g\) とする。ここで、
\(g^{\frac{p_1-1}{2}}\)
を考えると、生成元の定義上、\(g^{p_1-1}=1,\) \(g^x\neq1\:(1\leq x < p_1-1)\) なので、
\(\begin{eqnarray}
&&\:\:g^{\frac{p_1-1}{2}}&\neq1\\
&&\:\:(g^{\frac{p_1-1}{2}})^2&=1\\
\end{eqnarray}\)
であり、つまり、
\(g^{\frac{p_1-1}{2}}=-1\:(=p_1-1)\)
である。\(a^{2^rk}=-1\) が成り立つ \(a\) を、生成元 \(g\) を用いて、
\(a=g^x\:\:(1\leq x\leq p_1-1)\)
と表すと、
だが、\(p_1-1=2^{e_1}k_1\) なので、
\(g^{2^rkx}=g^{2^{e_1-1}k_1}\)
が成り立つ。ここで一般的に \((Z/pZ)^{*}\) の生成元を \(g\) とし、
\(g^s=g^t\)
なら、\(j\) を整数として、
\(\begin{eqnarray}
&&\:\:g^{p-1}&=1\\
&&\:\:g^{j(p-1)}&=1\\
\end{eqnarray}\)
なので、
\(g^s=g^{t+j(p-1)}\)
である。つまり、
\(s\equiv t\:\:(\mr{mod}\:p-1)\)
が成り立つ。従って、
\(2^rkx\equiv2^{e_1-1}k_1\:\:(\mr{mod}\:p_1-1)\)
であり、\((\br{E})\) 式は \((\br{D})\) 式と等価である。\((\br{E})\) 式を解いて \(x\) を求めると、そこから \(a=g^x\) で \(a\) が求まる。
ここで、\(r\geq e_1\) と仮定すると、\((\br{E})\) 式は、
\(2^rkx-2^{e_1-1}k_1\equiv0\:\:(\mr{mod}\:2^{e_1}k_1)\)
と書ける。この \((\br{F})\) 式の \((2^{r-e_1+1}kx-k_1)\) の項に着目すると、\(r-e_1+1\geq1\) であり、\(k_1\) は奇数なので「偶数 - 奇数」=「奇数」である。そうすると、\((\br{F})\) 式の左辺は \(2^{e_1-1}\) の奇数倍であり、法である \(2^{e_1}k_1\) では割り切れず、\((\br{F})\) 式は成り立たない。つまり、\(a^{2^rk}=-1\) の解は、\(r\geq e_1\) のときには無い。
一方、\(r < e_1\) のとき \((\br{E})\) 式は、
と書ける。この \((\br{F}\,')\) 式が成り立つためには、\((kx-2^{e_1-r-1}k_1)\) の項は約数として \(2^i\:(i\geq e_1-r\geq1)\) を持つ必要があるが(少なくとも偶数である必要)、\(kx\) と \(2^{e_1-r-1}k_1\) はともに奇数にも偶数にもなり得るので、 \((\br{F}\,')\) 式の成立可能性に問題はない。そこで、以降で \(r < e_1\) のときの \((\br{E})\) 式の解の個数を検討する。
において、
\(\begin{eqnarray}
&&\:\:h&=\mr{gcd}(k,\:k_1)\\
&&\:\:k\,'&=\dfrac{k}{h}\\
&&\:\:k_1{}^{\prime}&=\dfrac{k_1}{h}\\
\end{eqnarray}\)
とおく。\(k\,'\) と \(k_1{}^{\prime}\) は互いに素で、また、\(k,\:k_1\) が奇数なので、\(h,\:k\,',\:k_1{}^{\prime}\) は奇数である。\(r < e_1\) つまり \(r\leq e_1-1\) の条件があるので、\((\br{E})\) 式の両辺と法を \(2^rh\) で割ると、
となる。一般的に、
\(ax\equiv b\:\:(\mr{mod}\:m)\)
の合同方程式は、\(a\) が \(m\) と素なときには \(b\) の値にかかわらず解があって、その解は \(m\) を法として唯一である(下記)。
\((\br{G})\) 式 をみると、\(k\,'\) と \(k_1{}^{\prime}\) は互いに素であり、かつ奇数なので、\((\br{G})\) 式における \(k\,'\) と、法である \(2^{e_1-r}k_1{}^{\prime}\) は互いに素である。ということは、
\((\br{G})\) 式は、法 \(2^{e_1-r}k_1{}^{\prime}\) で唯一の解をもつ
ことになる。\((\br{G})\) 式は \((\br{E})\) 式の両辺と法を \(2^rh\) で割ったものであった。つまり、\((\br{G})\) 式の法は、
\(2^{e_1-r}k_1{}^{\prime}=\dfrac{2^{e_1}k_1}{2^rh}\)
である。ということは、\((\br{G})\) 式の、法 \(2^{e_1-r}k_1{}^{\prime}\) での唯一の解は、法 \(2^{e_1}k_1\) である \((\br{E})\) 式の解、\(2^rh=2^r\cdot\mr{gcd}(k,\:k_1)\) 個に対応する。\((\br{E})\) 式は \((\br{D})\) 式と等価なので、これで、
が証明できた。【証明終】
ここまでで、
\((Z/p_1Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は
\(r\geq e_1\) のとき \(0\) 個
\(r < e_1\) のとき \(2^r\cdot\mr{gcd}(k,\:k_1)\) 個
であることが分かりました。この議論は \((Z/p_2Z)^{*}\) のときにも全く同じようにできて、
\((Z/p_2Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は
\(r\geq e_2\) のとき \(0\) 個
\(r < e_2\) のとき \(2^r\cdot\mr{gcd}(k,\:k_2)\) 個
が言えます。この結果を踏まえて、
を求めます。これは、
\((Z/p_1p_2Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
の直積関係を利用すると、\(e_1 < e_2\) の関係を考慮して、
\(r < e_1\) のとき
\(\begin{eqnarray}
&&\:\: |A_2(r)|&=2^r\cdot\mr{gcd}(k,\:k_1)\cdot2^r\cdot\mr{gcd}(k,\:k_2)\\
&&&=4^r\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\\
\end{eqnarray}\)
\(r\geq e_1\) のとき
\(|A_2(r)|=0\)
となります。ここから \(|A_2|\) を計算するには、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
ですが、\(e_1\leq e\) の関係があるので、\(e-1\) までの総和は \(e_1-1\) までの総和に等しいことになります。つまり、
\(\begin{eqnarray}
&&\:\:|A_2|&=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\\
&&&=\displaystyle\sum_{r=0}^{e_1-1}|A_2(r)|\\
&&&=\displaystyle\sum_{r=0}^{e_1-1}4^r\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\\
\end{eqnarray}\)
の式が成り立ちます。この式に等比数列の総和である、
\(\displaystyle\sum_{r=0}^{e_1-1}4^r=\dfrac{4^{e_1}-1}{4-1}=\dfrac{4^{e_1}-1}{3}\)
を代入すると、
\(|A_2|=\dfrac{4^{e_1}-1}{3}\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
です。ここで、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
の関係を利用すると、
\(|A_2|\leq\dfrac{4^{e_1}-1}{3}k_1k_2\)
となります。ここまでの式は、\(e_1 < e_2\) でなくても \(e_1\leq e_2\) なら成り立つことが導出過程から分かります。
以上の計算で \(|M|\) を評価できます。
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq k_1k_2+\dfrac{4^{e_1}-1}{3}k_1k_2\\
\end{eqnarray}\)
この計算をもとに \(1\leq a\leq n-1\) の \(n-1\) 個のうちの \(|M|\) の割合を評価すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2}\\
&&&\leq\dfrac{1}{2^{e_1+e_2}}\left(1+\dfrac{4^{e_1}-1}{3}\right)\\
&&&=\dfrac{1}{2^{e_1+e_2}}\cdot\dfrac{2+4^{e_1}}{3}\\
\end{eqnarray}\)
となります。ここで、\(\bs{e_1 < e_2}\) なので、\(\bs{2e_1+1\leq e_1+e_2}\) です。従って、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{2e_1+1}}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{2+4^{e_1}}{6\cdot4^{e_1}}\\
\end{eqnarray}\)
ですが、この最後の式の最大値は \(e_1=1\) のときです。これを代入すると、
\(\dfrac{|M|}{n-1} < \dfrac{6}{24}=\dfrac{1}{4}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(e_1 < e_2\) のときに \(\dfrac{1}{4}\) 未満であることが証明されました。
2.2 \(e_1=e_2\) の場合
(1)が成立するとき
\(e_1 < e_2\) と全く同じ考え方で、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
です(\(k,\:k_1,\:k_2\) は奇数)。ここで、一般的には、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
が成り立ちますが、\(e_1=e_2\) だと、
\(\mr{gcd}(k,\:k_1)=k_1\)
\(\mr{gcd}(k,\:k_2)=k_2\)
が同時に成り立つことはありません。なぜなら、同時に成り立つとすると、
\(k_1\mid k\) かつ \(k_2\mid k\)
ですが、\(n-1=2^ek\) だったので、
\(k_1\mid(n-1)\) かつ \(k_2\mid(n-1)\)
です。ここで、\(n-1\) は
\(\begin{eqnarray}
&&\:\:n-1&=p_1p_2-1\\
&&&=(1+2^{e_1}k_1)\cdot p_2-1\\
&&&\equiv p_2-1\:\:(\mr{mod}\:k_1)\\
\end{eqnarray}\)
となりますが、\(k_1\mid(n-1)\) なので、
\(k_1\mid(p_2-1)\)
\(k_1\mid2^{e_2}k_2\)
\(k_1\mid k_2\)
となります。まったく同様にして、
\(n-1\equiv p_1-1\:\:(\mr{mod}\:k_2)\)
\(k_2\mid(p_1-1)\)
\(k_2\mid2^{e_1}k_1\)
\(k_2\mid k_1\)
です。\(k_1\mid k_2\) かつ \(k_2\mid k_1\) ということは、\(k_1=k_2\) ですが、\(e_1=e_2\) なので、\(p_1=p_2\) となって矛盾します。つまり \(\mr{gcd}(k,\:k_1)=k_1\)、\(\mr{gcd}(k,\:k_2)=k_2\) が同時に成り立つことはありません。そこで、
\(\mr{gcd}(k,\:k_1) < k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
として一般性を失いません。ここで \(k_1\) を素因数分解したときに現れる最小の素数を \(q\:(q\geq3)\)とし、
\(k_1=q\cdot k_0\:\:(k_0\):奇数\()\)
と表します。そうすると、\(\mr{gcd}(k,\:k_1) < k_1\) なので、
\(\mr{gcd}(k,\:k_1)\leq k_0\)
が成り立ち、
\(\dfrac{k_1}{\mr{gcd}(k,\:k_1)}\geq\dfrac{k_1}{k_0}=q\geq3\)
となります。ここから、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
が得られます。そこで、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
をもとに、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
を評価すると、
\(|A_1|\leq\dfrac{1}{3}k_1k_2\)
となります。
(2)が成立するとき
このケースは \(e_1 < e_2\) で導出した、
\(|A_2|\leq\dfrac{4^{e_1}-1}{3}\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
までは全く同じです。ここで、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
によって評価すると、
\(|A_2|\leq\dfrac{1}{3}\cdot\dfrac{4^{e_1}-1}{3}k_1k_2\)
が成り立ちます。
以上の計算から \(|M|\) を評価すると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq\dfrac{1}{3}k_1k_2+\dfrac{1}{3}\cdot\dfrac{4^{e_1}-1}{3}k_1k_2\\
\end{eqnarray}\)
この計算をもとに \(1\leq a\leq n-1\) の \(n\) 個のうちの \(|M|\) の割合を計算すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2}\\
&&&\leq\dfrac{1}{2^{e_1+e_2}}\cdot\dfrac{1}{3}\left(1+\dfrac{4^{e_1}-1}{3}\right)\\
&&&=\dfrac{1}{2^{2e_1}}\cdot\dfrac{1}{3}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{1}{4^{e_1}}\cdot\dfrac{1}{3}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{1}{3}\left(\dfrac{2}{3\cdot4^{e_1}}+\dfrac{1}{3}\right)\\
\end{eqnarray}\)
となります。この最後の式の最大値は \(e_1=1\) のときです。代入すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{3}\left(\dfrac{1}{6}+\dfrac{1}{3}\right)\\
&&&=\dfrac{1}{6} < \dfrac{1}{4}\\
\end{eqnarray}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は、\(e_1=e_2\) のときにも \(\dfrac{1}{4}\) 未満であることが証明されました。
3. \(n=p_1\cdot p_2\cdot\cd\cdot p_m\:\:(\:m\geq3\:)\)
\(n\) が3個以上の相異なる奇素数の積に素因数分解される場合です。この場合も、基本的には \(n=p_1\cdot p_2\) のケースと(全く同じではないが)同様になります。Miller-Rabin の定理を再掲します。
以降、表記を見やすくするため、\(m=3\)、\(n=p_1\cdot p_2\cdot p_3\) の場合で記述します。既約剰余類群の同型関係、
\((Z/p_1p_2p_3Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\times(Z/p_3Z)^{*}\)
を利用して、問題を置き換えます。それぞれの群位数は、
\(\begin{eqnarray}
&&\:\:|(Z/p_1p_2p_3Z)^{*}|&=\varphi(p_1p_2p_3)\\
&&&=(p_1-1)(p_2-1)(p_3-1)\\
\end{eqnarray}\)
\(|(Z/p_1Z)^{*}|=\varphi(p_1)=p_1-1\)
\(|(Z/p_2Z)^{*}|=\varphi(p_2)=p_2-1\)
\(|(Z/p_3Z)^{*}|=\varphi(p_3)=p_3-1\)
であり、
\(|(Z/p_1p_2p_3Z)^{*}|=|(Z/p_1Z)^{*}|\cdot|(Z/p_2Z)^{*}|\cdot|(Z/p_3Z)^{*}|\)
が成り立ちます。Miller-Rabin の条件は次のように言い換えられます。
例によって、
\(p_1-1=2^{e_1}k_1\:\:(e_1\geq1,\:k_1\) は奇数\()\)
\(p_2-1=2^{e_2}k_2\:\:(e_2\geq1,\:k_2\) は奇数\()\)
\(p_3-1=2^{e_3}k_3\:\:(e_3\geq1,\:k_3\) は奇数\()\)
とおきますが、\(\bs{e_1}\) は \(\bs{e_1,\:e_2,\:e_3}\) のうちの最小とします。こう仮定して一般性を失うことはありません。この仮定のもとでは、
\(3e_1\leq e_1+e_2+e_3\)
が成り立ちます。等号は \(e_1=e_2=e_3\) の場合です。
(1)が成立するとき
(1) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_1\) とします。\(n=p_1\cdot p_2\) のケースと同様の計算によって、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\cdot\mr{gcd}(k,\:k_3)\)
となります。\(|A_1|\) の上限値を評価すると、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
\(\mr{gcd}(k,\:k_3)\leq k_3\)
なので、
\(|A_1|\leq k_1k_2k_3\)
が結論づけられます。
(2)が成立するとき
(2) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_2\) とします。\(n=p_1\cdot p_2\) のケースと同様の計算で、
\(|A_2|=\displaystyle\sum_{r=0}^{e_1-1}(2^r)^3\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\cdot\mr{gcd}(k,\:k_3)\)
です。この式に \(e_1\) だけが現れるのは、\(e_1\) が \(\{e_1,\:e_2,\:e_3\}\) の最小値だからです。ここで、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
\(\mr{gcd}(k,\:k_3)\leq k_3\)
の関係を利用します。また、等比数列の総和を計算すると、
\(\begin{eqnarray}
&&\:\:\displaystyle\sum_{r=0}^{e_1-1}(2^r)^3&=\displaystyle\sum_{r=0}^{e_1-1}(2^3)^r\\
&&&=\dfrac{(2^3)^{e_1}-1}{2^3-1}\\
\end{eqnarray}\)
です。まとめると、
\(|A_2|\leq\dfrac{2^{3e_1}-1}{2^3-1}\cdot k_1k_2k_3\)
が得られます。
以上をもとに \(|M|\) を評価すると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq k_1k_2k_3+\dfrac{2^{3e_1}-1}{2^3-1}\cdot k_1k_2k_3\\
\end{eqnarray}\)
です。この計算をもとに \(1\leq a\leq n-1\) の \(n-1\) 個のうちの \(|M|\) の割合を計算すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2p_3-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)(p_3-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2\cdot2^{e_3}k_3}\\
&&&\leq\dfrac{1}{2^{e_1+e_2+e_3}}\left(1+\dfrac{2^{3e_1}-1}{2^3-1}\right)\\
\end{eqnarray}\)
となります。ここで、\(3e_1\leq e_1+e_2+e_3\) です。従って、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{3e_1}}\left(1+\dfrac{2^{3e_1}-1}{2^3-1}\right)\\
&&&=\dfrac{6+2^{3e_1}}{7\cdot2^{3e_1}}\\
\end{eqnarray}\)
ですが、この最後の式は \(e_1\) の増大によって単調減少するので、その最大値は \(e_1=1\) のときです。これを代入すると、
\(\dfrac{|M|}{n-1} < \dfrac{6+8}{56}=\dfrac{1}{4}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(\dfrac{1}{4}\) 未満であることが確かめられました。
以上の表記は \(m=3\) の場合ですが、証明のプロセスを振り返ってみると、\(m\geq3\) のときは、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{m\cdot e_1}}\left(1+\displaystyle\sum_{r=0}^{e_1-1}(2^m)^r\right)\\
&&&=\dfrac{1}{2^{m\cdot e_1}}\left(1+\dfrac{2^{m\cdot e_1}-1}{2^m-1}\right)\\
&&&=\dfrac{2^m-2+2^{m\cdot e_1}}{(2^m-1)\cdot2^{m\cdot e_1}}\\
\end{eqnarray}\)
です。この式の右辺は \(e_1\) について単調減少なので、\(e_1=1\) を代入すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{2^m-2+2^m}{(2^m-1)\cdot2^m}\\
&&&=\dfrac{2\cdot(2^m-1)}{(2^m-1)\cdot2^m}\\
&&&=\dfrac{1}{2^{m-1}}\\
&&&\leq\dfrac{1}{4}\\
\end{eqnarray}\)
が \(m\geq3\) のすべてで成り立ちます。
ちなみに、カーマイケル数は必ず、\(p_1\cdot p_2\cdot\cd\cdot p_m\) \((\:m\geq3\:)\) の形をしていることが知られています。上の証明によって、\(n\) がカーマイケル数であったとしても Miller-Rabin の条件を満たす底 \(a\) は 全体の \(\dfrac{1}{4}\) 未満であることが分かります。
以上で、Miller-Rabin の定理が証明されました。
Miller-Rabin の定理を使って、実際に巨大素数を求めてみます。2048 ビットの RSA 暗号で使われる 1024 ビットの素数を求めます。1024 ビットは、\(2^{1023}\) ~ \(2^{1024}-1\) の数です。Python で整数 n が素数かどうかを判定する関数、miller_rabin(n) を次のようにシンプルに実装します。n が素数なら True、合成数なら False を返す関数です。反復回数は40回とします。
この関数を用いて作ったのは、次のようなプログラムです。
1つの実行例ですが、12個の素数が見つかり、最初に見つかったのは次に示す 308桁の素数でした。実行時間は Google Colaboratry の環境で約 30秒です。
何回か実行してみると、素数の桁数はほとんどが 309桁で、一部が 308桁です。これは \(\mr{log}_{10}2^{1023}\fallingdotseq307.95\) なので、そうなるはずです。また、1万個の n のうちの素数の数は 8~18 個程度となりました。実行結果について「素数定理」と「反復回数」の観点から考察します。
素数定理
数学では、\(x\) 以下の素数の個数を \(\pi(x)\) で表わします。素数定理によると、
\(\pi(x)\sim\dfrac{x}{\mr{log}(x)}\)
です。左辺と右辺をつなぐ \(\sim\) は、
左辺と右辺の比率 \(\longrightarrow\:1\:\:(x\longrightarrow\infty)\)
を意味します。以下、
\(\pi(x)=\dfrac{x}{\mr{log}(x)}\)
と考えて、m ビットの数に含まれる素数の割合を見積もります。m ビットの数の総数は \(2^{m-1}\) 個なので、m ビット数の素数割合は、
ですが、\(\dfrac{m-2}{m-1}\) を \(1\) と見なすと、簡潔に、
素数割合 \(=\dfrac{1}{\mr{log}2\cdot m}\)
です。この式に \(m=1024\) を代入すると、
素数割合 \(\fallingdotseq0.0014\)
となります。つまり、
と言えます。これは上の実験で、1万個の n のうちの素数の数は 8~18 個程度だったことに合致します。
反復回数
プログラムを少々変更して、
何回目の反復(iteration)で素数\(\cdot\)合成数の判定ができたか
を調べると、素数判定のときは当然 iteration = 40 ですが、
合成数判定のときの iteration = 1
であることが分かります(1万個の素数判定をする前提です)。つまり、\(n\) が合成数なら最初の計算で即、合成数と判明します。何回かの反復の後に合成数と判明することは、上の計算では無いのです。
この理由は、\(n\) が合成数だと「\(a\:(1\leq a\leq n-1)\) のなかで Miller-Rabin の条件を満たす底 \(a\) の比率は \(\tfrac{1}{4}\) 以下」という定理の \(\tfrac{1}{4}\) が(一般には)過大評価であることによります。たとえば、\(n\) が2つの異なる素数の積の場合、
\(\begin{eqnarray}
&&\:\:n&=p_1p_2\\
&&\:\:n-1&=2^ek\\
&&\:\:p_1-1&=2^{e_1}k_1\\
&&\:\:p_2-1&=2^{e_2}k_2\\
\end{eqnarray}\)
(\(e,e_1,e_2\geq1,\:\:k,k_1,k_2\) は奇数)
において \(\tfrac{1}{4}\) 以下の主な根拠は、
\(\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\leq k_1k_2\)
でした。ところが、この式で等号が成り立つのは、特に \(n\) が巨大だと、めったにありません。高々 10,000個程度の合成数を判定したとしても、Miller-Rabin の条件を満たす底 \(a\) が現れる確率はほとんどゼロに等しいのです。
ランダムに選んだ数 \(n\) のほとんどは(1024 ビットの数の場合 99.86 % は)合成数です。したがって「合成数を合成数だと速く判定する」のが素数判定アルゴリズムのポイントであり、反復回数をどうするかは全体の速度にそれほど関係ありません。このあたりの事情はフェルマの条件で素数判定をしても同じです。
ただし、フェルマの条件とは違って、ランダムに選んだ底 \(a\) が Miller-Rabin の条件を満たす確率が、\(n\) の値にかかわらず必ず \(\tfrac{1}{4}\) 以下であることが数学的に保証されています。そこが Miller-Rabin の素数判定アルゴリズムの価値なのでした。
今まで「高校数学で理解する・・・」という記事を何回か書きましたが、その中に暗号についての一連の記事があります。
No.310「高校数学で理解するRSA暗号の数理(1)」
No.311「高校数学で理解するRSA暗号の数理(2)」
No.313「高校数学で理解する公開鍵暗号の数理」
No.315「高校数学で理解する楕円曲線暗号の数理(1)」
No.316「高校数学で理解する楕円曲線暗号の数理(2)」
の5つです。これらは公開鍵暗号と、その中でも代表的な RSA暗号、楕円曲線暗号の数学的背景を書いたものです。情報通信をインフラとする現代社会は、この公開鍵暗号がなくては成り立ちません。"数学の社会応用" の典型的な例と言えるでしょう。
これらの暗号では、10進数で数10桁~数100桁の素数が必要です。ないしは、数10桁~数100桁の数が素数かどうかを判定する必要があります。
たとえば、マイナンバー・カードの認証に使われている RSA暗号の公開鍵は 2048ビットで、1024ビットの素数2つを掛け合わせて個人ごとに作られます。1024ビットということは \(2^{1023}\) ~ \(2^{1024}-1\) の数であり、10進では約300桁の巨大数です。素数を生成する式はないので、作るためには1024ビットの数をランダムに選び、それが素数かどうかを実用的な時間で判定する必要があります。
ビットコインのデジタル署名で使われているのは、256ビットの楕円曲線暗号です。この暗号の公開鍵は一般に公開されていますが(暗号の仕組みから個人ごとに作る必要はない)、この公開鍵を設計するときに必要なのは、256ビット=約80桁(10進)の数が素数かどうかを判定することです。
つまり、公開鍵暗号の基礎となっている技術が「素数判定」なのです。そこで今回は、素数判定の方法で一般的な「Miller-Rabin テスト」の数学的背景を書きます。Miller、Rabin は、このテストを考案した数学者2人の名前です。
前提知識
本論に入る前に前提知識について整理します。「高校数学で理解する・・・」というタイトルは「高校までで習う数学の知識だけを前提とする」という意味です。従って、その前提からはずれるものはすべて証明するのが基本方針です。
今回は、以前の「高校数学で理解する・・・」で証明した事項を前提知識とします。
・合同式
・フェルマの小定理
・中国剰余定理
・オイラー関数
・群
です。また、暗号の記事ではありませんが、No.355「高校数学で理解するガロア理論(2)」の次の事項も前提とします。
・剰余群
・既約剰余類群
・巡回群
・群の直積
・群の同型
以下、剰余群以下の事項について、素数判定に関わるところを簡単に復習します。
剰余群
整数の集合を \(Z\) で表し、整数 \(n\) の倍数の集合を \(nZ\) とします。また、
\(\ol{j_n}\)
は、\(\bs{n}\) で割った余りが \(\bs{j}\) である整数の集合とします(剰余類と呼ばれる)。たとえば、\(n=9,\:j=2\) とすると、\(\ol{2_9}\) は「\(9\) で割ったら \(2\) 余る整数の集合」で、
\(\ol{2_9}=\{\:\cd,\:-16,\:-7,\:2,\:11,\:20,\:29,\:\cd\:\}\)
です。剰余群 \(Z/nZ\) とは、
\(Z/nZ=\{\ol{0_n},\:\ol{1_n},\:\cd\:,\:\ol{(n-1)_n}\}\)
で示される「無限集合を元とする有限集合」です。\(n=9\) だと、
\(Z/9Z=\{\ol{0_9},\:\ol{1_9},\:\ol{2_9},\:\ol{3_9},\:\ol{4_9},\:\ol{5_9},\:\ol{6_9},\:\ol{7_9},\:\ol{8_9}\}\)
です。この集合の元の加算 \(+\) を、
\(\ol{i_n}+\ol{j_n}=\ol{(i+j)_n}\)
と定義すると(右辺は整数のたし算)、\(Z/nZ\) はこの演算について群の定義を満たし(=加法群)、この群を剰余群と呼びます。一般に有限群 \(G\) の元の数=群位数を \(|G|\) で表しますが、剰余群の群位数は、
\(|Z/nZ|=n\)
です。以降、剰余類と整数を同一視して、
\(Z/9Z=\{0,\:1,\:2,\:3,\:4,\:5,\:6,\:7,\:8\}\)
というように書きます。従って、\(1\) は 整数の \(1\) を表すことも、また、\(Z/nZ\) の元(= \(n\) で割ると \(1\) 余る数の集合= \(\ol{1_n}\))を表すこともあります。どちらかは文脈で決まります。
既約剰余類群
\(Z/nZ\) の元 \(\{0,\:1,\:\cd\:,\:j,\:\cd\:,\:n-1\}\) から \(\mr{gcd}(j,\:n)=1\) となる元(= \(n\) と素な元)だけを取り出した集合を既約剰余類群といい、\((Z/nZ)^{*}\) で表します。例をあげると、
\(\begin{eqnarray}
&&\:\:(Z/9Z)^{*}&=\{\ol{1_9},\:\ol{2_9},\:\ol{4_9},\:\ol{5_9},\:\ol{7_9},\:\ol{8_9}\}\\
&&&=\{\:1,\:2,\:4,\:5,\:7,\:8\:\}\\
\end{eqnarray}\)
です。この集合の、元と元との乗算 \(\cdot\) を、
\(\ol{i_n}\cdot\ol{j_n}=\ol{(ij)_n}\)
で定義すると(右辺の \(ij\) は整数の乗算)、\((Z/nZ)^{*}\) は乗算を演算とする群になります(=乗法群)。従って、任意の元 \(a\in(Z/nZ)^{*}\) の逆元 \(a^{-1}\) が存在して、
\(a\cdot a^{-1}=1\)
が成り立ちます。つまり乗算と除算が自由にできます。\((Z/9Z)^{*}\) の例では、
\(\begin{eqnarray}
&&\:\:1^{-1}&=1&&\\
&&\:\:2^{-1}&=5, &5^{-1}&=2\\
&&\:\:4^{-1}&=7, &7^{-1}&=4\\
&&\:\:8^{-1}&=8&&\\
\end{eqnarray}\)
です。\((Z/nZ)^{*}\) の群位数は、オイラー関数 \(\varphi\) を使って、
\((Z/nZ)^{*}=\varphi(n)\)
で表されます。\(\varphi(n)\) は「\(n\) 以下で \(n\) とは互いに素な数の個数」です。\(p,\:q\) を異なる素数とすると、
\(\begin{eqnarray}
&&\:\:\varphi(p)&=p-1\\
&&\:\:\varphi(pq)&=(p-1)(q-1)\\
&&\:\:\varphi(p^2)&=p(p-1)\\
\end{eqnarray}\)
などが成り立ちます。
巡回群
\(p\) を奇素数(\(p\neq2\))とすると、既約剰余類群 \((Z/pZ)^{*}\) は生成元 \(g\) をもちます。つまり、
\((Z/pZ)^{*}=\{\:g,\:g^2,\:g^,\:\cd\:,\:g^{p-1}=1\:\}\)
と表され、群位数は \(\varphi(p)=p-1\) です。このように、一つの生成元の累乗で全ての元が表せる群を巡回群と言います(\(1\) の次は再び \(g\) になって巡回する)。また、\(n\) が \(p\) の累乗、\(n=p^{\al}\:(\al\geq2)\) のときも \((Z/p^{\al}Z)^{*}\) は生成元をもつ巡回群です。\(\al=2\) のときの群位数は、
\(|(Z/p^2Z)^{*}|=\varphi(p^2)=p(p-1)\)
です。\((Z/9Z)^{*}\) の場合、群位数は \(\varphi(9)=6\) で、\(g=2\) と \(g=5\) が生成元になり、
\(\begin{eqnarray}
&&\:\:(Z/9Z)^{*}&=\{2,\:2^2=4,\:2^3=8,\:2^4=7,\:2^5=5,\:2^6=1\}\\
&&&=\{5,\:5^2=7,\:5^3=8,\:5^4=4,\:5^5=2,\:5^6=1\}\\
\end{eqnarray}\)
などと表せます。\(1,\:4,\:7,\:8\) は生成元ではありません。
群の直積、群の同型
\(G\) と \(H\) を有限群とし、その元を \(g_i\in G,\:h_j\in H\) として、2つの元のペア、
\((g_i,\:h_j)\) \((1\leq i\leq|G|,\:1\leq j\leq|H|)\)
を作るとき、すべてのペアを元とする集合を「群の直積」と言い、\(G\times H\) で表します。元と元の演算を \(g_i\) と \(h_i\) で個別に行うことで、直積も群になります。その群位数は、
\(|G\times H|=|G|\cdot|H|\)
です。
中国剰余定理によると、\(m,\:n\) が互いに素のとき、
\(x\equiv a\:\:(\mr{mod}\:m)\)
\(x\equiv b\:\:(\mr{mod}\:n)\)
の連立合同方程式は、\(mn\) を法として唯一の解を持ちます。\(x\) を \(m\) で割った余りを \(x_m\)、\(n\) で割った余りを \(x_n\) とし、
\(f\::\:x\:\longrightarrow\:(x_m,\:x_n)\)
の写像 \(f\) を定義すると、中国剰余定理によって \(f\) は1対1写像であり、かつ、
\(\begin{eqnarray}
&&\:\:f(xy)&=((xy)_m,\:\:(xy)_n)\\
&&&=((x_m\cdot y_m)_m,\:\:(x_n\cdot y_n)_n)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(x)f(y)&=(x_m,\:x_n)\:(y_m,\:y_n)\\
&&&=((x_m\cdot y_m)_m,\:\:(x_n\cdot y_n)_n)\\
\end{eqnarray}\)
なので、
\(f(xy)=f(x)f(y)\)
が成り立ちます。また同様に \(f(x+y)=f(x)+f(y)\) であり、\(f\) は演算を保存する同型写像です。従って、剰余群 \(Z/mnZ\) は、2つの群の直積との間で "群の同型" が成り立ち、
\(Z/mnZ\cong Z/mZ\times Z/nZ\)
です(=中国剰余定理の群による表現)。また 既約剰余類群 \((Z/mnZ)^{*}\) は、
\((Z/mnZ)^{*}\cong(Z/mZ)^{*}\times(Z/nZ)^{*}\)
と直積で表現できます。\(m,\:n\) がともに奇素数で \(m=p,\:n=q\:(\neq p)\)だと、
\((Z/pqZ)^{*}\cong(Z/pZ)^{*}\times(Z/qZ)^{*}\)
です。\((Z/pqZ)^{*}\) は巡回群でありませんが、2つの巡回群の直積で表現できることになります。
以上を前提として「Miller-Rabin テスト」のことを書きますが、これは「確率的素数判定アルゴリズム」の一種です。
| 確率的素数判定アルゴリズム |
「Miller-Rabin テスト」は「フェルマ・テスト」の発展形と言えるものです。そこでまず、「フェルマ・テスト」の原理になっている「フェルマの小定理」から始めます。
フェルマの小定理
素数がもつ重要な性質を示したのが、フェルマの小定理です。
フェルマの小定理 \(p\) を素数とすると、\(p\) と素な \(a\) について、 \(a^{p-1}\equiv1\:\:(\mr{mod}\:p)\) が成り立つ。 |
この定理の \(a\) を、指数関数の「底(base)」と呼びます。偶数の素数は \(2\) しかないので、以降、\(\bs{n}\) は \(\bs{3}\) 以上の奇数として素数判定を考えます。フェルマの小定理を素数判定用に少々言い換えると、次のように表現できます。
フェルマの小定理 \(n\) を \(3\) 以上の奇数とする。\(\bs{n}\) が素数であれば、\(\bs{1\leq a\leq n-1}\) であるすべての \(\bs{a}\) について、次の "フェルマの条件" が成り立つ。 フェルマの条件 \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) |
このフェルマの小定理の対偶は次のようになります。
フェルマの小定理の対偶 \(n\) が \(3\) 以上の奇数であるとき、\(\bs{1\leq a\leq n-1}\) であるどれか一つの \(\bs{a}\) について、 \(a^{n-1}\not\equiv1\:\:(\mr{mod}\:n)\) であれば(=フェルマの条件に反すれば)\(\bs{n}\) は合成数である。 |
\(n\) が \(3\) 以上の奇数の合成数のとき、\(1\leq a\leq n-1\) について、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
\(a^{n-1}\not\equiv1\:\:(\mr{mod}\:n)\)
のどちらになるのか、\(a\) ごとに検討してみます。もちろん \(a=1\) なら \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) です。また、\(a=n-1\:(=-1)\) でも、\(n-1\) が偶数なので、 \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) です。
また、\(a\) が \(n\) と互いに素でないとき、つまり \(\mr{gcd}(n,\:a)\neq1\) ときは \(a^{n-1}\not\equiv1\:\:(\mr{mod}\:n)\) です。なぜなら、\(a\) と \(n\) の最大公約数を \(d\:(\neq1)\) として、もし \(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) だとすると、
\(a^{n-1}=k\cdot n+1\:\:(k\) は整数\()\)
と表わせますが、
左辺について \(d\mid a^{n-1}\)
右辺について \(d\nmid(k\cdot n+1)\)
となってしまい、矛盾するからです。
\(a\neq1,\:n-1\)、 \(\mr{gcd}(n,\:a)=1\) のときにどうなるかは、\(a\) によって両方がありえます。ためにしに、\(n=21\) で計算してみると、
| \(1\) | \(1\) |
| \(2\) | \(4\) |
| \(3\) | \(9\) |
| \(4\) | \(16\) |
| \(5\) | \(4\) |
| \(6\) | \(15\) |
| \(7\) | \(7\) |
| \(8\) | \(1\) |
| \(9\) | \(18\) |
| \(10\) | \(16\) |
| \(11\) | \(16\) |
| \(12\) | \(18\) |
| \(13\) | \(1\) |
| \(14\) | \(7\) |
| \(15\) | \(15\) |
| \(16\) | \(4\) |
| \(17\) | \(16\) |
| \(18\) | \(9\) |
| \(19\) | \(4\) |
| \(20\) | \(1\) |
となります。色を塗った10個が \(a\neq1,\:n-1\)、 \(\mr{gcd}(n,\:a)=1\) のところですが、\(\equiv1\) \((a=8,\:13)\) と \(\not\equiv1\)(それ以外の8個)があることがわかります。とにかく、上の表で一つでも \(\bs{\not\equiv1}\) があれば、\(n\) は合成数だと判断できます。
このフェルマの小定理の対偶を利用して、巨大整数(数10桁~数100桁) \(n\) が素数かどうかを確率的に判定できます。つまり、\(1\leq a\leq n-1\) である数をランダムに、順々に選び、ある \(a\) がフェルマの条件に反すれば、その時点で \(n\) は合成数と判定します。何回か試行してすべての \(a\) がフェルマの条件に合致するなら(=合成数だと判定できなければ)、\(n\) は素数の可能性が高い。
しかし困ったことに「合成数でありながら、多数の \(\bs{a}\) でフェルマの条件を満たしてしまう \(\bs{n}\)」が存在します。"カーマイケル数" です。最小のカーマイケル数は \(561=3\cdot11\cdot17\) ですが、\(\mr{gcd}(561,\:a)=1\) であるすべての \(a\:\:(1\leq a\leq560)\) で、
\(a^{560}\equiv1\:\:(\mr{mod}\:561)\)
が成り立ちます。その理由ですが、\(a\) を \(3,\:11,\:17\) のすべてと素な任意の数(= \(561\) と素な任意の数)とすると、フェルマの小定理より、
\(\begin{eqnarray}
&&\:\:a^{2}&\equiv1\:\:(\mr{mod}\:3)\\
&&\:\:a^{10}&\equiv1\:\:(\mr{mod}\:11)\\
&&\:\:a^{16}&\equiv1\:\:(\mr{mod}\:17)\\
\end{eqnarray}\)
が成り立ちます。\(560\) は、\(2,\:10,\:16\) 全部の倍数なので、それぞれの合同式の両辺を適切に累乗すると、
\(a^{560}\equiv1\:\:(\mr{mod}\:3)\)
\(a^{560}\equiv1\:\:(\mr{mod}\:11)\)
\(a^{560}\equiv1\:\:(\mr{mod}\:17)\)
が成り立つ。そうすると、中国剰余定理により、
\(a^{560}\equiv1\:\:(\mr{mod}\:3\cdot11\cdot17)\)
が成り立ちます。\(560\) 以下で \(561\) と素な数の個数は、オイラー関数 \(\varphi(n)\)(= \(n\) 以下で \(n\) と素な数の個数)を使うと、
\(\begin{eqnarray}
&&\:\:\varphi(561)&=\varphi(3)\varphi(11)\varphi(17)\\
&&&=2\cdot10\cdot16=320\\
\end{eqnarray}\)
なので、\(\dfrac{320}{560}=\dfrac{4}{7}\)、つまり半数以上の \(a\) でフェルマの条件が満たされることになります。これを一般的に言うと、カーマイケル数 \(c\) が3個の素数 \(p,\:q,\:r\) の積の場合、
\(\begin{eqnarray}
&&\:\:c&=pqr\\
&&\:\:\varphi(c)&=(p-1)(q-1)(r-1)\\
\end{eqnarray}\)
なので、この2つの比は、\(p,\:q,\:r\) が大きくなると \(1\) に近づきます。それは、ほとんど全ての \(a\:\:(1\leq a\leq c-1)\) がフェルマの条件を満たすことを意味します。
カーマイケル数は、特に \(n\) が巨大だと極めて希です。Wikipedia によると、「\(1\) から \(10^{21}\) の間には \(20,138,200\) 個のカーマイケル数があり、これはおよそ \(5\cdot10^{13}\) 個にひとつの割合」だそうです。しかし、カーマイケル数が無限個あることも証明されています。\(n\) が "運悪く" カーマイケル数だと、フェルマ\(\cdot\)テストでは素数と判定されてしまう。つまり、フェルマの条件を使って素数を確率的に判定するアルゴリズムには問題があるわけです。
Miller-Rabin の条件
そこで、素数の条件として、フェルマの条件とは別のものを考えます。フェルマの条件、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
において、\(n\) が素数とすると、\(n-1\) は偶数です。そこで、
\(n-1=2^ek\) (\(e\geq1,\:k\) は奇数)
と表します。この表記を用いて、\(a^{n-1}-1\) という式を因数分解すると、
\(\begin{eqnarray}
&&\:\:a^{n-1}-1&=a^{2^ek}-1\\
&&&=(a^{2^{e-1}k})^2-1\\
&&&=(a^{2^{e-1}k}+1)(a^{2^{e-1}k}-1)\\
&&&=(a^{2^{e-1}k}+1)((a^{2^{e-2}k})^2-1)\\
&&&=(a^{2^{e-1}k}+1)(a^{2^{e-2}k}+1)(a^{2^{e-2}k}-1)\\
&&& \vdots\\
\end{eqnarray}\)
と続きます。結局、因数分解は、
| \(a^{n-1}-1=\) | \((a^{2^{e-1}k}\) | \(+1)\cdot\) | ||
| \((a^{2^{e-2}k}\) | \(+1)\cdot\) | |||
| \((a^{2^{e-3}k}\) | \(+1)\cdot\) | |||
| \(\vdots\) | ||||
| \((a^{2^2k}\) | \(+1)\cdot\) | |||
| \((a^{2k}\) | \(+1)\cdot\) | |||
| \((a^k\) | \(+1)\cdot(a^k-1)\) | \((\br{A})\) |
となります。これを \((\br{A})\) 式とします。\(n\) が素数のときは、フェルマの条件を変形すると、
\(a^{n-1}-1\equiv0\:\:(\mr{mod}\:n)\)
なので、フェルマの条件と等価な式は、
\((\br{A})\) 式の右辺 \(\equiv0\:\:(\mr{mod}\:n)\)
であり、ということは、
\((\br{A})\) 式の右辺の少なくとも1つの項 \(\equiv0\:\:(\mr{mod}\:n)\) |
が成立します。\(\bs{n}\) が素数であるのがポイントです。\(n\) が合成数ならこんなことは言えません。このことより、\(n\) が素数であるための新たな条件が導けます。次項です。
素数の条件(Miller-Rabin)
\(n\) を \(3\) 以上の奇数とし、 \(n-1=2^ek\) (\(e\geq1,\:k\) は奇数) と表されているものとする。このとき、\(\bs{n}\) が素数であれば、\(\bs{1\leq a\leq n-1}\) であるすべての \(\bs{a}\) について、次の Miller-Rabin の条件が成り立つ。 Miller-Rabin の条件 (1) \(a^k\equiv1\:\:(\mr{mod}\:n)\) もしくは (2) ある \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) |
\(a^{2^ik}\:\:(0\leq i\leq e-1)\) の \(e\) 個の数列を Miller-Rabin 系列と呼ぶことにします。
\(a^k,\:a^{2k},\:a^{4k},\:\cd\:,\:a^{2^{e-1}k}\)
です。この系列は、ある項の2乗が次の項になっています。従って \(\mr{mod}\:n\) でみて \(a^{2^rk}\equiv-1\) になれば、以降の項はすべて \(\equiv1\:(\mr{mod}\:n)\) になります。ということは、系列の中で \(\equiv-1\) となる項は「全く無い」か「一つだけある」のどちらかです。
ちなみに、Miller-Rabin による素数の条件の対偶は次の通りです。これを利用して合成数の判定ができます。
合成数の判定(対偶) \(n\) を \(3\) 以上の奇数とし、 \(n-1=2^ek\) (\(e\geq1,\:k\) は奇数) と表されているものとする。このとき、\(\bs{1\leq a\leq n-1}\) のある \(\bs{a}\) について、 (1) \(a^k\not\equiv1\:\:(\mr{mod}\:n)\) かつ (2) すべての \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\not\equiv-1\:\:(\mr{mod}\:n)\) が成り立てば、\(n\) は合成数である。 |
\(\bs{n}\) が素数であれば、フェルマーの条件と Miller-Rabin の条件は等価です。しかし、\(n\) が合成数のときは、フェルマの条件と Miller-Rabin の条件の意味が違ってきます。それが次です。
\(n\) が合成数のとき
\(n\) が合成数のときは、フェルマの条件から Miller-Rabin の条件を導くことはできません。なぜなら「\(n\)が素数」が導出のキーだからです。つまり、
| フェルマの条件を満たす底 \(a\) の集合を \(F\) | |
| Miller-Rabin の条件を満たす底 \(a\) の集合を \(M\) |
とすると、\(a\in F\) であっても \(a\in M\) とは限らない。しかし、\((\br{A})\) 式でわかるように \(a\in M\) なら必ず \(a\in F\) です。従って、
\(M\:\subset\:F\)
です。ということは、数 \(a\) についてのフェルマーの条件によって \(n\) が合成数だと判定できなくても(つまり \(a\in F\))、Miller-Rabin の条件で合成数と判定できる(つまり \(a\notin M\))可能性があることになります。つまり合成数の判定においては、Miller-Rabin の条件はフェルマーの条件より厳格です。
しかも Miller-Rabin の条件は、合成数を合成数だと判定できる確率(ないしは判定できない確率)が、\(\bs{n}\) の値にかかわらず示せるのです。それが次の定理です。
Miller-Rabin の定理
Miller-Rabin の定理 \(n\) を \(3\) 以上の奇数の合成数とする。また、\(n-1=2^ek\:\:(e\geq1,\:k\) は奇数\()\) と表されているものとする。このとき、 Miller-Rabin の条件 (1) \(a^k\equiv1\:\:(\mr{mod}\:n)\) もしくは (2) ある \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) を満たす底 \(a\:(1\leq a\leq n-1)\) は、\(\bs{n-1}\) 個のうちの \(\bs{1/4}\) 以下である。 |
\(\bs{n}\) がいかなる数であっても成り立つのがポイントです。実際に計算をしてみます。\(n\) を \(9\leq n < 10000\) である奇数の合成数とします。調べてみると、その総数は \(3771\)個です。そして、
\(L=\)Miller-Rabin の条件を満たす底 \(a\) の個数
\(P=\dfrac{L}{n-1}\)
\(P=\dfrac{L}{n-1}\)
とし、\(3771\)個の \(n\) のうち \(P\geq0.2\) のものをリストアップすると、次の5つだけです。
| \(9\) | \(3\) | \(1\) | \(2\) | \(0.25\) |
| \(91\) | \(1\) | \(45\) | \(18\) | \(0.20\) |
| \(703\) | \(1\) | \(351\) | \(162\) | \(0.23\) |
| \(1891\) | \(1\) | \(945\) | \(450\) | \(0.24\) |
| \(8911\) | \(1\) | \(4455\) | \(1782\) | \(0.20\) |
\(n=9\) のとき、\(P\) は最大値の \(0.25\) です。それ以降、\(n=1891\) のときに \(P\fallingdotseq0.24\) となりますが、\(0.25\) を越える \(n\) は( \(9\leq n < 10000\) では)無いことがわかります。そしてこの定理は、\(\bs{n}\) がいかなる奇数の合成数であっても \(\bs{P\leq0.25}\) と主張しているわけです。
これでまず言えることは、Miller-Rabin の条件にとっての「カーマイケル数のような数」はあり得ないことです。
さらにこの定理によって、素数判定の信頼度を示すことができます。比喩で言うと次のとおりです。
| 正方形の、中が見えない箱があり、玉が \(100\)個入っています。箱は「素数箱」と「合成数箱」の区別がありますが、そのどちらかは見た目で判別できません。ただし、素数箱なら\(100\)個の白玉が入っていて、合成数箱なら \(25\)個の白玉と \(75\)個の赤玉が入っています。 | |
| 箱の上面には穴があって、そこから手を入れて玉を取り出し、色を確認した後、玉を箱に戻す(そしてかき混ぜる)ことができます。この確認は繰り返しができて、その繰り返しで、箱が素数箱か合成数箱かを判断します。 | |
| 最初に取り出した玉が赤玉なら、箱は合成数箱だとわかります。しかし白玉だと、素数箱の可能性が高いものの、断言はできない。合成数箱でも白玉を取り出す確率が \(1/4\) あるからです。従って2回目の確認をします。 | |
| 2回続けて白だと、素数箱である可能性がぐんと高まります。もしそれが合成数箱だとすると、2回続けて白の確率は \(1/16\) しかないからです。もちろん2回目が赤だと合成数箱です。 | |
| このようにして、赤が出ればその時点で合成数箱と判断し、白が出続ければ確認を繰り返します。もし合成数箱だとすると、白が5回出続ける確率は \(1/1024\) であり、以降、どんどん減っていくので、ある回数で打ち切って素数箱と判断します。 |
以上の考え方で \(n\) の素数判定をするアルゴリズムが次です。
Miller-Rabin の素数判定アルゴリズム
|
\(r=40\) だとすると、Miller-Rabin の素数判定アルゴリズムで「素数と判定したにもかかわらず実は合成数」の確率は、
\(\dfrac{1}{4^{40}}\) 以下
であることが保証されます。\(4^{40}\) は、\(\fallingdotseq\:1.2\times10^{24}\) で、\(10\)進数で\(25\)桁の数です。あまりに巨大すぎて想像するのは難しいのですが、たとえば、1秒の \(100\)万分の \(1\) の時間は \(1\) マイクロ秒で、\(1\) 秒間に地球を \(7.5\)周する光が \(300\)メートルしか進まない時間です。一方、宇宙の年齢は \(138\)億年程度と言われています。この宇宙の年齢をマイクロ秒で表すと、\(4.4\times10^{23}\) マイクロ秒です。ということは、\(4^{40}\) はその3倍近い数字です。
\(\dfrac{1}{4^{40}}\) は、数学的には \(0\) ではありませんが、確率としては実用的に \(0\) です。以上が Miller-Rabin の素数判定の原理です。
以降、 なぜ \(\dfrac{1}{4}\) 以下であると言えるのか、その証明をします。
| Miller-Rabin の定理の証明 |
定理を再度述べると次の通りです。
Miller-Rabin の定理(再掲) \(n\) を \(3\) 以上の奇数の合成数とする。また、\(n-1=2^ek\:\:(e\geq1,\:k\) は奇数\()\) と表されているものとする。このとき、 Miller-Rabin の条件 (1) \(a^k\equiv1\:\:(\mr{mod}\:n)\) もしくは (2) ある \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) を満たす \(a\:(1\leq a\leq n-1)\) は、\(n-1\) 個のうちの \(1/4\) 以下である。 |
3つのケースにわけて証明します。以降の証明は、後藤・鈴木(首都大学東京)「Miller-Rabin素数判定法における誤り確率の上限」を参考にしました。
| \(n=p^2t\:\:(p\)は奇素数。\(t\geq1\) は奇数\()\)と表されるとき
\(n\) が奇素数の2乗で割り切れるときです。このことを、\(n\) が「平方因子」をもつ、と言います。\(t\) の素因数分解に \(p\) が現れてもかまいません。平方因子が複数個ある場合は、そのどれかを \(p\) とします。
| |
| \(n=p_1\cdot p_2\:(p_1,\:p_2\) は奇素数で \(p_1\neq p_2)\) | |
| \(n=p_1\cdot p_2\cdot\cd\cdot p_m\:(m\geq3\) 個の相異なる奇素数の積\()\) |
② ③ のケースは \(n\) が平方因子を持たないので ① と排他的であり、また ② と ③ も排他的です。いずれの場合も \(n\) が奇数なので、素因数に \(2\) は現れません。以降の3つのケースに分けた証明では、\(p\) を素数としたとき既約剰余類群 \((Z/pZ)^{*}\) 、\((Z/p^2Z)^{*}\) が巡回群であることを利用します。
1. \(n=p^2t\:\:(\:p\)は奇素数。\(t\geq1\) は奇数\()\)
Miller-Rabin の条件を満たす \(a\:(0\leq a\leq n-1)\) の集合を \(M\) とします。上で説明したように、\(n\) が合成数であったとしても Miller-Rabin の条件が成立すればフェルマの条件も成立します(\(n\) が合成数だとその逆は成り立たない)。従って、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\)
が成り立ちます。このフェルマの条件を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(F\) とすると、\(M\:\subset\:F\) なので元の数は、
\(|M|\leq|F|\)
です。さらに、\(p^2\mid n\)(= \(p^2\) が \(n\) を割り切る)なので、
\(a^{n-1}\equiv1\:\:(\mr{mod}\:p^2)\)
\((\br{B})\)
も同時に成り立ちます。\((\br{B})\) 式を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(R_1\) とすると、\(a\in F\) なら \(a\in R_1\) なので、
\(\begin{eqnarray}
&&\:\:F&\subset R_1\\
&&\:\:|F|&\leq|R_1|\\
\end{eqnarray}\)
が成り立ちます。\(|M|\leq|F|\) とあわせると、
\(|M|\leq|R_1|\)
です。次に、剰余群 \(Z/p^2Z\) の元 で \((\br{B})\) 式を満たす \(a\:(0\leq a\leq p^2-1)\) の集合を \(R_2\) とします。\(x\in R_2\) だとすると、\(\mr{mod}\:p^2\) では、
\(\begin{eqnarray}
&&\:\:x&=x+p^2\\
&&&=x+2p^2\\
&&& \vdots\\
&&&=x+(t-1)p^2\leq p^2t-1\\
\end{eqnarray}\)
です。つまり、\((\br{B})\) 式を満たす \(Z/p^2Z\) の元1個に対して、\((\br{B})\) 式を満たす、\(0\leq a\leq n-1\:(p^2t-1)\) の \(t\)個の数が対応します。従って、
\(t|R_2|=|R_1|\)
です。\(|M|\leq|R_1|\) とあわせると、
\(|M|\leq t|R_2|\)
です。
剰余群 \(Z/p^2Z\) の元で \((\br{B})\) 式を満たすのは、\(p^2\) と互いに素な元だけです。つまり、既約剰余類群 \((Z/p^2Z)^{*}\) の元で \((\br{B})\) 式を満たすものの集合が \(R_2\) であるとも言えます。以降、 \((Z/p^2Z)^{*}\) を使って \(R_2\) の元の数、\(|R_2|\) を見積もります。それには \((Z/p^2Z)^{*}\) が巡回群であることを利用します。
一般に、巡回群においては次が成り立ちます。この定理を \((\br{C})\) とします。
巡回群 \(G\)(群位数 \(d\))において、\(x^m=1\) を満たす \(x\) の個数は \(\mr{gcd}(m,\:d)\) 個である。
\((\br{C})\) |
【証明】
\(h=\mr{gcd}(m,\:d)\) とおく。位数 \(d\) の巡回群 \(G\) は、生成元 \(g\) を用いて、
\(G=\{g,\:g^2,\:g^3,\:\cd\:,\:g^{d-1},\:g^d=1\}\)
と表現できる。そこで \(x=g^i\:\:(1\leq i\leq d)\) と表すと、
\(\begin{eqnarray}
&&\:\:(g^i)^m&=1\\
&&\:\:g^{im}&=1\\
\end{eqnarray}\)
なので、\(im\) は群位数 \(d\) の整数倍である。つまり、
\(d\mid im\)
である。\(h=\mr{gcd}(m,\:d)\) として \(d\,'=\dfrac{d}{h}\) \(m\,'=\dfrac{m}{h}\) とおくと、
\(d\,'\mid im\,'\)
になるが、\(d\,'\) と \(m\,'\) は互いに素なので、
\(d\,'\mid i\)
である。つまり \(i\) は \(d\,'=\dfrac{d}{h}\) の倍数である。従って、\(1\leq i\leq d\) であることを考慮すると、
\(i=\dfrac{d}{h}\cdot j\:\:(1\leq j\leq h)\)
と表せる。つまり、\(x^m=1\) を満たす \(x\) の個数は \(h=\mr{gcd}(m,\:d)\) 個である。【証明終】
既約剰余類群 \((Z/p^2Z)^{*}\) は巡回群であり、群位数は\(\varphi(p^2)=p(p-1)\) です。従って、\((Z/p^2Z)^{*}\) の元で \(a^{n-1}=1\) を満たす元の数(\(=|R_2|\))は定理 \((\br{C})\) により、
\(\begin{eqnarray}
&&\:\:|R_2|&=\mr{gcd}(p(p-1),\:n-1)\\
&&&=\mr{gcd}(p(p-1),\:p^2t-1)\\
\end{eqnarray}\)
となります。ここで、\(p^2t-1\) は \(p\) で割り切れないので、
\(\mr{gcd}(p(p-1),\:p^2t-1)=\mr{gcd}(p-1,\:p^2t-1)\)
ですが、この式の右辺は \(p-1\) 以下です。従って、
\(|R_2|\leq p-1\)
です。\(|M|\leq t|R_2|\) とあわせると、
\(|M|\leq t(p-1)\)
が得られました。従って、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&\leq\dfrac{t(p-1)}{tp^2-1}\\
&&&=\dfrac{p-1}{p^2-\dfrac{1}{t}}\\
\end{eqnarray}\)
となります。定義によって \(t\geq1,\:p\geq3\) ですが、上式の右辺は \(t\) についても \(p\) についても単調減少です。従って右辺の最大値は \(t=1,\:p=3\) のときで、
\(\dfrac{t(p-1)}{tp^2-1}\leq\dfrac{1}{4}\)
です。結論として、
\(\dfrac{|M|}{n-1}\leq\dfrac{1}{4}\)
となり、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(\dfrac{1}{4}\) 未満であることが証明されました。
ちなみに、この証明はフェルマの条件しか使っていません。つまり、
\(n\) が平方因子をもつなら、\(1\leq a\leq n-1\) のなかでフェルマの条件を満たす数の比率は \(\tfrac{1}{4}\) 未満
と言えます。ということは、平方因子をもつ数はカーマイケル数にはなりえないことが分かります。
2. \(n=p_1\cdot p_2\:(\:p_1,\:p_2\) は奇素数で \(p_1\neq p_2\:)\)
Miller-Rabin の定理を再掲します。
Miller-Rabin の定理(再掲) \(n\) を \(3\) 以上の奇数の合成数とする。また、\(n-1=2^ek\:\:(e\geq1,\:k\) は奇数\()\) と表されているものとする。このとき、 Miller-Rabin の条件 (1) \(a^k\equiv1\:\:(\mr{mod}\:n)\) もしくは (2) ある \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) を満たす \(a\:(1\leq a\leq n-1)\) は、\(n-1\) 個のうちの \(1/4\) 以下である。 |
証明のポイントは2つあります。(2) の条件に関する Miller-Rabin 系列、
\(a^k,\:a^{2k},\:\:a^{4k},\:\cd\:,\:a^{(e-1)k}\)
を考えると、ある項の2乗が次の項なので、\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) となる項があれば、それ以降の項は全て \(\equiv1\) となります。つまり、\(a^{2^rk}\equiv-1\) となる項は1つしかありません。従って、\(r\) を一つ決めたときに \(a^{2^rk}\equiv-1\) を満たす \(a\) の集合を \(A_2(r)\) とし、(2) を満たすすべての \(a\) の集合を \(A_2\) とすると、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
が成り立ちます。さらに (1) の条件を満たす \(a\) の集合を \(A_1\) とすると、(1) と (2) は排他的です。従って、Miller-Rabin の条件を満たす \(a\) の集合を \(M\) とすると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&=|A_1|+\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\\
\end{eqnarray}\)
です。このことを以下の証明で利用します。もう一つの証明のポイントは、「1.\(\bs{n=p^2t\:\:(\:p}\) は奇素数。\(\bs{t\geq1}\) は奇数\(\bs{)}\)」での証明と同じように、巡回群の性質を利用することです。
まず前提として、Miller-Rabin の条件を満たす \(a\:(0\leq a\leq n-1)\) は、フェルマの条件、\(a^{n-1}\equiv1\:\:(\mr{mod}\:n)\) も満たしますが、これが成り立つ \(a\) は \(n\) とは素です。従って、既約剰余類群 \((Z/nZ)^{*}\:=\:(Z/p_1p_2Z)^{*}\) の範囲で \(a\) の個数を検討します。
もちろん、\(p_1\neq p_2\) なので、既約剰余類群 \((Z/p_1p_2Z)^{*}\) は巡回群ではありません。しかし \(p_1,\:p_2\) が互いに素なので、\((Z/p_1p_2Z)^{*}\) は2つの既約剰余類群の直積と同型であり、
\((Z/p_1p_2Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
と表せます。つまり、\(a\in(Z/p_1p_2Z)^{*}\) とし、
\(a\) を \(p_1\) で割った余りを \(a_{p_1}\)
\(a\) を \(p_2\) で割った余りを \(a_{p_2}\)
と書くと、\(a_{p_1}\in(Z/p_1Z)^{*},\:\:a_{p_2}\in(Z/p_2Z)^{*}\) ですが、ここで、
\(f\::\:a\:\longrightarrow\:(a_{p_1},\:a_{p_2})\)
の写像を定義すると、この写像は1対1(全単射)で、同型写像であり、上の「直積と同型」の式が成り立ちます。同型写像は \(f(xy)=f(x)f(y)\) というように演算を保存するので、演算してから写像した結果と写像してから演算した結果は同じです。
また、この \((Z/p_1Z)^{*}\) と \((Z/p_2Z)^{*}\) は、\(p_1\) と \(p_2\) が素数なので、生成元をもつ巡回群です。それぞれの群位数は、
\(\begin{eqnarray}
&&\:\:|(Z/p_1p_2Z)^{*}|&=\varphi(p_1p_2)\\
&&&=(p_1-1)(p_2-1)\\
\end{eqnarray}\)
\(|(Z/p_1Z)^{*}|=\varphi(p_1)=p_1-1\)
\(|(Z/p_2Z)^{*}|=\varphi(p_2)=p_2-1\)
であり、
\(|(Z/p_1p_2Z)^{*}|=|(Z/p_1Z)^{*}|\cdot|(Z/p_2Z)^{*}|\)
が成り立ちます。ここで \((Z/p_1Z)^{*}\) の任意の部分集合を \(H_1\)、\((Z/p_2Z)^{*}\) の任意の部分集合を \(H_2\) とします。
\(H_1\subset(Z/p_1Z)^{*}\)
\(H_2\subset(Z/p_2Z)^{*}\)
です。\((Z/p_1p_2Z)^{*}\) の元 \(a\) で、
\(a_{p_1}\in H_1\)
\(a_{p_2}\in H_2\)
となる \(a\) を考え、このような \(a\) の集合を \(H\) と書くと、
\(f\::\:a\:\longrightarrow\:(a_{p_1},\:\:a_{p_2})\)
の写像は1対1対応であり(=中国剰余定理)、集合の元の数については、
\(|H|=|H_1|\cdot|H_2|\)
が成り立ちます。
以上を踏まえて証明に進みます。一般に、
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\) なら
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\)
が言えます。また、\(p_1\) と \(p_2\) は互いに素なので、
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\) なら
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\)
も言えます。なぜなら、\(p_1\mid(x-y)\) かつ \(p_2\mid(x-y)\) なら、\(p_1p_2\mid(x-y)\) だからです。つまり、
\(x\equiv y\:\:(\mr{mod}\:p_1p_2)\)
\(x\equiv y\:\:(\mr{mod}\:p_1)\) かつ \(x\equiv y\:\:(\mr{mod}\:p_2)\)
の2つは、\(p_1,\:p_2\) が素数という前提では等価です。従って、Miller-Rabin の条件は次のように言い換えることができます。
\(n=p_1p_2,\:\:n-1=2^ek\) とするとき、 Miller-Rabin の条件(言い換え) (1) (1a) \(a^k\equiv1\:\:(\mr{mod}\:p_1)\) かつ (1b) \(a^k\equiv1\:\:(\mr{mod}\:p_2)\) もしくは、 (2) ある \(r\:(0\leq r\leq e-1)\) について、 (2a) \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_1)\) かつ (2b) \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_2)\) が成り立つ。 |
このように言い換えて、\((Z/p_1p_2Z)^{*}\) での問題を、\((Z/p_1Z)^{*}\) と \((Z/p_2Z)^{*}\) の問題に置き換えます。Miller-Rabin の条件を満たす、
| \((Z/p_1p_2Z)^{*}\) | の部分集合を \(M\) | |
| \((Z/p_1Z)^{*}\) | の部分集合を \(M_1\) | |
| \((Z/p_2Z)^{*}\) | の部分集合を \(M_2\) |
とすると、元の数については、
\(|M|=|M_1|\cdot|M_2|\)
が成り立ちます。以降、(1)\(,\) (2) の条件ごとに \(|M_1|\) と \(|M_2|\) を見積もることで、条件ごとの \(|M|\) を見積もり、そこから目的である \(|M|\) の数を評価します。(1)\(,\) (2) の条件ごとの \(M\) については、既に上で使ったように、
(1)を満たす \(M\) の部分集合を \(A_1\)
(2)を満たす \(M\) の部分集合を \(A_2\)
とします。
\(n-1=2^ek\) とおいたのと同じように、
\(p_1-1=2^{e_1}k_1\) (\(e_1\geq1,\:k_1\):奇数)
\(p_2-1=2^{e_2}k_2\) (\(e_2\geq1,\:k_2\):奇数)
とします。ここで、
\(e_1\leq e_2\)
とします。\(p_1\) と \(p_2\) は入れ替えてもよいので、こうすることで一般性は失われません。まず初めに、\(e,\:e_1,\:e_2\) の関係を整理しておきます。\(n-1=2^ek\) の式ですが、
\(\begin{eqnarray}
&&\:\:n-1&=p_1\cdot p_2-1\\
&&&=(2^{e_1}k_1+1)\cdot(2^{e_2}k_2+1)-1\\
&&&=2^{e_1+e_2}k_1k_2+2^{e_1}k_1+2^{e_2}k_2\\
&&&=2^{e_1}(2^{e_2}k_1k_2+k_1+2^{e_2-e_1}k_2)\\
\end{eqnarray}\)
と計算されます。この式を、
\(n-1=2^{e_1}\cdot K\)
\(K=2^{e_2}k_1k_2+k_1+2^{e_2-e_1}k_2\)
と表わすと、
\(e_1 < e_2\) のときは、\(K\) は奇数なので \(e=e_1\)
\(e_1=e_2\) のときは、\(K\) は偶数なので \(e > e_1\)
となり、いずれにせよ、
\(e_1\leq e\)
です。
ちなみに、\(n=p_1p_2\cd p_m\:\:(m\geq3)\) のときも同様で、
\(p_i-1=2^{e_i}k_i\:(3\leq i\leq m)\)
としたとき、\(e_1\) を \(e_i\:(3\leq i\leq m)\) の最小値とすると、\(e_1\leq e\) です。
\(p_i-1=2^{e_i}k_i\:(3\leq i\leq m)\)
としたとき、\(e_1\) を \(e_i\:(3\leq i\leq m)\) の最小値とすると、\(e_1\leq e\) です。
以降、
\(e_1 < e_2\)
\(e_1=e_2\)
の2つに分けて証明します。
2.1 \(e_1 < e_2\) の場合
(1)が成立するとき
(1) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_1\) とします。巡回群に関する定理 \((\br{C})\) により、\((Z/pZ)^{*}\) の群位数は \(p-1\) なので、
\(a^k=1\) となる \((Z/p_1Z)^{*}\) の元は \(\mr{gcd}(k,\:p_1-1)\) 個
\(a^k=1\) となる \((Z/p_2Z)^{*}\) の元は \(\mr{gcd}(k,\:p_2-1)\) 個
です。また、\(n=p_1p_2\) のとき、
\((Z/nZ)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
の同型が成り立つので、
\(\begin{eqnarray}
&&\:\:|A_1|&=\mr{gcd}(k,\:p_1-1)\cdot\mr{gcd}(k,\:p_2-1)\\
&&&=\mr{gcd}(k,\:2^{e_1}k_1)\cdot\mr{gcd}(k,\:2^{e_2}k_2)\\
\end{eqnarray}\)
です。ここで、\(k,\:k_1,\:k_2\) は全て奇数です。従って、
\(\mr{gcd}(k,\:2^{e_1}k_1)=\mr{gcd}(k,\:k_1)\)
\(\mr{gcd}(k,\:2^{e_2}k_2)=\mr{gcd}(k,\:k_2)\)
が成り立ち、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
となります。ここで \(|A_1|\) の上限値を評価すると、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
であり、
\(|A_1|\leq k_1k_2\)
が結論づけられます。
(2)が成立するとき
(2) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_2\) とします。まず、\(0\leq r\leq e-1\) である \(r\) を一つ固定して考え、
\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_1)\) かつ
\(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_2)\)
であるような集合を \(A_2(r)\) とします。そうすると、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
が成り立ちます。まず、次を証明します。
\((Z/p_1Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は \(r\geq e_1\) のとき \(0\) 個 \(r < e_1\) のとき \(2^r\cdot\mr{gcd}(k,\:k_1)\) 個 である。 |
【証明】
\((Z/p_1Z)^{*}\) は群位数 \(p_1-1\) の巡回群なので、その生成元を \(g\) とする。ここで、
\(g^{\frac{p_1-1}{2}}\)
を考えると、生成元の定義上、\(g^{p_1-1}=1,\) \(g^x\neq1\:(1\leq x < p_1-1)\) なので、
\(\begin{eqnarray}
&&\:\:g^{\frac{p_1-1}{2}}&\neq1\\
&&\:\:(g^{\frac{p_1-1}{2}})^2&=1\\
\end{eqnarray}\)
であり、つまり、
\(g^{\frac{p_1-1}{2}}=-1\:(=p_1-1)\)
である。\(a^{2^rk}=-1\) が成り立つ \(a\) を、生成元 \(g\) を用いて、
\(a=g^x\:\:(1\leq x\leq p_1-1)\)
と表すと、
\(a^{2^rk}=-1\)
\((g^x)^{2^rk}=g^{\frac{p_1-1}{2}}\) \((\br{D})\)
だが、\(p_1-1=2^{e_1}k_1\) なので、
\(g^{2^rkx}=g^{2^{e_1-1}k_1}\)
が成り立つ。ここで一般的に \((Z/pZ)^{*}\) の生成元を \(g\) とし、
\(g^s=g^t\)
なら、\(j\) を整数として、
\(\begin{eqnarray}
&&\:\:g^{p-1}&=1\\
&&\:\:g^{j(p-1)}&=1\\
\end{eqnarray}\)
なので、
\(g^s=g^{t+j(p-1)}\)
である。つまり、
\(s\equiv t\:\:(\mr{mod}\:p-1)\)
が成り立つ。従って、
\(2^rkx\equiv2^{e_1-1}k_1\:\:(\mr{mod}\:p_1-1)\)
\(2^rkx\equiv2^{e_1-1}k_1\:\:(\mr{mod}\:2^{e_1}k_1)\)
\((\br{E})\)
であり、\((\br{E})\) 式は \((\br{D})\) 式と等価である。\((\br{E})\) 式を解いて \(x\) を求めると、そこから \(a=g^x\) で \(a\) が求まる。
ここで、\(r\geq e_1\) と仮定すると、\((\br{E})\) 式は、
\(2^rkx-2^{e_1-1}k_1\equiv0\:\:(\mr{mod}\:2^{e_1}k_1)\)
\(2^{e_1-1}(2^{r-e_1+1}kx-k_1)\equiv0\:\:(\mr{mod}\:2^{e_1}k_1)\)
\((\br{F})\)
と書ける。この \((\br{F})\) 式の \((2^{r-e_1+1}kx-k_1)\) の項に着目すると、\(r-e_1+1\geq1\) であり、\(k_1\) は奇数なので「偶数 - 奇数」=「奇数」である。そうすると、\((\br{F})\) 式の左辺は \(2^{e_1-1}\) の奇数倍であり、法である \(2^{e_1}k_1\) では割り切れず、\((\br{F})\) 式は成り立たない。つまり、\(a^{2^rk}=-1\) の解は、\(r\geq e_1\) のときには無い。
一方、\(r < e_1\) のとき \((\br{E})\) 式は、
\(2^r(kx-2^{e_1-r-1}k_1)\equiv0\:\:(\mr{mod}\:2^{e_1}k_1)\)
\((\br{F}\,')\)
と書ける。この \((\br{F}\,')\) 式が成り立つためには、\((kx-2^{e_1-r-1}k_1)\) の項は約数として \(2^i\:(i\geq e_1-r\geq1)\) を持つ必要があるが(少なくとも偶数である必要)、\(kx\) と \(2^{e_1-r-1}k_1\) はともに奇数にも偶数にもなり得るので、 \((\br{F}\,')\) 式の成立可能性に問題はない。そこで、以降で \(r < e_1\) のときの \((\br{E})\) 式の解の個数を検討する。
\(2^rkx\equiv2^{e_1-1}k_1\:\:(\mr{mod}\:2^{e_1}k_1)\)
\((\br{E})\)
において、
\(\begin{eqnarray}
&&\:\:h&=\mr{gcd}(k,\:k_1)\\
&&\:\:k\,'&=\dfrac{k}{h}\\
&&\:\:k_1{}^{\prime}&=\dfrac{k_1}{h}\\
\end{eqnarray}\)
とおく。\(k\,'\) と \(k_1{}^{\prime}\) は互いに素で、また、\(k,\:k_1\) が奇数なので、\(h,\:k\,',\:k_1{}^{\prime}\) は奇数である。\(r < e_1\) つまり \(r\leq e_1-1\) の条件があるので、\((\br{E})\) 式の両辺と法を \(2^rh\) で割ると、
\(k\,'x\equiv2^{e_1-1-r}k_1{}^{\prime}\:\:(\mr{mod}\:2^{e_1-r}k_1{}^{\prime})\)
\((\br{G})\)
となる。一般的に、
\(ax\equiv b\:\:(\mr{mod}\:m)\)
の合同方程式は、\(a\) が \(m\) と素なときには \(b\) の値にかかわらず解があって、その解は \(m\) を法として唯一である(下記)。
一次不定方程式、
\(ax+my=b\)
は、\(\mr{gcd}(a,\:m)=1\) のときに解をもつ(No.355「高校数学で理解するガロア理論(2):不定方程式の解の存在:21C」参照)。この等式の両辺を \(\mr{mod}\:m\) でみると、
\(ax\equiv b\:\:(\mr{mod}\:m)\)
の合同方程式となる。この方程式に \(x_1,\:x_2\) の2つの解があるとすると、
\(ax_1\equiv b\:\:(\mr{mod}\:m)\)
\(ax_2\equiv b\:\:(\mr{mod}\:m)\)
\(a(x_1-x_2)\equiv0\:\:(\mr{mod}\:m)\)
となるが、\(\mr{gcd}(a,\:m)=1\) なので、
\(x_1\equiv x_2\:\:(\mr{mod}\:m)\)
となり、解は \(m\) を法として唯一である。
\(ax+my=b\)
は、\(\mr{gcd}(a,\:m)=1\) のときに解をもつ(No.355「高校数学で理解するガロア理論(2):不定方程式の解の存在:21C」参照)。この等式の両辺を \(\mr{mod}\:m\) でみると、
\(ax\equiv b\:\:(\mr{mod}\:m)\)
の合同方程式となる。この方程式に \(x_1,\:x_2\) の2つの解があるとすると、
\(ax_1\equiv b\:\:(\mr{mod}\:m)\)
\(ax_2\equiv b\:\:(\mr{mod}\:m)\)
\(a(x_1-x_2)\equiv0\:\:(\mr{mod}\:m)\)
となるが、\(\mr{gcd}(a,\:m)=1\) なので、
\(x_1\equiv x_2\:\:(\mr{mod}\:m)\)
となり、解は \(m\) を法として唯一である。
\((\br{G})\) 式 をみると、\(k\,'\) と \(k_1{}^{\prime}\) は互いに素であり、かつ奇数なので、\((\br{G})\) 式における \(k\,'\) と、法である \(2^{e_1-r}k_1{}^{\prime}\) は互いに素である。ということは、
\((\br{G})\) 式は、法 \(2^{e_1-r}k_1{}^{\prime}\) で唯一の解をもつ
ことになる。\((\br{G})\) 式は \((\br{E})\) 式の両辺と法を \(2^rh\) で割ったものであった。つまり、\((\br{G})\) 式の法は、
\(2^{e_1-r}k_1{}^{\prime}=\dfrac{2^{e_1}k_1}{2^rh}\)
である。ということは、\((\br{G})\) 式の、法 \(2^{e_1-r}k_1{}^{\prime}\) での唯一の解は、法 \(2^{e_1}k_1\) である \((\br{E})\) 式の解、\(2^rh=2^r\cdot\mr{gcd}(k,\:k_1)\) 個に対応する。\((\br{E})\) 式は \((\br{D})\) 式と等価なので、これで、
\(0\leq r\leq e-1\) である \(r\) を一つ固定して考えたとき、\((Z/p_1Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は
\(r\geq e_1\) のとき \(0\) 個
\(r < e_1\) のとき \(2^r\cdot\mr{gcd}(k,\:k_1)\) 個
\(r\geq e_1\) のとき \(0\) 個
\(r < e_1\) のとき \(2^r\cdot\mr{gcd}(k,\:k_1)\) 個
が証明できた。【証明終】
ここまでで、
\((Z/p_1Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は
\(r\geq e_1\) のとき \(0\) 個
\(r < e_1\) のとき \(2^r\cdot\mr{gcd}(k,\:k_1)\) 個
であることが分かりました。この議論は \((Z/p_2Z)^{*}\) のときにも全く同じようにできて、
\((Z/p_2Z)^{*}\) において \(a^{2^rk}=-1\) である \(a\) の個数は
\(r\geq e_2\) のとき \(0\) 個
\(r < e_2\) のとき \(2^r\cdot\mr{gcd}(k,\:k_2)\) 個
が言えます。この結果を踏まえて、
| \(|A_2(r)|\): | \((Z/p_1p_2Z)^{*}\) において | |
| \(a^{2^rk}=-1\) である \(a\) の個数 |
を求めます。これは、
\((Z/p_1p_2Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\)
の直積関係を利用すると、\(e_1 < e_2\) の関係を考慮して、
\(r < e_1\) のとき
\(\begin{eqnarray}
&&\:\: |A_2(r)|&=2^r\cdot\mr{gcd}(k,\:k_1)\cdot2^r\cdot\mr{gcd}(k,\:k_2)\\
&&&=4^r\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\\
\end{eqnarray}\)
\(r\geq e_1\) のとき
\(|A_2(r)|=0\)
となります。ここから \(|A_2|\) を計算するには、
\(|A_2|=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\)
ですが、\(e_1\leq e\) の関係があるので、\(e-1\) までの総和は \(e_1-1\) までの総和に等しいことになります。つまり、
\(\begin{eqnarray}
&&\:\:|A_2|&=\displaystyle\sum_{r=0}^{e-1}|A_2(r)|\\
&&&=\displaystyle\sum_{r=0}^{e_1-1}|A_2(r)|\\
&&&=\displaystyle\sum_{r=0}^{e_1-1}4^r\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\\
\end{eqnarray}\)
の式が成り立ちます。この式に等比数列の総和である、
\(\displaystyle\sum_{r=0}^{e_1-1}4^r=\dfrac{4^{e_1}-1}{4-1}=\dfrac{4^{e_1}-1}{3}\)
を代入すると、
\(|A_2|=\dfrac{4^{e_1}-1}{3}\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
です。ここで、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
の関係を利用すると、
\(|A_2|\leq\dfrac{4^{e_1}-1}{3}k_1k_2\)
となります。ここまでの式は、\(e_1 < e_2\) でなくても \(e_1\leq e_2\) なら成り立つことが導出過程から分かります。
以上の計算で \(|M|\) を評価できます。
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq k_1k_2+\dfrac{4^{e_1}-1}{3}k_1k_2\\
\end{eqnarray}\)
この計算をもとに \(1\leq a\leq n-1\) の \(n-1\) 個のうちの \(|M|\) の割合を評価すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2}\\
&&&\leq\dfrac{1}{2^{e_1+e_2}}\left(1+\dfrac{4^{e_1}-1}{3}\right)\\
&&&=\dfrac{1}{2^{e_1+e_2}}\cdot\dfrac{2+4^{e_1}}{3}\\
\end{eqnarray}\)
となります。ここで、\(\bs{e_1 < e_2}\) なので、\(\bs{2e_1+1\leq e_1+e_2}\) です。従って、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{2e_1+1}}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{2+4^{e_1}}{6\cdot4^{e_1}}\\
\end{eqnarray}\)
ですが、この最後の式の最大値は \(e_1=1\) のときです。これを代入すると、
\(\dfrac{|M|}{n-1} < \dfrac{6}{24}=\dfrac{1}{4}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(e_1 < e_2\) のときに \(\dfrac{1}{4}\) 未満であることが証明されました。
2.2 \(e_1=e_2\) の場合
(1)が成立するとき
\(e_1 < e_2\) と全く同じ考え方で、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
です(\(k,\:k_1,\:k_2\) は奇数)。ここで、一般的には、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
が成り立ちますが、\(e_1=e_2\) だと、
\(\mr{gcd}(k,\:k_1)=k_1\)
\(\mr{gcd}(k,\:k_2)=k_2\)
が同時に成り立つことはありません。なぜなら、同時に成り立つとすると、
\(k_1\mid k\) かつ \(k_2\mid k\)
ですが、\(n-1=2^ek\) だったので、
\(k_1\mid(n-1)\) かつ \(k_2\mid(n-1)\)
です。ここで、\(n-1\) は
\(\begin{eqnarray}
&&\:\:n-1&=p_1p_2-1\\
&&&=(1+2^{e_1}k_1)\cdot p_2-1\\
&&&\equiv p_2-1\:\:(\mr{mod}\:k_1)\\
\end{eqnarray}\)
となりますが、\(k_1\mid(n-1)\) なので、
\(k_1\mid(p_2-1)\)
\(k_1\mid2^{e_2}k_2\)
\(k_1\mid k_2\)
となります。まったく同様にして、
\(n-1\equiv p_1-1\:\:(\mr{mod}\:k_2)\)
\(k_2\mid(p_1-1)\)
\(k_2\mid2^{e_1}k_1\)
\(k_2\mid k_1\)
です。\(k_1\mid k_2\) かつ \(k_2\mid k_1\) ということは、\(k_1=k_2\) ですが、\(e_1=e_2\) なので、\(p_1=p_2\) となって矛盾します。つまり \(\mr{gcd}(k,\:k_1)=k_1\)、\(\mr{gcd}(k,\:k_2)=k_2\) が同時に成り立つことはありません。そこで、
\(\mr{gcd}(k,\:k_1) < k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
として一般性を失いません。ここで \(k_1\) を素因数分解したときに現れる最小の素数を \(q\:(q\geq3)\)とし、
\(k_1=q\cdot k_0\:\:(k_0\):奇数\()\)
と表します。そうすると、\(\mr{gcd}(k,\:k_1) < k_1\) なので、
\(\mr{gcd}(k,\:k_1)\leq k_0\)
が成り立ち、
\(\dfrac{k_1}{\mr{gcd}(k,\:k_1)}\geq\dfrac{k_1}{k_0}=q\geq3\)
となります。ここから、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
が得られます。そこで、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
をもとに、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
を評価すると、
\(|A_1|\leq\dfrac{1}{3}k_1k_2\)
となります。
(2)が成立するとき
このケースは \(e_1 < e_2\) で導出した、
\(|A_2|\leq\dfrac{4^{e_1}-1}{3}\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\)
までは全く同じです。ここで、
\(\mr{gcd}(k,\:k_1)\leq\dfrac{1}{3}k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
によって評価すると、
\(|A_2|\leq\dfrac{1}{3}\cdot\dfrac{4^{e_1}-1}{3}k_1k_2\)
が成り立ちます。
以上の計算から \(|M|\) を評価すると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq\dfrac{1}{3}k_1k_2+\dfrac{1}{3}\cdot\dfrac{4^{e_1}-1}{3}k_1k_2\\
\end{eqnarray}\)
この計算をもとに \(1\leq a\leq n-1\) の \(n\) 個のうちの \(|M|\) の割合を計算すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2}\\
&&&\leq\dfrac{1}{2^{e_1+e_2}}\cdot\dfrac{1}{3}\left(1+\dfrac{4^{e_1}-1}{3}\right)\\
&&&=\dfrac{1}{2^{2e_1}}\cdot\dfrac{1}{3}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{1}{4^{e_1}}\cdot\dfrac{1}{3}\cdot\dfrac{2+4^{e_1}}{3}\\
&&&=\dfrac{1}{3}\left(\dfrac{2}{3\cdot4^{e_1}}+\dfrac{1}{3}\right)\\
\end{eqnarray}\)
となります。この最後の式の最大値は \(e_1=1\) のときです。代入すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{3}\left(\dfrac{1}{6}+\dfrac{1}{3}\right)\\
&&&=\dfrac{1}{6} < \dfrac{1}{4}\\
\end{eqnarray}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は、\(e_1=e_2\) のときにも \(\dfrac{1}{4}\) 未満であることが証明されました。
3. \(n=p_1\cdot p_2\cdot\cd\cdot p_m\:\:(\:m\geq3\:)\)
\(n\) が3個以上の相異なる奇素数の積に素因数分解される場合です。この場合も、基本的には \(n=p_1\cdot p_2\) のケースと(全く同じではないが)同様になります。Miller-Rabin の定理を再掲します。
Miller-Rabin の定理(再掲) \(n\) を \(3\) 以上の奇数の合成数とする。また、\(n-1=2^ek\:\:(e\geq1,\:k\) は奇数\()\) と表されているものとする。このとき、 Miller-Rabin の条件 (1) \(a^k\equiv1\:\:(\mr{mod}\:n)\) もしくは (2) ある \(r\:(0\leq r\leq e-1)\) について、 \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:n)\) を満たす \(a\:(1\leq a\leq n-1)\) は、\(n-1\) 個のうちの \(1/4\) 以下である。 |
以降、表記を見やすくするため、\(m=3\)、\(n=p_1\cdot p_2\cdot p_3\) の場合で記述します。既約剰余類群の同型関係、
\((Z/p_1p_2p_3Z)^{*}\cong(Z/p_1Z)^{*}\times(Z/p_2Z)^{*}\times(Z/p_3Z)^{*}\)
を利用して、問題を置き換えます。それぞれの群位数は、
\(\begin{eqnarray}
&&\:\:|(Z/p_1p_2p_3Z)^{*}|&=\varphi(p_1p_2p_3)\\
&&&=(p_1-1)(p_2-1)(p_3-1)\\
\end{eqnarray}\)
\(|(Z/p_1Z)^{*}|=\varphi(p_1)=p_1-1\)
\(|(Z/p_2Z)^{*}|=\varphi(p_2)=p_2-1\)
\(|(Z/p_3Z)^{*}|=\varphi(p_3)=p_3-1\)
であり、
\(|(Z/p_1p_2p_3Z)^{*}|=|(Z/p_1Z)^{*}|\cdot|(Z/p_2Z)^{*}|\cdot|(Z/p_3Z)^{*}|\)
が成り立ちます。Miller-Rabin の条件は次のように言い換えられます。
\(n=p_1p_2p_3,\:\:n-1=2^ek\) とするとき、 (1) (1a) \(a^k\equiv1\:\:(\mr{mod}\:p_1)\) かつ (1b) \(a^k\equiv1\:\:(\mr{mod}\:p_2)\) かつ (1c) \(a^k\equiv1\:\:(\mr{mod}\:p_3)\) もしくは、 (2) ある \(r\:(0\leq r\leq e-1)\) について、 (2a) \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_1)\) かつ (2b) \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_2)\) かつ (2c) \(a^{2^rk}\equiv-1\:\:(\mr{mod}\:p_3)\) が成り立つ。 |
例によって、
\(p_1-1=2^{e_1}k_1\:\:(e_1\geq1,\:k_1\) は奇数\()\)
\(p_2-1=2^{e_2}k_2\:\:(e_2\geq1,\:k_2\) は奇数\()\)
\(p_3-1=2^{e_3}k_3\:\:(e_3\geq1,\:k_3\) は奇数\()\)
とおきますが、\(\bs{e_1}\) は \(\bs{e_1,\:e_2,\:e_3}\) のうちの最小とします。こう仮定して一般性を失うことはありません。この仮定のもとでは、
\(3e_1\leq e_1+e_2+e_3\)
が成り立ちます。等号は \(e_1=e_2=e_3\) の場合です。
(1)が成立するとき
(1) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_1\) とします。\(n=p_1\cdot p_2\) のケースと同様の計算によって、
\(|A_1|=\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\cdot\mr{gcd}(k,\:k_3)\)
となります。\(|A_1|\) の上限値を評価すると、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
\(\mr{gcd}(k,\:k_3)\leq k_3\)
なので、
\(|A_1|\leq k_1k_2k_3\)
が結論づけられます。
(2)が成立するとき
(2) を満たす \(a\:(1\leq a\leq n-1)\) の集合を \(A_2\) とします。\(n=p_1\cdot p_2\) のケースと同様の計算で、
\(|A_2|=\displaystyle\sum_{r=0}^{e_1-1}(2^r)^3\cdot\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\cdot\mr{gcd}(k,\:k_3)\)
です。この式に \(e_1\) だけが現れるのは、\(e_1\) が \(\{e_1,\:e_2,\:e_3\}\) の最小値だからです。ここで、
\(\mr{gcd}(k,\:k_1)\leq k_1\)
\(\mr{gcd}(k,\:k_2)\leq k_2\)
\(\mr{gcd}(k,\:k_3)\leq k_3\)
の関係を利用します。また、等比数列の総和を計算すると、
\(\begin{eqnarray}
&&\:\:\displaystyle\sum_{r=0}^{e_1-1}(2^r)^3&=\displaystyle\sum_{r=0}^{e_1-1}(2^3)^r\\
&&&=\dfrac{(2^3)^{e_1}-1}{2^3-1}\\
\end{eqnarray}\)
です。まとめると、
\(|A_2|\leq\dfrac{2^{3e_1}-1}{2^3-1}\cdot k_1k_2k_3\)
が得られます。
以上をもとに \(|M|\) を評価すると、
\(\begin{eqnarray}
&&\:\:|M|&=|A_1|+|A_2|\\
&&&\leq k_1k_2k_3+\dfrac{2^{3e_1}-1}{2^3-1}\cdot k_1k_2k_3\\
\end{eqnarray}\)
です。この計算をもとに \(1\leq a\leq n-1\) の \(n-1\) 個のうちの \(|M|\) の割合を計算すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}&=\dfrac{|M|}{p_1p_2p_3-1}\\
&&& < \dfrac{|M|}{(p_1-1)(p_2-1)(p_3-1)}\\
&&&=\dfrac{|M|}{2^{e_1}k_1\cdot2^{e_2}k_2\cdot2^{e_3}k_3}\\
&&&\leq\dfrac{1}{2^{e_1+e_2+e_3}}\left(1+\dfrac{2^{3e_1}-1}{2^3-1}\right)\\
\end{eqnarray}\)
となります。ここで、\(3e_1\leq e_1+e_2+e_3\) です。従って、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{3e_1}}\left(1+\dfrac{2^{3e_1}-1}{2^3-1}\right)\\
&&&=\dfrac{6+2^{3e_1}}{7\cdot2^{3e_1}}\\
\end{eqnarray}\)
ですが、この最後の式は \(e_1\) の増大によって単調減少するので、その最大値は \(e_1=1\) のときです。これを代入すると、
\(\dfrac{|M|}{n-1} < \dfrac{6+8}{56}=\dfrac{1}{4}\)
となって、\(1\leq a\leq n-1\) のなかで Miller-Rabin の条件を満たす数の比率は \(\dfrac{1}{4}\) 未満であることが確かめられました。
以上の表記は \(m=3\) の場合ですが、証明のプロセスを振り返ってみると、\(m\geq3\) のときは、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{1}{2^{m\cdot e_1}}\left(1+\displaystyle\sum_{r=0}^{e_1-1}(2^m)^r\right)\\
&&&=\dfrac{1}{2^{m\cdot e_1}}\left(1+\dfrac{2^{m\cdot e_1}-1}{2^m-1}\right)\\
&&&=\dfrac{2^m-2+2^{m\cdot e_1}}{(2^m-1)\cdot2^{m\cdot e_1}}\\
\end{eqnarray}\)
です。この式の右辺は \(e_1\) について単調減少なので、\(e_1=1\) を代入すると、
\(\begin{eqnarray}
&&\:\:\dfrac{|M|}{n-1}& < \dfrac{2^m-2+2^m}{(2^m-1)\cdot2^m}\\
&&&=\dfrac{2\cdot(2^m-1)}{(2^m-1)\cdot2^m}\\
&&&=\dfrac{1}{2^{m-1}}\\
&&&\leq\dfrac{1}{4}\\
\end{eqnarray}\)
が \(m\geq3\) のすべてで成り立ちます。
ちなみに、カーマイケル数は必ず、\(p_1\cdot p_2\cdot\cd\cdot p_m\) \((\:m\geq3\:)\) の形をしていることが知られています。上の証明によって、\(n\) がカーマイケル数であったとしても Miller-Rabin の条件を満たす底 \(a\) は 全体の \(\dfrac{1}{4}\) 未満であることが分かります。
以上で、Miller-Rabin の定理が証明されました。
| 1024 ビットの素数を求める |
Miller-Rabin の定理を使って、実際に巨大素数を求めてみます。2048 ビットの RSA 暗号で使われる 1024 ビットの素数を求めます。1024 ビットは、\(2^{1023}\) ~ \(2^{1024}-1\) の数です。Python で整数 n が素数かどうかを判定する関数、miller_rabin(n) を次のようにシンプルに実装します。n が素数なら True、合成数なら False を返す関数です。反復回数は40回とします。
from random import randint
def miller_rabin(n):
if n == 2:
return True
if n < 2 or n % 2 == 0:
return False
k = (n - 1) // 2
e = 1;
while k % 2 == 0:
e += 1
k = k // 2
iteration = 40
for _ in range(iteration):
if not mr_base(n, e, k):
return False
return True
def mr_base(n, e, k):
a = randint(1, n - 1)
b = pow(a, k, n)
if (b == 1) or (b == n - 1):
return True
else:
for _ in range(e - 1):
b = pow(b, 2, n)
if b == n - 1:
return True
return False
|
この関数を用いて作ったのは、次のようなプログラムです。
| \(2^{1023}\) ~ \(2^{1024}-1\) の間の乱数 \(n\) を \(10,000\)個、順々に発生させる。 | |
| miller_rabin(n) で \(n\) が素数かどうかを調べる。 | |
| 見つかった素数の個数をカウントする。 | |
| 最初に見つかった素数を出力する。 |
1つの実行例ですが、12個の素数が見つかり、最初に見つかったのは次に示す 308桁の素数でした。実行時間は Google Colaboratry の環境で約 30秒です。
94872061 3054580553 8024546417 0443276752 8208705264 5738921481
0677834138 4405922941 9044925712 7675055467 0399951005
3184840724 4107587320 1847375774 1842027537 2972168431
3292460096 0558147125 1513790454 1422818823 6684614711
0137905023 0947309459 7845156412 5542386383 6759057622
9952488549 9964568003 6095666702 5172908475 7410497807
何回か実行してみると、素数の桁数はほとんどが 309桁で、一部が 308桁です。これは \(\mr{log}_{10}2^{1023}\fallingdotseq307.95\) なので、そうなるはずです。また、1万個の n のうちの素数の数は 8~18 個程度となりました。実行結果について「素数定理」と「反復回数」の観点から考察します。
素数定理
数学では、\(x\) 以下の素数の個数を \(\pi(x)\) で表わします。素数定理によると、
\(\pi(x)\sim\dfrac{x}{\mr{log}(x)}\)
です。左辺と右辺をつなぐ \(\sim\) は、
左辺と右辺の比率 \(\longrightarrow\:1\:\:(x\longrightarrow\infty)\)
を意味します。以下、
\(\pi(x)=\dfrac{x}{\mr{log}(x)}\)
と考えて、m ビットの数に含まれる素数の割合を見積もります。m ビットの数の総数は \(2^{m-1}\) 個なので、m ビット数の素数割合は、
| 素数割合 | \(=\dfrac{1}{2^{m-1}}(\pi(2^m)-\pi(2^{m-1}))\) | |
| \(=\dfrac{1}{\mr{log}2\cdot m}\cdot\dfrac{m-2}{m-1}\) |
ですが、\(\dfrac{m-2}{m-1}\) を \(1\) と見なすと、簡潔に、
素数割合 \(=\dfrac{1}{\mr{log}2\cdot m}\)
です。この式に \(m=1024\) を代入すると、
素数割合 \(\fallingdotseq0.0014\)
となります。つまり、
1024 ビットの数、10,000個をランダムに選んで素数判定を行うと、0.14%=14 個程度の素数が見つかる
と言えます。これは上の実験で、1万個の n のうちの素数の数は 8~18 個程度だったことに合致します。
反復回数
プログラムを少々変更して、
何回目の反復(iteration)で素数\(\cdot\)合成数の判定ができたか
を調べると、素数判定のときは当然 iteration = 40 ですが、
合成数判定のときの iteration = 1
であることが分かります(1万個の素数判定をする前提です)。つまり、\(n\) が合成数なら最初の計算で即、合成数と判明します。何回かの反復の後に合成数と判明することは、上の計算では無いのです。
この理由は、\(n\) が合成数だと「\(a\:(1\leq a\leq n-1)\) のなかで Miller-Rabin の条件を満たす底 \(a\) の比率は \(\tfrac{1}{4}\) 以下」という定理の \(\tfrac{1}{4}\) が(一般には)過大評価であることによります。たとえば、\(n\) が2つの異なる素数の積の場合、
\(\begin{eqnarray}
&&\:\:n&=p_1p_2\\
&&\:\:n-1&=2^ek\\
&&\:\:p_1-1&=2^{e_1}k_1\\
&&\:\:p_2-1&=2^{e_2}k_2\\
\end{eqnarray}\)
(\(e,e_1,e_2\geq1,\:\:k,k_1,k_2\) は奇数)
において \(\tfrac{1}{4}\) 以下の主な根拠は、
\(\mr{gcd}(k,\:k_1)\cdot\mr{gcd}(k,\:k_2)\leq k_1k_2\)
でした。ところが、この式で等号が成り立つのは、特に \(n\) が巨大だと、めったにありません。高々 10,000個程度の合成数を判定したとしても、Miller-Rabin の条件を満たす底 \(a\) が現れる確率はほとんどゼロに等しいのです。
ランダムに選んだ数 \(n\) のほとんどは(1024 ビットの数の場合 99.86 % は)合成数です。したがって「合成数を合成数だと速く判定する」のが素数判定アルゴリズムのポイントであり、反復回数をどうするかは全体の速度にそれほど関係ありません。このあたりの事情はフェルマの条件で素数判定をしても同じです。
ただし、フェルマの条件とは違って、ランダムに選んだ底 \(a\) が Miller-Rabin の条件を満たす確率が、\(n\) の値にかかわらず必ず \(\tfrac{1}{4}\) 以下であることが数学的に保証されています。そこが Miller-Rabin の素数判定アルゴリズムの価値なのでした。
2024-03-18 18:23
nice!(0)
No.368 - 命のビザが欲しかった理由 [歴史]
No.201「ヴァイオリン弾きとポグロム」に関連する話です。No.201 の記事は、シャガール(1887-1985)の絵画『ヴァイオリン弾き』(1912)を、中野京子さんの解説で紹介したものでした。有名なミュージカルの発想のもとになったこの絵画には、ユダヤ人迫害の記憶が刻み込まれています。シャガールは帝政ロシアのユダヤ人強制居住地区(現、ベラルーシ)に生まれた人です。
絵のキーワードは "ポグロム" でした。ポグロムとは何か。No.201 で書いたことを要約すると次のようになるでしょう。
その、ナチスによるホロコーストに関係した有名な話があります。当時のリトアニアの日本領事代理だった杉原千畝が、ユダヤ人に日本通過ビザ(いわゆる "命のビザ")を発行し、ドイツによるホロコーストから救ったという件です。
この "命のビザ" について、先日の朝日新聞に大変興味深い記事が掲載されました。「ユダヤ難民は誰から逃れたかったのか」を追求した、東京理科大学の菅野教授の研究です。それを以下に紹介します。記事の見出しは、
杉原千畝「命のビザ」で異説
ユダヤ人が逃れたかったのはソ連?
(朝日新聞 2023年11月20日 夕刊)
です。朝日新聞編集委員・永井靖二氏の署名入り記事です。
難民は何から逃れたかったのか
まず記事の出だしでは、当時の状況と命のビザの経緯が簡潔に書かれています。
東京理科大学の菅野教授は、当時の1次資料のみを読み解き、ユダヤ難民が何から逃れたかったのかを突き止めました。
あらためて歴史的経緯を時系列にまとめると、次のようになります。
この経緯のポイントは次の3つでしょう。
ユダヤ難民がなぜ命のビザを欲しがったのか。それは記事にあるように「ソ連から逃れるため」というのが正解でしょう。もちろん、ドイツの "ユダヤ人狩り" は難民も知っていたはずです。しかし、当時は独ソ不可侵条約が結ばれていて、その一方の当事者であるソ連にリトアニアは占領されていました。当時、ドイツの脅威が直接的にリトアニアに及んだわけではありません。シンプルに考えても、リトアニアのユダヤ難民が恐れたのはドイツではなくソ連だった。
加えてロシア・ソ連では、シャガールの絵に象徴されるように、19世紀以来、ポグロムの嵐が吹き荒れていました。ユダヤ人がリトアニアを占領したソ連から逃れたかったのは当然でしょう。
通説の経緯
しかし日本では「ナチスの迫害から逃れるため」というのが通説になっています。この通説ができた経緯が記事に紹介されています。
記事にある杉原氏の覚え書きによると、ビザを発給したのはポーランド難民で、その一部がユダヤ人ということになります。では「ユダヤ人でないポーランド難民」は何から逃れたかったのかというと、それはソ連からということになります。
しかし日本では当初から、ユダヤ難民は「ナチス・ドイツに追われ」たことになっていました。記事にも、
とあります。杉原氏自身でさえ、ユダヤ人難民は「ナチスに捕まってガスの部屋へ放り込まれる」からビザを欲したのだと、1988年に語っているわけです。「ナチスの迫害から逃れるため」という通説ができるのは当然です。もちろん、時間がたつと記憶が曖昧になるのは誰しもあるわけです。
これは、1960年の新聞報道を含め、ナチス・ドイツによるユダヤ人ホロコーストが、如何に世界の人々にショックと強烈な印象を与えたかという証だと思います。そして重要な点は、ユダヤ人難民がソ連から逃れたかったにしろ、杉原氏の行為に対する評価は変わらないということです。
複合的な視点で見る必要性
ナチス・ドイツによるユダヤ人ホロコーストという惨劇を知ってしまうと、それに強く影響された視点でものごとを考えがちです。しかし、複合的な視点はどのようなことでも重要です。記事の中で内田樹氏が発言していました。
この内田氏の指摘は鋭いと思います。
杉原氏は外交官であり、日本の国益のために働くのが使命です。明治以降の日本政府がユダヤ人に融和的だっというのは、数々の証拠があります。外交官である杉原氏はそれを知っていたのでしょう。その "融和的" な姿勢の発端は、日露戦争におけるユダヤ人資本家からの戦費調達であり、その背景にはロシアにおけるポグロムがある。ユダヤ人資本家は、ロシアと戦おうとする日本を応援したわけです。
という「複合的な視点」が重要でしょう。一面的に歴史をみることはまずいし、「歴史から学ぶ」ことにもならないのです。
絵のキーワードは "ポグロム" でした。ポグロムとは何か。No.201 で書いたことを要約すると次のようになるでしょう。
| ポグロムはロシア語で、もともと「破壊」の意味だが、歴史用語としてはユダヤ人に対する集団的略奪・虐殺を指す。単なるユダヤ人差別ではない。 | |
| ポグロムに加わったのは都市下層民や貧農などの経済的弱者で、シナゴーグ(ユダヤ教の礼拝・集会堂)への放火や、店を襲っての金品強奪、暴行、レイプ、果ては惨殺に及んだ。 | |
| ポグロムはロシアだけの現象ではない。現代の国名で言うと、ドイツ、ポーランド、バルト3国、ロシア、ウクライナ、ベラルーシなどで、12世紀ごろから始まった。特に19世紀末からは各地でポグロムの嵐が吹き荒れた。 | |
| 嵐が吹き荒れるにつれ、ポグロムに警官や軍人も加わるようになり、政治性を帯びて組織化した。この頂点が、第2次世界大戦中のナチス・ドイツによるユダヤ人のホロコーストである。 |
|
この "命のビザ" について、先日の朝日新聞に大変興味深い記事が掲載されました。「ユダヤ難民は誰から逃れたかったのか」を追求した、東京理科大学の菅野教授の研究です。それを以下に紹介します。記事の見出しは、
杉原千畝「命のビザ」で異説
ユダヤ人が逃れたかったのはソ連?
(朝日新聞 2023年11月20日 夕刊)
です。朝日新聞編集委員・永井靖二氏の署名入り記事です。

|
杉原氏が発給した手書きのビザ。"敦賀上陸" とある。 |
(朝日新聞より) |
難民は何から逃れたかったのか
まず記事の出だしでは、当時の状況と命のビザの経緯が簡潔に書かれています。
|
東京理科大学の菅野教授は、当時の1次資料のみを読み解き、ユダヤ難民が何から逃れたかったのかを突き止めました。
|
あらためて歴史的経緯を時系列にまとめると、次のようになります。
| 独ソ不可侵条約が締結 | |
| ドイツがポーランドに侵攻(=第2次世界大戦が勃発)。ソ連も侵攻し、10月、ポーランドは独ソ両国によって分割された。 | |
| ソ連がリトアニアに進駐 | |
| 杉原がリトアニアでユダヤ人に計2140件のビザを発給 | |
| ソ連がリトアニアを併合 | |
| 独ソ戦開戦 | |
| アウシュビッツ収容所で毒ガスが初めて使われた |
この経緯のポイントは次の3つでしょう。
| 杉原氏が命のビザを発給したのは、ソ連がリトアニアに進駐して併合する、まさにその時期にあたる。 | |
| 独ソ戦が始まったのは、命のビザより10ヶ月あとである(もちろん独ソ戦が始まった以上、リトアニアにドイツ軍が押し寄せてくることは想定できる)。 | |
| アウシュビッツ(ポーランド)で毒ガスによるホロコーストが始まったのは、命のビザより1年後である。 |
ユダヤ難民がなぜ命のビザを欲しがったのか。それは記事にあるように「ソ連から逃れるため」というのが正解でしょう。もちろん、ドイツの "ユダヤ人狩り" は難民も知っていたはずです。しかし、当時は独ソ不可侵条約が結ばれていて、その一方の当事者であるソ連にリトアニアは占領されていました。当時、ドイツの脅威が直接的にリトアニアに及んだわけではありません。シンプルに考えても、リトアニアのユダヤ難民が恐れたのはドイツではなくソ連だった。
加えてロシア・ソ連では、シャガールの絵に象徴されるように、19世紀以来、ポグロムの嵐が吹き荒れていました。ユダヤ人がリトアニアを占領したソ連から逃れたかったのは当然でしょう。
通説の経緯
しかし日本では「ナチスの迫害から逃れるため」というのが通説になっています。この通説ができた経緯が記事に紹介されています。
|
記事にある杉原氏の覚え書きによると、ビザを発給したのはポーランド難民で、その一部がユダヤ人ということになります。では「ユダヤ人でないポーランド難民」は何から逃れたかったのかというと、それはソ連からということになります。
しかし日本では当初から、ユダヤ難民は「ナチス・ドイツに追われ」たことになっていました。記事にも、
| 日本を通過したユダヤ人難民について、1960年7月1日付の朝日新聞朝刊は「ドイツを追われ日本に来た」としていた。8月7日発行の週刊読売も「ナチスに追われ」たと書いていた。 | |
| 1988年9月、杉原氏はフジテレビのドキュメンタリーで、難民にビザを発給したのは「ナチスにひっ捕まって」「ガスの部屋へ放り込まれる」からだったと語った。 |
とあります。杉原氏自身でさえ、ユダヤ人難民は「ナチスに捕まってガスの部屋へ放り込まれる」からビザを欲したのだと、1988年に語っているわけです。「ナチスの迫害から逃れるため」という通説ができるのは当然です。もちろん、時間がたつと記憶が曖昧になるのは誰しもあるわけです。
これは、1960年の新聞報道を含め、ナチス・ドイツによるユダヤ人ホロコーストが、如何に世界の人々にショックと強烈な印象を与えたかという証だと思います。そして重要な点は、ユダヤ人難民がソ連から逃れたかったにしろ、杉原氏の行為に対する評価は変わらないということです。
複合的な視点で見る必要性
ナチス・ドイツによるユダヤ人ホロコーストという惨劇を知ってしまうと、それに強く影響された視点でものごとを考えがちです。しかし、複合的な視点はどのようなことでも重要です。記事の中で内田樹氏が発言していました。
|
この内田氏の指摘は鋭いと思います。
| 日本政府はユダヤ人に融和的な姿勢を保っていたから、杉原氏には道義心に加えて、国益への配慮もあったはずだ。 | |
| リトアニアではソ連への恐怖の方がナチスよりも強かったし、難民らには局面ごとに多様な外力が働いていた。 |
杉原氏は外交官であり、日本の国益のために働くのが使命です。明治以降の日本政府がユダヤ人に融和的だっというのは、数々の証拠があります。外交官である杉原氏はそれを知っていたのでしょう。その "融和的" な姿勢の発端は、日露戦争におけるユダヤ人資本家からの戦費調達であり、その背景にはロシアにおけるポグロムがある。ユダヤ人資本家は、ロシアと戦おうとする日本を応援したわけです。
杉原氏の「命のビザ」は、ソ連から逃れようとする「ユダヤ人を含む難民」に発給されたものであり、それは人道的配慮と日本の国益への配慮に合致するものであった
という「複合的な視点」が重要でしょう。一面的に歴史をみることはまずいし、「歴史から学ぶ」ことにもならないのです。
2023-12-09 07:59
nice!(0)
No.367 - 南部鉄器のティーポット [文化]
これまでの記事で、NHK総合で定期的に放映されているフランスの警察ドラマ「アストリッドとラファエル」から連想した話題を2つ書きました。
の2つです。今回もその継続で、このドラマに出てくるティーポットの話を書きます。
ダマン・フレール
パリのマレ地区のヴォージュ広場を囲む回廊の一角に、紅茶専門店、ダマン・フレール(Dammann Frères)の本店があります。ダマン・フレールは、17世紀のルイ14世の時代にフランスにおける紅茶の独占販売権を得たという老舗で、ホームページには次のようにあります。
ちなみに、フレールとはフランス語で兄弟の意味で、屋号は「ダマン兄弟」です。緑茶や中国茶も扱っているので「お茶専門店」というのが正確でしょう。
パリには4回ほど個人旅行をしましたが、2000年代初頭にダマン・フレールの本店に行ったことがあります。私の配偶者が是非行きたいということで、紅茶のティーバッグをお土産(いわゆる "バラマキ")にするためだったと思います。
店内に入ってみると、いかにも老舗という内装で、その "重厚感" が印象的でした。当時は日本人の店員さんがいたと思います。パリでも日本人観光客がメジャーな時代でした。
そして私が最も印象的だったのは、明らかに日本の南部鉄器と思われる "ティーポット"(日本で言う "急須")が売られていたことです。ただし、黒い鉄色ではなく、色がついていました。このような鉄器の "カラー急須" を見たのは初めてだったので、ちょっとびっくりしたわけです。
アストリッドの愛用品
「アストリッドとラファエル」には、アストリッドの愛用品として鉄器のカラーのティーポットが出てきます。次の画像は、シーズン1の第2話「呪われた家」のもので、アストリッドが勤務する犯罪資料局の執務机の様子です。上の図では、彼女が青色の鉄器のティーポットを取り出して机に置いています。茶筒と湯呑み茶碗もあるので、緑茶(日本茶)を入れるためのものでしょう。その下の画像では、実際にお茶を入れています。
アストリッドの自宅の様子が次の画像です。このティーポットも青色ですが、犯罪資料局に持ち込んだものとはデザインが違うようです。
次の画像もアストリッドの自宅ですが、このティーポットは緑っぽい色です。
そもそもこのドラマには、日本関連のものが数々登場します。アストリッドが常連客である日本食材店や、犯罪資料局にアストリッドが持ち込んだ半畳ほどの畳、箱根細工(と思われる)"からくり箱" などです。また、アストリッドの "恋人" はテツオ・タナカという日本からの留学生です。ドラマの制作サイドが日本市場を意識しているのでしょう。
しかし南部鉄器のティーポットに関して言うと、それがパリでいつでも買えるものだからこそ、ドラマに登場するのだと思います。20年ほど前にダマン・フレールで見た南部鉄器のカラーのティーポットは、現在でもフランスに愛好者がいることが分かります。
南部鉄器は鋳造なので、ガラスや磁器のティーポットに比べると熱容量が大きく、お茶が冷めにくい。おそらくそこが評価されているのだと思います。また、ヨーロッパにとっては、紅茶や緑茶はもともと東洋からの輸入品です。南部鉄器という "アジアン・テイスト" のアイテムが、お茶にマッチすると考える人もいそうです。
岩鋳
ところで、南部鉄器をヨーロッパに輸出した先駆者は、岩手県盛岡市の「岩鋳」という会社です。南部鉄器といえば江戸時代が発祥の由緒ある工芸品で、盛岡と水沢(奥州市)が生産の中心地です。水沢の会社では "及源" が有名です。
その岩鋳の鉄器が海外進出した経緯が「ダイアモンド・オンライン」(ダイアモンド社)に出ていました。興味深い話だったので、是非それを紹介したいと思います。「飛び立て、世界へ! 中小企業の海外進出奮闘記」と題する一連の記事の中の一つで、記事のタイトルは、
です。まず、少々意外だったのは、岩鋳の製品の半分は海外に販売され、ヨーロッパでは「イワチュー」(IWACHU)が鉄器の代名詞になっていることです。
ポイントを何点かにまとめると、次のようになるでしょう。
なお、中国や東南アジアでは、欧米とは違い、日本で伝統的な黒い急須や鉄瓶が売れるようです。
その岩鋳の海外進出は 1960年代から始まりました。そして本格的な販売がスタートしたのは、パリの紅茶専門店からの依頼が契機だったのです。
岩鋳にカラフルなティーポットの製作を依頼したパリの紅茶専門店は、マリアージュ・フレールだそうです。マリアージュもパリのマレ地区に本店があり、ダマンから近い距離です。南部鉄器のカラフルなティーポットは、マリアージュでまずヒットし、それがダマンを含む店に広まったということでしょう。
鉄にホーローをコーティングするのは従来からある技術です(各種のホーロー製品)。しかし、鋳造した鉄への着色は従来からの技術ではありません。「3年かけて着色法を開発した」とあるように、かなりの苦労の末に開発した製品だったようです。
そして、記事の最後にある、岩鋳の岩清水社長のコメントが印象的でした。
カラフルな鉄器の急須は、我々日本人からすると、女性客を狙ったのだろうと、暗黙に考えてしまいます。無骨な感じの黒の鉄器ではパリジェンヌにはウケないだろうと ・・・・・。依頼を受けた岩鋳の人たちも、おそらくそう考えたのではないでしょうか。
しかしそうではないのですね。岩鋳に依頼したパリの紅茶専門店のオーナーの考えでは「カラフルな鉄器なら重厚感があり男性にぴったり」なのです。少なくとも当初の発想はそうだった。
かなり意外ですが、まさに岩清水社長の言うように「市場の声に耳を澄まし、そこに自慢の技術を投入することが肝要」です。お茶を飲むのは日本(を含む東アジアの)文化であり、南部鉄器の急須もその文化の一部です。しかし、ダマン・フレールを見ても分かるように、フランスにおいても、お茶は数百年の伝統をもつ伝統文化なのです。文化の "押し売り" はうまく行かない。岩鋳はパリの紅茶専門店に導かれて、ニーズと技術のベストなマッチングを作り上げたことになります。
ドラマ「アストリッドとラファエル」に戻ると、アストリッドが愛用する青いティーポットは、実はフランスと日本の2つの文化の接点を示している象徴的なアイテムなのでした。
の2つです。今回もその継続で、このドラマに出てくるティーポットの話を書きます。
ダマン・フレール
パリのマレ地区のヴォージュ広場を囲む回廊の一角に、紅茶専門店、ダマン・フレール(Dammann Frères)の本店があります。ダマン・フレールは、17世紀のルイ14世の時代にフランスにおける紅茶の独占販売権を得たという老舗で、ホームページには次のようにあります。
|
ちなみに、フレールとはフランス語で兄弟の意味で、屋号は「ダマン兄弟」です。緑茶や中国茶も扱っているので「お茶専門店」というのが正確でしょう。
パリには4回ほど個人旅行をしましたが、2000年代初頭にダマン・フレールの本店に行ったことがあります。私の配偶者が是非行きたいということで、紅茶のティーバッグをお土産(いわゆる "バラマキ")にするためだったと思います。

|
ダマン・フレール本店の店内 |
(ダマンの公式ホームページより) |
店内に入ってみると、いかにも老舗という内装で、その "重厚感" が印象的でした。当時は日本人の店員さんがいたと思います。パリでも日本人観光客がメジャーな時代でした。
そして私が最も印象的だったのは、明らかに日本の南部鉄器と思われる "ティーポット"(日本で言う "急須")が売られていたことです。ただし、黒い鉄色ではなく、色がついていました。このような鉄器の "カラー急須" を見たのは初めてだったので、ちょっとびっくりしたわけです。

|
南部鉄器のカラーのティーポット |
ダマンで売られていたものではありません。「ダイアモンド・オンライン」のページより。 |
アストリッドの愛用品
「アストリッドとラファエル」には、アストリッドの愛用品として鉄器のカラーのティーポットが出てきます。次の画像は、シーズン1の第2話「呪われた家」のもので、アストリッドが勤務する犯罪資料局の執務机の様子です。上の図では、彼女が青色の鉄器のティーポットを取り出して机に置いています。茶筒と湯呑み茶碗もあるので、緑茶(日本茶)を入れるためのものでしょう。その下の画像では、実際にお茶を入れています。

|
アストリッドの青のティーポット |
シーズン1・第2話「呪われた家 前編」(2022.8.14)より |

|
お茶を入れるアストリッド |
シーズン1・第2話「呪われた家 後編」(2022.8.21)より |
アストリッドの自宅の様子が次の画像です。このティーポットも青色ですが、犯罪資料局に持ち込んだものとはデザインが違うようです。

|
アストリッドの自宅のティーポット(1) |
シーズン1・第6話「存在しない男」(2022.9.18)より |
次の画像もアストリッドの自宅ですが、このティーポットは緑っぽい色です。

|
アストリッドの自宅のティーポット(2) |
シーズン4・第3話「密猟者」(2024.1.28)より |
そもそもこのドラマには、日本関連のものが数々登場します。アストリッドが常連客である日本食材店や、犯罪資料局にアストリッドが持ち込んだ半畳ほどの畳、箱根細工(と思われる)"からくり箱" などです。また、アストリッドの "恋人" はテツオ・タナカという日本からの留学生です。ドラマの制作サイドが日本市場を意識しているのでしょう。
しかし南部鉄器のティーポットに関して言うと、それがパリでいつでも買えるものだからこそ、ドラマに登場するのだと思います。20年ほど前にダマン・フレールで見た南部鉄器のカラーのティーポットは、現在でもフランスに愛好者がいることが分かります。
南部鉄器は鋳造なので、ガラスや磁器のティーポットに比べると熱容量が大きく、お茶が冷めにくい。おそらくそこが評価されているのだと思います。また、ヨーロッパにとっては、紅茶や緑茶はもともと東洋からの輸入品です。南部鉄器という "アジアン・テイスト" のアイテムが、お茶にマッチすると考える人もいそうです。
岩鋳
ところで、南部鉄器をヨーロッパに輸出した先駆者は、岩手県盛岡市の「岩鋳」という会社です。南部鉄器といえば江戸時代が発祥の由緒ある工芸品で、盛岡と水沢(奥州市)が生産の中心地です。水沢の会社では "及源" が有名です。
その岩鋳の鉄器が海外進出した経緯が「ダイアモンド・オンライン」(ダイアモンド社)に出ていました。興味深い話だったので、是非それを紹介したいと思います。「飛び立て、世界へ! 中小企業の海外進出奮闘記」と題する一連の記事の中の一つで、記事のタイトルは、
です。まず、少々意外だったのは、岩鋳の製品の半分は海外に販売され、ヨーロッパでは「イワチュー」(IWACHU)が鉄器の代名詞になっていることです。
|

|
岩鋳のカラーの急須 「ダイアモンド・オンライン」より。 |
ポイントを何点かにまとめると、次のようになるでしょう。
| 岩鋳は、伝統的な鉄瓶や急須だけではなく、鍋やフライパンなどのキッチンウエアなど、年間約100万点の鉄器を生産していて、南部鉄器としては最大規模である。かつ、その半数が海外20ヵ国で販売されている。 | |
| 欧米市場では、赤やピンク、青、緑、オレンジなどのカラフルな急須が主力商品である。ヨーロッパでは「イワチュー」が鉄器の代名詞になっている。
ちなみに、岩鋳の海外ブランドは "IWACHU" であり、最初に人気に火がついたフランスでは、フランス語読みで「イワシュー」で通っているそうです。
| |
| 急須の着色はウレタン樹脂を使うが、鋳物らしい風合い = 鋳肌(いはだ、鉄の素材感)を活かしている。また内部はホーローをコーティングしている。
日本古来の急須とちがって、着色するのみならず、急須の内部にはホーロー加工がしてあります。鉄器の急須は、鉄分が溶けだして体にいいとか、お茶がまろやかになると言いますが、そういう効果は期待できないわけです。しかしこれは欧米のニーズに合わせた製品なのです。
もちろん、鋳肌が活きていると書いてあるように、ダマン・フレールで見たときも、一目でアラレ模様の南部鉄器だと分かるものでした。着色も、日本の伝統色を思わせる中間色で、鉄器にマッチしています。 |
なお、中国や東南アジアでは、欧米とは違い、日本で伝統的な黒い急須や鉄瓶が売れるようです。
その岩鋳の海外進出は 1960年代から始まりました。そして本格的な販売がスタートしたのは、パリの紅茶専門店からの依頼が契機だったのです。
|
岩鋳にカラフルなティーポットの製作を依頼したパリの紅茶専門店は、マリアージュ・フレールだそうです。マリアージュもパリのマレ地区に本店があり、ダマンから近い距離です。南部鉄器のカラフルなティーポットは、マリアージュでまずヒットし、それがダマンを含む店に広まったということでしょう。
鉄にホーローをコーティングするのは従来からある技術です(各種のホーロー製品)。しかし、鋳造した鉄への着色は従来からの技術ではありません。「3年かけて着色法を開発した」とあるように、かなりの苦労の末に開発した製品だったようです。
そして、記事の最後にある、岩鋳の岩清水社長のコメントが印象的でした。
|
カラフルな鉄器の急須は、我々日本人からすると、女性客を狙ったのだろうと、暗黙に考えてしまいます。無骨な感じの黒の鉄器ではパリジェンヌにはウケないだろうと ・・・・・。依頼を受けた岩鋳の人たちも、おそらくそう考えたのではないでしょうか。
しかしそうではないのですね。岩鋳に依頼したパリの紅茶専門店のオーナーの考えでは「カラフルな鉄器なら重厚感があり男性にぴったり」なのです。少なくとも当初の発想はそうだった。
かなり意外ですが、まさに岩清水社長の言うように「市場の声に耳を澄まし、そこに自慢の技術を投入することが肝要」です。お茶を飲むのは日本(を含む東アジアの)文化であり、南部鉄器の急須もその文化の一部です。しかし、ダマン・フレールを見ても分かるように、フランスにおいても、お茶は数百年の伝統をもつ伝統文化なのです。文化の "押し売り" はうまく行かない。岩鋳はパリの紅茶専門店に導かれて、ニーズと技術のベストなマッチングを作り上げたことになります。
ドラマ「アストリッドとラファエル」に戻ると、アストリッドが愛用する青いティーポットは、実はフランスと日本の2つの文化の接点を示している象徴的なアイテムなのでした。
2023-11-12 11:19
nice!(0)
No.366 - 高校数学で理解する ChatGPT の仕組み(2) [技術]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
Attention Is All You Need
Google社は、2017年に "Attention Is All You Need" という論文(以下、"論文" と記述)を発表し、"Transformer" という画期的な技術を提案しました。Transformer は機械翻訳で当時の世界最高性能を発揮し、これが OpenAI 社の GPT シリーズや ChatGPT につながりました。
Attention(アテンション)とは "注意" という意味で、Transformer に取り入れられている "注意機構"(Attetion mechanism)を指します。"Attention Is All You Need" を直訳すると、
「必要なのはアテンションだけ」
ですが、少々意訳すると、
「アテンションこそがすべて」
となるでしょう(蛇足ですが、ビートルズの "All You Need Is Love" を連想させる論文タイトルです)。
Transformer を訳すと "変換器" ですが、その名の通り「系列 A から系列 B への変換」を行います。系列 A = 日本語、系列 B = 英語、とすると和文英訳になります。第3章では、この Transformer の仕組みを説明をします。
全体のアーキテクチャ
Transformer のアーキテクチャの全体像が次図です(論文より)。以降、この絵の意味を順に説明します。
アーキテクチャを簡略化して書くと次のようになります。以下では「日本語 → 英語の機械翻訳」を例として Transformer の動作を説明します。
左側がエンコーダで、入力された日本語テキストを中間表現(=テキストの特徴を抽出した内部表現)に変換します。右側のデコーダは、中間表現を参照しつつ「次に生成すべき英単語」を推論します。
エンコーダ、デコーダとも、図で「ブロック」と書いた単位を積層した構造です。つまり、1つのブロックの出力が次のブロックへの入力になります。アーキテクチャの絵で「N x」と書いてあるのはその積層の意味(= N 倍)で、積層する数を \(N\) とすると、Transformer では、
\(N=6\)
です。エンコーダの中間表現は最終ブロックからの出力です。その出力がデコーダの全てのブロックへ伝わります。
訓練
多数の「日本語 \(\rightarrow\) 英語の翻訳データ」を用いて Transformer を訓練するとき、全体がどのように動くかを示したのが次の図です。
エンコーダには日本語の文(Input)が入力されます。デコーダからの出力は、英文の推論結果(確率)です。これを正しい英文(Output = 教師ラベル)と照らし合わして損失(交差エントロピー誤差)を計算し、誤差逆伝播を行ってニューラル・ネットワークの重みを更新します(前回参照)。デコーダの入力となるのは「右に1語だけずらした Output」です。アーキテクチャの図18 で shifted right と書いてあるのはその意味です。なお、実際に入力されるのは単語ではなくトークンの列です(前回参照)。
推論
訓練を終えた Transformer を使って日本語文を英語文に機械翻訳するときの動きは次図です。
エンコーダに日本語のテキストを入力し、中間表現を得ます。これは1回きりです。
デコーダには、生成すべき英語テキストの最初のトークン、[BOS](文の始まりを示す特殊トークン)を入力し、[BOS] の次にくるべきトークンの確率を推論します。最も確率が高いトークンを選ぶと [I] になるはずです。これが1回目の推論(#1)です。
2回目(#2)では [I] を入力し、[I] の次のトークンを推論します([am] となるはずです)。[BOS] から [I] を推論したときの情報はデコーダに残されているので、その部分を再計算する必要はありません。推論のためには、日本語文の全情報(エンコーダの中間表現)と、既に生成した英文([BOS] [I])を参照します。
このようにして順々に英文を生成していき、推論結果が [EOS](文の終了を示す特殊トークン)になるところで、翻訳が終了します。
アーキテクチャの詳細
用語と記号
トークンの語彙
トークンの語彙(vocabulary)のサイズ を \(V\) とします。トークンを識別する "トークンID" は \(1\)~\(V\) の数字です。
系列
Transformer への入力となるテキストは、Tokenizer でトークンID の列に変換されます。以降、Transformer への入力を "系列(sequece)" と呼びます。
系列はその最大サイズ \(S\) が決まっています(普通、数千程度)。入力が \(S\) より少ない場合、残りのトークンは無効トークン([PAD])としておき、そこの処理は回避するようにします。[PAD] を含めて、系列は長さ \(\bs{S}\) の固定長とします。
系列\(=\{\:t_1,\:t_2,\:\cd\:,\:t_S\:\}\)
\(t_i\):トークンID \((1\leq t_i\leq V)\)
Transformer の論文には語彙のサイズと系列のサイズが書いてありませんが、以降の説明では \(V\) と \(S\) を使います。
分散表現ベクトル
トークンの分散表現ベクトル(埋め込みベクトル)の次元を \(D\) とします。トークンID が \(t_i\) であるトークンの分散表現を \(\bs{x}_i\) とすると、
\(\bs{x}_i=\left(\begin{array}{r}x_1&x_2&\cd&x_D\\\end{array}\right)\) \([1\times D]\)
というようになり、系列をベクトル列で表現すると、
系列\(=\{\:\bs{x}_1,\:\bs{x}_2,\:\cd\:,\:\bs{x}_S\:\}\)
となります。なお、\(D\) 次元ベクトルを、\(1\)行 \(D\)列の配列とし、\([1\times D]\) で表わします(前回参照)。
なお、Transformer では \(D=512\) です。
以降、全体アーキテクチャの図に沿って、各レイヤー(計算処理)の説明をします。以降の説明での \(\bs{x}_i,\:\:\bs{y}_i\) は、
\(\bs{x}_i\):レイヤーへの入力
(系列の \(i\) 番目。\(1\leq i\leq S\))
\(\bs{y}_i\):レイヤーからの出力
(系列の \(i\) 番目。\(1\leq i\leq S\))
で、すべてのレイヤーに共通です。また、\(D\) 次元ベクトルを \([1\times D]\)、\(S\)行 \(D\)列の行列を \([S\times D]\) と書きます。
埋め込みベクトルの生成
このレイヤーの入出力を、
とすると、
\(\bs{y}_i=\bs{x}_i\cdot\bs{W}_{\large enc}\)
\([1\times D]=[1\times V]\cdot[V\times D]\)
で表現できます(前回の word2vec 参照)。もちろん、この行列演算を実際にする必要はなく、\(\bs{x}_i\) のトークンID を \(t_i\) とすると、
\(\bs{y}_i=\bs{W}_{\large enc}\) の \(t_i\) 行
です。\(\bs{W}_{\large enc}\) は Transformer の訓練を始める前に、あらかじめ(ニューラル・ネットワークを用いて)作成しておきます。従って、埋め込みベクトルの作成はテーブルの参照処理(table lookup)です。
位置エンコーディング
埋め込みベクトル(分散表現)に、トークンの位置を表す「位置符号ベクトル」を加算します。つまり、
とすると、
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
\([1\times D]=[1\times D]+[1\times D]\)
の単純加算です。位置符号ベクトル \(\bs{p}_i\) の要素を次の記号で表します。
\(p_{t,d}\)
\(t\) は \(0\) から始まる、トークンの位置
\((t=i-1,\:\:0\leq t\leq S-1)\)
\(d\) は \(0\) から始まる、ベクトル内の要素の位置
\((0\leq d\leq D-1)\)
この \(p_{t,d}\) の値は次のように定義されます。
\((0\leq k < \dfrac{D}{2},\:\:\:x=\dfrac{2k}{D},\:\:\:0\leq x < 1)\)
つまり、\(D=512\) とすると、
\(d\) が偶数の要素位置では \(\mr{sin}\) 波
(\(d=0,\:2,\:4,\:\cd\:,510\))
\(d\) が奇数の要素位置では \(\mr{cos}\) 波
(\(d=1,\:3,\:5\:\:\cd\:,511\))
で位置符号値を決めます。この \(\mr{sin}/\mr{cos}\)波の波長 λ は
λ\(=2\pi\cdot10000^x\)
であり、\(0\leq d < D\) の範囲で、
\(2\pi\leq\)λ\( < 2\pi\cdot10000\)
となります。この \(\mr{sin}/\mr{cos}\) 波を図示してみます。グラフをわかりやすくするために、\(D=512\) ではなく、
\(D=32\)
とし、ベクトルの要素 \(32\)個のうちの最初の6つ、
\(d=0,\:1,\:2,\:3,\:4,\:5\)
だけのグラフにします。グラフの
・横軸はトークンの位置 \(t\)
・縦軸は位置符号ベクトルの要素 \(p_{t,d}\)
です。
具体的に \(t=3\) のときのベクトルの要素 \(p_{3,d}\:\:(0\leq d\leq31)\) の \(0\leq d\leq5\) の部分を書いてみると、
\(p_{3,0}=\phantom{-}0.1411\)
\(p_{3,1}=-0.9900\)
\(p_{3,2}=\phantom{-}0.9933\)
\(p_{3,3}=-0.1160\)
\(p_{3,4}=\phantom{-}0.8126\)
\(p_{3,5}=\phantom{-}0.5828\)
となります(図22)。
言うまでもなく、言語モデルにとってトークンの位置はきわめて重要な情報です。位置をバラバラにすると意味をなさないテキストになるし、Bob loves Alice と Alice loves Bob では意味が逆です。従って、何らかの手段で「トークンの位置を考慮したモデル化」をしなければならない。
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
の式で、\(\bs{x}_i\) は「単語埋め込み」のアルゴリズムで作られ、似たような単語/トークンは類似したベクトルになります(前回参照)。それに対し \(\bs{p}_i\) の \(\mr{sin}/\mr{cos}\) 波は、言語処理とは全く無関係な数学の産物です。従って、加算結果である \(\bs{y}_i\) がどのような「意味」をもつベクトルなのか、説明しようとしても無理でしょう。全く異質なものの足し算をしているのだから ・・・・・・。それでいて、このやり方で全体として成り立つのが驚きです。
Transformer より以前の機械翻訳では、トークンの出現順に逐次処理をするアーキテクチャでした。つまり、1つのトークンの処理結果を利用しながら次のトークンを処理するという逐次処理によって、並び順に意味があるという言語の特質を捕らえていました。
それに対し、位置エンコーディングを取り入れた Transformer では、逐次処理の必要性がなくなり、系列のトークン全部の並列処理が可能になりました。この結果、同一計算の超並列処理ができる GPU(数千並列が可能) をフルに活用することで、実用的な大規模言語モデルが構築できるようになったわけです。位置エンコーディングにはそういう意味があります。
なお Transformer の論文にも書いてあるのですが、位置符号ベクトルを \(\mr{sin}/\mr{cos}\) 波のような「決めうち」で作らないで、「学習可能なパラメータ」としておき、Transformer を訓練する過程で決めるやり方があります。位置符号ベクトルを学習で決めるわけです。GPT はこの方法をとっています。
Single Head Attention : SHA
アテンション・レイヤー(Multi Head Attention : MHA)の説明をするために、まず "Single Head Attention : SHA" の処理論理を説明します。Transformer で実際に使われている MHA は、以下に説明する SHA の拡張版で、核となるアルゴリズムは同じです。
SHAの入出力は、それぞれ \(S\)個の \(D\)次元ベクトルであり、
入力 \(\bs{x}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
出力 \(\bs{y}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
ですが、系列の全体を1つの行列で表すことができます。1つのベクトルを行列の1行として、それを縦方向に \(S\)個並べて行列を作ります。つまり、
入力 \(\bs{X}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{x}_i\))
出力 \(\bs{Y}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{y}_i\))
とすると SHA は、
\(\bs{Y}=\mr{SHA}(\bs{X})\)
と書けます。アテンションの処理では、まず入力ベクトル \(\bs{x}_i\) を、
の組、( \(\bs{q}_i,\:\:\bs{k}_i,\:\:\bs{v}_i\) )に変換します。変換式は次の通りです。
ここで、\(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は学習で決まる変換行列です。系列全体についての Query/Key/Value(\(QKV\))を行列の形で表すと、
となります。SHA レイヤーからの出力、\(\bs{y}_i\:\:[1\times D]\) は、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の "重み付き和" (加重和)で求めます。加重和に使う重み、\(\bs{w}_i\:\:[1\times S]\) は次のように計算されます。
まず、クエリ・ベクトル \(\bs{q}_i\) とキー・ベクトル \(\bs{k}_j\:\:(1\leq j\leq S)\) の "スケール化内積(scaled dot product)" を計算し、\(S\)個のスカラー値を求めます。スケール化内積(\(\mr{SDP}\) と記述します)とは、2つの \(D\)次元ベクトル \(\bs{a}\) と \(\bs{b}\) の場合、
\(\mr{SDP}(\bs{a},\bs{b})=\dfrac{1}{\sqrt{D}}\bs{a}\bs{b}^T\)
\([1\times1]=[1\times D]\cdot[D\times1]\)
で定義されます。つまり、一般の内積(=スカラー値)を「ベクトルの次元数の平方根」で割ったものです。
\(\bs{q}_i\) と \(\bs{k}_j\:\:(1\leq j\leq S)\) のスケール化内積を順番に \(S\)個並べたベクトルを \(\bs{s}_i\:\:[1\times S]\) と書くと、スケール化内積の定義によって、
\(\bs{s}_i=\dfrac{1}{\sqrt{D}}\bs{q}_i\bs{K}^T\)
\([1\times S]=[1\times D]\cdot[D\times S]\)
です。そして、加重和を求めるときの重み \(\bs{w}_i\) は、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
\([1\times S]=\mr{Softmax}([1\times S])\)
とします。この \(S\)次元の重みベクトルを使って、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の加重和をとると、出力ベクトル \(\bs{y}_i\) は、
\(\bs{y}_i=\bs{w}_i\cdot\bs{V}\)
\([1\times D]=[1\times S]\cdot[S\times D]\)
となります。以上の計算プロセスを一つの式で書いてしまうと、
です。従って、SHA からの出力ベクトル \(\bs{y}_i\) を縦方向に並べた行列 \(\bs{Y}\) は、
\(\bs{Y}=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{Q}\cdot\bs{K}^T\right)\cdot\bs{V}\)
\([S\times D]=\mr{Softmax}([S\times D]\cdot[D\times S])\cdot[S\times D]\)
と表すことがきます。この表記で \(\mr{Softmax}\) 関数が作用するのは \([S\times S]\) の行列ですが、\(S\)個の行ごとに \(\bs{\mr{Softmax}}\) を計算します。
単なる内積ではなく「スケール化内積」を使う理由ですが、2つのベクトルの内積は、要素同士のかけ算を次元数 \(D\) 個だけ加算したものです。従って、ベクトル \(\bs{s}_i\) を、シンプルな内積を使って、
\(\bs{s}_i\:=\bs{q}_i\cdot\bs{K}^T\)
のように定義し、重み \(\bs{w}_i\) を、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
で求めると、\(D\) が大きいと \(\bs{s}_i\) の要素が大きくなり、その結果として \(\bs{w}_i\) はゼロに近いところに多くの要素が集まるようになります。これは \(\mr{Softmax}\) 関数の性質によります(前回参照)。こうなると勾配消失が起きやすくなり、訓練が収束しづらくなります。そのため「スケール化」するというのが論文の説明です。
もちろん、幾多の試行錯誤があり、その結果として決まったのが「スケール化内積で加重和の重みを計算する」というやり方だったのでしょう。
以上の計算でわかるように、注意機構(Attention machanism)とは、あるトークンを処理するときに、注意を向けるべきトークンと注意の強さを決め(それ自体が学習で決まる)、注意を向けた先の情報を集めてきて集積するものです。
しかも、注意機構は6層(\(N=6\)) に重ねられています。ということは、階層的な(多段階の) "注意の向け方" ができることになります。また、言語における単語と単語の関係性は多様です。動作\(\cdot\)動作主体、修飾\(\cdot\)被修飾、指示代名詞と指示されるもの(照応関係)など多岐に渡ります。それらのさまざまなタイプの関係性を、Transformer の訓練を通して、多層の注意機構が自動的に把握すると考えられるのです。
MHA : Multi Head Attention
SHA では、入力ベクトル \(\bs{x}_i\) から、1組の Query/Key/Value(\(QKV\)) ベクトルを抽出しましたが、Transformer で実際に使われているのは、
という処理です。これを Multi Head Attention : MHA と呼びます。この「それぞれについてのアテンション処理」のことを "head(ヘッド)" と言います。複数の head なので Multi Head です。このヘッドの数を \(H\) とし、
\(d=\dfrac{D}{H}\) (\(D\) は入出力ベクトルの次元)
とします(\(H\) は \(d\) が整数になるように選びます)。このとき、
です。つまり MHA は「複数の特徴を抽出し(一つの情報量は SHA より少ない)、それぞれの特徴について 独立した "注意機構" を働かせ、最後に統合してまとめる」仕組みです。なお、Transformer では、
\(H=8\)
\(d=\dfrac{D}{H}=\dfrac{512}{8}=64\)
です。
\(h\) 番目のヘッド \((1\leq h\leq H)\) に着目し、"注意機構" の計算プロセスを式で書くと、次のようになります。まず、\(h\) 番目のヘッドの \(QKV\) ベクトルの計算は、
です。系列全体について、\(h\) 番目のヘッドの \(QKV\) を行列の形で表すと、
です。\(h\) 番目のヘッドのアテンション処理は、SHA の場合と同様で、
となり、これを系列全体での表現にすると、
となります。行列 \(\bs{Y}^h\) は、\(h\) 番目のヘッドの出力ベクトル \(\bs{y}_i^h\:\:[1\times d]\) を、系列の数だけ縦に並べた行列です。
系列の \(i\) 番目の入力 \(\bs{x}_i\) に対する \(H\) 個の出力ベクトル
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
が求まったところで、これら \(H\) 個を単純結合して(=順に並べる)一つのベクトルにし、さらに Linear 変換をして最終出力にします。変換に使う行列は \(\bs{W}_O\:\:[D\times D]\) です。
Linear 変換は直前の単純結合(Concatenation)とセットになっています。つまり、ヘッドの順序を表す \(h\:\:(1\leq h\leq H)\) という数字には、"注意機構" における何らかの意味があるわけではありません。単にアテンション処理を \(H\) 個に分けた \(h\) 番目というだけです。従って、順に単純結合する、
\(\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\)
という操作の「結合順序」には意味が無いことになります。そこで結合した後で、学習可能なパラメータ \(\bs{W}_O\) で線型写像を行って、最適な出力ベクトルを求めるわけです。
エンコーダの MHA は、エンコーダ内に閉じたアテンションで、これを「自己アテンション」(Self Attention)と言います。一方、デコーダ側には自己アテンションの他に、エンコーダとデコーダにまたがるアテンションがあります。これを Source Target Attention と言います。このアテンションは、
します。これによってエンコーダからデコーダ側への情報の流れを作ります。日本語 → 英語の機械翻訳の場合だと、次に生成すべき英単語に関連して「注意を向けるべき日本語のトークンと、その注意の量」がここで決まります。
Multi Head Attention において、1つのベクトルから複数の \(QKV\) を取り出すことの意味は、おそらくトークンの「多義性」でしょう。その例ですが、英語で fine という語の代表的な意味を4つあげるとしたら、たとえば、
fine :
(1) 素晴らしい
(2) 晴れた
(3) 細かい
(4) 罰金
です(例です。(1) (2) は同類の意味)。単語の埋め込みベクトルは、似たような(あるいは同一ジャンルの)語は類似している(= コサイン類似度が 1 に近い)わけです(前回参照)。とすると、(1)~(4) の同一ジャンルの言葉は、それぞれ、
(1) good, excellent, ・・・・・・
(2) cloudy, rainy, ・・・・・・
(3) tiny, small, coarce, ・・・・・・
(4) penalty, guilty, ・・・・・・
などとなるはずです。fine がこれら4つのジャンルと類似性があるということは、fine の埋め込みベクトルおいて4つの意味が物理的に分散して配置されていると考えられます。さらにイタリア語まで考えると、
fine :
(5) 終わり
が加わります(イタリア映画の最後に出てくる語、ないしは音楽用語)。埋め込みベクトルは言語ごとに作るわけではないので、fine のベクトルはあくまで1つです。ということは、埋め込みベクトルには(この例では)5つの意味が分散して配置されているはずです。
この状況は、埋め込みベクトルから複数の \(QKV\) ベクトルを取り出し、それぞれについて独立したアテンション計算をするというアルゴリズムがマッチしていると考えられるのです。
Add & Norm
アーキテクチャの絵で5カ所にある「Add & Norm」は、ベクトルごとに「残差結合」と「レイヤー正規化」を行うレイヤーです(詳細は前回参照)。図で表すと以下です。
計算式は次のようになります。系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略します。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\begin{eqnarray}
&&\:\: \bs{x}=\{\:x_1, &x_2, &\cd\:, &x_D\:\}\\
&&\:\: \bs{y}=\{\:y_1, &y_2, &\cd\:, &y_D\:\}\\
\end{eqnarray}\)
\(x_k\:\:(1\leq k\leq D)\) の平均 : \(\mu\)
\(\mu=\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}x_k\)
\(x_k\:\:(1\leq k\leq D)\) の標準偏差 : \(\sg\)
\(\sg=\sqrt{\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}(x_k-\mu)^2}\)
とおくと、
です。ここで \(\bs{g}\) と \(\bs{b}\) は学習で決まるベクトル(=パラメータ)です。
Feed Forward Network
ベクトルごとに処理される、2層の全結合ニューラル\(\cdot\)ネットワークです。第1層の活性化関数は \(\mr{ReLU}\) で、第2層(出力層)には活性化関数がありません。3つのレイヤーで表現すると次の通りです。
ニューロンの数(=ベクトルの次元)は、
入力層:\(D\)
第1層:\(D_{ff}=4\times D\)
出力層:\(D\)
です。計算を式で表すと(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)、
\(\bs{y}=\mr{ReLU}(\bs{x}\bs{W}_1+\bs{b}_1)\cdot\bs{W}_2+\bs{b}_2\)
です。第1層の次元を入力\(\cdot\)出力層の4倍にとるのは、そのようにするのが Transformer の性能(たとえば、翻訳文の質)が最も向上するからです。GPT-3、ChatGPT も踏襲しています。
Masked Multi Head Attention
デコーダ側にある Masked Multi Head Attention の説明をします。系列のトークンの列を、
\(\{\:\bs{x}_1,\:\cd\:,\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\cd\:,\:\bs{x}_S\:\}\)
とし、いま \(\bs{x}_t\) に着目しているとします。
\(\bs{x}_i\:\:\:(1\leq i\leq t)\:\longrightarrow\) 過去のトークン
\(\bs{x}_i\:\:\:(t < i\leq S)\:\longrightarrow\) 未来のトークン
と呼ぶことにします。着目しているトークンを基準に、系列でそれ以前のトークンが「過去」、次以降のトークンが「未来」です。
日本語から英語に翻訳する Transformer を例にとると、デコーダの推論時には、英文のトークンを一つずつ推論していきます。つまり、
[BOS] \(\longrightarrow\) [I]
[BOS] [I] \(\longrightarrow\) [am]
[BOS] [I] [am] \(\longrightarrow\) [a]
[BOS] [I] [am] [a] \(\longrightarrow\) [cat]
[BOS] [I] [am] [a] [cat] \(\longrightarrow\) [EOS]
といった具合です(図21)。このときの各ステップにおけるアテンション処理は、当然ですが、末尾のトークンから生成済みのトークン(=過去のトークン)に対して行われます。つまり「トークンが注意を向ける先は常に過去のトークン」です。「すでに生成済みのトークンの情報だけから次にくるトークンを推論する」のがデコーダなので、これは当然です。
一方、デコーダの訓練時のことを考えると、
で(図20)、入力データとしては系列のトークンが全部与えられています。しかしここで未来のトークンに注意を向けてしまうと、推論時との不整合が起きてしまいます。そこで
という配慮が、デコーダ側のアテンション処理では必要になります。この配慮をした注意機構が Masked Multi Head Attention です。一方、エンコーダ側では、訓練時も推論時も、
[我が輩] [は] [猫] [で] [ある]
という系列が一括して与えられるので(図20、図21)、未来のトークンに注意を向けても問題ありません。またデコーダ側からエンコダー側に注意を向けるのもかまいません。
この「過去のトークンにだけ注意を向ける」ことを数式で表現するには、\([S\times S]\) のマスク行列、\(\bs{M}\) を次のように定義します。
\(\bs{M}=\left(\begin{array}{c}
0&\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}\\
\phantom{0}&\large\ddots&\phantom{0}&\huge\textrm{-}\infty&\phantom{0}\\
\phantom{0}&\phantom{0}&0&\phantom{0}&\phantom{0}\\
\phantom{0}&\huge0&\phantom{0}&\large\ddots&\phantom{0}\\
\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}&0\\
\end{array}\right)\) \([S\times S]\)
このマスク行列は、
です。これを、アテンションの計算式の \(\mr{Softmax}\) 関数の内側に足し込みます。\(h\) 番目のヘッドに着目したアテンションの計算式は、
でした。これに \(\bs{M}\) を足し込むと、
となります。\(\mr{Softmax}\) 関数は、ベクトル(上式では行列の1行)の各要素の \(\mr{exp}()\) をとります。従って、要素が \(-\infty\) だと \(\mr{exp}(-\infty)=0\) となり、\(\mr{Softmax}\) 関数にとってはその要素が無いのと同じことになります。
上式の \(\mr{Softmax}\) 関数の内側は \([S\times S]\) の行列ですが、縦方向が系列全体のクエリ・ベクトルに対応し、横方向が系列全体のキー・ベクトルに対応しています。そのため、マスク行列を足し込むと、アテンション処理において過去のトークンだけに注意が行き、未来のトークンには注意が行かない(=結果としてバリュー・ベクトルが加重和されない)ようになるのです。
こうして求めた行列 \(\bs{Y}^h\) の \(i\) 行目をベクトル、
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
とすると、これ以降の処理はマスク行列がない場合と同じです。つまり \(H\) 個のベクトル \([1\times d]\) を単純結合して一つのベクトル \([1\times D]\) にし、さらに Linear 変換をしてアテンション処理からの最終出力にします。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\)
\(\begin{eqnarray}
&&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\
&&&=[1\times D]\cdot[D\times D]\\
\end{eqnarray}\)
わざわざ \(\mr{exp}(-\infty)\) を持ち出してマスク行列を使うのは、話をややこしくするだけのようですが、マスク行列を使った Masked Multi Head Attention の計算式を見ると、線型変換と \(\mr{Softmax}\) 関数だけからできています。ということは、「過去のトークンだけに注意を向けるアテンション計算は微分可能」であり、誤差逆伝播の計算が成り立つことがわかります。
確率生成
Transformerのデコーダの最終部分は、推論結果である \(D\) 次元のベクトルを、語彙集合の中での確率ベクトルに変換する部分です。計算式で書くと、
\(\bs{y}=\mr{Softmax}(\bs{x}\cdot\bs{W}_{\large dec})\)
\([1\times V]=\mr{Softmax}([1\times D]\cdot[D\times V])\)
です(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)。\(\bs{W}_{\large dec}\) は、前回の word2vec のところに出てきた、\(D\)次元の埋め込みベクトルを \(V\) 次元の確率ベクトルに変換する行列です。
以上で Transformer のアーキテクチャの説明は終わりですが、全体を振り返ると、
ことがわかります。以降は、この中で鍵となる「アテンション」と「Feed Foward Network」についての補足です。
アテンションの意義
一般のニューラル・ネットワークにおいて、隣合った2つの層、\(\bs{x}\) と \(\bs{y}\) が同じニューロン数 \(D\) だとします。活性値を、
\(\begin{eqnarray}
&&\:\:\bs{x}=\{x_1, &x_2, &\cd\:,&x_D\}\\
&&\:\:\bs{y}=\{y_1, &y_2, &\cd\:,&y_D\}\\
\end{eqnarray}\)
とし、重み行列を \(\bs{W}\)、バイアスはなし、活性化関数を \(\mr{ReLU}\) とするると、
\(\bs{y}=\mr{ReLU}(\bs{x}\cdot\bs{W})\)
です。重み \(\bs{W}\) は誤差逆伝播法による訓練で決まり、推論時には一定の値です。Transformer のアテンション機構もこれと似ています。アテンションは、
入力ベクトル列 :\(\bs{x}_i\:\:\:(1\leq i\leq S)\)
出力ベクトル列 :\(\bs{y}_i\:\:\:(1\leq i\leq S)\)
の間の変換をする機構だからです。ニューラル\(\cdot\)ネットワークの活性値(実数値)がベクトルに置き換わったものと言えます。ヘッドが1つの場合(Single Head Attension)で図示すると、次の通りです。
しかし、この図は一般のニューラル\(\cdot\)ネットワークとは決定的に違います。重み行列 \(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は推論時には一定ですが、実際に \(\bs{x}_i\) と \(\bs{y}_i\) の関係性を決めているのは、クエリ・ベクトル \(\bs{Q}\) とキー・ベクトル \(\bs{K}\) であり、これは入力ベクトル列 \(\bs{x}_i\) の内容にもろに依存しているからです。つまり、
と言えます。\(\bs{x}_1\) の値を変えると、その影響は \(\bs{y}_i\:\:(1\leq i\leq S)\) の全体に及びます。それは、「\(x_1\) を変えると \(y_i\) の全部が変わる」という一般のニューラル\(\cdot\)ネットワークと同じではありません。一般のニューラル\(\cdot\)ネットワークを関数とみなすと、「関数は一定だが、入力が変わるから出力も変わる」のです。それに対して注意機構は「入力が変わると関数の形まで変わる」とみなすことができるでしょう。もちろん、実際には図25のように関数は一定なのですが、一般のニューラル\(\cdot\)ネットワークとの比較で言うと、そうみなせるということです。
この柔軟性とダイナミックな(動的な)性格が、Transformer に大きなアドバンテージをもたらしました。次章の GPT-3 / ChatGPT が実現している「本文中学習(In Context Learning)」はその一つです。ChatGPT では、プロンプトを変える、ないしは文言を追加すると、応答が大きく変わることがあります。また、欲しい応答の表現形式を例示したプロンプトをすると、その形式どおりのに応答がきたりします。あたかも、プロンプトからその場で学んだように見えるのが In Context Learning です。しかし、ニューラル・ネットワークのパラメータは、推論時にはあくまで一定であり、決してその場で学んでいるわけではありません。この "あたかも" を作り出しているのが "注意機構"です。
Feed Forward Network の意味
Transformer のアーキテクチャは、注意機構の後ろに Feed Forward Network(FFN) が接続され、このペアが多層に積み重ねられています。この FFN の意味は何でしょうか。
FFN は、注意機構と違ってベクトルごとの処理です。論文では "Position-wise(位置ごとの)Feed Forward Network" と書いてあります。ということは、系列の文脈には依存しないということです。つまり Transformer の訓練を通して、ベクトル(トークンの中間表現)が本来持っている性格や関連情報が、FFN の重みの中に蓄えられると考えられます。AI の専門家である、プリファードネットワークス社の共同創業者の岡野原大輔氏は、著書の『大規模言語モデルは新たな知能か』の中で次のように書いています。
岡野原氏が「多重パーセプトロン(Multi-Layer Perceptron : MLP)と書いているのは FFN のことです。ちなみに入力層(第0層)を含めて「三層」という言い方になっています。
ここで、FFN のパラメータ数を求めてみます。バイアスを無視すると、
\(\bs{W}_1\:\:[D\times D_{ff}]\)
\(\bs{W}_2\:\:[D_{ff}\times D]\)
\(D\) : 埋め込みベクトルの次元
\(D_{ff}=4D\)
なので、
FFN のパラメータ数\(=8D^2\)
です。一方、Multi Head Attention で、
\(H\) : ヘッドの数
\(d=\dfrac{D}{H}\)
とすると、\(h\)番目のヘッドの \(QKV\) を作る行列は、
\(\bs{W}_Q^h\) \([D\times d]\)
\(\bs{W}_K^h\) \([D\times d]\)
\(\bs{W}_V^h\) \([D\times d]\)
であり、これらを足すとパラメータ数は \(3Dd\) ですが、この組が \(H\) セットあるので、合計は \(3DdH=3D^2\) です。さらに、単純結合したあとの Linear 変換行列である、
\(\bs{W}_O\) \([D\times D]\)
が加わるので、結局、
MHA のパラメータ数\(=4D^2\)
です。ということは、
FFN のパラメータ数は、MHA のパラメータ数の2倍
ということになります。パラメータ数だけの単純比較はできませんが、FFN が極めて多い情報量=記憶を持っていることは確かでしょう。それが、大量の訓練データの中から関連する情報を記憶し、また推論時にそれを想起することを可能にしています。
論文のタイトルは "Attention Is All You Need" で、これは従来の機械翻訳の技術では補助的役割だった Attention を中心に据えたという意味でしょう。しかし技術の内実をみると、決して「アテンションがすべて」ではなく「アテンション機構と多重パーセプトロンの合わせ技」であり、しかもそれを多層に重ねたのが Transformer なのでした。
前回でニューラル・ネットワークの例とした多重パーセプトロンは、ニューラル・ネットワークの研究の歴史の中で最も由緒あるもので、1980年代に盛んに研究されました。それが、2010年代半ばから研究が始まった "アテンション機構" と合体して Transformer のアーキテクチャになり、さらには ChatGPT につながったのが興味深いところです。
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。ここではまず GPT-3 の仕組みを説明します。
GPT-3 のアーキテクチャ
GPT は Generative Pre-trained Transformer の略です。generative とは "生成型の"、pre-trained は ""事前学習済の" という意味で、Transformer は Google が 2017年に提案した Transformer を指します。
訳すると "事前学習済の生成型トランスフォーマー" となるでしょう。Transformer は「変換器」という意味でした。とすると「生成型の変換器」とは言葉が矛盾しているようですが、実は GPT は Transformer のアーキテクチャのデコーダ部分だけを使った大規模言語モデルです。だから「生成型変換器」なのです(下図)。
この「デコーダ部分だけを使う」という発想が、OpenAI の技術者の慧眼でした。デコーダだけで系列変換(機械翻訳、文章要約、質問応答、・・・・・・ )ができるはず、という発想が GPT に柔軟性と大きな能力を与えました。GPT-3 のアキテクチャーは以下のようです。
このアキテクチャーは、Transformer から「エンコーダとエンコーダ関連部分」を取り去ったものです。ただし、次が違います。
これらはいずれも、学習の安定化と高速化のための工夫です。さらに GPT-3 は Transformer に比べてモデルの規模が大きく拡大されています。
・埋め込みベクトルの次元 \(D=12288\)
\((\)Transformer \(:\:512\) の \(24\)倍\()\)
・デコーダブロックの積層数 \(N=96\)
\((\)Transformer \(:\:6\) の \(16\)倍\()\)
・アテンションのヘッドの数 \(H=96\)
\((\)Transformer \(:\:8\) の \(12\)倍\()\)
です。大規模言語モデルでは、モデルの規模と学習量の拡大を続けると、それにともなって性能(たとえば機械翻訳の精度)が上がり続けるという「スケール則」がみられました。これは一般の深層学習のニューラル\(\cdot\)ネットワークにはない特徴です。このスケール則を信じ、アーキテクチャをシンプルにしつつ、モデルの規模を「桁違いに」拡大した OpenAI 社と出資した会社(マイクロソフト)の勝利でしょう。
このアーキテクチャのパラメータ数をカウントしてみます。
とします。GPT-3 の具体的な数値は、
です(\(V\) の値については前回参照)。学習で決まる行列やベクトルを順にカウントしていくと次のとおりです。
(1) Embedding と確率生成
\(\bs{W}_{\large enc}\) \([V\times D]\)
\(\bs{W}_{\large dec}\) \([D\times V]\)
\(\rightarrow\) パラメータ数\(=2VD\)
(2) Positional Encoding
\(\bs{p}\) \([S\times D]\)
\(\rightarrow\) パラメータ数\(=SD\)
(3) Masked Multi Head Attention
\(\bs{W}_Q\) \([D\times D]\) ※
\(\bs{W}_K\) \([D\times D]\) ※
\(\bs{W}_V\) \([D\times D]\) ※
\(\bs{W}_O\) \([D\times D]\)
\(\rightarrow\) パラメータ数\(=4D^2\)
(4) Feed Forward Network
\(\rightarrow\) パラメタ数\(=8D^2+5D\)
(5) Layer Nomaliation (2レイヤー)
\(\bs{g}\) \([1\times D]\)
\(\bs{b}\) \([1\times D]\)
\(\rightarrow\) パラメタ数\(=2\times2D=4D\)
(3), (4), (5) は \(\times\:N\) に積層されていることに注意して総パラメータ数を計算すると、
総パラメータ数
\(=\:2VD+SD+N(4D^2+8D^2+5D+4D)\)
\(=\:2VD+SD+N(12D^2+9D)\)
\(=\) \(\bs{175,217,074,176}\)
となり、約 1752億となります。一般に言われているパラメータ数が 1750億というのは、英語の 175B(B = Billion = 10億)の日本語訳で、Billion 単位にしたパラメータ数です。
GPT-3 が系列の次のトークンを推論するとき、1752億のパラメータの全てを使った演算が行われます(図21)。40文字の日本語文章を 60トークンだとすると、 わずか 40文字の日本語文章を生成するために、1752億のパラメータの全てを使った演算が 60回行われるということです。
また、1752億のパラメータがすべて 32ビットの浮動小数点数(4バイト)だとすると、パラメータのためだけに、
653ギガバイト(1ギガ = \(1024^3\) 換算)
のメモリが必要になります。業務用コンピュータ・システムの開発経験者ならわかると思いますが、これだけのデータ量を常時抱えつつ、更新やリアルタイムの推論を行うシステムを開発・運用するのは、ちゃんとやればできるでしょうが、かなり大変そうな感じです。
GPT-3 のアーキテクチャを振り返ってみると、Transformer のデコーダ部分だけを採用したことによる、Transformer との違いがあることに気づきます。それは、
ことです。言うまでもなく、アテンション機構は Transformer / GPT-3 の "キモ" です。そのキモのところに違いがある。
人間の言語活動(発話・文章作成)では「過去の単語との整合性を考慮しつつ、未来の単語を想定して次の単語を決める」ことが多々あります。このことは、機械翻訳では、翻訳前の「原文」を処理するエンコーダ側の「過去と未来の両方に注意を向けるアテンション機構」で実現されています(Mask がない Multi Head Attention)。
しかし GPT-3 では様子が違ってきます。事前学習(次項)だけの GPT-3 で機械翻訳がなぜできるかというと、
[ 原文 ] を翻訳すると [ 翻訳文 ] です
といった対訳(に相当するデータ)が訓練データの中に多数あるからです(GPT-2 の論文による)。この「原文」の部分のアテンション処理において、「原文」の中の未来の単語に注意が向くことはありません(Masked Multi Head Attention しかないから)。このことにより翻訳の精度が Transformer とは違ってくる(精度が落ちる)と想定できます。
こういった "問題" は、大規模言語モデルを "超大規模" にすることで解決するというのが、GPT-3 の開発方針だと考えられます。1752億という膨大なパラメータ数が、それを表しています。
GPT-3 の訓練
GPT-3 の訓練は、
・WebText
・電子ブック
・Wikipedia
をもとに行われました。WebText は "訓練に使うべきではない" テキストを除外してあります。集められたテキストの量はトークンの数でカウントすると、
です。これらのテキストからランダムに選んだミニバッチを作り、「ミニバッチ勾配降下法」(前回参照)で訓練が行われました。但し、Wikipedia などの "信頼性が高いテキスト" は、より多くミニバッチに選ばれるような工夫がしてあります。訓練は、使われたテキストが、トークン数で延べ \(3000\)億になったところで打ち切られました。
訓練は、Transformer のデコーダのところでで説明したように「ひたすら次のトークンの予測をする」というものです。この「次のトークンの予測」について補足しますと、前回、GPT のトークン化のロジックである BPE(Byte Pair Encoding)のことを書きました。これによると、UTF-8 では改行も空白も文字として扱われるので、改行、空白のそれぞれにトークンID が割り当てられることになります。
これから言えることは、テキストを学習するということは、その意味内容だけでなく、テキストの表現形式も学習するということです。つまり、段落、字下げ、箇条書きなどの形式です。訓練が終わった 1752億のパラメータには、そういった "表現形式に関する知識" も含まれていることに注意すべきでしょう。
以上のように、一般的に入手できるテキストだけを使ってニューラル・ネットワークを訓練することを「事前学習」と言います。このような事前学習を行った上で、機械翻訳や質問応答などのタスク別に専用に作成した訓練データで「目的別学習」を行うのが、言語モデルの定番の学習手法です。あらかじめ事前学習を行った方が言語モデルの性能が良くなるからです。目的別学習を "ファイン・チューニング" と言います。
GPT-3 は、それまでの GPT、GPT-2 と違って、ファイン・チューニングなしの言語モデルを狙ったものです。つまり、
と言えるでしょう。実際 GPT-3 は、ファイン・チューニングを行った言語モデルと比較しても、"そこそこの"、ないしは "同等の" 性能であることが分かりました。もちろんファイン・チューニング済の言語モデルに劣るタスクも多々あります。しかし全体としては "そこそこの" 性能を示します。「ニューラル・ネットワークの超大規模化」と「大量の訓練データ」によってそれが可能であることを、GPT-3 は示したのでした。
ChatGPT
ChatGPT は GPT-3 のアーキテクチャと事前学習をもとに、さらに「目標駆動型学習」を追加したものです。ここでの目標駆動型学習とは「人間にとって好ましい応答の例を人間が作り、それを目標として、そこに近づくように学習する」という意味です。OpenAI 社は RLHF(Reinforcement Learning by Human Feedback:人間のフィードバックによる強化学習)と呼んでいます。これは一種のファイン・チューニングであると言えます。
この、目標駆動型学習をどうやるか、その詳細が OpenAI 社のノウハウでしょう。考えてみると、GPT-3 の(従って ChatGPT の)アーキテクチャはシンプルあり、これをシステム上に実現するのは、コンピュータ技術とAI技術、ハードウェアの調達(特にGPU)、そしてお金の問題です。事前学習に使う WebText にしても、世界中から集めて公開している団体があります(GPT-3 でも使われた Common Crawl)。お金がある(かつ投資意欲がある)大手IT企業なら、システム構築は難しくない。
しかし「人手で作った訓練データをもとに、人にとって違和感がない対話ができるまでに訓練する」のは、Transformer の性質や "癖 を熟知していないとできないと考えられます。そこにノウハウがあるはずです。
その目標駆動型学習の概要を、先ほど引用した岡野原氏の「大規模言語モデルは新たな知能か」では、次のような3つのステップで説明しています。この説明は専門用語を最小にした簡潔なものなので、以降これに沿って書きます。
この岡野原氏の説明を読み解くと、次のようになるでしょう。ラベラーとは訓練データ(教師ラベル)を作る人の意味です。
第1ステップは、機械学習の分野でいう「教師あり学習」です。ここで具体的にどのような訓練をしたのかは、OpenAI 社も公表していません。推測すると「望ましい対話」の例には、人間の質問に「答えられません」や「できません」と応答する訓練データも多数あるのではと思います。たとえば「反社会的行為を助長するような質問」の場合(爆弾の作り方など)です。
さらにこの第1ステップでは、特定のタイプのプロンプトに対して、あたかも ChatGPT が感情をもっているかのように応答する訓練が可能なはずです。それが「望ましい対話」だと OpenAI が判断すればそうなります。
第2ステップは2つのフェーズに分かれています。第1フェーズは、人手によるランキングの作成です。このとき「複数の異なるモデル」を使います。モデルとは言語モデルのことです。実は、GPT-3 を開発する過程においても、パラメータ数の違う複数の言語モデルが開発されていて、最終的に公開されたのが GPT-3 です。またパラメータ数が同じでも、訓練のやり方が違うとパラメータの値が違うので、モデルとしては別です。
このような複数の異なるモデルを選び(4つとします)、同じ入力(プロンプト。\(P\) で表します)に対して、4つの違った応答、\(A,\:B,\:C,\:D\) を得ます。ラベラーは、この \(P/A,\:P/B,\:P/C,\:P/D\) という4つの「プロンプト \(/\) 応答」にランク付けします( \(/\) はプロンプトのあとに応答が続くという意味です)。ランク付けが仮に、
\(P/A\: > \:P/B\: > \:P/C\: > \:P/D\)
だとします。現実問題としては4つのランク付けは難しいので、2つずつの6つのペアについて、どちらが良いかを決めます。ランク付けの基準について岡野原氏は書いていないのですが、OpenAI 社の公開資料によると、
・嘘やデマを含まない
・差別的・攻撃的な内容を含まない
・ユーザの役に立つ
という基準です。このような「ランク付けデータ」を大量に準備します。これは人に頼る "人海戦術" しかないので、アウトソーシングしたとしてもコストがかかります。
第2ステップの第2フェーズは、ランキングのデータをもとに自動評価システムを作ることが目的です。データを入力して評価値(強化学習の用語でいうと "報酬")を出力する関数(=自動評価システム)を \(\mr{Score}()\) と書くと、
\(\mr{Score}(P/A) > \mr{Score}(P/B) > \mr{Score}(P/C) > \mr{Score}(P/D)\)
となるように関数を決めます。これはニューラル・ネットワークを使って、訓練を繰り返して決めます(強化学習の用語で "報酬モデル")。ここで岡野原氏が指摘しているのは、\(\mr{Score}\) 関数への入力は、
だということです。従って、\(\mr{Score}(P/A)\) は、
\(\mr{Score}(\mr{InnerState}(P/A))\)
と書くべきでしょう。これによって「高精度に評価を推定できる」というのが岡野原氏の説明です。
第3ステップでは、この自動評価システムを使って、プロンプトに対する応答の評価値が最も高くなるように強化学習を行います。このステップには人手を介した評価はないので、大量のプロンプトで学習することができます。
ここで、言語モデル \(\al\) の内部状態を入力とする自動評価システムを \(\mr{Score}_{\large\:\al}\) とし、言語モデル \(\al\) を上記のように訓練した結果、言語モデル \(\beta\) になったとします。すると、同じ「プロンプト/応答」を投入したときの内部状態が、2つの言語モデルで違ってきます。つまり、
\(\mr{InnerState}_{\large\:\al}(P/A)\neq\mr{InnerState}_{\large\:\beta}(P/A)\)
です。ということは、
ことになります。つまり「第2ステップの第2フェーズ」と「第3ステップ」をループさせて繰り返すことができる。このとき、ラベラーが作ったランキングデータはそのまま使えます。このランキングが絶対評価ではなく相対評価だからです。以上のことから、
と言えます。岡野原氏が言っている「高精度に評価を推定できる」とは、こういった "共進化" も含めてのことだと考えられます。このように、目標駆動型学習で鍵となるのは、この「高精度の自動評価システム」です。
補足しますと、ChatGPT が公開された後は、利用者の実際のプロンプトとそれに対する ChatGPT の応答を膨大に集積できます(利用者が拒否しなければ)。この実際の「プロンプト/応答」データの中から自動評価システムの評価が低いものだけを集め、プロンプトへの応答の評価が高くなるように ChatGPT の強化学習ができることになります。ChatGPT から "でたらめな" 応答を引き出そうとする(そして成功すれば喜ぶ)人は多いでしょうから、強化学習のためのデータにはこと欠かないはずです。
以上が、岡野原氏の説明の "読み解き" です。
ここまでをまとめると、次のようになるでしょう。
このような GPT-3 の仕組みでは、計算や論理的推論は本質的にできません。簡単な計算(2桁整数同士のたし算、2次方程式を解くなど)ができる(ように見える)のは、それが訓練データにあるからです。また、正しい論理的推論ができたとしたら、類似の推論が訓練データの中にあるからです。
とはいえ、ChatGPT はバックに語と語の関係性についての膨大な "知識" をもっていて、それによって "規則性" や "ルール" の認識が内部にできているはずです。その中には「人が気づかない」「暗黙の」「意外なもの」があってもおかしくない。それにより、蓄積した知識を "混ぜ合わせて" 正しい推論、ないしは発見的な推論がきることもあり得るはずです。
さらに、人が普段話すのと同じように話せば、その膨大な "知識" が活用できるのは多大なメリットでしょう。もちろん "悪用" される可能性はいつでもありますが、そのことを踏まえつつ、使い方の発見や検討が今後も進むのでしょう。
人の問いかけに対する ChatGPT の応答は、いかにも人らしいものです。もちろん間違いや、変な答え、明らかに事実とは違う応答もあります。しかし、世界中から集めた知識の量は膨大で、言語の壁も越えています。
その "知識" は(GPT-3, ChatGPT では)1752億個のパラメータの中に埋め込まれています。量は膨大ですが、それを処理する仕組みはシンプルです。なぜこれでうまくいくのか、そこが驚異だし、その理由を理解することは難しいでしょう。
もちろん、その中身を解明しようとする研究は進むでしょうが、"理解" は難しいのではと思われます。というのも、「比較的シンプルな記述による、人にフレンドリーな説明」でないと、人は "理解" したとは思わないからです。
しかし考えてみると、我々が言語(母語)を習得でき、かつ自在に扱えるのはなぜか、その脳の働きは、Transformer / ChatGPT と極めて似ているのではないでしょうか。
前回の冒頭で紹介したように、慶応義塾大学の今井教授は、「ChatGPT の仕組み(=注意機構)は、幼児が言語を学習するプロセスと類似している」と指摘していました。今井教授は幼児の言語発達を研究する専門家なのでこの指摘になるのですが、実は Transformer / ChatGPT のやっていることは、幼児のみならず、我々が言葉(母語)を理解してきた(現に理解している)やりかたと酷似していることに気づきます。それは、
という言語理解のありようです。もちろん(外からの指摘による)「好ましくない言葉の使い方」であれば訂正します。しかし、学び方も含めて、我々は内発的・創発的に言葉を理解しています。それが我々の脳の働きの重要な一面です。
前回、Transformer がタンパク質の機能分析に使える(可能性がある)ことを書きましたが、さらにヒトの脳の(ある脳領域の)解明に役立つこともありそうです。
大規模言語モデルの外面的な機能は驚異的ですが、さらにその内部の「仕組み」を理解することで、その応用範囲が極めて広いことがわかるのでした。
(前回より続く)
この記事は、No.365「高校数学で理解する ChatGPT の仕組み(1)」の続きです。記号の使い方、用語の定義、ニューラル・ネットワークの基本事項、単語の分散表現などは、前回の内容を踏まえています。 |
| 3.Transformer |
Attention Is All You Need
Google社は、2017年に "Attention Is All You Need" という論文(以下、"論文" と記述)を発表し、"Transformer" という画期的な技術を提案しました。Transformer は機械翻訳で当時の世界最高性能を発揮し、これが OpenAI 社の GPT シリーズや ChatGPT につながりました。
Attention(アテンション)とは "注意" という意味で、Transformer に取り入れられている "注意機構"(Attetion mechanism)を指します。"Attention Is All You Need" を直訳すると、
「必要なのはアテンションだけ」
ですが、少々意訳すると、
「アテンションこそがすべて」
となるでしょう(蛇足ですが、ビートルズの "All You Need Is Love" を連想させる論文タイトルです)。
Transformer を訳すと "変換器" ですが、その名の通り「系列 A から系列 B への変換」を行います。系列 A = 日本語、系列 B = 英語、とすると和文英訳になります。第3章では、この Transformer の仕組みを説明をします。
全体のアーキテクチャ
Transformer のアーキテクチャの全体像が次図です(論文より)。以降、この絵の意味を順に説明します。
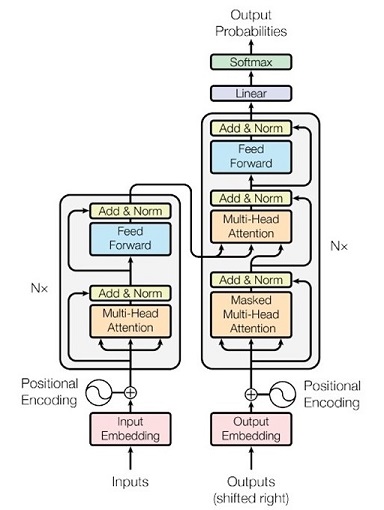
|
図18:Transformer のアーキテクチャ |
アーキテクチャを簡略化して書くと次のようになります。以下では「日本語 → 英語の機械翻訳」を例として Transformer の動作を説明します。
|
図19:アーキテクチャの簡略図 |
左側がエンコーダで、入力された日本語テキストを中間表現(=テキストの特徴を抽出した内部表現)に変換します。右側のデコーダは、中間表現を参照しつつ「次に生成すべき英単語」を推論します。
エンコーダ、デコーダとも、図で「ブロック」と書いた単位を積層した構造です。つまり、1つのブロックの出力が次のブロックへの入力になります。アーキテクチャの絵で「N x」と書いてあるのはその積層の意味(= N 倍)で、積層する数を \(N\) とすると、Transformer では、
\(N=6\)
です。エンコーダの中間表現は最終ブロックからの出力です。その出力がデコーダの全てのブロックへ伝わります。
訓練
多数の「日本語 \(\rightarrow\) 英語の翻訳データ」を用いて Transformer を訓練するとき、全体がどのように動くかを示したのが次の図です。
|
図20:Transformerの動作(訓練時) |
エンコーダには日本語の文(Input)が入力されます。デコーダからの出力は、英文の推論結果(確率)です。これを正しい英文(Output = 教師ラベル)と照らし合わして損失(交差エントロピー誤差)を計算し、誤差逆伝播を行ってニューラル・ネットワークの重みを更新します(前回参照)。デコーダの入力となるのは「右に1語だけずらした Output」です。アーキテクチャの図18 で shifted right と書いてあるのはその意味です。なお、実際に入力されるのは単語ではなくトークンの列です(前回参照)。
推論
訓練を終えた Transformer を使って日本語文を英語文に機械翻訳するときの動きは次図です。
|
図21:Transformerの動作(推論時) |
エンコーダに日本語のテキストを入力し、中間表現を得ます。これは1回きりです。
デコーダには、生成すべき英語テキストの最初のトークン、[BOS](文の始まりを示す特殊トークン)を入力し、[BOS] の次にくるべきトークンの確率を推論します。最も確率が高いトークンを選ぶと [I] になるはずです。これが1回目の推論(#1)です。
2回目(#2)では [I] を入力し、[I] の次のトークンを推論します([am] となるはずです)。[BOS] から [I] を推論したときの情報はデコーダに残されているので、その部分を再計算する必要はありません。推論のためには、日本語文の全情報(エンコーダの中間表現)と、既に生成した英文([BOS] [I])を参照します。
このようにして順々に英文を生成していき、推論結果が [EOS](文の終了を示す特殊トークン)になるところで、翻訳が終了します。
アーキテクチャの詳細
用語と記号
トークンの語彙
トークンの語彙(vocabulary)のサイズ を \(V\) とします。トークンを識別する "トークンID" は \(1\)~\(V\) の数字です。
系列
Transformer への入力となるテキストは、Tokenizer でトークンID の列に変換されます。以降、Transformer への入力を "系列(sequece)" と呼びます。
系列はその最大サイズ \(S\) が決まっています(普通、数千程度)。入力が \(S\) より少ない場合、残りのトークンは無効トークン([PAD])としておき、そこの処理は回避するようにします。[PAD] を含めて、系列は長さ \(\bs{S}\) の固定長とします。
系列\(=\{\:t_1,\:t_2,\:\cd\:,\:t_S\:\}\)
\(t_i\):トークンID \((1\leq t_i\leq V)\)
Transformer の論文には語彙のサイズと系列のサイズが書いてありませんが、以降の説明では \(V\) と \(S\) を使います。
分散表現ベクトル
トークンの分散表現ベクトル(埋め込みベクトル)の次元を \(D\) とします。トークンID が \(t_i\) であるトークンの分散表現を \(\bs{x}_i\) とすると、
\(\bs{x}_i=\left(\begin{array}{r}x_1&x_2&\cd&x_D\\\end{array}\right)\) \([1\times D]\)
というようになり、系列をベクトル列で表現すると、
系列\(=\{\:\bs{x}_1,\:\bs{x}_2,\:\cd\:,\:\bs{x}_S\:\}\)
となります。なお、\(D\) 次元ベクトルを、\(1\)行 \(D\)列の配列とし、\([1\times D]\) で表わします(前回参照)。
なお、Transformer では \(D=512\) です。
以降、全体アーキテクチャの図に沿って、各レイヤー(計算処理)の説明をします。以降の説明での \(\bs{x}_i,\:\:\bs{y}_i\) は、
\(\bs{x}_i\):レイヤーへの入力
(系列の \(i\) 番目。\(1\leq i\leq S\))
\(\bs{y}_i\):レイヤーからの出力
(系列の \(i\) 番目。\(1\leq i\leq S\))
で、すべてのレイヤーに共通です。また、\(D\) 次元ベクトルを \([1\times D]\)、\(S\)行 \(D\)列の行列を \([S\times D]\) と書きます。
埋め込みベクトルの生成
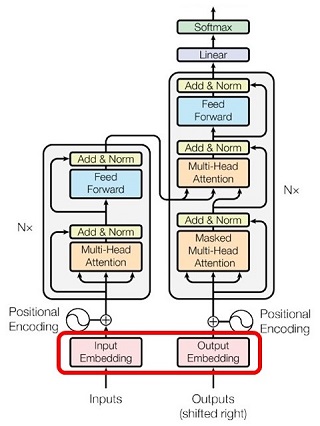
|
このレイヤーの入出力を、
| トークンID を one hot ベクトルにしたもの \([1\times V]\) | |
| 埋め込みベクトル \([1\times D]\) |
とすると、
\(\bs{y}_i=\bs{x}_i\cdot\bs{W}_{\large enc}\)
\([1\times D]=[1\times V]\cdot[V\times D]\)
で表現できます(前回の word2vec 参照)。もちろん、この行列演算を実際にする必要はなく、\(\bs{x}_i\) のトークンID を \(t_i\) とすると、
\(\bs{y}_i=\bs{W}_{\large enc}\) の \(t_i\) 行
です。\(\bs{W}_{\large enc}\) は Transformer の訓練を始める前に、あらかじめ(ニューラル・ネットワークを用いて)作成しておきます。従って、埋め込みベクトルの作成はテーブルの参照処理(table lookup)です。
位置エンコーディング
|
埋め込みベクトル(分散表現)に、トークンの位置を表す「位置符号ベクトル」を加算します。つまり、
| \(\bs{x}_i\):埋め込みベクトル | \([1\times D]\) | |
| \(\bs{p}_i\):位置符号ベクトル | \([1\times D]\) | |
| \(\bs{y}_i\):位置符号加算ベクトル | \([1\times D]\) |
とすると、
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
\([1\times D]=[1\times D]+[1\times D]\)
の単純加算です。位置符号ベクトル \(\bs{p}_i\) の要素を次の記号で表します。
\(p_{t,d}\)
\(t\) は \(0\) から始まる、トークンの位置
\((t=i-1,\:\:0\leq t\leq S-1)\)
\(d\) は \(0\) から始まる、ベクトル内の要素の位置
\((0\leq d\leq D-1)\)
この \(p_{t,d}\) の値は次のように定義されます。
| \(p_{t,2k}\) | \(=\mr{sin}\left(\dfrac{1}{10000^x}\cdot t\right)\) | |
| \(p_{t,2k+1}\) | \(=\mr{cos}\left(\dfrac{1}{10000^x}\cdot t\right)\) |
\((0\leq k < \dfrac{D}{2},\:\:\:x=\dfrac{2k}{D},\:\:\:0\leq x < 1)\)
つまり、\(D=512\) とすると、
\(d\) が偶数の要素位置では \(\mr{sin}\) 波
(\(d=0,\:2,\:4,\:\cd\:,510\))
\(d\) が奇数の要素位置では \(\mr{cos}\) 波
(\(d=1,\:3,\:5\:\:\cd\:,511\))
で位置符号値を決めます。この \(\mr{sin}/\mr{cos}\)波の波長 λ は
λ\(=2\pi\cdot10000^x\)
であり、\(0\leq d < D\) の範囲で、
\(2\pi\leq\)λ\( < 2\pi\cdot10000\)
となります。この \(\mr{sin}/\mr{cos}\) 波を図示してみます。グラフをわかりやすくするために、\(D=512\) ではなく、
\(D=32\)
とし、ベクトルの要素 \(32\)個のうちの最初の6つ、
\(d=0,\:1,\:2,\:3,\:4,\:5\)
だけのグラフにします。グラフの
・横軸はトークンの位置 \(t\)
・縦軸は位置符号ベクトルの要素 \(p_{t,d}\)
です。
|
図22:位置符号値を計算するための正弦・余弦波 |
図の黒丸は、\(t=3\) の位置符号ベクトルの、要素\(0\)~要素\(5\)(\(0\leq d\leq5\))を示す。 |
具体的に \(t=3\) のときのベクトルの要素 \(p_{3,d}\:\:(0\leq d\leq31)\) の \(0\leq d\leq5\) の部分を書いてみると、
\(p_{3,0}=\phantom{-}0.1411\)
\(p_{3,1}=-0.9900\)
\(p_{3,2}=\phantom{-}0.9933\)
\(p_{3,3}=-0.1160\)
\(p_{3,4}=\phantom{-}0.8126\)
\(p_{3,5}=\phantom{-}0.5828\)
となります(図22)。
言うまでもなく、言語モデルにとってトークンの位置はきわめて重要な情報です。位置をバラバラにすると意味をなさないテキストになるし、Bob loves Alice と Alice loves Bob では意味が逆です。従って、何らかの手段で「トークンの位置を考慮したモデル化」をしなければならない。
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
の式で、\(\bs{x}_i\) は「単語埋め込み」のアルゴリズムで作られ、似たような単語/トークンは類似したベクトルになります(前回参照)。それに対し \(\bs{p}_i\) の \(\mr{sin}/\mr{cos}\) 波は、言語処理とは全く無関係な数学の産物です。従って、加算結果である \(\bs{y}_i\) がどのような「意味」をもつベクトルなのか、説明しようとしても無理でしょう。全く異質なものの足し算をしているのだから ・・・・・・。それでいて、このやり方で全体として成り立つのが驚きです。
Transformer より以前の機械翻訳では、トークンの出現順に逐次処理をするアーキテクチャでした。つまり、1つのトークンの処理結果を利用しながら次のトークンを処理するという逐次処理によって、並び順に意味があるという言語の特質を捕らえていました。
それに対し、位置エンコーディングを取り入れた Transformer では、逐次処理の必要性がなくなり、系列のトークン全部の並列処理が可能になりました。この結果、同一計算の超並列処理ができる GPU(数千並列が可能) をフルに活用することで、実用的な大規模言語モデルが構築できるようになったわけです。位置エンコーディングにはそういう意味があります。
なお Transformer の論文にも書いてあるのですが、位置符号ベクトルを \(\mr{sin}/\mr{cos}\) 波のような「決めうち」で作らないで、「学習可能なパラメータ」としておき、Transformer を訓練する過程で決めるやり方があります。位置符号ベクトルを学習で決めるわけです。GPT はこの方法をとっています。
Single Head Attention : SHA
|
アテンション・レイヤー(Multi Head Attention : MHA)の説明をするために、まず "Single Head Attention : SHA" の処理論理を説明します。Transformer で実際に使われている MHA は、以下に説明する SHA の拡張版で、核となるアルゴリズムは同じです。
SHAの入出力は、それぞれ \(S\)個の \(D\)次元ベクトルであり、
入力 \(\bs{x}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
出力 \(\bs{y}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
ですが、系列の全体を1つの行列で表すことができます。1つのベクトルを行列の1行として、それを縦方向に \(S\)個並べて行列を作ります。つまり、
入力 \(\bs{X}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{x}_i\))
出力 \(\bs{Y}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{y}_i\))
とすると SHA は、
\(\bs{Y}=\mr{SHA}(\bs{X})\)
と書けます。アテンションの処理では、まず入力ベクトル \(\bs{x}_i\) を、
| ◆クエリ・ベクトル | \(\bs{q}_i\)(query:問合わせ) | |
| ◆キー・ベクトル | \(\bs{k}_i\)(key:鍵) | |
| ◆バリュー・ベクトル | \(\bs{v}_i\)(value:値) |
の組、( \(\bs{q}_i,\:\:\bs{k}_i,\:\:\bs{v}_i\) )に変換します。変換式は次の通りです。
\(\bs{q}_i=\bs{x}_i\cdot\bs{W}_Q\:\:\:(1\leq i\leq S)\) \(\bs{k}_i=\bs{x}_i\cdot\bs{W}_K\:\:\:(1\leq i\leq S)\) \(\bs{v}_i=\bs{x}_i\cdot\bs{W}_V\:\:\:(1\leq i\leq S)\) \([1\times D]=[1\times D]\cdot[D\times D]\) |
ここで、\(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は学習で決まる変換行列です。系列全体についての Query/Key/Value(\(QKV\))を行列の形で表すと、
\(\bs{Q}=\bs{X}\cdot\bs{W}_Q\) \(\bs{K}=\bs{X}\cdot\bs{W}_K\) \(\bs{V}=\bs{X}\cdot\bs{W}_V\) \([S\times D]=[S\times D]\cdot[D\times D]\) |
となります。SHA レイヤーからの出力、\(\bs{y}_i\:\:[1\times D]\) は、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の "重み付き和" (加重和)で求めます。加重和に使う重み、\(\bs{w}_i\:\:[1\times S]\) は次のように計算されます。
まず、クエリ・ベクトル \(\bs{q}_i\) とキー・ベクトル \(\bs{k}_j\:\:(1\leq j\leq S)\) の "スケール化内積(scaled dot product)" を計算し、\(S\)個のスカラー値を求めます。スケール化内積(\(\mr{SDP}\) と記述します)とは、2つの \(D\)次元ベクトル \(\bs{a}\) と \(\bs{b}\) の場合、
\(\mr{SDP}(\bs{a},\bs{b})=\dfrac{1}{\sqrt{D}}\bs{a}\bs{b}^T\)
\([1\times1]=[1\times D]\cdot[D\times1]\)
で定義されます。つまり、一般の内積(=スカラー値)を「ベクトルの次元数の平方根」で割ったものです。
\(\bs{q}_i\) と \(\bs{k}_j\:\:(1\leq j\leq S)\) のスケール化内積を順番に \(S\)個並べたベクトルを \(\bs{s}_i\:\:[1\times S]\) と書くと、スケール化内積の定義によって、
\(\bs{s}_i=\dfrac{1}{\sqrt{D}}\bs{q}_i\bs{K}^T\)
\([1\times S]=[1\times D]\cdot[D\times S]\)
です。そして、加重和を求めるときの重み \(\bs{w}_i\) は、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
\([1\times S]=\mr{Softmax}([1\times S])\)
とします。この \(S\)次元の重みベクトルを使って、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の加重和をとると、出力ベクトル \(\bs{y}_i\) は、
\(\bs{y}_i=\bs{w}_i\cdot\bs{V}\)
\([1\times D]=[1\times S]\cdot[S\times D]\)
となります。以上の計算プロセスを一つの式で書いてしまうと、
\(\bs{y}_i=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{q}_i\cdot\bs{K}^T\right)\cdot\bs{V}\) \([1\times D]=\mr{Softmax}([1\times D]\cdot[D\times S])\cdot[S\times D]\) |
です。従って、SHA からの出力ベクトル \(\bs{y}_i\) を縦方向に並べた行列 \(\bs{Y}\) は、
\(\bs{Y}=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{Q}\cdot\bs{K}^T\right)\cdot\bs{V}\)
\([S\times D]=\mr{Softmax}([S\times D]\cdot[D\times S])\cdot[S\times D]\)
と表すことがきます。この表記で \(\mr{Softmax}\) 関数が作用するのは \([S\times S]\) の行列ですが、\(S\)個の行ごとに \(\bs{\mr{Softmax}}\) を計算します。
単なる内積ではなく「スケール化内積」を使う理由ですが、2つのベクトルの内積は、要素同士のかけ算を次元数 \(D\) 個だけ加算したものです。従って、ベクトル \(\bs{s}_i\) を、シンプルな内積を使って、
\(\bs{s}_i\:=\bs{q}_i\cdot\bs{K}^T\)
のように定義し、重み \(\bs{w}_i\) を、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
で求めると、\(D\) が大きいと \(\bs{s}_i\) の要素が大きくなり、その結果として \(\bs{w}_i\) はゼロに近いところに多くの要素が集まるようになります。これは \(\mr{Softmax}\) 関数の性質によります(前回参照)。こうなると勾配消失が起きやすくなり、訓練が収束しづらくなります。そのため「スケール化」するというのが論文の説明です。
もちろん、幾多の試行錯誤があり、その結果として決まったのが「スケール化内積で加重和の重みを計算する」というやり方だったのでしょう。
以上の計算でわかるように、注意機構(Attention machanism)とは、あるトークンを処理するときに、注意を向けるべきトークンと注意の強さを決め(それ自体が学習で決まる)、注意を向けた先の情報を集めてきて集積するものです。
しかも、注意機構は6層(\(N=6\)) に重ねられています。ということは、階層的な(多段階の) "注意の向け方" ができることになります。また、言語における単語と単語の関係性は多様です。動作\(\cdot\)動作主体、修飾\(\cdot\)被修飾、指示代名詞と指示されるもの(照応関係)など多岐に渡ります。それらのさまざまなタイプの関係性を、Transformer の訓練を通して、多層の注意機構が自動的に把握すると考えられるのです。
MHA : Multi Head Attention
SHA では、入力ベクトル \(\bs{x}_i\) から、1組の Query/Key/Value(\(QKV\)) ベクトルを抽出しましたが、Transformer で実際に使われているのは、
| 1つの入力ベクトル \(\bs{x}_i\) から、複数組の違った \(\bs{QKV}\) ベクトルを抽出し、 | |
| それぞれについて独立に SHA と同等のアテンション処理をし、 | |
| 処理結果を単純結合(Concatenation)し、 | |
| 最後に線型変換をして出力ベクトルに \(\bs{y}_i\) する |
という処理です。これを Multi Head Attention : MHA と呼びます。この「それぞれについてのアテンション処理」のことを "head(ヘッド)" と言います。複数の head なので Multi Head です。このヘッドの数を \(H\) とし、
\(d=\dfrac{D}{H}\) (\(D\) は入出力ベクトルの次元)
とします(\(H\) は \(d\) が整数になるように選びます)。このとき、
\(\bs{x}_i\:\:[1\times D]\) から抽出される(複数組の)\(QKV\) ベクトルの次元はすべて \([1\times d]\)
です。つまり MHA は「複数の特徴を抽出し(一つの情報量は SHA より少ない)、それぞれの特徴について 独立した "注意機構" を働かせ、最後に統合してまとめる」仕組みです。なお、Transformer では、
\(H=8\)
\(d=\dfrac{D}{H}=\dfrac{512}{8}=64\)
です。
\(h\) 番目のヘッド \((1\leq h\leq H)\) に着目し、"注意機構" の計算プロセスを式で書くと、次のようになります。まず、\(h\) 番目のヘッドの \(QKV\) ベクトルの計算は、
\(\bs{q}_i^h=\bs{x}_i\cdot\bs{W}_Q^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \(\bs{k}_i^h=\bs{x}_i\cdot\bs{W}_K^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \(\bs{v}_i^h=\bs{x}_i\cdot\bs{W}_V^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \([1\times d]=[1\times D]\cdot[D\times d]\) |
です。系列全体について、\(h\) 番目のヘッドの \(QKV\) を行列の形で表すと、
\(\bs{Q}^h=\bs{X}\cdot\bs{W}_Q^h\) \(\bs{K}^h=\bs{X}\cdot\bs{W}_K^h\) \(\bs{V}^h=\bs{X}\cdot\bs{W}_V^h\) \([S\times d]=[S\times D]\cdot[D\times d]\) |
です。\(h\) 番目のヘッドのアテンション処理は、SHA の場合と同様で、
\(\bs{y}_i^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{q}_i^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([1\times d]=\mr{Softmax}([1\times d]\cdot[d\times S])\cdot[S\times d]\) |
となり、これを系列全体での表現にすると、
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S])\cdot[S\times d]\) |
となります。行列 \(\bs{Y}^h\) は、\(h\) 番目のヘッドの出力ベクトル \(\bs{y}_i^h\:\:[1\times d]\) を、系列の数だけ縦に並べた行列です。
系列の \(i\) 番目の入力 \(\bs{x}_i\) に対する \(H\) 個の出力ベクトル
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
が求まったところで、これら \(H\) 個を単純結合して(=順に並べる)一つのベクトルにし、さらに Linear 変換をして最終出力にします。変換に使う行列は \(\bs{W}_O\:\:[D\times D]\) です。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\) \(\begin{eqnarray} &&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\ &&&=[1\times D]\cdot[D\times D]\\ \end{eqnarray}\) |
Linear 変換は直前の単純結合(Concatenation)とセットになっています。つまり、ヘッドの順序を表す \(h\:\:(1\leq h\leq H)\) という数字には、"注意機構" における何らかの意味があるわけではありません。単にアテンション処理を \(H\) 個に分けた \(h\) 番目というだけです。従って、順に単純結合する、
\(\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\)
という操作の「結合順序」には意味が無いことになります。そこで結合した後で、学習可能なパラメータ \(\bs{W}_O\) で線型写像を行って、最適な出力ベクトルを求めるわけです。
エンコーダの MHA は、エンコーダ内に閉じたアテンションで、これを「自己アテンション」(Self Attention)と言います。一方、デコーダ側には自己アテンションの他に、エンコーダとデコーダにまたがるアテンションがあります。これを Source Target Attention と言います。このアテンションは、
| クエリは、デコーダ側のベクトルから生成し、 | |
| キーとバリューは、エンコーダ側のベクトルから生成 |
します。これによってエンコーダからデコーダ側への情報の流れを作ります。日本語 → 英語の機械翻訳の場合だと、次に生成すべき英単語に関連して「注意を向けるべき日本語のトークンと、その注意の量」がここで決まります。
Multi Head Attention において、1つのベクトルから複数の \(QKV\) を取り出すことの意味は、おそらくトークンの「多義性」でしょう。その例ですが、英語で fine という語の代表的な意味を4つあげるとしたら、たとえば、
fine :
(1) 素晴らしい
(2) 晴れた
(3) 細かい
(4) 罰金
です(例です。(1) (2) は同類の意味)。単語の埋め込みベクトルは、似たような(あるいは同一ジャンルの)語は類似している(= コサイン類似度が 1 に近い)わけです(前回参照)。とすると、(1)~(4) の同一ジャンルの言葉は、それぞれ、
(1) good, excellent, ・・・・・・
(2) cloudy, rainy, ・・・・・・
(3) tiny, small, coarce, ・・・・・・
(4) penalty, guilty, ・・・・・・
などとなるはずです。fine がこれら4つのジャンルと類似性があるということは、fine の埋め込みベクトルおいて4つの意味が物理的に分散して配置されていると考えられます。さらにイタリア語まで考えると、
fine :
(5) 終わり
が加わります(イタリア映画の最後に出てくる語、ないしは音楽用語)。埋め込みベクトルは言語ごとに作るわけではないので、fine のベクトルはあくまで1つです。ということは、埋め込みベクトルには(この例では)5つの意味が分散して配置されているはずです。
この状況は、埋め込みベクトルから複数の \(QKV\) ベクトルを取り出し、それぞれについて独立したアテンション計算をするというアルゴリズムがマッチしていると考えられるのです。
Add & Norm

|
アーキテクチャの絵で5カ所にある「Add & Norm」は、ベクトルごとに「残差結合」と「レイヤー正規化」を行うレイヤーです(詳細は前回参照)。図で表すと以下です。
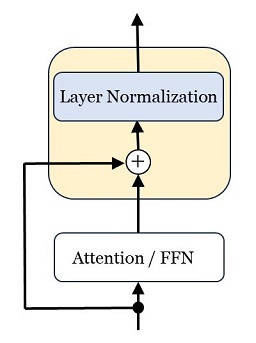
|
図23:残差結合とレイヤー正規化 |
計算式は次のようになります。系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略します。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\begin{eqnarray}
&&\:\: \bs{x}=\{\:x_1, &x_2, &\cd\:, &x_D\:\}\\
&&\:\: \bs{y}=\{\:y_1, &y_2, &\cd\:, &y_D\:\}\\
\end{eqnarray}\)
\(x_k\:\:(1\leq k\leq D)\) の平均 : \(\mu\)
\(\mu=\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}x_k\)
\(x_k\:\:(1\leq k\leq D)\) の標準偏差 : \(\sg\)
\(\sg=\sqrt{\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}(x_k-\mu)^2}\)
とおくと、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\) \([1\times D]=[1\times D]\odot[1\times D]+[1\times D]\) |
です。ここで \(\bs{g}\) と \(\bs{b}\) は学習で決まるベクトル(=パラメータ)です。
Feed Forward Network
|
ベクトルごとに処理される、2層の全結合ニューラル\(\cdot\)ネットワークです。第1層の活性化関数は \(\mr{ReLU}\) で、第2層(出力層)には活性化関数がありません。3つのレイヤーで表現すると次の通りです。
|
図24:Feed Forward Network |
ニューロンの数(=ベクトルの次元)は、
入力層:\(D\)
第1層:\(D_{ff}=4\times D\)
出力層:\(D\)
です。計算を式で表すと(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)、
\(\bs{y}=\mr{ReLU}(\bs{x}\bs{W}_1+\bs{b}_1)\cdot\bs{W}_2+\bs{b}_2\)
です。第1層の次元を入力\(\cdot\)出力層の4倍にとるのは、そのようにするのが Transformer の性能(たとえば、翻訳文の質)が最も向上するからです。GPT-3、ChatGPT も踏襲しています。
Masked Multi Head Attention
|
デコーダ側にある Masked Multi Head Attention の説明をします。系列のトークンの列を、
\(\{\:\bs{x}_1,\:\cd\:,\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\cd\:,\:\bs{x}_S\:\}\)
とし、いま \(\bs{x}_t\) に着目しているとします。
\(\bs{x}_i\:\:\:(1\leq i\leq t)\:\longrightarrow\) 過去のトークン
\(\bs{x}_i\:\:\:(t < i\leq S)\:\longrightarrow\) 未来のトークン
と呼ぶことにします。着目しているトークンを基準に、系列でそれ以前のトークンが「過去」、次以降のトークンが「未来」です。
日本語から英語に翻訳する Transformer を例にとると、デコーダの推論時には、英文のトークンを一つずつ推論していきます。つまり、
[BOS] \(\longrightarrow\) [I]
[BOS] [I] \(\longrightarrow\) [am]
[BOS] [I] [am] \(\longrightarrow\) [a]
[BOS] [I] [am] [a] \(\longrightarrow\) [cat]
[BOS] [I] [am] [a] [cat] \(\longrightarrow\) [EOS]
といった具合です(図21)。このときの各ステップにおけるアテンション処理は、当然ですが、末尾のトークンから生成済みのトークン(=過去のトークン)に対して行われます。つまり「トークンが注意を向ける先は常に過去のトークン」です。「すでに生成済みのトークンの情報だけから次にくるトークンを推論する」のがデコーダなので、これは当然です。
一方、デコーダの訓練時のことを考えると、
| (入力データ) | [BOS] | [I] | [am] | [a] | [cat] | |
| (教師ラベル) | [I] | [am] | [a] | [cat] | [EOS] |
で(図20)、入力データとしては系列のトークンが全部与えられています。しかしここで未来のトークンに注意を向けてしまうと、推論時との不整合が起きてしまいます。そこで
未来のトークンには注意を向けない。自分自身を含む過去のトークンにだけ注意を向ける
という配慮が、デコーダ側のアテンション処理では必要になります。この配慮をした注意機構が Masked Multi Head Attention です。一方、エンコーダ側では、訓練時も推論時も、
[我が輩] [は] [猫] [で] [ある]
という系列が一括して与えられるので(図20、図21)、未来のトークンに注意を向けても問題ありません。またデコーダ側からエンコダー側に注意を向けるのもかまいません。
この「過去のトークンにだけ注意を向ける」ことを数式で表現するには、\([S\times S]\) のマスク行列、\(\bs{M}\) を次のように定義します。
\(\bs{M}=\left(\begin{array}{c}
0&\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}\\
\phantom{0}&\large\ddots&\phantom{0}&\huge\textrm{-}\infty&\phantom{0}\\
\phantom{0}&\phantom{0}&0&\phantom{0}&\phantom{0}\\
\phantom{0}&\huge0&\phantom{0}&\large\ddots&\phantom{0}\\
\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}&0\\
\end{array}\right)\) \([S\times S]\)
このマスク行列は、
| 対角項:\(0\) | |
| 行列の左下(行番号\( > \)列番号):\(0\) | |
| 行列の右上(行番号\( < \)列番号):\(-\infty\) |
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S])\cdot[S\times d]\) |
でした。これに \(\bs{M}\) を足し込むと、
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T+\bs{M}\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S]+[S\times S])\cdot[S\times d]\) |
となります。\(\mr{Softmax}\) 関数は、ベクトル(上式では行列の1行)の各要素の \(\mr{exp}()\) をとります。従って、要素が \(-\infty\) だと \(\mr{exp}(-\infty)=0\) となり、\(\mr{Softmax}\) 関数にとってはその要素が無いのと同じことになります。
上式の \(\mr{Softmax}\) 関数の内側は \([S\times S]\) の行列ですが、縦方向が系列全体のクエリ・ベクトルに対応し、横方向が系列全体のキー・ベクトルに対応しています。そのため、マスク行列を足し込むと、アテンション処理において過去のトークンだけに注意が行き、未来のトークンには注意が行かない(=結果としてバリュー・ベクトルが加重和されない)ようになるのです。
こうして求めた行列 \(\bs{Y}^h\) の \(i\) 行目をベクトル、
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
とすると、これ以降の処理はマスク行列がない場合と同じです。つまり \(H\) 個のベクトル \([1\times d]\) を単純結合して一つのベクトル \([1\times D]\) にし、さらに Linear 変換をしてアテンション処理からの最終出力にします。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\)
\(\begin{eqnarray}
&&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\
&&&=[1\times D]\cdot[D\times D]\\
\end{eqnarray}\)
わざわざ \(\mr{exp}(-\infty)\) を持ち出してマスク行列を使うのは、話をややこしくするだけのようですが、マスク行列を使った Masked Multi Head Attention の計算式を見ると、線型変換と \(\mr{Softmax}\) 関数だけからできています。ということは、「過去のトークンだけに注意を向けるアテンション計算は微分可能」であり、誤差逆伝播の計算が成り立つことがわかります。
確率生成
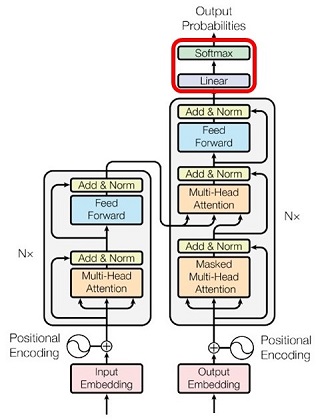
|
Transformerのデコーダの最終部分は、推論結果である \(D\) 次元のベクトルを、語彙集合の中での確率ベクトルに変換する部分です。計算式で書くと、
\(\bs{y}=\mr{Softmax}(\bs{x}\cdot\bs{W}_{\large dec})\)
\([1\times V]=\mr{Softmax}([1\times D]\cdot[D\times V])\)
です(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)。\(\bs{W}_{\large dec}\) は、前回の word2vec のところに出てきた、\(D\)次元の埋め込みベクトルを \(V\) 次元の確率ベクトルに変換する行列です。
以上で Transformer のアーキテクチャの説明は終わりですが、全体を振り返ると、
アテンションだけが系列全体に関わる処理であり、あとはすべてベクトル(トークン)ごとの処理である
ことがわかります。以降は、この中で鍵となる「アテンション」と「Feed Foward Network」についての補足です。
アテンションの意義
一般のニューラル・ネットワークにおいて、隣合った2つの層、\(\bs{x}\) と \(\bs{y}\) が同じニューロン数 \(D\) だとします。活性値を、
\(\begin{eqnarray}
&&\:\:\bs{x}=\{x_1, &x_2, &\cd\:,&x_D\}\\
&&\:\:\bs{y}=\{y_1, &y_2, &\cd\:,&y_D\}\\
\end{eqnarray}\)
とし、重み行列を \(\bs{W}\)、バイアスはなし、活性化関数を \(\mr{ReLU}\) とするると、
\(\bs{y}=\mr{ReLU}(\bs{x}\cdot\bs{W})\)
です。重み \(\bs{W}\) は誤差逆伝播法による訓練で決まり、推論時には一定の値です。Transformer のアテンション機構もこれと似ています。アテンションは、
入力ベクトル列 :\(\bs{x}_i\:\:\:(1\leq i\leq S)\)
出力ベクトル列 :\(\bs{y}_i\:\:\:(1\leq i\leq S)\)
の間の変換をする機構だからです。ニューラル\(\cdot\)ネットワークの活性値(実数値)がベクトルに置き換わったものと言えます。ヘッドが1つの場合(Single Head Attension)で図示すると、次の通りです。

|
図25:注意機構 |
ヘッドが1つの場合の計算処理である。ヘッドが複数の場合も本質は同じで、この計算処理を独立して複数個行ない、結果を結合して出力とする。 |
しかし、この図は一般のニューラル\(\cdot\)ネットワークとは決定的に違います。重み行列 \(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は推論時には一定ですが、実際に \(\bs{x}_i\) と \(\bs{y}_i\) の関係性を決めているのは、クエリ・ベクトル \(\bs{Q}\) とキー・ベクトル \(\bs{K}\) であり、これは入力ベクトル列 \(\bs{x}_i\) の内容にもろに依存しているからです。つまり、
注意機構により、ネットワークの "ありよう"(結合状態と結合強度)が、入力データの内容に依存して、ダイナミックに変化する
と言えます。\(\bs{x}_1\) の値を変えると、その影響は \(\bs{y}_i\:\:(1\leq i\leq S)\) の全体に及びます。それは、「\(x_1\) を変えると \(y_i\) の全部が変わる」という一般のニューラル\(\cdot\)ネットワークと同じではありません。一般のニューラル\(\cdot\)ネットワークを関数とみなすと、「関数は一定だが、入力が変わるから出力も変わる」のです。それに対して注意機構は「入力が変わると関数の形まで変わる」とみなすことができるでしょう。もちろん、実際には図25のように関数は一定なのですが、一般のニューラル\(\cdot\)ネットワークとの比較で言うと、そうみなせるということです。
この柔軟性とダイナミックな(動的な)性格が、Transformer に大きなアドバンテージをもたらしました。次章の GPT-3 / ChatGPT が実現している「本文中学習(In Context Learning)」はその一つです。ChatGPT では、プロンプトを変える、ないしは文言を追加すると、応答が大きく変わることがあります。また、欲しい応答の表現形式を例示したプロンプトをすると、その形式どおりのに応答がきたりします。あたかも、プロンプトからその場で学んだように見えるのが In Context Learning です。しかし、ニューラル・ネットワークのパラメータは、推論時にはあくまで一定であり、決してその場で学んでいるわけではありません。この "あたかも" を作り出しているのが "注意機構"です。
Feed Forward Network の意味
FFN は、注意機構と違ってベクトルごとの処理です。論文では "Position-wise(位置ごとの)Feed Forward Network" と書いてあります。ということは、系列の文脈には依存しないということです。つまり Transformer の訓練を通して、ベクトル(トークンの中間表現)が本来持っている性格や関連情報が、FFN の重みの中に蓄えられると考えられます。AI の専門家である、プリファードネットワークス社の共同創業者の岡野原大輔氏は、著書の『大規模言語モデルは新たな知能か』の中で次のように書いています。
|
岡野原氏が「多重パーセプトロン(Multi-Layer Perceptron : MLP)と書いているのは FFN のことです。ちなみに入力層(第0層)を含めて「三層」という言い方になっています。
ここで、FFN のパラメータ数を求めてみます。バイアスを無視すると、
\(\bs{W}_1\:\:[D\times D_{ff}]\)
\(\bs{W}_2\:\:[D_{ff}\times D]\)
\(D\) : 埋め込みベクトルの次元
\(D_{ff}=4D\)
なので、
FFN のパラメータ数\(=8D^2\)
です。一方、Multi Head Attention で、
\(H\) : ヘッドの数
\(d=\dfrac{D}{H}\)
とすると、\(h\)番目のヘッドの \(QKV\) を作る行列は、
\(\bs{W}_Q^h\) \([D\times d]\)
\(\bs{W}_K^h\) \([D\times d]\)
\(\bs{W}_V^h\) \([D\times d]\)
であり、これらを足すとパラメータ数は \(3Dd\) ですが、この組が \(H\) セットあるので、合計は \(3DdH=3D^2\) です。さらに、単純結合したあとの Linear 変換行列である、
\(\bs{W}_O\) \([D\times D]\)
が加わるので、結局、
MHA のパラメータ数\(=4D^2\)
です。ということは、
FFN のパラメータ数は、MHA のパラメータ数の2倍
ということになります。パラメータ数だけの単純比較はできませんが、FFN が極めて多い情報量=記憶を持っていることは確かでしょう。それが、大量の訓練データの中から関連する情報を記憶し、また推論時にそれを想起することを可能にしています。
論文のタイトルは "Attention Is All You Need" で、これは従来の機械翻訳の技術では補助的役割だった Attention を中心に据えたという意味でしょう。しかし技術の内実をみると、決して「アテンションがすべて」ではなく「アテンション機構と多重パーセプトロンの合わせ技」であり、しかもそれを多層に重ねたのが Transformer なのでした。
前回でニューラル・ネットワークの例とした多重パーセプトロンは、ニューラル・ネットワークの研究の歴史の中で最も由緒あるもので、1980年代に盛んに研究されました。それが、2010年代半ばから研究が始まった "アテンション機構" と合体して Transformer のアーキテクチャになり、さらには ChatGPT につながったのが興味深いところです。
| 4.GPT-3 と ChatGPT |
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。ここではまず GPT-3 の仕組みを説明します。
GPT-3 のアーキテクチャ
GPT は Generative Pre-trained Transformer の略です。generative とは "生成型の"、pre-trained は ""事前学習済の" という意味で、Transformer は Google が 2017年に提案した Transformer を指します。
訳すると "事前学習済の生成型トランスフォーマー" となるでしょう。Transformer は「変換器」という意味でした。とすると「生成型の変換器」とは言葉が矛盾しているようですが、実は GPT は Transformer のアーキテクチャのデコーダ部分だけを使った大規模言語モデルです。だから「生成型変換器」なのです(下図)。

|
GPT は上図の Transformer のアーキテクチャから赤枠の部分のみを使っている。 |
この「デコーダ部分だけを使う」という発想が、OpenAI の技術者の慧眼でした。デコーダだけで系列変換(機械翻訳、文章要約、質問応答、・・・・・・ )ができるはず、という発想が GPT に柔軟性と大きな能力を与えました。GPT-3 のアキテクチャーは以下のようです。
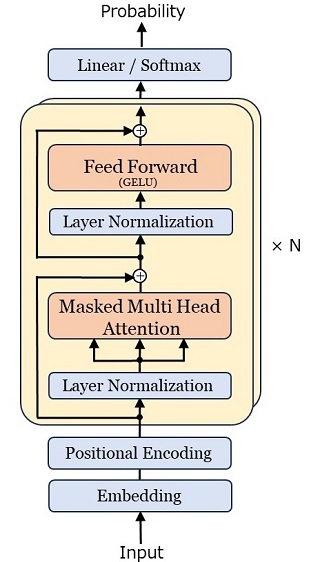
|
図26:GPT-3 のアーキテクチャ |
このアキテクチャーは、Transformer から「エンコーダとエンコーダ関連部分」を取り去ったものです。ただし、次が違います。
| Position Encoding における位置符号ベクトルは、学習で決まるパラメータとします。Transformer では固定的な \(\mr{sin}/\mr{cos}\) 波でした。 | |
| レイヤー正規化を Masked Multi Head Attetion と Feed Forward Network の直前に行います。Transformer では、それぞれの後にレイヤー正規化が配置されていました。 | |
| Feed Forward Network の活性化関数は \(\mr{GELU}\) を使います。Transformer では \(\mr{ReLU}\)です(\(\mr{GELU}\) については前回参照)。 |
これらはいずれも、学習の安定化と高速化のための工夫です。さらに GPT-3 は Transformer に比べてモデルの規模が大きく拡大されています。
・埋め込みベクトルの次元 \(D=12288\)
\((\)Transformer \(:\:512\) の \(24\)倍\()\)
・デコーダブロックの積層数 \(N=96\)
\((\)Transformer \(:\:6\) の \(16\)倍\()\)
・アテンションのヘッドの数 \(H=96\)
\((\)Transformer \(:\:8\) の \(12\)倍\()\)
です。大規模言語モデルでは、モデルの規模と学習量の拡大を続けると、それにともなって性能(たとえば機械翻訳の精度)が上がり続けるという「スケール則」がみられました。これは一般の深層学習のニューラル\(\cdot\)ネットワークにはない特徴です。このスケール則を信じ、アーキテクチャをシンプルにしつつ、モデルの規模を「桁違いに」拡大した OpenAI 社と出資した会社(マイクロソフト)の勝利でしょう。
このアーキテクチャのパラメータ数をカウントしてみます。
| ・トークンの語彙数 | \(V\) | |
| ・埋め込みベクトルの次元 | \(D\) | |
| ・系列の長さ | \(S\) | |
| ・デコーダの積層数 | \(N\) |
とします。GPT-3 の具体的な数値は、
| \(V\) | \(=50257\) | |
| \(D\) | \(=12288\) | |
| \(S\) | \(=\phantom{1}2048\) | |
| \(N\) | \(=\phantom{111}96\) |
です(\(V\) の値については前回参照)。学習で決まる行列やベクトルを順にカウントしていくと次のとおりです。
(1) Embedding と確率生成
\(\bs{W}_{\large enc}\) \([V\times D]\)
\(\bs{W}_{\large dec}\) \([D\times V]\)
\(\rightarrow\) パラメータ数\(=2VD\)
(2) Positional Encoding
\(\bs{p}\) \([S\times D]\)
\(\rightarrow\) パラメータ数\(=SD\)
(3) Masked Multi Head Attention
\(\bs{W}_Q\) \([D\times D]\) ※
\(\bs{W}_K\) \([D\times D]\) ※
\(\bs{W}_V\) \([D\times D]\) ※
\(\bs{W}_O\) \([D\times D]\)
\(\rightarrow\) パラメータ数\(=4D^2\)
※ GPT-3 のヘッドの数は \(H=96\) なので、\(\bs{W}_Q,\:\:\bs{W}_K,\:\bs{W}_V\) はそれぞれ \(96\)個の部分行列に分かれていますが、パラメータ数の全体は上式のとおりです。
(4) Feed Forward Network
| \(\bs{W}_1\) | \([D\times4D]\) | |
| \(\bs{b}_1\) | \([1\times4D]\) | |
| \(\bs{W}_2\) | \([4D\times D]\) | |
| \(\bs{b}_2\) | \([1\times D]\) |
\(\rightarrow\) パラメタ数\(=8D^2+5D\)
(5) Layer Nomaliation (2レイヤー)
\(\bs{g}\) \([1\times D]\)
\(\bs{b}\) \([1\times D]\)
\(\rightarrow\) パラメタ数\(=2\times2D=4D\)
(3), (4), (5) は \(\times\:N\) に積層されていることに注意して総パラメータ数を計算すると、
総パラメータ数
\(=\:2VD+SD+N(4D^2+8D^2+5D+4D)\)
\(=\:2VD+SD+N(12D^2+9D)\)
\(=\) \(\bs{175,217,074,176}\)
となり、約 1752億となります。一般に言われているパラメータ数が 1750億というのは、英語の 175B(B = Billion = 10億)の日本語訳で、Billion 単位にしたパラメータ数です。
GPT-3 が系列の次のトークンを推論するとき、1752億のパラメータの全てを使った演算が行われます(図21)。40文字の日本語文章を 60トークンだとすると、 わずか 40文字の日本語文章を生成するために、1752億のパラメータの全てを使った演算が 60回行われるということです。
また、1752億のパラメータがすべて 32ビットの浮動小数点数(4バイト)だとすると、パラメータのためだけに、
653ギガバイト(1ギガ = \(1024^3\) 換算)
のメモリが必要になります。業務用コンピュータ・システムの開発経験者ならわかると思いますが、これだけのデータ量を常時抱えつつ、更新やリアルタイムの推論を行うシステムを開発・運用するのは、ちゃんとやればできるでしょうが、かなり大変そうな感じです。
GPT-3 のアーキテクチャを振り返ってみると、Transformer のデコーダ部分だけを採用したことによる、Transformer との違いがあることに気づきます。それは、
Transformer には「過去と未来の両方に注意を向けるアテンション機構」と「過去にだけ注意を向けるアテンション機構」の両方があるが、GPT-3 には「過去にだけ注意を向けるアテンション機構」しかない
ことです。言うまでもなく、アテンション機構は Transformer / GPT-3 の "キモ" です。そのキモのところに違いがある。
人間の言語活動(発話・文章作成)では「過去の単語との整合性を考慮しつつ、未来の単語を想定して次の単語を決める」ことが多々あります。このことは、機械翻訳では、翻訳前の「原文」を処理するエンコーダ側の「過去と未来の両方に注意を向けるアテンション機構」で実現されています(Mask がない Multi Head Attention)。
しかし GPT-3 では様子が違ってきます。事前学習(次項)だけの GPT-3 で機械翻訳がなぜできるかというと、
[ 原文 ] を翻訳すると [ 翻訳文 ] です
といった対訳(に相当するデータ)が訓練データの中に多数あるからです(GPT-2 の論文による)。この「原文」の部分のアテンション処理において、「原文」の中の未来の単語に注意が向くことはありません(Masked Multi Head Attention しかないから)。このことにより翻訳の精度が Transformer とは違ってくる(精度が落ちる)と想定できます。
こういった "問題" は、大規模言語モデルを "超大規模" にすることで解決するというのが、GPT-3 の開発方針だと考えられます。1752億という膨大なパラメータ数が、それを表しています。
GPT-3 の訓練
GPT-3 の訓練は、
・WebText
・電子ブック
・Wikipedia
をもとに行われました。WebText は "訓練に使うべきではない" テキストを除外してあります。集められたテキストの量はトークンの数でカウントすると、
| ・WebText | \(4290\)億 | |
| ・電子ブック | \(\phantom{42}67\)億 | |
| ・Wikipedia | \(\phantom{42}30\)億 |
訓練は、Transformer のデコーダのところでで説明したように「ひたすら次のトークンの予測をする」というものです。この「次のトークンの予測」について補足しますと、前回、GPT のトークン化のロジックである BPE(Byte Pair Encoding)のことを書きました。これによると、UTF-8 では改行も空白も文字として扱われるので、改行、空白のそれぞれにトークンID が割り当てられることになります。
これから言えることは、テキストを学習するということは、その意味内容だけでなく、テキストの表現形式も学習するということです。つまり、段落、字下げ、箇条書きなどの形式です。訓練が終わった 1752億のパラメータには、そういった "表現形式に関する知識" も含まれていることに注意すべきでしょう。
以上のように、一般的に入手できるテキストだけを使ってニューラル・ネットワークを訓練することを「事前学習」と言います。このような事前学習を行った上で、機械翻訳や質問応答などのタスク別に専用に作成した訓練データで「目的別学習」を行うのが、言語モデルの定番の学習手法です。あらかじめ事前学習を行った方が言語モデルの性能が良くなるからです。目的別学習を "ファイン・チューニング" と言います。
GPT-3 は、それまでの GPT、GPT-2 と違って、ファイン・チューニングなしの言語モデルを狙ったものです。つまり、
事前学習済みの(=事前学習だけの)、生成型の(=デコーダだけの)トランスフォーマー
と言えるでしょう。実際 GPT-3 は、ファイン・チューニングを行った言語モデルと比較しても、"そこそこの"、ないしは "同等の" 性能であることが分かりました。もちろんファイン・チューニング済の言語モデルに劣るタスクも多々あります。しかし全体としては "そこそこの" 性能を示します。「ニューラル・ネットワークの超大規模化」と「大量の訓練データ」によってそれが可能であることを、GPT-3 は示したのでした。
ChatGPT
ChatGPT は GPT-3 のアーキテクチャと事前学習をもとに、さらに「目標駆動型学習」を追加したものです。ここでの目標駆動型学習とは「人間にとって好ましい応答の例を人間が作り、それを目標として、そこに近づくように学習する」という意味です。OpenAI 社は RLHF(Reinforcement Learning by Human Feedback:人間のフィードバックによる強化学習)と呼んでいます。これは一種のファイン・チューニングであると言えます。
この、目標駆動型学習をどうやるか、その詳細が OpenAI 社のノウハウでしょう。考えてみると、GPT-3 の(従って ChatGPT の)アーキテクチャはシンプルあり、これをシステム上に実現するのは、コンピュータ技術とAI技術、ハードウェアの調達(特にGPU)、そしてお金の問題です。事前学習に使う WebText にしても、世界中から集めて公開している団体があります(GPT-3 でも使われた Common Crawl)。お金がある(かつ投資意欲がある)大手IT企業なら、システム構築は難しくない。
しかし「人手で作った訓練データをもとに、人にとって違和感がない対話ができるまでに訓練する」のは、Transformer の性質や "癖 を熟知していないとできないと考えられます。そこにノウハウがあるはずです。
その目標駆動型学習の概要を、先ほど引用した岡野原氏の「大規模言語モデルは新たな知能か」では、次のような3つのステップで説明しています。この説明は専門用語を最小にした簡潔なものなので、以降これに沿って書きます。
|
この岡野原氏の説明を読み解くと、次のようになるでしょう。ラベラーとは訓練データ(教師ラベル)を作る人の意味です。
第1ステップは、機械学習の分野でいう「教師あり学習」です。ここで具体的にどのような訓練をしたのかは、OpenAI 社も公表していません。推測すると「望ましい対話」の例には、人間の質問に「答えられません」や「できません」と応答する訓練データも多数あるのではと思います。たとえば「反社会的行為を助長するような質問」の場合(爆弾の作り方など)です。
さらにこの第1ステップでは、特定のタイプのプロンプトに対して、あたかも ChatGPT が感情をもっているかのように応答する訓練が可能なはずです。それが「望ましい対話」だと OpenAI が判断すればそうなります。
第2ステップは2つのフェーズに分かれています。第1フェーズは、人手によるランキングの作成です。このとき「複数の異なるモデル」を使います。モデルとは言語モデルのことです。実は、GPT-3 を開発する過程においても、パラメータ数の違う複数の言語モデルが開発されていて、最終的に公開されたのが GPT-3 です。またパラメータ数が同じでも、訓練のやり方が違うとパラメータの値が違うので、モデルとしては別です。
このような複数の異なるモデルを選び(4つとします)、同じ入力(プロンプト。\(P\) で表します)に対して、4つの違った応答、\(A,\:B,\:C,\:D\) を得ます。ラベラーは、この \(P/A,\:P/B,\:P/C,\:P/D\) という4つの「プロンプト \(/\) 応答」にランク付けします( \(/\) はプロンプトのあとに応答が続くという意味です)。ランク付けが仮に、
\(P/A\: > \:P/B\: > \:P/C\: > \:P/D\)
だとします。現実問題としては4つのランク付けは難しいので、2つずつの6つのペアについて、どちらが良いかを決めます。ランク付けの基準について岡野原氏は書いていないのですが、OpenAI 社の公開資料によると、
・嘘やデマを含まない
・差別的・攻撃的な内容を含まない
・ユーザの役に立つ
という基準です。このような「ランク付けデータ」を大量に準備します。これは人に頼る "人海戦術" しかないので、アウトソーシングしたとしてもコストがかかります。
ちなみに、応答が「差別的・攻撃的な内容を含まない」というのは極めて重要です。というのも、過去に「AI を使った Chat システムが差別的発言をするようになり、公開中止に追い込まれる」という事件が何件か発生しているからです(2016年のマイクロソフト、2022年のメタなど)。
特に、メタ(旧フェイスブック)の Galactica 炎上事件(差別的応答による)は、システムの公開日が 2022年11月15日であり、ChatGPT の公開日(2022年11月30日)とほぼ同時期でした。メタがつまづき、ChatGPT がつまづかなかったのは、OpenAI 社が極めて慎重に「反倫理的・反社会的応答」を排除するように訓練したからと考えられます。
特に、メタ(旧フェイスブック)の Galactica 炎上事件(差別的応答による)は、システムの公開日が 2022年11月15日であり、ChatGPT の公開日(2022年11月30日)とほぼ同時期でした。メタがつまづき、ChatGPT がつまづかなかったのは、OpenAI 社が極めて慎重に「反倫理的・反社会的応答」を排除するように訓練したからと考えられます。
第2ステップの第2フェーズは、ランキングのデータをもとに自動評価システムを作ることが目的です。データを入力して評価値(強化学習の用語でいうと "報酬")を出力する関数(=自動評価システム)を \(\mr{Score}()\) と書くと、
\(\mr{Score}(P/A) > \mr{Score}(P/B) > \mr{Score}(P/C) > \mr{Score}(P/D)\)
となるように関数を決めます。これはニューラル・ネットワークを使って、訓練を繰り返して決めます(強化学習の用語で "報酬モデル")。ここで岡野原氏が指摘しているのは、\(\mr{Score}\) 関数への入力は、
ランキングをつけたデータそのものでなく、目標駆動型学習をしたい大規模言語モデル(この場合は GPT-3)にランキング済みデータを入力したときの、大規模言語モデルの内部状態
だということです。従って、\(\mr{Score}(P/A)\) は、
\(\mr{Score}(\mr{InnerState}(P/A))\)
と書くべきでしょう。これによって「高精度に評価を推定できる」というのが岡野原氏の説明です。
第3ステップでは、この自動評価システムを使って、プロンプトに対する応答の評価値が最も高くなるように強化学習を行います。このステップには人手を介した評価はないので、大量のプロンプトで学習することができます。
ここで、言語モデル \(\al\) の内部状態を入力とする自動評価システムを \(\mr{Score}_{\large\:\al}\) とし、言語モデル \(\al\) を上記のように訓練した結果、言語モデル \(\beta\) になったとします。すると、同じ「プロンプト/応答」を投入したときの内部状態が、2つの言語モデルで違ってきます。つまり、
\(\mr{InnerState}_{\large\:\al}(P/A)\neq\mr{InnerState}_{\large\:\beta}(P/A)\)
です。ということは、
\(\mr{InnerState}_{\large\:\beta}\) を入力とする、自動評価システム \(\mr{Score}_{\large\:\al}\) の改訂版、\(\mr{Score}_{\large\:\beta}\) が作れる
ことになります。つまり「第2ステップの第2フェーズ」と「第3ステップ」をループさせて繰り返すことができる。このとき、ラベラーが作ったランキングデータはそのまま使えます。このランキングが絶対評価ではなく相対評価だからです。以上のことから、
自動評価システムと言語モデルは、より正確な評価値を獲得するように "共進化" できる
と言えます。岡野原氏が言っている「高精度に評価を推定できる」とは、こういった "共進化" も含めてのことだと考えられます。このように、目標駆動型学習で鍵となるのは、この「高精度の自動評価システム」です。
補足しますと、ChatGPT が公開された後は、利用者の実際のプロンプトとそれに対する ChatGPT の応答を膨大に集積できます(利用者が拒否しなければ)。この実際の「プロンプト/応答」データの中から自動評価システムの評価が低いものだけを集め、プロンプトへの応答の評価が高くなるように ChatGPT の強化学習ができることになります。ChatGPT から "でたらめな" 応答を引き出そうとする(そして成功すれば喜ぶ)人は多いでしょうから、強化学習のためのデータにはこと欠かないはずです。
以上が、岡野原氏の説明の "読み解き" です。
ここまでをまとめると、次のようになるでしょう。
| GPT-3 は、ひたすら次の語を予測することに徹し、大量のテキストで訓練された大規模言語モデルである。その基盤技術は Transformer をシンプルにしたものであり、\(1752\)億のパラメータをもつ巨大ニューラル・ネットワークである。 | |
| ChatGPT は GPT-3 をベースに、人手で作った「人にとって好ましい応答例」を訓練データとして学習し、人と違和感なく会話できるようにした大規模言語モデルである。 |
このような GPT-3 の仕組みでは、計算や論理的推論は本質的にできません。簡単な計算(2桁整数同士のたし算、2次方程式を解くなど)ができる(ように見える)のは、それが訓練データにあるからです。また、正しい論理的推論ができたとしたら、類似の推論が訓練データの中にあるからです。
とはいえ、ChatGPT はバックに語と語の関係性についての膨大な "知識" をもっていて、それによって "規則性" や "ルール" の認識が内部にできているはずです。その中には「人が気づかない」「暗黙の」「意外なもの」があってもおかしくない。それにより、蓄積した知識を "混ぜ合わせて" 正しい推論、ないしは発見的な推論がきることもあり得るはずです。
さらに、人が普段話すのと同じように話せば、その膨大な "知識" が活用できるのは多大なメリットでしょう。もちろん "悪用" される可能性はいつでもありますが、そのことを踏まえつつ、使い方の発見や検討が今後も進むのでしょう。
| 言語の "理解" とは |
人の問いかけに対する ChatGPT の応答は、いかにも人らしいものです。もちろん間違いや、変な答え、明らかに事実とは違う応答もあります。しかし、世界中から集めた知識の量は膨大で、言語の壁も越えています。
その "知識" は(GPT-3, ChatGPT では)1752億個のパラメータの中に埋め込まれています。量は膨大ですが、それを処理する仕組みはシンプルです。なぜこれでうまくいくのか、そこが驚異だし、その理由を理解することは難しいでしょう。
もちろん、その中身を解明しようとする研究は進むでしょうが、"理解" は難しいのではと思われます。というのも、「比較的シンプルな記述による、人にフレンドリーな説明」でないと、人は "理解" したとは思わないからです。
しかし考えてみると、我々が言語(母語)を習得でき、かつ自在に扱えるのはなぜか、その脳の働きは、Transformer / ChatGPT と極めて似ているのではないでしょうか。
前回の冒頭で紹介したように、慶応義塾大学の今井教授は、「ChatGPT の仕組み(=注意機構)は、幼児が言語を学習するプロセスと類似している」と指摘していました。今井教授は幼児の言語発達を研究する専門家なのでこの指摘になるのですが、実は Transformer / ChatGPT のやっていることは、幼児のみならず、我々が言葉(母語)を理解してきた(現に理解している)やりかたと酷似していることに気づきます。それは、
外界からくる複雑な情報を丸ごと飲み込んで、ルールを知らないうちから活用する(活用できる)
という言語理解のありようです。もちろん(外からの指摘による)「好ましくない言葉の使い方」であれば訂正します。しかし、学び方も含めて、我々は内発的・創発的に言葉を理解しています。それが我々の脳の働きの重要な一面です。
前回、Transformer がタンパク質の機能分析に使える(可能性がある)ことを書きましたが、さらにヒトの脳の(ある脳領域の)解明に役立つこともありそうです。
大規模言語モデルの外面的な機能は驚異的ですが、さらにその内部の「仕組み」を理解することで、その応用範囲が極めて広いことがわかるのでした。
2023-10-06 07:39
nice!(0)
No.365 - 高校数学で理解する ChatGPT の仕組み(1) [技術]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
前回の No.364「言語の本質」の補足で紹介した新聞記事で、慶応義塾大学の今井教授は、
と指摘していました。メタ学習とは「学習のしかたを学習する」ことですが、 ChatGPT がそれをできる理由も「注意機構(Attention mechanism)」にあります。そこで今回は、その気になる ChatGPT の仕組みをまとめます。
今まで「高校数学で理解する ・・・・・・」というタイトルの記事をいくつか書きました。
の 13 の記事です。"高校数学で理解する" という言い方は、「高校までで習う数学だけを前提知識として説明する」という意味ですが、今回もそれに習います。もちろん、文部科学省の学習指導要領は年々変わるので、"おおよそ高校までの数学" が正しいでしょう。今回、前提とする知識は、
です。ChaGPT は "ニューラル・ネットワーク"、ないしは "深層学習(ディープ・ラーニング)" の技術を使った AI ですが、こういった知識は前提とはしないことにします。つまり、ニューラル・ネットワークについては、その基礎から(必要なものだけに絞って)順を追って説明します。
全体の構成
全体の構成は次の4つです
1.ニューラル・ネットワーク
2.自然言語のモデル化
3.Transformer
4.GPT-3 と ChatGPT
なお、この記事の作成には、Google と OpenAI の論文に加えて、以下を参考にしました。
◆岡野原 大輔(プリファードネットワークス)
「大規模言語モデルは新たな知能か」
(岩波書店 2023)
◆澁谷 崇(SONY)
「系列データモデリング (RNN/LSTM/Transformer)」
第7回「Transformer」
第12回「GPT-2, GPT-3」
(YouTube 動画)
記号
以降で使用する記号の意味は次の通りす。
ニューラル・ネットワークの例
2層から成るシンプルなニューラル・ネットワークの例が図1です。この例では隠れ層が1つだけですが、隠れ層は何層あってもかまいません(なお、入力層を含めて、これを "3層" のニューラル・ネットワークとする定義もあります)。
丸印は "ニューロン" で、各ニューロンは1つの値(活性値)をもちます。値は実数値で、32ビットの浮動小数点数が普通です。図1のニューロンの数は 3+4+3=10 個ですが、もちろんこの数は多くてもよく、実用的なネットワークでは数100万から億の単位になることがあります。
ニューロン間の矢印が "シナプス" で、一つのニューロンは、シナプスで結ばれている前の層のニューロンから値を受けとり、決められた演算をして自らの値を決めます(入力層を除く)。なお、"ニューロン" や "シナプス" は脳神経科学の用語に沿っています。
各層は、重み \(\bs{W}\)(行列)とバイアス \(\bs{b}\)(ベクトル)、活性化関数 \(f\) を持ちます。図1の場合、第1層の重みは \(\bs{W}\:\:[3\times4]\)、バイアスは \(\bs{b}\:\:[1\times4]\) で、
\(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}&w_{14}\\w_{21}&w_{22}&w_{23}&w_{24}\\w_{31}&w_{32}&w_{33}&w_{34}\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2&b_3&b_4\\\end{array}\right)\)
です。このとき、隠れ層(第1層)のニューロンの活性値、\(\bs{h}=\left(\begin{array}{r}h_1&h_2&h_3&h_4\\\end{array}\right)\) は、
\(h_1=f\:(\:x_1w_{11}+x_2w_{21}+x_3w_{31}+b_1\:)\)
\(h_2=f\:(\:x_1w_{12}+x_2w_{22}+x_3w_{32}+b_2\:)\)
\(h_3=f\:(\:x_1w_{13}+x_2w_{23}+x_3w_{33}+b_3\:)\)
\(h_4=f\:(\:x_1w_{14}+x_2w_{24}+x_3w_{34}+b_4\:)\)
の式で計算されます。ベクトルと行列で表示すると、
\(\bs{h}=f\:(\bs{x}\cdot\bs{W}+\bs{b})\)
になります。第2層も同様です。
このニューラル・ネットワークは、多重パーセプトロン(Multi Layer Perceptron : MLP)と呼ばれるタイプのもので、ニューラル・ネットワークの歴史の中では、古くから研究されている由緒のあるものです。
また上図の第1層、第2層は、すべてのニューロンが前層のすべてのニューロンとシナプスを持ってます。このような層を「全結合層」(Fully connected layer. FC-layer. FC層)と言います。全結合の多重パーセプトロンは Transformer や GPT で使われていて、重要な意味を持っています。
活性化関数 \(f\) は、隠れ層では、\(\mr{ReLU}\) 関数(Rectified Linear Unit:正規化線形ユニット)を使うのが普通です。\(\mr{ReLU}\) 関数は、
で定義される非線形関数です(図2)。以降での表記を簡潔にするため、単位ステップ関数 \(H(x)\) を用いて \(\mr{ReLU}\) 関数を表しておきます。単位ステップ関数は、
\(H(x)=1\:\:(x > 0)\)
\(H(x)=0\:\:(x\leq0)\)
で定義される関数で(図3)、ヘヴィサイド関数とも呼ばれます。\(H(x)\) の微分は、
\(H\,'(x)=0\:\:(x\neq0)\)
です。\(x=0\) において \(H(x)\) は不連続で、微分は定義できませんが、無理矢理、
\(H\,'(0)=0\)
と定義してしまうと、\(x\) の全域において、
\(H\,'(x)=0\)
となります。この \(H(x)\) を用いて \(\mr{ReLU}\) 関数を定義すると、
となり、微分は、
\(\dfrac{d}{dx}\mr{ReLU}(x)=H(x)\)
と表現できます。
出力層の活性化関数 \(f\,'\) は、ニューラル・ネットワークをどんな用途で使うかによって違ってきます。
ニューラル・ネットワークによる推論
ニューラル・ネットワークが扱う問題は、入力ベクトル \(\bs{x}\) をもとに出力ベクトル \(\bs{y}\) を "推論"(ないしは "推定"、"予測")する問題です。これには主に「回帰問題」と「分類問題」があります。
回帰問題で推論する \(\bs{y}\) は実数値(=連続値)です。たとえば、
・身長
・体重
・年齢
・男女の区別
・生体インピーダンス
から(\(=\bs{x}\))、
・体脂肪率
・筋肉量
・骨密度
を推定する(\(=\bs{y}\))といった例です(但し、市販の体組成計が AI を使っているわけではありません)。
一方、分類問題の例は、たとえば手書き数字を認識する問題です。この場合、多数の手書き数字の画像(をベクトルに変換した \(\bs{x}\))を「\(0\) のグループ」「\(1\) のグループ」・・・・・ というように分類していきます。このグループのことを AI では "クラス" と呼んでいます。つまり「クラス分類問題」です。
手書き数字の場合、明確に \(0\) ~ \(9\) のどれかに認識できればよいのですが、そうでない場合もある。たとえば、\(1\) なのか \(7\) なのか紛らわしい、\(0\) なのか \(6\) なのか曖昧、といったことが発生します。分類するのは、\(0\) ~ \(9\) のうちのどれかという「離散値の予測」であり、連続値とは違って、どうしても紛らわしい例が発生します。
従って、クラス分類問題(=離散値を予測する問題)では、出力ベクトル \(\bs{y}\) は確率です。手書き数字の認識では、\(\bs{y}\) は\(10\)次元の確率ベクトルで、たとえば、
となるように、ニューラル・ネットワークを設計します。確率なので、
\(0\leq y_i\leq1,\:\:\:\displaystyle\sum_{i=1}^{10}y_i=1\)
です。入力画像が \(1\) なのか \(7\) なのか紛らわしい場合、たとえば推定の例は、
\(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
です。これは、
\(1\) である確率が \(0.8\)
\(7\) である確率が \(0.2\)
を表します。クラス分類問題は「離散値を推論する問題」、すなわち「確率を推定する問題」であると言えます。
回帰問題の出力層の活性化関数は、恒等関数(=何もしない)とするのが普通です。一方、クラス分類問題の出力層の活性化関数は、出力 \(\bs{y}\) が確率として解釈できるような関数を選びます。それが \(\mr{Softmax}\) 関数です。
\(\mr{Softmax}\) 関数
\(\mr{Softmax}\) 関数によって、出力 \(\bs{y}\) が確率と解釈できるようになります。ベクトル \(\bs{x}\) を \(\mr{Softmax}\) 関数によって確率ベクトル \(\bs{y}\) に変換する式は、次のように定義できます。なお、ここでの \(\bs{x}\) は入力層の \(\bs{x}\) ではなく、一般的なベクトルを表します。
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(n\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{n}y_i=1\)
ここで使われている指数関数は、すぐに巨大な数になります。たとえば \(\mr{exp}(100)\) は\(10\)進で\(40\)桁以上の数で、\(32\)ビット浮動小数点の最大値(\(10\)進で\(40\)桁弱)を越えてしまいます。従って、\(\mr{Softmax}\) 関数の計算には工夫が必要で、それには \(\mr{Softmax}\) 関数の性質を利用します。
\(C\) を任意の実数値とし、\(n\)次元ベクトル \(\bs{z}\) を
\(z_i=x_i+C\)
と定義します。そして、
\(\bs{y}\,'=\mr{Softmax}(\bs{z})\)
と置くと、
\(\begin{eqnarray}
&&\:\:y_i\,'&=\dfrac{\mr{exp}(z_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(z_i)}=\dfrac{\mr{exp}(x_i+C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i+C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)\cdot\mr{exp}(C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\mr{exp}(C)\cdot\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\\
&&&=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}=y_i\\
\end{eqnarray}\)
となります。つまり \(x_i\:\:(1\leq i\leq n)\) の全部に定数 \(C\) を足しても、\(\mr{Softmax}\) 関数は変わりません。そこで、
\(C=-\mr{max}(x_1,\:x_2,\:\cd\:,x_n)\)
と置いて、
\(x_i\:\longleftarrow\:x_i+C\:\:(1\leq i\leq n)\)
と修正すると、\(x_i\) の最大値は \(0\) になります。従って、
\(0 < \mr{exp}(x_i)\leq1\)
の範囲で \(\mr{Softmax}\) 関数が計算可能になります。
大規模言語モデルと確率
クラス分類問題の出力ベクトル \(\bs{y}\) は確率でしたが、実は Transformer や GPT が実現している「大規模言語モデル」も "確率を推定するニューラル・ネットワーク" です。たとえば、
[今日] [は] [雨] [なの] [で]
というテキストに続く単語を推定します。仮に、日本語の日常用語の語彙数を5万語とすると、5万の単語すべてについて上のテキストに続く単語となる確率を、実例をもとに推定します。当然、「雨の日の行動」とか「雨の日の情景」、「雨の日の心理状態」、「雨の日に起こりうること」を描写・説明する単語の確率が高くなるわけです。たとえば名詞だけをとると、[家] [ビデオ] [映画] [傘] [犬] [洗濯] [祭] [運動会] などの確率が高く、[ニンジン] [牛] [鉛筆] などの確率は(雨の日とは関係があるとは思えないので)低いといった具合です(あくまで想定です)。
「大規模言語モデル」の重要な応用例(=タスク)である機械翻訳も同じです。日本語 → 英語の翻訳を例にとると、
[今日] [は] [晴れ] [です] [。] [BOS]
に続く英単語を推定します([BOS] は文の開始を示す特殊単語)。確率の高い単語から [it] を選んだとすると、次には、
[今日] [は] [晴れ] [です] [。] [BOS] [it]
に続く単語を推定します([is] になるはず)。こうやって進むのが機械翻訳です。
Transformer や GPT をごくごくシンプルに言えば、入力ベクトル \(\bs{x}\) はテキスト列、出力ベクトル \(\bs{y}\) は次に続く単語を示す確率ベクトル(次元は語彙数)です。
この記事は、Transformer、GPT、ChatGPT などの大規模言語モデルを説明するのが目的です。従って以降では、出力ベクトル \(\bs{y}\) は確率ベクトルであることを前提とします。
確率を推定するニューラル・ネットワーク
図1において、第1層(隠れ層)の活性化関数を \(\mr{ReLU}\)、第2層(出力層)の活性化関数を \(\mr{Softmax}\) とすると、図4になります。
図4の計算は、以下に示すような4段階の計算処理で表すことができます。
第1層
\(\bs{h}\,'=\bs{x}\cdot\bs{W}+\bs{b}\)
\(\bs{h}=\mr{ReLU}(\bs{h}\,')\)
第2層
\(\bs{y}\,'=\bs{h}\cdot\bs{W}\,'+\bs{b}\,'\)
\(\bs{y}=\mr{Softmax}(\bs{y}\,')\)
この4つの計算処理を「計算レイヤー」、略して「レイヤー」と呼び、図5のグラフで表現することにします。
レイヤー(layer)は日本語にすると「層」で、第1層や隠れ層の「層」と紛らわしいのですが、「レイヤー」と書いたときは "ある一定の計算処理" を示します。後ほど説明する Transformer や GPT は、図4のような単純な「層」では表現できない複雑な計算処理があります。従って "ある一定の計算処理 = レイヤー" とした方が、すべての場合を共通に表現できて都合が良いのです。
レイヤーの四角に向かう矢印は計算処理への入力を示し、四角から出る矢印は計算処理からの出力(計算結果)を示します。「レイヤーは一つの関数」と考えてもOKです。
図5の「Linear レイヤー」は、「Affine(アフィン)レイヤー」と呼ばれることが多いのですが、Transformer の論文で Linear があるので、そちらを採用します。
図5のネットワークがどうやって「学習可能なのか」を次に説明します。この「学習できる」ということが、ニューラル・ネットワークが成り立つ根幹です。
ニューラル・ネットワークの学習
重みとバイアスの初期値
まず、重み(\(\bs{W},\:\bs{W}\,'\))の初期値を乱数で与えます。この乱数は、前の層のニューロンの数を \(n\) とすると
の正規分布の乱数とするのが普通です。\(n=10,000\) とすると、標準偏差は \(0.01\) なので、
\(-\:0.01\) ~ \(0.01\)
の間にデータの多く(約 \(2/3\))が集まる乱数です。但し、\(\mr{ReLU}\) を活性化関数とする層(図4では第1層)の重みは、
の乱数とします。なお、バイアスの初期値は \(0\) とします。こういった初期値の与え方は、学習をスムーズに進めるためです。
損失と損失関数
初期値が決まったところで、訓練データの一つを、
\(\bs{x}\):入力データ
\(\bs{t}\):確率の正解データ
とします。この正解データのことを「教師ラベル」と呼びます。そして、ニューラル・ネットワークによる予測の確率 \(\bs{y}\) と、正解の確率である \(\bs{t}\) との差異を計算します。この差異を「損失(\(Loss\))」といい、\(L\) で表します。\(L\) は正のスカラー値です。
\(\bs{y}\) と \(\bs{t}\) から \(L\) を求めるのが「損失関数(Loss Function)」です。確率を予測する場合の損失関数は「交差エントロピー誤差(Cross Entropy Error : CEE)」とするのが普通で、次の式で表されます。
たとえば、先ほどの手書き数字の認識の「\(1\) または \(7\) という予測」を例にとって、その正解が \(1\) だとすると、
予測 \(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
正解 \(\bs{t}=\left(\begin{array}{r}1&0&0&0&0&0&0&0&0\\\end{array}\right)\) = 教師ラベル
です。なお、\(\mr{Softmax}\)関数の出力は \(0\) にはならないので、上の \(\bs{y}\) で \(0\) と書いた要素は、実際には微小値です。すると、
\(L=-\mr{log}\:0.8\fallingdotseq0.223\)
となります。損失関数を含めると、レイヤー構成は図6のようになります。
この図の重みとバイアスを少しだけ調整して、\(L\) を少しだけ \(0\) に近づけます。この調整を多数の学習データ(= \(\bs{x}\:\:\bs{t}\) のペア)で繰り返して、\(L\) を次第に \(0\) に近づけていくのが学習です。
勾配降下法
重みの調整には「勾配降下法(Gradient descent method)」を使います。図6の場合、損失 \(L\) は、ある関数 \(f\) を用いて、
\(L=f(\bs{x},\:\bs{W},\:\bs{b},\:\bs{W}\,',\:\bs{b}\,',\:\bs{t})\)
と表現できます。ここで、\(\bs{W}\) の一つの要素、\(w_{11}\) を例にとると、
を計算します。これはいわゆる微分ですが、多変数関数の微分なので、数学的には偏微分であり、
\(\dfrac{\partial L}{\partial w_{11}}\)
です。つまり、\(w_{11}\) 以外の変数をすべて固定しての(すべて定数とした上での)、\(w_{11}\) による微分です。
具体的な入力 \(\bs{x}\) のときの \(\dfrac{\partial L}{\partial w_{11}}\) が求まったとします。もし仮に、\(\dfrac{\partial L}{\partial w_{11}}\) が正の値だとしたら、\(w_{11}\) を少しだけ減らせば、\(L\) は少しだけ \(0\) に近づきます。もし \(\dfrac{\partial L}{\partial w_{11}}\) が負だとしたら、\(w_{11}\) を少しだけ増やせば、\(L\) は少しだけ \(0\) に近づきます。つまり、
更新式:\(w_{11}\:\longleftarrow\:w_{11}-\eta\cdot\dfrac{\partial L}{\partial w_{11}}\)
として重みを更新すればよいわけです。\(\eta\) は「少しだけ」を表す値で「学習率」といい、\(0.01\) とか \(0.001\) とかの値をあらかじめ決めておきます。この決め方は、学習の効率に大いに影響します。こういった更新を、すべての重みとバイアスに対して行います。
"学習で調整される値" を総称して「パラメータ」と言います。図6のパラメータは重みとバイアスですが、実用的なニューラル・ネットワークでは、それ以外にも更新されるパラメータがあります。
\(L\) の偏微分値をベクトルや行列単位でまとめたものを、次のように表記します。2次元のベクトル \(\bs{b}\) と、2行2列の行列 \(\bs{W}\) で例示すると、
\(\dfrac{\partial L}{\partial\bs{b}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial b_1}&\dfrac{\partial L}{\partial b_2}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{W}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\)
です。これを「勾配(gradient)」と言います。勾配を求めることでパラメータを少しづつ更新し、損失を少しづつ小さくしていく(=降下させる)のが勾配降下法です。
ミニバッチ勾配降下法
学習は次のように進みます。まず、すべての訓練データ(たとえば
数万件)から、数\(10\)~数\(100\)件(たとえば\(256\)件)の訓練データをランダムに選びます。この一群のデータを「ミニバッチ」と呼びます。ミニバッチの各訓練データによる確率の推定から損失を計算し、そこからすべてのパラメータの勾配と求め、その勾配ごとに "ミニバッチの平均値" をとります。その平均値に基づき、更新式に従って各パラメータを更新します。
ミニバッチによる更新が終わると、別のミニバッチをランダムに選び、更新を繰り返します。こうすると、損失は次第に減少していきますが、そのうち "頭打ち" になります。そこで更新を止めます。
このようなパラメータ更新のやり方を「ミニバッチ勾配降下法」と言います。一つの訓練データだけで更新しないのは、たまたまその訓練データが「外れデータ」(全体の傾向とは異質なデータ)だと、学習の進行に支障が出てくるからです。
訓練データをランダムに選択する方法を「確率的勾配降下法(Stochastic gradient method - SGD)」と言いますが、ミニバッチ勾配降下法は、その確率的勾配降下法の一種です。
誤差逆伝播法
ここで問題になるのは、すべてのパラメータの勾配をどうやって求めるかです。それに使われるのが「誤差逆伝播法(Back propagation)」です。その原理を、Linear レイヤーから説明します。
(1) Linear
図7で示すように、Linear レイヤーがあり、そのあとに何らかの計算処理が続いて、最終的に損失 \(L\) が求まったとします。\(\bs{x}\:\:\bs{y}\) はニューラル・ネットワークへの入力と出力ではなく、Linear レイヤーへの入力と出力の意味です。ここで、
と言えます。これが誤差逆伝播法の原理です。このことを、2次元ベクトル(\(\bs{x},\:\:\bs{b},\:\:\bs{y}\))、2行2列の配列(\(\bs{W}\))で例示します(\(N=2,\:M=2\) の場合)。
【Linear の計算式】
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+b_1\)
\(y_2=x_1w_{12}+x_2w_{22}+b_2\)
\(x_1\) が変化すると \(y_1,\:y_2\) が変化し、それが損失 \(L\) に影響することに注意して、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配を計算します。
【\(\bs{\bs{x}}\) の勾配】
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)\)
です。これをまとめると、
\(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\:\:\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T\)
となり、\(\bs{x}\) の勾配が求まります。
【\(\bs{\bs{W}}\) の勾配】
\(\dfrac{\partial L}{\partial w_{11}}=\dfrac{\partial y_1}{\partial w_{11}}\dfrac{\partial y_1}{\partial w_{11}}=x_1\dfrac{\partial y_1}{\partial w_{11}}\)
\(\dfrac{\partial L}{\partial w_{12}}=\dfrac{\partial y_2}{\partial w_{12}}\dfrac{\partial y_2}{\partial w_{12}}=x_1\dfrac{\partial y_2}{\partial w_{12}}\)
\(\dfrac{\partial L}{\partial w_{21}}=\dfrac{\partial y_1}{\partial w_{21}}\dfrac{\partial y_1}{\partial w_{21}}=x_2\dfrac{\partial y_1}{\partial w_{21}}\)
\(\dfrac{\partial L}{\partial w_{22}}=\dfrac{\partial y_2}{\partial w_{22}}\dfrac{\partial y_2}{\partial w_{22}}=x_2\dfrac{\partial y_2}{\partial w_{22}}\)
これらをまとめると、
となります。
【\(\bs{\bs{b}}\) の勾配】
以上の計算で求まった勾配をまとめて図示すると、図8になります。黒字(入力・出力とパラメータ)の下の赤字がパラメータの勾配で、右から左への矢印は、「レイヤーの出力の勾配が求まれば、レイヤーの入力の勾配が求まる」こと示します(= 逆伝播)。上での計算は2次元ベクトルと2行2列の配列で例示しましたが、図8のようなベクトル・配列で表示すると、\([1\times N]\) のベクトルと \([N\times M]\) の行列で成り立つことが確認できます。
(2) ReLU
\(\mr{ReLU}\) 関数は、
\(\mr{ReLU}(x_i)=x_i\:\:(x_i > 0)\)
\(\mr{ReLU}(x_i)=0\:\:\:(x_i\leq0)\)
であり、ベクトルの表現では、単位ステップ関数、
\(H(x)=1\:\:\:(x > 0)\)
\(H(x)=0\:\:\:(x\leq0)\)
と要素積 \(\odot\) を使って、
\(\mr{ReLU}(\bs{x})=H(\bs{x})\odot\bs{x}\)
と定義できます。従って、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=H(\bs{x})\odot\dfrac{\partial L}{\partial\bs{y}}\)
です。
(3) Softmax
\(\mr{Softmax}\) 関数の定義は、
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(N\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{N}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{N}y_i=1\)
です。勾配の計算を \(N=3\) の場合で例示します。
\(\dfrac{\partial L}{\partial x_1}=\dfrac{\partial y_1}{\partial x_1}\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\dfrac{\partial L}{\partial y_2}+\dfrac{\partial y_3}{\partial x_1}\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_1}=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_2}=y_2(1-y_2)\dfrac{\partial L}{\partial y_2}-y_2y_3\dfrac{\partial L}{\partial y_3}-y_2y_1\dfrac{\partial L}{\partial y_1}\)
\(\dfrac{\partial L}{\partial x_3}=y_3(1-y_3)\dfrac{\partial L}{\partial y_3}-y_3y_1\dfrac{\partial L}{\partial y_1}-y_3y_2\dfrac{\partial L}{\partial y_2}\)
(4) Cross Entropy Error - CEE
交差エントロピー誤差の定義は、
入力 \(\bs{y}\) \((1\times N)\)
入力 \(\bs{t}\) \((1\times N)\) 教師ラベル(正解データ)
出力 \(L\:(Loss)\)
とすると、
\(L=-\displaystyle\sum_{i=1}^{N}(t_i\mr{log}y_i)\)
で定義されます。従って、
\(\dfrac{\partial L}{\partial y_i}=-\dfrac{t_i}{y_i}\)
であり、\(N=3\) の場合を書くと、
\(\dfrac{\partial L}{\partial y_1}=-\dfrac{t_1}{y_1}\)
\(\dfrac{\partial L}{\partial y_2}=-\dfrac{t_2}{y_2}\)
\(\dfrac{\partial L}{\partial y_3}=-\dfrac{t_2}{y_3}\)
です。
(5) Softmax + CEE
\(\mr{Softmax}\) レイヤーの直後に交差エントロピー誤差のレイヤーを配置した場合を考えます。(3) と (4) の計算を合体させると、次のように計算できます。
計算の過程で、\(\bs{t}\) が確率ベクトルであることから、\(t_1+t_2+t_3=1\) を使いました。この計算は \(x_2,\:\:x_3\) についても全く同様にできます。それを含めてまとめると、
\(\dfrac{\partial L}{\partial x_1}=y_1-t_1\)
\(\dfrac{\partial L}{\partial x_2}=y_2-t_2\)
\(\dfrac{\partial L}{\partial x_3}=y_3-t_3\)
となります。この結果、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=\bs{y}-\bs{t}\)
という、大変シンプルな形になりました。これは任意の次元のベクトルで成り立ちます。実は、このようなシンプルな形になるように、\(\mr{Softmax}\) と 交差エントロピー誤差が設計されています。図示すると次の通りです。
ニューラル・ネットワークの誤差逆伝播
以上で「確率を推定するニューラル・ネットワーク」を構成する各レイヤーの誤差逆伝播が計算できました。これらをまとめると、次の図11になります。
ちなみに、第1層の重み \(\bs{W}\) の勾配は図11から陽に計算すると、次のようになります。
\(\dfrac{\partial L}{\partial\bs{W}}=\bs{x}^T(H(\bs{x}\bs{W}+\bs{b})\odot((\bs{y}-\bs{t})\bs{W}\,'))\)
このネットワークは隠れ層が1つだけというシンプルなものですが、今までの計算で分かるように、層数が何百層に増えたとしても、逆伝播を多段に重ねることで、誤差逆伝播法が成立します。
また、図11 で使っているレイヤーは、Linear、\(\mr{ReLU}\)、\(\mr{Softmax}\)、Cross Entropy Error ですが、これらを関数と見なしたとき、誤差逆伝播で使った数学的な前提は「関数がパラメータで微分可能」ということだけです。つまり、レイヤーの関数が微分可能である限り、誤差逆伝播法は有効です。
実は、実用的なニューラル・ネットワークで誤差逆伝播法をうまく機能させるためには、数々の工夫が必要です。また、一般に訓練データの数は膨大なので、学習速度を上げる工夫も必要です(以降でその一部を説明します)。上で述べた「初期値の選択」や「学習率」はその工夫の一つです。そういったことはありますが、ネットワークがいかに巨大になろうとも(大規模言語モデルはその巨大な典型です)、誤差逆伝播法は可能なことが分かっています。
以上が、「ニューラル・ネットワークが学習可能である」ということの原理です。
\(\mr{GELU}\)
最近の大規模言語モデル(GPT など)では、活性化関数 \(\mr{ReLU}\) の代わりに \(\mr{GELU}\) \((\)Gaussian Error Linear Unit:ガウス誤差線形ユニット\()\) が使われます。その方が、学習が効率的に進むことが分かったからです。
\(\mr{ReLU}\) は、\(H(x)\) を単位ステップ関数として、
\(\mr{ReLU}(x)=H(x)x\)
でしたが、\(\mr{GELU}\) は、
\(\mr{GELU}(x)=\Phi(x)x\)
で定義されます。\(\Phi(x)\) は標準正規分布(平均 \(0\)、標準偏差 \(1\))の累積分布関数です。標準正規分布の確率密度を \(f(x)\) とすると、
\(f(x)=\dfrac{1}{\sqrt{2\pi}}\mr{exp}\left(-\dfrac{x^2}{2}\right)\)
です(図12)。つまり \(x\) ~ \(x+dx\) である事象が発生する確率が \(f(x)dx\) です。また \(-\infty\) ~ \(\infty\) の範囲で積分すると \(1\) で、原点を中心に左右対称です。
この確率分布を \(-\infty\) から \(x\) まで積分したのが累積分布関数で、
\(\Phi(x)=\displaystyle\int_{-\infty}^{x}f(t)dt\)
です(図13)。これは正規分布に従うデータ値が \(x\) 以下になる確率です。これはガウスの誤差関数(Gaussian error function)\(\mr{Erf}\) を用いて表現できます。\(\Phi(0)=0.5\) となることを使って計算すると、
\(\begin{eqnarray}
&&\:\:\Phi(x)&=\displaystyle\int_{-\infty}^{x}f(t)dt\\
&&&=\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
\end{eqnarray}\)
\(t\:\rightarrow\:\sqrt{2}u\) の変数変換をすると、
\(\begin{eqnarray}
&&\:\:\phantom{\Phi(x)}&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)\sqrt{2}du\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)du\\
&&&=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\\
\end{eqnarray}\)
となります。ガウスの誤差関数、\(\mr{Erf}()\) の定義は
\(\mr{Erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_{0}^{x}\mr{exp}(-u^2)du\)
です。従って、
\(\Phi(x)=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\)
と表現できます。\(\mr{GELU}\) 関数の形は 図14 です。
\(\mr{GELU}\) は \(\mr{ReLU}\) と良く似ていますが、すべての点で微分可能であり、\(\mr{ReLU}\) のように微係数がジャンプするところがありません。このことが、大規模言語モデルの効率的な学習に役だっていると考えられます。
残差結合
Linear レイヤーを例にとります。入力を \(\bs{x}\)、出力を \(\bs{y}\) とし、入力と出力のベクトルの次元は同一とします。重みを \(\bs{W}\) とし、バイアス \(\bs{b}\) は省略します。通常の Linear レイヤーは、
\(\bs{y}=\bs{x}\bs{W}\)
ですが、
\(\bs{y}=\bs{x}\bs{W}+\bs{x}\)
とするのが、「残差結合(residual connection)」をもつ Linear レイヤーです。なお「残差接続」とも言います。また「スキップ接続(skip connection)」も同じ意味です。
誤差逆伝播を計算すると、\(\bs{x}\) の勾配は次のようになります。2次元ベクトルの場合で例示します。
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+x_1\)
\(y_2=x_1w_{12}+x_2w_{22}+x_2\)
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)+\dfrac{\partial L}{\partial y_2}\)
従って、
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T+\dfrac{\partial L}{\partial\bs{y}}\)
です。つまり、勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が、逆伝播でそのまま \(\dfrac{\partial L}{\partial\bs{x}}\) に伝わります(図\(16\))。
一般にニューラル・ネットワークの学習を続けると、重みがゼロに近づき、その結果 \(\dfrac{\partial L}{\partial\bs{x}}\) が \(0\) に近い小さな値となることがあります。\(\dfrac{\partial L}{\partial\bs{x}}\) は、その一つ前への逆伝播の入力となるので、多層のニューラル・ネットワークでこれが重なると、前の方の層の勾配が極小になり、重みが更新できないという事態になります。これが「勾配消失」で、ニューラル・ネットワークの学習が困難になります。
残差結合を用いると、この問題を解決できます。Transformer では残差結合が使われています。
正規化
Transformer で使われているもう一つのレイヤーが「レイヤー正規化(Layer Normalization)」です。これは、ベクトル \(\bs{x}\:[1\times N]\) の要素を、平均 \(0\)、標準偏差 \(1\) のベクトル \(\bs{y}\:[1\times N]\) の要素に置き換えるものです。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\mu=\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}x_i\)
\(\sg=\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\mu)^2}\)
とおくと、
\(y_i=\dfrac{1}{\sg}(x_i-\mu)\)
となります。実際にニューラル・ネットワークで使われるときには、さらにベクトルの要素ごとに線形変換をして、
\(y_i\:\longleftarrow\:g_iy_i+b_i\)
とします。ベクトルで表現すると、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\)
です。この \(\bs{g}\) と \(\bs{b}\) は学習可能なパラメータです。つまり、ニューラル・ネットワークの訓練のときに学習をして、最適値を決めます。もちろん、レイヤー正規化の式は微分可能なので、逆伝播計算が(少々複雑な式になりますが)可能です。
レイヤー正規化は、ニューラル・ネットワークを安定化させ、学習の効率化に役立ちます。その理由ですが、中間層の活性化関数で一般的な \(\mr{ReLU}\) 関数は、\(x=0\) の付近で非線型関数であり、それ以外では線型です。ニューラル・ネットワークは全体としては非線型関数で、そこにこそ意義があるのですが、その非線型性を生み出しているのは、\(x=0\) 付近の \(\mr{ReLU}\) 関数です。
従って、レイヤーの値を「ゼロ付近に集める」と、ニューラル・ネットワークの非線型性を強めることができ、これが学習の効率化につながります。その「ゼロ付近に集める」のがレイヤー正規化です。
以上の、
・\(\mr{ReLU}\) 関数(または \(\mr{GELU}\) 関数)
・残差結合
・正規化
は、大規模ニューラル・ネットワークを安定的に学習可能にするための必須技術であり、Transformer や GPT でも使われています。
単語への分解
自然言語で書かれたテキストをコンピュータで扱うとき、まずテキストを単語の系列に分解しなければなりません。系列とは「並び順に意味のある、同質の要素の集合」です。単語への分解は、単語の区切りを明示する英語(や、その他の欧米語)では容易です。文末を表すピリオドや、その他の記号も1つの単語と数えます。
日本語は単語の区切りがないので、形態素解析ソフトで単語に分解します。句読点、「、」などの記号も、それぞれ1単語と数えます。日本語の形態素解析ソフトは各種ありますが、オープンソースの MeCab が有名です。
大規模言語モデルは、世界中から集めた Webのテキスト(以下、WebText と言います)や Wikipedia、電子ブックなどを訓練データとして学習しますが、そこに出てくる単語を集めて「語彙の集合」を作ります。この集合のサイズを \(V\) とすると(たとえば、5万とか10万とかの値)、単語に \(1\)~\(V\) のユニークな番号を振ることができます。この番号を「単語ID」と呼びます。
なお、大規模言語モデルでは内部処理用として「特殊単語」も用います。以降の説明で使うのは、
[BOS] :文の開始
[EOS] :文の終了。ないしは文の区切り。
です。こうすると、テキスト \(\bs{T}\) は、
\(\bs{T}=\{x_1,\:x_2,\:x_3,\:\cd\:x_T\}\)
という単語IDの列で表現できることになります。もしこれが完結した文だとすると、\(x_1=\)[BOS]、\(x_T=\)[EOS] であり、複文だと途中にも [BOS] や [EOS] が出てくることになります。
単語IDは、その数字自体には意味がありません。また、語彙集合(要素数 \(V\))が増大すると単語IDの最大値も変化します。上の数字列は、あくまで「1時点での語彙集合をもとにして恣意的に付けられた数字の列」です。
分散表現
テキストをニュラール・ネットワークで扱うためには、すべての単語を、語彙集合のサイズにはよらない「固定長のベクトル」で表現するのが必須です。ここで使われるのが単語の「分散表現」で、固定長であるのみならず、"単語の意味もくみ取った" 表現です。ベクトルの次元は、たとば 512次元とか 1024次元です。
単語を分散表現にすることを "単語埋め込み"(word embedding)と言います。単語埋め込みの手法は各種ありますが、ここでは「word2vec」のアルゴリズムを例にとります。word2vec は、Google が2013年に提案したもので、実用的な分散表現の嚆矢となったものです。
word2vec に限りませんが、単語埋め込みのアルゴリズムの前提となっている仮定があります。それは、
というもので、これを「分布仮説」と言います。たとえば、英文を例にとり、「周囲」を仮に「前1語、後1語」とします。
[I] [ ] [beer]
という文で [ ] に入る1単語は何かです。1単語に限定すると、冠詞(a, the)は入れようがないので、入る単語は限定されます。たとえば、
などです。[ ] には「飲む」に関係した動詞か「嗜好」に関係した動詞が入る可能性が高い。少なくとも「私とビールの関わりについての動詞」です。つまり、入る単語は「前後の1語によって意味が限定される」わけです。もしこれが「前後5語」とか「前後10語」であると「似たような意味の単語」か、少なくとも「同じジャンルの単語」になるはずです。
word2vec という「単語埋め込みアルゴリズム」には2種類あり、「周囲の単語から中心の単語を推論する(CBOW)」と「中心の単語から周囲の単語を推論する(skip-gram)」の2つです。推論にはニューラル・ネットワークを使います。以下は CBOW(Continuous Bag of Words)のネットワーク・モデルで説明します。
word2vec(CBOW)
CBOW は「周囲の単語から中心の単語を推論する」ニューラル・ネットワークのモデルです。「周囲の単語」を "コンテクスト" と呼び、推論の対象とする単語を "ターゲット" と呼びます。
まず、コンテクストのサイズを決めます。ターゲットの前の \(c\) 語、ターゲットの後ろの \(c\) 語をコンテクストとする場合、この \(c\) を "ウィンドーサイズ" と呼びます。そして "ウィンドー" の中には \(2c\) 語のコンテクストと1つのターゲットが含まれます。そして、訓練データとする文の "ウィンドー" を1単語ずつずらしながら、コンテクストからターゲットを推論する学習を行います。
語彙集合の単語数を \(V\) とし、一つの文を、
\(\bs{T}=\{x_1,\:x_2,\:\cd x_T\}\)
\(x_i\) :単語ID \((1\leq x_i\leq V)\)
とします。そして、\(x_i\) に1対1に対応する、\(V\)次元の one hotベクトルを、
\(\bs{x}_i=\left(\begin{array}{r}a_1,&a_2,&a_3,&\cd&a_V\\\end{array}\right)\)
\(a_j=0\:\:(j\neq x_i)\)
\(a_j=1\:\:(j=x_i)\)
とします。つまり \(\bs{x}_i\) は、\(x_i\) 番目の要素だけが \(1\) で、他は全部 \(0\) の \(V\) 次元ベクトルです(1つだけ \(1\)、が "one hot" の意味です)。
例として、ウィンドーサイズを \(c=2\) とします。また分散表現の単語ベクトルの次元を \(D\) とします。この前提で、\(\bs{T}\) の中の \(t\) 番目の単語の one hotベクトルを推論するモデルが図17です。
\(\bs{T}=\{\:\cd,\:\bs{x}_{t-2},\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\bs{x}_{t+2},\:\cd\:\}\)
という単語の one hotベクトルの系列を想定したとき、 \(\bs{x}_t\) がターゲットの正解データ(=教師ラベル)であり、その他の4つがコンテクストです。
最初の MatMul (Matrix Multiply) レイヤーは、4つの one hotベクトル \(\bs{x}_i\) を入力とし、それぞれに重み行列 \(\bs{W}_{\large enc}\) をかけて、4つのベクトル \(\bs{h}_i\) を出力します(enc=encode)。つまり、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。Average レイヤーは、入力された複数ベクトルの平均をとり、一つのベクトル \(\bs{h}_t\) を出力します。この \(\bs{h}_t\) が \(\bs{x}_t\) の分散表現(= \(D\)次元ベクトル)です(というより、そうなるようにネットワークを訓練します)。
次の MatMul レイヤーで 重み \(\bs{W}_{\large dec}\) を掛け(dec=decode)、\(\mr{Softmax}\) レイヤーを通して、分散表現を \(V\) 次元の確率ベクトル \(\bs{y}_t\) に変換します。そして、教師ラベルである \(\bs{x}_t\) との間で交差エントロピー誤差を計算し、損失 \(L\) を求めます。
損失が求まれば、誤差逆伝播法で重み行列 \(\bs{W}_{\large enc}\) と \(\bs{W}_{\large dec}\) を修正します。この修正を、大量の文とそのすべてのウィンドーで行って、損失 \(L\) を最小化します。これがネットワークの訓練です。
訓練済みのネットワークでは、重み行列 \(\bs{W}_{\large enc}\:[V\times D]\) が、単語の分散表現の集積体になっています。つまり、one hot ベクトル \(\bs{x}_i\) の分散表現を \(\bs{h}_i\) とすると、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。\(\bs{x}_i\) の単語IDを \(x_i\) とすると、
\(\bs{h}_i=\bs{W}_{\large enc}\) の \(x_i\)行(\(1\)列から\(D\)列まで)
となります。
分散表現と単語の意味
「分布仮説」をもとに、ニューラル・ネットワークによる推論で得られた単語の分散表現ベクトルは、類似の意味の単語は類似のベクトルになる(ことが多い)ことが確認されています。たとえば、
year, month, day
などや、
car, automobile, vehicle
などです。ベクトルの類似は「コサイン類似度」で計測します。2つの2次元ベクトル、
\(\bs{a}=\left(\begin{array}{r}a_1&a_2\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
の場合で例示すると、
コサイン類似度\(=\dfrac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\)
で、2次元平面の2つのベクトルの角度(コサイン値)を求める式になります。この式の分子は内積(dot product)で、内積の定義式を変形したものです。この類似度を利用して「類推問題」が解けます。たとえば、
France : Paris = Japan : X
の X は何かという問題です。答えは Tokyo ですが、これを求めるには、分散表現ベクトルが類似しているという前提で、
となるはずなので、
X = France + Paris - Japan
であり、X を \(\bs{W}_{\large dec}\) と \(\mr{Softmax}\) 関数を使って確率ベクトルに変換すれば、確率が最も高い単語が Tokyo になるはずというわけです。
もちろん、分散表現ベクトルで類推問題を解くのは完璧ではありません。分散表現を作るときのウィンドーのサイズと訓練データの量にもよりますが、各種の類推問題を作って実際にテストをすると、60%~70% の正解率になるのが最大のようです。
言語モデル
分散表現ベクトルを用いて「言語モデル」を構築します。いま、一つの文を構成する単語の並び、
\(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T\)
があったとき(\(\bs{x}_1=\)[BOS]、\(\bs{x}_T=\)[EOS])、この文が存在する確率を、
\(P(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T)\)
で表します。文法として間違っている文の確率はゼロに近く、また文法としては合っていても、意味をなさない文の確率は低い。
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\( > \:P(\)[BOS],[学校],[は],[彼女],[へ],[行く],[EOS]\()\)
といった具合です。この「存在確率」は、次のような「条件付き確率」で表現できます。つまり、
\(P_1=P(\)[彼女] | [BOS]\()\)
:文頭が「彼女」である確率
\(P_2=P(\)[は] | [BOS],[彼女]\()\)
:「彼女」の次が「は」である確率
\(P_3=P(\)[学校] | [BOS],[彼女],[は]\()\)
:「彼女は」の次が「学校」である確率
\(P_4=P(\)[へ] | [BOS],[彼女],[は],[学校]\()\)
:「彼女は学校」の次が「へ」である確率
\(P_5=P(\)[行く] | [BOS],[彼女],[は],[学校],[へ]\()\)
:「彼女は学校へ」の次が「行く」である確率
\(P_6=P(\)[EOS] | [BOS],[彼女],[は],[学校],[へ],[行く]\()\)
:「彼女は学校へ行く」で文が終わる確率
とすると、
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\(=P_1\times P_2\times P_3\times P_4\times P_5\times P_6\)
となります。つまり、一般的に、
\(P(\bs{x}_{t+1}\:|\:\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_t)\)
が分かれば、言語モデルは決まります。平たく言うと、
それまでの単語の系列から、次にくる単語の確率を推測する
のが言語モデルと言えます。もちろん、次にくる可能性のある単語は1つではありません。語彙集合のすべての単語それぞれについて「次にくる」確率を予測します。
実は、Transformer や GPT、ChatGPT がやっていることは「次にくる単語の予測」であり、これを実現しているのが、「超大規模なニューラル・ネットワークで作った言語モデル」なのです。
トークン
今まで、ニューラル・ネットワークでテキストを扱うためには、テキストを単語に分解するとしてきました。しかし大規模言語モデルで実際にやっていることは、テキストを「トークン(token)」に分解し、そのトークンの分散表現ベクトルを求めてニューラル・ネットワークで処理することです。
トークンとは、基本的には「単語」ないしは「単語の一部」です。英語ですと、たとえば頻出単語は「単語=トークン」ですが、GPT-3 の例だと、トークンには、ed, ly, er, or, ing, ab, bi, co, dis, sub, pre, ible などの「単語の一部」が含まれます。GPT-3 のトークンの語彙数は約5万ですが、そのうち英語の完全な単語は約3000と言われています。通常使われる英単語は4万~5万なので、3000の単語で WebText や Wikipedia の全部を表すことは到底できません。つまり、単語の "切れ端" と単語の組み合わせ、ないしは単語の "切れ端" 同士の組み合わせでテキストを表現する必要があります。
たとえば「ディスコ音楽」などの disco という単語は、[dis] [co] と表現します。edible(食用の、食べられる、という意味)は、[ed] [ible] です。disco や edible は 3000 単語の中に入っていないようです。edible などは「基本的な英単語」と思えますが、あくまで WebText や Wikipedia に頻出するかどうかの判断によります。
また xylophone(木琴)は、[x] [yl] [ophone] です。このように、1文字がトークンになることもあります。"単語"、"単語の切れ端"、"文字" がトークンです。
BPEによるトークン化
テキストをトークンに変換することを「トークン化(tokenize)」、トークン化を行うソフトを tokenizer と言います。ここで GPT-3 のトークン化のアルゴリズムの概要をみてみます。
上の xylophone → [x] [yl] [ophone] で明快なのですが、トークン化は単語の意味とは無関係です。意味を言うなら xylo("木の" という意味の接頭語)+ phone(音)ですが、そういうこととは全く関係ありません。
GPT-2 の論文にそのアルゴリズムである BPE(Byte Pair Encoding)が書かれています(GPT-3 は GPT-2 と同じだと、GPT-3 の論文にあります)。
コンピュータで文字を表現するには文字コード(文字に数字を割り振ったもの)を使います。国際的に広く使われているのは unicode です。unicode を使うと各国語の文字が統一的に文字コードで表現できます。
unicode の数字をコンピュータでどう表すか、その表し方(=エンコーディング)には3種類ありますが、その一つが UTF-8 です。UTF-8 は1バイト(8ビット、10進数で 0~255)を単位とし、1~4バイトで1文字を表現する可変長のエンコーディングです(漢字の異字体は5バイト以上になります)。
UTF-8 でば、通常の英文に使われる英数字、特殊文字(空白 , . ? など)は1バイトで表します。一方、日本語の平仮名、カタカナ、漢字は3バイトです(一部の漢字は4バイト)。バイトは文字ではありません。あくまで文字を表現するためのコンピュータ用の数字です。
BPE ではまず、UTF-8 でエンコーディングされた大量のテキストを用意します。そして、1バイトの全パターンを256種類の基本トークンとして語彙に初期登録します。トークン ID は 1~256 とします。従って、英文における1文字の単語( I, a )や記号( , . ? ! など)は、この時点でトークンID が割り当てられたことになります。
次に、テキストの「トークンのペア」で、最も出現頻度の高いペアをみつけます。英語で最も出現頻度が高い単語は the で、トークンで表現すると [t] [h] [e] です。仮に、[t] [h] のペアがテキスト中で最も出現頻度が高いとします(説明のための仮定です)。そうすると、この2つのトークンを結合した [th] を新たなトークン(トークン ID=257)として語彙に登録します。以降、テキスト中の [t] [h] は [th] と見なします。
次に出現頻度の高いペアが [th] [e] だとすると、この2つを結合した [the] を新たなトークン(トークン ID=258)として語彙に登録します。この段階で the という単語がトークンの語彙に登録されたわけです(以上の [th] [the] のトークン ID は説明のための数字で、実際の GPT-3 のトークン ID は違います)。
以上のプロセスにおいてトークンは、「空白をまたがない」「空白で終わらない」「同一カテゴリの文字(英字、数字、特殊文字など)でしかペアを作らない」などの制約をもうけておきます。「カテゴリ」が何かは論文に書いていないので想定です。もちろんこれは、なるべく頻出単語をトークンにする工夫です。
これを「結合の最大回数」になるで繰り返します。GPT-2 / GPT-3 の場合、最大回数は 50,000 です。従って、最終的には、
256 + 50,000 + 1 = 50,257
のトークンの語彙ができあがることになります。最後の + 1 は文末の記号 [EOS] を特殊トークンとしているからです。
いったん語彙ができあがると、以降、この語彙を使ってすべてのテキストを同じアルゴズムでトークン化します。当然ですが、長いバイトのトークンからテキストに割り当てることになります。
大規模言語モデルの成立要件
GPT-3 のトークン化のロジックによると、すべての言語のすべてのテキストが 50,257個のトークンを使って、統一的に、もれなくトークン化できることになります。それはあたりまえで、1バイトのデータがすべてトークンとして登録してあるからです。テキストを UTF-8 で統一的に表せば可能なのです。
ここで、日本語がどうなるかです。日本語の unicode を UTF-8 で表すと、漢字・仮名・文章記号は3バイトです(一部の漢字は4バイト。また異字体は5バイト以上)。ということは、普通の漢字1字、仮名1字は1~3トークンで表されることになります。
実際、OpenAI 社が公開している GPT-3 の Tokenizer で試してみると、
仮名は1~2トークン
ほとんどの漢字は2~3トークン
となります。ちなみに、平仮名(清音、濁音、半濁音、計71文字種)のトークン数を調べてみると、
28 文字種:1トークン
43 文字種:2トークン
です。濁音で1トークンになるのは「が だ で」の3つだけですが、これは助詞として頻出するからでしょう。特別の場合は、仮名2文字で1トークンになるようです(スト、ーク、など)。1トークンになる漢字はごく少数のようで、たとえば「上」「田」「中」「一」「大」がそうです(他にもあると思います)。
以上をまとめると、何をトークンとするかは、
・単語
・単語の一部、ないしは文字の連なり
・文字
・バイト
がありうるわけですが、GPT-3 のトークンにはこれらが混在していて、規則性は全くないことになります。ここから何が言えるかと言うと、
ということです。もちろん、英語を扱うときのように頻出単語のトークン化ができれば、生成されるテキストのクオリティーが向上することは確かでしょう。しかし、単語単位のトークン化は必須ではない。つまり、
わけです。GPT-3(= ChatGPT の基盤となっているモデル)がそれを示しています。大規模言語モデルは、翻訳、文章要約、質問回答、おしゃべり(chat)などの多様なタスクに使えます。これらのタスクを実現する仕組みを作るには、言語学的知識は全く不要です。不要というより、言語学的知識を持ち込むことは邪魔になる。もちろん、「翻訳、文章要約、質問回答、おしゃべり」の実例や好ましい例が大量にあるのが条件です。
その GPT-3 のベースになっているのは、Google が提案した Transformer という技術です。ということは、次のようにも言えます。
これが言えるのなら、少々先走りますが、Transformer はタンパク質の機能分析にも使える(可能性がある)ことになります。タンパク質はアミノ酸が鎖状に1列に並んだもので、そのアミノ酸は20種類しかありません。
タンパク質は「20種の記号の系列」であり、それが生体内で特定の機能を果たします。多数のタンパク質のアミノ酸配列を Transformer で学習し、タンパク質の機能と照らし合わせることで、新たなタンパク質の設計に役立てるようなことができそうです。実は、こういった生化学分野での Transformer や言語モデルの利用は、今、世界でホットな研究テーマになっています。
もちろん、系列データはタンパク質の構造だけではありません。従来から AI で扱われてきた音声・音源データや、各種のセンサーから取得したデータがそうだし、分子生物学では DNA / RNA が「4文字で書かれた系列データ」と見なせます。現に米国では、DNA / RNA の塩基配列を学習した大規模言語モデルでウイルスの変異予測がされています。
Transformer は、もともと機械翻訳のために提案されたものでした。しかしそれは意外なことに、提案した Google も予想だにしなかった "奥深い" ものだった。ここに、大規模言語モデルのサイエンスとしての意義があるのです。
前回の No.364「言語の本質」の補足で紹介した新聞記事で、慶応義塾大学の今井教授は、
ChatGPT の「仕組み」(=注意機構)と「メタ学習」は、幼児が言語を学習するプロセスと類似している
と指摘していました。メタ学習とは「学習のしかたを学習する」ことですが、 ChatGPT がそれをできる理由も「注意機構(Attention mechanism)」にあります。そこで今回は、その気になる ChatGPT の仕組みをまとめます。
今まで「高校数学で理解する ・・・・・・」というタイトルの記事をいくつか書きました。
| 高校数学で理解するRSA暗号の数理 | |
| 高校数学で理解する公開鍵暗号の数理 | |
| 高校数学で理解する楕円曲線暗号の数理 | |
| 高校数学で理解する誕生日のパラドックス | |
| 高校数学で理解するレジ行列の数理 | |
| 高校数学で理解するガロア理論 |
の 13 の記事です。"高校数学で理解する" という言い方は、「高校までで習う数学だけを前提知識として説明する」という意味ですが、今回もそれに習います。もちろん、文部科学省の学習指導要領は年々変わるので、"おおよそ高校までの数学" が正しいでしょう。今回、前提とする知識は、
| 行列 | |
| ベクトル | |
| 指数関数、対数 | |
| 微分、積分 | |
| 標準偏差と正規分布(ガウス分布) |
全体の構成
全体の構成は次の4つです
1.ニューラル・ネットワーク
ニューラル・ネットワークの基礎から始まって、最も重要なポイントである「学習できる」ことを説明をします。
2.自然言語のモデル化
自然言語をニューラル・ネットワークで扱う際に必須である「単語の分散表現」を説明します。また、「言語モデル」と、ChatGPT で使われている「トークン」についても説明します。
3.Transformer
ChatGPT のベースになっている技術は、2017年に Google社が発表した Transformer です。この説明をします。
4.GPT-3 と ChatGPT
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。
ここでは GPT-3 の仕組み・技術内容を説明し、合わせて ChatGPT と GPT-3 の違いも説明します。
ここでは GPT-3 の仕組み・技術内容を説明し、合わせて ChatGPT と GPT-3 の違いも説明します。
なお、この記事の作成には、Google と OpenAI の論文に加えて、以下を参考にしました。
◆岡野原 大輔(プリファードネットワークス)
「大規模言語モデルは新たな知能か」
(岩波書店 2023)
◆澁谷 崇(SONY)
「系列データモデリング (RNN/LSTM/Transformer)」
第7回「Transformer」
第12回「GPT-2, GPT-3」
(YouTube 動画)
| 1.ニューラル・ネットワーク |
記号
以降で使用する記号の意味は次の通りす。
| ボールド体ではない、ノーマル書体の英大文字・小文字はスカラー値(ないしはスカラー変数)を表します。\(a,\:\:b,\:\:x,\:\:y,\:\:x_1,\:w_{12},\:\:M,\:\:N,\:\:L\) などです。 | |
| ボールド体の英大文字は行列を表します。\(\bs{W}\) などです。 \(N\) 行、\(M\) 列 の行列を \([N\times M]\) と表記します。\(\bs{W}\:[2\times3]\) は、2行3列の行列 \(\bs{W}\) で、 \(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}\\w_{21}&w_{22}&w_{23}\\\end{array}\right)\) です。 | |
| ボールド体の英小文字はベクトルを表します。ベクトルは「行ベクトル」で表現し、\(n\)次元のベクトル \(\bs{x}\) は、 \(\bs{x}=\left(\begin{array}{r}x_1&x_2&\cd&x_n\\\end{array}\right)\) です。この \(n\)次元のベクトルを、\(1\) 行 \(n\) 列の行列と同一視します。従って次元の表記は \(\bs{x}\:[1\times n]\) です。 | |
| 列ベクトルは、転置行列の記号(\({}^T\))を使って、 \(\bs{x}^T\) で表します。たとえば、3次元の列ベクトルは3次元の行ベクトルの転置を使って、 \(\bs{x}^T=\left(\begin{array}{r}x_1\\x_2\\x_3\\\end{array}\right)\:\:[3\times1]\) です。 | |
| 同一次元の2つのベクトル \(\bs{x}\:\:\bs{y}\) の内積(スカラー積、ドット積)は、 \(\bs{x}\bs{y}^T\) で表します。ドッド記号(\(\cdot\))は内積ではなく、行列の積(または実数値同士の積)です。ただし、一般的に行列の積は、\(\bs{x}\bs{y}^T\) のように積記号を省略します。 | |
| 同一次元の2つのベクトルの「対応する要素同士の積」で作ったベクトルを「要素積」(ないしはアダマール積)と呼び、\(\odot\) の記号で表します(一般的には \(\otimes\) の記号も使います)。\(n\)次元ベクトル同士の要素積は、 \(\left(\begin{array}{r}x_1&x_2&\cd&x_n\\\end{array}\right)\odot\left(\begin{array}{r}y_1&y_2&\cd&y_n\\\end{array}\right)\) \(=\left(\begin{array}{r}x_1y_1&x_2y_2&\cd&x_ny_n\\\end{array}\right)\) です。要素積は、行数・列数が同一の2つの行列にも適用します。 | |
| 指数関数、\(f(x)=e^x\) を、 \(f(x)=\mr{exp}(x)\) と表記します。 | |
| \(n\)次元ベクトルを \(\bs{x}=\{x_1\:x_2\:\cd\:x_n\}\) とし、1変数の関数 \(f(x)\) があるとき、ベクトル \(f(\bs{x})\) を、 \(f(\bs{x})=\left(\begin{array}{r}f(x_1)&f(x_2)&\cd&f(x_n)\\\end{array}\right)\) で定義します。 |
ニューラル・ネットワークの例
2層から成るシンプルなニューラル・ネットワークの例が図1です。この例では隠れ層が1つだけですが、隠れ層は何層あってもかまいません(なお、入力層を含めて、これを "3層" のニューラル・ネットワークとする定義もあります)。
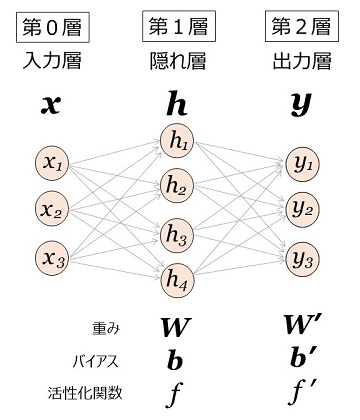
|
図1:ニューラル・ネットワーク |
丸印は "ニューロン" で、各ニューロンは1つの値(活性値)をもちます。値は実数値で、32ビットの浮動小数点数が普通です。図1のニューロンの数は 3+4+3=10 個ですが、もちろんこの数は多くてもよく、実用的なネットワークでは数100万から億の単位になることがあります。
ニューロン間の矢印が "シナプス" で、一つのニューロンは、シナプスで結ばれている前の層のニューロンから値を受けとり、決められた演算をして自らの値を決めます(入力層を除く)。なお、"ニューロン" や "シナプス" は脳神経科学の用語に沿っています。
各層は、重み \(\bs{W}\)(行列)とバイアス \(\bs{b}\)(ベクトル)、活性化関数 \(f\) を持ちます。図1の場合、第1層の重みは \(\bs{W}\:\:[3\times4]\)、バイアスは \(\bs{b}\:\:[1\times4]\) で、
\(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}&w_{14}\\w_{21}&w_{22}&w_{23}&w_{24}\\w_{31}&w_{32}&w_{33}&w_{34}\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2&b_3&b_4\\\end{array}\right)\)
です。このとき、隠れ層(第1層)のニューロンの活性値、\(\bs{h}=\left(\begin{array}{r}h_1&h_2&h_3&h_4\\\end{array}\right)\) は、
\(h_1=f\:(\:x_1w_{11}+x_2w_{21}+x_3w_{31}+b_1\:)\)
\(h_2=f\:(\:x_1w_{12}+x_2w_{22}+x_3w_{32}+b_2\:)\)
\(h_3=f\:(\:x_1w_{13}+x_2w_{23}+x_3w_{33}+b_3\:)\)
\(h_4=f\:(\:x_1w_{14}+x_2w_{24}+x_3w_{34}+b_4\:)\)
の式で計算されます。ベクトルと行列で表示すると、
\(\bs{h}=f\:(\bs{x}\cdot\bs{W}+\bs{b})\)
になります。第2層も同様です。
このニューラル・ネットワークは、多重パーセプトロン(Multi Layer Perceptron : MLP)と呼ばれるタイプのもので、ニューラル・ネットワークの歴史の中では、古くから研究されている由緒のあるものです。
また上図の第1層、第2層は、すべてのニューロンが前層のすべてのニューロンとシナプスを持ってます。このような層を「全結合層」(Fully connected layer. FC-layer. FC層)と言います。全結合の多重パーセプトロンは Transformer や GPT で使われていて、重要な意味を持っています。
|
\(\mr{ReLU}(x)=x\:\:(x > 0)\) \(\mr{ReLU}(x)=0\:\:(x\leq0)\) |
で定義される非線形関数です(図2)。以降での表記を簡潔にするため、単位ステップ関数 \(H(x)\) を用いて \(\mr{ReLU}\) 関数を表しておきます。単位ステップ関数は、
|
\(H(x)=0\:\:(x\leq0)\)
で定義される関数で(図3)、ヘヴィサイド関数とも呼ばれます。\(H(x)\) の微分は、
\(H\,'(x)=0\:\:(x\neq0)\)
です。\(x=0\) において \(H(x)\) は不連続で、微分は定義できませんが、無理矢理、
\(H\,'(0)=0\)
と定義してしまうと、\(x\) の全域において、
\(H\,'(x)=0\)
となります。この \(H(x)\) を用いて \(\mr{ReLU}\) 関数を定義すると、
\(\mr{ReLU}(x)=H(x)x\) |
となり、微分は、
\(\dfrac{d}{dx}\mr{ReLU}(x)=H(x)\)
と表現できます。
出力層の活性化関数 \(f\,'\) は、ニューラル・ネットワークをどんな用途で使うかによって違ってきます。
ニューラル・ネットワークによる推論
ニューラル・ネットワークが扱う問題は、入力ベクトル \(\bs{x}\) をもとに出力ベクトル \(\bs{y}\) を "推論"(ないしは "推定"、"予測")する問題です。これには主に「回帰問題」と「分類問題」があります。
回帰問題で推論する \(\bs{y}\) は実数値(=連続値)です。たとえば、
・身長
・体重
・年齢
・男女の区別
・生体インピーダンス
から(\(=\bs{x}\))、
・体脂肪率
・筋肉量
・骨密度
を推定する(\(=\bs{y}\))といった例です(但し、市販の体組成計が AI を使っているわけではありません)。
一方、分類問題の例は、たとえば手書き数字を認識する問題です。この場合、多数の手書き数字の画像(をベクトルに変換した \(\bs{x}\))を「\(0\) のグループ」「\(1\) のグループ」・・・・・ というように分類していきます。このグループのことを AI では "クラス" と呼んでいます。つまり「クラス分類問題」です。
手書き数字の場合、明確に \(0\) ~ \(9\) のどれかに認識できればよいのですが、そうでない場合もある。たとえば、\(1\) なのか \(7\) なのか紛らわしい、\(0\) なのか \(6\) なのか曖昧、といったことが発生します。分類するのは、\(0\) ~ \(9\) のうちのどれかという「離散値の予測」であり、連続値とは違って、どうしても紛らわしい例が発生します。
従って、クラス分類問題(=離散値を予測する問題)では、出力ベクトル \(\bs{y}\) は確率です。手書き数字の認識では、\(\bs{y}\) は\(10\)次元の確率ベクトルで、たとえば、
| \(y_1\) | :数字が \(1\) である確率 | |
| \(y_2\) | :数字が \(2\) である確率 | |
| \(\vdots\) | ||
| \(y_9\) | :数字が \(9\) である確率 | |
| \(y_{10}\) | :数字が \(0\) である確率 |
\(0\leq y_i\leq1,\:\:\:\displaystyle\sum_{i=1}^{10}y_i=1\)
です。入力画像が \(1\) なのか \(7\) なのか紛らわしい場合、たとえば推定の例は、
\(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
です。これは、
\(1\) である確率が \(0.8\)
\(7\) である確率が \(0.2\)
を表します。クラス分類問題は「離散値を推論する問題」、すなわち「確率を推定する問題」であると言えます。
回帰問題の出力層の活性化関数は、恒等関数(=何もしない)とするのが普通です。一方、クラス分類問題の出力層の活性化関数は、出力 \(\bs{y}\) が確率として解釈できるような関数を選びます。それが \(\mr{Softmax}\) 関数です。
\(\mr{Softmax}\) 関数
\(\mr{Softmax}\) 関数によって、出力 \(\bs{y}\) が確率と解釈できるようになります。ベクトル \(\bs{x}\) を \(\mr{Softmax}\) 関数によって確率ベクトル \(\bs{y}\) に変換する式は、次のように定義できます。なお、ここでの \(\bs{x}\) は入力層の \(\bs{x}\) ではなく、一般的なベクトルを表します。
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(n\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{n}y_i=1\)
ここで使われている指数関数は、すぐに巨大な数になります。たとえば \(\mr{exp}(100)\) は\(10\)進で\(40\)桁以上の数で、\(32\)ビット浮動小数点の最大値(\(10\)進で\(40\)桁弱)を越えてしまいます。従って、\(\mr{Softmax}\) 関数の計算には工夫が必要で、それには \(\mr{Softmax}\) 関数の性質を利用します。
\(C\) を任意の実数値とし、\(n\)次元ベクトル \(\bs{z}\) を
\(z_i=x_i+C\)
と定義します。そして、
\(\bs{y}\,'=\mr{Softmax}(\bs{z})\)
と置くと、
\(\begin{eqnarray}
&&\:\:y_i\,'&=\dfrac{\mr{exp}(z_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(z_i)}=\dfrac{\mr{exp}(x_i+C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i+C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)\cdot\mr{exp}(C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\mr{exp}(C)\cdot\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\\
&&&=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}=y_i\\
\end{eqnarray}\)
となります。つまり \(x_i\:\:(1\leq i\leq n)\) の全部に定数 \(C\) を足しても、\(\mr{Softmax}\) 関数は変わりません。そこで、
\(C=-\mr{max}(x_1,\:x_2,\:\cd\:,x_n)\)
と置いて、
\(x_i\:\longleftarrow\:x_i+C\:\:(1\leq i\leq n)\)
と修正すると、\(x_i\) の最大値は \(0\) になります。従って、
\(0 < \mr{exp}(x_i)\leq1\)
の範囲で \(\mr{Softmax}\) 関数が計算可能になります。
大規模言語モデルと確率
クラス分類問題の出力ベクトル \(\bs{y}\) は確率でしたが、実は Transformer や GPT が実現している「大規模言語モデル」も "確率を推定するニューラル・ネットワーク" です。たとえば、
[今日] [は] [雨] [なの] [で]
というテキストに続く単語を推定します。仮に、日本語の日常用語の語彙数を5万語とすると、5万の単語すべてについて上のテキストに続く単語となる確率を、実例をもとに推定します。当然、「雨の日の行動」とか「雨の日の情景」、「雨の日の心理状態」、「雨の日に起こりうること」を描写・説明する単語の確率が高くなるわけです。たとえば名詞だけをとると、[家] [ビデオ] [映画] [傘] [犬] [洗濯] [祭] [運動会] などの確率が高く、[ニンジン] [牛] [鉛筆] などの確率は(雨の日とは関係があるとは思えないので)低いといった具合です(あくまで想定です)。
「大規模言語モデル」の重要な応用例(=タスク)である機械翻訳も同じです。日本語 → 英語の翻訳を例にとると、
[今日] [は] [晴れ] [です] [。] [BOS]
に続く英単語を推定します([BOS] は文の開始を示す特殊単語)。確率の高い単語から [it] を選んだとすると、次には、
[今日] [は] [晴れ] [です] [。] [BOS] [it]
に続く単語を推定します([is] になるはず)。こうやって進むのが機械翻訳です。
Transformer や GPT をごくごくシンプルに言えば、入力ベクトル \(\bs{x}\) はテキスト列、出力ベクトル \(\bs{y}\) は次に続く単語を示す確率ベクトル(次元は語彙数)です。
この記事は、Transformer、GPT、ChatGPT などの大規模言語モデルを説明するのが目的です。従って以降では、出力ベクトル \(\bs{y}\) は確率ベクトルであることを前提とします。
確率を推定するニューラル・ネットワーク
図1において、第1層(隠れ層)の活性化関数を \(\mr{ReLU}\)、第2層(出力層)の活性化関数を \(\mr{Softmax}\) とすると、図4になります。
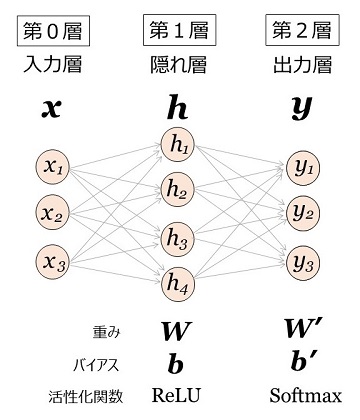
|
図4:ニューラル・ネットワーク (出力層は確率ベクトル) |
図4の計算は、以下に示すような4段階の計算処理で表すことができます。
第1層
\(\bs{h}\,'=\bs{x}\cdot\bs{W}+\bs{b}\)
\(\bs{h}=\mr{ReLU}(\bs{h}\,')\)
第2層
\(\bs{y}\,'=\bs{h}\cdot\bs{W}\,'+\bs{b}\,'\)
\(\bs{y}=\mr{Softmax}(\bs{y}\,')\)
この4つの計算処理を「計算レイヤー」、略して「レイヤー」と呼び、図5のグラフで表現することにします。
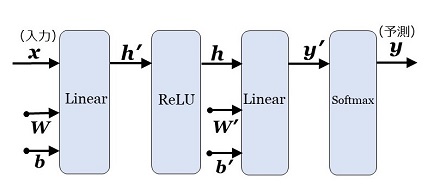
|
図5:クラス分類問題のレイヤー構成(推論時) |
レイヤー(layer)は日本語にすると「層」で、第1層や隠れ層の「層」と紛らわしいのですが、「レイヤー」と書いたときは "ある一定の計算処理" を示します。後ほど説明する Transformer や GPT は、図4のような単純な「層」では表現できない複雑な計算処理があります。従って "ある一定の計算処理 = レイヤー" とした方が、すべての場合を共通に表現できて都合が良いのです。
レイヤーの四角に向かう矢印は計算処理への入力を示し、四角から出る矢印は計算処理からの出力(計算結果)を示します。「レイヤーは一つの関数」と考えてもOKです。
図5の「Linear レイヤー」は、「Affine(アフィン)レイヤー」と呼ばれることが多いのですが、Transformer の論文で Linear があるので、そちらを採用します。
図5のネットワークがどうやって「学習可能なのか」を次に説明します。この「学習できる」ということが、ニューラル・ネットワークが成り立つ根幹です。
ニューラル・ネットワークの学習
重みとバイアスの初期値
まず、重み(\(\bs{W},\:\bs{W}\,'\))の初期値を乱数で与えます。この乱数は、前の層のニューロンの数を \(n\) とすると
| 平均 | \(=0\) | |
| 標準偏差 | \(=\sqrt{\dfrac{1}{n}}\) |
の正規分布の乱数とするのが普通です。\(n=10,000\) とすると、標準偏差は \(0.01\) なので、
\(-\:0.01\) ~ \(0.01\)
の間にデータの多く(約 \(2/3\))が集まる乱数です。但し、\(\mr{ReLU}\) を活性化関数とする層(図4では第1層)の重みは、
| 平均 | \(=0\) | |
| 標準偏差 | \(=\sqrt{\dfrac{2}{n}}\) |
の乱数とします。なお、バイアスの初期値は \(0\) とします。こういった初期値の与え方は、学習をスムーズに進めるためです。
損失と損失関数
初期値が決まったところで、訓練データの一つを、
\(\bs{x}\):入力データ
\(\bs{t}\):確率の正解データ
とします。この正解データのことを「教師ラベル」と呼びます。そして、ニューラル・ネットワークによる予測の確率 \(\bs{y}\) と、正解の確率である \(\bs{t}\) との差異を計算します。この差異を「損失(\(Loss\))」といい、\(L\) で表します。\(L\) は正のスカラー値です。
\(\bs{y}\) と \(\bs{t}\) から \(L\) を求めるのが「損失関数(Loss Function)」です。確率を予測する場合の損失関数は「交差エントロピー誤差(Cross Entropy Error : CEE)」とするのが普通で、次の式で表されます。
\(L=-\displaystyle\sum_{i=1}^{n}t_i\cdot\mr{log}\:y_i\) |
たとえば、先ほどの手書き数字の認識の「\(1\) または \(7\) という予測」を例にとって、その正解が \(1\) だとすると、
予測 \(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
正解 \(\bs{t}=\left(\begin{array}{r}1&0&0&0&0&0&0&0&0\\\end{array}\right)\) = 教師ラベル
です。なお、\(\mr{Softmax}\)関数の出力は \(0\) にはならないので、上の \(\bs{y}\) で \(0\) と書いた要素は、実際には微小値です。すると、
\(L=-\mr{log}\:0.8\fallingdotseq0.223\)
となります。損失関数を含めると、レイヤー構成は図6のようになります。
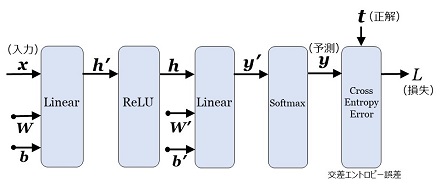
|
図6:クラス分類問題のレイヤー構成(学習時) |
この図の重みとバイアスを少しだけ調整して、\(L\) を少しだけ \(0\) に近づけます。この調整を多数の学習データ(= \(\bs{x}\:\:\bs{t}\) のペア)で繰り返して、\(L\) を次第に \(0\) に近づけていくのが学習です。
勾配降下法
重みの調整には「勾配降下法(Gradient descent method)」を使います。図6の場合、損失 \(L\) は、ある関数 \(f\) を用いて、
\(L=f(\bs{x},\:\bs{W},\:\bs{b},\:\bs{W}\,',\:\bs{b}\,',\:\bs{t})\)
と表現できます。ここで、\(\bs{W}\) の一つの要素、\(w_{11}\) を例にとると、
\(w_{11}\) を微小に増減させた場合、\(L\) はどのように増減するか、そのの \(w_{11}\) に対する変化の割合
を計算します。これはいわゆる微分ですが、多変数関数の微分なので、数学的には偏微分であり、
\(\dfrac{\partial L}{\partial w_{11}}\)
です。つまり、\(w_{11}\) 以外の変数をすべて固定しての(すべて定数とした上での)、\(w_{11}\) による微分です。
具体的な入力 \(\bs{x}\) のときの \(\dfrac{\partial L}{\partial w_{11}}\) が求まったとします。もし仮に、\(\dfrac{\partial L}{\partial w_{11}}\) が正の値だとしたら、\(w_{11}\) を少しだけ減らせば、\(L\) は少しだけ \(0\) に近づきます。もし \(\dfrac{\partial L}{\partial w_{11}}\) が負だとしたら、\(w_{11}\) を少しだけ増やせば、\(L\) は少しだけ \(0\) に近づきます。つまり、
更新式:\(w_{11}\:\longleftarrow\:w_{11}-\eta\cdot\dfrac{\partial L}{\partial w_{11}}\)
として重みを更新すればよいわけです。\(\eta\) は「少しだけ」を表す値で「学習率」といい、\(0.01\) とか \(0.001\) とかの値をあらかじめ決めておきます。この決め方は、学習の効率に大いに影響します。こういった更新を、すべての重みとバイアスに対して行います。
"学習で調整される値" を総称して「パラメータ」と言います。図6のパラメータは重みとバイアスですが、実用的なニューラル・ネットワークでは、それ以外にも更新されるパラメータがあります。
ちなみに、OpenAI 社の GPT\(-3\) のパラメータの総数は \(1750\)億個で、学習率は \(0.6\times10^{-4}\) です。
\(L\) の偏微分値をベクトルや行列単位でまとめたものを、次のように表記します。2次元のベクトル \(\bs{b}\) と、2行2列の行列 \(\bs{W}\) で例示すると、
\(\dfrac{\partial L}{\partial\bs{b}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial b_1}&\dfrac{\partial L}{\partial b_2}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{W}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\)
です。これを「勾配(gradient)」と言います。勾配を求めることでパラメータを少しづつ更新し、損失を少しづつ小さくしていく(=降下させる)のが勾配降下法です。
ミニバッチ勾配降下法
学習は次のように進みます。まず、すべての訓練データ(たとえば
数万件)から、数\(10\)~数\(100\)件(たとえば\(256\)件)の訓練データをランダムに選びます。この一群のデータを「ミニバッチ」と呼びます。ミニバッチの各訓練データによる確率の推定から損失を計算し、そこからすべてのパラメータの勾配と求め、その勾配ごとに "ミニバッチの平均値" をとります。その平均値に基づき、更新式に従って各パラメータを更新します。
ミニバッチによる更新が終わると、別のミニバッチをランダムに選び、更新を繰り返します。こうすると、損失は次第に減少していきますが、そのうち "頭打ち" になります。そこで更新を止めます。
このようなパラメータ更新のやり方を「ミニバッチ勾配降下法」と言います。一つの訓練データだけで更新しないのは、たまたまその訓練データが「外れデータ」(全体の傾向とは異質なデータ)だと、学習の進行に支障が出てくるからです。
訓練データをランダムに選択する方法を「確率的勾配降下法(Stochastic gradient method - SGD)」と言いますが、ミニバッチ勾配降下法は、その確率的勾配降下法の一種です。
誤差逆伝播法
ここで問題になるのは、すべてのパラメータの勾配をどうやって求めるかです。それに使われるのが「誤差逆伝播法(Back propagation)」です。その原理を、Linear レイヤーから説明します。
(1) Linear
|
図7:linear レイヤー |
入力 \(\bs{x}\) \([1\times N]\) \(\bs{W}\) \([N\times M]\) \(\bs{b}\) \([1\times M]\) 出力 \(\bs{y}\) \([1\times M]\) |
図7で示すように、Linear レイヤーがあり、そのあとに何らかの計算処理が続いて、最終的に損失 \(L\) が求まったとします。\(\bs{x}\:\:\bs{y}\) はニューラル・ネットワークへの入力と出力ではなく、Linear レイヤーへの入力と出力の意味です。ここで、
\(\bs{y}\) の勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が求まれば、合成関数の微分を使って、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配が求まる
と言えます。これが誤差逆伝播法の原理です。このことを、2次元ベクトル(\(\bs{x},\:\:\bs{b},\:\:\bs{y}\))、2行2列の配列(\(\bs{W}\))で例示します(\(N=2,\:M=2\) の場合)。
【Linear の計算式】
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+b_1\)
\(y_2=x_1w_{12}+x_2w_{22}+b_2\)
\(x_1\) が変化すると \(y_1,\:y_2\) が変化し、それが損失 \(L\) に影響することに注意して、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配を計算します。
【\(\bs{\bs{x}}\) の勾配】
| \(\dfrac{\partial L}{\partial x_1}\) | \(=\dfrac{\partial y_1}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_2}\) | |
| \(=\dfrac{\partial L}{\partial y_1}w_{11}+\dfrac{\partial L}{\partial y_2}w_{12}\) | ||
| \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}\\w_{12}\\\end{array}\right)\) |
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)\)
です。これをまとめると、
\(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\:\:\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T\)
となり、\(\bs{x}\) の勾配が求まります。
【\(\bs{\bs{W}}\) の勾配】
\(\dfrac{\partial L}{\partial w_{11}}=\dfrac{\partial y_1}{\partial w_{11}}\dfrac{\partial y_1}{\partial w_{11}}=x_1\dfrac{\partial y_1}{\partial w_{11}}\)
\(\dfrac{\partial L}{\partial w_{12}}=\dfrac{\partial y_2}{\partial w_{12}}\dfrac{\partial y_2}{\partial w_{12}}=x_1\dfrac{\partial y_2}{\partial w_{12}}\)
\(\dfrac{\partial L}{\partial w_{21}}=\dfrac{\partial y_1}{\partial w_{21}}\dfrac{\partial y_1}{\partial w_{21}}=x_2\dfrac{\partial y_1}{\partial w_{21}}\)
\(\dfrac{\partial L}{\partial w_{22}}=\dfrac{\partial y_2}{\partial w_{22}}\dfrac{\partial y_2}{\partial w_{22}}=x_2\dfrac{\partial y_2}{\partial w_{22}}\)
これらをまとめると、
| \(\dfrac{\partial L}{\partial\bs{W}}\) | \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\) | |
| \(=\left(\begin{array}{r}x_1\dfrac{\partial L}{\partial y_1}&x_1\dfrac{\partial L}{\partial y_2}\\x_2\dfrac{\partial L}{\partial y_1}&x_2\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) | ||
| \(=\left(\begin{array}{r}x_1\\x_2\\\end{array}\right)\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) | ||
| \(=\bs{x}^T\dfrac{\partial L}{\partial\bs{y}}\) |
となります。
【\(\bs{\bs{b}}\) の勾配】
| \(\dfrac{\partial L}{\partial b_1}\) | \(=\dfrac{\partial L}{\partial y_1}\) | |
| \(\dfrac{\partial L}{\partial b_2}\) | \(=\dfrac{\partial L}{\partial y_2}\) |
| \(\dfrac{\partial L}{\partial\bs{b}}\) | \(=\dfrac{\partial L}{\partial\bs{y}}\) |
以上の計算で求まった勾配をまとめて図示すると、図8になります。黒字(入力・出力とパラメータ)の下の赤字がパラメータの勾配で、右から左への矢印は、「レイヤーの出力の勾配が求まれば、レイヤーの入力の勾配が求まる」こと示します(= 逆伝播)。上での計算は2次元ベクトルと2行2列の配列で例示しましたが、図8のようなベクトル・配列で表示すると、\([1\times N]\) のベクトルと \([N\times M]\) の行列で成り立つことが確認できます。
|
図8:linear の誤差逆伝播 |
出力側の勾配が求まれば、そこから入力側の勾配はすべて求まる。これが誤差逆伝播の原理で、合成関数の微分のシンプルな応用である。 |
(2) ReLU
\(\mr{ReLU}\) 関数は、
\(\mr{ReLU}(x_i)=x_i\:\:(x_i > 0)\)
\(\mr{ReLU}(x_i)=0\:\:\:(x_i\leq0)\)
であり、ベクトルの表現では、単位ステップ関数、
\(H(x)=1\:\:\:(x > 0)\)
\(H(x)=0\:\:\:(x\leq0)\)
と要素積 \(\odot\) を使って、
\(\mr{ReLU}(\bs{x})=H(\bs{x})\odot\bs{x}\)
と定義できます。従って、勾配は、
| \(\dfrac{\partial L}{\partial x_i}=\dfrac{\partial L}{\partial y_i}\) | \((x_i > 0)\) | |
| \(\dfrac{\partial L}{\partial x_i}=0\) | \((x_i\leq0)\) |
\(\dfrac{\partial L}{\partial\bs{x}}=H(\bs{x})\odot\dfrac{\partial L}{\partial\bs{y}}\)
です。
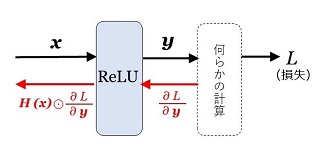
|
図9:ReLU の誤差逆伝播 |
(3) Softmax
\(\mr{Softmax}\) 関数の定義は、
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(N\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{N}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{N}y_i=1\)
です。勾配の計算を \(N=3\) の場合で例示します。
| \(S\) | \(=\mr{exp}(x_1)+\mr{exp}(x_2)+\mr{exp}(x_3)\) | |
| \(y_1\) | \(=\dfrac{\mr{exp}(x_1)}{S}\) | |
| \(y_2\) | \(=\dfrac{\mr{exp}(x_2)}{S}\) | |
| \(y_3\) | \(=\dfrac{\mr{exp}(x_3)}{S}\) |
\(\dfrac{\partial L}{\partial x_1}=\dfrac{\partial y_1}{\partial x_1}\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\dfrac{\partial L}{\partial y_2}+\dfrac{\partial y_3}{\partial x_1}\dfrac{\partial L}{\partial y_3}\)
| \(\dfrac{\partial y_1}{\partial x_1}\) | \(=\dfrac{\mr{exp}(x_1)}{S}-\dfrac{\mr{exp}(x_1)}{S^2}\mr{exp}(x_1)\) | |
| \(=y_1-y_1^2\) | ||
| \(=y_1(1-y_1)\) |
| \(\dfrac{\partial y_2}{\partial x_1}\) | \(=-\dfrac{\mr{exp}(x_2)}{S^2}\mr{exp}(x_1)\) | |
| \(=-y_1y_2\) |
| \(\dfrac{\partial y_3}{\partial x_1}\) | \(=-\dfrac{\mr{exp}(x_3)}{S^2}\mr{exp}(x_1)\) | |
| \(=-y_1y_3\) |
\(\dfrac{\partial L}{\partial x_1}=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_2}=y_2(1-y_2)\dfrac{\partial L}{\partial y_2}-y_2y_3\dfrac{\partial L}{\partial y_3}-y_2y_1\dfrac{\partial L}{\partial y_1}\)
\(\dfrac{\partial L}{\partial x_3}=y_3(1-y_3)\dfrac{\partial L}{\partial y_3}-y_3y_1\dfrac{\partial L}{\partial y_1}-y_3y_2\dfrac{\partial L}{\partial y_2}\)
(4) Cross Entropy Error - CEE
交差エントロピー誤差の定義は、
入力 \(\bs{y}\) \((1\times N)\)
入力 \(\bs{t}\) \((1\times N)\) 教師ラベル(正解データ)
出力 \(L\:(Loss)\)
とすると、
\(L=-\displaystyle\sum_{i=1}^{N}(t_i\mr{log}y_i)\)
で定義されます。従って、
\(\dfrac{\partial L}{\partial y_i}=-\dfrac{t_i}{y_i}\)
であり、\(N=3\) の場合を書くと、
\(\dfrac{\partial L}{\partial y_1}=-\dfrac{t_1}{y_1}\)
\(\dfrac{\partial L}{\partial y_2}=-\dfrac{t_2}{y_2}\)
\(\dfrac{\partial L}{\partial y_3}=-\dfrac{t_2}{y_3}\)
です。
(5) Softmax + CEE
\(\mr{Softmax}\) レイヤーの直後に交差エントロピー誤差のレイヤーを配置した場合を考えます。(3) と (4) の計算を合体させると、次のように計算できます。
| \(\dfrac{\partial L}{\partial x_1}\) | \(=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\) | |
| \(=-y_1(1-y_1)\dfrac{t_1}{y_1}+y_1y_2\dfrac{t_2}{y_2}+y_1y_3\dfrac{t_3}{y_3}\) | ||
| \(=-t_1+t_1y_1+y_1t_2+y_1t_3\) | ||
| \(=-t_1+t_1y_1+y_1(t_2+t_3)\) | ||
| \(=-t_1+t_1y_1+y_1(1-t_1)\) | ||
| \(=y_1-t_1\) |
計算の過程で、\(\bs{t}\) が確率ベクトルであることから、\(t_1+t_2+t_3=1\) を使いました。この計算は \(x_2,\:\:x_3\) についても全く同様にできます。それを含めてまとめると、
\(\dfrac{\partial L}{\partial x_1}=y_1-t_1\)
\(\dfrac{\partial L}{\partial x_2}=y_2-t_2\)
\(\dfrac{\partial L}{\partial x_3}=y_3-t_3\)
となります。この結果、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=\bs{y}-\bs{t}\)
という、大変シンプルな形になりました。これは任意の次元のベクトルで成り立ちます。実は、このようなシンプルな形になるように、\(\mr{Softmax}\) と 交差エントロピー誤差が設計されています。図示すると次の通りです。
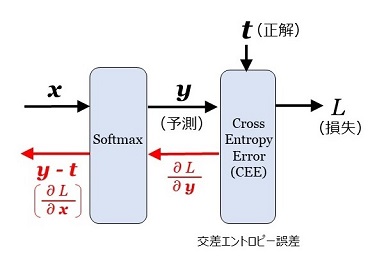
|
図10:Softmax + CEE の逆伝播 |
\(\mr{Softmax}\) 関数の後ろに交差エントロピー誤差を重ねると、\(\bs{x}\) の勾配は \(\bs{y}\) と \(\bs{t}\)(教師ラベル)から直接に求まる。 |
ニューラル・ネットワークの誤差逆伝播
以上で「確率を推定するニューラル・ネットワーク」を構成する各レイヤーの誤差逆伝播が計算できました。これらをまとめると、次の図11になります。
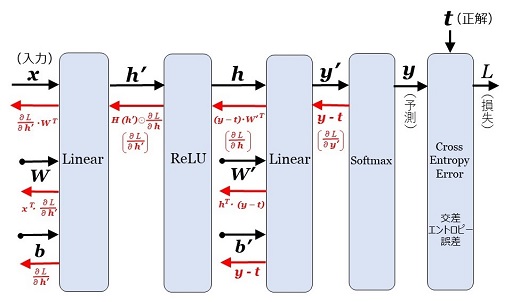
|
図11:クラス分類問題の誤差逆伝播 |
ちなみに、第1層の重み \(\bs{W}\) の勾配は図11から陽に計算すると、次のようになります。
\(\dfrac{\partial L}{\partial\bs{W}}=\bs{x}^T(H(\bs{x}\bs{W}+\bs{b})\odot((\bs{y}-\bs{t})\bs{W}\,'))\)
このネットワークは隠れ層が1つだけというシンプルなものですが、今までの計算で分かるように、層数が何百層に増えたとしても、逆伝播を多段に重ねることで、誤差逆伝播法が成立します。
また、図11 で使っているレイヤーは、Linear、\(\mr{ReLU}\)、\(\mr{Softmax}\)、Cross Entropy Error ですが、これらを関数と見なしたとき、誤差逆伝播で使った数学的な前提は「関数がパラメータで微分可能」ということだけです。つまり、レイヤーの関数が微分可能である限り、誤差逆伝播法は有効です。
実は、実用的なニューラル・ネットワークで誤差逆伝播法をうまく機能させるためには、数々の工夫が必要です。また、一般に訓練データの数は膨大なので、学習速度を上げる工夫も必要です(以降でその一部を説明します)。上で述べた「初期値の選択」や「学習率」はその工夫の一つです。そういったことはありますが、ネットワークがいかに巨大になろうとも(大規模言語モデルはその巨大な典型です)、誤差逆伝播法は可能なことが分かっています。
以上が、「ニューラル・ネットワークが学習可能である」ということの原理です。
\(\mr{GELU}\)
最近の大規模言語モデル(GPT など)では、活性化関数 \(\mr{ReLU}\) の代わりに \(\mr{GELU}\) \((\)Gaussian Error Linear Unit:ガウス誤差線形ユニット\()\) が使われます。その方が、学習が効率的に進むことが分かったからです。
|
\(\mr{ReLU}(x)=H(x)x\)
でしたが、\(\mr{GELU}\) は、
\(\mr{GELU}(x)=\Phi(x)x\)
で定義されます。\(\Phi(x)\) は標準正規分布(平均 \(0\)、標準偏差 \(1\))の累積分布関数です。標準正規分布の確率密度を \(f(x)\) とすると、
\(f(x)=\dfrac{1}{\sqrt{2\pi}}\mr{exp}\left(-\dfrac{x^2}{2}\right)\)
です(図12)。つまり \(x\) ~ \(x+dx\) である事象が発生する確率が \(f(x)dx\) です。また \(-\infty\) ~ \(\infty\) の範囲で積分すると \(1\) で、原点を中心に左右対称です。
|
\(\Phi(x)=\displaystyle\int_{-\infty}^{x}f(t)dt\)
です(図13)。これは正規分布に従うデータ値が \(x\) 以下になる確率です。これはガウスの誤差関数(Gaussian error function)\(\mr{Erf}\) を用いて表現できます。\(\Phi(0)=0.5\) となることを使って計算すると、
\(\begin{eqnarray}
&&\:\:\Phi(x)&=\displaystyle\int_{-\infty}^{x}f(t)dt\\
&&&=\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
\end{eqnarray}\)
\(t\:\rightarrow\:\sqrt{2}u\) の変数変換をすると、
\(\begin{eqnarray}
&&\:\:\phantom{\Phi(x)}&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)\sqrt{2}du\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)du\\
&&&=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\\
\end{eqnarray}\)
となります。ガウスの誤差関数、\(\mr{Erf}()\) の定義は
\(\mr{Erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_{0}^{x}\mr{exp}(-u^2)du\)
です。従って、
\(\Phi(x)=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\)
|
\(\mr{GELU}\) は \(\mr{ReLU}\) と良く似ていますが、すべての点で微分可能であり、\(\mr{ReLU}\) のように微係数がジャンプするところがありません。このことが、大規模言語モデルの効率的な学習に役だっていると考えられます。
残差結合
Linear レイヤーを例にとります。入力を \(\bs{x}\)、出力を \(\bs{y}\) とし、入力と出力のベクトルの次元は同一とします。重みを \(\bs{W}\) とし、バイアス \(\bs{b}\) は省略します。通常の Linear レイヤーは、
\(\bs{y}=\bs{x}\bs{W}\)
ですが、
\(\bs{y}=\bs{x}\bs{W}+\bs{x}\)
とするのが、「残差結合(residual connection)」をもつ Linear レイヤーです。なお「残差接続」とも言います。また「スキップ接続(skip connection)」も同じ意味です。

|
図15:残差結合 |
誤差逆伝播を計算すると、\(\bs{x}\) の勾配は次のようになります。2次元ベクトルの場合で例示します。
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+x_1\)
\(y_2=x_1w_{12}+x_2w_{22}+x_2\)
| \(\dfrac{\partial L}{\partial x_1}\) | \(=\dfrac{\partial y_1}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_2}\) | |
| \(=\dfrac{\partial L}{\partial y_1}w_{11}+\dfrac{\partial L}{\partial y_2}w_{12}+\dfrac{\partial L}{\partial y_1}\) | ||
| \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}\\w_{12}\\\end{array}\right)+\dfrac{\partial L}{\partial y_1}\) |
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)+\dfrac{\partial L}{\partial y_2}\)
従って、
| \(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\) | \(\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\) | |
| \(+\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) |
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T+\dfrac{\partial L}{\partial\bs{y}}\)
です。つまり、勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が、逆伝播でそのまま \(\dfrac{\partial L}{\partial\bs{x}}\) に伝わります(図\(16\))。

|
図16:残差結合の誤差逆伝播 |
一般にニューラル・ネットワークの学習を続けると、重みがゼロに近づき、その結果 \(\dfrac{\partial L}{\partial\bs{x}}\) が \(0\) に近い小さな値となることがあります。\(\dfrac{\partial L}{\partial\bs{x}}\) は、その一つ前への逆伝播の入力となるので、多層のニューラル・ネットワークでこれが重なると、前の方の層の勾配が極小になり、重みが更新できないという事態になります。これが「勾配消失」で、ニューラル・ネットワークの学習が困難になります。
残差結合を用いると、この問題を解決できます。Transformer では残差結合が使われています。
正規化
Transformer で使われているもう一つのレイヤーが「レイヤー正規化(Layer Normalization)」です。これは、ベクトル \(\bs{x}\:[1\times N]\) の要素を、平均 \(0\)、標準偏差 \(1\) のベクトル \(\bs{y}\:[1\times N]\) の要素に置き換えるものです。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
| \(x_i\) の平均 | : \(\mu\) | |
| \(x_i\) の標準偏差 | : \(\sg\) |
\(\mu=\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}x_i\)
\(\sg=\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\mu)^2}\)
とおくと、
\(y_i=\dfrac{1}{\sg}(x_i-\mu)\)
となります。実際にニューラル・ネットワークで使われるときには、さらにベクトルの要素ごとに線形変換をして、
\(y_i\:\longleftarrow\:g_iy_i+b_i\)
とします。ベクトルで表現すると、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\)
です。この \(\bs{g}\) と \(\bs{b}\) は学習可能なパラメータです。つまり、ニューラル・ネットワークの訓練のときに学習をして、最適値を決めます。もちろん、レイヤー正規化の式は微分可能なので、逆伝播計算が(少々複雑な式になりますが)可能です。
レイヤー正規化は、ニューラル・ネットワークを安定化させ、学習の効率化に役立ちます。その理由ですが、中間層の活性化関数で一般的な \(\mr{ReLU}\) 関数は、\(x=0\) の付近で非線型関数であり、それ以外では線型です。ニューラル・ネットワークは全体としては非線型関数で、そこにこそ意義があるのですが、その非線型性を生み出しているのは、\(x=0\) 付近の \(\mr{ReLU}\) 関数です。
従って、レイヤーの値を「ゼロ付近に集める」と、ニューラル・ネットワークの非線型性を強めることができ、これが学習の効率化につながります。その「ゼロ付近に集める」のがレイヤー正規化です。
以上の、
・\(\mr{ReLU}\) 関数(または \(\mr{GELU}\) 関数)
・残差結合
・正規化
は、大規模ニューラル・ネットワークを安定的に学習可能にするための必須技術であり、Transformer や GPT でも使われています。
| 2.自然言語のモデル化 |
単語への分解
自然言語で書かれたテキストをコンピュータで扱うとき、まずテキストを単語の系列に分解しなければなりません。系列とは「並び順に意味のある、同質の要素の集合」です。単語への分解は、単語の区切りを明示する英語(や、その他の欧米語)では容易です。文末を表すピリオドや、その他の記号も1つの単語と数えます。
日本語は単語の区切りがないので、形態素解析ソフトで単語に分解します。句読点、「、」などの記号も、それぞれ1単語と数えます。日本語の形態素解析ソフトは各種ありますが、オープンソースの MeCab が有名です。
大規模言語モデルは、世界中から集めた Webのテキスト(以下、WebText と言います)や Wikipedia、電子ブックなどを訓練データとして学習しますが、そこに出てくる単語を集めて「語彙の集合」を作ります。この集合のサイズを \(V\) とすると(たとえば、5万とか10万とかの値)、単語に \(1\)~\(V\) のユニークな番号を振ることができます。この番号を「単語ID」と呼びます。
なお、大規模言語モデルでは内部処理用として「特殊単語」も用います。以降の説明で使うのは、
[BOS] :文の開始
[EOS] :文の終了。ないしは文の区切り。
です。こうすると、テキスト \(\bs{T}\) は、
\(\bs{T}=\{x_1,\:x_2,\:x_3,\:\cd\:x_T\}\)
という単語IDの列で表現できることになります。もしこれが完結した文だとすると、\(x_1=\)[BOS]、\(x_T=\)[EOS] であり、複文だと途中にも [BOS] や [EOS] が出てくることになります。
単語IDは、その数字自体には意味がありません。また、語彙集合(要素数 \(V\))が増大すると単語IDの最大値も変化します。上の数字列は、あくまで「1時点での語彙集合をもとにして恣意的に付けられた数字の列」です。
分散表現
テキストをニュラール・ネットワークで扱うためには、すべての単語を、語彙集合のサイズにはよらない「固定長のベクトル」で表現するのが必須です。ここで使われるのが単語の「分散表現」で、固定長であるのみならず、"単語の意味もくみ取った" 表現です。ベクトルの次元は、たとば 512次元とか 1024次元です。
単語を分散表現にすることを "単語埋め込み"(word embedding)と言います。単語埋め込みの手法は各種ありますが、ここでは「word2vec」のアルゴリズムを例にとります。word2vec は、Google が2013年に提案したもので、実用的な分散表現の嚆矢となったものです。
word2vec に限りませんが、単語埋め込みのアルゴリズムの前提となっている仮定があります。それは、
単語の意味は、周囲の単語によって形成される
というもので、これを「分布仮説」と言います。たとえば、英文を例にとり、「周囲」を仮に「前1語、後1語」とします。
[I] [ ] [beer]
という文で [ ] に入る1単語は何かです。1単語に限定すると、冠詞(a, the)は入れようがないので、入る単語は限定されます。たとえば、
| [beer] (私はビール飲みます:習慣) | |
| [beer] (ビールはガブ飲みします:習慣) | |
| [beer] (ビールが大好きです:嗜好) | |
| [beer] (ビールは大嫌いです:嗜好) |
などです。[ ] には「飲む」に関係した動詞か「嗜好」に関係した動詞が入る可能性が高い。少なくとも「私とビールの関わりについての動詞」です。つまり、入る単語は「前後の1語によって意味が限定される」わけです。もしこれが「前後5語」とか「前後10語」であると「似たような意味の単語」か、少なくとも「同じジャンルの単語」になるはずです。
word2vec という「単語埋め込みアルゴリズム」には2種類あり、「周囲の単語から中心の単語を推論する(CBOW)」と「中心の単語から周囲の単語を推論する(skip-gram)」の2つです。推論にはニューラル・ネットワークを使います。以下は CBOW(Continuous Bag of Words)のネットワーク・モデルで説明します。
word2vec(CBOW)
CBOW は「周囲の単語から中心の単語を推論する」ニューラル・ネットワークのモデルです。「周囲の単語」を "コンテクスト" と呼び、推論の対象とする単語を "ターゲット" と呼びます。
まず、コンテクストのサイズを決めます。ターゲットの前の \(c\) 語、ターゲットの後ろの \(c\) 語をコンテクストとする場合、この \(c\) を "ウィンドーサイズ" と呼びます。そして "ウィンドー" の中には \(2c\) 語のコンテクストと1つのターゲットが含まれます。そして、訓練データとする文の "ウィンドー" を1単語ずつずらしながら、コンテクストからターゲットを推論する学習を行います。
語彙集合の単語数を \(V\) とし、一つの文を、
\(\bs{T}=\{x_1,\:x_2,\:\cd x_T\}\)
\(x_i\) :単語ID \((1\leq x_i\leq V)\)
とします。そして、\(x_i\) に1対1に対応する、\(V\)次元の one hotベクトルを、
\(\bs{x}_i=\left(\begin{array}{r}a_1,&a_2,&a_3,&\cd&a_V\\\end{array}\right)\)
\(a_j=0\:\:(j\neq x_i)\)
\(a_j=1\:\:(j=x_i)\)
とします。つまり \(\bs{x}_i\) は、\(x_i\) 番目の要素だけが \(1\) で、他は全部 \(0\) の \(V\) 次元ベクトルです(1つだけ \(1\)、が "one hot" の意味です)。
例として、ウィンドーサイズを \(c=2\) とします。また分散表現の単語ベクトルの次元を \(D\) とします。この前提で、\(\bs{T}\) の中の \(t\) 番目の単語の one hotベクトルを推論するモデルが図17です。
20E381AEE58D98E8AA9EE68EA8E8AB96E383A2E38387E383AB.jpg)
|
図17:word2vec(CBOW) の単語推論モデル |
\(\bs{T}=\{\:\cd,\:\bs{x}_{t-2},\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\bs{x}_{t+2},\:\cd\:\}\)
という単語の one hotベクトルの系列を想定したとき、 \(\bs{x}_t\) がターゲットの正解データ(=教師ラベル)であり、その他の4つがコンテクストです。
最初の MatMul (Matrix Multiply) レイヤーは、4つの one hotベクトル \(\bs{x}_i\) を入力とし、それぞれに重み行列 \(\bs{W}_{\large enc}\) をかけて、4つのベクトル \(\bs{h}_i\) を出力します(enc=encode)。つまり、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。Average レイヤーは、入力された複数ベクトルの平均をとり、一つのベクトル \(\bs{h}_t\) を出力します。この \(\bs{h}_t\) が \(\bs{x}_t\) の分散表現(= \(D\)次元ベクトル)です(というより、そうなるようにネットワークを訓練します)。
次の MatMul レイヤーで 重み \(\bs{W}_{\large dec}\) を掛け(dec=decode)、\(\mr{Softmax}\) レイヤーを通して、分散表現を \(V\) 次元の確率ベクトル \(\bs{y}_t\) に変換します。そして、教師ラベルである \(\bs{x}_t\) との間で交差エントロピー誤差を計算し、損失 \(L\) を求めます。
損失が求まれば、誤差逆伝播法で重み行列 \(\bs{W}_{\large enc}\) と \(\bs{W}_{\large dec}\) を修正します。この修正を、大量の文とそのすべてのウィンドーで行って、損失 \(L\) を最小化します。これがネットワークの訓練です。
訓練済みのネットワークでは、重み行列 \(\bs{W}_{\large enc}\:[V\times D]\) が、単語の分散表現の集積体になっています。つまり、one hot ベクトル \(\bs{x}_i\) の分散表現を \(\bs{h}_i\) とすると、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。\(\bs{x}_i\) の単語IDを \(x_i\) とすると、
\(\bs{h}_i=\bs{W}_{\large enc}\) の \(x_i\)行(\(1\)列から\(D\)列まで)
となります。
分散表現と単語の意味
「分布仮説」をもとに、ニューラル・ネットワークによる推論で得られた単語の分散表現ベクトルは、類似の意味の単語は類似のベクトルになる(ことが多い)ことが確認されています。たとえば、
year, month, day
などや、
car, automobile, vehicle
などです。ベクトルの類似は「コサイン類似度」で計測します。2つの2次元ベクトル、
\(\bs{a}=\left(\begin{array}{r}a_1&a_2\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
の場合で例示すると、
コサイン類似度\(=\dfrac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\)
で、2次元平面の2つのベクトルの角度(コサイン値)を求める式になります。この式の分子は内積(dot product)で、内積の定義式を変形したものです。この類似度を利用して「類推問題」が解けます。たとえば、
France : Paris = Japan : X
の X は何かという問題です。答えは Tokyo ですが、これを求めるには、分散表現ベクトルが類似しているという前提で、
| France | ≒ Japan | |
| Paris | ≒ X |
X = France + Paris - Japan
であり、X を \(\bs{W}_{\large dec}\) と \(\mr{Softmax}\) 関数を使って確率ベクトルに変換すれば、確率が最も高い単語が Tokyo になるはずというわけです。
もちろん、分散表現ベクトルで類推問題を解くのは完璧ではありません。分散表現を作るときのウィンドーのサイズと訓練データの量にもよりますが、各種の類推問題を作って実際にテストをすると、60%~70% の正解率になるのが最大のようです。
言語モデル
分散表現ベクトルを用いて「言語モデル」を構築します。いま、一つの文を構成する単語の並び、
\(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T\)
があったとき(\(\bs{x}_1=\)[BOS]、\(\bs{x}_T=\)[EOS])、この文が存在する確率を、
\(P(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T)\)
で表します。文法として間違っている文の確率はゼロに近く、また文法としては合っていても、意味をなさない文の確率は低い。
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\( > \:P(\)[BOS],[学校],[は],[彼女],[へ],[行く],[EOS]\()\)
といった具合です。この「存在確率」は、次のような「条件付き確率」で表現できます。つまり、
\(P_1=P(\)[彼女] | [BOS]\()\)
:文頭が「彼女」である確率
\(P_2=P(\)[は] | [BOS],[彼女]\()\)
:「彼女」の次が「は」である確率
\(P_3=P(\)[学校] | [BOS],[彼女],[は]\()\)
:「彼女は」の次が「学校」である確率
\(P_4=P(\)[へ] | [BOS],[彼女],[は],[学校]\()\)
:「彼女は学校」の次が「へ」である確率
\(P_5=P(\)[行く] | [BOS],[彼女],[は],[学校],[へ]\()\)
:「彼女は学校へ」の次が「行く」である確率
\(P_6=P(\)[EOS] | [BOS],[彼女],[は],[学校],[へ],[行く]\()\)
:「彼女は学校へ行く」で文が終わる確率
とすると、
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\(=P_1\times P_2\times P_3\times P_4\times P_5\times P_6\)
となります。つまり、一般的に、
\(P(\bs{x}_{t+1}\:|\:\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_t)\)
が分かれば、言語モデルは決まります。平たく言うと、
それまでの単語の系列から、次にくる単語の確率を推測する
のが言語モデルと言えます。もちろん、次にくる可能性のある単語は1つではありません。語彙集合のすべての単語それぞれについて「次にくる」確率を予測します。
実は、Transformer や GPT、ChatGPT がやっていることは「次にくる単語の予測」であり、これを実現しているのが、「超大規模なニューラル・ネットワークで作った言語モデル」なのです。
トークン
今まで、ニューラル・ネットワークでテキストを扱うためには、テキストを単語に分解するとしてきました。しかし大規模言語モデルで実際にやっていることは、テキストを「トークン(token)」に分解し、そのトークンの分散表現ベクトルを求めてニューラル・ネットワークで処理することです。
トークンとは、基本的には「単語」ないしは「単語の一部」です。英語ですと、たとえば頻出単語は「単語=トークン」ですが、GPT-3 の例だと、トークンには、ed, ly, er, or, ing, ab, bi, co, dis, sub, pre, ible などの「単語の一部」が含まれます。GPT-3 のトークンの語彙数は約5万ですが、そのうち英語の完全な単語は約3000と言われています。通常使われる英単語は4万~5万なので、3000の単語で WebText や Wikipedia の全部を表すことは到底できません。つまり、単語の "切れ端" と単語の組み合わせ、ないしは単語の "切れ端" 同士の組み合わせでテキストを表現する必要があります。
たとえば「ディスコ音楽」などの disco という単語は、[dis] [co] と表現します。edible(食用の、食べられる、という意味)は、[ed] [ible] です。disco や edible は 3000 単語の中に入っていないようです。edible などは「基本的な英単語」と思えますが、あくまで WebText や Wikipedia に頻出するかどうかの判断によります。
また xylophone(木琴)は、[x] [yl] [ophone] です。このように、1文字がトークンになることもあります。"単語"、"単語の切れ端"、"文字" がトークンです。
BPEによるトークン化
テキストをトークンに変換することを「トークン化(tokenize)」、トークン化を行うソフトを tokenizer と言います。ここで GPT-3 のトークン化のアルゴリズムの概要をみてみます。
上の xylophone → [x] [yl] [ophone] で明快なのですが、トークン化は単語の意味とは無関係です。意味を言うなら xylo("木の" という意味の接頭語)+ phone(音)ですが、そういうこととは全く関係ありません。
GPT-2 の論文にそのアルゴリズムである BPE(Byte Pair Encoding)が書かれています(GPT-3 は GPT-2 と同じだと、GPT-3 の論文にあります)。
コンピュータで文字を表現するには文字コード(文字に数字を割り振ったもの)を使います。国際的に広く使われているのは unicode です。unicode を使うと各国語の文字が統一的に文字コードで表現できます。
unicode の数字をコンピュータでどう表すか、その表し方(=エンコーディング)には3種類ありますが、その一つが UTF-8 です。UTF-8 は1バイト(8ビット、10進数で 0~255)を単位とし、1~4バイトで1文字を表現する可変長のエンコーディングです(漢字の異字体は5バイト以上になります)。
UTF-8 でば、通常の英文に使われる英数字、特殊文字(空白 , . ? など)は1バイトで表します。一方、日本語の平仮名、カタカナ、漢字は3バイトです(一部の漢字は4バイト)。バイトは文字ではありません。あくまで文字を表現するためのコンピュータ用の数字です。
BPE ではまず、UTF-8 でエンコーディングされた大量のテキストを用意します。そして、1バイトの全パターンを256種類の基本トークンとして語彙に初期登録します。トークン ID は 1~256 とします。従って、英文における1文字の単語( I, a )や記号( , . ? ! など)は、この時点でトークンID が割り当てられたことになります。
次に、テキストの「トークンのペア」で、最も出現頻度の高いペアをみつけます。英語で最も出現頻度が高い単語は the で、トークンで表現すると [t] [h] [e] です。仮に、[t] [h] のペアがテキスト中で最も出現頻度が高いとします(説明のための仮定です)。そうすると、この2つのトークンを結合した [th] を新たなトークン(トークン ID=257)として語彙に登録します。以降、テキスト中の [t] [h] は [th] と見なします。
次に出現頻度の高いペアが [th] [e] だとすると、この2つを結合した [the] を新たなトークン(トークン ID=258)として語彙に登録します。この段階で the という単語がトークンの語彙に登録されたわけです(以上の [th] [the] のトークン ID は説明のための数字で、実際の GPT-3 のトークン ID は違います)。
以上のプロセスにおいてトークンは、「空白をまたがない」「空白で終わらない」「同一カテゴリの文字(英字、数字、特殊文字など)でしかペアを作らない」などの制約をもうけておきます。「カテゴリ」が何かは論文に書いていないので想定です。もちろんこれは、なるべく頻出単語をトークンにする工夫です。
これを「結合の最大回数」になるで繰り返します。GPT-2 / GPT-3 の場合、最大回数は 50,000 です。従って、最終的には、
256 + 50,000 + 1 = 50,257
のトークンの語彙ができあがることになります。最後の + 1 は文末の記号 [EOS] を特殊トークンとしているからです。
いったん語彙ができあがると、以降、この語彙を使ってすべてのテキストを同じアルゴズムでトークン化します。当然ですが、長いバイトのトークンからテキストに割り当てることになります。
大規模言語モデルの成立要件
GPT-3 のトークン化のロジックによると、すべての言語のすべてのテキストが 50,257個のトークンを使って、統一的に、もれなくトークン化できることになります。それはあたりまえで、1バイトのデータがすべてトークンとして登録してあるからです。テキストを UTF-8 で統一的に表せば可能なのです。
ここで、日本語がどうなるかです。日本語の unicode を UTF-8 で表すと、漢字・仮名・文章記号は3バイトです(一部の漢字は4バイト。また異字体は5バイト以上)。ということは、普通の漢字1字、仮名1字は1~3トークンで表されることになります。
実際、OpenAI 社が公開している GPT-3 の Tokenizer で試してみると、
仮名は1~2トークン
ほとんどの漢字は2~3トークン
となります。ちなみに、平仮名(清音、濁音、半濁音、計71文字種)のトークン数を調べてみると、
28 文字種:1トークン
43 文字種:2トークン
です。濁音で1トークンになるのは「が だ で」の3つだけですが、これは助詞として頻出するからでしょう。特別の場合は、仮名2文字で1トークンになるようです(スト、ーク、など)。1トークンになる漢字はごく少数のようで、たとえば「上」「田」「中」「一」「大」がそうです(他にもあると思います)。
以上をまとめると、何をトークンとするかは、
・単語
・単語の一部、ないしは文字の連なり
・文字
・バイト
がありうるわけですが、GPT-3 のトークンにはこれらが混在していて、規則性は全くないことになります。ここから何が言えるかと言うと、
大規模言語モデルは、言語の文法や意味を関知しないのみならず、単語という概念さえなしでも成立しうる |
ということです。もちろん、英語を扱うときのように頻出単語のトークン化ができれば、生成されるテキストのクオリティーが向上することは確かでしょう。しかし、単語単位のトークン化は必須ではない。つまり、
単語の切れ端や文字どころか、文字を細分化した「バイト」をトークンとしても、その「バイト」には言語学的な意味が全く無いにもかかわらず、大規模言語モデルが、とりあえず成り立つ
わけです。GPT-3(= ChatGPT の基盤となっているモデル)がそれを示しています。大規模言語モデルは、翻訳、文章要約、質問回答、おしゃべり(chat)などの多様なタスクに使えます。これらのタスクを実現する仕組みを作るには、言語学的知識は全く不要です。不要というより、言語学的知識を持ち込むことは邪魔になる。もちろん、「翻訳、文章要約、質問回答、おしゃべり」の実例や好ましい例が大量にあるのが条件です。
その GPT-3 のベースになっているのは、Google が提案した Transformer という技術です。ということは、次のようにも言えます。
Transformer は「系列データ = 同質の記号・データが直列に並べられた、順序に意味のあるもの」であれば適用可能であり、その記号を文字としたのが大規模言語モデルである。もちろん、適用するには系列データの実例が大量にあることが必須である。 |
これが言えるのなら、少々先走りますが、Transformer はタンパク質の機能分析にも使える(可能性がある)ことになります。タンパク質はアミノ酸が鎖状に1列に並んだもので、そのアミノ酸は20種類しかありません。
タンパク質は「20種の記号の系列」であり、それが生体内で特定の機能を果たします。多数のタンパク質のアミノ酸配列を Transformer で学習し、タンパク質の機能と照らし合わせることで、新たなタンパク質の設計に役立てるようなことができそうです。実は、こういった生化学分野での Transformer や言語モデルの利用は、今、世界でホットな研究テーマになっています。
もちろん、系列データはタンパク質の構造だけではありません。従来から AI で扱われてきた音声・音源データや、各種のセンサーから取得したデータがそうだし、分子生物学では DNA / RNA が「4文字で書かれた系列データ」と見なせます。現に米国では、DNA / RNA の塩基配列を学習した大規模言語モデルでウイルスの変異予測がされています。
Transformer は、もともと機械翻訳のために提案されたものでした。しかしそれは意外なことに、提案した Google も予想だにしなかった "奥深い" ものだった。ここに、大規模言語モデルのサイエンスとしての意義があるのです。
(次回に続く)
タグ:正規分布 MLP ヘヴィサイド関数 単位ステップ関数 ReLU 活性化関数 多重パーセプトロン 標準偏差 積分 微分 指数関数 ベクトル 行列 ChatGPT 全結合 回帰問題 シナプス ニューロン GPT-3 GPT OpenAI Google transformer トークン 分散表現 大規模言語モデル 自然言語 バイアス 重み ニューラル・ネットワーク ガウス分布 分類問題 Softmax 損失 損失関数 交差エントロピー誤差 Cross Entropy Error 勾配 勾配降下法 ミニバッチ勾配降下法 確率的勾配降下法 誤差逆伝播法 標準正規分布 誤差関数 残差結合 GELU レイヤー正規化 パラメータ 単語埋め込み word2vec 分布仮説 コサイン類似度 BPE Byte Pair Encoding 系列データ バイト Unicode UTF-8 タンパク質 アミノ酸
2023-09-24 21:14
nice!(0)
No.364 - 言語の本質 [本]
No.344「算数文章題が解けない子どもたち」で、慶応義塾大学 環境情報学部教授の今井むつみ氏の同名の著作を紹介しました(著者は他に6名)。今回は、その今井氏が名古屋大学准教授の秋田喜美氏(言語心理学者)と執筆した『言語の本質 - ことばはどう生まれ、進化したか』(中公新書 2023。以下、"本書")を是非紹介したいと思います。共同執筆ですが、全体の核の部分は今井氏によるようです。
言うまでもなく、言語は極めて複雑なシステムです。それを、全くのゼロ(=赤ちゃん)から始まってヒトはどのように習得していくのか。本書はそのプロセスの解明を通して、言語の本質に迫ろうとしています。それは明らかに「ヒトとは何か」に通じます。
"言語の本質" とか "言葉とは何か" は、過去100年以上、世界の言語学者、人類学者、心理学者などが追求してきたものです。本書はその "壮大な" テーマを扱った本です。大風呂敷を広げた題名と思えるし、しかも新書版で約280ページというコンパクトさです。大丈夫なのか、見かけ倒しにならないのか、と疑ってしまいます。
しかし実際に読んでみると「言語の本質」というタイトルに恥じない出来映えの本だと思いました。読む立場としても幾多の発見があり、また個々の論旨の納得性も高い。以下に、内容の "さわり" を紹介します。
AI研究者との対話
本書で展開されている著者の問題意識のきっかけが、今井氏による「あとがき」に記されています。その部分を引用すると次の通りです。
少々意外なのですが、今井氏の問題意識の発端(の重要な点)は人工知能(AI)研究者との交流だったのですね。本書には、今井氏が自著の『ことばと思考』の冒頭部分を ChatGPT に英訳させた例が載っていて、今井氏は「ほとんど完璧」と書いています。しかし ChatGPT とヒトとの言葉の認識のあり方は全く違っていて、その違いも本書のテーマと結びついています。こういった記述は、今井氏の AI への関心が窺えます。
上の引用のキーワードは「記号接地(symbol grounding)」です。記号接地とは、記号(言語の場合は音の塊・並び)が人間の身体感覚(視覚、聴覚、触覚、心理感覚、・・・・・・ など)と結びつくことを言います。これが言語習得の第一歩だとするのが、本書の第1の主題です。それがオノマトペを例に説明されています。
オノマトペ
オノマトペとは、いわゆる擬音語、擬態語、擬情語(=「ワクワク」「ドキドキ」などの内的感覚・感情を表す語)の総称です。重複形が多いが、そればかりではありません(笑顔を表す擬態語に「ニコニコ」と「ニコッ」がある例)。オノマトペは、
感覚イメージを写し取る記号
と定義できます。ここでのキーワードは、まず「感覚」(視覚、聴覚、触覚、味覚など)です。オノマトペは、形容詞などと同じく "感覚" を表す言葉です。しかし形容詞には感覚("美しい")と、感覚ではないもの("正しい" などの理性的判断)の両方がありますが、感覚ではないオノマトペは考えにくい。"感覚" ではなく "感覚イメージ" と定義してあるのは、擬態語や擬情語を想定しているのでしょう。
もう一つのキーワードは「写し取る」です。表すもの(記号)と、それによって表されるものに類似性があるとき、その記号を「アイコン」と呼びます。アイコンは主として視覚によるもので、たとえばコンピュータ画面のゴミ箱のアイコンや、一般的に使われる笑顔のアイコン( ☺ )は、世界のだれが見てもゴミ箱や笑顔と見えます。
オノマトペもアイコンのように、表すもの(音形)と表されるもの(感覚イメージ)に類似性がある(=模倣性があると感じられる)記号です。このことを本書では "アイコン性" がある、と表現しています。"アイコン" ではなく "アイコン性" としてあるのは、視覚によるアイコンとは違って発音で "写し取る" ため、模倣性に限界があるからです。また、音による模倣は、言語体系がもつ母音・子音のバリエーションや音韻体系に大きく影響されます。アイコン、オノマトペ、オノマトペ以外の言葉の3つを対比させると、次のようになります。
音象徴
オノマトペを考える上で重要なことは、そもそも発音における "音" がアイコン性を帯びていることです。これを「音象徴」と言います。たとえば、清音と濁音の音象徴です。「コロコロ」より「ゴロゴロ」の方が大きくて重いものが転がる様子を表します。「サラサラ」より「ザラザラ」の方が荒くて不快な手触りを示す。「トントン」より「ドンドン」の方が、強い打撃が出すより大きな音を模倣します。g や z や d のような濁音は程度が大きいことを表し、またマイナスのニュアンスが伴いやすい音です。
母音の "あ" と "い" の音象徴もあります。打撃を表「パン」は平手でたたく感じで「ピン」は人差し指で弾くイメージであり、「パン」の方の打撃が大きい。水が飛び散る様子の「パチャパシャ」と「ピチャピチャ」も、「パチャパシャ」の方が飛び散る程度は大きいわけです。"あ" は大きいイメージと結びつき、"い" は小さいイメージと結びつきます。これは、発音のときの口腔の大きさに違いに起因します。
さらに、阻害音(p, t, k, s, d, g, z などの子音が入った音)は、硬く、尖って、角張ったイメージであり、共鳴音(m, n, y, r, w などの子音)は、柔らかく、なめらかで、丸っこい印象と結びつきます。この例として、次の図1を示して、
との質問をすると、多くの言語の多くの話者は「左側がマルマ」と答えます。
音象徴は、言語習得以前の赤ちゃんでも認められます。チリで行われた生後4ヶ月の赤ちゃんの実験では、親の膝の上に乗せられた赤ちゃんに、丸、楕円、四角、三角のどれかの図形を、大小をペアにしてスクリーン上に表示します。と同時に、様々な発音(音)を聞かせます。赤ちゃんの視線検知をすると、a を含む音を聞いたときは大きな図形の方を、i を含む音を聞いたときは小さな図形の方を見ることが分かりました。言語経験がほとんどない赤ちゃんですら、母音と図形大きさの関係に気づいているのです。
マルマとタケテの音象徴や、a と i の音象徴は、母語によらない共通性があります。しかし、ほとんどの音象徴は言語により個別です。たとえば、日本語においてカ行とタ行を含むオノマトペ、「カタカタ」「コトコト」「カチカチ」「コツコツ」は、いずれも硬いモノ同士の衝突音を表します。つまり、タ(t)、ト(t)、チ(ch)、ツ(ts)の子音が、音象徴で同じ意味と結びついている。
しかしこれは日本語ならではの音象徴です。たとえば英語では、titter は "忍び笑い"、chitter は "鳥のさえずり" で、t と ch が違う音象徴をもっています。
音がアイコン性をもつのが音象徴です。そしてアイコン性をもつ音の連なり=言葉がオノマトペであり、オノマトペが高度に発達した日本語や韓国語では、オノマトペこそ "身体で感じる感覚イメージを写し取る言葉" なのです。
言語の習得過程(1)
幼児の言語環境はオノマトペにあふれています。0歳児向けの絵本はオノマトペだけだし、0歳児・1歳児に対する親の語りかけもオノマトペが多用されます。そして2歳児以降になると、文や単語を修飾するオノマトペが増える。
そのオノマトペの発端が「音象徴」です。乳幼児は音象徴が認識できるかを著者が実験した結果が本書に書かれています。どうやって調べるのかというと、脳波の「N400 反応」をみます。
言葉を覚えたての1歳過ぎの幼児に知っている単語を聞かせ、同時にモノを見せたとき、単語とモノが合っているときと、単語とモノが違っているときでは脳波の反応が違います。たとえば、「イヌ」という音なのに絵はネコだとすると、音の始まりから400~500ミリ秒たったところで、脳の左右半球の真ん中付近の電位が下がります。これは大人でも単語と提示内容が不整合の場合にみられる反応で、N400反応と呼ばれています(N は Negative、400 は 400ミリ秒の意味)。
著者は、N400反応を利用して、言語習得前の生後11ヶ月の赤ちゃんのN400反応を調べました。次のような図形を用いた「モマ・キピ」実験です。
このように、ヒトの脳は音と対象の意味付けを生まれつき自然に行っています。これが、言葉の音(=記号)が身体に接地する第一歩になるのではないかというのが著者の意見です。
このことは、音の連なり(単語)にも意味があるという洞察につながります。さらには、対象それぞれに名前があるという "偉大な洞察" につながっていきます。
一般に、言葉の音からその意味を推測することはできません。「サカナ」という音の連なりは "魚" と何の関連性もありません。しかし、オノマトペは違います。「トントン」「ドンドン」(打撃音)や、「チョコチョコ」「ノシノシ」(歩く様子)などは、音が意味とつながっています。仮に「チョカチョカ」「ノスノス」とういう、現実には使われない "オノマトペ" を想定してみても、それが表す歩く様子は「チョコチョコ」「ノシノシ」と同じと感じられる。これは「サカナ」を「サカノ」にすると全く意味がとれなくなるのとは大違いです。
対象それぞれに名前があるというのは "偉大な洞察" だということを、著者はヘレン・ケラーのエピソードを引いて説明しています。
「ノスノス」実験
しかし、「対象それぞれに名前がある」という洞察から「語彙爆発」に向かうのは単純なことではありません。単純ではない一つの理由は、音の連なり(=言葉)で対象を説明されたとしても、その言葉が対象の「形」なのか「色」なのか「動作」なのかが曖昧だからです。実はここでも、感覚イメージを写し取るオノマトペが役だちます。著者は、3歳ぐらいの幼児に次の絵(図3)を見てせて動詞(=実際には使われない仮想的な動詞)を教える実験を紹介しています。
「ノスノス」は、人物を表すのではなく、動き(たとえば歩く)を表すのでもなく、動き方を表すのだと感覚的に分かるのです。このように、感覚と音が対応すると感じられる(アイコン性がある)オノマトペは言語学習の足場となり、手掛かりになるのです。
記号接地
もちろん、アイコン性のある言葉は言語学習の足場であって、最初の手掛かりに過ぎません。しかし言語という記号体系が意味を持つためには、基本的な一群の言葉の意味はどこかで感覚と接地(ground)していなければなりません。このことを指摘した認知科学者のハルナッドは、大人が中国語を学ぶ例をげて次のように説明しています。
辞書の定義だけから言葉の意味を理解しようとするのは、一度も地面に接地することなく「記号から記号への漂流」を続けるメリーゴーラウンドに乗っているようなものです。
その一方で、永遠に回り続けるメリーゴーラウンドを回避するためには、すべての言葉が身体感覚と接地している必要は全くありません。身体感覚とつながる言葉をある程度のボリュームで持っていれば、それらの言葉を組み合わせたり、それらとの対比や、また比喩や連想によって、直接の身体経験がなくても身体に接地したものとして言葉を覚えていくことができるのです。
身体感覚に接地する代表が音象徴であり、オノマトペですが、一般語にも音と意味の繋がりを感じるものがあることに注意すべきです。たとえば「かたい」「やわらかい」はオノマトペではありません。しかし「かたい」の k、t は硬い印象を与える音象徴があり(阻害音)、「やわらかい」は柔らかい印象の音象徴があります(共鳴音)。
「おおきい」「ちいさい」も同様で、大きい印象を与える "o" の長母音と、小さい印象を与える "i" が先頭音にあります。言葉を覚えたての幼児に親が絵本を読んで聞かせるとき、これらの言葉をどういう風に(大袈裟に)発音するかを想像してみたら、それは明確でしょう。
また「たたく(叩く)」「ふく(吹く)」「すう(吸う)」はオノマトペではありませんが、オノマトペの歴史研究によると、これらは「タッタッ」「フー」「スー」という擬音語に、古語における動詞化のための接尾辞「く」をつけたものです。「ひよこ」も、「ヒヨヒヨ」という擬音語に、可愛いものを表す接尾辞「こ」をつけたものです(「ワンコ」「ニャンコ」と同じ原理)。
こういった "隠れたオノマトペ" は非常にたくさんあり、"記号接地" の一助になっていると考えられます。また、このあたりはオノマトペが発達していない英語にも当てはまります。日本語なら「オノマトペ + 動詞」で表現するところを、英語では1語の動詞で表すのが一般的です。たとえば、英語の「話す・言う」ジャンルの言葉に、
などがありますが、これらは cha と チャにみられるように音象徴があります。
しかし、音象徴やオノマトペなどのアイコン性がある言葉があったとしても、基本的に言語は恣意的な記号の体系です。「日本国語大辞典」の見出し語は約50万語ですが、「日本語オノマトペ辞典」は、方言、古語を含んで 4500語です。多めに見積もったとしても、オノマトペは言葉の 1% に過ぎません。言語を習得するためには身体感覚とつながっているオノマトペから離れる必要があります。
そもそも言葉は抽象的で、記号とそれが表すものの関係は全く恣意的です。この恣意的な記号の膨大な体系をどうやって習得していくのか、それが本書の第2の主題です。
言語の習得過程(2)
子どもが言語を習得していく過程を観察すると「過剰一般化」の例がよくあります。具体的には、
の2つを学んだ子どもが、
事例がありました。「開ける」は多くの子どもが過剰一般化する有名な動詞です。上の例では子どもが "自分の欲しいモノや場所にアクセスしたいとき「あけて」と言えばよい" と過剰一般化したわけです。それは残念ながら、ミカンでは間違いになる(日本語環境では)。
英語の open も、多くの子どもが過剰一般化します。明かりやテレビをつけるときも "open" という子が多い。しかし中国語ではそれで正解です。中国語の「開」は、日本語の開けると同じ意味に加えて、電気をつけたり、パソコンのスイッチを入れたり、車を運転することにも使うからです(その "開" の意味の一部は漢字を通して日本語に入り、開始、開会、開業、開店、開校、開港、などと使われています。さすがに開車とは言いませんが)。
過剰一般化はあくまで "過剰" なので、子どもの暮らす言語環境では間違いです。しかし子どもは推論しているのです。みかんを剥くことも「あける」だろうと ・・・・・・。みかんの場合は間違いなので、親から「そういうときは、"むいて" と言うのよ」と直されるでしょう。しかしオモチャ箱のフタなら「あける」は正しいので、親は子どもの要望にそのまま応える。そのようにして子どもは言葉を覚えていく。
推論をするから過剰一般化が起きます。キーワードは "推論" であり、学習は丸暗記ではなく推論というステップを経たものなのです。その推論にもいろいろなタイプがありますが、言語習得の鍵となるのは「アブダクション推論」です。
アブダクション推論
論理学における推論は、一般には「演繹推論」と「帰納推論」ですが、アメリカの哲学者・パースはこれに加えて「アブダクション推論」を提唱しました。アブダクション推論は「仮説形成推論」とも言います。この3つの違いを本書での例で説明すると次の通りです(言い方を少々変えました)。
演繹推論
帰納推論
アブダクション推論
もちろん、常に正しい答えになるのは演繹推論だけです。しかし演繹推論は新しい知識を生みません。新しい知識を創造する(可能性がある)のは帰納推論とアブダクション推論です。
帰納推論は観察した事例での現象や性質が、その事例が属する集合の全体でも見い出されるとする推論です。つまり、部分を観察して全体に一般化する推論です。従って生み出される知識(= 一般化され普遍化された知識)は、部分としては既に観察されているものであり、とりたてて新しいものではありません。
それに対してアブダクション推論は、観察データを説明するための仮説を形成する推論です。この推論では、直接には観察できない何かを仮定し、直接観察したものとは違う種類の何かを推論します。従って、仮説が正しければ従来なかった新しい知識を獲得できます。上の例のアブダクション推論を分析すると、そもそも、
という仮説形成ができる理由は、もし A が正しいとすると、演繹推論(=常に正しい推論)によって、
が成り立つからです。つまり A → B を理解した上で、B から A を推論している(B → A)。アブダクション推論が「逆行推論」とも呼ばれるゆえんです。もちろん、A → B は常に正しいのですが、その反対の B → A が常に正しいわけではありません。従って A はあくまで「仮説」であって、仮説には検証が必要です。その検証をパスすると新知識の獲得になる。こういった類の推論がアブダクション推論 = 仮説形成推論です。
仮説形成推論の言語学習における役割について、本書ではヘレン・ケラーのエピソードも引きながら、次のように説明してあります。
「すべての対象には名前がある」という洞察は、さらに「名詞は形によって一般化される」「動詞は動作の類似性によって一般化される」という洞察につながっていきます。
アブダクション推論の具体例をもう少し考えてみます。子どものアブダクション推論は "言い間違い" によく現れます。たとえば、
と言った子どもがいました。もし大人が練乳を「イチゴの醤油だね」と言ったとしたら、それは意識的な比喩です。しかし子どもは「しょうゆ = 食品にかけておいしくするもの」という推論をした上で、"イチゴのしょうゆ" という "言い間違い" をしたわけです。
という間違いもあります。大人は「投げる」と「蹴る」は全く違う行為だと考えます。しかしよく考えてみると、両方とも「関節を曲げて伸ばすという行為によって何かを遠くへ飛ばす」という構造的類似性があります。子どもはその類似性による推論をして「足で投げる」になった。
言うまでもなく、アブダクション推論(と帰納推論)は常に検証・修正されなければなりせん。特に、アブダクション推論は過剰一般化と隣り合わせです。子どもは、ある時は推論=言い間違いを親から訂正され、またあるときは推論を親にすんなりと受け入れられ、そういう繰り返しで語彙を爆発的に増やしていくのです。
アブダクションの起源:ヒトと動物の違い
「すべての対象には名前がある」という気づきは、言語という記号体系を自分で構築していくための第1歩となる "偉大な" 洞察です。しかしこの洞察の背後には、暗黙に仮定されているもう一つの洞察があります。それは、
という洞察です。これはどういうことでしょうか。以下の説明では、モノをカタカナで、その発音をローマ字で記述します。
言葉を覚えたての幼児に、バナナとリンゴとミカンの名前を教えることを想定します。バナナを手にとって「これは banana」と教え、リンゴを手にとって「これは ringo」と教え、ミカンを手にとって「これは mikan」と教えます。何回かやると子どもは果物の名前を覚えます。そのあと、バナナを手にとって「これは ?」と問いかけると、子どもは「banana」と答える。リンゴ、ミカンについても同じです。つまり子どもは、バナナ → banana、リンゴ→ ringo、ミカン → mikan と覚えたわけです(モノ → 発音)。
この段階で、子どもの前にバナナとリンゴとミカンを置きます。そして「ringo はどれ?」と質問すると、こどもは間違いなくリンゴを手にするでしょう。バナナとミカンについても同じです。もし、自分の子どもがそれができない、つまり「ringo はどれ ?」と質問してもバナナを取ったりすると(あるいは、まごついて何もしないと)、親はショックを受けるでしょう。発達障害かと思ってパニックになるかもしれない。
子どもは、モノ → 発音 を習得すると、その裏で自動的に banana → バナナ、ringo→ リンゴ、mikan → ミカン という "逆の推論" をしています。これを「対称性推論」と言います。対象に名前があるということは、このような「形式(=名前)と対象の双方向性」を前提にしているのです。でないと "対象の名前" は意味がなくなる。
そんなこと当たり前だろうと思われるかもしれません。しかしそれは人間だから当たり前なのであって、動物では当たり前ではないのです。本書の著者の今井氏は、子どもが言葉を習得する過程を研究していますが、京都大学霊長類研究所の松沢教授とチンパンジー "アイ" の動画をみて驚愕しました。
人間は
記号→対象
を学習すると、同時に、
対象→記号
も学習します。つまり対象性推論を行います。もっと広く言うと、
XだからA
をもとに、
AだからX
という推論をします。たとえば、雨が降ったら道路が濡れる、という一般論をもとに、
と推論します。しかしこれはアブダクション推論であって、正確に言うと「雨が降ったという仮説形成をした」わけです。事実は、雨が降ったのではなく、向かいの家の人が水を撒いたのかもしれないし、放水車が通ったのかもしれない(そういった可能性はあくまで情況次第です)。
人間は「原因 → 結果」から「結果→原因」という推論をよくやります。もちろんこれは論理的には正しくない推論 = 非論理推論です。過剰一般化だともいえる。このようなアブダクション推論の一つとして、形式と対象の間の対称性推論があります。人間はそれを当然のように行う。しかし、動物は違います。
ヒトと祖先が同じであるチンパンジーはどうかというと「チンパンジーは種としては対称性推論をしない」ことが結論づけられています。ただし、京都大学霊長類研究所で "アイ" といっしょに飼育されていた "クロエ" という個体だけは対称性推論ができることが確認されています。
そこで疑問が起きます。ヒトの対称性推論はヒトがもともと持っている能力なのか、それともヒトが言語習得の過程で獲得する能力なのかです。今井氏は、前者が正しい、つまり、
という仮説をたて、それを検証するための実験を行いました。
乳児は対称性推論をするか
対象としたのは生後 8ヶ月の乳児、33人です。この段階の乳児は、音の連なりから単語(=音の固まり)を切り出す学習をしている段階で、知っている単語は極めて少なく、もし対称性推論ができたとしたら、それは言葉の学習の経験から得たものではないことが実証できます。
チンパンジーは対称性推論をするか
チンパンジーは他の動物と同じく、種としては対称性推論をしないことが分かっています。著者の今井氏は、乳児にやったのと同じ実験でこのことを確認しようと考えました。対象は京都大学霊長類研究所の7頭(成体)のチンパンジーです。
この実験は「チンパンジーは種としては対称性推論をしない」ことを再確認する結果となりました。ただし、非常に興味深いことに "クロエ" という個体だけは対称性推論をすることが示されました。これは京都大学霊長類研究所の以前の研究と整合的です。
この "クロエ" は「相互排他性推論」もできることが分かっています。相互排他性推論は、ヒトであれば言葉を覚えたての2歳以下の乳児でもできる推論です。つまり "コップ" という言葉は知っているが "ハニーディッパー" は知らない(=言葉もモノも知らない)子どもに対して、コップとハニーディッパーを目の前に置き「ハニーディッパーを取って」と言うと、子どもは躊躇なく、知らないはずのハニーディッパーを取ります。
つまり「未知の名前は自分が知らないものを指す」という推論が、2歳以下の子どもでもできるのです。これが相互排他性推論で、非論理推論と言えます。なぜなら「ピーラーを取って」でもハニーディッパーを取ることになるからです。ただし、「コップとハニーディッパーのどちらかを取ることが正しい」という前提があれば、極めて論理的な推論です。
"クロエ" だけが対称性推論や相互排他性推論といったアブダクション推論(=非論理推論)ができるということは、チンパンジーの中には少数の割合でそれができる個体がいると想像できます。ということは、アブダクション推論の萌芽がヒトとチンパンジーの共通祖先にすでにあり、ヒトの進化の過程でそれが徐々に形成され確立されていったという可能性が出てくるのです。
人類の進化
本書で、ヒトと動物の違いの説明があるのは「第7章 ヒトと動物を分かつもの」で、この章は全体のまとめである "終章" の前の最後の章です。その第7章の最後は「人類の進化」という見出しになっています。引用すると次の通りです。
人類(ホモ族)発祥の地・アフリカにおいて、チンパンジーは森に残り、霊長類で一般的な植物食、果実食に留まった。一方、東アフリカで乾燥化が進むサバンナの草原地帯に進出したホモ族は、そこでの狩猟採集というライフスタイルに突入し、そこから居住地を全世界に広げていった。それは、不確実な対象、直接の観察や経験が不可能な対象について推測・予測する必要がある生活であった。その結果、ヒトは言語を獲得して進化させ、その要因にアブダクション推論の進化があった、というのが本書の最後の論考ということになります。
「オノマトペ」から始まったはずの考察が、最後に「人類の進化」に行き着くのは驚きですが、そこが本書の魅力です。
感想
以上に紹介したのは本書(新書版で280ページ)の一部というか、"さわり" だけですが、「言語とは何か」を通して「ヒトとは何か」にまでに至る論考には感心しました。その際のキーワードは「記号接地」と「アブダクション推論」です。
「記号接地」に関しては、ヒトと AI の違いは何かが明確に答えられています。特に ChatGPT のような大規模言語モデルによる生成AI が創り出すテキストと人間の言語の違いです。逆にいうと ChatGPT が今後どういう方向を目指すのか、予想できると感じました。
「アブダクション推論」では、ヒトが他の動物と何が違うのか、その答え(の一つ)になっています。まさに「ヒトとは何か」に迫った論考で、特に「非論理的な推論をするからヒトなのだ」という主張です。アブダクション推論をはじめとする非論理的な推論は、言語システムの獲得に必須だし、また仮説形成が科学・技術の発達の原動力であることは言うまでもありません。
但し、その非論理的推論は、検証と修正にささえられています。言語獲得の場合は親との生活の中での(暗黙の)検証と修正の繰り返しだし、科学における仮説は、その正しさを証明する実験や分析が欠かせません。
原因から結果だけではなく、結果から原因を推論するのが人間の本性なのです。しかし検証と修正がない「結果 → 原因」推論は、社会レベルで考えると害悪をもたらします。そういった言説があふれている(メディアの発達がそれを加速している)のが現代社会という見立てもできると思いました。
本書は大変に有益な本ですが、残念なのは構成に難があることです。特に「第3章 オノマトペは言語か」です。ここでは、オノマトペは言語であるとの証明が長々と書かれています。
しかし、オノマトペがシスマティックに発達している日本語を使っている我々日本人にとって、オノマトペが言語なのはあたりまえです。おそらくオノマトペを "言語より一段低いもの" と見なす(ないしは "言語活動における枝葉末節" と見なす)欧米の言語学者への反論なのでしょうが、この章は余計でした。本書の英訳版を出すときに付け加えればよいと思いました。
さらに本書は、著者(今井氏)が過去からの探求の過程を振り返り、いろいろ考えると次々と疑問が沸いてくる、その疑問を解決してきた過程を発見的に書いている部分があります。それが悪いわけではありませんが、必然的に論旨が行き戻りすることがあり、もっとストレートに最新の研究成果に至る道を直線的に記述した方が、全体として分かりやすくなると思いました。ただ、これが本書の魅力と言えば魅力なのでしょう。
ともかく、本書は知的興奮を覚える本であり、久しぶりに読書の楽しみを味わいました。
本書の著者の今井むつみ氏が ChatGPT について書かれた文章を紹介します。子どもが言語を習得する過程に詳しい今井氏ならではの見方が出ています。
これは、岡野原大輔『大規模言語モデルは新たな知能か』(岩波書店 2023)の書評です。岡野原氏は日本の代表的なAI企業であるプリファード・ネットワークス社の共同創業者であり、同社の代表取締役最高研究責任者です。
「言語の本質」で展開されている議論に従うと、「ChatGPT は記号接地なしに、記号から記号への漂流を続ける生成 AI」です。それでも、ヒトとまともに会話したり、翻訳したりできます。今井氏も「言語の本質」の中で、"使わなければ損というレベルになっている" と評価していました。
しかし今井氏は、岡野原氏の「大規模言語モデルは新たな知能か」を読んで驚いたのでしょうね(たぶん)。ChatGPT の「注意機構」と「メタ学習」は、乳児が言語を獲得するプロセスと同じではないかと ・・・・・・。発達心理学のプロからすると、そう見えるのでしょう。
岡野原氏も本の中で書いていますが、メタ学習(学習のしかたを学習する)のポイントのなるのは「注意(Attention)機構」です。Google が開発した「トランスフォーマー」という技術は、この「注意機構」実装していました。それを利用して超大規模化モデルを作るとメタ学習まで可能になることを "偶発的に発見した"(岡野原氏)のが OpenAI です。Google や OpenAI の技術者が、当初は全く予想できなかったことが起こっている。
ヒトとは何かを突き詰めるためには、ヒトでないものも知らなければなりません。そのため「言語の本質」ではチンパンジーでの研究が書かれていました。しかし、大規模言語モデルによる生成AI も "ヒトでないもの" であり、しかもヒトと比較するレベルになっています。生成AIの研究がヒトとは何かを探求する一助になりうることを、今井氏の書評は言っているように思えました。
"言語の本質" とか "言葉とは何か" は、過去100年以上、世界の言語学者、人類学者、心理学者などが追求してきたものです。本書はその "壮大な" テーマを扱った本です。大風呂敷を広げた題名と思えるし、しかも新書版で約280ページというコンパクトさです。大丈夫なのか、見かけ倒しにならないのか、と疑ってしまいます。
しかし実際に読んでみると「言語の本質」というタイトルに恥じない出来映えの本だと思いました。読む立場としても幾多の発見があり、また個々の論旨の納得性も高い。以下に、内容の "さわり" を紹介します。
AI研究者との対話
本書で展開されている著者の問題意識のきっかけが、今井氏による「あとがき」に記されています。その部分を引用すると次の通りです。
| 以降の引用では、段落を増やしたところ、図の番号を修正したところや、漢数字を算用数字にしたところがあります。また下線は原文にはありません) |
|
少々意外なのですが、今井氏の問題意識の発端(の重要な点)は人工知能(AI)研究者との交流だったのですね。本書には、今井氏が自著の『ことばと思考』の冒頭部分を ChatGPT に英訳させた例が載っていて、今井氏は「ほとんど完璧」と書いています。しかし ChatGPT とヒトとの言葉の認識のあり方は全く違っていて、その違いも本書のテーマと結びついています。こういった記述は、今井氏の AI への関心が窺えます。
上の引用のキーワードは「記号接地(symbol grounding)」です。記号接地とは、記号(言語の場合は音の塊・並び)が人間の身体感覚(視覚、聴覚、触覚、心理感覚、・・・・・・ など)と結びつくことを言います。これが言語習得の第一歩だとするのが、本書の第1の主題です。それがオノマトペを例に説明されています。
オノマトペ
オノマトペとは、いわゆる擬音語、擬態語、擬情語(=「ワクワク」「ドキドキ」などの内的感覚・感情を表す語)の総称です。重複形が多いが、そればかりではありません(笑顔を表す擬態語に「ニコニコ」と「ニコッ」がある例)。オノマトペは、
感覚イメージを写し取る記号
と定義できます。ここでのキーワードは、まず「感覚」(視覚、聴覚、触覚、味覚など)です。オノマトペは、形容詞などと同じく "感覚" を表す言葉です。しかし形容詞には感覚("美しい")と、感覚ではないもの("正しい" などの理性的判断)の両方がありますが、感覚ではないオノマトペは考えにくい。"感覚" ではなく "感覚イメージ" と定義してあるのは、擬態語や擬情語を想定しているのでしょう。
もう一つのキーワードは「写し取る」です。表すもの(記号)と、それによって表されるものに類似性があるとき、その記号を「アイコン」と呼びます。アイコンは主として視覚によるもので、たとえばコンピュータ画面のゴミ箱のアイコンや、一般的に使われる笑顔のアイコン( ☺ )は、世界のだれが見てもゴミ箱や笑顔と見えます。
オノマトペもアイコンのように、表すもの(音形)と表されるもの(感覚イメージ)に類似性がある(=模倣性があると感じられる)記号です。このことを本書では "アイコン性" がある、と表現しています。"アイコン" ではなく "アイコン性" としてあるのは、視覚によるアイコンとは違って発音で "写し取る" ため、模倣性に限界があるからです。また、音による模倣は、言語体系がもつ母音・子音のバリエーションや音韻体系に大きく影響されます。アイコン、オノマトペ、オノマトペ以外の言葉の3つを対比させると、次のようになります。
| ☺ | アイコン (日本語話者以外も理解) |
| ニコニコ ニコッ |
アイコン性がある言葉 |
| えがお 笑顔 |
言葉 (日本語話者だけが理解) |
音象徴
オノマトペを考える上で重要なことは、そもそも発音における "音" がアイコン性を帯びていることです。これを「音象徴」と言います。たとえば、清音と濁音の音象徴です。「コロコロ」より「ゴロゴロ」の方が大きくて重いものが転がる様子を表します。「サラサラ」より「ザラザラ」の方が荒くて不快な手触りを示す。「トントン」より「ドンドン」の方が、強い打撃が出すより大きな音を模倣します。g や z や d のような濁音は程度が大きいことを表し、またマイナスのニュアンスが伴いやすい音です。
母音の "あ" と "い" の音象徴もあります。打撃を表「パン」は平手でたたく感じで「ピン」は人差し指で弾くイメージであり、「パン」の方の打撃が大きい。水が飛び散る様子の「パチャパシャ」と「ピチャピチャ」も、「パチャパシャ」の方が飛び散る程度は大きいわけです。"あ" は大きいイメージと結びつき、"い" は小さいイメージと結びつきます。これは、発音のときの口腔の大きさに違いに起因します。
さらに、阻害音(p, t, k, s, d, g, z などの子音が入った音)は、硬く、尖って、角張ったイメージであり、共鳴音(m, n, y, r, w などの子音)は、柔らかく、なめらかで、丸っこい印象と結びつきます。この例として、次の図1を示して、
| 一方が マルマ(maluma)で、一方が タケテ(takete)です。どちらがマルマで、どちらがタケテでしょうか」 |

|
図1:マルマとタケテ |
どちらが "マルマ" で、どちらが "タケテ" か |
音象徴は、言語習得以前の赤ちゃんでも認められます。チリで行われた生後4ヶ月の赤ちゃんの実験では、親の膝の上に乗せられた赤ちゃんに、丸、楕円、四角、三角のどれかの図形を、大小をペアにしてスクリーン上に表示します。と同時に、様々な発音(音)を聞かせます。赤ちゃんの視線検知をすると、a を含む音を聞いたときは大きな図形の方を、i を含む音を聞いたときは小さな図形の方を見ることが分かりました。言語経験がほとんどない赤ちゃんですら、母音と図形大きさの関係に気づいているのです。
マルマとタケテの音象徴や、a と i の音象徴は、母語によらない共通性があります。しかし、ほとんどの音象徴は言語により個別です。たとえば、日本語においてカ行とタ行を含むオノマトペ、「カタカタ」「コトコト」「カチカチ」「コツコツ」は、いずれも硬いモノ同士の衝突音を表します。つまり、タ(t)、ト(t)、チ(ch)、ツ(ts)の子音が、音象徴で同じ意味と結びついている。
しかしこれは日本語ならではの音象徴です。たとえば英語では、titter は "忍び笑い"、chitter は "鳥のさえずり" で、t と ch が違う音象徴をもっています。
音がアイコン性をもつのが音象徴です。そしてアイコン性をもつ音の連なり=言葉がオノマトペであり、オノマトペが高度に発達した日本語や韓国語では、オノマトペこそ "身体で感じる感覚イメージを写し取る言葉" なのです。
言語の習得過程(1)
幼児の言語環境はオノマトペにあふれています。0歳児向けの絵本はオノマトペだけだし、0歳児・1歳児に対する親の語りかけもオノマトペが多用されます。そして2歳児以降になると、文や単語を修飾するオノマトペが増える。
そのオノマトペの発端が「音象徴」です。乳幼児は音象徴が認識できるかを著者が実験した結果が本書に書かれています。どうやって調べるのかというと、脳波の「N400 反応」をみます。
言葉を覚えたての1歳過ぎの幼児に知っている単語を聞かせ、同時にモノを見せたとき、単語とモノが合っているときと、単語とモノが違っているときでは脳波の反応が違います。たとえば、「イヌ」という音なのに絵はネコだとすると、音の始まりから400~500ミリ秒たったところで、脳の左右半球の真ん中付近の電位が下がります。これは大人でも単語と提示内容が不整合の場合にみられる反応で、N400反応と呼ばれています(N は Negative、400 は 400ミリ秒の意味)。
著者は、N400反応を利用して、言語習得前の生後11ヶ月の赤ちゃんのN400反応を調べました。次のような図形を用いた「モマ・キピ」実験です。
|
図2:モマとキピ |
どちらが「モマ」で、どちらが「キピ」か |
|
このように、ヒトの脳は音と対象の意味付けを生まれつき自然に行っています。これが、言葉の音(=記号)が身体に接地する第一歩になるのではないかというのが著者の意見です。
このことは、音の連なり(単語)にも意味があるという洞察につながります。さらには、対象それぞれに名前があるという "偉大な洞察" につながっていきます。
一般に、言葉の音からその意味を推測することはできません。「サカナ」という音の連なりは "魚" と何の関連性もありません。しかし、オノマトペは違います。「トントン」「ドンドン」(打撃音)や、「チョコチョコ」「ノシノシ」(歩く様子)などは、音が意味とつながっています。仮に「チョカチョカ」「ノスノス」とういう、現実には使われない "オノマトペ" を想定してみても、それが表す歩く様子は「チョコチョコ」「ノシノシ」と同じと感じられる。これは「サカナ」を「サカノ」にすると全く意味がとれなくなるのとは大違いです。
対象それぞれに名前があるというのは "偉大な洞察" だということを、著者はヘレン・ケラーのエピソードを引いて説明しています。
|
「ノスノス」実験
しかし、「対象それぞれに名前がある」という洞察から「語彙爆発」に向かうのは単純なことではありません。単純ではない一つの理由は、音の連なり(=言葉)で対象を説明されたとしても、その言葉が対象の「形」なのか「色」なのか「動作」なのかが曖昧だからです。実はここでも、感覚イメージを写し取るオノマトペが役だちます。著者は、3歳ぐらいの幼児に次の絵(図3)を見てせて動詞(=実際には使われない仮想的な動詞)を教える実験を紹介しています。

|
図3:ノスノスしている |
ノスノスとはどういう動きを指す擬態語なのか |
|
「ノスノス」は、人物を表すのではなく、動き(たとえば歩く)を表すのでもなく、動き方を表すのだと感覚的に分かるのです。このように、感覚と音が対応すると感じられる(アイコン性がある)オノマトペは言語学習の足場となり、手掛かりになるのです。
記号接地
もちろん、アイコン性のある言葉は言語学習の足場であって、最初の手掛かりに過ぎません。しかし言語という記号体系が意味を持つためには、基本的な一群の言葉の意味はどこかで感覚と接地(ground)していなければなりません。このことを指摘した認知科学者のハルナッドは、大人が中国語を学ぶ例をげて次のように説明しています。
|
辞書の定義だけから言葉の意味を理解しようとするのは、一度も地面に接地することなく「記号から記号への漂流」を続けるメリーゴーラウンドに乗っているようなものです。
その一方で、永遠に回り続けるメリーゴーラウンドを回避するためには、すべての言葉が身体感覚と接地している必要は全くありません。身体感覚とつながる言葉をある程度のボリュームで持っていれば、それらの言葉を組み合わせたり、それらとの対比や、また比喩や連想によって、直接の身体経験がなくても身体に接地したものとして言葉を覚えていくことができるのです。
身体感覚に接地する代表が音象徴であり、オノマトペですが、一般語にも音と意味の繋がりを感じるものがあることに注意すべきです。たとえば「かたい」「やわらかい」はオノマトペではありません。しかし「かたい」の k、t は硬い印象を与える音象徴があり(阻害音)、「やわらかい」は柔らかい印象の音象徴があります(共鳴音)。
「おおきい」「ちいさい」も同様で、大きい印象を与える "o" の長母音と、小さい印象を与える "i" が先頭音にあります。言葉を覚えたての幼児に親が絵本を読んで聞かせるとき、これらの言葉をどういう風に(大袈裟に)発音するかを想像してみたら、それは明確でしょう。
また「たたく(叩く)」「ふく(吹く)」「すう(吸う)」はオノマトペではありませんが、オノマトペの歴史研究によると、これらは「タッタッ」「フー」「スー」という擬音語に、古語における動詞化のための接尾辞「く」をつけたものです。「ひよこ」も、「ヒヨヒヨ」という擬音語に、可愛いものを表す接尾辞「こ」をつけたものです(「ワンコ」「ニャンコ」と同じ原理)。
こういった "隠れたオノマトペ" は非常にたくさんあり、"記号接地" の一助になっていると考えられます。また、このあたりはオノマトペが発達していない英語にも当てはまります。日本語なら「オノマトペ + 動詞」で表現するところを、英語では1語の動詞で表すのが一般的です。たとえば、英語の「話す・言う」ジャンルの言葉に、
| (ペチャクチャ話す) | |
| (ヒソヒソ話す) | |
| (ブツブツ言う) | |
| (キャッと言う) |
などがありますが、これらは cha と チャにみられるように音象徴があります。
しかし、音象徴やオノマトペなどのアイコン性がある言葉があったとしても、基本的に言語は恣意的な記号の体系です。「日本国語大辞典」の見出し語は約50万語ですが、「日本語オノマトペ辞典」は、方言、古語を含んで 4500語です。多めに見積もったとしても、オノマトペは言葉の 1% に過ぎません。言語を習得するためには身体感覚とつながっているオノマトペから離れる必要があります。
そもそも言葉は抽象的で、記号とそれが表すものの関係は全く恣意的です。この恣意的な記号の膨大な体系をどうやって習得していくのか、それが本書の第2の主題です。
言語の習得過程(2)
子どもが言語を習得していく過程を観察すると「過剰一般化」の例がよくあります。具体的には、
| 閉まっているドアをあけて欲しいとき「あけて」と言う | |
| お菓子の袋をあけて欲しいとき「あけて」と言う |
の2つを学んだ子どもが、
| みかんを食べたいときにも「あけて」と言う |
事例がありました。「開ける」は多くの子どもが過剰一般化する有名な動詞です。上の例では子どもが "自分の欲しいモノや場所にアクセスしたいとき「あけて」と言えばよい" と過剰一般化したわけです。それは残念ながら、ミカンでは間違いになる(日本語環境では)。
英語の open も、多くの子どもが過剰一般化します。明かりやテレビをつけるときも "open" という子が多い。しかし中国語ではそれで正解です。中国語の「開」は、日本語の開けると同じ意味に加えて、電気をつけたり、パソコンのスイッチを入れたり、車を運転することにも使うからです(その "開" の意味の一部は漢字を通して日本語に入り、開始、開会、開業、開店、開校、開港、などと使われています。さすがに開車とは言いませんが)。
過剰一般化はあくまで "過剰" なので、子どもの暮らす言語環境では間違いです。しかし子どもは推論しているのです。みかんを剥くことも「あける」だろうと ・・・・・・。みかんの場合は間違いなので、親から「そういうときは、"むいて" と言うのよ」と直されるでしょう。しかしオモチャ箱のフタなら「あける」は正しいので、親は子どもの要望にそのまま応える。そのようにして子どもは言葉を覚えていく。
推論をするから過剰一般化が起きます。キーワードは "推論" であり、学習は丸暗記ではなく推論というステップを経たものなのです。その推論にもいろいろなタイプがありますが、言語習得の鍵となるのは「アブダクション推論」です。
アブダクション推論
論理学における推論は、一般には「演繹推論」と「帰納推論」ですが、アメリカの哲学者・パースはこれに加えて「アブダクション推論」を提唱しました。アブダクション推論は「仮説形成推論」とも言います。この3つの違いを本書での例で説明すると次の通りです(言い方を少々変えました)。
ちなみに、アブダクション(abduction)には「誘拐」「拉致」の意味があり(というより、それが第1義であり)、それとの混同を避けるため、「レトロダクション(retroduction)推論」が使われることも多いようです。
演繹推論
| この袋に入っている玉はすべて10g 以下である(一般論。前提)。 | |
| この玉は、この袋から取り出したものある(事実)。 | |
| この玉の重さは 10g 以下のはずだ(推論)。 |
帰納推論
| これらの玉はこの袋から取り出したものである(事実)。 | |
| これらの玉の重さはすべて 10g 以下である(事実)。 | |
| この袋に入っている玉は全部 10g 以下であろう(一般論の推論)。 |
アブダクション推論
| この袋に入っている玉はすべて10g 以下である(一般論。前提)。 | |
| これらの玉の重さはすべて 10g 以下である(事実)。 | |
| これらの玉はこの袋から取り出したものであろう(仮説形成)。 |
もちろん、常に正しい答えになるのは演繹推論だけです。しかし演繹推論は新しい知識を生みません。新しい知識を創造する(可能性がある)のは帰納推論とアブダクション推論です。
帰納推論は観察した事例での現象や性質が、その事例が属する集合の全体でも見い出されるとする推論です。つまり、部分を観察して全体に一般化する推論です。従って生み出される知識(= 一般化され普遍化された知識)は、部分としては既に観察されているものであり、とりたてて新しいものではありません。
それに対してアブダクション推論は、観察データを説明するための仮説を形成する推論です。この推論では、直接には観察できない何かを仮定し、直接観察したものとは違う種類の何かを推論します。従って、仮説が正しければ従来なかった新しい知識を獲得できます。上の例のアブダクション推論を分析すると、そもそも、
これらの玉はこの袋から取り出したものであろう(仮説形成=A)。
という仮説形成ができる理由は、もし A が正しいとすると、演繹推論(=常に正しい推論)によって、
これらの玉の重さはすべて 10g 以下である(観察された事実=B)
が成り立つからです。つまり A → B を理解した上で、B から A を推論している(B → A)。アブダクション推論が「逆行推論」とも呼ばれるゆえんです。もちろん、A → B は常に正しいのですが、その反対の B → A が常に正しいわけではありません。従って A はあくまで「仮説」であって、仮説には検証が必要です。その検証をパスすると新知識の獲得になる。こういった類の推論がアブダクション推論 = 仮説形成推論です。
仮説形成推論の言語学習における役割について、本書ではヘレン・ケラーのエピソードも引きながら、次のように説明してあります。
|
「すべての対象には名前がある」という洞察は、さらに「名詞は形によって一般化される」「動詞は動作の類似性によって一般化される」という洞察につながっていきます。
アブダクション推論の具体例をもう少し考えてみます。子どものアブダクション推論は "言い間違い" によく現れます。たとえば、
イチゴのしょうゆ(練乳の意味)
と言った子どもがいました。もし大人が練乳を「イチゴの醤油だね」と言ったとしたら、それは意識的な比喩です。しかし子どもは「しょうゆ = 食品にかけておいしくするもの」という推論をした上で、"イチゴのしょうゆ" という "言い間違い" をしたわけです。
足で投げる(蹴るの意味)
という間違いもあります。大人は「投げる」と「蹴る」は全く違う行為だと考えます。しかしよく考えてみると、両方とも「関節を曲げて伸ばすという行為によって何かを遠くへ飛ばす」という構造的類似性があります。子どもはその類似性による推論をして「足で投げる」になった。
言うまでもなく、アブダクション推論(と帰納推論)は常に検証・修正されなければなりせん。特に、アブダクション推論は過剰一般化と隣り合わせです。子どもは、ある時は推論=言い間違いを親から訂正され、またあるときは推論を親にすんなりと受け入れられ、そういう繰り返しで語彙を爆発的に増やしていくのです。
アブダクションの起源:ヒトと動物の違い
「すべての対象には名前がある」という気づきは、言語という記号体系を自分で構築していくための第1歩となる "偉大な" 洞察です。しかしこの洞察の背後には、暗黙に仮定されているもう一つの洞察があります。それは、
名前は形式と対象の双方向性から成り立っている
という洞察です。これはどういうことでしょうか。以下の説明では、モノをカタカナで、その発音をローマ字で記述します。
言葉を覚えたての幼児に、バナナとリンゴとミカンの名前を教えることを想定します。バナナを手にとって「これは banana」と教え、リンゴを手にとって「これは ringo」と教え、ミカンを手にとって「これは mikan」と教えます。何回かやると子どもは果物の名前を覚えます。そのあと、バナナを手にとって「これは ?」と問いかけると、子どもは「banana」と答える。リンゴ、ミカンについても同じです。つまり子どもは、バナナ → banana、リンゴ→ ringo、ミカン → mikan と覚えたわけです(モノ → 発音)。
この段階で、子どもの前にバナナとリンゴとミカンを置きます。そして「ringo はどれ?」と質問すると、こどもは間違いなくリンゴを手にするでしょう。バナナとミカンについても同じです。もし、自分の子どもがそれができない、つまり「ringo はどれ ?」と質問してもバナナを取ったりすると(あるいは、まごついて何もしないと)、親はショックを受けるでしょう。発達障害かと思ってパニックになるかもしれない。
子どもは、モノ → 発音 を習得すると、その裏で自動的に banana → バナナ、ringo→ リンゴ、mikan → ミカン という "逆の推論" をしています。これを「対称性推論」と言います。対象に名前があるということは、このような「形式(=名前)と対象の双方向性」を前提にしているのです。でないと "対象の名前" は意味がなくなる。
そんなこと当たり前だろうと思われるかもしれません。しかしそれは人間だから当たり前なのであって、動物では当たり前ではないのです。本書の著者の今井氏は、子どもが言葉を習得する過程を研究していますが、京都大学霊長類研究所の松沢教授とチンパンジー "アイ" の動画をみて驚愕しました。
|
人間は
記号→対象
を学習すると、同時に、
対象→記号
も学習します。つまり対象性推論を行います。もっと広く言うと、
XだからA
をもとに、
AだからX
という推論をします。たとえば、雨が降ったら道路が濡れる、という一般論をもとに、
家の前の道路が濡れていた → 雨が降ったのだろう
と推論します。しかしこれはアブダクション推論であって、正確に言うと「雨が降ったという仮説形成をした」わけです。事実は、雨が降ったのではなく、向かいの家の人が水を撒いたのかもしれないし、放水車が通ったのかもしれない(そういった可能性はあくまで情況次第です)。
人間は「原因 → 結果」から「結果→原因」という推論をよくやります。もちろんこれは論理的には正しくない推論 = 非論理推論です。過剰一般化だともいえる。このようなアブダクション推論の一つとして、形式と対象の間の対称性推論があります。人間はそれを当然のように行う。しかし、動物は違います。
|
ヒトと祖先が同じであるチンパンジーはどうかというと「チンパンジーは種としては対称性推論をしない」ことが結論づけられています。ただし、京都大学霊長類研究所で "アイ" といっしょに飼育されていた "クロエ" という個体だけは対称性推論ができることが確認されています。
そこで疑問が起きます。ヒトの対称性推論はヒトがもともと持っている能力なのか、それともヒトが言語習得の過程で獲得する能力なのかです。今井氏は、前者が正しい、つまり、
言葉を覚える前の乳児が対称性推論ができる
という仮説をたて、それを検証するための実験を行いました。
乳児は対称性推論をするか
対象としたのは生後 8ヶ月の乳児、33人です。この段階の乳児は、音の連なりから単語(=音の固まり)を切り出す学習をしている段階で、知っている単語は極めて少なく、もし対称性推論ができたとしたら、それは言葉の学習の経験から得たものではないことが実証できます。
|
図4:乳児の対称性推論の実験 |
|
チンパンジーは対称性推論をするか
チンパンジーは他の動物と同じく、種としては対称性推論をしないことが分かっています。著者の今井氏は、乳児にやったのと同じ実験でこのことを確認しようと考えました。対象は京都大学霊長類研究所の7頭(成体)のチンパンジーです。
|
この実験は「チンパンジーは種としては対称性推論をしない」ことを再確認する結果となりました。ただし、非常に興味深いことに "クロエ" という個体だけは対称性推論をすることが示されました。これは京都大学霊長類研究所の以前の研究と整合的です。
この "クロエ" は「相互排他性推論」もできることが分かっています。相互排他性推論は、ヒトであれば言葉を覚えたての2歳以下の乳児でもできる推論です。つまり "コップ" という言葉は知っているが "ハニーディッパー" は知らない(=言葉もモノも知らない)子どもに対して、コップとハニーディッパーを目の前に置き「ハニーディッパーを取って」と言うと、子どもは躊躇なく、知らないはずのハニーディッパーを取ります。
つまり「未知の名前は自分が知らないものを指す」という推論が、2歳以下の子どもでもできるのです。これが相互排他性推論で、非論理推論と言えます。なぜなら「ピーラーを取って」でもハニーディッパーを取ることになるからです。ただし、「コップとハニーディッパーのどちらかを取ることが正しい」という前提があれば、極めて論理的な推論です。
"クロエ" だけが対称性推論や相互排他性推論といったアブダクション推論(=非論理推論)ができるということは、チンパンジーの中には少数の割合でそれができる個体がいると想像できます。ということは、アブダクション推論の萌芽がヒトとチンパンジーの共通祖先にすでにあり、ヒトの進化の過程でそれが徐々に形成され確立されていったという可能性が出てくるのです。
本書にはない話ですが、NHK BSP の番組、ヒューマニエンス「"イヌ" ヒトの心を照らす存在」(2021年10月21日)で、麻布大学 獣医学部の菊水健史教授が "イヌは相互排他性推論をする" との主旨を語っておられました。
すべてのイヌ(ないしはほとんどのイヌ)なのか、一部のイヌなのかは覚えていません。ただこの番組は、家畜化に伴って現れたイヌの性質・性格や、ヒトとの類似性(幼形成熟など)、ヒトとイヌの深い絆の話だったので、「一般的に、訓練されたイヌは相互排他性推論をする」という主旨と考えられます。
本書で述べられているは、「一般に、動物は対称性推論をしない」ということでした。つまり「イヌは対称性推論をしない(できない)」ということになります。A → B を習得して 非A → 非B を推論するのが相互排他性推論ですが、対称性推論は B → A の推論であり、"逆行する推論" です。そこに難しさがあるのかもしれません。
すべてのイヌ(ないしはほとんどのイヌ)なのか、一部のイヌなのかは覚えていません。ただこの番組は、家畜化に伴って現れたイヌの性質・性格や、ヒトとの類似性(幼形成熟など)、ヒトとイヌの深い絆の話だったので、「一般的に、訓練されたイヌは相互排他性推論をする」という主旨と考えられます。
本書で述べられているは、「一般に、動物は対称性推論をしない」ということでした。つまり「イヌは対称性推論をしない(できない)」ということになります。A → B を習得して 非A → 非B を推論するのが相互排他性推論ですが、対称性推論は B → A の推論であり、"逆行する推論" です。そこに難しさがあるのかもしれません。
人類の進化
本書で、ヒトと動物の違いの説明があるのは「第7章 ヒトと動物を分かつもの」で、この章は全体のまとめである "終章" の前の最後の章です。その第7章の最後は「人類の進化」という見出しになっています。引用すると次の通りです。
|
人類(ホモ族)発祥の地・アフリカにおいて、チンパンジーは森に残り、霊長類で一般的な植物食、果実食に留まった。一方、東アフリカで乾燥化が進むサバンナの草原地帯に進出したホモ族は、そこでの狩猟採集というライフスタイルに突入し、そこから居住地を全世界に広げていった。それは、不確実な対象、直接の観察や経験が不可能な対象について推測・予測する必要がある生活であった。その結果、ヒトは言語を獲得して進化させ、その要因にアブダクション推論の進化があった、というのが本書の最後の論考ということになります。
「オノマトペ」から始まったはずの考察が、最後に「人類の進化」に行き着くのは驚きですが、そこが本書の魅力です。
感想
以上に紹介したのは本書(新書版で280ページ)の一部というか、"さわり" だけですが、「言語とは何か」を通して「ヒトとは何か」にまでに至る論考には感心しました。その際のキーワードは「記号接地」と「アブダクション推論」です。
「記号接地」に関しては、ヒトと AI の違いは何かが明確に答えられています。特に ChatGPT のような大規模言語モデルによる生成AI が創り出すテキストと人間の言語の違いです。逆にいうと ChatGPT が今後どういう方向を目指すのか、予想できると感じました。
「アブダクション推論」では、ヒトが他の動物と何が違うのか、その答え(の一つ)になっています。まさに「ヒトとは何か」に迫った論考で、特に「非論理的な推論をするからヒトなのだ」という主張です。アブダクション推論をはじめとする非論理的な推論は、言語システムの獲得に必須だし、また仮説形成が科学・技術の発達の原動力であることは言うまでもありません。
但し、その非論理的推論は、検証と修正にささえられています。言語獲得の場合は親との生活の中での(暗黙の)検証と修正の繰り返しだし、科学における仮説は、その正しさを証明する実験や分析が欠かせません。
原因から結果だけではなく、結果から原因を推論するのが人間の本性なのです。しかし検証と修正がない「結果 → 原因」推論は、社会レベルで考えると害悪をもたらします。そういった言説があふれている(メディアの発達がそれを加速している)のが現代社会という見立てもできると思いました。
本書は大変に有益な本ですが、残念なのは構成に難があることです。特に「第3章 オノマトペは言語か」です。ここでは、オノマトペは言語であるとの証明が長々と書かれています。
しかし、オノマトペがシスマティックに発達している日本語を使っている我々日本人にとって、オノマトペが言語なのはあたりまえです。おそらくオノマトペを "言語より一段低いもの" と見なす(ないしは "言語活動における枝葉末節" と見なす)欧米の言語学者への反論なのでしょうが、この章は余計でした。本書の英訳版を出すときに付け加えればよいと思いました。
さらに本書は、著者(今井氏)が過去からの探求の過程を振り返り、いろいろ考えると次々と疑問が沸いてくる、その疑問を解決してきた過程を発見的に書いている部分があります。それが悪いわけではありませんが、必然的に論旨が行き戻りすることがあり、もっとストレートに最新の研究成果に至る道を直線的に記述した方が、全体として分かりやすくなると思いました。ただ、これが本書の魅力と言えば魅力なのでしょう。
ともかく、本書は知的興奮を覚える本であり、久しぶりに読書の楽しみを味わいました。
| 補記:認知科学者がみる ChatGPT |
本書の著者の今井むつみ氏が ChatGPT について書かれた文章を紹介します。子どもが言語を習得する過程に詳しい今井氏ならではの見方が出ています。
これは、岡野原大輔『大規模言語モデルは新たな知能か』(岩波書店 2023)の書評です。岡野原氏は日本の代表的なAI企業であるプリファード・ネットワークス社の共同創業者であり、同社の代表取締役最高研究責任者です。
[この一冊] |
「言語の本質」で展開されている議論に従うと、「ChatGPT は記号接地なしに、記号から記号への漂流を続ける生成 AI」です。それでも、ヒトとまともに会話したり、翻訳したりできます。今井氏も「言語の本質」の中で、"使わなければ損というレベルになっている" と評価していました。
しかし今井氏は、岡野原氏の「大規模言語モデルは新たな知能か」を読んで驚いたのでしょうね(たぶん)。ChatGPT の「注意機構」と「メタ学習」は、乳児が言語を獲得するプロセスと同じではないかと ・・・・・・。発達心理学のプロからすると、そう見えるのでしょう。
岡野原氏も本の中で書いていますが、メタ学習(学習のしかたを学習する)のポイントのなるのは「注意(Attention)機構」です。Google が開発した「トランスフォーマー」という技術は、この「注意機構」実装していました。それを利用して超大規模化モデルを作るとメタ学習まで可能になることを "偶発的に発見した"(岡野原氏)のが OpenAI です。Google や OpenAI の技術者が、当初は全く予想できなかったことが起こっている。
ヒトとは何かを突き詰めるためには、ヒトでないものも知らなければなりません。そのため「言語の本質」ではチンパンジーでの研究が書かれていました。しかし、大規模言語モデルによる生成AI も "ヒトでないもの" であり、しかもヒトと比較するレベルになっています。生成AIの研究がヒトとは何かを探求する一助になりうることを、今井氏の書評は言っているように思えました。
(2023.8.26)
2023-08-26 09:08
nice!(0)
No.363 - 自閉スペクトラム症と生成AI [技術]
No.346「アストリッドが推理した呪われた家の秘密」で、NHK総合で放映中の「アストリッドとラファエル 文書係の事件簿」に関係した話を書きました("麦角菌" と『イーゼンハイムの祭壇画』の関係)。今回もその継続で、このドラマから思い出したことを書きます。現在、世界中で大きな話題になっている "生成AI" に関係した話です。
アストリッドとラファエル
「アストリッドとラファエル 文書係の事件簿」は、NHK総合 日曜日 23:00~ の枠で放映されているフランスの警察ドラマです。そのシーズン2の放映が2023年5月21日から始まりました。
アストリッドはパリの犯罪資料局に勤務する文書係の女性(俳優はサラ・モーテンセン)、ラファエルはパリ警視庁の刑事(警視)です(俳優はローラ・ドヴェール)。アストリッドは自閉スペクトラム症ですが、過去の犯罪資料に精通していて、また抜群の洞察力、推理力があります。一方のラファエルは、思い立ったらすぐに(捜査規律違反もいとわず)行動に移すタイプです。しかし正義感は人一倍強く、人間としての包容力もある女性刑事です。この全く対照的な2人がペアになって難事件を解決していくドラマです(サラ・モーテンセンの演技が素晴らしい)。
シーズン2 第6話「ゴーレム」(2023年6月25日)
この第6話で、ラファエル警視とペラン警部とアストリッドは、殺害された犯罪被害者が勤務していた AI 開発会社を事情聴取のために訪れます。会社の受付にはディスプレイ画面が設置されていて、受付嬢が写っていました。訪問者はその受付嬢と会話して、訪問相手を伝えたり、アポイントメントを確認します。もちろん殺人事件の捜査なのでアポなしであり、ラファエルとペランは受付を無視してオフィスの中に入っていきました。
しかしアストリッドはその受付嬢に興味を持ちました。実はそれはAIが創り出した "バーチャル受付嬢" で(名前はエヴ)、表情の変化や声は人間そっくりで、受付業務に必要な応対ができるのみならず、受付業務とは関係のない会話も来訪者とできて、質問に答えたりするのです。これは今で言うと、世界中で大きな話題になっている「大規模言語モデルによる生成AI」(ChatGPT や Bard など)と「画像生成AI」の複合体です。アストリッドは受付に留まって、エヴとの対話を続けました。
会社での事情聴取が終わったあと、アストリッドはラファエルの車で帰ります。そのときの2人の会話です。
エヴとの会話について、アストリッドの発言をまとめると、
となるでしょう。キーワードは「安心」と「共感」です。
自閉スペクトラム症(ASD)とは、自閉症やアスペルガー症など、かつては複数の診断名がついていたものを統合したものです。これらは境界線が引けるものではなく、光のスペクトルのように連続的に変化する症状がありうる。だから "スペクトラム" なのです。
NHKのホームページの「NHK健康チャネル」に簡潔な説明があります(https://www.nhk.or.jp/kenko/atc_346.html)。それによると自閉スペクトラム症は「自閉症」「高機能自閉症」「アスペルガー症候群」の総称であり、次のようになります。
このドラマにおいてアストリッドは極めて知的な人間として描かれています。記憶力は抜群だし、帰納的推論に長けていて、洞察力がある。そして強いこだわりがあります。その最たるものがパズルです。パズルを見ると解かずにはいられない。
ただし、人とのコミュニケーションが苦手で、その典型が人と共感できないことなのですね。その意味では、上の表ではアスペルガー症候群に近いわけですが、あくまで "スペクトラム" であって、簡単に分類できるものではありません。
ドラマは進行し、アストリッドは毎週参加している「社会力向上クラブ」の会合に出席しました。このクラブは、自閉スペクトラム症の人たち集まりで、主宰者はウィリアム・トマという人です。そのウィリアムとアストリッドの会話です。
アストリッドが「映画を見たり、詩を読んだり、夕日を見たときに、感動したことはありません。人工知能と同じです」と言っているのは、
ということであり、だから人工知能と同じなのです。知能の高低ではない。その意味で、ウィリアムとの会話は少々スレ違ってしまいました。アストリッドは、AI との会話が "安心で楽しかった" 自分がいて、そういう自分は AI と同じじゃないかと思い至り、それが自分が抱える問題だととらえたのです。
AI に心の相談をする
このドラマを見ていて、先日、新聞に掲載された東畑開人氏のコラムを思い出しました。
と題したコラムです。東畑開人氏は臨床心理士で、日本心理臨床学会常務理事です。
この中で東畑氏はまず、「何かあると、ひとまず ChatGPT に相談してしまう日々である」と書いています。見当違いな回答も多々あるが、
などとあります。東畑氏は臨床心理士であり、このコラムのテーマは「ChatGPT に心の問題、悩みを相談する」ということです。そのことについて、次にように書かれていました。
大規模言語モデル(LLM)を利用した生成AI については、今、さまざまな議論が行われていますが、この東畑氏のコメントは、生成AI と人々がどう関わるべきかについての本質(の一つ)をついたコメントだと思います。
アストリッドにとって、社会力向上クラブのメンバー以外で、何を言っても大丈夫と安心できる人間はごくわずかです。ラファエルと、シーズン2では、恋心を抱いたテツオ・タナカです(ちなみに彼も "夕日を見ても感動しない" と言ってました)。だからこそ、AI との対話が安心で心地よいものだったのです。
東畑氏のコメントに戻りますと、AIを活用したメンタルヘルスサービスが試みられているようです。
「AIを活用したメンタルヘルスサービス」は確かに有用と考えられます。但し、同時に "悪用されるリスク" も抱えているはずです。たとえば、心の悩みをもつ人を特定の宗教に "それとなく" "徐々に" 勧誘するようなAI が(作ろうと思えば)作れるでしょう。AI の訓練データ次第です。また極論すると "天国に行って楽になりましょう" 的な考えを植え付けることもできそうです。現にベルギーは AI メンタルサービスを使った人の自殺事件まで起きています。EU で議論されている生成AI の規制の検討はこういうことも踏まえているといいます。
人間は "心" をもっています。だから人と人とで共感できるし、困っている人を助けようともします。しかしそれと同時に、人を傷つけるようにも働きます。人間の "心" には AI にはない "弱さ"、"不安定さ"、"愚かさ" があるからです。
では、心の相談にとって人間と AI はどういう風に共存すべきか。その答えを東畑氏がもっているわけではないようですが、それは当然でしょう。そういった議論は、心の相談のみならず、各分野で始まったばかりなのだから。
ともかく、アストリッドが AI に抱いた「安心感」は、自閉スペクトラム症ではない健常者にとっても、"心の相談" を誰かにするときに必要な「安心感」に直結しています。東畑氏のコラムによって、そのことを強く感じました。
アストリッドとラファエル
「アストリッドとラファエル 文書係の事件簿」は、NHK総合 日曜日 23:00~ の枠で放映されているフランスの警察ドラマです。そのシーズン2の放映が2023年5月21日から始まりました。
アストリッドはパリの犯罪資料局に勤務する文書係の女性(俳優はサラ・モーテンセン)、ラファエルはパリ警視庁の刑事(警視)です(俳優はローラ・ドヴェール)。アストリッドは自閉スペクトラム症ですが、過去の犯罪資料に精通していて、また抜群の洞察力、推理力があります。一方のラファエルは、思い立ったらすぐに(捜査規律違反もいとわず)行動に移すタイプです。しかし正義感は人一倍強く、人間としての包容力もある女性刑事です。この全く対照的な2人がペアになって難事件を解決していくドラマです(サラ・モーテンセンの演技が素晴らしい)。
シーズン2 第6話「ゴーレム」(2023年6月25日)
この第6話で、ラファエル警視とペラン警部とアストリッドは、殺害された犯罪被害者が勤務していた AI 開発会社を事情聴取のために訪れます。会社の受付にはディスプレイ画面が設置されていて、受付嬢が写っていました。訪問者はその受付嬢と会話して、訪問相手を伝えたり、アポイントメントを確認します。もちろん殺人事件の捜査なのでアポなしであり、ラファエルとペランは受付を無視してオフィスの中に入っていきました。
しかしアストリッドはその受付嬢に興味を持ちました。実はそれはAIが創り出した "バーチャル受付嬢" で(名前はエヴ)、表情の変化や声は人間そっくりで、受付業務に必要な応対ができるのみならず、受付業務とは関係のない会話も来訪者とできて、質問に答えたりするのです。これは今で言うと、世界中で大きな話題になっている「大規模言語モデルによる生成AI」(ChatGPT や Bard など)と「画像生成AI」の複合体です。アストリッドは受付に留まって、エヴとの対話を続けました。
会社での事情聴取が終わったあと、アストリッドはラファエルの車で帰ります。そのときの2人の会話です。
|

|
エヴとの会話について、アストリッドの発言をまとめると、
| 的確な応答で、信頼できて、安心した。 | |
| 自閉スペクトラム症である私は、人と共感する能力がないとよく言われる。だからこそ、エヴとの会話が心地よかった。 |
となるでしょう。キーワードは「安心」と「共感」です。
自閉スペクトラム症(ASD)とは、自閉症やアスペルガー症など、かつては複数の診断名がついていたものを統合したものです。これらは境界線が引けるものではなく、光のスペクトルのように連続的に変化する症状がありうる。だから "スペクトラム" なのです。
NHKのホームページの「NHK健康チャネル」に簡潔な説明があります(https://www.nhk.or.jp/kenko/atc_346.html)。それによると自閉スペクトラム症は「自閉症」「高機能自閉症」「アスペルガー症候群」の総称であり、次のようになります。
| 自閉スペクトラム症 | |||
| 自閉症 | 症候群 |
||
| コミュニ | とても | 困難 | 少し困難 |
| 言葉の遅れ | ある | ある | ない |
| 知的障害 | ある | ない | ない |
| こだわり | ある | ある | ある |
このドラマにおいてアストリッドは極めて知的な人間として描かれています。記憶力は抜群だし、帰納的推論に長けていて、洞察力がある。そして強いこだわりがあります。その最たるものがパズルです。パズルを見ると解かずにはいられない。
ただし、人とのコミュニケーションが苦手で、その典型が人と共感できないことなのですね。その意味では、上の表ではアスペルガー症候群に近いわけですが、あくまで "スペクトラム" であって、簡単に分類できるものではありません。
ドラマは進行し、アストリッドは毎週参加している「社会力向上クラブ」の会合に出席しました。このクラブは、自閉スペクトラム症の人たち集まりで、主宰者はウィリアム・トマという人です。そのウィリアムとアストリッドの会話です。
|

|
アストリッドが「映画を見たり、詩を読んだり、夕日を見たときに、感動したことはありません。人工知能と同じです」と言っているのは、
普通の人が思っている "人間らしい心" がないと、他人からは思われる
ということであり、だから人工知能と同じなのです。知能の高低ではない。その意味で、ウィリアムとの会話は少々スレ違ってしまいました。アストリッドは、AI との会話が "安心で楽しかった" 自分がいて、そういう自分は AI と同じじゃないかと思い至り、それが自分が抱える問題だととらえたのです。
AI に心の相談をする
このドラマを見ていて、先日、新聞に掲載された東畑開人氏のコラムを思い出しました。
社会季評 AI に心の相談 弱さが生む人間の役割 朝日新聞(2023年6月22日) |
と題したコラムです。東畑開人氏は臨床心理士で、日本心理臨床学会常務理事です。
この中で東畑氏はまず、「何かあると、ひとまず ChatGPT に相談してしまう日々である」と書いています。見当違いな回答も多々あるが、
| 二日酔いの解決策を尋ねて、「お酒を飲まなければいいのです」と返ってきたときには脱力したが、 | |
| 悩みを打ち明けて、核心に迫るコメントをされたときには動揺した |
などとあります。東畑氏は臨床心理士であり、このコラムのテーマは「ChatGPT に心の問題、悩みを相談する」ということです。そのことについて、次にように書かれていました。
|
大規模言語モデル(LLM)を利用した生成AI については、今、さまざまな議論が行われていますが、この東畑氏のコメントは、生成AI と人々がどう関わるべきかについての本質(の一つ)をついたコメントだと思います。
アストリッドにとって、社会力向上クラブのメンバー以外で、何を言っても大丈夫と安心できる人間はごくわずかです。ラファエルと、シーズン2では、恋心を抱いたテツオ・タナカです(ちなみに彼も "夕日を見ても感動しない" と言ってました)。だからこそ、AI との対話が安心で心地よいものだったのです。
東畑氏のコメントに戻りますと、AIを活用したメンタルヘルスサービスが試みられているようです。
|
「AIを活用したメンタルヘルスサービス」は確かに有用と考えられます。但し、同時に "悪用されるリスク" も抱えているはずです。たとえば、心の悩みをもつ人を特定の宗教に "それとなく" "徐々に" 勧誘するようなAI が(作ろうと思えば)作れるでしょう。AI の訓練データ次第です。また極論すると "天国に行って楽になりましょう" 的な考えを植え付けることもできそうです。現にベルギーは AI メンタルサービスを使った人の自殺事件まで起きています。EU で議論されている生成AI の規制の検討はこういうことも踏まえているといいます。
人間は "心" をもっています。だから人と人とで共感できるし、困っている人を助けようともします。しかしそれと同時に、人を傷つけるようにも働きます。人間の "心" には AI にはない "弱さ"、"不安定さ"、"愚かさ" があるからです。
では、心の相談にとって人間と AI はどういう風に共存すべきか。その答えを東畑氏がもっているわけではないようですが、それは当然でしょう。そういった議論は、心の相談のみならず、各分野で始まったばかりなのだから。
ともかく、アストリッドが AI に抱いた「安心感」は、自閉スペクトラム症ではない健常者にとっても、"心の相談" を誰かにするときに必要な「安心感」に直結しています。東畑氏のコラムによって、そのことを強く感じました。
2023-07-15 10:38
nice!(0)
No.362 - ボロクソほめられた [文化]
先日の朝日新聞の「天声人語」で、以前に書いた記事、No.145「とても嬉しい」に関連した "言葉づかい" がテーマになっていました。今回は、No.145 の振り返りを含めて、その言葉づかいについて書きます。
「天声人語」:2023年 6月 11日
「天声人語」は例によって6段落の文章で、段落の区切りは▼で示されています。以下、段落の区切りを1行あけで引用します。
前例としての "とても"
注目したいのは、前半の3つの段落にある「ボロクソ」と「とても」です。女子中学生の「ボロクソほめられちゃった」という会話に驚いた天声人語子ですが(当然でしょう)、否定的な文脈で使う言葉を肯定的に使うのは過去に例があり、それが「とても」である。「とても」は、昔は否定的文脈で使われていて、そのエビデンスが芥川龍之介の文章にある。時が変われば正しい日本語も変化する、としているところです。
「天声人語」にあるように、「とても嬉しい」というような言い方が(東京地方で)広まった時期について、芥川龍之介が短文エッセイ集『澄江堂雑記』(1923 大正13)に書いています。「澄江堂」とは芥川龍之介自身の号です。
江戸時代の古典の(少々マニアックな)知識をさりげなく披露しつつ、三河言葉(=芥川の想像)が東京で使われるまでに200年かかったから「とても手間取つた」とのオチで終わるあたり、文章の芸が冴えています。ちなみに『猿蓑』は芭蕉一門の句集で、引用にあるように子尹は三河地方出身の俳人です。
それはともかく、芥川龍之介は「肯定的とても」が数年以前から東京で言われ出したと書いています。ということは、大正時代か明治末期からとなります。芥川龍之介は1892年(明治25年)に東京に生まれた人です。当然、小さい時から慣れた親しんだのは「とても出来ない」のような "否定的とても" であり、それが正しい標準語としての言葉使いと思っていたと想像できます。それは「とても嬉しい」のような "肯定的とても" が「田舎ことば」だとする書き方に暗示されています。
「とても」は否定的文脈で使うものだという言葉の規範意識は、芥川以降も続いていたようです。評論家・劇作家の山崎正和氏(1934-2020 。昭和9年-令和2年)は、丸谷才一氏との対談で次のように発言しています。
山崎正和氏が子供の頃というのは、昭和10年代から20年代半ばです。つまり、そのころ生きていた明治生まれの人(父方の祖母)には、「とても嬉しい」というような肯定的な使い方は誤用であるという規範意識が強くあった、ということなのです。少なくとも山崎家ではそうだった。今となっては想像できませんが ・・・・・・。
ところで、芥川龍之介のエッセイによって分かるのは「とても嬉しい」が明治末期、ないしは大正時代から東京で広まったことです。しかし、専門家の研究によると、遙か昔においては肯定的「とても」が一般的でした。
梅光学院大学・准教授の播磨桂子氏の論文に、『「とても」「全然」などにみられる副詞の用法変遷の一類型』(九州大学付属図書館)があり、そこに「とても」の歴史の研究があります。この論文によると「とても」の歴史は以下のように要約できます。
"肯定的とても" は、芥川龍之介が推測する三河方言ではなく、『平家物語』『太平記』『御伽草子』『好色一代女』にもある "由緒正しい" 言い方だったわけです。もちろん、由緒正しい言い方が方言だけに残るということもあり得ます。
ひょっとしたら、芥川はそれを知っていたのかもしれません。知っていながら「とても手間取つた」というオチに導くためにあえて『猿蓑』を持ち出した、つまり一種のジョークということも考えられると思います。
超・鬼・めちゃくちゃ
「とても」をいったん離れて、強調のための言葉について考えてみます。形容詞、動詞、名詞などを修飾して「程度が強いさま」を表す言葉を「強調詞」と呼ぶことにします。強調詞にはさまざまなもがあります。大変、非常に、全然、すごく、などがそのごく一部です。
漢字で書くと1字の「超」も、今ではあたりまえになりました。もちろんこれは超特急、超伝導など、名詞の接頭辞として由緒ある言葉で、「通常のレベルを遙かに超えた」という意味です。これが「超たのしい」「超カワイイ」などと使われるようになった(1960年代から広がったと言われています)。その「超」は、"本場" の中国に「逆輸出」され、「超好(超いい)」などと日常用語化しているといいます(日本経済新聞「NIKKEI プラス 1」2022年6月11日 による)。「超」はかなり "威力がある" 強調詞のようです。
漢字1字を訓読みで使う接頭辞もあって「鬼」がそうです。「鬼」はもともと名詞の接頭辞として「無慈悲」「冷酷」「恐ろしい」「巨大」「異形」「勇猛」「強い」などの意味を付加するものでした。「鬼将軍」「鬼軍曹」「鬼コーチ」「鬼検事」「鬼編集長」などです。栗の外皮を「鬼皮」と言いますが、強いという意味です。また「鬼」は動植物・生物の名前にも長らく使われてきました。同類と思われている生物同士の比較で、大きいものは「大・おお・オオ」を接頭辞として使いますが、それをさらに凌駕する大型種は「鬼・おに・オニ」を冠して呼びます。オニグモ(鬼蜘蛛)、オニユリ(鬼百合)、オニバス(鬼蓮)といった例です。
しかしこの数年、さらに進んで「鬼」を強調詞とする言い方が若者の間に出てきました。オニの部分をあえて漢字書くと、
・鬼かわいい
・鬼きれい
・鬼うまい(鬼おいしい)
・鬼むかつく
といった言い方です。もともとの「無慈悲」「冷酷」「恐ろしい」」「異形」などの否定的な意味はなくなり、「通常を凌駕するレベルである」ことだけが強調されています。これは「超」の使い方とそっくりです。この使い方が定着するのか、ないしは今後消えてしまうのかは分かりません。
さらに、もともと否定的文脈で使う「めちゃくちゃ」「めちゃめちゃ」「めっちゃ」「めちゃ」があります。「むちゃくちゃ」とも言います。これも江戸時代からある言葉で、漢字で書くと「滅茶苦茶」です。"混乱して、筋道がたたず、全く悪い状態" を指します言が、強調詞として使って「めちゃくちゃカワイイ」などと言います。
もともと否定的文脈で使う言葉という意味では、形容詞の「ものすごい(物凄い)」もそうです。これはもとは恐ろしいものに対してしか使わない言葉でした(西江雅之「ことばの課外授業」洋泉社 2003による)。確かに、青空文庫でこの言葉を検索すると、恐ろしいものの形容に使った文例しかありません。青空文庫は著作権が切れた(死後50年以上たった)作家の作品しかないので、「ものすごい美人」というような使い方は、少なくとも文章語としてはこの半世紀程度の間に広まった使い方であることは確実です(話し言葉としてはそれ以前から使われていたかもしれません)。
そこで「天声人語」の「ボロクソほめられた」です。これはもともと否定的文脈で使う言葉を、程度が大きいさまを表す強調詞とした典型的な例です。その意味で「とても」「めちゃくちゃ」「ものすごく」の系列につながっています。特に「めちゃくちゃ」に似ています。
と使うけども、
とも言います。であれば、
と使う一方で、
と言うのも、一般的ではないけれども、アリということでしょう。
強調詞の宿命
「とても」の変遷や、その他の言葉を見ていると、強調詞の "宿命" があるように思います。つまり、ある強調詞が広まってあたりまえに使われるようになると、それが "あまり強調しているようには感じられなくなる" という宿命です。
従って、新しい言葉が登場する。そのとき、否定的文脈で使われる言葉を肯定的に使ったり、名詞の接頭辞を形容詞を修飾する副詞に使ったりすると(超・鬼)、インパクトが強いわけです。特に、自分の思いや感情を吐露したい場合の話し言葉には、そういうインパクトが欲しい。そうして新語が使われだし、その結果一般的になってしまうと強調性が薄れ、また別の新語が使われ出す。
「天声人語」に引用された女子中学生の発言、「きのうさー、先生にさあ、ボロクソほめられちゃったんだ」も、よほど嬉しかったゆえの発言でしょう。天声人語子は「それにしても、あの女の子、うれしそうだったなあ」と書いていますが、今まで先生に誉められたことがなかったとか、あるいは、一生懸命努力して作ったモノとか努力して成し遂げたことを誉められたとか、内容は分からないけれど、そういうことが背景にあるのかも知れません。もちろん先生も言葉を重ねて誉めた。その子にとって「メッチャ、ほめられちゃった」や「チョー、ほめられちゃった」では、自分の感動を伝えるには不足なのです。
「ボロクソほめられた」は、一般的に広まることはないかもしれないけれど、個人的な言葉としては大いにアリだし、それは言葉の可能性の広さを表しているのだと思いました。
「天声人語」:2023年 6月 11日
「天声人語」は例によって6段落の文章で、段落の区切りは▼で示されています。以下、段落の区切りを1行あけで引用します。
|
前例としての "とても"
注目したいのは、前半の3つの段落にある「ボロクソ」と「とても」です。女子中学生の「ボロクソほめられちゃった」という会話に驚いた天声人語子ですが(当然でしょう)、否定的な文脈で使う言葉を肯定的に使うのは過去に例があり、それが「とても」である。「とても」は、昔は否定的文脈で使われていて、そのエビデンスが芥川龍之介の文章にある。時が変われば正しい日本語も変化する、としているところです。
「天声人語」にあるように、「とても嬉しい」というような言い方が(東京地方で)広まった時期について、芥川龍之介が短文エッセイ集『澄江堂雑記』(1923 大正13)に書いています。「澄江堂」とは芥川龍之介自身の号です。
|
江戸時代の古典の(少々マニアックな)知識をさりげなく披露しつつ、三河言葉(=芥川の想像)が東京で使われるまでに200年かかったから「とても手間取つた」とのオチで終わるあたり、文章の芸が冴えています。ちなみに『猿蓑』は芭蕉一門の句集で、引用にあるように子尹は三河地方出身の俳人です。
それはともかく、芥川龍之介は「肯定的とても」が数年以前から東京で言われ出したと書いています。ということは、大正時代か明治末期からとなります。芥川龍之介は1892年(明治25年)に東京に生まれた人です。当然、小さい時から慣れた親しんだのは「とても出来ない」のような "否定的とても" であり、それが正しい標準語としての言葉使いと思っていたと想像できます。それは「とても嬉しい」のような "肯定的とても" が「田舎ことば」だとする書き方に暗示されています。
「とても」は否定的文脈で使うものだという言葉の規範意識は、芥川以降も続いていたようです。評論家・劇作家の山崎正和氏(1934-2020 。昭和9年-令和2年)は、丸谷才一氏との対談で次のように発言しています。
|
山崎正和氏が子供の頃というのは、昭和10年代から20年代半ばです。つまり、そのころ生きていた明治生まれの人(父方の祖母)には、「とても嬉しい」というような肯定的な使い方は誤用であるという規範意識が強くあった、ということなのです。少なくとも山崎家ではそうだった。今となっては想像できませんが ・・・・・・。
ところで、芥川龍之介のエッセイによって分かるのは「とても嬉しい」が明治末期、ないしは大正時代から東京で広まったことです。しかし、専門家の研究によると、遙か昔においては肯定的「とても」が一般的でした。
梅光学院大学・准教授の播磨桂子氏の論文に、『「とても」「全然」などにみられる副詞の用法変遷の一類型』(九州大学付属図書館)があり、そこに「とても」の歴史の研究があります。この論文によると「とても」の歴史は以下のように要約できます。
| 「とても」は「とてもかくても」から生じたと考えられている。「とても」は平安時代から使われていて「どうしてもこうしても、どうせ、結局」という意味をもち、肯定表現にも否定表現にも用いられた。『平家物語』『太平記』『御伽草子』『好色一代女』などでの使用例がある。 | |
| しかし江戸時代になると否定語と呼応する使い方が増え、明治時代になると、もっぱら否定語と呼応するようになった。 | |
| さらに大正時代になると、肯定表現で程度を強調する使い方が広まり、否定語と呼応する使い方と共存するようになった。 | |
| 「否定」にも「肯定」にも使われる言葉が、ある時期から「否定」が優勢になり、その後「肯定」が復活する。このような「3段階」の歴史をもつ日本語の副詞は他にもあり、「全然」「断然」「なかなか」がそうである。 |
"肯定的とても" は、芥川龍之介が推測する三河方言ではなく、『平家物語』『太平記』『御伽草子』『好色一代女』にもある "由緒正しい" 言い方だったわけです。もちろん、由緒正しい言い方が方言だけに残るということもあり得ます。
ひょっとしたら、芥川はそれを知っていたのかもしれません。知っていながら「とても手間取つた」というオチに導くためにあえて『猿蓑』を持ち出した、つまり一種のジョークということも考えられると思います。
超・鬼・めちゃくちゃ
「とても」をいったん離れて、強調のための言葉について考えてみます。形容詞、動詞、名詞などを修飾して「程度が強いさま」を表す言葉を「強調詞」と呼ぶことにします。強調詞にはさまざまなもがあります。大変、非常に、全然、すごく、などがそのごく一部です。
漢字で書くと1字の「超」も、今ではあたりまえになりました。もちろんこれは超特急、超伝導など、名詞の接頭辞として由緒ある言葉で、「通常のレベルを遙かに超えた」という意味です。これが「超たのしい」「超カワイイ」などと使われるようになった(1960年代から広がったと言われています)。その「超」は、"本場" の中国に「逆輸出」され、「超好(超いい)」などと日常用語化しているといいます(日本経済新聞「NIKKEI プラス 1」2022年6月11日 による)。「超」はかなり "威力がある" 強調詞のようです。
漢字1字を訓読みで使う接頭辞もあって「鬼」がそうです。「鬼」はもともと名詞の接頭辞として「無慈悲」「冷酷」「恐ろしい」「巨大」「異形」「勇猛」「強い」などの意味を付加するものでした。「鬼将軍」「鬼軍曹」「鬼コーチ」「鬼検事」「鬼編集長」などです。栗の外皮を「鬼皮」と言いますが、強いという意味です。また「鬼」は動植物・生物の名前にも長らく使われてきました。同類と思われている生物同士の比較で、大きいものは「大・おお・オオ」を接頭辞として使いますが、それをさらに凌駕する大型種は「鬼・おに・オニ」を冠して呼びます。オニグモ(鬼蜘蛛)、オニユリ(鬼百合)、オニバス(鬼蓮)といった例です。
しかしこの数年、さらに進んで「鬼」を強調詞とする言い方が若者の間に出てきました。オニの部分をあえて漢字書くと、
・鬼かわいい
・鬼きれい
・鬼うまい(鬼おいしい)
・鬼むかつく
といった言い方です。もともとの「無慈悲」「冷酷」「恐ろしい」」「異形」などの否定的な意味はなくなり、「通常を凌駕するレベルである」ことだけが強調されています。これは「超」の使い方とそっくりです。この使い方が定着するのか、ないしは今後消えてしまうのかは分かりません。
さらに、もともと否定的文脈で使う「めちゃくちゃ」「めちゃめちゃ」「めっちゃ」「めちゃ」があります。「むちゃくちゃ」とも言います。これも江戸時代からある言葉で、漢字で書くと「滅茶苦茶」です。"混乱して、筋道がたたず、全く悪い状態" を指します言が、強調詞として使って「めちゃくちゃカワイイ」などと言います。
もともと否定的文脈で使う言葉という意味では、形容詞の「ものすごい(物凄い)」もそうです。これはもとは恐ろしいものに対してしか使わない言葉でした(西江雅之「ことばの課外授業」洋泉社 2003による)。確かに、青空文庫でこの言葉を検索すると、恐ろしいものの形容に使った文例しかありません。青空文庫は著作権が切れた(死後50年以上たった)作家の作品しかないので、「ものすごい美人」というような使い方は、少なくとも文章語としてはこの半世紀程度の間に広まった使い方であることは確実です(話し言葉としてはそれ以前から使われていたかもしれません)。
そこで「天声人語」の「ボロクソほめられた」です。これはもともと否定的文脈で使う言葉を、程度が大きいさまを表す強調詞とした典型的な例です。その意味で「とても」「めちゃくちゃ」「ものすごく」の系列につながっています。特に「めちゃくちゃ」に似ています。
| 彼は A氏のことをメチャクチャに言っていた。 |
| メチャクチャうれしかった |
| 彼の A氏についての評価はボロクソだった。 |
| ボロクソうれしかった |
強調詞の宿命
「とても」の変遷や、その他の言葉を見ていると、強調詞の "宿命" があるように思います。つまり、ある強調詞が広まってあたりまえに使われるようになると、それが "あまり強調しているようには感じられなくなる" という宿命です。
従って、新しい言葉が登場する。そのとき、否定的文脈で使われる言葉を肯定的に使ったり、名詞の接頭辞を形容詞を修飾する副詞に使ったりすると(超・鬼)、インパクトが強いわけです。特に、自分の思いや感情を吐露したい場合の話し言葉には、そういうインパクトが欲しい。そうして新語が使われだし、その結果一般的になってしまうと強調性が薄れ、また別の新語が使われ出す。
「天声人語」に引用された女子中学生の発言、「きのうさー、先生にさあ、ボロクソほめられちゃったんだ」も、よほど嬉しかったゆえの発言でしょう。天声人語子は「それにしても、あの女の子、うれしそうだったなあ」と書いていますが、今まで先生に誉められたことがなかったとか、あるいは、一生懸命努力して作ったモノとか努力して成し遂げたことを誉められたとか、内容は分からないけれど、そういうことが背景にあるのかも知れません。もちろん先生も言葉を重ねて誉めた。その子にとって「メッチャ、ほめられちゃった」や「チョー、ほめられちゃった」では、自分の感動を伝えるには不足なのです。
「ボロクソほめられた」は、一般的に広まることはないかもしれないけれど、個人的な言葉としては大いにアリだし、それは言葉の可能性の広さを表しているのだと思いました。
2023-07-01 14:16
nice!(0)
No.361 - 寄生生物が宿主を改変する [科学]
今まで、寄生生物が宿主(=寄生する相手)を操るというテーマに関連した記事を書きました。
の3つです。最初の No.348「蚊の嗅覚は超高性能」を要約すると、
でした。また No.350「寄生生物が行動をあやつる」は、次のようにまとめられます。
トキソプラズマは広範囲の動物に感染しますが、有性生殖ができるのは猫科の動物の体内だけです。トキソプラズマが動物の行動を改変するのは、猫科の動物に捕食されやすくするため(もともとそのためだった)と推測できます。
そのトキソプラズマについての記事が、No.352「トキソプラズマが行動をあやつる」です。何点かあげると、
などです。今回はその継続で、同じテーマについての新聞記事を取り上げます。朝日新聞 2023年2月~3月にかけて掲載された「寄生虫と人類」です。これは3回シリーズの記事で、その第2回(2023.3.3)と第3回(2023.3.10)を紹介します。今までと重複する部分もありますが、「寄生生物が宿主を改変する」ことを利用して医療に役立てようとする動きも紹介されています。
寄生生物の生き残り戦略
「寄生虫と人類」の第2回は、
との見出しです。例のトキソプラズマの話から始まります。
引用のようにトキソプラズマはヒトにも感染し、妊婦が初めて感染した場合、胎児が先天性トキソプラズマ症にかかることがあります。しかし、それ以上の影響があるのではと疑われています。つまり脳への影響です。脳への影響は動物で研究が進んでいます。
ネズミやオオカミにおけるトキソプラズマの影響は、No.350 や No.352 でも紹介した通りです。さらにトキソプラズマは、巧妙な仕掛けによって宿主の免疫系の攻撃から逃れるようなのです。
寄生虫は自らの生き残りのために宿主を改変しますが、そのことが自然生態系に大きな役割を持っている場合があります。その例が、No.350「寄生生物が行動をあやつる」で紹介したハリガネムシです。
No.350「寄生生物が行動をあやつる」に書いたように、佐藤准教授によると、渓流魚の餌の 60%(エネルギー換算)はハリガネムシが "連れてきた" 昆虫類でまかなわれているそうです。これだけでも重要ですが、上の引用によるとさらに「渓流魚に狙われる恐れが減った水生昆虫は藻類を食べるので、藻類が増えすぎない」とあります。ハリガネムシがカマドウマ(その他、カマキリ、キリギリスなど)に寄生することが、めぐりめぐって渓流の藻類が増えすぎないことにつながっている。生態系のバランスは誠に微妙だと思います。
寄生虫と病気治療
「寄生虫と人類」の第3回は、
との見出しです。ここでは寄生虫の生き残り戦略を解明して、それを人間の病気治療に役立てようとする研究が紹介されています。
記事に「マクロファージにがん細胞をどんどん食べさせるようにできるのではないか」とあります。これで思い出すのが、No.330「ウイルスでがんを治療する」です。これは、東京大学の藤堂教授が開発した "ウイルスによるがん治療薬" を紹介した記事でした。単純ヘルペスウイルス1型(HSV-1)の3つの遺伝子を改造し、がん細胞にだけ感染するようにすると、改造ヘルペスウイルスはがん細胞を次々と死滅させてゆく。
がん細胞を攻撃するのが難しい要因のひとつは、それが「自己」だからです。リーシュマニア原虫は寄生したマクロファージを改変して「自己」であるはずの赤血球だけを選択的に食べるようにします。その仕組みが解明できれば、がん細胞だけを食べるマクロファージを作れるかもしれません。
ヒトに感染する細菌やウイルスが、ヒトの免疫系からの攻撃を逃れるため、免疫の働きを押さえる制御性T細胞を誘導する(未分化のT細胞を制御性T細胞に変える)とか、制御性T細胞を活性化する話は、今までの記事で何回か書きました。
などです。細菌やウイルスが制御性T細胞を誘導するのであれば、遺伝子の数が多い寄生虫が同じことをできたとしても、むしろ当然という感じがします。
細菌やウイルスよりはるかに大きい寄生虫にヒトが対抗するためには、それを体内から排出するしかない。この仕組みを発動する免疫細胞が2010年に発見された(2型自然リンパ球、ILC2)という記事です。
寄生虫が多い環境では、このようなヒトの仕組みと、寄生虫が免疫から逃れようとする動き(制御性T細胞を生成するなど)が攻めぎ合っています。しかし、寄生虫がほとんどいない先進国の環境ではバランスが崩れ、ヒトの仕組みが不必要に発動して「自己」を攻撃してアレルギーの(一つの)原因になるわけです。
ヒト(ホモ・サピエンス)はアフリカのサバンナ地帯で進化してきたわけで、その環境とライフスタイル(狩猟採集)にマッチした DNA と体の造りになっています。サバンナでの狩猟採集に有利なように進化してきたのがヒトなのです。
もちろん現代で同じ環境で生きることはできません。しかし程度の差はあれ、「寄生生物と戦う環境、あるいは共生する環境」は、我々が健康に過ごすために必須だと感じる記事でした。
の3つです。最初の No.348「蚊の嗅覚は超高性能」を要約すると、
蚊がヒトを感知する仕組みは距離によって4種あり、その感度は極めて鋭敏である。
| |||||||||
| ある種のウイルスは、ネズミに感染すると一部のたんぱく質の働きを弱める。それによってアセトフェノンを作る微生物が皮膚で増え、この臭いが多くの蚊を呼び寄せる(中国・清華大学の研究)。 |
でした。また No.350「寄生生物が行動をあやつる」は、次のようにまとめられます。
| ハリガネムシは、カマキリに感染するとその行動を改変し、それによってカマキリは、深い水辺に反射した光の中に含まれる「水平偏光」に引き寄せられて水に飛び込む。ハリガネムシは水の中でカマキリの体から出て行き、そこで卵を生む。 | |
| トキソプラズマに感染したオオカミはリスクを冒す傾向が強く、群のリーダーになりやすい。 | |
| トキソプラズマに感染したネズミはネコの匂いも恐れずに近づく。 |
トキソプラズマは広範囲の動物に感染しますが、有性生殖ができるのは猫科の動物の体内だけです。トキソプラズマが動物の行動を改変するのは、猫科の動物に捕食されやすくするため(もともとそのためだった)と推測できます。
そのトキソプラズマについての記事が、No.352「トキソプラズマが行動をあやつる」です。何点かあげると、
| トキソプラズマに感染したネズミは、天敵である猫の匂いを忌避しなくなることが、実験によって証明された。 | |
| トキソプラズマに感染した人は、していない人に比べて交通事故にあう確率が 2.65 倍 高かった(チェコ大学。NHK BSP「超進化論 第3集」2023.1.8 による) | |
| トキソプラズマに感染したハイエナはライオンに襲われやすくなる(ナショナル・ジオグラフィック:2021.7.11 デジタル版)。 |
などです。今回はその継続で、同じテーマについての新聞記事を取り上げます。朝日新聞 2023年2月~3月にかけて掲載された「寄生虫と人類」です。これは3回シリーズの記事で、その第2回(2023.3.3)と第3回(2023.3.10)を紹介します。今までと重複する部分もありますが、「寄生生物が宿主を改変する」ことを利用して医療に役立てようとする動きも紹介されています。
寄生生物の生き残り戦略
「寄生虫と人類」の第2回は、
生物操り 都合のいい環境に
宿主の脳や免疫を制御 生態系に影響も
宿主の脳や免疫を制御 生態系に影響も
との見出しです。例のトキソプラズマの話から始まります。
|
|
トキソプラズマの拡散 |
(朝日新聞 2023.3.3 より) |
|
引用のようにトキソプラズマはヒトにも感染し、妊婦が初めて感染した場合、胎児が先天性トキソプラズマ症にかかることがあります。しかし、それ以上の影響があるのではと疑われています。つまり脳への影響です。脳への影響は動物で研究が進んでいます。
|
ネズミやオオカミにおけるトキソプラズマの影響は、No.350 や No.352 でも紹介した通りです。さらにトキソプラズマは、巧妙な仕掛けによって宿主の免疫系の攻撃から逃れるようなのです。
|
寄生虫は自らの生き残りのために宿主を改変しますが、そのことが自然生態系に大きな役割を持っている場合があります。その例が、No.350「寄生生物が行動をあやつる」で紹介したハリガネムシです。
|
No.350「寄生生物が行動をあやつる」に書いたように、佐藤准教授によると、渓流魚の餌の 60%(エネルギー換算)はハリガネムシが "連れてきた" 昆虫類でまかなわれているそうです。これだけでも重要ですが、上の引用によるとさらに「渓流魚に狙われる恐れが減った水生昆虫は藻類を食べるので、藻類が増えすぎない」とあります。ハリガネムシがカマドウマ(その他、カマキリ、キリギリスなど)に寄生することが、めぐりめぐって渓流の藻類が増えすぎないことにつながっている。生態系のバランスは誠に微妙だと思います。
寄生虫と病気治療
「寄生虫と人類」の第3回は、
「生き残り戦略」病気治療に光
宿主の免疫から攻撃逃れる仕組みを利用
宿主の免疫から攻撃逃れる仕組みを利用
との見出しです。ここでは寄生虫の生き残り戦略を解明して、それを人間の病気治療に役立てようとする研究が紹介されています。
|
記事に「マクロファージにがん細胞をどんどん食べさせるようにできるのではないか」とあります。これで思い出すのが、No.330「ウイルスでがんを治療する」です。これは、東京大学の藤堂教授が開発した "ウイルスによるがん治療薬" を紹介した記事でした。単純ヘルペスウイルス1型(HSV-1)の3つの遺伝子を改造し、がん細胞にだけ感染するようにすると、改造ヘルペスウイルスはがん細胞を次々と死滅させてゆく。
がん細胞を攻撃するのが難しい要因のひとつは、それが「自己」だからです。リーシュマニア原虫は寄生したマクロファージを改変して「自己」であるはずの赤血球だけを選択的に食べるようにします。その仕組みが解明できれば、がん細胞だけを食べるマクロファージを作れるかもしれません。
|
ヒトに感染する細菌やウイルスが、ヒトの免疫系からの攻撃を逃れるため、免疫の働きを押さえる制御性T細胞を誘導する(未分化のT細胞を制御性T細胞に変える)とか、制御性T細胞を活性化する話は、今までの記事で何回か書きました。
| 2010年には、自己免疫疾患を抑制する制御性T細胞の誘導に関係するバクテロイデス・フラジリスが、2011年には同様にこの制御性細胞を誘導するクロストリジウム属が発見された。─── No.70「自己と非自己の科学(2)」 | |
| 抗生物質のバンコマイシンで腸内細菌のクロストリジウム属を徐々に減らすと、ある時点で制御性T細胞が急減し、それが自己免疫疾患であるクローン病(=炎症性腸疾患)の発症を招く。─── No.120「"不在" という伝染病(2)」 | |
| エンテロウイルスに感染すると制御性T細胞の生成が刺激され、その細胞が成人期まで存続する。制御性T細胞は自己免疫性T細胞の生成を抑えることで1型糖尿病を防ぐ。─── No.229「糖尿病の発症をウイルスが抑止する」 |
などです。細菌やウイルスが制御性T細胞を誘導するのであれば、遺伝子の数が多い寄生虫が同じことをできたとしても、むしろ当然という感じがします。
|
細菌やウイルスよりはるかに大きい寄生虫にヒトが対抗するためには、それを体内から排出するしかない。この仕組みを発動する免疫細胞が2010年に発見された(2型自然リンパ球、ILC2)という記事です。
寄生虫が多い環境では、このようなヒトの仕組みと、寄生虫が免疫から逃れようとする動き(制御性T細胞を生成するなど)が攻めぎ合っています。しかし、寄生虫がほとんどいない先進国の環境ではバランスが崩れ、ヒトの仕組みが不必要に発動して「自己」を攻撃してアレルギーの(一つの)原因になるわけです。
|
ヒト(ホモ・サピエンス)はアフリカのサバンナ地帯で進化してきたわけで、その環境とライフスタイル(狩猟採集)にマッチした DNA と体の造りになっています。サバンナでの狩猟採集に有利なように進化してきたのがヒトなのです。
もちろん現代で同じ環境で生きることはできません。しかし程度の差はあれ、「寄生生物と戦う環境、あるいは共生する環境」は、我々が健康に過ごすために必須だと感じる記事でした。
2023-06-16 16:30
nice!(0)
No.360 - ヒトの進化と苦味 [科学]
今まで、ヒトと苦味の関係について2つの記事を書きました。
No.177「自己と非自己の科学:苦味受容体」
No.178「野菜は毒だから体によい」
の2つです。No.177「自己と非自己の科学:苦味受容体」を要約すると次の通りです。
五味と総称される、甘味・酸味・塩味・苦味・うま味のうち、苦味を除く4つは、その味を引き起こす物質が決まっています。
です。この4味を感じる味覚受容体はそれぞれ1種類です。しかし苦味を引き起こす物質は多様で、それに対応して苦味受容体も複数種類あります。そしてヒトは、本来危険のサインである苦味を楽しむ文化を作ってきました。
などは世界中に広まっています。ビールもそうでしょう。ホップを使ってわざわざ苦くしている。赤ワインの味は複雑ですが、味の魅力を作るポイントの一つが苦味(=ブドウの皮由来のタンニン)であることは間違いないでしょう。
ではなぜ、本来危険のサインである苦味を楽しむ文化が広まったのでしょうか。その理由の一端が分かるのが、No.178「野菜は毒だから体によい」です。要約すると、
上にある植物の毒素は、苦味と重ならないものもありますが(カプサイシン)、重なる部分も多い。つまり、植物由来の微量毒素を摂取することと、苦いものを食べる・飲むことは密接に関係していると考えられます。
ヒトの体は(小さな)ストレスや(小さな)ダメージから回復する機能を備えています。使わない機能は衰えるのが原則です。それが必要ないと体が判断するからです。ヒトは苦いものを食べる・飲むことで、体のストレス回復機能を常時活性化させておき、それが健康維持に役立つ ・・・・・・。そういう風に考えられます。
先日の日本経済新聞に、苦味とヒトの進化をまとめた記事が掲載されました(2023年4月30日 日経 STYLE)。ヒトにとっての苦味の意味が理解できる良い記事だと思ったので、紹介します。
苦味、命の恵み
日本経済新聞の記事は、
苦味、命の恵み
と題するもので、このタイトルのもとに、次の文が続きます。
記事は2つの部分に分かれています。
です。「郷土に根ざす文化の味わい」では、日本の郷土料理を支える苦味、特に山菜料理とその歴史の紹介でした。
以下は、第2部である「ヒトへの進化支える不思議」を紹介します。
ヒトへの進化支える不思議
苦味が本来危険のサインだとすると、子供が苦い食べ物を嫌うのはヒトに備わった正常な反応でしょう。しかし「食体験を積む中である種の苦みをおいしいと学習する」のはなぜでしょうか。これは少々不思議です。なぜ味覚が変化するのか。
たとえば、甘味を考えてみると、子供が甘いものが大好きなのは人類共通だと思います。しかし大人になると甘いものを嫌う人がでてきます(大人になっても甘いもの大好きという人もいるが)。これはなぜかというと「甘いものは体によくない」「糖質のとりすぎは健康を損ねる」という "知識" を獲得するためと考えられます。
塩味もそうです。塩は料理には欠かせないし、適度な塩分は体の維持に必須です。しかし年配になると塩味が強すぎるものを嫌う人が出てくる。これは、高血圧症などの生活習慣病のリスクを避けるという "知識" からくるのだと思います。その他、酢を使った料理や飲料を好むように変わったとしたら、それも健康に良いという知識によるのでしょう。
しかし苦味は違います。「苦味が健康に良い」という "知識" が広まっているとは思えません。それでもなおかつ大人になると苦味を好むのは、もちろん、コーヒーや緑茶やビールを飲むという文化・習慣が根付いていて、それに馴染むわけです。ではなぜそういう文化・習慣が根付いたかと言うと、体が苦いものを欲するようになるからではないでしょうか。
苦味は本来、危険のサインだけれど、長い進化や文化的伝統のなかで "安全な苦味" と分かっているものについては、その苦味にメリットがあることを自然と体得するのだと思います。
日経新聞の引用を続けます。
苦味の受容体は26種類、と書かれています。苦味物質がは多様であり、それに対応して苦味受容体の種類も多い。その多様性はヒトが進化の過程で獲得してきたものです。
NHK BS プレミアム ヒューマニエンス「"毒と薬" その攻防が進化を生む」(2023年1月31日 22:00~23:00)に早川さんが出演されて、苦味受容体の解説をされていました。それによると、霊長類の苦味受容体の種類は、
だそうです。この違いは何かというと、小型霊長類は主として昆虫食であるのに対し、大型霊長類は大きな体を維持するために苦味物質が含まれる植物の葉を食べるようになったからです。
ちなみに、ヒトとチンパンジーは約700万年前に共通の祖先から別れたのですが、その共通祖先の苦味受容体の種類数は28と推定されるそうです。つまりヒトは2種類失った。これはなぜなのでしょうか。
受容体の数を減らすことで、食べられる食物の選択肢を増やしたとの話ですが、それ以外に、肉食を始めたこと(約250~200万年前)や、加熱調理(約100万年前かそれ以前)によって、苦味を忌避する必要性が薄れたことも影響しているのでしょう。NHK の「ヒューマニエンス」でもそういう話がありました。
また、ヒトの苦味感覚には個人差があり、また苦味を受容するスタイルも多様です。
スタバのドリップコーヒーは苦くて飲めないという人がいます。私は平気ですが、飲めないという意見も理解できる。しかしそれほど "苦い" ものであっても、人々は砂糖を入れたり、ミルク、生クリームなどを入れたりして "苦味をマスキング" し、"何とかして" 飲もうとしてきた。これは、体が苦味を欲している、と考えるのが妥当だと思います。
さらに日経新聞には「料理にあえて苦味を加える」という、興味深い話があります。
辛味調味料である辛子や山葵を添える料理はいろいろあります。であれば、「ハーブソルトに、ビールの苦みや香りの元になるホップの成分を配合した」苦味調味料を添える料理があってもよいはずです。
考えてみると、焼いたり、炙ったり、焦げめをつけたりする料理がいろいろあります。これは、過度にならない苦味を足すことで食材の味をより引き立たせる意味も大きいのでしょう。さらに「稚鮎の天ぷら」のような料理を考えてみると、おいしさのポイントが鮎の内臓(ワタ)の苦味でであることは確かです。
ホップを使ったような "苦味調味料" は今まで無かったかもしれないが、実質的に同じ効果を得る料理はたくさんあるはずです。
冒頭に書いたように「苦味受容体は舌や口の中以外にも広く存在し、食べ物が直接接するはずのない鼻の苦味受容体は細菌の排除に役立っている」のは事実なので、「健康維持のために中高年になると、苦味物質を体が欲するようになる」というのが、サイエンスとしては正しいと思います。
以上のような話を読むと、野菜を品種改良して適度な苦味まで無くすとか、あるいは減少させるのは、ヒトと苦味の長い付き合いの本筋から全くはずれた行為と言えるでしょう。
要するに我々は、苦味とうまく付き合えばよいということです。
No.177「自己と非自己の科学:苦味受容体」
No.178「野菜は毒だから体によい」
の2つです。No.177「自己と非自己の科学:苦味受容体」を要約すると次の通りです。
| 苦味は本来、危険のサインである。 | |||||||
舌で苦味を感じるセンサー、苦味受容体は、鼻などの呼吸器系にもあり、細菌などの進入物から体を防御している。その働きは3つある。
| |||||||
| さらに、苦味受容体は呼吸器系だけでなく体のあちこちにあり(たとえば小腸)、免疫機能を果たしている。 |
五味と総称される、甘味・酸味・塩味・苦味・うま味のうち、苦味を除く4つは、その味を引き起こす物質が決まっています。
| :糖 | |
| :酸=水素イオン | |
| :塩=ナトリウムイオン | |
| :アミノ酸 |
です。この4味を感じる味覚受容体はそれぞれ1種類です。しかし苦味を引き起こす物質は多様で、それに対応して苦味受容体も複数種類あります。そしてヒトは、本来危険のサインである苦味を楽しむ文化を作ってきました。
| お茶を飲む文化 | |
| コーヒーを飲む文化 |
ではなぜ、本来危険のサインである苦味を楽しむ文化が広まったのでしょうか。その理由の一端が分かるのが、No.178「野菜は毒だから体によい」です。要約すると、
| 植物は、動物や昆虫に食べられまいとして、毒素を生成するものが多い。 | |||||||||||
植物の毒素のあるものは、微量であればヒトの体によい影響を及ぼす。代表的なものは、
| |||||||||||
| これらは微量なら体の細胞に適度なストレスを与え、細胞はそのストレスから回復しようとする(たとえば抗酸化物質の算出)。その回復機能の活性化が体に良い影響を与える。 |
上にある植物の毒素は、苦味と重ならないものもありますが(カプサイシン)、重なる部分も多い。つまり、植物由来の微量毒素を摂取することと、苦いものを食べる・飲むことは密接に関係していると考えられます。
ヒトの体は(小さな)ストレスや(小さな)ダメージから回復する機能を備えています。使わない機能は衰えるのが原則です。それが必要ないと体が判断するからです。ヒトは苦いものを食べる・飲むことで、体のストレス回復機能を常時活性化させておき、それが健康維持に役立つ ・・・・・・。そういう風に考えられます。
先日の日本経済新聞に、苦味とヒトの進化をまとめた記事が掲載されました(2023年4月30日 日経 STYLE)。ヒトにとっての苦味の意味が理解できる良い記事だと思ったので、紹介します。
苦味、命の恵み
日本経済新聞の記事は、
苦味、命の恵み
と題するもので、このタイトルのもとに、次の文が続きます。
|
記事は2つの部分に分かれています。
| 郷土に根ざす文化の味わい | |
| ヒトへの進化支える不思議 |
です。「郷土に根ざす文化の味わい」では、日本の郷土料理を支える苦味、特に山菜料理とその歴史の紹介でした。

|
埼玉県入間市の郷土料理店「ともん」で供される山菜。日本経済新聞より。 |
以下は、第2部である「ヒトへの進化支える不思議」を紹介します。
ヒトへの進化支える不思議
|
苦味が本来危険のサインだとすると、子供が苦い食べ物を嫌うのはヒトに備わった正常な反応でしょう。しかし「食体験を積む中である種の苦みをおいしいと学習する」のはなぜでしょうか。これは少々不思議です。なぜ味覚が変化するのか。
たとえば、甘味を考えてみると、子供が甘いものが大好きなのは人類共通だと思います。しかし大人になると甘いものを嫌う人がでてきます(大人になっても甘いもの大好きという人もいるが)。これはなぜかというと「甘いものは体によくない」「糖質のとりすぎは健康を損ねる」という "知識" を獲得するためと考えられます。
塩味もそうです。塩は料理には欠かせないし、適度な塩分は体の維持に必須です。しかし年配になると塩味が強すぎるものを嫌う人が出てくる。これは、高血圧症などの生活習慣病のリスクを避けるという "知識" からくるのだと思います。その他、酢を使った料理や飲料を好むように変わったとしたら、それも健康に良いという知識によるのでしょう。
しかし苦味は違います。「苦味が健康に良い」という "知識" が広まっているとは思えません。それでもなおかつ大人になると苦味を好むのは、もちろん、コーヒーや緑茶やビールを飲むという文化・習慣が根付いていて、それに馴染むわけです。ではなぜそういう文化・習慣が根付いたかと言うと、体が苦いものを欲するようになるからではないでしょうか。
苦味は本来、危険のサインだけれど、長い進化や文化的伝統のなかで "安全な苦味" と分かっているものについては、その苦味にメリットがあることを自然と体得するのだと思います。
日経新聞の引用を続けます。
|
苦味の受容体は26種類、と書かれています。苦味物質がは多様であり、それに対応して苦味受容体の種類も多い。その多様性はヒトが進化の過程で獲得してきたものです。
|
NHK BS プレミアム ヒューマニエンス「"毒と薬" その攻防が進化を生む」(2023年1月31日 22:00~23:00)に早川さんが出演されて、苦味受容体の解説をされていました。それによると、霊長類の苦味受容体の種類は、
小型霊長類
大型霊長類
| :20 | |
| :22 | |
| :16 |
| :25 | |
| :28 | |
| :26 |
だそうです。この違いは何かというと、小型霊長類は主として昆虫食であるのに対し、大型霊長類は大きな体を維持するために苦味物質が含まれる植物の葉を食べるようになったからです。
ちなみに、ヒトとチンパンジーは約700万年前に共通の祖先から別れたのですが、その共通祖先の苦味受容体の種類数は28と推定されるそうです。つまりヒトは2種類失った。これはなぜなのでしょうか。
|
受容体の数を減らすことで、食べられる食物の選択肢を増やしたとの話ですが、それ以外に、肉食を始めたこと(約250~200万年前)や、加熱調理(約100万年前かそれ以前)によって、苦味を忌避する必要性が薄れたことも影響しているのでしょう。NHK の「ヒューマニエンス」でもそういう話がありました。
また、ヒトの苦味感覚には個人差があり、また苦味を受容するスタイルも多様です。
|
スタバのドリップコーヒーは苦くて飲めないという人がいます。私は平気ですが、飲めないという意見も理解できる。しかしそれほど "苦い" ものであっても、人々は砂糖を入れたり、ミルク、生クリームなどを入れたりして "苦味をマスキング" し、"何とかして" 飲もうとしてきた。これは、体が苦味を欲している、と考えるのが妥当だと思います。
さらに日経新聞には「料理にあえて苦味を加える」という、興味深い話があります。
|

|
東京・北青山の「Hotel's」では、メインのステーキにホップの苦味が特徴のハーブソルトを添えて提供される。 |
辛味調味料である辛子や山葵を添える料理はいろいろあります。であれば、「ハーブソルトに、ビールの苦みや香りの元になるホップの成分を配合した」苦味調味料を添える料理があってもよいはずです。
考えてみると、焼いたり、炙ったり、焦げめをつけたりする料理がいろいろあります。これは、過度にならない苦味を足すことで食材の味をより引き立たせる意味も大きいのでしょう。さらに「稚鮎の天ぷら」のような料理を考えてみると、おいしさのポイントが鮎の内臓(ワタ)の苦味でであることは確かです。
ホップを使ったような "苦味調味料" は今まで無かったかもしれないが、実質的に同じ効果を得る料理はたくさんあるはずです。
|
冒頭に書いたように「苦味受容体は舌や口の中以外にも広く存在し、食べ物が直接接するはずのない鼻の苦味受容体は細菌の排除に役立っている」のは事実なので、「健康維持のために中高年になると、苦味物質を体が欲するようになる」というのが、サイエンスとしては正しいと思います。
|
以上のような話を読むと、野菜を品種改良して適度な苦味まで無くすとか、あるいは減少させるのは、ヒトと苦味の長い付き合いの本筋から全くはずれた行為と言えるでしょう。
要するに我々は、苦味とうまく付き合えばよいということです。
2023-05-27 08:41
nice!(0)
No.359 - 高校数学で理解するガロア理論(6) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
7.8 可解な5次方程式
大多数の5次方程式のガロア群は、対称群 \(S_5\) か 交代群 \(A_5\) であり、従って可解ではありません(65G)。しかし特別な形の5次方程式は可解です。
その可解な5次方程式として \(x^5-2=0\) を取り上げ、ガロア群を分析します。この方程式の根がべき根で表現できることはあたりまえだし、こんな "単純な" 方程式のガロア群を分析することに意味があるのかどうか、疑ってしまいます。
しかし、\(x^5-2=0\) のガロア群は可解な5次方程式のガロア群としては最も複雑なのです。方程式の "見た目の" 単純・複雑さと、ガロア群の単純・複雑さはリンクしません。以下で \(x^5-2\) のガロア群を計算します。
\(x^5-2\) のガロア群
\(1\) の原始\(5\)乗根の一つを \(\zeta\) とします。\(x^5-1=0\) は、
\((x-1)(x^4+x^3+x^2+x+1)=0\)
と因数分解できるので、\(\zeta\) は、
\(x^4+x^3+x^2+x+1=0\)
の根です。7.1節で計算したように、たとえば、
\(\zeta=\dfrac{1}{4}(-1+\sqrt{5}+i\sqrt{10+2\sqrt{5}})\)
です。また、
\(\al=\sqrt[5]{2}\)
とします。そうすると、\(x^5-2=0\) の解は、
\(\al,\:\:\al\zeta,\:\:\al\zeta^2,\:\:\al\zeta^3,\:\:\al\zeta^4\)
の5つです。\(f(x)=x^5-2\) の最小分解体 \(\bs{L}\) は、
\(\begin{eqnarray}
&&\:\:\bs{L}&=\bs{Q}(\al,\:\al\zeta,\:\al\zeta^2,\:\al\zeta^3,\:\al\zeta^4)\\
&&&=\bs{Q}(\zeta,\al)\\
\end{eqnarray}\)
です。この \(\bs{L}=\bs{Q}(\zeta,\al)\) は、\(\bs{F}=\bs{Q}(\zeta)\) として、
\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{L}\)
という、体の拡大で作られたものと見なせます。つまり \(\bs{L}=\bs{F}(\al)\) です。
\(\zeta\) の \(\bs{Q}\) 上最小多項式は、\(x^4+x^3+x^2+x+1\) という4次多項式なので、拡大次数は、
\([\:\bs{F}:\:\bs{Q}\:]=4\)
です。\(\bs{Q}(\zeta)\) は単拡大体であり、単拡大体の同型写像の定理(51G)によって、\(\zeta\) に作用する \(\bs{Q}\) 上の同型写像はちょうど \(4\)個あります。
\(\bs{L}=\bs{Q}(\zeta,\al)\) は \(\bs{F}=\bs{Q}(\zeta)\) 上の5次既約多項式 \(x^5-2\) の解 \(\al\) を \(\bs{F}\) に添加した単拡大体です。従って、
\([\:\bs{L}\::\:\bs{F}\:]=5\)
です。\(\bs{L}=\bs{F}(\al)\) も単拡大体であり、\(\al\) に作用する \(\bs{\bs{F}}\) 上の同型写像は \(5\)個です。
拡大次数の連鎖律(33H)により、
\([\:\bs{L}\::\:\bs{Q}\:]=[\:\bs{L}\::\:\bs{F}\:]\cdot[\:\bs{F}\::\:\bs{Q}\:]=20\)
がわかります。従って \(\mr{Gal}(\bs{L}/\bs{Q})\) の位数は \(20\) です。\(\bs{L}=\bs{Q}(\zeta,\al)\) の自己同型写像を\(20\)個見つければ、それが \(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\) です。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
自己同型写像は、方程式の解を共役な解に移します。\(\zeta\) は \(1\) の原始\(5\)乗根であり、4次方程式 \(x^4+x^3+x^2+x+1=0\) の解なので、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
が互いに共役です。そこで、自己同型写像 \(\tau_i\:(i=1,2,3,4)\) を、\(\zeta\) を \(\zeta^i\) に置き換える写像、つまり、
と定義します。これを、
\(\tau_i(\zeta)=\zeta^i\:\:(i=1,2,3,4)\)
と表記します。\(\tau_i\:(i=1,2,3,4)\) の集合を、
\(G_{\large t}=\{\tau_1,\:\tau_2,\:\tau_3,\:\tau_4\}\)
とすると、\(G_{\large t}\) は \(\bs{Q}(\zeta)\) の4つの自己同型写像の集合なので、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=G_{\large t}\)
です。恒等写像を \(e\) とすると、
\(\tau_1=e\)
ですが、
\(\tau_2(\zeta)=\zeta^2\)
\(\begin{eqnarray}
&&\:\:\tau_2^{\:2}(\zeta)&=\tau_2(\tau_2(\zeta))=\tau_2(\zeta^2)\\
&&&=\zeta^4=\tau_4(\zeta)\\
&&\:\:\tau_2^{\:3}(\zeta)&=\tau_2(\tau_2^2(\zeta))=\tau_2(\zeta^4)\\
&&&=\zeta^8=\zeta^3=\tau_3(\zeta)\\
&&\:\:\tau_2^{\:4}(\zeta)&=\zeta^{16}=\tau_1(\zeta)\\
\end{eqnarray}\)
と計算できるので、
\(\tau_1^{\:2}=\tau_4,\:\:\tau_1^{\:3}=\tau_3,\:\:\tau_1^{\:4}=e\)
となります。従って、\(\tau_2\) を \(\tau\) と書くと、
\(G_{\large t}=\{e,\:\tau,\:\tau^2,\:\tau^3\}\)
であり、\(G_{\large t}\) は \(\tau\)(= \(\tau_2\)) を生成元とする位数 \(4\) の巡回群で、既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と同型です。これは一般に \(1\) の原始\(n\)乗根を \(\zeta\) としたときに、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
という 6.3節の \(\bs{\bs{Q}(\zeta)}\)のガロア群の定理(63E)からもわかります。
\((\bs{Z}/5\bs{Z})^{*}\) の生成元は \(2,\:3\) です。従って、\(G_{\large t}\) の生成元は \(\tau_2,\:\tau_3\) です。\(\tau_4\) については、
\(\tau_4(\zeta)=\zeta^4\)
\(\begin{eqnarray}
&&\:\:\tau_4^{\:2}(\zeta)&=\tau_4(\tau_4(\zeta))=\tau_4(\zeta^4)\\
&&&=\zeta^{16}=\zeta\\
\end{eqnarray}\)
なので、\(\tau_4^{\:2}=\tau_1=e\) であり、生成元ではありません。
\(\mr{Gal}(\bs{F}(\al)/\bs{F})\)
\(\bs{L}=\bs{Q}(\zeta,\al)=\bs{F}(\al)\) は \(\bs{F}=\bs{Q}(\zeta)\) 上の既約方程式 \(x^5-2=0\) の解の一つである \(\al\) を \(\bs{F}\) に添加したべき根拡大体です。\(\bs{F}\) には \(1\)の原始5乗根 \(\zeta\) が含まれるので、\(\bs{F}(\al)/\bs{F}\) はガロア拡大、かつ巡回拡大です。\(\al\) と共役な方程式の根は、
\(\al,\:\:\al\zeta,\:\:\al\zeta^2,\:\:\al\zeta^3,\:\:\al\zeta^4\)
です。そこで \(\al\) に作用する自己同型写像 \(\sg_j\:(j=0,1,2,3,4)\) を、
と定義します。これを
\(\sg_j(\al)=\al\zeta^j\)
と書きます。\(\sg_j\) の集合を、
\(G_{\large s}=\{\sg_0,\:\sg_1,\:\sg_2,\:\sg_3,\:\sg_4\}\)
とすると、\(\mr{Gal}(\bs{F}(\al)/\bs{F})=G_{\large s}\) です。また、
\(\sg_0=e\)
\(\sg_1(\al)=\al\zeta\)
\(\sg_2(\al)=\al\zeta^2=\sg_1^{\:2}(\al)\)
\(\sg_3(\al)=\al\zeta^3=\sg_1^{\:3}(\al)\)
\(\sg_4(\al)=\al\zeta^4=\sg_1^{\:4}(\al)\)
です。\(\sg_1=\sg\) と書くと、
\(G_{\large s}=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\)
となって、\(G_{\large t}\) は \(\sg\) を生成元とする位数 \(5\) の巡回群であり、剰余群 \(\bs{Z}/5\bs{Z}\) と同型です。なお \(5\) は素数なので、\(\sg_1\) だけでなく、\(\sg_2,\:\sg_3,\:\sg_4\) も生成元です。
\(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\)
\(\sg_j\) を使って、\(\bs{F}=\bs{Q}(\zeta)\) の自己同型写像 \(\tau_i\) を \(\bs{L}=\bs{Q}(\zeta,\al)\) の自己同型写像に延長します。同型写像の延長定理(51H)により、\(\bs{Q}(\zeta,\al)\) の自己同型写像で、その作用を \(\bs{Q}(\zeta)\) に限定すると \(\tau_i\) に一致するものが必ず存在します。
\(\tau_i\) と \(\sg_j\) の合成写像を \(\sg_{ij}\) とし、
と定義します。\(\tau_i\) が先に作用します。すると、
\(\sg_{10}=\sg_0\cdot\tau_1=e\cdot e=e\)
\(\sg_{ij}(\zeta)=\tau_i(\zeta)=\zeta^i\)
\(\sg_{ij}(\al)=\sg_j(\al)=\al\zeta^j\)
となります。また、
\(\begin{eqnarray}
&&\:\:\sg_{ij}(\al\zeta)&=\sg_j\tau_i(\al\zeta)\\
&&&=\sg_j(\al\zeta^i)\\
&&&=\al\zeta^j\zeta^i\\
&&&=\al\zeta^{i+j}\\
\end{eqnarray}\)
です。このように定義した \(\sg_{ij}\) 同士の演算(=写像の合成)は \(\sg_{ij}\) で閉じています。\(\tau_i\) も \(\sg_j\) も5次方程式の解を共役な解に移す写像なので、その合成写像もまた、解を共役な解に移す写像ですが(=閉じている)、次のように計算で確認することができます。
\(\tau_i\:(i=1,2,3,4)\) は \(\tau(\)=\(\tau_2)\) を生成元とする巡回群で、\(\sg_j\:(j=0,1,2,3,4)\) は \(\sg(=\sg_1)\) を生成元とする巡回群です。ここで、
\(\tau\sg=\sg^2\tau\)
が成り立ちます。なぜなら、
\(\begin{eqnarray}
&&\:\:\tau\sg(\al\zeta)&=\tau_2\sg_1(\al\zeta)\\
&&&=\tau_2(\al\zeta\cdot\zeta)=\tau_2(\al\zeta^2)\\
&&&=\al\zeta^4\\
&&\:\:\sg^2\tau(\al\zeta)&=\sg_1^{\:2}\tau_2(\al\zeta)\\
&&&=\sg_1^{\:2}(\al\zeta^2)\\
&&&=\sg_1(\al\zeta\cdot\zeta^2)\\
&&&=\al\zeta\cdot\zeta\cdot\zeta^2\\
&&&=\al\zeta^4\\
\end{eqnarray}\)
と計算できるので、
\(\tau\sg(\al\zeta)=\sg^2\tau(\al\zeta)\)
が成り立つからです。\(\sg\) と \(\tau\) は可換ではありませんが(\(\tau\sg\neq\sg\tau\))、\(\tau\sg=\sg^2\tau\) という、いわば "弱可換性" があります("弱可換性" はここだけの言葉)。
\(\sg_{ij}\) の 2つの元 \(\sg_{ab},\:\sg_{cd}\) の合成写像は、
\(\sg_{cd}\sg_{ab}=\sg_d\tau_c\sg_b\tau_a=\sg_d(\tau_c\sg_b)\tau_a\)
ですが、\(\tau_c\sg_b\) の部分は、
\(\tau_c\sg_b=\tau\cd\tau\sg\cd\sg\)
の形をしています。この部分に弱可換性 \(\tau\sg=\sg^2\tau\) の関係を繰り返し使って、
\(\tau_c\sg_b=\sg\cd\sg\tau\cd\tau\)
の形に変形できます。ということは、
\(\sg_{cd}\sg_{ab}=\sg\cd\sg\tau\cd\tau\)
にまで変形できます。\(\sg^5=e,\:\tau^4=e\) なので、これは、
\(\sg_{cd}\sg_{ab}=\sg_j\tau_i\)
となる \(i,\:j\) が一意に決まることを示していて、合成写像は \(\sg_{ij}\) で閉じていることがわかります。
2つの写像、\(\sg_{ab}\) と \(\sg_{cd}\) の合成写像を具体的に計算してみると、
\(\begin{eqnarray}
&&\:\:\sg_{cd}\sg_{ab}(\al\zeta)&=\sg_{cd}(\al\zeta^{a+b})\\
&&&=\sg_d\tau_c(\al\zeta^{a+b})\\
&&&=\sg_d\al\zeta^{c(a+b)}\\
&&&=\al\zeta^{ac+bc+d}\\
\end{eqnarray}\)
\((1\leq a,c\leq4,\:\:0\leq b,d\leq4)\)
となります。四則演算はすべて有限体 \(\bs{F}_5\) で(= \(\mr{mod}\:5\) で)行います。
\(\sg_{(ac)(bc+d)}(\al\zeta)=\al\zeta^{ac+bc+d}\)
なので、
\(\sg_{cd}\sg_{ab}=\sg_{(ac)(bc+d)}\)
です。記述を見やすくするため、
と書きます。この記法を使うと、
[ \(c,\:d\) ][ \(a,\:b\) ]\(=\)[ \(ac,\:bc+d\) ]
となります。また、
[ \(a,\:b\) ][ \(a^{-1},\:-a^{-1}b\) ]
\(=\)[ \(aa^{-1},\:-aa^{-1}b+b\) ]
\(=\)[ \(1,\:0\) ]\(=e\)
[ \(a^{-1},\:-a^{-1}b\) ][ \(a,\:b\) ]
\(=\)[ \(a^{-1}a,\:a^{-1}b-a^{-1}b\) ]
\(=\)[ \(1,\:0\) ]\(=e\)
なので、[ \(a,\:b\) ] の逆元は、
[ \(a,\:b\) ]\(^{-1}=\)[ \(a^{-1},\:-a^{-1}b\) ]
です。\(a^{-1}\) は \(\bs{F}_5\)(ないしは\((\bs{Z}/5\bs{Z})^{*}\))での逆元で、\(1^{-1}=1\)、\(2^{-1}=3\)、\(3^{-1}=2\)、\(4^{-1}=4\) です。
以上で、演算で閉じていて、単位元と逆元の存在がいえるので、
\(\sg_{ij}\:\:(i=1,2,3,4)\:\:(j=0,1,2,3,4)\)
は群を構成することがわかります。
\(\sg_{ij}\) を共役な解の巡回置換で表現します。\(x^5-2=0\) の5つの解を \(1,\:2\:,3,\:4,\:5\) で表します。つまり、
\(1:\al,\:2:\al\zeta,\:3:\al\zeta^2,\:4:\al\zeta^3,\:5:\al\zeta^4\)
です。
\(\tau_i(\zeta)=\zeta^i\)
ですが、\(\zeta^5=1\) に注意して、\(\tau_i\) を巡回置換で表現すると、
\(\tau_1=\:e\)
\(\tau_2=(2,\:3,\:5,\:4)=\tau\)
\(\tau_3=(2,\:4,\:5,\:3)=\tau^3\)
\(\tau_4=(2,\:5)(3,\:4)=\tau^2\)
となります。同様にして、
\(\sg_j(\al)=\al\zeta^j\)
なので、
\(\sg_0=\:e\)
\(\sg_1=(1,\:2,\:3,\:4,\:5)=\sg\)
\(\sg_2=(1,\:3,\:5,\:2,\:4)=\sg^2\)
\(\sg_3=(1,\:4,\:2,\:5,\:3)=\sg^3\)
\(\sg_4=(1,\:5,\:4,\:3,\:2)=\sg^4\)
です。これらをもとに \(\sg_{ij}\) を計算すると、次のようになります。
\(\sg_{10}=\sg_0\tau_1=\:e\)
\(\sg_{20}=\sg_0\tau_2=(2,\:3,\:5,\:4)\)
\(\sg_{30}=\sg_0\tau_3=(2,\:4,\:5,\:3)\)
\(\sg_{40}=\sg_0\tau_4=(2,\:5)(3,\:4)\)
\(\sg_{11}=\sg_1\tau_1=(1,\:2,\:3,\:4,\:5)\)
\(\sg_{21}=\sg_1\tau_2=(1,\:2,\:4,\:3)\)
\(\sg_{31}=\sg_1\tau_3=(1,\:2,\:5,\:4)\)
\(\sg_{41}=\sg_1\tau_4=(1,\:2)(3,\:5)\)
\(\sg_{12}=\sg_2\tau_1=(1,\:3,\:5,\:2,\:4)\)
\(\sg_{22}=\sg_2\tau_2=(1,\:3,\:2,\:5)\)
\(\sg_{32}=\sg_2\tau_3=(1,\:3,\:4,\:2)\)
\(\sg_{42}=\sg_2\tau_4=(1,\:3)(4,\:5)\)
\(\sg_{13}=\sg_3\tau_1=(1,\:4,\:2,\:5,\:3)\)
\(\sg_{23}=\sg_3\tau_2=(1,\:4,\:5,\:2)\)
\(\sg_{33}=\sg_3\tau_3=(1,\:4,\:3,\:5)\)
\(\sg_{43}=\sg_3\tau_4=(1,\:4)(2,\:3)\)
\(\sg_{14}=\sg_4\tau_1=(1,\:5,\:4,\:3,\:2)\)
\(\sg_{24}=\sg_4\tau_2=(1,\:5,\:3,\:4)\)
\(\sg_{34}=\sg_4\tau_3=(1,\:5,\:2,\:3)\)
\(\sg_{44}=\sg_4\tau_4=(1,\:5)(2,\:4)\)
この巡回置換表示にもとづいて
[ \(c,\:d\) ][ \(a,\:b\) ]\(=\)[ \(ac,\:bc+d\) ]
を検証してみます。たとえば、
となるはずですが、
となって、確かに成り立っています。また逆元の式、
[ \(a,\:b\) ]\(^{-1}=\)[ \(a^{-1},\:-a^{-1}b\) ]
ですが、
となり、成り立っています。\(\bs{F}_5\) での演算では \(2^{-1}=3\) です。
以上により、
\(\begin{eqnarray}
&&\:\:G=\{\sg_{ij}\:| &i=1,2,3,4\\
&&&j=0,1,2,3,4\}\\
\end{eqnarray}\)
とおくと、
\(G=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\)
であることがわかりました。ここで、
\(G_{\large s}=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\)
は \(G\) の正規部分群になります。なぜなら、\(G_{\large s}=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta))\) なので、\(G_{\large s}\) の固定体は \(\bs{Q}(\zeta)\) です。一方、\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大なので、正規性定理(53C)によって \(G_{\large s}\) は \(G\) の正規部分群になるからです。
\(G_{\large s}\) が \(G\) の正規部分群であることは、計算でも確かめられます。"弱可換性" である、
\(\tau\sg=\sg^2\tau\)
の関係を使うと、
\(\begin{eqnarray}
&&\:\:\tau G_{\large s}&=\{\tau,\:\sg^2\tau,\:\sg^4\tau,\:\sg^6\tau,\:\sg^8\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau,\:\sg\tau,\:\sg^3\tau\}\\
&&&=\{e,\:\sg^2,\:\sg^4,\:\sg,\:\sg^3\}\cdot\tau\\
&&&=G_{\large s}\tau\\
\end{eqnarray}\)
が成り立ち、これを繰り返すと、
\(\tau^iG_{\large s}=G_{\large s}\tau^i\)
が成り立ちます。\(G\) の任意の元を \(\sg^j\tau^i\) とすると、
\(\begin{eqnarray}
&&\:\:(\sg^j\tau^i)G_{\large s}&=\sg^jG_{\large s}\tau^i\\
&&&=G_{\large s}(\sg^j\tau^i)\\
\end{eqnarray}\)
となって(\(\sg^j\) と \(G_{\large s}\) は可換です)、\(G_{\large s}\) が正規部分群の定義を満たします。
また、\(G\) の任意の元 \(x\) を \(x=\sg^j\tau^i\) とし、剰余群 \(G/G_{\large s}\) の任意の元 を \(xG_{\large s}\) とすると、
\(\begin{eqnarray}
&&\:\:xG_{\large s}&=(\sg^j\tau^i)G_{\large s}=\sg^jG_{\large s}\tau^i\\
&&&=G_{\large s}\tau^i\\
\end{eqnarray}\)
となりますが、\(G_{\large s}\tau^i=\tau^iG_{\large s}\) が成り立つので、
\(\begin{eqnarray}
&&\:\:(xG_{\large s})^4&=(G_{\large s}\tau^i)^4\\
&&&=(G_{\large s})^4(\tau^i)^4\\
&&&=G_{\large s}\\
\end{eqnarray}\)
となり、剰余群 \(G/G_{\large s}\) は位数 \(4\) の巡回群です。
もともと \(G_{\large s}=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta))\) であり、\(\bs{Q}(\zeta)\) の固定体は \(G_{\large s}\) でした。従って、
のガロア対応が得られました。\(G_{\large s}\) は \(G\) の正規部分群で \(G/G_{\large s}\) は巡回群、また \(G_{\large s}\) も巡回群です。従って \(G\) は可解群です。なお、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=G_{\large t}\) です。以上をまとめると、
\(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}))\)
\(=G\)
\(=\{\:\sg_{ij}\:\}=\{\:\sg_j\tau_i\:\}\)
\((i=1,2,3,4)\:\:(j=0,1,2,3,4)\)
\(\sg=(1,\:2,\:3,\:4,\:5)\)
\(\sg_0=e\)
\(\sg_1=\sg\)
\(\sg_2=\sg^2\)
\(\sg_3=\sg^3\)
\(\sg_4=\sg^4\)
\(\tau=(2,\:3,\:5,\:4)\)
\(\tau_1=e\)
\(\tau_2=\tau\)
\(\tau_3=\tau^3\)
\(\tau_4=\tau^2\)
\(\begin{eqnarray}
&&G_{\large s}&=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\\
&&&=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta)))\\
&&G_{\large t}&=\{e,\:\tau,\:\tau^2,\:\tau^3\}\\
&&&=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}))\\
\end{eqnarray}\)
となります。
位数 \(20\) の元、\(G=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\) は、(位数 \(20\)の)フロベニウス群という名前がついていて、\(F_{20}\) と表記します。フロベニウス群は、高々1点を固定する置換と恒等置換から成る群です。\(G\) は、固定する点がない \(\sg=(1,\:2,\:3,\:4,\:5)\) と、1点だけを固定する \(\tau=(2,\:3,\:5,\:4)\) の2つを生成元とする群なので、フロベニウス群です。この \(F_{20}\) の内部構造を調べます。
\(\tau_i\) には \(\{\tau_1=e,\:\tau_2,\:\tau_3,\:\tau_4\}\) の生成元とはならない \(\tau_4\) があります。\(\sg_i,\:\tau_j\) このような性格をもつのは \(\tau_4\) だけです。その \(\tau_4\) は、
\(\tau_4=(2,\:5)(3,\:4)\)
\(\tau_4^{\:2}=e\)
でした。つまり \(\{e,\:\tau_4\}\) は位数2の巡回群です。
ということは、\(\sg_1=\sg\) と \(t_4\) を生成元として、新たな群を定義できることになります。その群の元を \(\pi_{ij}\) とし、
\(\pi_{ij}=\sg^j\tau_4^i\:\:(i=0,1,\:\:j=0,\:1,\:2,\:3,\:4)\)
\(\begin{eqnarray}
&&\:\: \pi_{0j}&=\sg_j\\
&&\:\: \pi_{1j}&=\sg_j\cdot\tau_4\\
&&&=\sg_j\cdot(2,\:5)(3,\:4)\\
\end{eqnarray}\)
と定義すると、位数 \(10\) の群になります。具体的に計算してみると、
\(\pi_{00}=e\)
\(\pi_{01}=(1,\:2,\:3,\:4,\:5)\)
\(\pi_{02}=(1,\:3,\:5,\:2,\:4)\)
\(\pi_{03}=(1,\:4,\:2,\:5,\:3)\)
\(\pi_{04}=(1,\:5,\:4,\:3,\:2)\)
\(\pi_{10}=(2,\:5)(3,\:4)\)
\(\pi_{11}=(1,\:2)(3,\:5)\)
\(\pi_{12}=(1,\:3)(4,\:5)\)
\(\pi_{13}=(1,\:4)(2,\:3)\)
\(\pi_{24}=(1,\:5)(2,\:4)\)
となります。
この群は5次の2面体群であり、\(D_{10}\) で表します(\(D_5\) と書く流儀もある。幾何学の文脈では \(D_5\))。一般に 2面体群 \(D_{2n}\)(または \(D_n\))とは、裏表のある正\(n\)角形を元の形に一致するように移動する(=対称移動をする)ことを表す群です。正5角形の頂点に1から5の名前を一周する順につけると、たとえば \((1,\:2,\:3,\:4,\:5)\) は \(72^\circ\)の回転であり、\((2,\:5)(3,\:4)\) は頂点1を通る対称軸で折り返す対称移動です。3次の2面体群を1.3節で図示しました。
\(D_{10}\) は \(F_{20}\) の部分群で、位数は \(10\) です。位数が \(20\) の半分なので、半分の部分群は正規部分群の定理(65F)により、\(D_{10}\) は \(F_{20}\) の正規部分群であり、剰余群 \(F_{20}/D_{10}\) は位数が \(2\) なので巡回群です。
さらに \(D_{10}\) の部分群として \(\sg_i\:(i=0,1,2,3,4)\) があり、位数 \(5\) の巡回群です。位数 \(5\) の巡回群は \(C_5\) と表記されます。\(C_5\) の位数もまた \(D_{10}\) の半分なので、\(C_5\) は \(D_{10}\) の正規部分群であり、剰余群 \(D_{10}/C_5\) は巡回群です。結局、\(F_{20}\) には、
という部分群の列が存在することになり、これらすべてが可解列です。実は、可解な5次方程式のガロア群は、\(F_{20}\)、\(D_{10}\)、\(C_5\) の3つしかないことが知られています。以上のように \(x^5-2=0\) のガロア群は、可解なガロア群の全部を含んでいるのでした。
\(x^5+11x-44\)
一般的に、ある5次方程式が与えられたとき、そのガロア群を決定するには複雑な計算が必要です。また可解な5次方程式の解を、四則演算とべき根で表現するためのアルゴリズムも複雑です。これらは「可解性の必要十分条件を示す」というガロア理論の範囲を超えるので、この記事では省略します。可解な5次方程式の例をあげておきます。
\(x^5+11x-44=0\)
のガロア群は \(D_{10}\) であることが知られています。この方程式は実数解が1つで、虚数解が4つです。実数解を \(\al\) とし、Wolfram Alpha で \(\al\) の近似値と厳密値を求めてみると次のようになります。この厳密値は本当かと心配になりますが、検算してみると正しいことが分かります。
\(\begin{eqnarray}
&&\:\:\al&=1.8777502748964972576\cd\\
&&&=\dfrac{\sqrt[5]{11}}{(\sqrt[5]{5})^4}(\al_1+\al_2-\al_3+\al_4)\\
\end{eqnarray}\)
\(\al_1=\sqrt[5]{\phantom{-}75+50\sqrt{5}-12\sqrt{5-\sqrt{5}}-59\sqrt{5+\sqrt{5}}}\)
\(\al_2=\sqrt[5]{\phantom{-}75-50\sqrt{5}+59\sqrt{5-\sqrt{5}}-12\sqrt{5+\sqrt{5}}}\)
\(\al_3=\sqrt[5]{-75+50\sqrt{5}+59\sqrt{5-\sqrt{5}}-12\sqrt{5+\sqrt{5}}}\)
\(\al_4=\sqrt[5]{\phantom{-}75+50\sqrt{5}+12\sqrt{5-\sqrt{5}}+59\sqrt{5+\sqrt{5}}}\)
第5章から第7章まで、かなり長い証明のステップでしたが、可解性の必要条件(64B)、
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つ がべき根で表されているとする。\(f(x)\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) は可解群である。
と、可解性の十分条件(75A)、
体 \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{K}\) とする。\(\mr{Gal}(\bs{K}/\bs{F})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
および、具体的な5次方程式のガロア群の検討と合わせて、次が結論づけられました。
\(\bs{Q}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とする。方程式 \(f(x)=0\) の解が四則演算とべき根で表現できるための必要十分条件は、ガロア群
\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群であることである。
5次方程式のガロア群には、可解群でないものと可解群の両方がある。従って、任意の5次方程式の解を四則演算とべき根で統一的に表現する解の公式はない。
2.整数の群
2.1 整数
自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,\:b)\) で表す。自然数 \(a\) を \(b\) で割った余りを \(r\) とすると、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
\(0\) でない整数 \(a\) と \(b\) が互いに素とすると、1次不定方程式、
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) が互いに素、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
\(a,\:b\) を整数、\(n\) を自然数とする。\(a\) を \(n\) で割った余りと、\(b\) を \(n\) で割った余りが等しいとき、
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
\(a,\:b,\:c,\:d\) を整数、\(n,r\) を自然数とし、
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
である。
\(n_1\) と \(n_2\) を互いに素な自然数とする。\(a_1\) と \(a_2\) を、\(0\leq a_1 < n_1,\:0\leq a_2 < n_2\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
\(n_1,\:n_2,\:\cd\:,\:n_k\) を、どの2つをとっても互いに素な自然数とする。\(a_i\) を \(0\leq a_i < n_i\:\:(1\leq i\leq k)\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
2.2 群
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群(group)であると言う。
2.3 既約剰余類群
剰余群 \(\bs{Z}/n\bs{Z}\) から、代表元が \(n\) と互いに素なものだけを選び出したものを既約剰余類という。
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
2.4 有限体 \(\bs{\bs{F}_p}\)
\(\bs{F}_p\) 上の1次方程式、
\(ax+b=c\)
は1個の解をもつ。
\(\bs{F}_p\) 上の多項式を \(f(x)\) とする。
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
\(\bs{F}_p\) 上の \(n\)次多項式を \(f_n(x)\) とする。方程式、
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
2.5 既約剰余類群は巡回群
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
\((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とする。以下が成り立つ。
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
自然数 \(n\) と素な自然数 \(a\) について、
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
\(p\) を素数とする。\((\bs{Z}/p\bs{Z})^{*}\) において、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。
\(p\) を素数とするとき、\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在する。生成元とは、その位数が \((\bs{Z}/p\bs{Z})^{*}\) の群位数、\(p-1\) の元である。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
\(p\) を \(p\neq2\) の素数(=奇素数)とする。また、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
2のべき乗の既約剰余類群は、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である。
3.多項式と体
3.1 多項式
\(a(x)\) と \(b(x)\) が互いに素な多項式のとき、
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
有理数 \(\bs{Q}\) を係数とする多項式で、\(\bs{Q}\) の範囲ではそれ以上因数分解できない多項式を \(\bs{Q}\) 上で既約な多項式という。
整数係数の多項式 \(f(x)\) が \(\bs{Q}\) 上で(=有理数係数の多項式で)因数分解できれば、整数係数でも因数分解できる。
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式とすると、方程式 \(p(x)=0\) は(複素数の範囲で)重解を持たない。
\(\al\) を 方程式の解とする。\(\al\) を解としてもつ、体 \(\bs{Q}\) 上の方程式のうち、次数が最小の多項式を、\(\al\) の \(\bs{Q}\) 上の最小多項式と言う。
\(\bs{Q}\) 上の方程式、\(f(x)=0\) が \(\al\) を解としてもつとき、
の2つは同値である。
3.2 体
体 \(\bs{Q}\) 上の多項式 \(f(x)\) を、
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
\(\bs{Q}\) 上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大である。つまり \(\bs{K}\) の元 \(\theta\) があって、\(\bs{K}=\bs{Q}(\theta)\) となる。この \(\theta\) を原始元という。
ある代数的数 \(\al\) の \(\bs{Q}\) 上の最小多項式が \(n\)次多項式 \(f(x)\) であるとする。このとき 体 \(\bs{K}\) を、
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
3.3 線形空間
集合 \(V\) と 体 \(\bs{K}\) が次を満たすとき、\(V\) を \(\bs{\bs{K}}\) 上の線形空間(=ベクトル空間。linear space / vector space)と言う。
加算の定義
\(V\) の任意の元 \(u,\:v\) に対して \((u+v)\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
スカラー倍の定義
\(V\) の任意の元 \(u\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(ku\in V\) が定義されていて、加算との間に次の性質がある。\(u,\:v\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(mu)=(km)u\)
\((2)\:\:(k+m)u=ku+mu\)
\((3)\:\:k(u+v)=ku+kv\)
\((4)\:\:1v=v\)
1次独立
線形空間 \(V\) の元の組、\(\{v_1,v_2,\cd,v_n\}\) に対して、
\(a_1v_1+a_2v_2+\)..\(+a_nv_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{v_1,v_2,\cd,v_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{v_1,v_2,\cd,v_n\}\) に対して、
\(a_1v_1+a_2v_2+\)..\(+a_nv_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{v_1,v_2,\cd,v_n\}\) は1次従属であるという。
線形空間 \(V\) の元の組、\(\{v_1,v_2,\cd,v_n\}\) に対して、次の2つが満たされるとき、\(\{v_1,v_2,\cd,v_n\}\) を基底という。
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
\(\{u_1,u_2,\cd,u_m\}\) と \(\{v_1,v_2,\cd,v_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) である。
線形空間の基底に含まれる元の数が有限個のとき、その個数を線形空間の次元と言う。次元は基底の取り方によらない。
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。単拡大体である \(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間であり、\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) は \(\bs{Q}(\al)\) の基底である。
代数拡大体 \(\bs{F},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{K}\) であるとき、\(\bs{K}\) は \(\bs{F}\) 上の線形空間である。\(\bs{K}\) の次元を、\(\bs{K}\)の(\(\bs{F}\)からの)拡大次数といい、
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
代数拡大体 \(\bs{F},\:\bs{M},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{M}\:\subset\:\bs{K}\) であるとき、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
体 \(\bs{K}_0\) と 体 \(\bs{K}\) があり、\(\bs{K}_0\:\subset\:\bs{K}\) を満たしている。\(\bs{K}_0\) と \(\bs{K}\) が有限次元であり、その次元が同じであれば、\(\bs{K}_0=\bs{K}\) である。
4.一般の群
4.1 部分群\(\bs{\cdot}\)正規部分群、剰余類\(\bs{\cdot}\)剰余群
群 \(G\) の2つの部分集合を \(H,\:N\) とする。\(H\) と \(N\) の演算結果である \(G\) の部分集合、\(HN\) を次の式で定義する。
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
群 \(G\) の部分集合を \(N\) とし、\(N\) の任意の2つの元を \(x,\:y\) とする。
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
群 \(G\) の部分群を \(N\) とし、\(G\) の 元を \(x\) とすると、次の2つは同値である。
① \(xN\:=\:N\)
② \(x\:\in\:N\)
\(G\) の部分群を \(H,\:N\) とすると、\(H\cap N\) は部分群である。
有限群 \(G\) の位数を \(n\) とし( \(|G|=n\) )、\(H\) を \(G\) の部分群とする。\(H\) に左から \(G\) のすべての元、\(g_1,\:g_2,\:\cd\:,\:g_n\) かけて、集合、
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
群位数が素数の群は巡回群である。
有限群 \(G\) の部分群を \(H\) とする。\(G\) の全ての元 \(g\) について、
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
有限群 \(G\) の正規部分群を \(H\) とする。\(G\) の \(H\) による剰余類
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
巡回群の部分群による剰余群は巡回群である。
\(G\) の正規部分群を \(H\)、部分群を \(N\) とする。このとき、
が成り立つ。
4.2 準同型写像
群 \(G\) から群 \(G\,'\) への写像 \(f\) がある。\(G\) の任意の2つの元、\(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(G\) の元を \(f\) で移した元の集合を「\(f\) の像(image)」といい、\(\mr{Im}\:f\) と書く。\(\mr{Im}\:f\) を \(f(G)\) と書くこともある。
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。このとき
である。
群 \(G\) から群 \(G\,'\) への準同型写像を \(f\) とする。このとき \(\mr{Ker}\:f\) は \(G\) の正規部分群である。
4.3 同型定理
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(H=\mr{Ker}\:f\) とすると、\(G\) の \(H\) による剰余群は、\(G\) の \(f\) による像と同型である。つまり、
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
群 \(G\) の正規部分群を \(H\)、部分群を \(N\) とすると、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
5.ガロア群とガロア対応
5.1 体の同型写像
体 \(\bs{K}\) から 体 \(\bs{F}\) への写像 \(f\) が全単射であり、\(\bs{K}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
変数 \(x\) の多項式(係数は \(\bs{Q}\) の元)を分母・分子とする分数式を、\(\bs{Q}\) 上の有理式という。
体 \(\bs{K}\) と 体 \(\bs{F}\) は \(\bs{Q}\) を含むものとする。\(\sg\) を \(\bs{K}\) から \(\bs{F}\) への同型写像とし、\(a\) を \(\bs{K}\) の元とする。\(f(x)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}\,'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}\,'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とする。\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つを\(\al\)とし、\(\al\)は \(\bs{K}\) の元とする。すると \(\sg(\al)\) も \(f(x)=0\) の解である。
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とし、\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。方程式 \(f(x)=0\) の \(n\)個の解を \(\al_1,\al_2,\cd,\al_n\) とし、これらが全て \(\bs{K}\) に含まれるとする。
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(\al,\:\beta\) を方程式 \(f(x)=0\) の異なる解とする。
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(f(x)=0\) の全ての解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\) とする。このとき \(\bs{Q}(\al)\) に作用する同型写像は \(n\)個あり、それらは、
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
5.2 ガロア拡大とガロア群
ガロア拡大は次のように定義される。この2つの定義は同値である。
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\)、ガロア群を \(G\) とするとき、\([\:\bs{L}\::\:\bs{Q}\:]=|G|\) である。
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
\(\bs{K}\) を \(\bs{F}\) のガロア拡大体とし、\(\bs{M}\) を \(\bs{F}\subset\bs{M}\subset\bs{K}\) である任意の体(=中間体)とするとき、\(\bs{K}\) は \(\bs{M}\) のガロア拡大体でもある。
5.3 ガロア対応
体 \(\bs{F}\) 上の方程式の最小分解体(=ガロア拡大体)を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる。これを \(\bs{K}\) における \(H\) の固定体といい、\(\bs{K}(H)\) で表す(または \(\bs{K}^H\))。
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
\(\bs{F}\) のガロア拡大体を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の任意の部分群を \(H\) とし、\(H\) による \(\bs{K}\) の固定体 \(\bs{K}(H)\) を \(\bs{M}\) とする(次式)。
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とし、\(\mr{Gal}(\bs{K}/\bs{Q})=G\) とする。\(\bs{K}\) の中間体 \(\bs{M}\) と \(G\) の部分群 \(H\) がガロア対応になっているとする。このとき
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
6.可解性の必要条件
6.1 可解群
群 \(G\) から 単位元 \(e\) に至る部分群の列、
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、剰余群 \(H_i/H_{i+1}\) が巡回群であるとき、\(G\) を可解群(solvable group)と言う。
\(H_{i+1}\) が \(H_i\) の正規部分群であるとき、\(H_i\) を正規列と言う。また、\(H_i/H_{i+1}\) が巡回群のとき、\(H_i\) を可解列という。
巡回群は可解群である。また、巡回群の直積も可解群である。
可解群の部分群は可解群である。
可解群の準同型写像による像は可解群である。
このことより、
可解群の剰余群は可解群
であることが分かる。なぜなら、群 \(G\) の部分群を \(N\) とすると、\(G\) から \(G/N\) への自然準同型、つまり \(x\in G\) として、
\(x\:\longmapsto\:xN\)
の準同型写像を定義できるからである。
6.2 巡回拡大
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とする。\(\mr{Gal}(\bs{K}/\bs{Q})\) が巡回群のとき、\(\bs{K}/\bs{Q}\) を巡回拡大(cyclic extension)と言う。
\(\bs{Q}\) の拡大体を \(\bs{K}\) とする。
となる拡大列があって(\(k > 1\))、\(\bs{K}_{i+1}/\bs{K}_i\:(0\leq i < k)\) が巡回拡大のとき、\(\bs{K}/\bs{Q}\) は累巡回拡大であると言う。ただし、\(\bs{\bs{K}/\bs{Q}}\) が累巡回拡大だとしても、\(\bs{\bs{K}/\bs{Q}}\) がガロア拡大であるとは限らない。
\(\bs{Q}\) のガロア拡大を \(\bs{K}\)、そのガロア群を \(G\) とする。このとき、
の2つは同値である。
6.3 原始\(\bs{n}\)乗根を含む体とべき根拡大
1の原始\(n\)乗根を \(\zeta\) とする。このとき
・\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大
・\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\:\cong\:(\bs{Z}/n\bs{Z})^{*}\)
が成り立つ。
\(x^n-1=0\) の \(n\)個の解のうち、\(n\)乗して初めて \(1\) になる解を \(1\)の原始\(n\)乗根という。
原始\(n\)乗根は \(\varphi(n)\) 個ある。\(\varphi(n)\) はオイラー関数で、\(n\) と互いに素である \(n\) 以下の自然数の数を表す。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\zeta^m\:\:(1\leq m\leq n)\)
は、\(1\) の\(n\)乗根の全体を表す。また、
\(\zeta^m\:\:(\mr{gcd}(m,n)=1)\)
は、\(1\) の原始\(n\)乗根の全体を表す。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とする。\(\zeta\) の最小多項式を \(f(x)\) とし、\(k\) を \(n\) とは素な数とする。
このとき \(f(\zeta^k)=0\) である。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、\(\zeta\) の最小多項式を \(f(x)\) とすると、\(f(x)\) は円分多項式である。円分多項式とは、方程式 \(f(x)=0\) が \(\varphi(n)\) 個の解をもち、それらすべてが 原始\(n\)乗根 である多項式である。
従って、原始\(n\)乗根は互いに共役である。最小多項式は既約多項式なので、円分多項式は既約多項式である。
\(\bs{Q}\) に \(\zeta\) を添加した単拡大体 \(\bs{Q}(\zeta)\) は \(f(x)\) の最小分解体であり、\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大である。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
である。つまり \(1\) の原始\(n\)乗根の一つを \(\bs{Q}\) に添加した拡大体のガロア群は、既約剰余類群に同型である。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積と同型である。
従って、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は可解群であり(61B)、累巡回拡大である(62C)。
\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とするとき、\(\bs{K}(\sqrt[n]{a})\) を \(\bs{K}\) のべき根拡大(radical extension)と呼ぶ。
また、\(\bs{K}\) からのべき根拡大を繰り返して拡大体 \(\bs{F}\) ができるとき、\(\bs{F}/\bs{K}\) を累べき根拡大と言う。
\(1\) の原始\(n\)乗根を \(\zeta\) とし、\(\bs{K}\) に \(\zeta\) が含まれるとする。\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とし、\(\bs{L}=\bs{K}(\sqrt[n]{a})\) とすると、
が成り立つ。
6.4 可解性の必要条件
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つである \(\al\) がべき根で表されているとする。このとき「\(\bs{Q}\) のガロア拡大 \(\bs{E}\) で、\(\al\) を含み、\(\bs{E}/\bs{Q}\) が累巡回拡大」であるような 代数拡大体 \(\bs{E}\) が存在する。
\(\bs{Q}\) 上の \(n\)次既約方程式 \(f(x)=0\) の解の一つ がべき根で表されているとする。\(f(x)\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) は可解群である。
6.5 5次方程式の解の公式はない
すべての置換は共通文字を含まない巡回置換の積で表せる。
すべての置換は互換の積で表せる。
一つの置換を互換の積で表したとき、その互換の数は奇数か偶数かのどちらかに決まる。
\(S_n\) の元は同数の偶置換と奇置換から成る。従って、
\([\:S_n\::\:A_n\:]=2\)
である。
\(A_n\) は \(S_n\) の正規部分群であり、\(S_n/A_n\) は巡回群である。
交代群 \(A_n\) の任意の元は、3文字の巡回置換の積で表せる。
群 \(G\) の部分群を \(N\) とする。
\(|G|=2|N|\)
のとき(つまり 群の指数 \([G:N]=2\) のとき)、\(N\) は \(G\) の正規部分群である。
5次以上の対称群、\(S_n\:\:(n\geq5)\) は可解群ではない。
\(\bs{Q}\) の代数拡大体を \(\bs{K}\) とする。\(\bs{K}\) の任意の元である\(k\)5つの変数 \(b_1,b_2,b_3,b_4,b_5\) を根とする多項式を、
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
とし、\(\bs{Q}\) に \(a_0,a_1,a_2,a_3,a_4,\)を添加した代数拡大体を \(\bs{F}\) とする。つまり、
\(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\)
である。
このとき、\(\bs{K}\) の \(\bs{F}\) 上の ガロア群 \(G\) は5次対称群 \(S_5\) である。\(S_5\) は可解群ではないので(65G)、従って \(b_i\) を \(a_i\) のべき根で表すことはできない。
6.6 可解ではない5次方程式
群 \(G\) の位数 \(|G|\) が素数 \(p\) を約数にもつとき、\(g^p=e\:\:(g\neq e)\) となる \(G\) の元 \(g\) が存在する。つまり、\(G\) は位数 \(p\) の巡回群を部分群としてもつ。
\(f(x)\) を既約な5次多項式とする。方程式 \(f(x)=0\) が複素数解を2つ、実数解を3つもつなら、方程式は可解ではない。
7.可解性の十分条件
7.1 1の原始\(\bs{n}\)乗根
\(1\) の 原始\(n\)乗根はべき根で表現できる。
7.2 べき根拡大の十分条件のため補題
\(\bs{L}\) を \(\bs{K}\) のガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) を \(\sg\) で生成される位数 \(n\) の巡回群とする。式 \(g(x)\) を、
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
\(\zeta\) を \(1\) の原始\(n\)乗根とし、\(\zeta\)を含む代数体を \(\bs{K}\) とする。\(\bs{K}\) のガロア拡大体を \(\bs{L}\) とし、\(\mr{Gal}(\bs{L}/\bs{K})\) は \(\sg\) で生成される位数 \(n\) の巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。また \(f(x)\) を \(\bs{K}\) 上の \(n\)次既約多項式とし、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて、\(\bs{L}=\bs{K}(\theta)\) と表されているものとする。このとき、
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
7.3 べき根拡大の十分条件
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
7.4 べき根拡大と巡回拡大の同値性
\(1\) の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。また、\(\bs{K}\) の\(n\)次拡大体を \(\bs{L}\) とする( \([\:\bs{L}\::\:\bs{K}\:]=n\) )。
このとき、
の2つは同値である。
7.5 可解性の十分条件
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
| 7.可解性の十分条件(続き) |
7.8 可解な5次方程式
大多数の5次方程式のガロア群は、対称群 \(S_5\) か 交代群 \(A_5\) であり、従って可解ではありません(65G)。しかし特別な形の5次方程式は可解です。
|
しかし、\(x^5-2=0\) のガロア群は可解な5次方程式のガロア群としては最も複雑なのです。方程式の "見た目の" 単純・複雑さと、ガロア群の単純・複雑さはリンクしません。以下で \(x^5-2\) のガロア群を計算します。
\(x^5-2\) のガロア群
\(1\) の原始\(5\)乗根の一つを \(\zeta\) とします。\(x^5-1=0\) は、
\((x-1)(x^4+x^3+x^2+x+1)=0\)
と因数分解できるので、\(\zeta\) は、
\(x^4+x^3+x^2+x+1=0\)
の根です。7.1節で計算したように、たとえば、
\(\zeta=\dfrac{1}{4}(-1+\sqrt{5}+i\sqrt{10+2\sqrt{5}})\)
です。また、
\(\al=\sqrt[5]{2}\)
とします。そうすると、\(x^5-2=0\) の解は、
\(\al,\:\:\al\zeta,\:\:\al\zeta^2,\:\:\al\zeta^3,\:\:\al\zeta^4\)
の5つです。\(f(x)=x^5-2\) の最小分解体 \(\bs{L}\) は、
\(\begin{eqnarray}
&&\:\:\bs{L}&=\bs{Q}(\al,\:\al\zeta,\:\al\zeta^2,\:\al\zeta^3,\:\al\zeta^4)\\
&&&=\bs{Q}(\zeta,\al)\\
\end{eqnarray}\)
です。この \(\bs{L}=\bs{Q}(\zeta,\al)\) は、\(\bs{F}=\bs{Q}(\zeta)\) として、
\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{L}\)
という、体の拡大で作られたものと見なせます。つまり \(\bs{L}=\bs{F}(\al)\) です。
\(\zeta\) の \(\bs{Q}\) 上最小多項式は、\(x^4+x^3+x^2+x+1\) という4次多項式なので、拡大次数は、
\([\:\bs{F}:\:\bs{Q}\:]=4\)
です。\(\bs{Q}(\zeta)\) は単拡大体であり、単拡大体の同型写像の定理(51G)によって、\(\zeta\) に作用する \(\bs{Q}\) 上の同型写像はちょうど \(4\)個あります。
\(\bs{L}=\bs{Q}(\zeta,\al)\) は \(\bs{F}=\bs{Q}(\zeta)\) 上の5次既約多項式 \(x^5-2\) の解 \(\al\) を \(\bs{F}\) に添加した単拡大体です。従って、
\([\:\bs{L}\::\:\bs{F}\:]=5\)
です。\(\bs{L}=\bs{F}(\al)\) も単拡大体であり、\(\al\) に作用する \(\bs{\bs{F}}\) 上の同型写像は \(5\)個です。
拡大次数の連鎖律(33H)により、
\([\:\bs{L}\::\:\bs{Q}\:]=[\:\bs{L}\::\:\bs{F}\:]\cdot[\:\bs{F}\::\:\bs{Q}\:]=20\)
がわかります。従って \(\mr{Gal}(\bs{L}/\bs{Q})\) の位数は \(20\) です。\(\bs{L}=\bs{Q}(\zeta,\al)\) の自己同型写像を\(20\)個見つければ、それが \(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\) です。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
自己同型写像は、方程式の解を共役な解に移します。\(\zeta\) は \(1\) の原始\(5\)乗根であり、4次方程式 \(x^4+x^3+x^2+x+1=0\) の解なので、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
が互いに共役です。そこで、自己同型写像 \(\tau_i\:(i=1,2,3,4)\) を、\(\zeta\) を \(\zeta^i\) に置き換える写像、つまり、
\(\tau_i\::\:\zeta\:\longrightarrow\:\zeta^i\) |
\(\tau_i(\zeta)=\zeta^i\:\:(i=1,2,3,4)\)
と表記します。\(\tau_i\:(i=1,2,3,4)\) の集合を、
\(G_{\large t}=\{\tau_1,\:\tau_2,\:\tau_3,\:\tau_4\}\)
とすると、\(G_{\large t}\) は \(\bs{Q}(\zeta)\) の4つの自己同型写像の集合なので、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=G_{\large t}\)
です。恒等写像を \(e\) とすると、
\(\tau_1=e\)
ですが、
\(\tau_2(\zeta)=\zeta^2\)
\(\begin{eqnarray}
&&\:\:\tau_2^{\:2}(\zeta)&=\tau_2(\tau_2(\zeta))=\tau_2(\zeta^2)\\
&&&=\zeta^4=\tau_4(\zeta)\\
&&\:\:\tau_2^{\:3}(\zeta)&=\tau_2(\tau_2^2(\zeta))=\tau_2(\zeta^4)\\
&&&=\zeta^8=\zeta^3=\tau_3(\zeta)\\
&&\:\:\tau_2^{\:4}(\zeta)&=\zeta^{16}=\tau_1(\zeta)\\
\end{eqnarray}\)
と計算できるので、
\(\tau_1^{\:2}=\tau_4,\:\:\tau_1^{\:3}=\tau_3,\:\:\tau_1^{\:4}=e\)
となります。従って、\(\tau_2\) を \(\tau\) と書くと、
\(G_{\large t}=\{e,\:\tau,\:\tau^2,\:\tau^3\}\)
であり、\(G_{\large t}\) は \(\tau\)(= \(\tau_2\)) を生成元とする位数 \(4\) の巡回群で、既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と同型です。これは一般に \(1\) の原始\(n\)乗根を \(\zeta\) としたときに、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
という 6.3節の \(\bs{\bs{Q}(\zeta)}\)のガロア群の定理(63E)からもわかります。
\((\bs{Z}/5\bs{Z})^{*}\) の生成元は \(2,\:3\) です。従って、\(G_{\large t}\) の生成元は \(\tau_2,\:\tau_3\) です。\(\tau_4\) については、
\(\tau_4(\zeta)=\zeta^4\)
\(\begin{eqnarray}
&&\:\:\tau_4^{\:2}(\zeta)&=\tau_4(\tau_4(\zeta))=\tau_4(\zeta^4)\\
&&&=\zeta^{16}=\zeta\\
\end{eqnarray}\)
なので、\(\tau_4^{\:2}=\tau_1=e\) であり、生成元ではありません。
\(\mr{Gal}(\bs{F}(\al)/\bs{F})\)
\(\bs{L}=\bs{Q}(\zeta,\al)=\bs{F}(\al)\) は \(\bs{F}=\bs{Q}(\zeta)\) 上の既約方程式 \(x^5-2=0\) の解の一つである \(\al\) を \(\bs{F}\) に添加したべき根拡大体です。\(\bs{F}\) には \(1\)の原始5乗根 \(\zeta\) が含まれるので、\(\bs{F}(\al)/\bs{F}\) はガロア拡大、かつ巡回拡大です。\(\al\) と共役な方程式の根は、
\(\al,\:\:\al\zeta,\:\:\al\zeta^2,\:\:\al\zeta^3,\:\:\al\zeta^4\)
です。そこで \(\al\) に作用する自己同型写像 \(\sg_j\:(j=0,1,2,3,4)\) を、
\(\sg_j:\:\al\:\longrightarrow\:\al\zeta^j\) |
\(\sg_j(\al)=\al\zeta^j\)
と書きます。\(\sg_j\) の集合を、
\(G_{\large s}=\{\sg_0,\:\sg_1,\:\sg_2,\:\sg_3,\:\sg_4\}\)
とすると、\(\mr{Gal}(\bs{F}(\al)/\bs{F})=G_{\large s}\) です。また、
\(\sg_0=e\)
\(\sg_1(\al)=\al\zeta\)
\(\sg_2(\al)=\al\zeta^2=\sg_1^{\:2}(\al)\)
\(\sg_3(\al)=\al\zeta^3=\sg_1^{\:3}(\al)\)
\(\sg_4(\al)=\al\zeta^4=\sg_1^{\:4}(\al)\)
です。\(\sg_1=\sg\) と書くと、
\(G_{\large s}=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\)
となって、\(G_{\large t}\) は \(\sg\) を生成元とする位数 \(5\) の巡回群であり、剰余群 \(\bs{Z}/5\bs{Z}\) と同型です。なお \(5\) は素数なので、\(\sg_1\) だけでなく、\(\sg_2,\:\sg_3,\:\sg_4\) も生成元です。
\(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\)
\(\sg_j\) を使って、\(\bs{F}=\bs{Q}(\zeta)\) の自己同型写像 \(\tau_i\) を \(\bs{L}=\bs{Q}(\zeta,\al)\) の自己同型写像に延長します。同型写像の延長定理(51H)により、\(\bs{Q}(\zeta,\al)\) の自己同型写像で、その作用を \(\bs{Q}(\zeta)\) に限定すると \(\tau_i\) に一致するものが必ず存在します。
\(\tau_i\) と \(\sg_j\) の合成写像を \(\sg_{ij}\) とし、
\(\sg_{ij}=\sg_j\cdot\tau_i\) \((i=1,2,3,4)\:\:(j=0,1,2,3,4)\) |
\(\sg_{10}=\sg_0\cdot\tau_1=e\cdot e=e\)
\(\sg_{ij}(\zeta)=\tau_i(\zeta)=\zeta^i\)
\(\sg_{ij}(\al)=\sg_j(\al)=\al\zeta^j\)
となります。また、
\(\begin{eqnarray}
&&\:\:\sg_{ij}(\al\zeta)&=\sg_j\tau_i(\al\zeta)\\
&&&=\sg_j(\al\zeta^i)\\
&&&=\al\zeta^j\zeta^i\\
&&&=\al\zeta^{i+j}\\
\end{eqnarray}\)
です。このように定義した \(\sg_{ij}\) 同士の演算(=写像の合成)は \(\sg_{ij}\) で閉じています。\(\tau_i\) も \(\sg_j\) も5次方程式の解を共役な解に移す写像なので、その合成写像もまた、解を共役な解に移す写像ですが(=閉じている)、次のように計算で確認することができます。
\(\tau_i\:(i=1,2,3,4)\) は \(\tau(\)=\(\tau_2)\) を生成元とする巡回群で、\(\sg_j\:(j=0,1,2,3,4)\) は \(\sg(=\sg_1)\) を生成元とする巡回群です。ここで、
\(\tau\sg=\sg^2\tau\)
が成り立ちます。なぜなら、
\(\begin{eqnarray}
&&\:\:\tau\sg(\al\zeta)&=\tau_2\sg_1(\al\zeta)\\
&&&=\tau_2(\al\zeta\cdot\zeta)=\tau_2(\al\zeta^2)\\
&&&=\al\zeta^4\\
&&\:\:\sg^2\tau(\al\zeta)&=\sg_1^{\:2}\tau_2(\al\zeta)\\
&&&=\sg_1^{\:2}(\al\zeta^2)\\
&&&=\sg_1(\al\zeta\cdot\zeta^2)\\
&&&=\al\zeta\cdot\zeta\cdot\zeta^2\\
&&&=\al\zeta^4\\
\end{eqnarray}\)
と計算できるので、
\(\tau\sg(\al\zeta)=\sg^2\tau(\al\zeta)\)
が成り立つからです。\(\sg\) と \(\tau\) は可換ではありませんが(\(\tau\sg\neq\sg\tau\))、\(\tau\sg=\sg^2\tau\) という、いわば "弱可換性" があります("弱可換性" はここだけの言葉)。
なお、一般化すると、
\(\tau^i\sg^j=\sg^k\tau^i\:\:(k=2^{i}j)\)
と計算できます。
\(\tau^i\sg^j=\sg^k\tau^i\:\:(k=2^{i}j)\)
と計算できます。
\(\sg_{ij}\) の 2つの元 \(\sg_{ab},\:\sg_{cd}\) の合成写像は、
\(\sg_{cd}\sg_{ab}=\sg_d\tau_c\sg_b\tau_a=\sg_d(\tau_c\sg_b)\tau_a\)
ですが、\(\tau_c\sg_b\) の部分は、
\(\tau_c\sg_b=\tau\cd\tau\sg\cd\sg\)
の形をしています。この部分に弱可換性 \(\tau\sg=\sg^2\tau\) の関係を繰り返し使って、
\(\tau_c\sg_b=\sg\cd\sg\tau\cd\tau\)
の形に変形できます。ということは、
\(\sg_{cd}\sg_{ab}=\sg\cd\sg\tau\cd\tau\)
にまで変形できます。\(\sg^5=e,\:\tau^4=e\) なので、これは、
\(\sg_{cd}\sg_{ab}=\sg_j\tau_i\)
となる \(i,\:j\) が一意に決まることを示していて、合成写像は \(\sg_{ij}\) で閉じていることがわかります。
2つの写像、\(\sg_{ab}\) と \(\sg_{cd}\) の合成写像を具体的に計算してみると、
\(\begin{eqnarray}
&&\:\:\sg_{cd}\sg_{ab}(\al\zeta)&=\sg_{cd}(\al\zeta^{a+b})\\
&&&=\sg_d\tau_c(\al\zeta^{a+b})\\
&&&=\sg_d\al\zeta^{c(a+b)}\\
&&&=\al\zeta^{ac+bc+d}\\
\end{eqnarray}\)
\((1\leq a,c\leq4,\:\:0\leq b,d\leq4)\)
となります。四則演算はすべて有限体 \(\bs{F}_5\) で(= \(\mr{mod}\:5\) で)行います。
\(\sg_{(ac)(bc+d)}(\al\zeta)=\al\zeta^{ac+bc+d}\)
なので、
\(\sg_{cd}\sg_{ab}=\sg_{(ac)(bc+d)}\)
です。記述を見やすくするため、
\(\sg_{ij}=\)[ \(i,\:j\) ]
|
と書きます。この記法を使うと、
[ \(c,\:d\) ][ \(a,\:b\) ]\(=\)[ \(ac,\:bc+d\) ]
となります。また、
[ \(a,\:b\) ][ \(a^{-1},\:-a^{-1}b\) ]
\(=\)[ \(aa^{-1},\:-aa^{-1}b+b\) ]
\(=\)[ \(1,\:0\) ]\(=e\)
[ \(a^{-1},\:-a^{-1}b\) ][ \(a,\:b\) ]
\(=\)[ \(a^{-1}a,\:a^{-1}b-a^{-1}b\) ]
\(=\)[ \(1,\:0\) ]\(=e\)
なので、[ \(a,\:b\) ] の逆元は、
[ \(a,\:b\) ]\(^{-1}=\)[ \(a^{-1},\:-a^{-1}b\) ]
です。\(a^{-1}\) は \(\bs{F}_5\)(ないしは\((\bs{Z}/5\bs{Z})^{*}\))での逆元で、\(1^{-1}=1\)、\(2^{-1}=3\)、\(3^{-1}=2\)、\(4^{-1}=4\) です。
以上で、演算で閉じていて、単位元と逆元の存在がいえるので、
\(\sg_{ij}\:\:(i=1,2,3,4)\:\:(j=0,1,2,3,4)\)
は群を構成することがわかります。
\(\sg_{ij}\) を共役な解の巡回置換で表現します。\(x^5-2=0\) の5つの解を \(1,\:2\:,3,\:4,\:5\) で表します。つまり、
\(1:\al,\:2:\al\zeta,\:3:\al\zeta^2,\:4:\al\zeta^3,\:5:\al\zeta^4\)
です。
\(\tau_i(\zeta)=\zeta^i\)
ですが、\(\zeta^5=1\) に注意して、\(\tau_i\) を巡回置換で表現すると、
\(\tau_1=\:e\)
\(\tau_2=(2,\:3,\:5,\:4)=\tau\)
\(\tau_3=(2,\:4,\:5,\:3)=\tau^3\)
\(\tau_4=(2,\:5)(3,\:4)=\tau^2\)
となります。同様にして、
\(\sg_j(\al)=\al\zeta^j\)
なので、
\(\sg_0=\:e\)
\(\sg_1=(1,\:2,\:3,\:4,\:5)=\sg\)
\(\sg_2=(1,\:3,\:5,\:2,\:4)=\sg^2\)
\(\sg_3=(1,\:4,\:2,\:5,\:3)=\sg^3\)
\(\sg_4=(1,\:5,\:4,\:3,\:2)=\sg^4\)
です。これらをもとに \(\sg_{ij}\) を計算すると、次のようになります。
\(\sg_{10}=\sg_0\tau_1=\:e\)
\(\sg_{20}=\sg_0\tau_2=(2,\:3,\:5,\:4)\)
\(\sg_{30}=\sg_0\tau_3=(2,\:4,\:5,\:3)\)
\(\sg_{40}=\sg_0\tau_4=(2,\:5)(3,\:4)\)
\(\sg_{11}=\sg_1\tau_1=(1,\:2,\:3,\:4,\:5)\)
\(\sg_{21}=\sg_1\tau_2=(1,\:2,\:4,\:3)\)
\(\sg_{31}=\sg_1\tau_3=(1,\:2,\:5,\:4)\)
\(\sg_{41}=\sg_1\tau_4=(1,\:2)(3,\:5)\)
\(\sg_{12}=\sg_2\tau_1=(1,\:3,\:5,\:2,\:4)\)
\(\sg_{22}=\sg_2\tau_2=(1,\:3,\:2,\:5)\)
\(\sg_{32}=\sg_2\tau_3=(1,\:3,\:4,\:2)\)
\(\sg_{42}=\sg_2\tau_4=(1,\:3)(4,\:5)\)
\(\sg_{13}=\sg_3\tau_1=(1,\:4,\:2,\:5,\:3)\)
\(\sg_{23}=\sg_3\tau_2=(1,\:4,\:5,\:2)\)
\(\sg_{33}=\sg_3\tau_3=(1,\:4,\:3,\:5)\)
\(\sg_{43}=\sg_3\tau_4=(1,\:4)(2,\:3)\)
\(\sg_{14}=\sg_4\tau_1=(1,\:5,\:4,\:3,\:2)\)
\(\sg_{24}=\sg_4\tau_2=(1,\:5,\:3,\:4)\)
\(\sg_{34}=\sg_4\tau_3=(1,\:5,\:2,\:3)\)
\(\sg_{44}=\sg_4\tau_4=(1,\:5)(2,\:4)\)
この巡回置換表示にもとづいて
[ \(c,\:d\) ][ \(a,\:b\) ]\(=\)[ \(ac,\:bc+d\) ]
を検証してみます。たとえば、
| \(\sg_{23}\sg_{42}\) | \(=\)[ \(2,\:3\) ][ \(4,\:2\) ] | |
| \(=\)[ \(8,\:7\) ]\(=\)[ \(3,\:2\) ] | ||
| \(=\sg_{32}\) |
| \(\sg_{42}\) | \(=(1,\:3)(4,\:5)\) | |
| \(=\left(\begin{array}{c}1&2&3&4&5\\3&2&1&5&4\end{array}\right)\) | ||
| \(\sg_{23}\) | \(=(1,\:4,\:5,\:2)\) | |
| \(=\left(\begin{array}{c}3&2&1&5&4\\3&1&4&2&5\end{array}\right)\) |
| \(\sg_{23}\sg_{42}\) | \(=\left(\begin{array}{c}1&2&3&4&5\\3&1&4&2&5\end{array}\right)\) | |
| \(=(1\:3\:4\:2)=\sg_{32}\) |
となって、確かに成り立っています。また逆元の式、
[ \(a,\:b\) ]\(^{-1}=\)[ \(a^{-1},\:-a^{-1}b\) ]
ですが、
| \(\sg_{23}^{\:\:-1}\) | \(=\)[ \(2,\:3\) ]\(^{-1}\) | |
| \(=\)[ \(3,\:-3\cdot3\) ]\(=\)[ \(3,\:-9\) ] | ||
| \(=\)[ \(3,\:1\) ]\(=\sg_{31}\) | ||
| \(=(1,\:2,\:5,\:4)\) | ||
| \(\sg_{23}^{\:\:-1}\) | \(=(1,\:4,\:5,\:2)^{-1}\) | |
| \(=(2,\:5,\:4,\:1)\) | ||
| \(=(1,\:2,\:5,\:4)\) |
となり、成り立っています。\(\bs{F}_5\) での演算では \(2^{-1}=3\) です。
以上により、
\(\begin{eqnarray}
&&\:\:G=\{\sg_{ij}\:| &i=1,2,3,4\\
&&&j=0,1,2,3,4\}\\
\end{eqnarray}\)
とおくと、
\(G=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\)
であることがわかりました。ここで、
\(G_{\large s}=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\)
は \(G\) の正規部分群になります。なぜなら、\(G_{\large s}=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta))\) なので、\(G_{\large s}\) の固定体は \(\bs{Q}(\zeta)\) です。一方、\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大なので、正規性定理(53C)によって \(G_{\large s}\) は \(G\) の正規部分群になるからです。
\(G_{\large s}\) が \(G\) の正規部分群であることは、計算でも確かめられます。"弱可換性" である、
\(\tau\sg=\sg^2\tau\)
の関係を使うと、
\(\begin{eqnarray}
&&\:\:\tau G_{\large s}&=\{\tau,\:\sg^2\tau,\:\sg^4\tau,\:\sg^6\tau,\:\sg^8\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau,\:\sg\tau,\:\sg^3\tau\}\\
&&&=\{e,\:\sg^2,\:\sg^4,\:\sg,\:\sg^3\}\cdot\tau\\
&&&=G_{\large s}\tau\\
\end{eqnarray}\)
が成り立ち、これを繰り返すと、
\(\tau^iG_{\large s}=G_{\large s}\tau^i\)
が成り立ちます。\(G\) の任意の元を \(\sg^j\tau^i\) とすると、
\(\begin{eqnarray}
&&\:\:(\sg^j\tau^i)G_{\large s}&=\sg^jG_{\large s}\tau^i\\
&&&=G_{\large s}(\sg^j\tau^i)\\
\end{eqnarray}\)
となって(\(\sg^j\) と \(G_{\large s}\) は可換です)、\(G_{\large s}\) が正規部分群の定義を満たします。
また、\(G\) の任意の元 \(x\) を \(x=\sg^j\tau^i\) とし、剰余群 \(G/G_{\large s}\) の任意の元 を \(xG_{\large s}\) とすると、
\(\begin{eqnarray}
&&\:\:xG_{\large s}&=(\sg^j\tau^i)G_{\large s}=\sg^jG_{\large s}\tau^i\\
&&&=G_{\large s}\tau^i\\
\end{eqnarray}\)
となりますが、\(G_{\large s}\tau^i=\tau^iG_{\large s}\) が成り立つので、
\(\begin{eqnarray}
&&\:\:(xG_{\large s})^4&=(G_{\large s}\tau^i)^4\\
&&&=(G_{\large s})^4(\tau^i)^4\\
&&&=G_{\large s}\\
\end{eqnarray}\)
となり、剰余群 \(G/G_{\large s}\) は位数 \(4\) の巡回群です。
もともと \(G_{\large s}=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta))\) であり、\(\bs{Q}(\zeta)\) の固定体は \(G_{\large s}\) でした。従って、
| \(\bs{Q}\:\subset\:\bs{Q}(\zeta)\) | \(\subset\:\bs{Q}(\zeta,\al)\) | |
| \(G\:\sp\:G_{\large s}\) | \(\sp\:\{e\}\) |
のガロア対応が得られました。\(G_{\large s}\) は \(G\) の正規部分群で \(G/G_{\large s}\) は巡回群、また \(G_{\large s}\) も巡回群です。従って \(G\) は可解群です。なお、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=G_{\large t}\) です。以上をまとめると、
\(\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}))\)
\(=G\)
\(=\{\:\sg_{ij}\:\}=\{\:\sg_j\tau_i\:\}\)
\((i=1,2,3,4)\:\:(j=0,1,2,3,4)\)
\(\sg=(1,\:2,\:3,\:4,\:5)\)
\(\sg_0=e\)
\(\sg_1=\sg\)
\(\sg_2=\sg^2\)
\(\sg_3=\sg^3\)
\(\sg_4=\sg^4\)
\(\tau=(2,\:3,\:5,\:4)\)
\(\tau_1=e\)
\(\tau_2=\tau\)
\(\tau_3=\tau^3\)
\(\tau_4=\tau^2\)
\(\begin{eqnarray}
&&G_{\large s}&=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4\}\\
&&&=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q}(\zeta)))\\
&&G_{\large t}&=\{e,\:\tau,\:\tau^2,\:\tau^3\}\\
&&&=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}))\\
\end{eqnarray}\)
となります。
|
\(\bs{x^5-2=0}\) のガロア群(\(F_{20}\)) |
ガロア群 \(F_{20}\) の \(20\)個の元を、4つの5角形の頂点に配置した図。\((1,2,3,4,5)\) などはガロア群を構成する巡回置換を表す。また \(23451\) などは、その巡回置換によって \(12345\) を置換した結果を表す(白ヌキ数字は置換で不動の点)。この群の生成元は、色を付けた \((1,2,3,4,5)\) と \((2,3,5,4)\) である。 |
位数 \(20\) の元、\(G=\mr{Gal}(\bs{Q}(\zeta,\al)/\bs{Q})\) は、(位数 \(20\)の)フロベニウス群という名前がついていて、\(F_{20}\) と表記します。フロベニウス群は、高々1点を固定する置換と恒等置換から成る群です。\(G\) は、固定する点がない \(\sg=(1,\:2,\:3,\:4,\:5)\) と、1点だけを固定する \(\tau=(2,\:3,\:5,\:4)\) の2つを生成元とする群なので、フロベニウス群です。この \(F_{20}\) の内部構造を調べます。
\(\tau_i\) には \(\{\tau_1=e,\:\tau_2,\:\tau_3,\:\tau_4\}\) の生成元とはならない \(\tau_4\) があります。\(\sg_i,\:\tau_j\) このような性格をもつのは \(\tau_4\) だけです。その \(\tau_4\) は、
\(\tau_4=(2,\:5)(3,\:4)\)
\(\tau_4^{\:2}=e\)
でした。つまり \(\{e,\:\tau_4\}\) は位数2の巡回群です。
ということは、\(\sg_1=\sg\) と \(t_4\) を生成元として、新たな群を定義できることになります。その群の元を \(\pi_{ij}\) とし、
\(\pi_{ij}=\sg^j\tau_4^i\:\:(i=0,1,\:\:j=0,\:1,\:2,\:3,\:4)\)
\(\begin{eqnarray}
&&\:\: \pi_{0j}&=\sg_j\\
&&\:\: \pi_{1j}&=\sg_j\cdot\tau_4\\
&&&=\sg_j\cdot(2,\:5)(3,\:4)\\
\end{eqnarray}\)
と定義すると、位数 \(10\) の群になります。具体的に計算してみると、
\(\pi_{00}=e\)
\(\pi_{01}=(1,\:2,\:3,\:4,\:5)\)
\(\pi_{02}=(1,\:3,\:5,\:2,\:4)\)
\(\pi_{03}=(1,\:4,\:2,\:5,\:3)\)
\(\pi_{04}=(1,\:5,\:4,\:3,\:2)\)
\(\pi_{10}=(2,\:5)(3,\:4)\)
\(\pi_{11}=(1,\:2)(3,\:5)\)
\(\pi_{12}=(1,\:3)(4,\:5)\)
\(\pi_{13}=(1,\:4)(2,\:3)\)
\(\pi_{24}=(1,\:5)(2,\:4)\)
となります。
この群は5次の2面体群であり、\(D_{10}\) で表します(\(D_5\) と書く流儀もある。幾何学の文脈では \(D_5\))。一般に 2面体群 \(D_{2n}\)(または \(D_n\))とは、裏表のある正\(n\)角形を元の形に一致するように移動する(=対称移動をする)ことを表す群です。正5角形の頂点に1から5の名前を一周する順につけると、たとえば \((1,\:2,\:3,\:4,\:5)\) は \(72^\circ\)の回転であり、\((2,\:5)(3,\:4)\) は頂点1を通る対称軸で折り返す対称移動です。3次の2面体群を1.3節で図示しました。
\(D_{10}\) は \(F_{20}\) の部分群で、位数は \(10\) です。位数が \(20\) の半分なので、半分の部分群は正規部分群の定理(65F)により、\(D_{10}\) は \(F_{20}\) の正規部分群であり、剰余群 \(F_{20}/D_{10}\) は位数が \(2\) なので巡回群です。
さらに \(D_{10}\) の部分群として \(\sg_i\:(i=0,1,2,3,4)\) があり、位数 \(5\) の巡回群です。位数 \(5\) の巡回群は \(C_5\) と表記されます。\(C_5\) の位数もまた \(D_{10}\) の半分なので、\(C_5\) は \(D_{10}\) の正規部分群であり、剰余群 \(D_{10}/C_5\) は巡回群です。結局、\(F_{20}\) には、
| \(F_{20}\) | \(\sp\:C_5\:\sp\:\{\:e\:\}\) | |
| \(D_{10}\) | \(\sp\:C_5\:\sp\:\{\:e\:\}\) | |
| \(C_5\) | \(\sp\:\{\:e\:\}\) |
という部分群の列が存在することになり、これらすべてが可解列です。実は、可解な5次方程式のガロア群は、\(F_{20}\)、\(D_{10}\)、\(C_5\) の3つしかないことが知られています。以上のように \(x^5-2=0\) のガロア群は、可解なガロア群の全部を含んでいるのでした。
\(x^5+11x-44\)
|
\(x^5+11x-44=0\)
のガロア群は \(D_{10}\) であることが知られています。この方程式は実数解が1つで、虚数解が4つです。実数解を \(\al\) とし、Wolfram Alpha で \(\al\) の近似値と厳密値を求めてみると次のようになります。この厳密値は本当かと心配になりますが、検算してみると正しいことが分かります。
\(\begin{eqnarray}
&&\:\:\al&=1.8777502748964972576\cd\\
&&&=\dfrac{\sqrt[5]{11}}{(\sqrt[5]{5})^4}(\al_1+\al_2-\al_3+\al_4)\\
\end{eqnarray}\)
\(\al_1=\sqrt[5]{\phantom{-}75+50\sqrt{5}-12\sqrt{5-\sqrt{5}}-59\sqrt{5+\sqrt{5}}}\)
\(\al_2=\sqrt[5]{\phantom{-}75-50\sqrt{5}+59\sqrt{5-\sqrt{5}}-12\sqrt{5+\sqrt{5}}}\)
\(\al_3=\sqrt[5]{-75+50\sqrt{5}+59\sqrt{5-\sqrt{5}}-12\sqrt{5+\sqrt{5}}}\)
\(\al_4=\sqrt[5]{\phantom{-}75+50\sqrt{5}+12\sqrt{5-\sqrt{5}}+59\sqrt{5+\sqrt{5}}}\)
| 8.結論 |
第5章から第7章まで、かなり長い証明のステップでしたが、可解性の必要条件(64B)、
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つ がべき根で表されているとする。\(f(x)\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) は可解群である。
と、可解性の十分条件(75A)、
体 \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{K}\) とする。\(\mr{Gal}(\bs{K}/\bs{F})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
および、具体的な5次方程式のガロア群の検討と合わせて、次が結論づけられました。
\(\bs{Q}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とする。方程式 \(f(x)=0\) の解が四則演算とべき根で表現できるための必要十分条件は、ガロア群
\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群であることである。
5次方程式のガロア群には、可解群でないものと可解群の両方がある。従って、任意の5次方程式の解を四則演算とべき根で統一的に表現する解の公式はない。
(高校数学で理解するガロア理論:終)
| 定義\(\cdot\)定理一覧 |
2.整数の群
2.1 整数
| 互除法の原理(21A) |
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
| 不定方程式の解の存在(21B) |
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
| 不定方程式の解の存在(21C) |
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) が互いに素、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
| 法による演算の定義(21D) |
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
| 法による演算規則(21E) |
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
| \((1)\:a+c\) | \(\equiv b+d\) | \((\mr{mod}\:n)\) | |
| \((2)\:a-c\) | \(\equiv b-d\) | \((\mr{mod}\:n)\) | |
| \((3)\:ac\) | \(\equiv bd\) | \((\mr{mod}\:n)\) | |
| \((4)\:a^r\) | \(\equiv b^r\) | \((\mr{mod}\:n)\) |
| 中国剰余定理(21F) |
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
| 中国剰余定理・多連立(21G) |
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
2.2 群
| 群の定義(22A) |
| \(G\) の任意の元 \(x,\:y\) に対して演算(\(\cdot\)で表す)が定義されていて、\(x\cdot y\in G\) である。 | |
| 演算について結合法則が成り立つ。つまり、 \((x\cdot y)\cdot z=x\cdot(y\cdot z)\) | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot e=e\cdot x=x\) を満たす元 \(e\) が存在する。\(e\) を単位元という。 | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot y=y\cdot x=e\) となる元 \(y\) が存在する。\(y\) を \(x\) の逆元といい、\(x^{-1}\) と表す。 |
2.3 既約剰余類群
| 既約剰余類群(23A) |
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
2.4 有限体 \(\bs{\bs{F}_p}\)
| 有限体上の方程式1(24A) |
\(ax+b=c\)
は1個の解をもつ。
| 有限体上の方程式2(24B) |
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
| 有限体上の方程式3(24C) |
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
2.5 既約剰余類群は巡回群
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
| 位数の定理(25A) |
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
| オイラーの定理(25B) |
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
| 位数 \(d\) の元の数(25C) |
| 生成元の存在1(25D) |
なお、素数 \(p\) に対して、
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の「原始根」という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の「原始根」という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
| 生成元の探索アルゴリズム(25D’) |
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
| 生成元の存在2(25E) |
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
| 2のべき乗の既約剰余類群(25F) |
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
| 既約剰余類群の構造(25G) |
3.多項式と体
3.1 多項式
| 多項式の不定方程式(31A) |
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
| 既約多項式の定義(31B) |
| 整数係数多項式の既約性(31C) |
| 既約多項式と素数の類似性(31D) |
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
| 既約多項式の定理1(31E) |
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
| 既約多項式の定理2(31F) |
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
| 既約多項式の定理3(31G) |
| 最小多項式の定義(31H) |
| 最小多項式は既約多項式(31I) |
| \(f(x)\) が 体 \(\bs{Q}\) 上の既約多項式である | |
| \(f(x)\) が \(\al\) の \(\bs{Q}\) 上の最小多項式である |
の2つは同値である。
3.2 体
| 最小分解体の定義(32A) |
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
| 単拡大定理(32B) |
| 単拡大の体(32C) |
| \(\bs{K}\) | \(\overset{\text{ }}{=}\) | \(\{a_{n-1}\al^{n-1}+\)\(\:\cd\:+\)\(a_2\al^2+\)\(a_1\al+\)\(a_0\:|\:a_i\in\bs{Q}\:\}\) | |
| \((0\leq i\leq n-1)\) |
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
3.3 線形空間
| 線形空間の定義(33A) |
加算の定義
\(V\) の任意の元 \(u,\:v\) に対して \((u+v)\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
\(u+x=x\) となる \(x\) が存在する。これを \(0\) と書く。
\((2)\) 逆元の存在
\(u+x=0\) となる \(x\) が存在する。これを \(-u\) と書く。
\((3)\) 結合則が成り立つ
任意の元 \(u,\:v\:,w\) について、\((u+v)+w=u+(v+w)\)
\((4)\) 交換則が成り立つ
\(u+v=v+u\)
スカラー倍の定義
\(V\) の任意の元 \(u\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(ku\in V\) が定義されていて、加算との間に次の性質がある。\(u,\:v\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(mu)=(km)u\)
\((2)\:\:(k+m)u=ku+mu\)
\((3)\:\:k(u+v)=ku+kv\)
\((4)\:\:1v=v\)
| 1次独立と1次従属(33B) |
線形空間 \(V\) の元の組、\(\{v_1,v_2,\cd,v_n\}\) に対して、
\(a_1v_1+a_2v_2+\)..\(+a_nv_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{v_1,v_2,\cd,v_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{v_1,v_2,\cd,v_n\}\) に対して、
\(a_1v_1+a_2v_2+\)..\(+a_nv_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{v_1,v_2,\cd,v_n\}\) は1次従属であるという。
| 基底の定義(33C) |
| \({v_1,v_2,\cd,v_n}\) は1次独立である。 | |
| \(V\) の任意の元 \(v\) は、\(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) を選んで、
\(v=a_1v_1+a_2v_2+\)..\(+a_nv_n\)
と表せる。 |
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
| 基底の数の不変性(33D) |
| 次元の不変性(33E) |
| 単拡大体の基底(33F) |
| 拡大次数の定義(33G) |
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
| 拡大次数の連鎖律(33H) |
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
| 体の一致(33I) |
4.一般の群
4.1 部分群\(\bs{\cdot}\)正規部分群、剰余類\(\bs{\cdot}\)剰余群
| 部分集合の演算(41A) |
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
| 部分群の十分条件(41B) |
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
| 部分群の元の条件(41C) |
① \(xN\:=\:N\)
② \(x\:\in\:N\)
| 部分群の共通部分は部分群(41D) |
| 剰余類の定義(41E) |
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
群位数が素数の群は巡回群である。
| 正規部分群の定義(41F) |
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
| 剰余群の定義(41G) |
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
| 巡回群の剰余群は巡回群(41H) |
| 部分群と正規部分群(41I) |
(a) \(NH\) は \(G\) の部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
が成り立つ。
4.2 準同型写像
| 準同型写像と同型写像(42A) |
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
| 準同型写像の像と核(42B) |
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
| 核が単位元なら単射(42C) |
| \(\mr{Im}\:f\) | \(=\:G\,'\) | なら \(f\) は全射 | |
| \(\mr{Ker}\:f\) | \(=\:\{e\}\) | なら \(f\) は単射 |
である。
| 核は正規部分群(42D) |
4.3 同型定理
| 準同型定理(43A) |
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
| 第2同型定理(43B) |
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
5.ガロア群とガロア対応
5.1 体の同型写像
| 体の同型写像(51A) |
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
| 有理式の定義(51B) |
| 同型写像と有理式の順序交換(51C) |
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}\,'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}\,'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
| 同型写像での移り先(51D) |
| 同型写像による解の置換(51E) |
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
| 同型写像の存在(51F) |
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
| 単拡大体の同型写像(51G) |
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
| 同型写像の延長(51H) |
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
5.2 ガロア拡大とガロア群
| ガロア拡大(52A) |
| (最小分解体定義)体 \(\bs{F}\) 上の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とするとき、\(\bs{L}/\bs{F}\) をガロア拡大という。 | |
| (自己同型定義)体 \(\bs{F}\) の代数拡大体 \(\bs{K}\) があったとき、\(\bs{F}\) の元を不動にする \(\bs{K}\) の同型写像がすべて自己同型写像になるとき、\(\bs{K}/\bs{F}\) をガロア拡大という。 |
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
| 次数と位数の同一性(52B) |
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
| 中間体からのガロア拡大(52C) |
5.3 ガロア対応
| 固定体と固定群(53A) |
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
| ガロア対応(53B) |
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
| 正規性定理(53C) |
| \(\bs{M}/\bs{Q}\) がガロア拡大である | |
| \(H\)が\(G\)の正規部分群である |
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
6.可解性の必要条件
6.1 可解群
| 可解群の定義(61A) |
\(G=H_0\:\sp H_1\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{\:e\:\}\)
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、剰余群 \(H_i/H_{i+1}\) が巡回群であるとき、\(G\) を可解群(solvable group)と言う。
\(H_{i+1}\) が \(H_i\) の正規部分群であるとき、\(H_i\) を正規列と言う。また、\(H_i/H_{i+1}\) が巡回群のとき、\(H_i\) を可解列という。
| 巡回群は可解群(61B) |
| 可解群の部分群は可解群(61C) |
| 可解群の像は可解群(61D) |
このことより、
可解群の剰余群は可解群
であることが分かる。なぜなら、群 \(G\) の部分群を \(N\) とすると、\(G\) から \(G/N\) への自然準同型、つまり \(x\in G\) として、
\(x\:\longmapsto\:xN\)
の準同型写像を定義できるからである。
6.2 巡回拡大
| 巡回拡大の定義(62A) |
| 累巡回拡大の定義(62B) |
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{K}\)
となる拡大列があって(\(k > 1\))、\(\bs{K}_{i+1}/\bs{K}_i\:(0\leq i < k)\) が巡回拡大のとき、\(\bs{K}/\bs{Q}\) は累巡回拡大であると言う。ただし、\(\bs{\bs{K}/\bs{Q}}\) が累巡回拡大だとしても、\(\bs{\bs{K}/\bs{Q}}\) がガロア拡大であるとは限らない。
| 累巡回拡大ガロア群の可解性(62C) |
| \(G\) が可解群である | |
| \(\bs{K}/\bs{Q}\) が累巡回拡大である |
の2つは同値である。
6.3 原始\(\bs{n}\)乗根を含む体とべき根拡大
1の原始\(n\)乗根を \(\zeta\) とする。このとき
・\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大
・\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\:\cong\:(\bs{Z}/n\bs{Z})^{*}\)
が成り立つ。
| 原始n乗根の数(63A) |
原始\(n\)乗根は \(\varphi(n)\) 個ある。\(\varphi(n)\) はオイラー関数で、\(n\) と互いに素である \(n\) 以下の自然数の数を表す。
| 原始n乗根の累乗(63B) |
\(\zeta^m\:\:(1\leq m\leq n)\)
は、\(1\) の\(n\)乗根の全体を表す。また、
\(\zeta^m\:\:(\mr{gcd}(m,n)=1)\)
は、\(1\) の原始\(n\)乗根の全体を表す。
| 原始n乗根の最小多項式(63C) |
このとき \(f(\zeta^k)=0\) である。
| 円分多項式(63D) |
従って、原始\(n\)乗根は互いに共役である。最小多項式は既約多項式なので、円分多項式は既約多項式である。
\(\bs{Q}\) に \(\zeta\) を添加した単拡大体 \(\bs{Q}(\zeta)\) は \(f(x)\) の最小分解体であり、\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大である。
| Q(ζ)のガロア群(63E) |
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
である。つまり \(1\) の原始\(n\)乗根の一つを \(\bs{Q}\) に添加した拡大体のガロア群は、既約剰余類群に同型である。
| Q(ζ)のガロア群は巡回群(63F) |
従って、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は可解群であり(61B)、累巡回拡大である(62C)。
| べき根拡大の定義(63G) |
また、\(\bs{K}\) からのべき根拡大を繰り返して拡大体 \(\bs{F}\) ができるとき、\(\bs{F}/\bs{K}\) を累べき根拡大と言う。
| 原始n乗根を含むべき根拡大(63H) |
| \(\bs{L}/\bs{K}\) は巡回拡大である | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) の位数は \(n\) の約数である |
6.4 可解性の必要条件
| ガロア閉包の存在(64A) |
| 可解性の必要条件(64B) |
6.5 5次方程式の解の公式はない
| 置換は巡回置換の積(65A) |
| 置換は互換の積(65B) |
| 置換の偶奇性(65C) |
| 交代群は正規部分群(65D) |
\([\:S_n\::\:A_n\:]=2\)
である。
\(A_n\) は \(S_n\) の正規部分群であり、\(S_n/A_n\) は巡回群である。
| 交代群は3文字巡回置換の積(65E) |
| 半分の部分群は正規部分群(65F) |
\(|G|=2|N|\)
のとき(つまり 群の指数 \([G:N]=2\) のとき)、\(N\) は \(G\) の正規部分群である。
| 対称群の可解性(65G) |
| 5次方程式の解の公式はない(65H) |
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
とし、\(\bs{Q}\) に \(a_0,a_1,a_2,a_3,a_4,\)を添加した代数拡大体を \(\bs{F}\) とする。つまり、
\(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\)
である。
このとき、\(\bs{K}\) の \(\bs{F}\) 上の ガロア群 \(G\) は5次対称群 \(S_5\) である。\(S_5\) は可解群ではないので(65G)、従って \(b_i\) を \(a_i\) のべき根で表すことはできない。
6.6 可解ではない5次方程式
| コーシーの定理(66A) |
| 実数解が3つの5次方程式(66B) |
7.可解性の十分条件
7.1 1の原始\(\bs{n}\)乗根
| 原始n乗根はべき根で表現可能(71A) |
7.2 べき根拡大の十分条件のため補題
| べき根拡大の十分条件のため補題1(72A) |
| \(g(x)\) | \(\overset{\text{ }}{=}\) | \(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\) | |
| \((a_i\in\bs{L},\:1\leq i\leq n-1)\) |
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
| べき根拡大の十分条件のため補題2(72B) |
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
7.3 べき根拡大の十分条件
| べき根拡大の十分条件(73A) |
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
7.4 べき根拡大と巡回拡大の同値性
| べき根拡大と巡回拡大は同値(74A) |
このとき、
| \(\bs{L}/\bs{K}\) は巡回拡大である | |
| \(\bs{L}/\bs{K}\) はべき根拡大である。 |
7.5 可解性の十分条件
| 可解性の十分条件(75A) |
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
(定義・定理一覧:終)
2023-05-13 08:05
nice!(0)
No.358 - 高校数学で理解するガロア理論(5) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
第6章では、方程式が可解であれば(=解が四則演算とべき根で表現できれば)ガロア群が可解群であることをみました。第7章ではその逆、つまり、ガロア群が可解群であれば方程式が可解であることを証明します。
7.1 1の原始\(n\)乗根
可解性の十分条件を証明するために、まず、\(1\) の原始\(n\)乗根がべき根で表せることを証明します。このことを前提にした証明を最後で行うからです。念のために「1.1 方程式とその可解性」でのべき根の定義を振り返ると、
\(\sqrt[n]{\:a\:}\) (\(n=2\) の場合は \(\sqrt{\:a\:}\))
という表記は、
のでした。\(\sqrt{2}\) は \(1.4142\cd\) と \(-1.4142\cd\) のどちらかを表わすのではなく、\(1.4142\cd\) のことです。\(\sqrt[3]{2}\) は \(3\)乗して \(2\) になる3つの数のうちの正の実数(\(\fallingdotseq1.26\))を表わします。一方、\(\sqrt{-1\:}\) は\(2\)乗して \(-1\) になる2つの数のうちのどちらかで、その一方を \(i\) と書くと、もう一方が \(-i\) です。
この定義から、方程式 \(x^n-1=0\) の解を \(\sqrt[n]{\:1\:}\) と書くと、それは \(1\) のことです。従って、
ことを証明しておく必要があります。その証明はガロア理論とは無関係にできます。それが以下です。
\(1\) の 原始\(n\)乗根はべき根で表現できる。
[証明]
\(n\) についての数学的帰納法で証明する。\(n=2,\:3\) のときにべき根で表現できるのは根の公式で明らかである。また、原始4乗根は \(\pm i\) なので、\(n\leq4\) のとき題意は成り立つ。そこで、\(n\) 未満のときにべき根で表現できると仮定し、\(n\) のときにもべき根で表現できることを証明する。
\(n\) が合成数のときと素数のときに分ける。まず \(n\) が合成数なら、
\(n=s\cdot t\)
と表現できる。
\(1\) の原始\(s\)乗根を \(\zeta\)
\(1\) の原始\(t\)乗根を \(\eta\)
とし、\(X=x^{s}\) とおく。方程式 \(X^{t}-1=0\) の \(t\)個の解は \(\eta^k\:\:(0\leq k\leq t-1)\) と表わされる(63B)から、\(x^n-1\) は、
\(\begin{eqnarray}
&&\:\:x^n-1&=x^{st}-1=X^{t}-1\\
&&&=\displaystyle\prod_{k=0}^{t-1}(X-\eta^k)\\
&&&=\displaystyle\prod_{k=0}^{t-1}(x^{s}-\eta^k)\\
\end{eqnarray}\)
と因数分解できる。従って、方程式 \(x^n-1=0\) の解は、
\(x^{s}=\eta^k\:\:\:(0\leq k\leq t-1)\)
の解である。これを解くと、
\(x=\sqrt[s]{\eta^k}\cdot\zeta^j\:\:\:(0\leq j\leq s-1,\:\:0\leq k\leq t-1)\)
である(\(k=0\) のときは根号の規則に従って \(\sqrt[s]{1}=1\))。帰納法の仮定により、\(\zeta,\:\eta\) はべき根で表現できるから、上式により \(1\) の \(n\) 乗根はべき根で表現できる。従って原始\(n\)乗根もべき根で表現できる。
以降は \(n\) が素数の場合を証明する。\(n\) を \(p\)(= 素数)と表記する。以下では数式を見やすくするため \(p=5\) の場合を例示するが、証明の過程は一般性を失わない論理で進める。
位数 \(p-1\) の2つの巡回群、\((\bs{Z}/p\bs{Z})^{*}\) と \(\bs{Z}/(p-1)\bs{Z}\) の性質を利用する。\(p=5\) の場合は、位数 \(4\) の既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と、剰余群 \(\bs{Z}/4\bs{Z}\) である。
\(p\) が素数のとき、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は生成元をもつ(25D)。\((\bs{Z}/5\bs{Z})^{*}\) の生成元の一つは \(2\) である(もう一つは \(3\))。生成元を \(2\) とすると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
の巡回群となる。演算は乗算である。一方、\(\bs{Z}/4\bs{Z}\) は、演算が加算、生成元が \(1\)(または \(3\))の巡回群で、
\(\begin{eqnarray}
&&\:\:\bs{Z}/4\bs{Z}&=\{1,\:1+1,\:1+1+1,\:1+1+1+1\}\\
&&&=\{1,\:2,\:3,\:0\}\\
\end{eqnarray}\)
である。ここで、2つの変数 \(x,\:y\) をもつ関数を、
とおく。この関数は、4つある項の \(x,\:y\) の指数について、
\(y\) の指数は \([\:2,\:4,\:3,\:1\:]\) : \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン
\(x\) の指数は \([\:1,\:2,\:3,\:0\:]\) : \(\bs{Z}/4\bs{Z}\) の巡回パターン
となるようにしてある。
次に、2つの数 \(a,\:b\) を、
\(\begin{eqnarray}
&&\:\:a^5&=1\:(a\neq1)\\
&&\:\:b^4&=1\\
\end{eqnarray}\)
であるような数とする。\(a\) は \(1\) の原始5乗根でもよいし、その任意の累乗でもよい。とにかく \(a^5=1\:(a\neq1)\) を満たす数である。このとき、
\(a^5-1=0\)
\((a-1)(a^4+a^3+a^2+a+1)=0\)
なので、
\(a^4+a^3+a^2+a+1=0\) ないしは
\(a^4+a^3+a^2+a=-1\)
が成り立つ。\(b\) も \(1\) の原始4乗根か、その任意の累乗であるが、\(b=1\) であってもよい。
そうすると \(f(b,a)\) は、
\(f(b,a)=a^2b+a^4b^2+a^3b^3+a\)
\(a\) の指数は \([\:2,\:4,\:3,\:1\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
である。
次に \(f(b,a^2)\) を計算すると、
\(\begin{eqnarray}
&&\:\:f(b,a^2)&=a^4b+a^8b^2+a^6b^3+a^2\\
&&&=a^4+a^3b+a^1b^2+a^2b^3\\
\end{eqnarray}\)
\(a\) の指数は \([\:4,\:3,\:1,\:2\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
となる。
\(f(b,a^2)\) を \(f(b,a)\) と比べると、\(a\) の指数が \(1\) ステップだけ巡回している。ということは、\(b\) の指数も \([\:2,\:3,\:0,\:1\:]\) と \(1\) ステップだけ巡回させれば、\(a\) の指数と \(b\) の指数が同期することになり、\(f(b,a^2)\) の式は \(f(b,a)\) と同じものになる。同期させるには \(f(b,a^2)\) に \(b\) を掛ければよい。従って、
\(bf(b,a^2)=f(b,a)\)
である。
全く同様にして、
\(\begin{eqnarray}
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^8)&=b^3f(b,a^3)\\
&&&=f(b,a)\\
\end{eqnarray}\)
となる。まとめると、
\(\begin{eqnarray}
&&\:\:bf(b,a^2)&=f(b,a)\\
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^3)&=f(b,a)\\
\end{eqnarray}\)
である。\(b^4=1\) だから、各両辺を \(4\)乗すると、
\(f(b,a^2)^4=f(b,a)^4\)
\(f(b,a^4)^4=f(b,a)^4\)
\(f(b,a^3)^4=f(b,a)^4\)
の式を得る。
本題に戻って、次に \(f(b,a)^4\) を展開する。
であるが、このまま展開したのでは \(p=5\) のときに固有のものになり、一般性を失う。そこで、上式を展開して整理した形を、
とする。\(a^2,\:a^4,\:a^3,\:a\) の係数となっている \(h_i(b)\:(i=1,2,3,0)\) は \(b\) の多項式である。この展開形の決め方は次のように行う。
\((\br{B})\) 式においては、
であることに注意する。
次に \(f(b,a^2)^4\) を計算する。これは \((\br{B})\) 式において \(a\) を \(a^2\) に置き換えればよいから、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=h_1(b)a^4+h_2(b)a^8+h_3(b)a^6+h_0(b)a^2\\
&&&=h_1(b)a^4+h_2(b)a^3+h_3(b)a+h_0(b)a^2\\
\end{eqnarray}\)
となるが、これは \(f(b,a)^4\) において、
としたものと同じである。つまり、
\(f(b,a^2)^4=h_0(b)a^2+h_1(b)a^4+h_2(b)a^3+h_3(b)a\)
である。同様に、
\(f(b,a^4)^4=h_3(b)a^2+h_0(b)a^4+h_1(b)a^3+h_2(b)a\)
\(h_i(b)\) の添字 \(:\:[\:3,\:0,\:1,\:2\:]\)
\(f(b,a^3)^4=h_2(b)a^2+h_3(b)a^4+h_0(b)a^3+h_1(b)a\)
\(h_i(b)\) の添字 \(:\:[\:2,\:3,\:0,\:1\:]\)
である。
従って、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) において、\(a^j\:(j=2,4,3,1)\) の係数は \(h_k(b)\:(k=1,2,3,0)\) の全てを巡回する。つまり、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) の全部を足すと、\(a^j\:(j=2,4,3,1)\) の係数は全て同じになる。その計算をすると、
\(\displaystyle\sum_{i=1}^{4}f(b,a^i)^4\)
\(\begin{eqnarray}
&&\:\: =&(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&&\cdot(a^2+a^4+a^3+a)\\
\end{eqnarray}\)
となる。上式の左辺については、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=f(b,a)^4\\
&&\:\:f(b,a^4)^4&=f(b,a)^4\\
&&\:\:f(b,a^3)^4&=f(b,a)^4\\
\end{eqnarray}\)
だったので、左辺は \(4f(b,a)^4\) に等しい。また \(a^5-1=0\) なので \(a^2+a^4+a^3+a=-1\) である。従って、
\(4f(b,a)^4=-(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
である。ここで、
\(g(b)=-\dfrac{1}{4}\:(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
と定義すると、
を得る。\((\br{C})\) 式における \(\sqrt[4]{g(b)}\) とは「\(4\)乗すると \(g(b)\) になる数」という意味である。従って、実際には \(4\)次方程式の \(4\)つの解のどれかを表している。
なお、\(g(b)\) を具体的に計算すると、計算過程は省くが、
今までの計算をまとめると、
\(\begin{eqnarray}
&&\:\:a^5=1\:(a\neq1)&\\
&&\:\:b^4=1&\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(b,a)&=a^2b+a^4b^2+a^3b^3+a\\
&&\:\:f(b,a)^4&=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\\
&&\:\:g(b)&=-\dfrac{1}{4}(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&\:\:f(b,a)&=\sqrt[4]{g(b)}\\
\end{eqnarray}\)
である。この過程で、\(a,\:b\) については \(a^5=1\:(a\neq1),\:b^4=1\) という条件しか使っていない。従って、この条件が満たせれば \(a,\:b\) は任意である。そこで \(1\) の原始5乗根を \(\zeta\) とし、\(1\) の原始4乗根を \(\omega\) として、
\(a=\zeta\)
\(b=\omega^j\:\:(j=1,2,3,4)\)
とおく。\(b\) は \(1\) にもなりうる(\(\omega^4=1\))。なお、\(\omega\) は普通 \(1\) の原始3乗根の記号であるが、ここでは原始4乗根として使う。
すると、
という、4つの式が得られる。これは、
\(\zeta^2,\:\:\zeta^4,\:\:\zeta^3,\:\:\zeta\)
を4つの未知数とする連立1次方程式である。帰納法の仮定により \(\omega\) はべき根で表されているから、方程式を解いて \(\zeta\) が \(\omega\) のべき根(と四則演算)で表されば、証明が完成することになる。
\((\br{E})\) の連立方程式を具体的に書くと、
\(\zeta^2+\omega^j\zeta^4+(\omega^j)^2\zeta^3+(\omega^j)^3\zeta=\sqrt[4]{g(\omega^j)}\)
\((j=1,2,3,4)\)
であり、全てを陽に書くと、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta^2+\omega\:\:\zeta^4+(\omega\:\:)^2\zeta^3+(\omega\:\:)^3\zeta&=\sqrt[4]{g(\omega)}& \br{①}&\\
&&\zeta^2+\omega^2\zeta^4+(\omega^2)^2\zeta^3+(\omega^2)^3\zeta&=\sqrt[4]{g(\omega^2)}& \br{②}&\\
&&\zeta^2+\omega^3\zeta^4+(\omega^3)^2\zeta^3+(\omega^3)^3\zeta&=\sqrt[4]{g(\omega^3)}& \br{③}&\\
&&\zeta^2+\omega^4\zeta^4+(\omega^4)^2\zeta^3+(\omega^4)^3\zeta&=\sqrt[4]{g(\omega^4)}& \br{④}&\\
\end{eqnarray}
\end{array}\right.\)
となる。この連立方程式を解くため、\(\zeta\) の項だけを残し、他の未知数である \(\zeta^2,\:\zeta^4,\:\zeta^3\) の項を消去することを考える。そのために、
\(A\::\:\br{①}\times\omega\:+\:\br{②}\times\omega^2\:+\:\br{③}\times\omega^3\:+\:\br{④}\times\omega^4\)
とおくと、
\(A\) の左辺 \(=\)
\(\omega\:\:\zeta^2+(\omega\:\:)^2\zeta^4+(\omega\:\:)^3\zeta^3+(\omega\:\:)^4\zeta+\)
\(\omega^2\zeta^2+(\omega^2)^2\zeta^4+(\omega^2)^3\zeta^3+(\omega^2)^4\zeta+\)
\(\omega^3\zeta^2+(\omega^3)^2\zeta^4+(\omega^3)^3\zeta^3+(\omega^3)^4\zeta+\)
\(\omega^4\zeta^2+(\omega^4)^2\zeta^4+(\omega^4)^3\zeta^3+(\omega^4)^4\zeta\)
となる。\(\zeta\) の4つの項は、係数が \((\omega^j)^4=(\omega^4)^j=1\) であり、
\(\zeta\) の項の合計 \(=\:4\zeta\)
である。
\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数は、
\(\omega^j+\omega^{2j}+\omega^{3j}+\omega^{4j}\:\:(j=1,2,3)\)
である。\(\omega^4=1\) なので、
\(\omega^j+\omega^{2j}+\omega^{3j}+1\:\:(j=1,2,3)\)
の形をしている。\(\omega\) は \(1\) の原始4乗根であり、\(x^4-1=0\) の根である。\(x^4-1\) は、
\(x^4-1=(x-1)(x^3+x^2+x+1)\)
と因数分解されるから、\(\omega,\:\omega^2,\:\omega^3\) は方程式
\(x^3+x^2+x+1=0\)
の3つの根である。つまり、
\(x^3+x^2+x+1=(x-\omega)(x-\omega^2)(x-\omega^3)\)
と因数分解される。この式に \(x=\omega^j\:(j=1,2,3)\) を代入すると、
\((\omega^j)^3+(\omega^j)^2+\omega^j+1\)
\(\begin{eqnarray}
&&\:\: &=\omega^{3j}+\omega^{2j}+\omega^j+1\\
&&&=(\omega^j-\omega)(\omega^j-\omega^2)(\omega^j-\omega^3)\\
&&&=0\:\:(j=1,2,3)\\
\end{eqnarray}\)
となる。つまり、\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数、\(\omega^j+\omega^{2j}+\omega^{3j}+1\) は全て \(0\) ということである。以上をまとめると、\(A\) の左辺は \(\zeta\) の項だけが残り、
\(A\) の左辺 \(=\:4\zeta\)
である。一方、\(A\) 式の右辺は、
\(A\) の右辺 \(=\:\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
である。従って、
\(4\zeta=\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
\((\br{F})\) 式における \(\sqrt[4]{g(\omega^j)}\) とは「\(4\)乗すると \(g(\omega^j)\) になる数」という意味であり、\(4\)次方程式の\(4\)つの解のどれかである。従って、実際に \(\omega\) に数を入れて(この場合は \(1\) の原始4乗根だから \(i\) か \(-i\))計算するときには、\(\zeta^5=1\) になるように \((\br{F})\) 式の \(4\)つの項のそれぞれについて、\(4\)つの解のどれかを選択する必要がある。しかしそうであっても、\(\zeta\) が \(\omega\) の多項式のべき根と四則演算で表現できるということは変わらない。
これまでの論理展開では、\(p=5\) であることの特殊性は何も使っていない。唯一、使ったのは、\(p\) が素数であり、そのときに \((\bs{Z}/p\bs{Z})^{*}\) に生成元がある(25D)ということである。
従って、\(\zeta\) が \(1\) の原始\(p\)乗根であり、\(\omega\) が \(1\) の原始\((p-1)\)乗根であっても \((\br{F})\) 式は、\(4\) を \((p-1)\) に置き換えれば成り立つ。
帰納法の仮定により、\(1\) の原始\((p-1)\)乗根 \(\omega\) はべき根で表される。従って \((\br{F})\) 式から、\(1\) の原始\(p\)乗根 である \(\zeta\) もべき根で表される。[証明終]
ためしに \((\br{F})\) 式を使って、\(1\) の原始5乗根、\(\zeta\) を計算してみます。\(\omega\) は \(1\) の原始4乗根(の一つ)なので \(\omega=i\)(虚数単位)とすると、\((\br{D})\) 式も含めて、
\(\begin{eqnarray}
&&\:\:g(b)&=-16b^3+14b^2+4b-1 (\br{D})\\
&&\:\:b&=\omega^j\:\:(j=1,2,3,4)\\
&&&=\:\{\:i,\:-1,\:-i,\:1\:\}\\
&&\:\:g(\omega)&=-15+20i\\
&&\:\:g(\omega^2)&=25\\
&&\:\:g(\omega^3)&=-15-20i\\
&&\:\:g(\omega^4)&=1\\
\end{eqnarray}\)
となり、これらを \((\br{F})\) 式に代入すると、
\(\zeta=\dfrac{1}{4}(\sqrt[4]{1}-\sqrt[4]{25}+i(\sqrt[4]{-15+20i}-\sqrt[4]{-15-20i}))\)
となります。\(\sqrt[4]{\cd}\) は「\(4\)乗して \(\cd\) になる数」の意味です。この式を、
\(4\zeta=r+is\)
\(\begin{eqnarray}
&&\:\: r&=\sqrt[4]{1}-\sqrt[4]{25}\\
&&\:\: s&=\sqrt[4]{-15+20i}-\sqrt[4]{15-20i}\\
\end{eqnarray}\)
と表すことにします。そして \(\sqrt[4]{\cd}\) を \(\sqrt{\cd}\) に変換するために2乗すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=\pm6\pm2\sqrt{5}&\\
&&s^2=\pm10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
と計算できます。但し \(r^2+s^2=4\) の条件があるので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=6\pm2\sqrt{5}&\\
&&s^2=10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
となります(複合異順)。ここから \(r,\:s\) を求めると、\(r\) の方は2重根号をはずすことができて、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r=\pm(1+\sqrt{5}),\:\:s=\pm\sqrt{10-2\sqrt{5}}&\\
&&r=\pm(1-\sqrt{5}),\:\:s=\pm\sqrt{10+2\sqrt{5}}&\\
\end{eqnarray}
\end{array}\right.\)
の合計8つの解が求まります。このうちの4つは方程式 \(x^5-1=0\) の解 \((=\zeta)\) で、残りの4つは方程式 \(x^5+1=0\) の解 \((=-\zeta)\) です。\(\zeta\) を表記すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm i\sqrt{10+2\sqrt{5}}\right)&\\
&&\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm i\sqrt{10-2\sqrt{5}}\right)&\\
\end{eqnarray}
\end{array}\right.\)
の4つとなり、\(1\) の原始5乗根が求まりました。一般的な原始5乗根の計算方法とは違いますが、\((\br{F})\) 式によっても原始5乗根が求まることが確認できました。
7.2 べき根拡大の十分条件のため補題
ここでは「7.3 べき根拡大の十分条件」を証明するための補題を2つ証明します。以下に出てくる多項式 \(g(x)\) は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言います。
補題(1)
\(\bs{L}\) を \(\bs{K}\) のガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) を \(\sg\) で生成される位数 \(n\) の巡回群とする。式 \(g(x)\) を、
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
[証明]
\(\bs{L}\) が原始元 \(\theta\) によって \(\bs{L}=\bs{K}(\theta)\) と表されているとし(32B)、\(\theta\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式の定理(31I)により \(f(x)\) は既約多項式である。そうすると、\(\theta,\:\sg^i(\theta)\:(1\leq i\leq n-1)\) の \(n\)個は \(f(x)=0\) の解であり、既約多項式の定理3(31G)によって \(n\)個の解は全て異なる。つまり、
\(\theta-\sg^i(\theta)\neq0\:(1\leq i\leq n-1)\)
である。このことを踏まえて背理法で証明する。\(\bs{L}\) の任意の元 \(x\) について、
となるような \(\bs{L}\) の元 \(a_1,\:a_2,\:\cd\:,a_{n-1}\) が存在したとする。この \(g(x)=0\) の式から \(\sg^{n-1}(x)\) の項を消去することを考える。そのためにまず \(g(\theta x)\) を計算すると、
となる。この式から \(\sg^{n-1}(x)\) の項を消去するには、この式の \(\sg^{n-1}(x)\)の係数が \(a_{n-1}\sg^{n-1}(\theta)\) であり、また \(g(x)\) の \(\sg^{n-1}(x)\) の項の係数が \(a_{n-1}\) なので、
\(\sg^{n-1}(\theta)g(x)=0\)
の式を作って両辺から引けばよい。その計算をすると、
となる。ここで、\(x\) の係数である \((\theta-\sg^{n-1}(\theta))\) は、証明の最初に書いたように \(0\) ではない。そこで、全体を \((\theta-\sg^{n-1}(\theta))\) で割ると、
の形になる。ここで \(b_i\) は、
\(b_i=\dfrac{\sg^i(\theta)-\sg^{n-1}(\theta)}{\theta-\sg^{n-1}(\theta)}a_i\)
である。\((\br{B})\) 式は、基本的に \((\br{A})\) 式と同じで、\((\br{A})\) 式から \(\sg(x)^{n-1}\) の項を消去した形であり、\(x\) の最大次数の項は \(\sg(x)^{n-2}\) になっている。以上の、\((\br{A})\) から \((\br{B})\) への変換は繰り返し行えるから、\(n-2\) 回の変換を繰り返すと、
\(x+c_1\sg(x)=0\)
の形が得られる。この式にもう一度、\(n-1\) 回目の変換をすると、
となる。\(x\) は \(\bs{L}\) の任意の元だったから、\(\bs{L}\) のすべての元は \(0\) となってしまい、矛盾が生じた。従って背理法の仮定は誤りであり、\(\bs{L}\) の全ての元 \(x\) について、
補題(2)
\(\zeta\) を \(1\) の原始\(n\)乗根とし、\(\zeta\)を含む代数体を \(\bs{K}\) とする。\(\bs{K}\) のガロア拡大体を \(\bs{L}\) とし、\(\mr{Gal}(\bs{L}/\bs{K})\) は \(\sg\) で生成される位数 \(n\) の巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。また \(f(x)\) を \(\bs{K}\) 上の \(n\)次既約多項式とし、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて、\(\bs{L}=\bs{K}(\theta)\) と表されているものとする。このとき、
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
[証明]
\(g(x)\) の形は、べき根拡大の十分条件のため補題1(72A)で、
\(a_i=\zeta^{n-i}\:(1\leq i\leq n-1)\)
と置いたものである。\(\zeta\) は \(\bs{K}\) の元 = \(\bs{L}\) の元だから、補題(1)により \(\bs{L}\) の任意の元 \(x\) について \(g(x)=0\) となることはない。
この \(g(x)\) は次のような性質をもっている。まず \(\bs{K}\) の任意の元を \(a\) とすると、\(\mr{Gal}(\bs{L}/\bs{K})\) の 元 \(\sg\) は \(a\) を不動にするから、
\(\sg^i(a)=a\)
である。従って、\(g(a)\) を計算すると、
\(g(a)=ag(1)\)
となる。また、\(\bs{K}\) の任意の元を \(a\)、\(\bs{L}\) の任意の元を \(x\) とすると、
\(\sg^i(ax)=\sg^i(a)\sg^i(x)=a\sg^i(x)\)
なので、
\(g(ax)=ag(x)\)
である。さらに \(\bs{L}\) の任意の2つの元を \(x,\:y\) とすると、
\(\sg^i(x+y)=\sg^i(x)+\sg^i(y)\)
なので、
\(g(x+y)=g(x)+g(y)\)
である。
\(\bs{L}\) は、\(\bs{K}\) 上の既約多項式 \(f(x)\) を用いた方程式 \(f(x)=0\) の解 \(\theta\) の単拡大体 \(\bs{K}(\theta)\) だから、単拡大の体の定理(32C)により、\(\bs{L}\) の任意の元 \(x\) は、
\(x=b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1}\:(b^i\in\bs{K})\)
と表せる。\(g(x)\) の式にこの \(x\) を代入すると、
\(\begin{eqnarray}
&&\:\:g(x)&=g(b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1})\\
&&&=g(b_0)+g(b_1\theta)+g(b_2\theta^2)+\cd+g(b_{n-1}\theta^{n-1})\\
&&&=b_0g(1)+b_1g(\theta)+b_2g(\theta^2)+\cd+b_{n-1}g(\theta^{n-1})\\
\end{eqnarray}\)
となる。ここで、
\(g(1)=1+\zeta^{n-1}+\zeta^{n-2}+\cd+\zeta\)
だが、\(g(1)(1-\zeta)=\zeta^n-1=0\) なので \(g(1)=0\) である。従って、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) の全てが \(0\) だと、\(\bs{L}\) の全ての元 \(x\) について \(g(x)=0\) となり、矛盾が生じる。ゆえに、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち、少なくとも一つは \(0\) ではない。[証明終]
7.3 べき根拡大の十分条件
補題(1)と補題(2)を使って、体の拡大がべき根拡大になるための十分条件を証明します。
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
[証明]
\(\mr{Gal}(\bs{L}/\bs{K})\) は位数 \(n\) の巡回群なので、生成元を \(\sg\) とし、
\(\mr{Gal}(\bs{L}/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\sg^{n-1}\}\)
とする。\(\bs{L}\) の 元 \(c\) に対して、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
と定める。このとき \(\al\neq0\) となるように \(c\) を選べる。なぜなら、もし \(\al\neq0\) となる \(c\) が選べないとすると、\(\bs{L}\) の全ての元 \(x\) について、
\(x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\:\cd\:+\zeta\sg^{n-1}(x)=0\)
となるはずだが、これはべき根拡大の十分条件のため補題1(72A)、つまり、
\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない
において、\(a_1=\zeta^{n-1},\:a_2=\zeta^{n-2},\:\cd\:,a_{n-1}=\zeta\) と置いたことに相当し、そのような \(a_i\:(1\leq i\leq n-1)\) は存在しないとする補題1の結論に反するからである。またべき根拡大の十分条件のため補題2(72B)では、\(c\) の選び方の例が示されている。そこで、\(\al\neq0\) となるように \(c\) を選んだとする。
\(\sg\)は \(\bs{K}\) の元である \(\zeta\) を不変にするので、
\(\sg(\zeta^{n-i}\sg^i(c))=\zeta^{n-i}\sg^{i+1}(c)\)
である。これを用いて \(\sg(\al)\) を計算すると、
\(\sg(\al)\)
\(=\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta\sg^n(c)\)
\(=\zeta^n\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta c\)
\(=\zeta(\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\zeta^{n-3}\sg^3(c)+\:\cd+\zeta\sg^{n-1}(c)+c)\)
\(=\zeta\al\)
となる。計算では、\(\zeta^n=1\) であることと(第1項)、\(\sg^n=e\) なので \(\sg^n(c)=c\) となること(最終項)を用いた。
ここで、\(\al=\zeta\al\) となるのは、\(\al=0\) のときだけであるが、\(\al\neq0\) なので \(\al\neq\zeta\al\) である。つまり \(\sg(\al)\neq\al\) であり、\(\al\) は \(\sg\) を作用させると不変ではない。従って \(\al\) は \(\bs{K}\) の元ではない \(\bs{L}\) の元である。さらに \(\sg^i(\al)\) を求めていくと、
\(\begin{eqnarray}
&&\:\:\sg^2(\al)&=\sg(\sg(\al))=\sg(\zeta\al)=\zeta\sg(\al)=\zeta\zeta\al\\
&&&=\zeta^2\al\\
&&\:\:\sg^3(\al)&=\sg(\sg^2(\al))=\sg(\zeta^2\al)=\zeta^2\sg(\al)=\zeta^2\zeta\al\\
&&&=\zeta^3\al\\
\end{eqnarray}\)
というように計算でき、
\(\sg^i(\al)=\zeta^i\al\)
である。これを使うと、
\(\begin{eqnarray}
&&\:\:\sg(\al^n)&=\sg(\al)^n=(\zeta\al)^n=\zeta^n\al^n\\
&&&=\al^n\\
\end{eqnarray}\)
であり、\(\al^n\) は \(\sg\) を作用させても不変である。従って \(\al^n\) は \(\bs{K}\) の元である。そこで \(\al^n=a\:\:(a\in\bs{K})\) とおく。
方程式 \(x^n-a=0\) の解は、\(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al\) であり、\(x^n-a=0\) の \(\bs{K}\) 上の最小分解体は、\(\bs{K}\) には \(\zeta\) が含まれているから、
\(\bs{K}(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al)=\bs{K}(\al,\zeta)=\bs{K}(\al)\)
である。この式から、\(\bs{K}\) の同型写像による \(\al\) の移り先は全て \(\bs{K}(\al)\) に含まれることが分かる。従って \(\sg^i\:\:(1\leq i\leq n-1)\) はすべて \(\bs{K}(\al)\) の自己同型写像である。また、同型写像での移り先の定理(51D)により、同型写像は \(\al\) を共役な元に移すが、\(\al\) と共役な元は \(n-1\) 個しかない。従って \(\sg^i\) 以外に同型写像はない。つまり、
\(\mr{Gal}(\bs{K}(\al)/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\:\sg^{n-1}\}\)
であり、これは \(\mr{Gal}(\bs{L}/\bs{K})\) と同じである。次数と位数の同一性の定理(52B)により、ガロア群に含まれる自己同型写像の数は体の拡大次数に等しいから、
\([\:\bs{K}(\al)\::\:\bs{K}\:]=[\:\bs{L}\::\:\bs{K}\:]\)
である。もともと \(\al\) は \(\bs{L}\) の元だったので、\(\bs{K}(\al)\) の元は全て \(\bs{L}\) の元である。つまり、
\(\bs{K}(\al)\:\subset\:\bs{L}\)
であるが、\(\bs{K}(\al)\) と \(\bs{L}\) の線形空間の次元が等しいので、体の一致の定理(33I)により2つは一致し、
\(\bs{K}(\al)=\bs{L}\)
である。以上により、\(\bs{L}\) は \(\bs{K}\) の上の方程式 \(x^n-a=0\:(a\in\bs{K})\) の解の一つ \(\al\) を用いて \(\bs{L}=\bs{K}(\al)\) と表されるから、\(\bs{L}\) は \(\bs{K}\) の べき根拡大である。[証明終]
証明の過程で出てきた、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
の式は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言い、数学史においてはガロア理論より前に考えられたものです。この証明を振り返ってまとめてみると、
という条件のもとで、レゾルベントをうまく定義すると、
が成り立つという論理展開でした。つまりポイントは \(\bs{\al^n\in\bs{K}}\) のところであり、そういう \(\bs{\al\in\bs{L}}\) の存在が証明の核心です。
しかし、その鍵である \(\al\) を具体的に見つけようとすると、\(\al\) の式に現れる \(c\) を決めなければなりません。その \(c\) の値ですが、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて \(\bs{L}=\bs{K}(\theta)\) と表されているとき(= \(\theta\) が原始元のとき)、\(c=\theta\) にできることがべき根拡大の十分条件のため補題2(72B)に示されています。しかし、方程式の形から原始元が分かるわけではありません。
べき根拡大の十分条件(73A)は、その十分条件があればべき根拡大体の中に方程式の解が含まれる(= 方程式の解が四則演算とべき根で記述できる)ことだけを言っています。つまり四則演算とべき根で記述できる解の存在証明であり、そこが注意点です。
原始\(n\)乗根はべき根で表現可能
べき根拡大の十分条件(73A)を用いて原始\(\bs{n}\)乗根はべき根で表現可能(71A)であることを証明できます。(71A)ではガロア理論と関係なく証明しましたが、ガロア理論の枠組みを使っても証明できるということです。
まず \(n\) が合成数のとき、つまり \(n=s\cdot t\) と分解できるときには、原始\(n\)乗根は、原始\(s\)乗根と原始\(t\)乗根のべき根で表現できます(71A)。\(s\) や \(t\) が合成数なら、さらに "分解" を続けられるので、結局、\(n\) が素数 \(p\) のときに原始\(p\)乗根がべき根で表せることを示せればよいことになります。
いま、\(\bs{p}\) 未満の素数すべての原始\(\bs{n}\)乗根がべき根で表されると仮定します。これは帰納法の仮定です。原始\(p\)乗根を \(\eta\)(イータ) とし、その最小多項式を \(f(x)\) とすると、\(f(x)\) は既約多項式で、円分多項式です(63D)。原始\(p\)乗根は 方程式 \(x^p-1=0\) の \(1\) 以外の根なので、
\(x^p-1=(x-1)f(x)\)
であり、
\(f(x)=x^{p-1}+x^{p-2}+\:\cd\:+x+1\)
です。
原始\(p\)乗根による拡大体 \(\bs{Q}(\eta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\cong(\bs{Z}/p\bs{Z})^{*}\)
です(63E)。\((\bs{Z}/p\bs{Z})^{*}\) は位数 \((p-1)\) の巡回群で(25D)、\(\bs{Q}(\eta)/\bs{Q}\) の拡大次数は、\([\:\bs{Q}(\eta):\bs{Q}\:]=p-1\) です。原始\((p-1)\)乗根を \(\zeta\) とすると、\(\eta\notin\bs{Q}(\zeta)\) なので、\(\bs{Q}\) 上の既約多項式である \(f(x)\) は \(\bs{Q}(\zeta)\) 上でも既約多項式です。従って、
\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\cong\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\)
であり、\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\) も位数 \((p-1)\) の巡回群です。すると、べき根拡大の十分条件(73A)により、\(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta)\) はべき根拡大になります。つまり \(\eta\) は "有理数と \(\zeta\) の四則演算から成る式" のべき根で表現できます。
「\(p\) 未満の素数すべての原始\(n\)乗根がべき根で表される」という仮定により、\(\zeta\) はべき根で表現できます。従って \(\eta\) もべき根で表されます。
原始\(2\)乗根は \(-1\) であり、原始\(3\)乗根は根の公式によって、べき根で表現できます。従って帰納法により \(5\) 以上の素数 \(p\) の原始\(p\)乗根もべき根で表現できることが分かります。これで証明ができました。
ここで、原始\(\bs{n}\)乗根はべき根で表現可能(71A)とべき根拡大の十分条件(73A)の関係ですが、(73A)の証明の鍵になったのは、ラグランジュの分解式、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
でした。いま、原始\(5\)乗根を \(\eta\) とし、\(\bs{Q}(\eta)/\bs{Q}\) の巡回拡大を考えます。原始\(4\)乗根を \(\zeta\) とします(\(\zeta=i,\:-i\))。
\(\bs{Q}(\eta)\) の自己同型写像 \(\sg\) を、
\(\sg(\eta)=\eta^2\)
となる写像と定義します。そして、\(c=\eta,\:n=4\) を分解式に入れると、
\(\begin{eqnarray}
&&\:\:\al&=\eta+\zeta^3\sg(\eta)+\zeta^2\sg^2(\eta)+\zeta\sg^3(\eta)\\
&&&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
\end{eqnarray}\)
となります。このラグランジュの分解式と、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明で使った \(f(x,y)\) は本質的に同じものです。つまり
と定義すると、\(x,\:y\) の指数はそれぞれ、
\(x\) の指数:\([\:1,\:2,\:3,\:0\:]\)
\(\bs{Z}/4\bs{Z}\) の巡回パターン(生成元 \(=1\))
\(y\) の指数:\([\:3,\:4,\:2,\:1\:]\)
\((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン(生成元 \(=3\))
となります。(71A)では \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターンを \([\:2,\:4\:,3,\:1\:]\)(生成元 \(=2\))としたので式の形は少々違いますが、本質的に同じです。ここで、
\(x=\zeta,\:\:y=\eta\)
と置くと、
\(\begin{eqnarray}
&&\:\:f(x,y)&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
&&&=\al\\
\end{eqnarray}\)
となり、\(f(x,y)\) が ラグランジュの分解式と同じものであることが確認できました。つまり、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明は、
ものなのでした。
7.4 べき根拡大と巡回拡大の同値性
6.3節の "べき根拡大は巡回拡大である"(63H)と、7.3節の "巡回拡大はべき根拡大である"(73A)を合わせると、次にまとめることができます。
\(1\) の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。また、\(\bs{K}\) の\(n\)次拡大体を \(\bs{L}\) とする( \([\:\bs{L}\::\:\bs{K}\:]=n\) )。
このとき、
の2つは同値である。
\(\bs{1}\) の原始\(\bs{n}\)乗根が代数体に含まれるという条件をつけるのが巧妙なアイデアで、この条件によって可解性の必要十分条件が導けます。
7.5 可解性の十分条件
以上の準備をもとに、可解性の必要条件(64B)の逆である、可解性の十分条件の証明を行います。
代数拡大体 \(\bs{K}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とし、拡大次数を \([\:\bs{L}\::\:\bs{K}\:]=n\) とします。そして、ガロア群 \(\mr{Gal}(\bs{L}/\bs{K})\) が可解群であるとき、もし \(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるなら、べき根拡大と巡回拡大は同値の定理(74A)により、\(\bs{K}\) の巡回拡大とべき根拡大は同じことです。従って、
可解群 \(\rightarrow\) 累巡回拡大 \(\rightarrow\) 累べき根拡大 \(\rightarrow\) 可解
というルートで、方程式 \(f(x)=0\) の可解性が証明できます。しかし、\(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるとは限りません。\(\bs{K}\) が有理数体 \(\bs{Q}\) だとすると、そこに(原始2乗根以外の)原始\(n\)乗根はありません。しかし、このようなケースでも方程式の可解性が証明できます。それが以下です。
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
[証明]
\([\:\bs{L}\::\:\bs{K}\:]=n\:\:(|G|=n)\) とし、\(\zeta\) を \(1\) の原始\(n\)乗根とする。\(\bs{K}\) に \(\zeta\) を添加した拡大体 \(\bs{K}(\zeta)\)と、\(\bs{L}\) に \(\zeta\) を添加した拡大体 \(\bs{L}(\zeta)\) を考える。
\(\bs{L}(\zeta)\) は \(\bs{K}\) 上の方程式 \(f(x)(x^n-1)=0\) の最小分解体だから、\(\bs{L}(\zeta)/\bs{K}\) はガロア拡大である。
また \(\bs{K}(\zeta)\) は、\(\bs{K}\)のガロア拡大体 \(\bs{L}(\zeta)\) の中間体なので、中間体からのガロア拡大の定理(52C)によって、\(\bs{L}(\zeta)/\bs{K}(\zeta)\) もガロア拡大である。そこで、
\(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))=G\,'\)
とおく。
\(G\) の元を \(g\)、\(G\) の単位元を \(e\) とする。\(G\,'\)の元を \(g\,'\)、\(G\,'\) の単位元を \(e\,'\) とする。また、\(G\,'\) の元 \(g\,'\) を \(\bs{L}\) の元に限定して作用させるときの同型写像を \(\sg(g\,')\) とする。
\(g\,'\)は \(\bs{L}(\zeta)\) の自己同型写像だから、\(\bs{L}(\zeta)\) の元を共役な元に移す。従って 作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も \(\bs{L}\) の元を共役な元に移す。\(\bs{L}\) はガロア拡大体だから、\(\bs{L}\)の元の共役な元は \(\bs{L}\) に含まれる。従って \(\sg(g\,')\) は \(\bs{L}\) の自己同型写像である。
また \(g\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) の元だから、\(\bs{K}(\zeta)\) の元を固定する。従って、\(\bs{K}(\zeta)\) の部分集合である \(\bs{K}\) の元も固定する。ゆえに、\(g\,'\) の作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も、\(\bs{L}\) の部分集合である \(\bs{K}\) の元を固定する。
以上により \(\sg(g\,')\) は、\(\bs{K}\)の元を固定する \(\bs{L}\) の自己同型写像だから、\(\mr{Gal}(\bs{L}/\bs{K})\) の元、つまり \(G\) の元である。
\(\sg\) を \(G\,'\) から \(G\) への写像と見なして考える。\(G\,'\) の元 を \(g\,'\) とし、\(x\) を \(\bs{L}\) の元とすると、\(g\,'(x)=\sg(g\,')(x)\) である。つまり、作用する対象が \(\bs{L}\) の元なら、2つの写像、\(g\,'\) と \(\sg(g\,')\) は同じ効果を生む。
\(G\,'\)の任意の2つの元を \(g_1{}^{\prime},\:g_2{}^{\prime}\) とすると、\(g_1{}^{\prime}g_2{}^{\prime}\) も \(G\,'\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}(x)=g_1{}^{\prime}(\sg(g_2{}^{\prime})(x))\)
であるが、\(\sg(g_2{}^{\prime})(x)\) もまた \(\bs{L}\) の元だから、
\(\sg(g_1{}^{\prime}g_2{}^{\prime})=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})\)
となって、\(\sg\) は準同型写像(42A)である。
\(\sg(g\,')\) が \(G\) の元であり \(\sg\) が準同型写像なので、準同型写像の像と核の定理(42B)により、\(\sg\) による \(G\,'\) の 像 \(\sg(G\,')\) は \(G\) の部分群である。もちろん、\(G\) の部分群には \(G\) の自明な部分群である \(G\) 自身も含まれる。
いま、ある \(G\,'\) の元 \(h\) があって、\(\sg(h)=e\)(\(e\) は \(G\) の単位元)とする。つまり、\(h\) を \(\bs{L}\) に限定して適用すると、\(\bs{L}\) の元すべてを固定するものとする。
\(G\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) であり、そのすべての元は \(\bs{K}(\zeta)\) の元を固定する。従って、\(G\,'\) の元 \(h\) は \(\zeta\) も固定する。ということは、\(h\) は「\(\bs{L}\) の元すべてを固定し、かつ \(\zeta\) を固定する」から、\(\bs{L}(\zeta)\) の元すべてを固定する。つまり \(h\) は \(G\,'\) の単位元であり、\(h=e\,'\) である。
ゆえに、準同型写像の像と核(42B)における核の定義によって、
\(\mr{Ker}\:\sg=e\,'\)
であり、核が単位元なら単射の定理(42C)によって、\(\sg\) は単射である。このことから、準同型定理(43A)により、
\(G\,'/\mr{Ker}\:\sg\:\cong\:\sg(G\,')\)
すなわち、
\(G\,'\:\cong\:\sg(G\,')\)
である。つまり \(\bs{G\,'}\) は \(\bs{G}\) の部分群 \(\bs{\sg(G\,')}\) と同型である。
\(G\) は可解群なので、可解群の部分群は可解群の定理(61C)によって、\(G\) の部分群である \(\sg(G\,')\) も可解群であり、さらにそれと同型である \(G\,'\) も可解群である。\(G\,'\) が可解群なので、可解群の定義により \(G\,'\) から \(e\,'\) に至る部分群の列、
\(|G\,'|=m\) とおくと、\(G\,'\) は \(G\) の部分群である \(\sg(G\,')\) と同型なので、ラグランジュの定理(41E)によって、\(m\) は \(|G|=n\) の約数である。
ガロア対応(53B)による \(H_i\) の固定体を \(\bs{K}_i\) とすると、
\(\bs{L}(\zeta)/\bs{K}(\zeta)\) の拡大次数は、
\([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=|G\,'|=m\)
であり、\(n\) の約数である。
固定体の系列における一つの拡大 \(\bs{K}_{i+1}/\bs{K}_i\)を考える。その拡大次数 \([\:\bs{K}_{i+1}\::\:\bs{K}_i\:]=m_i\) は、拡大次数の連鎖律(33H)によって \([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=m\) の約数であり、従って \(n\) の約数である。
\(\bs{K}_i\) は \(1\) の原始\(n\)乗根 \(\zeta\) を含むから、\(\zeta^{\frac{n}{m_i}}\) も含んでいる。\(\zeta^{\frac{n}{m_i}}\) は \(1\) の原始\(m_i\)乗根である。つまり、\(\bs{K}_i\) は \(1\) の原始\(m_i\)乗根(\(m_i=[\:\bs{K}_{i+1}\::\:\bs{K}_i\:]\))を含む。従って、べき根拡大の十分条件の定理(73A)により、巡回拡大である \(\bs{K}_{i+1}/\bs{K}_i\) はべき根拡大である。
以上のことは \((0\leq i < k)\) のすべてで成り立つから、\(\bs{K}_i\) の系列は累べき根拡大である。
\(f(x)=0\) の解は \(\bs{L}\) に含まれるが、\(\bs{L}\:\subset\:\bs{L}(\zeta)\) だから \(f(x)=0\) の解は \(\bs{L}(\zeta)\) に含まれる。その \(\bs{L}(\zeta)\) は \(\bs{K}(\zeta)\) の累べき根拡大であり、また \(1\) の原始\(n\)乗根である \(\zeta\) は \(\bs{Q}\:(\in\bs{K})\) の元の四則演算とべき根で表現できるから(71A)、\(\bs{L}(\zeta)\) の元はすべて \(\bs{K}\) の元の四則演算とべき根で表現できる。従って \(f(x)=0\) の解も \(\bs{K}\) の元の四則演算とべき根で表現できる。[証明終]
この定理では「体 \(\bs{K}\) 上の方程式 \(f(x)=0\)」としましたが、もちろん、体 \(\bs{K}\) が 有理数体 \(\bs{Q}\) であっても同じです。以降、\(\bs{K}\) を \(\bs{Q}\) と書きます。
証明のポイントは、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) とし、\(G\,'=\mr{Gal}(\bs{L}(\zeta)/\bs{Q}(\zeta))\) とするとき、\(G\,'\) が \(G\) の部分群と同型であることです。たとえば、\(f(x)\) が既約な3次多項式だと、\(G\cong S_3\) か \(G\cong C_3\) であり、基本的に \(G\,'\cong G\) です。しかし、そうならない場合もあります。たとえば \(f(x)=x^3-2\) では \(G\cong S_3\) ですが、
\(\bs{Q}\:\subset\:\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\sqrt[3]{2})=\bs{L}\)
(\(\omega\) は \(1\) の原始3乗根)
という体の拡大列でわかるように、\(\bs{L}(\omega)=\bs{L}\) です。つまり、\(\bs{L}(\omega)/\bs{Q}(\omega)\) の拡大次数は \(3\) であり、\(\bs{L}/\bs{Q}\) の拡大次数の \(6\) とは違います。しかしそうであっても \(G\,'=\mr{Gal}(\bs{L}(\omega)/\bs{Q}(\omega))\cong C_3\) であり、\(G\,'\) は \(G\cong S_3\) の部分群と同型です。
\(G\,'\) は \(G\) の部分群と同型なので、\(G\) が可解群なら \(G\,'\) も可解群であり(61C)、\(\bs{L}(\omega)/\bs{Q}(\omega)\) は累巡回拡大であり(62C)、従って、累べき根拡大です(73A)。
さらに、\(1\) の原始\(n\)乗根が \(\bs{Q}\) の元の四則演算とべき根で表現できる(71A)ことも証明のポイントになっています。
この可解性の十分条件の定理(75A)によって、有理数係数の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) として、\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群のとき、\(f(x)=0\) の解は四則演算とべき根で表現可能なことが証明できました。
ここがゴールで「ガロア理論=可解性の必要十分条件」が完結しました。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
可解性の必要十分条件の証明は前節で尽きていますが、これ以降は可解な方程式の代表的なものを取り上げ、ガロア群の分析をします。まず最初は、
です。これらの方程式が可解であることは当然ですが、ガロア群の分析をすると正5角形と正\(17\)角形が定規とコンパスで作図できることを証明できます。
\(x^5-1=0\)
まず \(x^5-1=0\) の解を分析します。
\(x^5-1=(x-1)(x^4+x^3+x^2+x+1)\)
なので、\(1\) 以外の解を \(\zeta\) とすると、\(\zeta\) は4次方程式、
\(x^4+x^3+x^2+x+1=0\)
の解です。「7.1 1 の原始n乗根」で書いたように、この方程式の解は、
\(\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm\sqrt{-10-2\sqrt{5}}\right)\)
\(\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm\sqrt{-10+2\sqrt{5}}\right)\)
の4つであり、これが \(1\) の原始5乗根です。以下の論旨を明瞭にするために、虚数単位 \(i\) を使わずに、外側の \(\sqrt{\phantom{a}}\) の中を負の数にして記述しました。
この原始5乗根は、4次方程式の解であるにもかかわらず、四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現されています。なぜそうなるのか、それをガロア理論にのっとって説明します。実は、\(p\) を素数としたとき、
ことが知られています。定規というのは「目盛りのない、与えられた2点を通る直線を引くことだけができる道具」であり、コンパスというのは「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\cdot\)円弧を描くことだけができる道具」です。長さや角度を測ることはできません。作図可能の原理は次の項で説明します
\(f(x)=x^4+x^3+x^2+x+1\) とし、\(f(x)=0\) の解の一つを \(\zeta\) とすると、\(f(x)\) の最小分解体は \(\bs{Q}(\zeta)\) です。そのガロア群を、
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
と書くと、\(\zeta\) の最小多項式は \(f(x)\) なので(63C)、\(|G|=4\) です。また、\(\bs{\bs{Q}(\zeta)}\) のガロア群の定理(63E)により、\(G\) は既約剰余類群と同型で、
\(G\cong(\bs{Z}/5\bs{Z})^{*}\)
です。
\((\bs{Z}/5\bs{Z})^{*}=\{1,\:2,\:3,\:4\}\)
ですが、この群の生成元は \(2\) か \(3\) です。以下、生成元を \(2\) として話を進めると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
と表現できます。一方、\(f(x)=0\) の4つの解は、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
です。そこで、
\(\sg(\zeta)=\zeta^2\)
で定義される自己同型写像を考えると、ガロア群は、
\(G=\{\sg,\:\sg^2,\:\sg^3,\:\sg^4=e\}\)
となり、位数 \(4\) の巡回群、かつ可解群です。また、体の拡大次数は、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=4\)
です。
ガロア群 \(G\) には部分群が含まれています。つまり、
\(H=\{\sg^2,\:e\}\)
\(\sg^2(\zeta)=\zeta^4\)
と定義すると、\((\sg^2)^2=e\) なので \(H\) は部分群(\(\sg H=H\sg\) なので正規部分群)であり、位数 \(2\) の巡回群です。また、剰余群は、
\(G/H\cong\{e,\:\sg\}\)
です。従って、
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\)
は可解列です。ガロア対応の定理(53B)により、この可解列に対応する拡大体の列があって、
\(G\sp H\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}\subset\bs{Q}(\zeta)\)
となります。\(\bs{F}\) は \(H\) の固定体であり、\(\bs{Q}(\zeta)\) の中間体です。すると、正規性定理(53C)により、
\(\mr{Gal}(\bs{F}/\bs{Q})\cong G/H\)
なので、\(\mr{Gal}(\bs{F}/\bs{Q})\) は位数 \(2\) の巡回群です。またガロア群の定義により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\cong H\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\) も位数 \(2\) の巡回群です。従って、次数と位数の同一性の定理(52B)より拡大次数は、
であり、2つの拡大は巡回拡大です。原始2乗根(\(=-1\))は \(\bs{Q}\) に含まれるので、巡回拡大はべき根拡大です(73A)。拡大次数 \(2\) のべき根拡大を(一般的な数学用語ではありませんが)「平方根拡大」と呼ぶことにすると、
と結論づけられます。原始5乗根が四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できる理由がここにあります。
ここまでは、中間体 \(\bs{F}\) がどういう拡大体かに触れていませんが、\(\bs{F}\) を具体的に表現することもできます。\(\bs{F}\) は \(H=\{e,\:\sg^2\}\) の固定体なので、\(\bs{F}=\bs{Q}(\theta)\) として、
\(\sg^2(\theta)=\theta\)
となる \(\theta\) を探します。\(\theta\) の選び方には自由度があり、たとえば \(\theta=\zeta^4+\zeta\) としてもよいのですが、ここでは、
\(\theta=(\zeta^2-\zeta^3)(\zeta^4-\zeta)\)
とします。このように選ぶと、\(\sg^2(\zeta)=\zeta^4\) なので、
\(\begin{eqnarray}
&&\:\:\sg^2(\theta)&=(\zeta^8-\zeta^{12})(\zeta^{16}-\zeta^4)\\
&&&=(\zeta^3-\zeta^2)(\zeta-\zeta^4)=\theta\\
\end{eqnarray}\)
となって、\(\theta\) は \(\sg^2\) で不変です。と同時に、\(\sg(\zeta)=\zeta^2\) なので、
\(\begin{eqnarray}
&&\:\:\sg(\theta)&=(\zeta^4-\zeta^6)(\zeta^8-\zeta^2)\\
&&&=(\zeta^4-\zeta)(\zeta^3-\zeta^2)=-\theta\\
\end{eqnarray}\)
となります。ということは、
\(\sg(\theta^2)=(\sg(\theta))^2=(-\theta)^2=\theta^2\)
であり、\(\theta^2\) は \(\sg\) で不変、つまり \(G\) のすべての元で不変となり、\(\theta^2\) は有理数です。そこで、
\(\zeta^5=1\)
\(\zeta^4+\zeta^3+\zeta^2+\zeta+1=0\)
の関係を使って \(\theta^2\) を計算すると、
\(\begin{eqnarray}
&&\:\:\theta^2&=(\zeta^2-\zeta^3)^2(\zeta^4-\zeta)^2\\
&&&=(\zeta^4-2\zeta^5+\zeta^6)(\zeta^8-2\zeta^5+\zeta^2)\\
&&&=(\zeta^4-2+\zeta)(\zeta^3-2+\zeta^2)\\
&&&=\zeta^7-2\zeta^4+\zeta^6-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=\zeta^2-2\zeta^4+\zeta-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=-\zeta^4-\zeta^3-\zeta^2-\zeta+4\\
&&&=5\\
\end{eqnarray}\)
となり、確かに\(\theta^2\) は有理数であることが分かります。つまり、
\(\theta=\sqrt{5}\)
です。従ってガロア対応は、
となります。原始5乗根に \(\sqrt{-10+2\sqrt{5}}\) のような項が現れるのは、中間体が \(\bs{Q}(\sqrt{5})\) であるという、体の拡大構造からくるのでした。
ここまでの論証を振り返ってみると、
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
ことが分かります。この条件は \(p=3,\:5\) で成立しますが、その次に成立するのは \(p=17\) です。
\(x^{17}-1=0\)
\(1\) の原始\(17\)乗根を \(\zeta\) とします。\(p=17\) の最小原始根は \(3\) で(25D)、\((\bs{Z}/17\bs{Z})^{*}\) の位数は \(16\) です。\((\bs{Z}/17\bs{Z})^{*}\) において \(3\) の累乗は、
\(\phantom{1}3,\:\phantom{1}9,\:10,\:13,\:\phantom{1}5,\:15,\:11,\:16,\)
\(14,\:\phantom{1}8,\:\phantom{1}7,\:\phantom{1}4,\:12,\:\phantom{1}2,\:\phantom{1}6,\:\phantom{1}1\)
と、すべての元を巡回します。従って、
\(\sg(\zeta)=\zeta^3\)
という自己同型写像 \(\sg\) を定義すると、
\(G=\{\sg,\sg^2,\sg^3,\cd,\sg^{15},\sg^{16}=e\}\)
が \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) です。
\(x^5-1=0\) のときと同様の考察をすると、\(G\) には3つの部分群があります。
\(H_1=\{\sg^2,\sg^4,\sg^6,\sg^8,\sg^{10},\sg^{12},\sg^{14},e\}\)
\(\sg^2(\zeta)=\zeta^9\)
\(H_2=\{\sg^4,\sg^8,\sg^{12},e\}\)
\(\sg^4(\zeta)=\zeta^{13}\:\:(\phantom{1}9^2\equiv13\:\:(\mr{mod}\:17))\)
\(H_3=\{\sg^8,e\}\)
\(\sg^8(\zeta)=\zeta^{16}\:\:(13^2\equiv16\:\:(\mr{mod}\:17))\)
の3つで、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
は可解列です。ガロア対応の定理(53B)により、\(H_1,\:H_2,\:H_3\) にはそれぞれに対応した固定体 \(\bs{F}_1,\:\bs{F}_2,\:\bs{F}_3\) があって、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}_1\subset\bs{F}_2\subset\bs{F}_3\subset\bs{Q}(\zeta)\)
のガロア対応になります。\(\bs{Q}\) から \(\bs{Q}(\zeta)\) までの4つの拡大次数は、剰余群の位数に等しいのですべて \(2\) です。つまり、\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの「平方根拡大」を4回繰り返したものであり、原始\(17\)乗根は四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できます。従って正\(17\)角形は定規とコンパスで作図可能です。
これは、ドイツの大数学者\(\cdot\)ガウス(\(1777-1855\))が\(19\)才のときに発見した定理として有名です。
作図可能の原理
ここで改めて、平面上の図形が定規とコンパスで「作図可能」という意味を明確にします。ここで "定規" は「目盛りのない、与えられた2点を通る線を引くことだけができる道具」であり、"コンパス" は「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\bs{\cdot}\)円弧を描くことだけができる道具」でした。
平面上の図形は点と線でできています。線は2点を与えると描けるので、「作図可能」の意味は「平面上で作図可能な点とは何か」を定義することに帰着します。
平面を複素平面(\(=\bs{C}\))として考えます。以降、
の記号を使います。「作図可能」の意味は「複素平面上で作図可能な複素数(実数を含む)とは何か」を定義することです。
\(1,\:0\) は作図可能である。また複素平面の実軸と虚軸は作図できる。
任意の線分を単位長さとし、端点を \(1,\:0\) とします。2点を結ぶ直線が実軸で、\(0\) を通り実軸と垂直な直線を作図するとそれが虚軸です。
\(\al=a+b\:i\) とすると、\(a,\:b\) が作図可能なら \(\al\) も作図可能である。また、\(\al\) が作図可能なら \(a,\:b\) も作図可能である。
\(a\) が作図可能なら、\(-a\) も作図可能である。従って \(\al\) が作図可能なら \(-\al\) も作図可能である。
また \(a,\:b\) が作図可能なら \(a+b\) も作図可能である。従って、\(\al,\:\beta\) が作図可能なら \(\al+\beta\) も作図可能である。
\(a,\:b\) が作図可能なら \(ab\)も作図可能である。従って \(\al,\:\beta\) が作図可能なら \(\al\beta\) も作図可能である。
\(a\:\:(a\neq0)\) が作図可能なら \(a^{-1}\) も作図可能である。従って \(\al\:\:(\al\neq0)\) が作図可能なら \(\al^{-1}\) も作図可能である。
作図可能な \(\al\) を \(\al=a+b\:i\) とすると、
\(\al^{-1}=\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}\:i\)
です。\(a,\:b\) が作図可能なので、その四則演算の結果は作図可能です。従って \(\al^{-1}\) も作図可能です。
有理数 \(\bs{Q}\) は作図可能である。
実数のなかで作図可能な点は四則演算で閉じています。かつ、\(0,\:1\) は作図可能です。従って有理数は作図可能です。
\(a\) が正の実数のとき、\(\sqrt{a}\) は作図可能である。
\(a\) と \(-1\) を結ぶ線分を直径とする円を描き、虚軸との交点を \(x\cdot i\:(x\):実数) とすると、
\(1:x=x:a\)
なので、\(x=\pm\sqrt{a}\) です。従って \(\sqrt{a}\) は作図可能です。
\(\al\) を作図可能な複素数とするとき、\(\sqrt\al\) は作図可能である。
極形式を使って、
\(\al=r(\mr{cos}\theta+i\cdot\mr{sin}\theta)\)
とすると、\(r\) は作図可能であり、つまり \(\sqrt{r}\) も作図可能です。また、角 \(\theta\) を2等分する線も、定規とコンパスで作図可能です。従って \(\sqrt\al\) は作図可能です。
\(\al,\:\beta\) が作図可能な複素数とするとき、2次方程式 \(x^2+\al x+\beta=0\) の解は作図可能である。
ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能である。
2次方程式 \(x^2+\al x+\beta=0\) の解は、根の公式により、係数 \(\al,\:\beta\) の四則演算と平方根で表わされます。従って作図可能です。
定規とコンパスで作図可能な点は、作図可能な円や直線の交点として求まる点です。2次元 \(xy\) 平面( \(\bs{R}^2\) )で考えると、直線と直線の交点は1次方程式の解です。また円と直線の交点は2次方程式の解です。円と円の交点がどうかですが、\(a,\:b,\:c,\:d\) を実数として、2つの円の方程式を、
実数(\(a,\:b\))が作図可能と、複素数(\(a+bi\))が複素平面上で作図可能は同値です。従って、ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能です。
\(\bs{Q}\) の代数拡大体 \(\bs{K}\) があり、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{K}\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
を満たす \(\bs{Q}\) から \(\bs{K}\) の拡大列が存在するとき、\(\bs{K}\) の元
\(\al\in\bs{K}\)
は作図可能である。
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\) であれば、\(\bs{K}_{i+1}/\bs{K}_i\) は次数2のべき根拡大であり、
\(x^2-a=0\:\:\:(a\in\bs{K}_i)\)
の解、\(\sqrt{a}\) を用いて、
\(\bs{K}_{i+1}=\bs{K}_i(\sqrt{a})\)
と表されます。従って、\(\bs{K}_i\) の元が作図可能なら、\(\bs{K}_{i+1}\) の元は「作図可能な点の四則演算と平方根の組み合わせ」で表現できるので、作図可能です。体の拡大列の出発点である \(\bs{Q}\) の元は作図可能なので、到達点である \(\bs{K}\) の元も作図可能になります。
\(1\) の原始\(p\)乗根(\(p\):素数)を \(\zeta\) とすると、\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) の位数は \(p-1\) であり、それが2の累乗であれば、\(G\) の可解列にガロア対応する体の拡大系列、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{Q}(\zeta)\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
が存在します(前項での証明)。従って複素数平面上の点 \(\zeta\) は作図可能であり、正 \(p\)角形は作図可能です。条件に合致する素数は \(p=3\)、\(5\)、\(17\)、\(257\)、\(65537\)であることが知られています。これらの素数をフェルマ素数と呼びます。フェルマ素数 \(p\) とは、\(p-1\) が2の累乗であるような素数です。
さらに、一般の正 \(n\)角形が作図可能である条件は、次のようになります。
正 \(n\)角形は、
\(n=2^k\:\:\:(2\leq k)\)
\(n=2^k\cdot p_1p_2\cd p_r\:\:\:(0\leq k,\:\:1\leq r)\)
\(p_i\) は相異なるフェルマ素数
のとき、作図可能である。
[証明]
角度の2等分線は作図可能なので、\(n=2^k\:\:(2\leq k)\) のとき、正 \(n\)角形は作図可能である。と同時に、正 \(m\)角形が作図可能なとき、
\(n=2^k\cdot m\:\:(0\leq k)\)
とおくと、正 \(n\)角形は作図可能になる。\(p\) がフェルマ素数のとき、正 \(p\)角形は作図可能なので、
\(m_1\) と \(m_2\) を互いに素な3以上の数とするとき、正 \(m_1\) 角形と正 \(m_2\)角形が作図可能であれば、正 \(m\)角形(\(m=m_1m_2\))は作図可能である
ことが証明できれば十分である。
\(\theta,\:\theta_1,\:\theta_2\) を任意の角度とする。
\(\mr{sin}\theta=\sqrt{1-\mr{cos}^2\theta}\)
だから、\(\mr{cos}\theta\) が作図できれば \(\mr{sin}\theta\) も作図できる。また三角関数の加法定理より、
\(\mr{cos}(\theta_1+\theta_2)=\mr{cos}\theta_1\cdot\mr{cos}\theta_2-\mr{sin}\theta_1\cdot\mr{sin}\theta_2\)
なので、\(\mr{cos}\theta_1,\:\mr{cos}\theta_2\) が作図できれば \(\mr{cos}(\theta_1+\theta_2)\) も作図できる。このことから \(\mr{cos}\theta\) が作図できれば \(\mr{cos}(k\theta)\:\:(k\) は整数)も作図できる。
複素平面上で原点を中心とする半径1の円に正 \(m\)角形を描いたとき、その頂点の複素数は
\(\mr{cos}\left(\dfrac{2\pi}{m}k\right)+i\:\mr{sin}\left(\dfrac{2\pi}{m}k\right)\:\:(0\leq k\leq m-1)\)
である。\(k=1\) の点が作図できれば、残りの点が作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
が作図できれば、正 \(m\)角形は作図できる。
\(m_1\) と \(m_2\) は互いに素だから、不定方程式の解の存在の定理(21C)により、
\(k_1m_1+k_2m_2=1\)
を満たす \(k_1,\:k_2\) が存在する。両辺を \(m=m_1m_2\) で割ると
\(\dfrac{k_1}{m_2}+\dfrac{k_2}{m_1}=\dfrac{1}{m}\)
\(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2=\dfrac{2\pi}{m}\)
が得られる。正 \(m_1\)角形と正 \(m_2\)角形 は作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m_1}\right),\:\:\mr{cos}\left(\dfrac{2\pi}{m_2}\right)\)
は作図できる。従って
\(\mr{cos}\left(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2\right)\)
は作図でき、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
も作図できることになって、正 \(m\)角形は作図できる。[証明終]
証明の鍵は「\(m_1\) と \(m_2\) が互いに素」です。従って、正3角形が作図できても、正9角形は作図できません。正\(15\)角形なら作図できます。計算すると、作図可能な正 \(n\)角形(\(n\leq100\))は、
です。「正\(50\)角形は作図できないが、正\(51\)角形は作図できる」というのも不思議な感じがします。
7.7 巡回拡大はべき根拡大:3次方程式が解ける理由
この節では可解な方程式がなぜ解けるのかを、3次方程式を例にとってガロア理論で説明します。また3次方程式の根の公式をガロア理論に沿った形て導出します。「7.5 可解性の十分条件」で証明したことは、
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
でした。この証明の核となっているのは「7.3 べき根拡大の十分条件」であり、それは、
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
でした。このことを証明した論理展開は、次のようでした。
次の条件があるとする。
このとき、レゾルベント(分解式)を定義することで、
となる。
つまり、レゾルベントを使って、巡回拡大=べき根拡大(但し、体に \(1\) の原始\(n\)乗根が含まれることが条件)を証明したわけです。この証明プロセスを、具体的な3次方程式で順にたどります。まず、3次方程式のガロア群を再度整理します。
3次方程式のガロア群
3次方程式のガロア群は「1.3 ガロア群」で計算しましたが、改めて書きます。3次方程式のガロア群は、3次方程式の3つの解、\(\al,\:\beta,\gamma\) を入れ替える(置換する)群であり、一般的には、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
です。3つの解をそれぞれ \(1,\:2,\:3\) の文字で表し、巡回置換の記法(6.5節)で書くと、
で(\(\sg,\:\tau\) の演算は右から行う)、これは3次の対称群(\(S_3\)。6.5節)です。この群はもちろん可換群ではなく \(\tau\sg\neq\sg\tau\) ですが、\(\tau\sg\) を計算すると、
\(\tau\sg=(1,\:3)\)
であり、
\(\tau\sg=\sg^2\tau\)
との関係が成り立っています。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。ここで、
\(H=\{e,\:\sg,\:\sg^2\}\)
という \(G\) の部分群を考えると、\(H\) は巡回群であると同時に \(G\) の正規部分群です。"弱可換性" を使って検証してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
であり、同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つので \(H\) は \(G\) の正規部分群です。
\(G\) の \(H\) による剰余群は、
\(G/H=\{H,\tau H\}\)
であり、単位元は \(H\) で、
\((\tau H)^2=\tau H\tau H=\tau\tau HH=H\)
となる、位数\(2\) の巡回群です(\(G/H\cong C_2)\)。この結果、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
は可解列になり、\(G\) は可解群で、従って3次方程式は可解です(=四則演算とべき根で解が表現可能)。この節ではそれを具体例で確認していきます。
一方、「3.3 線形空間」の「代数拡大体の構造」で書いたように、3次方程式のガロア群が \(S_3\) ではなく、位数 \(3\) の巡回群( \(C_3\) )になる場合があります。それを再度整理します。
\(x^3+ax^2+bx+c=0\) の3次方程式は、\(x=X-\dfrac{a}{3}\) とおくと、
\(X^3+\left(b-\dfrac{a^2}{3}\right)X+\left(\dfrac{2}{27}a^3-\dfrac{1}{3}ab+c\right)=0\)
となって、2乗の項が消えます。従って以降、3次方程式を、
\(x^3+px+q=0\)
の形で扱います。
\(f(x)=x^3+px+q\)
とおき、\(f(x)\) は既約多項式とします。3次方程式の根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
であり、根と係数の関係から、
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=p\)
\(\al\beta\gamma=-q\)
です。3次方程式のガロア群が \(S_3\) か \(C_3\) かを決めるポイントとなるのは、
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
で定義される、根の差積と呼ばれる値です。差積は普通、\(\Delta\)(ギリシャ文字・デルタの大文字)で表しますが、後の説明の都合で \(\theta\) と書きます。差積は、任意の2つの根の互換で \(-\theta\) となるので、3つの根を \(\al,\:\beta,\:\gamma\) に割り当てる方法によって、\(\theta\) は2つの値をとり得ます。差積の2乗が判別式であり、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
です。つまり \(\theta=\sqrt{D}\) と書けますが、\(\sqrt{D}\) は「2乗して \(D\) となる2つの数のどちらか」の意味です。\(D\) は \(\al,\:\beta,\:\gamma\) の任意の置換で不変な対称式なので、3次方程式の係数である \(p,\:q\) で表すことができる有理数です。
その \(D\) を方程式の係数で表すために、\(f(x)\) を微分します。
\(f(x)=(x-\al)(x-\beta)(x-\gamma)\)
なので、
\(\begin{eqnarray}
&&\:\:f\,'(x)=&(x-\al)(x-\beta)+(x-\beta)(x-\gamma)+\\
&&&(x-\gamma)(x-\al)\\
\end{eqnarray}\)
であり、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\beta)=(\beta-\gamma)(\beta-\al)\)
\(f\,'(\gamma)=(\gamma-\al)(\gamma-\beta)\)
となります。従って、
\(D=-f\,'(\al)f\,'(\beta)f\,'(\gamma)\)
です。一方、
\(f\,'(x)=3x^2+p\)
なので、
\(D=-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\)
となります。ここからの計算を進めるために、次の2つの対称式を、根と係数の関係を使って \(p\) で表しておきます。
・\(\al^2+\beta^2+\gamma^2\)
\(=(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)\)
\(=-2p\)
・\(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2\)
\(=(\al\beta+\beta\gamma+\gamma\al)^2-2\al\beta\gamma(\al+\beta+\gamma)\)
\(=p^2\)
これを用いると、
\(\begin{eqnarray}
&&\:\:D&=&-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\\
&&&=&-27(\al\beta\gamma)^2-9(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2)p\\
&&&&-3(\al^2+\beta^2+\gamma^2)p^2-p^3\\
&&&=&-27q^2-9\cdot p^2\cdot p-3\cdot(-2p)\cdot p^2-p^3\\
&&&=&-4p^3-27q^2\\
\end{eqnarray}\)
と計算できます。つまり、
\(D=-4p^3-27q^2\)
です。ここでもし、\(D\) がある有理数 \(a\) の2乗(\(D=a^2\))なら、
\(\theta=\sqrt{D}=\pm a\)
となり、\(\theta\) は有理数です。\(\theta\) が有理数(\(\theta=\pm a\))の場合、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\al)=3\al^2+p\)
の関係があるので、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=-f\,'(\al)(\beta-\gamma)\\
&&&=-(3\al^2+p)(\beta-\gamma)\\
\end{eqnarray}\)
ですが、\(\theta=\pm a\) なので、
\(\beta-\gamma=\pm\dfrac{a}{3\al^2+p}\)
です。この式と、根と係数の関係である、
\(\beta+\gamma=-\al\)
を使うと、\(\bs{\beta}\) と \(\bs{\gamma}\) が \(\bs{\al}\) の有理式(=分母・分子が \(\bs{\al}\) の多項式)で表現できることになります。計算すると(\(\pm\)は省略して)、
\(\beta=\dfrac{2p\al+3q-a}{2(3\al^2+p)}\)
\(\gamma=\dfrac{2p\al+3q+a}{2(3\al^2+p)}\)
です(\(\beta\) と \(\gamma\) は逆でもよい)。\(\beta,\:\gamma\) が \(\al\) の有理式で表現できるので、
\(\bs{Q}(\al,\beta,\gamma)\subset\bs{Q}(\al)\)
であり、もちろん \(\bs{Q}(\al,\beta,\gamma)\sp\bs{Q}(\al)\) なので。
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
です。\(\bs{Q}(\al)\) のところは \(\bs{Q}(\beta)\) や \(\bs{Q}(\gamma)\) とすることができます。
つまり、\(\bs{Q}\) 上の既約多項式 \(f(x)=x^3+px+q\) の最小分解体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、方程式の解の一つである \(\al\) の(または \(\beta,\:\gamma\) の)単拡大体であり、単拡大体の基底の定理(33F)により \(\bs{L}\) の次元は \(3\) です。すると次数と位数の同一性(52B)により、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) の群位数は \(3\) です。従って、ラグランジュの定理(41E)により群位数が素数の群は巡回群なので、\(G\) は群位数 \(3\) の巡回群( \(C_3\) )です。
以上をまとめると、3次方程式の最小分解体のガロア群は、次のようになります。
前提として、
・\(f(x)=x^3+px+q\:\:(p,\:q\in\bs{Q})\)
( \(f(x)\) は既約多項式 )
・\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\)
・\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
・\(f(x)\) の最小分解体を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)
・\(G=\mr{Gal}(\bs{L}/\bs{Q})\)
とする。この前提のもとで、
\(\bs{\theta}\):有理数のとき
\(G\cong C_3\)
\(G=\{\:e,\:\sg,\:\sg^2\:\}\)
\(\sg=(1,\:2,\:3)\)
\(G\) は巡回群なので可解群
\(\bs{\theta}\):有理数でないとき
\(G\cong S_3\)
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
\(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\)
\(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列
\(G\) は可解群
なお、\((1,\:2,\:3)\:\:(2,\:3)\) の巡回置換は \((1,\:3,\:2)\:\:(1,\:2)\:\:(1,\:3)\) などとしても同じです。
\(C_3\::\:x^3-3x+1\)
まずガロア群が \(C_3\) の方程式 \(x^3-3x+1=0\) を取り上げ、巡回拡大がべき根拡大になる原理を確認します。この原理はガロア群が \(S_3\) のときにもそのまま応用できます。ちなみに \(C_3\) の方程式は \(p,\:q\) が \(-9\leq p\leq-1,\:\:1\leq q\leq9\) の整数だと、他に、
\(x^3-7x+6=0\:\:\:(D=400,\:\sqrt{D}=20)\)
\(x^3-7x+7=0\:\:\:(D=\phantom{0}49,\:\sqrt{D}=\phantom{0}7)\)
\(x^3-9x+9=0\:\:\:(D=729,\:\sqrt{D}=27)\)
があります。
\(x^3-3x+1=0\) の場合、\(p=-3,\:q=1\) なので、
\(\begin{eqnarray}
&&\:\:D&=-4p^3-27q^2=81=9^2\\
&&\:\:\theta&=\pm\sqrt{D}=\pm9\\
\end{eqnarray}\)
となります。3つの解を \(\al,\:\beta,\:\gamma\) とすると、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
で、\(\bs{L}\) の次元は \(3\) で、\(G=\mr{Gal}(\bs{L}/\bs{Q})\cong C_3\) です。
以下「7.3 べき根拡大の十分条件」の証明の論理に沿います。7.3 の証明では、体に \(1\) の原始\(n\)乗根が含まれているのが条件でした。そこで \(1\) の原始3乗根 を \(\omega\) とし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\:\al)=\bs{L}(\omega)\)
という体の拡大を考えます。\(\omega\) は \(x^2+x+1=0\) の2つある根のどちらかで、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
です。7.3 ではラグランジュのレゾルベントを \(\al\) と書きましたが、方程式の根の表記との重複を避けるため、ここでは \(S\) とします。そうするとレゾルベントは、
です。\(\bs{Q}(\omega,\:\al)\) は \(\bs{Q}(\omega)\) に \(\al\) を添加した単拡大体なので、べき根拡大の十分条件のため補題2(72B)に従って、\(c=\al\) と定めます。そうすると、
\(S=\al+\omega^2\sg(\al)+\omega\sg^2(\al)\)
となり、\(\al,\:\beta,\:\gamma\) で表すと、\((\br{A})\) 式は、
です。この \(S\) は \(\bs{Q}(\omega,\al,\beta,\gamma)\) の元ですが、
\(\bs{Q}(\omega,\al,\beta,\gamma)=\bs{Q}(\omega,\al)\)
なので、\(S\) は \(\bs{Q}(\omega,\al)\) の元であり、ということは、
\(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\al)\)
です。方程式の3つの解を \(\al,\:\beta,\:\gamma\) に割り当てる方法の数(\(=3!\) )により、\(S\) は6通りの可能性があります。
7.3 での証明のポイントは、\(\bs{S^3}\) が \(\bs{\bs{Q}(\omega)}\) の元である、というところでした。それを計算で確かめるため、もうひとつのレゾルベントを導入します。ガロア群 \(G=\{e,\sg,\sg^2\}\) は、\(\sg\) が生成元であると同時に、\(\sg^2\) も生成元です。レゾルベントの定義における \(\sg\) は \(G\) の生成元であることが条件でした(73A)。そこで \((\br{A})\) 式の \(\sg\) を \(\sg^2\) で置き換えた式を \(T\) とすると、
\(\begin{eqnarray}
&&\:\:T&=c+\omega^2\sg^2(c)+\omega\sg^4(c)\\
&&&=c+\omega^2\sg^2(c)+\omega\sg(c)\\
\end{eqnarray}\)
となります。この式で \(c=\al\) とおくと
\(T=\al+\omega\beta+\omega^2\gamma\)
です。\(S\) には6通りの可能性がありますが、\(S\) をそのうちの一つに決めると \(T\) は一意に決まります。ここで、
は \(\al,\:\beta,\:\gamma\) を未知数とする連立1次方程式なので、\(\al,\:\beta,\:\gamma\) を \(S\) と \(T\) の式で表せます。連立方程式を解くと、
\(\al=\dfrac{1}{3}(S+T)\)
です。さらに、\(S\) と \(T\) には特別の関係があります。
\(ST=(\al+\omega^2\beta+\omega\gamma)(\al+\omega\beta+\omega^2\gamma)\)
という式を考えると、
\(\begin{eqnarray}
&&\:\:ST&=&\al^2+\beta^2+\gamma^2+\\
&&&&(\omega^2+\omega)\al\beta+(\omega^4+\omega^2)\beta\gamma+(\omega^2+\omega)\gamma\al\\
&&&=&(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)+\\
&&&&(-\al\beta-\beta\gamma-\gamma\al)\\
&&&=&-3(\al\beta+\beta\gamma+\gamma\al)\\
&&&=&-3p\\
\end{eqnarray}\)
となり、つまり、
という関係です。上の式の変形では、根と係数の関係と \(\omega^2+\omega+1=0\)、および \(\omega^3=1\) を使いました。
次に、\(S^3\) を求めるために \(S^3+T^3\) を計算してみると、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=(S+T)(S^2-ST+T^2)\\
&&&=(S+T)(S+\omega T)(S+\omega^2T)\\
\end{eqnarray}\)
です。ここで \((\br{C})\) 式を変形すると、
が得られるので、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=3\al\cdot3\omega^2\beta\cdot3\omega\gamma\\
&&&=27\al\beta\gamma=-27q\\
\end{eqnarray}\)
となります。まとめると、
\(S^3+T^3=-27q\)
\(ST=-3p\)
であり、
\(S^3-\dfrac{27p^3}{S^3}+27q=0\)
です。つまり、
という \(S^3\) についての2次方程式を解くことで \(S^3\) が求まり、そこから \(S\) が求まります。\(S\) の値の可能性は6通りです。また \(T^3\) についても、
が成り立ちます。2次方程式、
の2つの解が \(S^3\) と \(T^3\) です。
ここまでの計算は \(x^3+px+q=0\) の形の既約方程式なら成り立ちます。ここで \(x^3-3x+1=0\) に即した、\(p=-3,\:q=1\) を \((\br{E})\) 式に入れると、
\((S^3)^2+27S^3+27^2=0\)
\(\begin{eqnarray}
&&\:\:S^3&=\dfrac{1}{2}\left(-27\pm\sqrt{27^2-4\cdot27^2}\right)\\
&&&=27\dfrac{-1\pm i\sqrt{3}}{2}\\
&&&=27\omega\\
\end{eqnarray}\)
となります。最後の式の \(\omega\) は、2つある \(1\) の原始3乗根のどちらか、という意味にとらえます。\(S^3=27\omega\) なら \(T^3=27\omega^2\) で、その逆でもよいわけです。
\((\br{C})\) 式と \((\br{D})\) 式により、\(\al\) は \(S\) と \(\omega\) の四則演算で表現できます。つまり、
\(\bs{Q}(\omega,\al)\subset\bs{Q}(\omega,\:S)\)
です。従って、さきほどの \(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\:\al)\) と合わせると、
\(\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\)
です。以上をまとめると、レゾルベント \(S\) について、
\(\begin{eqnarray}
&&\:\:S^3&\in\bs{Q}(\omega)\\
&&\:\:S&\in\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\\
\end{eqnarray}\)
です。つまり、
\(\bs{Q}(\omega)\) 上の方程式、
\(x^3-a=0\:\:(\:a=27\omega\in\bs{Q}(\omega)\:)\)
の解の一つ、\(\sqrt[3]{a}\) を \(\bs{Q}(\omega)\) に添加したのが \(\bs{Q}(\omega,\:\al)\)
であり、\(\bs{\bs{Q}(\omega,\:\al)}\) は \(\bs{\bs{Q}(\omega)}\) のべき根拡大体であることがわかりました。\(\bs{Q}(\omega,\:\al)\) は \(x^3-a=0\) の解、\(\sqrt[3]{a},\:\sqrt[3]{a}\:\omega,\:\sqrt[3]{a}\:\omega^2\) の全部を含むので、\(\bs{Q}(\omega)\) のガロア拡大体です。結論として、
ことになります。\(x^3-3x+1=0\) の場合、\(a=27\omega\) です。
巡回拡大がべき根拡大になることの証明のフォローはここまでですが、\(x^3-3x+1=0\) の解を具体的に求めることもできます。\(S^3=27\omega\) から、\(S=3\cdot\sqrt[3]{\omega}\) であり、また \(ST=9\) なので、
\(\begin{eqnarray}
&&\:\:\al&=\dfrac{1}{3}(S+T)=\dfrac{1}{3}\left(S+\dfrac{9}{S}\right)\\
&&&=\sqrt[3]{\omega}+\dfrac{1}{\sqrt[3]{\omega}}=\sqrt[3]{\omega}+\sqrt[3]{\omega^2}\\
&&&=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i}\\
\end{eqnarray}\)
が解の一つです。「1.3 ガロア群」の「ガロア群の例」に書いたように、
\(\al=1.53208888623796\:\cd\)
であり、正真正銘の正の実数ですが、\(\bs{\al}\) をべき根で表わそうとすると虚数単位が登場します。その理由がガロア理論から分かるのでした。
\(S_3\::\:x^3+px+q\)
方程式 \(x^3+px+q=0\) の係数を変数のままで扱い、ガロア群が \(S_3\) の方程式の一般論として話を進めます。3つの根を \(\al,\:\beta,\:\gamma\) とし(置換での表示では、それぞれ \(1,\:2,\:3\))、差積 \(\theta\) を、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=\sqrt{D}\\
&&\:\:D&=-4p^3-27q^2\\
\end{eqnarray}\)
と定義すると、\(\bs{\theta}\) が有理数でないとき、
となります(前述)。\(G\cong S_3\) は巡回群ではありません。しかし可解群なので "巡回群の入れ子構造" になっていて(=可解列が存在する)、「巡回拡大はべき根拡大」の定理(73A)を2段階に使うことで、方程式の解が四則演算とべき根で表現できることを証明できます。
まず、上記の可解列とガロア対応(53B)になっている「体の拡大列」は何かです。具体的には \(H\) の固定体は何かですが、それは \(\bs{Q}(\theta)\) です。実際、
\(\sg(\theta)=\theta,\:\:\sg^2(\theta)=\theta\)
なので、\(H\) のすべての元は \(\bs{Q}(\theta)\) の元を固定します。また、
\(\tau(\theta)=-\theta\)
なので、\(\tau\)(および \(\sg\tau,\:\sg^2\tau\))は \(\bs{Q}(\theta)\) の元 を固定しません。従って、\(H\) の固定体は \(\bs{Q}(\theta)\) です。つまり、\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) と書くと、
というガロア対応になっています。
次に体の拡大次元を検証します。まず、\(|G|=6\) なので、次数と位数の同一性(52B)により、\(\bs{L}/\bs{Q}\) の拡大次数は、
\([\:\bs{L}:\bs{Q}\:]=6\)
です。\(\bs{Q}(\theta)\) は \(\bs{Q}\) 上の既約な2次方程式、
\(x^2-D=0\)
の解である \(\theta\) で \(\bs{Q}\) を単拡大した体なので、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\theta):\bs{Q}\:]=2\)
です。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}:\bs{Q}\:]=[\:\bs{L}:\bs{Q}(\theta)\:]\cdot[\:\bs{Q}(\theta):\bs{Q}\:]\)
\([\:\bs{L}:\bs{Q}(\theta)\:]=3\)
となるはずです。\([\:\bs{L}:\bs{Q}(\theta)\:]=3\) であることを、具体的な体の拡大の様子を検証することで確かめます。2つのことを証明します。
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) とするとき、\(\bs{Q}(\theta,\al)=\bs{L}\) である。
[証明]
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\) だから、\(\theta\) は \(\al,\:\beta,\:\gamma\) で表現されている。従って
\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\)
である。この逆である、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であることを証明する。そのためには \(\beta,\:\gamma\) が「有理数と \(\theta,\:\al\) の四則演算」で表現できることを示せばよい。根と係数の関係により、
である。これを利用して \(\theta\) の定義式を変形すると、
\(\begin{eqnarray}
&&\:\:\theta=&(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=(\beta-\gamma)(-\al^2+(\beta+\gamma)\al-\beta\gamma)\\
&&&=(\beta-\gamma)\left(-\al^2-\al^2+\dfrac{q}{\al}\right)\\
&&&=(\beta-\gamma)\dfrac{-2\al^3+q}{\al}\\
\end{eqnarray}\)
となり、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であり、\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\) と合わせて、
\(\bs{Q}(\theta,\al)=\bs{Q}(\al,\beta,\gamma)\)
である。[証明終]
\(x^3+px+q\) は \(\bs{\bs{Q}(\theta)}\) 上の既約多項式である。
[証明]
\(\bs{Q}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解 \(\al\) による \(\bs{Q}\) の単拡大体 \(\bs{Q}(\al)\) を考えると、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\al):\bs{Q}\:]=3\)
である。従って \(\al\notin\bs{Q}(\theta)\) である。なぜなら、もし \(\al\in\bs{Q}(\theta)\) なら \(\bs{Q}(\theta)\) の次元は \(3\) 以上になるが、\([\:\bs{Q}(\theta):\bs{Q}\:]=2\) なので矛盾が生じるからである。同様に、\(\beta,\:\gamma\notin\bs{Q}(\theta)\) である。\(x^3+px+q\) は、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
と表されるから、\(x^3+px+q\) は \(\bs{Q}(\theta)\) 上では因数分解できない。つまり \(x^3+px+q\) は \(\bs{Q}(\theta)\) 上の既約多項式である。[証明終]
以上により、
ことが検証できました。これを踏まえて、3次方程式が解ける理由をガロア理論で説明します。ガロア対応である、
を2つの部分に分けます。
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\)
\(\mr{Gal}(\bs{Q}(\theta)/\bs{Q})\cong G/H\cong C_2\) であり、\(\bs{Q}(\theta)/\bs{Q}\) は巡回拡大で、拡大次数は \(2\) です。\(1\) の原始2乗根は \(-1\) であり、\(\bs{Q}\) に含まれています。従って \(\bs{Q}(\theta)/\bs{Q}\) はべき根拡大です。具体的には、
\(x^2-D=0\:\:(D\in\bs{Q})\)
\(D=-4p^3-27q^2\)
の解が \(\theta\) であり、
\(\theta=\sqrt{D}=\sqrt{-4p^3-27q^2}\)
です。これはレゾルベントを持ち出すまでもなく分かります。
\(\bs{Q}(\theta)\:\subset\:\bs{L}\)
\(\mr{Gal}(\bs{L}/\bs{Q}(\theta))=H\cong C_3\) であり、\(\bs{L}/\bs{Q}(\theta)\) は巡回拡大で、拡大次数は \(3\) です。また \(\bs{L}\) は \(\bs{Q}(\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体で、\(\bs{L}=\bs{Q}(\theta,\al)\) でした。
\(\bs{Q}(\theta)\) には(一般には)\(1\) の原始3乗根が含まれていません。そこで、\(\bs{L}/\bs{Q}(\theta)\) の体の拡大の代わりに、\(\bs{L}(\omega)/\bs{Q}(\omega,\theta)\) という拡大を考えます。
\(\bs{L}(\omega)=\bs{Q}(\omega,\theta,\al)\)
レゾルベント \(S,\:T\) を導入して \(S^3\) と \(T^3\) を求めます。計算は、方程式 \(x^3-3x+1=0\) のときと全く同じです。つまり、
\(\al=\dfrac{1}{3}(S+T)\)
です。方程式 \(x^3-3x+1=0\) の場合、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からの巡回拡大でしたが、\(x^3-3p+1q=0\) では \(\bs{Q}(\omega,\theta)\) からの巡回拡大であり、ガロア群が位数 \(3\) の巡回群であるという点では全く同じなのです。
\((\br{F})\) 式から \(X\) を求めると、
\(\begin{eqnarray}
&&\:\:X&=\dfrac{1}{2}\left(-27q\pm\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q\pm\sqrt{-27\theta^2}\right)\\
&&&=\dfrac{1}{2}(-27q\pm3\sqrt{3}i\cdot\theta)\\
\end{eqnarray}\)
となるので、
\(S^3=\dfrac{1}{2}(-27q+3\sqrt{3}i\cdot\theta)\)
\(T^3=\dfrac{1}{2}(-27q-3\sqrt{3}i\cdot\theta)\)
となります。\(S^3\) と \(T^3\) は逆でもかまいません。\(\omega\) は \(1\) の原始3乗根で、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
のどちらかです。従って、
\(\sqrt{3}i\in\bs{Q}(\omega,\theta)\)
です。つまり、
\(S^3,\:\:T^3\in\bs{Q}(\omega,\theta)\)
であることがわかりました。従って、\(S,\:T\) は \(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解ということになり、\(\bs{Q}(\omega,\theta,\:S)/\bs{Q}(\omega,\theta)\) の体の拡大を考えると、
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
であることが次のようにして分かります。つまり、\(\bs{Q}(\omega,\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解が \(\al,\:\beta,\:\gamma\) であり、\((\br{B})\) 式により \(S\) は \(\al,\:\beta,\:\gamma,\:\omega\) の四則演算で表されているので、
\(S\in\bs{Q}(\omega,\theta,\al,\beta,\gamma)\)
であり、また、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)\)
だったので、
\(S\in\bs{Q}(\omega,\theta,\al)\)
です。このことから、
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
です。
この説明は「7.3 べき根拡大の十分条件」の証明に従いましたが、3次方程式の場合は、\((\br{C})\) 式と \((\br{D})\) 式により、\(\al,\:\beta,\:\gamma\) が \(S\) と \(\omega\) の四則演算で表現できます。従って、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)\subset\bs{Q}(\omega,\theta,S)\)
\(\bs{Q}(\omega,\theta,\al)\subset\bs{Q}(\omega,\theta,S)\)
であり、
\(\bs{Q}(\omega,\theta,S)\subset\bs{Q}(\omega,\theta,\al)\)
と合わせて
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
である、とするのが簡便な説明になります。
以上をまとめると、
\(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解の一つ、\(S\) を \(\bs{Q}(\omega,\theta)\) に添加したべき根拡大体が \(\bs{Q}(\omega,\theta,\al)=\bs{L}(\omega)\) である
となり、体に \(\bs{\omega}\) が含まれる前提で、巡回拡大はべき根拡大であることが検証できました。ここから、\(\bs{L}(\omega)\) を \(\bs{Q}\) の拡大体として、方程式の係数 \(p,\:q\) を使って、できるだけ簡潔な形で表してみます。
\(\begin{eqnarray}
&&\:\:\theta&=\sqrt{-4p^3-27q^2}\\
&&&=6\cdot\sqrt{3}i\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\\
\end{eqnarray}\)
ですが、\(\sqrt{3}i\in\bs{Q}(\omega)\) なので、
\(\bs{Q}(\omega,\theta)=\bs{Q}\left(\omega,\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\)
と表せます。また、
\(\begin{eqnarray}
&&\:\:X^3&=\dfrac{1}{2}\left(-27q+\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q+27\cdot2\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
&&&=27\left(-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
\end{eqnarray}\)
なので、
\(S=3\cdot\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(T=3\cdot\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
が \(S,\:T\) です。\(\sqrt[3]{\phantom{I}\cd\phantom{I}}\) は3乗して \(\cd\) になる数の意味です。従って、\(S\) の選び方は3通りですが、\(S\) を一つに決めると、
\(ST=-3p\)
が成り立つように \(T\) を選ぶ必要があります。以上の \(S\) を用いて \(\bs{L}(\omega)\) を表すと、
\(\bs{L}(\omega)\)
\(=\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)=\bs{Q}(\omega,\theta,S)\)
\(=\bs{Q}\left(\omega,\:\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}},\:\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\right)\)
となります。この式が意味するところは、
ということです。べき根拡大の出発点は 有理数に \(\omega\) を添加した体です。「7.1 1の原始n乗根」で証明したように、原始\(n\)乗根はべき根で表現可能であり(71A)、もちろん \(\omega\) もそうです。これが3次方程式が解ける原理(一般化するとガロア群が可解群である方程式が解ける原理)です。補足すると、\(p=0\) のときは、
\(\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}=\pm\dfrac{q}{2}\in\bs{Q}\)
なので、べき根拡大は \(\sqrt[3]{\phantom{A}}\) の1回だけになります。
さらに、ここまでの計算で3次方程式の解も求まりました。解は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=\dfrac{1}{3}(S+T)&\\
&&\beta=\dfrac{1}{3}(\omega S+\omega^2T)&\\
&&\gamma=\dfrac{1}{3}(\omega^2S+\omega T)&\\
\end{eqnarray}
\end{array}\right.\)
であり、記号を、
\(S=3s\)
\(T=3t\)
に置き換えると、
3次方程式の解の公式
\(x^3+px+q=0\) の3つの解を \(\al,\:\beta,\:\gamma\) とする。
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=s+t&\\
&&\beta=\omega s+\omega^2t&\\
&&\gamma=\omega^2s+\omega t&\\
\end{eqnarray}
\end{array}\right.\)
\(s=\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(t=\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(st=-\dfrac{p}{3}\)
が、3次方程式の解の公式です。
3次方程式の解による体の拡大を振り返ってみます。\(\bs{Q}\) 上の既約な方程式 \(x^3+px+q=0\) の根を \(\al,\:\beta,\:\gamma\) とし、\(\bs{Q}\) の最小分解体 を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)、ガロア群を \(G=\mr{Gal}(\bs{L}/\bs{Q})\) とすると、
のガロア対応が成り立ちます。\(\bs{L}/\bs{Q}\) の拡大次数は \(6\)(\(|G|=6\))です。この、
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\subset\:\bs{L}\)
という体の拡大列で、\(\bs{Q}\:\subset\:\bs{Q}(\theta)\) のところはべき根拡大ですが、\(\bs{Q}(\theta)\:\subset\:\bs{L}\) は、\(\omega\in\bs{Q}(\theta)\) の場合を除き、べき根拡大ではありません。しかし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\theta)\:\subset\:\bs{L}(\omega)\)
なら、必ず、すべてがべき根拡大になります。従って、3次方程式の解は \(\bs{Q}(\omega)\) の元である「有理数と \(\omega\)」の四則演算・べき根で記述できます。
\(\omega\) は \(x^2+x+1=0\) の解なので、\([\:\bs{Q}(\omega):\bs{Q}\:]=2\) です。従って、拡大次数の連鎖律(33H)により、\(\omega\notin\bs{Q}(\theta)\) の条件で、
\([\:\bs{L}(\omega):\bs{Q}\:]=12\)
です。これは、\(\bs{Q}\) 上の多項式 \((x^3+px+q)(x^2+x+1)\) の最小分解体が \(\bs{L}(\omega)\) なので、\(\bs{Q}\) からの拡大次数は \(12\) であるとも言えます。3次方程式の「解」は、あくまで \(\bs{Q}\) の \(6\)次拡大体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) の中にありますが、「べき根で表された解」は \(\bs{Q}\) の \(12\)次拡大体 \(\bs{L}(\omega)\) の中にあるのです。
一見、矛盾しているようですが、そうではありません。ある代数拡大体 \(\bs{K}\) があったとして、\(a\) を \(\bs{K}\) の元とし、\(1\) の原始3乗根の一つを \(\omega\) とします。3次方程式、
\(x^3-a=0\:\:(a\in\bs{K})\)
は3つの解をもちます。そのうちのどれか一つを \(\sqrt[3]{a}\) と定義すると、3つの解(べき根)は、
\(\sqrt[3]{a},\:\:\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2\)
です。\(\sqrt[3]{a}\) では \(\omega\) が不要なように見えますが、それは表面上のことで、3つの解は、
\(\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2,\:\:\sqrt[3]{a}\:\omega^3\)
であるというのが正しい認識です。つまり \(\bs{\omega}\) は3つのべき根の関係性を規定していて、\(\sqrt[3]{a}\cdot\omega^i\:\:(i=1,2,3)\) という "ペアの形" によって3つの区別が可能になり、数式としての整合性が保てます。\(\sqrt[3]{\phantom{A}}\) という "曖昧さ" がある記号を用いる限り、\(\omega\) という、曖昧さを解消する "助手" が必然的に登場するのです。
| 7.可解性の十分条件 |
第6章では、方程式が可解であれば(=解が四則演算とべき根で表現できれば)ガロア群が可解群であることをみました。第7章ではその逆、つまり、ガロア群が可解群であれば方程式が可解であることを証明します。
7.1 1の原始\(n\)乗根
可解性の十分条件を証明するために、まず、\(1\) の原始\(n\)乗根がべき根で表せることを証明します。このことを前提にした証明を最後で行うからです。念のために「1.1 方程式とその可解性」でのべき根の定義を振り返ると、
\(\sqrt[n]{\:a\:}\) (\(n=2\) の場合は \(\sqrt{\:a\:}\))
という表記は、
| \(a\) が正の実数のとき、\(n\)乗して \(a\) になる正の実数を表わす | |
| \(a\) が負の実数や複素数の場合は、\(n\)乗して \(a\) になる数のどれかを表わす |
のでした。\(\sqrt{2}\) は \(1.4142\cd\) と \(-1.4142\cd\) のどちらかを表わすのではなく、\(1.4142\cd\) のことです。\(\sqrt[3]{2}\) は \(3\)乗して \(2\) になる3つの数のうちの正の実数(\(\fallingdotseq1.26\))を表わします。一方、\(\sqrt{-1\:}\) は\(2\)乗して \(-1\) になる2つの数のうちのどちらかで、その一方を \(i\) と書くと、もう一方が \(-i\) です。
この定義から、方程式 \(x^n-1=0\) の解を \(\sqrt[n]{\:1\:}\) と書くと、それは \(1\) のことです。従って、
\(1\) 以外の「\(n\)乗して \(1\) になる数」がべき根で表現できる
ことを証明しておく必要があります。その証明はガロア理論とは無関係にできます。それが以下です。
| (原始n乗根はべき根で表現可能:71A) |
\(1\) の 原始\(n\)乗根はべき根で表現できる。
[証明]
\(n\) についての数学的帰納法で証明する。\(n=2,\:3\) のときにべき根で表現できるのは根の公式で明らかである。また、原始4乗根は \(\pm i\) なので、\(n\leq4\) のとき題意は成り立つ。そこで、\(n\) 未満のときにべき根で表現できると仮定し、\(n\) のときにもべき根で表現できることを証明する。
\(n\) が合成数のときと素数のときに分ける。まず \(n\) が合成数なら、
\(n=s\cdot t\)
と表現できる。
\(1\) の原始\(s\)乗根を \(\zeta\)
\(1\) の原始\(t\)乗根を \(\eta\)
とし、\(X=x^{s}\) とおく。方程式 \(X^{t}-1=0\) の \(t\)個の解は \(\eta^k\:\:(0\leq k\leq t-1)\) と表わされる(63B)から、\(x^n-1\) は、
\(\begin{eqnarray}
&&\:\:x^n-1&=x^{st}-1=X^{t}-1\\
&&&=\displaystyle\prod_{k=0}^{t-1}(X-\eta^k)\\
&&&=\displaystyle\prod_{k=0}^{t-1}(x^{s}-\eta^k)\\
\end{eqnarray}\)
と因数分解できる。従って、方程式 \(x^n-1=0\) の解は、
\(x^{s}=\eta^k\:\:\:(0\leq k\leq t-1)\)
の解である。これを解くと、
\(x=\sqrt[s]{\eta^k}\cdot\zeta^j\:\:\:(0\leq j\leq s-1,\:\:0\leq k\leq t-1)\)
である(\(k=0\) のときは根号の規則に従って \(\sqrt[s]{1}=1\))。帰納法の仮定により、\(\zeta,\:\eta\) はべき根で表現できるから、上式により \(1\) の \(n\) 乗根はべき根で表現できる。従って原始\(n\)乗根もべき根で表現できる。
以降は \(n\) が素数の場合を証明する。\(n\) を \(p\)(= 素数)と表記する。以下では数式を見やすくするため \(p=5\) の場合を例示するが、証明の過程は一般性を失わない論理で進める。
位数 \(p-1\) の2つの巡回群、\((\bs{Z}/p\bs{Z})^{*}\) と \(\bs{Z}/(p-1)\bs{Z}\) の性質を利用する。\(p=5\) の場合は、位数 \(4\) の既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と、剰余群 \(\bs{Z}/4\bs{Z}\) である。
\(p\) が素数のとき、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は生成元をもつ(25D)。\((\bs{Z}/5\bs{Z})^{*}\) の生成元の一つは \(2\) である(もう一つは \(3\))。生成元を \(2\) とすると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
の巡回群となる。演算は乗算である。一方、\(\bs{Z}/4\bs{Z}\) は、演算が加算、生成元が \(1\)(または \(3\))の巡回群で、
\(\begin{eqnarray}
&&\:\:\bs{Z}/4\bs{Z}&=\{1,\:1+1,\:1+1+1,\:1+1+1+1\}\\
&&&=\{1,\:2,\:3,\:0\}\\
\end{eqnarray}\)
である。ここで、2つの変数 \(x,\:y\) をもつ関数を、
\(f(x,y)=y^2x+y^4x^2+y^3x^3+y\) |
とおく。この関数は、4つある項の \(x,\:y\) の指数について、
\(y\) の指数は \([\:2,\:4,\:3,\:1\:]\) : \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン
\(x\) の指数は \([\:1,\:2,\:3,\:0\:]\) : \(\bs{Z}/4\bs{Z}\) の巡回パターン
となるようにしてある。
次に、2つの数 \(a,\:b\) を、
\(\begin{eqnarray}
&&\:\:a^5&=1\:(a\neq1)\\
&&\:\:b^4&=1\\
\end{eqnarray}\)
であるような数とする。\(a\) は \(1\) の原始5乗根でもよいし、その任意の累乗でもよい。とにかく \(a^5=1\:(a\neq1)\) を満たす数である。このとき、
\(a^5-1=0\)
\((a-1)(a^4+a^3+a^2+a+1)=0\)
なので、
\(a^4+a^3+a^2+a+1=0\) ないしは
\(a^4+a^3+a^2+a=-1\)
が成り立つ。\(b\) も \(1\) の原始4乗根か、その任意の累乗であるが、\(b=1\) であってもよい。
そうすると \(f(b,a)\) は、
\(f(b,a)=a^2b+a^4b^2+a^3b^3+a\)
\(a\) の指数は \([\:2,\:4,\:3,\:1\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
である。
次に \(f(b,a^2)\) を計算すると、
\(\begin{eqnarray}
&&\:\:f(b,a^2)&=a^4b+a^8b^2+a^6b^3+a^2\\
&&&=a^4+a^3b+a^1b^2+a^2b^3\\
\end{eqnarray}\)
\(a\) の指数は \([\:4,\:3,\:1,\:2\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
となる。
\(f(b,a^2)\) を \(f(b,a)\) と比べると、\(a\) の指数が \(1\) ステップだけ巡回している。ということは、\(b\) の指数も \([\:2,\:3,\:0,\:1\:]\) と \(1\) ステップだけ巡回させれば、\(a\) の指数と \(b\) の指数が同期することになり、\(f(b,a^2)\) の式は \(f(b,a)\) と同じものになる。同期させるには \(f(b,a^2)\) に \(b\) を掛ければよい。従って、
\(bf(b,a^2)=f(b,a)\)
である。
全く同様にして、
\(\begin{eqnarray}
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^8)&=b^3f(b,a^3)\\
&&&=f(b,a)\\
\end{eqnarray}\)
となる。まとめると、
\(\begin{eqnarray}
&&\:\:bf(b,a^2)&=f(b,a)\\
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^3)&=f(b,a)\\
\end{eqnarray}\)
である。\(b^4=1\) だから、各両辺を \(4\)乗すると、
\(f(b,a^2)^4=f(b,a)^4\)
\(f(b,a^4)^4=f(b,a)^4\)
\(f(b,a^3)^4=f(b,a)^4\)
の式を得る。
本題から少々はずれるが、この仕組みは、\(a\) の指数が「\(2\) の乗算の巡回群」であるため、
\(a^k\:\rightarrow\:a^{2k}=(a^k)^2\)
と巡回し、\(b\) の指数は「\(1\) の足し算の巡回群」であるため、
\(b^k\:\rightarrow\:b^{k+1}=b\cdot b^k\)
と巡回することを利用したものである。
なお、\((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(2\) を選んだが、一般の \((\bs{Z}/p\bs{Z})^{*}\) では \(2\) が生成元とは限らない(25D)。その場合は任意の生成元を選んでよい。例えば \((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(3\) を選ぶと
\([\:3,\:3^2,\:3^3,\:3^4\:]=[\:3,\:4,\:2,\:1\:]\)
と巡回する。従って \(f(x,y)\) を、
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\)
と定義すると、\(y,\:a\) の指数は「\(3\) の乗算の巡回群」だから、
\(a^k\:\rightarrow\:a^{3k}=(a^k)^3\)
と巡回する(\(x,\:b\) については同じ)。つまり、
\(\begin{eqnarray} &&\:\:bf(b,a^3)&=f(b,a)\\ &&\:\:b^2f(b,a^4)&=f(b,a)\\ &&\:\:b^3f(b,a^2)&=f(b,a)\\ \end{eqnarray}\)
となり、
\(f(b,a^3)=f(b,a)^4\)
\(f(b,a^4)=f(b,a)^4\)
\(f(b,a^2)=f(b,a)^4\)
となり、同じ結果を得る。
\(a^k\:\rightarrow\:a^{2k}=(a^k)^2\)
と巡回し、\(b\) の指数は「\(1\) の足し算の巡回群」であるため、
\(b^k\:\rightarrow\:b^{k+1}=b\cdot b^k\)
と巡回することを利用したものである。
なお、\((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(2\) を選んだが、一般の \((\bs{Z}/p\bs{Z})^{*}\) では \(2\) が生成元とは限らない(25D)。その場合は任意の生成元を選んでよい。例えば \((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(3\) を選ぶと
\([\:3,\:3^2,\:3^3,\:3^4\:]=[\:3,\:4,\:2,\:1\:]\)
と巡回する。従って \(f(x,y)\) を、
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\)
と定義すると、\(y,\:a\) の指数は「\(3\) の乗算の巡回群」だから、
\(a^k\:\rightarrow\:a^{3k}=(a^k)^3\)
と巡回する(\(x,\:b\) については同じ)。つまり、
\(\begin{eqnarray} &&\:\:bf(b,a^3)&=f(b,a)\\ &&\:\:b^2f(b,a^4)&=f(b,a)\\ &&\:\:b^3f(b,a^2)&=f(b,a)\\ \end{eqnarray}\)
となり、
\(f(b,a^3)=f(b,a)^4\)
\(f(b,a^4)=f(b,a)^4\)
\(f(b,a^2)=f(b,a)^4\)
となり、同じ結果を得る。
本題に戻って、次に \(f(b,a)^4\) を展開する。
\(f(b,a)^4=(a^2b+a^4b^2+a^3b^3+a)^4\)
\((\br{A})\)
であるが、このまま展開したのでは \(p=5\) のときに固有のものになり、一般性を失う。そこで、上式を展開して整理した形を、
\(f(b,a)^4=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\)
\((\br{B})\)
とする。\(a^2,\:a^4,\:a^3,\:a\) の係数となっている \(h_i(b)\:(i=1,2,3,0)\) は \(b\) の多項式である。この展開形の決め方は次のように行う。
| \((\br{A})\) 式の次数は最大 \(a^{16}\) であるが、\(a^5=1\) の関係を利用して最大次数が \(a^4\) になるように「次数下げ」を行う。 | |
| そうすると、\(a\) を含まない \(b\) だけの項が出てくる。そこで、 \(1=-(a^4+a^3+a^2+a)\) の関係を利用し、\(b\) だけの項に \(-(a^4+a^3+a^2+a)\) を掛けて「次数上げ」を行う。 | |
| 以上の結果を、\(a^2,\:a^4,\:a^3,\:a\) ごとに整理したものを \((\br{B})\) とする。 |
\((\br{B})\) 式においては、
| \(a\) の指数 | \(:\:[\:2,\:4,\:3,\:1\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:1,\:2,\:3,\:0\:]\) |
次に \(f(b,a^2)^4\) を計算する。これは \((\br{B})\) 式において \(a\) を \(a^2\) に置き換えればよいから、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=h_1(b)a^4+h_2(b)a^8+h_3(b)a^6+h_0(b)a^2\\
&&&=h_1(b)a^4+h_2(b)a^3+h_3(b)a+h_0(b)a^2\\
\end{eqnarray}\)
| \(a\) の指数 | \(:\:[\:4,\:3,\:1,\:2\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:1,\:2,\:3,\:0\:]\) |
| \(a\) の指数 | \(:\:[\:2,\:4,\:3,\:1\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:0,\:1,\:2,\:3\:]\) |
\(f(b,a^2)^4=h_0(b)a^2+h_1(b)a^4+h_2(b)a^3+h_3(b)a\)
である。同様に、
\(f(b,a^4)^4=h_3(b)a^2+h_0(b)a^4+h_1(b)a^3+h_2(b)a\)
\(h_i(b)\) の添字 \(:\:[\:3,\:0,\:1,\:2\:]\)
\(f(b,a^3)^4=h_2(b)a^2+h_3(b)a^4+h_0(b)a^3+h_1(b)a\)
\(h_i(b)\) の添字 \(:\:[\:2,\:3,\:0,\:1\:]\)
である。
従って、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) において、\(a^j\:(j=2,4,3,1)\) の係数は \(h_k(b)\:(k=1,2,3,0)\) の全てを巡回する。つまり、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) の全部を足すと、\(a^j\:(j=2,4,3,1)\) の係数は全て同じになる。その計算をすると、
\(\displaystyle\sum_{i=1}^{4}f(b,a^i)^4\)
\(\begin{eqnarray}
&&\:\: =&(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&&\cdot(a^2+a^4+a^3+a)\\
\end{eqnarray}\)
となる。上式の左辺については、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=f(b,a)^4\\
&&\:\:f(b,a^4)^4&=f(b,a)^4\\
&&\:\:f(b,a^3)^4&=f(b,a)^4\\
\end{eqnarray}\)
だったので、左辺は \(4f(b,a)^4\) に等しい。また \(a^5-1=0\) なので \(a^2+a^4+a^3+a=-1\) である。従って、
\(4f(b,a)^4=-(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
である。ここで、
\(g(b)=-\dfrac{1}{4}\:(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
と定義すると、
| \(f(b,a)^4\) | \(=g(b)\) | ||
| \(f(b,a)\) | \(=\sqrt[4]{g(b)}\) | \((\br{C})\) |
を得る。\((\br{C})\) 式における \(\sqrt[4]{g(b)}\) とは「\(4\)乗すると \(g(b)\) になる数」という意味である。従って、実際には \(4\)次方程式の \(4\)つの解のどれかを表している。
なお、\(g(b)\) を具体的に計算すると、計算過程は省くが、
\(g(b)=-16b^3+14b^2+4b-1\)
となる。この表現は \(p=5\) のときのもので、一般論につながるものではない。 \((\br{D})\)
今までの計算をまとめると、
\(\begin{eqnarray}
&&\:\:a^5=1\:(a\neq1)&\\
&&\:\:b^4=1&\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(b,a)&=a^2b+a^4b^2+a^3b^3+a\\
&&\:\:f(b,a)^4&=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\\
&&\:\:g(b)&=-\dfrac{1}{4}(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&\:\:f(b,a)&=\sqrt[4]{g(b)}\\
\end{eqnarray}\)
である。この過程で、\(a,\:b\) については \(a^5=1\:(a\neq1),\:b^4=1\) という条件しか使っていない。従って、この条件が満たせれば \(a,\:b\) は任意である。そこで \(1\) の原始5乗根を \(\zeta\) とし、\(1\) の原始4乗根を \(\omega\) として、
\(a=\zeta\)
\(b=\omega^j\:\:(j=1,2,3,4)\)
とおく。\(b\) は \(1\) にもなりうる(\(\omega^4=1\))。なお、\(\omega\) は普通 \(1\) の原始3乗根の記号であるが、ここでは原始4乗根として使う。
すると、
\(f(\omega^j,\zeta)=\sqrt[4]{g(\omega^j)}\:\:(j=1,2,3,4)\)
\((\br{E})\)
という、4つの式が得られる。これは、
\(\zeta^2,\:\:\zeta^4,\:\:\zeta^3,\:\:\zeta\)
を4つの未知数とする連立1次方程式である。帰納法の仮定により \(\omega\) はべき根で表されているから、方程式を解いて \(\zeta\) が \(\omega\) のべき根(と四則演算)で表されば、証明が完成することになる。
\((\br{E})\) の連立方程式を具体的に書くと、
\(\zeta^2+\omega^j\zeta^4+(\omega^j)^2\zeta^3+(\omega^j)^3\zeta=\sqrt[4]{g(\omega^j)}\)
\((j=1,2,3,4)\)
であり、全てを陽に書くと、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta^2+\omega\:\:\zeta^4+(\omega\:\:)^2\zeta^3+(\omega\:\:)^3\zeta&=\sqrt[4]{g(\omega)}& \br{①}&\\
&&\zeta^2+\omega^2\zeta^4+(\omega^2)^2\zeta^3+(\omega^2)^3\zeta&=\sqrt[4]{g(\omega^2)}& \br{②}&\\
&&\zeta^2+\omega^3\zeta^4+(\omega^3)^2\zeta^3+(\omega^3)^3\zeta&=\sqrt[4]{g(\omega^3)}& \br{③}&\\
&&\zeta^2+\omega^4\zeta^4+(\omega^4)^2\zeta^3+(\omega^4)^3\zeta&=\sqrt[4]{g(\omega^4)}& \br{④}&\\
\end{eqnarray}
\end{array}\right.\)
となる。この連立方程式を解くため、\(\zeta\) の項だけを残し、他の未知数である \(\zeta^2,\:\zeta^4,\:\zeta^3\) の項を消去することを考える。そのために、
\(A\::\:\br{①}\times\omega\:+\:\br{②}\times\omega^2\:+\:\br{③}\times\omega^3\:+\:\br{④}\times\omega^4\)
とおくと、
\(A\) の左辺 \(=\)
\(\omega\:\:\zeta^2+(\omega\:\:)^2\zeta^4+(\omega\:\:)^3\zeta^3+(\omega\:\:)^4\zeta+\)
\(\omega^2\zeta^2+(\omega^2)^2\zeta^4+(\omega^2)^3\zeta^3+(\omega^2)^4\zeta+\)
\(\omega^3\zeta^2+(\omega^3)^2\zeta^4+(\omega^3)^3\zeta^3+(\omega^3)^4\zeta+\)
\(\omega^4\zeta^2+(\omega^4)^2\zeta^4+(\omega^4)^3\zeta^3+(\omega^4)^4\zeta\)
となる。\(\zeta\) の4つの項は、係数が \((\omega^j)^4=(\omega^4)^j=1\) であり、
\(\zeta\) の項の合計 \(=\:4\zeta\)
である。
\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数は、
\(\omega^j+\omega^{2j}+\omega^{3j}+\omega^{4j}\:\:(j=1,2,3)\)
である。\(\omega^4=1\) なので、
\(\omega^j+\omega^{2j}+\omega^{3j}+1\:\:(j=1,2,3)\)
の形をしている。\(\omega\) は \(1\) の原始4乗根であり、\(x^4-1=0\) の根である。\(x^4-1\) は、
\(x^4-1=(x-1)(x^3+x^2+x+1)\)
と因数分解されるから、\(\omega,\:\omega^2,\:\omega^3\) は方程式
\(x^3+x^2+x+1=0\)
の3つの根である。つまり、
\(x^3+x^2+x+1=(x-\omega)(x-\omega^2)(x-\omega^3)\)
と因数分解される。この式に \(x=\omega^j\:(j=1,2,3)\) を代入すると、
\((\omega^j)^3+(\omega^j)^2+\omega^j+1\)
\(\begin{eqnarray}
&&\:\: &=\omega^{3j}+\omega^{2j}+\omega^j+1\\
&&&=(\omega^j-\omega)(\omega^j-\omega^2)(\omega^j-\omega^3)\\
&&&=0\:\:(j=1,2,3)\\
\end{eqnarray}\)
となる。つまり、\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数、\(\omega^j+\omega^{2j}+\omega^{3j}+1\) は全て \(0\) ということである。以上をまとめると、\(A\) の左辺は \(\zeta\) の項だけが残り、
\(A\) の左辺 \(=\:4\zeta\)
である。一方、\(A\) 式の右辺は、
\(A\) の右辺 \(=\:\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
である。従って、
\(4\zeta=\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
\(\zeta=\dfrac{1}{4}\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
となり、\(\zeta\) が \(\omega\) の多項式のべき根として求まった。 \((\br{F})\)
\((\br{F})\) 式における \(\sqrt[4]{g(\omega^j)}\) とは「\(4\)乗すると \(g(\omega^j)\) になる数」という意味であり、\(4\)次方程式の\(4\)つの解のどれかである。従って、実際に \(\omega\) に数を入れて(この場合は \(1\) の原始4乗根だから \(i\) か \(-i\))計算するときには、\(\zeta^5=1\) になるように \((\br{F})\) 式の \(4\)つの項のそれぞれについて、\(4\)つの解のどれかを選択する必要がある。しかしそうであっても、\(\zeta\) が \(\omega\) の多項式のべき根と四則演算で表現できるということは変わらない。
これまでの論理展開では、\(p=5\) であることの特殊性は何も使っていない。唯一、使ったのは、\(p\) が素数であり、そのときに \((\bs{Z}/p\bs{Z})^{*}\) に生成元がある(25D)ということである。
従って、\(\zeta\) が \(1\) の原始\(p\)乗根であり、\(\omega\) が \(1\) の原始\((p-1)\)乗根であっても \((\br{F})\) 式は、\(4\) を \((p-1)\) に置き換えれば成り立つ。
帰納法の仮定により、\(1\) の原始\((p-1)\)乗根 \(\omega\) はべき根で表される。従って \((\br{F})\) 式から、\(1\) の原始\(p\)乗根 である \(\zeta\) もべき根で表される。[証明終]
ためしに \((\br{F})\) 式を使って、\(1\) の原始5乗根、\(\zeta\) を計算してみます。\(\omega\) は \(1\) の原始4乗根(の一つ)なので \(\omega=i\)(虚数単位)とすると、\((\br{D})\) 式も含めて、
\(\begin{eqnarray}
&&\:\:g(b)&=-16b^3+14b^2+4b-1 (\br{D})\\
&&\:\:b&=\omega^j\:\:(j=1,2,3,4)\\
&&&=\:\{\:i,\:-1,\:-i,\:1\:\}\\
&&\:\:g(\omega)&=-15+20i\\
&&\:\:g(\omega^2)&=25\\
&&\:\:g(\omega^3)&=-15-20i\\
&&\:\:g(\omega^4)&=1\\
\end{eqnarray}\)
となり、これらを \((\br{F})\) 式に代入すると、
\(\zeta=\dfrac{1}{4}(\sqrt[4]{1}-\sqrt[4]{25}+i(\sqrt[4]{-15+20i}-\sqrt[4]{-15-20i}))\)
となります。\(\sqrt[4]{\cd}\) は「\(4\)乗して \(\cd\) になる数」の意味です。この式を、
\(4\zeta=r+is\)
\(\begin{eqnarray}
&&\:\: r&=\sqrt[4]{1}-\sqrt[4]{25}\\
&&\:\: s&=\sqrt[4]{-15+20i}-\sqrt[4]{15-20i}\\
\end{eqnarray}\)
と表すことにします。そして \(\sqrt[4]{\cd}\) を \(\sqrt{\cd}\) に変換するために2乗すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=\pm6\pm2\sqrt{5}&\\
&&s^2=\pm10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
と計算できます。但し \(r^2+s^2=4\) の条件があるので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=6\pm2\sqrt{5}&\\
&&s^2=10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
となります(複合異順)。ここから \(r,\:s\) を求めると、\(r\) の方は2重根号をはずすことができて、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r=\pm(1+\sqrt{5}),\:\:s=\pm\sqrt{10-2\sqrt{5}}&\\
&&r=\pm(1-\sqrt{5}),\:\:s=\pm\sqrt{10+2\sqrt{5}}&\\
\end{eqnarray}
\end{array}\right.\)
の合計8つの解が求まります。このうちの4つは方程式 \(x^5-1=0\) の解 \((=\zeta)\) で、残りの4つは方程式 \(x^5+1=0\) の解 \((=-\zeta)\) です。\(\zeta\) を表記すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm i\sqrt{10+2\sqrt{5}}\right)&\\
&&\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm i\sqrt{10-2\sqrt{5}}\right)&\\
\end{eqnarray}
\end{array}\right.\)
の4つとなり、\(1\) の原始5乗根が求まりました。一般的な原始5乗根の計算方法とは違いますが、\((\br{F})\) 式によっても原始5乗根が求まることが確認できました。
7.2 べき根拡大の十分条件のため補題
ここでは「7.3 べき根拡大の十分条件」を証明するための補題を2つ証明します。以下に出てくる多項式 \(g(x)\) は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言います。
補題(1)
| (べき根拡大の十分条件のため補題1:72A) |
\(\bs{L}\) を \(\bs{K}\) のガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) を \(\sg\) で生成される位数 \(n\) の巡回群とする。式 \(g(x)\) を、
| \(g(x)\) | \(\overset{\text{ }}{=}\) | \(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\) | |
| \((a_i\in\bs{L},\:1\leq i\leq n-1)\) |
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
[証明]
\(\bs{L}\) が原始元 \(\theta\) によって \(\bs{L}=\bs{K}(\theta)\) と表されているとし(32B)、\(\theta\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式の定理(31I)により \(f(x)\) は既約多項式である。そうすると、\(\theta,\:\sg^i(\theta)\:(1\leq i\leq n-1)\) の \(n\)個は \(f(x)=0\) の解であり、既約多項式の定理3(31G)によって \(n\)個の解は全て異なる。つまり、
\(\theta-\sg^i(\theta)\neq0\:(1\leq i\leq n-1)\)
である。このことを踏まえて背理法で証明する。\(\bs{L}\) の任意の元 \(x\) について、
\(g(x)=x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
\((\br{A})\)
となるような \(\bs{L}\) の元 \(a_1,\:a_2,\:\cd\:,a_{n-1}\) が存在したとする。この \(g(x)=0\) の式から \(\sg^{n-1}(x)\) の項を消去することを考える。そのためにまず \(g(\theta x)\) を計算すると、
| \(g(\theta x)\) | \(\overset{\text{ }}{=}\) | \(\theta x+\)\(a_1\sg(\theta x)+\)\(a_2\sg^2(\theta x)+\)\(\:\cd\:+\)\(a_{n-1}\sg^{n-1}(\theta x)\) | |
| \(\overset{\text{ }}{=}\) | \(\theta x+\)\(a_1\sg(\theta)\sg(x)+\)\(a_2\sg^2(\theta)\sg^2(x)+\)\(\:\cd\:+\)\(a_{n-1}\sg^{n-1}(\theta)\sg^{n-1}(x)\) | ||
| \(\overset{\text{ }}{=}\) | \(0\) |
となる。この式から \(\sg^{n-1}(x)\) の項を消去するには、この式の \(\sg^{n-1}(x)\)の係数が \(a_{n-1}\sg^{n-1}(\theta)\) であり、また \(g(x)\) の \(\sg^{n-1}(x)\) の項の係数が \(a_{n-1}\) なので、
\(\sg^{n-1}(\theta)g(x)=0\)
の式を作って両辺から引けばよい。その計算をすると、
\(g(\theta x)-\sg^{n-1}(\theta)g(x)\)
| \(\overset{\text{ }}{=}\) | \((\theta-\sg^{n-1}(\theta))x+\)\((\sg(\theta)-\sg^{n-1}(\theta))a_1\sg(x)+\)\((\sg^2(\theta)-\sg^{n-1}(\theta))a_2\sg(x)^2+\)\(\:\cd\:+\)\((\sg^{n-2}(\theta)-\sg^{n-1}(\theta))a_{n-2}\sg(x)^{n-2}\) | ||
| \(\overset{\text{ }}{=}\) | \(0\) |
となる。ここで、\(x\) の係数である \((\theta-\sg^{n-1}(\theta))\) は、証明の最初に書いたように \(0\) ではない。そこで、全体を \((\theta-\sg^{n-1}(\theta))\) で割ると、
\(x+b_1\sg(x)+b_2\sg(x)^2+\:\cd\:+b_{n-2}\sg(x)^{n-2}=0\)
\((\br{B})\)
の形になる。ここで \(b_i\) は、
\(b_i=\dfrac{\sg^i(\theta)-\sg^{n-1}(\theta)}{\theta-\sg^{n-1}(\theta)}a_i\)
である。\((\br{B})\) 式は、基本的に \((\br{A})\) 式と同じで、\((\br{A})\) 式から \(\sg(x)^{n-1}\) の項を消去した形であり、\(x\) の最大次数の項は \(\sg(x)^{n-2}\) になっている。以上の、\((\br{A})\) から \((\br{B})\) への変換は繰り返し行えるから、\(n-2\) 回の変換を繰り返すと、
\(x+c_1\sg(x)=0\)
の形が得られる。この式にもう一度、\(n-1\) 回目の変換をすると、
\(\theta x+c_1\sg(\theta x)-\sg(\theta)(x+c_1\sg(x))=0\)
\(\theta x+c_1\sg(\theta)\sg(x)-\sg(\theta)x+c_1\sg(\theta)\sg(x)=0\)
\(\theta x-\sg(\theta)x=0\)
\((\theta-\sg(\theta))x=0\)
\(x=0\)
\(\theta x+c_1\sg(\theta)\sg(x)-\sg(\theta)x+c_1\sg(\theta)\sg(x)=0\)
\(\theta x-\sg(\theta)x=0\)
\((\theta-\sg(\theta))x=0\)
\(x=0\)
となる。\(x\) は \(\bs{L}\) の任意の元だったから、\(\bs{L}\) のすべての元は \(0\) となってしまい、矛盾が生じた。従って背理法の仮定は誤りであり、\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。[証明終]補題(2)
| (べき根拡大の十分条件のため補題2:72B) |
\(\zeta\) を \(1\) の原始\(n\)乗根とし、\(\zeta\)を含む代数体を \(\bs{K}\) とする。\(\bs{K}\) のガロア拡大体を \(\bs{L}\) とし、\(\mr{Gal}(\bs{L}/\bs{K})\) は \(\sg\) で生成される位数 \(n\) の巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。また \(f(x)\) を \(\bs{K}\) 上の \(n\)次既約多項式とし、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて、\(\bs{L}=\bs{K}(\theta)\) と表されているものとする。このとき、
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
[証明]
\(g(x)\) の形は、べき根拡大の十分条件のため補題1(72A)で、
\(a_i=\zeta^{n-i}\:(1\leq i\leq n-1)\)
と置いたものである。\(\zeta\) は \(\bs{K}\) の元 = \(\bs{L}\) の元だから、補題(1)により \(\bs{L}\) の任意の元 \(x\) について \(g(x)=0\) となることはない。
この \(g(x)\) は次のような性質をもっている。まず \(\bs{K}\) の任意の元を \(a\) とすると、\(\mr{Gal}(\bs{L}/\bs{K})\) の 元 \(\sg\) は \(a\) を不動にするから、
\(\sg^i(a)=a\)
である。従って、\(g(a)\) を計算すると、
\(g(a)=ag(1)\)
となる。また、\(\bs{K}\) の任意の元を \(a\)、\(\bs{L}\) の任意の元を \(x\) とすると、
\(\sg^i(ax)=\sg^i(a)\sg^i(x)=a\sg^i(x)\)
なので、
\(g(ax)=ag(x)\)
である。さらに \(\bs{L}\) の任意の2つの元を \(x,\:y\) とすると、
\(\sg^i(x+y)=\sg^i(x)+\sg^i(y)\)
なので、
\(g(x+y)=g(x)+g(y)\)
である。
\(\bs{L}\) は、\(\bs{K}\) 上の既約多項式 \(f(x)\) を用いた方程式 \(f(x)=0\) の解 \(\theta\) の単拡大体 \(\bs{K}(\theta)\) だから、単拡大の体の定理(32C)により、\(\bs{L}\) の任意の元 \(x\) は、
\(x=b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1}\:(b^i\in\bs{K})\)
と表せる。\(g(x)\) の式にこの \(x\) を代入すると、
\(\begin{eqnarray}
&&\:\:g(x)&=g(b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1})\\
&&&=g(b_0)+g(b_1\theta)+g(b_2\theta^2)+\cd+g(b_{n-1}\theta^{n-1})\\
&&&=b_0g(1)+b_1g(\theta)+b_2g(\theta^2)+\cd+b_{n-1}g(\theta^{n-1})\\
\end{eqnarray}\)
となる。ここで、
\(g(1)=1+\zeta^{n-1}+\zeta^{n-2}+\cd+\zeta\)
だが、\(g(1)(1-\zeta)=\zeta^n-1=0\) なので \(g(1)=0\) である。従って、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) の全てが \(0\) だと、\(\bs{L}\) の全ての元 \(x\) について \(g(x)=0\) となり、矛盾が生じる。ゆえに、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち、少なくとも一つは \(0\) ではない。[証明終]
7.3 べき根拡大の十分条件
補題(1)と補題(2)を使って、体の拡大がべき根拡大になるための十分条件を証明します。
| (べき根拡大の十分条件:73A) |
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
[証明]
\(\mr{Gal}(\bs{L}/\bs{K})\) は位数 \(n\) の巡回群なので、生成元を \(\sg\) とし、
\(\mr{Gal}(\bs{L}/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\sg^{n-1}\}\)
とする。\(\bs{L}\) の 元 \(c\) に対して、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
と定める。このとき \(\al\neq0\) となるように \(c\) を選べる。なぜなら、もし \(\al\neq0\) となる \(c\) が選べないとすると、\(\bs{L}\) の全ての元 \(x\) について、
\(x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\:\cd\:+\zeta\sg^{n-1}(x)=0\)
となるはずだが、これはべき根拡大の十分条件のため補題1(72A)、つまり、
\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない
において、\(a_1=\zeta^{n-1},\:a_2=\zeta^{n-2},\:\cd\:,a_{n-1}=\zeta\) と置いたことに相当し、そのような \(a_i\:(1\leq i\leq n-1)\) は存在しないとする補題1の結論に反するからである。またべき根拡大の十分条件のため補題2(72B)では、\(c\) の選び方の例が示されている。そこで、\(\al\neq0\) となるように \(c\) を選んだとする。
\(\sg\)は \(\bs{K}\) の元である \(\zeta\) を不変にするので、
\(\sg(\zeta^{n-i}\sg^i(c))=\zeta^{n-i}\sg^{i+1}(c)\)
である。これを用いて \(\sg(\al)\) を計算すると、
\(\sg(\al)\)
\(=\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta\sg^n(c)\)
\(=\zeta^n\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta c\)
\(=\zeta(\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\zeta^{n-3}\sg^3(c)+\:\cd+\zeta\sg^{n-1}(c)+c)\)
\(=\zeta\al\)
となる。計算では、\(\zeta^n=1\) であることと(第1項)、\(\sg^n=e\) なので \(\sg^n(c)=c\) となること(最終項)を用いた。
ここで、\(\al=\zeta\al\) となるのは、\(\al=0\) のときだけであるが、\(\al\neq0\) なので \(\al\neq\zeta\al\) である。つまり \(\sg(\al)\neq\al\) であり、\(\al\) は \(\sg\) を作用させると不変ではない。従って \(\al\) は \(\bs{K}\) の元ではない \(\bs{L}\) の元である。さらに \(\sg^i(\al)\) を求めていくと、
\(\begin{eqnarray}
&&\:\:\sg^2(\al)&=\sg(\sg(\al))=\sg(\zeta\al)=\zeta\sg(\al)=\zeta\zeta\al\\
&&&=\zeta^2\al\\
&&\:\:\sg^3(\al)&=\sg(\sg^2(\al))=\sg(\zeta^2\al)=\zeta^2\sg(\al)=\zeta^2\zeta\al\\
&&&=\zeta^3\al\\
\end{eqnarray}\)
というように計算でき、
\(\sg^i(\al)=\zeta^i\al\)
である。これを使うと、
\(\begin{eqnarray}
&&\:\:\sg(\al^n)&=\sg(\al)^n=(\zeta\al)^n=\zeta^n\al^n\\
&&&=\al^n\\
\end{eqnarray}\)
であり、\(\al^n\) は \(\sg\) を作用させても不変である。従って \(\al^n\) は \(\bs{K}\) の元である。そこで \(\al^n=a\:\:(a\in\bs{K})\) とおく。
方程式 \(x^n-a=0\) の解は、\(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al\) であり、\(x^n-a=0\) の \(\bs{K}\) 上の最小分解体は、\(\bs{K}\) には \(\zeta\) が含まれているから、
\(\bs{K}(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al)=\bs{K}(\al,\zeta)=\bs{K}(\al)\)
である。この式から、\(\bs{K}\) の同型写像による \(\al\) の移り先は全て \(\bs{K}(\al)\) に含まれることが分かる。従って \(\sg^i\:\:(1\leq i\leq n-1)\) はすべて \(\bs{K}(\al)\) の自己同型写像である。また、同型写像での移り先の定理(51D)により、同型写像は \(\al\) を共役な元に移すが、\(\al\) と共役な元は \(n-1\) 個しかない。従って \(\sg^i\) 以外に同型写像はない。つまり、
\(\mr{Gal}(\bs{K}(\al)/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\:\sg^{n-1}\}\)
であり、これは \(\mr{Gal}(\bs{L}/\bs{K})\) と同じである。次数と位数の同一性の定理(52B)により、ガロア群に含まれる自己同型写像の数は体の拡大次数に等しいから、
\([\:\bs{K}(\al)\::\:\bs{K}\:]=[\:\bs{L}\::\:\bs{K}\:]\)
である。もともと \(\al\) は \(\bs{L}\) の元だったので、\(\bs{K}(\al)\) の元は全て \(\bs{L}\) の元である。つまり、
\(\bs{K}(\al)\:\subset\:\bs{L}\)
であるが、\(\bs{K}(\al)\) と \(\bs{L}\) の線形空間の次元が等しいので、体の一致の定理(33I)により2つは一致し、
\(\bs{K}(\al)=\bs{L}\)
である。以上により、\(\bs{L}\) は \(\bs{K}\) の上の方程式 \(x^n-a=0\:(a\in\bs{K})\) の解の一つ \(\al\) を用いて \(\bs{L}=\bs{K}(\al)\) と表されるから、\(\bs{L}\) は \(\bs{K}\) の べき根拡大である。[証明終]
証明の過程で出てきた、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
の式は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言い、数学史においてはガロア理論より前に考えられたものです。この証明を振り返ってまとめてみると、
| \(\bs{L}\) は \(\bs{K}\) の代数拡大体であり、拡大次元は \(n\) である。 | |
| \(\bs{K}\) には \(1\) の原始\(n\)乗根が含まれている。 | |
| \(\bs{L}/\bs{K}\) はガロア拡大である。 | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) は巡回群である(=\(\bs{L}/\bs{K}\) は巡回拡大) |
という条件のもとで、レゾルベントをうまく定義すると、
| ある \(\bs{L}\) の元 \(\al\:(\notin\bs{K})\) が存在し、\(\al^n\) は \(\bs{K}\) の元である。 | |
| すなわち \(\al\) は、方程式 \(x^n-a=0\:\:(a\in\bs{K})\) の解である。 | |
| \(\bs{L}=\bs{K}(\al)\) であり、従って \(\bs{L}/\bs{K}\) はべき根拡大である。 |
が成り立つという論理展開でした。つまりポイントは \(\bs{\al^n\in\bs{K}}\) のところであり、そういう \(\bs{\al\in\bs{L}}\) の存在が証明の核心です。
しかし、その鍵である \(\al\) を具体的に見つけようとすると、\(\al\) の式に現れる \(c\) を決めなければなりません。その \(c\) の値ですが、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて \(\bs{L}=\bs{K}(\theta)\) と表されているとき(= \(\theta\) が原始元のとき)、\(c=\theta\) にできることがべき根拡大の十分条件のため補題2(72B)に示されています。しかし、方程式の形から原始元が分かるわけではありません。
べき根拡大の十分条件(73A)は、その十分条件があればべき根拡大体の中に方程式の解が含まれる(= 方程式の解が四則演算とべき根で記述できる)ことだけを言っています。つまり四則演算とべき根で記述できる解の存在証明であり、そこが注意点です。
原始\(n\)乗根はべき根で表現可能
べき根拡大の十分条件(73A)を用いて原始\(\bs{n}\)乗根はべき根で表現可能(71A)であることを証明できます。(71A)ではガロア理論と関係なく証明しましたが、ガロア理論の枠組みを使っても証明できるということです。
まず \(n\) が合成数のとき、つまり \(n=s\cdot t\) と分解できるときには、原始\(n\)乗根は、原始\(s\)乗根と原始\(t\)乗根のべき根で表現できます(71A)。\(s\) や \(t\) が合成数なら、さらに "分解" を続けられるので、結局、\(n\) が素数 \(p\) のときに原始\(p\)乗根がべき根で表せることを示せればよいことになります。
いま、\(\bs{p}\) 未満の素数すべての原始\(\bs{n}\)乗根がべき根で表されると仮定します。これは帰納法の仮定です。原始\(p\)乗根を \(\eta\)(イータ) とし、その最小多項式を \(f(x)\) とすると、\(f(x)\) は既約多項式で、円分多項式です(63D)。原始\(p\)乗根は 方程式 \(x^p-1=0\) の \(1\) 以外の根なので、
\(x^p-1=(x-1)f(x)\)
であり、
\(f(x)=x^{p-1}+x^{p-2}+\:\cd\:+x+1\)
です。
原始\(p\)乗根による拡大体 \(\bs{Q}(\eta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\cong(\bs{Z}/p\bs{Z})^{*}\)
です(63E)。\((\bs{Z}/p\bs{Z})^{*}\) は位数 \((p-1)\) の巡回群で(25D)、\(\bs{Q}(\eta)/\bs{Q}\) の拡大次数は、\([\:\bs{Q}(\eta):\bs{Q}\:]=p-1\) です。原始\((p-1)\)乗根を \(\zeta\) とすると、\(\eta\notin\bs{Q}(\zeta)\) なので、\(\bs{Q}\) 上の既約多項式である \(f(x)\) は \(\bs{Q}(\zeta)\) 上でも既約多項式です。従って、
\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\cong\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\)
であり、\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\) も位数 \((p-1)\) の巡回群です。すると、べき根拡大の十分条件(73A)により、\(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta)\) はべき根拡大になります。つまり \(\eta\) は "有理数と \(\zeta\) の四則演算から成る式" のべき根で表現できます。
「\(p\) 未満の素数すべての原始\(n\)乗根がべき根で表される」という仮定により、\(\zeta\) はべき根で表現できます。従って \(\eta\) もべき根で表されます。
原始\(2\)乗根は \(-1\) であり、原始\(3\)乗根は根の公式によって、べき根で表現できます。従って帰納法により \(5\) 以上の素数 \(p\) の原始\(p\)乗根もべき根で表現できることが分かります。これで証明ができました。
ここで、原始\(\bs{n}\)乗根はべき根で表現可能(71A)とべき根拡大の十分条件(73A)の関係ですが、(73A)の証明の鍵になったのは、ラグランジュの分解式、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
でした。いま、原始\(5\)乗根を \(\eta\) とし、\(\bs{Q}(\eta)/\bs{Q}\) の巡回拡大を考えます。原始\(4\)乗根を \(\zeta\) とします(\(\zeta=i,\:-i\))。
\(\bs{Q}(\eta)\) の自己同型写像 \(\sg\) を、
\(\sg(\eta)=\eta^2\)
となる写像と定義します。そして、\(c=\eta,\:n=4\) を分解式に入れると、
\(\begin{eqnarray}
&&\:\:\al&=\eta+\zeta^3\sg(\eta)+\zeta^2\sg^2(\eta)+\zeta\sg^3(\eta)\\
&&&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
\end{eqnarray}\)
となります。このラグランジュの分解式と、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明で使った \(f(x,y)\) は本質的に同じものです。つまり
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\) |
と定義すると、\(x,\:y\) の指数はそれぞれ、
\(x\) の指数:\([\:1,\:2,\:3,\:0\:]\)
\(\bs{Z}/4\bs{Z}\) の巡回パターン(生成元 \(=1\))
\(y\) の指数:\([\:3,\:4,\:2,\:1\:]\)
\((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン(生成元 \(=3\))
となります。(71A)では \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターンを \([\:2,\:4\:,3,\:1\:]\)(生成元 \(=2\))としたので式の形は少々違いますが、本質的に同じです。ここで、
\(x=\zeta,\:\:y=\eta\)
と置くと、
\(\begin{eqnarray}
&&\:\:f(x,y)&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
&&&=\al\\
\end{eqnarray}\)
となり、\(f(x,y)\) が ラグランジュの分解式と同じものであることが確認できました。つまり、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明は、
ラグランジュの分解式での証明(73A)と同じことを、"分解式"、"体"、"ガロア群" などの概念を使わずに証明し、かつ、\((p-1)\)乗根をもとに \(p\)乗根を求める計算式を示した
ものなのでした。
7.4 べき根拡大と巡回拡大の同値性
6.3節の "べき根拡大は巡回拡大である"(63H)と、7.3節の "巡回拡大はべき根拡大である"(73A)を合わせると、次にまとめることができます。
| (べき根拡大と巡回拡大は同値:74A) |
\(1\) の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。また、\(\bs{K}\) の\(n\)次拡大体を \(\bs{L}\) とする( \([\:\bs{L}\::\:\bs{K}\:]=n\) )。
このとき、
| \(\bs{L}/\bs{K}\) は巡回拡大である | |
| \(\bs{L}/\bs{K}\) はべき根拡大である。 |
\(\bs{1}\) の原始\(\bs{n}\)乗根が代数体に含まれるという条件をつけるのが巧妙なアイデアで、この条件によって可解性の必要十分条件が導けます。
7.5 可解性の十分条件
以上の準備をもとに、可解性の必要条件(64B)の逆である、可解性の十分条件の証明を行います。
代数拡大体 \(\bs{K}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とし、拡大次数を \([\:\bs{L}\::\:\bs{K}\:]=n\) とします。そして、ガロア群 \(\mr{Gal}(\bs{L}/\bs{K})\) が可解群であるとき、もし \(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるなら、べき根拡大と巡回拡大は同値の定理(74A)により、\(\bs{K}\) の巡回拡大とべき根拡大は同じことです。従って、
可解群 \(\rightarrow\) 累巡回拡大 \(\rightarrow\) 累べき根拡大 \(\rightarrow\) 可解
というルートで、方程式 \(f(x)=0\) の可解性が証明できます。しかし、\(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるとは限りません。\(\bs{K}\) が有理数体 \(\bs{Q}\) だとすると、そこに(原始2乗根以外の)原始\(n\)乗根はありません。しかし、このようなケースでも方程式の可解性が証明できます。それが以下です。
| (可解性の十分条件:75A) |
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
[証明]
\([\:\bs{L}\::\:\bs{K}\:]=n\:\:(|G|=n)\) とし、\(\zeta\) を \(1\) の原始\(n\)乗根とする。\(\bs{K}\) に \(\zeta\) を添加した拡大体 \(\bs{K}(\zeta)\)と、\(\bs{L}\) に \(\zeta\) を添加した拡大体 \(\bs{L}(\zeta)\) を考える。
\(\bs{L}(\zeta)\) は \(\bs{K}\) 上の方程式 \(f(x)(x^n-1)=0\) の最小分解体だから、\(\bs{L}(\zeta)/\bs{K}\) はガロア拡大である。
また \(\bs{K}(\zeta)\) は、\(\bs{K}\)のガロア拡大体 \(\bs{L}(\zeta)\) の中間体なので、中間体からのガロア拡大の定理(52C)によって、\(\bs{L}(\zeta)/\bs{K}(\zeta)\) もガロア拡大である。そこで、
\(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))=G\,'\)
とおく。
|
ポイントは、\(G\,'\) が \(G\) の部分群(\(G\) そのものも含む)と同型であることの証明である。これが成り立てば、① \(G\) は可解群なのでその部分群は可解群、② 可解群と同型な \(G\,'\) は可解群、③ \(G\,'\) が可解群なので \(\bs{L}(\zeta)/\bs{K}(\zeta)\) は累巡回拡大、④ \(\bs{K}(\zeta)\) は原始\(n\)乗根を含むので、累巡回拡大である \(\bs{L}(\zeta)/\bs{K}(\zeta)\) は累べき根拡大、が言える。 |
\(G\) の元を \(g\)、\(G\) の単位元を \(e\) とする。\(G\,'\)の元を \(g\,'\)、\(G\,'\) の単位元を \(e\,'\) とする。また、\(G\,'\) の元 \(g\,'\) を \(\bs{L}\) の元に限定して作用させるときの同型写像を \(\sg(g\,')\) とする。
\(g\,'\)は \(\bs{L}(\zeta)\) の自己同型写像だから、\(\bs{L}(\zeta)\) の元を共役な元に移す。従って 作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も \(\bs{L}\) の元を共役な元に移す。\(\bs{L}\) はガロア拡大体だから、\(\bs{L}\)の元の共役な元は \(\bs{L}\) に含まれる。従って \(\sg(g\,')\) は \(\bs{L}\) の自己同型写像である。
また \(g\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) の元だから、\(\bs{K}(\zeta)\) の元を固定する。従って、\(\bs{K}(\zeta)\) の部分集合である \(\bs{K}\) の元も固定する。ゆえに、\(g\,'\) の作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も、\(\bs{L}\) の部分集合である \(\bs{K}\) の元を固定する。
以上により \(\sg(g\,')\) は、\(\bs{K}\)の元を固定する \(\bs{L}\) の自己同型写像だから、\(\mr{Gal}(\bs{L}/\bs{K})\) の元、つまり \(G\) の元である。
\(\sg\) を \(G\,'\) から \(G\) への写像と見なして考える。\(G\,'\) の元 を \(g\,'\) とし、\(x\) を \(\bs{L}\) の元とすると、\(g\,'(x)=\sg(g\,')(x)\) である。つまり、作用する対象が \(\bs{L}\) の元なら、2つの写像、\(g\,'\) と \(\sg(g\,')\) は同じ効果を生む。
\(G\,'\)の任意の2つの元を \(g_1{}^{\prime},\:g_2{}^{\prime}\) とすると、\(g_1{}^{\prime}g_2{}^{\prime}\) も \(G\,'\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}(x)=\sg(g_1{}^{\prime}g_2{}^{\prime})(x)\)
である。左辺の \(g_2{}^{\prime}(x)\) は \(\sg(g_2{}^{\prime})(x)\) と同じなので、 \((\br{A})\)
\(g_1{}^{\prime}g_2{}^{\prime}(x)=g_1{}^{\prime}(\sg(g_2{}^{\prime})(x))\)
であるが、\(\sg(g_2{}^{\prime})(x)\) もまた \(\bs{L}\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}x=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})(x)\)
である。\((\br{A})\) と \((\br{B})\) より、 \((\br{B})\)
\(\sg(g_1{}^{\prime}g_2{}^{\prime})=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})\)
となって、\(\sg\) は準同型写像(42A)である。
\(\sg(g\,')\) が \(G\) の元であり \(\sg\) が準同型写像なので、準同型写像の像と核の定理(42B)により、\(\sg\) による \(G\,'\) の 像 \(\sg(G\,')\) は \(G\) の部分群である。もちろん、\(G\) の部分群には \(G\) の自明な部分群である \(G\) 自身も含まれる。
いま、ある \(G\,'\) の元 \(h\) があって、\(\sg(h)=e\)(\(e\) は \(G\) の単位元)とする。つまり、\(h\) を \(\bs{L}\) に限定して適用すると、\(\bs{L}\) の元すべてを固定するものとする。
\(G\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) であり、そのすべての元は \(\bs{K}(\zeta)\) の元を固定する。従って、\(G\,'\) の元 \(h\) は \(\zeta\) も固定する。ということは、\(h\) は「\(\bs{L}\) の元すべてを固定し、かつ \(\zeta\) を固定する」から、\(\bs{L}(\zeta)\) の元すべてを固定する。つまり \(h\) は \(G\,'\) の単位元であり、\(h=e\,'\) である。
ゆえに、準同型写像の像と核(42B)における核の定義によって、
\(\mr{Ker}\:\sg=e\,'\)
であり、核が単位元なら単射の定理(42C)によって、\(\sg\) は単射である。このことから、準同型定理(43A)により、
\(G\,'/\mr{Ker}\:\sg\:\cong\:\sg(G\,')\)
すなわち、
\(G\,'\:\cong\:\sg(G\,')\)
である。つまり \(\bs{G\,'}\) は \(\bs{G}\) の部分群 \(\bs{\sg(G\,')}\) と同型である。
\(G\) は可解群なので、可解群の部分群は可解群の定理(61C)によって、\(G\) の部分群である \(\sg(G\,')\) も可解群であり、さらにそれと同型である \(G\,'\) も可解群である。\(G\,'\) が可解群なので、可解群の定義により \(G\,'\) から \(e\,'\) に至る部分群の列、
\(G\,'=H_0\sp H_1\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{e\,'\}\)
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、\(H_i/H_{i+1}\) は巡回群である。\(|G\,'|=m\) とおくと、\(G\,'\) は \(G\) の部分群である \(\sg(G\,')\) と同型なので、ラグランジュの定理(41E)によって、\(m\) は \(|G|=n\) の約数である。
ガロア対応(53B)による \(H_i\) の固定体を \(\bs{K}_i\) とすると、
\(\bs{K}(\zeta)=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{L}(\zeta)\)
という固定体の系列が定義できる。\(H_i/H_{i+1}\) は巡回群なので、\(\bs{K}_{i+1}/\bs{K}_i\) は巡回拡大である。\(\bs{L}(\zeta)/\bs{K}(\zeta)\) の拡大次数は、
\([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=|G\,'|=m\)
であり、\(n\) の約数である。
固定体の系列における一つの拡大 \(\bs{K}_{i+1}/\bs{K}_i\)を考える。その拡大次数 \([\:\bs{K}_{i+1}\::\:\bs{K}_i\:]=m_i\) は、拡大次数の連鎖律(33H)によって \([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=m\) の約数であり、従って \(n\) の約数である。
\(\bs{K}_i\) は \(1\) の原始\(n\)乗根 \(\zeta\) を含むから、\(\zeta^{\frac{n}{m_i}}\) も含んでいる。\(\zeta^{\frac{n}{m_i}}\) は \(1\) の原始\(m_i\)乗根である。つまり、\(\bs{K}_i\) は \(1\) の原始\(m_i\)乗根(\(m_i=[\:\bs{K}_{i+1}\::\:\bs{K}_i\:]\))を含む。従って、べき根拡大の十分条件の定理(73A)により、巡回拡大である \(\bs{K}_{i+1}/\bs{K}_i\) はべき根拡大である。
以上のことは \((0\leq i < k)\) のすべてで成り立つから、\(\bs{K}_i\) の系列は累べき根拡大である。
\(f(x)=0\) の解は \(\bs{L}\) に含まれるが、\(\bs{L}\:\subset\:\bs{L}(\zeta)\) だから \(f(x)=0\) の解は \(\bs{L}(\zeta)\) に含まれる。その \(\bs{L}(\zeta)\) は \(\bs{K}(\zeta)\) の累べき根拡大であり、また \(1\) の原始\(n\)乗根である \(\zeta\) は \(\bs{Q}\:(\in\bs{K})\) の元の四則演算とべき根で表現できるから(71A)、\(\bs{L}(\zeta)\) の元はすべて \(\bs{K}\) の元の四則演算とべき根で表現できる。従って \(f(x)=0\) の解も \(\bs{K}\) の元の四則演算とべき根で表現できる。[証明終]
この定理では「体 \(\bs{K}\) 上の方程式 \(f(x)=0\)」としましたが、もちろん、体 \(\bs{K}\) が 有理数体 \(\bs{Q}\) であっても同じです。以降、\(\bs{K}\) を \(\bs{Q}\) と書きます。
証明のポイントは、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) とし、\(G\,'=\mr{Gal}(\bs{L}(\zeta)/\bs{Q}(\zeta))\) とするとき、\(G\,'\) が \(G\) の部分群と同型であることです。たとえば、\(f(x)\) が既約な3次多項式だと、\(G\cong S_3\) か \(G\cong C_3\) であり、基本的に \(G\,'\cong G\) です。しかし、そうならない場合もあります。たとえば \(f(x)=x^3-2\) では \(G\cong S_3\) ですが、
\(\bs{Q}\:\subset\:\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\sqrt[3]{2})=\bs{L}\)
(\(\omega\) は \(1\) の原始3乗根)
という体の拡大列でわかるように、\(\bs{L}(\omega)=\bs{L}\) です。つまり、\(\bs{L}(\omega)/\bs{Q}(\omega)\) の拡大次数は \(3\) であり、\(\bs{L}/\bs{Q}\) の拡大次数の \(6\) とは違います。しかしそうであっても \(G\,'=\mr{Gal}(\bs{L}(\omega)/\bs{Q}(\omega))\cong C_3\) であり、\(G\,'\) は \(G\cong S_3\) の部分群と同型です。
\(G\,'\) は \(G\) の部分群と同型なので、\(G\) が可解群なら \(G\,'\) も可解群であり(61C)、\(\bs{L}(\omega)/\bs{Q}(\omega)\) は累巡回拡大であり(62C)、従って、累べき根拡大です(73A)。
さらに、\(1\) の原始\(n\)乗根が \(\bs{Q}\) の元の四則演算とべき根で表現できる(71A)ことも証明のポイントになっています。
この可解性の十分条件の定理(75A)によって、有理数係数の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) として、\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群のとき、\(f(x)=0\) の解は四則演算とべき根で表現可能なことが証明できました。
ここがゴールで「ガロア理論=可解性の必要十分条件」が完結しました。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
可解性の必要十分条件の証明は前節で尽きていますが、これ以降は可解な方程式の代表的なものを取り上げ、ガロア群の分析をします。まず最初は、
| \(x^5\) | \(-1=0\) | |
| \(x^{17}\) | \(-1=0\) |
\(x^5-1=0\)
まず \(x^5-1=0\) の解を分析します。
\(x^5-1=(x-1)(x^4+x^3+x^2+x+1)\)
なので、\(1\) 以外の解を \(\zeta\) とすると、\(\zeta\) は4次方程式、
\(x^4+x^3+x^2+x+1=0\)
の解です。「7.1 1 の原始n乗根」で書いたように、この方程式の解は、
\(\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm\sqrt{-10-2\sqrt{5}}\right)\)
\(\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm\sqrt{-10+2\sqrt{5}}\right)\)
の4つであり、これが \(1\) の原始5乗根です。以下の論旨を明瞭にするために、虚数単位 \(i\) を使わずに、外側の \(\sqrt{\phantom{a}}\) の中を負の数にして記述しました。
この原始5乗根は、4次方程式の解であるにもかかわらず、四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現されています。なぜそうなるのか、それをガロア理論にのっとって説明します。実は、\(p\) を素数としたとき、
原始\(\bs{p}\)乗根が四則演算と平方根 \(\bs{\sqrt{\phantom{a}}}\) のみで表現できれば、正 \(\bs{p}\)角形は定規とコンパスで作図可能である
ことが知られています。定規というのは「目盛りのない、与えられた2点を通る直線を引くことだけができる道具」であり、コンパスというのは「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\cdot\)円弧を描くことだけができる道具」です。長さや角度を測ることはできません。作図可能の原理は次の項で説明します
\(f(x)=x^4+x^3+x^2+x+1\) とし、\(f(x)=0\) の解の一つを \(\zeta\) とすると、\(f(x)\) の最小分解体は \(\bs{Q}(\zeta)\) です。そのガロア群を、
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
と書くと、\(\zeta\) の最小多項式は \(f(x)\) なので(63C)、\(|G|=4\) です。また、\(\bs{\bs{Q}(\zeta)}\) のガロア群の定理(63E)により、\(G\) は既約剰余類群と同型で、
\(G\cong(\bs{Z}/5\bs{Z})^{*}\)
です。
\((\bs{Z}/5\bs{Z})^{*}=\{1,\:2,\:3,\:4\}\)
ですが、この群の生成元は \(2\) か \(3\) です。以下、生成元を \(2\) として話を進めると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
と表現できます。一方、\(f(x)=0\) の4つの解は、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
です。そこで、
\(\sg(\zeta)=\zeta^2\)
で定義される自己同型写像を考えると、ガロア群は、
\(G=\{\sg,\:\sg^2,\:\sg^3,\:\sg^4=e\}\)
となり、位数 \(4\) の巡回群、かつ可解群です。また、体の拡大次数は、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=4\)
です。
ガロア群 \(G\) には部分群が含まれています。つまり、
\(H=\{\sg^2,\:e\}\)
\(\sg^2(\zeta)=\zeta^4\)
と定義すると、\((\sg^2)^2=e\) なので \(H\) は部分群(\(\sg H=H\sg\) なので正規部分群)であり、位数 \(2\) の巡回群です。また、剰余群は、
\(G/H\cong\{e,\:\sg\}\)
です。従って、
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\)
| \(G/H\) | \(\cong\{e,\:\sg\}\) | :位数 \(2\) | |
| \(H/\{\:e\:\}\) | \(\cong H\) | :位数 \(2\) |
は可解列です。ガロア対応の定理(53B)により、この可解列に対応する拡大体の列があって、
\(G\sp H\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}\subset\bs{Q}(\zeta)\)
となります。\(\bs{F}\) は \(H\) の固定体であり、\(\bs{Q}(\zeta)\) の中間体です。すると、正規性定理(53C)により、
\(\mr{Gal}(\bs{F}/\bs{Q})\cong G/H\)
なので、\(\mr{Gal}(\bs{F}/\bs{Q})\) は位数 \(2\) の巡回群です。またガロア群の定義により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\cong H\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\) も位数 \(2\) の巡回群です。従って、次数と位数の同一性の定理(52B)より拡大次数は、
| \([\:\bs{F}\) | \(:\bs{Q}\:]=2\) | |
| \([\:\bs{Q}(\zeta)\) | \(:\bs{F}\:]=2\) |
\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの平方根拡大を2回繰り返したものである
と結論づけられます。原始5乗根が四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できる理由がここにあります。
ここまでは、中間体 \(\bs{F}\) がどういう拡大体かに触れていませんが、\(\bs{F}\) を具体的に表現することもできます。\(\bs{F}\) は \(H=\{e,\:\sg^2\}\) の固定体なので、\(\bs{F}=\bs{Q}(\theta)\) として、
\(\sg^2(\theta)=\theta\)
となる \(\theta\) を探します。\(\theta\) の選び方には自由度があり、たとえば \(\theta=\zeta^4+\zeta\) としてもよいのですが、ここでは、
\(\theta=(\zeta^2-\zeta^3)(\zeta^4-\zeta)\)
とします。このように選ぶと、\(\sg^2(\zeta)=\zeta^4\) なので、
\(\begin{eqnarray}
&&\:\:\sg^2(\theta)&=(\zeta^8-\zeta^{12})(\zeta^{16}-\zeta^4)\\
&&&=(\zeta^3-\zeta^2)(\zeta-\zeta^4)=\theta\\
\end{eqnarray}\)
となって、\(\theta\) は \(\sg^2\) で不変です。と同時に、\(\sg(\zeta)=\zeta^2\) なので、
\(\begin{eqnarray}
&&\:\:\sg(\theta)&=(\zeta^4-\zeta^6)(\zeta^8-\zeta^2)\\
&&&=(\zeta^4-\zeta)(\zeta^3-\zeta^2)=-\theta\\
\end{eqnarray}\)
となります。ということは、
\(\sg(\theta^2)=(\sg(\theta))^2=(-\theta)^2=\theta^2\)
であり、\(\theta^2\) は \(\sg\) で不変、つまり \(G\) のすべての元で不変となり、\(\theta^2\) は有理数です。そこで、
\(\zeta^5=1\)
\(\zeta^4+\zeta^3+\zeta^2+\zeta+1=0\)
の関係を使って \(\theta^2\) を計算すると、
\(\begin{eqnarray}
&&\:\:\theta^2&=(\zeta^2-\zeta^3)^2(\zeta^4-\zeta)^2\\
&&&=(\zeta^4-2\zeta^5+\zeta^6)(\zeta^8-2\zeta^5+\zeta^2)\\
&&&=(\zeta^4-2+\zeta)(\zeta^3-2+\zeta^2)\\
&&&=\zeta^7-2\zeta^4+\zeta^6-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=\zeta^2-2\zeta^4+\zeta-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=-\zeta^4-\zeta^3-\zeta^2-\zeta+4\\
&&&=5\\
\end{eqnarray}\)
となり、確かに\(\theta^2\) は有理数であることが分かります。つまり、
\(\theta=\sqrt{5}\)
です。従ってガロア対応は、
| \(G\sp H\) | \(\sp\{\:e\:\}\) | |
| \(\bs{Q}\subset\bs{Q}(\sqrt{5})\) | \(\subset\:\bs{Q}(\zeta)\) |
となります。原始5乗根に \(\sqrt{-10+2\sqrt{5}}\) のような項が現れるのは、中間体が \(\bs{Q}(\sqrt{5})\) であるという、体の拡大構造からくるのでした。
ここまでの論証を振り返ってみると、
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
ことが分かります。この条件は \(p=3,\:5\) で成立しますが、その次に成立するのは \(p=17\) です。
\(x^{17}-1=0\)
\(1\) の原始\(17\)乗根を \(\zeta\) とします。\(p=17\) の最小原始根は \(3\) で(25D)、\((\bs{Z}/17\bs{Z})^{*}\) の位数は \(16\) です。\((\bs{Z}/17\bs{Z})^{*}\) において \(3\) の累乗は、
\(\phantom{1}3,\:\phantom{1}9,\:10,\:13,\:\phantom{1}5,\:15,\:11,\:16,\)
\(14,\:\phantom{1}8,\:\phantom{1}7,\:\phantom{1}4,\:12,\:\phantom{1}2,\:\phantom{1}6,\:\phantom{1}1\)
と、すべての元を巡回します。従って、
\(\sg(\zeta)=\zeta^3\)
という自己同型写像 \(\sg\) を定義すると、
\(G=\{\sg,\sg^2,\sg^3,\cd,\sg^{15},\sg^{16}=e\}\)
が \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) です。
\(x^5-1=0\) のときと同様の考察をすると、\(G\) には3つの部分群があります。
\(H_1=\{\sg^2,\sg^4,\sg^6,\sg^8,\sg^{10},\sg^{12},\sg^{14},e\}\)
\(\sg^2(\zeta)=\zeta^9\)
\(H_2=\{\sg^4,\sg^8,\sg^{12},e\}\)
\(\sg^4(\zeta)=\zeta^{13}\:\:(\phantom{1}9^2\equiv13\:\:(\mr{mod}\:17))\)
\(H_3=\{\sg^8,e\}\)
\(\sg^8(\zeta)=\zeta^{16}\:\:(13^2\equiv16\:\:(\mr{mod}\:17))\)
の3つで、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
| \(G\) | \(/H_1\) | \(\cong\{\sg^{\phantom{2}},\:e\}\) | |
| \(H_1\) | \(/H_2\) | \(\cong\{\sg^2,\:e\}\) | |
| \(H_2\) | \(/H_3\) | \(\cong\{\sg^4,\:e\}\) | |
| \(H_3\) | \(/\{\:e\:\}\) | \(\cong\{\sg^8,\:e\}\) |
は可解列です。ガロア対応の定理(53B)により、\(H_1,\:H_2,\:H_3\) にはそれぞれに対応した固定体 \(\bs{F}_1,\:\bs{F}_2,\:\bs{F}_3\) があって、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}_1\subset\bs{F}_2\subset\bs{F}_3\subset\bs{Q}(\zeta)\)
のガロア対応になります。\(\bs{Q}\) から \(\bs{Q}(\zeta)\) までの4つの拡大次数は、剰余群の位数に等しいのですべて \(2\) です。つまり、\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの「平方根拡大」を4回繰り返したものであり、原始\(17\)乗根は四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できます。従って正\(17\)角形は定規とコンパスで作図可能です。
これは、ドイツの大数学者\(\cdot\)ガウス(\(1777-1855\))が\(19\)才のときに発見した定理として有名です。
作図可能の原理
ここで改めて、平面上の図形が定規とコンパスで「作図可能」という意味を明確にします。ここで "定規" は「目盛りのない、与えられた2点を通る線を引くことだけができる道具」であり、"コンパス" は「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\bs{\cdot}\)円弧を描くことだけができる道具」でした。
平面上の図形は点と線でできています。線は2点を与えると描けるので、「作図可能」の意味は「平面上で作図可能な点とは何か」を定義することに帰着します。
平面を複素平面(\(=\bs{C}\))として考えます。以降、
| \(a,\:b\) | \(\in\:\bs{R}\) | |
| \(\al,\:\beta\) | \(\in\:\bs{C}\) |
\(1,\:0\) は作図可能である。また複素平面の実軸と虚軸は作図できる。
|
任意の線分を単位長さとし、端点を \(1,\:0\) とします。2点を結ぶ直線が実軸で、\(0\) を通り実軸と垂直な直線を作図するとそれが虚軸です。
\(\al=a+b\:i\) とすると、\(a,\:b\) が作図可能なら \(\al\) も作図可能である。また、\(\al\) が作図可能なら \(a,\:b\) も作図可能である。
|
\(a\) が作図可能なら、\(-a\) も作図可能である。従って \(\al\) が作図可能なら \(-\al\) も作図可能である。
また \(a,\:b\) が作図可能なら \(a+b\) も作図可能である。従って、\(\al,\:\beta\) が作図可能なら \(\al+\beta\) も作図可能である。
|
\(a,\:b\) が作図可能なら \(ab\)も作図可能である。従って \(\al,\:\beta\) が作図可能なら \(\al\beta\) も作図可能である。
|
\(a\:\:(a\neq0)\) が作図可能なら \(a^{-1}\) も作図可能である。従って \(\al\:\:(\al\neq0)\) が作図可能なら \(\al^{-1}\) も作図可能である。
|
作図可能な \(\al\) を \(\al=a+b\:i\) とすると、
\(\al^{-1}=\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}\:i\)
です。\(a,\:b\) が作図可能なので、その四則演算の結果は作図可能です。従って \(\al^{-1}\) も作図可能です。
有理数 \(\bs{Q}\) は作図可能である。
実数のなかで作図可能な点は四則演算で閉じています。かつ、\(0,\:1\) は作図可能です。従って有理数は作図可能です。
\(a\) が正の実数のとき、\(\sqrt{a}\) は作図可能である。
|
\(a\) と \(-1\) を結ぶ線分を直径とする円を描き、虚軸との交点を \(x\cdot i\:(x\):実数) とすると、
\(1:x=x:a\)
なので、\(x=\pm\sqrt{a}\) です。従って \(\sqrt{a}\) は作図可能です。
\(\al\) を作図可能な複素数とするとき、\(\sqrt\al\) は作図可能である。
|
極形式を使って、
\(\al=r(\mr{cos}\theta+i\cdot\mr{sin}\theta)\)
とすると、\(r\) は作図可能であり、つまり \(\sqrt{r}\) も作図可能です。また、角 \(\theta\) を2等分する線も、定規とコンパスで作図可能です。従って \(\sqrt\al\) は作図可能です。
\(\al,\:\beta\) が作図可能な複素数とするとき、2次方程式 \(x^2+\al x+\beta=0\) の解は作図可能である。
ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能である。
2次方程式 \(x^2+\al x+\beta=0\) の解は、根の公式により、係数 \(\al,\:\beta\) の四則演算と平方根で表わされます。従って作図可能です。
定規とコンパスで作図可能な点は、作図可能な円や直線の交点として求まる点です。2次元 \(xy\) 平面( \(\bs{R}^2\) )で考えると、直線と直線の交点は1次方程式の解です。また円と直線の交点は2次方程式の解です。円と円の交点がどうかですが、\(a,\:b,\:c,\:d\) を実数として、2つの円の方程式を、
\(x^2+y^2=a^2\)
\((\br{A})\)
\((x-b)^2+(y-c)^2=d^2\)
とします。\((\br{A}),\:(\br{B})\) の両辺を引き算して整理すると、 \((\br{B})\)
\(2bx+2cy-(b^2+c^2+a^2-d^2)=0\)
という直線の方程式になります。2つの円の交点は \((\br{A}),\:(\br{C})\) の連立方程式の解であり、2次方程式の解です。つまり、作図可能な実数は、作図可能な実数を係数とする2次方程式(あるいは1次方程式)の解となる実数です。 \((\br{C})\)
実数(\(a,\:b\))が作図可能と、複素数(\(a+bi\))が複素平面上で作図可能は同値です。従って、ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能です。
\(\bs{Q}\) の代数拡大体 \(\bs{K}\) があり、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{K}\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
を満たす \(\bs{Q}\) から \(\bs{K}\) の拡大列が存在するとき、\(\bs{K}\) の元
\(\al\in\bs{K}\)
は作図可能である。
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\) であれば、\(\bs{K}_{i+1}/\bs{K}_i\) は次数2のべき根拡大であり、
\(x^2-a=0\:\:\:(a\in\bs{K}_i)\)
の解、\(\sqrt{a}\) を用いて、
\(\bs{K}_{i+1}=\bs{K}_i(\sqrt{a})\)
と表されます。従って、\(\bs{K}_i\) の元が作図可能なら、\(\bs{K}_{i+1}\) の元は「作図可能な点の四則演算と平方根の組み合わせ」で表現できるので、作図可能です。体の拡大列の出発点である \(\bs{Q}\) の元は作図可能なので、到達点である \(\bs{K}\) の元も作図可能になります。
\(1\) の原始\(p\)乗根(\(p\):素数)を \(\zeta\) とすると、\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) の位数は \(p-1\) であり、それが2の累乗であれば、\(G\) の可解列にガロア対応する体の拡大系列、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{Q}(\zeta)\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
が存在します(前項での証明)。従って複素数平面上の点 \(\zeta\) は作図可能であり、正 \(p\)角形は作図可能です。条件に合致する素数は \(p=3\)、\(5\)、\(17\)、\(257\)、\(65537\)であることが知られています。これらの素数をフェルマ素数と呼びます。フェルマ素数 \(p\) とは、\(p-1\) が2の累乗であるような素数です。
さらに、一般の正 \(n\)角形が作図可能である条件は、次のようになります。
正 \(n\)角形は、
\(n=2^k\:\:\:(2\leq k)\)
\(n=2^k\cdot p_1p_2\cd p_r\:\:\:(0\leq k,\:\:1\leq r)\)
\(p_i\) は相異なるフェルマ素数
のとき、作図可能である。
[証明]
角度の2等分線は作図可能なので、\(n=2^k\:\:(2\leq k)\) のとき、正 \(n\)角形は作図可能である。と同時に、正 \(m\)角形が作図可能なとき、
\(n=2^k\cdot m\:\:(0\leq k)\)
とおくと、正 \(n\)角形は作図可能になる。\(p\) がフェルマ素数のとき、正 \(p\)角形は作図可能なので、
\(m_1\) と \(m_2\) を互いに素な3以上の数とするとき、正 \(m_1\) 角形と正 \(m_2\)角形が作図可能であれば、正 \(m\)角形(\(m=m_1m_2\))は作図可能である
ことが証明できれば十分である。
\(\theta,\:\theta_1,\:\theta_2\) を任意の角度とする。
\(\mr{sin}\theta=\sqrt{1-\mr{cos}^2\theta}\)
だから、\(\mr{cos}\theta\) が作図できれば \(\mr{sin}\theta\) も作図できる。また三角関数の加法定理より、
\(\mr{cos}(\theta_1+\theta_2)=\mr{cos}\theta_1\cdot\mr{cos}\theta_2-\mr{sin}\theta_1\cdot\mr{sin}\theta_2\)
なので、\(\mr{cos}\theta_1,\:\mr{cos}\theta_2\) が作図できれば \(\mr{cos}(\theta_1+\theta_2)\) も作図できる。このことから \(\mr{cos}\theta\) が作図できれば \(\mr{cos}(k\theta)\:\:(k\) は整数)も作図できる。
複素平面上で原点を中心とする半径1の円に正 \(m\)角形を描いたとき、その頂点の複素数は
\(\mr{cos}\left(\dfrac{2\pi}{m}k\right)+i\:\mr{sin}\left(\dfrac{2\pi}{m}k\right)\:\:(0\leq k\leq m-1)\)
である。\(k=1\) の点が作図できれば、残りの点が作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
が作図できれば、正 \(m\)角形は作図できる。
\(m_1\) と \(m_2\) は互いに素だから、不定方程式の解の存在の定理(21C)により、
\(k_1m_1+k_2m_2=1\)
を満たす \(k_1,\:k_2\) が存在する。両辺を \(m=m_1m_2\) で割ると
\(\dfrac{k_1}{m_2}+\dfrac{k_2}{m_1}=\dfrac{1}{m}\)
\(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2=\dfrac{2\pi}{m}\)
が得られる。正 \(m_1\)角形と正 \(m_2\)角形 は作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m_1}\right),\:\:\mr{cos}\left(\dfrac{2\pi}{m_2}\right)\)
は作図できる。従って
\(\mr{cos}\left(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2\right)\)
は作図でき、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
も作図できることになって、正 \(m\)角形は作図できる。[証明終]
証明の鍵は「\(m_1\) と \(m_2\) が互いに素」です。従って、正3角形が作図できても、正9角形は作図できません。正\(15\)角形なら作図できます。計算すると、作図可能な正 \(n\)角形(\(n\leq100\))は、
| \(3\)、\(4\)、\(5\)、\(6\)、\(8\)、\(10\)、\(12\)、\(15\)、\(16\)、\(17\)、\(20\)、\(24\)、\(30\)、\(32\)、\(34\)、\(40\)、\(48\)、\(51\)、\(60\)、\(64\)、\(68\)、\(80\)、\(85\)、\(96\) |
です。「正\(50\)角形は作図できないが、正\(51\)角形は作図できる」というのも不思議な感じがします。
7.7 巡回拡大はべき根拡大:3次方程式が解ける理由
この節では可解な方程式がなぜ解けるのかを、3次方程式を例にとってガロア理論で説明します。また3次方程式の根の公式をガロア理論に沿った形て導出します。「7.5 可解性の十分条件」で証明したことは、
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
でした。この証明の核となっているのは「7.3 べき根拡大の十分条件」であり、それは、
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
でした。このことを証明した論理展開は、次のようでした。
次の条件があるとする。
| \(\bs{L}\) は \(\bs{K}\) の代数拡大体であり、拡大次元は \(n\) である。 | |
| \(\bs{K}\) には \(1\) の原始\(n\)乗根が含まれる。 | |
| \(\bs{L}/\bs{K}\) はガロア拡大である。 | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) は巡回群である(=\(\bs{L}/\bs{K}\) は巡回拡大) |
このとき、レゾルベント(分解式)を定義することで、
| \(\al^n\) が \(\bs{K}\) の元であるような \(\bs{L}\) の元 \(\al\) が存在する。すなわち、\(x^n-a=0\:\:(a\in\bs{K})\) の解が \(\al\in\bs{L}\) | |
| このとき \(\bs{L}=\bs{K}(\al)\) になり、従って \(\bs{L}/\bs{K}\) はべき根拡大 |
つまり、レゾルベントを使って、巡回拡大=べき根拡大(但し、体に \(1\) の原始\(n\)乗根が含まれることが条件)を証明したわけです。この証明プロセスを、具体的な3次方程式で順にたどります。まず、3次方程式のガロア群を再度整理します。
3次方程式のガロア群
3次方程式のガロア群は「1.3 ガロア群」で計算しましたが、改めて書きます。3次方程式のガロア群は、3次方程式の3つの解、\(\al,\:\beta,\gamma\) を入れ替える(置換する)群であり、一般的には、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
です。3つの解をそれぞれ \(1,\:2,\:3\) の文字で表し、巡回置換の記法(6.5節)で書くと、
| \(\sg\) | \(=(1,\:2,\:3)\) | |
| \(\sg^2\) | \(=(1,\:3,\:2)\) | |
| \(\tau\) | \(=(2,\:3)\) | |
| \(\sg\tau\) | \(=(1,\:2)\) | |
| \(\sg^2\tau\) | \(=(1,\:3)\) |
\(\tau\sg=(1,\:3)\)
であり、
\(\tau\sg=\sg^2\tau\)
との関係が成り立っています。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。ここで、
\(H=\{e,\:\sg,\:\sg^2\}\)
という \(G\) の部分群を考えると、\(H\) は巡回群であると同時に \(G\) の正規部分群です。"弱可換性" を使って検証してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
であり、同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つので \(H\) は \(G\) の正規部分群です。
\(G\) の \(H\) による剰余群は、
\(G/H=\{H,\tau H\}\)
であり、単位元は \(H\) で、
\((\tau H)^2=\tau H\tau H=\tau\tau HH=H\)
となる、位数\(2\) の巡回群です(\(G/H\cong C_2)\)。この結果、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
は可解列になり、\(G\) は可解群で、従って3次方程式は可解です(=四則演算とべき根で解が表現可能)。この節ではそれを具体例で確認していきます。
一方、「3.3 線形空間」の「代数拡大体の構造」で書いたように、3次方程式のガロア群が \(S_3\) ではなく、位数 \(3\) の巡回群( \(C_3\) )になる場合があります。それを再度整理します。
\(x^3+ax^2+bx+c=0\) の3次方程式は、\(x=X-\dfrac{a}{3}\) とおくと、
\(X^3+\left(b-\dfrac{a^2}{3}\right)X+\left(\dfrac{2}{27}a^3-\dfrac{1}{3}ab+c\right)=0\)
となって、2乗の項が消えます。従って以降、3次方程式を、
\(x^3+px+q=0\)
の形で扱います。
\(f(x)=x^3+px+q\)
とおき、\(f(x)\) は既約多項式とします。3次方程式の根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
であり、根と係数の関係から、
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=p\)
\(\al\beta\gamma=-q\)
です。3次方程式のガロア群が \(S_3\) か \(C_3\) かを決めるポイントとなるのは、
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
で定義される、根の差積と呼ばれる値です。差積は普通、\(\Delta\)(ギリシャ文字・デルタの大文字)で表しますが、後の説明の都合で \(\theta\) と書きます。差積は、任意の2つの根の互換で \(-\theta\) となるので、3つの根を \(\al,\:\beta,\:\gamma\) に割り当てる方法によって、\(\theta\) は2つの値をとり得ます。差積の2乗が判別式であり、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
です。つまり \(\theta=\sqrt{D}\) と書けますが、\(\sqrt{D}\) は「2乗して \(D\) となる2つの数のどちらか」の意味です。\(D\) は \(\al,\:\beta,\:\gamma\) の任意の置換で不変な対称式なので、3次方程式の係数である \(p,\:q\) で表すことができる有理数です。
その \(D\) を方程式の係数で表すために、\(f(x)\) を微分します。
\(f(x)=(x-\al)(x-\beta)(x-\gamma)\)
なので、
\(\begin{eqnarray}
&&\:\:f\,'(x)=&(x-\al)(x-\beta)+(x-\beta)(x-\gamma)+\\
&&&(x-\gamma)(x-\al)\\
\end{eqnarray}\)
であり、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\beta)=(\beta-\gamma)(\beta-\al)\)
\(f\,'(\gamma)=(\gamma-\al)(\gamma-\beta)\)
となります。従って、
\(D=-f\,'(\al)f\,'(\beta)f\,'(\gamma)\)
です。一方、
\(f\,'(x)=3x^2+p\)
なので、
\(D=-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\)
となります。ここからの計算を進めるために、次の2つの対称式を、根と係数の関係を使って \(p\) で表しておきます。
・\(\al^2+\beta^2+\gamma^2\)
\(=(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)\)
\(=-2p\)
・\(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2\)
\(=(\al\beta+\beta\gamma+\gamma\al)^2-2\al\beta\gamma(\al+\beta+\gamma)\)
\(=p^2\)
これを用いると、
\(\begin{eqnarray}
&&\:\:D&=&-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\\
&&&=&-27(\al\beta\gamma)^2-9(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2)p\\
&&&&-3(\al^2+\beta^2+\gamma^2)p^2-p^3\\
&&&=&-27q^2-9\cdot p^2\cdot p-3\cdot(-2p)\cdot p^2-p^3\\
&&&=&-4p^3-27q^2\\
\end{eqnarray}\)
と計算できます。つまり、
\(D=-4p^3-27q^2\)
です。ここでもし、\(D\) がある有理数 \(a\) の2乗(\(D=a^2\))なら、
\(\theta=\sqrt{D}=\pm a\)
となり、\(\theta\) は有理数です。\(\theta\) が有理数(\(\theta=\pm a\))の場合、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\al)=3\al^2+p\)
の関係があるので、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=-f\,'(\al)(\beta-\gamma)\\
&&&=-(3\al^2+p)(\beta-\gamma)\\
\end{eqnarray}\)
ですが、\(\theta=\pm a\) なので、
\(\beta-\gamma=\pm\dfrac{a}{3\al^2+p}\)
です。この式と、根と係数の関係である、
\(\beta+\gamma=-\al\)
を使うと、\(\bs{\beta}\) と \(\bs{\gamma}\) が \(\bs{\al}\) の有理式(=分母・分子が \(\bs{\al}\) の多項式)で表現できることになります。計算すると(\(\pm\)は省略して)、
\(\beta=\dfrac{2p\al+3q-a}{2(3\al^2+p)}\)
\(\gamma=\dfrac{2p\al+3q+a}{2(3\al^2+p)}\)
です(\(\beta\) と \(\gamma\) は逆でもよい)。\(\beta,\:\gamma\) が \(\al\) の有理式で表現できるので、
\(\bs{Q}(\al,\beta,\gamma)\subset\bs{Q}(\al)\)
であり、もちろん \(\bs{Q}(\al,\beta,\gamma)\sp\bs{Q}(\al)\) なので。
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
です。\(\bs{Q}(\al)\) のところは \(\bs{Q}(\beta)\) や \(\bs{Q}(\gamma)\) とすることができます。
つまり、\(\bs{Q}\) 上の既約多項式 \(f(x)=x^3+px+q\) の最小分解体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、方程式の解の一つである \(\al\) の(または \(\beta,\:\gamma\) の)単拡大体であり、単拡大体の基底の定理(33F)により \(\bs{L}\) の次元は \(3\) です。すると次数と位数の同一性(52B)により、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) の群位数は \(3\) です。従って、ラグランジュの定理(41E)により群位数が素数の群は巡回群なので、\(G\) は群位数 \(3\) の巡回群( \(C_3\) )です。
以上をまとめると、3次方程式の最小分解体のガロア群は、次のようになります。
前提として、
・\(f(x)=x^3+px+q\:\:(p,\:q\in\bs{Q})\)
( \(f(x)\) は既約多項式 )
・\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\)
・\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
・\(f(x)\) の最小分解体を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)
・\(G=\mr{Gal}(\bs{L}/\bs{Q})\)
とする。この前提のもとで、
\(\bs{\theta}\):有理数のとき
\(G\cong C_3\)
\(G=\{\:e,\:\sg,\:\sg^2\:\}\)
\(\sg=(1,\:2,\:3)\)
\(G\) は巡回群なので可解群
\(\bs{\theta}\):有理数でないとき
\(G\cong S_3\)
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
\(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\)
\(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列
| \(G/H\) | \(=\{H,\:\tau H\}\) | \(\cong C_2\) | |
| \(H/{e}\) | \(=H\) | \(\cong C_3\) |
なお、\((1,\:2,\:3)\:\:(2,\:3)\) の巡回置換は \((1,\:3,\:2)\:\:(1,\:2)\:\:(1,\:3)\) などとしても同じです。
\(C_3\::\:x^3-3x+1\)
まずガロア群が \(C_3\) の方程式 \(x^3-3x+1=0\) を取り上げ、巡回拡大がべき根拡大になる原理を確認します。この原理はガロア群が \(S_3\) のときにもそのまま応用できます。ちなみに \(C_3\) の方程式は \(p,\:q\) が \(-9\leq p\leq-1,\:\:1\leq q\leq9\) の整数だと、他に、
\(x^3-7x+6=0\:\:\:(D=400,\:\sqrt{D}=20)\)
\(x^3-7x+7=0\:\:\:(D=\phantom{0}49,\:\sqrt{D}=\phantom{0}7)\)
\(x^3-9x+9=0\:\:\:(D=729,\:\sqrt{D}=27)\)
があります。
\(x^3-3x+1=0\) の場合、\(p=-3,\:q=1\) なので、
\(\begin{eqnarray}
&&\:\:D&=-4p^3-27q^2=81=9^2\\
&&\:\:\theta&=\pm\sqrt{D}=\pm9\\
\end{eqnarray}\)
となります。3つの解を \(\al,\:\beta,\:\gamma\) とすると、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
で、\(\bs{L}\) の次元は \(3\) で、\(G=\mr{Gal}(\bs{L}/\bs{Q})\cong C_3\) です。
以下「7.3 べき根拡大の十分条件」の証明の論理に沿います。7.3 の証明では、体に \(1\) の原始\(n\)乗根が含まれているのが条件でした。そこで \(1\) の原始3乗根 を \(\omega\) とし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\:\al)=\bs{L}(\omega)\)
という体の拡大を考えます。\(\omega\) は \(x^2+x+1=0\) の2つある根のどちらかで、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
です。7.3 ではラグランジュのレゾルベントを \(\al\) と書きましたが、方程式の根の表記との重複を避けるため、ここでは \(S\) とします。そうするとレゾルベントは、
\(S=c+\omega^2\sg(c)+\omega\sg^2(c)\)
\((\br{A})\)
です。\(\bs{Q}(\omega,\:\al)\) は \(\bs{Q}(\omega)\) に \(\al\) を添加した単拡大体なので、べき根拡大の十分条件のため補題2(72B)に従って、\(c=\al\) と定めます。そうすると、
\(S=\al+\omega^2\sg(\al)+\omega\sg^2(\al)\)
となり、\(\al,\:\beta,\:\gamma\) で表すと、\((\br{A})\) 式は、
\(S=\al+\omega^2\beta+\omega\gamma\)
\((\br{B})\)
です。この \(S\) は \(\bs{Q}(\omega,\al,\beta,\gamma)\) の元ですが、
\(\bs{Q}(\omega,\al,\beta,\gamma)=\bs{Q}(\omega,\al)\)
なので、\(S\) は \(\bs{Q}(\omega,\al)\) の元であり、ということは、
\(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\al)\)
です。方程式の3つの解を \(\al,\:\beta,\:\gamma\) に割り当てる方法の数(\(=3!\) )により、\(S\) は6通りの可能性があります。
7.3 での証明のポイントは、\(\bs{S^3}\) が \(\bs{\bs{Q}(\omega)}\) の元である、というところでした。それを計算で確かめるため、もうひとつのレゾルベントを導入します。ガロア群 \(G=\{e,\sg,\sg^2\}\) は、\(\sg\) が生成元であると同時に、\(\sg^2\) も生成元です。レゾルベントの定義における \(\sg\) は \(G\) の生成元であることが条件でした(73A)。そこで \((\br{A})\) 式の \(\sg\) を \(\sg^2\) で置き換えた式を \(T\) とすると、
\(\begin{eqnarray}
&&\:\:T&=c+\omega^2\sg^2(c)+\omega\sg^4(c)\\
&&&=c+\omega^2\sg^2(c)+\omega\sg(c)\\
\end{eqnarray}\)
となります。この式で \(c=\al\) とおくと
\(T=\al+\omega\beta+\omega^2\gamma\)
です。\(S\) には6通りの可能性がありますが、\(S\) をそのうちの一つに決めると \(T\) は一意に決まります。ここで、
| \(\al+\omega^2\beta\) | \(+\omega\gamma\) | \(=S\) | |
| \(\al+\omega\beta\) | \(+\omega^2\gamma\) | \(=T\) | |
| \(\al+\beta\) | \(+\gamma\) | \(=0\) (根と係数の関係) |
\(\al=\dfrac{1}{3}(S+T)\)
\(\beta=\dfrac{1}{3}(\omega S+\omega^2T)\)
\(\gamma=\dfrac{1}{3}(\omega^2S+\omega T)\) \((\br{C})\)
です。さらに、\(S\) と \(T\) には特別の関係があります。
\(ST=(\al+\omega^2\beta+\omega\gamma)(\al+\omega\beta+\omega^2\gamma)\)
という式を考えると、
\(\begin{eqnarray}
&&\:\:ST&=&\al^2+\beta^2+\gamma^2+\\
&&&&(\omega^2+\omega)\al\beta+(\omega^4+\omega^2)\beta\gamma+(\omega^2+\omega)\gamma\al\\
&&&=&(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)+\\
&&&&(-\al\beta-\beta\gamma-\gamma\al)\\
&&&=&-3(\al\beta+\beta\gamma+\gamma\al)\\
&&&=&-3p\\
\end{eqnarray}\)
となり、つまり、
\(ST=-3p\)
\((\br{D})\)
という関係です。上の式の変形では、根と係数の関係と \(\omega^2+\omega+1=0\)、および \(\omega^3=1\) を使いました。
次に、\(S^3\) を求めるために \(S^3+T^3\) を計算してみると、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=(S+T)(S^2-ST+T^2)\\
&&&=(S+T)(S+\omega T)(S+\omega^2T)\\
\end{eqnarray}\)
です。ここで \((\br{C})\) 式を変形すると、
| \(3\al\) | \(=S+T\) | |
| \(3\omega^2\beta\) | \(=S+\omega T\) | |
| \(3\omega\gamma\) | \(=S+\omega^2T\) |
\(\begin{eqnarray}
&&\:\:S^3+T^3&=3\al\cdot3\omega^2\beta\cdot3\omega\gamma\\
&&&=27\al\beta\gamma=-27q\\
\end{eqnarray}\)
となります。まとめると、
\(S^3+T^3=-27q\)
\(ST=-3p\)
であり、
\(S^3-\dfrac{27p^3}{S^3}+27q=0\)
です。つまり、
\((S^3)^2+27qS^3-27p^3=0\)
\((\br{E})\)
という \(S^3\) についての2次方程式を解くことで \(S^3\) が求まり、そこから \(S\) が求まります。\(S\) の値の可能性は6通りです。また \(T^3\) についても、
\((T^3)^2+27qT^3-27p^3=0\)
\((\br{E}')\)
が成り立ちます。2次方程式、
\(X^2+27qX-27p^3=0\)
\((\br{F})\)
の2つの解が \(S^3\) と \(T^3\) です。
ここまでの計算は \(x^3+px+q=0\) の形の既約方程式なら成り立ちます。ここで \(x^3-3x+1=0\) に即した、\(p=-3,\:q=1\) を \((\br{E})\) 式に入れると、
\((S^3)^2+27S^3+27^2=0\)
\(\begin{eqnarray}
&&\:\:S^3&=\dfrac{1}{2}\left(-27\pm\sqrt{27^2-4\cdot27^2}\right)\\
&&&=27\dfrac{-1\pm i\sqrt{3}}{2}\\
&&&=27\omega\\
\end{eqnarray}\)
となります。最後の式の \(\omega\) は、2つある \(1\) の原始3乗根のどちらか、という意味にとらえます。\(S^3=27\omega\) なら \(T^3=27\omega^2\) で、その逆でもよいわけです。
\((\br{C})\) 式と \((\br{D})\) 式により、\(\al\) は \(S\) と \(\omega\) の四則演算で表現できます。つまり、
\(\bs{Q}(\omega,\al)\subset\bs{Q}(\omega,\:S)\)
です。従って、さきほどの \(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\:\al)\) と合わせると、
\(\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\)
です。以上をまとめると、レゾルベント \(S\) について、
\(\begin{eqnarray}
&&\:\:S^3&\in\bs{Q}(\omega)\\
&&\:\:S&\in\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\\
\end{eqnarray}\)
です。つまり、
\(\bs{Q}(\omega)\) 上の方程式、
\(x^3-a=0\:\:(\:a=27\omega\in\bs{Q}(\omega)\:)\)
の解の一つ、\(\sqrt[3]{a}\) を \(\bs{Q}(\omega)\) に添加したのが \(\bs{Q}(\omega,\:\al)\)
であり、\(\bs{\bs{Q}(\omega,\:\al)}\) は \(\bs{\bs{Q}(\omega)}\) のべき根拡大体であることがわかりました。\(\bs{Q}(\omega,\:\al)\) は \(x^3-a=0\) の解、\(\sqrt[3]{a},\:\sqrt[3]{a}\:\omega,\:\sqrt[3]{a}\:\omega^2\) の全部を含むので、\(\bs{Q}(\omega)\) のガロア拡大体です。結論として、
方程式 \(x^3-3x+1=0\) の解は、
の四則演算で表現できる
| 有理数 | |
| \(\omega\)(\(1\) の原始3乗根) | |
| \(\sqrt[3]{a}\:\:(\:a\in\bs{Q}(\omega)\:)\) |
ことになります。\(x^3-3x+1=0\) の場合、\(a=27\omega\) です。
巡回拡大がべき根拡大になることの証明のフォローはここまでですが、\(x^3-3x+1=0\) の解を具体的に求めることもできます。\(S^3=27\omega\) から、\(S=3\cdot\sqrt[3]{\omega}\) であり、また \(ST=9\) なので、
\(\begin{eqnarray}
&&\:\:\al&=\dfrac{1}{3}(S+T)=\dfrac{1}{3}\left(S+\dfrac{9}{S}\right)\\
&&&=\sqrt[3]{\omega}+\dfrac{1}{\sqrt[3]{\omega}}=\sqrt[3]{\omega}+\sqrt[3]{\omega^2}\\
&&&=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i}\\
\end{eqnarray}\)
が解の一つです。「1.3 ガロア群」の「ガロア群の例」に書いたように、
\(\al=1.53208888623796\:\cd\)
であり、正真正銘の正の実数ですが、\(\bs{\al}\) をべき根で表わそうとすると虚数単位が登場します。その理由がガロア理論から分かるのでした。
\(S_3\::\:x^3+px+q\)
方程式 \(x^3+px+q=0\) の係数を変数のままで扱い、ガロア群が \(S_3\) の方程式の一般論として話を進めます。3つの根を \(\al,\:\beta,\:\gamma\) とし(置換での表示では、それぞれ \(1,\:2,\:3\))、差積 \(\theta\) を、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=\sqrt{D}\\
&&\:\:D&=-4p^3-27q^2\\
\end{eqnarray}\)
と定義すると、\(\bs{\theta}\) が有理数でないとき、
\(G\cong S_3\) \(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\) \(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\) \(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群 \(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列 \(G/H=\{H,\:\tau H\}\cong C_2\) \(H/{\:e\:}=H\cong C_3\) \(G\) は可解群 |
となります(前述)。\(G\cong S_3\) は巡回群ではありません。しかし可解群なので "巡回群の入れ子構造" になっていて(=可解列が存在する)、「巡回拡大はべき根拡大」の定理(73A)を2段階に使うことで、方程式の解が四則演算とべき根で表現できることを証明できます。
まず、上記の可解列とガロア対応(53B)になっている「体の拡大列」は何かです。具体的には \(H\) の固定体は何かですが、それは \(\bs{Q}(\theta)\) です。実際、
\(\sg(\theta)=\theta,\:\:\sg^2(\theta)=\theta\)
なので、\(H\) のすべての元は \(\bs{Q}(\theta)\) の元を固定します。また、
\(\tau(\theta)=-\theta\)
なので、\(\tau\)(および \(\sg\tau,\:\sg^2\tau\))は \(\bs{Q}(\theta)\) の元 を固定しません。従って、\(H\) の固定体は \(\bs{Q}(\theta)\) です。つまり、\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) と書くと、
| \(G\:\sp\:H\:\) | \(\:\sp\:\{\:e\:\}\) | |
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\) | \(\:\subset\:\bs{L}\) |
というガロア対応になっています。
次に体の拡大次元を検証します。まず、\(|G|=6\) なので、次数と位数の同一性(52B)により、\(\bs{L}/\bs{Q}\) の拡大次数は、
\([\:\bs{L}:\bs{Q}\:]=6\)
です。\(\bs{Q}(\theta)\) は \(\bs{Q}\) 上の既約な2次方程式、
\(x^2-D=0\)
の解である \(\theta\) で \(\bs{Q}\) を単拡大した体なので、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\theta):\bs{Q}\:]=2\)
です。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}:\bs{Q}\:]=[\:\bs{L}:\bs{Q}(\theta)\:]\cdot[\:\bs{Q}(\theta):\bs{Q}\:]\)
\([\:\bs{L}:\bs{Q}(\theta)\:]=3\)
となるはずです。\([\:\bs{L}:\bs{Q}(\theta)\:]=3\) であることを、具体的な体の拡大の様子を検証することで確かめます。2つのことを証明します。
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) とするとき、\(\bs{Q}(\theta,\al)=\bs{L}\) である。
[証明]
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\) だから、\(\theta\) は \(\al,\:\beta,\:\gamma\) で表現されている。従って
\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\)
である。この逆である、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であることを証明する。そのためには \(\beta,\:\gamma\) が「有理数と \(\theta,\:\al\) の四則演算」で表現できることを示せばよい。根と係数の関係により、
\(\beta+\gamma=-\al\)
\(\beta\gamma=-\dfrac{q}{\al}\) \((\br{G})\)
である。これを利用して \(\theta\) の定義式を変形すると、
\(\begin{eqnarray}
&&\:\:\theta=&(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=(\beta-\gamma)(-\al^2+(\beta+\gamma)\al-\beta\gamma)\\
&&&=(\beta-\gamma)\left(-\al^2-\al^2+\dfrac{q}{\al}\right)\\
&&&=(\beta-\gamma)\dfrac{-2\al^3+q}{\al}\\
\end{eqnarray}\)
となり、
\(\beta-\gamma=\dfrac{\al\theta}{q-2\al^3}\)
である。\((\br{G})\) 式と \((\br{H})\) 式は \(\beta\) と \(\gamma\) についての連立1次方程式なので解が求まり、\(\beta\) と \(\gamma\) は \(\al,\:\theta,\:q\) の四則演算で表現できる。従って、 \((\br{H})\)
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であり、\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\) と合わせて、
\(\bs{Q}(\theta,\al)=\bs{Q}(\al,\beta,\gamma)\)
である。[証明終]
\(x^3+px+q\) は \(\bs{\bs{Q}(\theta)}\) 上の既約多項式である。
[証明]
\(\bs{Q}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解 \(\al\) による \(\bs{Q}\) の単拡大体 \(\bs{Q}(\al)\) を考えると、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\al):\bs{Q}\:]=3\)
である。従って \(\al\notin\bs{Q}(\theta)\) である。なぜなら、もし \(\al\in\bs{Q}(\theta)\) なら \(\bs{Q}(\theta)\) の次元は \(3\) 以上になるが、\([\:\bs{Q}(\theta):\bs{Q}\:]=2\) なので矛盾が生じるからである。同様に、\(\beta,\:\gamma\notin\bs{Q}(\theta)\) である。\(x^3+px+q\) は、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
と表されるから、\(x^3+px+q\) は \(\bs{Q}(\theta)\) 上では因数分解できない。つまり \(x^3+px+q\) は \(\bs{Q}(\theta)\) 上の既約多項式である。[証明終]
以上により、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、\(\bs{\bs{Q}(\theta)}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体、\(\bs{L}=\bs{Q}(\theta,\al)\) であり、その拡大次数は \([\:\bs{L}:\bs{Q}(\theta)\:]=\:3\) である
ことが検証できました。これを踏まえて、3次方程式が解ける理由をガロア理論で説明します。ガロア対応である、
| \(G\:\sp\:H\:\) | \(\:\sp\:\{\:e\:\}\) | |
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\) | \(\:\subset\:\bs{L}\) |
を2つの部分に分けます。
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\)
\(\mr{Gal}(\bs{Q}(\theta)/\bs{Q})\cong G/H\cong C_2\) であり、\(\bs{Q}(\theta)/\bs{Q}\) は巡回拡大で、拡大次数は \(2\) です。\(1\) の原始2乗根は \(-1\) であり、\(\bs{Q}\) に含まれています。従って \(\bs{Q}(\theta)/\bs{Q}\) はべき根拡大です。具体的には、
\(x^2-D=0\:\:(D\in\bs{Q})\)
\(D=-4p^3-27q^2\)
の解が \(\theta\) であり、
\(\theta=\sqrt{D}=\sqrt{-4p^3-27q^2}\)
です。これはレゾルベントを持ち出すまでもなく分かります。
\(\bs{Q}(\theta)\:\subset\:\bs{L}\)
\(\mr{Gal}(\bs{L}/\bs{Q}(\theta))=H\cong C_3\) であり、\(\bs{L}/\bs{Q}(\theta)\) は巡回拡大で、拡大次数は \(3\) です。また \(\bs{L}\) は \(\bs{Q}(\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体で、\(\bs{L}=\bs{Q}(\theta,\al)\) でした。
\(\bs{Q}(\theta)\) には(一般には)\(1\) の原始3乗根が含まれていません。そこで、\(\bs{L}/\bs{Q}(\theta)\) の体の拡大の代わりに、\(\bs{L}(\omega)/\bs{Q}(\omega,\theta)\) という拡大を考えます。
\(\bs{L}(\omega)=\bs{Q}(\omega,\theta,\al)\)
\([\:\bs{Q}(\omega,\theta,\al):\bs{Q}(\omega,\theta)\:]=3\)
です。 \((\br{I})\)
方程式によっては \(\theta\in\bs{Q}(\omega)\) の場合があります。たとえば、\(p=0\) だと、
\(\theta=\sqrt{-27q^2}=3\sqrt{3}i\cdot q\)
ですが、\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\) なので、\(\theta\in\bs{Q}(\omega)\) です。この場合は、
\(\bs{Q}(\omega,\theta)=\bs{Q}(\omega)=\bs{Q}(\theta)\)
ですが、\((\br{I})\) 式は成り立ちます。レゾルベント \(S,\:T\) を導入して \(S^3\) と \(T^3\) を求めます。計算は、方程式 \(x^3-3x+1=0\) のときと全く同じです。つまり、
\(S=\al+\omega^2\beta+\omega\gamma\)
\(T=\al+\omega\beta+\omega^2\gamma\) \((\br{B})\)
\(ST=-3p\)
\(S^3+T^3=-27q\) \((\br{D})\)
\(\al=\dfrac{1}{3}(S+T)\)
\(\beta=\dfrac{1}{3}(\omega S+\omega^2T)\)
\(\gamma=\dfrac{1}{3}(\omega^2S+\omega T)\) \((\br{C})\)
\(X^2+27qX-27p^3=0\)
の2つの解が \(S^3\) と \(T^3\) \((\br{F})\)
です。方程式 \(x^3-3x+1=0\) の場合、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からの巡回拡大でしたが、\(x^3-3p+1q=0\) では \(\bs{Q}(\omega,\theta)\) からの巡回拡大であり、ガロア群が位数 \(3\) の巡回群であるという点では全く同じなのです。
\((\br{F})\) 式から \(X\) を求めると、
\(\begin{eqnarray}
&&\:\:X&=\dfrac{1}{2}\left(-27q\pm\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q\pm\sqrt{-27\theta^2}\right)\\
&&&=\dfrac{1}{2}(-27q\pm3\sqrt{3}i\cdot\theta)\\
\end{eqnarray}\)
となるので、
\(S^3=\dfrac{1}{2}(-27q+3\sqrt{3}i\cdot\theta)\)
\(T^3=\dfrac{1}{2}(-27q-3\sqrt{3}i\cdot\theta)\)
となります。\(S^3\) と \(T^3\) は逆でもかまいません。\(\omega\) は \(1\) の原始3乗根で、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
のどちらかです。従って、
\(\sqrt{3}i\in\bs{Q}(\omega,\theta)\)
です。つまり、
\(S^3,\:\:T^3\in\bs{Q}(\omega,\theta)\)
であることがわかりました。従って、\(S,\:T\) は \(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解ということになり、\(\bs{Q}(\omega,\theta,\:S)/\bs{Q}(\omega,\theta)\) の体の拡大を考えると、
\([\:\bs{Q}(\omega,\theta,\:S):\bs{Q}(\omega,\theta)\:]=3\)
です。\(\bs{Q}(\omega,\theta,\:S)\) は \(\bs{Q}(\omega,\theta,\:T)\) としても同じことです。ここで、 \((\br{J})\)
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
であることが次のようにして分かります。つまり、\(\bs{Q}(\omega,\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解が \(\al,\:\beta,\:\gamma\) であり、\((\br{B})\) 式により \(S\) は \(\al,\:\beta,\:\gamma,\:\omega\) の四則演算で表されているので、
\(S\in\bs{Q}(\omega,\theta,\al,\beta,\gamma)\)
であり、また、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)\)
だったので、
\(S\in\bs{Q}(\omega,\theta,\al)\)
です。このことから、
\(\bs{Q}(\omega,\theta,\:S)\subset\bs{Q}(\omega,\theta,\:\al)\)
です。\((\br{I})\) 式と \((\br{J})\) 式により、\(\bs{Q}(\omega,\theta,\:S)\) と \(\bs{Q}(\omega,\theta,\:\al)\) の次元は等しく、かつ \((\br{K})\) 式の関係があるので、体の一致の定理(33I)により2つの体は一致し、 \((\br{K})\)
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
です。
この説明は「7.3 べき根拡大の十分条件」の証明に従いましたが、3次方程式の場合は、\((\br{C})\) 式と \((\br{D})\) 式により、\(\al,\:\beta,\:\gamma\) が \(S\) と \(\omega\) の四則演算で表現できます。従って、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)\subset\bs{Q}(\omega,\theta,S)\)
\(\bs{Q}(\omega,\theta,\al)\subset\bs{Q}(\omega,\theta,S)\)
であり、
\(\bs{Q}(\omega,\theta,S)\subset\bs{Q}(\omega,\theta,\al)\)
と合わせて
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
である、とするのが簡便な説明になります。
以上をまとめると、
\(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解の一つ、\(S\) を \(\bs{Q}(\omega,\theta)\) に添加したべき根拡大体が \(\bs{Q}(\omega,\theta,\al)=\bs{L}(\omega)\) である
となり、体に \(\bs{\omega}\) が含まれる前提で、巡回拡大はべき根拡大であることが検証できました。ここから、\(\bs{L}(\omega)\) を \(\bs{Q}\) の拡大体として、方程式の係数 \(p,\:q\) を使って、できるだけ簡潔な形で表してみます。
\(\begin{eqnarray}
&&\:\:\theta&=\sqrt{-4p^3-27q^2}\\
&&&=6\cdot\sqrt{3}i\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\\
\end{eqnarray}\)
ですが、\(\sqrt{3}i\in\bs{Q}(\omega)\) なので、
\(\bs{Q}(\omega,\theta)=\bs{Q}\left(\omega,\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\)
と表せます。また、
\(\begin{eqnarray}
&&\:\:X^3&=\dfrac{1}{2}\left(-27q+\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q+27\cdot2\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
&&&=27\left(-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
\end{eqnarray}\)
なので、
\(S=3\cdot\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(T=3\cdot\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
が \(S,\:T\) です。\(\sqrt[3]{\phantom{I}\cd\phantom{I}}\) は3乗して \(\cd\) になる数の意味です。従って、\(S\) の選び方は3通りですが、\(S\) を一つに決めると、
\(ST=-3p\)
が成り立つように \(T\) を選ぶ必要があります。以上の \(S\) を用いて \(\bs{L}(\omega)\) を表すと、
\(\bs{L}(\omega)\)
\(=\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)=\bs{Q}(\omega,\theta,S)\)
\(=\bs{Q}\left(\omega,\:\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}},\:\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\right)\)
となります。この式が意味するところは、
\(\dfrac{q^2}{4}+\dfrac{p^3}{27}\) が有理数なので、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からのべき根拡大を、\(\sqrt{\phantom{A}}\) と \(\sqrt[3]{\phantom{A}}\) の2回繰り返したものである
ということです。べき根拡大の出発点は 有理数に \(\omega\) を添加した体です。「7.1 1の原始n乗根」で証明したように、原始\(n\)乗根はべき根で表現可能であり(71A)、もちろん \(\omega\) もそうです。これが3次方程式が解ける原理(一般化するとガロア群が可解群である方程式が解ける原理)です。補足すると、\(p=0\) のときは、
\(\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}=\pm\dfrac{q}{2}\in\bs{Q}\)
なので、べき根拡大は \(\sqrt[3]{\phantom{A}}\) の1回だけになります。
さらに、ここまでの計算で3次方程式の解も求まりました。解は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=\dfrac{1}{3}(S+T)&\\
&&\beta=\dfrac{1}{3}(\omega S+\omega^2T)&\\
&&\gamma=\dfrac{1}{3}(\omega^2S+\omega T)&\\
\end{eqnarray}
\end{array}\right.\)
であり、記号を、
\(S=3s\)
\(T=3t\)
に置き換えると、
3次方程式の解の公式
\(x^3+px+q=0\) の3つの解を \(\al,\:\beta,\:\gamma\) とする。
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=s+t&\\
&&\beta=\omega s+\omega^2t&\\
&&\gamma=\omega^2s+\omega t&\\
\end{eqnarray}
\end{array}\right.\)
\(s=\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(t=\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(st=-\dfrac{p}{3}\)
が、3次方程式の解の公式です。
3次方程式の解による体の拡大を振り返ってみます。\(\bs{Q}\) 上の既約な方程式 \(x^3+px+q=0\) の根を \(\al,\:\beta,\:\gamma\) とし、\(\bs{Q}\) の最小分解体 を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)、ガロア群を \(G=\mr{Gal}(\bs{L}/\bs{Q})\) とすると、
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\:\) | \(\:\subset\:\bs{L}\) | |
| \(G\:\sp\:H\:\:\:\) | \(\:\sp\:\{\:e\:\}\) |
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\subset\:\bs{L}\)
という体の拡大列で、\(\bs{Q}\:\subset\:\bs{Q}(\theta)\) のところはべき根拡大ですが、\(\bs{Q}(\theta)\:\subset\:\bs{L}\) は、\(\omega\in\bs{Q}(\theta)\) の場合を除き、べき根拡大ではありません。しかし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\theta)\:\subset\:\bs{L}(\omega)\)
なら、必ず、すべてがべき根拡大になります。従って、3次方程式の解は \(\bs{Q}(\omega)\) の元である「有理数と \(\omega\)」の四則演算・べき根で記述できます。
\(\omega\) は \(x^2+x+1=0\) の解なので、\([\:\bs{Q}(\omega):\bs{Q}\:]=2\) です。従って、拡大次数の連鎖律(33H)により、\(\omega\notin\bs{Q}(\theta)\) の条件で、
\([\:\bs{L}(\omega):\bs{Q}\:]=12\)
です。これは、\(\bs{Q}\) 上の多項式 \((x^3+px+q)(x^2+x+1)\) の最小分解体が \(\bs{L}(\omega)\) なので、\(\bs{Q}\) からの拡大次数は \(12\) であるとも言えます。3次方程式の「解」は、あくまで \(\bs{Q}\) の \(6\)次拡大体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) の中にありますが、「べき根で表された解」は \(\bs{Q}\) の \(12\)次拡大体 \(\bs{L}(\omega)\) の中にあるのです。
一見、矛盾しているようですが、そうではありません。ある代数拡大体 \(\bs{K}\) があったとして、\(a\) を \(\bs{K}\) の元とし、\(1\) の原始3乗根の一つを \(\omega\) とします。3次方程式、
\(x^3-a=0\:\:(a\in\bs{K})\)
は3つの解をもちます。そのうちのどれか一つを \(\sqrt[3]{a}\) と定義すると、3つの解(べき根)は、
\(\sqrt[3]{a},\:\:\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2\)
です。\(\sqrt[3]{a}\) では \(\omega\) が不要なように見えますが、それは表面上のことで、3つの解は、
\(\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2,\:\:\sqrt[3]{a}\:\omega^3\)
であるというのが正しい認識です。つまり \(\bs{\omega}\) は3つのべき根の関係性を規定していて、\(\sqrt[3]{a}\cdot\omega^i\:\:(i=1,2,3)\) という "ペアの形" によって3つの区別が可能になり、数式としての整合性が保てます。\(\sqrt[3]{\phantom{A}}\) という "曖昧さ" がある記号を用いる限り、\(\omega\) という、曖昧さを解消する "助手" が必然的に登場するのです。
「7.7 巡回拡大はべき根拡大」終わり
(「7.可解性の十分条件」は次回に続く)
(「7.可解性の十分条件」は次回に続く)
2023-04-30 07:54
nice!(0)
No.357 - 高校数学で理解するガロア理論(4) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
6.1 可解群
正規部分群の概念、および剰余群と巡回群を使って「可解群」を定義します。可解群は純粋に群の性質として定義できますが、方程式の可解性と結びつきます。
群 \(G\) から 単位元 \(e\) に至る部分群の列、
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、剰余群 \(H_i/H_{i+1}\) が巡回群であるとき、\(G\) を可解群(solvable group)と言う。
\(H_{i+1}\) が \(H_i\) の正規部分群であるとき、\(H_i\) を正規列と言う。加えて、\(H_i/H_{i+1}\) が巡回群のとき、\(H_i\) を可解列という。
巡回群は可解群である。また、巡回群の直積も可解群である。
[証明]
群 \(G\) を巡回群とし、\(G\) から 単位元 \(e\) に至る部分群の列として、
\(G=H_0\:\sp\:H_1=\{\:e\:\}\)
をとる。\(H_1=\{\:e\:\}\) は \(H_0=G\) の正規部分群である。また、
\(H_0/H_1\:\cong\:H_0\:(=G)\)
であり、\(G\) は巡回群だから、\(H_0/H_1\) は巡回群である。従って \(G\) は可解群である。
3つの巡回群の直積 \(G\) で考える。\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\bs{Z}/k\bs{Z}\times\bs{Z}/m\bs{Z}\times\bs{Z}/n\bs{Z}\\
&&&=\{(a,b,c)\:|\:a\in\bs{Z}/k\bs{Z},\:b\in\bs{Z}/m\bs{Z},\:c\in\bs{Z}/n\bs{Z}\}\\
\end{eqnarray}\)
とする。このとき、
\(\begin{eqnarray}
&&\:\:&H_1&=\{(a,b,0)\:|\:a\in\bs{Z}/k\bs{Z},\:b\in\bs{Z}/m\bs{Z}\}\\
&&&H_2&=\{(a,0,0)\:|\:a\in\bs{Z}/k\bs{Z}\}\\
&&&\{e\}&=\{(0,0,0)\}\\
\end{eqnarray}\)
とおくと、
\(G\:\sp\:H_1\:\sp\:H_2\:\sp\:\{e\}\)
となる。巡回群は可換群であり、巡回群の直積 \(G\) も可換群である。従って、\(G\) の部分群である \(H_1,\:H_2\) も可換群であり、すなわち \(G\) の正規部分群である(41F)。
\(G\) の任意の2つの元を
\(g=(g_a,\:g_b,\:g_c)\)
\(h=(h_a,\:h_b,\:h_c)\)
とする。剰余類 \(g+H_1\) と \(h+H_1\) を考える。\((g_a,0,0)+H_1=H_1\)、\((0,g_b,0)+H_1=H_1\) だから、\((g_a,g_b,0)+H_1=H_1\) である。また同様に\((h_a,h_b,0)+H_1=H_1\) である。従って、\(g_c=h_c\) なら、\(g_a\)、\(g_b\)、\(h_a\)、\(h_b\) の値に関わらず \(g+H_1=h+H_1\) である。逆に、\(g_c\neq h_c\) なら \(g+H_1\neq h+H_1\) である。このことから剰余類の代表元(41E)として、\((0,0,0)\)、\((0,0,1)\)、\(\cd\)、\((0,0,n-1)\) の \(n\)個をとることができる。つまり、
\(\begin{eqnarray}
&&\:\:G/H_1=\{&(0,0,0)+H_1,\\
&&&(0,0,1)+H_1,\\
&&&(0,0,2)+H_1,\\
&&& \vdots\\
&&&(0,0,n-1)+H_1\}\\
\end{eqnarray}\)
である。これは \((0,0,1)+H_1\) を生成元とする位数 \(n\) の巡回群である。まったく同様の議論により、
\(\begin{eqnarray}
&&\:\:H_1/H_2=\{&(0,0,0)+H_2,\\
&&&(0,1,0)+H_2,\\
&&&(0,2,0)+H_2,\\
&&& \vdots\\
&&&(0,m-1,0)+H_2\}\\
\end{eqnarray}\)
であり、\(H_1/H_2\) は \((0,1,0)+H_2\) を生成元とする位数 \(m\) の巡回群である。以上により、
\(G=H_0\:\sp\:H_1\:\sp\:H_2\:\sp\:H_3=\{e\}\)
は、正規列であり、\(H_i/H_{i+1}\) が巡回群なので、\(G\) は可解群である。この議論は \(G\) が\(4\)個以上の巡回群の直積の場合でも全く同様に成り立つ。つまり、巡回群の直積は可解群である。[証明終]
可解群の部分群は可解群である。
[証明]
可解群を \(G\) とすると、可解群の定義により、
\(G=H_0\sp H_1\sp H_2\sp\cd H_{n-1}\sp H_n=\{e\}\)
という列で、\(H_{i+1}\) が \(H_i\) の正規部分群であり、\(H_i/H_{i+1}\) が巡回群のものが存在する。
ここで、\(G\) の任意の部分群を \(N\) としたとき、
\(N=N\cap H_0\sp N\cap H_1\sp N\cap H_2\sp\cd N\cap H_{n-1}\sp N\cap H_n=\{e\}\)
という集合の列を考える。部分群の共通部分は部分群の定理(41D)により、\(N\cap H_i\:(0\leq i\leq n)\) は \(G\) の部分群の列である。と同時に、これが可解列であることを以下で証明する。
列の \(N\cap H_{i-1}\sp N\cap H_i\) の部分を取り出して考える。\(H_i\) は \(H_{i-1}\) の正規部分群なので、\(H_{i-1}\) の任意の元 \(x\) について \(xH_i=H_ix\) が成り立つ。
\(N\cap H_{i-1}\) の任意の元を \(y\) とすると、\(y\in N\) かつ \(y\in H_{i-1}\) であるが、\(y\in N\) なので \(yN=Ny=N\) である。また \(y\in H_{i-1}\) なので、正規部分群の定義により、\(yH_i=H_iy\) が成り立つ。ゆえに、
\(y(N\cap H_i)=yN\cap yH_i=Ny\cap H_iy=(N\cap H_i)y\)
となり、定義によって \(\bs{N\cap H_i}\) は \(\bs{N\cap H_{i-1}}\) の正規部分群である。
次に第2同型定理(43B)によると、\(N\) が \(G\) の部分群、\(H\) が \(G\) の正規部分群のとき、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。\(N\) を \(N\cap H_{i-1}\) とし、\(H\) を \(H_i\) として定理を適用すると、
となる。ここで、\(H_i\:\subset\:H_{i-1}\) なので、\((N\cap H_{i-1})\cap H_i=N\cap H_i\) である。従って、
\(H_{i-1}H_i\:\subset\:H_{i-1}H_{i-1}\)
\((N\cap H_{i-1})H_i\:\subset\:H_{i-1}H_i\)
となるが、これと \((\br{C})\) 式を合わせると、
\((N\cap H_{i-1})H_i\:\subset\:H_{i-1}\)
となる。従って、\((N\cap H_{i-1})H_i\) と \(H_{i-1}\) の \(H_i\) による剰余類を考えると、
\((N\cap H_{i-1})H_i/H_i\:\subset\:H_{i-1}/H_i\)
の関係にある。これで、
以上の \((\br{A})\:\:(\br{A}\,')\:\:(\br{A}\,'')\) をあわせると、
\((N\cap H_{i-1})/(N\cap H_i)\:\cong\:H_{i-1}/H_i\) の部分群
である。\(G\) は可解群なので \(H_{i-1}/H_i\) は巡回群である。巡回群の部分群は巡回群なので、それと同型である \(\bs{(N\cap H_{i-1})/(N\cap H_i)}\) は巡回群である。まとめると、
\(N\cap H_i\) は \(N\cap H_{i-1}\) の正規部分群
\((N\cap H_{i-1})/(N\cap H_i)\) は巡回群
となる。このことは \(1\leq i\leq n\) のすべてで成り立つから、\(N\cap H_0\:=\:N\cap G\:=\:N\) は可解群である。つまり、可解群 \(G\) の任意の部分群 \(N\) は可解群である。[証明終]
可解群の準同型写像による像は可解群である。
このことより、
可解群の剰余群は可解群
であることが分かる。なぜなら、群 \(G\) の部分群を \(N\) とすると、\(G\) から \(G/N\) への自然準同型、つまり \(x\in G\) として、
\(x\:\longmapsto\:xN\)
の準同型写像を定義できるからである。
[証明]
可解群を \(G\) とすると、可解群の定義により、
\(G=H_0\sp H_1\sp\:H_2\sp\cd H_{n-1}\sp H_n=\{e\}\)
という列で、\(H_i\) が \(H_{i-1}\) の正規部分群であり、剰余群 \(H_{i-1}/H_i\) が巡回群の列(=可解列)が存在する。群 \(G\) に作用する準同型写像を \(\sg\) とすると、上記の可解列の \(\sg\) による像、
\(\sg\) による像の列から \(\sg(H_{i-1})\sp\sg(H_i)\) を取り出して考える。\(\sg\) を \(H_{i-1}\) から \(\sg(H_{i-1})\) への写像と考えると、\(\sg(H_{i-1})\) は \(\sg\) による \(H_{i-1}\) の像なので、\(\sg\) は全射である。従って、\(H_{i-1}\) の元 \(h\) を選ぶことによって \(\sg(h)\) で \(\sg(H_{i-1})\) の全ての元を表すことができる。
\(\sg(H_{i-1})\) の任意の元を \(\sg(h)\) とおくと、
\(\begin{eqnarray}
&&\:\:\sg(h)\sg(H_i)&=\sg(hH_i)=\sg(H_ih)\\
&&&=\sg(H_i)\sg(h)\\
\end{eqnarray}\)
であるから、\(\sg(H_i)\) は \(\sg(H_{i-1})\) の正規部分群である。つまり \((\br{D})\) は正規列である。従って、\(\sg(H_{i-1})\) の \(\sg(H_i)\) による剰余類は群であり、剰余群 \(\sg(H_{i-1})/\sg(H_i)\) になる。
次に、剰余群 \(\sg(H_{i-1})/\sg(H_i)\) が巡回群であることを示す。\(H_{i-1}\) の任意の元を \(x\) とし、剰余群 \(H_{i-1}/H_i\) の元を \(xH_i\) で表す。\(H_{i-1}/H_i\) から \(\sg(H_{i-1})/\sg(H_i)\) への写像 \(f\) を、
\(f\::\:xH_i\:\longmapsto\:\sg(x)\sg(H_i)\)
と定める。もし、剰余群 \(H_{i-1}/H_i\) の元が \(xH_i\) と \(yH_i\:(x,y\in H_{i-1})\) という異なる表現を持っているとすると、
\(xH_i=yH_i\)
\(\sg(xH_i)=\sg(yH_i)\)
\(\sg(x)\sg(H_i)=\sg(y)\sg(H_i)\)
であるが、\(f\) の定義によって、
\(f(xH_i)=\sg(x)\sg(H_i)\)
\(f(yH_i)=\sg(y)\sg(H_i)\)
であり、異なる表現の \(f\) による写像先は一致する。従って \(f\) は2つの剰余群の間の写像として矛盾なく定義されている。また \(f\) は、
\(\begin{eqnarray}
&&f(xH_iyH_i)&=f(xyH_iH_i)=f(xyH_i)\\
&&&=\sg(xy)\sg(H_i)=\sg(x)\sg(y)\sg(H_i)\\
&&&=\sg(x)\sg(y)\sg(H_iH_i)=\sg(x)\sg(yH_iH_i)\\
&&&=\sg(x)\sg(H_iyH_i)=\sg(x)\sg(H_i)\sg(yH_i)\\
&&&=\sg(xH_i)\sg(yH_i)=\sg(x)\sg(H_i)\sg(y)\sg(H_i)\\
&&&=f(xH_i)f(yH_i)\\
\end{eqnarray}\)
を満たすが、この式は \(xH_i\) と \(yH_i\) が剰余群 \(H_{i-1}/H_i\) の異なる元を表現していても成り立つ。従って \(f\) は準同型写像である(=\(\:\br{①}\:\))。また、\(f\) は \(H_{i-1}/H_i\) から \(\sg(H_{i-1})/\sg(H_i)\) への写像で、
\(f\::\:xH_i\:\longmapsto\:\sg(x)\sg(H_i)\)
と定義されたが、\(\sg(xH_i)=\sg(x)\sg(H_i)\) だから \(f\)は全射であり、
\(\mr{Im}\:f\:=\:\sg(H_{i-1})/\sg(H_i)\)
である(=\(\:\br{②}\:\))。\(\br{①}\) と \(\br{②}\)、および準同型定理(43A)により、
\((H_{i-1}/H_i)/\mr{Ker}\:f\:=\:\sg(H_{i-1})/\sg(H_i)\)
である。\(H_{i-1}/H_i\) は巡回群なので、巡回群の剰余群は巡回群の定理(41H)により、\((H_{i-1}/H_i)/\mr{Ker}\:f\) は巡回群である。従って、それと同型である \(\sg(H_{i-1})/\sg(H_i)\) も巡回群である。
結局、\((\br{D})\) は正規列であると同時に \(\sg(H_{i-1})/\sg(H_i)\) が巡回群なので、\(\sg(G)\) は可解群である。[証明終]
6.2 巡回拡大
巡回拡大
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とする。\(\mr{Gal}(\bs{K}/\bs{Q})\) が巡回群のとき、\(\bs{K}/\bs{Q}\) を巡回拡大(cyclic extension)と言う。
累巡回拡大
\(\bs{Q}\) の拡大体を \(\bs{K}\) とする。
となる拡大列があって(\(k > 1\))、\(\bs{K}_{i+1}/\bs{K}_i\:(0\leq i < k)\) が巡回拡大のとき、\(\bs{K}/\bs{Q}\) は累巡回拡大であると言う。ただし、\(\bs{\bs{K}/\bs{Q}}\) が累巡回拡大だとしても、\(\bs{\bs{K}/\bs{Q}}\) がガロア拡大であるとは限らない。
\(\bs{K}/\bs{Q}\) が累巡回拡大だとしてもガロア拡大であるとは限りません。たとえばシンプルな例で考えてみると、
\(\al=\sqrt{\sqrt{2}+1}\)
という代数的数があったとします。この式から \(\sqrt{\phantom{A}}\) を消去すると \(\al^4-2\al^2-1=0\) なので、\(\al\) の最小多項式 \(f(x)\) は、
\(f(x)=x^4-2x^2-1\)
です。\(f(x)\) は、
\(f(x)=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\)
と変形できるので、方程式 \(f(x)=0\) の解は
\(x=\pm\sqrt{\sqrt{2}+1},\:\:\pm i\sqrt{\sqrt{2}-1}\)
です。従って \(f(x)\) の最小分解体 \(\bs{L}\) は、
\(\bs{L}=\bs{Q}(\sqrt{\sqrt{2}+1},\:i\sqrt{\sqrt{2}-1})\)
であり、また、
\(\sqrt{\sqrt{2}+1}\cdot\sqrt{\sqrt{2}-1}=1\)
の関係があるので、
\(\bs{L}=\bs{Q}(i,\:\al)\)
と表現できます。\(\bs{L}/\bs{Q}\) はガロア拡大です。
一方、
\(\bs{K}=\bs{Q}(\al)\)
と定義すると、\(\bs{K}\) は \(f(x)=0\) の一つの解 \(\al\) だけによる単拡大体なので、\(\bs{K}/\bs{Q}\) はガロア拡大ではありません( \(\bs{Q}(\al)\neq\bs{Q}(i,\:\al)\) )。ここで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\al)=\bs{K}\)
という体の拡大列を考えます。\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解は \(\pm\sqrt{2}\) なので、\(\bs{Q}(\sqrt{2})/\bs{Q}\) はガロア拡大です。また、ガロア群は、
\(\mr{Gal}(\bs{Q}(\sqrt{2})/\bs{Q})=\{e,\:\sg\}\)
\(\sg(\sqrt{2})=-\sqrt{2}\)
\(\sg^2=e\)
なので巡回群であり、\(\bs{Q}(\sqrt{2})/\bs{Q}\) は巡回拡大です。
同様に、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-(\sqrt{2}+1)=0\) の解は \(\pm\al\) で、\(\bs{Q}(\sqrt{2},\al)\) は \(\bs{Q}(\sqrt{2})\) の巡回拡大です。\(\sqrt{2}=\al^2-1\) なので、\(\bs{Q}(\sqrt{2},\al)=\bs{Q}(\al)\) であり、\(\bs{Q}(\al)/\bs{Q}(\sqrt{2})\) が巡回拡大となります。
結局、\(\bs{K}/\bs{Q}\) は \(\bs{Q}(\sqrt{2})/\bs{Q},\:\:\bs{Q}(\al)/\bs{Q}(\sqrt{2})\) という2つの巡回拡大の列で表されるので、定義(62B)により累巡回拡大です。しかしそうであっても、\(\bs{K}/\bs{Q}\) は ガロア拡大ではないのです。
これがもし \(\al=\sqrt{2}+\sqrt{3}\) だとすると、\(2\) も \(3\) も \(\bs{Q}\) の元なので、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})=\bs{K}\)
の拡大列は累巡回拡大であり、かつ \(\bs{K}/\bs{Q}\) がガロア拡大です。
このように、\(\bs{K}/\bs{Q}\) が累巡回拡大だとしてもガロア拡大であるとは限らないのですが、もし \(\bs{K}/\bs{Q}\) が累巡回拡大でかつガロア拡大だとすると、\(\mr{Gal}(\bs{K}/\bs{Q})\) は可解群になります。それが、累巡回拡大と可解群を結びつける次の定理です。
累巡回拡大ガロア群の可解性
\(\bs{Q}\) のガロア拡大を \(\bs{K}\)、そのガロア群を \(G\) とする。このとき、
の2つは同値である。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) が可解群であることを示す部分群の列と、それとガロア対応をする体の拡大列を、
とする。\(G\) が可解群なので、\(H_{i+1}\) は \(H_i\) の正規部分群であり、\(H_{i+1}/H_i\:(0\leq i\leq k-1)\) は巡回群である。以降、\(H_i,\:H_{i+1}\) を取り出して考える。
\(H_i\:\sp\:H_{i+1}\:\sp\:\{e\}\)
\(\bs{F}_i\:\subset\:\bs{F}_{i+1}\:\subset\:\bs{K}\)
\(\bs{K}/\bs{Q}\) がガロア拡大なので、中間体からのガロア拡大の定理(52C)により、\(\bs{K}/\bs{F}_i\) もガロア拡大である。\(\bs{F}_i\) の固定群は \(H_i\) なので \(\mr{Gal}(\bs{K}/\bs{F}_i)=H_i\) である。同様に、\(\bs{K}/\bs{F}_{i+1}\) もガロア拡大であり、\(\mr{Gal}(\bs{K}/\bs{F}_{i+1})=H_{i+1}\) である。
ここで、\(H_{i+1}\) は \(H_i\) の正規部分群なので、正規性定理(53C)により \(\bs{F}_{i+1}/\bs{F}_i\) はガロア拡大であり、そのガロア群は、
\(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\cong H_i/H_{i+1}\)
となる。\(H_i/H_{i+1}\) は巡回群なので、それと同型の \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) も巡回群になる。従って、\(\bs{F}_{i+1}/\bs{F}_i\) は、「ガロア拡大で、かつ \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) が巡回群」なので、巡回拡大である。
以上が \(\bs{F}_i\:(0\leq i\leq k-1)\) で成り立つから、\(\bs{K}/\bs{Q}\) は累巡回拡大である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{K}\) が \(\bs{Q}\) の累巡回拡大であることを示す体の拡大列と、それとガロア対応する \(G\) の部分群の列を、
とする。\(\bs{F}_i\)と \(\bs{F}_{i+1}\) を取り出して考える。
\(\bs{F}_i\:\subset\:\bs{F}_{i+1}\:\subset\:\bs{K}\)
\(H_i\:\sp\:H_{i+1}\:\sp\:\{e\}\)
\(\bs{K}/\bs{Q}\) がガロア拡大なので、\(\bs{K}/\bs{F}_i\) も \(\bs{K}/\bs{F}_{i+1}\) もガロア拡大である。また \(\bs{F}_{i+1}/\bs{F}_i\) は巡回拡大なので、すなわちガロア拡大である。従って正規性定理(53C)により、\(H_{i+1}\) は \(H_i\) の正規部分群であり、
\(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\cong H_i/H_{i+1}\)
となる。\(\bs{F}_{i+1}/\bs{F}_i\) は巡回拡大なので \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) は巡回群であり、それと同型である \(H_i/H_{i+1}\) も巡回群である。まとめると「\(H_{i+1}\) は \(H_i\) の正規部分群であり、かつ \(H_i/H_{i+1}\) は巡回群」である。
このことは \(H_i\:(0\leq i\leq k-1)\) で成り立つから、定義によって \(G\) は可解群である。[証明終]
6.3 原始\(n\)乗根を含む体とべき根拡大
この節の目的は「1の原始\(\bs{n}\)乗根を含む体のべき根拡大」の性質を解明することです。そのためにまず、1の原始\(n\)乗根を \(\zeta\) を含む体 \(\bs{Q}(\zeta)\)に関する次の定理を数ステップに分けて証明します。
1の原始\(n\)乗根を \(\zeta\) とする。このとき
・\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大
・\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\:\cong\:(\bs{Z}/n\bs{Z})^{*}\)
が成り立つ。
\(1\) の原始\(n\)乗根
\(x^n-1=0\) の \(n\)個の解のうち、\(n\)乗して初めて \(1\) になる解を \(1\)の原始\(n\)乗根という。
原始\(n\)乗根は \(\varphi(n)\) 個ある。\(\varphi(n)\) はオイラー関数で、\(n\) と互いに素である \(n\) 以下の自然数の数を表す。
[証明]
まず、
\(\omega=\mr{cos}\dfrac{2\pi}{n}+i\:\mr{sin}\dfrac{2\pi}{n}\)
とおくと、明らかに \(\omega\) は原始\(n\)乗根である。さらに、
\(\omega^k=\mr{cos}\dfrac{2\pi k}{n}+i\:\mr{sin}\dfrac{2\pi k}{n}\:(1\leq k\leq n)\)
で \(1\) の\(n\)乗根の全体を表現できる。ここで \(\omega^k\) が原始\(n\)乗根になる条件を考える。いま、
\(\dfrac{2\pi k}{n}x=2\pi j\)
のときである。つまり、
\(\dfrac{k}{n}x=j\)
のときである。いま、\(k\) と \(n\) の最大公約数を \(d\) とすると( \(\mr{gcd}(k,n)=d\:)\)、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&k=sd&\\
&&n=td&\\
\end{eqnarray}
\end{array}\right.\)
と表せて、このとき \(s\) と \(t\) は互いに素である。これを使うと、
\(\dfrac{s}{t}x=j\)
のときに \(x\) は \((\br{A})\) 式を満たすことになる。\(s\) と \(t\) は互いに素であり、\(j\) は任意の整数だったから、\(x\) は \(t\) の倍数でなければならない。つまり、\(x\) は \(t=\dfrac{n}{d}\) の倍数である。ということは、\(x\) の最小値は \(\dfrac{n}{d}\) である。そして、\(\dfrac{n}{d}\) が \(n\) に等しいのは \(d=1\) の場合に限る。つまり \(\mr{gcd}(k,n)=1\) なら、\((\br{A})\) 式を満たす最小の \(x\) は \(n\) ということになる。従って、そのときに限り \(\omega^k\) は原始\(n\)乗根である。
\(\mr{gcd}(k,n)=1\) となる \(k\) は \(\varphi(n)\) 個あり、\(1\) の原始\(n\)乗根は \(\varphi(n)\) 個ある。[証明終]
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\zeta^m\:\:(1\leq m\leq n)\)
は、\(1\) の\(n\)乗根の全体を表す。また、
\(\zeta^m\:\:(\mr{gcd}(m,n)=1)\)
は、\(1\) の原始\(n\)乗根の全体を表す。
[証明]
\(\zeta^m\:(1\leq m\leq n)\) の \(n\) 個の値は全部異なっている。なぜなら、もし、 \(\zeta^j=\zeta^i\:(1\leq i < j\leq n)\)
だとすると、
\(\zeta^{j-i}=1\:(1\leq i < j\leq n)\)
となり、\(j-i < n\) だから、\(\zeta\) が原始\(n\)乗根という前提に反するからである。\(\zeta^m\:(1\leq m\leq n)\) は全部異なっているので、これら \(n\) 個の値は \(1\) の\(n\)乗根全体を表す。
\(\zeta\) は、\(\mr{gcd}(k,n)=1\) である \(k\) を用いて、
\(\zeta=\omega^k\)
\(\omega=\mr{cos}\dfrac{2\pi}{n}+i\:\mr{sin}\dfrac{2\pi}{n}\)
と表せる(63A)。すると
\(\zeta^m=(\omega^k)^m=\omega^{km}\)
である。\(\mr{gcd}(k,n)=1\) なので \(\mr{gcd}(m,n)=1\) なら \(\mr{gcd}(km,n)=1\) である。逆に、\(\mr{gcd}(km,n)=1\) が成り立つのは \(\mr{gcd}(m,n)=1\) のときに限る。従って、
\(\zeta^m\:(=\omega^{km})\)
は \(\mr{gcd}(m,n)=1\) のとき(かつ、そのときに限って)\(1\) の原始\(n\)乗根である。[証明終]
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とする。\(\zeta\) の最小多項式を \(f(x)\) とし、\(k\) を \(n\) とは素な数とする。
このとき \(f(\zeta^k)=0\) である。
[証明]
証明を2つのステップで行う
第1ステップ(\(p\) は \(\bs{n}\) と素な素数)
本論に入る前に、2つことを確認する。まず、\(p\) を素数とし \(a\) を \(p\) とは素な整数とするとき、\(a\neq0\) ならフェルマの小定理(25B)により、
\(a^{p-1}\equiv1\:(\mr{mod}\:p)\)
が成り立つ。この両辺に \(a\) をかけると、
次に、有限体 \(\bs{F}_p\) 上の多項式(係数が \(\bs{F}_p\) の元である多項式。「2.4 有限体」参照)についての定理である。\(p\) を素数とし \(x,\:y\) を変数とするとき、
\((x+y)^p=x^p+y^p\:\:\:[\bs{F}_p]\)
が成り立つ。その理由であるが、等式の左辺を整数係数として2項展開すると、
\(\begin{eqnarray}
&&\:\:(x+y)^p=&x^p+{}_{p}\mr{C}_{1}x^{p-1}y+\:\cd\:+{}_{p}\mr{C}_{p-1}xy^{p-1}+y^p\\
\end{eqnarray}\)
となる。この展開における \(x^p\) と \(y^p\) 以外の項の係数は、
\({}_{p}\mr{C}_{k}=\dfrac{p!}{k!\cdot(p-k)!}\:\:(1\leq k\leq p-1)\)
であるが、\(p\) が素数なので、分母の素因数に \(p\) はなく、分子の素因数にある \(p\) は分母で割り切れない。従って、
\({}_{p}\mr{C}_{k}\equiv0\:\:(\mr{mod}\:p)\:\:(1\leq k\leq p-1)\)
となり、\(\bs{F}_p\) 上の多項式としては、
\((x+y)^p=x^p+y^p\:\:\:[\bs{F}_p]\)
が成り立つ。
さらに、3変数、\(x,\:y,\:z\) では、
\(\begin{eqnarray}
&&\:\:(x+y+z)^p&=(x+y)^p+z^p\\
&&&=x^p+y^p+z^p\:\:\:[\bs{F}_p]\\
\end{eqnarray}\)
となり、これを繰り返すと \(n\) 変数に拡張できるのは明らかだから、\(x_1,\:\cd\:,\:x_n\) を変数として、
\((x_1+x_2+\:\cd\:+x_n)^p=\)
以上の \((\br{A})\) 式と \((\br{B})\) 式を前提として以下の本論を進める。
\(\zeta\) の最小多項式 \(f(x)\) は、最小多項式は既約多項式(31I)によって \(\bs{Q}\) 上の既約多項式である。\(\zeta\) は \(x^n-1=0\) と \(f(x)=0\) の共通の解だから、既約多項式の定理1(31E)により、\(x^n-1\) は \(f(x)\) で割り切れる。そこで、商の多項式を \(g(x)\) として、
とおく。この式の左辺の \(x^n-1\) は整数係数の多項式である。つまり上の式は、整数係数の多項式が \(\bs{Q}\) 上で(有理数係数の多項式として)因数分解できることになり、整数係数多項式の既約性の定理(31C)によって、\(x^n-1\) は整数係数の多項式で因数分解できる。従って、\(f(x)\) と \(g(x)\) は整数係数としてよい。ということは、\(f(x)\) と \(g(x)\) を有限体 \(\bs{F}_p\) 上の多項式と見なすこともできる。以降の証明にはこのことを使う。
\(p\) は \(n\) と互いに素だから \(\zeta^p\) も \(1\) の原始\(n\)乗根である(63B)。従って \((\br{C})\) 式に \(x=\zeta^p\) を代入すると、左辺は \(0\) だから、
\(f(\zeta^p)g(\zeta^p)=0\)
となり、\(f(\zeta^p)=0\) もしくは \(g(\zeta^p)=0\) である。
ここから、\(f(\zeta^p)=0\) であることを言うために背理法を使う。以下に \(f(\zeta^p)\neq0\) と仮定すると矛盾が生じることを証明する。
この背理法の仮定のもとでは \(g(\zeta^p)=0\) だから、\(\zeta\) は方程式 \(g(x^p)=0\) の解である。ということは、\(f(x)=0\) と \(g(x^p)=0\) は \(\zeta\) という共通の解をもつことになり、かつ \(f(x)\) は既約多項式であるから、既約多項式の定理1(31E)によって、\(g(x^p)\) は \(f(x)\) で割り切れる。その商を \(h(x)\) とすると、
\(g(x)\) を、
\(g(x)=a_mx^m+a_{m-1}x^{m-1}+\:\cd\:+\:a_1x+a_0\)
とし、これを \(\bs{F}_p\) 上の多項式とみなして \(g(x^p)\) を計算する。\((\br{A})\) 式を使って係数を \(\mr{mod}\:p\) でみると、
と変形できる。2行目への変形で \((\br{A})\) 式を用いた。
この最後の式は、\((\br{B})\) 式の右辺の \(x_1\) を \(a_mx^m\)、\(x_2\) を \(a_{m-1}x^{m-1}\)、\(\cd\:x_n\) を \(a_0\) と置き換えた形をしている。従って \((\br{B})\) 式を使うと、
となる。つまり \(g(x)\) を \(\bs{F}_p\) 上の多項式と見なすと、
\(f(x)\) は \(\bs{Q}\) 上の(整数係数の)既約多項式であった。しかし \(f(x)\) を \(\bs{F}_p\) 上の多項式と見なしたとき、それが既約多項式だとは限らない。たとえば \(x^2+1=0\) は \(\bs{Q}\) 上の既約多項式であるが、\(\bs{F}_5\) では、
\(x^2+1=(x-2)(x-3)\:\:\:[\bs{F}_5]\)
と因数分解できるから既約ではない。そこで、\(\bs{F}_p\) 上の多項式 \(f(x)\) を割り切る \(\bs{F}_p\) 上の既約多項式を \(q(x)\) とする。もし \(f(x)\) が \(\bs{F}_p\) 上でもなおかつ既約であれば \(q(x)=f(x)\) である。そうすると \(q(x)\) は \((\br{F})\) 式の右辺を割り切るから、左辺の \((g(x))^p\) も割り切る。ということは、既約多項式と素数の類似性(31D)によって、\(q(x)\) は \(g(x)\) を割り切る。
ここで \((\br{C})\) 式に戻って考えると、\((\br{C})\) 式は、
ここで \((\br{G})\) 式の両辺の導多項式(多項式の形式的微分)を求める。\(\bs{F}_p\) では距離が定義されていないので極限による微分の定義はできないが、形式的微分( \(x^k\:\rightarrow\:kx^{k-1}\) の変換)はできる。すると、
となる。
\((\br{G})\) 式と \((\br{H})\) 式により、\(\bs{F}_p\) 上の多項式として、
\(x^n-1\) と \(nx^{n-1}\) は共通の因数をもつ
ことになる。ここで矛盾が生じる。
なぜなら、\(n\) と \(p\) は互いに素だから、\(\bs{F}_p\) における \(n\) の逆数 \(n^{-1}\) がある。これを用いて \(x^n-1\) と \(nx^{n-1}\) に多項式の互除法を適用すると、
\(x^n-1=n^{-1}x(nx^{n-1})-1\:\:\:[\bs{F}_p]\)
となって、\(x^n-1\) と \(nx^{n-1}\) の最大公約数は \(-1\:(=p-1)\:\:[\bs{F}_p]\) という定数である。つまり、\(\bs{F}_p\) 上の多項式として、
\(x^n-1\) と \(nx^{n-1}\) は互いに素
である。これは明らかに矛盾している。この矛盾の発端は \(f(x)=0\) と \(g(x^p)=0\) が \(\zeta\) という共通の解をもつとしたことにあり、つまり \(g(\zeta^p)=0\) としたことにある。
従って、そもそもの仮定である \(f(\zeta^p)\neq0\) は間違っている。つまり \(f(\zeta^p)=0\) である。[第1ステップの証明終]
第2ステップ(\(k\) は \(\bs{n}\) と素な数)
\(k\) を \(n\) とは素な(しかし素数ではない)数とし、\(k\) の素因数分解を、
\(k=p_1p_2\cd p_m\)
とする。この形での素因数分解は、素因数が重複することもありうる。\(k\) は \(n\) と素だから、\(p_1,\:p_2,\:\cd\:,p_m\) のすべての素数は \(n\) と素である。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、第1ステップの \(p=p_1\) とする。\(p_1\) は \(n\) と素だから、原始\(\bs{n}\)乗根の累乗の定理(63B)により、\(\zeta^{p_1}\) も \(1\) の原始\(n\)乗根である。また、第1ステップの証明により、\(f(\zeta^{p_1})=0\) である。
次に、その \(\zeta^{p_1}\) を原始\(n\)乗根としてとりあげ、\(p=p_2\) とする。\(p_2\) は \(n\) と素だから、\((\zeta^{p_1})^{p_2}=\zeta^{p_1p_2}\) もまた原始\(n\)乗根になる(63B)。従って、第1ステップでの証明を適用して \(f(\zeta^{p_1p_2})=0\) である。
このプロセスは次々と続けることができる。結局 \(\zeta^{p_1p_2\:\cd\:p_m}=\zeta^k\) は \(1\) の原始\(n\)乗根であると同時に、\(f(\zeta^k)=0\) を満たす。\(k\) につけた条件は「\(n\) と互いに素」だけである。
原始\(\bs{n}\)乗根の累乗の定理(63B)により、\(k\) が \(n\) と素という条件で、\(\zeta^k\) は原始\(n\)乗根のすべてを表す。従って、\(f(x)=0\) は原始\(n\)乗根のすべてを解とする方程式である。[証明終]
この原始\(\bs{n}\)乗根の最小多項式の定理(63C)より、次の定理がすぐに導けます。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、\(\zeta\) の最小多項式を \(f(x)\) とすると、\(f(x)\) は円分多項式である。円分多項式とは、方程式 \(f(x)=0\) が \(\varphi(n)\) 個の解をもち、それらすべてが原始\(n\)乗根である多項式である。
従って、原始\(\bs{n}\)乗根は互いに共役である。最小多項式は既約多項式なので(31I)、円分多項式は既約多項式である。
\(\bs{Q}\) に \(\zeta\) を添加した単拡大体 \(\bs{Q}(\zeta)\) は円分多項式の最小分解体であり、\(\bs{\bs{Q}(\zeta)/\bs{Q}}\) はガロア拡大である。
\(\bs{Q}(\zeta)\)のガロア群
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
である。つまり \(1\) の原始\(n\)乗根の一つを \(\bs{Q}\) に添加した拡大体のガロア群は、既約剰余類群に同型である。
[証明]
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、最小多項式を \(f(x)\) とすると、円分多項式の定理(63D)により、\(f(x)=0\) の解は \(\varphi(n)=m\) 個の原始\(n\)乗根である。
原始\(n\)乗根を
\(\zeta^{k_i}\:(\:1\leq i\leq m,\:1\leq k_i\leq n\) かつ \(\mr{gcd}(k_i,n)=1\:)\)
と表すと、それらは互いに共役である。また、\(f(x)\) の最小分解体は、
\(\bs{Q}(\zeta^{k_1},\zeta^{k_2},\cd,\zeta^{k_m})=\bs{Q}(\zeta)\)
である。
\(\zeta\) に作用する同型写像 \(\sg\) を考えると、\(\sg\) は \(\zeta\) を共役な元に移すから、
\(\sg_{k_i}(\zeta)=\zeta^{k_i}\)
で \(m\) 個の同型写像が定義できる。この \(\sg\) による移り先はすべて \(\bs{Q}(\zeta)\) の元だから、\(\sg\) は \(\bs{Q}(\zeta)\) の自己同型写像である。また、\(\sg_{k_i}\) と \(\sg_{k_j}\) の積は、
\(\begin{eqnarray}
&&\:\:\sg_{k_i}(\sg_{k_j})&=\sg_{k_i}(\zeta^{k_j})\\
&&&=(\zeta^{k_j})^{k_i}\\
&&&=\zeta^{k_ik_j}\\
\end{eqnarray}\)
と計算できる。そこで \(\sg\) の演算規則を、
\(\sg_{k_i}\sg_{k_j}=\sg_{k_ik_j}\)
と定める。
ここで \(k_ik_j\) は、\(1\leq k_i,\:k_j\leq n\) かつ \(\mr{gcd}(k_i,n)=1\) かつ \(\mr{gcd}(k_j,n)=1\) だから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元であり、乗算で閉じている。すなわち \(\sg_{k_ik_j}\) は \(\sg\) のどれかである。つまり、自己同型写像である \(\sg\) は上の演算規則で群になり、ガロア群 \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) である。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) から \((\bs{Z}/n\bs{Z})^{*}\) への写像 \(f\) を、
で定めると、
が成り立つから、\(f\) は群の同型写像になる。従って、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) と \((\bs{Z}/n\bs{Z})^{*}\) は同型である。[証明終]
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型です(25G)。従って次の定理が得られます。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積と同型である。
従って、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は可解群であり(61B)、累巡回拡大である(62C)。
累巡回拡大は、可解性の必要条件を証明する重要ポイントです。そこで次に、\(\bs{Q}(\zeta)/\bs{Q}\) が累巡回拡大になる様子を、ガロア群の計算で示します。
円分拡大は累巡回拡大
\(1\) の原始\(n\)乗根 \(\zeta\) を \(\bs{Q}\) に添加する拡大、\(\bs{Q}(\zeta)/\bs{Q}\) を円分拡大と言います。\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積と同型で、従って 円分拡大 \(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大です。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) が巡回群の直積と同型になる理由は、既約剰余類群と同型であること、つまり、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
でした(63E)。その \((\bs{Z}/n\bs{Z})^{*}\) について振り返ってみると、次の通りです。\(\varphi\) はオイラー関数です。
\(\bs{n}\) が奇素数 \(\bs{p}\) 、ないしは奇素数 のべき乗のとき
(\(n=p^k,\:1\leq k\))(25D)(25E)
\((\bs{Z}/p^k\bs{Z})^{*}\) は生成元をもつ巡回群
群位数:\(\varphi(p^k)=p^{k-1}(p-1)\)
\(\bs{n}\) が2のべき乗のとき
(\(n=2^k,\:2\leq k\))(25F)
\((\bs{Z}/2^k\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{k-2}\bs{Z})\)
群位数:\(\varphi(2^k)=2^{k-1}\)
\(\bs{n=p^a\cdot q^b\cdot r^c}\)のとき
(\(p,\:q,\:r\) は素数)(25G)
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\)
群位数:\(\varphi(n)=\varphi(p^a)\varphi(q^b)\varphi(r^c)\)
もちろん最後の式は、素因数が4個以上でも同様に成り立ちます。以下、それぞれの例をあげます。
\(\zeta\) が 原始\(25\)乗根のとき
\(\zeta\) が 原始\(25\)乗根の(一つ)のとき、原始\(25\)乗根の全体は \(\zeta^k\:\:(\mr{gcd}(k,25)=1)\) で表され(63B)、その数は \(25\) と互いに素な自然数の数、\(\varphi(25)=20\) です。\(\bs{Q}(\zeta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/5^2\bs{Z})^{*}\)
でした(63E)。\((\bs{Z}/5\bs{Z})^{*}\) の最小の生成元は \(2\) ですが(25D)、ほどんどの場合、\((\bs{Z}/p\bs{Z})^{*}\) の生成元は同時に \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です(25E)。実際、\(2\) は \((\bs{Z}/25\bs{Z})^{*}\) の生成元であることが確認できます。
そこで、\(\bs{Q}(\zeta)\) の自己同型写像 \(\sg\) を、
\(\sg(\zeta)=\zeta^2\)
と定義すると、\(\sg^k(\zeta)\:\:(1\leq k\leq20)\) は、
\(\zeta^2,\:\zeta^4,\:\zeta^8,\:\zeta^{16},\:\zeta^7,\:\zeta^{14},\:\zeta^3,\:\zeta^6,\:\zeta^{12},\:\zeta^{24},\)
\(\zeta^{23},\:\zeta^{21},\:\zeta^{17},\:\zeta^9,\:\zeta^{18},\:\zeta^{11},\:\zeta^{22},\:\zeta^{19},\:\zeta^{13},\:\zeta\)
となって、原始\(25\)乗根の全部を尽くします。つまり、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=\{e,\:\sg,\:\sg^2,\:\cd,\:\sg^{19}\}\)
\(\sg(\zeta)=\zeta^2\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は位数 \(20\) の巡回群で、
\(\bs{Q}\:\subset\:\bs{Q}(\zeta)\)
は巡回拡大です。
\(\zeta\) が 原始\(16\)乗根のとき
原始\(16\)乗根は、自然数 \(k\) を \(16\) 以下の奇数として \(\zeta^k\) で表され、次の8個です。
\(\zeta,\:\zeta^3,\:\zeta^5,\:\zeta^7,\:\zeta^9,\:\zeta^{11},\:\zeta^{13},\:\zeta^{15}\)
ここで、\(n\) が2のべき乗のときの同型は、
\((\bs{Z}/16\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/4\bs{Z})\)
でした(25F)。つまり、\((\bs{Z}/16\bs{Z})^{*}\) は巡回群ではありませんが、位数 \(2\) の巡回群と位数 \(4\) の巡回群の直積に同型です。このことの証明(25F)を振り返ってみると、\(\mr{mod}\:16\) でみて \(5^k\:\:(0\leq k\leq3)\) は、
\(1,\:5,\:9,\:13\)
であり、\((\bs{Z}/16\bs{Z})^{*}\) の元のうちの「4で割って1余る数」が全部現れるのでした。そこで、\(\bs{Q}(\zeta)\) の自己同型写像 \(\sg\) を、
\(\sg(\zeta)=\zeta^5\)
と定義すると、\(\sg^k(\zeta)\:\:(0\leq k\leq3)\) は、
\(\zeta,\:\zeta^5,\:\zeta^9,\:\zeta^{13}\)
で、原始\(16\)乗根の半数を表現します。
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
\(H=\{e,\:\sg,\:\sg^2,\:\sg^3\}\)
と書くと、\(H\) は \(G\) の部分群で、\(H\) の位数 \(4\) は \(G\) の位数 \(8\) の半分です。
\(H\) の固定体を \(\bs{K}\) とします。
\(\sg(\zeta^4)=\sg(\zeta)^4=(\zeta^5)^4=\zeta^{20}\)
ですが、\(\zeta^{16}=1\) なので、
\(\sg(\zeta^4)=\zeta^4\)
です。\(\zeta^4\) は \(\sg\) で不変であり、従って \(\zeta^4\) は \(H\) のすべての元で不変です。\(\zeta^4\) は4乗して初めて \(1\) になる数で、\(1\) の原始4乗根、つまり \(i\)(または \(-i\)。\(i\) は虚数単位)です。つまり \(i\) は固定体 \(\bs{K}\) の元であり、
\(\bs{Q}(i)\:\subset\:\bs{K}\)
です。\(\bs{K}\) が \(H\) の固定体なので、ガロア対応は、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{Q}(\zeta)\)
です。ガロア対応の定理(53B)により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{K})=H\)
であり、次数と位数の同一性(52B)により、体の拡大次数はガロア群の位数と等しいので、
\([\:\bs{Q}(\zeta):\bs{K}\:]=|H|=4\)
です。また、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=\varphi(16)=8\)
なので、拡大次数の連鎖律(33H)により、
\([\:\bs{K}:\bs{Q}\:]=2\)
です。一方、\(i\) は既約な2次方程式 \(x^2+1=0\) の根なので、\([\:\bs{Q}(i):\bs{Q}\:]=2\) です。つまり \(\bs{K}\) と \(\bs{Q}(i)\) は次元(\(=\:2\))が一致し、かつ \(\bs{Q}(i)\:\subset\:\bs{K}\) なので、体の一致の定理(33I)によって、
\(\bs{K}=\bs{Q}(i)\)
です。まとめると、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}(i))\) は位数 \(4\) の巡回群であり、\(\bs{Q}(\zeta)/\bs{Q}(i)\) は巡回拡大です。
また、
\(\tau(i)=-i\)
と定義すると、\(\tau\) は \(\bs{Q}(i)\) の自己同型写像です。従って、
\(\mr{Gal}(\bs{Q}(i)/\bs{Q})=\{e,\:\tau\}\)
であり、\(\mr{Gal}(\bs{Q}(i)/\bs{Q})\) は位数 \(2\) の巡回群で、\(\bs{Q}(i)/\bs{Q}\) は巡回拡大です。
以上で、
\(\bs{Q}\:\subset\:\bs{Q}(i)\:\subset\:\bs{Q}(\zeta)\)
は2つの巡回拡大を連鎖させた累巡回拡大です。
\(\zeta\) が 原始\(360\)乗根のとき
\(n\) が複数の素因数をもつ一般的な場合を確認します。分かりやすいように \(n=360\) とします。\(360=2^3\cdot3^2\cdot5\) なので、既約剰余類群の構造の定理(25G)によって、
\((\bs{Z}/360\bs{Z})^{*}\cong(\bs{Z}/8\bs{Z})^{*}\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\)
です。右辺の群位数はそれぞれ、
\(|(\bs{Z}/8\bs{Z})^{*}|=\varphi(8)=4\)
\(|(\bs{Z}/9\bs{Z})^{*}|=\varphi(9)=6\)
\(|(\bs{Z}/5\bs{Z})^{*}|=\varphi(5)=4\)
なので、
\(|(\bs{Z}/360\bs{Z})^{*}|=4\cdot6\cdot4=96=\varphi(360)\)
です。ここで、
\(1\) の原始\(8\)乗根 \(:\:\zeta^{45}\)
\(1\) の原始\(9\)乗根 \(:\:\zeta^{40}\)
\(1\) の原始\(5\)乗根 \(:\:\zeta^{72}\)
ですが、これらを用いると、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
が成り立ちます。その理由ですが、
\(\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\subset\bs{Q}(\zeta)\)
であるのは当然として、その逆である、
\(\bs{Q}(\zeta)\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
も成り立つからです。なぜなら、
\(45x+40y+72z=1\)
の1次不定方程式を考えると、\(\mr{gcd}(45,40,72)=1\) なので不定方程式の解の存在の定理(21C)により必ず整数解があります。具体的には、
\(x=5,\:\:y=7,\:\:z=-7\)
が解(の一つ)です。従って、
\(\zeta=(\zeta^{45})^5\cdot(\zeta^{40})^7\cdot(\zeta^{72})^{-7}\)
であり、\(\zeta\) が \(\zeta^{45},\:\zeta^{40},\:\zeta^{72}\) の四則演算で表現できるので、
\(\bs{Q}(\zeta)\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
です。この結果、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
となります。
以上を踏まえると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) への体の拡大は、
\(\begin{eqnarray}
&&\:\:\bs{Q}&\subset\bs{Q}(\zeta^{45})\\
&&&\subset\bs{Q}(\zeta^{45},\zeta^{40})\\
&&&\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})=\bs{Q}(\zeta)\\
\end{eqnarray}\)
と、\(\bs{Q}\) からの単拡大を3回繰り返したものと言えます。以降で、それぞれの単拡大が巡回拡大になることを確認します。
\(\bs{Q}\:\subset\:\bs{Q}(\zeta^{45})\)
\(\zeta^{45}\) は原始\(8\)乗根なので、上で検討した原始\(16\)乗根の結果がそのまま使えます。つまり、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(\zeta^{45})\)
と表され、
\([\:\bs{Q}(i):\bs{Q}\:]=2\)
\([\:\bs{Q}(\zeta^{45}):\bs{Q}(i)\:]=2\)
\([\:\bs{Q}(\zeta^{45}):\bs{Q}\:]=4\)
であり、\(\mr{Gal}(\bs{Q}(i)/\bs{Q}),\:\mr{Gal}(\bs{Q}(\zeta^{45})/\bs{Q}(i))\) は位数2の巡回群です。原始8乗根は簡単に計算できて、たとえばその一つは、
\(\begin{eqnarray}
&&\:\:\zeta^{45}&=\mr{cos}\dfrac{\pi}{4}+i\:\mr{sin}\dfrac{\pi}{4}\\
&&&=\dfrac{1}{2}(\sqrt{2}+\sqrt{2}\:i)\\
\end{eqnarray}\)
なので、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(i,\sqrt{2})=\bs{Q}(\zeta^{45})\)
と表現することができます。この結果を使って、2つのガロア群 \(G_1\) と\(G_2\) の元を表現すると、
\(G_1=\mr{Gal}(\bs{Q}(i)/\bs{Q})=\{e,\:\sg_1\}\)
\(\sg_1(i)=-i\)
\(G_2=\mr{Gal}(\bs{Q}(\zeta^{45})/\bs{Q}(i))=\{e,\:\sg_2\}\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
となります。
\(\bs{Q}(\zeta^{45})\subset\bs{Q}(\zeta^{45},\zeta^{40})\)
\(\zeta^{40}\) は原始\(9\)乗根です。原始\(9\)乗根の一つを \(\al\) と書くと、原始\(9\)乗根の全体は \(1\)~\(8\) の数で \(9\) と素なものを選んで、
\(\al,\:\al^2,\:\al^4,\:\al^5,\:\al^7,\:\al^8\)
の6つになり、これらが共役な元です。\((\bs{Z}/9\bs{Z})^{*}\) の元は、
\((\bs{Z}/9\bs{Z})^{*}=\{1,\:2,\:4,\:5,\:7,\:8\}\)
ですが、生成元は \(2\) か \(5\) です。生成元として \(2\) を採用すると、\(2^k\:(\mr{mod}\:9)\:(1\leq k\leq6)\) は、
\(2,\:4,\:8,\:7,\:5,\:1\)
と、\((\bs{Z}/9\bs{Z})^{*}\) の元を巡回します。
\(G_3=\mr{Gal}(\bs{Q}(\zeta^{45},\zeta^{40})/\bs{Q}(\zeta^{45}))\)
と書くことにし、ガロア群 \(G_3\) の元 \(\sg\) を、
\(\sg(\al)=\al^2\)
と定義すると、
\(G_3=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4,\:\sg^5\}\)
となります。\(\al\) を \(\zeta\) で表すと、
ただし、ガロア群の定義によって \(\sg\) は \(\zeta^{45}\) を不動にします。従って、
\(40x\equiv80\:\:(\mr{mod}\:360)\)
\(45x\equiv45\:\:(\mr{mod}\:360)\)
\(x=65\)
です。当然ですが、\(65\)の累乗を \((\mr{mod}\:9)\) で計算してみると、
\(65^{\phantom{1}}\equiv2\:\:(\mr{mod}\:9)\)
\(65^2\equiv4\:\:(\mr{mod}\:9)\)
\(65^3\equiv8\:\:(\mr{mod}\:9)\)
\(65^4\equiv7\:\:(\mr{mod}\:9)\)
\(65^5\equiv5\:\:(\mr{mod}\:9)\)
\(65^6\equiv1\:\:(\mr{mod}\:9)\)
となって、\(2\) の累乗 \((\mr{mod}\:9)\) と一致します。\(\mr{mod}\:360\) に戻すと、
\(40\cdot65^{\phantom{1}}\equiv40\cdot2\:\:(\mr{mod}\:360)\)
\(40\cdot65^2\equiv40\cdot4\:\:(\mr{mod}\:360)\)
\(40\cdot65^3\equiv40\cdot8\:\:(\mr{mod}\:360)\)
\(40\cdot65^4\equiv40\cdot7\:\:(\mr{mod}\:360)\)
\(40\cdot65^5\equiv40\cdot5\:\:(\mr{mod}\:360)\)
\(40\cdot65^6\equiv40\phantom{\cdot5\:\:(}(\mr{mod}\:360)\)
です。この結果、
と定義すると、\(\sg_3\) は \(\al=\zeta^{40}\) を、
\(\sg_3^{\:\phantom{1}}(\al)=\al^2,\:\:\sg_3^{\:2}(\al)=\al^4,\:\:\sg_3^{\:3}(\al)=\al^8\)
\(\sg_3^{\:4}(\al)=\al^7,\:\:\sg_3^{\:5}(\al)=\al^5,\:\:\sg_3^{\:6}(\al)=\al\)
と巡回させます \((\zeta^{360}=1)\)。また、
\(65\cdot45=2925\equiv45\:\:(\mr{mod}\:360)\)
なので、
\(\sg_3(\zeta^{45})=\zeta^{45}\)
です。結局、
\(\begin{eqnarray}
&&\:\:G_3&=\mr{Gal}(\bs{Q}(\zeta^{45},\zeta^{40})/\bs{Q}(\zeta^{45}))\\
&&&=\{e,\:\sg_3,\:\sg_3^{\:2},\:\sg_3^{\:3},\:\sg_3^{\:4},\:\sg_3^{\:5}\}\\
\end{eqnarray}\)
\(\sg_3(\zeta)=\zeta^{65}\)
がガロア群です。
\(\bs{Q}(\zeta^{45},\zeta^{40})\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
\(\zeta^{72}\) は原始\(5\)乗根で、\((\bs{Z}/5\bs{Z})^{*}\) の生成元は \(2\) か \(3\) です。生成元として \(2\) を採用すると、ガロア群の元 \(\sg\) は、先ほどと同じように考えて、
ですが、これを簡単にして、
が得られます。この連立合同方程式も中国剰余定理\(\bs{\cdot}\)多連立(21G)によって、\(0\leq x < 9\cdot8\cdot5=360\) の範囲に唯一の解があります。それを求めると、
\(x=217\)
です。従って、
と定義すると、
\(G_4=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\)
\(\sg_4(\zeta)=\zeta^{217}\)
がガロア群になります。\(217^4\equiv1\:\:(\mr{mod}\:360)\) です。なお、
\(\bs{Q}(\zeta^{45},\zeta^{40})=\bs{Q}(\zeta^5)\)
と簡略化できます。なぜなら、\(40\) と \(45\) の最大公約数は \(5\) なので、
\(45x+40y=5\)
の1次不定方程式には整数解があり(21B)、具体的には、
\(x=1,\:\:y=-1\)
が解(の一つ)で、
\(\zeta^5=\zeta^{45}\cdot(\zeta^{40})^{-1}\)
と表せるからです。また、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
だったので、
\(\begin{eqnarray}
&&\:\:G_4&=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}(\zeta^5))\\
&&&=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\\
\end{eqnarray}\)
\(\sg_4(\zeta)=\zeta^{217}\)
と表記できます。\(G_4\) は位数 \(4\) の巡回群であり、\(\bs{Q}(\zeta)/\bs{Q}(\zeta^5)\) は巡回拡大です。さらに、
\(\begin{eqnarray}
&&\:\:\sg_4(\zeta^5)&=\zeta^{5\cdot217}=\zeta^{1085}\\
&&&=\zeta^{3\cdot360+5}=\zeta^5\\
\end{eqnarray}\)
なので、\(\sg_4\) が \(\zeta^5\) を固定することが確認できました。
以上の考察をまとめると、\(\zeta\) が \(1\) の原始\(360\)乗根のとき、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(\zeta^{45})\subset\bs{Q}(\zeta^5)\subset\bs{Q}(\zeta)\)
という、4段階の巡回拡大が得られました。\(i\) は原始\(4\)乗根なので、\(\bs{Q}(i)\) は \(\bs{Q}(\zeta^{90})\) と同じ意味です。それそれの拡大のガロア群を \(G_1,\:G_2,\:G_3,\:G_4\) とすると、
\(G_1=\{e,\:\sg_1\}\)
\(\sg_1(i)=-i\)
\(G_2=\{e,\:\sg_2\}\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
\(G_3=\{e,\:\sg_3,\:\sg_3^{\:2},\:\sg_3^{\:3},\:\sg_3^{\:4},\:\sg_3^{\:5}\}\)
\(\sg_3(\zeta)=\zeta^{65}\)
\(G_4=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\)
\(\sg_4(\zeta)=\zeta^{217}\)
であり、これらすべてが巡回群です。また、体の拡大次数はガロア群の位数と一致し、順に \(2,\:2,\:6,\:4\) です。以上のことは、\(\zeta\) を \(1\) の\(360\)乗根とするとき、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/360\bs{Z})^{*}\)
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/8\bs{Z})^{*}\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
であることの必然的な結果です。
以上のガロア群の計算を通して、\(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大であることが確認できました。
べき根拡大
\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とするとき、\(\bs{K}(\sqrt[n]{a})\) を \(\bs{K}\) のべき根拡大(radical extension)と呼ぶ。
また、\(\bs{K}\) からのべき根拡大を繰り返して拡大体 \(\bs{F}\) ができるとき、\(\bs{F}/\bs{K}\) を累べき根拡大と言う。
\(x^n-a\) は既約多項式とは限らないので、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) の拡大次数は \(n\) とは限りません。
また一般に、べき根拡大はガロア拡大ではありません。しかし \(\bs{K}\) に特別の条件(= \(\bs{K}\) に \(1\) の原始\(n\)乗根 \(\zeta\) が含まれる)があるときは、べき根拡大がガロア拡大、かつ巡回拡大になります。この「原始\(\bs{n}\)乗根を含む体からのべき根拡大」を考えるのが、ガロア理論の巧妙なアイデアです。
\(1\) の原始\(n\)乗根を含むべき根拡大
\(1\) の原始\(n\)乗根を \(\zeta\) とし、\(\bs{K}\) に \(\zeta\) が含まれるとする。\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とし、\(\bs{L}=\bs{K}(\sqrt[n]{a})\) とすると、
が成り立つ。
[証明]
\(\bs{K}(\sqrt[n]{a})\) 上の同型写像を \(\tau\) とする。\(x^n-a=0\) の解は、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\)
であり、\(\tau\) を \(\sqrt[n]{a}\) に作用させたときの移り先は、このうちのどれかである。もともと \(\bs{K}\) には \(1\) の原始\(n\)乗根 \(\zeta\) が 含まれているから、これらの移り先はすべて \(\bs{K}(\sqrt[n]{a})\) の元である。従って \(\tau\) は自己同型写像であり、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) はガロア拡大である。
次にガロア群 \(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) の元と、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) の拡大次数を求める。\(\sqrt[n]{a}\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式(31I)により \(f(x)\) は既約多項式であり、\(f(x)=0\) と \(x^n-a=0\) は共通の解 \(\sqrt[n]{a}\) を持つから、\(x^n-a=0\) は \(f(x)\) で割り切れる。従って \(f(x)=0\) の解は、\(x^n-a=0\) の解、\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\) の全部、またはその一部である。\(f(x)=0\) の解で、\(\sqrt[n]{a}\:\zeta^{t}\) の\(t\) が最小となる 正の数を \(d\:(1\leq d\leq n-1)\) とする。そして \(\bs{K}\) の元を固定する \(\bs{K}(\sqrt[n]{a})\) の同型写像、\(\sg\) を、
\(\sg(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{d}\)
と定義する。これは自己同型写像になるから、\(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) の元である。\(\sg\) は \(\bs{K}\) の元を固定するから \(\sg(\zeta)=\zeta\) である。これを用いて \(\sg^i(\sqrt[n]{a})\) を求めると、
\(\begin{eqnarray}
&&\:\:\sg^2(\sqrt[n]{a})&=\sg(\sg(\sqrt[n]{a}))=\sg(\sqrt[n]{a}\:\zeta^{d})=\sg(\sqrt[n]{a})\zeta^{d}\\
&&&=\sqrt[n]{a}\:\zeta^{d}\zeta^{d}=\sqrt[n]{a}\:\zeta^{2d}\\
&&\:\:\sg^3(\sqrt[n]{a})&=\sg(\sg^2(\sqrt[n]{a}))=\sg(\sqrt[n]{a}\:\zeta^{2d})=\sg(\sqrt[n]{a})\zeta^{2d}\\
&&&=\sqrt[n]{a}\:\zeta^{d}\zeta^{2}d=\sqrt[n]{a}\:\zeta^{3d}\\
\end{eqnarray}\)
となり、一般的には、
\(\sg^i(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{id}\:(1\leq i)\)
となる。\(i=n\) とおくと、
\(\sg^n(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{nd}=\sqrt[n]{a}\)
となるから、\(\sg^n=e\) である。
\(n\) を \(d\) で割ったときの商を \(s\)、余りを \(r\) とする。
\(n=sd+r\:(1 < s\leq n,\:0\leq r < d)\)
である。ここで \(\sg^i(\sqrt[n]{a})\) の \(i\) を \(n-s\) とおくと、
\(\begin{eqnarray}
&&\:\:\sg^{n-s}(\sqrt[n]{a})&=\sqrt[n]{a}\:\zeta^{nd-sd}\\
&&&=\sqrt[n]{a}\:\zeta^{n(d-1)+n-sd}\\
\end{eqnarray}\)
となる。\(\zeta^n=e\) なので、\(\zeta^{n(d-1)}=e\) であることを用いると、
\(\begin{eqnarray}
&&\:\:\sg^{n-s}(\sqrt[n]{a})&=\sqrt[n]{a}\:\zeta^{n-sd}\\
&&&=\sqrt[n]{a}\:\zeta^{r}\\
\end{eqnarray}\)
と計算できる。\(\sg^{s}\) はガロア群の元なので、\(\sg^{n-s}=\sg^{-s}\) もガロア群の元である。従って \(\sg^{n-s}(\sqrt[n]{a})\) は \(f(x)=0\) の解である。
ここでもし \(r\) がゼロでないとすると、\(1\) 以上、\(d\) 未満の数である \(r\) があって、\(\sqrt[n]{a}\:\zeta^{r}\) が \(f(x)=0\) の解となってしまう。しかしこれは、\(f(x)=0\) の解である \(\sqrt[n]{a}\:\zeta^{t}\) の \(t\) の最小値が \(d\) との仮定に反する。従って \(r=0\) である。
\(n=sd\) なので、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\)
の中に \(f(x)=0\) の解は \(s\) 個あり、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta^{d},\:\:\sqrt[n]{a}\:\zeta^{2d},\:\cd\:,\:\sqrt[n]{a}\:\zeta^{(s-1)d}\)
である。\(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) は位数 \(s\) の巡回群であり、位数は \(n\) の約数である。\(n\) が素数 \(p\) であれば、\(\mr{Gal}(\bs{K}(\sqrt[p]{a})/\bs{K})\) は \(p\)次の巡回群である。[証明終]
この定理から分かることは、あらかじめ必要な原始\(n\)乗根を "仕込んで" おけば、べき根拡大列は巡回拡大列になるということです。たとえば、べき根拡大の列、
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{L}\)
があり、\(\bs{K}/\bs{Q}\) の拡大次数を \(n_1\)、\(\bs{L}/\bs{K}\) の拡大次数を \(n_2\) とします。\(n_1,\:n_2\) の最小公倍数を \(n\)、\(1\) の原始\(n\)乗根を \(\zeta\) とします。そして、
\(\bs{Q}\:\subset\:\bs{Q}(\zeta)\:\subset\:\bs{K}\:\subset\:\bs{L}\)
の拡大列を考えると、\(\bs{Q}(\zeta)\) には、
\(1\) の原始\(n_1\)乗根 : \(\zeta^{\frac{n}{n_1}}\)
\(1\) の原始\(n_2\)乗根 : \(\zeta^{\frac{n}{n_2}}\)
が含まれているので、
となり、合わせると
\(\bs{L}/\bs{Q}\) : 累巡回拡大
になります。ここまでくると、可解性の必要条件の証明まであと一歩です。
6.4 可解性の必要条件
可解性の必要条件を証明する最終段階にきました。\(\bs{Q}\) 上の既約な方程式の解の一つを \(\al\) とし、\(\bs{K}=\bs{Q}(\al)\) の拡大体を考えます。\(\al\) が四則演算とべき根で表現できるということは、\(\bs{K}/\bs{Q}\) が累べき根拡大(63G)であるということです。ここが出発点です。そして証明の方針として、
の4つが密接に関係していることを示します。
まず、原始\(\bs{n}\)乗根を含むべき根拡大の定理(63H)により、累べき根拡大の拡大のステップに必要な原始\(n\)乗根の全種類をあらかじめ \(\bs{Q}\) に含めておけば、① 累べき根拡大は ② 累巡回拡大と同じことなります。
さらに、累巡回拡大ガロア群の可解性(62C)の定理により、もし \(\bs{K}/\bs{Q}\) が ③ ガロア拡大であれば、累巡回拡大 \(\bs{K}/\bs{Q}\) のガロア群 \(\mr{Gal}(\bs{K}/\bs{Q})\) は ④ 可解群です。
しかし、累巡回拡大の定義(62B)のところで書いたように、\(\bs{K}/\bs{Q}\) が累巡回拡大であってもガロア拡大であるとは限りません。そこで、
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{E}\)
となるような \(\bs{E}\) で、\(\bs{E}/\bs{Q}\) が累巡回拡大、かつガロア拡大である \(\bs{E}\) が必ず存在することを証明できれば、① \(\rightarrow\) ② \(\rightarrow\) ③ \(\rightarrow\) ④ が一気通貫でつながることになります。このような \(\bs{E}\)(そこには \(\al\) が含まれる)の存在を、累巡回拡大の定義(62B)の説明で書いたシンプルな例で考察します。
代数的数 \(\al\) を、
\(\al=\sqrt{\sqrt{2}+1}\)
とします。この \(\al\) は \(\bs{Q}\) 上の既約な方程式、
\(f(x)=x^4-2x^2-1=0\)
の解の一つです。この \(f(x)\) は \(\al\) の最小多項式です。ちなみに \(f(x)\) は、
\(f(x)=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\)
と変形できるので、方程式 \(f(x)=0\) の解は
\(x=\pm\sqrt{\sqrt{2}+1},\:\:\:\pm i\sqrt{\sqrt{2}-1}\)
の4つです。
\(\al\) を含む \(\bs{Q}\) の拡大体 \(\bs{Q}(\al)\) を考えます。\(\bs{Q}\:\subset\:\bs{Q}(\al)\) ですが、べき根拡大だけで表現すると、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\:\subset\:\bs{Q}(\sqrt{\sqrt{2}+1})\)
の累べき根拡大になります。つまり、\(\bs{Q}\) 上の方程式、
\(x^2-2=0\)
の解の一つ \(\sqrt{2}\) を \(\bs{Q}\) に添加してべき根拡大をし、\(\bs{Q}(\sqrt{2})\) 上の方程式、
\(x^2-(\sqrt{2}+1)=0\)
の解の一つ \(\sqrt{\sqrt{2}+1}\) を \(\bs{Q}(\sqrt{2})\) に添加したのが \(\bs{Q}(\sqrt{\sqrt{2}+1})\) です。2つのべき根拡大の拡大次数は2です。\(1\) の原始2乗根は \(-1\) なので、始めから \(\bs{Q}\) に含まれています。従って、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) は
・べき根拡大
・巡回拡大
\(\mr{Gal}(\bs{Q}(\sqrt{2})=\{\sg_1,\:\sg_2\}\)
\(\sg_1=e\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
・\(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) 上の多項式 \(x^2-2\) の最小分解体
となります。まったく同様に、
\(\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{\sqrt{2}+1})\) は
・べき根拡大
・巡回拡大
です。しかし、\(\bs{Q}(\sqrt{\sqrt{2}+1})/\bs{Q}\) がガロア拡大ではありません。というのも、\(\bs{Q}(\sqrt{\sqrt{2}+1})\) は \(\bs{Q}\) 上ではなく \(\bs{Q}(\sqrt{2})\) 上の方程式、
\(x^2-(\sqrt{2}+1)=0\)
の解の一つ \(\sqrt{\sqrt{2}+1}\) を \(\bs{Q}(\sqrt{2})\) に添加したものだからです。
そこで、\(\bs{Q}(\sqrt{2})\) 上の2つの方程式、
・\(x^2-\sg_1(\sqrt{2}+1)=0\)
・\(x^2-\sg_2(\sqrt{2}+1)=0\)
の解を順に \(\bs{Q}(\sqrt{2})\) に追加することにします。つまり、
・\(\sqrt{\phantom{-}\sqrt{2}+1}\)
・\(\sqrt{-\sqrt{2}+1}\)
の2つを \(\bs{Q}(\sqrt{2})\) に追加します。ガロア群は必ず単位元 \(e\) を含むので、\(\sg_1(\sqrt{2}+1)\) と \(\sg_2(\sqrt{2}+1)\) のどちらかは \(\al=\sqrt{\sqrt{2}+1}\) になります。この追加は2つともべき根拡大であり、巡回拡大です。こうして出来上がった拡大体を \(\bs{E}\) とすると、
\(\bs{E}=\bs{Q}(\sqrt{\sqrt{2}+1},\sqrt{-\sqrt{2}+1})\)
です。以上のことを別の観点で言うと、多項式 \(g(x)\) を、
\(g(x)=(x^2-\sg_1(\sqrt{2}+1))(x^2-\sg_2(\sqrt{2}+1))\)
と定義するとき、
\(g(x)=0\) の解を \(\bs{Q}(\sqrt{2})\) に追加したのが \(\bs{E}\)
ということになります。\(g(x)\) を計算すると、
\(\begin{eqnarray}
&&\:\:g(x)&=(x^2-\sg_1(\sqrt{2}+1))(x^2-\sg_2(\sqrt{2}+1))\\
&&&=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\\
&&&=x^4-2x^2-1\\
\end{eqnarray}\)
となり、\(g(x)\) は \(\bs{Q}\) 上の多項式です。なぜそうなるかと言うと、\(g(x)\) の係数は \(\sg_1(\sqrt{2}+1)\) と \(\sg_2(\sqrt{2}+1)\) の対称式で表されるからで、従ってガロア群の元 \(\sg_1,\:\sg_2\) を作用させても不変であり、つまり係数が有理数だからです。ここから得られる結論は、
\(\bs{E}\) は \(\bs{Q}\) 上の多項式 \(g(x)\) の最小分解体である
ということです。このことは、\(\al=\sqrt{\sqrt{2}+1}\) の最小多項式が \(x^4-2x^2-1=g(x)\) であったことからも確認できます。従ってガロア拡大の定義(52A)により、
\(\bs{E}/\bs{Q}\) はガロア拡大
です。まとめると、
\(\bs{Q}\:\subset\:\bs{Q}(\al)\:\subset\:\bs{E}\)
\(\bs{E}/\bs{Q}\) は累巡回拡大、かつガロア拡大
である \(\bs{E}\) の存在が証明できました。
以上は "2段階の2次拡大" という非常にシンプルな例ですが、このことを一般的に(多段階の \(n\)次拡大で)述べると次のようになります。
ガロア閉包
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つである \(\al\) がべき根で表されているとする。このとき「\(\bs{Q}\) のガロア拡大 \(\bs{E}\) で、\(\al\) を含み、\(\bs{E}/\bs{Q}\) が累巡回拡大」であるような 代数拡大体 \(\bs{E}\) が存在する。
[証明]
\(\bs{Q}\)上の方程式 \(f(x)=0\) の解の一つ \(\al\) がべき根で表されているとき、
となる、べき根拡大列 \(\bs{K}_i\) が存在する(= \(\bs{K}/\bs{Q}\) が累べき根拡大)。このべき根拡大列を修正して、
とできることを以下に示す。まず、\(n_i\:(0\leq i < k)\) の最小公倍数を \(n\) とし、\(1\) の原始\(n\)乗根を \(\zeta\) とする。そして、
\(\bs{F}_0=\bs{Q}(\zeta)\)
とおくと、\(\bs{K}_0(=\bs{Q})\:\subset\:\bs{F}_0\) であり、\(\bs{F}_0\) は \(1\) の原始\(n_i\)乗根 \((0\leq i < k)\) を全て含むことになる。
\(\bs{F}_0\) は \(\bs{Q}(\zeta)\) だから、\(\mr{Gal}(\bs{F}_0/\bs{Q})=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積に同型であり(63F)、従って可解群である(61B)。つまり、\(\bs{F}_0/\bs{Q}\) は累巡回拡大である(62C)。
次に、
\(\bs{F}_1=\bs{F}_0(\al_1)\)
とおく。\(\al_1\) は \(\bs{K}_0=\bs{Q}\) 上の方程式 \(x^{n_0}-a_0=0\:(a_0\in\bs{K}_0\:\subset\:\bs{F}_0)\) の根の一つで、\(\al_1=\sqrt[n_0]{a_0}\) であるから、\(\bs{F}_1\) は \(\bs{F}_0\) のべき根拡大になる。
すると、\(\bs{F}_0\)は \(1\) の原始\(n_0\)乗根を含むから、原始\(\bs{n}\)乗根を含むべき根拡大の定理(63H)により、\(\bs{F}_1/\bs{F}_0\) は巡回拡大である。この拡大次数は \([\bs{F}_1:\bs{F}_0]=[\bs{K}_1:\bs{K}_0(=\bs{Q})]=n_0\) である。
また \(\bs{F}_1\)は、\(\bs{Q}\) 上の方程式 \(x^{n_0}-a_0=0\) の解 \(\al_1\eta^j\)(\(\eta\) は \(1\) の原始\(n_0\)乗根。\(0\leq j < n_0\))をすべて含むから、\(\bs{F}_1/\bs{Q}\) はガロア拡大である。
次に \(\bs{K}_2\) を修正した \(\bs{F}_2\) を考える。\(\mr{Gal}(\bs{F}_1/\bs{Q})\) の元を \(\sg_j\:(1\leq j\leq m,\:\sg_1=e)\) の \(m\)個とする。
\(\al_2\) は \(x^{n_1}-a_1=0\:\:(a_1\in\bs{K}_1\:\subset\:\bs{F}_1)\) の根の一つであった。そこで、
\(\sg_j(a_1)\) \((1\leq j\leq m)\)
という \(m\)個の元をもとに、
\(x^{n_1}-\sg_j(a_1)=0\:(a_1\in\bs{K}_1\:\subset\:\bs{F}_1,\:\:1\leq j\leq m)\)
という \(m\)個の方程式群を考える。\(\sg_j\) の中には単位元 \(e\) が含まれるため、\(x^{n_1}-a_1=0\) も方程式群の中の一つである。
この \(m\)個の方程式の \(m\)個の解、
\(\sqrt[n_1]{\sg_j(a_1)}\) \((1\leq j\leq m)\)
を \(\bs{F}_1\) に順々に添加していき、最終的にできた体を \(\bs{F}_2\) とする。\(\bs{F}_1\) は \(1\) の原始 \(n_1\)乗根を含むから、\(\sqrt[n_1]{\sg_j(a_1)}\) \((1\leq j\leq m)\) の添加はすべて巡回拡大である(63H)。つまり、\(\bs{F}_2\) は \(\bs{F}_1\) の累巡回拡大である。\(\sg_j\) の中には単位元があるから、\(\bs{F}_2\) には \(\al_2=\sqrt[n_1]{a_1}\) を含む。
ここで多項式 \(g(x)\) を、
\(g(x)=\displaystyle\prod_{j=1}^{m}(x^{n_1}-\sg_j(a_1))\)
と定義する。\(\bs{F}_1\) は \(1\) の原始 \(n_1\)乗根を含むから、\(\bs{F}_2\) は \(g(x)=0\) のすべての解を \(\bs{F}_1\) に添加した拡大体である。
多項式 \(g(x)\) の係数は、根と係数の関係から \(\sg_j(a_1)\:\:(1\leq j\leq m)\) の対称式であり、係数に任意の \(\sg_j\:(=\mr{Gal}(\bs{F}_1/\bs{Q})\) の元\()\) を作用させても不変である。つまり係数は有理数であり、\(g(x)\) は \(\bs{Q}\) 上の多項式である。結局、\(\bs{F}_2\) は \(\bs{Q}\) 上の多項式 \(g(x)\) の最小分解体であり、\(\bs{F}_2/\bs{Q}\) はガロア拡大である(52A)。
まとめると、
で、かつ、
\(g(x)=\displaystyle\prod_{j=1}^{m}(x^{n_1}-\sg_j(a_1))\)
の条件で、\(g(x)=0\) のすべての解を \(\bs{F}_1\) に添加した拡大体を \(\bs{F}_2\) とすると、
となる。
この \(\bs{K}_i\) を \(\bs{F}_i\) に修正する操作は、\(\bs{K}_k\) を修正して \(\bs{F}_k\) にするまで続けることができる。従って、
とすることができる。[証明終]
\(1\) の原始\(n\)乗根を含む \(\bs{Q}(\zeta)\) からのべき根拡大を考えることによって、体の拡大が巡回拡大(=ガロア群が巡回群であるガロア拡大)になり(63H)、その繰り返しは累巡回拡大になります。しかし累巡回拡大が "全体としてガロア拡大になる" とは限りません(62B)。
そこで、ひと工夫して、\(\bs{\bs{F}_i}\) が常に \(\bs{\bs{Q}}\) 上の方程式 \(\bs{g(x)}\) の最小分解体で、かつ \(\bs{\al_i}\) を含むようにすると、\(\bs{F}_i/\bs{Q}\) が常にガロア拡大になっているので、\(\bs{E}/\bs{Q}\) もガロア拡大になります。しかも最終到達点である \(\bs{F}_k=\bs{E}\) の中には、元々の方程式の解である \(\al\) がある。このような \(\bs{E}\) の存在が重要です。この \(\bs{Q}(\zeta)\:\rightarrow\:\bs{E}\) の拡大を考えることで、単なるべき根拡大列だった \(\bs{Q}\:\rightarrow\:\bs{K}\) をガロア理論の俎上に乗せることができます。
一方、\(\bs{\bs{Q}(\zeta)/\bs{Q}}\) が累巡回拡大になるのは、全く別のロジックによります。つまり、\(\bs{Q}(\zeta)/\bs{Q}\) がガロア拡大で(63D)かつ、ガロア群が巡回群の直積に同型(63F)であり、従ってガロア群が可解群(61B)だからです。そうすると累巡回拡大ガロア群の可解性(62C)によって \(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大です。
以上の2つの合わせ技で、\(\bs{Q}\) から \(\bs{E}\) に至る累巡回拡大の列ができ、しかも \(\bs{E}/\bs{Q}\) がガロア拡大になっていて、次の可解性の必要条件の証明につながります。
可解性の必要条件
\(\bs{Q}\) 上の \(n\)次既約方程式 \(f(x)=0\) の解の一つ がべき根で表されているとする。\(f(x)\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) は可解群である。
[証明]
ガロア閉包の存在定理(64A)により、\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つがべき根で表されているとすると、
となるものが存在する。\(\bs{E}/\bs{Q}\) がガロア拡大なので、\(\mr{Gal}(\bs{E}/\bs{Q})\) による \(\al\) の移り先(\(f(x)=0\) の解)は \(\bs{E}\) に含まれる。最小分解体 \(\bs{L}\) は \(f(x)=0\) の \(n\)個の解を含む最小の体である。ゆえに \(\bs{E}\) は最小分解体 \(\bs{L}\) を含んでいる。
また、\(\bs{E}/\bs{Q}\) がガロア拡大ということは、中間体からのガロア拡大の定理(52C)により、\(\bs{E}/\bs{L}\) もガロア拡大である。従って、
\(\mr{Gal}(\bs{E}/\bs{Q})=G\)
\(\mr{Gal}(\bs{E}/\bs{L})=H\)
と書くと、
\(G\) \(\sp\) \(H\) \(\sp\) \(\{\:e\:\}\)
\(\bs{Q}\) \(\subset\) \(\bs{L}\) \(\subset\) \(\bs{E}\)
のガロア対応(53B)が成り立つ。
\(\bs{L}\) は \(\bs{Q}\) 上の既約多項式 \(f(x)\) の最小分解体だから、\(\bs{L}/\bs{Q}\) はガロア拡大である(52A)。ゆえに正規性定理(53C)により、\(H\) は \(G\) の正規部分群であり、
\(\mr{Gal}(\bs{L}/\bs{Q})\:\cong\:G/H\)
が成り立つ。
\(\bs{E}/\bs{Q}\) はガロア拡大かつ累巡回拡大だから、累巡回拡大ガロア群の可解性(62C)の定理によって \(G\) は可解群である。\(G\) が可解群なので、その剰余群である \(G/H\) も可解群である(61D)。従って、\(G/H\) と同型である \(\mr{Gal}(\bs{L}/\bs{Q})\) も可解群である。[証明終]
この定理の対偶をとると、
となります。これを用いて、非可解な5次方程式があることを証明できます。
6.5 5次方程式の解の公式はない
5次方程式には解の公式はないことをガロア理論で証明します。そのためにまず、対称群、交代群、置換の説明をします。
対称群 \(S_n\)
集合 \(\Omega_n=\{1,\:2,\:\cd\:n\}\) から \(\Omega_n\) への全単射写像(1対1写像)の全体を \(S_n\) と書き、\(n\)次の対称群(symmetric group)と言います。\(1,\:2,\:\cd\) は整数ではなく、集合の元を表す文字です。一般に集合 \(X\) から \(X\) への全単射写像を置換(permutation)と呼ぶので、\(S_n\) の元は \(n\) 個の文字の置換です。
\(S_n\) の元の一つを \(\sg\) とします。\(1\leq k\leq n\) とし、\(\sg\)による \(k\) の移り先を \(\sg(k)\) とすると、\(\sg\) は全単射写像なので、\(k\neq k\,'\) なら\(\sg(k)\neq\sg(k\,')\) です。従って、\((\sg(1),\sg(2),\cd,\sg(n))\) は、\((1,2,\cd n)\) の一つの順列になります。逆に、\((1,2,\cd n)\) の順列の一つを \((i_1,i_2,\cd i_n)\) とすると、\(\sg(k)=i_k\) で \(\Omega_n\) から \(\Omega_n\) への全単射写像が得られます。つまり \(S_n\) は \((1,2,\cd n)\) のすべての順列と同一視できます。
\(S_n\) の元の2つを \(\sg\)、\(\tau\) とし、\(\sg\) と \(\tau\) の合成写像 \(\sg\tau\) を、
\(\sg\tau(k)=\sg(\tau(k))\:\:(1\leq k\leq n)\)
で定義すると、\(\sg\tau\) も全単射写像なので \(S_n\) の元であり、\(S_n\) は群になります。単位元 \(e\) は \(e(k)=k\:(1\leq k\leq n)\) である恒等写像です。また、\(\sg\) は全単射写像なので逆写像 \(\sg^{-1}\) があり、群の定義を満たしています。
\(S_n\) は \((1,2,\cd n)\) のすべての順列と同一視できるので、その位数は
\(|S_n|=n\:!\)
です。\(S_n\) の元 \(\sg\) を、
\(\sg=\left(\begin{array}{c}1&2&\cd&n\\\sg(1)&\sg(2)&\cd&\sg(n)\end{array}\right)\)
と表します。この表記では縦の列が合っていればよく、並び順に意味はありません。これを使うと \(\sg\) の逆元は、
\(\sg^{-1}=\left(\begin{array}{c}\sg(1)&\sg(2)&\cd&\sg(n)\\1&2&\cd&n\end{array}\right)\)
です。
\(S_3\) の元を \(\sg_1,\sg_2,\:\cd\:\sg_6\) とし、具体的に書いてみると、
\(\sg_1=\left(\begin{array}{c}1&2&3\\1&2&3\end{array}\right)\) \(\sg_2=\left(\begin{array}{c}1&2&3\\2&3&1\end{array}\right)\)
\(\sg_3=\left(\begin{array}{c}1&2&3\\3&1&2\end{array}\right)\) \(\sg_4=\left(\begin{array}{c}1&2&3\\1&3&2\end{array}\right)\)
\(\sg_5=\left(\begin{array}{c}1&2&3\\3&2&1\end{array}\right)\) \(\sg_6=\left(\begin{array}{c}1&2&3\\2&1&3\end{array}\right)\)
となります。\(\sg_1\) は恒等置換 \(e\) です。なお \(S_3\) は、1.3節に出てきた3次の2面体群と同じものです。
巡回置換
\(S_n\) に現れる \(n\)文字からその一部を取り出します。例えば3つ取り出して、\(i,\:j,\:k\) とします。そして、
\(i\rightarrow j,\:\:j\rightarrow k,\:\:k\rightarrow i\)
と文字を循環させ、その他の文字は不動にする置換 \(\sg\) を考えます。これが巡回置換(cyclic permutation)です。
\(\sg=\left(\begin{array}{c}\cd&i&\cd&j&\cd&k&\cd\\\cd&j&\cd&k&\cd&i&\cd\end{array}\right)\)
と表せて、\(\cd\) の部分は不動です。これを簡略化して、
\(\sg=(i,\:j,\:k)\)
と表記します。\(\sg\) の逆元は、
です。一般に \(m\)文字の巡回置換 \((1\leq m\leq n)\) は、
\(\sg=(i_1,\:i_2,\:\cd\:,i_m)\)
です。長さ \(m\) の巡回置換、とも言います。逆元は文字の順序を逆順にした、
\(\sg^{-1}=(i_m,\:i_{m-1},\:\cd\:,i_1)\)
です。\(m\)文字の巡回置換を群としてとらえたとき、 \(C_m\) で表します。\(C_m\) は位数 \(m\) の巡回群で、可換群です。
特に、2文字の巡回置換を互換(transposition)と言います。巡回置換と互換について、次の定理が成り立ちます。
すべての置換は共通文字を含まない巡回置換の積で表せる。
[証明]
\(n\)次対称群 \(S_n\) の任意の元を \(\sg\) とすると、\(\sg\) は \(n\)文字の任意の置換である。\(n\)文字の中から \(\sg(a)\neq a\) である文字 \(a\) を選ぶ。そして \(\sg(a),\:\sg^2(a),\:\sg^3(a),\:\cd\) という、\(\sg\) による \(a\) の写像を繰り返す列を考える。\(\sg\)による \(a\) の移り先は最大 \(n\)個なので、列の中には、
\(\sg^j(a)=\sg^i(a)\:\:(i < j)\)
となる \(i,\:j\) が必ず出てくる。つまり、
\(\sg^{j-i}(a)=a\)
となる \(i,\:j\) が存在する。\(k_a\) を \(\sg^{k_a}(a)=a\) となる最小の数とすると、
\(\sg_1=(\sg(a),\:\sg^2(a),\:\cd\:,\sg^{k_a}(a))\)
の巡回置換と定義する。
もし仮に列 \((\br{A})\) が、\(\sg\) で変化する文字全部を尽くしているなら、題意は正しい。そうでないとき、列 \((\br{A})\) に現れない文字で \(\sg(b)\neq b\) である \(b\) を選ぶ。上と同様にして、
\(\sg_2=(\sg(b),\:\sg^2(b),\:\cd\:,\sg^{k_b}(b)=b)\)
という、2つ目の巡回置換が定義できる。列 \((\br{A})\) と \((\br{B})\) が \(\sg\) で変化する文字全部を尽くすなら、\(\sg=\sg_2\sg_1\) である。\(\sg_1\) と \(\sg_2\) に共通の文字は現れないので、\(\sg=\sg_1\sg_2\) と書いてもよい。
以上の操作は、\(\sg\) で変化する文字全部を尽くすまで繰り返すことができる。その繰り返し回数を \(m\) とすると、
\(\sg=\sg_1\sg_2\:\cd\:\sg_m\)
であり、任意の置換 \(\sg\) は巡回置換の積で表せることになる。なお、恒等置換 \(e\) は、
\(e=(i,\:j)^2\)
\(e=(i,\:j,\:k)^3\)
などであり、巡回置換の積で表せることに変わりはない。[証明終]
置換を巡回置換の積で表すと、例えば、
となります。
すべての置換は互換の積で表せる。
[証明]
巡回置換 \((1,\:2,\:3)\) は
\((1,\:2,\:3)=(1,\:3)(1,\:2)\)
と表せる(積は右から読む)。また、巡回置換 \((1,\:2,\:3\). \(4)\) は、
\((1,\:2,\:3,\:4)=(1,\:4)(1,\:3)(1,\:2)\)
である。一般に、
\((i_1,\:i_2,\:\cd\:,i_m)=(i_1,\:i_m)\:\cd\:(i_1,\:i_2)\)
である。このように巡回置換は互換の積で表せる。すべての置換は巡回置換の積で表せる(65A)ので、題意は正しい。[証明終]
交代群 \(A_n\)
一つの置換を互換の積で表す方法が一意に決まるわけではありません。たとえば、
です(積は右から読む)。ただし、積に現れる互換の数が偶数か奇数かは一意に決まります。
一つの置換を互換の積で表したとき、その互換の数は奇数か偶数かのどちらかに決まる。
[証明]
\(n\)変数の多項式 \(f(x_1,x_2,\cd,x_n)\) を、
\(f(x_1,x_2,\cd,x_n)=\displaystyle\prod_{1\leq i < j\leq n}^{}(x_i-x_j)\)
と定義する(差積と呼ばれる)。\(S_n\) の一つの元を \(\sg\) とし、\(\sg\) を \(f(x_1,x_2,\cd,x_n)\) に作用させることを、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=f(x_{\sg(1)},x_{\sg(2)},\cd,x_{\sg(n)})\)
と定義する。\(\sg\) が互換、つまり \(\sg=(i,\:j)\) であれば、
\((i,\:j)\cdot f(x_1,x_2,\cd,x_n)=-f(x_1,x_2,\cd,x_n)\)
となる。これはすべての互換で成り立つ。
\(\sg\) が \(k\)個の互換の積で表されていると、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=(-1)^kf(x_1,x_2,\cd,x_n)\)
である。もし、\(m\neq k\) として \(\sg\) が \(m\)個の互換の積で表せたとしたら、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=(-1)^mf(x_1,x_2,\cd,x_n)\)
である。従って、
\((-1)^k=(-1)^m\)
であり、\(k\) と \(m\) の偶奇は等しい。[証明終]
置換の偶奇性(65C)により、置換は2つのタイプに分けることができます。偶数個の互換の積で表す置換を偶置換(even permutaion)、奇数個の互換の積で表す置換を奇置換(odd permutaion)と言います。
偶置換の積は偶置換です。従って、\(S_n\) の偶置換の元を集めた集合は群になります。これを \(n\)次交代群(alternating group)といい、\(A_n\) で表します。
\(S_n\) の元は同数の偶置換と奇置換から成る。従って、
\([\:S_n\::\:A_n\:]=2\)
である。
\(A_n\) は \(S_n\) の正規部分群であり、\(S_n/A_n\) は巡回群である。
[証明]
\(B_n\) を \(S_n\) に含まれる奇置換の集合とする。\(S_n\) の任意の互換を \(\sg\) とすると、集合 \(\sg A_n\) のすべての元は奇置換だから、
\(\sg A_n\subset B_n\)
が成り立つ。それとは逆に、集合 \(\sg B_n\) のすべての元は偶置換だから、
\(\sg B_n\subset A_n\)
も成り立つ。この式に左から \(\sg\) を作用させると、
\(\sg^2B_n\subset\sg A_n\)
\(B_n\subset\sg A_n\)
となる。\(\sg A_n\subset B_n\) かつ \(B_n\subset\sg A_n\) なので、
\(B_n=\sg A_n\)
となり、\(B_n\) と \(A_n\) の元の数は等しい。\(S_n=A_n\cup B_n\) なので、
\([\:S_n\::\:A_n\:]=2\)
である。
\(S_n\) の部分群 \(A_n\) の元の数は \(S_n\) の元の数の半分なので、\(S_n\) は \(A_n\) の2つの左剰余類(または右剰余類)の和集合である。従って、\(B_n\) の 任意の元を \(b\) とすると、
(\(A_n\) の左剰余類) \(S_n=A_n\cup bA_n\:\:(A_n\cap bA_n=\phi)\)
(\(A_n\) の右剰余類) \(S_n=A_n\cup A_nb\:\:(A_n\cap A_nb=\phi)\)
となり、\(bA_n=A_nb\) である。また \(A_n\) の元 \(a\) については、\(A_n\) が群なので \(aA_n=A_n,\:A_na=A_n\) である。従って \(S_n\) の任意の元 \(\sg\) について \(\sg A_n=A_n\sg\) が成り立ち、\(A_n\) は \(S_n\) の正規部分群である。
\(A_n\) が正規部分群なので、\(S_n/A_n\) は剰余群である。\(S_n\) の任意の元を \(\sg\) とし、\(S_n/A_n\) の元を \(\sg A_n\) とすると、
\((\sg A_n)^2=\sg A_n\sg A_n=\sg\sg A_nA_n=\sg^2A_n\)
となるが、\(\sg A_n=B_n\) であり \(\sg B_n=A_n\) だから、\(\sg^2A_n=A_n\) である。つまり、
\((\sg A_n)^2=A_n\)
を満たす。\(A_n\) は 剰余群 \(S_n/A_n\) の単位元だから、\(S_n/A_n\) は巡回群でである。[証明終]
交代群 \(A_n\) の任意の元は、3文字の巡回置換の積で表せる。
[証明]
\(A_n\) の任意の元は偶数個の互換の積で表せる。この互換の積を2つずつ右から(ないしは左から)取り出すことを考える。2つの互換の積には4つの文字があるが、それには次の2つパターンがある。
異なる4文字
\((i,\:j)(k,\:m)\)
異なる3文字
\((i,\:j)(i,\:k)\)
異なる3文字のうち、\((i,\:j)(j,\:k)\) のパターンは、\(i\) を \(j\) と読み替え、\(j\) を \(i\) と読み替えると \((j,\:i)(i,\:k)\) となり、\((i,\:j)(i,\:k)\) と同じである。また、\((i,\:j)(k,\:i)\) や \((i,\:j)(k,\:j)\) も \((i,\:j)(i,\:k)\) と同じである。
異なる2文字から成る \((i,\:j)(i,\:j)\) は恒等互換なので無視してよい。
2つの互換の積の2パターンは、いずれも3文字の巡回置換の積で表せる。つまり、
\(\left(\begin{array}{c}i&j&k&m\\k&i&j&m\end{array}\right)=(i,\:k,\:j)\)
\(\left(\begin{array}{c}k&i&j&m\\j&i&m&k\end{array}\right)=(j,\:m,\:k)\)
\(\left(\begin{array}{c}i&j&k&m\\j&i&m&k\end{array}\right)=(i,\:j)(k,\:m)\)
なので、
\((i,\:j)(k,\:m)=(j,\:m,\:k)(i,\:k,\:j)\)
である。また、巡回置換を互換の積で表す標準的な方法(65B)から、
\((i,\:j)(i,\:k)=(i,\:k,\:j)\)
である。
\(A_n\) は「2つの互換の積」の積、で表現でき、「2つの互換の積」は「3文字の巡回置換の積」で表せるので、題意は正しい。[証明終]
なお、上の交代群は正規部分群(65D)の証明では、「交代群 \(A_n\) の元の数が、対称群 \(S_n\) の元の数の半分である」ことしか使っていません。従って次の定理が成り立ちます。
群 \(G\) の部分群を \(N\) とする。
\(|G|=2|N|\)
のとき(つまり 群の指数 \([G:N]=2\) のとき)、\(N\) は \(G\) の正規部分群である。
対称群の可解性
5次以上の対称群、\(S_n\:\:(n\geq5)\) は可解群ではない。
[証明]
\(S_n\) の交代群を \(A_n\) とする。\(A_n\) は \(S_n\) の部分群なので、もし \(A_n\) が可解群でなければ、可解群の部分群は可解群の定理(61C)の対偶により、\(S_n\) は可解群ではない。以下、\(A_n\) が可解群でないことを背理法で証明する。
\(A_n\) が可解群と仮定して矛盾を導く。\(A_n\) が可解群とすると、定義により \(A_n\) には正規部分群 \(N\:(N\neq A_n)\) があり、\(A_n/N\) が巡回群である。
\(A_n\) の任意の2つの元を \(x,\:y\) とし、剰余類 \(xN\) と \(yN\) を考える。\(A_n/N\) は巡回群なので可換群であり、\(xNyN=yNxN\) である。\(N\) は正規部分群なので、\(Ny=yN\)、\(Nx=xN\) であり、これを用いて \(xNyN=yNxN\) を変形していくと、
\(xNyN=yNxN\)
\(xyNN=yxNN\)
\(xyN=yxN\)
となる。この式に左から \(x^{-1}y^{-1}\) をかけると、
\(x^{-1}y^{-1}xyN=x^{-1}y^{-1}yxN\)
\(x^{-1}y^{-1}xyN=N\)
となる。部分群の元の条件の定理(41C)より、\(aN=N\) と \(a\in N\) は同値である。従って、
\(x^{-1}y^{-1}xy\in N\)
である。
一般に \(x^{-1}y^{-1}xy\) を \(x\) と \(y\) の交換子と呼ぶ。上の式の変形プロセスから言えることは、\(A_n\) の任意の2つの元(\(N\) の元である必要はない)の交換子は \(N\) の元になるということである。
\(S_n\:\:(n\geq5)\) の任意の3文字巡回置換を \((i,\:j,\:k)\) とする。
\((i,\:j,\:k)=(i,\:k)(i,\:j)\)
なので、\((i,\:j,\:k)\) は偶置換であり、
\((i,\:j,\:k)\in A_n\)
である。ここで、\(\bs{i,\:j,\:k}\) とは違う2つの文字 \(\bs{l,\:m}\) を選ぶ。\(\bs{n\geq5}\) ならこれは常に可能である。そして、
\(x=(i,\:m,\:j)\)
\(y=(i,\:l,\:k)\)
とし、\(x,\:y\) の交換子を作ってみる。計算すると以下のようになる。
\(x^{-1}y^{-1}xy\)
\(=(i,\:m,\:j)^{-1}(i,\:l,\:k)^{-1}(i,\:m,\:j)(i,\:l,\:k)\)
\(=(j,\:m,\:i)(k,\:l,\:i)(i,\:m,\:j)(i,\:l,\:k)\)
\(x^{-1}y^{-1}xy\)
\(=(j,\:m,\:i)(k,\:l,\:i)(i,\:m,\:j)(i,\:l,\:k)\)
\(=\left(\begin{array}{c}i&j&k&l&m\\j&k&i&l&m\end{array}\right)\)
\(=(i,\:j,\:k)\)
\(x^{-1}y^{-1}xy\in N\) なので、
\((i,\:j,\:k)\in N\)
である。つまり任意の3文字巡回置換は \(N\) に含まれる。
\(A_n\) のすべての元は3文字巡回置換の積で表される(65E)から、\(A_n\) は \(N\) の元の積で表せることになる。つまり、
\(A_n\subset N\)
だが、もともと \(N\) は \(A_n\) の部分集合だから、
\(A_n=N\)
である。これは \(N\neq A_n\) という仮定と矛盾する。従って、\(A_n\) の正規部分群 \(N\:(N\neq A_n)\) で、\(A_n/N\) が巡回群であるようなものはなく、\(A_n\) は可解群ではない。
\(S_n\:\:(n\geq5)\) は可解群ではない部分群 \(A_n\) をもつから、可解群の部分群は可解群の定理(61C)の対偶によって、\(S_n\) は可解群ではない。[証明終]
\(S_5\)(位数 \(120\)) や、その部分群 \(A_5\)(位数 \(60\))は可解群ではありません。しかし、「\(S_5\) のすべての部分群が可解群ではない」というわけではありません。\(S_5\) の部分群では、\(F_{20}\)(位数 \(20\))、\(D_{10}\)(位数 \(10\))、\(C_5\)(位数 \(5\))が可解群であることが知られています。これについては第7章で述べます。
一般5次方程式
5次方程式には代数的に解けるものと解けないものがあります。従って、全ての5次方程式に適用可能な根の公式はありません。5次方程式に根の公式がないことはガロア以前に証明されていたのですが、なぜ根の公式がないのか、その理由を明らかにしたのがガロア理論です。
係数が変数の方程式を「一般方程式」と言います。根の公式があるということは一般方程式が解けることを意味します。以下は、一般5次方程式が代数的に解けないことの証明ですが、この証明では係数が変数ではなく、解を変数としています。
\(\bs{Q}\) の代数拡大体を \(\bs{K}\) とする。\(\bs{K}\) の任意の元である5つの変数 \(b_1,b_2,b_3,b_4,b_5\) を根とする多項式を、
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
とし、\(\bs{Q}\) に \(a_0,a_1,a_2,a_3,a_4,\)を添加した代数拡大体を \(\bs{F}\) とする。つまり、
\(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\)
である。
このとき、\(\bs{K}\) の \(\bs{F}\) 上の ガロア群 \(G\) は5次対称群 \(S_5\) である。\(S_5\) は可解群ではないので(65G)、従って \(b_i\) を \(a_i\) のべき根で表すことはできない。
[証明]
代数拡大体 \(\bs{F}\) の作り方から、\(\bs{K}\) は \(\bs{F}\) 上の多項式 \(f(x)\) の最小分解体である。従って \(\bs{K}/\bs{F}\) はガロア拡大である。\(G=\mr{Gal}(\bs{K}/\bs{F})\) とおくと、\(G\) は \(\bs{F}\) の元を固定する自己同型写像が作る群である。
対称群 \(S_5\) の元の一つを \(s\) とし、
\(s=\left(\begin{array}{c}1&2&3&4&5\\s(1)&s(2)&s(3)&s(4)&s(5)\end{array}\right)\)
とする。このとき、
\(\sg(b_i)=b_{s(i)}\:\:(i=1,2,3,4,5)\)
で、\(b_i\) に作用する写像 \(\sg\) を定義する。そうすると \(\sg\) は \(f(x)=0\) の解 \(b_i\) を共役な解に移す写像だから、自己同型写像である。また、
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
の根と係数の関係から、
である。つまり \(a_i\:(0\leq i\leq4)\) は \(b_i\:(1\leq i\leq5)\) の対称式で表される。
従って、\(\sg(a_0)=a_0\)、\(\sg(a_1)=a_1\)、\(\sg(a_2)=a_2\)、\(\sg(a_3)=a_3\)、\(\sg(a_4)=a_4\) である。つまり \(\sg\) は \(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\) の元を固定する。従って \(\sg\) は \(\bs{F}\) の元を固定する \(\bs{K}\) の自己同型写像であり、\(G\) の元である。以上のことは \(S_5\) の任意の元 \(s\) について言えるから \(S_5\subset G\) である。
これを踏まえて \(\bs{F}\) 上の \(\bs{K}\) の拡大次数 \([\:\bs{K}\::\:\bs{F}\:]\) を考えると、\([\:\bs{K}\::\:\bs{F}\:]\) は \(\mr{Gal}(\bs{K}/\bs{F})\) の位数に等しいから、
\([\:\bs{K}\::\:\bs{F}\:]=|G|\geq|S_5|=5!=120\)
である。
次に、
という体の拡大列を考える。最初の拡大 \(\bs{F}\subset\bs{F}(b_1)\) をみると、\(b_1\) は \(\bs{F}\) 上の 5次方程式 \(f(x)=0\) の根だから、
\([\:\bs{F}(b_1)\::\:\bs{F}\:]\leq\mr{deg}\:f(x)\:=5\)
である。等号は \(f(x)\) が既約多項式のときである。さらに、\(b_2\) は
4次方程式 \(f(x)/(x-b_1)\) の根だから、
\([\:\bs{F}(b_1,b_2)\::\:\bs{F}(b_1)\:]\leq4\)
である。以上を順に続けると、体の拡大次数の連鎖律(33H)により、
\([\:\bs{K}\::\:\bs{F}\:]\)
である。従って、\([\:\bs{K}\::\:\bs{F}\:]\geq5!\) と合わせると \([\:\bs{K}\::\:\bs{F}\:]=5!\) であり、
\(|G|=|S_5|\)
となって、
\(G\cong S_5\)
である。つまり、一般5次方程式のガロア群は \(S_5\) と同型であることが証明できた。\(S_5\) は可解群ではないので(65G)、それと同型である \(G\) も可解群ではない。従って \(b_i\) を \(a_i\) のべき根で表すことはできず、一般5次方程式に解の公式はない。[証明終]
6.6 可解ではない5次方程式
5次方程式の全てに適用できる解の公式がないことは、ガロア以前に証明されていました(アーベル・ルフィニの定理)。しかしガロア理論によって、解の公式がないことの「原理」が明確になりました。つまり係数が変数である一般5次方程式は、解が四則演算とべき根で表現できる(=可解である)ための必要条件を満たさないから公式は作れないのです(65H)。
ということは、この「原理」を用いて、可解ではない、係数が数値の方程式を具体的に構成できることになります。それを以下で行います。そのためにまず、コーシーの定理を証明します。なお、コーシー(19世紀フランスの数学者)の名がついた定理はいくつかありますが、これは「群論のコーシーの定理」です。
コーシーの定理
群 \(G\) の位数 \(|G|\) が素数 \(p\) を約数にもつとき、\(g^p=e\:\:(g\neq e)\) となる \(G\) の元 \(g\) が存在する。つまり、\(G\) は位数 \(p\) の巡回群を部分群としてもつ。
[証明]
本論に入る前に、証明に使う定義を行う。\(X\) を、元の数が \(N\) の集合とし、そこから重複を許して \(n\)個の元を取り出して1列に並べた順列を考える。このような順列の集合を \(P\) とする。つまり、
\(P=\{\:(x_1,x_2,\cd,x_n)\:|\:x_i\in X\:\}\)
である。\((x_1,x_2,\cd,x_n)\) は並べる順序に意味がある、いわゆる重複順列で、集合 \(P\) の元の数は、
\(|P|=N^n\)
である。
\(P\) から自分自身 \(P\) への写像 \(\sg\) を、
\(\sg\::\:(x_1,x_2,\cd,x_n)\longmapsto(x_n,x_1,x_2,\cd,x_{n-1})\)
と定義する。最後尾の元を先頭に持ってくる "循環写像" である(ここだけの用語)。そうすると、集合 \(P\) の任意の元、\(\bs{a}\) について、
\(\sg^n(\bs{a})=\bs{a}\)
となり、\(\sg^n=e\) (\(e\::\) 恒等写像)である。
次に、集合 \(P\) のある元を \(\bs{a}\) としたとき、
\(\sg^d(\bs{a})=\bs{a}\)
となる最小の \(d\:\:(1\leq d\leq n)\) を、"\(\bs{a}\) の循環位数" と定義する(ここだけの用語)。そうすると、循環位数 \(\bs{d}\) は \(\bs{n}\) の約数になる。なぜなら、もし
\(n=kd+r\:\:(1\leq r < d)\)
だとすると、
\(\begin{eqnarray}
&&\:\:\sg^n(\bs{a})&=\sg^{kd+r}(\bs{a})\\
&&&=\sg^r((\sg^d)^k(\bs{a}))\\
&&&=\sg^r(\bs{a})\\
&&\:\:\sg^r(\bs{a})&=\bs{a}\\
\end{eqnarray}\)
となって、\(d\) が \(\sg^d(\bs{a})=\bs{a}\) となる最小の数ではなくなるからである。
循環位数の例をあげると、
\(\begin{eqnarray}
&&\:\:N&=6\\
&&\:\:X&=\{\:1,\:2,\:3,\:4,\:5,\:6\:\}\\
&&\:\:n&=6\\
\end{eqnarray}\)
の場合、
\(\bs{a}=(1,\:2,\:3,\:4,\:5,\:6)\:\:\rightarrow\:\:d=6\)
\(\bs{a}=(1,\:2,\:2,\:2,\:2,\:2)\:\:\rightarrow\:\:d=6\)
\(\bs{a}=(1,\:2,\:3,\:1,\:2,\:3)\:\:\rightarrow\:\:d=3\)
\(\bs{a}=(1,\:2,\:1,\:2,\:1,\:2)\:\:\rightarrow\:\:d=2\)
\(\bs{a}=(1,\:1,\:1,\:1,\:1,\:1)\:\:\rightarrow\:\:d=1\)
などである。以上を踏まえて本論に入る。
積が単位元になるような \(G\) の \(p\)個(\(p\):素数)の元の組の集合、
\(S\:=\:\{\:(x_1,x_2,\cd,x_p)\:\:|\:\:x_i\in G,\:x_1x_2\cd x_p=e\:\}\)
を考える。まず、\(S\) の元の数 \(|S|\) を求める。\(S\) の始めから \(p-1\) 個までの \(x_i\:(1\leq i\leq p-1)\) は、全く任意に選ぶことができる。なぜなら、そうしておいて
\(x_p=(x_1x_2\cd x_{p-1})^{-1}\)
とすれば、
\(x_1x_2\cd x_{p-1}x_p\)
\(=x_1x_2\cd x_{p-1}(x_1x_2\cd x_{p-1})^{-1}\)
\(=e\)
となり、\(S\) の元になるからである。\(x_i\:(1\leq i\leq p-1)\) の選び方はそのすべてについて \(|G|\) 通りあるから、
\(|S|=|G|^{p-1}\)
である。
次に、\(S\) の任意の元を \(\bs{a}\) とすると、\(\sg(\bs{a})\) もまた \(S\) の元になる。なぜなら、
\(\bs{a}=(x_1,x_2,\cd,x_p)\:\:\:(x_i\in G)\)
とおくと、
\(x_1x_2\cd x_{p-1}x_p=e\)
だが、この式に左から \(x_p\) をかけ、右から \(x_p^{-1}\) をかけると、
\(x_px_1x_2\cd x_{p-1}x_px_p^{-1}=x_pex_p^{-1}\)
\(x_px_1x_2\cd x_{p-1}=e\)
となり、これは \(\sg(\bs{a})\in S\) を意味しているからである。
\(S\) のすべての元に循環位数を割り振ると、\(\bs{p}\) が素数なので、循環位数は \(\bs{1}\) か \(\bs{p}\) のどちらかである。循環位数が \(1\) である \(S\) の元とは、
\((\overbrace{x,\:x,\:\cd\:,\:x}^{p\:個})\:\:(x\in G)\)
のように、\(G\) の同じ元を \(p\) 個並べたものである。また、循環位数が \(p\) の元とは、\(p\)個の \(G\) の元に1つでも違うものがあるような \(S\) の元である。
そこで、循環位数 \(p\) の \(S\) の元に着目する。その一つを \(\bs{a}_1\) とすると、
\(S_1=\{\bs{a}_1,\:\sg(\bs{a}_1),\:\sg^2(\bs{a}_1),\:\cd\:,\sg^{p-1}(\bs{a}_1)\}\)
は、すべて相異なる \(p\) 個 の \(S\) の元である。さらに、\(S_1\) に含まれない循環位数 \(p\) の元を \(\bs{a}_2\) とすると、
\(S_2=\{\bs{a}_2,\:\sg(\bs{a}_2),\:\sg^2(\bs{a}_2),\:\cd\:,\sg^{p-1}(\bs{a}_2)\}\)
も、すべて相異なる \(p\) 個 の \(S\) の元であり、しかも \(S_1\) とは重複しない。この操作は順々に繰り返せるから、いずれ循環位数 \(p\) の元は \(S_1,\:S_2,\:\cd\) でカバーできることとなる。循環位数 \(p\) の \(S\) の元の全部が、
\(S_1\:\cup\:S_2\:\cup\:\cd\:\cup\:S_q\)
と表現できたとしたら、その元の数は \(pq\) である。
循環位数 \(1\) の \(S\) の元の数は、\(S\) の元の数から循環位数 \(p\) の元の数を引いたものである。
\(|S|=|G|^{p-1}\)
だったから、\(p\) が \(|G|\) の約数である、つまり \(|G|\) が \(p\) の倍数であることに注意すると、
循環位数 \(1\) の元の数
\(=|G|^{p-1}-pq\equiv0\:\:(\mr{mod}\:p)\)
となる。この、循環位数 \(1\) の元の数は \(0\) ではない。なぜなら、
\((\overbrace{e,\:e,\:\cd\:,\:e}^{p\:個})\)
は 循環位数が \(1\) の元だからである。つまり、循環位数 \(1\) の元の数は \(p\) 以上の \(p\) の倍数である。従って、\(S\) には \((e,\:e,\:\cd\:,\:e)\) 以外に、
\((\overbrace{g,\:g,\:\cd\:,\:g}^{p\:個})\:\:\:\:(g\neq e,\:g\in G)\)
が必ず存在する。従って、
\(g^p=e\:\:(g\neq e)\)
である \(g\) が存在する。この式が成立するということは、\(g\) の位数は \(p\) の約数であるが、\(p\) が素数なので、\(g\) の位数は \(p\) である。従って、
\(\{\:g,\:g^2,\:\cd\:,g^{p-1},\:g^p=e\:\}\)
は位数 \(p\) の巡回群である。[証明終]
実数解3つの5次方程式は可解ではない
\(f(x)\) を既約な5次多項式とする。方程式 \(f(x)=0\) が複素数解を2つ、実数解を3つもつなら、方程式は可解ではない。
[証明]
\(f(x)=0\) の複素数解を \(\al_1,\:\al_2\)、実数解を \(\al_3,\:\al_4,\:\al_5\) とする。また、それらを \(\bs{Q}\) に付加した体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\al_3,\al_4,\al_5)\) とする。また、ガロア群 \(\mr{Gal}(\bs{L}/\bs{Q})\) を \(G\) と書く。
一般に、複素数 \(z=r+is\) が有理数係数の方程式の解なら、\(\ol{\,z\,}=r-is\) も解である。つまり \(z\) と \(\ol{\,z\,}\) は共役(同じ方程式の解同士)である(=共役複素数)。その理由は以下である。
まず、\(z_1\) と \(z_2\) を2つの複素数とすると、
\(\ol{z_1+z_2}=\ol{z_1}+\ol{z_2}\)
が成り立つ。また、
\(z_1=r+is\)
\(z_2=u+iv\)
とすると、
\(\begin{eqnarray}
&&\:\:z_1z_2&=ru-sv+i(su+rv)\\
&&\:\:\ol{z_1}\cdot\ol{z_2}&=(r-is)(u-iv)\\
&&&=ru-sv-i(su+rv)\\
\end{eqnarray}\)
なので、
\(\ol{z_1z_2}=\ol{z_1}\cdot\ol{z_2}\)
である。有理数係数の方程式を、3次方程式の例で、
\(x^3+ax^2+bx+c=0\)
とし、\(z\) をこの方程式の解だとすると、
\(z^3+az^2+bz+c=0\)
\(\ol{z^3+az^2+bz+c}=\ol{\,0\,}\)
\(\ol{z^3}+\ol{az^2}+\ol{bz}+\ol{\,c\,}=0\)
\(\ol{\,z\,}^3+\ol{\,a\,}\ol{\,z\,}^2+\ol{\,b\,}\ol{\,z\,}+c=0\)
\(\ol{\,z\,}^3+a\ol{\,z\,}^2+b\ol{\,z\,}+c=0\)
となって、\(\ol{\,z\,}\) も方程式の解である。もちろんこれは \(n\)次方程式でも成り立つ。
そこで、\(f(x)=0\) の複素数解 \(\al_1,\:\al_2\) を、
\(\al_1=a+ib\)
\(\al_2=a-ib\)
とする。ここで、複素数 \(r+is\) に作用する \(\bs{L}\) の写像を \(\tau\) を、
\(\tau(r+is)=r-is\)
と定める。そうすると、
\(\tau(\al_1)=\al_2,\:\tau(\al_2)=\al_1,\)
\(\tau(\al_3)=\al_3,\:\tau(\al_4)=\al_4,\:\tau(\al_5)=\al_5\)
となり(\(\al_3,\:\al_4,\:\al_5\) は実数なので \(\tau\) で不変)、\(\tau\) は \(f(x)=0\) の2つの解を入れ替えるから \(\bs{L}\) の自己同型写像になり(51E)、すなわち \(G\) の元である。\(\al_1\) を \(1\)、\(\al_2\) を \(2\) と書き、巡回置換の記法を使うと、
\(\tau=(1,\:2)\)
である。
一方、\(f(x)\) は既約多項式なので単拡大体の基底の定理(33F)により、\(\bs{Q}(\al_1)\) の次元は \(5\)、つまり \([\bs{Q}(\al_1)\::\:\bs{Q}]=5\) である。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}\::\:\bs{Q}\:]=[\:\bs{L}\::\:\bs{Q}(\al_1)\:][\bs{Q}(\al_1)\::\:\bs{Q}]\)
が成り立つので、\([\:\bs{L}\::\:\bs{Q}\:]\) は \(5\) の倍数である。\(|G|=[\:\bs{L}\::\:\bs{Q}\:]\) なので(52B)、ガロア群 \(G\) の位数は \(5\) を約数にもつ。
そうするとコーシーの定理(66A)より、\(G\) の部分群には位数 \(5\) の巡回群がある。それを、
\(H=\{\:\sg,\:\sg^2,\:\sg^3,\:\sg^4,\:\sg^5=e\:\}\)
とする。5つの解の置換の中で、位数 \(5\) の巡回群を生成する \(\sg\) は、巡回置換の記法で書くと、
\(\sg_1=(1,\:2\:,3,\:4,\:5)\)
\(\sg_2=(1,\:3\:,5,\:2,\:4)\)
\(\sg_3=(1,\:4\:,2,\:5,\:3)\)
\(\sg_4=(1,\:5\:,4,\:3,\:2)\)
の4つである。これらには、
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_3\)
\(\sg_1^{\:4}=\sg_4\)
の関係がある。そこで、\(G\) の中にある位数 \(5\) の巡回群は、
\(\sg=(1,\:2\:,3,\:4,\:5)\)
だとして一般性を失わない。そうすると、\(G\) の中には、
\(\tau=(1,\:2)\)
\(\sg=(1,\:2\:,3,\:4,\:5)\)
の2つの元があることになる。実は、
のである。それを証明する。
\(G\) は群なので \(\sg^{-1}\) も \(G\) に含まれる(\(\sg\) は位数 \(5\) の巡回群の元なので \(\sg^{-1}=\sg^4\))。まず、\(\sg\tau\sg^{-1}\) を計算してみると、
\(\sg\tau\sg^{-1}=(1,2,3,4,5)(1,2)(5,4,3,2,1)\)
なので、
\(\begin{eqnarray}
&&\:\:\sg\tau\sg^{-1}&=\left(\begin{array}{c}1&2&3&4&5\\1&3&2&4&5\end{array}\right)\\
&&&=(2,\:3)\\
\end{eqnarray}\)
となる。同様にして、
なので、
\(\begin{eqnarray}
&&\:\:\sg^2\tau\sg^{-2}&=\sg(\sg\tau\sg^{-1})\sg^{-1}\\
&&&=\sg\cdot(2,3)\cdot\sg^{-1}\\
&&&=\left(\begin{array}{c}1&2&3&4&5\\1&2&4&3&5\end{array}\right)\\
&&&=(3,\:4)\\
\end{eqnarray}\)
である。以下、
となる。つまり、
\((1,\:2)\)、\((2,\:3)\)、\((3,\:4)\)、\((1,\:5)\)
は \(G\) の元である。
一般に、
\((i,\:j)=(1,\:i)(1,\:j)(1,\:i)\)
である。なぜなら、
\(\begin{eqnarray}
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot1&=(1,\:i)(1,\:j)\cdot i\\
&&&=(1,\:i)\cdot i=1\\
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot i&=(1,\:i)(1,\:j)\cdot1\\
&&&=(1,\:i)\cdot j=j\\
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot j&=(1,\:i)(1,\:j)\cdot j\\
&&&=(1,\:i)\cdot1=i\\
\end{eqnarray}\)
が成り立つからである。従って、
\((2,\:3)=(1,\:2)(1,\:3)(1,\:2)\)
である。この両辺に左と右から \((1,\:2)\) をかけると、
\((1,\:2)(2,\:3)(1,\:2)=(1,\:3)\)
となり、\((2,\:3),\:(1,\:2)\) が \(G\) の元なので \((1,\:3)\) も \(G\) の元である。同様に、
\((3,\:4)=(1,\:3)(1,\:4)(1,\:3)\)
であるが、\((3,\:4),\:(1,\:3)\) が \(G\) の元なので、\((1,\:4)\) も \(G\) の元である。結局、
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
が \(G\) の元であることが分かった。
\(S_5\) は5文字の置換をすべて集めた集合である。すべての置換は互換の積で表せて(65B)、かつ任意の互換 \((i,\:j)\) は、
\((i,\:j)=(1,\:i)(1,\:j)(1,\:i)\)
と表せるから、5文字の置換はすべて、
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
という4つの互換の積で表現できる。つまり、\(S_5\) はこの4つの互換で生成できる。以上をまとめると、
\((1,\:2)\)、\((1,\:2\:,3,\:4,\:5)\)
\(\Downarrow\)
\((1,\:2)\)、\((2,\:3)\)、\((3,\:4)\)、\((1,\:5)\)
\(\Downarrow\)
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
\(\Downarrow\)
\(S_5\) のすべての元
という、"\(S_5\)を生成する連鎖" の存在が証明できた。従って \(G\cong S_5\) である。\(S_5\) は可解群ではない(65G)。従って、複素数解を2つ、実数解を3つもつ既約な5次方程式は可解ではない。[証明終]
この、実数解が3つの5次方程式の定理(66B)から、可解ではない5次方程式の実例を簡単に構成できます。たとえば、
\(f(x)=x^5-5x+a\)
とおき、\(f(x)=0\) の方程式を考えます。
\(f\,'(x)=5x^4-5\)
なので、\(f\,'(x)=0\) の実数解は \(1,\:-1\) の2つです。
\(f(\phantom{-}1)=a-4\)
\(f(-1)=a+4\)
なので、
\(a-4 < 0 < a+4\)
なら、\(f(x)=0\) には3つの実数解があります。この条件は、
\(-4 < a < 4\)
ですが、\(a=0\) のときは \(f(x)\) は既約多項式ではありません。また \(a=3,\:-3\) のときも、
\(x^5-5x+3=(x^2+x-1)(x^3-x^2+2x-3)\)
\(x^5-5x-3=(x^2-x-1)(x^3+x^2+2x+3)\)
と因数分解できるので、既約多項式ではありません。従って、
\(x^5-5x+2=0\)
\(x^5-5x+1=0\)
\(x^5-5x-1=0\)
\(x^5-5x-2=0\)
が可解ではない5次方程式の例(\(G\cong S_5\))であり、これらの方程式の解を四則演算とべき根で表すのは不可能です。
| 6.可解性の必要条件 |
6.1 可解群
正規部分群の概念、および剰余群と巡回群を使って「可解群」を定義します。可解群は純粋に群の性質として定義できますが、方程式の可解性と結びつきます。
| (可解群の定義:61A) |
群 \(G\) から 単位元 \(e\) に至る部分群の列、
\(G=H_0\:\sp H_1\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{\:e\:\}\)
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、剰余群 \(H_i/H_{i+1}\) が巡回群であるとき、\(G\) を可解群(solvable group)と言う。
\(H_{i+1}\) が \(H_i\) の正規部分群であるとき、\(H_i\) を正規列と言う。加えて、\(H_i/H_{i+1}\) が巡回群のとき、\(H_i\) を可解列という。
| (巡回群は可解群:61B) |
巡回群は可解群である。また、巡回群の直積も可解群である。
[証明]
群 \(G\) を巡回群とし、\(G\) から 単位元 \(e\) に至る部分群の列として、
\(G=H_0\:\sp\:H_1=\{\:e\:\}\)
をとる。\(H_1=\{\:e\:\}\) は \(H_0=G\) の正規部分群である。また、
\(H_0/H_1\:\cong\:H_0\:(=G)\)
であり、\(G\) は巡回群だから、\(H_0/H_1\) は巡回群である。従って \(G\) は可解群である。
3つの巡回群の直積 \(G\) で考える。\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\bs{Z}/k\bs{Z}\times\bs{Z}/m\bs{Z}\times\bs{Z}/n\bs{Z}\\
&&&=\{(a,b,c)\:|\:a\in\bs{Z}/k\bs{Z},\:b\in\bs{Z}/m\bs{Z},\:c\in\bs{Z}/n\bs{Z}\}\\
\end{eqnarray}\)
とする。このとき、
\(\begin{eqnarray}
&&\:\:&H_1&=\{(a,b,0)\:|\:a\in\bs{Z}/k\bs{Z},\:b\in\bs{Z}/m\bs{Z}\}\\
&&&H_2&=\{(a,0,0)\:|\:a\in\bs{Z}/k\bs{Z}\}\\
&&&\{e\}&=\{(0,0,0)\}\\
\end{eqnarray}\)
とおくと、
\(G\:\sp\:H_1\:\sp\:H_2\:\sp\:\{e\}\)
となる。巡回群は可換群であり、巡回群の直積 \(G\) も可換群である。従って、\(G\) の部分群である \(H_1,\:H_2\) も可換群であり、すなわち \(G\) の正規部分群である(41F)。
\(G\) の任意の2つの元を
\(g=(g_a,\:g_b,\:g_c)\)
\(h=(h_a,\:h_b,\:h_c)\)
とする。剰余類 \(g+H_1\) と \(h+H_1\) を考える。\((g_a,0,0)+H_1=H_1\)、\((0,g_b,0)+H_1=H_1\) だから、\((g_a,g_b,0)+H_1=H_1\) である。また同様に\((h_a,h_b,0)+H_1=H_1\) である。従って、\(g_c=h_c\) なら、\(g_a\)、\(g_b\)、\(h_a\)、\(h_b\) の値に関わらず \(g+H_1=h+H_1\) である。逆に、\(g_c\neq h_c\) なら \(g+H_1\neq h+H_1\) である。このことから剰余類の代表元(41E)として、\((0,0,0)\)、\((0,0,1)\)、\(\cd\)、\((0,0,n-1)\) の \(n\)個をとることができる。つまり、
\(\begin{eqnarray}
&&\:\:G/H_1=\{&(0,0,0)+H_1,\\
&&&(0,0,1)+H_1,\\
&&&(0,0,2)+H_1,\\
&&& \vdots\\
&&&(0,0,n-1)+H_1\}\\
\end{eqnarray}\)
である。これは \((0,0,1)+H_1\) を生成元とする位数 \(n\) の巡回群である。まったく同様の議論により、
\(\begin{eqnarray}
&&\:\:H_1/H_2=\{&(0,0,0)+H_2,\\
&&&(0,1,0)+H_2,\\
&&&(0,2,0)+H_2,\\
&&& \vdots\\
&&&(0,m-1,0)+H_2\}\\
\end{eqnarray}\)
であり、\(H_1/H_2\) は \((0,1,0)+H_2\) を生成元とする位数 \(m\) の巡回群である。以上により、
\(G=H_0\:\sp\:H_1\:\sp\:H_2\:\sp\:H_3=\{e\}\)
は、正規列であり、\(H_i/H_{i+1}\) が巡回群なので、\(G\) は可解群である。この議論は \(G\) が\(4\)個以上の巡回群の直積の場合でも全く同様に成り立つ。つまり、巡回群の直積は可解群である。[証明終]
| (可解群の部分群は可解群:61C) |
可解群の部分群は可解群である。
[証明]
可解群を \(G\) とすると、可解群の定義により、
\(G=H_0\sp H_1\sp H_2\sp\cd H_{n-1}\sp H_n=\{e\}\)
という列で、\(H_{i+1}\) が \(H_i\) の正規部分群であり、\(H_i/H_{i+1}\) が巡回群のものが存在する。
ここで、\(G\) の任意の部分群を \(N\) としたとき、
\(N=N\cap H_0\sp N\cap H_1\sp N\cap H_2\sp\cd N\cap H_{n-1}\sp N\cap H_n=\{e\}\)
という集合の列を考える。部分群の共通部分は部分群の定理(41D)により、\(N\cap H_i\:(0\leq i\leq n)\) は \(G\) の部分群の列である。と同時に、これが可解列であることを以下で証明する。
列の \(N\cap H_{i-1}\sp N\cap H_i\) の部分を取り出して考える。\(H_i\) は \(H_{i-1}\) の正規部分群なので、\(H_{i-1}\) の任意の元 \(x\) について \(xH_i=H_ix\) が成り立つ。
\(N\cap H_{i-1}\) の任意の元を \(y\) とすると、\(y\in N\) かつ \(y\in H_{i-1}\) であるが、\(y\in N\) なので \(yN=Ny=N\) である。また \(y\in H_{i-1}\) なので、正規部分群の定義により、\(yH_i=H_iy\) が成り立つ。ゆえに、
\(y(N\cap H_i)=yN\cap yH_i=Ny\cap H_iy=(N\cap H_i)y\)
となり、定義によって \(\bs{N\cap H_i}\) は \(\bs{N\cap H_{i-1}}\) の正規部分群である。
次に第2同型定理(43B)によると、\(N\) が \(G\) の部分群、\(H\) が \(G\) の正規部分群のとき、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。\(N\) を \(N\cap H_{i-1}\) とし、\(H\) を \(H_i\) として定理を適用すると、
\(N\cap H_{i-1}/((N\cap H_{i-1})\cap H_i)\:\cong\:(N\cap H_{i-1})H_i/H_i\)
\((\br{A})\)
となる。ここで、\(H_i\:\subset\:H_{i-1}\) なので、\((N\cap H_{i-1})\cap H_i=N\cap H_i\) である。従って、
\((\br{A})\) 式の左辺 \(=\:(N\cap H_{i-1})/(N\cap H_i)\)
となる。また、 \((\br{A}\,')\)
\((N\cap H_{i-1})\:\subset\:H_{i-1}\)
は常に成り立つ。さらに、\(H_i\:\subset\:H_{i-1}\) だから、この式に左から \(H_{i-1}\) をかけて、 \((\br{B})\)
\(H_{i-1}H_i\:\subset\:H_{i-1}H_{i-1}\)
\(H_{i-1}H_i\:\subset\:H_{i-1}\)
が成り立つ。\((\br{B})\) 式に右から \(H_i\) をかけると、 \((\br{C})\)
\((N\cap H_{i-1})H_i\:\subset\:H_{i-1}H_i\)
となるが、これと \((\br{C})\) 式を合わせると、
\((N\cap H_{i-1})H_i\:\subset\:H_{i-1}\)
となる。従って、\((N\cap H_{i-1})H_i\) と \(H_{i-1}\) の \(H_i\) による剰余類を考えると、
\((N\cap H_{i-1})H_i/H_i\:\subset\:H_{i-1}/H_i\)
の関係にある。これで、
\((\br{A})\) 式の右辺 \(=\:H_{i-1}/H_i\) の部分群
であることが分かった。 \((\br{A}\,'')\)
以上の \((\br{A})\:\:(\br{A}\,')\:\:(\br{A}\,'')\) をあわせると、
\((N\cap H_{i-1})/(N\cap H_i)\:\cong\:H_{i-1}/H_i\) の部分群
である。\(G\) は可解群なので \(H_{i-1}/H_i\) は巡回群である。巡回群の部分群は巡回群なので、それと同型である \(\bs{(N\cap H_{i-1})/(N\cap H_i)}\) は巡回群である。まとめると、
\(N\cap H_i\) は \(N\cap H_{i-1}\) の正規部分群
\((N\cap H_{i-1})/(N\cap H_i)\) は巡回群
となる。このことは \(1\leq i\leq n\) のすべてで成り立つから、\(N\cap H_0\:=\:N\cap G\:=\:N\) は可解群である。つまり、可解群 \(G\) の任意の部分群 \(N\) は可解群である。[証明終]
| (可解群の像は可解群:61D) |
可解群の準同型写像による像は可解群である。
このことより、
可解群の剰余群は可解群
であることが分かる。なぜなら、群 \(G\) の部分群を \(N\) とすると、\(G\) から \(G/N\) への自然準同型、つまり \(x\in G\) として、
\(x\:\longmapsto\:xN\)
の準同型写像を定義できるからである。
[証明]
可解群を \(G\) とすると、可解群の定義により、
\(G=H_0\sp H_1\sp\:H_2\sp\cd H_{n-1}\sp H_n=\{e\}\)
という列で、\(H_i\) が \(H_{i-1}\) の正規部分群であり、剰余群 \(H_{i-1}/H_i\) が巡回群の列(=可解列)が存在する。群 \(G\) に作用する準同型写像を \(\sg\) とすると、上記の可解列の \(\sg\) による像、
\(\sg(G)=\sg(H_0)\sp\sg(H_1)\sp\sg(H_2)\sp\cd\sg(H_{n-1})\sp\sg(H_n)\)
が正規列になっていることを以下に示す。 \((\br{D})\)
\(\sg\) による像の列から \(\sg(H_{i-1})\sp\sg(H_i)\) を取り出して考える。\(\sg\) を \(H_{i-1}\) から \(\sg(H_{i-1})\) への写像と考えると、\(\sg(H_{i-1})\) は \(\sg\) による \(H_{i-1}\) の像なので、\(\sg\) は全射である。従って、\(H_{i-1}\) の元 \(h\) を選ぶことによって \(\sg(h)\) で \(\sg(H_{i-1})\) の全ての元を表すことができる。
\(\sg(H_{i-1})\) の任意の元を \(\sg(h)\) とおくと、
\(\begin{eqnarray}
&&\:\:\sg(h)\sg(H_i)&=\sg(hH_i)=\sg(H_ih)\\
&&&=\sg(H_i)\sg(h)\\
\end{eqnarray}\)
であるから、\(\sg(H_i)\) は \(\sg(H_{i-1})\) の正規部分群である。つまり \((\br{D})\) は正規列である。従って、\(\sg(H_{i-1})\) の \(\sg(H_i)\) による剰余類は群であり、剰余群 \(\sg(H_{i-1})/\sg(H_i)\) になる。
次に、剰余群 \(\sg(H_{i-1})/\sg(H_i)\) が巡回群であることを示す。\(H_{i-1}\) の任意の元を \(x\) とし、剰余群 \(H_{i-1}/H_i\) の元を \(xH_i\) で表す。\(H_{i-1}/H_i\) から \(\sg(H_{i-1})/\sg(H_i)\) への写像 \(f\) を、
\(f\::\:xH_i\:\longmapsto\:\sg(x)\sg(H_i)\)
と定める。もし、剰余群 \(H_{i-1}/H_i\) の元が \(xH_i\) と \(yH_i\:(x,y\in H_{i-1})\) という異なる表現を持っているとすると、
\(xH_i=yH_i\)
\(\sg(xH_i)=\sg(yH_i)\)
\(\sg(x)\sg(H_i)=\sg(y)\sg(H_i)\)
であるが、\(f\) の定義によって、
\(f(xH_i)=\sg(x)\sg(H_i)\)
\(f(yH_i)=\sg(y)\sg(H_i)\)
であり、異なる表現の \(f\) による写像先は一致する。従って \(f\) は2つの剰余群の間の写像として矛盾なく定義されている。また \(f\) は、
\(\begin{eqnarray}
&&f(xH_iyH_i)&=f(xyH_iH_i)=f(xyH_i)\\
&&&=\sg(xy)\sg(H_i)=\sg(x)\sg(y)\sg(H_i)\\
&&&=\sg(x)\sg(y)\sg(H_iH_i)=\sg(x)\sg(yH_iH_i)\\
&&&=\sg(x)\sg(H_iyH_i)=\sg(x)\sg(H_i)\sg(yH_i)\\
&&&=\sg(xH_i)\sg(yH_i)=\sg(x)\sg(H_i)\sg(y)\sg(H_i)\\
&&&=f(xH_i)f(yH_i)\\
\end{eqnarray}\)
を満たすが、この式は \(xH_i\) と \(yH_i\) が剰余群 \(H_{i-1}/H_i\) の異なる元を表現していても成り立つ。従って \(f\) は準同型写像である(=\(\:\br{①}\:\))。また、\(f\) は \(H_{i-1}/H_i\) から \(\sg(H_{i-1})/\sg(H_i)\) への写像で、
\(f\::\:xH_i\:\longmapsto\:\sg(x)\sg(H_i)\)
と定義されたが、\(\sg(xH_i)=\sg(x)\sg(H_i)\) だから \(f\)は全射であり、
\(\mr{Im}\:f\:=\:\sg(H_{i-1})/\sg(H_i)\)
である(=\(\:\br{②}\:\))。\(\br{①}\) と \(\br{②}\)、および準同型定理(43A)により、
\((H_{i-1}/H_i)/\mr{Ker}\:f\:=\:\sg(H_{i-1})/\sg(H_i)\)
である。\(H_{i-1}/H_i\) は巡回群なので、巡回群の剰余群は巡回群の定理(41H)により、\((H_{i-1}/H_i)/\mr{Ker}\:f\) は巡回群である。従って、それと同型である \(\sg(H_{i-1})/\sg(H_i)\) も巡回群である。
結局、\((\br{D})\) は正規列であると同時に \(\sg(H_{i-1})/\sg(H_i)\) が巡回群なので、\(\sg(G)\) は可解群である。[証明終]
6.2 巡回拡大
巡回拡大
| (巡回拡大の定義:62A) |
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とする。\(\mr{Gal}(\bs{K}/\bs{Q})\) が巡回群のとき、\(\bs{K}/\bs{Q}\) を巡回拡大(cyclic extension)と言う。
累巡回拡大
| (累巡回拡大の定義:62B) |
\(\bs{Q}\) の拡大体を \(\bs{K}\) とする。
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{K}\)
となる拡大列があって(\(k > 1\))、\(\bs{K}_{i+1}/\bs{K}_i\:(0\leq i < k)\) が巡回拡大のとき、\(\bs{K}/\bs{Q}\) は累巡回拡大であると言う。ただし、\(\bs{\bs{K}/\bs{Q}}\) が累巡回拡大だとしても、\(\bs{\bs{K}/\bs{Q}}\) がガロア拡大であるとは限らない。
\(\bs{K}/\bs{Q}\) が累巡回拡大だとしてもガロア拡大であるとは限りません。たとえばシンプルな例で考えてみると、
\(\al=\sqrt{\sqrt{2}+1}\)
という代数的数があったとします。この式から \(\sqrt{\phantom{A}}\) を消去すると \(\al^4-2\al^2-1=0\) なので、\(\al\) の最小多項式 \(f(x)\) は、
\(f(x)=x^4-2x^2-1\)
です。\(f(x)\) は、
\(f(x)=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\)
と変形できるので、方程式 \(f(x)=0\) の解は
\(x=\pm\sqrt{\sqrt{2}+1},\:\:\pm i\sqrt{\sqrt{2}-1}\)
です。従って \(f(x)\) の最小分解体 \(\bs{L}\) は、
\(\bs{L}=\bs{Q}(\sqrt{\sqrt{2}+1},\:i\sqrt{\sqrt{2}-1})\)
であり、また、
\(\sqrt{\sqrt{2}+1}\cdot\sqrt{\sqrt{2}-1}=1\)
の関係があるので、
\(\bs{L}=\bs{Q}(i,\:\al)\)
と表現できます。\(\bs{L}/\bs{Q}\) はガロア拡大です。
一方、
\(\bs{K}=\bs{Q}(\al)\)
と定義すると、\(\bs{K}\) は \(f(x)=0\) の一つの解 \(\al\) だけによる単拡大体なので、\(\bs{K}/\bs{Q}\) はガロア拡大ではありません( \(\bs{Q}(\al)\neq\bs{Q}(i,\:\al)\) )。ここで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\al)=\bs{K}\)
という体の拡大列を考えます。\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解は \(\pm\sqrt{2}\) なので、\(\bs{Q}(\sqrt{2})/\bs{Q}\) はガロア拡大です。また、ガロア群は、
\(\mr{Gal}(\bs{Q}(\sqrt{2})/\bs{Q})=\{e,\:\sg\}\)
\(\sg(\sqrt{2})=-\sqrt{2}\)
\(\sg^2=e\)
なので巡回群であり、\(\bs{Q}(\sqrt{2})/\bs{Q}\) は巡回拡大です。
同様に、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-(\sqrt{2}+1)=0\) の解は \(\pm\al\) で、\(\bs{Q}(\sqrt{2},\al)\) は \(\bs{Q}(\sqrt{2})\) の巡回拡大です。\(\sqrt{2}=\al^2-1\) なので、\(\bs{Q}(\sqrt{2},\al)=\bs{Q}(\al)\) であり、\(\bs{Q}(\al)/\bs{Q}(\sqrt{2})\) が巡回拡大となります。
結局、\(\bs{K}/\bs{Q}\) は \(\bs{Q}(\sqrt{2})/\bs{Q},\:\:\bs{Q}(\al)/\bs{Q}(\sqrt{2})\) という2つの巡回拡大の列で表されるので、定義(62B)により累巡回拡大です。しかしそうであっても、\(\bs{K}/\bs{Q}\) は ガロア拡大ではないのです。
これがもし \(\al=\sqrt{2}+\sqrt{3}\) だとすると、\(2\) も \(3\) も \(\bs{Q}\) の元なので、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})=\bs{K}\)
の拡大列は累巡回拡大であり、かつ \(\bs{K}/\bs{Q}\) がガロア拡大です。
このように、\(\bs{K}/\bs{Q}\) が累巡回拡大だとしてもガロア拡大であるとは限らないのですが、もし \(\bs{K}/\bs{Q}\) が累巡回拡大でかつガロア拡大だとすると、\(\mr{Gal}(\bs{K}/\bs{Q})\) は可解群になります。それが、累巡回拡大と可解群を結びつける次の定理です。
累巡回拡大ガロア群の可解性
| (累巡回拡大ガロア群の可解性:62C) |
\(\bs{Q}\) のガロア拡大を \(\bs{K}\)、そのガロア群を \(G\) とする。このとき、
| \(G\) が可解群である | |
| \(\bs{K}/\bs{Q}\) が累巡回拡大である |
の2つは同値である。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) が可解群であることを示す部分群の列と、それとガロア対応をする体の拡大列を、
\(G=H_0\sp H_1\sp H_2\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{e\}\)
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_i\subset\bs{F}_{i+1}\subset\cd\subset\bs{F}_k=\bs{K}\)
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_i\subset\bs{F}_{i+1}\subset\cd\subset\bs{F}_k=\bs{K}\)
とする。\(G\) が可解群なので、\(H_{i+1}\) は \(H_i\) の正規部分群であり、\(H_{i+1}/H_i\:(0\leq i\leq k-1)\) は巡回群である。以降、\(H_i,\:H_{i+1}\) を取り出して考える。
\(H_i\:\sp\:H_{i+1}\:\sp\:\{e\}\)
\(\bs{F}_i\:\subset\:\bs{F}_{i+1}\:\subset\:\bs{K}\)
\(\bs{K}/\bs{Q}\) がガロア拡大なので、中間体からのガロア拡大の定理(52C)により、\(\bs{K}/\bs{F}_i\) もガロア拡大である。\(\bs{F}_i\) の固定群は \(H_i\) なので \(\mr{Gal}(\bs{K}/\bs{F}_i)=H_i\) である。同様に、\(\bs{K}/\bs{F}_{i+1}\) もガロア拡大であり、\(\mr{Gal}(\bs{K}/\bs{F}_{i+1})=H_{i+1}\) である。
ここで、\(H_{i+1}\) は \(H_i\) の正規部分群なので、正規性定理(53C)により \(\bs{F}_{i+1}/\bs{F}_i\) はガロア拡大であり、そのガロア群は、
\(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\cong H_i/H_{i+1}\)
となる。\(H_i/H_{i+1}\) は巡回群なので、それと同型の \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) も巡回群になる。従って、\(\bs{F}_{i+1}/\bs{F}_i\) は、「ガロア拡大で、かつ \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) が巡回群」なので、巡回拡大である。
以上が \(\bs{F}_i\:(0\leq i\leq k-1)\) で成り立つから、\(\bs{K}/\bs{Q}\) は累巡回拡大である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{K}\) が \(\bs{Q}\) の累巡回拡大であることを示す体の拡大列と、それとガロア対応する \(G\) の部分群の列を、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_i\subset\bs{F}_{i+1}\subset\cd\subset\bs{F}_k=\bs{K}\)
\(G=H_0\sp H_1\sp H_2\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{e\}\)
\(G=H_0\sp H_1\sp H_2\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{e\}\)
とする。\(\bs{F}_i\)と \(\bs{F}_{i+1}\) を取り出して考える。
\(\bs{F}_i\:\subset\:\bs{F}_{i+1}\:\subset\:\bs{K}\)
\(H_i\:\sp\:H_{i+1}\:\sp\:\{e\}\)
\(\bs{K}/\bs{Q}\) がガロア拡大なので、\(\bs{K}/\bs{F}_i\) も \(\bs{K}/\bs{F}_{i+1}\) もガロア拡大である。また \(\bs{F}_{i+1}/\bs{F}_i\) は巡回拡大なので、すなわちガロア拡大である。従って正規性定理(53C)により、\(H_{i+1}\) は \(H_i\) の正規部分群であり、
\(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\cong H_i/H_{i+1}\)
となる。\(\bs{F}_{i+1}/\bs{F}_i\) は巡回拡大なので \(\mr{Gal}(\bs{F}_{i+1}/\bs{F}_i)\) は巡回群であり、それと同型である \(H_i/H_{i+1}\) も巡回群である。まとめると「\(H_{i+1}\) は \(H_i\) の正規部分群であり、かつ \(H_i/H_{i+1}\) は巡回群」である。
このことは \(H_i\:(0\leq i\leq k-1)\) で成り立つから、定義によって \(G\) は可解群である。[証明終]
6.3 原始\(n\)乗根を含む体とべき根拡大
この節の目的は「1の原始\(\bs{n}\)乗根を含む体のべき根拡大」の性質を解明することです。そのためにまず、1の原始\(n\)乗根を \(\zeta\) を含む体 \(\bs{Q}(\zeta)\)に関する次の定理を数ステップに分けて証明します。
1の原始\(n\)乗根を \(\zeta\) とする。このとき
・\(\bs{Q}(\zeta)/\bs{Q}\) はガロア拡大
・\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\:\cong\:(\bs{Z}/n\bs{Z})^{*}\)
が成り立つ。
\(1\) の原始\(n\)乗根
| (原始n乗根の数:63A) |
\(x^n-1=0\) の \(n\)個の解のうち、\(n\)乗して初めて \(1\) になる解を \(1\)の原始\(n\)乗根という。
原始\(n\)乗根は \(\varphi(n)\) 個ある。\(\varphi(n)\) はオイラー関数で、\(n\) と互いに素である \(n\) 以下の自然数の数を表す。
[証明]
まず、
\(\omega=\mr{cos}\dfrac{2\pi}{n}+i\:\mr{sin}\dfrac{2\pi}{n}\)
とおくと、明らかに \(\omega\) は原始\(n\)乗根である。さらに、
\(\omega^k=\mr{cos}\dfrac{2\pi k}{n}+i\:\mr{sin}\dfrac{2\pi k}{n}\:(1\leq k\leq n)\)
で \(1\) の\(n\)乗根の全体を表現できる。ここで \(\omega^k\) が原始\(n\)乗根になる条件を考える。いま、
\((\omega^k)^x=1\:(1\leq x\leq n)\)
とすると、この式を満たす \(x\) の最小値が \(n\) であれば、\(\omega^k\) は原始\(n\)乗根である。これを満たす \(x\) は、\(j\) を任意の整数として、 \((\br{A})\)
\(\dfrac{2\pi k}{n}x=2\pi j\)
のときである。つまり、
\(\dfrac{k}{n}x=j\)
のときである。いま、\(k\) と \(n\) の最大公約数を \(d\) とすると( \(\mr{gcd}(k,n)=d\:)\)、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&k=sd&\\
&&n=td&\\
\end{eqnarray}
\end{array}\right.\)
と表せて、このとき \(s\) と \(t\) は互いに素である。これを使うと、
\(\dfrac{s}{t}x=j\)
のときに \(x\) は \((\br{A})\) 式を満たすことになる。\(s\) と \(t\) は互いに素であり、\(j\) は任意の整数だったから、\(x\) は \(t\) の倍数でなければならない。つまり、\(x\) は \(t=\dfrac{n}{d}\) の倍数である。ということは、\(x\) の最小値は \(\dfrac{n}{d}\) である。そして、\(\dfrac{n}{d}\) が \(n\) に等しいのは \(d=1\) の場合に限る。つまり \(\mr{gcd}(k,n)=1\) なら、\((\br{A})\) 式を満たす最小の \(x\) は \(n\) ということになる。従って、そのときに限り \(\omega^k\) は原始\(n\)乗根である。
\(\mr{gcd}(k,n)=1\) となる \(k\) は \(\varphi(n)\) 個あり、\(1\) の原始\(n\)乗根は \(\varphi(n)\) 個ある。[証明終]
| (原始n乗根の累乗:63B) |
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\zeta^m\:\:(1\leq m\leq n)\)
は、\(1\) の\(n\)乗根の全体を表す。また、
\(\zeta^m\:\:(\mr{gcd}(m,n)=1)\)
は、\(1\) の原始\(n\)乗根の全体を表す。
[証明]
\(\zeta^m\:(1\leq m\leq n)\) の \(n\) 個の値は全部異なっている。なぜなら、もし、 \(\zeta^j=\zeta^i\:(1\leq i < j\leq n)\)
だとすると、
\(\zeta^{j-i}=1\:(1\leq i < j\leq n)\)
となり、\(j-i < n\) だから、\(\zeta\) が原始\(n\)乗根という前提に反するからである。\(\zeta^m\:(1\leq m\leq n)\) は全部異なっているので、これら \(n\) 個の値は \(1\) の\(n\)乗根全体を表す。
\(\zeta\) は、\(\mr{gcd}(k,n)=1\) である \(k\) を用いて、
\(\zeta=\omega^k\)
\(\omega=\mr{cos}\dfrac{2\pi}{n}+i\:\mr{sin}\dfrac{2\pi}{n}\)
と表せる(63A)。すると
\(\zeta^m=(\omega^k)^m=\omega^{km}\)
である。\(\mr{gcd}(k,n)=1\) なので \(\mr{gcd}(m,n)=1\) なら \(\mr{gcd}(km,n)=1\) である。逆に、\(\mr{gcd}(km,n)=1\) が成り立つのは \(\mr{gcd}(m,n)=1\) のときに限る。従って、
\(\zeta^m\:(=\omega^{km})\)
は \(\mr{gcd}(m,n)=1\) のとき(かつ、そのときに限って)\(1\) の原始\(n\)乗根である。[証明終]
| (原始n乗根の最小多項式:63C) |
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とする。\(\zeta\) の最小多項式を \(f(x)\) とし、\(k\) を \(n\) とは素な数とする。
このとき \(f(\zeta^k)=0\) である。
[証明]
証明を2つのステップで行う
第1ステップ
\(p\) を \(\bs{n}\) と素な素数とし、\(k=p\) のとき題意が成り立つことを証明する。
第2ステップ
\(k\) を \(\bs{n}\) と素な数とし、第1ステップを使って題意が成り立つことを証明する。
第1ステップ(\(p\) は \(\bs{n}\) と素な素数)
本論に入る前に、2つことを確認する。まず、\(p\) を素数とし \(a\) を \(p\) とは素な整数とするとき、\(a\neq0\) ならフェルマの小定理(25B)により、
\(a^{p-1}\equiv1\:(\mr{mod}\:p)\)
が成り立つ。この両辺に \(a\) をかけると、
\(a^p\equiv a\:(\mr{mod}\:p)\)
となるが、この形の式にすると \(a=0,\:p\) でも成り立つ。つまり \(a\) が任意の整数のとき \((\br{A})\) 式が成り立つ。 \((\br{A})\)
次に、有限体 \(\bs{F}_p\) 上の多項式(係数が \(\bs{F}_p\) の元である多項式。「2.4 有限体」参照)についての定理である。\(p\) を素数とし \(x,\:y\) を変数とするとき、
\((x+y)^p=x^p+y^p\:\:\:[\bs{F}_p]\)
が成り立つ。その理由であるが、等式の左辺を整数係数として2項展開すると、
\(\begin{eqnarray}
&&\:\:(x+y)^p=&x^p+{}_{p}\mr{C}_{1}x^{p-1}y+\:\cd\:+{}_{p}\mr{C}_{p-1}xy^{p-1}+y^p\\
\end{eqnarray}\)
となる。この展開における \(x^p\) と \(y^p\) 以外の項の係数は、
\({}_{p}\mr{C}_{k}=\dfrac{p!}{k!\cdot(p-k)!}\:\:(1\leq k\leq p-1)\)
であるが、\(p\) が素数なので、分母の素因数に \(p\) はなく、分子の素因数にある \(p\) は分母で割り切れない。従って、
\({}_{p}\mr{C}_{k}\equiv0\:\:(\mr{mod}\:p)\:\:(1\leq k\leq p-1)\)
となり、\(\bs{F}_p\) 上の多項式としては、
\((x+y)^p=x^p+y^p\:\:\:[\bs{F}_p]\)
が成り立つ。
さらに、3変数、\(x,\:y,\:z\) では、
\(\begin{eqnarray}
&&\:\:(x+y+z)^p&=(x+y)^p+z^p\\
&&&=x^p+y^p+z^p\:\:\:[\bs{F}_p]\\
\end{eqnarray}\)
となり、これを繰り返すと \(n\) 変数に拡張できるのは明らかだから、\(x_1,\:\cd\:,\:x_n\) を変数として、
\((x_1+x_2+\:\cd\:+x_n)^p=\)
\(x_1^p+x_2^p+\:\cd\:+x_n^p\:\:\:[\bs{F}_p]\)
が成り立つ。 \((\br{B})\)
以上の \((\br{A})\) 式と \((\br{B})\) 式を前提として以下の本論を進める。
\(\zeta\) の最小多項式 \(f(x)\) は、最小多項式は既約多項式(31I)によって \(\bs{Q}\) 上の既約多項式である。\(\zeta\) は \(x^n-1=0\) と \(f(x)=0\) の共通の解だから、既約多項式の定理1(31E)により、\(x^n-1\) は \(f(x)\) で割り切れる。そこで、商の多項式を \(g(x)\) として、
\(x^n-1=f(x)g(x)\)
\((\br{C})\)
とおく。この式の左辺の \(x^n-1\) は整数係数の多項式である。つまり上の式は、整数係数の多項式が \(\bs{Q}\) 上で(有理数係数の多項式として)因数分解できることになり、整数係数多項式の既約性の定理(31C)によって、\(x^n-1\) は整数係数の多項式で因数分解できる。従って、\(f(x)\) と \(g(x)\) は整数係数としてよい。ということは、\(f(x)\) と \(g(x)\) を有限体 \(\bs{F}_p\) 上の多項式と見なすこともできる。以降の証明にはこのことを使う。
\(p\) は \(n\) と互いに素だから \(\zeta^p\) も \(1\) の原始\(n\)乗根である(63B)。従って \((\br{C})\) 式に \(x=\zeta^p\) を代入すると、左辺は \(0\) だから、
\(f(\zeta^p)g(\zeta^p)=0\)
となり、\(f(\zeta^p)=0\) もしくは \(g(\zeta^p)=0\) である。
ここから、\(f(\zeta^p)=0\) であることを言うために背理法を使う。以下に \(f(\zeta^p)\neq0\) と仮定すると矛盾が生じることを証明する。
この背理法の仮定のもとでは \(g(\zeta^p)=0\) だから、\(\zeta\) は方程式 \(g(x^p)=0\) の解である。ということは、\(f(x)=0\) と \(g(x^p)=0\) は \(\zeta\) という共通の解をもつことになり、かつ \(f(x)\) は既約多項式であるから、既約多項式の定理1(31E)によって、\(g(x^p)\) は \(f(x)\) で割り切れる。その商を \(h(x)\) とすると、
\(g(x^p)=f(x)h(x)\)
と表せる。\(h(x)\) も整数係数の多項式である。 \((\br{D})\)
\(g(x)\) を、
\(g(x)=a_mx^m+a_{m-1}x^{m-1}+\:\cd\:+\:a_1x+a_0\)
とし、これを \(\bs{F}_p\) 上の多項式とみなして \(g(x^p)\) を計算する。\((\br{A})\) 式を使って係数を \(\mr{mod}\:p\) でみると、
| \(g(x^p)\) | \(\overset{\text{ }}{=}\) | \(a_m(x^p)^m+a_{m-1}(x^p)^{m-1}+\:\cd\:+a_1(x^p)+a_0\) | |
| \(\overset{\text{ }}{=}\) | \(a_m^p(x^p)^m+a_{m-1}^p(x^p)^{m-1}+\:\cd\:+a_1^p(x^p)+a_0^p\) | ||
| \(\overset{\text{ }}{=}\) | \((a_mx^m)^p+(a_{m-1}x^{m-1})^p+\:\cd\:+(a_1x)^p+a_0^p\:\:\:[\bs{F}_p]\) |
この最後の式は、\((\br{B})\) 式の右辺の \(x_1\) を \(a_mx^m\)、\(x_2\) を \(a_{m-1}x^{m-1}\)、\(\cd\:x_n\) を \(a_0\) と置き換えた形をしている。従って \((\br{B})\) 式を使うと、
| \(g(x^p)\) | \(\overset{\text{ }}{=}\) | \((a_mx^m+a_{m-1}x^{m-1}+\:\cd\:+a_1x+a_0)^p\) | |
| \(\overset{\text{ }}{=}\) | \((g(x))^p\:\:\:[\bs{F}_p]\) |
\(g(x^p)=(g(x))^p\:\:\:[\bs{F}_p]\)
となる。同時に、\((\br{D})\) 式の \(f(x),\:h(x)\) も \(\bs{F}_p\) 上の多項式と見なして \((\br{E})\) 式 を \((\br{D})\) 式に代入すると、 \((\br{E})\)
\((g(x))^p=f(x)h(x)\:\:\:[\bs{F}_p]\)
が得られる。 \((\br{F})\)
\(f(x)\) は \(\bs{Q}\) 上の(整数係数の)既約多項式であった。しかし \(f(x)\) を \(\bs{F}_p\) 上の多項式と見なしたとき、それが既約多項式だとは限らない。たとえば \(x^2+1=0\) は \(\bs{Q}\) 上の既約多項式であるが、\(\bs{F}_5\) では、
\(x^2+1=(x-2)(x-3)\:\:\:[\bs{F}_5]\)
と因数分解できるから既約ではない。そこで、\(\bs{F}_p\) 上の多項式 \(f(x)\) を割り切る \(\bs{F}_p\) 上の既約多項式を \(q(x)\) とする。もし \(f(x)\) が \(\bs{F}_p\) 上でもなおかつ既約であれば \(q(x)=f(x)\) である。そうすると \(q(x)\) は \((\br{F})\) 式の右辺を割り切るから、左辺の \((g(x))^p\) も割り切る。ということは、既約多項式と素数の類似性(31D)によって、\(q(x)\) は \(g(x)\) を割り切る。
ここで \((\br{C})\) 式に戻って考えると、\((\br{C})\) 式は、
\(x^n-1=f(x)g(x)\)
であった。この式を \(\bs{F}_p\) 上の多項式とみなすと、\(f(x)\) と \(g(x)\) は共に \(q(x)\) という因数をもつから、\((\br{C})\) 式の右辺は \(q(x)^2\) という因数をもつ。従って \((\br{C})\) 式は、 \((\br{C})\)
\(x^n-1=q(x)^2\cdot r(x)\:\:\:[\bs{F}_p]\)
と書ける。\(r(x)\) は \(f(x)g(x)\) を \(q(x)^2\) で割ったときの商である。 \((\br{G})\)
ここで \((\br{G})\) 式の両辺の導多項式(多項式の形式的微分)を求める。\(\bs{F}_p\) では距離が定義されていないので極限による微分の定義はできないが、形式的微分( \(x^k\:\rightarrow\:kx^{k-1}\) の変換)はできる。すると、
| \(nx^{n-1}\) | \(=2q(x)q\,'(x)r(x)+q(x)^2\cdot r\,'(x)\) | ||
| \(=q(x)\cdot(2q\,'(x)r(x)+q(x)r\,'(x))\:\:\:[\bs{F}_p]\) | \((\br{H})\) |
\((\br{G})\) 式と \((\br{H})\) 式により、\(\bs{F}_p\) 上の多項式として、
\(x^n-1\) と \(nx^{n-1}\) は共通の因数をもつ
ことになる。ここで矛盾が生じる。
なぜなら、\(n\) と \(p\) は互いに素だから、\(\bs{F}_p\) における \(n\) の逆数 \(n^{-1}\) がある。これを用いて \(x^n-1\) と \(nx^{n-1}\) に多項式の互除法を適用すると、
\(x^n-1=n^{-1}x(nx^{n-1})-1\:\:\:[\bs{F}_p]\)
となって、\(x^n-1\) と \(nx^{n-1}\) の最大公約数は \(-1\:(=p-1)\:\:[\bs{F}_p]\) という定数である。つまり、\(\bs{F}_p\) 上の多項式として、
\(x^n-1\) と \(nx^{n-1}\) は互いに素
である。これは明らかに矛盾している。この矛盾の発端は \(f(x)=0\) と \(g(x^p)=0\) が \(\zeta\) という共通の解をもつとしたことにあり、つまり \(g(\zeta^p)=0\) としたことにある。
従って、そもそもの仮定である \(f(\zeta^p)\neq0\) は間違っている。つまり \(f(\zeta^p)=0\) である。[第1ステップの証明終]
第2ステップ(\(k\) は \(\bs{n}\) と素な数)
\(k\) を \(n\) とは素な(しかし素数ではない)数とし、\(k\) の素因数分解を、
\(k=p_1p_2\cd p_m\)
とする。この形での素因数分解は、素因数が重複することもありうる。\(k\) は \(n\) と素だから、\(p_1,\:p_2,\:\cd\:,p_m\) のすべての素数は \(n\) と素である。
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、第1ステップの \(p=p_1\) とする。\(p_1\) は \(n\) と素だから、原始\(\bs{n}\)乗根の累乗の定理(63B)により、\(\zeta^{p_1}\) も \(1\) の原始\(n\)乗根である。また、第1ステップの証明により、\(f(\zeta^{p_1})=0\) である。
次に、その \(\zeta^{p_1}\) を原始\(n\)乗根としてとりあげ、\(p=p_2\) とする。\(p_2\) は \(n\) と素だから、\((\zeta^{p_1})^{p_2}=\zeta^{p_1p_2}\) もまた原始\(n\)乗根になる(63B)。従って、第1ステップでの証明を適用して \(f(\zeta^{p_1p_2})=0\) である。
このプロセスは次々と続けることができる。結局 \(\zeta^{p_1p_2\:\cd\:p_m}=\zeta^k\) は \(1\) の原始\(n\)乗根であると同時に、\(f(\zeta^k)=0\) を満たす。\(k\) につけた条件は「\(n\) と互いに素」だけである。
原始\(\bs{n}\)乗根の累乗の定理(63B)により、\(k\) が \(n\) と素という条件で、\(\zeta^k\) は原始\(n\)乗根のすべてを表す。従って、\(f(x)=0\) は原始\(n\)乗根のすべてを解とする方程式である。[証明終]
この原始\(\bs{n}\)乗根の最小多項式の定理(63C)より、次の定理がすぐに導けます。
| (円分多項式:63D) |
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、\(\zeta\) の最小多項式を \(f(x)\) とすると、\(f(x)\) は円分多項式である。円分多項式とは、方程式 \(f(x)=0\) が \(\varphi(n)\) 個の解をもち、それらすべてが原始\(n\)乗根である多項式である。
従って、原始\(\bs{n}\)乗根は互いに共役である。最小多項式は既約多項式なので(31I)、円分多項式は既約多項式である。
\(\bs{Q}\) に \(\zeta\) を添加した単拡大体 \(\bs{Q}(\zeta)\) は円分多項式の最小分解体であり、\(\bs{\bs{Q}(\zeta)/\bs{Q}}\) はガロア拡大である。
\(\bs{Q}(\zeta)\)のガロア群
| (Q(ζ)のガロア群:63E) |
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
である。つまり \(1\) の原始\(n\)乗根の一つを \(\bs{Q}\) に添加した拡大体のガロア群は、既約剰余類群に同型である。
[証明]
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とし、最小多項式を \(f(x)\) とすると、円分多項式の定理(63D)により、\(f(x)=0\) の解は \(\varphi(n)=m\) 個の原始\(n\)乗根である。
原始\(n\)乗根を
\(\zeta^{k_i}\:(\:1\leq i\leq m,\:1\leq k_i\leq n\) かつ \(\mr{gcd}(k_i,n)=1\:)\)
と表すと、それらは互いに共役である。また、\(f(x)\) の最小分解体は、
\(\bs{Q}(\zeta^{k_1},\zeta^{k_2},\cd,\zeta^{k_m})=\bs{Q}(\zeta)\)
である。
\(\zeta\) に作用する同型写像 \(\sg\) を考えると、\(\sg\) は \(\zeta\) を共役な元に移すから、
\(\sg_{k_i}(\zeta)=\zeta^{k_i}\)
で \(m\) 個の同型写像が定義できる。この \(\sg\) による移り先はすべて \(\bs{Q}(\zeta)\) の元だから、\(\sg\) は \(\bs{Q}(\zeta)\) の自己同型写像である。また、\(\sg_{k_i}\) と \(\sg_{k_j}\) の積は、
\(\begin{eqnarray}
&&\:\:\sg_{k_i}(\sg_{k_j})&=\sg_{k_i}(\zeta^{k_j})\\
&&&=(\zeta^{k_j})^{k_i}\\
&&&=\zeta^{k_ik_j}\\
\end{eqnarray}\)
と計算できる。そこで \(\sg\) の演算規則を、
\(\sg_{k_i}\sg_{k_j}=\sg_{k_ik_j}\)
と定める。
ここで \(k_ik_j\) は、\(1\leq k_i,\:k_j\leq n\) かつ \(\mr{gcd}(k_i,n)=1\) かつ \(\mr{gcd}(k_j,n)=1\) だから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元であり、乗算で閉じている。すなわち \(\sg_{k_ik_j}\) は \(\sg\) のどれかである。つまり、自己同型写像である \(\sg\) は上の演算規則で群になり、ガロア群 \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) である。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) から \((\bs{Z}/n\bs{Z})^{*}\) への写像 \(f\) を、
| \(f\::\) | \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) | \(\longrightarrow\) | \((\bs{Z}/n\bs{Z})^{*}\) | |
| \(\sg_{k_i}\) | \(\longmapsto\) | \(k_i\) |
| \(f(\sg_{k_i}\sg_{k_j})\) | \(=f(\sg_{k_ik_j})\) | |
| \(=k_ik_j\) | ||
| \(f(\sg_{k_i})f(\sg_{k_j})\) | \(=k_ik_j\) |
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型です(25G)。従って次の定理が得られます。
| (Q(ζ)のガロア群は巡回群:63F) |
\(1\) の原始\(n\)乗根の一つを \(\zeta\) とすると、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積と同型である。
従って、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は可解群であり(61B)、累巡回拡大である(62C)。
累巡回拡大は、可解性の必要条件を証明する重要ポイントです。そこで次に、\(\bs{Q}(\zeta)/\bs{Q}\) が累巡回拡大になる様子を、ガロア群の計算で示します。
円分拡大は累巡回拡大
\(1\) の原始\(n\)乗根 \(\zeta\) を \(\bs{Q}\) に添加する拡大、\(\bs{Q}(\zeta)/\bs{Q}\) を円分拡大と言います。\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積と同型で、従って 円分拡大 \(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大です。
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) が巡回群の直積と同型になる理由は、既約剰余類群と同型であること、つまり、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/n\bs{Z})^{*}\)
でした(63E)。その \((\bs{Z}/n\bs{Z})^{*}\) について振り返ってみると、次の通りです。\(\varphi\) はオイラー関数です。
\(\bs{n}\) が奇素数 \(\bs{p}\) 、ないしは奇素数 のべき乗のとき
(\(n=p^k,\:1\leq k\))(25D)(25E)
\((\bs{Z}/p^k\bs{Z})^{*}\) は生成元をもつ巡回群
群位数:\(\varphi(p^k)=p^{k-1}(p-1)\)
\(\bs{n}\) が2のべき乗のとき
(\(n=2^k,\:2\leq k\))(25F)
\((\bs{Z}/2^k\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{k-2}\bs{Z})\)
群位数:\(\varphi(2^k)=2^{k-1}\)
\(\bs{n=p^a\cdot q^b\cdot r^c}\)のとき
(\(p,\:q,\:r\) は素数)(25G)
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\)
群位数:\(\varphi(n)=\varphi(p^a)\varphi(q^b)\varphi(r^c)\)
もちろん最後の式は、素因数が4個以上でも同様に成り立ちます。以下、それぞれの例をあげます。
\(\zeta\) が 原始\(25\)乗根のとき
\(\zeta\) が 原始\(25\)乗根の(一つ)のとき、原始\(25\)乗根の全体は \(\zeta^k\:\:(\mr{gcd}(k,25)=1)\) で表され(63B)、その数は \(25\) と互いに素な自然数の数、\(\varphi(25)=20\) です。\(\bs{Q}(\zeta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/5^2\bs{Z})^{*}\)
でした(63E)。\((\bs{Z}/5\bs{Z})^{*}\) の最小の生成元は \(2\) ですが(25D)、ほどんどの場合、\((\bs{Z}/p\bs{Z})^{*}\) の生成元は同時に \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です(25E)。実際、\(2\) は \((\bs{Z}/25\bs{Z})^{*}\) の生成元であることが確認できます。
そこで、\(\bs{Q}(\zeta)\) の自己同型写像 \(\sg\) を、
\(\sg(\zeta)=\zeta^2\)
と定義すると、\(\sg^k(\zeta)\:\:(1\leq k\leq20)\) は、
\(\zeta^2,\:\zeta^4,\:\zeta^8,\:\zeta^{16},\:\zeta^7,\:\zeta^{14},\:\zeta^3,\:\zeta^6,\:\zeta^{12},\:\zeta^{24},\)
\(\zeta^{23},\:\zeta^{21},\:\zeta^{17},\:\zeta^9,\:\zeta^{18},\:\zeta^{11},\:\zeta^{22},\:\zeta^{19},\:\zeta^{13},\:\zeta\)
となって、原始\(25\)乗根の全部を尽くします。つまり、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})=\{e,\:\sg,\:\sg^2,\:\cd,\:\sg^{19}\}\)
\(\sg(\zeta)=\zeta^2\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は位数 \(20\) の巡回群で、
\(\bs{Q}\:\subset\:\bs{Q}(\zeta)\)
は巡回拡大です。
\(\zeta\) が 原始\(16\)乗根のとき
原始\(16\)乗根は、自然数 \(k\) を \(16\) 以下の奇数として \(\zeta^k\) で表され、次の8個です。
\(\zeta,\:\zeta^3,\:\zeta^5,\:\zeta^7,\:\zeta^9,\:\zeta^{11},\:\zeta^{13},\:\zeta^{15}\)
ここで、\(n\) が2のべき乗のときの同型は、
\((\bs{Z}/16\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/4\bs{Z})\)
でした(25F)。つまり、\((\bs{Z}/16\bs{Z})^{*}\) は巡回群ではありませんが、位数 \(2\) の巡回群と位数 \(4\) の巡回群の直積に同型です。このことの証明(25F)を振り返ってみると、\(\mr{mod}\:16\) でみて \(5^k\:\:(0\leq k\leq3)\) は、
\(1,\:5,\:9,\:13\)
であり、\((\bs{Z}/16\bs{Z})^{*}\) の元のうちの「4で割って1余る数」が全部現れるのでした。そこで、\(\bs{Q}(\zeta)\) の自己同型写像 \(\sg\) を、
\(\sg(\zeta)=\zeta^5\)
と定義すると、\(\sg^k(\zeta)\:\:(0\leq k\leq3)\) は、
\(\zeta,\:\zeta^5,\:\zeta^9,\:\zeta^{13}\)
で、原始\(16\)乗根の半数を表現します。
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
\(H=\{e,\:\sg,\:\sg^2,\:\sg^3\}\)
と書くと、\(H\) は \(G\) の部分群で、\(H\) の位数 \(4\) は \(G\) の位数 \(8\) の半分です。
\(H\) の固定体を \(\bs{K}\) とします。
\(\sg(\zeta^4)=\sg(\zeta)^4=(\zeta^5)^4=\zeta^{20}\)
ですが、\(\zeta^{16}=1\) なので、
\(\sg(\zeta^4)=\zeta^4\)
です。\(\zeta^4\) は \(\sg\) で不変であり、従って \(\zeta^4\) は \(H\) のすべての元で不変です。\(\zeta^4\) は4乗して初めて \(1\) になる数で、\(1\) の原始4乗根、つまり \(i\)(または \(-i\)。\(i\) は虚数単位)です。つまり \(i\) は固定体 \(\bs{K}\) の元であり、
\(\bs{Q}(i)\:\subset\:\bs{K}\)
です。\(\bs{K}\) が \(H\) の固定体なので、ガロア対応は、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{Q}(\zeta)\)
です。ガロア対応の定理(53B)により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{K})=H\)
であり、次数と位数の同一性(52B)により、体の拡大次数はガロア群の位数と等しいので、
\([\:\bs{Q}(\zeta):\bs{K}\:]=|H|=4\)
です。また、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=\varphi(16)=8\)
なので、拡大次数の連鎖律(33H)により、
\([\:\bs{K}:\bs{Q}\:]=2\)
です。一方、\(i\) は既約な2次方程式 \(x^2+1=0\) の根なので、\([\:\bs{Q}(i):\bs{Q}\:]=2\) です。つまり \(\bs{K}\) と \(\bs{Q}(i)\) は次元(\(=\:2\))が一致し、かつ \(\bs{Q}(i)\:\subset\:\bs{K}\) なので、体の一致の定理(33I)によって、
\(\bs{K}=\bs{Q}(i)\)
です。まとめると、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}(i))\) は位数 \(4\) の巡回群であり、\(\bs{Q}(\zeta)/\bs{Q}(i)\) は巡回拡大です。
また、
\(\tau(i)=-i\)
と定義すると、\(\tau\) は \(\bs{Q}(i)\) の自己同型写像です。従って、
\(\mr{Gal}(\bs{Q}(i)/\bs{Q})=\{e,\:\tau\}\)
であり、\(\mr{Gal}(\bs{Q}(i)/\bs{Q})\) は位数 \(2\) の巡回群で、\(\bs{Q}(i)/\bs{Q}\) は巡回拡大です。
以上で、
\(\bs{Q}\:\subset\:\bs{Q}(i)\:\subset\:\bs{Q}(\zeta)\)
は2つの巡回拡大を連鎖させた累巡回拡大です。
\(\zeta\) が 原始\(360\)乗根のとき
\(n\) が複数の素因数をもつ一般的な場合を確認します。分かりやすいように \(n=360\) とします。\(360=2^3\cdot3^2\cdot5\) なので、既約剰余類群の構造の定理(25G)によって、
\((\bs{Z}/360\bs{Z})^{*}\cong(\bs{Z}/8\bs{Z})^{*}\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\)
です。右辺の群位数はそれぞれ、
\(|(\bs{Z}/8\bs{Z})^{*}|=\varphi(8)=4\)
\(|(\bs{Z}/9\bs{Z})^{*}|=\varphi(9)=6\)
\(|(\bs{Z}/5\bs{Z})^{*}|=\varphi(5)=4\)
なので、
\(|(\bs{Z}/360\bs{Z})^{*}|=4\cdot6\cdot4=96=\varphi(360)\)
です。ここで、
\(1\) の原始\(8\)乗根 \(:\:\zeta^{45}\)
\(1\) の原始\(9\)乗根 \(:\:\zeta^{40}\)
\(1\) の原始\(5\)乗根 \(:\:\zeta^{72}\)
ですが、これらを用いると、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
が成り立ちます。その理由ですが、
\(\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\subset\bs{Q}(\zeta)\)
であるのは当然として、その逆である、
\(\bs{Q}(\zeta)\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
も成り立つからです。なぜなら、
\(45x+40y+72z=1\)
の1次不定方程式を考えると、\(\mr{gcd}(45,40,72)=1\) なので不定方程式の解の存在の定理(21C)により必ず整数解があります。具体的には、
\(x=5,\:\:y=7,\:\:z=-7\)
が解(の一つ)です。従って、
\(\zeta=(\zeta^{45})^5\cdot(\zeta^{40})^7\cdot(\zeta^{72})^{-7}\)
であり、\(\zeta\) が \(\zeta^{45},\:\zeta^{40},\:\zeta^{72}\) の四則演算で表現できるので、
\(\bs{Q}(\zeta)\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
です。この結果、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
となります。
以上を踏まえると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) への体の拡大は、
\(\begin{eqnarray}
&&\:\:\bs{Q}&\subset\bs{Q}(\zeta^{45})\\
&&&\subset\bs{Q}(\zeta^{45},\zeta^{40})\\
&&&\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})=\bs{Q}(\zeta)\\
\end{eqnarray}\)
と、\(\bs{Q}\) からの単拡大を3回繰り返したものと言えます。以降で、それぞれの単拡大が巡回拡大になることを確認します。
\(\bs{Q}\:\subset\:\bs{Q}(\zeta^{45})\)
\(\zeta^{45}\) は原始\(8\)乗根なので、上で検討した原始\(16\)乗根の結果がそのまま使えます。つまり、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(\zeta^{45})\)
と表され、
\([\:\bs{Q}(i):\bs{Q}\:]=2\)
\([\:\bs{Q}(\zeta^{45}):\bs{Q}(i)\:]=2\)
\([\:\bs{Q}(\zeta^{45}):\bs{Q}\:]=4\)
であり、\(\mr{Gal}(\bs{Q}(i)/\bs{Q}),\:\mr{Gal}(\bs{Q}(\zeta^{45})/\bs{Q}(i))\) は位数2の巡回群です。原始8乗根は簡単に計算できて、たとえばその一つは、
\(\begin{eqnarray}
&&\:\:\zeta^{45}&=\mr{cos}\dfrac{\pi}{4}+i\:\mr{sin}\dfrac{\pi}{4}\\
&&&=\dfrac{1}{2}(\sqrt{2}+\sqrt{2}\:i)\\
\end{eqnarray}\)
なので、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(i,\sqrt{2})=\bs{Q}(\zeta^{45})\)
と表現することができます。この結果を使って、2つのガロア群 \(G_1\) と\(G_2\) の元を表現すると、
\(G_1=\mr{Gal}(\bs{Q}(i)/\bs{Q})=\{e,\:\sg_1\}\)
\(\sg_1(i)=-i\)
\(G_2=\mr{Gal}(\bs{Q}(\zeta^{45})/\bs{Q}(i))=\{e,\:\sg_2\}\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
となります。
\(\bs{Q}(\zeta^{45})\subset\bs{Q}(\zeta^{45},\zeta^{40})\)
\(\zeta^{40}\) は原始\(9\)乗根です。原始\(9\)乗根の一つを \(\al\) と書くと、原始\(9\)乗根の全体は \(1\)~\(8\) の数で \(9\) と素なものを選んで、
\(\al,\:\al^2,\:\al^4,\:\al^5,\:\al^7,\:\al^8\)
の6つになり、これらが共役な元です。\((\bs{Z}/9\bs{Z})^{*}\) の元は、
\((\bs{Z}/9\bs{Z})^{*}=\{1,\:2,\:4,\:5,\:7,\:8\}\)
ですが、生成元は \(2\) か \(5\) です。生成元として \(2\) を採用すると、\(2^k\:(\mr{mod}\:9)\:(1\leq k\leq6)\) は、
\(2,\:4,\:8,\:7,\:5,\:1\)
と、\((\bs{Z}/9\bs{Z})^{*}\) の元を巡回します。
\(G_3=\mr{Gal}(\bs{Q}(\zeta^{45},\zeta^{40})/\bs{Q}(\zeta^{45}))\)
と書くことにし、ガロア群 \(G_3\) の元 \(\sg\) を、
\(\sg(\al)=\al^2\)
と定義すると、
\(G_3=\{e,\:\sg,\:\sg^2,\:\sg^3,\:\sg^4,\:\sg^5\}\)
となります。\(\al\) を \(\zeta\) で表すと、
\(\sg(\zeta^{40})=\zeta^{80}\)
です。 \((\br{A})\)
ただし、ガロア群の定義によって \(\sg\) は \(\zeta^{45}\) を不動にします。従って、
\(\sg(\zeta^{45})=\zeta^{45}\)
を満たさなければなりません。ここで、\(\sg\) が \(\zeta\) に作用したとき、 \((\br{B})\)
\(\sg(\zeta)=\zeta^x\)
であると仮定します。すると \((\br{A})\) 式と \((\br{C})\) 式から、 \((\br{C})\)
\(40x\equiv80\:\:(\mr{mod}\:360)\)
\(x\equiv2\:\:(\mr{mod}\:9)\)
です。また、\((\br{B})\) 式と \((\br{C})\) 式から、 \((\br{D})\)
\(45x\equiv45\:\:(\mr{mod}\:360)\)
\(x\equiv1\:\:(\mr{mod}\:8)\)
です。\(9\) と \(8\) は互いに素です。そうすると中国剰余定理(21F)によって、\((\br{D})\) 式と \((\br{E})\) 式の連立合同方程式は \(0\leq x < 9\cdot8\) の範囲に唯一の解があります。それを求めると、 \((\br{E})\)
\(x=65\)
です。当然ですが、\(65\)の累乗を \((\mr{mod}\:9)\) で計算してみると、
\(65^{\phantom{1}}\equiv2\:\:(\mr{mod}\:9)\)
\(65^2\equiv4\:\:(\mr{mod}\:9)\)
\(65^3\equiv8\:\:(\mr{mod}\:9)\)
\(65^4\equiv7\:\:(\mr{mod}\:9)\)
\(65^5\equiv5\:\:(\mr{mod}\:9)\)
\(65^6\equiv1\:\:(\mr{mod}\:9)\)
となって、\(2\) の累乗 \((\mr{mod}\:9)\) と一致します。\(\mr{mod}\:360\) に戻すと、
\(40\cdot65^{\phantom{1}}\equiv40\cdot2\:\:(\mr{mod}\:360)\)
\(40\cdot65^2\equiv40\cdot4\:\:(\mr{mod}\:360)\)
\(40\cdot65^3\equiv40\cdot8\:\:(\mr{mod}\:360)\)
\(40\cdot65^4\equiv40\cdot7\:\:(\mr{mod}\:360)\)
\(40\cdot65^5\equiv40\cdot5\:\:(\mr{mod}\:360)\)
\(40\cdot65^6\equiv40\phantom{\cdot5\:\:(}(\mr{mod}\:360)\)
です。この結果、
\(\sg_3(\zeta)=\zeta^{65}\) |
\(\sg_3^{\:\phantom{1}}(\al)=\al^2,\:\:\sg_3^{\:2}(\al)=\al^4,\:\:\sg_3^{\:3}(\al)=\al^8\)
\(\sg_3^{\:4}(\al)=\al^7,\:\:\sg_3^{\:5}(\al)=\al^5,\:\:\sg_3^{\:6}(\al)=\al\)
と巡回させます \((\zeta^{360}=1)\)。また、
\(65\cdot45=2925\equiv45\:\:(\mr{mod}\:360)\)
なので、
\(\sg_3(\zeta^{45})=\zeta^{45}\)
です。結局、
\(\begin{eqnarray}
&&\:\:G_3&=\mr{Gal}(\bs{Q}(\zeta^{45},\zeta^{40})/\bs{Q}(\zeta^{45}))\\
&&&=\{e,\:\sg_3,\:\sg_3^{\:2},\:\sg_3^{\:3},\:\sg_3^{\:4},\:\sg_3^{\:5}\}\\
\end{eqnarray}\)
\(\sg_3(\zeta)=\zeta^{65}\)
がガロア群です。
\(\bs{Q}(\zeta^{45},\zeta^{40})\subset\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
\(\zeta^{72}\) は原始\(5\)乗根で、\((\bs{Z}/5\bs{Z})^{*}\) の生成元は \(2\) か \(3\) です。生成元として \(2\) を採用すると、ガロア群の元 \(\sg\) は、先ほどと同じように考えて、
\(\sg(\zeta^{72})=\zeta^{144}\)
です。また \(\sg\) は \(\zeta^{45}\) と \(\zeta^{40}\) を固定するので、 \((\br{A}\,')\)
\(\sg(\zeta^{45})=\zeta^{45},\:\:\:\sg(\zeta^{40})=\zeta^{40}\)
です。\(\sg\) が \(\zeta\) に作用したときに、 \((\br{B}\,')\)
\(\sg(\zeta)=\zeta^x\)
だとすると、\((\br{A}\,')\:\:(\br{B}\,')\) と \((\br{C})\) により、 \((\br{C})\)
| \(72x\equiv144\) | \((\mr{mod}\:360)\) | |
| \(45x\equiv45\) | \((\mr{mod}\:360)\) | |
| \(40x\equiv40\) | \((\mr{mod}\:360)\) |
| \(x\equiv2\) | \((\mr{mod}\:5)\) | |
| \(x\equiv1\) | \((\mr{mod}\:8)\) | |
| \(x\equiv1\) | \((\mr{mod}\:9)\) |
\(x=217\)
です。従って、
\(\sg_4(\zeta)=\zeta^{217}\) |
\(G_4=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\)
\(\sg_4(\zeta)=\zeta^{217}\)
がガロア群になります。\(217^4\equiv1\:\:(\mr{mod}\:360)\) です。なお、
\(\bs{Q}(\zeta^{45},\zeta^{40})=\bs{Q}(\zeta^5)\)
と簡略化できます。なぜなら、\(40\) と \(45\) の最大公約数は \(5\) なので、
\(45x+40y=5\)
の1次不定方程式には整数解があり(21B)、具体的には、
\(x=1,\:\:y=-1\)
が解(の一つ)で、
\(\zeta^5=\zeta^{45}\cdot(\zeta^{40})^{-1}\)
と表せるからです。また、
\(\bs{Q}(\zeta)=\bs{Q}(\zeta^{45},\zeta^{40},\zeta^{72})\)
だったので、
\(\begin{eqnarray}
&&\:\:G_4&=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q}(\zeta^5))\\
&&&=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\\
\end{eqnarray}\)
\(\sg_4(\zeta)=\zeta^{217}\)
と表記できます。\(G_4\) は位数 \(4\) の巡回群であり、\(\bs{Q}(\zeta)/\bs{Q}(\zeta^5)\) は巡回拡大です。さらに、
\(\begin{eqnarray}
&&\:\:\sg_4(\zeta^5)&=\zeta^{5\cdot217}=\zeta^{1085}\\
&&&=\zeta^{3\cdot360+5}=\zeta^5\\
\end{eqnarray}\)
なので、\(\sg_4\) が \(\zeta^5\) を固定することが確認できました。
以上の考察をまとめると、\(\zeta\) が \(1\) の原始\(360\)乗根のとき、
\(\bs{Q}\subset\bs{Q}(i)\subset\bs{Q}(\zeta^{45})\subset\bs{Q}(\zeta^5)\subset\bs{Q}(\zeta)\)
という、4段階の巡回拡大が得られました。\(i\) は原始\(4\)乗根なので、\(\bs{Q}(i)\) は \(\bs{Q}(\zeta^{90})\) と同じ意味です。それそれの拡大のガロア群を \(G_1,\:G_2,\:G_3,\:G_4\) とすると、
\(G_1=\{e,\:\sg_1\}\)
\(\sg_1(i)=-i\)
\(G_2=\{e,\:\sg_2\}\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
\(G_3=\{e,\:\sg_3,\:\sg_3^{\:2},\:\sg_3^{\:3},\:\sg_3^{\:4},\:\sg_3^{\:5}\}\)
\(\sg_3(\zeta)=\zeta^{65}\)
\(G_4=\{e,\:\sg_4,\:\sg_4^{\:2},\:\sg_4^{\:3}\}\)
\(\sg_4(\zeta)=\zeta^{217}\)
であり、これらすべてが巡回群です。また、体の拡大次数はガロア群の位数と一致し、順に \(2,\:2,\:6,\:4\) です。以上のことは、\(\zeta\) を \(1\) の\(360\)乗根とするとき、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\cong(\bs{Z}/360\bs{Z})^{*}\)
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/8\bs{Z})^{*}\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
であることの必然的な結果です。
以上のガロア群の計算を通して、\(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大であることが確認できました。
べき根拡大
| (べき根拡大の定義:63G) |
\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とするとき、\(\bs{K}(\sqrt[n]{a})\) を \(\bs{K}\) のべき根拡大(radical extension)と呼ぶ。
また、\(\bs{K}\) からのべき根拡大を繰り返して拡大体 \(\bs{F}\) ができるとき、\(\bs{F}/\bs{K}\) を累べき根拡大と言う。
\(x^n-a\) は既約多項式とは限らないので、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) の拡大次数は \(n\) とは限りません。
また一般に、べき根拡大はガロア拡大ではありません。しかし \(\bs{K}\) に特別の条件(= \(\bs{K}\) に \(1\) の原始\(n\)乗根 \(\zeta\) が含まれる)があるときは、べき根拡大がガロア拡大、かつ巡回拡大になります。この「原始\(\bs{n}\)乗根を含む体からのべき根拡大」を考えるのが、ガロア理論の巧妙なアイデアです。
\(1\) の原始\(n\)乗根を含むべき根拡大
| (原始n乗根を含むべき根拡大:63H) |
\(1\) の原始\(n\)乗根を \(\zeta\) とし、\(\bs{K}\) に \(\zeta\) が含まれるとする。\(\bs{K}\) 上の方程式 \(x^n-a=0\:(a\in\bs{K}\)、\(a\neq1)\) の解の一つで、\(\bs{K}\) に含まれないものを \(\sqrt[n]{a}\) とし、\(\bs{L}=\bs{K}(\sqrt[n]{a})\) とすると、
| \(\bs{L}/\bs{K}\) は巡回拡大である | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) の位数は \(n\) の約数である |
[証明]
\(\bs{K}(\sqrt[n]{a})\) 上の同型写像を \(\tau\) とする。\(x^n-a=0\) の解は、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\)
であり、\(\tau\) を \(\sqrt[n]{a}\) に作用させたときの移り先は、このうちのどれかである。もともと \(\bs{K}\) には \(1\) の原始\(n\)乗根 \(\zeta\) が 含まれているから、これらの移り先はすべて \(\bs{K}(\sqrt[n]{a})\) の元である。従って \(\tau\) は自己同型写像であり、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) はガロア拡大である。
次にガロア群 \(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) の元と、\(\bs{K}(\sqrt[n]{a})/\bs{K}\) の拡大次数を求める。\(\sqrt[n]{a}\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式(31I)により \(f(x)\) は既約多項式であり、\(f(x)=0\) と \(x^n-a=0\) は共通の解 \(\sqrt[n]{a}\) を持つから、\(x^n-a=0\) は \(f(x)\) で割り切れる。従って \(f(x)=0\) の解は、\(x^n-a=0\) の解、\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\) の全部、またはその一部である。\(f(x)=0\) の解で、\(\sqrt[n]{a}\:\zeta^{t}\) の\(t\) が最小となる 正の数を \(d\:(1\leq d\leq n-1)\) とする。そして \(\bs{K}\) の元を固定する \(\bs{K}(\sqrt[n]{a})\) の同型写像、\(\sg\) を、
\(\sg(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{d}\)
と定義する。これは自己同型写像になるから、\(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) の元である。\(\sg\) は \(\bs{K}\) の元を固定するから \(\sg(\zeta)=\zeta\) である。これを用いて \(\sg^i(\sqrt[n]{a})\) を求めると、
\(\begin{eqnarray}
&&\:\:\sg^2(\sqrt[n]{a})&=\sg(\sg(\sqrt[n]{a}))=\sg(\sqrt[n]{a}\:\zeta^{d})=\sg(\sqrt[n]{a})\zeta^{d}\\
&&&=\sqrt[n]{a}\:\zeta^{d}\zeta^{d}=\sqrt[n]{a}\:\zeta^{2d}\\
&&\:\:\sg^3(\sqrt[n]{a})&=\sg(\sg^2(\sqrt[n]{a}))=\sg(\sqrt[n]{a}\:\zeta^{2d})=\sg(\sqrt[n]{a})\zeta^{2d}\\
&&&=\sqrt[n]{a}\:\zeta^{d}\zeta^{2}d=\sqrt[n]{a}\:\zeta^{3d}\\
\end{eqnarray}\)
となり、一般的には、
\(\sg^i(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{id}\:(1\leq i)\)
となる。\(i=n\) とおくと、
\(\sg^n(\sqrt[n]{a})=\sqrt[n]{a}\:\zeta^{nd}=\sqrt[n]{a}\)
となるから、\(\sg^n=e\) である。
\(n\) を \(d\) で割ったときの商を \(s\)、余りを \(r\) とする。
\(n=sd+r\:(1 < s\leq n,\:0\leq r < d)\)
である。ここで \(\sg^i(\sqrt[n]{a})\) の \(i\) を \(n-s\) とおくと、
\(\begin{eqnarray}
&&\:\:\sg^{n-s}(\sqrt[n]{a})&=\sqrt[n]{a}\:\zeta^{nd-sd}\\
&&&=\sqrt[n]{a}\:\zeta^{n(d-1)+n-sd}\\
\end{eqnarray}\)
となる。\(\zeta^n=e\) なので、\(\zeta^{n(d-1)}=e\) であることを用いると、
\(\begin{eqnarray}
&&\:\:\sg^{n-s}(\sqrt[n]{a})&=\sqrt[n]{a}\:\zeta^{n-sd}\\
&&&=\sqrt[n]{a}\:\zeta^{r}\\
\end{eqnarray}\)
と計算できる。\(\sg^{s}\) はガロア群の元なので、\(\sg^{n-s}=\sg^{-s}\) もガロア群の元である。従って \(\sg^{n-s}(\sqrt[n]{a})\) は \(f(x)=0\) の解である。
ここでもし \(r\) がゼロでないとすると、\(1\) 以上、\(d\) 未満の数である \(r\) があって、\(\sqrt[n]{a}\:\zeta^{r}\) が \(f(x)=0\) の解となってしまう。しかしこれは、\(f(x)=0\) の解である \(\sqrt[n]{a}\:\zeta^{t}\) の \(t\) の最小値が \(d\) との仮定に反する。従って \(r=0\) である。
\(n=sd\) なので、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta,\:\sqrt[n]{a}\:\zeta^2,\:\cd\:,\:\sqrt[n]{a}\:\zeta^{n-1}\)
の中に \(f(x)=0\) の解は \(s\) 個あり、
\(\sqrt[n]{a},\:\sqrt[n]{a}\:\zeta^{d},\:\:\sqrt[n]{a}\:\zeta^{2d},\:\cd\:,\:\sqrt[n]{a}\:\zeta^{(s-1)d}\)
である。\(\mr{Gal}(\bs{K}(\sqrt[n]{a})/\bs{K})\) は位数 \(s\) の巡回群であり、位数は \(n\) の約数である。\(n\) が素数 \(p\) であれば、\(\mr{Gal}(\bs{K}(\sqrt[p]{a})/\bs{K})\) は \(p\)次の巡回群である。[証明終]
この定理から分かることは、あらかじめ必要な原始\(n\)乗根を "仕込んで" おけば、べき根拡大列は巡回拡大列になるということです。たとえば、べき根拡大の列、
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{L}\)
があり、\(\bs{K}/\bs{Q}\) の拡大次数を \(n_1\)、\(\bs{L}/\bs{K}\) の拡大次数を \(n_2\) とします。\(n_1,\:n_2\) の最小公倍数を \(n\)、\(1\) の原始\(n\)乗根を \(\zeta\) とします。そして、
\(\bs{Q}\:\subset\:\bs{Q}(\zeta)\:\subset\:\bs{K}\:\subset\:\bs{L}\)
の拡大列を考えると、\(\bs{Q}(\zeta)\) には、
\(1\) の原始\(n_1\)乗根 : \(\zeta^{\frac{n}{n_1}}\)
\(1\) の原始\(n_2\)乗根 : \(\zeta^{\frac{n}{n_2}}\)
が含まれているので、
| \(\bs{Q}(\zeta)/\bs{Q}\) | : 累巡回拡大(63F) | |
| \(\bs{K}/\bs{Q}(\zeta)\) | : 巡回拡大(63H) | |
| \(\bs{L}/\bs{K}\) | : 巡回拡大(63H) |
\(\bs{L}/\bs{Q}\) : 累巡回拡大
になります。ここまでくると、可解性の必要条件の証明まであと一歩です。
6.4 可解性の必要条件
可解性の必要条件を証明する最終段階にきました。\(\bs{Q}\) 上の既約な方程式の解の一つを \(\al\) とし、\(\bs{K}=\bs{Q}(\al)\) の拡大体を考えます。\(\al\) が四則演算とべき根で表現できるということは、\(\bs{K}/\bs{Q}\) が累べき根拡大(63G)であるということです。ここが出発点です。そして証明の方針として、
| \(\bs{K}/\bs{Q}\) が累べき根拡大 | |
| \(\bs{K}/\bs{Q}\) が累巡回拡大 | |
| ガロア拡大 | |
| ガロア群が可解群 |
の4つが密接に関係していることを示します。
まず、原始\(\bs{n}\)乗根を含むべき根拡大の定理(63H)により、累べき根拡大の拡大のステップに必要な原始\(n\)乗根の全種類をあらかじめ \(\bs{Q}\) に含めておけば、① 累べき根拡大は ② 累巡回拡大と同じことなります。
さらに、累巡回拡大ガロア群の可解性(62C)の定理により、もし \(\bs{K}/\bs{Q}\) が ③ ガロア拡大であれば、累巡回拡大 \(\bs{K}/\bs{Q}\) のガロア群 \(\mr{Gal}(\bs{K}/\bs{Q})\) は ④ 可解群です。
しかし、累巡回拡大の定義(62B)のところで書いたように、\(\bs{K}/\bs{Q}\) が累巡回拡大であってもガロア拡大であるとは限りません。そこで、
\(\bs{Q}\:\subset\:\bs{K}\:\subset\:\bs{E}\)
となるような \(\bs{E}\) で、\(\bs{E}/\bs{Q}\) が累巡回拡大、かつガロア拡大である \(\bs{E}\) が必ず存在することを証明できれば、① \(\rightarrow\) ② \(\rightarrow\) ③ \(\rightarrow\) ④ が一気通貫でつながることになります。このような \(\bs{E}\)(そこには \(\al\) が含まれる)の存在を、累巡回拡大の定義(62B)の説明で書いたシンプルな例で考察します。
代数的数 \(\al\) を、
\(\al=\sqrt{\sqrt{2}+1}\)
とします。この \(\al\) は \(\bs{Q}\) 上の既約な方程式、
\(f(x)=x^4-2x^2-1=0\)
の解の一つです。この \(f(x)\) は \(\al\) の最小多項式です。ちなみに \(f(x)\) は、
\(f(x)=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\)
と変形できるので、方程式 \(f(x)=0\) の解は
\(x=\pm\sqrt{\sqrt{2}+1},\:\:\:\pm i\sqrt{\sqrt{2}-1}\)
の4つです。
\(\al\) を含む \(\bs{Q}\) の拡大体 \(\bs{Q}(\al)\) を考えます。\(\bs{Q}\:\subset\:\bs{Q}(\al)\) ですが、べき根拡大だけで表現すると、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\:\subset\:\bs{Q}(\sqrt{\sqrt{2}+1})\)
の累べき根拡大になります。つまり、\(\bs{Q}\) 上の方程式、
\(x^2-2=0\)
の解の一つ \(\sqrt{2}\) を \(\bs{Q}\) に添加してべき根拡大をし、\(\bs{Q}(\sqrt{2})\) 上の方程式、
\(x^2-(\sqrt{2}+1)=0\)
の解の一つ \(\sqrt{\sqrt{2}+1}\) を \(\bs{Q}(\sqrt{2})\) に添加したのが \(\bs{Q}(\sqrt{\sqrt{2}+1})\) です。2つのべき根拡大の拡大次数は2です。\(1\) の原始2乗根は \(-1\) なので、始めから \(\bs{Q}\) に含まれています。従って、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) は
・べき根拡大
・巡回拡大
\(\mr{Gal}(\bs{Q}(\sqrt{2})=\{\sg_1,\:\sg_2\}\)
\(\sg_1=e\)
\(\sg_2(\sqrt{2})=-\sqrt{2}\)
・\(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) 上の多項式 \(x^2-2\) の最小分解体
となります。まったく同様に、
\(\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{\sqrt{2}+1})\) は
・べき根拡大
・巡回拡大
です。しかし、\(\bs{Q}(\sqrt{\sqrt{2}+1})/\bs{Q}\) がガロア拡大ではありません。というのも、\(\bs{Q}(\sqrt{\sqrt{2}+1})\) は \(\bs{Q}\) 上ではなく \(\bs{Q}(\sqrt{2})\) 上の方程式、
\(x^2-(\sqrt{2}+1)=0\)
の解の一つ \(\sqrt{\sqrt{2}+1}\) を \(\bs{Q}(\sqrt{2})\) に添加したものだからです。
そこで、\(\bs{Q}(\sqrt{2})\) 上の2つの方程式、
・\(x^2-\sg_1(\sqrt{2}+1)=0\)
・\(x^2-\sg_2(\sqrt{2}+1)=0\)
の解を順に \(\bs{Q}(\sqrt{2})\) に追加することにします。つまり、
・\(\sqrt{\phantom{-}\sqrt{2}+1}\)
・\(\sqrt{-\sqrt{2}+1}\)
の2つを \(\bs{Q}(\sqrt{2})\) に追加します。ガロア群は必ず単位元 \(e\) を含むので、\(\sg_1(\sqrt{2}+1)\) と \(\sg_2(\sqrt{2}+1)\) のどちらかは \(\al=\sqrt{\sqrt{2}+1}\) になります。この追加は2つともべき根拡大であり、巡回拡大です。こうして出来上がった拡大体を \(\bs{E}\) とすると、
\(\bs{E}=\bs{Q}(\sqrt{\sqrt{2}+1},\sqrt{-\sqrt{2}+1})\)
です。以上のことを別の観点で言うと、多項式 \(g(x)\) を、
\(g(x)=(x^2-\sg_1(\sqrt{2}+1))(x^2-\sg_2(\sqrt{2}+1))\)
と定義するとき、
\(g(x)=0\) の解を \(\bs{Q}(\sqrt{2})\) に追加したのが \(\bs{E}\)
ということになります。\(g(x)\) を計算すると、
\(\begin{eqnarray}
&&\:\:g(x)&=(x^2-\sg_1(\sqrt{2}+1))(x^2-\sg_2(\sqrt{2}+1))\\
&&&=(x^2-(\sqrt{2}+1))(x^2+(\sqrt{2}-1))\\
&&&=x^4-2x^2-1\\
\end{eqnarray}\)
となり、\(g(x)\) は \(\bs{Q}\) 上の多項式です。なぜそうなるかと言うと、\(g(x)\) の係数は \(\sg_1(\sqrt{2}+1)\) と \(\sg_2(\sqrt{2}+1)\) の対称式で表されるからで、従ってガロア群の元 \(\sg_1,\:\sg_2\) を作用させても不変であり、つまり係数が有理数だからです。ここから得られる結論は、
\(\bs{E}\) は \(\bs{Q}\) 上の多項式 \(g(x)\) の最小分解体である
ということです。このことは、\(\al=\sqrt{\sqrt{2}+1}\) の最小多項式が \(x^4-2x^2-1=g(x)\) であったことからも確認できます。従ってガロア拡大の定義(52A)により、
\(\bs{E}/\bs{Q}\) はガロア拡大
です。まとめると、
\(\bs{Q}\:\subset\:\bs{Q}(\al)\:\subset\:\bs{E}\)
\(\bs{E}/\bs{Q}\) は累巡回拡大、かつガロア拡大
である \(\bs{E}\) の存在が証明できました。
以上は "2段階の2次拡大" という非常にシンプルな例ですが、このことを一般的に(多段階の \(n\)次拡大で)述べると次のようになります。
ガロア閉包
| (ガロア閉包の存在:64A) |
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つである \(\al\) がべき根で表されているとする。このとき「\(\bs{Q}\) のガロア拡大 \(\bs{E}\) で、\(\al\) を含み、\(\bs{E}/\bs{Q}\) が累巡回拡大」であるような 代数拡大体 \(\bs{E}\) が存在する。
[証明]
\(\bs{Q}\)上の方程式 \(f(x)=0\) の解の一つ \(\al\) がべき根で表されているとき、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{K}\)
| \(\bs{K}_{i+1}=\bs{K}_i(\al_{i+1})\) | |
| \(\al_{i+1}\) は \(x^{n_i}-a_i=0\:(a_i\in\bs{K}_i)\) の根の一つ | |
| \([\bs{K}_{i+1}:\bs{K}_i]=n_i\) | |
| \(\al_k=\al\:\in\:\bs{K}_k=\bs{K}\) |
となる、べき根拡大列 \(\bs{K}_i\) が存在する(= \(\bs{K}/\bs{Q}\) が累べき根拡大)。このべき根拡大列を修正して、
\(\bs{Q}\subset\bs{F}_0\subset\bs{F}_1\subset\cd\subset\bs{F}_i\subset\bs{F}_{i+1}\subset\cd\subset\bs{F}_k=\bs{E}\)
| \(\bs{K}_i\:\subset\:\bs{F}_i\) | |
| \(\bs{F}_{i+1}/\bs{F}_i\) は累巡回拡大 | |
| \(\bs{E}/\bs{Q}\) はガロア拡大 | |
| \(\al_k=\al\:\in\:\bs{K}_k\:\subset\:\bs{F}_k=\bs{E}\) |
とできることを以下に示す。まず、\(n_i\:(0\leq i < k)\) の最小公倍数を \(n\) とし、\(1\) の原始\(n\)乗根を \(\zeta\) とする。そして、
\(\bs{F}_0=\bs{Q}(\zeta)\)
とおくと、\(\bs{K}_0(=\bs{Q})\:\subset\:\bs{F}_0\) であり、\(\bs{F}_0\) は \(1\) の原始\(n_i\)乗根 \((0\leq i < k)\) を全て含むことになる。
\(\bs{F}_0\) は \(\bs{Q}(\zeta)\) だから、\(\mr{Gal}(\bs{F}_0/\bs{Q})=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) は巡回群の直積に同型であり(63F)、従って可解群である(61B)。つまり、\(\bs{F}_0/\bs{Q}\) は累巡回拡大である(62C)。
次に、
\(\bs{F}_1=\bs{F}_0(\al_1)\)
とおく。\(\al_1\) は \(\bs{K}_0=\bs{Q}\) 上の方程式 \(x^{n_0}-a_0=0\:(a_0\in\bs{K}_0\:\subset\:\bs{F}_0)\) の根の一つで、\(\al_1=\sqrt[n_0]{a_0}\) であるから、\(\bs{F}_1\) は \(\bs{F}_0\) のべき根拡大になる。
すると、\(\bs{F}_0\)は \(1\) の原始\(n_0\)乗根を含むから、原始\(\bs{n}\)乗根を含むべき根拡大の定理(63H)により、\(\bs{F}_1/\bs{F}_0\) は巡回拡大である。この拡大次数は \([\bs{F}_1:\bs{F}_0]=[\bs{K}_1:\bs{K}_0(=\bs{Q})]=n_0\) である。
また \(\bs{F}_1\)は、\(\bs{Q}\) 上の方程式 \(x^{n_0}-a_0=0\) の解 \(\al_1\eta^j\)(\(\eta\) は \(1\) の原始\(n_0\)乗根。\(0\leq j < n_0\))をすべて含むから、\(\bs{F}_1/\bs{Q}\) はガロア拡大である。
次に \(\bs{K}_2\) を修正した \(\bs{F}_2\) を考える。\(\mr{Gal}(\bs{F}_1/\bs{Q})\) の元を \(\sg_j\:(1\leq j\leq m,\:\sg_1=e)\) の \(m\)個とする。
\(\al_2\) は \(x^{n_1}-a_1=0\:\:(a_1\in\bs{K}_1\:\subset\:\bs{F}_1)\) の根の一つであった。そこで、
\(\sg_j(a_1)\) \((1\leq j\leq m)\)
という \(m\)個の元をもとに、
\(x^{n_1}-\sg_j(a_1)=0\:(a_1\in\bs{K}_1\:\subset\:\bs{F}_1,\:\:1\leq j\leq m)\)
という \(m\)個の方程式群を考える。\(\sg_j\) の中には単位元 \(e\) が含まれるため、\(x^{n_1}-a_1=0\) も方程式群の中の一つである。
この \(m\)個の方程式の \(m\)個の解、
\(\sqrt[n_1]{\sg_j(a_1)}\) \((1\leq j\leq m)\)
を \(\bs{F}_1\) に順々に添加していき、最終的にできた体を \(\bs{F}_2\) とする。\(\bs{F}_1\) は \(1\) の原始 \(n_1\)乗根を含むから、\(\sqrt[n_1]{\sg_j(a_1)}\) \((1\leq j\leq m)\) の添加はすべて巡回拡大である(63H)。つまり、\(\bs{F}_2\) は \(\bs{F}_1\) の累巡回拡大である。\(\sg_j\) の中には単位元があるから、\(\bs{F}_2\) には \(\al_2=\sqrt[n_1]{a_1}\) を含む。
ここで多項式 \(g(x)\) を、
\(g(x)=\displaystyle\prod_{j=1}^{m}(x^{n_1}-\sg_j(a_1))\)
と定義する。\(\bs{F}_1\) は \(1\) の原始 \(n_1\)乗根を含むから、\(\bs{F}_2\) は \(g(x)=0\) のすべての解を \(\bs{F}_1\) に添加した拡大体である。
多項式 \(g(x)\) の係数は、根と係数の関係から \(\sg_j(a_1)\:\:(1\leq j\leq m)\) の対称式であり、係数に任意の \(\sg_j\:(=\mr{Gal}(\bs{F}_1/\bs{Q})\) の元\()\) を作用させても不変である。つまり係数は有理数であり、\(g(x)\) は \(\bs{Q}\) 上の多項式である。結局、\(\bs{F}_2\) は \(\bs{Q}\) 上の多項式 \(g(x)\) の最小分解体であり、\(\bs{F}_2/\bs{Q}\) はガロア拡大である(52A)。
まとめると、
| \(a_1\:\in\:\bs{K}_1\:\subset\:\bs{F}_1\) | |
| \(\bs{F}_1\) には \(1\) の原始\(n_1\)乗根が含まれる | |
| \(\al_2\) は \(x^{n_1}-a_1=0\) の根の一つ | |
| \(\mr{Gal}(\bs{F}_1/\bs{Q})\) の元が \(\sg_j\:(1\leq j\leq m,\:\:\:\sg_1=e)\) |
\(g(x)=\displaystyle\prod_{j=1}^{m}(x^{n_1}-\sg_j(a_1))\)
の条件で、\(g(x)=0\) のすべての解を \(\bs{F}_1\) に添加した拡大体を \(\bs{F}_2\) とすると、
| \(\bs{F}_2/\bs{F}_1\) 累巡回拡大 | |
| \(\bs{F}_2/\bs{Q}\) はガロア拡大 | |
| \(\al_2\:\in\:\bs{K}_2\:\subset\:\bs{F}_2\) |
この \(\bs{K}_i\) を \(\bs{F}_i\) に修正する操作は、\(\bs{K}_k\) を修正して \(\bs{F}_k\) にするまで続けることができる。従って、
\(\bs{Q}\subset\bs{F}_0\subset\bs{F}_1\subset\cd\subset\bs{F}_i\subset\bs{F}_{i+1}\subset\cd\subset\bs{F}_k=\bs{E}\)
の拡大列が存在し、| \(\bs{K}\:\subset\:\bs{F}_i\) | |
| \(\bs{F}_{i+1}/\bs{F}_i\) は累巡回拡大 | |
| \(\bs{F}_k/\bs{Q}\) はガロア拡大 | |
| \(\al_k=\al\:\in\:\bs{F}_k(=\bs{E})\) |
|
\(1\) の原始\(n\)乗根を含む \(\bs{Q}(\zeta)\) からのべき根拡大を考えることによって、体の拡大が巡回拡大(=ガロア群が巡回群であるガロア拡大)になり(63H)、その繰り返しは累巡回拡大になります。しかし累巡回拡大が "全体としてガロア拡大になる" とは限りません(62B)。
そこで、ひと工夫して、\(\bs{\bs{F}_i}\) が常に \(\bs{\bs{Q}}\) 上の方程式 \(\bs{g(x)}\) の最小分解体で、かつ \(\bs{\al_i}\) を含むようにすると、\(\bs{F}_i/\bs{Q}\) が常にガロア拡大になっているので、\(\bs{E}/\bs{Q}\) もガロア拡大になります。しかも最終到達点である \(\bs{F}_k=\bs{E}\) の中には、元々の方程式の解である \(\al\) がある。このような \(\bs{E}\) の存在が重要です。この \(\bs{Q}(\zeta)\:\rightarrow\:\bs{E}\) の拡大を考えることで、単なるべき根拡大列だった \(\bs{Q}\:\rightarrow\:\bs{K}\) をガロア理論の俎上に乗せることができます。
一方、\(\bs{\bs{Q}(\zeta)/\bs{Q}}\) が累巡回拡大になるのは、全く別のロジックによります。つまり、\(\bs{Q}(\zeta)/\bs{Q}\) がガロア拡大で(63D)かつ、ガロア群が巡回群の直積に同型(63F)であり、従ってガロア群が可解群(61B)だからです。そうすると累巡回拡大ガロア群の可解性(62C)によって \(\bs{Q}(\zeta)/\bs{Q}\) は累巡回拡大です。
以上の2つの合わせ技で、\(\bs{Q}\) から \(\bs{E}\) に至る累巡回拡大の列ができ、しかも \(\bs{E}/\bs{Q}\) がガロア拡大になっていて、次の可解性の必要条件の証明につながります。
可解性の必要条件
| (可解性の必要条件:64B) |
\(\bs{Q}\) 上の \(n\)次既約方程式 \(f(x)=0\) の解の一つ がべき根で表されているとする。\(f(x)\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) は可解群である。
[証明]
ガロア閉包の存在定理(64A)により、\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つがべき根で表されているとすると、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{E}\)
という拡大列で、| \(\bs{E}/\bs{Q}\) は累巡回拡大 | |
| \(\bs{E}/\bs{Q}\) はガロア拡大 | |
| \(\al\:\in\:\bs{E}\) |
また、\(\bs{E}/\bs{Q}\) がガロア拡大ということは、中間体からのガロア拡大の定理(52C)により、\(\bs{E}/\bs{L}\) もガロア拡大である。従って、
\(\mr{Gal}(\bs{E}/\bs{Q})=G\)
\(\mr{Gal}(\bs{E}/\bs{L})=H\)
と書くと、
\(G\) \(\sp\) \(H\) \(\sp\) \(\{\:e\:\}\)
\(\bs{Q}\) \(\subset\) \(\bs{L}\) \(\subset\) \(\bs{E}\)
のガロア対応(53B)が成り立つ。
\(\bs{L}\) は \(\bs{Q}\) 上の既約多項式 \(f(x)\) の最小分解体だから、\(\bs{L}/\bs{Q}\) はガロア拡大である(52A)。ゆえに正規性定理(53C)により、\(H\) は \(G\) の正規部分群であり、
\(\mr{Gal}(\bs{L}/\bs{Q})\:\cong\:G/H\)
が成り立つ。
\(\bs{E}/\bs{Q}\) はガロア拡大かつ累巡回拡大だから、累巡回拡大ガロア群の可解性(62C)の定理によって \(G\) は可解群である。\(G\) が可解群なので、その剰余群である \(G/H\) も可解群である(61D)。従って、\(G/H\) と同型である \(\mr{Gal}(\bs{L}/\bs{Q})\) も可解群である。[証明終]
この定理の対偶をとると、
\(\bs{Q}\) 上の既約方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とするとき、\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群でなければ、\(f(x)=0\) の解のすべてはべき根で表されない(=非可解)
となります。これを用いて、非可解な5次方程式があることを証明できます。
6.5 5次方程式の解の公式はない
5次方程式には解の公式はないことをガロア理論で証明します。そのためにまず、対称群、交代群、置換の説明をします。
対称群 \(S_n\)
集合 \(\Omega_n=\{1,\:2,\:\cd\:n\}\) から \(\Omega_n\) への全単射写像(1対1写像)の全体を \(S_n\) と書き、\(n\)次の対称群(symmetric group)と言います。\(1,\:2,\:\cd\) は整数ではなく、集合の元を表す文字です。一般に集合 \(X\) から \(X\) への全単射写像を置換(permutation)と呼ぶので、\(S_n\) の元は \(n\) 個の文字の置換です。
\(S_n\) の元の一つを \(\sg\) とします。\(1\leq k\leq n\) とし、\(\sg\)による \(k\) の移り先を \(\sg(k)\) とすると、\(\sg\) は全単射写像なので、\(k\neq k\,'\) なら\(\sg(k)\neq\sg(k\,')\) です。従って、\((\sg(1),\sg(2),\cd,\sg(n))\) は、\((1,2,\cd n)\) の一つの順列になります。逆に、\((1,2,\cd n)\) の順列の一つを \((i_1,i_2,\cd i_n)\) とすると、\(\sg(k)=i_k\) で \(\Omega_n\) から \(\Omega_n\) への全単射写像が得られます。つまり \(S_n\) は \((1,2,\cd n)\) のすべての順列と同一視できます。
\(S_n\) の元の2つを \(\sg\)、\(\tau\) とし、\(\sg\) と \(\tau\) の合成写像 \(\sg\tau\) を、
\(\sg\tau(k)=\sg(\tau(k))\:\:(1\leq k\leq n)\)
で定義すると、\(\sg\tau\) も全単射写像なので \(S_n\) の元であり、\(S_n\) は群になります。単位元 \(e\) は \(e(k)=k\:(1\leq k\leq n)\) である恒等写像です。また、\(\sg\) は全単射写像なので逆写像 \(\sg^{-1}\) があり、群の定義を満たしています。
\(S_n\) は \((1,2,\cd n)\) のすべての順列と同一視できるので、その位数は
\(|S_n|=n\:!\)
です。\(S_n\) の元 \(\sg\) を、
\(\sg=\left(\begin{array}{c}1&2&\cd&n\\\sg(1)&\sg(2)&\cd&\sg(n)\end{array}\right)\)
と表します。この表記では縦の列が合っていればよく、並び順に意味はありません。これを使うと \(\sg\) の逆元は、
\(\sg^{-1}=\left(\begin{array}{c}\sg(1)&\sg(2)&\cd&\sg(n)\\1&2&\cd&n\end{array}\right)\)
です。
\(S_3\) の元を \(\sg_1,\sg_2,\:\cd\:\sg_6\) とし、具体的に書いてみると、
\(\sg_1=\left(\begin{array}{c}1&2&3\\1&2&3\end{array}\right)\) \(\sg_2=\left(\begin{array}{c}1&2&3\\2&3&1\end{array}\right)\)
\(\sg_3=\left(\begin{array}{c}1&2&3\\3&1&2\end{array}\right)\) \(\sg_4=\left(\begin{array}{c}1&2&3\\1&3&2\end{array}\right)\)
\(\sg_5=\left(\begin{array}{c}1&2&3\\3&2&1\end{array}\right)\) \(\sg_6=\left(\begin{array}{c}1&2&3\\2&1&3\end{array}\right)\)
となります。\(\sg_1\) は恒等置換 \(e\) です。なお \(S_3\) は、1.3節に出てきた3次の2面体群と同じものです。
巡回置換
\(S_n\) に現れる \(n\)文字からその一部を取り出します。例えば3つ取り出して、\(i,\:j,\:k\) とします。そして、
\(i\rightarrow j,\:\:j\rightarrow k,\:\:k\rightarrow i\)
と文字を循環させ、その他の文字は不動にする置換 \(\sg\) を考えます。これが巡回置換(cyclic permutation)です。
\(\sg=\left(\begin{array}{c}\cd&i&\cd&j&\cd&k&\cd\\\cd&j&\cd&k&\cd&i&\cd\end{array}\right)\)
と表せて、\(\cd\) の部分は不動です。これを簡略化して、
\(\sg=(i,\:j,\:k)\)
と表記します。\(\sg\) の逆元は、
| \(\sg^{-1}\) | \(=(i,\:j,\:k)^{-1}\) | |
| \(=\left(\begin{array}{c}\cd&i&\cd&j&\cd&k&\cd\\\cd&j&\cd&k&\cd&i&\cd\end{array}\right)^{-1}\) | ||
| \(=\left(\begin{array}{c}\cd&j&\cd&k&\cd&i&\cd\\\cd&i&\cd&j&\cd&k&\cd\end{array}\right)\) | ||
| \(=\left(\begin{array}{c}\cd&i&\cd&j&\cd&k&\cd\\\cd&k&\cd&i&\cd&j&\cd\end{array}\right)\) | ||
| \(=(k,\:j,\:i)\) |
\(\sg=(i_1,\:i_2,\:\cd\:,i_m)\)
です。長さ \(m\) の巡回置換、とも言います。逆元は文字の順序を逆順にした、
\(\sg^{-1}=(i_m,\:i_{m-1},\:\cd\:,i_1)\)
です。\(m\)文字の巡回置換を群としてとらえたとき、 \(C_m\) で表します。\(C_m\) は位数 \(m\) の巡回群で、可換群です。
特に、2文字の巡回置換を互換(transposition)と言います。巡回置換と互換について、次の定理が成り立ちます。
| (置換は巡回置換の積:65A) |
すべての置換は共通文字を含まない巡回置換の積で表せる。
[証明]
\(n\)次対称群 \(S_n\) の任意の元を \(\sg\) とすると、\(\sg\) は \(n\)文字の任意の置換である。\(n\)文字の中から \(\sg(a)\neq a\) である文字 \(a\) を選ぶ。そして \(\sg(a),\:\sg^2(a),\:\sg^3(a),\:\cd\) という、\(\sg\) による \(a\) の写像を繰り返す列を考える。\(\sg\)による \(a\) の移り先は最大 \(n\)個なので、列の中には、
\(\sg^j(a)=\sg^i(a)\:\:(i < j)\)
となる \(i,\:j\) が必ず出てくる。つまり、
\(\sg^{j-i}(a)=a\)
となる \(i,\:j\) が存在する。\(k_a\) を \(\sg^{k_a}(a)=a\) となる最小の数とすると、
\(\sg(a),\:\sg^2(a),\:\cd\:,\sg^{k_a}(a)=a,\:\sg(a),\:\cd\)
となり、\(k_a+1\)番目で \(\sg(a)\) に戻って以降は巡回する。\(\sg_1\) を、 \((\br{A})\)
\(\sg_1=(\sg(a),\:\sg^2(a),\:\cd\:,\sg^{k_a}(a))\)
の巡回置換と定義する。
もし仮に列 \((\br{A})\) が、\(\sg\) で変化する文字全部を尽くしているなら、題意は正しい。そうでないとき、列 \((\br{A})\) に現れない文字で \(\sg(b)\neq b\) である \(b\) を選ぶ。上と同様にして、
\(\sg(b),\:\sg^2(b),\:\cd\:,\sg^{k_b}(b)=b\)
の列が作れる。\((\br{B})\) 列に \((\br{A})\) 列と同じ文字は現れない。なぜなら、もし列 \((\br{B})\) の \(\sg^i(b)\) が \((\br{A})\) 列に現れるとすると、\(\sg^i(b)\) に \(\sg\) による置換を繰り返すといずれは \(b\) になるから、\(b\) が \((\br{A})\) 列に現れることになってしまい、「列 \((\br{A})\) に現れない文字 \(b\)」ではなくなるからである。従って、 \((\br{B})\)
\(\sg_2=(\sg(b),\:\sg^2(b),\:\cd\:,\sg^{k_b}(b)=b)\)
という、2つ目の巡回置換が定義できる。列 \((\br{A})\) と \((\br{B})\) が \(\sg\) で変化する文字全部を尽くすなら、\(\sg=\sg_2\sg_1\) である。\(\sg_1\) と \(\sg_2\) に共通の文字は現れないので、\(\sg=\sg_1\sg_2\) と書いてもよい。
以上の操作は、\(\sg\) で変化する文字全部を尽くすまで繰り返すことができる。その繰り返し回数を \(m\) とすると、
\(\sg=\sg_1\sg_2\:\cd\:\sg_m\)
であり、任意の置換 \(\sg\) は巡回置換の積で表せることになる。なお、恒等置換 \(e\) は、
\(e=(i,\:j)^2\)
\(e=(i,\:j,\:k)^3\)
などであり、巡回置換の積で表せることに変わりはない。[証明終]
置換を巡回置換の積で表すと、例えば、
| \(\sg\) | \(=\left(\begin{array}{c}1&2&3&4&5&6\\1&4&5&6&3&2\end{array}\right)\) | |
| \(=(2,\:4,\:6)(3,\:5)\) |
| (置換は互換の積:65B) |
すべての置換は互換の積で表せる。
[証明]
巡回置換 \((1,\:2,\:3)\) は
\((1,\:2,\:3)=(1,\:3)(1,\:2)\)
と表せる(積は右から読む)。また、巡回置換 \((1,\:2,\:3\). \(4)\) は、
\((1,\:2,\:3,\:4)=(1,\:4)(1,\:3)(1,\:2)\)
である。一般に、
\((i_1,\:i_2,\:\cd\:,i_m)=(i_1,\:i_m)\:\cd\:(i_1,\:i_2)\)
である。このように巡回置換は互換の積で表せる。すべての置換は巡回置換の積で表せる(65A)ので、題意は正しい。[証明終]
交代群 \(A_n\)
一つの置換を互換の積で表す方法が一意に決まるわけではありません。たとえば、
| \((1,\:2,\:3)\) | \(=(1,\:3)(1,\:2)\) | |
| \(=(1,\:3)(2,\:3)(1,\:2)(1,\:3)\) |
| (置換の偶奇性:65C) |
一つの置換を互換の積で表したとき、その互換の数は奇数か偶数かのどちらかに決まる。
[証明]
\(n\)変数の多項式 \(f(x_1,x_2,\cd,x_n)\) を、
\(f(x_1,x_2,\cd,x_n)=\displaystyle\prod_{1\leq i < j\leq n}^{}(x_i-x_j)\)
と定義する(差積と呼ばれる)。\(S_n\) の一つの元を \(\sg\) とし、\(\sg\) を \(f(x_1,x_2,\cd,x_n)\) に作用させることを、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=f(x_{\sg(1)},x_{\sg(2)},\cd,x_{\sg(n)})\)
と定義する。\(\sg\) が互換、つまり \(\sg=(i,\:j)\) であれば、
\((i,\:j)\cdot f(x_1,x_2,\cd,x_n)=-f(x_1,x_2,\cd,x_n)\)
となる。これはすべての互換で成り立つ。
\(\sg\) が \(k\)個の互換の積で表されていると、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=(-1)^kf(x_1,x_2,\cd,x_n)\)
である。もし、\(m\neq k\) として \(\sg\) が \(m\)個の互換の積で表せたとしたら、
\(\sg\cdot f(x_1,x_2,\cd,x_n)=(-1)^mf(x_1,x_2,\cd,x_n)\)
である。従って、
\((-1)^k=(-1)^m\)
であり、\(k\) と \(m\) の偶奇は等しい。[証明終]
置換の偶奇性(65C)により、置換は2つのタイプに分けることができます。偶数個の互換の積で表す置換を偶置換(even permutaion)、奇数個の互換の積で表す置換を奇置換(odd permutaion)と言います。
偶置換の積は偶置換です。従って、\(S_n\) の偶置換の元を集めた集合は群になります。これを \(n\)次交代群(alternating group)といい、\(A_n\) で表します。
| (交代群は正規部分群:65D) |
\(S_n\) の元は同数の偶置換と奇置換から成る。従って、
\([\:S_n\::\:A_n\:]=2\)
である。
\(A_n\) は \(S_n\) の正規部分群であり、\(S_n/A_n\) は巡回群である。
[証明]
\(B_n\) を \(S_n\) に含まれる奇置換の集合とする。\(S_n\) の任意の互換を \(\sg\) とすると、集合 \(\sg A_n\) のすべての元は奇置換だから、
\(\sg A_n\subset B_n\)
が成り立つ。それとは逆に、集合 \(\sg B_n\) のすべての元は偶置換だから、
\(\sg B_n\subset A_n\)
も成り立つ。この式に左から \(\sg\) を作用させると、
\(\sg^2B_n\subset\sg A_n\)
\(B_n\subset\sg A_n\)
となる。\(\sg A_n\subset B_n\) かつ \(B_n\subset\sg A_n\) なので、
\(B_n=\sg A_n\)
となり、\(B_n\) と \(A_n\) の元の数は等しい。\(S_n=A_n\cup B_n\) なので、
\([\:S_n\::\:A_n\:]=2\)
である。
\(S_n\) の部分群 \(A_n\) の元の数は \(S_n\) の元の数の半分なので、\(S_n\) は \(A_n\) の2つの左剰余類(または右剰余類)の和集合である。従って、\(B_n\) の 任意の元を \(b\) とすると、
(\(A_n\) の左剰余類) \(S_n=A_n\cup bA_n\:\:(A_n\cap bA_n=\phi)\)
(\(A_n\) の右剰余類) \(S_n=A_n\cup A_nb\:\:(A_n\cap A_nb=\phi)\)
となり、\(bA_n=A_nb\) である。また \(A_n\) の元 \(a\) については、\(A_n\) が群なので \(aA_n=A_n,\:A_na=A_n\) である。従って \(S_n\) の任意の元 \(\sg\) について \(\sg A_n=A_n\sg\) が成り立ち、\(A_n\) は \(S_n\) の正規部分群である。
\(A_n\) が正規部分群なので、\(S_n/A_n\) は剰余群である。\(S_n\) の任意の元を \(\sg\) とし、\(S_n/A_n\) の元を \(\sg A_n\) とすると、
\((\sg A_n)^2=\sg A_n\sg A_n=\sg\sg A_nA_n=\sg^2A_n\)
となるが、\(\sg A_n=B_n\) であり \(\sg B_n=A_n\) だから、\(\sg^2A_n=A_n\) である。つまり、
\((\sg A_n)^2=A_n\)
を満たす。\(A_n\) は 剰余群 \(S_n/A_n\) の単位元だから、\(S_n/A_n\) は巡回群でである。[証明終]
| (交代群は3文字巡回置換の積:65E) |
交代群 \(A_n\) の任意の元は、3文字の巡回置換の積で表せる。
[証明]
\(A_n\) の任意の元は偶数個の互換の積で表せる。この互換の積を2つずつ右から(ないしは左から)取り出すことを考える。2つの互換の積には4つの文字があるが、それには次の2つパターンがある。
異なる4文字
\((i,\:j)(k,\:m)\)
異なる3文字
\((i,\:j)(i,\:k)\)
異なる3文字のうち、\((i,\:j)(j,\:k)\) のパターンは、\(i\) を \(j\) と読み替え、\(j\) を \(i\) と読み替えると \((j,\:i)(i,\:k)\) となり、\((i,\:j)(i,\:k)\) と同じである。また、\((i,\:j)(k,\:i)\) や \((i,\:j)(k,\:j)\) も \((i,\:j)(i,\:k)\) と同じである。
異なる2文字から成る \((i,\:j)(i,\:j)\) は恒等互換なので無視してよい。
2つの互換の積の2パターンは、いずれも3文字の巡回置換の積で表せる。つまり、
\(\left(\begin{array}{c}i&j&k&m\\k&i&j&m\end{array}\right)=(i,\:k,\:j)\)
\(\left(\begin{array}{c}k&i&j&m\\j&i&m&k\end{array}\right)=(j,\:m,\:k)\)
\(\left(\begin{array}{c}i&j&k&m\\j&i&m&k\end{array}\right)=(i,\:j)(k,\:m)\)
なので、
\((i,\:j)(k,\:m)=(j,\:m,\:k)(i,\:k,\:j)\)
である。また、巡回置換を互換の積で表す標準的な方法(65B)から、
\((i,\:j)(i,\:k)=(i,\:k,\:j)\)
である。
\(A_n\) は「2つの互換の積」の積、で表現でき、「2つの互換の積」は「3文字の巡回置換の積」で表せるので、題意は正しい。[証明終]
なお、上の交代群は正規部分群(65D)の証明では、「交代群 \(A_n\) の元の数が、対称群 \(S_n\) の元の数の半分である」ことしか使っていません。従って次の定理が成り立ちます。
| (半分の部分群は正規部分群:65F) |
群 \(G\) の部分群を \(N\) とする。
\(|G|=2|N|\)
のとき(つまり 群の指数 \([G:N]=2\) のとき)、\(N\) は \(G\) の正規部分群である。
対称群の可解性
| (対称群の可解性:65G) |
5次以上の対称群、\(S_n\:\:(n\geq5)\) は可解群ではない。
[証明]
\(S_n\) の交代群を \(A_n\) とする。\(A_n\) は \(S_n\) の部分群なので、もし \(A_n\) が可解群でなければ、可解群の部分群は可解群の定理(61C)の対偶により、\(S_n\) は可解群ではない。以下、\(A_n\) が可解群でないことを背理法で証明する。
\(A_n\) が可解群と仮定して矛盾を導く。\(A_n\) が可解群とすると、定義により \(A_n\) には正規部分群 \(N\:(N\neq A_n)\) があり、\(A_n/N\) が巡回群である。
\(A_n\) の任意の2つの元を \(x,\:y\) とし、剰余類 \(xN\) と \(yN\) を考える。\(A_n/N\) は巡回群なので可換群であり、\(xNyN=yNxN\) である。\(N\) は正規部分群なので、\(Ny=yN\)、\(Nx=xN\) であり、これを用いて \(xNyN=yNxN\) を変形していくと、
\(xNyN=yNxN\)
\(xyNN=yxNN\)
\(xyN=yxN\)
となる。この式に左から \(x^{-1}y^{-1}\) をかけると、
\(x^{-1}y^{-1}xyN=x^{-1}y^{-1}yxN\)
\(x^{-1}y^{-1}xyN=N\)
となる。部分群の元の条件の定理(41C)より、\(aN=N\) と \(a\in N\) は同値である。従って、
\(x^{-1}y^{-1}xy\in N\)
である。
一般に \(x^{-1}y^{-1}xy\) を \(x\) と \(y\) の交換子と呼ぶ。上の式の変形プロセスから言えることは、\(A_n\) の任意の2つの元(\(N\) の元である必要はない)の交換子は \(N\) の元になるということである。
\(S_n\:\:(n\geq5)\) の任意の3文字巡回置換を \((i,\:j,\:k)\) とする。
\((i,\:j,\:k)=(i,\:k)(i,\:j)\)
なので、\((i,\:j,\:k)\) は偶置換であり、
\((i,\:j,\:k)\in A_n\)
である。ここで、\(\bs{i,\:j,\:k}\) とは違う2つの文字 \(\bs{l,\:m}\) を選ぶ。\(\bs{n\geq5}\) ならこれは常に可能である。そして、
\(x=(i,\:m,\:j)\)
\(y=(i,\:l,\:k)\)
とし、\(x,\:y\) の交換子を作ってみる。計算すると以下のようになる。
\(x^{-1}y^{-1}xy\)
\(=(i,\:m,\:j)^{-1}(i,\:l,\:k)^{-1}(i,\:m,\:j)(i,\:l,\:k)\)
\(=(j,\:m,\:i)(k,\:l,\:i)(i,\:m,\:j)(i,\:l,\:k)\)
| \((i,\:l,\:k)\) | \(=\left(\begin{array}{c}i&j&k&l&m\\l&j&i&k&m\end{array}\right)\) | |
| \((i,\:m,\:j)\) | \(=\left(\begin{array}{c}l&j&i&k&m\\l&i&m&k&j\end{array}\right)\) | |
| \((k,\:l,\:i)\) | \(=\left(\begin{array}{c}l&i&m&k&j\\i&k&m&l&j\end{array}\right)\) | |
| \((j,\:m,\:i)\) | \(=\left(\begin{array}{c}i&k&m&l&j\\j&k&i&l&m\end{array}\right)\) |
\(x^{-1}y^{-1}xy\)
\(=(j,\:m,\:i)(k,\:l,\:i)(i,\:m,\:j)(i,\:l,\:k)\)
\(=\left(\begin{array}{c}i&j&k&l&m\\j&k&i&l&m\end{array}\right)\)
\(=(i,\:j,\:k)\)
\(x^{-1}y^{-1}xy\in N\) なので、
\((i,\:j,\:k)\in N\)
である。つまり任意の3文字巡回置換は \(N\) に含まれる。
\(A_n\) のすべての元は3文字巡回置換の積で表される(65E)から、\(A_n\) は \(N\) の元の積で表せることになる。つまり、
\(A_n\subset N\)
だが、もともと \(N\) は \(A_n\) の部分集合だから、
\(A_n=N\)
である。これは \(N\neq A_n\) という仮定と矛盾する。従って、\(A_n\) の正規部分群 \(N\:(N\neq A_n)\) で、\(A_n/N\) が巡回群であるようなものはなく、\(A_n\) は可解群ではない。
\(S_n\:\:(n\geq5)\) は可解群ではない部分群 \(A_n\) をもつから、可解群の部分群は可解群の定理(61C)の対偶によって、\(S_n\) は可解群ではない。[証明終]
\(S_5\)(位数 \(120\)) や、その部分群 \(A_5\)(位数 \(60\))は可解群ではありません。しかし、「\(S_5\) のすべての部分群が可解群ではない」というわけではありません。\(S_5\) の部分群では、\(F_{20}\)(位数 \(20\))、\(D_{10}\)(位数 \(10\))、\(C_5\)(位数 \(5\))が可解群であることが知られています。これについては第7章で述べます。
一般5次方程式
5次方程式には代数的に解けるものと解けないものがあります。従って、全ての5次方程式に適用可能な根の公式はありません。5次方程式に根の公式がないことはガロア以前に証明されていたのですが、なぜ根の公式がないのか、その理由を明らかにしたのがガロア理論です。
係数が変数の方程式を「一般方程式」と言います。根の公式があるということは一般方程式が解けることを意味します。以下は、一般5次方程式が代数的に解けないことの証明ですが、この証明では係数が変数ではなく、解を変数としています。
| (5次方程式の解の公式はない:65H) |
\(\bs{Q}\) の代数拡大体を \(\bs{K}\) とする。\(\bs{K}\) の任意の元である5つの変数 \(b_1,b_2,b_3,b_4,b_5\) を根とする多項式を、
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
とし、\(\bs{Q}\) に \(a_0,a_1,a_2,a_3,a_4,\)を添加した代数拡大体を \(\bs{F}\) とする。つまり、
\(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\)
である。
このとき、\(\bs{K}\) の \(\bs{F}\) 上の ガロア群 \(G\) は5次対称群 \(S_5\) である。\(S_5\) は可解群ではないので(65G)、従って \(b_i\) を \(a_i\) のべき根で表すことはできない。
[証明]
代数拡大体 \(\bs{F}\) の作り方から、\(\bs{K}\) は \(\bs{F}\) 上の多項式 \(f(x)\) の最小分解体である。従って \(\bs{K}/\bs{F}\) はガロア拡大である。\(G=\mr{Gal}(\bs{K}/\bs{F})\) とおくと、\(G\) は \(\bs{F}\) の元を固定する自己同型写像が作る群である。
対称群 \(S_5\) の元の一つを \(s\) とし、
\(s=\left(\begin{array}{c}1&2&3&4&5\\s(1)&s(2)&s(3)&s(4)&s(5)\end{array}\right)\)
とする。このとき、
\(\sg(b_i)=b_{s(i)}\:\:(i=1,2,3,4,5)\)
で、\(b_i\) に作用する写像 \(\sg\) を定義する。そうすると \(\sg\) は \(f(x)=0\) の解 \(b_i\) を共役な解に移す写像だから、自己同型写像である。また、
\(\begin{eqnarray}
&&\:\:f(x)&=(x-b_1)(x-b_2)(x-b_3)(x-b_4)(x-b_5)\:\:(b_i\in\bs{K})\\
&&&=x^5-a_4x^4+a_3x^3-a_2x^2+a_1x-a_0\\
\end{eqnarray}\)
の根と係数の関係から、
| \(a_4\) | \(\overset{\text{ }}{=}\) | \(b_1+b_2+b_3+b_4+b_5\) | |
| \(a_3\) | \(\overset{\text{ }}{=}\) | \(b_1b_2+b_1b_3+b_1b_4+b_1b_5+b_2b_3+b_2b_4+b_2b_5+b_3b_4+b_3b_5+b_4b_5\) | |
| \(a_2\) | \(\overset{\text{ }}{=}\) | \(b_1b_2b_3+\)\(b_1b_2b_4+\)\(b_1b_2b_5+\)\(b_1b_3b_4+\)\(b_1b_3b_5+\)\(b_1b_4b_5+\)\(b_2b_3b_4+\)\(b_2b_3b_5+\)\(b_2b_4b_5+\)\(b_3b_4b_5\) | |
| \(a_1\) | \(\overset{\text{ }}{=}\) | \(b_1b_2b_3b_4+b_1b_2b_3b_5+b_1b_2b_4b_5+b_1b_3b_4b_5+b_2b_3b_4b_5\) | |
| \(a_0\) | \(\overset{\text{ }}{=}\) | \(b_1b_2b_3b_4b_5\) |
従って、\(\sg(a_0)=a_0\)、\(\sg(a_1)=a_1\)、\(\sg(a_2)=a_2\)、\(\sg(a_3)=a_3\)、\(\sg(a_4)=a_4\) である。つまり \(\sg\) は \(\bs{F}=\bs{Q}(a_0,\:a_1,\:a_2,\:a_3,\:a_4)\) の元を固定する。従って \(\sg\) は \(\bs{F}\) の元を固定する \(\bs{K}\) の自己同型写像であり、\(G\) の元である。以上のことは \(S_5\) の任意の元 \(s\) について言えるから \(S_5\subset G\) である。
これを踏まえて \(\bs{F}\) 上の \(\bs{K}\) の拡大次数 \([\:\bs{K}\::\:\bs{F}\:]\) を考えると、\([\:\bs{K}\::\:\bs{F}\:]\) は \(\mr{Gal}(\bs{K}/\bs{F})\) の位数に等しいから、
\([\:\bs{K}\::\:\bs{F}\:]=|G|\geq|S_5|=5!=120\)
である。
次に、
| \(\bs{F}\subset\)\( \bs{F}(b_1)\subset\)\( \bs{F}(b_1,b_2)\subset\)\( \cd\subset\)\( \bs{F}(b_1,b_2,b_3,b_4,b_5)=\bs{K}\) |
\([\:\bs{F}(b_1)\::\:\bs{F}\:]\leq\mr{deg}\:f(x)\:=5\)
である。等号は \(f(x)\) が既約多項式のときである。さらに、\(b_2\) は
4次方程式 \(f(x)/(x-b_1)\) の根だから、
\([\:\bs{F}(b_1,b_2)\::\:\bs{F}(b_1)\:]\leq4\)
である。以上を順に続けると、体の拡大次数の連鎖律(33H)により、
\([\:\bs{K}\::\:\bs{F}\:]\)
| \(=\) | \([\:\bs{F}(b_1,b_2,b_3,b_4,b_5)\::\:\bs{F}\:]\) | ||
| \(=\) | \([\:\bs{F}(b_1,b_2,b_3,b_4,b_5)\::\:\bs{F}(b_1,b_2,b_3,b_4)\:]\cdot\) | ||
| \([\:\bs{F}(b_1,b_2,b_3,b_4)\::\:\bs{F}(b_1,b_2,b_3)\:]\cdot\) | |||
| \([\:\bs{F}(b_1,b_2,b_3)\::\:\bs{F}(b_1,b_2)\:]\cdot\) | |||
| \([\:\bs{F}(b_1,b_2)\::\:\bs{F}(b_1)\:]\cdot\) | |||
| \([\:\bs{F}(b_1)\::\:\bs{F}\:]\) | |||
| \(\leq\) | \(5\cdot4\cdot3\cdot2\cdot1=5!=120\) |
である。従って、\([\:\bs{K}\::\:\bs{F}\:]\geq5!\) と合わせると \([\:\bs{K}\::\:\bs{F}\:]=5!\) であり、
\(|G|=|S_5|\)
となって、
\(G\cong S_5\)
である。つまり、一般5次方程式のガロア群は \(S_5\) と同型であることが証明できた。\(S_5\) は可解群ではないので(65G)、それと同型である \(G\) も可解群ではない。従って \(b_i\) を \(a_i\) のべき根で表すことはできず、一般5次方程式に解の公式はない。[証明終]
6.6 可解ではない5次方程式
5次方程式の全てに適用できる解の公式がないことは、ガロア以前に証明されていました(アーベル・ルフィニの定理)。しかしガロア理論によって、解の公式がないことの「原理」が明確になりました。つまり係数が変数である一般5次方程式は、解が四則演算とべき根で表現できる(=可解である)ための必要条件を満たさないから公式は作れないのです(65H)。
ということは、この「原理」を用いて、可解ではない、係数が数値の方程式を具体的に構成できることになります。それを以下で行います。そのためにまず、コーシーの定理を証明します。なお、コーシー(19世紀フランスの数学者)の名がついた定理はいくつかありますが、これは「群論のコーシーの定理」です。
コーシーの定理
| (コーシーの定理:66A) |
群 \(G\) の位数 \(|G|\) が素数 \(p\) を約数にもつとき、\(g^p=e\:\:(g\neq e)\) となる \(G\) の元 \(g\) が存在する。つまり、\(G\) は位数 \(p\) の巡回群を部分群としてもつ。
[証明]
本論に入る前に、証明に使う定義を行う。\(X\) を、元の数が \(N\) の集合とし、そこから重複を許して \(n\)個の元を取り出して1列に並べた順列を考える。このような順列の集合を \(P\) とする。つまり、
\(P=\{\:(x_1,x_2,\cd,x_n)\:|\:x_i\in X\:\}\)
である。\((x_1,x_2,\cd,x_n)\) は並べる順序に意味がある、いわゆる重複順列で、集合 \(P\) の元の数は、
\(|P|=N^n\)
である。
\(P\) から自分自身 \(P\) への写像 \(\sg\) を、
\(\sg\::\:(x_1,x_2,\cd,x_n)\longmapsto(x_n,x_1,x_2,\cd,x_{n-1})\)
と定義する。最後尾の元を先頭に持ってくる "循環写像" である(ここだけの用語)。そうすると、集合 \(P\) の任意の元、\(\bs{a}\) について、
\(\sg^n(\bs{a})=\bs{a}\)
となり、\(\sg^n=e\) (\(e\::\) 恒等写像)である。
次に、集合 \(P\) のある元を \(\bs{a}\) としたとき、
\(\sg^d(\bs{a})=\bs{a}\)
となる最小の \(d\:\:(1\leq d\leq n)\) を、"\(\bs{a}\) の循環位数" と定義する(ここだけの用語)。そうすると、循環位数 \(\bs{d}\) は \(\bs{n}\) の約数になる。なぜなら、もし
\(n=kd+r\:\:(1\leq r < d)\)
だとすると、
\(\begin{eqnarray}
&&\:\:\sg^n(\bs{a})&=\sg^{kd+r}(\bs{a})\\
&&&=\sg^r((\sg^d)^k(\bs{a}))\\
&&&=\sg^r(\bs{a})\\
&&\:\:\sg^r(\bs{a})&=\bs{a}\\
\end{eqnarray}\)
となって、\(d\) が \(\sg^d(\bs{a})=\bs{a}\) となる最小の数ではなくなるからである。
循環位数の例をあげると、
\(\begin{eqnarray}
&&\:\:N&=6\\
&&\:\:X&=\{\:1,\:2,\:3,\:4,\:5,\:6\:\}\\
&&\:\:n&=6\\
\end{eqnarray}\)
の場合、
\(\bs{a}=(1,\:2,\:3,\:4,\:5,\:6)\:\:\rightarrow\:\:d=6\)
\(\bs{a}=(1,\:2,\:2,\:2,\:2,\:2)\:\:\rightarrow\:\:d=6\)
\(\bs{a}=(1,\:2,\:3,\:1,\:2,\:3)\:\:\rightarrow\:\:d=3\)
\(\bs{a}=(1,\:2,\:1,\:2,\:1,\:2)\:\:\rightarrow\:\:d=2\)
\(\bs{a}=(1,\:1,\:1,\:1,\:1,\:1)\:\:\rightarrow\:\:d=1\)
などである。以上を踏まえて本論に入る。
積が単位元になるような \(G\) の \(p\)個(\(p\):素数)の元の組の集合、
\(S\:=\:\{\:(x_1,x_2,\cd,x_p)\:\:|\:\:x_i\in G,\:x_1x_2\cd x_p=e\:\}\)
を考える。まず、\(S\) の元の数 \(|S|\) を求める。\(S\) の始めから \(p-1\) 個までの \(x_i\:(1\leq i\leq p-1)\) は、全く任意に選ぶことができる。なぜなら、そうしておいて
\(x_p=(x_1x_2\cd x_{p-1})^{-1}\)
とすれば、
\(x_1x_2\cd x_{p-1}x_p\)
\(=x_1x_2\cd x_{p-1}(x_1x_2\cd x_{p-1})^{-1}\)
\(=e\)
となり、\(S\) の元になるからである。\(x_i\:(1\leq i\leq p-1)\) の選び方はそのすべてについて \(|G|\) 通りあるから、
\(|S|=|G|^{p-1}\)
である。
次に、\(S\) の任意の元を \(\bs{a}\) とすると、\(\sg(\bs{a})\) もまた \(S\) の元になる。なぜなら、
\(\bs{a}=(x_1,x_2,\cd,x_p)\:\:\:(x_i\in G)\)
とおくと、
\(x_1x_2\cd x_{p-1}x_p=e\)
だが、この式に左から \(x_p\) をかけ、右から \(x_p^{-1}\) をかけると、
\(x_px_1x_2\cd x_{p-1}x_px_p^{-1}=x_pex_p^{-1}\)
\(x_px_1x_2\cd x_{p-1}=e\)
となり、これは \(\sg(\bs{a})\in S\) を意味しているからである。
\(S\) のすべての元に循環位数を割り振ると、\(\bs{p}\) が素数なので、循環位数は \(\bs{1}\) か \(\bs{p}\) のどちらかである。循環位数が \(1\) である \(S\) の元とは、
\((\overbrace{x,\:x,\:\cd\:,\:x}^{p\:個})\:\:(x\in G)\)
のように、\(G\) の同じ元を \(p\) 個並べたものである。また、循環位数が \(p\) の元とは、\(p\)個の \(G\) の元に1つでも違うものがあるような \(S\) の元である。
そこで、循環位数 \(p\) の \(S\) の元に着目する。その一つを \(\bs{a}_1\) とすると、
\(S_1=\{\bs{a}_1,\:\sg(\bs{a}_1),\:\sg^2(\bs{a}_1),\:\cd\:,\sg^{p-1}(\bs{a}_1)\}\)
は、すべて相異なる \(p\) 個 の \(S\) の元である。さらに、\(S_1\) に含まれない循環位数 \(p\) の元を \(\bs{a}_2\) とすると、
\(S_2=\{\bs{a}_2,\:\sg(\bs{a}_2),\:\sg^2(\bs{a}_2),\:\cd\:,\sg^{p-1}(\bs{a}_2)\}\)
も、すべて相異なる \(p\) 個 の \(S\) の元であり、しかも \(S_1\) とは重複しない。この操作は順々に繰り返せるから、いずれ循環位数 \(p\) の元は \(S_1,\:S_2,\:\cd\) でカバーできることとなる。循環位数 \(p\) の \(S\) の元の全部が、
\(S_1\:\cup\:S_2\:\cup\:\cd\:\cup\:S_q\)
と表現できたとしたら、その元の数は \(pq\) である。
循環位数 \(1\) の \(S\) の元の数は、\(S\) の元の数から循環位数 \(p\) の元の数を引いたものである。
\(|S|=|G|^{p-1}\)
だったから、\(p\) が \(|G|\) の約数である、つまり \(|G|\) が \(p\) の倍数であることに注意すると、
循環位数 \(1\) の元の数
\(=|G|^{p-1}-pq\equiv0\:\:(\mr{mod}\:p)\)
となる。この、循環位数 \(1\) の元の数は \(0\) ではない。なぜなら、
\((\overbrace{e,\:e,\:\cd\:,\:e}^{p\:個})\)
は 循環位数が \(1\) の元だからである。つまり、循環位数 \(1\) の元の数は \(p\) 以上の \(p\) の倍数である。従って、\(S\) には \((e,\:e,\:\cd\:,\:e)\) 以外に、
\((\overbrace{g,\:g,\:\cd\:,\:g}^{p\:個})\:\:\:\:(g\neq e,\:g\in G)\)
が必ず存在する。従って、
\(g^p=e\:\:(g\neq e)\)
である \(g\) が存在する。この式が成立するということは、\(g\) の位数は \(p\) の約数であるが、\(p\) が素数なので、\(g\) の位数は \(p\) である。従って、
\(\{\:g,\:g^2,\:\cd\:,g^{p-1},\:g^p=e\:\}\)
は位数 \(p\) の巡回群である。[証明終]
実数解3つの5次方程式は可解ではない
| (実数解が3つの5次方程式:66B) |
\(f(x)\) を既約な5次多項式とする。方程式 \(f(x)=0\) が複素数解を2つ、実数解を3つもつなら、方程式は可解ではない。
[証明]
\(f(x)=0\) の複素数解を \(\al_1,\:\al_2\)、実数解を \(\al_3,\:\al_4,\:\al_5\) とする。また、それらを \(\bs{Q}\) に付加した体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\al_3,\al_4,\al_5)\) とする。また、ガロア群 \(\mr{Gal}(\bs{L}/\bs{Q})\) を \(G\) と書く。
一般に、複素数 \(z=r+is\) が有理数係数の方程式の解なら、\(\ol{\,z\,}=r-is\) も解である。つまり \(z\) と \(\ol{\,z\,}\) は共役(同じ方程式の解同士)である(=共役複素数)。その理由は以下である。
まず、\(z_1\) と \(z_2\) を2つの複素数とすると、
\(\ol{z_1+z_2}=\ol{z_1}+\ol{z_2}\)
が成り立つ。また、
\(z_1=r+is\)
\(z_2=u+iv\)
とすると、
\(\begin{eqnarray}
&&\:\:z_1z_2&=ru-sv+i(su+rv)\\
&&\:\:\ol{z_1}\cdot\ol{z_2}&=(r-is)(u-iv)\\
&&&=ru-sv-i(su+rv)\\
\end{eqnarray}\)
なので、
\(\ol{z_1z_2}=\ol{z_1}\cdot\ol{z_2}\)
である。有理数係数の方程式を、3次方程式の例で、
\(x^3+ax^2+bx+c=0\)
とし、\(z\) をこの方程式の解だとすると、
\(z^3+az^2+bz+c=0\)
\(\ol{z^3+az^2+bz+c}=\ol{\,0\,}\)
\(\ol{z^3}+\ol{az^2}+\ol{bz}+\ol{\,c\,}=0\)
\(\ol{\,z\,}^3+\ol{\,a\,}\ol{\,z\,}^2+\ol{\,b\,}\ol{\,z\,}+c=0\)
\(\ol{\,z\,}^3+a\ol{\,z\,}^2+b\ol{\,z\,}+c=0\)
となって、\(\ol{\,z\,}\) も方程式の解である。もちろんこれは \(n\)次方程式でも成り立つ。
そこで、\(f(x)=0\) の複素数解 \(\al_1,\:\al_2\) を、
\(\al_1=a+ib\)
\(\al_2=a-ib\)
とする。ここで、複素数 \(r+is\) に作用する \(\bs{L}\) の写像を \(\tau\) を、
\(\tau(r+is)=r-is\)
と定める。そうすると、
\(\tau(\al_1)=\al_2,\:\tau(\al_2)=\al_1,\)
\(\tau(\al_3)=\al_3,\:\tau(\al_4)=\al_4,\:\tau(\al_5)=\al_5\)
となり(\(\al_3,\:\al_4,\:\al_5\) は実数なので \(\tau\) で不変)、\(\tau\) は \(f(x)=0\) の2つの解を入れ替えるから \(\bs{L}\) の自己同型写像になり(51E)、すなわち \(G\) の元である。\(\al_1\) を \(1\)、\(\al_2\) を \(2\) と書き、巡回置換の記法を使うと、
\(\tau=(1,\:2)\)
である。
一方、\(f(x)\) は既約多項式なので単拡大体の基底の定理(33F)により、\(\bs{Q}(\al_1)\) の次元は \(5\)、つまり \([\bs{Q}(\al_1)\::\:\bs{Q}]=5\) である。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}\::\:\bs{Q}\:]=[\:\bs{L}\::\:\bs{Q}(\al_1)\:][\bs{Q}(\al_1)\::\:\bs{Q}]\)
が成り立つので、\([\:\bs{L}\::\:\bs{Q}\:]\) は \(5\) の倍数である。\(|G|=[\:\bs{L}\::\:\bs{Q}\:]\) なので(52B)、ガロア群 \(G\) の位数は \(5\) を約数にもつ。
そうするとコーシーの定理(66A)より、\(G\) の部分群には位数 \(5\) の巡回群がある。それを、
\(H=\{\:\sg,\:\sg^2,\:\sg^3,\:\sg^4,\:\sg^5=e\:\}\)
とする。5つの解の置換の中で、位数 \(5\) の巡回群を生成する \(\sg\) は、巡回置換の記法で書くと、
\(\sg_1=(1,\:2\:,3,\:4,\:5)\)
\(\sg_2=(1,\:3\:,5,\:2,\:4)\)
\(\sg_3=(1,\:4\:,2,\:5,\:3)\)
\(\sg_4=(1,\:5\:,4,\:3,\:2)\)
の4つである。これらには、
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_3\)
\(\sg_1^{\:4}=\sg_4\)
の関係がある。そこで、\(G\) の中にある位数 \(5\) の巡回群は、
\(\sg=(1,\:2\:,3,\:4,\:5)\)
だとして一般性を失わない。そうすると、\(G\) の中には、
\(\tau=(1,\:2)\)
\(\sg=(1,\:2\:,3,\:4,\:5)\)
の2つの元があることになる。実は、
\(\tau,\:\sg\) から出発して、この2つの元とその逆元の演算を繰り返すことによって、5次対称群 \(\bs{S_5}\) の元が全部作り出せる
のである。それを証明する。
\(G\) は群なので \(\sg^{-1}\) も \(G\) に含まれる(\(\sg\) は位数 \(5\) の巡回群の元なので \(\sg^{-1}=\sg^4\))。まず、\(\sg\tau\sg^{-1}\) を計算してみると、
\(\sg\tau\sg^{-1}=(1,2,3,4,5)(1,2)(5,4,3,2,1)\)
| \((5,4,3,2,1)\) | \(=\left(\begin{array}{c}1&2&3&4&5\\5&1&2&3&4\end{array}\right)\) | |
| \((1\:2)\) | \(=\left(\begin{array}{c}5&1&2&3&4\\5&2&1&3&4\end{array}\right)\) | |
| \((1,2,3,4,5)\) | \(=\left(\begin{array}{c}5&2&1&3&4\\1&3&2&4&5\end{array}\right)\) |
\(\begin{eqnarray}
&&\:\:\sg\tau\sg^{-1}&=\left(\begin{array}{c}1&2&3&4&5\\1&3&2&4&5\end{array}\right)\\
&&&=(2,\:3)\\
\end{eqnarray}\)
となる。同様にして、
| \((5,4,3,2,1)\) | \(=\left(\begin{array}{c}1&2&3&4&5\\5&1&2&3&4\end{array}\right)\) | |
| \((2,\:3)\) | \(=\left(\begin{array}{c}5&1&2&3&4\\5&1&3&2&4\end{array}\right)\) | |
| \((1,2,3,4,5)\) | \(=\left(\begin{array}{c}5&1&3&2&4\\1&2&4&3&5\end{array}\right)\) |
\(\begin{eqnarray}
&&\:\:\sg^2\tau\sg^{-2}&=\sg(\sg\tau\sg^{-1})\sg^{-1}\\
&&&=\sg\cdot(2,3)\cdot\sg^{-1}\\
&&&=\left(\begin{array}{c}1&2&3&4&5\\1&2&4&3&5\end{array}\right)\\
&&&=(3,\:4)\\
\end{eqnarray}\)
である。以下、
| \((5,4,3,2,1)\) | \(=\left(\begin{array}{c}1&2&3&4&5\\5&1&2&3&4\end{array}\right)\) | |
| \((3,\:4)\) | \(=\left(\begin{array}{c}5&1&2&3&4\\5&1&2&4&3\end{array}\right)\) | |
| \((1,2,3,4,5)\) | \(=\left(\begin{array}{c}5&1&2&4&3\\1&2&3&5&4\end{array}\right)\) | |
| \(\rightarrow\:\sg^3\tau\sg^{-3}\) | \(=\left(\begin{array}{c}1&2&3&4&5\\1&2&3&5&4\end{array}\right)\) | |
| \(=(4,\:5)\) |
| \((5,4,3,2,1)\) | \(=\left(\begin{array}{c}1&2&3&4&5\\5&1&2&3&4\end{array}\right)\) | |
| \((4,\:5)\) | \(=\left(\begin{array}{c}5&1&2&3&4\\4&1&2&3&5\end{array}\right)\) | |
| \((1,2,3,4,5)\) | \(=\left(\begin{array}{c}4&1&2&3&5\\5&2&3&4&1\end{array}\right)\) | |
| \(\rightarrow\:\sg^4\tau\sg^{-4}\) | \(=\left(\begin{array}{c}1&2&3&4&5\\5&2&3&4&1\end{array}\right)\) | |
| \(=(1,\:5)\) |
\((1,\:2)\)、\((2,\:3)\)、\((3,\:4)\)、\((1,\:5)\)
は \(G\) の元である。
一般に、
\((i,\:j)=(1,\:i)(1,\:j)(1,\:i)\)
である。なぜなら、
\(\begin{eqnarray}
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot1&=(1,\:i)(1,\:j)\cdot i\\
&&&=(1,\:i)\cdot i=1\\
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot i&=(1,\:i)(1,\:j)\cdot1\\
&&&=(1,\:i)\cdot j=j\\
&&\:\:(1,\:i)(1,\:j)(1,\:i)\cdot j&=(1,\:i)(1,\:j)\cdot j\\
&&&=(1,\:i)\cdot1=i\\
\end{eqnarray}\)
が成り立つからである。従って、
\((2,\:3)=(1,\:2)(1,\:3)(1,\:2)\)
である。この両辺に左と右から \((1,\:2)\) をかけると、
\((1,\:2)(2,\:3)(1,\:2)=(1,\:3)\)
となり、\((2,\:3),\:(1,\:2)\) が \(G\) の元なので \((1,\:3)\) も \(G\) の元である。同様に、
\((3,\:4)=(1,\:3)(1,\:4)(1,\:3)\)
であるが、\((3,\:4),\:(1,\:3)\) が \(G\) の元なので、\((1,\:4)\) も \(G\) の元である。結局、
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
が \(G\) の元であることが分かった。
\(S_5\) は5文字の置換をすべて集めた集合である。すべての置換は互換の積で表せて(65B)、かつ任意の互換 \((i,\:j)\) は、
\((i,\:j)=(1,\:i)(1,\:j)(1,\:i)\)
と表せるから、5文字の置換はすべて、
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
という4つの互換の積で表現できる。つまり、\(S_5\) はこの4つの互換で生成できる。以上をまとめると、
\((1,\:2)\)、\((1,\:2\:,3,\:4,\:5)\)
\(\Downarrow\)
\((1,\:2)\)、\((2,\:3)\)、\((3,\:4)\)、\((1,\:5)\)
\(\Downarrow\)
\((1,\:2)\)、\((1,\:3)\)、\((1,\:4)\)、\((1,\:5)\)
\(\Downarrow\)
\(S_5\) のすべての元
という、"\(S_5\)を生成する連鎖" の存在が証明できた。従って \(G\cong S_5\) である。\(S_5\) は可解群ではない(65G)。従って、複素数解を2つ、実数解を3つもつ既約な5次方程式は可解ではない。[証明終]
この、実数解が3つの5次方程式の定理(66B)から、可解ではない5次方程式の実例を簡単に構成できます。たとえば、
\(f(x)=x^5-5x+a\)
とおき、\(f(x)=0\) の方程式を考えます。
\(f\,'(x)=5x^4-5\)
なので、\(f\,'(x)=0\) の実数解は \(1,\:-1\) の2つです。
\(f(\phantom{-}1)=a-4\)
\(f(-1)=a+4\)
なので、
\(a-4 < 0 < a+4\)
なら、\(f(x)=0\) には3つの実数解があります。この条件は、
\(-4 < a < 4\)
ですが、\(a=0\) のときは \(f(x)\) は既約多項式ではありません。また \(a=3,\:-3\) のときも、
\(x^5-5x+3=(x^2+x-1)(x^3-x^2+2x-3)\)
\(x^5-5x-3=(x^2-x-1)(x^3+x^2+2x+3)\)
と因数分解できるので、既約多項式ではありません。従って、
\(x^5-5x+2=0\)
\(x^5-5x+1=0\)
\(x^5-5x-1=0\)
\(x^5-5x-2=0\)
が可解ではない5次方程式の例(\(G\cong S_5\))であり、これらの方程式の解を四則演算とべき根で表すのは不可能です。

|
\(\bs{y=x^5-5x+1}\) のグラフ |
方程式 \(x^5-5x+1=0\) の3つの実数解を小さい方から \(\al,\beta,\gamma\) とし、数式処理ソフトそので近似解を求めると、 \(\al\fallingdotseq-1.5416516841045247594\) \(\beta\fallingdotseq\phantom{-}0.2000641026299753912\) \(\gamma\fallingdotseq\phantom{-}1.4405003973415600893\) である。近似解の精度を上げるのはいくらでも可能であり、方程式の形もシンプルだが、これらの解を四則演算とべき根で表すことはできない。グラフと近似解は WolframAlpha による。 |
「6.可解性の必要条件」終わり
(次回に続く)
(次回に続く)
2023-04-15 08:00
nice!(0)
No.356 - 高校数学で理解するガロア理論(3) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots} \newcommand{\fz}{0^{\tiny F}} \newcommand{\kz}{0^{\tiny K}} \newcommand{\fo}{1^{\tiny F}} \newcommand{\ko}{1^{\tiny K}}\)
3.3 線形空間
ガロア理論の一つの柱は、代数拡大体を線形空間(ベクトル空間)としてとらえることで、線形空間の「次元」や「基底」を使って理論が組み立てられています。線形空間には精緻な理論体系がありますが、ここではガロア理論に必要な事項の説明をします。
線形空間の定義
集合 \(V\) と 体 \(\bs{K}\) が次を満たすとき、\(V\) を \(\bs{\bs{K}}\) 上の線形空間(=ベクトル空間。linear space / vector space)と言う。
加算の定義
\(V\) の任意の元 \(\br{u},\:\br{v}\) に対して \((\br{u}+\br{v})\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
スカラー倍の定義
\(V\) の任意の元 \(\br{u}\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(k\br{u}\in V\) が定義されていて、加算との間に次の性質がある。\(\br{u},\:\br{v}\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(m\br{u})=(km)\br{u}\)
\((2)\:\:(k+m)\br{u}=k\br{u}+m\br{u}\)
\((3)\:\:k(\br{u}+\br{v})=k\br{u}+k\br{v}\)
\((4)\:\:1\br{v}=\br{v}\)
高校数学に出てくる "2次元ベクトル" とは、上記の定義の \(\bs{K}\) を \(\bs{R}\)(実数の体)とし、\(V\) を2つの実数のペアの集合 \(\{\:(x,y)\:|\:x,y\in\bs{R}\:\}\) とするベクトル空間(の要素)のことです。
上の定義の \(0\) は線形空間 \(V\) の元です。以下、\(V\) の単位元 \(0\)(= \(0\) ベクトル)と、体 \(\bs{K}\) の加法の単位元 \(0\) が混在しますが、文脈や式から明らかなので、同じ \(0\) で記述します。
1次独立と1次従属
1次独立
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次従属であるという。
基底
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、次の2つが満たされるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) を基底という。
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が基底だと、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) は基底ではありません。なぜなら、もし \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) が基底だとすると、
\(\br{v}_n=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}\)
と表せますが、これは、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}-\br{v}_n=0\)
ということであり、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が1次従属となってしまって、基底の要件を満たさなくなるからです。基底に、別の1つの元を加えるケースも同じことです。
\(\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) である。
[証明]
この定理の証明のために、まず次の補題を証明する。
[補題]
線形空間 \(V\) の任意の \(n\) 個の元を \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) とする(基底でなくてもよい)。線形空間 \(V\) の \(n+1\) 個の元 \(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) がすべて \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) の1次結合で表されるなら、\(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) は1次従属である。
数学的帰納法を使う。まず、\(n=1\) のとき、この定理は成り立つ。つまり、
\(\br{w}_1=k_1\br{u}_1\)
\(\br{w}_2=k_2\br{u}_1\)
と表されるなら、
\(k_2\br{w}_1-k_1\br{w}_2=0\)
であり、\(\br{w}_1\) と \(\br{w}_2\) は1次従属である。そこで、\(n\) が \(k\:\:(\geq1)\) のときに成り立つとし、\(n=k+1\) でも成り立つことを証明する。
以降、表記を見やすくするため、\(k=3\) の場合で記述する。ただし、一般性を失うことがないように記述する。\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) が、
\(\br{w}_1=a_{11}\br{u}_1+a_{12}\br{u}_2+a_{13}\br{u}_3\)
\(\br{w}_2=a_{21}\br{u}_1+a_{22}\br{u}_2+a_{23}\br{u}_3\)
\(\br{w}_3=a_{31}\br{u}_1+a_{32}\br{u}_2+a_{33}\br{u}_3\)
\(\br{w}_4=a_{41}\br{u}_1+a_{42}\br{u}_2+a_{43}\br{u}_3\)
と表せたとする。ここで \(\br{w}_4\) の係数に注目する。もし、
\(a_{41}=a_{42}=a_{43}=0\)
であれば、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属である。なぜなら、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3+b_4\br{w}_4=0\)
の式を満たす \(b_1,b_2,b_3,b_4\) は、
\(b_1=b_2=b_3=0\)
\(b_4\neq0\)
として実現でき、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属の定義を満たすからである。そこで、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つあるとする。それを \(a_{43}\) とし、
\(a_{43}\neq0\)
とする。この仮定で一般性を失うことはない。ここで、
\(\br{x}_i=\br{w}_i-\dfrac{a_{i3}}{a_{43}}\br{w}_4\:\:(i=1,2,3)\)
とおいて \(\br{u}_3\) の項を消去する。計算すると、
\(\begin{eqnarray}
&&\:\:\br{x}_1=&\left(a_{11}-\dfrac{a_{13}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{12}-\dfrac{a_{13}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_2=&\left(a_{21}-\dfrac{a_{23}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{22}-\dfrac{a_{23}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_3=&\left(a_{31}-\dfrac{a_{33}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{32}-\dfrac{a_{33}a_{42}}{a_{43}}\right)\br{u}_2\\
\end{eqnarray}\)
となる。そうすると、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は「線形空間 \(V\) の2つの元 \(\br{u}_1,\br{u}_2\) の1次結合で表された3つの元」である。従って、帰納法の仮定により、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は1次従属である。1次従属だから、
\(\br{x}_1=\br{w}_1-\dfrac{a_{13}}{a_{43}}\br{w}_4\)
\(\br{x}_2=\br{w}_2-\dfrac{a_{23}}{a_{43}}\br{w}_4\)
\(\br{x}_3=\br{w}_3-\dfrac{a_{33}}{a_{43}}\br{w}_4\)
だったから、これを \((\br{A})\) 式に代入すると、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3-\)
\(\dfrac{1}{a_{43}}(b_1a_{13}+b_2a_{23}+b_3a_{33})\br{w}_4=0\)
となる。この式における \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) の係数の少なくとも一つは \(0\) ではない。従って、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つある場合にも \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) は1次従属である。
以上で、線形空間 \(V\) の \(k=3\) 個の元(\(\br{u}_1,\br{u}_2,\br{u}_3\))の1次結合で、\(k+1=4\) 個の元(\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\))のすべてが表されば、その4個の元は1次従属であることが証明できた。\(k=3\) としたのは表記を見やすくするためであり、\(k=3\) であることの特殊性は使っていない。つまり、\(k\geq1\) のすべてで成り立つ。従って数学的帰納法により補題が正しいことが証明できた。[補題の証明終]
以上を踏まえて、\(A=\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(B=\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) となることを証明する。
もし仮に \(m < n\) だとすると、\(B\) の中から \((m+1)\) 個の元を選べる。それを \(B\:'=\{\br{v}_1,\br{v}_2,\cd,\br{v}_{m+1}\}\) とすると、\(A\) は 線形空間 \(V\) の基底だから、\(B\:'\) の元は \(A\) の元の1次結合で表現できる。つまり \(B\:'\) の \((m+1)\)個の元のすべては \(m\)個の元の1次結合で表されるから、[補題]によって \(B\:'\) は1次従属である。\(B\) は \(B\:'\) と同じものか、または \(B\:'\) に数個の元を付け加えたものだから、\(B\:'\) が1次従属なら \(B\) も1次従属である。しかし、\(B\) は線形空間 \(V\) の基底だから1次独立であり、矛盾が生じる。従って、\(m\geq n\) である。
もし仮に \(m > n\) だとしても、全く同様の考察により矛盾が生じる。従って、\(m\leq n\) である。この結果、\(m=n\) であることが証明できた。[証明終]
この基底の数の不変性の定理(33D)により、線形空間には次のように「次元」が定義できることになります。
次元
線形空間の基底に含まれる元の数が有限個のとき、その個数を線形空間の次元と言う。次元は基底の取り方によらない。
線形空間の次元や基底と、代数拡大体を結びつけるのが次の定理です。
単拡大体の基底
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。単拡大体である \(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間であり、\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) は \(\bs{Q}(\al)\) の基底である。
[証明]
\(\bs{Q}(\al)\) の基底であるための条件は、
の2つである。② は単拡大の体の定理(32C)で証明されているので、① を証明する。多項式 \(g(x)\) を、
\(g(x)=a_0+a_1x+a_2x^2+\cd+a_{n-1}x^{n-1}\)
とおく。\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立であることを言うには、
\(g(\al)=0\) であれば \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\)
を言えばよい。以降、背理法を使って証明する。\(g(\al)=0\) で、\(a_i\:\:(0\leq i\leq n-1)\) のうち、少なくとも1つはゼロでないと仮定する。
\(g(x)\) が定数(つまり \(a_0\) の項のみ)のときは、\(g(\al)=0\) なら \(a_0=0\) なので、「少なくとも1つはゼロでない」に反する。そこで \(g(x)\) は1次以上の多項式であるとする。
そうすると、2つの方程式 \(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) をもつことになる。しかし、\(f(x)\) は \(n\)次の既約多項式であり、\(g(x)\) は1次以上で \(n\)次未満の多項式である。既約多項式の定理2(31F)により、このような2つの方程式は共通の解を持たない。ゆえに矛盾が生じる。従って、\(g(\al)=0\) のとき \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\) であり、① が証明された。
基底の数が線形空間の次元であり、\(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間である。[証明終]
もし、\(f(x)\) が\(n\)次多項式だとしたら(既約多項式を含む)、\(\bs{Q}(\al)\) の次元は \(n\)以下になります。\(f(x)=0\) の解の一つ、\(\al\) の最小多項式(31H)を \(m\)次多項式である \(g(x)\) とすると、\(g(x)\) は既約多項式であり(31I)、\(\al\) は \(f(x)=0\) と \(g(x)=0\) の共通の解なので、既約多項式の定理1(31E)により \(f(x)\) は \(g(x)\) で割り切れます。つまり、
\(f(x)=h(x)g(x)\)
と書けるので、
\(\mr{deg}\:f(x)\:\geq\:\mr{deg}\:g(x)\)
\(n\:\geq\:m\)
ですが、単拡大体の基底の定理(33F)により \(\bs{Q}(\al)\) の次元は \(m\) なので、\(n\)以下です。
拡大次数とその連鎖律
方程式の解になる数が代数的数で、\(\bs{Q}\) に代数的数を添加した体が代数拡大体です。「3.2 体」の「単拡大の体」でとりあげた \(\bs{Q}(\al)\) は代数拡大体であり、次元は \(n\) でした(32C)。この次元を「体の拡大」の視点で考えてみます。
「体 \(\bs{K}\) 上の線形空間 \(V\)」の定義において、\(\bs{K}=\bs{Q}\) とし \(V=\bs{Q}\) とすると、「有理数体 \(\bs{Q}\) は、\(\bs{Q}\) 上の線形空間」であると言えます。\(\bs{Q}\) では加算もスカラー倍(=乗算)も定義されていて、可換だからです。線形空間の定義にある各種の演算は、体の演算の一部です。
線形空間 \(\bs{Q}\) の基底は、\(0\) ではない \(\bs{Q}\) の元 \(v\) です。\(0\) を含む \(\bs{Q}\) の任意の元を \(a\) とすると、
\(av=0\:\:\:(v\neq0)\)
が成り立つのは \(a=0\) しかないので \(v\) は1次独立であり、また \(av\) で全ての \(\bs{Q}\) の元が表されるからです。一方、\(0\) は、
\(a\cdot0=0\)
が \(0\) ではない \(a\) について成り立つので1次従属です。以上から、線形空間 \(\bs{Q}\) の基底として \(1\) を選ぶことにします。次元は \(1\) です。
\(\bs{Q}\) に \(\sqrt{2}\) を添加した \(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) の代数拡大体で、\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) です。\(\bs{Q}(\sqrt{2})\) は \(\bs{\bs{Q}}\) 上の線形空間です。\(\bs{Q}(\sqrt{2})\) の基底としては、まず \(1\) を選ぶことができます。\(1\) を \(\bs{Q}\) の元でスカラー倍すると、\(\bs{Q}(\sqrt{2})\) の部分集合である \(\bs{Q}\) の元の全てが表せます。
\(\bs{Q}(\sqrt{2})\) の元の全てを表現するためには、さらに基底に \(\sqrt{2}\) を追加します。\(\sqrt{2}\) は \(\bs{Q}\) の元の1次結合では表せないので、\(1\) と \(\sqrt{2}\) は 1次独立です。\(1,\:\sqrt{2}\) が \(\bs{Q}(\sqrt{2})\) の基底で、次元は \(2\) です。
さらに \(\bs{Q}(\sqrt{2})\) に \(\sqrt{3}\) を添加した代数拡大体 \(\bs{Q}(\sqrt{2},\sqrt{3})\) を考えてみると、\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間であり、基底は \(1,\:\sqrt{3}\) です。\(1\) と \(\sqrt{3}\) は 1次独立であり、\(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の全ての元は、\(\bs{\bs{Q}(\sqrt{2})}\) の元を係数とする \(\bs{1}\) と \(\bs{\sqrt{3}}\) の1次結合で表現できるからです。\(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間 \(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の次元は \(\bs{2}\) です。
ここで \(\bs{Q}(\sqrt{2},\sqrt{3})\) を \(\bs{\bs{Q}}\) 上の線形空間と考えると、その基底はまず、\(1,\:\sqrt{2},\:\sqrt{3}\) ですが、これだけでは不足で、\(\sqrt{6}\) を加える必要があります。\(\sqrt{6}\) は体としての演算(乗算)でできる数ですが、\(1,\:\sqrt{2},\:\sqrt{3}\) の1次結合では表現できないからです。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は \(1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\) であり、次元は \(4\) です。
ここまでの基底の表現はあくまで一例ですが、どういう基底を選ぼうと基底の数=次元は不変量であるというのが「次元の不変性」でした。以上の考察を踏まえて、拡大次数を定義し、拡大次数の連鎖律を証明します。
代数拡大体 \(\bs{F},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{K}\) であるとき、\(\bs{K}\) は \(\bs{F}\) 上の線形空間である。\(\bs{K}\) の次元を、\(\bs{K}\)の(\(\bs{F}\)からの)拡大次数といい、
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
代数拡大体 \(\bs{F},\:\bs{M},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{M}\:\subset\:\bs{K}\) であるとき、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
[証明]
\([\:\bs{M}\::\:\bs{F}\:]=m\)、\([\:\bs{K}\::\:\bs{M}\:]=n\) とする。以下、表記を見やすくするため、\(m=3,\:n=2\) の場合で記述する。もちろん一般性を失わないように記述する。
\(\bs{F}\) 上の線形空間 \(\bs{M}\) の基底を
\(u_1,\:u_2,\:u_3\)
とすると、\(\bs{M}\) の任意の元 \(b\) は、
\(b=a_1u_1+a_2u_2+a_3u_3\:\:(a_i\in\bs{F},\:u_i\in\bs{M},\:1\leq i\leq m)\)
と表せる。
\(\bs{M}\) 上の線形空間 \(\bs{K}\) の基底を
\(v_1,\:v_2\)
とすると、\(\bs{K}\) の任意の元 \(x\) は、
\(x=b_1v_1+b_2v_2\:\:(b_j\in\bs{M},\:v_j\in\bs{K},\:1\leq j\leq n)\)
と表せる。\(b_1,\:b_2\) を \(\bs{M}\) の基底 \(u_1,u_2,u_3\) で表すと、
\(b_1=a_{11}u_1+a_{21}u_2+a_{31}u_3\)
\(b_2=a_{12}u_1+a_{22}u_2+a_{32}u_3\)
\((\:a_{ij}\in\bs{F}\:)\)
となるが、これを用いて \(x\) を表すと、
\(\begin{eqnarray}
&&\:\:x=&a_{11}u_1v_1+a_{21}u_2v_1+a_{31}u_3v_1+\\
&&&a_{12}u_1v_2+a_{22}u_2v_2+a_{32}u_3v_2\\
\end{eqnarray}\)
となる。つまり、\(\bs{K}\) の任意の元は \(\bs{F}\) の元を係数とする、\(u_1v_1\)、\(u_2v_1\)、\(u_3v_1\)、\(u_1v_2\)、\(u_2v_2\)、\(u_3v_2\) の1次結合で表現できる。
ここで \(x=0\) とすると、
\((a_{11}u_1+a_{21}u_2+a_{31}u_3)v_1+\)
\((a_{12}u_1+a_{22}u_2+a_{32}u_3)v_2=0\)
であるが、\(v_1,v_2\) は \(\bs{K}\) の基底なので1次独立であり、従って、
\(a_{11}u_1+a_{21}u_2+a_{31}u_3=0\)
\(a_{12}u_1+a_{22}u_2+a_{32}u_3=0\)
である。すると、\(u_1,u_2,u_3\) は \(\bs{M}\) の基底なので1次独立であり、
\(a_{11}=a_{21}=a_{31}=a_{12}=a_{22}=a_{32}=0\)
である。従って、\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) は1次独立である。
\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) の \(mn\) 個の元は、
から、\(\bs{F}\) 上の線形空間 \(\bs{K}\) の基底であり、\(\bs{K}\) の次元は \(mn\) である。以上により、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
である。[証明終]
体の一致
2つの代数拡大体 \(\bs{F}\) と \(\bs{K}\) の次元が一致するとします。たとえば \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) の次元はいずれも \(2\) です。もちろん \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) は体として別物です。
それでは、\(\bs{F}\subset\bs{K}\) という関係があり、かつ \(\bs{F}\) と \(\bs{K}\) の次元が一致するとき、\(\bs{F}\) と \(\bs{K}\) は体として一致すると言えるのでしょうか。
これはイエスで、それを次に証明します。この定理は、ガロア理論の証明の過程において、2つの体が実は同じものであることを言うときに使われる論法です。証明の都合上、\(\bs{F}\) ではなく \(\bs{K}_0\) と書きます。
体 \(\bs{K}_0\) と 体 \(\bs{K}\) があり、\(\bs{K}_0\:\subset\:\bs{K}\) を満たしている。\(\bs{K}_0\) と \(\bs{K}\) が有限次元であり、その次元が同じであれば、\(\bs{K}_0=\bs{K}\) である。
[証明]
体 \(\bs{K}_0\) と \(\bs{K}\) を、\(\bs{Q}\) 上の線形空間と見なし、その次元を \(n\) とする。\(\bs{K}_0\) の基底を \(\{a_1,\:a_2,\:\cd\:,a_n\}\) とする。\(\bs{K}_0\) が \(\bs{K}\) の真部分集合である、つまり \(\bs{K}_0\:\subsetneq\:\bs{K}\) と仮定して、背理法で証明する。
\(\bs{K}_0\:\subsetneq\:\bs{K}\) だと、\(a_{n+1}\notin\bs{K}_0,\:a_{n+1}\in\bs{K}\) である元 \(a_{n+1}\) が存在する。この \(a_{n+1}\) は \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合では表せない。なぜなら、もし表せたとしたら、\(\bs{K}_0\) の全ての元は基底である \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されるので \(a_{n+1}\in\bs{K}_0\) になってしまうからである。
そこで、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) を考えると、この元の並びは1次独立である。なぜなら、もし1次従属だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n+a_{n+1}x_{n+1}=0\)
となる \(x_i\in\bs{Q}\:\:(1\leq i\leq n+1)\) があって、そのうち少なくとも一つは \(0\) ではない。もし \(x_{n+1}\neq0\) だとすると、\(a_{n+1}\) が \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されることになり、\(a_{n+1}\in\bs{K}_0\) となって矛盾が生じる。また \(x_{n+1}=0\) だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n=0\)
であるが、この場合は \(x_i\:\:(1\leq i\leq n)\) の中に少なくとも一つは \(0\) でないものがあることになり、\(\{a_1,\:a_2,\:\cd\:,a_n\}\) が基底である(=1次独立である)ことに矛盾する。従って \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は1次独立である。
\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表される全ての元の集合を \(\bs{K}_1\) とする。\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) はすべて \(\bs{K}\) の元であるから、\(\bs{K}_1\:\subset\:\bs{K}\) である。また \(\bs{K}_1\) の任意の元は1次独立である \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表されるから、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は \(\bs{K}_1\) の基底であり、すなわち \(\bs{K}_1\) の次元は \(n+1\) である。\(\bs{K}_1=\bs{K}\) なら \(\bs{K}\) の次元が \(n+1\) になって矛盾するから、\(\bs{K}_1\neq\bs{K}\) つまり \(\bs{K}_1\:\subsetneq\:\bs{K}\) である。
以上の論理を繰り返すと \(\bs{K}_2\:\subsetneq\:\bs{K}\) である \(n+2\) 次元の \(\bs{K}_2\) の存在を示せるが、この操作は無限に繰り返えせるから、\(\bs{K}\) は無限個の基底をもつ無限次元の体となる。これは \(\bs{K}\) の次元が有限次元の \(n\) であることに矛盾する。従って背理法の仮定は誤りであり、\(\bs{K}_0\:=\:\bs{K}\) である。[証明終]
代数拡大体の構造
多項式と代数拡大体の相互関係をまとめると次のようになります。
以下、例をいくつかあげます。
\(x^4-5x^2+6\)
\(f(x)\) を4次多項式、
\(f(x)=x^4-5x^2+6\)
とします。\(f(x)\) は、
\(f(x)=(x^2-2)(x^2-3)\)
と因数分解できるので既約多項式ではありません。また、
\(f(x)=(x-\sqrt{2})(x+\sqrt{2})(x-\sqrt{3})(x+\sqrt{3})\)
なので、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt{2},\sqrt{3})\)
です。\(\bs{Q}(\sqrt{2},\:\sqrt{3})\) は、\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) による拡大体を \(\bs{Q}(\sqrt{2})\) とし、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-3=0\) の解 \(\sqrt{3}\) による拡大体が \(\bs{Q}(\sqrt{2},\:\sqrt{3})\) であると見なせます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})\)
です。拡大次数は
\([\:\bs{Q}(\sqrt{2}):\bs{Q}\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}(\sqrt{2})\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}\:]=4\)
です。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は、
\(\begin{eqnarray}
&&\:\:B_1&=(\:1,\:\sqrt{2},\:1\cdot\sqrt{3},\:\sqrt{2}\cdot\sqrt{3}\:)\\
&&&=(\:1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\:)\\
\end{eqnarray}\)
とすることができます。
一方、
\(\theta=\sqrt{2}+\sqrt{3}\)
とおくと、
\(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\)
となります。なぜなら、
\(\sqrt{2}=\dfrac{1}{2}(\theta-\dfrac{1}{\theta})\)
\(\sqrt{3}=\dfrac{1}{2}(\theta+\dfrac{1}{\theta})\)
であり、\(\sqrt{2}\) と \(\sqrt{3}\) が \(\theta\) と有理数の加減乗除で表現できるからです。\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{Q}(\sqrt{2}+\sqrt{3})\) という単拡大体です。
\(\theta=\sqrt{2}+\sqrt{3}\) から根号を消去すると、
\(\theta^4-10\theta^2+1=0\)
となるので、\(\theta\)の最小多項式は、
\(g(x)=x^4-10x^2+1\)
であり、この \(g(x)\) は既約多項式です。\(y=x^2-5\) とおくと、
\(\begin{eqnarray}
&&\:\:g(x)&=y^2-24\\
&&&=(y-2\sqrt{6})(y+2\sqrt{6})\\
\end{eqnarray}\)
なので、
\(\begin{eqnarray}
&&\:\:g(x)&=&(x^2-5-2\sqrt{6})(x^2-5+2\sqrt{6})\\
&&&=&(x-\sqrt{2}-\sqrt{3})(x+\sqrt{2}-\sqrt{3})\cdot\\
&&&& (x-\sqrt{2}+\sqrt{3})(x+\sqrt{2}+\sqrt{3})\\
\end{eqnarray}\)
となり、\(g(x)=0\) の解は、\(\sqrt{2}+\sqrt{3}\)、\(-\sqrt{2}+\sqrt{3}\)、\(\sqrt{2}-\sqrt{3}\)、\(-\sqrt{2}-\sqrt{3}\) の4つです。その \(g(x)=0\) の解の一つが \(\theta=\sqrt{2}+\sqrt{3}\) なので、単拡大体の基底の定理(33F)を適用して、\(\bs{Q}(\theta)\) の基底を、
\(B_2=(\:1,\:\:\theta,\:\:\theta^2,\:\:\theta^3\:)\)
の4個に選ぶことができます。拡大次数は \([\:\bs{Q}(\theta):\bs{Q}\:]=4\) です。
\(B_1\) と \(B_2\) は、同じ体である \(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\) の基底なので、相互に1次結合で表現できます。\(B_2\) の1次結合で \(B_1\) を表現すると、
\(\sqrt{2}=\dfrac{1}{2}(\phantom{-}\theta^3-9\theta)\)
\(\sqrt{3}=\dfrac{1}{2}(-\theta^3+11\theta)\)
\(\sqrt{6}=\dfrac{1}{2}(\phantom{-}\theta^2-5)\)
となります。
\(x^3-2\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-2\)
とします。これは既約多項式です。
\(x^3-1=0\) 解で \(1\) でないもの一つを \(\omega\) とします(= \(1\) の原始\(3\)乗根)。
\(x^3-1=(x-1)(x^2+x+1)\)
なので \(\omega\) は、
\(\omega^2+\omega+1=0\)
を満たします。この2次方程式の解は2つありますが、
\(\omega=\dfrac{-1+\sqrt{3}\:i}{2}\)
とします。方程式 \(x^3-2=0\) の解は、
\(\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
の3つです、従って、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt[3]{2},\:\sqrt[3]{2}\omega,\:\sqrt[3]{2}\omega^2)=\bs{Q}(\sqrt[3]{2},\:\omega)\)
です。これは、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt[3]{2})\:\subset\:\bs{Q}(\sqrt[3]{2},\:\omega)\)
という構造をしています。基底は、単拡大体の基底の定理(33F)を順次適用して、
\(\bs{Q}(\sqrt[3]{2})\) の基底(\(\bs{Q}\) 上の線形空間)
\(1,\:\sqrt[3]{2},\:(\sqrt[3]{2})^2\)
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}(\sqrt[3]{2})\) 上の線形空間\()\)
\(1,\:\omega\)
です。これらを総合すると、
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}\) 上の線形空間\()\)
です。拡大次数は
\([\:\bs{Q}(\sqrt[3]{2}):\bs{Q}\:]=3\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}(\sqrt[3]{2})\:]=2\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}\:]=6\)
となります。
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の原始元 \(\theta\) を、
\(\theta=\sqrt[3]{2}+\omega\)
と選ぶことができます。なぜなら、計算は省きますが、
と表せるので、\(\bs{Q}\) に \(\sqrt[3]{2},\:\omega\) を添加した拡大体は \(\theta\) を添加した拡大体と同じものでからです。さらに、
\(\theta=\sqrt[3]{2}+\dfrac{-1+\sqrt{3}\:i}{2}\)
の式を2乗や3乗して \(i\) と根号を消去すると、計算過程は省きますが、
\(\theta^6+3\theta^5+6\theta^4+3\theta^3+9\theta+9=0\)
となります。従って、\(\theta\) の最小多項式を \(g(x)\) とすると、
\(g(x)=x^6+3x^5+6x^4+3x^3+9x+9\)
という6次多項式です。\(\bs{Q}(\sqrt[3]{2},\:\omega)\) は 6次方程式 \(g(x)=0\) の根の一つである \(\theta\) を使って、
\(\bs{Q}(\sqrt[3]{2},\:\omega)=\bs{Q}(\theta)\)
という単拡大体(次元は \(6\))と表現できます。
\(x^3-3x+1\)
「1.3 ガロア群」の「ガロア群の例」で書いたように、\(x^3-3x+1=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
の関係があり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できます。これにより、\(f(x)=x^3-3x+1\) の最小分解体は、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。基底は、たとえば \(1,\:\al,\:\al^2\) であり、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]=3\)
です。\(\al\) の最小多項式は、3次多項式である \(f(x)=x^3-3x+1\) です。
ちなみに、3次多項式の最小分解体の次元が \(3\) になる条件を書いておきます。まず、2次方程式の例ですが、
\(x^2+ax+b=0\)
の方程式の解を \(\al,\:\beta\) とすると、
\(x^2+ax+b=(x-\al)(x-\beta)\)
です。そうすると、根と係数の関係から、
\(a=-(\al+\beta)\)
\(b=\al\beta\)
です。ここで、判別式 \(\bs{D}\) を、
\(D=(\al-\beta)^2\)
と定義すると、
\(\begin{eqnarray}
&&\:\:D=&\al^2-2\al\beta+\beta^2\\
&&&=(\al+\beta)^2-4\al\beta\\
&&&=a^2-4b\\
\end{eqnarray}\)
となります。この判別式を使って解の状況がわかります。つまり、
以上を3次方程式に拡張できます。2乗の項がない既約な3次方程式を、
\(x^3+ax+b=0\)
とし、3つの根を \(\al,\:\beta,\:\gamma\) とすると、
\(\al\beta\gamma=-b\)
となります。3次方程式の判別式 \(D\) は、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
で定義されます。計算すると、
\(D=-4a^3-27b^2\)
となります。
ここで、\(D\) が、ある有理数 \(q\) の2乗の場合を考えます。つまり、
\(D=q^2\)
です。そうすると、
\((\br{A})\) 式の両辺を \(x\) で微分して \(x=\al\) を代入すると、
\(\beta=\dfrac{2a\al+3b-q}{2(3\al^2+a)}\)
\(\gamma=\dfrac{2a\al+3b+q}{2(3\al^2+a)}\)
です。式の形はともかく、要するに、
\(\beta\) と \(\gamma\) が \(\al\) の加減乗除で表現できる
わけです。このことは、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
であることを意味します。\(\bs{Q}(\al,\beta,\gamma)\) は、既約な3次方程式の根の一つである \(\al\) の単拡大体なので、その次元は \(3\) です。
まとめると、判別式 \(D\) が有理数の2乗であるとき、既約 \(3\)次多項式の最小分解体の次元が \(3\) になります。\(x^3-3x+1\) の場合、\(a=-3,\:b=1\) なので、
\(D=-4a^3-27b^2=81=9^2\)
となり、次元が \(3\) です。
既約多項式ではない3次多項式の拡大次数はもっと小さくなります。たとえば \((x-1)(x^2+2)\) の最小分解体は \(\bs{Q}(\sqrt{2}\:i)\) であり、拡大次数は \(2\) です。また \((x-2)^3\) の最小分解体は \(\bs{Q}\) そのもので、拡大次数は \(1\) です。
まとめると、3次多項式 \(f(x)\) の最小分解体の拡大次数は、\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]\:=\:6,\:3,\:2,\:1\)
の4種あることになります(この4種しかないことの理由は後の章にあります)。
ガロア理論の核心(第5章以降)に入る前の最後として、群についての各種の定義や定理を説明します。これらはいずれも第5章以降で必要になります。
4.1 部分群\(\cdot\)正規部分群、剰余類\(\cdot\)剰余群
部分集合の演算
以降の証明では集合の演算が多々出てきます。その定義は次の通りでです。これはあくまで群の "部分集合" に関するもので、それが部分群かどうかは別問題です。
群 \(G\) の2つの部分集合を \(H,\:N\) とする。\(H\) と \(N\) の演算結果である \(G\) の部分集合、\(HN\) を次の式で定義する。
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
部分群の定理
部分群に関する定理をいくつかあげます。これらはいずれも後の定理の証明の過程で使います。
部分群の十分条件
群 \(G\) の部分集合を \(N\) とし、\(N\) の任意の2つの元を \(x,\:y\) とする。
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
[証明]
\(N\) の元 \(x,\:y\) は \(G\) の元でもあるので、\(xy,\:x^{-1},\:y^{-1}\) は \(G\) の演算として定義されている。
\(y=x^{-1}\) とおくと \(xy=xx^{-1}=e\in N\) なので、\(N\) は単位元を含む。つまり、\(N\) は演算で閉じていて、単位元が存在し、逆元が \(N\) の元である。また結合則は \(G\) の元として成り立っている。従って \(N\) は \(G\) の部分群である。[証明終]
部分群の元の条件
群 \(G\) の部分群を \(N\) とし、\(G\) の 元を \(x\) とすると、次の2つは同値である。
① \(xN\:=\:N\)
② \(x\:\in\:N\)
[証明]
[① \(\bs{\Rightarrow}\) ②]
\(N\) には \(G\) の単位元 \(e\) が含まれるから、\(xe\) は \(xN\) に含まれる。
\(x=xe\in xN=N\) \(\Rightarrow\) \(x\in N\)
である。
[② \(\bs{\Rightarrow}\) ①]
\(x\in N\) とし、\(N\) の任意の元を \(a\) とすると、\(N\) は群だから \(xa\in\:N\) である。\(N\) の異なる2つの元を \(a,\:b\:\:(a\neq b)\) とすると、\(xa\neq xb\) である。なぜなら、もし \(xa=xb\) だとすると、\(x\) の逆元 \(x^{-1}\) を左からかけて \(a=b\) となり、矛盾するからである。以上により、\(xH\) は \(H\) の全ての元を含むから \(xH=H\) である。[証明終]
部分群の共通部分
\(G\) の部分群を \(H,\:N\) とすると、\(H\cap N\) は部分群である。
[証明]
\(G\) の部分群を \(H,\:N\) とし、\(H\cap N\) の任意の2つの元を \(x,\:y\) とすると、\(x,\:y\in H,\:\:x,\:y\in N\) なので、
\(xy\in H,\:x^{-1}\in H\)
\(xy\in N,\:x^{-1}\in N\)
であり、
\(xy\in H\cap N,\:x^{-1}\in H\cap N\)
となって、部分群の十分条件の定理(41B)により \(H\cap N\) は部分群である。[証明終]
剰余類
有限群 \(G\) の位数を \(n\) とし( \(|G|=n\) )、\(H\) を \(G\) の部分群とする。\(H\) に左から \(G\) のすべての元、\(g_1,\:g_2,\:\cd\:,\:g_n\) かけて、集合、
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
[証明]
\(|G|=[\:G\::\:H\:]\cdot|H|\) であることを証明する。2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとする。その共通な元が、\(x_1H\) では \(x_1h_i\)、\(x_2H\) では \(x_2h_j\) と表されているものとする。
\(x_1h_i=x_2h_j\)
左から \(x_2^{-1}\)、右から \(h_i^{-1}\) をかけると、
\(x_2^{-1}x_1h_ih_i^{-1}=x_2^{-1}x_2h_jh_i^{-1}\)
\(x_2^{-1}x_1=h_jh_i^{-1}\)
\(h_jh_i^{-1}\in H\) だから、
\(x_2^{-1}x_1\in H\)
を得る。部分群の元の条件の定理(41C)により、\(xH=H\) と \(x\in H\) は同値だから、
\(x_2^{-1}x_1H=H\)
となる。左から \(x_2\) をかけると、
\(x_1H=x_2H\)
を得る。これは、「2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとすると、2つの剰余類は一致する」ことを示している。従って、
である。\(H\) は 単位元 \(e\) を含むから、
\(g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
という和集合を作ると、そこには \(G\) のすべての元が含まれる。従って、
\(G=g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
である。剰余類 \(x_1H,\:x_2H,\:\cd\:x_dH\) は、\(g_1H,\:g_2H,\:\cd\:,g_nH\) を整理・分類したものだから、
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。この式の右辺の剰余類は共通の元がなく、それぞれの剰余類の元の数はすべて \(|H|\) だから、
\(|G|=d\cdot|H|\)
である。従ってラグランジュの定理、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
が成り立つ。[証明終]
ラグランジュの定理から、
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
ことがわかります。なぜなら、
\(H=\{e,\:g,\:g^2,\:\cd\:,\:g^{n-1}\}\)
とおくと、\(H\) は \(G\) の部分群(巡回群)になり、ラグランジュの定理によって \(|H|=n\) が \(|G|\) の約数になるからです。これは、位数の定理(25A)の[補題5]、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とし、\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
の一般化になっています。 \((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\)(\(\varphi\)はオイラー関数)なので、ラグランジュの定理はオイラーの定理やフェルマの小定理(25B)の一般化であるとも言えます。さらに、
群位数が素数の群は巡回群である。
こともわかります。なぜなら、群 \(G\) の位数を \(p\)(素数)とすると、単位元ではない \(G\) の任意の元 \(g\:(\neq e)\) の位数は \(p\) であり、つまり \(G\) は \(g\) を生成元とする位数 \(p\) の巡回群(\(C_p\))だからです。
次の「正規部分群」はガロア理論のキモといえる概念です。これは純粋に群の属性として定義できるのでここにあげますが、ガロア理論の核心である第5章以降で展開される論証の多くは正規部分群に関係しています。
正規部分群
有限群 \(G\) の部分群を \(H\) とする。\(G\) の全ての元 \(g\) について、
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
正規部分群 \(H\) の定義は、\(G\) の任意の元 \(g\) に対して、
\(gHg^{-1}=H\)
となる \(H\)、としても同じです。また 任意の \(h\in H\) について、
\(ghg^{-1}\in H\)
となる \(H\)、としても同じです。
剰余群
有限群 \(G\) の正規部分群を \(H\) とする。\(G\) の \(H\) による剰余類
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
[証明]
\(H\) が正規部分群のとき、剰余類が群になることを証明する。\(x_iH\) は \(G\) の剰余類なので、
\(G=x_1H\cup x_2H\cup\cd\cup x_dH\)
\((i\neq j\:のとき\:x_iH\cap x_jH=\phi)\)
と表されている。2つの剰余類、\(x_iH,\:x_jH\) の演算を行うと、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_iHx_jH=x_i(Hx_j)H\\
&&&=x_i(x_jH)H=x_ix_jHH\\
&&&=x_ix_j(HH)=x_ix_jH\\
\end{eqnarray}\)
つまり、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_ix_jH\\
\end{eqnarray}\)
となる。\(H\) は正規部分群なので \(Hx_j=x_jH\) であることと、\(H\) は部分群なので \(HH=H\) であることを用いた。
\(x_ix_j\) は \(G\) の元だから、\(x_ix_jH\) は \(G\) の剰余類のうちの一つである。従って \((x_iH)(x_jH)\) の演算は \(G\) の剰余類の中で閉じている。また、
\((x_iH\cdot x_jH)\cdot x_kH=x_ix_jH\cdot x_kH=x_ix_jx_kH\)
\(x_iH\cdot(x_jH\cdot x_kH)=x_iH\cdot x_jx_kH=x_ix_jx_kH\)
\((x_iH\cdot x_jH)\cdot x_kH=x_iH\cdot(x_jH\cdot x_kH)\)
であるから、結合法則が成り立っている。さらに、
\(H\cdot xh=eH\cdot xH=(ex)H=xH\)
\(xH\cdot H=xH\cdot eH=(xe)H=xH\)
なので、剰余類 \(H\) が単位元になる。また、
\(xH\cdot x^{-1}H=(xx^{-1})H=eH=H\)
\(x^{-1}H\cdot xH=(x^{-1}x)H=eH=H\)
であり、\(xH\) に対する逆元は \(x^{-1}H\) である。従って剰余類 \(G/H\) は群である。[証明終]
群の位数、元の位数、ラグランジュの定理、巡回群は、いずれも有限群の概念や定理です。しかし、剰余類、正規部分群、剰余群は、元の数が無限であっても成り立つ概念です。たとえば、整数の加法群 \(\bs{Z}\) は可換群なので、すべての部分群は正規部分群です。従って、\(n\) の倍数から成る部分群を \(n\bs{Z}\) とすると、\(\bs{Z}/n\bs{Z}\) は剰余群です。\(\bs{Z}/n\bs{Z}\) という表記は \(n\bs{Z}\) が \(\bs{Z}\) の正規部分群であることが暗黙の前提なのでした。
巡回群の部分群による剰余群は巡回群である。
[証明]
群 \(G\) を、位数 \(n\)、生成元 \(g\) の巡回群とし、その元を、
\(G\:=\:\{g,\:g^2,\:g^3,\:\cd,\:g^n=e\:\}\)
とする。\(G\) の部分群を \(H\) とし、\(H\) の元のうち \(g\) の指数が一番小さいものを \(g^{d}\:\:(1\leq d\leq n)\) とする。\(d=1\) なら \(H=G\) であり、また \(d=n\) なら \(H=\{\:e\:\}\) である。
\(n\) を \(d\) で割った商を \(q\)、余りを \(r\) とする。つまり、
\(n=qd+r\:\:(1\leq q\leq n,\:0\leq r < d)\)
とする。\(g^d\) は \(H\) の元だから その \(q\) 乗も \(H\) の元であり、
\((g^d)^q=g^{dq}\in H\)
である。また \(g^{dq}\) の逆元も \(H\) に含まれるから
\((g^{dq})^{-1}\in H\)
である。仮にもし \(1\leq r < d\) なら
\(g^{dq}g^{r}=g^{qd+r}=g^n=e\)
となるので、この式に左から \((g^{dq})^{-1}\) をかけると、
\(g^r=(g^{dq})^{-1}\in H\)
となり、\(d\) 未満の数 \(r\) が指数の \(g^r\) が \(H\) の元ということになるが、これは \(d\) が最小の指数であるという仮定に反する。従って \(r=0\) であり、\(qd=n\) である。つまり \(d\) と \(q\) は \(n\) の約数である。そうすると \(g^d\) を \(q\) 乗すると \(g^{dq}=g^n=e\) となるので、\(H\) は \(g^d\) を生成元とする位数 \(q\) の巡回群、
次に、剰余類 \(g^kH\:\:(1\leq k\leq n)\) を考える。\(k\) を \(d\) で割った商を \(m\)、余りを \(i\) とする。\(qd=n\) なので \(m\) の最大値は \(q\) であり、
\(k=md+i\) \((0\leq m\leq q,\:0\leq i < d)\)
と表現できる。以下、\(m,\:i\) の値によって3つに分ける。
\(k=i\:\:(m=0,\:1\leq i < d)\) のときは、\(H\) が単位元を含んでいるので、
\(g^k=g^i\in g^iH\)
である。
\(m\neq0,\:1\leq i < d\) のときは、
\(g^k=g^{md+i}=g^ig^{md}\)
となるが、\((\br{A})\) 式により、
\(g^{md}\in H\:\:(1\leq m\leq q)\)
なので、
\(g^ig^{md}\in g^iH\)
\(g^k\in g^iH\:\:(1\leq i < d)\)
となる。
また、\(m\neq0,\:i=0\) のときは、
\(g^k=g^{md}\in H\)
である。
結局、\(G\) の元 \(g^k\) は、\(\{\:H,\:g^iH\:\:(1\leq i < d)\:\}\) のどれかに含まれる。ここで、形式上 \(g^0H\:=\:H\) と定義すると、\(H,\:g^iH\) は、
\(g^iH\:=\:\{\:g^{i+md}\:|\:0\leq i < d,\:\:0\leq m\leq q\:\}\)
と表記できる。\(0\leq i,j < d,\:\:0\leq m_i,m_j\leq q\) で、\(i\neq j\) なら、
\(i+m_id\neq j+m_jd\)
なので、\(g^iH\) と \(g^jH\) に共通の元はなく、
\(g^iH\:\cap\:g^jH=\phi\:\:(i\neq j)\)
である。
以上より、巡回群 \(G\) は剰余類によって、
\(G=H\:\cup\:gH\:\cup\:g^2H\:\cup\:\cd\:\cup\:g^{d-1}\)
\(g^iH\:\cap\:g^jH=\phi\) \((i\neq j)\)
と分解できる。
\(H\) は \(G\) の正規部分群であった。従って \(G\) の \(H\) による剰余類は剰余群になり、
\(G/H=\{\:H,\:gH,\:g^2H,\:\cd\:,g^{d-1}H\:\}\)
である。ここで \(gH\) の累乗を調べると、
\((gH)^2=gHgH=ggHH=g^2H\)
\((gH)^3=gHgHgH=g^2HgH=g^2gHH=g^3H\)
のように計算でき、
\((gH)^i=g^iH\) \((1\leq i\leq d-1)\)
である。また、同じ計算によって、
\((gH)^d=g^dH\)
となるが、\(g^d\in H\) なので部分群の元の条件の定理(41C)により \(g^dH=H\) であり、つまり、
\((gH)^d=H\)
である。
以上により 剰余群 \(G/H\) は、
\(G/H=\{gH,\:(gH)^2,\:\cd\:,(gH)^{d-1},\:(gH)^{d}=H\}\)
と表され、生成元が \(gH\)、単位元が \(H\)、位数が \(d\) の巡回群である。[証明終]
部分群と正規部分群
\(G\) の正規部分群を \(H\)、部分群を \(N\) とする。このとき、
が成り立つ。
(a) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(NH\) は部分群である。
\(NH\) の任意の2つの元を
\(nx\:\:(n\in N,\:x\in H),\:\:my\:\:(m\in N,\:y\in H)\)
とすると、
\(nx\in nH,\:my\in mH\)
である。\(H\) は正規部分群だから、\(mH=Hm\) であることを用いると、
\((nx)(my)\in(nH)(mH)=nHmH=nmHH=nmH\)
となる。\(n,m\in N\) なので \(nm\in N\) であり、従って \(nmH\subset NH\) である。結局、
\((nx)(my)\in NH\)
となって、\(NH\) の2つの元の演算は \(NH\) で閉じていることが分かる(=\(\:\br{①}\:\))。
また一般に、\((xy)^{-1}=y^{-1}x^{-1}\) である。なぜなら、
\(xy(y^{-1}x^{-1})=x(yy^{-1})x^{-1}=xex^{-1}=xx^{-1}=e\)
\((y^{-1}x^{-1})xy=y^{-1}(x^{-1}x)y=y^{-1}ey=y^{-1}y=e\)
が成り立つからである。
\(G\) の部分群 \(N\) と正規部分群 \(H\) において、\(n\in N,\:x\in H\) とすると、\(n^{-1}\in N,\:x^{-1}\in H\) なので、
\((nx)^{-1}=x^{-1}n^{-1}\in Hn^{-1}\)
となるが、\(H\) が正規部分群なので、\(Hn^{-1}=n^{-1}H\)である。さらに、\(n^{-1}H\subset NH\) なので、結局、
\((nx)^{-1}\subset NH\)
となり、\(NH\) の任意の元 \(nx\) について逆元 \((nx)^{-1}\) が \(NH\) に含まれる(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) が成り立つので、部分群の十分条件の定理(41B)によって \(NH\) は \(G\) の部分群である。[証明終]
(b) の証明
\(G\) の正規部分群を \(H\)、部分群を \(N\) とするとき、\(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。\(N\) は \(G\) の 部分集合だから、\(N\) の任意の元 \(y\) についても、
\(yH=Hy\)
が成り立つ。従って \(H\) は \(N\) の正規部分群である。[証明終]
(c) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(N\cap H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。この式に右から \(x^{-1}\) をかけると、
\(xHx^{-1}=H\)
となる。これは、\(H\) の任意の元 \(h\) を決めると、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
となることを意味する。これは \(H\) が正規部分群であることの定義と等価である。以降、この形で \(N\cap H\) が正規部分群であることを証明する。
部分群 \(N\) の任意の元を \(y\)、正規部分群 \(H\) の任意の元を \(h\)、\(N\cap H\) の任意の元を \(n\) とする。\(y,\:y^{-1},\:n\) は全て \(N\) の元だから、
\(yny^{-1}\in N\)
である(=\(\:\br{①}\:\))。また \(H\) は \(G\) の正規部分群であるから、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
が成り立つ。ここで、\(G\:\sp\:N\) なので \(x=y\) とおくことができ、また \(H\:\sp\:N\cap H\) なので \(h=n\) とおくこともできる。従って、
\(yny^{-1}\in H\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、\(N\cap H\) の任意の元 \(n\) を決めると、\(N\) の全ての元 \(y\) について、
\(yny^{-1}\in N\cap H\)
となる。つまり \(N\cap H\) は \(N\) の正規部分群である。[証明終]
4.2 準同型写像
この節の写像の説明には「全射」「単射」「全単射」などの用語ができてます。その用語の意味は次の図の通りです。
準同型写像と同型写像
群 \(G\) から群 \(G\,'\) への写像 \(f\) がある。\(G\) の任意の2つの元、\(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
準同型写像の像と核
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(G\) の元を \(f\) で移した元の集合を「\(f\) の像(image)」といい、\(\mr{Im}\:f\) と書く。\(\mr{Im}\:f\) を \(f(G)\) と書くこともある。
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
[証明]
\(\mr{Im}\:f\) と \(\mr{Ker}\:f\) が群であることを証明する。
\(\mr{Im}\:f\) は群
\(\mr{Im}\:f\) の任意の2つの元を \(f(x),f(y)\:\:(x,y\in G)\) とすると、
\(f(x)f(y)=f(xy)\:\in\mr{Im}\:f\)
である(=\(\:\br{①}\:\))。
\(\mr{Im}\:f\) の任意の元 \(f(x)\) について、
\(f(e)f(x)=f(ex)=f(x)\)
\(f(x)f(e)=f(xe)=f(x)\)
なので、
\(f(e)=e\,'\)
である。\(G\) は群なので、任意の元 \(x\) について逆元 \(x^{-1}\) が存在する。
\(f(x)f(x^{-1})=f(xx^{-1})=f(e)=e\,'\)
\(f(x^{-1})f(x)=f(x^{-1}x)=f(e)=e\,'\)
であるから、
\(f(x)^{-1}=f(x^{-1})\:\in\mr{Im}\:f\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、部分群の十分条件の定理(41B)によって \(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(\mr{Ker}\:f\) は群
\(\mr{Ker}\:f\) の任意の元を \(x,\:y\) とすると、
\(f(xy)=f(x)f(y)=e\,'e\,'=e\,'\)
なので、
\(xy\:\in\mr{Ker}\:f\)
である(\(\:\br{③}\:\))。
また \(x\) は \(G\) の元だから \(x^{-1}\) が定義されている。
\(\begin{eqnarray}
&&\:\:f(x^{-1})&=f(x^{-1})e\,'=f(x^{-1})f(x)\\
&&&=f(x^{-1}x)=f(e)\\
&&&=e\,'\\
\end{eqnarray}\)
となるので、
\(x^{-1}\:\in\mr{Ker}\:f\)
である(\(\:\br{④}\:\))。\(\br{③}\:\:\br{④}\) より、部分群の十分条件の定理(41B)によって \(\mr{Ker}\:f\) は \(G\) の部分群である。[証明終]
核が単位元なら単射
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。このとき
である。
[証明]
"\(f\) は全射" については、全射の定義そのものである。
\(\mr{Ker}\:f\:=\:\{e\}\) とし、\(G\) の任意の2つの元を \(x,\:y\) とする。ここで、
\(f(x)=f(y)\)
であったとする。\(\mr{Im}\:f\) は群だから \(f(y)^{-1}\in\:\mr{Im}\:f\) である。上の式に左から \(f(y)^{-1}\) をかけると、
\(f(y)^{-1}f(x)=f(y)^{-1}f(y)\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)\in\:\mr{Ker}\:f\)
\(y^{-1}x=e\)
\(x=y\)
となる。\(f(x)=f(y)\) であれば \(x=y\) なので、\(f\) は単射である。[証明終]
核は正規部分群
群 \(G\) から群 \(G\,'\) への準同型写像を \(f\) とする。このとき \(\mr{Ker}\:f\) は \(G\) の正規部分群である。
[証明]
\(\mr{Ker}\:f\) を \(H\) と記述する。\(G\) の 任意の元を \(x\) とし、\(H\) の任意の元を \(y\) とする。すると、
\(\begin{eqnarray}
&&\:\:f(xyx^{-1})&=f(x)f(y)f(x^{-1})\\
&&&=f(x)e\,'f(x^{-1})=f(x)f(x^{-1})\\
&&&=f(xx^{-1})=f(e)=e\,'\\
\end{eqnarray}\)
と計算できるから、
\(xyx^{-1}\in H\)
である。\(y\) は \(H\) の任意の元だから、
\(xHx^{-1}\subset H\)
である。\(x\) は任意にとることができるので、\(x\) を \(x^{-1}\) に置き換えると、
\(x^{-1}Hx\subset H\)
を得る。この式に左から \(x\)、右から \(x^{-1}\) をかけると、
\(H\subset xHx^{-1}\)
となる。つまり
\(H\subset xHx^{-1}\subset H\)
\(xHx^{-1}=H\)
である。さらに右から \(x\) をかけると、
\(xH=Hx\)
となり、\(x\) は任意の \(G\) の元だから、\(H\:\:(=\mr{Ker}\:f)\) は \(G\) の正規部分群である。[証明終]
4.3 同型定理
準同型定理=第1同型定理
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(H=\mr{Ker}\:f\) とすると、\(G\) の \(H\) による剰余群は、\(G\) の \(f\) による像と同型である。つまり、
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
[証明]
\(H\:=\:\mr{Ker}\:f\) は、核は正規部分群の定理(42D)により、\(G\) の正規部分群である。従って剰余群 \(G/H\) が定義できる。\(G/H\) から \(\mr{Im}\:f\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G/H &\longrightarrow&\mr{Im}\:f\\
&&&xH &\longmapsto&f(x)\\
\end{eqnarray}\)
と定義する。まず、この写像が剰余類 \(xN\) の代表元 \(x\) のとりかたに依存しないこと、つまり \(xH=yH\) なら \(f(x)=f(y)\) であることを示す。\(xH=yH\) を変形すると、
\(xH=yH\)
\(y^{-1}xH=y^{-1}yH\)
\(y^{-1}xH=H\)
ゆえに部分群の元の条件の定理(41C)から \(y^{-1}x\in H\) である。そうすると、\(H\) は \(\mr{Ker}\:f\) のことだから、\(f(y^{-1}x)=e\,'\) である。これを変形すると、
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
となる。最後の変形では、準同型写像の像と核の定理(42B)の「\(\mr{Im}\:f\) は群」の証明から、\(f(y^{-1})=f(y)^{-1}\) であることを用いた。ここから、
\(f(y)^{-1}f(x)=e\,'\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(x)=f(y)\)
となり、\(f(x)=f(y)\) が証明できた。
以上の変形は逆も辿れる。つまり、
\(f(x)=f(y)\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1}x)\in H\)
\(y^{-1}xH=H\)
\(xH=yH\)
となる。これは \(f(x)=f(y)\) なら \(xH=yH\) であることを示していて、すなわち \(\sg\) は単射である。と同時に、\(\sg\) による写像の先は \(\mr{Im}\:f\) に限定しているので \(\sg\) は全射である。つまり \(\sg\) は 全単射である(=\(\:\br{①}\:\))。
さらに、
\(\begin{eqnarray}
&&\:\:\sg((xH)(yH))&=\sg(x(Hy)H)=\sg(x(yH)H)\\
&&&=\sg(xyH)=f(xy)=f(x)f(y)\\
&&&=\sg(xH)\sg(yH)\\
\end{eqnarray}\)
であり、つまり \(\sg((xH)(yH))=\sg(xH)\sg(yH)\) が成り立っている(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) により \(\sg\) は同型写像である。\(G/H\) から \(\mr{Im}\:f\) への同型写像が存在するから、
\(G/H\:\cong\:\mr{Im}\:f\)
である。[証明終]
第2同型定理
群 \(G\) の正規部分群を \(H\)、部分群を \(N\) とすると、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
[証明]
まず、部分群と正規部分群の定理(41I)により、\(G\) の正規部分群が \(H\)、部分群が \(N\) の場合、
である。従って剰余群の定義(41G)により、\(N/(N\cap H)\) および \(NH/H\) は剰余群となる。
\(G\) の任意の元を \(x,\:y\) とし、\(G\) から \(G/H\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G &\longrightarrow&G/H\\
&&&x &\longmapsto&xH\\
\end{eqnarray}\)
と定義する。この写像は、
\(\begin{eqnarray}
&&\:\:\sg(xy)&=xyH=xyHH=xHyH=(xH)(yH)\\
&&&=\sg(x)\sg(y)\\
\end{eqnarray}\)
を満たすから準同型写像である(ちなみに \(G\) とその正規部分群 \(H\) があるとき、上記の定義による \(\sg\) を自然準同型と呼ぶ)。
\(\sg\) の定義域は \(G\) であるが、\(\sg\) の定義域を \(G\) の部分群である \(N\) に制限した写像 \(\tau\)(タウ) を考える。\(N\) の任意の元を \(z\) とすると、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
&&&z &\longmapsto&zH\\
\end{eqnarray}\)
である。この \(\tau\) の像 \(\mr{Im}\:\tau\) を考えてみると、\(z\) が \(N\) の元のすべてを動くとき、\(\tau(z)=zH\) として出てくる \(G\) の元は \(NH\) の元である。つまり \(\tau\) は、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
として定義したが、\(\tau(z)\) が \(G/H\) の全てを尽くすわけではなく、全射ではない。写像による移り先は、\(G\) の部分群 \(NH\) を \(H\) で分類した剰余群、\(NH/H\) である。つまり \(\tau(N)=NH/H\) であり、
\(\mr{Im}\:\tau=NH/H\)
である。
次に準同型写像の核を考える。\(G/H\) の単位元は、
\(xH\cdot H=xH\)
\(H\cdot xH=HxH=xHH=xH\)
なので、\(H\) である。
\(G\) の元 \(x\) が \(\mr{Ker}\:\sg\) の元とする。つまり、
\(x\in\mr{Ker}\:\sg\)
とする。これは \(\sg(x)\) が \(G/H\) の単位元になるということだから、
\(\sg(x)=H\)
であり、\(\sg(x)=xH\) なので、
\(xH=H\)
である。これは部分群の元の条件の定理(41C)によって、
\(x\in H\)
と同値である。従って、
\(x\in\mr{Ker}\:\sg\)
\(x\in H\)
の2つは同値であり、つまり、
\(\mr{Ker}\:\sg=H\)
である。
\(\tau\) は \(\sg\) の定義域を \(N\) に制限したものなので、\(\mr{Ker}\:\tau\) は「\(\mr{Ker}\:\sg=H\) のうちで \(N\) に含まれるもの」であり、すなわち、
\(\mr{Ker}\:\tau=(N\cap H)\)
である。
ここで、\(\tau\) の定義である、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
に準同型定理(43A)を適用すると、
\(\begin{eqnarray}
&&\:\:N/(\mr{Ker}\:\tau) &\cong\:\mr{Im}\:\tau\\
&&\:\:N/(N\cap H) &\cong\:NH/H\\
\end{eqnarray}\)
となって、題意が成り立つ。[証明終]
第2同型定理を整数の剰余群で確認してみます。上の定理における \(G,\:H,\:N\) を、
\(G=\bs{Z}\)
\(H=10\bs{Z}\) (\(10\) の倍数)
\(N=\phantom{1}6\bs{Z}\) (\(\phantom{1}6\) の倍数)
の群とします。この群の演算は加算であり、可換群なので、\(\bs{Z}\) の部分群はすべて正規部分群です。
\(N\cap H\) は「\(10\) の倍数、かつ \(6\) の倍数」の集合なので、
\(N\cap H=30\bs{Z}\)
です。また \(NH\) は、\(10\) の倍数と\(6\) の倍数の加算の結果の集合です。つまり、
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
ですが、これが何を意味するかは不定方程式の解の存在の定理(21B)から分かります。定理を再掲すると、
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
です。\(c=kd\) なら、式を満たす \(x,\:y\) が必ず存在します。また任意の \(x,\:y\) について \(ax+by\) を計算すると、その結果の \(c\) は必ず \(c=kd\) の形になります。そうでなければ、\(c\) が最大公約数の倍数でないにも関わらず不定方程式が解をもつことになって定理に矛盾します。従って、\(ax+by=c\) の \(x,\:y\) を任意の整数とすると、\(c\) は \(a,\:b\) の "最大公約数の整数倍のすべて" になります。
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
とした場合、\(10\) と \(6\) の最大公約数は \(2\) なので、
\(NH=2\bs{Z}\)
です。この結果、
\(N/(N\cap H)\)
\(=6\bs{Z}/30\bs{Z}\)
\(=\{30\bs{Z},\:6+30\bs{Z},\:12+30\bs{Z},\:18+30\bs{Z},\:24+30\bs{Z}\}\)
\(NH/H\)
\(=2\bs{Z}/10\bs{Z}\)
\(=\{10\bs{Z},\:2+10\bs{Z},\:4+10\bs{Z},\:6+10\bs{Z},\:4+10\bs{Z}\}\)
となります。この2つの剰余群は位数 \(5\) の巡回群( \(C_5\) )で、\(\bs{Z}/5\bs{Z}\) に同型です。つまり、
であり、
\(N/(N\cap H)\:\cong\:NH/H\)
となって、第2同型定理が確認できました。
第2同型定理を数式で書くと何だか難しそうな感じがしますが、図にするといかにも自明なことという気がします。数学におけるイメージ図の威力が実感できます。
第2同型定理は、後ほど「可解群の部分群は可解群」という定理の証明に使います。「可解群の部分群は可解群」の定理は、5次方程式に可解でないものがあることを証明する際に鍵となる定理です。その第2同型定理は準同型定理を使って証明される、という構造になっているのでした。
2章から4章までは、多項式、体、線形空間、剰余類、群、剰余群、既約剰余類群、正規部分群といった、ガロア理論の基礎となる概念の説明でした。この第5章から、理論の核心に入っていきます。
5.1 体の同型写像
同型写像の定義
体 \(\bs{K}\) から 体 \(\bs{F}\) への写像 \(f\) が全単射であり、\(\bs{K}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
[証明]
上の定義による同型写像が、減法と除法を保存することを証明する。\(\bs{K}\) と \(\bs{F}\) は体だから、加法と乗法について群になっている。\(\bs{K}\) の加法の単位元を \(\kz\)、\(\bs{F}\) の加法の単位元を \(\fz\) とする。また、乗法の単位元をそれぞれ \(\ko\) と \(\fo\) とする。まず、\(f(\ko)=\fo\) で \(f(\kz)=\fz\) であることを示す。
\(f(x+y)=f(x)+f(y)\) において \(x=\kz,\:y=\kz\) とすると、
\(f(\kz+\kz)=f(\kz)+f(\kz)\)
\(f(\kz)=f(\kz)+f(\kz)\)
両辺に \(\bs{F}\) における \(f(\kz)\) の逆元 \(-f(\kz)\) を加えると、
\(f(\kz)+(-f(\kz))=f(\kz)\)
\(\fz=f(\kz)\)
となり、\(f(\kz)=\fz\) である。
\(f(xy)=f(x)f(y)\) において \(x=\ko,\:y=\ko\) とすると、
\(f(\ko\times\ko)=f(\ko)f(\ko)\)
\(f(\ko)=f(\ko)f(\ko)\)
両辺に \(\bs{F}\) における \(f(\ko)\) の逆元 \(-f(\ko)\) を加えると、
\(f(\ko)+(-f(\ko))=f(\ko)f(\ko)+(-f(\ko))\)
\(\fz=f(\ko)f(\ko)+(-f(\ko))\)
この式に現れているのは全て \(\bs{F}\) の元だから、分配則を使って、
\(f(\ko)(f(\ko)-\fo)=\fz\)
ここで \(f(\ko)=\fz\) と仮定すると、\(f(\kz)=\fz\)かつ \(f(\ko)=\fz\) となってしまい \(f\) が単射であることと矛盾する。従って \(f(\ko)\neq\fz\) である。上式の両辺を \(f(\ko)\) で割ると、
\(f(\ko)-\fo=\fz\)
\(f(\ko)=\fo\)
となる。
以上を踏まえると、同型写像が減法を保存することは次のようにしてわかる。\(\bs{K}\) は加法について群なので任意の元 \(x\in\bs{K}\) について逆元 \(-x\) がある。また \(\bs{F}\) も加法についても群だから \(f(x)\) の逆元 \(-f(x)\) がある。
\(f(-x)+f(x)=f(-x+x)=f(\kz)=\fz\)
両辺に \(-f(x)\) を足すと、
\(f(-x)+f(x)+(-f(x))=\fz+(-f(x))\)
\(f(-x)+\fz=\fz+(-f(x))\)
\(f(-x)=-f(x)\)
である。\(\bs{K}\) の任意の元を \(x,\:y\) とすると、
\(\begin{eqnarray}
&&\:\:f(x-y)&=f(x+(-y))\\
&&&=f(x)+f(-y)\\
&&&=f(x)+(-f(y))\\
&&&=f(x)-f(y)\\
\end{eqnarray}\)
となって、減法は保存されている。
除法を保存することは次のようにしてわかる。\(\bs{K}\) は乗法について群なので、任意の元 \(x\:\:(\neq\kz)\) について逆元 \(x^{-1}\) がある。\(\bs{F}\) も乗法についての群だから、\(f(x)\) の逆元である \(f(x)^{-1}\) がある。\(x\neq\kz\) なら \(f(x)\neq\fz\) なので逆元が定義できる。すると、
\(f(x^{-1})f(x)=f(x^{-1}x)=f(\ko)=\fo\)
である。この式の両辺に \(f(x)^{-1}\) をかけると、
\(f(x^{-1})f(x)f(x)^{-1}=\fo\times f(x)^{-1}\)
\(f(x^{-1})\times\fo=\fo\times f(x)^{-1}\)
\(f(x^{-1})=f(x)^{-1}\)
となる。\(\bs{K}\) の任意の元を \(x,\:y\:\:(y\neq\kz)\) とすると、
\(\begin{eqnarray}
&&\:\:f\left(\dfrac{x}{y}\right)&=f(xy^{-1})\\
&&&=f(x)f(y^{-1})\\
&&&=f(x)f(y)^{-1}\\
&&&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
となり、除法が保存されていることが分かる。
有理数の同型写像を考える。\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn\:個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)\\
&&&=n\\
\end{eqnarray}\)
なので、\(f(n)=n\) である。任意の有理数 \(a\) は、2つの整数 \(n\:(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるから、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は同型写像で不変である。[証明終]
同型写像と有理式の順序交換
変数 \(x\) の多項式(係数は \(\bs{Q}\) の元)を分母・分子とする分数式を、\(\bs{Q}\) 上の有理式という。
\(\bs{Q}\) 上の多項式は、有理数と \(x\) の加・減・乗算で作られる式です。一方、\(\bs{Q}\) 上の有理式とは、有理数と \(x\) の除算を含む四則演算で作られる式です。
体 \(\bs{K}\) と 体 \(\bs{F}\) は \(\bs{Q}\) を含むものとする。\(\sg\) を \(\bs{K}\) から \(\bs{F}\) への同型写像とし、\(a\) を \(\bs{K}\) の元とする。\(f(x)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
[証明]
\(a\in\bs{K},\:b_i\in\bs{Q},\:c_i\in\bs{Q}\) とし、1変数 \((=a)\) の2次多項式の分数式の場合を例に書くと、
\(\sg\left(\dfrac{b_2a^2+b_1a+b_0}{c_2a^2+c_1a+c_0}\right)\)
\(=\dfrac{\sg(b_2a^2+b_1a+b_0)}{\sg(c_2a^2+c_1a+c_0)}\)
\(=\dfrac{b_2\sg(a^2)+b_1\sg(a)+b_0}{c_2\sg(a^2)+c_1\sg(a)+c_0}\)
\(=\dfrac{b_2\sg(a)^2+b_1\sg(a)+b_0}{c_2\sg(a)^2+c_1\sg(a)+c_0}\)
であるから、題意は成り立つ。これは \(n\)次多項式の場合でも同じである。[証明終]
「同型写像と有理式は順序交換可能」は、\(\bs{Q}\) の拡大体の上の有理式でも成り立ちます。つまり、次が成り立ちます。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
同型写像は解を共役な解に移す
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とする。\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つを \(\al\) とし、\(\al\) は \(\bs{K}\) の元とする。すると \(\sg(\al)\) も \(f(x)=0\) の解である。
[証明]
\(\al\) は \(f(x)=0\) の解なので \(f(\al)=0\) が成り立つ。すると、
\(f(\sg(\al))=\sg(f(\al))=\sg(0)=0\)
となり、\(\sg(\al)\) も \(f(x)=0\) の解である。[証明終]
同じ方程式の解同士を「共役な解」「共役である」と言います。この定理により、同型写像は解を共役な解に移すこと分かります。
同型写像は解を入れ替える
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とし、\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。方程式 \(f(x)=0\) の \(n\)個の解を \(\al_1,\al_2,\cd,\al_n\) とし、これらが全て \(\bs{K}\) に含まれるとする。
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
[証明]
\(f(x)\) は既約多項式なので、方程式 \(f(x)=0\) は \(n\)個の解をもち、それらは全て異なる(31G)。同型写像は解を共役な解に移す(51D)ので、\(\sg(\al_i)\) も \(f(x)=0\) の解である。\(\sg\) は同型写像なので全単射であり、\(i\neq j\) なら \(\sg(\al_i)\neq\sg(\al_j)\) である。従って \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。[証明終]
同型写像を定義してその性質を述べてきましたが、あたかも「同型写像はあるのが当然」のような話でした。しかし、同型写像があったとしたらこういう性質をもつというのが正しく、同型写像が必ずあるとは証明していません。
同型写像の存在を示すには、第1章でやったように、\(\bs{Q}(\sqrt{2})\)において
\(\sg(\sqrt{2})=-\sqrt{2}\)
という写像を定義すると、体のすべての元について \(\sg\) は同型写像の定義を満たす、というような証明が必要です。それが次です。
単拡大体の同型写像の存在
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(\al,\:\beta\) を方程式 \(f(x)=0\) の異なる解とする。
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
[証明]
\(\bs{Q}(\al)\) の任意の元を \(a\)、\(\bs{Q}(\beta)\) の任意の元を \(b\) とする。単拡大体の基底の定理(33F)により、\(a,\:b\) は、
\(\begin{eqnarray}
&&\:\:\sg\:: &a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\\
&&&\longmapsto\:a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
と定義する。\(a=\al\) の場合は、\(a_1=1,\:a_i=0\:\:(i=0,\:2\leq i\leq n-1)\) だから、\(\sg(\al)=\beta\) である。以下、この \(\sg\) が同型写像であることを証明する。定義により(51A)同型写像であることは加法と乗法を保存することを言えばよい。
\(\bs{Q}(\al)\) の任意の2つの元を \(s,\:t\) とし、
\(p(x)=g(x)+h(x)\) とおくと、
\(p(\al)=g(\al)+h(\al)=s+t\)
である。また \(\sg\)の定義により、
\(\sg(p(\al))=p(\beta)\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\sg(s+t)&=\sg(p(\al))\\
&&&=p(\beta)\\
&&&=g(\beta)+h(\beta)\\
&&&=\sg(s)+\sg(t)\\
\end{eqnarray}\)
となり、加法は保存される。
\(g(x)h(x)\) を \(f(x)\) で割ったときの商を \(q(x)\)、余りを \(r(x)\) とすると、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。この式に \(x=\al,\:x=\beta\) のそれぞれを代入すると、\(f(\al)=0,\:f(\beta)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
\(g(\beta)h(\beta)=r(\beta)\)
となる。すると、
\(\begin{eqnarray}
&&\:\:\sg(st)&=\sg(g(\al)h(\al))\\
&&&=\sg(r(\al))=r(\sg(\al))\\
&&&=r(\beta)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:\sg(s)\sg(t)&=\sg(g(\al))\sg(h(\al))\\
&&&=g(\sg(\al))h(\sg(\al))\\
&&&=g(\beta)h(\beta)\\
&&&=r(\beta)\\
\end{eqnarray}\)
であり、
\(\sg(st)=\sg(s)\sg(t)\)
となって乗法も保存されている。従って \(\sg\) は同型写像である。
逆に、\(\bs{Q}(\al)\) に作用する同型写像 \(\tau\) があったとする。同型写像は \(\al\) を共役な元に移すので、その移り先の元を \(\beta\)、つまり \(\tau(\al)=\beta\) とする。\(\bs{Q}(\al)\) の任意の元 \(a\) に \(\tau\) を作用させると、
\(\begin{eqnarray}
&&\:\:\tau(a)&=\tau(a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0)\\
&&&=a_{n-1}\tau(\al^{n-1})+\:\cd\:+a_2\tau(\al^2)+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\tau(\al)^{n-1}+\:\cd\:+a_2\tau(\al)^2+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
となるので、同型写像はこの式を満たさなければならない。従って、上で定義した \(\sg\) が \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) の唯一の同型写像である。[証明終]
同型写像の存在(51F)を一般化すると、次のことが言えます。
単拡大体の同型写像は \(n\) 個
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(f(x)=0\) の全ての解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\) とする。このとき \(\bs{Q}(\al)\) に作用する同型写像は \(n\)個あり、それらは、
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
同型写像を別の視点で考えます。\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{K}\) といった体の拡大列があったとき、\(\bs{F}\) の同型写像と \(\bs{K}\) の同型写像には密接な関係があります。それが次の同型写像の延長の定理です。単拡大定理(32B)により、\(\bs{F}=\bs{Q}(\al)\)、\(\bs{K}=\bs{Q}(\al,\beta)\) としてよいので、その形を使います。
同型写像の延長
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
[証明]
\(\bs{Q}(\al)\) 上の \(m\)次既約多項式 \(g(x)\) を、
\(g(x)=x^m+a_1x^{m-1}+\cd+a_m\:\:(a_j\in\bs{Q}(\al))\)
とする。\(\beta\) は \(g(x)=0\) の解だから
\(g(\beta)=\beta^m+a_1\beta^{m-1}+\cd+a_m=0\)
である。また、多項式 \(\tau(g(x))\) を、
\(\tau(g(x))=x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_{m-1})x+\tau(a_m)\)
と定義し、方程式
\(\tau(g(x))=0\)
の解を \(t_j\:\:(0\leq j < m)\)とする。つまり \(\tau(g(t_j))=0\) である。
\(\bs{Q}(\al,\beta)\) は \(\bs{Q}(\al)\) 上の線形空間であり、単拡大体の基底の定理(33F)により、その基底を \(\{1,\:\beta,\:\beta^2,\:\cd\:\beta^{m-1}\}\) にとれるから、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) は、
と表せる。そこで、\(\bs{Q}(\al,\beta)\) の元に作用する写像 \(\sg_j\) を
と定義する。この定義における \(\sg_j\) は \(\bs{Q}(\al,\beta)\) の同型写像になる。同型写像になることは体の加算と乗算で示せればよい(51A)。\(\bs{Q}(\al,\beta)\) の2つの元を、
\(p=c_0+c_1\beta+c_2\beta^2\:+\cd+\:c_{m-1}\beta^{m-1}\:\:(c_j\in\:\bs{Q}(\al)\:)\)
\(q=d_0+d_1\beta+d_2\beta^2\:+\cd+\:d_{m-1}\beta^{m-1}\:\:(d_j\in\:\bs{Q}(\al)\:)\)
とし、2つの多項式を、
\(p(x)=c_0+c_1x+c_2x^2\:+\cd+\:c_{m-1}x^{m-1}\)
\(q(x)=d_0+d_1x+d_2x^2\:+\cd+\:d_{m-1}x^{m-1}\)
と定義する。加算で同型写像になるのは明白なので、乗算で同型写像になることを示す。
\(p(x)q(x)\) を \(g(x)\) で割ったときの商を \(t(x)\)、余りを \(r(x)\) とすると、
すると \(g(\beta)=0\) だから、
である。そうすると、\(\sg_j(pq)\) は \(\sg_j\) の定義により、
となる。
\(\tau\) は \(\bs{Q}(\al)\) の同型写像だから、\(\bs{Q}(\al)\) の元の有理式である \(s_j(c_j,d_j)\) に作用させると、同型写像と有理式の順序交換の定理(51C)により、
\(\tau(s_j(c_j,d_j))=s_j(\tau(c_j),\tau(d_j))\)
となる。従って、
である。
\(p(x)\) の係数 \(c_j\) を \(\tau(c_j)\) で置き換え、\(q(x)\) の係数 \(d_j\) を \(\tau(d_j)\) で置き換えた2つの多項式を、
\(\tau(p(x))=\tau(c_0)+\tau(c_1)x+\tau(c_2)x^2+\cd+\tau(c_{m-1})x^{m-1}\)
\(\tau(q(x))=\tau(d_0)+\tau(d_1)x+\tau(d_2)x^2+\cd+\tau(d_{m-1})x^{m-1}\)
とする。
\(\tau(p(x))\tau(q(x))\)を\(\tau(g(x))\)で割ったときの商を\(\tau(t(x))\)、余りを\(\tau(r(x))\)とする。つまり、
\(\tau(p(x))\tau(q(x))=\tau(g(x))\tau(t(x))+\tau(r(x))\)
である。\(c_j\) と \(d_j\) の有理式、\(s_j(c_j,d_j)\) を使って \(\tau(r(x))\) を表すと、
となる。\(\sg_j\) の定義により、
である。従って、
また、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) を、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表したとき、\(k\) が \(\bs{Q}(\al)\) の元だとすると \(k=b_0\:\:(b_0\in\bs{Q}(\al))\)、\(b_j=0\:\:(1\leq j < m)\) なので、
\(\sg_j(k)=\tau(b_0)=\tau(k)\)
となり、\(\sg_j\) の \(\bs{Q}(\al)\) の元に対する作用は \(\tau\) と一致する。従って、
\(\sg_j\) の定義式、
一方、\(\al\) は \(\bs{Q}\) 上の \(n\)次既約多項式 \(f(x)\) の解の一つだから、\(\bs{Q}(\al)\) の同型写像 \(\tau\) は \(n\)個ある。これを \(\tau_i\:\:(0\leq i < n)\) と書くと、それぞれの \(\tau_i\) に対して同型写像の拡張 \(\sg_{ij}\:\:(0\leq i < n,\:0\leq j < m)\) がある。従って \(\bs{Q}(\al,\beta)\) の 同型写像 \(\sg_{ij}\) は \(nm\)個ある。[証明終]
5.2 ガロア拡大とガロア群
ガロア拡大
ガロア拡大は次のように定義される。この2つの定義は同値である。
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
[① \(\bs{\Rightarrow}\) ②の証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。その解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{F}\) の元を不変にする \(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。
一方、\(\bs{L}\) は \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{F}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式(係数は \(\bs{F}\) の元)で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は \(\bs{F}\) の元)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させる。\(\bs{F}\) 係数の有理式と \(\bs{F}\) を不変にする同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移す(51D)から、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。
[② \(\bs{\Rightarrow}\) ①の証明]
単拡大定理(32B)により、\(\bs{K}\) は、\(\bs{K}\) の元 \(\theta\) を用いて \(\bs{K}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(f(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(f(x)\) は既約多項式である。また既約多項式の定理3(31G)により、方程式 \(f(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。
\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、\(\bs{F}\) 上の方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する。\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像は自己同型写像なので、\(\sg_i(\theta)=\theta_i\) は全て \(\bs{K}\) の元である。従って \(\bs{K}\) は \(\bs{F}\) 上の既約多項式 \(f(x)\) の解 \(\theta_i\) を用いて、
\(\begin{eqnarray}
&&\:\:\bs{K}&=\bs{F}(\theta)\\
&&&=\bs{F}(\theta_1,\:\theta_2,\:\cd,\:\theta_m)\\
\end{eqnarray}\)
と表される。\(\bs{K}\) は \(\bs{F}\) 上の既約多項式の最小分解体である。[証明終]
① の定義は、方程式の解のありようを議論するガロア理論にとっては "ノーマルな" 定義のように見えます。しかし ② のように方程式という言葉を全く使わない定義もメリットがあります。たとえば「次数が違う2つの方程式の解によるガロア拡大が同じ」ということは、いくらでもありうるからです。
また、ガロア拡大は次のような定義もできます。
方程式という言葉は使っていますが、拡大体から始まる定義です。言い換えると、\(\bs{K}\) がガロア拡大体のとき \(\bs{K}\) の任意の元に共役な元は \(\bs{K}\) に含まれるということです。
このように、互いに同値である多種の定義ができることがガロア理論の分かりにくいところですが、逆に「それだけ豊かな数学的内容を含んだ理論」とも言えるでしょう。
最小分解体の次数=ガロア群の位数
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\)、ガロア群を \(G\) とするとき、\([\:\bs{L}\::\:\bs{Q}\:]=|G|\) である。
[証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{Q}(\theta)\) と表すことができる。\(\theta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。ここで、\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{Q}\) の元を不変にするから、\(\bs{L}=\bs{Q}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。単拡大体 \(\bs{Q}(\theta)\) に作用する同型写像は \(m\)個だから(51G)、これが同型写像のすべてである。
一方、\(\bs{L}\) は \(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{Q}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は有理数)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させると、有理式と同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移すから(51D)、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。以上により、
\(\mr{Gal}(\bs{L}/\bs{Q})=\{\sg_1,\:\sg_2,\:\cd,\:\sg_m\}\)
であり、\(|G|=m\) である。
\(\theta\) の \(\bs{Q}\) 上の最小多項式(=既約多項式)の次数が \(m\) だから、単拡大体の基底の定理(33F)によって、最小分解体 \(\bs{L}=\bs{Q}(\theta)\) は \(\bs{Q}\) の \(m\)次拡大体であり、
\([\:\bs{L}\::\:\bs{Q}\:]=|G|\)
である。[証明終]
この定理では \(\bs{Q}\) としましたが、任意の代数拡大体 \(\bs{F}\) としても成り立ちます。また、最小分解体はガロア拡大体です。従って、最も一般的に言うと次のようになります。
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
中間体
\(\bs{K}\) を \(\bs{F}\) のガロア拡大体とし、\(\bs{M}\) を \(\bs{F}\subset\bs{M}\subset\bs{K}\) である任意の体(=中間体)とするとき、\(\bs{K}\) は \(\bs{M}\) のガロア拡大体でもある。
[証明]
最小分解体定義による
\(\bs{K}\) が \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であるとする。この方程式の解を \(\al_1,\:\al_2,\:\cd\:\al_n\) とすると、\(\bs{K}=\bs{F}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(\bs{F}\subset\bs{M}\subset\bs{L}\) なので、
\(\bs{F}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{M}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{K}(\al_1,\:\cd\:\al_n)=\bs{K}\)
となるが、すなわち、
\(\bs{F}\:\subset\:\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\:\subset\:\bs{K}\)
であり、\(\bs{K}=\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(f(x)=0\) は \(\bs{M}\) 上の方程式でもあるので、\(\bs{K}\) は \(\bs{M}\) 上の方程式の最小分解体であり、\(\bs{M}\) のガロア拡大体である。
自己同型定義による
\(\bs{L}\) の同型写像のうち、\(\bs{M}\) の元を固定する任意の同型写像を \(\sg\) とする。そうすると \(\sg\) は \(\bs{M}\) の部分集合である \(\bs{F}\) の元も固定する。\(\bs{L}\) は \(\bs{F}\) のガロア拡大体なので、\(\bs{F}\) の元を固定する \(\bs{L}\) の同型写像は自己同型写像である。従って \(\sg\) も自己同型写像であり、\(\bs{L}\) は \(\bs{M}\) のガロア拡大体である。[証明終]
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列があったとき、\(\bs{F}\subset\bs{K}\) がガロア拡大だと上の定理(52C)によって \(\bs{M}\subset\bs{K}\) もガロア拡大です。しかし、\(\bs{F}\subset\bs{M}\) がガロア拡大になるとは限りません。\(\bs{F}\subset\bs{M}\) がガロア拡大になるためには条件が必要で、その条件が満たされば、\(\bs{F}\subset\bs{M}\subset\bs{K}\) は「ガロア拡大の連鎖」になり、そのことが方程式の可解性と結びつきます。それが次の節の大きな主題です。
5.3 ガロア対応
固定体と固定群
体 \(\bs{F}\) 上の方程式の最小分解体(=ガロア拡大体)を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる。これを \(\bs{K}\) における \(H\) の固定体といい、\(\bs{K}(H)\) で表す(または \(\bs{K}^H\))。
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
[証明]
固定体と固定群の定義において、
の2点を証明する。
① の証明
\(\bs{M}\) が体であることを証明するには、四則演算で閉じていることを言えばよい(1.2 体)。\(\bs{M}\) の任意の2つの元を \(x,\:y\) とし、\(H\) の任意の元を \(\sg\) とする。\(x,\:y\) は \(\bs{K}\) の元でもあるから、
\(x+y\in\bs{K}\)
である。\(H\) の元 \(\sg\) は \(G\) の元でもあるから \(\sg(x+y)\) が定義できる。\(x,\:y\) は \(\bs{M}\) の元だから、\(H\) の元である \(\sg\) を作用させても不変であり、
\(\sg(x)=x\)
\(\sg(y)=y\)
である。すると、
\(\sg(x+y)=\sg(x)+\sg(y)=x+y\)
となって、\(x+y\) は \(\sg\) によって不変であり、
\(x+y\in\bs{M}\)
である。以上のことが加減乗除のすべてで成り立つことは明白だから、\(\bs{M}\) は四則演算で閉じていて、体である。
② の証明
\(\bs{M}\) の任意の元を \(x\)、\(H\) の2つの元を \(\sg,\:\tau\) とする。
\(\sg(x)=x\)
\(\tau(x)=x\)
である。すると、
\(\sg\tau(x)=\sg(\tau(x))=\sg(x)=x\)
となり、\(\sg\tau\in H\) となって、\(H\) の元は群演算で閉じている。
また \(H\) の元はもともと \(G\) の元なので、結合法則も成り立つ。\(G\) の単位元を \(e\) とすると、\(e(x)=x\) なので \(e\in H\) である。
さらに \(\sg\) は \(G\) の元なので、\(G\) の中に \(\sg^{-1}\) が存在する。すると、\(\sg(x)=x\) の両辺に左から \(\sg^{-1}\) をかけると、
\(\sg^{-1}\sg(x)=\sg^{-1}(x)\)
\(x=\sg^{-1}(x)\)
となり、
\(\sg^{-1}\in H\)
である。\(H\) は演算で閉じていて、結合法則が成り立ち、単位元と逆元が存在するので、群の定義(22A)を満たしている。[証明終]
以上の固定体と固定群の概念を用いると、次のガロア対応の定理が成り立ちます。以降の論証の基礎となる定理です。
ガロア対応の定理
\(\bs{F}\) のガロア拡大体を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の任意の部分群を \(H\) とし、\(H\) による \(\bs{K}\) の固定体 \(\bs{K}(H)\) を \(\bs{M}\) とする(次式)。
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
[証明]
\(G\) の任意の部分群である \(H\) は \(\bs{K}\) の部分集合 \(\bs{M}\) を固定する。一方、\(G(\bs{M})\) は \(\bs{M}\) を固定する \(G\) のすべての元の集合で、それが部分群になっている。従って、\(G(\bs{M})\) は \(H\) を含む。つまり
\(H\:\subset\:G(\bs{M})\)
であり、群位数は、
\(\bs{K}/\bs{F}\) はガロア拡大であり、\(\bs{M}\) はその中間体だから、中間体からのガロア拡大の定理(52C)によって、\(\bs{K}/\bs{M}\) はガロア拡大である。また、すべての代数拡大体は単拡大体だから(32B)、\(\bs{K}\) の元 \(\theta\) があって \(\bs{K}=\bs{F}(\theta)\) と表せる。これは、\(\bs{K}=\bs{M}(\theta)\) ということでもある。
\(H\) の \(|H|\) 個の元を \(\sg_i\:\:(1\leq i\leq|H|)\) とし、多項式
\(f(x)=\displaystyle\prod_{i=1}^{|H|}(x-\sg_i(\theta))\)
を考える。この多項式の次数は \(|H|\) である。\(\sg_i(\theta)\) は \(\theta\) の共役な元のどれかである。
\(f(x)\) を展開すると、その係数は \(\sg_i(\theta)\:\:(1\leq i\leq|H|)\) の対称式になる。また、\(\sg_i(\theta)\) に \(H\) の任意の元 \(\sg_k\) を作用させても、\(\sg_i\) は部分群だから演算で閉じており、\(\sg_i(\theta)\) を入れ替えるだけである(51E)。従って \(\sg_i(\theta)\) の対称式に \(\sg_k\) を作用させても不変である。つまり、\(H\) の任意の元は \(f(x)\) の係数を固定する。ということは、\(\bs{M}\) の定義(= \(H\) による \(\bs{K}\) の固定体が \(\bs{M}\))によって、\(f(x)\) の係数は \(\bs{M}\) の元である。
\(\sg_i\) は群だから単位元を含む。従って、
\(f(\theta)=\displaystyle\prod_{i=1}^{|H|}(\theta-\sg_i(\theta))=0\)
となり、\(\bs{\theta}\) は \(\bs{\bs{M}}\) 上の \(\bs{|H|}\) 次方程式 \(\bs{f(x)=0}\) の解の一つである。ゆえに \(\bs{M}\) から単拡大体 \(\bs{K}=\bs{M}(\theta)\) への拡大次数は、\(f(x)\) が \(\bs{M}\) 上の既約多項式なら単拡大体の基底の定理(33F)により \(|H|\) であり、一般には \(|H|\) 以下である。つまり、
\([\:\bs{K}\::\:\bs{M}\:]\leq|H|\)
である。次数と位数の同一性(52B)によると、拡大次数 \([\:\bs{K}\::\:\bs{M}\:]\) は、ガロア群 \(\mr{Gal}(\bs{K}/\bs{M})\) の位数に等しい。従って、
\(|\mr{Gal}(\bs{K}/\bs{M})|\leq|H|\)
\(|G(\bs{M})|=|H|\)
であり、\(G(\bs{M})\:\subset\:H\) と合わせると、
\(G(\bs{M})=H\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
である。[証明終]
証明の中に対称式という言葉が出てきます。対称式とは、
変数の任意の入れ替えで不変な多項式
です。2変数 \(x,\:y\) だと、
\(x+y,\:xy\)(ここまでが基本対称式)、\(x^2+y^2,\:\:(x-y)^2\)
などです。3変数 \(x,\:y\:,z\) だと、
\(x+y+z,\:xy+yz+zx,\:xyz\)(基本対称式)、\(((x-y)(y-z)(z-x))^2\)
などです。
対称式でよく出てくるのは、方程式の根と係数の関係です。たとえば、\(\bs{Q}\) 上の既約な3次多項式を \(f(x)\) をとし、\(f(x)=0\) の解を \(\al,\beta,\gamma\) とします。
\(\begin{eqnarray}
&&\:\:f(x)&=x^3-ax^2+bx-c\\
&&&=(x-\al)(x-\beta)(x-\gamma)\\
\end{eqnarray}\)
と書くと、
\(a=\al+\beta+\gamma\)
\(b=\al\beta+\beta\gamma+\gamma\al\)
\(c=\al\beta\gamma\)
と、係数が解の基本対称式で表現されます。
また ガロア群 \(\mr{Gal}(\bs{Q}(\al,\beta,\gamma)/\bs{Q})\) の任意の元 を \(\sg\) とします。\(\al,\beta,\gamma\) の任意の対称式を \(S(\al,\beta,\gamma)\in\bs{Q}(\al,\beta,\gamma)\) とすると、
\(\sg(S(\al,\beta,\gamma))=S(\al,\beta,\gamma)\)
です。ガロア群の元は自己同型写像であり、方程式の解を解の一つに置き換えるので、これが成り立ちます。自己同型写像を作用させて不変なのは有理数です(51A)。従って、\(S(\al,\beta,\gamma)\) は有理数です。もちろん \(f(x)\) が \(n\)次多項式であっても成り立ちます。
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列で \(\bs{F}\subset\bs{K}\) がガロア拡大のとき、\(\bs{M}\subset\bs{K}\) は自動的にガロア拡大ですが(52C)、ある条件があれば \(\bs{F}\subset\bs{M}\) もガロア拡大になって、\(\bs{F}\subset\bs{M}\subset\bs{K}\) が「ガロア拡大の連鎖」になります。その条件は「ガロア対応」と「正規部分群」の概念を用いて示されます。それが次の正規性定理です。次では \(\bs{Q}\) から始まる体の拡大列で記述しています。
正規性定理
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とし、\(\mr{Gal}(\bs{K}/\bs{Q})=G\) とする。\(\bs{K}\) の中間体 \(\bs{M}\) と \(G\) の部分群 \(H\) がガロア対応になっているとする。このとき
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) の任意の元を \(g\) とし、\(\bs{M}\) の任意の元を \(m\) とする。
\(\bs{M}\) が \(\bs{Q}\) のガロア拡大なので、\(m\) の共役な元は \(\bs{M}\) に含まれる。\(g\) は同型写像だから、\(\bs{K}\) の元を共役な元に移す(51D)。つまり、\(g\) を \(m\) に作用させると \(m\) と共役な元に移すことになり、 \(g(m)\in\bs{M}\) である。また \(g^{-1}\) も \(G\) の元だから \(g^{-1}(m)\in\bs{M}\) である。
\(H\) の任意の元を \(h\) とする。\(H\) は \(\bs{M}\) とガロア対応をしているから、\(h\) は \(\bs{M}\) の元を不動にする。ゆえに、
\(hg^{-1}(m)=g^{-1}(m)\)
である。従って、
\(ghg^{-1}(m)=gg^{-1}(m)=m\)
となり、\(ghg^{-1}\) は \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(gHg^{-1}\:\subset\:H\)
また、\(g(m)\) も \(\bs{M}\) の元なので、
\(hg(m)=g(m)\)
である。従って、
\(g^{-1}hg(m)=g^{-1}g(m)=m\)
となり、\(g^{-1}hg\) も \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(g^{-1}Hg\:\subset\:H\)
\(gH=Hg\)
となって、左剰余類と右剰余類が一致するから、\(H\) は \(G\) の正規部分群である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{M}\) の任意の元を \(m\) とする。同型写像の延長の定理(51H)により、\(\bs{M}\) の同型写像 \(s\) は \(\bs{K}\) の同型写像 \(g\) に延長できる。つまり、\(g\) を \(\bs{M}\) の元に限定して作用させたとき \(g(m)=s(m)\) となる \(g\) がある。
\(H\) の任意の元を \(h\) とすると、\(h\) は正規部分群の元なので、
\(g^{-1}hg\:\in\:H\)
である。従って、
\(g^{-1}hg(m)=m\)
\(hg(m)=g(m)\)
となり、\(g(m)\) は \(H\) の任意の元で不動である。
ガロア対応の原理により \(\bs{K}(H)=\bs{M}\) なので、
\(g(m)\:\in\:\bs{M}\)
となり、\(g(m)\) は \(H\) の固定体 \(\bs{M}\) の元である。
\(\bs{M}\)の元に \(g\) を作用させるときは \(g(m)\) は \(s(m)\) そのものなので、
\(s(m)\:\in\:\bs{M}\)
となる。
以上により、\(\bs{M}\) の同型写像による \(m\) の移り先(= \(m\) と共役な元)は \(\bs{M}\) に含まれることになり、\(\bs{M}/\bs{Q}\) はガロア拡大である。[証明終]
[\(\bs{\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H}\) の証明]
同型写像の延長の定理(51H)の証明で示したように、\(\bs{M}\) の同型写像 \(s\) を \(\bs{K}\) の同型写像に延長する可能性は複数ある。\(g_1\) と \(g_2\) を \(s\) の2つの延長とし、\(\bs{M}\)の元を \(m\) とする。\(g_1,\:g_2\) は、\(\bs{M}\) に限定して適用すると \(s\) に等しいから、
\(g_1(m)=s(m)\)
\(g_2(m)=s(m)\)
が成り立つ。
\(g_1^{-1}g_2\) を \(m\) に作用させると
\(\begin{eqnarray}
&&\:\:g_1^{-1}g_2(m)&=g_1^{-1}(s(m))\\
&&&=g_1^{-1}(g_1(m))=m\\
\end{eqnarray}\)
となり、\(g_1^{-1}g_2\) は \(\bs{M}\) の元を不動にする。よって、
\(g_1^{-1}g_2\in\:H\)
\(g_2\in\:g_1H\)
である。
つまり、\(g_2\) は \(H\) の剰余類の一つの集合 \(g_1H\) に入る。以上で、\(\bs{M}\) の同型写像 \(s\) は、同型写像の延長を通して 剰余類 \(G/H\) の一つを定めることが分かる。
逆に \(g_1\) と \(g_2\) が 剰余類 \(G/H\) の同じ集合に属すると、
\(g_2\in\:g_1H\)
\(g_1^{-1}g_2\in\:H\)
\(g_1^{-1}g_2(m)=m\)
\(g_2(m)=g_1(m)\)
となり、\(g_1\) と \(g_2\) は \(\bs{M}\) 上で全く同じ作用をする。従って、\(\bs{M}\) 上で \(g_1,\:g_2\) と同じ作用をする \(\mr{Gal}(\bs{M}/\bs{Q})\) の元 \(s\) を定められる。つまり、剰余類 \(G/H\) の一つの集合が \(\mr{Gal}(\bs{M}/\bs{Q})\) の元を一つ定める。
従って、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
である。[証明終]
| 3.多項式と体(続き) |
3.3 線形空間
ガロア理論の一つの柱は、代数拡大体を線形空間(ベクトル空間)としてとらえることで、線形空間の「次元」や「基底」を使って理論が組み立てられています。線形空間には精緻な理論体系がありますが、ここではガロア理論に必要な事項の説明をします。
線形空間の定義
| (線形空間の定義:33A) |
集合 \(V\) と 体 \(\bs{K}\) が次を満たすとき、\(V\) を \(\bs{\bs{K}}\) 上の線形空間(=ベクトル空間。linear space / vector space)と言う。
加算の定義
\(V\) の任意の元 \(\br{u},\:\br{v}\) に対して \((\br{u}+\br{v})\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
\(\br{u}+\br{x}=\br{x}\) となる \(\br{x}\) が存在する。これを \(0\) と書く。
\((2)\) 逆元の存在
\(\br{u}+\br{x}=0\) となる \(\br{x}\) が存在する。これを \(-\br{u}\) と書く。
\((3)\) 結合則が成り立つ
任意の元 \(\br{u},\:\br{v}\:,\br{w}\) について、\((\br{u}+\br{v})+\br{w}=\br{u}+(\br{v}+\br{w})\)
\((4)\) 交換則が成り立つ
\(\br{u}+\br{v}=\br{v}+\br{u}\)
スカラー倍の定義
\(V\) の任意の元 \(\br{u}\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(k\br{u}\in V\) が定義されていて、加算との間に次の性質がある。\(\br{u},\:\br{v}\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(m\br{u})=(km)\br{u}\)
\((2)\:\:(k+m)\br{u}=k\br{u}+m\br{u}\)
\((3)\:\:k(\br{u}+\br{v})=k\br{u}+k\br{v}\)
\((4)\:\:1\br{v}=\br{v}\)
高校数学に出てくる "2次元ベクトル" とは、上記の定義の \(\bs{K}\) を \(\bs{R}\)(実数の体)とし、\(V\) を2つの実数のペアの集合 \(\{\:(x,y)\:|\:x,y\in\bs{R}\:\}\) とするベクトル空間(の要素)のことです。
上の定義の \(0\) は線形空間 \(V\) の元です。以下、\(V\) の単位元 \(0\)(= \(0\) ベクトル)と、体 \(\bs{K}\) の加法の単位元 \(0\) が混在しますが、文脈や式から明らかなので、同じ \(0\) で記述します。
1次独立と1次従属
| (1次独立と1次従属:33B) |
1次独立
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次従属であるという。
基底
| (基底の定義:33C) |
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、次の2つが満たされるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) を基底という。
| \({\br{v}_1,\br{v}_2,\cd,\br{v}_n}\) は1次独立である。 | |
| \(V\) の任意の元 \(\br{v}\) は、\(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) を選んで、
\(\br{v}=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n\)
と表せる。 |
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が基底だと、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) は基底ではありません。なぜなら、もし \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) が基底だとすると、
\(\br{v}_n=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}\)
と表せますが、これは、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}-\br{v}_n=0\)
ということであり、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が1次従属となってしまって、基底の要件を満たさなくなるからです。基底に、別の1つの元を加えるケースも同じことです。
| (基底の数の不変性:33D) |
\(\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) である。
[証明]
この定理の証明のために、まず次の補題を証明する。
[補題]
線形空間 \(V\) の任意の \(n\) 個の元を \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) とする(基底でなくてもよい)。線形空間 \(V\) の \(n+1\) 個の元 \(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) がすべて \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) の1次結合で表されるなら、\(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) は1次従属である。
数学的帰納法を使う。まず、\(n=1\) のとき、この定理は成り立つ。つまり、
\(\br{w}_1=k_1\br{u}_1\)
\(\br{w}_2=k_2\br{u}_1\)
と表されるなら、
\(k_2\br{w}_1-k_1\br{w}_2=0\)
であり、\(\br{w}_1\) と \(\br{w}_2\) は1次従属である。そこで、\(n\) が \(k\:\:(\geq1)\) のときに成り立つとし、\(n=k+1\) でも成り立つことを証明する。
以降、表記を見やすくするため、\(k=3\) の場合で記述する。ただし、一般性を失うことがないように記述する。\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) が、
\(\br{w}_1=a_{11}\br{u}_1+a_{12}\br{u}_2+a_{13}\br{u}_3\)
\(\br{w}_2=a_{21}\br{u}_1+a_{22}\br{u}_2+a_{23}\br{u}_3\)
\(\br{w}_3=a_{31}\br{u}_1+a_{32}\br{u}_2+a_{33}\br{u}_3\)
\(\br{w}_4=a_{41}\br{u}_1+a_{42}\br{u}_2+a_{43}\br{u}_3\)
と表せたとする。ここで \(\br{w}_4\) の係数に注目する。もし、
\(a_{41}=a_{42}=a_{43}=0\)
であれば、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属である。なぜなら、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3+b_4\br{w}_4=0\)
の式を満たす \(b_1,b_2,b_3,b_4\) は、
\(b_1=b_2=b_3=0\)
\(b_4\neq0\)
として実現でき、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属の定義を満たすからである。そこで、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つあるとする。それを \(a_{43}\) とし、
\(a_{43}\neq0\)
とする。この仮定で一般性を失うことはない。ここで、
\(\br{x}_i=\br{w}_i-\dfrac{a_{i3}}{a_{43}}\br{w}_4\:\:(i=1,2,3)\)
とおいて \(\br{u}_3\) の項を消去する。計算すると、
\(\begin{eqnarray}
&&\:\:\br{x}_1=&\left(a_{11}-\dfrac{a_{13}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{12}-\dfrac{a_{13}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_2=&\left(a_{21}-\dfrac{a_{23}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{22}-\dfrac{a_{23}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_3=&\left(a_{31}-\dfrac{a_{33}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{32}-\dfrac{a_{33}a_{42}}{a_{43}}\right)\br{u}_2\\
\end{eqnarray}\)
となる。そうすると、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は「線形空間 \(V\) の2つの元 \(\br{u}_1,\br{u}_2\) の1次結合で表された3つの元」である。従って、帰納法の仮定により、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は1次従属である。1次従属だから、
\(b_1\br{x}_1+b_2\br{x}_2+b_3\br{x}_3=0\)
となる少なくとも一つは \(0\) ではない \(b_1,\:b_2,\:b_3\) がある。 \((\br{A})\)
\(\br{x}_1=\br{w}_1-\dfrac{a_{13}}{a_{43}}\br{w}_4\)
\(\br{x}_2=\br{w}_2-\dfrac{a_{23}}{a_{43}}\br{w}_4\)
\(\br{x}_3=\br{w}_3-\dfrac{a_{33}}{a_{43}}\br{w}_4\)
だったから、これを \((\br{A})\) 式に代入すると、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3-\)
\(\dfrac{1}{a_{43}}(b_1a_{13}+b_2a_{23}+b_3a_{33})\br{w}_4=0\)
となる。この式における \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) の係数の少なくとも一つは \(0\) ではない。従って、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つある場合にも \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) は1次従属である。
以上で、線形空間 \(V\) の \(k=3\) 個の元(\(\br{u}_1,\br{u}_2,\br{u}_3\))の1次結合で、\(k+1=4\) 個の元(\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\))のすべてが表されば、その4個の元は1次従属であることが証明できた。\(k=3\) としたのは表記を見やすくするためであり、\(k=3\) であることの特殊性は使っていない。つまり、\(k\geq1\) のすべてで成り立つ。従って数学的帰納法により補題が正しいことが証明できた。[補題の証明終]
以上を踏まえて、\(A=\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(B=\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) となることを証明する。
もし仮に \(m < n\) だとすると、\(B\) の中から \((m+1)\) 個の元を選べる。それを \(B\:'=\{\br{v}_1,\br{v}_2,\cd,\br{v}_{m+1}\}\) とすると、\(A\) は 線形空間 \(V\) の基底だから、\(B\:'\) の元は \(A\) の元の1次結合で表現できる。つまり \(B\:'\) の \((m+1)\)個の元のすべては \(m\)個の元の1次結合で表されるから、[補題]によって \(B\:'\) は1次従属である。\(B\) は \(B\:'\) と同じものか、または \(B\:'\) に数個の元を付け加えたものだから、\(B\:'\) が1次従属なら \(B\) も1次従属である。しかし、\(B\) は線形空間 \(V\) の基底だから1次独立であり、矛盾が生じる。従って、\(m\geq n\) である。
もし仮に \(m > n\) だとしても、全く同様の考察により矛盾が生じる。従って、\(m\leq n\) である。この結果、\(m=n\) であることが証明できた。[証明終]
この基底の数の不変性の定理(33D)により、線形空間には次のように「次元」が定義できることになります。
次元
| (次元の不変性:33E) |
線形空間の基底に含まれる元の数が有限個のとき、その個数を線形空間の次元と言う。次元は基底の取り方によらない。
線形空間の次元や基底と、代数拡大体を結びつけるのが次の定理です。
単拡大体の基底
| (単拡大体の基底:33F) |
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。単拡大体である \(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間であり、\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) は \(\bs{Q}(\al)\) の基底である。
[証明]
\(\bs{Q}(\al)\) の基底であるための条件は、
| \(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立である | |
| \(\bs{Q}(\al)\) の任意の元が \(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) の1次結合で表される |
の2つである。② は単拡大の体の定理(32C)で証明されているので、① を証明する。多項式 \(g(x)\) を、
\(g(x)=a_0+a_1x+a_2x^2+\cd+a_{n-1}x^{n-1}\)
とおく。\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立であることを言うには、
\(g(\al)=0\) であれば \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\)
を言えばよい。以降、背理法を使って証明する。\(g(\al)=0\) で、\(a_i\:\:(0\leq i\leq n-1)\) のうち、少なくとも1つはゼロでないと仮定する。
\(g(x)\) が定数(つまり \(a_0\) の項のみ)のときは、\(g(\al)=0\) なら \(a_0=0\) なので、「少なくとも1つはゼロでない」に反する。そこで \(g(x)\) は1次以上の多項式であるとする。
そうすると、2つの方程式 \(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) をもつことになる。しかし、\(f(x)\) は \(n\)次の既約多項式であり、\(g(x)\) は1次以上で \(n\)次未満の多項式である。既約多項式の定理2(31F)により、このような2つの方程式は共通の解を持たない。ゆえに矛盾が生じる。従って、\(g(\al)=0\) のとき \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\) であり、① が証明された。
基底の数が線形空間の次元であり、\(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間である。[証明終]
もし、\(f(x)\) が\(n\)次多項式だとしたら(既約多項式を含む)、\(\bs{Q}(\al)\) の次元は \(n\)以下になります。\(f(x)=0\) の解の一つ、\(\al\) の最小多項式(31H)を \(m\)次多項式である \(g(x)\) とすると、\(g(x)\) は既約多項式であり(31I)、\(\al\) は \(f(x)=0\) と \(g(x)=0\) の共通の解なので、既約多項式の定理1(31E)により \(f(x)\) は \(g(x)\) で割り切れます。つまり、
\(f(x)=h(x)g(x)\)
と書けるので、
\(\mr{deg}\:f(x)\:\geq\:\mr{deg}\:g(x)\)
\(n\:\geq\:m\)
ですが、単拡大体の基底の定理(33F)により \(\bs{Q}(\al)\) の次元は \(m\) なので、\(n\)以下です。
拡大次数とその連鎖律
方程式の解になる数が代数的数で、\(\bs{Q}\) に代数的数を添加した体が代数拡大体です。「3.2 体」の「単拡大の体」でとりあげた \(\bs{Q}(\al)\) は代数拡大体であり、次元は \(n\) でした(32C)。この次元を「体の拡大」の視点で考えてみます。
「体 \(\bs{K}\) 上の線形空間 \(V\)」の定義において、\(\bs{K}=\bs{Q}\) とし \(V=\bs{Q}\) とすると、「有理数体 \(\bs{Q}\) は、\(\bs{Q}\) 上の線形空間」であると言えます。\(\bs{Q}\) では加算もスカラー倍(=乗算)も定義されていて、可換だからです。線形空間の定義にある各種の演算は、体の演算の一部です。
線形空間 \(\bs{Q}\) の基底は、\(0\) ではない \(\bs{Q}\) の元 \(v\) です。\(0\) を含む \(\bs{Q}\) の任意の元を \(a\) とすると、
\(av=0\:\:\:(v\neq0)\)
が成り立つのは \(a=0\) しかないので \(v\) は1次独立であり、また \(av\) で全ての \(\bs{Q}\) の元が表されるからです。一方、\(0\) は、
\(a\cdot0=0\)
が \(0\) ではない \(a\) について成り立つので1次従属です。以上から、線形空間 \(\bs{Q}\) の基底として \(1\) を選ぶことにします。次元は \(1\) です。
\(\bs{Q}\) に \(\sqrt{2}\) を添加した \(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) の代数拡大体で、\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) です。\(\bs{Q}(\sqrt{2})\) は \(\bs{\bs{Q}}\) 上の線形空間です。\(\bs{Q}(\sqrt{2})\) の基底としては、まず \(1\) を選ぶことができます。\(1\) を \(\bs{Q}\) の元でスカラー倍すると、\(\bs{Q}(\sqrt{2})\) の部分集合である \(\bs{Q}\) の元の全てが表せます。
\(\bs{Q}(\sqrt{2})\) の元の全てを表現するためには、さらに基底に \(\sqrt{2}\) を追加します。\(\sqrt{2}\) は \(\bs{Q}\) の元の1次結合では表せないので、\(1\) と \(\sqrt{2}\) は 1次独立です。\(1,\:\sqrt{2}\) が \(\bs{Q}(\sqrt{2})\) の基底で、次元は \(2\) です。
さらに \(\bs{Q}(\sqrt{2})\) に \(\sqrt{3}\) を添加した代数拡大体 \(\bs{Q}(\sqrt{2},\sqrt{3})\) を考えてみると、\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間であり、基底は \(1,\:\sqrt{3}\) です。\(1\) と \(\sqrt{3}\) は 1次独立であり、\(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の全ての元は、\(\bs{\bs{Q}(\sqrt{2})}\) の元を係数とする \(\bs{1}\) と \(\bs{\sqrt{3}}\) の1次結合で表現できるからです。\(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間 \(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の次元は \(\bs{2}\) です。
ここで \(\bs{Q}(\sqrt{2},\sqrt{3})\) を \(\bs{\bs{Q}}\) 上の線形空間と考えると、その基底はまず、\(1,\:\sqrt{2},\:\sqrt{3}\) ですが、これだけでは不足で、\(\sqrt{6}\) を加える必要があります。\(\sqrt{6}\) は体としての演算(乗算)でできる数ですが、\(1,\:\sqrt{2},\:\sqrt{3}\) の1次結合では表現できないからです。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は \(1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\) であり、次元は \(4\) です。
ここまでの基底の表現はあくまで一例ですが、どういう基底を選ぼうと基底の数=次元は不変量であるというのが「次元の不変性」でした。以上の考察を踏まえて、拡大次数を定義し、拡大次数の連鎖律を証明します。
| (拡大次数の定義:33G) |
代数拡大体 \(\bs{F},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{K}\) であるとき、\(\bs{K}\) は \(\bs{F}\) 上の線形空間である。\(\bs{K}\) の次元を、\(\bs{K}\)の(\(\bs{F}\)からの)拡大次数といい、
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
| (拡大次数の連鎖律:33H) |
代数拡大体 \(\bs{F},\:\bs{M},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{M}\:\subset\:\bs{K}\) であるとき、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
[証明]
\([\:\bs{M}\::\:\bs{F}\:]=m\)、\([\:\bs{K}\::\:\bs{M}\:]=n\) とする。以下、表記を見やすくするため、\(m=3,\:n=2\) の場合で記述する。もちろん一般性を失わないように記述する。
\(\bs{F}\) 上の線形空間 \(\bs{M}\) の基底を
\(u_1,\:u_2,\:u_3\)
とすると、\(\bs{M}\) の任意の元 \(b\) は、
\(b=a_1u_1+a_2u_2+a_3u_3\:\:(a_i\in\bs{F},\:u_i\in\bs{M},\:1\leq i\leq m)\)
と表せる。
\(\bs{M}\) 上の線形空間 \(\bs{K}\) の基底を
\(v_1,\:v_2\)
とすると、\(\bs{K}\) の任意の元 \(x\) は、
\(x=b_1v_1+b_2v_2\:\:(b_j\in\bs{M},\:v_j\in\bs{K},\:1\leq j\leq n)\)
と表せる。\(b_1,\:b_2\) を \(\bs{M}\) の基底 \(u_1,u_2,u_3\) で表すと、
\(b_1=a_{11}u_1+a_{21}u_2+a_{31}u_3\)
\(b_2=a_{12}u_1+a_{22}u_2+a_{32}u_3\)
\((\:a_{ij}\in\bs{F}\:)\)
となるが、これを用いて \(x\) を表すと、
\(\begin{eqnarray}
&&\:\:x=&a_{11}u_1v_1+a_{21}u_2v_1+a_{31}u_3v_1+\\
&&&a_{12}u_1v_2+a_{22}u_2v_2+a_{32}u_3v_2\\
\end{eqnarray}\)
となる。つまり、\(\bs{K}\) の任意の元は \(\bs{F}\) の元を係数とする、\(u_1v_1\)、\(u_2v_1\)、\(u_3v_1\)、\(u_1v_2\)、\(u_2v_2\)、\(u_3v_2\) の1次結合で表現できる。
ここで \(x=0\) とすると、
\((a_{11}u_1+a_{21}u_2+a_{31}u_3)v_1+\)
\((a_{12}u_1+a_{22}u_2+a_{32}u_3)v_2=0\)
であるが、\(v_1,v_2\) は \(\bs{K}\) の基底なので1次独立であり、従って、
\(a_{11}u_1+a_{21}u_2+a_{31}u_3=0\)
\(a_{12}u_1+a_{22}u_2+a_{32}u_3=0\)
である。すると、\(u_1,u_2,u_3\) は \(\bs{M}\) の基底なので1次独立であり、
\(a_{11}=a_{21}=a_{31}=a_{12}=a_{22}=a_{32}=0\)
である。従って、\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) は1次独立である。
\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) の \(mn\) 個の元は、
| 1次独立 | |
| \(\bs{F}\) の元を係数とする1次結合で \(\bs{K}\) の元のすべてを表せる |
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
である。[証明終]
体の一致
2つの代数拡大体 \(\bs{F}\) と \(\bs{K}\) の次元が一致するとします。たとえば \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) の次元はいずれも \(2\) です。もちろん \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) は体として別物です。
それでは、\(\bs{F}\subset\bs{K}\) という関係があり、かつ \(\bs{F}\) と \(\bs{K}\) の次元が一致するとき、\(\bs{F}\) と \(\bs{K}\) は体として一致すると言えるのでしょうか。
これはイエスで、それを次に証明します。この定理は、ガロア理論の証明の過程において、2つの体が実は同じものであることを言うときに使われる論法です。証明の都合上、\(\bs{F}\) ではなく \(\bs{K}_0\) と書きます。
| (体の一致:33I) |
体 \(\bs{K}_0\) と 体 \(\bs{K}\) があり、\(\bs{K}_0\:\subset\:\bs{K}\) を満たしている。\(\bs{K}_0\) と \(\bs{K}\) が有限次元であり、その次元が同じであれば、\(\bs{K}_0=\bs{K}\) である。
[証明]
体 \(\bs{K}_0\) と \(\bs{K}\) を、\(\bs{Q}\) 上の線形空間と見なし、その次元を \(n\) とする。\(\bs{K}_0\) の基底を \(\{a_1,\:a_2,\:\cd\:,a_n\}\) とする。\(\bs{K}_0\) が \(\bs{K}\) の真部分集合である、つまり \(\bs{K}_0\:\subsetneq\:\bs{K}\) と仮定して、背理法で証明する。
\(\bs{K}_0\:\subsetneq\:\bs{K}\) だと、\(a_{n+1}\notin\bs{K}_0,\:a_{n+1}\in\bs{K}\) である元 \(a_{n+1}\) が存在する。この \(a_{n+1}\) は \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合では表せない。なぜなら、もし表せたとしたら、\(\bs{K}_0\) の全ての元は基底である \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されるので \(a_{n+1}\in\bs{K}_0\) になってしまうからである。
そこで、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) を考えると、この元の並びは1次独立である。なぜなら、もし1次従属だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n+a_{n+1}x_{n+1}=0\)
となる \(x_i\in\bs{Q}\:\:(1\leq i\leq n+1)\) があって、そのうち少なくとも一つは \(0\) ではない。もし \(x_{n+1}\neq0\) だとすると、\(a_{n+1}\) が \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されることになり、\(a_{n+1}\in\bs{K}_0\) となって矛盾が生じる。また \(x_{n+1}=0\) だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n=0\)
であるが、この場合は \(x_i\:\:(1\leq i\leq n)\) の中に少なくとも一つは \(0\) でないものがあることになり、\(\{a_1,\:a_2,\:\cd\:,a_n\}\) が基底である(=1次独立である)ことに矛盾する。従って \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は1次独立である。
\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表される全ての元の集合を \(\bs{K}_1\) とする。\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) はすべて \(\bs{K}\) の元であるから、\(\bs{K}_1\:\subset\:\bs{K}\) である。また \(\bs{K}_1\) の任意の元は1次独立である \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表されるから、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は \(\bs{K}_1\) の基底であり、すなわち \(\bs{K}_1\) の次元は \(n+1\) である。\(\bs{K}_1=\bs{K}\) なら \(\bs{K}\) の次元が \(n+1\) になって矛盾するから、\(\bs{K}_1\neq\bs{K}\) つまり \(\bs{K}_1\:\subsetneq\:\bs{K}\) である。
以上の論理を繰り返すと \(\bs{K}_2\:\subsetneq\:\bs{K}\) である \(n+2\) 次元の \(\bs{K}_2\) の存在を示せるが、この操作は無限に繰り返えせるから、\(\bs{K}\) は無限個の基底をもつ無限次元の体となる。これは \(\bs{K}\) の次元が有限次元の \(n\) であることに矛盾する。従って背理法の仮定は誤りであり、\(\bs{K}_0\:=\:\bs{K}\) である。[証明終]
代数拡大体の構造
多項式と代数拡大体の相互関係をまとめると次のようになります。
| 体 \(\bs{Q}\) 上の\(\bs{n}\)次多項式 \(f(x)\) が(複素数の範囲で) \(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\) と因数分解できるとき、 \(\bs{Q}(\al_1,\:\:\al_2,\:\:\cd\:\:,\:\:\al_n)\) を \(f(x)\) の最小分解体と言う(32A)。つまり、\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体が最小分解体である。 | |
| すべての代数拡大体は単拡大体である(32B)。従って最小分解体も単拡大体である。つまり原始元 \(\theta\) があって、\(\bs{Q}(\theta)\) と表せる。 | |
| \(\theta\) の最小多項式を \(\bs{m}\)次多項式の \(g(x)\) とすると、\(g(x)\) は既約多項式である(31I)。 | |
| 方程式 \(g(x)=0\) の解の一つが \(\theta\) であるから、 \(1,\:\:\theta,\:\:\theta^2,\:\:\cd,\:\:\theta^{m-1}\) の \(m\)個の元は \(\bs{Q}(\theta)\) の基底である(33F)。つまり \(\bs{Q}(\theta)\) は \(m\)次元である。従って、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\) も \(m\)次元である。 |
以下、例をいくつかあげます。
\(x^4-5x^2+6\)
\(f(x)\) を4次多項式、
\(f(x)=x^4-5x^2+6\)
とします。\(f(x)\) は、
\(f(x)=(x^2-2)(x^2-3)\)
と因数分解できるので既約多項式ではありません。また、
\(f(x)=(x-\sqrt{2})(x+\sqrt{2})(x-\sqrt{3})(x+\sqrt{3})\)
なので、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt{2},\sqrt{3})\)
です。\(\bs{Q}(\sqrt{2},\:\sqrt{3})\) は、\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) による拡大体を \(\bs{Q}(\sqrt{2})\) とし、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-3=0\) の解 \(\sqrt{3}\) による拡大体が \(\bs{Q}(\sqrt{2},\:\sqrt{3})\) であると見なせます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})\)
です。拡大次数は
\([\:\bs{Q}(\sqrt{2}):\bs{Q}\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}(\sqrt{2})\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}\:]=4\)
です。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は、
\(\begin{eqnarray}
&&\:\:B_1&=(\:1,\:\sqrt{2},\:1\cdot\sqrt{3},\:\sqrt{2}\cdot\sqrt{3}\:)\\
&&&=(\:1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\:)\\
\end{eqnarray}\)
とすることができます。
一方、
\(\theta=\sqrt{2}+\sqrt{3}\)
とおくと、
\(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\)
となります。なぜなら、
\(\sqrt{2}=\dfrac{1}{2}(\theta-\dfrac{1}{\theta})\)
\(\sqrt{3}=\dfrac{1}{2}(\theta+\dfrac{1}{\theta})\)
であり、\(\sqrt{2}\) と \(\sqrt{3}\) が \(\theta\) と有理数の加減乗除で表現できるからです。\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{Q}(\sqrt{2}+\sqrt{3})\) という単拡大体です。
\(\theta=\sqrt{2}+\sqrt{3}\) から根号を消去すると、
\(\theta^4-10\theta^2+1=0\)
となるので、\(\theta\)の最小多項式は、
\(g(x)=x^4-10x^2+1\)
であり、この \(g(x)\) は既約多項式です。\(y=x^2-5\) とおくと、
\(\begin{eqnarray}
&&\:\:g(x)&=y^2-24\\
&&&=(y-2\sqrt{6})(y+2\sqrt{6})\\
\end{eqnarray}\)
なので、
\(\begin{eqnarray}
&&\:\:g(x)&=&(x^2-5-2\sqrt{6})(x^2-5+2\sqrt{6})\\
&&&=&(x-\sqrt{2}-\sqrt{3})(x+\sqrt{2}-\sqrt{3})\cdot\\
&&&& (x-\sqrt{2}+\sqrt{3})(x+\sqrt{2}+\sqrt{3})\\
\end{eqnarray}\)
となり、\(g(x)=0\) の解は、\(\sqrt{2}+\sqrt{3}\)、\(-\sqrt{2}+\sqrt{3}\)、\(\sqrt{2}-\sqrt{3}\)、\(-\sqrt{2}-\sqrt{3}\) の4つです。その \(g(x)=0\) の解の一つが \(\theta=\sqrt{2}+\sqrt{3}\) なので、単拡大体の基底の定理(33F)を適用して、\(\bs{Q}(\theta)\) の基底を、
\(B_2=(\:1,\:\:\theta,\:\:\theta^2,\:\:\theta^3\:)\)
の4個に選ぶことができます。拡大次数は \([\:\bs{Q}(\theta):\bs{Q}\:]=4\) です。
\(B_1\) と \(B_2\) は、同じ体である \(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\) の基底なので、相互に1次結合で表現できます。\(B_2\) の1次結合で \(B_1\) を表現すると、
\(\sqrt{2}=\dfrac{1}{2}(\phantom{-}\theta^3-9\theta)\)
\(\sqrt{3}=\dfrac{1}{2}(-\theta^3+11\theta)\)
\(\sqrt{6}=\dfrac{1}{2}(\phantom{-}\theta^2-5)\)
となります。
\(x^3-2\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-2\)
とします。これは既約多項式です。
\(x^3-1=0\) 解で \(1\) でないもの一つを \(\omega\) とします(= \(1\) の原始\(3\)乗根)。
\(x^3-1=(x-1)(x^2+x+1)\)
なので \(\omega\) は、
\(\omega^2+\omega+1=0\)
を満たします。この2次方程式の解は2つありますが、
\(\omega=\dfrac{-1+\sqrt{3}\:i}{2}\)
とします。方程式 \(x^3-2=0\) の解は、
\(\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
の3つです、従って、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt[3]{2},\:\sqrt[3]{2}\omega,\:\sqrt[3]{2}\omega^2)=\bs{Q}(\sqrt[3]{2},\:\omega)\)
です。これは、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt[3]{2})\:\subset\:\bs{Q}(\sqrt[3]{2},\:\omega)\)
という構造をしています。基底は、単拡大体の基底の定理(33F)を順次適用して、
\(\bs{Q}(\sqrt[3]{2})\) の基底(\(\bs{Q}\) 上の線形空間)
\(1,\:\sqrt[3]{2},\:(\sqrt[3]{2})^2\)
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}(\sqrt[3]{2})\) 上の線形空間\()\)
\(1,\:\omega\)
です。これらを総合すると、
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}\) 上の線形空間\()\)
| \(1,\) | \(\sqrt[3]{2},\) | \((\sqrt[3]{2})^2,\) | |
| \(\omega,\) | \(\sqrt[3]{2}\omega,\) | \((\sqrt[3]{2})^2\omega\) |
\([\:\bs{Q}(\sqrt[3]{2}):\bs{Q}\:]=3\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}(\sqrt[3]{2})\:]=2\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}\:]=6\)
となります。
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の原始元 \(\theta\) を、
\(\theta=\sqrt[3]{2}+\omega\)
と選ぶことができます。なぜなら、計算は省きますが、
| \(\sqrt[3]{2}\) | \(=\dfrac{1}{9}(\) | \(2\theta^5+3\theta^4+6\theta^3-6\theta^2+9\theta\) | \(+18)\) | |
| \(\omega\) | \(=\dfrac{1}{9}(-\) | \(2\theta^5-3\theta^4-6\theta^3+6\theta^2\) | \(-18)\) |
\(\theta=\sqrt[3]{2}+\dfrac{-1+\sqrt{3}\:i}{2}\)
の式を2乗や3乗して \(i\) と根号を消去すると、計算過程は省きますが、
\(\theta^6+3\theta^5+6\theta^4+3\theta^3+9\theta+9=0\)
となります。従って、\(\theta\) の最小多項式を \(g(x)\) とすると、
\(g(x)=x^6+3x^5+6x^4+3x^3+9x+9\)
という6次多項式です。\(\bs{Q}(\sqrt[3]{2},\:\omega)\) は 6次方程式 \(g(x)=0\) の根の一つである \(\theta\) を使って、
\(\bs{Q}(\sqrt[3]{2},\:\omega)=\bs{Q}(\theta)\)
という単拡大体(次元は \(6\))と表現できます。
\(x^3-3x+1\)
「1.3 ガロア群」の「ガロア群の例」で書いたように、\(x^3-3x+1=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
の関係があり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できます。これにより、\(f(x)=x^3-3x+1\) の最小分解体は、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。基底は、たとえば \(1,\:\al,\:\al^2\) であり、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]=3\)
です。\(\al\) の最小多項式は、3次多項式である \(f(x)=x^3-3x+1\) です。
ちなみに、3次多項式の最小分解体の次元が \(3\) になる条件を書いておきます。まず、2次方程式の例ですが、
\(x^2+ax+b=0\)
の方程式の解を \(\al,\:\beta\) とすると、
\(x^2+ax+b=(x-\al)(x-\beta)\)
です。そうすると、根と係数の関係から、
\(a=-(\al+\beta)\)
\(b=\al\beta\)
です。ここで、判別式 \(\bs{D}\) を、
\(D=(\al-\beta)^2\)
と定義すると、
\(\begin{eqnarray}
&&\:\:D=&\al^2-2\al\beta+\beta^2\\
&&&=(\al+\beta)^2-4\al\beta\\
&&&=a^2-4b\\
\end{eqnarray}\)
となります。この判別式を使って解の状況がわかります。つまり、
\(\cdot D\:\geq\:0\) なら2つの実数解(重根は2と数える)
\(\cdot D\:\geq\:0\) で \(\sqrt{D}\) が有理数なら、2つの有理数解
をもちます。\(\cdot D\:\geq\:0\) で \(\sqrt{D}\) が有理数なら、2つの有理数解
以上を3次方程式に拡張できます。2乗の項がない既約な3次方程式を、
\(x^3+ax+b=0\)
とし、3つの根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+ax+b=(x-\al)(x-\beta)(x-\gamma)\)
\((\br{A})\)
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=a\) \((\br{B})\)
\(\al\beta\gamma=-b\)
となります。3次方程式の判別式 \(D\) は、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
で定義されます。計算すると、
\(D=-4a^3-27b^2\)
となります。
ここで、\(D\) が、ある有理数 \(q\) の2乗の場合を考えます。つまり、
\(D=q^2\)
です。そうすると、
\(q=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
です(\(-q\) でも成り立ちますが割愛します)。 \((\br{C})\)
\((\br{A})\) 式の両辺を \(x\) で微分して \(x=\al\) を代入すると、
\(3\al^2+a=(\al-\beta)(\al-\gamma)\)
が得られます。\((\br{C})\) 式と \((\br{D})\) 式の両辺同士を割り算すると、 \((\br{D})\)
\(\dfrac{q}{3\al^2+a}=-(\beta-\gamma)\)
となります。そうすると、\((\br{B})\) 式と \((\br{E})\) 式を用いて、\(\beta\) と \(\gamma\) を \(\al\) の式として表現できます。その結果は、 \((\br{E})\)
\(\beta=\dfrac{2a\al+3b-q}{2(3\al^2+a)}\)
\(\gamma=\dfrac{2a\al+3b+q}{2(3\al^2+a)}\)
です。式の形はともかく、要するに、
\(\beta\) と \(\gamma\) が \(\al\) の加減乗除で表現できる
わけです。このことは、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
であることを意味します。\(\bs{Q}(\al,\beta,\gamma)\) は、既約な3次方程式の根の一つである \(\al\) の単拡大体なので、その次元は \(3\) です。
まとめると、判別式 \(D\) が有理数の2乗であるとき、既約 \(3\)次多項式の最小分解体の次元が \(3\) になります。\(x^3-3x+1\) の場合、\(a=-3,\:b=1\) なので、
\(D=-4a^3-27b^2=81=9^2\)
となり、次元が \(3\) です。
既約多項式ではない3次多項式の拡大次数はもっと小さくなります。たとえば \((x-1)(x^2+2)\) の最小分解体は \(\bs{Q}(\sqrt{2}\:i)\) であり、拡大次数は \(2\) です。また \((x-2)^3\) の最小分解体は \(\bs{Q}\) そのもので、拡大次数は \(1\) です。
まとめると、3次多項式 \(f(x)\) の最小分解体の拡大次数は、\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]\:=\:6,\:3,\:2,\:1\)
の4種あることになります(この4種しかないことの理由は後の章にあります)。
| 4.一般の群 |
ガロア理論の核心(第5章以降)に入る前の最後として、群についての各種の定義や定理を説明します。これらはいずれも第5章以降で必要になります。
4.1 部分群\(\cdot\)正規部分群、剰余類\(\cdot\)剰余群
部分集合の演算
以降の証明では集合の演算が多々出てきます。その定義は次の通りでです。これはあくまで群の "部分集合" に関するもので、それが部分群かどうかは別問題です。
| (部分集合の演算:41A) |
群 \(G\) の2つの部分集合を \(H,\:N\) とする。\(H\) と \(N\) の演算結果である \(G\) の部分集合、\(HN\) を次の式で定義する。
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
部分群の定理
部分群に関する定理をいくつかあげます。これらはいずれも後の定理の証明の過程で使います。
部分群の十分条件
| (部分群の十分条件:41B) |
群 \(G\) の部分集合を \(N\) とし、\(N\) の任意の2つの元を \(x,\:y\) とする。
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
[証明]
\(N\) の元 \(x,\:y\) は \(G\) の元でもあるので、\(xy,\:x^{-1},\:y^{-1}\) は \(G\) の演算として定義されている。
\(y=x^{-1}\) とおくと \(xy=xx^{-1}=e\in N\) なので、\(N\) は単位元を含む。つまり、\(N\) は演算で閉じていて、単位元が存在し、逆元が \(N\) の元である。また結合則は \(G\) の元として成り立っている。従って \(N\) は \(G\) の部分群である。[証明終]
部分群の元の条件
| (部分群の元の条件:41C) |
群 \(G\) の部分群を \(N\) とし、\(G\) の 元を \(x\) とすると、次の2つは同値である。
① \(xN\:=\:N\)
② \(x\:\in\:N\)
[証明]
[① \(\bs{\Rightarrow}\) ②]
\(N\) には \(G\) の単位元 \(e\) が含まれるから、\(xe\) は \(xN\) に含まれる。
\(x=xe\in xN=N\) \(\Rightarrow\) \(x\in N\)
である。
[② \(\bs{\Rightarrow}\) ①]
\(x\in N\) とし、\(N\) の任意の元を \(a\) とすると、\(N\) は群だから \(xa\in\:N\) である。\(N\) の異なる2つの元を \(a,\:b\:\:(a\neq b)\) とすると、\(xa\neq xb\) である。なぜなら、もし \(xa=xb\) だとすると、\(x\) の逆元 \(x^{-1}\) を左からかけて \(a=b\) となり、矛盾するからである。以上により、\(xH\) は \(H\) の全ての元を含むから \(xH=H\) である。[証明終]
部分群の共通部分
| (部分群の共通部分は部分群:41D) |
\(G\) の部分群を \(H,\:N\) とすると、\(H\cap N\) は部分群である。
[証明]
\(G\) の部分群を \(H,\:N\) とし、\(H\cap N\) の任意の2つの元を \(x,\:y\) とすると、\(x,\:y\in H,\:\:x,\:y\in N\) なので、
\(xy\in H,\:x^{-1}\in H\)
\(xy\in N,\:x^{-1}\in N\)
であり、
\(xy\in H\cap N,\:x^{-1}\in H\cap N\)
となって、部分群の十分条件の定理(41B)により \(H\cap N\) は部分群である。[証明終]
剰余類
| (剰余類の定義:41E) |
有限群 \(G\) の位数を \(n\) とし( \(|G|=n\) )、\(H\) を \(G\) の部分群とする。\(H\) に左から \(G\) のすべての元、\(g_1,\:g_2,\:\cd\:,\:g_n\) かけて、集合、
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
[証明]
\(|G|=[\:G\::\:H\:]\cdot|H|\) であることを証明する。2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとする。その共通な元が、\(x_1H\) では \(x_1h_i\)、\(x_2H\) では \(x_2h_j\) と表されているものとする。
\(x_1h_i=x_2h_j\)
左から \(x_2^{-1}\)、右から \(h_i^{-1}\) をかけると、
\(x_2^{-1}x_1h_ih_i^{-1}=x_2^{-1}x_2h_jh_i^{-1}\)
\(x_2^{-1}x_1=h_jh_i^{-1}\)
\(h_jh_i^{-1}\in H\) だから、
\(x_2^{-1}x_1\in H\)
を得る。部分群の元の条件の定理(41C)により、\(xH=H\) と \(x\in H\) は同値だから、
\(x_2^{-1}x_1H=H\)
となる。左から \(x_2\) をかけると、
\(x_1H=x_2H\)
を得る。これは、「2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとすると、2つの剰余類は一致する」ことを示している。従って、
2つの剰余類 \(x_1H\) と \(x_2H\) は、\(x_1H=x_2H\) か \(x_1H\cap x_2H=\phi\) のどちらか
である。\(H\) は 単位元 \(e\) を含むから、
\(g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
という和集合を作ると、そこには \(G\) のすべての元が含まれる。従って、
\(G=g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
である。剰余類 \(x_1H,\:x_2H,\:\cd\:x_dH\) は、\(g_1H,\:g_2H,\:\cd\:,g_nH\) を整理・分類したものだから、
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。この式の右辺の剰余類は共通の元がなく、それぞれの剰余類の元の数はすべて \(|H|\) だから、
\(|G|=d\cdot|H|\)
である。従ってラグランジュの定理、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
が成り立つ。[証明終]
ラグランジュの定理から、
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
ことがわかります。なぜなら、
\(H=\{e,\:g,\:g^2,\:\cd\:,\:g^{n-1}\}\)
とおくと、\(H\) は \(G\) の部分群(巡回群)になり、ラグランジュの定理によって \(|H|=n\) が \(|G|\) の約数になるからです。これは、位数の定理(25A)の[補題5]、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とし、\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
の一般化になっています。 \((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\)(\(\varphi\)はオイラー関数)なので、ラグランジュの定理はオイラーの定理やフェルマの小定理(25B)の一般化であるとも言えます。さらに、
群位数が素数の群は巡回群である。
こともわかります。なぜなら、群 \(G\) の位数を \(p\)(素数)とすると、単位元ではない \(G\) の任意の元 \(g\:(\neq e)\) の位数は \(p\) であり、つまり \(G\) は \(g\) を生成元とする位数 \(p\) の巡回群(\(C_p\))だからです。
次の「正規部分群」はガロア理論のキモといえる概念です。これは純粋に群の属性として定義できるのでここにあげますが、ガロア理論の核心である第5章以降で展開される論証の多くは正規部分群に関係しています。
正規部分群
| (正規部分群の定義:41F) |
有限群 \(G\) の部分群を \(H\) とする。\(G\) の全ての元 \(g\) について、
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
正規部分群 \(H\) の定義は、\(G\) の任意の元 \(g\) に対して、
\(gHg^{-1}=H\)
となる \(H\)、としても同じです。また 任意の \(h\in H\) について、
\(ghg^{-1}\in H\)
となる \(H\)、としても同じです。
剰余群
| (剰余群の定義:41G) |
有限群 \(G\) の正規部分群を \(H\) とする。\(G\) の \(H\) による剰余類
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
[証明]
\(H\) が正規部分群のとき、剰余類が群になることを証明する。\(x_iH\) は \(G\) の剰余類なので、
\(G=x_1H\cup x_2H\cup\cd\cup x_dH\)
\((i\neq j\:のとき\:x_iH\cap x_jH=\phi)\)
と表されている。2つの剰余類、\(x_iH,\:x_jH\) の演算を行うと、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_iHx_jH=x_i(Hx_j)H\\
&&&=x_i(x_jH)H=x_ix_jHH\\
&&&=x_ix_j(HH)=x_ix_jH\\
\end{eqnarray}\)
つまり、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_ix_jH\\
\end{eqnarray}\)
となる。\(H\) は正規部分群なので \(Hx_j=x_jH\) であることと、\(H\) は部分群なので \(HH=H\) であることを用いた。
\(x_ix_j\) は \(G\) の元だから、\(x_ix_jH\) は \(G\) の剰余類のうちの一つである。従って \((x_iH)(x_jH)\) の演算は \(G\) の剰余類の中で閉じている。また、
\((x_iH\cdot x_jH)\cdot x_kH=x_ix_jH\cdot x_kH=x_ix_jx_kH\)
\(x_iH\cdot(x_jH\cdot x_kH)=x_iH\cdot x_jx_kH=x_ix_jx_kH\)
\((x_iH\cdot x_jH)\cdot x_kH=x_iH\cdot(x_jH\cdot x_kH)\)
であるから、結合法則が成り立っている。さらに、
\(H\cdot xh=eH\cdot xH=(ex)H=xH\)
\(xH\cdot H=xH\cdot eH=(xe)H=xH\)
なので、剰余類 \(H\) が単位元になる。また、
\(xH\cdot x^{-1}H=(xx^{-1})H=eH=H\)
\(x^{-1}H\cdot xH=(x^{-1}x)H=eH=H\)
であり、\(xH\) に対する逆元は \(x^{-1}H\) である。従って剰余類 \(G/H\) は群である。[証明終]
群の位数、元の位数、ラグランジュの定理、巡回群は、いずれも有限群の概念や定理です。しかし、剰余類、正規部分群、剰余群は、元の数が無限であっても成り立つ概念です。たとえば、整数の加法群 \(\bs{Z}\) は可換群なので、すべての部分群は正規部分群です。従って、\(n\) の倍数から成る部分群を \(n\bs{Z}\) とすると、\(\bs{Z}/n\bs{Z}\) は剰余群です。\(\bs{Z}/n\bs{Z}\) という表記は \(n\bs{Z}\) が \(\bs{Z}\) の正規部分群であることが暗黙の前提なのでした。
| (巡回群の剰余群は巡回群:41H) |
巡回群の部分群による剰余群は巡回群である。
[証明]
群 \(G\) を、位数 \(n\)、生成元 \(g\) の巡回群とし、その元を、
\(G\:=\:\{g,\:g^2,\:g^3,\:\cd,\:g^n=e\:\}\)
とする。\(G\) の部分群を \(H\) とし、\(H\) の元のうち \(g\) の指数が一番小さいものを \(g^{d}\:\:(1\leq d\leq n)\) とする。\(d=1\) なら \(H=G\) であり、また \(d=n\) なら \(H=\{\:e\:\}\) である。
\(n\) を \(d\) で割った商を \(q\)、余りを \(r\) とする。つまり、
\(n=qd+r\:\:(1\leq q\leq n,\:0\leq r < d)\)
とする。\(g^d\) は \(H\) の元だから その \(q\) 乗も \(H\) の元であり、
\((g^d)^q=g^{dq}\in H\)
である。また \(g^{dq}\) の逆元も \(H\) に含まれるから
\((g^{dq})^{-1}\in H\)
である。仮にもし \(1\leq r < d\) なら
\(g^{dq}g^{r}=g^{qd+r}=g^n=e\)
となるので、この式に左から \((g^{dq})^{-1}\) をかけると、
\(g^r=(g^{dq})^{-1}\in H\)
となり、\(d\) 未満の数 \(r\) が指数の \(g^r\) が \(H\) の元ということになるが、これは \(d\) が最小の指数であるという仮定に反する。従って \(r=0\) であり、\(qd=n\) である。つまり \(d\) と \(q\) は \(n\) の約数である。そうすると \(g^d\) を \(q\) 乗すると \(g^{dq}=g^n=e\) となるので、\(H\) は \(g^d\) を生成元とする位数 \(q\) の巡回群、
\(H=\{\:g^{d},\:g^{2d},\:\cd,\:g^{qd}=g^n=e\:\}\)
である。また、\(G\) は巡回群、つまり可換群だから、その部分群である \(H\) は \(G\) の正規部分群である。 \((\br{A})\)
次に、剰余類 \(g^kH\:\:(1\leq k\leq n)\) を考える。\(k\) を \(d\) で割った商を \(m\)、余りを \(i\) とする。\(qd=n\) なので \(m\) の最大値は \(q\) であり、
\(k=md+i\) \((0\leq m\leq q,\:0\leq i < d)\)
と表現できる。以下、\(m,\:i\) の値によって3つに分ける。
\(k=i\:\:(m=0,\:1\leq i < d)\) のときは、\(H\) が単位元を含んでいるので、
\(g^k=g^i\in g^iH\)
である。
\(m\neq0,\:1\leq i < d\) のときは、
\(g^k=g^{md+i}=g^ig^{md}\)
となるが、\((\br{A})\) 式により、
\(g^{md}\in H\:\:(1\leq m\leq q)\)
なので、
\(g^ig^{md}\in g^iH\)
\(g^k\in g^iH\:\:(1\leq i < d)\)
となる。
また、\(m\neq0,\:i=0\) のときは、
\(g^k=g^{md}\in H\)
である。
結局、\(G\) の元 \(g^k\) は、\(\{\:H,\:g^iH\:\:(1\leq i < d)\:\}\) のどれかに含まれる。ここで、形式上 \(g^0H\:=\:H\) と定義すると、\(H,\:g^iH\) は、
\(g^iH\:=\:\{\:g^{i+md}\:|\:0\leq i < d,\:\:0\leq m\leq q\:\}\)
と表記できる。\(0\leq i,j < d,\:\:0\leq m_i,m_j\leq q\) で、\(i\neq j\) なら、
\(i+m_id\neq j+m_jd\)
なので、\(g^iH\) と \(g^jH\) に共通の元はなく、
\(g^iH\:\cap\:g^jH=\phi\:\:(i\neq j)\)
である。
以上より、巡回群 \(G\) は剰余類によって、
\(G=H\:\cup\:gH\:\cup\:g^2H\:\cup\:\cd\:\cup\:g^{d-1}\)
\(g^iH\:\cap\:g^jH=\phi\) \((i\neq j)\)
と分解できる。
\(H\) は \(G\) の正規部分群であった。従って \(G\) の \(H\) による剰余類は剰余群になり、
\(G/H=\{\:H,\:gH,\:g^2H,\:\cd\:,g^{d-1}H\:\}\)
である。ここで \(gH\) の累乗を調べると、
\((gH)^2=gHgH=ggHH=g^2H\)
\((gH)^3=gHgHgH=g^2HgH=g^2gHH=g^3H\)
のように計算でき、
\((gH)^i=g^iH\) \((1\leq i\leq d-1)\)
である。また、同じ計算によって、
\((gH)^d=g^dH\)
となるが、\(g^d\in H\) なので部分群の元の条件の定理(41C)により \(g^dH=H\) であり、つまり、
\((gH)^d=H\)
である。
以上により 剰余群 \(G/H\) は、
\(G/H=\{gH,\:(gH)^2,\:\cd\:,(gH)^{d-1},\:(gH)^{d}=H\}\)
と表され、生成元が \(gH\)、単位元が \(H\)、位数が \(d\) の巡回群である。[証明終]
部分群と正規部分群
| (部分群と正規部分群:41I) |
\(G\) の正規部分群を \(H\)、部分群を \(N\) とする。このとき、
(a) \(NH\) は \(G\) の部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
が成り立つ。
(a) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(NH\) は部分群である。
\(NH\) の任意の2つの元を
\(nx\:\:(n\in N,\:x\in H),\:\:my\:\:(m\in N,\:y\in H)\)
とすると、
\(nx\in nH,\:my\in mH\)
である。\(H\) は正規部分群だから、\(mH=Hm\) であることを用いると、
\((nx)(my)\in(nH)(mH)=nHmH=nmHH=nmH\)
となる。\(n,m\in N\) なので \(nm\in N\) であり、従って \(nmH\subset NH\) である。結局、
\((nx)(my)\in NH\)
となって、\(NH\) の2つの元の演算は \(NH\) で閉じていることが分かる(=\(\:\br{①}\:\))。
また一般に、\((xy)^{-1}=y^{-1}x^{-1}\) である。なぜなら、
\(xy(y^{-1}x^{-1})=x(yy^{-1})x^{-1}=xex^{-1}=xx^{-1}=e\)
\((y^{-1}x^{-1})xy=y^{-1}(x^{-1}x)y=y^{-1}ey=y^{-1}y=e\)
が成り立つからである。
\(G\) の部分群 \(N\) と正規部分群 \(H\) において、\(n\in N,\:x\in H\) とすると、\(n^{-1}\in N,\:x^{-1}\in H\) なので、
\((nx)^{-1}=x^{-1}n^{-1}\in Hn^{-1}\)
となるが、\(H\) が正規部分群なので、\(Hn^{-1}=n^{-1}H\)である。さらに、\(n^{-1}H\subset NH\) なので、結局、
\((nx)^{-1}\subset NH\)
となり、\(NH\) の任意の元 \(nx\) について逆元 \((nx)^{-1}\) が \(NH\) に含まれる(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) が成り立つので、部分群の十分条件の定理(41B)によって \(NH\) は \(G\) の部分群である。[証明終]
(b) の証明
\(G\) の正規部分群を \(H\)、部分群を \(N\) とするとき、\(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。\(N\) は \(G\) の 部分集合だから、\(N\) の任意の元 \(y\) についても、
\(yH=Hy\)
が成り立つ。従って \(H\) は \(N\) の正規部分群である。[証明終]
(c) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(N\cap H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。この式に右から \(x^{-1}\) をかけると、
\(xHx^{-1}=H\)
となる。これは、\(H\) の任意の元 \(h\) を決めると、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
となることを意味する。これは \(H\) が正規部分群であることの定義と等価である。以降、この形で \(N\cap H\) が正規部分群であることを証明する。
部分群 \(N\) の任意の元を \(y\)、正規部分群 \(H\) の任意の元を \(h\)、\(N\cap H\) の任意の元を \(n\) とする。\(y,\:y^{-1},\:n\) は全て \(N\) の元だから、
\(yny^{-1}\in N\)
である(=\(\:\br{①}\:\))。また \(H\) は \(G\) の正規部分群であるから、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
が成り立つ。ここで、\(G\:\sp\:N\) なので \(x=y\) とおくことができ、また \(H\:\sp\:N\cap H\) なので \(h=n\) とおくこともできる。従って、
\(yny^{-1}\in H\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、\(N\cap H\) の任意の元 \(n\) を決めると、\(N\) の全ての元 \(y\) について、
\(yny^{-1}\in N\cap H\)
となる。つまり \(N\cap H\) は \(N\) の正規部分群である。[証明終]
4.2 準同型写像
この節の写像の説明には「全射」「単射」「全単射」などの用語ができてます。その用語の意味は次の図の通りです。
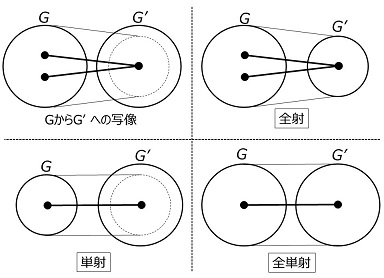
|
全射:\(G\,'\)の任意の元 \(y\) について \(f(x)=y\) となる \(x\in G\) がある。 単射:\(x\neq y\:(x,y\in G)\) なら \(f(x)\neq f(y)\)。 全単射:全射かつ単射。 |
準同型写像と同型写像
| (準同型写像と同型写像:42A) |
群 \(G\) から群 \(G\,'\) への写像 \(f\) がある。\(G\) の任意の2つの元、\(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
準同型写像の像と核
| (準同型写像の像と核:42B) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(G\) の元を \(f\) で移した元の集合を「\(f\) の像(image)」といい、\(\mr{Im}\:f\) と書く。\(\mr{Im}\:f\) を \(f(G)\) と書くこともある。
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
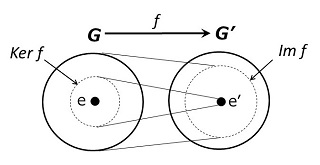
|
[証明]
\(\mr{Im}\:f\) と \(\mr{Ker}\:f\) が群であることを証明する。
\(\mr{Im}\:f\) は群
\(\mr{Im}\:f\) の任意の2つの元を \(f(x),f(y)\:\:(x,y\in G)\) とすると、
\(f(x)f(y)=f(xy)\:\in\mr{Im}\:f\)
である(=\(\:\br{①}\:\))。
\(\mr{Im}\:f\) の任意の元 \(f(x)\) について、
\(f(e)f(x)=f(ex)=f(x)\)
\(f(x)f(e)=f(xe)=f(x)\)
なので、
\(f(e)=e\,'\)
である。\(G\) は群なので、任意の元 \(x\) について逆元 \(x^{-1}\) が存在する。
\(f(x)f(x^{-1})=f(xx^{-1})=f(e)=e\,'\)
\(f(x^{-1})f(x)=f(x^{-1}x)=f(e)=e\,'\)
であるから、
\(f(x)^{-1}=f(x^{-1})\:\in\mr{Im}\:f\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、部分群の十分条件の定理(41B)によって \(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(\mr{Ker}\:f\) は群
\(\mr{Ker}\:f\) の任意の元を \(x,\:y\) とすると、
\(f(xy)=f(x)f(y)=e\,'e\,'=e\,'\)
なので、
\(xy\:\in\mr{Ker}\:f\)
である(\(\:\br{③}\:\))。
また \(x\) は \(G\) の元だから \(x^{-1}\) が定義されている。
\(\begin{eqnarray}
&&\:\:f(x^{-1})&=f(x^{-1})e\,'=f(x^{-1})f(x)\\
&&&=f(x^{-1}x)=f(e)\\
&&&=e\,'\\
\end{eqnarray}\)
となるので、
\(x^{-1}\:\in\mr{Ker}\:f\)
である(\(\:\br{④}\:\))。\(\br{③}\:\:\br{④}\) より、部分群の十分条件の定理(41B)によって \(\mr{Ker}\:f\) は \(G\) の部分群である。[証明終]
核が単位元なら単射
| (核が単位元なら単射:42C) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。このとき
| \(\mr{Im}\:f\) | \(=\:G\,'\) | なら \(f\) は全射 | |
| \(\mr{Ker}\:f\) | \(=\:\{e\}\) | なら \(f\) は単射 |
である。
[証明]
"\(f\) は全射" については、全射の定義そのものである。
\(\mr{Ker}\:f\:=\:\{e\}\) とし、\(G\) の任意の2つの元を \(x,\:y\) とする。ここで、
\(f(x)=f(y)\)
であったとする。\(\mr{Im}\:f\) は群だから \(f(y)^{-1}\in\:\mr{Im}\:f\) である。上の式に左から \(f(y)^{-1}\) をかけると、
\(f(y)^{-1}f(x)=f(y)^{-1}f(y)\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)\in\:\mr{Ker}\:f\)
\(y^{-1}x=e\)
\(x=y\)
となる。\(f(x)=f(y)\) であれば \(x=y\) なので、\(f\) は単射である。[証明終]
核は正規部分群
| (核は正規部分群:42D) |
群 \(G\) から群 \(G\,'\) への準同型写像を \(f\) とする。このとき \(\mr{Ker}\:f\) は \(G\) の正規部分群である。
[証明]
\(\mr{Ker}\:f\) を \(H\) と記述する。\(G\) の 任意の元を \(x\) とし、\(H\) の任意の元を \(y\) とする。すると、
\(\begin{eqnarray}
&&\:\:f(xyx^{-1})&=f(x)f(y)f(x^{-1})\\
&&&=f(x)e\,'f(x^{-1})=f(x)f(x^{-1})\\
&&&=f(xx^{-1})=f(e)=e\,'\\
\end{eqnarray}\)
と計算できるから、
\(xyx^{-1}\in H\)
である。\(y\) は \(H\) の任意の元だから、
\(xHx^{-1}\subset H\)
である。\(x\) は任意にとることができるので、\(x\) を \(x^{-1}\) に置き換えると、
\(x^{-1}Hx\subset H\)
を得る。この式に左から \(x\)、右から \(x^{-1}\) をかけると、
\(H\subset xHx^{-1}\)
となる。つまり
\(H\subset xHx^{-1}\subset H\)
\(xHx^{-1}=H\)
である。さらに右から \(x\) をかけると、
\(xH=Hx\)
となり、\(x\) は任意の \(G\) の元だから、\(H\:\:(=\mr{Ker}\:f)\) は \(G\) の正規部分群である。[証明終]
4.3 同型定理
準同型定理=第1同型定理
| (準同型定理:43A) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(H=\mr{Ker}\:f\) とすると、\(G\) の \(H\) による剰余群は、\(G\) の \(f\) による像と同型である。つまり、
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
[証明]
\(H\:=\:\mr{Ker}\:f\) は、核は正規部分群の定理(42D)により、\(G\) の正規部分群である。従って剰余群 \(G/H\) が定義できる。\(G/H\) から \(\mr{Im}\:f\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G/H &\longrightarrow&\mr{Im}\:f\\
&&&xH &\longmapsto&f(x)\\
\end{eqnarray}\)
と定義する。まず、この写像が剰余類 \(xN\) の代表元 \(x\) のとりかたに依存しないこと、つまり \(xH=yH\) なら \(f(x)=f(y)\) であることを示す。\(xH=yH\) を変形すると、
\(xH=yH\)
\(y^{-1}xH=y^{-1}yH\)
\(y^{-1}xH=H\)
ゆえに部分群の元の条件の定理(41C)から \(y^{-1}x\in H\) である。そうすると、\(H\) は \(\mr{Ker}\:f\) のことだから、\(f(y^{-1}x)=e\,'\) である。これを変形すると、
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
となる。最後の変形では、準同型写像の像と核の定理(42B)の「\(\mr{Im}\:f\) は群」の証明から、\(f(y^{-1})=f(y)^{-1}\) であることを用いた。ここから、
\(f(y)^{-1}f(x)=e\,'\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(x)=f(y)\)
となり、\(f(x)=f(y)\) が証明できた。
以上の変形は逆も辿れる。つまり、
\(f(x)=f(y)\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1}x)\in H\)
\(y^{-1}xH=H\)
\(xH=yH\)
となる。これは \(f(x)=f(y)\) なら \(xH=yH\) であることを示していて、すなわち \(\sg\) は単射である。と同時に、\(\sg\) による写像の先は \(\mr{Im}\:f\) に限定しているので \(\sg\) は全射である。つまり \(\sg\) は 全単射である(=\(\:\br{①}\:\))。
さらに、
\(\begin{eqnarray}
&&\:\:\sg((xH)(yH))&=\sg(x(Hy)H)=\sg(x(yH)H)\\
&&&=\sg(xyH)=f(xy)=f(x)f(y)\\
&&&=\sg(xH)\sg(yH)\\
\end{eqnarray}\)
であり、つまり \(\sg((xH)(yH))=\sg(xH)\sg(yH)\) が成り立っている(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) により \(\sg\) は同型写像である。\(G/H\) から \(\mr{Im}\:f\) への同型写像が存在するから、
\(G/H\:\cong\:\mr{Im}\:f\)
である。[証明終]
第2同型定理
| (第2同型定理:43B) |
群 \(G\) の正規部分群を \(H\)、部分群を \(N\) とすると、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
|
[証明]
まず、部分群と正規部分群の定理(41I)により、\(G\) の正規部分群が \(H\)、部分群が \(N\) の場合、
| \(N\cap H\) は \(N\) の正規部分群 | |
| \(NH\) は \(G\) の部分群 | |
| \(G\:\sp\:NH\:\sp\:H\) なので、\(H\) は \(NH\) の正規部分群 |
\(G\) の任意の元を \(x,\:y\) とし、\(G\) から \(G/H\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G &\longrightarrow&G/H\\
&&&x &\longmapsto&xH\\
\end{eqnarray}\)
と定義する。この写像は、
\(\begin{eqnarray}
&&\:\:\sg(xy)&=xyH=xyHH=xHyH=(xH)(yH)\\
&&&=\sg(x)\sg(y)\\
\end{eqnarray}\)
を満たすから準同型写像である(ちなみに \(G\) とその正規部分群 \(H\) があるとき、上記の定義による \(\sg\) を自然準同型と呼ぶ)。
\(\sg\) の定義域は \(G\) であるが、\(\sg\) の定義域を \(G\) の部分群である \(N\) に制限した写像 \(\tau\)(タウ) を考える。\(N\) の任意の元を \(z\) とすると、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
&&&z &\longmapsto&zH\\
\end{eqnarray}\)
である。この \(\tau\) の像 \(\mr{Im}\:\tau\) を考えてみると、\(z\) が \(N\) の元のすべてを動くとき、\(\tau(z)=zH\) として出てくる \(G\) の元は \(NH\) の元である。つまり \(\tau\) は、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
として定義したが、\(\tau(z)\) が \(G/H\) の全てを尽くすわけではなく、全射ではない。写像による移り先は、\(G\) の部分群 \(NH\) を \(H\) で分類した剰余群、\(NH/H\) である。つまり \(\tau(N)=NH/H\) であり、
\(\mr{Im}\:\tau=NH/H\)
である。
次に準同型写像の核を考える。\(G/H\) の単位元は、
\(xH\cdot H=xH\)
\(H\cdot xH=HxH=xHH=xH\)
なので、\(H\) である。
\(G\) の元 \(x\) が \(\mr{Ker}\:\sg\) の元とする。つまり、
\(x\in\mr{Ker}\:\sg\)
とする。これは \(\sg(x)\) が \(G/H\) の単位元になるということだから、
\(\sg(x)=H\)
であり、\(\sg(x)=xH\) なので、
\(xH=H\)
である。これは部分群の元の条件の定理(41C)によって、
\(x\in H\)
と同値である。従って、
\(x\in\mr{Ker}\:\sg\)
\(x\in H\)
の2つは同値であり、つまり、
\(\mr{Ker}\:\sg=H\)
である。
\(\tau\) は \(\sg\) の定義域を \(N\) に制限したものなので、\(\mr{Ker}\:\tau\) は「\(\mr{Ker}\:\sg=H\) のうちで \(N\) に含まれるもの」であり、すなわち、
\(\mr{Ker}\:\tau=(N\cap H)\)
である。
ここで、\(\tau\) の定義である、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
に準同型定理(43A)を適用すると、
\(\begin{eqnarray}
&&\:\:N/(\mr{Ker}\:\tau) &\cong\:\mr{Im}\:\tau\\
&&\:\:N/(N\cap H) &\cong\:NH/H\\
\end{eqnarray}\)
となって、題意が成り立つ。[証明終]
第2同型定理を整数の剰余群で確認してみます。上の定理における \(G,\:H,\:N\) を、
\(G=\bs{Z}\)
\(H=10\bs{Z}\) (\(10\) の倍数)
\(N=\phantom{1}6\bs{Z}\) (\(\phantom{1}6\) の倍数)
の群とします。この群の演算は加算であり、可換群なので、\(\bs{Z}\) の部分群はすべて正規部分群です。
\(N\cap H\) は「\(10\) の倍数、かつ \(6\) の倍数」の集合なので、
\(N\cap H=30\bs{Z}\)
です。また \(NH\) は、\(10\) の倍数と\(6\) の倍数の加算の結果の集合です。つまり、
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
ですが、これが何を意味するかは不定方程式の解の存在の定理(21B)から分かります。定理を再掲すると、
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
です。\(c=kd\) なら、式を満たす \(x,\:y\) が必ず存在します。また任意の \(x,\:y\) について \(ax+by\) を計算すると、その結果の \(c\) は必ず \(c=kd\) の形になります。そうでなければ、\(c\) が最大公約数の倍数でないにも関わらず不定方程式が解をもつことになって定理に矛盾します。従って、\(ax+by=c\) の \(x,\:y\) を任意の整数とすると、\(c\) は \(a,\:b\) の "最大公約数の整数倍のすべて" になります。
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
とした場合、\(10\) と \(6\) の最大公約数は \(2\) なので、
\(NH=2\bs{Z}\)
です。この結果、
\(N/(N\cap H)\)
\(=6\bs{Z}/30\bs{Z}\)
\(=\{30\bs{Z},\:6+30\bs{Z},\:12+30\bs{Z},\:18+30\bs{Z},\:24+30\bs{Z}\}\)
\(NH/H\)
\(=2\bs{Z}/10\bs{Z}\)
\(=\{10\bs{Z},\:2+10\bs{Z},\:4+10\bs{Z},\:6+10\bs{Z},\:4+10\bs{Z}\}\)
となります。この2つの剰余群は位数 \(5\) の巡回群( \(C_5\) )で、\(\bs{Z}/5\bs{Z}\) に同型です。つまり、
| \(N/(N\cap H)\) | \(\cong\:\bs{Z}/5\bs{Z}\) | |
| \(NH/H\) | \(\cong\:\bs{Z}/5\bs{Z}\) |
\(N/(N\cap H)\:\cong\:NH/H\)
となって、第2同型定理が確認できました。
|
第2同型定理 : \(\bs{6\bs{Z}/30\bs{Z}\:\cong\:2\bs{Z}/10\bs{Z}}\) |
この図をみると、\(NH/H=2\bs{Z}/10\bs{Z}\) と \(N/(N\cap H)=6\bs{Z}/30\bs{Z}\) が同型であることがヴィジュアルにイメージできる。両方とも位数 \(5\) の巡回群である。 |
第2同型定理を数式で書くと何だか難しそうな感じがしますが、図にするといかにも自明なことという気がします。数学におけるイメージ図の威力が実感できます。
第2同型定理は、後ほど「可解群の部分群は可解群」という定理の証明に使います。「可解群の部分群は可解群」の定理は、5次方程式に可解でないものがあることを証明する際に鍵となる定理です。その第2同型定理は準同型定理を使って証明される、という構造になっているのでした。
| 5.ガロア群とガロア対応 |
2章から4章までは、多項式、体、線形空間、剰余類、群、剰余群、既約剰余類群、正規部分群といった、ガロア理論の基礎となる概念の説明でした。この第5章から、理論の核心に入っていきます。
5.1 体の同型写像
同型写像の定義
| (体の同型写像:51A) |
体 \(\bs{K}\) から 体 \(\bs{F}\) への写像 \(f\) が全単射であり、\(\bs{K}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
[証明]
上の定義による同型写像が、減法と除法を保存することを証明する。\(\bs{K}\) と \(\bs{F}\) は体だから、加法と乗法について群になっている。\(\bs{K}\) の加法の単位元を \(\kz\)、\(\bs{F}\) の加法の単位元を \(\fz\) とする。また、乗法の単位元をそれぞれ \(\ko\) と \(\fo\) とする。まず、\(f(\ko)=\fo\) で \(f(\kz)=\fz\) であることを示す。
\(f(x+y)=f(x)+f(y)\) において \(x=\kz,\:y=\kz\) とすると、
\(f(\kz+\kz)=f(\kz)+f(\kz)\)
\(f(\kz)=f(\kz)+f(\kz)\)
両辺に \(\bs{F}\) における \(f(\kz)\) の逆元 \(-f(\kz)\) を加えると、
\(f(\kz)+(-f(\kz))=f(\kz)\)
\(\fz=f(\kz)\)
となり、\(f(\kz)=\fz\) である。
\(f(xy)=f(x)f(y)\) において \(x=\ko,\:y=\ko\) とすると、
\(f(\ko\times\ko)=f(\ko)f(\ko)\)
\(f(\ko)=f(\ko)f(\ko)\)
両辺に \(\bs{F}\) における \(f(\ko)\) の逆元 \(-f(\ko)\) を加えると、
\(f(\ko)+(-f(\ko))=f(\ko)f(\ko)+(-f(\ko))\)
\(\fz=f(\ko)f(\ko)+(-f(\ko))\)
この式に現れているのは全て \(\bs{F}\) の元だから、分配則を使って、
\(f(\ko)(f(\ko)-\fo)=\fz\)
ここで \(f(\ko)=\fz\) と仮定すると、\(f(\kz)=\fz\)かつ \(f(\ko)=\fz\) となってしまい \(f\) が単射であることと矛盾する。従って \(f(\ko)\neq\fz\) である。上式の両辺を \(f(\ko)\) で割ると、
\(f(\ko)-\fo=\fz\)
\(f(\ko)=\fo\)
となる。
以上を踏まえると、同型写像が減法を保存することは次のようにしてわかる。\(\bs{K}\) は加法について群なので任意の元 \(x\in\bs{K}\) について逆元 \(-x\) がある。また \(\bs{F}\) も加法についても群だから \(f(x)\) の逆元 \(-f(x)\) がある。
\(f(-x)+f(x)=f(-x+x)=f(\kz)=\fz\)
両辺に \(-f(x)\) を足すと、
\(f(-x)+f(x)+(-f(x))=\fz+(-f(x))\)
\(f(-x)+\fz=\fz+(-f(x))\)
\(f(-x)=-f(x)\)
である。\(\bs{K}\) の任意の元を \(x,\:y\) とすると、
\(\begin{eqnarray}
&&\:\:f(x-y)&=f(x+(-y))\\
&&&=f(x)+f(-y)\\
&&&=f(x)+(-f(y))\\
&&&=f(x)-f(y)\\
\end{eqnarray}\)
となって、減法は保存されている。
除法を保存することは次のようにしてわかる。\(\bs{K}\) は乗法について群なので、任意の元 \(x\:\:(\neq\kz)\) について逆元 \(x^{-1}\) がある。\(\bs{F}\) も乗法についての群だから、\(f(x)\) の逆元である \(f(x)^{-1}\) がある。\(x\neq\kz\) なら \(f(x)\neq\fz\) なので逆元が定義できる。すると、
\(f(x^{-1})f(x)=f(x^{-1}x)=f(\ko)=\fo\)
である。この式の両辺に \(f(x)^{-1}\) をかけると、
\(f(x^{-1})f(x)f(x)^{-1}=\fo\times f(x)^{-1}\)
\(f(x^{-1})\times\fo=\fo\times f(x)^{-1}\)
\(f(x^{-1})=f(x)^{-1}\)
となる。\(\bs{K}\) の任意の元を \(x,\:y\:\:(y\neq\kz)\) とすると、
\(\begin{eqnarray}
&&\:\:f\left(\dfrac{x}{y}\right)&=f(xy^{-1})\\
&&&=f(x)f(y^{-1})\\
&&&=f(x)f(y)^{-1}\\
&&&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
となり、除法が保存されていることが分かる。
有理数の同型写像を考える。\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn\:個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)\\
&&&=n\\
\end{eqnarray}\)
なので、\(f(n)=n\) である。任意の有理数 \(a\) は、2つの整数 \(n\:(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるから、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は同型写像で不変である。[証明終]
同型写像と有理式の順序交換
| (有理式の定義:51B) |
変数 \(x\) の多項式(係数は \(\bs{Q}\) の元)を分母・分子とする分数式を、\(\bs{Q}\) 上の有理式という。
\(\bs{Q}\) 上の多項式は、有理数と \(x\) の加・減・乗算で作られる式です。一方、\(\bs{Q}\) 上の有理式とは、有理数と \(x\) の除算を含む四則演算で作られる式です。
| (同型写像と有理式の順序交換:51C) |
体 \(\bs{K}\) と 体 \(\bs{F}\) は \(\bs{Q}\) を含むものとする。\(\sg\) を \(\bs{K}\) から \(\bs{F}\) への同型写像とし、\(a\) を \(\bs{K}\) の元とする。\(f(x)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
[証明]
\(a\in\bs{K},\:b_i\in\bs{Q},\:c_i\in\bs{Q}\) とし、1変数 \((=a)\) の2次多項式の分数式の場合を例に書くと、
\(\sg\left(\dfrac{b_2a^2+b_1a+b_0}{c_2a^2+c_1a+c_0}\right)\)
\(=\dfrac{\sg(b_2a^2+b_1a+b_0)}{\sg(c_2a^2+c_1a+c_0)}\)
\(=\dfrac{b_2\sg(a^2)+b_1\sg(a)+b_0}{c_2\sg(a^2)+c_1\sg(a)+c_0}\)
\(=\dfrac{b_2\sg(a)^2+b_1\sg(a)+b_0}{c_2\sg(a)^2+c_1\sg(a)+c_0}\)
であるから、題意は成り立つ。これは \(n\)次多項式の場合でも同じである。[証明終]
「同型写像と有理式は順序交換可能」は、\(\bs{Q}\) の拡大体の上の有理式でも成り立ちます。つまり、次が成り立ちます。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
同型写像は解を共役な解に移す
| (同型写像での移り先:51D) |
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とする。\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つを \(\al\) とし、\(\al\) は \(\bs{K}\) の元とする。すると \(\sg(\al)\) も \(f(x)=0\) の解である。
[証明]
\(\al\) は \(f(x)=0\) の解なので \(f(\al)=0\) が成り立つ。すると、
\(f(\sg(\al))=\sg(f(\al))=\sg(0)=0\)
となり、\(\sg(\al)\) も \(f(x)=0\) の解である。[証明終]
同じ方程式の解同士を「共役な解」「共役である」と言います。この定理により、同型写像は解を共役な解に移すこと分かります。
同型写像は解を入れ替える
| (同型写像による解の置換:51E) |
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とし、\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。方程式 \(f(x)=0\) の \(n\)個の解を \(\al_1,\al_2,\cd,\al_n\) とし、これらが全て \(\bs{K}\) に含まれるとする。
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
[証明]
\(f(x)\) は既約多項式なので、方程式 \(f(x)=0\) は \(n\)個の解をもち、それらは全て異なる(31G)。同型写像は解を共役な解に移す(51D)ので、\(\sg(\al_i)\) も \(f(x)=0\) の解である。\(\sg\) は同型写像なので全単射であり、\(i\neq j\) なら \(\sg(\al_i)\neq\sg(\al_j)\) である。従って \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。[証明終]
同型写像を定義してその性質を述べてきましたが、あたかも「同型写像はあるのが当然」のような話でした。しかし、同型写像があったとしたらこういう性質をもつというのが正しく、同型写像が必ずあるとは証明していません。
同型写像の存在を示すには、第1章でやったように、\(\bs{Q}(\sqrt{2})\)において
\(\sg(\sqrt{2})=-\sqrt{2}\)
という写像を定義すると、体のすべての元について \(\sg\) は同型写像の定義を満たす、というような証明が必要です。それが次です。
単拡大体の同型写像の存在
| (同型写像の存在:51F) |
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(\al,\:\beta\) を方程式 \(f(x)=0\) の異なる解とする。
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
[証明]
\(\bs{Q}(\al)\) の任意の元を \(a\)、\(\bs{Q}(\beta)\) の任意の元を \(b\) とする。単拡大体の基底の定理(33F)により、\(a,\:b\) は、
\(a=a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\:\:(a_i\in\bs{Q})\)
\(b=b_{n-1}\beta^{n-1}+\:\cd\:+b_2\beta^2+b_1\beta+b_0\:\:(b_i\in\bs{Q})\)
の形に一意に表される。ここで \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への同型写像 \(\sg\) を、\(b=b_{n-1}\beta^{n-1}+\:\cd\:+b_2\beta^2+b_1\beta+b_0\:\:(b_i\in\bs{Q})\)
\(\begin{eqnarray}
&&\:\:\sg\:: &a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\\
&&&\longmapsto\:a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
と定義する。\(a=\al\) の場合は、\(a_1=1,\:a_i=0\:\:(i=0,\:2\leq i\leq n-1)\) だから、\(\sg(\al)=\beta\) である。以下、この \(\sg\) が同型写像であることを証明する。定義により(51A)同型写像であることは加法と乗法を保存することを言えばよい。
\(\bs{Q}(\al)\) の任意の2つの元を \(s,\:t\) とし、
\(s=s_{n-1}\al^{n-1}+\:\cd\:+s_2\al^2+s_1\al+s_0\)
\(t=t_{n-1}\al^{n-1}+\:\cd\:+t_2\al^2+t_1\al+t_0\)
とする。また多項式 \(g(x)\) と \(h(x)\) を、\(t=t_{n-1}\al^{n-1}+\:\cd\:+t_2\al^2+t_1\al+t_0\)
\(g(x)=s_{n-1}x^{n-1}+\:\cd\:+s_2x^2+s_1x+s_0\)
\(h(x)=t_{n-1}x^{n-1}+\:\cd\:+t_2x^2+t_1x+t_0\)
と定義する。\(s_i,t_i\in\bs{Q}\) であり、\(s=g(\al),\:t=h(\al)\) である。また \(\sg\) の定義により \(\sg(s)=g(\beta),\:\sg(t)=h(\beta)\) である。\(h(x)=t_{n-1}x^{n-1}+\:\cd\:+t_2x^2+t_1x+t_0\)
\(p(x)=g(x)+h(x)\) とおくと、
\(p(\al)=g(\al)+h(\al)=s+t\)
である。また \(\sg\)の定義により、
\(\sg(p(\al))=p(\beta)\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\sg(s+t)&=\sg(p(\al))\\
&&&=p(\beta)\\
&&&=g(\beta)+h(\beta)\\
&&&=\sg(s)+\sg(t)\\
\end{eqnarray}\)
となり、加法は保存される。
\(g(x)h(x)\) を \(f(x)\) で割ったときの商を \(q(x)\)、余りを \(r(x)\) とすると、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。この式に \(x=\al,\:x=\beta\) のそれぞれを代入すると、\(f(\al)=0,\:f(\beta)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
\(g(\beta)h(\beta)=r(\beta)\)
となる。すると、
\(\begin{eqnarray}
&&\:\:\sg(st)&=\sg(g(\al)h(\al))\\
&&&=\sg(r(\al))=r(\sg(\al))\\
&&&=r(\beta)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:\sg(s)\sg(t)&=\sg(g(\al))\sg(h(\al))\\
&&&=g(\sg(\al))h(\sg(\al))\\
&&&=g(\beta)h(\beta)\\
&&&=r(\beta)\\
\end{eqnarray}\)
であり、
\(\sg(st)=\sg(s)\sg(t)\)
となって乗法も保存されている。従って \(\sg\) は同型写像である。
逆に、\(\bs{Q}(\al)\) に作用する同型写像 \(\tau\) があったとする。同型写像は \(\al\) を共役な元に移すので、その移り先の元を \(\beta\)、つまり \(\tau(\al)=\beta\) とする。\(\bs{Q}(\al)\) の任意の元 \(a\) に \(\tau\) を作用させると、
\(\begin{eqnarray}
&&\:\:\tau(a)&=\tau(a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0)\\
&&&=a_{n-1}\tau(\al^{n-1})+\:\cd\:+a_2\tau(\al^2)+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\tau(\al)^{n-1}+\:\cd\:+a_2\tau(\al)^2+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
となるので、同型写像はこの式を満たさなければならない。従って、上で定義した \(\sg\) が \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) の唯一の同型写像である。[証明終]
同型写像の存在(51F)を一般化すると、次のことが言えます。
単拡大体の同型写像は \(n\) 個
| (単拡大体の同型写像:51G) |
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(f(x)=0\) の全ての解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\) とする。このとき \(\bs{Q}(\al)\) に作用する同型写像は \(n\)個あり、それらは、
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
同型写像を別の視点で考えます。\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{K}\) といった体の拡大列があったとき、\(\bs{F}\) の同型写像と \(\bs{K}\) の同型写像には密接な関係があります。それが次の同型写像の延長の定理です。単拡大定理(32B)により、\(\bs{F}=\bs{Q}(\al)\)、\(\bs{K}=\bs{Q}(\al,\beta)\) としてよいので、その形を使います。
同型写像の延長
| (同型写像の延長:51H) |
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
[証明]
\(\bs{Q}(\al)\) 上の \(m\)次既約多項式 \(g(x)\) を、
\(g(x)=x^m+a_1x^{m-1}+\cd+a_m\:\:(a_j\in\bs{Q}(\al))\)
とする。\(\beta\) は \(g(x)=0\) の解だから
\(g(\beta)=\beta^m+a_1\beta^{m-1}+\cd+a_m=0\)
である。また、多項式 \(\tau(g(x))\) を、
\(\tau(g(x))=x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_{m-1})x+\tau(a_m)\)
と定義し、方程式
\(\tau(g(x))=0\)
の解を \(t_j\:\:(0\leq j < m)\)とする。つまり \(\tau(g(t_j))=0\) である。
\(\bs{Q}(\al,\beta)\) は \(\bs{Q}(\al)\) 上の線形空間であり、単拡大体の基底の定理(33F)により、その基底を \(\{1,\:\beta,\:\beta^2,\:\cd\:\beta^{m-1}\}\) にとれるから、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) は、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表せる。そこで、\(\bs{Q}(\al,\beta)\) の元に作用する写像 \(\sg_j\) を
\(\sg_j(k)=\tau(b_0)+\tau(b_1)t_j+\tau(b_2)t_j^2+\cd+\tau(b_{m-1})t_j^{m-1}\)
と定義する。この定義における \(\sg_j\) は \(\bs{Q}(\al,\beta)\) の同型写像になる。同型写像になることは体の加算と乗算で示せればよい(51A)。\(\bs{Q}(\al,\beta)\) の2つの元を、
\(p=c_0+c_1\beta+c_2\beta^2\:+\cd+\:c_{m-1}\beta^{m-1}\:\:(c_j\in\:\bs{Q}(\al)\:)\)
\(q=d_0+d_1\beta+d_2\beta^2\:+\cd+\:d_{m-1}\beta^{m-1}\:\:(d_j\in\:\bs{Q}(\al)\:)\)
とし、2つの多項式を、
\(p(x)=c_0+c_1x+c_2x^2\:+\cd+\:c_{m-1}x^{m-1}\)
\(q(x)=d_0+d_1x+d_2x^2\:+\cd+\:d_{m-1}x^{m-1}\)
と定義する。加算で同型写像になるのは明白なので、乗算で同型写像になることを示す。
\(p(x)q(x)\) を \(g(x)\) で割ったときの商を \(t(x)\)、余りを \(r(x)\) とすると、
\(p(x)q(x)=t(x)g(x)+r(x)\)
と書ける。ここで \(s_j()\) は \(c_j,\:d_j\:\:(0\leq j\leq m-1)\)の有理式である。\(()\) の中を全部書くと \(s_j(c_0,c_1,\cd,c_{m-1},d_0,d_1,\cd,d_{m-1})\) という \(2m\)個の \(\bs{Q}(\al)\) の元の有理式を表わしていて、それを簡略表記している。| \(r(x)\) | \(\overset{\text{ }}{=}\) | \(s_0(c_j,d_j)+s_1(c_j,d_j)x+s_2(c_j,d_j)x^2+\cd+s_{m-1}(c_j,d_j)x^{m-1}\) |
すると \(g(\beta)=0\) だから、
| \(pq\) | \(\overset{\text{ }}{=}\) | \(p(\beta)q(\beta)\) | |
| \(\overset{\text{ }}{=}\) | \(r(\beta)\) | ||
| \(\overset{\text{ }}{=}\) | \(s_0(c_j,d_j)+\)\(s_1(c_j,d_j)\beta+\)\(s_2(c_j,d_j)\beta^2\:+\)\(\cd+\)\(s_{m-1}(c_j,d_j)\beta^{m-1}\) |
| \(\sg_j(pq)\) | \(\overset{\text{ }}{=}\) | \(\tau(s_0(c_j,d_j))+\)\(\tau(s_1(c_j,d_j))t_j+\)\(\tau(s_2(c_j,d_j))t_j^2+\)\(\cd+\)\(\tau(s_{m-1}(c_j,d_j))t_j^{m-1}\) |
\(\tau\) は \(\bs{Q}(\al)\) の同型写像だから、\(\bs{Q}(\al)\) の元の有理式である \(s_j(c_j,d_j)\) に作用させると、同型写像と有理式の順序交換の定理(51C)により、
\(\tau(s_j(c_j,d_j))=s_j(\tau(c_j),\tau(d_j))\)
となる。従って、
| \(\sg_j(pq)\) | \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))t_j\:+\)\(s_2(\tau(c_j),\tau(d_j))t_j^2+\)\(\cd+\)\(s_{m-1}(\tau(c_j),\tau(d_j))t_j^{m-1}\) |
\(p(x)\) の係数 \(c_j\) を \(\tau(c_j)\) で置き換え、\(q(x)\) の係数 \(d_j\) を \(\tau(d_j)\) で置き換えた2つの多項式を、
\(\tau(p(x))=\tau(c_0)+\tau(c_1)x+\tau(c_2)x^2+\cd+\tau(c_{m-1})x^{m-1}\)
\(\tau(q(x))=\tau(d_0)+\tau(d_1)x+\tau(d_2)x^2+\cd+\tau(d_{m-1})x^{m-1}\)
とする。
\(\tau(p(x))\tau(q(x))\)を\(\tau(g(x))\)で割ったときの商を\(\tau(t(x))\)、余りを\(\tau(r(x))\)とする。つまり、
\(\tau(p(x))\tau(q(x))=\tau(g(x))\tau(t(x))+\tau(r(x))\)
である。\(c_j\) と \(d_j\) の有理式、\(s_j(c_j,d_j)\) を使って \(\tau(r(x))\) を表すと、
| \(\tau(r(x))\) | \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))x+\)\(s_2(\tau(c_j),\tau(d_j))x^2\:+\)\(\cd+\)\(s_{m-1}(\tau(c_j),\tau(d_j))x^{m-1}\) |
| \(\sg_j(p)\) | \(\overset{\text{ }}{=}\) | \(\tau(c_0)+\)\(\tau(c_1)t_j+\)\(\tau(c_2)t_j^2+\)\(\cd+\)\(\tau(c_{m-1})t_j^{m-1}\) | |
| \(\overset{\text{ }}{=}\) | \(\tau(p(t_j))\) | ||
| \(\sg_j(q)\) | \(\overset{\text{ }}{=}\) | \(\tau(d_0)+\)\(\tau(d_1)t_j+\)\(\tau(d_2)t_j^2+\)\(\cd+\)\(\tau(d_{m-1})t_j^{m-1}\) | |
| \(\overset{\text{ }}{=}\) | \(\tau(q(t_j))\) |
\(\sg_j(p)\sg_j(q)\)
となり、\(\sg_j\) は同型写像の定義を満たしている。| \(\overset{\text{ }}{=}\) | \(\tau(p(t_j))\tau(q(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(\tau(f(t_j))\tau(t(t_j))+\tau(r(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(\tau(r(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))t_j+\)\(s_2(\tau(c_j),\tau(d_j))t_j^2+\)\(\cd+\)\(s_{n-1}(\tau(c_j),\tau(d_j))t_j^{m-1}\) | ||
| \(\overset{\text{ }}{=}\) | \(\sg_j(pq)\) |
また、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) を、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表したとき、\(k\) が \(\bs{Q}(\al)\) の元だとすると \(k=b_0\:\:(b_0\in\bs{Q}(\al))\)、\(b_j=0\:\:(1\leq j < m)\) なので、
\(\sg_j(k)=\tau(b_0)=\tau(k)\)
となり、\(\sg_j\) の \(\bs{Q}(\al)\) の元に対する作用は \(\tau\) と一致する。従って、
\(\sg_j\)は、その作用を \(\bs{Q}(\al)\) に限定したとき \(\tau\) と一致する \(\bs{Q}(\al,\beta)\) の同型写像
であり、\(\bs{Q}(\al)\) の同型写像 \(\tau\) の延長である。\(\sg_j\) の定義式、
\(\sg_j(k)=\tau(b_0)+\tau(b_1)t_j+\tau(b_2)t_j^2+\cd+\tau(b_{m-1})t_j^{m-1}\)
における \(t_j\) は、 \(\bs{Q}(\al)\) 上の \(m\)次方程式、
\(x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_m)=0\)
の解であった。従って \(t_j\) の選択肢は \(m\) 個あり、\(\bs{Q}(\al)\) の同型写像 \(\tau\) の延長は \(m\) 個ある。一方、\(\al\) は \(\bs{Q}\) 上の \(n\)次既約多項式 \(f(x)\) の解の一つだから、\(\bs{Q}(\al)\) の同型写像 \(\tau\) は \(n\)個ある。これを \(\tau_i\:\:(0\leq i < n)\) と書くと、それぞれの \(\tau_i\) に対して同型写像の拡張 \(\sg_{ij}\:\:(0\leq i < n,\:0\leq j < m)\) がある。従って \(\bs{Q}(\al,\beta)\) の 同型写像 \(\sg_{ij}\) は \(nm\)個ある。[証明終]
5.2 ガロア拡大とガロア群
ガロア拡大
| (ガロア拡大:52A) |
ガロア拡大は次のように定義される。この2つの定義は同値である。
| (最小分解体定義)体 \(\bs{F}\) 上の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とするとき、\(\bs{L}/\bs{F}\) をガロア拡大という。 | |
| (自己同型定義)体 \(\bs{F}\) の代数拡大体 \(\bs{K}\) があったとき、\(\bs{F}\) の元を不動にする \(\bs{K}\) の同型写像がすべて自己同型写像になるとき、\(\bs{K}/\bs{F}\) をガロア拡大という。 |
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
[① \(\bs{\Rightarrow}\) ②の証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。その解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{F}\) の元を不変にする \(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。
一方、\(\bs{L}\) は \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{F}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式(係数は \(\bs{F}\) の元)で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は \(\bs{F}\) の元)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させる。\(\bs{F}\) 係数の有理式と \(\bs{F}\) を不変にする同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移す(51D)から、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。
[② \(\bs{\Rightarrow}\) ①の証明]
単拡大定理(32B)により、\(\bs{K}\) は、\(\bs{K}\) の元 \(\theta\) を用いて \(\bs{K}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(f(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(f(x)\) は既約多項式である。また既約多項式の定理3(31G)により、方程式 \(f(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。
\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、\(\bs{F}\) 上の方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する。\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像は自己同型写像なので、\(\sg_i(\theta)=\theta_i\) は全て \(\bs{K}\) の元である。従って \(\bs{K}\) は \(\bs{F}\) 上の既約多項式 \(f(x)\) の解 \(\theta_i\) を用いて、
\(\begin{eqnarray}
&&\:\:\bs{K}&=\bs{F}(\theta)\\
&&&=\bs{F}(\theta_1,\:\theta_2,\:\cd,\:\theta_m)\\
\end{eqnarray}\)
と表される。\(\bs{K}\) は \(\bs{F}\) 上の既約多項式の最小分解体である。[証明終]
① の定義は、方程式の解のありようを議論するガロア理論にとっては "ノーマルな" 定義のように見えます。しかし ② のように方程式という言葉を全く使わない定義もメリットがあります。たとえば「次数が違う2つの方程式の解によるガロア拡大が同じ」ということは、いくらでもありうるからです。
また、ガロア拡大は次のような定義もできます。
| (正規拡大定義)体 \(\bs{F}\) の代数拡大体 \(\bs{K}\) があったとき、\(\bs{K}\) の任意の元の \(\bs{F}\) 上の最小多項式を \(f(x)\) とする。\(f(x)=0\) のすべての解が \(\bs{K}\) の元のとき、\(\bs{K}\) を \(\bs{F}\) の正規拡大と言う。ガロア拡大とは正規拡大のことである。 |
方程式という言葉は使っていますが、拡大体から始まる定義です。言い換えると、\(\bs{K}\) がガロア拡大体のとき \(\bs{K}\) の任意の元に共役な元は \(\bs{K}\) に含まれるということです。
このように、互いに同値である多種の定義ができることがガロア理論の分かりにくいところですが、逆に「それだけ豊かな数学的内容を含んだ理論」とも言えるでしょう。
最小分解体の次数=ガロア群の位数
| (次数と位数の同一性:52B) |
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\)、ガロア群を \(G\) とするとき、\([\:\bs{L}\::\:\bs{Q}\:]=|G|\) である。
[証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{Q}(\theta)\) と表すことができる。\(\theta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。ここで、\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{Q}\) の元を不変にするから、\(\bs{L}=\bs{Q}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。単拡大体 \(\bs{Q}(\theta)\) に作用する同型写像は \(m\)個だから(51G)、これが同型写像のすべてである。
一方、\(\bs{L}\) は \(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{Q}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は有理数)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させると、有理式と同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移すから(51D)、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。以上により、
\(\mr{Gal}(\bs{L}/\bs{Q})=\{\sg_1,\:\sg_2,\:\cd,\:\sg_m\}\)
であり、\(|G|=m\) である。
\(\theta\) の \(\bs{Q}\) 上の最小多項式(=既約多項式)の次数が \(m\) だから、単拡大体の基底の定理(33F)によって、最小分解体 \(\bs{L}=\bs{Q}(\theta)\) は \(\bs{Q}\) の \(m\)次拡大体であり、
\([\:\bs{L}\::\:\bs{Q}\:]=|G|\)
である。[証明終]
この定理では \(\bs{Q}\) としましたが、任意の代数拡大体 \(\bs{F}\) としても成り立ちます。また、最小分解体はガロア拡大体です。従って、最も一般的に言うと次のようになります。
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
中間体
| (中間体からのガロア拡大:52C) |
\(\bs{K}\) を \(\bs{F}\) のガロア拡大体とし、\(\bs{M}\) を \(\bs{F}\subset\bs{M}\subset\bs{K}\) である任意の体(=中間体)とするとき、\(\bs{K}\) は \(\bs{M}\) のガロア拡大体でもある。
[証明]
最小分解体定義による
\(\bs{K}\) が \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であるとする。この方程式の解を \(\al_1,\:\al_2,\:\cd\:\al_n\) とすると、\(\bs{K}=\bs{F}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(\bs{F}\subset\bs{M}\subset\bs{L}\) なので、
\(\bs{F}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{M}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{K}(\al_1,\:\cd\:\al_n)=\bs{K}\)
となるが、すなわち、
\(\bs{F}\:\subset\:\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\:\subset\:\bs{K}\)
であり、\(\bs{K}=\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(f(x)=0\) は \(\bs{M}\) 上の方程式でもあるので、\(\bs{K}\) は \(\bs{M}\) 上の方程式の最小分解体であり、\(\bs{M}\) のガロア拡大体である。
自己同型定義による
\(\bs{L}\) の同型写像のうち、\(\bs{M}\) の元を固定する任意の同型写像を \(\sg\) とする。そうすると \(\sg\) は \(\bs{M}\) の部分集合である \(\bs{F}\) の元も固定する。\(\bs{L}\) は \(\bs{F}\) のガロア拡大体なので、\(\bs{F}\) の元を固定する \(\bs{L}\) の同型写像は自己同型写像である。従って \(\sg\) も自己同型写像であり、\(\bs{L}\) は \(\bs{M}\) のガロア拡大体である。[証明終]
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列があったとき、\(\bs{F}\subset\bs{K}\) がガロア拡大だと上の定理(52C)によって \(\bs{M}\subset\bs{K}\) もガロア拡大です。しかし、\(\bs{F}\subset\bs{M}\) がガロア拡大になるとは限りません。\(\bs{F}\subset\bs{M}\) がガロア拡大になるためには条件が必要で、その条件が満たされば、\(\bs{F}\subset\bs{M}\subset\bs{K}\) は「ガロア拡大の連鎖」になり、そのことが方程式の可解性と結びつきます。それが次の節の大きな主題です。
5.3 ガロア対応
固定体と固定群
| (固定体と固定群:53A) |
体 \(\bs{F}\) 上の方程式の最小分解体(=ガロア拡大体)を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる。これを \(\bs{K}\) における \(H\) の固定体といい、\(\bs{K}(H)\) で表す(または \(\bs{K}^H\))。
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
[証明]
固定体と固定群の定義において、
| \(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる | |
| \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる |
の2点を証明する。
① の証明
\(\bs{M}\) が体であることを証明するには、四則演算で閉じていることを言えばよい(1.2 体)。\(\bs{M}\) の任意の2つの元を \(x,\:y\) とし、\(H\) の任意の元を \(\sg\) とする。\(x,\:y\) は \(\bs{K}\) の元でもあるから、
\(x+y\in\bs{K}\)
である。\(H\) の元 \(\sg\) は \(G\) の元でもあるから \(\sg(x+y)\) が定義できる。\(x,\:y\) は \(\bs{M}\) の元だから、\(H\) の元である \(\sg\) を作用させても不変であり、
\(\sg(x)=x\)
\(\sg(y)=y\)
である。すると、
\(\sg(x+y)=\sg(x)+\sg(y)=x+y\)
となって、\(x+y\) は \(\sg\) によって不変であり、
\(x+y\in\bs{M}\)
である。以上のことが加減乗除のすべてで成り立つことは明白だから、\(\bs{M}\) は四則演算で閉じていて、体である。
② の証明
\(\bs{M}\) の任意の元を \(x\)、\(H\) の2つの元を \(\sg,\:\tau\) とする。
\(\sg(x)=x\)
\(\tau(x)=x\)
である。すると、
\(\sg\tau(x)=\sg(\tau(x))=\sg(x)=x\)
となり、\(\sg\tau\in H\) となって、\(H\) の元は群演算で閉じている。
また \(H\) の元はもともと \(G\) の元なので、結合法則も成り立つ。\(G\) の単位元を \(e\) とすると、\(e(x)=x\) なので \(e\in H\) である。
さらに \(\sg\) は \(G\) の元なので、\(G\) の中に \(\sg^{-1}\) が存在する。すると、\(\sg(x)=x\) の両辺に左から \(\sg^{-1}\) をかけると、
\(\sg^{-1}\sg(x)=\sg^{-1}(x)\)
\(x=\sg^{-1}(x)\)
となり、
\(\sg^{-1}\in H\)
である。\(H\) は演算で閉じていて、結合法則が成り立ち、単位元と逆元が存在するので、群の定義(22A)を満たしている。[証明終]
以上の固定体と固定群の概念を用いると、次のガロア対応の定理が成り立ちます。以降の論証の基礎となる定理です。
ガロア対応の定理
| (ガロア対応:53B) |
\(\bs{F}\) のガロア拡大体を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の任意の部分群を \(H\) とし、\(H\) による \(\bs{K}\) の固定体 \(\bs{K}(H)\) を \(\bs{M}\) とする(次式)。
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
[証明]
\(G\) の任意の部分群である \(H\) は \(\bs{K}\) の部分集合 \(\bs{M}\) を固定する。一方、\(G(\bs{M})\) は \(\bs{M}\) を固定する \(G\) のすべての元の集合で、それが部分群になっている。従って、\(G(\bs{M})\) は \(H\) を含む。つまり
\(H\:\subset\:G(\bs{M})\)
であり、群位数は、
\(|H|\:\leq\:|G(\bs{M})|\)
である。 \((\br{A})\)
\(\bs{K}/\bs{F}\) はガロア拡大であり、\(\bs{M}\) はその中間体だから、中間体からのガロア拡大の定理(52C)によって、\(\bs{K}/\bs{M}\) はガロア拡大である。また、すべての代数拡大体は単拡大体だから(32B)、\(\bs{K}\) の元 \(\theta\) があって \(\bs{K}=\bs{F}(\theta)\) と表せる。これは、\(\bs{K}=\bs{M}(\theta)\) ということでもある。
\(H\) の \(|H|\) 個の元を \(\sg_i\:\:(1\leq i\leq|H|)\) とし、多項式
\(f(x)=\displaystyle\prod_{i=1}^{|H|}(x-\sg_i(\theta))\)
を考える。この多項式の次数は \(|H|\) である。\(\sg_i(\theta)\) は \(\theta\) の共役な元のどれかである。
\(f(x)\) を展開すると、その係数は \(\sg_i(\theta)\:\:(1\leq i\leq|H|)\) の対称式になる。また、\(\sg_i(\theta)\) に \(H\) の任意の元 \(\sg_k\) を作用させても、\(\sg_i\) は部分群だから演算で閉じており、\(\sg_i(\theta)\) を入れ替えるだけである(51E)。従って \(\sg_i(\theta)\) の対称式に \(\sg_k\) を作用させても不変である。つまり、\(H\) の任意の元は \(f(x)\) の係数を固定する。ということは、\(\bs{M}\) の定義(= \(H\) による \(\bs{K}\) の固定体が \(\bs{M}\))によって、\(f(x)\) の係数は \(\bs{M}\) の元である。
\(\sg_i\) は群だから単位元を含む。従って、
\(f(\theta)=\displaystyle\prod_{i=1}^{|H|}(\theta-\sg_i(\theta))=0\)
となり、\(\bs{\theta}\) は \(\bs{\bs{M}}\) 上の \(\bs{|H|}\) 次方程式 \(\bs{f(x)=0}\) の解の一つである。ゆえに \(\bs{M}\) から単拡大体 \(\bs{K}=\bs{M}(\theta)\) への拡大次数は、\(f(x)\) が \(\bs{M}\) 上の既約多項式なら単拡大体の基底の定理(33F)により \(|H|\) であり、一般には \(|H|\) 以下である。つまり、
\([\:\bs{K}\::\:\bs{M}\:]\leq|H|\)
である。次数と位数の同一性(52B)によると、拡大次数 \([\:\bs{K}\::\:\bs{M}\:]\) は、ガロア群 \(\mr{Gal}(\bs{K}/\bs{M})\) の位数に等しい。従って、
\(|\mr{Gal}(\bs{K}/\bs{M})|\leq|H|\)
\(|G(\bs{M})|\leq|H|\)
となる。\((\br{A})\) と \((\br{B})\) により、 \((\br{B})\)
\(|G(\bs{M})|=|H|\)
であり、\(G(\bs{M})\:\subset\:H\) と合わせると、
\(G(\bs{M})=H\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
である。[証明終]
証明の中に対称式という言葉が出てきます。対称式とは、
変数の任意の入れ替えで不変な多項式
です。2変数 \(x,\:y\) だと、
\(x+y,\:xy\)(ここまでが基本対称式)、\(x^2+y^2,\:\:(x-y)^2\)
などです。3変数 \(x,\:y\:,z\) だと、
\(x+y+z,\:xy+yz+zx,\:xyz\)(基本対称式)、\(((x-y)(y-z)(z-x))^2\)
などです。
対称式でよく出てくるのは、方程式の根と係数の関係です。たとえば、\(\bs{Q}\) 上の既約な3次多項式を \(f(x)\) をとし、\(f(x)=0\) の解を \(\al,\beta,\gamma\) とします。
\(\begin{eqnarray}
&&\:\:f(x)&=x^3-ax^2+bx-c\\
&&&=(x-\al)(x-\beta)(x-\gamma)\\
\end{eqnarray}\)
と書くと、
\(a=\al+\beta+\gamma\)
\(b=\al\beta+\beta\gamma+\gamma\al\)
\(c=\al\beta\gamma\)
と、係数が解の基本対称式で表現されます。
また ガロア群 \(\mr{Gal}(\bs{Q}(\al,\beta,\gamma)/\bs{Q})\) の任意の元 を \(\sg\) とします。\(\al,\beta,\gamma\) の任意の対称式を \(S(\al,\beta,\gamma)\in\bs{Q}(\al,\beta,\gamma)\) とすると、
\(\sg(S(\al,\beta,\gamma))=S(\al,\beta,\gamma)\)
です。ガロア群の元は自己同型写像であり、方程式の解を解の一つに置き換えるので、これが成り立ちます。自己同型写像を作用させて不変なのは有理数です(51A)。従って、\(S(\al,\beta,\gamma)\) は有理数です。もちろん \(f(x)\) が \(n\)次多項式であっても成り立ちます。
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列で \(\bs{F}\subset\bs{K}\) がガロア拡大のとき、\(\bs{M}\subset\bs{K}\) は自動的にガロア拡大ですが(52C)、ある条件があれば \(\bs{F}\subset\bs{M}\) もガロア拡大になって、\(\bs{F}\subset\bs{M}\subset\bs{K}\) が「ガロア拡大の連鎖」になります。その条件は「ガロア対応」と「正規部分群」の概念を用いて示されます。それが次の正規性定理です。次では \(\bs{Q}\) から始まる体の拡大列で記述しています。
正規性定理
| (正規性定理:53C) |
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とし、\(\mr{Gal}(\bs{K}/\bs{Q})=G\) とする。\(\bs{K}\) の中間体 \(\bs{M}\) と \(G\) の部分群 \(H\) がガロア対応になっているとする。このとき
| \(\bs{M}/\bs{Q}\) がガロア拡大である | |
| \(H\)が\(G\)の正規部分群である |
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) の任意の元を \(g\) とし、\(\bs{M}\) の任意の元を \(m\) とする。
\(\bs{M}\) が \(\bs{Q}\) のガロア拡大なので、\(m\) の共役な元は \(\bs{M}\) に含まれる。\(g\) は同型写像だから、\(\bs{K}\) の元を共役な元に移す(51D)。つまり、\(g\) を \(m\) に作用させると \(m\) と共役な元に移すことになり、 \(g(m)\in\bs{M}\) である。また \(g^{-1}\) も \(G\) の元だから \(g^{-1}(m)\in\bs{M}\) である。
\(H\) の任意の元を \(h\) とする。\(H\) は \(\bs{M}\) とガロア対応をしているから、\(h\) は \(\bs{M}\) の元を不動にする。ゆえに、
\(hg^{-1}(m)=g^{-1}(m)\)
である。従って、
\(ghg^{-1}(m)=gg^{-1}(m)=m\)
となり、\(ghg^{-1}\) は \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(gHg^{-1}\:\subset\:H\)
\(gH\:\subset\:Hg\)
が成り立つ。 \((\br{C})\)
また、\(g(m)\) も \(\bs{M}\) の元なので、
\(hg(m)=g(m)\)
である。従って、
\(g^{-1}hg(m)=g^{-1}g(m)=m\)
となり、\(g^{-1}hg\) も \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(g^{-1}Hg\:\subset\:H\)
\(Hg\:\subset\:gH\)
が成り立つ。\((\br{C})\) と \((\br{D})\) により、 \((\br{D})\)
\(gH=Hg\)
となって、左剰余類と右剰余類が一致するから、\(H\) は \(G\) の正規部分群である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{M}\) の任意の元を \(m\) とする。同型写像の延長の定理(51H)により、\(\bs{M}\) の同型写像 \(s\) は \(\bs{K}\) の同型写像 \(g\) に延長できる。つまり、\(g\) を \(\bs{M}\) の元に限定して作用させたとき \(g(m)=s(m)\) となる \(g\) がある。
\(H\) の任意の元を \(h\) とすると、\(h\) は正規部分群の元なので、
\(g^{-1}hg\:\in\:H\)
である。従って、
\(g^{-1}hg(m)=m\)
\(hg(m)=g(m)\)
となり、\(g(m)\) は \(H\) の任意の元で不動である。
ガロア対応の原理により \(\bs{K}(H)=\bs{M}\) なので、
\(g(m)\:\in\:\bs{M}\)
となり、\(g(m)\) は \(H\) の固定体 \(\bs{M}\) の元である。
\(\bs{M}\)の元に \(g\) を作用させるときは \(g(m)\) は \(s(m)\) そのものなので、
\(s(m)\:\in\:\bs{M}\)
となる。
以上により、\(\bs{M}\) の同型写像による \(m\) の移り先(= \(m\) と共役な元)は \(\bs{M}\) に含まれることになり、\(\bs{M}/\bs{Q}\) はガロア拡大である。[証明終]
[\(\bs{\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H}\) の証明]
同型写像の延長の定理(51H)の証明で示したように、\(\bs{M}\) の同型写像 \(s\) を \(\bs{K}\) の同型写像に延長する可能性は複数ある。\(g_1\) と \(g_2\) を \(s\) の2つの延長とし、\(\bs{M}\)の元を \(m\) とする。\(g_1,\:g_2\) は、\(\bs{M}\) に限定して適用すると \(s\) に等しいから、
\(g_1(m)=s(m)\)
\(g_2(m)=s(m)\)
が成り立つ。
\(g_1^{-1}g_2\) を \(m\) に作用させると
\(\begin{eqnarray}
&&\:\:g_1^{-1}g_2(m)&=g_1^{-1}(s(m))\\
&&&=g_1^{-1}(g_1(m))=m\\
\end{eqnarray}\)
となり、\(g_1^{-1}g_2\) は \(\bs{M}\) の元を不動にする。よって、
\(g_1^{-1}g_2\in\:H\)
\(g_2\in\:g_1H\)
である。
つまり、\(g_2\) は \(H\) の剰余類の一つの集合 \(g_1H\) に入る。以上で、\(\bs{M}\) の同型写像 \(s\) は、同型写像の延長を通して 剰余類 \(G/H\) の一つを定めることが分かる。
逆に \(g_1\) と \(g_2\) が 剰余類 \(G/H\) の同じ集合に属すると、
\(g_2\in\:g_1H\)
\(g_1^{-1}g_2\in\:H\)
\(g_1^{-1}g_2(m)=m\)
\(g_2(m)=g_1(m)\)
となり、\(g_1\) と \(g_2\) は \(\bs{M}\) 上で全く同じ作用をする。従って、\(\bs{M}\) 上で \(g_1,\:g_2\) と同じ作用をする \(\mr{Gal}(\bs{M}/\bs{Q})\) の元 \(s\) を定められる。つまり、剰余類 \(G/H\) の一つの集合が \(\mr{Gal}(\bs{M}/\bs{Q})\) の元を一つ定める。
従って、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
である。[証明終]
「5.ガロア群とガロア対応」終わり
(次回に続く)
(次回に続く)
2023-04-01 08:44
nice!(0)
No.355 - 高校数学で理解するガロア理論(2) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
「2.整数の群」「3.多項式と体」「4.一般の群」の3つの章は、第5章以下のガロア理論の核心に入るための準備です。
第2章の目的は2つあり、一つは整数を素材にして「群」と、それに関連した「剰余類」「剰余群」「既約剰余類」など、ガロア理論の理解に必要な概念を説明することです。
もう一つは、第2章の最後にある「既約剰余類群は巡回群の直積と同型である」という定理を証明することです。この定理はガロア理論の最終段階(6.可解性の必要条件)で必要なピースになります。
まず、"整数の群" に入る前に、整数論の基礎ともいえる「ユークリッドの互除法」「不定方程式」「法による演算」「中国剰余定理」から始めます。これらは後の定理の証明にしばしば使います。
2.1 整数
ユークリッドの互除法
自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,\:b)\) で表す。自然数 \(a\) を \(b\) で割った余りを \(r\) とすると、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
[証明]
記述を簡略化するため、最大公約数を、
\(\mr{gcd}(a,\:b)=x\)
\(\mr{gcd}(b,\:r)=y\)
で表す。\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とすると、
\(a=pb+r\) \((0\leq r < b)\)
と書ける。\(a\) と \(pb\) は \(x\) で割り切れるから、\(r\) も \(x\) で割り切れる。つまり \(x\) は \(r\) の約数である。\(x\) は \(b\) の約数でもあるから、\(x\) は \(b\) と \(r\) の公約数である。公約数は \(b\) と \(r\) の最大公約数 \(y\) 以下だから、
\(x\leq y\)
である。
一方、\(pb\) と \(r\) は \(y\) で割り切れるから、\(y\) は \(a\) の約数である。\(y\) は \(b\) の約数でもあるから、\(y\) は \(a\) と \(b\) の公約数である。公約数は \(a\) と \(b\) の最大公約数以下だから、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので \(x=y\)、つまり、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。[証明終]
この原理を利用して \(\mr{gcd}(a,\:b)\) を求めることができます。もし \(a\) が \(b\) で割り切れるなら \(\mr{gcd}(a,\:b)=b\) です。そうでないなら、\(a\) を \(b\) で割った余り \(r\) を求め、
新 \(a\:\longleftarrow\:b\)
新 \(b\:\longleftarrow\:r\)
と定義し直して、\(a\) が \(b\) で割り切れるかどうかを見ます。こうして次々と \(a\) と \(b\) のペアを作っていけば(=互除法)、\(b\) は単調減少していくので、いずれ \(a\) が \(b\) で割り切れるときがきます。なかなか割り切れなくても、\(b\) が \(1\) までくると絶対に割り切れる。つまり、
\(\mr{gcd}(a,\:b)=b\)
となるのが最終段階で、そのときの \(b\) が最大公約数です。\(b\) が \(1\) までになってしまったら、最大公約数は \(\bs{1}\)、つまり \(\bs{a}\) と \(\bs{b}\) は互いに素です。
ちなみに、ユークリッドの互除法で a と b の最大公約数を求める関数 EUCLID を Python で記述すると次のようになります。
% は Python の剰余演算子で、a % b は「a を b で割った余り」の意味です(定理の記述では \(r\))。つまり、このコードは、
gcd( a, b )=gcd( b, a % b )
という互除法の原理(21A)をストレートに書いたものです(a と b の大小に関係なく動作します)。こういったアルゴリズムはプログラミング言語で記述した方がシンプルでわかりやすくなります。
互除法は多項式の演算にも適用できます。多項式は整数と同じように割り算はできませんが余り算はできるからです。多項式の性質を理解するときに互除法は必須になります。
1次不定方程式
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
[証明]
1次不定方程式が整数解を持つとしたら、方程式の左辺は \(d\) で割り切れる、つまり \(d\) の倍数だから、右辺の \(c\) も \(d\) の倍数である。このことの対偶は「\(c\) が \(d\) の倍数でなければ方程式は整数解を持たない」なので、題意の「そうでなければ整数解を持たない」が証明されたことになる。従って以降は「\(c=kd\) (\(k\) は整数)と表せるなら方程式は整数解を持つ」ことを証明する。まず、変数が2つの場合である。
係数の \(a\) と \(b\) に互除法(21A)を適用し、それと同時に \(x,\:y\) の変数を変換して方程式を変形していく。まず、\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とする。
\(a=pb+r\)
である。互除法の次のステップの係数と変数を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1=b&\\
&&b_1=r&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_1=px+y&\\
&&y_1=x&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(x,\:y\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x=y_1&\\
&&y=x_1-py_1&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(\begin{eqnarray}
&&\:\:a_1x_1+b_1y_1&=b(px+y)+rx\\
&&&=pbx+by+rx\\
&&&=(pb+r)x+by\\
&&&=ax+by\\
\end{eqnarray}\)
と計算できるので、不定方程式は、
\(a_1x_1+b_1y_1=c\)
となり、係数の値がより小さい方程式に変形できる。互除法の原理(21A)により、\(a_1\) と \(b_1\) の最大公約数は \(d\) のままである。この方程式の \(x_1,\:y_1\) が求まれば、\(\br{③}\) を使って \(x,\:y\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i\) を \(b_i\) で割った商と余りを、
\(a_i=p_ib_i+r_i\)
のように求め、互除法の次のステップを、
\(a_{i+1}=b_i\)
\(b_{i+1}=r_i\)
\(x_{i+1}=p_ix_i+y_i\)
\(y_{i+1}=x_i\)
とすることで続けていける。このように、係数に互除法の適用を繰り返し、同時に変数を変換していく。そして互除法の最終段階で、
\(a_nx_n+b_ny_n=c\)
となったとする。この段階では \(a_n\) は \(b_n\) で割り切れ、そのときの \(b_n\) は最大公約数 \(d\) である。つまり。
\(a_nx_n+dy_n=c\)
である。もし \(c\) が \(d\) の倍数であれば、つまり \(c=kd\) (\(k\) は整数)なら、
\(x_n=0\)
\(y_n=k\)
という整数解を必ずもつ。従って、変数の変換過程を逆にたどって \(x,\:y\) が求まる。以上で2変数の場合に題意が正しいことが証明でき、同時に1次不定方程式の解を求めるアルゴリズムも明らかになった。
ちなみに、一次不定方程式の解の一つを求めるアルゴリズムを Python の関数で記述すると、次のようにシンプルです。
数学的帰納法を使って、3変数以上の場合を証明する。\(n=2\) の場合に成り立つことを示したので、\(n=k\) の場合に成り立つと仮定する。つまり、
と仮定する。\(n=k+1\) の場合の不定方程式を、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k+a_{k+1}x_{k+1}=c_{k+1}\)
\(\begin{eqnarray}
&&\:\: d_k&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\\
&&\:\: d_{k+1}&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k,\:a_{k+1})\\
\end{eqnarray}\)
とし、この方程式が整数解をもつ条件を調べる。方程式を移項すると、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_{k+1}-a_{k+1}x_{k+1}\)
となるが、この不定方程式が整数解をもつのは、数学的帰納法の仮定によって、
左辺\(=d_k\) の整数倍
のときである。つまり、
\(c_{k+1}-a_{k+1}x_{k+1}=d_k\cdot y\)
という、2つの変数 \(x_{k+1},\:y\) の不定方程式が整数解をもつときである。式を移項すると、
\(a_{k+1}x_{k+1}+d_k\cdot y=c_{k+1}\)
であるが、これは証明済みの \(n=2\) のときの定理によって、
\(c_{k+1}=m\cdot\mr{gcd}(d_k,\:a_{k+1})\) (\(m\) は整数)
の場合に整数解をもつ。ここで、
\(\mr{gcd}(d_k,\:a_{k+1})=d_{k+1}\)
なので、
\(c_{k+1}=m\cdot d_{k+1}\) (\(m\) は整数)
の場合にのみ、\(n=k+1\) の不定方程式は整数解をもつことになる。
つまり、\(n=k\) のときに題意が成り立つと仮定すると、\(n=k+1\) のときにも成り立つ。\(n=2\) のときには成り立つから、\(n\geq3\) でも成り立つ。[証明終]
重要なのは、係数が互いに素な場合です。不定方程式の解の存在(21B)から、次の定理がすぐに出てきます。
\(0\) でない整数 \(a\) と \(b\) が互いに素とすると、1次不定方程式、
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) の最大公約数が \(1\)、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
互除法と同じように、不定方程式の解の存在定理 (21B)と(21C)も、多項式の性質を理解する上で重要です。
法による演算
\(a,\:b\) を整数、\(n\) を自然数とする。\(a\) を \(n\) で割った余りと、\(b\) を \(n\) で割った余りが等しいとき、
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
法による演算の規則は、さまざまありますが、主なものは次の通りです。このような演算を以降の説明で適時使います。
\(a,\:b,\:c,\:d\) を整数、\(n,r\) を自然数とし、
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
である。
中国剰余定理
\(n_1\) と \(n_2\) を互いに素な自然数とする。\(a_1\) と \(a_2\) を、\(0\leq a_1 < n_1,\:0\leq a_2 < n_2\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
[証明]
もし \(x\) と \(y\:\:(y\leq x)\) が連立方程式を満たすとすると、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(y\equiv a_1\:\:(\mr{mod}\:n_1)\)
なので、
\(x-y\equiv0\:\:(\mr{mod}\:n_1)\)
であり、\(x-y\) は \(n_1\) で割り切れる。同様にして \(x-y\) は \(n_2\) でも割り切れる。\(n_1\) と \(n_2\) は互いに素なので、\(x-y\) は \(n_1n_2\) で割り切れる。従って \(x-y\) は \(n_1n_2\) の倍数であり、
である。従って連立方程式に解があるとしたら \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり \(0\leq x < n_1n_2\) の範囲で唯一に決まる。
\(n_1,\:n_2\) は互いに素なので、不定方程式の解の存在定理(21C)により、
\(n_1m_1+n_2m_2=1\)
を満たす \(m_1,\:m_2\) が存在する。ここで、
\(x=a_2n_1m_1+a_1n_2m_2\)
とおくと、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2n_1m_1+a_1(1-n_1m_1)\\
&&&=a_1+n_1m_1(a_2-a_1)\\
&&&\equiv a_1\:\:(\mr{mod}\:n_1)\\
\end{eqnarray}\)
であり、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2(1-n_2m_2)+a_1n_2m_2\\
&&&=a_2+n_2m_2(a_1-a_2)\\
&&&\equiv a_2\:\:(\mr{mod}\:n_2)\\
\end{eqnarray}\)
なので、\(x\) は連立方程式の解である。この解は、上での証明のとおり \(\mr{mod}\:n_1n_2\) でみて唯一である。[証明終]
中国剰余定理は3数以上に拡張できて、次が成り立ちます。
\(n_1,\:n_2,\:\cd\:,\:n_k\) を、どの2つをとっても互いに素な自然数とする。\(a_i\) を \(0\leq a_i < n_i\:\:(1\leq i\leq k)\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
[証明]
自然数 \(N\) を
\(N=n_1n_2\cd n_k\)
と定義する。
\(\mr{gcd}\left(\dfrac{N}{n_i},n_i\right)=1\:\:\:(1\leq i\leq k)\)
なので、不定方程式の解の存在の定理(21C)により、
\(\dfrac{N}{n_i}s_i+n_it_i=1\:\:\:(1\leq i\leq k)\)
を満たす整数解、\(s_i,\:t_i\:\:(1\leq i\leq k)\) が存在する。
\(x=\displaystyle\sum_{i=1}^{k}a_i\dfrac{N}{n_i}s_i\)
と定義すると、\(j\neq i\) である \(j\) について、
\(\dfrac{N}{n_j}\equiv0\:\:(\mr{mod}\:n_i)\)
だから、\(\mr{mod}\:n_i\) でみると、\(x\) を定義する総和記号のなかは \(i\) の項だけが残る。つまり、
\(\begin{eqnarray}
&&\:\:x&\equiv a_i\dfrac{N}{n_i}s_i\:\:(\mr{mod}\:n_i)\\
&&&=a_i(1-n_it_i)\\
&&&\equiv a_i\:\:(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となって、\(x\) は連立合同方程式の解である。
連立合同方程式に2つの解、\(x,\:y\) があったとすると、
\(\begin{eqnarray}
&&\:\:x-y&\equiv a_i-a_i &(\mr{mod}\:n_i)\\
&&&=0 &(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となり、\(x-y\) は \(n_i\) の倍数である。これは \(1\leq i\leq k\) のすべての \(i\) で成り立ち、また \(n_i\:\:(1\leq i\leq k)\) は、どの2つをとっても互いに素である(=共通な因数が全くない)から、\(x-y\) は \(N\) の倍数である。従って、
\(x\equiv y\:\:(\mr{mod}\:N)\)
であり、\(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。[証明終]
2.2 群
これ以降、整数を素材に「群」と、それに関連した概念の説明をします。まず、群の定義からです。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群(group)であると言う。
整数 \(\bs{Z}\)
整数の集合を \(\bs{Z}\) と書きます。\(\bs{Z}\) は「加法(足し算)を演算とする群」になります。単位元は \(0\) で、元 \(x\) の逆元は \(-x\) です。この群の元の数は無限なので「無限群」です。
整数の加法は、\(x+y=y+x\) と演算の順序を入れ替えることができます。このような群が可換群です。アーベル群とも言います。
なお、有理数は \(\bs{Q}\)、実数は \(\bs{R}\)、複素数は \(\bs{C}\) で表しますが、\(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) は、\(\bs{Z}\) を同じように加法に関して群です(=加法群)。と同時に \(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) から加法の単位元 \(0\) を除くと、乗法に関しても群になります。その単位元は \(1\) です。
部分群 \(n\bs{Z}\)
群 \(G\) の部分集合 \(H\) が、\(G\) と同じ演算で群としての定義を満たすとき、\(H\) を部分群(subgroup)と言います。
\(G\) の単位元 \(e\) だけから成る部分集合 \(\{\:e\:\}\) は群としての定義を満たし、部分群です。また \(G\) そのものも "\(G\)の部分集合" であり、部分群です。これらを \(G\) の自明な部分群と言います。
\(\bs{Z}\) の元の一つを \(n\) とし(\(n\neq0\))、\(n\) の倍数の集合を \(n\bs{Z}\) と表記します。\(n\bs{Z}\) は加法を演算として群の定義を満たすので、\(\bs{Z}\) の部分群です。\(n\bs{Z}\) も無限群かつ可換群です。たとえば \(n=6\) とすると、
\(6\bs{Z}=\{\cd,\:-6,\:0,\:6,\:12,\:18,\:\cd\}\)
です。
剰余類と剰余群
部分群を用いて、元の数が有限個である有限群を作ることができます。一般に、群 \(G\) の部分群を \(H\) とするとき(演算を "\(\cdot\)" とします)、\(G\) の任意の元 \(g\) を取り出して、
\(g\cdot H\)
とした集合を剰余類(coset / residue class)と言います。これは「\(g\) と、集合 \(H\) のすべての元を演算した結果の集合」の意味です。
\(\bs{Z}\) と その部分群 \(6\bs{Z}\) を例にとると、\(\bs{Z}\) の任意の元を \(i\) として、
\(i+6\bs{Z}\)
が剰余類です。具体的にその集合を書くと、
\(\vdots\)
\(0+6\bs{Z}=\{\cd,\:-6,\:\:0,\:\phantom{1}6,\:12,\:18,\:\cd\}\)
\(1+6\bs{Z}=\{\cd,\:-5,\:\:1,\:\phantom{1}7,\:13,\:19,\:\cd\}\)
\(2+6\bs{Z}=\{\cd,\:-4,\:\:2,\:\phantom{1}8,\:14,\:20,\:\cd\}\)
\(3+6\bs{Z}=\{\cd,\:-3,\:\:3,\:\phantom{1}9,\:15,\:21,\:\cd\}\)
\(4+6\bs{Z}=\{\cd,\:-2,\:\:4,\:10,\:16,\:22,\:\cd\}\)
\(5+6\bs{Z}=\{\cd,\:-1,\:\:5,\:11,\:17,\:23,\:\cd\}\)
\(6+6\bs{Z}=\{\cd,\:\phantom{-}0,\:\:6,\:12,\:18,\:24,\:\cd\}\)
\(7+6\bs{Z}=\{\cd,\:\phantom{-}1,\:\:7,\:13,\:19,\:25,\:\cd\}\)
\(\vdots\)
などです。以降、剰余類 \(i+6\bs{Z}\) を \(\ol{\,i\,}\) と記述します。つまり、
\(\ol{\,i\,}=i+6\bs{Z}\)
です。上の表示を見ると分かるように、たとえば \(\ol{\,1\,}\) と \(\ol{\,7\,}\) は集合として同じものです。さらに、
\(\cd=\ol{-11}=\ol{-5}=\ol{\,1\,}=\ol{\,7\,}=\ol{13}=\cd\)
であり、これらは同じ集合です。これらの集合の中から一つの元を選んで「代表元」と呼ぶことにします。以降、分かりやすいように \(1\) を代表元とします。その他の剰余類についても同じようにすると、部分群 \(6\bs{Z}\) による剰余類は、
\(\ol{\,0\,},\:\ol{\,1\,},\:\ol{\,2\,},\:\ol{\,3\,},\:\ol{\,4\,},\:\ol{\,5\,}\)
の6つで表されることになります。これらの剰余類には重複がありません。また、全部の和集合をとると \(\bs{Z}\) になります。記号で書くと、\(\phi\) を空集合として、
\(\ol{\,i\,}\:\cap\:\ol{\,j\,}\:=\:\phi\:\:(0\leq i,\:j\leq6,\:i\neq j)\)
\(\bs{Z}=\ol{\,0\,}\:\cup\:\ol{\,1\,}\:\cup\:\ol{\,2\,}\:\cup\:\ol{\,3\,}\:\cup\:\ol{\,4\,}\:\cup\:\ol{\,5\,}\)
です。別の見方をすると、\(i,\:j\) を任意の整数するとき、
と言えます。平たく言うと、\(n\)(上の例では \(6\))で割った余りが同じ整数を集めたものが剰余類です。"剰余" という用語はそこからきています。
剰余類のうち、\(\ol{\,0\,}\) は \(\bs{Z}\) の部分群ですが、\(\ol{\,i\,}\:(i\neq0)\) の集合は \(\bs{Z}\) の部分群ではありません。集合の元と元のたし算が集合を "はみ出す" からです。しかし、剰余類同士の演算(=集合と集合の演算)を定義することにより、剰余類を元とする群を構成できます。それが次です。
剰余類に加算を定義できます。つまり、\(\ol{\,i\,}+\ol{\,j\,}\) を、
\(\ol{\,i\,}+\ol{\,j\,}=\ol{(\:i+j\:)}\) (右辺の \(+\) は整数の加算)
と定義すると、この演算の定義で剰余類は群になり、
\(\bs{Z}/n\bs{Z}\)
と表します。この群の元は集合(=剰余類)です。この群を剰余群(あるいは商群。quotient group)と言います。元の数は有限なので有限群です。また演算が整数の加算なので可換であり、「有限可換群」です。
一般に、有限群 \(G\) の元の数を群の位数(order)と呼び、
\(|G|\) あるいは \(\#G\)
で表します。剰余群では、
です。
生成元と巡回群
剰余群 \(\bs{Z}/n\bs{Z}\) は、元 \(\ol{\,1\,}\) だけをもとに群演算を繰り返すことによって、すべての元を作り出すことができます。\(\bs{Z}/6\bs{Z}\) を例にとると、
\(\ol{\,2\,}=\ol{\,1\,}+\ol{\,1\,}\)
\(\ol{\,3\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
などであり
\(\ol{\,0\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
です。群にこのような元がある場合、それを生成元(generator)と呼びます。\(\bs{Z}/6\bs{Z}\) の場合は \(\ol{\,1\,}\) のほかに \(\ol{\,5\,}\) も生成元です。\(\ol{\,i\,}\) を \(k\) 個加算することを、\(k\cdot\ol{\,i\,}\) と書くことにします。
\(k\cdot\ol{\,i\,}=\overbrace{\ol{\,i\,}+\ol{\,i\,}+\cd+\ol{\,i\,}}^{k\:個加算}\)
です。\(\ol{\,5\,}\) については、
\(1\cdot\ol{\,5\,}=\ol{\,5\,},\:\:2\cdot\ol{\,5\,}=\ol{\,4\,},\:\:3\cdot\ol{\,5\,}=\ol{\,3\,}\)
\(4\cdot\ol{\,5\,}=\ol{\,2\,},\:\:5\cdot\ol{\,5\,}=\ol{\,1\,},\:\:6\cdot\ol{\,5\,}=\ol{\,0\,}\)
のように、\(\ol{\,5\,}\) を起点として全部の元が生成され、\(\ol{\,5\,}\) が生成元であることがわかります。
剰余群 \(\bs{Z}/n\bs{Z}\) においては、\(1\leq g < n\) である整数 \(g\) が \(n\) と互いに素であるとき、\(\ol{\,g\,}\) は生成元になります。その理由ですが、
\(i\cdot\ol{\,g\,}=j\cdot\ol{\,g\,}\)
だとすると、これは、法 \(n\) における整数の合同式で、
\(ig\equiv jg\:\:(\mr{mod}\:n)\)
を意味します。つまり、
\((j-i)g\equiv0\:\:(\mr{mod}\:n)\)
ですが、\(g\) が \(n\) と互いに素なため、\((j-i)\) は \(n\) で割り切れなければなりません。しかし \(1\leq(j-i)\leq(n-1)\) なので、矛盾します。従って、\(n\) 個の剰余類の列 \((\br{A})\) は、全て違ったものです。剰余群 \(\bs{Z}/n\bs{Z}\) の群位数は \(n\) なので、\((\br{A})\) は \(\bs{Z}/n\bs{Z}\) の全ての元であり、従って \(\ol{\,g\,}\) は生成元です。
\(n\) が素数 \(p\) の場合は、\(p\) 未満の自然数はすべて \(p\) と互いに素なので、単位元 \(\ol{\,0\,}\) を除く \(\bs{Z}/p\bs{Z}\) の元が生成元になります。
\(k\) 個の \(\ol{\,i\,}\) の群演算をして初めて、結果が単位元 \(\ol{\,0\,}\) になるときの \(k\) を、\(\ol{\,i\,}\) の位数(order)といいます。群の位数と紛らわしいですが、これは群の「元の位数」です。\(\bs{Z}/6\bs{Z}\) の場合、「元 \(\rightarrow\) 位数」の対応は、
\(\ol{\,0\,}\:\rightarrow\:1,\:\:\ol{\,1\,}\:\rightarrow\:6,\:\:\ol{\,2\,}\:\rightarrow\:3\)
\(\ol{\,3\,}\:\rightarrow\:2,\:\:\ol{\,4\,}\:\rightarrow\:3,\:\:\ol{\,5\,}\:\rightarrow\:6\)
です。位数という用語を使うと、生成元とは「位数が群位数に等しい元」のことです。
群 \(G\) が一つの生成元から生成されるとき、\(G\) を巡回群(cyclic group)と言います。\(\bs{Z}/10\bs{Z}\) の例をとると、\(10\) と互いに素な数を考えて、生成元は \(\ol{\,1\,},\:\ol{\,3\,},\:\ol{\,7\,},\:\ol{\,9\,}\) の4つです。従って、たとえば \(\ol{\,7\,}\) 同士の加算を繰り返すと、
というように、\(\bs{Z}/10\bs{Z}\) の全ての元が現れたあとに再び \(\ol{\,7\,}\) に戻って "巡回" します。"巡回" 群と呼ばれるゆえんです。
群の直積
\(G,\:H\) を群とします。\(G\) の任意の元 \(g\) と \(H\) の任意の元 \(h\) のペア \((g,\:h)\) 作り、このペアを元とする集合を考えます。以降、群の演算を表す "\(\cdot\)" を省略します。
集合の任意2つの元を、
\(a=(g_a,\:h_a)\)
\(b=(g_b,\:h_b)\)
とし、\(a\) と \(b\) の演算を、
\(ab=(g_ag_b,\:h_ah_b)\)
で定義すると、この集合は群となります。この群を \(G\) と \(H\) の直積といい、
\(G\times H\)
で表します。有限群の場合、群の位数は、
\(|G\times H|=|G|\cdot|H|\) (\(\cdot\) は整数のかけ算)
です。以上は2つの群の直積ですが、同様に3つ以上の群の直積も定義できます。
群の同型
\(G\) と \(H\) を群とします。\(G\) から \(H\) への1対1の写像 \(f\) で、\(G\) の任意の2つの元 \(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つ写像があるとき、\(G\) と \(H\) は「同型である」といい、
\(G\cong H\)
と表します。同型であるということは、2つの群の元が1対1対応するのみならず、元の演算前、演算後も1対1対応していることを意味します。従って同型である群は「同じもの」と見なせます。
\(\bs{Z}/15\bs{Z}\) で群の同型の例を示します。ここでは、整数 \(i\) を 整数 \(a\) で割った余りを \(i_a\) と書きます。\(\bs{Z}/15\bs{Z}\) の任意の元 \(i\:\:(0\leq i\leq14)\) について、写像 \(f\) を、
\(f\::\:i\:\longmapsto\:(i_3,\:i_5)\)
で定めると、\(f\) は \(\bs{Z}/15\bs{Z}\) から \((\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\) への同型写像になります。
そのことを確かめると、まず \(i\) を決めれば \(i_3,\:i_5\) は一意に決まります。また\(i_3,\:i_5\) を決めると、\(3\) と \(5\) は互いに素なので、中国剰余定理(21F)により、\(0\leq i\leq14\) の範囲で \(i\) が一意に決まります。つまり \(f\) は1対1写像(数学用語で "全単射")です。また、2つの元 \(i,\:j\) について
\(\begin{eqnarray}
&&\:\:f(i+j)&=(\:(i+j)_3,\:(i+j)_5\:)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i)+f(j)&=(i_3,\:i_5)+(j_3,\:j_5)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i+j)&=f(i)+f(j)\\
\end{eqnarray}\)
が成り立つので、\(f\) は同型写像の要件を満たします。従って、
\(\bs{Z}/15\bs{Z}\cong(\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\)
です。一般に、\(a\) と \(b\) を互いに素な自然数とすると、
\(\bs{Z}/(ab)\bs{Z}\cong(\bs{Z}/a\bs{Z})\times(\bs{Z}/b\bs{Z})\)
です。これは2つの数だけでなく、\(n\) が \(k\)個の数 \(a_1,\:a_2,\:\cd\:a_k\) の積で表され、かつ、\(a_1,\:a_2,\:\cd\:a_k\) のどの2つをとっても互いに素なときには、中国剰余定理・多連立(21G)によって、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/a_1\bs{Z})\times(\bs{Z}/a_2\bs{Z})\times\cd\times(\bs{Z}/a_k\bs{Z})\)
が成り立ちます。一般に 自然数 \(n\) は \(p_i\) を素数として、
\(n=p_1^{n_1}p_2^{n_2}\cd p_k^{n_k}\)
と素因数分解され、\(p_i^{n_i}\:\:(1\leq i\leq k)\) はどの2つをとっても互いに素なので、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/p_1^{n_1}\bs{Z})\times(\bs{Z}/p_2^{n_2}\bs{Z})\times\cd\times(\bs{Z}/p_k^{n_k}\bs{Z})\)
成り立ちます。
2.3 既約剰余類群
2.2 節の剰余群は、整数の加算を演算の定義とする群でした。これに対して、整数の乗算を演算の定義とする群が構成できます。それが既約剰余類群です。
剰余群 \(\bs{Z}/n\bs{Z}\) から、代表元が \(n\) と互いに素なものだけを選び出したものを既約剰余類という。
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
[証明]
「既約剰余類」は、乗算に関して群になることを証明する。まず例をあげると、\((\bs{Z}/10\bs{Z})^{*}\) の元は \(10\) と互いに素な代表元をもつ \(1,\:3,\:7,\:9\) である。この元の乗算による演算表を作ると、
となって、演算は閉じていて、単元 \(1\) があり、逆元があることがわかる( \(3^{-1}=7,\:7^{-1}=3,\:9^{-1}=9\) である\()\)。つまり群として成り立っている。
一般に、\(a,\:b\) が \(n\) と素だとすると、\(ab\) も \(n\) と素なので、\((\bs{Z}/n\bs{Z})^{*}\) は乗算で閉じている。また、不定方程式の解の存在定理(21C)により、
\(ax+ny=1\)
を満たす \(x,\:y\) が存在する。この式の両辺を \(\mr{mod}\:n\) でみると、
\(ax\equiv1\:\:(\mr{mod}\:n)\)
となる。この方程式の解の一つ(=特殊解)を \(x_0\) とし、\(k\) を整数として、\(x=x_0+kn\) とおくと\(,\)
\(\begin{eqnarray}
&&\:\:ax&=a(x_0+kn)\\
&&&=ax_0+akn\\
&&&\equiv1\:\:(\mr{mod}\:n)\\
\end{eqnarray}\)
なので、\(x\) も解である。従って解を \(1\leq x < n\) の範囲で選ぶことができる。つまり、\((\bs{Z}/n\bs{Z})^{*}\) の元 \(a\) に対して逆元が定義できることになり、\((\bs{Z}/n\bs{Z})^{*}\) は群である。[証明終]
2.4 有限体 \(\bs{F}_p\)
\(\bs{Z}/p\bs{Z}\) は体
剰余群 \(\bs{Z}/n\bs{Z}\) において \(n\) が素数 \(p\) である \(\bs{Z}/p\bs{Z}\) を考えます。\(p\) 未満の自然数は \(p\) と互いに素なので、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は、\(\bs{Z}/p\bs{Z}\) から 加法の単位元 \(0\) を除いたものになります。つまり \(\bs{Z}/p\bs{Z}\) は加法について群であり、\(\bs{Z}/p\bs{Z}\:-\:\{\:0\:\}\) が乗法について群になっている。このような集合を体(field)と言います。
体とは加減乗除ができて、加法と乗法を結びつける分配則、
\(a(b+c)=ab+ac\)
が成り立つ集合です。\(\bs{Z}/p\bs{Z}\) は整数の演算をもとに定義されているので分配則が成り立ちます。
\(\bs{\bs{Z}/p\bs{Z}}\) を体としてみるとき、\(\bs{\bs{F}_p}\) と表記します。有理数 \(\bs{Q}\)、実数 \(\bs{R}\)、複素数 \(\bs{C}\) は体ですが、これらは無限集合です。一方、\(\bs{F}_p\) は有限集合なので有限体です。
有限体 \(\bs{F}_p\) における定数、変数、多項式、方程式の計算は、有理数/実数/複素数と同じようにできます。以下、今後の証明に使うので、\(\bs{F}_p\) 上の多項式と方程式を説明します。つまり、係数が \(\bs{F}_p\) の数である多項式や方程式です。
有限体の多項式と方程式
\(\bs{F}_p\) 上の多項式は、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:\:(a_i\in\bs{F}_p)\)
です。見た目は整数係数の多項式ですが、係数は \(\bs{F}_p\) の元です。\(\bs{F}_p\) は体なので、\(\bs{F}_p\) 上の多項式は加減算\(\cdot\)乗算\(\cdot\)余りをともなう除算(=剰余算、余り算)が、\(\bs{Q}\) 上の多項式と同じようにできます。従ってこれらの演算にもとづいた概念、定理は、\(\bs{Q}\) 上の多項式の場合と同じです。つまり、
などです(なお、多項式\(\cdot\)方程式についてのこれらの概念や定理は「3.1 多項式」で説明します)。
たとえば、\(\bs{F}_5\) における多項式、\(x^2+1\) は、
\(x^2+1=(x-2)(x-3)\) [\(\bs{F}_5\)]
と、2つの1次多項式に因数分解できます。
\(\begin{eqnarray}
&&\:\:(x-2)(x-3)&=x^2-5x+6\\
&&&=x^2+1\\
\end{eqnarray}\)
が成り立つからです。従って、方程式、
\(x^2+1=0\) [\(\bs{F}_5\)]
の解は、\(x=2,\:3\) です。
一方、\(\bs{F}_7\) において \(x^2+1\) はこれ以上因数分解できない多項式です。なぜなら、
\(f(x)=x^2+1\) [\(\bs{F}_7\)]
とおくと、
\(f(k)\neq0\:\:(0\leq k\leq6)\) [\(\bs{F}_7\)]
だからです。もちろん剰余算(余り算)はできて、\(x^2+1\) を \(x-2\) で割ると、
\(x^2+1=(x-2)(x+2)+5\) [\(\bs{F}_7\)]
と計算できます。これは \(f(2)=5\)、つまり \(f(x)\) を \(x-2\) で割った余りは \(5\)、を意味します。
以上を踏まえて、\(\bs{F}_p\) 上の多項式\(\cdot\)方程式に関する次の定理を証明します(次節の定理の証明に使います)。方程式の "解" は "\(\bs{F}_p\) における解" の意味です。
\(\bs{F}_p\) 上の1次方程式、
\(ax+b=c\)
は1個の解をもつ。
[証明]
両辺に \(b\) の加法の逆元 \(-b\) を加えると、
\(ax=c+(-b)\)
となり、この両辺に 乗法の逆元 \(a^{-1}\) を掛けると、
\(x=a^{-1}(c+(-b))\)
となり、唯一の解が求まる。[証明終]
\(\bs{F}_p\) 上の多項式を \(f(x)\) とする。
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
[証明]
\(f(x)\) を \(x-a\) で割った商を \(g(x)\)、余りを \(b\) とする。
\(f(x)=(x-a)g(x)+b\)
であるが、\(f(a)=0\) なので \(b=0\) である。従って、
\(f(x)=(x-a)g(x)\)
と表され、\(f(x)\) は \(x-a\) で割り切れる。[証明終]
\(\bs{F}_p\) 上の \(n\)次多項式を \(f_n(x)\) とする。方程式、
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
[証明]
\(n\) に関する数学的帰納法を使う。\(\bs{F}_p\) 上 の1次方程式の解は1個だから(24A)、題意は成り立つ。\(n\) 以下で題意が成り立つと仮定する。
\(\bs{F}_p\) 上の \(n+1\) 次方程式 \(f_{n+1}(x)=0\) の解がなければ、\(n+1\) でも題意は成り立っている。もし1個の解 \(a\) があるとすると\(f_{n+1}(a)=0\) なので、\(f_{n+1}(x)\) は \(x-a\) で割り切れる(24B)。つまり、
\(f_{n+1}(x)=(x-a)g(x)\)
となるが、\(g(x)\) は \(n\)次多項式だから、方程式、
\(g(x)=0\)
の解は高々 \(n\) 個である。従って、\(f_{n+1}(x)=0\) の解は高々 \(n+1\) 個である。ゆえに帰納法により題意は正しい。[証明終]
2.5 既約剰余類群は巡回群
2.5 節の目的は、2章の最終目的である、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
という定理を証明することです。証明には少々長いステップが必要ですが、この定理はガロア理論の最終段階で必要になります。まず、群の「元の位数」の性質から始めます。
位数
\((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とする。以下が成り立つ。
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
[証明]
[補題1]
\((\bs{Z}/n\bs{Z})^{*}\) は有限群だから、\(a^j=a^i\:\:(i < j)\) となる \(i,\:j\) は必ず存在する。\(a^{-i}\) を両辺に掛けると \(a^{j-i}=1\) となり\(a^x=1\) となる \(x\) が必ず存在する。従って \(a\) の位数が定義できる。
[補題2]
\(a^j=a^i\:\:(1\leq i < j\leq d)\) となる \(i,\:j\) があったとすると、両辺に \(a^{-1}\) を掛けて \(a^{j-i}=1\) となるが、\(j-i < d\) だから、\(a^x=1\) となる最小の \(x\) が \(d\) ということと矛盾する。従って、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。
[補題3]
\(a^i\:\:(1\leq i\leq d)\) を \(d\) 乗すると、
\((a^i)^d=(a^d)^i=1\)
であり、これら \(d\) 個の元はすべて \(d\) 乗すると \(1\) になる。
一方、\(d\) 乗すると \(1\) になる 元は 有限体 \(\bs{F}_p\) 上の \(d\) 次方程式 \(x^d-1=0\) の解であるが、有限体上の方程式3の定理(24C)により、\(d\) 次方程式の解の数は高々 \(d\) 個である。従って、\(a^i\:\:(1\leq i\leq d)\) の \(d\) 個の元は、\(d\) 乗すると \(1\) になる 元のすべてである。
[補題4]
\(x\) を \(d\) で割った商を \(q\:\:(1\leq q)\)、余りを \(r\:\:(0\leq r < d)\)とすると、
\(\begin{eqnarray}
&&\:\:a^{qd+r}&=1\\
&&\:\:(a^d)^q\cdot a^r&=1\\
&&\:\:a^r=1&\\
\end{eqnarray}\)
となるが、もし \(r\neq0\) なら、\(d\) より小さい数 \(r\) で \(a^r=1\) となり、これは \(a\) の位数が \(d\) であることと矛盾する。従って \(r=0\) であり、\(x\) は \(d\) の倍数である。
[補題5]
\((\bs{Z}/n\bs{Z})^{*}\) を \(G\) と書く。集合 \(A\) を、
\(A=\{a,\:a^2,\:\cd\:,\:a^d=1\}\)
とする。もし \(|G|=d\) なら、題意は満たされている。
\(d < |G|\) の場合、\(A\) に含まれない \(G\) の元の一つを \(b_1\) とし、
\(A_1=\{b_1a,\:b_1a^2,\:\cd\:,\:b_1a^d\}\)
とする。この \(A_1\) に \(A\) と共通な元はない。なぜならもし、
\(a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-j}\) をかけて、
\(a^{i-j}=b_1\)
となるが、左辺は \(A\) の元であり、右辺の \(b_1\) が \(A\) の元となって矛盾するからである。もし \(A\) と \(A_1\) で \(G\) の元を尽くしているなら、\(|G|=2d\) であり、題意は満たされている。
そうでない場合、\(A\) と \(A_1\) に含まれない \(G\) の元の一つを \(b_2\) とし、
\(A_2=\{b_2a,\:b_2a^2,\:\cd\:,\:b_2a^d\}\)
とする。上の論理と同じで \(A_2\) と \(A\) に共通な元はない。のみならず、\(A_2\) と \(A_1\) に共通な元もない。なぜなら、もし、
\(b_2a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-i}\) をかけて、
\(b_2=b_1a^{j-i}\)
となるが、\(a^{j-i}\) は \(A\) の元だから、\(b_1a^{j-i}\) は \(A_1\) の元であり、\(b_2\) が \(A_1\) の元ということになって矛盾するからである。もし \(A,\:A_1,\:A_2\) で \(G\) の元を尽くしているなら、\(|G|=3d\) であり、題意は満たされている。
そうでない場合、この操作を続けていくと、\(G\) は有限群だから、ちょうど \(G\) の元が尽くされたところで、操作は止まる。最後に作った部分集合が \(A_n\) だったとすると \(|G|=(1+n)d\) であり、\(a\) の位数 \(d\) は群位数の約数である。
\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) なので(23A)、位数の定理(25A)の[補題5]から、次のフェルマの小定理とオイラーの定理が成り立つことがわかります。
自然数 \(n\) と素な自然数 \(a\) について、
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
生成元の存在1
\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在し、従って巡回群であることを証明します。まず、特定の位数 \(d\) をもつ元の数に関する定理からです。
\(p\) を素数とする。\((\bs{Z}/p\bs{Z})^{*}\) において、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。
[証明]
[補題1]により、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元に位数が定義できる。その位数は[補題5]により、群位数 \((p-1)\) の約数である。
\((p-1)\) の任意の約数を \(d\) とし、位数 \(d\) の元 \(a\) があったとする。[補題3]により、\(d\)乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d(=1)\)
の「\(a\) 系列」がそのすべてである。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は、\(d\)乗すると \(1\) になるから、\(a\) 以外の位数 \(d\) の元も「\(a\) 系列」の中に含まれている。
ここで、\(\mr{gcd}(j,d)\neq1\) である \(j\:\:(1 < j\leq d)\) をとると、\(a^j\) の位数は \(d\) より小さくなる。なぜなら、\(\mr{gcd}(j,d)=c\:( > 1)\) とすると、2つの数 \(s,\:t\) を選んで、
\(j=c\cdot s\:\:(s < j)\)
\(d=c\cdot t\:\:(t < d)\)
と表されるが、そうすると、
\((a^j)t=a^{cst}=(a^d)^s=1\)
で、\(a^j\) の位数は \(t\) 以下だが、\(t < d\) なので \(a^j\) の位数は \(d\) より小さくなるからである。
一方、\(\mr{gcd}(j,d)\neq1\) である(=\(d\) と素な)\(j\:\:(1\leq j < d)\) をとると、\(a^j\) の位数は \(d\) になる。その理由は以下である。
\((a^j)^x\:\:(1\leq x\leq d)\) が \(x\) の値によってどう変わるかを調べると、まず、\(x=d\) のときは、
\((a^j)^x=(a^j)^d=(a^d)^j=1\)
である。
次に \(1\leq x < d\) のときは \(jx\) は \(d\) の倍数でない。なぜなら、\(j\) は \(d\) と素なため、もし \(jx\) が \(d\) の倍数だとすると、\(x\) が \(d\) の倍数ということになり、\(1\leq x < d\) に反するからである。従って、ある数 \(s,\:t\) を選んで、
\(jx=t\cdot d+s\:\:(0 < s < d)\)
と表せる。そうすると、
\((a^j)^x=a^{td+s}=(a^d)^t\cdot a^s=a^s\)
となるが、\(a\) の位数は \(d\) だから、\(d\) 未満の数 \(s\) で \(a^s\) が \(1\) になることはない。従って \(a^s\neq1\) であり、
\((a^j)^x\neq1\:\:(1\leq x < d)\)
である。
以上により
が分かったので、 \(a^j\) の位数は \(d\) である。\(j\) は \(\mr{gcd}(j,d)\neq1\) だったから、\(j\) のとりうる値は \(\varphi(d)\) 個ある。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は「\(a\) 系列」に含まれるから、\((\bs{Z}/p\bs{Z})^{*}\) に位数 \(\bs{d}\) の元があるとしたら、その数は \(\varphi(d)\) 個である。
まとめると、\((p-1)\) の任意の約数を \(d\) とし、\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元の数を \(\#\mr{ord}(d)\) と表記すると、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
が成り立つ。ここで \(d|(p-1)\) は、\((p-1)\) のすべての約数 \(d\) についての和をとる意味である。
次に、オイラー関数についてオイラー関数の総和の定理が成り立つことを証明する。
(オイラー関数の総和)
\(n\) を任意の自然数とするとき、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。\(d|n\) は、\(n\) のすべての約数 \(d\) についての和をとる。
[証明]
まず、次の2点に注意する。2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
\(\dfrac{a}{\mr{gcd}(a,b)}\) と \(\dfrac{b}{\mr{gcd}(a,b)}\) は互いに素
である。これは最大公約数の定義そのものである。
次に、\(n\) の約数の一つを \(a\) とし、\(n=a\cdot b\) と表すと、\(b\) もまた \(n\) の約数の一つである。\(n\) に \(r\) 個の約数、\(a_i\:\:(1\leq i\leq r)\) があるとき、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、\(b_i\:\:(1\leq i\leq r)\) もまた \(n\) の \(r\) 個の約数である。つまり、\(b_i\) は \(a_i\) を並び替えたものである。
以上の2点を前提に、まず \(n=12\) の場合で考察する。いま、\(1\) から \(12\) までの \(12\) 個の整数を「\(12\) との最大公約数で分類する」ことを考える。\(12\) の約数 \(d\) は、\(1,\:2,\:3,\:4,\:6,\:12\) の6つである。\(12\) との最大公約数が \(d\) である集合を \(S_d\) とすると、
となる。各集合に含まれる整数の個数を \(\#S_d\) として順に見ていくと、まず、オイラー関数の定義より、
\(\#S_1=\varphi(12)\)
である。
次に、\(12\) との最大公約数が \(2\) の集合、\(S_2=\{\:2,\:10\:\}\) を考える。\(\{\:2,\:10\:\}\) を \(2\) で割り算した \(\{\:1,\:5\:\}\) のそれぞれは、最大公約数の定義により、\(12\) を \(2\) で割り算した \(6\) と互いに素である。従って、
\(\#S_2=\varphi(6)\)
である。同様に他の集合についても、
となる。\(S_d\) は \(12\) 個の整数を分類したものだったので、そこに含まれる整数の個数の総和は \(12\) である。これにより、
となる。総和の記号で書くと、
\(\displaystyle\sum_{d|12}^{}\varphi(d)=12\)
である。
以上の考察は \(n=12\) の場合であるが、\(12\) に特別な意味はない。従って一般の \(n\) の場合も同様となる。
\(n\) が \(r\) 個の約数をもつとし、それらを \(a_i\:\:(1\leq i\leq r)\) とする。集合 \(S\) を \(1\) から \(n\) の \(n\) 個の整数の集合とし、その部分集合 \(S_i\) を、
\(S_i\):\(n\) との最大公約数が \(a_i\) である \(S\) の元の集合
とする。このとき、\(S_i\) の任意の元を \(x\) とすると、
\(\dfrac{x}{a_i}\) と \(\dfrac{n}{a_i}\) は互いに素
である。そもそも、そうなる \(x\) を集めたのが \(S_i\) であった。このことから、
\(S_i\) の元の個数は \(\dfrac{n}{a_i}\) と素である \(S\) の元の個数
ということになる。\(S_i\) の元の個数を \(\#S_i\) と書くと、
\(\#S_i=\varphi\left(\dfrac{n}{a_i}\right)\)
である。ここで \(b_i\) を、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、
\(\#S_i=\varphi(b_i)\)
となるが、この \(b_i\:\:(1\leq i\leq r)\) は \(n\) の約数のすべてであり、\(a_i\) を並び替えたものである。式の両辺の \((1\leq i\leq r)\) の総和をとると、\(\#S_i\) の総和は \(S\) の元の数なので、
左辺\(=\displaystyle\sum_{i=1}^{r}\#S_i=n\)
である。一方、右辺の総和は、
\(\begin{eqnarray}
&&\:\:右辺&=\displaystyle\sum_{i=1}^{r}\varphi(b_i)=\displaystyle\sum_{i=1}^{r}\varphi(a_i)\\
&&&=\displaystyle\sum_{d|n}^{}\varphi(d)\\
\end{eqnarray}\)
となって、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。
\((p-1)\) の約数に戻ると、オイラー関数の総和の定理より、
\(\displaystyle\sum_{d|(p-1)}^{}\varphi(d)=p-1\)
である。一方、位数 \(d\) の元の総和は、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
であった。この2点から、
\(\#\mr{ord}(d)=\varphi(d)\)
が結論づけられる。\(\#\mr{ord}(d)=0\) となる \((p-1)\) の約数 \(d\) は無い。もしあるとすると矛盾が生じる。
従って \((\bs{Z}/p\bs{Z})^{*}\) においては、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。[証明終]
この位数 \(\bs{d}\) の元の数の定理(25C)により、次の生成元の存在1が成り立つことが分かります。
\(p\) を素数とするとき、\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在する。生成元とは、その位数が \((\bs{Z}/p\bs{Z})^{*}\) の群位数、\(p-1\) の元である。
ちなみに、\(100\)以下の素数 \(p\)(\(2\) を除く \(24\)個)について、原始根の数 = \(\varphi(p-1)\) と最小の原始根をパソコンで計算すると、次のようになります。
この表を見ると、\(2\) が最小原始根になることが多いのがわかります。全体の半分(\(12\)個の素数)でそうです。そうでなれければ素数が多い。ただし、\(p=41\) のときの \(6\) のように、合成数が最小原始根になる場合もあります。
\((\bs{Z}/p\bs{Z})^{*}\) の生成元を求める計算式はありません。しかし生成元を求めるアルゴリズムはあって、それが次です。これは、少なくとも一つの生成元が存在する証明になっています。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
この証明のために2つの補題を証明する。以下において、
・\(a\) は \(b\) を割り切る
・\(a\) は \(b\) の約数である
・\(b\) は \(a\) で割り切れる
・\(b\) は \(a\) の倍数である
ことを、
\(a|b\)
と記述する。また \(a\) と \(b\) の最大値を、
\(\mr{max}(a,\:b)\)
と表す。
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[証明]
\(a\) と \(b\) を素因数分解したときに現れるすべての素数を小さい方から順に並べて、
\(p_1,\:p_2,\:\cd\:,\:p_n\)
とする。この素数の列を用いて、\(a\) と \(b\) を、
\(a=p_1^{a_1}\cdot p_2^{a_2}\cdot\cd\cdot p_n^{a_n}\)
\(b=p_1^{b_1}\cdot p_2^{b_2}\cdot\cd\cdot p_n^{b_n}\)
と素因数分解する。もちろんこの表現では \(a_i=0\) や \(b_i=0\) もありうる。ここで、
\(c_i=\mr{max}(a_i,\:b_i)\:\:\:(1\leq i\leq n)\)
と定義すると、\(a,\:b\) の最小公倍数は、
\(\mr{lcm}(a,b)=p_1^{c_1}\cdot p_2^{c_2}\cdot\cd\cdot p_n^{c_n}\)
である。また、
と定義して(\(1\leq i\leq n\))、
\(a\,'=p_1^{\al_1}\cdot p_2^{\al_2}\cd\cd p_n^{\al_n}\)
とおくと、
\(a\,'|a\)
である。同様に、
\(b\,'=p_1^{\beta_1}\cdot p_2^{\beta_2}\cdot\cd\cdot p_n^{\beta_n}\)
とおくと、
\(b\,'|b\)
である。このように \(a\,'\) と \(b\,'\) を決めると、
\(a\,'b\,'=\mr{lcm}(a,b)\)
となり、\(a\,'\) と \(b\,'\) に共通の素因数はないから、
\(\mr{gcd}(a\,',b\,')=1\)
である。[補題6の証明終]
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[証明]
\(\mr{gcd}(k,d)\) を \(g\) と書き、
\(k\,'=\dfrac{k}{g}\)
\(d\,'=\dfrac{d}{g}\)
とすると、
\(k=k\,'\cdot g\)
\(d=d\,'\cdot g\)
\(\mr{gcd}(k\,',d\,')=1\)
と表せる。\(a^k\) の位数を調べるため、
\((a^k)^x=1\)
とおくと、
\(a^{kx}=1\)
なので、[補題4](25A)により、
\(d|(kx)\)
である。つまり、
\((d\,'g)|(k\,'gx)\)
\(d\,'|k\,'x\)
となる。すると、\(\mr{gcd}(k\,',d\,')=1\) なので、
\(d\,'|x\)
が成り立つ。\(d\,'|x\) が成り立つ \(x\) の最小値は \(d\,'\) であり、\(x\) の最小値はすなわち \(a^k\) の位数 \(e\) だから、\(e=d\,'\) である。つまり、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。[補題7の証明終]
[補題6]と[補題7]を用いて、生成元の探索アルゴリズム(25D’)を証明します。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
[証明]
\(a\) の累乗の列、
\(a,\:a^2,\:a^3,\:\cd,\:a^d=1\)
は \(d\)個の異なる元である。\(d < p-1\)(群位数)なので、この列に含まれない任意の元を \(b\) とし、\(b\) の位数を \(e\) とする。[補題3](25A)により、\(d\) 乗して \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は \(a\) の累乗の列で尽されているから、\(b^d\neq1\) である。従って \(b\) の位数 \(e\) は \(d\) の約数ではない。もちろん \(e > 1\) である。以降、証明を2つのケースに分ける。
\(\bs{(1)\:\:\mr{gcd}(d,e)=1}\) のとき
このとき、\(ab\) の位数が \(d\) より大きいことを以下で証明する。\(ab\) の位数を調べるために、
\((ab)^x=1\)
とおく。両辺を \(d\)乗すると、
\((ab)^{dx}=1\)
であり、また \(a^d=1\) から \((a^d)^x=1\) だから、
\(b^{dx}=(a^d)^xb^{dx}=(ab)^{dx}=1\)
となり、[補題4](25A)により \(dx\) は \(b\) の位数 \(e\) の倍数である。つまり、
\(e|dx\)
である。すると、\(\mr{gcd}(d,e)=1\) により、
\(e|x\)
となる。同様に、
\((ab)^{ex}=1\)
\(b^e=1\)
だから、
\(a^{ex}=a^{ex}(b^e)^x=(ab)^{ex}=1\)
となり、\(ex\) は \(a\) の位数 \(d\) の倍数である。つまり、
\(d|ex\)
である。すると \(\mr{gcd}(d,e)=1\) により、
\(d|x\)
である。以上の結果、\(e|x\) かつ \(d|x\) であり、
\((de)|x\)
が成り立つ。つまり \(x\) の最小値は \(de\) である。\((ab)^x=1\) となる \(x\) の最小値が \(ab\) の位数だから、
\(ab\) の位数\(=de\)
となる。\(e > 1\) なので、\(ab\) は位数が \(d\) より大きい元である。
\(\bs{(2)\:\:\mr{gcd}(d,e)\neq1}\) のとき
[補題6]により、2つの数、\(d\,',\:e\,'\) をとって、
\(d\,'|d\)
\(e\,'|e\)
\(\mr{gcd}(d\,',e\,')=1\)
\(\mr{lcm}(d,e)=d\,'e\,'\)
となるようにできる。
\(\mr{gcd}\left(\dfrac{d}{d\,'},d\right)=\dfrac{d}{d\,'}\)
だから、[補題7]を使って、
\(a^{{}^{\frac{d}{d\,'}}}\) の位数 \(=\dfrac{d}{\mr{gcd}\left(\dfrac{d}{d\,'},d\right)}=d\,'\)
であり、同様に、
\(b^{{}^{\frac{e}{e\,'}}}\) の位数 \(=\dfrac{e}{\mr{gcd}\left(\dfrac{e}{e\,'},e\right)}=e\,'\)
である。\(\mr{gcd}(d\,',e\,')=1\) だから、
\(c=a^{{}^{\frac{d}{d\,'}}}\cdot b^{{}^{\frac{e}{e\,'}}}\)
とおくと、\(\bs{(1)}\) を使って、
となるが、\(e\) は \(d\) の約数ではないため、
\(\mr{lcm}(d,e) > d\)
である。つまり、\(c\) は位数が \(d\) より大きい元である。[証明終]
生成元の存在2
以降で \((\bs{Z}/p^n\bs{Z})^{*}\) にも生成元が存在することを証明します(ただし、\(p\neq2\))。まず、その証明に使う[補題8]を証明します。整数についての定理です。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
[証明]
表記を分かりやすくするため、まず \(m=1\) のときに成り立つことを証明する。\(m=1\) のときに[補題8]は、
[補題8]\(\bs{m=1}\)
\(p\) を奇素数とし、\(k\) を \(p\) と素な数( \(\mr{gcd}(k,p)=1\) )とする。このとき、
\((1+kp)^p=1+k\,'p^2\)
と表すことができて、\(k\,'\) は \(p\) と素である。
となる。\((1+kp)^p\) を2項定理で展開すると、
\((1+kp)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp+{}_{p}\mr{C}_{2}(kp)^2+{}_{p}\mr{C}_{3}(kp)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp)^{p-1}+(kp)^p\\
&&\:\: =&1+p^2(k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2})\\
&&\:\: =&1+k\,'p^2\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2}\\
\end{eqnarray}\)
となる。\(k\,'\) の第3項(\({}_{p}\mr{C}_{3}k^3p\))以降は \(p\) の指数が \(1\) 以上だから \(p\) で割り切れる。第2項の \(p\) に関係した式は、
\({}_{p}\mr{C}_{2}=\dfrac{p(p-1)}{2}\)
であるが、\(\bs{p}\) が奇素数(\(\bs{p\neq2}\))であるため、この第2項も \(p\) で割り切れる(\(p\) が奇数だと \(p\) で割り切れる)。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。
次に \(m\geq2\) のときであるが、\(m=1\) のときの上の証明において \(p\) を \(p^m\) に置き換えれば、同様の計算で証明できる。\((1+kp^m)^p\) を2項定理で展開すると、
\((1+kp^m)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp^m+{}_{p}\mr{C}_{2}(kp^m)^2+{}_{p}\mr{C}_{3}(kp^m)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp^m)^{p-1}+(kp^m)^p\\
&&\:\: =&1+p^{m+1}(k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1})\\
&&\:\: =&1+k\,'p^{m+1}\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1}\\
\end{eqnarray}\)
\(k\,'\) の第2項以降は \(m\geq2\) なので \(p\) の指数は \(1\) 以上であり、\(p\) で割り切れる。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は、第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。以上の結論として、題意が成り立つ。[証明終]
生成元の存在1の定理(25D)と[補題8]を用いて、\((\bs{Z}/p^n\bs{Z})^{*}\) に生成元が存在することを証明します。
\(p\) を \(p\neq2\) の素数(=奇素数)とする。また、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
[証明]
フェルマの小定理(25B)により、\((\bs{Z}/p\bs{Z})^{*}\) の任意の元は \((p-1)\) 乗すると \(1\) になる。従って、整数の記法で、
\(g^{p-1}=1+kp\)
と書ける。以降、
・\(k\) の素因数に \(p\) を含まないとき
・\(k\) の素因数に \(p\) を含むとき
の2つに分けて証明する。
\(k\) の素因数に \(p\) を含まないとき
この場合は以下が成り立つ。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
[証明(その1)]
\(g\) は \(p\) と互いに素なので \((\bs{Z}/p^n\bs{Z})^{*}\) の元でもある。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は、既約剰余類群の定義によって \(\varphi(p^n)\) である。\(p^n\) 以下で \(p\) で割り切れる数は、\(p^n\) を含んで \(\dfrac{p^n}{p}=p^{n-1}\) 個あるから、
\(\begin{eqnarray}
&&\:\:\varphi(p^n)&=p^n-p^{n-1}\\
&&&=p^{n-1}(p-1)\\
\end{eqnarray}\)
である。従って、オイラーの定理(25B)より、
\(g^{p^{n-1}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
が成り立つ。記述の簡素化のために、
\(h=g^{p-1}\)
とおく。
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
である。
仮定によって \(h\) は、
\(h=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表される。この \(h\) に対して "\(p\)乗する" 操作を \((n-1)\) 回繰り返すと、[補題8]を次々に使って、次のように計算できる。
この結果から、
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
であることがわかる。この式は \(n\geq1\) のすべての \(n\) で成り立つ。
従って、\(h^x\equiv1\:\:(\mr{mod}\:p^n)\) となる最小の \(x\) は \(p^{n-1}\) の約数であり、\((n-1)\) 個の \(p^i\:\:(1\leq i\leq n-1)\) のどれかである。
しかし、上の計算過程を見ると、
であって、\(1\leq i\leq n-2\) であれば右辺の \(k_i\cdot p^{i+1}\) は \(p^n\) で割り切れない。つまり、
\(h^{p^i}\not\equiv1\:\:(\mr{mod}\:p^n)\:\:(1\leq i\leq n-2)\)
である。従って、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
\(h\) は \(g^{p-1}\) であった。ゆえに、\(g\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その1)終]
\(k\) の素因数に \(p\) を含むとき
\(g^{p-1}=1+kp\) と表したときの \(k\) の素因数に \(p\) を含む場合、ある数 \(k\,''\) があって、
\(g^{p-1}=1+k\,''\cdot p^m\:\:(m\geq2)\)
\(\mr{gcd}(k\,'',p)=1\)
と表すことができる。ここで \(k\,''\) を改めて \(k\) と書くと、次が成り立つ。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
[証明(その2)]
\((g+p)^{p-1}\) を2項定理で展開する。
\((g+p)^{p-1}\)
\(=1+p(kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2})\)
\(=1+k\,'p\)
\(k\,'=kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2}\)
\(m\geq2\) なので、\(k\,'\) の第2項以外はすべて \(p\) で割り切れる。第2項は \((p-1)g^{p-2}\) だが、\((p-1)\) も \(g^{p-2}\) も \(p\) で割り切れない。つまり \(k\,'\) は第2項だけが唯一、\(p\) で割り切れないから、
\(\mr{gcd}(k\,',p)=1\)
である。まとめると、
\((g+p)^{p-1}=1+k\,'p\)
\(\mr{gcd}(k\,',p)=1\)
と表すことができる。ここで、
\(h=1+k\,'p\)
と書くと、[補題8]を次々と使うことで、次の計算が成り立つ。
この計算は「\(\bs{k}\) の素因数に \(\bs{p}\) を含まないとき」と全く同じである。従って、そのときの結論を踏襲できて、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
その \(h\) は、
\(h=1+k\,'p=(g+p)^{p-1}\)
であった。\(h\) が \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になるのだから、\(g+p\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その2)終]
以上により、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とすると、\(g\) か \(g+p\) のどちらかは \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。従って \((\bs{Z}/p^n\bs{Z})^{*}\) には生成元があり、群位数 \(p^{n-1}(p-1)\) の巡回群である。[証明終]
ちなみに、\(h=g^{p-1}\) とし、
\(h=1+kp^2\)
\(\mr{gcd}(k,p)=1\)
と表されているときは \(g+p\) が生成元ですが、\(\bs{g}\) は生成元ではありません。なぜなら[補題8]を次々と使うと、
となり、\(h\) を \(p^{n-1}\) 乗する前の \(h^{p^{n-2}}\) の段階で、
\(h^{p^{n-2}}\equiv1\:\:(\mr{mod}\:p^n)\)
\(\longrightarrow\:g^{p^{n-2}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
となってしまいます。つまり \(g\) は生成元ではないのです。\(g^{p-1}=1+kp^m\:\:(m > 2)\) と表されるときも同じです。
実は、\((\bs{Z}/p\bs{Z})^{*}\) の生成元を \(g\) とすると、ほとんどの場合で \(g\) は \((\bs{Z}/p^2\bs{Z})^{*}\) の(従って \((\bs{Z}/p^n\bs{Z})^{*}\) の)生成元になります。生成元の存在1であげた、\(100\) 以下の素数 \(p\) の最小原始根の表ですが、そのすべては \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です。それどころか「\(100\) 以下の素数 \(p\) の原始根が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならない」というケースは、計算してみると次の4つしかありません。
\(p=29,\:g=14\)
\(p=37,\:g=18\)
\(p=43,\:g=19\)
\(p=71,\:g=11\)
たとえば \(p=29\) の場合、\(\varphi(28)=12\) なので原始根 \(g\) は \(12\)個あります。リストすると、
\(g=2,\:3,\:8,\:10,\:11,\:14,\:15,\:18,\:19,\:21,\:26,\:27\)
の \(12\)個です。\(p^2=841\) であり、\((\bs{Z}/p^2\bs{Z})^{*}\) は \((\bs{Z}/841\bs{Z})^{*}\) のことです。その \((\bs{Z}/841\bs{Z})^{*}\) の群位数は、
\(\varphi(p^2)=p(p-1)=29\cdot28=812\)
です。
\(g\) のうち、\(14\) を除く \(11\)個の位数は \(812\) です。ところが \(14\) だけは違って、
\(14^{28}\equiv1\:\:(\mr{mod}\:841)\)
となり、位数は \(28\) です。もちろんこの場合でも、生成元の存在2(25E)の証明プロセスにあるように、
\(g+p=14+29=43\)
の位数は \(812\) で、\((\bs{Z}/841\bs{Z})^{*}\) の生成元です。以上をまとめると、
となります。
生成元の存在2(25E)の証明は、[補題8]の証明での \(\bs{{}_{p}\mr{C}_{2}}\) が \(\bs{p}\) で割り切れることがポイントになっていて、\(p\neq2\) である素数(奇素数)のときには成り立ちますが、\(p=2\) のときには成り立ちません。\(p=2\) では生成元が存在しないのです。
しかし \(p=2\) のとき、つまり \((\bs{Z}/2^n\bs{Z})^{*}\) は、生成元をもつ2つの巡回群の直積と同型であることが証明できます。
2のべき乗の既約剰余類群
2のべき乗の既約剰余類群は、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[証明]
まず \(n=5\) の場合である \((\bs{Z}/32\bs{Z})^{*}\) で考察する。
\((\bs{Z}/32\bs{Z})^{*}\) の元とは、\(1\) から \(31\) までの奇数の集合である。この奇数から「\(4\)で割ると \(1\) 余る奇数」を取り出して、集合 \(A\) とする。
\(A=\{1,\:5,\:9,\:13,\:17,\:21,\:25,\:29\}\)
である。集合 \(A\) の要素の数は、\(32/4=8\) である。ここで、
\(5\equiv1\:\:(\mr{mod}\:4)\)
であることに着目する。この両辺を \(k\) 乗(\(0\leq k\))すると、
\(5^k\equiv1\:\:(\mr{mod}\:4)\)
だから(21E)、\(5^k\) は「\(4\)で割ると \(1\) 余る奇数」である。ここで、\(5^k\) を \(32\) で割った余りを \(j\) とする。つまり、
\(5^k\equiv j\:\:(\mr{mod}\:32)\:\:(0\leq k,\:1\leq j\leq31)\)
である。すると \(j\) は「\(32\)未満の、\(4\)で割ると \(1\) 余る奇数」であり、\(A\) に含まれている。そこでもし、
\(5^x\equiv1\:\:(\mr{mod}\:32)\)
を満たす最小の \(x\)(つまり \(\mr{mod}\:32\) での \(5\) の位数)が \(8\) であれば、位数の定理(25A)の[補題2]によって「\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) はすべて異なる」から、それらは \(A\) そのものである。実際に計算してみると、
となって、\(\mr{mod}\:32\) での \(5\) の位数は \(8\) であり、\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) には \(A\) の元がすべて現れる。これは \(A\) が巡回群と同型であることを示している。
一方、\((\bs{Z}/32\bs{Z})^{*}\) の元から「\(4\)で割ると \(3\) 余る奇数」を取り出し、それを集合 \(B\) とすると、
\(B=\{3,\:7,\:11,\:15,\:19,\:23,\:27,\:31\}\)
である。ここで、\(A=\{4k+1\:|\:0\leq k\leq7\}\) と記述し、\(i=7-k\:\:(k=7-i)\) と定義すると、
\(\begin{eqnarray}
&&\:\:(-1)\cdot A&=\{-4k-1 &|\:0\leq k\leq7\}\\
&&&=\{-4(7-i)-1 &|\:0\leq i\leq7\}\\
&&&=\{4i+3-32 &|\:0\leq i\leq7\}\\
\end{eqnarray}\)
だから、\(\mr{mod}\:32\) でみると、
\(B\equiv(-1)\cdot A\)
である。\((-1)\cdot A\) は、集合 \(A\) の要素すべてに \(-1\) を掛けた集合の意味である。
\((\bs{Z}/32\bs{Z})^{*}\) の元は \(A\) と \(B\) の和であり、\(A\) と \(B\) に重複はない。従って、\((\bs{Z}/32\bs{Z})^{*}\) の元は、\(\mr{mod}\:32\) でみて、
\((-1)^j\cdot5^k\:\:(j=0,1)\) \((0\leq k\leq7)\)
の形に一意に表現できる。\(j=0\) の場合は \(A\) を、\(j=1\) なら \(B\) を表している。
\(\mr{mod}\:32\) でみて、\(5^k\) は群位数 \(8\) の巡回群であり、\((-1)^j\) は群位数 \(2\) の巡回群である。従って、\((\bs{Z}/32\bs{Z})^{*}\) は2つの巡回群の直積で表現できることになる。このことが成り立つキーポイントは、
\(\mr{mod}\:32\) でみた \(5\) の位数が \(\dfrac{32}{4}=8\)
ということである。もしこれが \(2^5=32\) だけでなく \(2^n\:\:(2\leq n)\) で成り立てば、一般論に拡張できる。その、\(2^n\) で成り立つことは、次のように、[補題9]として証明できる。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
[証明]
数学的帰納法で証明する。題意は \(n=2\) のときに成り立つので( \(5\equiv1\:\:(\mr{mod}\:4)\) )、\(n\) で成り立つと仮定し、\(n+1\) でも成り立つことを証明する。\(\mr{mod}\:2^{n+1}\) での \(5\) の位数を調べるため、
一般に \(a\equiv b\:\:(\mr{mod}\:p^n)\) なら、\(1\leq i < n\) とするとき \(a\equiv b\:\:(\mr{mod}\:p^i)\) である。従って \((\br{A})\) 式が成り立つとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^n)\)
も成り立つ。帰納法の仮定により \(\mr{mod}\:2^n\) での \(5\) の位数は \(2^{n-2}\) だから、位数の定理(25A)の[補題4]により \(x\) は \(2^{n-2}\) の倍数である。
従って \(x\) の最小値は \(2^{n-2}\) だが、\(x\) を \(2^{n-2}\) とすると \((\br{A})\) 式が成り立たない。なぜなら、
\((\br{A})\) 式の \(x\) は \(2^{n-2}\) の倍数であるが、\(x=2^{n-2}\) では \((\br{A})\) 式が成り立たないことが分かった。その次に小さな \(x\) の倍数は \(x=2\cdot2^{n-2}=2^{n-1}\) であり、これを \((\br{A})\) 式に入れると、
左辺\(=5^{2^{n-1}}\)
である。一方、\((\br{B})\) 式の両辺を2乗すると、
\(\begin{eqnarray}
&&\:\:5^{2^{n-1}}&\equiv(1+2^n)^2\:\:(\mr{mod}\:2^{n+1})\\
&&&=1+2^{n+1}+2^{2n}\\
&&&\equiv1\:\:(\mr{mod}\:2^{n+1})\\
\end{eqnarray}\)
であるから、\(x=2^{n-1}\) のとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
が成り立つ。つまり \((\br{A})\) 式が成り立つ \(x\) の最小値は \(2^{n-1}\) であり、\(5\) の \(\mr{mod}\:2^{n+1}\) での位数は \(2^{n-1}\) である。これで、帰納法によって[補題9]が正しいことが証明できた。[補題9の証明終]
[補題9]が正しいので、\(n=5\) の例で展開した論理により、\((\bs{Z}/2^n\bs{Z})^{*}\) の元は、\(\mr{mod}\:2^n\) でみて、
\((-1)^j5^k\:\:(j=0,1,\:\:0\leq k\leq2^{n-2}-1)\)
の形に一意に表現できることが分かった。
ここで、\((\bs{Z}/2^n\bs{Z})^{*}\) から \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) への写像 \(f\) を、
で定める。\((\bs{Z}/2^n\bs{Z})^{*}\) の群演算は乗算であり、\((\bs{Z}/2\bs{Z})\) と \((\bs{Z}/2^{n-2}\bs{Z})\) の群演算は加算であることに注意すると、\((\bs{Z}/2^n\bs{Z})^{*}\) の2つの元 \((-1)^j5^k\)、\((-1)^l5^m\) について、
\(\begin{eqnarray}
&&\:\:f((-1)^j5^k\cdot(-1)^l5^m)&=f((-1)^{j+l}5^{k+m})\\
&&&=(j+l,\:k+m)\\
&&\:\:f((-1)^j5^k)+f((-1)^l5^m)&=(j,k)+(l,m)\\
&&&=(j+l,\:k+m)\\
\end{eqnarray}\)
\(f((-1)^j5^k\cdot(-1)^l5^m)=f((-1)^j5^k)+f((-1)^l5^m)\)
となり、\(f\) は同型写像の要件を満たしている。従って、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
であり、\((\bs{Z}/2^n\bs{Z})^{*}\) は、群位数 \(2\) と群位数 \(2^{n-2}\) の2つの巡回群の直積に同型である。[証明終]
既約剰余類群の構造
ここまでの準備を行うと、既約剰余類群の構造を明らかにできます。これが第2章のゴールです。
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である。
[証明]
以下の記述では、
・\(a_j\) は \(a\) を \(j\) で割った余り
・\((a+b)_j\) は \((a+b)\) を \(j\) で割った余り
を表す。
\(j\) と \(k\) を 互いに素な整数 \((2\leq j,k)\) とする。\(a\) を \(\bs{Z}/(jk)\bs{Z}\) の元とし \((0\leq a\leq jk-1)\)、\(\bs{Z}/(jk)\bs{Z}\) から \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) への写像、\(f\) を次のように定義する。
\(j\) と \(k\) が 互いに素なので、中国剰余定理(21F)により、任意に選んだ \(a_j\) と \(a_k\) から \(a\) が一意に決まる。つまり、\(f\) は1対1写像(数学用語で "全単射")である。また、\(a\) とは別の \(\bs{Z}/(jk)\bs{Z}\) の元を \(b\) とすると、
\(\begin{eqnarray}
&&\:\:f(a+b)&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a)+f(b)&=(a_j,\:a_k)+(b_j,\:b_k)\\
&&&=(a_j+b_j,\:a_k+b_k)\\
&&&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a+b)&=f(a)+f(b)\\
\end{eqnarray}\)
となり、\(f\) は同型写像である。
いま、\(\mr{gcd}(a,jk)=1\)(\(a\) が \(jk\) と素)だとすると、既約剰余類群の定義により、\(a\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) の元である。
ここで一般的に、
\(\mr{gcd}(a,jk)=1\) なら
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\)
である。また \(\mr{gcd}(a,j)=1\) なら \(\mr{gcd}(j,a_j)=1\) である。なぜなら互除法の原理(21A)によって、\(a\) と \(j\) の公約数は \(j\) と \(a_j\) の公約数だからである。
従って、
\(\mr{gcd}(j,a_j)=1\) かつ \(\mr{gcd}(k,a_k)=1\)
になる。つまり、\(a_j\) は \((\bs{Z}/j\bs{Z})^{*}\) の元であり、\(a_k\) は \((\bs{Z}/k\bs{Z})^{*}\) の元である。また、
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\) なら
\(\mr{gcd}(a,jk)=1\)
も成り立つので、任意の \((\bs{Z}/j\bs{Z})^{*}\) の元と \((\bs{Z}/k\bs{Z})^{*}\) の元を決めれば、\((\bs{Z}/(jk)\bs{Z})^{*}\) の元が定まる。
さらに、既約剰余類群の群演算は乗算であるが、
\(\begin{eqnarray}
&&\:\:a_j\cdot b_j&=(a\cdot b)_j\\
&&\:\:a_k\cdot b_k&=(a\cdot b)_k\\
\end{eqnarray}\)
が成り立つので、
\(f(ab)=f(a)f(b)\)
であり、\(f\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) から \((\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\) への同型写像でもある。従って、\(j\) と \(k\) が互いに素という条件のもとで、
いま、\(p,\:q\) を2つの素数とし、\(n\) の素因数分解が、
\(n=p^a\cdot q^b\)
だとする。このとき \((\br{C})\) 式で \(j=p^a,\:k=q^b\) とおくと、
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\)
となる。さらに、\(p,\:q,\:r\) を3つの素数とし、
\(n=p^a\cdot q^b\cdot r^c\)
と表せたとする。\((\br{C})\) 式で \(j=p^a\cdot q^b,\:k=r^c\) とおくと、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/n\bs{Z})^{*}&\cong(\bs{Z}/(p^aq^b)\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
&&&\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
\end{eqnarray}\)
となる。\(n\) の素因数の数が4以上に増えてもこの操作は繰り返せるから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \((\bs{Z}/p^a\bs{Z})^{*}\) の形の既約剰余類群の直積と同型である。
\((\bs{Z}/p^a\bs{Z})^{*}\) は、\(p=2\) のときは2のべき乗の既約剰余類群の定理(25F)により、2つの巡回群の直積と同型である。また、\(p\neq2\) の素数のときは生成元の存在2の定理(25E)により、それ自体が巡回群である。従って、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \(n\) の値にかかわらず、巡回群の直積と同型である。[証明終]
具体例として、たとえば \(n=360\) とすると、\(n=2^3\cdot3^2\cdot5\) なので、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/2^3\bs{Z})^{*}\times(\bs{Z}/3^2\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
となり、\((\bs{Z}/360\bs{Z})^{*}\) は4つの巡回群の直積と同型です。
「既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型」(25G)は、ガロア理論の証明で次のように使います。\(1\) の \(n\)乗根(\(x^n-1=0\) の解)のうち、\(n\)乗して初めて \(1\) になるものを「\(1\) の原始\(n\)乗根」といいます。それを \(\zeta\) とすると、
となり、④が証明できます。① と ③ は別途証明します。④ の「\(\bs{Q}(\zeta)\) のガロア群は可解群」が重要で、方程式の可解性の必要条件を証明するときの一つのポイントになります。
ガロア理論では方程式の解を含む「体」の特性を分析することで、方程式が代数的に解けるかどうかを調べます。第3章ではその「体」と、方程式の元になる「多項式」に関する重要な定義と定理を説明します。
3.1 多項式
ガロア理論で対象とする多項式は、1つの変数(未知数)をもつ、有理数係数の多項式です。それを、
で表します。\(\bs{f(x)}\) の「\(\bs{0}\) でない最高次の係数 \(\bs{n}\)」を、多項式の「次数」といい、\(\bs{\mr{deg}\:f(x)}\) で表します。通常、\(\mr{deg}\:f(x)\geq1\) ですが、便宜上、\(a_0\) 以外の係数が \(0\) の場合(=定数項のみの場合)も多項式と呼び「\(\bs{0}\) 次多項式」とします。また、全ての係数が \(0\) の場合を「\(\bs{0}\) 多項式(零多項式)」と呼びます。
多項式 \(a(x)\) を 多項式 \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とすると、
\(a(x)=p(x)b(x)+r(x)\)
\((\:\mr{deg}\:r(x) < \mr{deg}\:b(x)\:)\)
です。整数のときと同じように互除法(21A)を用い、次に \(b(x)\) を \(r(x)\) で割って余りを求める操作を繰り返すと、\(\mr{deg}\:r(x)\) が単調減少するので、いずれ \(b(x)\) が \(r(x)\) で割り切れるとき(=互除法の最終段階)がきます。\(r(x)\) が \(0\) 次多項式(=定数)なら、\(b(x)\) は \(r(x)\) で割り切れるので、最終段階は必ずあります。
\(b(x)\) が \(r(x)\) で割り切れるとき、\(r(x)\) が \(a(x)\) と \(b(x)\) の「最大公約数」です。実際は "数" ではなく多項式なので、「最大公約式」や「最大公約因子」といった言い方もありますが、一般的には「最大公約数」で通っています。
最大公約数が定数(\(0\) 次多項式)のとき、\(a(x)\) と \(b(x)\) は互いに素である、といいます。このとき、整数における不定方程式の解の存在定理(21C)と同様の、次の定理が成り立ちます。
不定方程式
\(a(x)\) と \(b(x)\) が互いに素な多項式のとき、
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
[証明]
\(a(x)\) と \(b(x)\) に互除法(21A)を適用して次数を下げ、同時に \(f(x),\:g(x)\) を変換して同等の方程式に変形していく。\(a(x)\) を \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とする。
\(a(x)=p(x)b(x)+r(x)\)
\(\mr{deg}\:r(x) < \mr{deg}\:b(x)\)
である。互除法の次のステップの \(a_1(x),\:b_1(x)\)、\(f_1(x),\:g_1(x)\) を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1(x)=b(x)&\\
&&b_1(x)=r(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f_1(x)=p(x)f(x)+g(x)&\\
&&g_1(x)=f(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(f(x),\:g(x)\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f(x)=g_1(x)&\\
&&g(x)=f_1(x)-p(x)g_1(x)&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(a_1(x)f_1(x)+b_1(x)g_1(x)\)
\(=b(x)(p(x)f(x)+g(x))+r(x)f(x)\)
\(=p(x)b(x)f(x)+b(x)g(x)+r(x)f(x)\)
\(=(p(x)b(x)+r(x))f(x)+b(x)g(x)\)
\(=a(x)f(x)+b(x)g(x)\)
と計算できるので、不定方程式は、
\(a_1(x)f_1(x)+b_1(x)g_1(x)=1\)
となり、係数多項式 \(a_1(x),\:b_1(x)\) の次数が元々の \(a(x),\:b(x)\) より小さな方程式に変形できる。この方程式の解である \(f_1(x),\:g_1(x)\) が求まれば、\(\br{③}\) を使って \(f(x),\:g(x)\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i(x)\) を \(b_i(x)\) で割った商と余りを、
\(a_i(x)=p_i(x)b_i(x)+r_i(x)\)
\((\:\mr{deg}\:r_i(x) < \mr{deg}\:b_i(x)\:)\)
のように求め、次のステップを、
\(a_{i+1}(x)=b_i(x)\)
\(b_{i+1}(x)=r_i(x)\)
\(f_{i+1}(x)=p_i(x)f_i(x)+g_i(x)\)
\(g_{i+1}(x)=f_i(x)\)
とすることで、互除法を続けていける。このように係数多項式 \(a(x),\:b(x)\) の剰余算を繰り返し、同時に変数多項式 \(f(x),\:g(x)\) を変換していくと、この過程で \(\mr{deg}\:r_i(x)\) は単調減少していく。そして互除法の最終段階で、
\(a_n(x)f_n(x)+b_n(x)g_n(x)=1\)
となったとする。元々の \(a(x)\) と \(b(x)\) は互いに素だったから、この段階の \(b_n(x)\) は \(0\) 次多項式=定数である。その定数を \(c\) とすると、
\(a_n(x)f_n(x)+cg_n(x)=1\)
となるが、この不定方程式の解は、
\(f_n(x)=0\)
\(g_n(x)=\dfrac{1}{c}\)
である。この解を起点として \(f_i(x),\:g_i(x)\:\:(1\leq i\leq n)\) の変換過程を逆にたどると \(f(x),\:g(x)\) が求まる。
次に、
\(\mr{deg}\:g(x) < \mr{deg}\:a(x)\)
であるように選べることを示す。\(g(x)\) を \(a(x)\) で割った商を \(q(x)\)、余りを \(s(x)\) とする。
\(g(x)=q(x)a(x)+s(x)\)
\(s(x)=g(x)-q(x)a(x)\)
である。ここで、
\(F(x)=f(x)+b(x)q(x)\)
\(G(x)=s(x)\)
とおくと、
\(a(x)F(x)+b(x)G(x)\)
\(\begin{eqnarray}
&&\:\: =&a(x)(f(x)+b(x)q(x))+b(x)s(x)\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)(g(x)-q(x)a(x))\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)g(x)-b(x)q(x)a(x)\\
&&\:\: =&a(x)f(x)+b(x)g(x)\\
\end{eqnarray}\)
となるので、
\(a(x)f(x)+b(x)g(x)=1\)
であれば、
\(a(x)F(x)+b(x)G(x)=1\)
である。つまり \(f(x),\:g(x)\) が不定方程式の解であれば、\(F(x),\:G(x)\)も解である。\(\mr{deg}\:G(x)=\mr{deg}\:s(x) < \mr{deg}\:a(x)\) なので、\(F(x),\:G(x)\) が題意を満たす解である。
\((\br{A})\) 式を満たす \(f(x),\:g(x)\) が求まったとする。\((\br{A})\) 式の両辺に \(h(x)\) を掛けると、
\(a(x)f(x)h(x)+b(x)g(x)h(x)=h(x)\)
となる。
\(F(x)=f(x)h(x)\)
\(G(x)=g(x)h(x)\)
とおくと、\(F(x),\:G(x)\) は不定方程式、
\(a(x)F(x)+b(x)G(x)=h(x)\)
の解である。\((\br{A})\) 式の解を \(\mr{deg}\:g(x) < \mr{deg}\:a(x)\) となるように選べることを上で証明したが、この過程において方程式の右辺は無関係であった。従って、全く同じプロセスをたどることで、
\(\mr{deg}\:G(x) < \mr{deg}\:a(x)\)
とすることができる。[証明終]
既約多項式
有理数係数の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解がべき根で表現できるために必要十分条件を述べるのがガロア理論です。
このとき、多項式が有理数の範囲で因数分解できるのであれば、\(f(x)=0\) は、たとえば \(g(x)h(x)=0\)、\(g(x)=0,\:h(x)=0\) となって、より次数の低い方程式の問題に還元されてしまいます。これでは、たとえば \(f(x)\) が5次多項式だとしても、5次方程式の問題ではなくなる。
従って、方程式の解の議論をするときには「因数分解できない多項式」の議論をすればよいことになります。それが既約多項式です。
有理数 \(\bs{Q}\) を係数とする多項式で、\(\bs{Q}\) の範囲ではそれ以上因数分解できない多項式を \(\bs{Q}\) 上で既約な多項式という。
たとえば多項式 \(x^2-2\) は \(\bs{Q}\) 上では因数分解できませんが、\(\bs{R}\) 上では \((x-\sqrt{2})(x+\sqrt{2})\) と因数分解できます。\(x^2+2\) は \(\bs{R}\) 上では因数分解できませんが、\(\bs{C}\) 上では \((x-\sqrt{2}i)(x+\sqrt{2}i)\) と因数分解できます。「代数学の基本定理」によると、\(n\)次方程式は 複素数の範囲で\(n\)個の解をもつので、\(\bs{C}\) 上の既約多項式は1次多項式しかないことになります。つまり、既約多項式を議論するときには「どの体での既約多項式か」を明確にする必要があります。
なお、以降の説明において、\(f(x)\) を既約多項式とするとき、方程式 \(f(x)=0\) を「既約方程式」と記述することがあります。
以下、既約多項式の性質を調べますが、その前に次の定理を証明します。
整数係数の多項式 \(f(x)\) が \(\bs{Q}\) 上で(=有理数係数の多項式で)因数分解できれば、整数係数でも因数分解できる。
この定理の対偶をとると、
となります。有理数係数の多項式は、各係数を整数の分数で表現可能で、その分母の最小公倍数を多項式全体に掛けると整数係数の多項式になります。従って、ある多項式が既約かどうかという議論は整数係数の範囲で考えればよいことになり、話が随分シンプルになります。
これを証明するために、まず次の補題を証明します。
[補題]
2つの整数係数の多項式、\(g(x),\:\:h(x)\) があり、ともに係数の最大公約数は \(1\) とする。このとき、
\(r(x)=g(x)h(x)\)
で定義される多項式 \(r(x)\) の係数の最大公約数も \(1\) である。
[証明]
背理法を使う。\(r(x)\) の係数の最大公約数が \(2\) 以上と仮定する。最大公約数を素因数分解したときに現れる素数の一つを \(\bs{p}\) とする。
\(r(x)=a_0+a_1x+a_2x^2+\cd+a_nx^n\)
とおくと、\(a_i\:\:(0\leq i\leq n)\) のすべては \(p\) で割り切れる。ここで、
\(g(x)=b_0+b_1x+b_2x^2+\cd+b_mx^m\)
\(h(x)=c_0+c_1x+c_2x^2+\cd+c_kx^k\)
とすると、\(g(x)\) の係数の最大公約数は \(1\) なので、係数のすべてが \(p\) で割り切れることはなく、少なくとも \(1\) つの係数は \(p\) で割り切れない。ここで、\(p\) で割り切れない \(g(x)\) の係数のうち \(x\) の次数が最小の係数を考える。以降の数式を見やすくするため、\(b_2\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。このとき \(b_0,\:b_1\) は \(p\) で割り切れる。
全く同様にして \(h(x)\) に関しては、\(c_3\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。つまり \(c_0,\:c_1,\:c_2\) は \(p\) で割り切れる。
ここで、\(r(x)=g(x)h(x)\) の等式の \(x^5\) の係数を比較する。左辺の \(x^5\) の項は \(a_5x^5\) であるが、背理法の仮定によって係数 \(a_5\) は \(p\) で割り切れる。
一方、右辺の \(g(x)h(x)\) の \(x^5\) の項は、
\((b_0c_5+b_1c_4+b_2c_3+b_3c_2+b_4c_1+b_5c_0)x^5\)
であるが、この係数のうち \(b_2c_3\) は 素数 \(p\) で割り切れない。なぜなら、\(b_2\) も \(c_3\) も素数 \(p\) で割り切れないので、\(b_2c_3\) を素因数分解しても \(p\) が現れないからである。一方、\(b_2c_3\) 以外の5つの項は、\(b_0,\:b_1,\:c_0,\:c_1,\:c_2\) のいずれかを因数にもつから、\(p\) で割り切れる。従って、唯一、 \(b_2c_3\) だけが \(p\) で割り切れないので、右辺全体としては \(p\) で割り切れない。
ということは、\(r(x)=g(x)h(x)\) の等式は \(x^5\) の項に関して右辺が \(p\) で割り切れ、左辺が \(p\) で割り切れないことになり、矛盾が生じる。
表記を見やすくするために、\(b_2\) と \(c_3\) が素数 \(p\) で割り切れない最小の次数の係数としたが、これを \(b_i\:\:(0\leq i\leq m)\) と \(c_j\:\:(0\leq j\leq k)\) としても全く同じであり、左辺の \(x^{i+j}\) の係数である \(a_{i+j}\) が \(p\) で割り切れる(=背理法の仮定)にもかかわらず、右辺の \(x^{i+j}\) の係数が \(p\) で割り切れないという矛盾が生じる。
従って背理法の仮定は間違っていて、\(r(x)\) の係数すべてを割り切る素数はなく、係数の最大公約数は \(1\) である。[補題の証明終]
この補題を用いて、整数係数多項式の既約性の定理(31C)を証明します。
[証明]
整数係数の多項式 \(f(x)\) が、2つの有理数係数の多項式 \(g(x)\) と \(h(x)\) に因数分解されたとする。
\(f(x)=df_r(x)\)
であり、\(f_r(x)\) の係数の最大公約数は \(1\) である。
\(g(x)\) の係数は有理数(=整数の分数)であるが、適当な整数 \(m_g\) をかけることによって整数係数の多項式 \(m_gg(x)\) にすることができる。この多項式 \(m_gg(x)\) の係数の最大公約数を \(d_g\) とし、\(m_gg(x)\) の各係数を \(d_g\) で割った多項式を \(g_r(x)\) とする。
\(m_gg(x)=d_gg_r(x)\)
であり、\(g_r(x)\) の係数の最大公約数は \(1\) である。
同様に、\(h(x)\) の係数は有理数であるが、適当な整数 \(m_h\) をかけることによって整数係数の多項式 \(m_hh(x)\) にすることができる。この \(m_hh(x)\) の係数の最大公約数を \(d_h\) とし、\(m_hh(x)\) の各係数を \(d_h\) で割った多項式を \(h_r(x)\) とする。
\(m_hh(x)=d_hh_r(x)\)
であり、\(h_r(x)\) の係数の最大公約数は \(1\) である。
以上にもとづいて \((\br{B})\) 式を書き換えると、
となる。ここで、
\((\br{D})\) 式を \((\br{C})\) 式に代入すると、
(整数)\(\times\)(係数の最大公約数が \(1\) の整数係数多項式)
と表現する方法は1種類しかない。従って \((\br{E})\) 式の両辺の係数と多項式は同じものであり、多項式の部分は、
\(\begin{eqnarray}
&&\:\:f_r(x)&=r(x)\\
&&&=g_r(x)\cdot h_r(x)\\
\end{eqnarray}\)
である。従って \(f(x)=df_r(x)\) を使って、
\(f(x)=(dg_r(x))\cdot h_r(x)\)
と表現できる。結局、\(f(x)\) は整数係数の2つの多項式に因数分解できることになり、題意が証明された。[証明終]
この定理があるため、有理数係数の既約多項式を議論するときには、整数係数の既約多項式 \(f(x)\) を議論し、\(f(x)=0\) の解を調べればよいことになります。これ以降の説明では整数係数の方程式の例だけが出てきますが、その理由は整数係数の例で十分だからです。
多項式の不定方程式の定理(31A)のように、多項式は整数とのアナロジーがあります。そのアナロジーで言うと、既約多項式は整数における素数に相当します。例えば次の定理が成り立ちます。
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
[証明]
\(f(x)\) が \(p(x)\) で割り切れないとする。\(f(x)\) と \(p(x)\) は互いに素なので、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x),\:b(x)\) が存在する。両辺に \(g(x)\) を掛けると、
\(g(x)f(x)a(x)+g(x)p(x)b(x)=g(x)\)
となる。\(g(x)f(x)\) は \(p(x)\) で割り切れるので、
\(g(x)f(x)=p(x)h(x)\)
と書ける。これを代入して、
\(p(x)h(x)a(x)+g(x)p(x)b(x)=g(x)\)
\(p(x)\cdot(h(x)a(x)+g(x)b(x))=g(x)\)
となり、\(g(x)\) は \(p(x)\) で割り切れる。従って \(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。[証明終]
この定理の \(f(x)\) を \(g(x)\) に置き換えると次が言えます。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
\(a\) を整数とし、\(a^2\) が \(3\) で割り切れれば、\(a\) は \(3\) で割り切れます。しかし \(a^2\) が \(4\) で割り切れたとしても \(a\) が \(4\) で割り切れるとは限らない。これと既約多項式のアナロジーが成り立っています。
以下、既約多項式がもつ重要な性質を3つあげます。最初の3つは方程式に関するものです。
既約多項式の性質
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
[証明]
\(f(x)\) は \(p(x)\) で割り切れないと仮定して背理法で証明する。\(f(x)\) が \(p(x)\) で割り切れないのなら、\(f(x)\) と \(p(x)\) は互いに素である。なぜなら、もし互いに素でないとすると、1次式以上の多項式 \(h(x)\) があって、
\(f(x)=f_1(x)h(x)\)
\(p(x)=p_1(x)h(x)\)
と表現できるが、\(p(x)\) は既約多項式なので \(p_1(x)=1\) であり、つまり \(h(x)=p(x)\) である。そうすると \(f(x)=f_1(x)p(x)\) となり、\(f(x)\) は \(p(x)\) で割り切れることになって矛盾するからである。つまり、\(f(x)\) が \(p(x)\) で割り切れないのなら \(f(x)\) と \(p(x)\) は互いに素である。
\(f(x)\) と \(p(x)\) が互いに素なら、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x)\)、\(b(x)\) が存在する。そこで、方程式 \(p(x)=0\) と \(f(x)=0\) の共通の解を \(\al\in\bs{C}\) とし、この式に代入すると、左辺\(=0\) となって矛盾する。
従って、\(f(x)\) は \(p(x)\) で割り切れないとの仮定は矛盾を導くから、仮定は誤りであり、\(f(x)\) は \(p(x)\) で割り切れる。[証明終]
この定理は重要なことを言っています。\(\bs{Q}\) 上の方程式の解になる数を代数的数といいます。\(f(x)\) を既約多項式とし、ある代数的数 \(\al\) が \(f(x)=0\) の解とします。
もし、既約多項式 \(f(x)\) 以外の多項式 \(g(x)\) があって、\(g(x)=0\) の解の一つが\(\al\) だとすると、上記の定理により \(g(x)\) は \(f(x)\) で割り切れます。\(g(x)\) の次数が \(f(x)\) の次数と同じとすると、\(g(x)\) は \(f(x)\) の定数倍の既約多項式です。\(g(x)\) の次数が \(f(x)\) の次数より大きいとすると、\(g(x)\) は既約多項式ではありません。
つまり、\(\al\) を方程式の解とするとき、\(\bs{f(\al)=0}\) である既約多項式 \(\bs{f(x)}\) は、定数倍を除いて一意に決まることがわかります。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
[証明]
既約多項式の定理1(31E)により、もし方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば \(f(x)\) は \(p(x)\) で割り切れるので、多項式 \(h(x)\)(定数の場合を含む)を用いて
\(f(x)=p(x)h(x)\)
と表現できる。従って、
\(f(x)\) の次数 \(\geq\:p(x)\)の次数
である。つまり、
この定理は、既約多項式の定理1(31E)と同じことを別の視点で述べたものです。「3.2 体」の「単拡大体の基底」で、既約多項式の定理2(31F)を使った証明を行います。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式とすると、方程式 \(p(x)=0\) は(複素数の範囲で)重解を持たない。
[証明]
方程式 \(p(x)=0\) が重解 \(\al\) を持つとすると、
\(p(x)=(x-\al)^2q(x)\)
となる。これを微分すると、
\(p\,'(x)=2(x-\al)q(x)+(x-\al)^2q\,'(x)\)
となる。以上の2式に \(\al\) を代入すると、
となる。つまり、
・既約多項式 \(p(x)\) の次数は \(2\) 以上
・\(p\,'(x)\) の次数は \(2\) 未満
であるにもかかわらず共通の解 \(\al\) を持つことになり、既約多項式の定理2(31F)に反して矛盾が生じる。従って方程式 \(p(x)=0\) は重解を持たない。[証明終]
この定理も重要です。以降で行う証明の中には「\(n\)次既約方程式 \(f(x)=0\) の \(n\) 個の解を \(\al_1,\al_2,\cd,\al_n\) とする」といった、「\(n\)次方程式は \(\bs{n}\) 個の異なった解を持つのが当然」のような記述が出てきますが、\(\bs{f(x)}\) が既約多項式ならこの定理で保証されているからです。
最小多項式
\(\al\) を 方程式の解とする。\(\al\) を解としてもつ、体 \(\bs{Q}\) 上の方程式のうち、次数が最小の多項式を、\(\al\) の \(\bs{Q}\) 上の最小多項式と言う。
\(\bs{Q}\) 上の方程式、\(f(x)=0\) が \(\al\) を解としてもつとき、
の2つは同値である。
[② \(\bs{\Rightarrow}\) ① の証明]
最小多項式 \(f(x)\) が既約多項式でなければ、\(f(x)=g(x)h(x)\) となる \(\bs{Q}\) 係数の多項式 \(g(x)\)、\(h(x)\) が存在する。\(x\) に \(\al\) を代入すると、
\(f(\al)=g(\al)h(\al)=0\)
となり、少なくとも \(g(\al)=0\)、\(h(\al)=0\) のどちらかは成り立つ。従って、\(f(x)\) より次数の低い多項式で \(\al\) を解にもつものが存在することになり、\(f(x)\) が最小次数であるという、最小多項式の定義に反する。従って \(f(x)\) は既約多項式である。
[① \(\bs{\Rightarrow}\) ② の証明]
\(g(x)\) を \(\al\) の \(\bs{Q}\) 上の最小多項式とする。すると、\(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) を持つことになり、\(f(x)\) は既約多項式なので、既約多項式の定理1(31E)により \(g(x)\) は \(f(x)\) で割り切れる。従って \(g(x)\) は多項式 \(h(x)\) を用いて、
\(g(x)=h(x)f(x)\)
と表せる。② \(\Rightarrow\) ①の証明により、最小多項式は既約多項式なので、\(g(x)\) は既約多項式である。既約多項式が \(1\)次多項式以上の因数をもつことはない。従って \(h(x)\) は \(0\)次多項式=定数である。ということは、\(f(x)\) も \(\al\) の最小多項式である。[証明終]
方程式 \(f(x)=0\) の解が \(\al\) である( \(f(\al)=0\) )という場合、方程式がまずあって、その解を考えます。しかしその逆、つまり代数的数 \(\al\) があり、\(\al\) を解にもつような方程式は何かと考えるのが最小多項式です。これは、ガロア理論でしばしば出てきます。
3.2 体
「体」とは何かを「1.2 体」で説明しました。それを前提として、ガロア理論に必要な「体」についての定義\(\cdot\)定理を説明します。
最小分解体
体 \(\bs{Q}\) 上の多項式 \(f(x)\) を、
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
この最小分解体は、あとに出てくるガロア拡大体と直結している重要な概念です。
\(\bs{Q}\) 上の方程式の解が四則演算とべき根で表されるかどうか、と言った場合、既約多項式だけを考えれば十分です。しかし最小分解体は、既約でない多項式をも含んだ定義です。ガロア理論でしばしば出てくるのは \(1\) の \(n\)乗根を求める、
\(x^n-1=0\)
という方程式ですが、左辺は因数分解ができるので既約多項式ではありません。最小分解体の定義は、一般の多項式としておく方が都合が良いのです。
単拡大定理
\(\bs{Q}\) 上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大である。つまり \(\bs{K}\) の元 \(\theta\) があって、\(\bs{K}=\bs{Q}(\theta)\) となる。この \(\theta\) を原始元という。
[証明]
\(\bs{Q}\) 上の方程式の解を \(\al\)、\(\beta\) とし、
\(\theta=\al+c\beta\:\:(c\in\bs{Q})\)
とおく。すると、\(\al+c\beta\) と有理数の四則演算で作れる数は、\(\al,\:\beta,\) 有理数の四則演算で作れるから、
\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。次に、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
が成り立つような \(c\) が存在することを示す。
\(\al\) の \(\bs{Q}\) 上の最小多項式を \(f(x)\) とし、\(\beta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とする。そして、
\(f(x)=0\) の解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\)
\(g(x)=0\) の解を \(\beta_1=\beta,\:\beta_2,\:\cd\:,\beta_m\)
とする。ここで、
\(h(x)=f(\al+c\beta-cx)\)
とおくと、
\(h(\beta)=f(\al)=0\)
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\:\:(2\leq i\leq m)\)
となる。
\(c\) は有理数であり、無数に選べるので、\(\al+c\beta-c\beta_i\:\:(2\leq i\leq m)\) のどれもが \(\al_1,\:\al_2,\:\cd\:,\al_n\) と一致しないようにできる。具体的には、もし \(\al_j\:\:(1\leq j\leq n)\) と一致したとしたら、
\(\al_j=\al+c\beta-c\beta_i\)
\(c=-\dfrac{\al-\al_j}{\beta-\beta_i}\)
なので、\(i\) と \(j\) を \((2\leq i\leq m,\:\:1\leq j\leq n)\) の範囲で振って \(n(m-1)\) 個の \(c\) を計算し、これら以外の値を選べばよい。このように \(c\) を選んだとする。そうすると \(\al+c\beta-c\beta_i\) は方程式 \(f(x)=0\) の解にはなり得ないので、
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\neq0\:\:(2\leq i\leq m)\)
であり、\(g(x)=0\) と \(h(x)=0\) の共通解は \(\beta=\beta_1\) のみになる。
そうすると \(h(x)\) と \(g(x)\) は唯一の共通の因数 \((x-\beta)\) をもつので、\(h(x)\) と \(g(x)\) に互除法(21A)を適用すると、\(k\) をある有理数として最後は \(k(x-\beta)\) で割り切れる。
\(g(x)\) は \(\bs{Q}\) 上の多項式だから、すなわち \(\bs{Q}(\al+c\beta)\) 上の多項式である。また、\(h(x)\) は \(h(x)=f(\al+c\beta-cx)\) と定義されるが、\(f(x)\) が \(\bs{Q}\) 上の多項式なので、\(h(x)\) は \(\bs{Q}(\al+c\beta)\) 上の多項式である。つまり \(h(x)\) も \(g(x)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。
従って、互除法の最終結果である \(k(x-\beta)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。これは、
\(k,\:k\beta\:\in\:\bs{Q}(\al+c\beta)\)
であることを意味しており、従って、
\(\beta\:\in\:\bs{Q}(\al+c\beta)\)
となる。また \(\al\) も、
\(\al=(\al+c\beta)-c\beta\:\in\:\bs{Q}(\al+c\beta)\)
である。この結果、\(\al\)、\(\beta\) の両方が \((\al+c\beta)\) の四則演算で表現できることになり、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。従って、\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\theta)\) と合わせて、
\(\bs{Q}(\al,\beta)=\bs{Q}(\theta)\)
が結論づけられた。
以上を繰り返し適用すると、\(\bs{Q}\) に添加する方程式の解は \(\al,\:\beta,\:\gamma,\:\cd\) と増やしていける。従って、
ことが証明できた。[証明終]
「すべての代数拡大体は単拡大である」というのは、ちょっと驚くような定理です。方程式の解を複数添加した体は、このような性質をもっています。方程式の解の議論をするときに解を含む体の性質で議論することのメリットは、このような単拡大定理が使えることにも現れています。次の「単拡大の体」に関する定理も、単拡大定理があることで任意の代数拡大体につながっています。
なお、上の証明で本質的な役割を果たしているのはユークリッドの互除法が成り立つ原理(21A)です。互除法の "奥の深さ" がわかります。
単拡大の体
ある代数的数 \(\al\) の \(\bs{Q}\) 上の最小多項式が \(n\)次多項式 \(f(x)\) であるとする。このとき 体 \(\bs{K}\) を、
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
[証明]
\(\bs{K}\) が四則演算で閉じていて体であることを証明する。\(\bs{K}\) の元は「\(\bs{Q}\) 上の、\(\al\) の \(n-1\) 次以下の式」で表されるので、\(\bs{K}\) の任意の2つの元を、\(\bs{Q}\) 上の \(n-1\) 次以下の2つの多項式 \(g(x),\:h(x)\) を用いて、\(g(\al),\:h(\al)\) とする。
\(g(\al)+h(\al),\:g(\al)-h(\al)\) は \(\al\) の \(n-1\) 次以下の式なので、\(\bs{K}\) は加減について閉じている。
乗法で閉じていることを言うため、\(g(x)h(x)\) を \(f(x)\) で割った商を \(q(x)\)、余りを \(r(x)\) とする。つまり、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。\(x=\al\) を代入すると、\(f(\al)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
となる。\(r(x)\) は \(f(x)\) で割ったときの余りなので、次数は \(f(x)\) の次数 \(n\) よりも小さく、\(n-1\) 以下である。従って、\(g(\al)h(\al)\) は \(\al\) の \(n-1\) 次以下の式になり、\(\bs{K}\) は乗法で閉じている。
除法で閉じていることは、\(h(\al)\neq0\) のとき、\(\dfrac{g(\al)}{h(\al)}\) が \(\bs{Q}\) 上の「\(\al\) の \(n-1\) 次以下の多項式」で表されることを示せればよい。\(s(x),\:t(x)\) を未知の多項式とし、次の不定方程式を立てる。
\(f(x)s(x)+h(x)t(x)=g(x)\)
\(f(x)\) は最小多項式なので、最小多項式は既約多項式の定理(31I)により既約多項式である。また、\(h(x)\) は \(f(x)\) で割り切れない。なぜなら、もし \(h(x)\) が \(f(x)\) で割り切れるとすると、\(h(x)=u(x)f(x)\) と書けるが、これに \(\al\) を代入すると \(h(\al)=u(\al)f(\al)=0\) となり、\(h(\al)\neq0\) に矛盾するからである。
\(h(x)\) が、既約多項式である \(f(x)\) で割り切れないので、\(h(x)\) と \(f(x)\) は互いに素である。すると、多項式の不定方程式の定理(31A)により、上記の不定方程式を満たす \(s(x),\:t(x)\) が存在して、\(t(x)\) を \(n-1\) 次以下にとることができる。不定方程式に \(x=\al\) を代入すると、
\(h(\al)t(\al)=g(\al)\)
\(\dfrac{g(\al)}{h(\al)}=t(\al)\)
となり、除法でも閉じていることが分かった。つまり \(\bs{K}\) は体である。
\(\bs{Q}(\al)\) は「有理数と\(\al\)」の四則演算で生成される全ての数から成る体である。\(\bs{K}\) の元は有理数と \(\al\) の四則演算で表現され、それは元の間の四則演算で完全に閉じている。従って \(\bs{K}=\bs{Q}(\al)\) である。
表現の一意性は次のようにして証明できる。もし \(\bs{Q}(\al)\) の元について \(g(\al)\) と\(h(\al)\) の2通りの表し方があったとする。つまり、
\(g(\al)=h(\al)\)
\(g(\al)-h(\al)=0\)
とする。\(g(x)-h(x)\) が1次式以上だと仮定すると、\(n-1\)次以下の方程式 \(g(x)-h(x)=0\) が \(\al\) を解にもつことになる。つまり \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解 \(\al\) を持つ。一方、\(f(x)\) は \(n\)次既約多項式であり、\(g(x)-h(x)\) は \(n-1\) 次以下の多項式である。この場合、既約多項式の定理2(31F)によって、方程式 \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解を持たない。従って矛盾が生じる。つまり \(g(x)-h(x)\) は1次式以上ではありえない。\(g(x)-h(x)\) は \(0\)次多項式=定数である。
\(g(x)-h(x)\) が定数であれば、\(g(\al)-h(\al)=0\) なので、その定数は \(0\) しかない。つまり \(g(x)\) と \(h(x)\) の係数は全く一致する。従って表現は一意である。[証明終]
単拡大定理(32B)と、この単拡大の体の定理(32C)を合わせると、
ことになります。このことは、分子\(\cdot\)分母が \(\al\) の多項式である分数式があったとしても、分数を取り払った \(\al\) の多項式に変換できることを意味します。1.2 節の「方程式の解を含む体」で触れた "分母の有理化" が、どんなに複雑な分母であっても常に可能であることが分かります。
| 2.整数の群 |
「2.整数の群」「3.多項式と体」「4.一般の群」の3つの章は、第5章以下のガロア理論の核心に入るための準備です。
第2章の目的は2つあり、一つは整数を素材にして「群」と、それに関連した「剰余類」「剰余群」「既約剰余類」など、ガロア理論の理解に必要な概念を説明することです。
もう一つは、第2章の最後にある「既約剰余類群は巡回群の直積と同型である」という定理を証明することです。この定理はガロア理論の最終段階(6.可解性の必要条件)で必要なピースになります。
まず、"整数の群" に入る前に、整数論の基礎ともいえる「ユークリッドの互除法」「不定方程式」「法による演算」「中国剰余定理」から始めます。これらは後の定理の証明にしばしば使います。
2.1 整数
ユークリッドの互除法
| (互除法の原理:21A) |
自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,\:b)\) で表す。自然数 \(a\) を \(b\) で割った余りを \(r\) とすると、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
[証明]
記述を簡略化するため、最大公約数を、
\(\mr{gcd}(a,\:b)=x\)
\(\mr{gcd}(b,\:r)=y\)
で表す。\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とすると、
\(a=pb+r\) \((0\leq r < b)\)
と書ける。\(a\) と \(pb\) は \(x\) で割り切れるから、\(r\) も \(x\) で割り切れる。つまり \(x\) は \(r\) の約数である。\(x\) は \(b\) の約数でもあるから、\(x\) は \(b\) と \(r\) の公約数である。公約数は \(b\) と \(r\) の最大公約数 \(y\) 以下だから、
\(x\leq y\)
である。
一方、\(pb\) と \(r\) は \(y\) で割り切れるから、\(y\) は \(a\) の約数である。\(y\) は \(b\) の約数でもあるから、\(y\) は \(a\) と \(b\) の公約数である。公約数は \(a\) と \(b\) の最大公約数以下だから、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので \(x=y\)、つまり、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。[証明終]
この原理を利用して \(\mr{gcd}(a,\:b)\) を求めることができます。もし \(a\) が \(b\) で割り切れるなら \(\mr{gcd}(a,\:b)=b\) です。そうでないなら、\(a\) を \(b\) で割った余り \(r\) を求め、
新 \(a\:\longleftarrow\:b\)
新 \(b\:\longleftarrow\:r\)
と定義し直して、\(a\) が \(b\) で割り切れるかどうかを見ます。こうして次々と \(a\) と \(b\) のペアを作っていけば(=互除法)、\(b\) は単調減少していくので、いずれ \(a\) が \(b\) で割り切れるときがきます。なかなか割り切れなくても、\(b\) が \(1\) までくると絶対に割り切れる。つまり、
\(\mr{gcd}(a,\:b)=b\)
となるのが最終段階で、そのときの \(b\) が最大公約数です。\(b\) が \(1\) までになってしまったら、最大公約数は \(\bs{1}\)、つまり \(\bs{a}\) と \(\bs{b}\) は互いに素です。
ちなみに、ユークリッドの互除法で a と b の最大公約数を求める関数 EUCLID を Python で記述すると次のようになります。
def EUCLID(a, b): if a % b == 0: return b else: return EUCLID(b, a % b) |
% は Python の剰余演算子で、a % b は「a を b で割った余り」の意味です(定理の記述では \(r\))。つまり、このコードは、
gcd( a, b )=gcd( b, a % b )
という互除法の原理(21A)をストレートに書いたものです(a と b の大小に関係なく動作します)。こういったアルゴリズムはプログラミング言語で記述した方がシンプルでわかりやすくなります。
互除法は多項式の演算にも適用できます。多項式は整数と同じように割り算はできませんが余り算はできるからです。多項式の性質を理解するときに互除法は必須になります。
1次不定方程式
| (不定方程式の解の存在:21B) |
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
[証明]
1次不定方程式が整数解を持つとしたら、方程式の左辺は \(d\) で割り切れる、つまり \(d\) の倍数だから、右辺の \(c\) も \(d\) の倍数である。このことの対偶は「\(c\) が \(d\) の倍数でなければ方程式は整数解を持たない」なので、題意の「そうでなければ整数解を持たない」が証明されたことになる。従って以降は「\(c=kd\) (\(k\) は整数)と表せるなら方程式は整数解を持つ」ことを証明する。まず、変数が2つの場合である。
係数の \(a\) と \(b\) に互除法(21A)を適用し、それと同時に \(x,\:y\) の変数を変換して方程式を変形していく。まず、\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とする。
\(a=pb+r\)
である。互除法の次のステップの係数と変数を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1=b&\\
&&b_1=r&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_1=px+y&\\
&&y_1=x&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(x,\:y\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x=y_1&\\
&&y=x_1-py_1&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(\begin{eqnarray}
&&\:\:a_1x_1+b_1y_1&=b(px+y)+rx\\
&&&=pbx+by+rx\\
&&&=(pb+r)x+by\\
&&&=ax+by\\
\end{eqnarray}\)
と計算できるので、不定方程式は、
\(a_1x_1+b_1y_1=c\)
となり、係数の値がより小さい方程式に変形できる。互除法の原理(21A)により、\(a_1\) と \(b_1\) の最大公約数は \(d\) のままである。この方程式の \(x_1,\:y_1\) が求まれば、\(\br{③}\) を使って \(x,\:y\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i\) を \(b_i\) で割った商と余りを、
\(a_i=p_ib_i+r_i\)
のように求め、互除法の次のステップを、
\(a_{i+1}=b_i\)
\(b_{i+1}=r_i\)
\(x_{i+1}=p_ix_i+y_i\)
\(y_{i+1}=x_i\)
とすることで続けていける。このように、係数に互除法の適用を繰り返し、同時に変数を変換していく。そして互除法の最終段階で、
\(a_nx_n+b_ny_n=c\)
となったとする。この段階では \(a_n\) は \(b_n\) で割り切れ、そのときの \(b_n\) は最大公約数 \(d\) である。つまり。
\(a_nx_n+dy_n=c\)
である。もし \(c\) が \(d\) の倍数であれば、つまり \(c=kd\) (\(k\) は整数)なら、
\(x_n=0\)
\(y_n=k\)
という整数解を必ずもつ。従って、変数の変換過程を逆にたどって \(x,\:y\) が求まる。以上で2変数の場合に題意が正しいことが証明でき、同時に1次不定方程式の解を求めるアルゴリズムも明らかになった。
ちなみに、一次不定方程式の解の一つを求めるアルゴリズムを Python の関数で記述すると、次のようにシンプルです。
def LinearDiophantineEq(a, b, c): def extendedEUCLID(a, b): # gcd(a,b) と ax+by=gcd(a,b) の解を求める r = a % b # % は剰余演算 if r == 0: return {"x": 0, "y": 1, "gcd": b} else: x, y, gcd = extendedEUCLID(b, r).values() p = a // b # // は切捨て除算 return {"x": y, "y": x - p * y, "gcd": gcd} x, y, gcd = extendedEUCLID(a, b).values() k = c // gcd if( k != c / gcd ): return None # 解なし else: return [x * k, y * k] # x, y のペアを返す |
数学的帰納法を使って、3変数以上の場合を証明する。\(n=2\) の場合に成り立つことを示したので、\(n=k\) の場合に成り立つと仮定する。つまり、
\(k\) 変数の不定方程式を、 \(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_k\) (\(a_i\) は \(0\) 以外の整数) \(d_k=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\) とするとき、 \(c_k=md_k\) (\(m\) は整数) なら整数解がある。 |
と仮定する。\(n=k+1\) の場合の不定方程式を、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k+a_{k+1}x_{k+1}=c_{k+1}\)
\(\begin{eqnarray}
&&\:\: d_k&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\\
&&\:\: d_{k+1}&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k,\:a_{k+1})\\
\end{eqnarray}\)
とし、この方程式が整数解をもつ条件を調べる。方程式を移項すると、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_{k+1}-a_{k+1}x_{k+1}\)
となるが、この不定方程式が整数解をもつのは、数学的帰納法の仮定によって、
左辺\(=d_k\) の整数倍
のときである。つまり、
\(c_{k+1}-a_{k+1}x_{k+1}=d_k\cdot y\)
という、2つの変数 \(x_{k+1},\:y\) の不定方程式が整数解をもつときである。式を移項すると、
\(a_{k+1}x_{k+1}+d_k\cdot y=c_{k+1}\)
であるが、これは証明済みの \(n=2\) のときの定理によって、
\(c_{k+1}=m\cdot\mr{gcd}(d_k,\:a_{k+1})\) (\(m\) は整数)
の場合に整数解をもつ。ここで、
\(\mr{gcd}(d_k,\:a_{k+1})=d_{k+1}\)
なので、
\(c_{k+1}=m\cdot d_{k+1}\) (\(m\) は整数)
の場合にのみ、\(n=k+1\) の不定方程式は整数解をもつことになる。
つまり、\(n=k\) のときに題意が成り立つと仮定すると、\(n=k+1\) のときにも成り立つ。\(n=2\) のときには成り立つから、\(n\geq3\) でも成り立つ。[証明終]
重要なのは、係数が互いに素な場合です。不定方程式の解の存在(21B)から、次の定理がすぐに出てきます。
| (不定方程式の解の存在:21C) |
\(0\) でない整数 \(a\) と \(b\) が互いに素とすると、1次不定方程式、
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) の最大公約数が \(1\)、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
互除法と同じように、不定方程式の解の存在定理 (21B)と(21C)も、多項式の性質を理解する上で重要です。
法による演算
| (法による演算の定義:21D) |
\(a,\:b\) を整数、\(n\) を自然数とする。\(a\) を \(n\) で割った余りと、\(b\) を \(n\) で割った余りが等しいとき、
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
法による演算の規則は、さまざまありますが、主なものは次の通りです。このような演算を以降の説明で適時使います。
| (法による演算規則:21E) |
\(a,\:b,\:c,\:d\) を整数、\(n,r\) を自然数とし、
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
| \((1)\:a+c\) | \(\equiv b+d\) | \((\mr{mod}\:n)\) | |
| \((2)\:a-c\) | \(\equiv b-d\) | \((\mr{mod}\:n)\) | |
| \((3)\:ac\) | \(\equiv bd\) | \((\mr{mod}\:n)\) | |
| \((4)\:a^r\) | \(\equiv b^r\) | \((\mr{mod}\:n)\) |
中国剰余定理
| (中国剰余定理:21F) |
\(n_1\) と \(n_2\) を互いに素な自然数とする。\(a_1\) と \(a_2\) を、\(0\leq a_1 < n_1,\:0\leq a_2 < n_2\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
[証明]
もし \(x\) と \(y\:\:(y\leq x)\) が連立方程式を満たすとすると、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(y\equiv a_1\:\:(\mr{mod}\:n_1)\)
なので、
\(x-y\equiv0\:\:(\mr{mod}\:n_1)\)
であり、\(x-y\) は \(n_1\) で割り切れる。同様にして \(x-y\) は \(n_2\) でも割り切れる。\(n_1\) と \(n_2\) は互いに素なので、\(x-y\) は \(n_1n_2\) で割り切れる。従って \(x-y\) は \(n_1n_2\) の倍数であり、
| \(x-y\equiv0\) | \((\mr{mod}\:n_1n_2)\) | |
| \(x\equiv y\) | \((\mr{mod}\:n_1n_2)\) |
\(n_1,\:n_2\) は互いに素なので、不定方程式の解の存在定理(21C)により、
\(n_1m_1+n_2m_2=1\)
を満たす \(m_1,\:m_2\) が存在する。ここで、
\(x=a_2n_1m_1+a_1n_2m_2\)
とおくと、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2n_1m_1+a_1(1-n_1m_1)\\
&&&=a_1+n_1m_1(a_2-a_1)\\
&&&\equiv a_1\:\:(\mr{mod}\:n_1)\\
\end{eqnarray}\)
であり、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2(1-n_2m_2)+a_1n_2m_2\\
&&&=a_2+n_2m_2(a_1-a_2)\\
&&&\equiv a_2\:\:(\mr{mod}\:n_2)\\
\end{eqnarray}\)
なので、\(x\) は連立方程式の解である。この解は、上での証明のとおり \(\mr{mod}\:n_1n_2\) でみて唯一である。[証明終]
中国剰余定理は3数以上に拡張できて、次が成り立ちます。
| (中国剰余定理・多連立:21G) |
\(n_1,\:n_2,\:\cd\:,\:n_k\) を、どの2つをとっても互いに素な自然数とする。\(a_i\) を \(0\leq a_i < n_i\:\:(1\leq i\leq k)\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
[証明]
自然数 \(N\) を
\(N=n_1n_2\cd n_k\)
と定義する。
\(\mr{gcd}\left(\dfrac{N}{n_i},n_i\right)=1\:\:\:(1\leq i\leq k)\)
なので、不定方程式の解の存在の定理(21C)により、
\(\dfrac{N}{n_i}s_i+n_it_i=1\:\:\:(1\leq i\leq k)\)
を満たす整数解、\(s_i,\:t_i\:\:(1\leq i\leq k)\) が存在する。
\(x=\displaystyle\sum_{i=1}^{k}a_i\dfrac{N}{n_i}s_i\)
と定義すると、\(j\neq i\) である \(j\) について、
\(\dfrac{N}{n_j}\equiv0\:\:(\mr{mod}\:n_i)\)
だから、\(\mr{mod}\:n_i\) でみると、\(x\) を定義する総和記号のなかは \(i\) の項だけが残る。つまり、
\(\begin{eqnarray}
&&\:\:x&\equiv a_i\dfrac{N}{n_i}s_i\:\:(\mr{mod}\:n_i)\\
&&&=a_i(1-n_it_i)\\
&&&\equiv a_i\:\:(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となって、\(x\) は連立合同方程式の解である。
連立合同方程式に2つの解、\(x,\:y\) があったとすると、
\(\begin{eqnarray}
&&\:\:x-y&\equiv a_i-a_i &(\mr{mod}\:n_i)\\
&&&=0 &(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となり、\(x-y\) は \(n_i\) の倍数である。これは \(1\leq i\leq k\) のすべての \(i\) で成り立ち、また \(n_i\:\:(1\leq i\leq k)\) は、どの2つをとっても互いに素である(=共通な因数が全くない)から、\(x-y\) は \(N\) の倍数である。従って、
\(x\equiv y\:\:(\mr{mod}\:N)\)
であり、\(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。[証明終]
2.2 群
これ以降、整数を素材に「群」と、それに関連した概念の説明をします。まず、群の定義からです。
群の定義
| (群の定義:22A) |
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群(group)であると言う。
| \(G\) の任意の元 \(x,\:y\) に対して演算(\(\cdot\)で表す)が定義されていて、\(x\cdot y\in G\) である。 | |
| 演算について結合法則が成り立つ。つまり、 \((x\cdot y)\cdot z=x\cdot(y\cdot z)\) | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot e=e\cdot x=x\) を満たす元 \(e\) が存在する。\(e\) を単位元という。 | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot y=y\cdot x=e\) となる元 \(y\) が存在する。\(y\) を \(x\) の逆元といい、\(x^{-1}\) と表す。 |
整数 \(\bs{Z}\)
整数の集合を \(\bs{Z}\) と書きます。\(\bs{Z}\) は「加法(足し算)を演算とする群」になります。単位元は \(0\) で、元 \(x\) の逆元は \(-x\) です。この群の元の数は無限なので「無限群」です。
整数の加法は、\(x+y=y+x\) と演算の順序を入れ替えることができます。このような群が可換群です。アーベル群とも言います。
なお、有理数は \(\bs{Q}\)、実数は \(\bs{R}\)、複素数は \(\bs{C}\) で表しますが、\(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) は、\(\bs{Z}\) を同じように加法に関して群です(=加法群)。と同時に \(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) から加法の単位元 \(0\) を除くと、乗法に関しても群になります。その単位元は \(1\) です。
部分群 \(n\bs{Z}\)
群 \(G\) の部分集合 \(H\) が、\(G\) と同じ演算で群としての定義を満たすとき、\(H\) を部分群(subgroup)と言います。
\(G\) の単位元 \(e\) だけから成る部分集合 \(\{\:e\:\}\) は群としての定義を満たし、部分群です。また \(G\) そのものも "\(G\)の部分集合" であり、部分群です。これらを \(G\) の自明な部分群と言います。
\(\bs{Z}\) の元の一つを \(n\) とし(\(n\neq0\))、\(n\) の倍数の集合を \(n\bs{Z}\) と表記します。\(n\bs{Z}\) は加法を演算として群の定義を満たすので、\(\bs{Z}\) の部分群です。\(n\bs{Z}\) も無限群かつ可換群です。たとえば \(n=6\) とすると、
\(6\bs{Z}=\{\cd,\:-6,\:0,\:6,\:12,\:18,\:\cd\}\)
です。
剰余類と剰余群
部分群を用いて、元の数が有限個である有限群を作ることができます。一般に、群 \(G\) の部分群を \(H\) とするとき(演算を "\(\cdot\)" とします)、\(G\) の任意の元 \(g\) を取り出して、
\(g\cdot H\)
とした集合を剰余類(coset / residue class)と言います。これは「\(g\) と、集合 \(H\) のすべての元を演算した結果の集合」の意味です。
\(\bs{Z}\) と その部分群 \(6\bs{Z}\) を例にとると、\(\bs{Z}\) の任意の元を \(i\) として、
\(i+6\bs{Z}\)
が剰余類です。具体的にその集合を書くと、
\(\vdots\)
\(0+6\bs{Z}=\{\cd,\:-6,\:\:0,\:\phantom{1}6,\:12,\:18,\:\cd\}\)
\(1+6\bs{Z}=\{\cd,\:-5,\:\:1,\:\phantom{1}7,\:13,\:19,\:\cd\}\)
\(2+6\bs{Z}=\{\cd,\:-4,\:\:2,\:\phantom{1}8,\:14,\:20,\:\cd\}\)
\(3+6\bs{Z}=\{\cd,\:-3,\:\:3,\:\phantom{1}9,\:15,\:21,\:\cd\}\)
\(4+6\bs{Z}=\{\cd,\:-2,\:\:4,\:10,\:16,\:22,\:\cd\}\)
\(5+6\bs{Z}=\{\cd,\:-1,\:\:5,\:11,\:17,\:23,\:\cd\}\)
\(6+6\bs{Z}=\{\cd,\:\phantom{-}0,\:\:6,\:12,\:18,\:24,\:\cd\}\)
\(7+6\bs{Z}=\{\cd,\:\phantom{-}1,\:\:7,\:13,\:19,\:25,\:\cd\}\)
\(\vdots\)
などです。以降、剰余類 \(i+6\bs{Z}\) を \(\ol{\,i\,}\) と記述します。つまり、
\(\ol{\,i\,}=i+6\bs{Z}\)
です。上の表示を見ると分かるように、たとえば \(\ol{\,1\,}\) と \(\ol{\,7\,}\) は集合として同じものです。さらに、
\(\cd=\ol{-11}=\ol{-5}=\ol{\,1\,}=\ol{\,7\,}=\ol{13}=\cd\)
であり、これらは同じ集合です。これらの集合の中から一つの元を選んで「代表元」と呼ぶことにします。以降、分かりやすいように \(1\) を代表元とします。その他の剰余類についても同じようにすると、部分群 \(6\bs{Z}\) による剰余類は、
\(\ol{\,0\,},\:\ol{\,1\,},\:\ol{\,2\,},\:\ol{\,3\,},\:\ol{\,4\,},\:\ol{\,5\,}\)
の6つで表されることになります。これらの剰余類には重複がありません。また、全部の和集合をとると \(\bs{Z}\) になります。記号で書くと、\(\phi\) を空集合として、
\(\ol{\,i\,}\:\cap\:\ol{\,j\,}\:=\:\phi\:\:(0\leq i,\:j\leq6,\:i\neq j)\)
\(\bs{Z}=\ol{\,0\,}\:\cup\:\ol{\,1\,}\:\cup\:\ol{\,2\,}\:\cup\:\ol{\,3\,}\:\cup\:\ol{\,4\,}\:\cup\:\ol{\,5\,}\)
です。別の見方をすると、\(i,\:j\) を任意の整数するとき、
| \(\ol{\,i\,}\) と \(\ol{\,j\,}\) の元は「全く同じ」か「全く重複しない」のどちらかである | |
| \(\bs{Z}\) は剰余類で分類される |
と言えます。平たく言うと、\(n\)(上の例では \(6\))で割った余りが同じ整数を集めたものが剰余類です。"剰余" という用語はそこからきています。
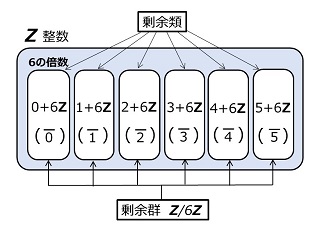
|
剰余類と剰余群 |
整数 \(\bs{Z}\) の部分集合 \(6\bs{Z}\)(\(6\)の倍数の集合)から、\(\ol{\,i\,}=i+6\bs{Z}\) \((0\leq i\leq5)\) の定義で6つの「剰余類」が作れる。これらに重複はなく、\(\bs{Z}\) はこの6つで "分類" される。 整数 \(i,\:j,\:k\) に \(i+j=k\) の関係があるとき、\(\ol{\,i\,}+\ol{\,j\,}=\ol{\,k\,}\) で剰余類の加算を定義すると、この定義で剰余類は群となる。この群を「剰余群」と呼び \(\bs{Z}/6\bs{Z}\) で表わす(単位元は \(\ol{\,0\,}\))。この群では \(\ol{\,3\,}+\ol{\,5\,}=\ol{\,2\,}\) などの演算になるが、これは整数の合同式 \(3+5\equiv2\) \((\mr{mod}\:6)\) と同一視できる。 |
剰余類のうち、\(\ol{\,0\,}\) は \(\bs{Z}\) の部分群ですが、\(\ol{\,i\,}\:(i\neq0)\) の集合は \(\bs{Z}\) の部分群ではありません。集合の元と元のたし算が集合を "はみ出す" からです。しかし、剰余類同士の演算(=集合と集合の演算)を定義することにより、剰余類を元とする群を構成できます。それが次です。
剰余類に加算を定義できます。つまり、\(\ol{\,i\,}+\ol{\,j\,}\) を、
\(\ol{\,i\,}+\ol{\,j\,}=\ol{(\:i+j\:)}\) (右辺の \(+\) は整数の加算)
と定義すると、この演算の定義で剰余類は群になり、
\(\bs{Z}/n\bs{Z}\)
と表します。この群の元は集合(=剰余類)です。この群を剰余群(あるいは商群。quotient group)と言います。元の数は有限なので有限群です。また演算が整数の加算なので可換であり、「有限可換群」です。
\(\bs{Z}/n\bs{Z}\) という記法では、\(\bs{Z}\) も \(n\bs{Z}\) も群(この場合は加法群)です。一般に「群\(/\)部分群」と書けば、剰余群(商群)の意味です。これに対して「拡大体\(/\)体」は "体の拡大" を意味します。 \(\bs{Q}(\al)/\bs{Q}\) などです。
一般に、有限群 \(G\) の元の数を群の位数(order)と呼び、
\(|G|\) あるいは \(\#G\)
で表します。剰余群では、
| \(|(\bs{Z}/n\bs{Z})|\) | \(=n\) | |
| \(\#(\bs{Z}/n\bs{Z})\) | \(=n\) |
生成元と巡回群
剰余群 \(\bs{Z}/n\bs{Z}\) は、元 \(\ol{\,1\,}\) だけをもとに群演算を繰り返すことによって、すべての元を作り出すことができます。\(\bs{Z}/6\bs{Z}\) を例にとると、
\(\ol{\,2\,}=\ol{\,1\,}+\ol{\,1\,}\)
\(\ol{\,3\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
などであり
\(\ol{\,0\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
です。群にこのような元がある場合、それを生成元(generator)と呼びます。\(\bs{Z}/6\bs{Z}\) の場合は \(\ol{\,1\,}\) のほかに \(\ol{\,5\,}\) も生成元です。\(\ol{\,i\,}\) を \(k\) 個加算することを、\(k\cdot\ol{\,i\,}\) と書くことにします。
\(k\cdot\ol{\,i\,}=\overbrace{\ol{\,i\,}+\ol{\,i\,}+\cd+\ol{\,i\,}}^{k\:個加算}\)
です。\(\ol{\,5\,}\) については、
\(1\cdot\ol{\,5\,}=\ol{\,5\,},\:\:2\cdot\ol{\,5\,}=\ol{\,4\,},\:\:3\cdot\ol{\,5\,}=\ol{\,3\,}\)
\(4\cdot\ol{\,5\,}=\ol{\,2\,},\:\:5\cdot\ol{\,5\,}=\ol{\,1\,},\:\:6\cdot\ol{\,5\,}=\ol{\,0\,}\)
のように、\(\ol{\,5\,}\) を起点として全部の元が生成され、\(\ol{\,5\,}\) が生成元であることがわかります。
剰余群 \(\bs{Z}/n\bs{Z}\) においては、\(1\leq g < n\) である整数 \(g\) が \(n\) と互いに素であるとき、\(\ol{\,g\,}\) は生成元になります。その理由ですが、
\(\ol{\,g\,},\:\:2\cdot\ol{\,g\,},\:\:3\cdot\ol{\,g\,},\:\cd\:,\:n\cdot\ol{\,g\,}\)
という \(n\) 個の剰余類の列を考えると、これらは全て違ったものだからです。なぜなら、もし \(1\leq i < j\leq n\) である \(i,\:j\) について、 \((\br{A})\)
\(i\cdot\ol{\,g\,}=j\cdot\ol{\,g\,}\)
だとすると、これは、法 \(n\) における整数の合同式で、
\(ig\equiv jg\:\:(\mr{mod}\:n)\)
を意味します。つまり、
\((j-i)g\equiv0\:\:(\mr{mod}\:n)\)
ですが、\(g\) が \(n\) と互いに素なため、\((j-i)\) は \(n\) で割り切れなければなりません。しかし \(1\leq(j-i)\leq(n-1)\) なので、矛盾します。従って、\(n\) 個の剰余類の列 \((\br{A})\) は、全て違ったものです。剰余群 \(\bs{Z}/n\bs{Z}\) の群位数は \(n\) なので、\((\br{A})\) は \(\bs{Z}/n\bs{Z}\) の全ての元であり、従って \(\ol{\,g\,}\) は生成元です。
\(n\) が素数 \(p\) の場合は、\(p\) 未満の自然数はすべて \(p\) と互いに素なので、単位元 \(\ol{\,0\,}\) を除く \(\bs{Z}/p\bs{Z}\) の元が生成元になります。
\(k\) 個の \(\ol{\,i\,}\) の群演算をして初めて、結果が単位元 \(\ol{\,0\,}\) になるときの \(k\) を、\(\ol{\,i\,}\) の位数(order)といいます。群の位数と紛らわしいですが、これは群の「元の位数」です。\(\bs{Z}/6\bs{Z}\) の場合、「元 \(\rightarrow\) 位数」の対応は、
\(\ol{\,0\,}\:\rightarrow\:1,\:\:\ol{\,1\,}\:\rightarrow\:6,\:\:\ol{\,2\,}\:\rightarrow\:3\)
\(\ol{\,3\,}\:\rightarrow\:2,\:\:\ol{\,4\,}\:\rightarrow\:3,\:\:\ol{\,5\,}\:\rightarrow\:6\)
です。位数という用語を使うと、生成元とは「位数が群位数に等しい元」のことです。
群 \(G\) が一つの生成元から生成されるとき、\(G\) を巡回群(cyclic group)と言います。\(\bs{Z}/10\bs{Z}\) の例をとると、\(10\) と互いに素な数を考えて、生成元は \(\ol{\,1\,},\:\ol{\,3\,},\:\ol{\,7\,},\:\ol{\,9\,}\) の4つです。従って、たとえば \(\ol{\,7\,}\) 同士の加算を繰り返すと、
| \(\ol{\,7\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,1\,}\:\rightarrow\)\( \:\ol{\,8\,}\:\rightarrow\)\( \:\ol{\,5\,}\:\rightarrow\)\( \:\ol{\,2\,}\:\rightarrow\)\( \:\ol{\,9\,}\:\rightarrow\)\( \:\ol{\,6\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,0\,}\:\rightarrow\)\( \:\ol{\,7\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,1\,}\:\rightarrow\)\( \:\ol{\,8\,}\:\rightarrow\)\( \:\cd\) |
群の直積
\(G,\:H\) を群とします。\(G\) の任意の元 \(g\) と \(H\) の任意の元 \(h\) のペア \((g,\:h)\) 作り、このペアを元とする集合を考えます。以降、群の演算を表す "\(\cdot\)" を省略します。
集合の任意2つの元を、
\(a=(g_a,\:h_a)\)
\(b=(g_b,\:h_b)\)
とし、\(a\) と \(b\) の演算を、
\(ab=(g_ag_b,\:h_ah_b)\)
| \(g_ag_b\) | は \(G\) での群演算 | |
| \(h_ah_b\) | は \(H\) での群演算 |
\(G\times H\)
で表します。有限群の場合、群の位数は、
\(|G\times H|=|G|\cdot|H|\) (\(\cdot\) は整数のかけ算)
です。以上は2つの群の直積ですが、同様に3つ以上の群の直積も定義できます。
群の同型
\(G\) と \(H\) を群とします。\(G\) から \(H\) への1対1の写像 \(f\) で、\(G\) の任意の2つの元 \(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
| \(xy\) は群 \(G\) の演算、\(f(x)f(y)\) は群 \(H\) の演算) |
\(G\cong H\)
と表します。同型であるということは、2つの群の元が1対1対応するのみならず、元の演算前、演算後も1対1対応していることを意味します。従って同型である群は「同じもの」と見なせます。
以降、剰余類を表す \(\bs{\ol{\,i\,}}\) のバーを省略して \(\bs{i}\) と書きます。従って \(i\) は整数か剰余類のどちらかを示しますが、2つは同一視できます。 |
\(\bs{Z}/15\bs{Z}\) で群の同型の例を示します。ここでは、整数 \(i\) を 整数 \(a\) で割った余りを \(i_a\) と書きます。\(\bs{Z}/15\bs{Z}\) の任意の元 \(i\:\:(0\leq i\leq14)\) について、写像 \(f\) を、
\(f\::\:i\:\longmapsto\:(i_3,\:i_5)\)
で定めると、\(f\) は \(\bs{Z}/15\bs{Z}\) から \((\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\) への同型写像になります。
そのことを確かめると、まず \(i\) を決めれば \(i_3,\:i_5\) は一意に決まります。また\(i_3,\:i_5\) を決めると、\(3\) と \(5\) は互いに素なので、中国剰余定理(21F)により、\(0\leq i\leq14\) の範囲で \(i\) が一意に決まります。つまり \(f\) は1対1写像(数学用語で "全単射")です。また、2つの元 \(i,\:j\) について
\(\begin{eqnarray}
&&\:\:f(i+j)&=(\:(i+j)_3,\:(i+j)_5\:)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i)+f(j)&=(i_3,\:i_5)+(j_3,\:j_5)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i+j)&=f(i)+f(j)\\
\end{eqnarray}\)
が成り立つので、\(f\) は同型写像の要件を満たします。従って、
\(\bs{Z}/15\bs{Z}\cong(\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\)
です。一般に、\(a\) と \(b\) を互いに素な自然数とすると、
\(\bs{Z}/(ab)\bs{Z}\cong(\bs{Z}/a\bs{Z})\times(\bs{Z}/b\bs{Z})\)
です。これは2つの数だけでなく、\(n\) が \(k\)個の数 \(a_1,\:a_2,\:\cd\:a_k\) の積で表され、かつ、\(a_1,\:a_2,\:\cd\:a_k\) のどの2つをとっても互いに素なときには、中国剰余定理・多連立(21G)によって、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/a_1\bs{Z})\times(\bs{Z}/a_2\bs{Z})\times\cd\times(\bs{Z}/a_k\bs{Z})\)
が成り立ちます。一般に 自然数 \(n\) は \(p_i\) を素数として、
\(n=p_1^{n_1}p_2^{n_2}\cd p_k^{n_k}\)
と素因数分解され、\(p_i^{n_i}\:\:(1\leq i\leq k)\) はどの2つをとっても互いに素なので、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/p_1^{n_1}\bs{Z})\times(\bs{Z}/p_2^{n_2}\bs{Z})\times\cd\times(\bs{Z}/p_k^{n_k}\bs{Z})\)
成り立ちます。
2.3 既約剰余類群
2.2 節の剰余群は、整数の加算を演算の定義とする群でした。これに対して、整数の乗算を演算の定義とする群が構成できます。それが既約剰余類群です。
| (既約剰余類群:23A) |
剰余群 \(\bs{Z}/n\bs{Z}\) から、代表元が \(n\) と互いに素なものだけを選び出したものを既約剰余類という。
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
[証明]
「既約剰余類」は、乗算に関して群になることを証明する。まず例をあげると、\((\bs{Z}/10\bs{Z})^{*}\) の元は \(10\) と互いに素な代表元をもつ \(1,\:3,\:7,\:9\) である。この元の乗算による演算表を作ると、
\(\begin{array}{r|rrrr}
&1&3&7&9\\ \hline
1&1&3&7&9\\
3&3&9&1&7\\
7&7&1&9&3\\
9&9&7&3&1\\
\end{array}\)
となって、演算は閉じていて、単元 \(1\) があり、逆元があることがわかる( \(3^{-1}=7,\:7^{-1}=3,\:9^{-1}=9\) である\()\)。つまり群として成り立っている。
一般に、\(a,\:b\) が \(n\) と素だとすると、\(ab\) も \(n\) と素なので、\((\bs{Z}/n\bs{Z})^{*}\) は乗算で閉じている。また、不定方程式の解の存在定理(21C)により、
\(ax+ny=1\)
を満たす \(x,\:y\) が存在する。この式の両辺を \(\mr{mod}\:n\) でみると、
\(ax\equiv1\:\:(\mr{mod}\:n)\)
となる。この方程式の解の一つ(=特殊解)を \(x_0\) とし、\(k\) を整数として、\(x=x_0+kn\) とおくと\(,\)
\(\begin{eqnarray}
&&\:\:ax&=a(x_0+kn)\\
&&&=ax_0+akn\\
&&&\equiv1\:\:(\mr{mod}\:n)\\
\end{eqnarray}\)
なので、\(x\) も解である。従って解を \(1\leq x < n\) の範囲で選ぶことができる。つまり、\((\bs{Z}/n\bs{Z})^{*}\) の元 \(a\) に対して逆元が定義できることになり、\((\bs{Z}/n\bs{Z})^{*}\) は群である。[証明終]
2.4 有限体 \(\bs{F}_p\)
\(\bs{Z}/p\bs{Z}\) は体
剰余群 \(\bs{Z}/n\bs{Z}\) において \(n\) が素数 \(p\) である \(\bs{Z}/p\bs{Z}\) を考えます。\(p\) 未満の自然数は \(p\) と互いに素なので、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は、\(\bs{Z}/p\bs{Z}\) から 加法の単位元 \(0\) を除いたものになります。つまり \(\bs{Z}/p\bs{Z}\) は加法について群であり、\(\bs{Z}/p\bs{Z}\:-\:\{\:0\:\}\) が乗法について群になっている。このような集合を体(field)と言います。
体とは加減乗除ができて、加法と乗法を結びつける分配則、
\(a(b+c)=ab+ac\)
が成り立つ集合です。\(\bs{Z}/p\bs{Z}\) は整数の演算をもとに定義されているので分配則が成り立ちます。
\(\bs{\bs{Z}/p\bs{Z}}\) を体としてみるとき、\(\bs{\bs{F}_p}\) と表記します。有理数 \(\bs{Q}\)、実数 \(\bs{R}\)、複素数 \(\bs{C}\) は体ですが、これらは無限集合です。一方、\(\bs{F}_p\) は有限集合なので有限体です。
有限体 \(\bs{F}_p\) における定数、変数、多項式、方程式の計算は、有理数/実数/複素数と同じようにできます。以下、今後の証明に使うので、\(\bs{F}_p\) 上の多項式と方程式を説明します。つまり、係数が \(\bs{F}_p\) の数である多項式や方程式です。
有限体の多項式と方程式
\(\bs{F}_p\) 上の多項式は、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:\:(a_i\in\bs{F}_p)\)
です。見た目は整数係数の多項式ですが、係数は \(\bs{F}_p\) の元です。\(\bs{F}_p\) は体なので、\(\bs{F}_p\) 上の多項式は加減算\(\cdot\)乗算\(\cdot\)余りをともなう除算(=剰余算、余り算)が、\(\bs{Q}\) 上の多項式と同じようにできます。従ってこれらの演算にもとづいた概念、定理は、\(\bs{Q}\) 上の多項式の場合と同じです。つまり、
| 因数分解 | |
| 割り切れる、割り切れないの概念 | |
| 最大公約数(共通に割り切る最大次数の多項式) | |
| 互除法による最大公約数の計算 | |
| 互いに素の概念(最大公約数が定数) | |
| 多項式の不定方程式(31A) | |
| 既約多項式(31B) | |
| 既約多項式と素数の類似性(31D) |
などです(なお、多項式\(\cdot\)方程式についてのこれらの概念や定理は「3.1 多項式」で説明します)。
たとえば、\(\bs{F}_5\) における多項式、\(x^2+1\) は、
\(x^2+1=(x-2)(x-3)\) [\(\bs{F}_5\)]
と、2つの1次多項式に因数分解できます。
\(\begin{eqnarray}
&&\:\:(x-2)(x-3)&=x^2-5x+6\\
&&&=x^2+1\\
\end{eqnarray}\)
が成り立つからです。従って、方程式、
\(x^2+1=0\) [\(\bs{F}_5\)]
の解は、\(x=2,\:3\) です。
一方、\(\bs{F}_7\) において \(x^2+1\) はこれ以上因数分解できない多項式です。なぜなら、
\(f(x)=x^2+1\) [\(\bs{F}_7\)]
とおくと、
\(f(k)\neq0\:\:(0\leq k\leq6)\) [\(\bs{F}_7\)]
だからです。もちろん剰余算(余り算)はできて、\(x^2+1\) を \(x-2\) で割ると、
\(x^2+1=(x-2)(x+2)+5\) [\(\bs{F}_7\)]
と計算できます。これは \(f(2)=5\)、つまり \(f(x)\) を \(x-2\) で割った余りは \(5\)、を意味します。
以上を踏まえて、\(\bs{F}_p\) 上の多項式\(\cdot\)方程式に関する次の定理を証明します(次節の定理の証明に使います)。方程式の "解" は "\(\bs{F}_p\) における解" の意味です。
| (有限体上の方程式1:24A) |
\(\bs{F}_p\) 上の1次方程式、
\(ax+b=c\)
は1個の解をもつ。
[証明]
両辺に \(b\) の加法の逆元 \(-b\) を加えると、
\(ax=c+(-b)\)
となり、この両辺に 乗法の逆元 \(a^{-1}\) を掛けると、
\(x=a^{-1}(c+(-b))\)
となり、唯一の解が求まる。[証明終]
| (有限体上の方程式2:24B) |
\(\bs{F}_p\) 上の多項式を \(f(x)\) とする。
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
[証明]
\(f(x)\) を \(x-a\) で割った商を \(g(x)\)、余りを \(b\) とする。
\(f(x)=(x-a)g(x)+b\)
であるが、\(f(a)=0\) なので \(b=0\) である。従って、
\(f(x)=(x-a)g(x)\)
と表され、\(f(x)\) は \(x-a\) で割り切れる。[証明終]
| (有限体上の方程式3:24C) |
\(\bs{F}_p\) 上の \(n\)次多項式を \(f_n(x)\) とする。方程式、
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
[証明]
\(n\) に関する数学的帰納法を使う。\(\bs{F}_p\) 上 の1次方程式の解は1個だから(24A)、題意は成り立つ。\(n\) 以下で題意が成り立つと仮定する。
\(\bs{F}_p\) 上の \(n+1\) 次方程式 \(f_{n+1}(x)=0\) の解がなければ、\(n+1\) でも題意は成り立っている。もし1個の解 \(a\) があるとすると\(f_{n+1}(a)=0\) なので、\(f_{n+1}(x)\) は \(x-a\) で割り切れる(24B)。つまり、
\(f_{n+1}(x)=(x-a)g(x)\)
となるが、\(g(x)\) は \(n\)次多項式だから、方程式、
\(g(x)=0\)
の解は高々 \(n\) 個である。従って、\(f_{n+1}(x)=0\) の解は高々 \(n+1\) 個である。ゆえに帰納法により題意は正しい。[証明終]
2.5 既約剰余類群は巡回群
2.5 節の目的は、2章の最終目的である、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
という定理を証明することです。証明には少々長いステップが必要ですが、この定理はガロア理論の最終段階で必要になります。まず、群の「元の位数」の性質から始めます。
位数
| (位数の定理:25A) |
\((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とする。以下が成り立つ。
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
[証明]
[補題1]
\((\bs{Z}/n\bs{Z})^{*}\) は有限群だから、\(a^j=a^i\:\:(i < j)\) となる \(i,\:j\) は必ず存在する。\(a^{-i}\) を両辺に掛けると \(a^{j-i}=1\) となり\(a^x=1\) となる \(x\) が必ず存在する。従って \(a\) の位数が定義できる。
[補題2]
\(a^j=a^i\:\:(1\leq i < j\leq d)\) となる \(i,\:j\) があったとすると、両辺に \(a^{-1}\) を掛けて \(a^{j-i}=1\) となるが、\(j-i < d\) だから、\(a^x=1\) となる最小の \(x\) が \(d\) ということと矛盾する。従って、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。
[補題3]
\(a^i\:\:(1\leq i\leq d)\) を \(d\) 乗すると、
\((a^i)^d=(a^d)^i=1\)
であり、これら \(d\) 個の元はすべて \(d\) 乗すると \(1\) になる。
一方、\(d\) 乗すると \(1\) になる 元は 有限体 \(\bs{F}_p\) 上の \(d\) 次方程式 \(x^d-1=0\) の解であるが、有限体上の方程式3の定理(24C)により、\(d\) 次方程式の解の数は高々 \(d\) 個である。従って、\(a^i\:\:(1\leq i\leq d)\) の \(d\) 個の元は、\(d\) 乗すると \(1\) になる 元のすべてである。
[補題4]
\(x\) を \(d\) で割った商を \(q\:\:(1\leq q)\)、余りを \(r\:\:(0\leq r < d)\)とすると、
\(\begin{eqnarray}
&&\:\:a^{qd+r}&=1\\
&&\:\:(a^d)^q\cdot a^r&=1\\
&&\:\:a^r=1&\\
\end{eqnarray}\)
となるが、もし \(r\neq0\) なら、\(d\) より小さい数 \(r\) で \(a^r=1\) となり、これは \(a\) の位数が \(d\) であることと矛盾する。従って \(r=0\) であり、\(x\) は \(d\) の倍数である。
[補題5]
\((\bs{Z}/n\bs{Z})^{*}\) を \(G\) と書く。集合 \(A\) を、
\(A=\{a,\:a^2,\:\cd\:,\:a^d=1\}\)
とする。もし \(|G|=d\) なら、題意は満たされている。
\(d < |G|\) の場合、\(A\) に含まれない \(G\) の元の一つを \(b_1\) とし、
\(A_1=\{b_1a,\:b_1a^2,\:\cd\:,\:b_1a^d\}\)
とする。この \(A_1\) に \(A\) と共通な元はない。なぜならもし、
\(a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-j}\) をかけて、
\(a^{i-j}=b_1\)
となるが、左辺は \(A\) の元であり、右辺の \(b_1\) が \(A\) の元となって矛盾するからである。もし \(A\) と \(A_1\) で \(G\) の元を尽くしているなら、\(|G|=2d\) であり、題意は満たされている。
そうでない場合、\(A\) と \(A_1\) に含まれない \(G\) の元の一つを \(b_2\) とし、
\(A_2=\{b_2a,\:b_2a^2,\:\cd\:,\:b_2a^d\}\)
とする。上の論理と同じで \(A_2\) と \(A\) に共通な元はない。のみならず、\(A_2\) と \(A_1\) に共通な元もない。なぜなら、もし、
\(b_2a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-i}\) をかけて、
\(b_2=b_1a^{j-i}\)
となるが、\(a^{j-i}\) は \(A\) の元だから、\(b_1a^{j-i}\) は \(A_1\) の元であり、\(b_2\) が \(A_1\) の元ということになって矛盾するからである。もし \(A,\:A_1,\:A_2\) で \(G\) の元を尽くしているなら、\(|G|=3d\) であり、題意は満たされている。
そうでない場合、この操作を続けていくと、\(G\) は有限群だから、ちょうど \(G\) の元が尽くされたところで、操作は止まる。最後に作った部分集合が \(A_n\) だったとすると \(|G|=(1+n)d\) であり、\(a\) の位数 \(d\) は群位数の約数である。
\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) なので(23A)、位数の定理(25A)の[補題5]から、次のフェルマの小定理とオイラーの定理が成り立つことがわかります。
| (オイラーの定理:25B) |
自然数 \(n\) と素な自然数 \(a\) について、
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
生成元の存在1
\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在し、従って巡回群であることを証明します。まず、特定の位数 \(d\) をもつ元の数に関する定理からです。
| (位数 \(d\) の元の数:25C) |
\(p\) を素数とする。\((\bs{Z}/p\bs{Z})^{*}\) において、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。
[証明]
[補題1]により、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元に位数が定義できる。その位数は[補題5]により、群位数 \((p-1)\) の約数である。
\((p-1)\) の任意の約数を \(d\) とし、位数 \(d\) の元 \(a\) があったとする。[補題3]により、\(d\)乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d(=1)\)
の「\(a\) 系列」がそのすべてである。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は、\(d\)乗すると \(1\) になるから、\(a\) 以外の位数 \(d\) の元も「\(a\) 系列」の中に含まれている。
ここで、\(\mr{gcd}(j,d)\neq1\) である \(j\:\:(1 < j\leq d)\) をとると、\(a^j\) の位数は \(d\) より小さくなる。なぜなら、\(\mr{gcd}(j,d)=c\:( > 1)\) とすると、2つの数 \(s,\:t\) を選んで、
\(j=c\cdot s\:\:(s < j)\)
\(d=c\cdot t\:\:(t < d)\)
と表されるが、そうすると、
\((a^j)t=a^{cst}=(a^d)^s=1\)
で、\(a^j\) の位数は \(t\) 以下だが、\(t < d\) なので \(a^j\) の位数は \(d\) より小さくなるからである。
一方、\(\mr{gcd}(j,d)\neq1\) である(=\(d\) と素な)\(j\:\:(1\leq j < d)\) をとると、\(a^j\) の位数は \(d\) になる。その理由は以下である。
\((a^j)^x\:\:(1\leq x\leq d)\) が \(x\) の値によってどう変わるかを調べると、まず、\(x=d\) のときは、
\((a^j)^x=(a^j)^d=(a^d)^j=1\)
である。
次に \(1\leq x < d\) のときは \(jx\) は \(d\) の倍数でない。なぜなら、\(j\) は \(d\) と素なため、もし \(jx\) が \(d\) の倍数だとすると、\(x\) が \(d\) の倍数ということになり、\(1\leq x < d\) に反するからである。従って、ある数 \(s,\:t\) を選んで、
\(jx=t\cdot d+s\:\:(0 < s < d)\)
と表せる。そうすると、
\((a^j)^x=a^{td+s}=(a^d)^t\cdot a^s=a^s\)
となるが、\(a\) の位数は \(d\) だから、\(d\) 未満の数 \(s\) で \(a^s\) が \(1\) になることはない。従って \(a^s\neq1\) であり、
\((a^j)^x\neq1\:\:(1\leq x < d)\)
である。
以上により
| \((a^j)^x\neq1\) | \((1\leq x < d)\) | |
| \((a^j)^x=1\) | \((x=d)\) |
まとめると、\((p-1)\) の任意の約数を \(d\) とし、\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元の数を \(\#\mr{ord}(d)\) と表記すると、
\(\#\mr{ord}(d)=\left\{
\begin{array}{l}
\begin{eqnarray}
&&\varphi(d)&\\
&&0&\\
\end{eqnarray}
\end{array}\right.\)
のどちらかである。また、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元には位数が定義でき、\((\bs{Z}/p\bs{Z})^{*}\) の \((p-1)\) 個の元は位数で分類できるから、\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
が成り立つ。ここで \(d|(p-1)\) は、\((p-1)\) のすべての約数 \(d\) についての和をとる意味である。
次に、オイラー関数についてオイラー関数の総和の定理が成り立つことを証明する。
(オイラー関数の総和)
\(n\) を任意の自然数とするとき、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。\(d|n\) は、\(n\) のすべての約数 \(d\) についての和をとる。
[証明]
まず、次の2点に注意する。2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
\(\dfrac{a}{\mr{gcd}(a,b)}\) と \(\dfrac{b}{\mr{gcd}(a,b)}\) は互いに素
である。これは最大公約数の定義そのものである。
次に、\(n\) の約数の一つを \(a\) とし、\(n=a\cdot b\) と表すと、\(b\) もまた \(n\) の約数の一つである。\(n\) に \(r\) 個の約数、\(a_i\:\:(1\leq i\leq r)\) があるとき、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、\(b_i\:\:(1\leq i\leq r)\) もまた \(n\) の \(r\) 個の約数である。つまり、\(b_i\) は \(a_i\) を並び替えたものである。
以上の2点を前提に、まず \(n=12\) の場合で考察する。いま、\(1\) から \(12\) までの \(12\) 個の整数を「\(12\) との最大公約数で分類する」ことを考える。\(12\) の約数 \(d\) は、\(1,\:2,\:3,\:4,\:6,\:12\) の6つである。\(12\) との最大公約数が \(d\) である集合を \(S_d\) とすると、
| \(S_1\) | \(=\{\:1,\:5\:,7\:,11\:\}\) | |
| \(S_2\) | \(=\{\:2,\:10\:\}\) | |
| \(S_3\) | \(=\{\:3,\:9\:\}\) | |
| \(S_4\) | \(=\{\:4,\:8\:\}\) | |
| \(S_6\) | \(=\{\:6\:\}\) | |
| \(S_{12}\) | \(=\{\:12\:\}\) |
となる。各集合に含まれる整数の個数を \(\#S_d\) として順に見ていくと、まず、オイラー関数の定義より、
\(\#S_1=\varphi(12)\)
である。
次に、\(12\) との最大公約数が \(2\) の集合、\(S_2=\{\:2,\:10\:\}\) を考える。\(\{\:2,\:10\:\}\) を \(2\) で割り算した \(\{\:1,\:5\:\}\) のそれぞれは、最大公約数の定義により、\(12\) を \(2\) で割り算した \(6\) と互いに素である。従って、
\(\#S_2=\varphi(6)\)
である。同様に他の集合についても、
| \(\#S_2\) | \(=\varphi(4)\) | |
| \(\#S_4\) | \(=\varphi(3)\) | |
| \(\#S_6\) | \(=\varphi(2)\) | |
| \(\#S_{12}\) | \(=\varphi(1)\) |
| \(\varphi(12)+\varphi(6)+\varphi(4)+\varphi(3)+\varphi(2)+\varphi(1)=12\) |
\(\displaystyle\sum_{d|12}^{}\varphi(d)=12\)
である。
以上の考察は \(n=12\) の場合であるが、\(12\) に特別な意味はない。従って一般の \(n\) の場合も同様となる。
\(n\) が \(r\) 個の約数をもつとし、それらを \(a_i\:\:(1\leq i\leq r)\) とする。集合 \(S\) を \(1\) から \(n\) の \(n\) 個の整数の集合とし、その部分集合 \(S_i\) を、
\(S_i\):\(n\) との最大公約数が \(a_i\) である \(S\) の元の集合
とする。このとき、\(S_i\) の任意の元を \(x\) とすると、
\(\dfrac{x}{a_i}\) と \(\dfrac{n}{a_i}\) は互いに素
である。そもそも、そうなる \(x\) を集めたのが \(S_i\) であった。このことから、
\(S_i\) の元の個数は \(\dfrac{n}{a_i}\) と素である \(S\) の元の個数
ということになる。\(S_i\) の元の個数を \(\#S_i\) と書くと、
\(\#S_i=\varphi\left(\dfrac{n}{a_i}\right)\)
である。ここで \(b_i\) を、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、
\(\#S_i=\varphi(b_i)\)
となるが、この \(b_i\:\:(1\leq i\leq r)\) は \(n\) の約数のすべてであり、\(a_i\) を並び替えたものである。式の両辺の \((1\leq i\leq r)\) の総和をとると、\(\#S_i\) の総和は \(S\) の元の数なので、
左辺\(=\displaystyle\sum_{i=1}^{r}\#S_i=n\)
である。一方、右辺の総和は、
\(\begin{eqnarray}
&&\:\:右辺&=\displaystyle\sum_{i=1}^{r}\varphi(b_i)=\displaystyle\sum_{i=1}^{r}\varphi(a_i)\\
&&&=\displaystyle\sum_{d|n}^{}\varphi(d)\\
\end{eqnarray}\)
となって、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。
\((p-1)\) の約数に戻ると、オイラー関数の総和の定理より、
\(\displaystyle\sum_{d|(p-1)}^{}\varphi(d)=p-1\)
である。一方、位数 \(d\) の元の総和は、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
であった。この2点から、
\(\#\mr{ord}(d)=\varphi(d)\)
が結論づけられる。\(\#\mr{ord}(d)=0\) となる \((p-1)\) の約数 \(d\) は無い。もしあるとすると矛盾が生じる。
従って \((\bs{Z}/p\bs{Z})^{*}\) においては、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。[証明終]
この位数 \(\bs{d}\) の元の数の定理(25C)により、次の生成元の存在1が成り立つことが分かります。
| (生成元の存在1:25D) |
\(p\) を素数とするとき、\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在する。生成元とは、その位数が \((\bs{Z}/p\bs{Z})^{*}\) の群位数、\(p-1\) の元である。
なお、素数 \(p\) に対して、
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の原始根(primitive root)という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の原始根(primitive root)という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
ちなみに、\(100\)以下の素数 \(p\)(\(2\) を除く \(24\)個)について、原始根の数 = \(\varphi(p-1)\) と最小の原始根をパソコンで計算すると、次のようになります。
|
|
この表を見ると、\(2\) が最小原始根になることが多いのがわかります。全体の半分(\(12\)個の素数)でそうです。そうでなれければ素数が多い。ただし、\(p=41\) のときの \(6\) のように、合成数が最小原始根になる場合もあります。
\((\bs{Z}/p\bs{Z})^{*}\) の生成元を求める計算式はありません。しかし生成元を求めるアルゴリズムはあって、それが次です。これは、少なくとも一つの生成元が存在する証明になっています。
| (生成元の探索アルゴリズム:25D’) |
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
この証明のために2つの補題を証明する。以下において、
・\(a\) は \(b\) を割り切る
・\(a\) は \(b\) の約数である
・\(b\) は \(a\) で割り切れる
・\(b\) は \(a\) の倍数である
ことを、
\(a|b\)
と記述する。また \(a\) と \(b\) の最大値を、
\(\mr{max}(a,\:b)\)
と表す。
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[証明]
\(a\) と \(b\) を素因数分解したときに現れるすべての素数を小さい方から順に並べて、
\(p_1,\:p_2,\:\cd\:,\:p_n\)
とする。この素数の列を用いて、\(a\) と \(b\) を、
\(a=p_1^{a_1}\cdot p_2^{a_2}\cdot\cd\cdot p_n^{a_n}\)
\(b=p_1^{b_1}\cdot p_2^{b_2}\cdot\cd\cdot p_n^{b_n}\)
と素因数分解する。もちろんこの表現では \(a_i=0\) や \(b_i=0\) もありうる。ここで、
\(c_i=\mr{max}(a_i,\:b_i)\:\:\:(1\leq i\leq n)\)
と定義すると、\(a,\:b\) の最小公倍数は、
\(\mr{lcm}(a,b)=p_1^{c_1}\cdot p_2^{c_2}\cdot\cd\cdot p_n^{c_n}\)
である。また、
\(\al_i=\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_i\:\:\:(a_i\geq b_i)&\\
&&0\:\:\:\:(a_i < b_i)&\\
\end{eqnarray}
\end{array}\right.\)
\(\beta_i=\left\{
\begin{array}{l}
\begin{eqnarray}
&&0\:\:\:\:(a_i\geq b_i)&\\
&&b_i\:\:\:(a_i < b_i)&\\
\end{eqnarray}
\end{array}\right.\)
と定義して(\(1\leq i\leq n\))、
\(a\,'=p_1^{\al_1}\cdot p_2^{\al_2}\cd\cd p_n^{\al_n}\)
とおくと、
\(a\,'|a\)
である。同様に、
\(b\,'=p_1^{\beta_1}\cdot p_2^{\beta_2}\cdot\cd\cdot p_n^{\beta_n}\)
とおくと、
\(b\,'|b\)
である。このように \(a\,'\) と \(b\,'\) を決めると、
\(a\,'b\,'=\mr{lcm}(a,b)\)
となり、\(a\,'\) と \(b\,'\) に共通の素因数はないから、
\(\mr{gcd}(a\,',b\,')=1\)
である。[補題6の証明終]
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[証明]
\(\mr{gcd}(k,d)\) を \(g\) と書き、
\(k\,'=\dfrac{k}{g}\)
\(d\,'=\dfrac{d}{g}\)
とすると、
\(k=k\,'\cdot g\)
\(d=d\,'\cdot g\)
\(\mr{gcd}(k\,',d\,')=1\)
と表せる。\(a^k\) の位数を調べるため、
\((a^k)^x=1\)
とおくと、
\(a^{kx}=1\)
なので、[補題4](25A)により、
\(d|(kx)\)
である。つまり、
\((d\,'g)|(k\,'gx)\)
\(d\,'|k\,'x\)
となる。すると、\(\mr{gcd}(k\,',d\,')=1\) なので、
\(d\,'|x\)
が成り立つ。\(d\,'|x\) が成り立つ \(x\) の最小値は \(d\,'\) であり、\(x\) の最小値はすなわち \(a^k\) の位数 \(e\) だから、\(e=d\,'\) である。つまり、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。[補題7の証明終]
[補題6]と[補題7]を用いて、生成元の探索アルゴリズム(25D’)を証明します。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
[証明]
\(a\) の累乗の列、
\(a,\:a^2,\:a^3,\:\cd,\:a^d=1\)
は \(d\)個の異なる元である。\(d < p-1\)(群位数)なので、この列に含まれない任意の元を \(b\) とし、\(b\) の位数を \(e\) とする。[補題3](25A)により、\(d\) 乗して \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は \(a\) の累乗の列で尽されているから、\(b^d\neq1\) である。従って \(b\) の位数 \(e\) は \(d\) の約数ではない。もちろん \(e > 1\) である。以降、証明を2つのケースに分ける。
\(\bs{(1)\:\:\mr{gcd}(d,e)=1}\) のとき
このとき、\(ab\) の位数が \(d\) より大きいことを以下で証明する。\(ab\) の位数を調べるために、
\((ab)^x=1\)
とおく。両辺を \(d\)乗すると、
\((ab)^{dx}=1\)
であり、また \(a^d=1\) から \((a^d)^x=1\) だから、
\(b^{dx}=(a^d)^xb^{dx}=(ab)^{dx}=1\)
となり、[補題4](25A)により \(dx\) は \(b\) の位数 \(e\) の倍数である。つまり、
\(e|dx\)
である。すると、\(\mr{gcd}(d,e)=1\) により、
\(e|x\)
となる。同様に、
\((ab)^{ex}=1\)
\(b^e=1\)
だから、
\(a^{ex}=a^{ex}(b^e)^x=(ab)^{ex}=1\)
となり、\(ex\) は \(a\) の位数 \(d\) の倍数である。つまり、
\(d|ex\)
である。すると \(\mr{gcd}(d,e)=1\) により、
\(d|x\)
である。以上の結果、\(e|x\) かつ \(d|x\) であり、
\((de)|x\)
が成り立つ。つまり \(x\) の最小値は \(de\) である。\((ab)^x=1\) となる \(x\) の最小値が \(ab\) の位数だから、
\(ab\) の位数\(=de\)
となる。\(e > 1\) なので、\(ab\) は位数が \(d\) より大きい元である。
\(\bs{(2)\:\:\mr{gcd}(d,e)\neq1}\) のとき
[補題6]により、2つの数、\(d\,',\:e\,'\) をとって、
\(d\,'|d\)
\(e\,'|e\)
\(\mr{gcd}(d\,',e\,')=1\)
\(\mr{lcm}(d,e)=d\,'e\,'\)
となるようにできる。
\(\mr{gcd}\left(\dfrac{d}{d\,'},d\right)=\dfrac{d}{d\,'}\)
だから、[補題7]を使って、
\(a^{{}^{\frac{d}{d\,'}}}\) の位数 \(=\dfrac{d}{\mr{gcd}\left(\dfrac{d}{d\,'},d\right)}=d\,'\)
であり、同様に、
\(b^{{}^{\frac{e}{e\,'}}}\) の位数 \(=\dfrac{e}{\mr{gcd}\left(\dfrac{e}{e\,'},e\right)}=e\,'\)
である。\(\mr{gcd}(d\,',e\,')=1\) だから、
\(c=a^{{}^{\frac{d}{d\,'}}}\cdot b^{{}^{\frac{e}{e\,'}}}\)
とおくと、\(\bs{(1)}\) を使って、
| \(c\) の位数 | \(=d\,'e\,'\) | |
| \(=\mr{lcm}(d,e)\) |
\(\mr{lcm}(d,e) > d\)
である。つまり、\(c\) は位数が \(d\) より大きい元である。[証明終]
生成元の存在2
以降で \((\bs{Z}/p^n\bs{Z})^{*}\) にも生成元が存在することを証明します(ただし、\(p\neq2\))。まず、その証明に使う[補題8]を証明します。整数についての定理です。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
[証明]
表記を分かりやすくするため、まず \(m=1\) のときに成り立つことを証明する。\(m=1\) のときに[補題8]は、
[補題8]\(\bs{m=1}\)
\(p\) を奇素数とし、\(k\) を \(p\) と素な数( \(\mr{gcd}(k,p)=1\) )とする。このとき、
\((1+kp)^p=1+k\,'p^2\)
と表すことができて、\(k\,'\) は \(p\) と素である。
となる。\((1+kp)^p\) を2項定理で展開すると、
\((1+kp)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp+{}_{p}\mr{C}_{2}(kp)^2+{}_{p}\mr{C}_{3}(kp)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp)^{p-1}+(kp)^p\\
&&\:\: =&1+p^2(k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2})\\
&&\:\: =&1+k\,'p^2\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2}\\
\end{eqnarray}\)
となる。\(k\,'\) の第3項(\({}_{p}\mr{C}_{3}k^3p\))以降は \(p\) の指数が \(1\) 以上だから \(p\) で割り切れる。第2項の \(p\) に関係した式は、
\({}_{p}\mr{C}_{2}=\dfrac{p(p-1)}{2}\)
であるが、\(\bs{p}\) が奇素数(\(\bs{p\neq2}\))であるため、この第2項も \(p\) で割り切れる(\(p\) が奇数だと \(p\) で割り切れる)。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。
次に \(m\geq2\) のときであるが、\(m=1\) のときの上の証明において \(p\) を \(p^m\) に置き換えれば、同様の計算で証明できる。\((1+kp^m)^p\) を2項定理で展開すると、
\((1+kp^m)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp^m+{}_{p}\mr{C}_{2}(kp^m)^2+{}_{p}\mr{C}_{3}(kp^m)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp^m)^{p-1}+(kp^m)^p\\
&&\:\: =&1+p^{m+1}(k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1})\\
&&\:\: =&1+k\,'p^{m+1}\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1}\\
\end{eqnarray}\)
\(k\,'\) の第2項以降は \(m\geq2\) なので \(p\) の指数は \(1\) 以上であり、\(p\) で割り切れる。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は、第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。以上の結論として、題意が成り立つ。[証明終]
生成元の存在1の定理(25D)と[補題8]を用いて、\((\bs{Z}/p^n\bs{Z})^{*}\) に生成元が存在することを証明します。
| (生成元の存在2:25E) |
\(p\) を \(p\neq2\) の素数(=奇素数)とする。また、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
[証明]
フェルマの小定理(25B)により、\((\bs{Z}/p\bs{Z})^{*}\) の任意の元は \((p-1)\) 乗すると \(1\) になる。従って、整数の記法で、
\(g^{p-1}=1+kp\)
と書ける。以降、
・\(k\) の素因数に \(p\) を含まないとき
・\(k\) の素因数に \(p\) を含むとき
の2つに分けて証明する。
\(k\) の素因数に \(p\) を含まないとき
この場合は以下が成り立つ。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
[証明(その1)]
\(g\) は \(p\) と互いに素なので \((\bs{Z}/p^n\bs{Z})^{*}\) の元でもある。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は、既約剰余類群の定義によって \(\varphi(p^n)\) である。\(p^n\) 以下で \(p\) で割り切れる数は、\(p^n\) を含んで \(\dfrac{p^n}{p}=p^{n-1}\) 個あるから、
\(\begin{eqnarray}
&&\:\:\varphi(p^n)&=p^n-p^{n-1}\\
&&&=p^{n-1}(p-1)\\
\end{eqnarray}\)
である。従って、オイラーの定理(25B)より、
\(g^{p^{n-1}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
が成り立つ。記述の簡素化のために、
\(h=g^{p-1}\)
とおく。
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
である。
仮定によって \(h\) は、
\(h=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表される。この \(h\) に対して "\(p\)乗する" 操作を \((n-1)\) 回繰り返すと、[補題8]を次々に使って、次のように計算できる。
| \(h^p\) | \(=1+k_1p^2\) | \(\mr{gcd}(k_1,p)=1\) | ||
| \(h^{p^2}\) | \(=(1+k_1p^2)^p\) | \(=1+k_2p^3\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^3)^p\) | \(=1+k_3p^4\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-2})^p\) | \(=1+k_{n-2}p^{n-1}\) | \(\mr{gcd}(k_{n-2},p)=1\) | |
| \(h^{p^{n-1}}\) | \(=(1+k_{n-2}p^{n-1})^p\) | \(=1+k_{n-1}p^n\) | \(\mr{gcd}(k_{n-1},p)=1\) |
この結果から、
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
であることがわかる。この式は \(n\geq1\) のすべての \(n\) で成り立つ。
従って、\(h^x\equiv1\:\:(\mr{mod}\:p^n)\) となる最小の \(x\) は \(p^{n-1}\) の約数であり、\((n-1)\) 個の \(p^i\:\:(1\leq i\leq n-1)\) のどれかである。
しかし、上の計算過程を見ると、
| \(h^{p^i}-1=k_i\cdot p^{i+1}\) | \((\mr{gcd}(k_i,p)=1)\) | |
| \((1\leq i\leq n-1)\) |
\(h^{p^i}\not\equiv1\:\:(\mr{mod}\:p^n)\:\:(1\leq i\leq n-2)\)
である。従って、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
\(h\) は \(g^{p-1}\) であった。ゆえに、\(g\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その1)終]
\(k\) の素因数に \(p\) を含むとき
\(g^{p-1}=1+kp\) と表したときの \(k\) の素因数に \(p\) を含む場合、ある数 \(k\,''\) があって、
\(g^{p-1}=1+k\,''\cdot p^m\:\:(m\geq2)\)
\(\mr{gcd}(k\,'',p)=1\)
と表すことができる。ここで \(k\,''\) を改めて \(k\) と書くと、次が成り立つ。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
[証明(その2)]
\((g+p)^{p-1}\) を2項定理で展開する。
\((g+p)^{p-1}\)
| \(=g^{p-1}\) | \(+{}_{p-1}\mr{C}_{1}g^{p-2}p+{}_{p-1}\mr{C}_{2}g^{p-3}p^2+\:\cd\:+p^{p-1}\) | |
| \(=1+kp^m\) | \(+{}_{p-1}\mr{C}_{1}g^{p-2}p+{}_{p-1}\mr{C}_{2}g^{p-3}p^2+\:\cd\:+p^{p-1}\) |
\(=1+k\,'p\)
\(k\,'=kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2}\)
\(m\geq2\) なので、\(k\,'\) の第2項以外はすべて \(p\) で割り切れる。第2項は \((p-1)g^{p-2}\) だが、\((p-1)\) も \(g^{p-2}\) も \(p\) で割り切れない。つまり \(k\,'\) は第2項だけが唯一、\(p\) で割り切れないから、
\(\mr{gcd}(k\,',p)=1\)
である。まとめると、
\((g+p)^{p-1}=1+k\,'p\)
\(\mr{gcd}(k\,',p)=1\)
と表すことができる。ここで、
\(h=1+k\,'p\)
と書くと、[補題8]を次々と使うことで、次の計算が成り立つ。
| \(h^p\) | \(=1+k_1p^2\) | \(\mr{gcd}(k_1,p)=1\) | ||
| \(h^{p^2}\) | \(=(1+k_1p^2)^p\) | \(=1+k_2p^3\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^3)^p\) | \(=1+k_3p^4\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-2})^p\) | \(=1+k_{n-2}p^{n-1}\) | \(\mr{gcd}(k_{n-2},p)=1\) | |
| \(h^{p^{n-1}}\) | \(=(1+k_{n-2}p^{n-1})^p\) | \(=1+k_{n-1}p^n\) | \(\mr{gcd}(k_{n-1},p)=1\) |
この計算は「\(\bs{k}\) の素因数に \(\bs{p}\) を含まないとき」と全く同じである。従って、そのときの結論を踏襲できて、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
その \(h\) は、
\(h=1+k\,'p=(g+p)^{p-1}\)
であった。\(h\) が \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になるのだから、\(g+p\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その2)終]
以上により、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とすると、\(g\) か \(g+p\) のどちらかは \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。従って \((\bs{Z}/p^n\bs{Z})^{*}\) には生成元があり、群位数 \(p^{n-1}(p-1)\) の巡回群である。[証明終]
ちなみに、\(h=g^{p-1}\) とし、
\(h=1+kp^2\)
\(\mr{gcd}(k,p)=1\)
と表されているときは \(g+p\) が生成元ですが、\(\bs{g}\) は生成元ではありません。なぜなら[補題8]を次々と使うと、
| \(h^p\) | \(=(1+kp^2)^p\) | \(=1+k_1p^3\) | \(\mr{gcd}(k_1,p)=1\) | |
| \(h^{p^2}\) | \(=(1+k_1p^3)^p\) | \(=1+k_2p^4\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^4)^p\) | \(=1+k_3p^5\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-1})^p\) | \(=1+k_{n-2}p^n\) | \(\mr{gcd}(k_{n-2},p)=1\) |
となり、\(h\) を \(p^{n-1}\) 乗する前の \(h^{p^{n-2}}\) の段階で、
\(h^{p^{n-2}}\equiv1\:\:(\mr{mod}\:p^n)\)
\(\longrightarrow\:g^{p^{n-2}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
となってしまいます。つまり \(g\) は生成元ではないのです。\(g^{p-1}=1+kp^m\:\:(m > 2)\) と表されるときも同じです。
実は、\((\bs{Z}/p\bs{Z})^{*}\) の生成元を \(g\) とすると、ほとんどの場合で \(g\) は \((\bs{Z}/p^2\bs{Z})^{*}\) の(従って \((\bs{Z}/p^n\bs{Z})^{*}\) の)生成元になります。生成元の存在1であげた、\(100\) 以下の素数 \(p\) の最小原始根の表ですが、そのすべては \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です。それどころか「\(100\) 以下の素数 \(p\) の原始根が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならない」というケースは、計算してみると次の4つしかありません。
\(p=29,\:g=14\)
\(p=37,\:g=18\)
\(p=43,\:g=19\)
\(p=71,\:g=11\)
たとえば \(p=29\) の場合、\(\varphi(28)=12\) なので原始根 \(g\) は \(12\)個あります。リストすると、
\(g=2,\:3,\:8,\:10,\:11,\:14,\:15,\:18,\:19,\:21,\:26,\:27\)
の \(12\)個です。\(p^2=841\) であり、\((\bs{Z}/p^2\bs{Z})^{*}\) は \((\bs{Z}/841\bs{Z})^{*}\) のことです。その \((\bs{Z}/841\bs{Z})^{*}\) の群位数は、
\(\varphi(p^2)=p(p-1)=29\cdot28=812\)
です。
\(g\) のうち、\(14\) を除く \(11\)個の位数は \(812\) です。ところが \(14\) だけは違って、
\(14^{28}\equiv1\:\:(\mr{mod}\:841)\)
となり、位数は \(28\) です。もちろんこの場合でも、生成元の存在2(25E)の証明プロセスにあるように、
\(g+p=14+29=43\)
の位数は \(812\) で、\((\bs{Z}/841\bs{Z})^{*}\) の生成元です。以上をまとめると、
\(100\) 以下の素数を \(p\) とするとき、\((\bs{Z}/p\bs{Z})^{*}\) の生成元 \(g\) は、\(p=29,\:37,\:43,\:71\) のときを除いて、すべてが \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元であり、\(p=29,\:37,\:43,\:71\) の場合でも \(g\) が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならないケースは、それぞれについて1つしかない
となります。
生成元の存在2(25E)の証明は、[補題8]の証明での \(\bs{{}_{p}\mr{C}_{2}}\) が \(\bs{p}\) で割り切れることがポイントになっていて、\(p\neq2\) である素数(奇素数)のときには成り立ちますが、\(p=2\) のときには成り立ちません。\(p=2\) では生成元が存在しないのです。
しかし \(p=2\) のとき、つまり \((\bs{Z}/2^n\bs{Z})^{*}\) は、生成元をもつ2つの巡回群の直積と同型であることが証明できます。
以降、整数 \(a\) について、 \(a^x\equiv1\:\:(\mr{mod}\:n)\) となる最小の \(x\:(\geq1)\) が存在するとき、\(x\) を「\(\bs{\mr{mod}\:n}\) での \(\bs{a}\) の位数」あるいは「\(a\) の位数 \((\mr{mod}\:n)\)」と呼びます。 |
2のべき乗の既約剰余類群
| (2のべき乗の既約剰余類群:25F) |
2のべき乗の既約剰余類群は、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[証明]
まず \(n=5\) の場合である \((\bs{Z}/32\bs{Z})^{*}\) で考察する。
\((\bs{Z}/32\bs{Z})^{*}\) の元とは、\(1\) から \(31\) までの奇数の集合である。この奇数から「\(4\)で割ると \(1\) 余る奇数」を取り出して、集合 \(A\) とする。
\(A=\{1,\:5,\:9,\:13,\:17,\:21,\:25,\:29\}\)
である。集合 \(A\) の要素の数は、\(32/4=8\) である。ここで、
\(5\equiv1\:\:(\mr{mod}\:4)\)
であることに着目する。この両辺を \(k\) 乗(\(0\leq k\))すると、
\(5^k\equiv1\:\:(\mr{mod}\:4)\)
だから(21E)、\(5^k\) は「\(4\)で割ると \(1\) 余る奇数」である。ここで、\(5^k\) を \(32\) で割った余りを \(j\) とする。つまり、
\(5^k\equiv j\:\:(\mr{mod}\:32)\:\:(0\leq k,\:1\leq j\leq31)\)
である。すると \(j\) は「\(32\)未満の、\(4\)で割ると \(1\) 余る奇数」であり、\(A\) に含まれている。そこでもし、
\(5^x\equiv1\:\:(\mr{mod}\:32)\)
を満たす最小の \(x\)(つまり \(\mr{mod}\:32\) での \(5\) の位数)が \(8\) であれば、位数の定理(25A)の[補題2]によって「\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) はすべて異なる」から、それらは \(A\) そのものである。実際に計算してみると、
| \(5^0\equiv\:1\) | \((\mr{mod}\:32)\) | |
| \(5^1\equiv\:5\) | \((\mr{mod}\:32)\) | |
| \(5^2\equiv25\) | \((\mr{mod}\:32)\) | |
| \(5^3\equiv29\) | \((\mr{mod}\:32)\) | |
| \(5^4\equiv17\) | \((\mr{mod}\:32)\) | |
| \(5^5\equiv21\) | \((\mr{mod}\:32)\) | |
| \(5^6\equiv\:9\) | \((\mr{mod}\:32)\) | |
| \(5^7\equiv13\) | \((\mr{mod}\:32)\) | |
| \(5^8\equiv\:1\) | \((\mr{mod}\:32)\) |
となって、\(\mr{mod}\:32\) での \(5\) の位数は \(8\) であり、\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) には \(A\) の元がすべて現れる。これは \(A\) が巡回群と同型であることを示している。
一方、\((\bs{Z}/32\bs{Z})^{*}\) の元から「\(4\)で割ると \(3\) 余る奇数」を取り出し、それを集合 \(B\) とすると、
\(B=\{3,\:7,\:11,\:15,\:19,\:23,\:27,\:31\}\)
である。ここで、\(A=\{4k+1\:|\:0\leq k\leq7\}\) と記述し、\(i=7-k\:\:(k=7-i)\) と定義すると、
\(\begin{eqnarray}
&&\:\:(-1)\cdot A&=\{-4k-1 &|\:0\leq k\leq7\}\\
&&&=\{-4(7-i)-1 &|\:0\leq i\leq7\}\\
&&&=\{4i+3-32 &|\:0\leq i\leq7\}\\
\end{eqnarray}\)
だから、\(\mr{mod}\:32\) でみると、
\(B\equiv(-1)\cdot A\)
である。\((-1)\cdot A\) は、集合 \(A\) の要素すべてに \(-1\) を掛けた集合の意味である。
\((\bs{Z}/32\bs{Z})^{*}\) の元は \(A\) と \(B\) の和であり、\(A\) と \(B\) に重複はない。従って、\((\bs{Z}/32\bs{Z})^{*}\) の元は、\(\mr{mod}\:32\) でみて、
\((-1)^j\cdot5^k\:\:(j=0,1)\) \((0\leq k\leq7)\)
の形に一意に表現できる。\(j=0\) の場合は \(A\) を、\(j=1\) なら \(B\) を表している。
\(\mr{mod}\:32\) でみて、\(5^k\) は群位数 \(8\) の巡回群であり、\((-1)^j\) は群位数 \(2\) の巡回群である。従って、\((\bs{Z}/32\bs{Z})^{*}\) は2つの巡回群の直積で表現できることになる。このことが成り立つキーポイントは、
\(\mr{mod}\:32\) でみた \(5\) の位数が \(\dfrac{32}{4}=8\)
ということである。もしこれが \(2^5=32\) だけでなく \(2^n\:\:(2\leq n)\) で成り立てば、一般論に拡張できる。その、\(2^n\) で成り立つことは、次のように、[補題9]として証明できる。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
[証明]
数学的帰納法で証明する。題意は \(n=2\) のときに成り立つので( \(5\equiv1\:\:(\mr{mod}\:4)\) )、\(n\) で成り立つと仮定し、\(n+1\) でも成り立つことを証明する。\(\mr{mod}\:2^{n+1}\) での \(5\) の位数を調べるため、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
を満たす \(x\) について考察する。\(x\) の最小値が \(2^{n-1}\) であれば、[補題9]が証明されたことになる。 \((\br{A})\)
一般に \(a\equiv b\:\:(\mr{mod}\:p^n)\) なら、\(1\leq i < n\) とするとき \(a\equiv b\:\:(\mr{mod}\:p^i)\) である。従って \((\br{A})\) 式が成り立つとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^n)\)
も成り立つ。帰納法の仮定により \(\mr{mod}\:2^n\) での \(5\) の位数は \(2^{n-2}\) だから、位数の定理(25A)の[補題4]により \(x\) は \(2^{n-2}\) の倍数である。
従って \(x\) の最小値は \(2^{n-2}\) だが、\(x\) を \(2^{n-2}\) とすると \((\br{A})\) 式が成り立たない。なぜなら、
\(5^{2^{n-2}}\equiv1+2^n\:\:(\mr{mod}\:2^{n+1})\)
が言えるからである。 \((\br{B})\)
\((\br{B})\) 式が正しい理由を数学的帰納法で説明すると、\(n=2\) のとき \((\br{B})\) 式は \(5\equiv5\:\:(\mr{mod}\:8)\) だから成り立っている。そこで、ある整数 \(k\) を用いて \((\br{B})\) 式を等式化すると、
\(5^{2^{n-2}}+k2^{n+1}=1+2^n\)
となる。記述を見やすくするため \(5^{2^{n-2}}=\al\) とおくと、
\(\al+k2^{n+1}=1+2^n\)
である。この両辺を2乗すると、
\((\al+k2^{n+1})^2=(1+2^n)^2\)
\(\al^2+\al k2^{n+2}+k^22^{2n+2}=1+2^{n+1}+2^{2n}\)
となる。\(2\leq n\) のときは \(n+2\leq2n\) なので、両辺を \(\mr{mod}\:2^{n+2}\) でみると、左辺の第2項、第3項、右辺の第3項は \(0\) である。従って、
\(\al^2\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
\(5^{2^{n-1}}\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
となり、\((\br{B})\) 式は \(n\) を \(n+1\) に置き換えても成り立つ。従って \((\br{B})\) 式は正しい。
\(5^{2^{n-2}}+k2^{n+1}=1+2^n\)
となる。記述を見やすくするため \(5^{2^{n-2}}=\al\) とおくと、
\(\al+k2^{n+1}=1+2^n\)
である。この両辺を2乗すると、
\((\al+k2^{n+1})^2=(1+2^n)^2\)
\(\al^2+\al k2^{n+2}+k^22^{2n+2}=1+2^{n+1}+2^{2n}\)
となる。\(2\leq n\) のときは \(n+2\leq2n\) なので、両辺を \(\mr{mod}\:2^{n+2}\) でみると、左辺の第2項、第3項、右辺の第3項は \(0\) である。従って、
\(\al^2\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
\(5^{2^{n-1}}\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
となり、\((\br{B})\) 式は \(n\) を \(n+1\) に置き換えても成り立つ。従って \((\br{B})\) 式は正しい。
\((\br{A})\) 式の \(x\) は \(2^{n-2}\) の倍数であるが、\(x=2^{n-2}\) では \((\br{A})\) 式が成り立たないことが分かった。その次に小さな \(x\) の倍数は \(x=2\cdot2^{n-2}=2^{n-1}\) であり、これを \((\br{A})\) 式に入れると、
左辺\(=5^{2^{n-1}}\)
である。一方、\((\br{B})\) 式の両辺を2乗すると、
\(\begin{eqnarray}
&&\:\:5^{2^{n-1}}&\equiv(1+2^n)^2\:\:(\mr{mod}\:2^{n+1})\\
&&&=1+2^{n+1}+2^{2n}\\
&&&\equiv1\:\:(\mr{mod}\:2^{n+1})\\
\end{eqnarray}\)
であるから、\(x=2^{n-1}\) のとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
が成り立つ。つまり \((\br{A})\) 式が成り立つ \(x\) の最小値は \(2^{n-1}\) であり、\(5\) の \(\mr{mod}\:2^{n+1}\) での位数は \(2^{n-1}\) である。これで、帰納法によって[補題9]が正しいことが証明できた。[補題9の証明終]
[補題9]が正しいので、\(n=5\) の例で展開した論理により、\((\bs{Z}/2^n\bs{Z})^{*}\) の元は、\(\mr{mod}\:2^n\) でみて、
\((-1)^j5^k\:\:(j=0,1,\:\:0\leq k\leq2^{n-2}-1)\)
の形に一意に表現できることが分かった。
ここで、\((\bs{Z}/2^n\bs{Z})^{*}\) から \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) への写像 \(f\) を、
| \(f\::\) | \((\bs{Z}/2^n\bs{Z})^{*}\) | \(\longrightarrow\) | \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) | |
| \((-1)^j5^k\) | \(\longmapsto\) | \((j,\:k)\) |
\(\begin{eqnarray}
&&\:\:f((-1)^j5^k\cdot(-1)^l5^m)&=f((-1)^{j+l}5^{k+m})\\
&&&=(j+l,\:k+m)\\
&&\:\:f((-1)^j5^k)+f((-1)^l5^m)&=(j,k)+(l,m)\\
&&&=(j+l,\:k+m)\\
\end{eqnarray}\)
\(f((-1)^j5^k\cdot(-1)^l5^m)=f((-1)^j5^k)+f((-1)^l5^m)\)
となり、\(f\) は同型写像の要件を満たしている。従って、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
であり、\((\bs{Z}/2^n\bs{Z})^{*}\) は、群位数 \(2\) と群位数 \(2^{n-2}\) の2つの巡回群の直積に同型である。[証明終]
既約剰余類群の構造
ここまでの準備を行うと、既約剰余類群の構造を明らかにできます。これが第2章のゴールです。
| (既約剰余類群の構造:25G) |
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である。
[証明]
以下の記述では、
・\(a_j\) は \(a\) を \(j\) で割った余り
・\((a+b)_j\) は \((a+b)\) を \(j\) で割った余り
を表す。
\(j\) と \(k\) を 互いに素な整数 \((2\leq j,k)\) とする。\(a\) を \(\bs{Z}/(jk)\bs{Z}\) の元とし \((0\leq a\leq jk-1)\)、\(\bs{Z}/(jk)\bs{Z}\) から \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) への写像、\(f\) を次のように定義する。
| \(f\::\) | \(\bs{Z}/(jk)\bs{Z}\) | \(\longrightarrow\) | \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) | |
| \(a\) | \(\longmapsto\) | \((a_j,\:a_k)\) |
\(j\) と \(k\) が 互いに素なので、中国剰余定理(21F)により、任意に選んだ \(a_j\) と \(a_k\) から \(a\) が一意に決まる。つまり、\(f\) は1対1写像(数学用語で "全単射")である。また、\(a\) とは別の \(\bs{Z}/(jk)\bs{Z}\) の元を \(b\) とすると、
\(\begin{eqnarray}
&&\:\:f(a+b)&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a)+f(b)&=(a_j,\:a_k)+(b_j,\:b_k)\\
&&&=(a_j+b_j,\:a_k+b_k)\\
&&&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a+b)&=f(a)+f(b)\\
\end{eqnarray}\)
となり、\(f\) は同型写像である。
いま、\(\mr{gcd}(a,jk)=1\)(\(a\) が \(jk\) と素)だとすると、既約剰余類群の定義により、\(a\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) の元である。
ここで一般的に、
\(\mr{gcd}(a,jk)=1\) なら
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\)
である。また \(\mr{gcd}(a,j)=1\) なら \(\mr{gcd}(j,a_j)=1\) である。なぜなら互除法の原理(21A)によって、\(a\) と \(j\) の公約数は \(j\) と \(a_j\) の公約数だからである。
従って、
\(\mr{gcd}(j,a_j)=1\) かつ \(\mr{gcd}(k,a_k)=1\)
になる。つまり、\(a_j\) は \((\bs{Z}/j\bs{Z})^{*}\) の元であり、\(a_k\) は \((\bs{Z}/k\bs{Z})^{*}\) の元である。また、
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\) なら
\(\mr{gcd}(a,jk)=1\)
も成り立つので、任意の \((\bs{Z}/j\bs{Z})^{*}\) の元と \((\bs{Z}/k\bs{Z})^{*}\) の元を決めれば、\((\bs{Z}/(jk)\bs{Z})^{*}\) の元が定まる。
さらに、既約剰余類群の群演算は乗算であるが、
\(\begin{eqnarray}
&&\:\:a_j\cdot b_j&=(a\cdot b)_j\\
&&\:\:a_k\cdot b_k&=(a\cdot b)_k\\
\end{eqnarray}\)
が成り立つので、
\(f(ab)=f(a)f(b)\)
であり、\(f\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) から \((\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\) への同型写像でもある。従って、\(j\) と \(k\) が互いに素という条件のもとで、
\((\bs{Z}/(jk)\bs{Z})^{*}\cong(\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\)
である。 \((\br{C})\)
いま、\(p,\:q\) を2つの素数とし、\(n\) の素因数分解が、
\(n=p^a\cdot q^b\)
だとする。このとき \((\br{C})\) 式で \(j=p^a,\:k=q^b\) とおくと、
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\)
となる。さらに、\(p,\:q,\:r\) を3つの素数とし、
\(n=p^a\cdot q^b\cdot r^c\)
と表せたとする。\((\br{C})\) 式で \(j=p^a\cdot q^b,\:k=r^c\) とおくと、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/n\bs{Z})^{*}&\cong(\bs{Z}/(p^aq^b)\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
&&&\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
\end{eqnarray}\)
となる。\(n\) の素因数の数が4以上に増えてもこの操作は繰り返せるから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \((\bs{Z}/p^a\bs{Z})^{*}\) の形の既約剰余類群の直積と同型である。
\((\bs{Z}/p^a\bs{Z})^{*}\) は、\(p=2\) のときは2のべき乗の既約剰余類群の定理(25F)により、2つの巡回群の直積と同型である。また、\(p\neq2\) の素数のときは生成元の存在2の定理(25E)により、それ自体が巡回群である。従って、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \(n\) の値にかかわらず、巡回群の直積と同型である。[証明終]
具体例として、たとえば \(n=360\) とすると、\(n=2^3\cdot3^2\cdot5\) なので、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/2^3\bs{Z})^{*}\times(\bs{Z}/3^2\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
となり、\((\bs{Z}/360\bs{Z})^{*}\) は4つの巡回群の直積と同型です。
「既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型」(25G)は、ガロア理論の証明で次のように使います。\(1\) の \(n\)乗根(\(x^n-1=0\) の解)のうち、\(n\)乗して初めて \(1\) になるものを「\(1\) の原始\(n\)乗根」といいます。それを \(\zeta\) とすると、
| \(\bs{Q}(\zeta)\) のガロア群は \((\bs{Z}/n\bs{Z})^{*}\) と同型である。 | |
| \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型である(25G)。 | |
| 巡回群の直積は可解群である。 | |
| \(\bs{Q}(\zeta)\) のガロア群は可解群である。 |
となり、④が証明できます。① と ③ は別途証明します。④ の「\(\bs{Q}(\zeta)\) のガロア群は可解群」が重要で、方程式の可解性の必要条件を証明するときの一つのポイントになります。
| 3.多項式と体 |
ガロア理論では方程式の解を含む「体」の特性を分析することで、方程式が代数的に解けるかどうかを調べます。第3章ではその「体」と、方程式の元になる「多項式」に関する重要な定義と定理を説明します。
3.1 多項式
ガロア理論で対象とする多項式は、1つの変数(未知数)をもつ、有理数係数の多項式です。それを、
| \(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:(a_i\in\bs{Q})\) |
で表します。\(\bs{f(x)}\) の「\(\bs{0}\) でない最高次の係数 \(\bs{n}\)」を、多項式の「次数」といい、\(\bs{\mr{deg}\:f(x)}\) で表します。通常、\(\mr{deg}\:f(x)\geq1\) ですが、便宜上、\(a_0\) 以外の係数が \(0\) の場合(=定数項のみの場合)も多項式と呼び「\(\bs{0}\) 次多項式」とします。また、全ての係数が \(0\) の場合を「\(\bs{0}\) 多項式(零多項式)」と呼びます。
多項式 \(a(x)\) を 多項式 \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とすると、
\(a(x)=p(x)b(x)+r(x)\)
\((\:\mr{deg}\:r(x) < \mr{deg}\:b(x)\:)\)
です。整数のときと同じように互除法(21A)を用い、次に \(b(x)\) を \(r(x)\) で割って余りを求める操作を繰り返すと、\(\mr{deg}\:r(x)\) が単調減少するので、いずれ \(b(x)\) が \(r(x)\) で割り切れるとき(=互除法の最終段階)がきます。\(r(x)\) が \(0\) 次多項式(=定数)なら、\(b(x)\) は \(r(x)\) で割り切れるので、最終段階は必ずあります。
\(b(x)\) が \(r(x)\) で割り切れるとき、\(r(x)\) が \(a(x)\) と \(b(x)\) の「最大公約数」です。実際は "数" ではなく多項式なので、「最大公約式」や「最大公約因子」といった言い方もありますが、一般的には「最大公約数」で通っています。
最大公約数が定数(\(0\) 次多項式)のとき、\(a(x)\) と \(b(x)\) は互いに素である、といいます。このとき、整数における不定方程式の解の存在定理(21C)と同様の、次の定理が成り立ちます。
不定方程式
| (多項式の不定方程式:31A) |
\(a(x)\) と \(b(x)\) が互いに素な多項式のとき、
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
[証明]
\(a(x)\) と \(b(x)\) に互除法(21A)を適用して次数を下げ、同時に \(f(x),\:g(x)\) を変換して同等の方程式に変形していく。\(a(x)\) を \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とする。
\(a(x)=p(x)b(x)+r(x)\)
\(\mr{deg}\:r(x) < \mr{deg}\:b(x)\)
である。互除法の次のステップの \(a_1(x),\:b_1(x)\)、\(f_1(x),\:g_1(x)\) を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1(x)=b(x)&\\
&&b_1(x)=r(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f_1(x)=p(x)f(x)+g(x)&\\
&&g_1(x)=f(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(f(x),\:g(x)\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f(x)=g_1(x)&\\
&&g(x)=f_1(x)-p(x)g_1(x)&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(a_1(x)f_1(x)+b_1(x)g_1(x)\)
\(=b(x)(p(x)f(x)+g(x))+r(x)f(x)\)
\(=p(x)b(x)f(x)+b(x)g(x)+r(x)f(x)\)
\(=(p(x)b(x)+r(x))f(x)+b(x)g(x)\)
\(=a(x)f(x)+b(x)g(x)\)
と計算できるので、不定方程式は、
\(a_1(x)f_1(x)+b_1(x)g_1(x)=1\)
となり、係数多項式 \(a_1(x),\:b_1(x)\) の次数が元々の \(a(x),\:b(x)\) より小さな方程式に変形できる。この方程式の解である \(f_1(x),\:g_1(x)\) が求まれば、\(\br{③}\) を使って \(f(x),\:g(x)\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i(x)\) を \(b_i(x)\) で割った商と余りを、
\(a_i(x)=p_i(x)b_i(x)+r_i(x)\)
\((\:\mr{deg}\:r_i(x) < \mr{deg}\:b_i(x)\:)\)
のように求め、次のステップを、
\(a_{i+1}(x)=b_i(x)\)
\(b_{i+1}(x)=r_i(x)\)
\(f_{i+1}(x)=p_i(x)f_i(x)+g_i(x)\)
\(g_{i+1}(x)=f_i(x)\)
とすることで、互除法を続けていける。このように係数多項式 \(a(x),\:b(x)\) の剰余算を繰り返し、同時に変数多項式 \(f(x),\:g(x)\) を変換していくと、この過程で \(\mr{deg}\:r_i(x)\) は単調減少していく。そして互除法の最終段階で、
\(a_n(x)f_n(x)+b_n(x)g_n(x)=1\)
となったとする。元々の \(a(x)\) と \(b(x)\) は互いに素だったから、この段階の \(b_n(x)\) は \(0\) 次多項式=定数である。その定数を \(c\) とすると、
\(a_n(x)f_n(x)+cg_n(x)=1\)
となるが、この不定方程式の解は、
\(f_n(x)=0\)
\(g_n(x)=\dfrac{1}{c}\)
である。この解を起点として \(f_i(x),\:g_i(x)\:\:(1\leq i\leq n)\) の変換過程を逆にたどると \(f(x),\:g(x)\) が求まる。
次に、
\(a(x)f(x)+b(x)g(x)=1\)
の解が、 \((\br{A})\)
\(\mr{deg}\:g(x) < \mr{deg}\:a(x)\)
であるように選べることを示す。\(g(x)\) を \(a(x)\) で割った商を \(q(x)\)、余りを \(s(x)\) とする。
\(g(x)=q(x)a(x)+s(x)\)
\(s(x)=g(x)-q(x)a(x)\)
である。ここで、
\(F(x)=f(x)+b(x)q(x)\)
\(G(x)=s(x)\)
とおくと、
\(a(x)F(x)+b(x)G(x)\)
\(\begin{eqnarray}
&&\:\: =&a(x)(f(x)+b(x)q(x))+b(x)s(x)\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)(g(x)-q(x)a(x))\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)g(x)-b(x)q(x)a(x)\\
&&\:\: =&a(x)f(x)+b(x)g(x)\\
\end{eqnarray}\)
となるので、
\(a(x)f(x)+b(x)g(x)=1\)
であれば、
\(a(x)F(x)+b(x)G(x)=1\)
である。つまり \(f(x),\:g(x)\) が不定方程式の解であれば、\(F(x),\:G(x)\)も解である。\(\mr{deg}\:G(x)=\mr{deg}\:s(x) < \mr{deg}\:a(x)\) なので、\(F(x),\:G(x)\) が題意を満たす解である。
\((\br{A})\) 式を満たす \(f(x),\:g(x)\) が求まったとする。\((\br{A})\) 式の両辺に \(h(x)\) を掛けると、
\(a(x)f(x)h(x)+b(x)g(x)h(x)=h(x)\)
となる。
\(F(x)=f(x)h(x)\)
\(G(x)=g(x)h(x)\)
とおくと、\(F(x),\:G(x)\) は不定方程式、
\(a(x)F(x)+b(x)G(x)=h(x)\)
の解である。\((\br{A})\) 式の解を \(\mr{deg}\:g(x) < \mr{deg}\:a(x)\) となるように選べることを上で証明したが、この過程において方程式の右辺は無関係であった。従って、全く同じプロセスをたどることで、
\(\mr{deg}\:G(x) < \mr{deg}\:a(x)\)
とすることができる。[証明終]
既約多項式
有理数係数の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解がべき根で表現できるために必要十分条件を述べるのがガロア理論です。
このとき、多項式が有理数の範囲で因数分解できるのであれば、\(f(x)=0\) は、たとえば \(g(x)h(x)=0\)、\(g(x)=0,\:h(x)=0\) となって、より次数の低い方程式の問題に還元されてしまいます。これでは、たとえば \(f(x)\) が5次多項式だとしても、5次方程式の問題ではなくなる。
従って、方程式の解の議論をするときには「因数分解できない多項式」の議論をすればよいことになります。それが既約多項式です。
| (既約多項式の定義:31B) |
有理数 \(\bs{Q}\) を係数とする多項式で、\(\bs{Q}\) の範囲ではそれ以上因数分解できない多項式を \(\bs{Q}\) 上で既約な多項式という。
たとえば多項式 \(x^2-2\) は \(\bs{Q}\) 上では因数分解できませんが、\(\bs{R}\) 上では \((x-\sqrt{2})(x+\sqrt{2})\) と因数分解できます。\(x^2+2\) は \(\bs{R}\) 上では因数分解できませんが、\(\bs{C}\) 上では \((x-\sqrt{2}i)(x+\sqrt{2}i)\) と因数分解できます。「代数学の基本定理」によると、\(n\)次方程式は 複素数の範囲で\(n\)個の解をもつので、\(\bs{C}\) 上の既約多項式は1次多項式しかないことになります。つまり、既約多項式を議論するときには「どの体での既約多項式か」を明確にする必要があります。
なお、以降の説明において、\(f(x)\) を既約多項式とするとき、方程式 \(f(x)=0\) を「既約方程式」と記述することがあります。
以下、既約多項式の性質を調べますが、その前に次の定理を証明します。
| (整数係数多項式の既約性:31C) |
整数係数の多項式 \(f(x)\) が \(\bs{Q}\) 上で(=有理数係数の多項式で)因数分解できれば、整数係数でも因数分解できる。
この定理の対偶をとると、
整数係数の多項式 \(f(x)\) が整数係数で因数分解できなければ、有理数係数でも因数分解できず、つまり \(f(x)\) は既約多項式である
となります。有理数係数の多項式は、各係数を整数の分数で表現可能で、その分母の最小公倍数を多項式全体に掛けると整数係数の多項式になります。従って、ある多項式が既約かどうかという議論は整数係数の範囲で考えればよいことになり、話が随分シンプルになります。
これを証明するために、まず次の補題を証明します。
[補題]
2つの整数係数の多項式、\(g(x),\:\:h(x)\) があり、ともに係数の最大公約数は \(1\) とする。このとき、
\(r(x)=g(x)h(x)\)
で定義される多項式 \(r(x)\) の係数の最大公約数も \(1\) である。
[証明]
背理法を使う。\(r(x)\) の係数の最大公約数が \(2\) 以上と仮定する。最大公約数を素因数分解したときに現れる素数の一つを \(\bs{p}\) とする。
\(r(x)=a_0+a_1x+a_2x^2+\cd+a_nx^n\)
とおくと、\(a_i\:\:(0\leq i\leq n)\) のすべては \(p\) で割り切れる。ここで、
\(g(x)=b_0+b_1x+b_2x^2+\cd+b_mx^m\)
\(h(x)=c_0+c_1x+c_2x^2+\cd+c_kx^k\)
とすると、\(g(x)\) の係数の最大公約数は \(1\) なので、係数のすべてが \(p\) で割り切れることはなく、少なくとも \(1\) つの係数は \(p\) で割り切れない。ここで、\(p\) で割り切れない \(g(x)\) の係数のうち \(x\) の次数が最小の係数を考える。以降の数式を見やすくするため、\(b_2\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。このとき \(b_0,\:b_1\) は \(p\) で割り切れる。
全く同様にして \(h(x)\) に関しては、\(c_3\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。つまり \(c_0,\:c_1,\:c_2\) は \(p\) で割り切れる。
ここで、\(r(x)=g(x)h(x)\) の等式の \(x^5\) の係数を比較する。左辺の \(x^5\) の項は \(a_5x^5\) であるが、背理法の仮定によって係数 \(a_5\) は \(p\) で割り切れる。
一方、右辺の \(g(x)h(x)\) の \(x^5\) の項は、
\((b_0c_5+b_1c_4+b_2c_3+b_3c_2+b_4c_1+b_5c_0)x^5\)
であるが、この係数のうち \(b_2c_3\) は 素数 \(p\) で割り切れない。なぜなら、\(b_2\) も \(c_3\) も素数 \(p\) で割り切れないので、\(b_2c_3\) を素因数分解しても \(p\) が現れないからである。一方、\(b_2c_3\) 以外の5つの項は、\(b_0,\:b_1,\:c_0,\:c_1,\:c_2\) のいずれかを因数にもつから、\(p\) で割り切れる。従って、唯一、 \(b_2c_3\) だけが \(p\) で割り切れないので、右辺全体としては \(p\) で割り切れない。
ということは、\(r(x)=g(x)h(x)\) の等式は \(x^5\) の項に関して右辺が \(p\) で割り切れ、左辺が \(p\) で割り切れないことになり、矛盾が生じる。
表記を見やすくするために、\(b_2\) と \(c_3\) が素数 \(p\) で割り切れない最小の次数の係数としたが、これを \(b_i\:\:(0\leq i\leq m)\) と \(c_j\:\:(0\leq j\leq k)\) としても全く同じであり、左辺の \(x^{i+j}\) の係数である \(a_{i+j}\) が \(p\) で割り切れる(=背理法の仮定)にもかかわらず、右辺の \(x^{i+j}\) の係数が \(p\) で割り切れないという矛盾が生じる。
従って背理法の仮定は間違っていて、\(r(x)\) の係数すべてを割り切る素数はなく、係数の最大公約数は \(1\) である。[補題の証明終]
この補題を用いて、整数係数多項式の既約性の定理(31C)を証明します。
[証明]
整数係数の多項式 \(f(x)\) が、2つの有理数係数の多項式 \(g(x)\) と \(h(x)\) に因数分解されたとする。
\(f(x)=g(x)h(x)\)
\(f(x)\) の係数の最大公約数を \(d\) とし、全部の係数を \(d\) で割って作った多項式を \(f_r(x)\) とする。つまり、 \((\br{B})\)
\(f(x)=df_r(x)\)
であり、\(f_r(x)\) の係数の最大公約数は \(1\) である。
\(g(x)\) の係数は有理数(=整数の分数)であるが、適当な整数 \(m_g\) をかけることによって整数係数の多項式 \(m_gg(x)\) にすることができる。この多項式 \(m_gg(x)\) の係数の最大公約数を \(d_g\) とし、\(m_gg(x)\) の各係数を \(d_g\) で割った多項式を \(g_r(x)\) とする。
\(m_gg(x)=d_gg_r(x)\)
であり、\(g_r(x)\) の係数の最大公約数は \(1\) である。
同様に、\(h(x)\) の係数は有理数であるが、適当な整数 \(m_h\) をかけることによって整数係数の多項式 \(m_hh(x)\) にすることができる。この \(m_hh(x)\) の係数の最大公約数を \(d_h\) とし、\(m_hh(x)\) の各係数を \(d_h\) で割った多項式を \(h_r(x)\) とする。
\(m_hh(x)=d_hh_r(x)\)
であり、\(h_r(x)\) の係数の最大公約数は \(1\) である。
以上にもとづいて \((\br{B})\) 式を書き換えると、
| \(df_r(x)\) | \(=\dfrac{d_g}{m_g}g_r(x)\cdot\dfrac{d_h}{m_h}h_r(x)\) | ||
| \(=\dfrac{d_gd_h}{m_gm_h}g_r(x)\cdot h_r(x)\) | \((\br{C})\) |
\(g_r(x)\cdot h_r(x)=r(x)\)
と定義すると、[補題]により、多項式 \(r(x)\) の係数の最大公約数は \(1\) である。 \((\br{D})\)
\((\br{D})\) 式を \((\br{C})\) 式に代入すると、
\(df_r(x)=\dfrac{d_gd_h}{m_gm_h}r(x)\)
となる。この式で \(f_r(x)\) と \(r(x)\) はともに係数の最大公約数が \(1\) であるが、整数係数の多項式を、 \((\br{E})\)
(整数)\(\times\)(係数の最大公約数が \(1\) の整数係数多項式)
と表現する方法は1種類しかない。従って \((\br{E})\) 式の両辺の係数と多項式は同じものであり、多項式の部分は、
\(\begin{eqnarray}
&&\:\:f_r(x)&=r(x)\\
&&&=g_r(x)\cdot h_r(x)\\
\end{eqnarray}\)
である。従って \(f(x)=df_r(x)\) を使って、
\(f(x)=(dg_r(x))\cdot h_r(x)\)
と表現できる。結局、\(f(x)\) は整数係数の2つの多項式に因数分解できることになり、題意が証明された。[証明終]
この定理があるため、有理数係数の既約多項式を議論するときには、整数係数の既約多項式 \(f(x)\) を議論し、\(f(x)=0\) の解を調べればよいことになります。これ以降の説明では整数係数の方程式の例だけが出てきますが、その理由は整数係数の例で十分だからです。
多項式の不定方程式の定理(31A)のように、多項式は整数とのアナロジーがあります。そのアナロジーで言うと、既約多項式は整数における素数に相当します。例えば次の定理が成り立ちます。
| (既約多項式と素数の類似性:31D) |
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
[証明]
\(f(x)\) が \(p(x)\) で割り切れないとする。\(f(x)\) と \(p(x)\) は互いに素なので、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x),\:b(x)\) が存在する。両辺に \(g(x)\) を掛けると、
\(g(x)f(x)a(x)+g(x)p(x)b(x)=g(x)\)
となる。\(g(x)f(x)\) は \(p(x)\) で割り切れるので、
\(g(x)f(x)=p(x)h(x)\)
と書ける。これを代入して、
\(p(x)h(x)a(x)+g(x)p(x)b(x)=g(x)\)
\(p(x)\cdot(h(x)a(x)+g(x)b(x))=g(x)\)
となり、\(g(x)\) は \(p(x)\) で割り切れる。従って \(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。[証明終]
この定理の \(f(x)\) を \(g(x)\) に置き換えると次が言えます。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
\(a\) を整数とし、\(a^2\) が \(3\) で割り切れれば、\(a\) は \(3\) で割り切れます。しかし \(a^2\) が \(4\) で割り切れたとしても \(a\) が \(4\) で割り切れるとは限らない。これと既約多項式のアナロジーが成り立っています。
以下、既約多項式がもつ重要な性質を3つあげます。最初の3つは方程式に関するものです。
既約多項式の性質
| (既約多項式の定理1:31E) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
[証明]
\(f(x)\) は \(p(x)\) で割り切れないと仮定して背理法で証明する。\(f(x)\) が \(p(x)\) で割り切れないのなら、\(f(x)\) と \(p(x)\) は互いに素である。なぜなら、もし互いに素でないとすると、1次式以上の多項式 \(h(x)\) があって、
\(f(x)=f_1(x)h(x)\)
\(p(x)=p_1(x)h(x)\)
と表現できるが、\(p(x)\) は既約多項式なので \(p_1(x)=1\) であり、つまり \(h(x)=p(x)\) である。そうすると \(f(x)=f_1(x)p(x)\) となり、\(f(x)\) は \(p(x)\) で割り切れることになって矛盾するからである。つまり、\(f(x)\) が \(p(x)\) で割り切れないのなら \(f(x)\) と \(p(x)\) は互いに素である。
\(f(x)\) と \(p(x)\) が互いに素なら、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x)\)、\(b(x)\) が存在する。そこで、方程式 \(p(x)=0\) と \(f(x)=0\) の共通の解を \(\al\in\bs{C}\) とし、この式に代入すると、左辺\(=0\) となって矛盾する。
従って、\(f(x)\) は \(p(x)\) で割り切れないとの仮定は矛盾を導くから、仮定は誤りであり、\(f(x)\) は \(p(x)\) で割り切れる。[証明終]
この定理は重要なことを言っています。\(\bs{Q}\) 上の方程式の解になる数を代数的数といいます。\(f(x)\) を既約多項式とし、ある代数的数 \(\al\) が \(f(x)=0\) の解とします。
もし、既約多項式 \(f(x)\) 以外の多項式 \(g(x)\) があって、\(g(x)=0\) の解の一つが\(\al\) だとすると、上記の定理により \(g(x)\) は \(f(x)\) で割り切れます。\(g(x)\) の次数が \(f(x)\) の次数と同じとすると、\(g(x)\) は \(f(x)\) の定数倍の既約多項式です。\(g(x)\) の次数が \(f(x)\) の次数より大きいとすると、\(g(x)\) は既約多項式ではありません。
つまり、\(\al\) を方程式の解とするとき、\(\bs{f(\al)=0}\) である既約多項式 \(\bs{f(x)}\) は、定数倍を除いて一意に決まることがわかります。
| (既約多項式の定理2:31F) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
[証明]
既約多項式の定理1(31E)により、もし方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば \(f(x)\) は \(p(x)\) で割り切れるので、多項式 \(h(x)\)(定数の場合を含む)を用いて
\(f(x)=p(x)h(x)\)
と表現できる。従って、
\(f(x)\) の次数 \(\geq\:p(x)\)の次数
である。つまり、
方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば、\(f(x)\) の次数 \(\geq\:p(x)\)の次数である
と言えるが、この対偶をとると、
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は共通の解を持たない
となる。[証明終]この定理は、既約多項式の定理1(31E)と同じことを別の視点で述べたものです。「3.2 体」の「単拡大体の基底」で、既約多項式の定理2(31F)を使った証明を行います。
| (既約多項式の定理3:31G) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式とすると、方程式 \(p(x)=0\) は(複素数の範囲で)重解を持たない。
[証明]
方程式 \(p(x)=0\) が重解 \(\al\) を持つとすると、
\(p(x)=(x-\al)^2q(x)\)
となる。これを微分すると、
\(p\,'(x)=2(x-\al)q(x)+(x-\al)^2q\,'(x)\)
となる。以上の2式に \(\al\) を代入すると、
| \(p(\al)\) | \(=0\) | |
| \(p\,'(\al)\) | \(=0\) |
・既約多項式 \(p(x)\) の次数は \(2\) 以上
・\(p\,'(x)\) の次数は \(2\) 未満
であるにもかかわらず共通の解 \(\al\) を持つことになり、既約多項式の定理2(31F)に反して矛盾が生じる。従って方程式 \(p(x)=0\) は重解を持たない。[証明終]
この定理も重要です。以降で行う証明の中には「\(n\)次既約方程式 \(f(x)=0\) の \(n\) 個の解を \(\al_1,\al_2,\cd,\al_n\) とする」といった、「\(n\)次方程式は \(\bs{n}\) 個の異なった解を持つのが当然」のような記述が出てきますが、\(\bs{f(x)}\) が既約多項式ならこの定理で保証されているからです。
最小多項式
| (最小多項式の定義:31H) |
\(\al\) を 方程式の解とする。\(\al\) を解としてもつ、体 \(\bs{Q}\) 上の方程式のうち、次数が最小の多項式を、\(\al\) の \(\bs{Q}\) 上の最小多項式と言う。
| (最小多項式は既約多項式:31I) |
\(\bs{Q}\) 上の方程式、\(f(x)=0\) が \(\al\) を解としてもつとき、
| \(f(x)\) が 体 \(\bs{Q}\) 上の既約多項式である | |
| \(f(x)\) が \(\al\) の \(\bs{Q}\) 上の最小多項式である |
の2つは同値である。
[② \(\bs{\Rightarrow}\) ① の証明]
最小多項式 \(f(x)\) が既約多項式でなければ、\(f(x)=g(x)h(x)\) となる \(\bs{Q}\) 係数の多項式 \(g(x)\)、\(h(x)\) が存在する。\(x\) に \(\al\) を代入すると、
\(f(\al)=g(\al)h(\al)=0\)
となり、少なくとも \(g(\al)=0\)、\(h(\al)=0\) のどちらかは成り立つ。従って、\(f(x)\) より次数の低い多項式で \(\al\) を解にもつものが存在することになり、\(f(x)\) が最小次数であるという、最小多項式の定義に反する。従って \(f(x)\) は既約多項式である。
[① \(\bs{\Rightarrow}\) ② の証明]
\(g(x)\) を \(\al\) の \(\bs{Q}\) 上の最小多項式とする。すると、\(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) を持つことになり、\(f(x)\) は既約多項式なので、既約多項式の定理1(31E)により \(g(x)\) は \(f(x)\) で割り切れる。従って \(g(x)\) は多項式 \(h(x)\) を用いて、
\(g(x)=h(x)f(x)\)
と表せる。② \(\Rightarrow\) ①の証明により、最小多項式は既約多項式なので、\(g(x)\) は既約多項式である。既約多項式が \(1\)次多項式以上の因数をもつことはない。従って \(h(x)\) は \(0\)次多項式=定数である。ということは、\(f(x)\) も \(\al\) の最小多項式である。[証明終]
方程式 \(f(x)=0\) の解が \(\al\) である( \(f(\al)=0\) )という場合、方程式がまずあって、その解を考えます。しかしその逆、つまり代数的数 \(\al\) があり、\(\al\) を解にもつような方程式は何かと考えるのが最小多項式です。これは、ガロア理論でしばしば出てきます。
3.2 体
「体」とは何かを「1.2 体」で説明しました。それを前提として、ガロア理論に必要な「体」についての定義\(\cdot\)定理を説明します。
最小分解体
| (最小分解体の定義:32A) |
体 \(\bs{Q}\) 上の多項式 \(f(x)\) を、
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
この最小分解体は、あとに出てくるガロア拡大体と直結している重要な概念です。
\(\bs{Q}\) 上の方程式の解が四則演算とべき根で表されるかどうか、と言った場合、既約多項式だけを考えれば十分です。しかし最小分解体は、既約でない多項式をも含んだ定義です。ガロア理論でしばしば出てくるのは \(1\) の \(n\)乗根を求める、
\(x^n-1=0\)
という方程式ですが、左辺は因数分解ができるので既約多項式ではありません。最小分解体の定義は、一般の多項式としておく方が都合が良いのです。
単拡大定理
| (単拡大定理:32B) |
\(\bs{Q}\) 上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大である。つまり \(\bs{K}\) の元 \(\theta\) があって、\(\bs{K}=\bs{Q}(\theta)\) となる。この \(\theta\) を原始元という。
[証明]
\(\bs{Q}\) 上の方程式の解を \(\al\)、\(\beta\) とし、
\(\theta=\al+c\beta\:\:(c\in\bs{Q})\)
とおく。すると、\(\al+c\beta\) と有理数の四則演算で作れる数は、\(\al,\:\beta,\) 有理数の四則演算で作れるから、
\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。次に、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
が成り立つような \(c\) が存在することを示す。
\(\al\) の \(\bs{Q}\) 上の最小多項式を \(f(x)\) とし、\(\beta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とする。そして、
\(f(x)=0\) の解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\)
\(g(x)=0\) の解を \(\beta_1=\beta,\:\beta_2,\:\cd\:,\beta_m\)
とする。ここで、
\(h(x)=f(\al+c\beta-cx)\)
とおくと、
\(h(\beta)=f(\al)=0\)
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\:\:(2\leq i\leq m)\)
となる。
\(c\) は有理数であり、無数に選べるので、\(\al+c\beta-c\beta_i\:\:(2\leq i\leq m)\) のどれもが \(\al_1,\:\al_2,\:\cd\:,\al_n\) と一致しないようにできる。具体的には、もし \(\al_j\:\:(1\leq j\leq n)\) と一致したとしたら、
\(\al_j=\al+c\beta-c\beta_i\)
\(c=-\dfrac{\al-\al_j}{\beta-\beta_i}\)
なので、\(i\) と \(j\) を \((2\leq i\leq m,\:\:1\leq j\leq n)\) の範囲で振って \(n(m-1)\) 個の \(c\) を計算し、これら以外の値を選べばよい。このように \(c\) を選んだとする。そうすると \(\al+c\beta-c\beta_i\) は方程式 \(f(x)=0\) の解にはなり得ないので、
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\neq0\:\:(2\leq i\leq m)\)
であり、\(g(x)=0\) と \(h(x)=0\) の共通解は \(\beta=\beta_1\) のみになる。
そうすると \(h(x)\) と \(g(x)\) は唯一の共通の因数 \((x-\beta)\) をもつので、\(h(x)\) と \(g(x)\) に互除法(21A)を適用すると、\(k\) をある有理数として最後は \(k(x-\beta)\) で割り切れる。
\(g(x)\) は \(\bs{Q}\) 上の多項式だから、すなわち \(\bs{Q}(\al+c\beta)\) 上の多項式である。また、\(h(x)\) は \(h(x)=f(\al+c\beta-cx)\) と定義されるが、\(f(x)\) が \(\bs{Q}\) 上の多項式なので、\(h(x)\) は \(\bs{Q}(\al+c\beta)\) 上の多項式である。つまり \(h(x)\) も \(g(x)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。
従って、互除法の最終結果である \(k(x-\beta)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。これは、
\(k,\:k\beta\:\in\:\bs{Q}(\al+c\beta)\)
であることを意味しており、従って、
\(\beta\:\in\:\bs{Q}(\al+c\beta)\)
となる。また \(\al\) も、
\(\al=(\al+c\beta)-c\beta\:\in\:\bs{Q}(\al+c\beta)\)
である。この結果、\(\al\)、\(\beta\) の両方が \((\al+c\beta)\) の四則演算で表現できることになり、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。従って、\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\theta)\) と合わせて、
\(\bs{Q}(\al,\beta)=\bs{Q}(\theta)\)
が結論づけられた。
以上を繰り返し適用すると、\(\bs{Q}\) に添加する方程式の解は \(\al,\:\beta,\:\gamma,\:\cd\) と増やしていける。従って、
\(\bs{Q}\)上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大であり、ある \(\bs{K}\) の元 \(\theta\) を使って \(\bs{K}=\bs{Q}(\theta)\) と表せる
ことが証明できた。[証明終]
「すべての代数拡大体は単拡大である」というのは、ちょっと驚くような定理です。方程式の解を複数添加した体は、このような性質をもっています。方程式の解の議論をするときに解を含む体の性質で議論することのメリットは、このような単拡大定理が使えることにも現れています。次の「単拡大の体」に関する定理も、単拡大定理があることで任意の代数拡大体につながっています。
なお、上の証明で本質的な役割を果たしているのはユークリッドの互除法が成り立つ原理(21A)です。互除法の "奥の深さ" がわかります。
単拡大の体
| (単拡大の体:32C) |
ある代数的数 \(\al\) の \(\bs{Q}\) 上の最小多項式が \(n\)次多項式 \(f(x)\) であるとする。このとき 体 \(\bs{K}\) を、
| \(\bs{K}\) | \(\overset{\text{ }}{=}\) | \(\{a_{n-1}\al^{n-1}+\)\(\:\cd\:+\)\(a_2\al^2+\)\(a_1\al+\)\(a_0\:|\:a_i\in\bs{Q}\:\}\) | |
| \((0\leq i\leq n-1)\) |
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
[証明]
\(\bs{K}\) が四則演算で閉じていて体であることを証明する。\(\bs{K}\) の元は「\(\bs{Q}\) 上の、\(\al\) の \(n-1\) 次以下の式」で表されるので、\(\bs{K}\) の任意の2つの元を、\(\bs{Q}\) 上の \(n-1\) 次以下の2つの多項式 \(g(x),\:h(x)\) を用いて、\(g(\al),\:h(\al)\) とする。
\(g(\al)+h(\al),\:g(\al)-h(\al)\) は \(\al\) の \(n-1\) 次以下の式なので、\(\bs{K}\) は加減について閉じている。
乗法で閉じていることを言うため、\(g(x)h(x)\) を \(f(x)\) で割った商を \(q(x)\)、余りを \(r(x)\) とする。つまり、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。\(x=\al\) を代入すると、\(f(\al)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
となる。\(r(x)\) は \(f(x)\) で割ったときの余りなので、次数は \(f(x)\) の次数 \(n\) よりも小さく、\(n-1\) 以下である。従って、\(g(\al)h(\al)\) は \(\al\) の \(n-1\) 次以下の式になり、\(\bs{K}\) は乗法で閉じている。
除法で閉じていることは、\(h(\al)\neq0\) のとき、\(\dfrac{g(\al)}{h(\al)}\) が \(\bs{Q}\) 上の「\(\al\) の \(n-1\) 次以下の多項式」で表されることを示せればよい。\(s(x),\:t(x)\) を未知の多項式とし、次の不定方程式を立てる。
\(f(x)s(x)+h(x)t(x)=g(x)\)
\(f(x)\) は最小多項式なので、最小多項式は既約多項式の定理(31I)により既約多項式である。また、\(h(x)\) は \(f(x)\) で割り切れない。なぜなら、もし \(h(x)\) が \(f(x)\) で割り切れるとすると、\(h(x)=u(x)f(x)\) と書けるが、これに \(\al\) を代入すると \(h(\al)=u(\al)f(\al)=0\) となり、\(h(\al)\neq0\) に矛盾するからである。
\(h(x)\) が、既約多項式である \(f(x)\) で割り切れないので、\(h(x)\) と \(f(x)\) は互いに素である。すると、多項式の不定方程式の定理(31A)により、上記の不定方程式を満たす \(s(x),\:t(x)\) が存在して、\(t(x)\) を \(n-1\) 次以下にとることができる。不定方程式に \(x=\al\) を代入すると、
\(h(\al)t(\al)=g(\al)\)
\(\dfrac{g(\al)}{h(\al)}=t(\al)\)
となり、除法でも閉じていることが分かった。つまり \(\bs{K}\) は体である。
\(\bs{Q}(\al)\) は「有理数と\(\al\)」の四則演算で生成される全ての数から成る体である。\(\bs{K}\) の元は有理数と \(\al\) の四則演算で表現され、それは元の間の四則演算で完全に閉じている。従って \(\bs{K}=\bs{Q}(\al)\) である。
表現の一意性は次のようにして証明できる。もし \(\bs{Q}(\al)\) の元について \(g(\al)\) と\(h(\al)\) の2通りの表し方があったとする。つまり、
\(g(\al)=h(\al)\)
\(g(\al)-h(\al)=0\)
とする。\(g(x)-h(x)\) が1次式以上だと仮定すると、\(n-1\)次以下の方程式 \(g(x)-h(x)=0\) が \(\al\) を解にもつことになる。つまり \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解 \(\al\) を持つ。一方、\(f(x)\) は \(n\)次既約多項式であり、\(g(x)-h(x)\) は \(n-1\) 次以下の多項式である。この場合、既約多項式の定理2(31F)によって、方程式 \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解を持たない。従って矛盾が生じる。つまり \(g(x)-h(x)\) は1次式以上ではありえない。\(g(x)-h(x)\) は \(0\)次多項式=定数である。
\(g(x)-h(x)\) が定数であれば、\(g(\al)-h(\al)=0\) なので、その定数は \(0\) しかない。つまり \(g(x)\) と \(h(x)\) の係数は全く一致する。従って表現は一意である。[証明終]
単拡大定理(32B)と、この単拡大の体の定理(32C)を合わせると、
代数拡大体のすべて元は、ある代数的数 \(\al\) の多項式で一意に表せる
ことになります。このことは、分子\(\cdot\)分母が \(\al\) の多項式である分数式があったとしても、分数を取り払った \(\al\) の多項式に変換できることを意味します。1.2 節の「方程式の解を含む体」で触れた "分母の有理化" が、どんなに複雑な分母であっても常に可能であることが分かります。
「3.2 体」終わり
(「3.多項式と体」は次回に続く)
(「3.多項式と体」は次回に続く)
2023-03-18 08:22
nice!(0)
No.354 - 高校数学で理解するガロア理論(1) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
今までに「高校数学で理解する ・・・・・・」と題した記事を何回か書きました。
の7つの記事です。「高校数学で理解する」という言葉の意味は、「高校までで習う数学の知識をベースに説明する」ということです。今回はそのシリーズの続編で、ガロア理論をテーマにします。その第1回目です。
ここで言う「ガロア理論」とは、
とし、その範囲に限定します。これが、そもそもの理論の発端であり、19世紀に夭折したフランスの数学者、ガロアが数学史に残した功績でした。
例によって、前提知識は高校までで習う数学に限定し、そこに含まれない定理は全部証明することにします。ただし、複素数と複素平面の知識は前提とします。また集合論の記号(\(\in\:\:\subset\:\:\sp\:\:\cup\:\:\cap\) など)を適時使います。さらに「すべての方程式は複素数の範囲に解をもつ」という "代数学の基本定理" は、証明はしませんが前提です。
以降の記述では、次の3つの本を特に参考にしました。
全体の内容は以下です。「高校の数学に含まれない定理は全部証明する」方針なので、証明の完結までにはかなりの論証が必要です。そのため、全体は少々長くなります。第1章は、その全体像を俯瞰したもので、第2章からが本論です。
方程式が解けるための必要十分条件の導出は、そこに至るためにかなり長いステップの証明が必要で、論理に論理を積み重ねる必要があります。そこでまず第1章で、証明の枠組みがどうなっているか、全体のアウトラインを説明します。
これは証明そのものではないし、数学的に曖昧なところもあります。しかし、ガロア理論の理解の道筋を示す意味で、2章からの本論の理解の助けになると思います。
1.1 方程式とその可解性
方程式
\(f(x)\) を、有理数を係数にもつ1変数の \(n\)次多項式とします。有理数の集合を \(\bs{Q}\) で表すので、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\)
\((\:a_n\neq0,\:a_i\in\bs{Q}\:)\)
と定義できます。以降のガロア理論で問題にする \(n\)次方程式とは、
\(f(x)=0\)
で表されるものです。これを \(\bs{\bs{Q}}\) 上の(=係数が有理数の)\(n\)次方程式といいます。
代数学の基本定理によると、複素数係数の方程式は複素数の集合 \(\bs{C}\) の中に必ず解をもちます。もちろん、有理数係数の方程式も複素数の集合 \(\bs{C}\) の中に解を持ちます。
有理数係数の方程式の解となる数を代数的数と呼びます。実数や複素数には代数的数でない数があり、たとえば円周率 \(\pi\) や、自然対数の底 \(e\) が有名です。
方程式の可解性
方程式の解が四則演算とべき根(\(\sqrt[n]{a}\))の組み合わせで記述できるとき、その方程式は、
・代数的に解ける
・代数的解法がある
・可解である
と言います(同じ意味です)。べき根(冪根)は累乗根ともいいます。
まず大切なところですが、べき根の定義を明確にしておきます。
\(\sqrt[n]{a}\:\:(\:a\in\bs{C}\:)\)
とは \(n\) 乗して \(a\) になる数の意味ですが、\(a\) が正の実数の場合、「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちの正の実数を表わす」とします。
そして \(a\) が正の実数以外の、負の実数や複素数の場合は「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちのどれかを表わす」とします。"どれか" とするのは、\(n\) 乗して \(a\) になる複数の数を区別する方法がないからです。たとえば \(\sqrt{-1}\) は「2乗して \(-1\) になる2つの数のどちらか」であり、その一方を \(i\) と書くと、もう一方が \(-i\) です。2つの数のどちらが \(i\) かを決めることはできません。複素平面で上の方が \(i\) のように見えますが、それは話が逆で、\(i\) とした方を上に書くのが複素平面です。
従って、方程式の解をべき根で書くときには注意が必要です。たとえば仮想的な例ですが、
\(\sqrt[3]{p}\:+\:\sqrt[3]{q}\)
という記述があったとき、3乗すると \(p,\:q\) になる数のどれでもよい場合もあります。3乗して特定の数になる数は基本的に3つあるので、3\(\times\)3=9種 のどれでもよい場合もあります。しかし、たとえば、
\(\sqrt[3]{p}\cdot\sqrt[3]{q}=r\) であること
といった付帯条件が付いている(付ける必要がある)場合もある。そうすると \(p,\:q\) の選び方には制約が出てきます。べき根が複数の中の何を指すのか、その選択には注意が必要です。
方程式の可解性に戻りますと、
ですが(2次方程式はもちろん可解です)、
のです。従って、2次・3次・4次方程式では解の公式、つまり任意の(=係数が変数の)方程式の解を示す公式がありますが、5次以上の方程式には解の公式がありません。
もちろん、可解でない方程式の解が求まらないわけではありません。現代では数値計算ソフトウェアを使って、いくらでも詳しい精度で解を求めることができます。ただ、その解が四則演算とべき根では表せないと言っているのです。
べき根 \(\sqrt[n]{a}\) は \(n\)乗の逆関数です。方程式が \(\bs{n}\)乗の組み合わせでできているのに、解が \(\bs{n}\)乗の逆関数で表現できない(場合がある)というのは少々不思議ですが、数の世界はそうなっているのです。
それでは、方程式がどういう条件だったら可解で、どういう条件だったら可解でないのか、その必要十分条件は何かが問題になってきます。その必要十分条件を示したのがガロア理論です。
1.2 体
体とは
ガロア理論の出発点は、方程式の解の特性を考えるときに「方程式の解を含む体」を考えて、体の性質でもって解の特性を語ることにあります。
体(field)とは、加減乗除の四則演算が成り立ち、加法と乗法を結びつける分配則が成り立つ集合です。分配則とは \(a(b+c)=ab+ac\) となることです。
は体で、これらは \(\bs{Q}\:\subset\:\bs{R}\:\subset\:\bs{C}\) の関係にあります。\(\bs{Z}\) で表す整数の集合は体ではありません。除算の結果が有理数になって、整数にはならないからです。一般に、集合の要素同士の演算結果がその集合の要素になるとき、集合はその演算に関して「閉じている」と言います。整数は加減乗算で閉じていますが、除算では閉じていません。
\(\bs{Q},\:\bs{R},\:\bs{C}\) はいずれも複素数の集合 \(\bs{C}\) の部分集合であり、これらを数体と呼びます。\(\bs{C}\) は四則演算と分配則が成り立つので、その部分集合は四則演算ができて分配則が成り立ちます。従って、部分集合が体(=数体)である条件は、四則演算で閉じていることです。
数体はこの3つだけではありません。ガロア理論で問題にするのは、方程式の解を含む体です。
方程式の解を含む体
有理数係数の \(n\)次方程式 \(f(x)=0\) の一つの解を\(\al\:(\al\notin\bs{Q})\) とするとき、\(\bs{Q}\) と \(\al\)を含む最小の集合で体の定義を満たすものを \(\bs{Q}(\al)\) と書きます。これは、有理数と \(\bs{\al}\) の四則演算で作り出せるすべの数の集合です。四則演算は何回繰り返してもかまいません。
\(\bs{Q}\) をもとにして \(\bs{Q}(\al)\) を作るのが体の拡大(extension)で、\(\bs{Q}(\al)\) を \(\bs{Q}\) の拡大体といい、「\(\bs{Q}\) に \(\al\) を添加した(ないしは付加した)体」ということもあります。\(\al\) は代数的数なので、\(\bs{Q}\) の代数拡大体ともいいます。集合の包括関係は \(\bs{Q}\:\subset\:\bs{Q}(\al)\) です。この拡大のことを \(\bs{Q}(\al)/\bs{Q}\) と書きます。「拡大体\(/\)元の体」の形です。
当然、\(\bs{Q}\) に複数の代数的数を付加した体も考えられて、
\(\bs{Q}(\al,\:\beta,\:\gamma,\:\cd)\)
というように書きます。\(\al,\:\beta,\:\gamma,\:\cd\) が違った方程式の解であってもかまいません。
例として \(x^2-2=0\) の解での一つである \(\sqrt{2}\) を付加した \(\bs{Q}(\sqrt{2})\) を考えます。この体の任意の数 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
で表されます。この表現は四則演算で閉じています。加算・減算・乗算で閉じているのはすぐにわかります。また除算でも閉じています。というのも、分母の有理化のテクニックを使うと、
\(\dfrac{1}{a+b\sqrt{2}}=\dfrac{a}{a^2-2b^2}-\dfrac{b}{a^2-2b^2}\sqrt{2}\)
となって、\(a+b\sqrt{2}\) の形になるからです(\(a,b\in\bs{Q}\) なので \(a^2\neq2b^2\) です)。従って、乗算で閉じているので除算でも閉じていることになります。上の有理化は方程式の解を一つだけ添加した体の場合ですが、複数の解を添加した体でも有理化は常に可能です。このことは別途きっちりと証明します。
べき根拡大
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) という体の拡大を一般化します。\(\bs{Q}\) 上の \(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{Q})\)
の解の一つで、\(\bs{Q}\) に属さないものを \(\al\) としたとき、
\(\bs{Q}(\al)\)
を \(\bs{Q}\) のべき根拡大体といい、\(\bs{Q}\) から \(\bs{Q}(\al)\) を作ることをべき根拡大(radical extension)といいます。さらにもっと一般化して、体 \(\bs{F}\) があったとき、\(\bs{F}\) 上の(=\(\bs{F}\) 係数の)\(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{F})\)
の解の一つで、\(\bs{F}\) に属さないものを \(\al\) としたとき、
\(\bs{F}(\al)\)
が \(\bs{F}\) のべき根拡大体です。
ここで、ある代数的数 \(\al\) を、
\(\al=\sqrt{3+\sqrt{2}}\)
とします。これは四則演算とべき根で表現された代数的数です。これを変形すると、
\(\al^2-3=\sqrt{2}\)
\(\al^4-6\al^2+7=0\)
となるので、\(\al\) は方程式
\(x^4-6x^2+7=0\)
という4次方程式の解の一つです。そこで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{3+\sqrt{2}})\)
という体の拡大を考えたとき、この拡大は、
の、2ステップの拡大と考えることができます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\:\sqrt{3+\sqrt{2}})\)
という体の拡大です。そうすると各ステップが、\(x^n-a=0\) というタイプの方程式の解による体の拡大=べき根拡大になります。つまり「べき根拡大の系列」ができます。このことを一般化していうと、
方程式 \(f(x)=0\) の解の一つを \(\al\) とするとき、\(\al\) が四則演算とべき根で書けるなら、\(\bs{Q}\) から始まって \(\bs{Q}(\al\))に到達する「べき根拡大の系列」が存在する
となります。ガロア理論では、\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体を考えます。それを \(\bs{Q}\) のガロア拡大体といいます。つまり、\(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\al_n)\) です。この記法を使うと、
\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}\) から始まって \(\bs{Q}(\al_1,\:\cd\:,\al_n)\) に到達する「べき根拡大の系列」が存在するなら、\(f(x)=0\) は可解である
と言えるわけです。式で書くと、
\(\bs{F}_0=\bs{Q},\:\:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\)
として、
であり、かつ、
1.3 ガロア群
そのガロア群を説明するために、まず群(group)とは何か、その定義を明確にしておきます。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群であると言う。
たとえば、有理数の集合 \(\bs{Q}\) は、加法という演算に関して群になります。単位元は \(0\) で、\(a\) の逆元は \(-a\) です。また、有理数の集合から \(0\) を除いた集合は、乗法という演算で群になります。単位元は \(1\) で、\(a\) の逆元は \(a^{-1}\) です。これらは無限個の元をもつ無限群であり、また \(ab=ba\) が成り立つ可換群(アーベル群とも言う)です。
元の数が有限個の有限群もあります。たとえば、裏表のある正3角形を、もとの形と重なるように回転移動する、ないしは対称軸で折り返すという "操作" は群になります。頂点に番号を付け、時計回りに \(1,\:2,\:3\) とします。この操作は6個あって、それに \(e\)、\(\sg\)(シグマ)、\(\tau\)(タウ)の記号をつけて列挙すると、
となります。「時計回りに \(120^\circ\)回転する」のは「反時計回りに \(240^\circ\)回転する」のと頂点番号が同じになるので \(\sg_2\) と同じものとします。「時計回りに \(240^\circ\)回転する」も同様です。
そこで、集合 \(G\) を、
\(G=\{e,\:\sg_1,\:\sg_2,\:\tau_1,\:\tau_2,\:\tau_3\:\}\)
とすると、この集合は「操作を続けてやるという演算」で群になります。なぜなら、
が成り立つからです。\(G\) は有限群です。有限群に含まれる元の数を、群の位数と呼び、\(|G|\) または \(\#G\) で表します。
この \(G\) は可換群ではありません。\(\tau_i\) がからむ演算を実際にやってみると、
\(\tau_1\sg_1=\tau_2,\:\:\sg_1\tau_1=\tau_3\)
\(\tau_2\tau_1=\sg_2,\:\:\tau_1\tau_2=\sg_1\)
などとなり、演算順序を変えると結果が違ってきます(演算は右を先に行う)。この群では \(\sg_1\) と \(\sg_2\) の演算だけが可換です。
正3角形を対称移動する操作の群は、結局、\(1,\:2,\:3\) という3つの文字を置き換える(=置換する)操作と同じです。この置換の数は3文字の順列なので \(3\:!\) 個です。従って、
という対応関係がつきます。\(G\) をこのような文字の置き換えととらえるとき、置換群といいます。一方、正3角形の対称移動ととらえたときは(3次の)2面体群です。"2面体" というのは、裏表がある、裏返せるという意味です。
体の自己同型写像
ガロア群とは「体の自己同型写像がつくる群」です。まず、自己同型写像(automorphism)の定義をします。次において、体 \(\bs{F}\) は \(\bs{Q}\) の代数拡大体とします。
体 \(\bs{F}\) から 体 \(\bs{F}\) への写像(=自分自身への写像)\(f\) が1対1写像であり、\(\bs{F}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(x-y)&=f(x)-f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
&&\:\:f\left(\dfrac{x}{y}\right)&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体 \(\bs{F}\) の自己同型写像という。
体 \(\bs{F}\) の部分集合である有理数体 \(\bs{Q}\) の元、\(a\) に対しては、
\(f(a)=a\)
である。つまり、有理数は自己同型写像で不変である。
この定義でわかるように、自己同型写像とは、四則演算してから写像しても、写像してから四則演算しても同じになる写像です。このことを簡潔に、四則演算を保存する写像と表現します。なお、定義にある「1対1写像」とは、
の2条件を満たす写像です。この定義の「有理数は自己同型写像で不変」のところは次のように証明できます。
\(f(x+y)=f(x)+f(y)\) において \(x=0,\:y=0\) とすると、
\(f(0+0)=f(0)+f(0)\)
\(f(0)=f(0)+f(0)\)
なので、
\(f(0)=0\)
です。また、\(f(xy)=f(x)f(y)\) において \(x=1,\:y=1\) とすると、
\(f(1\cdot1)=f(1)f(1)\)
\(f(1)=f(1)f(1)\)
となり、\(f(1)=0\) か \(f(1)=1\) です。しかし \(f(1)=0\) とすると \(f(0)=0\) かつ \(f(1)=0\) となってしまい、\(f\) が「1対1写像である」という定義に反します。従って、
\(f(1)=1\)
です。次に、\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn 個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)=n\\
\end{eqnarray}\)
なので、
\(f(n)=n\)
です。任意の有理数 \(a\) は、2つの整数 \(n(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるので、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は自己同型写像で不変である(=自己同型写像は有理数を固定する)ことがわかります。
どんな体においても恒等写像 \(e\) は常に自己同型写像です。従って「すべての自己同型写像が有理数に対しては恒等写像として働く」ということは、「有理数体 \(\bs{Q}\) の自己同型写像は恒等写像 \(e\) しかない」ことになります。
しかし、\(\bs{Q}\) の代数拡大体 \(\bs{F}\) については、\(e\) を含む複数個の自己同型写像があります。そして、この複数個の自己同型写像の集合は群になり、それがガロア群です。具体的な例で説明します。
ガロア群の例
\(x^2-2=0\)
上で説明したように、この方程式に対応したガロア拡大体は \(\bs{Q}(\sqrt{2})\) であり、 \(\bs{Q}(\sqrt{2})\) の任意の元 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
と表せます。ここで写像 \(\sg\) を「\(\sqrt{2}\) を \(-\sqrt{2}\) に置き換える写像」つまり、
\(\sg\::\:\sqrt{2}\:\longmapsto\:-\sqrt{2}\)
と定義します。これを、
\(\sg(\sqrt{2})=-\sqrt{2}\)
と表記します。この定義によって \(\sg\) は \(\bs{Q}(\sqrt{2})\) の自己同型写像になります。
そのことを確認しますが、記述を見やすくするため \(a,\:b\) を変数ではなく具体的な数値で書きます。もちろん、一般性を失わないようにする前提です。
\(\begin{eqnarray}
&&\:\:x&=2+3\sqrt{2}\\
&&\:\:y&=5-4\sqrt{2}\\
\end{eqnarray}\)
とすると、
\(\begin{eqnarray}
&&\:\:\sg(x+y)&=\sg(7-\sqrt{2})=7+\sqrt{2}\\
&&\:\:\sg(x)+\sg(y)&=(2-3\sqrt{2})+(5+4\sqrt{2})\\
&&&=7+\sqrt{2}\\
\end{eqnarray}\)
なので、\(\sg\)は加算を保存しています。減算についても同じです。また、
\(\sg(xy)\)
\(=\sg(2\cdot5-3\cdot4\cdot2+3\cdot5\sqrt{2}-2\cdot4\sqrt{2})\)
\(=\sg(-14+7\sqrt{2})\)
\(=-14-7\sqrt{2}\)
\(\sg(x)\sg(y)\)
\(=(2-3\sqrt{2})(5+4\sqrt{2})\)
\(=2\cdot5-3\cdot4\cdot2-3\cdot5\sqrt{2}+2\cdot4\sqrt{2}\)
\(=-14-7\sqrt{2}\)
なので、\(\sg\) は乗算を保存します。さらに、
\(\begin{eqnarray}
&&\:\:\dfrac{x}{y}&=\dfrac{2+3\sqrt{2}}{5-4\sqrt{2}}\\
&&&=\dfrac{(2+3\sqrt{2})(5+4\sqrt{2})}{(5-4\sqrt{2})(5+4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}-\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
なので、
\(\sg\left(\dfrac{x}{y}\right)=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\)
です。一方、
\(\begin{eqnarray}
&&\:\:\dfrac{\sg(x)}{\sg(y)}&=\dfrac{2-3\sqrt{2}}{5+4\sqrt{2}}\\
&&&=\dfrac{(2-3\sqrt{2})(5-4\sqrt{2})}{(5+4\sqrt{2})(5-4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
です。従って、
\(\sg\left(\dfrac{x}{y}\right)=\dfrac{\sg(x)}{\sg(y)}\)
となって、除算も保存しています。以上は具体的数値での計算ですが、\(a,\:b\) を変数としても成り立つことは、上の計算プロセスを追ってみると分かります。
このようになる理由は、\(\bs{\sg}\) が 方程式の解を、解のどれかに置き換える写像だからです。つまり、\(x^2-2=0\) の解は \(\sqrt{2}\) と \(-\sqrt{2}\) ですが、
\(\sg(\phantom{-}\sqrt{2})=-\sqrt{2}\)
\(\sg(-\sqrt{2})=\phantom{-}\sqrt{2}\)
となります。ここで「解を、解のどれかに置き換える」という表現は「解を自分自身に置き換える」ことも含みます。
このことは、\(x^2-2=0\) という "特別な" 方程式だけでなく、一般の2次方程で成り立ちます。2次方程式、
\(x^2+px+q=0\)
の解を \(\al,\:\beta\) とし、共に有理数ではないとします(\(\al,\:\beta\notin\bs{Q}\))。\(\bs{Q}\) の代数拡大体、\(\bs{Q}(\al,\beta)\) の自己同型写像を \(\sg\) とします。\(\al\) は、
\(\al^2+p\al+q=0\)
を満たしますが、この式の両辺に対して \(\sg\) による写像を行うと、
\(\sg(\al^2+p\al+q)=\sg(0)\)
\(\sg(\al)^2+p\sg(\al)+q=0\)
となります。\(\sg\) は四則演算を保存し、また \(\sg(0)=0\) だからこうなります。ということは、\(\sg(\al)\) は元の2次方程式の解です。従って、
\(\sg(\al)=\al\)
\(\sg(\al)=\beta\)
のどちらかです。\(\beta\) についても全く同じことが言えて、
\(\sg(\beta)=\beta\)
\(\sg(\beta)=\al\)
のどちらかです。従って \(\bs{Q}(\al,\beta)\) の自己同型写像 は、
\(e\)(恒等写像)
\(\sg(\al)=\beta\) となる写像
の2種類です。ここで、\(\sg\) を \(\sg(\al)=\beta\) となる写像と規定すると、必然的に \(\sg(\beta)=\al\) になります。なぜなら、もし \(\sg(\beta)=\beta\) だとすると、\(\sg(\al)=\beta\) かつ \(\sg(\beta)=\beta\) になり、\(\sg\) が1対1写像であるという、そもそもの自己同型写像の定義に反するからです。2次方程式の解による代数拡大体の自己同型写像は、恒等写像と「2つの解を入れ替える写像」の2つです。
ここで、自己同型写像 \(e,\:\sg\) の集合を \(G\) とします。つまり、
\(G=\{e,\:\sg\}\)
です。そうすると、\(G\) は群になります。\(e\) という恒等写像があり、
\(\sg^2(\al)=\sg(\sg(\al))=\sg(\beta)=\al\)
なので、
\(\sg^2=e\)
\(\sg^{-1}=\sg\)
となって、逆元があるからです。この \(G\) が \(\bs{Q}(\al,\beta)\) のガロア群です。しかもこのガロア群は、\(\sg\) の(群の要素としての)累乗をとっていくと、
\(\sg,\:\sg^2=e,\:\sg^3=\sg,\:\sg^4=e,\:\cd\)
というように1つの元を出発点として巡回します。このような群を巡回群(cyclic group)といいます。この場合、\(G\) は位数 \(2\) の巡回群です。位数 \(2\) の巡回群を \(C_2\) と表現します。
\(C_2\) は \(\sg,\:e,\:\sg,\:e,\:\cd\) と、2つの元が交互に現れるだけなので、"巡回感" が薄いかもしれませんが、位数 \(3\) の巡回群(\(C_3\))になると "巡回してる感" が出てきます。それが次の方程式の例です。
\(x^3-3x+1=0\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-3x+1\)
とします。
と計算できるので、方程式 \(f(x)=0\) は、\(2\) と \(1\) の間、\(1\) と \(0\) の間、\(-1\) と \(-2\) の間に3つの実数解があります。それを大きい順に \(\al,\:\beta,\:\gamma\) とします。
です。この \(\al,\:\beta,\:\gamma\) を実際に求めてみます。いずれの解も絶対値が \(2\) より小さいので、\(\theta\) を角度を表す変数として、
\(x=2\mr{cos}\theta\:\:(0\leq\theta\leq\pi)\)
とおいて \(x\) から \(\theta\) へ変数を変換すると、
\(f(x)=8\mr{cos}^3\theta-6\mr{cos}\theta+1\)
となります。ここで3倍角の公式、
\(\mr{cos}3\theta=4\mr{cos}^3\theta-3\mr{cos}\theta\)
を使うと、
\(f(x)=2\mr{cos}3\theta+1\)
となります。このことから \(f(x)=0\) の解は、
\(2\mr{cos}3\theta+1=0\)
\(\mr{cos}3\theta=-\dfrac{1}{2}\:\:(0\leq3\theta\leq3\pi)\)
を満たします。従って、
です。ここから、\(\theta_0=\dfrac{2\pi}{9}\) として、
\(\al=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}\theta_0\)
\(\beta=2\mr{cos}\dfrac{4\pi}{9}=2\mr{cos}2\theta_0\)
\(\gamma=2\mr{cos}\dfrac{8\pi}{9}=2\mr{cos}4\theta_0\)
\((\theta_0=\dfrac{2\pi}{9})\)
が求まります。なお、
\(\begin{eqnarray}
&&\:\:\al&=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}(2\pi-\dfrac{2\pi}{9})\\
&&&=2\mr{cos}\dfrac{16\pi}{9}=2\mr{cos}8\theta_0\\
\end{eqnarray}\)
です。ここで倍角の公式、
\(\mr{cos}2\theta=2\mr{cos}^2\theta-1\)
を使うと、
\(\begin{eqnarray}
&&\:\:\beta&=2\mr{cos}2\theta_0=2(2\mr{cos}^2\theta_0-1)\\
&&&=4\mr{cos}^2\theta_0-2=\al^2-2\\
\end{eqnarray}\)
となります。同様にして、
\(\begin{eqnarray}
&&\:\:\gamma&=2\mr{cos}4\theta_0=\beta^2-2\\
&&&=(\al^2-2)^2-2\\
&&\:\:\al&=2\mr{cos}8\theta_0=\gamma^2-2\\
&&&=(\beta^2-2)^2-2\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:\beta&=\al^2-2\\
&&&=(\gamma^2-2)^2-2\\
\end{eqnarray}\)
であることも分かります。従って、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
となり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できることになります。方程式 \(x^3-3x+1=0\) は、3つの解の間に "特別な関係" があります。
ここまで、\(\al,\:\beta,\:\gamma\) を求めると言っても三角関数で表示しただけであり、四則演算とべき根で表したわけではありません。しかし、\(\al,\:\beta,\:\gamma\) の "特別な関係" を使ってガロア群を求めることができます。それが次です。
\(\bs{Q}\) に \(x^3-3x+1=0\) の3つの解、\(\al,\:\beta,\:\gamma\) を添加した代数拡大体 \(\bs{Q}(\al,\beta,\gamma)\) を調べます。\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できるので、
\(\bs{Q}(\al,\:\beta,\:\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。以下、\(\bs{Q}(\al)\) で語ることにすると、\(\bs{Q}(\al)\) の任意の元 \(x\) は、
\(x=a\al^2+b\al+c\:\:(a,b,c\in\bs{Q})\)
という "標準形" で表されます。なぜなら、\(\al^3-3\al+1=0\)、つまり\(\al^3=3\al-1\) という関係があるので、四則演算の結果で現れる \(\al^3\) 以上の項は \(\al^2\) 以下に「次数下げ」ができるからです。
"標準形" で表現できる数が、加算、減算、乗算で閉じていることは明白でしょう。乗算の結果も「次数下げ」で "標準形" になります。除算が問題ですが、例えば、\(x=\al^2+\al+1\) の場合、
\(\begin{eqnarray}
&&\:\:\dfrac{1}{x}&=\dfrac{1}{\al^2+\al+1}\\
&&&=-\dfrac{3}{19}\al^2-\dfrac{2}{19}\al+\dfrac{14}{19}\\
\end{eqnarray}\)
というように "分母の有理化" ができるので、除算でも閉じています。この有理化の例を検算してみると、
(\(\al^2+\al+1)(-3\al^2-2\al+14)\)
\(\begin{eqnarray}
&&\:\: &=&-3\al^4-2\al^3+14\al^2-3\al^3-2\al^2+14\al\\
&&&& -3\al^2-2\al+14\\
&&&=&-3\al^4-5\al^3+9\al^2+12\al+14\\
&&&=&-3\al(\al^3-3\al+1)-5\al^3+15\al+14\\
&&&=&-5(\al^3-3\al+1)+19\\
&&&=&19\\
\end{eqnarray}\)
となって、正しい結果です。この検算で分かるように、分母の有理化は \(\al\) が方程式の解であること、つまり \(\al^3-3\al+1=0\) という関係だけをもとにしています。もちろん、\(x=a\al^2+b\al+c\) という任意の数で分母の有理化が可能です(ややこしい式になりますが)。このように、\(\bs{Q}(\al)=\bs{Q}(\al,\:\beta,\:\gamma)\) は体の定義を満たすことが確認できました。
次に \(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\) の自己同型写像を調べます。自己同型写像は、方程式の解を、解のどれかに移します。そこで \(\al\) に作用する自己同型写像を考えると、これには3つあります。
\(\sg_0(\al)=\al\)
\(\sg_1(\al)=\beta\)
\(\sg_2(\al)=\gamma\)
の \(\sg_0,\:\sg_1,\:\sg_2\) です。\(\sg_1\) は、\(\beta=\al^2-2\) なので、
\(\sg_1(\al)=\al^2-2\)
であり、\(\al\) を \(\al^2-2\) に置き換える写像です。
ここで \(\al\) に \(\sg_1\) を2回作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1^{\:2}(\al)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1(\al^2-2)\\
&&&=\sg_1(\al)^2-\sg_1(2)\\
&&&=\beta^2-2=\gamma\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:\sg_2(\al)&=\gamma\\
&&\:\:\sg_1^{\:2}(\al)&=\gamma\\
\end{eqnarray}\)
なので、
\(\sg_1^{\:2}=\sg_2\)
であることが分かります。
次に、\(\sg_1\) を \(\beta\) に作用させてみると、
\(\begin{eqnarray}
&&\:\:\sg_1(\beta)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1^{\:2}(\al)\\
&&&=\sg_2(\al)=\gamma\\
\end{eqnarray}\)
となります。また \(\sg_1\) を \(\gamma\) に作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1(\gamma)&=\sg_1(\beta^2-2)\\
&&&=\sg_1(\beta)^2-\sg_1(2)\\
&&&=\gamma^2-2=\al\\
\end{eqnarray}\)
となります。
\(\sg_2\) についても同様の計算をしてみると、
\(\begin{eqnarray}
&&\:\:\sg_2(\beta)&=\sg_1^{\:2}(\beta)\\
&&&=\sg_1(\sg_1(\beta))\\
&&&=\sg_1(\gamma)=\al\\
&&\:\:\sg_2(\gamma)&=\sg_1^{\:2}(\gamma)\\
&&&=\sg_1(\sg_1(\gamma))\\
&&&=\sg_1(\al)=\beta\\
\end{eqnarray}\)
です。
さらに、\(\sg_0(\al)=\al\) である \(\sg_0\) については、\(\beta\) と \(\gamma\) が \(\al\) の式で表されているので \(\sg_0(\beta)=\beta\)、\(\sg_0(\gamma)=\gamma\) であり、また、自己同型写像は有理数を固定するので、\(\sg_0\) は \(\bs{Q}(\al,\beta,\gamma)\) のすべての元を固定する恒等写像 \(e\) です。
まとめると、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つになります。この3つは、
\(e\::\) 恒等写像
\(\sg_1(\al)=\beta\)、\(\sg_1(\beta)=\gamma\)、\(\sg_1(\gamma)=\al\)
\(\sg_2(\al)=\gamma\)、\(\sg_2(\beta)=\al\)、\(\sg_2(\gamma)=\beta\)
というように、\(x^3-3x+1=0\) の3つの解を入れ替えます。また、
\(\sg_1\sg_2=\sg_2\sg_1=e\)
\(\sg_1^{-1}=\sg_2,\:\:\sg_2^{-1}=\sg_1\)
であることも分かりました。
解の入れ替えは他に3種が考えられます。つまり一つの解を固定し他の2つを入れ替える写像\(\cdot\)3種ですが、一つの解で他の2つの解が表されているので、一つの解を固定する写像は全部の解を固定します。「一つの解を固定し、他の2つを入れ替える写像」は、この方程式の場合は存在しません。従って、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つがすべてです。
\(G=\{e,\:\sg_1,\:\sg_2\}\) とすると、\(G\) は \(\bs{Q}(\al,\beta,\gamma)\) のガロア群になります。しかも \(\sg_2=\sg_1^{\:2}\)、\(\sg_2\sg_1=\sg_1^{\:3}=e\) の関係があります。ここで \(\sg_1\) をあらためて \(\sg\) と書くと、
が \(\bs{Q}(\al,\beta,\gamma)\) のガロア群です。\(\sg\) は、
で定義される自己同型写像です。
この \(G\) は位数 \(3\) の巡回群(\(C_3\) で表される)です。そして、ガロア群が巡回群であるというのが、方程式が可解であるための条件の一つなのです。
ちなみに、数式処理ソフトウェアを使って \(x^3-3x+1=0\) の解のうちの最大である \(\al\) を計算してみると、
\(\al=1.53208888623796\) ・・・
です。一方、3次方程式の根の公式を使って \(\al\) の厳密解を求めると、
\(\al=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{-3}}{2}}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{-3}}{2}}\)
となります。\(\sqrt{3}\:i\) と書かずにあえて \(\sqrt{-3}\) としました。この式はこれ以上簡略化できないし、また根号の中のマイナスを無くした表現にもできません。
つまり \(\al\) は、正真正銘の正の実数であるにもかかわらず、代数的に(=四則演算とべき根で)表そうとすると虚数を登場させざるを得ないわけです。
数学史をみると、そもそも虚数の必要性が認識されたのは3次方程式の解の表現からでした。そして、ガロア理論によると \(\bs{\sqrt{-3}=\sqrt{3}\:i}\) が現れるのは必然なのです。その理由はガロア理論の全体を理解することでわかります。
自己同型写像は方程式の解を入れ替えます("入れ替えない" を含む)。一般の3次方程式の場合、この入れ替えは \(3\:!\:=\:6\) 通りあります。解を \(1\:2\:3\) の文字で表すと、
の6通りです。入れ替えない、全部入れ替える(2個)、2つだけを入れ替える(3個)の6通りです。この6つの自己同型写像をもつ方程式の例が次です。
\(x^3-2=0\)
この方程式を解くため「\(1\) の原始 \(3\)乗根」を定義します(一般には、\(\bs{1}\) の原始\(\bs{n}\)乗根)。「\(1\) の原始 \(3\)乗根」とは、3乗して初めて \(1\) になる数です。これは \(x^3-1=0\) の根ですが、
\(x^3-1=(x-1)(x^2+x+1)\)
と因数分解できるので、\(1\) の原始 \(3\)乗根は2次方程式、
\(x^2+x+1=0\)
の、2つある解の両方です。そのどちらか一方を \(\omega\) とすると \(\omega^2\) も2次方程式を満たす原始 \(3\)乗根です。\(\omega,\:\omega^2\) を具体的に書くと、
です。逆でもかまいません。\(x^3-1=0\) の根は、
\(1,\:\:\omega,\:\:\omega^2\)
です。
これを使って方程式 \(x^3-2=0\) を解くと、
\(x^3-2=0\)
\(\left(\dfrac{x}{\sqrt[3]{2}}\right)^3=1\)
\(\dfrac{x}{\sqrt[3]{2}}=1,\:\:\omega,\:\:\omega^2\)
\(x=\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
と求まります。以降、\(\al=\sqrt[3]{2}\) とします。方程式 \(x^3-2=0\) の3つの解は、
\(\al,\:\:\al\omega,\:\:\al\omega^2\)
であり、これらを含む \(\bs{Q}\) の代数拡大体は、
\(\bs{Q}(\al,\:\al\omega,\:\al\omega^2)=\bs{Q}(\omega,\:\al)\)
です。この体のガロア群を調べます。
まず、写像 \(\tau\) を、
\(\tau(\omega)=\omega^2,\:\:\tau(\al)=\al\)
で定義される写像とします。この \(\tau\) は、
\(\tau(\al\omega)=\al\tau(\omega)=\al\omega^2\)
\(\tau(\al\omega^2)=\al\tau(\omega^2)=\al\omega^4=\al\omega\)
と、\(\al\omega\) と \(\al\omega^2\) を入れ替える自己同型写像です。\(\tau^2=e\) なので、
\(\{e,\:\tau\}\)
は位数 \(2\) の巡回群(\(C_2\))です。
次に、写像 \(\sg\) を、
\(\sg_i(\al)=\al\omega^i\:\:(i=0,1,2)\)
\(\sg_i(\omega)=\omega\)
と定義します。すると、
となって、\(\sg_i\) は解を、3つの解のどれかに移す写像です。また、
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_0\)
であることもわかります。\(\sg_0\) は恒等写像です。改めて、
\(\sg_0=e\)
\(\sg_1=\sg\)
と書くと、
\(\sg_i=\{e,\:\sg,\:\sg^2\}\)
であり、これは位数 \(3\) の巡回群(\(C_3\))です。
次に \(\{e,\:\tau\}\) の上に \(\{e,\:\sg,\:\sg^2\}\) を組み合わせた集合、\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\{\:\{e,\:\sg,\:\sg^2\}e,\:\{e,\:\sg,\:\sg^2\}\tau\}\\
&&&=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\\
\end{eqnarray}\)
と定義します。\(\sg\)、\(\tau\) の演算は右から順に行います。この \(G\) には恒等写像=単位元 \(e\) があり、次のように群の条件を満たします。
演算で閉じている
\(G\) は「写像を続けて行う」という演算に関して閉じています。なぜなら、\(\sg\) も \(\tau\) も3つの解を入れ替える写像であり、いくら続けてやっても3つの解を入れ替えることに変わりないからです。また3つの解を入れ替える写像は最大6つですが、\(G\) の位数は \(6\) であり、要素同士を演算すると \(G\) のどれかになります。
逆元がある
\(\sg\) と \(\tau\) の定義から
は明確ですが、\(\sg\tau,\:\sg^2\tau\) はどうかという問題です。ここで、\(\tau\sg\) を計算してみると、
となります。実はこれは \(\sg^2\tau\) と全く同じ写像です。確かめると、
となって、全く同じ写像だとわかります。
\(\sg\) と \(\tau\) は可換ではなく、
\(\tau\sg\neq\sg\tau\)
です。しかし、上の計算で分かるように、
\(\tau\sg=\sg^2\tau\)
という関係が成り立っています。いわば "弱い可換性" です。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。この弱可換性を使って計算すると、
\(\begin{eqnarray}
&&\:\:(\sg\tau)(\sg\tau)&=\sg(\tau\sg)\tau=\sg(\sg^2\tau)\tau\\
&&&=\sg^3\tau^2=e\\
&&\:\:(\sg^2\tau)(\sg^2\tau)&=\sg^2(\tau\sg)(\sg\tau)\\
&&&=\sg^2(\sg^2\tau)(\sg\tau)\\
&&&=\sg^4(\tau\sg)\tau=\sg^4(\sg^2\tau)\tau\\
&&&=\sg^6\tau^2=e\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:(\sg\tau)^{-1}&=\sg\tau\\
&&\:\:(\sg^2\tau)^{-1}&=\sg^2\tau\\
\end{eqnarray}\)
となって、すべての元の逆元が存在することが分かりました。以上により \(G\) は群であり、方程式 \(x^3-2=0\) の3つの解を含む代数拡大体、\(\bs{Q}(\omega,\al)\:\:(\al=\sqrt[3]{2})\) のガロア群は \(G\) です。
\(G\) の元が3つの解をどのように入れ替えるかをまとめます。3つの文字 \(1\:2\:3\) を使って、
とすると、
となり、これは正3角形の対称移動の群(3次の2面体群)と同じものです。
しかし重要なことは、\(G\) が \(\{e,\:\tau\}\) と \(\{e,\:\sg,\:\sg^2\}\) という2つの巡回群の "2階建て構造" になっていることです。"2階建て構造" というのはここだけの言葉で、数学用語ではありません。数学的にきっちりとした定義は別途行います。
実は、方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のときも、方程式は可解になります。このことをより正確に言うと以下のようになります。
可解群
方程式 \(x^3-2=0\) のガロア群、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
の性質をさらに調べます。この中の、\(\{e,\:\sg,\:\sg^2\}\) は、それだけで群を構成しています。つまり \(G\) の部分群(subgroup)です。これに \(H\) という名前をつけて、
\(H=\{e,\:\sg,\:\sg^2\}\)
とします。この \(H\) に左から \(\tau\) をかけて \(\tau H\) を作ります。\(\tau H\) とは、\(H\) のすべての元に左から \(\tau\) をかけた集合の意味です。弱可換性である \(\tau\sg=\sg^2\tau\) に注意して \(\tau H\) を計算してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
です。同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、
任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つ
わけです。このような性質をもつ部分群 \(H\) を、\(G\) の正規部分群(normal subgroup)と言います。ちなみに \(\{e,\:\tau\}\) も \(G\) の部分群(=巡回群)ですが、\(\sg\tau\neq\tau\sg\) なので、これは \(G\) の正規部分群ではありません。
上の例の場合、\(H\) は巡回群でしたが、\(\{e,\:\tau\}\) がそうであるように、巡回群だからといって正規部分群になるわけではありません。正規部分群はあくまで \(G\)(全体)と \(H\)(部分)の関係性に依存します。正規部分群が巡回群のこともある、というのが正しい認識です。
正規部分群 \(H\) の任意の元 \(h\) は、\(G\) の任意の元 \(x\) と可換ではありません。しかし、\(H\) の別の元 \(h\,'\) との間で \(xh=h\,'x\) が成り立ちます。つまり \(H\) は、\(G\) の任意の元とグループとして可換なのです。\(H\) の元は \(G\) の任意の元と弱い可換性がある、ともいえるでしょう。
そこで、方程式の可解性と正規部分群の関係です。\(x^3-2=0\) のガロア群のところで、
としました。しかしこれは少々曖昧な表現で、正確には、
です。そして、上の言い方の最後、「ただしその正規部分群が巡回群であること」の部分は、必ずしも巡回群でなくてもよいのです。つまり、ガロア群が "巡回群と正規部分群Aの2階建て構造" であり、その "正規部分群Aが、巡回群と正規部分群B(=巡回群)の2階建て構造" でもよいのです。いわば、正規部分群を介した巡回群の入れ子構造です。この入れ子の "深さ" は何段階でもかまいません。"正規部分群を介する" のは多段階でもよい。まとめると、
わけです。この正規部分群という概念が、ガロア理論の最大のキモです。先ほどの例の正規部分群 \(H=\{e,\:\sg,\:\sg^2\}\) は巡回群でしたが、一般に正規部分群は巡回群ではありません。そのため、"正規部分群を介した巡回群の入れ子構造" が重要な意味をもつのです。
方程式 \(x^3-3x+1=0\) のところで書いたように、ガロア群が巡回群であれば方程式は可解でした。ここまでのことを踏まえて可解群の定義をすると、
となります。可解群とは "ほぼ巡回群" であり、"広義の巡回群" だとも言えるでしょう。巡回群は、一つの元の演算だけで群のすべての元が作り出せるという "最もシンプルな" 群です。可解群は巡回群より広い概念ですが、"かなりシンプルな" 群です。このかなりのシンプルさが方程式の可解性と関わっているのです。
可解群という概念は、ガロア群とは関係なく純粋に群の特性として定義することが可能です。もちろん可解というネーミングでわかるように、方程式の可解性と直結しています。なお、可解群の数学的に厳密な定義は別途きちっとやります(第6章)。
1.4 可解性の必要十分条件
ガロア理論は、
というものでした。そこに、正規部分群の概念を利用した可解群という概念を持ち込むと、方程式の可解性の必要十分条件が導けます。
可解性の必要条件
\(n\)次方程式 \(f(x)\) の解を\(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
があるとしたら、\(\bs{L}\) のガロア群は可解群である。
なぜそう言えるのかの証明は、かなりのステップが必要です。それは別途やりますが、ここで重要なのは上の定理の対偶です。上の定理の対偶は、
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{L}\) のガロア群が可解群でなければ、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
は存在しない。
となります。\(\bs{\bs{Q}}\) から始まるべき根拡大の連続で \(\bs{\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)}\) に到達できないということは、すなわち \(\bs{\al_1,\al_2,\:\cd\:,\al_n}\) が四則演算とべき根では表現できないということに他なりません。ガロア群が可解群ということが、方程式が "代数的に解ける" ための必要条件なのです。
2・3・4次方程式のガロア群はすべて可解群ですが、5次方程式のガロア群は可解群であるものとそうでないものがあります。だから5次方程式の解の公式(=あらゆる5次方程式に通用する公式)はないのです。
ここで定義を振り返ってみると、可解群は、巡回群か、正規部分群を介した巡回群の入れ子構造の群でした。方程式の "解ける解けない" が問題になるのは5次方程式です。実は、可解な5次方程式のガロア群は、巡回群か "巡回群と正規部分群(=巡回群)の2階建て" です(そのような5次方程式もかなりのレア・ケースですが)。可解な5次方程式を考える限り、"正規部分群を介した巡回群の入れ子構造" の "入れ子" は、1段階の非常にシンプルなものに過ぎないのです。
しかし、ある5次方程式が可解でないことを証明するには正規部分群が威力を発揮します。つまり、その5次方程式のガロア群に "正規部分群を介した巡回群の入れ子構造"がないことを言えばよいのですが、そもそも正規部分群がないことを証明してしまえば、その5次方程式は可解ではなくなるからです。そして実際に、ある特定の5次方程式が可解でないことの証明に使われるのは、その5次方程式のガロア群に正規部分群がないということなのです。先ほど「正規部分群という概念がガロア理論の最大のキモ」としたのは、そういう意味を含みます。
可解性の十分条件
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。また、\(1\) の原始\(n\)乗根を \(\zeta\) とする。
\(\bs{L}\) のガロア群が可解群であれば、\(\bs{Q}(\zeta)\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}(\zeta)=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
が存在する。
なぜそう言えるのか、また、なぜここに突然 \(1\) の原始\(n\)乗根が登場するのかは、別途厳密に証明します。この定理で言えることは、「ガロア群が可解群であれば、\(n\)次方程式の解は、有理数と \(\zeta\) の四則演算・べき根の組み合わせで表現できる」ということです。
ここで \(1\) の原始 \(n\)乗根である \(\zeta\) が問題になります。実は、\(1\) の原始 \(n\)乗根は有理数の四則演算とべき根で表現できることがガロア理論とは無関係に証明できます(その証明も別途やります。ガロア理論で証明することもできます)。従って、方程式は可解なのです。
方程式が代数的に解けるキーワードは可解群です。巡回群は代表的な可解群であり、ガロア群が巡回群だと方程式をべき根で解く手法が存在します。ガロア群が巡回群の入れ子構造でも、その手法を多段階に使うことによって、\(\bs{Q}\) から始まるべき根拡大の系列で方程式の解を含む代数拡大体に到達できます。可解性の十分条件の証明は、そのような組み立てになっています。
以上の必要条件と十分条件を組み合わせると、以下が言えます。
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
\(n\)次方程式 \(f(x)=0\) が可解である、つまり四則演算とべき根で解が表現できるための必要十分条件は、\(\bs{L}\) のガロア群(= 自己同型写像が作る群)が可解群であることである。
ガロア理論は、方程式が解けるための必要十分条件を示すものです。従って、ある方程式が可解であることの証明、あるいは逆に、可解でないことの証明はできます。しかし、可解である方程式の解を、具体的に四則演算とべき根で求めるための実用的なアルゴリズムを示しているわけではありません。そこが注意点です。
ここまで、方程式の可解性の必要十分条件を解き明かすガロア理論の全体構造、アウトラインを説明しました。以降ではこれを精密化し、数学的に正しい、首尾一貫した証明にしていきます。目次にあるように、全体は次の8章から成ります。
1.証明の枠組み
2.整数の群
3.多項式と体
4.一般の群
5.ガロア群とガロア対応
6.可解性の必要条件
7.可解性の十分条件
8.結論
第5章から第7章までが、ガロア理論の核心の部分です。第2章から第4章までは、核心部分の証明に使う各種の定義や定理の説明です。この部分がかなり長いのは、高校までで習う数学(いわゆる "受験数学" ではない、教科書ベースの数学)だけを前提知識とし、そうでないものは全部証明するという方針によります。
今までに「高校数学で理解する ・・・・・・」と題した記事を何回か書きました。
No.310 - 高校数学で理解するRSA暗号の数理(1)
No.311 - 高校数学で理解するRSA暗号の数理(2)
No.313 - 高校数学で理解する公開鍵暗号の数理
No.315 - 高校数学で理解する楕円曲線暗号の数理(1)
No.316 - 高校数学で理解する楕円曲線暗号の数理(2)
No.325 - 高校数学で理解する誕生日のパラドックス
No.329 - 高校数学で理解するレジ行列の数理
No.311 - 高校数学で理解するRSA暗号の数理(2)
No.313 - 高校数学で理解する公開鍵暗号の数理
No.315 - 高校数学で理解する楕円曲線暗号の数理(1)
No.316 - 高校数学で理解する楕円曲線暗号の数理(2)
No.325 - 高校数学で理解する誕生日のパラドックス
No.329 - 高校数学で理解するレジ行列の数理
の7つの記事です。「高校数学で理解する」という言葉の意味は、「高校までで習う数学の知識をベースに説明する」ということです。今回はそのシリーズの続編で、ガロア理論をテーマにします。その第1回目です。
ここで言う「ガロア理論」とは、
方程式の解が四則演算記号と \(n\)乗根の記号(\(\sqrt[n]{a}\))で表現できる(=方程式が "解ける")ための必要十分条件を示す理論
とし、その範囲に限定します。これが、そもそもの理論の発端であり、19世紀に夭折したフランスの数学者、ガロアが数学史に残した功績でした。
例によって、前提知識は高校までで習う数学に限定し、そこに含まれない定理は全部証明することにします。ただし、複素数と複素平面の知識は前提とします。また集合論の記号(\(\in\:\:\subset\:\:\sp\:\:\cup\:\:\cap\) など)を適時使います。さらに「すべての方程式は複素数の範囲に解をもつ」という "代数学の基本定理" は、証明はしませんが前提です。
以降の記述では、次の3つの本を特に参考にしました。
草場 公邦 『ガロワと方程式』(朝倉書店 1989)
石井 俊全 『ガロア理論の頂を踏む』(ベレ出版 2013)
加藤 文元 『ガロア理論 12講』(KADOKAWA 2022)
石井 俊全 『ガロア理論の頂を踏む』(ベレ出版 2013)
加藤 文元 『ガロア理論 12講』(KADOKAWA 2022)
全体の内容は以下です。「高校の数学に含まれない定理は全部証明する」方針なので、証明の完結までにはかなりの論証が必要です。そのため、全体は少々長くなります。第1章は、その全体像を俯瞰したもので、第2章からが本論です。
|
| 1.証明の枠組み |
方程式が解けるための必要十分条件の導出は、そこに至るためにかなり長いステップの証明が必要で、論理に論理を積み重ねる必要があります。そこでまず第1章で、証明の枠組みがどうなっているか、全体のアウトラインを説明します。
これは証明そのものではないし、数学的に曖昧なところもあります。しかし、ガロア理論の理解の道筋を示す意味で、2章からの本論の理解の助けになると思います。
1.1 方程式とその可解性
方程式
\(f(x)\) を、有理数を係数にもつ1変数の \(n\)次多項式とします。有理数の集合を \(\bs{Q}\) で表すので、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\)
\((\:a_n\neq0,\:a_i\in\bs{Q}\:)\)
と定義できます。以降のガロア理論で問題にする \(n\)次方程式とは、
\(f(x)=0\)
で表されるものです。これを \(\bs{\bs{Q}}\) 上の(=係数が有理数の)\(n\)次方程式といいます。
代数学の基本定理によると、複素数係数の方程式は複素数の集合 \(\bs{C}\) の中に必ず解をもちます。もちろん、有理数係数の方程式も複素数の集合 \(\bs{C}\) の中に解を持ちます。
有理数係数の方程式の解となる数を代数的数と呼びます。実数や複素数には代数的数でない数があり、たとえば円周率 \(\pi\) や、自然対数の底 \(e\) が有名です。
方程式の可解性
方程式の解が四則演算とべき根(\(\sqrt[n]{a}\))の組み合わせで記述できるとき、その方程式は、
・代数的に解ける
・代数的解法がある
・可解である
と言います(同じ意味です)。べき根(冪根)は累乗根ともいいます。
まず大切なところですが、べき根の定義を明確にしておきます。
\(\sqrt[n]{a}\:\:(\:a\in\bs{C}\:)\)
とは \(n\) 乗して \(a\) になる数の意味ですが、\(a\) が正の実数の場合、「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちの正の実数を表わす」とします。
そして \(a\) が正の実数以外の、負の実数や複素数の場合は「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちのどれかを表わす」とします。"どれか" とするのは、\(n\) 乗して \(a\) になる複数の数を区別する方法がないからです。たとえば \(\sqrt{-1}\) は「2乗して \(-1\) になる2つの数のどちらか」であり、その一方を \(i\) と書くと、もう一方が \(-i\) です。2つの数のどちらが \(i\) かを決めることはできません。複素平面で上の方が \(i\) のように見えますが、それは話が逆で、\(i\) とした方を上に書くのが複素平面です。
従って、方程式の解をべき根で書くときには注意が必要です。たとえば仮想的な例ですが、
\(\sqrt[3]{p}\:+\:\sqrt[3]{q}\)
という記述があったとき、3乗すると \(p,\:q\) になる数のどれでもよい場合もあります。3乗して特定の数になる数は基本的に3つあるので、3\(\times\)3=9種 のどれでもよい場合もあります。しかし、たとえば、
\(\sqrt[3]{p}\cdot\sqrt[3]{q}=r\) であること
といった付帯条件が付いている(付ける必要がある)場合もある。そうすると \(p,\:q\) の選び方には制約が出てきます。べき根が複数の中の何を指すのか、その選択には注意が必要です。
方程式の可解性に戻りますと、
| すべての3次方程式は可解 | |
| すべての4次方程式は可解 |
| 5次方程式には(ないしは5次以上の方程式には)可解であるものと可解でないものがある |
もちろん、可解でない方程式の解が求まらないわけではありません。現代では数値計算ソフトウェアを使って、いくらでも詳しい精度で解を求めることができます。ただ、その解が四則演算とべき根では表せないと言っているのです。
べき根 \(\sqrt[n]{a}\) は \(n\)乗の逆関数です。方程式が \(\bs{n}\)乗の組み合わせでできているのに、解が \(\bs{n}\)乗の逆関数で表現できない(場合がある)というのは少々不思議ですが、数の世界はそうなっているのです。
それでは、方程式がどういう条件だったら可解で、どういう条件だったら可解でないのか、その必要十分条件は何かが問題になってきます。その必要十分条件を示したのがガロア理論です。
1.2 体
体とは
ガロア理論の出発点は、方程式の解の特性を考えるときに「方程式の解を含む体」を考えて、体の性質でもって解の特性を語ることにあります。
体(field)とは、加減乗除の四則演算が成り立ち、加法と乗法を結びつける分配則が成り立つ集合です。分配則とは \(a(b+c)=ab+ac\) となることです。
| ・有理数 | (\(\bs{Q}\) で表す) | |
| ・実数 | (\(\bs{R}\) で表す) | |
| ・複素数 | (\(\bs{C}\) で表す) |
\(\bs{Q},\:\bs{R},\:\bs{C}\) はいずれも複素数の集合 \(\bs{C}\) の部分集合であり、これらを数体と呼びます。\(\bs{C}\) は四則演算と分配則が成り立つので、その部分集合は四則演算ができて分配則が成り立ちます。従って、部分集合が体(=数体)である条件は、四則演算で閉じていることです。
数体はこの3つだけではありません。ガロア理論で問題にするのは、方程式の解を含む体です。
方程式の解を含む体
有理数係数の \(n\)次方程式 \(f(x)=0\) の一つの解を\(\al\:(\al\notin\bs{Q})\) とするとき、\(\bs{Q}\) と \(\al\)を含む最小の集合で体の定義を満たすものを \(\bs{Q}(\al)\) と書きます。これは、有理数と \(\bs{\al}\) の四則演算で作り出せるすべの数の集合です。四則演算は何回繰り返してもかまいません。
\(\bs{Q}\) をもとにして \(\bs{Q}(\al)\) を作るのが体の拡大(extension)で、\(\bs{Q}(\al)\) を \(\bs{Q}\) の拡大体といい、「\(\bs{Q}\) に \(\al\) を添加した(ないしは付加した)体」ということもあります。\(\al\) は代数的数なので、\(\bs{Q}\) の代数拡大体ともいいます。集合の包括関係は \(\bs{Q}\:\subset\:\bs{Q}(\al)\) です。この拡大のことを \(\bs{Q}(\al)/\bs{Q}\) と書きます。「拡大体\(/\)元の体」の形です。
当然、\(\bs{Q}\) に複数の代数的数を付加した体も考えられて、
\(\bs{Q}(\al,\:\beta,\:\gamma,\:\cd)\)
というように書きます。\(\al,\:\beta,\:\gamma,\:\cd\) が違った方程式の解であってもかまいません。
例として \(x^2-2=0\) の解での一つである \(\sqrt{2}\) を付加した \(\bs{Q}(\sqrt{2})\) を考えます。この体の任意の数 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
で表されます。この表現は四則演算で閉じています。加算・減算・乗算で閉じているのはすぐにわかります。また除算でも閉じています。というのも、分母の有理化のテクニックを使うと、
\(\dfrac{1}{a+b\sqrt{2}}=\dfrac{a}{a^2-2b^2}-\dfrac{b}{a^2-2b^2}\sqrt{2}\)
となって、\(a+b\sqrt{2}\) の形になるからです(\(a,b\in\bs{Q}\) なので \(a^2\neq2b^2\) です)。従って、乗算で閉じているので除算でも閉じていることになります。上の有理化は方程式の解を一つだけ添加した体の場合ですが、複数の解を添加した体でも有理化は常に可能です。このことは別途きっちりと証明します。
べき根拡大
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) という体の拡大を一般化します。\(\bs{Q}\) 上の \(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{Q})\)
の解の一つで、\(\bs{Q}\) に属さないものを \(\al\) としたとき、
\(\bs{Q}(\al)\)
を \(\bs{Q}\) のべき根拡大体といい、\(\bs{Q}\) から \(\bs{Q}(\al)\) を作ることをべき根拡大(radical extension)といいます。さらにもっと一般化して、体 \(\bs{F}\) があったとき、\(\bs{F}\) 上の(=\(\bs{F}\) 係数の)\(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{F})\)
の解の一つで、\(\bs{F}\) に属さないものを \(\al\) としたとき、
\(\bs{F}(\al)\)
が \(\bs{F}\) のべき根拡大体です。
ここで、ある代数的数 \(\al\) を、
\(\al=\sqrt{3+\sqrt{2}}\)
とします。これは四則演算とべき根で表現された代数的数です。これを変形すると、
\(\al^2-3=\sqrt{2}\)
\(\al^4-6\al^2+7=0\)
となるので、\(\al\) は方程式
\(x^4-6x^2+7=0\)
という4次方程式の解の一つです。そこで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{3+\sqrt{2}})\)
という体の拡大を考えたとき、この拡大は、
| \(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) を \(\bs{Q}\) に付加して体を拡大 | |
| 次に、\(\bs{\bs{Q}(\sqrt{2})}\) 上の方程式 \(\bs{x^2-(3+\sqrt{2})=0}\) の解 \(\sqrt{3+\sqrt{2}}\) を \(\bs{Q}(\sqrt{2})\) に付加して体を拡大 |
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\:\sqrt{3+\sqrt{2}})\)
という体の拡大です。そうすると各ステップが、\(x^n-a=0\) というタイプの方程式の解による体の拡大=べき根拡大になります。つまり「べき根拡大の系列」ができます。このことを一般化していうと、
方程式 \(f(x)=0\) の解の一つを \(\al\) とするとき、\(\al\) が四則演算とべき根で書けるなら、\(\bs{Q}\) から始まって \(\bs{Q}(\al\))に到達する「べき根拡大の系列」が存在する
となります。ガロア理論では、\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体を考えます。それを \(\bs{Q}\) のガロア拡大体といいます。つまり、\(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\al_n)\) です。この記法を使うと、
\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}\) から始まって \(\bs{Q}(\al_1,\:\cd\:,\al_n)\) に到達する「べき根拡大の系列」が存在するなら、\(f(x)=0\) は可解である
と言えるわけです。式で書くと、
\(\bs{F}_0=\bs{Q},\:\:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\)
として、
| \(\bs{Q}=\bs{F}_0\:\subset\)\( \:\bs{F}_1\:\subset\)\( \:\bs{F}_2\:\subset\)\( \:\cd\:\subset\)\( \:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\) |
各ステップの拡大 \(\bs{F}_{i+1}/\bs{F}_i\) が全部べき根拡大
の条件が成立するとき、\(f(x)=0\) は可解です。これが成り立つのはどういう場合なのか、その条件を、\(\bs{Q}(\al_1,\:\cd\:,\al_n)\) というガロア拡大体に "背後霊" のように付帯している "群"(=ガロア群)の性質で説明するのがガロア理論です。1.3 ガロア群
そのガロア群を説明するために、まず群(group)とは何か、その定義を明確にしておきます。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群であると言う。
| \(G\) の任意の元 \(x,\:y\) に対して演算(\(\cdot\)で表す)が定義されていて、\(x\cdot y\in G\) である。 | |
| 演算について結合法則が成り立つ。つまり、 \((x\cdot y)\cdot z=x\cdot(y\cdot z)\) | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot e=e\cdot x=x\) を満たす元 \(e\) が存在する。\(e\) を単位元という。 | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot y=y\cdot x=e\) となる元 \(y\) が存在する。\(y\) を \(x\) の逆元といい、\(x^{-1}\) と表す。 |
たとえば、有理数の集合 \(\bs{Q}\) は、加法という演算に関して群になります。単位元は \(0\) で、\(a\) の逆元は \(-a\) です。また、有理数の集合から \(0\) を除いた集合は、乗法という演算で群になります。単位元は \(1\) で、\(a\) の逆元は \(a^{-1}\) です。これらは無限個の元をもつ無限群であり、また \(ab=ba\) が成り立つ可換群(アーベル群とも言う)です。
元の数が有限個の有限群もあります。たとえば、裏表のある正3角形を、もとの形と重なるように回転移動する、ないしは対称軸で折り返すという "操作" は群になります。頂点に番号を付け、時計回りに \(1,\:2,\:3\) とします。この操作は6個あって、それに \(e\)、\(\sg\)(シグマ)、\(\tau\)(タウ)の記号をつけて列挙すると、
| ① 何もしない | \(=\:e\) | |
| ② 反時計回りに \(120^\circ\)回転する | \(=\:\sg_1\) | |
| ③ 反時計回りに \(240^\circ\)回転する | \(=\:\sg_2\) | |
| ④ 頂点 \(1\) を通る対称軸で折り返す | \(=\:\tau_1\) | |
| ⑤ 頂点 \(2\) を通る対称軸で折り返す | \(=\:\tau_2\) | |
| ⑥ 頂点 \(3\) を通る対称軸で折り返す | \(=\:\tau_3\) |
|
そこで、集合 \(G\) を、
\(G=\{e,\:\sg_1,\:\sg_2,\:\tau_1,\:\tau_2,\:\tau_3\:\}\)
とすると、この集合は「操作を続けてやるという演算」で群になります。なぜなら、
| 操作を続けてやっても元の配置と重なるのは間違いないので、演算で閉じている。 | |
| 単位元 \(e\) がある。 | |
| 逆元がある。つまり、 \(\sg_2\sg_1=\sg_1\sg_2=e\) : \(360^\circ\)回転すると元に戻る \(\tau_1\tau_1=e,\:\tau_2\tau_2=e,\:\tau_3\tau_3=e\) : 2回折り返すと元に戻る |
この \(G\) は可換群ではありません。\(\tau_i\) がからむ演算を実際にやってみると、
\(\tau_1\sg_1=\tau_2,\:\:\sg_1\tau_1=\tau_3\)
\(\tau_2\tau_1=\sg_2,\:\:\tau_1\tau_2=\sg_1\)
などとなり、演算順序を変えると結果が違ってきます(演算は右を先に行う)。この群では \(\sg_1\) と \(\sg_2\) の演算だけが可換です。
正3角形を対称移動する操作の群は、結局、\(1,\:2,\:3\) という3つの文字を置き換える(=置換する)操作と同じです。この置換の数は3文字の順列なので \(3\:!\) 個です。従って、
| \(e\) | \(:\:1\:2\:3\:\longmapsto\:1\:2\:3\) | |
| \(\sg_1\) | \(:\:1\:2\:3\:\longmapsto\:2\:3\:1\) | |
| \(\sg_2\) | \(:\:1\:2\:3\:\longmapsto\:3\:1\:2\) | |
| \(\tau_1\) | \(:\:1\:2\:3\:\longmapsto\:1\:3\:2\) | |
| \(\tau_2\) | \(:\:1\:2\:3\:\longmapsto\:3\:2\:1\) | |
| \(\tau_3\) | \(:\:1\:2\:3\:\longmapsto\:2\:1\:3\) |
体の自己同型写像
ガロア群とは「体の自己同型写像がつくる群」です。まず、自己同型写像(automorphism)の定義をします。次において、体 \(\bs{F}\) は \(\bs{Q}\) の代数拡大体とします。
体 \(\bs{F}\) から 体 \(\bs{F}\) への写像(=自分自身への写像)\(f\) が1対1写像であり、\(\bs{F}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(x-y)&=f(x)-f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
&&\:\:f\left(\dfrac{x}{y}\right)&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体 \(\bs{F}\) の自己同型写像という。
体 \(\bs{F}\) の部分集合である有理数体 \(\bs{Q}\) の元、\(a\) に対しては、
\(f(a)=a\)
である。つまり、有理数は自己同型写像で不変である。
この定義でわかるように、自己同型写像とは、四則演算してから写像しても、写像してから四則演算しても同じになる写像です。このことを簡潔に、四則演算を保存する写像と表現します。なお、定義にある「1対1写像」とは、
| \(x\neq y\) なら \(f(x)\neq f(y)\) | |
| 任意の \(y\) について \(f(x)=y\) となる \(x\) がある |
\(f(x+y)=f(x)+f(y)\) において \(x=0,\:y=0\) とすると、
\(f(0+0)=f(0)+f(0)\)
\(f(0)=f(0)+f(0)\)
なので、
\(f(0)=0\)
です。また、\(f(xy)=f(x)f(y)\) において \(x=1,\:y=1\) とすると、
\(f(1\cdot1)=f(1)f(1)\)
\(f(1)=f(1)f(1)\)
となり、\(f(1)=0\) か \(f(1)=1\) です。しかし \(f(1)=0\) とすると \(f(0)=0\) かつ \(f(1)=0\) となってしまい、\(f\) が「1対1写像である」という定義に反します。従って、
\(f(1)=1\)
です。次に、\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn 個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)=n\\
\end{eqnarray}\)
なので、
\(f(n)=n\)
です。任意の有理数 \(a\) は、2つの整数 \(n(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるので、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は自己同型写像で不変である(=自己同型写像は有理数を固定する)ことがわかります。
どんな体においても恒等写像 \(e\) は常に自己同型写像です。従って「すべての自己同型写像が有理数に対しては恒等写像として働く」ということは、「有理数体 \(\bs{Q}\) の自己同型写像は恒等写像 \(e\) しかない」ことになります。
しかし、\(\bs{Q}\) の代数拡大体 \(\bs{F}\) については、\(e\) を含む複数個の自己同型写像があります。そして、この複数個の自己同型写像の集合は群になり、それがガロア群です。具体的な例で説明します。
ガロア群の例
\(x^2-2=0\)
上で説明したように、この方程式に対応したガロア拡大体は \(\bs{Q}(\sqrt{2})\) であり、 \(\bs{Q}(\sqrt{2})\) の任意の元 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
と表せます。ここで写像 \(\sg\) を「\(\sqrt{2}\) を \(-\sqrt{2}\) に置き換える写像」つまり、
\(\sg\::\:\sqrt{2}\:\longmapsto\:-\sqrt{2}\)
と定義します。これを、
\(\sg(\sqrt{2})=-\sqrt{2}\)
と表記します。この定義によって \(\sg\) は \(\bs{Q}(\sqrt{2})\) の自己同型写像になります。
そのことを確認しますが、記述を見やすくするため \(a,\:b\) を変数ではなく具体的な数値で書きます。もちろん、一般性を失わないようにする前提です。
\(\begin{eqnarray}
&&\:\:x&=2+3\sqrt{2}\\
&&\:\:y&=5-4\sqrt{2}\\
\end{eqnarray}\)
とすると、
\(\begin{eqnarray}
&&\:\:\sg(x+y)&=\sg(7-\sqrt{2})=7+\sqrt{2}\\
&&\:\:\sg(x)+\sg(y)&=(2-3\sqrt{2})+(5+4\sqrt{2})\\
&&&=7+\sqrt{2}\\
\end{eqnarray}\)
なので、\(\sg\)は加算を保存しています。減算についても同じです。また、
\(\sg(xy)\)
\(=\sg(2\cdot5-3\cdot4\cdot2+3\cdot5\sqrt{2}-2\cdot4\sqrt{2})\)
\(=\sg(-14+7\sqrt{2})\)
\(=-14-7\sqrt{2}\)
\(\sg(x)\sg(y)\)
\(=(2-3\sqrt{2})(5+4\sqrt{2})\)
\(=2\cdot5-3\cdot4\cdot2-3\cdot5\sqrt{2}+2\cdot4\sqrt{2}\)
\(=-14-7\sqrt{2}\)
なので、\(\sg\) は乗算を保存します。さらに、
\(\begin{eqnarray}
&&\:\:\dfrac{x}{y}&=\dfrac{2+3\sqrt{2}}{5-4\sqrt{2}}\\
&&&=\dfrac{(2+3\sqrt{2})(5+4\sqrt{2})}{(5-4\sqrt{2})(5+4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}-\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
なので、
\(\sg\left(\dfrac{x}{y}\right)=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\)
です。一方、
\(\begin{eqnarray}
&&\:\:\dfrac{\sg(x)}{\sg(y)}&=\dfrac{2-3\sqrt{2}}{5+4\sqrt{2}}\\
&&&=\dfrac{(2-3\sqrt{2})(5-4\sqrt{2})}{(5+4\sqrt{2})(5-4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
です。従って、
\(\sg\left(\dfrac{x}{y}\right)=\dfrac{\sg(x)}{\sg(y)}\)
となって、除算も保存しています。以上は具体的数値での計算ですが、\(a,\:b\) を変数としても成り立つことは、上の計算プロセスを追ってみると分かります。
このようになる理由は、\(\bs{\sg}\) が 方程式の解を、解のどれかに置き換える写像だからです。つまり、\(x^2-2=0\) の解は \(\sqrt{2}\) と \(-\sqrt{2}\) ですが、
\(\sg(\phantom{-}\sqrt{2})=-\sqrt{2}\)
\(\sg(-\sqrt{2})=\phantom{-}\sqrt{2}\)
となります。ここで「解を、解のどれかに置き換える」という表現は「解を自分自身に置き換える」ことも含みます。
このことは、\(x^2-2=0\) という "特別な" 方程式だけでなく、一般の2次方程で成り立ちます。2次方程式、
\(x^2+px+q=0\)
の解を \(\al,\:\beta\) とし、共に有理数ではないとします(\(\al,\:\beta\notin\bs{Q}\))。\(\bs{Q}\) の代数拡大体、\(\bs{Q}(\al,\beta)\) の自己同型写像を \(\sg\) とします。\(\al\) は、
\(\al^2+p\al+q=0\)
を満たしますが、この式の両辺に対して \(\sg\) による写像を行うと、
\(\sg(\al^2+p\al+q)=\sg(0)\)
\(\sg(\al)^2+p\sg(\al)+q=0\)
となります。\(\sg\) は四則演算を保存し、また \(\sg(0)=0\) だからこうなります。ということは、\(\sg(\al)\) は元の2次方程式の解です。従って、
\(\sg(\al)=\al\)
\(\sg(\al)=\beta\)
のどちらかです。\(\beta\) についても全く同じことが言えて、
\(\sg(\beta)=\beta\)
\(\sg(\beta)=\al\)
のどちらかです。従って \(\bs{Q}(\al,\beta)\) の自己同型写像 は、
\(e\)(恒等写像)
\(\sg(\al)=\beta\) となる写像
の2種類です。ここで、\(\sg\) を \(\sg(\al)=\beta\) となる写像と規定すると、必然的に \(\sg(\beta)=\al\) になります。なぜなら、もし \(\sg(\beta)=\beta\) だとすると、\(\sg(\al)=\beta\) かつ \(\sg(\beta)=\beta\) になり、\(\sg\) が1対1写像であるという、そもそもの自己同型写像の定義に反するからです。2次方程式の解による代数拡大体の自己同型写像は、恒等写像と「2つの解を入れ替える写像」の2つです。
ここで、自己同型写像 \(e,\:\sg\) の集合を \(G\) とします。つまり、
\(G=\{e,\:\sg\}\)
です。そうすると、\(G\) は群になります。\(e\) という恒等写像があり、
\(\sg^2(\al)=\sg(\sg(\al))=\sg(\beta)=\al\)
なので、
\(\sg^2=e\)
\(\sg^{-1}=\sg\)
となって、逆元があるからです。この \(G\) が \(\bs{Q}(\al,\beta)\) のガロア群です。しかもこのガロア群は、\(\sg\) の(群の要素としての)累乗をとっていくと、
\(\sg,\:\sg^2=e,\:\sg^3=\sg,\:\sg^4=e,\:\cd\)
というように1つの元を出発点として巡回します。このような群を巡回群(cyclic group)といいます。この場合、\(G\) は位数 \(2\) の巡回群です。位数 \(2\) の巡回群を \(C_2\) と表現します。
\(C_2\) は \(\sg,\:e,\:\sg,\:e,\:\cd\) と、2つの元が交互に現れるだけなので、"巡回感" が薄いかもしれませんが、位数 \(3\) の巡回群(\(C_3\))になると "巡回してる感" が出てきます。それが次の方程式の例です。
\(x^3-3x+1=0\)
|
\(f(x)=x^3-3x+1\)
とします。
| \(f(\phantom{-}2)\) | \(=\phantom{-}3\) | |
| \(f(\phantom{-}1)\) | \(=-1\) | |
| \(f(\phantom{-}0)\) | \(=\phantom{-}1\) | |
| \(f(-1)\) | \(=\phantom{-}3\) | |
| \(f(-2)\) | \(=-1\) |
| \(\phantom{-}1\) | \( < \al< \phantom{-}2\) | |
| \(\phantom{-}0\) | \( < \beta< \phantom{-}1\) | |
| \(-2\) | \( < \gamma< -1\) |
\(x=2\mr{cos}\theta\:\:(0\leq\theta\leq\pi)\)
とおいて \(x\) から \(\theta\) へ変数を変換すると、
\(f(x)=8\mr{cos}^3\theta-6\mr{cos}\theta+1\)
となります。ここで3倍角の公式、
\(\mr{cos}3\theta=4\mr{cos}^3\theta-3\mr{cos}\theta\)
を使うと、
\(f(x)=2\mr{cos}3\theta+1\)
となります。このことから \(f(x)=0\) の解は、
\(2\mr{cos}3\theta+1=0\)
\(\mr{cos}3\theta=-\dfrac{1}{2}\:\:(0\leq3\theta\leq3\pi)\)
を満たします。従って、
| \(3\theta\) | \(=\dfrac{2\pi}{3},\:\dfrac{4\pi}{3},\:\dfrac{8\pi}{3}\) | |
| \(\theta\) | \(=\dfrac{2\pi}{9},\:\dfrac{4\pi}{9},\:\dfrac{8\pi}{9}\) |
\(\al=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}\theta_0\)
\(\beta=2\mr{cos}\dfrac{4\pi}{9}=2\mr{cos}2\theta_0\)
\(\gamma=2\mr{cos}\dfrac{8\pi}{9}=2\mr{cos}4\theta_0\)
\((\theta_0=\dfrac{2\pi}{9})\)
が求まります。なお、
\(\begin{eqnarray}
&&\:\:\al&=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}(2\pi-\dfrac{2\pi}{9})\\
&&&=2\mr{cos}\dfrac{16\pi}{9}=2\mr{cos}8\theta_0\\
\end{eqnarray}\)
です。ここで倍角の公式、
\(\mr{cos}2\theta=2\mr{cos}^2\theta-1\)
を使うと、
\(\begin{eqnarray}
&&\:\:\beta&=2\mr{cos}2\theta_0=2(2\mr{cos}^2\theta_0-1)\\
&&&=4\mr{cos}^2\theta_0-2=\al^2-2\\
\end{eqnarray}\)
となります。同様にして、
\(\begin{eqnarray}
&&\:\:\gamma&=2\mr{cos}4\theta_0=\beta^2-2\\
&&&=(\al^2-2)^2-2\\
&&\:\:\al&=2\mr{cos}8\theta_0=\gamma^2-2\\
&&&=(\beta^2-2)^2-2\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:\beta&=\al^2-2\\
&&&=(\gamma^2-2)^2-2\\
\end{eqnarray}\)
であることも分かります。従って、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
となり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できることになります。方程式 \(x^3-3x+1=0\) は、3つの解の間に "特別な関係" があります。
ここまで、\(\al,\:\beta,\:\gamma\) を求めると言っても三角関数で表示しただけであり、四則演算とべき根で表したわけではありません。しかし、\(\al,\:\beta,\:\gamma\) の "特別な関係" を使ってガロア群を求めることができます。それが次です。
\(\bs{Q}\) に \(x^3-3x+1=0\) の3つの解、\(\al,\:\beta,\:\gamma\) を添加した代数拡大体 \(\bs{Q}(\al,\beta,\gamma)\) を調べます。\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できるので、
\(\bs{Q}(\al,\:\beta,\:\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。以下、\(\bs{Q}(\al)\) で語ることにすると、\(\bs{Q}(\al)\) の任意の元 \(x\) は、
\(x=a\al^2+b\al+c\:\:(a,b,c\in\bs{Q})\)
という "標準形" で表されます。なぜなら、\(\al^3-3\al+1=0\)、つまり\(\al^3=3\al-1\) という関係があるので、四則演算の結果で現れる \(\al^3\) 以上の項は \(\al^2\) 以下に「次数下げ」ができるからです。
"標準形" で表現できる数が、加算、減算、乗算で閉じていることは明白でしょう。乗算の結果も「次数下げ」で "標準形" になります。除算が問題ですが、例えば、\(x=\al^2+\al+1\) の場合、
\(\begin{eqnarray}
&&\:\:\dfrac{1}{x}&=\dfrac{1}{\al^2+\al+1}\\
&&&=-\dfrac{3}{19}\al^2-\dfrac{2}{19}\al+\dfrac{14}{19}\\
\end{eqnarray}\)
というように "分母の有理化" ができるので、除算でも閉じています。この有理化の例を検算してみると、
(\(\al^2+\al+1)(-3\al^2-2\al+14)\)
\(\begin{eqnarray}
&&\:\: &=&-3\al^4-2\al^3+14\al^2-3\al^3-2\al^2+14\al\\
&&&& -3\al^2-2\al+14\\
&&&=&-3\al^4-5\al^3+9\al^2+12\al+14\\
&&&=&-3\al(\al^3-3\al+1)-5\al^3+15\al+14\\
&&&=&-5(\al^3-3\al+1)+19\\
&&&=&19\\
\end{eqnarray}\)
となって、正しい結果です。この検算で分かるように、分母の有理化は \(\al\) が方程式の解であること、つまり \(\al^3-3\al+1=0\) という関係だけをもとにしています。もちろん、\(x=a\al^2+b\al+c\) という任意の数で分母の有理化が可能です(ややこしい式になりますが)。このように、\(\bs{Q}(\al)=\bs{Q}(\al,\:\beta,\:\gamma)\) は体の定義を満たすことが確認できました。
次に \(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\) の自己同型写像を調べます。自己同型写像は、方程式の解を、解のどれかに移します。そこで \(\al\) に作用する自己同型写像を考えると、これには3つあります。
\(\sg_0(\al)=\al\)
\(\sg_1(\al)=\beta\)
\(\sg_2(\al)=\gamma\)
の \(\sg_0,\:\sg_1,\:\sg_2\) です。\(\sg_1\) は、\(\beta=\al^2-2\) なので、
\(\sg_1(\al)=\al^2-2\)
であり、\(\al\) を \(\al^2-2\) に置き換える写像です。
ここで \(\al\) に \(\sg_1\) を2回作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1^{\:2}(\al)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1(\al^2-2)\\
&&&=\sg_1(\al)^2-\sg_1(2)\\
&&&=\beta^2-2=\gamma\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:\sg_2(\al)&=\gamma\\
&&\:\:\sg_1^{\:2}(\al)&=\gamma\\
\end{eqnarray}\)
なので、
\(\sg_1^{\:2}=\sg_2\)
であることが分かります。
次に、\(\sg_1\) を \(\beta\) に作用させてみると、
\(\begin{eqnarray}
&&\:\:\sg_1(\beta)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1^{\:2}(\al)\\
&&&=\sg_2(\al)=\gamma\\
\end{eqnarray}\)
となります。また \(\sg_1\) を \(\gamma\) に作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1(\gamma)&=\sg_1(\beta^2-2)\\
&&&=\sg_1(\beta)^2-\sg_1(2)\\
&&&=\gamma^2-2=\al\\
\end{eqnarray}\)
となります。
\(\sg_2\) についても同様の計算をしてみると、
\(\begin{eqnarray}
&&\:\:\sg_2(\beta)&=\sg_1^{\:2}(\beta)\\
&&&=\sg_1(\sg_1(\beta))\\
&&&=\sg_1(\gamma)=\al\\
&&\:\:\sg_2(\gamma)&=\sg_1^{\:2}(\gamma)\\
&&&=\sg_1(\sg_1(\gamma))\\
&&&=\sg_1(\al)=\beta\\
\end{eqnarray}\)
です。
さらに、\(\sg_0(\al)=\al\) である \(\sg_0\) については、\(\beta\) と \(\gamma\) が \(\al\) の式で表されているので \(\sg_0(\beta)=\beta\)、\(\sg_0(\gamma)=\gamma\) であり、また、自己同型写像は有理数を固定するので、\(\sg_0\) は \(\bs{Q}(\al,\beta,\gamma)\) のすべての元を固定する恒等写像 \(e\) です。
まとめると、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つになります。この3つは、
\(e\::\) 恒等写像
\(\sg_1(\al)=\beta\)、\(\sg_1(\beta)=\gamma\)、\(\sg_1(\gamma)=\al\)
\(\sg_2(\al)=\gamma\)、\(\sg_2(\beta)=\al\)、\(\sg_2(\gamma)=\beta\)
というように、\(x^3-3x+1=0\) の3つの解を入れ替えます。また、
\(\sg_1\sg_2=\sg_2\sg_1=e\)
\(\sg_1^{-1}=\sg_2,\:\:\sg_2^{-1}=\sg_1\)
であることも分かりました。
解の入れ替えは他に3種が考えられます。つまり一つの解を固定し他の2つを入れ替える写像\(\cdot\)3種ですが、一つの解で他の2つの解が表されているので、一つの解を固定する写像は全部の解を固定します。「一つの解を固定し、他の2つを入れ替える写像」は、この方程式の場合は存在しません。従って、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つがすべてです。
\(G=\{e,\:\sg_1,\:\sg_2\}\) とすると、\(G\) は \(\bs{Q}(\al,\beta,\gamma)\) のガロア群になります。しかも \(\sg_2=\sg_1^{\:2}\)、\(\sg_2\sg_1=\sg_1^{\:3}=e\) の関係があります。ここで \(\sg_1\) をあらためて \(\sg\) と書くと、
\(G=\{e,\:\sg,\:\sg^2\}\) |
が \(\bs{Q}(\al,\beta,\gamma)\) のガロア群です。\(\sg\) は、
\(\begin{eqnarray}
&&\sg\:: &\al\longmapsto\beta\\
&&&\beta\longmapsto\gamma\\
&&&\gamma\longmapsto\al\\
\end{eqnarray}\) |
で定義される自己同型写像です。
この \(G\) は位数 \(3\) の巡回群(\(C_3\) で表される)です。そして、ガロア群が巡回群であるというのが、方程式が可解であるための条件の一つなのです。
ちなみに、数式処理ソフトウェアを使って \(x^3-3x+1=0\) の解のうちの最大である \(\al\) を計算してみると、
\(\al=1.53208888623796\) ・・・
です。一方、3次方程式の根の公式を使って \(\al\) の厳密解を求めると、
\(\al=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{-3}}{2}}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{-3}}{2}}\)
となります。\(\sqrt{3}\:i\) と書かずにあえて \(\sqrt{-3}\) としました。この式はこれ以上簡略化できないし、また根号の中のマイナスを無くした表現にもできません。
つまり \(\al\) は、正真正銘の正の実数であるにもかかわらず、代数的に(=四則演算とべき根で)表そうとすると虚数を登場させざるを得ないわけです。
ただし、3次方程式の実数解のすべてに虚数 \(i\) が登場するわけではありません。3次方程式の実数解は、\(i\) なしで表わされるものと、\(i\) が必須の場合があります。このことは、任意の3次方程式の解を表わす公式には必ず \(\bs{i}\) が含まれることを意味します。
数学史をみると、そもそも虚数の必要性が認識されたのは3次方程式の解の表現からでした。そして、ガロア理論によると \(\bs{\sqrt{-3}=\sqrt{3}\:i}\) が現れるのは必然なのです。その理由はガロア理論の全体を理解することでわかります。
自己同型写像は方程式の解を入れ替えます("入れ替えない" を含む)。一般の3次方程式の場合、この入れ替えは \(3\:!\:=\:6\) 通りあります。解を \(1\:2\:3\) の文字で表すと、
| \(1\:2\:3\) | \(\longmapsto\:1\:2\:3\) | |
| \(\longmapsto\:2\:3\:1,\:\:3\:1\:2\) | ||
| \(\longmapsto\:1\:3\:2,\:\:3\:2\:1,\:\:2\:1\:3\) |
\(x^3-2=0\)
この方程式を解くため「\(1\) の原始 \(3\)乗根」を定義します(一般には、\(\bs{1}\) の原始\(\bs{n}\)乗根)。「\(1\) の原始 \(3\)乗根」とは、3乗して初めて \(1\) になる数です。これは \(x^3-1=0\) の根ですが、
\(x^3-1=(x-1)(x^2+x+1)\)
と因数分解できるので、\(1\) の原始 \(3\)乗根は2次方程式、
\(x^2+x+1=0\)
の、2つある解の両方です。そのどちらか一方を \(\omega\) とすると \(\omega^2\) も2次方程式を満たす原始 \(3\)乗根です。\(\omega,\:\omega^2\) を具体的に書くと、
| \(\omega\) | \(=\dfrac{-1+\sqrt{3}i}{2}\) | |
| \(\omega^2\) | \(=\dfrac{-1-\sqrt{3}i}{2}\) |
\(1,\:\:\omega,\:\:\omega^2\)
です。
|
\(x^3-2=0\)
\(\left(\dfrac{x}{\sqrt[3]{2}}\right)^3=1\)
\(\dfrac{x}{\sqrt[3]{2}}=1,\:\:\omega,\:\:\omega^2\)
\(x=\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
と求まります。以降、\(\al=\sqrt[3]{2}\) とします。方程式 \(x^3-2=0\) の3つの解は、
\(\al,\:\:\al\omega,\:\:\al\omega^2\)
であり、これらを含む \(\bs{Q}\) の代数拡大体は、
\(\bs{Q}(\al,\:\al\omega,\:\al\omega^2)=\bs{Q}(\omega,\:\al)\)
です。この体のガロア群を調べます。
まず、写像 \(\tau\) を、
\(\tau(\omega)=\omega^2,\:\:\tau(\al)=\al\)
で定義される写像とします。この \(\tau\) は、
\(\tau(\al\omega)=\al\tau(\omega)=\al\omega^2\)
\(\tau(\al\omega^2)=\al\tau(\omega^2)=\al\omega^4=\al\omega\)
と、\(\al\omega\) と \(\al\omega^2\) を入れ替える自己同型写像です。\(\tau^2=e\) なので、
\(\{e,\:\tau\}\)
は位数 \(2\) の巡回群(\(C_2\))です。
次に、写像 \(\sg\) を、
\(\sg_i(\al)=\al\omega^i\:\:(i=0,1,2)\)
\(\sg_i(\omega)=\omega\)
と定義します。すると、
| \(\sg_0(\al)\) | \(=\al\) | |
| \(\sg_0(\al\omega)\) | \(=\al\omega\) | |
| \(\sg_0(\al\omega^2)\) | \(=\al\omega^2\) | |
| \(\sg_1(\al)\) | \(=\al\omega\) | |
| \(\sg_1(\al\omega)\) | \(=\al\omega^2\) | |
| \(\sg_1(\al\omega^2)\) | \(=\al\omega^3=\al\) | |
| \(\sg_2(\al)\) | \(=\al\omega^2\) | |
| \(\sg_2(\al\omega)\) | \(=\al\omega^3=\al\) | |
| \(\sg_2(\al\omega^2)\) | \(=\al\omega^4=\al\omega\) |
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_0\)
であることもわかります。\(\sg_0\) は恒等写像です。改めて、
\(\sg_0=e\)
\(\sg_1=\sg\)
と書くと、
\(\sg_i=\{e,\:\sg,\:\sg^2\}\)
であり、これは位数 \(3\) の巡回群(\(C_3\))です。
次に \(\{e,\:\tau\}\) の上に \(\{e,\:\sg,\:\sg^2\}\) を組み合わせた集合、\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\{\:\{e,\:\sg,\:\sg^2\}e,\:\{e,\:\sg,\:\sg^2\}\tau\}\\
&&&=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\\
\end{eqnarray}\)
と定義します。\(\sg\)、\(\tau\) の演算は右から順に行います。この \(G\) には恒等写像=単位元 \(e\) があり、次のように群の条件を満たします。
演算で閉じている
\(G\) は「写像を続けて行う」という演算に関して閉じています。なぜなら、\(\sg\) も \(\tau\) も3つの解を入れ替える写像であり、いくら続けてやっても3つの解を入れ替えることに変わりないからです。また3つの解を入れ替える写像は最大6つですが、\(G\) の位数は \(6\) であり、要素同士を演算すると \(G\) のどれかになります。
逆元がある
\(\sg\) と \(\tau\) の定義から
| \(\sg^{-1}\) | \(=\sg^2\) | |
| \((\sg^2)^{-1}\) | \(=\sg\) | |
| \(\tau^{-1}\) | \(=\tau\) |
| \(\tau\sg(\al)\) | \(=\tau(\al\omega)\) | \(=\al\omega^2\) | |
| \(\tau\sg(\al\omega)\) | \(=\tau(\al\omega^2)\) | \(=\al\omega^4=\al\omega\) | |
| \(\tau\sg(\al\omega^2)\) | \(=\tau(\al\omega^3)\) | \(=\tau(\al)=\al\) |
| \(\sg^2\tau(\al)\) | \(=\sg^2(\al)=\sg(\sg(\al))\) | |
| \(=\sg(\al\omega)=\al\omega^2\) | ||
| \(\sg^2\tau(\al\omega)\) | \(=\sg^2(\al\omega^2)=\sg(\sg(\al\omega^2))\) | |
| \(=\sg(\al\omega^3)=\sg(\al)=\al\omega\) | ||
| \(\sg^2\tau(\al\omega^2)\) | \(=\sg^2(\al\omega^4)=\sg^2(\al\omega)\) | |
| \(=\sg(\sg(\al\omega))=\sg(\al\omega^2)\) | ||
| \(=\al\omega^3=\al\) |
\(\sg\) と \(\tau\) は可換ではなく、
\(\tau\sg\neq\sg\tau\)
です。しかし、上の計算で分かるように、
\(\tau\sg=\sg^2\tau\)
という関係が成り立っています。いわば "弱い可換性" です。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。この弱可換性を使って計算すると、
\(\begin{eqnarray}
&&\:\:(\sg\tau)(\sg\tau)&=\sg(\tau\sg)\tau=\sg(\sg^2\tau)\tau\\
&&&=\sg^3\tau^2=e\\
&&\:\:(\sg^2\tau)(\sg^2\tau)&=\sg^2(\tau\sg)(\sg\tau)\\
&&&=\sg^2(\sg^2\tau)(\sg\tau)\\
&&&=\sg^4(\tau\sg)\tau=\sg^4(\sg^2\tau)\tau\\
&&&=\sg^6\tau^2=e\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:(\sg\tau)^{-1}&=\sg\tau\\
&&\:\:(\sg^2\tau)^{-1}&=\sg^2\tau\\
\end{eqnarray}\)
となって、すべての元の逆元が存在することが分かりました。以上により \(G\) は群であり、方程式 \(x^3-2=0\) の3つの解を含む代数拡大体、\(\bs{Q}(\omega,\al)\:\:(\al=\sqrt[3]{2})\) のガロア群は \(G\) です。
\(G\) の元が3つの解をどのように入れ替えるかをまとめます。3つの文字 \(1\:2\:3\) を使って、
\(1\::\:\al\)、 \(2\::\:\al\omega\)、 \(3\::\:\al\omega^2\) |
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\) \(\begin{eqnarray} &&e &:\:1\:2\:3\:\longmapsto\:1\:2\:3\\ &&\sg&:\:1\:2\:3\:\longmapsto\:2\:3\:1\\ &&\sg^2 &:\:1\:2\:3\:\longmapsto\:3\:1\:2\\ &&\tau&:\:1\:2\:3\:\longmapsto\:1\:3\:2\\ &&\sg\tau&:\:1\:2\:3\:\longmapsto\:2\:1\:3\\ &&\sg^2\tau&:\:1\:2\:3\:\longmapsto\:3\:2\:1\\ \end{eqnarray}\) |
となり、これは正3角形の対称移動の群(3次の2面体群)と同じものです。
しかし重要なことは、\(G\) が \(\{e,\:\tau\}\) と \(\{e,\:\sg,\:\sg^2\}\) という2つの巡回群の "2階建て構造" になっていることです。"2階建て構造" というのはここだけの言葉で、数学用語ではありません。数学的にきっちりとした定義は別途行います。
実は、方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のときも、方程式は可解になります。このことをより正確に言うと以下のようになります。
可解群
方程式 \(x^3-2=0\) のガロア群、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
の性質をさらに調べます。この中の、\(\{e,\:\sg,\:\sg^2\}\) は、それだけで群を構成しています。つまり \(G\) の部分群(subgroup)です。これに \(H\) という名前をつけて、
\(H=\{e,\:\sg,\:\sg^2\}\)
とします。この \(H\) に左から \(\tau\) をかけて \(\tau H\) を作ります。\(\tau H\) とは、\(H\) のすべての元に左から \(\tau\) をかけた集合の意味です。弱可換性である \(\tau\sg=\sg^2\tau\) に注意して \(\tau H\) を計算してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
です。同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、
任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つ
わけです。このような性質をもつ部分群 \(H\) を、\(G\) の正規部分群(normal subgroup)と言います。ちなみに \(\{e,\:\tau\}\) も \(G\) の部分群(=巡回群)ですが、\(\sg\tau\neq\tau\sg\) なので、これは \(G\) の正規部分群ではありません。
上の例の場合、\(H\) は巡回群でしたが、\(\{e,\:\tau\}\) がそうであるように、巡回群だからといって正規部分群になるわけではありません。正規部分群はあくまで \(G\)(全体)と \(H\)(部分)の関係性に依存します。正規部分群が巡回群のこともある、というのが正しい認識です。
正規部分群 \(H\) の任意の元 \(h\) は、\(G\) の任意の元 \(x\) と可換ではありません。しかし、\(H\) の別の元 \(h\,'\) との間で \(xh=h\,'x\) が成り立ちます。つまり \(H\) は、\(G\) の任意の元とグループとして可換なのです。\(H\) の元は \(G\) の任意の元と弱い可換性がある、ともいえるでしょう。
そこで、方程式の可解性と正規部分群の関係です。\(x^3-2=0\) のガロア群のところで、
方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のとき、方程式は可解になる
としました。しかしこれは少々曖昧な表現で、正確には、
方程式の解を含む代数拡大体のガロア群が "巡回群と正規部分群の2階建て構造" のときに方程式は可解になる。ただしその正規部分群が巡回群であること
です。そして、上の言い方の最後、「ただしその正規部分群が巡回群であること」の部分は、必ずしも巡回群でなくてもよいのです。つまり、ガロア群が "巡回群と正規部分群Aの2階建て構造" であり、その "正規部分群Aが、巡回群と正規部分群B(=巡回群)の2階建て構造" でもよいのです。いわば、正規部分群を介した巡回群の入れ子構造です。この入れ子の "深さ" は何段階でもかまいません。"正規部分群を介する" のは多段階でもよい。まとめると、
方程式の解を含む代数拡大体のガロア群が、正規部分群を介した "巡回群の入れ子構造" になっているとき、方程式は可解である
わけです。この正規部分群という概念が、ガロア理論の最大のキモです。先ほどの例の正規部分群 \(H=\{e,\:\sg,\:\sg^2\}\) は巡回群でしたが、一般に正規部分群は巡回群ではありません。そのため、"正規部分群を介した巡回群の入れ子構造" が重要な意味をもつのです。
方程式 \(x^3-3x+1=0\) のところで書いたように、ガロア群が巡回群であれば方程式は可解でした。ここまでのことを踏まえて可解群の定義をすると、
ガロア群が、巡回群か、正規部分群を介した巡回群の入れ子構造のとき、その群を可解群という
となります。可解群とは "ほぼ巡回群" であり、"広義の巡回群" だとも言えるでしょう。巡回群は、一つの元の演算だけで群のすべての元が作り出せるという "最もシンプルな" 群です。可解群は巡回群より広い概念ですが、"かなりシンプルな" 群です。このかなりのシンプルさが方程式の可解性と関わっているのです。
|
正規部分群を介した巡回群の入れ子構造 |
可解群の「正規部分群を介した巡回群の入れ子構造」のイメージを図にしたものである。入れ子の深さは何段階でもよく、最後は正規部分群=巡回群で終わる。数学的には、巡回群 \(C_1\) は、\(C_1=G/H_1\) で定義される剰余群(商群)であり、また \(C_2=H_1/H_2\)、\(C_3=H_2/H_3\) である。各段階で剰余群が巡回群になるのが「入れ子構造」の条件である。 可解群は、方程式とは関係なく、純粋に群の構造として定義できる。ガロア理論では「方程式の解が四則演算とべき根で記述できるか」という問題が、群の構造の議論に置き換えられている。なお、この図はあくまでイメージであり、可解群の正確な定義は別途行う(第6章)。 |
可解群という概念は、ガロア群とは関係なく純粋に群の特性として定義することが可能です。もちろん可解というネーミングでわかるように、方程式の可解性と直結しています。なお、可解群の数学的に厳密な定義は別途きちっとやります(第6章)。
1.4 可解性の必要十分条件
ガロア理論は、
| 方程式の解の特性を「方程式の解を含む体の性質」で語る | |
| 「方程式の解を含む体の性質」を「体に付随した群=ガロア群の性質」で語る |
可解性の必要条件
\(n\)次方程式 \(f(x)\) の解を\(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
があるとしたら、\(\bs{L}\) のガロア群は可解群である。
なぜそう言えるのかの証明は、かなりのステップが必要です。それは別途やりますが、ここで重要なのは上の定理の対偶です。上の定理の対偶は、
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{L}\) のガロア群が可解群でなければ、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
は存在しない。
となります。\(\bs{\bs{Q}}\) から始まるべき根拡大の連続で \(\bs{\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)}\) に到達できないということは、すなわち \(\bs{\al_1,\al_2,\:\cd\:,\al_n}\) が四則演算とべき根では表現できないということに他なりません。ガロア群が可解群ということが、方程式が "代数的に解ける" ための必要条件なのです。
2・3・4次方程式のガロア群はすべて可解群ですが、5次方程式のガロア群は可解群であるものとそうでないものがあります。だから5次方程式の解の公式(=あらゆる5次方程式に通用する公式)はないのです。
ここで定義を振り返ってみると、可解群は、巡回群か、正規部分群を介した巡回群の入れ子構造の群でした。方程式の "解ける解けない" が問題になるのは5次方程式です。実は、可解な5次方程式のガロア群は、巡回群か "巡回群と正規部分群(=巡回群)の2階建て" です(そのような5次方程式もかなりのレア・ケースですが)。可解な5次方程式を考える限り、"正規部分群を介した巡回群の入れ子構造" の "入れ子" は、1段階の非常にシンプルなものに過ぎないのです。
しかし、ある5次方程式が可解でないことを証明するには正規部分群が威力を発揮します。つまり、その5次方程式のガロア群に "正規部分群を介した巡回群の入れ子構造"がないことを言えばよいのですが、そもそも正規部分群がないことを証明してしまえば、その5次方程式は可解ではなくなるからです。そして実際に、ある特定の5次方程式が可解でないことの証明に使われるのは、その5次方程式のガロア群に正規部分群がないということなのです。先ほど「正規部分群という概念がガロア理論の最大のキモ」としたのは、そういう意味を含みます。
可解性の十分条件
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。また、\(1\) の原始\(n\)乗根を \(\zeta\) とする。
\(\bs{L}\) のガロア群が可解群であれば、\(\bs{Q}(\zeta)\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}(\zeta)=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
が存在する。
なぜそう言えるのか、また、なぜここに突然 \(1\) の原始\(n\)乗根が登場するのかは、別途厳密に証明します。この定理で言えることは、「ガロア群が可解群であれば、\(n\)次方程式の解は、有理数と \(\zeta\) の四則演算・べき根の組み合わせで表現できる」ということです。
ここで \(1\) の原始 \(n\)乗根である \(\zeta\) が問題になります。実は、\(1\) の原始 \(n\)乗根は有理数の四則演算とべき根で表現できることがガロア理論とは無関係に証明できます(その証明も別途やります。ガロア理論で証明することもできます)。従って、方程式は可解なのです。
方程式が代数的に解けるキーワードは可解群です。巡回群は代表的な可解群であり、ガロア群が巡回群だと方程式をべき根で解く手法が存在します。ガロア群が巡回群の入れ子構造でも、その手法を多段階に使うことによって、\(\bs{Q}\) から始まるべき根拡大の系列で方程式の解を含む代数拡大体に到達できます。可解性の十分条件の証明は、そのような組み立てになっています。
以上の必要条件と十分条件を組み合わせると、以下が言えます。
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
\(n\)次方程式 \(f(x)=0\) が可解である、つまり四則演算とべき根で解が表現できるための必要十分条件は、\(\bs{L}\) のガロア群(= 自己同型写像が作る群)が可解群であることである。
ガロア理論は、方程式が解けるための必要十分条件を示すものです。従って、ある方程式が可解であることの証明、あるいは逆に、可解でないことの証明はできます。しかし、可解である方程式の解を、具体的に四則演算とべき根で求めるための実用的なアルゴリズムを示しているわけではありません。そこが注意点です。
ここまで、方程式の可解性の必要十分条件を解き明かすガロア理論の全体構造、アウトラインを説明しました。以降ではこれを精密化し、数学的に正しい、首尾一貫した証明にしていきます。目次にあるように、全体は次の8章から成ります。
1.証明の枠組み
2.整数の群
3.多項式と体
4.一般の群
5.ガロア群とガロア対応
6.可解性の必要条件
7.可解性の十分条件
8.結論
第5章から第7章までが、ガロア理論の核心の部分です。第2章から第4章までは、核心部分の証明に使う各種の定義や定理の説明です。この部分がかなり長いのは、高校までで習う数学(いわゆる "受験数学" ではない、教科書ベースの数学)だけを前提知識とし、そうでないものは全部証明するという方針によります。
「1.証明の枠組み」 終わり
(次回に続く)
(次回に続く)
2023-03-04 11:47
nice!(0)
No.353 - ウイルスがうつ病のリスクを高める [科学]
前回の No.352「トキソプラズマが行動をあやつる」で、トキソプラズマという微生物が人間の脳に影響を与え、人間の行動を変容させるのではという仮説を紹介しました。哺乳類に対しては、オオカミやハイエナの例、また、マウスでの実験で影響が明らかなので、人間に対してもそうだと考えるのが妥当なわけです。
これに関連してですが、微生物(=ウイルス)が人間の脳に影響を与え、その結果うつ病の発症リスクが高まるという研究がテレビ番組で放送されました。今回はその話です。
番組は、2022年10月4日放送の「ヒューマニエンス 49億年のたくらみ」(NHK BS プレミアム)で、その中での東京慈恵会医科大学のウイルス学者・近藤一博教授の研究です。大変興味深かったので、以下に番組のナレーションと近藤教授の話を再録します。
HHV-6 がうつ病のリスクを高める
【ナレーション】
過度の疲労が続くと起こりやすくなるうつ病。その発症に関係していると近藤さんが考えているのが、ヒトヘルペスウイルス6、通称 HHV-6。これまでは、赤ちゃんに突発性発疹を引き起こすことだけが知られてきた。HHV-6 は、私たちのほぼ 100% が体内に宿しているが、大人になってからは健康被害を引き起こすことはないと言われてきた。
しかし近藤さんは、HHV-6 はうつ病と深いつながりがあると考えている。
【近藤教授】
うつ病患者の血液を調べますと、HHV-6 が作り出す SITH-1(シス・ワン)というタンパク質が、健康な人に比べて明らかに大量に作られているということがわかりました。
【ナレーション】
これは健康な人とうつ病患者で、HHV-6 が作り出す SITH-1 タンパク質の量を比べたもの。はっきりと、うつ病患者の方が多いことが見てとれる。
【近藤教授】
このタンパク質が疲労によるストレス反応を増幅させて、うつ病を起こしやすくするのではないかと考えています。
【ナレーション】
近藤さんが考えるうつ病発症のメカニズムを見てみよう。HHV-6 は、普段は血液中の免疫細胞、マクロファージの中に潜伏感染している。疲労によって細胞にストレスがかかると、再活性化して増殖。血液を通じて唾液に集まる。しかしこの時は何の症状も起こさない。
うつ病のリスクが高まるのは、HHV-6 が唾液を通じて脳の近くにある嗅球に感染したあと。そこで HHV-6 は SITH-1 を作り出す。それが脳のストレス反応を高め、疲労などのストレスに敏感に反応するようになる。
すると人は不安をより強く感じるようになり、うつ病を発症するリスクが高まるというのだ。
【近藤教授】
我々は、どうやって この HHV-6、SITH-1 がうつ病を引き起こすのか、もう見つけているので、それを治す薬を今開発しているところです。
(うつ病は過去のものになりつつあるのかという質問に)
うつ病というのは心理的な要素も大きいのです。我々が見つけているのはうつ病の素因、いわゆる生物学的な要因というのですけど、これと、いわゆる悩みとかそういう心理的な要因が重なってうつ病が起こってくるので、この要素が強い人と、もっと心理的な要素が強い人でちょっと違うんですね。
(その、SITH-1 の要素を取り除いてやると、うつ病が楽になるのではという質問に対して)
だいぶ楽になります。うつ病の主な症状は、「抑うつ」と「喜びの消失」(何をやっても楽しくない)、それからもう一つは「疲労感」なんです。このうちの「喜びの消失」と「疲労感」、こがれ実は HHV-6、SITH-1 が関係していると我々は考えているのです。
(ウイルスということは、ワクチンで対処できるのでは、という質問に対して)
ワクチンで全員から HHV-6 を除いてしまうことは、必ずしも人間の進化上は得策ではない。実は、我々が考えている SITH-1 のメカニズムは、必ずしも悪いことばかりではないんですね。いわゆる、性格的に言うとすごく真面目な性格を作り出すんですね。周りの環境に敏感に反応できて自分の生存確率を上げることができる。人が生存していれば中に住んでいる HHV-6 も残るので、両得の関係できていたんですね。
ところが今の時代はストレスが強すぎるので、不安を誘導してうつ病を増やしたりするのですね。
【藤井アナウンサー】
もともとは宿主を長生きさせたいというウイルスの戦略だったのに、ちょっと今の時代にはマッチしなくって、うつ病を引き起こしてしまっているていう感じなんでしょうか。
【近藤教授】
そうなんです。時代が悪いんですよ。
微生物の精神面への影響
微生物が体に好影響、あるいは悪影響を与えるというのは常識です。であれば、脳に影響して人間の精神活動が変わる(変わりうる)のは当然そうかなという感想です。トキソプラズマやHHV-6 はそのほんの一角なのでしょう。今後、類似の研究が進むのではと思いました。
ちなみに SITH-1 の Sith(シス)は、スターウォーズに出てきます。つまり、銀河のエネルギーである「フォース」の "ダークサイド"を操る、ジェダイの敵対者集団です。この名前をウイルスが出すタンパク質につけたのは近藤教授のようで、ユーモアのある方だと思いました。
これに関連してですが、微生物(=ウイルス)が人間の脳に影響を与え、その結果うつ病の発症リスクが高まるという研究がテレビ番組で放送されました。今回はその話です。
番組は、2022年10月4日放送の「ヒューマニエンス 49億年のたくらみ」(NHK BS プレミアム)で、その中での東京慈恵会医科大学のウイルス学者・近藤一博教授の研究です。大変興味深かったので、以下に番組のナレーションと近藤教授の話を再録します。
HHV-6 がうつ病のリスクを高める
【ナレーション】
過度の疲労が続くと起こりやすくなるうつ病。その発症に関係していると近藤さんが考えているのが、ヒトヘルペスウイルス6、通称 HHV-6。これまでは、赤ちゃんに突発性発疹を引き起こすことだけが知られてきた。HHV-6 は、私たちのほぼ 100% が体内に宿しているが、大人になってからは健康被害を引き起こすことはないと言われてきた。
しかし近藤さんは、HHV-6 はうつ病と深いつながりがあると考えている。
【近藤教授】
うつ病患者の血液を調べますと、HHV-6 が作り出す SITH-1(シス・ワン)というタンパク質が、健康な人に比べて明らかに大量に作られているということがわかりました。
|
(NHK BSプレミアムより) |
【ナレーション】
これは健康な人とうつ病患者で、HHV-6 が作り出す SITH-1 タンパク質の量を比べたもの。はっきりと、うつ病患者の方が多いことが見てとれる。
【近藤教授】
このタンパク質が疲労によるストレス反応を増幅させて、うつ病を起こしやすくするのではないかと考えています。
【ナレーション】
近藤さんが考えるうつ病発症のメカニズムを見てみよう。HHV-6 は、普段は血液中の免疫細胞、マクロファージの中に潜伏感染している。疲労によって細胞にストレスがかかると、再活性化して増殖。血液を通じて唾液に集まる。しかしこの時は何の症状も起こさない。
|
(NHK BSプレミアムより) |
うつ病のリスクが高まるのは、HHV-6 が唾液を通じて脳の近くにある嗅球に感染したあと。そこで HHV-6 は SITH-1 を作り出す。それが脳のストレス反応を高め、疲労などのストレスに敏感に反応するようになる。
すると人は不安をより強く感じるようになり、うつ病を発症するリスクが高まるというのだ。
【近藤教授】
我々は、どうやって この HHV-6、SITH-1 がうつ病を引き起こすのか、もう見つけているので、それを治す薬を今開発しているところです。
(うつ病は過去のものになりつつあるのかという質問に)
うつ病というのは心理的な要素も大きいのです。我々が見つけているのはうつ病の素因、いわゆる生物学的な要因というのですけど、これと、いわゆる悩みとかそういう心理的な要因が重なってうつ病が起こってくるので、この要素が強い人と、もっと心理的な要素が強い人でちょっと違うんですね。
(その、SITH-1 の要素を取り除いてやると、うつ病が楽になるのではという質問に対して)
だいぶ楽になります。うつ病の主な症状は、「抑うつ」と「喜びの消失」(何をやっても楽しくない)、それからもう一つは「疲労感」なんです。このうちの「喜びの消失」と「疲労感」、こがれ実は HHV-6、SITH-1 が関係していると我々は考えているのです。
(ウイルスということは、ワクチンで対処できるのでは、という質問に対して)
ワクチンで全員から HHV-6 を除いてしまうことは、必ずしも人間の進化上は得策ではない。実は、我々が考えている SITH-1 のメカニズムは、必ずしも悪いことばかりではないんですね。いわゆる、性格的に言うとすごく真面目な性格を作り出すんですね。周りの環境に敏感に反応できて自分の生存確率を上げることができる。人が生存していれば中に住んでいる HHV-6 も残るので、両得の関係できていたんですね。
ところが今の時代はストレスが強すぎるので、不安を誘導してうつ病を増やしたりするのですね。
【藤井アナウンサー】
もともとは宿主を長生きさせたいというウイルスの戦略だったのに、ちょっと今の時代にはマッチしなくって、うつ病を引き起こしてしまっているていう感じなんでしょうか。
【近藤教授】
そうなんです。時代が悪いんですよ。
微生物の精神面への影響
微生物が体に好影響、あるいは悪影響を与えるというのは常識です。であれば、脳に影響して人間の精神活動が変わる(変わりうる)のは当然そうかなという感想です。トキソプラズマやHHV-6 はそのほんの一角なのでしょう。今後、類似の研究が進むのではと思いました。
ちなみに SITH-1 の Sith(シス)は、スターウォーズに出てきます。つまり、銀河のエネルギーである「フォース」の "ダークサイド"を操る、ジェダイの敵対者集団です。この名前をウイルスが出すタンパク質につけたのは近藤教授のようで、ユーモアのある方だと思いました。
2023-02-18 07:58
nice!(0)
No.352 - トキソプラズマが行動をあやつる [科学]
No.350「寄生生物が行動をあやつる」で、トキソプラズマの話を書きました。今回はその補足です。トキソプラズマは単細胞の原生生物ですが、N0.350 の要点は次の通りでした。
この、トキソプラズマが感染した動物の行動をあやつることに関して、NHK BSプレミアムの番組の中で詳しく紹介されていました。
です。今回はその番組からトキソプラズマの部分を紹介します。
超進化論・すべては微生物から始まった
【ナレーション(廣瀬智美アナウンサー)】
微生物は、ひょっとしたら意志をもっているのではないか。そう、思わせるような研究報告が相次いでいます。何と、感染した生き物の脳を操って自分の味方にしてしまうというのです。
ことの主役はトキソプラズマ。哺乳類や鳥類に感染する微生物です。人間に感染しても、胎児を除けば、ほとんど影響がないと考えられてきました。
チェコ・カレル大学のフレグルさん。トキソプラズマの驚くべき能力を明らかにしました。
【ヤロスラフ・フレグル】
(チェコ・カレル大学 進化生物学者)
トキソプラズマは他の生き物を巧みに操ります。ネズミや人間の行動を変えてしまうのです。
【ナレーション】
ネズミや人間の行動を変える ? それを明らかにしたのがのが、こんな実験。ネズミを入れたケースの中にさまざまな匂いを置きます。ネズミの仲間、住み慣れた藁、そして天敵である猫の匂いです。
まずは、感染していないネズミをこのケースの中に入れます。それほど動き回らず、慎重に様子をうかがっているようです。苦手な猫の匂いも、確かめには行くものの、やはり、あまり寄りつきません。結局、住み慣れた藁や、何もない場所に長く滞在し、猫の匂いを置いた区画にいた時間は全体の 11% でした。
ところが、トキソプラズマに感染したネズミの場合、おやっ、苦手なはずの猫の匂いに近寄っています。
今回の実験では、猫の匂いの近くにいた時間が、先ほどの3倍。トキソプラズマに感染したネズミは、良く言えば大胆、悪く言えば慎重さに欠ける行動をとるようになるのです。
いったいなぜ、こんなことが起きるのか。実は、トキソプラズマには猫科の動物の体内でのみ子孫を増やせるという性質があります。ネズミに感染してしまうと、子孫は増やせない。そこで、ネズミの脳の働きを攪乱させ、猫に食べられやすくなるように操っているのではないかと考えられるのです。
【ヤロスラフ・フレグル】
こうしてトキソプラズマは、自分にとって子孫を残せる場所、つまり猫科の動物の胃袋にたどり着くことができます。なかなか洗練された戦略でしょう ? 高度な知性があるようにすら思えます。
【ナレーション】
では、人間がトキソプラズマに感染した場合にも、行動に変化は出るのでしょうか ───。ひょっとすると、大胆さが幸いして、企業の経営者などに向いているのではないかなど、さまざまな仮説が語られています。
一方、フレグルさんがデータを分析したところ、思いもよらない傾向が浮かび上がりました。それは交通事故。何と、感染した人は、していない人に比べて、事故の割合が 2.65 倍 高かったのです。行動を大胆に変化させるというトキソプラズマの働きが人間にも影響していると、フレグルさんは考えています。
【ヤロスラフ・フレグル】
感染者の行動や振る舞いは、体内にいる微生物に左右されていると考えられます。性格や人格というのは、私たちにとって一番大事で誇りに思う部分でもあるでしょう。しかし実際には、遺伝や環境に操られています。微生物たちも、その環境の一つと考えるべきなのです。
トキソプラズマ関連の番組のナレーションはここまでです。
微生物と脳の働き
トキソプラズマが感染した哺乳類の行動を変えるというのは、さまざまな報告があるようです。番組で紹介されたのはネズミでの実験ですが、ナショナル・ジオグラフィック(2021.7.11 デジタル版)によると、トキソプラズマに感染したハイエナはライオンに近づき過ぎて、ライオンに襲われやすくなるそうです。
人間に感染している微生物は、それが人間と共生しているかどうかは別にして、身体に影響を与える(ことがある)のは常識です。だとすると、脳にも影響を与えると考えられます。性格やパーソナリティは遺伝と環境に影響されます。その環境の一部が微生物です。脳が感染している微生物に影響される(ことがある)のは、むしろ当然だと考えられます。
病気も含む「人間の精神のありよう」と微生物の関係は、今後の研究が進む分野であると思いました。
| トキソプラズマは猫科の動物が最終宿主であり、そこでしか有性生殖できない。 | |
| トキソプラズマは人間を含む幅広い哺乳類や鳥類に感染し(= 哺乳類や鳥類は中間宿主)、無性生殖(=分裂)を行う。 | |
| トキソプラズマは感染した動物の行動を変える。狼は攻撃的になり、群のリーダになりやすい(仮説)。ネズミは猫を恐れなくなる。 |
この、トキソプラズマが感染した動物の行動をあやつることに関して、NHK BSプレミアムの番組の中で詳しく紹介されていました。
超進化論 第3集
すべては微生物から始まった
~ 見えないスーパーパワー ~
すべては微生物から始まった
~ 見えないスーパーパワー ~
| NHK BSP 2023年1月8日) |
です。今回はその番組からトキソプラズマの部分を紹介します。
超進化論・すべては微生物から始まった
【ナレーション(廣瀬智美アナウンサー)】
微生物は、ひょっとしたら意志をもっているのではないか。そう、思わせるような研究報告が相次いでいます。何と、感染した生き物の脳を操って自分の味方にしてしまうというのです。
ことの主役はトキソプラズマ。哺乳類や鳥類に感染する微生物です。人間に感染しても、胎児を除けば、ほとんど影響がないと考えられてきました。
チェコ・カレル大学のフレグルさん。トキソプラズマの驚くべき能力を明らかにしました。
【ヤロスラフ・フレグル】
(チェコ・カレル大学 進化生物学者)
トキソプラズマは他の生き物を巧みに操ります。ネズミや人間の行動を変えてしまうのです。
【ナレーション】
ネズミや人間の行動を変える ? それを明らかにしたのがのが、こんな実験。ネズミを入れたケースの中にさまざまな匂いを置きます。ネズミの仲間、住み慣れた藁、そして天敵である猫の匂いです。
まずは、感染していないネズミをこのケースの中に入れます。それほど動き回らず、慎重に様子をうかがっているようです。苦手な猫の匂いも、確かめには行くものの、やはり、あまり寄りつきません。結局、住み慣れた藁や、何もない場所に長く滞在し、猫の匂いを置いた区画にいた時間は全体の 11% でした。
ところが、トキソプラズマに感染したネズミの場合、おやっ、苦手なはずの猫の匂いに近寄っています。
|
3つの匂いを入れた瓶を用意し、この上から撮った画面の左上には「自分の住処の匂い」、左下に「他のネズミの匂い」、右上に「天敵の猫の匂い」を置く。右下には何も置かない。この状態でネズミの4つの区画の滞在時間を調べる。 (上図)トキソプラズマに感染していないネズミは、左上「自分の住処の匂い」、右下「何も置かない」の滞在時間が長くなった。 (下図)トキソプラズマに感染したネズミでは、右上「天敵の猫の匂い」の区画に最も長く滞在した。 |
(NHK BSプレミアムより) |
今回の実験では、猫の匂いの近くにいた時間が、先ほどの3倍。トキソプラズマに感染したネズミは、良く言えば大胆、悪く言えば慎重さに欠ける行動をとるようになるのです。
いったいなぜ、こんなことが起きるのか。実は、トキソプラズマには猫科の動物の体内でのみ子孫を増やせるという性質があります。ネズミに感染してしまうと、子孫は増やせない。そこで、ネズミの脳の働きを攪乱させ、猫に食べられやすくなるように操っているのではないかと考えられるのです。
【ヤロスラフ・フレグル】
こうしてトキソプラズマは、自分にとって子孫を残せる場所、つまり猫科の動物の胃袋にたどり着くことができます。なかなか洗練された戦略でしょう ? 高度な知性があるようにすら思えます。
【ナレーション】
では、人間がトキソプラズマに感染した場合にも、行動に変化は出るのでしょうか ───。ひょっとすると、大胆さが幸いして、企業の経営者などに向いているのではないかなど、さまざまな仮説が語られています。
一方、フレグルさんがデータを分析したところ、思いもよらない傾向が浮かび上がりました。それは交通事故。何と、感染した人は、していない人に比べて、事故の割合が 2.65 倍 高かったのです。行動を大胆に変化させるというトキソプラズマの働きが人間にも影響していると、フレグルさんは考えています。
|
(NHK BSプレミアムより) |
【ヤロスラフ・フレグル】
感染者の行動や振る舞いは、体内にいる微生物に左右されていると考えられます。性格や人格というのは、私たちにとって一番大事で誇りに思う部分でもあるでしょう。しかし実際には、遺伝や環境に操られています。微生物たちも、その環境の一つと考えるべきなのです。
トキソプラズマ関連の番組のナレーションはここまでです。
微生物と脳の働き
トキソプラズマが感染した哺乳類の行動を変えるというのは、さまざまな報告があるようです。番組で紹介されたのはネズミでの実験ですが、ナショナル・ジオグラフィック(2021.7.11 デジタル版)によると、トキソプラズマに感染したハイエナはライオンに近づき過ぎて、ライオンに襲われやすくなるそうです。
人間に感染している微生物は、それが人間と共生しているかどうかは別にして、身体に影響を与える(ことがある)のは常識です。だとすると、脳にも影響を与えると考えられます。性格やパーソナリティは遺伝と環境に影響されます。その環境の一部が微生物です。脳が感染している微生物に影響される(ことがある)のは、むしろ当然だと考えられます。
病気も含む「人間の精神のありよう」と微生物の関係は、今後の研究が進む分野であると思いました。
2023-01-28 08:05
nice!(1)
No.351 - 運動しても痩せないのはなぜか [科学]
No.221「なぜ痩せられないのか」で、「日経サイエンス」に掲載されたデューク大学のハーマン・ポンツァー准教授の論文を紹介しました。進化人類学者のポンツァーは、身体活動量が全く違うアフリカの狩猟採集民・ハッザ族とアメリカの都市生活者のエネルギー消費を比較し、それがほぼ同じであることを立証していました。運動によるエネルギー消費で減量を目指しても、その効果は無いか、限定的です。
もちろん、運動は健康維持に役立ちます。というより、健康維持のためには運動が必須です。そのことは、
で紹介しました。以上の話の発端となったポンツァー准教授が著した単行本が出版されました。
です。No.221 と重複する内容もありますが、単行本なのでさすがに詳しく記述してあります。今回はこの本(以下、本書)の内容をかいつまんで紹介します。なお、原題は、
BURN
です。直訳すると、
"燃焼"
となるでしょう(試訳)。
代謝
本書のメインテーマは、原書の題名や副題にあるように "カロリーの燃焼"、つまり「代謝」です。我々が健康を維持するには、体の仕組みを理解することが必須で、その重要なものが代謝です。
代謝とは、体内の細胞(人間では約37兆)のすべての "活動" ないしは "働き" を言います。細胞が種々の仕事をするにはエネルギーが必要で、我々はそのエネルギーを食物から得ています。エネルギー源となる食物成分の基本は、炭水化物(糖類)、脂質、タンパク質で、それらは体内で分解され、呼吸で得た酸素で "燃焼させて" エネルギーを得ている。燃焼の産物である二酸化炭素は呼吸で排出します。
もちろんエネルギーは、グリコーゲンや脂肪として蓄積でき、必要に応じてエネルギーに転換されます。タンパク質はアミノ酸に分解されて主に筋肉やその他の組織になりますが、必要ならブドウ糖に転換されてエネルギー源になります(=糖再生)。
体内のネルギー源は、最終的にはすべて ATP(アデノシン3リン酸)という分子になります。ATP は極小の充電式バッテリーのようなもので、ATP が ADP(アデノシン2リン酸)に変化するときにエネルギーが放出され、ADP にエネルギーを "チャージ" すると ATP に変化します。ATP は体内の「エネルギー通貨」です。
エネルギーとは、一言でいうと "仕事をする能力" で、多様な形をとります。高いところにある物質がもつ「位置エネルギー」、食物に含まれる分子の「化学エネルギー」、燃焼や太陽光の「熱エネルギー」、電気・電波などの「電磁波エネルギー」などです。
エネルギーを計る単位は、カロリー(cal。食品)とジュール(記号は J。食品以外)があります。1カロリーは1ミリリットルの水の温度を1度上げるのに必要なエネルギーで、カロリーの1000倍がキロカロリーです。栄養学ではキロカロリー(kcal)を使うのが伝統的です。
ジュールは、1ニュートン(N)の力で物体を力の方向に1メートル(m)動かすのに必要なエネルギーです。1キログラムの物体に働く重力が 9.8 N なので、1N は 102g の物体に働く重力です。ジュールはエネルギー(またはその等価物。仕事、熱量、電気量、など)を表す国際単位系です。ジュールの値を4で割ると、およそのカロリーになります(1 cal = 4.128 J)。欧州諸国では食品にジュールを使う国が多くあります。
ヒトにとって、エネルギーは通貨に似ています。我々は通貨を外部から得て、それをさまざまな目的のために消費します。一度消費した通貨は別の目的に消費することはできません。通貨は貯蔵することが可能です。また、モノを買うために消費した通貨は、そのモノを売るという形で再び通貨に変えることも可能です。
以上、ざっくり表現すると「代謝」とは「エネルギー消費」のことだといえます。
我々は何もしないときでも一定のエネルギーを消費し続けています。これが基礎代謝(BMR。Basic Metabolic Rate)で、安静時のエネルギー消費量です。厳密には、
におけるエネルギー消費量です。空腹を条件とするのは、消化のためにエネルギーを消費するからです。また快適な気温という条件は、寒いと体を暖かく保つためにエネルギーを消費するからです。
基礎代謝は体重に依存します(その他のエネルギー消費も体重に依存する)。人間の1日あたりの基礎代謝は、おおよそ次の式で計算できます(本書に記載の推定式)。
基礎代謝量(1日あたり。キロカロリー)
この式の体重はポンド表示です。kg表示の体重をポンドにするには2.2倍(1/0.45 倍)する必要があります。この式で具体的に計算してみると、
となって、よく言われる「男性:1500kcal 程度、女性:1200 kcal 程度」とほぼ同じ数字です。ただし、基礎代謝は人によって(体脂肪率や筋肉量が影響)、または年齢によって(加齢で低下)± 200 程度の差異があります。
我々が何らかの活動をすると、基礎代謝以外のエネルギーを消費します。これは「代謝当量 = METs(メッツ)」という単位で表されます(MET=Metabolic Equivalent of Task)。1 METs とは「1時間に体重1キログラムあたり1キロカロリーを消費」することを言います。1 METs は BMR にほぼ等しい値です
各種活動のエネルギー・コストを調べると分かることがあります。それは、運動で消費するエネルギーが意外に(がっかりするほど)少ないことです。150ポンド(68kg)の成人で考えると、1万歩(8キロ程度)歩いたときの消費エネルギーはおよそ250 kcalです。これは炭酸飲料1本分(240 kcal)、ビッグマック半分(270 kcal)に過ぎません(もちろん炭酸飲料には低カロリーのものもある)。
本書に興味深いグラフがあります。それは「ランニング・歩行・水泳・自転車のエネルギーコスト」が速度によってどう変わるかを示したものです。
注目すべきは、ランニングと歩行のエネルギー消費の違いです。上記の表は、横軸 x が速度で、縦軸 y は1マイルを移動するときのエネルギー消費量(="燃費")です。歩行は、一定距離を歩くのに最もエネルギー消費が少ない速度があり、y は x の2乗に比例しています。しかしランニングの燃費は速度にほとんど無関係で、y は x に単純比例し、その比例定数はわずかです。
歩行では体の重心が上下します。しかしランニングは、足のバネによって上下動が少なく、足の骨の作りもスムーズに前進できる構造をしている。ヒトは2足走行に適した体の作りなのです。なお、水泳、自転車は、流体(水・空気)の抵抗で歩行やランニングとは違った様相を呈します。
ここまでが「代謝」を巡る序論です。では、代謝という視点でヒトをみたらどうなるか。まずヒトを含む霊長類の話からです。
霊長類のエネルギー消費
霊長類は哺乳類の一種ですが、他の哺乳類と比較してエネルギー消費が少ない種です。たとえば、ヒト(成人)の1日のエネルギー消費量は普通、2500~3000 kcal 程度ですが、ヒトと同程度の大きさの哺乳類は 5000 kcal を越えます。ヒトを含む霊長類(ゴリラ、オランウータン、チンパンジーとボノボ、ヒト)は、哺乳類の中ではエネルギーの消費量が少ない、つまり代謝の速度が低いのです。
代謝は成長と密接な関係があります。霊長類は進化のある時点で代謝が低下し、成長・繁殖・老化に時間がかかるようになった。つまり、ゆっくりとしたライフサイクルをおくるようになったわけです。イヌの1年は人間の7年に相当するなどと言いますが、そのことを指しています。
ヒトを除く霊長類のライフスタイルをみると、類人猿はベジタリアンです。シロアリなども食べますが、基本的に植物食です。植物を食べる種は移動距離が少なくて済みます。類人猿のBMR(体重あたり)は、他の哺乳類のBMRとあまり変わらないのですが、植物食が中心で移動距離は少なく、エネルギー消費が少なく、代謝の速度が遅く、ゆっくりと成長して繁殖するように進化したのです。
しかし、霊長類の中でヒトは少々違います。ヒトは霊長類で比べるとエネルギー消費が多いのです。1日のエネルギー消費量は、110kg のオランウータン(オス)で2050 kcal、55kg のオランウータン(メス)で1600 kcal 程度です。これは、同体重のヒトに比べて約30%少ない値です。霊長類4科(チンパンジー・ボノボ、オランウータン、ゴリラ、ヒト)の中でヒトは他の3科と比較して、体重差を補正すると、20%~50%エネルギー消費が多い種なのです。
それはなぜそうなったのでしょうか。
社会的狩猟採集者としてのヒト
ヒトは200万年ほど前に、他の霊長類にはない行動を始めました、それが狩猟による肉食です。小動物だけではなく、シマウマなどの大型哺乳類も標的にする狩猟です。植物食とは違って、狩猟はかなりの身体活動を伴います。
さらにヒトは、根にデンプンを含む野生植物の塊茎を、道具を使い土を掘って採集して食物としました。これも身体活動が伴います。
現代の東アフリカには、農業や牧畜を一切行わず、狩猟採集だけで生活をしている部族がいます。ハッザ族はその一つですが、彼らも大型哺乳類を狩り(男性)、塊茎を採集する(女性)狩猟採集民です。
シマウマやキリンなどの大型哺乳類を狩って肉食をするということは、仲間で狩りをし、その肉を仲間で分配することが前提です。一人での狩りの成功は難しいし、一人が独占して食べる獲物としては大き過ぎるからです。
この「分配」が「代謝の向上」とセットになってヒトは進化しました。分配を伴う狩猟採集は「社会的狩猟採集」と呼べます。この社会的狩猟採集というライフスタイルにより、類人猿よりも多くのエネルギーを摂取し、かつ消費することが可能になりました。
これで可能になった大きなポイントが脳の発達です。「社会的狩猟採集」を始めたホモ属は、それ以前のアウストラロピテクスより20%以上も脳の体積が増加したことが確かめられています。
ヒトが社会的狩猟採集に適した進化を遂げたことの別の現れが、持久力の向上です。持久力の指標である「最大酸素摂取量」は、ヒトはチンパンジーの4倍あります。ざっくり言って、ヒトの持久力は霊長類(類人猿)の4倍です。持久力があると遠距離の狩猟が可能です。哺乳類をどこまでも追いかけ、獲物が弱ったところで(=人間で言う "熱中症" になったところで)仕留める「持久狩猟」も可能になりました。
さらに火の使用がエネルギー摂取量を大きくしました。加熱調理をすると食物の構造や化学的性質が変わり、栄養を摂取しやすくなります。たとえば、加熱調理したジャガイモは、生で食べるより2倍のエネルギーをとれます。
また火の使用は社会的狩猟採集というライフスタイルの質を向上させました。火で槍の先を硬くする、火でタールを溶かして石斧を作る、暖をとってエネルギー消費を押さえる、などの効果です。
一方、ヒトの代謝量が向上したことにはマイナス面もあります。それは代謝性疾患にかかるリスクで、肥満、2型糖尿病、心臓疾患などが代表的なものです。ただし狩猟採集民であるハッザ族ではこういった代謝性疾患はありません。活発な身体活動というライフスタイルがなくなったとき、リスクが表面化するのです。
こういった進化をとげてきたヒトのエネルギーを消費は身体活動量によってどう変わるのでしょうか。それが次です。
制限的日時消費カロリーモデル
人間が一定期間(たとえば1日)でどれだけエネルギーを消費するかは、従来は「要因加算法」で計算されてきました。これは、
という仮定にもとづくものです。いかにも妥当な仮定にみえますが、これは根拠がない全くの空論であることが分かってきました。
それは、技術革新により消費エネルギーの厳密測定が可能になったからです。この技術が「2重標識水法」です。これは水素の同位元素である「重水素」と、酸素の同位元素である「酸素18」でできた水(=2重標識水)を使うものです。
アフリカの狩猟採集民であるハッザ族と、現代アメリカ人のエネルギー消費量を調査したグラフがあります。それをみると、ハッザ族と現代アメリカ人は身体活動量が大きく違うにもかかわらず、エネルギー消費量は同じです。
ハッザ族だけではありません。世界各地のさまざまなライフスタイルの民族を比較しても、エネルギー消費量は同じだという証拠が積み上がってきました。
では、同じ人が身体活動を変えると、エネルギー消費量はどう変化するのでしょうか。このわかりやすい例がオランダで行われた「ハーフマラソン研究」です。これは、
というものです。
以下、「ハーフマラソン研究」で判明したことを本書から引用します(なお、以降の引用では段落を増やしたところがあります)。
ハーフマラソンに向けての練習で消費したエネルギーの分だけ、身体のどこかのエネルギー消費が減り、トータルとしてのエネルギー消費がほぼ一定に保たれる。ヒトの体はそういうふうにできている(=そのように進化してきた)のです。これがエネルギー消費に関する「制限的日時消費カロリーモデル」です。
この種の研究は多数行われています。プログラムの期間や運動の強度によっていくらか結果は異なりますが、ほとんどの場合、制限的日次カロリー消費モデルに沿ったものとなっています。
運動が体によい理由
「制限的日時消費カロリーモデル」によって、運動が体によい理由の一つが見えてきます。このモデルをわかりやすく図示したのが次の図です。
運動でエネルギーを消費すると、必須ではない体の活動 = カロリーが余っているときにすればよい活動が制限され、体の維持に必須の活動はできるだけ守られます。つまり、運動はエネルギーの配分バランスを変えることになります。配分バランスの変化の結果、「体に悪影響を及ぼすエネルギー消費」が少なくなる。それは主として3つあります。
炎症
一つは「炎症」です。体に細菌やウイルス、あるいはダニのような寄生生物が進入すると、免疫細胞がその部位に集結し、異物を排除します。外見的にはその部位が腫れる。これが体の炎症反応です。これは侵入者に対処するための必須の仕組みです。
しかし炎症反応が真の標的を見誤り、花粉のように無害のものや、あるいは自己の細胞を攻撃するようになると、アレルギー、関節炎、動脈疾患などの広範囲の症状を引き起こします。それが脳の視床下部に影響すると、過食や、その他の体の調節異常を起こします。
定期的な運動が慢性炎症の抑制に効果的であることは、ずいぶん前から指摘されてきました。運動でカロリーを消費すると、体は残ったカロリーを倹約して使うようになります。運動は、炎症反応が本来の標的に対して働くように仕向け、免疫系が不要な活動にエネルギーを使うことを抑制します。
ストレス反応
何らかの緊急事態に遭遇したときや、普通ではない状況に陥ったときには、アドレナリンやコルチゾールが分泌されてストレス反応が起こります。これは緊急事態に対応するための正常な反応です。
しかし炎症と同じで、ストレス反応が間違って引き起こされたり、いつまでも続いたりすると、健康に重大な影響を及ぼします。
運動は気分を改善し、ストレスを軽減します。運動することによってストレス反応の大きさが押さえられるからです。中程度の鬱病患者の治療として運動が使われることもあります。
生殖ホルモン
運動を続けると生殖ホルモン(男性ホルモン、女性ホルモン)の分泌量が減ります。
生殖ホルモンの分泌量の低下は、子供の数という面ではマイナスです。ハッザ族では避妊は行われず、大家族が望まれますが、女性が子供を生む間隔は3~4年です。一方、アメリカでは、授乳中であれ、もし希望すれば1~2年おきに出産が可能です。これはアメリカの母親の方が身体活動レベルが低く、高カロリー食品を容易に摂取できるので、ハッザ族の女性よりも出産にエネルギーを回すことができ、出産後の回復も早いからです。
しかし、生殖ホルモンのレベルが高いと生殖系のがん(乳がんや前立腺がん)のリスク要因になります。運動はそのリスクを低下させます。むしろ、身体活動が高く、生殖ホルモンの分泌量が低下している状態の方が、ヒトの体の本来の姿と言えます。運動は本来の姿に戻します。
もちろん過度の運動による生殖ホルモンの低下は問題を引き起こします。女性であれば生理が止まったりすることがあります。
運動が健康に良いのは、以上に述べたような代謝からの要因(=エネルギー使用バランスの変化による要因)だけでありません。本書から、健康によい理由の部分(数々の研究から引用したもの)を引用します。
まとめ
本書の重要ポイントをまとめると、次のようになるでしょう。
痩せることを目標にして運動をはじめてはみたものの、思ったように痩せないので運動をやめた、というようなことがあるとしたら、これほど本末転倒なことはないわけです。
ヒトは、身体活動レベルが高いのが通常状態であり、それは「社会的狩猟採集」というライフスタイルに適合するように進化した結果です。つまり、ヒトの体の基本的なしくみは、東アフリカのサバンナで作られ、それは今も変わっていない(=体はまだサバンナにいる)と言えるでしょう。
サバンナでの映画上映
本書に、著者たちがアフリカのサバンナに住むハッザ族のキャンプに泊まりこんでフィールド調査をしたときのエピソードが出てきます。印象的な文章だったので、それを紹介します。
著者たちはパソコンを使って、ある自然ドキュメンタリー映画をハッザ族に見せました。映画の一場面は、動物たちが集まるサバンナの水飲み場です。その夜の映像です。
我々は「人間によって管理された自然」を体験しますが、そうではない自然、「さまざまな種が集まっていて、自分もその寄せ集めの一部にすぎない自然」に身を置いたことはないのですね(普通の人は)。そのことが思い起こされる文章でした。
もちろん、運動は健康維持に役立ちます。というより、健康維持のためには運動が必須です。そのことは、
で紹介しました。以上の話の発端となったポンツァー准教授が著した単行本が出版されました。
運動しても痩せないのはなぜか
代謝の最新科学が示す「それでも運動すべき理由」
ハーマン・ポンツァー(Herman Pontzer)著
(小巻靖子・訳 草思社 2022)
代謝の最新科学が示す「それでも運動すべき理由」
ハーマン・ポンツァー(Herman Pontzer)著
(小巻靖子・訳 草思社 2022)
です。No.221 と重複する内容もありますが、単行本なのでさすがに詳しく記述してあります。今回はこの本(以下、本書)の内容をかいつまんで紹介します。なお、原題は、
BURN
New Research Blows the Lid Off
How We Really Burn Calories, Lose Weight, and Stay Healthy
How We Really Burn Calories, Lose Weight, and Stay Healthy
です。直訳すると、
"燃焼"
目から鱗の最新研究
カロリーの消費、減量、健康維持の真実
カロリーの消費、減量、健康維持の真実
となるでしょう(試訳)。
代謝
本書のメインテーマは、原書の題名や副題にあるように "カロリーの燃焼"、つまり「代謝」です。我々が健康を維持するには、体の仕組みを理解することが必須で、その重要なものが代謝です。
| 代謝とは |
|
もちろんエネルギーは、グリコーゲンや脂肪として蓄積でき、必要に応じてエネルギーに転換されます。タンパク質はアミノ酸に分解されて主に筋肉やその他の組織になりますが、必要ならブドウ糖に転換されてエネルギー源になります(=糖再生)。
体内のネルギー源は、最終的にはすべて ATP(アデノシン3リン酸)という分子になります。ATP は極小の充電式バッテリーのようなもので、ATP が ADP(アデノシン2リン酸)に変化するときにエネルギーが放出され、ADP にエネルギーを "チャージ" すると ATP に変化します。ATP は体内の「エネルギー通貨」です。
| エネルギー |
エネルギーとは、一言でいうと "仕事をする能力" で、多様な形をとります。高いところにある物質がもつ「位置エネルギー」、食物に含まれる分子の「化学エネルギー」、燃焼や太陽光の「熱エネルギー」、電気・電波などの「電磁波エネルギー」などです。
エネルギーを計る単位は、カロリー(cal。食品)とジュール(記号は J。食品以外)があります。1カロリーは1ミリリットルの水の温度を1度上げるのに必要なエネルギーで、カロリーの1000倍がキロカロリーです。栄養学ではキロカロリー(kcal)を使うのが伝統的です。
ジュールは、1ニュートン(N)の力で物体を力の方向に1メートル(m)動かすのに必要なエネルギーです。1キログラムの物体に働く重力が 9.8 N なので、1N は 102g の物体に働く重力です。ジュールはエネルギー(またはその等価物。仕事、熱量、電気量、など)を表す国際単位系です。ジュールの値を4で割ると、およそのカロリーになります(1 cal = 4.128 J)。欧州諸国では食品にジュールを使う国が多くあります。
ヒトにとって、エネルギーは通貨に似ています。我々は通貨を外部から得て、それをさまざまな目的のために消費します。一度消費した通貨は別の目的に消費することはできません。通貨は貯蔵することが可能です。また、モノを買うために消費した通貨は、そのモノを売るという形で再び通貨に変えることも可能です。
以上、ざっくり表現すると「代謝」とは「エネルギー消費」のことだといえます。
| 基礎代謝 BMR |
我々は何もしないときでも一定のエネルギーを消費し続けています。これが基礎代謝(BMR。Basic Metabolic Rate)で、安静時のエネルギー消費量です。厳密には、
| 早朝、空腹で(過去6時間に食事をしていない) | |
| 快適な気温で | |
| 横たわって、覚めてはいるが安静状態 |
におけるエネルギー消費量です。空腹を条件とするのは、消化のためにエネルギーを消費するからです。また快適な気温という条件は、寒いと体を暖かく保つためにエネルギーを消費するからです。
基礎代謝は体重に依存します(その他のエネルギー消費も体重に依存する)。人間の1日あたりの基礎代謝は、おおよそ次の式で計算できます(本書に記載の推定式)。
基礎代謝量(1日あたり。キロカロリー)
| 成人男性 : 7×体重 + 551 | |
| 成人女性 : 5×体重 + 607 |
この式の体重はポンド表示です。kg表示の体重をポンドにするには2.2倍(1/0.45 倍)する必要があります。この式で具体的に計算してみると、
成人男性(体重 65kg)→ 1550 kcal/日
成人女性(体重 55kg)→ 1200 kcal/日
成人女性(体重 55kg)→ 1200 kcal/日
となって、よく言われる「男性:1500kcal 程度、女性:1200 kcal 程度」とほぼ同じ数字です。ただし、基礎代謝は人によって(体脂肪率や筋肉量が影響)、または年齢によって(加齢で低下)± 200 程度の差異があります。
| 代謝当量 メッツ - METs |
我々が何らかの活動をすると、基礎代謝以外のエネルギーを消費します。これは「代謝当量 = METs(メッツ)」という単位で表されます(MET=Metabolic Equivalent of Task)。1 METs とは「1時間に体重1キログラムあたり1キロカロリーを消費」することを言います。1 METs は BMR にほぼ等しい値です
各種活動のエネルギー・コスト
| 活動 | メッツ | 備考 |
| 安静 | 1.0 | 睡眠はもう少し低く、0.95 メッツ |
| 座る | 1.3 | 読む、テレビを見る、コンピュータ作業も同じ |
| 立つ | 1.8 | 両足 |
| ヨガ | 2.5 | ハタ・ヨガ |
| 歩く | 3.0 | 2.5マイル(4 km)/時。硬い、平らな地面 |
| スポーツ | サッカー、バスケットボール、テニスなどの有酸素運動 | |
| 家事 | 掃除、洗濯、モップがけなど | |
| アメリカ海軍特殊部隊の訓練、ボクシング、舟を懸命に漕ぐなど |
(本書の表を引用)
各種活動のエネルギー・コストを調べると分かることがあります。それは、運動で消費するエネルギーが意外に(がっかりするほど)少ないことです。150ポンド(68kg)の成人で考えると、1万歩(8キロ程度)歩いたときの消費エネルギーはおよそ250 kcalです。これは炭酸飲料1本分(240 kcal)、ビッグマック半分(270 kcal)に過ぎません(もちろん炭酸飲料には低カロリーのものもある)。
本書に興味深いグラフがあります。それは「ランニング・歩行・水泳・自転車のエネルギーコスト」が速度によってどう変わるかを示したものです。

|
ランニング・歩行・水泳・自転車のエネルギーコスト |
横軸 x は速度。縦軸 y は1マイルを移動するときのエネルギー消費量 |
注目すべきは、ランニングと歩行のエネルギー消費の違いです。上記の表は、横軸 x が速度で、縦軸 y は1マイルを移動するときのエネルギー消費量(="燃費")です。歩行は、一定距離を歩くのに最もエネルギー消費が少ない速度があり、y は x の2乗に比例しています。しかしランニングの燃費は速度にほとんど無関係で、y は x に単純比例し、その比例定数はわずかです。
歩行では体の重心が上下します。しかしランニングは、足のバネによって上下動が少なく、足の骨の作りもスムーズに前進できる構造をしている。ヒトは2足走行に適した体の作りなのです。なお、水泳、自転車は、流体(水・空気)の抵抗で歩行やランニングとは違った様相を呈します。
ここまでが「代謝」を巡る序論です。では、代謝という視点でヒトをみたらどうなるか。まずヒトを含む霊長類の話からです。
霊長類のエネルギー消費
霊長類は哺乳類の一種ですが、他の哺乳類と比較してエネルギー消費が少ない種です。たとえば、ヒト(成人)の1日のエネルギー消費量は普通、2500~3000 kcal 程度ですが、ヒトと同程度の大きさの哺乳類は 5000 kcal を越えます。ヒトを含む霊長類(ゴリラ、オランウータン、チンパンジーとボノボ、ヒト)は、哺乳類の中ではエネルギーの消費量が少ない、つまり代謝の速度が低いのです。
代謝は成長と密接な関係があります。霊長類は進化のある時点で代謝が低下し、成長・繁殖・老化に時間がかかるようになった。つまり、ゆっくりとしたライフサイクルをおくるようになったわけです。イヌの1年は人間の7年に相当するなどと言いますが、そのことを指しています。
|
動物によるエネルギー消費の違い |
哺乳類(非霊長類)と鳥類は、霊長類より1日のエネルギー消費量がはるかに多い。 |
ヒトを除く霊長類のライフスタイルをみると、類人猿はベジタリアンです。シロアリなども食べますが、基本的に植物食です。植物を食べる種は移動距離が少なくて済みます。類人猿のBMR(体重あたり)は、他の哺乳類のBMRとあまり変わらないのですが、植物食が中心で移動距離は少なく、エネルギー消費が少なく、代謝の速度が遅く、ゆっくりと成長して繁殖するように進化したのです。
しかし、霊長類の中でヒトは少々違います。ヒトは霊長類で比べるとエネルギー消費が多いのです。1日のエネルギー消費量は、110kg のオランウータン(オス)で2050 kcal、55kg のオランウータン(メス)で1600 kcal 程度です。これは、同体重のヒトに比べて約30%少ない値です。霊長類4科(チンパンジー・ボノボ、オランウータン、ゴリラ、ヒト)の中でヒトは他の3科と比較して、体重差を補正すると、20%~50%エネルギー消費が多い種なのです。
それはなぜそうなったのでしょうか。
社会的狩猟採集者としてのヒト
ヒトは200万年ほど前に、他の霊長類にはない行動を始めました、それが狩猟による肉食です。小動物だけではなく、シマウマなどの大型哺乳類も標的にする狩猟です。植物食とは違って、狩猟はかなりの身体活動を伴います。
さらにヒトは、根にデンプンを含む野生植物の塊茎を、道具を使い土を掘って採集して食物としました。これも身体活動が伴います。
現代の東アフリカには、農業や牧畜を一切行わず、狩猟採集だけで生活をしている部族がいます。ハッザ族はその一つですが、彼らも大型哺乳類を狩り(男性)、塊茎を採集する(女性)狩猟採集民です。
シマウマやキリンなどの大型哺乳類を狩って肉食をするということは、仲間で狩りをし、その肉を仲間で分配することが前提です。一人での狩りの成功は難しいし、一人が独占して食べる獲物としては大き過ぎるからです。
この「分配」が「代謝の向上」とセットになってヒトは進化しました。分配を伴う狩猟採集は「社会的狩猟採集」と呼べます。この社会的狩猟採集というライフスタイルにより、類人猿よりも多くのエネルギーを摂取し、かつ消費することが可能になりました。
|
代謝革命 |
ヒトは社会性と採食行動を一体化させ、余分の食料を仲間で分配する。これにより消費できるカロリー量が増え、長い寿命、多くの子孫、大きな脳、活発な活動などにつながった。 |
これで可能になった大きなポイントが脳の発達です。「社会的狩猟採集」を始めたホモ属は、それ以前のアウストラロピテクスより20%以上も脳の体積が増加したことが確かめられています。
ヒトが社会的狩猟採集に適した進化を遂げたことの別の現れが、持久力の向上です。持久力の指標である「最大酸素摂取量」は、ヒトはチンパンジーの4倍あります。ざっくり言って、ヒトの持久力は霊長類(類人猿)の4倍です。持久力があると遠距離の狩猟が可能です。哺乳類をどこまでも追いかけ、獲物が弱ったところで(=人間で言う "熱中症" になったところで)仕留める「持久狩猟」も可能になりました。
さらに火の使用がエネルギー摂取量を大きくしました。加熱調理をすると食物の構造や化学的性質が変わり、栄養を摂取しやすくなります。たとえば、加熱調理したジャガイモは、生で食べるより2倍のエネルギーをとれます。
また火の使用は社会的狩猟採集というライフスタイルの質を向上させました。火で槍の先を硬くする、火でタールを溶かして石斧を作る、暖をとってエネルギー消費を押さえる、などの効果です。
一方、ヒトの代謝量が向上したことにはマイナス面もあります。それは代謝性疾患にかかるリスクで、肥満、2型糖尿病、心臓疾患などが代表的なものです。ただし狩猟採集民であるハッザ族ではこういった代謝性疾患はありません。活発な身体活動というライフスタイルがなくなったとき、リスクが表面化するのです。
こういった進化をとげてきたヒトのエネルギーを消費は身体活動量によってどう変わるのでしょうか。それが次です。
制限的日時消費カロリーモデル
人間が一定期間(たとえば1日)でどれだけエネルギーを消費するかは、従来は「要因加算法」で計算されてきました。これは、
基礎代謝量(BMR)に、消化に必要なエネルギーと、身体活動に必要なエネルギーを加えたものが総エネルギー消費量である
という仮定にもとづくものです。いかにも妥当な仮定にみえますが、これは根拠がない全くの空論であることが分かってきました。
それは、技術革新により消費エネルギーの厳密測定が可能になったからです。この技術が「2重標識水法」です。これは水素の同位元素である「重水素」と、酸素の同位元素である「酸素18」でできた水(=2重標識水)を使うものです。
なお、2重標識水法の解説を No.221「なぜ痩せられないのか」に書きました。また、霊長類などのエネルギー消費の厳密測定も2重標識水法で初めて可能になりました。
アフリカの狩猟採集民であるハッザ族と、現代アメリカ人のエネルギー消費量を調査したグラフがあります。それをみると、ハッザ族と現代アメリカ人は身体活動量が大きく違うにもかかわらず、エネルギー消費量は同じです。
|
カロリー消費量の比較(ハッザ族と先進国) |
丸は男性、四角は女性を表す。灰色の丸・四角の一つ一つは、先進国の男性集団・女性集団のカロリー消費量を調査した結果を示していて、それが多数プロットされている。黒い曲線が男性・女性の近似曲線である。 一方、ハッザ族の成人のカロリー消費量は黒い丸と四角である。これは黒い曲線の近辺にあり、先進国の数々の集団と同じであることを示している。 |
ハッザ族だけではありません。世界各地のさまざまなライフスタイルの民族を比較しても、エネルギー消費量は同じだという証拠が積み上がってきました。
では、同じ人が身体活動を変えると、エネルギー消費量はどう変化するのでしょうか。このわかりやすい例がオランダで行われた「ハーフマラソン研究」です。これは、
運動を全くしていなかった男女をプログラムに参加させ、1年間かけてハーフマラソンを走れるようにする
というものです。
|
要因加算法とハーフマラソン研究 |
上の図は要因加算法の仮定で、「その他」となっているのは基礎代謝や消化のエネルギー消費などである。これに身体活動のエネルギーを加算したものが総エネルギー消費だとする。しかしこれには根拠が全くない。 下の図はオランダで行われたハーフマラソン研究の結果である。ランニングの時間が延びても、エネルギー消費量はほぼ変わらない。 |
以下、「ハーフマラソン研究」で判明したことを本書から引用します(なお、以降の引用では段落を増やしたところがあります)。
|
ハーフマラソンに向けての練習で消費したエネルギーの分だけ、身体のどこかのエネルギー消費が減り、トータルとしてのエネルギー消費がほぼ一定に保たれる。ヒトの体はそういうふうにできている(=そのように進化してきた)のです。これがエネルギー消費に関する「制限的日時消費カロリーモデル」です。
この種の研究は多数行われています。プログラムの期間や運動の強度によっていくらか結果は異なりますが、ほとんどの場合、制限的日次カロリー消費モデルに沿ったものとなっています。
運動が体によい理由
「制限的日時消費カロリーモデル」によって、運動が体によい理由の一つが見えてきます。このモデルをわかりやすく図示したのが次の図です。
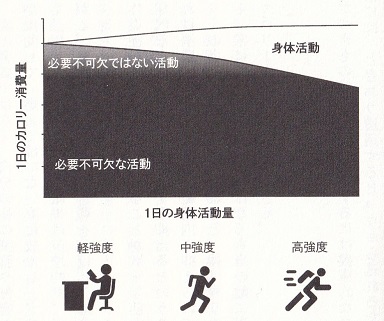
|
身体活動量とカロリー消費 |
運動でエネルギーを消費すると、必須ではない体の活動 = カロリーが余っているときにすればよい活動が制限され、体の維持に必須の活動はできるだけ守られます。つまり、運動はエネルギーの配分バランスを変えることになります。配分バランスの変化の結果、「体に悪影響を及ぼすエネルギー消費」が少なくなる。それは主として3つあります。
炎症
一つは「炎症」です。体に細菌やウイルス、あるいはダニのような寄生生物が進入すると、免疫細胞がその部位に集結し、異物を排除します。外見的にはその部位が腫れる。これが体の炎症反応です。これは侵入者に対処するための必須の仕組みです。
しかし炎症反応が真の標的を見誤り、花粉のように無害のものや、あるいは自己の細胞を攻撃するようになると、アレルギー、関節炎、動脈疾患などの広範囲の症状を引き起こします。それが脳の視床下部に影響すると、過食や、その他の体の調節異常を起こします。
定期的な運動が慢性炎症の抑制に効果的であることは、ずいぶん前から指摘されてきました。運動でカロリーを消費すると、体は残ったカロリーを倹約して使うようになります。運動は、炎症反応が本来の標的に対して働くように仕向け、免疫系が不要な活動にエネルギーを使うことを抑制します。
ストレス反応
何らかの緊急事態に遭遇したときや、普通ではない状況に陥ったときには、アドレナリンやコルチゾールが分泌されてストレス反応が起こります。これは緊急事態に対応するための正常な反応です。
しかし炎症と同じで、ストレス反応が間違って引き起こされたり、いつまでも続いたりすると、健康に重大な影響を及ぼします。
運動は気分を改善し、ストレスを軽減します。運動することによってストレス反応の大きさが押さえられるからです。中程度の鬱病患者の治療として運動が使われることもあります。
生殖ホルモン
運動を続けると生殖ホルモン(男性ホルモン、女性ホルモン)の分泌量が減ります。
生殖ホルモンの分泌量の低下は、子供の数という面ではマイナスです。ハッザ族では避妊は行われず、大家族が望まれますが、女性が子供を生む間隔は3~4年です。一方、アメリカでは、授乳中であれ、もし希望すれば1~2年おきに出産が可能です。これはアメリカの母親の方が身体活動レベルが低く、高カロリー食品を容易に摂取できるので、ハッザ族の女性よりも出産にエネルギーを回すことができ、出産後の回復も早いからです。
しかし、生殖ホルモンのレベルが高いと生殖系のがん(乳がんや前立腺がん)のリスク要因になります。運動はそのリスクを低下させます。むしろ、身体活動が高く、生殖ホルモンの分泌量が低下している状態の方が、ヒトの体の本来の姿と言えます。運動は本来の姿に戻します。
もちろん過度の運動による生殖ホルモンの低下は問題を引き起こします。女性であれば生理が止まったりすることがあります。
運動が健康に良いのは、以上に述べたような代謝からの要因(=エネルギー使用バランスの変化による要因)だけでありません。本書から、健康によい理由の部分(数々の研究から引用したもの)を引用します。
|
|
まとめ
本書の重要ポイントをまとめると、次のようになるでしょう。
| 運動しても痩せないからこそ、運動する意義(の一つ)がある。それは運動によって体内のエネルギー消費=代謝のバランスが変化し、その変化が健康維持に役立つからである。 | |
| もちろん、代謝の視点以外からも、運動(活発な身体活動)は、数々の理由で健康維持のために必須である。 |
痩せることを目標にして運動をはじめてはみたものの、思ったように痩せないので運動をやめた、というようなことがあるとしたら、これほど本末転倒なことはないわけです。
ヒトは、身体活動レベルが高いのが通常状態であり、それは「社会的狩猟採集」というライフスタイルに適合するように進化した結果です。つまり、ヒトの体の基本的なしくみは、東アフリカのサバンナで作られ、それは今も変わっていない(=体はまだサバンナにいる)と言えるでしょう。
サバンナでの映画上映
本書に、著者たちがアフリカのサバンナに住むハッザ族のキャンプに泊まりこんでフィールド調査をしたときのエピソードが出てきます。印象的な文章だったので、それを紹介します。
著者たちはパソコンを使って、ある自然ドキュメンタリー映画をハッザ族に見せました。映画の一場面は、動物たちが集まるサバンナの水飲み場です。その夜の映像です。
|
我々は「人間によって管理された自然」を体験しますが、そうではない自然、「さまざまな種が集まっていて、自分もその寄せ集めの一部にすぎない自然」に身を置いたことはないのですね(普通の人は)。そのことが思い起こされる文章でした。
2023-01-07 12:12
nice!(0)
No.350 - 寄生生物が行動をあやつる [科学]
No.348、No.349 に続いて寄生の話です。No.348「蚊の嗅覚は超高性能」では、
との主旨を書きました。ウイルスの生き残り(ないしはコピーの拡散)戦略は誠に巧妙です。また、No.349「蜂殺し遺伝子」は、
との主旨でした。ウイルスにとって寄生パチは宿主(=芋虫)をめぐる競争相手です。従って競争相手を排除する仕組みを発達させたのです。
こういったウイルス、もっと広くとらえると「寄生体」は、この2例のように宿主の "体質" を変えることがあり、さらにそれだけでなく、宿主の行動をコントロールするケースがあることが知られています。そのような「宿主の行動を操る寄生体」として、カマキリにの寄生するハリガネムシの例を紹介します。ハリガネムシ(針金虫)とは、その名のとおり針金のような形の虫で、カマキリをはじめとする各種の昆虫に寄生します。
最強ハンター カマキリ
2022年11月7日のNHK BSプレミアムの番組、ワイルドライフ「鳥を襲う最強ハンター カマキリ 究極の技」で、驚きの映像が2つ紹介されました。一つは、カマキリが小鳥のベニヒワを襲う(=狩る)映像です。
能登半島の北、約50kmの位置にある舳倉島(石川県輪島市)は、世界的にも有名な渡り鳥の中継地で、その季節になるとバード・ウォッチャーの人たちで賑わいます。この島に生息するカマキリは、小鳥の一種であるベニヒワを襲うことがあるのです。放映された映像では、カマキリは草の上の方でじっと待ち、たまたま近くにベニヒワがとまると、そっとベニヒワの死角から忍び寄って、ベニヒワの後頭部に "カマ" を突き立てる。
映像ではカマキリが "狩り" に失敗したケースと成功したケースの両方が映し出されていました。成功したケースでは、ベニヒワはカマキリと一緒に地上に墜落して羽をバタつかせています。誠に驚くべき映像(=世界初)で、これを撮影した番組スタッフの執念に感心しました。
しかし、この番組ではもう一つの驚くべき映像がありました。泳げないカマキリが川に飛び込んで "自殺" する瞬間をとらえた映像です。このカマキリの行動は以前から知られていましたが、動画でとらえたのは初めてのようです。これは寄生体にからんでいるので、以下、この部分をそのまま紹介します。
カマキリの "自殺"
【ナレーション(首藤奈知子アナウンサー)】
昆虫界最強ハンター、カマキリ。でも、意外な原因で命を落とすことがあります。私たちは、その驚きの瞬間を目撃しました。
川に近づくハラビロカマキリ。水面をじっと見つめ ・・・・・・ なんと、飛び込んでしまいました。泳げないカマキリが自ら水に飛び込むなんて ・・・・・・ 。いったいなぜ、こんなことが起きたんでしょうか。
この謎の行動について研究を続けている佐藤拓哉博士。実はカマキリはある動物に操られているのだと言います。
佐藤博士が手のひらに乗せているヒモのようなもの。寄生虫のハリガネムシです。これがカマキリの体内に入り込んで動きを操っていたんです。
【佐藤拓哉博士(京都大学生態学研究センター、准教授)】
ハリガネムシは、普段はあまり歩かないカマキリを、活動量が上がるようなタンパク質を出したり、光に応答してしまうようなタンパク質を出したりして、川や池に飛び込ませる。いわば洗脳してしまうような状態になると言われています。
【ナレーション】
何とも恐ろしいハリガネムシ。でも、なぜ水に飛び込むよう、仕向けるのでしょうか。
その理由はハリガネムシの暮らしにあります。ハリガネムシの一生は川の中で始まります。春、卵からかえった幼生は、川底に潜んで暮らします。カゲロウなどの幼虫が川底で食事をするとき、偶然、口から吸い込まれると、殻に包まれた状態に変化し、休眠状態に入ります。
やがて幼虫は羽化して森へ。それを待ち受けるのがカマキリ ・・・・・・ つかまえました(カマキリがカゲロウをつかまえるシーンが挿入される) ・・・・・・。するとハリガネムシはカマキリの体内へ移動。眠りから覚め、成長していきます。
でも、子孫を残すためには水中で産卵しなければなりません。そこで、神経を混乱させる物質を出してカマキリを操ります。こうして乗っ取られた状態になったカマキリは、川へ飛び込んでしまうんです。ハリガネムシは水に入るとカマキリの体から出て行きます。
最近の研究で、カマキリは飛び込む場所までハリガネムシにコントロールされているという、衝撃の事実が明らかになりました。
【佐藤拓哉博士】
これまでは、ハリガネムシに寄生されたカマキリは、水の反射光のキラキラ、明るさですね、明るさに引き寄せられると言われていたんですけれども、実際には自然界には水たまりとか、葉っぱに反射するキラキラ明るい所とか、いろんなものがあるわけですけど、そういう所にいちいち感染したカマキリが引き寄せられていると、川に戻れないというふうになってしまいます。
【ナレーション】
ハリガネムシに寄生されたカマキリが飛び込むのは、きまって川の深い所。佐藤博士たちは長年の研究の末、この謎をついに解き明かしました。
【佐藤拓哉博士】
ハリガネムシに感染したカマキリは、深い水辺に反射した光の中に含まれる「水平偏光」に引き寄せられて川に飛び込んでいるというようなことが分かってきました。
【ナレーション】
水平偏光とは、深い水中からの反射光に多く含まれる光の一種です。肉眼では見ることができませんが、特殊なカメラで覗いてみると、水平偏光が強い場所は赤っぽく写ります。浅い川では一見キラキラして見えますが、赤い部分はほとんどありません。一方、深い川は暗く見えますが、赤い部分が多いことが分かります。
ハリガネムシの繁殖に適しているのは深い川の中。寄生されたカマキリは、水平偏光の強い深い川に引き寄せられ、飛び込んでいたんです。
カマキリの命の奪う寄生虫、ハリガネムシ。研究を進めるうち、意外な事実も見えてきました。
【佐藤拓哉博士】
ハリガネムシは森の虫をつれて川に入ると、産卵をして死んでいくんですが、その過程で大量に入った森の虫が川の魚の餌になっている。つまり、ハリガネムシがいると森から川に大きなエネルギーの流れが起きるというようなことに気づいたんです。
【ナレーション】
寄生されたカマキリなどの昆虫は、川に飛び込んだあと魚に食べられることがよくあります。そうした昆虫たちが川の生態系に大きな役割を果たしているのです。
【佐藤拓哉博士】
調べてみると、調査した川に棲んでいる渓流魚が1年間に消費するエネルギーの約6割を、ハリガネムシが森から連れてきた虫によって担われているということが分かってきました。1年の6割をハリガネムシが担っているというのは、これは森と川がものすごく強くハリガネムシのおかげで繋がっているというようなことで、すごく驚きでした。
【ナレーション】
陸と川との思わぬ繋がり。それを支えているのは、カマキリなどの昆虫たちだったのです。
カマキリに寄生したハリガネムシが、カマキリの神経を混乱させ、川の深いところを選んで飛び込むように操っている、というのは驚きの事実です。さらにもう一つの驚きは、こうしたハリガネムシの生活史が渓流魚の餌の供給を支えていて、エネルギー・ベースでは餌の6割にも相当する、ということです。
このカマキリとハリガネムシの話は、2022年12月4日の日本経済新聞にも載っていました。ただし記事のメインは「オオカミを操る寄生体」です。次にそれを紹介します。
オオカミ、寄生体がボス指名
その日本経済新聞のコラム記事は、
と題するものです。寄生体が操るのは、カマキリといった昆虫ではななく、なんとオオカミだというのです。
記事でいう「目を疑うような内容」とは「ある種の寄生体を宿すオオカミはリスクを冒す傾向が強くリーダーになりやすい」という調査結果です。その寄生体が次に書いてあります。
この研究はオオカミが「トキソプラズマに感染する」ことと「群れのリーダーになる」ことの間に強い相関関係があることを示したものです。しかし、相関関係があるからといって因果関係があるとは限りません。上に引用にもあるように、「トキソプラズマがオオカミを操って攻撃性を高める」というのはあくまで仮説です。しかし、あとで出てきますが、トキソプラズマが感染した動物の性格を変える例はほかにもあり、このオオカミの例は因果関係を疑わせるものなのです。
この寄生体の介入が、オオカミのボスを決めるだけならまだしも、それによる影響がオオカミの群に及ぶのでは、というのが研究チームの懸念です。
トキソプラズマが感染したネズミは
トキソプラズマ(単細胞の原生生物)は、ネコ科の動物の腸が本来の住処であり、有性生殖するのはそこだけです。他の動物にも感染しますが、無性生殖しかできない。
トキソプラズマが感染したネズミがどうなるか、という話が次に出てきます。
ネズミがネコに食べられやすくなったら、ネズミの体内のトキソプラズマは「故郷」に帰れるし、ネコにとっては食料が増えて好都合です。そういうふうにトキソプラズマがネズミを操っているのです。
「この世界には様々な陰の支配者がおり、予想以上に大きな力を振るっている」と記事にもありました。その別の例が、NHK の番組にあった「カマキリを操るハリガネムシ」です。
カマキリを操るハリガネムシ
「ハリガネムシが寄生したカマキリ」は、さきほどの「トキソプラズマが寄生したネズミ = ネコに食べられやすい」とそっくりです。両方とも、寄生体にとって都合のよいように宿主の行動が変わるという意味でそっくりなのです。
人間とトキソプラズマ
「この世界には様々な陰の支配者がおり、予想以上に大きな力を振るっている」としたら、人間も無関係ではありえません。
従来、精神疾患は、遺伝的な要因や、本人が受けた精神的ストレスの要因が研究されてきましたが、最近注目されているのは微生物との関係です。一つは腸内細菌が脳に与える影響であり、もう一つは脳に潜む微生物・寄生体です。
最近の NHK BSプレミアムの番組ですが、2022年10月4日放送の「ヒューマニエンス」で、東京慈恵会医科大学のウイルス学者・近藤一博教授が、
との主旨を語っておられました。HHV-6 は赤ちゃんに突発性発疹を起こすウイルスで、ヒトに対する影響はそれしかないと思われてきましたが、実は成人にも影響し、鬱病のリスク増大要因になるのです。
「自然界における寄生体は、予想以上に大きな力をもっている」のかもしれません。ヒトに寄生する生物が、ヒトの性格や行動、精神的な傾向に与える影響は、今後研究が進む分野だと思いました。
本文中に書いた、
ことについて、その行動の謎を遺伝子レベルで解明しようとする研究がされています。日本経済新聞の記事から引用します。
ある種のウイルスは、宿主(= ウイルスが感染している生物)を、蚊の嗅覚に感知されやすいように変化させ、蚊の媒介によるウイルスの拡散が起こりやすくしている
との主旨を書きました。ウイルスの生き残り(ないしはコピーの拡散)戦略は誠に巧妙です。また、No.349「蜂殺し遺伝子」は、
ウイルスが芋虫に感染すると、その芋虫は寄生バチの卵や幼虫を死滅させるタンパク質を生成し、これによってハチに寄生される確率が下がる。このタンパク質を生成する「蜂殺し遺伝子」はウイルスがもたらす
との主旨でした。ウイルスにとって寄生パチは宿主(=芋虫)をめぐる競争相手です。従って競争相手を排除する仕組みを発達させたのです。
こういったウイルス、もっと広くとらえると「寄生体」は、この2例のように宿主の "体質" を変えることがあり、さらにそれだけでなく、宿主の行動をコントロールするケースがあることが知られています。そのような「宿主の行動を操る寄生体」として、カマキリにの寄生するハリガネムシの例を紹介します。ハリガネムシ(針金虫)とは、その名のとおり針金のような形の虫で、カマキリをはじめとする各種の昆虫に寄生します。
最強ハンター カマキリ
2022年11月7日のNHK BSプレミアムの番組、ワイルドライフ「鳥を襲う最強ハンター カマキリ 究極の技」で、驚きの映像が2つ紹介されました。一つは、カマキリが小鳥のベニヒワを襲う(=狩る)映像です。
能登半島の北、約50kmの位置にある舳倉島(石川県輪島市)は、世界的にも有名な渡り鳥の中継地で、その季節になるとバード・ウォッチャーの人たちで賑わいます。この島に生息するカマキリは、小鳥の一種であるベニヒワを襲うことがあるのです。放映された映像では、カマキリは草の上の方でじっと待ち、たまたま近くにベニヒワがとまると、そっとベニヒワの死角から忍び寄って、ベニヒワの後頭部に "カマ" を突き立てる。
映像ではカマキリが "狩り" に失敗したケースと成功したケースの両方が映し出されていました。成功したケースでは、ベニヒワはカマキリと一緒に地上に墜落して羽をバタつかせています。誠に驚くべき映像(=世界初)で、これを撮影した番組スタッフの執念に感心しました。
しかし、この番組ではもう一つの驚くべき映像がありました。泳げないカマキリが川に飛び込んで "自殺" する瞬間をとらえた映像です。このカマキリの行動は以前から知られていましたが、動画でとらえたのは初めてのようです。これは寄生体にからんでいるので、以下、この部分をそのまま紹介します。
カマキリの "自殺"
【ナレーション(首藤奈知子アナウンサー)】
昆虫界最強ハンター、カマキリ。でも、意外な原因で命を落とすことがあります。私たちは、その驚きの瞬間を目撃しました。
川に近づくハラビロカマキリ。水面をじっと見つめ ・・・・・・ なんと、飛び込んでしまいました。泳げないカマキリが自ら水に飛び込むなんて ・・・・・・ 。いったいなぜ、こんなことが起きたんでしょうか。


|
川に飛び込むハラビロカマキリ(番組より) |
この謎の行動について研究を続けている佐藤拓哉博士。実はカマキリはある動物に操られているのだと言います。
佐藤博士が手のひらに乗せているヒモのようなもの。寄生虫のハリガネムシです。これがカマキリの体内に入り込んで動きを操っていたんです。

|
佐藤博士が川で採取したハリガネムシを示している(番組より) |
【佐藤拓哉博士(京都大学生態学研究センター、准教授)】
ハリガネムシは、普段はあまり歩かないカマキリを、活動量が上がるようなタンパク質を出したり、光に応答してしまうようなタンパク質を出したりして、川や池に飛び込ませる。いわば洗脳してしまうような状態になると言われています。
【ナレーション】
何とも恐ろしいハリガネムシ。でも、なぜ水に飛び込むよう、仕向けるのでしょうか。
その理由はハリガネムシの暮らしにあります。ハリガネムシの一生は川の中で始まります。春、卵からかえった幼生は、川底に潜んで暮らします。カゲロウなどの幼虫が川底で食事をするとき、偶然、口から吸い込まれると、殻に包まれた状態に変化し、休眠状態に入ります。
やがて幼虫は羽化して森へ。それを待ち受けるのがカマキリ ・・・・・・ つかまえました(カマキリがカゲロウをつかまえるシーンが挿入される) ・・・・・・。するとハリガネムシはカマキリの体内へ移動。眠りから覚め、成長していきます。
でも、子孫を残すためには水中で産卵しなければなりません。そこで、神経を混乱させる物質を出してカマキリを操ります。こうして乗っ取られた状態になったカマキリは、川へ飛び込んでしまうんです。ハリガネムシは水に入るとカマキリの体から出て行きます。

|
水中でカマキリの体内から出てくるハリガネムシ(番組より) |
最近の研究で、カマキリは飛び込む場所までハリガネムシにコントロールされているという、衝撃の事実が明らかになりました。
【佐藤拓哉博士】
これまでは、ハリガネムシに寄生されたカマキリは、水の反射光のキラキラ、明るさですね、明るさに引き寄せられると言われていたんですけれども、実際には自然界には水たまりとか、葉っぱに反射するキラキラ明るい所とか、いろんなものがあるわけですけど、そういう所にいちいち感染したカマキリが引き寄せられていると、川に戻れないというふうになってしまいます。
【ナレーション】
ハリガネムシに寄生されたカマキリが飛び込むのは、きまって川の深い所。佐藤博士たちは長年の研究の末、この謎をついに解き明かしました。
【佐藤拓哉博士】
ハリガネムシに感染したカマキリは、深い水辺に反射した光の中に含まれる「水平偏光」に引き寄せられて川に飛び込んでいるというようなことが分かってきました。
【ナレーション】
水平偏光とは、深い水中からの反射光に多く含まれる光の一種です。肉眼では見ることができませんが、特殊なカメラで覗いてみると、水平偏光が強い場所は赤っぽく写ります。浅い川では一見キラキラして見えますが、赤い部分はほとんどありません。一方、深い川は暗く見えますが、赤い部分が多いことが分かります。
ハリガネムシの繁殖に適しているのは深い川の中。寄生されたカマキリは、水平偏光の強い深い川に引き寄せられ、飛び込んでいたんです。
カマキリの命の奪う寄生虫、ハリガネムシ。研究を進めるうち、意外な事実も見えてきました。
【佐藤拓哉博士】
ハリガネムシは森の虫をつれて川に入ると、産卵をして死んでいくんですが、その過程で大量に入った森の虫が川の魚の餌になっている。つまり、ハリガネムシがいると森から川に大きなエネルギーの流れが起きるというようなことに気づいたんです。
【ナレーション】
寄生されたカマキリなどの昆虫は、川に飛び込んだあと魚に食べられることがよくあります。そうした昆虫たちが川の生態系に大きな役割を果たしているのです。
【佐藤拓哉博士】
調べてみると、調査した川に棲んでいる渓流魚が1年間に消費するエネルギーの約6割を、ハリガネムシが森から連れてきた虫によって担われているということが分かってきました。1年の6割をハリガネムシが担っているというのは、これは森と川がものすごく強くハリガネムシのおかげで繋がっているというようなことで、すごく驚きでした。
【ナレーション】
陸と川との思わぬ繋がり。それを支えているのは、カマキリなどの昆虫たちだったのです。
カマキリに寄生したハリガネムシが、カマキリの神経を混乱させ、川の深いところを選んで飛び込むように操っている、というのは驚きの事実です。さらにもう一つの驚きは、こうしたハリガネムシの生活史が渓流魚の餌の供給を支えていて、エネルギー・ベースでは餌の6割にも相当する、ということです。
このカマキリとハリガネムシの話は、2022年12月4日の日本経済新聞にも載っていました。ただし記事のメインは「オオカミを操る寄生体」です。次にそれを紹介します。
オオカミ、寄生体がボス指名
その日本経済新聞のコラム記事は、
オオカミ、寄生体がボス指名
感染で脳操作、野心かきたてる
感染で脳操作、野心かきたてる
と題するものです。寄生体が操るのは、カマキリといった昆虫ではななく、なんとオオカミだというのです。
|

|
オオカミは群れる. (日本経済新聞より) |
記事でいう「目を疑うような内容」とは「ある種の寄生体を宿すオオカミはリスクを冒す傾向が強くリーダーになりやすい」という調査結果です。その寄生体が次に書いてあります。
|
この研究はオオカミが「トキソプラズマに感染する」ことと「群れのリーダーになる」ことの間に強い相関関係があることを示したものです。しかし、相関関係があるからといって因果関係があるとは限りません。上に引用にもあるように、「トキソプラズマがオオカミを操って攻撃性を高める」というのはあくまで仮説です。しかし、あとで出てきますが、トキソプラズマが感染した動物の性格を変える例はほかにもあり、このオオカミの例は因果関係を疑わせるものなのです。
この寄生体の介入が、オオカミのボスを決めるだけならまだしも、それによる影響がオオカミの群に及ぶのでは、というのが研究チームの懸念です。
|
トキソプラズマが感染したネズミは
トキソプラズマ(単細胞の原生生物)は、ネコ科の動物の腸が本来の住処であり、有性生殖するのはそこだけです。他の動物にも感染しますが、無性生殖しかできない。
トキソプラズマが感染したネズミがどうなるか、という話が次に出てきます。
|
ネズミがネコに食べられやすくなったら、ネズミの体内のトキソプラズマは「故郷」に帰れるし、ネコにとっては食料が増えて好都合です。そういうふうにトキソプラズマがネズミを操っているのです。
「この世界には様々な陰の支配者がおり、予想以上に大きな力を振るっている」と記事にもありました。その別の例が、NHK の番組にあった「カマキリを操るハリガネムシ」です。
カマキリを操るハリガネムシ
|
「ハリガネムシが寄生したカマキリ」は、さきほどの「トキソプラズマが寄生したネズミ = ネコに食べられやすい」とそっくりです。両方とも、寄生体にとって都合のよいように宿主の行動が変わるという意味でそっくりなのです。
|
寄生生物が行動を操る (日本経済新聞より) |
人間とトキソプラズマ
「この世界には様々な陰の支配者がおり、予想以上に大きな力を振るっている」としたら、人間も無関係ではありえません。
|
従来、精神疾患は、遺伝的な要因や、本人が受けた精神的ストレスの要因が研究されてきましたが、最近注目されているのは微生物との関係です。一つは腸内細菌が脳に与える影響であり、もう一つは脳に潜む微生物・寄生体です。
最近の NHK BSプレミアムの番組ですが、2022年10月4日放送の「ヒューマニエンス」で、東京慈恵会医科大学のウイルス学者・近藤一博教授が、
ヒトに潜伏感染するヘルペス・ウイルスの一種、ヒトヘルペスウイルス6型(HHV-6)が、鬱病の発症リスクを高める
との主旨を語っておられました。HHV-6 は赤ちゃんに突発性発疹を起こすウイルスで、ヒトに対する影響はそれしかないと思われてきましたが、実は成人にも影響し、鬱病のリスク増大要因になるのです。
「自然界における寄生体は、予想以上に大きな力をもっている」のかもしれません。ヒトに寄生する生物が、ヒトの性格や行動、精神的な傾向に与える影響は、今後研究が進む分野だと思いました。
| 補記:ハリガネムシとカマキリ |
本文中に書いた、
カマキリに寄生したハリガネムシが、カマキリの神経を混乱させ、川の深いところを選んで飛び込むように操る
ことについて、その行動の謎を遺伝子レベルで解明しようとする研究がされています。日本経済新聞の記事から引用します。
|
2022-12-17 08:10
nice!(0)
No.349 - 蜂殺し遺伝子 [科学]
前回の No.348「蚊の嗅覚は超高性能」で、
との主旨を書きました。ウイルスの生き残り(ないしはコピーの拡散)戦略は誠に巧妙です。
これは、2022年9月17日の日本経済新聞の記事から紹介したものですが、その1年ほど前の日経新聞にも「ウイルスの巧妙な戦略」の記事があったことを思い出しました。今回はその内容を紹介します。
と題した記事です。以下の引用は、日経デジタル(2021年8月21日 2:00)からです。
補食寄生
まず、この記事の前提は「補食寄生」です。ほとんどの寄生者は宿主(= 寄生する相手)と共存しますが、補食寄生とは最終的に宿主を殺してしまう寄生です。
蜂の仲間には補食寄生を行う種が多々ありますが、最も "高度な" 寄生者として「エメラルドゴキブリバチ」が知られています。多くの補食寄生者は特定の1種の昆虫を宿主とします。エメラルドゴキブリバチの宿主は、ゴキブリの1種のワモンゴキブリ(輪紋ゴキブリ)です。日経サイエンス 2021年7月号の記事「エメラルドゴキブリバチは3度毒針を刺す」(K.C.カタニア:バンダービルト大学・米 テネシー州)によると、エメラルドゴキブリバチは次のように行動します。
誠に驚くべき "高度な" 補食寄生者です。動きが活発なゴキブリの成虫に寄生する(卵を産みつける)ため、神経毒を3回注入し、しかもそれぞれ目的が違うというのは、ちょっと信じ難いような進化の結果です。
これほどまでの蜂はエメラルドゴキブリバチしか知られていないようです。つまり、ほとんどの補食寄生者はもっと "簡単な" やりかたをします。つまり、寄生する相手は昆虫の、
が普通で、動かないものか、動きが鈍いものです。そして日経新聞にあったのは幼虫(芋虫)のケースで、そこに、蜂だけなくウイルスが絡んできます。
蜂殺し遺伝子の発見
以上の「補食寄生」を踏まえて、日本経済新聞 2021年8日22日 の「蜂殺し遺伝子」の話を紹介します。蜂と芋虫の「寄生・被寄生」関係に割って入るウイルスがあるのです。
ウイルスと芋虫とハチの種が書いてないのですが、当然、昆虫のみに感染する、ある特定のウイルスです。そのウイルスは多種の芋虫に感染するのでしょう。芋虫・ハチの補食寄生の関係は特定の種同士かもしれないが、補食寄生は多くのハチにみられる現象なので、ウイルスが感染した芋虫もハチが卵を産みつける可能性が高い。そう理解できます。
アポトーシス
補食寄生に続く第2のキーワードは「アポトーシス」です。アポトーシスとは、いわば細胞の "自殺" ですが、ウイルスがもたらした遺伝子が、ハチの卵のアポトーシスを引き起こしているようなのです。
よく知られているように、ウイルスは自分の遺伝子を宿主の細胞に送り込み、その遺伝子は細胞が本来持っていなかった "モノ" 作り出します。それは普通、ウイルスの複製ですが、この場合は「寄生バチの卵や幼虫のアポトーシスを引き起こすタンパク質」も作り出す。そう理解できます。
芋虫にとっては「命を奪う寄生バチよりも体調不良で済むウイルスの方がマシ」なのでしょう。またウイルスからすると「助け舟を出しながら、芋虫を増殖に利用するのが狙い」です。仲井教授は仮説としてそう考えています。
進化的軍拡競争
さらに第3のキーワードは「進化的軍拡競争」です。つまり、生物が競争関係や敵対関係になると、互いに相手の形質を上回るような "進化の競争" が始まります。
ウイルスと芋虫は、互いにメリットを与え合う「共存関係」にある、と理解できます。
ウイルスと生物
記事の最後には、ウイルスと生物の関係についてのマクロ的な解説があり、安定状態では共存が保たれるが、不安定な競合関係ではウイルスは脅威になるということが説明されていました。
以下は記事の感想です。この「蜂殺し遺伝子」の話は、前回の No.348「蚊の嗅覚は超高性能」に書いた、東京慈恵会医科大学の近藤教授の発言を思い起こさせます。再掲すると以下です。
「ウイルスの策略を知るには多くの生物が織りなす生態系への理解が不可欠」と、日経新聞の記事の最後にありました。人間のウイルスについての理解は、マクロ的にみると "始まったばかり" か、それが言い過ぎなら "初期段階にある" と言えるのでしょう。
ある種のウイルスは、宿主(= ウイルスが感染している生物)を "蚊の嗅覚に感知されやすいように" 変化させ、蚊の媒介によるウイルスの拡散が起こりやすくしている
との主旨を書きました。ウイルスの生き残り(ないしはコピーの拡散)戦略は誠に巧妙です。
これは、2022年9月17日の日本経済新聞の記事から紹介したものですが、その1年ほど前の日経新聞にも「ウイルスの巧妙な戦略」の記事があったことを思い出しました。今回はその内容を紹介します。
ウイルスの脅威、競合相手にも
「感染者」横取り阻む
日本経済新聞(2021年8日22日)
「感染者」横取り阻む
日本経済新聞(2021年8日22日)
と題した記事です。以下の引用は、日経デジタル(2021年8月21日 2:00)からです。
補食寄生
まず、この記事の前提は「補食寄生」です。ほとんどの寄生者は宿主(= 寄生する相手)と共存しますが、補食寄生とは最終的に宿主を殺してしまう寄生です。
|
| エメラルドゴキブリバチのメスは、ワモンゴキブリを見つけると、ゴキブリの腹にある「第1胸神経節」に針を刺し、毒素を注入する。これによってゴキブリの前足が一時的に麻痺する。 | |
| エメラルドゴキブリバチは前足が麻痺したゴキブリの喉から2度目の針を刺し、脳に毒素を注入する。これによってゴキブリは動けなくなる(ゾンビ化する)。 | |
| ハチはゴキブリを閉じ込めるための適当な穴を探しに出かける。見つけたあと、ゴキブリを引っ張って穴の中に入れる。 | |
| ハチはゴキブリの「第2胸神経節」に3度目の針を刺し、毒素を注入する。これによってゴキブリの運動神経が活性化し、中足が開く。 | |
| ハチは、開いた中足の関節のつけ根にある薄い膜の上に卵を産みつける。その後、穴から出て石などで蓋をする。 | |
| 孵化した幼虫は、進入可能な唯一の部分である薄い膜を破ってゴキブリの体内に潜り込む。そしてゴキブリの体を食べて成長し、繭を作る。40~60日後に成虫がゴキブリの体から出てくる。 |
誠に驚くべき "高度な" 補食寄生者です。動きが活発なゴキブリの成虫に寄生する(卵を産みつける)ため、神経毒を3回注入し、しかもそれぞれ目的が違うというのは、ちょっと信じ難いような進化の結果です。
これほどまでの蜂はエメラルドゴキブリバチしか知られていないようです。つまり、ほとんどの補食寄生者はもっと "簡単な" やりかたをします。つまり、寄生する相手は昆虫の、
| 卵 | |
| 蛹 | |
| 幼虫(芋虫) |
が普通で、動かないものか、動きが鈍いものです。そして日経新聞にあったのは幼虫(芋虫)のケースで、そこに、蜂だけなくウイルスが絡んできます。
蜂殺し遺伝子の発見
以上の「補食寄生」を踏まえて、日本経済新聞 2021年8日22日 の「蜂殺し遺伝子」の話を紹介します。蜂と芋虫の「寄生・被寄生」関係に割って入るウイルスがあるのです。
|

|
アワヨトウの幼虫に卵を産みつける寄生バチ「カリヤコマユバチ」。東京農工大学提供。 |
日本経済新聞(2021年8日22日)より |
ウイルスと芋虫とハチの種が書いてないのですが、当然、昆虫のみに感染する、ある特定のウイルスです。そのウイルスは多種の芋虫に感染するのでしょう。芋虫・ハチの補食寄生の関係は特定の種同士かもしれないが、補食寄生は多くのハチにみられる現象なので、ウイルスが感染した芋虫もハチが卵を産みつける可能性が高い。そう理解できます。
アポトーシス
補食寄生に続く第2のキーワードは「アポトーシス」です。アポトーシスとは、いわば細胞の "自殺" ですが、ウイルスがもたらした遺伝子が、ハチの卵のアポトーシスを引き起こしているようなのです。
|
|
芋虫をめぐる2つの寄生者の競争イメージ 日本経済新聞(2021年8日22日)より |
よく知られているように、ウイルスは自分の遺伝子を宿主の細胞に送り込み、その遺伝子は細胞が本来持っていなかった "モノ" 作り出します。それは普通、ウイルスの複製ですが、この場合は「寄生バチの卵や幼虫のアポトーシスを引き起こすタンパク質」も作り出す。そう理解できます。
芋虫にとっては「命を奪う寄生バチよりも体調不良で済むウイルスの方がマシ」なのでしょう。またウイルスからすると「助け舟を出しながら、芋虫を増殖に利用するのが狙い」です。仲井教授は仮説としてそう考えています。
進化的軍拡競争
さらに第3のキーワードは「進化的軍拡競争」です。つまり、生物が競争関係や敵対関係になると、互いに相手の形質を上回るような "進化の競争" が始まります。

|
「進化的軍拡競争」の例 |
日本経済新聞(2021年8日22日)より |
|
ウイルスと芋虫は、互いにメリットを与え合う「共存関係」にある、と理解できます。
ウイルスと生物
記事の最後には、ウイルスと生物の関係についてのマクロ的な解説があり、安定状態では共存が保たれるが、不安定な競合関係ではウイルスは脅威になるということが説明されていました。
|
以下は記事の感想です。この「蜂殺し遺伝子」の話は、前回の No.348「蚊の嗅覚は超高性能」に書いた、東京慈恵会医科大学の近藤教授の発言を思い起こさせます。再掲すると以下です。
|
「ウイルスの策略を知るには多くの生物が織りなす生態系への理解が不可欠」と、日経新聞の記事の最後にありました。人間のウイルスについての理解は、マクロ的にみると "始まったばかり" か、それが言い過ぎなら "初期段階にある" と言えるのでしょう。
2022-11-07 16:11
nice!(0)
No.348 - 蚊の嗅覚は超高性能 [科学]
今まで何回か生物の "共生" について書きました。たとえば、
では、アフリカのサバンナにすむノドグロミツオシエという鳥が動物を蜂の巣へ誘導する行動が、かつてアフリカにいた絶滅人類との共生関係で成立したのではないかとする、ハーバード大学のランガム教授の仮説を紹介しました。また、
では、人体に住む常在菌(特に腸内細菌)が、人体に数々のメリットを与えていることをみました。
生物界における共生、ないしは依存関係で最も知られているのは、植物と昆虫の関係でしょう。植物は昆虫によって受粉・交配し、昆虫は蜜などを得る(=栄養として子孫を残すことに役立つ)という関係です。植物は昆虫にきてもらう為にいろんな手を尽くします。
オーストラリアに自生するある種のランは、特定の蜂のメスに擬態し、その蜂のオスが間違えて交尾にやってくると、可動する雄蕊で花粉を蜂の背中につけるものがあります。こうなると、ランが蜂を「利用している」という印象になりますが、進化のプロセスが作り出したしくみは誠に奥深いというか、非常に巧妙だと思わざるを得ません。
ところで最近、植物と昆虫の関係に似た話が日本経済新聞に載っていました。それは「ウイルス」と、ウイルスを動物間で媒介する「蚊」の関係です。ちょっと信じがたいような内容だったので、それを紹介したいと思います。中国の清華大学のチームの成果です。
ウイルスが蚊をおびき寄せる
以下は、日本経済新聞のサイエンスエディター、加藤宏志氏の署名がある記事です。
記事を書いた加藤氏は「信じ難い内容」としていますが、確かにそうです。内容は主に動物実験ですが、「患者のにおい成分も蚊を引き寄せた」とあるように、ウイルスに感染した患者のにおい成分は、普通の人のにおい成分よりも蚊を引きつけた(そういう実験をした)ということでしょう。記事には実験(検証)に使ったウイルスの種類が書いてありませんが、特定のウイルスで実験したのだと推測します。特定のウイルスだとしても巧妙なしくみです。
しかし、冒頭に書いた「特定のランと特定の蜂」の関係のように、ウイルスも含めた生命体が子孫を残す、ないしは子孫を増やすやりかたは巧妙です。しかもウイルスは単独では死滅するしかなく、宿主に寄生して数を増やすしかない。ということは、現在生き残っているウイルスは "極めて巧妙精緻な" やりかたで数を増やしてきた、ないしは、生き残ってきた、死滅しなかったと想像できます。上の記事のような状況があったとしても、不思議ではありません。
そして、このウイルスの "策略" が成り立つ要因は、「蚊の嗅覚が異常に鋭い」ということなのです。
記事によると蚊の嗅覚は、「生物界の共通原則」を逸脱しているようです。
書いてある内容がちょっと専門的でわかりにくいのですが、調べてみると、生物界に共通する嗅覚のしくみは、まず臭いを検知する1つの受容体をもつ嗅細胞があり、そこからニューロン(神経繊維)が出て、臭いを判断して脳に送る嗅覚糸球体へと繋がっている。この対応は「1:1:1」が原則である。しかし蚊は複数の受容体を嗅細胞が持っているので原則からはずれる。そう解釈できます。これが蚊の鋭い嗅覚にどうつながるのか、その解明はこれからのようです。
蚊の嗅覚の鋭さについては、記事に次のような例が書いてありました。
BSテレ東「居間からサイエンス」(2022年10月17日)によると、人間を殺す生物ランキング(年間死者数)は、
(出典:ビル&メリンダ・ゲイツ財団)
だそうです。もちろん、感染症の流行や戦争で死者数は変動するでしょうが、この数字はそういうことがない "定常状態" の値だと推測します。日本経済新聞の記事もこう結ばれていました。
蚊の能力
記事に登場した東京慈恵会医科大学の嘉糠洋陸教授は、NHK Eテレの、サイエンス ZERO「恐ろしくも華麗な "蚊" - 秘められた力を解明せよ」(2022年9月25日)に出演されました。
この番組ではまず、世界で最も人の命を奪っている生物は蚊、だとし、蚊が媒介する感染症で奪われる命は、年間、世界で72万人と紹介しています(ビル&メリンダ・ゲイツ財団の値と同じ)。感染症としてはマラリア、デング熱が代表的で、そのほかに日本脳炎や西ナイル熱もあります。最も人の命を奪っている生物だからこそ、蚊は世界中で研究されているのです。この番組の中で嘉糠教授は次のような内容を語っておられました。
1メートル以内に蚊をおびき寄せるもののうち、① 二酸化炭素、③ 熱(赤外線)は、ヒトによる違いがないはずです。問題は ② の「臭い」で、これはヒトによって微妙に違うはずです。
日本経済新聞にあった嘉糠教授の「A 氏を好む蚊は B 氏が同席していても『無き者』として扱い、A 氏の血を吸う。その場に1人なら、好みにはこだわらない」との発言をみても、蚊が臭い(= ヒトが放出する化学物質)の微妙な違いを検知していることをうかがわせます。なお、10メートル離れても感知できる ① 二酸化炭素 も、嗅覚の働きです。
蚊を忌避する新戦略
「嗅覚を惑わしさえすれば刺されない。こんな希望は最新の研究で落胆に変わる。」と記事にあるように、蚊の臭いを感知する能力は極めて鋭敏なため、嗅覚を混乱させて蚊から逃れようとするのは困難なようです。
しかし最近、全く新しい原理で蚊を忌避する方法が開発されました。サイエンス ZEROに登場した、花王・パーソナルヘルスケア研究所の仲川喬雄氏が次のような内容を語っていました。
物理的作用で蚊を忌避する発想、蚊が肌にとまってもよいが刺されないとする考え方が斬新です。肌につける各種の液を長年研究してきた花王の技術力がベースにあるのでしょう。この花王の新商品は、ひょっとしたらマラリア蔓延国にとっての救世主になるかもしれません。
ウイルスの策略
話を最初のウイルスに戻します。蚊は人間を利用して子孫を残そうとし、そのために人間を感知する能力を高度に発達させました。一方、"蚊に刺される運命にある" 人間は、何とかそれを回避しようと(蚊が媒介する感染症による死者を減らそうと)知恵を絞っている。しかし、この "人間と蚊の戦い" の上を行くのがウイルスかもしれません。
同じ NHK の番組ですが、2022年10月4日放送の「ヒューマニエンス」(BSプレミアム)で、東京慈恵会医科大学のウイルス学者・近藤教授が次のように語っていました。
新型コロナウイルスとの "戦い" に人間がてこずるのはあたりまえなのでしょう。また、完全撲滅は難しいのでしょう。ただ、近藤教授は「まだまだ勝てない」と言っていて「勝てない」という表現ではありません。ウイルスには(そしてヒトには)未解明のことが多々あるということだと思います。もちろん蚊についても ・・・・・・。
では、アフリカのサバンナにすむノドグロミツオシエという鳥が動物を蜂の巣へ誘導する行動が、かつてアフリカにいた絶滅人類との共生関係で成立したのではないかとする、ハーバード大学のランガム教授の仮説を紹介しました。また、
では、人体に住む常在菌(特に腸内細菌)が、人体に数々のメリットを与えていることをみました。
生物界における共生、ないしは依存関係で最も知られているのは、植物と昆虫の関係でしょう。植物は昆虫によって受粉・交配し、昆虫は蜜などを得る(=栄養として子孫を残すことに役立つ)という関係です。植物は昆虫にきてもらう為にいろんな手を尽くします。
オーストラリアに自生するある種のランは、特定の蜂のメスに擬態し、その蜂のオスが間違えて交尾にやってくると、可動する雄蕊で花粉を蜂の背中につけるものがあります。こうなると、ランが蜂を「利用している」という印象になりますが、進化のプロセスが作り出したしくみは誠に奥深いというか、非常に巧妙だと思わざるを得ません。
ところで最近、植物と昆虫の関係に似た話が日本経済新聞に載っていました。それは「ウイルス」と、ウイルスを動物間で媒介する「蚊」の関係です。ちょっと信じがたいような内容だったので、それを紹介したいと思います。中国の清華大学のチームの成果です。
ウイルスが蚊をおびき寄せる
以下は、日本経済新聞のサイエンスエディター、加藤宏志氏の署名がある記事です。
|
|
上の内容を図に表したもの。ウイルスが蚊を宿主におびき寄せ、他の宿主に感染を広げるチャンスを増やす。日本経済新聞(2022年9月18日)より。 |
記事を書いた加藤氏は「信じ難い内容」としていますが、確かにそうです。内容は主に動物実験ですが、「患者のにおい成分も蚊を引き寄せた」とあるように、ウイルスに感染した患者のにおい成分は、普通の人のにおい成分よりも蚊を引きつけた(そういう実験をした)ということでしょう。記事には実験(検証)に使ったウイルスの種類が書いてありませんが、特定のウイルスで実験したのだと推測します。特定のウイルスだとしても巧妙なしくみです。
しかし、冒頭に書いた「特定のランと特定の蜂」の関係のように、ウイルスも含めた生命体が子孫を残す、ないしは子孫を増やすやりかたは巧妙です。しかもウイルスは単独では死滅するしかなく、宿主に寄生して数を増やすしかない。ということは、現在生き残っているウイルスは "極めて巧妙精緻な" やりかたで数を増やしてきた、ないしは、生き残ってきた、死滅しなかったと想像できます。上の記事のような状況があったとしても、不思議ではありません。
そして、このウイルスの "策略" が成り立つ要因は、「蚊の嗅覚が異常に鋭い」ということなのです。
|
記事によると蚊の嗅覚は、「生物界の共通原則」を逸脱しているようです。
|
書いてある内容がちょっと専門的でわかりにくいのですが、調べてみると、生物界に共通する嗅覚のしくみは、まず臭いを検知する1つの受容体をもつ嗅細胞があり、そこからニューロン(神経繊維)が出て、臭いを判断して脳に送る嗅覚糸球体へと繋がっている。この対応は「1:1:1」が原則である。しかし蚊は複数の受容体を嗅細胞が持っているので原則からはずれる。そう解釈できます。これが蚊の鋭い嗅覚にどうつながるのか、その解明はこれからのようです。
蚊の嗅覚の鋭さについては、記事に次のような例が書いてありました。
|
BSテレ東「居間からサイエンス」(2022年10月17日)によると、人間を殺す生物ランキング(年間死者数)は、
| 1位 | 蚊 | 72万人 |
| 2位 | 人間 | 47万人 |
| 3位 | ヘビ | 5万人 |
だそうです。もちろん、感染症の流行や戦争で死者数は変動するでしょうが、この数字はそういうことがない "定常状態" の値だと推測します。日本経済新聞の記事もこう結ばれていました。
|
蚊の能力
記事に登場した東京慈恵会医科大学の嘉糠洋陸教授は、NHK Eテレの、サイエンス ZERO「恐ろしくも華麗な "蚊" - 秘められた力を解明せよ」(2022年9月25日)に出演されました。
この番組ではまず、世界で最も人の命を奪っている生物は蚊、だとし、蚊が媒介する感染症で奪われる命は、年間、世界で72万人と紹介しています(ビル&メリンダ・ゲイツ財団の値と同じ)。感染症としてはマラリア、デング熱が代表的で、そのほかに日本脳炎や西ナイル熱もあります。最も人の命を奪っている生物だからこそ、蚊は世界中で研究されているのです。この番組の中で嘉糠教授は次のような内容を語っておられました。
| 全ての蚊が血を吸うのではない。日本にいる蚊で血を吸うのは 110種類中の3割である。またオスの蚊は血を吸わない。血を吸わない蚊は花の蜜などで栄養をとる。 | |||||||||
| メスの蚊で、しかも交配済みのメスが血を吸う。未交配のメスは血を吸わない。 | |||||||||
| 血液は栄養豊富なサプリメントである。蚊は血液を濃縮して濾しとったタンパク質で卵を作る。そうすることで効率良く、迅速に卵を作れる。つまり次の世代をどんどん作れる。 | |||||||||
| 吸血する蚊の一種、ヒトスジシマカは、1回の吸血で200個前後の卵を生む。血を吸わない蚊はだいたい40~50個である。 | |||||||||
| 人間は蚊に刺される運命にある。動物はたくさんの毛で覆われていて皮膚も厚く、蚊にとっては刺しにくい生き物だ。人間は毛が少なくて皮膚も薄く、蚊にとっては「どうぞ血を吸ってください」という生き物である。 | |||||||||
| 現代は歴史上、人口が最も多い時期にある。従って蚊も生命の歴史上、最も数が多い時期にある。 | |||||||||
蚊が人間を感知する仕組みは、距離によって4種ある。
| |||||||||
| 血液型が O型の人は、他の血液型の人より2倍程度、蚊に刺されやすい。我々も野外で研究用の蚊を集めるときに、O型の大学院生を "おとり" にして、その学生に寄ってくる蚊を捕獲したりする。なぜ O型が刺され易いのかは最新科学でもまだ謎である。 |
1メートル以内に蚊をおびき寄せるもののうち、① 二酸化炭素、③ 熱(赤外線)は、ヒトによる違いがないはずです。問題は ② の「臭い」で、これはヒトによって微妙に違うはずです。
日本経済新聞にあった嘉糠教授の「A 氏を好む蚊は B 氏が同席していても『無き者』として扱い、A 氏の血を吸う。その場に1人なら、好みにはこだわらない」との発言をみても、蚊が臭い(= ヒトが放出する化学物質)の微妙な違いを検知していることをうかがわせます。なお、10メートル離れても感知できる ① 二酸化炭素 も、嗅覚の働きです。
蚊を忌避する新戦略
「嗅覚を惑わしさえすれば刺されない。こんな希望は最新の研究で落胆に変わる。」と記事にあるように、蚊の臭いを感知する能力は極めて鋭敏なため、嗅覚を混乱させて蚊から逃れようとするのは困難なようです。
しかし最近、全く新しい原理で蚊を忌避する方法が開発されました。サイエンス ZEROに登場した、花王・パーソナルヘルスケア研究所の仲川喬雄氏が次のような内容を語っていました。
| 蚊の足には微細構造があり、超撥水性がある。つまり、微細構造の中に空気が入り込み、水に浮くことができる。そのような超撥水性の足は、逆に、水と正反対の性質をもつオイルに馴染みやすい。 | |
| 化粧品や日用品に使われる低粘度のシリコンオイルを肌に塗布すると、蚊が肌にとまったとき、毛細管現象で微細構造の中にオイルが吸い上げられる。その結果、オイルの表面張力で蚊の足を下に引き込む力が発生する(蚊に作用する重力の80%以上)。 | |
| この力を蚊は敏感に感知し、一瞬で肌から離れる。 | |
| この原理を使った忌避剤を、すでにタイで商品化した。 |
物理的作用で蚊を忌避する発想、蚊が肌にとまってもよいが刺されないとする考え方が斬新です。肌につける各種の液を長年研究してきた花王の技術力がベースにあるのでしょう。この花王の新商品は、ひょっとしたらマラリア蔓延国にとっての救世主になるかもしれません。
ウイルスの策略
話を最初のウイルスに戻します。蚊は人間を利用して子孫を残そうとし、そのために人間を感知する能力を高度に発達させました。一方、"蚊に刺される運命にある" 人間は、何とかそれを回避しようと(蚊が媒介する感染症による死者を減らそうと)知恵を絞っている。しかし、この "人間と蚊の戦い" の上を行くのがウイルスかもしれません。
同じ NHK の番組ですが、2022年10月4日放送の「ヒューマニエンス」(BSプレミアム)で、東京慈恵会医科大学のウイルス学者・近藤教授が次のように語っていました。
|
新型コロナウイルスとの "戦い" に人間がてこずるのはあたりまえなのでしょう。また、完全撲滅は難しいのでしょう。ただ、近藤教授は「まだまだ勝てない」と言っていて「勝てない」という表現ではありません。ウイルスには(そしてヒトには)未解明のことが多々あるということだと思います。もちろん蚊についても ・・・・・・。
2022-10-23 08:54
nice!(0)
No.347 - 少なくともひとりは火曜日生まれの女の子 [科学]
No.149「我々は直感に裏切られる」と No.325「高校数学で理解する誕生日のパラドックス」でとりあげた「誕生日のパラドックス」から話を始めます。
有名な「誕生日のパラドックス」は「バースデー・パラドックス」とも言われ、
というものです。これは正確に言うとパラドックスではなく "疑似パラドックス" です。パラドックスとは「一見すると妥当そうに思える推論から、受け入れがたい結論が導かれること」ですが、疑似パラドックスは「数学的には全く正しいが、人間の直感に反するように感じられる結論」です。
この "疑似パラドックス" が成り立つ理由を一般化して言うと、「確率が直感に反することが多々ある」でしょう。さらにもっと一般化すると「確率は難しい」ということだと思います。裏から言うと「誤った確率の使い方は人を誤解に導く」ともなるでしょう。誤っていることが往々にして分からないからです。
我々は「コインを投げたとき、表が出る確率は 1/2」とか「サイコロを振ったとき 1の目が出る確率は 1/6」のように、"確率を理解している" と思っているかもしれません。「2つのサイコロを振ったとき、2つとも 1 の目が出る確率は 1/36」もよいでしょう。しかし、我々が常識の範囲で理解できるのは、せいぜいこのあたりまでで、ちょっと込み入ってくると手に負えなくなってしまうようなのです。
イアン・スチュアート著「不確実性を飼いならす ── 予測不能な世界を読み解く科学」(徳田 功訳。白揚社 2021)を読んでいたら、確率に関することがいろいろ出ていました。イアン・スチュアートは世界的に著名なイギリスの数学者です。その本の文章をちょっと紹介します。
イアン・スチュアートは「確率に対する人間の直感は絶望的」の典型例として、まず、モンティ・ホール問題をあげています。
モンティ・ホール問題
モンティ・ホール問題は確率に関する有名な問題です。モンティ・ホールとは、かつてのアメリカのテレビのゲーム・ショー番組「取引しよう」の初代司会者の名前です。
そのテレビ番組で行われたのは次のようなゲームです。3つの独立した部屋があり、前面にドアがあって閉じられています。3つの部屋のうちの1つには特別賞のクルマが、残りの2つには残念賞のヤギが隠されています。
クルマを当てたい回答者が一つのドアを選びます。ドアが開けられた時点で、そこにあるものはクルマであれヤギであれ、回答者のものになります。
そのとき司会者は、回答者が選ばなかった2つのドアのうち、ヤギがいる一つのドアを開けてヤギを見せます。そして回答者に「選ぶドアを変更してもよい」と言って、選び直しの機会を与えます。
クルマが欲しい回答者はどうすべきでしょうか。これが問題です。
クルマがあるのは、最初に回答者が選んだドアか、まだ開けられていないもう一つのドアか、そのどちらかです。従って「選び直しても、選び直さなかったとしても、クルマが当たる確率は同じ」と考えてしまいそうです。実際に回答者になって現場にいたとしたら、直感はそうでしょう。
さらに回答者としては「心理的な」直感も働く可能性が高い。つまり、司会者がわざわざ一つのドアをあけて「選び直してもよい」と言ったということは、選び直すように誘導しているに違いないと思う直感です。この2つの直感によって、回答者は選び直さない可能性の方が大きいと考えられます。
しかし真実は全く違います。クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高いのが正解です。
これは次のように考えると分かります。ドアを A、B、C の3つとし、最初に回答者が A を選んだとします。クルマがあるのは A、B、C のどれかであり、この3つのケースの確率は全く同じです。
クルマが A にある確率は 1/3 です。この場合は「選び直さない方がよい」わけです。司会者が B か C のドアをあけてヤギを見せたとしても「選び直さない方がよい」のは変わらない。司会者がドアをあけたことでクルマは移動しないからです。
クルマが B にある確率は 1/3 であり、この場合は「選び直した方がよい」わけです。司会者が C のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらない。選び直すとしたら B しかありません。つまり、この場合は選び直すと必ずクルマをゲットできることになります。
クルマが C にある確率も 1/3 で、この場合も「選び直した方がよい」わけです。司会者が B のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらないし、選び直すと必ずクルマをゲットできます。司会者が、わざわざ選び直しの対象としての B を除外してくれたのだから ・・・・・・。
以上で「選び直さない方がよい」ケースは3回に1回起こり、「選び直した方がよい」ケースは3回に2回起こります。この状況は、最初に回答者が選んだドアが B でも C でも全く同じです。
従って、クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高い、となります。
納得できたでしょうか。
NHK総合の「笑わない数学」の「確率論」(2022年9月21日放送)では、この問題を実際に実験していました。3つの箱の一つに景品を隠す実験です。回答者役と司会者役を2組用意し、一方の回答者は「必ず選び直す」、もう一方の回答者は「必ず選び直さない」とします。それぞれ100回の試行した結果、景品をゲットできた数は、
でした。選び直した方が2倍有利という確率論の結果が(実験であるがゆえの誤差を含みつつ)実証されたわけです。実験は大切です。
それでも、なぜそうなるのか納得できないという人もいるのではないでしょうか。
ドアが10個だとしたら
イアン・スチュアートの本では、それでも納得できないという人のために、ある仮想実験による説明をしています。トランプの52枚のカードを使ったものですが、同じことなので「10個のドア」に焼き直して紹介します。もちろん、実際にはあり得ない仮想実験です。
モンティ・ホール問題と基本的に同じです。ただしドアは10個あります。そのうちの一つにクルマが隠されていて、残りの9個には何もありません(ヤギを9匹用意するのは大変なので)。
あなたは司会者から1つのドアを選ぶように言われます。もしそこにクルマがあったとしたら、あなたのものになります。何もなければ、賞品は無しです。
1つのドアを選んだあなたはどう考えるでしょうか。「クルマが隠されているドアを選ぶ確率は 1/10 である。これは、まず当たらないな」と考えるのが普通でしょう。10回チャレンジしてようやく1回当たるかどうかという確率です。ほとんど無理と思うでしょう。
ところがです。司会者はあなたが選ばなかった9個ドアから8個を選び、それを次々と空けて、そこには何もないことを示したのです。そしてこう宣告します。「あなたが選んだドアのほかに、まだ閉じらているドアが1つあります。今からドアの選択を変えるチャンスをあげましょう。変えても、変えなくてもどちらでもよい。どうしますか?」
・・・・・・ という状況だったら、あなたは間違いなくドアの選択を変えるはずです。だってそうでしょう。最初に選択したドアにクルマがある確率は 1/10 で、ほぼハズレです。選択しなかった9個のドアのどれかにクルマがある確率は 9/10 です。ほどんどの場合、その9個のうちのどれかにクルマがあると、誰にでもわかる。
しかし、その9個のドアのうちの8個にはクルマがないことが分かってしまった。わざわざ司会者がそう示してくれたのです。とすると、残りの1個に高い確率でクルマがあるに違いない。確率的には、選択を変えた方が変えないよりも9倍、クルマをゲットできる可能性が高いことになります。
この「10枚のドア」の状況は、モンティ・ホール問題の「3枚のドア」と全く同じ構造をしています。「10枚のドア」ではなく「100枚のドア」でも問題の構造は同じです。100枚のドアだと、ドアの選択を変えると 99% の確率でクルマがゲットできる。つまり、ほぼ確実にクルマがもらえることになります。
2人とも女の子の確率
イアン・スチュアートの本ではさらに「確率と人間の直感」を考える問題として、
という問題と、その変形問題が示されています。まず前提として、子どもがいたとき、それが「男の子」か「女の子」かはどちらかに決まっているとします。常識的にはあたりまえなのですが、生物学的には男女の区別が曖昧というケースもあって、必ずしも正しくはない。しかしこういった生物学的な議論は無しにして、男か女のどちらであるとします。
さらに一番重要なのは、男の子が生まれる確率と女の子が生まれる確率は全く同じ、という前提です。これも生物学的にはそうではなく、人間においても男が生まれる確率がわずかに大きいことが知られています。また「男女の産み分け」も行われていて、そうなると半々だとはますます言えなくなります。しかしそういったことは一切抜きにして「男の子が生まれる確率と女の子が生まれる確率は全く同じ」が前提です。
さらに以下の説明で使うのでコメントしますが、2人の子どもを「第1子」と「第2子」と表現します。同時に生まれた双子だったとしても、兄・姉/弟・妹の区別をするので、兄・姉と呼ばれている子を「第1子」とします。
以上の前提のもと「スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか」という質問に対する答えは 1/4 が正解です。これは多くの人が納得でしょう。
高校などで、確率を習い始めの生徒がよくやる間違いは、子どもの組み合わせは「2人とも男」「男女一人ずつ」「2人とも女」の3つだから、答えは 1/3 とする間違いです。
この手の間違いを防止するために、ちょっと数学的になりますが、イアン・スチュアートの本にある「標本空間」と「標的事象」で考えてみます。
「標本空間」とは「起こりうる全ての事象をもれなく集めた集合」であり、「標的事象」とは、いま確率を問題にしている事象のことです。スミス夫妻の問題の場合の「標本空間」と「標的事象」を図で表すと、次のようになります。左側の青が「標本空間」、右側の赤が「標的事象」です。
図で分かるように、標本空間には4つの事象があり、その確率は同じです。標的事象(2人とも女の子)は1つですから、答えは 1/4 です。
少なくともひとりは女の子
問題を少し変えます。
この問題では、標的事象(2人とも女の子)は前の問題と同じですが「少なくともひとりは女の子」という情報が追加されたため、標本空間が変化します。標本空間は3つ、標的事象は1つですから、答えは 1/3 です。
ここまでは納得の範囲ではないでしょうか。少なくともひとりは女の子という情報が追加されたために、2人とも女の子の確率が上がった。最初の問題では 1/4 だった確率が 1/3 になる。直感とも合っているはずです。しかし問題になるのはこの次です。
少なくともひとりは火曜日生まれの女の子
さらに問題を少し変えます。
前提として「子どもが生まれる曜日はどの曜日も同じ確率」とします。この前提は現実社会では必ずしも正しくなく、「どの曜日もほぼ同じ確率」が正しいのですが、問題としては「同じ」とします。
この問題の答えは 13/27 です。えっ! と思うでしょう。"火曜日生まれの" という "些細な" 情報が追加されただけで、確率は劇的に変わってしまった。13/27 というと、ほぼ 1/2 の値です。1/4 が 1/3 になったよりも変化が大きい。全く直感に反しています。
そして、全く直感に反しているため、これは理にかなっていない、間違っている、と感じるのではないでしょうか。生まれた曜日など確率に関係ないと考える方が理にかなっている ・・・・・・。
しかし 13/27 は正しいのです。それは標本空間と標的事象を作ってみればわかります。この問題の標本空間を作るため、男女のそれぞれを曜日で7分割した図を用意します。
この図には 14 × 14 = 196 のマス目があります。もし単に「2人の子どもがいます」なら、この196の事象が起きる確率は全く同じです。
この図に「少なくともひとりは火曜日生まれの女の子」という条件を加味した標本空間を青く塗ってみると次の通りとなります。
さらに、この標本空間の中に含まれる標的事象(=2人も女の子)を赤で塗ると、次の図になります。
標本空間のマス目の数は 27、標本空間の中の標的事象のマス目の数は 13 なので、問題の解答は 13/27 です。問題には「火曜日」としましたが、これが何曜日であっても答は同じです。
これは、いわゆる「条件付き確率」です。
の条件では、女の子は「ひとりの可能性」と「2人の可能性」があって、2人の可能性は 1/3 です。この場合、2人の女の子を区別できる情報はありません。
これに「女の子が2人だった場合に、その2人を区別できる可能性を高める情報」が付け加えられると、その区別可能性が高いほど2人である確率は高まります。たとえば、"火曜日に生まれた" より区別可能性が高い情報を付け加えた例ですが、
という問題にすると、第1子はひとりしかいないので、答えは 1/2 となります。"火曜日生まれ" だと、2人とも火曜日生まれの可能性があって、必ずしも2人を区別できない。"第1子" は2人の女の子を区別するのに絶対に確実な情報です。
少なくともひとりは女の子だけれど、それが第1子か第2子かという情報(やその他の情報)が全くない状況では、確率が 1/3 に減ってしまうのです。
"火曜日に生まれた" より区別可能性が低い情報を付け加えた例を作ってみます(これはイアン・ステュアートの本にはありません)。男女とも血液型が A 型である確率を統計的に 50% とすると、
の答えは、3/7 になり、13/27 と 1/3 の間の数になります。
確率は直感に反する
最初の「モンティ・ホール問題」は直感に反するように思えます。ただ、3つのドアではなく「10個のドア」とか「100個のドア」で説明されると、なるほどそうかという気にもなる。
しかし「少なくともひとりは火曜日生まれの女の子」問題は、いくら理論的に説明されても直感的には納得できません。
この話の教訓は「"正しい確率" は理解が難しい」ということであり、「"正しい確率" が直感に反するのは、むしろ当然」ぐらいに思った方がよいということだと思います。
このことを全く逆から言うと、「確率を持ち出して、そこからいかにも直感に合致する結論を主張する言説」があったとしたら、サイコロの目とかコインの裏表のように誰がみても明らかなものを除いて、そもそもその持ち出された "確率" なるものが怪しいのでは、と疑ってみた方がよいと言えるでしょう。
なぜなら、イアン・ステュアートが言っているように「確率に対する人間の直感は絶望的」であり、平たく言うと "正しい確率は直感と合致しない" のだから ・・・・・・。
有名な「誕生日のパラドックス」は「バースデー・パラドックス」とも言われ、
23人のクラスで同じ誕生日のペアがいる確率は 0.5 を超える
というものです。これは正確に言うとパラドックスではなく "疑似パラドックス" です。パラドックスとは「一見すると妥当そうに思える推論から、受け入れがたい結論が導かれること」ですが、疑似パラドックスは「数学的には全く正しいが、人間の直感に反するように感じられる結論」です。
この "疑似パラドックス" が成り立つ理由を一般化して言うと、「確率が直感に反することが多々ある」でしょう。さらにもっと一般化すると「確率は難しい」ということだと思います。裏から言うと「誤った確率の使い方は人を誤解に導く」ともなるでしょう。誤っていることが往々にして分からないからです。
イアン・スチュアート著「不確実性を飼いならす ── 予測不能な世界を読み解く科学」(徳田 功訳。白揚社 2021)を読んでいたら、確率に関することがいろいろ出ていました。イアン・スチュアートは世界的に著名なイギリスの数学者です。その本の文章をちょっと紹介します。
|
イアン・スチュアートは「確率に対する人間の直感は絶望的」の典型例として、まず、モンティ・ホール問題をあげています。
モンティ・ホール問題
モンティ・ホール問題は確率に関する有名な問題です。モンティ・ホールとは、かつてのアメリカのテレビのゲーム・ショー番組「取引しよう」の初代司会者の名前です。
そのテレビ番組で行われたのは次のようなゲームです。3つの独立した部屋があり、前面にドアがあって閉じられています。3つの部屋のうちの1つには特別賞のクルマが、残りの2つには残念賞のヤギが隠されています。
クルマを当てたい回答者が一つのドアを選びます。ドアが開けられた時点で、そこにあるものはクルマであれヤギであれ、回答者のものになります。
そのとき司会者は、回答者が選ばなかった2つのドアのうち、ヤギがいる一つのドアを開けてヤギを見せます。そして回答者に「選ぶドアを変更してもよい」と言って、選び直しの機会を与えます。
クルマが欲しい回答者はどうすべきでしょうか。これが問題です。
クルマがあるのは、最初に回答者が選んだドアか、まだ開けられていないもう一つのドアか、そのどちらかです。従って「選び直しても、選び直さなかったとしても、クルマが当たる確率は同じ」と考えてしまいそうです。実際に回答者になって現場にいたとしたら、直感はそうでしょう。
さらに回答者としては「心理的な」直感も働く可能性が高い。つまり、司会者がわざわざ一つのドアをあけて「選び直してもよい」と言ったということは、選び直すように誘導しているに違いないと思う直感です。この2つの直感によって、回答者は選び直さない可能性の方が大きいと考えられます。
しかし真実は全く違います。クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高いのが正解です。
これは次のように考えると分かります。ドアを A、B、C の3つとし、最初に回答者が A を選んだとします。クルマがあるのは A、B、C のどれかであり、この3つのケースの確率は全く同じです。
クルマが A にある確率は 1/3 です。この場合は「選び直さない方がよい」わけです。司会者が B か C のドアをあけてヤギを見せたとしても「選び直さない方がよい」のは変わらない。司会者がドアをあけたことでクルマは移動しないからです。
クルマが B にある確率は 1/3 であり、この場合は「選び直した方がよい」わけです。司会者が C のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらない。選び直すとしたら B しかありません。つまり、この場合は選び直すと必ずクルマをゲットできることになります。
クルマが C にある確率も 1/3 で、この場合も「選び直した方がよい」わけです。司会者が B のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらないし、選び直すと必ずクルマをゲットできます。司会者が、わざわざ選び直しの対象としての B を除外してくれたのだから ・・・・・・。
以上で「選び直さない方がよい」ケースは3回に1回起こり、「選び直した方がよい」ケースは3回に2回起こります。この状況は、最初に回答者が選んだドアが B でも C でも全く同じです。
従って、クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高い、となります。
納得できたでしょうか。
NHK総合の「笑わない数学」の「確率論」(2022年9月21日放送)では、この問題を実際に実験していました。3つの箱の一つに景品を隠す実験です。回答者役と司会者役を2組用意し、一方の回答者は「必ず選び直す」、もう一方の回答者は「必ず選び直さない」とします。それぞれ100回の試行した結果、景品をゲットできた数は、
| : 70回 | |
| : 33回 |
でした。選び直した方が2倍有利という確率論の結果が(実験であるがゆえの誤差を含みつつ)実証されたわけです。実験は大切です。
それでも、なぜそうなるのか納得できないという人もいるのではないでしょうか。
ドアが10個だとしたら
イアン・スチュアートの本では、それでも納得できないという人のために、ある仮想実験による説明をしています。トランプの52枚のカードを使ったものですが、同じことなので「10個のドア」に焼き直して紹介します。もちろん、実際にはあり得ない仮想実験です。
モンティ・ホール問題と基本的に同じです。ただしドアは10個あります。そのうちの一つにクルマが隠されていて、残りの9個には何もありません(ヤギを9匹用意するのは大変なので)。
あなたは司会者から1つのドアを選ぶように言われます。もしそこにクルマがあったとしたら、あなたのものになります。何もなければ、賞品は無しです。
1つのドアを選んだあなたはどう考えるでしょうか。「クルマが隠されているドアを選ぶ確率は 1/10 である。これは、まず当たらないな」と考えるのが普通でしょう。10回チャレンジしてようやく1回当たるかどうかという確率です。ほとんど無理と思うでしょう。
ところがです。司会者はあなたが選ばなかった9個ドアから8個を選び、それを次々と空けて、そこには何もないことを示したのです。そしてこう宣告します。「あなたが選んだドアのほかに、まだ閉じらているドアが1つあります。今からドアの選択を変えるチャンスをあげましょう。変えても、変えなくてもどちらでもよい。どうしますか?」
・・・・・・ という状況だったら、あなたは間違いなくドアの選択を変えるはずです。だってそうでしょう。最初に選択したドアにクルマがある確率は 1/10 で、ほぼハズレです。選択しなかった9個のドアのどれかにクルマがある確率は 9/10 です。ほどんどの場合、その9個のうちのどれかにクルマがあると、誰にでもわかる。
しかし、その9個のドアのうちの8個にはクルマがないことが分かってしまった。わざわざ司会者がそう示してくれたのです。とすると、残りの1個に高い確率でクルマがあるに違いない。確率的には、選択を変えた方が変えないよりも9倍、クルマをゲットできる可能性が高いことになります。
この「10枚のドア」の状況は、モンティ・ホール問題の「3枚のドア」と全く同じ構造をしています。「10枚のドア」ではなく「100枚のドア」でも問題の構造は同じです。100枚のドアだと、ドアの選択を変えると 99% の確率でクルマがゲットできる。つまり、ほぼ確実にクルマがもらえることになります。
2人とも女の子の確率
イアン・スチュアートの本ではさらに「確率と人間の直感」を考える問題として、
スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか。 |
という問題と、その変形問題が示されています。まず前提として、子どもがいたとき、それが「男の子」か「女の子」かはどちらかに決まっているとします。常識的にはあたりまえなのですが、生物学的には男女の区別が曖昧というケースもあって、必ずしも正しくはない。しかしこういった生物学的な議論は無しにして、男か女のどちらであるとします。
さらに一番重要なのは、男の子が生まれる確率と女の子が生まれる確率は全く同じ、という前提です。これも生物学的にはそうではなく、人間においても男が生まれる確率がわずかに大きいことが知られています。また「男女の産み分け」も行われていて、そうなると半々だとはますます言えなくなります。しかしそういったことは一切抜きにして「男の子が生まれる確率と女の子が生まれる確率は全く同じ」が前提です。
さらに以下の説明で使うのでコメントしますが、2人の子どもを「第1子」と「第2子」と表現します。同時に生まれた双子だったとしても、兄・姉/弟・妹の区別をするので、兄・姉と呼ばれている子を「第1子」とします。
以上の前提のもと「スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか」という質問に対する答えは 1/4 が正解です。これは多くの人が納得でしょう。
高校などで、確率を習い始めの生徒がよくやる間違いは、子どもの組み合わせは「2人とも男」「男女一人ずつ」「2人とも女」の3つだから、答えは 1/3 とする間違いです。
この手の間違いを防止するために、ちょっと数学的になりますが、イアン・スチュアートの本にある「標本空間」と「標的事象」で考えてみます。
「標本空間」とは「起こりうる全ての事象をもれなく集めた集合」であり、「標的事象」とは、いま確率を問題にしている事象のことです。スミス夫妻の問題の場合の「標本空間」と「標的事象」を図で表すと、次のようになります。左側の青が「標本空間」、右側の赤が「標的事象」です。
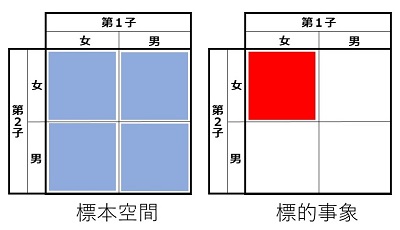
|
「2人の子どもがいます」の標本空間(左、青)と「2人とも女の子」に相当する標的事象(右、赤) |
図で分かるように、標本空間には4つの事象があり、その確率は同じです。標的事象(2人とも女の子)は1つですから、答えは 1/4 です。
少なくともひとりは女の子
問題を少し変えます。
スミス夫妻には2人の子どもがいて、少なくともひとりは女の子です。2人とも女の子である確率はどれだけですか。 |
この問題では、標的事象(2人とも女の子)は前の問題と同じですが「少なくともひとりは女の子」という情報が追加されたため、標本空間が変化します。標本空間は3つ、標的事象は1つですから、答えは 1/3 です。
|
「2人の子どもがいて、少なくともひとりは女の子」の標本空間(左、青)と「2人とも女の子」に相当する標的事象(右、赤) |
ここまでは納得の範囲ではないでしょうか。少なくともひとりは女の子という情報が追加されたために、2人とも女の子の確率が上がった。最初の問題では 1/4 だった確率が 1/3 になる。直感とも合っているはずです。しかし問題になるのはこの次です。
少なくともひとりは火曜日生まれの女の子
さらに問題を少し変えます。
スミス夫妻には2人の子どもがいて、少なくともひとりは火曜日生まれの女の子です。2人とも女の子である確率はどれだけですか。 |
前提として「子どもが生まれる曜日はどの曜日も同じ確率」とします。この前提は現実社会では必ずしも正しくなく、「どの曜日もほぼ同じ確率」が正しいのですが、問題としては「同じ」とします。
この問題の答えは 13/27 です。えっ! と思うでしょう。"火曜日生まれの" という "些細な" 情報が追加されただけで、確率は劇的に変わってしまった。13/27 というと、ほぼ 1/2 の値です。1/4 が 1/3 になったよりも変化が大きい。全く直感に反しています。
そして、全く直感に反しているため、これは理にかなっていない、間違っている、と感じるのではないでしょうか。生まれた曜日など確率に関係ないと考える方が理にかなっている ・・・・・・。
しかし 13/27 は正しいのです。それは標本空間と標的事象を作ってみればわかります。この問題の標本空間を作るため、男女のそれぞれを曜日で7分割した図を用意します。
|
男女のそれぞれを曜日で7分割した図。これは「2人の子どもがいます」という条件だけなら、この 14 × 14 = 196 のマス目の確率は全く同じである。 |
この図には 14 × 14 = 196 のマス目があります。もし単に「2人の子どもがいます」なら、この196の事象が起きる確率は全く同じです。
この図に「少なくともひとりは火曜日生まれの女の子」という条件を加味した標本空間を青く塗ってみると次の通りとなります。
|
「2人の子どもがいます。少なくとも一人は火曜日生まれの女の子」の標本空間。マス目は 27 になる。 |
さらに、この標本空間の中に含まれる標的事象(=2人も女の子)を赤で塗ると、次の図になります。
|
標本空間の中で「2人とも女の子」に相当する標的事象。マス目は 13 である。 |
標本空間のマス目の数は 27、標本空間の中の標的事象のマス目の数は 13 なので、問題の解答は 13/27 です。問題には「火曜日」としましたが、これが何曜日であっても答は同じです。
これは、いわゆる「条件付き確率」です。
少なくとも一人は女の子
の条件では、女の子は「ひとりの可能性」と「2人の可能性」があって、2人の可能性は 1/3 です。この場合、2人の女の子を区別できる情報はありません。
これに「女の子が2人だった場合に、その2人を区別できる可能性を高める情報」が付け加えられると、その区別可能性が高いほど2人である確率は高まります。たとえば、"火曜日に生まれた" より区別可能性が高い情報を付け加えた例ですが、
スミス夫妻には2人の子どもがいて、少なくとも一人は第1子の女の子です。2人とも女の子である確率はどれだけですか。 |
という問題にすると、第1子はひとりしかいないので、答えは 1/2 となります。"火曜日生まれ" だと、2人とも火曜日生まれの可能性があって、必ずしも2人を区別できない。"第1子" は2人の女の子を区別するのに絶対に確実な情報です。
少なくともひとりは女の子だけれど、それが第1子か第2子かという情報(やその他の情報)が全くない状況では、確率が 1/3 に減ってしまうのです。
"火曜日に生まれた" より区別可能性が低い情報を付け加えた例を作ってみます(これはイアン・ステュアートの本にはありません)。男女とも血液型が A 型である確率を統計的に 50% とすると、
スミス夫妻には2人の子どもがいて、少なくとも一人は血液型がA型の女の子です。2人とも女の子である確率はどれだけですか。 |
の答えは、3/7 になり、13/27 と 1/3 の間の数になります。
確率は直感に反する
最初の「モンティ・ホール問題」は直感に反するように思えます。ただ、3つのドアではなく「10個のドア」とか「100個のドア」で説明されると、なるほどそうかという気にもなる。
しかし「少なくともひとりは火曜日生まれの女の子」問題は、いくら理論的に説明されても直感的には納得できません。
この話の教訓は「"正しい確率" は理解が難しい」ということであり、「"正しい確率" が直感に反するのは、むしろ当然」ぐらいに思った方がよいということだと思います。
このことを全く逆から言うと、「確率を持ち出して、そこからいかにも直感に合致する結論を主張する言説」があったとしたら、サイコロの目とかコインの裏表のように誰がみても明らかなものを除いて、そもそもその持ち出された "確率" なるものが怪しいのでは、と疑ってみた方がよいと言えるでしょう。
なぜなら、イアン・ステュアートが言っているように「確率に対する人間の直感は絶望的」であり、平たく言うと "正しい確率は直感と合致しない" のだから ・・・・・・。
2022-10-09 09:31
nice!(0)
No.346 - アストリッドが推理した呪われた家の秘密 [アート]
このブログでは数々の絵画について書きましたが、その最初は、No.19「ベラスケスの "怖い絵"」で取り上げた「インノケンティウス10世の肖像」で、中野京子さんの『怖い絵』(2007)にある解説を引用しました。この絵はローマで実際に見たことがあり、また中野さんの解説が秀逸で、印象的だったのです。
『怖い絵』には興味深々の解説が多く、読み返すこともあるのですが、最近、あるテレビドラマを見ていて『怖い絵』にあった別の絵を思い出しました。15~16世紀のドイツの画家・グリューネヴァルトが描いた『イーゼンハイムの祭壇画』です。今回はそのことを書きます。
テレビドラマとは、NHK総合で放映中の「アストリッドとラファエル 文書係の事件簿」です。
アストリッドとラファエル
「アストリッドとラファエル 文書係の事件簿」は、NHK総合 日曜日 23:00~ の枠で放映されているフランスの警察ドラマです。
アストリッドはパリの犯罪資料局に勤務する文書係の女性(俳優はサラ・モーテンセン)、ラファエルはパリ警視庁の刑事(警視)です(俳優はローラ・ドヴェール)。アストリッドは自閉スペクトラム症ですが、過去の犯罪資料に精通していて、また抜群の洞察力があります。一方のラファエルは、思い立ったらすぐに(捜査規律違反もいとわず)行動に移すタイプです。しかし正義感は人一倍強く、人間としての包容力もある女性刑事です。この全く対照的な2人がペアになって難事件を解決していくドラマです(サラ・モーテンセンの演技が素晴らしいと思います。彼女の演技だけでも番組を見る価値があります)。
呪われた家
このドラマのシリーズで「呪われた家」というストーリーが2回に分けて放映されました(前編:2022年8月14日、後編:8月21日)。このストーリーでの重要な舞台は、パリにある "呪われた家" との噂がある屋敷です。この屋敷の歴史について、アストリッドが過去の資料を調べてラファエルに説明するシーンがあります。台詞を抜き出すと以下です。以下に出てくる "リボー" とは、突然、行方不明になった屋敷の主です。

呪われた家の秘密
実は、"呪われた家" には隠されていた地下室がありました。ラファエルが封印を破って地下室に最初に入ったとき、ラファエルは幻影を見ます。
その後、ラファエルとアストリッドが地下室を詳しく調ているときです。アストリッドは地下室の隅に放置されたままの袋を見つけました。
"呪われた家" を出たアストリッドは、あることが閃いたようで、「犯罪資料局に戻らなければ。今すぐに」と言います。ラファエルも同行しました。
キーワードは麦角菌です。その麦角菌と関係する有名な絵画がフランスにあります。
麦角菌
LSD(Lysergic acid diethylamid)は強い幻覚作用をもち、日本をはじめ各国で麻薬として禁止されている薬物です。ラファエルが「リゼルギン酸ジエチルアミド」とアストリッドから聞いてすぐ LSD だと分かったのは、それが刑事の必須知識である禁止薬物だからです。
LSDは人工的に合成されますが、もともと麦角菌に含まれる「麦角アルカロイド」の研究から生まれたものでした。麦角アルカロイドの中のリゼルギン酸から LSD が生成されることもあります。
アルカロイドとは、主に植物や菌が生成する有機化合物の総称ですが、麦角アルカロイドの人への影響は幻覚だけでありません。Wikipedia から引用すると、次のとおりです。
麦角アルカロイドが人にもたらすさまざまな症状を「麦角中毒」といいます。そして「麦角中毒」は、アストリッドが指摘した1951年のポン・サン・テスプリ(Pont-Saint-Esprit。南フランスの小さな町)での事件(実際にあった事件です)より遙か昔から、ヨーロッパでしばしば起こっていました。そして中世ヨーロッパでは、麦角中毒のことを人々は「聖アントニウス病」ないしは「聖アントニウスの火」と呼んでいました。
その「聖アントニウス病」と密接に関係した絵が、ドイツの画家・グリューネヴァルトが描いた『イーゼンハイムの祭壇画』(1515年頃)です。イエスの磔刑を描いていますが、イエスを最も酷い姿で描いた絵として有名です。
イーゼンハイムの祭壇画
中野京子さんの『怖い絵』(2007)にある『イーゼンハイムの祭壇画』の解説を紹介します。
上に引用にあるように、聖アントニウス病が麦角中毒だと分かるのは17世紀終わりです。ということは、それ以前の中世、たとえば『イーゼンハイムの祭壇画』が描かれた16世紀では、そんなことは誰も知らない。当時、聖アントニウス病を治すには、転地療養や旅(巡礼)が良いとされたようですが、それは食事が変わって、いつも食べている「麦角菌入りのライ麦パン」を食べなくなったからなのでしょう。
では、麦角中毒がなぜ「聖アントニウス病」と呼ばれたのか。そして、イーゼンハイム(現在のストラスブール近郊の町)の修道院にあった『イーゼンハイムの祭壇画』が、なぜ「聖アントニウス病」と関係するのか。中野さんの解説が続きます。
このあと中野さんは、当時、聖アントニウス病にかかった村人が、同じ症状の人をさそって、5人でイーゼンハイムへ巡礼に出かける旅路を、村人目線で、想像で書いています。同行の人は次々と行き倒れ、イーゼンハイムに近づいたときには、村人一人になっていました。
要するに『イーゼンハイムの祭壇画』は、たとえば、当時、聖アントニウス病に罹患し、イーゼンハイムの修道院にやっとの思いでたどり着いた巡礼者の気持ちを想像してみないと、その価値の一端すら分からないと言っているのですね。
このあとは、祭壇画の詳細な解説です。登場人物はイエス、聖母マリア、イエスの弟子の聖ヨハネ、マグダラのマリア、洗礼者聖ヨハネ、聖セバスティアヌス、聖アントニウスなどです。
コルマールのウンターリンデン美術館
「イーゼンハイムの祭壇画」は現在、解体された状態で、フランスのアルザス地方の都市、コルマールにあるウンターリンデン美術館にあります。
コルマールは一度だけ行ったことがありますが、その時はツアー旅行だったので、美術館のところまで来たときには閉館時間を過ぎていました。残念でしたが、ツアー旅行なので仕方ありません。なお、コルマールは、ジブリ映画『ハウルの動く城』のモデルになったとも言われる美しい街です。ウンターリンデン美術館とは関係なく、十分に訪問する価値がある街です。
『怖い絵』には興味深々の解説が多く、読み返すこともあるのですが、最近、あるテレビドラマを見ていて『怖い絵』にあった別の絵を思い出しました。15~16世紀のドイツの画家・グリューネヴァルトが描いた『イーゼンハイムの祭壇画』です。今回はそのことを書きます。
テレビドラマとは、NHK総合で放映中の「アストリッドとラファエル 文書係の事件簿」です。
アストリッドとラファエル
「アストリッドとラファエル 文書係の事件簿」は、NHK総合 日曜日 23:00~ の枠で放映されているフランスの警察ドラマです。
アストリッドはパリの犯罪資料局に勤務する文書係の女性(俳優はサラ・モーテンセン)、ラファエルはパリ警視庁の刑事(警視)です(俳優はローラ・ドヴェール)。アストリッドは自閉スペクトラム症ですが、過去の犯罪資料に精通していて、また抜群の洞察力があります。一方のラファエルは、思い立ったらすぐに(捜査規律違反もいとわず)行動に移すタイプです。しかし正義感は人一倍強く、人間としての包容力もある女性刑事です。この全く対照的な2人がペアになって難事件を解決していくドラマです(サラ・モーテンセンの演技が素晴らしいと思います。彼女の演技だけでも番組を見る価値があります)。
呪われた家
このドラマのシリーズで「呪われた家」というストーリーが2回に分けて放映されました(前編:2022年8月14日、後編:8月21日)。このストーリーでの重要な舞台は、パリにある "呪われた家" との噂がある屋敷です。この屋敷の歴史について、アストリッドが過去の資料を調べてラファエルに説明するシーンがあります。台詞を抜き出すと以下です。以下に出てくる "リボー" とは、突然、行方不明になった屋敷の主です。
|

呪われた家の秘密
実は、"呪われた家" には隠されていた地下室がありました。ラファエルが封印を破って地下室に最初に入ったとき、ラファエルは幻影を見ます。
その後、ラファエルとアストリッドが地下室を詳しく調ているときです。アストリッドは地下室の隅に放置されたままの袋を見つけました。
|
"呪われた家" を出たアストリッドは、あることが閃いたようで、「犯罪資料局に戻らなければ。今すぐに」と言います。ラファエルも同行しました。
|
キーワードは麦角菌です。その麦角菌と関係する有名な絵画がフランスにあります。
麦角菌
LSD(Lysergic acid diethylamid)は強い幻覚作用をもち、日本をはじめ各国で麻薬として禁止されている薬物です。ラファエルが「リゼルギン酸ジエチルアミド」とアストリッドから聞いてすぐ LSD だと分かったのは、それが刑事の必須知識である禁止薬物だからです。
LSDは人工的に合成されますが、もともと麦角菌に含まれる「麦角アルカロイド」の研究から生まれたものでした。麦角アルカロイドの中のリゼルギン酸から LSD が生成されることもあります。
アルカロイドとは、主に植物や菌が生成する有機化合物の総称ですが、麦角アルカロイドの人への影響は幻覚だけでありません。Wikipedia から引用すると、次のとおりです。
|
麦角アルカロイドが人にもたらすさまざまな症状を「麦角中毒」といいます。そして「麦角中毒」は、アストリッドが指摘した1951年のポン・サン・テスプリ(Pont-Saint-Esprit。南フランスの小さな町)での事件(実際にあった事件です)より遙か昔から、ヨーロッパでしばしば起こっていました。そして中世ヨーロッパでは、麦角中毒のことを人々は「聖アントニウス病」ないしは「聖アントニウスの火」と呼んでいました。
その「聖アントニウス病」と密接に関係した絵が、ドイツの画家・グリューネヴァルトが描いた『イーゼンハイムの祭壇画』(1515年頃)です。イエスの磔刑を描いていますが、イエスを最も酷い姿で描いた絵として有名です。
イーゼンハイムの祭壇画
中野京子さんの『怖い絵』(2007)にある『イーゼンハイムの祭壇画』の解説を紹介します。
 |
マティアス・グリューネヴァルト(1470/75 - 1528) 「イーゼンハイムの祭壇画 第1面」(1515年頃) |
ウンターリンデン美術館(仏) |
|
|
では、麦角中毒がなぜ「聖アントニウス病」と呼ばれたのか。そして、イーゼンハイム(現在のストラスブール近郊の町)の修道院にあった『イーゼンハイムの祭壇画』が、なぜ「聖アントニウス病」と関係するのか。中野さんの解説が続きます。
|
このあと中野さんは、当時、聖アントニウス病にかかった村人が、同じ症状の人をさそって、5人でイーゼンハイムへ巡礼に出かける旅路を、村人目線で、想像で書いています。同行の人は次々と行き倒れ、イーゼンハイムに近づいたときには、村人一人になっていました。
|
要するに『イーゼンハイムの祭壇画』は、たとえば、当時、聖アントニウス病に罹患し、イーゼンハイムの修道院にやっとの思いでたどり着いた巡礼者の気持ちを想像してみないと、その価値の一端すら分からないと言っているのですね。
|
このあとは、祭壇画の詳細な解説です。登場人物はイエス、聖母マリア、イエスの弟子の聖ヨハネ、マグダラのマリア、洗礼者聖ヨハネ、聖セバスティアヌス、聖アントニウスなどです。
 |
マティアス・グリューネヴァルト 「イーゼンハイムの祭壇画 第1面」 |
|
 |
マティアス・グリューネヴァルト 「イーゼンハイムの祭壇画 第2面」 |
ウンターリンデン美術館(仏) |
|
コルマールのウンターリンデン美術館
「イーゼンハイムの祭壇画」は現在、解体された状態で、フランスのアルザス地方の都市、コルマールにあるウンターリンデン美術館にあります。
コルマールは一度だけ行ったことがありますが、その時はツアー旅行だったので、美術館のところまで来たときには閉館時間を過ぎていました。残念でしたが、ツアー旅行なので仕方ありません。なお、コルマールは、ジブリ映画『ハウルの動く城』のモデルになったとも言われる美しい街です。ウンターリンデン美術館とは関係なく、十分に訪問する価値がある街です。
2022-09-24 07:30
nice!(0)
No.345 - "恐怖" による生態系の復活 [科学]
No.126-127「捕食者なき世界」の続きです。No.126-127は、生態系における捕食者の重要性を、ウィリアム・ソウルゼンバーグ著「捕食者なき世界」(文春文庫 2014)に沿って紹介したものでした。
生態系において捕食者(例えば肉食獣)が、乱獲などの何らかの原因で不在になると、被捕食者(例えば草食動物)が増え過ぎ、そのことによって植物相が減少する。最悪の場合は草食動物もかえって数が減って生態系の荒廃が起こり得る。このようなことが、豊富な実例とともに示されていました。
生態系における「捕食・被捕食」の関係は、動植物の種が複雑に絡み合うネットワークを形成していて、そのネットワークには「不在になると他の種に連鎖的な影響を及ぼす種」(= キーストーン種。キーストーンは "要石" の意味)があります。食物連鎖の頂点に位置する肉食獣は代表的なキーストーン種なのでした。
ところで、最近の NHK BS1 のドキュメンタリーで、人的要因によって激変してしまった生態系を、捕食者の再導入によって元に戻そうとするプロジェクトが放映されました。その番組は、
です。今回はこの番組の概要を紹介します。日本語題名に「"恐怖" でよみがえる」とあり、また原題の意味は「自然の要素としての "恐怖"」です。つまり "恐怖" が重要なテーマになっています。これは、
という意味です。このことは以降の概要で詳しく出てきます。プロジェクトの主役 = 捕食者は、アフリカに住むイヌに似た肉食獣の "リカオン" です。
ゴロンゴーザ国立公園とその荒廃
東アフリカのモザンビークにあるゴロンゴーザ国立公園は、アフリカの国立公園の中でも特に豊かな自然に恵まれている公園です。
モザンビークでは独立後、1970年代から15年以上ものあいだ、政府軍と反政府勢力の激しい内戦が続きました。この内戦による犠牲者は 100万人にのぼるとされています。
この内戦のあいだ、ゴロンゴーザ国立公園は反政府勢力の格好の隠れ家になり、戦場にもなったので、荒廃してしまいました。戦乱と密猟によって大型の哺乳類の数が激減してしまったのです。20年前の調査では、大型の哺乳類の数が内戦前に比べて 1/10 以下に減少していました。たとえば、
といった悲惨な状況です。ゴロンゴーザ国立公園の復活は不可能だと思われました。
しかし希望がありました。それは豊かな自然環境です。ゴロンゴーザ国立公園は、サバンナ、林、氾濫原、湖、川、熱帯雨林などがモザイク状に入り組んでいます。この自然環境がそのまま残っていたのです。
ゴロンゴーザ再生プロジェクト
世界各地からも専門家が集まって官民共同の「ゴロンゴーザ再生プロジェクト」が結成されました。このプロジェクトによって、大きく数を減らした動物の一部は他の地域から持ち込まれました。こうした努力の結果、動物の生息数は回復しつつあります。特に、草食動物の生息数は内戦前に近づきつつあります。
素晴らしいことのよう思えますが、専門家の判断によると健全な生態系の回復ではありません。動物によって増え方に偏りがあり、以前のような多様性が失われたのです。たとえば、一部の動物だけが急速に数を増やしています。中でも、ウォーターバックの数が爆発的に増えました。生息総数は6万頭に迫る勢いで、これは内戦前の10倍以上です。
「多種多様な生き物がそれぞれに適した場所で生息し、全体として安定した生態系を作っている」という、本来あるべき姿ではないのです。なぜ動物の数が偏るのでしょうか。この問題の解決策を探るべく、ゴロンゴーザ再生プロジェクトでは生態系の地道な調査をはじめました。
ブッシュバックの奇妙な行動
生態系の調査で判明したことの一つに、アンテロープ(=レイヨウ)の一種で、本来警戒心が強いブッシュバックの奇妙な行動があります。ブッシュバックはその名のとおり、本来なら茂みに隠れて暮らします。しかし林を離れて、開けた氾濫原に行動範囲を広げていました。より栄養がある食べ物を求めて氾濫原に踏み出したと考えられました。
草食動物がどの種類の草を食べているのか、糞を採取して調べること可能です。3年間で3000以上ものブッシュバックの糞が集められ、アメリカのプリンストン大学に送られました。含まれる植物のDNA分析の結果、氾濫原のブッシュバックは林の中の個体より栄養価の高い草を食べていることが分かりました。その結果、氾濫原に踏み出したブッシュバックは体が大きくなり、子どももたくさん作れるのです。
草食動物の食性変化
プロジェクトではさらに、ゴロンゴーザ国立の主な草食動物が何を食べているかを分析し、ケニアの似たような国立公園と比較しました。ケニアの草食動物は、種によって食べるものがはっきり分かれていました。一方、ゴロンゴーザでは複数の種が同じ物を食べていました。
動物たちがあらゆる場所に進出し好きなものを食べるようになった結果、食性における "種の境界線" が崩壊していたのです。こうなると過度の争いが起き、生態系が崩れてきます。
捕食者の不足
根本原因は2つの不足でした。「捕食者」と「恐怖」です。ゴロンゴーザにおける捕食者は、ライオン、ハイエナ、ヒョウ、チータ、リカオンでしたが、内戦が続いた結果、わずかなライオンを除いて姿を消しました。この結果、草食動物が "恐怖心"、つまり「他の動物の餌食になることを恐れる気持ち」を忘れたのです。
本来、動物は捕食者の存在を意識し、襲われたときに不利になるような環境や地形を避けて行動範囲を決めています。
このことを昆虫で明らかにした実験があります。森の中の草地に2種のネットを設置し、1種のネットにはバッタだけ、もう1種のネットにはバッタとその天敵の蜘蛛をいれます。そうすると、蜘蛛がいるネットのバッタは天敵から身を隠すのに適した植物を食べるので、体が小さくなりました。一方、蜘蛛がいないネットのバッタは、栄養が豊富な植物を食べるので体が大きくなり、繁殖数を増やしました。つまり「捕食されにくい行動」と「子孫を多く残す行動」のトレードオフ関係がみられたのです。
プロジェクトでは、ゴロンゴーザの生態系の荒廃を回復させるため、捕食者の再導入が計画されました。実は25年前、米国のイエローストーン国立公園ににオオカミが再導入され、成果をあげていました(No.126-127「捕食者なき世界」参照)。
しかしゴロンゴーザの動物は、もう何世代も捕食者のいない環境が続いています。果たして、今でも捕食者を恐れる行動をとるのでしょうか。
そこでまず、氾濫原のブッシュバックがヒョウの声に反応するかどうかの実験が行われました。ヒョウの声を録音し、氾濫原にスピーカーを設置して、何日かはただの雑音を流し、別の日にヒョウの声を流しました。すると、ヒョウの声でブッシュバックの行動が一変し、生息域を変えてヒョウの声を避けるようになったのです。
声だけで変化を起こせるのなら、本物の捕食者はもっと大きな変化を起こせるはずです。これで捕食者の再導入が決まりました。捕食者として選ばれたのはリカオンです。
リカオンの再導入
リカオンは体にまだら模様があり、格好はイヌに似ています。しかし約150万年前にオオカミから枝分かれしてアフリカ大陸で独自の進化をとげた動物で、イヌやオオカミとは全く別の動物です。その生息数はアフリカ全土で7000頭以下に減少していて、絶滅の危機にあります。リカオンがゴロンゴーザ国立公園で最後に確認されたのは30年以上も前でした。
ゴロンゴーザ国立公園から800キロ離れた南アフリカの動物保護区から、14頭のリカオンが運ばれました。遺伝的な多様性を重視して、これらのリカオンは異なる群から選ばれた14頭です。
14頭のリカオンは、まず、ゴロンゴーザ国立公園に作られた囲いの中で共に過ごしました。この過程で群としての一体感が醸成され、リーダーのリカオンも決まっていきました。そして8週間後、囲いの扉が開けられ、公園に放たれました。
リカオンには発信器がつけられ、行動をつぶさに追跡できます。またブッシュバックにも多くの発信器がつけらています。リカオンとブッシュバックの糞の分析すると何を食べたかが分かる。つまり、リカオンの再導入による生態系の変化が詳細に分析できるのです。その意味で、この再導入は生態学における歴史的な実験です。また、順調にいけば、絶滅危惧種であるリカオンの繁殖につながる可能性もあります。
ゴロンゴーザ国立公園でのリカオン
プロジェクトの努力で、ライオンの生息数は150頭にまで回復していました。ゴロンゴーザにおけるライオンの狩りの基本は「待ち伏せ」です。ライオンは林と氾濫原の間の背の高い草が茂るところに単独で潜み、そこを通る動物を狙うのです。
一方、リカオンの狩りは集団による狩りです。氾濫原のような開けた場所で草食動物を狙います。かつ、リカオンはライオンを避けます。ライオンに殺されることもあるからです。生態系の回復のためには、異なったテリトリーで獲物をねらう複数の捕食者が必要です。
リカオンの群は、平均で1日2頭以上のアンテロープ(ブッシュバックなど)をしとめます。ゴロンゴーザの今の状況では、食べ物に全く困らないはずです。
ゴロンゴーザの14頭のリカオンを追跡する過程で、繁殖が確認できました。まず、11頭の子どもが生まれました。その次には8頭の子どもが生まれました。さらに群の一部が独立して別の群ができ、その別の群でも8頭の子どもが生まれました。ゴロンゴーザのリカオンは、総計40頭以上の2つの群になり、存在感を増しました。
さらに、ライオンがあまり狙わない動物をしとめていることも分かってきました。そのため、動物の警戒心が強くなり、動物の行動が変わりました。
リカオンの糞を分析すると、狩りの獲物の半分以上はブッシュバックだとわかりました。ブッシュバックはいずれ氾濫原から撤退し、今よりも栄養状態が劣るようになると想定できます。プロジェクトの成果は数年経たないと確定できませんが、希望がもてるスタートです。
さらに、プロジェクトのメンバーにとって嬉しい知らせがありました。ゴロンゴーザ国立公園では10年以上目撃されていなかったヒョウが目撃されたのです。それだけ、ゴロンゴーザには自然が残っていたということです。ヒョウは自力で復活を果たすかもしれません。
14頭のリカオンが放たれてから1年後、さらに15頭が到着しました。これはリカオンの遺伝的な偏りを防ぎ、ゴロンゴーザにさらなる "恐怖" をもたらすためです。将来的には他の捕食者の導入も検討されています。
感想
ゴロンゴーザ再生プロジェクトに関わる生態学者、動物学者の地道な努力の積み重ねが印象的でした。たとえば、本文に引用した「ゴロンゴーザとケニアにおける草食動物(5種)の食性の違い」ですが、各種の草食動物の糞を多数に集め、植物のサンプルも大量に集め、それらをDNA分析して、食性の違いを明らかにしています。大変な作業です。こういうことを地道に、かつ定期的にやることが、ゴロンゴーザ再生プロジェクト(リカオンの再導入はその一つ)の成果を、エビデンスとともに示せるということでしょう。
いったん崩れた生態系を元に戻すのは、おいそれとできるものではなく、時間とコストがかかります。しかしそれにチャレンジする学者がいる。そのことが実感できたドキュメンタリーでした。
生態系において捕食者(例えば肉食獣)が、乱獲などの何らかの原因で不在になると、被捕食者(例えば草食動物)が増え過ぎ、そのことによって植物相が減少する。最悪の場合は草食動物もかえって数が減って生態系の荒廃が起こり得る。このようなことが、豊富な実例とともに示されていました。
生態系における「捕食・被捕食」の関係は、動植物の種が複雑に絡み合うネットワークを形成していて、そのネットワークには「不在になると他の種に連鎖的な影響を及ぼす種」(= キーストーン種。キーストーンは "要石" の意味)があります。食物連鎖の頂点に位置する肉食獣は代表的なキーストーン種なのでした。
ところで、最近の NHK BS1 のドキュメンタリーで、人的要因によって激変してしまった生態系を、捕食者の再導入によって元に戻そうとするプロジェクトが放映されました。その番組は、
NHK BS1 BS世界のドキュメンタリー
| 2022年8月9日 15:00~15:45) | |
| "恐怖" でよみがえる野生の王国」 | |
| Nature's Fear Factor) 制作:Tangled Bank Studios(米国 2020) |
です。今回はこの番組の概要を紹介します。日本語題名に「"恐怖" でよみがえる」とあり、また原題の意味は「自然の要素としての "恐怖"」です。つまり "恐怖" が重要なテーマになっています。これは、
| 捕食者は、単に被捕食者を殺して食べるだけでなく、被捕食者に常に "恐怖" を与えており、そのことによって被捕食者の行動は制限され、これが生態系維持の重要な要素になっている」 |
という意味です。このことは以降の概要で詳しく出てきます。プロジェクトの主役 = 捕食者は、アフリカに住むイヌに似た肉食獣の "リカオン" です。
ゴロンゴーザ国立公園とその荒廃
東アフリカのモザンビークにあるゴロンゴーザ国立公園は、アフリカの国立公園の中でも特に豊かな自然に恵まれている公園です。

|
ゴロンゴーザ国立公園 |
サバンナ、林、氾濫原、湖、川、熱帯雨林などが複雑に入り組んだ自然生態系を成している。番組より。 |
モザンビークでは独立後、1970年代から15年以上ものあいだ、政府軍と反政府勢力の激しい内戦が続きました。この内戦による犠牲者は 100万人にのぼるとされています。
この内戦のあいだ、ゴロンゴーザ国立公園は反政府勢力の格好の隠れ家になり、戦場にもなったので、荒廃してしまいました。戦乱と密猟によって大型の哺乳類の数が激減してしまったのです。20年前の調査では、大型の哺乳類の数が内戦前に比べて 1/10 以下に減少していました。たとえば、
| : 2500 → 250 | |
| : 3500 → 100未満 | |
| : 200 → 10 | |
| : 3500 → 0 | |
| : 6500 → 0 | |
| : 14000 → 0 |
といった悲惨な状況です。ゴロンゴーザ国立公園の復活は不可能だと思われました。
しかし希望がありました。それは豊かな自然環境です。ゴロンゴーザ国立公園は、サバンナ、林、氾濫原、湖、川、熱帯雨林などがモザイク状に入り組んでいます。この自然環境がそのまま残っていたのです。
ゴロンゴーザ再生プロジェクト
世界各地からも専門家が集まって官民共同の「ゴロンゴーザ再生プロジェクト」が結成されました。このプロジェクトによって、大きく数を減らした動物の一部は他の地域から持ち込まれました。こうした努力の結果、動物の生息数は回復しつつあります。特に、草食動物の生息数は内戦前に近づきつつあります。
素晴らしいことのよう思えますが、専門家の判断によると健全な生態系の回復ではありません。動物によって増え方に偏りがあり、以前のような多様性が失われたのです。たとえば、一部の動物だけが急速に数を増やしています。中でも、ウォーターバックの数が爆発的に増えました。生息総数は6万頭に迫る勢いで、これは内戦前の10倍以上です。

|
ウォーターバック(雌) |
(Wikipedia) |
「多種多様な生き物がそれぞれに適した場所で生息し、全体として安定した生態系を作っている」という、本来あるべき姿ではないのです。なぜ動物の数が偏るのでしょうか。この問題の解決策を探るべく、ゴロンゴーザ再生プロジェクトでは生態系の地道な調査をはじめました。
ブッシュバックの奇妙な行動
生態系の調査で判明したことの一つに、アンテロープ(=レイヨウ)の一種で、本来警戒心が強いブッシュバックの奇妙な行動があります。ブッシュバックはその名のとおり、本来なら茂みに隠れて暮らします。しかし林を離れて、開けた氾濫原に行動範囲を広げていました。より栄養がある食べ物を求めて氾濫原に踏み出したと考えられました。

|
ブッシュバック(雌) |
(Wikipedia) |
草食動物がどの種類の草を食べているのか、糞を採取して調べること可能です。3年間で3000以上ものブッシュバックの糞が集められ、アメリカのプリンストン大学に送られました。含まれる植物のDNA分析の結果、氾濫原のブッシュバックは林の中の個体より栄養価の高い草を食べていることが分かりました。その結果、氾濫原に踏み出したブッシュバックは体が大きくなり、子どももたくさん作れるのです。
草食動物の食性変化
プロジェクトではさらに、ゴロンゴーザ国立の主な草食動物が何を食べているかを分析し、ケニアの似たような国立公園と比較しました。ケニアの草食動物は、種によって食べるものがはっきり分かれていました。一方、ゴロンゴーザでは複数の種が同じ物を食べていました。

|
草食動物の食性の比較 |
[ケニア(左)とゴロンゴーザ(右)] |
色の違いは草食動物の種を表し、ブッシュバック、ウォーターバック、リードバック、インパラ、オリビの5種である。点は個体で、個体が食べた草の種類によって3次元グラフにプロットし、それをある方向から2次元的に見たのが上の図である。ケニアの5種の草食動物は食性が分離しているが、ゴロンゴーザでは食性が重なっている。番組より。 |
動物たちがあらゆる場所に進出し好きなものを食べるようになった結果、食性における "種の境界線" が崩壊していたのです。こうなると過度の争いが起き、生態系が崩れてきます。
捕食者の不足
根本原因は2つの不足でした。「捕食者」と「恐怖」です。ゴロンゴーザにおける捕食者は、ライオン、ハイエナ、ヒョウ、チータ、リカオンでしたが、内戦が続いた結果、わずかなライオンを除いて姿を消しました。この結果、草食動物が "恐怖心"、つまり「他の動物の餌食になることを恐れる気持ち」を忘れたのです。
|
本来、動物は捕食者の存在を意識し、襲われたときに不利になるような環境や地形を避けて行動範囲を決めています。
このことを昆虫で明らかにした実験があります。森の中の草地に2種のネットを設置し、1種のネットにはバッタだけ、もう1種のネットにはバッタとその天敵の蜘蛛をいれます。そうすると、蜘蛛がいるネットのバッタは天敵から身を隠すのに適した植物を食べるので、体が小さくなりました。一方、蜘蛛がいないネットのバッタは、栄養が豊富な植物を食べるので体が大きくなり、繁殖数を増やしました。つまり「捕食されにくい行動」と「子孫を多く残す行動」のトレードオフ関係がみられたのです。
プロジェクトでは、ゴロンゴーザの生態系の荒廃を回復させるため、捕食者の再導入が計画されました。実は25年前、米国のイエローストーン国立公園ににオオカミが再導入され、成果をあげていました(No.126-127「捕食者なき世界」参照)。
しかしゴロンゴーザの動物は、もう何世代も捕食者のいない環境が続いています。果たして、今でも捕食者を恐れる行動をとるのでしょうか。

|
氾濫原に進出したブッシュバック。番組より。 |
そこでまず、氾濫原のブッシュバックがヒョウの声に反応するかどうかの実験が行われました。ヒョウの声を録音し、氾濫原にスピーカーを設置して、何日かはただの雑音を流し、別の日にヒョウの声を流しました。すると、ヒョウの声でブッシュバックの行動が一変し、生息域を変えてヒョウの声を避けるようになったのです。
声だけで変化を起こせるのなら、本物の捕食者はもっと大きな変化を起こせるはずです。これで捕食者の再導入が決まりました。捕食者として選ばれたのはリカオンです。
リカオンの再導入

|
リカオン |
(Wikipedia) |
リカオンは体にまだら模様があり、格好はイヌに似ています。しかし約150万年前にオオカミから枝分かれしてアフリカ大陸で独自の進化をとげた動物で、イヌやオオカミとは全く別の動物です。その生息数はアフリカ全土で7000頭以下に減少していて、絶滅の危機にあります。リカオンがゴロンゴーザ国立公園で最後に確認されたのは30年以上も前でした。
ゴロンゴーザ国立公園から800キロ離れた南アフリカの動物保護区から、14頭のリカオンが運ばれました。遺伝的な多様性を重視して、これらのリカオンは異なる群から選ばれた14頭です。
14頭のリカオンは、まず、ゴロンゴーザ国立公園に作られた囲いの中で共に過ごしました。この過程で群としての一体感が醸成され、リーダーのリカオンも決まっていきました。そして8週間後、囲いの扉が開けられ、公園に放たれました。
リカオンには発信器がつけられ、行動をつぶさに追跡できます。またブッシュバックにも多くの発信器がつけらています。リカオンとブッシュバックの糞の分析すると何を食べたかが分かる。つまり、リカオンの再導入による生態系の変化が詳細に分析できるのです。その意味で、この再導入は生態学における歴史的な実験です。また、順調にいけば、絶滅危惧種であるリカオンの繁殖につながる可能性もあります。
ゴロンゴーザ国立公園でのリカオン
プロジェクトの努力で、ライオンの生息数は150頭にまで回復していました。ゴロンゴーザにおけるライオンの狩りの基本は「待ち伏せ」です。ライオンは林と氾濫原の間の背の高い草が茂るところに単独で潜み、そこを通る動物を狙うのです。
一方、リカオンの狩りは集団による狩りです。氾濫原のような開けた場所で草食動物を狙います。かつ、リカオンはライオンを避けます。ライオンに殺されることもあるからです。生態系の回復のためには、異なったテリトリーで獲物をねらう複数の捕食者が必要です。
リカオンの群は、平均で1日2頭以上のアンテロープ(ブッシュバックなど)をしとめます。ゴロンゴーザの今の状況では、食べ物に全く困らないはずです。
ゴロンゴーザの14頭のリカオンを追跡する過程で、繁殖が確認できました。まず、11頭の子どもが生まれました。その次には8頭の子どもが生まれました。さらに群の一部が独立して別の群ができ、その別の群でも8頭の子どもが生まれました。ゴロンゴーザのリカオンは、総計40頭以上の2つの群になり、存在感を増しました。

|
ゴロンゴーザ国立公園で数を増やしたリカオン。親にまじって子どもが写っている。番組より。 |
さらに、ライオンがあまり狙わない動物をしとめていることも分かってきました。そのため、動物の警戒心が強くなり、動物の行動が変わりました。
リカオンの糞を分析すると、狩りの獲物の半分以上はブッシュバックだとわかりました。ブッシュバックはいずれ氾濫原から撤退し、今よりも栄養状態が劣るようになると想定できます。プロジェクトの成果は数年経たないと確定できませんが、希望がもてるスタートです。
さらに、プロジェクトのメンバーにとって嬉しい知らせがありました。ゴロンゴーザ国立公園では10年以上目撃されていなかったヒョウが目撃されたのです。それだけ、ゴロンゴーザには自然が残っていたということです。ヒョウは自力で復活を果たすかもしれません。
14頭のリカオンが放たれてから1年後、さらに15頭が到着しました。これはリカオンの遺伝的な偏りを防ぎ、ゴロンゴーザにさらなる "恐怖" をもたらすためです。将来的には他の捕食者の導入も検討されています。
感想
ゴロンゴーザ再生プロジェクトに関わる生態学者、動物学者の地道な努力の積み重ねが印象的でした。たとえば、本文に引用した「ゴロンゴーザとケニアにおける草食動物(5種)の食性の違い」ですが、各種の草食動物の糞を多数に集め、植物のサンプルも大量に集め、それらをDNA分析して、食性の違いを明らかにしています。大変な作業です。こういうことを地道に、かつ定期的にやることが、ゴロンゴーザ再生プロジェクト(リカオンの再導入はその一つ)の成果を、エビデンスとともに示せるということでしょう。
いったん崩れた生態系を元に戻すのは、おいそれとできるものではなく、時間とコストがかかります。しかしそれにチャレンジする学者がいる。そのことが実感できたドキュメンタリーでした。
2022-09-10 11:58
nice!(0)
No.344 - 算数文章題が解けない子どもたち [社会]
No.234「教科書が読めない子どもたち」は、国立情報学研究所の新井紀子教授が中心になって実施した「全国読解力調査」(対象は中学・高校生)を紹介したものでした。
この調査の経緯ですが、新井教授は日本数学会の教育委員長として、大学1年生を対象に「大学生数学基本調査」を実施しました。というのも、大学に勤める数学系の教員の多くが、入学してくる学生の学力低下を肌で感じていたからです。この数学基本調査で浮かび上がったのは、そもそも「誤答する学生の多くは問題文の意味を理解できていないのでは」という疑問だったのです。
そこで本格的に子どもたちの読解力を調べたのが「全国読解力調査」でした。その結果は No.234 に概要を紹介した通りです。
ところで最近、小学生の学力の実態を詳細に調べた本が出版されました。慶応義塾大学 環境情報学部教授の今井むつみ氏(他6名)の「算数文章題が解けない子どもたち ── ことば・思考の力と学力不振」(岩波書店 2022年6月)です(以下「本書」と記述)。新井教授の本とよく似た(文法構造が全く同じの)題名ですが、触発されたのかもしれません。
新井教授は数学者ですが、本書の今井教授は心理学者であり、認知科学(特に言語の発達)や教育心理学が専門です。いわば、読解力を含む「学力」とは何かを研究するプロフェッショナルです。そのテーマは「算数文章題」で、対象は小学3年生・4年生・5年生です。
私は教育関係者ではないし、小学生ないしは就学前の子どもがあるわけでもありません。しかしこの本を大変に興味深く読みました。その理由は、
と感じたからです。著者にそこまでの意図はなかったと思いますが、そういう風にも読める。ということは、要するに "良い本" だということです。そこで是非とも、本書の "さわり" を紹介したいと思います。以下の引用では、原文にはない下線や段落を追加したところがあります。また引用した問題文の漢字には、本書ではルビがふってありますが、省略しました。
問題意識
まず、本書の冒頭に次のように書いてあります。
著者(たち)は広島県教育委員会から「小学生の学力のベースとなる能力を測定し、学力不振の原因を明らかにすることができるアセスメントテストの作成」を依頼されました。県教委からは次のようにあったそうです(この引用の太字と下線は原文通りです)。
その「つまずいている子どもが なぜつまずいているのか」を知る目的で、著者は認知科学と教育心理学の長年の研究成果をもとに、2種類の「たつじんテスト」を開発しました。
の2つです。そして
の成績と「たつじんテスト」の成績の相関関係を統計的に明らかにしました。また、相関関係をみるだけでなく、子どもたちの誤答を詳細に分析し「なぜつまずいているのか」を明らかにしました。この詳細分析が最も重要な点だと言えるでしょう。
本書には「算数文章題テスト」と、2つの「たつじんテスト」の内容、誤答の分析、「算数文章題テスト」と「たつじんテスト」の相関関係、学力を育てる家庭環境とは何かなどが書かれています。それを順に紹介します。
算数文章題テスト
算数文章題テストは、広島県福山市の3つの小学校の3・4・5年生を対象に行われました。調査参加人数は、3年生:167人、4年生:148人、5年生:173人でした。問題は3・4年生用と5年生用に分かれています。
3・4年生用の算数文章題は8問です。いずれも教科書からとられたもので、
です。具体的な問題は次の通りでした。
これらの問題の正答率は次の通りでした。
本書では、このような全体の成績だけでなく、誤答を個別に分析し、誤答を導いた要因(= 子どもの認知のあり方)を推測しています。その例を2つ紹介します。
問題1(列の並び順)
問題1は小学1年の教科書から採られた問題ですが、正答率が衝撃的に低くなりました。3年生の正答率は30%を切り、4年生でも半分程度しか正解できていません
ちなみに、同じ問題を5年生もやりましたが、正答率は72.3% でした。つまり5年生になっても3割の子どもが間違えたわけで、これも衝撃的です。3・4年生の代表的な誤答を調べると次のようになります。まず、
という回答をした子がいます。2桁と1桁の掛け算は正確にできていますが、このタイプの子どもは「文の意味を深く考えず、問題文にある数字を全部使って式を立て、計算をして、何でもよいから答えを出そうという文章題解決に対する考え方を子どもがもっている可能性が高い」(本書)わけです。
そもそも「問題文の状況のイメージを式にできない」子どもがいることも分かりました。問題文のイメージをつかむために、回答用紙に図を描いた子どもはたくさんいます。つまり、14人の列の一人一人を ○ で描いた子どもです。しかしそれをやっても、問題文を正しく絵に出来ない子どもがいる。文章に書かれていることの意味を読み取れないのです。さらに、誤答の中に、
というのがありました。問題文に現れる人数を表す数字は 14 と 7 の2つだけです。従って上のような式になった。この子は「文章に現れる数字(だけ)を使って回答しなければならないという誤ったスキーマ」を持っていると考えられます。
ここで言うスキーマとは認知心理学の用語で「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。言うまでもなく正しい式は、
ですが、式には人数として 1 という、文章には現れない数字が必要であり、それを文章から読み取る必要があるわけです。
また、14 - 7 = 7 (答)7人 という回答をした子どもの中には、正しい図を描いた子もいました。このような誤答は「メタ認知能力」が働いていないと考えられます。
メタ認知能力とは「自分をちょっと離れたところから俯瞰的に眺め、自分の知識の状態や行動を客観的に認知する能力」のことです。批判的思考ができる能力と言ってもよいでしょう。7人が正しい答えかどうか、正しい図を書いているのだから「振り返ってみれば」分かるはずなのです。
問題2(必要ケーキ数)
この問題で多かった誤答の例を2つあげると次のようです。まず、
という答です。この回答は、問題文にある最初の2つの数字だけをみて、しかも問題文を勝手に読み替えています。つまり「ケーキを 4つ入れた箱から 2つを配ると何個残りますか」というような問題に読み替えている。問題文の読み取りが全くできていません。
という答もありました。もちろん問題2の正答は、
ですが、4 × 2 = 8、8 × 3 = 24 という2段階の思考が必要です。このような「マルチステップの認知処理上の負荷を回避する」傾向が誤答を招いた例がよくありした。
本書に「作業記憶と実行機能をうまく働かせられていない」と書いてあります。この問題に正答するためには、4 × 2 = 8 の「8こ」をいったん「作業記憶」にいれ、次には作業記憶の 8 と問題文の 3 だけに着目して(4 と 2 は忘れて)掛け算をする必要があります。心理学で言う「実行機能」の重要な側面は「必要な情報だけに集中し、余計な情報を無視できる認知機能」です。誤答する子どもはこれができないと考えられます。
5年生用の算数文章題は8問です。このうち問題1、4、5、6は3・4年生用の問題と共通です。まとめると次の通りです。
正答率は次の通りでした。
問題12:お菓子の量の問題
誤答の分析から1つだけを紹介します。問題12「お菓子の量の問題」に次のような回答がありました。以下の(図)は、回答用紙の(図)欄に子どもが書いたコメントです。
この回答を書いた子どもは増量の意味が分かっています。30% が 0.3 だということも分かっている。「答は増えるはずだ」という「メタ認知」もちゃんと働いています。しかも、小数での割り算(250 ÷ 0.3)もできて、おおよそですが合っています。何と、本当は掛け算にすべきだということまで分かっている!! そこまで分かっているにも関わらず、正しい立式ができていません。言うまでもなく正しい式は、
ですが、この問題の文章に 1.3 という数字はありません。この子は 30% 増量が 1.3 倍だということが思いつかなかったのです。ないしは2番目の立式のような「マルチステップの思考」ができなかったのです。
この例のように、算数文章題が苦手な子どもは「文章に書かれていない数字を常識で補って推論する」ことがとても苦手です。読解力で大切なのは「文章で使われている言葉の意味をきちんと理解し、常識を含む自分の知識で "行間を補う"」ことなのですが、誤答した多くの子どもはそれができないのです。
算数文章題の誤答分析
以上は3つの誤答の例ですが、3・4・5年生の誤答の全体を分析すると次のようになります。
まず、典型的な誤答では、小数や分数などの数の概念が理解できていないことが顕著でした。小数や分数を理解するためには、整数・分数・小数という演算間の関係性の理解、つまり「数」という "システム" の理解が必要ですが、それが全くできていないのです。つまり「数」の知識が「システム化された数の知識」になっていない。
また時間の計算においては「秒・分・時間・日」の単位変換が苦手なことが顕著でした(3・4・5年生の問題4の正解率参照)。これも「秒・分・時間・日」の概念をバラバラに覚えているだけで「システム化された知識」になっていないのが原因と考えられます。
また、しばしばある誤答の理由は、文章の読みとり(=読解)ができず、従って文章に描かれている状況がイメージできないという点です。その「読解ができない」ことの最大の要因は、推論能力が足りないことです。文章に書かれていないことを、自分のスキーマに従って補って推論する力が足りないのです。
さらに、多くの子供たちが「足し算とかけ算は数を大きくする、引き算と割り算は数を小さくするという誤ったスキーマ」をもっていることが見て取れました。
「誤ったスキーマ」の最たるものが「数はモノを数えるためにある」というスキーマです。数学用語を使うと「すべての数は自然数である」というスキーマです。このスキーマをもっていると、分数・小数の理解が阻害され、その結果として誤答を生み出す。
以上のような要因に加え、作業記憶が必要なマルチステップの問題や、実行機能(ある部分だけを注視して他を無視するなど)が必要な問題では、それによる「認知的負荷」が複合的に加わって、それが誤答を生み出しています。認知的負荷が高いと誤ったスキーマが顔を出す傾向も顕著でした。
ことばのたつじん
「ことばのたつじん」は、算数文章題に答えるための "基礎的な学力" と想定できる「言語力」の測定をするものです。これには、
の3つがあります。
これは "一般的な語彙力" をみるテストで、
の3種があります。「ことばの意味」は30問からなり、そのうちの25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。その例をあげます。
標準問題の例
チャレンジ問題の例
「にていることば」も30問からなり、25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。
標準問題の例
チャレンジ問題の例
「あてはまることば」は、慣用句や慣習的な比喩表現、一つの語から連想される "共起語" の知識をみるものです。29問の「標準問題」(3つの選択肢から1つの正解を選ぶ)と、5問の「チャレンジ問題」(4つの選択肢から2つの正解を選ぶ)から成ります。その例をあげます。
標準問題の例
チャレンジ問題の例
特に成績が悪かった問題の一つは、「ことばのいみ」の中の「期間」を正解とする、次の標準問題でした。
3年生の正答率は「きかん(=正解)」が64%、「きげん」が26%、4年生では「きかん(=正解)」が75%、「きげん」が23% でした。「きかん」と「きげん」と誤答するのは、
といった要因が複合していると推測されます。これらの要因があると正答率が下がるのは「にていることば」でも同様でした。本書に次のような記述があります。
①「語彙の深さと広さ」は一般的な語彙の知識のテストでしたが、②「空間・時間のことば」は、"空間ことば"(前後左右など)と "時間ことば"(2日前、5日後、1週間先など)に絞って、それらを状況に応じて柔軟かつ的確に運用できるかをみるテストです。その例を引用します。
宝物さがし問題(自分と同じ視点)
宝物さがし問題(自分と逆の視点)
この2つの問題の正答率は
でした。全般的に「空間ことば」の問題では、単純な質問では正しく答えられる子どもが多いのですが、上に引用した「宝探し問題」、特に「自分と逆の視点」では正答率が下がります。
「自分と逆の視点」に正解するためには、「視点変更能力」(= 自分以外の視点でものごとを見る力)や、「作業記憶」を使う認知能力、自分の視点を抑制する「実行機能」が必要です。つまり問題解決に必要な情報全体に目配りをしつつ部分を統合する必要があり、それが、部分部分の知識を「生きた知識」として活用できることなのです。
「生きた知識」を持っているかどうかは、他の情報との統合を必要とする "認知の負荷が高い状況" で、個々のことばの知識を本当に使えるのかを評価する必要があることがわかります。
カレンダー問題
上の例では「ちょうど一週間後」を聞いていますが、問題の全体では「あした・ちょうど一週間後・きのう・2日前・5日後・来週の月曜日・ちょうど1週間前・先週の月曜日・5日先・2日後・1週間先・2日先・5日前」の13種の日が、カレンダーでどの日に当たるかを質問しました。
著者は「この問題の正答率の低さに驚いた」と書いています。正答率の低い原因は、時間の関係を表す「前」「後」「先」が "分かりにくい" からです。その理由を著者は次のように書いています。
「先」ということばも曲者です。「さっき言ったでしょう」の「先」は過去ですが、「1週間さき」の「先」は未来です。また、同じ漢字を使う「先週」は過去です。耳からの言葉で覚えた子どもが「さっき」と「さき」を混同するのは分かるし、同じ「先」を使う「先週」を未来だと誤認するのも分かるのです。ちなみに、日本語を母語としない外国人にとって「先」にはとても苦労するそうです。
時間は目に見えない抽象概念であり、もともと子どもには理解しづらいものです。それに加え、日本語では「未来 → 過去」と「過去 → 未来」という2種のモデルが存在し、大人はそれを混在して使っています。子どもが "時間ことば" の理解や使用に苦労するのは当然なのです。
日常的な動作を表す動詞について、システム化された「生きた知識」をもっているかをテストするものです。たとえば、
というような、( )を埋める問題です。このタイプの問題に正答するためには、類似概念を日本語がどのように分割しているかを知っていなければなりません。たとえば身につける動作は、帽子なら「かぶる」、上着なら「きる」、パンツや靴なら「はく」です。かつ、動詞の活用の形(=文法)と統合して答える必要があります。システム化された「生きた知識」があってこそ正答できるのです。
「動作のことば」の回答を分析すると、問題ごとに正解率が大きく違うことがわかります。そして正解率が低いのは「チーズを縦に(裂いて)います」「草を鎌で(刈って)います」などの問題です。これらの動作は、小学生が日常生活で見たり、自分で行ったりすることが少ない動詞です。だから正答率が低い。
逆に、これらの動作の動詞を知っていて的確に使える子どもは、日常会話だけでなく、本などから語彙を学んでいると考えられるのです。
「ことばのたつじん」と学力の関係
「ことばのたつじん」と「算数文章題」の得点の相関係数は次のとおりでした。
この相関係数はすべて 0.1% の水準で統計的に有意(その値が偶然によってもたらされる確率が0.1% 以下)でした。
この表を見ると「ことばのたつじん」と学力(この場合は算数文章題)とが、極めて強い相関関係にあることがわかります。特に「空間・時間のことば」です。この傾向は標準学力テスト(国語・算数)との相関係数と同様でした。
かんがえるたつじん
「かず・かたち・かんがえるたつじん」(略称:かんがえるたつじん)は、子どもの思考力のアセスメントです。
の3部から構成されています。
大問1:整数の数直線上の相対位置
0 から 100 までの数直線の上に、与えられた数のだいたいの位置の目印を書き込む問題です。たとえば 18 と提示されたら、それは 20 に近いので、数直線をだいたい 5 分割して、それよりちょっと 0 に近いところに目印をつける、といった感じです。4つの小問(提示数:18, 71, 4, 23)があります。
これは「整数は相対的な大きさを示す」というスキーマを子どもたちが持っているかどうかを見るものです。このスキーマを理解していない子どもは、18 と提示されると定規を取り出して 18mm のところに目印をつけたりします。誤答をする少なからぬ子どもがそうしていました。
大問2:小数・分数の大小関係
どちらが大きいかを問う問題です。12の小問があります。5年生の平均正答率とともに引用します。
小問10、小問11、小問12 は「ケーキの12こ分と13こ分ではどちらがたくさん食べることができますか」のような "文章題" になっています。
特に正答率が悪いのは、小問2, 7, 8 です。小問2 と「同程度に難しいはず」の小問3 の正答率が高いのは(小問2 の正答率より 35% も跳ね上がっている)、小問3では「たまたま分母の数も分子の数も大きい方が大きい」からだと考えられます。
このデータは、少なからぬ子どもが分数や小数の概念的理解ができていないことを示しています。また分数や小数が、いかに直感的にとらえどころがないものかも示しています。
大問3:心的数直線上での小数・分数の相対位置
0 から 1 までの数直線があり、10分割した目盛りがついています。与えられた小数や分数が数直線上のどの位置にあるかの目印をつける問題です。6つの小問があります。
特に成績の悪かったのは、12と25でした。5年生の平均正答率では、12が 46.0%、25が 31.3% でした。
12は日常生活で頻繁に使われます。しかし正答できない子どもは、「ケーキ」のような具体的なモノが与えられずに、「1を基準にしたときにそれに対してどの割合の量なのか」という純粋な「数」としての理解ができていないのです。
25の正答率が異様に低いのは、0 から 1 の数直線に10分割した目盛りが振ってあるからです。つまり正答するためには「2目盛りを1単位としてそれが2つ」という心的操作をしなければならない。これが問題を特に難しくしています。
「1」には、モノを数えるときに「1個ある」という意味と、任意のモノを「1」として、それを分割したり比較のしたりするときの基準の意味があります。「数はモノを数えるもの」という誤ったスキーマを持っていると「基準としての1」が理解できません。この理解なしに分数や小数の意味は理解できないのです。
また大問2・大問3の誤答分析からは、誤答する子どもたちが整数・分数・小数をバラバラに理解していて、それらの関連付けがされていないことがわかります。分数の単元で分数だけ、小数の単元で小数だけという現在の小学校の教え方では「システム化」された知識の習得は難しいのです。
図形の問題です。図形を折る、隠す、回転させるという操作を心の中でできるかどうかです。具体的な問題の例をあげます。
大問4:図形を折ったときのイメージ
大問5:図形の隠れた部分のイメージ

大問6:図形を回転させたときのイメージ
これらの問題に正解するためには「複数のことを同時に処理しなければない」わけです。誤答を分析すると、一つの状況なら楽にできる心的操作が、複数のことを同時に処理しなければらない状況では破綻してしまい、その結果、問題解決に失敗する傾向が見て取れました。
また大問6に顕著ですが、正答する子どもは図形に補助線を引き、補助線が回転後にどうなるかを考えて答を出しています。つまり、図形の回転は認知的負荷が高いのを直感し、負荷を軽減する方略を自分で考えられたので正解できたのです。問題解決のための方略を自分で考えられるのが "できる" 子どもの特徴だと言えます。
「推論」が学力と関係しているという分析は本書のこれまでにもにありましたが、ここでは推論だけを純粋にとりあげます。問題の例を以下にあげます。
大問7:推移的推論
大問8:複数次元の変化を伴う類推

大問9:実行機能を伴う拡張的類推

大問9の例に関してですが、この場合の実行機能とは、注意点を取捨選択し、不要な注意点を抑制し、必要に応じて注意点を切り替えられる機能です。またこの例では見本のペアとその向きを常に短期記憶におきつつ、図の中から同じ関係のペアを見いだす必要があります。
絵の中には関係するものが複数あります。たとえば、木は葉っぱや鳥や鋸と関係がある。また糸だと、関係するのはハサミと針です。つまり「見本のペアの関係ではない関係への注意」を抑制する必要がある。これができて正解することができます。
以上の「かんがえるたつじん」と「算数文章題」の得点の相関係数は、0.37~0.48 で、高いものでした。最も高かったのが大問8(複数次元の変化を伴う類推)で、その次が 大問2(小数・分数の大小関係)でした。
算数文章題と「たつじん」テストの相関
本書には、次の6つの「たつじんテスト」、
「ことばのたつじん」
「かず・かたち・かんがえるたつじん」
の成績と、算数文章題の成績の相関係数を計算した表が本書にあります。それをみると、3・4年生では6つのテスト中5つが0.5を超え(「動作のことば」だけが0.38)、5年生では5つが 0.39~0.47の範囲になっています(「動作のことば」だけが0.3)。またすべてにおいて、0.1% 水準で有意(=全く偶然にその相関係数になるのは 0.1% 以下の確率)になっています。
ただ、6つの「たつじんテスト」は相互に相関関係があるはずなので、1つのテストが算数文章題と相関をもつと、それにつられて関係のある他のテストも算数文章題と相関します。つまり、どの「たつじんテスト」が算数文章題の成績に "利いて" いるのかは、相関係数だけでは分かりません。
そこで本書には、重回帰分析(説明変数=「たつじんテスト」の成績6種、被説明変数=算数文章題の成績)の結果が載っています。それによると、算数文章題の成績に最も寄与しているのが「空間・時間のことば」でした。これは国語と算数の標準学力テストでも同じでした。
従来からの心理学の研究で、言語能力が学力と深い関わりを持っていることが分かっていて、このことは広く受け入れられています。しかし想定されている「言語能力」とは「語彙のサイズ」(=どれだけ多くの言葉を知っているか)でした。
しかし今回の研究から、「語彙の広さと深さ」よりも「空間・時間のことばの運用」の方が頑健に「学力」を説明することがわかりました。このことは、教育現場で当たり前のようにして使われいている「言語能力」の考え方を見直す必要があることを示しています。
重回帰分析の結果から、「空間・時間のことば」の次には「推論の力」が算数文章題の成績に寄与していることも分かりました。その次が「整数・分数・小数の概念」です。
つまづきの原因
本書では全体の「まとめ」として「第6章:学習のつまずきの原因」と題した章があり、各種のテストでの誤答を分析した結果を総括し、これをもとに教育関係者への提言がされています。この中から「つまずきの原因」の何点かを紹介します。まず、
ことです。これは「たし算・引き算・かけ算・割り算」の関係性が理解できず、それぞれの計算手続きは分かるものの、問題解決に有効に使える知識になってないという意味です。それぞれの単元での学習結果が断片的な知識となっていて「数の世界の、計算というシステム」としての理解になっていない。また、
のもつまずきの原因です。算数文章題の場合、誤ったスキーマの根は一つです。それは「数はモノを数えるためのもの」というスキーマです。このスキーマをもっていると「1」が「全体を表すもの」あるいは「単位を表すもの」という概念が受け入れられません。
「足し算とかけ算は数を増やす計算」と「引き算と割り算は数を減らす計算」という誤ったスキーマもよく見られたものです。これは、まず「増やす計算」と「減らす計算」でそれぞれを教えるからだと考えれます。子どもたちは誤ったスキーマを自分で作り出してしまうのです。
似ているのが「割り算は必ず割り切れる」というスキーマです。これも 12÷4 のような割り切れる数の計算が最初に導入されるからです。誤ったスキーマをもってしまうと、答えが整数にならない割り算を教えられても、なかなか受け入れることができません。本書には「永遠の後出しじゃんけん」という表現を使って次のように書いてあります。
さらに、
のも、つまづきの要因です。「たつじんテスト」で最も強く学力を予測していたのは「空間・時間ことば」でしたが、前・後・左・右はまさに相対的であり、誰を基準にするか、どの点を基準にするかで変わってきます。
また、数直線上に与えられた数の位置を示すには、0~100 あるいは 0~1 というスケールの中で相対的に考える必要がありますが、これができない子どもが多数いました。著者は「驚くほど多かったのはショックだった」と書いています。これは「数」という概念の核である「数の相対性」が理解できていないことを端的に示しています。
「相対的にものごとを見る」ことは「視点を柔軟に変更・変換できる」ことと深い関係があります。そして視点変更の柔軟性は、ことばの多義性の理解につながります。「1」はモノが1個のことであるというスキーマをもった子どもが、「1」は「子ども 140人」でも「水 50リットル」でもよい、「全体」ないしは「単位」を表すものだという認識に進むためには、過去のスキーマの抜本的な修正が必要です。「相対的にものごとを見る能力」=「視点変更の柔軟性」は、誤ったスキーマを修正できる力に関わっています。そして誤ったスキーマを自ら修正できる力は、知識を発展させるための最重要の能力なのです。
その他、本書では
などが総括としてまとめられています。
ほんものの学力を生む家庭環境
本書では付録として、テストをうけた児童の保護者に44項目のアンケート調査をし、その結果と子どもの学力(たつじんテストと、国語・算数の標準学力テスト)の相関を示した大変に興味深い表が載っています。44項目の質問は、子どもの基本的生活習慣、家庭学習、しつけの考え方、読書習慣、小学校に入る前のひらがな・数字への関心、小学校に入る前の時間・ひらがな・数字の家庭教育など、多岐にわたります。
これらの中で、最も学力との相関が強かったのは「読書習慣・読み聞かせ」に関する3項目と、「家庭内の本の冊数」に関する2項目でした。その次に相関が強かったのは小学校入学前の「ひらがな・数字への興味・関心」の2項目と「時間・ひらがな・数字の教育」3項目でした。この結果から著者は次のように記しています。
本書の感想
最初に書いたように、本書は、
と思いました。つまり我々大人が社会で生きていく際に必要な思考力の重要な要素を示しているように感じたのです。
たとえばその一つは、「ある目的や機能を遂行する何か」を「システムとしてみる力」です。「システム」として捉えるということは、「何か」が複数のサブシステムからなり、それぞれのサブシステムは固有の目的や機能を持っている。それが有機的かつ相互依存的に結合してシステムとしての目的や機能を果たす。そのサブシステムは、さらに下位の要素からなる、という見方です。これは社会におけるさまざまな組織、自治体、ハードウェア、サービスの仕組み、プロジェクト、学問体系 ・・・・・ などなどを理解し、それらを構築・運用・発展させていく上で必須でしょう。
「相対的に考える」のも重要です。他者からみてどう見えるか、第3者の視点ではどうか、全体を俯瞰するとどうなるのか、対立項が何なのか、全体との対比で部分をみるとどうなるのか、という視点です。
そして、相対的に考える思考力は「スキーマを修正する力」につながります。本書のキーワードの一つである "スキーマ" とは「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。人は必ず何らかのスキーマに基づいて判断します。そして社会において個人が持つ「誤ったスキーマ」の典型は「自らの成功体験からくるスキーマ」です。社会環境が変化すると、そのスキーマには捨てなければならない部分や付け加えなければならないものが出てくる。本書に「スキーマを自ら修正できる力は、知識を発展させるための最重要の能力」とありますが、全くその通りです。
さらに「抽象的に考える」ことの重要性です。"良く練られた" 抽象的考えは、より一般性があり、より普遍的で、従ってよりパワーを発揮します。「抽象的でよく分からない、具体的にはどういうことか」というリクエストに答えて具体例を提示することは重要ですが、それは抽象的考えを理解する手だてとして重要なのです。
子どもは小学校から(公式に)抽象の世界に踏み出します。「言葉・語彙」がそうだし「数」がそうです。本書からの引用を再掲しますと、
とありました。抽象性の大きな壁である「9歳の壁」を乗り越えた子どもは、その次の段階へと行けます。これは中学校・高校・大学と「学び」を続ける限り、抽象性の壁を乗り越えることが繰り返されるはずです。だとすると、社会に出てからも繰り返されるはずだし、学校での「学び」はその訓練とも考えられます。
ともかく、10歳前後の小学生の誤答分析から明らかになった「学力」や「思考力」の源泉は、大人の社会に直結していると思いました。
分数は直感的に理解しづらい
最後に一つ、「分数は直感的に理解しづらい」ということの実例を書いておきます。
本書の「かんがえるたつじん ① 整数・分数・小数の概念」の「大問2:小数・分数の大小関係」のところで、テストの結果データの分析として「多くの子どもたちが、分数や小数の概念的な理解ができていない」と書かれていました。そして「これは、正答できない子どもたちの努力が足りないと片づけてよい問題ではない。分数・小数がいかに直感的に捉えどころがないものかを示すデータなのである」とも書いてありました。
分数で言うと、12や13は「任意の」モノを「1」としたとき、それを「均等に」2分割、あるいは3分割した数です。この「任意の」と「均等に」が非常に抽象的で、捉えどころがないのです。
我々大人は分数を理解していると思っているし、それを使えると思っています。大小関係も分かると自信を持っている。しかし本来「分数は直感的に捉えどころがない」のなら、それは大人にとってもそうであり、ほとんどの場合は正しく使えたとしても、何かの拍子に「捉えどころのなさ」が顔を出すはずです。
そのことを実例で示したような記述が本書にありました。「かんがえるたつじん ① 整数・分数・小数の概念」の「大問1:整数の数直線上の相対的位置」の説明のところです。どのような問題かを著者が説明した文章です。
えっ! と思いましたが、何度読み直しても、これでは 23 あたりに目印をつけることになります。本書に書いてある採点方法だと、5点満点の 3点(ないしは4点)です。
本書の著者は大学教授の方々、計7名で、原稿は著者の間で何回もレビューし、見直し、確認したはずです。岩波書店に渡った後も、原稿や校正刷りの各段階での何回ものチェックがされたはずです。それでも「100を4分割すると20」になってしまう。どの段階でこうなったかは不明ですが ・・・・・・。
これは単にケアレスミスというより、そもそも「14が分かりにくいから、ないしは15や20100が分かりにくいから」、つまり「分数は抽象的で理解しづらい概念」ということを示していると思います。子どもが算数文章題につまずく理由、その理由の一端を本書が "身をもって" 示しているのでした。
この調査の経緯ですが、新井教授は日本数学会の教育委員長として、大学1年生を対象に「大学生数学基本調査」を実施しました。というのも、大学に勤める数学系の教員の多くが、入学してくる学生の学力低下を肌で感じていたからです。この数学基本調査で浮かび上がったのは、そもそも「誤答する学生の多くは問題文の意味を理解できていないのでは」という疑問だったのです。
そこで本格的に子どもたちの読解力を調べたのが「全国読解力調査」でした。その結果は No.234 に概要を紹介した通りです。
ところで最近、小学生の学力の実態を詳細に調べた本が出版されました。慶応義塾大学 環境情報学部教授の今井むつみ氏(他6名)の「算数文章題が解けない子どもたち ── ことば・思考の力と学力不振」(岩波書店 2022年6月)です(以下「本書」と記述)。新井教授の本とよく似た(文法構造が全く同じの)題名ですが、触発されたのかもしれません。

|
新井教授は数学者ですが、本書の今井教授は心理学者であり、認知科学(特に言語の発達)や教育心理学が専門です。いわば、読解力を含む「学力」とは何かを研究するプロフェッショナルです。そのテーマは「算数文章題」で、対象は小学3年生・4年生・5年生です。
私は教育関係者ではないし、小学生ないしは就学前の子どもがあるわけでもありません。しかしこの本を大変に興味深く読みました。その理由は、
小学生の「算数文章題における学力とは何か」の探求を通して、「人間の思考力とは何か」や「考える力の本質は何か」という問題に迫っている
と感じたからです。著者にそこまでの意図はなかったと思いますが、そういう風にも読める。ということは、要するに "良い本" だということです。そこで是非とも、本書の "さわり" を紹介したいと思います。以下の引用では、原文にはない下線や段落を追加したところがあります。また引用した問題文の漢字には、本書ではルビがふってありますが、省略しました。
問題意識
まず、本書の冒頭に次のように書いてあります。
|
著者(たち)は広島県教育委員会から「小学生の学力のベースとなる能力を測定し、学力不振の原因を明らかにすることができるアセスメントテストの作成」を依頼されました。県教委からは次のようにあったそうです(この引用の太字と下線は原文通りです)。
|
その「つまずいている子どもが なぜつまずいているのか」を知る目的で、著者は認知科学と教育心理学の長年の研究成果をもとに、2種類の「たつじんテスト」を開発しました。
| ことばのたつじん」
→ ことばに関する知識を測る
| |
| かず・かたち・かんがえるたつじん」 | |
| 略称「かんがえるたつじん」)
→ 数と図形に関する知識と推論能力を測る
|
の2つです。そして
| 算数文章題テスト | |
| 主として教科書にある算数文章題) | |
| 国語・算数の標準学力テスト |
の成績と「たつじんテスト」の成績の相関関係を統計的に明らかにしました。また、相関関係をみるだけでなく、子どもたちの誤答を詳細に分析し「なぜつまずいているのか」を明らかにしました。この詳細分析が最も重要な点だと言えるでしょう。
本書には「算数文章題テスト」と、2つの「たつじんテスト」の内容、誤答の分析、「算数文章題テスト」と「たつじんテスト」の相関関係、学力を育てる家庭環境とは何かなどが書かれています。それを順に紹介します。
算数文章題テスト
算数文章題テストは、広島県福山市の3つの小学校の3・4・5年生を対象に行われました。調査参加人数は、3年生:167人、4年生:148人、5年生:173人でした。問題は3・4年生用と5年生用に分かれています。
| 3・4年生:問題とテスト結果 |
3・4年生用の算数文章題は8問です。いずれも教科書からとられたもので、
| :1年生の教科書 | |
| :3年生の教科書 |
です。具体的な問題は次の通りでした。
|
問題1 (順番) | 子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
|
問題2 (かけ算) | ケーキを4こずつ入れたはこを、1人に2はこずつ3人にくばります。ケーキは、全部で何こいりますか。 |
|
問題3 (時間の引き算1) | けんさんは、午前9時 20 分に家を出て、午前10時40分に遊園地へ着きました。家から遊園地まで、何時間何分かかりましたか。 |
|
問題4 (時間の引き算2) | えりさんは、山道を5時間10分歩きました。山をのぼるのに歩いた時間は、2時間 50 分です。山をくだるのに歩いた時間は、何時間何分ですか。 |
|
問題5 (割り算) | 1まいの画用紙から、カードが8まい作れます。45まいのカードを作るには、画用紙は何まいいりますか。 |
|
問題6 (分数) | りんさんが、ジュースを37L(リットル)のんだので、残りは27L(リットル)になりました。 はじめにジュースは、何 L(リットル)ありましたか。 |
|
問題7 (小数) | リボンが4m ありました。けんたさんが、何m か切り取ったので、リボンは1.7m になりました。けんたさんは、何m 切り取りましたか。 |
|
問題8 (倍率) | なおきさんのテープの長さは、えりさんのテープの長さの4 倍で、48 cm です。えりさんのテープの長さは何cm ですか。 |
これらの問題の正答率は次の通りでした。
| 3年生 | 4年生 | |
| 問題1 順番 | 28.1% | 53.4% |
| 問題2 かけ算 | 57.5% | 72.5% |
| 問題3 時間の引き算1 | 56.0% | 63.4% |
| 問題4 時間の引き算2 | 17.7% | 26.0% |
| 問題5 割り算 | 41.1% | 48.9% |
| 問題6 分数 | 84.4% | 87.0% |
| 問題7 小数 | 48.2% | 63.4% |
| 問題8 倍率 | 45.0% | 62.6% |
本書では、このような全体の成績だけでなく、誤答を個別に分析し、誤答を導いた要因(= 子どもの認知のあり方)を推測しています。その例を2つ紹介します。
問題1(列の並び順)
子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
問題1は小学1年の教科書から採られた問題ですが、正答率が衝撃的に低くなりました。3年生の正答率は30%を切り、4年生でも半分程度しか正解できていません
ちなみに、同じ問題を5年生もやりましたが、正答率は72.3% でした。つまり5年生になっても3割の子どもが間違えたわけで、これも衝撃的です。3・4年生の代表的な誤答を調べると次のようになります。まず、
(式)14 × 7 = 98 (答)98人 |
という回答をした子がいます。2桁と1桁の掛け算は正確にできていますが、このタイプの子どもは「文の意味を深く考えず、問題文にある数字を全部使って式を立て、計算をして、何でもよいから答えを出そうという文章題解決に対する考え方を子どもがもっている可能性が高い」(本書)わけです。
そもそも「問題文の状況のイメージを式にできない」子どもがいることも分かりました。問題文のイメージをつかむために、回答用紙に図を描いた子どもはたくさんいます。つまり、14人の列の一人一人を ○ で描いた子どもです。しかしそれをやっても、問題文を正しく絵に出来ない子どもがいる。文章に書かれていることの意味を読み取れないのです。さらに、誤答の中に、
(式)14 - 7 = 7 (答)7人 |
というのがありました。問題文に現れる人数を表す数字は 14 と 7 の2つだけです。従って上のような式になった。この子は「文章に現れる数字(だけ)を使って回答しなければならないという誤ったスキーマ」を持っていると考えられます。
ここで言うスキーマとは認知心理学の用語で「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。言うまでもなく正しい式は、
14 - 7 - 1 = 6 |
ですが、式には人数として 1 という、文章には現れない数字が必要であり、それを文章から読み取る必要があるわけです。
また、14 - 7 = 7 (答)7人 という回答をした子どもの中には、正しい図を描いた子もいました。このような誤答は「メタ認知能力」が働いていないと考えられます。
メタ認知能力とは「自分をちょっと離れたところから俯瞰的に眺め、自分の知識の状態や行動を客観的に認知する能力」のことです。批判的思考ができる能力と言ってもよいでしょう。7人が正しい答えかどうか、正しい図を書いているのだから「振り返ってみれば」分かるはずなのです。
問題2(必要ケーキ数)
ケーキを4こずつ入れたはこを、1人に2はこずつ3人にくばります。ケーキは、全部で何こいりますか。 |
この問題で多かった誤答の例を2つあげると次のようです。まず、
(式)4 - 2 = 2 (答)2こ |
という答です。この回答は、問題文にある最初の2つの数字だけをみて、しかも問題文を勝手に読み替えています。つまり「ケーキを 4つ入れた箱から 2つを配ると何個残りますか」というような問題に読み替えている。問題文の読み取りが全くできていません。
(式)4 × 3 = 12 (答)12こ |
という答もありました。もちろん問題2の正答は、
(式)4 × 2 × 3 = 24 (答)24こ |
ですが、4 × 2 = 8、8 × 3 = 24 という2段階の思考が必要です。このような「マルチステップの認知処理上の負荷を回避する」傾向が誤答を招いた例がよくありした。
本書に「作業記憶と実行機能をうまく働かせられていない」と書いてあります。この問題に正答するためには、4 × 2 = 8 の「8こ」をいったん「作業記憶」にいれ、次には作業記憶の 8 と問題文の 3 だけに着目して(4 と 2 は忘れて)掛け算をする必要があります。心理学で言う「実行機能」の重要な側面は「必要な情報だけに集中し、余計な情報を無視できる認知機能」です。誤答する子どもはこれができないと考えられます。
| 5年生:問題とテスト結果 |
5年生用の算数文章題は8問です。このうち問題1、4、5、6は3・4年生用の問題と共通です。まとめると次の通りです。
| :1年生の教科書 | |
| :3年生の教科書 | |
| :5年生の教科書、および作問したもの |
|
問題1 (順番) | 子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
|
問題4 (時間の引き算2) | えりさんは、山道を5時間10分歩きました。山をのぼるのに歩いた時間は、2時間 50 分です。山をくだるのに歩いた時間は、何時間何分ですか。 |
|
問題5 (割り算) | 1まいの画用紙から、カードが8まい作れます。45まいのカードを作るには、画用紙は何まいいりますか。 |
|
問題6 (分数) | りんさんが、ジュースを37 L(リットル)のんだので、残りは27L(リットル)になりました。 はじめにジュースは、何 L(リットル)ありましたか。 |
|
問題9 (距離の計算) | えみさんの家から学校までの距離は 3.6km で、あきらさんの家から学校までの距離より35km 遠いそうです。あきらさんの家から学校までは、何km ですか。 |
|
問題10 | こうたさんの学校の今年の児童数は 476人で、10年前の 200% に当たります。10年前の児童数は何人ですか。 |
|
問題11 | 2時間で108km 走る電車があります。この電車は、3時間で何km 進みますか。 |
|
問題12 (倍率・増量) | 250g入りのお菓子が、30%増量して売られるそうです。お菓子の量は、何gになりますか。 |
正答率は次の通りでした。
| 5年生 | |
| 問題1 順番 | 72.3% |
| 問題4 時間の引き算2 | 53.9% |
| 問題5 割り算 | 59.6% |
| 問題6 分数 | 87.2% |
| 問題9 距離の計算 | 17.7% |
| 問題10 倍率・割り戻し | 55.3% |
| 問題11 速さと距離の計算 | 66.7% |
| 問題12 倍率・増量 | 37.6% |
問題12:お菓子の量の問題
250g入りのお菓子が、30%増量して売られるそうです。お菓子の量は、何gになりますか。 |
誤答の分析から1つだけを紹介します。問題12「お菓子の量の問題」に次のような回答がありました。以下の(図)は、回答用紙の(図)欄に子どもが書いたコメントです。
(式)250 ÷ 0.3 = 800 (答え)800g (図)
ふつうならかけだけど かけにしてしまうと逆に減ってしまうので(0.3だから)÷ にしてふやす
|
この回答を書いた子どもは増量の意味が分かっています。30% が 0.3 だということも分かっている。「答は増えるはずだ」という「メタ認知」もちゃんと働いています。しかも、小数での割り算(250 ÷ 0.3)もできて、おおよそですが合っています。何と、本当は掛け算にすべきだということまで分かっている!! そこまで分かっているにも関わらず、正しい立式ができていません。言うまでもなく正しい式は、
250 × 1.3 = 325 ないしは、 250 × 0.3 = 75 250 + 75 = 325 |
ですが、この問題の文章に 1.3 という数字はありません。この子は 30% 増量が 1.3 倍だということが思いつかなかったのです。ないしは2番目の立式のような「マルチステップの思考」ができなかったのです。
この例のように、算数文章題が苦手な子どもは「文章に書かれていない数字を常識で補って推論する」ことがとても苦手です。読解力で大切なのは「文章で使われている言葉の意味をきちんと理解し、常識を含む自分の知識で "行間を補う"」ことなのですが、誤答した多くの子どもはそれができないのです。
算数文章題の誤答分析
以上は3つの誤答の例ですが、3・4・5年生の誤答の全体を分析すると次のようになります。
まず、典型的な誤答では、小数や分数などの数の概念が理解できていないことが顕著でした。小数や分数を理解するためには、整数・分数・小数という演算間の関係性の理解、つまり「数」という "システム" の理解が必要ですが、それが全くできていないのです。つまり「数」の知識が「システム化された数の知識」になっていない。
また時間の計算においては「秒・分・時間・日」の単位変換が苦手なことが顕著でした(3・4・5年生の問題4の正解率参照)。これも「秒・分・時間・日」の概念をバラバラに覚えているだけで「システム化された知識」になっていないのが原因と考えられます。
また、しばしばある誤答の理由は、文章の読みとり(=読解)ができず、従って文章に描かれている状況がイメージできないという点です。その「読解ができない」ことの最大の要因は、推論能力が足りないことです。文章に書かれていないことを、自分のスキーマに従って補って推論する力が足りないのです。
さらに、多くの子供たちが「足し算とかけ算は数を大きくする、引き算と割り算は数を小さくするという誤ったスキーマ」をもっていることが見て取れました。
「誤ったスキーマ」の最たるものが「数はモノを数えるためにある」というスキーマです。数学用語を使うと「すべての数は自然数である」というスキーマです。このスキーマをもっていると、分数・小数の理解が阻害され、その結果として誤答を生み出す。
以上のような要因に加え、作業記憶が必要なマルチステップの問題や、実行機能(ある部分だけを注視して他を無視するなど)が必要な問題では、それによる「認知的負荷」が複合的に加わって、それが誤答を生み出しています。認知的負荷が高いと誤ったスキーマが顔を出す傾向も顕著でした。
ことばのたつじん
「ことばのたつじん」は、算数文章題に答えるための "基礎的な学力" と想定できる「言語力」の測定をするものです。これには、
| 「語彙の深さと広さ」 | |
| 「空間・時間のことば」 | |
| 「動作のことば」 |
の3つがあります。
| ①「語彙の深さと広さ」 |
これは "一般的な語彙力" をみるテストで、
| ことばのいみ」 | |
| にていることば」 | |
| あてはまることば」 |
の3種があります。「ことばの意味」は30問からなり、そのうちの25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。その例をあげます。
標準問題の例
ねんどなどを 力を 入れて よく まぜること 1. まぶす 2. たたく 3. こねる |
チャレンジ問題の例
おゆが じゅうぶんに あつくなること 1. ほてる 2. ふっとうする 3. わく 4. こみあげる |
「にていることば」も30問からなり、25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。
標準問題の例
ひかくする : もちものを ひかくします。 1. ならべます 2. くらべます 3. しらべます |
チャレンジ問題の例
まず : まず 手を あらいましょう 1. 後で 2. 先に 3. はじめに 4. いちどに |
「あてはまることば」は、慣用句や慣習的な比喩表現、一つの語から連想される "共起語" の知識をみるものです。29問の「標準問題」(3つの選択肢から1つの正解を選ぶ)と、5問の「チャレンジ問題」(4つの選択肢から2つの正解を選ぶ)から成ります。その例をあげます。
標準問題の例
あつい( )を よせています。 1. しんらい 2. 親切 3. しんじつ |
チャレンジ問題の例
( )が 広いです。 1. 顔 2. かかと 3. きもち 4. 心 |
特に成績が悪かった問題の一つは、「ことばのいみ」の中の「期間」を正解とする、次の標準問題でした。
ある日から そのあとの ある日まで 何かが つづくこと 1. きげん 2. きかん 3. しゅるい |
3年生の正答率は「きかん(=正解)」が64%、「きげん」が26%、4年生では「きかん(=正解)」が75%、「きげん」が23% でした。「きかん」と「きげん」と誤答するのは、
| 発音の類似 | |
| 意味の類似 | |
| 漢語である | |
| 抽象名詞である | |
| そもそも時間の概念が抽象概念である |
といった要因が複合していると推測されます。これらの要因があると正答率が下がるのは「にていることば」でも同様でした。本書に次のような記述があります。
|
| ②「空間・時間のことば」 |
①「語彙の深さと広さ」は一般的な語彙の知識のテストでしたが、②「空間・時間のことば」は、"空間ことば"(前後左右など)と "時間ことば"(2日前、5日後、1週間先など)に絞って、それらを状況に応じて柔軟かつ的確に運用できるかをみるテストです。その例を引用します。
宝物さがし問題(自分と同じ視点)
あなたは 友だちと いっしょに 町に 来ました  あなたが ほんやの 手前の 道を 右に まがると たからものがあります。 たからものは どこですか。 1ばん 2ばん 3ばん 4ばん |
宝物さがし問題(自分と逆の視点)
あなたは 友だちと いっしょに 町に 来ました  あなたが さいしょの こうさてんで 右に まがると たからものがあります。 たからものは どこですか。 1ばん 2ばん 3ばん 4ばん |
この2つの問題の正答率は
| 同じ視点 | 逆の視点 | |
| 3年生 | 59.1% | 42.7% |
| 4年生 | 72.8% | 55.0% |
でした。全般的に「空間ことば」の問題では、単純な質問では正しく答えられる子どもが多いのですが、上に引用した「宝探し問題」、特に「自分と逆の視点」では正答率が下がります。
「自分と逆の視点」に正解するためには、「視点変更能力」(= 自分以外の視点でものごとを見る力)や、「作業記憶」を使う認知能力、自分の視点を抑制する「実行機能」が必要です。つまり問題解決に必要な情報全体に目配りをしつつ部分を統合する必要があり、それが、部分部分の知識を「生きた知識」として活用できることなのです。
「生きた知識」を持っているかどうかは、他の情報との統合を必要とする "認知の負荷が高い状況" で、個々のことばの知識を本当に使えるのかを評価する必要があることがわかります。
カレンダー問題
りんちゃんの たん生日は 3月14日です。たん生日の ちょうど 一週間後は おわかれ会です。カレンダーの 中から おわかれ会の日を 一つ えらび ○をしましょう。  |
上の例では「ちょうど一週間後」を聞いていますが、問題の全体では「あした・ちょうど一週間後・きのう・2日前・5日後・来週の月曜日・ちょうど1週間前・先週の月曜日・5日先・2日後・1週間先・2日先・5日前」の13種の日が、カレンダーでどの日に当たるかを質問しました。
著者は「この問題の正答率の低さに驚いた」と書いています。正答率の低い原因は、時間の関係を表す「前」「後」「先」が "分かりにくい" からです。その理由を著者は次のように書いています。
|
|
2つの時間モデル |
上のモデルでは、過去から未来への時の流れに乗って、自分が未来に向かって進んでいく。下のモデルは、未来から過去に流れる時の流れを、自分が客観的視点から観察している。この2つのモデルで「前」の意味は逆転する。日本語では2つのモデルを混在して使う。 |
「先」ということばも曲者です。「さっき言ったでしょう」の「先」は過去ですが、「1週間さき」の「先」は未来です。また、同じ漢字を使う「先週」は過去です。耳からの言葉で覚えた子どもが「さっき」と「さき」を混同するのは分かるし、同じ「先」を使う「先週」を未来だと誤認するのも分かるのです。ちなみに、日本語を母語としない外国人にとって「先」にはとても苦労するそうです。
時間は目に見えない抽象概念であり、もともと子どもには理解しづらいものです。それに加え、日本語では「未来 → 過去」と「過去 → 未来」という2種のモデルが存在し、大人はそれを混在して使っています。子どもが "時間ことば" の理解や使用に苦労するのは当然なのです。
| ③「動作のことば」 |
日常的な動作を表す動詞について、システム化された「生きた知識」をもっているかをテストするものです。たとえば、
何をしていますか。  ぼうしを 頭に( )います。 |
というような、( )を埋める問題です。このタイプの問題に正答するためには、類似概念を日本語がどのように分割しているかを知っていなければなりません。たとえば身につける動作は、帽子なら「かぶる」、上着なら「きる」、パンツや靴なら「はく」です。かつ、動詞の活用の形(=文法)と統合して答える必要があります。システム化された「生きた知識」があってこそ正答できるのです。
「動作のことば」の回答を分析すると、問題ごとに正解率が大きく違うことがわかります。そして正解率が低いのは「チーズを縦に(裂いて)います」「草を鎌で(刈って)います」などの問題です。これらの動作は、小学生が日常生活で見たり、自分で行ったりすることが少ない動詞です。だから正答率が低い。
逆に、これらの動作の動詞を知っていて的確に使える子どもは、日常会話だけでなく、本などから語彙を学んでいると考えられるのです。
「ことばのたつじん」と学力の関係
「ことばのたつじん」と「算数文章題」の得点の相関係数は次のとおりでした。
| 3年生 | 4年生 | 5年生 | |
| ①語彙の深さと広さ | 0.49 | 0.58 | 0.44 |
| ②空間・時間のことば | 0.58 | 0.67 | 0.47 |
| ③動作のことば | 0.34 | 0.35 | 0.30 |
この相関係数はすべて 0.1% の水準で統計的に有意(その値が偶然によってもたらされる確率が0.1% 以下)でした。
この表を見ると「ことばのたつじん」と学力(この場合は算数文章題)とが、極めて強い相関関係にあることがわかります。特に「空間・時間のことば」です。この傾向は標準学力テスト(国語・算数)との相関係数と同様でした。
|
かんがえるたつじん
「かず・かたち・かんがえるたつじん」(略称:かんがえるたつじん)は、子どもの思考力のアセスメントです。
| 整数・分数・小数の概念 | |
| 図形イメージの心的操作 | |
| 推論の力 |
の3部から構成されています。
| ①整数・分数・小数の概念 |
大問1:整数の数直線上の相対位置
0 から 100 までの数直線の上に、与えられた数のだいたいの位置の目印を書き込む問題です。たとえば 18 と提示されたら、それは 20 に近いので、数直線をだいたい 5 分割して、それよりちょっと 0 に近いところに目印をつける、といった感じです。4つの小問(提示数:18, 71, 4, 23)があります。
これは「整数は相対的な大きさを示す」というスキーマを子どもたちが持っているかどうかを見るものです。このスキーマを理解していない子どもは、18 と提示されると定規を取り出して 18mm のところに目印をつけたりします。誤答をする少なからぬ子どもがそうしていました。
大問2:小数・分数の大小関係
どちらが大きいかを問う問題です。12の小問があります。5年生の平均正答率とともに引用します。
| 小問1 | 13と23 | 94.0% |
| 小問2 | 12と13 | 49.7% |
| 小問3 | 23と12 | 85.9% |
| 小問4 | 0.3 と 0.1 | 96.6% |
| 小問5 | 1 と 0.9 | 98.7% |
| 小問6 | 1.5 と 2 | 99.3% |
| 小問7 | 0.5 と13 | 42.3% |
| 小問8 | 12と 0.7 | 54.4% |
| 小問9 | 0.2 と12 | 82.6% |
| 小問10 | 12と13 | 78.5% |
| 小問11 | 13と23 | 71.8% |
| 小問12 | 13と14 | 69.1% |
小問10、小問11、小問12 は「ケーキの12こ分と13こ分ではどちらがたくさん食べることができますか」のような "文章題" になっています。
特に正答率が悪いのは、小問2, 7, 8 です。小問2 と「同程度に難しいはず」の小問3 の正答率が高いのは(小問2 の正答率より 35% も跳ね上がっている)、小問3では「たまたま分母の数も分子の数も大きい方が大きい」からだと考えられます。
このデータは、少なからぬ子どもが分数や小数の概念的理解ができていないことを示しています。また分数や小数が、いかに直感的にとらえどころがないものかも示しています。
大問3:心的数直線上での小数・分数の相対位置
0 から 1 までの数直線があり、10分割した目盛りがついています。与えられた小数や分数が数直線上のどの位置にあるかの目印をつける問題です。6つの小問があります。
特に成績の悪かったのは、12と25でした。5年生の平均正答率では、12が 46.0%、25が 31.3% でした。
12は日常生活で頻繁に使われます。しかし正答できない子どもは、「ケーキ」のような具体的なモノが与えられずに、「1を基準にしたときにそれに対してどの割合の量なのか」という純粋な「数」としての理解ができていないのです。
25の正答率が異様に低いのは、0 から 1 の数直線に10分割した目盛りが振ってあるからです。つまり正答するためには「2目盛りを1単位としてそれが2つ」という心的操作をしなければならない。これが問題を特に難しくしています。
「1」には、モノを数えるときに「1個ある」という意味と、任意のモノを「1」として、それを分割したり比較のしたりするときの基準の意味があります。「数はモノを数えるもの」という誤ったスキーマを持っていると「基準としての1」が理解できません。この理解なしに分数や小数の意味は理解できないのです。
また大問2・大問3の誤答分析からは、誤答する子どもたちが整数・分数・小数をバラバラに理解していて、それらの関連付けがされていないことがわかります。分数の単元で分数だけ、小数の単元で小数だけという現在の小学校の教え方では「システム化」された知識の習得は難しいのです。
| ②図形イメージの心的操作 |
図形の問題です。図形を折る、隠す、回転させるという操作を心の中でできるかどうかです。具体的な問題の例をあげます。
大問4:図形を折ったときのイメージ

大問5:図形の隠れた部分のイメージ

大問6:図形を回転させたときのイメージ

これらの問題に正解するためには「複数のことを同時に処理しなければない」わけです。誤答を分析すると、一つの状況なら楽にできる心的操作が、複数のことを同時に処理しなければらない状況では破綻してしまい、その結果、問題解決に失敗する傾向が見て取れました。
また大問6に顕著ですが、正答する子どもは図形に補助線を引き、補助線が回転後にどうなるかを考えて答を出しています。つまり、図形の回転は認知的負荷が高いのを直感し、負荷を軽減する方略を自分で考えられたので正解できたのです。問題解決のための方略を自分で考えられるのが "できる" 子どもの特徴だと言えます。
| ③推論の力 |
「推論」が学力と関係しているという分析は本書のこれまでにもにありましたが、ここでは推論だけを純粋にとりあげます。問題の例を以下にあげます。
大問7:推移的推論

大問8:複数次元の変化を伴う類推

大問9:実行機能を伴う拡張的類推

大問9の例に関してですが、この場合の実行機能とは、注意点を取捨選択し、不要な注意点を抑制し、必要に応じて注意点を切り替えられる機能です。またこの例では見本のペアとその向きを常に短期記憶におきつつ、図の中から同じ関係のペアを見いだす必要があります。
絵の中には関係するものが複数あります。たとえば、木は葉っぱや鳥や鋸と関係がある。また糸だと、関係するのはハサミと針です。つまり「見本のペアの関係ではない関係への注意」を抑制する必要がある。これができて正解することができます。
以上の「かんがえるたつじん」と「算数文章題」の得点の相関係数は、0.37~0.48 で、高いものでした。最も高かったのが大問8(複数次元の変化を伴う類推)で、その次が 大問2(小数・分数の大小関係)でした。
算数文章題と「たつじん」テストの相関
本書には、次の6つの「たつじんテスト」、
「ことばのたつじん」
| 語彙の深さと広さ | |
| 空間・時間のことば | |
| 動作のことば |
| 整数・分数・小数の概念 | |
| 図形イメージの心的操作 | |
| 推論の力 |
の成績と、算数文章題の成績の相関係数を計算した表が本書にあります。それをみると、3・4年生では6つのテスト中5つが0.5を超え(「動作のことば」だけが0.38)、5年生では5つが 0.39~0.47の範囲になっています(「動作のことば」だけが0.3)。またすべてにおいて、0.1% 水準で有意(=全く偶然にその相関係数になるのは 0.1% 以下の確率)になっています。
ただ、6つの「たつじんテスト」は相互に相関関係があるはずなので、1つのテストが算数文章題と相関をもつと、それにつられて関係のある他のテストも算数文章題と相関します。つまり、どの「たつじんテスト」が算数文章題の成績に "利いて" いるのかは、相関係数だけでは分かりません。
そこで本書には、重回帰分析(説明変数=「たつじんテスト」の成績6種、被説明変数=算数文章題の成績)の結果が載っています。それによると、算数文章題の成績に最も寄与しているのが「空間・時間のことば」でした。これは国語と算数の標準学力テストでも同じでした。
従来からの心理学の研究で、言語能力が学力と深い関わりを持っていることが分かっていて、このことは広く受け入れられています。しかし想定されている「言語能力」とは「語彙のサイズ」(=どれだけ多くの言葉を知っているか)でした。
しかし今回の研究から、「語彙の広さと深さ」よりも「空間・時間のことばの運用」の方が頑健に「学力」を説明することがわかりました。このことは、教育現場で当たり前のようにして使われいている「言語能力」の考え方を見直す必要があることを示しています。
重回帰分析の結果から、「空間・時間のことば」の次には「推論の力」が算数文章題の成績に寄与していることも分かりました。その次が「整数・分数・小数の概念」です。
つまづきの原因
本書では全体の「まとめ」として「第6章:学習のつまずきの原因」と題した章があり、各種のテストでの誤答を分析した結果を総括し、これをもとに教育関係者への提言がされています。この中から「つまずきの原因」の何点かを紹介します。まず、
知識が断片的でシステムの一部になっていない
ことです。これは「たし算・引き算・かけ算・割り算」の関係性が理解できず、それぞれの計算手続きは分かるものの、問題解決に有効に使える知識になってないという意味です。それぞれの単元での学習結果が断片的な知識となっていて「数の世界の、計算というシステム」としての理解になっていない。また、
誤ったスキーマをもっている
のもつまずきの原因です。算数文章題の場合、誤ったスキーマの根は一つです。それは「数はモノを数えるためのもの」というスキーマです。このスキーマをもっていると「1」が「全体を表すもの」あるいは「単位を表すもの」という概念が受け入れられません。
「足し算とかけ算は数を増やす計算」と「引き算と割り算は数を減らす計算」という誤ったスキーマもよく見られたものです。これは、まず「増やす計算」と「減らす計算」でそれぞれを教えるからだと考えれます。子どもたちは誤ったスキーマを自分で作り出してしまうのです。
似ているのが「割り算は必ず割り切れる」というスキーマです。これも 12÷4 のような割り切れる数の計算が最初に導入されるからです。誤ったスキーマをもってしまうと、答えが整数にならない割り算を教えられても、なかなか受け入れることができません。本書には「永遠の後出しじゃんけん」という表現を使って次のように書いてあります。
|
さらに、
相対的にものごとを見ることができない
のも、つまづきの要因です。「たつじんテスト」で最も強く学力を予測していたのは「空間・時間ことば」でしたが、前・後・左・右はまさに相対的であり、誰を基準にするか、どの点を基準にするかで変わってきます。
また、数直線上に与えられた数の位置を示すには、0~100 あるいは 0~1 というスケールの中で相対的に考える必要がありますが、これができない子どもが多数いました。著者は「驚くほど多かったのはショックだった」と書いています。これは「数」という概念の核である「数の相対性」が理解できていないことを端的に示しています。
「相対的にものごとを見る」ことは「視点を柔軟に変更・変換できる」ことと深い関係があります。そして視点変更の柔軟性は、ことばの多義性の理解につながります。「1」はモノが1個のことであるというスキーマをもった子どもが、「1」は「子ども 140人」でも「水 50リットル」でもよい、「全体」ないしは「単位」を表すものだという認識に進むためには、過去のスキーマの抜本的な修正が必要です。「相対的にものごとを見る能力」=「視点変更の柔軟性」は、誤ったスキーマを修正できる力に関わっています。そして誤ったスキーマを自ら修正できる力は、知識を発展させるための最重要の能力なのです。
その他、本書では
| 認知処理能力をコントロールしながら推論する力が弱い、また推論で行間を埋められない | |
| メタ知識が働かず、答えのモニタリングができない | |
| 学習無力感をもっている。何のために算数を学ぶのか分からず、算数の意味を感じ取れていない |
などが総括としてまとめられています。
ほんものの学力を生む家庭環境
本書では付録として、テストをうけた児童の保護者に44項目のアンケート調査をし、その結果と子どもの学力(たつじんテストと、国語・算数の標準学力テスト)の相関を示した大変に興味深い表が載っています。44項目の質問は、子どもの基本的生活習慣、家庭学習、しつけの考え方、読書習慣、小学校に入る前のひらがな・数字への関心、小学校に入る前の時間・ひらがな・数字の家庭教育など、多岐にわたります。
これらの中で、最も学力との相関が強かったのは「読書習慣・読み聞かせ」に関する3項目と、「家庭内の本の冊数」に関する2項目でした。その次に相関が強かったのは小学校入学前の「ひらがな・数字への興味・関心」の2項目と「時間・ひらがな・数字の教育」3項目でした。この結果から著者は次のように記しています。
|
本書の感想
最初に書いたように、本書は、
小学生の「算数文章題における学力とは何か」の探求を通して、「人間の思考力とは何か」や「考える力の本質は何か」という問題に迫っている
と思いました。つまり我々大人が社会で生きていく際に必要な思考力の重要な要素を示しているように感じたのです。
たとえばその一つは、「ある目的や機能を遂行する何か」を「システムとしてみる力」です。「システム」として捉えるということは、「何か」が複数のサブシステムからなり、それぞれのサブシステムは固有の目的や機能を持っている。それが有機的かつ相互依存的に結合してシステムとしての目的や機能を果たす。そのサブシステムは、さらに下位の要素からなる、という見方です。これは社会におけるさまざまな組織、自治体、ハードウェア、サービスの仕組み、プロジェクト、学問体系 ・・・・・ などなどを理解し、それらを構築・運用・発展させていく上で必須でしょう。
「相対的に考える」のも重要です。他者からみてどう見えるか、第3者の視点ではどうか、全体を俯瞰するとどうなるのか、対立項が何なのか、全体との対比で部分をみるとどうなるのか、という視点です。
そして、相対的に考える思考力は「スキーマを修正する力」につながります。本書のキーワードの一つである "スキーマ" とは「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。人は必ず何らかのスキーマに基づいて判断します。そして社会において個人が持つ「誤ったスキーマ」の典型は「自らの成功体験からくるスキーマ」です。社会環境が変化すると、そのスキーマには捨てなければならない部分や付け加えなければならないものが出てくる。本書に「スキーマを自ら修正できる力は、知識を発展させるための最重要の能力」とありますが、全くその通りです。
さらに「抽象的に考える」ことの重要性です。"良く練られた" 抽象的考えは、より一般性があり、より普遍的で、従ってよりパワーを発揮します。「抽象的でよく分からない、具体的にはどういうことか」というリクエストに答えて具体例を提示することは重要ですが、それは抽象的考えを理解する手だてとして重要なのです。
子どもは小学校から(公式に)抽象の世界に踏み出します。「言葉・語彙」がそうだし「数」がそうです。本書からの引用を再掲しますと、
|
とありました。抽象性の大きな壁である「9歳の壁」を乗り越えた子どもは、その次の段階へと行けます。これは中学校・高校・大学と「学び」を続ける限り、抽象性の壁を乗り越えることが繰り返されるはずです。だとすると、社会に出てからも繰り返されるはずだし、学校での「学び」はその訓練とも考えられます。
ともかく、10歳前後の小学生の誤答分析から明らかになった「学力」や「思考力」の源泉は、大人の社会に直結していると思いました。
分数は直感的に理解しづらい
最後に一つ、「分数は直感的に理解しづらい」ということの実例を書いておきます。
本書の「かんがえるたつじん ① 整数・分数・小数の概念」の「大問2:小数・分数の大小関係」のところで、テストの結果データの分析として「多くの子どもたちが、分数や小数の概念的な理解ができていない」と書かれていました。そして「これは、正答できない子どもたちの努力が足りないと片づけてよい問題ではない。分数・小数がいかに直感的に捉えどころがないものかを示すデータなのである」とも書いてありました。
分数で言うと、12や13は「任意の」モノを「1」としたとき、それを「均等に」2分割、あるいは3分割した数です。この「任意の」と「均等に」が非常に抽象的で、捉えどころがないのです。
我々大人は分数を理解していると思っているし、それを使えると思っています。大小関係も分かると自信を持っている。しかし本来「分数は直感的に捉えどころがない」のなら、それは大人にとってもそうであり、ほとんどの場合は正しく使えたとしても、何かの拍子に「捉えどころのなさ」が顔を出すはずです。
そのことを実例で示したような記述が本書にありました。「かんがえるたつじん ① 整数・分数・小数の概念」の「大問1:整数の数直線上の相対的位置」の説明のところです。どのような問題かを著者が説明した文章です。
|
えっ! と思いましたが、何度読み直しても、これでは 23 あたりに目印をつけることになります。本書に書いてある採点方法だと、5点満点の 3点(ないしは4点)です。
本書の著者は大学教授の方々、計7名で、原稿は著者の間で何回もレビューし、見直し、確認したはずです。岩波書店に渡った後も、原稿や校正刷りの各段階での何回ものチェックがされたはずです。それでも「100を4分割すると20」になってしまう。どの段階でこうなったかは不明ですが ・・・・・・。
これは単にケアレスミスというより、そもそも「14が分かりにくいから、ないしは15や20100が分かりにくいから」、つまり「分数は抽象的で理解しづらい概念」ということを示していると思います。子どもが算数文章題につまずく理由、その理由の一端を本書が "身をもって" 示しているのでした。
2022-08-31 18:25
nice!(0)
No.343 - マルタとマリア [アート]
No.341「ベラスケス:卵を料理する老婆」は、スコットランド国立美術館が所蔵するベラスケスの「卵を料理する老婆」(2022年に初来日。東京都美術館)の感想を書いたものでした。ベラスケスが10代で描いた作品ですが(19歳頃)、リアリズムの描法も全体構図も完璧で、かつ、後のベラスケス作品に見られる「人間の尊厳を描く」という、画家の最良の特質が早くも現れている作品でした。
この「卵を料理する老婆」で思い出した作品があるので、今回はそのことを書きます。ロンドン・ナショナル・ギャラリーが所蔵する「マルタとマリアの家のキリスト」です。この絵もベラスケスが10代の作品で、また、2020年に日本で開催された「ロンドン・ナショナル・ギャラリー展」で展示されました。
新約聖書のマルタとマリア
まず絵の題についてです。「マルタとマリアの家のキリスト」は新約聖書に出てくる話で、聖書から引用すると次のようです。原文にあるルビは最小限に省略にしました。
このエピソードには不可解なところがあります。以前の記事(No.41)でとりあげましたが、社会学者の橋爪大三郎氏と大澤真幸氏の対談本「ふしぎなキリスト教」(講談社現代新書 2011)には次のように出てきます。
この箇所に違和感を持った人は多いらしく、大澤氏によると、中世の大神学者・エックハルトもそうで、強引な解釈をしているようです。普通のキリスト教徒が読んでも不可解に思えるのは間違いありません。
この大澤氏の問いかけに対して、橋爪氏は次のように答えています。これは橋爪氏の独自解釈というわけではなく、一般的なようです。
これもちょっと強引な、ないしは一面的な解釈で、上の引用に続く部分を読むと、大澤氏も納得していないようです。なぜ強引かというと「イエスを本当に歓迎しているんだったら、マリアの役割とマルタの役割が両方必要だと理解できる」というのはマリアに対しても言えるからです。だとしたら、「いいほうをとった」マリアの方に、マルタに対する「気遣い」があってもよいはずです。一言、マルタに言葉をかけるとか ・・・・・・。両方の役割が必要だと理解していなかったという点では、マリアもマルタも同じなのです。
もちろん、「世俗的仕事」と「信仰」のどちらかを取れと二者択一で言われたなら「信仰」とすべきなのでしょう。イエスは「無くてはならぬものは多くはない。いや、ひとつだけである」と言っています。信仰に生きることの重要性です。ただ、二者択一でない "解決策" もあるはずで、たとえばマルタとマリアの2人で接待の準備をし、そのあと2人でイエスの言葉を聴くこともできる。別に現代人ではなくても、そう考えるはずです。
というわけで、違和感が残るというか、不可解さが拭えないのは当然で、従って、この話をもとに絵画を制作する場合もさまざまな立場がありうることが想定されます。
ここからが本題です。ベラスケスはどう図像化したのか。
ベラスケス:マルタとマリアの家のキリスト
まずこの絵の特徴は「二重空間」の絵だということです。手前の "空間" には厨房で働く娘と老婆がいます。老婆は明らかに「卵を料理する老婆」と同じモデルです。娘は何となく泣きそうな感じで、老婆は後ろの "空間" を指さして娘に何かを言っています。
一方、後ろの "空間" にはキリストとマルタとマリアが描かれています。マリアは座ってキリストの言葉を聴いています。立っているのがマルタでしょうが、彼女がどういう態度を示しているのか、絵を見ただけでは判然としません。この後ろの "空間" については、
という3つの解釈があるそうです。ただ "鏡" という解釈には無理があると思われます。というのも、このような大きな鏡、しかも四角い平面鏡は、キリストの時代にも、この絵が描かれた17世紀にも稀少、ないしはまずないからです。平面鏡のためには平面ガラスが必要ですが、作るためには高度な技術が必要です。それは、ベラスケスの「ラス・メニーナス」に描かれたスペイン宮殿の鏡も "小ぶりで丸みを帯びている" ことからも分かります。仮に四角い平面鏡があったとしても、国王の宮殿ならともかく、庶民の厨房に掛けるようなものではないでしょう。
隣の別の部屋という解釈はどうでしょうか。後ろの "空間" が別の部屋ということは、厨房に四角い "窓" があいていて、そこから向こうの部屋が見えるということになります。このような作りの厨房は考えにくいと思います。
ということで、後ろの "空間" は絵とするのが妥当でしょう。この絵が描かれた17世紀には、新約聖書の「マルタとマリア」の解釈として「世俗的な生」と「信仰の生」の両方が大切だと考えられていたようです。ということは、厨房を手伝わないマリアの態度に不平をもらしたマルタはよくない、厨房の仕事も大切だという "戒め" として絵が掛けてあると解釈できます。
娘はなんだか涙目で、不満そうな顔をしています。ニンニクを金属製器具ですりつぶしているようですが、老婆に厨房での仕事について何らかの厳しい注意、ないしは叱責ををされた。それで不満そうな涙目になった。それを見た老婆は「マルタとマリア」の絵を指さして、不満をもつのはよくない、調理は大切で立派な仕事だと諭している、そういう光景に見えます。
とは言うものの、後ろの "空間" が「鏡」か「別の部屋」か「絵」かは、画家にとってはどうでもよいのでしょう。つまり、後ろの "空間" はこの絵が「マルタとマリアの家のキリスト」を描いたと言うための "口実" であって、画家の本当の狙いは「厨房を描く」ことだったと考えられるのです。特に、前景にある「金属製の器具」「4匹の魚」「2つの卵」、その他、器具の前にあるニンニクなどです。これらのリアリズムに徹した描写が、この絵の最大のポイントと思えます。魚の部分図を以下に掲げます。
絵の最大の狙いが静物の描写にあることは、この魚を描いた部分を見るだけでも一目瞭然だと思います。そして画家の第2の狙いをあげるとすると、庶民の労働を描くことでしょう。
さまざまな解釈を生む絵がありますが、絵そのものが画家の意図を雄弁に語っているケースがあります。この絵もそうだと思います。
余談ですが、このベラスケスの作品から、ある浮世絵を思い出しました。歌川国貞の「江戸百景の内 三廻」です(No.295「タンギー爺さんの画中画」の「補記」に画像を掲載)。題名だけを見ると風景画です。しかし、隅田川河畔の三廻神社が描かれているのは画面の左上の小さな四角(浮世絵の用語では "こま")の中だけで、本当の画題は中央に大きく描かれている女性、つまり美人画である、という浮世絵(いわゆる "こま絵")です。
この状況はベラスケスの「マルタとマリアの家のキリスト」にそっくりです。世の東西に関わらず、似たような発想の絵があるものです。
フェルメール
ベラスケスを離れて、同じ新約聖書のシーンを描いた作品を振り返ってみます。その有名作品として、「卵を料理する老婆」と同じくスコットランド国立美術館が所蔵するフェルメールの「マルタとマリアの家のキリスト」があります。この絵も 2018年のフェルメール展で展示されました(上野の森美術館)。
フェルメールが20代前半の初期の作品です。フェルメールは画家としての初期に宗教画を描き、その後は宗教画を離れて風俗画(と風景画)を描くようになったことで知られています。
この絵はベラスケスと違って、聖書に登場する3者だけを描いています。左に描かれているのがマリアで、キリストの話に聞き入っています。中央に描かれているのはマルタで、キリストにパンを差し出しています。聖書通りだとマルタはここでキリストに不平を言い、キリストはマリアを指さしつつマルタを諭しているはずです。
しかしそうだとしても、マルタの不平の表現は抑制されています。それよりも、パンを差し出す、つまりキリストを接待している表現の方を強く感じる。また、マルタは三角形の安定した構図の中心に描かれています。光の当て方も含めて、彼女が構図の焦点のように感じられます。
この絵は、聖書のストーリーを忠実に再現したと説明されれば、そう見えないことはない。しかし聖書とは裏腹に、マリアはキリストの話に聴き入り、マルタは厨房で仕事をしたあと(ないしは仕事の途中で)キリストを接待するという "調和的な状況" が描かれているとも見える。つまり「活動的なマルタ」と「瞑想的なマリア」が人間の両面を表し、かつ、構図の焦点であるマルタの重要性 = 世俗的な労働の大切さが強調されているようです。
おそらくこれは画家の(ないしは当時のオランダ社会の)聖書解釈を反映しているのだと思います。
ウテワール
そのフェルメールの絵より約70年前に描かれた「マルタとマリア」を主題にした絵があります。同じオランダの画家、ウテワールの「台所のメイド」です。
この絵については、東京都美術館の学芸員、高城靖之氏が日本経済新聞に解説を書いていました。それを引用します。
この絵で奥の部屋に描かれているマルタ、マリア、キリストは、まさに聖書の記述に従っています。というのも、マルタがマリアの態度に怒っているそぶりだからです。彼女は鍋を持ったまま、キリストとマリアのところに出てきて怒っている。
しかしベラスケスと同じで、この絵の主題はマルタとマリアの家のメイドを主人公にした前景の厨房です。そこには「静物」として、鳥、串、魚、肉、野菜、チーズ、パン、ワインの注がれたグラス、陶器、金属食器といった、質感の異なるさまざまなものがあり、高城氏が書いているように「質感や色彩を巧みに描き分けている画家の描写力」が見事です。その "静物の質感表現" こそ、この絵の第1のポイントでしょう。
そして第2のポイントは、鳥を串に刺しているメイド(高城氏の文章では女中)の表現です。腕と指を見ても分かるように、彼女はいかにもたくましく、働き者で、厨房での仕事を次々とこなし、家の食卓を一手に引き受けているような感じです。しかも調理に喜びをもって取り組んでいるように見える。労働は尊い、というメッセージ性を感じます。
以上の「マルタとマリア」の3作品に共通するのは、
と言えるでしょう。一見して "不可解" な新約聖書のエピソードを画題にすることで、宗教画の変貌がわかる3作品だと思います。
この「卵を料理する老婆」で思い出した作品があるので、今回はそのことを書きます。ロンドン・ナショナル・ギャラリーが所蔵する「マルタとマリアの家のキリスト」です。この絵もベラスケスが10代の作品で、また、2020年に日本で開催された「ロンドン・ナショナル・ギャラリー展」で展示されました。
新約聖書のマルタとマリア
まず絵の題についてです。「マルタとマリアの家のキリスト」は新約聖書に出てくる話で、聖書から引用すると次のようです。原文にあるルビは最小限に省略にしました。
|
このエピソードには不可解なところがあります。以前の記事(No.41)でとりあげましたが、社会学者の橋爪大三郎氏と大澤真幸氏の対談本「ふしぎなキリスト教」(講談社現代新書 2011)には次のように出てきます。
|
この箇所に違和感を持った人は多いらしく、大澤氏によると、中世の大神学者・エックハルトもそうで、強引な解釈をしているようです。普通のキリスト教徒が読んでも不可解に思えるのは間違いありません。
この大澤氏の問いかけに対して、橋爪氏は次のように答えています。これは橋爪氏の独自解釈というわけではなく、一般的なようです。
|
これもちょっと強引な、ないしは一面的な解釈で、上の引用に続く部分を読むと、大澤氏も納得していないようです。なぜ強引かというと「イエスを本当に歓迎しているんだったら、マリアの役割とマルタの役割が両方必要だと理解できる」というのはマリアに対しても言えるからです。だとしたら、「いいほうをとった」マリアの方に、マルタに対する「気遣い」があってもよいはずです。一言、マルタに言葉をかけるとか ・・・・・・。両方の役割が必要だと理解していなかったという点では、マリアもマルタも同じなのです。
もちろん、「世俗的仕事」と「信仰」のどちらかを取れと二者択一で言われたなら「信仰」とすべきなのでしょう。イエスは「無くてはならぬものは多くはない。いや、ひとつだけである」と言っています。信仰に生きることの重要性です。ただ、二者択一でない "解決策" もあるはずで、たとえばマルタとマリアの2人で接待の準備をし、そのあと2人でイエスの言葉を聴くこともできる。別に現代人ではなくても、そう考えるはずです。
というわけで、違和感が残るというか、不可解さが拭えないのは当然で、従って、この話をもとに絵画を制作する場合もさまざまな立場がありうることが想定されます。
ここからが本題です。ベラスケスはどう図像化したのか。
ベラスケス:マルタとマリアの家のキリスト

|
デイエゴ・ベラスケス(1599-1660) 「マルタとマリアの家のキリスト」(1618頃) |
ロンドン・ナショナル・ギャラリー |
まずこの絵の特徴は「二重空間」の絵だということです。手前の "空間" には厨房で働く娘と老婆がいます。老婆は明らかに「卵を料理する老婆」と同じモデルです。娘は何となく泣きそうな感じで、老婆は後ろの "空間" を指さして娘に何かを言っています。
一方、後ろの "空間" にはキリストとマルタとマリアが描かれています。マリアは座ってキリストの言葉を聴いています。立っているのがマルタでしょうが、彼女がどういう態度を示しているのか、絵を見ただけでは判然としません。この後ろの "空間" については、
| 隣の別の部屋 | |
| 壁に掛けられた鏡 | |
| 絵 |
という3つの解釈があるそうです。ただ "鏡" という解釈には無理があると思われます。というのも、このような大きな鏡、しかも四角い平面鏡は、キリストの時代にも、この絵が描かれた17世紀にも稀少、ないしはまずないからです。平面鏡のためには平面ガラスが必要ですが、作るためには高度な技術が必要です。それは、ベラスケスの「ラス・メニーナス」に描かれたスペイン宮殿の鏡も "小ぶりで丸みを帯びている" ことからも分かります。仮に四角い平面鏡があったとしても、国王の宮殿ならともかく、庶民の厨房に掛けるようなものではないでしょう。
隣の別の部屋という解釈はどうでしょうか。後ろの "空間" が別の部屋ということは、厨房に四角い "窓" があいていて、そこから向こうの部屋が見えるということになります。このような作りの厨房は考えにくいと思います。
ということで、後ろの "空間" は絵とするのが妥当でしょう。この絵が描かれた17世紀には、新約聖書の「マルタとマリア」の解釈として「世俗的な生」と「信仰の生」の両方が大切だと考えられていたようです。ということは、厨房を手伝わないマリアの態度に不平をもらしたマルタはよくない、厨房の仕事も大切だという "戒め" として絵が掛けてあると解釈できます。
娘はなんだか涙目で、不満そうな顔をしています。ニンニクを金属製器具ですりつぶしているようですが、老婆に厨房での仕事について何らかの厳しい注意、ないしは叱責ををされた。それで不満そうな涙目になった。それを見た老婆は「マルタとマリア」の絵を指さして、不満をもつのはよくない、調理は大切で立派な仕事だと諭している、そういう光景に見えます。
とは言うものの、後ろの "空間" が「鏡」か「別の部屋」か「絵」かは、画家にとってはどうでもよいのでしょう。つまり、後ろの "空間" はこの絵が「マルタとマリアの家のキリスト」を描いたと言うための "口実" であって、画家の本当の狙いは「厨房を描く」ことだったと考えられるのです。特に、前景にある「金属製の器具」「4匹の魚」「2つの卵」、その他、器具の前にあるニンニクなどです。これらのリアリズムに徹した描写が、この絵の最大のポイントと思えます。魚の部分図を以下に掲げます。

|
絵の最大の狙いが静物の描写にあることは、この魚を描いた部分を見るだけでも一目瞭然だと思います。そして画家の第2の狙いをあげるとすると、庶民の労働を描くことでしょう。
さまざまな解釈を生む絵がありますが、絵そのものが画家の意図を雄弁に語っているケースがあります。この絵もそうだと思います。
余談ですが、このベラスケスの作品から、ある浮世絵を思い出しました。歌川国貞の「江戸百景の内 三廻」です(No.295「タンギー爺さんの画中画」の「補記」に画像を掲載)。題名だけを見ると風景画です。しかし、隅田川河畔の三廻神社が描かれているのは画面の左上の小さな四角(浮世絵の用語では "こま")の中だけで、本当の画題は中央に大きく描かれている女性、つまり美人画である、という浮世絵(いわゆる "こま絵")です。
この状況はベラスケスの「マルタとマリアの家のキリスト」にそっくりです。世の東西に関わらず、似たような発想の絵があるものです。
フェルメール
ベラスケスを離れて、同じ新約聖書のシーンを描いた作品を振り返ってみます。その有名作品として、「卵を料理する老婆」と同じくスコットランド国立美術館が所蔵するフェルメールの「マルタとマリアの家のキリスト」があります。この絵も 2018年のフェルメール展で展示されました(上野の森美術館)。

|
ヨハネス・フェルメール(1632-1675) 「マルタとマリアの家のキリスト」(1654/55) |
スコットランド国立美術館 |
フェルメールが20代前半の初期の作品です。フェルメールは画家としての初期に宗教画を描き、その後は宗教画を離れて風俗画(と風景画)を描くようになったことで知られています。
この絵はベラスケスと違って、聖書に登場する3者だけを描いています。左に描かれているのがマリアで、キリストの話に聞き入っています。中央に描かれているのはマルタで、キリストにパンを差し出しています。聖書通りだとマルタはここでキリストに不平を言い、キリストはマリアを指さしつつマルタを諭しているはずです。
しかしそうだとしても、マルタの不平の表現は抑制されています。それよりも、パンを差し出す、つまりキリストを接待している表現の方を強く感じる。また、マルタは三角形の安定した構図の中心に描かれています。光の当て方も含めて、彼女が構図の焦点のように感じられます。
この絵は、聖書のストーリーを忠実に再現したと説明されれば、そう見えないことはない。しかし聖書とは裏腹に、マリアはキリストの話に聴き入り、マルタは厨房で仕事をしたあと(ないしは仕事の途中で)キリストを接待するという "調和的な状況" が描かれているとも見える。つまり「活動的なマルタ」と「瞑想的なマリア」が人間の両面を表し、かつ、構図の焦点であるマルタの重要性 = 世俗的な労働の大切さが強調されているようです。
おそらくこれは画家の(ないしは当時のオランダ社会の)聖書解釈を反映しているのだと思います。
ウテワール
そのフェルメールの絵より約70年前に描かれた「マルタとマリア」を主題にした絵があります。同じオランダの画家、ウテワールの「台所のメイド」です。

|
ヨアヒム・ウテワール(1566-1638) 「台所のメイド」(1620/25) |
ユトレヒト中央美術館(オランダ) |
この絵については、東京都美術館の学芸員、高城靖之氏が日本経済新聞に解説を書いていました。それを引用します。
|
この絵で奥の部屋に描かれているマルタ、マリア、キリストは、まさに聖書の記述に従っています。というのも、マルタがマリアの態度に怒っているそぶりだからです。彼女は鍋を持ったまま、キリストとマリアのところに出てきて怒っている。
しかしベラスケスと同じで、この絵の主題はマルタとマリアの家のメイドを主人公にした前景の厨房です。そこには「静物」として、鳥、串、魚、肉、野菜、チーズ、パン、ワインの注がれたグラス、陶器、金属食器といった、質感の異なるさまざまなものがあり、高城氏が書いているように「質感や色彩を巧みに描き分けている画家の描写力」が見事です。その "静物の質感表現" こそ、この絵の第1のポイントでしょう。
そして第2のポイントは、鳥を串に刺しているメイド(高城氏の文章では女中)の表現です。腕と指を見ても分かるように、彼女はいかにもたくましく、働き者で、厨房での仕事を次々とこなし、家の食卓を一手に引き受けているような感じです。しかも調理に喜びをもって取り組んでいるように見える。労働は尊い、というメッセージ性を感じます。
以上の「マルタとマリア」の3作品に共通するのは、
| 労働は大切という考え(3作品) | |
| 聖書を "引き合いに" して厨房を描く。特に、静物の質感を油絵の技術を駆使して描き分ける(ウテワールとベラスケス) |
と言えるでしょう。一見して "不可解" な新約聖書のエピソードを画題にすることで、宗教画の変貌がわかる3作品だと思います。
2022-08-13 11:22
nice!(0)
No.342 - ヒトは自己家畜化で進化した [科学]
No.299「優しさが生き残りの条件だった」は、雑誌・日経サイエンス2020年11月号に掲載された、米・デューク大学のブライアン・ヘア(Brian Hare)とヴァネッサ・ウッズ(Vanessa Woods)による「優しくなければ生き残れない」と題した論文の紹介でした。これは、人類(=ホモ族)の中でホモ・サピエンス(=現生人類)だけが生き残って地球上で繁栄した理由を説明する "自己家畜化仮説" を紹介したものです。
"自己家畜化仮説" の有力な証拠となったのは、旧ソ連の遺伝学者、ドミトリ・ベリャーエフ(1917-1985)が始め、現在も続いている「キツネの家畜化実験」です。この実験のことは No.211「狐は犬になれる」に書きました。この実験がなければ "自己家畜化仮説" は生まれなかったと思われます。"自己家畜化" というと、なんだか "おどろおどろしい" 語感がありますが、進化人類学で定義された言葉です。
ところで、ブライアン・ヘアとヴァネッサ・ウッズ(以下「著者」と記述)の論文の原題は「Survival of the Friendliest」(Scientific American誌)です。直訳すると「最も友好的なものが生き残る」という意味です。これはもちろん、進化論で言われる "Survival of the Fittest"(適者生存)の "もじり" です。適者生存とは、自然環境・生存環境に最も適した生物が生き残ることで生物が変化(=進化)し、多様化してきたという、進化論の原理を表現しています。それをもじって "the friendliest=最も友好的な者" としたわけです。
その著者は論文と同じ題名の本を2020年に出版し、2022年に日本語訳が出版されました。
Brian Hare & Vanessa Woods
"Survival of the Friendliest"
ブライアン・ヘア、ヴァネッサ・ウッズ
「ヒトは <家畜化> して進化した」
藤原多伽夫 訳(白揚社 2022.6)
です(以下「本書」と記述)。今回はこの本の内容の一部を紹介します。もちろん、論文と基本のところの主旨は同じなのですが、単行本ならではの詳細な記述もあります。
問題提起:ホモ・サピエンスの大変化
現生人類(=ホモ・サピエンス。以下ヒト、または人間)がアフリカで誕生したのは、およそ20万年~30万年前です。その時、すでに少なくとも4種の人類が生存していて世界に拡散していました。その中で最も古いのはホモ・エレクトスで、180万年前にはアフリカを出てユーラシア大陸に散らばっていました。ホモ・サピエンスが誕生したときに使った道具にハンドアックス(握斧)がありますが、それは150万年前にホモ・エレクトスが考案したものとほぼ同様の石器でした。
75,000年前(氷河期)の時点で考えると、当時最も繁栄していた人類はネアンデルタール人です。ネアンデルタール人の脳はヒトと同じかそれより大きく、身長はヒトと同じくらいでしたが、体重はヒトより重かった。彼らは長い槍で獲物を狩る優秀なハンターでした。
著者は「75,000年前に、どの人類がその後の不確かな気候のもとで生き残れるかについて賭けをしたなら、ネアンデルタール人が本命だっただろう」と書いています。しかし、5万年前になると状況は明らかにヒトに有利になってきました。著者はその例として、ヒトが作り出した道具を紹介しています。
ヒトはアフリカを出て、またたく間にユーラシア大陸に拡散し、さらに東南アジアの島からオーストラリア大陸に到達しました。
25,000年前までに、ヒトは数百人規模で野営地に定住し、調理用の道具や竈を作り、骨製の細い針を使って毛皮で防寒用の衣服を作りました。また、海から何百キロも離れたところで貝殻の装飾品が見つかりますが、これは社会的ネットワークの存在を示しています。定住地の岩には生き生きとした動物の絵を描きました。
これらをまとめて著者は「行動が現代化した」と書いています。つまり当時のヒトは現代人と同じようなみかけであり、似たような行動をとっていたわけです。
5万年前以降のヒトの大変化はどのようにして起きたのでしょうか。なぜヒト(現世人類)だけに起きたのでしょうか。これが本書の問題提起です。その一番の理由を、著者はヒトが獲得した「協力的コミュニケーション」の能力だとしています。
著者の言う「協力的コミュニケーション」とは、他者に対する(特殊なタイプの)友好性です。この友好性が進化した要因が「自己家畜化」です。
しかしながら、友好性を獲得すると同時にヒトは "非人間化した他者" に対する残虐性も発揮するようになりました。日本語訳の副題に「私たちはなぜ寛容で残酷な生き物になったのか」とあるのはそのことです。
以上が全体の主旨ですが、以降は自己家畜化仮説を裏付けるエビデンスです。その一つは、ヒトが生来持っている「協力的コミュニケーション」で、それは "他者の考えについて考える" 能力です。
"他者の考えについて考える" 能力
ヒトの「協力的コミュニケーション」の最初の発揮として、著者は赤ちゃんの頃から始まる "指さし" 行動を取り上げています。
心理学では「心の理論(Theory of Mind)」という用語が使われます。これは他者の心や意図を推察する能力のことです。指さしは「心の理論」の入り口です。
イヌは "指さし" の意図を読める
「他者が行う指さしを見て、その意図を推察できる能力」は、他の動物ではどうなのでしょうか。たとえば、人間に最も近いとされるチンパンジーです。著者がマイケル(マイク)・トマセロ博士のもとで行った研究が書かれています。
チンパンジーが食べ物を得るためには「人間との協調」と「人間とのコミュニケーション」が同時にできなければなりません。チンパンジーにとってはこれが難しい。
しかしイヌはできるのです。著者は自分の愛犬(名はオレオ)で実験したときのことが書かれています。
著者はイヌが「指さしの意図を理解している」のではない可能性(たとえば餌の臭いを感知している)を調べるため、さまざまな実験を繰り返しました。もちろん自分の愛犬以外にも、イヌの一時預かり所に出向いて実験を繰り返しましたが、いずれの場合もイヌはパスしました。イヌはチンパンジーと違って、試行錯誤で指の方向に餌があることを学ぶのではないのです。
人間の赤ちゃんとイヌに共通するこの「協力的コミュニケーション」の能力は、どのようにして発達したのでしょうか。イヌは氷河期にオオカミの先祖をヒトが家畜化したものと考えられています。この家畜化の過程で能力を獲得した(能力が進化した)と考えることができます。
実は、このことを検証するのに格好の素材があります。それは旧ソ連の遺伝学者、ドミトリ・ベリャーエフが始めた "キツネを家畜化する実験" です。この実験は No.211「狐は犬になれる」で紹介しましたが、もちろん本書にも詳しく書かれています。
友好的であることの力:キツネの家畜化実験
著書はドミトリ・ベリャーエフの実験の記述の前に、兄のニコライのことから始めています。兄のことは初めて知りました。
著者はベリャーエフの実験を「20世紀の行動遺伝学の金字塔」と書いていますが、まさにその通りでしょう。
ベリャーエフ(1917-1985)は人生のあいだこの実験を続け、彼の死後はリュドミラ・トルート(1933 -)が実験を引き継ぎました。
動物は家畜化すると、さまざまな形質が共通して現れることが知られています。これらは、人間の都合によってそれぞれの形質が選別されてきたと考えられてきました。
家畜化にともなって、一見ランダムに見えるさまざまな形質がまとまって現れます。これらを「家畜化症候群」と呼ぶことがあります。ベリャーエフは、たった一つの条件でこのような家畜化が起こると考えたのです。それは、ダーウィン以来、誰一人として思いつかなかった天才的な考えであり、それが正しいことが実験で明らかになったのです。
著者は、ベリャーエフの弟子であるリュドミラ・トルートが現在も行っているシベリアの実験場を訪問しました。その時のことが書かれています。
友好的というキツネの行動が遺伝的なものであることを示すために、ベリャーエフとリュドミラは次のような実験をしました。
しかし、産んだ母親も育てた母親も結果には影響しませんでした。友好的なキツネは受精したときから、普通のキツネよりも友好的だったのです。"友好的という行動が遺伝する" わけです。
キツネの指さし実験
実は、著者がキツネの飼育施設を訪問したのは見学だけが目的ではありませんでした。イヌでやったような「指さし実験」をするためだったのです。
その実験をするために「友好的な子キツネのグループ」と「普通の子キツネのグループ」を用意します。まず、生後数週間の普通の子キツネを10匹程度選び、著者の助手(ナタリー)に慣れさせます。この時期の子キツネは人間を恐れる機構が発達していないので、慣れさせることができます。そしてボウル状の容器の下に餌を隠し、その餌を見つけられるように訓練します。これが「普通の子キツネのグループ」とします。
また「友好的な子キツネのグループ」としては、生後3~4ヶ月の、友好的として選別されたばかりのキツネを選びました。
9週間に渡ってヒトに慣れさせる(=社会化)訓練をしたにもかかわらず、普通のキツネは指さしジェスチャーの意図を理解できなかったのです。一方、友好的なキツネはどうだったか。
友好的なキツネは、"指さしに反応して餌を見つける" というゲームを一度もやったことがなかったにもかかわらず、イヌ並みの成績をあげたのです。このことは、
ということを意味します。
オオカミがやってきてイヌになった
以上を踏まえて、オオカミが家畜化されてイヌになったプロセスはどのように推測できるでしょうか。
一般に想定されているシナリオでは、農耕民がオオカミの子を何匹か捕まえて住居に持ち帰り、従順な子を繁殖させてイヌにした、というものです。しかしこのシナリオは非現実的です。というのも、遺伝子の研究からオオカミの家畜化は農耕の開始より前、遅くとも1万年前には始まっていたからです。つまりオオカミの家畜化が始まったのは氷河時代と考えられるのです。
著者が考える「オオカミがイヌになったシナリオ」は次の通りで、これが "自己家畜化" です。
そして、このような家畜化がヒトにも起こった。つまり、
とするのが「自己家畜化仮説」です。
自己家畜化仮説の証拠はあるか
では、ホモ・サピエンスに自己家畜化のプロセスがあったという証拠はあるのでしょうか。
家畜化された動物は、ヒトに友好的になると同時に身体に特徴的な変化が現れます。ロシアの友好的なキツネでは、選抜によってホルモンに変化が生じました。こうしたホルモンがキツネの成長の仕方(身体と行動)を変えたのです。
ヒトにも外見や行動の発達を調整するホルモンがあります。その一つのテストステロンは、濃度が高いと他のホルモンとの相互作用で攻撃性が高まります。同時に、成長期にテストステロンの濃度が高いと眉弓(眉のところの弓形の骨。眉弓骨)の突起が高くなります。
ホモ・サピエンスの頭蓋骨の化石、1421点を調査したところ、更新世後期(38000年前~1万年前)の眉弓の突起は、更新世中期(20万年前~9万年前)のものより 平均で 40% 低くなっていました。
アンドロゲンというホルモンがあります。妊娠中にこのホルモンの濃度が高いと、人差し指の長さに対する薬指の長さ(= 2D:4D 比)が長くなる傾向にあります。2D:4D 比が小さいと「男性化した」と見なせて、危険を冒す度合いや攻撃性が高まります。
研究によると、更新世中期のホモ・サピエンスの2D:4D 比は現代人より小さく、より「男性的」であったことが分かりました。またそれよりさらに男性的なのがネアンデルタール人でした。つまりホモ・サピエンスは現代人になる過程において、2D:4D 比が高まり、より女性的になったと言えます。
家畜化が身体に与える影響の一つが「脳の小型化」です。脳が小型化すれば頭蓋骨も小さくなります。ヒトの知能が最も発達したのは過去2万年です。農耕が始まる前の1万年と始まって以降の1万年を比較すると、平均で頭蓋骨容量が 5% 小さくなっていました。
家畜化された動物の脳を小さくする最大の要因は、セロトニンというホルモンです。キツネの家畜化実験でもわかるように、家畜化された動物の攻撃性が低下するにつて、体内のセロトニン濃度が増加します。このホルモンが高まると友好的な感情が高まることが知られています。
以上が、化石資料がら類推できる家畜化=友好性の発達の例ですが、著者はこれとは別に、ヒトの「協力的コミュニケーション」を発達させた要因として「白い強膜」をあげています。強膜とは眼球の外側の白い皮膜のことで、眼球の前方で角膜とつながっています。いわゆる「しろ目」のことです。
強膜が白いのはヒトの特徴です。霊長類の中で白い強膜をもっている(=強膜を黒くする色素を失った)のは、ヒトだけです。白い強膜だと視線を感じることができ、アイコンタクトが可能で、他者の視線を追うこともでき、「協力的コミュニケーション」にピッタリなのです。
友好性が新たな攻撃性を生んだ
ヒトは自己家畜化の過程において、自分の属する集団を想定し、その集団を家族のように感じる能力を発達させました。一度も合ったことがない他者でも、その他者が仲間かどうかを見分け、同じ集団に属していると認識するこができます。著者は、こういった集団アイデンティティーの発達を促したのが、オキシトシンというホルモンだと推定しています。
しかし、このことは「集団に属さないと認識した他者」への、新たな攻撃性を生むことになりました。
人間は、自分の集団ではないと認識した他者を「非人間化」できます。そして非人間化した他者に対してはどんな暴力をふるうこともできる。これは今までもそうだったし、現在、その傾向がますます高まっています。
しかし、集団のアイデンティティー認識は、生物学的根拠のあるものではありません。その認識は人間が変えられる。著者は、同じ集団であると認識する一番の鍵は "接触" だと主張しています。人と人の接触がまず必要で、それが第1歩です。
本書全体を通して
本書は次の2つの論を並行して進めるという体裁をとっています。
の2点です。今まで紹介したのは ① の部分です。しかし著者が本を書いた意図は ② の部分も大いにあるのです。
進化人類学の立場から ② に踏み込むことは、論を広げすぎのように感じます。しかし「友好性をもつ人間が集まったとき、最大のパフォーマンスを発揮できる」というのは全くの事実です。それが、進化人類学の視点からも裏付けられて、友好性をもつからこそヒトはヒトになったと言える。そうであれば、現在の世界の状況に対して是非とも発言したいと思ったのは理解できます。
本書の原題は、最初に書いたように、
ですが、これはヒトが生き残って繁栄した理由であると同時に、現在の人類が今後地球上で "サバイバル" できる鍵である。そう著者は言いたいのだと思いました。
"自己家畜化仮説" の有力な証拠となったのは、旧ソ連の遺伝学者、ドミトリ・ベリャーエフ(1917-1985)が始め、現在も続いている「キツネの家畜化実験」です。この実験のことは No.211「狐は犬になれる」に書きました。この実験がなければ "自己家畜化仮説" は生まれなかったと思われます。"自己家畜化" というと、なんだか "おどろおどろしい" 語感がありますが、進化人類学で定義された言葉です。
ところで、ブライアン・ヘアとヴァネッサ・ウッズ(以下「著者」と記述)の論文の原題は「Survival of the Friendliest」(Scientific American誌)です。直訳すると「最も友好的なものが生き残る」という意味です。これはもちろん、進化論で言われる "Survival of the Fittest"(適者生存)の "もじり" です。適者生存とは、自然環境・生存環境に最も適した生物が生き残ることで生物が変化(=進化)し、多様化してきたという、進化論の原理を表現しています。それをもじって "the friendliest=最も友好的な者" としたわけです。
その著者は論文と同じ題名の本を2020年に出版し、2022年に日本語訳が出版されました。
Brian Hare & Vanessa Woods
"Survival of the Friendliest"
| Understanding Our Origins and Rediscovering Our Common Humanity(我々の起源を理解し、我々に共通な人間性を再発見する) |
ブライアン・ヘア、ヴァネッサ・ウッズ
「ヒトは <家畜化> して進化した」
| 私たちはなぜ寛容で残酷な生き物になったのか |
です(以下「本書」と記述)。今回はこの本の内容の一部を紹介します。もちろん、論文と基本のところの主旨は同じなのですが、単行本ならではの詳細な記述もあります。
以下の引用では原則として漢数字を算用数字に直しました。また段落を増やしたところがあります。
問題提起:ホモ・サピエンスの大変化
|
75,000年前(氷河期)の時点で考えると、当時最も繁栄していた人類はネアンデルタール人です。ネアンデルタール人の脳はヒトと同じかそれより大きく、身長はヒトと同じくらいでしたが、体重はヒトより重かった。彼らは長い槍で獲物を狩る優秀なハンターでした。
|
著者は「75,000年前に、どの人類がその後の不確かな気候のもとで生き残れるかについて賭けをしたなら、ネアンデルタール人が本命だっただろう」と書いています。しかし、5万年前になると状況は明らかにヒトに有利になってきました。著者はその例として、ヒトが作り出した道具を紹介しています。
|
ヒトはアフリカを出て、またたく間にユーラシア大陸に拡散し、さらに東南アジアの島からオーストラリア大陸に到達しました。
|
25,000年前までに、ヒトは数百人規模で野営地に定住し、調理用の道具や竈を作り、骨製の細い針を使って毛皮で防寒用の衣服を作りました。また、海から何百キロも離れたところで貝殻の装飾品が見つかりますが、これは社会的ネットワークの存在を示しています。定住地の岩には生き生きとした動物の絵を描きました。
これらをまとめて著者は「行動が現代化した」と書いています。つまり当時のヒトは現代人と同じようなみかけであり、似たような行動をとっていたわけです。
5万年前以降のヒトの大変化はどのようにして起きたのでしょうか。なぜヒト(現世人類)だけに起きたのでしょうか。これが本書の問題提起です。その一番の理由を、著者はヒトが獲得した「協力的コミュニケーション」の能力だとしています。
|
著者の言う「協力的コミュニケーション」とは、他者に対する(特殊なタイプの)友好性です。この友好性が進化した要因が「自己家畜化」です。
|
しかしながら、友好性を獲得すると同時にヒトは "非人間化した他者" に対する残虐性も発揮するようになりました。日本語訳の副題に「私たちはなぜ寛容で残酷な生き物になったのか」とあるのはそのことです。
|
以上が全体の主旨ですが、以降は自己家畜化仮説を裏付けるエビデンスです。その一つは、ヒトが生来持っている「協力的コミュニケーション」で、それは "他者の考えについて考える" 能力です。
"他者の考えについて考える" 能力
ヒトの「協力的コミュニケーション」の最初の発揮として、著者は赤ちゃんの頃から始まる "指さし" 行動を取り上げています。
|
心理学では「心の理論(Theory of Mind)」という用語が使われます。これは他者の心や意図を推察する能力のことです。指さしは「心の理論」の入り口です。
|
イヌは "指さし" の意図を読める
「他者が行う指さしを見て、その意図を推察できる能力」は、他の動物ではどうなのでしょうか。たとえば、人間に最も近いとされるチンパンジーです。著者がマイケル(マイク)・トマセロ博士のもとで行った研究が書かれています。
|
チンパンジーが食べ物を得るためには「人間との協調」と「人間とのコミュニケーション」が同時にできなければなりません。チンパンジーにとってはこれが難しい。
しかしイヌはできるのです。著者は自分の愛犬(名はオレオ)で実験したときのことが書かれています。
|
著者はイヌが「指さしの意図を理解している」のではない可能性(たとえば餌の臭いを感知している)を調べるため、さまざまな実験を繰り返しました。もちろん自分の愛犬以外にも、イヌの一時預かり所に出向いて実験を繰り返しましたが、いずれの場合もイヌはパスしました。イヌはチンパンジーと違って、試行錯誤で指の方向に餌があることを学ぶのではないのです。
|
人間の赤ちゃんとイヌに共通するこの「協力的コミュニケーション」の能力は、どのようにして発達したのでしょうか。イヌは氷河期にオオカミの先祖をヒトが家畜化したものと考えられています。この家畜化の過程で能力を獲得した(能力が進化した)と考えることができます。
実は、このことを検証するのに格好の素材があります。それは旧ソ連の遺伝学者、ドミトリ・ベリャーエフが始めた "キツネを家畜化する実験" です。この実験は No.211「狐は犬になれる」で紹介しましたが、もちろん本書にも詳しく書かれています。
友好的であることの力:キツネの家畜化実験
著書はドミトリ・ベリャーエフの実験の記述の前に、兄のニコライのことから始めています。兄のことは初めて知りました。
|
著者はベリャーエフの実験を「20世紀の行動遺伝学の金字塔」と書いていますが、まさにその通りでしょう。
|
ベリャーエフ(1917-1985)は人生のあいだこの実験を続け、彼の死後はリュドミラ・トルート(1933 -)が実験を引き継ぎました。
動物は家畜化すると、さまざまな形質が共通して現れることが知られています。これらは、人間の都合によってそれぞれの形質が選別されてきたと考えられてきました。
|
家畜化による変化と特徴 |
動物を家畜化することで、さざまな形質、特徴が共通して現れる。これらを「家畜化症候群」と呼ぶことがある。図は本書の p.58-59 から引用。 |
|
家畜化にともなって、一見ランダムに見えるさまざまな形質がまとまって現れます。これらを「家畜化症候群」と呼ぶことがあります。ベリャーエフは、たった一つの条件でこのような家畜化が起こると考えたのです。それは、ダーウィン以来、誰一人として思いつかなかった天才的な考えであり、それが正しいことが実験で明らかになったのです。
著者は、ベリャーエフの弟子であるリュドミラ・トルートが現在も行っているシベリアの実験場を訪問しました。その時のことが書かれています。
|
友好的というキツネの行動が遺伝的なものであることを示すために、ベリャーエフとリュドミラは次のような実験をしました。
| 友好的なキツネの子を、誕生時に普通のキツネの子と取り替え、普通のキツネの子が友好的な母親の行動に影響されるかどうかを見る。 | |
| 友好的なキツネの受精卵を普通のキツネの子宮に移植する。 | |
| 普通のキツネの受精卵を、友好的なキツネの子宮に移植する。 |
しかし、産んだ母親も育てた母親も結果には影響しませんでした。友好的なキツネは受精したときから、普通のキツネよりも友好的だったのです。"友好的という行動が遺伝する" わけです。
キツネの指さし実験
実は、著者がキツネの飼育施設を訪問したのは見学だけが目的ではありませんでした。イヌでやったような「指さし実験」をするためだったのです。
その実験をするために「友好的な子キツネのグループ」と「普通の子キツネのグループ」を用意します。まず、生後数週間の普通の子キツネを10匹程度選び、著者の助手(ナタリー)に慣れさせます。この時期の子キツネは人間を恐れる機構が発達していないので、慣れさせることができます。そしてボウル状の容器の下に餌を隠し、その餌を見つけられるように訓練します。これが「普通の子キツネのグループ」とします。
また「友好的な子キツネのグループ」としては、生後3~4ヶ月の、友好的として選別されたばかりのキツネを選びました。
|
9週間に渡ってヒトに慣れさせる(=社会化)訓練をしたにもかかわらず、普通のキツネは指さしジェスチャーの意図を理解できなかったのです。一方、友好的なキツネはどうだったか。
|
友好的なキツネは、"指さしに反応して餌を見つける" というゲームを一度もやったことがなかったにもかかわらず、イヌ並みの成績をあげたのです。このことは、
ヒトに対して友好的という、たった一つの基準で選別してきたキツネは、数々の家畜化症候群を発現させるとともに、協力的コミュニケーションの能力を獲得した
ということを意味します。
オオカミがやってきてイヌになった
以上を踏まえて、オオカミが家畜化されてイヌになったプロセスはどのように推測できるでしょうか。
一般に想定されているシナリオでは、農耕民がオオカミの子を何匹か捕まえて住居に持ち帰り、従順な子を繁殖させてイヌにした、というものです。しかしこのシナリオは非現実的です。というのも、遺伝子の研究からオオカミの家畜化は農耕の開始より前、遅くとも1万年前には始まっていたからです。つまりオオカミの家畜化が始まったのは氷河時代と考えられるのです。
著者が考える「オオカミがイヌになったシナリオ」は次の通りで、これが "自己家畜化" です。
|
そして、このような家畜化がヒトにも起こった。つまり、
| 友好的な個体が選別されていくと(=家畜化すると)、社会的能力(協力的コミュニケーションなど)が発達する。 | |
| 社会的能力をもつ個体がより有利で生き残りやすくなる条件があると、自然選択による家畜化、つまり自己家畜化が起きる。 | |
| ホモ・サピエンスは自己家畜化の過程を経て生き残り、繁栄した。 |
とするのが「自己家畜化仮説」です。
自己家畜化仮説の証拠はあるか
では、ホモ・サピエンスに自己家畜化のプロセスがあったという証拠はあるのでしょうか。
家畜化された動物は、ヒトに友好的になると同時に身体に特徴的な変化が現れます。ロシアの友好的なキツネでは、選抜によってホルモンに変化が生じました。こうしたホルモンがキツネの成長の仕方(身体と行動)を変えたのです。
ヒトにも外見や行動の発達を調整するホルモンがあります。その一つのテストステロンは、濃度が高いと他のホルモンとの相互作用で攻撃性が高まります。同時に、成長期にテストステロンの濃度が高いと眉弓(眉のところの弓形の骨。眉弓骨)の突起が高くなります。
ホモ・サピエンスの頭蓋骨の化石、1421点を調査したところ、更新世後期(38000年前~1万年前)の眉弓の突起は、更新世中期(20万年前~9万年前)のものより 平均で 40% 低くなっていました。
アンドロゲンというホルモンがあります。妊娠中にこのホルモンの濃度が高いと、人差し指の長さに対する薬指の長さ(= 2D:4D 比)が長くなる傾向にあります。2D:4D 比が小さいと「男性化した」と見なせて、危険を冒す度合いや攻撃性が高まります。
研究によると、更新世中期のホモ・サピエンスの2D:4D 比は現代人より小さく、より「男性的」であったことが分かりました。またそれよりさらに男性的なのがネアンデルタール人でした。つまりホモ・サピエンスは現代人になる過程において、2D:4D 比が高まり、より女性的になったと言えます。
家畜化が身体に与える影響の一つが「脳の小型化」です。脳が小型化すれば頭蓋骨も小さくなります。ヒトの知能が最も発達したのは過去2万年です。農耕が始まる前の1万年と始まって以降の1万年を比較すると、平均で頭蓋骨容量が 5% 小さくなっていました。
家畜化された動物の脳を小さくする最大の要因は、セロトニンというホルモンです。キツネの家畜化実験でもわかるように、家畜化された動物の攻撃性が低下するにつて、体内のセロトニン濃度が増加します。このホルモンが高まると友好的な感情が高まることが知られています。
以上が、化石資料がら類推できる家畜化=友好性の発達の例ですが、著者はこれとは別に、ヒトの「協力的コミュニケーション」を発達させた要因として「白い強膜」をあげています。強膜とは眼球の外側の白い皮膜のことで、眼球の前方で角膜とつながっています。いわゆる「しろ目」のことです。
強膜が白いのはヒトの特徴です。霊長類の中で白い強膜をもっている(=強膜を黒くする色素を失った)のは、ヒトだけです。白い強膜だと視線を感じることができ、アイコンタクトが可能で、他者の視線を追うこともでき、「協力的コミュニケーション」にピッタリなのです。
友好性が新たな攻撃性を生んだ
ヒトは自己家畜化の過程において、自分の属する集団を想定し、その集団を家族のように感じる能力を発達させました。一度も合ったことがない他者でも、その他者が仲間かどうかを見分け、同じ集団に属していると認識するこができます。著者は、こういった集団アイデンティティーの発達を促したのが、オキシトシンというホルモンだと推定しています。
|
しかし、このことは「集団に属さないと認識した他者」への、新たな攻撃性を生むことになりました。
|
人間は、自分の集団ではないと認識した他者を「非人間化」できます。そして非人間化した他者に対してはどんな暴力をふるうこともできる。これは今までもそうだったし、現在、その傾向がますます高まっています。
しかし、集団のアイデンティティー認識は、生物学的根拠のあるものではありません。その認識は人間が変えられる。著者は、同じ集団であると認識する一番の鍵は "接触" だと主張しています。人と人の接触がまず必要で、それが第1歩です。
本書全体を通して
本書は次の2つの論を並行して進めるという体裁をとっています。
| ヒトは自己家畜化(=友好性をもつ個体が自然選択される)の過程を経て生き残り、社会を作り、繁栄した。と同時に、他者に対する新たな攻撃性を持ってしまった。 | |
| 現在、世界で起こっている(特にアメリカで起こっている)暴力、差別、分断を憂い、それを解決する提言を行う。 |
の2点です。今まで紹介したのは ① の部分です。しかし著者が本を書いた意図は ② の部分も大いにあるのです。
進化人類学の立場から ② に踏み込むことは、論を広げすぎのように感じます。しかし「友好性をもつ人間が集まったとき、最大のパフォーマンスを発揮できる」というのは全くの事実です。それが、進化人類学の視点からも裏付けられて、友好性をもつからこそヒトはヒトになったと言える。そうであれば、現在の世界の状況に対して是非とも発言したいと思ったのは理解できます。
本書の原題は、最初に書いたように、
Survival of the Friendliest
ですが、これはヒトが生き残って繁栄した理由であると同時に、現在の人類が今後地球上で "サバイバル" できる鍵である。そう著者は言いたいのだと思いました。
2022-07-31 08:58
nice!(0)
No.341 - ベラスケス:卵を料理する老婆 [アート]
今まで何回か書いたベラスケスについての記事の続きです。2022年4月22日 ~ 7月3日まで、東京都美術館で「スコットランド国立美術館展」が開催され、ベラスケスの「卵を料理する老婆」が展示されました。初来日です。今回はこの絵について書きます。
卵を料理する老婆
この絵は、No.230「消えたベラスケス(1)」で紹介しました。No.230 は、英国の美術評論家、ローラ・カミングの著書「消えたベラスケス」の内容を紹介したものです。この中で著者は、8歳のときに両親に連れられて行ったエディンバラのスコットランド国立美術館で見たのがこの絵だった、と書いていました。彼女の父親は画家です。画家はこの絵を8歳になった娘に見せた。8歳であればこの絵の素晴らしさが理解できると信じたのでしょう。案の定、これはローラ・カミングにとっての特別な体験だったようで、ここから彼女の "ベラスケス愛" が始まった。そして後年、「消えたベラスケス」のような本を書くに至った。そいういうことだと思います。
No.230 に続いて、「卵を料理する老婆」について書かれたローラ・カミングの文章再度引用します。
老婆が作っている卵料理は「ウエボ・フリート」(Huevo frito。スペイン風目玉焼き)です。「ウエボ」が "卵"、「フリート」は "揚げた" という意味で、現代のスペインでも作ります。ニンニクを入れたオリーブオイルを鍋にたっぷり入れ、卵を割って、上からスプーンでオリーブオイルをかけながら揚げるように焼きます。この絵の真鍮の容器と道具はニンニクを磨り潰すためのものでしょう。「目玉焼き」よりは「目玉揚げ」「揚げ卵」と言った方が実態に即しているでしょう。
驚くべき精緻さで描かれた物たちの中でも、ひときわ目立つのがこのウエボ・フリートの卵です。液体から半液体、半固体、固体へと変化する様子がとらえられています。絵には数々の "静物" が描かれていますが、鍋の中で固まりつつある卵は、その "静物" の一つです。しかしそれは、変化しつつある "動的実体" です。まるで時間の経過を画面に捉えたようです。一般に絵画では人物やモノ、自然の「動き」を描くことで時間経過を捉えるのはよくありますが、この絵は動かないものの動き =「物体が変質するという動き」が描かれている。そこがポイントです。
そのウエボ・フリートを作っている老婆は、3個目の卵を鍋に入れようとしています。少年はガラス瓶を持っていますが、おそらくオリーブオイルが入っているのでしょう。それをこれから老婆のスプーンの注ごうとしている(ないしは指示があれば注ごうと待ち構えている)ようです。この調理の動作が2つめの「動き」です。それに加えて、絵には数々のアイテムが描かれています。つまり、
などで、それぞれの質感が完璧に描き分けられています。もちろん、質感表現と言うなら最初にあげた「固まりつつある卵」がその筆頭です。モノの質感表現に挑んだ絵画は過去から現在までヤマほどありますが、「熱によって変質しつあるタンパク質の表現」をやってのけた絵画は(そしてそれに成功した絵画は)、これが唯一ではないでしょうか。
一方、構図をみると、この絵の構造線は、
の2つです。数々の事物と人物が描かれているものの、この2つの構造線によって安定感のある画面構成になっています。また、左からの光によるコントラストの強い明暗の使い方はカラヴァッジョを思わせます。
人間の尊厳を描く
「卵を料理する老婆」を特徴づけるのは、まずそれぞれの事物のリアルな描写であり、次に、構図と光の使い方ですが、されにこれらを越えて「人間を描く」という視点で見ても傑作です。この点について、朝日新聞に的確な紹介があったので引用します。
松沢記者(文化くらし報道部)の文章を要約すると、この絵から感じられるのは、
の2つということでしょう。人間の存在や尊厳をありのままにとらえた絵、というのは、まさにその通りだと思います。
画家が10代で描いた絵
この絵は画家が10代の時に描いた作品です。ローラ・カミングの本には18歳とありますが、19歳という説もあります。しかし10代であることには違いない。そして、ベラスケスの10代の絵にはもう1つの傑作があります。No.230 で画像を引用した、
です。この絵にはモデルとして「卵を料理する老婆」と同じ少年が登場します。
No.190「画家が10代で描いた絵」で、日本の美術館の絵を中心に10代の作品を取り上げましたが、「作品として完成している」「完璧なリアリズム」「人間の尊厳を描く」という3点で、このベラスケスの2作品に勝るものはないでしょう。ピカソもかなわない感じがします。
No.230 にあったように、これらの作品は画家が自分の技量を誇示するために描いたものと推定されます。じっさい「セビーリャの水売り」は、ベラスケスがマドリードを訪問する際に持参しています(No.230)。つまり「売り込み」です。しかし、たとえ目的がそうだったにせよ、鑑賞者の心をうつ作品になる。技量はもちろんだが、それだけではないと感じさせる一枚になる。アートとは不思議なものだと思います。
なお、ベラスケスに関する過去の記事は以下のとおりです。
卵を料理する老婆

|
ディエゴ・ベラスケス 「卵を料理する老婆」(1618) |
(100.5cm × 119.5cm) スコットランド国立美術館 |
この絵は、No.230「消えたベラスケス(1)」で紹介しました。No.230 は、英国の美術評論家、ローラ・カミングの著書「消えたベラスケス」の内容を紹介したものです。この中で著者は、8歳のときに両親に連れられて行ったエディンバラのスコットランド国立美術館で見たのがこの絵だった、と書いていました。彼女の父親は画家です。画家はこの絵を8歳になった娘に見せた。8歳であればこの絵の素晴らしさが理解できると信じたのでしょう。案の定、これはローラ・カミングにとっての特別な体験だったようで、ここから彼女の "ベラスケス愛" が始まった。そして後年、「消えたベラスケス」のような本を書くに至った。そいういうことだと思います。
No.230 に続いて、「卵を料理する老婆」について書かれたローラ・カミングの文章再度引用します。
|
老婆が作っている卵料理は「ウエボ・フリート」(Huevo frito。スペイン風目玉焼き)です。「ウエボ」が "卵"、「フリート」は "揚げた" という意味で、現代のスペインでも作ります。ニンニクを入れたオリーブオイルを鍋にたっぷり入れ、卵を割って、上からスプーンでオリーブオイルをかけながら揚げるように焼きます。この絵の真鍮の容器と道具はニンニクを磨り潰すためのものでしょう。「目玉焼き」よりは「目玉揚げ」「揚げ卵」と言った方が実態に即しているでしょう。
|
そのウエボ・フリートを作っている老婆は、3個目の卵を鍋に入れようとしています。少年はガラス瓶を持っていますが、おそらくオリーブオイルが入っているのでしょう。それをこれから老婆のスプーンの注ごうとしている(ないしは指示があれば注ごうと待ち構えている)ようです。この調理の動作が2つめの「動き」です。それに加えて、絵には数々のアイテムが描かれています。つまり、
| ニンニク | |
| タマネギ | |
| 茶色の鍋 | |
| 陶器のコンロ(わずかに火が見える) | |
| 白い鉢と壷 | |
| 銀のナイフ | |
| 真鍮の容器と器具 | |
| 鉄の容器 | |
| メロン | |
| ガラス容器 | |
| 籠 |
などで、それぞれの質感が完璧に描き分けられています。もちろん、質感表現と言うなら最初にあげた「固まりつつある卵」がその筆頭です。モノの質感表現に挑んだ絵画は過去から現在までヤマほどありますが、「熱によって変質しつあるタンパク質の表現」をやってのけた絵画は(そしてそれに成功した絵画は)、これが唯一ではないでしょうか。
一方、構図をみると、この絵の構造線は、
| 老婆の体の中心を通る縦の線 | |
| 左上からスロープ状に曲線を描いて右下に至る放物線 |
の2つです。数々の事物と人物が描かれているものの、この2つの構造線によって安定感のある画面構成になっています。また、左からの光によるコントラストの強い明暗の使い方はカラヴァッジョを思わせます。
人間の尊厳を描く
「卵を料理する老婆」を特徴づけるのは、まずそれぞれの事物のリアルな描写であり、次に、構図と光の使い方ですが、されにこれらを越えて「人間を描く」という視点で見ても傑作です。この点について、朝日新聞に的確な紹介があったので引用します。

|
ディエゴ・ベラスケス 「卵を料理する老婆」(1618) |
|
松沢記者(文化くらし報道部)の文章を要約すると、この絵から感じられるのは、
| 油で熱せられた卵が固まりつつある瞬間の描写や、数々の食材や日用品の質感の違いを描き分ける、完璧なリアリズム | |
| 単なるリアリズムを超え、人間の存在や尊厳をありのままにとらえる技量 |
の2つということでしょう。人間の存在や尊厳をありのままにとらえた絵、というのは、まさにその通りだと思います。
画家が10代で描いた絵
この絵は画家が10代の時に描いた作品です。ローラ・カミングの本には18歳とありますが、19歳という説もあります。しかし10代であることには違いない。そして、ベラスケスの10代の絵にはもう1つの傑作があります。No.230 で画像を引用した、
| セビーリャの水売り」 | |
| ウェリントン・コレクション:英国) |
です。この絵にはモデルとして「卵を料理する老婆」と同じ少年が登場します。
No.190「画家が10代で描いた絵」で、日本の美術館の絵を中心に10代の作品を取り上げましたが、「作品として完成している」「完璧なリアリズム」「人間の尊厳を描く」という3点で、このベラスケスの2作品に勝るものはないでしょう。ピカソもかなわない感じがします。
No.230 にあったように、これらの作品は画家が自分の技量を誇示するために描いたものと推定されます。じっさい「セビーリャの水売り」は、ベラスケスがマドリードを訪問する際に持参しています(No.230)。つまり「売り込み」です。しかし、たとえ目的がそうだったにせよ、鑑賞者の心をうつ作品になる。技量はもちろんだが、それだけではないと感じさせる一枚になる。アートとは不思議なものだと思います。
2022-07-16 07:58
nice!(0)
No.340 - 中島みゆきの詩(20)キツネ狩りの歌 [音楽]
今回は「中島みゆきの詩」シリーズの続きですが、No.64「中島みゆきの詩(1)自立する言葉」の中で一部を引用した《キツネ狩りの歌》を取り上げます。この詩は、数ある中島作品の中でも最も "不思議な" というか、解釈にとまどう詩の一つだと思うからです。
キツネ狩りの歌
《キツネ狩りの歌》は、7作目のオリジナルアルバム「生きていてもいいですか」(1980)第3曲として収録されている楽曲で、その詩は次のようです。
《キツネ狩りの歌》をめぐる3つの層
この詩の解釈ですが、「タイトル」「寓話」「象徴」の3つの層で考えてみたいと思います。
まず第1は「タイトル」です。"キツネ狩り" が何を意味するかですが、言葉をそのまま素直に受け取ると、これはイギリス伝統のキツネ狩り(Fox hunting)でしょう。イギリスの貴族が赤い派手な狩猟服を着込み、多数の猟犬を引きつれて、馬を駆って野生のキツネを追いたてる。銃は使わず、あくまで馬と猟犬でキツネを追い詰め、最後はキツネが猟犬に食い殺される ・・・・・・。いわゆる "スポーツ・ハンティング" の一種ですが、イギリスでは動物愛護の精神にもとる残酷な行為ということで2004年に禁止されました。
ということは、《キツネ狩りの歌》が発表された当時(1980年)では堂々と行われていたということになります。ちなみに《キツネ狩りの歌》の曲は、トランペットのファンファーレのような響きで始まります。これは実際のキツネ狩りで合図に使われるラッパ(Fox hunting horn)を模したように聞こえます。
第2の層は「寓話」で、それも日本の民話か昔話風のものです。日本では昔からキツネやタヌキが "別のものに化ける" ないしは "人を化かす" という伝承があります。その一方で、キツネに関しては "神獣・霊的動物" として敬う伝統もある(全国にある稲荷神社が典型)。その "別のものに化ける" ないしは "人を化かす" という伝承の中に、次のような骨子の民話がなかったでしょうか(タヌキを例にとります)。
このような骨子の話を読んだ記憶があります。どこだったか思い出せないのですが、ともかく、こういったたぐいの(= これに近いストーリーの)民話はいかにもありそうです。《キツネ狩りの歌》にある、
などの表現から感じるのは「民話・昔話仕立ての寓話」という雰囲気です。
第3の層は「象徴」です。「キツネ狩り」や、その他、この詩に現れるさまざまな言葉が "何かの象徴になっている" という雰囲気です。思い出すのが《あぶな坂》です。
《あぶな坂》は、中島さんの第1作のアルバムである「私の声が聞こえますか」(1976)の第1曲です。当時、中島さんは24歳ですが、詩の内容は新進気鋭のシンガーソングライターのファーストアルバムの第1曲とはとても思えないほど不思議で、異次元的で、一種異様な感じがしないでもない。
No.64「中島みゆきの詩(1)自立する言葉」ではこの詩を「象徴詩」という文脈でとらえました。つまり「あぶな坂」「坂」「越える」「橋」「こわす」「なじる」「落ちる」などの言葉は、何らかの象徴になっているわけです。当然、作者がこの詩を書いたときの "思い" はあるのだろうけれど、象徴である以上、聴く人がどう受け取るかは自由である。そういった詩です。思い返すと、中島さんは「中島みゆき 全歌集」の序文に、次のように書いていました。
「私一人のものでしかない」のだけれど「すでに私のものではない」という二面性を綴った文章です。平たく言うと「詩を書いたときの思いやこだわりはあるのだけれど(それは作者一人の全く個人的なものだけれど)、詩をどう受け取るかは受け取る側の解釈に任されている」ということでしょう。これは「中島みゆき 全歌集」全体についての文章ですが、《あぶな坂》はまさにそういう感じの詩になっています。
《キツネ狩りの歌》も同じでしょう。キツネ狩りという「イギリス貴族の遊び」を背景に「寓話仕立ての詩」を作り上げていますが、そこに配置されている数々の言葉は、総体として "何かの" 象徴になっている。それが何かは、受け取る側の解釈に依存している ・・・・・・。そういうことだと思います。
では、"何かの" 象徴だとすると、それは何でしょうか。受け手としては解釈の自由があるわけで、それを考える上で参考にしたいのが、この詩を読む(ないしは楽曲として聴く)たびに連想する童話、宮沢賢治の「注文の多い料理店」です。
宮沢賢治「注文の多い料理店」
「注文の多い料理店」は、宮沢賢治の生前に出版された唯一の童話集である『注文の多い料理店』(大正13年。1924)の9編の中の1つです。童話集のタイトルになっていることから、賢治にとっては "思いのこもった" 作品なのでしょう。
以下にあらすじを書きますが、この童話は "ミステリー仕立て" です。従って本来、あらすじや結末を明かすべきではないとも思いますが、非常に有名な作品なので、引用とともに書くことにします。まず、冒頭は次のように始まります。
主人公は2人の紳士です。上の引用では分かりませんが、2人は東京からやってきたことが最後に明かされます。その2人がイギリス風の格好をして山にやってきた。どの山とは書いていませんが、宮沢賢治の故郷、岩手(賢治の言い方だとイーハトヴ)の山を想定するのがよいでしょう。その山奥で地元の猟師をガイドとして雇ってスポーツ・ハンティングをする。そういった情景です。
ところが上の引用の最後にあるように、2人の紳士はガイドの猟師とはぐれてしまった。戻ろうとしますが、戻り道が分からなくなります。そしてふと見ると、立派な西洋風の家があったのです。その玄関に近づくと、表札がかかっていました。
2人はホッとして、ちょうどよかった、ここで食事をしようと玄関の扉に近づくと、そこには、
との掲示がありました。玄関をあけると扉の内側には、
とあります。中は廊下になっていて、進むとまた扉があり、
とあります。その扉の内側には、
とありました。さらに廊下は続き、次の扉には、
と書いてあります。廊下と扉はさらに続きます。それぞれの扉には、
と、順に書いてありました。さらに次の扉には、
とあり、その裏側には、
とあります。2人はこれらの注文について、それぞれに合理的な理由を考え、一応のところ納得した上で従ってきました。この次からは宮沢賢治の文章を引用します。
2人は逃げだそうと入ってきた扉を開けようとしますが、扉は堅く閉まっていて動きません。おまけに前方の扉のかぎ穴からは、2つの目玉が2人の方を覗いています。
その時です。後ろの扉を突き破って、あの白熊のような2匹の犬が飛び込んできました。かぎ穴の目玉はたちまちなくなり、2匹の犬は前の扉に飛びつきます。扉は開き、犬はその中に駆け込んでいきました。
2人はやっと安心し、猟師の持ってきた団子を食べました。そして東京へと帰っていきました。しかし、恐怖で紙屑のようにくしゃくしゃになった2人の顔は元の通りにはなりませんでした。
都市文明への反感
宮沢賢治は童話集『注文の多い料理店』の出版にあたって、宣伝のためのちらしを書いています。 "『注文の多い料理店』新刊案内" と題したものですが、その中で童話「注文の多い料理店」について次のようにあります。
その通りなのでしょう。都市文明とそこに暮らす富裕層を代表するのが、東京からイーハトーヴにやってきた2人の紳士です。イギリス風の(つまり日本ではあまり見かけない)狩猟服に身を包み、地元の猟師(= 生活の糧として猟をする人)を雇ってガイドにつけ、スポーツ・ハンティングをする。鹿の横腹に銃弾を命中させればクルクルまわってドタッと倒れる、それが痛快だなどと話しています。
しかしそんな富裕層の紳士も、ガイドを見失い、山猫軒の "親方"(経営者のことを宮沢賢治は "親方" と書いています)の策略で無防備な姿にされ、我が身の危機が迫っていると分かると、恐怖に顔をひきつらせて泣き叫ぶだけなのです。「二人は泣いて泣いて泣いて泣いて泣きました」などの "戯画的" な表現は、文明の力、金の力で強そうにしている人間も、その内実は中身のない自立できない人間であり、それが真実の姿であるといったところでしょう。
それを徹底的に揶揄したような話の組み立てが、賢治の言う「都会文明と放恣な階級とに対するやむにやまれない反感」だと思います。もっと大きな構えで言うと、都会と地方、文明と自然の対立であり、権力や資産に乏しい「地方・自然」サイドからの「都会・文明」への反撃が「注文の多い料理店」だと思います。
ただ、根底がそうだとしても、この童話には物語としての工夫があります。それは料理店サイドから客に注文を次々出すという、少々奇想天外なストーリーです。また、親方の策略は "やりすぎ" が高じてボロが出て、それを子分に批判されるのもちょっと予想外の展開です。"策に溺れる" と言ったらいいのでしょうか。さらに物語のクライマックスでは、すべてが霧散解消し、話の全体は2人の紳士が見た幻影のような書き方がされています。都市文明と富裕層への反感とは言いながら、これらの点が不思議な魅力を物語に与え、名作とされているのだと思います。
連想の理由
《キツネ狩りの歌》から「注文の多い料理店」を連想するのには理由があります。まず、
という作品の基本的なコンセプトが非常に似ていることです。これは一目瞭然でしょう。さらに共通するのは、ちょっと意外なキーワードとしての、
です。キツネ狩りはイギリスの伝統だし、「注文の多い料理店」の冒頭の最初の文章には "イギリス" が出てきます。そこには「イギリスの兵隊のかたちをして」とありますが、この「兵隊」はイギリスの近衛兵だと想定します。つまり、バッキンガム宮殿で見かける赤い軍服の兵隊です。これはキツネ狩りで貴族が着込む狩猟服にそっくりです。この共通する "イギリス" は偶然なのでしょうか。
付け加えるなら、「注文に多い料理店」は "言葉の多義性" あるいは "ダブル・ミーニング" を巧みに取り入れた童話です。タイトルの「注文」がそうだし、上の引用中にある「すぐたべられます」も、日本語では「可能」と「受け身」が同一表現(レル・ラレル)ということを利用したダブル・ミーニングになっています。このような多義性を利用することは、まさしく中島さんが詩を書く上で得意とするところです。宮沢賢治の「注文の多い料理店」は "中島みゆき好み" の作品という気がします。
中島さんが《キツネ狩りの歌》を書くときに「注文の多い料理店」が念頭にあったのか、ないしは意識したのか、それは分かりません。しかし、受け手には "解釈の自由" があります。その前提で、「注文の多い料理店」を念頭に置いて《キツネ狩りの歌》を解釈したらどうなるかです。
「キツネ狩りの歌」の主題
「注文の多い料理店」を "補助線" として《キツネ狩りの歌》を解釈したらどうなるでしょうか。それを簡潔に言うと、
という "警句" と考えたいと思います。ここで "享楽" としたのは「酒」「乾杯」などの言葉が詩にあるからです。
「力を過信して行動する人」と「その犠牲なるものたち」の対比は、それを具体化すると、大きなものから小さなものまで、社会のさまざまな側面にあるでしょう。「富める者」と「貧しい者」もそうだし、「男性社会」における「弱い立場としての女性」と考えてもよい。最も大きくとらえれば「文明化を押し進める人類」と、それによって「収奪される自然環境」です。
ここで《キツネ狩りの歌》が「生きていてもいいですか」というアルバムの収録曲だという点から考えてみます。"生きていてもいいですか" という表現は、アルバムの第7曲である《エレーン》の詩の中に出てきます。つまり《エレーン》がアルバム「生きていてもいいですか」のタイトル・チューンになっている。その《エレーン》は、中島みゆきさんの知り合いだった外国人娼婦をモデルにした曲です。この女性のことは、小説集「女歌」の中の「街の女」に書かれていて、最後は惨殺されるという衝撃的な話です。ちょうどキツネ狩りにおけるキツネのように ・・・・・・。
また、アルバムの最終曲は「異国」で、詩には "二度と来るなと唾を吐く町 / 私がそこで生きてたことさえ / 覚えもないねと町が云うなら / 臨終の際にもそこは異国だ" といったたぐいの表現に満ちています。この詩が《エレーン》と関係していることは明白でしょう。
といったことから考えると、《キツネ狩りの歌》の「犠牲になるもの」は「弱い立場としての女性」かつ「社会のアウトサイダー」と受け取るのが最もしっくりきます。アルバムの最初の曲が「うらみ・ます」で、そこには "ふられたての女くらい だましやすいものはないんだってね / あんた誰と賭けていたの あたしの心はいくらだったの" という、一度聴いたら忘れられないフレーズがあって、それはアルバム全体におけるの "女性の視点" を強調しているようです。
とはいえ、中島さんの詩を "狭く受け取る" と誤解してしまうことがあります。《キツネ狩りの歌》はあくまで「力を過信して行動する人」と「その犠牲なるものたち」の対比という構図でとらえ、具体的に何を想定するかは多様な解釈ができるとしておくのがよいのでしょう。
ただ、一つ確実に言えることは《キツネ狩りの歌》で強く感じる、キツネを狩る人 = 力を過信して行動する人に対するシニカルな目です。浮かれていると自滅しますよ、墓穴を掘ることになりますよ、誰も助けてくれないけどいいんですか ・・・・・ というような「突き放した見方」を感じる。
中島さんの詩には「小さなもの」や「弱い存在」、「マイナーなもの」「疎外されたもの」の側に立って、世の中の真実を見据えた作品がいろいろあります。この詩もその一つでしょう。それをシニカルに言語化した作品、それが《キツネ狩りの歌》だと思います。
おそらく、宮沢賢治をリスペクトする文学者やアーティスト、クリエーターは大変多いと想像されます。中島さんがその一人であっても何の不思議もありません。しかし中島さんは、単にリスペクトするだけでなく、宮沢賢治にインスパイアされた作品を作っているのですね。夜会「24時着 0時発」(2004年初演)です。
この作品の基本テーマは、題名の「24時着 0時発」=「1日の終わりは始まり」=「地球の自転」で明確なように "永劫回帰" であり、それはすでに『時代』で示されているものです。そして、この作品のもう一つ発想の源泉が『銀河鉄道の夜』です。YAMAHA のサイトでの「24時着 0時発」(DVD作品)の紹介コピーは次のようになっています。
『銀河鉄道の夜』を愛するアーティストは多数いるでしょうが、それをもとに作品まで作った人はそう多くはないと思います。何となく、中島さんの "宮沢賢治愛" が伝わってくるような感じがする。
だとすると、《キツネ狩りの歌》が『注文の多い料理店』を踏まえているというのは、単なる憶測を超えていると思います。
中島みゆきさんが、夜会「24時着 0時発」と宮沢賢治との関係を語った発言があるので、それを紹介します。以下の内容はすべて、Webサイト「中島みゆき研究所」からのものです。この個人サイトを運営されている阿部忠義氏に感謝します。
2011年10月29日、NHK BSプレミアムで「宮沢賢治の音楽会 ~ 3.11との協奏曲 ~」が放映されました。内容は「中島みゆき研究所」の解説によると、
です。その "中島みゆきのコメント"(声の出演) が以下です。
"企画の途中で宮沢賢治と同じだと気づいた" との主旨を語っておられますが、これは本当なのでしょうか。ひょっとしたら、初めから『銀河鉄道の夜』へのオマージュを作りたかったのでは、とも思いました(たぶん、そうです)。
とにかく、中島さんの "宮沢賢治愛" を感じざるを得ないコメントであることは確かだと思います。
なお、中島みゆきさんの詩についての記事の一覧が、No.35「中島みゆき:時代」の「補記2」にあります。
キツネ狩りの歌
《キツネ狩りの歌》は、7作目のオリジナルアルバム「生きていてもいいですか」(1980)第3曲として収録されている楽曲で、その詩は次のようです。
|


|
中島みゆき 「生きていてもいいですか」(1980) |
(画像は表と裏のジャケット) |
① うらみ・ます ② 泣きたい夜に ③ キツネ狩りの歌 ④ 蕎麦屋 ⑤ 船を出すのなら九月 ⑥ ~インストゥルメンタル~ ⑦ エレーン ⑧ 異国 |
《キツネ狩りの歌》をめぐる3つの層
この詩の解釈ですが、「タイトル」「寓話」「象徴」の3つの層で考えてみたいと思います。
まず第1は「タイトル」です。"キツネ狩り" が何を意味するかですが、言葉をそのまま素直に受け取ると、これはイギリス伝統のキツネ狩り(Fox hunting)でしょう。イギリスの貴族が赤い派手な狩猟服を着込み、多数の猟犬を引きつれて、馬を駆って野生のキツネを追いたてる。銃は使わず、あくまで馬と猟犬でキツネを追い詰め、最後はキツネが猟犬に食い殺される ・・・・・・。いわゆる "スポーツ・ハンティング" の一種ですが、イギリスでは動物愛護の精神にもとる残酷な行為ということで2004年に禁止されました。
ということは、《キツネ狩りの歌》が発表された当時(1980年)では堂々と行われていたということになります。ちなみに《キツネ狩りの歌》の曲は、トランペットのファンファーレのような響きで始まります。これは実際のキツネ狩りで合図に使われるラッパ(Fox hunting horn)を模したように聞こえます。
第2の層は「寓話」で、それも日本の民話か昔話風のものです。日本では昔からキツネやタヌキが "別のものに化ける" ないしは "人を化かす" という伝承があります。その一方で、キツネに関しては "神獣・霊的動物" として敬う伝統もある(全国にある稲荷神社が典型)。その "別のものに化ける" ないしは "人を化かす" という伝承の中に、次のような骨子の民話がなかったでしょうか(タヌキを例にとります)。
数人の仲間と一緒に、野山にタヌキ狩りに出かけた。運良くタヌキをしとめ、それをタヌキ汁にして食べようとした。仲間たちが鍋と火の準備をしているが、何だか様子がおかしい。ふと見ると、仲間の後ろ姿から尻尾がのぞいている。実は "仲間" はタヌキが化けたもので、自分を鍋で食べようとしていたのだ。恐怖に駆られて一目散に逃げ出した。里の近くで本当の仲間と合流したが、自分の慌てた姿を見て怪訝な顔をされた ・・・・・・。
このような骨子の話を読んだ記憶があります。どこだったか思い出せないのですが、ともかく、こういったたぐいの(= これに近いストーリーの)民話はいかにもありそうです。《キツネ狩りの歌》にある、
| ただ生きて戻れたら、ね | |
| 妙にひげは長くないか | |
| グラスあげているのがキツネだったりするから |
などの表現から感じるのは「民話・昔話仕立ての寓話」という雰囲気です。
第3の層は「象徴」です。「キツネ狩り」や、その他、この詩に現れるさまざまな言葉が "何かの象徴になっている" という雰囲気です。思い出すのが《あぶな坂》です。
|
《あぶな坂》は、中島さんの第1作のアルバムである「私の声が聞こえますか」(1976)の第1曲です。当時、中島さんは24歳ですが、詩の内容は新進気鋭のシンガーソングライターのファーストアルバムの第1曲とはとても思えないほど不思議で、異次元的で、一種異様な感じがしないでもない。
No.64「中島みゆきの詩(1)自立する言葉」ではこの詩を「象徴詩」という文脈でとらえました。つまり「あぶな坂」「坂」「越える」「橋」「こわす」「なじる」「落ちる」などの言葉は、何らかの象徴になっているわけです。当然、作者がこの詩を書いたときの "思い" はあるのだろうけれど、象徴である以上、聴く人がどう受け取るかは自由である。そういった詩です。思い返すと、中島さんは「中島みゆき 全歌集」の序文に、次のように書いていました。
|
|
《キツネ狩りの歌》も同じでしょう。キツネ狩りという「イギリス貴族の遊び」を背景に「寓話仕立ての詩」を作り上げていますが、そこに配置されている数々の言葉は、総体として "何かの" 象徴になっている。それが何かは、受け取る側の解釈に依存している ・・・・・・。そういうことだと思います。
では、"何かの" 象徴だとすると、それは何でしょうか。受け手としては解釈の自由があるわけで、それを考える上で参考にしたいのが、この詩を読む(ないしは楽曲として聴く)たびに連想する童話、宮沢賢治の「注文の多い料理店」です。
宮沢賢治「注文の多い料理店」
「注文の多い料理店」は、宮沢賢治の生前に出版された唯一の童話集である『注文の多い料理店』(大正13年。1924)の9編の中の1つです。童話集のタイトルになっていることから、賢治にとっては "思いのこもった" 作品なのでしょう。
以下にあらすじを書きますが、この童話は "ミステリー仕立て" です。従って本来、あらすじや結末を明かすべきではないとも思いますが、非常に有名な作品なので、引用とともに書くことにします。まず、冒頭は次のように始まります。

|
童話「注文の多い料理店」の中扉(初版本) (角川文庫 1996) |
|
引用した角川文庫では、初版本の旧仮名使いを新仮名遣いに直してあります。なお上の引用で、ルビは「宮沢賢治全集 8」(筑摩文庫 1986)による初版本のルビに従いました。以下、同じです。
主人公は2人の紳士です。上の引用では分かりませんが、2人は東京からやってきたことが最後に明かされます。その2人がイギリス風の格好をして山にやってきた。どの山とは書いていませんが、宮沢賢治の故郷、岩手(賢治の言い方だとイーハトヴ)の山を想定するのがよいでしょう。その山奥で地元の猟師をガイドとして雇ってスポーツ・ハンティングをする。そういった情景です。
ところが上の引用の最後にあるように、2人の紳士はガイドの猟師とはぐれてしまった。戻ろうとしますが、戻り道が分からなくなります。そしてふと見ると、立派な西洋風の家があったのです。その玄関に近づくと、表札がかかっていました。
RESTAURANT
西洋料理店 WILDCAT HOUSE 山猫軒 |

|
童話「注文の多い料理店」の挿画(初版本) (角川文庫 1996) |
2人はホッとして、ちょうどよかった、ここで食事をしようと玄関の扉に近づくと、そこには、
| どなたでもどうかお入りください。決してご遠慮はありません。」 |
| ことに太ったお方や若いお方は、大歓迎いたします。」 |
| 当軒は注文の多い料理店ですからどうかそこはご承知ください」 |
| 注文はずいぶん多いでしょうがどうか一々こらえてください」 |
| お客さまがた、ここで髪をきちんとして、それからはきものの泥を落としてください。」 |
| 鉄砲と弾丸をここへ置いてください。」 | |
| どうか帽子と外套と靴をおとり下さい。」 | |
| ネクタイピン、カフスボタン、眼鏡、財布、その他金物類、ことに尖ったものは、みんなここに置いてください。」 |
| 壷の中のクリームを顔や手足にすっかり塗ってください。」 |
| クリームをよく塗りましたか。耳にもよく塗りましたか。」 |
|
2人は逃げだそうと入ってきた扉を開けようとしますが、扉は堅く閉まっていて動きません。おまけに前方の扉のかぎ穴からは、2つの目玉が2人の方を覗いています。
|
その時です。後ろの扉を突き破って、あの白熊のような2匹の犬が飛び込んできました。かぎ穴の目玉はたちまちなくなり、2匹の犬は前の扉に飛びつきます。扉は開き、犬はその中に駆け込んでいきました。
|
2人はやっと安心し、猟師の持ってきた団子を食べました。そして東京へと帰っていきました。しかし、恐怖で紙屑のようにくしゃくしゃになった2人の顔は元の通りにはなりませんでした。
都市文明への反感
宮沢賢治は童話集『注文の多い料理店』の出版にあたって、宣伝のためのちらしを書いています。 "『注文の多い料理店』新刊案内" と題したものですが、その中で童話「注文の多い料理店」について次のようにあります。
|
その通りなのでしょう。都市文明とそこに暮らす富裕層を代表するのが、東京からイーハトーヴにやってきた2人の紳士です。イギリス風の(つまり日本ではあまり見かけない)狩猟服に身を包み、地元の猟師(= 生活の糧として猟をする人)を雇ってガイドにつけ、スポーツ・ハンティングをする。鹿の横腹に銃弾を命中させればクルクルまわってドタッと倒れる、それが痛快だなどと話しています。
しかしそんな富裕層の紳士も、ガイドを見失い、山猫軒の "親方"(経営者のことを宮沢賢治は "親方" と書いています)の策略で無防備な姿にされ、我が身の危機が迫っていると分かると、恐怖に顔をひきつらせて泣き叫ぶだけなのです。「二人は泣いて泣いて泣いて泣いて泣きました」などの "戯画的" な表現は、文明の力、金の力で強そうにしている人間も、その内実は中身のない自立できない人間であり、それが真実の姿であるといったところでしょう。
それを徹底的に揶揄したような話の組み立てが、賢治の言う「都会文明と放恣な階級とに対するやむにやまれない反感」だと思います。もっと大きな構えで言うと、都会と地方、文明と自然の対立であり、権力や資産に乏しい「地方・自然」サイドからの「都会・文明」への反撃が「注文の多い料理店」だと思います。
ただ、根底がそうだとしても、この童話には物語としての工夫があります。それは料理店サイドから客に注文を次々出すという、少々奇想天外なストーリーです。また、親方の策略は "やりすぎ" が高じてボロが出て、それを子分に批判されるのもちょっと予想外の展開です。"策に溺れる" と言ったらいいのでしょうか。さらに物語のクライマックスでは、すべてが霧散解消し、話の全体は2人の紳士が見た幻影のような書き方がされています。都市文明と富裕層への反感とは言いながら、これらの点が不思議な魅力を物語に与え、名作とされているのだと思います。
連想の理由
《キツネ狩りの歌》から「注文の多い料理店」を連想するのには理由があります。まず、
動物を狩る人間が、狩られるはずの動物に騙されて命が危うくなる
という作品の基本的なコンセプトが非常に似ていることです。これは一目瞭然でしょう。さらに共通するのは、ちょっと意外なキーワードとしての、
イギリス
です。キツネ狩りはイギリスの伝統だし、「注文の多い料理店」の冒頭の最初の文章には "イギリス" が出てきます。そこには「イギリスの兵隊のかたちをして」とありますが、この「兵隊」はイギリスの近衛兵だと想定します。つまり、バッキンガム宮殿で見かける赤い軍服の兵隊です。これはキツネ狩りで貴族が着込む狩猟服にそっくりです。この共通する "イギリス" は偶然なのでしょうか。
付け加えるなら、「注文に多い料理店」は "言葉の多義性" あるいは "ダブル・ミーニング" を巧みに取り入れた童話です。タイトルの「注文」がそうだし、上の引用中にある「すぐたべられます」も、日本語では「可能」と「受け身」が同一表現(レル・ラレル)ということを利用したダブル・ミーニングになっています。このような多義性を利用することは、まさしく中島さんが詩を書く上で得意とするところです。宮沢賢治の「注文の多い料理店」は "中島みゆき好み" の作品という気がします。
中島さんが《キツネ狩りの歌》を書くときに「注文の多い料理店」が念頭にあったのか、ないしは意識したのか、それは分かりません。しかし、受け手には "解釈の自由" があります。その前提で、「注文の多い料理店」を念頭に置いて《キツネ狩りの歌》を解釈したらどうなるかです。
「キツネ狩りの歌」の主題
「注文の多い料理店」を "補助線" として《キツネ狩りの歌》を解釈したらどうなるでしょうか。それを簡潔に言うと、
自分の力(権力、権威、地位、財力など)を過信して行動し、享楽にふけっていると、その力の犠牲になるものたちからの "しっぺ返し" を食らう
という "警句" と考えたいと思います。ここで "享楽" としたのは「酒」「乾杯」などの言葉が詩にあるからです。
「力を過信して行動する人」と「その犠牲なるものたち」の対比は、それを具体化すると、大きなものから小さなものまで、社会のさまざまな側面にあるでしょう。「富める者」と「貧しい者」もそうだし、「男性社会」における「弱い立場としての女性」と考えてもよい。最も大きくとらえれば「文明化を押し進める人類」と、それによって「収奪される自然環境」です。
ここで《キツネ狩りの歌》が「生きていてもいいですか」というアルバムの収録曲だという点から考えてみます。"生きていてもいいですか" という表現は、アルバムの第7曲である《エレーン》の詩の中に出てきます。つまり《エレーン》がアルバム「生きていてもいいですか」のタイトル・チューンになっている。その《エレーン》は、中島みゆきさんの知り合いだった外国人娼婦をモデルにした曲です。この女性のことは、小説集「女歌」の中の「街の女」に書かれていて、最後は惨殺されるという衝撃的な話です。ちょうどキツネ狩りにおけるキツネのように ・・・・・・。
また、アルバムの最終曲は「異国」で、詩には "二度と来るなと唾を吐く町 / 私がそこで生きてたことさえ / 覚えもないねと町が云うなら / 臨終の際にもそこは異国だ" といったたぐいの表現に満ちています。この詩が《エレーン》と関係していることは明白でしょう。
といったことから考えると、《キツネ狩りの歌》の「犠牲になるもの」は「弱い立場としての女性」かつ「社会のアウトサイダー」と受け取るのが最もしっくりきます。アルバムの最初の曲が「うらみ・ます」で、そこには "ふられたての女くらい だましやすいものはないんだってね / あんた誰と賭けていたの あたしの心はいくらだったの" という、一度聴いたら忘れられないフレーズがあって、それはアルバム全体におけるの "女性の視点" を強調しているようです。
とはいえ、中島さんの詩を "狭く受け取る" と誤解してしまうことがあります。《キツネ狩りの歌》はあくまで「力を過信して行動する人」と「その犠牲なるものたち」の対比という構図でとらえ、具体的に何を想定するかは多様な解釈ができるとしておくのがよいのでしょう。
ただ、一つ確実に言えることは《キツネ狩りの歌》で強く感じる、キツネを狩る人 = 力を過信して行動する人に対するシニカルな目です。浮かれていると自滅しますよ、墓穴を掘ることになりますよ、誰も助けてくれないけどいいんですか ・・・・・ というような「突き放した見方」を感じる。
中島さんの詩には「小さなもの」や「弱い存在」、「マイナーなもの」「疎外されたもの」の側に立って、世の中の真実を見据えた作品がいろいろあります。この詩もその一つでしょう。それをシニカルに言語化した作品、それが《キツネ狩りの歌》だと思います。
おそらく、宮沢賢治をリスペクトする文学者やアーティスト、クリエーターは大変多いと想像されます。中島さんがその一人であっても何の不思議もありません。しかし中島さんは、単にリスペクトするだけでなく、宮沢賢治にインスパイアされた作品を作っているのですね。夜会「24時着 0時発」(2004年初演)です。
この作品の基本テーマは、題名の「24時着 0時発」=「1日の終わりは始まり」=「地球の自転」で明確なように "永劫回帰" であり、それはすでに『時代』で示されているものです。そして、この作品のもう一つ発想の源泉が『銀河鉄道の夜』です。YAMAHA のサイトでの「24時着 0時発」(DVD作品)の紹介コピーは次のようになっています。
舞台は、主人公“あかり”が、過労のため生死をさまよう間に不思議な夢を見るところから物語が始まる。河を上る鮭の遡上を宮沢賢治の「銀河鉄道の夜」になぞらえ、そこに主人公の人生を重ね合わせてゆく。
『銀河鉄道の夜』を愛するアーティストは多数いるでしょうが、それをもとに作品まで作った人はそう多くはないと思います。何となく、中島さんの "宮沢賢治愛" が伝わってくるような感じがする。
だとすると、《キツネ狩りの歌》が『注文の多い料理店』を踏まえているというのは、単なる憶測を超えていると思います。
| 補記:24時着 0時発 |
中島みゆきさんが、夜会「24時着 0時発」と宮沢賢治との関係を語った発言があるので、それを紹介します。以下の内容はすべて、Webサイト「中島みゆき研究所」からのものです。この個人サイトを運営されている阿部忠義氏に感謝します。
2011年10月29日、NHK BSプレミアムで「宮沢賢治の音楽会 ~ 3.11との協奏曲 ~」が放映されました。内容は「中島みゆき研究所」の解説によると、
2011年10月22日(土)~ 10月30日(日)まで、NHK BSプレミアムで放送される特集「きらり!東北の秋」の3週目に放送される特別番組。宮沢賢治が生涯に残した20曲あまりの歌の魅力を現代のミュージシャン、アーティストたちの歌と朗読で堪能する。宮沢賢治の「銀河鉄道の夜」をモチーフにした「夜会VOL.14 ─ 24時着00時発」から、中島みゆきのコメント(B.G.M.『サヨナラ・コンニチハ』)と中島みゆきが少年 "ジョバンニ" に扮し『命のリレー』を唄った映像が流れた。
です。その "中島みゆきのコメント"(声の出演) が以下です。
|
"企画の途中で宮沢賢治と同じだと気づいた" との主旨を語っておられますが、これは本当なのでしょうか。ひょっとしたら、初めから『銀河鉄道の夜』へのオマージュを作りたかったのでは、とも思いました(たぶん、そうです)。
とにかく、中島さんの "宮沢賢治愛" を感じざるを得ないコメントであることは確かだと思います。
2022-07-02 09:49
nice!(1)
前の30件 | -









.jpg)




