No.316 - 高校数学で理解する楕円曲線暗号の数理(2) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
16. 楕円曲線上の点
有限体 \(\bs{F}_p\) の元 \(x\) と \(y\) のぺア \((x,\:y)\) の集合を \(\bs{F}_p^{\:2}\) と記述します。集合 \(\bs{F}_p^{\:2}\) の元で楕円曲線上の "点" はどれだけあるでしょうか。まず、楕円曲線の式を満たす \(\bs{F}_p^{\:2}\) の元がどのように計算できるかを調べます。
平方数と平方根
楕円曲線の式を、
と書くとき、\(z\)(\(z\neq0\))が \(\bs{F}_p\) での平方数なら、\(y\) の解が2つ求まります。ここで、次の命題が成立します。
\(\bs{F}_p\) で考えているので「平方数」と書きましたが、整数の世界では平方剰余です。つまり、\(x^2=a\:(\mr{mod}\:n)\) となるような \(x\) が存在する \(a\) が「\(n\) を法とする平方剰余」です。16.1 の証明ですが、12.1(No.313)により、\(z\) は \(\bs{F}_p^{*}\) の生成元(の一つ)を \(g\) として、
と表現できます。つまり、命題の条件は、
です。このとき \(k\) は偶数のはずです。なぜなら、もし \(k\) が奇数だとすると、\(k\dfrac{p-1}{2}\) は \(p-1\) で割り切れないので、
と表現できます。すると、
となり、\(g^t=1\:(1\leq t < p-1)\) になりますが、これは \(g\) が生成元であることと矛盾します。従って \(k\) は偶数です。そうすると \(k=2m\) とおいて、
となり、\(z\) は平方数になります。逆に、
と表現されるとすると、フェルマの小定理 3.1をつかって、
となり、\(\bs{z^{\frac{p-1}{2}}=1}\) と 「\(\bs{z}\) が平方数」は同値であることが証明できました。
なお、フェルマの小定理によって、 \((z^{\frac{p-1}{2}})^2=1\) なので、\(z^{\frac{p-1}{2}}\) は \(1\) か \(-1(=p-1)\) のどちらかです。従って、
ということになります。「平方数ではない」は、整数の世界では「平方非剰余」です。
平方根を求める
\(z\) は平方数だとわかったとき、実際に \(\bs{F}_p\) で \(y\)(= \(z\) の平方根)を求める手段が必要になります。整数であれば平方根を求めるのは容易ですが、\(\bs{F}_p\) ではそうはいきません。特に、楕円曲線暗号で使われる \(p\) は10進数で数10桁以上の巨大素数なので、総当たりで求めたり、解の存在範囲を限定していって求めるわけにはいかないのです。以下が解を求めるアルゴリズムです。
\(p\equiv3\:(\mr{mod}\:4)\) の場合
この場合は
が解の一つとなります(もう一つの解は \(-y\) で、つまり \(p-y\))。確認してみると、
となって、確かに \(y\) が解であることがわかります。
\(p\equiv1\:(\mr{mod}\:4)\) の場合
この場合は「トネリ-シャンクスのアルゴリズム」で解を求めることができます(Tonelli は19世紀イタリア、Shanks は20世紀米国の数学者)。以下のアルゴリズムは Wikipedia を参考にしました。
\(p\equiv1\:(\mr{mod}\:4)\) の場合、\(p-1\) は \(4\) の倍数です。\(p-1\) を素因数分解したときの \(2\) のべき乗を \(S\) とすると、\(p-1\) は、
と表現できます。ここで、\(\bs{F}_p\) において平方数ではない数 \(w\) を(どれでもよいから)一つ選びます。つまり、
\(w^{\frac{p-1}{2}}=-1\)
となる数 \(w\) です。\(\bs{F}_p\) においては平方数とそうでない数が半々なので、この選択は容易です。次に、4つの数を、
と定義します。このように定義すると、\(c_0,\:\:t_0,\:\:y_0\) は次の「性質」を持ちます。
\(\begin{eqnarray}
&&\:\:(c_0)^{2^{S_0-1}}&=(w^Q)^{2^{S-1}}\\
&&&=w^{Q\cdot2^{S-1}}\\
&&&=w^{\frac{p-1}{2}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_0)^{2^{S_0-1}}&=(z^Q)^{2^{S-1}}\\
&&&=z^{Q\cdot2^{S-1}}\\
&&&=z^{\frac{p-1}{2}}\\
&&&=1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:y_0^{\:2}&=\left(z^{\frac{Q+1}{2}}\right)^2\\
&&&=z^{Q+1}\\
&&&=t_0\cdot z\\
\end{eqnarray}\)
まとめると、
です。もし、\(t_0=1\) なら、3番目の式により \(z\) の平方根は \(y_0\) および \(-y_0\:(=p-y_0)\) ですが、そうはなりません。\(S_0=1\) なら \(t_0=1\) となりますが、\(S_0=S\geq2\) だからです。
そこで、\(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) の4数の組の列 \((i=0,\:1,\:2,\:\cd\:)\) を順次作り、上記の「性質」を保ちつつ、ある時点で \(t_i=1\) になることを目指します。\(t_i=1\) になったとしたら、そのときの \(\pm y_i\) が \(z\) の平方根です。\(i=1\) に対応する4数の組は次のようにします。
このように定義すると、次のように「性質」が保たれることが分かります。
\(\begin{eqnarray}
&&\:\:(c_1)^{2^{S_1-1}}&=\left((c_0)^{2^{S_0-S_1}}\right)^{2^{S_1-1}}\\
&&&=(c_0)^{2^{S_0-1}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_1)^{2^{S_1-1}}&=(t_0)^{2^{S_1-1}}\cdot\left((c_0)^{2^{S_0-S_1}}\right)^{2^{S_1-1}}\\
&&&=(t_0)^{2^{S_1-1}}\cdot(c_0)^{2^{S_0-1}}\\
&&&=-(t_0)^{2^{S_1-1}}\\
\end{eqnarray}\)
ここで、最後の式からマイナスを取って、
\((t_0)^{2^{S_1-1}}=X\)
とおくと、\(S_1\) の定義から \((t_0)^{2^{S_1}}=1\) なので、
\(X^2=(t_0)^{2^{S_1}}=1\)
となり、\(X\) は \(\bs{F}_p\) における方程式 \(X^2=1\) の解です。つまり、
\(X=1,\:-1\)
です。ところが \(X=1\) とすると、
\((t_0)^{2^{S_1-1}}=1\)
となりますが、\(S_1\) は \(0 < S_1 < S_0\) で \((t_0)^{2^{S_1}}=1\) を満たす最小の数と定義したにも関わらず、\(S_1\) より小さい \(S_1-1\) が定義を満たすことになってしまって矛盾します。従って \(X=-1\) であり、結局、
\(\begin{eqnarray}
&&\:\:(t_1)^{2^{S_1-1}}&=-X\\
&&&=1\\
\end{eqnarray}\)
となります。さらに、
\(\begin{eqnarray}
&&(y_1)^2&=(y_0)^2\cdot\left((c_0)^{2^{S_0-S_1-1}}\right)^2\\
&&&=t_0\cdot z\cdot(c_0)^{2^{S_0-S_1}}\\
&&&=t_0\cdot(c_0)^{2^{S_0-S_1}}\cdot z\\
&&&=t_1\cdot z\\
\end{eqnarray}\)
と計算できます。まとめると、
となって、\(i=1\) においても「性質」が成り立つことが分かりました。ここで仮に、\(\bs{t_1=1}\) なら \(\bs{(y_1)^2=z}\) となって、\(\bs{z}\) の平方根は \(\bs{\pm y_1}\) になります。
この計算で重要なことは \(S_1 < S_0\) であり、同様のやり方で \(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) \((i=0,\:1,\:2,\:\cd\:)\) の4数の組の列を順次作っていくと、\(\bs{S_i}\) は単調減少することです。さらに、\(S_i=1\) なら \(t_i=1\) になることもポイントです。
以上のプロセスを進めて、\(i=0,\:1,\:2,\:3,\:\cd\) のとき、
と定義すると、
の「性質」が成り立つことを数学的帰納法で証明します。\(i=0,\:1\) で成り立つことは上で既に確認しました。\(i\) のときに「性質」が成り立つと仮定すると、\(i+1\) でも成り立つことが次のように分かります。基本的には上の \(i=1\) での計算と同じです。
\(\begin{eqnarray}
&&\:\:(c_{i+1})^{2^{S_{i+1}-1}}&=\left((c_i)^{2^{S_i-S_{i+1}}}\right)^{2^{S_{i+1}-1}}\\
&&&=(c_i)^{2^{S_i-1}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_{i+1})^{2^{S_{i+1}-1}}&=(t_i)^{2^{S_{i+1}-1}}\cdot\left((c_i)^{2^{S_i-S_{i+1}}}\right)^{2^{S_{i+1}-1}}\\
&&&=(t_i)^{2^{S_{i+1}-1}}\cdot(c_i)^{2^{S_i-1}}\\
&&&=-(t_i)^{2^{S_{i+1}-1}}\\
\end{eqnarray}\)
ここで、
\((t_i)^{2^{S_{i+1}-1}}=X\)
とおくと、\(S_{i+1}\) の定義によって \((t_i)^{2^{S_{i+1}}}=1\) なので、
\(X^2=(t_i)^{2^{S_{i+1}}}=1\)
となり、\(X\) は \(\bs{F}_p\) における方程式 \(X^2=1\) の解です。つまり、
\(X=1,\:-1\)
です。ところが \(X=1\) とすると、
\((t_i)^{2^{S_{i+1}-1}}=1\)
となりますが、\(S_{i+1}\) は \(0 < S_{i+1} < S_i\) で \((t_i)^{2^{S_{i+1}}}=1\) を満たす最小の数としたにも関わらず、\(S_{i+1}\) より小さい \(S_{i+1}-1\) が定義を満たすことになってしまい、矛盾します。従って \(X=-1\) であり、
\(\begin{eqnarray}
&&\:\:(t_{i+1})^{2^{S_{i+1}-1}}&=-X\\
&&&=1\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:(y_{i+1})^2&=(y_i)^2\cdot\left((c_i)^{2^{S_i-S_{i+1}-1}}\right)^2\\
&&&=t_i\cdot z\cdot(c_i)^{2^{S_i-S_{i+1}}}\\
&&&=t_i\cdot(c_i)^{2^{S_i-S_{i+1}}}\cdot z\\
&&&=t_{i+1}\cdot z\\
\end{eqnarray}\)
と計算できます。まとめると
となり、\(i\) のときに成り立つと仮定すると \(i+1\) でも成り立つことが分かりました。これで、\(i=0,\:1,\:2,\:3,\:\cd\) で成り立つことが数学的帰納法で証明できました。
\(i=0,\:1,\:2,\:3,\:\cd\) のどこかで \(t_i=1\) となれば、そのときの \(\pm y_i\) が \(z\) の平方根です。\(S_i\) は単調減少であり、かつ、\(S_i=1\) なら \(t_i=1\) です。\(t_i=1\) となる \(i\) がなかなか見つからなくても、\(S_i\) が \(1\) まで減少すれば必ず見つかるので、\(z\) の平方根が求まります。
このアルゴリズムを実験してみます。4 で割って1余る素数 \(p\) として、 \(p=2^S+1\) 型の素数を選びます。\(S=8\) のとき \(p=257\) は素数なので、
\(p=257,\:\:Q=1,\:\:S=8\)
とおきます。計算してみると \(\bs{F}_{257}\) において \(11,\:13\) は平方数です。また、平方数でない数として \(3\) を選ぶことができます。そこでまず、
\(p=257,\:\:Q=1,\:\:S=8,\)
\(z=11,\:\:w=3\)
とおくと、
\(\begin{eqnarray}
&&\:\:S_0&=S&=8\\
&&\:\:c_0&=w^Q&=3\\
&&\:\:t_0&=z^Q&=11\\
&&\:\:y_0&=z^{\frac{Q+1}{2}}&=11\\
\end{eqnarray}\)
が初期値です。ここからアルゴリズムに沿って \(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) \((i=1,\:2,\:\cd\:)\) を計算してみると、結果は、
となり、\(\bs{F}_{257}\) における \(11\) の平方根の1つは \(221\) と求まりました。もう1つは \(257-221=36\) です。実際、
\(221^2=48841=190\cdot257+11\)
\(\phantom{2}36^2=\phantom{4}1296=\phantom{25}5\cdot257+11\)
なので正しい結果です。\(z=13\) もやってみると、
となり、\(\bs{F}_{257}\) における \(13\) の平方根(の1つ)は \(28\) です。
\(28^2=784=3\cdot257+13\)
であり、アルゴリズムの確認ができました。
楕円曲線上の点の総数
\(\bs{F}_p\) 上の楕円曲線、\(E(a,\:b,\:p)\) の点の数がどの程度になるのでしょうか。以降、群 \(E(a,\:b,\:p)\) の元の数(群位数)を \(\#E\) と書きます。前回の No.315「高校数学で理解する楕円曲線暗号の数理(1)」の最後にあげた例だと、
でした。この \(\#E(a,\:b,\:p)\) を評価する式があります。「ハッセの定理」です(Helmut Hasse は20世紀ドイツの数学者)。この定理によると、
であり、\(\#E\) は \(p+1\) の周辺、\(\pm2\sqrt{p}\) の範囲です。この意味を考えてみます。\(\bs{F}_p\) 上の楕円曲線を
で表わし、\(\bs{F}_p\) において \(z\) を \(0\) から \(p-1\) まで振ったときの \(y^2=z\) の解の総数を求めます。\(z\) を、\(\bs{F}_p^{*}\) の生成元 \(g\) を使って、
と表すと、
となり、\(\bs{F}_p^{\:2}\) における解、\((z,\:y)\) の総数は \(p\) となります。では、\(\bs{F}_p^{\:2}\) における楕円曲線上の点、\((x,\:y)\) の総数はどうなるでしょうか。\(x\) が \(\bs{F}_p\) の全ての元に渡るとき、\(z\) が \(\bs{F}_p\) で均等にバラつくとは限りません。しかし \((x,\:y)\) の総数は「だいたい \(p\) に近い値」だと考えられます。
つまり、群 \(E(a,\:b,\:p)\) の元で、零元 \(\mathcal{O}\) 以外の \(\bs{F}_p^{\:2}\) に属するものは、だいたい \(p\) 個あると考えられる。従って \(\#E\) は 零元 \(\mathcal{O}\) を含んで \(p+1\) に近い値だと考えられます。これが「ハッセの定理」の直感的理解です。
別の観点から言うと、任意に選んだ \(x\) に対して、もし \(z\) が平方数なら \(y\) が2つ存在し、楕円曲線上の点が2つ求まります。ハッセの定理から言えることは、そうなる確率は、任意の \(x\) についてほぼ \(0.5\) ということです。\(p\) が大きくなると、\(p+1\) に対する \(2\sqrt{p}\) の比率は極めて小さくなるからです。
\(\#E\) を具体的に求めるアルゴリズムは、1985年にオランダ出身の数学者、レネ・ショーフ(Rene Schoof。英語読みでスクーフとも書かれる)が開発しました。その「ショーフのアルゴリズム」は、数学用語で言うと最初の「決定論的多項式時間アルゴリズム」です。平たく言うと「計算結果が100%正しいと数学的に保証される(=決定論的)計算可能な(=多項式時間)アルゴリズム」です。「ショーフのアルゴリズム」の具体的内容は、ここでは割愛します。
17. 楕円曲線暗号
楕円曲線暗号を構成する上で必要になるのが、有限群における「位数」の概念です。次の位数の話はすべての有限群に共通するので、群の演算を乗法的に書くことにします(掛け算、冪乗、単位元 \(e\)、などの記法を使います)。No.315 でやったように、演算を加法と考えても全く同じことになります。
位数
元の数が有限個の群 \(G\) を「有限群」といい、その元の個数を「群位数(group order)」と呼びます。群位数を \(|G|\) と表します。群の演算則だけから次のことが言えます。
単位元 \(e\) でない群 \(G\) の元を \(a\) とします。\(a\) の冪乗 \(a^n(1\leq n)\) の \(n\) を増やしていくと、ある時点で \(a^n=e\) となります。その理由ですが、
という \(|G|\) 個の元を考えてみます。もし \(|G|\) 個が全て相異なると、どれかが \(e\) のはずです。全てが相異なる元ではないとき、
となったとすると、両辺に \(a\) の逆元を \(i\) 回掛けて、
が得られます。\(1\leq j-i < |G|\) なので、この範囲に \(e\) があります。そこで、つぎのように元 \(a\) の位数を定義できます。
さらに、元の位数については次の命題が成り立ちます。
これはラグランジュの定理と呼ばれるものです。この定理が成り立つ理由は次の通りです。有限群 \(G\) の任意の元を \(a\) とし、集合 \(A\) を、
とします。集合 \(A\) の元は全て相異なります。なぜなら、もし、
となったとすると、両辺に \(a\) の逆元を \(i\) 回掛けて、
となり、\(d\) が \(a^d=e\) となる最小の数であるという位数の定義に反するからです。さらに、集合 \(A\) の任意の元の逆元は集合 \(A\) に含まれます。つまり、\(a^d=e\) なので \(a^j(1\leq j < d)\) に対して \(a^{d-j}(1\leq d-j < d)\) が逆元です(ということは集合 \(A\) もまた群であり、これを \(G\) の部分群と言います)。
集合 \(A\) が \(G\) の全ての元を尽くしているなら 17.2 は成立します。そこで、集合 \(A\) に含まれない \(G\) の元があったとし、それを \(b_1\) とします。集合 \(A\) の全ての元に左から \(b_1\) を掛けて、集合 \(B_1\) を作ります。つまり、
です。集合 \(A\) の元は全て相異なるので、集合 \(B_1\) の元も全て相異なります。さらに、集合 \(B_1\) の元で集合 \(A\) の元と同じものはありません。なぜなら、もし、
だとすると、\(a^i\) の逆元、\(a^{d-i}\)を右から掛けて、
となりますが、\(1\leq j-i < d\) なので、これは \(b_1\) が集合 \(A\) の元であることを意味していて仮定に反します。つまり、集合 \(B_1\) の元で集合 \(A\) の元と同じものはありません。
集合 \(A\) と \(B_1\) で \(G\) の元の全てを尽くしているなら、\(2d=|G|\) となって 17.2 は証明できたことになります。そうではない場合、集合 \(A\) と \(B_1\) に含まれない \(G\) の元の一つを \(b_2\) として、集合 \(B_2\) を、
と定義します。そうすると先ほど同じように、集合 \(B_2\) の元は全て相異なり、かつ、集合 \(A\) との重複はありません。さらに、集合 \(B_2\) の元は集合 \(B_1\) の元とも重複しません。なぜなら、もし、
だとすると、\(a^i\) の逆元、\(a^{d-i}\)を右から掛けて、
となりますが、\(1\leq j-i < d\) なので、\(b_2\) が 集合 \(B_1\) の元という意味になり仮定に反します。つまり、集合 \(B_2\)の元は集合 \(B_1\) の元と重複しません。
以上の操作は \(G\) の元が残っている限り \(B_3B_4\:\cd\) と続けられます。そしてある時点で 残っている \(G\) の元がちょうど切りのよいところで無くなるはずです。\(B_{n-1}\) まで作ったときに \(G\) の元の全てを尽くしたとしたら、\(n_d=|G|\) です。これで 17.2 が証明できました。17.2 から直ちに次の2つが結論づけられます。
これは、群位数 \(|G|\) が 元 \(a\) の位数の倍数なのでそうなります。\(p\) を素数とし、\(G\) が \(p\) 未満の自然数からなる乗法群 \(\bs{F}_p^{*}\) だとすると、\(|G|=p-1\) なので、フェルマの小定理( 3.1 )そのものです。
また、\(n\) 未満の自然数で \(n\) と互いに素なものの集合を \(G\) とすると、\(G\) は \(\mr{mod}n\) の乗算に関して閉じた集合になり、逆元も定義できるので(2.3 参照)、群となります(= 既約剰余類群)。オイラー関数を用いると \(|G|=\varphi(n)\) と表せて、オイラーの定理( 7.1 )になります。
つまり 17.3 は、フェルマの小定理の一般化であると同時に、フェルマの小定理を一般化したオイラーの定理をさらに一般化したものと言えるでしょう。
素数の約数は \(1\) と素数自身しかないので、単位元以外の元の位数は群位数に等しくなります。従って、群位数が素数の群では任意の元 \(a\) の冪乗が群全体に "バラける" ことになります。
楕円曲線暗号の構成
スカラー倍
ここから具体的な楕円曲線暗号のしくみに入ります。楕円曲線上の \(\bs{F}_p^{\:2}\) の点と零元 \(\mathcal{O}\) が作る加法群を \(E(a,\:b,\:p)\) とし、その群位数を \(\#E\) と書きます。楕円曲線暗号では \(E(a,\:b,\:p)\) における「スカラー倍」の演算を利用します。
楕円曲線上の \(\bs{F}_p^{\:2}\) の点の一つを \(G=(G_x,\:G_y)\) とし、\(d\) を \(G\) の位数、\(n\) を \(1\leq n\) の整数とします。\(G\) の \(n\) 倍(=スカラー倍)を \(nG\) と書き、
と定義します。この定義から、
です。また、\((dk)G=\mathcal{O}\) \((k=1,\:2,\:3,\:\cd)\) です。スカラー倍は「倍」という名前がついているため、整数と楕円曲線上の点の掛け算のように誤解しそうですが、掛け算ではありません。
です。従って、\(n,\:\:m\) を整数とすると次のような式が成り立ちます。
\((1)\) 式には、整数の乗算とスカラー倍が混在しています。また \((2)\) 式に整数の加算の \(+\) と、楕円曲線上の点の加算の \(+\) が混在していますが、意味するところは明確でしょう。さらに、
も成り立ちます。つまり、スカラー倍の "スカラー" の部分が式の場合、\(d\) を法とする演算でよいことになります。\(d\) は素数なので \(d\) を \(q\) と書くと、 "スカラー" 部分の式は有限体 \(\bs{F}_q\) での演算と言えます。たとえば \((4)\) は、
と記述できます。
\(nG\) を求める計算は、\(E(a,\:b,\:p)\) の2倍式と加法式を使って可能です。例として \(133G\) の場合だと、\(133=2^7+2^2+1\) なので、
となります。つまり、\(E(a,\:b,\:p)\) の2倍式を7回使って、
と順次計算し、加法式を2回使うと \(133G\) が求まります。これは \(n\) がたとえ巨大数であっても可能です。\(2^{256}\) は10進数で約80桁(256ビット)の巨大数ですが、それでも256回程度の2倍算と最大で256回程度の加算をすれば \(nG\) が求まります。このあたりは 4.2 の「冪剰余の計算アルゴリズム」と同じです。もちろん冪剰余と違って、2倍算も加算も単純な掛け算ではありません。\(E(a,\:b,\:p)\) の群演算は、定義式どおりの少々ややこしい式です。しかし計算が可能なことは確かです。
離散対数
スカラー倍の演算を、
\(P=nG\)
とします。上に書いたように、この計算は高速に可能ですが、その逆、つまり \(P\) と \(G\) を知って \(n\) 求めるのは困難になります。この \(n\) を求める問題を、加法群 \(E(a,\:b,\:p)\) における「離散対数問題」と呼びます。離散対数問題を解くのが不可能になるのは、\(G\) の位数 \(d\) が10進数で数10桁以上といった巨大数の場合です。その場合、\(P\) は \(d\) 種のバリエーションをとるので、\(n\) を求めるのは不可能になります。
位数 \(d\) が巨大数である \(G\) を求める方法の一つは、\(p\) を巨大な素数とし、群位数 \(\#E\) も素数であるような \(E(a,\:b,\:p)\) を選ぶことです。そうすると 17.4 により、零元 \(\mathcal{O}\) 以外の \(E(a,\:b,\:p)\) の全ての元の位数 \(d\) は \(\#E\) になり、その \(\#E\) は \(p+1\) の近辺にあるので、\(G\) をどのように選ぼうとも位数 \(d\) は巨大素数になります。
\(\#E\) が素数である \(E(a,\:b,\:p)\) では、任意の元 \(P\) と \(G\) について、\(nG=P\) となる \(n\) が唯一存在することになります。このことを、
と書くと、\(G\) は実数における通常の対数の "底(base)" に相当します。\(G\) は \(E(a,\:b,\:p)\) の元 = \(\bs{F}_p^{\:2}\) の元なので、\(G\) を「ベースポイント(base point)」と呼びます。このペースポイントを含め、楕円曲線暗号では、
が公開されます。そして暗号化通信では、\(d\) より小さい数 \(k\) をランダムに選び
とします。公開鍵だけを知っても秘密鍵は計算できない。これが楕円曲線暗号の原理です。なお、 \(\#E\) が 素数でなくても、位数 \(d\) が巨大素数である \(G\) を選ぶことで、楕円曲線暗号は成立します。
スカラー倍のイメージをつかむため、\(p\) がごく小さい数の場合で実験してみます。計算してみると、\(p=29,\:\:a=-1(=28),\:\:b=1\) のとき \(\#E=37\) となって、群位数が素数になります。\(y^2=x^3-x+1\) の解の一つは \((0,\:1)\) なので、これをベースポイント \(G\) としてスカラー倍を順次計算してみると次の通りとなります。
群位数が素数なので \(G\) の位数は \(37\) となり、群位数と一致します。この計算を \(\bs{F}_p^{\:2}\) の平面に表示すると次の通りです。\(G\) と \(36G\) は赤丸、\(2G\) ~ \(35G\) は黒丸です。矢印は加算を示し、赤矢印は \(G+G\) と \(35G+G\) の加算です。
スカラー倍を繰り返すごとに "楕円曲線" 上の合計\(36\)点を通り、それが乱雑に変化することが分かります。
振り返ってみると、RSA暗号(No.311)の安全性は巨大数の因数分解の困難性に依存しているのでした。またディフィー・ヘルマンの鍵交換(No.313)は、乗法群 \(\bs{F}_p^{*}\) における離散対数問題を解くことの困難性に依存しています。これらに使われる演算はいずれも整数の乗除算です。それに対して楕円曲線暗号に使われるのは、整数の乗除算よりは遙かに複雑な、楕円曲線上の加法群における「加算」です。ここに楕円曲線暗号の解読しにくさの要因があります。
実用的な楕円曲線暗号で公開するパラメータをどうやって作るか、その一例をあげます。
\(\#E\) が素数なので、\(G\) の位数 \(d\) は \(\#E\) に等しくなります。なお、\(\#E\) がたまたま \(p\) と一致すると離散対数問題が解けることが分かっているので、③ でそのようなケースを排除しておきます。
この決め方では、群位数 \(\#E\) の計算と素数判定を繰り返すことになり、多大な計算時間がかかることは想像に難くありません。しかしパラメータは1度計算すれば暗号通信の仕様として公開し、皆がそれを使えばいいわけです。最初の1回だけの計算時間より、その後の通信の安全性の方が重要です。
楕円曲線暗号のパラメータの一例を次に掲げます。secp160r1 という名称で公開されているパラメータです。群位数 \(\#E\:( > p)\) は素数です。\(p,\:\#E\) ともに10進で49桁の数です。
secp160r1
ちなみに、計算してみると、
\(\dfrac{\#E-(p+1)}{2\sqrt{p}}\fallingdotseq0.978\)
であり、\(\#E\) は「ハッセの定理」の上限付近にあります。
楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)
楕円曲線暗号とは、以上のような「有限体上の楕円曲線が構成する加法群を利用した暗号方式」の総称です。その例として、ディフィー・ヘルマンの鍵共有(= DH、No.313「高校数学で理解する公開鍵暗号の数理」参照)を楕円曲線暗号で実現できます(ECDH と略称される)。鍵共有のプロセスは次のように進みます。しかるべき「公開鍵センター」が、皆が使う公開鍵として、
をオープンにして(暗号通信の仕様書として公開して)おきます。以下のスカラー倍演算はすべて \(\bs{F}_p\) で行います。Alice と Bob が秘密鍵を共有したい場合、
します。乱数 \(k_A\) は Alice の秘密鍵として秘匿します。次に同様に、
します。もちろん \(k_B\) は秘匿します。そして、
とします。この作り方から \(K_A=K_B=K\) となるので、楕円曲線上の点である秘密鍵 \(K\) を共有できたことになり、以降はこれを使って暗号化通信(公開鍵ではない、高速な暗号化通信)を行います。使った秘密鍵は通信が終わったら捨てます。もちろん、\(K=(K_x,\:K_y)\) の \(K_x\) だけを秘密鍵としてもよいわけです。
原理は、オリジナルのディフィー・ヘルマンの鍵交換(DH)と全く同じです。ただ、オリジナルが \(\bs{F}_p^{*}\) での離散対数問題を利用していたのに対し、ECDH は \(E(a,\:b,\:p)\) での離散対数問題を利用した暗号であることが違います。
メッセージ伝送とデジタル署名
以降、前提として、
が公開されているものとします。
メッセージ伝送
楕円曲線暗号によるメッセージ伝送方式の例として「楕円曲線 ElGamal 暗号」をとりあげます。これは、\(\bs{F}_p\) における離散対数問題を利用した ElGamal 暗号(No.313「高校数学で理解する公開鍵暗号の数理」の「13. 離散対数暗号」参照)の「楕円曲線版」です。
この暗号では、送るべきメッセージを \(m\)(=整数)とするとき、\(m\) を \(\bs{F}_p\) 上の楕円曲線の点 \(M=(x,\:y)\) と対応付けます。その対応付けの方法は送信者と受信者であらかじめ合意しておく必要があります。そのやり方の例として、\(m\) を \(\dfrac{d}{100}\) 未満の数となるように選びます。そして、
\(x=m\cdot100+i\:\:(i=0,\:1,\:2,\:\cd,\:99)\)
の \(100\) 個の中から、
\(x^3+ax+b\)
が平方数となるような \(x\) を選びます。\(x\) の約半数は \(y^2=x^3+ax+b\) を満たす \(y\) があるので、\(100\)個を試せば必ず \(x\) が見つかります。そこで \(x^3+ax+b\) の平方根を計算して \(y\) を求め、
\(M=(x,\:y)\)
を伝送するメッセージとします(\(y\) は2つありますが、どちらかを選びます)。\(M\) から \(m\) への復元は、\([\cd]\) を \(\cd\) を超えない最大の整数(=ガウス記号)として、
\(m=\left[\dfrac{x}{100}\right]\)
で可能です(=切り捨て除算)。この \(100\) に大きな意味はなく、コンピュータで実装するときには演算回数を減らすために \(2^n\) となる数を選ぶのがベターでしょう。
楕円曲線 ElGamal 暗号によるメッセージ伝送は次のように進みます。Bob から Alice にメッセージ \(m\) を送る例です。
まず、Alice と Bob は「楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)」を使って秘密鍵 \(k_A\) と \(k_B\) を決め、公開鍵 \(k_AG\) と \(k_BG\) を交換しておきます。
Bob の暗号化手順
Alice の復号化手順
デジタル署名
Bob から Alice にメッセージ \(m\) (楕円曲線上の点としては \(M\))を送るとき、次のようにしてデジタル署名を付加できます。ベースポイント \(\bs{G}\) の位数 \(\bs{d}\) は素数ですが、この素数を \(\bs{q}\) とも書き、スカラー倍における "スカラー部分の演算" を有限体 \(\bs{\bs{F}_q}\) での演算として表記します。また、ハッシュ関数を \(H(\:)\) と書きます(No.311「高校数学で理解するRSA暗号の数理(2)」の "補記" 参照)。
Bob の署名手順
Alice の検証手順
このデジタル署名のアルゴリズムは、ECDSA (Elliptic Curve Digital Signature Algorithm) と呼ばれるもので、メッセージ \(m\) の暗号化方式が「楕円曲線 ElGamal 暗号」でなくても通用します。一般に、メッセージ伝送方式とデジタル署名方式は独立です。
上にも書いたように、楕円曲線暗号とは「有限体上の楕円曲線が構成する加法群を利用した暗号方式」の総称です。「楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)」や「楕円 ElGamal 暗号」以外にも種々の方式が提案され、実用化されています。
18. 結合則が成り立つことの検証と証明
前回の No.315 で、"結合則が成り立つ" ことの証明を後回しにしたので、ここに書きます。楕円曲線暗号は、楕円曲線上の有理点が群になることに依存した暗号です。その "群" であることの要件の一つは結合則が成り立つことであり、楕円曲線暗号の数学的背景として是非とも確認しておきたいところです。
楕円曲線上の3点について、
\((P_1+P_2)+P_3=P_1+(P_2+P_3)\)
となるのが結合則ですが、加法は数式で示されています。そこでまず、数式を使って簡単な例で確かめてみます。
数式による確認(トライアル)
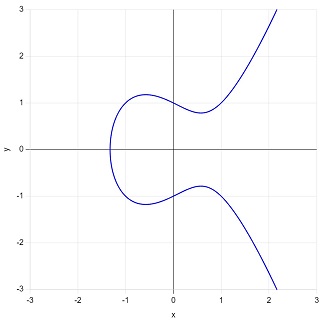
図15:楕円曲線の例2
\(y^2=x^3-x+1\)
楕円曲線として、No.315 の図15でとりあげた、
\(y^2=x^3-x+1\)
を例とし、この楕円曲線上に2つの固定点と1つの任意点を取って計算してみます。使う記号は次の通りです。
\(P_1=(0,\:1)\)
\(P_2=(p,\:q)\:\:\:(q^2=p^3-p+1)\)
\(P_3=(1,\:1)\)
\(P_4=P_1+P_2\)
\(P_5=P_4+P_3=(P_1+P_2)+P_3\)
\(P_6=P_2+P_3\)
\(P_7=P_1+P_6=P_1+(P_2+P_3)\)
\(P_5=P_7\) が示せれば結合則が成り立っています。以下、No.315 の加法式(第2形)、
を使って計算を進めると次のようになります。
途中、\(x_5\) の計算で \(q^2\) を \(p^2-p+1\) で置き換えました。さらに、\(\lambda_4=\dfrac{p^2-1}{q+1}\) を使って \(\lambda_5\) の式から \(\lambda_4\) を消去すると、
\(\lambda_5=\dfrac{-p^2+2q+3}{(p+1)(q+1)}\)
となります。これを用いて \(y_5\) を計算すると、
となり、\(P_5=(x_5,\:y_5)\) が求まりました。
ここで \(\lambda_6=\dfrac{p^2+p}{q+1}\) を使って \(\lambda_7\) の式から \(\lambda_6\) を消去すると、
\(\lambda_7=-\dfrac{2(p^2+p-q-1)}{(p+1)(q+1)}\)
となります。この \(\lambda_7\) を使って \(y_7\) を計算すると、
となり、\(P_7=(x_7,\:y_7)\) が求まりました。以上の計算で、\(P_5=(\)\(x_5,\:y_5\)\()\) と \(P_7=(\)\(x_7,\:y_7\)\()\) は同じ点であることが分かり、この例では結合則が検証できました。
もちろんこれで結合則が証明できたわけではありません。しかし上の検証から分かるように、加法式によって結合則を証明するには計算が膨大になると推測できます。そこで次に、数式処理ソフトを使って証明します。
数式による証明(SymPy)
再度、記号の定義をはっきりさせます。
群の要件の一つである結合則を証明するために、楕円曲線上の3点を、\(P_1,\:\:P_2,\:\:P_3\) とし、
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とします。
\(y_1^2=x_1^3+ax_1+b\)
\(y_2^2=x_2^3+ax_2+b\)
\(y_3^2=x_3^3+ax_3+b\)
です。このとき、
\((P_1+P_2)+P_3=P_1+(P_2+P_3)\)
であれば結合則が成り立ちます。これを示すため、\(P_4,\:P_5,\:P_6,\:P_7\) を、
\(P_1+P_2=P_4\)
\(P_4+P_3=P_5\)
\(P_2+P_3=P_6\)
\(P_1+P_6=P_7\)
\(P_i=(x_i,\:y_i)\:\:(4\leq i\leq7)\)
と定義して、
\(P_5\:=\:P_7\)
であることを証明します。そのためには、
\(x_5=x_7\)
を示せれば十分です。以降で、Python のライブラリ SymPy の数式処理機能を使って、\(x_5=x_7\) であることを証明します。そのためのコードと実行結果を掲げますが、ポイントは、
\(y_i^2=x_i^3+ax_i+b\:\:(1\leq i\leq3)\)
の関係を使って、計算途中の要所要所で、\(y_1,\:y_2,\:y_3\) の2乗以上の項を無くすことです。次のコードでは ellipse_substitute 関数がそれを行っています。
実行結果
この実行結果より、\(x_5\) と \(x_7\) の差異は厳密に \(0\) であり、\(x_5=x_7\) であることが証明されました。
このコードの ellipse_substitute 関数の補足ですが、SymPy のメソッドの cancel は、式を有理式の形(\(\tfrac{p}{q}\) の形。\(p,\:q\) は多項式)にととのえます。また subs は、式を別の式(ないしは値)で置き換えます。従って、関数は次の処理をします。
\(y_i^4\) の置き換えは、\(y_i^2\) の置き換えと同時に SymPy で処理されます。\(y_i^5\) 以上の項は、このコードでは発生しません。ちなみに、\(x_5\) と \(x_7\) を有理式の形で、
\(x_5=\dfrac{A}{B},\:\:x_7=\dfrac{C}{D}\)
と表わしたときの \(A,\:B,\:C,\:D\) は次の通りです。\(A,\:C\) は72項、\(B,\:D\) は40項もあるので手計算は無理ですが、SymPy で確認すると \(AD=BC\) が成り立っています。
\(A=x_1^4x_2^2x_3+\)\(x_1^4x_2x_3^2+\)\(6x_1^3x_2^3x_3-\)\(x_1^3x_2^2x_3^2+\)\(x_1^2x_2^4x_3-\)\(x_1^2x_2^3x_3^2+\)\(x_1x_2^4x_3^2+\)\(y_1y_2(-2ax_1^2+\)\(4ax_1x_2-\)\(4ax_1x_3-\)\(2ax_2^2-\)\(4ax_2x_3-\)\(8bx_3-\)\(4x_1^2x_2x_3-\)\(2x_1^2x_3^2-\)\(4x_1x_2^2x_3+\)\(4x_1x_2x_3^2-\)\(2x_2^2x_3^2)+\)\(y_1y_3(2ax_1^2+\)\(4ax_1x_2-\)\(6ax_2^2+\)\(8bx_1-\)\(8bx_2+\)\(6x_1^2x_2^2-\)\(4x_1x_2^3-\)\(2x_2^4)+\)\(y_2y_3(-6ax_1^2+\)\(4ax_1x_2+\)\(2ax_2^2-\)\(8bx_1+\)\(8bx_2-\)\(2x_1^4-\)\(4x_1^3x_2+\)\(6x_1^2x_2^2)+\)\(a^2(x_1^3-\)\(x_1^2x_2+\)\(x_1^2x_3-\)\(x_1x_2^2+\)\(6x_1x_2x_3+\)\(x_2^3+\)\(x_2^2x_3)+\)\(2ab(x_1^2-\)\(2x_1x_2+\)\(4x_1x_3+\)\(x_2^2+\)\(4x_2x_3)+\)\(8b^2x_3+\)\(a(x_1^4x_2+\)\(x_1^4x_3-\)\(x_1^3x_2^2+\)\(2x_1^3x_2x_3+\)\(x_1^3x_3^2-\)\(x_1^2x_2^3+\)\(10x_1^2x_2^2x_3-\)\(x_1^2x_2x_3^2+\)\(x_1x_2^4+\)\(2x_1x_2^3x_3-\)\(x_1x_2^2x_3^2+\)\(x_2^4x_3+\)\(x_2^3x_3^2)+\)\(2b(x_1^4-\)\(4x_1^3x_2+\)\(2x_1^3x_3+\)\(6x_1^2x_2^2+\)\(2x_1^2x_2x_3+\)\(x_1^2x_3^2-\)\(4x_1x_2^3+\)\(2x_1x_2^2x_3-\)\(2x_1x_2x_3^2+\)\(x_2^4+\)\(2x_2^3x_3+\)\(x_2^2x_3^2)\)
\(B=x_1^4x_2^2-\)\(2x_1^4x_2x_3+\)\(x_1^4x_3^2+\)\(6x_1^3x_2^3+\)\(2x_1^3x_2^2x_3-\)\(4x_1^3x_2x_3^2+\)\(x_1^2x_2^4+\)\(2x_1^2x_2^3x_3+\)\(6x_1^2x_2^2x_3^2-\)\(2x_1x_2^4x_3-\)\(4x_1x_2^3x_3^2+\)\(x_2^4x_3^2+\)\(y_1y_2(-4ax_1-\)\(4ax_2-\)\(8b-\)\(4x_1^2x_2+\)\(4x_1^2x_3-\)\(4x_1x_2^2-\)\(8x_1x_2x_3+\)\(4x_2^2x_3)+\)\(a^2(x_1^2+\)\(6x_1x_2+\)\(x_2^2)+\)\(8ab(x_1+\)\(x_2)+\)\(8b^2+\)\(2a(3x_1^3x_2-\)\(x_1^3x_3+\)\(2x_1^2x_2^2+\)\(x_1^2x_2x_3+\)\(3x_1x_2^3+\)\(x_1x_2^2x_3-\)\(x_2^3x_3)+\)\(4b(x_1^3+\)\(x_1^2x_2-\)\(x_1^2x_3+\)\(x_1x_2^2+\)\(2x_1x_2x_3+\)\(x_2^3-\)\(x_2^2x_3)\)
\(C=x_1^2x_2^4x_3-\)\(x_1^2x_2^3x_3^2-\)\(x_1^2x_2^2x_3^3+\)\(x_1^2x_2x_3^4+\)\(x_1x_2^4x_3^2+\)\(6x_1x_2^3x_3^3+\)\(x_1x_2^2x_3^4+\)\(y_1y_2(2ax_2^2+\)\(4ax_2x_3-\)\(6ax_3^2+\)\(8bx_2-\)\(8bx_3+\)\(6x_2^2x_3^2-\)\(4x_2x_3^3-\)\(2x_3^4)+\)\(y_1y_3(-6ax_2^2+\)\(4ax_2x_3+\)\(2ax_3^2-\)\(8bx_2+\)\(8bx_3-\)\(2x_2^4-\)\(4x_2^3x_3+\)\(6x_2^2x_3^2)+\)\(y_2y_3(-4ax_1x_2-\)\(4ax_1x_3-\)\(2ax_2^2+\)\(4ax_2x_3-\)\(2ax_3^2-\)\(8bx_1-\)\(2x_1^2x_2^2+\)\(4x_1^2x_2x_3-\)\(2x_1^2x_3^2-\)\(4x_1x_2^2x_3-\)\(4x_1x_2x_3^2)+\)\(a^2(x_1x_2^2+\)\(6x_1x_2x_3+\)\(x_1x_3^2+\)\(x_2^3-\)\(x_2^2x_3-\)\(x_2x_3^2+\)\(x_3^3)+\)\(2ab(4x_1x_2+\)\(4x_1x_3+\)\(x_2^2-\)\(2x_2x_3+\)\(x_3^2)+\)\(8b^2x_1+\)\(a(x_1^2x_2^3-\)\(x_1^2x_2^2x_3-\)\(x_1^2x_2x_3^2+\)\(x_1^2x_3^3+\)\(x_1x_2^4+\)\(2x_1x_2^3x_3+\)\(10x_1x_2^2x_3^2+\)\(2x_1x_2x_3^3+\)\(x_1x_3^4+\)\(x_2^4x_3-\)\(x_2^3x_3^2-\)\(x_2^2x_3^3+\)\(x_2x_3^4)+\)\(2b(x_1^2x_2^2-\)\(2x_1^2x_2x_3+\)\(x_1^2x_3^2+\)\(2x_1x_2^3+\)\(2x_1x_2^2x_3+\)\(2x_1x_2x_3^2+\)\(2x_1x_3^3+\)\(x_2^4-\)\(4x_2^3x_3+\)\(6x_2^2x_3^2-\)\(4x_2x_3^3+\)\(x_3^4)\)
\(D=x_1^2x_2^4-\)\(4x_1^2x_2^3x_3+\)\(6x_1^2x_2^2x_3^2-\)\(4x_1^2x_2x_3^3+\)\(x_1^2x_3^4-\)\(2x_1x_2^4x_3+\)\(2x_1x_2^3x_3^2+\)\(2x_1x_2^2x_3^3-\)\(2x_1x_2x_3^4+\)\(x_2^4x_3^2+\)\(6x_2^3x_3^3+\)\(x_2^2x_3^4+\)\(y_2y_3(-4ax_2-\)\(4ax_3-\)\(8b+\)\(4x_1x_2^2-\)\(8x_1x_2x_3+\)\(4x_1x_3^2-\)\(4x_2^2x_3-\)\(4x_2x_3^2)+\)\(a^2(x_2^2+\)\(6x_2x_3+\)\(x_3^2)+\)\(8ab(x_2+\)\(x_3)+\)\(8b^2+\)\(2a(-\)\(x_1x_2^3+\)\(x_1x_2^2x_3+\)\(x_1x_2x_3^2-\)\(x_1x_3^3+\)\(3x_2^3x_3+\)\(2x_2^2x_3^2+\)\(3x_2x_3^3)+\)\(4b(-\)\(x_1x_2^2+\)\(2x_1x_2x_3-\)\(x_1x_3^2+\)\(x_2^3+\)\(x_2^2x_3+\)\(x_2x_3^2+\)\(x_3^3)\)
3次曲線による証明
コンピュータを使った(=数式処理ソフトによる)証明では、なんとなく、証明した気になりません。その理由は、SymPy が正しい(バグがない)ことに依存しているからです。そこで以下は、シルヴァーマン、テイト著「楕円曲線論入門」にある証明を紹介します。これは、楕円曲線を含む3次曲線の性質を用いた証明で、本質をついた議論になっています。
結合則が成り立つのは、楕円曲線上の加法を「3次曲線と直線の交点」で決めていることに理由があります。「楕円曲線論入門」に、結合則が成り立つことを示した次の図があります。加法群の零元 \(\mathcal{O}\) を楕円曲線上にとった場合の図です。
楕円曲線上に点 \(P\)、\(Q\)、\(R\) をとったとき、
となるのが結合則ですが、
です。ここで \(\!*\!\) の記号は、\(A\!*\!B\) と書くと \(A\) と \(B\) を結ぶ直線が楕円曲線と交わる点(で \(A\)、\(B\) 以外の点)の意味です。\(\mathcal{O}\) は零元でした。従って、結合則を証明するためには、
が証明できればよいことになります。言葉で書くと、
となります。上の図はそれを表しています。以下の証明では同じことですが、次を示します。
これは楕円曲線上の2点、\((P+Q)\!*\!R\) と \(P\!*\!(Q+R)\) が等しい(= 図11)ことと同じなので、以降は 18.1 が成り立つことを示します。そのためにまず、次の命題 18.2 を証明します。この証明の筋道は「楕円曲線論入門」に書かれているものです。
これは「ケーレー・バカラック(Cayley-Bacharach)の定理」と呼ばれるものの一部です(Cayleyは英国、Bacharachはドイツの数学者。バカラックは英語読み。いずれも19世紀)。この定理は、
というもので、その3次元曲線の場合が 18.2 です。ここで言う3次曲線とは次の一般形で表される "3次曲線のすべて" であり、楕円曲線もその一部です。
\([\)3次曲線の一般形\(]\)
\(ax^3+bx^2y+cxy^2+dy^3+ex^2+fxy+gy^2+hx+iy+j=0\)
10個の係数(=パラメータ)、\(a,\:b,\:\:\cd\:,\:i,\:j\) を決めると3次曲線が一つ決まります。もちろん、各係数を定数倍した曲線は同じ曲線です。つまり、この形の3次曲線の係数は実質的に "9次元" と言えます。3次曲線なので \(a,\:b,\:c,\:d\) のうち少なくとも一つは \(0\) でないものがあります。その係数で全体を割れば、係数の数は9個になることからもわかります。9次元なので「相異なる8点を通る3次曲線」は無数にあります。
そこで、相異なる8点を通る3次曲線が一般的にどういう式で表現できるかを考えます。相異なる8点の座標を、
とします。まず、3次曲線が \(P_1\) を通るということは、10個のパラメータは次の制約条件を満足しなければなりません。
\(x_1^3a+x_1^2y_1b+x_1y_1^2c+y_1^3d+x_1^2e+x_1y_1f+y_1^2g+x_1h+y_1i+j=0\)
これは 10個の変数 \(a\) ~ \(j\) についての線型方程式(1次方程式)なので、係数を変数の前に記述しました。同様にして、3次曲線が \(P_2\) から \(P_8\) を通ることから7個の制約条件が得られます。これらをまとめると、
の、合計8つの制約条件が得られます。8個の点を通る3次曲線の10個のパラメータは、この8つの制約条件(連立1次方程式)を満たさなければなりません。ということは、\(10-8=2\) で、これらのパラメータは、制約条件のない自由な2つのパラメータで表現できることになります。
たとえば \(a\) と \(b\) を "2つのパラメータ" に選ぶと、残りの \(c\) ~ \(j\) は、\(\al_na+\beta_nb\:(n=c\:\cd\:j)\) という「\(a\) と \(b\) の1次式」で表現できます(\(\al_n,\:\beta_n\) は連立1次方程式の係数で決まる値)。しかしこれでは \(a=0\) かつ \(b=0\) のときに、すべてのパラメータが \(\bs{0}\) という自明な解しか得られません。\(x^3\) の項と \(x^2y\) の項がない3次曲線はいくらでもありうるので、自明ではない解の中に \(a=0,\:b=0\) となるものは当然あるはずです。つまり、\(\al_na+\beta_nb\) の形は連立1次方程式の解の全部は表していません。
では、上記の連立1次方程式の「自明ではない解すべてを表す一般解」はどういう形でしょうか。それには8つの方程式を満たす独立な数値の組(=連立1次方程式の解)を2組用意します。つまり無数にある解の中から2つをピックアップし、それをベクトル表現で、
とします。"独立" とはこの場合、2つの数値群が異なった3次曲線を表現しているということです。そして、同時に \(0\) にはならない新たな2つのパラメータを導入します。それを \(\lambda_1,\:\:\lambda_2\) とすると、
が連立1次方程式の一般解(不定解)になります。自由な2つのパラメータの1次式で表現されていて、8つの方程式を満たすことが明らかだからです。この一般解をもとに3次曲線の方程式を表現します。そこで、
の2つの関数を考えると、\(f_1=0\) の3次曲線と \(f_1=0\) の3次曲線は、共に8点を通ります。従って、
は8点を通り、2つの自由なパラメータで表現された3次曲線群です。従って、これが \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) を通るすべての3次曲線を表す一般形です。
以上を踏まえて命題 18.2 を検討します。命題を再掲すると、
でした。この前半の2つの3次曲線の関数式を
とします。\(F_1=0\) も \(F_2=0\) も9点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_9\) を通る3次曲線です。従って \(F_1=0\) と \(F_2=0\) は \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通る2つの3次曲線でもある。ということは、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通るすべての3次曲線は、
で表されます。従って、命題の後半に出てくる別の3次曲線 \(D\) が \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通るとすると、\(D\) は \(F=\lambda_1F_1+\lambda_2F_2=0\) で表現できます。
ここでよく考えてみると、3次曲線 \(F=0\) は9点目の \(P_9\) を通るのでした。従って \(D\) も \(P_9\) を通ります。これで 18.2 が成り立つことが証明できました。以上を振り返ってまとめると次のようになります。
この "まとめ" で述べているように、8つの点を通る3次曲線は無数に存在します。8つの点を通る3次曲線は(一般には)一意に定まりません。そこで点を1つ増やすと、9つの点を通る3次曲線は(一般には)一意に定まります(9次元だから)。しかし、その9点が「2つの3次曲線の交点である9点」なら状況が変わります。その9点は独立ではなく、8点が決まれば残りの1点は自動的に決まる。従って、8点を通るすべての3次曲線は残りの1点も通ることになります。この例を図で示すと次の通りです。2つの3次曲線、\(C_1\) と \(C_2\) を、
\(C_1\::\)
\(C_2\::\)
とします。この2つの3次曲線は9つの点、\(P_1\) ~ \(P_9\) で交差します。それを正確に図示すると図19の通りです。
ここで、\(C_1,\:C_2\) とは別の、\(P_1\) ~ \(P_8\) の8つの点を通る3次曲線を作ると、それも \(P_9\) を通ります(図20)。図20 で、黄・緑・青の3つの3次曲線がその例です。
18.2 を踏まえて、楕円曲線の加法群で結合則が成り立つことを証明しますが、証明のポイントは、相異なる3つの直線を "3次曲線" として扱うことです。この扱いがなぜ可能かと言うと、3つの直線を、
としたとき、
からです。もちろん、\(F_L=0\) という曲線の方程式は、3次曲線の一般形の係数 \(a,\:b,\:\:\cd\:,\:i,\:j\) に特別の関係を持ち込んだものです。だからこそ3つの直線を表現しているわけです(数学用語で言うと "退化した" 3次曲線)。しかし特別の関係があるとしても 18.2 を証明した議論の筋道には全く影響しません。
具体的な例をあげると、次の通りです。まず、3次曲線との交点が3つある直線を2つ描き(赤で示す)、交点を \(P_1,\:P_2,\:P_3\)、\(P_4,\:P_5,\:P_6\) とします(図21)。
次に、\(P_1\) と \(P_4\) を結ぶ直線と、\(P_3\) と \(P_6\) を結ぶ直線を緑で描き、3次曲線との交点をそれぞれ \(P_7,\:\:P_8\) とします(図22)。
こうした上で、\(P_2\) と \(P_5\) を結ぶ直線を緑で、\(P_7\) と \(P_8\) を結ぶ直線を赤で描きます(図23)。
ここで、
\(C_1\) : 3次曲線
\(C_2\) : 赤の3直線
\(C_3\) : 緑の3直線
とすると、\(C_1,\:\:C_2,\:\:C_3\) の 3つの "3次曲線" はすべて \(P_1\) ~ \(P_8\) の8点を通ります。すると 18.2 によって、この3つの "3次曲線" ははすべて、\(P_1\) ~ \(P_8\) 以外の、ある特別な点(=図23の点線丸印)を通ります。言い換えると、
ことになります。
以上を踏まえて、結合則を証明すべき図11を再掲します。図11 と図23 は数学的に全く同じであることが、以降の証明のポイントです。
証明すべきことは 18.1 の、
でした。図11で、
とすると、\(C_1\)(点線) と \(C_2\)(実線)は次の9つの点を通ります。
\(C_1\) と \(C_2\) が9つの点を通るのはそういう風に作図したからです。一方、楕円曲線は \(T\) 以外の \(P_1\) ~ \(P_8\) の8点を通ります。なぜならその8点は楕円曲線上の点として作ったからです。ところが \(T\) だけは違っていて、楕円曲線上の点として作ったのではなく2直線の交点です。しかし 18.2 によって楕円曲線は \(T\) も通ることになります。
これで、楕円曲線上の有理点が作る加法群で結合則が成り立つことの証明が完成しました。
零元を無限遠点にとる加法群ではどうなるでしょうか。この場合は「射影平面での3次曲線」を考える必要があります。射影平面での3次曲線の一般形は、
\([\)射影平面における3次曲線の一般形\(]\)
\(AX^3+BX^2Y+CXY^2+DY^3+EX^2Z+FXYZ+GY^2Z+\)
\(HXZ^2+IYZ^2+JZ^3=0\)
ですが、証明の筋道は \(xy\) 平面と全く同じです。というのも、証明のコアのところは「10変数の連立1次方程式(方程式数が8)の不定解が、一般形でどう表現できるか」であり、曲線方程式の未知数が \((x,\:y)\) の2つであっても \((X,\:Y,\:Z)\) の3つであっても証明の論理に影響がないからです。
というわけで、楕円曲線暗号で実際に使われる「無限遠点を零元にした加法群」においても結合則が成り立つのでした。
19. パスカルの定理
最後に余談ですが、18.2(ケーレー・バカラックの定理)から証明できる別の定理があります。「パスカルの定理」です。これはパスカルが16歳のときに発表した「円錐曲線試論」にあります。最も一般的な形で言うと次の通りです。
これは非常に美しい定理です。どんな円錐曲線かを言っていないし(円、楕円、放物線、双曲線)、円錐曲線上の6点の位置も、その順序も何も言ってない。それにもかかわらず「同一直線上にある」という、シンプルで強い断定が結論にくる ・・・・・・。個人的経験を言うと、高校生時代にこの定理を知ってその "不思議さ" が印象的だったことを覚えています。
この定理の例を図24と図25、図26に示します。\(Q_1\) を \(P_7\)、\(Q_2\) を \(P_8\)、\(Q_3\) を \(T\) と書きました。円錐曲線が円か楕円であり、6点を円・楕円の周上に順に(= 一周するように)とった場合には、パスカルの定理は、
と簡潔に表現できます(図24)。図25の楕円上の点の位置は図24と同じですが、名前付けが違います。しかし3点が同一線上に並ぶのは同じです。このように6点は楕円上のどの位置にどの順序で配置してもよいわけです。
定理の証明は次の通りです。3次曲線、\(C_1,\:\:C_2,\:\:D\) を、
とします。\(C_1\) と \(C_2\) は 、\(P_1\) ~ \(P_8\) と \(T\) を通ります。そういう風に作図したからです。一方、\(D\) は \(P_1\) ~ \(P_8\) を通ります。そうすると 18.2 より \(D\) は \(T\) も通ります。\(D\) は \(P_7\) と \(P_8\) を通るように作図しましたが、\(T\) を通るようには作図していません。それでも \(T\) を通る。
その \(T\) は、\(D\) の円錐曲線部分にはありません。なぜなら、\(T\) は直線 \(P_3P_4\) 上に(ないしは直線 \(P_6P_1\) 上に)ありますが、円錐曲線と直線の交点は高々2つであり、\(P_3,\:\:P_4\) が(ないしは \(P_6,\:\:P_1\) が)すでに円錐曲線上にあるからです。従って \(T\) は \(D\) の直線部分にあるしかない。これで証明が終わりました。
パスカルの定理のよくある証明は、円の場合に補助円を用いて証明し、それを "斜めから見たら" 楕円でも成り立つ、とするものです。しかしこの定理は、すべての円錐曲線(=2次曲線の一般形、\(ax^2+bxy+cy^2+dx+ey+f=0\) で表される曲線)で成り立つことが上の証明から分かります。
ちなみに、パスカルの定理は「円錐曲線」を「2直線」に置き換えても、交点ができるように点を配置すれば成り立ちます(パップスの定理と呼ばれる。パップスは4世紀のアレキサンドリアの数学者)。
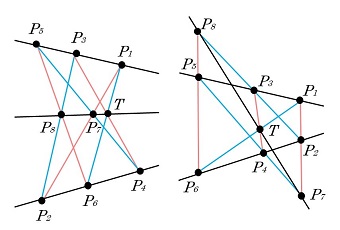
図27 パップスの定理
軸を含む平面で円錐を2分割すると(平行でない)2直線になり、それは(退化した)円錐曲線とも言えますが、たとえ平行な2直線であっても2次曲線の一般形で表現できるので定理は成り立ちます。
楕円曲線暗号は「楕円曲線上の有理点による加法群」の上に作られた暗号ですが、
のでした。
補足:素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
(前回の No.315 より続く)
16. 楕円曲線上の点
有限体 \(\bs{F}_p\) の元 \(x\) と \(y\) のぺア \((x,\:y)\) の集合を \(\bs{F}_p^{\:2}\) と記述します。集合 \(\bs{F}_p^{\:2}\) の元で楕円曲線上の "点" はどれだけあるでしょうか。まず、楕円曲線の式を満たす \(\bs{F}_p^{\:2}\) の元がどのように計算できるかを調べます。
平方数と平方根
楕円曲線の式を、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=z&\\
&&z=x^3+ax+b&\\
\end{eqnarray}
\end{array}\right.\)
と書くとき、\(z\)(\(z\neq0\))が \(\bs{F}_p\) での平方数なら、\(y\) の解が2つ求まります。ここで、次の命題が成立します。
| 16.1 | 平方数である条件 |
|
\(z\) を \(0\) ではない \(\bs{F}_p\) の元とする。
\(z^{\frac{p-1}{2}}=1\) であるとき(かつ、そのときに限り)\(z\) は平方数である(= オイラーの規準)。 | |
\(\bs{F}_p\) で考えているので「平方数」と書きましたが、整数の世界では平方剰余です。つまり、\(x^2=a\:(\mr{mod}\:n)\) となるような \(x\) が存在する \(a\) が「\(n\) を法とする平方剰余」です。16.1 の証明ですが、12.1(No.313)により、\(z\) は \(\bs{F}_p^{*}\) の生成元(の一つ)を \(g\) として、
\(z=g^k\)
と表現できます。つまり、命題の条件は、
\(g^{k\frac{p-1}{2}}=1\)
です。このとき \(k\) は偶数のはずです。なぜなら、もし \(k\) が奇数だとすると、\(k\dfrac{p-1}{2}\) は \(p-1\) で割り切れないので、
\(k\dfrac{p-1}{2}=s(p-1)+t\)
\((1\leq t < p-1)\)
\((1\leq t < p-1)\)
と表現できます。すると、
\(\begin{eqnarray}
&&g^{k\frac{p-1}{2}}&=g^{s(p-1)+t}\\
&&&=(g^{p-1})^s\cdot g^t=g^t\\
\end{eqnarray}\)
となり、\(g^t=1\:(1\leq t < p-1)\) になりますが、これは \(g\) が生成元であることと矛盾します。従って \(k\) は偶数です。そうすると \(k=2m\) とおいて、
\(z=(g^m)^2\)
となり、\(z\) は平方数になります。逆に、
\(z=y^2\)
と表現されるとすると、フェルマの小定理 3.1をつかって、
\(\begin{eqnarray}
&&z^{\frac{p-1}{2}}&=(y^2)^{\frac{p-1}{2}}\\
&&&=y^{p-1}\\
&&&=1\\
\end{eqnarray}\)
となり、\(\bs{z^{\frac{p-1}{2}}=1}\) と 「\(\bs{z}\) が平方数」は同値であることが証明できました。
なお、フェルマの小定理によって、 \((z^{\frac{p-1}{2}})^2=1\) なので、\(z^{\frac{p-1}{2}}\) は \(1\) か \(-1(=p-1)\) のどちらかです。従って、
\(z^{\frac{p-1}{2}}=\phantom{-}1\) のとき、\(z\) は平方数
\(z^{\frac{p-1}{2}}=-1\) のとき、\(z\) は平方数ではない
\(z^{\frac{p-1}{2}}=-1\) のとき、\(z\) は平方数ではない
ということになります。「平方数ではない」は、整数の世界では「平方非剰余」です。
平方根を求める
\(z\) は平方数だとわかったとき、実際に \(\bs{F}_p\) で \(y\)(= \(z\) の平方根)を求める手段が必要になります。整数であれば平方根を求めるのは容易ですが、\(\bs{F}_p\) ではそうはいきません。特に、楕円曲線暗号で使われる \(p\) は10進数で数10桁以上の巨大素数なので、総当たりで求めたり、解の存在範囲を限定していって求めるわけにはいかないのです。以下が解を求めるアルゴリズムです。
\(p\equiv3\:(\mr{mod}\:4)\) の場合
この場合は
\(y=z^{\frac{p+1}{4}}\)
が解の一つとなります(もう一つの解は \(-y\) で、つまり \(p-y\))。確認してみると、
\(\begin{eqnarray}
&&y^2&=\left(z^{\frac{p+1}{4}}\right)^2=z^{\frac{p+1}{2}}\\
&&&=z^{\frac{p-1}{2}}\cdot z=z\\
\end{eqnarray}\)
となって、確かに \(y\) が解であることがわかります。
\(p\equiv1\:(\mr{mod}\:4)\) の場合
この場合は「トネリ-シャンクスのアルゴリズム」で解を求めることができます(Tonelli は19世紀イタリア、Shanks は20世紀米国の数学者)。以下のアルゴリズムは Wikipedia を参考にしました。
\(p\equiv1\:(\mr{mod}\:4)\) の場合、\(p-1\) は \(4\) の倍数です。\(p-1\) を素因数分解したときの \(2\) のべき乗を \(S\) とすると、\(p-1\) は、
\(p-1=Q\cdot2^S\) \(Q\) は奇数、 \(S\geq2\) |
と表現できます。ここで、\(\bs{F}_p\) において平方数ではない数 \(w\) を(どれでもよいから)一つ選びます。つまり、
\(w^{\frac{p-1}{2}}=-1\)
となる数 \(w\) です。\(\bs{F}_p\) においては平方数とそうでない数が半々なので、この選択は容易です。次に、4つの数を、
\(\begin{eqnarray}
&&S_0&=S\\
&&c_0&=w^Q\\
&&t_0&=z^Q\\
&&y_0&=z^{\frac{Q+1}{2}}\\
\end{eqnarray}\) |
と定義します。このように定義すると、\(c_0,\:\:t_0,\:\:y_0\) は次の「性質」を持ちます。
\(\begin{eqnarray}
&&\:\:(c_0)^{2^{S_0-1}}&=(w^Q)^{2^{S-1}}\\
&&&=w^{Q\cdot2^{S-1}}\\
&&&=w^{\frac{p-1}{2}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_0)^{2^{S_0-1}}&=(z^Q)^{2^{S-1}}\\
&&&=z^{Q\cdot2^{S-1}}\\
&&&=z^{\frac{p-1}{2}}\\
&&&=1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:y_0^{\:2}&=\left(z^{\frac{Q+1}{2}}\right)^2\\
&&&=z^{Q+1}\\
&&&=t_0\cdot z\\
\end{eqnarray}\)
まとめると、
\(\begin{eqnarray}
&&(c_0)^{2^{S_0-1}}&=-1\\
&&(t_0)^{2^{S_0-1}}&=\phantom{-}1\\
&&(y_0)^2&=t_0\cdot z\\
\end{eqnarray}\) |
です。もし、\(t_0=1\) なら、3番目の式により \(z\) の平方根は \(y_0\) および \(-y_0\:(=p-y_0)\) ですが、そうはなりません。\(S_0=1\) なら \(t_0=1\) となりますが、\(S_0=S\geq2\) だからです。
そこで、\(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) の4数の組の列 \((i=0,\:1,\:2,\:\cd\:)\) を順次作り、上記の「性質」を保ちつつ、ある時点で \(t_i=1\) になることを目指します。\(t_i=1\) になったとしたら、そのときの \(\pm y_i\) が \(z\) の平方根です。\(i=1\) に対応する4数の組は次のようにします。
\(S_1\) : \(0 < S_1 < S_0\) で、\((t_0)^{2^{S_1}}=1\) を満たす最小の数
\(S_1=S_0-1\) と置くと、\((t_0)^{2^{S_0-1}}=1\) だったので、\(S_0-1\) は \(S_1\) の候補です。もしこれが最小なら \(S_1\) そのものです。従って条件に合う \(S_1\) を必ず選ぶことができます。
\(\begin{eqnarray} &&c_1&=(c_0)^{2^{S_0-S_1}}\\ &&t_1&=t_0\cdot(c_0)^{2^{S_0-S_1}}\\ &&y_1&=y_0\cdot(c_0)^{2^{S_0-S_1-1}}\\ \end{eqnarray}\) |
このように定義すると、次のように「性質」が保たれることが分かります。
\(\begin{eqnarray}
&&\:\:(c_1)^{2^{S_1-1}}&=\left((c_0)^{2^{S_0-S_1}}\right)^{2^{S_1-1}}\\
&&&=(c_0)^{2^{S_0-1}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_1)^{2^{S_1-1}}&=(t_0)^{2^{S_1-1}}\cdot\left((c_0)^{2^{S_0-S_1}}\right)^{2^{S_1-1}}\\
&&&=(t_0)^{2^{S_1-1}}\cdot(c_0)^{2^{S_0-1}}\\
&&&=-(t_0)^{2^{S_1-1}}\\
\end{eqnarray}\)
ここで、最後の式からマイナスを取って、
\((t_0)^{2^{S_1-1}}=X\)
とおくと、\(S_1\) の定義から \((t_0)^{2^{S_1}}=1\) なので、
\(X^2=(t_0)^{2^{S_1}}=1\)
となり、\(X\) は \(\bs{F}_p\) における方程式 \(X^2=1\) の解です。つまり、
\(X=1,\:-1\)
です。ところが \(X=1\) とすると、
\((t_0)^{2^{S_1-1}}=1\)
となりますが、\(S_1\) は \(0 < S_1 < S_0\) で \((t_0)^{2^{S_1}}=1\) を満たす最小の数と定義したにも関わらず、\(S_1\) より小さい \(S_1-1\) が定義を満たすことになってしまって矛盾します。従って \(X=-1\) であり、結局、
\(\begin{eqnarray}
&&\:\:(t_1)^{2^{S_1-1}}&=-X\\
&&&=1\\
\end{eqnarray}\)
となります。さらに、
\(\begin{eqnarray}
&&(y_1)^2&=(y_0)^2\cdot\left((c_0)^{2^{S_0-S_1-1}}\right)^2\\
&&&=t_0\cdot z\cdot(c_0)^{2^{S_0-S_1}}\\
&&&=t_0\cdot(c_0)^{2^{S_0-S_1}}\cdot z\\
&&&=t_1\cdot z\\
\end{eqnarray}\)
と計算できます。まとめると、
\(\begin{eqnarray}
&&(c_1)^{2^{S_1-1}}&=-1\\
&&(t_1)^{2^{S_1-1}}&=\phantom{-}1\\
&&(y_1)^2&=t_1\cdot z\\
\end{eqnarray}\) |
となって、\(i=1\) においても「性質」が成り立つことが分かりました。ここで仮に、\(\bs{t_1=1}\) なら \(\bs{(y_1)^2=z}\) となって、\(\bs{z}\) の平方根は \(\bs{\pm y_1}\) になります。
この計算で重要なことは \(S_1 < S_0\) であり、同様のやり方で \(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) \((i=0,\:1,\:2,\:\cd\:)\) の4数の組の列を順次作っていくと、\(\bs{S_i}\) は単調減少することです。さらに、\(S_i=1\) なら \(t_i=1\) になることもポイントです。
以上のプロセスを進めて、\(i=0,\:1,\:2,\:3,\:\cd\) のとき、
\(S_{i+1}\) : \(0 < S_{i+1} < S_i\) で、\((t_i)^{2^{S_{i+1}}}=1\) を満たす最小の数 \(\begin{eqnarray} &&c_{i+1}&=(c_i)^{2^{S_i-S_{i+1}}}\\ &&t_{i+1}&=t_i\cdot(c_i)^{2^{S_i-S_{i+1}}}\\ &&y_{i+1}&=y_i\cdot(c_i)^{2^{S_i-S_{i+1}-1}}\\ \end{eqnarray}\) |
と定義すると、
\(\begin{eqnarray}
&&(c_i)^{2^{S_i-1}}&=-1\\
&&(t_i)^{2^{S_i-1}}&=\phantom{-}1\\
&&(y_i)^2&=t_i\cdot z\\
\end{eqnarray}\) |
の「性質」が成り立つことを数学的帰納法で証明します。\(i=0,\:1\) で成り立つことは上で既に確認しました。\(i\) のときに「性質」が成り立つと仮定すると、\(i+1\) でも成り立つことが次のように分かります。基本的には上の \(i=1\) での計算と同じです。
\(\begin{eqnarray}
&&\:\:(c_{i+1})^{2^{S_{i+1}-1}}&=\left((c_i)^{2^{S_i-S_{i+1}}}\right)^{2^{S_{i+1}-1}}\\
&&&=(c_i)^{2^{S_i-1}}\\
&&&=-1\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:(t_{i+1})^{2^{S_{i+1}-1}}&=(t_i)^{2^{S_{i+1}-1}}\cdot\left((c_i)^{2^{S_i-S_{i+1}}}\right)^{2^{S_{i+1}-1}}\\
&&&=(t_i)^{2^{S_{i+1}-1}}\cdot(c_i)^{2^{S_i-1}}\\
&&&=-(t_i)^{2^{S_{i+1}-1}}\\
\end{eqnarray}\)
ここで、
\((t_i)^{2^{S_{i+1}-1}}=X\)
とおくと、\(S_{i+1}\) の定義によって \((t_i)^{2^{S_{i+1}}}=1\) なので、
\(X^2=(t_i)^{2^{S_{i+1}}}=1\)
となり、\(X\) は \(\bs{F}_p\) における方程式 \(X^2=1\) の解です。つまり、
\(X=1,\:-1\)
です。ところが \(X=1\) とすると、
\((t_i)^{2^{S_{i+1}-1}}=1\)
となりますが、\(S_{i+1}\) は \(0 < S_{i+1} < S_i\) で \((t_i)^{2^{S_{i+1}}}=1\) を満たす最小の数としたにも関わらず、\(S_{i+1}\) より小さい \(S_{i+1}-1\) が定義を満たすことになってしまい、矛盾します。従って \(X=-1\) であり、
\(\begin{eqnarray}
&&\:\:(t_{i+1})^{2^{S_{i+1}-1}}&=-X\\
&&&=1\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:(y_{i+1})^2&=(y_i)^2\cdot\left((c_i)^{2^{S_i-S_{i+1}-1}}\right)^2\\
&&&=t_i\cdot z\cdot(c_i)^{2^{S_i-S_{i+1}}}\\
&&&=t_i\cdot(c_i)^{2^{S_i-S_{i+1}}}\cdot z\\
&&&=t_{i+1}\cdot z\\
\end{eqnarray}\)
と計算できます。まとめると
\(\begin{eqnarray}
&&(c_{i+1})^{2^{S_{i+1}-1}}&=-1\\
&&(t_{i+1})^{2^{S_{i+1}-1}}&=\phantom{-}1\\
&&(y_{i+1})^2&=t_{i+1}\cdot z\\
\end{eqnarray}\) |
となり、\(i\) のときに成り立つと仮定すると \(i+1\) でも成り立つことが分かりました。これで、\(i=0,\:1,\:2,\:3,\:\cd\) で成り立つことが数学的帰納法で証明できました。
\(i=0,\:1,\:2,\:3,\:\cd\) のどこかで \(t_i=1\) となれば、そのときの \(\pm y_i\) が \(z\) の平方根です。\(S_i\) は単調減少であり、かつ、\(S_i=1\) なら \(t_i=1\) です。\(t_i=1\) となる \(i\) がなかなか見つからなくても、\(S_i\) が \(1\) まで減少すれば必ず見つかるので、\(z\) の平方根が求まります。
このアルゴリズムを実験してみます。4 で割って1余る素数 \(p\) として、 \(p=2^S+1\) 型の素数を選びます。\(S=8\) のとき \(p=257\) は素数なので、
\(p=257,\:\:Q=1,\:\:S=8\)
とおきます。計算してみると \(\bs{F}_{257}\) において \(11,\:13\) は平方数です。また、平方数でない数として \(3\) を選ぶことができます。そこでまず、
\(p=257,\:\:Q=1,\:\:S=8,\)
\(z=11,\:\:w=3\)
とおくと、
\(\begin{eqnarray}
&&\:\:S_0&=S&=8\\
&&\:\:c_0&=w^Q&=3\\
&&\:\:t_0&=z^Q&=11\\
&&\:\:y_0&=z^{\frac{Q+1}{2}}&=11\\
\end{eqnarray}\)
が初期値です。ここからアルゴリズムに沿って \(\{\:S_i,\) \(c_i,\) \(t_i,\) \(y_i\:\}\) \((i=1,\:2,\:\cd\:)\) を計算してみると、結果は、
| \(0\) | \(8\) | \(3\) | \(11\) | \(11\) |
| \(1\) | \(6\) | \(81\) | \(120\) | \(99\) |
| \(2\) | \(5\) | \(136\) | \(129\) | \(52\) |
| \(3\) | \(4\) | \(249\) | \(253\) | \(133\) |
| \(4\) | \(3\) | \(64\) | \(1\) | \(221\) |
となり、\(\bs{F}_{257}\) における \(11\) の平方根の1つは \(221\) と求まりました。もう1つは \(257-221=36\) です。実際、
\(221^2=48841=190\cdot257+11\)
\(\phantom{2}36^2=\phantom{4}1296=\phantom{25}5\cdot257+11\)
なので正しい結果です。\(z=13\) もやってみると、
| \(0\) | \(8\) | \(3\) | \(13\) | \(13\) |
| \(1\) | \(7\) | \(9\) | \(117\) | \(39\) |
| \(2\) | \(6\) | \(81\) | \(225\) | \(94\) |
| \(3\) | \(4\) | \(249\) | \(256\) | \(191\) |
| \(4\) | \(1\) | \(256\) | \(1\) | \(28\) |
となり、\(\bs{F}_{257}\) における \(13\) の平方根(の1つ)は \(28\) です。
\(28^2=784=3\cdot257+13\)
であり、アルゴリズムの確認ができました。
楕円曲線上の点の総数
\(\bs{F}_p\) 上の楕円曲線、\(E(a,\:b,\:p)\) の点の数がどの程度になるのでしょうか。以降、群 \(E(a,\:b,\:p)\) の元の数(群位数)を \(\#E\) と書きます。前回の No.315「高校数学で理解する楕円曲線暗号の数理(1)」の最後にあげた例だと、
\(\#E(2,\:4,\:109)=127\)
| \(\bs{F}_{109}\) 上の楕円曲線 \(y^2=x^3+2x+4\) の点の数は無限遠点を含んで \(127\)) |
でした。この \(\#E(a,\:b,\:p)\) を評価する式があります。「ハッセの定理」です(Helmut Hasse は20世紀ドイツの数学者)。この定理によると、
\(p+1-2\sqrt{p}\leq\#E\leq p+1+2\sqrt{p}\)
であり、\(\#E\) は \(p+1\) の周辺、\(\pm2\sqrt{p}\) の範囲です。この意味を考えてみます。\(\bs{F}_p\) 上の楕円曲線を
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=z&\\
&&z=x^3+ax+b&\\
\end{eqnarray}
\end{array}\right.\)
で表わし、\(\bs{F}_p\) において \(z\) を \(0\) から \(p-1\) まで振ったときの \(y^2=z\) の解の総数を求めます。\(z\) を、\(\bs{F}_p^{*}\) の生成元 \(g\) を使って、
\(z=\left\{
\begin{array}{l}
\begin{eqnarray}
&&0&\\
&&g^k\:\:(k=1,\:2,\:\:\cd\:,\:p-1)&\\
\end{eqnarray}
\end{array}\right.\)
と表すと、
| \(z=0\) のとき、解は\(1\)個 | |
| \(k\) が偶数のとき、解は\(2\)個 | |
| \(k\) が奇数のとき、解は無し |
となり、\(\bs{F}_p^{\:2}\) における解、\((z,\:y)\) の総数は \(p\) となります。では、\(\bs{F}_p^{\:2}\) における楕円曲線上の点、\((x,\:y)\) の総数はどうなるでしょうか。\(x\) が \(\bs{F}_p\) の全ての元に渡るとき、\(z\) が \(\bs{F}_p\) で均等にバラつくとは限りません。しかし \((x,\:y)\) の総数は「だいたい \(p\) に近い値」だと考えられます。
つまり、群 \(E(a,\:b,\:p)\) の元で、零元 \(\mathcal{O}\) 以外の \(\bs{F}_p^{\:2}\) に属するものは、だいたい \(p\) 個あると考えられる。従って \(\#E\) は 零元 \(\mathcal{O}\) を含んで \(p+1\) に近い値だと考えられます。これが「ハッセの定理」の直感的理解です。
別の観点から言うと、任意に選んだ \(x\) に対して、もし \(z\) が平方数なら \(y\) が2つ存在し、楕円曲線上の点が2つ求まります。ハッセの定理から言えることは、そうなる確率は、任意の \(x\) についてほぼ \(0.5\) ということです。\(p\) が大きくなると、\(p+1\) に対する \(2\sqrt{p}\) の比率は極めて小さくなるからです。
\(\#E\) を具体的に求めるアルゴリズムは、1985年にオランダ出身の数学者、レネ・ショーフ(Rene Schoof。英語読みでスクーフとも書かれる)が開発しました。その「ショーフのアルゴリズム」は、数学用語で言うと最初の「決定論的多項式時間アルゴリズム」です。平たく言うと「計算結果が100%正しいと数学的に保証される(=決定論的)計算可能な(=多項式時間)アルゴリズム」です。「ショーフのアルゴリズム」の具体的内容は、ここでは割愛します。
17. 楕円曲線暗号
楕円曲線暗号を構成する上で必要になるのが、有限群における「位数」の概念です。次の位数の話はすべての有限群に共通するので、群の演算を乗法的に書くことにします(掛け算、冪乗、単位元 \(e\)、などの記法を使います)。No.315 でやったように、演算を加法と考えても全く同じことになります。
位数
元の数が有限個の群 \(G\) を「有限群」といい、その元の個数を「群位数(group order)」と呼びます。群位数を \(|G|\) と表します。群の演算則だけから次のことが言えます。
単位元 \(e\) でない群 \(G\) の元を \(a\) とします。\(a\) の冪乗 \(a^n(1\leq n)\) の \(n\) を増やしていくと、ある時点で \(a^n=e\) となります。その理由ですが、
\(a^1,\:a^2,\:\:\cd\:,\:a^{|G|}\)
という \(|G|\) 個の元を考えてみます。もし \(|G|\) 個が全て相異なると、どれかが \(e\) のはずです。全てが相異なる元ではないとき、
\(a^j=a^i(1\leq i < j\leq|G|)\)
となったとすると、両辺に \(a\) の逆元を \(i\) 回掛けて、
\(a^{j-i}=e\)
が得られます。\(1\leq j-i < |G|\) なので、この範囲に \(e\) があります。そこで、つぎのように元 \(a\) の位数を定義できます。
| 17.1 | 位数の定義 |
|
有限群 \(G\) の任意の元 \(a\) について、
\(a^d=e\) r となる最小の\(d\) を \(a\) の "位数(order)" と言う。 | |
さらに、元の位数については次の命題が成り立ちます。
| 17.2 | 位数と群位数 |
|
有限群 \(G\) の任意の元 \(a\) の位数を \(d\) とすると、\(d\) は群位数 \(|G|\) の約数である。 | |
これはラグランジュの定理と呼ばれるものです。この定理が成り立つ理由は次の通りです。有限群 \(G\) の任意の元を \(a\) とし、集合 \(A\) を、
\(A=(a^1,\:a^2,\:\cd\:,\:a^d=e)\)
とします。集合 \(A\) の元は全て相異なります。なぜなら、もし、
\(a^j=a^i(1\leq i < j\leq d)\)
となったとすると、両辺に \(a\) の逆元を \(i\) 回掛けて、
\(a^{j-i}=e\)
となり、\(d\) が \(a^d=e\) となる最小の数であるという位数の定義に反するからです。さらに、集合 \(A\) の任意の元の逆元は集合 \(A\) に含まれます。つまり、\(a^d=e\) なので \(a^j(1\leq j < d)\) に対して \(a^{d-j}(1\leq d-j < d)\) が逆元です(ということは集合 \(A\) もまた群であり、これを \(G\) の部分群と言います)。
集合 \(A\) が \(G\) の全ての元を尽くしているなら 17.2 は成立します。そこで、集合 \(A\) に含まれない \(G\) の元があったとし、それを \(b_1\) とします。集合 \(A\) の全ての元に左から \(b_1\) を掛けて、集合 \(B_1\) を作ります。つまり、
\(B_1=(b_1a^1,\:b_1a^2,\:\cd\:,\:b_1a^d)\)
です。集合 \(A\) の元は全て相異なるので、集合 \(B_1\) の元も全て相異なります。さらに、集合 \(B_1\) の元で集合 \(A\) の元と同じものはありません。なぜなら、もし、
\(b_1a^i=a^j(1\leq i < j\leq d)\)
だとすると、\(a^i\) の逆元、\(a^{d-i}\)を右から掛けて、
\(b_1a^d=a^{d-i+j}\)
\(b_1=a^{d-i+j}=a^{j-i}\)
\(b_1=a^{d-i+j}=a^{j-i}\)
となりますが、\(1\leq j-i < d\) なので、これは \(b_1\) が集合 \(A\) の元であることを意味していて仮定に反します。つまり、集合 \(B_1\) の元で集合 \(A\) の元と同じものはありません。
集合 \(A\) と \(B_1\) で \(G\) の元の全てを尽くしているなら、\(2d=|G|\) となって 17.2 は証明できたことになります。そうではない場合、集合 \(A\) と \(B_1\) に含まれない \(G\) の元の一つを \(b_2\) として、集合 \(B_2\) を、
\(B_2=(b_2a^1,\:b_2a^2,\:\cd\:,\:b_2a^d)\)
と定義します。そうすると先ほど同じように、集合 \(B_2\) の元は全て相異なり、かつ、集合 \(A\) との重複はありません。さらに、集合 \(B_2\) の元は集合 \(B_1\) の元とも重複しません。なぜなら、もし、
\(b_2a^i=b_1a^j(1\leq i < j\leq d)\)
だとすると、\(a^i\) の逆元、\(a^{d-i}\)を右から掛けて、
\(b_2=b_1a^{d-i+j}=b_1a^{j-i}\)
となりますが、\(1\leq j-i < d\) なので、\(b_2\) が 集合 \(B_1\) の元という意味になり仮定に反します。つまり、集合 \(B_2\)の元は集合 \(B_1\) の元と重複しません。
以上の操作は \(G\) の元が残っている限り \(B_3B_4\:\cd\) と続けられます。そしてある時点で 残っている \(G\) の元がちょうど切りのよいところで無くなるはずです。\(B_{n-1}\) まで作ったときに \(G\) の元の全てを尽くしたとしたら、\(n_d=|G|\) です。これで 17.2 が証明できました。17.2 から直ちに次の2つが結論づけられます。
| 17.3 | |
|
有限群 \(G\) の任意の元 \(a\) について、
\(a^{|G|}=e\) である。 | |
これは、群位数 \(|G|\) が 元 \(a\) の位数の倍数なのでそうなります。\(p\) を素数とし、\(G\) が \(p\) 未満の自然数からなる乗法群 \(\bs{F}_p^{*}\) だとすると、\(|G|=p-1\) なので、フェルマの小定理( 3.1 )そのものです。
また、\(n\) 未満の自然数で \(n\) と互いに素なものの集合を \(G\) とすると、\(G\) は \(\mr{mod}n\) の乗算に関して閉じた集合になり、逆元も定義できるので(2.3 参照)、群となります(= 既約剰余類群)。オイラー関数を用いると \(|G|=\varphi(n)\) と表せて、オイラーの定理( 7.1 )になります。
つまり 17.3 は、フェルマの小定理の一般化であると同時に、フェルマの小定理を一般化したオイラーの定理をさらに一般化したものと言えるでしょう。
| 17.4 | 群位数が素数の群 |
|
有限群 \(G\) の群位数 \(|G|\) が素数だとすると、
単位元 \(e\) を除く \(G\) の全ての元の位数は \(|G|\) である。 | |
素数の約数は \(1\) と素数自身しかないので、単位元以外の元の位数は群位数に等しくなります。従って、群位数が素数の群では任意の元 \(a\) の冪乗が群全体に "バラける" ことになります。
楕円曲線暗号の構成
スカラー倍
ここから具体的な楕円曲線暗号のしくみに入ります。楕円曲線上の \(\bs{F}_p^{\:2}\) の点と零元 \(\mathcal{O}\) が作る加法群を \(E(a,\:b,\:p)\) とし、その群位数を \(\#E\) と書きます。楕円曲線暗号では \(E(a,\:b,\:p)\) における「スカラー倍」の演算を利用します。
楕円曲線上の \(\bs{F}_p^{\:2}\) の点の一つを \(G=(G_x,\:G_y)\) とし、\(d\) を \(G\) の位数、\(n\) を \(1\leq n\) の整数とします。\(G\) の \(n\) 倍(=スカラー倍)を \(nG\) と書き、
\(nG=\overbrace{G+G+\:\cd\:+G}^{n}\)
と定義します。この定義から、
\(dG=\mathcal{O}\)(零元)
です。また、\((dk)G=\mathcal{O}\) \((k=1,\:2,\:3,\:\cd)\) です。スカラー倍は「倍」という名前がついているため、整数と楕円曲線上の点の掛け算のように誤解しそうですが、掛け算ではありません。
\(\bs{nG}\) は、\(\bs{\bs{F}_p}\) 上の楕円曲線の点 \(\bs{G}\) を、楕円曲線の加法式を使って \(\bs{n}\) 回加算した結果という意味
です。従って、\(n,\:\:m\) を整数とすると次のような式が成り立ちます。
\((1)\:\:n(mG)=(nm)G=(mn)G=m(nG)\)
\((2)\:\:(n+m)G=nG+mG\)
\((2)\:\:(n+m)G=nG+mG\)
\((1)\) 式には、整数の乗算とスカラー倍が混在しています。また \((2)\) 式に整数の加算の \(+\) と、楕円曲線上の点の加算の \(+\) が混在していますが、意味するところは明確でしょう。さらに、
\((3)\:\:n\equiv m\:\:(\mr{mod}\:d)\) なら \(nG=mG\)
\((4)\:\:nm\equiv1\:\:(\mr{mod}\:d)\) なら \(m(nG)=G\)
\((4)\:\:nm\equiv1\:\:(\mr{mod}\:d)\) なら \(m(nG)=G\)
も成り立ちます。つまり、スカラー倍の "スカラー" の部分が式の場合、\(d\) を法とする演算でよいことになります。\(d\) は素数なので \(d\) を \(q\) と書くと、 "スカラー" 部分の式は有限体 \(\bs{F}_q\) での演算と言えます。たとえば \((4)\) は、
\((4)\:\:n^{-1}(nG)=G\)
と記述できます。
\(nG\) を求める計算は、\(E(a,\:b,\:p)\) の2倍式と加法式を使って可能です。例として \(133G\) の場合だと、\(133=2^7+2^2+1\) なので、
\(133G=2^7G+2^2G+G\)
となります。つまり、\(E(a,\:b,\:p)\) の2倍式を7回使って、
\(2^1G,\:\:2^2G,\:\:\cd\:\:,\:\:2^6G,\:\:2^7G\)
と順次計算し、加法式を2回使うと \(133G\) が求まります。これは \(n\) がたとえ巨大数であっても可能です。\(2^{256}\) は10進数で約80桁(256ビット)の巨大数ですが、それでも256回程度の2倍算と最大で256回程度の加算をすれば \(nG\) が求まります。このあたりは 4.2 の「冪剰余の計算アルゴリズム」と同じです。もちろん冪剰余と違って、2倍算も加算も単純な掛け算ではありません。\(E(a,\:b,\:p)\) の群演算は、定義式どおりの少々ややこしい式です。しかし計算が可能なことは確かです。
離散対数
スカラー倍の演算を、
\(P=nG\)
とします。上に書いたように、この計算は高速に可能ですが、その逆、つまり \(P\) と \(G\) を知って \(n\) 求めるのは困難になります。この \(n\) を求める問題を、加法群 \(E(a,\:b,\:p)\) における「離散対数問題」と呼びます。離散対数問題を解くのが不可能になるのは、\(G\) の位数 \(d\) が10進数で数10桁以上といった巨大数の場合です。その場合、\(P\) は \(d\) 種のバリエーションをとるので、\(n\) を求めるのは不可能になります。
位数 \(d\) が巨大数である \(G\) を求める方法の一つは、\(p\) を巨大な素数とし、群位数 \(\#E\) も素数であるような \(E(a,\:b,\:p)\) を選ぶことです。そうすると 17.4 により、零元 \(\mathcal{O}\) 以外の \(E(a,\:b,\:p)\) の全ての元の位数 \(d\) は \(\#E\) になり、その \(\#E\) は \(p+1\) の近辺にあるので、\(G\) をどのように選ぼうとも位数 \(d\) は巨大素数になります。
\(\#E\) が素数である \(E(a,\:b,\:p)\) では、任意の元 \(P\) と \(G\) について、\(nG=P\) となる \(n\) が唯一存在することになります。このことを、
\(\mr{log}_GP=n\)
と書くと、\(G\) は実数における通常の対数の "底(base)" に相当します。\(G\) は \(E(a,\:b,\:p)\) の元 = \(\bs{F}_p^{\:2}\) の元なので、\(G\) を「ベースポイント(base point)」と呼びます。このペースポイントを含め、楕円曲線暗号では、
| \(E(a,\:b,\:p)\) : 楕円曲線 | |
| \(G=(G_x,\:G_y)\) : ベースポイント | |
| \(d\) : \(G\) の位数(素数) |
が公開されます。そして暗号化通信では、\(d\) より小さい数 \(k\) をランダムに選び
| 公開鍵 : \(kG\) | |
| 秘密鍵 : \(k\) |
とします。公開鍵だけを知っても秘密鍵は計算できない。これが楕円曲線暗号の原理です。なお、 \(\#E\) が 素数でなくても、位数 \(d\) が巨大素数である \(G\) を選ぶことで、楕円曲線暗号は成立します。
スカラー倍のイメージをつかむため、\(p\) がごく小さい数の場合で実験してみます。計算してみると、\(p=29,\:\:a=-1(=28),\:\:b=1\) のとき \(\#E=37\) となって、群位数が素数になります。\(y^2=x^3-x+1\) の解の一つは \((0,\:1)\) なので、これをベースポイント \(G\) としてスカラー倍を順次計算してみると次の通りとなります。
| \(\phantom{11}G=(\:\phantom{1}0,\phantom{1}1\:)\) | \(19G=(\:10,11\:)\) |
| \(\phantom{1}2G=(\:22,10\:)\) | \(20G=(\:20,\phantom{1}8\:)\) |
| \(\phantom{1}3G=(\:27,13\:)\) | \(21G=(\:25,12\:)\) |
| \(\phantom{1}4G=(\:\phantom{1}9,24\:)\) | \(22G=(\:17,24\:)\) |
| \(\phantom{1}5G=(\:14,18\:)\) | \(23G=(\:\phantom{1}5,11\:)\) |
| \(\phantom{1}6G=(\:11,25\:)\) | \(24G=(\:28,\phantom{1}1\:)\) |
| \(\phantom{1}7G=(\:23,20\:)\) | \(25G=(\:\phantom{1}1,28\:)\) |
| \(\phantom{1}8G=(\:12,\phantom{1}8\:)\) | \(26G=(\:\phantom{1}3,\phantom{1}5\:)\) |
| \(\phantom{1}9G=(\:26,\phantom{1}8\:)\) | \(27G=(\:\phantom{1}2,\phantom{1}6\:)\) |
| \(10G=(\:\phantom{1}2,23\:)\) | \(28G=(\:26,21\:)\) |
| \(11G=(\:\phantom{1}3,24\:)\) | \(29G=(\:12,21\:)\) |
| \(12G=(\:\phantom{1}1,\phantom{1}1\:)\) | \(30G=(\:23,\phantom{1}9\:)\) |
| \(13G=(\:28,28\:)\) | \(31G=(\:11,\phantom{1}4\:)\) |
| \(14G=(\:\phantom{1}5,18\:)\) | \(32G=(\:14,11\:)\) |
| \(15G=(\:17,\phantom{1}5\:)\) | \(33G=(\:\phantom{1}9,\phantom{1}5\:)\) |
| \(16G=(\:25,17\:)\) | \(34G=(\:27,16\:)\) |
| \(17G=(\:20,21\:)\) | \(35G=(\:22,19\:)\) |
| \(18G=(\:10,18\:)\) | \(36G=(\:\phantom{1}0,28\:)\) |
| \(37G=\mathcal{O}\) |
群位数が素数なので \(G\) の位数は \(37\) となり、群位数と一致します。この計算を \(\bs{F}_p^{\:2}\) の平面に表示すると次の通りです。\(G\) と \(36G\) は赤丸、\(2G\) ~ \(35G\) は黒丸です。矢印は加算を示し、赤矢印は \(G+G\) と \(35G+G\) の加算です。

|
図18:\(\bs{E(-1,\:1,\:29)}\)(零元を除く)
\(\#E=37,\:\:G=(0,\:1),\:\:d=37\) |
スカラー倍を繰り返すごとに "楕円曲線" 上の合計\(36\)点を通り、それが乱雑に変化することが分かります。
振り返ってみると、RSA暗号(No.311)の安全性は巨大数の因数分解の困難性に依存しているのでした。またディフィー・ヘルマンの鍵交換(No.313)は、乗法群 \(\bs{F}_p^{*}\) における離散対数問題を解くことの困難性に依存しています。これらに使われる演算はいずれも整数の乗除算です。それに対して楕円曲線暗号に使われるのは、整数の乗除算よりは遙かに複雑な、楕円曲線上の加法群における「加算」です。ここに楕円曲線暗号の解読しにくさの要因があります。
実用的な楕円曲線暗号で公開するパラメータをどうやって作るか、その一例をあげます。
|
\(\#E\) が素数なので、\(G\) の位数 \(d\) は \(\#E\) に等しくなります。なお、\(\#E\) がたまたま \(p\) と一致すると離散対数問題が解けることが分かっているので、③ でそのようなケースを排除しておきます。
この決め方では、群位数 \(\#E\) の計算と素数判定を繰り返すことになり、多大な計算時間がかかることは想像に難くありません。しかしパラメータは1度計算すれば暗号通信の仕様として公開し、皆がそれを使えばいいわけです。最初の1回だけの計算時間より、その後の通信の安全性の方が重要です。
楕円曲線暗号のパラメータの一例を次に掲げます。secp160r1 という名称で公開されているパラメータです。群位数 \(\#E\:( > p)\) は素数です。\(p,\:\#E\) ともに10進で49桁の数です。
secp160r1
\(\begin{eqnarray}
&&p=&1461501637330902918203684\\
&&&832716283019653785059327\\
&&& (=2^{160}-2^{31}-1)\\
&&&\\
&&a=&1461501637330902918203684\\
&&&832716283019653785059324\\
&&& (=p-3)\\
&&b=&1632357913061681105466049\\
&&&19403271579530548345413\\
&&&\\
&&\#E=&1461501637330902918203687\\
&&&197606826779884643492439\\
&&&\\
&&G_x=&4258262317238883504465415\\
&&&92701409065913635568770\\
&&G_y=&2035201141629041078739914\\
&&&57957346892027982641970\\
&&&\\
&&d=&1461501637330902918203687\\
&&&197606826779884643492439\\
&&& (=\#E)\\
\end{eqnarray}\)
ちなみに、計算してみると、
\(\dfrac{\#E-(p+1)}{2\sqrt{p}}\fallingdotseq0.978\)
であり、\(\#E\) は「ハッセの定理」の上限付近にあります。
楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)
楕円曲線暗号とは、以上のような「有限体上の楕円曲線が構成する加法群を利用した暗号方式」の総称です。その例として、ディフィー・ヘルマンの鍵共有(= DH、No.313「高校数学で理解する公開鍵暗号の数理」参照)を楕円曲線暗号で実現できます(ECDH と略称される)。鍵共有のプロセスは次のように進みます。しかるべき「公開鍵センター」が、皆が使う公開鍵として、
| \(E(a,\:b,\:p)\) : 楕円曲線 | |
| \(G=(G_x,\:G_y)\) : ベースポイント | |
| \(d\) : \(G\) の位数(素数) |
をオープンにして(暗号通信の仕様書として公開して)おきます。以下のスカラー倍演算はすべて \(\bs{F}_p\) で行います。Alice と Bob が秘密鍵を共有したい場合、
暗号文による通信の開始にあたって、Alice は \(0 < k_A < d\) である乱数 \(k_A\) を発生させ、\(k_AG\) を Alice の公開鍵として(盗聴されている通信路を介して) Bob に送付
します。乱数 \(k_A\) は Alice の秘密鍵として秘匿します。次に同様に、
Bob は \(0 < k_B < d\) である乱数 \(k_B\) を発生させ、\(k_BG\) を Bob の公開鍵として(盗聴されている通信路を介して) Alice に送付
します。もちろん \(k_B\) は秘匿します。そして、
Alice は \(K_A=k_Ak_BG\) を共有の秘密鍵
Bob は \(K_B=k_Bk_AG\) を共有の秘密鍵
Bob は \(K_B=k_Bk_AG\) を共有の秘密鍵
とします。この作り方から \(K_A=K_B=K\) となるので、楕円曲線上の点である秘密鍵 \(K\) を共有できたことになり、以降はこれを使って暗号化通信(公開鍵ではない、高速な暗号化通信)を行います。使った秘密鍵は通信が終わったら捨てます。もちろん、\(K=(K_x,\:K_y)\) の \(K_x\) だけを秘密鍵としてもよいわけです。
原理は、オリジナルのディフィー・ヘルマンの鍵交換(DH)と全く同じです。ただ、オリジナルが \(\bs{F}_p^{*}\) での離散対数問題を利用していたのに対し、ECDH は \(E(a,\:b,\:p)\) での離散対数問題を利用した暗号であることが違います。
メッセージ伝送とデジタル署名
以降、前提として、
| \(E(a,\:b,\:p)\) : 楕円曲線 | |
| \(G=(G_x,\:G_y)\) : ベースポイント | |
| \(d\) : \(G\) の位数(素数) |
が公開されているものとします。
メッセージ伝送
楕円曲線暗号によるメッセージ伝送方式の例として「楕円曲線 ElGamal 暗号」をとりあげます。これは、\(\bs{F}_p\) における離散対数問題を利用した ElGamal 暗号(No.313「高校数学で理解する公開鍵暗号の数理」の「13. 離散対数暗号」参照)の「楕円曲線版」です。
この暗号では、送るべきメッセージを \(m\)(=整数)とするとき、\(m\) を \(\bs{F}_p\) 上の楕円曲線の点 \(M=(x,\:y)\) と対応付けます。その対応付けの方法は送信者と受信者であらかじめ合意しておく必要があります。そのやり方の例として、\(m\) を \(\dfrac{d}{100}\) 未満の数となるように選びます。そして、
\(x=m\cdot100+i\:\:(i=0,\:1,\:2,\:\cd,\:99)\)
の \(100\) 個の中から、
\(x^3+ax+b\)
が平方数となるような \(x\) を選びます。\(x\) の約半数は \(y^2=x^3+ax+b\) を満たす \(y\) があるので、\(100\)個を試せば必ず \(x\) が見つかります。そこで \(x^3+ax+b\) の平方根を計算して \(y\) を求め、
\(M=(x,\:y)\)
を伝送するメッセージとします(\(y\) は2つありますが、どちらかを選びます)。\(M\) から \(m\) への復元は、\([\cd]\) を \(\cd\) を超えない最大の整数(=ガウス記号)として、
\(m=\left[\dfrac{x}{100}\right]\)
で可能です(=切り捨て除算)。この \(100\) に大きな意味はなく、コンピュータで実装するときには演算回数を減らすために \(2^n\) となる数を選ぶのがベターでしょう。
楕円曲線 ElGamal 暗号によるメッセージ伝送は次のように進みます。Bob から Alice にメッセージ \(m\) を送る例です。
まず、Alice と Bob は「楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)」を使って秘密鍵 \(k_A\) と \(k_B\) を決め、公開鍵 \(k_AG\) と \(k_BG\) を交換しておきます。
Bob の暗号化手順
| \(m\) を楕円曲線上の点 \(M\) に変換する。 | |
| \(0 < k < d\) である乱数 \(k\) を発生させる。 | |
| 楕円曲線上の2点、\(M_1=kG\)、 \(M_2=M+kk_AG\) を計算し、\((M_1,\:\:M_2)\) のペア を暗号化メッセージとして Alice に送る。 | |
| 送信が終わると \(k\) は捨てる。 |
Alice の復号化手順
| 暗号の作り方から \(\begin{eqnarray} &&\:\:M&=M_2-kk_AG\\ &&&=M_2-k_AM_1\\ \end{eqnarray}\) なので、\(M_2-k_AM_1\) を計算して \(M\) を求める。この計算は \(k_A\) を知っている Alice にしかできない。 | |
| \(M\) から メッセージ \(m\) を復元する。 |
デジタル署名
Bob から Alice にメッセージ \(m\) (楕円曲線上の点としては \(M\))を送るとき、次のようにしてデジタル署名を付加できます。ベースポイント \(\bs{G}\) の位数 \(\bs{d}\) は素数ですが、この素数を \(\bs{q}\) とも書き、スカラー倍における "スカラー部分の演算" を有限体 \(\bs{\bs{F}_q}\) での演算として表記します。また、ハッシュ関数を \(H(\:)\) と書きます(No.311「高校数学で理解するRSA暗号の数理(2)」の "補記" 参照)。
Bob の署名手順
| \(1 < k < q-1\) である乱数を発生させる。 | |
| \(kG\) を計算し、\(kG=(x,\:y)\) とおく。 | |
| メッセージ \(m\) から ハッシュ値 \(h=H(m)\) を得る。\(H()\) は安全なハッシュ関数。 | |
| \(s=(h+xk_B)\cdot k^{-1}\) を計算して \((x,\:s)\) をデジタル署名として Alice に送る。\(k_B\) は Bob の秘密鍵、\(k^{-1}\) は \(\bs{F}_q\) での \(k\) の逆数である。この計算は、秘密鍵とメッセージの両方を知っている者だけができる。なお、\(1 < k < q-1\) なので \(\bs{F}_q\) において \(k\neq k^{-1}\) である。 | |
| 送信が終わったら、乱数の \(k\) は捨てる。 |
Alice の検証手順
| 受け取ったメッセージ \(m\) から ハッシュ値 \(h=H(m)\) を計算する。 | |
| \(h\)、Bob の署名 \((x,\:s)\)、ベースポイント \(G\)、Bob の公開鍵 \(k_BG\) から、次のスカラー倍計算を行って \(R\) を求める(スカラー部分の演算は \(\bs{F}_q\) での演算)。 \(R=(R_x,\:R_y)=s^{-1}(hG+x(k_BG))\)
ここで、
\(\begin{eqnarray} &&\:\:s^{-1}&=((h+xk_B)\cdot k^{-1})^{-1}\\ &&&=k\cdot(h+xk_B)^{-1}\\ \end{eqnarray}\) である。また、スカラー倍の計算部分は、 \(hG+x(k_BG)=(h+xk_B)G\) と変形できる。従って、\(R\) は、 \(\begin{eqnarray} &&\:\:R&=k\cdot(h+xk_B)^{-1}\cdot(h+xk_B)G\\ &&&=kG=(x,\:y)\\ \end{eqnarray}\) となるから、\((R_x,\:R_y)=(x,\:y)\) のはずである。 | |
| 受け取った署名の \(x\) を見て、\(x=R_x\) なら署名は Bob のものであり、かつ、メッセージは改竄されていないことが確証できる。 |
このデジタル署名のアルゴリズムは、ECDSA (Elliptic Curve Digital Signature Algorithm) と呼ばれるもので、メッセージ \(m\) の暗号化方式が「楕円曲線 ElGamal 暗号」でなくても通用します。一般に、メッセージ伝送方式とデジタル署名方式は独立です。
上にも書いたように、楕円曲線暗号とは「有限体上の楕円曲線が構成する加法群を利用した暗号方式」の総称です。「楕円曲線暗号版ディフィー・ヘルマンの鍵交換(ECDH)」や「楕円 ElGamal 暗号」以外にも種々の方式が提案され、実用化されています。
18. 結合則が成り立つことの検証と証明
前回の No.315 で、"結合則が成り立つ" ことの証明を後回しにしたので、ここに書きます。楕円曲線暗号は、楕円曲線上の有理点が群になることに依存した暗号です。その "群" であることの要件の一つは結合則が成り立つことであり、楕円曲線暗号の数学的背景として是非とも確認しておきたいところです。
楕円曲線上の3点について、
\((P_1+P_2)+P_3=P_1+(P_2+P_3)\)
となるのが結合則ですが、加法は数式で示されています。そこでまず、数式を使って簡単な例で確かめてみます。
数式による確認(トライアル)

図15:楕円曲線の例2
\(y^2=x^3-x+1\)
楕円曲線として、No.315 の図15でとりあげた、
\(y^2=x^3-x+1\)
を例とし、この楕円曲線上に2つの固定点と1つの任意点を取って計算してみます。使う記号は次の通りです。
\(P_1=(0,\:1)\)
\(P_2=(p,\:q)\:\:\:(q^2=p^3-p+1)\)
\(P_3=(1,\:1)\)
\(P_4=P_1+P_2\)
\(P_5=P_4+P_3=(P_1+P_2)+P_3\)
\(P_6=P_2+P_3\)
\(P_7=P_1+P_6=P_1+(P_2+P_3)\)
\(P_5=P_7\) が示せれば結合則が成り立っています。以下、No.315 の加法式(第2形)、
\(P_0=P_1+P_2\)
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_0=\lambda^2-x_1-x_2&\\
&&y_0=\lambda(x_1-x_0)-y_1&\\
&&\lambda=\dfrac{x_1^2+x_1x_2+x_2^2-1}{y_1+y_2}&\\
\end{eqnarray}
\end{array}\right.\)
を使って計算を進めると次のようになります。
| \(P_4\) | \(=(x_4,\:y_4)=P_1+P_2\) | |
| \(=(0,\:1)+(p,\:q)\) | ||
| \(\lambda_4\) | \(=\dfrac{p^2-1}{q+1}\) | |
| \(x_4\) | \(=\lambda_4^2-p\) | |
| \(y_4\) | \(=-\lambda_4x_4-1\) | |
| \(=\lambda_4p-\lambda_4^3-1\) |
| \(P_5\) | \(=\) | \((x_5,\:y_5)\) | |
| \(=\) | \(P_4+P_3=P_3+P_4\) | ||
| \(=\) | \((1,\:1)+(x_4,\:y_4)\) | ||
| \(\lambda_5\) | \(=\) | \(\dfrac{x_4^2+x_4}{\lambda_4p-\lambda_4^3}=\dfrac{p-\lambda_4^2-1}{\lambda_4}\) |
| \(x_5\) | \(=\) | \(\lambda_5^2-x_4-1\) | |
| \(=\) | \(\lambda_5^2-\lambda_4^2+p-1\) | ||
| \(=\) | \(\dfrac{-p^2+2q+3}{(p+1)^2}\) |
途中、\(x_5\) の計算で \(q^2\) を \(p^2-p+1\) で置き換えました。さらに、\(\lambda_4=\dfrac{p^2-1}{q+1}\) を使って \(\lambda_5\) の式から \(\lambda_4\) を消去すると、
\(\lambda_5=\dfrac{-p^2+2q+3}{(p+1)(q+1)}\)
となります。これを用いて \(y_5\) を計算すると、
| \(y_5\) | \(=\) | \(\lambda_5(1-x_5)-1\) | |
| \(=\) | \(\tfrac{p^2(x_5-1)-p(q+1)-2qx_5+q-3x_5+2}{(p+1)(q+1)}\) | ||
| \(=\) | \(\tfrac{-2p^4-p^3(q+7)+p^2(3q+5)+p(q+7)-11(q+1)}{(p+1)^3(q+1)}\) |
となり、\(P_5=(x_5,\:y_5)\) が求まりました。
| \(P_6\) | \(=\) | \((x_6,\:y_6)\) | |
| \(=\) | \(P_2+P_3=P_3+P_2\) | ||
| \(=\) | \((1,\:1)+(p,\:q)\) | ||
| \(\lambda_6\) | \(=\) | \(\dfrac{p^2+p}{q+1}\) | |
| \(x_6\) | \(=\) | \(\lambda_6^2-p-1\) | |
| \(y_6\) | \(=\) | \(\lambda_6(1-x_6)-1\) | |
| \(=\) | \(\lambda_6(p+2-\lambda_6^2)-1\) |
| \(P_7\) | \(=\) | \((x_7,\:y_7)=P_1+P_6\) | |
| \(=\) | \((0,\:1)+(x_6,\:y_6)\) | ||
| \(\lambda_7\) | \(=\) | \(\dfrac{x_6^2-1}{y_6+1}=\dfrac{(\lambda_6^2-p-1)^2-1}{\lambda_6(p+2-\lambda_6^2)}\) |
| \(x_7\) | \(=\) | \(\lambda_7^2-x_6\) | |
| \(=\) | \(\lambda_7^2-\lambda_6^2+p+1\) | ||
| \(=\) | \(\dfrac{p^2}{\lambda_6^2}-p+1\) | ||
| \(=\) | \(\dfrac{-p^2+2q+3}{(p+1)^2}\) |
ここで \(\lambda_6=\dfrac{p^2+p}{q+1}\) を使って \(\lambda_7\) の式から \(\lambda_6\) を消去すると、
\(\lambda_7=-\dfrac{2(p^2+p-q-1)}{(p+1)(q+1)}\)
となります。この \(\lambda_7\) を使って \(y_7\) を計算すると、
| \(y_7\) | \(=\) | \(-\lambda_7x_7-1\) | |
| \(=\) | \(\tfrac{p^2(\lambda_7-1)-2p-(2q+3)\lambda_7-1}{(p+1)^2}\) | ||
| \(=\) | \(\tfrac{-2p^4-p^3(q+7)+p^2(3q+5)+p(q+7)-11(q+1)}{(p+1)^3(q+1)}\) |
となり、\(P_7=(x_7,\:y_7)\) が求まりました。以上の計算で、\(P_5=(\)\(x_5,\:y_5\)\()\) と \(P_7=(\)\(x_7,\:y_7\)\()\) は同じ点であることが分かり、この例では結合則が検証できました。
もちろんこれで結合則が証明できたわけではありません。しかし上の検証から分かるように、加法式によって結合則を証明するには計算が膨大になると推測できます。そこで次に、数式処理ソフトを使って証明します。
数式による証明(SymPy)
再度、記号の定義をはっきりさせます。
楕円曲線上の有理点の加法式 楕円曲線、\(y^2=x^3+ax+b\)上の有理点を、 \(P_1=(x_1,\:y_1)\) \(P_2=(x_2,\:y_2)\) \(y_1^2=x_1^3+ax_1+b\) \(y_2^2=x_2^3+ax_2+b\) とし、\(P_0\) を \(P_0=P_1+P_2\) \(P_0=(x_0,\:y_0)\) \(\lambda=\dfrac{y_2-y_1}{x_2-x_1}\) \(x_0=\lambda^2-x_1-x_2\) \(y_0=\lambda(x_1-x_0)-y_1\) と定義する。楕円曲線上の有理点はこの加法によって群となる(従って、結合則が成り立つ)。 |
群の要件の一つである結合則を証明するために、楕円曲線上の3点を、\(P_1,\:\:P_2,\:\:P_3\) とし、
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とします。
\(y_1^2=x_1^3+ax_1+b\)
\(y_2^2=x_2^3+ax_2+b\)
\(y_3^2=x_3^3+ax_3+b\)
です。このとき、
\((P_1+P_2)+P_3=P_1+(P_2+P_3)\)
であれば結合則が成り立ちます。これを示すため、\(P_4,\:P_5,\:P_6,\:P_7\) を、
\(P_1+P_2=P_4\)
\(P_4+P_3=P_5\)
\(P_2+P_3=P_6\)
\(P_1+P_6=P_7\)
\(P_i=(x_i,\:y_i)\:\:(4\leq i\leq7)\)
と定義して、
\(P_5\:=\:P_7\)
であることを証明します。そのためには、
\(x_5=x_7\)
を示せれば十分です。以降で、Python のライブラリ SymPy の数式処理機能を使って、\(x_5=x_7\) であることを証明します。そのためのコードと実行結果を掲げますが、ポイントは、
\(y_i^2=x_i^3+ax_i+b\:\:(1\leq i\leq3)\)
の関係を使って、計算途中の要所要所で、\(y_1,\:y_2,\:y_3\) の2乗以上の項を無くすことです。次のコードでは ellipse_substitute 関数がそれを行っています。
import sympy as sy
x_1, y_1 = sy.symbols('x_1, y_1')
x_2, y_2 = sy.symbols('x_2, y_2')
x_3, y_3 = sy.symbols('x_3, y_3')
a , b = sy.symbols('a, b')
P_1 = [x_1, y_1]
P_2 = [x_2, y_2]
P_3 = [x_3, y_3]
def ellipse_add(P1, P2):
x1, y1 = P1
x2, y2 = P2
L = (y2 - y1)/(x2 - x1)
x = L**2 - x1 - x2
y = L*(x1 - x) - y1
return [x, y]
def ellipse_substitute(expr):
w = sy.cancel(expr)
y_1sq = x_1**3 + a*x_1 + b
w = w.subs(y_1**3, y_1sq*y_1)
w = w.subs(y_1**2, y_1sq)
y_2sq = x_2**3 + a*x_2 + b
w = w.subs(y_2**3, y_2sq*y_2)
w = w.subs(y_2**2, y_2sq)
y_3sq = x_3**3 + a*x_3 + b
w = w.subs(y_3**3, y_3sq*y_3)
w = w.subs(y_3**2, y_3sq)
return sy.cancel(w)
P_4 = ellipse_add(P_1, P_2)
P_5 = ellipse_add(P_4, P_3)
x_5 = ellipse_substitute(P_5[0])
P_6 = ellipse_add(P_2, P_3)
P_7 = ellipse_add(P_1, P_6)
x_7 = ellipse_substitute(P_7[0])
diff = ellipse_substitute(x_5 - x_7)
print(f"x_5 - x_7 = {diff}")
|
実行結果
x_5 - x_7 = 0
|
この実行結果より、\(x_5\) と \(x_7\) の差異は厳密に \(0\) であり、\(x_5=x_7\) であることが証明されました。
このコードの ellipse_substitute 関数の補足ですが、SymPy のメソッドの cancel は、式を有理式の形(\(\tfrac{p}{q}\) の形。\(p,\:q\) は多項式)にととのえます。また subs は、式を別の式(ないしは値)で置き換えます。従って、関数は次の処理をします。
| 入力を有理式に変換する。 | |
| \(y_i^3\) の項を \((x_i^3+ax_i+b)y_i\) に置き換える | |
| \(y_i^2\) の項を \((x_i^3+ax_i+b)\) に置き換える | |
| 有理式に変換した結果を返す |
\(y_i^4\) の置き換えは、\(y_i^2\) の置き換えと同時に SymPy で処理されます。\(y_i^5\) 以上の項は、このコードでは発生しません。ちなみに、\(x_5\) と \(x_7\) を有理式の形で、
\(x_5=\dfrac{A}{B},\:\:x_7=\dfrac{C}{D}\)
と表わしたときの \(A,\:B,\:C,\:D\) は次の通りです。\(A,\:C\) は72項、\(B,\:D\) は40項もあるので手計算は無理ですが、SymPy で確認すると \(AD=BC\) が成り立っています。
\(A=x_1^4x_2^2x_3+\)\(x_1^4x_2x_3^2+\)\(6x_1^3x_2^3x_3-\)\(x_1^3x_2^2x_3^2+\)\(x_1^2x_2^4x_3-\)\(x_1^2x_2^3x_3^2+\)\(x_1x_2^4x_3^2+\)\(y_1y_2(-2ax_1^2+\)\(4ax_1x_2-\)\(4ax_1x_3-\)\(2ax_2^2-\)\(4ax_2x_3-\)\(8bx_3-\)\(4x_1^2x_2x_3-\)\(2x_1^2x_3^2-\)\(4x_1x_2^2x_3+\)\(4x_1x_2x_3^2-\)\(2x_2^2x_3^2)+\)\(y_1y_3(2ax_1^2+\)\(4ax_1x_2-\)\(6ax_2^2+\)\(8bx_1-\)\(8bx_2+\)\(6x_1^2x_2^2-\)\(4x_1x_2^3-\)\(2x_2^4)+\)\(y_2y_3(-6ax_1^2+\)\(4ax_1x_2+\)\(2ax_2^2-\)\(8bx_1+\)\(8bx_2-\)\(2x_1^4-\)\(4x_1^3x_2+\)\(6x_1^2x_2^2)+\)\(a^2(x_1^3-\)\(x_1^2x_2+\)\(x_1^2x_3-\)\(x_1x_2^2+\)\(6x_1x_2x_3+\)\(x_2^3+\)\(x_2^2x_3)+\)\(2ab(x_1^2-\)\(2x_1x_2+\)\(4x_1x_3+\)\(x_2^2+\)\(4x_2x_3)+\)\(8b^2x_3+\)\(a(x_1^4x_2+\)\(x_1^4x_3-\)\(x_1^3x_2^2+\)\(2x_1^3x_2x_3+\)\(x_1^3x_3^2-\)\(x_1^2x_2^3+\)\(10x_1^2x_2^2x_3-\)\(x_1^2x_2x_3^2+\)\(x_1x_2^4+\)\(2x_1x_2^3x_3-\)\(x_1x_2^2x_3^2+\)\(x_2^4x_3+\)\(x_2^3x_3^2)+\)\(2b(x_1^4-\)\(4x_1^3x_2+\)\(2x_1^3x_3+\)\(6x_1^2x_2^2+\)\(2x_1^2x_2x_3+\)\(x_1^2x_3^2-\)\(4x_1x_2^3+\)\(2x_1x_2^2x_3-\)\(2x_1x_2x_3^2+\)\(x_2^4+\)\(2x_2^3x_3+\)\(x_2^2x_3^2)\)
\(B=x_1^4x_2^2-\)\(2x_1^4x_2x_3+\)\(x_1^4x_3^2+\)\(6x_1^3x_2^3+\)\(2x_1^3x_2^2x_3-\)\(4x_1^3x_2x_3^2+\)\(x_1^2x_2^4+\)\(2x_1^2x_2^3x_3+\)\(6x_1^2x_2^2x_3^2-\)\(2x_1x_2^4x_3-\)\(4x_1x_2^3x_3^2+\)\(x_2^4x_3^2+\)\(y_1y_2(-4ax_1-\)\(4ax_2-\)\(8b-\)\(4x_1^2x_2+\)\(4x_1^2x_3-\)\(4x_1x_2^2-\)\(8x_1x_2x_3+\)\(4x_2^2x_3)+\)\(a^2(x_1^2+\)\(6x_1x_2+\)\(x_2^2)+\)\(8ab(x_1+\)\(x_2)+\)\(8b^2+\)\(2a(3x_1^3x_2-\)\(x_1^3x_3+\)\(2x_1^2x_2^2+\)\(x_1^2x_2x_3+\)\(3x_1x_2^3+\)\(x_1x_2^2x_3-\)\(x_2^3x_3)+\)\(4b(x_1^3+\)\(x_1^2x_2-\)\(x_1^2x_3+\)\(x_1x_2^2+\)\(2x_1x_2x_3+\)\(x_2^3-\)\(x_2^2x_3)\)
\(C=x_1^2x_2^4x_3-\)\(x_1^2x_2^3x_3^2-\)\(x_1^2x_2^2x_3^3+\)\(x_1^2x_2x_3^4+\)\(x_1x_2^4x_3^2+\)\(6x_1x_2^3x_3^3+\)\(x_1x_2^2x_3^4+\)\(y_1y_2(2ax_2^2+\)\(4ax_2x_3-\)\(6ax_3^2+\)\(8bx_2-\)\(8bx_3+\)\(6x_2^2x_3^2-\)\(4x_2x_3^3-\)\(2x_3^4)+\)\(y_1y_3(-6ax_2^2+\)\(4ax_2x_3+\)\(2ax_3^2-\)\(8bx_2+\)\(8bx_3-\)\(2x_2^4-\)\(4x_2^3x_3+\)\(6x_2^2x_3^2)+\)\(y_2y_3(-4ax_1x_2-\)\(4ax_1x_3-\)\(2ax_2^2+\)\(4ax_2x_3-\)\(2ax_3^2-\)\(8bx_1-\)\(2x_1^2x_2^2+\)\(4x_1^2x_2x_3-\)\(2x_1^2x_3^2-\)\(4x_1x_2^2x_3-\)\(4x_1x_2x_3^2)+\)\(a^2(x_1x_2^2+\)\(6x_1x_2x_3+\)\(x_1x_3^2+\)\(x_2^3-\)\(x_2^2x_3-\)\(x_2x_3^2+\)\(x_3^3)+\)\(2ab(4x_1x_2+\)\(4x_1x_3+\)\(x_2^2-\)\(2x_2x_3+\)\(x_3^2)+\)\(8b^2x_1+\)\(a(x_1^2x_2^3-\)\(x_1^2x_2^2x_3-\)\(x_1^2x_2x_3^2+\)\(x_1^2x_3^3+\)\(x_1x_2^4+\)\(2x_1x_2^3x_3+\)\(10x_1x_2^2x_3^2+\)\(2x_1x_2x_3^3+\)\(x_1x_3^4+\)\(x_2^4x_3-\)\(x_2^3x_3^2-\)\(x_2^2x_3^3+\)\(x_2x_3^4)+\)\(2b(x_1^2x_2^2-\)\(2x_1^2x_2x_3+\)\(x_1^2x_3^2+\)\(2x_1x_2^3+\)\(2x_1x_2^2x_3+\)\(2x_1x_2x_3^2+\)\(2x_1x_3^3+\)\(x_2^4-\)\(4x_2^3x_3+\)\(6x_2^2x_3^2-\)\(4x_2x_3^3+\)\(x_3^4)\)
\(D=x_1^2x_2^4-\)\(4x_1^2x_2^3x_3+\)\(6x_1^2x_2^2x_3^2-\)\(4x_1^2x_2x_3^3+\)\(x_1^2x_3^4-\)\(2x_1x_2^4x_3+\)\(2x_1x_2^3x_3^2+\)\(2x_1x_2^2x_3^3-\)\(2x_1x_2x_3^4+\)\(x_2^4x_3^2+\)\(6x_2^3x_3^3+\)\(x_2^2x_3^4+\)\(y_2y_3(-4ax_2-\)\(4ax_3-\)\(8b+\)\(4x_1x_2^2-\)\(8x_1x_2x_3+\)\(4x_1x_3^2-\)\(4x_2^2x_3-\)\(4x_2x_3^2)+\)\(a^2(x_2^2+\)\(6x_2x_3+\)\(x_3^2)+\)\(8ab(x_2+\)\(x_3)+\)\(8b^2+\)\(2a(-\)\(x_1x_2^3+\)\(x_1x_2^2x_3+\)\(x_1x_2x_3^2-\)\(x_1x_3^3+\)\(3x_2^3x_3+\)\(2x_2^2x_3^2+\)\(3x_2x_3^3)+\)\(4b(-\)\(x_1x_2^2+\)\(2x_1x_2x_3-\)\(x_1x_3^2+\)\(x_2^3+\)\(x_2^2x_3+\)\(x_2x_3^2+\)\(x_3^3)\)
3次曲線による証明
コンピュータを使った(=数式処理ソフトによる)証明では、なんとなく、証明した気になりません。その理由は、SymPy が正しい(バグがない)ことに依存しているからです。そこで以下は、シルヴァーマン、テイト著「楕円曲線論入門」にある証明を紹介します。これは、楕円曲線を含む3次曲線の性質を用いた証明で、本質をついた議論になっています。
結合則が成り立つのは、楕円曲線上の加法を「3次曲線と直線の交点」で決めていることに理由があります。「楕円曲線論入門」に、結合則が成り立つことを示した次の図があります。加法群の零元 \(\mathcal{O}\) を楕円曲線上にとった場合の図です。
 |
図11:結合則 |
「楕円曲線論入門」より引用 |
|
\((P+Q)+R=P+(Q+R)\)
となるのが結合則ですが、
\((P+Q)+R=((P+Q)\!*\!R)*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
です。ここで \(\!*\!\) の記号は、\(A\!*\!B\) と書くと \(A\) と \(B\) を結ぶ直線が楕円曲線と交わる点(で \(A\)、\(B\) 以外の点)の意味です。\(\mathcal{O}\) は零元でした。従って、結合則を証明するためには、
\((P+Q)\!*\!R=P\!*\!(Q+R)\)
が証明できればよいことになります。言葉で書くと、
\(P+Q\) と \(R\) を通る直線が楕円曲線と交わる点を \(T_1\) とし、\(P\) と \(Q+R\) を通る直線が楕円曲線と交わる点を \(T_2\) とすると、 \(T_1\) と \(T_2\) は同じ点である |
となります。上の図はそれを表しています。以下の証明では同じことですが、次を示します。
| 18.1 | 結合則 |
|
\(P+Q\) と \(R\) を結ぶ直線と、\(Q+R\) と \(P\) を結ぶ直線の交点を \(T\) とすると、楕円曲線は \(T\) を通る。 | |
これは楕円曲線上の2点、\((P+Q)\!*\!R\) と \(P\!*\!(Q+R)\) が等しい(= 図11)ことと同じなので、以降は 18.1 が成り立つことを示します。そのためにまず、次の命題 18.2 を証明します。この証明の筋道は「楕円曲線論入門」に書かれているものです。
| 18.2 | 3つの3次曲線の交差 |
|
2つの3次曲線、\(C_1\) と \(C_2\) が相異なる9点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_9\) を通るとする。 別の3次曲線 \(D\) が 9点のうちの8点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) を通るとき、\(D\) は \(P_9\) も通る。 | |
これは「ケーレー・バカラック(Cayley-Bacharach)の定理」と呼ばれるものの一部です(Cayleyは英国、Bacharachはドイツの数学者。バカラックは英語読み。いずれも19世紀)。この定理は、
\(d_1\)次曲線と \(d_2\)次曲線が \(d_1d_2\)個の異なる交点で交わるとき、別の \((d_1+d_2-3)\)次曲線が交点のうちの \((d_1d_2-1)\)個を通ると、その別の曲線は残りの\(1\)点も通る
というもので、その3次元曲線の場合が 18.2 です。ここで言う3次曲線とは次の一般形で表される "3次曲線のすべて" であり、楕円曲線もその一部です。
\([\)3次曲線の一般形\(]\)
\(ax^3+bx^2y+cxy^2+dy^3+ex^2+fxy+gy^2+hx+iy+j=0\)
10個の係数(=パラメータ)、\(a,\:b,\:\:\cd\:,\:i,\:j\) を決めると3次曲線が一つ決まります。もちろん、各係数を定数倍した曲線は同じ曲線です。つまり、この形の3次曲線の係数は実質的に "9次元" と言えます。3次曲線なので \(a,\:b,\:c,\:d\) のうち少なくとも一つは \(0\) でないものがあります。その係数で全体を割れば、係数の数は9個になることからもわかります。9次元なので「相異なる8点を通る3次曲線」は無数にあります。
そこで、相異なる8点を通る3次曲線が一般的にどういう式で表現できるかを考えます。相異なる8点の座標を、
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(\vdots\)
\(P_8=(x_8,\:y_8)\)
\(P_2=(x_2,\:y_2)\)
\(\vdots\)
\(P_8=(x_8,\:y_8)\)
とします。まず、3次曲線が \(P_1\) を通るということは、10個のパラメータは次の制約条件を満足しなければなりません。
\(x_1^3a+x_1^2y_1b+x_1y_1^2c+y_1^3d+x_1^2e+x_1y_1f+y_1^2g+x_1h+y_1i+j=0\)
これは 10個の変数 \(a\) ~ \(j\) についての線型方程式(1次方程式)なので、係数を変数の前に記述しました。同様にして、3次曲線が \(P_2\) から \(P_8\) を通ることから7個の制約条件が得られます。これらをまとめると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_1^3a+x_1^2y_1b+\:\cd\:+y_1i+j=0&\\
&&x_2^3a+x_2^2y_2b+\:\cd\:+y_2i+j=0&\\
&&\:\:\vdots&\\
&&x_8^3a+x_8^2y_8b+\:\cd\:+y_8i+j=0&\\
\end{eqnarray}
\end{array}\right.\)
の、合計8つの制約条件が得られます。8個の点を通る3次曲線の10個のパラメータは、この8つの制約条件(連立1次方程式)を満たさなければなりません。ということは、\(10-8=2\) で、これらのパラメータは、制約条件のない自由な2つのパラメータで表現できることになります。
たとえば \(a\) と \(b\) を "2つのパラメータ" に選ぶと、残りの \(c\) ~ \(j\) は、\(\al_na+\beta_nb\:(n=c\:\cd\:j)\) という「\(a\) と \(b\) の1次式」で表現できます(\(\al_n,\:\beta_n\) は連立1次方程式の係数で決まる値)。しかしこれでは \(a=0\) かつ \(b=0\) のときに、すべてのパラメータが \(\bs{0}\) という自明な解しか得られません。\(x^3\) の項と \(x^2y\) の項がない3次曲線はいくらでもありうるので、自明ではない解の中に \(a=0,\:b=0\) となるものは当然あるはずです。つまり、\(\al_na+\beta_nb\) の形は連立1次方程式の解の全部は表していません。
では、上記の連立1次方程式の「自明ではない解すべてを表す一般解」はどういう形でしょうか。それには8つの方程式を満たす独立な数値の組(=連立1次方程式の解)を2組用意します。つまり無数にある解の中から2つをピックアップし、それをベクトル表現で、
\(\bs{V}_1=(a_1,\:b_1,\:\cd\:,\:j_1)\)
\(\bs{V}_2=(a_2,\:b_2,\:\cd\:,\:j_2)\)
\(\bs{V}_2=(a_2,\:b_2,\:\cd\:,\:j_2)\)
とします。"独立" とはこの場合、2つの数値群が異なった3次曲線を表現しているということです。そして、同時に \(0\) にはならない新たな2つのパラメータを導入します。それを \(\lambda_1,\:\:\lambda_2\) とすると、
\(\lambda_1\bs{V}_1+\lambda_2\bs{V}_2\)
が連立1次方程式の一般解(不定解)になります。自由な2つのパラメータの1次式で表現されていて、8つの方程式を満たすことが明らかだからです。この一般解をもとに3次曲線の方程式を表現します。そこで、
\(\begin{eqnarray}
&&f_1=&a_1x^3+b_1x^2y+\:\cd\\
&&&\cd\:+h_1x+i_1y+j_1\\
&&f_2=&a_2x^3+b_2x^2y+\:\cd\\
&&&\cd\:+h_2x+i_2y+j_2\\
\end{eqnarray}\)
の2つの関数を考えると、\(f_1=0\) の3次曲線と \(f_1=0\) の3次曲線は、共に8点を通ります。従って、
\(\lambda_1f_1+\lambda_2f_2=0\)
は8点を通り、2つの自由なパラメータで表現された3次曲線群です。従って、これが \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) を通るすべての3次曲線を表す一般形です。
以上を踏まえて命題 18.2 を検討します。命題を再掲すると、
2つの3次曲線、\(C_1\) と \(C_2\) が相異なる9点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_9\) を通るとする。 別の3次曲線 \(D\) が 9点のうちの8点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) を通るとき、\(D\) は \(P_9\) も通る。 |
でした。この前半の2つの3次曲線の関数式を
\(C_1\::\:F_1=0\)
\(C_2\::\:F_2=0\)
\(C_2\::\:F_2=0\)
とします。\(F_1=0\) も \(F_2=0\) も9点、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_9\) を通る3次曲線です。従って \(F_1=0\) と \(F_2=0\) は \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通る2つの3次曲線でもある。ということは、\(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通るすべての3次曲線は、
\(F=\lambda_1F_1+\lambda_2F_2=0\)
で表されます。従って、命題の後半に出てくる別の3次曲線 \(D\) が \(P_1,\:\:P_2,\:\:\cd\:,\:\:P_8\) の8点を通るとすると、\(D\) は \(F=\lambda_1F_1+\lambda_2F_2=0\) で表現できます。
ここでよく考えてみると、3次曲線 \(F=0\) は9点目の \(P_9\) を通るのでした。従って \(D\) も \(P_9\) を通ります。これで 18.2 が成り立つことが証明できました。以上を振り返ってまとめると次のようになります。
|
この "まとめ" で述べているように、8つの点を通る3次曲線は無数に存在します。8つの点を通る3次曲線は(一般には)一意に定まりません。そこで点を1つ増やすと、9つの点を通る3次曲線は(一般には)一意に定まります(9次元だから)。しかし、その9点が「2つの3次曲線の交点である9点」なら状況が変わります。その9点は独立ではなく、8点が決まれば残りの1点は自動的に決まる。従って、8点を通るすべての3次曲線は残りの1点も通ることになります。この例を図で示すと次の通りです。2つの3次曲線、\(C_1\) と \(C_2\) を、
\(C_1\::\)
\(x^3+\tfrac{1}{20}xy^2+\tfrac{1}{10}y^3-\tfrac{1}{10}x^2+\tfrac{1}{10}y^2-3x-y-\tfrac{2}{5}=0\)
\(C_2\::\)
\(\tfrac{1}{10}x^3+\tfrac{1}{20}x^2y+y^3+\tfrac{1}{10}x^2-\tfrac{1}{10}y^2-x-3y-\tfrac{2}{5}=0\)
とします。この2つの3次曲線は9つの点、\(P_1\) ~ \(P_9\) で交差します。それを正確に図示すると図19の通りです。
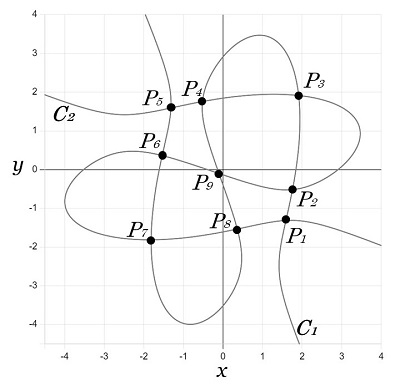
|
図19:9点で交差する2つの3次曲線、\(\bs{C_1,\:C_2}\) |
ここで、\(C_1,\:C_2\) とは別の、\(P_1\) ~ \(P_8\) の8つの点を通る3次曲線を作ると、それも \(P_9\) を通ります(図20)。図20 で、黄・緑・青の3つの3次曲線がその例です。
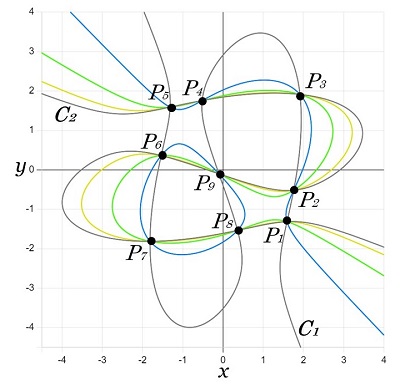
|
図20:8点を通る3次曲線は9点目も通る |
8点(たとえば \(P_1\) ~ \(P_8\))を通る3次曲線は \(P_9\) も通る(黄・緑・青の3つの曲線の例)。青色の3次曲線は2つの成分があるが、9点を通っている。 一般に3次曲線は(独立な)9点から一意に決まる(2次曲線の場合は5点から一意に決まる)。しかし、その9点が2つの3次曲線の交点であるとき、その9点は独立ではなく、8点が決まれば残りの1点は決まってしまう。つまり、9点のうちの8点を通る全ての3次曲線は、残りの1点も通る。 |
18.2 を踏まえて、楕円曲線の加法群で結合則が成り立つことを証明しますが、証明のポイントは、相異なる3つの直線を "3次曲線" として扱うことです。この扱いがなぜ可能かと言うと、3つの直線を、
\(f_1=a_1x+b_1y+c_1=0\)
\(f_2=a_2x+b_2y+c_2=0\)
\(f_3=a_3x+b_3y+c_3=0\)
\(f_2=a_2x+b_2y+c_2=0\)
\(f_3=a_3x+b_3y+c_3=0\)
としたとき、
\(F_L=f_1\cdot f_2\cdot f_3=0\) で表される2次元平面上の点の集合は3つの直線を表しているが、3次曲線の一般形であることに違いはない
からです。もちろん、\(F_L=0\) という曲線の方程式は、3次曲線の一般形の係数 \(a,\:b,\:\:\cd\:,\:i,\:j\) に特別の関係を持ち込んだものです。だからこそ3つの直線を表現しているわけです(数学用語で言うと "退化した" 3次曲線)。しかし特別の関係があるとしても 18.2 を証明した議論の筋道には全く影響しません。
具体的な例をあげると、次の通りです。まず、3次曲線との交点が3つある直線を2つ描き(赤で示す)、交点を \(P_1,\:P_2,\:P_3\)、\(P_4,\:P_5,\:P_6\) とします(図21)。
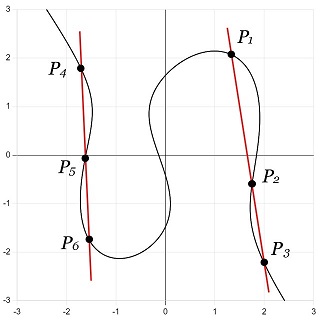
|
図21:3次曲線と2直線の交点(1) |
次に、\(P_1\) と \(P_4\) を結ぶ直線と、\(P_3\) と \(P_6\) を結ぶ直線を緑で描き、3次曲線との交点をそれぞれ \(P_7,\:\:P_8\) とします(図22)。

|
図22:3次曲線と2直線の交点(2) |
こうした上で、\(P_2\) と \(P_5\) を結ぶ直線を緑で、\(P_7\) と \(P_8\) を結ぶ直線を赤で描きます(図23)。
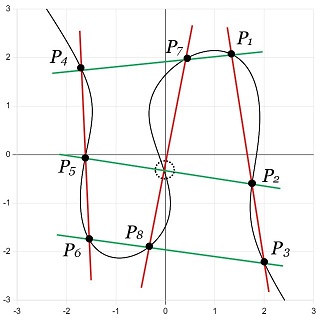
|
図23:3次曲線と2組の3直線の交点 |
ここで、
\(C_1\) : 3次曲線
\(C_2\) : 赤の3直線
\(C_3\) : 緑の3直線
とすると、\(C_1,\:\:C_2,\:\:C_3\) の 3つの "3次曲線" はすべて \(P_1\) ~ \(P_8\) の8点を通ります。すると 18.2 によって、この3つの "3次曲線" ははすべて、\(P_1\) ~ \(P_8\) 以外の、ある特別な点(=図23の点線丸印)を通ります。言い換えると、
直線 \(\bs{P_2\:P_5}\) と直線 \(\bs{P_7\:P_8}\) の交点は3次曲線上にある
ことになります。
以上を踏まえて、結合則を証明すべき図11を再掲します。図11 と図23 は数学的に全く同じであることが、以降の証明のポイントです。

|
図11:結合則 |
「楕円曲線論入門」より引用 |
証明すべきことは 18.1 の、
\(P+Q\) と \(R\) を結ぶ直線と、\(Q+R\) と \(P\) を結ぶ直線の交点を \(T\) とすると、楕円曲線は \(T\) を通る。 |
でした。図11で、
\(C_1\) : 点線の3直線から成る "3次曲線"
\(C_2\) : 実線の3直線から成る "3次曲線"
\(C_2\) : 実線の3直線から成る "3次曲線"
とすると、\(C_1\)(点線) と \(C_2\)(実線)は次の9つの点を通ります。
| \(\mathcal{O}\) | |
| \(P\) | |
| \(Q\) | |
| \(R\) | |
| \(P\!*\!Q\) | |
| \(Q\!*\!R\) | |
| \(P+Q\) | |
| \(Q+R\) | |
| \(P+Q\) と \(R\) を結ぶ直線と、\(Q+R\) と \(P\) を結ぶ直線の交点 |
\(C_1\) と \(C_2\) が9つの点を通るのはそういう風に作図したからです。一方、楕円曲線は \(T\) 以外の \(P_1\) ~ \(P_8\) の8点を通ります。なぜならその8点は楕円曲線上の点として作ったからです。ところが \(T\) だけは違っていて、楕円曲線上の点として作ったのではなく2直線の交点です。しかし 18.2 によって楕円曲線は \(T\) も通ることになります。
これで、楕円曲線上の有理点が作る加法群で結合則が成り立つことの証明が完成しました。
零元を無限遠点にとる加法群ではどうなるでしょうか。この場合は「射影平面での3次曲線」を考える必要があります。射影平面での3次曲線の一般形は、
\([\)射影平面における3次曲線の一般形\(]\)
\(AX^3+BX^2Y+CXY^2+DY^3+EX^2Z+FXYZ+GY^2Z+\)
\(HXZ^2+IYZ^2+JZ^3=0\)
ですが、証明の筋道は \(xy\) 平面と全く同じです。というのも、証明のコアのところは「10変数の連立1次方程式(方程式数が8)の不定解が、一般形でどう表現できるか」であり、曲線方程式の未知数が \((x,\:y)\) の2つであっても \((X,\:Y,\:Z)\) の3つであっても証明の論理に影響がないからです。
というわけで、楕円曲線暗号で実際に使われる「無限遠点を零元にした加法群」においても結合則が成り立つのでした。
19. パスカルの定理
最後に余談ですが、18.2(ケーレー・バカラックの定理)から証明できる別の定理があります。「パスカルの定理」です。これはパスカルが16歳のときに発表した「円錐曲線試論」にあります。最も一般的な形で言うと次の通りです。
| 19.1 | パスカルの定理 |
|
円錐曲線上に異なる6点、\(P_1\) ~ \(P_6\) をとる。
直線 \(P_1P_2\) と \(P_4P_5\) の交点を \(Q_1\) 直線 \(P_2P_3\) と \(P_5P_6\) の交点を \(Q_2\) 直線 \(P_3P_4\) と \(P_6P_1\) の交点を \(Q_3\) とすると、\(Q_1,\:\:Q_2,\:\:Q_3\) は同一直線上にある。 | |
これは非常に美しい定理です。どんな円錐曲線かを言っていないし(円、楕円、放物線、双曲線)、円錐曲線上の6点の位置も、その順序も何も言ってない。それにもかかわらず「同一直線上にある」という、シンプルで強い断定が結論にくる ・・・・・・。個人的経験を言うと、高校生時代にこの定理を知ってその "不思議さ" が印象的だったことを覚えています。
この定理の例を図24と図25、図26に示します。\(Q_1\) を \(P_7\)、\(Q_2\) を \(P_8\)、\(Q_3\) を \(T\) と書きました。円錐曲線が円か楕円であり、6点を円・楕円の周上に順に(= 一周するように)とった場合には、パスカルの定理は、
円・楕円に内接する6角形の対辺が作る2直線の交点3つは同一直線上にある
と簡潔に表現できます(図24)。図25の楕円上の点の位置は図24と同じですが、名前付けが違います。しかし3点が同一線上に並ぶのは同じです。このように6点は楕円上のどの位置にどの順序で配置してもよいわけです。
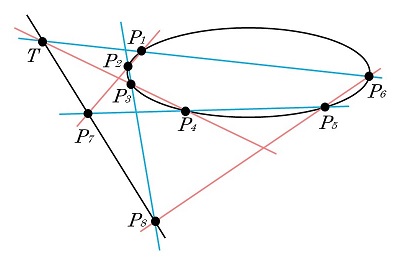
|
図24 パスカルの定理(1)楕円 |

|
図25 パスカルの定理(2)楕円 |
\(P_1\) ~ \(P_6\) の座標を図24と同じにし、名前付けを変えた。 |
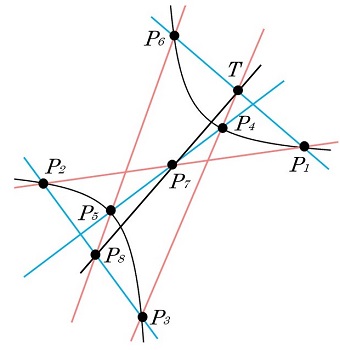
|
図26 パスカルの定理(3)双曲線 |
定理の証明は次の通りです。3次曲線、\(C_1,\:\:C_2,\:\:D\) を、
| 赤色の "3次曲線" | |
| 青色の "3次曲線" | |
| \(P_7\) と \(P_8\) を(\(T\) とは関係なく)結んだ直線と円錐曲線が作る、黒色の "3次曲線" |
とします。\(C_1\) と \(C_2\) は 、\(P_1\) ~ \(P_8\) と \(T\) を通ります。そういう風に作図したからです。一方、\(D\) は \(P_1\) ~ \(P_8\) を通ります。そうすると 18.2 より \(D\) は \(T\) も通ります。\(D\) は \(P_7\) と \(P_8\) を通るように作図しましたが、\(T\) を通るようには作図していません。それでも \(T\) を通る。
その \(T\) は、\(D\) の円錐曲線部分にはありません。なぜなら、\(T\) は直線 \(P_3P_4\) 上に(ないしは直線 \(P_6P_1\) 上に)ありますが、円錐曲線と直線の交点は高々2つであり、\(P_3,\:\:P_4\) が(ないしは \(P_6,\:\:P_1\) が)すでに円錐曲線上にあるからです。従って \(T\) は \(D\) の直線部分にあるしかない。これで証明が終わりました。
パスカルの定理のよくある証明は、円の場合に補助円を用いて証明し、それを "斜めから見たら" 楕円でも成り立つ、とするものです。しかしこの定理は、すべての円錐曲線(=2次曲線の一般形、\(ax^2+bxy+cy^2+dx+ey+f=0\) で表される曲線)で成り立つことが上の証明から分かります。
ちなみに、パスカルの定理は「円錐曲線」を「2直線」に置き換えても、交点ができるように点を配置すれば成り立ちます(パップスの定理と呼ばれる。パップスは4世紀のアレキサンドリアの数学者)。

図27 パップスの定理
軸を含む平面で円錐を2分割すると(平行でない)2直線になり、それは(退化した)円錐曲線とも言えますが、たとえ平行な2直線であっても2次曲線の一般形で表現できるので定理は成り立ちます。
楕円曲線暗号は「楕円曲線上の有理点による加法群」の上に作られた暗号ですが、
楕円曲線上の有理点で加法群を構成できることと、パスカルの定理が成り立つことには、意外にも共通の数学的理由がある
のでした。
補足:素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
(2024.3.18)
2021-07-24 10:52
nice!(0)
No.315 - 高校数学で理解する楕円曲線暗号の数理(1) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
このブログでは、インターネットをはじめとする情報通信インフラで使われている「公開鍵暗号」について、今まで3回にわたって書きました。
の3つです。今回はその継続として、公開鍵暗号の一種で広く使われている「楕円曲線暗号」について、その数学的な背景を書きます。楕円曲線暗号は、1985年に米国 IBM の Victor Miller と米国 Washington 大学の Neal Koblitz によって独立に提案されました。暗号に限らず科学技術の世界では、同時期に同じアイディアが独立に考案されるというケースが見られます。
例によって高校レベルの数学知識だけを前提にし、証明なしに用いる定理や命題はないものとします。ただし、No.310、No.311、No.313 の内容やそこで証明した定理は既知とします。特にその中の、
です。なお、楕円曲線(Elliptic Curve)は、2次曲線である楕円(Ellipse)とは関係ありません。楕円の弧長を積分で求める時に出てくる数式なのでその名があるだけです。暗号の名を楕円暗号とするむきもありますが、誤解されるでしょう。楕円曲線暗号(Elliptic Curve Cryptography)が正しい言い方です。
15. 楕円曲線(Elliptic Curve)とは
楕円曲線とは、次の式で表される平面3次曲線です。
係数の \(a\) と \(b\) は有理数とします。楕円曲線の式の「標準形」と呼ばれるものは何種類かありますが、上式はその最も簡単な形です。楕円曲線暗号ではこの形を使うので、以降、楕円曲線といえばこの形で表される3次曲線とします。Wikipedia に非常にわかりやすい「楕円曲線のカタログ」が載っているのでそれを引用します。
図でわかるように楕円曲線は成分(= ひとつながりの曲線)が1つのものと2つのもの(その1つは閉じた曲線)があります。この違いは何でしょうか。また、図の中にある \(a=0,\:b=0\) の曲線は、実は楕円曲線ではありません。このあたりの説明は以降の通りです。楕円曲線の \(x\) の式を、
と書きます。\(y=f(x)\) のグラフは少なくとも1回、\(x\) 軸を横切るので、\(f(x)=0\) の3次方程式は少なくとも1つの実数解を持ちます。この3次方程式が3つの異なる実数解を持つ条件を調べます。関数 \(f(x)\) が極値をとるとしたら、そのときの \(x\) は方程式、
の解です。この解を \(x_1\) と \(x_2\) とすると、
です。\(x\) がこの値をとるときの2つの極値がゼロでなく、符号が逆であれば、\(f(x)=0\) は3つの異なる実数解をもちます。つまりその条件は、
です。\(x_1,\:x_2\) を入れて計算してみると、この条件は、
となります。不等号の向きが逆なら実数解は1つだけです。この不等号の左辺は「3次方程式の判別式」の符号を逆にしたものです。3次方程式の判別式 \(D\) は、いま扱っている楕円曲線の式の場合、
です。従って、
となります。この2つのケースで楕円曲線をを図示すると、図2(\(a=-2,\:b=1\))、図3(\(a=-2,\:b=2\))のようになります。
ここで \(D=0\) のときにどうなるかを調べてみます。不定方程式、
の整数解を求めるために、\(a=-3k^2\:(0\leq k)\) と置くと、
が解です。\(k=0,\:1\) とすると、
が解のうちの3組です。まず、\((a,\:b)=(0,\:0)\) のとき曲線の式は、
となり、図4のように「尖点」をもつ曲線となります(Wikipedia の "楕円曲線のカタログ" にあったものです)。尖点では微係数が定まらず、曲線の接線が引けません。
\((a,\:b)=(-3,\:2)\) のときの曲線の式は、
となり、図5のように「結節点」をもつ自己交差曲線となります。結節点において接線は引けますが、2種類あって一意に定まりません。
\((a,\:b)=(-3,-2)\) のときの曲線の式は、
となり、図6のように \((-1,\:0)\) に「孤立点」が発生します。この孤立点でも接線は引けません。
尖点、結節点、孤立点を曲線の「特異点」と言い、特異点をもつ3次曲線を特異3次曲線と言います。そして特異3次曲線は \(y^2=x^3+ax+b\) の形であっても楕円曲線とは言いません。つまり、楕円曲線の正確な定義は次の通りです。
この定義による楕円曲線は "なめらか" であり、曲線上の全ての点で唯一の接線が引けます。以降、この楕円曲線の性質を調べていきます。
楕円曲線暗号は「楕円曲線上の点の加法群」で構成する暗号です。そこでまず、No.313 でも触れた「群(group)」とは何かを復習します。
群の定義
群(\(G\) で表します)とは、何らかの2項演算 "\(\circ\)" が定義された集合です。演算が定義されているとは、集合 \(G\) の任意の2つの元(同じ元であってもよい)、\(a\)、\(b\) を演算した結果の \(a\circ b\) が \(G\) の元であることを意味します。この2項演算は次の3つの条件を満たす必要があります。この「条件を満たす2項演算が定義された集合」が群 \(G\) です。
演算 "\(\circ\)" を乗算と考えるとき、\(G\) を乗法群といいます。乗法群では2項演算を \(a\times b,\:\:a\cdot b,\:\:ab\) などと書きます。単位元は \(1\) と書くこともあります。また、逆元 \(b\) は \(a^{-1}\) です。同一の \(n\) 個の元 \(a\) に対して演算 "\(\circ\)" を \(n-1\) 回行った結果は \(a^n\) で「累乗(あるいは冪乗)」と呼びます。
演算 "\(\circ\)" を加算と考えるとき、\(G\) を加法群といいます。加法群では2項演算を \(a+b\) と書きます。加法群の単位元を零元と呼び、\(0\) と書くことがあります。また逆元 \(b\) は \(-a\) です。同一の \(n\) 個の元 \(a\) に対して演算 \(\circ\) を行った結果は \(na\)で「スカラー倍」と呼びます。
乗法群か加法群かは多分に "言葉の綾" の面があり、どちらがイメージしやすいかによります。但し、加法群と言った場合は暗黙に可換則、\(a\circ b=b\circ a\) が成り立つ群を言います。可換則が成り立つ群を、ノルウェーの数学者 Abel の名前をとって「アーベル群」と呼びます。もちろん「乗法」や「加法」のイメージとは結びつきにくい群もたくさんあります。
楕円曲線上の有理点
楕円曲線上の有理点からなる加法群を構成することができます。有理点とは、楕円曲線上の点、\((x_0,\:y_0)\) で、\(x_0\) も \(y_0\) も有理数の点です。一般に、楕円曲線が有理点を持つかどうかを有限回の手続きで決定する方法は知られていません。しかし、1個か2個の有理点があれば、次のような手続きで次々と有理点を見つけることができます。以下の記述では \(P\)、\(Q\)、\(R\) などを有理点とし、
と定義します。ここでの " \(\!*\!\) " は乗算の記号ではなく「" \(\!*\!\) " の前後に書かれた楕円曲線上の点ではない、もう一つの直線と楕円曲線の交点」の意味です。
図7で、\(P\!*\!Q\) も \(P\!*\!P\) も有理点です。なぜなら、係数が有理数の3次曲線と直線の交点を求める式は3次方程式になりますが、3次方程式の2つの異なる根が有理数なら(図7の左の \(P\) と \(Q\))、もうひとつの根 \(P\!*\!Q\) も有理数だからです。もう1つが有理数でないと(=無理数や複素数)、3次曲線の係数が有理数という前提に反します。同じように3次方程式の重根(図7の右の \(P\))が有理数だと、もう一つの根も有理数です。
つまり、楕円曲線上に1つ、ないしは2つの有理点があったとしたら、上記の操作で有理点を増やしていけます(但し有理点が無限個なのか有限個なのかは楕円曲線によります)。そこで有理点の存在を前提として以下の議論を進めます。
楕円曲線上の有理点が作る加法群
楕円曲線上の有理点を "群" にするためには、そこに何らかの演算を定義する必要がありますが、その定義を次のようにします。加法群なので演算を \(+\) と書きます。
群演算
零元
この演算における零元 \(\mathcal{O}\) が、群の零元の条件を満たしているかどうかを検証すると、
となって、零元の条件を満たしていることがわかります(図9)。もちろん、\(\mathcal{O}+P=P\) です。
逆元
逆元は次のように定義します。零元 \(\mathcal{O}\) における接線が楕円曲線と交わる点を \(S\) とします。まず、
です。そして 点 \(Q\) と \(S\) を結ぶ直線が再び楕円曲線を交わる点を、\(Q\) の逆元(= \(-Q\))とします。つまり、
です。このように定義すると
となり、群の逆元の条件を満たすことがわかります(図10)。\(S\) と \(\mathcal{O}\) を結ぶ直線は \(\mathcal{O}\) で2回交差するので、\(S*\mathcal{O}=\mathcal{O}\) です。
結合則
群を構成するためには、以上の群演算の定義が結合則を満たしていななければなりません。楕円曲線上に点 \(P\)、\(Q\)、\(R\) をとったとき、
となるのが結合則ですが、
なので、
が示せればよいことになります。「楕円曲線論入門」にはこのことを示した図が載っています(図11)。
\((P+Q)\!*\!R\) の点と \(P\!*\!(Q+R)\) の点が、楕円曲線上で同一の点になることの証明は少々複雑なので「18. 結合則が成り立つことの検証と証明」にまわします。
以上のように楕円曲線上の有理点は、直線との交点を使って加法と逆元をうまく定義することで "群" になることがわかりました。ここで注意すべきは、零元は楕円曲線上の任意の有理点でよいことです。これを利用し「零元=無限遠点」としたのが、実用的に使われる楕円曲線上の加法群です。
無限遠点を零元とする加法群
以下では「対称点」という言葉を使いますが、
ことにします。楕円曲線は \(x\) 軸について対称なので、点 \(P\) を \(x\) 軸で "折り返した" 点が \(P\) の対称点です。\(y=0\) となる点が楕円曲線上に1つ、または3つありますが、その点の対称点は同じ点です。
次に「\(y\) 軸方向の無限遠点」を導入し、「楕円曲線上の有理点と無限遠点を合わせた集合」に群を定義します。ここからは無限遠点を \(\mathcal{O}\) と書きます。
無限遠点は図に表せないのでイメージしにくいのですが、\(\bs{y}\) 軸方向の無限遠に \(\bs{\mathcal{O}}\) があると考えます。\(y\) 軸の正方向でも負の方向でもかまいません。
楕円曲線上の点 \(P\) を \(P=(x_p,\:y_p)\) とし、\(x_p\) をどんどん大きくすると、楕円曲線の式では \(x^3\) の項が支配的になるので、\(y_p^2=x_p^3\) と近似できます。つまり \(y_p=\pm x_p^{1.5}\) となり、\(x_p\) が大きいと \(y_p\) は \(y\) 軸の遙か上方(と下方)になります。この極限が無限遠点 \(\mathcal{O}\) と考えます。さらに、
と考えます。この \(\bs{y}\) 軸方向の無限遠点 \(\bs{\mathcal{O}}\) を零元とする群を構成します。
群演算
まず、群演算の加法ですが、
と定義します(図12)。
こうすると、\(P\!*\!Q\) と \(P+Q\) を結ぶ直線は \(y\) 軸と平行になり、それは無限遠点 \(\mathcal{O}\) で楕円曲線と交差します。つまり、
です。この定義は 零元を楕円曲線上の点にとった図8と合致します。この加法の定義で \(\mathcal{O}\) が群の零元の要件を満たしているかを検証すると、
となって要件を満たしていることがわかります。\(P*\mathcal{O}\) は \(P\) の対称点ですが、\(P\) の対称点と \(\mathcal{O}\) を結ぶ直線が楕円曲線と交差する点は \(P\) なので上式が成立します。これは楕円曲線上に \(\mathcal{O}\) をとった図9と同じです。さらに逆元ですが、\(Q\) が楕円曲線上にあったとき、
と定義します(図13)。
こうすると、
となりますが、\(\mathcal{O}*\mathcal{O}=\mathcal{O}\)(=無限遠点の対称点は無限遠点)との自然な定義を行うと、
となって逆元の要件を満たします。結合則についても零元を楕円曲線上にとった場合(図11)と同じ様に成立します。「18. 結合則が成り立つことの検証と証明」でそのこと書きます。
射影平面
無限遠点は図で表現できず、何だか "怪しげな" 感じがしますが、数学的に厳密に定義できます。それには射影平面を使います。
平面 \((x,\:y)\) に対し、3つの数 \((X,\:Y,\:Z)\) で表される "平面" を射影平面と言います。3つの数がありますが3次元空間ではありません。ただし \((0,\:0,\:0)\) の点は除きます。また、
と定義します。\(xy\) 平面から射影平面の対応は、
とし、その逆の対応は、
です。この対応からわかるように、射影平面には \(xy\) 平面にない点が含まれています(\(Z=0\) の点)。
射影平面での楕円曲線の式は、\(xy\) 平面の楕円曲線の式で、\(x=\dfrac{X}{Z},\:\:y=\dfrac{Y}{Z}\) とおき、全体に \(Z^3\) をかけて同次化(=変数項の合計次数をそろえる)します。その結果、
の同次方程式が、射影平面での楕円曲線になります。ためしに、図2の楕円曲線(\(a=-2,\:b=1\))と \(y\) 軸との交点を計算してみると、\(xy\) 平面では、
の連立方程式を解いて、\((0,\pm1)\) となります。一方、射影平面では、\(x=0\) は \(X=0\) なので、
が、楕円曲線と直線の交点を求める連立式になります。この解は、\(\al\) と \(\beta\) を \(0\) ではない数として、\((0,\al,\pm\al),\:(0,\beta,\:0)\) です。射影平面の同値関係を利用すると、
が楕円曲線と直線の交点になり、交点は3つあることになります。ここで \(xy\) 平面の交点には現れなかった \((0,\:1,\:0)\) が \(y\) 軸方向の無限遠点です。これを一般化すると次のようになります。つまり、楕円曲線と \(y\) 軸に平行な直線の式を、
とすると、これに対応する射影平面の式は、
です。\((0,\:1,\:0)\) はこの2式を必ず満たします。つまり全ての楕円曲線は \((0,\:1,\:0)\) を通り、全ての \(y\) 軸に平行な直線は \((0,\:1,\:0)\) を通る。従って、楕円曲線と\(y\) 軸に平行な直線は(\(y\) 軸方向の)無限遠点で交わることになります。
楕円曲線の計算には現れませんが、無限遠点にもいろいろあって、\((1,\:0,\:0)\) は \(x\) 軸方向の無限遠点、\((\al,\:\beta,\:0)\) は任意方向の無限遠点です(\(\al\)、\(\beta\) は \(0\) ではない数)。
\(xy\) 平面の2直線は、平行なときには交点がありませんが、射影平面の2直線は必ず1点で交わります。また射影平面の楕円曲線の1点を通る直線は、楕円曲線と必ず3点で交わります(直線が楕円曲線の接線の場合は、接点での交差数を2と数えます)。このように、交差を統一的に扱えるのが射影平面の特徴の一つです。
以上のような数学的裏付けのもとに導入したのが無限遠点です。これを \(xy\) 平面では、
とイメージしてよいわけです。
加法式・2倍式
楕円曲線上の加法を計算式で表します。楕円曲線上の3点を次のように定義します。
とします。\(P_1\) と \(P_2\) を結ぶ直線を \(y=\lambda x+\mu\) とすると、連立方程式、
の解が \(P_1,\:P_2,\:(x_3,-y_3)\) です。この2つの式から \(y\) を消去すると、
が得られますが、この式は、
と同一のはずです。そこで \(x^2\) の係数を比較すると、
が得られます。つまり、
となります。この \(x_3\) を直線の式に入れると、
ですが、\(y_1=\lambda x_1+\mu\) なので \(\mu\) を消去すると、
となります。これが基本の加法式です。これを \(P_1\) と \(P_2\) の配置パターンごとにまとめると、次の通りです。
\(x_1\neq x_2\) のとき
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
この場合は \(P_1\) と \(P_2\) を通る直線は \(P_1\) における楕円曲線の接線となり、直線の傾き \(\lambda\) は上の式のままでは計算できません。そこで \(y^2=x^3+ax+b\) を \(x\) で微分すると
なので、
となります。\(x_2\) を \(x_1\) に置き換えてまとめると、
が \(P_1+P_1\) の計算式です。これは \(P_1\) の "2倍"(一般にはスカラー倍)であり、\(2P_1\) と書きます。
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
この場合、\(P_2=-P_1\) なので、定義により
です。
なお、\(P_1\) と \(P_2\) は、楕円曲線の定義式、
を満たしますが、この左辺と右辺のそれぞれを引き算すると、
となって \(\lambda\) の別の表現が得られますが、これは \(x_1=x_2\) でも使えます。従って「加法式(第2形)」を次のようにも表現できます。
\(y_1+y_2\neq0\) のとき
\(y_1+y_2=0\) のとき
楕円曲線の具体例
楕円曲線とその有理点、加法則の適用例として、整数係数の3つの楕円曲線を調べてみます。以後の記述では、\(P=(x,\:y)\) とするとき、\(nP,\:-P,\:-nP\) の記述を使いますが、それぞれの定義は、
です。また、\(nP=(x_n,\:y_n)\) とすると、加法の定義から \(-nP=(x_n,-y_n)\) です。
\(y^2=x^3+1\)
この楕円曲線上の有理点は、次の5つの整点(= 座標値が整数の点)です。
ここで、群の演算式を使って \(nP_1\) を計算してみると、
となります。\(P_1\) は 6倍する(= 6個加算する)と \(\mathcal{O}\)(=零元)になる。このことを「\(P_1\) の位数(order)が \(6\) である」と言います。また、
なので、\(P_2\) の位数は \(3\) です。同様にして、\(P_3\)~\(P_5\) の位数はそれぞれ \(2,\:\:3,\:\:6\) になります。
楕円曲線 \(y^2=x^3+1\) の有理点は \(P_1\)~\(P_5\) の点しかありません。また位数が有限値なので、これらは有限位数の点です。これらの点と 零元 \(\mathcal{O}\) を合わせて群を構成します。
しかし楕円曲線上の有理点が有限位数をもつとは限りません。それが次の例です。
\(y^2=x^3-x+1\)
方程式 \(y^2=x^3-x+1\) の整数解を調べると、手計算で \((-1,\pm1),\) \((0,\pm1),\) \((1,\pm1),\) \((3,\pm5),\) \((5,\pm11)\) の\(10\)個の解が容易に見つかります。今、\(P_1=(1,\:1)\) とし、\(nP_1\) を順に計算してみると、次のようになります。
途中で \((56,-419)\) という、手計算では分からない整点が現れました。計算してみると、
となって、確かにこれが楕円曲線上の点であることが分かります。\(15P_1\) までの結果を掲げましたが、この計算は \(\mathcal{O}\)(= 零元)で終わることがなく、無限に続きます。つまり、\(P_1=(1,\:1)\) は無限位数の点です。
さらに、同様の計算を\(-P_1=(1,-1)\) から始めると、\(y\) 座標の符号が逆転した点列、\(-nP_1\) が得られます。そして実は、
ことが分かっています。\(0P_1=\mathcal{O}\) と定義すれば、楕円曲線で定義された加法群の元は \(mP_1\)(\(m\) は整数)の形で表現できるとも言えます。この性質を有限生成と言い、\(P_1\) を生成元(generator)と呼びます。一般には、生成元は複数個あります。つまり楕円曲線上の有理点は \(r\) 個の有理点 \(Q_i\) を使って、
の形で表現できます。この \(r\) を楕円曲線の階数(rank)と言います。なお、有限個の有理点しかもたない 図14 のような楕円曲線の階数は \(0\) とします。
楕円曲線 \(y^2=x^3-x+1\) の階数は \(1\) です。そして今までの結果から、階数が \(1\) の楕円曲線の有理点と零点 \(\mathcal{O}\) は、加法に関して整数(= 正の自然数と負の自然数と \(0\))と全く同じ構造をもつことが分かります。ただ、楕円曲線の有理点の加法は普通の整数の加法よりよほど複雑な演算です。これが楕円曲線暗号を作るときの基礎となっています。
\(y^2=x^3-4x+1\)
この楕円曲線の階数は \(2\) です。従って生成元は2つで、
です。曲線上には無限個の有理点がありますが、すべてはこの2つの生成元から「有限生成」されます。無限個の有理点のうち、生成元を含めて 22個が整点ですが(\(y\) 座標の正負を無視すると 11個)、もちろんそれらの整点も生成元で表現できます。実際に計算してみると以下の通りです。
もちろん、計算していくと上記の整点だけでなく有理点が次々と生成され、それが無限に続きます。上の計算で \(P_1,\:P_2\) の符号を逆転させると \(y\) 座標の符号が逆の整点が得られます。たとえば、
です。以上を含めてこの楕円曲線の整点は、
となります。最大の整点は \((1274,\pm45473)\) ですが、実際に計算してみると、
となって、楕円曲線上の点であることが確認できます。この最大の整点を2つの生成元に分けて、それぞれを計算してみると、
となりますが、この2つの有理点を楕円曲線の加法式で \(8P_1+3P_2\) とすると整点である \((1274,\:-45473)\) が現れるのも不思議な感じがします。
以上の「楕円曲線の有理点から成る加法群」を踏まえ、これ以降は楕円曲線暗号で使われる「有限体上の楕円曲線による加法群」に移ります。
有限体上の楕円曲線による加法群
以降に出てくる有限体 \(\bs{F}_p\) と 乗法群 \(\bs{F}_p^{*}\) については、No.313「高校数学で理解する公開鍵暗号の数理:10. 有限体と乗法群」 で定義したものです。
楕円曲線暗号に使われる楕円曲線は、有限体 \(\bs{F}_p\) で定義された "曲線" で、次の式を満たすものです。
\(x\)、\(y\)、\(a\)、\(b\) は全て \(\bs{F}_p\) の元です。「この式を満たす全ての \((x,\:y)\) と 零点 \(\mathcal{O}\) の集合」に対して演算を定義して群を構成します。演算を加法と考えて \(+\) と書きます。この "曲線" 上の3点を、
とするとき、群の演算式は次のように定義されます。
\(x_1\neq x_2\) のとき
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
つまり、実数平面の有理点と無限遠点(=零元)で構成された群の演算式と全く同じです。もちろん加減乗除は \(\bs{F}_p\) で行います。これが群になる理由は、有理数体(有理数全体の集合)も有限体 \(\bs{F}_p\) も「体」であり、加減乗除は全く同一形式で記述できるからです。ただ、有理数体と違って \(\bs{F}_p\) の元の数は有限個であり、群の元の数も有限個(=有限群)です。以降、\(\bs{\bs{F}_p}\) 上の楕円曲線、\(\bs{y^2=x^3+ax+b}\) による有限群を \(\bs{E(a,\:b,\:p)}\) と表記します。
\(\bs{F}_p\) 上の楕円曲線は、もはや "曲線" の形をしていませんが、これを可視化した図を次に示します。有限体 \(F_{109}\) 上の "楕円曲線"、\(y^2=x^3+2x+4\) の例です。
以上が「有限体上の楕円曲線が作る加法群」で、楕円曲線暗号はこの加法群で構成されます。その話を次回にします。
このブログでは、インターネットをはじめとする情報通信インフラで使われている「公開鍵暗号」について、今まで3回にわたって書きました。
の3つです。今回はその継続として、公開鍵暗号の一種で広く使われている「楕円曲線暗号」について、その数学的な背景を書きます。楕円曲線暗号は、1985年に米国 IBM の Victor Miller と米国 Washington 大学の Neal Koblitz によって独立に提案されました。暗号に限らず科学技術の世界では、同時期に同じアイディアが独立に考案されるというケースが見られます。
例によって高校レベルの数学知識だけを前提にし、証明なしに用いる定理や命題はないものとします。ただし、No.310、No.311、No.313 の内容やそこで証明した定理は既知とします。特にその中の、
です。なお、楕円曲線(Elliptic Curve)は、2次曲線である楕円(Ellipse)とは関係ありません。楕円の弧長を積分で求める時に出てくる数式なのでその名があるだけです。暗号の名を楕円暗号とするむきもありますが、誤解されるでしょう。楕円曲線暗号(Elliptic Curve Cryptography)が正しい言い方です。
15. 楕円曲線(Elliptic Curve)とは
楕円曲線とは、次の式で表される平面3次曲線です。
\(y^2=x^3+ax+b\)
係数の \(a\) と \(b\) は有理数とします。楕円曲線の式の「標準形」と呼ばれるものは何種類かありますが、上式はその最も簡単な形です。楕円曲線暗号ではこの形を使うので、以降、楕円曲線といえばこの形で表される3次曲線とします。Wikipedia に非常にわかりやすい「楕円曲線のカタログ」が載っているのでそれを引用します。
| \(b=-1\) | \(b=\phantom{-}0\) | \(b=\phantom{-}1\) | \(b=\phantom{-}2\) | |
| \(a=-2\) |

|
|||
| \(a=-1\) | ||||
| \(a=\phantom{-}0\) | ||||
| \(a=\phantom{-}1\) | ||||
図1:楕円曲線のカタログ
| ||||
Wikipediaより。楕円曲線には曲線の "成分" が1つのものと2つのものがある。なお、この図で \(a=b=0\) だけは楕円曲線ではない(後述)。
| ||||
図でわかるように楕円曲線は成分(= ひとつながりの曲線)が1つのものと2つのもの(その1つは閉じた曲線)があります。この違いは何でしょうか。また、図の中にある \(a=0,\:b=0\) の曲線は、実は楕円曲線ではありません。このあたりの説明は以降の通りです。楕円曲線の \(x\) の式を、
\(x^3+ax+b=f(x)\)
と書きます。\(y=f(x)\) のグラフは少なくとも1回、\(x\) 軸を横切るので、\(f(x)=0\) の3次方程式は少なくとも1つの実数解を持ちます。この3次方程式が3つの異なる実数解を持つ条件を調べます。関数 \(f(x)\) が極値をとるとしたら、そのときの \(x\) は方程式、
\(f^{'}(x)=0\)
の解です。この解を \(x_1\) と \(x_2\) とすると、
\(x_1=\phantom{-}\sqrt{\dfrac{-a}{3}}\)
\(x_2=-\sqrt{\dfrac{-a}{3}}\)
\(x_2=-\sqrt{\dfrac{-a}{3}}\)
です。\(x\) がこの値をとるときの2つの極値がゼロでなく、符号が逆であれば、\(f(x)=0\) は3つの異なる実数解をもちます。つまりその条件は、
\(f(x_1)\cdot f(x_2) < 0\)
です。\(x_1,\:x_2\) を入れて計算してみると、この条件は、
\(4a^3+27b^2 < 0\)
となります。不等号の向きが逆なら実数解は1つだけです。この不等号の左辺は「3次方程式の判別式」の符号を逆にしたものです。3次方程式の判別式 \(D\) は、いま扱っている楕円曲線の式の場合、
\(D=-(4a^3+27b^2)\)
です。従って、
| \(D > 0\) のとき、\(f(x)=0\) は3つの実数解をもち、楕円曲線で \(y=0\) となる点は3つある。このとき楕円曲線の成分は2つになる(図2)。 | |
| \(D < 0\) のとき、\(f(x)=0\) の実数解は1つであり、楕円曲線で \(y=0\) の点も1つである。このとき楕円曲線の成分は1つになる(図3)。 |
となります。この2つのケースで楕円曲線をを図示すると、図2(\(a=-2,\:b=1\))、図3(\(a=-2,\:b=2\))のようになります。

|
図2:成分が2つの楕円曲線 \(y^2=x^3-2x+1\) |
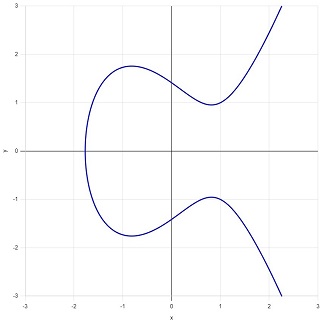
|
図3:成分が1つの楕円曲線 \(y^2=x^3-2x+2\) |
ここで \(D=0\) のときにどうなるかを調べてみます。不定方程式、
\(4a^3+27b^2=0\)
の整数解を求めるために、\(a=-3k^2\:(0\leq k)\) と置くと、
\(a=-3k^2\)
\(b=\pm2k^2\)
\(b=\pm2k^2\)
が解です。\(k=0,\:1\) とすると、
\((a,\:b)=(0,\:0),\:\:(-3,\:2),\:\:(-3,-2)\)
が解のうちの3組です。まず、\((a,\:b)=(0,\:0)\) のとき曲線の式は、
\(y^2=x^3\)
となり、図4のように「尖点」をもつ曲線となります(Wikipedia の "楕円曲線のカタログ" にあったものです)。尖点では微係数が定まらず、曲線の接線が引けません。
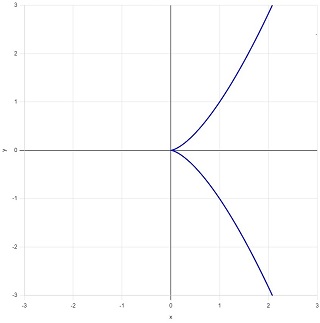
|
図4:尖点をもつ3次曲線 \(y^2=x^3\) |
\((a,\:b)=(-3,\:2)\) のときの曲線の式は、
\(\begin{eqnarray}
&&y^2&=x^3-3x+2\\
&&&=(x+2)(x-1)^2\\
\end{eqnarray}\)
となり、図5のように「結節点」をもつ自己交差曲線となります。結節点において接線は引けますが、2種類あって一意に定まりません。
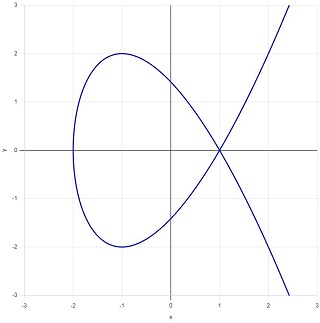
|
図5:結節点をもつ3次曲線 \(y^2=x^3-3x+2\) |
\((a,\:b)=(-3,-2)\) のときの曲線の式は、
\(\begin{eqnarray}
&&y^2&=x^3-3x-2\\
&&&=(x-2)(x+1)^2\\
\end{eqnarray}\)
となり、図6のように \((-1,\:0)\) に「孤立点」が発生します。この孤立点でも接線は引けません。
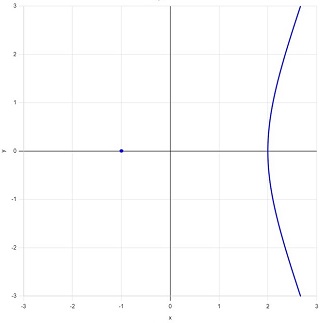
|
図6:孤立点をもつ3次曲線 \(y^2=x^3-3x-2\) |
尖点、結節点、孤立点を曲線の「特異点」と言い、特異点をもつ3次曲線を特異3次曲線と言います。そして特異3次曲線は \(y^2=x^3+ax+b\) の形であっても楕円曲線とは言いません。つまり、楕円曲線の正確な定義は次の通りです。
| 15.1 | 楕円曲線の定義 |
|
次の式で表される平面曲線を楕円曲線と言う。
\(y^2=x^3+ax+b\) \((4a^3+27b^2\neq0)\) | |
この定義による楕円曲線は "なめらか" であり、曲線上の全ての点で唯一の接線が引けます。以降、この楕円曲線の性質を調べていきます。
楕円曲線暗号は「楕円曲線上の点の加法群」で構成する暗号です。そこでまず、No.313 でも触れた「群(group)」とは何かを復習します。
群の定義
群(\(G\) で表します)とは、何らかの2項演算 "\(\circ\)" が定義された集合です。演算が定義されているとは、集合 \(G\) の任意の2つの元(同じ元であってもよい)、\(a\)、\(b\) を演算した結果の \(a\circ b\) が \(G\) の元であることを意味します。この2項演算は次の3つの条件を満たす必要があります。この「条件を満たす2項演算が定義された集合」が群 \(G\) です。
| \(a\circ e=e\circ a=a\) となる元 \(e\) が存在 | |
| \(a\circ b=b\circ a=e\) となる \(b\) が、任意の \(a\) について存在 | |
| \((a\circ b)\circ c=a\circ(b\circ c)\) |
演算 "\(\circ\)" を乗算と考えるとき、\(G\) を乗法群といいます。乗法群では2項演算を \(a\times b,\:\:a\cdot b,\:\:ab\) などと書きます。単位元は \(1\) と書くこともあります。また、逆元 \(b\) は \(a^{-1}\) です。同一の \(n\) 個の元 \(a\) に対して演算 "\(\circ\)" を \(n-1\) 回行った結果は \(a^n\) で「累乗(あるいは冪乗)」と呼びます。
演算 "\(\circ\)" を加算と考えるとき、\(G\) を加法群といいます。加法群では2項演算を \(a+b\) と書きます。加法群の単位元を零元と呼び、\(0\) と書くことがあります。また逆元 \(b\) は \(-a\) です。同一の \(n\) 個の元 \(a\) に対して演算 \(\circ\) を行った結果は \(na\)で「スカラー倍」と呼びます。
乗法群か加法群かは多分に "言葉の綾" の面があり、どちらがイメージしやすいかによります。但し、加法群と言った場合は暗黙に可換則、\(a\circ b=b\circ a\) が成り立つ群を言います。可換則が成り立つ群を、ノルウェーの数学者 Abel の名前をとって「アーベル群」と呼びます。もちろん「乗法」や「加法」のイメージとは結びつきにくい群もたくさんあります。
楕円曲線上の有理点
楕円曲線上の有理点からなる加法群を構成することができます。有理点とは、楕円曲線上の点、\((x_0,\:y_0)\) で、\(x_0\) も \(y_0\) も有理数の点です。一般に、楕円曲線が有理点を持つかどうかを有限回の手続きで決定する方法は知られていません。しかし、1個か2個の有理点があれば、次のような手続きで次々と有理点を見つけることができます。以下の記述では \(P\)、\(Q\)、\(R\) などを有理点とし、
| \(P\) と \(Q\) を結ぶ直線がふたたび楕円曲線と交わる点を \(P\!*\!Q\)(図7の左) | |
| \(P\) 点における接線が楕円曲線と交わる点を \(P\!*\!P\)(図7の右) |
と定義します。ここでの " \(\!*\!\) " は乗算の記号ではなく「" \(\!*\!\) " の前後に書かれた楕円曲線上の点ではない、もう一つの直線と楕円曲線の交点」の意味です。
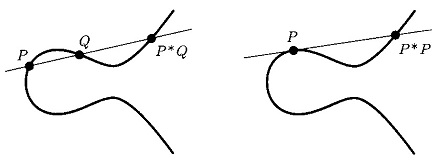
|
図7:楕円曲線上の有理点 |
J.H.シルヴァーマン、J.テイト著「楕円曲線論入門」(シュプリンガー・フェアラーク東京 \(1995\))より引用 |
|
つまり、楕円曲線上に1つ、ないしは2つの有理点があったとしたら、上記の操作で有理点を増やしていけます(但し有理点が無限個なのか有限個なのかは楕円曲線によります)。そこで有理点の存在を前提として以下の議論を進めます。
なお、楕円曲線暗号で使う加法群は「有限体上の楕円曲線における加法群」であり、有理点を見つけるアルゴリズムがあります(後述)。もちろん有理点の数は有限個です。
楕円曲線上の有理点が作る加法群
楕円曲線上の有理点を "群" にするためには、そこに何らかの演算を定義する必要がありますが、その定義を次のようにします。加法群なので演算を \(+\) と書きます。
群演算
| 任意の有理点を零元(= \(\mathcal{O}\) )とする。 | |
| \(P\) と \(Q\) を楕円曲線上の有理点とするとき、点 \(P\!*\!Q\) と \(\mathcal{O}\) を結ぶ直線が再び楕円曲線と交わる点を \(P+Q\) とする。つまり、
\(P+Q=(P\!*\!Q)*\mathcal{O}\)
とする。 |
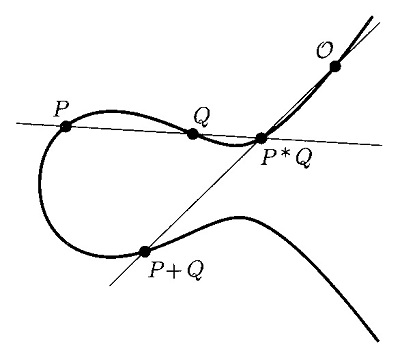
|
図8:楕円曲線上の群演算 |
シルヴァーマン、テイト「楕円曲線論入門」より引用。零元の記号には、英大文字 \(O\) の筆記体 \(\mathcal{O}\) が使ってある。以下同様 |
零元
この演算における零元 \(\mathcal{O}\) が、群の零元の条件を満たしているかどうかを検証すると、
\(P+\mathcal{O}=(P*\mathcal{O})*\mathcal{O}=P\)
となって、零元の条件を満たしていることがわかります(図9)。もちろん、\(\mathcal{O}+P=P\) です。
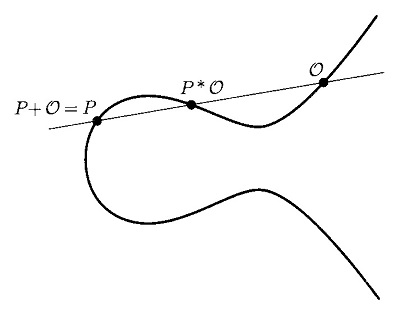
|
図9:\(\bs{\mathcal{O}}\) が零元であることの検証 |
「楕円曲線論入門」より引用 |
逆元
逆元は次のように定義します。零元 \(\mathcal{O}\) における接線が楕円曲線と交わる点を \(S\) とします。まず、
\(S=\mathcal{O}*\mathcal{O}\)
です。そして 点 \(Q\) と \(S\) を結ぶ直線が再び楕円曲線を交わる点を、\(Q\) の逆元(= \(-Q\))とします。つまり、
\(-Q=Q\!*\!S\)
です。このように定義すると
\(\begin{eqnarray}
&&Q+(-Q)&=(Q\!*\!(-Q))*\mathcal{O}\\
&&&=S*\mathcal{O}\\
&&&=\mathcal{O}\\
\end{eqnarray}\)
となり、群の逆元の条件を満たすことがわかります(図10)。\(S\) と \(\mathcal{O}\) を結ぶ直線は \(\mathcal{O}\) で2回交差するので、\(S*\mathcal{O}=\mathcal{O}\) です。
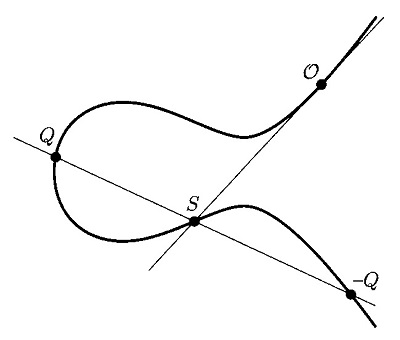
|
図10:点の逆元 |
「楕円曲線論入門」より引用 |
結合則
群を構成するためには、以上の群演算の定義が結合則を満たしていななければなりません。楕円曲線上に点 \(P\)、\(Q\)、\(R\) をとったとき、
\((P+Q)+R=P+(Q+R)\)
となるのが結合則ですが、
\((P+Q)+R=((P+Q)\!*\!R)*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
なので、
\((P+Q)\!*\!R=P\!*\!(Q+R)\)
が示せればよいことになります。「楕円曲線論入門」にはこのことを示した図が載っています(図11)。

|
図11:結合則の検証 |
「楕円曲線論入門」より引用 |
\((P+Q)\!*\!R\) の点と \(P\!*\!(Q+R)\) の点が、楕円曲線上で同一の点になることの証明は少々複雑なので「18. 結合則が成り立つことの検証と証明」にまわします。
以上のように楕円曲線上の有理点は、直線との交点を使って加法と逆元をうまく定義することで "群" になることがわかりました。ここで注意すべきは、零元は楕円曲線上の任意の有理点でよいことです。これを利用し「零元=無限遠点」としたのが、実用的に使われる楕円曲線上の加法群です。
無限遠点を零元とする加法群
以下では「対称点」という言葉を使いますが、
\(P=(x_p,\:y_p)\) とするとき、点 \((x_p,\:-y_p)\) を\(P\) の対称点と呼ぶ
ことにします。楕円曲線は \(x\) 軸について対称なので、点 \(P\) を \(x\) 軸で "折り返した" 点が \(P\) の対称点です。\(y=0\) となる点が楕円曲線上に1つ、または3つありますが、その点の対称点は同じ点です。
次に「\(y\) 軸方向の無限遠点」を導入し、「楕円曲線上の有理点と無限遠点を合わせた集合」に群を定義します。ここからは無限遠点を \(\mathcal{O}\) と書きます。
無限遠点は図に表せないのでイメージしにくいのですが、\(\bs{y}\) 軸方向の無限遠に \(\bs{\mathcal{O}}\) があると考えます。\(y\) 軸の正方向でも負の方向でもかまいません。
楕円曲線上の点 \(P\) を \(P=(x_p,\:y_p)\) とし、\(x_p\) をどんどん大きくすると、楕円曲線の式では \(x^3\) の項が支配的になるので、\(y_p^2=x_p^3\) と近似できます。つまり \(y_p=\pm x_p^{1.5}\) となり、\(x_p\) が大きいと \(y_p\) は \(y\) 軸の遙か上方(と下方)になります。この極限が無限遠点 \(\mathcal{O}\) と考えます。さらに、
楕円曲線上の任意の点 \(P\) を通る \(y\) 軸に平行な直線を引くと、その直線は \(P\) の対称点で楕円曲線と交差すると同時に、無限遠点 \(\mathcal{O}\) でも交差する
と考えます。この \(\bs{y}\) 軸方向の無限遠点 \(\bs{\mathcal{O}}\) を零元とする群を構成します。
群演算
まず、群演算の加法ですが、
\(P+Q=P\!*\!Q\) の対称点
と定義します(図12)。
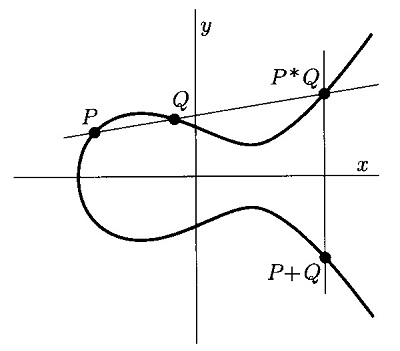
|
図12:加法則 |
「楕円曲線論入門」より引用 |
こうすると、\(P\!*\!Q\) と \(P+Q\) を結ぶ直線は \(y\) 軸と平行になり、それは無限遠点 \(\mathcal{O}\) で楕円曲線と交差します。つまり、
\(P+Q=(P\!*\!Q)*\mathcal{O}\)
です。この定義は 零元を楕円曲線上の点にとった図8と合致します。この加法の定義で \(\mathcal{O}\) が群の零元の要件を満たしているかを検証すると、
\(P+\mathcal{O}=(P*\mathcal{O})*\mathcal{O}=P\)
となって要件を満たしていることがわかります。\(P*\mathcal{O}\) は \(P\) の対称点ですが、\(P\) の対称点と \(\mathcal{O}\) を結ぶ直線が楕円曲線と交差する点は \(P\) なので上式が成立します。これは楕円曲線上に \(\mathcal{O}\) をとった図9と同じです。さらに逆元ですが、\(Q\) が楕円曲線上にあったとき、
\(Q\) の対称点が \(Q\) の逆元(\(-Q\) と表記)
と定義します(図13)。
|
図13:逆元 |
「楕円曲線論入門」より引用 |
こうすると、
\(\begin{eqnarray}
&&Q+(-Q)&=(Q\!*\!(-Q))*\mathcal{O}\\
&&&=\mathcal{O}*\mathcal{O}\\
\end{eqnarray}\)
となりますが、\(\mathcal{O}*\mathcal{O}=\mathcal{O}\)(=無限遠点の対称点は無限遠点)との自然な定義を行うと、
\(Q+(-Q)=\mathcal{O}\)
となって逆元の要件を満たします。結合則についても零元を楕円曲線上にとった場合(図11)と同じ様に成立します。「18. 結合則が成り立つことの検証と証明」でそのこと書きます。
射影平面
無限遠点は図で表現できず、何だか "怪しげな" 感じがしますが、数学的に厳密に定義できます。それには射影平面を使います。
平面 \((x,\:y)\) に対し、3つの数 \((X,\:Y,\:Z)\) で表される "平面" を射影平面と言います。3つの数がありますが3次元空間ではありません。ただし \((0,\:0,\:0)\) の点は除きます。また、
\(\lambda\neq0\)とするとき
\((X,\:Y,\:Z)\) と \((\lambda X,\lambda Y,\lambda Z)\) は同じものである(同値である)
\((X,\:Y,\:Z)\) と \((\lambda X,\lambda Y,\lambda Z)\) は同じものである(同値である)
と定義します。\(xy\) 平面から射影平面の対応は、
\((x,\:y)\longrightarrow(x,\:y,\:1)\)
とし、その逆の対応は、
\(Z\neq0\) のとき
\((X,\:Y,\:Z)\longrightarrow\left(\dfrac{X}{Z},\dfrac{Y}{Z}\right)\)
\((X,\:Y,\:Z)\longrightarrow\left(\dfrac{X}{Z},\dfrac{Y}{Z}\right)\)
です。この対応からわかるように、射影平面には \(xy\) 平面にない点が含まれています(\(Z=0\) の点)。
射影平面での楕円曲線の式は、\(xy\) 平面の楕円曲線の式で、\(x=\dfrac{X}{Z},\:\:y=\dfrac{Y}{Z}\) とおき、全体に \(Z^3\) をかけて同次化(=変数項の合計次数をそろえる)します。その結果、
\(Y^2Z=X^3+aXZ^2+bZ^3\)
の同次方程式が、射影平面での楕円曲線になります。ためしに、図2の楕円曲線(\(a=-2,\:b=1\))と \(y\) 軸との交点を計算してみると、\(xy\) 平面では、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3-2x+1&\\
&&x=0&\\
\end{eqnarray}
\end{array}\right.\)
の連立方程式を解いて、\((0,\pm1)\) となります。一方、射影平面では、\(x=0\) は \(X=0\) なので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&Y^2Z=X^3-2XZ^2+Z^3&\\
&&X=0&\\
\end{eqnarray}
\end{array}\right.\)
が、楕円曲線と直線の交点を求める連立式になります。この解は、\(\al\) と \(\beta\) を \(0\) ではない数として、\((0,\al,\pm\al),\:(0,\beta,\:0)\) です。射影平面の同値関係を利用すると、
\((0,\:\pm1,\:1)\)
\((0,\:1,\:0)\)
\((0,\:1,\:0)\)
が楕円曲線と直線の交点になり、交点は3つあることになります。ここで \(xy\) 平面の交点には現れなかった \((0,\:1,\:0)\) が \(y\) 軸方向の無限遠点です。これを一般化すると次のようになります。つまり、楕円曲線と \(y\) 軸に平行な直線の式を、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3+ax+b&\\
&&x=c&\\
\end{eqnarray}
\end{array}\right.\)
とすると、これに対応する射影平面の式は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&Y^2Z=X^3+aXZ^2+bZ^3&\\
&&X=cZ&\\
\end{eqnarray}
\end{array}\right.\)
です。\((0,\:1,\:0)\) はこの2式を必ず満たします。つまり全ての楕円曲線は \((0,\:1,\:0)\) を通り、全ての \(y\) 軸に平行な直線は \((0,\:1,\:0)\) を通る。従って、楕円曲線と\(y\) 軸に平行な直線は(\(y\) 軸方向の)無限遠点で交わることになります。
楕円曲線の計算には現れませんが、無限遠点にもいろいろあって、\((1,\:0,\:0)\) は \(x\) 軸方向の無限遠点、\((\al,\:\beta,\:0)\) は任意方向の無限遠点です(\(\al\)、\(\beta\) は \(0\) ではない数)。
\(xy\) 平面の2直線は、平行なときには交点がありませんが、射影平面の2直線は必ず1点で交わります。また射影平面の楕円曲線の1点を通る直線は、楕円曲線と必ず3点で交わります(直線が楕円曲線の接線の場合は、接点での交差数を2と数えます)。このように、交差を統一的に扱えるのが射影平面の特徴の一つです。
以上のような数学的裏付けのもとに導入したのが無限遠点です。これを \(xy\) 平面では、
| \(y\) 軸方向の無限遠のところに無限遠点 \(\mathcal{O}\) がある | |
| 楕円曲線は \(\mathcal{O}\) を通る | |
| \(y\) 軸に平行な直線は \(\mathcal{O}\) で楕円曲線と交わる |
とイメージしてよいわけです。
加法式・2倍式
楕円曲線上の加法を計算式で表します。楕円曲線上の3点を次のように定義します。
\(P_1+P_2=P_3\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とします。\(P_1\) と \(P_2\) を結ぶ直線を \(y=\lambda x+\mu\) とすると、連立方程式、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3+ax+b&\\
&&y=\lambda x+\mu&\\
\end{eqnarray}
\end{array}\right.\)
の解が \(P_1,\:P_2,\:(x_3,-y_3)\) です。この2つの式から \(y\) を消去すると、
\(x^3+ax+b-(\lambda x+\mu)^2=0\)
が得られますが、この式は、
\((x-x_1)(x-x_2)(x-x_3)=0\)
と同一のはずです。そこで \(x^2\) の係数を比較すると、
\(-\lambda^2=-x_1-x_2-x_3\)
が得られます。つまり、
\(x_3=\lambda^2-x_1-x_2\)
となります。この \(x_3\) を直線の式に入れると、
\(-y_3=\lambda x_3+\mu\)
ですが、\(y_1=\lambda x_1+\mu\) なので \(\mu\) を消去すると、
\(y_3=-y_1+\lambda(x_1-x_3)\)
となります。これが基本の加法式です。これを \(P_1\) と \(P_2\) の配置パターンごとにまとめると、次の通りです。
\(x_1\neq x_2\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{y_2-y_1}{x_2-x_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
この場合は \(P_1\) と \(P_2\) を通る直線は \(P_1\) における楕円曲線の接線となり、直線の傾き \(\lambda\) は上の式のままでは計算できません。そこで \(y^2=x^3+ax+b\) を \(x\) で微分すると
\(2y\dfrac{dy}{dx}=3x^2+a\)
なので、
\(\lambda=\dfrac{3x_1^2+a}{2y_1}\)
となります。\(x_2\) を \(x_1\) に置き換えてまとめると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-2x_1&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{3x_1^2+a}{2y_1}&\\
\end{eqnarray}
\end{array}\right.\)
が \(P_1+P_1\) の計算式です。これは \(P_1\) の "2倍"(一般にはスカラー倍)であり、\(2P_1\) と書きます。
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
この場合、\(P_2=-P_1\) なので、定義により
\(P_1+P_2=\mathcal{O}\)
です。
なお、\(P_1\) と \(P_2\) は、楕円曲線の定義式、
\(y_1^2=x_1^3+ax_1+b\)
\(y_2^2=x_2^3+ax_2+b\)
\(y_2^2=x_2^3+ax_2+b\)
を満たしますが、この左辺と右辺のそれぞれを引き算すると、
\((y_1+y_2)(y_1-y_2)=\)
\((x_1-x_2)(x_1^2+x_1x_2+x_2^2)+a(x_1-x_2)\)
\((x_1-x_2)(x_1^2+x_1x_2+x_2^2)+a(x_1-x_2)\)
\(\begin{eqnarray}
&&\dfrac{y_1-y_2}{x_1-x_2}&=\dfrac{x_1^2+x_1x_2+x_2^2+a}{y_1+y_2}\\
&&&=\lambda\\
\end{eqnarray}\)
となって \(\lambda\) の別の表現が得られますが、これは \(x_1=x_2\) でも使えます。従って「加法式(第2形)」を次のようにも表現できます。
\(y_1+y_2\neq0\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{x_1^2+x_1x_2+x_2^2+a}{y_1+y_2}&\\
\end{eqnarray}
\end{array}\right.\)
\(y_1+y_2=0\) のとき
\(P_1+P_2=\mathcal{O}\)
楕円曲線の具体例
楕円曲線とその有理点、加法則の適用例として、整数係数の3つの楕円曲線を調べてみます。以後の記述では、\(P=(x,\:y)\) とするとき、\(nP,\:-P,\:-nP\) の記述を使いますが、それぞれの定義は、
\(\phantom{-}nP=\overbrace{P+P+\:\cd+P}^{n}\)
\(\phantom{n}-\!\!P=(x,-y)\)
\(-nP=\overbrace{(-P)+(-P)+\:\cd+(-P)}^{n}\)
\(\phantom{n}-\!\!P=(x,-y)\)
\(-nP=\overbrace{(-P)+(-P)+\:\cd+(-P)}^{n}\)
です。また、\(nP=(x_n,\:y_n)\) とすると、加法の定義から \(-nP=(x_n,-y_n)\) です。
\(y^2=x^3+1\)
|
図14:楕円曲線の例1 \(y^2=x^3+1\) |
この楕円曲線上の有理点は、次の5つの整点(= 座標値が整数の点)です。
\(P_1=(\phantom{-}2,\phantom{-}3)\)
\(P_2=(\phantom{-}0,\phantom{-}1)\)
\(P_3=(-1,\phantom{-}0)\)
\(P_4=(\phantom{-}0,-1)\)
\(P_5=(\phantom{-}2,-3)\)
\(P_2=(\phantom{-}0,\phantom{-}1)\)
\(P_3=(-1,\phantom{-}0)\)
\(P_4=(\phantom{-}0,-1)\)
\(P_5=(\phantom{-}2,-3)\)
ここで、群の演算式を使って \(nP_1\) を計算してみると、
\(2P_1=(\phantom{-}0,\phantom{-}1)=P_2\)
\(3P_1=(-1,\phantom{-}0)=P_3\)
\(4P_1=(\phantom{-}0,-1)=P_4\)
\(5P_1=(\phantom{-}2,-3)=P_5\)
\(6P_1=\mathcal{O}\)
\(3P_1=(-1,\phantom{-}0)=P_3\)
\(4P_1=(\phantom{-}0,-1)=P_4\)
\(5P_1=(\phantom{-}2,-3)=P_5\)
\(6P_1=\mathcal{O}\)
となります。\(P_1\) は 6倍する(= 6個加算する)と \(\mathcal{O}\)(=零元)になる。このことを「\(P_1\) の位数(order)が \(6\) である」と言います。また、
\(3(P_2)=3(2P_1)=6P_1=\mathcal{O}\)
なので、\(P_2\) の位数は \(3\) です。同様にして、\(P_3\)~\(P_5\) の位数はそれぞれ \(2,\:\:3,\:\:6\) になります。
楕円曲線 \(y^2=x^3+1\) の有理点は \(P_1\)~\(P_5\) の点しかありません。また位数が有限値なので、これらは有限位数の点です。これらの点と 零元 \(\mathcal{O}\) を合わせて群を構成します。
しかし楕円曲線上の有理点が有限位数をもつとは限りません。それが次の例です。
\(y^2=x^3-x+1\)

|
図15:楕円曲線の例2 \(y^2=x^3-x+1\) |
方程式 \(y^2=x^3-x+1\) の整数解を調べると、手計算で \((-1,\pm1),\) \((0,\pm1),\) \((1,\pm1),\) \((3,\pm5),\) \((5,\pm11)\) の\(10\)個の解が容易に見つかります。今、\(P_1=(1,\:1)\) とし、\(nP_1\) を順に計算してみると、次のようになります。
\(\begin{eqnarray}
&&\phantom{1}1P_1&=(\phantom{-}1,\phantom{-}1)\\
&&\phantom{1}2P_1&=(-1,\phantom{-}1)\\
&&\phantom{1}3P_1&=(\phantom{-}0,-1)\\
&&\phantom{1}4P_1&=(\phantom{-}3,-5)\\
&&\phantom{1}5P_1&=(\phantom{-}5,\,\,11)\\
&&\phantom{1}6P_1&=\left(\phantom{-}\dfrac{1}{4},\phantom{-}\dfrac{7}{8}\right)\\
&&\phantom{1}7P_1&=\left(-\dfrac{11}{9},-\dfrac{17}{27}\right)\\
&&\phantom{1}8P_1&=\left(\phantom{-}\dfrac{19}{25},-\dfrac{103}{125}\right)\\
&&\phantom{1}9P_1&=(56,-419)\\
&&10P_1&=\left(\dfrac{159}{121},\dfrac{1861}{1331}\right)\\
&&&=\left(\dfrac{3\cdot53}{11^2},\dfrac{1861}{11^3}\right)\\
&&&\fallingdotseq(1.31405,1.39820)\\
&&11P_1&=\left(-\dfrac{255}{361},\dfrac{7981}{6859}\right)\\
&&&=\left(-\dfrac{3\cdot5\cdot17}{19^2},\dfrac{23\cdot347}{19^3}\right)\\
&&&\fallingdotseq(-0.70637,1.16358)\\
&&12P_1&=\left(-\dfrac{223}{784},-\dfrac{24655}{21952}\right)\\
&&&=\left(-\dfrac{223}{2^4\cdot7^2},-\dfrac{5\cdot4931}{2^6\cdot7^3}\right)\\
&&&\fallingdotseq(-0.28444,-1.12313)\\
&&13P_1&=\left(\dfrac{5665}{2809},-\dfrac{399083}{148877}\right)\\
&&&=\left(\dfrac{5\cdot11\cdot103}{53^2},-\dfrac{43\cdot9281}{53^3}\right)\\
&&&\fallingdotseq(2.01673,-2.68062)\\
&&14P_1&=\left(\dfrac{26239}{2601},\dfrac{4231459}{132651}\right)\\
&&&=\left(\dfrac{19\cdot1381}{3^2\cdot17^2},\dfrac{4231459}{3^2\cdot17^2}\right)\\
&&&\fallingdotseq(10.08804,31.89919)\\
&&15P_1&=\left(\dfrac{23464}{49729},\dfrac{8824453}{11089567}\right)\\
&&&=\left(\dfrac{2^3\cdot7\cdot419}{223^2},\dfrac{11\cdot59\cdot13597}{223^2}\right)\\
&&&\fallingdotseq(0.47183,0.79574)\\
\end{eqnarray}\)
途中で \((56,-419)\) という、手計算では分からない整点が現れました。計算してみると、
\(56^3-56+1=175561=419^2\)
となって、確かにこれが楕円曲線上の点であることが分かります。\(15P_1\) までの結果を掲げましたが、この計算は \(\mathcal{O}\)(= 零元)で終わることがなく、無限に続きます。つまり、\(P_1=(1,\:1)\) は無限位数の点です。
さらに、同様の計算を\(-P_1=(1,-1)\) から始めると、\(y\) 座標の符号が逆転した点列、\(-nP_1\) が得られます。そして実は、
楕円曲線 \(y^2=x^3-x+1\) の有理点の全ては、
\(mP_1\)(\(m\)は正負の整数)
の形で表現できることが分かっています。\(0P_1=\mathcal{O}\) と定義すれば、楕円曲線で定義された加法群の元は \(mP_1\)(\(m\) は整数)の形で表現できるとも言えます。この性質を有限生成と言い、\(P_1\) を生成元(generator)と呼びます。一般には、生成元は複数個あります。つまり楕円曲線上の有理点は \(r\) 個の有理点 \(Q_i\) を使って、
\(m_1Q_1+m_2Q_2+\:\cd+m_rQ_r\)
の形で表現できます。この \(r\) を楕円曲線の階数(rank)と言います。なお、有限個の有理点しかもたない 図14 のような楕円曲線の階数は \(0\) とします。
楕円曲線 \(y^2=x^3-x+1\) の階数は \(1\) です。そして今までの結果から、階数が \(1\) の楕円曲線の有理点と零点 \(\mathcal{O}\) は、加法に関して整数(= 正の自然数と負の自然数と \(0\))と全く同じ構造をもつことが分かります。ただ、楕円曲線の有理点の加法は普通の整数の加法よりよほど複雑な演算です。これが楕円曲線暗号を作るときの基礎となっています。
\(y^2=x^3-4x+1\)
|
図16:楕円曲線の例3 \(y^2=x^3-4x+1\) |
この楕円曲線の階数は \(2\) です。従って生成元は2つで、
\(P_1=(0,\:1)\)
\(P_2=(3,\:4)\)
\(P_2=(3,\:4)\)
です。曲線上には無限個の有理点がありますが、すべてはこの2つの生成元から「有限生成」されます。無限個の有理点のうち、生成元を含めて 22個が整点ですが(\(y\) 座標の正負を無視すると 11個)、もちろんそれらの整点も生成元で表現できます。実際に計算してみると以下の通りです。
\(\phantom{9}P_1+\phantom{9}P_2=(-2,\:1)\)
\(2P_1\,\,\,\phantom{+9P_2}=(4,\:7)\)
\(2P_1-\phantom{9}P_2=(114,-1217)\)
\(2P_1+\phantom{9}P_2=(2,-1)\)
\(2P_1+2P_2=(20,-89)\)
\(3P_1+\phantom{9}P_2=(-1,-2)\)
\(4P_1+\phantom{9}P_2=(10,-31)\)
\(4P_1+2P_2=(12,\:41)\)
\(8P_1+3P_2=(1274,-45473)\)
\(2P_1\,\,\,\phantom{+9P_2}=(4,\:7)\)
\(2P_1-\phantom{9}P_2=(114,-1217)\)
\(2P_1+\phantom{9}P_2=(2,-1)\)
\(2P_1+2P_2=(20,-89)\)
\(3P_1+\phantom{9}P_2=(-1,-2)\)
\(4P_1+\phantom{9}P_2=(10,-31)\)
\(4P_1+2P_2=(12,\:41)\)
\(8P_1+3P_2=(1274,-45473)\)
もちろん、計算していくと上記の整点だけでなく有理点が次々と生成され、それが無限に続きます。上の計算で \(P_1,\:P_2\) の符号を逆転させると \(y\) 座標の符号が逆の整点が得られます。たとえば、
\(-2P_1-P_2=(2,\:1)\)
\(-2P_1+P_2=(114,\:1217)\)
\(-2P_1+P_2=(114,\:1217)\)
です。以上を含めてこの楕円曲線の整点は、
\((-2,\pm1),\) \((-1,\pm2),\) \((0,\pm1),\) \((2,\pm1),\) \((3,\pm4),\) \((4,\pm7),\) \((10,\pm31),\) \((12,\pm41),\) \((20,\pm89),\) \((114,\pm1217),\) \((1274,\pm45473)\)
となります。最大の整点は \((1274,\pm45473)\) ですが、実際に計算してみると、
\(1274^3-4\cdot1274+1\)
\(=2067793729\)
\(=37^2\cdot1229^2\)
\(=45473^2\)
\(=2067793729\)
\(=37^2\cdot1229^2\)
\(=45473^2\)
となって、楕円曲線上の点であることが確認できます。この最大の整点を2つの生成元に分けて、それぞれを計算してみると、
\(\begin{eqnarray}
&&8P_1&=\left(\dfrac{59965740}{625681},\dfrac{464259138209}{494913671}\right)\\
&&&=\left(\dfrac{2^2\cdot3^2\cdot5\cdot79\cdot4217}{7^2\cdot113^2},\dfrac{455419\cdot1019411}{7^3\cdot113^3}\right)\\
&&3P_2&=\left(\dfrac{130403}{2209},-\dfrac{47063372}{103823}\right)\\
&&&=\left(\dfrac{7\cdot13\cdot1433}{47^2},-\dfrac{2^2\cdot353\cdot33331}{47^3}\right)\\
\end{eqnarray}\)
となりますが、この2つの有理点を楕円曲線の加法式で \(8P_1+3P_2\) とすると整点である \((1274,\:-45473)\) が現れるのも不思議な感じがします。
以上の「楕円曲線の有理点から成る加法群」を踏まえ、これ以降は楕円曲線暗号で使われる「有限体上の楕円曲線による加法群」に移ります。
有限体上の楕円曲線による加法群
以降に出てくる有限体 \(\bs{F}_p\) と 乗法群 \(\bs{F}_p^{*}\) については、No.313「高校数学で理解する公開鍵暗号の数理:10. 有限体と乗法群」 で定義したものです。
楕円曲線暗号に使われる楕円曲線は、有限体 \(\bs{F}_p\) で定義された "曲線" で、次の式を満たすものです。
\(y^2=x^3+ax+b\)
\((4a^3+27b^2\neq0)\)
\((4a^3+27b^2\neq0)\)
\(x\)、\(y\)、\(a\)、\(b\) は全て \(\bs{F}_p\) の元です。「この式を満たす全ての \((x,\:y)\) と 零点 \(\mathcal{O}\) の集合」に対して演算を定義して群を構成します。演算を加法と考えて \(+\) と書きます。この "曲線" 上の3点を、
\(P_1+P_2=P_3\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とするとき、群の演算式は次のように定義されます。
\(x_1\neq x_2\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{y_2-y_1}{x_2-x_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-2x_1&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{3x_1^2+a}{2y_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
\(P_1+P_2=\mathcal{O}\)
つまり、実数平面の有理点と無限遠点(=零元)で構成された群の演算式と全く同じです。もちろん加減乗除は \(\bs{F}_p\) で行います。これが群になる理由は、有理数体(有理数全体の集合)も有限体 \(\bs{F}_p\) も「体」であり、加減乗除は全く同一形式で記述できるからです。ただ、有理数体と違って \(\bs{F}_p\) の元の数は有限個であり、群の元の数も有限個(=有限群)です。以降、\(\bs{\bs{F}_p}\) 上の楕円曲線、\(\bs{y^2=x^3+ax+b}\) による有限群を \(\bs{E(a,\:b,\:p)}\) と表記します。
\(\bs{F}_p\) 上の楕円曲線は、もはや "曲線" の形をしていませんが、これを可視化した図を次に示します。有限体 \(F_{109}\) 上の "楕円曲線"、\(y^2=x^3+2x+4\) の例です。
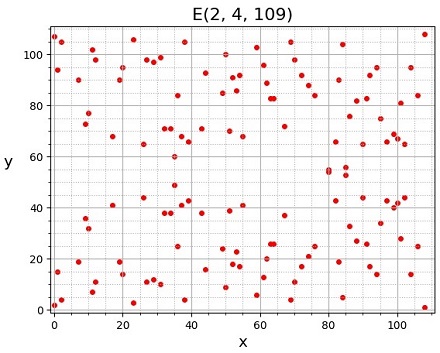
|
図17:有限体上の "楕円曲線" \(E(2,\:4,\:109)\) \(F_{109},\:\:\:y^2=x^3+2x+4\) |
赤丸が "楕円曲線上の点" を表し、計 \(126\) 個ある。零元(無限遠点 \(\mathcal{O}\))と合わせて群の元の総数は \(127\)(=素数)である。このような、群位数が素数の楕円曲線を利用して暗号を構成できる(次回参照)。 |
以上が「有限体上の楕円曲線が作る加法群」で、楕円曲線暗号はこの加法群で構成されます。その話を次回にします。
(次回に続く)
2021-07-11 08:37
nice!(0)




