No.325 - 高校数学で理解する誕生日のパラドックス [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
「高校数学で理解する・・・」というタイトルで、今まで５つの記事書きました。
ですが、いずれも現代のインターネット社会における情報通信の基礎となっている "公開鍵暗号" の数理を、高校レベルの数学だけを前提知識として述べたものでした。
今回はその「高校数学で理解する\(\cdot\cdot\cdot\)」の続きですが、公開鍵暗号よりは断然軽い話題で、No.149「我々は直感に裏切られる」でとりあげた「誕生日のパラドックス」をもう一度、考察します。No.149 では「バースデー\(\cdot\)パラドックス」と書いたもので、よく知られた話です。
誕生日のパラドックス
誕生日のパラドックスとは、
というものです。一瞬、えっ！ と思ってしまいますが、数学的には全く正しい。普通、パラドックスと言うと「絶対に不可能なことが可能なように思えてしまう」ないしは、「あり得ないことがあり得るように見えてしまう」ことを言いますが、この誕生日のパラドックスはそれとは違う「疑似パラドックス」です。つまり、
です。以下、１年を365日に固定して考えることにし、
の記号を使うと、
なので、\(\ol{\,B\,}(365,23)\) を計算すればよいことになります。「23人のクラスの、誕生日のすべての組み合わせ（\(=X\)）」は、365種類のものから重複を許して23個を並べる順列、いわゆる「重複順列」で、
です。一方、「23人のクラスの、誕生日がすべて違う組み合わせ（\(=Y\)）」は、出席番号１番の人は 365通り、２番の人は 364通り、３番の人は 363通りで、以下、出席番号23番の人は 343通り（\(=\:365\:-\:23\:+\:1\)）です。これを全部掛け合わせたのが \(Y\) ですが、これは 365通りのものから23個を選んで並べる順列であり、「順列\(\cdot\)組み合わせ」の記号を用いると、
です。\(X\) と \(Y\) の値を実際に計算してみると、両方とも59桁の数字になり、
です。従って、\(\dfrac{Y}{X}\) を計算すると、
となります。つまり、
となって、誕生日が同じ人がいる確率は確かに 0.5 を超えます。ちなみに「誕生日が同じ人がいる確率が 0.9 を超えるクラスの人数」を探ってみると、
なので、その答は 41人ということになります。誕生日は365通りです。41人というと、その約9分の1です。9分の1の人数を集めるとほぼ確実に誕生日が同じ人がいるというのは、23人と並んでかなり意外ではないでしょうか。このあたりの状況をグラフにしたのが下図です。
カジノ・ゲーム
誕生日のパラドックスを応用した、次のような "カジノ・ゲーム" を想定しても、"直感との乖離" が明らかになると思います。あなたはカジノで掛け金を積んでディーラーと対決します。
このゲームは、あなた（客）にとって有利でしょうか、それとも不利でしょうか。あなたが勝つ確率はどれぐらいでしょうか。
あなたは（おそらく）次のように考えると思います。２回目に「引いてはいけないカード」は１枚しかない。これは自分が圧倒的に有利である。また３回目も２枚だけを引かなければよい。つまり有利だ。最後の10回目を考えると「引いてはいけない」カードが９枚あるが「引いてもいいカード」は44枚もある。確かに９枚のどれかを引いてしまうこともあるだろうが、まだ随分自分が有利のはずである。もちろん、１回のチャレンジだったら負けることもあるだろうが、10回もやれば自分がかなり有利なはずだ ･･････。
しかし、事実は違います。誕生日のパラドックスにより、この賭は客が不利です。客が引いた10枚の全部が違うカードである確率は、さきほどの記号を使うと、
です。この値を計算してみると、
となり、客が勝つ確率は 40% しかありません。ディーラーは客の1.5倍の確率で勝つのです。この賭は引く枚数が少ないほど客が有利になるのは当然なので、枚数を変えて計算してみると、
となって、引く枚数が９枚でもまだ客が不利です。８枚になって初めて客が有利になることが分かります。誕生日のパラドックスの言葉を使うと「53枚のカードから１枚引いて戻す操作を９回繰り返すと、一致するカードを引く確率が 0.5を超える」となります。
８枚で客が有利、９枚で客が不利というこの結果は直感と合っているでしょうか。「23人のクラスには同じ誕生日の人が 0.5 以上の確率でいる」よりは意外性がありませんが、それでもまだ直感に合わない感じがします。
サイコロ・ゲーム
カードはジョーカーも含めて 53枚あります。この 53 という数字をもっと減らしたらどうなるでしょうか。次のような「サイコロ・ゲーム」を考えてみます。
２回だと有利なことはすぐに分かります。４回だと、運よく３回まで同じ目が出なかったとして、４回目に出すべき目は３種であり、つまり半分の確率で３回目までとは違う目が出ます。ただし２回目、３回目で同じ目が出ることがあるので、それを勘案するとトータルとしては不利です。４回だと不利というのも直感と合っているでしょう。
では、３回ならどうか。直感では「微妙だが、有利」ではないでしょうか。実際に計算してみると
となり、確かに（わずかに）有利なことが分かります。
以上をまとめると、モノのパターンの数が
となると思います。この理由を数学的に探っていきます。
誕生日関数を近似する
はじめの方で、
と定義しましたが、これを一般化して
とします。この \(B(n,k)\) を「誕生日関数」と呼ぶことにします。変数が２個の関数です。そうすると、
となります。この \(\ol{\,B\,}(n,k)\) を \(n\) と \(k\) の簡便な多項式で近似することを考えます。\(\ol{\,B\,}(n,k)\) を展開すると、
となります。ここで、\(x\) の絶対値が \(1\) よりかなり小さく \(0\) に近いとき、
と近似できることを利用します。\(f(x)=e^x\) とおくと
なので、\(1+x\) は \(x=0\) における \(e^x\) の接線の方程式になっています。この近似の精度をいくつかの値で試算してみると、
となり、\(x\) が \(0.2\) 程度でも誤差は \(2\%\) 弱で、\(x\) が小さくなると誤差は急速に小さくなります。ちなみにこの近似は \(e^x\) のマクローリン展開、
の第２項までに相当します。マクローリン展開は高校数学では出てこないと思いますが、意味するところは明快です。この、
とする近似で \(\ol{\,B\,}(n,k)\) を表現したものを "第１近似" と呼ぶことにし、それを \(\ol{\,B\,}_{app_1}(n,k)\) で表すと、\(\ol{\,B\,}(n,k)\) の展開式から、
となります。従って、
となって、誕生日関数の近似式ができました。
誕生日の定理
以上の計算結果を踏まえて、誕生日のパラドックスに関する命題を導きます。つまり、
という問いの答がどうなるかという命題です。この答の数を \(P_5\) とすると、誕生日の場合（\(n=365\)）\(P_5=23\) です。\(B_{app_1}(n,k)\) を使って、
の不等式を解くと \(P_5\) が求まりますが、\(P_5\) を簡便な式で求めるため、\(\ol{\,B\,}(n,k)\) の "第２近似" を、
とします。つまり、\(\ol{\,B\,}_{app_1}(n,k)\) の \(k(k-1)\) を \(k^2\) で置き換えたものです。 この "第２近似" の誤差は、
程度です。この第２近似を使うと、\(P_5\) を求める不等式は、
となります。これを解くと、
となります。定数の計算をすると、おおよそ、
となります。つまり次の「誕生日の定理」が成り立ちます。
近似計算をしているので、\(1.177\) のところは \(1.18\) でもよいでしょう。試しに、誕生日のパラドックスとカジノ・ゲームを例に誕生日の定理を使ってみると、
となり、それぞれ 23 と 9 で一致するペアが存在する確率が 50% を超えることがわかります。これは前にやった正確計算と合致しています。ちなみに、
という問いの答えを \(P_9\) とすると、
となります。これを解くと、
となり、定数の計算をすると、おおよそ、
となります。\(2.146\) は \(1.177\) の約 \(1.8\) 倍です。従って、次の「誕生日の定理（補足）」が成り立ちます。
誕生日のパラドックスとカジノ\(\cdot\)ゲームで計算してみると、
となり、それぞれ 41 と 16 で一致するペアが存在する確率が 90% を超えることがわかります。これは前にやった正確計算と合致しています。
このように、\(\bs{n}\)通りのパターンがあるものを何個集めたら一致するペアがある確率が一定数を超えるか、という質問の答えは、\(\bs{n}\) に比例するのではなく \(\bs{n}\)の平方根に比例します。\(\bs{n}\) が大きくなっても \(\bs{n}\)の平方根はさほど大きくならない。このあたりに誕生日のパラドックスの原因がありそうです。
５色のサイコロ
誕生日よりもっとパターンの多い例で考えてみます。
誕生日の定理を使って答を計算してみると
となります。つまり、
というわけです。出る目のパターンは 7776通りもあります。それでも、100回そこそこで同じパターンが現れる確率が50%を越すことが分かります。なお厳密計算をすると、確率 50% と 90% を超えるのはそれぞれ 105回と 189回です。
誕生日のパラドックス
５色のサイコロのように、パターンの数が多いほど同一パターンが現れるに必要な個数は、パターンの数に比べて小さくなります。しかし "数が多いほど" と言っても、その多さが直感的に理解できないとパラドックスとは感じられないはずです。
その意味で、誕生日のパターンが 365 というのは、適度に多い数で、誰もがその多さの程度を直感的に理解できる数です。そこに誕生日のパラドックスの意味があるのでした。
「高校数学で理解する・・・」というタイトルで、今まで５つの記事書きました。
| 高校数学で理解するRSA暗号の数理 | |
| 高校数学で理解する公開鍵暗号の数理 | |
| 高校数学で理解する楕円曲線暗号の数理 |
ですが、いずれも現代のインターネット社会における情報通信の基礎となっている "公開鍵暗号" の数理を、高校レベルの数学だけを前提知識として述べたものでした。
今回はその「高校数学で理解する\(\cdot\cdot\cdot\)」の続きですが、公開鍵暗号よりは断然軽い話題で、No.149「我々は直感に裏切られる」でとりあげた「誕生日のパラドックス」をもう一度、考察します。No.149 では「バースデー\(\cdot\)パラドックス」と書いたもので、よく知られた話です。
誕生日のパラドックス
誕生日のパラドックスとは、
誕生日のパラドックス 23人のクラスで誕生日が同じ人がいる確率は 0.5 を越える |
というものです。一瞬、えっ！ と思ってしまいますが、数学的には全く正しい。普通、パラドックスと言うと「絶対に不可能なことが可能なように思えてしまう」ないしは、「あり得ないことがあり得るように見えてしまう」ことを言いますが、この誕生日のパラドックスはそれとは違う「疑似パラドックス」です。つまり、
疑似パラドックス
| 直感に反するが、数学的には矛盾がなく正しい命題 |
です。以下、１年を365日に固定して考えることにし、
\(B(365,23)\)
| 23人のクラスで誕生日が同じ人がいる確率 |
\(\ol{\,B\,}(365,23)\)
| 23人のクラスで誕生日が同じ人がいない確率 |
の記号を使うと、
\(B(365,23)=1-\ol{\,B\,}(365,23)\)
なので、\(\ol{\,B\,}(365,23)\) を計算すればよいことになります。「23人のクラスの、誕生日のすべての組み合わせ（\(=X\)）」は、365種類のものから重複を許して23個を並べる順列、いわゆる「重複順列」で、
\(X=365^{23}\)
です。一方、「23人のクラスの、誕生日がすべて違う組み合わせ（\(=Y\)）」は、出席番号１番の人は 365通り、２番の人は 364通り、３番の人は 363通りで、以下、出席番号23番の人は 343通り（\(=\:365\:-\:23\:+\:1\)）です。これを全部掛け合わせたのが \(Y\) ですが、これは 365通りのものから23個を選んで並べる順列であり、「順列\(\cdot\)組み合わせ」の記号を用いると、
\(Y={}_{365}\,P_{23}\)
です。\(X\) と \(Y\) の値を実際に計算してみると、両方とも59桁の数字になり、
\(\begin{eqnarray}
&&X=&\phantom{9}856516793,5315032123\\
&&&6814267844,3951526893\\
&&&5462236404,4189453125\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&Y=&\phantom{9}422008193,0209235987\\
&&&2395663074,9089572537\\
&&&4976070077,6448000000\\
\end{eqnarray}\)
です。従って、\(\dfrac{Y}{X}\) を計算すると、
\(\begin{eqnarray}
&&\ol{\,B\,}(365,23)&=\dfrac{{}_{365}P_{23}}{365^{23}}\\
&&&=\dfrac{Y}{X}\\
&&&=\:0.49270277\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&B(365,23)&=1-\ol{\,B\,}(365,23)\\
&&&=\:0.50729723\\
\end{eqnarray}\)
となって、誕生日が同じ人がいる確率は確かに 0.5 を超えます。ちなみに「誕生日が同じ人がいる確率が 0.9 を超えるクラスの人数」を探ってみると、
\(B(365,40)=0.89123180\)
\(B(365,41)=0.90315161\)
\(B(365,41)=0.90315161\)
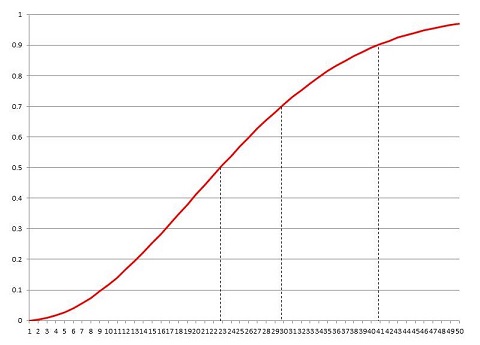
なので、その答は 41人ということになります。誕生日は365通りです。41人というと、その約9分の1です。9分の1の人数を集めるとほぼ確実に誕生日が同じ人がいるというのは、23人と並んでかなり意外ではないでしょうか。このあたりの状況をグラフにしたのが下図です。
|
誕生日のパラドックス |
横軸はクラスの人数で、縦軸は少なくとも１組の誕生日が同じ生徒がいる確率。23人クラスで確率は 0.5 を超える。30人クラスで 0.7 を超え、41人クラスで 0.9 を超える。 |
カジノ・ゲーム
誕生日のパラドックスを応用した、次のような "カジノ・ゲーム" を想定しても、"直感との乖離" が明らかになると思います。あなたはカジノで掛け金を積んでディーラーと対決します。
|
このゲームは、あなた（客）にとって有利でしょうか、それとも不利でしょうか。あなたが勝つ確率はどれぐらいでしょうか。
あなたは（おそらく）次のように考えると思います。２回目に「引いてはいけないカード」は１枚しかない。これは自分が圧倒的に有利である。また３回目も２枚だけを引かなければよい。つまり有利だ。最後の10回目を考えると「引いてはいけない」カードが９枚あるが「引いてもいいカード」は44枚もある。確かに９枚のどれかを引いてしまうこともあるだろうが、まだ随分自分が有利のはずである。もちろん、１回のチャレンジだったら負けることもあるだろうが、10回もやれば自分がかなり有利なはずだ ･･････。
しかし、事実は違います。誕生日のパラドックスにより、この賭は客が不利です。客が引いた10枚の全部が違うカードである確率は、さきほどの記号を使うと、
\(\ol{\,B\,}(53,10)\)
です。この値を計算してみると、
\(\begin{eqnarray}
&&\ol{\,B\,}(53,10)&=\dfrac{{}_{53}P_{10}}{53^{10}}\\
&&&=\dfrac{\:7075833,2701056000\:}{\:17488747,0365513049\:}\\
&&&=0.40459349\\
\end{eqnarray}\)
となり、客が勝つ確率は 40% しかありません。ディーラーは客の1.5倍の確率で勝つのです。この賭は引く枚数が少ないほど客が有利になるのは当然なので、枚数を変えて計算してみると、
\(\ol{\,B\,}(53,9)=\:0.48735125\)
\(\ol{\,B\,}(53,8)=\:0.57399147\)
\(\ol{\,B\,}(53,8)=\:0.57399147\)
となって、引く枚数が９枚でもまだ客が不利です。８枚になって初めて客が有利になることが分かります。誕生日のパラドックスの言葉を使うと「53枚のカードから１枚引いて戻す操作を９回繰り返すと、一致するカードを引く確率が 0.5を超える」となります。
ちなみに、「41人クラスでは同じ誕生日のペアがいる確率が 0.9 を超える」ことに相当する値、「53枚のカードから１枚引いて戻す操作を繰り返すとき、一致するカードを引く確率が 0.9 を超える回数」を計算すると、
なので、その答えは 16回となります。16という数字はカードの総数の3分の1以下ですが、それだけ引くとほぼ確実に同じカードを引いてしまうわけです。
\(\ol{\,B\,}(53,15)=\:0.11175468\)
\(\ol{\,B\,}(53,16)=\:0.08012600\)
\(\ol{\,B\,}(53,16)=\:0.08012600\)
なので、その答えは 16回となります。16という数字はカードの総数の3分の1以下ですが、それだけ引くとほぼ確実に同じカードを引いてしまうわけです。
８枚で客が有利、９枚で客が不利というこの結果は直感と合っているでしょうか。「23人のクラスには同じ誕生日の人が 0.5 以上の確率でいる」よりは意外性がありませんが、それでもまだ直感に合わない感じがします。
サイコロ・ゲーム
カードはジョーカーも含めて 53枚あります。この 53 という数字をもっと減らしたらどうなるでしょうか。次のような「サイコロ・ゲーム」を考えてみます。
あらかじめ決められた回数だけサイコロを振って、同じ目が出なければあなたの勝ちとします。サイコロを振る回数が、 \(\cdot\)２回 \(\cdot\)３回 \(\cdot\)４回 のとき、それぞれあなたは有利でしょうか。それとも不利でしょうか。 |
|
２回だと有利なことはすぐに分かります。４回だと、運よく３回まで同じ目が出なかったとして、４回目に出すべき目は３種であり、つまり半分の確率で３回目までとは違う目が出ます。ただし２回目、３回目で同じ目が出ることがあるので、それを勘案するとトータルとしては不利です。４回だと不利というのも直感と合っているでしょう。
では、３回ならどうか。直感では「微妙だが、有利」ではないでしょうか。実際に計算してみると
\(\ol{\,B\,}(6,3)=\dfrac{5}{9}\)
となり、確かに（わずかに）有利なことが分かります。
以上をまとめると、モノのパターンの数が
| ・ | 6 | → 直感どおり | |
| ・ | 53 | → 直感からずれる | |
| ・ | 365 | → 直感と合わない、意外 |
となると思います。この理由を数学的に探っていきます。
誕生日関数を近似する
はじめの方で、
\(B(365,23)\)
\(\ol{\,B\,}(365,23)\)
＝ 23 人のクラスで誕生日が同じ人がいる確率
\(\ol{\,B\,}(365,23)\)
＝ 23 人のクラスで誕生日が同じ人がいない確率
と定義しましたが、これを一般化して
\(B(n,k)\)
\(\ol{\,B\,}(n,k)\)
＝ \(n\) 通りのパターンがあるものを \(k\) 個集めたとき、一致するペアがある確率
\(\ol{\,B\,}(n,k)\)
＝ \(n\) 通りのパターンがあるものを \(k\) 個集めたとき、一致するペアがない確率
とします。この \(B(n,k)\) を「誕生日関数」と呼ぶことにします。変数が２個の関数です。そうすると、
\(B(n,k)=1-\ol{\,B\,}(n,k)\)
\(\ol{\,B\,}(n,k)=\dfrac{{}_nP_k}{n^k}\)
\(\ol{\,B\,}(n,k)=\dfrac{{}_nP_k}{n^k}\)
となります。この \(\ol{\,B\,}(n,k)\) を \(n\) と \(k\) の簡便な多項式で近似することを考えます。\(\ol{\,B\,}(n,k)\) を展開すると、
\(\begin{eqnarray}
&&\ol{\,B\,}(n,k)&=\dfrac{n_{n-1}(n-2)\:\cd\:(n-k+1)}{n^k}\\
&&&\\
&&&=\left(1-\dfrac{1}{n}\right)\left(1-\dfrac{2}{n}\right)\:\cd\:\left(1-\dfrac{k-1}{n}\right)\\
\end{eqnarray}\)
となります。ここで、\(x\) の絶対値が \(1\) よりかなり小さく \(0\) に近いとき、
\(e^x\fallingdotseq1+x\)
と近似できることを利用します。\(f(x)=e^x\) とおくと
\(\begin{eqnarray}
&&f(0)&=1\\
&&f^{'}(0)&=1\\
\end{eqnarray}\)
なので、\(1+x\) は \(x=0\) における \(e^x\) の接線の方程式になっています。この近似の精度をいくつかの値で試算してみると、
\(\begin{eqnarray}
&&\dfrac{e^{0.2}}{1+0.2}&=1.01783\\
&&\dfrac{e^{0.1}}{1+0.1}&=1.00407\\
&&\dfrac{e^{0.05}}{1+0.05}&=1.00121\\
&&\dfrac{e^{0.02}}{1+0.02}&=1.00019\\
&&\dfrac{e^{0.01}}{1+0.01}&=1.00005\\
\end{eqnarray}\)
となり、\(x\) が \(0.2\) 程度でも誤差は \(2\%\) 弱で、\(x\) が小さくなると誤差は急速に小さくなります。ちなみにこの近似は \(e^x\) のマクローリン展開、
\(e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\:\cd\)
の第２項までに相当します。マクローリン展開は高校数学では出てこないと思いますが、意味するところは明快です。この、
\(1+x\fallingdotseq e^x\)
とする近似で \(\ol{\,B\,}(n,k)\) を表現したものを "第１近似" と呼ぶことにし、それを \(\ol{\,B\,}_{app_1}(n,k)\) で表すと、\(\ol{\,B\,}(n,k)\) の展開式から、
\(\ol{\,B\,}_{app_1}(n,k)\)
\(=e^{-\frac{1}{n}}\cdot e^{-\frac{2}{n}}\cdot\:\cd\:\cdot e^{-\frac{k-1}{n}}\)
\(=e^{-\frac{k(k-1)}{2n}}\)
\(=e^{-\frac{1}{n}}\cdot e^{-\frac{2}{n}}\cdot\:\cd\:\cdot e^{-\frac{k-1}{n}}\)
\(=e^{-\frac{k(k-1)}{2n}}\)
となります。従って、
\(B_{app_1}(n,k)=1-e^{-\frac{k(k-1)}{2n}}\)
となって、誕生日関数の近似式ができました。
誕生日の定理
以上の計算結果を踏まえて、誕生日のパラドックスに関する命題を導きます。つまり、
n 通りのパターンがあるものを何個以上集めたら、一致するペアがある確率が0.5を超えるか
という問いの答がどうなるかという命題です。この答の数を \(P_5\) とすると、誕生日の場合（\(n=365\)）\(P_5=23\) です。\(B_{app_1}(n,k)\) を使って、
\(0.5 < 1-e^{-\frac{P_5(P_5-1)}{2n}}\)
の不等式を解くと \(P_5\) が求まりますが、\(P_5\) を簡便な式で求めるため、\(\ol{\,B\,}(n,k)\) の "第２近似" を、
\(\ol{\,B\,}_{app_2}(n,k)=e^{-\frac{k^2}{2n}}\)
とします。つまり、\(\ol{\,B\,}_{app_1}(n,k)\) の \(k(k-1)\) を \(k^2\) で置き換えたものです。 この "第２近似" の誤差は、
| \(\ol{\,B\,}(53,9)\) | \(=0.48735125\) | |
| \(\ol{\,B\,}_{app_2}(53,9)\) | \(=0.46572917\) | |
| （誤差：\(4.4\%\)） |
| \(\ol{\,B\,}(365,23)\) | \(=0.49270277\) | |
| \(\ol{\,B\,}_{app_2}(365,23)\) | \(=0.48449048\) | |
| （誤差：\(1.7\%\)） |
程度です。この第２近似を使うと、\(P_5\) を求める不等式は、
\(0.5\: < 1-e^{-\frac{P_5^{\:2}}{2n}}\)
となります。これを解くと、
\(P_5 > \sqrt{2\mr{log}{2}}\sqrt{n}\)
となります。定数の計算をすると、おおよそ、
\(P_5 > 1.177\sqrt{n}\)
となります。つまり次の「誕生日の定理」が成り立ちます。
誕生日の定理 \(n\) 通りのパターンがあるものを 約 \(1.177\sqrt{n}\) 個集めると、一致するペアが存在する確率が \(50\%\) を越える |
近似計算をしているので、\(1.177\) のところは \(1.18\) でもよいでしょう。試しに、誕生日のパラドックスとカジノ・ゲームを例に誕生日の定理を使ってみると、
\(\begin{eqnarray}
&&1.177\sqrt{365}&=22.49\\
&&1.177\sqrt{53}&=8.57\\
\end{eqnarray}\)
となり、それぞれ 23 と 9 で一致するペアが存在する確率が 50% を超えることがわかります。これは前にやった正確計算と合致しています。ちなみに、
n 通りのパターンがあるものを何個以上集めたら、一致するペアがある確率が0.9を超えるか
という問いの答えを \(P_9\) とすると、
\(0.9\: < 1-e^{-\frac{P_9^{\:2}}{2n}}\)
となります。これを解くと、
\(P_9 > \sqrt{2\mr{log}{10}}\sqrt{n}\)
となり、定数の計算をすると、おおよそ、
\(P_9 > 2.146\sqrt{n}\)
となります。\(2.146\) は \(1.177\) の約 \(1.8\) 倍です。従って、次の「誕生日の定理（補足）」が成り立ちます。
誕生日の定理（補足） \(n\) 通りのパターンがあるものを約\(2.146\sqrt{n}\) 個集めると、一致するペアが存在する確率が \(90\%\) を越える。 「一致するペアが存在する確率が \(50\%\) を越える個数」の約\(1.8\)倍の個数を集めると、確率は \(90\%\) を超えて、ほぼ確実に一致するペアが存在する。 |
誕生日のパラドックスとカジノ\(\cdot\)ゲームで計算してみると、
\(\begin{eqnarray}
&&2.146\sqrt{365}&=40.99\\
&&2.146\sqrt{53}&=15.62\\
\end{eqnarray}\)
となり、それぞれ 41 と 16 で一致するペアが存在する確率が 90% を超えることがわかります。これは前にやった正確計算と合致しています。
このように、\(\bs{n}\)通りのパターンがあるものを何個集めたら一致するペアがある確率が一定数を超えるか、という質問の答えは、\(\bs{n}\) に比例するのではなく \(\bs{n}\)の平方根に比例します。\(\bs{n}\) が大きくなっても \(\bs{n}\)の平方根はさほど大きくならない。このあたりに誕生日のパラドックスの原因がありそうです。
５色のサイコロ
誕生日よりもっとパターンの多い例で考えてみます。
５つのサイコロがあり、それぞれ白、赤、青、緑、黒に色分けされています。 この５色のサイコロを同時に振ったとき、出る目のパターンは、\(6^5=7776\) 通りです。 では、５色のサイコロを同時に振ることを何回繰り返したら、全く同じパターンが現れるでしょうか。 |
|
白、赤、青、緑、黒の５つのサイコロを同時に振ると、出る目のパターンは 7776 通りになる。 |
誕生日の定理を使って答を計算してみると
\(\begin{eqnarray}
&&1.177\sqrt{7776}&=103.79\\
&&2.146\sqrt{7776}&=189.24\\
\end{eqnarray}\)
となります。つまり、
| ５色のサイコロを104回振ると、同じパターンが現れる確率が50%を超える。 | |
| ５色のサイコロを190回振ると、その確率は90%を超え、ほぼ確実に同じパターンが現れる。 |
というわけです。出る目のパターンは 7776通りもあります。それでも、100回そこそこで同じパターンが現れる確率が50%を越すことが分かります。なお厳密計算をすると、確率 50% と 90% を超えるのはそれぞれ 105回と 189回です。
誕生日のパラドックス
５色のサイコロのように、パターンの数が多いほど同一パターンが現れるに必要な個数は、パターンの数に比べて小さくなります。しかし "数が多いほど" と言っても、その多さが直感的に理解できないとパラドックスとは感じられないはずです。
その意味で、誕生日のパターンが 365 というのは、適度に多い数で、誰もがその多さの程度を直感的に理解できる数です。そこに誕生日のパラドックスの意味があるのでした。
2021-11-27 11:24
nice!(0)
No.324 - 役割語というバーチャル日本語 [文化]
このブログの第１回目は、
でした。宮崎駿監督の『千と千尋の神隠し』には、ドイツの作家・プロイスラーの小説『クラバート』に影響を受けた部分があるという話から始まって、『クラバート』のあらすじを紹介し、『千と千尋の神隠し』との関係を探ったものです。
その発端の『千と千尋の神隠し』ですが、最近の新聞に登場人物の言葉使いについての興味深い話題が載っていました。今回は是非ともそれを紹介したいと思います。
役割語
キーワードは、大阪大学教授で日本語学者の金水敏氏が提唱した概念である "役割語" です。役割語とは何か、朝日新聞の記事から引用します。
小説、漫画、アニメ、戯曲（演劇）、童話、外国人の発言の翻訳などにおいては、
が使われることが多いわけです。これが役割語で、金水教授が提唱して研究されてきた概念です。金水教授は『千と千尋の神隠し』を例に、次のように説明しています。
金水教授は、湯婆婆が「おばあさん語」を使うと言っています。新聞記事にはありませんが、その一例をあげます。千尋が初めて湯婆婆の "執務室" で湯婆婆と対峙する場面です。
「男性語」を使うリンの言葉遣いの一例は次です。湯屋で働くことになった千尋を、先輩であるリンが部屋に案内する場面です。
せりふだけを読むと千尋は男性と会話しているかようですが、リンは女性です。この言葉遣いについて金水教授は「強い少女像を際だたせるために、あえてジェンダー観をずらした役割語が使われている」と分析しているのでした。
お茶の水博士の「知っておる」
金水さんの役割語という概念の発端は、手塚治虫の「鉄腕アトム」に出てくるお茶の水博士の言葉遣いだったと言います。
ここに至って、宮崎駿監督がアニメで「役割語」を多用する背景が分かります。「役割語」は漫画の "神様" である手塚治虫が使っている。だから当然使う。しかもそれは江戸時代にルーツをもつ長い文化的伝統があり、手塚治虫以前の漫画家も多々使ってきた。そういうことだと思います。
ステレオタイプとしての役割語
我々は日常生活の中で、人間を性別、職業、年齢、人種などで分類しがちですが、その分類（＝カテゴリー）に属する人間が共通して持っていると信じられている特徴を "ステレオタイプ" と言います。役割語はこのステレオタイプの概念と密接に関係しています。
上の引用に、
とあります。役割語の理解を深めるために「外国人のインタビューの翻訳」の想定例を一つ作ってみます。アメリカのある地方の伝統的なハロウィーン事情を取材した日本のTV番組があったとします。自宅の台所でクッキーを焼いている女性にカメラ・インタビューをし、その女性の発言を翻訳し、女性アナウンサーが "吹き替え"をするとします。その翻訳は次のようになるはずです。
女性アナウンサーはこのような「女性語の語尾」で、思い入れたっぷりに（少々の "演技" を交えながら）アナウンスするでしょう。アメリカ人女性を日本の女性アナウンサーが吹き替えるのは自然です。しかし言葉遣いに関しては、インタビューされた人が英語で女性語を使っているはずがないのです。
お菓子を作るのが趣味の男性もいるので、クッキーを焼いているのが男性だとします。それを翻訳して日本の男性アナウンサーが吹き替えると、
この程度の "事実や意見ををすらすら述べる英語"では形容詞や間投詞はなく、また外国TV局のインタビューなのでスラングもなく、従って女性だろうと男性だろうとほぼ同じ英語のはずです。しかし日本語では、男性なら上のような男性語の語尾で翻訳される。
こういった翻訳は日本のリアル社会で使われる言葉とは必ずしも一致しません。たとえば、上の女性の翻訳で使った「なのよ」「あげるの」という語尾ですが、リアル社会では男性も使います。特に東京中心の地方です。ちなみに私は男性ですが、明らかに使っています。しかし創作物では女性が使う。例外はいろいろあるでしょうが、この語尾は "役割語としての女性語" と言ってよいと思います。つまり、女性「らしさ」の強調ための言葉です。
以上のように、日本語の創作物においては、リアル会話とは必ずしも一致しない「女性語」「男性語」という役割語があります。役割語は、リアル社会で話される日常語とは別次元の「ヴァーチャル日本語」です。これが上の引用で「役割語は言語上のステレオタイプ」と言っている意味です。つまり
という概念が創作物の中で形作られ、それが暗黙に根付いています。それは手っ取り早くキャラクターを造形するのに役立つかもしれないが、時代の要請にマッチしないステレオタイプとなることもある。上の引用はそう言っているのでした。
ところで、金水教授は役割語について一冊の本を書いています。
です。以降はこの本（以下「本書」と記述）に沿って、朝日新聞の記事をもう一度振り返ってみます。
お茶の水博士の「博士語」
手塚治虫の「鉄腕アトム」に出てくるお茶の水博士は、つぎのようにしゃべります。
このようなじゃべり方は、お茶の水博士だけでなく、作家も発表年も違う多くの漫画に認められます。これを仮に「博士語」としておきます。「博士語」を標準語と比較すると次の通りです。
この博士語と標準語の対比は、日本の東西方言の対立とよく重なります。日本の方言をさまざまな特徴で分類していくと、多くの特徴が東西に分かれて分布します。分布の境界線は、北は富山県と新潟県の境あたりで、そこから日本アルプス（岐阜と富山の県境）を経由し、南は（言葉によって違うが）愛知県から静岡県東部に抜ける線です。この境界線で分かれる「西日本方言」と「東日本方言」の特徴を対比すると次の通りです。
この表と「博士語：標準語の対応表」をみると、博士語は西日本方言よく似ています。ただし違いもある。本書では博士語について、西日本方言との違いを次のように指摘しています。
つまり博士語は、文法的に現代西日本方言の特徴を部分的にもっていると言えます。もちろん、お茶の水博士をはじめとする漫画に登場する博士が西日本出身のキャラクターと想定されているわけではありません。ではなぜ、漫画の博士は西日本方言を（部分的に）しゃべるのでしょうか。
老人語
実は、漫画の中の博士の言葉を調べていくと、博士語を使わない博士もいることに気づきます。この相違を調べると、博士語を使う博士は "老人的特徴" がはっきりした博士（頭が禿げている、白髪など）だと分かります。その反対に、髪が黒い比較的若い博士は博士語をしゃべらない。つまり、博士語は老人語の一種だったのです。
老人語には、上の博士語であげた例のほかに、「お前も働いとるしのう」というときの「のう」といった終助詞も含まれます。ちなみに「のう」も西日本方言です。こういった老人語（と、その一種としての博士語）のルーツをさかのぼると江戸時代の言語事情に行き着くというのが金水教授の研究で、それは朝日新聞の記事にあるとおりです。本書には次のように書かれています。
金水教授は「言葉づかいをしていたのであろう」や「目立ったと思われる」というように、断定を避けた言い方をしていますが、これは戯作や歌舞伎の文献の言葉遣いから話されていた言葉を推定しているからでしょう。
こうした経緯をもつ老人語の "文化的伝統" の現れが、『千と千尋の神隠し』の湯婆婆なのでした。
老人語について、金水教授はさらに深く分析しています。つまり創作物語の中において、
です。その "特別な役割" とは何か。教授の分析によると、老人語の話し手はおおむね次の３つの類型に分けられます。
この類型からすると、博士語はまさに a. の役割を表すものと言えるでしょう。老人語の話し手は物語の中で特定の役割を与えられた人物である ･･････。これが老人語の（ひいては役割語の）根幹です。そして金水教授は神話学者、ジョセフ・キャンベルの「ヒーローの旅」との関連を指摘しています。
キャンベルは世界各国の神話を分析し、ヒーロー（男性・女性を含む）が出会う "一定の役割をもった人物" と、その "人物との出会いを含む出来事" の時間的配置に一定の類型があることを見い出しました。これが「ヒーローの旅」で、次のようなものです。〈〉が一定の役割をもった人物、「」が出来事です。
この「ヒーローの旅」という物語の構造は、映画、演劇、小説などで、冒険活劇、SF、ミステリー、ラブロマンスなどのジャンルを問わずに活用されてきました。逆に言うと、人気を博した物語は「ヒーローの旅」の構造を全面的、ないしは部分的に持っています。端的な例は「スター・ウォーズ」です。
そして金水教授の指摘は、「ヒーローの旅」の "一定の役割をもった人物" と "日本の物語における老人語の話し手の類型" が、次のような対応関係にあることです。
『千と千尋の神隠し』に即していうと、「ヒーローの旅」における〈影〉＝「b. 悪知恵と不思議な力によって主人公を陥れ、苦しめる悪の化身」＝ 湯婆婆、ということでしょう。湯婆婆を "悪の化身" とは言い過ぎでしょうが、物語の類型におけるポジションとしてはそういうことです。
言うまでもなく「ヒーローの旅」という物語の構造は（日本を含む）世界共通のものです。従って、外国の物語で「ヒーローの旅」の構造をもち、そこに年配の〈助言者〉か〈影〉か〈トリックスター〉が出てきたときは、日本語では老人語で翻訳されることになります。本書では「ハリーポッター」のダンブルドアが〈助言者〉の典型としてあげられています。次はダンブルドアのハリーに対する発言です。
このように日本語訳のハリー・ポッターにおいて、魔法学校の校長・ダンブルドアは老人語で訳されています。
ちなみに、本書にはありませんが、上に引用したダンブルドアの発言は、原書では以下です。
「ハリー・ポッター」は若年層も対象とするファンタジーであり、非常に分かりやすい "標準の" 英語です。念のために、ハリーの発話がどう訳されているかを見てみます。上のダンブルドアの発言の後の方で、出典にあるルビは省略しました。
原書のこの部分の英語は次の通りです。
この引用で分かるように、ハリーの英語とダンブルドアの英語は "同質" です。文法的にも同じだし、特徴ある単語を使うわけでもない。同質だけど、ダンブルドアと違ってハリーの日本語訳はストレートな標準語です。"僕" にみられるような男性語がありますが、それはリアルな会話でも男性が使うので役割語ではありません。
それと比較して、日本語訳されたダンブルドアは「じゃ」「のう」「おる」などの西日本方言の特徴を部分的に使うのです。しかも、現実に日本の老人が使う言葉ではありません。断定に「じゃ」を使う地域が日本にありまりすが、老人が「じゃ」を使う地域なら老若男女を問わず「じゃ」を使います。高齢者になったら「じゃ」を使い出すなんてことはあり得ない。
「ハリー・ポッター」のダンブルドアは、物語の中では〈助言者〉のポジションの高齢者です。だから日本語訳では西日本方言の特徴を部分的にもつ老人語が割り当てられる。役割語の典型といえるでしょう。
そして、我々はそのことに疑問をもつことはありません。読んでも、何の違和感も抱かない。その理由は、そういう風に "教育されてきた" からです。もちろん学校で習ったわけではありません。絵本、童話、マンガ、アニメなど、子どもが接するメディアにおいて、キャラクターを際だたせる言葉としての役割語が多用されていて、そのことによって「暗黙の教育」を受けてきたわけです。
子どもが接するメディアにおいて役割語が多用されるという事実は、ステレオタイプで人物を描くという役割語の性格を表しています。そのため、大人向けの小説やリアルなTVドラマ、映画などで役割語（たとえば老人語や博士語）が使われることはあまりありません。役割語を多用すると、人物描写が重要な文学や脚本としての価値が薄くなるからです。
我々は日本語を学ぶと同時に、リアルな会話では使わない「ヴァーチャル日本語」を学んできたと言えるでしょう。
本書に戻ります。「ハリー・ポッター」の日本語訳では、老人語を話すダンブルドアとは対照的に、ハリーは標準語で訳されていました。このことは、標準語が一般的な日本語だからという以上の意味があるようです。
当然、ハリー・ポッターは日本語の標準語で翻訳されるし、千尋の言葉は「特徴がないことが特徴」となるわけです。
この "標準語" の対立概念は "非標準語" ＝ 方言ですが、本書では「田舎ことば」という役割語が説明されています。それが次です。
田舎ことば
劇作家・木下順二（1914-2006）の代表作に『夕鶴』があります。昔話の「鶴の恩返し」に題材をとった物語で、登場人物は、
です。この劇において、与ひょう、運ず、惣どの３人は、次のような「田舎ことば」を話します。
この引用にある「だ」は東日本方言の特徴ですが、「いとしゅうて」と打ち消しの「ん」は西日本方言の特徴です。また「そげな」は九州でよく聞かれる言い方です。つまりこの３人の会話は、どこの方言ということもない、いかにも田舎くさい言葉に聞こえる表現をまぜて作った「ニセ方言」なのです。
一方、つうのせりふは次のように完璧な標準語（の女性語）というべき表現になっています。
実は、劇作家の木下順二は、３人の男たちが使う「ニセ方言」を意図的に使っているのです。次のように発言しています。
金水教授は次のように分析しています。
この〈田舎ことば〉は、外国文学の翻訳にも使われます。その例は物語に白人と黒人が登場する場合で、金水教授は『風と共に去りぬ』をあげています。
ちなみに「ハリー・ポッター」と違って「風と共に去りぬ」の場合、スカーレットは標準英語を話すのに対して、ディルシーは黒人英語というか、南北戦争当時の黒人奴隷が話す英語です。マーガレット・ミッチェルはそこを "ちゃんと" 書いているのです。たとえば、上に引用した会話の原文は次の通りです。
ディルシーの Thankee は Thank you だし、gives は 正しくは give です。従って日本語訳において、スカーレットとディルシーの発話を "違うことばで" 訳するのは合理性があると言えます。しかしその「黒人英語」を日本語の「田舎ことば」で訳する背景は、まさに金水教授の示した図式どおりでしょう。
役割語に偏見と差別が忍び込む
新聞記事の紹介のところで書いた "ステレオタイプ" をもう一度とりあげます。我々は日常生活の中で人間を性別、職業、年齢、人種などで分類しがちですが、その分類（＝カテゴリー）に属する人間が共通して持っていると信じられている特徴を "ステレオタイプ" と言います。
カテゴリーによる認識は、我々が生活する上で必須だと言えるでしょう。役割語は "言語上のステレオタイプ" であり、"カテゴリー・ベース" の発話記述です。役割語が子ども向けの創作物にしばしば使われるのは、カテゴリー・ベースの記述で人物像を分かりやすく子どもに伝えられるからです。しかしその一方で、ステレオタイプには偏見や差別が忍び込みます。
本書には、役割語が偏見と差別に結びついた典型例として〈アルヨことば〉が分析されています。〈アルヨことば〉とは、
のように文末述語に直接「ある」または「あるよ」がつく言い方です。本書では、この〈アルヨことば〉が、日清戦争から日中戦争に至る過程において中国人に対する偏見・差別とセットで発達し（前者の例）、それが戦後にも引き継がれた（後者の例 ＝ Dr.スランプ）ことが明らかにされています。金水教授は本書の最後のページで次のように述べています。
まとめ
以上が金水教授の著書「ヴァーチャル日本語 役割語の謎」の "さわり" ですが、さらに要約すると次のようになるでしょう。
我々はヴァーチャルとリアルを区別できない
以下は役割語について、特に金水教授の著書「ヴァーチャル日本語 役割語の謎」についての感想です。
最近、IT技術を使ったヴァーチャル・リアリティ（VR。Virtual Reality。仮想現実）が、ゲーム、エンターテインメント、ビジネスにおける 3D シミュレータなどで広まっています。金水教授は本書の "はしがき" のところで「現実」と「仮想現実」について次のように述べています。
我々は「現実」と「仮想現実」を本誌的に区別できない ･･････。これは真実を突いています。
実生活で使う言葉や、アナウンサーが使う言葉を「リアル言語」だとすると、役割語は「ヴァーチャル言語」です。従って、役割語で作られるキャラクターの世界は「仮想現実」です。「仮想現実」だけれど、我々はそれを「現実」と区別できず、暗黙に（あくまで暗黙に）現実だと思ってしまう。
この "区別できない" ことは、どういう効果を生むでしょうか。役割語としての「男性語」と「女性語」の例で考えてみると、『千と千尋の神隠し』に登場する少女・リンは男性語を使うのでした。金水教授は「リンは "いつか湯屋を出たい" という強い意志を持っているキャラクター」であり「強い少女像を際だたせるために、あえてジェンダー観をずらした役割語が使われている」と指摘していました。
つまり我々は「男性語を使う ＝ 強い意志をもつ存在」というキャラクター像を暗黙に受け入れていて、それに何の疑問も感じないのです。そのことを大前提として、リンのせりふが成り立っている。もちろん宮崎監督は、強い少女像を際だたせるためにリンに男性語を割り当てたのでしょう。それは、子どもを対象とするアニメのキャラクター設定としては自然だし、まっとうだと思います。
しかしアニメを含む創作物において、男性語を使う少女・リンのような存在はまれであり、男性語を使い手のほとんどは少年や男性です。つまり我々は「男性 ＝ 強い意志をもった自立する存在」というようなイメージを、役割語が使われる仮想現実の世界で受け入れてしまっているのではないでしょうか。それと反対に、女性語を使うのは「保護すべき弱い存在」というキャラクターだと、無意識に感じているのではないか。それを役割語が補強している。
これが仮想現実の世界に閉じていればよいのですが、我々は「現実」と「仮想現実」を本誌的に区別できないのです。従って、役割語によるキャラクター像が現実においてもそうだと無意識に思ってしまう。本質的に区別できないのだから ･･････。
そのような認識が現実の実態とは違うのは明白です。強い意志の女性もいれば、弱い男性もいる。しかし実態とは全く別に、役割語は「男性は男性らしく、女性は女性らしく」とか「男性は論理的で女性は感情的」とか「男性と女性は社会的役割が違う」といった考えや概念が暗黙に忍び込む素地を作っているのではないでしょうか。
そうなると、男性・女性という生物学的な差異を越えて偏見につながるだろうし、ひいては差別を生む誘因になりかねない。ここまで「男性語」と「女性語」の例で書きましたが、ほかの役割語も、その役割語で与えられたキャラクター像（仮想現実）によっては同じ効果を生むでしょう。
我々は言葉によって世界を切り取り、言葉によって世界の構造の認識しています。と同時に、我々は仮想現実と現実を本質的に区別できません。この２つが重なると、物語の中の言葉によるキャラクター像が偏見や差別を助長するという "不都合" を生むことがありうる。しかもその言葉（＝役割語）は、日本人である限り幼少の頃から刷り込まれたものです。
そういった不都合を回避する第一歩は、刷り込まれていることの認識である。そう思いました。
役割語としての方言
以降は余談で、役割語という概念について気付いた点です。金水教授の本には「田舎言葉としての"ニセ方言"」が出てきますが、以下は "真の" 方言の話です。
もちろん方言は「それを話す人が該当地方に住んでいる」、もしくは「該当地方の出身である」ということを示します。たとえば、関西地方が舞台のドラマでは役者が関西弁を話し、関東が舞台のドラマで関西弁を話す人がいたとしたらその人は関西出身であることを示す、といった具合です。
しかし、こと関西弁・関西言葉については、単なる方言以上の役割があるように感じます。その理由は、戦国時代を扱った歴史ドラマの配役では、関西人だけが方言（＝関西言葉）を使うからです。しかも使うのは、文化人（たとえば千利休）、商人（たとえば堺の豪商）、京の公家に限られます。関西出身の武士、例えば明智光秀（近江）や黒田官兵衛（播磨）が関西言葉を使うドラマの記憶はありません。
もちろん戦国歴史ドラマにおいて、武士は標準語（をベースにしたドラマ用の武家言葉）で話すのが普通です。徳川家康や羽柴秀吉は三河弁を使わないし、織田信長は尾張弁を使わない。と同時に、三河や尾張の有力商人が登場したとして、その人たちも方言（＝三河弁や尾張弁）を使うことはないと思うのです。
明智光秀や黒田官兵衛がドラマにおける "武士としての言葉" を使ったとしてもおかしくはありません。その一方で、堺の豪商や茶人は関西言葉を話すのです。
戦国歴史ドラマにおいて、関西言葉は特別なポジションを与えられているのではないでしょうか。つまり「文化と経済を担う人物が使う言葉」という位置づけで、これも役割語といってよいと思います。
さらに「幕末から明治維新にかけての歴史ドラマ」では、別のタイプの役割語があると思います。「特定の人物像と結びついた特徴ある言葉遣い」ではなく、「特定の人物と結びついた特徴ある言葉遣い」です。
つまり、幕末の歴史ドラマで「おいどん」とか「ごわす」という言葉遣いをする人物がいたとしたら、それは間違いなく西郷隆盛です。「おいどん」は鹿児島弁の１人称ですね。だとすると、大久保利道も村田新八も自分のことを「おいどん」と言っていいはずなのに、そうは言わない感じがします。「おいどん」という自称は西郷隆盛という特定の人物を示す役割語となっているのではないでしょうか。
同様に、語尾に「ぜよ」を使う人物がいたとしたら、それは確実に坂本龍馬でしょう。これは土佐弁なので、土佐藩の中岡慎太郎や後藤象二郎も「ぜよ」を使うはずなのに、龍馬だけが「ぜよ」と言う気がします。
最近は歴史ドラマをあまり見なくなったので、近年の役者・俳優のせりふがどうなっているのか、確定的なことはわかりません。ただ、「特定の人物と結びついた」タイプの役割語もあるのではと思います。
でした。宮崎駿監督の『千と千尋の神隠し』には、ドイツの作家・プロイスラーの小説『クラバート』に影響を受けた部分があるという話から始まって、『クラバート』のあらすじを紹介し、『千と千尋の神隠し』との関係を探ったものです。
その発端の『千と千尋の神隠し』ですが、最近の新聞に登場人物の言葉使いについての興味深い話題が載っていました。今回は是非ともそれを紹介したいと思います。
なお、以下に掲げる引用において下線は原文にはありません。また段落を増やしたところがあります。
役割語
キーワードは、大阪大学教授で日本語学者の金水敏氏が提唱した概念である "役割語" です。役割語とは何か、朝日新聞の記事から引用します。
|
小説、漫画、アニメ、戯曲（演劇）、童話、外国人の発言の翻訳などにおいては、
特定の人物像と結びついた特徴ある言葉遣い
が使われることが多いわけです。これが役割語で、金水教授が提唱して研究されてきた概念です。金水教授は『千と千尋の神隠し』を例に、次のように説明しています。
|
金水教授は、湯婆婆が「おばあさん語」を使うと言っています。新聞記事にはありませんが、その一例をあげます。千尋が初めて湯婆婆の "執務室" で湯婆婆と対峙する場面です。
|
|
「男性語」を使うリンの言葉遣いの一例は次です。湯屋で働くことになった千尋を、先輩であるリンが部屋に案内する場面です。
|
|
せりふだけを読むと千尋は男性と会話しているかようですが、リンは女性です。この言葉遣いについて金水教授は「強い少女像を際だたせるために、あえてジェンダー観をずらした役割語が使われている」と分析しているのでした。
お茶の水博士の「知っておる」
金水さんの役割語という概念の発端は、手塚治虫の「鉄腕アトム」に出てくるお茶の水博士の言葉遣いだったと言います。
|
ここに至って、宮崎駿監督がアニメで「役割語」を多用する背景が分かります。「役割語」は漫画の "神様" である手塚治虫が使っている。だから当然使う。しかもそれは江戸時代にルーツをもつ長い文化的伝統があり、手塚治虫以前の漫画家も多々使ってきた。そういうことだと思います。
ステレオタイプとしての役割語
我々は日常生活の中で、人間を性別、職業、年齢、人種などで分類しがちですが、その分類（＝カテゴリー）に属する人間が共通して持っていると信じられている特徴を "ステレオタイプ" と言います。役割語はこのステレオタイプの概念と密接に関係しています。
|
上の引用に、
| 役割語は）外国人のインタビューの翻訳でも多用される |
とあります。役割語の理解を深めるために「外国人のインタビューの翻訳」の想定例を一つ作ってみます。アメリカのある地方の伝統的なハロウィーン事情を取材した日本のTV番組があったとします。自宅の台所でクッキーを焼いている女性にカメラ・インタビューをし、その女性の発言を翻訳し、女性アナウンサーが "吹き替え"をするとします。その翻訳は次のようになるはずです。
| こうやって毎年クッキーを自分で焼いて、ハロウィーンの日にやってくる子どもたちにあげるの。子どもたちの喜ぶ顔を見るのが楽しみなのよ。この地区の住人の親睦にも役だっていると思うわ」 |
女性アナウンサーはこのような「女性語の語尾」で、思い入れたっぷりに（少々の "演技" を交えながら）アナウンスするでしょう。アメリカ人女性を日本の女性アナウンサーが吹き替えるのは自然です。しかし言葉遣いに関しては、インタビューされた人が英語で女性語を使っているはずがないのです。
お菓子を作るのが趣味の男性もいるので、クッキーを焼いているのが男性だとします。それを翻訳して日本の男性アナウンサーが吹き替えると、
| こうやって毎年クッキーを自分で焼いて、ハロウィーンの日にやってくる子どもたちにあげるんだ。子どもたちの喜ぶ顔を見るのが楽しみなのさ。この地区の住人の親睦にも役だっていると思うよ」 |
この程度の "事実や意見ををすらすら述べる英語"では形容詞や間投詞はなく、また外国TV局のインタビューなのでスラングもなく、従って女性だろうと男性だろうとほぼ同じ英語のはずです。しかし日本語では、男性なら上のような男性語の語尾で翻訳される。
こういった翻訳は日本のリアル社会で使われる言葉とは必ずしも一致しません。たとえば、上の女性の翻訳で使った「なのよ」「あげるの」という語尾ですが、リアル社会では男性も使います。特に東京中心の地方です。ちなみに私は男性ですが、明らかに使っています。しかし創作物では女性が使う。例外はいろいろあるでしょうが、この語尾は "役割語としての女性語" と言ってよいと思います。つまり、女性「らしさ」の強調ための言葉です。
以上のように、日本語の創作物においては、リアル会話とは必ずしも一致しない「女性語」「男性語」という役割語があります。役割語は、リアル社会で話される日常語とは別次元の「ヴァーチャル日本語」です。これが上の引用で「役割語は言語上のステレオタイプ」と言っている意味です。つまり
| 女性語を使う人 → 女性 | |
| 女性 → 女性語を使う → 女性らしい |
という概念が創作物の中で形作られ、それが暗黙に根付いています。それは手っ取り早くキャラクターを造形するのに役立つかもしれないが、時代の要請にマッチしないステレオタイプとなることもある。上の引用はそう言っているのでした。
ところで、金水教授は役割語について一冊の本を書いています。
金水敏「ヴァーチャル日本語 役割語の謎」（岩波書店 2003）
です。以降はこの本（以下「本書」と記述）に沿って、朝日新聞の記事をもう一度振り返ってみます。
お茶の水博士の「博士語」
手塚治虫の「鉄腕アトム」に出てくるお茶の水博士は、つぎのようにしゃべります。
| 親じゃと？ わしはアトムの親がわりになっとるわい！」 | |
| アトムどうじゃ」 | |
| 人間のふりをして煙にとっつかれてみんか」 |
このようなじゃべり方は、お茶の水博士だけでなく、作家も発表年も違う多くの漫画に認められます。これを仮に「博士語」としておきます。「博士語」を標準語と比較すると次の通りです。
| 博士語 | 標準語 | |
| 断定 | 親代わりじゃ | 親代わりだ |
| 打ち消し | 知らん、知らぬ | 知らない |
| 人間の存在 | おる | いる |
| 進行、状態 | 知っておる 知っとる | 知っている 知ってる |
この博士語と標準語の対比は、日本の東西方言の対立とよく重なります。日本の方言をさまざまな特徴で分類していくと、多くの特徴が東西に分かれて分布します。分布の境界線は、北は富山県と新潟県の境あたりで、そこから日本アルプス（岐阜と富山の県境）を経由し、南は（言葉によって違うが）愛知県から静岡県東部に抜ける線です。この境界線で分かれる「西日本方言」と「東日本方言」の特徴を対比すると次の通りです。
| 西日本方言 | 東日本方言 | |
| 断定 | 雨じゃ、雨や | 雨だ |
| 打ち消し | 知らん 知らへん | 知らない 知らねえ |
| 人間の存在 | おる | いる |
| 進行、状態 | 降っておる 降っとる 降りよる | 降っている 降ってる |
| 形容詞連用形 | 赤うなる | 赤くなる |
| 一段動詞命令形 | 起きい | 起きろ |
| サ変動詞命令形 | せえ、など | しろ、など |
この表と「博士語：標準語の対応表」をみると、博士語は西日本方言よく似ています。ただし違いもある。本書では博士語について、西日本方言との違いを次のように指摘しています。
| お茶の水博士は断定に「じゃ」を使うが、「だ」を使うこともかなり多い。つまりフレーバー的に時々「じゃ」を使う。 | |
| 形容詞連用形の「赤うなる」などの、いわゆるウ音便はあまり用いない。 | |
| 西日本方言の中でも、断定の「雨や」、打ち消しの「知らへん」は用いない。 |
つまり博士語は、文法的に現代西日本方言の特徴を部分的にもっていると言えます。もちろん、お茶の水博士をはじめとする漫画に登場する博士が西日本出身のキャラクターと想定されているわけではありません。ではなぜ、漫画の博士は西日本方言を（部分的に）しゃべるのでしょうか。
老人語
|
老人語には、上の博士語であげた例のほかに、「お前も働いとるしのう」というときの「のう」といった終助詞も含まれます。ちなみに「のう」も西日本方言です。こういった老人語（と、その一種としての博士語）のルーツをさかのぼると江戸時代の言語事情に行き着くというのが金水教授の研究で、それは朝日新聞の記事にあるとおりです。本書には次のように書かれています。
|
金水教授は「言葉づかいをしていたのであろう」や「目立ったと思われる」というように、断定を避けた言い方をしていますが、これは戯作や歌舞伎の文献の言葉遣いから話されていた言葉を推定しているからでしょう。
こうした経緯をもつ老人語の "文化的伝統" の現れが、『千と千尋の神隠し』の湯婆婆なのでした。
老人語について、金水教授はさらに深く分析しています。つまり創作物語の中において、
|
です。その "特別な役割" とは何か。教授の分析によると、老人語の話し手はおおむね次の３つの類型に分けられます。
| 主人公に知恵と教訓を授け、教え、導く助言者 | |
| 悪知恵と不思議な力によって主人公を陥れ、苦しめる悪の化身（例：白雪姫の女王や眠り姫の魔女） | |
| 老耄ゆえの勘違いや失敗を繰り返し、主人公やその周辺の人物を混乱させ、時に和ませ、関係調整役として働く人物（例：「ちびまる子ちゃん」のともぞうじいさん） |
この類型からすると、博士語はまさに a. の役割を表すものと言えるでしょう。老人語の話し手は物語の中で特定の役割を与えられた人物である ･･････。これが老人語の（ひいては役割語の）根幹です。そして金水教授は神話学者、ジョセフ・キャンベルの「ヒーローの旅」との関連を指摘しています。
キャンベルは世界各国の神話を分析し、ヒーロー（男性・女性を含む）が出会う "一定の役割をもった人物" と、その "人物との出会いを含む出来事" の時間的配置に一定の類型があることを見い出しました。これが「ヒーローの旅」で、次のようなものです。〈〉が一定の役割をもった人物、「」が出来事です。
| 「普通の生活」をしていた〈ヒーロー〉が、ある日、異界の〈使者〉から「冒険への呼び出し」を受ける。 | |
| 〈ヒーロー〉はいったんこの「呼び出しを拒絶」するが、老人の〈助言者〉に導かれ、励まされ、力を授かり、旅立つ。 | |
| 〈ヒーロー〉は「最初の関門」にさしかかり、〈関門の番人〉に「試練」を与えられる。その過程で〈味方〉と〈敵〉が明らかになる。 | |
| 〈敵〉は〈ヒーロー〉を呪い、苦しめようとする〈影〉の部下であったり、〈影〉そのものであったりする。 | |
| 〈トリックスター〉は、いたずらや失敗で〈ヒーロー〉たちを混乱させ、笑わせ、変化の必要性に気づかせる。 | |
| 〈変容する者〉は〈ヒーロー〉にとって異性の誘惑者で、〈ヒーロー〉は彼／彼女の心を読み取ることができず、疑惑に悩まされる。 | |
| やがて〈ヒーロー〉は「深奥の洞窟への進入」を試み、「苦難」をくぐり抜け、宝の「剣（報酬）をつかみ取る」。 | |
| 〈ヒーロー〉は「帰還への道」をたどるが、その途中で死に直面し、そして「再生」を果たす。その後「神秘の妙薬を携えて帰還」する。 |
この「ヒーローの旅」という物語の構造は、映画、演劇、小説などで、冒険活劇、SF、ミステリー、ラブロマンスなどのジャンルを問わずに活用されてきました。逆に言うと、人気を博した物語は「ヒーローの旅」の構造を全面的、ないしは部分的に持っています。端的な例は「スター・ウォーズ」です。
そして金水教授の指摘は、「ヒーローの旅」の "一定の役割をもった人物" と "日本の物語における老人語の話し手の類型" が、次のような対応関係にあることです。
a. → 〈助言者〉
b. → 〈影〉
c. → 〈トリックスター〉
b. → 〈影〉
c. → 〈トリックスター〉
『千と千尋の神隠し』に即していうと、「ヒーローの旅」における〈影〉＝「b. 悪知恵と不思議な力によって主人公を陥れ、苦しめる悪の化身」＝ 湯婆婆、ということでしょう。湯婆婆を "悪の化身" とは言い過ぎでしょうが、物語の類型におけるポジションとしてはそういうことです。
言うまでもなく「ヒーローの旅」という物語の構造は（日本を含む）世界共通のものです。従って、外国の物語で「ヒーローの旅」の構造をもち、そこに年配の〈助言者〉か〈影〉か〈トリックスター〉が出てきたときは、日本語では老人語で翻訳されることになります。本書では「ハリーポッター」のダンブルドアが〈助言者〉の典型としてあげられています。次はダンブルドアのハリーに対する発言です。
|
|
映画版「ハリー・ポッターと賢者の石」（2001）に登場するアルバス・ダンブルドア。演じたのはリチャード・ハリスである。なお、リチャード・ハリスは次作の「ハリー・ポッターと秘密の部屋」（2002）でもダンブルドアを演じたが、それが遺作となった。 |
このように日本語訳のハリー・ポッターにおいて、魔法学校の校長・ダンブルドアは老人語で訳されています。
ちなみに、本書にはありませんが、上に引用したダンブルドアの発言は、原書では以下です。
|
「ハリー・ポッター」は若年層も対象とするファンタジーであり、非常に分かりやすい "標準の" 英語です。念のために、ハリーの発話がどう訳されているかを見てみます。上のダンブルドアの発言の後の方で、出典にあるルビは省略しました。
|
原書のこの部分の英語は次の通りです。
|
この引用で分かるように、ハリーの英語とダンブルドアの英語は "同質" です。文法的にも同じだし、特徴ある単語を使うわけでもない。同質だけど、ダンブルドアと違ってハリーの日本語訳はストレートな標準語です。"僕" にみられるような男性語がありますが、それはリアルな会話でも男性が使うので役割語ではありません。
それと比較して、日本語訳されたダンブルドアは「じゃ」「のう」「おる」などの西日本方言の特徴を部分的に使うのです。しかも、現実に日本の老人が使う言葉ではありません。断定に「じゃ」を使う地域が日本にありまりすが、老人が「じゃ」を使う地域なら老若男女を問わず「じゃ」を使います。高齢者になったら「じゃ」を使い出すなんてことはあり得ない。
完全な蛇足ですが、私の配偶者（女性）は広島出身で、高校まで広島で育ち、関西の大学に入学しました。すると、周りの男子学生（ほとんどが関西出身）から「じゃろ の ◎◎ ちゃん」（◎◎ は彼女の名前）とのあだ名を付けられたそうです。関西の男子学生にとって、20歳前の若い女性が「じゃろ」を連発するのは印象的だったに違いありません（＝ "カワイーイ！"）。もちろん彼女の両親も「じゃろ」を使っていました。ちなみに断定の「じゃ」には、地域によって「じゃろ」「じゃん」「じゃけん」などの変化形があります。
「ハリー・ポッター」のダンブルドアは、物語の中では〈助言者〉のポジションの高齢者です。だから日本語訳では西日本方言の特徴を部分的にもつ老人語が割り当てられる。役割語の典型といえるでしょう。
そして、我々はそのことに疑問をもつことはありません。読んでも、何の違和感も抱かない。その理由は、そういう風に "教育されてきた" からです。もちろん学校で習ったわけではありません。絵本、童話、マンガ、アニメなど、子どもが接するメディアにおいて、キャラクターを際だたせる言葉としての役割語が多用されていて、そのことによって「暗黙の教育」を受けてきたわけです。
子どもが接するメディアにおいて役割語が多用されるという事実は、ステレオタイプで人物を描くという役割語の性格を表しています。そのため、大人向けの小説やリアルなTVドラマ、映画などで役割語（たとえば老人語や博士語）が使われることはあまりありません。役割語を多用すると、人物描写が重要な文学や脚本としての価値が薄くなるからです。
我々は日本語を学ぶと同時に、リアルな会話では使わない「ヴァーチャル日本語」を学んできたと言えるでしょう。
本書に戻ります。「ハリー・ポッター」の日本語訳では、老人語を話すダンブルドアとは対照的に、ハリーは標準語で訳されていました。このことは、標準語が一般的な日本語だからという以上の意味があるようです。
|
当然、ハリー・ポッターは日本語の標準語で翻訳されるし、千尋の言葉は「特徴がないことが特徴」となるわけです。
この "標準語" の対立概念は "非標準語" ＝ 方言ですが、本書では「田舎ことば」という役割語が説明されています。それが次です。
田舎ことば
劇作家・木下順二（1914-2006）の代表作に『夕鶴』があります。昔話の「鶴の恩返し」に題材をとった物語で、登場人物は、
| ： 鶴の化身 | |
| ： 鶴を助けた農民 | |
| ： 与ひょうの悪友 |
です。この劇において、与ひょう、運ず、惣どの３人は、次のような「田舎ことば」を話します。
|
この引用にある「だ」は東日本方言の特徴ですが、「いとしゅうて」と打ち消しの「ん」は西日本方言の特徴です。また「そげな」は九州でよく聞かれる言い方です。つまりこの３人の会話は、どこの方言ということもない、いかにも田舎くさい言葉に聞こえる表現をまぜて作った「ニセ方言」なのです。
一方、つうのせりふは次のように完璧な標準語（の女性語）というべき表現になっています。
|
実は、劇作家の木下順二は、３人の男たちが使う「ニセ方言」を意図的に使っているのです。次のように発言しています。
|
金水教授は次のように分析しています。
|
この〈田舎ことば〉は、外国文学の翻訳にも使われます。その例は物語に白人と黒人が登場する場合で、金水教授は『風と共に去りぬ』をあげています。
|
ちなみに「ハリー・ポッター」と違って「風と共に去りぬ」の場合、スカーレットは標準英語を話すのに対して、ディルシーは黒人英語というか、南北戦争当時の黒人奴隷が話す英語です。マーガレット・ミッチェルはそこを "ちゃんと" 書いているのです。たとえば、上に引用した会話の原文は次の通りです。
|
ディルシーの Thankee は Thank you だし、gives は 正しくは give です。従って日本語訳において、スカーレットとディルシーの発話を "違うことばで" 訳するのは合理性があると言えます。しかしその「黒人英語」を日本語の「田舎ことば」で訳する背景は、まさに金水教授の示した図式どおりでしょう。
役割語に偏見と差別が忍び込む
新聞記事の紹介のところで書いた "ステレオタイプ" をもう一度とりあげます。我々は日常生活の中で人間を性別、職業、年齢、人種などで分類しがちですが、その分類（＝カテゴリー）に属する人間が共通して持っていると信じられている特徴を "ステレオタイプ" と言います。
|
カテゴリーによる認識は、我々が生活する上で必須だと言えるでしょう。役割語は "言語上のステレオタイプ" であり、"カテゴリー・ベース" の発話記述です。役割語が子ども向けの創作物にしばしば使われるのは、カテゴリー・ベースの記述で人物像を分かりやすく子どもに伝えられるからです。しかしその一方で、ステレオタイプには偏見や差別が忍び込みます。
|
本書には、役割語が偏見と差別に結びついた典型例として〈アルヨことば〉が分析されています。〈アルヨことば〉とは、
| 隊長たいへんあるよ 日本軍がきたある」 | |
| こ こんにちは わたちたち こんどひっこちてきた摘（つん）一家ある」 |
のように文末述語に直接「ある」または「あるよ」がつく言い方です。本書では、この〈アルヨことば〉が、日清戦争から日中戦争に至る過程において中国人に対する偏見・差別とセットで発達し（前者の例）、それが戦後にも引き継がれた（後者の例 ＝ Dr.スランプ）ことが明らかにされています。金水教授は本書の最後のページで次のように述べています。
|
まとめ
以上が金水教授の著書「ヴァーチャル日本語 役割語の謎」の "さわり" ですが、さらに要約すると次のようになるでしょう。
| 役割語とは、各種の創作物で使われる「特定の人物像と結びついた特徴ある言葉遣い」である。 | |
| これには、老人語、男性語、女性語、上司語（ "見積書を作ってくれたまえ" ）、お嬢様ことば（ "そうですわよ、わたくしが存じておりますわ" ）、田舎ことば、異人ことば（アルヨことば、など）などがある。 | |
| 役割語は必ずしも現実とは一致しない。それどころか、老人語のように現実には決して話されない言葉もある。方言をまぜこぜにした田舎ことばも、現実に話す人はいない。 | |
| 役割語を使うと "手っ取り早く" 人物像を提示できる。つまり、人物像の詳細な書き込みや描写の必要がない。そのため、子ども向けの創作物に多用される。大人向けの創作物で多用されるとしたら、その創作物は "B級作品" である。 | |
| 役割語は学校で習ったわけではなく、誰かに教えてもらったのでもない。しかし、日本で日本語で生活する皆が理解している。それは絵本から始まって、小さいときから役割語を刷り込まれてきたからである。 | |
| 人間（および事物）をカテゴリーに分類し、カテゴリーに属する集団がある特徴を共通して持っていると信じられているとき、それをステレオタイプと言う。役割語は言語上のステレオタイプである。役割語による発話は、カテゴリー・ベースの記述である。 | |
| カテゴリーによる人間や事物の認識は、我々が生活していく上で必須のものであるが、反面、そこに偏見や差別が忍び込む。我々は役割語による人物認識を見直し、暗黙に偏った見方に陥っているのではないかを反省し、豊かな言葉と認識を取り戻すべきである。 |
我々はヴァーチャルとリアルを区別できない
以下は役割語について、特に金水教授の著書「ヴァーチャル日本語 役割語の謎」についての感想です。
最近、IT技術を使ったヴァーチャル・リアリティ（VR。Virtual Reality。仮想現実）が、ゲーム、エンターテインメント、ビジネスにおける 3D シミュレータなどで広まっています。金水教授は本書の "はしがき" のところで「現実」と「仮想現実」について次のように述べています。
|
我々は「現実」と「仮想現実」を本誌的に区別できない ･･････。これは真実を突いています。
実生活で使う言葉や、アナウンサーが使う言葉を「リアル言語」だとすると、役割語は「ヴァーチャル言語」です。従って、役割語で作られるキャラクターの世界は「仮想現実」です。「仮想現実」だけれど、我々はそれを「現実」と区別できず、暗黙に（あくまで暗黙に）現実だと思ってしまう。
この "区別できない" ことは、どういう効果を生むでしょうか。役割語としての「男性語」と「女性語」の例で考えてみると、『千と千尋の神隠し』に登場する少女・リンは男性語を使うのでした。金水教授は「リンは "いつか湯屋を出たい" という強い意志を持っているキャラクター」であり「強い少女像を際だたせるために、あえてジェンダー観をずらした役割語が使われている」と指摘していました。
つまり我々は「男性語を使う ＝ 強い意志をもつ存在」というキャラクター像を暗黙に受け入れていて、それに何の疑問も感じないのです。そのことを大前提として、リンのせりふが成り立っている。もちろん宮崎監督は、強い少女像を際だたせるためにリンに男性語を割り当てたのでしょう。それは、子どもを対象とするアニメのキャラクター設定としては自然だし、まっとうだと思います。
しかしアニメを含む創作物において、男性語を使う少女・リンのような存在はまれであり、男性語を使い手のほとんどは少年や男性です。つまり我々は「男性 ＝ 強い意志をもった自立する存在」というようなイメージを、役割語が使われる仮想現実の世界で受け入れてしまっているのではないでしょうか。それと反対に、女性語を使うのは「保護すべき弱い存在」というキャラクターだと、無意識に感じているのではないか。それを役割語が補強している。
これが仮想現実の世界に閉じていればよいのですが、我々は「現実」と「仮想現実」を本誌的に区別できないのです。従って、役割語によるキャラクター像が現実においてもそうだと無意識に思ってしまう。本質的に区別できないのだから ･･････。
そのような認識が現実の実態とは違うのは明白です。強い意志の女性もいれば、弱い男性もいる。しかし実態とは全く別に、役割語は「男性は男性らしく、女性は女性らしく」とか「男性は論理的で女性は感情的」とか「男性と女性は社会的役割が違う」といった考えや概念が暗黙に忍び込む素地を作っているのではないでしょうか。
そうなると、男性・女性という生物学的な差異を越えて偏見につながるだろうし、ひいては差別を生む誘因になりかねない。ここまで「男性語」と「女性語」の例で書きましたが、ほかの役割語も、その役割語で与えられたキャラクター像（仮想現実）によっては同じ効果を生むでしょう。
我々は言葉によって世界を切り取り、言葉によって世界の構造の認識しています。と同時に、我々は仮想現実と現実を本質的に区別できません。この２つが重なると、物語の中の言葉によるキャラクター像が偏見や差別を助長するという "不都合" を生むことがありうる。しかもその言葉（＝役割語）は、日本人である限り幼少の頃から刷り込まれたものです。
そういった不都合を回避する第一歩は、刷り込まれていることの認識である。そう思いました。
役割語としての方言
以降は余談で、役割語という概念について気付いた点です。金水教授の本には「田舎言葉としての"ニセ方言"」が出てきますが、以下は "真の" 方言の話です。
もちろん方言は「それを話す人が該当地方に住んでいる」、もしくは「該当地方の出身である」ということを示します。たとえば、関西地方が舞台のドラマでは役者が関西弁を話し、関東が舞台のドラマで関西弁を話す人がいたとしたらその人は関西出身であることを示す、といった具合です。
しかし、こと関西弁・関西言葉については、単なる方言以上の役割があるように感じます。その理由は、戦国時代を扱った歴史ドラマの配役では、関西人だけが方言（＝関西言葉）を使うからです。しかも使うのは、文化人（たとえば千利休）、商人（たとえば堺の豪商）、京の公家に限られます。関西出身の武士、例えば明智光秀（近江）や黒田官兵衛（播磨）が関西言葉を使うドラマの記憶はありません。
もちろん戦国歴史ドラマにおいて、武士は標準語（をベースにしたドラマ用の武家言葉）で話すのが普通です。徳川家康や羽柴秀吉は三河弁を使わないし、織田信長は尾張弁を使わない。と同時に、三河や尾張の有力商人が登場したとして、その人たちも方言（＝三河弁や尾張弁）を使うことはないと思うのです。
明智光秀や黒田官兵衛がドラマにおける "武士としての言葉" を使ったとしてもおかしくはありません。その一方で、堺の豪商や茶人は関西言葉を話すのです。
戦国歴史ドラマにおいて、関西言葉は特別なポジションを与えられているのではないでしょうか。つまり「文化と経済を担う人物が使う言葉」という位置づけで、これも役割語といってよいと思います。
| 特定の人物と結びついた言葉 |
さらに「幕末から明治維新にかけての歴史ドラマ」では、別のタイプの役割語があると思います。「特定の人物像と結びついた特徴ある言葉遣い」ではなく、「特定の人物と結びついた特徴ある言葉遣い」です。
つまり、幕末の歴史ドラマで「おいどん」とか「ごわす」という言葉遣いをする人物がいたとしたら、それは間違いなく西郷隆盛です。「おいどん」は鹿児島弁の１人称ですね。だとすると、大久保利道も村田新八も自分のことを「おいどん」と言っていいはずなのに、そうは言わない感じがします。「おいどん」という自称は西郷隆盛という特定の人物を示す役割語となっているのではないでしょうか。
同様に、語尾に「ぜよ」を使う人物がいたとしたら、それは確実に坂本龍馬でしょう。これは土佐弁なので、土佐藩の中岡慎太郎や後藤象二郎も「ぜよ」を使うはずなのに、龍馬だけが「ぜよ」と言う気がします。
最近は歴史ドラマをあまり見なくなったので、近年の役者・俳優のせりふがどうなっているのか、確定的なことはわかりません。ただ、「特定の人物と結びついた」タイプの役割語もあるのではと思います。
2021-11-13 08:25
nice!(0)
