No.325 - 高校数学で理解する誕生日のパラドックス [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
「高校数学で理解する・・・」というタイトルで、今まで5つの記事書きました。
ですが、いずれも現代のインターネット社会における情報通信の基礎となっている "公開鍵暗号" の数理を、高校レベルの数学だけを前提知識として述べたものでした。
今回はその「高校数学で理解する\(\cdot\cdot\cdot\)」の続きですが、公開鍵暗号よりは断然軽い話題で、No.149「我々は直感に裏切られる」でとりあげた「誕生日のパラドックス」をもう一度、考察します。No.149 では「バースデー\(\cdot\)パラドックス」と書いたもので、よく知られた話です。
誕生日のパラドックス
誕生日のパラドックスとは、
というものです。一瞬、えっ! と思ってしまいますが、数学的には全く正しい。普通、パラドックスと言うと「絶対に不可能なことが可能なように思えてしまう」ないしは、「あり得ないことがあり得るように見えてしまう」ことを言いますが、この誕生日のパラドックスはそれとは違う「疑似パラドックス」です。つまり、
です。以下、1年を365日に固定して考えることにし、
の記号を使うと、
なので、\(\ol{\,B\,}(365,23)\) を計算すればよいことになります。「23人のクラスの、誕生日のすべての組み合わせ(\(=X\))」は、365種類のものから重複を許して23個を並べる順列、いわゆる「重複順列」で、
です。一方、「23人のクラスの、誕生日がすべて違う組み合わせ(\(=Y\))」は、出席番号1番の人は 365通り、2番の人は 364通り、3番の人は 363通りで、以下、出席番号23番の人は 343通り(\(=\:365\:-\:23\:+\:1\))です。これを全部掛け合わせたのが \(Y\) ですが、これは 365通りのものから23個を選んで並べる順列であり、「順列\(\cdot\)組み合わせ」の記号を用いると、
です。\(X\) と \(Y\) の値を実際に計算してみると、両方とも59桁の数字になり、
です。従って、\(\dfrac{Y}{X}\) を計算すると、
となります。つまり、
となって、誕生日が同じ人がいる確率は確かに 0.5 を超えます。ちなみに「誕生日が同じ人がいる確率が 0.9 を超えるクラスの人数」を探ってみると、
なので、その答は 41人ということになります。誕生日は365通りです。41人というと、その約9分の1です。9分の1の人数を集めるとほぼ確実に誕生日が同じ人がいるというのは、23人と並んでかなり意外ではないでしょうか。このあたりの状況をグラフにしたのが下図です。
カジノ・ゲーム
誕生日のパラドックスを応用した、次のような "カジノ・ゲーム" を想定しても、"直感との乖離" が明らかになると思います。あなたはカジノで掛け金を積んでディーラーと対決します。

このゲームは、あなた(客)にとって有利でしょうか、それとも不利でしょうか。あなたが勝つ確率はどれぐらいでしょうか。
あなたは(おそらく)次のように考えると思います。2回目に「引いてはいけないカード」は1枚しかない。これは自分が圧倒的に有利である。また3回目も2枚だけを引かなければよい。つまり有利だ。最後の10回目を考えると「引いてはいけない」カードが9枚あるが「引いてもいいカード」は44枚もある。確かに9枚のどれかを引いてしまうこともあるだろうが、まだ随分自分が有利のはずである。もちろん、1回のチャレンジだったら負けることもあるだろうが、10回もやれば自分がかなり有利なはずだ ・・・・・・。
しかし、事実は違います。誕生日のパラドックスにより、この賭は客が不利です。客が引いた10枚の全部が違うカードである確率は、さきほどの記号を使うと、
です。この値を計算してみると、
となり、客が勝つ確率は 40% しかありません。ディーラーは客の1.5倍の確率で勝つのです。この賭は引く枚数が少ないほど客が有利になるのは当然なので、枚数を変えて計算してみると、
となって、引く枚数が9枚でもまだ客が不利です。8枚になって初めて客が有利になることが分かります。誕生日のパラドックスの言葉を使うと「53枚のカードから1枚引いて戻す操作を9回繰り返すと、一致するカードを引く確率が 0.5を超える」となります。
8枚で客が有利、9枚で客が不利というこの結果は直感と合っているでしょうか。「23人のクラスには同じ誕生日の人が 0.5 以上の確率でいる」よりは意外性がありませんが、それでもまだ直感に合わない感じがします。
サイコロ・ゲーム
カードはジョーカーも含めて 53枚あります。この 53 という数字をもっと減らしたらどうなるでしょうか。次のような「サイコロ・ゲーム」を考えてみます。
2回だと有利なことはすぐに分かります。4回だと、運よく3回まで同じ目が出なかったとして、4回目に出すべき目は3種であり、つまり半分の確率で3回目までとは違う目が出ます。ただし2回目、3回目で同じ目が出ることがあるので、それを勘案するとトータルとしては不利です。4回だと不利というのも直感と合っているでしょう。
では、3回ならどうか。直感では「微妙だが、有利」ではないでしょうか。実際に計算してみると
となり、確かに(わずかに)有利なことが分かります。
以上をまとめると、モノのパターンの数が
となると思います。この理由を数学的に探っていきます。
誕生日関数を近似する
はじめの方で、
と定義しましたが、これを一般化して
とします。この \(B(n,k)\) を「誕生日関数」と呼ぶことにします。変数が2個の関数です。そうすると、
となります。この \(\ol{\,B\,}(n,k)\) を \(n\) と \(k\) の簡便な多項式で近似することを考えます。\(\ol{\,B\,}(n,k)\) を展開すると、
となります。ここで、\(x\) の絶対値が \(1\) よりかなり小さく \(0\) に近いとき、
と近似できることを利用します。\(f(x)=e^x\) とおくと
なので、\(1+x\) は \(x=0\) における \(e^x\) の接線の方程式になっています。この近似の精度をいくつかの値で試算してみると、
となり、\(x\) が \(0.2\) 程度でも誤差は \(2\%\) 弱で、\(x\) が小さくなると誤差は急速に小さくなります。ちなみにこの近似は \(e^x\) のマクローリン展開、
の第2項までに相当します。マクローリン展開は高校数学では出てこないと思いますが、意味するところは明快です。この、
とする近似で \(\ol{\,B\,}(n,k)\) を表現したものを "第1近似" と呼ぶことにし、それを \(\ol{\,B\,}_{app_1}(n,k)\) で表すと、\(\ol{\,B\,}(n,k)\) の展開式から、
となります。従って、
となって、誕生日関数の近似式ができました。
誕生日の定理
以上の計算結果を踏まえて、誕生日のパラドックスに関する命題を導きます。つまり、
という問いの答がどうなるかという命題です。この答の数を \(P_5\) とすると、誕生日の場合(\(n=365\))\(P_5=23\) です。\(B_{app_1}(n,k)\) を使って、
の不等式を解くと \(P_5\) が求まりますが、\(P_5\) を簡便な式で求めるため、\(\ol{\,B\,}(n,k)\) の "第2近似" を、
とします。つまり、\(\ol{\,B\,}_{app_1}(n,k)\) の \(k(k-1)\) を \(k^2\) で置き換えたものです。 この "第2近似" の誤差は、
程度です。この第2近似を使うと、\(P_5\) を求める不等式は、
となります。これを解くと、
となります。定数の計算をすると、おおよそ、
となります。つまり次の「誕生日の定理」が成り立ちます。
近似計算をしているので、\(1.177\) のところは \(1.18\) でもよいでしょう。試しに、誕生日のパラドックスとカジノ・ゲームを例に誕生日の定理を使ってみると、
となり、それぞれ 23 と 9 で一致するペアが存在する確率が 50% を超えることがわかります。これは前にやった正確計算と合致しています。ちなみに、
という問いの答えを \(P_9\) とすると、
となります。これを解くと、
となり、定数の計算をすると、おおよそ、
となります。\(2.146\) は \(1.177\) の約 \(1.8\) 倍です。従って、次の「誕生日の定理(補足)」が成り立ちます。
誕生日のパラドックスとカジノ\(\cdot\)ゲームで計算してみると、
となり、それぞれ 41 と 16 で一致するペアが存在する確率が 90% を超えることがわかります。これは前にやった正確計算と合致しています。
このように、\(\bs{n}\)通りのパターンがあるものを何個集めたら一致するペアがある確率が一定数を超えるか、という質問の答えは、\(\bs{n}\) に比例するのではなく \(\bs{n}\)の平方根に比例します。\(\bs{n}\) が大きくなっても \(\bs{n}\)の平方根はさほど大きくならない。このあたりに誕生日のパラドックスの原因がありそうです。
5色のサイコロ
誕生日よりもっとパターンの多い例で考えてみます。
誕生日の定理を使って答を計算してみると
となります。つまり、
というわけです。出る目のパターンは 7776通りもあります。それでも、100回そこそこで同じパターンが現れる確率が50%を越すことが分かります。なお厳密計算をすると、確率 50% と 90% を超えるのはそれぞれ 105回と 189回です。
誕生日のパラドックス
5色のサイコロのように、パターンの数が多いほど同一パターンが現れるに必要な個数は、パターンの数に比べて小さくなります。しかし "数が多いほど" と言っても、その多さが直感的に理解できないとパラドックスとは感じられないはずです。
その意味で、誕生日のパターンが 365 というのは、適度に多い数で、誰もがその多さの程度を直感的に理解できる数です。そこに誕生日のパラドックスの意味があるのでした。
「高校数学で理解する・・・」というタイトルで、今まで5つの記事書きました。
| 高校数学で理解するRSA暗号の数理 | |
| 高校数学で理解する公開鍵暗号の数理 | |
| 高校数学で理解する楕円曲線暗号の数理 |
ですが、いずれも現代のインターネット社会における情報通信の基礎となっている "公開鍵暗号" の数理を、高校レベルの数学だけを前提知識として述べたものでした。
今回はその「高校数学で理解する\(\cdot\cdot\cdot\)」の続きですが、公開鍵暗号よりは断然軽い話題で、No.149「我々は直感に裏切られる」でとりあげた「誕生日のパラドックス」をもう一度、考察します。No.149 では「バースデー\(\cdot\)パラドックス」と書いたもので、よく知られた話です。
誕生日のパラドックス
誕生日のパラドックスとは、
誕生日のパラドックス 23人のクラスで誕生日が同じ人がいる確率は 0.5 を越える |
というものです。一瞬、えっ! と思ってしまいますが、数学的には全く正しい。普通、パラドックスと言うと「絶対に不可能なことが可能なように思えてしまう」ないしは、「あり得ないことがあり得るように見えてしまう」ことを言いますが、この誕生日のパラドックスはそれとは違う「疑似パラドックス」です。つまり、
疑似パラドックス
| 直感に反するが、数学的には矛盾がなく正しい命題 |
です。以下、1年を365日に固定して考えることにし、
\(B(365,23)\)
| 23人のクラスで誕生日が同じ人がいる確率 |
\(\ol{\,B\,}(365,23)\)
| 23人のクラスで誕生日が同じ人がいない確率 |
の記号を使うと、
\(B(365,23)=1-\ol{\,B\,}(365,23)\)
なので、\(\ol{\,B\,}(365,23)\) を計算すればよいことになります。「23人のクラスの、誕生日のすべての組み合わせ(\(=X\))」は、365種類のものから重複を許して23個を並べる順列、いわゆる「重複順列」で、
\(X=365^{23}\)
です。一方、「23人のクラスの、誕生日がすべて違う組み合わせ(\(=Y\))」は、出席番号1番の人は 365通り、2番の人は 364通り、3番の人は 363通りで、以下、出席番号23番の人は 343通り(\(=\:365\:-\:23\:+\:1\))です。これを全部掛け合わせたのが \(Y\) ですが、これは 365通りのものから23個を選んで並べる順列であり、「順列\(\cdot\)組み合わせ」の記号を用いると、
\(Y={}_{365}\,P_{23}\)
です。\(X\) と \(Y\) の値を実際に計算してみると、両方とも59桁の数字になり、
\(\begin{eqnarray}
&&X=&\phantom{9}856516793,5315032123\\
&&&6814267844,3951526893\\
&&&5462236404,4189453125\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&Y=&\phantom{9}422008193,0209235987\\
&&&2395663074,9089572537\\
&&&4976070077,6448000000\\
\end{eqnarray}\)
です。従って、\(\dfrac{Y}{X}\) を計算すると、
\(\begin{eqnarray}
&&\ol{\,B\,}(365,23)&=\dfrac{{}_{365}P_{23}}{365^{23}}\\
&&&=\dfrac{Y}{X}\\
&&&=\:0.49270277\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&B(365,23)&=1-\ol{\,B\,}(365,23)\\
&&&=\:0.50729723\\
\end{eqnarray}\)
となって、誕生日が同じ人がいる確率は確かに 0.5 を超えます。ちなみに「誕生日が同じ人がいる確率が 0.9 を超えるクラスの人数」を探ってみると、
\(B(365,40)=0.89123180\)
\(B(365,41)=0.90315161\)
\(B(365,41)=0.90315161\)
なので、その答は 41人ということになります。誕生日は365通りです。41人というと、その約9分の1です。9分の1の人数を集めるとほぼ確実に誕生日が同じ人がいるというのは、23人と並んでかなり意外ではないでしょうか。このあたりの状況をグラフにしたのが下図です。
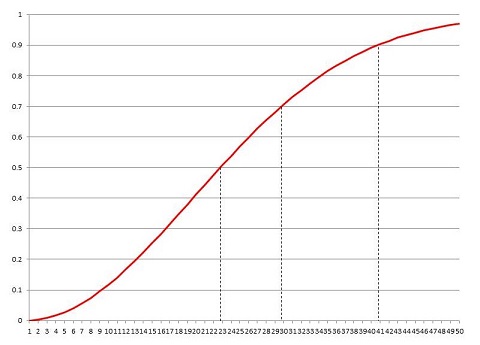
|
誕生日のパラドックス |
横軸はクラスの人数で、縦軸は少なくとも1組の誕生日が同じ生徒がいる確率。23人クラスで確率は 0.5 を超える。30人クラスで 0.7 を超え、41人クラスで 0.9 を超える。 |
カジノ・ゲーム
誕生日のパラドックスを応用した、次のような "カジノ・ゲーム" を想定しても、"直感との乖離" が明らかになると思います。あなたはカジノで掛け金を積んでディーラーと対決します。
|

このゲームは、あなた(客)にとって有利でしょうか、それとも不利でしょうか。あなたが勝つ確率はどれぐらいでしょうか。
あなたは(おそらく)次のように考えると思います。2回目に「引いてはいけないカード」は1枚しかない。これは自分が圧倒的に有利である。また3回目も2枚だけを引かなければよい。つまり有利だ。最後の10回目を考えると「引いてはいけない」カードが9枚あるが「引いてもいいカード」は44枚もある。確かに9枚のどれかを引いてしまうこともあるだろうが、まだ随分自分が有利のはずである。もちろん、1回のチャレンジだったら負けることもあるだろうが、10回もやれば自分がかなり有利なはずだ ・・・・・・。
しかし、事実は違います。誕生日のパラドックスにより、この賭は客が不利です。客が引いた10枚の全部が違うカードである確率は、さきほどの記号を使うと、
\(\ol{\,B\,}(53,10)\)
です。この値を計算してみると、
\(\begin{eqnarray}
&&\ol{\,B\,}(53,10)&=\dfrac{{}_{53}P_{10}}{53^{10}}\\
&&&=\dfrac{\:7075833,2701056000\:}{\:17488747,0365513049\:}\\
&&&=0.40459349\\
\end{eqnarray}\)
となり、客が勝つ確率は 40% しかありません。ディーラーは客の1.5倍の確率で勝つのです。この賭は引く枚数が少ないほど客が有利になるのは当然なので、枚数を変えて計算してみると、
\(\ol{\,B\,}(53,9)=\:0.48735125\)
\(\ol{\,B\,}(53,8)=\:0.57399147\)
\(\ol{\,B\,}(53,8)=\:0.57399147\)
となって、引く枚数が9枚でもまだ客が不利です。8枚になって初めて客が有利になることが分かります。誕生日のパラドックスの言葉を使うと「53枚のカードから1枚引いて戻す操作を9回繰り返すと、一致するカードを引く確率が 0.5を超える」となります。
ちなみに、「41人クラスでは同じ誕生日のペアがいる確率が 0.9 を超える」ことに相当する値、「53枚のカードから1枚引いて戻す操作を繰り返すとき、一致するカードを引く確率が 0.9 を超える回数」を計算すると、
なので、その答えは 16回となります。16という数字はカードの総数の3分の1以下ですが、それだけ引くとほぼ確実に同じカードを引いてしまうわけです。
\(\ol{\,B\,}(53,15)=\:0.11175468\)
\(\ol{\,B\,}(53,16)=\:0.08012600\)
\(\ol{\,B\,}(53,16)=\:0.08012600\)
なので、その答えは 16回となります。16という数字はカードの総数の3分の1以下ですが、それだけ引くとほぼ確実に同じカードを引いてしまうわけです。
8枚で客が有利、9枚で客が不利というこの結果は直感と合っているでしょうか。「23人のクラスには同じ誕生日の人が 0.5 以上の確率でいる」よりは意外性がありませんが、それでもまだ直感に合わない感じがします。
サイコロ・ゲーム
カードはジョーカーも含めて 53枚あります。この 53 という数字をもっと減らしたらどうなるでしょうか。次のような「サイコロ・ゲーム」を考えてみます。
あらかじめ決められた回数だけサイコロを振って、同じ目が出なければあなたの勝ちとします。サイコロを振る回数が、 \(\cdot\)2回 \(\cdot\)3回 \(\cdot\)4回 のとき、それぞれあなたは有利でしょうか。それとも不利でしょうか。 |

|
2回だと有利なことはすぐに分かります。4回だと、運よく3回まで同じ目が出なかったとして、4回目に出すべき目は3種であり、つまり半分の確率で3回目までとは違う目が出ます。ただし2回目、3回目で同じ目が出ることがあるので、それを勘案するとトータルとしては不利です。4回だと不利というのも直感と合っているでしょう。
では、3回ならどうか。直感では「微妙だが、有利」ではないでしょうか。実際に計算してみると
\(\ol{\,B\,}(6,3)=\dfrac{5}{9}\)
となり、確かに(わずかに)有利なことが分かります。
以上をまとめると、モノのパターンの数が
| ・ | 6 | → 直感どおり | |
| ・ | 53 | → 直感からずれる | |
| ・ | 365 | → 直感と合わない、意外 |
となると思います。この理由を数学的に探っていきます。
誕生日関数を近似する
はじめの方で、
\(B(365,23)\)
\(\ol{\,B\,}(365,23)\)
= 23 人のクラスで誕生日が同じ人がいる確率
\(\ol{\,B\,}(365,23)\)
= 23 人のクラスで誕生日が同じ人がいない確率
と定義しましたが、これを一般化して
\(B(n,k)\)
\(\ol{\,B\,}(n,k)\)
= \(n\) 通りのパターンがあるものを \(k\) 個集めたとき、一致するペアがある確率
\(\ol{\,B\,}(n,k)\)
= \(n\) 通りのパターンがあるものを \(k\) 個集めたとき、一致するペアがない確率
とします。この \(B(n,k)\) を「誕生日関数」と呼ぶことにします。変数が2個の関数です。そうすると、
\(B(n,k)=1-\ol{\,B\,}(n,k)\)
\(\ol{\,B\,}(n,k)=\dfrac{{}_nP_k}{n^k}\)
\(\ol{\,B\,}(n,k)=\dfrac{{}_nP_k}{n^k}\)
となります。この \(\ol{\,B\,}(n,k)\) を \(n\) と \(k\) の簡便な多項式で近似することを考えます。\(\ol{\,B\,}(n,k)\) を展開すると、
\(\begin{eqnarray}
&&\ol{\,B\,}(n,k)&=\dfrac{n_{n-1}(n-2)\:\cd\:(n-k+1)}{n^k}\\
&&&\\
&&&=\left(1-\dfrac{1}{n}\right)\left(1-\dfrac{2}{n}\right)\:\cd\:\left(1-\dfrac{k-1}{n}\right)\\
\end{eqnarray}\)
となります。ここで、\(x\) の絶対値が \(1\) よりかなり小さく \(0\) に近いとき、
\(e^x\fallingdotseq1+x\)
と近似できることを利用します。\(f(x)=e^x\) とおくと
\(\begin{eqnarray}
&&f(0)&=1\\
&&f^{'}(0)&=1\\
\end{eqnarray}\)
なので、\(1+x\) は \(x=0\) における \(e^x\) の接線の方程式になっています。この近似の精度をいくつかの値で試算してみると、
\(\begin{eqnarray}
&&\dfrac{e^{0.2}}{1+0.2}&=1.01783\\
&&\dfrac{e^{0.1}}{1+0.1}&=1.00407\\
&&\dfrac{e^{0.05}}{1+0.05}&=1.00121\\
&&\dfrac{e^{0.02}}{1+0.02}&=1.00019\\
&&\dfrac{e^{0.01}}{1+0.01}&=1.00005\\
\end{eqnarray}\)
となり、\(x\) が \(0.2\) 程度でも誤差は \(2\%\) 弱で、\(x\) が小さくなると誤差は急速に小さくなります。ちなみにこの近似は \(e^x\) のマクローリン展開、
\(e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\:\cd\)
の第2項までに相当します。マクローリン展開は高校数学では出てこないと思いますが、意味するところは明快です。この、
\(1+x\fallingdotseq e^x\)
とする近似で \(\ol{\,B\,}(n,k)\) を表現したものを "第1近似" と呼ぶことにし、それを \(\ol{\,B\,}_{app_1}(n,k)\) で表すと、\(\ol{\,B\,}(n,k)\) の展開式から、
\(\ol{\,B\,}_{app_1}(n,k)\)
\(=e^{-\frac{1}{n}}\cdot e^{-\frac{2}{n}}\cdot\:\cd\:\cdot e^{-\frac{k-1}{n}}\)
\(=e^{-\frac{k(k-1)}{2n}}\)
\(=e^{-\frac{1}{n}}\cdot e^{-\frac{2}{n}}\cdot\:\cd\:\cdot e^{-\frac{k-1}{n}}\)
\(=e^{-\frac{k(k-1)}{2n}}\)
となります。従って、
\(B_{app_1}(n,k)=1-e^{-\frac{k(k-1)}{2n}}\)
となって、誕生日関数の近似式ができました。
誕生日の定理
以上の計算結果を踏まえて、誕生日のパラドックスに関する命題を導きます。つまり、
n 通りのパターンがあるものを何個以上集めたら、一致するペアがある確率が0.5を超えるか
という問いの答がどうなるかという命題です。この答の数を \(P_5\) とすると、誕生日の場合(\(n=365\))\(P_5=23\) です。\(B_{app_1}(n,k)\) を使って、
\(0.5 < 1-e^{-\frac{P_5(P_5-1)}{2n}}\)
の不等式を解くと \(P_5\) が求まりますが、\(P_5\) を簡便な式で求めるため、\(\ol{\,B\,}(n,k)\) の "第2近似" を、
\(\ol{\,B\,}_{app_2}(n,k)=e^{-\frac{k^2}{2n}}\)
とします。つまり、\(\ol{\,B\,}_{app_1}(n,k)\) の \(k(k-1)\) を \(k^2\) で置き換えたものです。 この "第2近似" の誤差は、
| \(\ol{\,B\,}(53,9)\) | \(=0.48735125\) | |
| \(\ol{\,B\,}_{app_2}(53,9)\) | \(=0.46572917\) | |
| (誤差:\(4.4\%\)) |
| \(\ol{\,B\,}(365,23)\) | \(=0.49270277\) | |
| \(\ol{\,B\,}_{app_2}(365,23)\) | \(=0.48449048\) | |
| (誤差:\(1.7\%\)) |
程度です。この第2近似を使うと、\(P_5\) を求める不等式は、
\(0.5\: < 1-e^{-\frac{P_5^{\:2}}{2n}}\)
となります。これを解くと、
\(P_5 > \sqrt{2\mr{log}{2}}\sqrt{n}\)
となります。定数の計算をすると、おおよそ、
\(P_5 > 1.177\sqrt{n}\)
となります。つまり次の「誕生日の定理」が成り立ちます。
誕生日の定理 \(n\) 通りのパターンがあるものを 約 \(1.177\sqrt{n}\) 個集めると、一致するペアが存在する確率が \(50\%\) を越える |
近似計算をしているので、\(1.177\) のところは \(1.18\) でもよいでしょう。試しに、誕生日のパラドックスとカジノ・ゲームを例に誕生日の定理を使ってみると、
\(\begin{eqnarray}
&&1.177\sqrt{365}&=22.49\\
&&1.177\sqrt{53}&=8.57\\
\end{eqnarray}\)
となり、それぞれ 23 と 9 で一致するペアが存在する確率が 50% を超えることがわかります。これは前にやった正確計算と合致しています。ちなみに、
n 通りのパターンがあるものを何個以上集めたら、一致するペアがある確率が0.9を超えるか
という問いの答えを \(P_9\) とすると、
\(0.9\: < 1-e^{-\frac{P_9^{\:2}}{2n}}\)
となります。これを解くと、
\(P_9 > \sqrt{2\mr{log}{10}}\sqrt{n}\)
となり、定数の計算をすると、おおよそ、
\(P_9 > 2.146\sqrt{n}\)
となります。\(2.146\) は \(1.177\) の約 \(1.8\) 倍です。従って、次の「誕生日の定理(補足)」が成り立ちます。
誕生日の定理(補足) \(n\) 通りのパターンがあるものを約\(2.146\sqrt{n}\) 個集めると、一致するペアが存在する確率が \(90\%\) を越える。 「一致するペアが存在する確率が \(50\%\) を越える個数」の約\(1.8\)倍の個数を集めると、確率は \(90\%\) を超えて、ほぼ確実に一致するペアが存在する。 |
誕生日のパラドックスとカジノ\(\cdot\)ゲームで計算してみると、
\(\begin{eqnarray}
&&2.146\sqrt{365}&=40.99\\
&&2.146\sqrt{53}&=15.62\\
\end{eqnarray}\)
となり、それぞれ 41 と 16 で一致するペアが存在する確率が 90% を超えることがわかります。これは前にやった正確計算と合致しています。
このように、\(\bs{n}\)通りのパターンがあるものを何個集めたら一致するペアがある確率が一定数を超えるか、という質問の答えは、\(\bs{n}\) に比例するのではなく \(\bs{n}\)の平方根に比例します。\(\bs{n}\) が大きくなっても \(\bs{n}\)の平方根はさほど大きくならない。このあたりに誕生日のパラドックスの原因がありそうです。
5色のサイコロ
誕生日よりもっとパターンの多い例で考えてみます。
5つのサイコロがあり、それぞれ白、赤、青、緑、黒に色分けされています。 この5色のサイコロを同時に振ったとき、出る目のパターンは、\(6^5=7776\) 通りです。 では、5色のサイコロを同時に振ることを何回繰り返したら、全く同じパターンが現れるでしょうか。 |

|
白、赤、青、緑、黒の5つのサイコロを同時に振ると、出る目のパターンは 7776 通りになる。 |
誕生日の定理を使って答を計算してみると
\(\begin{eqnarray}
&&1.177\sqrt{7776}&=103.79\\
&&2.146\sqrt{7776}&=189.24\\
\end{eqnarray}\)
となります。つまり、
| 5色のサイコロを104回振ると、同じパターンが現れる確率が50%を超える。 | |
| 5色のサイコロを190回振ると、その確率は90%を超え、ほぼ確実に同じパターンが現れる。 |
というわけです。出る目のパターンは 7776通りもあります。それでも、100回そこそこで同じパターンが現れる確率が50%を越すことが分かります。なお厳密計算をすると、確率 50% と 90% を超えるのはそれぞれ 105回と 189回です。
誕生日のパラドックス
5色のサイコロのように、パターンの数が多いほど同一パターンが現れるに必要な個数は、パターンの数に比べて小さくなります。しかし "数が多いほど" と言っても、その多さが直感的に理解できないとパラドックスとは感じられないはずです。
その意味で、誕生日のパターンが 365 というのは、適度に多い数で、誰もがその多さの程度を直感的に理解できる数です。そこに誕生日のパラドックスの意味があるのでした。
2021-11-27 11:24
nice!(0)



