No.312 - ダブル・レインボー [アート]
先日、新聞を読んでいたらダブル・レインボー(二重の虹。二重虹)のことが出ていました。そして、以前にこのブログで引用した絵画を思い出しました。今回はそのことを書きます。
二重の虹
まず、ダブル・レインボーについて書かれた朝日新聞の記事を引用します。以降の引用において下線は原文にはありません。
ダブル・レインボーは私も2~3度、見たことがあります。最近では2年ほど前です。早朝、海岸の遊歩道を朝日を背に西に向かって歩いているときに、くっきりと見えました。雨上がりの、湿気のある空気がたちこめている雰囲気だったと記憶しています。
引用した記事には、ダブル・レインボーが見える条件として「豊富な水滴」「強い太陽光」とあります。確かにそうだと思いますが、私の感じではもう一つ条件があって、それは「暗い背景」だと思います。外側の副虹は内側の主虹に比べて輝度が随分低いわけです。記事にあるように、太陽光が水滴で2回反射するからです。従って、ダブル・レインボーの背景の空(や風景)は、できるだけ暗い方が虹が見えやすい。
私の経験した海岸の遊歩道でも、東の空は雲もなく明るいのに、虹が見える西の空は薄灰色の雲が立ちこめていました。黒雲だともっとはっきりと見えたのでしょう。普通の虹でも背景が重要だと思いますが、輝度が低いダブル・レインボー(の外側の虹)では一層重要である、そう思います。
ともかく、ダブル・レインボーは珍しい現象です。記事の見出しである「5分間の奇跡」の "奇跡" というのは少々言い過ぎだと思いますが、日常生活では滅多にお目にかかれない気象現象なのは確かでしょう。以下にダブル・レインボーが見える原理を示した図を引用しておきます。
このダブル・レインボーで思い出す芸術作品が、パリのオルセー美術館が所蔵しているミレーの『春』という作品です。
ジャン = フランソワ・ミレー
左上に虹が描かれています。うっかりすると見過ごしそうですが、この虹はダブル・レインボーです。
近景は畑でしょうか。小道があって木立があります。遠方には林が見える。画面の下や左の方は暗いが、近景の半分から向こうの林にまで光が当たっています。雨上がりの光景なのでしょう。遠方の空には、雨を降らせたと思われる黒雲が立ちこめ、空は暗い。その黒雲を背景に、かすかに副虹が見えるダブル・レインボーがかかっています。黒雲の薄暗さが虹を引き立てていて、この雰囲気はダブル・レインボーを実際に見た経験とも合っています。虹の位置関係からすると、背後から強い光があたっているはずです。それは夕日を思わせます。
この絵の題名は『春』なので、春の情景なのでしょう。だけど、何となく幻想的な雰囲気です。手前から遠方に「暗・明・暗」と変化していて、暗と明の世界の同居というか、2つの世界の狭間の光景のような感じがあります。
そして ・・・・・・。
よく見ると、奥の木立のそばに人物が描かれています。さらにもっとよく見ると、空には白い鳥が飛んでいる。これについて三菱一号館美術館の上席学芸員、安井裕雄氏が日本経済新聞にコラムを書いていました。
この絵には、うっかりすると見過ごしてしまいそうなアイテムが3つ描かれています。① ダブル・レインボー、② 人物、③ 鳥、の3つです。そして三菱一号館美術館 上席学芸員の安井氏によると、人物はミレーの腕の中で息を引き取ったテオドール・ルソーであり、鳥は天へと召されていくルソーの魂の象徴だというのです。テオドール・ルソーの没年は1867年です(55歳)。つまりこの絵はミレーが、亡くなったルソーの思い出を込めて描いたということになります。
とすると、これは少々複雑な絵です。バルビゾンのミレー家の裏の畑という現実の光景がベースなのだろうけれど、そこに幻想の光景が重ね合わされている。この複雑性が見る人の想像力を刺激するのでしょう。その刺激を受けた一人が黒澤明監督です。
黒澤 明
ミレーの『春』に触発された映画の一シーンがあります。黒澤明監督(1910-1998)の『夢』(1990)の一場面です。『夢』は8話からなるオムニバス映画で、その第1話が『日照り雨』です。その1シーンがこの映画のポスターになりました。
近景は美しい花畑で、遠くには暗い山と空、その間をつなぐようにかかる虹、そこに向かうように少年が立っています。このシーンがミレーの『春』へのオマージュです。その『日照り雨』は、次のような話です。
これを教訓話として考えると「人間は自然を乱すことなく、人間は自然界の掟に従って生きなければならない」ということでしょう。しかしそういう風に考えるよりも、これは黒澤監督の夢の実写化です。"不気味さ・怖さ" と "美しさ" が入り交じった幻想の世界と考えておけばよいのだと思います。
そこで、もう一度、ミレーの『春』をみると、手前は暗いがその向こうから林までに光が当たっています。まるでそのあたりがスポットライトに照らされているようです。これは虹の見える条件(=背後からの強い光)とはちょっと違う感じがする。
黒澤監督は、ミレーの『春』は現実の光景ではない、幻想の光景だと感じたのではないかと思います。『夢』は、黒澤監督が見た夢を映像化したものです。当然、現実そのものではないファンタジーの世界です。それがミレーの『春』とシンクロした。黒澤監督はもともと画家志望です。自作を展覧会に出品したこともあります。映画監督になってからも、絵コンテを自ら大量に描いたことで有名です。ミレーの絵が好きだったのかどうかは知りませんが、絵画から何かを感じることには長けていたと考えられます。
話を、ダブル・レインボーに戻します。しかしなぜ『春』に、滅多に見ることがないダブルレインボーが "微かに" 描かれているのでしょうか。黒澤明監督は "一重の普通の虹" で映像化しています。『春』も普通の虹でよいはずです。ここに描かれたダブル・レインボーも幻想の光景なのでしょうか。
しかし、これは現実の光景からヒントを得たのだと考えられます。つまり画家は、バルビゾンの自宅の裏庭から畑ごしにダブルレインボーを見たのだと推察します。というの、も『春』と構図がほぼ同じの『虹』という絵が残っているからです。
パステルで描かれたダブル・レインボー
その『春』とほぼ同じ構図のパステル画が、ポルトガルの首都・リスボンのグルベンキアン美術館にあります。No.192「グルベンキアン美術館」で引用しましたが、ここに再掲します。
この絵の題名は『虹』です。その題名どおり、ダブル・レインボーがくっきりと描かれている。これは実際に画家が自宅の裏の畑の方向を見た光景がもとになっていると考えられます。ミレーは、奇跡とは言わないまでも、滅多に出現しないダブル・レインボーを自宅から見て感じ入るところがあった。
このパステル画は、油彩画の『春』とほぼ同じ構図です。ただ、違いもあります。まず、奥の木立へと続く小道が描かれていません。また、空を飛ぶ白い鳥もいない。ただし、奥の木立のそばに小さく人物が描かれているところは共通しています。
ダブル・レインボーないしはもっと一般的に虹が、フランスでどういう象徴性で考えられているのかは知りません。しかし常識的に考えて悪い意味ではないと想像します。意味があるとしたら「幸運」とか「吉兆」でしょう。しかも滅多に見られないダブル・レインボーとなると、その象徴性が倍加されるはずです。
ミレーは珍しいダブル・レインボーを自宅の裏の畑から見て、亡くなったテオドール・ルソーの魂に重ね合わせたのではないでしょうか。だから奥の木立のそばにそっと人物(=ルソー)を描き込んだ。
画家が同じ構図のパステル画と油絵を制作するという場合、パステル画が先行すると考えるのが普通でしょう。パステル画を制作し、それをもとに油絵バージョンを描く。ミレーの『虹』と『春』の2作の場合もそうだったのではと想像します。
そして油絵にするとき、画家は2つのアイテムを追加した。一つは白い3羽の鳥で、これは天国に召されたルソーの魂です。そしてもう一つは、手前から人物のそばの木立へと続く小道です。この道はミレーとルソーの "絆" を象徴しているのではと思います。と同時に、ダブル・レインボーを画題の中心ではなく、構図の中に盛り込まれた1つの要素の位置づけにした。
オルセー美術館の公式サイトによると、この『春』は、テオドール・ルソーのパトロンだったフレデリック・アルトマンという人の依頼で制作された「四季、4部作」の一枚です(完成は1873年)。そして、『夏』『秋』『冬(未完)』の3作は "ミレーらしい" 農民の農作業が画題ですが、『春』だけは違っていて(一見すると)風景画です。しかしその「一見すると風景画」に秘密がある。
"春" は自然と生命が息を吹き返す時期であり、四季の始まりです。亡くなったテオドール・ルソーの思い出として描くには、"春" がピッタリだったのだと思います。
本文の冒頭に引用した朝日新聞のダブル・レインボーの写真は2021年4月8日のものでしたが、それから1ヶ月もたたない2021年5月2日の日本経済新聞(NIKKEI The STYLE)に虹の写真が掲載されました。「虹が立つ草原を行く」と題されたもので、タンザニアのセレンゲティ国立公園で撮影されたものです。草原を行く「ヌーの群れ」と「虹」のツーショット写真です。
この写真をよく見ると、実はうっすらと副虹が写っているのですね。ほんの微かですが ・・・・・・。つまり、ダブル・レインボーの写真ということになります。日経の読者の方も、気がつかなかった人が多いのではないでしょうか。
この写真でよく分かるのは「ダブル・レインボーは程度問題」ということです。くっきりと見える場合もあれば(=滅多にない)、全く見えないこともあり(=ほとんどの場合)、その間には無限の段階がある。我々も虹を見たとき、実は外側にある、ほんの微かな副虹を見逃していることがあるのではないでしょうか。そう感じさせるセレンゲティ国立公園の写真でした。
二重の虹
まず、ダブル・レインボーについて書かれた朝日新聞の記事を引用します。以降の引用において下線は原文にはありません。
|
ダブル・レインボーは私も2~3度、見たことがあります。最近では2年ほど前です。早朝、海岸の遊歩道を朝日を背に西に向かって歩いているときに、くっきりと見えました。雨上がりの、湿気のある空気がたちこめている雰囲気だったと記憶しています。
引用した記事には、ダブル・レインボーが見える条件として「豊富な水滴」「強い太陽光」とあります。確かにそうだと思いますが、私の感じではもう一つ条件があって、それは「暗い背景」だと思います。外側の副虹は内側の主虹に比べて輝度が随分低いわけです。記事にあるように、太陽光が水滴で2回反射するからです。従って、ダブル・レインボーの背景の空(や風景)は、できるだけ暗い方が虹が見えやすい。
私の経験した海岸の遊歩道でも、東の空は雲もなく明るいのに、虹が見える西の空は薄灰色の雲が立ちこめていました。黒雲だともっとはっきりと見えたのでしょう。普通の虹でも背景が重要だと思いますが、輝度が低いダブル・レインボー(の外側の虹)では一層重要である、そう思います。
ともかく、ダブル・レインボーは珍しい現象です。記事の見出しである「5分間の奇跡」の "奇跡" というのは少々言い過ぎだと思いますが、日常生活では滅多にお目にかかれない気象現象なのは確かでしょう。以下にダブル・レインボーが見える原理を示した図を引用しておきます。
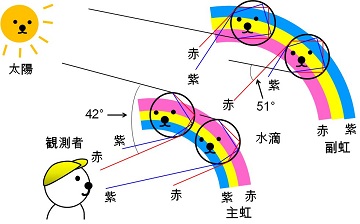
|
ダブル・レインボーが見える原理 |
光の反射によってできる光線の角度は、主虹(1回反射)が約42度、2回反射した副虹は約51度で、副虹の方が角度が大きい。従って副虹が外側に見える。気象庁の荒木健太郎博士の Twitter より引用した。ちなみに荒木博士は新海誠監督の「天気の子」の気象監修をされた方である(No.271)。 |
このダブル・レインボーで思い出す芸術作品が、パリのオルセー美術館が所蔵しているミレーの『春』という作品です。
ジャン = フランソワ・ミレー

|
ジャン = フランソワ・ミレー (1814-1875) 「春」(1868-73) |
オルセー美術館 (フランス、パリ) |
左上に虹が描かれています。うっかりすると見過ごしそうですが、この虹はダブル・レインボーです。
近景は畑でしょうか。小道があって木立があります。遠方には林が見える。画面の下や左の方は暗いが、近景の半分から向こうの林にまで光が当たっています。雨上がりの光景なのでしょう。遠方の空には、雨を降らせたと思われる黒雲が立ちこめ、空は暗い。その黒雲を背景に、かすかに副虹が見えるダブル・レインボーがかかっています。黒雲の薄暗さが虹を引き立てていて、この雰囲気はダブル・レインボーを実際に見た経験とも合っています。虹の位置関係からすると、背後から強い光があたっているはずです。それは夕日を思わせます。
この絵の題名は『春』なので、春の情景なのでしょう。だけど、何となく幻想的な雰囲気です。手前から遠方に「暗・明・暗」と変化していて、暗と明の世界の同居というか、2つの世界の狭間の光景のような感じがあります。
そして ・・・・・・。
よく見ると、奥の木立のそばに人物が描かれています。さらにもっとよく見ると、空には白い鳥が飛んでいる。これについて三菱一号館美術館の上席学芸員、安井裕雄氏が日本経済新聞にコラムを書いていました。
|
この絵には、うっかりすると見過ごしてしまいそうなアイテムが3つ描かれています。① ダブル・レインボー、② 人物、③ 鳥、の3つです。そして三菱一号館美術館 上席学芸員の安井氏によると、人物はミレーの腕の中で息を引き取ったテオドール・ルソーであり、鳥は天へと召されていくルソーの魂の象徴だというのです。テオドール・ルソーの没年は1867年です(55歳)。つまりこの絵はミレーが、亡くなったルソーの思い出を込めて描いたということになります。
とすると、これは少々複雑な絵です。バルビゾンのミレー家の裏の畑という現実の光景がベースなのだろうけれど、そこに幻想の光景が重ね合わされている。この複雑性が見る人の想像力を刺激するのでしょう。その刺激を受けた一人が黒澤明監督です。
黒澤 明
ミレーの『春』に触発された映画の一シーンがあります。黒澤明監督(1910-1998)の『夢』(1990)の一場面です。『夢』は8話からなるオムニバス映画で、その第1話が『日照り雨』です。その1シーンがこの映画のポスターになりました。

|
黒澤明監督作品 「夢」(1990) |
近景は美しい花畑で、遠くには暗い山と空、その間をつなぐようにかかる虹、そこに向かうように少年が立っています。このシーンがミレーの『春』へのオマージュです。その『日照り雨』は、次のような話です。
立派な門構えの家から少年が遊びに出ようとしたとき、太陽は出ているのに急に雨が降り出した。少年は母親から「こんな日照り雨の日には狐の嫁入りがある。狐はそれを見られるのが嫌だから、見てしまうと恐ろしいことが起こりますよ」と警告される。
余計に好奇心に駆られた少年は森に分け入り、狐の嫁入りを見てしまう。そして家に帰ったとき、門には母親が恐い顔をして立っていて、少年に短刀を差し出した ・・・・・・。
余計に好奇心に駆られた少年は森に分け入り、狐の嫁入りを見てしまう。そして家に帰ったとき、門には母親が恐い顔をして立っていて、少年に短刀を差し出した ・・・・・・。
これを教訓話として考えると「人間は自然を乱すことなく、人間は自然界の掟に従って生きなければならない」ということでしょう。しかしそういう風に考えるよりも、これは黒澤監督の夢の実写化です。"不気味さ・怖さ" と "美しさ" が入り交じった幻想の世界と考えておけばよいのだと思います。
そこで、もう一度、ミレーの『春』をみると、手前は暗いがその向こうから林までに光が当たっています。まるでそのあたりがスポットライトに照らされているようです。これは虹の見える条件(=背後からの強い光)とはちょっと違う感じがする。
黒澤監督は、ミレーの『春』は現実の光景ではない、幻想の光景だと感じたのではないかと思います。『夢』は、黒澤監督が見た夢を映像化したものです。当然、現実そのものではないファンタジーの世界です。それがミレーの『春』とシンクロした。黒澤監督はもともと画家志望です。自作を展覧会に出品したこともあります。映画監督になってからも、絵コンテを自ら大量に描いたことで有名です。ミレーの絵が好きだったのかどうかは知りませんが、絵画から何かを感じることには長けていたと考えられます。
余談ですが、絵画からインスピレーションを得た映画として、以前にリドリー・スコット監督の2作品を紹介しました。ジェロームの絵画『差し下おろされた親指』からヒントを得た映画『グラディエーター』(No.203)と、ホッパーの『ナイトホークス』に影響された『ブレードランナー』(No.288)です。黒澤監督とスコット監督は似ていて、2人とも画家としての素養があり、また自ら映画の絵コンテを作成しました。
話を、ダブル・レインボーに戻します。しかしなぜ『春』に、滅多に見ることがないダブルレインボーが "微かに" 描かれているのでしょうか。黒澤明監督は "一重の普通の虹" で映像化しています。『春』も普通の虹でよいはずです。ここに描かれたダブル・レインボーも幻想の光景なのでしょうか。
しかし、これは現実の光景からヒントを得たのだと考えられます。つまり画家は、バルビゾンの自宅の裏庭から畑ごしにダブルレインボーを見たのだと推察します。というの、も『春』と構図がほぼ同じの『虹』という絵が残っているからです。
パステルで描かれたダブル・レインボー
その『春』とほぼ同じ構図のパステル画が、ポルトガルの首都・リスボンのグルベンキアン美術館にあります。No.192「グルベンキアン美術館」で引用しましたが、ここに再掲します。

|
ジャン = フランソワ・ミレー 「虹」(1872/73) |
グルベンキアン美術館 (ポルトガル、リスボン) |
この絵の題名は『虹』です。その題名どおり、ダブル・レインボーがくっきりと描かれている。これは実際に画家が自宅の裏の畑の方向を見た光景がもとになっていると考えられます。ミレーは、奇跡とは言わないまでも、滅多に出現しないダブル・レインボーを自宅から見て感じ入るところがあった。
このパステル画は、油彩画の『春』とほぼ同じ構図です。ただ、違いもあります。まず、奥の木立へと続く小道が描かれていません。また、空を飛ぶ白い鳥もいない。ただし、奥の木立のそばに小さく人物が描かれているところは共通しています。
ダブル・レインボーないしはもっと一般的に虹が、フランスでどういう象徴性で考えられているのかは知りません。しかし常識的に考えて悪い意味ではないと想像します。意味があるとしたら「幸運」とか「吉兆」でしょう。しかも滅多に見られないダブル・レインボーとなると、その象徴性が倍加されるはずです。
ミレーは珍しいダブル・レインボーを自宅の裏の畑から見て、亡くなったテオドール・ルソーの魂に重ね合わせたのではないでしょうか。だから奥の木立のそばにそっと人物(=ルソー)を描き込んだ。
画家が同じ構図のパステル画と油絵を制作するという場合、パステル画が先行すると考えるのが普通でしょう。パステル画を制作し、それをもとに油絵バージョンを描く。ミレーの『虹』と『春』の2作の場合もそうだったのではと想像します。
そして油絵にするとき、画家は2つのアイテムを追加した。一つは白い3羽の鳥で、これは天国に召されたルソーの魂です。そしてもう一つは、手前から人物のそばの木立へと続く小道です。この道はミレーとルソーの "絆" を象徴しているのではと思います。と同時に、ダブル・レインボーを画題の中心ではなく、構図の中に盛り込まれた1つの要素の位置づけにした。
オルセー美術館の公式サイトによると、この『春』は、テオドール・ルソーのパトロンだったフレデリック・アルトマンという人の依頼で制作された「四季、4部作」の一枚です(完成は1873年)。そして、『夏』『秋』『冬(未完)』の3作は "ミレーらしい" 農民の農作業が画題ですが、『春』だけは違っていて(一見すると)風景画です。しかしその「一見すると風景画」に秘密がある。
"春" は自然と生命が息を吹き返す時期であり、四季の始まりです。亡くなったテオドール・ルソーの思い出として描くには、"春" がピッタリだったのだと思います。
| 補記:セレンゲティの虹 |
本文の冒頭に引用した朝日新聞のダブル・レインボーの写真は2021年4月8日のものでしたが、それから1ヶ月もたたない2021年5月2日の日本経済新聞(NIKKEI The STYLE)に虹の写真が掲載されました。「虹が立つ草原を行く」と題されたもので、タンザニアのセレンゲティ国立公園で撮影されたものです。草原を行く「ヌーの群れ」と「虹」のツーショット写真です。

|
「虹がたつ草原を行く タンザニア」 |
(日本経済新聞 2021.5.2) |
この写真をよく見ると、実はうっすらと副虹が写っているのですね。ほんの微かですが ・・・・・・。つまり、ダブル・レインボーの写真ということになります。日経の読者の方も、気がつかなかった人が多いのではないでしょうか。
この写真でよく分かるのは「ダブル・レインボーは程度問題」ということです。くっきりと見える場合もあれば(=滅多にない)、全く見えないこともあり(=ほとんどの場合)、その間には無限の段階がある。我々も虹を見たとき、実は外側にある、ほんの微かな副虹を見逃していることがあるのではないでしょうか。そう感じさせるセレンゲティ国立公園の写真でした。
2021-05-29 11:43
nice!(0)
No.311 - 高校数学で理解するRSA暗号の数理(2) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
4. RSA暗号の証明
RSA暗号において、暗号化・復号化に必要なのは公開鍵の \((e,\:n)\) と 秘密鍵の \(d\) であり、それらを生成するのに使った \(p\) と \(q\) は不要です。というより、\(p\) と \(q\) ないしは \((p-1)(q-1)\) が漏れると暗号が破られてしまうので、これらの数は鍵を生成した後は破棄(情報を安全に抹消)する必要があります。
以下に、上の「復号化の式」が成り立つことを証明します。まず合同式の累乗 1.2 を使って「暗号化の式」の両辺を \(d\) 乗すると、
となります。ここで、\(de\equiv1\:(\mr{mod}\:(p-1)(q-1))\) なので、\(de=k(p-1)(q-1)+1\) と表現できます。従って、
となります。累乗を分解すると、
です。一方、フェルマの小定理 3.1 により、
となります。合同式の累乗の定理 1.2 により、この式の両辺を \(q-1\) 乗すると、
が得られます。さらに、フェルマの小定理 3.1 により、
ですが、両辺を \(p-1\) 乗して、
となります。ここで、\(p\) と \(q\) は互いに素なので、1.5 の合同式の定理を \((3),\:(4)\)に適用すると、
を導くことができます。この式の両辺を 1.2 を使って \(k\) 乗すると、
であり、さらに両辺に合同式の乗算 1.1c を使って \(P\) をかけると、
となります。従って、\((1),\:(2),\:(5)\) を合わせると、
となり、RSA暗号の復号化の式が証明できました。
最小公倍数
以上の証明の過程を改めて振り返ってみると、「\(m\) が \((p-1)\) の倍数であり、かつ \((q-1)\) の倍数」であれば、RSA暗号は成立することが分かります。つまり「\(m\) が \((p-1)\) と \((q-1)\) の公倍数」であれば成立する。そのような \(m\) は、
の2通りに表現できます。すると、\(de\equiv1\:(\mr{mod}\:m)\) なので、
と2通りに表せます。ここから、
となって、平文が復元できます。この考察から分かるのは、\(m\) の最小値は「\((p-1)\) と \((q-1)\) の最小公倍数」ということです。最小公倍数を \(\mr{lcm}\) で表すと、
であればRSA暗号は成立します。そして一般に、
です。最大公約数・\(\mr{gcd}\) は「2. ユークリッドの互除法」を使って高速に計算できるので \(p\) や \(q\) が巨大数であっても最小公倍数・\(\mr{lcm}\) は計算可能です。
累乗の剰余を求めるアルゴリズム
RSA暗号では、暗号化と復号化で "累乗(冪乗)の剰余"(冪剰余と呼ぶ)を求める計算が出てきます。この計算で使う公開鍵 \((e,\:n)\) も秘密鍵 \(d\) も、また平文や暗号文も、実用的には\(10\)進数で\(300\)桁とか、そういった巨大な数です。
しかし巨大な数であっても、累乗の剰余計算ができるアルゴリズムがあります。その一つとして、ここでは「2分割法」で説明します。前回の「RSA暗号の例題」であげた、
の例で説明します。考え方としては「2.ユークリッドの互除法」と同じで、問題をより "小さな問題" に置き換えるというものです。つまり、\(133\)乗を求める代わりに
が求まったとしたら、\(C\) は、
で計算できます。さらに、その \(C_1\) は、
が求まったとしたら、
で計算できます。この2分割を次々と続けていくと、\(82\)の\(16\)乗、\(8\)乗、\(4\)乗、\(2\)乗、\(1\)乗を \(143\) で割った剰余が求まれば良いことになります。これを逆にたどって電卓で \(82^k\) \(\mathbf{mod}\) \(143\:(k=1,\) \(2,\) \(4,\) \(8,\) \(16,\) \(33,\) \(66,\) \(133)\) を順次計算してみると、
となり、答の \(4\) が求まりました。これをプログラム言語で記述すると次の通りです。
次はこのアルゴリズムの補足説明です。
\(e,\:n,\:d\) が10進数で300桁程度の巨大数とします。\(2^{1000}\) は約300桁の数なので、"2分割法" を使うと1000回程度の剰余計算を繰り返すこと答が求まります。この程度の計算は現在のコンピュータで可能です。ただし可能といっても 1000回の繰り返しはさすがに大変なので、実用的にはこれを高速化する手法がいろいろと開発されています。
「2. ユークリッドの互除法」で、公開鍵 \((e,\:n)\) の \(e\) と秘密鍵 \(d\) について、たとえ巨大数であっても高速に算出できることを書きました。それに加えて、暗号化・復号化で使われる「巨大数の累乗の剰余計算」も算出可能であり、RSA暗号の全体が "計算可能" であることが証明できました。
今までのまとめ
実用的な RSA暗号を構成するときに必要なのは、巨大な素数 \(p,\:q\) (\(10\)進数で150桁程度かそれ以上)です。こういった素数をどうやって作り出すか、また素数であることの判定をどうやってするかの計算手法については割愛します。
今までのRSA暗号についての説明全体をまとめると、以下の2点になるでしょう。
RSA暗号は現代の情報化社会にとって必須のものであり、社会インフラの重要な構成要素です。それは、数学が実用的に、かつ直接的に社会に役立っている例なのでした。
RSA暗号の成立性の証明はこれまでで尽きていますが、以降はRSA暗号と関係が深い「オイラー関数」を説明し、次に「オイラーの定理」を導いて、そこからRSA暗号の原理を導出します。まずその前提としての「中国剰余定理」です。
5. 中国剰余定理
5~6世紀頃の中国で成立した算術書『孫子算経』に、
という問題が書かれています。答は23ですが、これを一般化した定理を「中国剰余定理」と呼んでいます。
\(x_1\) と \(x_2\) の2つの解があったとします。すると、\(\mr{mod}\:m_1\) の式から、
となり、1.1b により、
となります。同様に、\(\mr{mod}\:m_2\) の式から、
が言えます。\(m_1\) と \(m_2\) は互いに素なので、ここで 1.5 を適用すると、
となります。以上のことは \(m_3\) から \(m_k\) までの全ての式についても言えるので、1.5 を順次適用することにより、
となります。つまり、
です。従って、解 \(x\) が複数あったとしても、それらは全て \(M\) を法として合同になります\((\)= 解は \(M\) を法として唯一)。
ここで
とおくと、\(\mr{gcd}(m_i,M_i)=1\) なので、2.3 により、
となる \(N_i\) が存在します。これを使って、
とおくと、それが解になります。なぜなら \(M_i\) の作り方から \(i\) 番目の項以外の項は \(m_i\) で割り切れるので、\(i\) 番目の項単独で「\(m_i\) を法として \(x\) と合同」になります。つまり、
です。一方、合同の性質の 1.4 において \(y=1\) とおくと 1.4 は、
となります。1.4 の「\(x\) が \(m\) と互いに素」という条件は、\(x\equiv1\:(\mr{mod}\:m)\) で満たされています。このことを適用すると、
という2つの条件から、
となります。これが全ての \(i\) について成り立つ。従って \(x\) が解であることが証明できました。また前段で証明したように全ての解は \(M\) を法として合同なので、\(x\) が唯一の解です。
中国剰余定理の意味を直感的に理解するために、\(k=2\)、\(m_1=3\)、\(m_2=4\)、\(M=12\) とし、\(x\) の全て解についての対応表を作ってみると次の通りになります。
この表をみると、\(0,\:1,\:2\) を繰り返し並べ(\(\mr{mod}\:3\) の列)、\(0,\:1,\:2,\:3\) を繰り返し並べると(\(\mr{mod}\:4\) の列)、\(3\) と \(4\) が互いに素の関係にあるために、\((0,\:0)\) は \(3\times4=12\) 回繰り返さないと現れないことが分かります。その間、\(x\) は\(12\)未満の全ての数をとり、 \((\mr{mod}\:3,\:\mr{mod}\:4)\) の全ての組み合わせが現れる。このため、 \((\mr{mod}\:3,\:\mr{mod}\:4)\) の1つの組み合わせに対して解 \(x\) が唯一になるわけです。この状況は \(k\) の値にかかわらず、\(m_i\:(1\leq i\leq k)\) のどの2つをとっても互いに素である限り変わらない。
「互いに素」なゆえに成立するこのイメージは、次のオイラー関数の証明に役立ちます。
6. オイラー関数
オイラー(1707-1783)はスイスのバーゼルに生まれた18世紀ヨーロッパの大数学者です。その業績は多岐に渡り、オイラー ・・・(何とか)という定理や公式、関数、数式、等式、図などがどっさりとあります。
以下の「オイラー関数」は、一般に関数名をギリシャ文字の \(\varphi\)(ファイ)で表記するので「オイラーの \(\varphi\) 関数」とも呼ばれています。数論ではたびたび出てくる関数です。
余談ですが、オイラーは20歳台後半で右目を失明しました。ここに掲載した肖像画にもそれが現れています。
まず 6.1a ですが、素数 \(p\) は \(p\) 未満のすべての自然数と互いに素です。従って、\(\varphi(p)=p-1\) です。
次に \(pq\) 以下の数で、\(p\) で割り切れるのは \(pq\) を含んで \(q\) 個、\(q\) で割り切れるのは \(pq\) を含んで \(p\) 個です。\(pq\) 以下の数の全体は \(pq\) 個なので、\(pq\) 以下の数で \(p\) でも \(q\) でも割り切れない数の個数(= \(pq\) と互いに素な数の個数)は、
です(6.1b)。上の式の1行目で、\(-p\) と \(-q\) には \(pq\) の分が重複しているので \(+1\) してあります。
さらに、\(p^{\al}\) 以下の数で、\(p\) の倍数は全て \(p^{\al}\) と共通の約数 \(p\) を持ちます。\(p^{\al}\) 以下の \(p\) の倍数の個数は \(p^{\al}\) を含んで、
なので、\(\varphi(p^{\al})\)は、
となります(6.1c)。このオイラー関数に関しては、次の「乗法性」が重要です。
一般に、関数のこのような性質を "乗法性"、このような関数を "乗法的関数" と呼んでいます。証明は3段階で行います。キーワードは「中国剰余定理」と「1対1対応」です。
第1段
\(0\leq i < m\)、\(0\leq j < n\) である数を選び \((i,j)\) のペアを作ります。\(i\) の選択肢は \(m\) 個、\(j\) の選択肢は \(n\) 個で、それぞれ独立して選ぶので、相異なる \((i,j)\) のペアの数は \(mn\) 個です。
仮定により \(m\) と \(n\) は互いに素です。従って、それぞれの \((i,j)\) のペアについて中国剰余定理 5.1 により、
を同時に満たす \(x\) が、\(mn\) を法として唯一存在します。つまり \(0\leq x < mn\) の範囲では \(x\) が一意に決まります。これは \(\bs{(i,j)}\) のペアに \(\bs{x}\) を対応づけられることを意味します。
逆に、\(0\leq x < mn\) である \(x\) を1つ選ぶと、それに対して \(\mr{mod}\:m\) と \(\mr{mod}\:n\) を求めて \((i,j)\) のペアと対応づけられる。つまり、
ことになります。
第2段
第1段の方法で作った「1対1に対応する \((i,j)\) のペアと \(x\)」については、
になります。なぜなら、もし \(x\) と \(m\) に共通の約数 \(a\) があったとすると(= \(a|x\) でかつ \(a|m\) )、中国剰余定理の前提から
と表せるので \(a|i\) となり、\(a\) が \(i\) と \(m\) の共通の約数にもなってしまって「\(i\) が \(m\) と素」という仮定に反するからです。全く同様に、
です。この2つを合わせると、
になります。「\(x\) が \(m\) と \(n\) の2つの数と素」であることは「\(x\) が \(mn\) と素」ということに他なりません。つまり、
です。その逆に「\(x\) が \(mn\) と素」であるなら「\(x\) は \(m\) と \(n\) の2つの数と素」です。そうすると中国剰余定理の前提から「\(i\) は \(m\) と素」でかつ「\(j\) は \(n\) と素」になります。つまり、まとめると、
ことになります。そして1対1の対応関係がつく集合の要素の数は等しい。ここが証明の根幹です。
第3段
オイラー関数の定義により、
です。\(i\) と \(j\) は独立に選んでいるので、
です。さらにオイラー関数の定義により、
になります。第2段で証明したように「\(i\) が \(m\) と素」で「\(j\) が \(n\) と素」である \((i,j)\) のペアと、\(mn\) と素である \(x\) は1対1の対応関係にあります。従ってその個数は等しく、
となって、証明が完成しました。
オイラー関数の乗法性を直感的に理解するために、中国剰余定理のところであげた表を使って \(\varphi(12)=\varphi(3)\varphi(4)\) のイメージを示したのが次です。\(●\) 印を付けたのはそれぞれ、\(12,\:3,\:4\) とは素な数です。
このオイラー関数の乗法性(6.2)と素数の累乗のオイラー関数値(6.1c)を用いると、一般の自然数 \(N\) のオイラー関数値を求めることができます。つまり素因数分解の一意性により、\(p_i\) を素数として、
と表現できます。ここでオイラー関数の乗法性(6.2)を繰り返して使うと、
となります。また、素数の累乗のオイラー関数値(6.1c)によって、
です。以上を合わせると、任意の数 \(N\) のオイラー関数値を求める公式は、
となります。つまり、\(N\) の素因数分解ができれば \(\varphi(N)\) は簡単に求まります。逆に言うと\(\bs{N}\) の素因数分解が困難なら \(\bs{\varphi(N)}\) を求めるのも困難になる。このことが RSA暗号が成立する背景となっています。
ちなみに、上のオイラー関数の公式の末尾の形(色を塗った部分)は、オイラーより以前に江戸時代の和算家・久留島義太(? - 1758)が発見しています。久留島義太は、関孝和、建部賢弘とともに三大和算家と呼ばれた人ですが、自分では書物を残すことがなかったので、業績は知人や弟子がまとめたものにしかありません。その一人、仙台藩の天文学者・戸板保佑の『久氏遺稿』の中に公式の記述ができます(鳴海 風「小説になる江戸時代の数学者」- 日本数学会「市民講演会」2007.3.31 による)。
その書物には \(\varphi(360)\) を求める例示があります(暗算でも出来ます)。つまり \(360=6\cdot6\cdot10\) なので素因数は \(2,\:3,\:5\) だけです。従って \(360\) を \(2\cdot3\cdot5=30\) で割って(答は \(12\))、\(1\cdot2\cdot4=8\) を掛けると \(\varphi(360)=96\) が求まる。このことが書かれています。この求め方は公式そのものです。
公式には \(p_i\) の累乗の部分(\(\al^i\))が全く現れません。ちょっと不思議な感じもする公式です。
日本の数学者の中には「久留島・オイラーの関数」と呼ぶ人もいます。"オイラー何とか" という名前の定理や公式はいろいろあるので、その方が分かりやすいかもしれません。
7. オイラーによるフェルマの小定理の一般化(オイラーの定理)
オイラー関数を使うと、オイラーが発見した「一般化されたフェルマの小定理」の証明ができます。
\(a\) や \(m\) に何らかの制約があるわけではなく、2つの数が「互いに素」という条件だけで成立する美しい定理です。これがフェルマの小定理の一般化であることは、\(p\) を素数として \(m=p\) とおけばフェルマの小定理そのものになることから分かります。
この証明を2段階に分けて行います。まず第1段階で \(m\) が素数の累乗の時に成立することを証明し、第2段階でその結果を使って \(m\) が一般の数の場合を証明します。
\(\al\) についての数学的帰納法で証明します。まず \(\al=1\) のときはフェルマの小定理そのものなので成立します。次に \(\al=k-1\:(k\geq2)\) のときに成立すると仮定します。つまり、
が成り立つとします。そうすると、ある数 \(b\) が存在して、
と表現できます。この式の左辺に 6.1c(素数の累乗のオイラー関数値)を適用すると、
となります。この両辺を \(p\) 乗し、右辺は2項定理で展開すると、
が得られます。この展開した右辺において、第2項は \({}_p\,C_1=p\) なので \(bp^k\) となり、\(p^k\) で割り切れます。また第3項以降は \(2\leq i\leq p\) として \({}_p\,C_ib^ip^{(k-1)i}\) と表せますが、\(k,\:i\geq2\) のとき \((k-1)(i-1)\geq1\) であり、この式を変形すると \((k-1)i\geq k\) となるので、第3項以降も \(p^k\) で割り切れます。つまり、展開した第1項の \(1\) 以外は \(p^k\) で割り切れることになります。従って、
となります。この結果、7.2 は \(\al=k-1\) のときに成立するなら \(\al=k\) のときにも成立することが証明でき、数学的帰納法が完成しました。
7.2 を使って 7.1 を証明します。\(p_i\) を相異なる素数とし、任意の数 \(m\) を、
とおきます。すると 7.2 により、\(1\leq i\leq r\) のそれぞれの \(i\) において、
が成立します。ここで、
とおくと、オイラー関数の乗法性(6.2)により、
となります。ここで、この式と合同式の累乗(1.2)を使って \((1)\) 式の両辺を \(\varphi\:(n_i)\) 乗すると、
が得られました。\((2)\) 式は \(1\leq i\leq r\) の \(i\) においてそれぞれ成立します。\(p_i\) は相異なる素数だったので、ここで 1.5 を順次適用すると、
となり、7.1 が正しいことが証明されました。
7.1 の証明の過程を振り返ってみると、次の 7.3 が成り立つことが分かります。
これは 7.1 の証明の後半(= 7.2 を使って証明する部分)からすぐに分かります。\(\psi(m)\) の定義から、
と書き表すことができます。一方 7.2 より、
が成り立ちます。この合同式の両辺を 1.2(合同式の累乗) に従って \(k_i\) 乗すると、
となり、これから、
が得られます。この式は \(1\leq i\leq r\) であるすべての \(i\) について成立し、また \(p_i^{\al_i}\) は互いに素なので、1.5 を順次適用することで、
となり、7.3 が証明できました。この証明の過程から、\(\psi(m)\) が最小公倍数でなくても、公倍数であれば成立することが分かります。なお \(\psi(m)\) は一般的な表記ではなく、ここで便宜上使った記号です。
オイラーの定理(7.1)と、オイラーの定理・その2(7.3)を
として具体的に書いてみると次の通りです。
オイラーの定理の別証明
いままでは「オイラー関数の乗法性」を導出して、それをもとにオイラーの定理(とその最小公倍数版)を証明しました。しかし単にオイラーの定理だけを証明したいのなら、以下のようにフェルマの小定理(3.1)のときと同じ論法で可能です。
\(n\) 以下の自然数で \(n\) と互いに素である \(\varphi(n)\) 個の数を、数列として、
と並べます。これらはすべて相異なる数です。次に \(n\) とは素な数 \(a\) を選び、数列の全部にかけ算をして新たな数列、
を作ります。そして、それぞれの数を \(n\) で割った剰余を \(r_i\) とします。つまり、
です。\(a\) も \(b_i\) も \(n\) と素なので \(r_i\) が \(0\) になることはなく、\(1\leq r_i < n\) です。そして、このようにすると\(\bs{r_i}\) は全て \(\bs{n}\) と素になります。なぜなら、剰余の式を、
とするとき、\(r_i\) と \(n\) に共通の約数があるなら、その約数は \(ab_i\) の約数にもなり「\(a\) も \(b_i\) も \(n\) と互いに素」という、そもそもの仮定に反するからです。
さらに、\(1\leq i,\:\:j\leq\varphi(n)\) である \(i,\:j\) について、
になります。なぜなら、もし \(r_i=r_j\) とすると、1.1b(合同式の減算)より、
です。仮定より \(a\) は \(n\) と互いに素なので 1.3 により(\(1.3\) で \(b=0\) の場合)、
となりますが、\(1\leq b_i,\:\:b_j\leq n\) なので、
となり、\(b_1,\:\:b_2,\:\:b_3,\:\cd\:,b_{\varphi(n)}\) が相異なる数という仮定に反してしまうからです。つまり\(i\neq j\) であれば、必ず \(r_i\neq r_j\) です。
ということは、\(\varphi(n)\) 個の数、\(r_i\) は「すべてが \(n\) とは素である、相異なる数」であり、つまり \(\varphi(n)\) 個の数、\(b_i\)を並び替えたものです。従って、
と書くとすると、
となります。そこで、1.1c(合同式の乗算)を上の \(\varphi(n)\) 個の合同式に適用して左辺と右辺を全てかけ合わせると、
が得られます。ここで、そもそもの定義から \(B\) は \(n\) と素なので 1.3 を使うと、
となって証明が完成しました。
8. RSA暗号の一般形
オイラー関数とオイラーの定理(オイラーによるフェルマの小定理の一般化)を用いると、RSA暗号(4.1)の一般形を次のように記述できます。
この一般形にすると、復号化の式の証明はいたってシンプルになります。\(de=k\varphi(n)+1\)とおくと、
となり証明できます。\(d,\:\:e\) を入れ替えても成り立ちます。最後の式の変形のところでは 7.1 と 1.2(合同式の累乗)を使っています。また 7.3 で証明したように、\(\varphi(n)\) の代わりに \(\psi(n)\) (= \(n\) の素因数それぞれのオイラー関数値の最小公倍数)としても、RSA暗号の一般形は成立します。
実際のRSA暗号は \(p\) と \(q\) を素数として \(n=pq\) とおいたものですが(6.1b)、数学的には \(n\) の素因数分解が分かると(素因数の累乗があってもよい) \(\varphi(n)\) はすぐに計算できるので(6. オイラー関数)暗号が構成できることになります。それが 8.1 の一般形の意味です。
しかし実用的な暗号のためには、素因数分解が困難であり(= \(n\) の素因数ができるだけ大きな数であり)、また暗号化・復号化の高速計算のためには \(n\) が小さいほど良いので、RSA暗号がその最適解なのでした。
全体のまとめ
最後に、RSA暗号についての説明全体をまとめると、以下のようになるでしょう。
この最後の点が、ここに「RSA暗号の数理」を掲載した目的でした。
補足1:デジタル署名
公開鍵暗号は暗号化の鍵を公開するため、誰でも通信相手の公開鍵を使って暗号を作れます。\(A\) さんと \(B\) さんが RSA暗号で暗号化通信をするとし、
とします。\(B\) から \(A\) にメッセージ \(M\) を送るには、
\(M^{\:\large e_{\overset{\:}{A}}}\equiv C\:\:(\mr{mod}\:n_A)\)
となる暗号文 \(C\) を送ればよく、\(C\) は \(d_A\) を知っている人しか解読できません。しかし、秘密鍵 \(d_A\) でしか解読できない暗号文は誰にでも作れます。つまり "なりすまし" ができる。\(A\) としては確かに \(B\) から来た暗号文だという確証が必要です。この確証を得る手段がないと、公開鍵暗号は成立しません。
その確証の手段が「デジタル署名」で、これは「ハッシュ関数」という技術にもとづいて作ります。
ハッシュ関数
ハッシュ関数は「任意長の入力データを固定長のハッシュ値に変換する関数」です。固定長は、たとえば256ビットです。これは暗号学的に信頼できる標準的なものがあって、アメリカ国立標準技術研究所(NIST)によって公開されている SHA-2、SHA-3 がその例です(SHA : Secure Hash Algorithm)。
ハッシュ関数には「入力メッセージのわずかな違いも、出力されるハッシュ値に大きな変化を及ぼす」という特性があります。SHA-2 の仕様の一つである SHA256(ハッシュ値:256ビット)で実際にやってみると、
A rolling stone gathers no moss.
A rolling stone gathers no moss
という2つの文章の違いは、最後にピリオドがあるか(前)、無いか(後)だけですが、2つのハッシュ値を16進数で並べて書くと、
4F73D0D6A45EF8B201707281CB421EE90413D4C1A5CA846BABF502A4BB202DE8 709EAFF33947303FBBC0810DD8F099C317BACC057F4BF91E081DB2B099457FCA
であり、全く違うことが分かります。もし入力データが同じであれば、ハッシュ関数は厳密に同じハッシュ値を出力します。
安全なハッシュ関数の条件は、まずハッシュ値から入力データを推測できないことです(=一方向性)。また、同じハッシュ値をもつ別の入力データを推測できないことです(=衝突困難性)。SHA-2、SHA-3 はそのような条件をクリアした、安全なアルゴリズムです。
以降、ハッシュ関数を \(H(\:)\) と書きます。RSA暗号を使ったデジタル署名のアルゴリズムは次の通りです。
デジタル署名
\(B\) から \(A\) にメッセージ \(M\) を送る手順です。
RSA暗号は暗号化と復号化が対称形の計算なので、デジタル署名の作成と検証はシンプルです。
補足2:素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
(前回から続く)
4. RSA暗号の証明
| 4.1 | RSA暗号 |
|
RSA暗号の公開鍵・秘密鍵の作成方法と暗号化・復号化の計算式を定理として記述すると次の通りです。 \(p\) と \(q\) を相異なる素数とし、\(n=pq\) とする。 \(e\) を \(m=(p-1)(q-1)\) と素な数、\(d\) を、\(de\equiv1\:(\mr{mod}\:m)\) を満たす数とする。この前提で、 暗号化:\(P^e\equiv C\:(\mr{mod}\:n)\) ならば 復号化:\(C^d\equiv P\:(\mr{mod}\:n)\) である。 ( \(P\):平文。\(C\):暗号文 ) | |
RSA暗号において、暗号化・復号化に必要なのは公開鍵の \((e,\:n)\) と 秘密鍵の \(d\) であり、それらを生成するのに使った \(p\) と \(q\) は不要です。というより、\(p\) と \(q\) ないしは \((p-1)(q-1)\) が漏れると暗号が破られてしまうので、これらの数は鍵を生成した後は破棄(情報を安全に抹消)する必要があります。
以下に、上の「復号化の式」が成り立つことを証明します。まず合同式の累乗 1.2 を使って「暗号化の式」の両辺を \(d\) 乗すると、
\(C^d\equiv P^{de}\:(\mr{mod}\:pq)\) \(\cd\:(1)\)
となります。ここで、\(de\equiv1\:(\mr{mod}\:(p-1)(q-1))\) なので、\(de=k(p-1)(q-1)+1\) と表現できます。従って、
\(P^{de}=P^{k(p-1)(q-1)+1}\)
となります。累乗を分解すると、
\(P^{de}=(P^{(p-1)(q-1)})^k\:\cdot\:P\) \(\cd\:(2)\)
です。一方、フェルマの小定理 3.1 により、
\(P^{p-1}\equiv1\:(\mr{mod}\:p)\)
となります。合同式の累乗の定理 1.2 により、この式の両辺を \(q-1\) 乗すると、
\(P^{(p-1)(q-1)}\equiv1\:(\mr{mod}\:p)\) \(\cd\:(3)\)
が得られます。さらに、フェルマの小定理 3.1 により、
\(P^{q-1}\equiv1\:(\mr{mod}\:q)\)
ですが、両辺を \(p-1\) 乗して、
\(P^{(p-1)(q-1)}\equiv1\:(\mr{mod}\:q)\) \(\cd\:(4)\)
となります。ここで、\(p\) と \(q\) は互いに素なので、1.5 の合同式の定理を \((3),\:(4)\)に適用すると、
\(P^{(p-1)(q-1)}\equiv1\:(\mr{mod}\:pq)\)
を導くことができます。この式の両辺を 1.2 を使って \(k\) 乗すると、
\((P^{(p-1)(q-1)})^k\equiv1\:(\mr{mod}\:pq)\)
であり、さらに両辺に合同式の乗算 1.1c を使って \(P\) をかけると、
\((P^{(p-1)(q-1)})^k\:\cdot\:P\equiv P\:(\mr{mod}\:pq)\) \(\cd\:(5)\)
となります。従って、\((1),\:(2),\:(5)\) を合わせると、
\(C^d\equiv P\:(\mr{mod}\:pq)\)
となり、RSA暗号の復号化の式が証明できました。
最小公倍数
以上の証明の過程を改めて振り返ってみると、「\(m\) が \((p-1)\) の倍数であり、かつ \((q-1)\) の倍数」であれば、RSA暗号は成立することが分かります。つまり「\(m\) が \((p-1)\) と \((q-1)\) の公倍数」であれば成立する。そのような \(m\) は、
\(m=n_p(p-1)\)
\(m=n_q(q-1)\)
\(m=n_q(q-1)\)
の2通りに表現できます。すると、\(de\equiv1\:(\mr{mod}\:m)\) なので、
\(de=k_p(p-1)+1\)
\(de=k_q(q-1)+1\)
\(de=k_q(q-1)+1\)
と2通りに表せます。ここから、
\(P^{de}=P^{k_p(p-1)+1}\)
\(\phantom{P^{de}}=P\cdot(P^{p-1})^{k_p}\)
\(\phantom{P^{de}}\equiv P\:(\mr{mod}\:p)\)
\(P^{de}=P^{k_q(q-1)+1}\)
\(\phantom{P^{de}}=P\cdot(P^{q-1})^{k_q}\)
\(\phantom{P^{de}}\equiv P\:(\mr{mod}\:q)\)
\(P^{de}\equiv P\:(\mr{mod}\:pq)\)
\(C^{d\phantom{e}}\equiv P\:(\mr{mod}\:pq)\)
\(\phantom{P^{de}}=P\cdot(P^{p-1})^{k_p}\)
\(\phantom{P^{de}}\equiv P\:(\mr{mod}\:p)\)
\(P^{de}=P^{k_q(q-1)+1}\)
\(\phantom{P^{de}}=P\cdot(P^{q-1})^{k_q}\)
\(\phantom{P^{de}}\equiv P\:(\mr{mod}\:q)\)
\(P^{de}\equiv P\:(\mr{mod}\:pq)\)
\(C^{d\phantom{e}}\equiv P\:(\mr{mod}\:pq)\)
となって、平文が復元できます。この考察から分かるのは、\(m\) の最小値は「\((p-1)\) と \((q-1)\) の最小公倍数」ということです。最小公倍数を \(\mr{lcm}\) で表すと、
\(m=\mr{lcm}(p-1,q-1)\)
であればRSA暗号は成立します。そして一般に、
\(\mr{lcm}(a,b)=\dfrac{a\times b}{\mr{gcd}(a,b)}\)
です。最大公約数・\(\mr{gcd}\) は「2. ユークリッドの互除法」を使って高速に計算できるので \(p\) や \(q\) が巨大数であっても最小公倍数・\(\mr{lcm}\) は計算可能です。
累乗の剰余を求めるアルゴリズム
RSA暗号では、暗号化と復号化で "累乗(冪乗)の剰余"(冪剰余と呼ぶ)を求める計算が出てきます。この計算で使う公開鍵 \((e,\:n)\) も秘密鍵 \(d\) も、また平文や暗号文も、実用的には\(10\)進数で\(300\)桁とか、そういった巨大な数です。
しかし巨大な数であっても、累乗の剰余計算ができるアルゴリズムがあります。その一つとして、ここでは「2分割法」で説明します。前回の「RSA暗号の例題」であげた、
\(C=82^{133}\) \(\mathbf{mod}\) \(143=4\)
の例で説明します。考え方としては「2.ユークリッドの互除法」と同じで、問題をより "小さな問題" に置き換えるというものです。つまり、\(133\)乗を求める代わりに
\(C_1=82^{66}\) \(\mathbf{mod}\) \(143\)
が求まったとしたら、\(C\) は、
\(C=(C_1\cdot C_1\cdot82)\) \(\mathbf{mod}\) \(143\)
で計算できます。さらに、その \(C_1\) は、
\(C_2=82^{33}\) \(\mathbf{mod}\) \(143\)
が求まったとしたら、
\(C_1=(C_2\cdot C_2)\) \(\mathbf{mod}\) \(143\)
で計算できます。この2分割を次々と続けていくと、\(82\)の\(16\)乗、\(8\)乗、\(4\)乗、\(2\)乗、\(1\)乗を \(143\) で割った剰余が求まれば良いことになります。これを逆にたどって電卓で \(82^k\) \(\mathbf{mod}\) \(143\:(k=1,\) \(2,\) \(4,\) \(8,\) \(16,\) \(33,\) \(66,\) \(133)\) を順次計算してみると、
| \(\,82^k\) | \(\mathbf{mod}\) \(143\) |
| \(\,82^1\) | \(82\,\) |
| \(\,82^2\) | \(3\,\) |
| \(\,82^4\) | \(9\,\) |
| \(\,82^8\) | \(81\,\) |
| \(\,82^{16}\) | \(126\,\) |
| \(\,82^{33}\) | \(103\,\) |
| \(\,82^{66}\) | \(27\,\) |
| \(\,82^{133}\) | \(4\,\) |
となり、答の \(4\) が求まりました。これをプログラム言語で記述すると次の通りです。
| 4.2 | 2分割法による冪剰余計算 | ||||||||||||||||||
|
\(P^e\) \(\mathbf{mod}\) \(n\) を求める関数 RSA(Javascriptで記述)。
| |||||||||||||||||||
次はこのアルゴリズムの補足説明です。
| e が 1 なら P % n が答なので、それを関数値として返す。% は Javascript の剰余演算子で、\(P\) \(\mathbf{mod}\) \(n\) と同じ意味。 | |
| e が 1 でないときは、e を半分(約半分)にして答を求める。Math.floor() は小数点以下を切り捨てる Javascript の組み込み関数。Javascript では実数と整数の区別がないので必要。 | |
| その "半分の答" を2乗し、剰余を求めて仮の答 c とする。 | |
| e が偶数なら c が正しい答。それを関数値として返す。 | |
| e が奇数なら c にさらに P を掛け、剰余を求めて関数値として返す。 |
\(e,\:n,\:d\) が10進数で300桁程度の巨大数とします。\(2^{1000}\) は約300桁の数なので、"2分割法" を使うと1000回程度の剰余計算を繰り返すこと答が求まります。この程度の計算は現在のコンピュータで可能です。ただし可能といっても 1000回の繰り返しはさすがに大変なので、実用的にはこれを高速化する手法がいろいろと開発されています。
「2. ユークリッドの互除法」で、公開鍵 \((e,\:n)\) の \(e\) と秘密鍵 \(d\) について、たとえ巨大数であっても高速に算出できることを書きました。それに加えて、暗号化・復号化で使われる「巨大数の累乗の剰余計算」も算出可能であり、RSA暗号の全体が "計算可能" であることが証明できました。
今までのまとめ
実用的な RSA暗号を構成するときに必要なのは、巨大な素数 \(p,\:q\) (\(10\)進数で150桁程度かそれ以上)です。こういった素数をどうやって作り出すか、また素数であることの判定をどうやってするかの計算手法については割愛します。
今までのRSA暗号についての説明全体をまとめると、以下の2点になるでしょう。
| RSA暗号は数論(整数論)の基礎から構成されている(合同、ユークリッドの互除法、フェルマの小定理、・・・・・)。 | |
| RSA暗号における公開鍵・秘密鍵の生成式、暗号化・復号化の式は、実用的に計算可能である。 |
RSA暗号は現代の情報化社会にとって必須のものであり、社会インフラの重要な構成要素です。それは、数学が実用的に、かつ直接的に社会に役立っている例なのでした。
| RSA暗号とオイラー関数・オイラーの定理 |
RSA暗号の成立性の証明はこれまでで尽きていますが、以降はRSA暗号と関係が深い「オイラー関数」を説明し、次に「オイラーの定理」を導いて、そこからRSA暗号の原理を導出します。まずその前提としての「中国剰余定理」です。
5. 中国剰余定理
5~6世紀頃の中国で成立した算術書『孫子算経』に、
3で割ると2余り
5で割ると3余り
7で割ると2余る数は何か
5で割ると3余り
7で割ると2余る数は何か
という問題が書かれています。答は23ですが、これを一般化した定理を「中国剰余定理」と呼んでいます。
| 5.1 | 中国剰余定理 |
|
与えられた \(k\) 個の整数、\(m_1,\:m_2,\:\cd,\:m_k\) は、どの2つをとっても互いに素とする。このとき任意に与えられた\(k\) 個の整数、\(a_1,\:a_2,\:\cd\:,\:a_k\) についての \(k\) 個の式、
\(x\equiv a_1\:(\mr{mod}\:m_1)\) \(x\equiv a_2\:(\mr{mod}\:m_2)\) \(\vdots\) \(x\equiv a_k\:(\mr{mod}\:m_k)\) を同時に満たす解 \(x\) が存在し、この解は \(M=m_1m_2\:\cd\:m_k\)を法として唯一である。 | |
\(x_1\) と \(x_2\) の2つの解があったとします。すると、\(\mr{mod}\:m_1\) の式から、
\(x_1\equiv a_1\:(\mr{mod}\:m_1)\)
\(x_2\equiv a_1\:(\mr{mod}\:m_1)\)
\(x_2\equiv a_1\:(\mr{mod}\:m_1)\)
となり、1.1b により、
\(x_1-x_2\equiv0\:(\mr{mod}\:m_1)\)
となります。同様に、\(\mr{mod}\:m_2\) の式から、
\(x_1-x_2\equiv0\:(\mr{mod}\:m_2)\)
が言えます。\(m_1\) と \(m_2\) は互いに素なので、ここで 1.5 を適用すると、
\(x_1-x_2\equiv0\:(\mr{mod}\:m_1m_2)\)
となります。以上のことは \(m_3\) から \(m_k\) までの全ての式についても言えるので、1.5 を順次適用することにより、
\(x_1-x_2\equiv0\:(\mr{mod}\:m_1m_2\:\cd\:m_k)\)
となります。つまり、
\(x_1\equiv x_2\:(\mr{mod}\:M)\)
です。従って、解 \(x\) が複数あったとしても、それらは全て \(M\) を法として合同になります\((\)= 解は \(M\) を法として唯一)。
ここで
\(M_i=\dfrac{M}{m_i}\)
とおくと、\(\mr{gcd}(m_i,M_i)=1\) なので、2.3 により、
\(M_i\cdot N_i\equiv1\:(\mr{mod}\:m_i)\)
となる \(N_i\) が存在します。これを使って、
\(x=\displaystyle\sum_{i=1}^{k}a_iM_iN_i\)
とおくと、それが解になります。なぜなら \(M_i\) の作り方から \(i\) 番目の項以外の項は \(m_i\) で割り切れるので、\(i\) 番目の項単独で「\(m_i\) を法として \(x\) と合同」になります。つまり、
\(x\equiv a_iM_iN_i\:(\mr{mod}\:m_i)\)
です。一方、合同の性質の 1.4 において \(y=1\) とおくと 1.4 は、
\(ax\equiv b\:(\mr{mod}\:m)\) かつ、
\(\phantom{a}x\equiv1\:(\mr{mod}\:m)\) のとき、
\(a\phantom{x}\equiv b\:(\mr{mod}\:m)\)
\(\phantom{a}x\equiv1\:(\mr{mod}\:m)\) のとき、
\(a\phantom{x}\equiv b\:(\mr{mod}\:m)\)
となります。1.4 の「\(x\) が \(m\) と互いに素」という条件は、\(x\equiv1\:(\mr{mod}\:m)\) で満たされています。このことを適用すると、
\(x\equiv a_iM_iN_i\:(\mr{mod}\:m_i)\)
\(M_i\cdot N_i\equiv1\:(\mr{mod}\:m_i)\)
\(M_i\cdot N_i\equiv1\:(\mr{mod}\:m_i)\)
という2つの条件から、
\(x\equiv a_i\:(\mr{mod}\:m_i)\)
となります。これが全ての \(i\) について成り立つ。従って \(x\) が解であることが証明できました。また前段で証明したように全ての解は \(M\) を法として合同なので、\(x\) が唯一の解です。
中国剰余定理の意味を直感的に理解するために、\(k=2\)、\(m_1=3\)、\(m_2=4\)、\(M=12\) とし、\(x\) の全て解についての対応表を作ってみると次の通りになります。
| \(\overset{\:}{x}\,\) | \(\mr{mod}\:3\) | \(\mr{mod}\:4\) |
| \(\,0\,\) | \(0\,\) | \(0\,\) |
| \(\,1\,\) | \(1\,\) | \(1\,\) |
| \(\,2\,\) | \(2\,\) | \(2\,\) |
| \(\,3\,\) | \(0\,\) | \(3\,\) |
| \(\,4\,\) | \(1\,\) | \(0\,\) |
| \(\,5\,\) | \(2\,\) | \(1\,\) |
| \(\,6\,\) | \(0\,\) | \(2\,\) |
| \(\,7\,\) | \(1\,\) | \(3\,\) |
| \(\,8\,\) | \(2\,\) | \(0\,\) |
| \(\,9\,\) | \(0\,\) | \(1\,\) |
| \(\,10\,\) | \(1\,\) | \(2\,\) |
| \(\,11\,\) | \(2\,\) | \(3\,\) |
この表をみると、\(0,\:1,\:2\) を繰り返し並べ(\(\mr{mod}\:3\) の列)、\(0,\:1,\:2,\:3\) を繰り返し並べると(\(\mr{mod}\:4\) の列)、\(3\) と \(4\) が互いに素の関係にあるために、\((0,\:0)\) は \(3\times4=12\) 回繰り返さないと現れないことが分かります。その間、\(x\) は\(12\)未満の全ての数をとり、 \((\mr{mod}\:3,\:\mr{mod}\:4)\) の全ての組み合わせが現れる。このため、 \((\mr{mod}\:3,\:\mr{mod}\:4)\) の1つの組み合わせに対して解 \(x\) が唯一になるわけです。この状況は \(k\) の値にかかわらず、\(m_i\:(1\leq i\leq k)\) のどの2つをとっても互いに素である限り変わらない。
「互いに素」なゆえに成立するこのイメージは、次のオイラー関数の証明に役立ちます。
6. オイラー関数
|
以下の「オイラー関数」は、一般に関数名をギリシャ文字の \(\varphi\)(ファイ)で表記するので「オイラーの \(\varphi\) 関数」とも呼ばれています。数論ではたびたび出てくる関数です。
余談ですが、オイラーは20歳台後半で右目を失明しました。ここに掲載した肖像画にもそれが現れています。
| 6.1 | オイラー関数 |
|
オイラー関数 \(\varphi\) の定義は以下のとおり。
\(\varphi(m)\) : \(m\) 以下で、\(m\) とは互いに素な自然数の個数 \(p\)、\(q\) を相異なる素数とするとき、オイラー関数は次の性質をもつ。 (素数のオイラー関数値) 6.1a \(\varphi(p)=p-1\) (素数の積のオイラー関数値) 6.1b \(\varphi(pq)=(p-1)(q-1)\) (素数の累乗のオイラー関数値) 6.1c \(\varphi(p^{\al})=p^{\al}-p^{\al-1}\) なお「互いに素」は、すなわち「最大公約数が \(1\)」であり、\(\mr{gcd}(1,1)=1\)なので、\(\varphi(1)=1\)。 | |
まず 6.1a ですが、素数 \(p\) は \(p\) 未満のすべての自然数と互いに素です。従って、\(\varphi(p)=p-1\) です。
次に \(pq\) 以下の数で、\(p\) で割り切れるのは \(pq\) を含んで \(q\) 個、\(q\) で割り切れるのは \(pq\) を含んで \(p\) 個です。\(pq\) 以下の数の全体は \(pq\) 個なので、\(pq\) 以下の数で \(p\) でも \(q\) でも割り切れない数の個数(= \(pq\) と互いに素な数の個数)は、
\(\varphi(pq)=pq-p-q+1\)
\(\phantom{\varphi(pq)}=(p-1)(q-1)\)
\(\phantom{\varphi(pq)}=(p-1)(q-1)\)
です(6.1b)。上の式の1行目で、\(-p\) と \(-q\) には \(pq\) の分が重複しているので \(+1\) してあります。
さらに、\(p^{\al}\) 以下の数で、\(p\) の倍数は全て \(p^{\al}\) と共通の約数 \(p\) を持ちます。\(p^{\al}\) 以下の \(p\) の倍数の個数は \(p^{\al}\) を含んで、
\(\dfrac{p^{\al}}{p}=p^{\al-1}\)
なので、\(\varphi(p^{\al})\)は、
\(\varphi(p^{\al})=p^{\al}-p^{\al-1}\)
となります(6.1c)。このオイラー関数に関しては、次の「乗法性」が重要です。
| 6.2 | オイラー関数の乗法性 |
|
\(\mr{gcd}(m,n)=1\)( \(m\) と \(n\) は互いに素 )のとき \(\varphi(mn)=\varphi(m)\varphi(n)\) | |
一般に、関数のこのような性質を "乗法性"、このような関数を "乗法的関数" と呼んでいます。証明は3段階で行います。キーワードは「中国剰余定理」と「1対1対応」です。
第1段
\(0\leq i < m\)、\(0\leq j < n\) である数を選び \((i,j)\) のペアを作ります。\(i\) の選択肢は \(m\) 個、\(j\) の選択肢は \(n\) 個で、それぞれ独立して選ぶので、相異なる \((i,j)\) のペアの数は \(mn\) 個です。
仮定により \(m\) と \(n\) は互いに素です。従って、それぞれの \((i,j)\) のペアについて中国剰余定理 5.1 により、
\(x\equiv i\:(\mr{mod}\:m)\)
\(x\equiv j\:(\mr{mod}\:n)\)
\(x\equiv j\:(\mr{mod}\:n)\)
を同時に満たす \(x\) が、\(mn\) を法として唯一存在します。つまり \(0\leq x < mn\) の範囲では \(x\) が一意に決まります。これは \(\bs{(i,j)}\) のペアに \(\bs{x}\) を対応づけられることを意味します。
逆に、\(0\leq x < mn\) である \(x\) を1つ選ぶと、それに対して \(\mr{mod}\:m\) と \(\mr{mod}\:n\) を求めて \((i,j)\) のペアと対応づけられる。つまり、
\(mn\) 個の \((i,j)\) のペアと \(mn\) 個の \(x\) の間に1対1対応が作れる
ことになります。
第2段
第1段の方法で作った「1対1に対応する \((i,j)\) のペアと \(x\)」については、
\(i\) が \(m\) と素であるなら、\(x\) も \(m\) と素
になります。なぜなら、もし \(x\) と \(m\) に共通の約数 \(a\) があったとすると(= \(a|x\) でかつ \(a|m\) )、中国剰余定理の前提から
\(x=km+i\)
と表せるので \(a|i\) となり、\(a\) が \(i\) と \(m\) の共通の約数にもなってしまって「\(i\) が \(m\) と素」という仮定に反するからです。全く同様に、
\(j\) が \(n\) と素であるなら、\(x\) も \(n\) と素
です。この2つを合わせると、
\((i,j)\) のペアにおいて「\(i\) が \(m\) と素」で、かつ「\(j\) が \(n\) と素」であれば、「1対1対応がつけられた \(x\) は \(m\) と \(n\) の2つの数と素」
になります。「\(x\) が \(m\) と \(n\) の2つの数と素」であることは「\(x\) が \(mn\) と素」ということに他なりません。つまり、
\((i,j)\) のペアで「\(i\) が \(m\) と素」であり、かつ「\(j\) が \(n\) と素」であれば「\((i,j)\) と1対1対応がつけられた \(x\) は \(mn\) と素」
です。その逆に「\(x\) が \(mn\) と素」であるなら「\(x\) は \(m\) と \(n\) の2つの数と素」です。そうすると中国剰余定理の前提から「\(i\) は \(m\) と素」でかつ「\(j\) は \(n\) と素」になります。つまり、まとめると、
\((i,j)\) のペアのうち「\(i\) が \(m\) と素で、\(j\) が \(n\) と素であるペア」は、「\(mn\) と素である \(x\)」と1対1の対応関係がつけられる
ことになります。そして1対1の対応関係がつく集合の要素の数は等しい。ここが証明の根幹です。
第3段
オイラー関数の定義により、
\(m\) と素である \(i\) の個数は \(\varphi(m)\)
\(n\) と素である \(j\) の個数は \(\varphi(n)\)
\(n\) と素である \(j\) の個数は \(\varphi(n)\)
です。\(i\) と \(j\) は独立に選んでいるので、
\((i,j)\) のペアのうち、「\(i\) が \(m\) と素」で「\(j\) が \(n\) と素」のペアの個数は、\(\varphi(m)\varphi(n)\)
です。さらにオイラー関数の定義により、
\(mn\) と素な \(x\) の個数は \(\varphi(mn)\)
になります。第2段で証明したように「\(i\) が \(m\) と素」で「\(j\) が \(n\) と素」である \((i,j)\) のペアと、\(mn\) と素である \(x\) は1対1の対応関係にあります。従ってその個数は等しく、
\(\varphi(mn)=\varphi(m)\varphi(n)\)
となって、証明が完成しました。
オイラー関数の乗法性を直感的に理解するために、中国剰余定理のところであげた表を使って \(\varphi(12)=\varphi(3)\varphi(4)\) のイメージを示したのが次です。\(●\) 印を付けたのはそれぞれ、\(12,\:3,\:4\) とは素な数です。
| \(mn=12\) | \(m=3\) | \(n=4\) |
| \(0\,\) | \(0\,\) | \(0\,\) |
| \(●\:1\,\) | \(●\:1\,\) | \(●\:1\,\) |
| \(\phantom{●}2\,\) | \(●\:2\,\) | \(\phantom{●}2\,\) |
| \(\phantom{●}3\,\) | \(\phantom{●}0\,\) | \(●\:3\,\) |
| \(\phantom{●}4\,\) | \(●\:1\,\) | \(\phantom{●}0\,\) |
| \(●\:5\,\) | \(●\:2\,\) | \(●\:1\,\) |
| \(\phantom{●}6\,\) | \(\phantom{●}0\,\) | \(\phantom{●}2\,\) |
| \(●\:7\,\) | \(●\:1\,\) | \(●\:3\,\) |
| \(\phantom{●}8\,\) | \(●\:2\,\) | \(\phantom{●}0\,\) |
| \(\phantom{●}9\,\) | \(\phantom{●}0\,\) | \(●\:1\,\) |
| \(\phantom{●}0\,\) | \(●\:1\,\) | \(\phantom{●}2\,\) |
| \(●11\,\) | \(●\:2\,\) | \(●\:3\,\) |
このオイラー関数の乗法性(6.2)と素数の累乗のオイラー関数値(6.1c)を用いると、一般の自然数 \(N\) のオイラー関数値を求めることができます。つまり素因数分解の一意性により、\(p_i\) を素数として、
\(N=p_1^{\al_1}\:p_2^{\al_2}\:\cd\:p_r^{\al_r}\)
と表現できます。ここでオイラー関数の乗法性(6.2)を繰り返して使うと、
\(\varphi(N)=\varphi(p_1^{\al_1})\:\varphi(p_2^{\al_2})\:\cd\:\varphi(p_r^{\al_r})\)
となります。また、素数の累乗のオイラー関数値(6.1c)によって、
\(\varphi(p_i^{\al_i})=p_i^{\al_i}-p_i^{\al_i-1}\)
です。以上を合わせると、任意の数 \(N\) のオイラー関数値を求める公式は、
| \(\varphi(N)\) | \(=\) | \((p_1^{\al_1}-p_1^{\al_1-1})\cdot\:\cd\:\cdot(p_r^{\al_r}-p_r^{\al_r-1})\) | |
| \(=\) | \(\dfrac{p_1^{\al_1}}{p_1}(p_1-1)\cdot\:\cd\:\cdot\dfrac{p_r^{\al_r}}{p_r}(p_r-1)\) | ||
| \(=\) | \(\dfrac{N}{p_1p_2\:\cd\:p_r}\cdot(p_1-1)\cdot\:\cd\:\cdot(p_r-1)\) |
となります。つまり、\(N\) の素因数分解ができれば \(\varphi(N)\) は簡単に求まります。逆に言うと\(\bs{N}\) の素因数分解が困難なら \(\bs{\varphi(N)}\) を求めるのも困難になる。このことが RSA暗号が成立する背景となっています。
ちなみに、上のオイラー関数の公式の末尾の形(色を塗った部分)は、オイラーより以前に江戸時代の和算家・久留島義太(? - 1758)が発見しています。久留島義太は、関孝和、建部賢弘とともに三大和算家と呼ばれた人ですが、自分では書物を残すことがなかったので、業績は知人や弟子がまとめたものにしかありません。その一人、仙台藩の天文学者・戸板保佑の『久氏遺稿』の中に公式の記述ができます(鳴海 風「小説になる江戸時代の数学者」- 日本数学会「市民講演会」2007.3.31 による)。
その書物には \(\varphi(360)\) を求める例示があります(暗算でも出来ます)。つまり \(360=6\cdot6\cdot10\) なので素因数は \(2,\:3,\:5\) だけです。従って \(360\) を \(2\cdot3\cdot5=30\) で割って(答は \(12\))、\(1\cdot2\cdot4=8\) を掛けると \(\varphi(360)=96\) が求まる。このことが書かれています。この求め方は公式そのものです。
公式には \(p_i\) の累乗の部分(\(\al^i\))が全く現れません。ちょっと不思議な感じもする公式です。
日本の数学者の中には「久留島・オイラーの関数」と呼ぶ人もいます。"オイラー何とか" という名前の定理や公式はいろいろあるので、その方が分かりやすいかもしれません。
7. オイラーによるフェルマの小定理の一般化(オイラーの定理)
オイラー関数を使うと、オイラーが発見した「一般化されたフェルマの小定理」の証明ができます。
| 7.1 | オイラーの定理 |
|
\(a\) を \(m\) とは素な数とするとき \(a^{\varphi(m)}\equiv1\:(\mr{mod}\:m)\) | |
\(a\) や \(m\) に何らかの制約があるわけではなく、2つの数が「互いに素」という条件だけで成立する美しい定理です。これがフェルマの小定理の一般化であることは、\(p\) を素数として \(m=p\) とおけばフェルマの小定理そのものになることから分かります。
この証明を2段階に分けて行います。まず第1段階で \(m\) が素数の累乗の時に成立することを証明し、第2段階でその結果を使って \(m\) が一般の数の場合を証明します。
| 7.2 | |
|
\(p\) を素数とする。 \(m=p^{\al}\) のとき、7.1 は成り立つ。 | |
\(\al\) についての数学的帰納法で証明します。まず \(\al=1\) のときはフェルマの小定理そのものなので成立します。次に \(\al=k-1\:(k\geq2)\) のときに成立すると仮定します。つまり、
\(a^{\varphi(p^{k-1})}\equiv1\:(\mr{mod}\:p^{k-1})\)
が成り立つとします。そうすると、ある数 \(b\) が存在して、
\(a^{\varphi(p^{k-1})}=1+bp^{k-1}\)
と表現できます。この式の左辺に 6.1c(素数の累乗のオイラー関数値)を適用すると、
\(a^{p^{k-1}-p^{k-2}}=1+bp^{k-1}\)
となります。この両辺を \(p\) 乗し、右辺は2項定理で展開すると、
\(\begin{eqnarray}
&&a^{p^k-p^{k-1}}&=(1+bp^{k-1})^p\\
&&&=1+{}_p\,C_1(bp^{k-1})^1\\
&&&\phantom{=1}+{}_p\,C_2(bp^{k-1})^2+\:\cd\\
\end{eqnarray}\)
が得られます。この展開した右辺において、第2項は \({}_p\,C_1=p\) なので \(bp^k\) となり、\(p^k\) で割り切れます。また第3項以降は \(2\leq i\leq p\) として \({}_p\,C_ib^ip^{(k-1)i}\) と表せますが、\(k,\:i\geq2\) のとき \((k-1)(i-1)\geq1\) であり、この式を変形すると \((k-1)i\geq k\) となるので、第3項以降も \(p^k\) で割り切れます。つまり、展開した第1項の \(1\) 以外は \(p^k\) で割り切れることになります。従って、
\(\begin{eqnarray}
&&a^{p^k-p^{k-1}}&\equiv1\:(\mr{mod}\:p^k)\\
&&a^{\varphi(p^k)}&\equiv1\:(\mr{mod}\:p^k)\\
\end{eqnarray}\)
となります。この結果、7.2 は \(\al=k-1\) のときに成立するなら \(\al=k\) のときにも成立することが証明でき、数学的帰納法が完成しました。
7.2 を使って 7.1 を証明します。\(p_i\) を相異なる素数とし、任意の数 \(m\) を、
\(m=p_1^{\al_1}\:p_2^{\al_2}\:\cd\:p_r^{\al_r}\)
とおきます。すると 7.2 により、\(1\leq i\leq r\) のそれぞれの \(i\) において、
\(a^{\varphi(p^{\al_i})}\equiv1\:(\mr{mod}\:p^{\al_i})\) \(\cd\:(1)\)
が成立します。ここで、
\(n_i=\dfrac{m}{p^{\al_i}}\) \((m=n_i\cdot p^{\al_i})\)
とおくと、オイラー関数の乗法性(6.2)により、
\(\varphi(m)=\:\varphi(n_i)\:\varphi(p^{\al_i})\)
となります。ここで、この式と合同式の累乗(1.2)を使って \((1)\) 式の両辺を \(\varphi\:(n_i)\) 乗すると、
\(a^{\varphi(m)}\equiv1\:(\mr{mod}\:p^{\al_i})\) \(\cd\:(2)\)
が得られました。\((2)\) 式は \(1\leq i\leq r\) の \(i\) においてそれぞれ成立します。\(p_i\) は相異なる素数だったので、ここで 1.5 を順次適用すると、
\(a^{\varphi(m)}\equiv1\:(\mr{mod}\:m)\)
となり、7.1 が正しいことが証明されました。
7.1 の証明の過程を振り返ってみると、次の 7.3 が成り立つことが分かります。
| 7.3 | オイラーの定理・その2 |
|
任意の数 \(m\) の素因数分解を、相異なる素数 \(p_i(1\leq i\leq r)\) を使って、
\(m=p_1^{\al_1}p_2^{\al_2}\:\cd\:p_r^{\al_r}\) と表す。\(\psi(m)\) を \(r\) 個の \(\varphi(p_i^{\al_i})\) の最小公倍数とする(\(\psi\) はギリシャ文字のプサイ)。つまり、
\(\psi(m)=\mr{lcm}(\varphi(p_1^{\al_1}),\:\cd\:,\varphi(p_r^{\al_r}))\) とすると、\(m\) と素である数 \(a\) について、
\(a^{\psi(m)}\equiv1\:(\mr{mod}\:m)\) が成り立つ(\(\mr{lcm}=\) 最小公倍数)。 | |
これは 7.1 の証明の後半(= 7.2 を使って証明する部分)からすぐに分かります。\(\psi(m)\) の定義から、
\(\psi(m)=k_i\cdot\varphi(p_i^{\al_i})\:\:(1\leq i\leq r)\)
と書き表すことができます。一方 7.2 より、
\(a^{\varphi(p_i^{\al_i})}\equiv1\:(\mr{mod}\:p_i^{\al_i})\)
が成り立ちます。この合同式の両辺を 1.2(合同式の累乗) に従って \(k_i\) 乗すると、
\(a^{k_i\varphi(p_i^{\al_i})}\equiv1\:(\mr{mod}\:p_i^{\al_i})\)
となり、これから、
\(a^{\psi(m)}\equiv1\:(\mr{mod}\:p_i^{\al_i})\)
が得られます。この式は \(1\leq i\leq r\) であるすべての \(i\) について成立し、また \(p_i^{\al_i}\) は互いに素なので、1.5 を順次適用することで、
\(a^{\psi(m)}\equiv1\:(\mr{mod}\:m)\)
となり、7.3 が証明できました。この証明の過程から、\(\psi(m)\) が最小公倍数でなくても、公倍数であれば成立することが分かります。なお \(\psi(m)\) は一般的な表記ではなく、ここで便宜上使った記号です。
オイラーの定理(7.1)と、オイラーの定理・その2(7.3)を
\(\begin{eqnarray}
&&m&=3\cdot7=21\\
&&a&=2\\
\end{eqnarray}\)
として具体的に書いてみると次の通りです。
\(\begin{eqnarray}
&&\varphi(m)&=\varphi(3)\cdot\varphi(7)\\
&&&=2\cdot6\\
&&&=12\\
&&&\\
&&2^{12}&=4096\\
&&&=195\cdot21+1\\
&&&\equiv1\:(\mr{mod}\:21)\\
&&&\\
&&\psi(m)&=\mr{lcm}(\varphi(3),\varphi(7))\\
&&&=\mr{lcm}(2,6)\\
&&&=6\\
&&&\\
&&2^6&=64\\
&&&=3\cdot21+1\\
&&&\equiv1\:(\mr{mod}\:21)\\
\end{eqnarray}\)
オイラーの定理の別証明
いままでは「オイラー関数の乗法性」を導出して、それをもとにオイラーの定理(とその最小公倍数版)を証明しました。しかし単にオイラーの定理だけを証明したいのなら、以下のようにフェルマの小定理(3.1)のときと同じ論法で可能です。
\(n\) 以下の自然数で \(n\) と互いに素である \(\varphi(n)\) 個の数を、数列として、
\(b_1,\:\:b_2,\:\:b_3,\:\cd\:,\:b_{\varphi(n)}\)
と並べます。これらはすべて相異なる数です。次に \(n\) とは素な数 \(a\) を選び、数列の全部にかけ算をして新たな数列、
\(ab_1,\:\:ab_2,\:\:ab_3,\:\cd\:,\:ab_{\varphi(n)}\)
を作ります。そして、それぞれの数を \(n\) で割った剰余を \(r_i\) とします。つまり、
\(\begin{eqnarray}
&&ab_1&\equiv r_1\:(\mr{mod}\:n)\\
&&ab_2&\equiv r_2\:(\mr{mod}\:n)\\
&&ab_2&\equiv r_3\:(\mr{mod}\:n)\\
&&&\vdots\\
&&ab_{\varphi(n)}&\equiv r_{\varphi(n)}\:(\mr{mod}\:n)\\
\end{eqnarray}\)
です。\(a\) も \(b_i\) も \(n\) と素なので \(r_i\) が \(0\) になることはなく、\(1\leq r_i < n\) です。そして、このようにすると\(\bs{r_i}\) は全て \(\bs{n}\) と素になります。なぜなら、剰余の式を、
\(ab_i=k_in+r_i\)
とするとき、\(r_i\) と \(n\) に共通の約数があるなら、その約数は \(ab_i\) の約数にもなり「\(a\) も \(b_i\) も \(n\) と互いに素」という、そもそもの仮定に反するからです。
さらに、\(1\leq i,\:\:j\leq\varphi(n)\) である \(i,\:j\) について、
\(i\neq j\) であれば、必ず \(r_i\neq r_j\)
になります。なぜなら、もし \(r_i=r_j\) とすると、1.1b(合同式の減算)より、
\(a(b_i-b_j)\equiv0\:(\mr{mod}\:n)\)
です。仮定より \(a\) は \(n\) と互いに素なので 1.3 により(\(1.3\) で \(b=0\) の場合)、
\((b_i-b_j)\equiv0\:(\mr{mod}\:n)\)
となりますが、\(1\leq b_i,\:\:b_j\leq n\) なので、
\(b_i=b_j\)
となり、\(b_1,\:\:b_2,\:\:b_3,\:\cd\:,b_{\varphi(n)}\) が相異なる数という仮定に反してしまうからです。つまり\(i\neq j\) であれば、必ず \(r_i\neq r_j\) です。
ということは、\(\varphi(n)\) 個の数、\(r_i\) は「すべてが \(n\) とは素である、相異なる数」であり、つまり \(\varphi(n)\) 個の数、\(b_i\)を並び替えたものです。従って、
\(r_i\) を全部かけ算したものを \(R\)
\(b_i\) を全部かけ算したものを \(B\)
\(b_i\) を全部かけ算したものを \(B\)
と書くとすると、
\(R=B\)
\((r_1r_2\:\cd\:r_{\varphi(n)}=b_1b_2\:\cd\:b_{\varphi(n)})\)
\((r_1r_2\:\cd\:r_{\varphi(n)}=b_1b_2\:\cd\:b_{\varphi(n)})\)
となります。そこで、1.1c(合同式の乗算)を上の \(\varphi(n)\) 個の合同式に適用して左辺と右辺を全てかけ合わせると、
\(a^{\varphi(n)}\cdot B\equiv R\:(\mr{mod}\:n)\) つまり、
\(a^{\varphi(n)}\cdot B\equiv B\:(\mr{mod}\:n)\)
\(a^{\varphi(n)}\cdot B\equiv B\:(\mr{mod}\:n)\)
が得られます。ここで、そもそもの定義から \(B\) は \(n\) と素なので 1.3 を使うと、
\(a^{\varphi(n)}\equiv1\:(\mr{mod}\:n)\)
となって証明が完成しました。
8. RSA暗号の一般形
オイラー関数とオイラーの定理(オイラーによるフェルマの小定理の一般化)を用いると、RSA暗号(4.1)の一般形を次のように記述できます。
| 8.1 | RSA暗号の一般形 |
|
\(n\) を任意の自然数とし、\(e\:,d\) を、 \(de\equiv1\:(\mr{mod}\:\varphi(n))\) を満たす数とする。この前提で、 暗号化:\(P^e\equiv C\:(\mr{mod}\:n)\) ならば 復号化:\(C^d\equiv P\:(\mr{mod}\:n)\) である。また、 暗号化:\(P^e\equiv C\:(\mr{mod}\:n)\) ならば 復号化:\(C^d\equiv P\:(\mr{mod}\:n)\) も成り立つ。 | |
この一般形にすると、復号化の式の証明はいたってシンプルになります。\(de=k\varphi(n)+1\)とおくと、
\(C^d\equiv P^{de}\:(\mr{mod}\:n)\)
\(\phantom{C^d}=P^{k\varphi(n)+1}\)
\(\phantom{C^d}=P\cdot(P^{\varphi(n)})^k\)
\(\phantom{C^d}\equiv P\:(\mr{mod}\:n)\)
\(\phantom{C^d}=P^{k\varphi(n)+1}\)
\(\phantom{C^d}=P\cdot(P^{\varphi(n)})^k\)
\(\phantom{C^d}\equiv P\:(\mr{mod}\:n)\)
となり証明できます。\(d,\:\:e\) を入れ替えても成り立ちます。最後の式の変形のところでは 7.1 と 1.2(合同式の累乗)を使っています。また 7.3 で証明したように、\(\varphi(n)\) の代わりに \(\psi(n)\) (= \(n\) の素因数それぞれのオイラー関数値の最小公倍数)としても、RSA暗号の一般形は成立します。
実際のRSA暗号は \(p\) と \(q\) を素数として \(n=pq\) とおいたものですが(6.1b)、数学的には \(n\) の素因数分解が分かると(素因数の累乗があってもよい) \(\varphi(n)\) はすぐに計算できるので(6. オイラー関数)暗号が構成できることになります。それが 8.1 の一般形の意味です。
しかし実用的な暗号のためには、素因数分解が困難であり(= \(n\) の素因数ができるだけ大きな数であり)、また暗号化・復号化の高速計算のためには \(n\) が小さいほど良いので、RSA暗号がその最適解なのでした。
全体のまとめ
最後に、RSA暗号についての説明全体をまとめると、以下のようになるでしょう。
| RSA暗号は数論(整数論)の基礎から構成されている。その基礎には、ユークリッド、孫子算経、フェルマ、オイラーなどによる数学史の重要な発見が詰まっている。 | |
| RSA暗号における公開鍵・秘密鍵の生成式、暗号化・復号化の式には巨大数の演算が現れるが、それは実用的に計算可能である。 | |
| RSA暗号の原理は、整数の "加減乗除" と "累乗(冪乗)" の知識をベースとして、そこから論理を積み重ねることで理解可能である。つまり「高校数学程度の知識で理解」できる。 |
この最後の点が、ここに「RSA暗号の数理」を掲載した目的でした。
補足1:デジタル署名
公開鍵暗号は暗号化の鍵を公開するため、誰でも通信相手の公開鍵を使って暗号を作れます。\(A\) さんと \(B\) さんが RSA暗号で暗号化通信をするとし、
\(A\) 公開鍵 \((e_A,\:\:n_A)\)、秘密鍵 \(d_A\) \(B\) 公開鍵 \((e_B,\:\:n_B)\)、秘密鍵 \(d_B\) |
とします。\(B\) から \(A\) にメッセージ \(M\) を送るには、
\(M^{\:\large e_{\overset{\:}{A}}}\equiv C\:\:(\mr{mod}\:n_A)\)
となる暗号文 \(C\) を送ればよく、\(C\) は \(d_A\) を知っている人しか解読できません。しかし、秘密鍵 \(d_A\) でしか解読できない暗号文は誰にでも作れます。つまり "なりすまし" ができる。\(A\) としては確かに \(B\) から来た暗号文だという確証が必要です。この確証を得る手段がないと、公開鍵暗号は成立しません。
その確証の手段が「デジタル署名」で、これは「ハッシュ関数」という技術にもとづいて作ります。
ハッシュ関数
ハッシュ関数は「任意長の入力データを固定長のハッシュ値に変換する関数」です。固定長は、たとえば256ビットです。これは暗号学的に信頼できる標準的なものがあって、アメリカ国立標準技術研究所(NIST)によって公開されている SHA-2、SHA-3 がその例です(SHA : Secure Hash Algorithm)。
ハッシュ関数には「入力メッセージのわずかな違いも、出力されるハッシュ値に大きな変化を及ぼす」という特性があります。SHA-2 の仕様の一つである SHA256(ハッシュ値:256ビット)で実際にやってみると、
A rolling stone gathers no moss.
A rolling stone gathers no moss
という2つの文章の違いは、最後にピリオドがあるか(前)、無いか(後)だけですが、2つのハッシュ値を16進数で並べて書くと、
4F73D0D6A45EF8B201707281CB421EE90413D4C1A5CA846BABF502A4BB202DE8 709EAFF33947303FBBC0810DD8F099C317BACC057F4BF91E081DB2B099457FCA
であり、全く違うことが分かります。もし入力データが同じであれば、ハッシュ関数は厳密に同じハッシュ値を出力します。
安全なハッシュ関数の条件は、まずハッシュ値から入力データを推測できないことです(=一方向性)。また、同じハッシュ値をもつ別の入力データを推測できないことです(=衝突困難性)。SHA-2、SHA-3 はそのような条件をクリアした、安全なアルゴリズムです。
以降、ハッシュ関数を \(H(\:)\) と書きます。RSA暗号を使ったデジタル署名のアルゴリズムは次の通りです。
デジタル署名
\(B\) から \(A\) にメッセージ \(M\) を送る手順です。
\(\bs{B}\) の署名手順
\(\bs{A}\) の検証手順
|
RSA暗号は暗号化と復号化が対称形の計算なので、デジタル署名の作成と検証はシンプルです。
補足2:素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
(2024.3.18)
2021-05-15 11:49
nice!(0)
No.310 - 高校数学で理解するRSA暗号の数理(1) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
No.235「三角関数を学ぶ理由」では、私たちが学校で勉強を学ぶ目的の一つが「論理的に考える力を養う」こととし、その典型例として数学をとりあげました。数学は「論理のみで成り立っている」からです。そのことを改めて示すために \(\mr{sin}\:\theta\) の微分が \(\mr{cos}\:\theta\) になることを、三角関数のそもそもの定義に立ち返って証明しました。
今回はその継続・発展で、別の数学の問題を取り上げます。現代社会で広く使われている公開鍵暗号(その中の RSA暗号)です。これを取り上げる理由 は、
の3点です。以下の文章は元々別の目的のために作ったものですが、ここに掲載することにします。
公開鍵暗号
公開鍵暗号とは、
というタイプの暗号です。公開鍵暗号のメリットは多々ありますが、一番のメリットは「鍵を配送するコストがかからない」ことです。全ての鍵を秘匿する暗号だと、その鍵をどうやって配送して暗号化をしたい人に届けるかが大きな問題となります。暗号化通信で配送するというのは解決になりません。その暗号化通信の暗号鍵をどうやって配送するかという問題が残るからです。
公開鍵暗号では暗号化のための鍵がオープンなので、配送のコストはゼロです。暗号文を受け取りたい人が公開鍵と秘密鍵を生成し、公開鍵をオープンにすると誰でもその人に暗号文を送ることができます。
公開鍵暗号の設計の最大のポイントは、あたりまえですが、公開鍵から秘密鍵を推定したり導出したりできないことです。まさにそこに数学が使われていて、暗号文を解読できないようになっています。この「暗号化の鍵を公開してしまう」という革新的なアイデアというか、まさに "究極の逆転の発想" を論文として発表したのは、当時スタンフォード大学の研究者だったディフィー(米)とヘルマン(米)で、1976年のことでした。
そのディフィーとヘルマンのアイデアに基づいた最初の暗号が RSA暗号で、現代でも盛んに使われています。これは 1978年に MIT のリベスト(米)、シャミア(イスラエル)、エーデルマン(米)の3人のよって発明され、3人の頭文字をとって RSA と呼ばれています。
実はこの RSA暗号は、実用として何に使ったらいいのか、発表当時は使い道が分からなかったといいます。それが現代ではインターネットによる通信の重要技術として広く使われている。これにはコンピュータの処理速度の飛躍的向上も貢献しています。革新的な技術は、その応用環境が整った時点で、後から実用化される。よくあることです。
以下、このRSA暗号の数理を順に見ていきます。
RSA暗号の例題
まずRSA暗号はどういうものか、それを極めて簡単な例題で説明します。
平文(=暗号化する文)を \(P\) で、またそれを暗号化した暗号文を \(C\) で表します。例題として平文は1文字だけの英字で、それを整数に変換したものとします。RSA暗号にちなんで大文字の R の1文字だけを平文の例とします。コンピュータで使われる ASCII(アスキー)コードでは、英大文字・英小文字・数字・特殊記号を \(1\)~\(128\) の数で表すので、それを使って数字化すると R は 82 です。つまり、
が例題の平文です。公開鍵は2つの数字のペア \((e,n)\)、秘密鍵は一つの数字 \(d\) で、例題としては、
とします。この公開鍵と秘密鍵の作り方は後で述べます。平文から暗号文への変換(=暗号化)と、暗号文から平文への変換(=復号化)を次の計算で行います。以降の記述では、\(\bs{a}\) を \(\bs{b}\) で割った余り(=剰余)を "\(\bs{a\:\mr{mod}\:b}\)" と書きます(プログラム言語や EXCEL で \(\mr{mod}(a,\:b)\) と書くのと同じ意味です)。
例題の平文、\(P=82\) をこの暗号化の式に入れると、
となり、平文 "\(82\)" に対する暗号文は "\(4\)" です。\(82^{133}\) は巨大な数ですが、剰余を求めるときにこの巨大数を計算する必要は全くありません。上の程度の計算なら電卓でも簡単にできます。そのやり方は後ほど示します(「4. RSA暗号の証明」)。暗号文の復号化は、暗号文 "\(4\)" を復号化の式に入れると、
となり、元の平文である "\(82\)" が復元できました。なお、この例では平文をわずか1文字(\(2^7\) 以下の数字)としましたが、実際に使われる暗号では \(2^{1024}\) 程度(10進で約300桁程度)の数字です(= 平文を数字化したもの。平文が長い場合は複数に分割する)。また、公開鍵 \((e,\:n)\) と秘密鍵 \(d\) も同程度の大きさの数字です。
この計算で暗号化と復号化が可能なのは、公開鍵と秘密鍵の作り方に工夫があるからです。まず \(n=143\) は2つの素数 \(p=11\) と \(q=13\) の積です。
また \(e\) は、\(e\) と \((p-1)(q-1)=120=2^3\cdot3\cdot5\) との最大公約数が \(1\) であるように決めてあります。\(e=133=7\cdot19\) なので、\(133\) と \(120\) との共通の約数は \(1\) だけです。さらに秘密鍵である \(d\) は、
となるように決めてあります。\(37\cdot133=4921=41\cdot120+1\) なので成り立っています。後で説明しますが、\(e\) と \((p-1)(q-1)\) との最大公約数が \(1\) なので、このような \(d\) が必ず存在します。このように鍵を仕込んでおくと暗号化と復号化が可能になる。そのことを証明するのが、本記事の目的です。その証明を、前提とする数学知識を最小限にしてやってみたいと思います。
公開鍵暗号は「公開鍵から秘密鍵が導出できない」ことが必須です。RSA暗号では、\(n=p\cdot q\) と素因数分解ができれば、
の式を解いて \(d\) が求まります。しかし実用で使われるRSA暗号は最低でも \(n\) の桁数が10進数で300桁程度です(2進数で 1024ビット程度。平文も同等の長さ)。この程度の大きさの整数の素因数分解は超高速コンピュータをもってしても困難です。もしコンピュータの速度がさらに向上するなら、鍵の桁数をさらに大きくすればよい。この素因数分解の困難性が、RSA暗号が成り立つ理由です。
以降でRSA暗号の暗号化と復号化の式が成り立つことの証明を行います。さらに、単に成り立つことだけでなく、RSA暗号に関わる各種の式が計算可能であることの説明をします。"式が正しい" ことと、その "式が実用的に計算可能である" ことは違うからです。素因数分解がまさにその例です。
まず、整数の性質についての用語の定義からです。用語は RSA暗号の式の証明に必要なものだけに絞ります。以降に現れる "数" やそれを表す記号は、ほとんど場合は整数のことですが、自然数( \(1\) 以上の整数)を意味する場合もあります。どちらかは文脈から明らかなので、いちいち断りなく使います。
準備:用語の定義
割り切る・約数・因数・最大公約数
整数 \(N\) を \(a\) で割ったときの余りがゼロのとき、\(\bs{N}\) は \(\bs{a}\) で割り切れると言い、また、\(\bs{a}\) は \(\bs{N}\) を割り切ると言います。このことを記号を使って、
と書きます。またこのときの \(a\) を \(N\) の約数と呼びます。\(N|N\) と \(1|N\) は常に成り立つので、\(1\) と \(N\) は \(N\) の約数です。
\(N\) が 2つ以上の数の積で表されるとき、そのおのおのの数を \(N\) の因数と呼びます。因数は約数と同じものですが、見方の違いと言えるでしょう。
2つの数、\(N\) と \(M\) があったとき、共通の約数を公約数と言います。また、公約数のうち最大のものを最大公約数と呼び、\(\mr{gcd}(N,M)\) で表します。
素数と素因数分解
\(2\) 以上の整数 \(N\) の約数が \(1\) と \(N\) のみのとき、\(N\) を素数と言い、そうでない数を合成数と言います。合成数は \(1\) と \(N\) 以外の約数を持ちます。約数(=因数)が素数のとき、それを素因数と呼びます。\(N\) が素数の場合は \(N\) が素因数です。
合成数は素因数の積で表現できます(=素因数分解)。なぜなら、定義によって合成数 \(N\) は、\(1\) でも \(N\) でもない数 \(a\) と \(b\) を使って \(N=a\cdot b\) と表現(=分解)できますが、\(a\) や \(b\) が合成数なら、さらに分解を繰り返すことによって最終的には素数の積にたどり着くからです。なお便宜上、素数はそれ自身が素因数分解であるとします。
「素数」と「大きな数の素因数分解の困難性」が RSA暗号の基礎になっているのは、例題で説明した通りです。
素因数分解の一意性
素因数分解は、かけ算の順序を無視して一意に決まります(=素因数分解の一意性)。これは自明のように思えますが、証明をすると次の通りです。
いま(かけ算の順序は無視して)異なった2種類の素数列の積で表現できる合成数がある(=素因数分解が一意ではない)と仮定します。すると、そのような最小の数、\(N\) があるはずです。このとき \(N\) は、\(p_i\) と \(q_i\) を素数として、
と表現できます。ここで \(p_1\) に着目すると \(p_1|N\) なので、\(p_1|q_i\) となる \(q_i\) があるはずです。かけ算の順序は無視するので、\(p_1|q_1\) として一般性を失いません。ところが \(q_1\) は素数なので、\(q_1=p_1\) しかあり得ない。そこで式の全体を \(p_1\) で割ると、
となります。これは \(\dfrac{N}{p_1}\) が2つの異なった形に素因数分解できることを示しています。ところが \(\dfrac{N}{p_1}\) は \(N\) より小さい数なので「\(N\) が2つの異なった形に素因数分解できる最小の数」ということに矛盾します。従って「2つの異なった形で素因数分解できる数がある」という仮定が誤りであり、素因数分解の一意性が示されました。
互いに素
整数 \(N\) と 整数 \(M\) の最大公約数が \(1\) のとき、つまり \(\mr{gcd}(N,M)=1\) のとき、「\(N\) と \(M\) は互いに素である」と言います。これは \(N\) と \(M\) が共通の素因数を持たないことと同じです。なお、\(\mr{gcd}(N,1)=1\) は常に成り立つので、\(1\) は他の数と互いに素です。
以降の、RSA暗号の証明に至るプロセスでは「互いに素」に関連した数々の定理や証明が出てきます。RSA暗号は「素数」と「互いに素」の上に構築された暗号です。
用語の定義はここまでです。以降はRSA暗号の成立性の証明に入ります。まず、数の "合同" の概念からです。
1. 合同
合同の概念はRSA暗号の根幹の一つです。\(m\) を \(2\) 以上の整数とするとき、2つの整数 \(a,\:b\) について
\(\bs{a}\) と \(\bs{b}\) は \(\bs{m}\) を法として合同であると言い、
と書きます。少々ややこしいですが、はじめに書いたように "\(a\) \(\mathbf{mod}\) \(b\)" とすると「\(a\) を \(b\) で割った余り」の意味です。以下に、合同の性質でRSA暗号の証明に必要なものをあげます。
これらの性質は、それぞれの数を、
というように書いて計算をすればすぐにわかります。たとえば 1.1c(合同式の乗算)を証明するには、\(a\) と \(c\) の式をかけ算し、\(b\) と \(d\) の式をかけ算して、
が得られますが、2つの数が共に \(m\) で割り切れると、その差も \(m\) で割り切れます。従って、
となります。
これは 1.1c で、\(c=a\)、\(d=b\) とおいて 1.1c を "繰り返して使う" ことでわかります。"繰り返して使う" ことを証明として書くなら数学的帰納法になるでしょう。以降は「互いに素」に関連した合同の性質です。
合同の定義により
となります。ここで一般的に次の 1.3a が成り立つことに注意します。
\(m\) と \(x\) は互いに素なので、\(m\) と \(x\) に共通の素因数はありません。従って、\(m\) を素因数分解したときに現れる素因数は、すべて \(n\) の素因数のはずです。でないと、\(m|xn\) とはならないからです。従って \(m|n\) となります。このことを \(m|x(a-b)\) に適用すると、
となり、1.3 が証明されました。1.3 は以降の証明にたびたび出てくる重要な定理です。1.3 を一般化したのが次の 1.4 です。
\(a,\:b,\:x,\:y\) を、\(m\) と 剰余 \(r\) を使って次のように表します。
このようにおくと、\(ax\equiv by\:(\mr{mod}\:m)\) より、
となります。一方、\(r\) と \(m\) は互いに素です。なぜなら、もし \(r\) と \(m\) が \(1\) ではない共通の約数 \(c\) をもつとすると、上の \(x\) の式から \(c\) は \(x\) の約数にもなり、\(x\) と \(m\) が互いに素ではなくなるからです。また、\(y\) の式から \(c\) は \(y\) の約数でもあり、\(y\) と \(m\) が互いに素という前提にも反します。このように \(r\) と \(m\) は互いに素なので 1.3 を使って、
となりますが、\(0\leq\:r_a,\:r_b\: < m\) なので、\(r_a=r_b\) となり、
が示されました。
\(a\equiv b\:(\mr{mod}\:m)\) なので、合同の定義から \(m|(a-b)\) です。また、\(a\equiv b\:(\mr{mod}\:n)\) なので、合同の定義から \(n|(a-b)\) であり、\(a-b=k_1n\) と表せます。この式の \(a-b\) を \(m|(a-b)\) に代入すると、
となります。\(m\) と \(n\) は互いに素なので 1.3a を使うと、
となり、従って \(k_1=k_2m\) と表せることになります。この \(k_1\) を \(a-b=k_1n\) に代入すると、
となって 1.5 が証明できました。
合同には数々の性質や定理がありますが、RSA暗号の証明に必要なものは以上です。次に、2つの数の最大公約数を求める「ユークリッドの互除法」です。これは最大公約数を求める計算方法というだけでなく、RSA暗号において公開鍵と秘密鍵を生成する際に必須のものです。
2. ユークリッドの互除法
ユークリッドの互除法は 2つの自然数(\(a\) と \(b\)。\(a > b\) とします)の最大公約数を求める計算方法です。これはユークリッドの数学書である『原論』にあります。『原論』は紀元前 300年頃の成立といいますから、2300年ほど前の書物ということになります。
この計算方法では、割り算(除算)を何ステップか繰り返します。割り算において被除数(=割られる数)と除数(=割る数)、商(=答)、剰余(=余り)の関係は、
ですが、まず第1ステップとして、
とおき、
の計算をして、商1と剰余1を求めます。次に第2ステップとして、
とおいて割り算を行い、商2と剰余2を求めます。つまり、
です。この「除数と剰余を新たな被除数と除数にして割り算をする」ステップを次々と繰り返して行くと、剰余は次第に小さくなっていき、ついには剰余がゼロ(= 被除数が除数で割り切れる)となります。この時点での除数(= 一つ前のステップの剰余)が \(a\) と \(b\) の最大公約数です。
なぜそうなるのかが以下ですが、ポイントは割り算の式から明らかなように「被除数と除数の公約数は、剰余の約数でもある」ことです。つまり \(a\) と \(b\) の約数であるという性質が剰余に引き継がれ、それは割り算のステップを繰り返してもずっと続きます。しかも、剰余はステップが進むにつれて小さくなっていくので、最大公約数に近づく。そして割り切れたときの除数(一つ前のステップの剰余)は、約数であると同時に最大の約数である。おおまかにはそのような理解です。
\(a\) と \(b\)(\(a > b\))の公約数を \(x\) とします。すると、\(x|a\) かつ \(x|b\) なので、\((1)\) 式から \(x|r_1\) になります。この \(x|r_1\) と \(x|b\) から \((2)\) 式を使って \(x|r_2\) が得られます。
その次には \(x|r_1\) 、\(x|r_2\) 、\((3)\) 式から \(x|r_3\) になる。以上を最後まで繰り返すと、次のようになります。
以上のように、最終的には \(x|r_i\) となり、
ことが示せました。同時に、
ことも分かります。
次に、ユークリッドの互除法の最終プロセスに現れる剰余は、全てのステップの剰余の約数になっていることを示します。このことを最終ステップから順に遡って検証すると、
となり、\(r_i|b\) かつ \(r_i|a\)、つまり、
ことが示せました。
従って、
の2つから、\(\mr{gcd}(a,b)=r_i\) が証明できました。
計算量
RSA暗号にとってのユークリッドの互除法の意味ですが、次の2つが重要です。まず第1に「2つの数の最大公約数は、素因数分解なしに計算できる」ことです。これはすなわち「2つの数が互いに素であることが素因数分解なしに示せる」ことも意味します。
我々が普通、学校で習う最大公約数の求め方は、2つの数を素因数分解して共通の素因数を探すというものでした。共通のものがなければ最大公約数は \(1\)(=互いに素)です。しかし、数が巨大になると素因数分解が困難になります(それがRSA暗号が成り立つゆえんです)。ユークリッドの互除法を使うと「最大公約数」や「互いに素」が素因数分解なしに示せるのです。
第2は、ユークリッドの互除法が高速に計算できることです。ユークリッドの互除法では、一つのステップの剰余が次のステップの除数になります。次のステップの剰余は除数より小さいので、
となりますが、\(r_{i+1}\) が \(0\) に近いと計算は急速に収束します。また \(r_{i+1}\) が \(r_i\) に近い場合でも、その次のステップの商が大きくなり、\(r_{i+2}\) が \(0\) に近くなるので、計算は収束することになります。従って、最も計算が長引くのは、\(r_{i+1}\) が \(r_i\) の半分程度で、それが連続する場合だと推測できます。
実は、ユークリッドの互除法のステップが最も長くなるケースが知られています。それは 割り算の商が常に \(1\) になるケースで、\(a\) と \(b\) が(たまたま)フィボナッチ数列の隣り合う2項だとそうなります。フィボナッチ数列とは、
で定義される数列で、実際に書いてみると、
です。いま、\(a=144\)、\(b=89\) としてユークリッドの互除法の計算をしてみると
となって、10ステップかかります。剰余が減る割合が常に 0.6 倍程度で、なかなか減りません。商が常に 1 なのでこうなります。しかし、なかなか減らないが毎回 0.6 倍程度にはなり、マクロ的には急速に小さくなる。証明は省略しますが、\(a\) と \(b\) が\(10\)進で \(N\) 桁の数字でフィボナッチ数列の隣り合う2項だった場合でも、ユークリッドの互除法は \(5\times N\) ステップ以下で終了します。
これは a とb が300桁程度の数字のとき、それが偶然にもフィボナッチ級数の隣り合う2項であるという最悪の最悪の場合でも 1500回の割り算で終了することを意味します。この程度の計算はもちろんコンピュータで可能です。
本題に戻ります。最初の「RSA暗号の例題」のところで公開鍵の作り方を書きました。まず2つの素数、\(p\) と \(q\) を選び、\(n=p\cdot q\) とします。次に、\((p-1)(q-1)\) との最大公約数が \(1\) であるような数(=互いに素)を選び、それを \(e\) とします。その \((e,\:n)\) のペアを公開鍵とするのでした。
\(n\) と同程度の大きさの数、\(e\) をランダムに選んだとき、その \(e\) が \((p-1)(q-1)\) と互いに素であるかどうかは、ユークリッドの互除法で検証可能です。そしてこの検証は \(p\) と \(q\) が巨大な数であっても可能です。つまりユークリッドの互除法は公開鍵が現実に作成できるという数学的根拠になっています。
アルゴリズム
2.1 において、\(a\) と \(b\) の最大公約数は \(r_i\) でしたが、この \(r_i\) は \((1)\)式における \(b\) と \(r_1\) の最大公約数にもなります。なぜなら、\(b\) と \(r_1\) の最大公約数を求めるためには \((2)\)式から互除法の計算を始めればよく、その結果は \(r_i\) になるからです。これは次を意味します。
つまり、ユークリッドの互除法は
ものといえます。この置き換えは次々と可能で、置き換えるたびに問題がより "小さく" なっていく。これがユークリッドの互除法の原理です。ここで改めて 2.1a の証明をすると、次の通りです。
もちろん、\(b|a\) であれば \(\mr{gcd}(a,b)=b\) です。
ユークリッドの互除法は "世界最古のアルゴリズム" と言われています。そして、アルゴリズムを記述するのに最適な言語はプログラミング言語です。2.1a の原理に基づき、ユークリッドの互除法で最大公約数を計算するプログラムを掲げます。
① の "%" は Javascript の剰余演算子で、"a % b" は "a を b で割った余り" という意味です(a \(\mathbf{mod}\) b と同じ)。なお、このプログラムは a<b でも動作します。
もちろん、Javascript でなくても、C++ でも Python でも記述できます。このようにプログラムで書くと簡潔になって、ユークリッドの互除法というアルゴリズムの本質がクリアにわかります。
拡張ユークリッドの互除法
ユークリッドの互除法の "副産物" として、次の定理が成り立ちます。
この定理の証明ですが、ユークリッドの互除法の計算過程を振り返ると、
でした。ここで \((1)\) を変形して、
とします。\(u_1=1,\:\:v_1=-q_1\) です。次に、今求めた \(r_1\) と \((2)\) を使うと、
の形に表せることになります。\(u_2=-q_2,\:\:v_2=1+q_1q_2\) です。さらに、求まった \(r_1\) と \(r_2\) と \((3)\) を使って、
と表せることが分かります。このステップを順に続けていって \((i)\) まで到達すると、
となることがわかります。\(r_i=\mr{gcd}(a,b)\) だったので、2.2 が証明できました。\(u\) と \(v\) のうち、一つは正の整数、もう一つはゼロか負の整数です。一つがゼロであるのは、\(a=b\) のときです。なお、2.2 を満たす \(u\)、\(v\) に、
を満たす \(u\)、\(v\) をそれぞれ足し込んでも 2.2 が成立することが明白です。つまり 2.2 を満たす \(u\)、\(v\) は1組というわけではありません。なお、2.2 は次のように言い換えることができます。
拡張ユークリッドの互除法のアルゴリズム
ユークリッドの互除法を拡張して、\(a\) と \(b\) が与えられたとき、\(\mr{gcd}(a,b)\) と、
を満たす \(u\) と \(v\)(=無数にある解のうちの一つのペア)を同時に計算してしまうアルゴリズムを考えてみます。
考え方は 2.1b のユークリッドの互除法と同じで、解くべき問題を「等価でより小さな問題」に置き換えます。そのために \(a=qb+r\) とおくと、2.1a より、
なので、問題は次のように書き換えられます。
ここで、未知数の \(u\) と \(v\) を次のように変換します。
これを代入して式を整理すると
となり、"小さな問題" に変換することができました。この考え方でアルゴリズムを記述すると次のとおりです。
以下は、このアルゴリズムの補足説明です。
この拡張ユークリッドの互除法のアルゴリズムは、2.1b のユークリッドのアルゴリズムとほぼ同じです。ただし、\(u\) と \(v\) の計算のために変数を変換しているので、最大公約数を計算したあとに元の変数値を求める必要があります(=⑤)。そこが違います。
このことから、拡張ユークリッドの互除法の計算量は、ユークリッドの互除法のほぼ2倍だと推測できます。計算は少々複雑になりますが、たとえ \(\bs{a}\) や \(\bs{b}\) が巨大な数であっても、コンピュータで高速に計算できる。このことは次の「整数の逆数」の項で述べるように、RSA暗号にとっての重要ポイントになります。
整数の逆数
2.2 から導かれる次の定理は、RSA暗号にとって重要です。
2.2 において \(a\)と互いに素な数 \(m\) を選び、\(b=m\) とおくと、\(\mr{gcd}(a,m)=1\) なので、適当な \(u\) と \(v\) をとることにより、
とすることができます。すなわち、
となり、2.3 が示されました。このとき \(a\cdot u\) は \(m\) と互いに素であり、また \(a\) と \(m\) は互いに素なので、\(b\) も \(m\) と互いに素になります。また、\(b_1\) と \(b_2\) の2つの解があるとすると、
となり、\(a\) と \(m\) は互いに素なので 1.3a より、
となります。従って、\(1\leq b < m\) の範囲に \(b\) があり、かつ、この範囲で \(b\) は一意に定まります。\(m\) を法として \(b\) と合同な数も解であることは明白ですが、それらの解は \(m\) を法として唯一です。
2.3 の "逆数" を計算するアルゴリズムは、拡張ユークリッドの互除法2.2 のアルゴリズム(2.2b)と基本的に同じです。
①で、extdEUCLID のアルゴリズム(2.2b)を使って u を求め、それを m 未満の自然数に直して答えの b を求めています。( b + m )% m は b が負の場合の配慮です。このアルゴリズムは正確に言うと、a と m が与えられたとき、
となる \(b\) を求めるアルゴリズムです。\(a\) と \(m\) が互いに素でなくても成立します。
この "逆数の存在定理" は RSA暗号において秘密鍵の算出に使われています。冒頭の「RSA暗号の例題」に書いたように、RSA暗号の公開鍵と秘密鍵は、まず秘密の2つの素数 \(p\) と \(q\) を決め、
とします。そして \(e\) を、
となるように決め、\(n\) と \(e\) を公開鍵とするのでした。そして秘密鍵 \(d\) を、
を満たす数とします。この秘密鍵 \(d\) の計算は、\(\mr{mod}\:(p-1)(q-1)\) の世界で \(e\) の逆数を求めていることに他なりません。逆数の存在が保証されるのは、\(e\) を \((p-1)(q-1)\) と互いに素という条件で決めたからです。さらに、この逆数の計算アルゴリズムは 2.2b の拡張ユークリッドの互除法と同じなので高速に計算できることが重要ポイントです。
普通、整数の "逆数"は(整数の範囲で)定義できません( \(1\) 以外は)。しかし、"\(\mr{mod}\:m\) の合同の世界" では、\(m\) と互いに素な数 \(a\) に対して逆数が定義できることになります。つまり整数の範囲で「割り算」が定義できる。
たとえば \(\mr{mod}\:10\) の世界では \(7\times3=1\) であり、\(7\) の逆数は \(3\) です。割り算は逆数のかけ算なので、たとえば \(8\div7=8\times3=4\)(\(\mr{mod}\:10\) の世界)といった演算が定義できます。"検算" をすると \(4\times7=8\)(\(\mr{mod}\:10\) の世界)なので合っています。
\(\mr{mod}\:10\) の場合は実用的な意味はありませんが、\(p\) を素数としたとき「\(\mr{mod}\:p\) の世界」は大変重要です。というのも \(p\) 未満の自然数はすべて \(p\) と互いに素だからです。つまり \(p\) 未満の全ての自然数に対して "逆数" が定義できます。
2.3b はほとんど 2.3 と同じです。「異なる \(a\) に対する逆数 \(b\) は異なる」というところですが、もし \(1\leq i < j < p\) である \(i\) と \(j\) に対して、
となったとすると、
ですが、\((j-i)\) も \(b\) も \(p\) と素なので矛盾します。異なる \(a\) に対する逆数 \(b\) は異なります。
このように逆数が存在するということは、\(p\) 未満の2つの自然数の "除算" が定義できます。さらに、\(0\) と \(p\) 未満の自然数を合わせると加減乗除が行えることになります。
加減乗除が定義された集合を「体(Field)」と呼びます。有理数、実数、複素数は「体」ですが、「\(0\) と \(p\) 未満の自然数」も体になります。これを \(\bs{F}_p\) と表記します。この集合の要素の数は有限個なので「有限体」です。 \(\bs{F}_{13}\) の場合(\(\mr{mod}\:13\))で "逆数" の計算をしてみると、
となり、\(0\) 以外の \(\bs{F}_{13}\) の要素は、その逆数(=逆元)と1対1に対応していることがわかります。
\(\bs{F}_p\) においては "整数" の加減乗除を "自由かつ厳密に" 行うことができます。これは、全ての情報を2進数に帰着させて扱うデジタル・コンピュータとの相性がよい。このため、公開鍵暗号の中には \(\bs{F}_p\) の演算を利用したものがあります。
なお、\(p\) を素数としたとき「\(p\) 未満の自然数はすべて \(p\) と互いに素」ということは「\((p-1)\:!\) と \(p\) は互いに素」ということです(" \(!\) " は階乗記号)。これは次の「フェルマの小定理」の証明に出てきます。
3. フェルマの小定理
フェルマの小定理は RSA暗号の根幹にかかわるものです。フェルマは17世紀フランスの大数学者(1607-1665)で、有名なフェルマの最終定理(大定理)と区別するために「小定理」の名があります。
これは少々意外な定理です。我々が高校までで習う素数は、自身と \(1\) 以外の約数を持たない数という定義か、素因数分解の定理か、そういうものです。「素数がもつ性質」に言及した定理はあまり思い浮かばない。しかしフェルマの小定理は、素数であれば必ずこうなると言っているわけです。これは次のように証明できます。
\(1,\:2,\:3,\:\cd\:,\:p-1\) のそれぞれに \(a\) をかけて、
という数列を作ります。そして、それぞれの数を \(p\) で割った剰余を \(b_i\) とします。つまり、
です。\(p\) は素数なので \(1\) から \((p-1)\) までの数は \(p\) と素であり、また \(a\) は仮定により \(p\) と素です。従って \(b_i\) が \(0\) になることはなく、\(1\leq b_i\leq\:(p-1)\) です。このとき、\(1\leq i,\:\:j\leq\:(p-1)\) である \(i,\:j\) について、
になります。なぜなら、もし \(b_i=b_j\) とすると、1.1b(合同式の減算)より、
です。仮定より \(a\) は \(p\) と互いに素なので、1.3 により(\(1.3\) で \(b=0\) の場合)、
となりますが、\(1\leq i,\:\:j\leq\:(p-1)\) なので、
となり仮定に反します。つまり\(i\neq j\) であれば、必ず \(b_i\neq b_j\) です。ということは、\((p-1)\) 個の数、\(b_i(1\leq i\leq p-1)\) は全て違う数であり、つまり、\((1,\:2,\:3,\:\cd\:,\:p-1)\) を並び替えたものです。従って、\(b_i\) を全部かけ算すると、
となります。そこで、1.1c(合同式の乗算)を上の \((p-1)\) 個の合同式に適用して左辺と右辺を全てかけ合わせてしまうと、
となります。ここで、\(p\) は素数なので \(p\) と \((p-1)!\) は互いに素です。すると 1.3 により、
となり、証明が完成しました。
No.235「三角関数を学ぶ理由」では、私たちが学校で勉強を学ぶ目的の一つが「論理的に考える力を養う」こととし、その典型例として数学をとりあげました。数学は「論理のみで成り立っている」からです。そのことを改めて示すために \(\mr{sin}\:\theta\) の微分が \(\mr{cos}\:\theta\) になることを、三角関数のそもそもの定義に立ち返って証明しました。
今回はその継続・発展で、別の数学の問題を取り上げます。現代社会で広く使われている公開鍵暗号(その中の RSA暗号)です。これを取り上げる理由 は、
| 2000年にわたる数学(数論 = 整数論)の基礎の上に作られた暗号である。 | |
| インターネットの重要技術の一つであり、現代社会のインフラとなっている。 | |
| 高校生程度の前提知識があれば、論理的思考を積み重ねることで十分に理解できる(= タイトルの「高校数学で理解する」の意味)。 |
の3点です。以下の文章は元々別の目的のために作ったものですが、ここに掲載することにします。
公開鍵暗号
公開鍵暗号とは、
| 暗号化の手順と、そこで使用する暗号化のための "鍵" が公開されている(その鍵が "公開鍵")。 | |
| 暗号文を解読するための手順も公開されているが、それに使う "鍵" は秘匿されている(その鍵が "秘密鍵")。 |
というタイプの暗号です。公開鍵暗号のメリットは多々ありますが、一番のメリットは「鍵を配送するコストがかからない」ことです。全ての鍵を秘匿する暗号だと、その鍵をどうやって配送して暗号化をしたい人に届けるかが大きな問題となります。暗号化通信で配送するというのは解決になりません。その暗号化通信の暗号鍵をどうやって配送するかという問題が残るからです。
公開鍵暗号では暗号化のための鍵がオープンなので、配送のコストはゼロです。暗号文を受け取りたい人が公開鍵と秘密鍵を生成し、公開鍵をオープンにすると誰でもその人に暗号文を送ることができます。
公開鍵暗号の設計の最大のポイントは、あたりまえですが、公開鍵から秘密鍵を推定したり導出したりできないことです。まさにそこに数学が使われていて、暗号文を解読できないようになっています。この「暗号化の鍵を公開してしまう」という革新的なアイデアというか、まさに "究極の逆転の発想" を論文として発表したのは、当時スタンフォード大学の研究者だったディフィー(米)とヘルマン(米)で、1976年のことでした。

|
ディフィーとヘルマンは公開鍵暗号の発明の功績で、コンピュータ・サイエンス分野のノーベル賞といわれるチューリング賞を 2015年に受賞した。 |
そのディフィーとヘルマンのアイデアに基づいた最初の暗号が RSA暗号で、現代でも盛んに使われています。これは 1978年に MIT のリベスト(米)、シャミア(イスラエル)、エーデルマン(米)の3人のよって発明され、3人の頭文字をとって RSA と呼ばれています。
実はこの RSA暗号は、実用として何に使ったらいいのか、発表当時は使い道が分からなかったといいます。それが現代ではインターネットによる通信の重要技術として広く使われている。これにはコンピュータの処理速度の飛躍的向上も貢献しています。革新的な技術は、その応用環境が整った時点で、後から実用化される。よくあることです。

|
RSA暗号を発明した3人は、チューリング賞を 2002年に受賞している。 |
以下、このRSA暗号の数理を順に見ていきます。
RSA暗号の例題
まずRSA暗号はどういうものか、それを極めて簡単な例題で説明します。
平文(=暗号化する文)を \(P\) で、またそれを暗号化した暗号文を \(C\) で表します。例題として平文は1文字だけの英字で、それを整数に変換したものとします。RSA暗号にちなんで大文字の R の1文字だけを平文の例とします。コンピュータで使われる ASCII(アスキー)コードでは、英大文字・英小文字・数字・特殊記号を \(1\)~\(128\) の数で表すので、それを使って数字化すると R は 82 です。つまり、
\(P=82\)
が例題の平文です。公開鍵は2つの数字のペア \((e,n)\)、秘密鍵は一つの数字 \(d\) で、例題としては、
公開鍵 : \(e=133,\:n=143\)
秘密鍵 : \(d=37\)
秘密鍵 : \(d=37\)
とします。この公開鍵と秘密鍵の作り方は後で述べます。平文から暗号文への変換(=暗号化)と、暗号文から平文への変換(=復号化)を次の計算で行います。以降の記述では、\(\bs{a}\) を \(\bs{b}\) で割った余り(=剰余)を "\(\bs{a\:\mr{mod}\:b}\)" と書きます(プログラム言語や EXCEL で \(\mr{mod}(a,\:b)\) と書くのと同じ意味です)。
暗号化 : \(C=P^e\) \(\mathbf{mod}\) \(n\)
復号化 : \(P=C^d\) \(\mathbf{mod}\) \(n\)
復号化 : \(P=C^d\) \(\mathbf{mod}\) \(n\)
例題の平文、\(P=82\) をこの暗号化の式に入れると、
\(C=82^{133}\) \(\mathbf{mod}\) \(143=4\)
となり、平文 "\(82\)" に対する暗号文は "\(4\)" です。\(82^{133}\) は巨大な数ですが、剰余を求めるときにこの巨大数を計算する必要は全くありません。上の程度の計算なら電卓でも簡単にできます。そのやり方は後ほど示します(「4. RSA暗号の証明」)。暗号文の復号化は、暗号文 "\(4\)" を復号化の式に入れると、
\(P=4^{37}\) \(\mathbf{mod}\) \(143=82\)
となり、元の平文である "\(82\)" が復元できました。なお、この例では平文をわずか1文字(\(2^7\) 以下の数字)としましたが、実際に使われる暗号では \(2^{1024}\) 程度(10進で約300桁程度)の数字です(= 平文を数字化したもの。平文が長い場合は複数に分割する)。また、公開鍵 \((e,\:n)\) と秘密鍵 \(d\) も同程度の大きさの数字です。
この計算で暗号化と復号化が可能なのは、公開鍵と秘密鍵の作り方に工夫があるからです。まず \(n=143\) は2つの素数 \(p=11\) と \(q=13\) の積です。
また \(e\) は、\(e\) と \((p-1)(q-1)=120=2^3\cdot3\cdot5\) との最大公約数が \(1\) であるように決めてあります。\(e=133=7\cdot19\) なので、\(133\) と \(120\) との共通の約数は \(1\) だけです。さらに秘密鍵である \(d\) は、
\(d\cdot e\) \(\mathbf{mod}\) \((p-1)(q-1)=1\)
となるように決めてあります。\(37\cdot133=4921=41\cdot120+1\) なので成り立っています。後で説明しますが、\(e\) と \((p-1)(q-1)\) との最大公約数が \(1\) なので、このような \(d\) が必ず存在します。このように鍵を仕込んでおくと暗号化と復号化が可能になる。そのことを証明するのが、本記事の目的です。その証明を、前提とする数学知識を最小限にしてやってみたいと思います。
公開鍵暗号は「公開鍵から秘密鍵が導出できない」ことが必須です。RSA暗号では、\(n=p\cdot q\) と素因数分解ができれば、
\(d\cdot e\) \(\mathbf{mod}\) \((p-1)(q-1)=1\)
の式を解いて \(d\) が求まります。しかし実用で使われるRSA暗号は最低でも \(n\) の桁数が10進数で300桁程度です(2進数で 1024ビット程度。平文も同等の長さ)。この程度の大きさの整数の素因数分解は超高速コンピュータをもってしても困難です。もしコンピュータの速度がさらに向上するなら、鍵の桁数をさらに大きくすればよい。この素因数分解の困難性が、RSA暗号が成り立つ理由です。
以降でRSA暗号の暗号化と復号化の式が成り立つことの証明を行います。さらに、単に成り立つことだけでなく、RSA暗号に関わる各種の式が計算可能であることの説明をします。"式が正しい" ことと、その "式が実用的に計算可能である" ことは違うからです。素因数分解がまさにその例です。
まず、整数の性質についての用語の定義からです。用語は RSA暗号の式の証明に必要なものだけに絞ります。以降に現れる "数" やそれを表す記号は、ほとんど場合は整数のことですが、自然数( \(1\) 以上の整数)を意味する場合もあります。どちらかは文脈から明らかなので、いちいち断りなく使います。
準備:用語の定義
割り切る・約数・因数・最大公約数
整数 \(N\) を \(a\) で割ったときの余りがゼロのとき、\(\bs{N}\) は \(\bs{a}\) で割り切れると言い、また、\(\bs{a}\) は \(\bs{N}\) を割り切ると言います。このことを記号を使って、
\(a|N\)
と書きます。またこのときの \(a\) を \(N\) の約数と呼びます。\(N|N\) と \(1|N\) は常に成り立つので、\(1\) と \(N\) は \(N\) の約数です。
\(N\) が 2つ以上の数の積で表されるとき、そのおのおのの数を \(N\) の因数と呼びます。因数は約数と同じものですが、見方の違いと言えるでしょう。
2つの数、\(N\) と \(M\) があったとき、共通の約数を公約数と言います。また、公約数のうち最大のものを最大公約数と呼び、\(\mr{gcd}(N,M)\) で表します。
素数と素因数分解
\(2\) 以上の整数 \(N\) の約数が \(1\) と \(N\) のみのとき、\(N\) を素数と言い、そうでない数を合成数と言います。合成数は \(1\) と \(N\) 以外の約数を持ちます。約数(=因数)が素数のとき、それを素因数と呼びます。\(N\) が素数の場合は \(N\) が素因数です。
合成数は素因数の積で表現できます(=素因数分解)。なぜなら、定義によって合成数 \(N\) は、\(1\) でも \(N\) でもない数 \(a\) と \(b\) を使って \(N=a\cdot b\) と表現(=分解)できますが、\(a\) や \(b\) が合成数なら、さらに分解を繰り返すことによって最終的には素数の積にたどり着くからです。なお便宜上、素数はそれ自身が素因数分解であるとします。
「素数」と「大きな数の素因数分解の困難性」が RSA暗号の基礎になっているのは、例題で説明した通りです。
素因数分解の一意性
素因数分解は、かけ算の順序を無視して一意に決まります(=素因数分解の一意性)。これは自明のように思えますが、証明をすると次の通りです。
いま(かけ算の順序は無視して)異なった2種類の素数列の積で表現できる合成数がある(=素因数分解が一意ではない)と仮定します。すると、そのような最小の数、\(N\) があるはずです。このとき \(N\) は、\(p_i\) と \(q_i\) を素数として、
\(N=p_1\:p_2\:p_3\:\cd\:p_r=q_1\:q_2\:q_3\:\cd\:q_s\)
と表現できます。ここで \(p_1\) に着目すると \(p_1|N\) なので、\(p_1|q_i\) となる \(q_i\) があるはずです。かけ算の順序は無視するので、\(p_1|q_1\) として一般性を失いません。ところが \(q_1\) は素数なので、\(q_1=p_1\) しかあり得ない。そこで式の全体を \(p_1\) で割ると、
\(\dfrac{N}{p_1}=p_2\:p_3\:\cd\:p_r=q_2\:q_3\:\cd\:q_s\)
となります。これは \(\dfrac{N}{p_1}\) が2つの異なった形に素因数分解できることを示しています。ところが \(\dfrac{N}{p_1}\) は \(N\) より小さい数なので「\(N\) が2つの異なった形に素因数分解できる最小の数」ということに矛盾します。従って「2つの異なった形で素因数分解できる数がある」という仮定が誤りであり、素因数分解の一意性が示されました。
互いに素
整数 \(N\) と 整数 \(M\) の最大公約数が \(1\) のとき、つまり \(\mr{gcd}(N,M)=1\) のとき、「\(N\) と \(M\) は互いに素である」と言います。これは \(N\) と \(M\) が共通の素因数を持たないことと同じです。なお、\(\mr{gcd}(N,1)=1\) は常に成り立つので、\(1\) は他の数と互いに素です。
以降の、RSA暗号の証明に至るプロセスでは「互いに素」に関連した数々の定理や証明が出てきます。RSA暗号は「素数」と「互いに素」の上に構築された暗号です。
用語の定義はここまでです。以降はRSA暗号の成立性の証明に入ります。まず、数の "合同" の概念からです。
1. 合同
合同の概念はRSA暗号の根幹の一つです。\(m\) を \(2\) 以上の整数とするとき、2つの整数 \(a,\:b\) について
| \(a\) を \(m\) で割ったときの余りと、\(b\) を \(m\) で割ったときの余りが等しいとき、あるいは同じことですが、 | |
| \((a-b)\) が \(m\) で割り切れるとき、つまり \(m|(a-b)\) のとき、 |
\(\bs{a}\) と \(\bs{b}\) は \(\bs{m}\) を法として合同であると言い、
\(a\equiv b\:(\mr{mod}\:m)\)
と書きます。少々ややこしいですが、はじめに書いたように "\(a\) \(\mathbf{mod}\) \(b\)" とすると「\(a\) を \(b\) で割った余り」の意味です。以下に、合同の性質でRSA暗号の証明に必要なものをあげます。
| 1.1 | |
|
\(a\equiv b\:(\mr{mod}\:m)\) かつ、 \(c\equiv d\:(\mr{mod}\:m)\) のとき、 1.1a \(a+c\equiv b+d\:(\mr{mod}\:m)\) 1.1b \(a-c\equiv b-d\:(\mr{mod}\:m)\) 1.1c \(ac\equiv bd\:(\mr{mod}\:m)\) | |
これらの性質は、それぞれの数を、
\(\begin{eqnarray}
&&a&=k_a\cdot m+r_1\\
&&b&=k_b\cdot m+r_1\\
&&c&=k_c\cdot m+r_2\\
&&d&=k_d\cdot m+r_2\\
\end{eqnarray}\)
というように書いて計算をすればすぐにわかります。たとえば 1.1c(合同式の乗算)を証明するには、\(a\) と \(c\) の式をかけ算し、\(b\) と \(d\) の式をかけ算して、
\(m|(ac-r_1r_2)\)
\(m|(bd-r_1r_2)\)
\(m|(bd-r_1r_2)\)
が得られますが、2つの数が共に \(m\) で割り切れると、その差も \(m\) で割り切れます。従って、
\(m|((ac-r_1r_2)-(bd-r_1r_2))\)
\(m|(ac-bd)\)
\(ac\equiv bd\:(\mr{mod}\:m)\)
\(m|(ac-bd)\)
\(ac\equiv bd\:(\mr{mod}\:m)\)
となります。
| 1.2 | 合同式の累乗(冪乗) |
|
\(a\equiv b\:(\mr{mod}\:m)\) なら、\(2\)以上の \(r\) について、 \(a^r\equiv b^r\:(\mr{mod}\:m)\) である。 | |
これは 1.1c で、\(c=a\)、\(d=b\) とおいて 1.1c を "繰り返して使う" ことでわかります。"繰り返して使う" ことを証明として書くなら数学的帰納法になるでしょう。以降は「互いに素」に関連した合同の性質です。
| 1.3 | 互いに素(1) |
|
\(ax\equiv bx\:(\mr{mod}\:m)\) かつ、 \(x\) と \(m\) が互いに素なら、 \(a\equiv b\:(\mr{mod}\:m)\) | |
合同の定義により
\(m|(ax-bx)\)
\(m|x(a-b)\)
\(m|x(a-b)\)
となります。ここで一般的に次の 1.3a が成り立つことに注意します。
| 1.3a | |
|
\(m\) は \(x\) と互いに素とする。 \(m|xn\) ならば \(m|n\) | |
\(m\) と \(x\) は互いに素なので、\(m\) と \(x\) に共通の素因数はありません。従って、\(m\) を素因数分解したときに現れる素因数は、すべて \(n\) の素因数のはずです。でないと、\(m|xn\) とはならないからです。従って \(m|n\) となります。このことを \(m|x(a-b)\) に適用すると、
\(m|(a-b)\)
\(a\equiv b\:(\mr{mod}\:m)\)
\(a\equiv b\:(\mr{mod}\:m)\)
となり、1.3 が証明されました。1.3 は以降の証明にたびたび出てくる重要な定理です。1.3 を一般化したのが次の 1.4 です。
| 1.4 | 互いに素(2) |
|
\(ax\equiv by\:(\mr{mod}\:m)\) かつ、 \(\phantom{a}x\equiv\phantom{b}y\:(\mr{mod}\:m)\) かつ、 \(x\) と \(y\) は \(m\) と互いに素なら、 \(a\equiv b\:(\mr{mod}\:m)\) | |
\(a,\:b,\:x,\:y\) を、\(m\) と 剰余 \(r\) を使って次のように表します。
\(\begin{eqnarray}
&&a&=k_a\cdot m+r_a\\
&&b&=k_b\cdot m+r_b\\
&&x&=k_x\cdot m+r\\
&&y&=k_y\cdot m+r\\
\end{eqnarray}\)
\((0\leq\:r_a,\:r_b,\:r\: < m)\)
\((0\leq\:r_a,\:r_b,\:r\: < m)\)
このようにおくと、\(ax\equiv by\:(\mr{mod}\:m)\) より、
\(r\cdot r_a\equiv r\cdot r_b\:(\mr{mod}\:m)\)
となります。一方、\(r\) と \(m\) は互いに素です。なぜなら、もし \(r\) と \(m\) が \(1\) ではない共通の約数 \(c\) をもつとすると、上の \(x\) の式から \(c\) は \(x\) の約数にもなり、\(x\) と \(m\) が互いに素ではなくなるからです。また、\(y\) の式から \(c\) は \(y\) の約数でもあり、\(y\) と \(m\) が互いに素という前提にも反します。このように \(r\) と \(m\) は互いに素なので 1.3 を使って、
\(r_a\equiv r_b\:(\mr{mod}\:m)\)
となりますが、\(0\leq\:r_a,\:r_b\: < m\) なので、\(r_a=r_b\) となり、
\(a\equiv b\:(\mr{mod}\:m)\)
が示されました。
| 1.5 | 互いに素(3) |
|
\(m\) と \(n\) は互いに素とする。 \(a\equiv b\:(\mr{mod}\:m)\) かつ、 \(a\equiv b\:(\mr{mod}\:n)\) なら、 \(a\equiv b\:(\mr{mod}\:mn)\) | |
\(a\equiv b\:(\mr{mod}\:m)\) なので、合同の定義から \(m|(a-b)\) です。また、\(a\equiv b\:(\mr{mod}\:n)\) なので、合同の定義から \(n|(a-b)\) であり、\(a-b=k_1n\) と表せます。この式の \(a-b\) を \(m|(a-b)\) に代入すると、
\(m|k_1n\)
となります。\(m\) と \(n\) は互いに素なので 1.3a を使うと、
\(m|k_1\)
となり、従って \(k_1=k_2m\) と表せることになります。この \(k_1\) を \(a-b=k_1n\) に代入すると、
\(a-b=k_2mn\)
\(mn|(a-b)\)
\(a\equiv b\:(\mr{mod}\:mn)\)
\(mn|(a-b)\)
\(a\equiv b\:(\mr{mod}\:mn)\)
となって 1.5 が証明できました。
合同には数々の性質や定理がありますが、RSA暗号の証明に必要なものは以上です。次に、2つの数の最大公約数を求める「ユークリッドの互除法」です。これは最大公約数を求める計算方法というだけでなく、RSA暗号において公開鍵と秘密鍵を生成する際に必須のものです。
2. ユークリッドの互除法
ユークリッドの互除法は 2つの自然数(\(a\) と \(b\)。\(a > b\) とします)の最大公約数を求める計算方法です。これはユークリッドの数学書である『原論』にあります。『原論』は紀元前 300年頃の成立といいますから、2300年ほど前の書物ということになります。
この計算方法では、割り算(除算)を何ステップか繰り返します。割り算において被除数(=割られる数)と除数(=割る数)、商(=答)、剰余(=余り)の関係は、
被除数 = 商 \(\times\) 除数 + 剰余
ですが、まず第1ステップとして、
| 被除数1 | = \(a\) | |
| 除数1 | = \(b\) |
とおき、
被除数1 = 商1 \(\times\) 除数1 + 剰余1
の計算をして、商1と剰余1を求めます。次に第2ステップとして、
| 被除数2 | = 除数1 | |
| 除数2 | = 剰余1 |
とおいて割り算を行い、商2と剰余2を求めます。つまり、
被除数2 = 商2 \(\times\) 除数2 + 剰余2
です。この「除数と剰余を新たな被除数と除数にして割り算をする」ステップを次々と繰り返して行くと、剰余は次第に小さくなっていき、ついには剰余がゼロ(= 被除数が除数で割り切れる)となります。この時点での除数(= 一つ前のステップの剰余)が \(a\) と \(b\) の最大公約数です。
なぜそうなるのかが以下ですが、ポイントは割り算の式から明らかなように「被除数と除数の公約数は、剰余の約数でもある」ことです。つまり \(a\) と \(b\) の約数であるという性質が剰余に引き継がれ、それは割り算のステップを繰り返してもずっと続きます。しかも、剰余はステップが進むにつれて小さくなっていくので、最大公約数に近づく。そして割り切れたときの除数(一つ前のステップの剰余)は、約数であると同時に最大の約数である。おおまかにはそのような理解です。
| 2.1 | ユークリッドの互除法 |
|
\(a\)と \(b\) を自然数とし、\(a > b\) とする。
\(\begin{eqnarray}
&&a&=q_1\cdot b_1+r_1 &\cd\:(1)\\
&&b&=q_2\cdot r_1+r_2 &\cd\:(2)\\
&&r_1&=q_3\cdot r_2+r_3 &\cd\:(3)\\
&&r_2&=q_4\cdot r_3+r_4 &\cd\:(4)\\
&&&\vdots&\\
&&r_{i-4}&=q_{i-2}\cdot r_{i-3}+r_{i-2} &\cd\:(i-2)\\
&&r_{i-3}&=q_{i-1}\cdot r_{i-2}+r_{i-1} &\cd\:(i-1)\\
&&r_{i-2}&=q_{i\phantom{-0}}\cdot r_{i-1}+r_{i\phantom{-0}} &\cd\:(i)\\
&&r_{i-1}&=q_{i+1}\cdot r_i &\cd\:(i+1)\\
\end{eqnarray}\) となったとき、
\(\mr{gcd}(a,b)=r_i\) である。 | |
\(a\) と \(b\)(\(a > b\))の公約数を \(x\) とします。すると、\(x|a\) かつ \(x|b\) なので、\((1)\) 式から \(x|r_1\) になります。この \(x|r_1\) と \(x|b\) から \((2)\) 式を使って \(x|r_2\) が得られます。
その次には \(x|r_1\) 、\(x|r_2\) 、\((3)\) 式から \(x|r_3\) になる。以上を最後まで繰り返すと、次のようになります。
\(\begin{eqnarray}
&&x|a, &x|b, &(1)式&\rightarrow x|r_1\\
&&x|b, &x|r_1, &(2)式&\rightarrow x|r_2\\
&&x|r_1, &x|r_2, &(3)式&\rightarrow x|r_3\\
&&&\vdots&&\\
&&x|r_{i-4}, &x|r_{i-3}, &(i-2)式&\rightarrow x|r_{i-2}\\
&&x|r_{i-3}, &x|r_{i-2}, &(i-1)式&\rightarrow x|r_{i-1}\\
&&x|r_{i-2}, &x|r_{i-1}, &(i)式&\rightarrow x|r_i\\
\end{eqnarray}\)
以上のように、最終的には \(x|r_i\) となり、
\(a\) と \(b\) の公約数は \(r_i\) の約数である
ことが示せました。同時に、
\(a\) と \(b\) の公約数の最大値は \(r_i\) である
ことも分かります。
次に、ユークリッドの互除法の最終プロセスに現れる剰余は、全てのステップの剰余の約数になっていることを示します。このことを最終ステップから順に遡って検証すると、
\(\begin{eqnarray}
&&&&(i+1)式&\rightarrow r_i|r_{i-1}\\
&&r_i|r_{i-1},&&(i)式&\rightarrow r_i|r_{i-2}\\
&&r_i|r_{i-2},&r_i|r_{i-1},&(i-1)式&\rightarrow r_i|r_{i-3}\\
&&r_i|r_{i-3},&r_i|r_{i-2},&(i-2)式&\rightarrow r_i|r_{i-4}\\
&&&\vdots&&\\
&&r_i|r_2,&r_i|r_3,&(3)式&\rightarrow r_i|r_1\\
&&r_i|r_1,&r_i|r_2,&(2)式&\rightarrow r_i|b\\
&&r_i|b,&r_i|r_1,&(1)式&\rightarrow r_i|a\\
\end{eqnarray}\)
となり、\(r_i|b\) かつ \(r_i|a\)、つまり、
\(r_i\) は \(a\) と \(b\) の公約数である
ことが示せました。
従って、
| \(r_i\) は \(a\) と \(b\) の公約数である | |
| \(a\) と \(b\) の公約数の最大値は \(r_i\) である |
の2つから、\(\mr{gcd}(a,b)=r_i\) が証明できました。
計算量
RSA暗号にとってのユークリッドの互除法の意味ですが、次の2つが重要です。まず第1に「2つの数の最大公約数は、素因数分解なしに計算できる」ことです。これはすなわち「2つの数が互いに素であることが素因数分解なしに示せる」ことも意味します。
我々が普通、学校で習う最大公約数の求め方は、2つの数を素因数分解して共通の素因数を探すというものでした。共通のものがなければ最大公約数は \(1\)(=互いに素)です。しかし、数が巨大になると素因数分解が困難になります(それがRSA暗号が成り立つゆえんです)。ユークリッドの互除法を使うと「最大公約数」や「互いに素」が素因数分解なしに示せるのです。
第2は、ユークリッドの互除法が高速に計算できることです。ユークリッドの互除法では、一つのステップの剰余が次のステップの除数になります。次のステップの剰余は除数より小さいので、
\(0 < r_{i+1} < r_i\)
となりますが、\(r_{i+1}\) が \(0\) に近いと計算は急速に収束します。また \(r_{i+1}\) が \(r_i\) に近い場合でも、その次のステップの商が大きくなり、\(r_{i+2}\) が \(0\) に近くなるので、計算は収束することになります。従って、最も計算が長引くのは、\(r_{i+1}\) が \(r_i\) の半分程度で、それが連続する場合だと推測できます。
実は、ユークリッドの互除法のステップが最も長くなるケースが知られています。それは 割り算の商が常に \(1\) になるケースで、\(a\) と \(b\) が(たまたま)フィボナッチ数列の隣り合う2項だとそうなります。フィボナッチ数列とは、
\(F_0=0,\) \(F_1=1\)
\(F_{n+2}=F_{n+1}+F_n\)
\(F_{n+2}=F_{n+1}+F_n\)
で定義される数列で、実際に書いてみると、
\(0,\:1,\:1,\:2,\:3,\:5,\:8,\:13,\:21,\:34,\:55,\:89,\:\cd\)
です。いま、\(a=144\)、\(b=89\) としてユークリッドの互除法の計算をしてみると
\(144=1\cdot89+55\)
\(\phantom{1}89=1\cdot55+34\)
\(\phantom{1}55=1\cdot34+21\)
\(\phantom{1}34=1\cdot21+13\)
\(\phantom{1}21=1\cdot13+\phantom{1}8\)
\(\phantom{1}13=1\cdot\phantom{1}8+\phantom{1}5\)
\(\phantom{11}8=1\cdot\phantom{1}5+\phantom{1}3\)
\(\phantom{11}5=1\cdot\phantom{1}3+\phantom{1}2\)
\(\phantom{11}3=1\cdot\phantom{1}2+\phantom{1}1\)
\(\phantom{11}2=2\cdot\phantom{1}1\)
\(\phantom{1}89=1\cdot55+34\)
\(\phantom{1}55=1\cdot34+21\)
\(\phantom{1}34=1\cdot21+13\)
\(\phantom{1}21=1\cdot13+\phantom{1}8\)
\(\phantom{1}13=1\cdot\phantom{1}8+\phantom{1}5\)
\(\phantom{11}8=1\cdot\phantom{1}5+\phantom{1}3\)
\(\phantom{11}5=1\cdot\phantom{1}3+\phantom{1}2\)
\(\phantom{11}3=1\cdot\phantom{1}2+\phantom{1}1\)
\(\phantom{11}2=2\cdot\phantom{1}1\)
となって、10ステップかかります。剰余が減る割合が常に 0.6 倍程度で、なかなか減りません。商が常に 1 なのでこうなります。しかし、なかなか減らないが毎回 0.6 倍程度にはなり、マクロ的には急速に小さくなる。証明は省略しますが、\(a\) と \(b\) が\(10\)進で \(N\) 桁の数字でフィボナッチ数列の隣り合う2項だった場合でも、ユークリッドの互除法は \(5\times N\) ステップ以下で終了します。
これは a とb が300桁程度の数字のとき、それが偶然にもフィボナッチ級数の隣り合う2項であるという最悪の最悪の場合でも 1500回の割り算で終了することを意味します。この程度の計算はもちろんコンピュータで可能です。
本題に戻ります。最初の「RSA暗号の例題」のところで公開鍵の作り方を書きました。まず2つの素数、\(p\) と \(q\) を選び、\(n=p\cdot q\) とします。次に、\((p-1)(q-1)\) との最大公約数が \(1\) であるような数(=互いに素)を選び、それを \(e\) とします。その \((e,\:n)\) のペアを公開鍵とするのでした。
\(n\) と同程度の大きさの数、\(e\) をランダムに選んだとき、その \(e\) が \((p-1)(q-1)\) と互いに素であるかどうかは、ユークリッドの互除法で検証可能です。そしてこの検証は \(p\) と \(q\) が巨大な数であっても可能です。つまりユークリッドの互除法は公開鍵が現実に作成できるという数学的根拠になっています。
アルゴリズム
2.1 において、\(a\) と \(b\) の最大公約数は \(r_i\) でしたが、この \(r_i\) は \((1)\)式における \(b\) と \(r_1\) の最大公約数にもなります。なぜなら、\(b\) と \(r_1\) の最大公約数を求めるためには \((2)\)式から互除法の計算を始めればよく、その結果は \(r_i\) になるからです。これは次を意味します。
| 2.1a | 互除法の原理 |
|
\(a\)と \(b\) を自然数とし、\(a > b\) とする。\(a\) を
\(a=q\cdot b+r\:\:(1\leq q,\:0 < r)\) と書き表せるとき、
\(\mr{gcd}(a,b)=\mr{gcd}(b,r)\) である。 | |
つまり、ユークリッドの互除法は
| \(a\) と \(b\) の最大公約数を求める問題」を「より小さな数である \(b\) と \(r\) の最大公約数を求める問題」に置き換える |
ものといえます。この置き換えは次々と可能で、置き換えるたびに問題がより "小さく" なっていく。これがユークリッドの互除法の原理です。ここで改めて 2.1a の証明をすると、次の通りです。
【証明】
表記を見やすくするため、
\(\mr{gcd}(a,b)=x\)
\(\mr{gcd}(b,r)=y\)
と書く。
\(x|a,\:\:x|b\) であり、\(a=q\cdot b+r\) から \(x|r\) である。従って、\(x\) は \(b\) と \(r\) の公約数である。公約数は最大公約数より以下なので、
\(x\leq y\)
が成り立つ。一方、\(y|b,\:\:y|r\) なので \(y|a\) である。つまり \(y\) は \(a\) と \(b\) の公約数である。公約数は最大公約数以下なので、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので、
\(x=y\) つまり
\(\mr{gcd}(a,b)=\mr{gcd}(b,r)\)
である。
\(\mr{gcd}(a,b)=x\)
\(\mr{gcd}(b,r)=y\)
と書く。
\(x|a,\:\:x|b\) であり、\(a=q\cdot b+r\) から \(x|r\) である。従って、\(x\) は \(b\) と \(r\) の公約数である。公約数は最大公約数より以下なので、
\(x\leq y\)
が成り立つ。一方、\(y|b,\:\:y|r\) なので \(y|a\) である。つまり \(y\) は \(a\) と \(b\) の公約数である。公約数は最大公約数以下なので、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので、
\(x=y\) つまり
\(\mr{gcd}(a,b)=\mr{gcd}(b,r)\)
である。
もちろん、\(b|a\) であれば \(\mr{gcd}(a,b)=b\) です。
ユークリッドの互除法は "世界最古のアルゴリズム" と言われています。そして、アルゴリズムを記述するのに最適な言語はプログラミング言語です。2.1a の原理に基づき、ユークリッドの互除法で最大公約数を計算するプログラムを掲げます。
| 2.1b | アルゴリズム |
|
ユークリッドの互除法で a と b の最大公約数を求める関数 EUCLID(Javascriptで記述) function EUCLID( a, b ) { if( a % b == 0 ) // ① return b; else return EUCLID( b, a % b ); } | |
① の "%" は Javascript の剰余演算子で、"a % b" は "a を b で割った余り" という意味です(a \(\mathbf{mod}\) b と同じ)。なお、このプログラムは a<b でも動作します。
もちろん、Javascript でなくても、C++ でも Python でも記述できます。このようにプログラムで書くと簡潔になって、ユークリッドの互除法というアルゴリズムの本質がクリアにわかります。
拡張ユークリッドの互除法
ユークリッドの互除法の "副産物" として、次の定理が成り立ちます。
| 2.2 | |
|
\(a\) と \(b\) を自然数とする。このとき適当な整数 \(u\)、\(v\) をとって、
\(\mr{gcd}(a,b)=u\cdot a+v\cdot b\) と表せる。 | |
この定理の証明ですが、ユークリッドの互除法の計算過程を振り返ると、
\(\begin{eqnarray}
&&a&=q_1\cdot b_1+r_1 &\cd\:(1)\\
&&b&=q_2\cdot r_1+r_2 &\cd\:(2)\\
&&r_1&=q_3\cdot r_2+r_3 &\cd\:(3)\\
&&r_2&=q_4\cdot r_3+r_4 &\cd\:(4)\\
&&&\vdots&\\
&&r_{i-4}&=q_{i-2}\cdot r_{i-3}+r_{i-2} &\cd\:(i-2)\\
&&r_{i-3}&=q_{i-1}\cdot r_{i-2}+r_{i-1} &\cd\:(i-1)\\
&&r_{i-2}&=q_{i\phantom{-0}}\cdot r_{i-1}+r_{i\phantom{-0}} &\cd\:(i)\\
&&r_{i-1}&=q_{i+1}\cdot r_i &\cd\:(i+1)\\
\end{eqnarray}\)
でした。ここで \((1)\) を変形して、
\(r_1=u_1\cdot a+v_1\cdot b\)
とします。\(u_1=1,\:\:v_1=-q_1\) です。次に、今求めた \(r_1\) と \((2)\) を使うと、
\(r_2=u_2\cdot a+v_2\cdot b\)
の形に表せることになります。\(u_2=-q_2,\:\:v_2=1+q_1q_2\) です。さらに、求まった \(r_1\) と \(r_2\) と \((3)\) を使って、
\(r_3=u_3\cdot a+v_3\cdot b\)
と表せることが分かります。このステップを順に続けていって \((i)\) まで到達すると、
\(r_i=u\cdot a+v\cdot b\)
\(u,\:v\) は \(q_j\:(1\leq j\leq i)\) の式
\(u,\:v\) は \(q_j\:(1\leq j\leq i)\) の式
となることがわかります。\(r_i=\mr{gcd}(a,b)\) だったので、2.2 が証明できました。\(u\) と \(v\) のうち、一つは正の整数、もう一つはゼロか負の整数です。一つがゼロであるのは、\(a=b\) のときです。なお、2.2 を満たす \(u\)、\(v\) に、
\(u\cdot a+v\cdot b=0\)
を満たす \(u\)、\(v\) をそれぞれ足し込んでも 2.2 が成立することが明白です。つまり 2.2 を満たす \(u\)、\(v\) は1組というわけではありません。なお、2.2 は次のように言い換えることができます。
| 2.2a | 不定方程式の整数解 |
|
\(a\) と \(b\) を自然数とする。このとき、不定方程式
\(ax+by=\mr{gcd}(a,b)\) は整数解をもつ。 | |
拡張ユークリッドの互除法のアルゴリズム
ユークリッドの互除法を拡張して、\(a\) と \(b\) が与えられたとき、\(\mr{gcd}(a,b)\) と、
\(au+bv=\mr{gcd}(a,b)\)
を満たす \(u\) と \(v\)(=無数にある解のうちの一つのペア)を同時に計算してしまうアルゴリズムを考えてみます。
考え方は 2.1b のユークリッドの互除法と同じで、解くべき問題を「等価でより小さな問題」に置き換えます。そのために \(a=qb+r\) とおくと、2.1a より、
\(\mr{gcd}(a,b)=\mr{gcd}(b,r)\)
なので、問題は次のように書き換えられます。
\((qb+r)u+bv=\mr{gcd}(b,r)\)
ここで、未知数の \(u\) と \(v\) を次のように変換します。
\(u=V\)
\(v=U-qV\)
\(v=U-qV\)
これを代入して式を整理すると
\(bU+rV=\mr{gcd}(b,r)\)
となり、"小さな問題" に変換することができました。この考え方でアルゴリズムを記述すると次のとおりです。
| 2.2b | 拡張ユークリッドの互除法 | ||||||||||||||||||||||||||||
|
\(a\) と \(b\) から拡張ユークリッドの互除法で(\(u,\:v,\) 最大公約数)の3つを同時に求める関数 extdEUCLID(Javascriptで記述)
| |||||||||||||||||||||||||||||
以下は、このアルゴリズムの補足説明です。
| var:変数の宣言。%:剰余演算子。 | |
| a が b で割り切れるなら解が求まる。自然な解を関数値として返す。関数値は3つの変数(u, v, gcd)をひとまとめにしたオブジェクト。 | |
| 商を求め、小数点以下を切り捨て整数化する。Javascript には実数・整数の区別がないので整数化(組み込み関数の Math.floor)が必要。 | |
| 小さな問題として計算する。 | |
| 変数を元に戻して、関数値(u, v, gcd)を返す。 |
この拡張ユークリッドの互除法のアルゴリズムは、2.1b のユークリッドのアルゴリズムとほぼ同じです。ただし、\(u\) と \(v\) の計算のために変数を変換しているので、最大公約数を計算したあとに元の変数値を求める必要があります(=⑤)。そこが違います。
このことから、拡張ユークリッドの互除法の計算量は、ユークリッドの互除法のほぼ2倍だと推測できます。計算は少々複雑になりますが、たとえ \(\bs{a}\) や \(\bs{b}\) が巨大な数であっても、コンピュータで高速に計算できる。このことは次の「整数の逆数」の項で述べるように、RSA暗号にとっての重要ポイントになります。
整数の逆数
2.2 から導かれる次の定理は、RSA暗号にとって重要です。
| 2.3 | 逆数の存在 |
|
\(\mr{gcd}(a,m)=1\) なら(= \(a\) と \(m\) が互いに素なら)、
\(a\cdot b\equiv1\:(\mr{mod}\:m)\) となる \(b\) が存在する。この \(b\) は \(m\) と互いに素であり、\(1\leq b < m\) の範囲では一意に定まる(= \(m\) を法として唯一)。 | |
2.2 において \(a\)と互いに素な数 \(m\) を選び、\(b=m\) とおくと、\(\mr{gcd}(a,m)=1\) なので、適当な \(u\) と \(v\) をとることにより、
\(u\cdot a+v\cdot m=1\)
とすることができます。すなわち、
\(a\cdot u\equiv1\:(\mr{mod}\:m)\)
となり、2.3 が示されました。このとき \(a\cdot u\) は \(m\) と互いに素であり、また \(a\) と \(m\) は互いに素なので、\(b\) も \(m\) と互いに素になります。また、\(b_1\) と \(b_2\) の2つの解があるとすると、
\(a\cdot b_1\equiv1\:(\mr{mod}\:m)\)
\(a\cdot b_2\equiv1\:(\mr{mod}\:m)\)
\(a(b_1-b_2)\equiv0\:(\mr{mod}\:m)\)
\(m|a(b_1-b_2)\)
\(a\cdot b_2\equiv1\:(\mr{mod}\:m)\)
\(a(b_1-b_2)\equiv0\:(\mr{mod}\:m)\)
\(m|a(b_1-b_2)\)
となり、\(a\) と \(m\) は互いに素なので 1.3a より、
\(m|(b_1-b_2)\)
\(b_1\equiv b_2\:(\mr{mod}\:m)\)
\(b_1\equiv b_2\:(\mr{mod}\:m)\)
となります。従って、\(1\leq b < m\) の範囲に \(b\) があり、かつ、この範囲で \(b\) は一意に定まります。\(m\) を法として \(b\) と合同な数も解であることは明白ですが、それらの解は \(m\) を法として唯一です。
2.3 の "逆数" を計算するアルゴリズムは、拡張ユークリッドの互除法2.2 のアルゴリズム(2.2b)と基本的に同じです。
| 2.3a | 逆数の計算アルゴリズム |
|
\(m\) を法とする \(a\) の逆数を求める関数 INVERSE(Javascriptで記述) function INVERSE( a, m ) { var b = extdEUCLID( a, m ).u % m; // ① return ( b + m ) % m; // function extdEUCLID( a, b ) { var r = a % b; if( r == 0 ) return { u : 0, v : 1, gcd : b }; else { var q = Math.floor( a / b ); var s = extdEUCLID( b, r ); return { u : s.v, v : (s.u - q * s.v), gcd : s.gcd }; } } // extdEUCLID 終わり // } // INVERSE 終わり | |
①で、extdEUCLID のアルゴリズム(2.2b)を使って u を求め、それを m 未満の自然数に直して答えの b を求めています。( b + m )% m は b が負の場合の配慮です。このアルゴリズムは正確に言うと、a と m が与えられたとき、
\(a\cdot b\equiv\mr{gcd}(a,m)\:\:(\mr{mod}\:m)\)
となる \(b\) を求めるアルゴリズムです。\(a\) と \(m\) が互いに素でなくても成立します。
この "逆数の存在定理" は RSA暗号において秘密鍵の算出に使われています。冒頭の「RSA暗号の例題」に書いたように、RSA暗号の公開鍵と秘密鍵は、まず秘密の2つの素数 \(p\) と \(q\) を決め、
\(n=p\cdot q\)
とします。そして \(e\) を、
\(\mr{gcd}(e,\:(p-1)(q-1))=1\)
となるように決め、\(n\) と \(e\) を公開鍵とするのでした。そして秘密鍵 \(d\) を、
\(d\cdot e\equiv1\:(\mr{mod}\:(p-1)(q-1))\)
を満たす数とします。この秘密鍵 \(d\) の計算は、\(\mr{mod}\:(p-1)(q-1)\) の世界で \(e\) の逆数を求めていることに他なりません。逆数の存在が保証されるのは、\(e\) を \((p-1)(q-1)\) と互いに素という条件で決めたからです。さらに、この逆数の計算アルゴリズムは 2.2b の拡張ユークリッドの互除法と同じなので高速に計算できることが重要ポイントです。
普通、整数の "逆数"は(整数の範囲で)定義できません( \(1\) 以外は)。しかし、"\(\mr{mod}\:m\) の合同の世界" では、\(m\) と互いに素な数 \(a\) に対して逆数が定義できることになります。つまり整数の範囲で「割り算」が定義できる。
たとえば \(\mr{mod}\:10\) の世界では \(7\times3=1\) であり、\(7\) の逆数は \(3\) です。割り算は逆数のかけ算なので、たとえば \(8\div7=8\times3=4\)(\(\mr{mod}\:10\) の世界)といった演算が定義できます。"検算" をすると \(4\times7=8\)(\(\mr{mod}\:10\) の世界)なので合っています。
\(\mr{mod}\:10\) の場合は実用的な意味はありませんが、\(p\) を素数としたとき「\(\mr{mod}\:p\) の世界」は大変重要です。というのも \(p\) 未満の自然数はすべて \(p\) と互いに素だからです。つまり \(p\) 未満の全ての自然数に対して "逆数" が定義できます。
| 2.3b | 逆数の存在:法が素数 |
|
\(p\) を素数とする。\(p\) 未満の自然数 \(a\) に対して、
\(a\cdot b\equiv1\:(\mr{mod}\:p)\) を満たす逆数 \(b\) が \(1\leq b < p\) の範囲で一意に定まる。また、異なる \(a\) に対する逆数 \(b\) は異なる。 | |
2.3b はほとんど 2.3 と同じです。「異なる \(a\) に対する逆数 \(b\) は異なる」というところですが、もし \(1\leq i < j < p\) である \(i\) と \(j\) に対して、
\(i\cdot b\equiv1\:(\mr{mod}\:p)\)
\(j\cdot b\equiv1\:(\mr{mod}\:p)\)
\(j\cdot b\equiv1\:(\mr{mod}\:p)\)
となったとすると、
\((j-i)\cdot b\equiv0\:(\mr{mod}\:p)\)
ですが、\((j-i)\) も \(b\) も \(p\) と素なので矛盾します。異なる \(a\) に対する逆数 \(b\) は異なります。
このように逆数が存在するということは、\(p\) 未満の2つの自然数の "除算" が定義できます。さらに、\(0\) と \(p\) 未満の自然数を合わせると加減乗除が行えることになります。
加減乗除が定義された集合を「体(Field)」と呼びます。有理数、実数、複素数は「体」ですが、「\(0\) と \(p\) 未満の自然数」も体になります。これを \(\bs{F}_p\) と表記します。この集合の要素の数は有限個なので「有限体」です。 \(\bs{F}_{13}\) の場合(\(\mr{mod}\:13\))で "逆数" の計算をしてみると、
\(\phantom{1}1\cdot\phantom{1}1\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}2\cdot\phantom{1}7\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}3\cdot\phantom{1}9\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}4\cdot10\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}5\cdot\phantom{1}8\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}6\cdot11\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}7\cdot\phantom{1}2\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}8\cdot\phantom{1}5\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}9\cdot\phantom{1}3\equiv1\:(\mr{mod}\:13)\)
\(10\cdot\phantom{1}4\equiv1\:(\mr{mod}\:13)\)
\(11\cdot\phantom{1}6\equiv1\:(\mr{mod}\:13)\)
\(12\cdot12\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}2\cdot\phantom{1}7\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}3\cdot\phantom{1}9\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}4\cdot10\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}5\cdot\phantom{1}8\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}6\cdot11\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}7\cdot\phantom{1}2\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}8\cdot\phantom{1}5\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}9\cdot\phantom{1}3\equiv1\:(\mr{mod}\:13)\)
\(10\cdot\phantom{1}4\equiv1\:(\mr{mod}\:13)\)
\(11\cdot\phantom{1}6\equiv1\:(\mr{mod}\:13)\)
\(12\cdot12\equiv1\:(\mr{mod}\:13)\)
となり、\(0\) 以外の \(\bs{F}_{13}\) の要素は、その逆数(=逆元)と1対1に対応していることがわかります。
\(\bs{F}_p\) においては "整数" の加減乗除を "自由かつ厳密に" 行うことができます。これは、全ての情報を2進数に帰着させて扱うデジタル・コンピュータとの相性がよい。このため、公開鍵暗号の中には \(\bs{F}_p\) の演算を利用したものがあります。
なお、\(p\) を素数としたとき「\(p\) 未満の自然数はすべて \(p\) と互いに素」ということは「\((p-1)\:!\) と \(p\) は互いに素」ということです(" \(!\) " は階乗記号)。これは次の「フェルマの小定理」の証明に出てきます。
3. フェルマの小定理
フェルマの小定理は RSA暗号の根幹にかかわるものです。フェルマは17世紀フランスの大数学者(1607-1665)で、有名なフェルマの最終定理(大定理)と区別するために「小定理」の名があります。
| 3.1 | フェルマの小定理 |
|
\(p\) を素数とし、\(a\) を \(p\) とは素な数とすると、
\(a^{p-1}\equiv1\:(\mr{mod}\:p)\) が成り立つ。 | |
これは少々意外な定理です。我々が高校までで習う素数は、自身と \(1\) 以外の約数を持たない数という定義か、素因数分解の定理か、そういうものです。「素数がもつ性質」に言及した定理はあまり思い浮かばない。しかしフェルマの小定理は、素数であれば必ずこうなると言っているわけです。これは次のように証明できます。
\(1,\:2,\:3,\:\cd\:,\:p-1\) のそれぞれに \(a\) をかけて、
\(a,\:2a,\:3a,\:\cd\:,\:(p-1)a\)
という数列を作ります。そして、それぞれの数を \(p\) で割った剰余を \(b_i\) とします。つまり、
\(\begin{eqnarray}
&&a&\equiv b_1 &(\mr{mod}\:p)\\
&&2a&\equiv b_2 &(\mr{mod}\:p)\\
&&3a&\equiv b_3 &(\mr{mod}\:p)\\
&&&\vdots&\\
&&(p-1)a&\equiv b_{p-1} &(\mr{mod}\:p)\\
\end{eqnarray}\)
です。\(p\) は素数なので \(1\) から \((p-1)\) までの数は \(p\) と素であり、また \(a\) は仮定により \(p\) と素です。従って \(b_i\) が \(0\) になることはなく、\(1\leq b_i\leq\:(p-1)\) です。このとき、\(1\leq i,\:\:j\leq\:(p-1)\) である \(i,\:j\) について、
\(i\neq j\) であれば、必ず \(b_i\neq b_j\)
になります。なぜなら、もし \(b_i=b_j\) とすると、1.1b(合同式の減算)より、
\((i-j)a\equiv0\:(\mr{mod}\:p)\)
です。仮定より \(a\) は \(p\) と互いに素なので、1.3 により(\(1.3\) で \(b=0\) の場合)、
\((i-j)\equiv0\:(\mr{mod}\:p)\)
となりますが、\(1\leq i,\:\:j\leq\:(p-1)\) なので、
\(i=j\)
となり仮定に反します。つまり\(i\neq j\) であれば、必ず \(b_i\neq b_j\) です。ということは、\((p-1)\) 個の数、\(b_i(1\leq i\leq p-1)\) は全て違う数であり、つまり、\((1,\:2,\:3,\:\cd\:,\:p-1)\) を並び替えたものです。従って、\(b_i\) を全部かけ算すると、
\(b_1\:b_2\:b_3\:\cd\:b_{p-1}=(p-1)\:!\)
となります。そこで、1.1c(合同式の乗算)を上の \((p-1)\) 個の合同式に適用して左辺と右辺を全てかけ合わせてしまうと、
\((p-1)\:!\cdot a^{p-1}\)
| \(\equiv b_1\:b_2\:b_3\:\cd\:b_{p-1}\) | \((\mr{mod}\:p)\) | |
| \(\equiv(p-1)\:!\) | \((\mr{mod}\:p)\) |
となります。ここで、\(p\) は素数なので \(p\) と \((p-1)!\) は互いに素です。すると 1.3 により、
\(a^{p-1}\equiv1\:(\mr{mod}\:p)\)
となり、証明が完成しました。
(次回に続く)
2021-05-01 11:00
nice!(0)





