No.358 - 高校数学で理解するガロア理論(5) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
第6章では、方程式が可解であれば(=解が四則演算とべき根で表現できれば)ガロア群が可解群であることをみました。第7章ではその逆、つまり、ガロア群が可解群であれば方程式が可解であることを証明します。
7.1 1の原始\(n\)乗根
可解性の十分条件を証明するために、まず、\(1\) の原始\(n\)乗根がべき根で表せることを証明します。このことを前提にした証明を最後で行うからです。念のために「1.1 方程式とその可解性」でのべき根の定義を振り返ると、
\(\sqrt[n]{\:a\:}\) (\(n=2\) の場合は \(\sqrt{\:a\:}\))
という表記は、
のでした。\(\sqrt{2}\) は \(1.4142\cd\) と \(-1.4142\cd\) のどちらかを表わすのではなく、\(1.4142\cd\) のことです。\(\sqrt[3]{2}\) は \(3\)乗して \(2\) になる3つの数のうちの正の実数(\(\fallingdotseq1.26\))を表わします。一方、\(\sqrt{-1\:}\) は\(2\)乗して \(-1\) になる2つの数のうちのどちらかで、その一方を \(i\) と書くと、もう一方が \(-i\) です。
この定義から、方程式 \(x^n-1=0\) の解を \(\sqrt[n]{\:1\:}\) と書くと、それは \(1\) のことです。従って、
ことを証明しておく必要があります。その証明はガロア理論とは無関係にできます。それが以下です。
\(1\) の 原始\(n\)乗根はべき根で表現できる。
[証明]
\(n\) についての数学的帰納法で証明する。\(n=2,\:3\) のときにべき根で表現できるのは根の公式で明らかである。また、原始4乗根は \(\pm i\) なので、\(n\leq4\) のとき題意は成り立つ。そこで、\(n\) 未満のときにべき根で表現できると仮定し、\(n\) のときにもべき根で表現できることを証明する。
\(n\) が合成数のときと素数のときに分ける。まず \(n\) が合成数なら、
\(n=s\cdot t\)
と表現できる。
\(1\) の原始\(s\)乗根を \(\zeta\)
\(1\) の原始\(t\)乗根を \(\eta\)
とし、\(X=x^{s}\) とおく。方程式 \(X^{t}-1=0\) の \(t\)個の解は \(\eta^k\:\:(0\leq k\leq t-1)\) と表わされる(63B)から、\(x^n-1\) は、
\(\begin{eqnarray}
&&\:\:x^n-1&=x^{st}-1=X^{t}-1\\
&&&=\displaystyle\prod_{k=0}^{t-1}(X-\eta^k)\\
&&&=\displaystyle\prod_{k=0}^{t-1}(x^{s}-\eta^k)\\
\end{eqnarray}\)
と因数分解できる。従って、方程式 \(x^n-1=0\) の解は、
\(x^{s}=\eta^k\:\:\:(0\leq k\leq t-1)\)
の解である。これを解くと、
\(x=\sqrt[s]{\eta^k}\cdot\zeta^j\:\:\:(0\leq j\leq s-1,\:\:0\leq k\leq t-1)\)
である(\(k=0\) のときは根号の規則に従って \(\sqrt[s]{1}=1\))。帰納法の仮定により、\(\zeta,\:\eta\) はべき根で表現できるから、上式により \(1\) の \(n\) 乗根はべき根で表現できる。従って原始\(n\)乗根もべき根で表現できる。
以降は \(n\) が素数の場合を証明する。\(n\) を \(p\)(= 素数)と表記する。以下では数式を見やすくするため \(p=5\) の場合を例示するが、証明の過程は一般性を失わない論理で進める。
位数 \(p-1\) の2つの巡回群、\((\bs{Z}/p\bs{Z})^{*}\) と \(\bs{Z}/(p-1)\bs{Z}\) の性質を利用する。\(p=5\) の場合は、位数 \(4\) の既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と、剰余群 \(\bs{Z}/4\bs{Z}\) である。
\(p\) が素数のとき、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は生成元をもつ(25D)。\((\bs{Z}/5\bs{Z})^{*}\) の生成元の一つは \(2\) である(もう一つは \(3\))。生成元を \(2\) とすると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
の巡回群となる。演算は乗算である。一方、\(\bs{Z}/4\bs{Z}\) は、演算が加算、生成元が \(1\)(または \(3\))の巡回群で、
\(\begin{eqnarray}
&&\:\:\bs{Z}/4\bs{Z}&=\{1,\:1+1,\:1+1+1,\:1+1+1+1\}\\
&&&=\{1,\:2,\:3,\:0\}\\
\end{eqnarray}\)
である。ここで、2つの変数 \(x,\:y\) をもつ関数を、
とおく。この関数は、4つある項の \(x,\:y\) の指数について、
\(y\) の指数は \([\:2,\:4,\:3,\:1\:]\) : \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン
\(x\) の指数は \([\:1,\:2,\:3,\:0\:]\) : \(\bs{Z}/4\bs{Z}\) の巡回パターン
となるようにしてある。
次に、2つの数 \(a,\:b\) を、
\(\begin{eqnarray}
&&\:\:a^5&=1\:(a\neq1)\\
&&\:\:b^4&=1\\
\end{eqnarray}\)
であるような数とする。\(a\) は \(1\) の原始5乗根でもよいし、その任意の累乗でもよい。とにかく \(a^5=1\:(a\neq1)\) を満たす数である。このとき、
\(a^5-1=0\)
\((a-1)(a^4+a^3+a^2+a+1)=0\)
なので、
\(a^4+a^3+a^2+a+1=0\) ないしは
\(a^4+a^3+a^2+a=-1\)
が成り立つ。\(b\) も \(1\) の原始4乗根か、その任意の累乗であるが、\(b=1\) であってもよい。
そうすると \(f(b,a)\) は、
\(f(b,a)=a^2b+a^4b^2+a^3b^3+a\)
\(a\) の指数は \([\:2,\:4,\:3,\:1\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
である。
次に \(f(b,a^2)\) を計算すると、
\(\begin{eqnarray}
&&\:\:f(b,a^2)&=a^4b+a^8b^2+a^6b^3+a^2\\
&&&=a^4+a^3b+a^1b^2+a^2b^3\\
\end{eqnarray}\)
\(a\) の指数は \([\:4,\:3,\:1,\:2\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
となる。
\(f(b,a^2)\) を \(f(b,a)\) と比べると、\(a\) の指数が \(1\) ステップだけ巡回している。ということは、\(b\) の指数も \([\:2,\:3,\:0,\:1\:]\) と \(1\) ステップだけ巡回させれば、\(a\) の指数と \(b\) の指数が同期することになり、\(f(b,a^2)\) の式は \(f(b,a)\) と同じものになる。同期させるには \(f(b,a^2)\) に \(b\) を掛ければよい。従って、
\(bf(b,a^2)=f(b,a)\)
である。
全く同様にして、
\(\begin{eqnarray}
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^8)&=b^3f(b,a^3)\\
&&&=f(b,a)\\
\end{eqnarray}\)
となる。まとめると、
\(\begin{eqnarray}
&&\:\:bf(b,a^2)&=f(b,a)\\
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^3)&=f(b,a)\\
\end{eqnarray}\)
である。\(b^4=1\) だから、各両辺を \(4\)乗すると、
\(f(b,a^2)^4=f(b,a)^4\)
\(f(b,a^4)^4=f(b,a)^4\)
\(f(b,a^3)^4=f(b,a)^4\)
の式を得る。
本題に戻って、次に \(f(b,a)^4\) を展開する。
であるが、このまま展開したのでは \(p=5\) のときに固有のものになり、一般性を失う。そこで、上式を展開して整理した形を、
とする。\(a^2,\:a^4,\:a^3,\:a\) の係数となっている \(h_i(b)\:(i=1,2,3,0)\) は \(b\) の多項式である。この展開形の決め方は次のように行う。
\((\br{B})\) 式においては、
であることに注意する。
次に \(f(b,a^2)^4\) を計算する。これは \((\br{B})\) 式において \(a\) を \(a^2\) に置き換えればよいから、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=h_1(b)a^4+h_2(b)a^8+h_3(b)a^6+h_0(b)a^2\\
&&&=h_1(b)a^4+h_2(b)a^3+h_3(b)a+h_0(b)a^2\\
\end{eqnarray}\)
となるが、これは \(f(b,a)^4\) において、
としたものと同じである。つまり、
\(f(b,a^2)^4=h_0(b)a^2+h_1(b)a^4+h_2(b)a^3+h_3(b)a\)
である。同様に、
\(f(b,a^4)^4=h_3(b)a^2+h_0(b)a^4+h_1(b)a^3+h_2(b)a\)
\(h_i(b)\) の添字 \(:\:[\:3,\:0,\:1,\:2\:]\)
\(f(b,a^3)^4=h_2(b)a^2+h_3(b)a^4+h_0(b)a^3+h_1(b)a\)
\(h_i(b)\) の添字 \(:\:[\:2,\:3,\:0,\:1\:]\)
である。
従って、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) において、\(a^j\:(j=2,4,3,1)\) の係数は \(h_k(b)\:(k=1,2,3,0)\) の全てを巡回する。つまり、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) の全部を足すと、\(a^j\:(j=2,4,3,1)\) の係数は全て同じになる。その計算をすると、
\(\displaystyle\sum_{i=1}^{4}f(b,a^i)^4\)
\(\begin{eqnarray}
&&\:\: =&(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&&\cdot(a^2+a^4+a^3+a)\\
\end{eqnarray}\)
となる。上式の左辺については、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=f(b,a)^4\\
&&\:\:f(b,a^4)^4&=f(b,a)^4\\
&&\:\:f(b,a^3)^4&=f(b,a)^4\\
\end{eqnarray}\)
だったので、左辺は \(4f(b,a)^4\) に等しい。また \(a^5-1=0\) なので \(a^2+a^4+a^3+a=-1\) である。従って、
\(4f(b,a)^4=-(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
である。ここで、
\(g(b)=-\dfrac{1}{4}\:(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
と定義すると、
を得る。\((\br{C})\) 式における \(\sqrt[4]{g(b)}\) とは「\(4\)乗すると \(g(b)\) になる数」という意味である。従って、実際には \(4\)次方程式の \(4\)つの解のどれかを表している。
なお、\(g(b)\) を具体的に計算すると、計算過程は省くが、
今までの計算をまとめると、
\(\begin{eqnarray}
&&\:\:a^5=1\:(a\neq1)&\\
&&\:\:b^4=1&\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(b,a)&=a^2b+a^4b^2+a^3b^3+a\\
&&\:\:f(b,a)^4&=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\\
&&\:\:g(b)&=-\dfrac{1}{4}(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&\:\:f(b,a)&=\sqrt[4]{g(b)}\\
\end{eqnarray}\)
である。この過程で、\(a,\:b\) については \(a^5=1\:(a\neq1),\:b^4=1\) という条件しか使っていない。従って、この条件が満たせれば \(a,\:b\) は任意である。そこで \(1\) の原始5乗根を \(\zeta\) とし、\(1\) の原始4乗根を \(\omega\) として、
\(a=\zeta\)
\(b=\omega^j\:\:(j=1,2,3,4)\)
とおく。\(b\) は \(1\) にもなりうる(\(\omega^4=1\))。なお、\(\omega\) は普通 \(1\) の原始3乗根の記号であるが、ここでは原始4乗根として使う。
すると、
という、4つの式が得られる。これは、
\(\zeta^2,\:\:\zeta^4,\:\:\zeta^3,\:\:\zeta\)
を4つの未知数とする連立1次方程式である。帰納法の仮定により \(\omega\) はべき根で表されているから、方程式を解いて \(\zeta\) が \(\omega\) のべき根(と四則演算)で表されば、証明が完成することになる。
\((\br{E})\) の連立方程式を具体的に書くと、
\(\zeta^2+\omega^j\zeta^4+(\omega^j)^2\zeta^3+(\omega^j)^3\zeta=\sqrt[4]{g(\omega^j)}\)
\((j=1,2,3,4)\)
であり、全てを陽に書くと、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta^2+\omega\:\:\zeta^4+(\omega\:\:)^2\zeta^3+(\omega\:\:)^3\zeta&=\sqrt[4]{g(\omega)}& \br{①}&\\
&&\zeta^2+\omega^2\zeta^4+(\omega^2)^2\zeta^3+(\omega^2)^3\zeta&=\sqrt[4]{g(\omega^2)}& \br{②}&\\
&&\zeta^2+\omega^3\zeta^4+(\omega^3)^2\zeta^3+(\omega^3)^3\zeta&=\sqrt[4]{g(\omega^3)}& \br{③}&\\
&&\zeta^2+\omega^4\zeta^4+(\omega^4)^2\zeta^3+(\omega^4)^3\zeta&=\sqrt[4]{g(\omega^4)}& \br{④}&\\
\end{eqnarray}
\end{array}\right.\)
となる。この連立方程式を解くため、\(\zeta\) の項だけを残し、他の未知数である \(\zeta^2,\:\zeta^4,\:\zeta^3\) の項を消去することを考える。そのために、
\(A\::\:\br{①}\times\omega\:+\:\br{②}\times\omega^2\:+\:\br{③}\times\omega^3\:+\:\br{④}\times\omega^4\)
とおくと、
\(A\) の左辺 \(=\)
\(\omega\:\:\zeta^2+(\omega\:\:)^2\zeta^4+(\omega\:\:)^3\zeta^3+(\omega\:\:)^4\zeta+\)
\(\omega^2\zeta^2+(\omega^2)^2\zeta^4+(\omega^2)^3\zeta^3+(\omega^2)^4\zeta+\)
\(\omega^3\zeta^2+(\omega^3)^2\zeta^4+(\omega^3)^3\zeta^3+(\omega^3)^4\zeta+\)
\(\omega^4\zeta^2+(\omega^4)^2\zeta^4+(\omega^4)^3\zeta^3+(\omega^4)^4\zeta\)
となる。\(\zeta\) の4つの項は、係数が \((\omega^j)^4=(\omega^4)^j=1\) であり、
\(\zeta\) の項の合計 \(=\:4\zeta\)
である。
\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数は、
\(\omega^j+\omega^{2j}+\omega^{3j}+\omega^{4j}\:\:(j=1,2,3)\)
である。\(\omega^4=1\) なので、
\(\omega^j+\omega^{2j}+\omega^{3j}+1\:\:(j=1,2,3)\)
の形をしている。\(\omega\) は \(1\) の原始4乗根であり、\(x^4-1=0\) の根である。\(x^4-1\) は、
\(x^4-1=(x-1)(x^3+x^2+x+1)\)
と因数分解されるから、\(\omega,\:\omega^2,\:\omega^3\) は方程式
\(x^3+x^2+x+1=0\)
の3つの根である。つまり、
\(x^3+x^2+x+1=(x-\omega)(x-\omega^2)(x-\omega^3)\)
と因数分解される。この式に \(x=\omega^j\:(j=1,2,3)\) を代入すると、
\((\omega^j)^3+(\omega^j)^2+\omega^j+1\)
\(\begin{eqnarray}
&&\:\: &=\omega^{3j}+\omega^{2j}+\omega^j+1\\
&&&=(\omega^j-\omega)(\omega^j-\omega^2)(\omega^j-\omega^3)\\
&&&=0\:\:(j=1,2,3)\\
\end{eqnarray}\)
となる。つまり、\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数、\(\omega^j+\omega^{2j}+\omega^{3j}+1\) は全て \(0\) ということである。以上をまとめると、\(A\) の左辺は \(\zeta\) の項だけが残り、
\(A\) の左辺 \(=\:4\zeta\)
である。一方、\(A\) 式の右辺は、
\(A\) の右辺 \(=\:\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
である。従って、
\(4\zeta=\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
\((\br{F})\) 式における \(\sqrt[4]{g(\omega^j)}\) とは「\(4\)乗すると \(g(\omega^j)\) になる数」という意味であり、\(4\)次方程式の\(4\)つの解のどれかである。従って、実際に \(\omega\) に数を入れて(この場合は \(1\) の原始4乗根だから \(i\) か \(-i\))計算するときには、\(\zeta^5=1\) になるように \((\br{F})\) 式の \(4\)つの項のそれぞれについて、\(4\)つの解のどれかを選択する必要がある。しかしそうであっても、\(\zeta\) が \(\omega\) の多項式のべき根と四則演算で表現できるということは変わらない。
これまでの論理展開では、\(p=5\) であることの特殊性は何も使っていない。唯一、使ったのは、\(p\) が素数であり、そのときに \((\bs{Z}/p\bs{Z})^{*}\) に生成元がある(25D)ということである。
従って、\(\zeta\) が \(1\) の原始\(p\)乗根であり、\(\omega\) が \(1\) の原始\((p-1)\)乗根であっても \((\br{F})\) 式は、\(4\) を \((p-1)\) に置き換えれば成り立つ。
帰納法の仮定により、\(1\) の原始\((p-1)\)乗根 \(\omega\) はべき根で表される。従って \((\br{F})\) 式から、\(1\) の原始\(p\)乗根 である \(\zeta\) もべき根で表される。[証明終]
ためしに \((\br{F})\) 式を使って、\(1\) の原始5乗根、\(\zeta\) を計算してみます。\(\omega\) は \(1\) の原始4乗根(の一つ)なので \(\omega=i\)(虚数単位)とすると、\((\br{D})\) 式も含めて、
\(\begin{eqnarray}
&&\:\:g(b)&=-16b^3+14b^2+4b-1 (\br{D})\\
&&\:\:b&=\omega^j\:\:(j=1,2,3,4)\\
&&&=\:\{\:i,\:-1,\:-i,\:1\:\}\\
&&\:\:g(\omega)&=-15+20i\\
&&\:\:g(\omega^2)&=25\\
&&\:\:g(\omega^3)&=-15-20i\\
&&\:\:g(\omega^4)&=1\\
\end{eqnarray}\)
となり、これらを \((\br{F})\) 式に代入すると、
\(\zeta=\dfrac{1}{4}(\sqrt[4]{1}-\sqrt[4]{25}+i(\sqrt[4]{-15+20i}-\sqrt[4]{-15-20i}))\)
となります。\(\sqrt[4]{\cd}\) は「\(4\)乗して \(\cd\) になる数」の意味です。この式を、
\(4\zeta=r+is\)
\(\begin{eqnarray}
&&\:\: r&=\sqrt[4]{1}-\sqrt[4]{25}\\
&&\:\: s&=\sqrt[4]{-15+20i}-\sqrt[4]{15-20i}\\
\end{eqnarray}\)
と表すことにします。そして \(\sqrt[4]{\cd}\) を \(\sqrt{\cd}\) に変換するために2乗すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=\pm6\pm2\sqrt{5}&\\
&&s^2=\pm10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
と計算できます。但し \(r^2+s^2=4\) の条件があるので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=6\pm2\sqrt{5}&\\
&&s^2=10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
となります(複合異順)。ここから \(r,\:s\) を求めると、\(r\) の方は2重根号をはずすことができて、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r=\pm(1+\sqrt{5}),\:\:s=\pm\sqrt{10-2\sqrt{5}}&\\
&&r=\pm(1-\sqrt{5}),\:\:s=\pm\sqrt{10+2\sqrt{5}}&\\
\end{eqnarray}
\end{array}\right.\)
の合計8つの解が求まります。このうちの4つは方程式 \(x^5-1=0\) の解 \((=\zeta)\) で、残りの4つは方程式 \(x^5+1=0\) の解 \((=-\zeta)\) です。\(\zeta\) を表記すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm i\sqrt{10+2\sqrt{5}}\right)&\\
&&\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm i\sqrt{10-2\sqrt{5}}\right)&\\
\end{eqnarray}
\end{array}\right.\)
の4つとなり、\(1\) の原始5乗根が求まりました。一般的な原始5乗根の計算方法とは違いますが、\((\br{F})\) 式によっても原始5乗根が求まることが確認できました。
7.2 べき根拡大の十分条件のため補題
ここでは「7.3 べき根拡大の十分条件」を証明するための補題を2つ証明します。以下に出てくる多項式 \(g(x)\) は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言います。
補題(1)
\(\bs{L}\) を \(\bs{K}\) のガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) を \(\sg\) で生成される位数 \(n\) の巡回群とする。式 \(g(x)\) を、
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
[証明]
\(\bs{L}\) が原始元 \(\theta\) によって \(\bs{L}=\bs{K}(\theta)\) と表されているとし(32B)、\(\theta\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式の定理(31I)により \(f(x)\) は既約多項式である。そうすると、\(\theta,\:\sg^i(\theta)\:(1\leq i\leq n-1)\) の \(n\)個は \(f(x)=0\) の解であり、既約多項式の定理3(31G)によって \(n\)個の解は全て異なる。つまり、
\(\theta-\sg^i(\theta)\neq0\:(1\leq i\leq n-1)\)
である。このことを踏まえて背理法で証明する。\(\bs{L}\) の任意の元 \(x\) について、
となるような \(\bs{L}\) の元 \(a_1,\:a_2,\:\cd\:,a_{n-1}\) が存在したとする。この \(g(x)=0\) の式から \(\sg^{n-1}(x)\) の項を消去することを考える。そのためにまず \(g(\theta x)\) を計算すると、
となる。この式から \(\sg^{n-1}(x)\) の項を消去するには、この式の \(\sg^{n-1}(x)\)の係数が \(a_{n-1}\sg^{n-1}(\theta)\) であり、また \(g(x)\) の \(\sg^{n-1}(x)\) の項の係数が \(a_{n-1}\) なので、
\(\sg^{n-1}(\theta)g(x)=0\)
の式を作って両辺から引けばよい。その計算をすると、
となる。ここで、\(x\) の係数である \((\theta-\sg^{n-1}(\theta))\) は、証明の最初に書いたように \(0\) ではない。そこで、全体を \((\theta-\sg^{n-1}(\theta))\) で割ると、
の形になる。ここで \(b_i\) は、
\(b_i=\dfrac{\sg^i(\theta)-\sg^{n-1}(\theta)}{\theta-\sg^{n-1}(\theta)}a_i\)
である。\((\br{B})\) 式は、基本的に \((\br{A})\) 式と同じで、\((\br{A})\) 式から \(\sg(x)^{n-1}\) の項を消去した形であり、\(x\) の最大次数の項は \(\sg(x)^{n-2}\) になっている。以上の、\((\br{A})\) から \((\br{B})\) への変換は繰り返し行えるから、\(n-2\) 回の変換を繰り返すと、
\(x+c_1\sg(x)=0\)
の形が得られる。この式にもう一度、\(n-1\) 回目の変換をすると、
となる。\(x\) は \(\bs{L}\) の任意の元だったから、\(\bs{L}\) のすべての元は \(0\) となってしまい、矛盾が生じた。従って背理法の仮定は誤りであり、\(\bs{L}\) の全ての元 \(x\) について、
補題(2)
\(\zeta\) を \(1\) の原始\(n\)乗根とし、\(\zeta\)を含む代数体を \(\bs{K}\) とする。\(\bs{K}\) のガロア拡大体を \(\bs{L}\) とし、\(\mr{Gal}(\bs{L}/\bs{K})\) は \(\sg\) で生成される位数 \(n\) の巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。また \(f(x)\) を \(\bs{K}\) 上の \(n\)次既約多項式とし、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて、\(\bs{L}=\bs{K}(\theta)\) と表されているものとする。このとき、
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
[証明]
\(g(x)\) の形は、べき根拡大の十分条件のため補題1(72A)で、
\(a_i=\zeta^{n-i}\:(1\leq i\leq n-1)\)
と置いたものである。\(\zeta\) は \(\bs{K}\) の元 = \(\bs{L}\) の元だから、補題(1)により \(\bs{L}\) の任意の元 \(x\) について \(g(x)=0\) となることはない。
この \(g(x)\) は次のような性質をもっている。まず \(\bs{K}\) の任意の元を \(a\) とすると、\(\mr{Gal}(\bs{L}/\bs{K})\) の 元 \(\sg\) は \(a\) を不動にするから、
\(\sg^i(a)=a\)
である。従って、\(g(a)\) を計算すると、
\(g(a)=ag(1)\)
となる。また、\(\bs{K}\) の任意の元を \(a\)、\(\bs{L}\) の任意の元を \(x\) とすると、
\(\sg^i(ax)=\sg^i(a)\sg^i(x)=a\sg^i(x)\)
なので、
\(g(ax)=ag(x)\)
である。さらに \(\bs{L}\) の任意の2つの元を \(x,\:y\) とすると、
\(\sg^i(x+y)=\sg^i(x)+\sg^i(y)\)
なので、
\(g(x+y)=g(x)+g(y)\)
である。
\(\bs{L}\) は、\(\bs{K}\) 上の既約多項式 \(f(x)\) を用いた方程式 \(f(x)=0\) の解 \(\theta\) の単拡大体 \(\bs{K}(\theta)\) だから、単拡大の体の定理(32C)により、\(\bs{L}\) の任意の元 \(x\) は、
\(x=b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1}\:(b^i\in\bs{K})\)
と表せる。\(g(x)\) の式にこの \(x\) を代入すると、
\(\begin{eqnarray}
&&\:\:g(x)&=g(b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1})\\
&&&=g(b_0)+g(b_1\theta)+g(b_2\theta^2)+\cd+g(b_{n-1}\theta^{n-1})\\
&&&=b_0g(1)+b_1g(\theta)+b_2g(\theta^2)+\cd+b_{n-1}g(\theta^{n-1})\\
\end{eqnarray}\)
となる。ここで、
\(g(1)=1+\zeta^{n-1}+\zeta^{n-2}+\cd+\zeta\)
だが、\(g(1)(1-\zeta)=\zeta^n-1=0\) なので \(g(1)=0\) である。従って、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) の全てが \(0\) だと、\(\bs{L}\) の全ての元 \(x\) について \(g(x)=0\) となり、矛盾が生じる。ゆえに、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち、少なくとも一つは \(0\) ではない。[証明終]
7.3 べき根拡大の十分条件
補題(1)と補題(2)を使って、体の拡大がべき根拡大になるための十分条件を証明します。
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
[証明]
\(\mr{Gal}(\bs{L}/\bs{K})\) は位数 \(n\) の巡回群なので、生成元を \(\sg\) とし、
\(\mr{Gal}(\bs{L}/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\sg^{n-1}\}\)
とする。\(\bs{L}\) の 元 \(c\) に対して、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
と定める。このとき \(\al\neq0\) となるように \(c\) を選べる。なぜなら、もし \(\al\neq0\) となる \(c\) が選べないとすると、\(\bs{L}\) の全ての元 \(x\) について、
\(x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\:\cd\:+\zeta\sg^{n-1}(x)=0\)
となるはずだが、これはべき根拡大の十分条件のため補題1(72A)、つまり、
\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない
において、\(a_1=\zeta^{n-1},\:a_2=\zeta^{n-2},\:\cd\:,a_{n-1}=\zeta\) と置いたことに相当し、そのような \(a_i\:(1\leq i\leq n-1)\) は存在しないとする補題1の結論に反するからである。またべき根拡大の十分条件のため補題2(72B)では、\(c\) の選び方の例が示されている。そこで、\(\al\neq0\) となるように \(c\) を選んだとする。
\(\sg\)は \(\bs{K}\) の元である \(\zeta\) を不変にするので、
\(\sg(\zeta^{n-i}\sg^i(c))=\zeta^{n-i}\sg^{i+1}(c)\)
である。これを用いて \(\sg(\al)\) を計算すると、
\(\sg(\al)\)
\(=\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta\sg^n(c)\)
\(=\zeta^n\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta c\)
\(=\zeta(\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\zeta^{n-3}\sg^3(c)+\:\cd+\zeta\sg^{n-1}(c)+c)\)
\(=\zeta\al\)
となる。計算では、\(\zeta^n=1\) であることと(第1項)、\(\sg^n=e\) なので \(\sg^n(c)=c\) となること(最終項)を用いた。
ここで、\(\al=\zeta\al\) となるのは、\(\al=0\) のときだけであるが、\(\al\neq0\) なので \(\al\neq\zeta\al\) である。つまり \(\sg(\al)\neq\al\) であり、\(\al\) は \(\sg\) を作用させると不変ではない。従って \(\al\) は \(\bs{K}\) の元ではない \(\bs{L}\) の元である。さらに \(\sg^i(\al)\) を求めていくと、
\(\begin{eqnarray}
&&\:\:\sg^2(\al)&=\sg(\sg(\al))=\sg(\zeta\al)=\zeta\sg(\al)=\zeta\zeta\al\\
&&&=\zeta^2\al\\
&&\:\:\sg^3(\al)&=\sg(\sg^2(\al))=\sg(\zeta^2\al)=\zeta^2\sg(\al)=\zeta^2\zeta\al\\
&&&=\zeta^3\al\\
\end{eqnarray}\)
というように計算でき、
\(\sg^i(\al)=\zeta^i\al\)
である。これを使うと、
\(\begin{eqnarray}
&&\:\:\sg(\al^n)&=\sg(\al)^n=(\zeta\al)^n=\zeta^n\al^n\\
&&&=\al^n\\
\end{eqnarray}\)
であり、\(\al^n\) は \(\sg\) を作用させても不変である。従って \(\al^n\) は \(\bs{K}\) の元である。そこで \(\al^n=a\:\:(a\in\bs{K})\) とおく。
方程式 \(x^n-a=0\) の解は、\(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al\) であり、\(x^n-a=0\) の \(\bs{K}\) 上の最小分解体は、\(\bs{K}\) には \(\zeta\) が含まれているから、
\(\bs{K}(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al)=\bs{K}(\al,\zeta)=\bs{K}(\al)\)
である。この式から、\(\bs{K}\) の同型写像による \(\al\) の移り先は全て \(\bs{K}(\al)\) に含まれることが分かる。従って \(\sg^i\:\:(1\leq i\leq n-1)\) はすべて \(\bs{K}(\al)\) の自己同型写像である。また、同型写像での移り先の定理(51D)により、同型写像は \(\al\) を共役な元に移すが、\(\al\) と共役な元は \(n-1\) 個しかない。従って \(\sg^i\) 以外に同型写像はない。つまり、
\(\mr{Gal}(\bs{K}(\al)/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\:\sg^{n-1}\}\)
であり、これは \(\mr{Gal}(\bs{L}/\bs{K})\) と同じである。次数と位数の同一性の定理(52B)により、ガロア群に含まれる自己同型写像の数は体の拡大次数に等しいから、
\([\:\bs{K}(\al)\::\:\bs{K}\:]=[\:\bs{L}\::\:\bs{K}\:]\)
である。もともと \(\al\) は \(\bs{L}\) の元だったので、\(\bs{K}(\al)\) の元は全て \(\bs{L}\) の元である。つまり、
\(\bs{K}(\al)\:\subset\:\bs{L}\)
であるが、\(\bs{K}(\al)\) と \(\bs{L}\) の線形空間の次元が等しいので、体の一致の定理(33I)により2つは一致し、
\(\bs{K}(\al)=\bs{L}\)
である。以上により、\(\bs{L}\) は \(\bs{K}\) の上の方程式 \(x^n-a=0\:(a\in\bs{K})\) の解の一つ \(\al\) を用いて \(\bs{L}=\bs{K}(\al)\) と表されるから、\(\bs{L}\) は \(\bs{K}\) の べき根拡大である。[証明終]
証明の過程で出てきた、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
の式は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言い、数学史においてはガロア理論より前に考えられたものです。この証明を振り返ってまとめてみると、
という条件のもとで、レゾルベントをうまく定義すると、
が成り立つという論理展開でした。つまりポイントは \(\bs{\al^n\in\bs{K}}\) のところであり、そういう \(\bs{\al\in\bs{L}}\) の存在が証明の核心です。
しかし、その鍵である \(\al\) を具体的に見つけようとすると、\(\al\) の式に現れる \(c\) を決めなければなりません。その \(c\) の値ですが、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて \(\bs{L}=\bs{K}(\theta)\) と表されているとき(= \(\theta\) が原始元のとき)、\(c=\theta\) にできることがべき根拡大の十分条件のため補題2(72B)に示されています。しかし、方程式の形から原始元が分かるわけではありません。
べき根拡大の十分条件(73A)は、その十分条件があればべき根拡大体の中に方程式の解が含まれる(= 方程式の解が四則演算とべき根で記述できる)ことだけを言っています。つまり四則演算とべき根で記述できる解の存在証明であり、そこが注意点です。
原始\(n\)乗根はべき根で表現可能
べき根拡大の十分条件(73A)を用いて原始\(\bs{n}\)乗根はべき根で表現可能(71A)であることを証明できます。(71A)ではガロア理論と関係なく証明しましたが、ガロア理論の枠組みを使っても証明できるということです。
まず \(n\) が合成数のとき、つまり \(n=s\cdot t\) と分解できるときには、原始\(n\)乗根は、原始\(s\)乗根と原始\(t\)乗根のべき根で表現できます(71A)。\(s\) や \(t\) が合成数なら、さらに "分解" を続けられるので、結局、\(n\) が素数 \(p\) のときに原始\(p\)乗根がべき根で表せることを示せればよいことになります。
いま、\(\bs{p}\) 未満の素数すべての原始\(\bs{n}\)乗根がべき根で表されると仮定します。これは帰納法の仮定です。原始\(p\)乗根を \(\eta\)(イータ) とし、その最小多項式を \(f(x)\) とすると、\(f(x)\) は既約多項式で、円分多項式です(63D)。原始\(p\)乗根は 方程式 \(x^p-1=0\) の \(1\) 以外の根なので、
\(x^p-1=(x-1)f(x)\)
であり、
\(f(x)=x^{p-1}+x^{p-2}+\:\cd\:+x+1\)
です。
原始\(p\)乗根による拡大体 \(\bs{Q}(\eta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\cong(\bs{Z}/p\bs{Z})^{*}\)
です(63E)。\((\bs{Z}/p\bs{Z})^{*}\) は位数 \((p-1)\) の巡回群で(25D)、\(\bs{Q}(\eta)/\bs{Q}\) の拡大次数は、\([\:\bs{Q}(\eta):\bs{Q}\:]=p-1\) です。原始\((p-1)\)乗根を \(\zeta\) とすると、\(\eta\notin\bs{Q}(\zeta)\) なので、\(\bs{Q}\) 上の既約多項式である \(f(x)\) は \(\bs{Q}(\zeta)\) 上でも既約多項式です。従って、
\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\cong\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\)
であり、\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\) も位数 \((p-1)\) の巡回群です。すると、べき根拡大の十分条件(73A)により、\(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta)\) はべき根拡大になります。つまり \(\eta\) は "有理数と \(\zeta\) の四則演算から成る式" のべき根で表現できます。
「\(p\) 未満の素数すべての原始\(n\)乗根がべき根で表される」という仮定により、\(\zeta\) はべき根で表現できます。従って \(\eta\) もべき根で表されます。
原始\(2\)乗根は \(-1\) であり、原始\(3\)乗根は根の公式によって、べき根で表現できます。従って帰納法により \(5\) 以上の素数 \(p\) の原始\(p\)乗根もべき根で表現できることが分かります。これで証明ができました。
ここで、原始\(\bs{n}\)乗根はべき根で表現可能(71A)とべき根拡大の十分条件(73A)の関係ですが、(73A)の証明の鍵になったのは、ラグランジュの分解式、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
でした。いま、原始\(5\)乗根を \(\eta\) とし、\(\bs{Q}(\eta)/\bs{Q}\) の巡回拡大を考えます。原始\(4\)乗根を \(\zeta\) とします(\(\zeta=i,\:-i\))。
\(\bs{Q}(\eta)\) の自己同型写像 \(\sg\) を、
\(\sg(\eta)=\eta^2\)
となる写像と定義します。そして、\(c=\eta,\:n=4\) を分解式に入れると、
\(\begin{eqnarray}
&&\:\:\al&=\eta+\zeta^3\sg(\eta)+\zeta^2\sg^2(\eta)+\zeta\sg^3(\eta)\\
&&&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
\end{eqnarray}\)
となります。このラグランジュの分解式と、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明で使った \(f(x,y)\) は本質的に同じものです。つまり
と定義すると、\(x,\:y\) の指数はそれぞれ、
\(x\) の指数:\([\:1,\:2,\:3,\:0\:]\)
\(\bs{Z}/4\bs{Z}\) の巡回パターン(生成元 \(=1\))
\(y\) の指数:\([\:3,\:4,\:2,\:1\:]\)
\((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン(生成元 \(=3\))
となります。(71A)では \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターンを \([\:2,\:4\:,3,\:1\:]\)(生成元 \(=2\))としたので式の形は少々違いますが、本質的に同じです。ここで、
\(x=\zeta,\:\:y=\eta\)
と置くと、
\(\begin{eqnarray}
&&\:\:f(x,y)&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
&&&=\al\\
\end{eqnarray}\)
となり、\(f(x,y)\) が ラグランジュの分解式と同じものであることが確認できました。つまり、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明は、
ものなのでした。
7.4 べき根拡大と巡回拡大の同値性
6.3節の "べき根拡大は巡回拡大である"(63H)と、7.3節の "巡回拡大はべき根拡大である"(73A)を合わせると、次にまとめることができます。
\(1\) の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。また、\(\bs{K}\) の\(n\)次拡大体を \(\bs{L}\) とする( \([\:\bs{L}\::\:\bs{K}\:]=n\) )。
このとき、
の2つは同値である。
\(\bs{1}\) の原始\(\bs{n}\)乗根が代数体に含まれるという条件をつけるのが巧妙なアイデアで、この条件によって可解性の必要十分条件が導けます。
7.5 可解性の十分条件
以上の準備をもとに、可解性の必要条件(64B)の逆である、可解性の十分条件の証明を行います。
代数拡大体 \(\bs{K}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とし、拡大次数を \([\:\bs{L}\::\:\bs{K}\:]=n\) とします。そして、ガロア群 \(\mr{Gal}(\bs{L}/\bs{K})\) が可解群であるとき、もし \(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるなら、べき根拡大と巡回拡大は同値の定理(74A)により、\(\bs{K}\) の巡回拡大とべき根拡大は同じことです。従って、
可解群 \(\rightarrow\) 累巡回拡大 \(\rightarrow\) 累べき根拡大 \(\rightarrow\) 可解
というルートで、方程式 \(f(x)=0\) の可解性が証明できます。しかし、\(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるとは限りません。\(\bs{K}\) が有理数体 \(\bs{Q}\) だとすると、そこに(原始2乗根以外の)原始\(n\)乗根はありません。しかし、このようなケースでも方程式の可解性が証明できます。それが以下です。
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
[証明]
\([\:\bs{L}\::\:\bs{K}\:]=n\:\:(|G|=n)\) とし、\(\zeta\) を \(1\) の原始\(n\)乗根とする。\(\bs{K}\) に \(\zeta\) を添加した拡大体 \(\bs{K}(\zeta)\)と、\(\bs{L}\) に \(\zeta\) を添加した拡大体 \(\bs{L}(\zeta)\) を考える。
\(\bs{L}(\zeta)\) は \(\bs{K}\) 上の方程式 \(f(x)(x^n-1)=0\) の最小分解体だから、\(\bs{L}(\zeta)/\bs{K}\) はガロア拡大である。
また \(\bs{K}(\zeta)\) は、\(\bs{K}\)のガロア拡大体 \(\bs{L}(\zeta)\) の中間体なので、中間体からのガロア拡大の定理(52C)によって、\(\bs{L}(\zeta)/\bs{K}(\zeta)\) もガロア拡大である。そこで、
\(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))=G\,'\)
とおく。
\(G\) の元を \(g\)、\(G\) の単位元を \(e\) とする。\(G\,'\)の元を \(g\,'\)、\(G\,'\) の単位元を \(e\,'\) とする。また、\(G\,'\) の元 \(g\,'\) を \(\bs{L}\) の元に限定して作用させるときの同型写像を \(\sg(g\,')\) とする。
\(g\,'\)は \(\bs{L}(\zeta)\) の自己同型写像だから、\(\bs{L}(\zeta)\) の元を共役な元に移す。従って 作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も \(\bs{L}\) の元を共役な元に移す。\(\bs{L}\) はガロア拡大体だから、\(\bs{L}\)の元の共役な元は \(\bs{L}\) に含まれる。従って \(\sg(g\,')\) は \(\bs{L}\) の自己同型写像である。
また \(g\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) の元だから、\(\bs{K}(\zeta)\) の元を固定する。従って、\(\bs{K}(\zeta)\) の部分集合である \(\bs{K}\) の元も固定する。ゆえに、\(g\,'\) の作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も、\(\bs{L}\) の部分集合である \(\bs{K}\) の元を固定する。
以上により \(\sg(g\,')\) は、\(\bs{K}\)の元を固定する \(\bs{L}\) の自己同型写像だから、\(\mr{Gal}(\bs{L}/\bs{K})\) の元、つまり \(G\) の元である。
\(\sg\) を \(G\,'\) から \(G\) への写像と見なして考える。\(G\,'\) の元 を \(g\,'\) とし、\(x\) を \(\bs{L}\) の元とすると、\(g\,'(x)=\sg(g\,')(x)\) である。つまり、作用する対象が \(\bs{L}\) の元なら、2つの写像、\(g\,'\) と \(\sg(g\,')\) は同じ効果を生む。
\(G\,'\)の任意の2つの元を \(g_1{}^{\prime},\:g_2{}^{\prime}\) とすると、\(g_1{}^{\prime}g_2{}^{\prime}\) も \(G\,'\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}(x)=g_1{}^{\prime}(\sg(g_2{}^{\prime})(x))\)
であるが、\(\sg(g_2{}^{\prime})(x)\) もまた \(\bs{L}\) の元だから、
\(\sg(g_1{}^{\prime}g_2{}^{\prime})=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})\)
となって、\(\sg\) は準同型写像(42A)である。
\(\sg(g\,')\) が \(G\) の元であり \(\sg\) が準同型写像なので、準同型写像の像と核の定理(42B)により、\(\sg\) による \(G\,'\) の 像 \(\sg(G\,')\) は \(G\) の部分群である。もちろん、\(G\) の部分群には \(G\) の自明な部分群である \(G\) 自身も含まれる。
いま、ある \(G\,'\) の元 \(h\) があって、\(\sg(h)=e\)(\(e\) は \(G\) の単位元)とする。つまり、\(h\) を \(\bs{L}\) に限定して適用すると、\(\bs{L}\) の元すべてを固定するものとする。
\(G\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) であり、そのすべての元は \(\bs{K}(\zeta)\) の元を固定する。従って、\(G\,'\) の元 \(h\) は \(\zeta\) も固定する。ということは、\(h\) は「\(\bs{L}\) の元すべてを固定し、かつ \(\zeta\) を固定する」から、\(\bs{L}(\zeta)\) の元すべてを固定する。つまり \(h\) は \(G\,'\) の単位元であり、\(h=e\,'\) である。
ゆえに、準同型写像の像と核(42B)における核の定義によって、
\(\mr{Ker}\:\sg=e\,'\)
であり、核が単位元なら単射の定理(42C)によって、\(\sg\) は単射である。このことから、準同型定理(43A)により、
\(G\,'/\mr{Ker}\:\sg\:\cong\:\sg(G\,')\)
すなわち、
\(G\,'\:\cong\:\sg(G\,')\)
である。つまり \(\bs{G\,'}\) は \(\bs{G}\) の部分群 \(\bs{\sg(G\,')}\) と同型である。
\(G\) は可解群なので、可解群の部分群は可解群の定理(61C)によって、\(G\) の部分群である \(\sg(G\,')\) も可解群であり、さらにそれと同型である \(G\,'\) も可解群である。\(G\,'\) が可解群なので、可解群の定義により \(G\,'\) から \(e\,'\) に至る部分群の列、
\(|G\,'|=m\) とおくと、\(G\,'\) は \(G\) の部分群である \(\sg(G\,')\) と同型なので、ラグランジュの定理(41E)によって、\(m\) は \(|G|=n\) の約数である。
ガロア対応(53B)による \(H_i\) の固定体を \(\bs{K}_i\) とすると、
\(\bs{L}(\zeta)/\bs{K}(\zeta)\) の拡大次数は、
\([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=|G\,'|=m\)
であり、\(n\) の約数である。
固定体の系列における一つの拡大 \(\bs{K}_{i+1}/\bs{K}_i\)を考える。その拡大次数 \([\:\bs{K}_{i+1}\::\:\bs{K}_i\:]=m_i\) は、拡大次数の連鎖律(33H)によって \([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=m\) の約数であり、従って \(n\) の約数である。
\(\bs{K}_i\) は \(1\) の原始\(n\)乗根 \(\zeta\) を含むから、\(\zeta^{\frac{n}{m_i}}\) も含んでいる。\(\zeta^{\frac{n}{m_i}}\) は \(1\) の原始\(m_i\)乗根である。つまり、\(\bs{K}_i\) は \(1\) の原始\(m_i\)乗根(\(m_i=[\:\bs{K}_{i+1}\::\:\bs{K}_i\:]\))を含む。従って、べき根拡大の十分条件の定理(73A)により、巡回拡大である \(\bs{K}_{i+1}/\bs{K}_i\) はべき根拡大である。
以上のことは \((0\leq i < k)\) のすべてで成り立つから、\(\bs{K}_i\) の系列は累べき根拡大である。
\(f(x)=0\) の解は \(\bs{L}\) に含まれるが、\(\bs{L}\:\subset\:\bs{L}(\zeta)\) だから \(f(x)=0\) の解は \(\bs{L}(\zeta)\) に含まれる。その \(\bs{L}(\zeta)\) は \(\bs{K}(\zeta)\) の累べき根拡大であり、また \(1\) の原始\(n\)乗根である \(\zeta\) は \(\bs{Q}\:(\in\bs{K})\) の元の四則演算とべき根で表現できるから(71A)、\(\bs{L}(\zeta)\) の元はすべて \(\bs{K}\) の元の四則演算とべき根で表現できる。従って \(f(x)=0\) の解も \(\bs{K}\) の元の四則演算とべき根で表現できる。[証明終]
この定理では「体 \(\bs{K}\) 上の方程式 \(f(x)=0\)」としましたが、もちろん、体 \(\bs{K}\) が 有理数体 \(\bs{Q}\) であっても同じです。以降、\(\bs{K}\) を \(\bs{Q}\) と書きます。
証明のポイントは、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) とし、\(G\,'=\mr{Gal}(\bs{L}(\zeta)/\bs{Q}(\zeta))\) とするとき、\(G\,'\) が \(G\) の部分群と同型であることです。たとえば、\(f(x)\) が既約な3次多項式だと、\(G\cong S_3\) か \(G\cong C_3\) であり、基本的に \(G\,'\cong G\) です。しかし、そうならない場合もあります。たとえば \(f(x)=x^3-2\) では \(G\cong S_3\) ですが、
\(\bs{Q}\:\subset\:\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\sqrt[3]{2})=\bs{L}\)
(\(\omega\) は \(1\) の原始3乗根)
という体の拡大列でわかるように、\(\bs{L}(\omega)=\bs{L}\) です。つまり、\(\bs{L}(\omega)/\bs{Q}(\omega)\) の拡大次数は \(3\) であり、\(\bs{L}/\bs{Q}\) の拡大次数の \(6\) とは違います。しかしそうであっても \(G\,'=\mr{Gal}(\bs{L}(\omega)/\bs{Q}(\omega))\cong C_3\) であり、\(G\,'\) は \(G\cong S_3\) の部分群と同型です。
\(G\,'\) は \(G\) の部分群と同型なので、\(G\) が可解群なら \(G\,'\) も可解群であり(61C)、\(\bs{L}(\omega)/\bs{Q}(\omega)\) は累巡回拡大であり(62C)、従って、累べき根拡大です(73A)。
さらに、\(1\) の原始\(n\)乗根が \(\bs{Q}\) の元の四則演算とべき根で表現できる(71A)ことも証明のポイントになっています。
この可解性の十分条件の定理(75A)によって、有理数係数の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) として、\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群のとき、\(f(x)=0\) の解は四則演算とべき根で表現可能なことが証明できました。
ここがゴールで「ガロア理論=可解性の必要十分条件」が完結しました。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
可解性の必要十分条件の証明は前節で尽きていますが、これ以降は可解な方程式の代表的なものを取り上げ、ガロア群の分析をします。まず最初は、
です。これらの方程式が可解であることは当然ですが、ガロア群の分析をすると正5角形と正\(17\)角形が定規とコンパスで作図できることを証明できます。
\(x^5-1=0\)
まず \(x^5-1=0\) の解を分析します。
\(x^5-1=(x-1)(x^4+x^3+x^2+x+1)\)
なので、\(1\) 以外の解を \(\zeta\) とすると、\(\zeta\) は4次方程式、
\(x^4+x^3+x^2+x+1=0\)
の解です。「7.1 1 の原始n乗根」で書いたように、この方程式の解は、
\(\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm\sqrt{-10-2\sqrt{5}}\right)\)
\(\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm\sqrt{-10+2\sqrt{5}}\right)\)
の4つであり、これが \(1\) の原始5乗根です。以下の論旨を明瞭にするために、虚数単位 \(i\) を使わずに、外側の \(\sqrt{\phantom{a}}\) の中を負の数にして記述しました。
この原始5乗根は、4次方程式の解であるにもかかわらず、四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現されています。なぜそうなるのか、それをガロア理論にのっとって説明します。実は、\(p\) を素数としたとき、
ことが知られています。定規というのは「目盛りのない、与えられた2点を通る直線を引くことだけができる道具」であり、コンパスというのは「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\cdot\)円弧を描くことだけができる道具」です。長さや角度を測ることはできません。作図可能の原理は次の項で説明します
\(f(x)=x^4+x^3+x^2+x+1\) とし、\(f(x)=0\) の解の一つを \(\zeta\) とすると、\(f(x)\) の最小分解体は \(\bs{Q}(\zeta)\) です。そのガロア群を、
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
と書くと、\(\zeta\) の最小多項式は \(f(x)\) なので(63C)、\(|G|=4\) です。また、\(\bs{\bs{Q}(\zeta)}\) のガロア群の定理(63E)により、\(G\) は既約剰余類群と同型で、
\(G\cong(\bs{Z}/5\bs{Z})^{*}\)
です。
\((\bs{Z}/5\bs{Z})^{*}=\{1,\:2,\:3,\:4\}\)
ですが、この群の生成元は \(2\) か \(3\) です。以下、生成元を \(2\) として話を進めると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
と表現できます。一方、\(f(x)=0\) の4つの解は、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
です。そこで、
\(\sg(\zeta)=\zeta^2\)
で定義される自己同型写像を考えると、ガロア群は、
\(G=\{\sg,\:\sg^2,\:\sg^3,\:\sg^4=e\}\)
となり、位数 \(4\) の巡回群、かつ可解群です。また、体の拡大次数は、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=4\)
です。
ガロア群 \(G\) には部分群が含まれています。つまり、
\(H=\{\sg^2,\:e\}\)
\(\sg^2(\zeta)=\zeta^4\)
と定義すると、\((\sg^2)^2=e\) なので \(H\) は部分群(\(\sg H=H\sg\) なので正規部分群)であり、位数 \(2\) の巡回群です。また、剰余群は、
\(G/H\cong\{e,\:\sg\}\)
です。従って、
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\)
は可解列です。ガロア対応の定理(53B)により、この可解列に対応する拡大体の列があって、
\(G\sp H\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}\subset\bs{Q}(\zeta)\)
となります。\(\bs{F}\) は \(H\) の固定体であり、\(\bs{Q}(\zeta)\) の中間体です。すると、正規性定理(53C)により、
\(\mr{Gal}(\bs{F}/\bs{Q})\cong G/H\)
なので、\(\mr{Gal}(\bs{F}/\bs{Q})\) は位数 \(2\) の巡回群です。またガロア群の定義により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\cong H\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\) も位数 \(2\) の巡回群です。従って、次数と位数の同一性の定理(52B)より拡大次数は、
であり、2つの拡大は巡回拡大です。原始2乗根(\(=-1\))は \(\bs{Q}\) に含まれるので、巡回拡大はべき根拡大です(73A)。拡大次数 \(2\) のべき根拡大を(一般的な数学用語ではありませんが)「平方根拡大」と呼ぶことにすると、
と結論づけられます。原始5乗根が四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できる理由がここにあります。
ここまでは、中間体 \(\bs{F}\) がどういう拡大体かに触れていませんが、\(\bs{F}\) を具体的に表現することもできます。\(\bs{F}\) は \(H=\{e,\:\sg^2\}\) の固定体なので、\(\bs{F}=\bs{Q}(\theta)\) として、
\(\sg^2(\theta)=\theta\)
となる \(\theta\) を探します。\(\theta\) の選び方には自由度があり、たとえば \(\theta=\zeta^4+\zeta\) としてもよいのですが、ここでは、
\(\theta=(\zeta^2-\zeta^3)(\zeta^4-\zeta)\)
とします。このように選ぶと、\(\sg^2(\zeta)=\zeta^4\) なので、
\(\begin{eqnarray}
&&\:\:\sg^2(\theta)&=(\zeta^8-\zeta^{12})(\zeta^{16}-\zeta^4)\\
&&&=(\zeta^3-\zeta^2)(\zeta-\zeta^4)=\theta\\
\end{eqnarray}\)
となって、\(\theta\) は \(\sg^2\) で不変です。と同時に、\(\sg(\zeta)=\zeta^2\) なので、
\(\begin{eqnarray}
&&\:\:\sg(\theta)&=(\zeta^4-\zeta^6)(\zeta^8-\zeta^2)\\
&&&=(\zeta^4-\zeta)(\zeta^3-\zeta^2)=-\theta\\
\end{eqnarray}\)
となります。ということは、
\(\sg(\theta^2)=(\sg(\theta))^2=(-\theta)^2=\theta^2\)
であり、\(\theta^2\) は \(\sg\) で不変、つまり \(G\) のすべての元で不変となり、\(\theta^2\) は有理数です。そこで、
\(\zeta^5=1\)
\(\zeta^4+\zeta^3+\zeta^2+\zeta+1=0\)
の関係を使って \(\theta^2\) を計算すると、
\(\begin{eqnarray}
&&\:\:\theta^2&=(\zeta^2-\zeta^3)^2(\zeta^4-\zeta)^2\\
&&&=(\zeta^4-2\zeta^5+\zeta^6)(\zeta^8-2\zeta^5+\zeta^2)\\
&&&=(\zeta^4-2+\zeta)(\zeta^3-2+\zeta^2)\\
&&&=\zeta^7-2\zeta^4+\zeta^6-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=\zeta^2-2\zeta^4+\zeta-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=-\zeta^4-\zeta^3-\zeta^2-\zeta+4\\
&&&=5\\
\end{eqnarray}\)
となり、確かに\(\theta^2\) は有理数であることが分かります。つまり、
\(\theta=\sqrt{5}\)
です。従ってガロア対応は、
となります。原始5乗根に \(\sqrt{-10+2\sqrt{5}}\) のような項が現れるのは、中間体が \(\bs{Q}(\sqrt{5})\) であるという、体の拡大構造からくるのでした。
ここまでの論証を振り返ってみると、
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
ことが分かります。この条件は \(p=3,\:5\) で成立しますが、その次に成立するのは \(p=17\) です。
\(x^{17}-1=0\)
\(1\) の原始\(17\)乗根を \(\zeta\) とします。\(p=17\) の最小原始根は \(3\) で(25D)、\((\bs{Z}/17\bs{Z})^{*}\) の位数は \(16\) です。\((\bs{Z}/17\bs{Z})^{*}\) において \(3\) の累乗は、
\(\phantom{1}3,\:\phantom{1}9,\:10,\:13,\:\phantom{1}5,\:15,\:11,\:16,\)
\(14,\:\phantom{1}8,\:\phantom{1}7,\:\phantom{1}4,\:12,\:\phantom{1}2,\:\phantom{1}6,\:\phantom{1}1\)
と、すべての元を巡回します。従って、
\(\sg(\zeta)=\zeta^3\)
という自己同型写像 \(\sg\) を定義すると、
\(G=\{\sg,\sg^2,\sg^3,\cd,\sg^{15},\sg^{16}=e\}\)
が \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) です。
\(x^5-1=0\) のときと同様の考察をすると、\(G\) には3つの部分群があります。
\(H_1=\{\sg^2,\sg^4,\sg^6,\sg^8,\sg^{10},\sg^{12},\sg^{14},e\}\)
\(\sg^2(\zeta)=\zeta^9\)
\(H_2=\{\sg^4,\sg^8,\sg^{12},e\}\)
\(\sg^4(\zeta)=\zeta^{13}\:\:(\phantom{1}9^2\equiv13\:\:(\mr{mod}\:17))\)
\(H_3=\{\sg^8,e\}\)
\(\sg^8(\zeta)=\zeta^{16}\:\:(13^2\equiv16\:\:(\mr{mod}\:17))\)
の3つで、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
は可解列です。ガロア対応の定理(53B)により、\(H_1,\:H_2,\:H_3\) にはそれぞれに対応した固定体 \(\bs{F}_1,\:\bs{F}_2,\:\bs{F}_3\) があって、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}_1\subset\bs{F}_2\subset\bs{F}_3\subset\bs{Q}(\zeta)\)
のガロア対応になります。\(\bs{Q}\) から \(\bs{Q}(\zeta)\) までの4つの拡大次数は、剰余群の位数に等しいのですべて \(2\) です。つまり、\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの「平方根拡大」を4回繰り返したものであり、原始\(17\)乗根は四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できます。従って正\(17\)角形は定規とコンパスで作図可能です。
これは、ドイツの大数学者\(\cdot\)ガウス(\(1777-1855\))が\(19\)才のときに発見した定理として有名です。
作図可能の原理
ここで改めて、平面上の図形が定規とコンパスで「作図可能」という意味を明確にします。ここで "定規" は「目盛りのない、与えられた2点を通る線を引くことだけができる道具」であり、"コンパス" は「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\bs{\cdot}\)円弧を描くことだけができる道具」でした。
平面上の図形は点と線でできています。線は2点を与えると描けるので、「作図可能」の意味は「平面上で作図可能な点とは何か」を定義することに帰着します。
平面を複素平面(\(=\bs{C}\))として考えます。以降、
の記号を使います。「作図可能」の意味は「複素平面上で作図可能な複素数(実数を含む)とは何か」を定義することです。
\(1,\:0\) は作図可能である。また複素平面の実軸と虚軸は作図できる。
任意の線分を単位長さとし、端点を \(1,\:0\) とします。2点を結ぶ直線が実軸で、\(0\) を通り実軸と垂直な直線を作図するとそれが虚軸です。
\(\al=a+b\:i\) とすると、\(a,\:b\) が作図可能なら \(\al\) も作図可能である。また、\(\al\) が作図可能なら \(a,\:b\) も作図可能である。
\(a\) が作図可能なら、\(-a\) も作図可能である。従って \(\al\) が作図可能なら \(-\al\) も作図可能である。
また \(a,\:b\) が作図可能なら \(a+b\) も作図可能である。従って、\(\al,\:\beta\) が作図可能なら \(\al+\beta\) も作図可能である。
\(a,\:b\) が作図可能なら \(ab\)も作図可能である。従って \(\al,\:\beta\) が作図可能なら \(\al\beta\) も作図可能である。
\(a\:\:(a\neq0)\) が作図可能なら \(a^{-1}\) も作図可能である。従って \(\al\:\:(\al\neq0)\) が作図可能なら \(\al^{-1}\) も作図可能である。
作図可能な \(\al\) を \(\al=a+b\:i\) とすると、
\(\al^{-1}=\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}\:i\)
です。\(a,\:b\) が作図可能なので、その四則演算の結果は作図可能です。従って \(\al^{-1}\) も作図可能です。
有理数 \(\bs{Q}\) は作図可能である。
実数のなかで作図可能な点は四則演算で閉じています。かつ、\(0,\:1\) は作図可能です。従って有理数は作図可能です。
\(a\) が正の実数のとき、\(\sqrt{a}\) は作図可能である。
\(a\) と \(-1\) を結ぶ線分を直径とする円を描き、虚軸との交点を \(x\cdot i\:(x\):実数) とすると、
\(1:x=x:a\)
なので、\(x=\pm\sqrt{a}\) です。従って \(\sqrt{a}\) は作図可能です。
\(\al\) を作図可能な複素数とするとき、\(\sqrt\al\) は作図可能である。
極形式を使って、
\(\al=r(\mr{cos}\theta+i\cdot\mr{sin}\theta)\)
とすると、\(r\) は作図可能であり、つまり \(\sqrt{r}\) も作図可能です。また、角 \(\theta\) を2等分する線も、定規とコンパスで作図可能です。従って \(\sqrt\al\) は作図可能です。
\(\al,\:\beta\) が作図可能な複素数とするとき、2次方程式 \(x^2+\al x+\beta=0\) の解は作図可能である。
ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能である。
2次方程式 \(x^2+\al x+\beta=0\) の解は、根の公式により、係数 \(\al,\:\beta\) の四則演算と平方根で表わされます。従って作図可能です。
定規とコンパスで作図可能な点は、作図可能な円や直線の交点として求まる点です。2次元 \(xy\) 平面( \(\bs{R}^2\) )で考えると、直線と直線の交点は1次方程式の解です。また円と直線の交点は2次方程式の解です。円と円の交点がどうかですが、\(a,\:b,\:c,\:d\) を実数として、2つの円の方程式を、
実数(\(a,\:b\))が作図可能と、複素数(\(a+bi\))が複素平面上で作図可能は同値です。従って、ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能です。
\(\bs{Q}\) の代数拡大体 \(\bs{K}\) があり、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{K}\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
を満たす \(\bs{Q}\) から \(\bs{K}\) の拡大列が存在するとき、\(\bs{K}\) の元
\(\al\in\bs{K}\)
は作図可能である。
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\) であれば、\(\bs{K}_{i+1}/\bs{K}_i\) は次数2のべき根拡大であり、
\(x^2-a=0\:\:\:(a\in\bs{K}_i)\)
の解、\(\sqrt{a}\) を用いて、
\(\bs{K}_{i+1}=\bs{K}_i(\sqrt{a})\)
と表されます。従って、\(\bs{K}_i\) の元が作図可能なら、\(\bs{K}_{i+1}\) の元は「作図可能な点の四則演算と平方根の組み合わせ」で表現できるので、作図可能です。体の拡大列の出発点である \(\bs{Q}\) の元は作図可能なので、到達点である \(\bs{K}\) の元も作図可能になります。
\(1\) の原始\(p\)乗根(\(p\):素数)を \(\zeta\) とすると、\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) の位数は \(p-1\) であり、それが2の累乗であれば、\(G\) の可解列にガロア対応する体の拡大系列、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{Q}(\zeta)\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
が存在します(前項での証明)。従って複素数平面上の点 \(\zeta\) は作図可能であり、正 \(p\)角形は作図可能です。条件に合致する素数は \(p=3\)、\(5\)、\(17\)、\(257\)、\(65537\)であることが知られています。これらの素数をフェルマ素数と呼びます。フェルマ素数 \(p\) とは、\(p-1\) が2の累乗であるような素数です。
さらに、一般の正 \(n\)角形が作図可能である条件は、次のようになります。
正 \(n\)角形は、
\(n=2^k\:\:\:(2\leq k)\)
\(n=2^k\cdot p_1p_2\cd p_r\:\:\:(0\leq k,\:\:1\leq r)\)
\(p_i\) は相異なるフェルマ素数
のとき、作図可能である。
[証明]
角度の2等分線は作図可能なので、\(n=2^k\:\:(2\leq k)\) のとき、正 \(n\)角形は作図可能である。と同時に、正 \(m\)角形が作図可能なとき、
\(n=2^k\cdot m\:\:(0\leq k)\)
とおくと、正 \(n\)角形は作図可能になる。\(p\) がフェルマ素数のとき、正 \(p\)角形は作図可能なので、
\(m_1\) と \(m_2\) を互いに素な3以上の数とするとき、正 \(m_1\) 角形と正 \(m_2\)角形が作図可能であれば、正 \(m\)角形(\(m=m_1m_2\))は作図可能である
ことが証明できれば十分である。
\(\theta,\:\theta_1,\:\theta_2\) を任意の角度とする。
\(\mr{sin}\theta=\sqrt{1-\mr{cos}^2\theta}\)
だから、\(\mr{cos}\theta\) が作図できれば \(\mr{sin}\theta\) も作図できる。また三角関数の加法定理より、
\(\mr{cos}(\theta_1+\theta_2)=\mr{cos}\theta_1\cdot\mr{cos}\theta_2-\mr{sin}\theta_1\cdot\mr{sin}\theta_2\)
なので、\(\mr{cos}\theta_1,\:\mr{cos}\theta_2\) が作図できれば \(\mr{cos}(\theta_1+\theta_2)\) も作図できる。このことから \(\mr{cos}\theta\) が作図できれば \(\mr{cos}(k\theta)\:\:(k\) は整数)も作図できる。
複素平面上で原点を中心とする半径1の円に正 \(m\)角形を描いたとき、その頂点の複素数は
\(\mr{cos}\left(\dfrac{2\pi}{m}k\right)+i\:\mr{sin}\left(\dfrac{2\pi}{m}k\right)\:\:(0\leq k\leq m-1)\)
である。\(k=1\) の点が作図できれば、残りの点が作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
が作図できれば、正 \(m\)角形は作図できる。
\(m_1\) と \(m_2\) は互いに素だから、不定方程式の解の存在の定理(21C)により、
\(k_1m_1+k_2m_2=1\)
を満たす \(k_1,\:k_2\) が存在する。両辺を \(m=m_1m_2\) で割ると
\(\dfrac{k_1}{m_2}+\dfrac{k_2}{m_1}=\dfrac{1}{m}\)
\(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2=\dfrac{2\pi}{m}\)
が得られる。正 \(m_1\)角形と正 \(m_2\)角形 は作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m_1}\right),\:\:\mr{cos}\left(\dfrac{2\pi}{m_2}\right)\)
は作図できる。従って
\(\mr{cos}\left(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2\right)\)
は作図でき、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
も作図できることになって、正 \(m\)角形は作図できる。[証明終]
証明の鍵は「\(m_1\) と \(m_2\) が互いに素」です。従って、正3角形が作図できても、正9角形は作図できません。正\(15\)角形なら作図できます。計算すると、作図可能な正 \(n\)角形(\(n\leq100\))は、
です。「正\(50\)角形は作図できないが、正\(51\)角形は作図できる」というのも不思議な感じがします。
7.7 巡回拡大はべき根拡大:3次方程式が解ける理由
この節では可解な方程式がなぜ解けるのかを、3次方程式を例にとってガロア理論で説明します。また3次方程式の根の公式をガロア理論に沿った形て導出します。「7.5 可解性の十分条件」で証明したことは、
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
でした。この証明の核となっているのは「7.3 べき根拡大の十分条件」であり、それは、
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
でした。このことを証明した論理展開は、次のようでした。
次の条件があるとする。
このとき、レゾルベント(分解式)を定義することで、
となる。
つまり、レゾルベントを使って、巡回拡大=べき根拡大(但し、体に \(1\) の原始\(n\)乗根が含まれることが条件)を証明したわけです。この証明プロセスを、具体的な3次方程式で順にたどります。まず、3次方程式のガロア群を再度整理します。
3次方程式のガロア群
3次方程式のガロア群は「1.3 ガロア群」で計算しましたが、改めて書きます。3次方程式のガロア群は、3次方程式の3つの解、\(\al,\:\beta,\gamma\) を入れ替える(置換する)群であり、一般的には、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
です。3つの解をそれぞれ \(1,\:2,\:3\) の文字で表し、巡回置換の記法(6.5節)で書くと、
で(\(\sg,\:\tau\) の演算は右から行う)、これは3次の対称群(\(S_3\)。6.5節)です。この群はもちろん可換群ではなく \(\tau\sg\neq\sg\tau\) ですが、\(\tau\sg\) を計算すると、
\(\tau\sg=(1,\:3)\)
であり、
\(\tau\sg=\sg^2\tau\)
との関係が成り立っています。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。ここで、
\(H=\{e,\:\sg,\:\sg^2\}\)
という \(G\) の部分群を考えると、\(H\) は巡回群であると同時に \(G\) の正規部分群です。"弱可換性" を使って検証してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
であり、同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つので \(H\) は \(G\) の正規部分群です。
\(G\) の \(H\) による剰余群は、
\(G/H=\{H,\tau H\}\)
であり、単位元は \(H\) で、
\((\tau H)^2=\tau H\tau H=\tau\tau HH=H\)
となる、位数\(2\) の巡回群です(\(G/H\cong C_2)\)。この結果、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
は可解列になり、\(G\) は可解群で、従って3次方程式は可解です(=四則演算とべき根で解が表現可能)。この節ではそれを具体例で確認していきます。
一方、「3.3 線形空間」の「代数拡大体の構造」で書いたように、3次方程式のガロア群が \(S_3\) ではなく、位数 \(3\) の巡回群( \(C_3\) )になる場合があります。それを再度整理します。
\(x^3+ax^2+bx+c=0\) の3次方程式は、\(x=X-\dfrac{a}{3}\) とおくと、
\(X^3+\left(b-\dfrac{a^2}{3}\right)X+\left(\dfrac{2}{27}a^3-\dfrac{1}{3}ab+c\right)=0\)
となって、2乗の項が消えます。従って以降、3次方程式を、
\(x^3+px+q=0\)
の形で扱います。
\(f(x)=x^3+px+q\)
とおき、\(f(x)\) は既約多項式とします。3次方程式の根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
であり、根と係数の関係から、
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=p\)
\(\al\beta\gamma=-q\)
です。3次方程式のガロア群が \(S_3\) か \(C_3\) かを決めるポイントとなるのは、
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
で定義される、根の差積と呼ばれる値です。差積は普通、\(\Delta\)(ギリシャ文字・デルタの大文字)で表しますが、後の説明の都合で \(\theta\) と書きます。差積は、任意の2つの根の互換で \(-\theta\) となるので、3つの根を \(\al,\:\beta,\:\gamma\) に割り当てる方法によって、\(\theta\) は2つの値をとり得ます。差積の2乗が判別式であり、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
です。つまり \(\theta=\sqrt{D}\) と書けますが、\(\sqrt{D}\) は「2乗して \(D\) となる2つの数のどちらか」の意味です。\(D\) は \(\al,\:\beta,\:\gamma\) の任意の置換で不変な対称式なので、3次方程式の係数である \(p,\:q\) で表すことができる有理数です。
その \(D\) を方程式の係数で表すために、\(f(x)\) を微分します。
\(f(x)=(x-\al)(x-\beta)(x-\gamma)\)
なので、
\(\begin{eqnarray}
&&\:\:f\,'(x)=&(x-\al)(x-\beta)+(x-\beta)(x-\gamma)+\\
&&&(x-\gamma)(x-\al)\\
\end{eqnarray}\)
であり、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\beta)=(\beta-\gamma)(\beta-\al)\)
\(f\,'(\gamma)=(\gamma-\al)(\gamma-\beta)\)
となります。従って、
\(D=-f\,'(\al)f\,'(\beta)f\,'(\gamma)\)
です。一方、
\(f\,'(x)=3x^2+p\)
なので、
\(D=-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\)
となります。ここからの計算を進めるために、次の2つの対称式を、根と係数の関係を使って \(p\) で表しておきます。
・\(\al^2+\beta^2+\gamma^2\)
\(=(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)\)
\(=-2p\)
・\(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2\)
\(=(\al\beta+\beta\gamma+\gamma\al)^2-2\al\beta\gamma(\al+\beta+\gamma)\)
\(=p^2\)
これを用いると、
\(\begin{eqnarray}
&&\:\:D&=&-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\\
&&&=&-27(\al\beta\gamma)^2-9(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2)p\\
&&&&-3(\al^2+\beta^2+\gamma^2)p^2-p^3\\
&&&=&-27q^2-9\cdot p^2\cdot p-3\cdot(-2p)\cdot p^2-p^3\\
&&&=&-4p^3-27q^2\\
\end{eqnarray}\)
と計算できます。つまり、
\(D=-4p^3-27q^2\)
です。ここでもし、\(D\) がある有理数 \(a\) の2乗(\(D=a^2\))なら、
\(\theta=\sqrt{D}=\pm a\)
となり、\(\theta\) は有理数です。\(\theta\) が有理数(\(\theta=\pm a\))の場合、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\al)=3\al^2+p\)
の関係があるので、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=-f\,'(\al)(\beta-\gamma)\\
&&&=-(3\al^2+p)(\beta-\gamma)\\
\end{eqnarray}\)
ですが、\(\theta=\pm a\) なので、
\(\beta-\gamma=\pm\dfrac{a}{3\al^2+p}\)
です。この式と、根と係数の関係である、
\(\beta+\gamma=-\al\)
を使うと、\(\bs{\beta}\) と \(\bs{\gamma}\) が \(\bs{\al}\) の有理式(=分母・分子が \(\bs{\al}\) の多項式)で表現できることになります。計算すると(\(\pm\)は省略して)、
\(\beta=\dfrac{2p\al+3q-a}{2(3\al^2+p)}\)
\(\gamma=\dfrac{2p\al+3q+a}{2(3\al^2+p)}\)
です(\(\beta\) と \(\gamma\) は逆でもよい)。\(\beta,\:\gamma\) が \(\al\) の有理式で表現できるので、
\(\bs{Q}(\al,\beta,\gamma)\subset\bs{Q}(\al)\)
であり、もちろん \(\bs{Q}(\al,\beta,\gamma)\sp\bs{Q}(\al)\) なので。
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
です。\(\bs{Q}(\al)\) のところは \(\bs{Q}(\beta)\) や \(\bs{Q}(\gamma)\) とすることができます。
つまり、\(\bs{Q}\) 上の既約多項式 \(f(x)=x^3+px+q\) の最小分解体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、方程式の解の一つである \(\al\) の(または \(\beta,\:\gamma\) の)単拡大体であり、単拡大体の基底の定理(33F)により \(\bs{L}\) の次元は \(3\) です。すると次数と位数の同一性(52B)により、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) の群位数は \(3\) です。従って、ラグランジュの定理(41E)により群位数が素数の群は巡回群なので、\(G\) は群位数 \(3\) の巡回群( \(C_3\) )です。
以上をまとめると、3次方程式の最小分解体のガロア群は、次のようになります。
前提として、
・\(f(x)=x^3+px+q\:\:(p,\:q\in\bs{Q})\)
( \(f(x)\) は既約多項式 )
・\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\)
・\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
・\(f(x)\) の最小分解体を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)
・\(G=\mr{Gal}(\bs{L}/\bs{Q})\)
とする。この前提のもとで、
\(\bs{\theta}\):有理数のとき
\(G\cong C_3\)
\(G=\{\:e,\:\sg,\:\sg^2\:\}\)
\(\sg=(1,\:2,\:3)\)
\(G\) は巡回群なので可解群
\(\bs{\theta}\):有理数でないとき
\(G\cong S_3\)
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
\(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\)
\(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列
\(G\) は可解群
なお、\((1,\:2,\:3)\:\:(2,\:3)\) の巡回置換は \((1,\:3,\:2)\:\:(1,\:2)\:\:(1,\:3)\) などとしても同じです。
\(C_3\::\:x^3-3x+1\)
まずガロア群が \(C_3\) の方程式 \(x^3-3x+1=0\) を取り上げ、巡回拡大がべき根拡大になる原理を確認します。この原理はガロア群が \(S_3\) のときにもそのまま応用できます。ちなみに \(C_3\) の方程式は \(p,\:q\) が \(-9\leq p\leq-1,\:\:1\leq q\leq9\) の整数だと、他に、
\(x^3-7x+6=0\:\:\:(D=400,\:\sqrt{D}=20)\)
\(x^3-7x+7=0\:\:\:(D=\phantom{0}49,\:\sqrt{D}=\phantom{0}7)\)
\(x^3-9x+9=0\:\:\:(D=729,\:\sqrt{D}=27)\)
があります。
\(x^3-3x+1=0\) の場合、\(p=-3,\:q=1\) なので、
\(\begin{eqnarray}
&&\:\:D&=-4p^3-27q^2=81=9^2\\
&&\:\:\theta&=\pm\sqrt{D}=\pm9\\
\end{eqnarray}\)
となります。3つの解を \(\al,\:\beta,\:\gamma\) とすると、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
で、\(\bs{L}\) の次元は \(3\) で、\(G=\mr{Gal}(\bs{L}/\bs{Q})\cong C_3\) です。
以下「7.3 べき根拡大の十分条件」の証明の論理に沿います。7.3 の証明では、体に \(1\) の原始\(n\)乗根が含まれているのが条件でした。そこで \(1\) の原始3乗根 を \(\omega\) とし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\:\al)=\bs{L}(\omega)\)
という体の拡大を考えます。\(\omega\) は \(x^2+x+1=0\) の2つある根のどちらかで、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
です。7.3 ではラグランジュのレゾルベントを \(\al\) と書きましたが、方程式の根の表記との重複を避けるため、ここでは \(S\) とします。そうするとレゾルベントは、
です。\(\bs{Q}(\omega,\:\al)\) は \(\bs{Q}(\omega)\) に \(\al\) を添加した単拡大体なので、べき根拡大の十分条件のため補題2(72B)に従って、\(c=\al\) と定めます。そうすると、
\(S=\al+\omega^2\sg(\al)+\omega\sg^2(\al)\)
となり、\(\al,\:\beta,\:\gamma\) で表すと、\((\br{A})\) 式は、
です。この \(S\) は \(\bs{Q}(\omega,\al,\beta,\gamma)\) の元ですが、
\(\bs{Q}(\omega,\al,\beta,\gamma)=\bs{Q}(\omega,\al)\)
なので、\(S\) は \(\bs{Q}(\omega,\al)\) の元であり、ということは、
\(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\al)\)
です。方程式の3つの解を \(\al,\:\beta,\:\gamma\) に割り当てる方法の数(\(=3!\) )により、\(S\) は6通りの可能性があります。
7.3 での証明のポイントは、\(\bs{S^3}\) が \(\bs{\bs{Q}(\omega)}\) の元である、というところでした。それを計算で確かめるため、もうひとつのレゾルベントを導入します。ガロア群 \(G=\{e,\sg,\sg^2\}\) は、\(\sg\) が生成元であると同時に、\(\sg^2\) も生成元です。レゾルベントの定義における \(\sg\) は \(G\) の生成元であることが条件でした(73A)。そこで \((\br{A})\) 式の \(\sg\) を \(\sg^2\) で置き換えた式を \(T\) とすると、
\(\begin{eqnarray}
&&\:\:T&=c+\omega^2\sg^2(c)+\omega\sg^4(c)\\
&&&=c+\omega^2\sg^2(c)+\omega\sg(c)\\
\end{eqnarray}\)
となります。この式で \(c=\al\) とおくと
\(T=\al+\omega\beta+\omega^2\gamma\)
です。\(S\) には6通りの可能性がありますが、\(S\) をそのうちの一つに決めると \(T\) は一意に決まります。ここで、
は \(\al,\:\beta,\:\gamma\) を未知数とする連立1次方程式なので、\(\al,\:\beta,\:\gamma\) を \(S\) と \(T\) の式で表せます。連立方程式を解くと、
\(\al=\dfrac{1}{3}(S+T)\)
です。さらに、\(S\) と \(T\) には特別の関係があります。
\(ST=(\al+\omega^2\beta+\omega\gamma)(\al+\omega\beta+\omega^2\gamma)\)
という式を考えると、
\(\begin{eqnarray}
&&\:\:ST&=&\al^2+\beta^2+\gamma^2+\\
&&&&(\omega^2+\omega)\al\beta+(\omega^4+\omega^2)\beta\gamma+(\omega^2+\omega)\gamma\al\\
&&&=&(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)+\\
&&&&(-\al\beta-\beta\gamma-\gamma\al)\\
&&&=&-3(\al\beta+\beta\gamma+\gamma\al)\\
&&&=&-3p\\
\end{eqnarray}\)
となり、つまり、
という関係です。上の式の変形では、根と係数の関係と \(\omega^2+\omega+1=0\)、および \(\omega^3=1\) を使いました。
次に、\(S^3\) を求めるために \(S^3+T^3\) を計算してみると、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=(S+T)(S^2-ST+T^2)\\
&&&=(S+T)(S+\omega T)(S+\omega^2T)\\
\end{eqnarray}\)
です。ここで \((\br{C})\) 式を変形すると、
が得られるので、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=3\al\cdot3\omega^2\beta\cdot3\omega\gamma\\
&&&=27\al\beta\gamma=-27q\\
\end{eqnarray}\)
となります。まとめると、
\(S^3+T^3=-27q\)
\(ST=-3p\)
であり、
\(S^3-\dfrac{27p^3}{S^3}+27q=0\)
です。つまり、
という \(S^3\) についての2次方程式を解くことで \(S^3\) が求まり、そこから \(S\) が求まります。\(S\) の値の可能性は6通りです。また \(T^3\) についても、
が成り立ちます。2次方程式、
の2つの解が \(S^3\) と \(T^3\) です。
ここまでの計算は \(x^3+px+q=0\) の形の既約方程式なら成り立ちます。ここで \(x^3-3x+1=0\) に即した、\(p=-3,\:q=1\) を \((\br{E})\) 式に入れると、
\((S^3)^2+27S^3+27^2=0\)
\(\begin{eqnarray}
&&\:\:S^3&=\dfrac{1}{2}\left(-27\pm\sqrt{27^2-4\cdot27^2}\right)\\
&&&=27\dfrac{-1\pm i\sqrt{3}}{2}\\
&&&=27\omega\\
\end{eqnarray}\)
となります。最後の式の \(\omega\) は、2つある \(1\) の原始3乗根のどちらか、という意味にとらえます。\(S^3=27\omega\) なら \(T^3=27\omega^2\) で、その逆でもよいわけです。
\((\br{C})\) 式と \((\br{D})\) 式により、\(\al\) は \(S\) と \(\omega\) の四則演算で表現できます。つまり、
\(\bs{Q}(\omega,\al)\subset\bs{Q}(\omega,\:S)\)
です。従って、さきほどの \(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\:\al)\) と合わせると、
\(\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\)
です。以上をまとめると、レゾルベント \(S\) について、
\(\begin{eqnarray}
&&\:\:S^3&\in\bs{Q}(\omega)\\
&&\:\:S&\in\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\\
\end{eqnarray}\)
です。つまり、
\(\bs{Q}(\omega)\) 上の方程式、
\(x^3-a=0\:\:(\:a=27\omega\in\bs{Q}(\omega)\:)\)
の解の一つ、\(\sqrt[3]{a}\) を \(\bs{Q}(\omega)\) に添加したのが \(\bs{Q}(\omega,\:\al)\)
であり、\(\bs{\bs{Q}(\omega,\:\al)}\) は \(\bs{\bs{Q}(\omega)}\) のべき根拡大体であることがわかりました。\(\bs{Q}(\omega,\:\al)\) は \(x^3-a=0\) の解、\(\sqrt[3]{a},\:\sqrt[3]{a}\:\omega,\:\sqrt[3]{a}\:\omega^2\) の全部を含むので、\(\bs{Q}(\omega)\) のガロア拡大体です。結論として、
ことになります。\(x^3-3x+1=0\) の場合、\(a=27\omega\) です。
巡回拡大がべき根拡大になることの証明のフォローはここまでですが、\(x^3-3x+1=0\) の解を具体的に求めることもできます。\(S^3=27\omega\) から、\(S=3\cdot\sqrt[3]{\omega}\) であり、また \(ST=9\) なので、
\(\begin{eqnarray}
&&\:\:\al&=\dfrac{1}{3}(S+T)=\dfrac{1}{3}\left(S+\dfrac{9}{S}\right)\\
&&&=\sqrt[3]{\omega}+\dfrac{1}{\sqrt[3]{\omega}}=\sqrt[3]{\omega}+\sqrt[3]{\omega^2}\\
&&&=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i}\\
\end{eqnarray}\)
が解の一つです。「1.3 ガロア群」の「ガロア群の例」に書いたように、
\(\al=1.53208888623796\:\cd\)
であり、正真正銘の正の実数ですが、\(\bs{\al}\) をべき根で表わそうとすると虚数単位が登場します。その理由がガロア理論から分かるのでした。
\(S_3\::\:x^3+px+q\)
方程式 \(x^3+px+q=0\) の係数を変数のままで扱い、ガロア群が \(S_3\) の方程式の一般論として話を進めます。3つの根を \(\al,\:\beta,\:\gamma\) とし(置換での表示では、それぞれ \(1,\:2,\:3\))、差積 \(\theta\) を、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=\sqrt{D}\\
&&\:\:D&=-4p^3-27q^2\\
\end{eqnarray}\)
と定義すると、\(\bs{\theta}\) が有理数でないとき、
となります(前述)。\(G\cong S_3\) は巡回群ではありません。しかし可解群なので "巡回群の入れ子構造" になっていて(=可解列が存在する)、「巡回拡大はべき根拡大」の定理(73A)を2段階に使うことで、方程式の解が四則演算とべき根で表現できることを証明できます。
まず、上記の可解列とガロア対応(53B)になっている「体の拡大列」は何かです。具体的には \(H\) の固定体は何かですが、それは \(\bs{Q}(\theta)\) です。実際、
\(\sg(\theta)=\theta,\:\:\sg^2(\theta)=\theta\)
なので、\(H\) のすべての元は \(\bs{Q}(\theta)\) の元を固定します。また、
\(\tau(\theta)=-\theta\)
なので、\(\tau\)(および \(\sg\tau,\:\sg^2\tau\))は \(\bs{Q}(\theta)\) の元 を固定しません。従って、\(H\) の固定体は \(\bs{Q}(\theta)\) です。つまり、\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) と書くと、
というガロア対応になっています。
次に体の拡大次元を検証します。まず、\(|G|=6\) なので、次数と位数の同一性(52B)により、\(\bs{L}/\bs{Q}\) の拡大次数は、
\([\:\bs{L}:\bs{Q}\:]=6\)
です。\(\bs{Q}(\theta)\) は \(\bs{Q}\) 上の既約な2次方程式、
\(x^2-D=0\)
の解である \(\theta\) で \(\bs{Q}\) を単拡大した体なので、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\theta):\bs{Q}\:]=2\)
です。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}:\bs{Q}\:]=[\:\bs{L}:\bs{Q}(\theta)\:]\cdot[\:\bs{Q}(\theta):\bs{Q}\:]\)
\([\:\bs{L}:\bs{Q}(\theta)\:]=3\)
となるはずです。\([\:\bs{L}:\bs{Q}(\theta)\:]=3\) であることを、具体的な体の拡大の様子を検証することで確かめます。2つのことを証明します。
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) とするとき、\(\bs{Q}(\theta,\al)=\bs{L}\) である。
[証明]
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\) だから、\(\theta\) は \(\al,\:\beta,\:\gamma\) で表現されている。従って
\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\)
である。この逆である、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であることを証明する。そのためには \(\beta,\:\gamma\) が「有理数と \(\theta,\:\al\) の四則演算」で表現できることを示せばよい。根と係数の関係により、
である。これを利用して \(\theta\) の定義式を変形すると、
\(\begin{eqnarray}
&&\:\:\theta=&(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=(\beta-\gamma)(-\al^2+(\beta+\gamma)\al-\beta\gamma)\\
&&&=(\beta-\gamma)\left(-\al^2-\al^2+\dfrac{q}{\al}\right)\\
&&&=(\beta-\gamma)\dfrac{-2\al^3+q}{\al}\\
\end{eqnarray}\)
となり、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であり、\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\) と合わせて、
\(\bs{Q}(\theta,\al)=\bs{Q}(\al,\beta,\gamma)\)
である。[証明終]
\(x^3+px+q\) は \(\bs{\bs{Q}(\theta)}\) 上の既約多項式である。
[証明]
\(\bs{Q}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解 \(\al\) による \(\bs{Q}\) の単拡大体 \(\bs{Q}(\al)\) を考えると、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\al):\bs{Q}\:]=3\)
である。従って \(\al\notin\bs{Q}(\theta)\) である。なぜなら、もし \(\al\in\bs{Q}(\theta)\) なら \(\bs{Q}(\theta)\) の次元は \(3\) 以上になるが、\([\:\bs{Q}(\theta):\bs{Q}\:]=2\) なので矛盾が生じるからである。同様に、\(\beta,\:\gamma\notin\bs{Q}(\theta)\) である。\(x^3+px+q\) は、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
と表されるから、\(x^3+px+q\) は \(\bs{Q}(\theta)\) 上では因数分解できない。つまり \(x^3+px+q\) は \(\bs{Q}(\theta)\) 上の既約多項式である。[証明終]
以上により、
ことが検証できました。これを踏まえて、3次方程式が解ける理由をガロア理論で説明します。ガロア対応である、
を2つの部分に分けます。
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\)
\(\mr{Gal}(\bs{Q}(\theta)/\bs{Q})\cong G/H\cong C_2\) であり、\(\bs{Q}(\theta)/\bs{Q}\) は巡回拡大で、拡大次数は \(2\) です。\(1\) の原始2乗根は \(-1\) であり、\(\bs{Q}\) に含まれています。従って \(\bs{Q}(\theta)/\bs{Q}\) はべき根拡大です。具体的には、
\(x^2-D=0\:\:(D\in\bs{Q})\)
\(D=-4p^3-27q^2\)
の解が \(\theta\) であり、
\(\theta=\sqrt{D}=\sqrt{-4p^3-27q^2}\)
です。これはレゾルベントを持ち出すまでもなく分かります。
\(\bs{Q}(\theta)\:\subset\:\bs{L}\)
\(\mr{Gal}(\bs{L}/\bs{Q}(\theta))=H\cong C_3\) であり、\(\bs{L}/\bs{Q}(\theta)\) は巡回拡大で、拡大次数は \(3\) です。また \(\bs{L}\) は \(\bs{Q}(\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体で、\(\bs{L}=\bs{Q}(\theta,\al)\) でした。
\(\bs{Q}(\theta)\) には(一般には)\(1\) の原始3乗根が含まれていません。そこで、\(\bs{L}/\bs{Q}(\theta)\) の体の拡大の代わりに、\(\bs{L}(\omega)/\bs{Q}(\omega,\theta)\) という拡大を考えます。
\(\bs{L}(\omega)=\bs{Q}(\omega,\theta,\al)\)
レゾルベント \(S,\:T\) を導入して \(S^3\) と \(T^3\) を求めます。計算は、方程式 \(x^3-3x+1=0\) のときと全く同じです。つまり、
\(\al=\dfrac{1}{3}(S+T)\)
です。方程式 \(x^3-3x+1=0\) の場合、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からの巡回拡大でしたが、\(x^3-3p+1q=0\) では \(\bs{Q}(\omega,\theta)\) からの巡回拡大であり、ガロア群が位数 \(3\) の巡回群であるという点では全く同じなのです。
\((\br{F})\) 式から \(X\) を求めると、
\(\begin{eqnarray}
&&\:\:X&=\dfrac{1}{2}\left(-27q\pm\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q\pm\sqrt{-27\theta^2}\right)\\
&&&=\dfrac{1}{2}(-27q\pm3\sqrt{3}i\cdot\theta)\\
\end{eqnarray}\)
となるので、
\(S^3=\dfrac{1}{2}(-27q+3\sqrt{3}i\cdot\theta)\)
\(T^3=\dfrac{1}{2}(-27q-3\sqrt{3}i\cdot\theta)\)
となります。\(S^3\) と \(T^3\) は逆でもかまいません。\(\omega\) は \(1\) の原始3乗根で、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
のどちらかです。従って、
\(\sqrt{3}i\in\bs{Q}(\omega,\theta)\)
です。つまり、
\(S^3,\:\:T^3\in\bs{Q}(\omega,\theta)\)
であることがわかりました。従って、\(S,\:T\) は \(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解ということになり、\(\bs{Q}(\omega,\theta,\:S)/\bs{Q}(\omega,\theta)\) の体の拡大を考えると、
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
であることが次のようにして分かります。つまり、\(\bs{Q}(\omega,\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解が \(\al,\:\beta,\:\gamma\) であり、\((\br{B})\) 式により \(S\) は \(\al,\:\beta,\:\gamma,\:\omega\) の四則演算で表されているので、
\(S\in\bs{Q}(\omega,\theta,\al,\beta,\gamma)\)
であり、また、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)\)
だったので、
\(S\in\bs{Q}(\omega,\theta,\al)\)
です。このことから、
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
です。
この説明は「7.3 べき根拡大の十分条件」の証明に従いましたが、3次方程式の場合は、\((\br{C})\) 式と \((\br{D})\) 式により、\(\al,\:\beta,\:\gamma\) が \(S\) と \(\omega\) の四則演算で表現できます。従って、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)\subset\bs{Q}(\omega,\theta,S)\)
\(\bs{Q}(\omega,\theta,\al)\subset\bs{Q}(\omega,\theta,S)\)
であり、
\(\bs{Q}(\omega,\theta,S)\subset\bs{Q}(\omega,\theta,\al)\)
と合わせて
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
である、とするのが簡便な説明になります。
以上をまとめると、
\(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解の一つ、\(S\) を \(\bs{Q}(\omega,\theta)\) に添加したべき根拡大体が \(\bs{Q}(\omega,\theta,\al)=\bs{L}(\omega)\) である
となり、体に \(\bs{\omega}\) が含まれる前提で、巡回拡大はべき根拡大であることが検証できました。ここから、\(\bs{L}(\omega)\) を \(\bs{Q}\) の拡大体として、方程式の係数 \(p,\:q\) を使って、できるだけ簡潔な形で表してみます。
\(\begin{eqnarray}
&&\:\:\theta&=\sqrt{-4p^3-27q^2}\\
&&&=6\cdot\sqrt{3}i\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\\
\end{eqnarray}\)
ですが、\(\sqrt{3}i\in\bs{Q}(\omega)\) なので、
\(\bs{Q}(\omega,\theta)=\bs{Q}\left(\omega,\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\)
と表せます。また、
\(\begin{eqnarray}
&&\:\:X^3&=\dfrac{1}{2}\left(-27q+\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q+27\cdot2\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
&&&=27\left(-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
\end{eqnarray}\)
なので、
\(S=3\cdot\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(T=3\cdot\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
が \(S,\:T\) です。\(\sqrt[3]{\phantom{I}\cd\phantom{I}}\) は3乗して \(\cd\) になる数の意味です。従って、\(S\) の選び方は3通りですが、\(S\) を一つに決めると、
\(ST=-3p\)
が成り立つように \(T\) を選ぶ必要があります。以上の \(S\) を用いて \(\bs{L}(\omega)\) を表すと、
\(\bs{L}(\omega)\)
\(=\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)=\bs{Q}(\omega,\theta,S)\)
\(=\bs{Q}\left(\omega,\:\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}},\:\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\right)\)
となります。この式が意味するところは、
ということです。べき根拡大の出発点は 有理数に \(\omega\) を添加した体です。「7.1 1の原始n乗根」で証明したように、原始\(n\)乗根はべき根で表現可能であり(71A)、もちろん \(\omega\) もそうです。これが3次方程式が解ける原理(一般化するとガロア群が可解群である方程式が解ける原理)です。補足すると、\(p=0\) のときは、
\(\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}=\pm\dfrac{q}{2}\in\bs{Q}\)
なので、べき根拡大は \(\sqrt[3]{\phantom{A}}\) の1回だけになります。
さらに、ここまでの計算で3次方程式の解も求まりました。解は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=\dfrac{1}{3}(S+T)&\\
&&\beta=\dfrac{1}{3}(\omega S+\omega^2T)&\\
&&\gamma=\dfrac{1}{3}(\omega^2S+\omega T)&\\
\end{eqnarray}
\end{array}\right.\)
であり、記号を、
\(S=3s\)
\(T=3t\)
に置き換えると、
3次方程式の解の公式
\(x^3+px+q=0\) の3つの解を \(\al,\:\beta,\:\gamma\) とする。
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=s+t&\\
&&\beta=\omega s+\omega^2t&\\
&&\gamma=\omega^2s+\omega t&\\
\end{eqnarray}
\end{array}\right.\)
\(s=\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(t=\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(st=-\dfrac{p}{3}\)
が、3次方程式の解の公式です。
3次方程式の解による体の拡大を振り返ってみます。\(\bs{Q}\) 上の既約な方程式 \(x^3+px+q=0\) の根を \(\al,\:\beta,\:\gamma\) とし、\(\bs{Q}\) の最小分解体 を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)、ガロア群を \(G=\mr{Gal}(\bs{L}/\bs{Q})\) とすると、
のガロア対応が成り立ちます。\(\bs{L}/\bs{Q}\) の拡大次数は \(6\)(\(|G|=6\))です。この、
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\subset\:\bs{L}\)
という体の拡大列で、\(\bs{Q}\:\subset\:\bs{Q}(\theta)\) のところはべき根拡大ですが、\(\bs{Q}(\theta)\:\subset\:\bs{L}\) は、\(\omega\in\bs{Q}(\theta)\) の場合を除き、べき根拡大ではありません。しかし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\theta)\:\subset\:\bs{L}(\omega)\)
なら、必ず、すべてがべき根拡大になります。従って、3次方程式の解は \(\bs{Q}(\omega)\) の元である「有理数と \(\omega\)」の四則演算・べき根で記述できます。
\(\omega\) は \(x^2+x+1=0\) の解なので、\([\:\bs{Q}(\omega):\bs{Q}\:]=2\) です。従って、拡大次数の連鎖律(33H)により、\(\omega\notin\bs{Q}(\theta)\) の条件で、
\([\:\bs{L}(\omega):\bs{Q}\:]=12\)
です。これは、\(\bs{Q}\) 上の多項式 \((x^3+px+q)(x^2+x+1)\) の最小分解体が \(\bs{L}(\omega)\) なので、\(\bs{Q}\) からの拡大次数は \(12\) であるとも言えます。3次方程式の「解」は、あくまで \(\bs{Q}\) の \(6\)次拡大体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) の中にありますが、「べき根で表された解」は \(\bs{Q}\) の \(12\)次拡大体 \(\bs{L}(\omega)\) の中にあるのです。
一見、矛盾しているようですが、そうではありません。ある代数拡大体 \(\bs{K}\) があったとして、\(a\) を \(\bs{K}\) の元とし、\(1\) の原始3乗根の一つを \(\omega\) とします。3次方程式、
\(x^3-a=0\:\:(a\in\bs{K})\)
は3つの解をもちます。そのうちのどれか一つを \(\sqrt[3]{a}\) と定義すると、3つの解(べき根)は、
\(\sqrt[3]{a},\:\:\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2\)
です。\(\sqrt[3]{a}\) では \(\omega\) が不要なように見えますが、それは表面上のことで、3つの解は、
\(\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2,\:\:\sqrt[3]{a}\:\omega^3\)
であるというのが正しい認識です。つまり \(\bs{\omega}\) は3つのべき根の関係性を規定していて、\(\sqrt[3]{a}\cdot\omega^i\:\:(i=1,2,3)\) という "ペアの形" によって3つの区別が可能になり、数式としての整合性が保てます。\(\sqrt[3]{\phantom{A}}\) という "曖昧さ" がある記号を用いる限り、\(\omega\) という、曖昧さを解消する "助手" が必然的に登場するのです。
| 7.可解性の十分条件 |
第6章では、方程式が可解であれば(=解が四則演算とべき根で表現できれば)ガロア群が可解群であることをみました。第7章ではその逆、つまり、ガロア群が可解群であれば方程式が可解であることを証明します。
7.1 1の原始\(n\)乗根
可解性の十分条件を証明するために、まず、\(1\) の原始\(n\)乗根がべき根で表せることを証明します。このことを前提にした証明を最後で行うからです。念のために「1.1 方程式とその可解性」でのべき根の定義を振り返ると、
\(\sqrt[n]{\:a\:}\) (\(n=2\) の場合は \(\sqrt{\:a\:}\))
という表記は、
| \(a\) が正の実数のとき、\(n\)乗して \(a\) になる正の実数を表わす | |
| \(a\) が負の実数や複素数の場合は、\(n\)乗して \(a\) になる数のどれかを表わす |
のでした。\(\sqrt{2}\) は \(1.4142\cd\) と \(-1.4142\cd\) のどちらかを表わすのではなく、\(1.4142\cd\) のことです。\(\sqrt[3]{2}\) は \(3\)乗して \(2\) になる3つの数のうちの正の実数(\(\fallingdotseq1.26\))を表わします。一方、\(\sqrt{-1\:}\) は\(2\)乗して \(-1\) になる2つの数のうちのどちらかで、その一方を \(i\) と書くと、もう一方が \(-i\) です。
この定義から、方程式 \(x^n-1=0\) の解を \(\sqrt[n]{\:1\:}\) と書くと、それは \(1\) のことです。従って、
\(1\) 以外の「\(n\)乗して \(1\) になる数」がべき根で表現できる
ことを証明しておく必要があります。その証明はガロア理論とは無関係にできます。それが以下です。
| (原始n乗根はべき根で表現可能:71A) |
\(1\) の 原始\(n\)乗根はべき根で表現できる。
[証明]
\(n\) についての数学的帰納法で証明する。\(n=2,\:3\) のときにべき根で表現できるのは根の公式で明らかである。また、原始4乗根は \(\pm i\) なので、\(n\leq4\) のとき題意は成り立つ。そこで、\(n\) 未満のときにべき根で表現できると仮定し、\(n\) のときにもべき根で表現できることを証明する。
\(n\) が合成数のときと素数のときに分ける。まず \(n\) が合成数なら、
\(n=s\cdot t\)
と表現できる。
\(1\) の原始\(s\)乗根を \(\zeta\)
\(1\) の原始\(t\)乗根を \(\eta\)
とし、\(X=x^{s}\) とおく。方程式 \(X^{t}-1=0\) の \(t\)個の解は \(\eta^k\:\:(0\leq k\leq t-1)\) と表わされる(63B)から、\(x^n-1\) は、
\(\begin{eqnarray}
&&\:\:x^n-1&=x^{st}-1=X^{t}-1\\
&&&=\displaystyle\prod_{k=0}^{t-1}(X-\eta^k)\\
&&&=\displaystyle\prod_{k=0}^{t-1}(x^{s}-\eta^k)\\
\end{eqnarray}\)
と因数分解できる。従って、方程式 \(x^n-1=0\) の解は、
\(x^{s}=\eta^k\:\:\:(0\leq k\leq t-1)\)
の解である。これを解くと、
\(x=\sqrt[s]{\eta^k}\cdot\zeta^j\:\:\:(0\leq j\leq s-1,\:\:0\leq k\leq t-1)\)
である(\(k=0\) のときは根号の規則に従って \(\sqrt[s]{1}=1\))。帰納法の仮定により、\(\zeta,\:\eta\) はべき根で表現できるから、上式により \(1\) の \(n\) 乗根はべき根で表現できる。従って原始\(n\)乗根もべき根で表現できる。
以降は \(n\) が素数の場合を証明する。\(n\) を \(p\)(= 素数)と表記する。以下では数式を見やすくするため \(p=5\) の場合を例示するが、証明の過程は一般性を失わない論理で進める。
位数 \(p-1\) の2つの巡回群、\((\bs{Z}/p\bs{Z})^{*}\) と \(\bs{Z}/(p-1)\bs{Z}\) の性質を利用する。\(p=5\) の場合は、位数 \(4\) の既約剰余類群 \((\bs{Z}/5\bs{Z})^{*}\) と、剰余群 \(\bs{Z}/4\bs{Z}\) である。
\(p\) が素数のとき、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は生成元をもつ(25D)。\((\bs{Z}/5\bs{Z})^{*}\) の生成元の一つは \(2\) である(もう一つは \(3\))。生成元を \(2\) とすると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
の巡回群となる。演算は乗算である。一方、\(\bs{Z}/4\bs{Z}\) は、演算が加算、生成元が \(1\)(または \(3\))の巡回群で、
\(\begin{eqnarray}
&&\:\:\bs{Z}/4\bs{Z}&=\{1,\:1+1,\:1+1+1,\:1+1+1+1\}\\
&&&=\{1,\:2,\:3,\:0\}\\
\end{eqnarray}\)
である。ここで、2つの変数 \(x,\:y\) をもつ関数を、
\(f(x,y)=y^2x+y^4x^2+y^3x^3+y\) |
とおく。この関数は、4つある項の \(x,\:y\) の指数について、
\(y\) の指数は \([\:2,\:4,\:3,\:1\:]\) : \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン
\(x\) の指数は \([\:1,\:2,\:3,\:0\:]\) : \(\bs{Z}/4\bs{Z}\) の巡回パターン
となるようにしてある。
次に、2つの数 \(a,\:b\) を、
\(\begin{eqnarray}
&&\:\:a^5&=1\:(a\neq1)\\
&&\:\:b^4&=1\\
\end{eqnarray}\)
であるような数とする。\(a\) は \(1\) の原始5乗根でもよいし、その任意の累乗でもよい。とにかく \(a^5=1\:(a\neq1)\) を満たす数である。このとき、
\(a^5-1=0\)
\((a-1)(a^4+a^3+a^2+a+1)=0\)
なので、
\(a^4+a^3+a^2+a+1=0\) ないしは
\(a^4+a^3+a^2+a=-1\)
が成り立つ。\(b\) も \(1\) の原始4乗根か、その任意の累乗であるが、\(b=1\) であってもよい。
そうすると \(f(b,a)\) は、
\(f(b,a)=a^2b+a^4b^2+a^3b^3+a\)
\(a\) の指数は \([\:2,\:4,\:3,\:1\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
である。
次に \(f(b,a^2)\) を計算すると、
\(\begin{eqnarray}
&&\:\:f(b,a^2)&=a^4b+a^8b^2+a^6b^3+a^2\\
&&&=a^4+a^3b+a^1b^2+a^2b^3\\
\end{eqnarray}\)
\(a\) の指数は \([\:4,\:3,\:1,\:2\:]\)
\(b\) の指数は \([\:1,\:2,\:3,\:0\:]\)
となる。
\(f(b,a^2)\) を \(f(b,a)\) と比べると、\(a\) の指数が \(1\) ステップだけ巡回している。ということは、\(b\) の指数も \([\:2,\:3,\:0,\:1\:]\) と \(1\) ステップだけ巡回させれば、\(a\) の指数と \(b\) の指数が同期することになり、\(f(b,a^2)\) の式は \(f(b,a)\) と同じものになる。同期させるには \(f(b,a^2)\) に \(b\) を掛ければよい。従って、
\(bf(b,a^2)=f(b,a)\)
である。
全く同様にして、
\(\begin{eqnarray}
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^8)&=b^3f(b,a^3)\\
&&&=f(b,a)\\
\end{eqnarray}\)
となる。まとめると、
\(\begin{eqnarray}
&&\:\:bf(b,a^2)&=f(b,a)\\
&&\:\:b^2f(b,a^4)&=f(b,a)\\
&&\:\:b^3f(b,a^3)&=f(b,a)\\
\end{eqnarray}\)
である。\(b^4=1\) だから、各両辺を \(4\)乗すると、
\(f(b,a^2)^4=f(b,a)^4\)
\(f(b,a^4)^4=f(b,a)^4\)
\(f(b,a^3)^4=f(b,a)^4\)
の式を得る。
本題から少々はずれるが、この仕組みは、\(a\) の指数が「\(2\) の乗算の巡回群」であるため、
\(a^k\:\rightarrow\:a^{2k}=(a^k)^2\)
と巡回し、\(b\) の指数は「\(1\) の足し算の巡回群」であるため、
\(b^k\:\rightarrow\:b^{k+1}=b\cdot b^k\)
と巡回することを利用したものである。
なお、\((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(2\) を選んだが、一般の \((\bs{Z}/p\bs{Z})^{*}\) では \(2\) が生成元とは限らない(25D)。その場合は任意の生成元を選んでよい。例えば \((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(3\) を選ぶと
\([\:3,\:3^2,\:3^3,\:3^4\:]=[\:3,\:4,\:2,\:1\:]\)
と巡回する。従って \(f(x,y)\) を、
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\)
と定義すると、\(y,\:a\) の指数は「\(3\) の乗算の巡回群」だから、
\(a^k\:\rightarrow\:a^{3k}=(a^k)^3\)
と巡回する(\(x,\:b\) については同じ)。つまり、
\(\begin{eqnarray} &&\:\:bf(b,a^3)&=f(b,a)\\ &&\:\:b^2f(b,a^4)&=f(b,a)\\ &&\:\:b^3f(b,a^2)&=f(b,a)\\ \end{eqnarray}\)
となり、
\(f(b,a^3)=f(b,a)^4\)
\(f(b,a^4)=f(b,a)^4\)
\(f(b,a^2)=f(b,a)^4\)
となり、同じ結果を得る。
\(a^k\:\rightarrow\:a^{2k}=(a^k)^2\)
と巡回し、\(b\) の指数は「\(1\) の足し算の巡回群」であるため、
\(b^k\:\rightarrow\:b^{k+1}=b\cdot b^k\)
と巡回することを利用したものである。
なお、\((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(2\) を選んだが、一般の \((\bs{Z}/p\bs{Z})^{*}\) では \(2\) が生成元とは限らない(25D)。その場合は任意の生成元を選んでよい。例えば \((\bs{Z}/5\bs{Z})^{*}\) の生成元として \(3\) を選ぶと
\([\:3,\:3^2,\:3^3,\:3^4\:]=[\:3,\:4,\:2,\:1\:]\)
と巡回する。従って \(f(x,y)\) を、
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\)
と定義すると、\(y,\:a\) の指数は「\(3\) の乗算の巡回群」だから、
\(a^k\:\rightarrow\:a^{3k}=(a^k)^3\)
と巡回する(\(x,\:b\) については同じ)。つまり、
\(\begin{eqnarray} &&\:\:bf(b,a^3)&=f(b,a)\\ &&\:\:b^2f(b,a^4)&=f(b,a)\\ &&\:\:b^3f(b,a^2)&=f(b,a)\\ \end{eqnarray}\)
となり、
\(f(b,a^3)=f(b,a)^4\)
\(f(b,a^4)=f(b,a)^4\)
\(f(b,a^2)=f(b,a)^4\)
となり、同じ結果を得る。
本題に戻って、次に \(f(b,a)^4\) を展開する。
\(f(b,a)^4=(a^2b+a^4b^2+a^3b^3+a)^4\)
\((\br{A})\)
であるが、このまま展開したのでは \(p=5\) のときに固有のものになり、一般性を失う。そこで、上式を展開して整理した形を、
\(f(b,a)^4=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\)
\((\br{B})\)
とする。\(a^2,\:a^4,\:a^3,\:a\) の係数となっている \(h_i(b)\:(i=1,2,3,0)\) は \(b\) の多項式である。この展開形の決め方は次のように行う。
| \((\br{A})\) 式の次数は最大 \(a^{16}\) であるが、\(a^5=1\) の関係を利用して最大次数が \(a^4\) になるように「次数下げ」を行う。 | |
| そうすると、\(a\) を含まない \(b\) だけの項が出てくる。そこで、 \(1=-(a^4+a^3+a^2+a)\) の関係を利用し、\(b\) だけの項に \(-(a^4+a^3+a^2+a)\) を掛けて「次数上げ」を行う。 | |
| 以上の結果を、\(a^2,\:a^4,\:a^3,\:a\) ごとに整理したものを \((\br{B})\) とする。 |
\((\br{B})\) 式においては、
| \(a\) の指数 | \(:\:[\:2,\:4,\:3,\:1\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:1,\:2,\:3,\:0\:]\) |
次に \(f(b,a^2)^4\) を計算する。これは \((\br{B})\) 式において \(a\) を \(a^2\) に置き換えればよいから、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=h_1(b)a^4+h_2(b)a^8+h_3(b)a^6+h_0(b)a^2\\
&&&=h_1(b)a^4+h_2(b)a^3+h_3(b)a+h_0(b)a^2\\
\end{eqnarray}\)
| \(a\) の指数 | \(:\:[\:4,\:3,\:1,\:2\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:1,\:2,\:3,\:0\:]\) |
| \(a\) の指数 | \(:\:[\:2,\:4,\:3,\:1\:]\) | |
| \(h_i(b)\) の添字 | \(:\:[\:0,\:1,\:2,\:3\:]\) |
\(f(b,a^2)^4=h_0(b)a^2+h_1(b)a^4+h_2(b)a^3+h_3(b)a\)
である。同様に、
\(f(b,a^4)^4=h_3(b)a^2+h_0(b)a^4+h_1(b)a^3+h_2(b)a\)
\(h_i(b)\) の添字 \(:\:[\:3,\:0,\:1,\:2\:]\)
\(f(b,a^3)^4=h_2(b)a^2+h_3(b)a^4+h_0(b)a^3+h_1(b)a\)
\(h_i(b)\) の添字 \(:\:[\:2,\:3,\:0,\:1\:]\)
である。
従って、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) において、\(a^j\:(j=2,4,3,1)\) の係数は \(h_k(b)\:(k=1,2,3,0)\) の全てを巡回する。つまり、\(f(b,a^i)^4\:\:(i=1,2,4,3)\) の全部を足すと、\(a^j\:(j=2,4,3,1)\) の係数は全て同じになる。その計算をすると、
\(\displaystyle\sum_{i=1}^{4}f(b,a^i)^4\)
\(\begin{eqnarray}
&&\:\: =&(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&&\cdot(a^2+a^4+a^3+a)\\
\end{eqnarray}\)
となる。上式の左辺については、
\(\begin{eqnarray}
&&\:\:f(b,a^2)^4&=f(b,a)^4\\
&&\:\:f(b,a^4)^4&=f(b,a)^4\\
&&\:\:f(b,a^3)^4&=f(b,a)^4\\
\end{eqnarray}\)
だったので、左辺は \(4f(b,a)^4\) に等しい。また \(a^5-1=0\) なので \(a^2+a^4+a^3+a=-1\) である。従って、
\(4f(b,a)^4=-(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
である。ここで、
\(g(b)=-\dfrac{1}{4}\:(h_1(b)+h_2(b)+h_3(b)+h_0(b))\)
と定義すると、
| \(f(b,a)^4\) | \(=g(b)\) | ||
| \(f(b,a)\) | \(=\sqrt[4]{g(b)}\) | \((\br{C})\) |
を得る。\((\br{C})\) 式における \(\sqrt[4]{g(b)}\) とは「\(4\)乗すると \(g(b)\) になる数」という意味である。従って、実際には \(4\)次方程式の \(4\)つの解のどれかを表している。
なお、\(g(b)\) を具体的に計算すると、計算過程は省くが、
\(g(b)=-16b^3+14b^2+4b-1\)
となる。この表現は \(p=5\) のときのもので、一般論につながるものではない。 \((\br{D})\)
今までの計算をまとめると、
\(\begin{eqnarray}
&&\:\:a^5=1\:(a\neq1)&\\
&&\:\:b^4=1&\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:f(b,a)&=a^2b+a^4b^2+a^3b^3+a\\
&&\:\:f(b,a)^4&=h_1(b)a^2+h_2(b)a^4+h_3(b)a^3+h_0(b)a\\
&&\:\:g(b)&=-\dfrac{1}{4}(h_1(b)+h_2(b)+h_3(b)+h_0(b))\\
&&\:\:f(b,a)&=\sqrt[4]{g(b)}\\
\end{eqnarray}\)
である。この過程で、\(a,\:b\) については \(a^5=1\:(a\neq1),\:b^4=1\) という条件しか使っていない。従って、この条件が満たせれば \(a,\:b\) は任意である。そこで \(1\) の原始5乗根を \(\zeta\) とし、\(1\) の原始4乗根を \(\omega\) として、
\(a=\zeta\)
\(b=\omega^j\:\:(j=1,2,3,4)\)
とおく。\(b\) は \(1\) にもなりうる(\(\omega^4=1\))。なお、\(\omega\) は普通 \(1\) の原始3乗根の記号であるが、ここでは原始4乗根として使う。
すると、
\(f(\omega^j,\zeta)=\sqrt[4]{g(\omega^j)}\:\:(j=1,2,3,4)\)
\((\br{E})\)
という、4つの式が得られる。これは、
\(\zeta^2,\:\:\zeta^4,\:\:\zeta^3,\:\:\zeta\)
を4つの未知数とする連立1次方程式である。帰納法の仮定により \(\omega\) はべき根で表されているから、方程式を解いて \(\zeta\) が \(\omega\) のべき根(と四則演算)で表されば、証明が完成することになる。
\((\br{E})\) の連立方程式を具体的に書くと、
\(\zeta^2+\omega^j\zeta^4+(\omega^j)^2\zeta^3+(\omega^j)^3\zeta=\sqrt[4]{g(\omega^j)}\)
\((j=1,2,3,4)\)
であり、全てを陽に書くと、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta^2+\omega\:\:\zeta^4+(\omega\:\:)^2\zeta^3+(\omega\:\:)^3\zeta&=\sqrt[4]{g(\omega)}& \br{①}&\\
&&\zeta^2+\omega^2\zeta^4+(\omega^2)^2\zeta^3+(\omega^2)^3\zeta&=\sqrt[4]{g(\omega^2)}& \br{②}&\\
&&\zeta^2+\omega^3\zeta^4+(\omega^3)^2\zeta^3+(\omega^3)^3\zeta&=\sqrt[4]{g(\omega^3)}& \br{③}&\\
&&\zeta^2+\omega^4\zeta^4+(\omega^4)^2\zeta^3+(\omega^4)^3\zeta&=\sqrt[4]{g(\omega^4)}& \br{④}&\\
\end{eqnarray}
\end{array}\right.\)
となる。この連立方程式を解くため、\(\zeta\) の項だけを残し、他の未知数である \(\zeta^2,\:\zeta^4,\:\zeta^3\) の項を消去することを考える。そのために、
\(A\::\:\br{①}\times\omega\:+\:\br{②}\times\omega^2\:+\:\br{③}\times\omega^3\:+\:\br{④}\times\omega^4\)
とおくと、
\(A\) の左辺 \(=\)
\(\omega\:\:\zeta^2+(\omega\:\:)^2\zeta^4+(\omega\:\:)^3\zeta^3+(\omega\:\:)^4\zeta+\)
\(\omega^2\zeta^2+(\omega^2)^2\zeta^4+(\omega^2)^3\zeta^3+(\omega^2)^4\zeta+\)
\(\omega^3\zeta^2+(\omega^3)^2\zeta^4+(\omega^3)^3\zeta^3+(\omega^3)^4\zeta+\)
\(\omega^4\zeta^2+(\omega^4)^2\zeta^4+(\omega^4)^3\zeta^3+(\omega^4)^4\zeta\)
となる。\(\zeta\) の4つの項は、係数が \((\omega^j)^4=(\omega^4)^j=1\) であり、
\(\zeta\) の項の合計 \(=\:4\zeta\)
である。
\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数は、
\(\omega^j+\omega^{2j}+\omega^{3j}+\omega^{4j}\:\:(j=1,2,3)\)
である。\(\omega^4=1\) なので、
\(\omega^j+\omega^{2j}+\omega^{3j}+1\:\:(j=1,2,3)\)
の形をしている。\(\omega\) は \(1\) の原始4乗根であり、\(x^4-1=0\) の根である。\(x^4-1\) は、
\(x^4-1=(x-1)(x^3+x^2+x+1)\)
と因数分解されるから、\(\omega,\:\omega^2,\:\omega^3\) は方程式
\(x^3+x^2+x+1=0\)
の3つの根である。つまり、
\(x^3+x^2+x+1=(x-\omega)(x-\omega^2)(x-\omega^3)\)
と因数分解される。この式に \(x=\omega^j\:(j=1,2,3)\) を代入すると、
\((\omega^j)^3+(\omega^j)^2+\omega^j+1\)
\(\begin{eqnarray}
&&\:\: &=\omega^{3j}+\omega^{2j}+\omega^j+1\\
&&&=(\omega^j-\omega)(\omega^j-\omega^2)(\omega^j-\omega^3)\\
&&&=0\:\:(j=1,2,3)\\
\end{eqnarray}\)
となる。つまり、\(\zeta^2,\:\zeta^4,\:\zeta^3\) の項の係数、\(\omega^j+\omega^{2j}+\omega^{3j}+1\) は全て \(0\) ということである。以上をまとめると、\(A\) の左辺は \(\zeta\) の項だけが残り、
\(A\) の左辺 \(=\:4\zeta\)
である。一方、\(A\) 式の右辺は、
\(A\) の右辺 \(=\:\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
である。従って、
\(4\zeta=\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
\(\zeta=\dfrac{1}{4}\displaystyle\sum_{j=1}^{4}\omega^j\sqrt[4]{g(\omega^j)}\)
となり、\(\zeta\) が \(\omega\) の多項式のべき根として求まった。 \((\br{F})\)
\((\br{F})\) 式における \(\sqrt[4]{g(\omega^j)}\) とは「\(4\)乗すると \(g(\omega^j)\) になる数」という意味であり、\(4\)次方程式の\(4\)つの解のどれかである。従って、実際に \(\omega\) に数を入れて(この場合は \(1\) の原始4乗根だから \(i\) か \(-i\))計算するときには、\(\zeta^5=1\) になるように \((\br{F})\) 式の \(4\)つの項のそれぞれについて、\(4\)つの解のどれかを選択する必要がある。しかしそうであっても、\(\zeta\) が \(\omega\) の多項式のべき根と四則演算で表現できるということは変わらない。
これまでの論理展開では、\(p=5\) であることの特殊性は何も使っていない。唯一、使ったのは、\(p\) が素数であり、そのときに \((\bs{Z}/p\bs{Z})^{*}\) に生成元がある(25D)ということである。
従って、\(\zeta\) が \(1\) の原始\(p\)乗根であり、\(\omega\) が \(1\) の原始\((p-1)\)乗根であっても \((\br{F})\) 式は、\(4\) を \((p-1)\) に置き換えれば成り立つ。
帰納法の仮定により、\(1\) の原始\((p-1)\)乗根 \(\omega\) はべき根で表される。従って \((\br{F})\) 式から、\(1\) の原始\(p\)乗根 である \(\zeta\) もべき根で表される。[証明終]
ためしに \((\br{F})\) 式を使って、\(1\) の原始5乗根、\(\zeta\) を計算してみます。\(\omega\) は \(1\) の原始4乗根(の一つ)なので \(\omega=i\)(虚数単位)とすると、\((\br{D})\) 式も含めて、
\(\begin{eqnarray}
&&\:\:g(b)&=-16b^3+14b^2+4b-1 (\br{D})\\
&&\:\:b&=\omega^j\:\:(j=1,2,3,4)\\
&&&=\:\{\:i,\:-1,\:-i,\:1\:\}\\
&&\:\:g(\omega)&=-15+20i\\
&&\:\:g(\omega^2)&=25\\
&&\:\:g(\omega^3)&=-15-20i\\
&&\:\:g(\omega^4)&=1\\
\end{eqnarray}\)
となり、これらを \((\br{F})\) 式に代入すると、
\(\zeta=\dfrac{1}{4}(\sqrt[4]{1}-\sqrt[4]{25}+i(\sqrt[4]{-15+20i}-\sqrt[4]{-15-20i}))\)
となります。\(\sqrt[4]{\cd}\) は「\(4\)乗して \(\cd\) になる数」の意味です。この式を、
\(4\zeta=r+is\)
\(\begin{eqnarray}
&&\:\: r&=\sqrt[4]{1}-\sqrt[4]{25}\\
&&\:\: s&=\sqrt[4]{-15+20i}-\sqrt[4]{15-20i}\\
\end{eqnarray}\)
と表すことにします。そして \(\sqrt[4]{\cd}\) を \(\sqrt{\cd}\) に変換するために2乗すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=\pm6\pm2\sqrt{5}&\\
&&s^2=\pm10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
と計算できます。但し \(r^2+s^2=4\) の条件があるので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r^2=6\pm2\sqrt{5}&\\
&&s^2=10\pm2\sqrt{5}&\\
\end{eqnarray}
\end{array}\right.\)
となります(複合異順)。ここから \(r,\:s\) を求めると、\(r\) の方は2重根号をはずすことができて、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&r=\pm(1+\sqrt{5}),\:\:s=\pm\sqrt{10-2\sqrt{5}}&\\
&&r=\pm(1-\sqrt{5}),\:\:s=\pm\sqrt{10+2\sqrt{5}}&\\
\end{eqnarray}
\end{array}\right.\)
の合計8つの解が求まります。このうちの4つは方程式 \(x^5-1=0\) の解 \((=\zeta)\) で、残りの4つは方程式 \(x^5+1=0\) の解 \((=-\zeta)\) です。\(\zeta\) を表記すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm i\sqrt{10+2\sqrt{5}}\right)&\\
&&\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm i\sqrt{10-2\sqrt{5}}\right)&\\
\end{eqnarray}
\end{array}\right.\)
の4つとなり、\(1\) の原始5乗根が求まりました。一般的な原始5乗根の計算方法とは違いますが、\((\br{F})\) 式によっても原始5乗根が求まることが確認できました。
7.2 べき根拡大の十分条件のため補題
ここでは「7.3 べき根拡大の十分条件」を証明するための補題を2つ証明します。以下に出てくる多項式 \(g(x)\) は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言います。
補題(1)
| (べき根拡大の十分条件のため補題1:72A) |
\(\bs{L}\) を \(\bs{K}\) のガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) を \(\sg\) で生成される位数 \(n\) の巡回群とする。式 \(g(x)\) を、
| \(g(x)\) | \(\overset{\text{ }}{=}\) | \(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\) | |
| \((a_i\in\bs{L},\:1\leq i\leq n-1)\) |
と定義する。このとき、\(\bs{L}\) の全ての元 \(x\) について、\(g(x)=0\) となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。
[証明]
\(\bs{L}\) が原始元 \(\theta\) によって \(\bs{L}=\bs{K}(\theta)\) と表されているとし(32B)、\(\theta\) の \(\bs{K}\) 上の最小多項式を \(f(x)\) とする。最小多項式は既約多項式の定理(31I)により \(f(x)\) は既約多項式である。そうすると、\(\theta,\:\sg^i(\theta)\:(1\leq i\leq n-1)\) の \(n\)個は \(f(x)=0\) の解であり、既約多項式の定理3(31G)によって \(n\)個の解は全て異なる。つまり、
\(\theta-\sg^i(\theta)\neq0\:(1\leq i\leq n-1)\)
である。このことを踏まえて背理法で証明する。\(\bs{L}\) の任意の元 \(x\) について、
\(g(x)=x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
\((\br{A})\)
となるような \(\bs{L}\) の元 \(a_1,\:a_2,\:\cd\:,a_{n-1}\) が存在したとする。この \(g(x)=0\) の式から \(\sg^{n-1}(x)\) の項を消去することを考える。そのためにまず \(g(\theta x)\) を計算すると、
| \(g(\theta x)\) | \(\overset{\text{ }}{=}\) | \(\theta x+\)\(a_1\sg(\theta x)+\)\(a_2\sg^2(\theta x)+\)\(\:\cd\:+\)\(a_{n-1}\sg^{n-1}(\theta x)\) | |
| \(\overset{\text{ }}{=}\) | \(\theta x+\)\(a_1\sg(\theta)\sg(x)+\)\(a_2\sg^2(\theta)\sg^2(x)+\)\(\:\cd\:+\)\(a_{n-1}\sg^{n-1}(\theta)\sg^{n-1}(x)\) | ||
| \(\overset{\text{ }}{=}\) | \(0\) |
となる。この式から \(\sg^{n-1}(x)\) の項を消去するには、この式の \(\sg^{n-1}(x)\)の係数が \(a_{n-1}\sg^{n-1}(\theta)\) であり、また \(g(x)\) の \(\sg^{n-1}(x)\) の項の係数が \(a_{n-1}\) なので、
\(\sg^{n-1}(\theta)g(x)=0\)
の式を作って両辺から引けばよい。その計算をすると、
\(g(\theta x)-\sg^{n-1}(\theta)g(x)\)
| \(\overset{\text{ }}{=}\) | \((\theta-\sg^{n-1}(\theta))x+\)\((\sg(\theta)-\sg^{n-1}(\theta))a_1\sg(x)+\)\((\sg^2(\theta)-\sg^{n-1}(\theta))a_2\sg(x)^2+\)\(\:\cd\:+\)\((\sg^{n-2}(\theta)-\sg^{n-1}(\theta))a_{n-2}\sg(x)^{n-2}\) | ||
| \(\overset{\text{ }}{=}\) | \(0\) |
となる。ここで、\(x\) の係数である \((\theta-\sg^{n-1}(\theta))\) は、証明の最初に書いたように \(0\) ではない。そこで、全体を \((\theta-\sg^{n-1}(\theta))\) で割ると、
\(x+b_1\sg(x)+b_2\sg(x)^2+\:\cd\:+b_{n-2}\sg(x)^{n-2}=0\)
\((\br{B})\)
の形になる。ここで \(b_i\) は、
\(b_i=\dfrac{\sg^i(\theta)-\sg^{n-1}(\theta)}{\theta-\sg^{n-1}(\theta)}a_i\)
である。\((\br{B})\) 式は、基本的に \((\br{A})\) 式と同じで、\((\br{A})\) 式から \(\sg(x)^{n-1}\) の項を消去した形であり、\(x\) の最大次数の項は \(\sg(x)^{n-2}\) になっている。以上の、\((\br{A})\) から \((\br{B})\) への変換は繰り返し行えるから、\(n-2\) 回の変換を繰り返すと、
\(x+c_1\sg(x)=0\)
の形が得られる。この式にもう一度、\(n-1\) 回目の変換をすると、
\(\theta x+c_1\sg(\theta x)-\sg(\theta)(x+c_1\sg(x))=0\)
\(\theta x+c_1\sg(\theta)\sg(x)-\sg(\theta)x+c_1\sg(\theta)\sg(x)=0\)
\(\theta x-\sg(\theta)x=0\)
\((\theta-\sg(\theta))x=0\)
\(x=0\)
\(\theta x+c_1\sg(\theta)\sg(x)-\sg(\theta)x+c_1\sg(\theta)\sg(x)=0\)
\(\theta x-\sg(\theta)x=0\)
\((\theta-\sg(\theta))x=0\)
\(x=0\)
となる。\(x\) は \(\bs{L}\) の任意の元だったから、\(\bs{L}\) のすべての元は \(0\) となってしまい、矛盾が生じた。従って背理法の仮定は誤りであり、\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない。[証明終]補題(2)
| (べき根拡大の十分条件のため補題2:72B) |
\(\zeta\) を \(1\) の原始\(n\)乗根とし、\(\zeta\)を含む代数体を \(\bs{K}\) とする。\(\bs{K}\) のガロア拡大体を \(\bs{L}\) とし、\(\mr{Gal}(\bs{L}/\bs{K})\) は \(\sg\) で生成される位数 \(n\) の巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。また \(f(x)\) を \(\bs{K}\) 上の \(n\)次既約多項式とし、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて、\(\bs{L}=\bs{K}(\theta)\) と表されているものとする。このとき、
\(g(x)=x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\cd+\zeta\sg^{n-1}(x)\)
とおくと、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち少なくとも一つは \(0\) ではない。
[証明]
\(g(x)\) の形は、べき根拡大の十分条件のため補題1(72A)で、
\(a_i=\zeta^{n-i}\:(1\leq i\leq n-1)\)
と置いたものである。\(\zeta\) は \(\bs{K}\) の元 = \(\bs{L}\) の元だから、補題(1)により \(\bs{L}\) の任意の元 \(x\) について \(g(x)=0\) となることはない。
この \(g(x)\) は次のような性質をもっている。まず \(\bs{K}\) の任意の元を \(a\) とすると、\(\mr{Gal}(\bs{L}/\bs{K})\) の 元 \(\sg\) は \(a\) を不動にするから、
\(\sg^i(a)=a\)
である。従って、\(g(a)\) を計算すると、
\(g(a)=ag(1)\)
となる。また、\(\bs{K}\) の任意の元を \(a\)、\(\bs{L}\) の任意の元を \(x\) とすると、
\(\sg^i(ax)=\sg^i(a)\sg^i(x)=a\sg^i(x)\)
なので、
\(g(ax)=ag(x)\)
である。さらに \(\bs{L}\) の任意の2つの元を \(x,\:y\) とすると、
\(\sg^i(x+y)=\sg^i(x)+\sg^i(y)\)
なので、
\(g(x+y)=g(x)+g(y)\)
である。
\(\bs{L}\) は、\(\bs{K}\) 上の既約多項式 \(f(x)\) を用いた方程式 \(f(x)=0\) の解 \(\theta\) の単拡大体 \(\bs{K}(\theta)\) だから、単拡大の体の定理(32C)により、\(\bs{L}\) の任意の元 \(x\) は、
\(x=b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1}\:(b^i\in\bs{K})\)
と表せる。\(g(x)\) の式にこの \(x\) を代入すると、
\(\begin{eqnarray}
&&\:\:g(x)&=g(b_0+b_1\theta+b_2\theta^2+\cd+b_{n-1}\theta^{n-1})\\
&&&=g(b_0)+g(b_1\theta)+g(b_2\theta^2)+\cd+g(b_{n-1}\theta^{n-1})\\
&&&=b_0g(1)+b_1g(\theta)+b_2g(\theta^2)+\cd+b_{n-1}g(\theta^{n-1})\\
\end{eqnarray}\)
となる。ここで、
\(g(1)=1+\zeta^{n-1}+\zeta^{n-2}+\cd+\zeta\)
だが、\(g(1)(1-\zeta)=\zeta^n-1=0\) なので \(g(1)=0\) である。従って、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) の全てが \(0\) だと、\(\bs{L}\) の全ての元 \(x\) について \(g(x)=0\) となり、矛盾が生じる。ゆえに、\(g(\theta),\:g(\theta^2),\:\cd\:,g(\theta^{n-1})\) のうち、少なくとも一つは \(0\) ではない。[証明終]
7.3 べき根拡大の十分条件
補題(1)と補題(2)を使って、体の拡大がべき根拡大になるための十分条件を証明します。
| (べき根拡大の十分条件:73A) |
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。
このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
[証明]
\(\mr{Gal}(\bs{L}/\bs{K})\) は位数 \(n\) の巡回群なので、生成元を \(\sg\) とし、
\(\mr{Gal}(\bs{L}/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\sg^{n-1}\}\)
とする。\(\bs{L}\) の 元 \(c\) に対して、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
と定める。このとき \(\al\neq0\) となるように \(c\) を選べる。なぜなら、もし \(\al\neq0\) となる \(c\) が選べないとすると、\(\bs{L}\) の全ての元 \(x\) について、
\(x+\zeta^{n-1}\sg(x)+\zeta^{n-2}\sg^2(x)+\:\cd\:+\zeta\sg^{n-1}(x)=0\)
となるはずだが、これはべき根拡大の十分条件のため補題1(72A)、つまり、
\(\bs{L}\) の全ての元 \(x\) について、
\(x+a_1\sg(x)+a_2\sg^2(x)+\:\cd\:+a_{n-1}\sg^{n-1}(x)=0\)
となるような \(\bs{L}\) の元、\(a_1,\:a_2,\:\cd\:,a_{n-1}\) は存在しない
において、\(a_1=\zeta^{n-1},\:a_2=\zeta^{n-2},\:\cd\:,a_{n-1}=\zeta\) と置いたことに相当し、そのような \(a_i\:(1\leq i\leq n-1)\) は存在しないとする補題1の結論に反するからである。またべき根拡大の十分条件のため補題2(72B)では、\(c\) の選び方の例が示されている。そこで、\(\al\neq0\) となるように \(c\) を選んだとする。
\(\sg\)は \(\bs{K}\) の元である \(\zeta\) を不変にするので、
\(\sg(\zeta^{n-i}\sg^i(c))=\zeta^{n-i}\sg^{i+1}(c)\)
である。これを用いて \(\sg(\al)\) を計算すると、
\(\sg(\al)\)
\(=\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta\sg^n(c)\)
\(=\zeta^n\sg(c)+\zeta^{n-1}\sg^2(c)+\zeta^{n-2}\sg^3(c)+\:\cd+\zeta^2\sg^{n-1}(c)+\zeta c\)
\(=\zeta(\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\zeta^{n-3}\sg^3(c)+\:\cd+\zeta\sg^{n-1}(c)+c)\)
\(=\zeta\al\)
となる。計算では、\(\zeta^n=1\) であることと(第1項)、\(\sg^n=e\) なので \(\sg^n(c)=c\) となること(最終項)を用いた。
ここで、\(\al=\zeta\al\) となるのは、\(\al=0\) のときだけであるが、\(\al\neq0\) なので \(\al\neq\zeta\al\) である。つまり \(\sg(\al)\neq\al\) であり、\(\al\) は \(\sg\) を作用させると不変ではない。従って \(\al\) は \(\bs{K}\) の元ではない \(\bs{L}\) の元である。さらに \(\sg^i(\al)\) を求めていくと、
\(\begin{eqnarray}
&&\:\:\sg^2(\al)&=\sg(\sg(\al))=\sg(\zeta\al)=\zeta\sg(\al)=\zeta\zeta\al\\
&&&=\zeta^2\al\\
&&\:\:\sg^3(\al)&=\sg(\sg^2(\al))=\sg(\zeta^2\al)=\zeta^2\sg(\al)=\zeta^2\zeta\al\\
&&&=\zeta^3\al\\
\end{eqnarray}\)
というように計算でき、
\(\sg^i(\al)=\zeta^i\al\)
である。これを使うと、
\(\begin{eqnarray}
&&\:\:\sg(\al^n)&=\sg(\al)^n=(\zeta\al)^n=\zeta^n\al^n\\
&&&=\al^n\\
\end{eqnarray}\)
であり、\(\al^n\) は \(\sg\) を作用させても不変である。従って \(\al^n\) は \(\bs{K}\) の元である。そこで \(\al^n=a\:\:(a\in\bs{K})\) とおく。
方程式 \(x^n-a=0\) の解は、\(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al\) であり、\(x^n-a=0\) の \(\bs{K}\) 上の最小分解体は、\(\bs{K}\) には \(\zeta\) が含まれているから、
\(\bs{K}(\al,\:\zeta\al,\:\zeta^2\al,\:\cd,\:\zeta^{n-1}\al)=\bs{K}(\al,\zeta)=\bs{K}(\al)\)
である。この式から、\(\bs{K}\) の同型写像による \(\al\) の移り先は全て \(\bs{K}(\al)\) に含まれることが分かる。従って \(\sg^i\:\:(1\leq i\leq n-1)\) はすべて \(\bs{K}(\al)\) の自己同型写像である。また、同型写像での移り先の定理(51D)により、同型写像は \(\al\) を共役な元に移すが、\(\al\) と共役な元は \(n-1\) 個しかない。従って \(\sg^i\) 以外に同型写像はない。つまり、
\(\mr{Gal}(\bs{K}(\al)/\bs{K})=\{e,\:\sg,\:\sg^2,\:\cd\:,\:\sg^{n-1}\}\)
であり、これは \(\mr{Gal}(\bs{L}/\bs{K})\) と同じである。次数と位数の同一性の定理(52B)により、ガロア群に含まれる自己同型写像の数は体の拡大次数に等しいから、
\([\:\bs{K}(\al)\::\:\bs{K}\:]=[\:\bs{L}\::\:\bs{K}\:]\)
である。もともと \(\al\) は \(\bs{L}\) の元だったので、\(\bs{K}(\al)\) の元は全て \(\bs{L}\) の元である。つまり、
\(\bs{K}(\al)\:\subset\:\bs{L}\)
であるが、\(\bs{K}(\al)\) と \(\bs{L}\) の線形空間の次元が等しいので、体の一致の定理(33I)により2つは一致し、
\(\bs{K}(\al)=\bs{L}\)
である。以上により、\(\bs{L}\) は \(\bs{K}\) の上の方程式 \(x^n-a=0\:(a\in\bs{K})\) の解の一つ \(\al\) を用いて \(\bs{L}=\bs{K}(\al)\) と表されるから、\(\bs{L}\) は \(\bs{K}\) の べき根拡大である。[証明終]
証明の過程で出てきた、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
の式は、方程式を解くために考えられた「ラグランジュの分解式」と呼ばれるものです。分解式はレゾルベント(resolvent)とも言い、数学史においてはガロア理論より前に考えられたものです。この証明を振り返ってまとめてみると、
| \(\bs{L}\) は \(\bs{K}\) の代数拡大体であり、拡大次元は \(n\) である。 | |
| \(\bs{K}\) には \(1\) の原始\(n\)乗根が含まれている。 | |
| \(\bs{L}/\bs{K}\) はガロア拡大である。 | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) は巡回群である(=\(\bs{L}/\bs{K}\) は巡回拡大) |
という条件のもとで、レゾルベントをうまく定義すると、
| ある \(\bs{L}\) の元 \(\al\:(\notin\bs{K})\) が存在し、\(\al^n\) は \(\bs{K}\) の元である。 | |
| すなわち \(\al\) は、方程式 \(x^n-a=0\:\:(a\in\bs{K})\) の解である。 | |
| \(\bs{L}=\bs{K}(\al)\) であり、従って \(\bs{L}/\bs{K}\) はべき根拡大である。 |
が成り立つという論理展開でした。つまりポイントは \(\bs{\al^n\in\bs{K}}\) のところであり、そういう \(\bs{\al\in\bs{L}}\) の存在が証明の核心です。
しかし、その鍵である \(\al\) を具体的に見つけようとすると、\(\al\) の式に現れる \(c\) を決めなければなりません。その \(c\) の値ですが、\(\bs{L}\) が方程式 \(f(x)=0\) の解 \(\theta\) を用いて \(\bs{L}=\bs{K}(\theta)\) と表されているとき(= \(\theta\) が原始元のとき)、\(c=\theta\) にできることがべき根拡大の十分条件のため補題2(72B)に示されています。しかし、方程式の形から原始元が分かるわけではありません。
べき根拡大の十分条件(73A)は、その十分条件があればべき根拡大体の中に方程式の解が含まれる(= 方程式の解が四則演算とべき根で記述できる)ことだけを言っています。つまり四則演算とべき根で記述できる解の存在証明であり、そこが注意点です。
原始\(n\)乗根はべき根で表現可能
べき根拡大の十分条件(73A)を用いて原始\(\bs{n}\)乗根はべき根で表現可能(71A)であることを証明できます。(71A)ではガロア理論と関係なく証明しましたが、ガロア理論の枠組みを使っても証明できるということです。
まず \(n\) が合成数のとき、つまり \(n=s\cdot t\) と分解できるときには、原始\(n\)乗根は、原始\(s\)乗根と原始\(t\)乗根のべき根で表現できます(71A)。\(s\) や \(t\) が合成数なら、さらに "分解" を続けられるので、結局、\(n\) が素数 \(p\) のときに原始\(p\)乗根がべき根で表せることを示せればよいことになります。
いま、\(\bs{p}\) 未満の素数すべての原始\(\bs{n}\)乗根がべき根で表されると仮定します。これは帰納法の仮定です。原始\(p\)乗根を \(\eta\)(イータ) とし、その最小多項式を \(f(x)\) とすると、\(f(x)\) は既約多項式で、円分多項式です(63D)。原始\(p\)乗根は 方程式 \(x^p-1=0\) の \(1\) 以外の根なので、
\(x^p-1=(x-1)f(x)\)
であり、
\(f(x)=x^{p-1}+x^{p-2}+\:\cd\:+x+1\)
です。
原始\(p\)乗根による拡大体 \(\bs{Q}(\eta)\) のガロア群は、
\(\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\cong(\bs{Z}/p\bs{Z})^{*}\)
です(63E)。\((\bs{Z}/p\bs{Z})^{*}\) は位数 \((p-1)\) の巡回群で(25D)、\(\bs{Q}(\eta)/\bs{Q}\) の拡大次数は、\([\:\bs{Q}(\eta):\bs{Q}\:]=p-1\) です。原始\((p-1)\)乗根を \(\zeta\) とすると、\(\eta\notin\bs{Q}(\zeta)\) なので、\(\bs{Q}\) 上の既約多項式である \(f(x)\) は \(\bs{Q}(\zeta)\) 上でも既約多項式です。従って、
\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\cong\mr{Gal}(\bs{Q}(\eta)/\bs{Q})\)
であり、\(\mr{Gal}(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta))\) も位数 \((p-1)\) の巡回群です。すると、べき根拡大の十分条件(73A)により、\(\bs{Q}(\zeta,\eta)/\bs{Q}(\zeta)\) はべき根拡大になります。つまり \(\eta\) は "有理数と \(\zeta\) の四則演算から成る式" のべき根で表現できます。
「\(p\) 未満の素数すべての原始\(n\)乗根がべき根で表される」という仮定により、\(\zeta\) はべき根で表現できます。従って \(\eta\) もべき根で表されます。
原始\(2\)乗根は \(-1\) であり、原始\(3\)乗根は根の公式によって、べき根で表現できます。従って帰納法により \(5\) 以上の素数 \(p\) の原始\(p\)乗根もべき根で表現できることが分かります。これで証明ができました。
ここで、原始\(\bs{n}\)乗根はべき根で表現可能(71A)とべき根拡大の十分条件(73A)の関係ですが、(73A)の証明の鍵になったのは、ラグランジュの分解式、
\(\al=c+\zeta^{n-1}\sg(c)+\zeta^{n-2}\sg^2(c)+\:\cd+\zeta^2\sg^{n-2}(c)+\zeta\sg^{n-1}(c)\)
でした。いま、原始\(5\)乗根を \(\eta\) とし、\(\bs{Q}(\eta)/\bs{Q}\) の巡回拡大を考えます。原始\(4\)乗根を \(\zeta\) とします(\(\zeta=i,\:-i\))。
\(\bs{Q}(\eta)\) の自己同型写像 \(\sg\) を、
\(\sg(\eta)=\eta^2\)
となる写像と定義します。そして、\(c=\eta,\:n=4\) を分解式に入れると、
\(\begin{eqnarray}
&&\:\:\al&=\eta+\zeta^3\sg(\eta)+\zeta^2\sg^2(\eta)+\zeta\sg^3(\eta)\\
&&&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
\end{eqnarray}\)
となります。このラグランジュの分解式と、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明で使った \(f(x,y)\) は本質的に同じものです。つまり
\(f(x,y)=y^3x+y^4x^2+y^2x^3+y\) |
と定義すると、\(x,\:y\) の指数はそれぞれ、
\(x\) の指数:\([\:1,\:2,\:3,\:0\:]\)
\(\bs{Z}/4\bs{Z}\) の巡回パターン(生成元 \(=1\))
\(y\) の指数:\([\:3,\:4,\:2,\:1\:]\)
\((\bs{Z}/5\bs{Z})^{*}\) の巡回パターン(生成元 \(=3\))
となります。(71A)では \((\bs{Z}/5\bs{Z})^{*}\) の巡回パターンを \([\:2,\:4\:,3,\:1\:]\)(生成元 \(=2\))としたので式の形は少々違いますが、本質的に同じです。ここで、
\(x=\zeta,\:\:y=\eta\)
と置くと、
\(\begin{eqnarray}
&&\:\:f(x,y)&=\eta+\zeta^3\eta^2+\zeta^2\eta^4+\zeta\eta^3\\
&&&=\al\\
\end{eqnarray}\)
となり、\(f(x,y)\) が ラグランジュの分解式と同じものであることが確認できました。つまり、原始\(\bs{n}\)乗根はべき根で表現可能(71A)の証明は、
ラグランジュの分解式での証明(73A)と同じことを、"分解式"、"体"、"ガロア群" などの概念を使わずに証明し、かつ、\((p-1)\)乗根をもとに \(p\)乗根を求める計算式を示した
ものなのでした。
7.4 べき根拡大と巡回拡大の同値性
6.3節の "べき根拡大は巡回拡大である"(63H)と、7.3節の "巡回拡大はべき根拡大である"(73A)を合わせると、次にまとめることができます。
| (べき根拡大と巡回拡大は同値:74A) |
\(1\) の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。また、\(\bs{K}\) の\(n\)次拡大体を \(\bs{L}\) とする( \([\:\bs{L}\::\:\bs{K}\:]=n\) )。
このとき、
| \(\bs{L}/\bs{K}\) は巡回拡大である | |
| \(\bs{L}/\bs{K}\) はべき根拡大である。 |
\(\bs{1}\) の原始\(\bs{n}\)乗根が代数体に含まれるという条件をつけるのが巧妙なアイデアで、この条件によって可解性の必要十分条件が導けます。
7.5 可解性の十分条件
以上の準備をもとに、可解性の必要条件(64B)の逆である、可解性の十分条件の証明を行います。
代数拡大体 \(\bs{K}\) 上の多項式 \(f(x)\) の最小分解体を \(\bs{L}\) とし、拡大次数を \([\:\bs{L}\::\:\bs{K}\:]=n\) とします。そして、ガロア群 \(\mr{Gal}(\bs{L}/\bs{K})\) が可解群であるとき、もし \(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるなら、べき根拡大と巡回拡大は同値の定理(74A)により、\(\bs{K}\) の巡回拡大とべき根拡大は同じことです。従って、
可解群 \(\rightarrow\) 累巡回拡大 \(\rightarrow\) 累べき根拡大 \(\rightarrow\) 可解
というルートで、方程式 \(f(x)=0\) の可解性が証明できます。しかし、\(\bs{K}\) に \(1\) の原始\(n\)乗根が含まれるとは限りません。\(\bs{K}\) が有理数体 \(\bs{Q}\) だとすると、そこに(原始2乗根以外の)原始\(n\)乗根はありません。しかし、このようなケースでも方程式の可解性が証明できます。それが以下です。
| (可解性の十分条件:75A) |
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。
このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
[証明]
\([\:\bs{L}\::\:\bs{K}\:]=n\:\:(|G|=n)\) とし、\(\zeta\) を \(1\) の原始\(n\)乗根とする。\(\bs{K}\) に \(\zeta\) を添加した拡大体 \(\bs{K}(\zeta)\)と、\(\bs{L}\) に \(\zeta\) を添加した拡大体 \(\bs{L}(\zeta)\) を考える。
\(\bs{L}(\zeta)\) は \(\bs{K}\) 上の方程式 \(f(x)(x^n-1)=0\) の最小分解体だから、\(\bs{L}(\zeta)/\bs{K}\) はガロア拡大である。
また \(\bs{K}(\zeta)\) は、\(\bs{K}\)のガロア拡大体 \(\bs{L}(\zeta)\) の中間体なので、中間体からのガロア拡大の定理(52C)によって、\(\bs{L}(\zeta)/\bs{K}(\zeta)\) もガロア拡大である。そこで、
\(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))=G\,'\)
とおく。
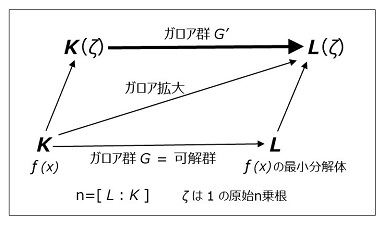
|
ポイントは、\(G\,'\) が \(G\) の部分群(\(G\) そのものも含む)と同型であることの証明である。これが成り立てば、① \(G\) は可解群なのでその部分群は可解群、② 可解群と同型な \(G\,'\) は可解群、③ \(G\,'\) が可解群なので \(\bs{L}(\zeta)/\bs{K}(\zeta)\) は累巡回拡大、④ \(\bs{K}(\zeta)\) は原始\(n\)乗根を含むので、累巡回拡大である \(\bs{L}(\zeta)/\bs{K}(\zeta)\) は累べき根拡大、が言える。 |
\(G\) の元を \(g\)、\(G\) の単位元を \(e\) とする。\(G\,'\)の元を \(g\,'\)、\(G\,'\) の単位元を \(e\,'\) とする。また、\(G\,'\) の元 \(g\,'\) を \(\bs{L}\) の元に限定して作用させるときの同型写像を \(\sg(g\,')\) とする。
\(g\,'\)は \(\bs{L}(\zeta)\) の自己同型写像だから、\(\bs{L}(\zeta)\) の元を共役な元に移す。従って 作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も \(\bs{L}\) の元を共役な元に移す。\(\bs{L}\) はガロア拡大体だから、\(\bs{L}\)の元の共役な元は \(\bs{L}\) に含まれる。従って \(\sg(g\,')\) は \(\bs{L}\) の自己同型写像である。
また \(g\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) の元だから、\(\bs{K}(\zeta)\) の元を固定する。従って、\(\bs{K}(\zeta)\) の部分集合である \(\bs{K}\) の元も固定する。ゆえに、\(g\,'\) の作用範囲を \(\bs{L}\) に限定した \(\sg(g\,')\) も、\(\bs{L}\) の部分集合である \(\bs{K}\) の元を固定する。
以上により \(\sg(g\,')\) は、\(\bs{K}\)の元を固定する \(\bs{L}\) の自己同型写像だから、\(\mr{Gal}(\bs{L}/\bs{K})\) の元、つまり \(G\) の元である。
\(\sg\) を \(G\,'\) から \(G\) への写像と見なして考える。\(G\,'\) の元 を \(g\,'\) とし、\(x\) を \(\bs{L}\) の元とすると、\(g\,'(x)=\sg(g\,')(x)\) である。つまり、作用する対象が \(\bs{L}\) の元なら、2つの写像、\(g\,'\) と \(\sg(g\,')\) は同じ効果を生む。
\(G\,'\)の任意の2つの元を \(g_1{}^{\prime},\:g_2{}^{\prime}\) とすると、\(g_1{}^{\prime}g_2{}^{\prime}\) も \(G\,'\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}(x)=\sg(g_1{}^{\prime}g_2{}^{\prime})(x)\)
である。左辺の \(g_2{}^{\prime}(x)\) は \(\sg(g_2{}^{\prime})(x)\) と同じなので、 \((\br{A})\)
\(g_1{}^{\prime}g_2{}^{\prime}(x)=g_1{}^{\prime}(\sg(g_2{}^{\prime})(x))\)
であるが、\(\sg(g_2{}^{\prime})(x)\) もまた \(\bs{L}\) の元だから、
\(g_1{}^{\prime}g_2{}^{\prime}x=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})(x)\)
である。\((\br{A})\) と \((\br{B})\) より、 \((\br{B})\)
\(\sg(g_1{}^{\prime}g_2{}^{\prime})=\sg(g_1{}^{\prime})\sg(g_2{}^{\prime})\)
となって、\(\sg\) は準同型写像(42A)である。
\(\sg(g\,')\) が \(G\) の元であり \(\sg\) が準同型写像なので、準同型写像の像と核の定理(42B)により、\(\sg\) による \(G\,'\) の 像 \(\sg(G\,')\) は \(G\) の部分群である。もちろん、\(G\) の部分群には \(G\) の自明な部分群である \(G\) 自身も含まれる。
いま、ある \(G\,'\) の元 \(h\) があって、\(\sg(h)=e\)(\(e\) は \(G\) の単位元)とする。つまり、\(h\) を \(\bs{L}\) に限定して適用すると、\(\bs{L}\) の元すべてを固定するものとする。
\(G\,'\) は \(\mr{Gal}(\bs{L}(\zeta)/\bs{K}(\zeta))\) であり、そのすべての元は \(\bs{K}(\zeta)\) の元を固定する。従って、\(G\,'\) の元 \(h\) は \(\zeta\) も固定する。ということは、\(h\) は「\(\bs{L}\) の元すべてを固定し、かつ \(\zeta\) を固定する」から、\(\bs{L}(\zeta)\) の元すべてを固定する。つまり \(h\) は \(G\,'\) の単位元であり、\(h=e\,'\) である。
ゆえに、準同型写像の像と核(42B)における核の定義によって、
\(\mr{Ker}\:\sg=e\,'\)
であり、核が単位元なら単射の定理(42C)によって、\(\sg\) は単射である。このことから、準同型定理(43A)により、
\(G\,'/\mr{Ker}\:\sg\:\cong\:\sg(G\,')\)
すなわち、
\(G\,'\:\cong\:\sg(G\,')\)
である。つまり \(\bs{G\,'}\) は \(\bs{G}\) の部分群 \(\bs{\sg(G\,')}\) と同型である。
\(G\) は可解群なので、可解群の部分群は可解群の定理(61C)によって、\(G\) の部分群である \(\sg(G\,')\) も可解群であり、さらにそれと同型である \(G\,'\) も可解群である。\(G\,'\) が可解群なので、可解群の定義により \(G\,'\) から \(e\,'\) に至る部分群の列、
\(G\,'=H_0\sp H_1\sp\cd\sp H_i\sp H_{i+1}\sp\cd\sp H_k=\{e\,'\}\)
があって、\(H_{i+1}\) は \(H_i\) の正規部分群であり、\(H_i/H_{i+1}\) は巡回群である。\(|G\,'|=m\) とおくと、\(G\,'\) は \(G\) の部分群である \(\sg(G\,')\) と同型なので、ラグランジュの定理(41E)によって、\(m\) は \(|G|=n\) の約数である。
ガロア対応(53B)による \(H_i\) の固定体を \(\bs{K}_i\) とすると、
\(\bs{K}(\zeta)=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_k=\bs{L}(\zeta)\)
という固定体の系列が定義できる。\(H_i/H_{i+1}\) は巡回群なので、\(\bs{K}_{i+1}/\bs{K}_i\) は巡回拡大である。\(\bs{L}(\zeta)/\bs{K}(\zeta)\) の拡大次数は、
\([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=|G\,'|=m\)
であり、\(n\) の約数である。
固定体の系列における一つの拡大 \(\bs{K}_{i+1}/\bs{K}_i\)を考える。その拡大次数 \([\:\bs{K}_{i+1}\::\:\bs{K}_i\:]=m_i\) は、拡大次数の連鎖律(33H)によって \([\:\bs{L}(\zeta)\::\:\bs{K}(\zeta)\:]=m\) の約数であり、従って \(n\) の約数である。
\(\bs{K}_i\) は \(1\) の原始\(n\)乗根 \(\zeta\) を含むから、\(\zeta^{\frac{n}{m_i}}\) も含んでいる。\(\zeta^{\frac{n}{m_i}}\) は \(1\) の原始\(m_i\)乗根である。つまり、\(\bs{K}_i\) は \(1\) の原始\(m_i\)乗根(\(m_i=[\:\bs{K}_{i+1}\::\:\bs{K}_i\:]\))を含む。従って、べき根拡大の十分条件の定理(73A)により、巡回拡大である \(\bs{K}_{i+1}/\bs{K}_i\) はべき根拡大である。
以上のことは \((0\leq i < k)\) のすべてで成り立つから、\(\bs{K}_i\) の系列は累べき根拡大である。
\(f(x)=0\) の解は \(\bs{L}\) に含まれるが、\(\bs{L}\:\subset\:\bs{L}(\zeta)\) だから \(f(x)=0\) の解は \(\bs{L}(\zeta)\) に含まれる。その \(\bs{L}(\zeta)\) は \(\bs{K}(\zeta)\) の累べき根拡大であり、また \(1\) の原始\(n\)乗根である \(\zeta\) は \(\bs{Q}\:(\in\bs{K})\) の元の四則演算とべき根で表現できるから(71A)、\(\bs{L}(\zeta)\) の元はすべて \(\bs{K}\) の元の四則演算とべき根で表現できる。従って \(f(x)=0\) の解も \(\bs{K}\) の元の四則演算とべき根で表現できる。[証明終]
この定理では「体 \(\bs{K}\) 上の方程式 \(f(x)=0\)」としましたが、もちろん、体 \(\bs{K}\) が 有理数体 \(\bs{Q}\) であっても同じです。以降、\(\bs{K}\) を \(\bs{Q}\) と書きます。
証明のポイントは、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) とし、\(G\,'=\mr{Gal}(\bs{L}(\zeta)/\bs{Q}(\zeta))\) とするとき、\(G\,'\) が \(G\) の部分群と同型であることです。たとえば、\(f(x)\) が既約な3次多項式だと、\(G\cong S_3\) か \(G\cong C_3\) であり、基本的に \(G\,'\cong G\) です。しかし、そうならない場合もあります。たとえば \(f(x)=x^3-2\) では \(G\cong S_3\) ですが、
\(\bs{Q}\:\subset\:\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\sqrt[3]{2})=\bs{L}\)
(\(\omega\) は \(1\) の原始3乗根)
という体の拡大列でわかるように、\(\bs{L}(\omega)=\bs{L}\) です。つまり、\(\bs{L}(\omega)/\bs{Q}(\omega)\) の拡大次数は \(3\) であり、\(\bs{L}/\bs{Q}\) の拡大次数の \(6\) とは違います。しかしそうであっても \(G\,'=\mr{Gal}(\bs{L}(\omega)/\bs{Q}(\omega))\cong C_3\) であり、\(G\,'\) は \(G\cong S_3\) の部分群と同型です。
\(G\,'\) は \(G\) の部分群と同型なので、\(G\) が可解群なら \(G\,'\) も可解群であり(61C)、\(\bs{L}(\omega)/\bs{Q}(\omega)\) は累巡回拡大であり(62C)、従って、累べき根拡大です(73A)。
さらに、\(1\) の原始\(n\)乗根が \(\bs{Q}\) の元の四則演算とべき根で表現できる(71A)ことも証明のポイントになっています。
この可解性の十分条件の定理(75A)によって、有理数係数の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) として、\(\mr{Gal}(\bs{L}/\bs{Q})\) が可解群のとき、\(f(x)=0\) の解は四則演算とべき根で表現可能なことが証明できました。
ここがゴールで「ガロア理論=可解性の必要十分条件」が完結しました。
7.6 位数2の巡回拡大は平方根拡大:正5角形が作図できる理由
可解性の必要十分条件の証明は前節で尽きていますが、これ以降は可解な方程式の代表的なものを取り上げ、ガロア群の分析をします。まず最初は、
| \(x^5\) | \(-1=0\) | |
| \(x^{17}\) | \(-1=0\) |
\(x^5-1=0\)
まず \(x^5-1=0\) の解を分析します。
\(x^5-1=(x-1)(x^4+x^3+x^2+x+1)\)
なので、\(1\) 以外の解を \(\zeta\) とすると、\(\zeta\) は4次方程式、
\(x^4+x^3+x^2+x+1=0\)
の解です。「7.1 1 の原始n乗根」で書いたように、この方程式の解は、
\(\zeta=\dfrac{1}{4}\left(-1+\sqrt{5}\pm\sqrt{-10-2\sqrt{5}}\right)\)
\(\zeta=\dfrac{1}{4}\left(-1-\sqrt{5}\pm\sqrt{-10+2\sqrt{5}}\right)\)
の4つであり、これが \(1\) の原始5乗根です。以下の論旨を明瞭にするために、虚数単位 \(i\) を使わずに、外側の \(\sqrt{\phantom{a}}\) の中を負の数にして記述しました。
この原始5乗根は、4次方程式の解であるにもかかわらず、四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現されています。なぜそうなるのか、それをガロア理論にのっとって説明します。実は、\(p\) を素数としたとき、
原始\(\bs{p}\)乗根が四則演算と平方根 \(\bs{\sqrt{\phantom{a}}}\) のみで表現できれば、正 \(\bs{p}\)角形は定規とコンパスで作図可能である
ことが知られています。定規というのは「目盛りのない、与えられた2点を通る直線を引くことだけができる道具」であり、コンパスというのは「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\cdot\)円弧を描くことだけができる道具」です。長さや角度を測ることはできません。作図可能の原理は次の項で説明します
\(f(x)=x^4+x^3+x^2+x+1\) とし、\(f(x)=0\) の解の一つを \(\zeta\) とすると、\(f(x)\) の最小分解体は \(\bs{Q}(\zeta)\) です。そのガロア群を、
\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\)
と書くと、\(\zeta\) の最小多項式は \(f(x)\) なので(63C)、\(|G|=4\) です。また、\(\bs{\bs{Q}(\zeta)}\) のガロア群の定理(63E)により、\(G\) は既約剰余類群と同型で、
\(G\cong(\bs{Z}/5\bs{Z})^{*}\)
です。
\((\bs{Z}/5\bs{Z})^{*}=\{1,\:2,\:3,\:4\}\)
ですが、この群の生成元は \(2\) か \(3\) です。以下、生成元を \(2\) として話を進めると、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/5\bs{Z})^{*}&=\{2,\:2^2,\:2^3,\:2^4\}\\
&&&=\{2,\:4,\:3,\:1\}\\
\end{eqnarray}\)
と表現できます。一方、\(f(x)=0\) の4つの解は、
\(\zeta,\:\:\zeta^2,\:\:\zeta^3,\:\:\zeta^4\)
です。そこで、
\(\sg(\zeta)=\zeta^2\)
で定義される自己同型写像を考えると、ガロア群は、
\(G=\{\sg,\:\sg^2,\:\sg^3,\:\sg^4=e\}\)
となり、位数 \(4\) の巡回群、かつ可解群です。また、体の拡大次数は、
\([\:\bs{Q}(\zeta):\bs{Q}\:]=4\)
です。
ガロア群 \(G\) には部分群が含まれています。つまり、
\(H=\{\sg^2,\:e\}\)
\(\sg^2(\zeta)=\zeta^4\)
と定義すると、\((\sg^2)^2=e\) なので \(H\) は部分群(\(\sg H=H\sg\) なので正規部分群)であり、位数 \(2\) の巡回群です。また、剰余群は、
\(G/H\cong\{e,\:\sg\}\)
です。従って、
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\)
| \(G/H\) | \(\cong\{e,\:\sg\}\) | :位数 \(2\) | |
| \(H/\{\:e\:\}\) | \(\cong H\) | :位数 \(2\) |
は可解列です。ガロア対応の定理(53B)により、この可解列に対応する拡大体の列があって、
\(G\sp H\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}\subset\bs{Q}(\zeta)\)
となります。\(\bs{F}\) は \(H\) の固定体であり、\(\bs{Q}(\zeta)\) の中間体です。すると、正規性定理(53C)により、
\(\mr{Gal}(\bs{F}/\bs{Q})\cong G/H\)
なので、\(\mr{Gal}(\bs{F}/\bs{Q})\) は位数 \(2\) の巡回群です。またガロア群の定義により、
\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\cong H\)
であり、\(\mr{Gal}(\bs{Q}(\zeta)/\bs{F})\) も位数 \(2\) の巡回群です。従って、次数と位数の同一性の定理(52B)より拡大次数は、
| \([\:\bs{F}\) | \(:\bs{Q}\:]=2\) | |
| \([\:\bs{Q}(\zeta)\) | \(:\bs{F}\:]=2\) |
\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの平方根拡大を2回繰り返したものである
と結論づけられます。原始5乗根が四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できる理由がここにあります。
ここまでは、中間体 \(\bs{F}\) がどういう拡大体かに触れていませんが、\(\bs{F}\) を具体的に表現することもできます。\(\bs{F}\) は \(H=\{e,\:\sg^2\}\) の固定体なので、\(\bs{F}=\bs{Q}(\theta)\) として、
\(\sg^2(\theta)=\theta\)
となる \(\theta\) を探します。\(\theta\) の選び方には自由度があり、たとえば \(\theta=\zeta^4+\zeta\) としてもよいのですが、ここでは、
\(\theta=(\zeta^2-\zeta^3)(\zeta^4-\zeta)\)
とします。このように選ぶと、\(\sg^2(\zeta)=\zeta^4\) なので、
\(\begin{eqnarray}
&&\:\:\sg^2(\theta)&=(\zeta^8-\zeta^{12})(\zeta^{16}-\zeta^4)\\
&&&=(\zeta^3-\zeta^2)(\zeta-\zeta^4)=\theta\\
\end{eqnarray}\)
となって、\(\theta\) は \(\sg^2\) で不変です。と同時に、\(\sg(\zeta)=\zeta^2\) なので、
\(\begin{eqnarray}
&&\:\:\sg(\theta)&=(\zeta^4-\zeta^6)(\zeta^8-\zeta^2)\\
&&&=(\zeta^4-\zeta)(\zeta^3-\zeta^2)=-\theta\\
\end{eqnarray}\)
となります。ということは、
\(\sg(\theta^2)=(\sg(\theta))^2=(-\theta)^2=\theta^2\)
であり、\(\theta^2\) は \(\sg\) で不変、つまり \(G\) のすべての元で不変となり、\(\theta^2\) は有理数です。そこで、
\(\zeta^5=1\)
\(\zeta^4+\zeta^3+\zeta^2+\zeta+1=0\)
の関係を使って \(\theta^2\) を計算すると、
\(\begin{eqnarray}
&&\:\:\theta^2&=(\zeta^2-\zeta^3)^2(\zeta^4-\zeta)^2\\
&&&=(\zeta^4-2\zeta^5+\zeta^6)(\zeta^8-2\zeta^5+\zeta^2)\\
&&&=(\zeta^4-2+\zeta)(\zeta^3-2+\zeta^2)\\
&&&=\zeta^7-2\zeta^4+\zeta^6-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=\zeta^2-2\zeta^4+\zeta-2\zeta^3+4-2\zeta^2+\zeta^4-2\zeta+\zeta^3\\
&&&=-\zeta^4-\zeta^3-\zeta^2-\zeta+4\\
&&&=5\\
\end{eqnarray}\)
となり、確かに\(\theta^2\) は有理数であることが分かります。つまり、
\(\theta=\sqrt{5}\)
です。従ってガロア対応は、
| \(G\sp H\) | \(\sp\{\:e\:\}\) | |
| \(\bs{Q}\subset\bs{Q}(\sqrt{5})\) | \(\subset\:\bs{Q}(\zeta)\) |
となります。原始5乗根に \(\sqrt{-10+2\sqrt{5}}\) のような項が現れるのは、中間体が \(\bs{Q}(\sqrt{5})\) であるという、体の拡大構造からくるのでした。
ここまでの論証を振り返ってみると、
\(p\) を素数とし、原始\(p\)乗根を \(\zeta\) とすると、
\(|\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})|=|(\bs{Z}/p\bs{Z})^{*}|=p-1\)
なので、
\(p-1=2^k\:\:(1\leq k)\)
の条件があると、\(\bs{Q}\) から \(\bs{Q}(\zeta)\) に至る「平方根拡大」の列が存在し、\(\zeta\) は四則演算と平方根 \(\sqrt{\phantom{a}}\) だけで表現できる。従って 正 \(p\)角形は定規とコンパスで作図可能である
ことが分かります。この条件は \(p=3,\:5\) で成立しますが、その次に成立するのは \(p=17\) です。
\(x^{17}-1=0\)
\(1\) の原始\(17\)乗根を \(\zeta\) とします。\(p=17\) の最小原始根は \(3\) で(25D)、\((\bs{Z}/17\bs{Z})^{*}\) の位数は \(16\) です。\((\bs{Z}/17\bs{Z})^{*}\) において \(3\) の累乗は、
\(\phantom{1}3,\:\phantom{1}9,\:10,\:13,\:\phantom{1}5,\:15,\:11,\:16,\)
\(14,\:\phantom{1}8,\:\phantom{1}7,\:\phantom{1}4,\:12,\:\phantom{1}2,\:\phantom{1}6,\:\phantom{1}1\)
と、すべての元を巡回します。従って、
\(\sg(\zeta)=\zeta^3\)
という自己同型写像 \(\sg\) を定義すると、
\(G=\{\sg,\sg^2,\sg^3,\cd,\sg^{15},\sg^{16}=e\}\)
が \(\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) です。
\(x^5-1=0\) のときと同様の考察をすると、\(G\) には3つの部分群があります。
\(H_1=\{\sg^2,\sg^4,\sg^6,\sg^8,\sg^{10},\sg^{12},\sg^{14},e\}\)
\(\sg^2(\zeta)=\zeta^9\)
\(H_2=\{\sg^4,\sg^8,\sg^{12},e\}\)
\(\sg^4(\zeta)=\zeta^{13}\:\:(\phantom{1}9^2\equiv13\:\:(\mr{mod}\:17))\)
\(H_3=\{\sg^8,e\}\)
\(\sg^8(\zeta)=\zeta^{16}\:\:(13^2\equiv16\:\:(\mr{mod}\:17))\)
の3つで、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
| \(G\) | \(/H_1\) | \(\cong\{\sg^{\phantom{2}},\:e\}\) | |
| \(H_1\) | \(/H_2\) | \(\cong\{\sg^2,\:e\}\) | |
| \(H_2\) | \(/H_3\) | \(\cong\{\sg^4,\:e\}\) | |
| \(H_3\) | \(/\{\:e\:\}\) | \(\cong\{\sg^8,\:e\}\) |
は可解列です。ガロア対応の定理(53B)により、\(H_1,\:H_2,\:H_3\) にはそれぞれに対応した固定体 \(\bs{F}_1,\:\bs{F}_2,\:\bs{F}_3\) があって、
\(G\sp H_1\sp H_2\sp H_3\sp\{\:e\:\}\)
\(\bs{Q}\subset\bs{F}_1\subset\bs{F}_2\subset\bs{F}_3\subset\bs{Q}(\zeta)\)
のガロア対応になります。\(\bs{Q}\) から \(\bs{Q}(\zeta)\) までの4つの拡大次数は、剰余群の位数に等しいのですべて \(2\) です。つまり、\(\bs{\bs{Q}(\zeta)}\) は \(\bs{\bs{Q}}\) からの「平方根拡大」を4回繰り返したものであり、原始\(17\)乗根は四則演算と平方根 \(\sqrt{\phantom{a}}\) のみを使って表現できます。従って正\(17\)角形は定規とコンパスで作図可能です。
これは、ドイツの大数学者\(\cdot\)ガウス(\(1777-1855\))が\(19\)才のときに発見した定理として有名です。
作図可能の原理
ここで改めて、平面上の図形が定規とコンパスで「作図可能」という意味を明確にします。ここで "定規" は「目盛りのない、与えられた2点を通る線を引くことだけができる道具」であり、"コンパス" は「角度目盛りのない、与えられた2点のうちの1点を中心として別の点を通る円\(\bs{\cdot}\)円弧を描くことだけができる道具」でした。
平面上の図形は点と線でできています。線は2点を与えると描けるので、「作図可能」の意味は「平面上で作図可能な点とは何か」を定義することに帰着します。
平面を複素平面(\(=\bs{C}\))として考えます。以降、
| \(a,\:b\) | \(\in\:\bs{R}\) | |
| \(\al,\:\beta\) | \(\in\:\bs{C}\) |
\(1,\:0\) は作図可能である。また複素平面の実軸と虚軸は作図できる。
|
任意の線分を単位長さとし、端点を \(1,\:0\) とします。2点を結ぶ直線が実軸で、\(0\) を通り実軸と垂直な直線を作図するとそれが虚軸です。
\(\al=a+b\:i\) とすると、\(a,\:b\) が作図可能なら \(\al\) も作図可能である。また、\(\al\) が作図可能なら \(a,\:b\) も作図可能である。
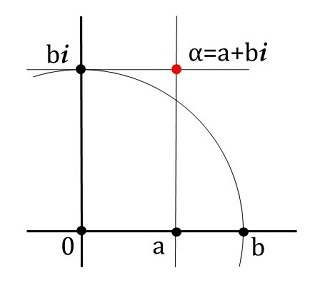
|
\(a\) が作図可能なら、\(-a\) も作図可能である。従って \(\al\) が作図可能なら \(-\al\) も作図可能である。
また \(a,\:b\) が作図可能なら \(a+b\) も作図可能である。従って、\(\al,\:\beta\) が作図可能なら \(\al+\beta\) も作図可能である。
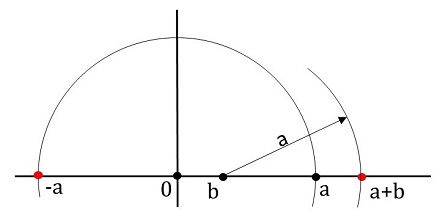
|
\(a,\:b\) が作図可能なら \(ab\)も作図可能である。従って \(\al,\:\beta\) が作図可能なら \(\al\beta\) も作図可能である。
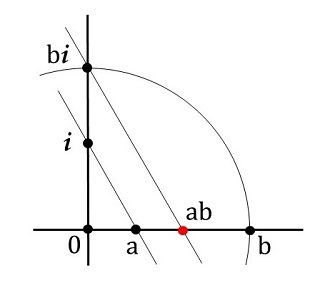
|
\(a\:\:(a\neq0)\) が作図可能なら \(a^{-1}\) も作図可能である。従って \(\al\:\:(\al\neq0)\) が作図可能なら \(\al^{-1}\) も作図可能である。
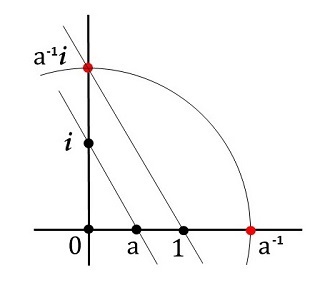
|
作図可能な \(\al\) を \(\al=a+b\:i\) とすると、
\(\al^{-1}=\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}\:i\)
です。\(a,\:b\) が作図可能なので、その四則演算の結果は作図可能です。従って \(\al^{-1}\) も作図可能です。
有理数 \(\bs{Q}\) は作図可能である。
実数のなかで作図可能な点は四則演算で閉じています。かつ、\(0,\:1\) は作図可能です。従って有理数は作図可能です。
\(a\) が正の実数のとき、\(\sqrt{a}\) は作図可能である。
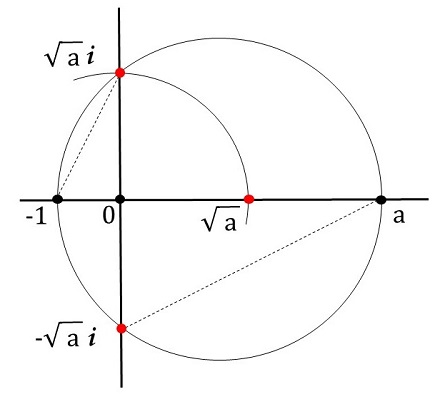
|
\(a\) と \(-1\) を結ぶ線分を直径とする円を描き、虚軸との交点を \(x\cdot i\:(x\):実数) とすると、
\(1:x=x:a\)
なので、\(x=\pm\sqrt{a}\) です。従って \(\sqrt{a}\) は作図可能です。
\(\al\) を作図可能な複素数とするとき、\(\sqrt\al\) は作図可能である。
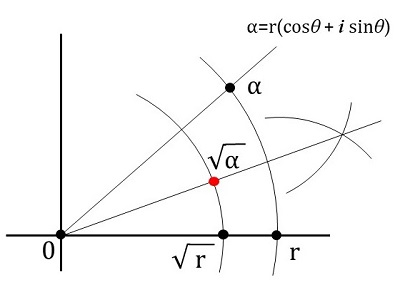
|
極形式を使って、
\(\al=r(\mr{cos}\theta+i\cdot\mr{sin}\theta)\)
とすると、\(r\) は作図可能であり、つまり \(\sqrt{r}\) も作図可能です。また、角 \(\theta\) を2等分する線も、定規とコンパスで作図可能です。従って \(\sqrt\al\) は作図可能です。
\(\al,\:\beta\) が作図可能な複素数とするとき、2次方程式 \(x^2+\al x+\beta=0\) の解は作図可能である。
ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能である。
2次方程式 \(x^2+\al x+\beta=0\) の解は、根の公式により、係数 \(\al,\:\beta\) の四則演算と平方根で表わされます。従って作図可能です。
定規とコンパスで作図可能な点は、作図可能な円や直線の交点として求まる点です。2次元 \(xy\) 平面( \(\bs{R}^2\) )で考えると、直線と直線の交点は1次方程式の解です。また円と直線の交点は2次方程式の解です。円と円の交点がどうかですが、\(a,\:b,\:c,\:d\) を実数として、2つの円の方程式を、
\(x^2+y^2=a^2\)
\((\br{A})\)
\((x-b)^2+(y-c)^2=d^2\)
とします。\((\br{A}),\:(\br{B})\) の両辺を引き算して整理すると、 \((\br{B})\)
\(2bx+2cy-(b^2+c^2+a^2-d^2)=0\)
という直線の方程式になります。2つの円の交点は \((\br{A}),\:(\br{C})\) の連立方程式の解であり、2次方程式の解です。つまり、作図可能な実数は、作図可能な実数を係数とする2次方程式(あるいは1次方程式)の解となる実数です。 \((\br{C})\)
実数(\(a,\:b\))が作図可能と、複素数(\(a+bi\))が複素平面上で作図可能は同値です。従って、ある複素数 \(\al\) は、作図可能な複素数を係数とする2次方程式、あるいは1次方程式の解となるときのみ、作図可能です。
\(\bs{Q}\) の代数拡大体 \(\bs{K}\) があり、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{K}\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
を満たす \(\bs{Q}\) から \(\bs{K}\) の拡大列が存在するとき、\(\bs{K}\) の元
\(\al\in\bs{K}\)
は作図可能である。
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\) であれば、\(\bs{K}_{i+1}/\bs{K}_i\) は次数2のべき根拡大であり、
\(x^2-a=0\:\:\:(a\in\bs{K}_i)\)
の解、\(\sqrt{a}\) を用いて、
\(\bs{K}_{i+1}=\bs{K}_i(\sqrt{a})\)
と表されます。従って、\(\bs{K}_i\) の元が作図可能なら、\(\bs{K}_{i+1}\) の元は「作図可能な点の四則演算と平方根の組み合わせ」で表現できるので、作図可能です。体の拡大列の出発点である \(\bs{Q}\) の元は作図可能なので、到達点である \(\bs{K}\) の元も作図可能になります。
\(1\) の原始\(p\)乗根(\(p\):素数)を \(\zeta\) とすると、\(G=\mr{Gal}(\bs{Q}(\zeta)/\bs{Q})\) の位数は \(p-1\) であり、それが2の累乗であれば、\(G\) の可解列にガロア対応する体の拡大系列、
\(\bs{Q}=\bs{K}_0\subset\bs{K}_1\subset\cd\subset\bs{K}_i\subset\bs{K}_{i+1}\subset\cd\subset\bs{K}_n=\bs{Q}(\zeta)\)
\([\:\bs{K}_{i+1}:\bs{K}_i\:]=2\:\:(0\leq i < n)\)
が存在します(前項での証明)。従って複素数平面上の点 \(\zeta\) は作図可能であり、正 \(p\)角形は作図可能です。条件に合致する素数は \(p=3\)、\(5\)、\(17\)、\(257\)、\(65537\)であることが知られています。これらの素数をフェルマ素数と呼びます。フェルマ素数 \(p\) とは、\(p-1\) が2の累乗であるような素数です。
さらに、一般の正 \(n\)角形が作図可能である条件は、次のようになります。
正 \(n\)角形は、
\(n=2^k\:\:\:(2\leq k)\)
\(n=2^k\cdot p_1p_2\cd p_r\:\:\:(0\leq k,\:\:1\leq r)\)
\(p_i\) は相異なるフェルマ素数
のとき、作図可能である。
[証明]
角度の2等分線は作図可能なので、\(n=2^k\:\:(2\leq k)\) のとき、正 \(n\)角形は作図可能である。と同時に、正 \(m\)角形が作図可能なとき、
\(n=2^k\cdot m\:\:(0\leq k)\)
とおくと、正 \(n\)角形は作図可能になる。\(p\) がフェルマ素数のとき、正 \(p\)角形は作図可能なので、
\(m_1\) と \(m_2\) を互いに素な3以上の数とするとき、正 \(m_1\) 角形と正 \(m_2\)角形が作図可能であれば、正 \(m\)角形(\(m=m_1m_2\))は作図可能である
ことが証明できれば十分である。
\(\theta,\:\theta_1,\:\theta_2\) を任意の角度とする。
\(\mr{sin}\theta=\sqrt{1-\mr{cos}^2\theta}\)
だから、\(\mr{cos}\theta\) が作図できれば \(\mr{sin}\theta\) も作図できる。また三角関数の加法定理より、
\(\mr{cos}(\theta_1+\theta_2)=\mr{cos}\theta_1\cdot\mr{cos}\theta_2-\mr{sin}\theta_1\cdot\mr{sin}\theta_2\)
なので、\(\mr{cos}\theta_1,\:\mr{cos}\theta_2\) が作図できれば \(\mr{cos}(\theta_1+\theta_2)\) も作図できる。このことから \(\mr{cos}\theta\) が作図できれば \(\mr{cos}(k\theta)\:\:(k\) は整数)も作図できる。
複素平面上で原点を中心とする半径1の円に正 \(m\)角形を描いたとき、その頂点の複素数は
\(\mr{cos}\left(\dfrac{2\pi}{m}k\right)+i\:\mr{sin}\left(\dfrac{2\pi}{m}k\right)\:\:(0\leq k\leq m-1)\)
である。\(k=1\) の点が作図できれば、残りの点が作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
が作図できれば、正 \(m\)角形は作図できる。
\(m_1\) と \(m_2\) は互いに素だから、不定方程式の解の存在の定理(21C)により、
\(k_1m_1+k_2m_2=1\)
を満たす \(k_1,\:k_2\) が存在する。両辺を \(m=m_1m_2\) で割ると
\(\dfrac{k_1}{m_2}+\dfrac{k_2}{m_1}=\dfrac{1}{m}\)
\(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2=\dfrac{2\pi}{m}\)
が得られる。正 \(m_1\)角形と正 \(m_2\)角形 は作図できるから、
\(\mr{cos}\left(\dfrac{2\pi}{m_1}\right),\:\:\mr{cos}\left(\dfrac{2\pi}{m_2}\right)\)
は作図できる。従って
\(\mr{cos}\left(\dfrac{2\pi}{m_2}k_1+\dfrac{2\pi}{m_1}k_2\right)\)
は作図でき、
\(\mr{cos}\left(\dfrac{2\pi}{m}\right)\)
も作図できることになって、正 \(m\)角形は作図できる。[証明終]
証明の鍵は「\(m_1\) と \(m_2\) が互いに素」です。従って、正3角形が作図できても、正9角形は作図できません。正\(15\)角形なら作図できます。計算すると、作図可能な正 \(n\)角形(\(n\leq100\))は、
| \(3\)、\(4\)、\(5\)、\(6\)、\(8\)、\(10\)、\(12\)、\(15\)、\(16\)、\(17\)、\(20\)、\(24\)、\(30\)、\(32\)、\(34\)、\(40\)、\(48\)、\(51\)、\(60\)、\(64\)、\(68\)、\(80\)、\(85\)、\(96\) |
です。「正\(50\)角形は作図できないが、正\(51\)角形は作図できる」というのも不思議な感じがします。
7.7 巡回拡大はべき根拡大:3次方程式が解ける理由
この節では可解な方程式がなぜ解けるのかを、3次方程式を例にとってガロア理論で説明します。また3次方程式の根の公式をガロア理論に沿った形て導出します。「7.5 可解性の十分条件」で証明したことは、
体 \(\bs{K}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とする。\(\mr{Gal}(\bs{L}/\bs{K})=G\) とし、\(G\) は可解群とする。このとき \(f(x)=0\) の解は四則演算とべき根で表現できる。
でした。この証明の核となっているのは「7.3 べき根拡大の十分条件」であり、それは、
1の原始\(n\)乗根を \(\zeta\) とし、代数体 \(\bs{\bs{K}}\) には \(\bs{\zeta}\) が含まれるとする。\(\bs{L}/\bs{K}\) をガロア拡大とし、\(\mr{Gal}(\bs{L}/\bs{K})\) が巡回群とする(= \(\bs{L}/\bs{K}\) が巡回拡大)。拡大次数は \([\bs{L}:\bs{K}]=n\) とする。このとき、\(\bs{L}\) は \(\bs{K}\) のべき根拡大である。
でした。このことを証明した論理展開は、次のようでした。
次の条件があるとする。
| \(\bs{L}\) は \(\bs{K}\) の代数拡大体であり、拡大次元は \(n\) である。 | |
| \(\bs{K}\) には \(1\) の原始\(n\)乗根が含まれる。 | |
| \(\bs{L}/\bs{K}\) はガロア拡大である。 | |
| \(\mr{Gal}(\bs{L}/\bs{K})\) は巡回群である(=\(\bs{L}/\bs{K}\) は巡回拡大) |
このとき、レゾルベント(分解式)を定義することで、
| \(\al^n\) が \(\bs{K}\) の元であるような \(\bs{L}\) の元 \(\al\) が存在する。すなわち、\(x^n-a=0\:\:(a\in\bs{K})\) の解が \(\al\in\bs{L}\) | |
| このとき \(\bs{L}=\bs{K}(\al)\) になり、従って \(\bs{L}/\bs{K}\) はべき根拡大 |
つまり、レゾルベントを使って、巡回拡大=べき根拡大(但し、体に \(1\) の原始\(n\)乗根が含まれることが条件)を証明したわけです。この証明プロセスを、具体的な3次方程式で順にたどります。まず、3次方程式のガロア群を再度整理します。
3次方程式のガロア群
3次方程式のガロア群は「1.3 ガロア群」で計算しましたが、改めて書きます。3次方程式のガロア群は、3次方程式の3つの解、\(\al,\:\beta,\gamma\) を入れ替える(置換する)群であり、一般的には、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
です。3つの解をそれぞれ \(1,\:2,\:3\) の文字で表し、巡回置換の記法(6.5節)で書くと、
| \(\sg\) | \(=(1,\:2,\:3)\) | |
| \(\sg^2\) | \(=(1,\:3,\:2)\) | |
| \(\tau\) | \(=(2,\:3)\) | |
| \(\sg\tau\) | \(=(1,\:2)\) | |
| \(\sg^2\tau\) | \(=(1,\:3)\) |
\(\tau\sg=(1,\:3)\)
であり、
\(\tau\sg=\sg^2\tau\)
との関係が成り立っています。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。ここで、
\(H=\{e,\:\sg,\:\sg^2\}\)
という \(G\) の部分群を考えると、\(H\) は巡回群であると同時に \(G\) の正規部分群です。"弱可換性" を使って検証してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
であり、同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つので \(H\) は \(G\) の正規部分群です。
\(G\) の \(H\) による剰余群は、
\(G/H=\{H,\tau H\}\)
であり、単位元は \(H\) で、
\((\tau H)^2=\tau H\tau H=\tau\tau HH=H\)
となる、位数\(2\) の巡回群です(\(G/H\cong C_2)\)。この結果、
\(G\:\sp\:H\:\sp\:\{\:e\:\}\)
は可解列になり、\(G\) は可解群で、従って3次方程式は可解です(=四則演算とべき根で解が表現可能)。この節ではそれを具体例で確認していきます。
一方、「3.3 線形空間」の「代数拡大体の構造」で書いたように、3次方程式のガロア群が \(S_3\) ではなく、位数 \(3\) の巡回群( \(C_3\) )になる場合があります。それを再度整理します。
\(x^3+ax^2+bx+c=0\) の3次方程式は、\(x=X-\dfrac{a}{3}\) とおくと、
\(X^3+\left(b-\dfrac{a^2}{3}\right)X+\left(\dfrac{2}{27}a^3-\dfrac{1}{3}ab+c\right)=0\)
となって、2乗の項が消えます。従って以降、3次方程式を、
\(x^3+px+q=0\)
の形で扱います。
\(f(x)=x^3+px+q\)
とおき、\(f(x)\) は既約多項式とします。3次方程式の根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
であり、根と係数の関係から、
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=p\)
\(\al\beta\gamma=-q\)
です。3次方程式のガロア群が \(S_3\) か \(C_3\) かを決めるポイントとなるのは、
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
で定義される、根の差積と呼ばれる値です。差積は普通、\(\Delta\)(ギリシャ文字・デルタの大文字)で表しますが、後の説明の都合で \(\theta\) と書きます。差積は、任意の2つの根の互換で \(-\theta\) となるので、3つの根を \(\al,\:\beta,\:\gamma\) に割り当てる方法によって、\(\theta\) は2つの値をとり得ます。差積の2乗が判別式であり、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
です。つまり \(\theta=\sqrt{D}\) と書けますが、\(\sqrt{D}\) は「2乗して \(D\) となる2つの数のどちらか」の意味です。\(D\) は \(\al,\:\beta,\:\gamma\) の任意の置換で不変な対称式なので、3次方程式の係数である \(p,\:q\) で表すことができる有理数です。
その \(D\) を方程式の係数で表すために、\(f(x)\) を微分します。
\(f(x)=(x-\al)(x-\beta)(x-\gamma)\)
なので、
\(\begin{eqnarray}
&&\:\:f\,'(x)=&(x-\al)(x-\beta)+(x-\beta)(x-\gamma)+\\
&&&(x-\gamma)(x-\al)\\
\end{eqnarray}\)
であり、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\beta)=(\beta-\gamma)(\beta-\al)\)
\(f\,'(\gamma)=(\gamma-\al)(\gamma-\beta)\)
となります。従って、
\(D=-f\,'(\al)f\,'(\beta)f\,'(\gamma)\)
です。一方、
\(f\,'(x)=3x^2+p\)
なので、
\(D=-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\)
となります。ここからの計算を進めるために、次の2つの対称式を、根と係数の関係を使って \(p\) で表しておきます。
・\(\al^2+\beta^2+\gamma^2\)
\(=(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)\)
\(=-2p\)
・\(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2\)
\(=(\al\beta+\beta\gamma+\gamma\al)^2-2\al\beta\gamma(\al+\beta+\gamma)\)
\(=p^2\)
これを用いると、
\(\begin{eqnarray}
&&\:\:D&=&-(3\al^2+p)(3\beta^2+p)(3\gamma^2+p)\\
&&&=&-27(\al\beta\gamma)^2-9(\al^2\beta^2+\beta^2\gamma^2+\gamma^2\al^2)p\\
&&&&-3(\al^2+\beta^2+\gamma^2)p^2-p^3\\
&&&=&-27q^2-9\cdot p^2\cdot p-3\cdot(-2p)\cdot p^2-p^3\\
&&&=&-4p^3-27q^2\\
\end{eqnarray}\)
と計算できます。つまり、
\(D=-4p^3-27q^2\)
です。ここでもし、\(D\) がある有理数 \(a\) の2乗(\(D=a^2\))なら、
\(\theta=\sqrt{D}=\pm a\)
となり、\(\theta\) は有理数です。\(\theta\) が有理数(\(\theta=\pm a\))の場合、
\(f\,'(\al)=(\al-\beta)(\al-\gamma)\)
\(f\,'(\al)=3\al^2+p\)
の関係があるので、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=-f\,'(\al)(\beta-\gamma)\\
&&&=-(3\al^2+p)(\beta-\gamma)\\
\end{eqnarray}\)
ですが、\(\theta=\pm a\) なので、
\(\beta-\gamma=\pm\dfrac{a}{3\al^2+p}\)
です。この式と、根と係数の関係である、
\(\beta+\gamma=-\al\)
を使うと、\(\bs{\beta}\) と \(\bs{\gamma}\) が \(\bs{\al}\) の有理式(=分母・分子が \(\bs{\al}\) の多項式)で表現できることになります。計算すると(\(\pm\)は省略して)、
\(\beta=\dfrac{2p\al+3q-a}{2(3\al^2+p)}\)
\(\gamma=\dfrac{2p\al+3q+a}{2(3\al^2+p)}\)
です(\(\beta\) と \(\gamma\) は逆でもよい)。\(\beta,\:\gamma\) が \(\al\) の有理式で表現できるので、
\(\bs{Q}(\al,\beta,\gamma)\subset\bs{Q}(\al)\)
であり、もちろん \(\bs{Q}(\al,\beta,\gamma)\sp\bs{Q}(\al)\) なので。
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
です。\(\bs{Q}(\al)\) のところは \(\bs{Q}(\beta)\) や \(\bs{Q}(\gamma)\) とすることができます。
つまり、\(\bs{Q}\) 上の既約多項式 \(f(x)=x^3+px+q\) の最小分解体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、方程式の解の一つである \(\al\) の(または \(\beta,\:\gamma\) の)単拡大体であり、単拡大体の基底の定理(33F)により \(\bs{L}\) の次元は \(3\) です。すると次数と位数の同一性(52B)により、\(G=\mr{Gal}(\bs{L}/\bs{Q})\) の群位数は \(3\) です。従って、ラグランジュの定理(41E)により群位数が素数の群は巡回群なので、\(G\) は群位数 \(3\) の巡回群( \(C_3\) )です。
以上をまとめると、3次方程式の最小分解体のガロア群は、次のようになります。
前提として、
・\(f(x)=x^3+px+q\:\:(p,\:q\in\bs{Q})\)
( \(f(x)\) は既約多項式 )
・\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\)
・\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
・\(f(x)\) の最小分解体を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)
・\(G=\mr{Gal}(\bs{L}/\bs{Q})\)
とする。この前提のもとで、
\(\bs{\theta}\):有理数のとき
\(G\cong C_3\)
\(G=\{\:e,\:\sg,\:\sg^2\:\}\)
\(\sg=(1,\:2,\:3)\)
\(G\) は巡回群なので可解群
\(\bs{\theta}\):有理数でないとき
\(G\cong S_3\)
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
\(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\)
\(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群
\(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列
| \(G/H\) | \(=\{H,\:\tau H\}\) | \(\cong C_2\) | |
| \(H/{e}\) | \(=H\) | \(\cong C_3\) |
なお、\((1,\:2,\:3)\:\:(2,\:3)\) の巡回置換は \((1,\:3,\:2)\:\:(1,\:2)\:\:(1,\:3)\) などとしても同じです。
\(C_3\::\:x^3-3x+1\)
まずガロア群が \(C_3\) の方程式 \(x^3-3x+1=0\) を取り上げ、巡回拡大がべき根拡大になる原理を確認します。この原理はガロア群が \(S_3\) のときにもそのまま応用できます。ちなみに \(C_3\) の方程式は \(p,\:q\) が \(-9\leq p\leq-1,\:\:1\leq q\leq9\) の整数だと、他に、
\(x^3-7x+6=0\:\:\:(D=400,\:\sqrt{D}=20)\)
\(x^3-7x+7=0\:\:\:(D=\phantom{0}49,\:\sqrt{D}=\phantom{0}7)\)
\(x^3-9x+9=0\:\:\:(D=729,\:\sqrt{D}=27)\)
があります。
\(x^3-3x+1=0\) の場合、\(p=-3,\:q=1\) なので、
\(\begin{eqnarray}
&&\:\:D&=-4p^3-27q^2=81=9^2\\
&&\:\:\theta&=\pm\sqrt{D}=\pm9\\
\end{eqnarray}\)
となります。3つの解を \(\al,\:\beta,\:\gamma\) とすると、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
で、\(\bs{L}\) の次元は \(3\) で、\(G=\mr{Gal}(\bs{L}/\bs{Q})\cong C_3\) です。
以下「7.3 べき根拡大の十分条件」の証明の論理に沿います。7.3 の証明では、体に \(1\) の原始\(n\)乗根が含まれているのが条件でした。そこで \(1\) の原始3乗根 を \(\omega\) とし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\:\al)=\bs{L}(\omega)\)
という体の拡大を考えます。\(\omega\) は \(x^2+x+1=0\) の2つある根のどちらかで、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
です。7.3 ではラグランジュのレゾルベントを \(\al\) と書きましたが、方程式の根の表記との重複を避けるため、ここでは \(S\) とします。そうするとレゾルベントは、
\(S=c+\omega^2\sg(c)+\omega\sg^2(c)\)
\((\br{A})\)
です。\(\bs{Q}(\omega,\:\al)\) は \(\bs{Q}(\omega)\) に \(\al\) を添加した単拡大体なので、べき根拡大の十分条件のため補題2(72B)に従って、\(c=\al\) と定めます。そうすると、
\(S=\al+\omega^2\sg(\al)+\omega\sg^2(\al)\)
となり、\(\al,\:\beta,\:\gamma\) で表すと、\((\br{A})\) 式は、
\(S=\al+\omega^2\beta+\omega\gamma\)
\((\br{B})\)
です。この \(S\) は \(\bs{Q}(\omega,\al,\beta,\gamma)\) の元ですが、
\(\bs{Q}(\omega,\al,\beta,\gamma)=\bs{Q}(\omega,\al)\)
なので、\(S\) は \(\bs{Q}(\omega,\al)\) の元であり、ということは、
\(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\al)\)
です。方程式の3つの解を \(\al,\:\beta,\:\gamma\) に割り当てる方法の数(\(=3!\) )により、\(S\) は6通りの可能性があります。
7.3 での証明のポイントは、\(\bs{S^3}\) が \(\bs{\bs{Q}(\omega)}\) の元である、というところでした。それを計算で確かめるため、もうひとつのレゾルベントを導入します。ガロア群 \(G=\{e,\sg,\sg^2\}\) は、\(\sg\) が生成元であると同時に、\(\sg^2\) も生成元です。レゾルベントの定義における \(\sg\) は \(G\) の生成元であることが条件でした(73A)。そこで \((\br{A})\) 式の \(\sg\) を \(\sg^2\) で置き換えた式を \(T\) とすると、
\(\begin{eqnarray}
&&\:\:T&=c+\omega^2\sg^2(c)+\omega\sg^4(c)\\
&&&=c+\omega^2\sg^2(c)+\omega\sg(c)\\
\end{eqnarray}\)
となります。この式で \(c=\al\) とおくと
\(T=\al+\omega\beta+\omega^2\gamma\)
です。\(S\) には6通りの可能性がありますが、\(S\) をそのうちの一つに決めると \(T\) は一意に決まります。ここで、
| \(\al+\omega^2\beta\) | \(+\omega\gamma\) | \(=S\) | |
| \(\al+\omega\beta\) | \(+\omega^2\gamma\) | \(=T\) | |
| \(\al+\beta\) | \(+\gamma\) | \(=0\) (根と係数の関係) |
\(\al=\dfrac{1}{3}(S+T)\)
\(\beta=\dfrac{1}{3}(\omega S+\omega^2T)\)
\(\gamma=\dfrac{1}{3}(\omega^2S+\omega T)\) \((\br{C})\)
です。さらに、\(S\) と \(T\) には特別の関係があります。
\(ST=(\al+\omega^2\beta+\omega\gamma)(\al+\omega\beta+\omega^2\gamma)\)
という式を考えると、
\(\begin{eqnarray}
&&\:\:ST&=&\al^2+\beta^2+\gamma^2+\\
&&&&(\omega^2+\omega)\al\beta+(\omega^4+\omega^2)\beta\gamma+(\omega^2+\omega)\gamma\al\\
&&&=&(\al+\beta+\gamma)^2-2(\al\beta+\beta\gamma+\gamma\al)+\\
&&&&(-\al\beta-\beta\gamma-\gamma\al)\\
&&&=&-3(\al\beta+\beta\gamma+\gamma\al)\\
&&&=&-3p\\
\end{eqnarray}\)
となり、つまり、
\(ST=-3p\)
\((\br{D})\)
という関係です。上の式の変形では、根と係数の関係と \(\omega^2+\omega+1=0\)、および \(\omega^3=1\) を使いました。
次に、\(S^3\) を求めるために \(S^3+T^3\) を計算してみると、
\(\begin{eqnarray}
&&\:\:S^3+T^3&=(S+T)(S^2-ST+T^2)\\
&&&=(S+T)(S+\omega T)(S+\omega^2T)\\
\end{eqnarray}\)
です。ここで \((\br{C})\) 式を変形すると、
| \(3\al\) | \(=S+T\) | |
| \(3\omega^2\beta\) | \(=S+\omega T\) | |
| \(3\omega\gamma\) | \(=S+\omega^2T\) |
\(\begin{eqnarray}
&&\:\:S^3+T^3&=3\al\cdot3\omega^2\beta\cdot3\omega\gamma\\
&&&=27\al\beta\gamma=-27q\\
\end{eqnarray}\)
となります。まとめると、
\(S^3+T^3=-27q\)
\(ST=-3p\)
であり、
\(S^3-\dfrac{27p^3}{S^3}+27q=0\)
です。つまり、
\((S^3)^2+27qS^3-27p^3=0\)
\((\br{E})\)
という \(S^3\) についての2次方程式を解くことで \(S^3\) が求まり、そこから \(S\) が求まります。\(S\) の値の可能性は6通りです。また \(T^3\) についても、
\((T^3)^2+27qT^3-27p^3=0\)
\((\br{E}')\)
が成り立ちます。2次方程式、
\(X^2+27qX-27p^3=0\)
\((\br{F})\)
の2つの解が \(S^3\) と \(T^3\) です。
ここまでの計算は \(x^3+px+q=0\) の形の既約方程式なら成り立ちます。ここで \(x^3-3x+1=0\) に即した、\(p=-3,\:q=1\) を \((\br{E})\) 式に入れると、
\((S^3)^2+27S^3+27^2=0\)
\(\begin{eqnarray}
&&\:\:S^3&=\dfrac{1}{2}\left(-27\pm\sqrt{27^2-4\cdot27^2}\right)\\
&&&=27\dfrac{-1\pm i\sqrt{3}}{2}\\
&&&=27\omega\\
\end{eqnarray}\)
となります。最後の式の \(\omega\) は、2つある \(1\) の原始3乗根のどちらか、という意味にとらえます。\(S^3=27\omega\) なら \(T^3=27\omega^2\) で、その逆でもよいわけです。
\((\br{C})\) 式と \((\br{D})\) 式により、\(\al\) は \(S\) と \(\omega\) の四則演算で表現できます。つまり、
\(\bs{Q}(\omega,\al)\subset\bs{Q}(\omega,\:S)\)
です。従って、さきほどの \(\bs{Q}(\omega,\:S)\subset\bs{Q}(\omega,\:\al)\) と合わせると、
\(\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\)
です。以上をまとめると、レゾルベント \(S\) について、
\(\begin{eqnarray}
&&\:\:S^3&\in\bs{Q}(\omega)\\
&&\:\:S&\in\bs{Q}(\omega,\:S)=\bs{Q}(\omega,\:\al)\\
\end{eqnarray}\)
です。つまり、
\(\bs{Q}(\omega)\) 上の方程式、
\(x^3-a=0\:\:(\:a=27\omega\in\bs{Q}(\omega)\:)\)
の解の一つ、\(\sqrt[3]{a}\) を \(\bs{Q}(\omega)\) に添加したのが \(\bs{Q}(\omega,\:\al)\)
であり、\(\bs{\bs{Q}(\omega,\:\al)}\) は \(\bs{\bs{Q}(\omega)}\) のべき根拡大体であることがわかりました。\(\bs{Q}(\omega,\:\al)\) は \(x^3-a=0\) の解、\(\sqrt[3]{a},\:\sqrt[3]{a}\:\omega,\:\sqrt[3]{a}\:\omega^2\) の全部を含むので、\(\bs{Q}(\omega)\) のガロア拡大体です。結論として、
方程式 \(x^3-3x+1=0\) の解は、
の四則演算で表現できる
| 有理数 | |
| \(\omega\)(\(1\) の原始3乗根) | |
| \(\sqrt[3]{a}\:\:(\:a\in\bs{Q}(\omega)\:)\) |
ことになります。\(x^3-3x+1=0\) の場合、\(a=27\omega\) です。
巡回拡大がべき根拡大になることの証明のフォローはここまでですが、\(x^3-3x+1=0\) の解を具体的に求めることもできます。\(S^3=27\omega\) から、\(S=3\cdot\sqrt[3]{\omega}\) であり、また \(ST=9\) なので、
\(\begin{eqnarray}
&&\:\:\al&=\dfrac{1}{3}(S+T)=\dfrac{1}{3}\left(S+\dfrac{9}{S}\right)\\
&&&=\sqrt[3]{\omega}+\dfrac{1}{\sqrt[3]{\omega}}=\sqrt[3]{\omega}+\sqrt[3]{\omega^2}\\
&&&=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i}\\
\end{eqnarray}\)
が解の一つです。「1.3 ガロア群」の「ガロア群の例」に書いたように、
\(\al=1.53208888623796\:\cd\)
であり、正真正銘の正の実数ですが、\(\bs{\al}\) をべき根で表わそうとすると虚数単位が登場します。その理由がガロア理論から分かるのでした。
\(S_3\::\:x^3+px+q\)
方程式 \(x^3+px+q=0\) の係数を変数のままで扱い、ガロア群が \(S_3\) の方程式の一般論として話を進めます。3つの根を \(\al,\:\beta,\:\gamma\) とし(置換での表示では、それぞれ \(1,\:2,\:3\))、差積 \(\theta\) を、
\(\begin{eqnarray}
&&\:\:\theta&=(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=\sqrt{D}\\
&&\:\:D&=-4p^3-27q^2\\
\end{eqnarray}\)
と定義すると、\(\bs{\theta}\) が有理数でないとき、
\(G\cong S_3\) \(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\) \(\sg=(1,\:2,\:3)\:\:\tau=(2,\:3)\) \(H=\{e,\:\sg,\:\sg^2\}\) は \(G\) の正規部分群 \(G\:\sp\:H\:\:\sp\:\{\:e\:\}\) は可解列 \(G/H=\{H,\:\tau H\}\cong C_2\) \(H/{\:e\:}=H\cong C_3\) \(G\) は可解群 |
となります(前述)。\(G\cong S_3\) は巡回群ではありません。しかし可解群なので "巡回群の入れ子構造" になっていて(=可解列が存在する)、「巡回拡大はべき根拡大」の定理(73A)を2段階に使うことで、方程式の解が四則演算とべき根で表現できることを証明できます。
まず、上記の可解列とガロア対応(53B)になっている「体の拡大列」は何かです。具体的には \(H\) の固定体は何かですが、それは \(\bs{Q}(\theta)\) です。実際、
\(\sg(\theta)=\theta,\:\:\sg^2(\theta)=\theta\)
なので、\(H\) のすべての元は \(\bs{Q}(\theta)\) の元を固定します。また、
\(\tau(\theta)=-\theta\)
なので、\(\tau\)(および \(\sg\tau,\:\sg^2\tau\))は \(\bs{Q}(\theta)\) の元 を固定しません。従って、\(H\) の固定体は \(\bs{Q}(\theta)\) です。つまり、\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) と書くと、
| \(G\:\sp\:H\:\) | \(\:\sp\:\{\:e\:\}\) | |
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\) | \(\:\subset\:\bs{L}\) |
というガロア対応になっています。
次に体の拡大次元を検証します。まず、\(|G|=6\) なので、次数と位数の同一性(52B)により、\(\bs{L}/\bs{Q}\) の拡大次数は、
\([\:\bs{L}:\bs{Q}\:]=6\)
です。\(\bs{Q}(\theta)\) は \(\bs{Q}\) 上の既約な2次方程式、
\(x^2-D=0\)
の解である \(\theta\) で \(\bs{Q}\) を単拡大した体なので、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\theta):\bs{Q}\:]=2\)
です。そうすると、拡大次数の連鎖律(33H)により、
\([\:\bs{L}:\bs{Q}\:]=[\:\bs{L}:\bs{Q}(\theta)\:]\cdot[\:\bs{Q}(\theta):\bs{Q}\:]\)
\([\:\bs{L}:\bs{Q}(\theta)\:]=3\)
となるはずです。\([\:\bs{L}:\bs{Q}(\theta)\:]=3\) であることを、具体的な体の拡大の様子を検証することで確かめます。2つのことを証明します。
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) とするとき、\(\bs{Q}(\theta,\al)=\bs{L}\) である。
[証明]
\(\theta=(\al-\beta)(\beta-\gamma)(\gamma-\al)\) だから、\(\theta\) は \(\al,\:\beta,\:\gamma\) で表現されている。従って
\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\)
である。この逆である、
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であることを証明する。そのためには \(\beta,\:\gamma\) が「有理数と \(\theta,\:\al\) の四則演算」で表現できることを示せばよい。根と係数の関係により、
\(\beta+\gamma=-\al\)
\(\beta\gamma=-\dfrac{q}{\al}\) \((\br{G})\)
である。これを利用して \(\theta\) の定義式を変形すると、
\(\begin{eqnarray}
&&\:\:\theta=&(\al-\beta)(\beta-\gamma)(\gamma-\al)\\
&&&=(\beta-\gamma)(-\al^2+(\beta+\gamma)\al-\beta\gamma)\\
&&&=(\beta-\gamma)\left(-\al^2-\al^2+\dfrac{q}{\al}\right)\\
&&&=(\beta-\gamma)\dfrac{-2\al^3+q}{\al}\\
\end{eqnarray}\)
となり、
\(\beta-\gamma=\dfrac{\al\theta}{q-2\al^3}\)
である。\((\br{G})\) 式と \((\br{H})\) 式は \(\beta\) と \(\gamma\) についての連立1次方程式なので解が求まり、\(\beta\) と \(\gamma\) は \(\al,\:\theta,\:q\) の四則演算で表現できる。従って、 \((\br{H})\)
\(\bs{Q}(\al,\beta,\gamma)\:\subset\:\bs{Q}(\theta,\al)\)
であり、\(\bs{Q}(\theta,\al)\:\subset\:\bs{Q}(\al,\beta,\gamma)\) と合わせて、
\(\bs{Q}(\theta,\al)=\bs{Q}(\al,\beta,\gamma)\)
である。[証明終]
\(x^3+px+q\) は \(\bs{\bs{Q}(\theta)}\) 上の既約多項式である。
[証明]
\(\bs{Q}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解 \(\al\) による \(\bs{Q}\) の単拡大体 \(\bs{Q}(\al)\) を考えると、単拡大体の基底の定理(33F)により、
\([\:\bs{Q}(\al):\bs{Q}\:]=3\)
である。従って \(\al\notin\bs{Q}(\theta)\) である。なぜなら、もし \(\al\in\bs{Q}(\theta)\) なら \(\bs{Q}(\theta)\) の次元は \(3\) 以上になるが、\([\:\bs{Q}(\theta):\bs{Q}\:]=2\) なので矛盾が生じるからである。同様に、\(\beta,\:\gamma\notin\bs{Q}(\theta)\) である。\(x^3+px+q\) は、
\(x^3+px+q=(x-\al)(x-\beta)(x-\gamma)\)
と表されるから、\(x^3+px+q\) は \(\bs{Q}(\theta)\) 上では因数分解できない。つまり \(x^3+px+q\) は \(\bs{Q}(\theta)\) 上の既約多項式である。[証明終]
以上により、
\(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) は、\(\bs{\bs{Q}(\theta)}\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体、\(\bs{L}=\bs{Q}(\theta,\al)\) であり、その拡大次数は \([\:\bs{L}:\bs{Q}(\theta)\:]=\:3\) である
ことが検証できました。これを踏まえて、3次方程式が解ける理由をガロア理論で説明します。ガロア対応である、
| \(G\:\sp\:H\:\) | \(\:\sp\:\{\:e\:\}\) | |
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\) | \(\:\subset\:\bs{L}\) |
を2つの部分に分けます。
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\)
\(\mr{Gal}(\bs{Q}(\theta)/\bs{Q})\cong G/H\cong C_2\) であり、\(\bs{Q}(\theta)/\bs{Q}\) は巡回拡大で、拡大次数は \(2\) です。\(1\) の原始2乗根は \(-1\) であり、\(\bs{Q}\) に含まれています。従って \(\bs{Q}(\theta)/\bs{Q}\) はべき根拡大です。具体的には、
\(x^2-D=0\:\:(D\in\bs{Q})\)
\(D=-4p^3-27q^2\)
の解が \(\theta\) であり、
\(\theta=\sqrt{D}=\sqrt{-4p^3-27q^2}\)
です。これはレゾルベントを持ち出すまでもなく分かります。
\(\bs{Q}(\theta)\:\subset\:\bs{L}\)
\(\mr{Gal}(\bs{L}/\bs{Q}(\theta))=H\cong C_3\) であり、\(\bs{L}/\bs{Q}(\theta)\) は巡回拡大で、拡大次数は \(3\) です。また \(\bs{L}\) は \(\bs{Q}(\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解の一つである \(\al\) を \(\bs{Q}(\theta)\) に添加した単拡大体で、\(\bs{L}=\bs{Q}(\theta,\al)\) でした。
\(\bs{Q}(\theta)\) には(一般には)\(1\) の原始3乗根が含まれていません。そこで、\(\bs{L}/\bs{Q}(\theta)\) の体の拡大の代わりに、\(\bs{L}(\omega)/\bs{Q}(\omega,\theta)\) という拡大を考えます。
\(\bs{L}(\omega)=\bs{Q}(\omega,\theta,\al)\)
\([\:\bs{Q}(\omega,\theta,\al):\bs{Q}(\omega,\theta)\:]=3\)
です。 \((\br{I})\)
方程式によっては \(\theta\in\bs{Q}(\omega)\) の場合があります。たとえば、\(p=0\) だと、
\(\theta=\sqrt{-27q^2}=3\sqrt{3}i\cdot q\)
ですが、\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\) なので、\(\theta\in\bs{Q}(\omega)\) です。この場合は、
\(\bs{Q}(\omega,\theta)=\bs{Q}(\omega)=\bs{Q}(\theta)\)
ですが、\((\br{I})\) 式は成り立ちます。レゾルベント \(S,\:T\) を導入して \(S^3\) と \(T^3\) を求めます。計算は、方程式 \(x^3-3x+1=0\) のときと全く同じです。つまり、
\(S=\al+\omega^2\beta+\omega\gamma\)
\(T=\al+\omega\beta+\omega^2\gamma\) \((\br{B})\)
\(ST=-3p\)
\(S^3+T^3=-27q\) \((\br{D})\)
\(\al=\dfrac{1}{3}(S+T)\)
\(\beta=\dfrac{1}{3}(\omega S+\omega^2T)\)
\(\gamma=\dfrac{1}{3}(\omega^2S+\omega T)\) \((\br{C})\)
\(X^2+27qX-27p^3=0\)
の2つの解が \(S^3\) と \(T^3\) \((\br{F})\)
です。方程式 \(x^3-3x+1=0\) の場合、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からの巡回拡大でしたが、\(x^3-3p+1q=0\) では \(\bs{Q}(\omega,\theta)\) からの巡回拡大であり、ガロア群が位数 \(3\) の巡回群であるという点では全く同じなのです。
\((\br{F})\) 式から \(X\) を求めると、
\(\begin{eqnarray}
&&\:\:X&=\dfrac{1}{2}\left(-27q\pm\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q\pm\sqrt{-27\theta^2}\right)\\
&&&=\dfrac{1}{2}(-27q\pm3\sqrt{3}i\cdot\theta)\\
\end{eqnarray}\)
となるので、
\(S^3=\dfrac{1}{2}(-27q+3\sqrt{3}i\cdot\theta)\)
\(T^3=\dfrac{1}{2}(-27q-3\sqrt{3}i\cdot\theta)\)
となります。\(S^3\) と \(T^3\) は逆でもかまいません。\(\omega\) は \(1\) の原始3乗根で、
\(\omega=\dfrac{1}{2}(-1\pm\sqrt{3}i)\)
のどちらかです。従って、
\(\sqrt{3}i\in\bs{Q}(\omega,\theta)\)
です。つまり、
\(S^3,\:\:T^3\in\bs{Q}(\omega,\theta)\)
であることがわかりました。従って、\(S,\:T\) は \(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解ということになり、\(\bs{Q}(\omega,\theta,\:S)/\bs{Q}(\omega,\theta)\) の体の拡大を考えると、
\([\:\bs{Q}(\omega,\theta,\:S):\bs{Q}(\omega,\theta)\:]=3\)
です。\(\bs{Q}(\omega,\theta,\:S)\) は \(\bs{Q}(\omega,\theta,\:T)\) としても同じことです。ここで、 \((\br{J})\)
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
であることが次のようにして分かります。つまり、\(\bs{Q}(\omega,\theta)\) 上の既約な3次方程式 \(x^3+px+q=0\) の解が \(\al,\:\beta,\:\gamma\) であり、\((\br{B})\) 式により \(S\) は \(\al,\:\beta,\:\gamma,\:\omega\) の四則演算で表されているので、
\(S\in\bs{Q}(\omega,\theta,\al,\beta,\gamma)\)
であり、また、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)\)
だったので、
\(S\in\bs{Q}(\omega,\theta,\al)\)
です。このことから、
\(\bs{Q}(\omega,\theta,\:S)\subset\bs{Q}(\omega,\theta,\:\al)\)
です。\((\br{I})\) 式と \((\br{J})\) 式により、\(\bs{Q}(\omega,\theta,\:S)\) と \(\bs{Q}(\omega,\theta,\:\al)\) の次元は等しく、かつ \((\br{K})\) 式の関係があるので、体の一致の定理(33I)により2つの体は一致し、 \((\br{K})\)
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
です。
この説明は「7.3 べき根拡大の十分条件」の証明に従いましたが、3次方程式の場合は、\((\br{C})\) 式と \((\br{D})\) 式により、\(\al,\:\beta,\:\gamma\) が \(S\) と \(\omega\) の四則演算で表現できます。従って、
\(\bs{Q}(\omega,\theta,\al,\beta,\gamma)\subset\bs{Q}(\omega,\theta,S)\)
\(\bs{Q}(\omega,\theta,\al)\subset\bs{Q}(\omega,\theta,S)\)
であり、
\(\bs{Q}(\omega,\theta,S)\subset\bs{Q}(\omega,\theta,\al)\)
と合わせて
\(\bs{Q}(\omega,\theta,\:S)=\bs{Q}(\omega,\theta,\:\al)\)
である、とするのが簡便な説明になります。
以上をまとめると、
\(\bs{Q}(\omega,\theta)\) 上の3次方程式、\(x^3-a=0\:\:(a\in\bs{Q}(\omega,\theta))\) の解の一つ、\(S\) を \(\bs{Q}(\omega,\theta)\) に添加したべき根拡大体が \(\bs{Q}(\omega,\theta,\al)=\bs{L}(\omega)\) である
となり、体に \(\bs{\omega}\) が含まれる前提で、巡回拡大はべき根拡大であることが検証できました。ここから、\(\bs{L}(\omega)\) を \(\bs{Q}\) の拡大体として、方程式の係数 \(p,\:q\) を使って、できるだけ簡潔な形で表してみます。
\(\begin{eqnarray}
&&\:\:\theta&=\sqrt{-4p^3-27q^2}\\
&&&=6\cdot\sqrt{3}i\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\\
\end{eqnarray}\)
ですが、\(\sqrt{3}i\in\bs{Q}(\omega)\) なので、
\(\bs{Q}(\omega,\theta)=\bs{Q}\left(\omega,\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\)
と表せます。また、
\(\begin{eqnarray}
&&\:\:X^3&=\dfrac{1}{2}\left(-27q+\sqrt{27^2q^2+27\cdot4p^3}\right)\\
&&&=\dfrac{1}{2}\left(-27q+27\cdot2\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
&&&=27\left(-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}\right)\\
\end{eqnarray}\)
なので、
\(S=3\cdot\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(T=3\cdot\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
が \(S,\:T\) です。\(\sqrt[3]{\phantom{I}\cd\phantom{I}}\) は3乗して \(\cd\) になる数の意味です。従って、\(S\) の選び方は3通りですが、\(S\) を一つに決めると、
\(ST=-3p\)
が成り立つように \(T\) を選ぶ必要があります。以上の \(S\) を用いて \(\bs{L}(\omega)\) を表すと、
\(\bs{L}(\omega)\)
\(=\bs{Q}(\omega,\theta,\al,\beta,\gamma)=\bs{Q}(\omega,\theta,\al)=\bs{Q}(\omega,\theta,S)\)
\(=\bs{Q}\left(\omega,\:\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}},\:\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\right)\)
となります。この式が意味するところは、
\(\dfrac{q^2}{4}+\dfrac{p^3}{27}\) が有理数なので、\(\bs{L}(\omega)\) は \(\bs{Q}(\omega)\) からのべき根拡大を、\(\sqrt{\phantom{A}}\) と \(\sqrt[3]{\phantom{A}}\) の2回繰り返したものである
ということです。べき根拡大の出発点は 有理数に \(\omega\) を添加した体です。「7.1 1の原始n乗根」で証明したように、原始\(n\)乗根はべき根で表現可能であり(71A)、もちろん \(\omega\) もそうです。これが3次方程式が解ける原理(一般化するとガロア群が可解群である方程式が解ける原理)です。補足すると、\(p=0\) のときは、
\(\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}=\pm\dfrac{q}{2}\in\bs{Q}\)
なので、べき根拡大は \(\sqrt[3]{\phantom{A}}\) の1回だけになります。
さらに、ここまでの計算で3次方程式の解も求まりました。解は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=\dfrac{1}{3}(S+T)&\\
&&\beta=\dfrac{1}{3}(\omega S+\omega^2T)&\\
&&\gamma=\dfrac{1}{3}(\omega^2S+\omega T)&\\
\end{eqnarray}
\end{array}\right.\)
であり、記号を、
\(S=3s\)
\(T=3t\)
に置き換えると、
3次方程式の解の公式
\(x^3+px+q=0\) の3つの解を \(\al,\:\beta,\:\gamma\) とする。
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\al=s+t&\\
&&\beta=\omega s+\omega^2t&\\
&&\gamma=\omega^2s+\omega t&\\
\end{eqnarray}
\end{array}\right.\)
\(s=\sqrt[3]{-\dfrac{q}{2}+\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(t=\sqrt[3]{-\dfrac{q}{2}-\sqrt{\dfrac{q^2}{4}+\dfrac{p^3}{27}}}\)
\(st=-\dfrac{p}{3}\)
が、3次方程式の解の公式です。
3次方程式の解による体の拡大を振り返ってみます。\(\bs{Q}\) 上の既約な方程式 \(x^3+px+q=0\) の根を \(\al,\:\beta,\:\gamma\) とし、\(\bs{Q}\) の最小分解体 を \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\)、ガロア群を \(G=\mr{Gal}(\bs{L}/\bs{Q})\) とすると、
| \(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\:\) | \(\:\subset\:\bs{L}\) | |
| \(G\:\sp\:H\:\:\:\) | \(\:\sp\:\{\:e\:\}\) |
\(\bs{Q}\:\subset\:\bs{Q}(\theta)\:\subset\:\bs{L}\)
という体の拡大列で、\(\bs{Q}\:\subset\:\bs{Q}(\theta)\) のところはべき根拡大ですが、\(\bs{Q}(\theta)\:\subset\:\bs{L}\) は、\(\omega\in\bs{Q}(\theta)\) の場合を除き、べき根拡大ではありません。しかし、
\(\bs{Q}(\omega)\:\subset\:\bs{Q}(\omega,\theta)\:\subset\:\bs{L}(\omega)\)
なら、必ず、すべてがべき根拡大になります。従って、3次方程式の解は \(\bs{Q}(\omega)\) の元である「有理数と \(\omega\)」の四則演算・べき根で記述できます。
\(\omega\) は \(x^2+x+1=0\) の解なので、\([\:\bs{Q}(\omega):\bs{Q}\:]=2\) です。従って、拡大次数の連鎖律(33H)により、\(\omega\notin\bs{Q}(\theta)\) の条件で、
\([\:\bs{L}(\omega):\bs{Q}\:]=12\)
です。これは、\(\bs{Q}\) 上の多項式 \((x^3+px+q)(x^2+x+1)\) の最小分解体が \(\bs{L}(\omega)\) なので、\(\bs{Q}\) からの拡大次数は \(12\) であるとも言えます。3次方程式の「解」は、あくまで \(\bs{Q}\) の \(6\)次拡大体 \(\bs{L}=\bs{Q}(\al,\beta,\gamma)\) の中にありますが、「べき根で表された解」は \(\bs{Q}\) の \(12\)次拡大体 \(\bs{L}(\omega)\) の中にあるのです。
一見、矛盾しているようですが、そうではありません。ある代数拡大体 \(\bs{K}\) があったとして、\(a\) を \(\bs{K}\) の元とし、\(1\) の原始3乗根の一つを \(\omega\) とします。3次方程式、
\(x^3-a=0\:\:(a\in\bs{K})\)
は3つの解をもちます。そのうちのどれか一つを \(\sqrt[3]{a}\) と定義すると、3つの解(べき根)は、
\(\sqrt[3]{a},\:\:\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2\)
です。\(\sqrt[3]{a}\) では \(\omega\) が不要なように見えますが、それは表面上のことで、3つの解は、
\(\sqrt[3]{a}\:\omega,\:\:\sqrt[3]{a}\:\omega^2,\:\:\sqrt[3]{a}\:\omega^3\)
であるというのが正しい認識です。つまり \(\bs{\omega}\) は3つのべき根の関係性を規定していて、\(\sqrt[3]{a}\cdot\omega^i\:\:(i=1,2,3)\) という "ペアの形" によって3つの区別が可能になり、数式としての整合性が保てます。\(\sqrt[3]{\phantom{A}}\) という "曖昧さ" がある記号を用いる限り、\(\omega\) という、曖昧さを解消する "助手" が必然的に登場するのです。
「7.7 巡回拡大はべき根拡大」終わり
(「7.可解性の十分条件」は次回に続く)
(「7.可解性の十分条件」は次回に続く)
2023-04-30 07:54
nice!(0)



