No.314 - 人体に380兆のウイルス [科学]
No.307-308「人体の9割は細菌」で、ヒトは体内や皮膚に棲む微生物と共存していることを書きました。これら微生物には、もちろんヒトに有害な事象を引き起こすものもありますが、ヒトの役に立ったり、ヒトの免疫機構を調整しているものもある。人体は微生物と共存することを前提に成り立っています。
No.307-308での "微生物" は、題名にあるように主に細菌でした。しかし忘れてはいけない微生物のジャンルはウイルスです。そして人体はウイルスとも共存しています。人体に共存する微生物の総体(=微生物叢)をマイクロバイオーム(Microbiome。厳密にはヒトマイクロバイオーム)と言いますが、ウイルスの総体(=ウイルス叢)をバイローム(Virome。ヒトバイローム)と言います。言葉がややこしいのですが、マイクロバイオームの一部としてバイロームがあると考えてよいでしょう。
ウイルスというと、病気を引き起こす "ヒトの敵" というイメージが強いわけです。新型コロナウイルスがまさにそうだし、No.302「ワクチン接種の推奨中止で4000人が死亡」でとりあげたのは、子宮頸癌を引き起こすヒトパピローマウイルス(HPV)とそのワクチンの話でした(HPV は他の癌の原因にもなりうる)。大きな社会問題にもなった肝炎を引き起こすウイルスがあるし、エイズもウイルスの感染で発症する病気です。もちろんインフルエンザもウイルスが原因です。
しかしウイルスの中にはヒトに "好ましい" 影響を与えるものもあります。その好例が、No.229「糖尿病の発症をウイルスが抑止する」で紹介したある種のウイルスで、膵臓がこのウイルスに感染していると、遺伝性の自己免疫疾患である1型糖尿病の発症が抑止されるのでした。
人体と共存する細菌に "善玉菌" と "悪玉菌" があるように、ウイルスにも "善玉ウイルス" と "悪玉ウイルス" があることが想定されます。では、ヒトの "ウイルス叢" = "バイローム" の全体像はどうなっているのか。その探求が、この10年ほどの間に進んできました。ただ、この種の研究はまだ始まったばかりであり、本格的なバイロームの解明はこれからと言えます。
そのバイローム研究の最新状況を紹介した雑誌記事があったので、No.307-308「人体の9割は細菌」の続きとして紹介したいと思います。記事の題は「あなたの中にいる380兆のウイルス」で、日経サイエンス 2021年7月号に掲載されたものです。著者はカリフォルニア大学サンディエゴ校の病理学者、 デヴィッド・プライド(David Pride)准教授です。これは Scientific American 誌 2020年12月号の「The Viruses Inside You」を翻訳したものです。
ウイルスは人体の一部
新型コロナウイルス(ウイルス名:SARS-Cov-2)の影響もあり「ウイルスは病気をもたらすもの」という認識が一般的でしょう。しかし病気でなくても、普段からヒトの体内には何兆個ものウイルスが存在しています。このことは研究者の共通認識になってきました。
ヒトの細胞の総数は、最新の研究では約37兆個といわれています(赤血球を除くと約11兆個)。ヒトと共存している細菌は、数からいうと腸内細菌がほとんど(9割以上)で、ざっと100兆個といわれています。その細菌より多数のウイルスが体内にいることとになります。ウイルスの大きさが細菌の大きさの100~1000分の1であることを考えると、これは驚くに当たらないでしょう。これらの細菌やウイルスの数は、今後の研究の進展に従って増加することが考えられます。
これらのウイルスは、皮膚表面を含む体内のあらゆる場所に生息しており、脳の脊髄からも発見されています。
No.307-308「人体の9割は細菌」で書いたように、細菌のマイクロバイオームは赤ちゃんが生まれるその時点から形成されます。また母乳にも細菌が含まれていて、それが赤ちゃんに伝わる。このような状況はウイルスのバイロームでも同じのようです。
細菌と同じように、人のバイロームは、その人の「個人情報」になります。しかもこの個人情報は、人から人へと伝播しやすいという性質があります。新型コロナウイルスやインフルエンザウイルスの呼吸器系に感染するウイルスは、咳などの飛沫でも容易に伝播するのです。
要するに、同居人の間でのウイルスの伝播(バイロームの共有)は、性関係(=ロマンチックな関係)のあるなしには影響されないわけです。
細菌に感染するファージ
ウイルスは自前の増殖機能がないため、細胞に感染することで増えて広がっていきます。実は、ヒトの体内にいるウイルスの多くは、ヒトの細胞ではなく、体内に生息する細菌に感染するウイルスです。このタイプのウイルスをバクテリオファージ(略してファージ)と呼びます。
ファージは細菌と共存しているとも言えます。ということは、ヒトと共存する細菌の中にヒトに有益な作用をもたらすものがあるように、ファージの中にも細菌を "助ける" ものがあってもおかしくありません。
抗生物質は細菌に作用するだけで、ウイルスは影響を受けません。従って「細菌が抗生物質に抵抗するのを助ける遺伝子」をファージが運ぶとしたら、ファージの生存環境を確保し、ファージ自身の生存を促進するという "目的" しかないわけです。
人体細胞に感染するウイルス
もちろん細菌に感染するファージだけでなく、ヒトの細胞に直接感染するウイルスもあります。
普段は何もせずに感染しているウイルスが、ヒトの免疫機能の低下などにより急に病原性を発揮することがあります。このような状況を「日和見感染」といいます。また、何らかのウイルスが感染してヒトの免疫系がそれと戦っているときに、別の細菌やウイルスに感染することがあります。これを「共感染」と呼びます。
新型コロナ感染症でも重症者に共感染がみられます。黄色ブドウ球菌や肺炎レンサ球菌などによる "細菌性続発性肺炎" や "菌血症"(血液中に細菌が増える症状)です。また、インフルエンザウイルスやアデノウイルスなどの "ウイルス性共感染" も観察されています。さらに、既にバイローム中にいるエプスタイン・バーウイルス(EBウイルス)やサイトメガロウイルスが活性化される可能性もあります。ヒトの免疫系が新型コロナウイルスと戦っているその体内は、これらの細菌やウイルスが大増殖しやすい状態になっているわけです。
いま出てきた "EBウイルス" と "サイトメガロウイルス" は、ヘルペスウイルスの一種です。ヘルペスウイルスは約100種のウイルスの総称で、そのうちの9種がヒトに感染します。日本人でも半数以上の人が感染しています。このウイルスはヒトの神経節に "潜伏感染" し、そうなると増殖も何もしないので免疫系に攻撃されることがありません。しかし何らかのトリガーで活性化し、帯状疱疹や水痘(水ぼうそう)、口唇ヘルペスなどを引き起こします。
ヘルペスウイルスはそれ以外にも数々の病気とかかわっているのではと疑われています。その一つがアルツハイマー病です。
この引用にある「2018年の研究」を報じたニュース記事が次です。
ファージを医療に応用する
ウイルスを医療に役立てようとする研究が進められています。というのも、ファージは細菌に入り込み、細菌の機構を利用して増殖し、細菌を破壊して飛び出すからです。ファージを利用して病気の原因菌を排除しようとするのは自然な流れでしょう。その焦点は、抗生物質が効かない耐性菌の対策です。雑誌記事から2つ引用します。
ファージ医療は耐性菌対策の "切り札" だと、著者は書いてます。薬(抗生物質)が効かない病原菌を排除するためには、細菌に感染するファージを利用するのが切り札になるわけです。
バイロームとヒトの健康
ヒトのマイクロバイオーム(細菌)が健康と密接な関係があるように、バイロームもそうであることが十分考えられます。マウスによる実験では細菌の変化とウイルスの変化が同時に起こることが観察されています。ヒトにおいても、歯周病と炎症性腸疾患を発症とバイロームの変化が同時におこる場合があることがわかっています。
今後、ヒトの健康に影響を与えるカテゴリーのウイルスを "操作" して、疾患から我々の体を守る新たな方法がみつかることが期待されています。
以上が、日経サイエンス 2021年7月号に掲載された「あなたの中にいる380兆のウイルス」の概要です。ここから以降は、この記事に関連した最近の日本での話題をとりあげます。
ウイルスを医療に応用する
日経サイエンスの記事には、細菌に感染するファージを利用して病気の原因菌を人体から排除する "ファージ医療" のことが書かれていました。
ということは、人体から排除したいヒトの細胞を破壊するには、人体細胞に感染するウイルスを使えばよい、ということになります。人体から排除したいヒトの細胞とは、つまり癌細胞です。
癌治療にウイルスを使う研究は世界で行われてきましたが、2021年6月10日に東京大学医科学研究所の藤堂具紀教授は、ウイルスを使った治療薬が承認される見通しになったと発表しました。日本製としては初の承認です。
この発表の20日ほど前の朝日新聞デジタルには、癌のウイルス治療の歴史や背景を含めた解説がありました。以下です。
ヘルペスウイルスは潜伏感染をし、突如として病気を引き起こすというウイルスです。しかも日経サイエンスの記事にあったように、脳にも感染するヘルペスウイルスはアルツハイマー病の原因になるのではと疑われています。そのウイルスで癌細胞を攻撃するというのは、まさに「毒をもって毒を制する」ことの典型でしょう。
今回の承認は「悪性神経膠腫」の治療用ですが、前立腺がんなど、ほかの癌への応用の研究も進んでいるようです。東京大医科学研究所のホームページに詳しい説明がありますが、それを読むと、今回のヘルペスウイルス改変型ウイルスはすべての癌に効果があるとしか思えないのですね。
2020年に「癌の光免疫療法」が日本で承認され、"第5の癌療法" として注目されました(既存の4つとは、手術・化学・放射線・免疫の各療法)。ウイルス療法が "第6の癌療法" になること期待したいものです。
本文に引用した藤堂教授の研究成果が、2021年7月5日の日本経済新聞にも掲載されました。本文と重複する部分もありますが、治験結果などの重要な情報もあるので全文を引用しておきます。下線は原文にはありません。
No.307-308での "微生物" は、題名にあるように主に細菌でした。しかし忘れてはいけない微生物のジャンルはウイルスです。そして人体はウイルスとも共存しています。人体に共存する微生物の総体(=微生物叢)をマイクロバイオーム(Microbiome。厳密にはヒトマイクロバイオーム)と言いますが、ウイルスの総体(=ウイルス叢)をバイローム(Virome。ヒトバイローム)と言います。言葉がややこしいのですが、マイクロバイオームの一部としてバイロームがあると考えてよいでしょう。
ウイルスというと、病気を引き起こす "ヒトの敵" というイメージが強いわけです。新型コロナウイルスがまさにそうだし、No.302「ワクチン接種の推奨中止で4000人が死亡」でとりあげたのは、子宮頸癌を引き起こすヒトパピローマウイルス(HPV)とそのワクチンの話でした(HPV は他の癌の原因にもなりうる)。大きな社会問題にもなった肝炎を引き起こすウイルスがあるし、エイズもウイルスの感染で発症する病気です。もちろんインフルエンザもウイルスが原因です。
しかしウイルスの中にはヒトに "好ましい" 影響を与えるものもあります。その好例が、No.229「糖尿病の発症をウイルスが抑止する」で紹介したある種のウイルスで、膵臓がこのウイルスに感染していると、遺伝性の自己免疫疾患である1型糖尿病の発症が抑止されるのでした。
|
そのバイローム研究の最新状況を紹介した雑誌記事があったので、No.307-308「人体の9割は細菌」の続きとして紹介したいと思います。記事の題は「あなたの中にいる380兆のウイルス」で、日経サイエンス 2021年7月号に掲載されたものです。著者はカリフォルニア大学サンディエゴ校の病理学者、 デヴィッド・プライド(David Pride)准教授です。これは Scientific American 誌 2020年12月号の「The Viruses Inside You」を翻訳したものです。
ウイルスは人体の一部
新型コロナウイルス(ウイルス名:SARS-Cov-2)の影響もあり「ウイルスは病気をもたらすもの」という認識が一般的でしょう。しかし病気でなくても、普段からヒトの体内には何兆個ものウイルスが存在しています。このことは研究者の共通認識になってきました。
|
ヒトの細胞の総数は、最新の研究では約37兆個といわれています(赤血球を除くと約11兆個)。ヒトと共存している細菌は、数からいうと腸内細菌がほとんど(9割以上)で、ざっと100兆個といわれています。その細菌より多数のウイルスが体内にいることとになります。ウイルスの大きさが細菌の大きさの100~1000分の1であることを考えると、これは驚くに当たらないでしょう。これらの細菌やウイルスの数は、今後の研究の進展に従って増加することが考えられます。
|
これらのウイルスは、皮膚表面を含む体内のあらゆる場所に生息しており、脳の脊髄からも発見されています。
|
No.307-308「人体の9割は細菌」で書いたように、細菌のマイクロバイオームは赤ちゃんが生まれるその時点から形成されます。また母乳にも細菌が含まれていて、それが赤ちゃんに伝わる。このような状況はウイルスのバイロームでも同じのようです。
|
細菌と同じように、人のバイロームは、その人の「個人情報」になります。しかもこの個人情報は、人から人へと伝播しやすいという性質があります。新型コロナウイルスやインフルエンザウイルスの呼吸器系に感染するウイルスは、咳などの飛沫でも容易に伝播するのです。
|
要するに、同居人の間でのウイルスの伝播(バイロームの共有)は、性関係(=ロマンチックな関係)のあるなしには影響されないわけです。
細菌に感染するファージ
ウイルスは自前の増殖機能がないため、細胞に感染することで増えて広がっていきます。実は、ヒトの体内にいるウイルスの多くは、ヒトの細胞ではなく、体内に生息する細菌に感染するウイルスです。このタイプのウイルスをバクテリオファージ(略してファージ)と呼びます。
|
ファージは細菌と共存しているとも言えます。ということは、ヒトと共存する細菌の中にヒトに有益な作用をもたらすものがあるように、ファージの中にも細菌を "助ける" ものがあってもおかしくありません。
|
抗生物質は細菌に作用するだけで、ウイルスは影響を受けません。従って「細菌が抗生物質に抵抗するのを助ける遺伝子」をファージが運ぶとしたら、ファージの生存環境を確保し、ファージ自身の生存を促進するという "目的" しかないわけです。
人体細胞に感染するウイルス
もちろん細菌に感染するファージだけでなく、ヒトの細胞に直接感染するウイルスもあります。
|
普段は何もせずに感染しているウイルスが、ヒトの免疫機能の低下などにより急に病原性を発揮することがあります。このような状況を「日和見感染」といいます。また、何らかのウイルスが感染してヒトの免疫系がそれと戦っているときに、別の細菌やウイルスに感染することがあります。これを「共感染」と呼びます。
新型コロナ感染症でも重症者に共感染がみられます。黄色ブドウ球菌や肺炎レンサ球菌などによる "細菌性続発性肺炎" や "菌血症"(血液中に細菌が増える症状)です。また、インフルエンザウイルスやアデノウイルスなどの "ウイルス性共感染" も観察されています。さらに、既にバイローム中にいるエプスタイン・バーウイルス(EBウイルス)やサイトメガロウイルスが活性化される可能性もあります。ヒトの免疫系が新型コロナウイルスと戦っているその体内は、これらの細菌やウイルスが大増殖しやすい状態になっているわけです。
いま出てきた "EBウイルス" と "サイトメガロウイルス" は、ヘルペスウイルスの一種です。ヘルペスウイルスは約100種のウイルスの総称で、そのうちの9種がヒトに感染します。日本人でも半数以上の人が感染しています。このウイルスはヒトの神経節に "潜伏感染" し、そうなると増殖も何もしないので免疫系に攻撃されることがありません。しかし何らかのトリガーで活性化し、帯状疱疹や水痘(水ぼうそう)、口唇ヘルペスなどを引き起こします。
ヘルペスウイルスはそれ以外にも数々の病気とかかわっているのではと疑われています。その一つがアルツハイマー病です。
|
この引用にある「2018年の研究」を報じたニュース記事が次です。
|
ファージを医療に応用する
ウイルスを医療に役立てようとする研究が進められています。というのも、ファージは細菌に入り込み、細菌の機構を利用して増殖し、細菌を破壊して飛び出すからです。ファージを利用して病気の原因菌を排除しようとするのは自然な流れでしょう。その焦点は、抗生物質が効かない耐性菌の対策です。雑誌記事から2つ引用します。
|
|
ファージ医療は耐性菌対策の "切り札" だと、著者は書いてます。薬(抗生物質)が効かない病原菌を排除するためには、細菌に感染するファージを利用するのが切り札になるわけです。
バイロームとヒトの健康
ヒトのマイクロバイオーム(細菌)が健康と密接な関係があるように、バイロームもそうであることが十分考えられます。マウスによる実験では細菌の変化とウイルスの変化が同時に起こることが観察されています。ヒトにおいても、歯周病と炎症性腸疾患を発症とバイロームの変化が同時におこる場合があることがわかっています。
今後、ヒトの健康に影響を与えるカテゴリーのウイルスを "操作" して、疾患から我々の体を守る新たな方法がみつかることが期待されています。
以上が、日経サイエンス 2021年7月号に掲載された「あなたの中にいる380兆のウイルス」の概要です。ここから以降は、この記事に関連した最近の日本での話題をとりあげます。
ウイルスを医療に応用する
日経サイエンスの記事には、細菌に感染するファージを利用して病気の原因菌を人体から排除する "ファージ医療" のことが書かれていました。
ということは、人体から排除したいヒトの細胞を破壊するには、人体細胞に感染するウイルスを使えばよい、ということになります。人体から排除したいヒトの細胞とは、つまり癌細胞です。
癌治療にウイルスを使う研究は世界で行われてきましたが、2021年6月10日に東京大学医科学研究所の藤堂具紀教授は、ウイルスを使った治療薬が承認される見通しになったと発表しました。日本製としては初の承認です。
|
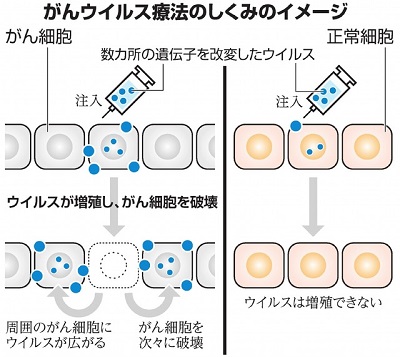
この発表の20日ほど前の朝日新聞デジタルには、癌のウイルス治療の歴史や背景を含めた解説がありました。以下です。
|
|
癌のウイルス治療のイメージ |
(朝日新聞デジタル 2021.5.24 より) |
ヘルペスウイルスは潜伏感染をし、突如として病気を引き起こすというウイルスです。しかも日経サイエンスの記事にあったように、脳にも感染するヘルペスウイルスはアルツハイマー病の原因になるのではと疑われています。そのウイルスで癌細胞を攻撃するというのは、まさに「毒をもって毒を制する」ことの典型でしょう。
今回の承認は「悪性神経膠腫」の治療用ですが、前立腺がんなど、ほかの癌への応用の研究も進んでいるようです。東京大医科学研究所のホームページに詳しい説明がありますが、それを読むと、今回のヘルペスウイルス改変型ウイルスはすべての癌に効果があるとしか思えないのですね。
2020年に「癌の光免疫療法」が日本で承認され、"第5の癌療法" として注目されました(既存の4つとは、手術・化学・放射線・免疫の各療法)。ウイルス療法が "第6の癌療法" になること期待したいものです。
| 補記 |
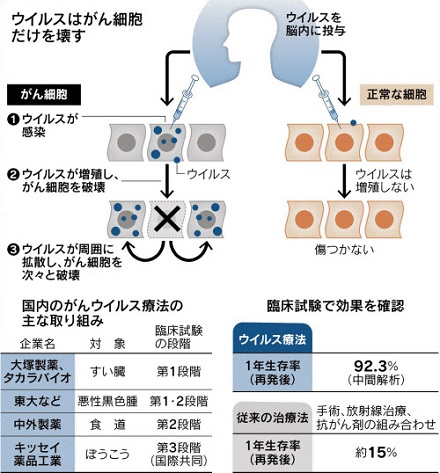
本文に引用した藤堂教授の研究成果が、2021年7月5日の日本経済新聞にも掲載されました。本文と重複する部分もありますが、治験結果などの重要な情報もあるので全文を引用しておきます。下線は原文にはありません。
|
|
日本経済新聞 2021.7.5 より |
(2021.7.7)
2021-06-27 08:01
nice!(0)
No.313 - 高校数学で理解する公開鍵暗号の数理 [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
No.310-311「高校数学で理解するRSA暗号の数理」の続きです。公開鍵暗号の "老舗" である RSA暗号は、1978年に MIT の研究者であったリベスト(米)、シャミア(イスラエル)、エーデルマン(米)の3人によって発明されました(RSAは3人の頭文字)。3人はこの功績によって2002年のチューリング賞を受賞しました。チューリング賞は計算機科学分野の国際学会である ACM(Association of Computing Machinary)が毎年授与している賞で、この分野では最高の栄誉とされているものです。
しかし公開鍵暗号そのもののアイデアを最初に提示したのは、スタンフォード大学の研究者だったディフィー(米)とヘルマン(米)で、1976年のことでした。2人も 2015年にチューリング賞を受賞しています。この「鍵を公開する」という、画期的というか逆転の発想である公開鍵暗号の登場以降、暗号の研究は一変してしまいました。そして RSA暗号のみならず各種の公開鍵暗号が開発され、現代のインターネットの基盤になっています。たとえばインターネットのWebサーバへのアクセス(閲覧やフォーム入力など)で使われる SSL/TSL という暗号化通信(https:// のサイトで使われる)は、まさに公開鍵方式を使っています。
今回はその公開鍵暗号を "発明した" ディフィーとヘルマンに敬意を表して、彼らが発表した「鍵共有システム」の内容と、その数学的背景を書いてみたいと思います。また、それと数学的な関連が深い「離散対数暗号」にも触れます。
ディフィーとヘルマンが提出したアイデアは「公開鍵を使って秘密鍵を安全に共有する」ものでした。これは「ディフィー・ヘルマンの鍵共有」と呼ばれていて、現在でも使われています。そこでまず「秘密鍵の共有」の意義を振り返ってみたいと思います。
秘密鍵の共有
古今東西、様々な暗号化方式が開発・使用されてきましたが「秘密鍵の共有による暗号」(=共通鍵暗号)が基本です。その中でも「一回限りの乱数表」は安全(=解読されない)と証明されている暗号です。この場合、乱数表が秘密鍵に相当します。
英大文字・小文字、数字、英文に使われる特殊文字を、\(0\) ~ \(127\) の数字でコード化するとします。いま、\(n\) 文字以下の平文をコード化して暗号文にしたいとき、「一回限りの乱数表」として必要なのは、\(0\) ~ \(127\) の値をとる乱数が \(n\) 個並んだ表です。さらに、
とするとき、「乱数 \(r_i\) の値に依存して、\(a_i\) を \(b_i\) に1対1に変換する関数 \(f\)」を決めておきます。そうすると、
の変換で暗号文 \(b_i\) が得られます。この関数 \(f\) は \(128\times128\) の コード変換テーブルでもいいし、\((a_i+r_i)\:\mr{mod}\:128\) のような四則演算でもよい。とにかく \(r_i\) が違えば別の1対1変換になる関数が条件で、そうすれば逆変換で複号化が可能です。
この関数を秘密にする必要はなく、オープンにしてもかまいません。この暗号が安全な理由は、
の2点によります。もちろん乱数が "真の乱数" であることも重要です。しかし、上の2点を守るためには秘密鍵(乱数表)の長さが膨大になります。使い終わった乱数表のページを破って捨てなければならないからです。そこで実用的には、暗号文のやりとりを始める前に秘密鍵を共有しておき、暗号化はその「秘密鍵にもとづいた何らかの暗号化方式」で行うことになります。こうすると平文の長さが秘密鍵より長くなるので、絶対に安全とは言えなくなります。そこで、解読しにくい(=強度の高い)暗号化方式の必要性があり、これをめぐって様々な方式が作られてきました。
しかし問題は、最初の「秘密鍵の共有」をどうやってやるかです。結局、秘密鍵を印刷し、アタッシュケースに入れて相手に持参するというような、スパイ映画にでも出てきそうな方法しか本質的には無いわけです。どういうやり方をとるにせよ「秘密鍵の共有」には多大なコストがかかる。
No.310-311「高校数学で理解する RSA 暗号の数理」で書いた公開鍵暗号の価値はそういうところにあります。つまり、RSA暗号における暗号化・複号化は巨大な数の "冪剰余" を求める計算になり、これはこれで計算機負荷が高い。そこで、まずRSA暗号を使って秘密鍵を生成・共有しておき、以降はその秘密鍵を使う高速な(= 計算機負荷の低い)暗号化・複号化方式で通信をするやり方が多くとられます(=ハイブリッド暗号)。もちろんその秘密鍵は通信が一段落したら捨てて、次の通信では新たな秘密鍵を生成して共有するわけです。これは他の公開鍵暗号でも同じです。
その、"公開鍵を使って秘密鍵を共有する" ことを最初に提唱したのが「ディフィー・ヘルマンの鍵共有」でした。そしてこれが、そもそもの「公開鍵の発明」になりました。この鍵共有は、
ためのアルゴリズムです。どうしてそんなことができるのかが、以降です。
9. ディフィー・ヘルマンの鍵共有
ディフィー・ヘルマンの鍵共有は次のように進みます。まず「公開鍵センター」が "皆が使う公開鍵"として、
のペアを公開しておきます。次に、\(A\) さんと \(B\) さんが秘密鍵を共有したい場合、
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。次に同様に、
します。もちろん \(b\) は秘匿します。そして、
とします。この作り方から \(G_a=G_b\) となるので、秘密鍵 \(G=g^{ab}\:(\mr{mod}\:p)\) が共有できたことになり、以降はこれを使って暗号化通信を行います。大切なことは \(A\) は \(B\) の秘密鍵(\(b\))を知らないし、\(B\) は \(A\) の秘密鍵(\(a\))を知らないことです。それでも秘密鍵 \(G\)(\(=G_a=G_b\))を共有できるわけです。
以上の仕組みにおいて通信路が盗聴されたとしても安全なのは、\(A\) の公開鍵 \(g^a\) から \(a\) を求めるのが困難なことと、同様に \(g^b\) から \(b\) を求めるのが困難なことです。なぜ困難かとい言うと、一つは \(\bs{p}\) が巨大な素数だからであり(\(10\)進数で数百桁か \(1000\)桁以上)、また \(\bs{g}\) が「生成元」(原始根ともいう)だからです。
以降でその「生成元」とは何か、盗聴者が公開鍵から \(A\) と \(B\) の秘密鍵(\(a\) と \(b\))をなぜ計算できないのかという、ディフィー・ヘルマンの鍵共有の数学的背景を概観します。以下の説明では「高校数学程度の知識だけ」を前提としますが(= タイトルの "高校数学で理解する" の意味)、No.310-311「高校数学で理解するRSA暗号の数理」での各種説明は既知とします。特に、
の知識を前提とします。
10. 有限体(\(\bs{F}_p\))と乗法群(\(\bs{F}_p^{*}\))
一般に加減乗除が定義された集合を "体(Field)" と言います。有理数、実数、複素数は "体" です。さらに No.310「高校数学で理解するRSA暗号の数理(1)」の終わりの方に書いたように、\(p\) を素数とし、\(p\) 未満の自然数と \(0\) を合わせた集合も "体" となり、\(\bs{F}_p\) で表します。この集合は元の数が有限なので、有限体です。
\(\bs{F}_p\) における演算は、加算・減算・乗算については普通の整数のように行い、その答に対して \((\mr{mod}\:p)\) の演算を行って「答と合同である \(\bs{F}_p\) の元」を求めて演算結果にします(\(\bs{F}_p\) は、ここでは \(\bs{Z}/p\bs{Z}\) で表される "整数の剰余類の集合" と同じ意味)。
除算は逆数(=逆元)を乗算する演算で行います。\(\bs{F}_p\) においては 2.3b により、\(0\) 以外の元に対して逆元(逆数)が存在します。2.3b を再掲すると次の通りです。
No.310 でやったように、\(\bs{F}_{13}\) の場合で "逆数" がどうなっているかを(= かけ算で \(1\) になる場合を)計算してみると、
となります。以上のことから、\(\bs{F}_p\) においては加減乗除が定義できて有限体となるわけです。
ここで \(\bs{F}_p\) から \(0\) 元 を除いた「\(p\) 未満の自然数の集合」を考えると、この集合では乗算と除算が定義できます。従って、この集合は「乗法群」になり、\(\bs{F}_p^{\:*}\) と表記します。ちなみに "群(group)" とは、何らかの二項演算 \(\times\) があって、
の3つの条件を満たす、"演算が定義された集合" です。以降の記述は、すべて乗法群 \(\bs{F}_p^{\:*}\) での演算とします。従って \(\equiv\) は \(=\) と書き、 \((\mr{mod}\:p)\) は記述しません。
11. 位数(order)
\(\bs{F}_p^{\:*}\) における冪乗がどうなっているか、その例として \(\bs{F}_{13}^{\:*}\) で計算してみます。まず、フェルマの小定理(3.1)により、\(\bs{F}_{13}^{\:*}\) の元 \(a\) について、
が成り立ちます。つまり、すべての元は \(12\) 乗すると \(1\) になる。では、冪乗が \(1\) になるためには必ず \(12\) 乗しなければならないのでしょうか。ためしに \(5\) の冪乗を(\(\bs{F}_{13}^{\:*}\) で)計算してみると、
となって、\(5^4\) で \(1\) になり、あとはそれが繰り返えされて、\(5^{12}\) に至ってフェルマの小定理が示す \(1\) になることがわかります。一方、\(2\) の冪乗は、
となり、フェルマの小定理が示す \(a^{12}=1\) より小さな冪乗では \(1\) になりません。この "冪乗に関する元の振る舞いの違い" が以降のテーマです。
位数の定義
"冪乗に関する元の振る舞いの違い" を表すために、\(\bs{F}_p^{\:*}\) の各元に対して「位数(order)」を定義します。
フェルマの小定理により \(a^{p-1}=1\) であることが保証されているので、すべての元について何らかの位数が定義できます。先ほどの \(\bs{F}_{13}^{\:*}\) の例だと、
です。位数になりうる数は、最小 \(1\)(\(a=1\) の場合)、最大 \((p-1)\) の間で、次のようになります。
なぜなら、元 \(a\) の位数が \(d\) であるとき、\(a\) の冪乗を順々に作っていくと \(d\) 乗ごとに \(1\) になります。一方、フェルマの小定理によって \(a\) の \((p-1)\) 乗は必ず \(1\) になるので、\(d\) が \((p-1)\) の約数でないと矛盾が生じます。つまり、位数のバリエーションは \((p-1)\) の約数の個数しかありません。
このことは直感的理解が可能ですが、次の命題はステップを踏んだ証明が必要です。
位数が \(d\) の元の個数
これは、\((p-1)\) の約数 \(d\) について、\(d\) の位数をもつ \(\bs{F}_p^{\:*}\) の元が \(\varphi(d)\) 個あることを主張するものではありません。そうではなく、もし位数 \(\bs{d}\) の元があったとしたら、そのような元は \(\varphi(d)\) 個あると言っています。11.3 を証明するために、位数 \(\bs{d}\) の元 \(\bs{a}\) があったとして、その \(a\) の冪乗からなる次の数列を作ってみます。
以降、これを、
と表記し、この \(d\) 個の数列の性質を調べます。
\(1\leq i,\:j\leq d\) として、もし
となったとします。両辺を \(a^i\) で割ると(= \(a^i\) の逆元を乗算すると)、
となりますが、\((j-i) < d\) なので、これは「\(a\) 冪乗が \(1\) になる最小の冪数が \(d\)」という位数の定義に反します。従って \(a^k\:(1\leq k\leq d)\) はすべて異なっています。
これは \((a^k)^d=(a^d)^k=1\) ということです。
\(d\) 乗すると \(1\) になる元は \(x^d=1\) という \(\bs{F}_p^{\:*}\) における式を満たします。これはすなわち、有限体 \(\bs{F}_p\) における \(d\) 次方程式 \(x^d-1=0\) の解です。
一般に、有限体 \(\bs{F}_p\) において「\(n\)次方程式の解の数は高々 \(n\)個」という命題が成立します。数学的帰納法で考えると、まず \(1\)次方程式、\(a_1x+a_0=0\) の解が \(1\)個なのは明らかなので \(n=k\) の時に命題が成り立つと仮定します。そして \((k+1)\) 次多項式を、
とし、方程式 \(f_{k+1}(x)=0\) が解 \(\al\) をもったとします。すると \(f_{k+1}(\al)=0\) なので、\(g_k(x)\) を \(k\)次多項式として、
と表現できます。なぜなら \((1\leq i\leq k+1)\) の範囲で、
の因数分解が成り立つからです。帰納法の仮定により方程式 \(g_k(x)=0\) の解の数は高々 \(k\)個です。つまり 方程式 \(f_{k+1}(x)=0\) の解の数は高々 \(k+1\) 個であり、命題は \(n=k+1\) でも成立して帰納法による証明ができました。従って有限体 \(\bs{F}_p\) における \(d\) 次方程式 \(x^d-1=0\) の解は 高々 \(d\) 個です。
\(a^k\:(1\leq k\leq d)\) は、
でした。このような元は \(\bs{F}_p^{\:*}\) の中に高々 \(d\) 個しかありません。従って、\(d\) 乗 すると \(1\) になる \(\bs{F}_p^{\:*}\) の元は \(a^k\:(1\leq k\leq d)\) の \(d\) 個がそのすべてということになります。
位数 \(d\) の元は \(d\) 乗すると \(1\) になります。一方、11.3c より \(d\) 乗すると \(1\) になる元は \(a^k\:(1\leq k\leq d)\) がそのすべてです。つまり位数 \(d\) の元があったとしたら、それは \(a^k\:(1\leq k\leq d)\) に含まれることになります。
これはもちろん、\(a^k\:(1\leq k\leq d)\) のすべての元の位数が \(d\) ということではありません。各元の位数は \(d\) かもしれないが、そうでない(= 位数が \(d\) より小さい)かもしれない。ここで、\(a^k\:(1\leq k\leq d)\) の各元の位数は次のように分類できます。
\(\mr{gcd}(j,d)=c > 1\) とします。すると、2つの数 \(s\) と \(t\) を選んで、
と書き表せます。ここで、\(a^j\) の \(t\) 乗をとると、
となり、\(a^j\) の位数は \(t\) 以下であることが分かりますが、\(t < d\) だったので、\(a^j\) の位数は \(d\) より小さいことになります。
\((a^j)^k\:(1\leq k\leq d)\) がどうなるかを調べます。まず、\(k=d\) のときは、11.3b により \((a^j)^k=1\) です。
次に \(1\leq k < d\) の場合ですが、このとき \(jk\) は \(d\) の倍数とはなりません。なぜなら、もし \(d\) の倍数だとすると \(d|(jk)\) ですが、\(j\) と \(d\) は互いに素なため、1.3a により \(d|k\) となって矛盾が生じるからです。従って、ある数 \(s\) と \(t\) を選んで。
と表すことができます。そうすると、
となります。\(s < d\) なので位数の定義により \(a^s\) は \(1\) にはならないのです。まとめると、
となり、定義により \(a^j\) の位数は \(d\) です。結局、11.3e と 11.3f により、次のことが分かります。
11.3e と 11.3f により、\(\mr{gcd}(j,d)=1\) である \(j\:(1\leq j < d)\) の場合だけ(= \(j\) が \(d\) と素なときだけ)\(a^j\) の位数は \(d\) であり、それ以外の \(a^j\) の位数は \(d\) より小さいことが分かりました。オイラー関数の定義から、\(\bs{d}\) 以下で \(\bs{d}\) と素な数は \(\bs{\varphi(d)}\) 個です。つまり 11.3g が成り立ちます。
以上の 11.3d と 11.3g、つまり、\(\bs{F}_p^{\:*}\) の元 \(a\) の位数を \(d\) とするとき、
11.3d
11.3g
の2つから、
11.3
が証明できました。
ここまでの考察を次のようにまとめることができます。
ここで 位数 \(d\) の元の個数を \(\#\mr{ord}(d)\) と書くことにします。\(\#\mr{ord}(d)=\varphi(d)\)、もしくは \(\#\mr{ord}(d)=0\) です。\(d\) は \((p-1)\) の約数 のどれかでした。この記号を使うと次の通りとなります。
\(\bs{F}_p^{\:*}\) の元のすべてに位数が定義できます。ということは \(\bs{F}_p^{\:*}\) の元を位数によってグループに分類できます。従って、各グループの元の個数の総和をとると、\(\bs{F}_p^{\:*}\) の元の個数である \(p-1\) になる。11.4 の総和の式はそのことを言っています。
そこで次に、\((p-1)\) の個々の約数 \(d\) について \(\#\mr{ord}(d)\) が \(\varphi(d)\) か \(0\) かが問題になりますが、それは次の「オイラー関数の総和定理」から分かります。
オイラー関数の総和定理
この "総和定理" は、特に \(\bs{F}_p^{\:*}\) や位数とは関係がなく、自然数一般についての定理です。この定理を証明する前提として、次の2つに注意します。まず、2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
です。これは最大公約数の定義そのものであり、そういう風に決めたのが最大公約数でした。2番目に、\(N\) の約数の一つが \(a\) だとすると \(N=a\cdot b\) と表せますが、当然、\(b\) も \(N\) の約数の一つです。いま、\(N\) が \(r\) 個の約数をもつとします。すると、
と言えます。この2つを前提に、まず \(N=12\) の場合で考えます。いま、\(1\) から \(12\) の \(12\) 個の整数を「\(12\)との最大公約数で分類する」ことを考えます。\(12\) の約数 \(d\) は、\(1\)、\(2\)、\(3\)、\(4\)、\(6\)、\(12\) の \(6\) つです。従って \(1\) から \(12\) の数を、\((S_1,S_2,S_3,S_4,S_6,S_{12})\) の \(6\) つのグループに分類します。すると各グループに含まれる整数は、
となります。いま、各グループに含まれる整数の個数を \(\#S_d\) で表して、各グループの個数がどうなるかを見ていきます。まず、
です。\(S_1\) に含まれるのは、\(12\)との最大公約数が \(1\) の整数(= \(12\) と素な整数)なので、オイラー関数の定義により \(\#S_1\) は \(\varphi(12)=4\) です。
次に、\(S_2\) に含まれる整数 \((2,10)\)を、\(12\) との最大公約数の \(2\) で割り算した \((1,5)\) を考えると、これらの整数は \(12\) を \(2\) で割り算した \(6\) と互いに素です。これは上に書いたように最大公約数の定義そのものです。従って、
となります。同様にして、残りのグループについては、
となります。\(S_d\) は \(12\)個 の整数を分類したものだったので、そこに含まれる整数の総数は \(12\) です。これにより、
が証明できました。これを総和の記号で書くと、
です。
以上の説明では \(N=12\) としましたが、\(12\) という数に特別な意味はありません。従って、一般の \(N\) の場合にも同様に証明ができます。
\(N\) が \(r\) 個の約数をもつとし、それらを \(a_i\:(1\leq i\leq r)\) とします。集合 \(S\) の元を \(1\) から \(N\) の 整数 \(N\) 個とし、これらの \(S\) の元を「\(N\) との最大公約数で \(r\) 個の部分集合に分ける」ことを考えます。つまり、\(S\) の部分集合 \(S_i\:(1\leq i\leq r)\) を、
とします。このとき \(S_i\) の任意の元を \(k\) とすると、最大公約数の定義により、
になります。そもそも、そのような元 \(k\) を集めたのが \(S_i\) なのでした。このことから、
ということになります。\(\bs{S_i}\) の元の個数を \(\bs{\#S_i}\) と書くと、
になります。ここで \(b_i\) を、
と定義すると、
となりますが、上に書いたように、この \(b_i\) は \(r\) 個の \(N\) の約数のすべてであり、つまり \(a_i\) を並び替えたものです。
ここで上式の両辺の \(1\) から \(r\) までの総和をとります。まず左辺の総和ですが、\(S_i\) は \(S\) を分類したものだったので、\(\#S_i\) の総和は \(S\) の元の総数である \(N\) と等しくなります。つまり左辺の総和は、
です。一方、右辺の総和は、
です。以上の左辺と右辺の総和が等しいことにより、11.5 の
が証明できました。
位数 \(d\) の元の存在定理
11.5 の "オイラー関数の総和定理" と 11.4 を合わせると、次の命題が証明できます。
11.4 を振り返ってみると、
でした。しかし 11.5 のオイラー関数の総和定理で \(N=p-1\) とおくと、
となります。これが何を意味するかというと、
ということです。ある位数 \(d\) をもつ元の個数が \(0\) だとするとオイラーの総和定理(11.5)が成り立たなくなるからです。位数 \(d\) をもつ元の個数は \(\varphi(d)\) 個しかあり得ない。つまり、\(\#\mr{ord}(d)=\varphi(d)\) です。これで 11.6 の証明ができました。この 11.6 から生成元の存在が証明でき、その個数が分かります。
12. 生成元と離散対数
11.6 からすぐに、次の「生成元の存在定理」が成り立ちます。これは\(19\)世紀ドイツの大数学者、ガウスが証明したものです。
11.6 によると、\((p-1)\) の約数 \(d\) のすべてについて位数 \(d\) をもつ元が存在します。\((p-1)\) の約数の一つが \((p-1)\) なので、位数が \((p-1)\) の元が必ず存在します。これが生成元で、その個数は \(\varphi(p-1)\) です。
生成元は原始根(primitive root)とも言います。「11. 位数(order)」の最初に書いた例だと、\(\bs{F}_{13}^{\:*}\) において \(2\) の位数は \(12\) であり、生成元(の一つ)なのでした。計算してみると \(6\)、\(7\)、\(11\) も生成元で、\(\bs{F}_{13}^{\:*}\) の生成元の個数は、合計 \(\varphi(12)=4\) です。
とにかく、\(\bs{F}_p^{\:*}\) の任意の元(= \(\bs{1}\) から \(\bs{p-1}\) の元)は生成元 \(\bs{g}\) の冪乗で表現でるきるわけです。つまり、次が成り立ちます。
対数は普通、実数で定義されるものですが、\(\mr{log}_g\:a\) はそれと同等のことを整数で定義しています。実数は連続値ですが、整数は離散値をとります。そのため「離散対数」の呼び名があります。
実数の対数を計算する手法はいろいろありますが(初等的にはマクローリン級数など)、離散対数を計算する効率的手法は知られていません。特に、\(\bs{F}_p^{\:*}\) において \(p\) が巨大な素数だと、実質的に計算が不可能になります。ここが、ディフィー・ヘルマンの鍵共有が成り立つ原理です。ディフィー・ヘルマンの鍵共有を、振り返ってみると次の通りです。まず、
のペアを「皆が使う公開鍵」として公開しておきます。演算は \(\bs{F}_p^{\:*}\) で行います。\(A\) さんと \(B\) さんが秘密鍵を共有したい場合、
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。次に同様に、
します。もちろん \(b\) は秘匿します。そして、
とします。この作り方から \(G_a=G_b\) となるので、秘密鍵 \(G=g^{ab}\)を共有できたことになり、以降はこれを使って暗号化通信を行います。\(g\) が生成元であるため、\(g^a\) や \(g^b\) は、
ことになります。「\(g\) は小さな生成元」と書きましたが、生成元はたくさんあり(\(\varphi(p-1)\) 個もある!)、\(\bs{F}_{13}^{\:*}\) の場合のように \(2\) が生成元となる場合が多い。その場合は \(g=2\) として問題ありません(小さい生成元の方が実用的には冪剰余を計算しやすい。特に \(2\))。生成元として \(2\) を選んだとしても、巨大な数で冪乗をすると結果が "バラける" ことが数学的に保証されているからです。
離散対数を計算する効率的な手法は知られていないため、\(p\) が 10進数で数百桁とか1000桁以上の数だと、\(g^a\) や \(g^b\) から \(a\) や \(b\) を知ることが実質的に不可能になります。これがディフィー・ヘルマンの鍵共有の原理です。
13. 離散対数暗号
ディフィー・ヘルマンの鍵共有の原理を使って、暗号化されたメッセージ伝送とデジタル署名ができます。ElGamal 暗号と呼ばれているもので、「離散対数暗号」の一種です。まず前提として、
のペアを「皆が使う公開鍵」として公開しておきます。
メッセージ伝送
以下の演算はすべて \(\bs{F}_p^{\:*}\) で行います。\(B\) さんから \(A\) さんにメッセージ \(M\) を暗号化して送りたい場合、次のようにします。
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。\(B\) がメッセージ \(M\) を暗号文にして \(A\) に送る場合、
します。このペアを受け取ると、
します。複号化は \(g^{ak}\) の逆数(逆元)を乗算しますが、No.310 の「拡張ユークリッドの互除法」の 2.3a に書いたように、逆数の計算はたとえ \(g^{ak}\) や \(p\) が巨大数であっても効率的に可能です。
デジタル署名
\(A\) さん
秘密鍵 : \(a\)
公開鍵 : \(g^a\)
\(B\) さん
秘密鍵 : \(b\)
公開鍵 : \(g^b\)
とします。また、ハッシュ関数を \(H(\:)\) と書きます(ハッシュ関数については No.311「高校数学で理解するRSA暗号の数理(2)」の "補記" 参照)。\(B\) さんから \(A\) さんにメッセージ \(M\) を送るとき、デジタル署名の手順は次のように進みます。
\(B\) の署名
\(A\) の検証
離散対数暗号(ElGamal 暗号)は、公開鍵暗号としてメジャーではありませんが、「暗号化鍵を公開してメッセージ伝送とデジタル署名を成立させる」ことの原理を端的に表わすものと言えます。
14. 生成元であることの証明
「ディフィー・ヘルマンの鍵共有」や「離散対数暗号」を実現するためには、巨大な素数 \(p\) に対する \(\bs{F}_p^{\:*}\) の生成元(のどれか)を知らなければなりません。これはどのように可能でしょうか。まず、
ので、\((p-1)\) の素因数分解ができたとすると約数が分かり、位数の候補がリストアップできます。
一般に \(d\) が 元 \(a\)(\(\neq1\)。以降、\(a\neq1\) とします)の位数であることの証明は手間がかかります。\(a\) の \(d\) 乗が \(1\) になったとしても \(d\) が \(a\) の位数だとは限りません。\(d\) よりも小さな数 \(e\) で \(a^e=1\) となるかもしれないからです。しかし、\(\bs{d}\) が \(\bs{a}\) の位数ではないことは簡単に証明できます。
を示せばよいからです。従って、\(a\) が \(\bs{F}_p^{\:*}\) の生成元であることを示すためには、\((p-1)\) の約数のうち \((p-1)\) 以外のすべての約数 \(d\) について、\(a^d\neq1\) であることを示せればよい。すると消去法で、\(a\) の位数は \((p-1)\) になります。この考えに基づき、簡単のために \(\bs{F}_{73}^{\:*}\) で考えると、
なので \((p-1)\) の約数は \(1\) と \(72\) を含めて \(4\times3=12\) 個あります。従って \(72\) と \(1\) を除いた \(10\) 個の約数 \(d\) について
であれば、\(a\) の位数は \(72\) しかありえず、\(a\) は \(\bs{F}_{73}^{\:*}\) の生成元です。しかし実は、これでは「計算のやりすぎ」になります。この場合、
の2つだけが成り立てば、\(a\) の位数は \(72\) になります。なぜかというと、一般に次の命題が成立するからです。
\(e\) が \(d\) の約数だとすると、ある数 \(k\) があって \(d=ke\) と表せます。このとき、
です。このことの対偶をとると
となり、これはつまり、
ことを意味します。\(p-1=72\) の場合、\(72\) を除く \(72\)(\(=2^3\cdot3^2\))の約数は、すべて \(24\)(\(=2^3\cdot3^1\)) か \(36\)(\(=2^2\cdot3^2\))のどちらかの(あるいは両方の)約数になります。従って、
が示せれば、\(72\) を除く \(72\) のすべての約数 \(d\) について、
となり、\(d\) は \(a\) の位数ではありません。この結果、\(a\) の位数は \(72\) しかあり得ず、\(a\) は \(\bs{F}_{73}^{\:*}\) の生成元であることになります。以上の考察を一般化すると、次の命題が成立します。
\((p-1)\) の約数で、\((p-1)\) 以外の任意の約数を \(d\) とし、
と表します。ここで \(\beta_i\) は、
です。そうすると、\(d\) は \((p-1)\) 以外の \((p-1)\) の約数なので、
ことになります。なぜなら、もしそのような \(k\) がなければ \(d=p-1\) だからです。そのような \(k\) について、命題 14.2 で定義した、
に着目すると、\(d\) は \(m_k\) の約数になります。なぜなら、\(d\) と \(m_k\) の「素因数ごとの冪乗数」を比較してみると、
であり、\(d\) のすべての素因数の冪乗数は \(m_k\) の素因数の冪乗数以下です。つまり \(m_k\) は \(d\) で割り切れ、\(d\) は \(m_k\) の約数ということになります。
一方、命題 14.2 の仮定により、
なので \(m_k\) は \(g\) の位数ではありません。従って、\(m_k\) の約数である \(d\) も 14.1 により \(g\) の位数とはなりません。
\(d\) は \((p-1)\) 以外の任意の \((p-1)\) の約数でした。ということは、\((p-1)\) 以外の \((p-1)\) の約数は \(g\) の位数ではない。つまり消去法で、\(g\) の位数は \((p-1)\) であり、\(g\) は \(\bs{F}_p^{\:*}\) の生成元であることが証明されました。
実際に生成元を求める
\(\bs{F}_p^{\:*}\) の元 \(g\) をとったとき、それが生成元かどうかは 14.2 によって確かめることができます。しかしここで問題は、実用的なディフィー・ヘルマンの鍵共有では \(p\) が巨大な素数であり、\((p-1)\) の素因数分解が実質的に不可能なことです。巨大数の素因数分解が困難なことは、まさにRSA暗号(No.310-311「高校数学で理解するRSA暗号の数理」)が成立する根拠でした。
そこで実際に生成元を求めるためには、\(p\) を "作為的に" 決める必要があります。まず前提となるのは、ある数 \(p\) が素数であるかどうかの判定法は種々あって(ミラー\(\cdot\)ラビン素数判定法、など)、\(p\) が巨大数であっても判定可能なことです。この前提のもとに、簡単な方法の例を一つあげますと、次の関係にあるような3つの数 \(p\)、\(q\)、\(e\) を決めます。
\(p\) と \(q\) は10進数で数百桁から1000桁以上の巨大素数(= 奇数)、\(e\) はたとえば100 以下の(もっと絞れば 10 以下の)偶数です。具体的には、まず \(q\) をランダムに選んで素数判定をし、素数であれば 次に \(e\) を選んで \(p\) が素数かどうかを判定するというプロセスになります。
こうすると \((p-1)\) の素因数分解は簡単にできるので、\(\bs{F}_p^{\:*}\) の任意の元 \(g\) が生成元かどうかは 14.2 で判定できます。具体的には \(g=2\) から始めて 順次 \(g\) を増やしていって生成元を探索することになるでしょう。
以上は一つの例ですが、実際に実務で使う \(p\) と \(g\) については \(g=2\) であると、コンピュータによる計算上、都合がよいわけです。従って、\(2\) が生成元になる前提で \(p\) を探索することになるでしょう。
ちなみに、現在、ディフィー・ヘルマンの鍵共有が実際に使われている例をあげておきます。インターネットを介してリモートのコンピュータ同士が安全に通信するための SSH(Secure Shell)という規格がありますが、そこで使われている公開鍵の一つ "diffie-hellman-group14-sha1"(2048ビットの素数 \(p\) と生成元 \(g\))を次に掲げます。これはインターネットの規格文書(RFC)に記載されています(RFC3526。16進表示)。この \(p\) は \(p=2q+1\) の形の素数で、10進では617桁です。10進表示と16進表示を以下に掲げます( \([\cd]\) はガウス記号で \(\cd\) を超えない最大の整数)。
diffie-hellman-group14-sha1(2048 bit)
\(p\:=\:2^{2048}-2^{1984}-1+2^{64}([2^{1918}\pi]+124476)\)
= 3231700 6071311007
3003389139 2642382824 8817941241 1402391128 4200975140
0741706634 3542226196 8941736356 9347117901 7379097041
9175460587 3209195028 8537589861 8562215321 2175412514
9017745202 7023579607 8236248884 2461894775 8764110592
8646099411 7232454266 2252219323 0540919037 6805242355
1912567971 5870117001 0580558776 5103886184 7280257976
0549035697 3256152616 7081339361 7995413364 7655916036
8317896729 0731783845 8968063967 1900977202 1941686472
2587103141 1336429319 5361934716 3653320971 7077448227
9885885653 6920864529 6636077250 2689555059 2836275112
1174096972 9980684105 5435958486 6583291642 1362182310
7899099944 8652468262 4169720359 1185250704 5361090559
=
FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D
C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F
83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D
670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B
E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9
DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510
15728E5A 8AACAA68 FFFFFFFF FFFFFFFF
\(g\:=\:2\)
ディフィー・ヘルマンの鍵共有の安全性ですが、離散対数問題を効率的に解くアルゴリズムはないと、数学的に証明されているわけではありません。ただ、RSA暗号の根拠になっている素因数分解のアルゴリズムと同じように、こういった数論の極めて基本的で、昔からある普遍的な問題は、世界の多くの数学者が関わってきています。それでも効率的に解くアルゴリズムは知られていません。ブログのタイトルを「高校数学で理解する」とましたが、そのような基礎的な数学しか使っていないからこそ暗号が成り立っている。そう言えると思います。
ディフィー・ヘルマンの鍵共有は公開鍵暗号の発端となったものですが、上にあげたように現在でも使われています(DHと略記される)。ただ、公開鍵暗号の優秀性は、「解読の困難性」と「暗号化・複号化計算の容易性」という二律背反の要求をいかに両立させるかにあります。その意味で、ディフィー・ヘルマン以降、各種の公開鍵暗号が開発されてきました。離散対数問題を使った暗号で言うと、よく使われるのは "楕円暗号(楕円曲線暗号)" です。これは「楕円曲線上の有理点がつくる "加法群" での離散対数問題」を利用した暗号です。しかし基本的な考え方はディフィー・ヘルマンの鍵共有と同じです。その意味で、公開鍵暗号の発端となった発明の意義は、今も続いているのでした。
まとめ
以上の 「ディフィー・ヘルマンの鍵共有」および「離散対数暗号」をまとめると、次のようになるでしょう。
No.310-311 のRSA暗号と同じく、この最後の点がこの記事の目的なのでした。
素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
No.310-311「高校数学で理解するRSA暗号の数理」の続きです。公開鍵暗号の "老舗" である RSA暗号は、1978年に MIT の研究者であったリベスト(米)、シャミア(イスラエル)、エーデルマン(米)の3人によって発明されました(RSAは3人の頭文字)。3人はこの功績によって2002年のチューリング賞を受賞しました。チューリング賞は計算機科学分野の国際学会である ACM(Association of Computing Machinary)が毎年授与している賞で、この分野では最高の栄誉とされているものです。
しかし公開鍵暗号そのもののアイデアを最初に提示したのは、スタンフォード大学の研究者だったディフィー(米)とヘルマン(米)で、1976年のことでした。2人も 2015年にチューリング賞を受賞しています。この「鍵を公開する」という、画期的というか逆転の発想である公開鍵暗号の登場以降、暗号の研究は一変してしまいました。そして RSA暗号のみならず各種の公開鍵暗号が開発され、現代のインターネットの基盤になっています。たとえばインターネットのWebサーバへのアクセス(閲覧やフォーム入力など)で使われる SSL/TSL という暗号化通信(https:// のサイトで使われる)は、まさに公開鍵方式を使っています。
今回はその公開鍵暗号を "発明した" ディフィーとヘルマンに敬意を表して、彼らが発表した「鍵共有システム」の内容と、その数学的背景を書いてみたいと思います。また、それと数学的な関連が深い「離散対数暗号」にも触れます。

|
ACM(Association of Computing Machinary)のサイトには、歴代のチューリング賞の受賞者の紹介ページがある。2015年の受賞者はディフィーとヘルマンで、受賞理由として「公開鍵暗号の発明」と書かれている。 |
ディフィーとヘルマンが提出したアイデアは「公開鍵を使って秘密鍵を安全に共有する」ものでした。これは「ディフィー・ヘルマンの鍵共有」と呼ばれていて、現在でも使われています。そこでまず「秘密鍵の共有」の意義を振り返ってみたいと思います。
秘密鍵の共有
古今東西、様々な暗号化方式が開発・使用されてきましたが「秘密鍵の共有による暗号」(=共通鍵暗号)が基本です。その中でも「一回限りの乱数表」は安全(=解読されない)と証明されている暗号です。この場合、乱数表が秘密鍵に相当します。
英大文字・小文字、数字、英文に使われる特殊文字を、\(0\) ~ \(127\) の数字でコード化するとします。いま、\(n\) 文字以下の平文をコード化して暗号文にしたいとき、「一回限りの乱数表」として必要なのは、\(0\) ~ \(127\) の値をとる乱数が \(n\) 個並んだ表です。さらに、
コード化した平文 : \(a_i\)
乱数表(秘密鍵) : \(r_i\)
暗号文 : \(b_i\)
乱数表(秘密鍵) : \(r_i\)
暗号文 : \(b_i\)
\(1\leq i\leq n\)
\(0\leq a_i,\:r_i,\:b_i\leq127\)
\(0\leq a_i,\:r_i,\:b_i\leq127\)
とするとき、「乱数 \(r_i\) の値に依存して、\(a_i\) を \(b_i\) に1対1に変換する関数 \(f\)」を決めておきます。そうすると、
\(b_i=f(a_i,\:r_i)\)
の変換で暗号文 \(b_i\) が得られます。この関数 \(f\) は \(128\times128\) の コード変換テーブルでもいいし、\((a_i+r_i)\:\mr{mod}\:128\) のような四則演算でもよい。とにかく \(r_i\) が違えば別の1対1変換になる関数が条件で、そうすれば逆変換で複号化が可能です。
関数 \(f\) としてよく使われるのは排他的論理和(Exclusive OR, XOR)です。これはビットごとに排他的論理和(ビットが一致すれば 0, 相違すれば 1)をとるもので、その関数を \(f_{XOR}(\:)\) で表わすと、
となり、暗号化・復号化がシンプルです。
\(b_i=f_{XOR}(a_i,\:r_i)\) なら
\(a_i=f_{XOR}(b_i,\:r_i)\)
\(a_i=f_{XOR}(b_i,\:r_i)\)
となり、暗号化・復号化がシンプルです。
この関数を秘密にする必要はなく、オープンにしてもかまいません。この暗号が安全な理由は、
| 秘密鍵(=乱数表)の長さが平文と同じ | |
| 秘密鍵は1回限り=使い終わったら捨てる |
の2点によります。もちろん乱数が "真の乱数" であることも重要です。しかし、上の2点を守るためには秘密鍵(乱数表)の長さが膨大になります。使い終わった乱数表のページを破って捨てなければならないからです。そこで実用的には、暗号文のやりとりを始める前に秘密鍵を共有しておき、暗号化はその「秘密鍵にもとづいた何らかの暗号化方式」で行うことになります。こうすると平文の長さが秘密鍵より長くなるので、絶対に安全とは言えなくなります。そこで、解読しにくい(=強度の高い)暗号化方式の必要性があり、これをめぐって様々な方式が作られてきました。
しかし問題は、最初の「秘密鍵の共有」をどうやってやるかです。結局、秘密鍵を印刷し、アタッシュケースに入れて相手に持参するというような、スパイ映画にでも出てきそうな方法しか本質的には無いわけです。どういうやり方をとるにせよ「秘密鍵の共有」には多大なコストがかかる。
No.310-311「高校数学で理解する RSA 暗号の数理」で書いた公開鍵暗号の価値はそういうところにあります。つまり、RSA暗号における暗号化・複号化は巨大な数の "冪剰余" を求める計算になり、これはこれで計算機負荷が高い。そこで、まずRSA暗号を使って秘密鍵を生成・共有しておき、以降はその秘密鍵を使う高速な(= 計算機負荷の低い)暗号化・複号化方式で通信をするやり方が多くとられます(=ハイブリッド暗号)。もちろんその秘密鍵は通信が一段落したら捨てて、次の通信では新たな秘密鍵を生成して共有するわけです。これは他の公開鍵暗号でも同じです。
その、"公開鍵を使って秘密鍵を共有する" ことを最初に提唱したのが「ディフィー・ヘルマンの鍵共有」でした。そしてこれが、そもそもの「公開鍵の発明」になりました。この鍵共有は、
盗聴されている通信路を使って情報をやりとりすることで、秘密鍵の共有を安全に実現する
ためのアルゴリズムです。どうしてそんなことができるのかが、以降です。
9. ディフィー・ヘルマンの鍵共有
ディフィー・ヘルマンの鍵共有は次のように進みます。まず「公開鍵センター」が "皆が使う公開鍵"として、
\((p,\:g)\)
| \(p\)は巨大な素数 | |
| \(g\)は小さな整数 |
のペアを公開しておきます。次に、\(A\) さんと \(B\) さんが秘密鍵を共有したい場合、
\(A\) は、\(1 < a < (p-1)\) である乱数 \(a\) を発生させ、\(g^a\:(\mr{mod}\:p)\) を \(A\) の公開鍵として(盗聴されている通信路を介して) \(B\) に送付
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。次に同様に、
\(B\) は、\(1 < b < (p-1)\) である乱数 \(b\) を発生させ、\(g^b\:(\mr{mod}\:p)\) を \(B\) の公開鍵として(盗聴されている通信路を介して) \(A\) に送付
します。もちろん \(b\) は秘匿します。そして、
\(A\) は \(G_a=(g^b)^a\:(\mr{mod}\:p)\) を共有の秘密鍵
\(B\) は \(G_b=(g^a)^b\:(\mr{mod}\:p)\) を共有の秘密鍵
\(B\) は \(G_b=(g^a)^b\:(\mr{mod}\:p)\) を共有の秘密鍵
とします。この作り方から \(G_a=G_b\) となるので、秘密鍵 \(G=g^{ab}\:(\mr{mod}\:p)\) が共有できたことになり、以降はこれを使って暗号化通信を行います。大切なことは \(A\) は \(B\) の秘密鍵(\(b\))を知らないし、\(B\) は \(A\) の秘密鍵(\(a\))を知らないことです。それでも秘密鍵 \(G\)(\(=G_a=G_b\))を共有できるわけです。
ちなみに、以上のプロセスに出てくる \(g^a\:(\mr{mod}\:p)\) などの "冪剰余" の計算ですが、たとえ \(a\) や \(p\) が巨大数であっても効率的に計算できることを、No.311「高校数学で理解するRSA暗号の数理(2)」の「累乗の剰余を求めるアルゴリズム」で書きました。
以上の仕組みにおいて通信路が盗聴されたとしても安全なのは、\(A\) の公開鍵 \(g^a\) から \(a\) を求めるのが困難なことと、同様に \(g^b\) から \(b\) を求めるのが困難なことです。なぜ困難かとい言うと、一つは \(\bs{p}\) が巨大な素数だからであり(\(10\)進数で数百桁か \(1000\)桁以上)、また \(\bs{g}\) が「生成元」(原始根ともいう)だからです。
以降でその「生成元」とは何か、盗聴者が公開鍵から \(A\) と \(B\) の秘密鍵(\(a\) と \(b\))をなぜ計算できないのかという、ディフィー・ヘルマンの鍵共有の数学的背景を概観します。以下の説明では「高校数学程度の知識だけ」を前提としますが(= タイトルの "高校数学で理解する" の意味)、No.310-311「高校数学で理解するRSA暗号の数理」での各種説明は既知とします。特に、
の知識を前提とします。
10. 有限体(\(\bs{F}_p\))と乗法群(\(\bs{F}_p^{*}\))
一般に加減乗除が定義された集合を "体(Field)" と言います。有理数、実数、複素数は "体" です。さらに No.310「高校数学で理解するRSA暗号の数理(1)」の終わりの方に書いたように、\(p\) を素数とし、\(p\) 未満の自然数と \(0\) を合わせた集合も "体" となり、\(\bs{F}_p\) で表します。この集合は元の数が有限なので、有限体です。
\(\bs{F}_p\) における演算は、加算・減算・乗算については普通の整数のように行い、その答に対して \((\mr{mod}\:p)\) の演算を行って「答と合同である \(\bs{F}_p\) の元」を求めて演算結果にします(\(\bs{F}_p\) は、ここでは \(\bs{Z}/p\bs{Z}\) で表される "整数の剰余類の集合" と同じ意味)。
除算は逆数(=逆元)を乗算する演算で行います。\(\bs{F}_p\) においては 2.3b により、\(0\) 以外の元に対して逆元(逆数)が存在します。2.3b を再掲すると次の通りです。
| 2.3b | 逆数の存在:法が素数 |
|
\(p\) を素数とする。\(p\) 未満の自然数 \(a\) に対して、
\(a\cdot b\equiv1\:(\mr{mod}\:p)\) を満たす逆数 \(b\) が \(1\leq b < p\) の範囲で一意に定まる。また、異なる \(a\) に対する逆数 \(b\) は異なる。 | |
No.310 でやったように、\(\bs{F}_{13}\) の場合で "逆数" がどうなっているかを(= かけ算で \(1\) になる場合を)計算してみると、
\(\phantom{1}1\cdot\phantom{1}1\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}2\cdot\phantom{1}7\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}3\cdot\phantom{1}9\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}4\cdot10\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}5\cdot\phantom{1}8\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}6\cdot11\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}7\cdot\phantom{1}2\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}8\cdot\phantom{1}5\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}9\cdot\phantom{1}3\equiv1\:(\mr{mod}\:13)\)
\(10\cdot\phantom{1}4\equiv1\:(\mr{mod}\:13)\)
\(11\cdot\phantom{1}6\equiv1\:(\mr{mod}\:13)\)
\(12\cdot12\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}2\cdot\phantom{1}7\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}3\cdot\phantom{1}9\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}4\cdot10\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}5\cdot\phantom{1}8\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}6\cdot11\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}7\cdot\phantom{1}2\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}8\cdot\phantom{1}5\equiv1\:(\mr{mod}\:13)\)
\(\phantom{1}9\cdot\phantom{1}3\equiv1\:(\mr{mod}\:13)\)
\(10\cdot\phantom{1}4\equiv1\:(\mr{mod}\:13)\)
\(11\cdot\phantom{1}6\equiv1\:(\mr{mod}\:13)\)
\(12\cdot12\equiv1\:(\mr{mod}\:13)\)
となります。以上のことから、\(\bs{F}_p\) においては加減乗除が定義できて有限体となるわけです。
ここで \(\bs{F}_p\) から \(0\) 元 を除いた「\(p\) 未満の自然数の集合」を考えると、この集合では乗算と除算が定義できます。従って、この集合は「乗法群」になり、\(\bs{F}_p^{\:*}\) と表記します。ちなみに "群(group)" とは、何らかの二項演算 \(\times\) があって、
| \((a\times b)\times c=a\times(b\times c)\) | |
| \(a\times1=1\times a=a\) となる元 \(1\) が存在 | |
| \(a\times b=b\times a=1\) となる \(b\) が、任意の \(a\) について存在 |
の3つの条件を満たす、"演算が定義された集合" です。以降の記述は、すべて乗法群 \(\bs{F}_p^{\:*}\) での演算とします。従って \(\equiv\) は \(=\) と書き、 \((\mr{mod}\:p)\) は記述しません。
11. 位数(order)
\(\bs{F}_p^{\:*}\) における冪乗がどうなっているか、その例として \(\bs{F}_{13}^{\:*}\) で計算してみます。まず、フェルマの小定理(3.1)により、\(\bs{F}_{13}^{\:*}\) の元 \(a\) について、
\(a^{12}=1\)
が成り立ちます。つまり、すべての元は \(12\) 乗すると \(1\) になる。では、冪乗が \(1\) になるためには必ず \(12\) 乗しなければならないのでしょうか。ためしに \(5\) の冪乗を(\(\bs{F}_{13}^{\:*}\) で)計算してみると、
\(\begin{eqnarray}
&&5^1&=\phantom{1}5\\
&&5^2&=12\\
&&5^3&=\phantom{1}8\\
&&5^4&=\phantom{1}1\\
&&5^5&=\phantom{1}5\\
&&5^6&=12\\
&&5^7&=\phantom{1}8\\
&&5^8&=\phantom{1}1\\
&&5^9&=\phantom{1}5\\
&&5^{10}&=12\\
&&5^{11}&=\phantom{1}8\\
&&5^{12}&=\phantom{1}1\\
\end{eqnarray}\)
となって、\(5^4\) で \(1\) になり、あとはそれが繰り返えされて、\(5^{12}\) に至ってフェルマの小定理が示す \(1\) になることがわかります。一方、\(2\) の冪乗は、
\(\begin{eqnarray}
&&2^1&=\phantom{1}2\\
&&2^2&=\phantom{1}4\\
&&2^3&=\phantom{1}8\\
&&2^4&=\phantom{1}3\\
&&2^5&=\phantom{1}6\\
&&2^6&=12\\
&&2^7&=11\\
&&2^8&=\phantom{1}9\\
&&2^9&=\phantom{1}5\\
&&2^{10}&=10\\
&&2^{11}&=\phantom{1}7\\
&&2^{12}&=\phantom{1}1\\
\end{eqnarray}\)
となり、フェルマの小定理が示す \(a^{12}=1\) より小さな冪乗では \(1\) になりません。この "冪乗に関する元の振る舞いの違い" が以降のテーマです。
位数の定義
"冪乗に関する元の振る舞いの違い" を表すために、\(\bs{F}_p^{\:*}\) の各元に対して「位数(order)」を定義します。
| 11.1 | 位数の定義 |
|
\(\bs{F}_p^{\:*}\) の元 \(a\) について、
\(a^k=1\) となる最小の \(k\) を \(a\) の "位数(order)" と言う。 | |
フェルマの小定理により \(a^{p-1}=1\) であることが保証されているので、すべての元について何らかの位数が定義できます。先ほどの \(\bs{F}_{13}^{\:*}\) の例だと、
\(5\) の位数は \(4\)
\(2\) の位数は \(12\)
\(2\) の位数は \(12\)
です。位数になりうる数は、最小 \(1\)(\(a=1\) の場合)、最大 \((p-1)\) の間で、次のようになります。
| 11.2 | 位数がとりうる値 |
|
\(d\) が \(\bs{F}_p^{\:*}\) のある元の位数とすると、\(d\) は \((p-1)\) の約数である。 | |
なぜなら、元 \(a\) の位数が \(d\) であるとき、\(a\) の冪乗を順々に作っていくと \(d\) 乗ごとに \(1\) になります。一方、フェルマの小定理によって \(a\) の \((p-1)\) 乗は必ず \(1\) になるので、\(d\) が \((p-1)\) の約数でないと矛盾が生じます。つまり、位数のバリエーションは \((p-1)\) の約数の個数しかありません。
このことは直感的理解が可能ですが、次の命題はステップを踏んだ証明が必要です。
位数が \(d\) の元の個数
| 11.3 | |
|
\((p-1)\) の約数の一つ \(d\) の位数をもつ \(\bs{F}_p^{\:*}\) の元があったとすると、位数 \(d\) の元は \(\varphi(d)\) 個ある。\(\varphi(d)\) はオイラー関数。 | |
これは、\((p-1)\) の約数 \(d\) について、\(d\) の位数をもつ \(\bs{F}_p^{\:*}\) の元が \(\varphi(d)\) 個あることを主張するものではありません。そうではなく、もし位数 \(\bs{d}\) の元があったとしたら、そのような元は \(\varphi(d)\) 個あると言っています。11.3 を証明するために、位数 \(\bs{d}\) の元 \(\bs{a}\) があったとして、その \(a\) の冪乗からなる次の数列を作ってみます。
\(a^1,\:a^2,\:a^3,\:\cd\:,\:a^d(=1)\)
以降、これを、
\(a^k\:(1\leq k\leq d)\)
と表記し、この \(d\) 個の数列の性質を調べます。
| 11.3a | |
|
\(a^k\:(1\leq k\leq d)\) の \(d\) 個の元はすべて異なる。 | |
\(1\leq i,\:j\leq d\) として、もし
\(a^j=a^i\)
となったとします。両辺を \(a^i\) で割ると(= \(a^i\) の逆元を乗算すると)、
\(a^{j-i}=1\)
となりますが、\((j-i) < d\) なので、これは「\(a\) 冪乗が \(1\) になる最小の冪数が \(d\)」という位数の定義に反します。従って \(a^k\:(1\leq k\leq d)\) はすべて異なっています。
| 11.3b | |
|
\(a^k\:(1\leq k\leq d)\) の \(d\) 個の元は、すべて \(d\) 乗 すると \(1\) になる。 | |
これは \((a^k)^d=(a^d)^k=1\) ということです。
| 11.3c | |
|
\(d\) 乗すると \(1\) になる \(\bs{F}_p^{\:*}\) の元は、\(a^k\:(1\leq k\leq d)\) がそのすべてである。 | |
\(d\) 乗すると \(1\) になる元は \(x^d=1\) という \(\bs{F}_p^{\:*}\) における式を満たします。これはすなわち、有限体 \(\bs{F}_p\) における \(d\) 次方程式 \(x^d-1=0\) の解です。
一般に、有限体 \(\bs{F}_p\) において「\(n\)次方程式の解の数は高々 \(n\)個」という命題が成立します。数学的帰納法で考えると、まず \(1\)次方程式、\(a_1x+a_0=0\) の解が \(1\)個なのは明らかなので \(n=k\) の時に命題が成り立つと仮定します。そして \((k+1)\) 次多項式を、
\(f_{k+1}(x)=a_{k+1}x^{k+1}+a_kx^k+\:\cd+a_1x+a_0\)
\((a_{k+1}\neq0)\)
\((a_{k+1}\neq0)\)
とし、方程式 \(f_{k+1}(x)=0\) が解 \(\al\) をもったとします。すると \(f_{k+1}(\al)=0\) なので、\(g_k(x)\) を \(k\)次多項式として、
\(\begin{eqnarray}
&&f_{k+1}(x)&=f_{k+1}(x)-f_{k+1}(\al)\\
&&&=(x-\al)g_k(x)\\
\end{eqnarray}\)
と表現できます。なぜなら \((1\leq i\leq k+1)\) の範囲で、
\(\begin{eqnarray}
&&x^i-\al^i=(x-\al)&(x^{i-1}+\al^1x^{i-2}+\:\cd\\
&&&\al^{i-2}x+\al^{i-1})\\
\end{eqnarray}\)
の因数分解が成り立つからです。帰納法の仮定により方程式 \(g_k(x)=0\) の解の数は高々 \(k\)個です。つまり 方程式 \(f_{k+1}(x)=0\) の解の数は高々 \(k+1\) 個であり、命題は \(n=k+1\) でも成立して帰納法による証明ができました。従って有限体 \(\bs{F}_p\) における \(d\) 次方程式 \(x^d-1=0\) の解は 高々 \(d\) 個です。
\(a^k\:(1\leq k\leq d)\) は、
| \(d\) 個の、すべてが相異なる元であり(11.3a) | |
| \(d\) 乗すれば \(1\)(11.3b) |
でした。このような元は \(\bs{F}_p^{\:*}\) の中に高々 \(d\) 個しかありません。従って、\(d\) 乗 すると \(1\) になる \(\bs{F}_p^{\:*}\) の元は \(a^k\:(1\leq k\leq d)\) の \(d\) 個がそのすべてということになります。
| 11.3d | |
|
\(\bs{F}_p^{\:*}\) において位数 \(d\) の元があったとしたら、それは \(a^k\:(1\leq k\leq d)\) の中に含まれている。 | |
位数 \(d\) の元は \(d\) 乗すると \(1\) になります。一方、11.3c より \(d\) 乗すると \(1\) になる元は \(a^k\:(1\leq k\leq d)\) がそのすべてです。つまり位数 \(d\) の元があったとしたら、それは \(a^k\:(1\leq k\leq d)\) に含まれることになります。
これはもちろん、\(a^k\:(1\leq k\leq d)\) のすべての元の位数が \(d\) ということではありません。各元の位数は \(d\) かもしれないが、そうでない(= 位数が \(d\) より小さい)かもしれない。ここで、\(a^k\:(1\leq k\leq d)\) の各元の位数は次のように分類できます。
| 11.3e | |
|
\(\mr{gcd}(j,d)\neq1\) である \(j\:(1\leq j\leq d)\) をとると、\(a^j\) の位数は \(d\) より小さい。 | |
\(\mr{gcd}(j,d)=c > 1\) とします。すると、2つの数 \(s\) と \(t\) を選んで、
\(j=cs\:(s < j)\)
\(d=ct\:(t < d)\)
\(d=ct\:(t < d)\)
と書き表せます。ここで、\(a^j\) の \(t\) 乗をとると、
\((a^j)^t=a^{cst}=(a^d)^s=1\)
となり、\(a^j\) の位数は \(t\) 以下であることが分かりますが、\(t < d\) だったので、\(a^j\) の位数は \(d\) より小さいことになります。
| 11.3f | |
|
\(\mr{gcd}(j,d)=1\) である \(j\:(1\leq j < d)\) をとると、\(a^j\) の位数は \(d\) である。 | |
\((a^j)^k\:(1\leq k\leq d)\) がどうなるかを調べます。まず、\(k=d\) のときは、11.3b により \((a^j)^k=1\) です。
次に \(1\leq k < d\) の場合ですが、このとき \(jk\) は \(d\) の倍数とはなりません。なぜなら、もし \(d\) の倍数だとすると \(d|(jk)\) ですが、\(j\) と \(d\) は互いに素なため、1.3a により \(d|k\) となって矛盾が生じるからです。従って、ある数 \(s\) と \(t\) を選んで。
\(jk=td+s\:(0 < s < d)\)
と表すことができます。そうすると、
\((a^j)^k=a^{td+s}\)
\(\phantom{(a^j)^k}=(a^d)^t\cdot a^s\)
\(\phantom{(a^j)^k}=a^s\neq1\)
\(\phantom{(a^j)^k}=(a^d)^t\cdot a^s\)
\(\phantom{(a^j)^k}=a^s\neq1\)
となります。\(s < d\) なので位数の定義により \(a^s\) は \(1\) にはならないのです。まとめると、
\(\begin{eqnarray}
&&(a^j)^k&\neq1 &(1\leq k < d)\\
&&(a^j)^k&=1 &(k=d)\\
\end{eqnarray}\)
となり、定義により \(a^j\) の位数は \(d\) です。結局、11.3e と 11.3f により、次のことが分かります。
| 11.3g | |
|
\(a^k\:(1\leq k\leq d)\) の中には 位数 \(d\) の元が \(\varphi(d)\) 個ある。 | |
11.3e と 11.3f により、\(\mr{gcd}(j,d)=1\) である \(j\:(1\leq j < d)\) の場合だけ(= \(j\) が \(d\) と素なときだけ)\(a^j\) の位数は \(d\) であり、それ以外の \(a^j\) の位数は \(d\) より小さいことが分かりました。オイラー関数の定義から、\(\bs{d}\) 以下で \(\bs{d}\) と素な数は \(\bs{\varphi(d)}\) 個です。つまり 11.3g が成り立ちます。
以上の 11.3d と 11.3g、つまり、\(\bs{F}_p^{\:*}\) の元 \(a\) の位数を \(d\) とするとき、
11.3d
\(\bs{F}_p^{\:*}\) において位数 \(d\) の元があったとしたら、それは \(a^k\:(1\leq k\leq d)\) の中に含まれる。
11.3g
\(a^k\:(1\leq k\leq d)\) の中には 位数 \(d\) の元が \(\varphi(d)\) 個ある。
の2つから、
11.3
\((p-1)\) の約数の一つ \(d\) の位数をもつ \(\bs{F}_p^{\:*}\) の元があったとすると、位数 \(d\) の元は \(\varphi(d)\) 個ある。
が証明できました。
ここまでの考察を次のようにまとめることができます。
| \(\bs{F}_p^{\:*}\) の各元の位数は \((p-1)\) の約数である(│.2) | |
| 位数 \(d\) の元の個数は \(\varphi(d)\) か \(0\) である(11.3)。 |
ここで 位数 \(d\) の元の個数を \(\#\mr{ord}(d)\) と書くことにします。\(\#\mr{ord}(d)=\varphi(d)\)、もしくは \(\#\mr{ord}(d)=0\) です。\(d\) は \((p-1)\) の約数 のどれかでした。この記号を使うと次の通りとなります。
| 11.4 | |||||
|
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
| |||||
\(\bs{F}_p^{\:*}\) の元のすべてに位数が定義できます。ということは \(\bs{F}_p^{\:*}\) の元を位数によってグループに分類できます。従って、各グループの元の個数の総和をとると、\(\bs{F}_p^{\:*}\) の元の個数である \(p-1\) になる。11.4 の総和の式はそのことを言っています。
そこで次に、\((p-1)\) の個々の約数 \(d\) について \(\#\mr{ord}(d)\) が \(\varphi(d)\) か \(0\) かが問題になりますが、それは次の「オイラー関数の総和定理」から分かります。
オイラー関数の総和定理
| 11.5 | オイラー関数の総和 |
|
\(N\) を任意の自然数とするとき、
\(\displaystyle\sum_{d|N}^{}\varphi(d)=N\) が成り立つ。\(d|N\) は \(N\) の約数 \(d\) すべてについての総和をとる。 | |
この "総和定理" は、特に \(\bs{F}_p^{\:*}\) や位数とは関係がなく、自然数一般についての定理です。この定理を証明する前提として、次の2つに注意します。まず、2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
\(\dfrac{a}{\mr{gcd}(a,b)}\) と \(\dfrac{b}{\mr{gcd}(a,b)}\) は互いに素
です。これは最大公約数の定義そのものであり、そういう風に決めたのが最大公約数でした。2番目に、\(N\) の約数の一つが \(a\) だとすると \(N=a\cdot b\) と表せますが、当然、\(b\) も \(N\) の約数の一つです。いま、\(N\) が \(r\) 個の約数をもつとします。すると、
\(a_i\:(1\leq i\leq r)\) が \(N\) のすべての約数であれば、\(b_i=\dfrac{N}{a_i}\:(1\leq i\leq r)\) も \(N\) のすべての約数であり、つまり \(b_i\) は \(a_i\) を並び替えたものである
と言えます。この2つを前提に、まず \(N=12\) の場合で考えます。いま、\(1\) から \(12\) の \(12\) 個の整数を「\(12\)との最大公約数で分類する」ことを考えます。\(12\) の約数 \(d\) は、\(1\)、\(2\)、\(3\)、\(4\)、\(6\)、\(12\) の \(6\) つです。従って \(1\) から \(12\) の数を、\((S_1,S_2,S_3,S_4,S_6,S_{12})\) の \(6\) つのグループに分類します。すると各グループに含まれる整数は、
\(\begin{eqnarray}
&&S_1&=(1,5,7,11)\\
&&S_2&=(2,10)\\
&&S_3&=(3,9)\\
&&S_4&=(4,8)\\
&&S_6&=(6)\\
&&S_{12}&=(12)\\
\end{eqnarray}\)
となります。いま、各グループに含まれる整数の個数を \(\#S_d\) で表して、各グループの個数がどうなるかを見ていきます。まず、
\(\#S_1=\varphi(12)\)
です。\(S_1\) に含まれるのは、\(12\)との最大公約数が \(1\) の整数(= \(12\) と素な整数)なので、オイラー関数の定義により \(\#S_1\) は \(\varphi(12)=4\) です。
次に、\(S_2\) に含まれる整数 \((2,10)\)を、\(12\) との最大公約数の \(2\) で割り算した \((1,5)\) を考えると、これらの整数は \(12\) を \(2\) で割り算した \(6\) と互いに素です。これは上に書いたように最大公約数の定義そのものです。従って、
\(\#S_2=\varphi(6)\)
となります。同様にして、残りのグループについては、
\(\begin{eqnarray}
&&\#S_3&=\varphi(4)\\
&&\#S_4&=\varphi(3)\\
&&\#S_6&=\varphi(2)\\
&&\#S_{12}&=\varphi(1)\\
\end{eqnarray}\)
となります。\(S_d\) は \(12\)個 の整数を分類したものだったので、そこに含まれる整数の総数は \(12\) です。これにより、
\(\varphi(12)+\varphi(6)+\varphi(4)+\varphi(3)+\varphi(2)+\varphi(1)=12\)
が証明できました。これを総和の記号で書くと、
\(\displaystyle\sum_{d|12}^{}\varphi(d)=12\)
です。
以上の説明では \(N=12\) としましたが、\(12\) という数に特別な意味はありません。従って、一般の \(N\) の場合にも同様に証明ができます。
\(N\) が \(r\) 個の約数をもつとし、それらを \(a_i\:(1\leq i\leq r)\) とします。集合 \(S\) の元を \(1\) から \(N\) の 整数 \(N\) 個とし、これらの \(S\) の元を「\(N\) との最大公約数で \(r\) 個の部分集合に分ける」ことを考えます。つまり、\(S\) の部分集合 \(S_i\:(1\leq i\leq r)\) を、
\(S_i\):\(N\) との最大公約数が \(a_i\) である \(S\) の元の集合
とします。このとき \(S_i\) の任意の元を \(k\) とすると、最大公約数の定義により、
\(\dfrac{k}{a_i}\) は \(\dfrac{N}{a_i}\) と互いに素
になります。そもそも、そのような元 \(k\) を集めたのが \(S_i\) なのでした。このことから、
\(S_i\) の元の個数は、\(\dfrac{N}{a_i}\) と素である \(S\) の元の個数
ということになります。\(\bs{S_i}\) の元の個数を \(\bs{\#S_i}\) と書くと、
\(\#S_i=\varphi\left(\dfrac{N}{a_i}\right)\)
になります。ここで \(b_i\) を、
\(b_i=\dfrac{N}{a_i}\:(1\leq i\leq r)\)
と定義すると、
\(\#S_i=\varphi(b_i)\)
となりますが、上に書いたように、この \(b_i\) は \(r\) 個の \(N\) の約数のすべてであり、つまり \(a_i\) を並び替えたものです。
ここで上式の両辺の \(1\) から \(r\) までの総和をとります。まず左辺の総和ですが、\(S_i\) は \(S\) を分類したものだったので、\(\#S_i\) の総和は \(S\) の元の総数である \(N\) と等しくなります。つまり左辺の総和は、
\(\displaystyle\sum_{i=1}^{r}\#S_i=N\)
です。一方、右辺の総和は、
\(\begin{eqnarray}
&&\displaystyle\sum_{i=1}^{r}\varphi(b_i)&=\displaystyle\sum_{i=1}^{r}\varphi(a_i)\\
&&&=\displaystyle\sum_{d|N}^{}\varphi(d)\\
\end{eqnarray}\)
です。以上の左辺と右辺の総和が等しいことにより、11.5 の
\(\displaystyle\sum_{d|N}^{}\varphi(d)=N\)
が証明できました。
位数 \(d\) の元の存在定理
11.5 の "オイラー関数の総和定理" と 11.4 を合わせると、次の命題が証明できます。
| 11.6 | |
|
\(\bs{F}_p^{\:*}\) において、\(\bs{(p-1)}\) の約数 \(\bs{d}\) のすべてについて位数 \(\bs{d}\) をもつ元が存在し、その個数は \(\bs{\varphi(d)}\) 個である。 | |
11.4 を振り返ってみると、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
| \(\#\mr{ord}(d)\) は位数 \(d\) の元の個数で、\(\varphi(d)\) か \(0\) |
でした。しかし 11.5 のオイラー関数の総和定理で \(N=p-1\) とおくと、
\(\displaystyle\sum_{d|(p-1)}^{}\varphi(d)=p-1\)
となります。これが何を意味するかというと、
\(\bs{F}_p^{\:*}\) においては、\((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) をもつ元の個数が \(0\) になることはない。位数 \(d\) をもつ元の個数は \(\varphi(d)\) 個である
ということです。ある位数 \(d\) をもつ元の個数が \(0\) だとするとオイラーの総和定理(11.5)が成り立たなくなるからです。位数 \(d\) をもつ元の個数は \(\varphi(d)\) 個しかあり得ない。つまり、\(\#\mr{ord}(d)=\varphi(d)\) です。これで 11.6 の証明ができました。この 11.6 から生成元の存在が証明でき、その個数が分かります。
12. 生成元と離散対数
11.6 からすぐに、次の「生成元の存在定理」が成り立ちます。これは\(19\)世紀ドイツの大数学者、ガウスが証明したものです。
| 12.1 | 生成元の存在 |
|
\(\bs{F}_p^{\:*}\) においては、位数が \((p-1)\) の元 \(g\) が \(\varphi(p-1)\) 個存在する。 \(g^k(1\leq k\leq p-1)\) はすべて相違し、総数が \((p-1)\) 個である \(\bs{F}_p^{\:*}\) の元のすべてを尽くす。この \(g\) を \(\bs{F}_p^{\:*}\) の生成元(generator)と呼ぶ。 | |
11.6 によると、\((p-1)\) の約数 \(d\) のすべてについて位数 \(d\) をもつ元が存在します。\((p-1)\) の約数の一つが \((p-1)\) なので、位数が \((p-1)\) の元が必ず存在します。これが生成元で、その個数は \(\varphi(p-1)\) です。
生成元は原始根(primitive root)とも言います。「11. 位数(order)」の最初に書いた例だと、\(\bs{F}_{13}^{\:*}\) において \(2\) の位数は \(12\) であり、生成元(の一つ)なのでした。計算してみると \(6\)、\(7\)、\(11\) も生成元で、\(\bs{F}_{13}^{\:*}\) の生成元の個数は、合計 \(\varphi(12)=4\) です。
とにかく、\(\bs{F}_p^{\:*}\) の任意の元(= \(\bs{1}\) から \(\bs{p-1}\) の元)は生成元 \(\bs{g}\) の冪乗で表現でるきるわけです。つまり、次が成り立ちます。
| 12.2 | 離散対数 |
|
\(g\) を \(\bs{F}_p^{\:*}\) の生成元とする。\(\bs{F}_p^{\:*}\) の任意の元 \(a\) について、
\(g^b=a\) となる元 \(b\) が一意に定まる。\(b\) を \(a\) の離散対数と呼び、
\(\mr{log}_g\:a=b\) で表す。\(g\) は離散対数の "底" である。 | |
対数は普通、実数で定義されるものですが、\(\mr{log}_g\:a\) はそれと同等のことを整数で定義しています。実数は連続値ですが、整数は離散値をとります。そのため「離散対数」の呼び名があります。
実数の対数を計算する手法はいろいろありますが(初等的にはマクローリン級数など)、離散対数を計算する効率的手法は知られていません。特に、\(\bs{F}_p^{\:*}\) において \(p\) が巨大な素数だと、実質的に計算が不可能になります。ここが、ディフィー・ヘルマンの鍵共有が成り立つ原理です。ディフィー・ヘルマンの鍵共有を、振り返ってみると次の通りです。まず、
\((p,\:g)\)
| \(p\)は巨大な素数 | |
| \(g\)は小さな生成元 |
のペアを「皆が使う公開鍵」として公開しておきます。演算は \(\bs{F}_p^{\:*}\) で行います。\(A\) さんと \(B\) さんが秘密鍵を共有したい場合、
\(A\) は \(1 < a < (p-1)\) である乱数 \(a\) を発生させ、\(g^a\) を \(A\) の公開鍵として(盗聴されている通信路を介して) \(B\) に送付
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。次に同様に、
\(B\) は \(1 < b < (p-1)\) である乱数 \(b\) を発生させ、\(g^b\) を \(B\) の公開鍵として(盗聴されている通信路を介して) \(A\) に送付
します。もちろん \(b\) は秘匿します。そして、
\(A\) は \(G_a=(g^b)^a\) を共有の秘密鍵
\(B\) は \(G_b=(g^a)^b\) を共有の秘密鍵
\(B\) は \(G_b=(g^a)^b\) を共有の秘密鍵
とします。この作り方から \(G_a=G_b\) となるので、秘密鍵 \(G=g^{ab}\)を共有できたことになり、以降はこれを使って暗号化通信を行います。\(g\) が生成元であるため、\(g^a\) や \(g^b\) は、
\(1 < g^a,\:g^b < (p-1)\) の範囲に "バラける"
ことになります。「\(g\) は小さな生成元」と書きましたが、生成元はたくさんあり(\(\varphi(p-1)\) 個もある!)、\(\bs{F}_{13}^{\:*}\) の場合のように \(2\) が生成元となる場合が多い。その場合は \(g=2\) として問題ありません(小さい生成元の方が実用的には冪剰余を計算しやすい。特に \(2\))。生成元として \(2\) を選んだとしても、巨大な数で冪乗をすると結果が "バラける" ことが数学的に保証されているからです。
離散対数を計算する効率的な手法は知られていないため、\(p\) が 10進数で数百桁とか1000桁以上の数だと、\(g^a\) や \(g^b\) から \(a\) や \(b\) を知ることが実質的に不可能になります。これがディフィー・ヘルマンの鍵共有の原理です。
13. 離散対数暗号
ディフィー・ヘルマンの鍵共有の原理を使って、暗号化されたメッセージ伝送とデジタル署名ができます。ElGamal 暗号と呼ばれているもので、「離散対数暗号」の一種です。まず前提として、
\((p,\:g)\)
| \(p\) は巨大な素数 | |
| \(g\) は \(\bs{F}_p^{\:*}\) の生成元 |
のペアを「皆が使う公開鍵」として公開しておきます。
メッセージ伝送
以下の演算はすべて \(\bs{F}_p^{\:*}\) で行います。\(B\) さんから \(A\) さんにメッセージ \(M\) を暗号化して送りたい場合、次のようにします。
\(A\) は \(1 < a < p-1\) である乱数 \(a\) を発生させ、\(g^a\) を \(A\) の公開鍵として \(B\) に送付、ないしは公開
します。乱数 \(a\) は \(A\) の秘密鍵として秘匿します。\(B\) がメッセージ \(M\) を暗号文にして \(A\) に送る場合、
\(B\) は(暗号文を送るたびに)\(1 < k < p-1\) である乱数 \(k\) を発生させ、\((g^k,\:\:M\cdot g^{ak})\) のペアを生成して \(A\) に送付
します。このペアを受け取ると、
\(A\) は \(g^k\) と自分の秘密鍵 \(a\) から \(g^{ak}\) を計算できます。これを使ってメッセージ \(M\) を復号化
します。複号化は \(g^{ak}\) の逆数(逆元)を乗算しますが、No.310 の「拡張ユークリッドの互除法」の 2.3a に書いたように、逆数の計算はたとえ \(g^{ak}\) や \(p\) が巨大数であっても効率的に可能です。
デジタル署名
\(A\) さん
秘密鍵 : \(a\)
公開鍵 : \(g^a\)
\(B\) さん
秘密鍵 : \(b\)
公開鍵 : \(g^b\)
とします。また、ハッシュ関数を \(H(\:)\) と書きます(ハッシュ関数については No.311「高校数学で理解するRSA暗号の数理(2)」の "補記" 参照)。\(B\) さんから \(A\) さんにメッセージ \(M\) を送るとき、デジタル署名の手順は次のように進みます。
\(B\) の署名
| \(0 < k < p-1\) で、\(\mr{gcd}(k,\:p-1)=1\) となる \(k\) をランダムに選ぶ。これはユークリッドの互除法を使って計算できる。 | |
| \(kx\equiv1\:\:(\mr{mod}\:p-1)\) となる \(x\:\:(1 < x < p-1)\) を求める。これも「拡張ユークリッドの互除法」2.3aで計算できる。以降、\(x=k^{-1}\) と表記する。 | |
| \(r\equiv g^k\:\:(\mr{mod}\:p)\) となる \(r\:\:(0 < r < p)\) を計算する。 | |
| メッセージ \(M\) のハッシュ値、\(h=H(M)\) を計算する。 | |
| \(s\equiv(h-rb)k^{-1}\:\:(\mr{mod}\:p-1)\) となる \(s\:\:(0 < s < p-1)\) を計算する。\(s\) がたまたま \(0\) なら、\(k\) の選択からやり直す。この計算は秘密鍵 \(b\) を知っている \(B\) にしかできない。 | |
| \((r,\:s)\) をデジタル署名として、メッセージ \(M\) とともに、暗号化通信で \(A\) に送付する。 |
\(A\) の検証
| 復号化したメッセージ \(M\) からハッシュ値 \(h=H(M)\) を計算する。 | |
| \(g^h\:\:(\mr{mod}\:p)\) を計算する。\(s\) の作り方から、
\(s\equiv(h-rb)k^{-1}\:\:(\mr{mod}\:p-1)\)
なので、両辺に \(k\) を掛けて変形すると、
\(\begin{eqnarray}
&&sk&\equiv h-rb &(\mr{mod}\:p-1)\\
&&h&\equiv sk+rb &(\mr{mod}\:p-1)\\
\end{eqnarray}\)
となる。従って、
\(h=n(p-1)+sk+rb\)
と書ける。このことと、フェルマの小定理(3.1)から \(g^{p-1}\equiv1\:\:(\mr{mod}\:p)\) なので、\(g^h\) は、
\(\begin{eqnarray}
&&g^h&=g^{n(p-1)}\cdot g^{sk}\cdot g^{rb}&\\
&&&\equiv g^{sk}\cdot g^{rb} &(\mr{mod}\:p)\\
&&&=(g^k)^s\cdot g^{rb} &(\mr{mod}\:p)\\
&&&=r^s\cdot(g^b)^r &(\mr{mod}\:p)\\
\end{eqnarray}\)
となるはずである。この最後の式において、\(\bs{r,\:s}\) は送られてきた \(\bs{B}\) の署名、\(\bs{g^b}\) は \(\bs{B}\) の公開鍵なので、すべて \(\bs{A}\) が知りうる値である。 | |
| \(g^h\equiv r^s\cdot(g^b)^r\:\:(\mr{mod}\:p)\) なら、署名は確かに \(B\) のものであり(= 公開鍵 \(g^b\) に対応した秘密鍵 \(b\) を知っている人の署名であり)、かつ、メッセージ \(M\) は改竄されていないと確証できる。 |
離散対数暗号(ElGamal 暗号)は、公開鍵暗号としてメジャーではありませんが、「暗号化鍵を公開してメッセージ伝送とデジタル署名を成立させる」ことの原理を端的に表わすものと言えます。
14. 生成元であることの証明
「ディフィー・ヘルマンの鍵共有」や「離散対数暗号」を実現するためには、巨大な素数 \(p\) に対する \(\bs{F}_p^{\:*}\) の生成元(のどれか)を知らなければなりません。これはどのように可能でしょうか。まず、
| 生成元は位数が \((p-1)\) の元であり (12.1) | |
| 位数は \((p-1)\) の約数に限られる (11.2) |
ので、\((p-1)\) の素因数分解ができたとすると約数が分かり、位数の候補がリストアップできます。
一般に \(d\) が 元 \(a\)(\(\neq1\)。以降、\(a\neq1\) とします)の位数であることの証明は手間がかかります。\(a\) の \(d\) 乗が \(1\) になったとしても \(d\) が \(a\) の位数だとは限りません。\(d\) よりも小さな数 \(e\) で \(a^e=1\) となるかもしれないからです。しかし、\(\bs{d}\) が \(\bs{a}\) の位数ではないことは簡単に証明できます。
\(a^d\neq1\)
を示せばよいからです。従って、\(a\) が \(\bs{F}_p^{\:*}\) の生成元であることを示すためには、\((p-1)\) の約数のうち \((p-1)\) 以外のすべての約数 \(d\) について、\(a^d\neq1\) であることを示せればよい。すると消去法で、\(a\) の位数は \((p-1)\) になります。この考えに基づき、簡単のために \(\bs{F}_{73}^{\:*}\) で考えると、
\(p-1=72=2^3\cdot3^2\)
なので \((p-1)\) の約数は \(1\) と \(72\) を含めて \(4\times3=12\) 個あります。従って \(72\) と \(1\) を除いた \(10\) 個の約数 \(d\) について
\(a^d\neq1\)
であれば、\(a\) の位数は \(72\) しかありえず、\(a\) は \(\bs{F}_{73}^{\:*}\) の生成元です。しかし実は、これでは「計算のやりすぎ」になります。この場合、
\(a^{24}\neq1\)
\(a^{36}\neq1\)
\(a^{36}\neq1\)
の2つだけが成り立てば、\(a\) の位数は \(72\) になります。なぜかというと、一般に次の命題が成立するからです。
| 14.1 | |
|
\(\bs{F}_p^{\:*}\) において、\(d\) が \(\bs{a}\) の位数ではないとすると、\(\bs{d}\) の任意の約数 \(\bs{e}\) も \(\bs{a}\) の位数ではない。 | |
\(e\) が \(d\) の約数だとすると、ある数 \(k\) があって \(d=ke\) と表せます。このとき、
\(a^e=1\) であるなら
\(a^d=a^{ke}=(a^e)^k=1\)
\(a^d=a^{ke}=(a^e)^k=1\)
です。このことの対偶をとると
\(a^d\neq1\) であるなら
\(a^e\neq1\)
\(a^e\neq1\)
となり、これはつまり、
\(d\) が \(a\) の位数でないなら、\(d\) の任意の約数 \(e\) も \(a\) の位数ではない
ことを意味します。\(p-1=72\) の場合、\(72\) を除く \(72\)(\(=2^3\cdot3^2\))の約数は、すべて \(24\)(\(=2^3\cdot3^1\)) か \(36\)(\(=2^2\cdot3^2\))のどちらかの(あるいは両方の)約数になります。従って、
\(a^{24}\neq1\)
\(a^{36}\neq1\)
\(a^{36}\neq1\)
が示せれば、\(72\) を除く \(72\) のすべての約数 \(d\) について、
\(a^d\neq1\)
となり、\(d\) は \(a\) の位数ではありません。この結果、\(a\) の位数は \(72\) しかあり得ず、\(a\) は \(\bs{F}_{73}^{\:*}\) の生成元であることになります。以上の考察を一般化すると、次の命題が成立します。
| 14.2 | |
|
\(p\) を素数とし、\((p-1)\) の素因数分解を、\(q_i\:(1\leq i\leq r)\) を素因数として、
\(p-1=q_1^{\al_1}\:q_2^{\al_2}\:\cd\:q_r^{\al_r}\) と表す。ここで、
\(m_i=\dfrac{p-1}{q_i}\) とおくと、もし \(1\) から \(r\) までのすべての \(i\) について、
\(g^{m_i}\neq1\:\:(1\leq i\leq r)\) が成り立つなら、\(g\) は \(\bs{F}_p^{\:*}\) の生成元である。 | |
\((p-1)\) の約数で、\((p-1)\) 以外の任意の約数を \(d\) とし、
\(d=q_1^{\beta_1}\:q_2^{\beta_2}\:\cd\:q_r^{\beta_r}\)
と表します。ここで \(\beta_i\) は、
\(0\leq\beta_i\leq\al_i\:(1\leq i\leq r)\)
です。そうすると、\(d\) は \((p-1)\) 以外の \((p-1)\) の約数なので、
\(d\) の素因数分解の中には、\(\beta_k < \al_k\) となる \(k\:(1\leq k\leq r)\) が少なくとも1つある
ことになります。なぜなら、もしそのような \(k\) がなければ \(d=p-1\) だからです。そのような \(k\) について、命題 14.2 で定義した、
\(m_k=\dfrac{p-1}{q_k}\)
に着目すると、\(d\) は \(m_k\) の約数になります。なぜなら、\(d\) と \(m_k\) の「素因数ごとの冪乗数」を比較してみると、
\(\beta_i\leq\al_i\:\:(1\leq i\leq r,\:i\neq k)\)
\(\beta_k\leq\al_k-1\) (仮定により \(\beta_k < \al_k\) だから)
\(\beta_k\leq\al_k-1\) (仮定により \(\beta_k < \al_k\) だから)
であり、\(d\) のすべての素因数の冪乗数は \(m_k\) の素因数の冪乗数以下です。つまり \(m_k\) は \(d\) で割り切れ、\(d\) は \(m_k\) の約数ということになります。
一方、命題 14.2 の仮定により、
\(g^{m_k}\neq1\)
なので \(m_k\) は \(g\) の位数ではありません。従って、\(m_k\) の約数である \(d\) も 14.1 により \(g\) の位数とはなりません。
\(d\) は \((p-1)\) 以外の任意の \((p-1)\) の約数でした。ということは、\((p-1)\) 以外の \((p-1)\) の約数は \(g\) の位数ではない。つまり消去法で、\(g\) の位数は \((p-1)\) であり、\(g\) は \(\bs{F}_p^{\:*}\) の生成元であることが証明されました。
実際に生成元を求める
\(\bs{F}_p^{\:*}\) の元 \(g\) をとったとき、それが生成元かどうかは 14.2 によって確かめることができます。しかしここで問題は、実用的なディフィー・ヘルマンの鍵共有では \(p\) が巨大な素数であり、\((p-1)\) の素因数分解が実質的に不可能なことです。巨大数の素因数分解が困難なことは、まさにRSA暗号(No.310-311「高校数学で理解するRSA暗号の数理」)が成立する根拠でした。
そこで実際に生成元を求めるためには、\(p\) を "作為的に" 決める必要があります。まず前提となるのは、ある数 \(p\) が素数であるかどうかの判定法は種々あって(ミラー\(\cdot\)ラビン素数判定法、など)、\(p\) が巨大数であっても判定可能なことです。この前提のもとに、簡単な方法の例を一つあげますと、次の関係にあるような3つの数 \(p\)、\(q\)、\(e\) を決めます。
\(p=eq+1\)
| \(p\)、\(q\) は巨大素数 | |
| \(e\) は小さな偶数 |
\(p\) と \(q\) は10進数で数百桁から1000桁以上の巨大素数(= 奇数)、\(e\) はたとえば100 以下の(もっと絞れば 10 以下の)偶数です。具体的には、まず \(q\) をランダムに選んで素数判定をし、素数であれば 次に \(e\) を選んで \(p\) が素数かどうかを判定するというプロセスになります。
こうすると \((p-1)\) の素因数分解は簡単にできるので、\(\bs{F}_p^{\:*}\) の任意の元 \(g\) が生成元かどうかは 14.2 で判定できます。具体的には \(g=2\) から始めて 順次 \(g\) を増やしていって生成元を探索することになるでしょう。
以上は一つの例ですが、実際に実務で使う \(p\) と \(g\) については \(g=2\) であると、コンピュータによる計算上、都合がよいわけです。従って、\(2\) が生成元になる前提で \(p\) を探索することになるでしょう。
ちなみに、現在、ディフィー・ヘルマンの鍵共有が実際に使われている例をあげておきます。インターネットを介してリモートのコンピュータ同士が安全に通信するための SSH(Secure Shell)という規格がありますが、そこで使われている公開鍵の一つ "diffie-hellman-group14-sha1"(2048ビットの素数 \(p\) と生成元 \(g\))を次に掲げます。これはインターネットの規格文書(RFC)に記載されています(RFC3526。16進表示)。この \(p\) は \(p=2q+1\) の形の素数で、10進では617桁です。10進表示と16進表示を以下に掲げます( \([\cd]\) はガウス記号で \(\cd\) を超えない最大の整数)。
diffie-hellman-group14-sha1(2048 bit)
\(p\:=\:2^{2048}-2^{1984}-1+2^{64}([2^{1918}\pi]+124476)\)
= 3231700 6071311007
3003389139 2642382824 8817941241 1402391128 4200975140
0741706634 3542226196 8941736356 9347117901 7379097041
9175460587 3209195028 8537589861 8562215321 2175412514
9017745202 7023579607 8236248884 2461894775 8764110592
8646099411 7232454266 2252219323 0540919037 6805242355
1912567971 5870117001 0580558776 5103886184 7280257976
0549035697 3256152616 7081339361 7995413364 7655916036
8317896729 0731783845 8968063967 1900977202 1941686472
2587103141 1336429319 5361934716 3653320971 7077448227
9885885653 6920864529 6636077250 2689555059 2836275112
1174096972 9980684105 5435958486 6583291642 1362182310
7899099944 8652468262 4169720359 1185250704 5361090559
=
FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D
C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F
83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D
670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B
E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9
DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510
15728E5A 8AACAA68 FFFFFFFF FFFFFFFF
\(g\:=\:2\)
ディフィー・ヘルマンの鍵共有の安全性ですが、離散対数問題を効率的に解くアルゴリズムはないと、数学的に証明されているわけではありません。ただ、RSA暗号の根拠になっている素因数分解のアルゴリズムと同じように、こういった数論の極めて基本的で、昔からある普遍的な問題は、世界の多くの数学者が関わってきています。それでも効率的に解くアルゴリズムは知られていません。ブログのタイトルを「高校数学で理解する」とましたが、そのような基礎的な数学しか使っていないからこそ暗号が成り立っている。そう言えると思います。
ディフィー・ヘルマンの鍵共有は公開鍵暗号の発端となったものですが、上にあげたように現在でも使われています(DHと略記される)。ただ、公開鍵暗号の優秀性は、「解読の困難性」と「暗号化・複号化計算の容易性」という二律背反の要求をいかに両立させるかにあります。その意味で、ディフィー・ヘルマン以降、各種の公開鍵暗号が開発されてきました。離散対数問題を使った暗号で言うと、よく使われるのは "楕円暗号(楕円曲線暗号)" です。これは「楕円曲線上の有理点がつくる "加法群" での離散対数問題」を利用した暗号です。しかし基本的な考え方はディフィー・ヘルマンの鍵共有と同じです。その意味で、公開鍵暗号の発端となった発明の意義は、今も続いているのでした。
まとめ
以上の 「ディフィー・ヘルマンの鍵共有」および「離散対数暗号」をまとめると、次のようになるでしょう。
| 公開鍵暗号の発端となった "ディフィー・ヘルマンの鍵共有" は、離散対数問題を解く困難さ(=実質的に不可能)を根拠とする暗号である。 | |
| 「ディフィー・ヘルマンの鍵共有」や「離散対数暗号」は、有限体(乗法群)やその生成元の存在など(オイラー、ガウスにさかのぼる)数論の基本のところをベースにできている。 | |
| RSA暗号(No.310-311)から通して振り返ってみると、そこでの前提知識は加減乗除と冪乗のルール程度であり、そこから論理を積み重ねていって公開鍵暗号の成立性が証明できる。つまり高校数学程度の知識があれば十分理解できる。 |
No.310-311 のRSA暗号と同じく、この最後の点がこの記事の目的なのでした。
素数判定アルゴリズム
公開鍵暗号で使われる巨大素数の判定アルゴリズム(ミラー・ラビン法)を、
No.369「高校数学で理解する素数判定の数理」
に書きました。
(2024.3.18)
2021-06-12 12:59
nice!(0)




