No.366 - 高校数学で理解する ChatGPT の仕組み(2) [技術]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
Attention Is All You Need
Google社は、2017年に "Attention Is All You Need" という論文(以下、"論文" と記述)を発表し、"Transformer" という画期的な技術を提案しました。Transformer は機械翻訳で当時の世界最高性能を発揮し、これが OpenAI 社の GPT シリーズや ChatGPT につながりました。
Attention(アテンション)とは "注意" という意味で、Transformer に取り入れられている "注意機構"(Attetion mechanism)を指します。"Attention Is All You Need" を直訳すると、
「必要なのはアテンションだけ」
ですが、少々意訳すると、
「アテンションこそがすべて」
となるでしょう(蛇足ですが、ビートルズの "All You Need Is Love" を連想させる論文タイトルです)。
Transformer を訳すと "変換器" ですが、その名の通り「系列 A から系列 B への変換」を行います。系列 A = 日本語、系列 B = 英語、とすると和文英訳になります。第3章では、この Transformer の仕組みを説明をします。
全体のアーキテクチャ
Transformer のアーキテクチャの全体像が次図です(論文より)。以降、この絵の意味を順に説明します。
アーキテクチャを簡略化して書くと次のようになります。以下では「日本語 → 英語の機械翻訳」を例として Transformer の動作を説明します。
左側がエンコーダで、入力された日本語テキストを中間表現(=テキストの特徴を抽出した内部表現)に変換します。右側のデコーダは、中間表現を参照しつつ「次に生成すべき英単語」を推論します。
エンコーダ、デコーダとも、図で「ブロック」と書いた単位を積層した構造です。つまり、1つのブロックの出力が次のブロックへの入力になります。アーキテクチャの絵で「N x」と書いてあるのはその積層の意味(= N 倍)で、積層する数を \(N\) とすると、Transformer では、
\(N=6\)
です。エンコーダの中間表現は最終ブロックからの出力です。その出力がデコーダの全てのブロックへ伝わります。
訓練
多数の「日本語 \(\rightarrow\) 英語の翻訳データ」を用いて Transformer を訓練するとき、全体がどのように動くかを示したのが次の図です。
エンコーダには日本語の文(Input)が入力されます。デコーダからの出力は、英文の推論結果(確率)です。これを正しい英文(Output = 教師ラベル)と照らし合わして損失(交差エントロピー誤差)を計算し、誤差逆伝播を行ってニューラル・ネットワークの重みを更新します(前回参照)。デコーダの入力となるのは「右に1語だけずらした Output」です。アーキテクチャの図18 で shifted right と書いてあるのはその意味です。なお、実際に入力されるのは単語ではなくトークンの列です(前回参照)。
推論
訓練を終えた Transformer を使って日本語文を英語文に機械翻訳するときの動きは次図です。
エンコーダに日本語のテキストを入力し、中間表現を得ます。これは1回きりです。
デコーダには、生成すべき英語テキストの最初のトークン、[BOS](文の始まりを示す特殊トークン)を入力し、[BOS] の次にくるべきトークンの確率を推論します。最も確率が高いトークンを選ぶと [I] になるはずです。これが1回目の推論(#1)です。
2回目(#2)では [I] を入力し、[I] の次のトークンを推論します([am] となるはずです)。[BOS] から [I] を推論したときの情報はデコーダに残されているので、その部分を再計算する必要はありません。推論のためには、日本語文の全情報(エンコーダの中間表現)と、既に生成した英文([BOS] [I])を参照します。
このようにして順々に英文を生成していき、推論結果が [EOS](文の終了を示す特殊トークン)になるところで、翻訳が終了します。
アーキテクチャの詳細
用語と記号
トークンの語彙
トークンの語彙(vocabulary)のサイズ を \(V\) とします。トークンを識別する "トークンID" は \(1\)~\(V\) の数字です。
系列
Transformer への入力となるテキストは、Tokenizer でトークンID の列に変換されます。以降、Transformer への入力を "系列(sequece)" と呼びます。
系列はその最大サイズ \(S\) が決まっています(普通、数千程度)。入力が \(S\) より少ない場合、残りのトークンは無効トークン([PAD])としておき、そこの処理は回避するようにします。[PAD] を含めて、系列は長さ \(\bs{S}\) の固定長とします。
系列\(=\{\:t_1,\:t_2,\:\cd\:,\:t_S\:\}\)
\(t_i\):トークンID \((1\leq t_i\leq V)\)
Transformer の論文には語彙のサイズと系列のサイズが書いてありませんが、以降の説明では \(V\) と \(S\) を使います。
分散表現ベクトル
トークンの分散表現ベクトル(埋め込みベクトル)の次元を \(D\) とします。トークンID が \(t_i\) であるトークンの分散表現を \(\bs{x}_i\) とすると、
\(\bs{x}_i=\left(\begin{array}{r}x_1&x_2&\cd&x_D\\\end{array}\right)\) \([1\times D]\)
というようになり、系列をベクトル列で表現すると、
系列\(=\{\:\bs{x}_1,\:\bs{x}_2,\:\cd\:,\:\bs{x}_S\:\}\)
となります。なお、\(D\) 次元ベクトルを、\(1\)行 \(D\)列の配列とし、\([1\times D]\) で表わします(前回参照)。
なお、Transformer では \(D=512\) です。
以降、全体アーキテクチャの図に沿って、各レイヤー(計算処理)の説明をします。以降の説明での \(\bs{x}_i,\:\:\bs{y}_i\) は、
\(\bs{x}_i\):レイヤーへの入力
(系列の \(i\) 番目。\(1\leq i\leq S\))
\(\bs{y}_i\):レイヤーからの出力
(系列の \(i\) 番目。\(1\leq i\leq S\))
で、すべてのレイヤーに共通です。また、\(D\) 次元ベクトルを \([1\times D]\)、\(S\)行 \(D\)列の行列を \([S\times D]\) と書きます。
埋め込みベクトルの生成
このレイヤーの入出力を、
とすると、
\(\bs{y}_i=\bs{x}_i\cdot\bs{W}_{\large enc}\)
\([1\times D]=[1\times V]\cdot[V\times D]\)
で表現できます(前回の word2vec 参照)。もちろん、この行列演算を実際にする必要はなく、\(\bs{x}_i\) のトークンID を \(t_i\) とすると、
\(\bs{y}_i=\bs{W}_{\large enc}\) の \(t_i\) 行
です。\(\bs{W}_{\large enc}\) は Transformer の訓練を始める前に、あらかじめ(ニューラル・ネットワークを用いて)作成しておきます。従って、埋め込みベクトルの作成はテーブルの参照処理(table lookup)です。
位置エンコーディング
埋め込みベクトル(分散表現)に、トークンの位置を表す「位置符号ベクトル」を加算します。つまり、
とすると、
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
\([1\times D]=[1\times D]+[1\times D]\)
の単純加算です。位置符号ベクトル \(\bs{p}_i\) の要素を次の記号で表します。
\(p_{t,d}\)
\(t\) は \(0\) から始まる、トークンの位置
\((t=i-1,\:\:0\leq t\leq S-1)\)
\(d\) は \(0\) から始まる、ベクトル内の要素の位置
\((0\leq d\leq D-1)\)
この \(p_{t,d}\) の値は次のように定義されます。
\((0\leq k < \dfrac{D}{2},\:\:\:x=\dfrac{2k}{D},\:\:\:0\leq x < 1)\)
つまり、\(D=512\) とすると、
\(d\) が偶数の要素位置では \(\mr{sin}\) 波
(\(d=0,\:2,\:4,\:\cd\:,510\))
\(d\) が奇数の要素位置では \(\mr{cos}\) 波
(\(d=1,\:3,\:5\:\:\cd\:,511\))
で位置符号値を決めます。この \(\mr{sin}/\mr{cos}\)波の波長 λ は
λ\(=2\pi\cdot10000^x\)
であり、\(0\leq d < D\) の範囲で、
\(2\pi\leq\)λ\( < 2\pi\cdot10000\)
となります。この \(\mr{sin}/\mr{cos}\) 波を図示してみます。グラフをわかりやすくするために、\(D=512\) ではなく、
\(D=32\)
とし、ベクトルの要素 \(32\)個のうちの最初の6つ、
\(d=0,\:1,\:2,\:3,\:4,\:5\)
だけのグラフにします。グラフの
・横軸はトークンの位置 \(t\)
・縦軸は位置符号ベクトルの要素 \(p_{t,d}\)
です。
具体的に \(t=3\) のときのベクトルの要素 \(p_{3,d}\:\:(0\leq d\leq31)\) の \(0\leq d\leq5\) の部分を書いてみると、
\(p_{3,0}=\phantom{-}0.1411\)
\(p_{3,1}=-0.9900\)
\(p_{3,2}=\phantom{-}0.9933\)
\(p_{3,3}=-0.1160\)
\(p_{3,4}=\phantom{-}0.8126\)
\(p_{3,5}=\phantom{-}0.5828\)
となります(図22)。
言うまでもなく、言語モデルにとってトークンの位置はきわめて重要な情報です。位置をバラバラにすると意味をなさないテキストになるし、Bob loves Alice と Alice loves Bob では意味が逆です。従って、何らかの手段で「トークンの位置を考慮したモデル化」をしなければならない。
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
の式で、\(\bs{x}_i\) は「単語埋め込み」のアルゴリズムで作られ、似たような単語/トークンは類似したベクトルになります(前回参照)。それに対し \(\bs{p}_i\) の \(\mr{sin}/\mr{cos}\) 波は、言語処理とは全く無関係な数学の産物です。従って、加算結果である \(\bs{y}_i\) がどのような「意味」をもつベクトルなのか、説明しようとしても無理でしょう。全く異質なものの足し算をしているのだから ・・・・・・。それでいて、このやり方で全体として成り立つのが驚きです。
Transformer より以前の機械翻訳では、トークンの出現順に逐次処理をするアーキテクチャでした。つまり、1つのトークンの処理結果を利用しながら次のトークンを処理するという逐次処理によって、並び順に意味があるという言語の特質を捕らえていました。
それに対し、位置エンコーディングを取り入れた Transformer では、逐次処理の必要性がなくなり、系列のトークン全部の並列処理が可能になりました。この結果、同一計算の超並列処理ができる GPU(数千並列が可能) をフルに活用することで、実用的な大規模言語モデルが構築できるようになったわけです。位置エンコーディングにはそういう意味があります。
なお Transformer の論文にも書いてあるのですが、位置符号ベクトルを \(\mr{sin}/\mr{cos}\) 波のような「決めうち」で作らないで、「学習可能なパラメータ」としておき、Transformer を訓練する過程で決めるやり方があります。位置符号ベクトルを学習で決めるわけです。GPT はこの方法をとっています。
Single Head Attention : SHA
アテンション・レイヤー(Multi Head Attention : MHA)の説明をするために、まず "Single Head Attention : SHA" の処理論理を説明します。Transformer で実際に使われている MHA は、以下に説明する SHA の拡張版で、核となるアルゴリズムは同じです。
SHAの入出力は、それぞれ \(S\)個の \(D\)次元ベクトルであり、
入力 \(\bs{x}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
出力 \(\bs{y}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
ですが、系列の全体を1つの行列で表すことができます。1つのベクトルを行列の1行として、それを縦方向に \(S\)個並べて行列を作ります。つまり、
入力 \(\bs{X}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{x}_i\))
出力 \(\bs{Y}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{y}_i\))
とすると SHA は、
\(\bs{Y}=\mr{SHA}(\bs{X})\)
と書けます。アテンションの処理では、まず入力ベクトル \(\bs{x}_i\) を、
の組、( \(\bs{q}_i,\:\:\bs{k}_i,\:\:\bs{v}_i\) )に変換します。変換式は次の通りです。
ここで、\(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は学習で決まる変換行列です。系列全体についての Query/Key/Value(\(QKV\))を行列の形で表すと、
となります。SHA レイヤーからの出力、\(\bs{y}_i\:\:[1\times D]\) は、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の "重み付き和" (加重和)で求めます。加重和に使う重み、\(\bs{w}_i\:\:[1\times S]\) は次のように計算されます。
まず、クエリ・ベクトル \(\bs{q}_i\) とキー・ベクトル \(\bs{k}_j\:\:(1\leq j\leq S)\) の "スケール化内積(scaled dot product)" を計算し、\(S\)個のスカラー値を求めます。スケール化内積(\(\mr{SDP}\) と記述します)とは、2つの \(D\)次元ベクトル \(\bs{a}\) と \(\bs{b}\) の場合、
\(\mr{SDP}(\bs{a},\bs{b})=\dfrac{1}{\sqrt{D}}\bs{a}\bs{b}^T\)
\([1\times1]=[1\times D]\cdot[D\times1]\)
で定義されます。つまり、一般の内積(=スカラー値)を「ベクトルの次元数の平方根」で割ったものです。
\(\bs{q}_i\) と \(\bs{k}_j\:\:(1\leq j\leq S)\) のスケール化内積を順番に \(S\)個並べたベクトルを \(\bs{s}_i\:\:[1\times S]\) と書くと、スケール化内積の定義によって、
\(\bs{s}_i=\dfrac{1}{\sqrt{D}}\bs{q}_i\bs{K}^T\)
\([1\times S]=[1\times D]\cdot[D\times S]\)
です。そして、加重和を求めるときの重み \(\bs{w}_i\) は、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
\([1\times S]=\mr{Softmax}([1\times S])\)
とします。この \(S\)次元の重みベクトルを使って、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の加重和をとると、出力ベクトル \(\bs{y}_i\) は、
\(\bs{y}_i=\bs{w}_i\cdot\bs{V}\)
\([1\times D]=[1\times S]\cdot[S\times D]\)
となります。以上の計算プロセスを一つの式で書いてしまうと、
です。従って、SHA からの出力ベクトル \(\bs{y}_i\) を縦方向に並べた行列 \(\bs{Y}\) は、
\(\bs{Y}=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{Q}\cdot\bs{K}^T\right)\cdot\bs{V}\)
\([S\times D]=\mr{Softmax}([S\times D]\cdot[D\times S])\cdot[S\times D]\)
と表すことがきます。この表記で \(\mr{Softmax}\) 関数が作用するのは \([S\times S]\) の行列ですが、\(S\)個の行ごとに \(\bs{\mr{Softmax}}\) を計算します。
単なる内積ではなく「スケール化内積」を使う理由ですが、2つのベクトルの内積は、要素同士のかけ算を次元数 \(D\) 個だけ加算したものです。従って、ベクトル \(\bs{s}_i\) を、シンプルな内積を使って、
\(\bs{s}_i\:=\bs{q}_i\cdot\bs{K}^T\)
のように定義し、重み \(\bs{w}_i\) を、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
で求めると、\(D\) が大きいと \(\bs{s}_i\) の要素が大きくなり、その結果として \(\bs{w}_i\) はゼロに近いところに多くの要素が集まるようになります。これは \(\mr{Softmax}\) 関数の性質によります(前回参照)。こうなると勾配消失が起きやすくなり、訓練が収束しづらくなります。そのため「スケール化」するというのが論文の説明です。
もちろん、幾多の試行錯誤があり、その結果として決まったのが「スケール化内積で加重和の重みを計算する」というやり方だったのでしょう。
以上の計算でわかるように、注意機構(Attention machanism)とは、あるトークンを処理するときに、注意を向けるべきトークンと注意の強さを決め(それ自体が学習で決まる)、注意を向けた先の情報を集めてきて集積するものです。
しかも、注意機構は6層(\(N=6\)) に重ねられています。ということは、階層的な(多段階の) "注意の向け方" ができることになります。また、言語における単語と単語の関係性は多様です。動作\(\cdot\)動作主体、修飾\(\cdot\)被修飾、指示代名詞と指示されるもの(照応関係)など多岐に渡ります。それらのさまざまなタイプの関係性を、Transformer の訓練を通して、多層の注意機構が自動的に把握すると考えられるのです。
MHA : Multi Head Attention
SHA では、入力ベクトル \(\bs{x}_i\) から、1組の Query/Key/Value(\(QKV\)) ベクトルを抽出しましたが、Transformer で実際に使われているのは、
という処理です。これを Multi Head Attention : MHA と呼びます。この「それぞれについてのアテンション処理」のことを "head(ヘッド)" と言います。複数の head なので Multi Head です。このヘッドの数を \(H\) とし、
\(d=\dfrac{D}{H}\) (\(D\) は入出力ベクトルの次元)
とします(\(H\) は \(d\) が整数になるように選びます)。このとき、
です。つまり MHA は「複数の特徴を抽出し(一つの情報量は SHA より少ない)、それぞれの特徴について 独立した "注意機構" を働かせ、最後に統合してまとめる」仕組みです。なお、Transformer では、
\(H=8\)
\(d=\dfrac{D}{H}=\dfrac{512}{8}=64\)
です。
\(h\) 番目のヘッド \((1\leq h\leq H)\) に着目し、"注意機構" の計算プロセスを式で書くと、次のようになります。まず、\(h\) 番目のヘッドの \(QKV\) ベクトルの計算は、
です。系列全体について、\(h\) 番目のヘッドの \(QKV\) を行列の形で表すと、
です。\(h\) 番目のヘッドのアテンション処理は、SHA の場合と同様で、
となり、これを系列全体での表現にすると、
となります。行列 \(\bs{Y}^h\) は、\(h\) 番目のヘッドの出力ベクトル \(\bs{y}_i^h\:\:[1\times d]\) を、系列の数だけ縦に並べた行列です。
系列の \(i\) 番目の入力 \(\bs{x}_i\) に対する \(H\) 個の出力ベクトル
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
が求まったところで、これら \(H\) 個を単純結合して(=順に並べる)一つのベクトルにし、さらに Linear 変換をして最終出力にします。変換に使う行列は \(\bs{W}_O\:\:[D\times D]\) です。
Linear 変換は直前の単純結合(Concatenation)とセットになっています。つまり、ヘッドの順序を表す \(h\:\:(1\leq h\leq H)\) という数字には、"注意機構" における何らかの意味があるわけではありません。単にアテンション処理を \(H\) 個に分けた \(h\) 番目というだけです。従って、順に単純結合する、
\(\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\)
という操作の「結合順序」には意味が無いことになります。そこで結合した後で、学習可能なパラメータ \(\bs{W}_O\) で線型写像を行って、最適な出力ベクトルを求めるわけです。
エンコーダの MHA は、エンコーダ内に閉じたアテンションで、これを「自己アテンション」(Self Attention)と言います。一方、デコーダ側には自己アテンションの他に、エンコーダとデコーダにまたがるアテンションがあります。これを Source Target Attention と言います。このアテンションは、
します。これによってエンコーダからデコーダ側への情報の流れを作ります。日本語 → 英語の機械翻訳の場合だと、次に生成すべき英単語に関連して「注意を向けるべき日本語のトークンと、その注意の量」がここで決まります。
Multi Head Attention において、1つのベクトルから複数の \(QKV\) を取り出すことの意味は、おそらくトークンの「多義性」でしょう。その例ですが、英語で fine という語の代表的な意味を4つあげるとしたら、たとえば、
fine :
(1) 素晴らしい
(2) 晴れた
(3) 細かい
(4) 罰金
です(例です。(1) (2) は同類の意味)。単語の埋め込みベクトルは、似たような(あるいは同一ジャンルの)語は類似している(= コサイン類似度が 1 に近い)わけです(前回参照)。とすると、(1)~(4) の同一ジャンルの言葉は、それぞれ、
(1) good, excellent, ・・・・・・
(2) cloudy, rainy, ・・・・・・
(3) tiny, small, coarce, ・・・・・・
(4) penalty, guilty, ・・・・・・
などとなるはずです。fine がこれら4つのジャンルと類似性があるということは、fine の埋め込みベクトルおいて4つの意味が物理的に分散して配置されていると考えられます。さらにイタリア語まで考えると、
fine :
(5) 終わり
が加わります(イタリア映画の最後に出てくる語、ないしは音楽用語)。埋め込みベクトルは言語ごとに作るわけではないので、fine のベクトルはあくまで1つです。ということは、埋め込みベクトルには(この例では)5つの意味が分散して配置されているはずです。
この状況は、埋め込みベクトルから複数の \(QKV\) ベクトルを取り出し、それぞれについて独立したアテンション計算をするというアルゴリズムがマッチしていると考えられるのです。
Add & Norm
アーキテクチャの絵で5カ所にある「Add & Norm」は、ベクトルごとに「残差結合」と「レイヤー正規化」を行うレイヤーです(詳細は前回参照)。図で表すと以下です。
計算式は次のようになります。系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略します。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\begin{eqnarray}
&&\:\: \bs{x}=\{\:x_1, &x_2, &\cd\:, &x_D\:\}\\
&&\:\: \bs{y}=\{\:y_1, &y_2, &\cd\:, &y_D\:\}\\
\end{eqnarray}\)
\(x_k\:\:(1\leq k\leq D)\) の平均 : \(\mu\)
\(\mu=\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}x_k\)
\(x_k\:\:(1\leq k\leq D)\) の標準偏差 : \(\sg\)
\(\sg=\sqrt{\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}(x_k-\mu)^2}\)
とおくと、
です。ここで \(\bs{g}\) と \(\bs{b}\) は学習で決まるベクトル(=パラメータ)です。
Feed Forward Network
ベクトルごとに処理される、2層の全結合ニューラル\(\cdot\)ネットワークです。第1層の活性化関数は \(\mr{ReLU}\) で、第2層(出力層)には活性化関数がありません。3つのレイヤーで表現すると次の通りです。
ニューロンの数(=ベクトルの次元)は、
入力層:\(D\)
第1層:\(D_{ff}=4\times D\)
出力層:\(D\)
です。計算を式で表すと(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)、
\(\bs{y}=\mr{ReLU}(\bs{x}\bs{W}_1+\bs{b}_1)\cdot\bs{W}_2+\bs{b}_2\)
です。第1層の次元を入力\(\cdot\)出力層の4倍にとるのは、そのようにするのが Transformer の性能(たとえば、翻訳文の質)が最も向上するからです。GPT-3、ChatGPT も踏襲しています。
Masked Multi Head Attention
デコーダ側にある Masked Multi Head Attention の説明をします。系列のトークンの列を、
\(\{\:\bs{x}_1,\:\cd\:,\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\cd\:,\:\bs{x}_S\:\}\)
とし、いま \(\bs{x}_t\) に着目しているとします。
\(\bs{x}_i\:\:\:(1\leq i\leq t)\:\longrightarrow\) 過去のトークン
\(\bs{x}_i\:\:\:(t < i\leq S)\:\longrightarrow\) 未来のトークン
と呼ぶことにします。着目しているトークンを基準に、系列でそれ以前のトークンが「過去」、次以降のトークンが「未来」です。
日本語から英語に翻訳する Transformer を例にとると、デコーダの推論時には、英文のトークンを一つずつ推論していきます。つまり、
[BOS] \(\longrightarrow\) [I]
[BOS] [I] \(\longrightarrow\) [am]
[BOS] [I] [am] \(\longrightarrow\) [a]
[BOS] [I] [am] [a] \(\longrightarrow\) [cat]
[BOS] [I] [am] [a] [cat] \(\longrightarrow\) [EOS]
といった具合です(図21)。このときの各ステップにおけるアテンション処理は、当然ですが、末尾のトークンから生成済みのトークン(=過去のトークン)に対して行われます。つまり「トークンが注意を向ける先は常に過去のトークン」です。「すでに生成済みのトークンの情報だけから次にくるトークンを推論する」のがデコーダなので、これは当然です。
一方、デコーダの訓練時のことを考えると、
で(図20)、入力データとしては系列のトークンが全部与えられています。しかしここで未来のトークンに注意を向けてしまうと、推論時との不整合が起きてしまいます。そこで
という配慮が、デコーダ側のアテンション処理では必要になります。この配慮をした注意機構が Masked Multi Head Attention です。一方、エンコーダ側では、訓練時も推論時も、
[我が輩] [は] [猫] [で] [ある]
という系列が一括して与えられるので(図20、図21)、未来のトークンに注意を向けても問題ありません。またデコーダ側からエンコダー側に注意を向けるのもかまいません。
この「過去のトークンにだけ注意を向ける」ことを数式で表現するには、\([S\times S]\) のマスク行列、\(\bs{M}\) を次のように定義します。
\(\bs{M}=\left(\begin{array}{c}
0&\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}\\
\phantom{0}&\large\ddots&\phantom{0}&\huge\textrm{-}\infty&\phantom{0}\\
\phantom{0}&\phantom{0}&0&\phantom{0}&\phantom{0}\\
\phantom{0}&\huge0&\phantom{0}&\large\ddots&\phantom{0}\\
\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}&0\\
\end{array}\right)\) \([S\times S]\)
このマスク行列は、
です。これを、アテンションの計算式の \(\mr{Softmax}\) 関数の内側に足し込みます。\(h\) 番目のヘッドに着目したアテンションの計算式は、
でした。これに \(\bs{M}\) を足し込むと、
となります。\(\mr{Softmax}\) 関数は、ベクトル(上式では行列の1行)の各要素の \(\mr{exp}()\) をとります。従って、要素が \(-\infty\) だと \(\mr{exp}(-\infty)=0\) となり、\(\mr{Softmax}\) 関数にとってはその要素が無いのと同じことになります。
上式の \(\mr{Softmax}\) 関数の内側は \([S\times S]\) の行列ですが、縦方向が系列全体のクエリ・ベクトルに対応し、横方向が系列全体のキー・ベクトルに対応しています。そのため、マスク行列を足し込むと、アテンション処理において過去のトークンだけに注意が行き、未来のトークンには注意が行かない(=結果としてバリュー・ベクトルが加重和されない)ようになるのです。
こうして求めた行列 \(\bs{Y}^h\) の \(i\) 行目をベクトル、
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
とすると、これ以降の処理はマスク行列がない場合と同じです。つまり \(H\) 個のベクトル \([1\times d]\) を単純結合して一つのベクトル \([1\times D]\) にし、さらに Linear 変換をしてアテンション処理からの最終出力にします。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\)
\(\begin{eqnarray}
&&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\
&&&=[1\times D]\cdot[D\times D]\\
\end{eqnarray}\)
わざわざ \(\mr{exp}(-\infty)\) を持ち出してマスク行列を使うのは、話をややこしくするだけのようですが、マスク行列を使った Masked Multi Head Attention の計算式を見ると、線型変換と \(\mr{Softmax}\) 関数だけからできています。ということは、「過去のトークンだけに注意を向けるアテンション計算は微分可能」であり、誤差逆伝播の計算が成り立つことがわかります。
確率生成
Transformerのデコーダの最終部分は、推論結果である \(D\) 次元のベクトルを、語彙集合の中での確率ベクトルに変換する部分です。計算式で書くと、
\(\bs{y}=\mr{Softmax}(\bs{x}\cdot\bs{W}_{\large dec})\)
\([1\times V]=\mr{Softmax}([1\times D]\cdot[D\times V])\)
です(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)。\(\bs{W}_{\large dec}\) は、前回の word2vec のところに出てきた、\(D\)次元の埋め込みベクトルを \(V\) 次元の確率ベクトルに変換する行列です。
以上で Transformer のアーキテクチャの説明は終わりですが、全体を振り返ると、
ことがわかります。以降は、この中で鍵となる「アテンション」と「Feed Foward Network」についての補足です。
アテンションの意義
一般のニューラル・ネットワークにおいて、隣合った2つの層、\(\bs{x}\) と \(\bs{y}\) が同じニューロン数 \(D\) だとします。活性値を、
\(\begin{eqnarray}
&&\:\:\bs{x}=\{x_1, &x_2, &\cd\:,&x_D\}\\
&&\:\:\bs{y}=\{y_1, &y_2, &\cd\:,&y_D\}\\
\end{eqnarray}\)
とし、重み行列を \(\bs{W}\)、バイアスはなし、活性化関数を \(\mr{ReLU}\) とするると、
\(\bs{y}=\mr{ReLU}(\bs{x}\cdot\bs{W})\)
です。重み \(\bs{W}\) は誤差逆伝播法による訓練で決まり、推論時には一定の値です。Transformer のアテンション機構もこれと似ています。アテンションは、
入力ベクトル列 :\(\bs{x}_i\:\:\:(1\leq i\leq S)\)
出力ベクトル列 :\(\bs{y}_i\:\:\:(1\leq i\leq S)\)
の間の変換をする機構だからです。ニューラル\(\cdot\)ネットワークの活性値(実数値)がベクトルに置き換わったものと言えます。ヘッドが1つの場合(Single Head Attension)で図示すると、次の通りです。
しかし、この図は一般のニューラル\(\cdot\)ネットワークとは決定的に違います。重み行列 \(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は推論時には一定ですが、実際に \(\bs{x}_i\) と \(\bs{y}_i\) の関係性を決めているのは、クエリ・ベクトル \(\bs{Q}\) とキー・ベクトル \(\bs{K}\) であり、これは入力ベクトル列 \(\bs{x}_i\) の内容にもろに依存しているからです。つまり、
と言えます。\(\bs{x}_1\) の値を変えると、その影響は \(\bs{y}_i\:\:(1\leq i\leq S)\) の全体に及びます。それは、「\(x_1\) を変えると \(y_i\) の全部が変わる」という一般のニューラル\(\cdot\)ネットワークと同じではありません。一般のニューラル\(\cdot\)ネットワークを関数とみなすと、「関数は一定だが、入力が変わるから出力も変わる」のです。それに対して注意機構は「入力が変わると関数の形まで変わる」とみなすことができるでしょう。もちろん、実際には図25のように関数は一定なのですが、一般のニューラル\(\cdot\)ネットワークとの比較で言うと、そうみなせるということです。
この柔軟性とダイナミックな(動的な)性格が、Transformer に大きなアドバンテージをもたらしました。次章の GPT-3 / ChatGPT が実現している「本文中学習(In Context Learning)」はその一つです。ChatGPT では、プロンプトを変える、ないしは文言を追加すると、応答が大きく変わることがあります。また、欲しい応答の表現形式を例示したプロンプトをすると、その形式どおりのに応答がきたりします。あたかも、プロンプトからその場で学んだように見えるのが In Context Learning です。しかし、ニューラル・ネットワークのパラメータは、推論時にはあくまで一定であり、決してその場で学んでいるわけではありません。この "あたかも" を作り出しているのが "注意機構"です。
Feed Forward Network の意味
Transformer のアーキテクチャは、注意機構の後ろに Feed Forward Network(FFN) が接続され、このペアが多層に積み重ねられています。この FFN の意味は何でしょうか。
FFN は、注意機構と違ってベクトルごとの処理です。論文では "Position-wise(位置ごとの)Feed Forward Network" と書いてあります。ということは、系列の文脈には依存しないということです。つまり Transformer の訓練を通して、ベクトル(トークンの中間表現)が本来持っている性格や関連情報が、FFN の重みの中に蓄えられると考えられます。AI の専門家である、プリファードネットワークス社の共同創業者の岡野原大輔氏は、著書の『大規模言語モデルは新たな知能か』の中で次のように書いています。
岡野原氏が「多重パーセプトロン(Multi-Layer Perceptron : MLP)と書いているのは FFN のことです。ちなみに入力層(第0層)を含めて「三層」という言い方になっています。
ここで、FFN のパラメータ数を求めてみます。バイアスを無視すると、
\(\bs{W}_1\:\:[D\times D_{ff}]\)
\(\bs{W}_2\:\:[D_{ff}\times D]\)
\(D\) : 埋め込みベクトルの次元
\(D_{ff}=4D\)
なので、
FFN のパラメータ数\(=8D^2\)
です。一方、Multi Head Attention で、
\(H\) : ヘッドの数
\(d=\dfrac{D}{H}\)
とすると、\(h\)番目のヘッドの \(QKV\) を作る行列は、
\(\bs{W}_Q^h\) \([D\times d]\)
\(\bs{W}_K^h\) \([D\times d]\)
\(\bs{W}_V^h\) \([D\times d]\)
であり、これらを足すとパラメータ数は \(3Dd\) ですが、この組が \(H\) セットあるので、合計は \(3DdH=3D^2\) です。さらに、単純結合したあとの Linear 変換行列である、
\(\bs{W}_O\) \([D\times D]\)
が加わるので、結局、
MHA のパラメータ数\(=4D^2\)
です。ということは、
FFN のパラメータ数は、MHA のパラメータ数の2倍
ということになります。パラメータ数だけの単純比較はできませんが、FFN が極めて多い情報量=記憶を持っていることは確かでしょう。それが、大量の訓練データの中から関連する情報を記憶し、また推論時にそれを想起することを可能にしています。
論文のタイトルは "Attention Is All You Need" で、これは従来の機械翻訳の技術では補助的役割だった Attention を中心に据えたという意味でしょう。しかし技術の内実をみると、決して「アテンションがすべて」ではなく「アテンション機構と多重パーセプトロンの合わせ技」であり、しかもそれを多層に重ねたのが Transformer なのでした。
前回でニューラル・ネットワークの例とした多重パーセプトロンは、ニューラル・ネットワークの研究の歴史の中で最も由緒あるもので、1980年代に盛んに研究されました。それが、2010年代半ばから研究が始まった "アテンション機構" と合体して Transformer のアーキテクチャになり、さらには ChatGPT につながったのが興味深いところです。
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。ここではまず GPT-3 の仕組みを説明します。
GPT-3 のアーキテクチャ
GPT は Generative Pre-trained Transformer の略です。generative とは "生成型の"、pre-trained は ""事前学習済の" という意味で、Transformer は Google が 2017年に提案した Transformer を指します。
訳すると "事前学習済の生成型トランスフォーマー" となるでしょう。Transformer は「変換器」という意味でした。とすると「生成型の変換器」とは言葉が矛盾しているようですが、実は GPT は Transformer のアーキテクチャのデコーダ部分だけを使った大規模言語モデルです。だから「生成型変換器」なのです(下図)。
この「デコーダ部分だけを使う」という発想が、OpenAI の技術者の慧眼でした。デコーダだけで系列変換(機械翻訳、文章要約、質問応答、・・・・・・ )ができるはず、という発想が GPT に柔軟性と大きな能力を与えました。GPT-3 のアキテクチャーは以下のようです。
このアキテクチャーは、Transformer から「エンコーダとエンコーダ関連部分」を取り去ったものです。ただし、次が違います。
これらはいずれも、学習の安定化と高速化のための工夫です。さらに GPT-3 は Transformer に比べてモデルの規模が大きく拡大されています。
・埋め込みベクトルの次元 \(D=12288\)
\((\)Transformer \(:\:512\) の \(24\)倍\()\)
・デコーダブロックの積層数 \(N=96\)
\((\)Transformer \(:\:6\) の \(16\)倍\()\)
・アテンションのヘッドの数 \(H=96\)
\((\)Transformer \(:\:8\) の \(12\)倍\()\)
です。大規模言語モデルでは、モデルの規模と学習量の拡大を続けると、それにともなって性能(たとえば機械翻訳の精度)が上がり続けるという「スケール則」がみられました。これは一般の深層学習のニューラル\(\cdot\)ネットワークにはない特徴です。このスケール則を信じ、アーキテクチャをシンプルにしつつ、モデルの規模を「桁違いに」拡大した OpenAI 社と出資した会社(マイクロソフト)の勝利でしょう。
このアーキテクチャのパラメータ数をカウントしてみます。
とします。GPT-3 の具体的な数値は、
です(\(V\) の値については前回参照)。学習で決まる行列やベクトルを順にカウントしていくと次のとおりです。
(1) Embedding と確率生成
\(\bs{W}_{\large enc}\) \([V\times D]\)
\(\bs{W}_{\large dec}\) \([D\times V]\)
\(\rightarrow\) パラメータ数\(=2VD\)
(2) Positional Encoding
\(\bs{p}\) \([S\times D]\)
\(\rightarrow\) パラメータ数\(=SD\)
(3) Masked Multi Head Attention
\(\bs{W}_Q\) \([D\times D]\) ※
\(\bs{W}_K\) \([D\times D]\) ※
\(\bs{W}_V\) \([D\times D]\) ※
\(\bs{W}_O\) \([D\times D]\)
\(\rightarrow\) パラメータ数\(=4D^2\)
(4) Feed Forward Network
\(\rightarrow\) パラメタ数\(=8D^2+5D\)
(5) Layer Nomaliation (2レイヤー)
\(\bs{g}\) \([1\times D]\)
\(\bs{b}\) \([1\times D]\)
\(\rightarrow\) パラメタ数\(=2\times2D=4D\)
(3), (4), (5) は \(\times\:N\) に積層されていることに注意して総パラメータ数を計算すると、
総パラメータ数
\(=\:2VD+SD+N(4D^2+8D^2+5D+4D)\)
\(=\:2VD+SD+N(12D^2+9D)\)
\(=\) \(\bs{175,217,074,176}\)
となり、約 1752億となります。一般に言われているパラメータ数が 1750億というのは、英語の 175B(B = Billion = 10億)の日本語訳で、Billion 単位にしたパラメータ数です。
GPT-3 が系列の次のトークンを推論するとき、1752億のパラメータの全てを使った演算が行われます(図21)。40文字の日本語文章を 60トークンだとすると、 わずか 40文字の日本語文章を生成するために、1752億のパラメータの全てを使った演算が 60回行われるということです。
また、1752億のパラメータがすべて 32ビットの浮動小数点数(4バイト)だとすると、パラメータのためだけに、
653ギガバイト(1ギガ = \(1024^3\) 換算)
のメモリが必要になります。業務用コンピュータ・システムの開発経験者ならわかると思いますが、これだけのデータ量を常時抱えつつ、更新やリアルタイムの推論を行うシステムを開発・運用するのは、ちゃんとやればできるでしょうが、かなり大変そうな感じです。
GPT-3 のアーキテクチャを振り返ってみると、Transformer のデコーダ部分だけを採用したことによる、Transformer との違いがあることに気づきます。それは、
ことです。言うまでもなく、アテンション機構は Transformer / GPT-3 の "キモ" です。そのキモのところに違いがある。
人間の言語活動(発話・文章作成)では「過去の単語との整合性を考慮しつつ、未来の単語を想定して次の単語を決める」ことが多々あります。このことは、機械翻訳では、翻訳前の「原文」を処理するエンコーダ側の「過去と未来の両方に注意を向けるアテンション機構」で実現されています(Mask がない Multi Head Attention)。
しかし GPT-3 では様子が違ってきます。事前学習(次項)だけの GPT-3 で機械翻訳がなぜできるかというと、
[ 原文 ] を翻訳すると [ 翻訳文 ] です
といった対訳(に相当するデータ)が訓練データの中に多数あるからです(GPT-2 の論文による)。この「原文」の部分のアテンション処理において、「原文」の中の未来の単語に注意が向くことはありません(Masked Multi Head Attention しかないから)。このことにより翻訳の精度が Transformer とは違ってくる(精度が落ちる)と想定できます。
こういった "問題" は、大規模言語モデルを "超大規模" にすることで解決するというのが、GPT-3 の開発方針だと考えられます。1752億という膨大なパラメータ数が、それを表しています。
GPT-3 の訓練
GPT-3 の訓練は、
・WebText
・電子ブック
・Wikipedia
をもとに行われました。WebText は "訓練に使うべきではない" テキストを除外してあります。集められたテキストの量はトークンの数でカウントすると、
です。これらのテキストからランダムに選んだミニバッチを作り、「ミニバッチ勾配降下法」(前回参照)で訓練が行われました。但し、Wikipedia などの "信頼性が高いテキスト" は、より多くミニバッチに選ばれるような工夫がしてあります。訓練は、使われたテキストが、トークン数で延べ \(3000\)億になったところで打ち切られました。
訓練は、Transformer のデコーダのところでで説明したように「ひたすら次のトークンの予測をする」というものです。この「次のトークンの予測」について補足しますと、前回、GPT のトークン化のロジックである BPE(Byte Pair Encoding)のことを書きました。これによると、UTF-8 では改行も空白も文字として扱われるので、改行、空白のそれぞれにトークンID が割り当てられることになります。
これから言えることは、テキストを学習するということは、その意味内容だけでなく、テキストの表現形式も学習するということです。つまり、段落、字下げ、箇条書きなどの形式です。訓練が終わった 1752億のパラメータには、そういった "表現形式に関する知識" も含まれていることに注意すべきでしょう。
以上のように、一般的に入手できるテキストだけを使ってニューラル・ネットワークを訓練することを「事前学習」と言います。このような事前学習を行った上で、機械翻訳や質問応答などのタスク別に専用に作成した訓練データで「目的別学習」を行うのが、言語モデルの定番の学習手法です。あらかじめ事前学習を行った方が言語モデルの性能が良くなるからです。目的別学習を "ファイン・チューニング" と言います。
GPT-3 は、それまでの GPT、GPT-2 と違って、ファイン・チューニングなしの言語モデルを狙ったものです。つまり、
と言えるでしょう。実際 GPT-3 は、ファイン・チューニングを行った言語モデルと比較しても、"そこそこの"、ないしは "同等の" 性能であることが分かりました。もちろんファイン・チューニング済の言語モデルに劣るタスクも多々あります。しかし全体としては "そこそこの" 性能を示します。「ニューラル・ネットワークの超大規模化」と「大量の訓練データ」によってそれが可能であることを、GPT-3 は示したのでした。
ChatGPT
ChatGPT は GPT-3 のアーキテクチャと事前学習をもとに、さらに「目標駆動型学習」を追加したものです。ここでの目標駆動型学習とは「人間にとって好ましい応答の例を人間が作り、それを目標として、そこに近づくように学習する」という意味です。OpenAI 社は RLHF(Reinforcement Learning by Human Feedback:人間のフィードバックによる強化学習)と呼んでいます。これは一種のファイン・チューニングであると言えます。
この、目標駆動型学習をどうやるか、その詳細が OpenAI 社のノウハウでしょう。考えてみると、GPT-3 の(従って ChatGPT の)アーキテクチャはシンプルあり、これをシステム上に実現するのは、コンピュータ技術とAI技術、ハードウェアの調達(特にGPU)、そしてお金の問題です。事前学習に使う WebText にしても、世界中から集めて公開している団体があります(GPT-3 でも使われた Common Crawl)。お金がある(かつ投資意欲がある)大手IT企業なら、システム構築は難しくない。
しかし「人手で作った訓練データをもとに、人にとって違和感がない対話ができるまでに訓練する」のは、Transformer の性質や "癖 を熟知していないとできないと考えられます。そこにノウハウがあるはずです。
その目標駆動型学習の概要を、先ほど引用した岡野原氏の「大規模言語モデルは新たな知能か」では、次のような3つのステップで説明しています。この説明は専門用語を最小にした簡潔なものなので、以降これに沿って書きます。
この岡野原氏の説明を読み解くと、次のようになるでしょう。ラベラーとは訓練データ(教師ラベル)を作る人の意味です。
第1ステップは、機械学習の分野でいう「教師あり学習」です。ここで具体的にどのような訓練をしたのかは、OpenAI 社も公表していません。推測すると「望ましい対話」の例には、人間の質問に「答えられません」や「できません」と応答する訓練データも多数あるのではと思います。たとえば「反社会的行為を助長するような質問」の場合(爆弾の作り方など)です。
さらにこの第1ステップでは、特定のタイプのプロンプトに対して、あたかも ChatGPT が感情をもっているかのように応答する訓練が可能なはずです。それが「望ましい対話」だと OpenAI が判断すればそうなります。
第2ステップは2つのフェーズに分かれています。第1フェーズは、人手によるランキングの作成です。このとき「複数の異なるモデル」を使います。モデルとは言語モデルのことです。実は、GPT-3 を開発する過程においても、パラメータ数の違う複数の言語モデルが開発されていて、最終的に公開されたのが GPT-3 です。またパラメータ数が同じでも、訓練のやり方が違うとパラメータの値が違うので、モデルとしては別です。
このような複数の異なるモデルを選び(4つとします)、同じ入力(プロンプト。\(P\) で表します)に対して、4つの違った応答、\(A,\:B,\:C,\:D\) を得ます。ラベラーは、この \(P/A,\:P/B,\:P/C,\:P/D\) という4つの「プロンプト \(/\) 応答」にランク付けします( \(/\) はプロンプトのあとに応答が続くという意味です)。ランク付けが仮に、
\(P/A\: > \:P/B\: > \:P/C\: > \:P/D\)
だとします。現実問題としては4つのランク付けは難しいので、2つずつの6つのペアについて、どちらが良いかを決めます。ランク付けの基準について岡野原氏は書いていないのですが、OpenAI 社の公開資料によると、
・嘘やデマを含まない
・差別的・攻撃的な内容を含まない
・ユーザの役に立つ
という基準です。このような「ランク付けデータ」を大量に準備します。これは人に頼る "人海戦術" しかないので、アウトソーシングしたとしてもコストがかかります。
第2ステップの第2フェーズは、ランキングのデータをもとに自動評価システムを作ることが目的です。データを入力して評価値(強化学習の用語でいうと "報酬")を出力する関数(=自動評価システム)を \(\mr{Score}()\) と書くと、
\(\mr{Score}(P/A) > \mr{Score}(P/B) > \mr{Score}(P/C) > \mr{Score}(P/D)\)
となるように関数を決めます。これはニューラル・ネットワークを使って、訓練を繰り返して決めます(強化学習の用語で "報酬モデル")。ここで岡野原氏が指摘しているのは、\(\mr{Score}\) 関数への入力は、
だということです。従って、\(\mr{Score}(P/A)\) は、
\(\mr{Score}(\mr{InnerState}(P/A))\)
と書くべきでしょう。これによって「高精度に評価を推定できる」というのが岡野原氏の説明です。
第3ステップでは、この自動評価システムを使って、プロンプトに対する応答の評価値が最も高くなるように強化学習を行います。このステップには人手を介した評価はないので、大量のプロンプトで学習することができます。
ここで、言語モデル \(\al\) の内部状態を入力とする自動評価システムを \(\mr{Score}_{\large\:\al}\) とし、言語モデル \(\al\) を上記のように訓練した結果、言語モデル \(\beta\) になったとします。すると、同じ「プロンプト/応答」を投入したときの内部状態が、2つの言語モデルで違ってきます。つまり、
\(\mr{InnerState}_{\large\:\al}(P/A)\neq\mr{InnerState}_{\large\:\beta}(P/A)\)
です。ということは、
ことになります。つまり「第2ステップの第2フェーズ」と「第3ステップ」をループさせて繰り返すことができる。このとき、ラベラーが作ったランキングデータはそのまま使えます。このランキングが絶対評価ではなく相対評価だからです。以上のことから、
と言えます。岡野原氏が言っている「高精度に評価を推定できる」とは、こういった "共進化" も含めてのことだと考えられます。このように、目標駆動型学習で鍵となるのは、この「高精度の自動評価システム」です。
補足しますと、ChatGPT が公開された後は、利用者の実際のプロンプトとそれに対する ChatGPT の応答を膨大に集積できます(利用者が拒否しなければ)。この実際の「プロンプト/応答」データの中から自動評価システムの評価が低いものだけを集め、プロンプトへの応答の評価が高くなるように ChatGPT の強化学習ができることになります。ChatGPT から "でたらめな" 応答を引き出そうとする(そして成功すれば喜ぶ)人は多いでしょうから、強化学習のためのデータにはこと欠かないはずです。
以上が、岡野原氏の説明の "読み解き" です。
ここまでをまとめると、次のようになるでしょう。
このような GPT-3 の仕組みでは、計算や論理的推論は本質的にできません。簡単な計算(2桁整数同士のたし算、2次方程式を解くなど)ができる(ように見える)のは、それが訓練データにあるからです。また、正しい論理的推論ができたとしたら、類似の推論が訓練データの中にあるからです。
とはいえ、ChatGPT はバックに語と語の関係性についての膨大な "知識" をもっていて、それによって "規則性" や "ルール" の認識が内部にできているはずです。その中には「人が気づかない」「暗黙の」「意外なもの」があってもおかしくない。それにより、蓄積した知識を "混ぜ合わせて" 正しい推論、ないしは発見的な推論がきることもあり得るはずです。
さらに、人が普段話すのと同じように話せば、その膨大な "知識" が活用できるのは多大なメリットでしょう。もちろん "悪用" される可能性はいつでもありますが、そのことを踏まえつつ、使い方の発見や検討が今後も進むのでしょう。
人の問いかけに対する ChatGPT の応答は、いかにも人らしいものです。もちろん間違いや、変な答え、明らかに事実とは違う応答もあります。しかし、世界中から集めた知識の量は膨大で、言語の壁も越えています。
その "知識" は(GPT-3, ChatGPT では)1752億個のパラメータの中に埋め込まれています。量は膨大ですが、それを処理する仕組みはシンプルです。なぜこれでうまくいくのか、そこが驚異だし、その理由を理解することは難しいでしょう。
もちろん、その中身を解明しようとする研究は進むでしょうが、"理解" は難しいのではと思われます。というのも、「比較的シンプルな記述による、人にフレンドリーな説明」でないと、人は "理解" したとは思わないからです。
しかし考えてみると、我々が言語(母語)を習得でき、かつ自在に扱えるのはなぜか、その脳の働きは、Transformer / ChatGPT と極めて似ているのではないでしょうか。
前回の冒頭で紹介したように、慶応義塾大学の今井教授は、「ChatGPT の仕組み(=注意機構)は、幼児が言語を学習するプロセスと類似している」と指摘していました。今井教授は幼児の言語発達を研究する専門家なのでこの指摘になるのですが、実は Transformer / ChatGPT のやっていることは、幼児のみならず、我々が言葉(母語)を理解してきた(現に理解している)やりかたと酷似していることに気づきます。それは、
という言語理解のありようです。もちろん(外からの指摘による)「好ましくない言葉の使い方」であれば訂正します。しかし、学び方も含めて、我々は内発的・創発的に言葉を理解しています。それが我々の脳の働きの重要な一面です。
前回、Transformer がタンパク質の機能分析に使える(可能性がある)ことを書きましたが、さらにヒトの脳の(ある脳領域の)解明に役立つこともありそうです。
大規模言語モデルの外面的な機能は驚異的ですが、さらにその内部の「仕組み」を理解することで、その応用範囲が極めて広いことがわかるのでした。
(前回より続く)
この記事は、No.365「高校数学で理解する ChatGPT の仕組み(1)」の続きです。記号の使い方、用語の定義、ニューラル・ネットワークの基本事項、単語の分散表現などは、前回の内容を踏まえています。 |
| 3.Transformer |
Attention Is All You Need
Google社は、2017年に "Attention Is All You Need" という論文(以下、"論文" と記述)を発表し、"Transformer" という画期的な技術を提案しました。Transformer は機械翻訳で当時の世界最高性能を発揮し、これが OpenAI 社の GPT シリーズや ChatGPT につながりました。
Attention(アテンション)とは "注意" という意味で、Transformer に取り入れられている "注意機構"(Attetion mechanism)を指します。"Attention Is All You Need" を直訳すると、
「必要なのはアテンションだけ」
ですが、少々意訳すると、
「アテンションこそがすべて」
となるでしょう(蛇足ですが、ビートルズの "All You Need Is Love" を連想させる論文タイトルです)。
Transformer を訳すと "変換器" ですが、その名の通り「系列 A から系列 B への変換」を行います。系列 A = 日本語、系列 B = 英語、とすると和文英訳になります。第3章では、この Transformer の仕組みを説明をします。
全体のアーキテクチャ
Transformer のアーキテクチャの全体像が次図です(論文より)。以降、この絵の意味を順に説明します。
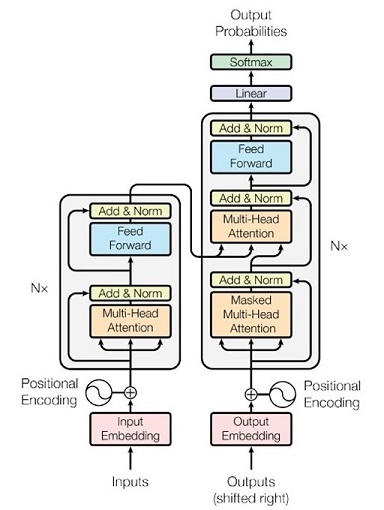
|
図18:Transformer のアーキテクチャ |
アーキテクチャを簡略化して書くと次のようになります。以下では「日本語 → 英語の機械翻訳」を例として Transformer の動作を説明します。
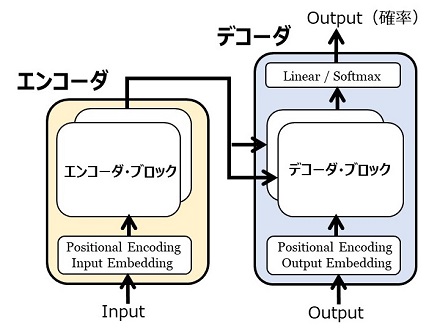
|
図19:アーキテクチャの簡略図 |
左側がエンコーダで、入力された日本語テキストを中間表現(=テキストの特徴を抽出した内部表現)に変換します。右側のデコーダは、中間表現を参照しつつ「次に生成すべき英単語」を推論します。
エンコーダ、デコーダとも、図で「ブロック」と書いた単位を積層した構造です。つまり、1つのブロックの出力が次のブロックへの入力になります。アーキテクチャの絵で「N x」と書いてあるのはその積層の意味(= N 倍)で、積層する数を \(N\) とすると、Transformer では、
\(N=6\)
です。エンコーダの中間表現は最終ブロックからの出力です。その出力がデコーダの全てのブロックへ伝わります。
訓練
多数の「日本語 \(\rightarrow\) 英語の翻訳データ」を用いて Transformer を訓練するとき、全体がどのように動くかを示したのが次の図です。
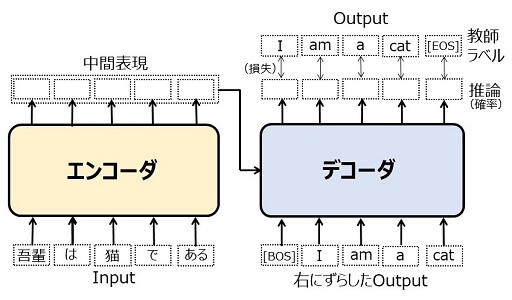
|
図20:Transformerの動作(訓練時) |
エンコーダには日本語の文(Input)が入力されます。デコーダからの出力は、英文の推論結果(確率)です。これを正しい英文(Output = 教師ラベル)と照らし合わして損失(交差エントロピー誤差)を計算し、誤差逆伝播を行ってニューラル・ネットワークの重みを更新します(前回参照)。デコーダの入力となるのは「右に1語だけずらした Output」です。アーキテクチャの図18 で shifted right と書いてあるのはその意味です。なお、実際に入力されるのは単語ではなくトークンの列です(前回参照)。
推論
訓練を終えた Transformer を使って日本語文を英語文に機械翻訳するときの動きは次図です。
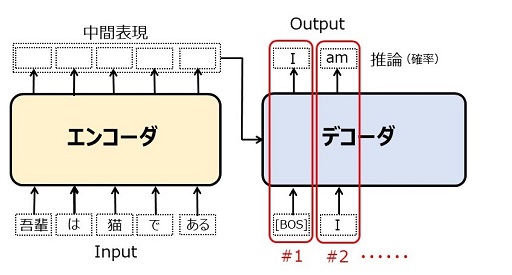
|
図21:Transformerの動作(推論時) |
エンコーダに日本語のテキストを入力し、中間表現を得ます。これは1回きりです。
デコーダには、生成すべき英語テキストの最初のトークン、[BOS](文の始まりを示す特殊トークン)を入力し、[BOS] の次にくるべきトークンの確率を推論します。最も確率が高いトークンを選ぶと [I] になるはずです。これが1回目の推論(#1)です。
2回目(#2)では [I] を入力し、[I] の次のトークンを推論します([am] となるはずです)。[BOS] から [I] を推論したときの情報はデコーダに残されているので、その部分を再計算する必要はありません。推論のためには、日本語文の全情報(エンコーダの中間表現)と、既に生成した英文([BOS] [I])を参照します。
このようにして順々に英文を生成していき、推論結果が [EOS](文の終了を示す特殊トークン)になるところで、翻訳が終了します。
アーキテクチャの詳細
用語と記号
トークンの語彙
トークンの語彙(vocabulary)のサイズ を \(V\) とします。トークンを識別する "トークンID" は \(1\)~\(V\) の数字です。
系列
Transformer への入力となるテキストは、Tokenizer でトークンID の列に変換されます。以降、Transformer への入力を "系列(sequece)" と呼びます。
系列はその最大サイズ \(S\) が決まっています(普通、数千程度)。入力が \(S\) より少ない場合、残りのトークンは無効トークン([PAD])としておき、そこの処理は回避するようにします。[PAD] を含めて、系列は長さ \(\bs{S}\) の固定長とします。
系列\(=\{\:t_1,\:t_2,\:\cd\:,\:t_S\:\}\)
\(t_i\):トークンID \((1\leq t_i\leq V)\)
Transformer の論文には語彙のサイズと系列のサイズが書いてありませんが、以降の説明では \(V\) と \(S\) を使います。
分散表現ベクトル
トークンの分散表現ベクトル(埋め込みベクトル)の次元を \(D\) とします。トークンID が \(t_i\) であるトークンの分散表現を \(\bs{x}_i\) とすると、
\(\bs{x}_i=\left(\begin{array}{r}x_1&x_2&\cd&x_D\\\end{array}\right)\) \([1\times D]\)
というようになり、系列をベクトル列で表現すると、
系列\(=\{\:\bs{x}_1,\:\bs{x}_2,\:\cd\:,\:\bs{x}_S\:\}\)
となります。なお、\(D\) 次元ベクトルを、\(1\)行 \(D\)列の配列とし、\([1\times D]\) で表わします(前回参照)。
なお、Transformer では \(D=512\) です。
以降、全体アーキテクチャの図に沿って、各レイヤー(計算処理)の説明をします。以降の説明での \(\bs{x}_i,\:\:\bs{y}_i\) は、
\(\bs{x}_i\):レイヤーへの入力
(系列の \(i\) 番目。\(1\leq i\leq S\))
\(\bs{y}_i\):レイヤーからの出力
(系列の \(i\) 番目。\(1\leq i\leq S\))
で、すべてのレイヤーに共通です。また、\(D\) 次元ベクトルを \([1\times D]\)、\(S\)行 \(D\)列の行列を \([S\times D]\) と書きます。
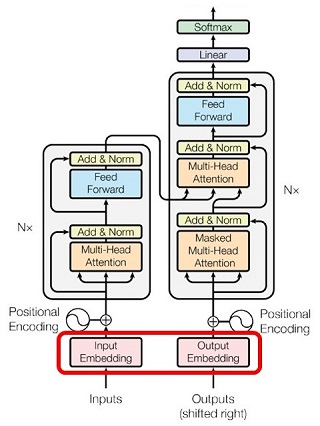
埋め込みベクトルの生成
|
このレイヤーの入出力を、
| トークンID を one hot ベクトルにしたもの \([1\times V]\) | |
| 埋め込みベクトル \([1\times D]\) |
とすると、
\(\bs{y}_i=\bs{x}_i\cdot\bs{W}_{\large enc}\)
\([1\times D]=[1\times V]\cdot[V\times D]\)
で表現できます(前回の word2vec 参照)。もちろん、この行列演算を実際にする必要はなく、\(\bs{x}_i\) のトークンID を \(t_i\) とすると、
\(\bs{y}_i=\bs{W}_{\large enc}\) の \(t_i\) 行
です。\(\bs{W}_{\large enc}\) は Transformer の訓練を始める前に、あらかじめ(ニューラル・ネットワークを用いて)作成しておきます。従って、埋め込みベクトルの作成はテーブルの参照処理(table lookup)です。
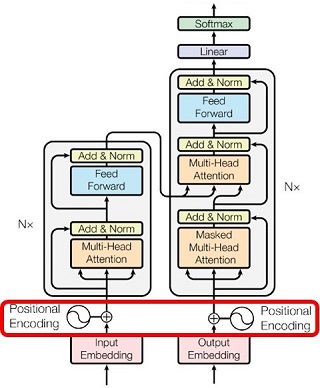
位置エンコーディング
|
埋め込みベクトル(分散表現)に、トークンの位置を表す「位置符号ベクトル」を加算します。つまり、
| \(\bs{x}_i\):埋め込みベクトル | \([1\times D]\) | |
| \(\bs{p}_i\):位置符号ベクトル | \([1\times D]\) | |
| \(\bs{y}_i\):位置符号加算ベクトル | \([1\times D]\) |
とすると、
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
\([1\times D]=[1\times D]+[1\times D]\)
の単純加算です。位置符号ベクトル \(\bs{p}_i\) の要素を次の記号で表します。
\(p_{t,d}\)
\(t\) は \(0\) から始まる、トークンの位置
\((t=i-1,\:\:0\leq t\leq S-1)\)
\(d\) は \(0\) から始まる、ベクトル内の要素の位置
\((0\leq d\leq D-1)\)
この \(p_{t,d}\) の値は次のように定義されます。
| \(p_{t,2k}\) | \(=\mr{sin}\left(\dfrac{1}{10000^x}\cdot t\right)\) | |
| \(p_{t,2k+1}\) | \(=\mr{cos}\left(\dfrac{1}{10000^x}\cdot t\right)\) |
\((0\leq k < \dfrac{D}{2},\:\:\:x=\dfrac{2k}{D},\:\:\:0\leq x < 1)\)
つまり、\(D=512\) とすると、
\(d\) が偶数の要素位置では \(\mr{sin}\) 波
(\(d=0,\:2,\:4,\:\cd\:,510\))
\(d\) が奇数の要素位置では \(\mr{cos}\) 波
(\(d=1,\:3,\:5\:\:\cd\:,511\))
で位置符号値を決めます。この \(\mr{sin}/\mr{cos}\)波の波長 λ は
λ\(=2\pi\cdot10000^x\)
であり、\(0\leq d < D\) の範囲で、
\(2\pi\leq\)λ\( < 2\pi\cdot10000\)
となります。この \(\mr{sin}/\mr{cos}\) 波を図示してみます。グラフをわかりやすくするために、\(D=512\) ではなく、
\(D=32\)
とし、ベクトルの要素 \(32\)個のうちの最初の6つ、
\(d=0,\:1,\:2,\:3,\:4,\:5\)
だけのグラフにします。グラフの
・横軸はトークンの位置 \(t\)
・縦軸は位置符号ベクトルの要素 \(p_{t,d}\)
です。
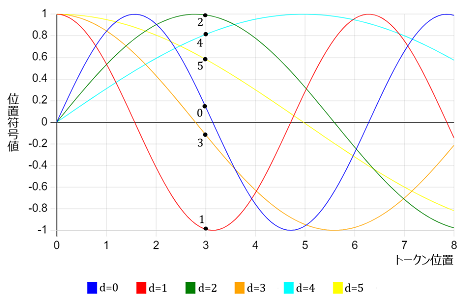
|
図22:位置符号値を計算するための正弦・余弦波 |
図の黒丸は、\(t=3\) の位置符号ベクトルの、要素\(0\)~要素\(5\)(\(0\leq d\leq5\))を示す。 |
具体的に \(t=3\) のときのベクトルの要素 \(p_{3,d}\:\:(0\leq d\leq31)\) の \(0\leq d\leq5\) の部分を書いてみると、
\(p_{3,0}=\phantom{-}0.1411\)
\(p_{3,1}=-0.9900\)
\(p_{3,2}=\phantom{-}0.9933\)
\(p_{3,3}=-0.1160\)
\(p_{3,4}=\phantom{-}0.8126\)
\(p_{3,5}=\phantom{-}0.5828\)
となります(図22)。
言うまでもなく、言語モデルにとってトークンの位置はきわめて重要な情報です。位置をバラバラにすると意味をなさないテキストになるし、Bob loves Alice と Alice loves Bob では意味が逆です。従って、何らかの手段で「トークンの位置を考慮したモデル化」をしなければならない。
\(\bs{y}_i=\bs{x}_i+\bs{p}_i\:\:\:(1\leq i\leq S)\)
の式で、\(\bs{x}_i\) は「単語埋め込み」のアルゴリズムで作られ、似たような単語/トークンは類似したベクトルになります(前回参照)。それに対し \(\bs{p}_i\) の \(\mr{sin}/\mr{cos}\) 波は、言語処理とは全く無関係な数学の産物です。従って、加算結果である \(\bs{y}_i\) がどのような「意味」をもつベクトルなのか、説明しようとしても無理でしょう。全く異質なものの足し算をしているのだから ・・・・・・。それでいて、このやり方で全体として成り立つのが驚きです。
Transformer より以前の機械翻訳では、トークンの出現順に逐次処理をするアーキテクチャでした。つまり、1つのトークンの処理結果を利用しながら次のトークンを処理するという逐次処理によって、並び順に意味があるという言語の特質を捕らえていました。
それに対し、位置エンコーディングを取り入れた Transformer では、逐次処理の必要性がなくなり、系列のトークン全部の並列処理が可能になりました。この結果、同一計算の超並列処理ができる GPU(数千並列が可能) をフルに活用することで、実用的な大規模言語モデルが構築できるようになったわけです。位置エンコーディングにはそういう意味があります。
なお Transformer の論文にも書いてあるのですが、位置符号ベクトルを \(\mr{sin}/\mr{cos}\) 波のような「決めうち」で作らないで、「学習可能なパラメータ」としておき、Transformer を訓練する過程で決めるやり方があります。位置符号ベクトルを学習で決めるわけです。GPT はこの方法をとっています。
Single Head Attention : SHA
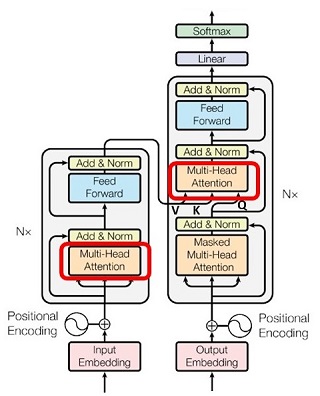
|
アテンション・レイヤー(Multi Head Attention : MHA)の説明をするために、まず "Single Head Attention : SHA" の処理論理を説明します。Transformer で実際に使われている MHA は、以下に説明する SHA の拡張版で、核となるアルゴリズムは同じです。
SHAの入出力は、それぞれ \(S\)個の \(D\)次元ベクトルであり、
入力 \(\bs{x}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
出力 \(\bs{y}_i\:\:[1\times D]\:\:(1\leq i\leq S)\)
ですが、系列の全体を1つの行列で表すことができます。1つのベクトルを行列の1行として、それを縦方向に \(S\)個並べて行列を作ります。つまり、
入力 \(\bs{X}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{x}_i\))
出力 \(\bs{Y}\:\:[S\times D]\) (\(i\) 番目の行が \(\bs{y}_i\))
とすると SHA は、
\(\bs{Y}=\mr{SHA}(\bs{X})\)
と書けます。アテンションの処理では、まず入力ベクトル \(\bs{x}_i\) を、
| ◆クエリ・ベクトル | \(\bs{q}_i\)(query:問合わせ) | |
| ◆キー・ベクトル | \(\bs{k}_i\)(key:鍵) | |
| ◆バリュー・ベクトル | \(\bs{v}_i\)(value:値) |
の組、( \(\bs{q}_i,\:\:\bs{k}_i,\:\:\bs{v}_i\) )に変換します。変換式は次の通りです。
\(\bs{q}_i=\bs{x}_i\cdot\bs{W}_Q\:\:\:(1\leq i\leq S)\) \(\bs{k}_i=\bs{x}_i\cdot\bs{W}_K\:\:\:(1\leq i\leq S)\) \(\bs{v}_i=\bs{x}_i\cdot\bs{W}_V\:\:\:(1\leq i\leq S)\) \([1\times D]=[1\times D]\cdot[D\times D]\) |
ここで、\(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は学習で決まる変換行列です。系列全体についての Query/Key/Value(\(QKV\))を行列の形で表すと、
\(\bs{Q}=\bs{X}\cdot\bs{W}_Q\) \(\bs{K}=\bs{X}\cdot\bs{W}_K\) \(\bs{V}=\bs{X}\cdot\bs{W}_V\) \([S\times D]=[S\times D]\cdot[D\times D]\) |
となります。SHA レイヤーからの出力、\(\bs{y}_i\:\:[1\times D]\) は、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の "重み付き和" (加重和)で求めます。加重和に使う重み、\(\bs{w}_i\:\:[1\times S]\) は次のように計算されます。
まず、クエリ・ベクトル \(\bs{q}_i\) とキー・ベクトル \(\bs{k}_j\:\:(1\leq j\leq S)\) の "スケール化内積(scaled dot product)" を計算し、\(S\)個のスカラー値を求めます。スケール化内積(\(\mr{SDP}\) と記述します)とは、2つの \(D\)次元ベクトル \(\bs{a}\) と \(\bs{b}\) の場合、
\(\mr{SDP}(\bs{a},\bs{b})=\dfrac{1}{\sqrt{D}}\bs{a}\bs{b}^T\)
\([1\times1]=[1\times D]\cdot[D\times1]\)
で定義されます。つまり、一般の内積(=スカラー値)を「ベクトルの次元数の平方根」で割ったものです。
\(\bs{q}_i\) と \(\bs{k}_j\:\:(1\leq j\leq S)\) のスケール化内積を順番に \(S\)個並べたベクトルを \(\bs{s}_i\:\:[1\times S]\) と書くと、スケール化内積の定義によって、
\(\bs{s}_i=\dfrac{1}{\sqrt{D}}\bs{q}_i\bs{K}^T\)
\([1\times S]=[1\times D]\cdot[D\times S]\)
です。そして、加重和を求めるときの重み \(\bs{w}_i\) は、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
\([1\times S]=\mr{Softmax}([1\times S])\)
とします。この \(S\)次元の重みベクトルを使って、\(S\)個のバリュー・ベクトル \(\bs{v}_j\:\:(1\leq j\leq S)\) の加重和をとると、出力ベクトル \(\bs{y}_i\) は、
\(\bs{y}_i=\bs{w}_i\cdot\bs{V}\)
\([1\times D]=[1\times S]\cdot[S\times D]\)
となります。以上の計算プロセスを一つの式で書いてしまうと、
\(\bs{y}_i=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{q}_i\cdot\bs{K}^T\right)\cdot\bs{V}\) \([1\times D]=\mr{Softmax}([1\times D]\cdot[D\times S])\cdot[S\times D]\) |
です。従って、SHA からの出力ベクトル \(\bs{y}_i\) を縦方向に並べた行列 \(\bs{Y}\) は、
\(\bs{Y}=\mr{Softmax}\left(\dfrac{1}{\sqrt{D}}\bs{Q}\cdot\bs{K}^T\right)\cdot\bs{V}\)
\([S\times D]=\mr{Softmax}([S\times D]\cdot[D\times S])\cdot[S\times D]\)
と表すことがきます。この表記で \(\mr{Softmax}\) 関数が作用するのは \([S\times S]\) の行列ですが、\(S\)個の行ごとに \(\bs{\mr{Softmax}}\) を計算します。
単なる内積ではなく「スケール化内積」を使う理由ですが、2つのベクトルの内積は、要素同士のかけ算を次元数 \(D\) 個だけ加算したものです。従って、ベクトル \(\bs{s}_i\) を、シンプルな内積を使って、
\(\bs{s}_i\:=\bs{q}_i\cdot\bs{K}^T\)
のように定義し、重み \(\bs{w}_i\) を、
\(\bs{w}_i=\mr{Softmax}(\bs{s}_i)\)
で求めると、\(D\) が大きいと \(\bs{s}_i\) の要素が大きくなり、その結果として \(\bs{w}_i\) はゼロに近いところに多くの要素が集まるようになります。これは \(\mr{Softmax}\) 関数の性質によります(前回参照)。こうなると勾配消失が起きやすくなり、訓練が収束しづらくなります。そのため「スケール化」するというのが論文の説明です。
もちろん、幾多の試行錯誤があり、その結果として決まったのが「スケール化内積で加重和の重みを計算する」というやり方だったのでしょう。
以上の計算でわかるように、注意機構(Attention machanism)とは、あるトークンを処理するときに、注意を向けるべきトークンと注意の強さを決め(それ自体が学習で決まる)、注意を向けた先の情報を集めてきて集積するものです。
しかも、注意機構は6層(\(N=6\)) に重ねられています。ということは、階層的な(多段階の) "注意の向け方" ができることになります。また、言語における単語と単語の関係性は多様です。動作\(\cdot\)動作主体、修飾\(\cdot\)被修飾、指示代名詞と指示されるもの(照応関係)など多岐に渡ります。それらのさまざまなタイプの関係性を、Transformer の訓練を通して、多層の注意機構が自動的に把握すると考えられるのです。
MHA : Multi Head Attention
SHA では、入力ベクトル \(\bs{x}_i\) から、1組の Query/Key/Value(\(QKV\)) ベクトルを抽出しましたが、Transformer で実際に使われているのは、
| 1つの入力ベクトル \(\bs{x}_i\) から、複数組の違った \(\bs{QKV}\) ベクトルを抽出し、 | |
| それぞれについて独立に SHA と同等のアテンション処理をし、 | |
| 処理結果を単純結合(Concatenation)し、 | |
| 最後に線型変換をして出力ベクトルに \(\bs{y}_i\) する |
という処理です。これを Multi Head Attention : MHA と呼びます。この「それぞれについてのアテンション処理」のことを "head(ヘッド)" と言います。複数の head なので Multi Head です。このヘッドの数を \(H\) とし、
\(d=\dfrac{D}{H}\) (\(D\) は入出力ベクトルの次元)
とします(\(H\) は \(d\) が整数になるように選びます)。このとき、
\(\bs{x}_i\:\:[1\times D]\) から抽出される(複数組の)\(QKV\) ベクトルの次元はすべて \([1\times d]\)
です。つまり MHA は「複数の特徴を抽出し(一つの情報量は SHA より少ない)、それぞれの特徴について 独立した "注意機構" を働かせ、最後に統合してまとめる」仕組みです。なお、Transformer では、
\(H=8\)
\(d=\dfrac{D}{H}=\dfrac{512}{8}=64\)
です。
\(h\) 番目のヘッド \((1\leq h\leq H)\) に着目し、"注意機構" の計算プロセスを式で書くと、次のようになります。まず、\(h\) 番目のヘッドの \(QKV\) ベクトルの計算は、
\(\bs{q}_i^h=\bs{x}_i\cdot\bs{W}_Q^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \(\bs{k}_i^h=\bs{x}_i\cdot\bs{W}_K^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \(\bs{v}_i^h=\bs{x}_i\cdot\bs{W}_V^h\:\:\:(1\leq i\leq S,\:\:1\leq h\leq H)\) \([1\times d]=[1\times D]\cdot[D\times d]\) |
です。系列全体について、\(h\) 番目のヘッドの \(QKV\) を行列の形で表すと、
\(\bs{Q}^h=\bs{X}\cdot\bs{W}_Q^h\) \(\bs{K}^h=\bs{X}\cdot\bs{W}_K^h\) \(\bs{V}^h=\bs{X}\cdot\bs{W}_V^h\) \([S\times d]=[S\times D]\cdot[D\times d]\) |
です。\(h\) 番目のヘッドのアテンション処理は、SHA の場合と同様で、
\(\bs{y}_i^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{q}_i^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([1\times d]=\mr{Softmax}([1\times d]\cdot[d\times S])\cdot[S\times d]\) |
となり、これを系列全体での表現にすると、
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S])\cdot[S\times d]\) |
となります。行列 \(\bs{Y}^h\) は、\(h\) 番目のヘッドの出力ベクトル \(\bs{y}_i^h\:\:[1\times d]\) を、系列の数だけ縦に並べた行列です。
系列の \(i\) 番目の入力 \(\bs{x}_i\) に対する \(H\) 個の出力ベクトル
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
が求まったところで、これら \(H\) 個を単純結合して(=順に並べる)一つのベクトルにし、さらに Linear 変換をして最終出力にします。変換に使う行列は \(\bs{W}_O\:\:[D\times D]\) です。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\) \(\begin{eqnarray} &&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\ &&&=[1\times D]\cdot[D\times D]\\ \end{eqnarray}\) |
Linear 変換は直前の単純結合(Concatenation)とセットになっています。つまり、ヘッドの順序を表す \(h\:\:(1\leq h\leq H)\) という数字には、"注意機構" における何らかの意味があるわけではありません。単にアテンション処理を \(H\) 個に分けた \(h\) 番目というだけです。従って、順に単純結合する、
\(\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\)
という操作の「結合順序」には意味が無いことになります。そこで結合した後で、学習可能なパラメータ \(\bs{W}_O\) で線型写像を行って、最適な出力ベクトルを求めるわけです。
エンコーダの MHA は、エンコーダ内に閉じたアテンションで、これを「自己アテンション」(Self Attention)と言います。一方、デコーダ側には自己アテンションの他に、エンコーダとデコーダにまたがるアテンションがあります。これを Source Target Attention と言います。このアテンションは、
| クエリは、デコーダ側のベクトルから生成し、 | |
| キーとバリューは、エンコーダ側のベクトルから生成 |
します。これによってエンコーダからデコーダ側への情報の流れを作ります。日本語 → 英語の機械翻訳の場合だと、次に生成すべき英単語に関連して「注意を向けるべき日本語のトークンと、その注意の量」がここで決まります。
Multi Head Attention において、1つのベクトルから複数の \(QKV\) を取り出すことの意味は、おそらくトークンの「多義性」でしょう。その例ですが、英語で fine という語の代表的な意味を4つあげるとしたら、たとえば、
fine :
(1) 素晴らしい
(2) 晴れた
(3) 細かい
(4) 罰金
です(例です。(1) (2) は同類の意味)。単語の埋め込みベクトルは、似たような(あるいは同一ジャンルの)語は類似している(= コサイン類似度が 1 に近い)わけです(前回参照)。とすると、(1)~(4) の同一ジャンルの言葉は、それぞれ、
(1) good, excellent, ・・・・・・
(2) cloudy, rainy, ・・・・・・
(3) tiny, small, coarce, ・・・・・・
(4) penalty, guilty, ・・・・・・
などとなるはずです。fine がこれら4つのジャンルと類似性があるということは、fine の埋め込みベクトルおいて4つの意味が物理的に分散して配置されていると考えられます。さらにイタリア語まで考えると、
fine :
(5) 終わり
が加わります(イタリア映画の最後に出てくる語、ないしは音楽用語)。埋め込みベクトルは言語ごとに作るわけではないので、fine のベクトルはあくまで1つです。ということは、埋め込みベクトルには(この例では)5つの意味が分散して配置されているはずです。
この状況は、埋め込みベクトルから複数の \(QKV\) ベクトルを取り出し、それぞれについて独立したアテンション計算をするというアルゴリズムがマッチしていると考えられるのです。
Add & Norm
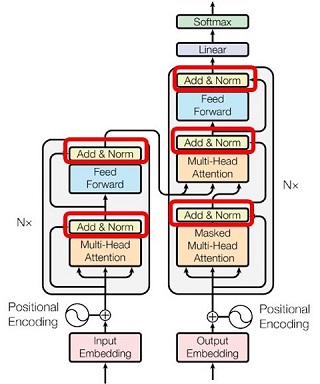
|
アーキテクチャの絵で5カ所にある「Add & Norm」は、ベクトルごとに「残差結合」と「レイヤー正規化」を行うレイヤーです(詳細は前回参照)。図で表すと以下です。
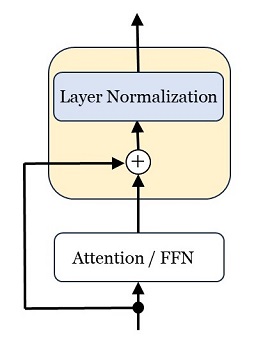
|
図23:残差結合とレイヤー正規化 |
計算式は次のようになります。系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略します。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\begin{eqnarray}
&&\:\: \bs{x}=\{\:x_1, &x_2, &\cd\:, &x_D\:\}\\
&&\:\: \bs{y}=\{\:y_1, &y_2, &\cd\:, &y_D\:\}\\
\end{eqnarray}\)
\(x_k\:\:(1\leq k\leq D)\) の平均 : \(\mu\)
\(\mu=\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}x_k\)
\(x_k\:\:(1\leq k\leq D)\) の標準偏差 : \(\sg\)
\(\sg=\sqrt{\dfrac{1}{D}\displaystyle\sum_{k=1}^{D}(x_k-\mu)^2}\)
とおくと、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\) \([1\times D]=[1\times D]\odot[1\times D]+[1\times D]\) |
です。ここで \(\bs{g}\) と \(\bs{b}\) は学習で決まるベクトル(=パラメータ)です。
Feed Forward Network
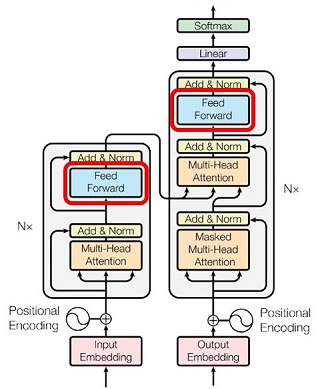
|
ベクトルごとに処理される、2層の全結合ニューラル\(\cdot\)ネットワークです。第1層の活性化関数は \(\mr{ReLU}\) で、第2層(出力層)には活性化関数がありません。3つのレイヤーで表現すると次の通りです。
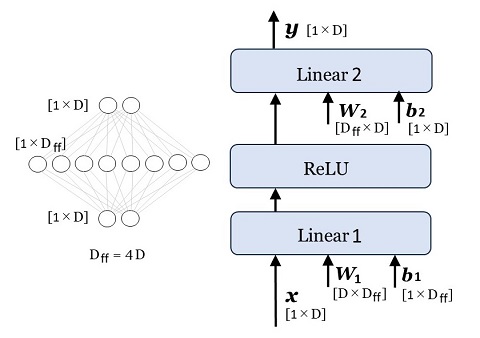
|
図24:Feed Forward Network |
ニューロンの数(=ベクトルの次元)は、
入力層:\(D\)
第1層:\(D_{ff}=4\times D\)
出力層:\(D\)
です。計算を式で表すと(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)、
\(\bs{y}=\mr{ReLU}(\bs{x}\bs{W}_1+\bs{b}_1)\cdot\bs{W}_2+\bs{b}_2\)
です。第1層の次元を入力\(\cdot\)出力層の4倍にとるのは、そのようにするのが Transformer の性能(たとえば、翻訳文の質)が最も向上するからです。GPT-3、ChatGPT も踏襲しています。
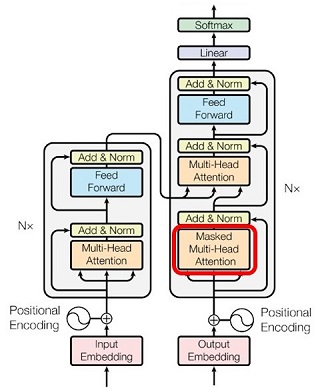
Masked Multi Head Attention
|
デコーダ側にある Masked Multi Head Attention の説明をします。系列のトークンの列を、
\(\{\:\bs{x}_1,\:\cd\:,\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\cd\:,\:\bs{x}_S\:\}\)
とし、いま \(\bs{x}_t\) に着目しているとします。
\(\bs{x}_i\:\:\:(1\leq i\leq t)\:\longrightarrow\) 過去のトークン
\(\bs{x}_i\:\:\:(t < i\leq S)\:\longrightarrow\) 未来のトークン
と呼ぶことにします。着目しているトークンを基準に、系列でそれ以前のトークンが「過去」、次以降のトークンが「未来」です。
日本語から英語に翻訳する Transformer を例にとると、デコーダの推論時には、英文のトークンを一つずつ推論していきます。つまり、
[BOS] \(\longrightarrow\) [I]
[BOS] [I] \(\longrightarrow\) [am]
[BOS] [I] [am] \(\longrightarrow\) [a]
[BOS] [I] [am] [a] \(\longrightarrow\) [cat]
[BOS] [I] [am] [a] [cat] \(\longrightarrow\) [EOS]
といった具合です(図21)。このときの各ステップにおけるアテンション処理は、当然ですが、末尾のトークンから生成済みのトークン(=過去のトークン)に対して行われます。つまり「トークンが注意を向ける先は常に過去のトークン」です。「すでに生成済みのトークンの情報だけから次にくるトークンを推論する」のがデコーダなので、これは当然です。
一方、デコーダの訓練時のことを考えると、
| (入力データ) | [BOS] | [I] | [am] | [a] | [cat] | |
| (教師ラベル) | [I] | [am] | [a] | [cat] | [EOS] |
で(図20)、入力データとしては系列のトークンが全部与えられています。しかしここで未来のトークンに注意を向けてしまうと、推論時との不整合が起きてしまいます。そこで
未来のトークンには注意を向けない。自分自身を含む過去のトークンにだけ注意を向ける
という配慮が、デコーダ側のアテンション処理では必要になります。この配慮をした注意機構が Masked Multi Head Attention です。一方、エンコーダ側では、訓練時も推論時も、
[我が輩] [は] [猫] [で] [ある]
という系列が一括して与えられるので(図20、図21)、未来のトークンに注意を向けても問題ありません。またデコーダ側からエンコダー側に注意を向けるのもかまいません。
この「過去のトークンにだけ注意を向ける」ことを数式で表現するには、\([S\times S]\) のマスク行列、\(\bs{M}\) を次のように定義します。
\(\bs{M}=\left(\begin{array}{c}
0&\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}\\
\phantom{0}&\large\ddots&\phantom{0}&\huge\textrm{-}\infty&\phantom{0}\\
\phantom{0}&\phantom{0}&0&\phantom{0}&\phantom{0}\\
\phantom{0}&\huge0&\phantom{0}&\large\ddots&\phantom{0}\\
\phantom{0}&\phantom{0}&\phantom{0}&\phantom{0}&0\\
\end{array}\right)\) \([S\times S]\)
このマスク行列は、
| 対角項:\(0\) | |
| 行列の左下(行番号\( > \)列番号):\(0\) | |
| 行列の右上(行番号\( < \)列番号):\(-\infty\) |
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S])\cdot[S\times d]\) |
でした。これに \(\bs{M}\) を足し込むと、
\(\bs{Y}^h=\mr{Softmax}\left(\dfrac{1}{\sqrt{d}}\bs{Q}^h\cdot(\bs{K}^h)^T+\bs{M}\right)\cdot\bs{V}^h\) \([S\times d]=\mr{Softmax}([S\times d]\cdot[d\times S]+[S\times S])\cdot[S\times d]\) |
となります。\(\mr{Softmax}\) 関数は、ベクトル(上式では行列の1行)の各要素の \(\mr{exp}()\) をとります。従って、要素が \(-\infty\) だと \(\mr{exp}(-\infty)=0\) となり、\(\mr{Softmax}\) 関数にとってはその要素が無いのと同じことになります。
上式の \(\mr{Softmax}\) 関数の内側は \([S\times S]\) の行列ですが、縦方向が系列全体のクエリ・ベクトルに対応し、横方向が系列全体のキー・ベクトルに対応しています。そのため、マスク行列を足し込むと、アテンション処理において過去のトークンだけに注意が行き、未来のトークンには注意が行かない(=結果としてバリュー・ベクトルが加重和されない)ようになるのです。
こうして求めた行列 \(\bs{Y}^h\) の \(i\) 行目をベクトル、
\(\bs{y}_i^h\:\:[1\times d]\:\:(1\leq h\leq H)\)
とすると、これ以降の処理はマスク行列がない場合と同じです。つまり \(H\) 個のベクトル \([1\times d]\) を単純結合して一つのベクトル \([1\times D]\) にし、さらに Linear 変換をしてアテンション処理からの最終出力にします。
\(\bs{y}_i=\mr{Concat}(\bs{y}_i^1,\:\bs{y}_i^2,\:\cd,\:\bs{y}_i^H)\cdot\bs{W}_O\)
\(\begin{eqnarray}
&&\:\: [1\times D]&=\mr{Concat}([1\times d],\:\cd\:)\cdot[D\times D]\\
&&&=[1\times D]\cdot[D\times D]\\
\end{eqnarray}\)
わざわざ \(\mr{exp}(-\infty)\) を持ち出してマスク行列を使うのは、話をややこしくするだけのようですが、マスク行列を使った Masked Multi Head Attention の計算式を見ると、線型変換と \(\mr{Softmax}\) 関数だけからできています。ということは、「過去のトークンだけに注意を向けるアテンション計算は微分可能」であり、誤差逆伝播の計算が成り立つことがわかります。
確率生成
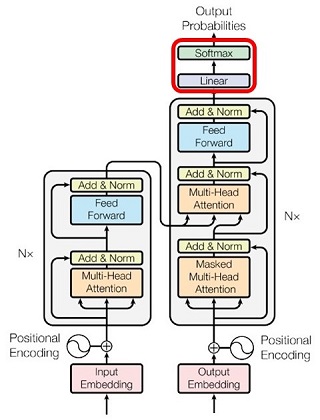
|
Transformerのデコーダの最終部分は、推論結果である \(D\) 次元のベクトルを、語彙集合の中での確率ベクトルに変換する部分です。計算式で書くと、
\(\bs{y}=\mr{Softmax}(\bs{x}\cdot\bs{W}_{\large dec})\)
\([1\times V]=\mr{Softmax}([1\times D]\cdot[D\times V])\)
です(系列の \(i\) 番目を示す \(\bs{x}_i,\:\:\bs{y}_i\) の \(i\) は省略)。\(\bs{W}_{\large dec}\) は、前回の word2vec のところに出てきた、\(D\)次元の埋め込みベクトルを \(V\) 次元の確率ベクトルに変換する行列です。
以上で Transformer のアーキテクチャの説明は終わりですが、全体を振り返ると、
アテンションだけが系列全体に関わる処理であり、あとはすべてベクトル(トークン)ごとの処理である
ことがわかります。以降は、この中で鍵となる「アテンション」と「Feed Foward Network」についての補足です。
アテンションの意義
一般のニューラル・ネットワークにおいて、隣合った2つの層、\(\bs{x}\) と \(\bs{y}\) が同じニューロン数 \(D\) だとします。活性値を、
\(\begin{eqnarray}
&&\:\:\bs{x}=\{x_1, &x_2, &\cd\:,&x_D\}\\
&&\:\:\bs{y}=\{y_1, &y_2, &\cd\:,&y_D\}\\
\end{eqnarray}\)
とし、重み行列を \(\bs{W}\)、バイアスはなし、活性化関数を \(\mr{ReLU}\) とするると、
\(\bs{y}=\mr{ReLU}(\bs{x}\cdot\bs{W})\)
です。重み \(\bs{W}\) は誤差逆伝播法による訓練で決まり、推論時には一定の値です。Transformer のアテンション機構もこれと似ています。アテンションは、
入力ベクトル列 :\(\bs{x}_i\:\:\:(1\leq i\leq S)\)
出力ベクトル列 :\(\bs{y}_i\:\:\:(1\leq i\leq S)\)
の間の変換をする機構だからです。ニューラル\(\cdot\)ネットワークの活性値(実数値)がベクトルに置き換わったものと言えます。ヘッドが1つの場合(Single Head Attension)で図示すると、次の通りです。
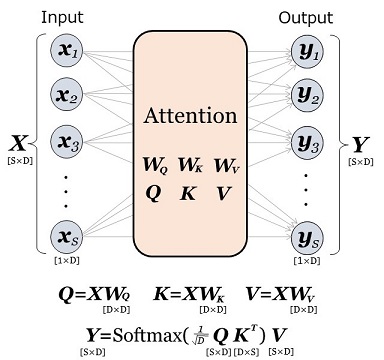
|
図25:注意機構 |
ヘッドが1つの場合の計算処理である。ヘッドが複数の場合も本質は同じで、この計算処理を独立して複数個行ない、結果を結合して出力とする。 |
しかし、この図は一般のニューラル\(\cdot\)ネットワークとは決定的に違います。重み行列 \(\bs{W}_Q,\:\:\bs{W}_K,\:\:\bs{W}_V\) は推論時には一定ですが、実際に \(\bs{x}_i\) と \(\bs{y}_i\) の関係性を決めているのは、クエリ・ベクトル \(\bs{Q}\) とキー・ベクトル \(\bs{K}\) であり、これは入力ベクトル列 \(\bs{x}_i\) の内容にもろに依存しているからです。つまり、
注意機構により、ネットワークの "ありよう"(結合状態と結合強度)が、入力データの内容に依存して、ダイナミックに変化する
と言えます。\(\bs{x}_1\) の値を変えると、その影響は \(\bs{y}_i\:\:(1\leq i\leq S)\) の全体に及びます。それは、「\(x_1\) を変えると \(y_i\) の全部が変わる」という一般のニューラル\(\cdot\)ネットワークと同じではありません。一般のニューラル\(\cdot\)ネットワークを関数とみなすと、「関数は一定だが、入力が変わるから出力も変わる」のです。それに対して注意機構は「入力が変わると関数の形まで変わる」とみなすことができるでしょう。もちろん、実際には図25のように関数は一定なのですが、一般のニューラル\(\cdot\)ネットワークとの比較で言うと、そうみなせるということです。
この柔軟性とダイナミックな(動的な)性格が、Transformer に大きなアドバンテージをもたらしました。次章の GPT-3 / ChatGPT が実現している「本文中学習(In Context Learning)」はその一つです。ChatGPT では、プロンプトを変える、ないしは文言を追加すると、応答が大きく変わることがあります。また、欲しい応答の表現形式を例示したプロンプトをすると、その形式どおりのに応答がきたりします。あたかも、プロンプトからその場で学んだように見えるのが In Context Learning です。しかし、ニューラル・ネットワークのパラメータは、推論時にはあくまで一定であり、決してその場で学んでいるわけではありません。この "あたかも" を作り出しているのが "注意機構"です。
Feed Forward Network の意味
FFN は、注意機構と違ってベクトルごとの処理です。論文では "Position-wise(位置ごとの)Feed Forward Network" と書いてあります。ということは、系列の文脈には依存しないということです。つまり Transformer の訓練を通して、ベクトル(トークンの中間表現)が本来持っている性格や関連情報が、FFN の重みの中に蓄えられると考えられます。AI の専門家である、プリファードネットワークス社の共同創業者の岡野原大輔氏は、著書の『大規模言語モデルは新たな知能か』の中で次のように書いています。
|
岡野原氏が「多重パーセプトロン(Multi-Layer Perceptron : MLP)と書いているのは FFN のことです。ちなみに入力層(第0層)を含めて「三層」という言い方になっています。
ここで、FFN のパラメータ数を求めてみます。バイアスを無視すると、
\(\bs{W}_1\:\:[D\times D_{ff}]\)
\(\bs{W}_2\:\:[D_{ff}\times D]\)
\(D\) : 埋め込みベクトルの次元
\(D_{ff}=4D\)
なので、
FFN のパラメータ数\(=8D^2\)
です。一方、Multi Head Attention で、
\(H\) : ヘッドの数
\(d=\dfrac{D}{H}\)
とすると、\(h\)番目のヘッドの \(QKV\) を作る行列は、
\(\bs{W}_Q^h\) \([D\times d]\)
\(\bs{W}_K^h\) \([D\times d]\)
\(\bs{W}_V^h\) \([D\times d]\)
であり、これらを足すとパラメータ数は \(3Dd\) ですが、この組が \(H\) セットあるので、合計は \(3DdH=3D^2\) です。さらに、単純結合したあとの Linear 変換行列である、
\(\bs{W}_O\) \([D\times D]\)
が加わるので、結局、
MHA のパラメータ数\(=4D^2\)
です。ということは、
FFN のパラメータ数は、MHA のパラメータ数の2倍
ということになります。パラメータ数だけの単純比較はできませんが、FFN が極めて多い情報量=記憶を持っていることは確かでしょう。それが、大量の訓練データの中から関連する情報を記憶し、また推論時にそれを想起することを可能にしています。
論文のタイトルは "Attention Is All You Need" で、これは従来の機械翻訳の技術では補助的役割だった Attention を中心に据えたという意味でしょう。しかし技術の内実をみると、決して「アテンションがすべて」ではなく「アテンション機構と多重パーセプトロンの合わせ技」であり、しかもそれを多層に重ねたのが Transformer なのでした。
前回でニューラル・ネットワークの例とした多重パーセプトロンは、ニューラル・ネットワークの研究の歴史の中で最も由緒あるもので、1980年代に盛んに研究されました。それが、2010年代半ばから研究が始まった "アテンション機構" と合体して Transformer のアーキテクチャになり、さらには ChatGPT につながったのが興味深いところです。
| 4.GPT-3 と ChatGPT |
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。ここではまず GPT-3 の仕組みを説明します。
GPT-3 のアーキテクチャ
GPT は Generative Pre-trained Transformer の略です。generative とは "生成型の"、pre-trained は ""事前学習済の" という意味で、Transformer は Google が 2017年に提案した Transformer を指します。
訳すると "事前学習済の生成型トランスフォーマー" となるでしょう。Transformer は「変換器」という意味でした。とすると「生成型の変換器」とは言葉が矛盾しているようですが、実は GPT は Transformer のアーキテクチャのデコーダ部分だけを使った大規模言語モデルです。だから「生成型変換器」なのです(下図)。
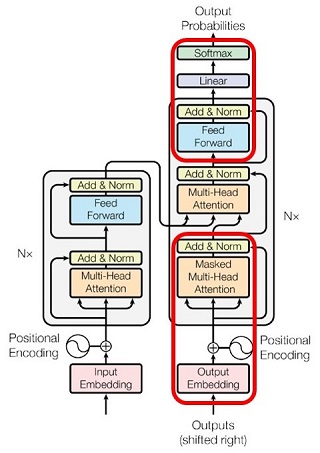
|
GPT は上図の Transformer のアーキテクチャから赤枠の部分のみを使っている。 |
この「デコーダ部分だけを使う」という発想が、OpenAI の技術者の慧眼でした。デコーダだけで系列変換(機械翻訳、文章要約、質問応答、・・・・・・ )ができるはず、という発想が GPT に柔軟性と大きな能力を与えました。GPT-3 のアキテクチャーは以下のようです。
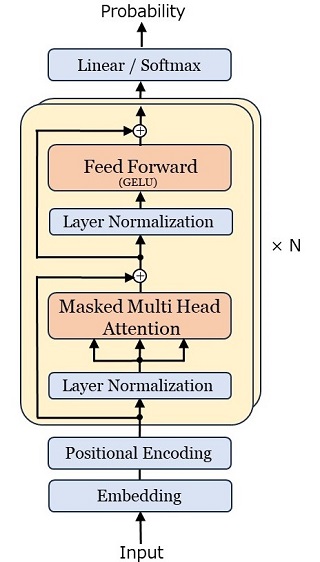
|
図26:GPT-3 のアーキテクチャ |
このアキテクチャーは、Transformer から「エンコーダとエンコーダ関連部分」を取り去ったものです。ただし、次が違います。
| Position Encoding における位置符号ベクトルは、学習で決まるパラメータとします。Transformer では固定的な \(\mr{sin}/\mr{cos}\) 波でした。 | |
| レイヤー正規化を Masked Multi Head Attetion と Feed Forward Network の直前に行います。Transformer では、それぞれの後にレイヤー正規化が配置されていました。 | |
| Feed Forward Network の活性化関数は \(\mr{GELU}\) を使います。Transformer では \(\mr{ReLU}\)です(\(\mr{GELU}\) については前回参照)。 |
これらはいずれも、学習の安定化と高速化のための工夫です。さらに GPT-3 は Transformer に比べてモデルの規模が大きく拡大されています。
・埋め込みベクトルの次元 \(D=12288\)
\((\)Transformer \(:\:512\) の \(24\)倍\()\)
・デコーダブロックの積層数 \(N=96\)
\((\)Transformer \(:\:6\) の \(16\)倍\()\)
・アテンションのヘッドの数 \(H=96\)
\((\)Transformer \(:\:8\) の \(12\)倍\()\)
です。大規模言語モデルでは、モデルの規模と学習量の拡大を続けると、それにともなって性能(たとえば機械翻訳の精度)が上がり続けるという「スケール則」がみられました。これは一般の深層学習のニューラル\(\cdot\)ネットワークにはない特徴です。このスケール則を信じ、アーキテクチャをシンプルにしつつ、モデルの規模を「桁違いに」拡大した OpenAI 社と出資した会社(マイクロソフト)の勝利でしょう。
このアーキテクチャのパラメータ数をカウントしてみます。
| ・トークンの語彙数 | \(V\) | |
| ・埋め込みベクトルの次元 | \(D\) | |
| ・系列の長さ | \(S\) | |
| ・デコーダの積層数 | \(N\) |
とします。GPT-3 の具体的な数値は、
| \(V\) | \(=50257\) | |
| \(D\) | \(=12288\) | |
| \(S\) | \(=\phantom{1}2048\) | |
| \(N\) | \(=\phantom{111}96\) |
です(\(V\) の値については前回参照)。学習で決まる行列やベクトルを順にカウントしていくと次のとおりです。
(1) Embedding と確率生成
\(\bs{W}_{\large enc}\) \([V\times D]\)
\(\bs{W}_{\large dec}\) \([D\times V]\)
\(\rightarrow\) パラメータ数\(=2VD\)
(2) Positional Encoding
\(\bs{p}\) \([S\times D]\)
\(\rightarrow\) パラメータ数\(=SD\)
(3) Masked Multi Head Attention
\(\bs{W}_Q\) \([D\times D]\) ※
\(\bs{W}_K\) \([D\times D]\) ※
\(\bs{W}_V\) \([D\times D]\) ※
\(\bs{W}_O\) \([D\times D]\)
\(\rightarrow\) パラメータ数\(=4D^2\)
※ GPT-3 のヘッドの数は \(H=96\) なので、\(\bs{W}_Q,\:\:\bs{W}_K,\:\bs{W}_V\) はそれぞれ \(96\)個の部分行列に分かれていますが、パラメータ数の全体は上式のとおりです。
(4) Feed Forward Network
| \(\bs{W}_1\) | \([D\times4D]\) | |
| \(\bs{b}_1\) | \([1\times4D]\) | |
| \(\bs{W}_2\) | \([4D\times D]\) | |
| \(\bs{b}_2\) | \([1\times D]\) |
\(\rightarrow\) パラメタ数\(=8D^2+5D\)
(5) Layer Nomaliation (2レイヤー)
\(\bs{g}\) \([1\times D]\)
\(\bs{b}\) \([1\times D]\)
\(\rightarrow\) パラメタ数\(=2\times2D=4D\)
(3), (4), (5) は \(\times\:N\) に積層されていることに注意して総パラメータ数を計算すると、
総パラメータ数
\(=\:2VD+SD+N(4D^2+8D^2+5D+4D)\)
\(=\:2VD+SD+N(12D^2+9D)\)
\(=\) \(\bs{175,217,074,176}\)
となり、約 1752億となります。一般に言われているパラメータ数が 1750億というのは、英語の 175B(B = Billion = 10億)の日本語訳で、Billion 単位にしたパラメータ数です。
GPT-3 が系列の次のトークンを推論するとき、1752億のパラメータの全てを使った演算が行われます(図21)。40文字の日本語文章を 60トークンだとすると、 わずか 40文字の日本語文章を生成するために、1752億のパラメータの全てを使った演算が 60回行われるということです。
また、1752億のパラメータがすべて 32ビットの浮動小数点数(4バイト)だとすると、パラメータのためだけに、
653ギガバイト(1ギガ = \(1024^3\) 換算)
のメモリが必要になります。業務用コンピュータ・システムの開発経験者ならわかると思いますが、これだけのデータ量を常時抱えつつ、更新やリアルタイムの推論を行うシステムを開発・運用するのは、ちゃんとやればできるでしょうが、かなり大変そうな感じです。
GPT-3 のアーキテクチャを振り返ってみると、Transformer のデコーダ部分だけを採用したことによる、Transformer との違いがあることに気づきます。それは、
Transformer には「過去と未来の両方に注意を向けるアテンション機構」と「過去にだけ注意を向けるアテンション機構」の両方があるが、GPT-3 には「過去にだけ注意を向けるアテンション機構」しかない
ことです。言うまでもなく、アテンション機構は Transformer / GPT-3 の "キモ" です。そのキモのところに違いがある。
人間の言語活動(発話・文章作成)では「過去の単語との整合性を考慮しつつ、未来の単語を想定して次の単語を決める」ことが多々あります。このことは、機械翻訳では、翻訳前の「原文」を処理するエンコーダ側の「過去と未来の両方に注意を向けるアテンション機構」で実現されています(Mask がない Multi Head Attention)。
しかし GPT-3 では様子が違ってきます。事前学習(次項)だけの GPT-3 で機械翻訳がなぜできるかというと、
[ 原文 ] を翻訳すると [ 翻訳文 ] です
といった対訳(に相当するデータ)が訓練データの中に多数あるからです(GPT-2 の論文による)。この「原文」の部分のアテンション処理において、「原文」の中の未来の単語に注意が向くことはありません(Masked Multi Head Attention しかないから)。このことにより翻訳の精度が Transformer とは違ってくる(精度が落ちる)と想定できます。
こういった "問題" は、大規模言語モデルを "超大規模" にすることで解決するというのが、GPT-3 の開発方針だと考えられます。1752億という膨大なパラメータ数が、それを表しています。
GPT-3 の訓練
GPT-3 の訓練は、
・WebText
・電子ブック
・Wikipedia
をもとに行われました。WebText は "訓練に使うべきではない" テキストを除外してあります。集められたテキストの量はトークンの数でカウントすると、
| ・WebText | \(4290\)億 | |
| ・電子ブック | \(\phantom{42}67\)億 | |
| ・Wikipedia | \(\phantom{42}30\)億 |
訓練は、Transformer のデコーダのところでで説明したように「ひたすら次のトークンの予測をする」というものです。この「次のトークンの予測」について補足しますと、前回、GPT のトークン化のロジックである BPE(Byte Pair Encoding)のことを書きました。これによると、UTF-8 では改行も空白も文字として扱われるので、改行、空白のそれぞれにトークンID が割り当てられることになります。
これから言えることは、テキストを学習するということは、その意味内容だけでなく、テキストの表現形式も学習するということです。つまり、段落、字下げ、箇条書きなどの形式です。訓練が終わった 1752億のパラメータには、そういった "表現形式に関する知識" も含まれていることに注意すべきでしょう。
以上のように、一般的に入手できるテキストだけを使ってニューラル・ネットワークを訓練することを「事前学習」と言います。このような事前学習を行った上で、機械翻訳や質問応答などのタスク別に専用に作成した訓練データで「目的別学習」を行うのが、言語モデルの定番の学習手法です。あらかじめ事前学習を行った方が言語モデルの性能が良くなるからです。目的別学習を "ファイン・チューニング" と言います。
GPT-3 は、それまでの GPT、GPT-2 と違って、ファイン・チューニングなしの言語モデルを狙ったものです。つまり、
事前学習済みの(=事前学習だけの)、生成型の(=デコーダだけの)トランスフォーマー
と言えるでしょう。実際 GPT-3 は、ファイン・チューニングを行った言語モデルと比較しても、"そこそこの"、ないしは "同等の" 性能であることが分かりました。もちろんファイン・チューニング済の言語モデルに劣るタスクも多々あります。しかし全体としては "そこそこの" 性能を示します。「ニューラル・ネットワークの超大規模化」と「大量の訓練データ」によってそれが可能であることを、GPT-3 は示したのでした。
ChatGPT
ChatGPT は GPT-3 のアーキテクチャと事前学習をもとに、さらに「目標駆動型学習」を追加したものです。ここでの目標駆動型学習とは「人間にとって好ましい応答の例を人間が作り、それを目標として、そこに近づくように学習する」という意味です。OpenAI 社は RLHF(Reinforcement Learning by Human Feedback:人間のフィードバックによる強化学習)と呼んでいます。これは一種のファイン・チューニングであると言えます。
この、目標駆動型学習をどうやるか、その詳細が OpenAI 社のノウハウでしょう。考えてみると、GPT-3 の(従って ChatGPT の)アーキテクチャはシンプルあり、これをシステム上に実現するのは、コンピュータ技術とAI技術、ハードウェアの調達(特にGPU)、そしてお金の問題です。事前学習に使う WebText にしても、世界中から集めて公開している団体があります(GPT-3 でも使われた Common Crawl)。お金がある(かつ投資意欲がある)大手IT企業なら、システム構築は難しくない。
しかし「人手で作った訓練データをもとに、人にとって違和感がない対話ができるまでに訓練する」のは、Transformer の性質や "癖 を熟知していないとできないと考えられます。そこにノウハウがあるはずです。
その目標駆動型学習の概要を、先ほど引用した岡野原氏の「大規模言語モデルは新たな知能か」では、次のような3つのステップで説明しています。この説明は専門用語を最小にした簡潔なものなので、以降これに沿って書きます。
|
この岡野原氏の説明を読み解くと、次のようになるでしょう。ラベラーとは訓練データ(教師ラベル)を作る人の意味です。
第1ステップは、機械学習の分野でいう「教師あり学習」です。ここで具体的にどのような訓練をしたのかは、OpenAI 社も公表していません。推測すると「望ましい対話」の例には、人間の質問に「答えられません」や「できません」と応答する訓練データも多数あるのではと思います。たとえば「反社会的行為を助長するような質問」の場合(爆弾の作り方など)です。
さらにこの第1ステップでは、特定のタイプのプロンプトに対して、あたかも ChatGPT が感情をもっているかのように応答する訓練が可能なはずです。それが「望ましい対話」だと OpenAI が判断すればそうなります。
第2ステップは2つのフェーズに分かれています。第1フェーズは、人手によるランキングの作成です。このとき「複数の異なるモデル」を使います。モデルとは言語モデルのことです。実は、GPT-3 を開発する過程においても、パラメータ数の違う複数の言語モデルが開発されていて、最終的に公開されたのが GPT-3 です。またパラメータ数が同じでも、訓練のやり方が違うとパラメータの値が違うので、モデルとしては別です。
このような複数の異なるモデルを選び(4つとします)、同じ入力(プロンプト。\(P\) で表します)に対して、4つの違った応答、\(A,\:B,\:C,\:D\) を得ます。ラベラーは、この \(P/A,\:P/B,\:P/C,\:P/D\) という4つの「プロンプト \(/\) 応答」にランク付けします( \(/\) はプロンプトのあとに応答が続くという意味です)。ランク付けが仮に、
\(P/A\: > \:P/B\: > \:P/C\: > \:P/D\)
だとします。現実問題としては4つのランク付けは難しいので、2つずつの6つのペアについて、どちらが良いかを決めます。ランク付けの基準について岡野原氏は書いていないのですが、OpenAI 社の公開資料によると、
・嘘やデマを含まない
・差別的・攻撃的な内容を含まない
・ユーザの役に立つ
という基準です。このような「ランク付けデータ」を大量に準備します。これは人に頼る "人海戦術" しかないので、アウトソーシングしたとしてもコストがかかります。
ちなみに、応答が「差別的・攻撃的な内容を含まない」というのは極めて重要です。というのも、過去に「AI を使った Chat システムが差別的発言をするようになり、公開中止に追い込まれる」という事件が何件か発生しているからです(2016年のマイクロソフト、2022年のメタなど)。
特に、メタ(旧フェイスブック)の Galactica 炎上事件(差別的応答による)は、システムの公開日が 2022年11月15日であり、ChatGPT の公開日(2022年11月30日)とほぼ同時期でした。メタがつまづき、ChatGPT がつまづかなかったのは、OpenAI 社が極めて慎重に「反倫理的・反社会的応答」を排除するように訓練したからと考えられます。
特に、メタ(旧フェイスブック)の Galactica 炎上事件(差別的応答による)は、システムの公開日が 2022年11月15日であり、ChatGPT の公開日(2022年11月30日)とほぼ同時期でした。メタがつまづき、ChatGPT がつまづかなかったのは、OpenAI 社が極めて慎重に「反倫理的・反社会的応答」を排除するように訓練したからと考えられます。
第2ステップの第2フェーズは、ランキングのデータをもとに自動評価システムを作ることが目的です。データを入力して評価値(強化学習の用語でいうと "報酬")を出力する関数(=自動評価システム)を \(\mr{Score}()\) と書くと、
\(\mr{Score}(P/A) > \mr{Score}(P/B) > \mr{Score}(P/C) > \mr{Score}(P/D)\)
となるように関数を決めます。これはニューラル・ネットワークを使って、訓練を繰り返して決めます(強化学習の用語で "報酬モデル")。ここで岡野原氏が指摘しているのは、\(\mr{Score}\) 関数への入力は、
ランキングをつけたデータそのものでなく、目標駆動型学習をしたい大規模言語モデル(この場合は GPT-3)にランキング済みデータを入力したときの、大規模言語モデルの内部状態
だということです。従って、\(\mr{Score}(P/A)\) は、
\(\mr{Score}(\mr{InnerState}(P/A))\)
と書くべきでしょう。これによって「高精度に評価を推定できる」というのが岡野原氏の説明です。
第3ステップでは、この自動評価システムを使って、プロンプトに対する応答の評価値が最も高くなるように強化学習を行います。このステップには人手を介した評価はないので、大量のプロンプトで学習することができます。
ここで、言語モデル \(\al\) の内部状態を入力とする自動評価システムを \(\mr{Score}_{\large\:\al}\) とし、言語モデル \(\al\) を上記のように訓練した結果、言語モデル \(\beta\) になったとします。すると、同じ「プロンプト/応答」を投入したときの内部状態が、2つの言語モデルで違ってきます。つまり、
\(\mr{InnerState}_{\large\:\al}(P/A)\neq\mr{InnerState}_{\large\:\beta}(P/A)\)
です。ということは、
\(\mr{InnerState}_{\large\:\beta}\) を入力とする、自動評価システム \(\mr{Score}_{\large\:\al}\) の改訂版、\(\mr{Score}_{\large\:\beta}\) が作れる
ことになります。つまり「第2ステップの第2フェーズ」と「第3ステップ」をループさせて繰り返すことができる。このとき、ラベラーが作ったランキングデータはそのまま使えます。このランキングが絶対評価ではなく相対評価だからです。以上のことから、
自動評価システムと言語モデルは、より正確な評価値を獲得するように "共進化" できる
と言えます。岡野原氏が言っている「高精度に評価を推定できる」とは、こういった "共進化" も含めてのことだと考えられます。このように、目標駆動型学習で鍵となるのは、この「高精度の自動評価システム」です。
補足しますと、ChatGPT が公開された後は、利用者の実際のプロンプトとそれに対する ChatGPT の応答を膨大に集積できます(利用者が拒否しなければ)。この実際の「プロンプト/応答」データの中から自動評価システムの評価が低いものだけを集め、プロンプトへの応答の評価が高くなるように ChatGPT の強化学習ができることになります。ChatGPT から "でたらめな" 応答を引き出そうとする(そして成功すれば喜ぶ)人は多いでしょうから、強化学習のためのデータにはこと欠かないはずです。
以上が、岡野原氏の説明の "読み解き" です。
ここまでをまとめると、次のようになるでしょう。
| GPT-3 は、ひたすら次の語を予測することに徹し、大量のテキストで訓練された大規模言語モデルである。その基盤技術は Transformer をシンプルにしたものであり、\(1752\)億のパラメータをもつ巨大ニューラル・ネットワークである。 | |
| ChatGPT は GPT-3 をベースに、人手で作った「人にとって好ましい応答例」を訓練データとして学習し、人と違和感なく会話できるようにした大規模言語モデルである。 |
このような GPT-3 の仕組みでは、計算や論理的推論は本質的にできません。簡単な計算(2桁整数同士のたし算、2次方程式を解くなど)ができる(ように見える)のは、それが訓練データにあるからです。また、正しい論理的推論ができたとしたら、類似の推論が訓練データの中にあるからです。
とはいえ、ChatGPT はバックに語と語の関係性についての膨大な "知識" をもっていて、それによって "規則性" や "ルール" の認識が内部にできているはずです。その中には「人が気づかない」「暗黙の」「意外なもの」があってもおかしくない。それにより、蓄積した知識を "混ぜ合わせて" 正しい推論、ないしは発見的な推論がきることもあり得るはずです。
さらに、人が普段話すのと同じように話せば、その膨大な "知識" が活用できるのは多大なメリットでしょう。もちろん "悪用" される可能性はいつでもありますが、そのことを踏まえつつ、使い方の発見や検討が今後も進むのでしょう。
| 言語の "理解" とは |
人の問いかけに対する ChatGPT の応答は、いかにも人らしいものです。もちろん間違いや、変な答え、明らかに事実とは違う応答もあります。しかし、世界中から集めた知識の量は膨大で、言語の壁も越えています。
その "知識" は(GPT-3, ChatGPT では)1752億個のパラメータの中に埋め込まれています。量は膨大ですが、それを処理する仕組みはシンプルです。なぜこれでうまくいくのか、そこが驚異だし、その理由を理解することは難しいでしょう。
もちろん、その中身を解明しようとする研究は進むでしょうが、"理解" は難しいのではと思われます。というのも、「比較的シンプルな記述による、人にフレンドリーな説明」でないと、人は "理解" したとは思わないからです。
しかし考えてみると、我々が言語(母語)を習得でき、かつ自在に扱えるのはなぜか、その脳の働きは、Transformer / ChatGPT と極めて似ているのではないでしょうか。
前回の冒頭で紹介したように、慶応義塾大学の今井教授は、「ChatGPT の仕組み(=注意機構)は、幼児が言語を学習するプロセスと類似している」と指摘していました。今井教授は幼児の言語発達を研究する専門家なのでこの指摘になるのですが、実は Transformer / ChatGPT のやっていることは、幼児のみならず、我々が言葉(母語)を理解してきた(現に理解している)やりかたと酷似していることに気づきます。それは、
外界からくる複雑な情報を丸ごと飲み込んで、ルールを知らないうちから活用する(活用できる)
という言語理解のありようです。もちろん(外からの指摘による)「好ましくない言葉の使い方」であれば訂正します。しかし、学び方も含めて、我々は内発的・創発的に言葉を理解しています。それが我々の脳の働きの重要な一面です。
前回、Transformer がタンパク質の機能分析に使える(可能性がある)ことを書きましたが、さらにヒトの脳の(ある脳領域の)解明に役立つこともありそうです。
大規模言語モデルの外面的な機能は驚異的ですが、さらにその内部の「仕組み」を理解することで、その応用範囲が極めて広いことがわかるのでした。
2023-10-06 07:39
nice!(0)




