No.365 - 高校数学で理解する ChatGPT の仕組み(1) [技術]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
前回の No.364「言語の本質」の補足で紹介した新聞記事で、慶応義塾大学の今井教授は、
と指摘していました。メタ学習とは「学習のしかたを学習する」ことですが、 ChatGPT がそれをできる理由も「注意機構(Attention mechanism)」にあります。そこで今回は、その気になる ChatGPT の仕組みをまとめます。
今まで「高校数学で理解する ・・・・・・」というタイトルの記事をいくつか書きました。
の 13 の記事です。"高校数学で理解する" という言い方は、「高校までで習う数学だけを前提知識として説明する」という意味ですが、今回もそれに習います。もちろん、文部科学省の学習指導要領は年々変わるので、"おおよそ高校までの数学" が正しいでしょう。今回、前提とする知識は、
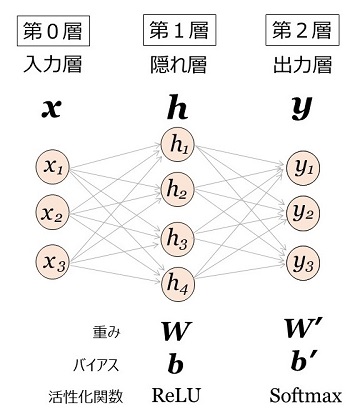
です。ChaGPT は "ニューラル・ネットワーク"、ないしは "深層学習(ディープ・ラーニング)" の技術を使った AI ですが、こういった知識は前提とはしないことにします。つまり、ニューラル・ネットワークについては、その基礎から(必要なものだけに絞って)順を追って説明します。
全体の構成
全体の構成は次の4つです
1.ニューラル・ネットワーク
2.自然言語のモデル化
3.Transformer
4.GPT-3 と ChatGPT
なお、この記事の作成には、Google と OpenAI の論文に加えて、以下を参考にしました。
◆岡野原 大輔(プリファードネットワークス)
「大規模言語モデルは新たな知能か」
(岩波書店 2023)
◆澁谷 崇(SONY)
「系列データモデリング (RNN/LSTM/Transformer)」
第7回「Transformer」
第12回「GPT-2, GPT-3」
(YouTube 動画)
記号
以降で使用する記号の意味は次の通りす。
ニューラル・ネットワークの例
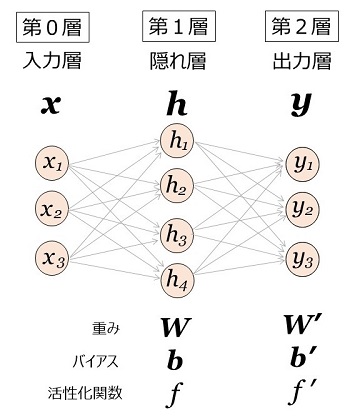
2層から成るシンプルなニューラル・ネットワークの例が図1です。この例では隠れ層が1つだけですが、隠れ層は何層あってもかまいません(なお、入力層を含めて、これを "3層" のニューラル・ネットワークとする定義もあります)。
丸印は "ニューロン" で、各ニューロンは1つの値(活性値)をもちます。値は実数値で、32ビットの浮動小数点数が普通です。図1のニューロンの数は 3+4+3=10 個ですが、もちろんこの数は多くてもよく、実用的なネットワークでは数100万から億の単位になることがあります。
ニューロン間の矢印が "シナプス" で、一つのニューロンは、シナプスで結ばれている前の層のニューロンから値を受けとり、決められた演算をして自らの値を決めます(入力層を除く)。なお、"ニューロン" や "シナプス" は脳神経科学の用語に沿っています。
各層は、重み \(\bs{W}\)(行列)とバイアス \(\bs{b}\)(ベクトル)、活性化関数 \(f\) を持ちます。図1の場合、第1層の重みは \(\bs{W}\:\:[3\times4]\)、バイアスは \(\bs{b}\:\:[1\times4]\) で、
\(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}&w_{14}\\w_{21}&w_{22}&w_{23}&w_{24}\\w_{31}&w_{32}&w_{33}&w_{34}\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2&b_3&b_4\\\end{array}\right)\)
です。このとき、隠れ層(第1層)のニューロンの活性値、\(\bs{h}=\left(\begin{array}{r}h_1&h_2&h_3&h_4\\\end{array}\right)\) は、
\(h_1=f\:(\:x_1w_{11}+x_2w_{21}+x_3w_{31}+b_1\:)\)
\(h_2=f\:(\:x_1w_{12}+x_2w_{22}+x_3w_{32}+b_2\:)\)
\(h_3=f\:(\:x_1w_{13}+x_2w_{23}+x_3w_{33}+b_3\:)\)
\(h_4=f\:(\:x_1w_{14}+x_2w_{24}+x_3w_{34}+b_4\:)\)
の式で計算されます。ベクトルと行列で表示すると、
\(\bs{h}=f\:(\bs{x}\cdot\bs{W}+\bs{b})\)
になります。第2層も同様です。
このニューラル・ネットワークは、多重パーセプトロン(Multi Layer Perceptron : MLP)と呼ばれるタイプのもので、ニューラル・ネットワークの歴史の中では、古くから研究されている由緒のあるものです。
また上図の第1層、第2層は、すべてのニューロンが前層のすべてのニューロンとシナプスを持ってます。このような層を「全結合層」(Fully connected layer. FC-layer. FC層)と言います。全結合の多重パーセプトロンは Transformer や GPT で使われていて、重要な意味を持っています。
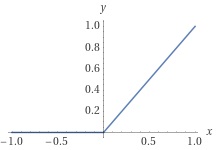
活性化関数 \(f\) は、隠れ層では、\(\mr{ReLU}\) 関数(Rectified Linear Unit:正規化線形ユニット)を使うのが普通です。\(\mr{ReLU}\) 関数は、
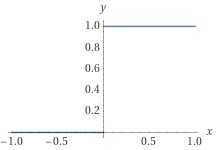
で定義される非線形関数です(図2)。以降での表記を簡潔にするため、単位ステップ関数 \(H(x)\) を用いて \(\mr{ReLU}\) 関数を表しておきます。単位ステップ関数は、
\(H(x)=1\:\:(x > 0)\)
\(H(x)=0\:\:(x\leq0)\)
で定義される関数で(図3)、ヘヴィサイド関数とも呼ばれます。\(H(x)\) の微分は、
\(H\,'(x)=0\:\:(x\neq0)\)
です。\(x=0\) において \(H(x)\) は不連続で、微分は定義できませんが、無理矢理、
\(H\,'(0)=0\)
と定義してしまうと、\(x\) の全域において、
\(H\,'(x)=0\)
となります。この \(H(x)\) を用いて \(\mr{ReLU}\) 関数を定義すると、
となり、微分は、
\(\dfrac{d}{dx}\mr{ReLU}(x)=H(x)\)
と表現できます。
出力層の活性化関数 \(f\,'\) は、ニューラル・ネットワークをどんな用途で使うかによって違ってきます。
ニューラル・ネットワークによる推論
ニューラル・ネットワークが扱う問題は、入力ベクトル \(\bs{x}\) をもとに出力ベクトル \(\bs{y}\) を "推論"(ないしは "推定"、"予測")する問題です。これには主に「回帰問題」と「分類問題」があります。
回帰問題で推論する \(\bs{y}\) は実数値(=連続値)です。たとえば、
・身長
・体重
・年齢
・男女の区別
・生体インピーダンス
から(\(=\bs{x}\))、
・体脂肪率
・筋肉量
・骨密度
を推定する(\(=\bs{y}\))といった例です(但し、市販の体組成計が AI を使っているわけではありません)。
一方、分類問題の例は、たとえば手書き数字を認識する問題です。この場合、多数の手書き数字の画像(をベクトルに変換した \(\bs{x}\))を「\(0\) のグループ」「\(1\) のグループ」・・・・・ というように分類していきます。このグループのことを AI では "クラス" と呼んでいます。つまり「クラス分類問題」です。
手書き数字の場合、明確に \(0\) ~ \(9\) のどれかに認識できればよいのですが、そうでない場合もある。たとえば、\(1\) なのか \(7\) なのか紛らわしい、\(0\) なのか \(6\) なのか曖昧、といったことが発生します。分類するのは、\(0\) ~ \(9\) のうちのどれかという「離散値の予測」であり、連続値とは違って、どうしても紛らわしい例が発生します。
従って、クラス分類問題(=離散値を予測する問題)では、出力ベクトル \(\bs{y}\) は確率です。手書き数字の認識では、\(\bs{y}\) は\(10\)次元の確率ベクトルで、たとえば、
となるように、ニューラル・ネットワークを設計します。確率なので、
\(0\leq y_i\leq1,\:\:\:\displaystyle\sum_{i=1}^{10}y_i=1\)
です。入力画像が \(1\) なのか \(7\) なのか紛らわしい場合、たとえば推定の例は、
\(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
です。これは、
\(1\) である確率が \(0.8\)
\(7\) である確率が \(0.2\)
を表します。クラス分類問題は「離散値を推論する問題」、すなわち「確率を推定する問題」であると言えます。
回帰問題の出力層の活性化関数は、恒等関数(=何もしない)とするのが普通です。一方、クラス分類問題の出力層の活性化関数は、出力 \(\bs{y}\) が確率として解釈できるような関数を選びます。それが \(\mr{Softmax}\) 関数です。
\(\mr{Softmax}\) 関数
\(\mr{Softmax}\) 関数によって、出力 \(\bs{y}\) が確率と解釈できるようになります。ベクトル \(\bs{x}\) を \(\mr{Softmax}\) 関数によって確率ベクトル \(\bs{y}\) に変換する式は、次のように定義できます。なお、ここでの \(\bs{x}\) は入力層の \(\bs{x}\) ではなく、一般的なベクトルを表します。
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(n\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{n}y_i=1\)
ここで使われている指数関数は、すぐに巨大な数になります。たとえば \(\mr{exp}(100)\) は\(10\)進で\(40\)桁以上の数で、\(32\)ビット浮動小数点の最大値(\(10\)進で\(40\)桁弱)を越えてしまいます。従って、\(\mr{Softmax}\) 関数の計算には工夫が必要で、それには \(\mr{Softmax}\) 関数の性質を利用します。
\(C\) を任意の実数値とし、\(n\)次元ベクトル \(\bs{z}\) を
\(z_i=x_i+C\)
と定義します。そして、
\(\bs{y}\,'=\mr{Softmax}(\bs{z})\)
と置くと、
\(\begin{eqnarray}
&&\:\:y_i\,'&=\dfrac{\mr{exp}(z_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(z_i)}=\dfrac{\mr{exp}(x_i+C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i+C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)\cdot\mr{exp}(C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\mr{exp}(C)\cdot\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\\
&&&=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}=y_i\\
\end{eqnarray}\)
となります。つまり \(x_i\:\:(1\leq i\leq n)\) の全部に定数 \(C\) を足しても、\(\mr{Softmax}\) 関数は変わりません。そこで、
\(C=-\mr{max}(x_1,\:x_2,\:\cd\:,x_n)\)
と置いて、
\(x_i\:\longleftarrow\:x_i+C\:\:(1\leq i\leq n)\)
と修正すると、\(x_i\) の最大値は \(0\) になります。従って、
\(0 < \mr{exp}(x_i)\leq1\)
の範囲で \(\mr{Softmax}\) 関数が計算可能になります。
大規模言語モデルと確率
クラス分類問題の出力ベクトル \(\bs{y}\) は確率でしたが、実は Transformer や GPT が実現している「大規模言語モデル」も "確率を推定するニューラル・ネットワーク" です。たとえば、
[今日] [は] [雨] [なの] [で]
というテキストに続く単語を推定します。仮に、日本語の日常用語の語彙数を5万語とすると、5万の単語すべてについて上のテキストに続く単語となる確率を、実例をもとに推定します。当然、「雨の日の行動」とか「雨の日の情景」、「雨の日の心理状態」、「雨の日に起こりうること」を描写・説明する単語の確率が高くなるわけです。たとえば名詞だけをとると、[家] [ビデオ] [映画] [傘] [犬] [洗濯] [祭] [運動会] などの確率が高く、[ニンジン] [牛] [鉛筆] などの確率は(雨の日とは関係があるとは思えないので)低いといった具合です(あくまで想定です)。
「大規模言語モデル」の重要な応用例(=タスク)である機械翻訳も同じです。日本語 → 英語の翻訳を例にとると、
[今日] [は] [晴れ] [です] [。] [BOS]
に続く英単語を推定します([BOS] は文の開始を示す特殊単語)。確率の高い単語から [it] を選んだとすると、次には、
[今日] [は] [晴れ] [です] [。] [BOS] [it]
に続く単語を推定します([is] になるはず)。こうやって進むのが機械翻訳です。
Transformer や GPT をごくごくシンプルに言えば、入力ベクトル \(\bs{x}\) はテキスト列、出力ベクトル \(\bs{y}\) は次に続く単語を示す確率ベクトル(次元は語彙数)です。
この記事は、Transformer、GPT、ChatGPT などの大規模言語モデルを説明するのが目的です。従って以降では、出力ベクトル \(\bs{y}\) は確率ベクトルであることを前提とします。
確率を推定するニューラル・ネットワーク
図1において、第1層(隠れ層)の活性化関数を \(\mr{ReLU}\)、第2層(出力層)の活性化関数を \(\mr{Softmax}\) とすると、図4になります。
図4の計算は、以下に示すような4段階の計算処理で表すことができます。
第1層
\(\bs{h}\,'=\bs{x}\cdot\bs{W}+\bs{b}\)
\(\bs{h}=\mr{ReLU}(\bs{h}\,')\)
第2層
\(\bs{y}\,'=\bs{h}\cdot\bs{W}\,'+\bs{b}\,'\)
\(\bs{y}=\mr{Softmax}(\bs{y}\,')\)
この4つの計算処理を「計算レイヤー」、略して「レイヤー」と呼び、図5のグラフで表現することにします。
レイヤー(layer)は日本語にすると「層」で、第1層や隠れ層の「層」と紛らわしいのですが、「レイヤー」と書いたときは "ある一定の計算処理" を示します。後ほど説明する Transformer や GPT は、図4のような単純な「層」では表現できない複雑な計算処理があります。従って "ある一定の計算処理 = レイヤー" とした方が、すべての場合を共通に表現できて都合が良いのです。
レイヤーの四角に向かう矢印は計算処理への入力を示し、四角から出る矢印は計算処理からの出力(計算結果)を示します。「レイヤーは一つの関数」と考えてもOKです。
図5の「Linear レイヤー」は、「Affine(アフィン)レイヤー」と呼ばれることが多いのですが、Transformer の論文で Linear があるので、そちらを採用します。
図5のネットワークがどうやって「学習可能なのか」を次に説明します。この「学習できる」ということが、ニューラル・ネットワークが成り立つ根幹です。
ニューラル・ネットワークの学習
重みとバイアスの初期値
まず、重み(\(\bs{W},\:\bs{W}\,'\))の初期値を乱数で与えます。この乱数は、前の層のニューロンの数を \(n\) とすると
の正規分布の乱数とするのが普通です。\(n=10,000\) とすると、標準偏差は \(0.01\) なので、
\(-\:0.01\) ~ \(0.01\)
の間にデータの多く(約 \(2/3\))が集まる乱数です。但し、\(\mr{ReLU}\) を活性化関数とする層(図4では第1層)の重みは、
の乱数とします。なお、バイアスの初期値は \(0\) とします。こういった初期値の与え方は、学習をスムーズに進めるためです。
損失と損失関数
初期値が決まったところで、訓練データの一つを、
\(\bs{x}\):入力データ
\(\bs{t}\):確率の正解データ
とします。この正解データのことを「教師ラベル」と呼びます。そして、ニューラル・ネットワークによる予測の確率 \(\bs{y}\) と、正解の確率である \(\bs{t}\) との差異を計算します。この差異を「損失(\(Loss\))」といい、\(L\) で表します。\(L\) は正のスカラー値です。
\(\bs{y}\) と \(\bs{t}\) から \(L\) を求めるのが「損失関数(Loss Function)」です。確率を予測する場合の損失関数は「交差エントロピー誤差(Cross Entropy Error : CEE)」とするのが普通で、次の式で表されます。
たとえば、先ほどの手書き数字の認識の「\(1\) または \(7\) という予測」を例にとって、その正解が \(1\) だとすると、
予測 \(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
正解 \(\bs{t}=\left(\begin{array}{r}1&0&0&0&0&0&0&0&0\\\end{array}\right)\) = 教師ラベル
です。なお、\(\mr{Softmax}\)関数の出力は \(0\) にはならないので、上の \(\bs{y}\) で \(0\) と書いた要素は、実際には微小値です。すると、
\(L=-\mr{log}\:0.8\fallingdotseq0.223\)
となります。損失関数を含めると、レイヤー構成は図6のようになります。
この図の重みとバイアスを少しだけ調整して、\(L\) を少しだけ \(0\) に近づけます。この調整を多数の学習データ(= \(\bs{x}\:\:\bs{t}\) のペア)で繰り返して、\(L\) を次第に \(0\) に近づけていくのが学習です。
勾配降下法
重みの調整には「勾配降下法(Gradient descent method)」を使います。図6の場合、損失 \(L\) は、ある関数 \(f\) を用いて、
\(L=f(\bs{x},\:\bs{W},\:\bs{b},\:\bs{W}\,',\:\bs{b}\,',\:\bs{t})\)
と表現できます。ここで、\(\bs{W}\) の一つの要素、\(w_{11}\) を例にとると、
を計算します。これはいわゆる微分ですが、多変数関数の微分なので、数学的には偏微分であり、
\(\dfrac{\partial L}{\partial w_{11}}\)
です。つまり、\(w_{11}\) 以外の変数をすべて固定しての(すべて定数とした上での)、\(w_{11}\) による微分です。
具体的な入力 \(\bs{x}\) のときの \(\dfrac{\partial L}{\partial w_{11}}\) が求まったとします。もし仮に、\(\dfrac{\partial L}{\partial w_{11}}\) が正の値だとしたら、\(w_{11}\) を少しだけ減らせば、\(L\) は少しだけ \(0\) に近づきます。もし \(\dfrac{\partial L}{\partial w_{11}}\) が負だとしたら、\(w_{11}\) を少しだけ増やせば、\(L\) は少しだけ \(0\) に近づきます。つまり、
更新式:\(w_{11}\:\longleftarrow\:w_{11}-\eta\cdot\dfrac{\partial L}{\partial w_{11}}\)
として重みを更新すればよいわけです。\(\eta\) は「少しだけ」を表す値で「学習率」といい、\(0.01\) とか \(0.001\) とかの値をあらかじめ決めておきます。この決め方は、学習の効率に大いに影響します。こういった更新を、すべての重みとバイアスに対して行います。
"学習で調整される値" を総称して「パラメータ」と言います。図6のパラメータは重みとバイアスですが、実用的なニューラル・ネットワークでは、それ以外にも更新されるパラメータがあります。
\(L\) の偏微分値をベクトルや行列単位でまとめたものを、次のように表記します。2次元のベクトル \(\bs{b}\) と、2行2列の行列 \(\bs{W}\) で例示すると、
\(\dfrac{\partial L}{\partial\bs{b}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial b_1}&\dfrac{\partial L}{\partial b_2}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{W}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\)
です。これを「勾配(gradient)」と言います。勾配を求めることでパラメータを少しづつ更新し、損失を少しづつ小さくしていく(=降下させる)のが勾配降下法です。
ミニバッチ勾配降下法
学習は次のように進みます。まず、すべての訓練データ(たとえば
数万件)から、数\(10\)~数\(100\)件(たとえば\(256\)件)の訓練データをランダムに選びます。この一群のデータを「ミニバッチ」と呼びます。ミニバッチの各訓練データによる確率の推定から損失を計算し、そこからすべてのパラメータの勾配と求め、その勾配ごとに "ミニバッチの平均値" をとります。その平均値に基づき、更新式に従って各パラメータを更新します。
ミニバッチによる更新が終わると、別のミニバッチをランダムに選び、更新を繰り返します。こうすると、損失は次第に減少していきますが、そのうち "頭打ち" になります。そこで更新を止めます。
このようなパラメータ更新のやり方を「ミニバッチ勾配降下法」と言います。一つの訓練データだけで更新しないのは、たまたまその訓練データが「外れデータ」(全体の傾向とは異質なデータ)だと、学習の進行に支障が出てくるからです。
訓練データをランダムに選択する方法を「確率的勾配降下法(Stochastic gradient method - SGD)」と言いますが、ミニバッチ勾配降下法は、その確率的勾配降下法の一種です。
誤差逆伝播法
ここで問題になるのは、すべてのパラメータの勾配をどうやって求めるかです。それに使われるのが「誤差逆伝播法(Back propagation)」です。その原理を、Linear レイヤーから説明します。
(1) Linear
図7で示すように、Linear レイヤーがあり、そのあとに何らかの計算処理が続いて、最終的に損失 \(L\) が求まったとします。\(\bs{x}\:\:\bs{y}\) はニューラル・ネットワークへの入力と出力ではなく、Linear レイヤーへの入力と出力の意味です。ここで、
と言えます。これが誤差逆伝播法の原理です。このことを、2次元ベクトル(\(\bs{x},\:\:\bs{b},\:\:\bs{y}\))、2行2列の配列(\(\bs{W}\))で例示します(\(N=2,\:M=2\) の場合)。
【Linear の計算式】
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+b_1\)
\(y_2=x_1w_{12}+x_2w_{22}+b_2\)
\(x_1\) が変化すると \(y_1,\:y_2\) が変化し、それが損失 \(L\) に影響することに注意して、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配を計算します。
【\(\bs{\bs{x}}\) の勾配】
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)\)
です。これをまとめると、
\(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\:\:\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T\)
となり、\(\bs{x}\) の勾配が求まります。
【\(\bs{\bs{W}}\) の勾配】
\(\dfrac{\partial L}{\partial w_{11}}=\dfrac{\partial y_1}{\partial w_{11}}\dfrac{\partial y_1}{\partial w_{11}}=x_1\dfrac{\partial y_1}{\partial w_{11}}\)
\(\dfrac{\partial L}{\partial w_{12}}=\dfrac{\partial y_2}{\partial w_{12}}\dfrac{\partial y_2}{\partial w_{12}}=x_1\dfrac{\partial y_2}{\partial w_{12}}\)
\(\dfrac{\partial L}{\partial w_{21}}=\dfrac{\partial y_1}{\partial w_{21}}\dfrac{\partial y_1}{\partial w_{21}}=x_2\dfrac{\partial y_1}{\partial w_{21}}\)
\(\dfrac{\partial L}{\partial w_{22}}=\dfrac{\partial y_2}{\partial w_{22}}\dfrac{\partial y_2}{\partial w_{22}}=x_2\dfrac{\partial y_2}{\partial w_{22}}\)
これらをまとめると、
となります。
【\(\bs{\bs{b}}\) の勾配】
以上の計算で求まった勾配をまとめて図示すると、図8になります。黒字(入力・出力とパラメータ)の下の赤字がパラメータの勾配で、右から左への矢印は、「レイヤーの出力の勾配が求まれば、レイヤーの入力の勾配が求まる」こと示します(= 逆伝播)。上での計算は2次元ベクトルと2行2列の配列で例示しましたが、図8のようなベクトル・配列で表示すると、\([1\times N]\) のベクトルと \([N\times M]\) の行列で成り立つことが確認できます。
(2) ReLU
\(\mr{ReLU}\) 関数は、
\(\mr{ReLU}(x_i)=x_i\:\:(x_i > 0)\)
\(\mr{ReLU}(x_i)=0\:\:\:(x_i\leq0)\)
であり、ベクトルの表現では、単位ステップ関数、
\(H(x)=1\:\:\:(x > 0)\)
\(H(x)=0\:\:\:(x\leq0)\)
と要素積 \(\odot\) を使って、
\(\mr{ReLU}(\bs{x})=H(\bs{x})\odot\bs{x}\)
と定義できます。従って、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=H(\bs{x})\odot\dfrac{\partial L}{\partial\bs{y}}\)
です。
(3) Softmax
\(\mr{Softmax}\) 関数の定義は、
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(N\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{N}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{N}y_i=1\)
です。勾配の計算を \(N=3\) の場合で例示します。
\(\dfrac{\partial L}{\partial x_1}=\dfrac{\partial y_1}{\partial x_1}\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\dfrac{\partial L}{\partial y_2}+\dfrac{\partial y_3}{\partial x_1}\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_1}=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_2}=y_2(1-y_2)\dfrac{\partial L}{\partial y_2}-y_2y_3\dfrac{\partial L}{\partial y_3}-y_2y_1\dfrac{\partial L}{\partial y_1}\)
\(\dfrac{\partial L}{\partial x_3}=y_3(1-y_3)\dfrac{\partial L}{\partial y_3}-y_3y_1\dfrac{\partial L}{\partial y_1}-y_3y_2\dfrac{\partial L}{\partial y_2}\)
(4) Cross Entropy Error - CEE
交差エントロピー誤差の定義は、
入力 \(\bs{y}\) \((1\times N)\)
入力 \(\bs{t}\) \((1\times N)\) 教師ラベル(正解データ)
出力 \(L\:(Loss)\)
とすると、
\(L=-\displaystyle\sum_{i=1}^{N}(t_i\mr{log}y_i)\)
で定義されます。従って、
\(\dfrac{\partial L}{\partial y_i}=-\dfrac{t_i}{y_i}\)
であり、\(N=3\) の場合を書くと、
\(\dfrac{\partial L}{\partial y_1}=-\dfrac{t_1}{y_1}\)
\(\dfrac{\partial L}{\partial y_2}=-\dfrac{t_2}{y_2}\)
\(\dfrac{\partial L}{\partial y_3}=-\dfrac{t_2}{y_3}\)
です。
(5) Softmax + CEE
\(\mr{Softmax}\) レイヤーの直後に交差エントロピー誤差のレイヤーを配置した場合を考えます。(3) と (4) の計算を合体させると、次のように計算できます。
計算の過程で、\(\bs{t}\) が確率ベクトルであることから、\(t_1+t_2+t_3=1\) を使いました。この計算は \(x_2,\:\:x_3\) についても全く同様にできます。それを含めてまとめると、
\(\dfrac{\partial L}{\partial x_1}=y_1-t_1\)
\(\dfrac{\partial L}{\partial x_2}=y_2-t_2\)
\(\dfrac{\partial L}{\partial x_3}=y_3-t_3\)
となります。この結果、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=\bs{y}-\bs{t}\)
という、大変シンプルな形になりました。これは任意の次元のベクトルで成り立ちます。実は、このようなシンプルな形になるように、\(\mr{Softmax}\) と 交差エントロピー誤差が設計されています。図示すると次の通りです。
ニューラル・ネットワークの誤差逆伝播
以上で「確率を推定するニューラル・ネットワーク」を構成する各レイヤーの誤差逆伝播が計算できました。これらをまとめると、次の図11になります。
ちなみに、第1層の重み \(\bs{W}\) の勾配は図11から陽に計算すると、次のようになります。
\(\dfrac{\partial L}{\partial\bs{W}}=\bs{x}^T(H(\bs{x}\bs{W}+\bs{b})\odot((\bs{y}-\bs{t})\bs{W}\,'))\)
このネットワークは隠れ層が1つだけというシンプルなものですが、今までの計算で分かるように、層数が何百層に増えたとしても、逆伝播を多段に重ねることで、誤差逆伝播法が成立します。
また、図11 で使っているレイヤーは、Linear、\(\mr{ReLU}\)、\(\mr{Softmax}\)、Cross Entropy Error ですが、これらを関数と見なしたとき、誤差逆伝播で使った数学的な前提は「関数がパラメータで微分可能」ということだけです。つまり、レイヤーの関数が微分可能である限り、誤差逆伝播法は有効です。
実は、実用的なニューラル・ネットワークで誤差逆伝播法をうまく機能させるためには、数々の工夫が必要です。また、一般に訓練データの数は膨大なので、学習速度を上げる工夫も必要です(以降でその一部を説明します)。上で述べた「初期値の選択」や「学習率」はその工夫の一つです。そういったことはありますが、ネットワークがいかに巨大になろうとも(大規模言語モデルはその巨大な典型です)、誤差逆伝播法は可能なことが分かっています。
以上が、「ニューラル・ネットワークが学習可能である」ということの原理です。
\(\mr{GELU}\)
最近の大規模言語モデル(GPT など)では、活性化関数 \(\mr{ReLU}\) の代わりに \(\mr{GELU}\) \((\)Gaussian Error Linear Unit:ガウス誤差線形ユニット\()\) が使われます。その方が、学習が効率的に進むことが分かったからです。
\(\mr{ReLU}\) は、\(H(x)\) を単位ステップ関数として、
\(\mr{ReLU}(x)=H(x)x\)
でしたが、\(\mr{GELU}\) は、
\(\mr{GELU}(x)=\Phi(x)x\)
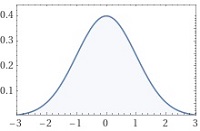
で定義されます。\(\Phi(x)\) は標準正規分布(平均 \(0\)、標準偏差 \(1\))の累積分布関数です。標準正規分布の確率密度を \(f(x)\) とすると、
\(f(x)=\dfrac{1}{\sqrt{2\pi}}\mr{exp}\left(-\dfrac{x^2}{2}\right)\)
です(図12)。つまり \(x\) ~ \(x+dx\) である事象が発生する確率が \(f(x)dx\) です。また \(-\infty\) ~ \(\infty\) の範囲で積分すると \(1\) で、原点を中心に左右対称です。
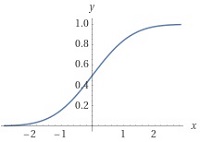
この確率分布を \(-\infty\) から \(x\) まで積分したのが累積分布関数で、
\(\Phi(x)=\displaystyle\int_{-\infty}^{x}f(t)dt\)
です(図13)。これは正規分布に従うデータ値が \(x\) 以下になる確率です。これはガウスの誤差関数(Gaussian error function)\(\mr{Erf}\) を用いて表現できます。\(\Phi(0)=0.5\) となることを使って計算すると、
\(\begin{eqnarray}
&&\:\:\Phi(x)&=\displaystyle\int_{-\infty}^{x}f(t)dt\\
&&&=\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
\end{eqnarray}\)
\(t\:\rightarrow\:\sqrt{2}u\) の変数変換をすると、
\(\begin{eqnarray}
&&\:\:\phantom{\Phi(x)}&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)\sqrt{2}du\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)du\\
&&&=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\\
\end{eqnarray}\)
となります。ガウスの誤差関数、\(\mr{Erf}()\) の定義は
\(\mr{Erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_{0}^{x}\mr{exp}(-u^2)du\)
です。従って、
\(\Phi(x)=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\)
と表現できます。\(\mr{GELU}\) 関数の形は 図14 です。
\(\mr{GELU}\) は \(\mr{ReLU}\) と良く似ていますが、すべての点で微分可能であり、\(\mr{ReLU}\) のように微係数がジャンプするところがありません。このことが、大規模言語モデルの効率的な学習に役だっていると考えられます。
残差結合
Linear レイヤーを例にとります。入力を \(\bs{x}\)、出力を \(\bs{y}\) とし、入力と出力のベクトルの次元は同一とします。重みを \(\bs{W}\) とし、バイアス \(\bs{b}\) は省略します。通常の Linear レイヤーは、
\(\bs{y}=\bs{x}\bs{W}\)
ですが、
\(\bs{y}=\bs{x}\bs{W}+\bs{x}\)
とするのが、「残差結合(residual connection)」をもつ Linear レイヤーです。なお「残差接続」とも言います。また「スキップ接続(skip connection)」も同じ意味です。
誤差逆伝播を計算すると、\(\bs{x}\) の勾配は次のようになります。2次元ベクトルの場合で例示します。
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+x_1\)
\(y_2=x_1w_{12}+x_2w_{22}+x_2\)
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)+\dfrac{\partial L}{\partial y_2}\)
従って、
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T+\dfrac{\partial L}{\partial\bs{y}}\)
です。つまり、勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が、逆伝播でそのまま \(\dfrac{\partial L}{\partial\bs{x}}\) に伝わります(図\(16\))。
一般にニューラル・ネットワークの学習を続けると、重みがゼロに近づき、その結果 \(\dfrac{\partial L}{\partial\bs{x}}\) が \(0\) に近い小さな値となることがあります。\(\dfrac{\partial L}{\partial\bs{x}}\) は、その一つ前への逆伝播の入力となるので、多層のニューラル・ネットワークでこれが重なると、前の方の層の勾配が極小になり、重みが更新できないという事態になります。これが「勾配消失」で、ニューラル・ネットワークの学習が困難になります。
残差結合を用いると、この問題を解決できます。Transformer では残差結合が使われています。
正規化
Transformer で使われているもう一つのレイヤーが「レイヤー正規化(Layer Normalization)」です。これは、ベクトル \(\bs{x}\:[1\times N]\) の要素を、平均 \(0\)、標準偏差 \(1\) のベクトル \(\bs{y}\:[1\times N]\) の要素に置き換えるものです。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
\(\mu=\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}x_i\)
\(\sg=\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\mu)^2}\)
とおくと、
\(y_i=\dfrac{1}{\sg}(x_i-\mu)\)
となります。実際にニューラル・ネットワークで使われるときには、さらにベクトルの要素ごとに線形変換をして、
\(y_i\:\longleftarrow\:g_iy_i+b_i\)
とします。ベクトルで表現すると、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\)
です。この \(\bs{g}\) と \(\bs{b}\) は学習可能なパラメータです。つまり、ニューラル・ネットワークの訓練のときに学習をして、最適値を決めます。もちろん、レイヤー正規化の式は微分可能なので、逆伝播計算が(少々複雑な式になりますが)可能です。
レイヤー正規化は、ニューラル・ネットワークを安定化させ、学習の効率化に役立ちます。その理由ですが、中間層の活性化関数で一般的な \(\mr{ReLU}\) 関数は、\(x=0\) の付近で非線型関数であり、それ以外では線型です。ニューラル・ネットワークは全体としては非線型関数で、そこにこそ意義があるのですが、その非線型性を生み出しているのは、\(x=0\) 付近の \(\mr{ReLU}\) 関数です。
従って、レイヤーの値を「ゼロ付近に集める」と、ニューラル・ネットワークの非線型性を強めることができ、これが学習の効率化につながります。その「ゼロ付近に集める」のがレイヤー正規化です。
以上の、
・\(\mr{ReLU}\) 関数(または \(\mr{GELU}\) 関数)
・残差結合
・正規化
は、大規模ニューラル・ネットワークを安定的に学習可能にするための必須技術であり、Transformer や GPT でも使われています。
単語への分解
自然言語で書かれたテキストをコンピュータで扱うとき、まずテキストを単語の系列に分解しなければなりません。系列とは「並び順に意味のある、同質の要素の集合」です。単語への分解は、単語の区切りを明示する英語(や、その他の欧米語)では容易です。文末を表すピリオドや、その他の記号も1つの単語と数えます。
日本語は単語の区切りがないので、形態素解析ソフトで単語に分解します。句読点、「、」などの記号も、それぞれ1単語と数えます。日本語の形態素解析ソフトは各種ありますが、オープンソースの MeCab が有名です。
大規模言語モデルは、世界中から集めた Webのテキスト(以下、WebText と言います)や Wikipedia、電子ブックなどを訓練データとして学習しますが、そこに出てくる単語を集めて「語彙の集合」を作ります。この集合のサイズを \(V\) とすると(たとえば、5万とか10万とかの値)、単語に \(1\)~\(V\) のユニークな番号を振ることができます。この番号を「単語ID」と呼びます。
なお、大規模言語モデルでは内部処理用として「特殊単語」も用います。以降の説明で使うのは、
[BOS] :文の開始
[EOS] :文の終了。ないしは文の区切り。
です。こうすると、テキスト \(\bs{T}\) は、
\(\bs{T}=\{x_1,\:x_2,\:x_3,\:\cd\:x_T\}\)
という単語IDの列で表現できることになります。もしこれが完結した文だとすると、\(x_1=\)[BOS]、\(x_T=\)[EOS] であり、複文だと途中にも [BOS] や [EOS] が出てくることになります。
単語IDは、その数字自体には意味がありません。また、語彙集合(要素数 \(V\))が増大すると単語IDの最大値も変化します。上の数字列は、あくまで「1時点での語彙集合をもとにして恣意的に付けられた数字の列」です。
分散表現
テキストをニュラール・ネットワークで扱うためには、すべての単語を、語彙集合のサイズにはよらない「固定長のベクトル」で表現するのが必須です。ここで使われるのが単語の「分散表現」で、固定長であるのみならず、"単語の意味もくみ取った" 表現です。ベクトルの次元は、たとば 512次元とか 1024次元です。
単語を分散表現にすることを "単語埋め込み"(word embedding)と言います。単語埋め込みの手法は各種ありますが、ここでは「word2vec」のアルゴリズムを例にとります。word2vec は、Google が2013年に提案したもので、実用的な分散表現の嚆矢となったものです。
word2vec に限りませんが、単語埋め込みのアルゴリズムの前提となっている仮定があります。それは、
というもので、これを「分布仮説」と言います。たとえば、英文を例にとり、「周囲」を仮に「前1語、後1語」とします。
[I] [ ] [beer]
という文で [ ] に入る1単語は何かです。1単語に限定すると、冠詞(a, the)は入れようがないので、入る単語は限定されます。たとえば、
などです。[ ] には「飲む」に関係した動詞か「嗜好」に関係した動詞が入る可能性が高い。少なくとも「私とビールの関わりについての動詞」です。つまり、入る単語は「前後の1語によって意味が限定される」わけです。もしこれが「前後5語」とか「前後10語」であると「似たような意味の単語」か、少なくとも「同じジャンルの単語」になるはずです。
word2vec という「単語埋め込みアルゴリズム」には2種類あり、「周囲の単語から中心の単語を推論する(CBOW)」と「中心の単語から周囲の単語を推論する(skip-gram)」の2つです。推論にはニューラル・ネットワークを使います。以下は CBOW(Continuous Bag of Words)のネットワーク・モデルで説明します。
word2vec(CBOW)
CBOW は「周囲の単語から中心の単語を推論する」ニューラル・ネットワークのモデルです。「周囲の単語」を "コンテクスト" と呼び、推論の対象とする単語を "ターゲット" と呼びます。
まず、コンテクストのサイズを決めます。ターゲットの前の \(c\) 語、ターゲットの後ろの \(c\) 語をコンテクストとする場合、この \(c\) を "ウィンドーサイズ" と呼びます。そして "ウィンドー" の中には \(2c\) 語のコンテクストと1つのターゲットが含まれます。そして、訓練データとする文の "ウィンドー" を1単語ずつずらしながら、コンテクストからターゲットを推論する学習を行います。
語彙集合の単語数を \(V\) とし、一つの文を、
\(\bs{T}=\{x_1,\:x_2,\:\cd x_T\}\)
\(x_i\) :単語ID \((1\leq x_i\leq V)\)
とします。そして、\(x_i\) に1対1に対応する、\(V\)次元の one hotベクトルを、
\(\bs{x}_i=\left(\begin{array}{r}a_1,&a_2,&a_3,&\cd&a_V\\\end{array}\right)\)
\(a_j=0\:\:(j\neq x_i)\)
\(a_j=1\:\:(j=x_i)\)
とします。つまり \(\bs{x}_i\) は、\(x_i\) 番目の要素だけが \(1\) で、他は全部 \(0\) の \(V\) 次元ベクトルです(1つだけ \(1\)、が "one hot" の意味です)。
例として、ウィンドーサイズを \(c=2\) とします。また分散表現の単語ベクトルの次元を \(D\) とします。この前提で、\(\bs{T}\) の中の \(t\) 番目の単語の one hotベクトルを推論するモデルが図17です。
\(\bs{T}=\{\:\cd,\:\bs{x}_{t-2},\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\bs{x}_{t+2},\:\cd\:\}\)
という単語の one hotベクトルの系列を想定したとき、 \(\bs{x}_t\) がターゲットの正解データ(=教師ラベル)であり、その他の4つがコンテクストです。
最初の MatMul (Matrix Multiply) レイヤーは、4つの one hotベクトル \(\bs{x}_i\) を入力とし、それぞれに重み行列 \(\bs{W}_{\large enc}\) をかけて、4つのベクトル \(\bs{h}_i\) を出力します(enc=encode)。つまり、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。Average レイヤーは、入力された複数ベクトルの平均をとり、一つのベクトル \(\bs{h}_t\) を出力します。この \(\bs{h}_t\) が \(\bs{x}_t\) の分散表現(= \(D\)次元ベクトル)です(というより、そうなるようにネットワークを訓練します)。
次の MatMul レイヤーで 重み \(\bs{W}_{\large dec}\) を掛け(dec=decode)、\(\mr{Softmax}\) レイヤーを通して、分散表現を \(V\) 次元の確率ベクトル \(\bs{y}_t\) に変換します。そして、教師ラベルである \(\bs{x}_t\) との間で交差エントロピー誤差を計算し、損失 \(L\) を求めます。
損失が求まれば、誤差逆伝播法で重み行列 \(\bs{W}_{\large enc}\) と \(\bs{W}_{\large dec}\) を修正します。この修正を、大量の文とそのすべてのウィンドーで行って、損失 \(L\) を最小化します。これがネットワークの訓練です。
訓練済みのネットワークでは、重み行列 \(\bs{W}_{\large enc}\:[V\times D]\) が、単語の分散表現の集積体になっています。つまり、one hot ベクトル \(\bs{x}_i\) の分散表現を \(\bs{h}_i\) とすると、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。\(\bs{x}_i\) の単語IDを \(x_i\) とすると、
\(\bs{h}_i=\bs{W}_{\large enc}\) の \(x_i\)行(\(1\)列から\(D\)列まで)
となります。
分散表現と単語の意味
「分布仮説」をもとに、ニューラル・ネットワークによる推論で得られた単語の分散表現ベクトルは、類似の意味の単語は類似のベクトルになる(ことが多い)ことが確認されています。たとえば、
year, month, day
などや、
car, automobile, vehicle
などです。ベクトルの類似は「コサイン類似度」で計測します。2つの2次元ベクトル、
\(\bs{a}=\left(\begin{array}{r}a_1&a_2\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
の場合で例示すると、
コサイン類似度\(=\dfrac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\)
で、2次元平面の2つのベクトルの角度(コサイン値)を求める式になります。この式の分子は内積(dot product)で、内積の定義式を変形したものです。この類似度を利用して「類推問題」が解けます。たとえば、
France : Paris = Japan : X
の X は何かという問題です。答えは Tokyo ですが、これを求めるには、分散表現ベクトルが類似しているという前提で、
となるはずなので、
X = France + Paris - Japan
であり、X を \(\bs{W}_{\large dec}\) と \(\mr{Softmax}\) 関数を使って確率ベクトルに変換すれば、確率が最も高い単語が Tokyo になるはずというわけです。
もちろん、分散表現ベクトルで類推問題を解くのは完璧ではありません。分散表現を作るときのウィンドーのサイズと訓練データの量にもよりますが、各種の類推問題を作って実際にテストをすると、60%~70% の正解率になるのが最大のようです。
言語モデル
分散表現ベクトルを用いて「言語モデル」を構築します。いま、一つの文を構成する単語の並び、
\(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T\)
があったとき(\(\bs{x}_1=\)[BOS]、\(\bs{x}_T=\)[EOS])、この文が存在する確率を、
\(P(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T)\)
で表します。文法として間違っている文の確率はゼロに近く、また文法としては合っていても、意味をなさない文の確率は低い。
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\( > \:P(\)[BOS],[学校],[は],[彼女],[へ],[行く],[EOS]\()\)
といった具合です。この「存在確率」は、次のような「条件付き確率」で表現できます。つまり、
\(P_1=P(\)[彼女] | [BOS]\()\)
:文頭が「彼女」である確率
\(P_2=P(\)[は] | [BOS],[彼女]\()\)
:「彼女」の次が「は」である確率
\(P_3=P(\)[学校] | [BOS],[彼女],[は]\()\)
:「彼女は」の次が「学校」である確率
\(P_4=P(\)[へ] | [BOS],[彼女],[は],[学校]\()\)
:「彼女は学校」の次が「へ」である確率
\(P_5=P(\)[行く] | [BOS],[彼女],[は],[学校],[へ]\()\)
:「彼女は学校へ」の次が「行く」である確率
\(P_6=P(\)[EOS] | [BOS],[彼女],[は],[学校],[へ],[行く]\()\)
:「彼女は学校へ行く」で文が終わる確率
とすると、
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\(=P_1\times P_2\times P_3\times P_4\times P_5\times P_6\)
となります。つまり、一般的に、
\(P(\bs{x}_{t+1}\:|\:\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_t)\)
が分かれば、言語モデルは決まります。平たく言うと、
それまでの単語の系列から、次にくる単語の確率を推測する
のが言語モデルと言えます。もちろん、次にくる可能性のある単語は1つではありません。語彙集合のすべての単語それぞれについて「次にくる」確率を予測します。
実は、Transformer や GPT、ChatGPT がやっていることは「次にくる単語の予測」であり、これを実現しているのが、「超大規模なニューラル・ネットワークで作った言語モデル」なのです。
トークン
今まで、ニューラル・ネットワークでテキストを扱うためには、テキストを単語に分解するとしてきました。しかし大規模言語モデルで実際にやっていることは、テキストを「トークン(token)」に分解し、そのトークンの分散表現ベクトルを求めてニューラル・ネットワークで処理することです。
トークンとは、基本的には「単語」ないしは「単語の一部」です。英語ですと、たとえば頻出単語は「単語=トークン」ですが、GPT-3 の例だと、トークンには、ed, ly, er, or, ing, ab, bi, co, dis, sub, pre, ible などの「単語の一部」が含まれます。GPT-3 のトークンの語彙数は約5万ですが、そのうち英語の完全な単語は約3000と言われています。通常使われる英単語は4万~5万なので、3000の単語で WebText や Wikipedia の全部を表すことは到底できません。つまり、単語の "切れ端" と単語の組み合わせ、ないしは単語の "切れ端" 同士の組み合わせでテキストを表現する必要があります。
たとえば「ディスコ音楽」などの disco という単語は、[dis] [co] と表現します。edible(食用の、食べられる、という意味)は、[ed] [ible] です。disco や edible は 3000 単語の中に入っていないようです。edible などは「基本的な英単語」と思えますが、あくまで WebText や Wikipedia に頻出するかどうかの判断によります。
また xylophone(木琴)は、[x] [yl] [ophone] です。このように、1文字がトークンになることもあります。"単語"、"単語の切れ端"、"文字" がトークンです。
BPEによるトークン化
テキストをトークンに変換することを「トークン化(tokenize)」、トークン化を行うソフトを tokenizer と言います。ここで GPT-3 のトークン化のアルゴリズムの概要をみてみます。
上の xylophone → [x] [yl] [ophone] で明快なのですが、トークン化は単語の意味とは無関係です。意味を言うなら xylo("木の" という意味の接頭語)+ phone(音)ですが、そういうこととは全く関係ありません。
GPT-2 の論文にそのアルゴリズムである BPE(Byte Pair Encoding)が書かれています(GPT-3 は GPT-2 と同じだと、GPT-3 の論文にあります)。
コンピュータで文字を表現するには文字コード(文字に数字を割り振ったもの)を使います。国際的に広く使われているのは unicode です。unicode を使うと各国語の文字が統一的に文字コードで表現できます。
unicode の数字をコンピュータでどう表すか、その表し方(=エンコーディング)には3種類ありますが、その一つが UTF-8 です。UTF-8 は1バイト(8ビット、10進数で 0~255)を単位とし、1~4バイトで1文字を表現する可変長のエンコーディングです(漢字の異字体は5バイト以上になります)。
UTF-8 でば、通常の英文に使われる英数字、特殊文字(空白 , . ? など)は1バイトで表します。一方、日本語の平仮名、カタカナ、漢字は3バイトです(一部の漢字は4バイト)。バイトは文字ではありません。あくまで文字を表現するためのコンピュータ用の数字です。
BPE ではまず、UTF-8 でエンコーディングされた大量のテキストを用意します。そして、1バイトの全パターンを256種類の基本トークンとして語彙に初期登録します。トークン ID は 1~256 とします。従って、英文における1文字の単語( I, a )や記号( , . ? ! など)は、この時点でトークンID が割り当てられたことになります。
次に、テキストの「トークンのペア」で、最も出現頻度の高いペアをみつけます。英語で最も出現頻度が高い単語は the で、トークンで表現すると [t] [h] [e] です。仮に、[t] [h] のペアがテキスト中で最も出現頻度が高いとします(説明のための仮定です)。そうすると、この2つのトークンを結合した [th] を新たなトークン(トークン ID=257)として語彙に登録します。以降、テキスト中の [t] [h] は [th] と見なします。
次に出現頻度の高いペアが [th] [e] だとすると、この2つを結合した [the] を新たなトークン(トークン ID=258)として語彙に登録します。この段階で the という単語がトークンの語彙に登録されたわけです(以上の [th] [the] のトークン ID は説明のための数字で、実際の GPT-3 のトークン ID は違います)。
以上のプロセスにおいてトークンは、「空白をまたがない」「空白で終わらない」「同一カテゴリの文字(英字、数字、特殊文字など)でしかペアを作らない」などの制約をもうけておきます。「カテゴリ」が何かは論文に書いていないので想定です。もちろんこれは、なるべく頻出単語をトークンにする工夫です。
これを「結合の最大回数」になるで繰り返します。GPT-2 / GPT-3 の場合、最大回数は 50,000 です。従って、最終的には、
256 + 50,000 + 1 = 50,257
のトークンの語彙ができあがることになります。最後の + 1 は文末の記号 [EOS] を特殊トークンとしているからです。
いったん語彙ができあがると、以降、この語彙を使ってすべてのテキストを同じアルゴズムでトークン化します。当然ですが、長いバイトのトークンからテキストに割り当てることになります。
大規模言語モデルの成立要件
GPT-3 のトークン化のロジックによると、すべての言語のすべてのテキストが 50,257個のトークンを使って、統一的に、もれなくトークン化できることになります。それはあたりまえで、1バイトのデータがすべてトークンとして登録してあるからです。テキストを UTF-8 で統一的に表せば可能なのです。
ここで、日本語がどうなるかです。日本語の unicode を UTF-8 で表すと、漢字・仮名・文章記号は3バイトです(一部の漢字は4バイト。また異字体は5バイト以上)。ということは、普通の漢字1字、仮名1字は1~3トークンで表されることになります。
実際、OpenAI 社が公開している GPT-3 の Tokenizer で試してみると、
仮名は1~2トークン
ほとんどの漢字は2~3トークン
となります。ちなみに、平仮名(清音、濁音、半濁音、計71文字種)のトークン数を調べてみると、
28 文字種:1トークン
43 文字種:2トークン
です。濁音で1トークンになるのは「が だ で」の3つだけですが、これは助詞として頻出するからでしょう。特別の場合は、仮名2文字で1トークンになるようです(スト、ーク、など)。1トークンになる漢字はごく少数のようで、たとえば「上」「田」「中」「一」「大」がそうです(他にもあると思います)。
以上をまとめると、何をトークンとするかは、
・単語
・単語の一部、ないしは文字の連なり
・文字
・バイト
がありうるわけですが、GPT-3 のトークンにはこれらが混在していて、規則性は全くないことになります。ここから何が言えるかと言うと、
ということです。もちろん、英語を扱うときのように頻出単語のトークン化ができれば、生成されるテキストのクオリティーが向上することは確かでしょう。しかし、単語単位のトークン化は必須ではない。つまり、
わけです。GPT-3(= ChatGPT の基盤となっているモデル)がそれを示しています。大規模言語モデルは、翻訳、文章要約、質問回答、おしゃべり(chat)などの多様なタスクに使えます。これらのタスクを実現する仕組みを作るには、言語学的知識は全く不要です。不要というより、言語学的知識を持ち込むことは邪魔になる。もちろん、「翻訳、文章要約、質問回答、おしゃべり」の実例や好ましい例が大量にあるのが条件です。
その GPT-3 のベースになっているのは、Google が提案した Transformer という技術です。ということは、次のようにも言えます。
これが言えるのなら、少々先走りますが、Transformer はタンパク質の機能分析にも使える(可能性がある)ことになります。タンパク質はアミノ酸が鎖状に1列に並んだもので、そのアミノ酸は20種類しかありません。
タンパク質は「20種の記号の系列」であり、それが生体内で特定の機能を果たします。多数のタンパク質のアミノ酸配列を Transformer で学習し、タンパク質の機能と照らし合わせることで、新たなタンパク質の設計に役立てるようなことができそうです。実は、こういった生化学分野での Transformer や言語モデルの利用は、今、世界でホットな研究テーマになっています。
もちろん、系列データはタンパク質の構造だけではありません。従来から AI で扱われてきた音声・音源データや、各種のセンサーから取得したデータがそうだし、分子生物学では DNA / RNA が「4文字で書かれた系列データ」と見なせます。現に米国では、DNA / RNA の塩基配列を学習した大規模言語モデルでウイルスの変異予測がされています。
Transformer は、もともと機械翻訳のために提案されたものでした。しかしそれは意外なことに、提案した Google も予想だにしなかった "奥深い" ものだった。ここに、大規模言語モデルのサイエンスとしての意義があるのです。
前回の No.364「言語の本質」の補足で紹介した新聞記事で、慶応義塾大学の今井教授は、
ChatGPT の「仕組み」(=注意機構)と「メタ学習」は、幼児が言語を学習するプロセスと類似している
と指摘していました。メタ学習とは「学習のしかたを学習する」ことですが、 ChatGPT がそれをできる理由も「注意機構(Attention mechanism)」にあります。そこで今回は、その気になる ChatGPT の仕組みをまとめます。
今まで「高校数学で理解する ・・・・・・」というタイトルの記事をいくつか書きました。
| 高校数学で理解するRSA暗号の数理 | |
| 高校数学で理解する公開鍵暗号の数理 | |
| 高校数学で理解する楕円曲線暗号の数理 | |
| 高校数学で理解する誕生日のパラドックス | |
| 高校数学で理解するレジ行列の数理 | |
| 高校数学で理解するガロア理論 |
の 13 の記事です。"高校数学で理解する" という言い方は、「高校までで習う数学だけを前提知識として説明する」という意味ですが、今回もそれに習います。もちろん、文部科学省の学習指導要領は年々変わるので、"おおよそ高校までの数学" が正しいでしょう。今回、前提とする知識は、
| 行列 | |
| ベクトル | |
| 指数関数、対数 | |
| 微分、積分 | |
| 標準偏差と正規分布(ガウス分布) |
全体の構成
全体の構成は次の4つです
1.ニューラル・ネットワーク
ニューラル・ネットワークの基礎から始まって、最も重要なポイントである「学習できる」ことを説明をします。
2.自然言語のモデル化
自然言語をニューラル・ネットワークで扱う際に必須である「単語の分散表現」を説明します。また、「言語モデル」と、ChatGPT で使われている「トークン」についても説明します。
3.Transformer
ChatGPT のベースになっている技術は、2017年に Google社が発表した Transformer です。この説明をします。
4.GPT-3 と ChatGPT
OpenAI 社は、GPT(2018)、GPT-2(2019)、GPT-3(2020)、ChatGPT(2022)と発表してきましたが、技術内容が論文で公開されているのは GPT-3 までです。また、ChatGPT の大規模言語モデルは GPT-3 と同じ仕組みであり、大幅に学習を追加して一般公開できるようにしたのが ChatGPT です。
ここでは GPT-3 の仕組み・技術内容を説明し、合わせて ChatGPT と GPT-3 の違いも説明します。
ここでは GPT-3 の仕組み・技術内容を説明し、合わせて ChatGPT と GPT-3 の違いも説明します。
なお、この記事の作成には、Google と OpenAI の論文に加えて、以下を参考にしました。
◆岡野原 大輔(プリファードネットワークス)
「大規模言語モデルは新たな知能か」
(岩波書店 2023)
◆澁谷 崇(SONY)
「系列データモデリング (RNN/LSTM/Transformer)」
第7回「Transformer」
第12回「GPT-2, GPT-3」
(YouTube 動画)
| 1.ニューラル・ネットワーク |
記号
以降で使用する記号の意味は次の通りす。
| ボールド体ではない、ノーマル書体の英大文字・小文字はスカラー値(ないしはスカラー変数)を表します。\(a,\:\:b,\:\:x,\:\:y,\:\:x_1,\:w_{12},\:\:M,\:\:N,\:\:L\) などです。 | |
| ボールド体の英大文字は行列を表します。\(\bs{W}\) などです。 \(N\) 行、\(M\) 列 の行列を \([N\times M]\) と表記します。\(\bs{W}\:[2\times3]\) は、2行3列の行列 \(\bs{W}\) で、 \(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}\\w_{21}&w_{22}&w_{23}\\\end{array}\right)\) です。 | |
| ボールド体の英小文字はベクトルを表します。ベクトルは「行ベクトル」で表現し、\(n\)次元のベクトル \(\bs{x}\) は、 \(\bs{x}=\left(\begin{array}{r}x_1&x_2&\cd&x_n\\\end{array}\right)\) です。この \(n\)次元のベクトルを、\(1\) 行 \(n\) 列の行列と同一視します。従って次元の表記は \(\bs{x}\:[1\times n]\) です。 | |
| 列ベクトルは、転置行列の記号(\({}^T\))を使って、 \(\bs{x}^T\) で表します。たとえば、3次元の列ベクトルは3次元の行ベクトルの転置を使って、 \(\bs{x}^T=\left(\begin{array}{r}x_1\\x_2\\x_3\\\end{array}\right)\:\:[3\times1]\) です。 | |
| 同一次元の2つのベクトル \(\bs{x}\:\:\bs{y}\) の内積(スカラー積、ドット積)は、 \(\bs{x}\bs{y}^T\) で表します。ドッド記号(\(\cdot\))は内積ではなく、行列の積(または実数値同士の積)です。ただし、一般的に行列の積は、\(\bs{x}\bs{y}^T\) のように積記号を省略します。 | |
| 同一次元の2つのベクトルの「対応する要素同士の積」で作ったベクトルを「要素積」(ないしはアダマール積)と呼び、\(\odot\) の記号で表します(一般的には \(\otimes\) の記号も使います)。\(n\)次元ベクトル同士の要素積は、 \(\left(\begin{array}{r}x_1&x_2&\cd&x_n\\\end{array}\right)\odot\left(\begin{array}{r}y_1&y_2&\cd&y_n\\\end{array}\right)\) \(=\left(\begin{array}{r}x_1y_1&x_2y_2&\cd&x_ny_n\\\end{array}\right)\) です。要素積は、行数・列数が同一の2つの行列にも適用します。 | |
| 指数関数、\(f(x)=e^x\) を、 \(f(x)=\mr{exp}(x)\) と表記します。 | |
| \(n\)次元ベクトルを \(\bs{x}=\{x_1\:x_2\:\cd\:x_n\}\) とし、1変数の関数 \(f(x)\) があるとき、ベクトル \(f(\bs{x})\) を、 \(f(\bs{x})=\left(\begin{array}{r}f(x_1)&f(x_2)&\cd&f(x_n)\\\end{array}\right)\) で定義します。 |
ニューラル・ネットワークの例
2層から成るシンプルなニューラル・ネットワークの例が図1です。この例では隠れ層が1つだけですが、隠れ層は何層あってもかまいません(なお、入力層を含めて、これを "3層" のニューラル・ネットワークとする定義もあります)。
|
図1:ニューラル・ネットワーク |
丸印は "ニューロン" で、各ニューロンは1つの値(活性値)をもちます。値は実数値で、32ビットの浮動小数点数が普通です。図1のニューロンの数は 3+4+3=10 個ですが、もちろんこの数は多くてもよく、実用的なネットワークでは数100万から億の単位になることがあります。
ニューロン間の矢印が "シナプス" で、一つのニューロンは、シナプスで結ばれている前の層のニューロンから値を受けとり、決められた演算をして自らの値を決めます(入力層を除く)。なお、"ニューロン" や "シナプス" は脳神経科学の用語に沿っています。
各層は、重み \(\bs{W}\)(行列)とバイアス \(\bs{b}\)(ベクトル)、活性化関数 \(f\) を持ちます。図1の場合、第1層の重みは \(\bs{W}\:\:[3\times4]\)、バイアスは \(\bs{b}\:\:[1\times4]\) で、
\(\bs{W}=\left(\begin{array}{r}w_{11}&w_{12}&w_{13}&w_{14}\\w_{21}&w_{22}&w_{23}&w_{24}\\w_{31}&w_{32}&w_{33}&w_{34}\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2&b_3&b_4\\\end{array}\right)\)
です。このとき、隠れ層(第1層)のニューロンの活性値、\(\bs{h}=\left(\begin{array}{r}h_1&h_2&h_3&h_4\\\end{array}\right)\) は、
\(h_1=f\:(\:x_1w_{11}+x_2w_{21}+x_3w_{31}+b_1\:)\)
\(h_2=f\:(\:x_1w_{12}+x_2w_{22}+x_3w_{32}+b_2\:)\)
\(h_3=f\:(\:x_1w_{13}+x_2w_{23}+x_3w_{33}+b_3\:)\)
\(h_4=f\:(\:x_1w_{14}+x_2w_{24}+x_3w_{34}+b_4\:)\)
の式で計算されます。ベクトルと行列で表示すると、
\(\bs{h}=f\:(\bs{x}\cdot\bs{W}+\bs{b})\)
になります。第2層も同様です。
このニューラル・ネットワークは、多重パーセプトロン(Multi Layer Perceptron : MLP)と呼ばれるタイプのもので、ニューラル・ネットワークの歴史の中では、古くから研究されている由緒のあるものです。
また上図の第1層、第2層は、すべてのニューロンが前層のすべてのニューロンとシナプスを持ってます。このような層を「全結合層」(Fully connected layer. FC-layer. FC層)と言います。全結合の多重パーセプトロンは Transformer や GPT で使われていて、重要な意味を持っています。
|
\(\mr{ReLU}(x)=x\:\:(x > 0)\) \(\mr{ReLU}(x)=0\:\:(x\leq0)\) |
で定義される非線形関数です(図2)。以降での表記を簡潔にするため、単位ステップ関数 \(H(x)\) を用いて \(\mr{ReLU}\) 関数を表しておきます。単位ステップ関数は、
|
\(H(x)=0\:\:(x\leq0)\)
で定義される関数で(図3)、ヘヴィサイド関数とも呼ばれます。\(H(x)\) の微分は、
\(H\,'(x)=0\:\:(x\neq0)\)
です。\(x=0\) において \(H(x)\) は不連続で、微分は定義できませんが、無理矢理、
\(H\,'(0)=0\)
と定義してしまうと、\(x\) の全域において、
\(H\,'(x)=0\)
となります。この \(H(x)\) を用いて \(\mr{ReLU}\) 関数を定義すると、
\(\mr{ReLU}(x)=H(x)x\) |
となり、微分は、
\(\dfrac{d}{dx}\mr{ReLU}(x)=H(x)\)
と表現できます。
出力層の活性化関数 \(f\,'\) は、ニューラル・ネットワークをどんな用途で使うかによって違ってきます。
ニューラル・ネットワークによる推論
ニューラル・ネットワークが扱う問題は、入力ベクトル \(\bs{x}\) をもとに出力ベクトル \(\bs{y}\) を "推論"(ないしは "推定"、"予測")する問題です。これには主に「回帰問題」と「分類問題」があります。
回帰問題で推論する \(\bs{y}\) は実数値(=連続値)です。たとえば、
・身長
・体重
・年齢
・男女の区別
・生体インピーダンス
から(\(=\bs{x}\))、
・体脂肪率
・筋肉量
・骨密度
を推定する(\(=\bs{y}\))といった例です(但し、市販の体組成計が AI を使っているわけではありません)。
一方、分類問題の例は、たとえば手書き数字を認識する問題です。この場合、多数の手書き数字の画像(をベクトルに変換した \(\bs{x}\))を「\(0\) のグループ」「\(1\) のグループ」・・・・・ というように分類していきます。このグループのことを AI では "クラス" と呼んでいます。つまり「クラス分類問題」です。
手書き数字の場合、明確に \(0\) ~ \(9\) のどれかに認識できればよいのですが、そうでない場合もある。たとえば、\(1\) なのか \(7\) なのか紛らわしい、\(0\) なのか \(6\) なのか曖昧、といったことが発生します。分類するのは、\(0\) ~ \(9\) のうちのどれかという「離散値の予測」であり、連続値とは違って、どうしても紛らわしい例が発生します。
従って、クラス分類問題(=離散値を予測する問題)では、出力ベクトル \(\bs{y}\) は確率です。手書き数字の認識では、\(\bs{y}\) は\(10\)次元の確率ベクトルで、たとえば、
| \(y_1\) | :数字が \(1\) である確率 | |
| \(y_2\) | :数字が \(2\) である確率 | |
| \(\vdots\) | ||
| \(y_9\) | :数字が \(9\) である確率 | |
| \(y_{10}\) | :数字が \(0\) である確率 |
\(0\leq y_i\leq1,\:\:\:\displaystyle\sum_{i=1}^{10}y_i=1\)
です。入力画像が \(1\) なのか \(7\) なのか紛らわしい場合、たとえば推定の例は、
\(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
です。これは、
\(1\) である確率が \(0.8\)
\(7\) である確率が \(0.2\)
を表します。クラス分類問題は「離散値を推論する問題」、すなわち「確率を推定する問題」であると言えます。
回帰問題の出力層の活性化関数は、恒等関数(=何もしない)とするのが普通です。一方、クラス分類問題の出力層の活性化関数は、出力 \(\bs{y}\) が確率として解釈できるような関数を選びます。それが \(\mr{Softmax}\) 関数です。
\(\mr{Softmax}\) 関数
\(\mr{Softmax}\) 関数によって、出力 \(\bs{y}\) が確率と解釈できるようになります。ベクトル \(\bs{x}\) を \(\mr{Softmax}\) 関数によって確率ベクトル \(\bs{y}\) に変換する式は、次のように定義できます。なお、ここでの \(\bs{x}\) は入力層の \(\bs{x}\) ではなく、一般的なベクトルを表します。
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(n\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{n}y_i=1\)
ここで使われている指数関数は、すぐに巨大な数になります。たとえば \(\mr{exp}(100)\) は\(10\)進で\(40\)桁以上の数で、\(32\)ビット浮動小数点の最大値(\(10\)進で\(40\)桁弱)を越えてしまいます。従って、\(\mr{Softmax}\) 関数の計算には工夫が必要で、それには \(\mr{Softmax}\) 関数の性質を利用します。
\(C\) を任意の実数値とし、\(n\)次元ベクトル \(\bs{z}\) を
\(z_i=x_i+C\)
と定義します。そして、
\(\bs{y}\,'=\mr{Softmax}(\bs{z})\)
と置くと、
\(\begin{eqnarray}
&&\:\:y_i\,'&=\dfrac{\mr{exp}(z_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(z_i)}=\dfrac{\mr{exp}(x_i+C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i+C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)\cdot\mr{exp}(C)}\\
&&&=\dfrac{\mr{exp}(x_i)\cdot\mr{exp}(C)}{\mr{exp}(C)\cdot\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}\\
&&&=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{n}\mr{exp}(x_i)}=y_i\\
\end{eqnarray}\)
となります。つまり \(x_i\:\:(1\leq i\leq n)\) の全部に定数 \(C\) を足しても、\(\mr{Softmax}\) 関数は変わりません。そこで、
\(C=-\mr{max}(x_1,\:x_2,\:\cd\:,x_n)\)
と置いて、
\(x_i\:\longleftarrow\:x_i+C\:\:(1\leq i\leq n)\)
と修正すると、\(x_i\) の最大値は \(0\) になります。従って、
\(0 < \mr{exp}(x_i)\leq1\)
の範囲で \(\mr{Softmax}\) 関数が計算可能になります。
大規模言語モデルと確率
クラス分類問題の出力ベクトル \(\bs{y}\) は確率でしたが、実は Transformer や GPT が実現している「大規模言語モデル」も "確率を推定するニューラル・ネットワーク" です。たとえば、
[今日] [は] [雨] [なの] [で]
というテキストに続く単語を推定します。仮に、日本語の日常用語の語彙数を5万語とすると、5万の単語すべてについて上のテキストに続く単語となる確率を、実例をもとに推定します。当然、「雨の日の行動」とか「雨の日の情景」、「雨の日の心理状態」、「雨の日に起こりうること」を描写・説明する単語の確率が高くなるわけです。たとえば名詞だけをとると、[家] [ビデオ] [映画] [傘] [犬] [洗濯] [祭] [運動会] などの確率が高く、[ニンジン] [牛] [鉛筆] などの確率は(雨の日とは関係があるとは思えないので)低いといった具合です(あくまで想定です)。
「大規模言語モデル」の重要な応用例(=タスク)である機械翻訳も同じです。日本語 → 英語の翻訳を例にとると、
[今日] [は] [晴れ] [です] [。] [BOS]
に続く英単語を推定します([BOS] は文の開始を示す特殊単語)。確率の高い単語から [it] を選んだとすると、次には、
[今日] [は] [晴れ] [です] [。] [BOS] [it]
に続く単語を推定します([is] になるはず)。こうやって進むのが機械翻訳です。
Transformer や GPT をごくごくシンプルに言えば、入力ベクトル \(\bs{x}\) はテキスト列、出力ベクトル \(\bs{y}\) は次に続く単語を示す確率ベクトル(次元は語彙数)です。
この記事は、Transformer、GPT、ChatGPT などの大規模言語モデルを説明するのが目的です。従って以降では、出力ベクトル \(\bs{y}\) は確率ベクトルであることを前提とします。
確率を推定するニューラル・ネットワーク
図1において、第1層(隠れ層)の活性化関数を \(\mr{ReLU}\)、第2層(出力層)の活性化関数を \(\mr{Softmax}\) とすると、図4になります。
|
図4:ニューラル・ネットワーク (出力層は確率ベクトル) |
図4の計算は、以下に示すような4段階の計算処理で表すことができます。
第1層
\(\bs{h}\,'=\bs{x}\cdot\bs{W}+\bs{b}\)
\(\bs{h}=\mr{ReLU}(\bs{h}\,')\)
第2層
\(\bs{y}\,'=\bs{h}\cdot\bs{W}\,'+\bs{b}\,'\)
\(\bs{y}=\mr{Softmax}(\bs{y}\,')\)
この4つの計算処理を「計算レイヤー」、略して「レイヤー」と呼び、図5のグラフで表現することにします。
|
図5:クラス分類問題のレイヤー構成(推論時) |
レイヤー(layer)は日本語にすると「層」で、第1層や隠れ層の「層」と紛らわしいのですが、「レイヤー」と書いたときは "ある一定の計算処理" を示します。後ほど説明する Transformer や GPT は、図4のような単純な「層」では表現できない複雑な計算処理があります。従って "ある一定の計算処理 = レイヤー" とした方が、すべての場合を共通に表現できて都合が良いのです。
レイヤーの四角に向かう矢印は計算処理への入力を示し、四角から出る矢印は計算処理からの出力(計算結果)を示します。「レイヤーは一つの関数」と考えてもOKです。
図5の「Linear レイヤー」は、「Affine(アフィン)レイヤー」と呼ばれることが多いのですが、Transformer の論文で Linear があるので、そちらを採用します。
図5のネットワークがどうやって「学習可能なのか」を次に説明します。この「学習できる」ということが、ニューラル・ネットワークが成り立つ根幹です。
ニューラル・ネットワークの学習
重みとバイアスの初期値
まず、重み(\(\bs{W},\:\bs{W}\,'\))の初期値を乱数で与えます。この乱数は、前の層のニューロンの数を \(n\) とすると
| 平均 | \(=0\) | |
| 標準偏差 | \(=\sqrt{\dfrac{1}{n}}\) |
の正規分布の乱数とするのが普通です。\(n=10,000\) とすると、標準偏差は \(0.01\) なので、
\(-\:0.01\) ~ \(0.01\)
の間にデータの多く(約 \(2/3\))が集まる乱数です。但し、\(\mr{ReLU}\) を活性化関数とする層(図4では第1層)の重みは、
| 平均 | \(=0\) | |
| 標準偏差 | \(=\sqrt{\dfrac{2}{n}}\) |
の乱数とします。なお、バイアスの初期値は \(0\) とします。こういった初期値の与え方は、学習をスムーズに進めるためです。
損失と損失関数
初期値が決まったところで、訓練データの一つを、
\(\bs{x}\):入力データ
\(\bs{t}\):確率の正解データ
とします。この正解データのことを「教師ラベル」と呼びます。そして、ニューラル・ネットワークによる予測の確率 \(\bs{y}\) と、正解の確率である \(\bs{t}\) との差異を計算します。この差異を「損失(\(Loss\))」といい、\(L\) で表します。\(L\) は正のスカラー値です。
\(\bs{y}\) と \(\bs{t}\) から \(L\) を求めるのが「損失関数(Loss Function)」です。確率を予測する場合の損失関数は「交差エントロピー誤差(Cross Entropy Error : CEE)」とするのが普通で、次の式で表されます。
\(L=-\displaystyle\sum_{i=1}^{n}t_i\cdot\mr{log}\:y_i\) |
たとえば、先ほどの手書き数字の認識の「\(1\) または \(7\) という予測」を例にとって、その正解が \(1\) だとすると、
予測 \(\bs{y}=\left(\begin{array}{r}0.8&0&0&0&0&0&0.2&0&0&0\\\end{array}\right)\)
正解 \(\bs{t}=\left(\begin{array}{r}1&0&0&0&0&0&0&0&0\\\end{array}\right)\) = 教師ラベル
です。なお、\(\mr{Softmax}\)関数の出力は \(0\) にはならないので、上の \(\bs{y}\) で \(0\) と書いた要素は、実際には微小値です。すると、
\(L=-\mr{log}\:0.8\fallingdotseq0.223\)
となります。損失関数を含めると、レイヤー構成は図6のようになります。
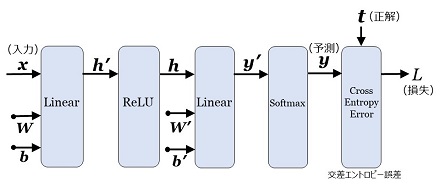
|
図6:クラス分類問題のレイヤー構成(学習時) |
この図の重みとバイアスを少しだけ調整して、\(L\) を少しだけ \(0\) に近づけます。この調整を多数の学習データ(= \(\bs{x}\:\:\bs{t}\) のペア)で繰り返して、\(L\) を次第に \(0\) に近づけていくのが学習です。
勾配降下法
重みの調整には「勾配降下法(Gradient descent method)」を使います。図6の場合、損失 \(L\) は、ある関数 \(f\) を用いて、
\(L=f(\bs{x},\:\bs{W},\:\bs{b},\:\bs{W}\,',\:\bs{b}\,',\:\bs{t})\)
と表現できます。ここで、\(\bs{W}\) の一つの要素、\(w_{11}\) を例にとると、
\(w_{11}\) を微小に増減させた場合、\(L\) はどのように増減するか、そのの \(w_{11}\) に対する変化の割合
を計算します。これはいわゆる微分ですが、多変数関数の微分なので、数学的には偏微分であり、
\(\dfrac{\partial L}{\partial w_{11}}\)
です。つまり、\(w_{11}\) 以外の変数をすべて固定しての(すべて定数とした上での)、\(w_{11}\) による微分です。
具体的な入力 \(\bs{x}\) のときの \(\dfrac{\partial L}{\partial w_{11}}\) が求まったとします。もし仮に、\(\dfrac{\partial L}{\partial w_{11}}\) が正の値だとしたら、\(w_{11}\) を少しだけ減らせば、\(L\) は少しだけ \(0\) に近づきます。もし \(\dfrac{\partial L}{\partial w_{11}}\) が負だとしたら、\(w_{11}\) を少しだけ増やせば、\(L\) は少しだけ \(0\) に近づきます。つまり、
更新式:\(w_{11}\:\longleftarrow\:w_{11}-\eta\cdot\dfrac{\partial L}{\partial w_{11}}\)
として重みを更新すればよいわけです。\(\eta\) は「少しだけ」を表す値で「学習率」といい、\(0.01\) とか \(0.001\) とかの値をあらかじめ決めておきます。この決め方は、学習の効率に大いに影響します。こういった更新を、すべての重みとバイアスに対して行います。
"学習で調整される値" を総称して「パラメータ」と言います。図6のパラメータは重みとバイアスですが、実用的なニューラル・ネットワークでは、それ以外にも更新されるパラメータがあります。
ちなみに、OpenAI 社の GPT\(-3\) のパラメータの総数は \(1750\)億個で、学習率は \(0.6\times10^{-4}\) です。
\(L\) の偏微分値をベクトルや行列単位でまとめたものを、次のように表記します。2次元のベクトル \(\bs{b}\) と、2行2列の行列 \(\bs{W}\) で例示すると、
\(\dfrac{\partial L}{\partial\bs{b}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial b_1}&\dfrac{\partial L}{\partial b_2}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{W}}=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\)
です。これを「勾配(gradient)」と言います。勾配を求めることでパラメータを少しづつ更新し、損失を少しづつ小さくしていく(=降下させる)のが勾配降下法です。
ミニバッチ勾配降下法
学習は次のように進みます。まず、すべての訓練データ(たとえば
数万件)から、数\(10\)~数\(100\)件(たとえば\(256\)件)の訓練データをランダムに選びます。この一群のデータを「ミニバッチ」と呼びます。ミニバッチの各訓練データによる確率の推定から損失を計算し、そこからすべてのパラメータの勾配と求め、その勾配ごとに "ミニバッチの平均値" をとります。その平均値に基づき、更新式に従って各パラメータを更新します。
ミニバッチによる更新が終わると、別のミニバッチをランダムに選び、更新を繰り返します。こうすると、損失は次第に減少していきますが、そのうち "頭打ち" になります。そこで更新を止めます。
このようなパラメータ更新のやり方を「ミニバッチ勾配降下法」と言います。一つの訓練データだけで更新しないのは、たまたまその訓練データが「外れデータ」(全体の傾向とは異質なデータ)だと、学習の進行に支障が出てくるからです。
訓練データをランダムに選択する方法を「確率的勾配降下法(Stochastic gradient method - SGD)」と言いますが、ミニバッチ勾配降下法は、その確率的勾配降下法の一種です。
誤差逆伝播法
ここで問題になるのは、すべてのパラメータの勾配をどうやって求めるかです。それに使われるのが「誤差逆伝播法(Back propagation)」です。その原理を、Linear レイヤーから説明します。
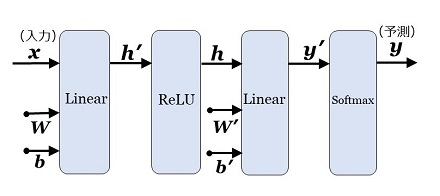
(1) Linear
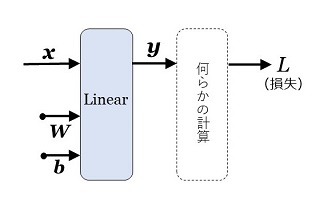
|
図7:linear レイヤー |
入力 \(\bs{x}\) \([1\times N]\) \(\bs{W}\) \([N\times M]\) \(\bs{b}\) \([1\times M]\) 出力 \(\bs{y}\) \([1\times M]\) |
図7で示すように、Linear レイヤーがあり、そのあとに何らかの計算処理が続いて、最終的に損失 \(L\) が求まったとします。\(\bs{x}\:\:\bs{y}\) はニューラル・ネットワークへの入力と出力ではなく、Linear レイヤーへの入力と出力の意味です。ここで、
\(\bs{y}\) の勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が求まれば、合成関数の微分を使って、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配が求まる
と言えます。これが誤差逆伝播法の原理です。このことを、2次元ベクトル(\(\bs{x},\:\:\bs{b},\:\:\bs{y}\))、2行2列の配列(\(\bs{W}\))で例示します(\(N=2,\:M=2\) の場合)。
【Linear の計算式】
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+b_1\)
\(y_2=x_1w_{12}+x_2w_{22}+b_2\)
\(x_1\) が変化すると \(y_1,\:y_2\) が変化し、それが損失 \(L\) に影響することに注意して、\(\bs{x},\:\:\bs{W},\:\:\bs{b}\) の勾配を計算します。
【\(\bs{\bs{x}}\) の勾配】
| \(\dfrac{\partial L}{\partial x_1}\) | \(=\dfrac{\partial y_1}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_2}\) | |
| \(=\dfrac{\partial L}{\partial y_1}w_{11}+\dfrac{\partial L}{\partial y_2}w_{12}\) | ||
| \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}\\w_{12}\\\end{array}\right)\) |
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)\)
です。これをまとめると、
\(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\:\:\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\)
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T\)
となり、\(\bs{x}\) の勾配が求まります。
【\(\bs{\bs{W}}\) の勾配】
\(\dfrac{\partial L}{\partial w_{11}}=\dfrac{\partial y_1}{\partial w_{11}}\dfrac{\partial y_1}{\partial w_{11}}=x_1\dfrac{\partial y_1}{\partial w_{11}}\)
\(\dfrac{\partial L}{\partial w_{12}}=\dfrac{\partial y_2}{\partial w_{12}}\dfrac{\partial y_2}{\partial w_{12}}=x_1\dfrac{\partial y_2}{\partial w_{12}}\)
\(\dfrac{\partial L}{\partial w_{21}}=\dfrac{\partial y_1}{\partial w_{21}}\dfrac{\partial y_1}{\partial w_{21}}=x_2\dfrac{\partial y_1}{\partial w_{21}}\)
\(\dfrac{\partial L}{\partial w_{22}}=\dfrac{\partial y_2}{\partial w_{22}}\dfrac{\partial y_2}{\partial w_{22}}=x_2\dfrac{\partial y_2}{\partial w_{22}}\)
これらをまとめると、
| \(\dfrac{\partial L}{\partial\bs{W}}\) | \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial w_{11}}&\dfrac{\partial L}{\partial w_{12}}\\\dfrac{\partial L}{\partial w_{21}}&\dfrac{\partial L}{\partial w_{22}}\\\end{array}\right)\) | |
| \(=\left(\begin{array}{r}x_1\dfrac{\partial L}{\partial y_1}&x_1\dfrac{\partial L}{\partial y_2}\\x_2\dfrac{\partial L}{\partial y_1}&x_2\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) | ||
| \(=\left(\begin{array}{r}x_1\\x_2\\\end{array}\right)\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) | ||
| \(=\bs{x}^T\dfrac{\partial L}{\partial\bs{y}}\) |
となります。
【\(\bs{\bs{b}}\) の勾配】
| \(\dfrac{\partial L}{\partial b_1}\) | \(=\dfrac{\partial L}{\partial y_1}\) | |
| \(\dfrac{\partial L}{\partial b_2}\) | \(=\dfrac{\partial L}{\partial y_2}\) |
| \(\dfrac{\partial L}{\partial\bs{b}}\) | \(=\dfrac{\partial L}{\partial\bs{y}}\) |
以上の計算で求まった勾配をまとめて図示すると、図8になります。黒字(入力・出力とパラメータ)の下の赤字がパラメータの勾配で、右から左への矢印は、「レイヤーの出力の勾配が求まれば、レイヤーの入力の勾配が求まる」こと示します(= 逆伝播)。上での計算は2次元ベクトルと2行2列の配列で例示しましたが、図8のようなベクトル・配列で表示すると、\([1\times N]\) のベクトルと \([N\times M]\) の行列で成り立つことが確認できます。
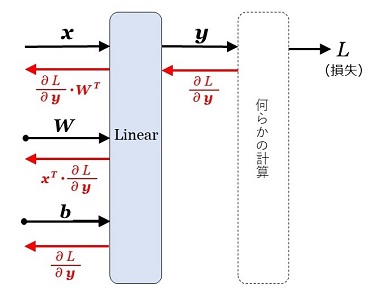
|
図8:linear の誤差逆伝播 |
出力側の勾配が求まれば、そこから入力側の勾配はすべて求まる。これが誤差逆伝播の原理で、合成関数の微分のシンプルな応用である。 |
(2) ReLU
\(\mr{ReLU}\) 関数は、
\(\mr{ReLU}(x_i)=x_i\:\:(x_i > 0)\)
\(\mr{ReLU}(x_i)=0\:\:\:(x_i\leq0)\)
であり、ベクトルの表現では、単位ステップ関数、
\(H(x)=1\:\:\:(x > 0)\)
\(H(x)=0\:\:\:(x\leq0)\)
と要素積 \(\odot\) を使って、
\(\mr{ReLU}(\bs{x})=H(\bs{x})\odot\bs{x}\)
と定義できます。従って、勾配は、
| \(\dfrac{\partial L}{\partial x_i}=\dfrac{\partial L}{\partial y_i}\) | \((x_i > 0)\) | |
| \(\dfrac{\partial L}{\partial x_i}=0\) | \((x_i\leq0)\) |
\(\dfrac{\partial L}{\partial\bs{x}}=H(\bs{x})\odot\dfrac{\partial L}{\partial\bs{y}}\)
です。
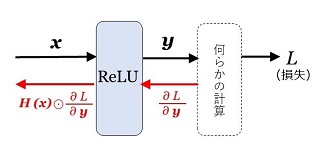
|
図9:ReLU の誤差逆伝播 |
(3) Softmax
\(\mr{Softmax}\) 関数の定義は、
\(\bs{y}=\mr{Softmax}(\bs{x})\)
(\(\bs{x}\:\:\bs{y}\) は \(N\)次元ベクトル)
\(y_i=\dfrac{\mr{exp}(x_i)}{\displaystyle\sum_{i=1}^{N}\mr{exp}(x_i)}\)
\(0 < y_i < 1,\:\:\:\displaystyle\sum_{i=1}^{N}y_i=1\)
です。勾配の計算を \(N=3\) の場合で例示します。
| \(S\) | \(=\mr{exp}(x_1)+\mr{exp}(x_2)+\mr{exp}(x_3)\) | |
| \(y_1\) | \(=\dfrac{\mr{exp}(x_1)}{S}\) | |
| \(y_2\) | \(=\dfrac{\mr{exp}(x_2)}{S}\) | |
| \(y_3\) | \(=\dfrac{\mr{exp}(x_3)}{S}\) |
\(\dfrac{\partial L}{\partial x_1}=\dfrac{\partial y_1}{\partial x_1}\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\dfrac{\partial L}{\partial y_2}+\dfrac{\partial y_3}{\partial x_1}\dfrac{\partial L}{\partial y_3}\)
| \(\dfrac{\partial y_1}{\partial x_1}\) | \(=\dfrac{\mr{exp}(x_1)}{S}-\dfrac{\mr{exp}(x_1)}{S^2}\mr{exp}(x_1)\) | |
| \(=y_1-y_1^2\) | ||
| \(=y_1(1-y_1)\) |
| \(\dfrac{\partial y_2}{\partial x_1}\) | \(=-\dfrac{\mr{exp}(x_2)}{S^2}\mr{exp}(x_1)\) | |
| \(=-y_1y_2\) |
| \(\dfrac{\partial y_3}{\partial x_1}\) | \(=-\dfrac{\mr{exp}(x_3)}{S^2}\mr{exp}(x_1)\) | |
| \(=-y_1y_3\) |
\(\dfrac{\partial L}{\partial x_1}=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\)
\(\dfrac{\partial L}{\partial x_2}=y_2(1-y_2)\dfrac{\partial L}{\partial y_2}-y_2y_3\dfrac{\partial L}{\partial y_3}-y_2y_1\dfrac{\partial L}{\partial y_1}\)
\(\dfrac{\partial L}{\partial x_3}=y_3(1-y_3)\dfrac{\partial L}{\partial y_3}-y_3y_1\dfrac{\partial L}{\partial y_1}-y_3y_2\dfrac{\partial L}{\partial y_2}\)
(4) Cross Entropy Error - CEE
交差エントロピー誤差の定義は、
入力 \(\bs{y}\) \((1\times N)\)
入力 \(\bs{t}\) \((1\times N)\) 教師ラベル(正解データ)
出力 \(L\:(Loss)\)
とすると、
\(L=-\displaystyle\sum_{i=1}^{N}(t_i\mr{log}y_i)\)
で定義されます。従って、
\(\dfrac{\partial L}{\partial y_i}=-\dfrac{t_i}{y_i}\)
であり、\(N=3\) の場合を書くと、
\(\dfrac{\partial L}{\partial y_1}=-\dfrac{t_1}{y_1}\)
\(\dfrac{\partial L}{\partial y_2}=-\dfrac{t_2}{y_2}\)
\(\dfrac{\partial L}{\partial y_3}=-\dfrac{t_2}{y_3}\)
です。
(5) Softmax + CEE
\(\mr{Softmax}\) レイヤーの直後に交差エントロピー誤差のレイヤーを配置した場合を考えます。(3) と (4) の計算を合体させると、次のように計算できます。
| \(\dfrac{\partial L}{\partial x_1}\) | \(=y_1(1-y_1)\dfrac{\partial L}{\partial y_1}-y_1y_2\dfrac{\partial L}{\partial y_2}-y_1y_3\dfrac{\partial L}{\partial y_3}\) | |
| \(=-y_1(1-y_1)\dfrac{t_1}{y_1}+y_1y_2\dfrac{t_2}{y_2}+y_1y_3\dfrac{t_3}{y_3}\) | ||
| \(=-t_1+t_1y_1+y_1t_2+y_1t_3\) | ||
| \(=-t_1+t_1y_1+y_1(t_2+t_3)\) | ||
| \(=-t_1+t_1y_1+y_1(1-t_1)\) | ||
| \(=y_1-t_1\) |
計算の過程で、\(\bs{t}\) が確率ベクトルであることから、\(t_1+t_2+t_3=1\) を使いました。この計算は \(x_2,\:\:x_3\) についても全く同様にできます。それを含めてまとめると、
\(\dfrac{\partial L}{\partial x_1}=y_1-t_1\)
\(\dfrac{\partial L}{\partial x_2}=y_2-t_2\)
\(\dfrac{\partial L}{\partial x_3}=y_3-t_3\)
となります。この結果、勾配は、
\(\dfrac{\partial L}{\partial\bs{x}}=\bs{y}-\bs{t}\)
という、大変シンプルな形になりました。これは任意の次元のベクトルで成り立ちます。実は、このようなシンプルな形になるように、\(\mr{Softmax}\) と 交差エントロピー誤差が設計されています。図示すると次の通りです。
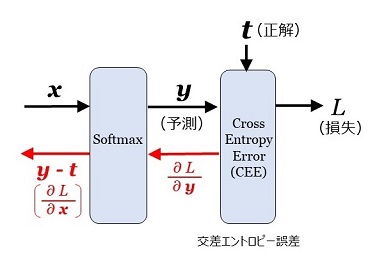
|
図10:Softmax + CEE の逆伝播 |
\(\mr{Softmax}\) 関数の後ろに交差エントロピー誤差を重ねると、\(\bs{x}\) の勾配は \(\bs{y}\) と \(\bs{t}\)(教師ラベル)から直接に求まる。 |
ニューラル・ネットワークの誤差逆伝播
以上で「確率を推定するニューラル・ネットワーク」を構成する各レイヤーの誤差逆伝播が計算できました。これらをまとめると、次の図11になります。
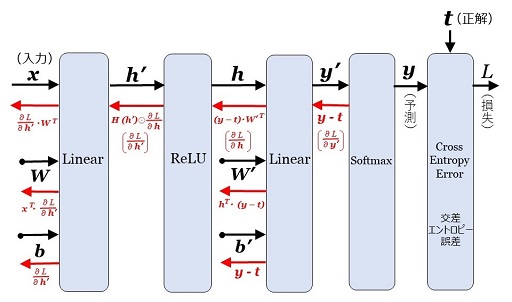
|
図11:クラス分類問題の誤差逆伝播 |
ちなみに、第1層の重み \(\bs{W}\) の勾配は図11から陽に計算すると、次のようになります。
\(\dfrac{\partial L}{\partial\bs{W}}=\bs{x}^T(H(\bs{x}\bs{W}+\bs{b})\odot((\bs{y}-\bs{t})\bs{W}\,'))\)
このネットワークは隠れ層が1つだけというシンプルなものですが、今までの計算で分かるように、層数が何百層に増えたとしても、逆伝播を多段に重ねることで、誤差逆伝播法が成立します。
また、図11 で使っているレイヤーは、Linear、\(\mr{ReLU}\)、\(\mr{Softmax}\)、Cross Entropy Error ですが、これらを関数と見なしたとき、誤差逆伝播で使った数学的な前提は「関数がパラメータで微分可能」ということだけです。つまり、レイヤーの関数が微分可能である限り、誤差逆伝播法は有効です。
実は、実用的なニューラル・ネットワークで誤差逆伝播法をうまく機能させるためには、数々の工夫が必要です。また、一般に訓練データの数は膨大なので、学習速度を上げる工夫も必要です(以降でその一部を説明します)。上で述べた「初期値の選択」や「学習率」はその工夫の一つです。そういったことはありますが、ネットワークがいかに巨大になろうとも(大規模言語モデルはその巨大な典型です)、誤差逆伝播法は可能なことが分かっています。
以上が、「ニューラル・ネットワークが学習可能である」ということの原理です。
\(\mr{GELU}\)
最近の大規模言語モデル(GPT など)では、活性化関数 \(\mr{ReLU}\) の代わりに \(\mr{GELU}\) \((\)Gaussian Error Linear Unit:ガウス誤差線形ユニット\()\) が使われます。その方が、学習が効率的に進むことが分かったからです。
|
\(\mr{ReLU}(x)=H(x)x\)
でしたが、\(\mr{GELU}\) は、
\(\mr{GELU}(x)=\Phi(x)x\)
で定義されます。\(\Phi(x)\) は標準正規分布(平均 \(0\)、標準偏差 \(1\))の累積分布関数です。標準正規分布の確率密度を \(f(x)\) とすると、
\(f(x)=\dfrac{1}{\sqrt{2\pi}}\mr{exp}\left(-\dfrac{x^2}{2}\right)\)
です(図12)。つまり \(x\) ~ \(x+dx\) である事象が発生する確率が \(f(x)dx\) です。また \(-\infty\) ~ \(\infty\) の範囲で積分すると \(1\) で、原点を中心に左右対称です。
|
\(\Phi(x)=\displaystyle\int_{-\infty}^{x}f(t)dt\)
です(図13)。これは正規分布に従うデータ値が \(x\) 以下になる確率です。これはガウスの誤差関数(Gaussian error function)\(\mr{Erf}\) を用いて表現できます。\(\Phi(0)=0.5\) となることを使って計算すると、
\(\begin{eqnarray}
&&\:\:\Phi(x)&=\displaystyle\int_{-\infty}^{x}f(t)dt\\
&&&=\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{x}\mr{exp}\left(-\dfrac{t^2}{2}\right)dt\\
\end{eqnarray}\)
\(t\:\rightarrow\:\sqrt{2}u\) の変数変換をすると、
\(\begin{eqnarray}
&&\:\:\phantom{\Phi(x)}&=\dfrac{1}{2}+\dfrac{1}{\sqrt{2\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)\sqrt{2}du\\
&&&=\dfrac{1}{2}+\dfrac{1}{\sqrt{\pi}}\displaystyle\int_{0}^{\tiny\dfrac{x}{\sqrt{2}}}\mr{exp}(-u^2)du\\
&&&=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\\
\end{eqnarray}\)
となります。ガウスの誤差関数、\(\mr{Erf}()\) の定義は
\(\mr{Erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_{0}^{x}\mr{exp}(-u^2)du\)
です。従って、
\(\Phi(x)=\dfrac{1}{2}\left(1+\mr{Erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)\)
|
\(\mr{GELU}\) は \(\mr{ReLU}\) と良く似ていますが、すべての点で微分可能であり、\(\mr{ReLU}\) のように微係数がジャンプするところがありません。このことが、大規模言語モデルの効率的な学習に役だっていると考えられます。
残差結合
Linear レイヤーを例にとります。入力を \(\bs{x}\)、出力を \(\bs{y}\) とし、入力と出力のベクトルの次元は同一とします。重みを \(\bs{W}\) とし、バイアス \(\bs{b}\) は省略します。通常の Linear レイヤーは、
\(\bs{y}=\bs{x}\bs{W}\)
ですが、
\(\bs{y}=\bs{x}\bs{W}+\bs{x}\)
とするのが、「残差結合(residual connection)」をもつ Linear レイヤーです。なお「残差接続」とも言います。また「スキップ接続(skip connection)」も同じ意味です。
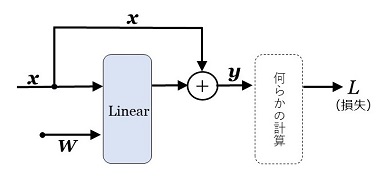
|
図15:残差結合 |
誤差逆伝播を計算すると、\(\bs{x}\) の勾配は次のようになります。2次元ベクトルの場合で例示します。
\(\left(\begin{array}{r}y_1&y_2\\\end{array}\right)=\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\cdot\left(\begin{array}{r}w_{11}&w_{12}\\w_{21}&w_{22}\\\end{array}\right)+\left(\begin{array}{r}x_1&x_2\\\end{array}\right)\)
\(y_1=x_1w_{11}+x_2w_{21}+x_1\)
\(y_2=x_1w_{12}+x_2w_{22}+x_2\)
| \(\dfrac{\partial L}{\partial x_1}\) | \(=\dfrac{\partial y_1}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_1}+\dfrac{\partial y_2}{\partial x_1}\cdot\dfrac{\partial L}{\partial y_2}\) | |
| \(=\dfrac{\partial L}{\partial y_1}w_{11}+\dfrac{\partial L}{\partial y_2}w_{12}+\dfrac{\partial L}{\partial y_1}\) | ||
| \(=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}\\w_{12}\\\end{array}\right)+\dfrac{\partial L}{\partial y_1}\) |
同様にして、
\(\dfrac{\partial L}{\partial x_2}=\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{21}\\w_{22}\\\end{array}\right)+\dfrac{\partial L}{\partial y_2}\)
従って、
| \(\left(\begin{array}{r}\dfrac{\partial L}{\partial x_1}&\dfrac{\partial L}{\partial x_2}\\\end{array}\right)=\) | \(\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\left(\begin{array}{r}w_{11}&w_{21}\\w_{12}&w_{22}\\\end{array}\right)\) | |
| \(+\:\left(\begin{array}{r}\dfrac{\partial L}{\partial y_1}&\dfrac{\partial L}{\partial y_2}\\\end{array}\right)\) |
\(\dfrac{\partial L}{\partial\bs{x}}=\dfrac{\partial L}{\partial\bs{y}}\cdot\bs{W}^T+\dfrac{\partial L}{\partial\bs{y}}\)
です。つまり、勾配 \(\dfrac{\partial L}{\partial\bs{y}}\) が、逆伝播でそのまま \(\dfrac{\partial L}{\partial\bs{x}}\) に伝わります(図\(16\))。
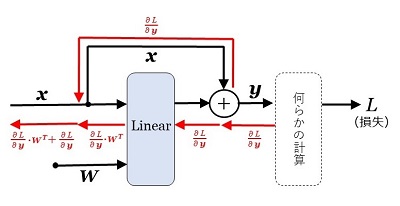
|
図16:残差結合の誤差逆伝播 |
一般にニューラル・ネットワークの学習を続けると、重みがゼロに近づき、その結果 \(\dfrac{\partial L}{\partial\bs{x}}\) が \(0\) に近い小さな値となることがあります。\(\dfrac{\partial L}{\partial\bs{x}}\) は、その一つ前への逆伝播の入力となるので、多層のニューラル・ネットワークでこれが重なると、前の方の層の勾配が極小になり、重みが更新できないという事態になります。これが「勾配消失」で、ニューラル・ネットワークの学習が困難になります。
残差結合を用いると、この問題を解決できます。Transformer では残差結合が使われています。
正規化
Transformer で使われているもう一つのレイヤーが「レイヤー正規化(Layer Normalization)」です。これは、ベクトル \(\bs{x}\:[1\times N]\) の要素を、平均 \(0\)、標準偏差 \(1\) のベクトル \(\bs{y}\:[1\times N]\) の要素に置き換えるものです。
\(\bs{y}=\mr{LayerNormalization}(\bs{x})\)
| \(x_i\) の平均 | : \(\mu\) | |
| \(x_i\) の標準偏差 | : \(\sg\) |
\(\mu=\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}x_i\)
\(\sg=\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\mu)^2}\)
とおくと、
\(y_i=\dfrac{1}{\sg}(x_i-\mu)\)
となります。実際にニューラル・ネットワークで使われるときには、さらにベクトルの要素ごとに線形変換をして、
\(y_i\:\longleftarrow\:g_iy_i+b_i\)
とします。ベクトルで表現すると、
\(\bs{y}=\dfrac{1}{\sg}\bs{g}\odot(\bs{x}-\mu)+\bs{b}\)
です。この \(\bs{g}\) と \(\bs{b}\) は学習可能なパラメータです。つまり、ニューラル・ネットワークの訓練のときに学習をして、最適値を決めます。もちろん、レイヤー正規化の式は微分可能なので、逆伝播計算が(少々複雑な式になりますが)可能です。
レイヤー正規化は、ニューラル・ネットワークを安定化させ、学習の効率化に役立ちます。その理由ですが、中間層の活性化関数で一般的な \(\mr{ReLU}\) 関数は、\(x=0\) の付近で非線型関数であり、それ以外では線型です。ニューラル・ネットワークは全体としては非線型関数で、そこにこそ意義があるのですが、その非線型性を生み出しているのは、\(x=0\) 付近の \(\mr{ReLU}\) 関数です。
従って、レイヤーの値を「ゼロ付近に集める」と、ニューラル・ネットワークの非線型性を強めることができ、これが学習の効率化につながります。その「ゼロ付近に集める」のがレイヤー正規化です。
以上の、
・\(\mr{ReLU}\) 関数(または \(\mr{GELU}\) 関数)
・残差結合
・正規化
は、大規模ニューラル・ネットワークを安定的に学習可能にするための必須技術であり、Transformer や GPT でも使われています。
| 2.自然言語のモデル化 |
単語への分解
自然言語で書かれたテキストをコンピュータで扱うとき、まずテキストを単語の系列に分解しなければなりません。系列とは「並び順に意味のある、同質の要素の集合」です。単語への分解は、単語の区切りを明示する英語(や、その他の欧米語)では容易です。文末を表すピリオドや、その他の記号も1つの単語と数えます。
日本語は単語の区切りがないので、形態素解析ソフトで単語に分解します。句読点、「、」などの記号も、それぞれ1単語と数えます。日本語の形態素解析ソフトは各種ありますが、オープンソースの MeCab が有名です。
大規模言語モデルは、世界中から集めた Webのテキスト(以下、WebText と言います)や Wikipedia、電子ブックなどを訓練データとして学習しますが、そこに出てくる単語を集めて「語彙の集合」を作ります。この集合のサイズを \(V\) とすると(たとえば、5万とか10万とかの値)、単語に \(1\)~\(V\) のユニークな番号を振ることができます。この番号を「単語ID」と呼びます。
なお、大規模言語モデルでは内部処理用として「特殊単語」も用います。以降の説明で使うのは、
[BOS] :文の開始
[EOS] :文の終了。ないしは文の区切り。
です。こうすると、テキスト \(\bs{T}\) は、
\(\bs{T}=\{x_1,\:x_2,\:x_3,\:\cd\:x_T\}\)
という単語IDの列で表現できることになります。もしこれが完結した文だとすると、\(x_1=\)[BOS]、\(x_T=\)[EOS] であり、複文だと途中にも [BOS] や [EOS] が出てくることになります。
単語IDは、その数字自体には意味がありません。また、語彙集合(要素数 \(V\))が増大すると単語IDの最大値も変化します。上の数字列は、あくまで「1時点での語彙集合をもとにして恣意的に付けられた数字の列」です。
分散表現
テキストをニュラール・ネットワークで扱うためには、すべての単語を、語彙集合のサイズにはよらない「固定長のベクトル」で表現するのが必須です。ここで使われるのが単語の「分散表現」で、固定長であるのみならず、"単語の意味もくみ取った" 表現です。ベクトルの次元は、たとば 512次元とか 1024次元です。
単語を分散表現にすることを "単語埋め込み"(word embedding)と言います。単語埋め込みの手法は各種ありますが、ここでは「word2vec」のアルゴリズムを例にとります。word2vec は、Google が2013年に提案したもので、実用的な分散表現の嚆矢となったものです。
word2vec に限りませんが、単語埋め込みのアルゴリズムの前提となっている仮定があります。それは、
単語の意味は、周囲の単語によって形成される
というもので、これを「分布仮説」と言います。たとえば、英文を例にとり、「周囲」を仮に「前1語、後1語」とします。
[I] [ ] [beer]
という文で [ ] に入る1単語は何かです。1単語に限定すると、冠詞(a, the)は入れようがないので、入る単語は限定されます。たとえば、
| [beer] (私はビール飲みます:習慣) | |
| [beer] (ビールはガブ飲みします:習慣) | |
| [beer] (ビールが大好きです:嗜好) | |
| [beer] (ビールは大嫌いです:嗜好) |
などです。[ ] には「飲む」に関係した動詞か「嗜好」に関係した動詞が入る可能性が高い。少なくとも「私とビールの関わりについての動詞」です。つまり、入る単語は「前後の1語によって意味が限定される」わけです。もしこれが「前後5語」とか「前後10語」であると「似たような意味の単語」か、少なくとも「同じジャンルの単語」になるはずです。
word2vec という「単語埋め込みアルゴリズム」には2種類あり、「周囲の単語から中心の単語を推論する(CBOW)」と「中心の単語から周囲の単語を推論する(skip-gram)」の2つです。推論にはニューラル・ネットワークを使います。以下は CBOW(Continuous Bag of Words)のネットワーク・モデルで説明します。
word2vec(CBOW)
CBOW は「周囲の単語から中心の単語を推論する」ニューラル・ネットワークのモデルです。「周囲の単語」を "コンテクスト" と呼び、推論の対象とする単語を "ターゲット" と呼びます。
まず、コンテクストのサイズを決めます。ターゲットの前の \(c\) 語、ターゲットの後ろの \(c\) 語をコンテクストとする場合、この \(c\) を "ウィンドーサイズ" と呼びます。そして "ウィンドー" の中には \(2c\) 語のコンテクストと1つのターゲットが含まれます。そして、訓練データとする文の "ウィンドー" を1単語ずつずらしながら、コンテクストからターゲットを推論する学習を行います。
語彙集合の単語数を \(V\) とし、一つの文を、
\(\bs{T}=\{x_1,\:x_2,\:\cd x_T\}\)
\(x_i\) :単語ID \((1\leq x_i\leq V)\)
とします。そして、\(x_i\) に1対1に対応する、\(V\)次元の one hotベクトルを、
\(\bs{x}_i=\left(\begin{array}{r}a_1,&a_2,&a_3,&\cd&a_V\\\end{array}\right)\)
\(a_j=0\:\:(j\neq x_i)\)
\(a_j=1\:\:(j=x_i)\)
とします。つまり \(\bs{x}_i\) は、\(x_i\) 番目の要素だけが \(1\) で、他は全部 \(0\) の \(V\) 次元ベクトルです(1つだけ \(1\)、が "one hot" の意味です)。
例として、ウィンドーサイズを \(c=2\) とします。また分散表現の単語ベクトルの次元を \(D\) とします。この前提で、\(\bs{T}\) の中の \(t\) 番目の単語の one hotベクトルを推論するモデルが図17です。
20E381AEE58D98E8AA9EE68EA8E8AB96E383A2E38387E383AB.jpg)
|
図17:word2vec(CBOW) の単語推論モデル |
\(\bs{T}=\{\:\cd,\:\bs{x}_{t-2},\:\bs{x}_{t-1},\:\bs{x}_t,\:\bs{x}_{t+1},\:\bs{x}_{t+2},\:\cd\:\}\)
という単語の one hotベクトルの系列を想定したとき、 \(\bs{x}_t\) がターゲットの正解データ(=教師ラベル)であり、その他の4つがコンテクストです。
最初の MatMul (Matrix Multiply) レイヤーは、4つの one hotベクトル \(\bs{x}_i\) を入力とし、それぞれに重み行列 \(\bs{W}_{\large enc}\) をかけて、4つのベクトル \(\bs{h}_i\) を出力します(enc=encode)。つまり、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。Average レイヤーは、入力された複数ベクトルの平均をとり、一つのベクトル \(\bs{h}_t\) を出力します。この \(\bs{h}_t\) が \(\bs{x}_t\) の分散表現(= \(D\)次元ベクトル)です(というより、そうなるようにネットワークを訓練します)。
次の MatMul レイヤーで 重み \(\bs{W}_{\large dec}\) を掛け(dec=decode)、\(\mr{Softmax}\) レイヤーを通して、分散表現を \(V\) 次元の確率ベクトル \(\bs{y}_t\) に変換します。そして、教師ラベルである \(\bs{x}_t\) との間で交差エントロピー誤差を計算し、損失 \(L\) を求めます。
損失が求まれば、誤差逆伝播法で重み行列 \(\bs{W}_{\large enc}\) と \(\bs{W}_{\large dec}\) を修正します。この修正を、大量の文とそのすべてのウィンドーで行って、損失 \(L\) を最小化します。これがネットワークの訓練です。
訓練済みのネットワークでは、重み行列 \(\bs{W}_{\large enc}\:[V\times D]\) が、単語の分散表現の集積体になっています。つまり、one hot ベクトル \(\bs{x}_i\) の分散表現を \(\bs{h}_i\) とすると、
\(\bs{h}_i=\bs{x}_i\cdot\:\bs{W}_{\large enc}\)
です。\(\bs{x}_i\) の単語IDを \(x_i\) とすると、
\(\bs{h}_i=\bs{W}_{\large enc}\) の \(x_i\)行(\(1\)列から\(D\)列まで)
となります。
分散表現と単語の意味
「分布仮説」をもとに、ニューラル・ネットワークによる推論で得られた単語の分散表現ベクトルは、類似の意味の単語は類似のベクトルになる(ことが多い)ことが確認されています。たとえば、
year, month, day
などや、
car, automobile, vehicle
などです。ベクトルの類似は「コサイン類似度」で計測します。2つの2次元ベクトル、
\(\bs{a}=\left(\begin{array}{r}a_1&a_2\\\end{array}\right)\)
\(\bs{b}=\left(\begin{array}{r}b_1&b_2\\\end{array}\right)\)
の場合で例示すると、
コサイン類似度\(=\dfrac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}\)
で、2次元平面の2つのベクトルの角度(コサイン値)を求める式になります。この式の分子は内積(dot product)で、内積の定義式を変形したものです。この類似度を利用して「類推問題」が解けます。たとえば、
France : Paris = Japan : X
の X は何かという問題です。答えは Tokyo ですが、これを求めるには、分散表現ベクトルが類似しているという前提で、
| France | ≒ Japan | |
| Paris | ≒ X |
X = France + Paris - Japan
であり、X を \(\bs{W}_{\large dec}\) と \(\mr{Softmax}\) 関数を使って確率ベクトルに変換すれば、確率が最も高い単語が Tokyo になるはずというわけです。
もちろん、分散表現ベクトルで類推問題を解くのは完璧ではありません。分散表現を作るときのウィンドーのサイズと訓練データの量にもよりますが、各種の類推問題を作って実際にテストをすると、60%~70% の正解率になるのが最大のようです。
言語モデル
分散表現ベクトルを用いて「言語モデル」を構築します。いま、一つの文を構成する単語の並び、
\(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T\)
があったとき(\(\bs{x}_1=\)[BOS]、\(\bs{x}_T=\)[EOS])、この文が存在する確率を、
\(P(\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_T)\)
で表します。文法として間違っている文の確率はゼロに近く、また文法としては合っていても、意味をなさない文の確率は低い。
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\( > \:P(\)[BOS],[学校],[は],[彼女],[へ],[行く],[EOS]\()\)
といった具合です。この「存在確率」は、次のような「条件付き確率」で表現できます。つまり、
\(P_1=P(\)[彼女] | [BOS]\()\)
:文頭が「彼女」である確率
\(P_2=P(\)[は] | [BOS],[彼女]\()\)
:「彼女」の次が「は」である確率
\(P_3=P(\)[学校] | [BOS],[彼女],[は]\()\)
:「彼女は」の次が「学校」である確率
\(P_4=P(\)[へ] | [BOS],[彼女],[は],[学校]\()\)
:「彼女は学校」の次が「へ」である確率
\(P_5=P(\)[行く] | [BOS],[彼女],[は],[学校],[へ]\()\)
:「彼女は学校へ」の次が「行く」である確率
\(P_6=P(\)[EOS] | [BOS],[彼女],[は],[学校],[へ],[行く]\()\)
:「彼女は学校へ行く」で文が終わる確率
とすると、
\(P(\)[BOS],[彼女],[は],[学校],[へ],[行く],[EOS]\()\)
\(=P_1\times P_2\times P_3\times P_4\times P_5\times P_6\)
となります。つまり、一般的に、
\(P(\bs{x}_{t+1}\:|\:\bs{x}_1,\:\bs{x}_2,\:\bs{x}_3,\:\cd\:,\:\bs{x}_t)\)
が分かれば、言語モデルは決まります。平たく言うと、
それまでの単語の系列から、次にくる単語の確率を推測する
のが言語モデルと言えます。もちろん、次にくる可能性のある単語は1つではありません。語彙集合のすべての単語それぞれについて「次にくる」確率を予測します。
実は、Transformer や GPT、ChatGPT がやっていることは「次にくる単語の予測」であり、これを実現しているのが、「超大規模なニューラル・ネットワークで作った言語モデル」なのです。
トークン
今まで、ニューラル・ネットワークでテキストを扱うためには、テキストを単語に分解するとしてきました。しかし大規模言語モデルで実際にやっていることは、テキストを「トークン(token)」に分解し、そのトークンの分散表現ベクトルを求めてニューラル・ネットワークで処理することです。
トークンとは、基本的には「単語」ないしは「単語の一部」です。英語ですと、たとえば頻出単語は「単語=トークン」ですが、GPT-3 の例だと、トークンには、ed, ly, er, or, ing, ab, bi, co, dis, sub, pre, ible などの「単語の一部」が含まれます。GPT-3 のトークンの語彙数は約5万ですが、そのうち英語の完全な単語は約3000と言われています。通常使われる英単語は4万~5万なので、3000の単語で WebText や Wikipedia の全部を表すことは到底できません。つまり、単語の "切れ端" と単語の組み合わせ、ないしは単語の "切れ端" 同士の組み合わせでテキストを表現する必要があります。
たとえば「ディスコ音楽」などの disco という単語は、[dis] [co] と表現します。edible(食用の、食べられる、という意味)は、[ed] [ible] です。disco や edible は 3000 単語の中に入っていないようです。edible などは「基本的な英単語」と思えますが、あくまで WebText や Wikipedia に頻出するかどうかの判断によります。
また xylophone(木琴)は、[x] [yl] [ophone] です。このように、1文字がトークンになることもあります。"単語"、"単語の切れ端"、"文字" がトークンです。
BPEによるトークン化
テキストをトークンに変換することを「トークン化(tokenize)」、トークン化を行うソフトを tokenizer と言います。ここで GPT-3 のトークン化のアルゴリズムの概要をみてみます。
上の xylophone → [x] [yl] [ophone] で明快なのですが、トークン化は単語の意味とは無関係です。意味を言うなら xylo("木の" という意味の接頭語)+ phone(音)ですが、そういうこととは全く関係ありません。
GPT-2 の論文にそのアルゴリズムである BPE(Byte Pair Encoding)が書かれています(GPT-3 は GPT-2 と同じだと、GPT-3 の論文にあります)。
コンピュータで文字を表現するには文字コード(文字に数字を割り振ったもの)を使います。国際的に広く使われているのは unicode です。unicode を使うと各国語の文字が統一的に文字コードで表現できます。
unicode の数字をコンピュータでどう表すか、その表し方(=エンコーディング)には3種類ありますが、その一つが UTF-8 です。UTF-8 は1バイト(8ビット、10進数で 0~255)を単位とし、1~4バイトで1文字を表現する可変長のエンコーディングです(漢字の異字体は5バイト以上になります)。
UTF-8 でば、通常の英文に使われる英数字、特殊文字(空白 , . ? など)は1バイトで表します。一方、日本語の平仮名、カタカナ、漢字は3バイトです(一部の漢字は4バイト)。バイトは文字ではありません。あくまで文字を表現するためのコンピュータ用の数字です。
BPE ではまず、UTF-8 でエンコーディングされた大量のテキストを用意します。そして、1バイトの全パターンを256種類の基本トークンとして語彙に初期登録します。トークン ID は 1~256 とします。従って、英文における1文字の単語( I, a )や記号( , . ? ! など)は、この時点でトークンID が割り当てられたことになります。
次に、テキストの「トークンのペア」で、最も出現頻度の高いペアをみつけます。英語で最も出現頻度が高い単語は the で、トークンで表現すると [t] [h] [e] です。仮に、[t] [h] のペアがテキスト中で最も出現頻度が高いとします(説明のための仮定です)。そうすると、この2つのトークンを結合した [th] を新たなトークン(トークン ID=257)として語彙に登録します。以降、テキスト中の [t] [h] は [th] と見なします。
次に出現頻度の高いペアが [th] [e] だとすると、この2つを結合した [the] を新たなトークン(トークン ID=258)として語彙に登録します。この段階で the という単語がトークンの語彙に登録されたわけです(以上の [th] [the] のトークン ID は説明のための数字で、実際の GPT-3 のトークン ID は違います)。
以上のプロセスにおいてトークンは、「空白をまたがない」「空白で終わらない」「同一カテゴリの文字(英字、数字、特殊文字など)でしかペアを作らない」などの制約をもうけておきます。「カテゴリ」が何かは論文に書いていないので想定です。もちろんこれは、なるべく頻出単語をトークンにする工夫です。
これを「結合の最大回数」になるで繰り返します。GPT-2 / GPT-3 の場合、最大回数は 50,000 です。従って、最終的には、
256 + 50,000 + 1 = 50,257
のトークンの語彙ができあがることになります。最後の + 1 は文末の記号 [EOS] を特殊トークンとしているからです。
いったん語彙ができあがると、以降、この語彙を使ってすべてのテキストを同じアルゴズムでトークン化します。当然ですが、長いバイトのトークンからテキストに割り当てることになります。
大規模言語モデルの成立要件
GPT-3 のトークン化のロジックによると、すべての言語のすべてのテキストが 50,257個のトークンを使って、統一的に、もれなくトークン化できることになります。それはあたりまえで、1バイトのデータがすべてトークンとして登録してあるからです。テキストを UTF-8 で統一的に表せば可能なのです。
ここで、日本語がどうなるかです。日本語の unicode を UTF-8 で表すと、漢字・仮名・文章記号は3バイトです(一部の漢字は4バイト。また異字体は5バイト以上)。ということは、普通の漢字1字、仮名1字は1~3トークンで表されることになります。
実際、OpenAI 社が公開している GPT-3 の Tokenizer で試してみると、
仮名は1~2トークン
ほとんどの漢字は2~3トークン
となります。ちなみに、平仮名(清音、濁音、半濁音、計71文字種)のトークン数を調べてみると、
28 文字種:1トークン
43 文字種:2トークン
です。濁音で1トークンになるのは「が だ で」の3つだけですが、これは助詞として頻出するからでしょう。特別の場合は、仮名2文字で1トークンになるようです(スト、ーク、など)。1トークンになる漢字はごく少数のようで、たとえば「上」「田」「中」「一」「大」がそうです(他にもあると思います)。
以上をまとめると、何をトークンとするかは、
・単語
・単語の一部、ないしは文字の連なり
・文字
・バイト
がありうるわけですが、GPT-3 のトークンにはこれらが混在していて、規則性は全くないことになります。ここから何が言えるかと言うと、
大規模言語モデルは、言語の文法や意味を関知しないのみならず、単語という概念さえなしでも成立しうる |
ということです。もちろん、英語を扱うときのように頻出単語のトークン化ができれば、生成されるテキストのクオリティーが向上することは確かでしょう。しかし、単語単位のトークン化は必須ではない。つまり、
単語の切れ端や文字どころか、文字を細分化した「バイト」をトークンとしても、その「バイト」には言語学的な意味が全く無いにもかかわらず、大規模言語モデルが、とりあえず成り立つ
わけです。GPT-3(= ChatGPT の基盤となっているモデル)がそれを示しています。大規模言語モデルは、翻訳、文章要約、質問回答、おしゃべり(chat)などの多様なタスクに使えます。これらのタスクを実現する仕組みを作るには、言語学的知識は全く不要です。不要というより、言語学的知識を持ち込むことは邪魔になる。もちろん、「翻訳、文章要約、質問回答、おしゃべり」の実例や好ましい例が大量にあるのが条件です。
その GPT-3 のベースになっているのは、Google が提案した Transformer という技術です。ということは、次のようにも言えます。
Transformer は「系列データ = 同質の記号・データが直列に並べられた、順序に意味のあるもの」であれば適用可能であり、その記号を文字としたのが大規模言語モデルである。もちろん、適用するには系列データの実例が大量にあることが必須である。 |
これが言えるのなら、少々先走りますが、Transformer はタンパク質の機能分析にも使える(可能性がある)ことになります。タンパク質はアミノ酸が鎖状に1列に並んだもので、そのアミノ酸は20種類しかありません。
タンパク質は「20種の記号の系列」であり、それが生体内で特定の機能を果たします。多数のタンパク質のアミノ酸配列を Transformer で学習し、タンパク質の機能と照らし合わせることで、新たなタンパク質の設計に役立てるようなことができそうです。実は、こういった生化学分野での Transformer や言語モデルの利用は、今、世界でホットな研究テーマになっています。
もちろん、系列データはタンパク質の構造だけではありません。従来から AI で扱われてきた音声・音源データや、各種のセンサーから取得したデータがそうだし、分子生物学では DNA / RNA が「4文字で書かれた系列データ」と見なせます。現に米国では、DNA / RNA の塩基配列を学習した大規模言語モデルでウイルスの変異予測がされています。
Transformer は、もともと機械翻訳のために提案されたものでした。しかしそれは意外なことに、提案した Google も予想だにしなかった "奥深い" ものだった。ここに、大規模言語モデルのサイエンスとしての意義があるのです。
(次回に続く)
タグ:正規分布 MLP ヘヴィサイド関数 単位ステップ関数 ReLU 活性化関数 多重パーセプトロン 標準偏差 積分 微分 指数関数 ベクトル 行列 ChatGPT 全結合 回帰問題 シナプス ニューロン GPT-3 GPT OpenAI Google transformer トークン 分散表現 大規模言語モデル 自然言語 バイアス 重み ニューラル・ネットワーク ガウス分布 分類問題 Softmax 損失 損失関数 交差エントロピー誤差 Cross Entropy Error 勾配 勾配降下法 ミニバッチ勾配降下法 確率的勾配降下法 誤差逆伝播法 標準正規分布 誤差関数 残差結合 GELU レイヤー正規化 パラメータ 単語埋め込み word2vec 分布仮説 コサイン類似度 BPE Byte Pair Encoding 系列データ バイト Unicode UTF-8 タンパク質 アミノ酸
2023-09-24 21:14
nice!(0)