No.315 - 高校数学で理解する楕円曲線暗号の数理(1) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
このブログでは、インターネットをはじめとする情報通信インフラで使われている「公開鍵暗号」について、今まで3回にわたって書きました。
の3つです。今回はその継続として、公開鍵暗号の一種で広く使われている「楕円曲線暗号」について、その数学的な背景を書きます。楕円曲線暗号は、1985年に米国 IBM の Victor Miller と米国 Washington 大学の Neal Koblitz によって独立に提案されました。暗号に限らず科学技術の世界では、同時期に同じアイディアが独立に考案されるというケースが見られます。
例によって高校レベルの数学知識だけを前提にし、証明なしに用いる定理や命題はないものとします。ただし、No.310、No.311、No.313 の内容やそこで証明した定理は既知とします。特にその中の、
です。なお、楕円曲線(Elliptic Curve)は、2次曲線である楕円(Ellipse)とは関係ありません。楕円の弧長を積分で求める時に出てくる数式なのでその名があるだけです。暗号の名を楕円暗号とするむきもありますが、誤解されるでしょう。楕円曲線暗号(Elliptic Curve Cryptography)が正しい言い方です。
15. 楕円曲線(Elliptic Curve)とは
楕円曲線とは、次の式で表される平面3次曲線です。
係数の \(a\) と \(b\) は有理数とします。楕円曲線の式の「標準形」と呼ばれるものは何種類かありますが、上式はその最も簡単な形です。楕円曲線暗号ではこの形を使うので、以降、楕円曲線といえばこの形で表される3次曲線とします。Wikipedia に非常にわかりやすい「楕円曲線のカタログ」が載っているのでそれを引用します。
図でわかるように楕円曲線は成分(= ひとつながりの曲線)が1つのものと2つのもの(その1つは閉じた曲線)があります。この違いは何でしょうか。また、図の中にある \(a=0,\:b=0\) の曲線は、実は楕円曲線ではありません。このあたりの説明は以降の通りです。楕円曲線の \(x\) の式を、
と書きます。\(y=f(x)\) のグラフは少なくとも1回、\(x\) 軸を横切るので、\(f(x)=0\) の3次方程式は少なくとも1つの実数解を持ちます。この3次方程式が3つの異なる実数解を持つ条件を調べます。関数 \(f(x)\) が極値をとるとしたら、そのときの \(x\) は方程式、
の解です。この解を \(x_1\) と \(x_2\) とすると、
です。\(x\) がこの値をとるときの2つの極値がゼロでなく、符号が逆であれば、\(f(x)=0\) は3つの異なる実数解をもちます。つまりその条件は、
です。\(x_1,\:x_2\) を入れて計算してみると、この条件は、
となります。不等号の向きが逆なら実数解は1つだけです。この不等号の左辺は「3次方程式の判別式」の符号を逆にしたものです。3次方程式の判別式 \(D\) は、いま扱っている楕円曲線の式の場合、
です。従って、
となります。この2つのケースで楕円曲線をを図示すると、図2(\(a=-2,\:b=1\))、図3(\(a=-2,\:b=2\))のようになります。
ここで \(D=0\) のときにどうなるかを調べてみます。不定方程式、
の整数解を求めるために、\(a=-3k^2\:(0\leq k)\) と置くと、
が解です。\(k=0,\:1\) とすると、
が解のうちの3組です。まず、\((a,\:b)=(0,\:0)\) のとき曲線の式は、
となり、図4のように「尖点」をもつ曲線となります(Wikipedia の "楕円曲線のカタログ" にあったものです)。尖点では微係数が定まらず、曲線の接線が引けません。
\((a,\:b)=(-3,\:2)\) のときの曲線の式は、
となり、図5のように「結節点」をもつ自己交差曲線となります。結節点において接線は引けますが、2種類あって一意に定まりません。
\((a,\:b)=(-3,-2)\) のときの曲線の式は、
となり、図6のように \((-1,\:0)\) に「孤立点」が発生します。この孤立点でも接線は引けません。
尖点、結節点、孤立点を曲線の「特異点」と言い、特異点をもつ3次曲線を特異3次曲線と言います。そして特異3次曲線は \(y^2=x^3+ax+b\) の形であっても楕円曲線とは言いません。つまり、楕円曲線の正確な定義は次の通りです。
この定義による楕円曲線は "なめらか" であり、曲線上の全ての点で唯一の接線が引けます。以降、この楕円曲線の性質を調べていきます。
楕円曲線暗号は「楕円曲線上の点の加法群」で構成する暗号です。そこでまず、No.313 でも触れた「群(group)」とは何かを復習します。
群の定義
群(\(G\) で表します)とは、何らかの2項演算 "\(\circ\)" が定義された集合です。演算が定義されているとは、集合 \(G\) の任意の2つの元(同じ元であってもよい)、\(a\)、\(b\) を演算した結果の \(a\circ b\) が \(G\) の元であることを意味します。この2項演算は次の3つの条件を満たす必要があります。この「条件を満たす2項演算が定義された集合」が群 \(G\) です。
演算 "\(\circ\)" を乗算と考えるとき、\(G\) を乗法群といいます。乗法群では2項演算を \(a\times b,\:\:a\cdot b,\:\:ab\) などと書きます。単位元は \(1\) と書くこともあります。また、逆元 \(b\) は \(a^{-1}\) です。同一の \(n\) 個の元 \(a\) に対して演算 "\(\circ\)" を \(n-1\) 回行った結果は \(a^n\) で「累乗(あるいは冪乗)」と呼びます。
演算 "\(\circ\)" を加算と考えるとき、\(G\) を加法群といいます。加法群では2項演算を \(a+b\) と書きます。加法群の単位元を零元と呼び、\(0\) と書くことがあります。また逆元 \(b\) は \(-a\) です。同一の \(n\) 個の元 \(a\) に対して演算 \(\circ\) を行った結果は \(na\)で「スカラー倍」と呼びます。
乗法群か加法群かは多分に "言葉の綾" の面があり、どちらがイメージしやすいかによります。但し、加法群と言った場合は暗黙に可換則、\(a\circ b=b\circ a\) が成り立つ群を言います。可換則が成り立つ群を、ノルウェーの数学者 Abel の名前をとって「アーベル群」と呼びます。もちろん「乗法」や「加法」のイメージとは結びつきにくい群もたくさんあります。
楕円曲線上の有理点
楕円曲線上の有理点からなる加法群を構成することができます。有理点とは、楕円曲線上の点、\((x_0,\:y_0)\) で、\(x_0\) も \(y_0\) も有理数の点です。一般に、楕円曲線が有理点を持つかどうかを有限回の手続きで決定する方法は知られていません。しかし、1個か2個の有理点があれば、次のような手続きで次々と有理点を見つけることができます。以下の記述では \(P\)、\(Q\)、\(R\) などを有理点とし、
と定義します。ここでの " \(\!*\!\) " は乗算の記号ではなく「" \(\!*\!\) " の前後に書かれた楕円曲線上の点ではない、もう一つの直線と楕円曲線の交点」の意味です。
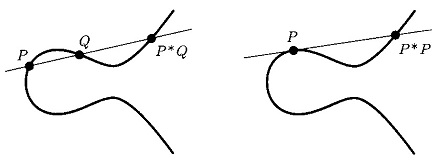
図7で、\(P\!*\!Q\) も \(P\!*\!P\) も有理点です。なぜなら、係数が有理数の3次曲線と直線の交点を求める式は3次方程式になりますが、3次方程式の2つの異なる根が有理数なら(図7の左の \(P\) と \(Q\))、もうひとつの根 \(P\!*\!Q\) も有理数だからです。もう1つが有理数でないと(=無理数や複素数)、3次曲線の係数が有理数という前提に反します。同じように3次方程式の重根(図7の右の \(P\))が有理数だと、もう一つの根も有理数です。
つまり、楕円曲線上に1つ、ないしは2つの有理点があったとしたら、上記の操作で有理点を増やしていけます(但し有理点が無限個なのか有限個なのかは楕円曲線によります)。そこで有理点の存在を前提として以下の議論を進めます。
楕円曲線上の有理点が作る加法群
楕円曲線上の有理点を "群" にするためには、そこに何らかの演算を定義する必要がありますが、その定義を次のようにします。加法群なので演算を \(+\) と書きます。
群演算
零元
この演算における零元 \(\mathcal{O}\) が、群の零元の条件を満たしているかどうかを検証すると、
となって、零元の条件を満たしていることがわかります(図9)。もちろん、\(\mathcal{O}+P=P\) です。
逆元
逆元は次のように定義します。零元 \(\mathcal{O}\) における接線が楕円曲線と交わる点を \(S\) とします。まず、
です。そして 点 \(Q\) と \(S\) を結ぶ直線が再び楕円曲線を交わる点を、\(Q\) の逆元(= \(-Q\))とします。つまり、
です。このように定義すると
となり、群の逆元の条件を満たすことがわかります(図10)。\(S\) と \(\mathcal{O}\) を結ぶ直線は \(\mathcal{O}\) で2回交差するので、\(S*\mathcal{O}=\mathcal{O}\) です。
結合則
群を構成するためには、以上の群演算の定義が結合則を満たしていななければなりません。楕円曲線上に点 \(P\)、\(Q\)、\(R\) をとったとき、
となるのが結合則ですが、
なので、
が示せればよいことになります。「楕円曲線論入門」にはこのことを示した図が載っています(図11)。
\((P+Q)\!*\!R\) の点と \(P\!*\!(Q+R)\) の点が、楕円曲線上で同一の点になることの証明は少々複雑なので「18. 結合則が成り立つことの検証と証明」にまわします。
以上のように楕円曲線上の有理点は、直線との交点を使って加法と逆元をうまく定義することで "群" になることがわかりました。ここで注意すべきは、零元は楕円曲線上の任意の有理点でよいことです。これを利用し「零元=無限遠点」としたのが、実用的に使われる楕円曲線上の加法群です。
無限遠点を零元とする加法群
以下では「対称点」という言葉を使いますが、
ことにします。楕円曲線は \(x\) 軸について対称なので、点 \(P\) を \(x\) 軸で "折り返した" 点が \(P\) の対称点です。\(y=0\) となる点が楕円曲線上に1つ、または3つありますが、その点の対称点は同じ点です。
次に「\(y\) 軸方向の無限遠点」を導入し、「楕円曲線上の有理点と無限遠点を合わせた集合」に群を定義します。ここからは無限遠点を \(\mathcal{O}\) と書きます。
無限遠点は図に表せないのでイメージしにくいのですが、\(\bs{y}\) 軸方向の無限遠に \(\bs{\mathcal{O}}\) があると考えます。\(y\) 軸の正方向でも負の方向でもかまいません。
楕円曲線上の点 \(P\) を \(P=(x_p,\:y_p)\) とし、\(x_p\) をどんどん大きくすると、楕円曲線の式では \(x^3\) の項が支配的になるので、\(y_p^2=x_p^3\) と近似できます。つまり \(y_p=\pm x_p^{1.5}\) となり、\(x_p\) が大きいと \(y_p\) は \(y\) 軸の遙か上方(と下方)になります。この極限が無限遠点 \(\mathcal{O}\) と考えます。さらに、
と考えます。この \(\bs{y}\) 軸方向の無限遠点 \(\bs{\mathcal{O}}\) を零元とする群を構成します。
群演算
まず、群演算の加法ですが、
と定義します(図12)。
こうすると、\(P\!*\!Q\) と \(P+Q\) を結ぶ直線は \(y\) 軸と平行になり、それは無限遠点 \(\mathcal{O}\) で楕円曲線と交差します。つまり、
です。この定義は 零元を楕円曲線上の点にとった図8と合致します。この加法の定義で \(\mathcal{O}\) が群の零元の要件を満たしているかを検証すると、
となって要件を満たしていることがわかります。\(P*\mathcal{O}\) は \(P\) の対称点ですが、\(P\) の対称点と \(\mathcal{O}\) を結ぶ直線が楕円曲線と交差する点は \(P\) なので上式が成立します。これは楕円曲線上に \(\mathcal{O}\) をとった図9と同じです。さらに逆元ですが、\(Q\) が楕円曲線上にあったとき、
と定義します(図13)。
こうすると、
となりますが、\(\mathcal{O}*\mathcal{O}=\mathcal{O}\)(=無限遠点の対称点は無限遠点)との自然な定義を行うと、
となって逆元の要件を満たします。結合則についても零元を楕円曲線上にとった場合(図11)と同じ様に成立します。「18. 結合則が成り立つことの検証と証明」でそのこと書きます。
射影平面
無限遠点は図で表現できず、何だか "怪しげな" 感じがしますが、数学的に厳密に定義できます。それには射影平面を使います。
平面 \((x,\:y)\) に対し、3つの数 \((X,\:Y,\:Z)\) で表される "平面" を射影平面と言います。3つの数がありますが3次元空間ではありません。ただし \((0,\:0,\:0)\) の点は除きます。また、
と定義します。\(xy\) 平面から射影平面の対応は、
とし、その逆の対応は、
です。この対応からわかるように、射影平面には \(xy\) 平面にない点が含まれています(\(Z=0\) の点)。
射影平面での楕円曲線の式は、\(xy\) 平面の楕円曲線の式で、\(x=\dfrac{X}{Z},\:\:y=\dfrac{Y}{Z}\) とおき、全体に \(Z^3\) をかけて同次化(=変数項の合計次数をそろえる)します。その結果、
の同次方程式が、射影平面での楕円曲線になります。ためしに、図2の楕円曲線(\(a=-2,\:b=1\))と \(y\) 軸との交点を計算してみると、\(xy\) 平面では、
の連立方程式を解いて、\((0,\pm1)\) となります。一方、射影平面では、\(x=0\) は \(X=0\) なので、
が、楕円曲線と直線の交点を求める連立式になります。この解は、\(\al\) と \(\beta\) を \(0\) ではない数として、\((0,\al,\pm\al),\:(0,\beta,\:0)\) です。射影平面の同値関係を利用すると、
が楕円曲線と直線の交点になり、交点は3つあることになります。ここで \(xy\) 平面の交点には現れなかった \((0,\:1,\:0)\) が \(y\) 軸方向の無限遠点です。これを一般化すると次のようになります。つまり、楕円曲線と \(y\) 軸に平行な直線の式を、
とすると、これに対応する射影平面の式は、
です。\((0,\:1,\:0)\) はこの2式を必ず満たします。つまり全ての楕円曲線は \((0,\:1,\:0)\) を通り、全ての \(y\) 軸に平行な直線は \((0,\:1,\:0)\) を通る。従って、楕円曲線と\(y\) 軸に平行な直線は(\(y\) 軸方向の)無限遠点で交わることになります。
楕円曲線の計算には現れませんが、無限遠点にもいろいろあって、\((1,\:0,\:0)\) は \(x\) 軸方向の無限遠点、\((\al,\:\beta,\:0)\) は任意方向の無限遠点です(\(\al\)、\(\beta\) は \(0\) ではない数)。
\(xy\) 平面の2直線は、平行なときには交点がありませんが、射影平面の2直線は必ず1点で交わります。また射影平面の楕円曲線の1点を通る直線は、楕円曲線と必ず3点で交わります(直線が楕円曲線の接線の場合は、接点での交差数を2と数えます)。このように、交差を統一的に扱えるのが射影平面の特徴の一つです。
以上のような数学的裏付けのもとに導入したのが無限遠点です。これを \(xy\) 平面では、
とイメージしてよいわけです。
加法式・2倍式
楕円曲線上の加法を計算式で表します。楕円曲線上の3点を次のように定義します。
とします。\(P_1\) と \(P_2\) を結ぶ直線を \(y=\lambda x+\mu\) とすると、連立方程式、
の解が \(P_1,\:P_2,\:(x_3,-y_3)\) です。この2つの式から \(y\) を消去すると、
が得られますが、この式は、
と同一のはずです。そこで \(x^2\) の係数を比較すると、
が得られます。つまり、
となります。この \(x_3\) を直線の式に入れると、
ですが、\(y_1=\lambda x_1+\mu\) なので \(\mu\) を消去すると、
となります。これが基本の加法式です。これを \(P_1\) と \(P_2\) の配置パターンごとにまとめると、次の通りです。
\(x_1\neq x_2\) のとき
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
この場合は \(P_1\) と \(P_2\) を通る直線は \(P_1\) における楕円曲線の接線となり、直線の傾き \(\lambda\) は上の式のままでは計算できません。そこで \(y^2=x^3+ax+b\) を \(x\) で微分すると
なので、
となります。\(x_2\) を \(x_1\) に置き換えてまとめると、
が \(P_1+P_1\) の計算式です。これは \(P_1\) の "2倍"(一般にはスカラー倍)であり、\(2P_1\) と書きます。
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
この場合、\(P_2=-P_1\) なので、定義により
です。
なお、\(P_1\) と \(P_2\) は、楕円曲線の定義式、
を満たしますが、この左辺と右辺のそれぞれを引き算すると、
となって \(\lambda\) の別の表現が得られますが、これは \(x_1=x_2\) でも使えます。従って「加法式(第2形)」を次のようにも表現できます。
\(y_1+y_2\neq0\) のとき
\(y_1+y_2=0\) のとき
楕円曲線の具体例
楕円曲線とその有理点、加法則の適用例として、整数係数の3つの楕円曲線を調べてみます。以後の記述では、\(P=(x,\:y)\) とするとき、\(nP,\:-P,\:-nP\) の記述を使いますが、それぞれの定義は、
です。また、\(nP=(x_n,\:y_n)\) とすると、加法の定義から \(-nP=(x_n,-y_n)\) です。
\(y^2=x^3+1\)
この楕円曲線上の有理点は、次の5つの整点(= 座標値が整数の点)です。
ここで、群の演算式を使って \(nP_1\) を計算してみると、
となります。\(P_1\) は 6倍する(= 6個加算する)と \(\mathcal{O}\)(=零元)になる。このことを「\(P_1\) の位数(order)が \(6\) である」と言います。また、
なので、\(P_2\) の位数は \(3\) です。同様にして、\(P_3\)~\(P_5\) の位数はそれぞれ \(2,\:\:3,\:\:6\) になります。
楕円曲線 \(y^2=x^3+1\) の有理点は \(P_1\)~\(P_5\) の点しかありません。また位数が有限値なので、これらは有限位数の点です。これらの点と 零元 \(\mathcal{O}\) を合わせて群を構成します。
しかし楕円曲線上の有理点が有限位数をもつとは限りません。それが次の例です。
\(y^2=x^3-x+1\)
方程式 \(y^2=x^3-x+1\) の整数解を調べると、手計算で \((-1,\pm1),\) \((0,\pm1),\) \((1,\pm1),\) \((3,\pm5),\) \((5,\pm11)\) の\(10\)個の解が容易に見つかります。今、\(P_1=(1,\:1)\) とし、\(nP_1\) を順に計算してみると、次のようになります。
途中で \((56,-419)\) という、手計算では分からない整点が現れました。計算してみると、
となって、確かにこれが楕円曲線上の点であることが分かります。\(15P_1\) までの結果を掲げましたが、この計算は \(\mathcal{O}\)(= 零元)で終わることがなく、無限に続きます。つまり、\(P_1=(1,\:1)\) は無限位数の点です。
さらに、同様の計算を\(-P_1=(1,-1)\) から始めると、\(y\) 座標の符号が逆転した点列、\(-nP_1\) が得られます。そして実は、
ことが分かっています。\(0P_1=\mathcal{O}\) と定義すれば、楕円曲線で定義された加法群の元は \(mP_1\)(\(m\) は整数)の形で表現できるとも言えます。この性質を有限生成と言い、\(P_1\) を生成元(generator)と呼びます。一般には、生成元は複数個あります。つまり楕円曲線上の有理点は \(r\) 個の有理点 \(Q_i\) を使って、
の形で表現できます。この \(r\) を楕円曲線の階数(rank)と言います。なお、有限個の有理点しかもたない 図14 のような楕円曲線の階数は \(0\) とします。
楕円曲線 \(y^2=x^3-x+1\) の階数は \(1\) です。そして今までの結果から、階数が \(1\) の楕円曲線の有理点と零点 \(\mathcal{O}\) は、加法に関して整数(= 正の自然数と負の自然数と \(0\))と全く同じ構造をもつことが分かります。ただ、楕円曲線の有理点の加法は普通の整数の加法よりよほど複雑な演算です。これが楕円曲線暗号を作るときの基礎となっています。
\(y^2=x^3-4x+1\)
この楕円曲線の階数は \(2\) です。従って生成元は2つで、
です。曲線上には無限個の有理点がありますが、すべてはこの2つの生成元から「有限生成」されます。無限個の有理点のうち、生成元を含めて 22個が整点ですが(\(y\) 座標の正負を無視すると 11個)、もちろんそれらの整点も生成元で表現できます。実際に計算してみると以下の通りです。
もちろん、計算していくと上記の整点だけでなく有理点が次々と生成され、それが無限に続きます。上の計算で \(P_1,\:P_2\) の符号を逆転させると \(y\) 座標の符号が逆の整点が得られます。たとえば、
です。以上を含めてこの楕円曲線の整点は、
となります。最大の整点は \((1274,\pm45473)\) ですが、実際に計算してみると、
となって、楕円曲線上の点であることが確認できます。この最大の整点を2つの生成元に分けて、それぞれを計算してみると、
となりますが、この2つの有理点を楕円曲線の加法式で \(8P_1+3P_2\) とすると整点である \((1274,\:-45473)\) が現れるのも不思議な感じがします。
以上の「楕円曲線の有理点から成る加法群」を踏まえ、これ以降は楕円曲線暗号で使われる「有限体上の楕円曲線による加法群」に移ります。
有限体上の楕円曲線による加法群
以降に出てくる有限体 \(\bs{F}_p\) と 乗法群 \(\bs{F}_p^{*}\) については、No.313「高校数学で理解する公開鍵暗号の数理:10. 有限体と乗法群」 で定義したものです。
楕円曲線暗号に使われる楕円曲線は、有限体 \(\bs{F}_p\) で定義された "曲線" で、次の式を満たすものです。
\(x\)、\(y\)、\(a\)、\(b\) は全て \(\bs{F}_p\) の元です。「この式を満たす全ての \((x,\:y)\) と 零点 \(\mathcal{O}\) の集合」に対して演算を定義して群を構成します。演算を加法と考えて \(+\) と書きます。この "曲線" 上の3点を、
とするとき、群の演算式は次のように定義されます。
\(x_1\neq x_2\) のとき
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
つまり、実数平面の有理点と無限遠点(=零元)で構成された群の演算式と全く同じです。もちろん加減乗除は \(\bs{F}_p\) で行います。これが群になる理由は、有理数体(有理数全体の集合)も有限体 \(\bs{F}_p\) も「体」であり、加減乗除は全く同一形式で記述できるからです。ただ、有理数体と違って \(\bs{F}_p\) の元の数は有限個であり、群の元の数も有限個(=有限群)です。以降、\(\bs{\bs{F}_p}\) 上の楕円曲線、\(\bs{y^2=x^3+ax+b}\) による有限群を \(\bs{E(a,\:b,\:p)}\) と表記します。
\(\bs{F}_p\) 上の楕円曲線は、もはや "曲線" の形をしていませんが、これを可視化した図を次に示します。有限体 \(F_{109}\) 上の "楕円曲線"、\(y^2=x^3+2x+4\) の例です。
以上が「有限体上の楕円曲線が作る加法群」で、楕円曲線暗号はこの加法群で構成されます。その話を次回にします。
このブログでは、インターネットをはじめとする情報通信インフラで使われている「公開鍵暗号」について、今まで3回にわたって書きました。
の3つです。今回はその継続として、公開鍵暗号の一種で広く使われている「楕円曲線暗号」について、その数学的な背景を書きます。楕円曲線暗号は、1985年に米国 IBM の Victor Miller と米国 Washington 大学の Neal Koblitz によって独立に提案されました。暗号に限らず科学技術の世界では、同時期に同じアイディアが独立に考案されるというケースが見られます。
例によって高校レベルの数学知識だけを前提にし、証明なしに用いる定理や命題はないものとします。ただし、No.310、No.311、No.313 の内容やそこで証明した定理は既知とします。特にその中の、
です。なお、楕円曲線(Elliptic Curve)は、2次曲線である楕円(Ellipse)とは関係ありません。楕円の弧長を積分で求める時に出てくる数式なのでその名があるだけです。暗号の名を楕円暗号とするむきもありますが、誤解されるでしょう。楕円曲線暗号(Elliptic Curve Cryptography)が正しい言い方です。
15. 楕円曲線(Elliptic Curve)とは
楕円曲線とは、次の式で表される平面3次曲線です。
\(y^2=x^3+ax+b\)
係数の \(a\) と \(b\) は有理数とします。楕円曲線の式の「標準形」と呼ばれるものは何種類かありますが、上式はその最も簡単な形です。楕円曲線暗号ではこの形を使うので、以降、楕円曲線といえばこの形で表される3次曲線とします。Wikipedia に非常にわかりやすい「楕円曲線のカタログ」が載っているのでそれを引用します。
| \(b=-1\) | \(b=\phantom{-}0\) | \(b=\phantom{-}1\) | \(b=\phantom{-}2\) | |
| \(a=-2\) |

|
|||
| \(a=-1\) | ||||
| \(a=\phantom{-}0\) | ||||
| \(a=\phantom{-}1\) | ||||
図1:楕円曲線のカタログ
| ||||
Wikipediaより。楕円曲線には曲線の "成分" が1つのものと2つのものがある。なお、この図で \(a=b=0\) だけは楕円曲線ではない(後述)。
| ||||
図でわかるように楕円曲線は成分(= ひとつながりの曲線)が1つのものと2つのもの(その1つは閉じた曲線)があります。この違いは何でしょうか。また、図の中にある \(a=0,\:b=0\) の曲線は、実は楕円曲線ではありません。このあたりの説明は以降の通りです。楕円曲線の \(x\) の式を、
\(x^3+ax+b=f(x)\)
と書きます。\(y=f(x)\) のグラフは少なくとも1回、\(x\) 軸を横切るので、\(f(x)=0\) の3次方程式は少なくとも1つの実数解を持ちます。この3次方程式が3つの異なる実数解を持つ条件を調べます。関数 \(f(x)\) が極値をとるとしたら、そのときの \(x\) は方程式、
\(f^{'}(x)=0\)
の解です。この解を \(x_1\) と \(x_2\) とすると、
\(x_1=\phantom{-}\sqrt{\dfrac{-a}{3}}\)
\(x_2=-\sqrt{\dfrac{-a}{3}}\)
\(x_2=-\sqrt{\dfrac{-a}{3}}\)
です。\(x\) がこの値をとるときの2つの極値がゼロでなく、符号が逆であれば、\(f(x)=0\) は3つの異なる実数解をもちます。つまりその条件は、
\(f(x_1)\cdot f(x_2) < 0\)
です。\(x_1,\:x_2\) を入れて計算してみると、この条件は、
\(4a^3+27b^2 < 0\)
となります。不等号の向きが逆なら実数解は1つだけです。この不等号の左辺は「3次方程式の判別式」の符号を逆にしたものです。3次方程式の判別式 \(D\) は、いま扱っている楕円曲線の式の場合、
\(D=-(4a^3+27b^2)\)
です。従って、
| \(D > 0\) のとき、\(f(x)=0\) は3つの実数解をもち、楕円曲線で \(y=0\) となる点は3つある。このとき楕円曲線の成分は2つになる(図2)。 | |
| \(D < 0\) のとき、\(f(x)=0\) の実数解は1つであり、楕円曲線で \(y=0\) の点も1つである。このとき楕円曲線の成分は1つになる(図3)。 |
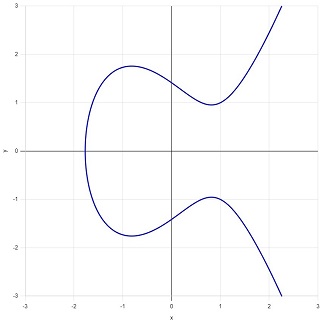
となります。この2つのケースで楕円曲線をを図示すると、図2(\(a=-2,\:b=1\))、図3(\(a=-2,\:b=2\))のようになります。

|
図2:成分が2つの楕円曲線 \(y^2=x^3-2x+1\) |
|
図3:成分が1つの楕円曲線 \(y^2=x^3-2x+2\) |
ここで \(D=0\) のときにどうなるかを調べてみます。不定方程式、
\(4a^3+27b^2=0\)
の整数解を求めるために、\(a=-3k^2\:(0\leq k)\) と置くと、
\(a=-3k^2\)
\(b=\pm2k^2\)
\(b=\pm2k^2\)
が解です。\(k=0,\:1\) とすると、
\((a,\:b)=(0,\:0),\:\:(-3,\:2),\:\:(-3,-2)\)
が解のうちの3組です。まず、\((a,\:b)=(0,\:0)\) のとき曲線の式は、
\(y^2=x^3\)
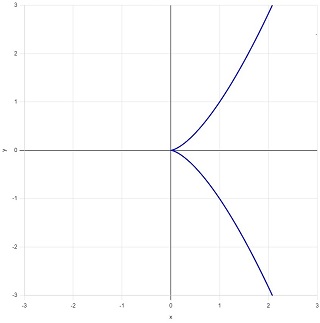
となり、図4のように「尖点」をもつ曲線となります(Wikipedia の "楕円曲線のカタログ" にあったものです)。尖点では微係数が定まらず、曲線の接線が引けません。
|
図4:尖点をもつ3次曲線 \(y^2=x^3\) |
\((a,\:b)=(-3,\:2)\) のときの曲線の式は、
\(\begin{eqnarray}
&&y^2&=x^3-3x+2\\
&&&=(x+2)(x-1)^2\\
\end{eqnarray}\)
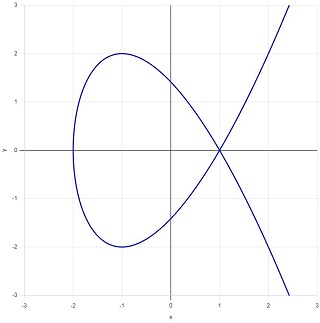
となり、図5のように「結節点」をもつ自己交差曲線となります。結節点において接線は引けますが、2種類あって一意に定まりません。
|
図5:結節点をもつ3次曲線 \(y^2=x^3-3x+2\) |
\((a,\:b)=(-3,-2)\) のときの曲線の式は、
\(\begin{eqnarray}
&&y^2&=x^3-3x-2\\
&&&=(x-2)(x+1)^2\\
\end{eqnarray}\)
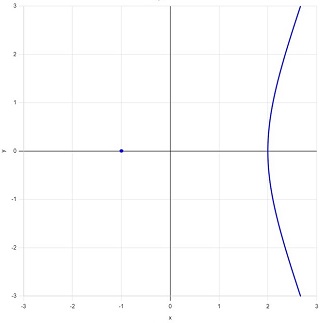
となり、図6のように \((-1,\:0)\) に「孤立点」が発生します。この孤立点でも接線は引けません。
|
図6:孤立点をもつ3次曲線 \(y^2=x^3-3x-2\) |
尖点、結節点、孤立点を曲線の「特異点」と言い、特異点をもつ3次曲線を特異3次曲線と言います。そして特異3次曲線は \(y^2=x^3+ax+b\) の形であっても楕円曲線とは言いません。つまり、楕円曲線の正確な定義は次の通りです。
| 15.1 | 楕円曲線の定義 |
|
次の式で表される平面曲線を楕円曲線と言う。
\(y^2=x^3+ax+b\) \((4a^3+27b^2\neq0)\) | |
この定義による楕円曲線は "なめらか" であり、曲線上の全ての点で唯一の接線が引けます。以降、この楕円曲線の性質を調べていきます。
楕円曲線暗号は「楕円曲線上の点の加法群」で構成する暗号です。そこでまず、No.313 でも触れた「群(group)」とは何かを復習します。
群の定義
群(\(G\) で表します)とは、何らかの2項演算 "\(\circ\)" が定義された集合です。演算が定義されているとは、集合 \(G\) の任意の2つの元(同じ元であってもよい)、\(a\)、\(b\) を演算した結果の \(a\circ b\) が \(G\) の元であることを意味します。この2項演算は次の3つの条件を満たす必要があります。この「条件を満たす2項演算が定義された集合」が群 \(G\) です。
| \(a\circ e=e\circ a=a\) となる元 \(e\) が存在 | |
| \(a\circ b=b\circ a=e\) となる \(b\) が、任意の \(a\) について存在 | |
| \((a\circ b)\circ c=a\circ(b\circ c)\) |
演算 "\(\circ\)" を乗算と考えるとき、\(G\) を乗法群といいます。乗法群では2項演算を \(a\times b,\:\:a\cdot b,\:\:ab\) などと書きます。単位元は \(1\) と書くこともあります。また、逆元 \(b\) は \(a^{-1}\) です。同一の \(n\) 個の元 \(a\) に対して演算 "\(\circ\)" を \(n-1\) 回行った結果は \(a^n\) で「累乗(あるいは冪乗)」と呼びます。
演算 "\(\circ\)" を加算と考えるとき、\(G\) を加法群といいます。加法群では2項演算を \(a+b\) と書きます。加法群の単位元を零元と呼び、\(0\) と書くことがあります。また逆元 \(b\) は \(-a\) です。同一の \(n\) 個の元 \(a\) に対して演算 \(\circ\) を行った結果は \(na\)で「スカラー倍」と呼びます。
乗法群か加法群かは多分に "言葉の綾" の面があり、どちらがイメージしやすいかによります。但し、加法群と言った場合は暗黙に可換則、\(a\circ b=b\circ a\) が成り立つ群を言います。可換則が成り立つ群を、ノルウェーの数学者 Abel の名前をとって「アーベル群」と呼びます。もちろん「乗法」や「加法」のイメージとは結びつきにくい群もたくさんあります。
楕円曲線上の有理点
楕円曲線上の有理点からなる加法群を構成することができます。有理点とは、楕円曲線上の点、\((x_0,\:y_0)\) で、\(x_0\) も \(y_0\) も有理数の点です。一般に、楕円曲線が有理点を持つかどうかを有限回の手続きで決定する方法は知られていません。しかし、1個か2個の有理点があれば、次のような手続きで次々と有理点を見つけることができます。以下の記述では \(P\)、\(Q\)、\(R\) などを有理点とし、
| \(P\) と \(Q\) を結ぶ直線がふたたび楕円曲線と交わる点を \(P\!*\!Q\)(図7の左) | |
| \(P\) 点における接線が楕円曲線と交わる点を \(P\!*\!P\)(図7の右) |
と定義します。ここでの " \(\!*\!\) " は乗算の記号ではなく「" \(\!*\!\) " の前後に書かれた楕円曲線上の点ではない、もう一つの直線と楕円曲線の交点」の意味です。
|
図7:楕円曲線上の有理点 |
J.H.シルヴァーマン、J.テイト著「楕円曲線論入門」(シュプリンガー・フェアラーク東京 \(1995\))より引用 |
|
つまり、楕円曲線上に1つ、ないしは2つの有理点があったとしたら、上記の操作で有理点を増やしていけます(但し有理点が無限個なのか有限個なのかは楕円曲線によります)。そこで有理点の存在を前提として以下の議論を進めます。
なお、楕円曲線暗号で使う加法群は「有限体上の楕円曲線における加法群」であり、有理点を見つけるアルゴリズムがあります(後述)。もちろん有理点の数は有限個です。
楕円曲線上の有理点が作る加法群
楕円曲線上の有理点を "群" にするためには、そこに何らかの演算を定義する必要がありますが、その定義を次のようにします。加法群なので演算を \(+\) と書きます。
群演算
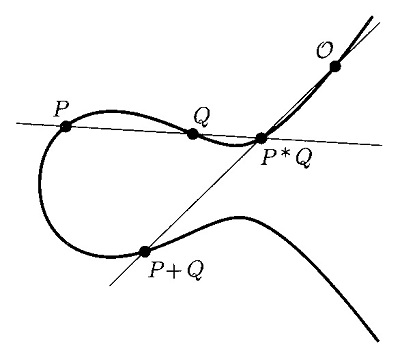
| 任意の有理点を零元(= \(\mathcal{O}\) )とする。 | |
| \(P\) と \(Q\) を楕円曲線上の有理点とするとき、点 \(P\!*\!Q\) と \(\mathcal{O}\) を結ぶ直線が再び楕円曲線と交わる点を \(P+Q\) とする。つまり、
\(P+Q=(P\!*\!Q)*\mathcal{O}\)
とする。 |
|
図8:楕円曲線上の群演算 |
シルヴァーマン、テイト「楕円曲線論入門」より引用。零元の記号には、英大文字 \(O\) の筆記体 \(\mathcal{O}\) が使ってある。以下同様 |
零元
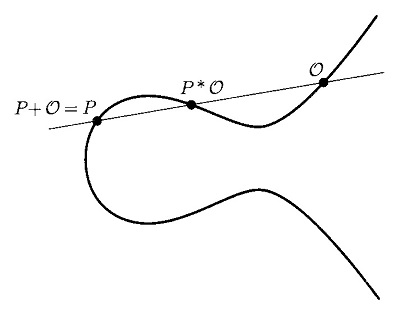
この演算における零元 \(\mathcal{O}\) が、群の零元の条件を満たしているかどうかを検証すると、
\(P+\mathcal{O}=(P*\mathcal{O})*\mathcal{O}=P\)
となって、零元の条件を満たしていることがわかります(図9)。もちろん、\(\mathcal{O}+P=P\) です。
|
図9:\(\bs{\mathcal{O}}\) が零元であることの検証 |
「楕円曲線論入門」より引用 |
逆元
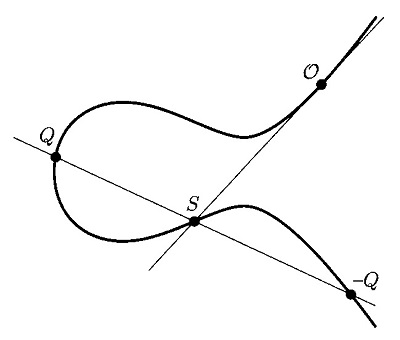
逆元は次のように定義します。零元 \(\mathcal{O}\) における接線が楕円曲線と交わる点を \(S\) とします。まず、
\(S=\mathcal{O}*\mathcal{O}\)
です。そして 点 \(Q\) と \(S\) を結ぶ直線が再び楕円曲線を交わる点を、\(Q\) の逆元(= \(-Q\))とします。つまり、
\(-Q=Q\!*\!S\)
です。このように定義すると
\(\begin{eqnarray}
&&Q+(-Q)&=(Q\!*\!(-Q))*\mathcal{O}\\
&&&=S*\mathcal{O}\\
&&&=\mathcal{O}\\
\end{eqnarray}\)
となり、群の逆元の条件を満たすことがわかります(図10)。\(S\) と \(\mathcal{O}\) を結ぶ直線は \(\mathcal{O}\) で2回交差するので、\(S*\mathcal{O}=\mathcal{O}\) です。
|
図10:点の逆元 |
「楕円曲線論入門」より引用 |
結合則
群を構成するためには、以上の群演算の定義が結合則を満たしていななければなりません。楕円曲線上に点 \(P\)、\(Q\)、\(R\) をとったとき、
\((P+Q)+R=P+(Q+R)\)
となるのが結合則ですが、
\((P+Q)+R=((P+Q)\!*\!R)*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
\(P+(Q+R)=(P\!*\!(Q+R))*\mathcal{O}\)
なので、
\((P+Q)\!*\!R=P\!*\!(Q+R)\)
が示せればよいことになります。「楕円曲線論入門」にはこのことを示した図が載っています(図11)。

|
図11:結合則の検証 |
「楕円曲線論入門」より引用 |
\((P+Q)\!*\!R\) の点と \(P\!*\!(Q+R)\) の点が、楕円曲線上で同一の点になることの証明は少々複雑なので「18. 結合則が成り立つことの検証と証明」にまわします。
以上のように楕円曲線上の有理点は、直線との交点を使って加法と逆元をうまく定義することで "群" になることがわかりました。ここで注意すべきは、零元は楕円曲線上の任意の有理点でよいことです。これを利用し「零元=無限遠点」としたのが、実用的に使われる楕円曲線上の加法群です。
無限遠点を零元とする加法群
以下では「対称点」という言葉を使いますが、
\(P=(x_p,\:y_p)\) とするとき、点 \((x_p,\:-y_p)\) を\(P\) の対称点と呼ぶ
ことにします。楕円曲線は \(x\) 軸について対称なので、点 \(P\) を \(x\) 軸で "折り返した" 点が \(P\) の対称点です。\(y=0\) となる点が楕円曲線上に1つ、または3つありますが、その点の対称点は同じ点です。
次に「\(y\) 軸方向の無限遠点」を導入し、「楕円曲線上の有理点と無限遠点を合わせた集合」に群を定義します。ここからは無限遠点を \(\mathcal{O}\) と書きます。
無限遠点は図に表せないのでイメージしにくいのですが、\(\bs{y}\) 軸方向の無限遠に \(\bs{\mathcal{O}}\) があると考えます。\(y\) 軸の正方向でも負の方向でもかまいません。
楕円曲線上の点 \(P\) を \(P=(x_p,\:y_p)\) とし、\(x_p\) をどんどん大きくすると、楕円曲線の式では \(x^3\) の項が支配的になるので、\(y_p^2=x_p^3\) と近似できます。つまり \(y_p=\pm x_p^{1.5}\) となり、\(x_p\) が大きいと \(y_p\) は \(y\) 軸の遙か上方(と下方)になります。この極限が無限遠点 \(\mathcal{O}\) と考えます。さらに、
楕円曲線上の任意の点 \(P\) を通る \(y\) 軸に平行な直線を引くと、その直線は \(P\) の対称点で楕円曲線と交差すると同時に、無限遠点 \(\mathcal{O}\) でも交差する
と考えます。この \(\bs{y}\) 軸方向の無限遠点 \(\bs{\mathcal{O}}\) を零元とする群を構成します。
群演算
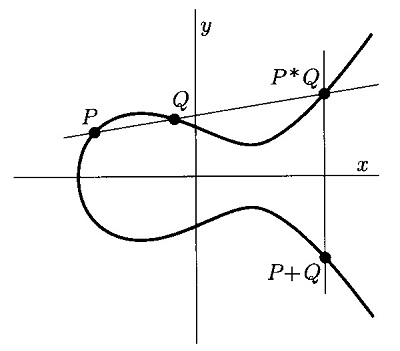
まず、群演算の加法ですが、
\(P+Q=P\!*\!Q\) の対称点
と定義します(図12)。
|
図12:加法則 |
「楕円曲線論入門」より引用 |
こうすると、\(P\!*\!Q\) と \(P+Q\) を結ぶ直線は \(y\) 軸と平行になり、それは無限遠点 \(\mathcal{O}\) で楕円曲線と交差します。つまり、
\(P+Q=(P\!*\!Q)*\mathcal{O}\)
です。この定義は 零元を楕円曲線上の点にとった図8と合致します。この加法の定義で \(\mathcal{O}\) が群の零元の要件を満たしているかを検証すると、
\(P+\mathcal{O}=(P*\mathcal{O})*\mathcal{O}=P\)
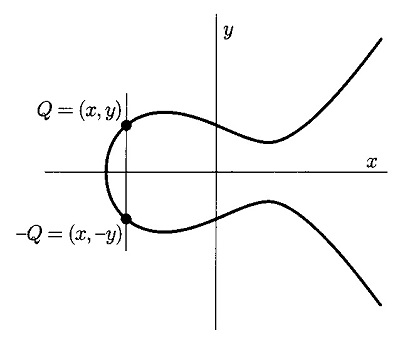
となって要件を満たしていることがわかります。\(P*\mathcal{O}\) は \(P\) の対称点ですが、\(P\) の対称点と \(\mathcal{O}\) を結ぶ直線が楕円曲線と交差する点は \(P\) なので上式が成立します。これは楕円曲線上に \(\mathcal{O}\) をとった図9と同じです。さらに逆元ですが、\(Q\) が楕円曲線上にあったとき、
\(Q\) の対称点が \(Q\) の逆元(\(-Q\) と表記)
と定義します(図13)。
|
図13:逆元 |
「楕円曲線論入門」より引用 |
こうすると、
\(\begin{eqnarray}
&&Q+(-Q)&=(Q\!*\!(-Q))*\mathcal{O}\\
&&&=\mathcal{O}*\mathcal{O}\\
\end{eqnarray}\)
となりますが、\(\mathcal{O}*\mathcal{O}=\mathcal{O}\)(=無限遠点の対称点は無限遠点)との自然な定義を行うと、
\(Q+(-Q)=\mathcal{O}\)
となって逆元の要件を満たします。結合則についても零元を楕円曲線上にとった場合(図11)と同じ様に成立します。「18. 結合則が成り立つことの検証と証明」でそのこと書きます。
射影平面
無限遠点は図で表現できず、何だか "怪しげな" 感じがしますが、数学的に厳密に定義できます。それには射影平面を使います。
平面 \((x,\:y)\) に対し、3つの数 \((X,\:Y,\:Z)\) で表される "平面" を射影平面と言います。3つの数がありますが3次元空間ではありません。ただし \((0,\:0,\:0)\) の点は除きます。また、
\(\lambda\neq0\)とするとき
\((X,\:Y,\:Z)\) と \((\lambda X,\lambda Y,\lambda Z)\) は同じものである(同値である)
\((X,\:Y,\:Z)\) と \((\lambda X,\lambda Y,\lambda Z)\) は同じものである(同値である)
と定義します。\(xy\) 平面から射影平面の対応は、
\((x,\:y)\longrightarrow(x,\:y,\:1)\)
とし、その逆の対応は、
\(Z\neq0\) のとき
\((X,\:Y,\:Z)\longrightarrow\left(\dfrac{X}{Z},\dfrac{Y}{Z}\right)\)
\((X,\:Y,\:Z)\longrightarrow\left(\dfrac{X}{Z},\dfrac{Y}{Z}\right)\)
です。この対応からわかるように、射影平面には \(xy\) 平面にない点が含まれています(\(Z=0\) の点)。
射影平面での楕円曲線の式は、\(xy\) 平面の楕円曲線の式で、\(x=\dfrac{X}{Z},\:\:y=\dfrac{Y}{Z}\) とおき、全体に \(Z^3\) をかけて同次化(=変数項の合計次数をそろえる)します。その結果、
\(Y^2Z=X^3+aXZ^2+bZ^3\)
の同次方程式が、射影平面での楕円曲線になります。ためしに、図2の楕円曲線(\(a=-2,\:b=1\))と \(y\) 軸との交点を計算してみると、\(xy\) 平面では、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3-2x+1&\\
&&x=0&\\
\end{eqnarray}
\end{array}\right.\)
の連立方程式を解いて、\((0,\pm1)\) となります。一方、射影平面では、\(x=0\) は \(X=0\) なので、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&Y^2Z=X^3-2XZ^2+Z^3&\\
&&X=0&\\
\end{eqnarray}
\end{array}\right.\)
が、楕円曲線と直線の交点を求める連立式になります。この解は、\(\al\) と \(\beta\) を \(0\) ではない数として、\((0,\al,\pm\al),\:(0,\beta,\:0)\) です。射影平面の同値関係を利用すると、
\((0,\:\pm1,\:1)\)
\((0,\:1,\:0)\)
\((0,\:1,\:0)\)
が楕円曲線と直線の交点になり、交点は3つあることになります。ここで \(xy\) 平面の交点には現れなかった \((0,\:1,\:0)\) が \(y\) 軸方向の無限遠点です。これを一般化すると次のようになります。つまり、楕円曲線と \(y\) 軸に平行な直線の式を、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3+ax+b&\\
&&x=c&\\
\end{eqnarray}
\end{array}\right.\)
とすると、これに対応する射影平面の式は、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&Y^2Z=X^3+aXZ^2+bZ^3&\\
&&X=cZ&\\
\end{eqnarray}
\end{array}\right.\)
です。\((0,\:1,\:0)\) はこの2式を必ず満たします。つまり全ての楕円曲線は \((0,\:1,\:0)\) を通り、全ての \(y\) 軸に平行な直線は \((0,\:1,\:0)\) を通る。従って、楕円曲線と\(y\) 軸に平行な直線は(\(y\) 軸方向の)無限遠点で交わることになります。
楕円曲線の計算には現れませんが、無限遠点にもいろいろあって、\((1,\:0,\:0)\) は \(x\) 軸方向の無限遠点、\((\al,\:\beta,\:0)\) は任意方向の無限遠点です(\(\al\)、\(\beta\) は \(0\) ではない数)。
\(xy\) 平面の2直線は、平行なときには交点がありませんが、射影平面の2直線は必ず1点で交わります。また射影平面の楕円曲線の1点を通る直線は、楕円曲線と必ず3点で交わります(直線が楕円曲線の接線の場合は、接点での交差数を2と数えます)。このように、交差を統一的に扱えるのが射影平面の特徴の一つです。
以上のような数学的裏付けのもとに導入したのが無限遠点です。これを \(xy\) 平面では、
| \(y\) 軸方向の無限遠のところに無限遠点 \(\mathcal{O}\) がある | |
| 楕円曲線は \(\mathcal{O}\) を通る | |
| \(y\) 軸に平行な直線は \(\mathcal{O}\) で楕円曲線と交わる |
とイメージしてよいわけです。
加法式・2倍式
楕円曲線上の加法を計算式で表します。楕円曲線上の3点を次のように定義します。
\(P_1+P_2=P_3\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とします。\(P_1\) と \(P_2\) を結ぶ直線を \(y=\lambda x+\mu\) とすると、連立方程式、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&y^2=x^3+ax+b&\\
&&y=\lambda x+\mu&\\
\end{eqnarray}
\end{array}\right.\)
の解が \(P_1,\:P_2,\:(x_3,-y_3)\) です。この2つの式から \(y\) を消去すると、
\(x^3+ax+b-(\lambda x+\mu)^2=0\)
が得られますが、この式は、
\((x-x_1)(x-x_2)(x-x_3)=0\)
と同一のはずです。そこで \(x^2\) の係数を比較すると、
\(-\lambda^2=-x_1-x_2-x_3\)
が得られます。つまり、
\(x_3=\lambda^2-x_1-x_2\)
となります。この \(x_3\) を直線の式に入れると、
\(-y_3=\lambda x_3+\mu\)
ですが、\(y_1=\lambda x_1+\mu\) なので \(\mu\) を消去すると、
\(y_3=-y_1+\lambda(x_1-x_3)\)
となります。これが基本の加法式です。これを \(P_1\) と \(P_2\) の配置パターンごとにまとめると、次の通りです。
\(x_1\neq x_2\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{y_2-y_1}{x_2-x_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
この場合は \(P_1\) と \(P_2\) を通る直線は \(P_1\) における楕円曲線の接線となり、直線の傾き \(\lambda\) は上の式のままでは計算できません。そこで \(y^2=x^3+ax+b\) を \(x\) で微分すると
\(2y\dfrac{dy}{dx}=3x^2+a\)
なので、
\(\lambda=\dfrac{3x_1^2+a}{2y_1}\)
となります。\(x_2\) を \(x_1\) に置き換えてまとめると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-2x_1&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{3x_1^2+a}{2y_1}&\\
\end{eqnarray}
\end{array}\right.\)
が \(P_1+P_1\) の計算式です。これは \(P_1\) の "2倍"(一般にはスカラー倍)であり、\(2P_1\) と書きます。
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
この場合、\(P_2=-P_1\) なので、定義により
\(P_1+P_2=\mathcal{O}\)
です。
なお、\(P_1\) と \(P_2\) は、楕円曲線の定義式、
\(y_1^2=x_1^3+ax_1+b\)
\(y_2^2=x_2^3+ax_2+b\)
\(y_2^2=x_2^3+ax_2+b\)
を満たしますが、この左辺と右辺のそれぞれを引き算すると、
\((y_1+y_2)(y_1-y_2)=\)
\((x_1-x_2)(x_1^2+x_1x_2+x_2^2)+a(x_1-x_2)\)
\((x_1-x_2)(x_1^2+x_1x_2+x_2^2)+a(x_1-x_2)\)
\(\begin{eqnarray}
&&\dfrac{y_1-y_2}{x_1-x_2}&=\dfrac{x_1^2+x_1x_2+x_2^2+a}{y_1+y_2}\\
&&&=\lambda\\
\end{eqnarray}\)
となって \(\lambda\) の別の表現が得られますが、これは \(x_1=x_2\) でも使えます。従って「加法式(第2形)」を次のようにも表現できます。
\(y_1+y_2\neq0\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{x_1^2+x_1x_2+x_2^2+a}{y_1+y_2}&\\
\end{eqnarray}
\end{array}\right.\)
\(y_1+y_2=0\) のとき
\(P_1+P_2=\mathcal{O}\)
楕円曲線の具体例
楕円曲線とその有理点、加法則の適用例として、整数係数の3つの楕円曲線を調べてみます。以後の記述では、\(P=(x,\:y)\) とするとき、\(nP,\:-P,\:-nP\) の記述を使いますが、それぞれの定義は、
\(\phantom{-}nP=\overbrace{P+P+\:\cd+P}^{n}\)
\(\phantom{n}-\!\!P=(x,-y)\)
\(-nP=\overbrace{(-P)+(-P)+\:\cd+(-P)}^{n}\)
\(\phantom{n}-\!\!P=(x,-y)\)
\(-nP=\overbrace{(-P)+(-P)+\:\cd+(-P)}^{n}\)
です。また、\(nP=(x_n,\:y_n)\) とすると、加法の定義から \(-nP=(x_n,-y_n)\) です。
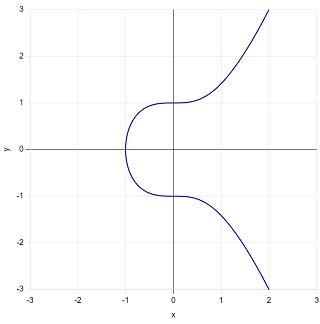
\(y^2=x^3+1\)
|
図14:楕円曲線の例1 \(y^2=x^3+1\) |
この楕円曲線上の有理点は、次の5つの整点(= 座標値が整数の点)です。
\(P_1=(\phantom{-}2,\phantom{-}3)\)
\(P_2=(\phantom{-}0,\phantom{-}1)\)
\(P_3=(-1,\phantom{-}0)\)
\(P_4=(\phantom{-}0,-1)\)
\(P_5=(\phantom{-}2,-3)\)
\(P_2=(\phantom{-}0,\phantom{-}1)\)
\(P_3=(-1,\phantom{-}0)\)
\(P_4=(\phantom{-}0,-1)\)
\(P_5=(\phantom{-}2,-3)\)
ここで、群の演算式を使って \(nP_1\) を計算してみると、
\(2P_1=(\phantom{-}0,\phantom{-}1)=P_2\)
\(3P_1=(-1,\phantom{-}0)=P_3\)
\(4P_1=(\phantom{-}0,-1)=P_4\)
\(5P_1=(\phantom{-}2,-3)=P_5\)
\(6P_1=\mathcal{O}\)
\(3P_1=(-1,\phantom{-}0)=P_3\)
\(4P_1=(\phantom{-}0,-1)=P_4\)
\(5P_1=(\phantom{-}2,-3)=P_5\)
\(6P_1=\mathcal{O}\)
となります。\(P_1\) は 6倍する(= 6個加算する)と \(\mathcal{O}\)(=零元)になる。このことを「\(P_1\) の位数(order)が \(6\) である」と言います。また、
\(3(P_2)=3(2P_1)=6P_1=\mathcal{O}\)
なので、\(P_2\) の位数は \(3\) です。同様にして、\(P_3\)~\(P_5\) の位数はそれぞれ \(2,\:\:3,\:\:6\) になります。
楕円曲線 \(y^2=x^3+1\) の有理点は \(P_1\)~\(P_5\) の点しかありません。また位数が有限値なので、これらは有限位数の点です。これらの点と 零元 \(\mathcal{O}\) を合わせて群を構成します。
しかし楕円曲線上の有理点が有限位数をもつとは限りません。それが次の例です。
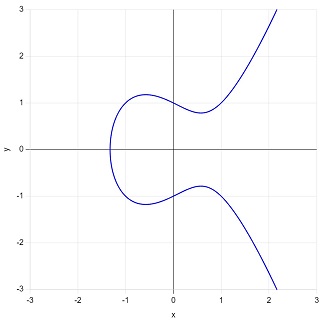
\(y^2=x^3-x+1\)
|
図15:楕円曲線の例2 \(y^2=x^3-x+1\) |
方程式 \(y^2=x^3-x+1\) の整数解を調べると、手計算で \((-1,\pm1),\) \((0,\pm1),\) \((1,\pm1),\) \((3,\pm5),\) \((5,\pm11)\) の\(10\)個の解が容易に見つかります。今、\(P_1=(1,\:1)\) とし、\(nP_1\) を順に計算してみると、次のようになります。
\(\begin{eqnarray}
&&\phantom{1}1P_1&=(\phantom{-}1,\phantom{-}1)\\
&&\phantom{1}2P_1&=(-1,\phantom{-}1)\\
&&\phantom{1}3P_1&=(\phantom{-}0,-1)\\
&&\phantom{1}4P_1&=(\phantom{-}3,-5)\\
&&\phantom{1}5P_1&=(\phantom{-}5,\,\,11)\\
&&\phantom{1}6P_1&=\left(\phantom{-}\dfrac{1}{4},\phantom{-}\dfrac{7}{8}\right)\\
&&\phantom{1}7P_1&=\left(-\dfrac{11}{9},-\dfrac{17}{27}\right)\\
&&\phantom{1}8P_1&=\left(\phantom{-}\dfrac{19}{25},-\dfrac{103}{125}\right)\\
&&\phantom{1}9P_1&=(56,-419)\\
&&10P_1&=\left(\dfrac{159}{121},\dfrac{1861}{1331}\right)\\
&&&=\left(\dfrac{3\cdot53}{11^2},\dfrac{1861}{11^3}\right)\\
&&&\fallingdotseq(1.31405,1.39820)\\
&&11P_1&=\left(-\dfrac{255}{361},\dfrac{7981}{6859}\right)\\
&&&=\left(-\dfrac{3\cdot5\cdot17}{19^2},\dfrac{23\cdot347}{19^3}\right)\\
&&&\fallingdotseq(-0.70637,1.16358)\\
&&12P_1&=\left(-\dfrac{223}{784},-\dfrac{24655}{21952}\right)\\
&&&=\left(-\dfrac{223}{2^4\cdot7^2},-\dfrac{5\cdot4931}{2^6\cdot7^3}\right)\\
&&&\fallingdotseq(-0.28444,-1.12313)\\
&&13P_1&=\left(\dfrac{5665}{2809},-\dfrac{399083}{148877}\right)\\
&&&=\left(\dfrac{5\cdot11\cdot103}{53^2},-\dfrac{43\cdot9281}{53^3}\right)\\
&&&\fallingdotseq(2.01673,-2.68062)\\
&&14P_1&=\left(\dfrac{26239}{2601},\dfrac{4231459}{132651}\right)\\
&&&=\left(\dfrac{19\cdot1381}{3^2\cdot17^2},\dfrac{4231459}{3^2\cdot17^2}\right)\\
&&&\fallingdotseq(10.08804,31.89919)\\
&&15P_1&=\left(\dfrac{23464}{49729},\dfrac{8824453}{11089567}\right)\\
&&&=\left(\dfrac{2^3\cdot7\cdot419}{223^2},\dfrac{11\cdot59\cdot13597}{223^2}\right)\\
&&&\fallingdotseq(0.47183,0.79574)\\
\end{eqnarray}\)
途中で \((56,-419)\) という、手計算では分からない整点が現れました。計算してみると、
\(56^3-56+1=175561=419^2\)
となって、確かにこれが楕円曲線上の点であることが分かります。\(15P_1\) までの結果を掲げましたが、この計算は \(\mathcal{O}\)(= 零元)で終わることがなく、無限に続きます。つまり、\(P_1=(1,\:1)\) は無限位数の点です。
さらに、同様の計算を\(-P_1=(1,-1)\) から始めると、\(y\) 座標の符号が逆転した点列、\(-nP_1\) が得られます。そして実は、
楕円曲線 \(y^2=x^3-x+1\) の有理点の全ては、
\(mP_1\)(\(m\)は正負の整数)
の形で表現できることが分かっています。\(0P_1=\mathcal{O}\) と定義すれば、楕円曲線で定義された加法群の元は \(mP_1\)(\(m\) は整数)の形で表現できるとも言えます。この性質を有限生成と言い、\(P_1\) を生成元(generator)と呼びます。一般には、生成元は複数個あります。つまり楕円曲線上の有理点は \(r\) 個の有理点 \(Q_i\) を使って、
\(m_1Q_1+m_2Q_2+\:\cd+m_rQ_r\)
の形で表現できます。この \(r\) を楕円曲線の階数(rank)と言います。なお、有限個の有理点しかもたない 図14 のような楕円曲線の階数は \(0\) とします。
楕円曲線 \(y^2=x^3-x+1\) の階数は \(1\) です。そして今までの結果から、階数が \(1\) の楕円曲線の有理点と零点 \(\mathcal{O}\) は、加法に関して整数(= 正の自然数と負の自然数と \(0\))と全く同じ構造をもつことが分かります。ただ、楕円曲線の有理点の加法は普通の整数の加法よりよほど複雑な演算です。これが楕円曲線暗号を作るときの基礎となっています。
\(y^2=x^3-4x+1\)
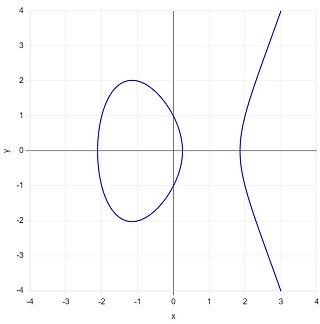
|
図16:楕円曲線の例3 \(y^2=x^3-4x+1\) |
この楕円曲線の階数は \(2\) です。従って生成元は2つで、
\(P_1=(0,\:1)\)
\(P_2=(3,\:4)\)
\(P_2=(3,\:4)\)
です。曲線上には無限個の有理点がありますが、すべてはこの2つの生成元から「有限生成」されます。無限個の有理点のうち、生成元を含めて 22個が整点ですが(\(y\) 座標の正負を無視すると 11個)、もちろんそれらの整点も生成元で表現できます。実際に計算してみると以下の通りです。
\(\phantom{9}P_1+\phantom{9}P_2=(-2,\:1)\)
\(2P_1\,\,\,\phantom{+9P_2}=(4,\:7)\)
\(2P_1-\phantom{9}P_2=(114,-1217)\)
\(2P_1+\phantom{9}P_2=(2,-1)\)
\(2P_1+2P_2=(20,-89)\)
\(3P_1+\phantom{9}P_2=(-1,-2)\)
\(4P_1+\phantom{9}P_2=(10,-31)\)
\(4P_1+2P_2=(12,\:41)\)
\(8P_1+3P_2=(1274,-45473)\)
\(2P_1\,\,\,\phantom{+9P_2}=(4,\:7)\)
\(2P_1-\phantom{9}P_2=(114,-1217)\)
\(2P_1+\phantom{9}P_2=(2,-1)\)
\(2P_1+2P_2=(20,-89)\)
\(3P_1+\phantom{9}P_2=(-1,-2)\)
\(4P_1+\phantom{9}P_2=(10,-31)\)
\(4P_1+2P_2=(12,\:41)\)
\(8P_1+3P_2=(1274,-45473)\)
もちろん、計算していくと上記の整点だけでなく有理点が次々と生成され、それが無限に続きます。上の計算で \(P_1,\:P_2\) の符号を逆転させると \(y\) 座標の符号が逆の整点が得られます。たとえば、
\(-2P_1-P_2=(2,\:1)\)
\(-2P_1+P_2=(114,\:1217)\)
\(-2P_1+P_2=(114,\:1217)\)
です。以上を含めてこの楕円曲線の整点は、
\((-2,\pm1),\) \((-1,\pm2),\) \((0,\pm1),\) \((2,\pm1),\) \((3,\pm4),\) \((4,\pm7),\) \((10,\pm31),\) \((12,\pm41),\) \((20,\pm89),\) \((114,\pm1217),\) \((1274,\pm45473)\)
となります。最大の整点は \((1274,\pm45473)\) ですが、実際に計算してみると、
\(1274^3-4\cdot1274+1\)
\(=2067793729\)
\(=37^2\cdot1229^2\)
\(=45473^2\)
\(=2067793729\)
\(=37^2\cdot1229^2\)
\(=45473^2\)
となって、楕円曲線上の点であることが確認できます。この最大の整点を2つの生成元に分けて、それぞれを計算してみると、
\(\begin{eqnarray}
&&8P_1&=\left(\dfrac{59965740}{625681},\dfrac{464259138209}{494913671}\right)\\
&&&=\left(\dfrac{2^2\cdot3^2\cdot5\cdot79\cdot4217}{7^2\cdot113^2},\dfrac{455419\cdot1019411}{7^3\cdot113^3}\right)\\
&&3P_2&=\left(\dfrac{130403}{2209},-\dfrac{47063372}{103823}\right)\\
&&&=\left(\dfrac{7\cdot13\cdot1433}{47^2},-\dfrac{2^2\cdot353\cdot33331}{47^3}\right)\\
\end{eqnarray}\)
となりますが、この2つの有理点を楕円曲線の加法式で \(8P_1+3P_2\) とすると整点である \((1274,\:-45473)\) が現れるのも不思議な感じがします。
以上の「楕円曲線の有理点から成る加法群」を踏まえ、これ以降は楕円曲線暗号で使われる「有限体上の楕円曲線による加法群」に移ります。
有限体上の楕円曲線による加法群
以降に出てくる有限体 \(\bs{F}_p\) と 乗法群 \(\bs{F}_p^{*}\) については、No.313「高校数学で理解する公開鍵暗号の数理:10. 有限体と乗法群」 で定義したものです。
楕円曲線暗号に使われる楕円曲線は、有限体 \(\bs{F}_p\) で定義された "曲線" で、次の式を満たすものです。
\(y^2=x^3+ax+b\)
\((4a^3+27b^2\neq0)\)
\((4a^3+27b^2\neq0)\)
\(x\)、\(y\)、\(a\)、\(b\) は全て \(\bs{F}_p\) の元です。「この式を満たす全ての \((x,\:y)\) と 零点 \(\mathcal{O}\) の集合」に対して演算を定義して群を構成します。演算を加法と考えて \(+\) と書きます。この "曲線" 上の3点を、
\(P_1+P_2=P_3\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
\(P_1=(x_1,\:y_1)\)
\(P_2=(x_2,\:y_2)\)
\(P_3=(x_3,\:y_3)\)
とするとき、群の演算式は次のように定義されます。
\(x_1\neq x_2\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-x_1-x_2&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{y_2-y_1}{x_2-x_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1=y_2\neq0\) のとき
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_3=\lambda^2-2x_1&\\
&&y_3=\lambda(x_1-x_3)-y_1&\\
&&\lambda=\dfrac{3x_1^2+a}{2y_1}&\\
\end{eqnarray}
\end{array}\right.\)
\(x_1=x_2,\:y_1\neq y_2\) のとき、あるいは \(y_1=y_2=0\) のとき
\(P_1+P_2=\mathcal{O}\)
つまり、実数平面の有理点と無限遠点(=零元)で構成された群の演算式と全く同じです。もちろん加減乗除は \(\bs{F}_p\) で行います。これが群になる理由は、有理数体(有理数全体の集合)も有限体 \(\bs{F}_p\) も「体」であり、加減乗除は全く同一形式で記述できるからです。ただ、有理数体と違って \(\bs{F}_p\) の元の数は有限個であり、群の元の数も有限個(=有限群)です。以降、\(\bs{\bs{F}_p}\) 上の楕円曲線、\(\bs{y^2=x^3+ax+b}\) による有限群を \(\bs{E(a,\:b,\:p)}\) と表記します。
\(\bs{F}_p\) 上の楕円曲線は、もはや "曲線" の形をしていませんが、これを可視化した図を次に示します。有限体 \(F_{109}\) 上の "楕円曲線"、\(y^2=x^3+2x+4\) の例です。
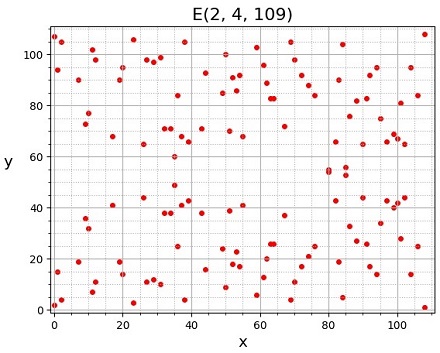
|
図17:有限体上の "楕円曲線" \(E(2,\:4,\:109)\) \(F_{109},\:\:\:y^2=x^3+2x+4\) |
赤丸が "楕円曲線上の点" を表し、計 \(126\) 個ある。零元(無限遠点 \(\mathcal{O}\))と合わせて群の元の総数は \(127\)(=素数)である。このような、群位数が素数の楕円曲線を利用して暗号を構成できる(次回参照)。 |
以上が「有限体上の楕円曲線が作る加法群」で、楕円曲線暗号はこの加法群で構成されます。その話を次回にします。
(次回に続く)
2021-07-11 08:37
nice!(0)




