No.355 - 高校数学で理解するガロア理論(2) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
「2.整数の群」「3.多項式と体」「4.一般の群」の3つの章は、第5章以下のガロア理論の核心に入るための準備です。
第2章の目的は2つあり、一つは整数を素材にして「群」と、それに関連した「剰余類」「剰余群」「既約剰余類」など、ガロア理論の理解に必要な概念を説明することです。
もう一つは、第2章の最後にある「既約剰余類群は巡回群の直積と同型である」という定理を証明することです。この定理はガロア理論の最終段階(6.可解性の必要条件)で必要なピースになります。
まず、"整数の群" に入る前に、整数論の基礎ともいえる「ユークリッドの互除法」「不定方程式」「法による演算」「中国剰余定理」から始めます。これらは後の定理の証明にしばしば使います。
2.1 整数
ユークリッドの互除法
自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,\:b)\) で表す。自然数 \(a\) を \(b\) で割った余りを \(r\) とすると、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
[証明]
記述を簡略化するため、最大公約数を、
\(\mr{gcd}(a,\:b)=x\)
\(\mr{gcd}(b,\:r)=y\)
で表す。\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とすると、
\(a=pb+r\) \((0\leq r < b)\)
と書ける。\(a\) と \(pb\) は \(x\) で割り切れるから、\(r\) も \(x\) で割り切れる。つまり \(x\) は \(r\) の約数である。\(x\) は \(b\) の約数でもあるから、\(x\) は \(b\) と \(r\) の公約数である。公約数は \(b\) と \(r\) の最大公約数 \(y\) 以下だから、
\(x\leq y\)
である。
一方、\(pb\) と \(r\) は \(y\) で割り切れるから、\(y\) は \(a\) の約数である。\(y\) は \(b\) の約数でもあるから、\(y\) は \(a\) と \(b\) の公約数である。公約数は \(a\) と \(b\) の最大公約数以下だから、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので \(x=y\)、つまり、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。[証明終]
この原理を利用して \(\mr{gcd}(a,\:b)\) を求めることができます。もし \(a\) が \(b\) で割り切れるなら \(\mr{gcd}(a,\:b)=b\) です。そうでないなら、\(a\) を \(b\) で割った余り \(r\) を求め、
新 \(a\:\longleftarrow\:b\)
新 \(b\:\longleftarrow\:r\)
と定義し直して、\(a\) が \(b\) で割り切れるかどうかを見ます。こうして次々と \(a\) と \(b\) のペアを作っていけば(=互除法)、\(b\) は単調減少していくので、いずれ \(a\) が \(b\) で割り切れるときがきます。なかなか割り切れなくても、\(b\) が \(1\) までくると絶対に割り切れる。つまり、
\(\mr{gcd}(a,\:b)=b\)
となるのが最終段階で、そのときの \(b\) が最大公約数です。\(b\) が \(1\) までになってしまったら、最大公約数は \(\bs{1}\)、つまり \(\bs{a}\) と \(\bs{b}\) は互いに素です。
ちなみに、ユークリッドの互除法で a と b の最大公約数を求める関数 EUCLID を Python で記述すると次のようになります。
% は Python の剰余演算子で、a % b は「a を b で割った余り」の意味です(定理の記述では \(r\))。つまり、このコードは、
gcd( a, b )=gcd( b, a % b )
という互除法の原理(21A)をストレートに書いたものです(a と b の大小に関係なく動作します)。こういったアルゴリズムはプログラミング言語で記述した方がシンプルでわかりやすくなります。
互除法は多項式の演算にも適用できます。多項式は整数と同じように割り算はできませんが余り算はできるからです。多項式の性質を理解するときに互除法は必須になります。
1次不定方程式
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
[証明]
1次不定方程式が整数解を持つとしたら、方程式の左辺は \(d\) で割り切れる、つまり \(d\) の倍数だから、右辺の \(c\) も \(d\) の倍数である。このことの対偶は「\(c\) が \(d\) の倍数でなければ方程式は整数解を持たない」なので、題意の「そうでなければ整数解を持たない」が証明されたことになる。従って以降は「\(c=kd\) (\(k\) は整数)と表せるなら方程式は整数解を持つ」ことを証明する。まず、変数が2つの場合である。
係数の \(a\) と \(b\) に互除法(21A)を適用し、それと同時に \(x,\:y\) の変数を変換して方程式を変形していく。まず、\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とする。
\(a=pb+r\)
である。互除法の次のステップの係数と変数を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1=b&\\
&&b_1=r&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_1=px+y&\\
&&y_1=x&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(x,\:y\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x=y_1&\\
&&y=x_1-py_1&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(\begin{eqnarray}
&&\:\:a_1x_1+b_1y_1&=b(px+y)+rx\\
&&&=pbx+by+rx\\
&&&=(pb+r)x+by\\
&&&=ax+by\\
\end{eqnarray}\)
と計算できるので、不定方程式は、
\(a_1x_1+b_1y_1=c\)
となり、係数の値がより小さい方程式に変形できる。互除法の原理(21A)により、\(a_1\) と \(b_1\) の最大公約数は \(d\) のままである。この方程式の \(x_1,\:y_1\) が求まれば、\(\br{③}\) を使って \(x,\:y\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i\) を \(b_i\) で割った商と余りを、
\(a_i=p_ib_i+r_i\)
のように求め、互除法の次のステップを、
\(a_{i+1}=b_i\)
\(b_{i+1}=r_i\)
\(x_{i+1}=p_ix_i+y_i\)
\(y_{i+1}=x_i\)
とすることで続けていける。このように、係数に互除法の適用を繰り返し、同時に変数を変換していく。そして互除法の最終段階で、
\(a_nx_n+b_ny_n=c\)
となったとする。この段階では \(a_n\) は \(b_n\) で割り切れ、そのときの \(b_n\) は最大公約数 \(d\) である。つまり。
\(a_nx_n+dy_n=c\)
である。もし \(c\) が \(d\) の倍数であれば、つまり \(c=kd\) (\(k\) は整数)なら、
\(x_n=0\)
\(y_n=k\)
という整数解を必ずもつ。従って、変数の変換過程を逆にたどって \(x,\:y\) が求まる。以上で2変数の場合に題意が正しいことが証明でき、同時に1次不定方程式の解を求めるアルゴリズムも明らかになった。
ちなみに、一次不定方程式の解の一つを求めるアルゴリズムを Python の関数で記述すると、次のようにシンプルです。
数学的帰納法を使って、3変数以上の場合を証明する。\(n=2\) の場合に成り立つことを示したので、\(n=k\) の場合に成り立つと仮定する。つまり、
と仮定する。\(n=k+1\) の場合の不定方程式を、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k+a_{k+1}x_{k+1}=c_{k+1}\)
\(\begin{eqnarray}
&&\:\: d_k&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\\
&&\:\: d_{k+1}&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k,\:a_{k+1})\\
\end{eqnarray}\)
とし、この方程式が整数解をもつ条件を調べる。方程式を移項すると、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_{k+1}-a_{k+1}x_{k+1}\)
となるが、この不定方程式が整数解をもつのは、数学的帰納法の仮定によって、
左辺\(=d_k\) の整数倍
のときである。つまり、
\(c_{k+1}-a_{k+1}x_{k+1}=d_k\cdot y\)
という、2つの変数 \(x_{k+1},\:y\) の不定方程式が整数解をもつときである。式を移項すると、
\(a_{k+1}x_{k+1}+d_k\cdot y=c_{k+1}\)
であるが、これは証明済みの \(n=2\) のときの定理によって、
\(c_{k+1}=m\cdot\mr{gcd}(d_k,\:a_{k+1})\) (\(m\) は整数)
の場合に整数解をもつ。ここで、
\(\mr{gcd}(d_k,\:a_{k+1})=d_{k+1}\)
なので、
\(c_{k+1}=m\cdot d_{k+1}\) (\(m\) は整数)
の場合にのみ、\(n=k+1\) の不定方程式は整数解をもつことになる。
つまり、\(n=k\) のときに題意が成り立つと仮定すると、\(n=k+1\) のときにも成り立つ。\(n=2\) のときには成り立つから、\(n\geq3\) でも成り立つ。[証明終]
重要なのは、係数が互いに素な場合です。不定方程式の解の存在(21B)から、次の定理がすぐに出てきます。
\(0\) でない整数 \(a\) と \(b\) が互いに素とすると、1次不定方程式、
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) の最大公約数が \(1\)、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
互除法と同じように、不定方程式の解の存在定理 (21B)と(21C)も、多項式の性質を理解する上で重要です。
法による演算
\(a,\:b\) を整数、\(n\) を自然数とする。\(a\) を \(n\) で割った余りと、\(b\) を \(n\) で割った余りが等しいとき、
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
法による演算の規則は、さまざまありますが、主なものは次の通りです。このような演算を以降の説明で適時使います。
\(a,\:b,\:c,\:d\) を整数、\(n,r\) を自然数とし、
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
である。
中国剰余定理
\(n_1\) と \(n_2\) を互いに素な自然数とする。\(a_1\) と \(a_2\) を、\(0\leq a_1 < n_1,\:0\leq a_2 < n_2\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
[証明]
もし \(x\) と \(y\:\:(y\leq x)\) が連立方程式を満たすとすると、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(y\equiv a_1\:\:(\mr{mod}\:n_1)\)
なので、
\(x-y\equiv0\:\:(\mr{mod}\:n_1)\)
であり、\(x-y\) は \(n_1\) で割り切れる。同様にして \(x-y\) は \(n_2\) でも割り切れる。\(n_1\) と \(n_2\) は互いに素なので、\(x-y\) は \(n_1n_2\) で割り切れる。従って \(x-y\) は \(n_1n_2\) の倍数であり、
である。従って連立方程式に解があるとしたら \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり \(0\leq x < n_1n_2\) の範囲で唯一に決まる。
\(n_1,\:n_2\) は互いに素なので、不定方程式の解の存在定理(21C)により、
\(n_1m_1+n_2m_2=1\)
を満たす \(m_1,\:m_2\) が存在する。ここで、
\(x=a_2n_1m_1+a_1n_2m_2\)
とおくと、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2n_1m_1+a_1(1-n_1m_1)\\
&&&=a_1+n_1m_1(a_2-a_1)\\
&&&\equiv a_1\:\:(\mr{mod}\:n_1)\\
\end{eqnarray}\)
であり、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2(1-n_2m_2)+a_1n_2m_2\\
&&&=a_2+n_2m_2(a_1-a_2)\\
&&&\equiv a_2\:\:(\mr{mod}\:n_2)\\
\end{eqnarray}\)
なので、\(x\) は連立方程式の解である。この解は、上での証明のとおり \(\mr{mod}\:n_1n_2\) でみて唯一である。[証明終]
中国剰余定理は3数以上に拡張できて、次が成り立ちます。
\(n_1,\:n_2,\:\cd\:,\:n_k\) を、どの2つをとっても互いに素な自然数とする。\(a_i\) を \(0\leq a_i < n_i\:\:(1\leq i\leq k)\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
[証明]
自然数 \(N\) を
\(N=n_1n_2\cd n_k\)
と定義する。
\(\mr{gcd}\left(\dfrac{N}{n_i},n_i\right)=1\:\:\:(1\leq i\leq k)\)
なので、不定方程式の解の存在の定理(21C)により、
\(\dfrac{N}{n_i}s_i+n_it_i=1\:\:\:(1\leq i\leq k)\)
を満たす整数解、\(s_i,\:t_i\:\:(1\leq i\leq k)\) が存在する。
\(x=\displaystyle\sum_{i=1}^{k}a_i\dfrac{N}{n_i}s_i\)
と定義すると、\(j\neq i\) である \(j\) について、
\(\dfrac{N}{n_j}\equiv0\:\:(\mr{mod}\:n_i)\)
だから、\(\mr{mod}\:n_i\) でみると、\(x\) を定義する総和記号のなかは \(i\) の項だけが残る。つまり、
\(\begin{eqnarray}
&&\:\:x&\equiv a_i\dfrac{N}{n_i}s_i\:\:(\mr{mod}\:n_i)\\
&&&=a_i(1-n_it_i)\\
&&&\equiv a_i\:\:(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となって、\(x\) は連立合同方程式の解である。
連立合同方程式に2つの解、\(x,\:y\) があったとすると、
\(\begin{eqnarray}
&&\:\:x-y&\equiv a_i-a_i &(\mr{mod}\:n_i)\\
&&&=0 &(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となり、\(x-y\) は \(n_i\) の倍数である。これは \(1\leq i\leq k\) のすべての \(i\) で成り立ち、また \(n_i\:\:(1\leq i\leq k)\) は、どの2つをとっても互いに素である(=共通な因数が全くない)から、\(x-y\) は \(N\) の倍数である。従って、
\(x\equiv y\:\:(\mr{mod}\:N)\)
であり、\(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。[証明終]
2.2 群
これ以降、整数を素材に「群」と、それに関連した概念の説明をします。まず、群の定義からです。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群(group)であると言う。
整数 \(\bs{Z}\)
整数の集合を \(\bs{Z}\) と書きます。\(\bs{Z}\) は「加法(足し算)を演算とする群」になります。単位元は \(0\) で、元 \(x\) の逆元は \(-x\) です。この群の元の数は無限なので「無限群」です。
整数の加法は、\(x+y=y+x\) と演算の順序を入れ替えることができます。このような群が可換群です。アーベル群とも言います。
なお、有理数は \(\bs{Q}\)、実数は \(\bs{R}\)、複素数は \(\bs{C}\) で表しますが、\(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) は、\(\bs{Z}\) を同じように加法に関して群です(=加法群)。と同時に \(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) から加法の単位元 \(0\) を除くと、乗法に関しても群になります。その単位元は \(1\) です。
部分群 \(n\bs{Z}\)
群 \(G\) の部分集合 \(H\) が、\(G\) と同じ演算で群としての定義を満たすとき、\(H\) を部分群(subgroup)と言います。
\(G\) の単位元 \(e\) だけから成る部分集合 \(\{\:e\:\}\) は群としての定義を満たし、部分群です。また \(G\) そのものも "\(G\)の部分集合" であり、部分群です。これらを \(G\) の自明な部分群と言います。
\(\bs{Z}\) の元の一つを \(n\) とし(\(n\neq0\))、\(n\) の倍数の集合を \(n\bs{Z}\) と表記します。\(n\bs{Z}\) は加法を演算として群の定義を満たすので、\(\bs{Z}\) の部分群です。\(n\bs{Z}\) も無限群かつ可換群です。たとえば \(n=6\) とすると、
\(6\bs{Z}=\{\cd,\:-6,\:0,\:6,\:12,\:18,\:\cd\}\)
です。
剰余類と剰余群
部分群を用いて、元の数が有限個である有限群を作ることができます。一般に、群 \(G\) の部分群を \(H\) とするとき(演算を "\(\cdot\)" とします)、\(G\) の任意の元 \(g\) を取り出して、
\(g\cdot H\)
とした集合を剰余類(coset / residue class)と言います。これは「\(g\) と、集合 \(H\) のすべての元を演算した結果の集合」の意味です。
\(\bs{Z}\) と その部分群 \(6\bs{Z}\) を例にとると、\(\bs{Z}\) の任意の元を \(i\) として、
\(i+6\bs{Z}\)
が剰余類です。具体的にその集合を書くと、
\(\vdots\)
\(0+6\bs{Z}=\{\cd,\:-6,\:\:0,\:\phantom{1}6,\:12,\:18,\:\cd\}\)
\(1+6\bs{Z}=\{\cd,\:-5,\:\:1,\:\phantom{1}7,\:13,\:19,\:\cd\}\)
\(2+6\bs{Z}=\{\cd,\:-4,\:\:2,\:\phantom{1}8,\:14,\:20,\:\cd\}\)
\(3+6\bs{Z}=\{\cd,\:-3,\:\:3,\:\phantom{1}9,\:15,\:21,\:\cd\}\)
\(4+6\bs{Z}=\{\cd,\:-2,\:\:4,\:10,\:16,\:22,\:\cd\}\)
\(5+6\bs{Z}=\{\cd,\:-1,\:\:5,\:11,\:17,\:23,\:\cd\}\)
\(6+6\bs{Z}=\{\cd,\:\phantom{-}0,\:\:6,\:12,\:18,\:24,\:\cd\}\)
\(7+6\bs{Z}=\{\cd,\:\phantom{-}1,\:\:7,\:13,\:19,\:25,\:\cd\}\)
\(\vdots\)
などです。以降、剰余類 \(i+6\bs{Z}\) を \(\ol{\,i\,}\) と記述します。つまり、
\(\ol{\,i\,}=i+6\bs{Z}\)
です。上の表示を見ると分かるように、たとえば \(\ol{\,1\,}\) と \(\ol{\,7\,}\) は集合として同じものです。さらに、
\(\cd=\ol{-11}=\ol{-5}=\ol{\,1\,}=\ol{\,7\,}=\ol{13}=\cd\)
であり、これらは同じ集合です。これらの集合の中から一つの元を選んで「代表元」と呼ぶことにします。以降、分かりやすいように \(1\) を代表元とします。その他の剰余類についても同じようにすると、部分群 \(6\bs{Z}\) による剰余類は、
\(\ol{\,0\,},\:\ol{\,1\,},\:\ol{\,2\,},\:\ol{\,3\,},\:\ol{\,4\,},\:\ol{\,5\,}\)
の6つで表されることになります。これらの剰余類には重複がありません。また、全部の和集合をとると \(\bs{Z}\) になります。記号で書くと、\(\phi\) を空集合として、
\(\ol{\,i\,}\:\cap\:\ol{\,j\,}\:=\:\phi\:\:(0\leq i,\:j\leq6,\:i\neq j)\)
\(\bs{Z}=\ol{\,0\,}\:\cup\:\ol{\,1\,}\:\cup\:\ol{\,2\,}\:\cup\:\ol{\,3\,}\:\cup\:\ol{\,4\,}\:\cup\:\ol{\,5\,}\)
です。別の見方をすると、\(i,\:j\) を任意の整数するとき、
と言えます。平たく言うと、\(n\)(上の例では \(6\))で割った余りが同じ整数を集めたものが剰余類です。"剰余" という用語はそこからきています。
剰余類のうち、\(\ol{\,0\,}\) は \(\bs{Z}\) の部分群ですが、\(\ol{\,i\,}\:(i\neq0)\) の集合は \(\bs{Z}\) の部分群ではありません。集合の元と元のたし算が集合を "はみ出す" からです。しかし、剰余類同士の演算(=集合と集合の演算)を定義することにより、剰余類を元とする群を構成できます。それが次です。
剰余類に加算を定義できます。つまり、\(\ol{\,i\,}+\ol{\,j\,}\) を、
\(\ol{\,i\,}+\ol{\,j\,}=\ol{(\:i+j\:)}\) (右辺の \(+\) は整数の加算)
と定義すると、この演算の定義で剰余類は群になり、
\(\bs{Z}/n\bs{Z}\)
と表します。この群の元は集合(=剰余類)です。この群を剰余群(あるいは商群。quotient group)と言います。元の数は有限なので有限群です。また演算が整数の加算なので可換であり、「有限可換群」です。
一般に、有限群 \(G\) の元の数を群の位数(order)と呼び、
\(|G|\) あるいは \(\#G\)
で表します。剰余群では、
です。
生成元と巡回群
剰余群 \(\bs{Z}/n\bs{Z}\) は、元 \(\ol{\,1\,}\) だけをもとに群演算を繰り返すことによって、すべての元を作り出すことができます。\(\bs{Z}/6\bs{Z}\) を例にとると、
\(\ol{\,2\,}=\ol{\,1\,}+\ol{\,1\,}\)
\(\ol{\,3\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
などであり
\(\ol{\,0\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
です。群にこのような元がある場合、それを生成元(generator)と呼びます。\(\bs{Z}/6\bs{Z}\) の場合は \(\ol{\,1\,}\) のほかに \(\ol{\,5\,}\) も生成元です。\(\ol{\,i\,}\) を \(k\) 個加算することを、\(k\cdot\ol{\,i\,}\) と書くことにします。
\(k\cdot\ol{\,i\,}=\overbrace{\ol{\,i\,}+\ol{\,i\,}+\cd+\ol{\,i\,}}^{k\:個加算}\)
です。\(\ol{\,5\,}\) については、
\(1\cdot\ol{\,5\,}=\ol{\,5\,},\:\:2\cdot\ol{\,5\,}=\ol{\,4\,},\:\:3\cdot\ol{\,5\,}=\ol{\,3\,}\)
\(4\cdot\ol{\,5\,}=\ol{\,2\,},\:\:5\cdot\ol{\,5\,}=\ol{\,1\,},\:\:6\cdot\ol{\,5\,}=\ol{\,0\,}\)
のように、\(\ol{\,5\,}\) を起点として全部の元が生成され、\(\ol{\,5\,}\) が生成元であることがわかります。
剰余群 \(\bs{Z}/n\bs{Z}\) においては、\(1\leq g < n\) である整数 \(g\) が \(n\) と互いに素であるとき、\(\ol{\,g\,}\) は生成元になります。その理由ですが、
\(i\cdot\ol{\,g\,}=j\cdot\ol{\,g\,}\)
だとすると、これは、法 \(n\) における整数の合同式で、
\(ig\equiv jg\:\:(\mr{mod}\:n)\)
を意味します。つまり、
\((j-i)g\equiv0\:\:(\mr{mod}\:n)\)
ですが、\(g\) が \(n\) と互いに素なため、\((j-i)\) は \(n\) で割り切れなければなりません。しかし \(1\leq(j-i)\leq(n-1)\) なので、矛盾します。従って、\(n\) 個の剰余類の列 \((\br{A})\) は、全て違ったものです。剰余群 \(\bs{Z}/n\bs{Z}\) の群位数は \(n\) なので、\((\br{A})\) は \(\bs{Z}/n\bs{Z}\) の全ての元であり、従って \(\ol{\,g\,}\) は生成元です。
\(n\) が素数 \(p\) の場合は、\(p\) 未満の自然数はすべて \(p\) と互いに素なので、単位元 \(\ol{\,0\,}\) を除く \(\bs{Z}/p\bs{Z}\) の元が生成元になります。
\(k\) 個の \(\ol{\,i\,}\) の群演算をして初めて、結果が単位元 \(\ol{\,0\,}\) になるときの \(k\) を、\(\ol{\,i\,}\) の位数(order)といいます。群の位数と紛らわしいですが、これは群の「元の位数」です。\(\bs{Z}/6\bs{Z}\) の場合、「元 \(\rightarrow\) 位数」の対応は、
\(\ol{\,0\,}\:\rightarrow\:1,\:\:\ol{\,1\,}\:\rightarrow\:6,\:\:\ol{\,2\,}\:\rightarrow\:3\)
\(\ol{\,3\,}\:\rightarrow\:2,\:\:\ol{\,4\,}\:\rightarrow\:3,\:\:\ol{\,5\,}\:\rightarrow\:6\)
です。位数という用語を使うと、生成元とは「位数が群位数に等しい元」のことです。
群 \(G\) が一つの生成元から生成されるとき、\(G\) を巡回群(cyclic group)と言います。\(\bs{Z}/10\bs{Z}\) の例をとると、\(10\) と互いに素な数を考えて、生成元は \(\ol{\,1\,},\:\ol{\,3\,},\:\ol{\,7\,},\:\ol{\,9\,}\) の4つです。従って、たとえば \(\ol{\,7\,}\) 同士の加算を繰り返すと、
というように、\(\bs{Z}/10\bs{Z}\) の全ての元が現れたあとに再び \(\ol{\,7\,}\) に戻って "巡回" します。"巡回" 群と呼ばれるゆえんです。
群の直積
\(G,\:H\) を群とします。\(G\) の任意の元 \(g\) と \(H\) の任意の元 \(h\) のペア \((g,\:h)\) 作り、このペアを元とする集合を考えます。以降、群の演算を表す "\(\cdot\)" を省略します。
集合の任意2つの元を、
\(a=(g_a,\:h_a)\)
\(b=(g_b,\:h_b)\)
とし、\(a\) と \(b\) の演算を、
\(ab=(g_ag_b,\:h_ah_b)\)
で定義すると、この集合は群となります。この群を \(G\) と \(H\) の直積といい、
\(G\times H\)
で表します。有限群の場合、群の位数は、
\(|G\times H|=|G|\cdot|H|\) (\(\cdot\) は整数のかけ算)
です。以上は2つの群の直積ですが、同様に3つ以上の群の直積も定義できます。
群の同型
\(G\) と \(H\) を群とします。\(G\) から \(H\) への1対1の写像 \(f\) で、\(G\) の任意の2つの元 \(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つ写像があるとき、\(G\) と \(H\) は「同型である」といい、
\(G\cong H\)
と表します。同型であるということは、2つの群の元が1対1対応するのみならず、元の演算前、演算後も1対1対応していることを意味します。従って同型である群は「同じもの」と見なせます。
\(\bs{Z}/15\bs{Z}\) で群の同型の例を示します。ここでは、整数 \(i\) を 整数 \(a\) で割った余りを \(i_a\) と書きます。\(\bs{Z}/15\bs{Z}\) の任意の元 \(i\:\:(0\leq i\leq14)\) について、写像 \(f\) を、
\(f\::\:i\:\longmapsto\:(i_3,\:i_5)\)
で定めると、\(f\) は \(\bs{Z}/15\bs{Z}\) から \((\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\) への同型写像になります。
そのことを確かめると、まず \(i\) を決めれば \(i_3,\:i_5\) は一意に決まります。また\(i_3,\:i_5\) を決めると、\(3\) と \(5\) は互いに素なので、中国剰余定理(21F)により、\(0\leq i\leq14\) の範囲で \(i\) が一意に決まります。つまり \(f\) は1対1写像(数学用語で "全単射")です。また、2つの元 \(i,\:j\) について
\(\begin{eqnarray}
&&\:\:f(i+j)&=(\:(i+j)_3,\:(i+j)_5\:)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i)+f(j)&=(i_3,\:i_5)+(j_3,\:j_5)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i+j)&=f(i)+f(j)\\
\end{eqnarray}\)
が成り立つので、\(f\) は同型写像の要件を満たします。従って、
\(\bs{Z}/15\bs{Z}\cong(\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\)
です。一般に、\(a\) と \(b\) を互いに素な自然数とすると、
\(\bs{Z}/(ab)\bs{Z}\cong(\bs{Z}/a\bs{Z})\times(\bs{Z}/b\bs{Z})\)
です。これは2つの数だけでなく、\(n\) が \(k\)個の数 \(a_1,\:a_2,\:\cd\:a_k\) の積で表され、かつ、\(a_1,\:a_2,\:\cd\:a_k\) のどの2つをとっても互いに素なときには、中国剰余定理・多連立(21G)によって、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/a_1\bs{Z})\times(\bs{Z}/a_2\bs{Z})\times\cd\times(\bs{Z}/a_k\bs{Z})\)
が成り立ちます。一般に 自然数 \(n\) は \(p_i\) を素数として、
\(n=p_1^{n_1}p_2^{n_2}\cd p_k^{n_k}\)
と素因数分解され、\(p_i^{n_i}\:\:(1\leq i\leq k)\) はどの2つをとっても互いに素なので、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/p_1^{n_1}\bs{Z})\times(\bs{Z}/p_2^{n_2}\bs{Z})\times\cd\times(\bs{Z}/p_k^{n_k}\bs{Z})\)
成り立ちます。
2.3 既約剰余類群
2.2 節の剰余群は、整数の加算を演算の定義とする群でした。これに対して、整数の乗算を演算の定義とする群が構成できます。それが既約剰余類群です。
剰余群 \(\bs{Z}/n\bs{Z}\) から、代表元が \(n\) と互いに素なものだけを選び出したものを既約剰余類という。
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
[証明]
「既約剰余類」は、乗算に関して群になることを証明する。まず例をあげると、\((\bs{Z}/10\bs{Z})^{*}\) の元は \(10\) と互いに素な代表元をもつ \(1,\:3,\:7,\:9\) である。この元の乗算による演算表を作ると、
となって、演算は閉じていて、単元 \(1\) があり、逆元があることがわかる( \(3^{-1}=7,\:7^{-1}=3,\:9^{-1}=9\) である\()\)。つまり群として成り立っている。
一般に、\(a,\:b\) が \(n\) と素だとすると、\(ab\) も \(n\) と素なので、\((\bs{Z}/n\bs{Z})^{*}\) は乗算で閉じている。また、不定方程式の解の存在定理(21C)により、
\(ax+ny=1\)
を満たす \(x,\:y\) が存在する。この式の両辺を \(\mr{mod}\:n\) でみると、
\(ax\equiv1\:\:(\mr{mod}\:n)\)
となる。この方程式の解の一つ(=特殊解)を \(x_0\) とし、\(k\) を整数として、\(x=x_0+kn\) とおくと\(,\)
\(\begin{eqnarray}
&&\:\:ax&=a(x_0+kn)\\
&&&=ax_0+akn\\
&&&\equiv1\:\:(\mr{mod}\:n)\\
\end{eqnarray}\)
なので、\(x\) も解である。従って解を \(1\leq x < n\) の範囲で選ぶことができる。つまり、\((\bs{Z}/n\bs{Z})^{*}\) の元 \(a\) に対して逆元が定義できることになり、\((\bs{Z}/n\bs{Z})^{*}\) は群である。[証明終]
2.4 有限体 \(\bs{F}_p\)
\(\bs{Z}/p\bs{Z}\) は体
剰余群 \(\bs{Z}/n\bs{Z}\) において \(n\) が素数 \(p\) である \(\bs{Z}/p\bs{Z}\) を考えます。\(p\) 未満の自然数は \(p\) と互いに素なので、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は、\(\bs{Z}/p\bs{Z}\) から 加法の単位元 \(0\) を除いたものになります。つまり \(\bs{Z}/p\bs{Z}\) は加法について群であり、\(\bs{Z}/p\bs{Z}\:-\:\{\:0\:\}\) が乗法について群になっている。このような集合を体(field)と言います。
体とは加減乗除ができて、加法と乗法を結びつける分配則、
\(a(b+c)=ab+ac\)
が成り立つ集合です。\(\bs{Z}/p\bs{Z}\) は整数の演算をもとに定義されているので分配則が成り立ちます。
\(\bs{\bs{Z}/p\bs{Z}}\) を体としてみるとき、\(\bs{\bs{F}_p}\) と表記します。有理数 \(\bs{Q}\)、実数 \(\bs{R}\)、複素数 \(\bs{C}\) は体ですが、これらは無限集合です。一方、\(\bs{F}_p\) は有限集合なので有限体です。
有限体 \(\bs{F}_p\) における定数、変数、多項式、方程式の計算は、有理数/実数/複素数と同じようにできます。以下、今後の証明に使うので、\(\bs{F}_p\) 上の多項式と方程式を説明します。つまり、係数が \(\bs{F}_p\) の数である多項式や方程式です。
有限体の多項式と方程式
\(\bs{F}_p\) 上の多項式は、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:\:(a_i\in\bs{F}_p)\)
です。見た目は整数係数の多項式ですが、係数は \(\bs{F}_p\) の元です。\(\bs{F}_p\) は体なので、\(\bs{F}_p\) 上の多項式は加減算\(\cdot\)乗算\(\cdot\)余りをともなう除算(=剰余算、余り算)が、\(\bs{Q}\) 上の多項式と同じようにできます。従ってこれらの演算にもとづいた概念、定理は、\(\bs{Q}\) 上の多項式の場合と同じです。つまり、
などです(なお、多項式\(\cdot\)方程式についてのこれらの概念や定理は「3.1 多項式」で説明します)。
たとえば、\(\bs{F}_5\) における多項式、\(x^2+1\) は、
\(x^2+1=(x-2)(x-3)\) [\(\bs{F}_5\)]
と、2つの1次多項式に因数分解できます。
\(\begin{eqnarray}
&&\:\:(x-2)(x-3)&=x^2-5x+6\\
&&&=x^2+1\\
\end{eqnarray}\)
が成り立つからです。従って、方程式、
\(x^2+1=0\) [\(\bs{F}_5\)]
の解は、\(x=2,\:3\) です。
一方、\(\bs{F}_7\) において \(x^2+1\) はこれ以上因数分解できない多項式です。なぜなら、
\(f(x)=x^2+1\) [\(\bs{F}_7\)]
とおくと、
\(f(k)\neq0\:\:(0\leq k\leq6)\) [\(\bs{F}_7\)]
だからです。もちろん剰余算(余り算)はできて、\(x^2+1\) を \(x-2\) で割ると、
\(x^2+1=(x-2)(x+2)+5\) [\(\bs{F}_7\)]
と計算できます。これは \(f(2)=5\)、つまり \(f(x)\) を \(x-2\) で割った余りは \(5\)、を意味します。
以上を踏まえて、\(\bs{F}_p\) 上の多項式\(\cdot\)方程式に関する次の定理を証明します(次節の定理の証明に使います)。方程式の "解" は "\(\bs{F}_p\) における解" の意味です。
\(\bs{F}_p\) 上の1次方程式、
\(ax+b=c\)
は1個の解をもつ。
[証明]
両辺に \(b\) の加法の逆元 \(-b\) を加えると、
\(ax=c+(-b)\)
となり、この両辺に 乗法の逆元 \(a^{-1}\) を掛けると、
\(x=a^{-1}(c+(-b))\)
となり、唯一の解が求まる。[証明終]
\(\bs{F}_p\) 上の多項式を \(f(x)\) とする。
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
[証明]
\(f(x)\) を \(x-a\) で割った商を \(g(x)\)、余りを \(b\) とする。
\(f(x)=(x-a)g(x)+b\)
であるが、\(f(a)=0\) なので \(b=0\) である。従って、
\(f(x)=(x-a)g(x)\)
と表され、\(f(x)\) は \(x-a\) で割り切れる。[証明終]
\(\bs{F}_p\) 上の \(n\)次多項式を \(f_n(x)\) とする。方程式、
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
[証明]
\(n\) に関する数学的帰納法を使う。\(\bs{F}_p\) 上 の1次方程式の解は1個だから(24A)、題意は成り立つ。\(n\) 以下で題意が成り立つと仮定する。
\(\bs{F}_p\) 上の \(n+1\) 次方程式 \(f_{n+1}(x)=0\) の解がなければ、\(n+1\) でも題意は成り立っている。もし1個の解 \(a\) があるとすると\(f_{n+1}(a)=0\) なので、\(f_{n+1}(x)\) は \(x-a\) で割り切れる(24B)。つまり、
\(f_{n+1}(x)=(x-a)g(x)\)
となるが、\(g(x)\) は \(n\)次多項式だから、方程式、
\(g(x)=0\)
の解は高々 \(n\) 個である。従って、\(f_{n+1}(x)=0\) の解は高々 \(n+1\) 個である。ゆえに帰納法により題意は正しい。[証明終]
2.5 既約剰余類群は巡回群
2.5 節の目的は、2章の最終目的である、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
という定理を証明することです。証明には少々長いステップが必要ですが、この定理はガロア理論の最終段階で必要になります。まず、群の「元の位数」の性質から始めます。
位数
\((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とする。以下が成り立つ。
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
[証明]
[補題1]
\((\bs{Z}/n\bs{Z})^{*}\) は有限群だから、\(a^j=a^i\:\:(i < j)\) となる \(i,\:j\) は必ず存在する。\(a^{-i}\) を両辺に掛けると \(a^{j-i}=1\) となり\(a^x=1\) となる \(x\) が必ず存在する。従って \(a\) の位数が定義できる。
[補題2]
\(a^j=a^i\:\:(1\leq i < j\leq d)\) となる \(i,\:j\) があったとすると、両辺に \(a^{-1}\) を掛けて \(a^{j-i}=1\) となるが、\(j-i < d\) だから、\(a^x=1\) となる最小の \(x\) が \(d\) ということと矛盾する。従って、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。
[補題3]
\(a^i\:\:(1\leq i\leq d)\) を \(d\) 乗すると、
\((a^i)^d=(a^d)^i=1\)
であり、これら \(d\) 個の元はすべて \(d\) 乗すると \(1\) になる。
一方、\(d\) 乗すると \(1\) になる 元は 有限体 \(\bs{F}_p\) 上の \(d\) 次方程式 \(x^d-1=0\) の解であるが、有限体上の方程式3の定理(24C)により、\(d\) 次方程式の解の数は高々 \(d\) 個である。従って、\(a^i\:\:(1\leq i\leq d)\) の \(d\) 個の元は、\(d\) 乗すると \(1\) になる 元のすべてである。
[補題4]
\(x\) を \(d\) で割った商を \(q\:\:(1\leq q)\)、余りを \(r\:\:(0\leq r < d)\)とすると、
\(\begin{eqnarray}
&&\:\:a^{qd+r}&=1\\
&&\:\:(a^d)^q\cdot a^r&=1\\
&&\:\:a^r=1&\\
\end{eqnarray}\)
となるが、もし \(r\neq0\) なら、\(d\) より小さい数 \(r\) で \(a^r=1\) となり、これは \(a\) の位数が \(d\) であることと矛盾する。従って \(r=0\) であり、\(x\) は \(d\) の倍数である。
[補題5]
\((\bs{Z}/n\bs{Z})^{*}\) を \(G\) と書く。集合 \(A\) を、
\(A=\{a,\:a^2,\:\cd\:,\:a^d=1\}\)
とする。もし \(|G|=d\) なら、題意は満たされている。
\(d < |G|\) の場合、\(A\) に含まれない \(G\) の元の一つを \(b_1\) とし、
\(A_1=\{b_1a,\:b_1a^2,\:\cd\:,\:b_1a^d\}\)
とする。この \(A_1\) に \(A\) と共通な元はない。なぜならもし、
\(a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-j}\) をかけて、
\(a^{i-j}=b_1\)
となるが、左辺は \(A\) の元であり、右辺の \(b_1\) が \(A\) の元となって矛盾するからである。もし \(A\) と \(A_1\) で \(G\) の元を尽くしているなら、\(|G|=2d\) であり、題意は満たされている。
そうでない場合、\(A\) と \(A_1\) に含まれない \(G\) の元の一つを \(b_2\) とし、
\(A_2=\{b_2a,\:b_2a^2,\:\cd\:,\:b_2a^d\}\)
とする。上の論理と同じで \(A_2\) と \(A\) に共通な元はない。のみならず、\(A_2\) と \(A_1\) に共通な元もない。なぜなら、もし、
\(b_2a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-i}\) をかけて、
\(b_2=b_1a^{j-i}\)
となるが、\(a^{j-i}\) は \(A\) の元だから、\(b_1a^{j-i}\) は \(A_1\) の元であり、\(b_2\) が \(A_1\) の元ということになって矛盾するからである。もし \(A,\:A_1,\:A_2\) で \(G\) の元を尽くしているなら、\(|G|=3d\) であり、題意は満たされている。
そうでない場合、この操作を続けていくと、\(G\) は有限群だから、ちょうど \(G\) の元が尽くされたところで、操作は止まる。最後に作った部分集合が \(A_n\) だったとすると \(|G|=(1+n)d\) であり、\(a\) の位数 \(d\) は群位数の約数である。
\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) なので(23A)、位数の定理(25A)の[補題5]から、次のフェルマの小定理とオイラーの定理が成り立つことがわかります。
自然数 \(n\) と素な自然数 \(a\) について、
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
生成元の存在1
\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在し、従って巡回群であることを証明します。まず、特定の位数 \(d\) をもつ元の数に関する定理からです。
\(p\) を素数とする。\((\bs{Z}/p\bs{Z})^{*}\) において、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。
[証明]
[補題1]により、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元に位数が定義できる。その位数は[補題5]により、群位数 \((p-1)\) の約数である。
\((p-1)\) の任意の約数を \(d\) とし、位数 \(d\) の元 \(a\) があったとする。[補題3]により、\(d\)乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d(=1)\)
の「\(a\) 系列」がそのすべてである。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は、\(d\)乗すると \(1\) になるから、\(a\) 以外の位数 \(d\) の元も「\(a\) 系列」の中に含まれている。
ここで、\(\mr{gcd}(j,d)\neq1\) である \(j\:\:(1 < j\leq d)\) をとると、\(a^j\) の位数は \(d\) より小さくなる。なぜなら、\(\mr{gcd}(j,d)=c\:( > 1)\) とすると、2つの数 \(s,\:t\) を選んで、
\(j=c\cdot s\:\:(s < j)\)
\(d=c\cdot t\:\:(t < d)\)
と表されるが、そうすると、
\((a^j)t=a^{cst}=(a^d)^s=1\)
で、\(a^j\) の位数は \(t\) 以下だが、\(t < d\) なので \(a^j\) の位数は \(d\) より小さくなるからである。
一方、\(\mr{gcd}(j,d)\neq1\) である(=\(d\) と素な)\(j\:\:(1\leq j < d)\) をとると、\(a^j\) の位数は \(d\) になる。その理由は以下である。
\((a^j)^x\:\:(1\leq x\leq d)\) が \(x\) の値によってどう変わるかを調べると、まず、\(x=d\) のときは、
\((a^j)^x=(a^j)^d=(a^d)^j=1\)
である。
次に \(1\leq x < d\) のときは \(jx\) は \(d\) の倍数でない。なぜなら、\(j\) は \(d\) と素なため、もし \(jx\) が \(d\) の倍数だとすると、\(x\) が \(d\) の倍数ということになり、\(1\leq x < d\) に反するからである。従って、ある数 \(s,\:t\) を選んで、
\(jx=t\cdot d+s\:\:(0 < s < d)\)
と表せる。そうすると、
\((a^j)^x=a^{td+s}=(a^d)^t\cdot a^s=a^s\)
となるが、\(a\) の位数は \(d\) だから、\(d\) 未満の数 \(s\) で \(a^s\) が \(1\) になることはない。従って \(a^s\neq1\) であり、
\((a^j)^x\neq1\:\:(1\leq x < d)\)
である。
以上により
が分かったので、 \(a^j\) の位数は \(d\) である。\(j\) は \(\mr{gcd}(j,d)\neq1\) だったから、\(j\) のとりうる値は \(\varphi(d)\) 個ある。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は「\(a\) 系列」に含まれるから、\((\bs{Z}/p\bs{Z})^{*}\) に位数 \(\bs{d}\) の元があるとしたら、その数は \(\varphi(d)\) 個である。
まとめると、\((p-1)\) の任意の約数を \(d\) とし、\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元の数を \(\#\mr{ord}(d)\) と表記すると、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
が成り立つ。ここで \(d|(p-1)\) は、\((p-1)\) のすべての約数 \(d\) についての和をとる意味である。
次に、オイラー関数についてオイラー関数の総和の定理が成り立つことを証明する。
(オイラー関数の総和)
\(n\) を任意の自然数とするとき、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。\(d|n\) は、\(n\) のすべての約数 \(d\) についての和をとる。
[証明]
まず、次の2点に注意する。2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
\(\dfrac{a}{\mr{gcd}(a,b)}\) と \(\dfrac{b}{\mr{gcd}(a,b)}\) は互いに素
である。これは最大公約数の定義そのものである。
次に、\(n\) の約数の一つを \(a\) とし、\(n=a\cdot b\) と表すと、\(b\) もまた \(n\) の約数の一つである。\(n\) に \(r\) 個の約数、\(a_i\:\:(1\leq i\leq r)\) があるとき、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、\(b_i\:\:(1\leq i\leq r)\) もまた \(n\) の \(r\) 個の約数である。つまり、\(b_i\) は \(a_i\) を並び替えたものである。
以上の2点を前提に、まず \(n=12\) の場合で考察する。いま、\(1\) から \(12\) までの \(12\) 個の整数を「\(12\) との最大公約数で分類する」ことを考える。\(12\) の約数 \(d\) は、\(1,\:2,\:3,\:4,\:6,\:12\) の6つである。\(12\) との最大公約数が \(d\) である集合を \(S_d\) とすると、
となる。各集合に含まれる整数の個数を \(\#S_d\) として順に見ていくと、まず、オイラー関数の定義より、
\(\#S_1=\varphi(12)\)
である。
次に、\(12\) との最大公約数が \(2\) の集合、\(S_2=\{\:2,\:10\:\}\) を考える。\(\{\:2,\:10\:\}\) を \(2\) で割り算した \(\{\:1,\:5\:\}\) のそれぞれは、最大公約数の定義により、\(12\) を \(2\) で割り算した \(6\) と互いに素である。従って、
\(\#S_2=\varphi(6)\)
である。同様に他の集合についても、
となる。\(S_d\) は \(12\) 個の整数を分類したものだったので、そこに含まれる整数の個数の総和は \(12\) である。これにより、
となる。総和の記号で書くと、
\(\displaystyle\sum_{d|12}^{}\varphi(d)=12\)
である。
以上の考察は \(n=12\) の場合であるが、\(12\) に特別な意味はない。従って一般の \(n\) の場合も同様となる。
\(n\) が \(r\) 個の約数をもつとし、それらを \(a_i\:\:(1\leq i\leq r)\) とする。集合 \(S\) を \(1\) から \(n\) の \(n\) 個の整数の集合とし、その部分集合 \(S_i\) を、
\(S_i\):\(n\) との最大公約数が \(a_i\) である \(S\) の元の集合
とする。このとき、\(S_i\) の任意の元を \(x\) とすると、
\(\dfrac{x}{a_i}\) と \(\dfrac{n}{a_i}\) は互いに素
である。そもそも、そうなる \(x\) を集めたのが \(S_i\) であった。このことから、
\(S_i\) の元の個数は \(\dfrac{n}{a_i}\) と素である \(S\) の元の個数
ということになる。\(S_i\) の元の個数を \(\#S_i\) と書くと、
\(\#S_i=\varphi\left(\dfrac{n}{a_i}\right)\)
である。ここで \(b_i\) を、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、
\(\#S_i=\varphi(b_i)\)
となるが、この \(b_i\:\:(1\leq i\leq r)\) は \(n\) の約数のすべてであり、\(a_i\) を並び替えたものである。式の両辺の \((1\leq i\leq r)\) の総和をとると、\(\#S_i\) の総和は \(S\) の元の数なので、
左辺\(=\displaystyle\sum_{i=1}^{r}\#S_i=n\)
である。一方、右辺の総和は、
\(\begin{eqnarray}
&&\:\:右辺&=\displaystyle\sum_{i=1}^{r}\varphi(b_i)=\displaystyle\sum_{i=1}^{r}\varphi(a_i)\\
&&&=\displaystyle\sum_{d|n}^{}\varphi(d)\\
\end{eqnarray}\)
となって、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。
\((p-1)\) の約数に戻ると、オイラー関数の総和の定理より、
\(\displaystyle\sum_{d|(p-1)}^{}\varphi(d)=p-1\)
である。一方、位数 \(d\) の元の総和は、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
であった。この2点から、
\(\#\mr{ord}(d)=\varphi(d)\)
が結論づけられる。\(\#\mr{ord}(d)=0\) となる \((p-1)\) の約数 \(d\) は無い。もしあるとすると矛盾が生じる。
従って \((\bs{Z}/p\bs{Z})^{*}\) においては、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。[証明終]
この位数 \(\bs{d}\) の元の数の定理(25C)により、次の生成元の存在1が成り立つことが分かります。
\(p\) を素数とするとき、\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在する。生成元とは、その位数が \((\bs{Z}/p\bs{Z})^{*}\) の群位数、\(p-1\) の元である。
ちなみに、\(100\)以下の素数 \(p\)(\(2\) を除く \(24\)個)について、原始根の数 = \(\varphi(p-1)\) と最小の原始根をパソコンで計算すると、次のようになります。
この表を見ると、\(2\) が最小原始根になることが多いのがわかります。全体の半分(\(12\)個の素数)でそうです。そうでなれければ素数が多い。ただし、\(p=41\) のときの \(6\) のように、合成数が最小原始根になる場合もあります。
\((\bs{Z}/p\bs{Z})^{*}\) の生成元を求める計算式はありません。しかし生成元を求めるアルゴリズムはあって、それが次です。これは、少なくとも一つの生成元が存在する証明になっています。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
この証明のために2つの補題を証明する。以下において、
・\(a\) は \(b\) を割り切る
・\(a\) は \(b\) の約数である
・\(b\) は \(a\) で割り切れる
・\(b\) は \(a\) の倍数である
ことを、
\(a|b\)
と記述する。また \(a\) と \(b\) の最大値を、
\(\mr{max}(a,\:b)\)
と表す。
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[証明]
\(a\) と \(b\) を素因数分解したときに現れるすべての素数を小さい方から順に並べて、
\(p_1,\:p_2,\:\cd\:,\:p_n\)
とする。この素数の列を用いて、\(a\) と \(b\) を、
\(a=p_1^{a_1}\cdot p_2^{a_2}\cdot\cd\cdot p_n^{a_n}\)
\(b=p_1^{b_1}\cdot p_2^{b_2}\cdot\cd\cdot p_n^{b_n}\)
と素因数分解する。もちろんこの表現では \(a_i=0\) や \(b_i=0\) もありうる。ここで、
\(c_i=\mr{max}(a_i,\:b_i)\:\:\:(1\leq i\leq n)\)
と定義すると、\(a,\:b\) の最小公倍数は、
\(\mr{lcm}(a,b)=p_1^{c_1}\cdot p_2^{c_2}\cdot\cd\cdot p_n^{c_n}\)
である。また、
と定義して(\(1\leq i\leq n\))、
\(a\,'=p_1^{\al_1}\cdot p_2^{\al_2}\cd\cd p_n^{\al_n}\)
とおくと、
\(a\,'|a\)
である。同様に、
\(b\,'=p_1^{\beta_1}\cdot p_2^{\beta_2}\cdot\cd\cdot p_n^{\beta_n}\)
とおくと、
\(b\,'|b\)
である。このように \(a\,'\) と \(b\,'\) を決めると、
\(a\,'b\,'=\mr{lcm}(a,b)\)
となり、\(a\,'\) と \(b\,'\) に共通の素因数はないから、
\(\mr{gcd}(a\,',b\,')=1\)
である。[補題6の証明終]
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[証明]
\(\mr{gcd}(k,d)\) を \(g\) と書き、
\(k\,'=\dfrac{k}{g}\)
\(d\,'=\dfrac{d}{g}\)
とすると、
\(k=k\,'\cdot g\)
\(d=d\,'\cdot g\)
\(\mr{gcd}(k\,',d\,')=1\)
と表せる。\(a^k\) の位数を調べるため、
\((a^k)^x=1\)
とおくと、
\(a^{kx}=1\)
なので、[補題4](25A)により、
\(d|(kx)\)
である。つまり、
\((d\,'g)|(k\,'gx)\)
\(d\,'|k\,'x\)
となる。すると、\(\mr{gcd}(k\,',d\,')=1\) なので、
\(d\,'|x\)
が成り立つ。\(d\,'|x\) が成り立つ \(x\) の最小値は \(d\,'\) であり、\(x\) の最小値はすなわち \(a^k\) の位数 \(e\) だから、\(e=d\,'\) である。つまり、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。[補題7の証明終]
[補題6]と[補題7]を用いて、生成元の探索アルゴリズム(25D’)を証明します。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
[証明]
\(a\) の累乗の列、
\(a,\:a^2,\:a^3,\:\cd,\:a^d=1\)
は \(d\)個の異なる元である。\(d < p-1\)(群位数)なので、この列に含まれない任意の元を \(b\) とし、\(b\) の位数を \(e\) とする。[補題3](25A)により、\(d\) 乗して \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は \(a\) の累乗の列で尽されているから、\(b^d\neq1\) である。従って \(b\) の位数 \(e\) は \(d\) の約数ではない。もちろん \(e > 1\) である。以降、証明を2つのケースに分ける。
\(\bs{(1)\:\:\mr{gcd}(d,e)=1}\) のとき
このとき、\(ab\) の位数が \(d\) より大きいことを以下で証明する。\(ab\) の位数を調べるために、
\((ab)^x=1\)
とおく。両辺を \(d\)乗すると、
\((ab)^{dx}=1\)
であり、また \(a^d=1\) から \((a^d)^x=1\) だから、
\(b^{dx}=(a^d)^xb^{dx}=(ab)^{dx}=1\)
となり、[補題4](25A)により \(dx\) は \(b\) の位数 \(e\) の倍数である。つまり、
\(e|dx\)
である。すると、\(\mr{gcd}(d,e)=1\) により、
\(e|x\)
となる。同様に、
\((ab)^{ex}=1\)
\(b^e=1\)
だから、
\(a^{ex}=a^{ex}(b^e)^x=(ab)^{ex}=1\)
となり、\(ex\) は \(a\) の位数 \(d\) の倍数である。つまり、
\(d|ex\)
である。すると \(\mr{gcd}(d,e)=1\) により、
\(d|x\)
である。以上の結果、\(e|x\) かつ \(d|x\) であり、
\((de)|x\)
が成り立つ。つまり \(x\) の最小値は \(de\) である。\((ab)^x=1\) となる \(x\) の最小値が \(ab\) の位数だから、
\(ab\) の位数\(=de\)
となる。\(e > 1\) なので、\(ab\) は位数が \(d\) より大きい元である。
\(\bs{(2)\:\:\mr{gcd}(d,e)\neq1}\) のとき
[補題6]により、2つの数、\(d\,',\:e\,'\) をとって、
\(d\,'|d\)
\(e\,'|e\)
\(\mr{gcd}(d\,',e\,')=1\)
\(\mr{lcm}(d,e)=d\,'e\,'\)
となるようにできる。
\(\mr{gcd}\left(\dfrac{d}{d\,'},d\right)=\dfrac{d}{d\,'}\)
だから、[補題7]を使って、
\(a^{{}^{\frac{d}{d\,'}}}\) の位数 \(=\dfrac{d}{\mr{gcd}\left(\dfrac{d}{d\,'},d\right)}=d\,'\)
であり、同様に、
\(b^{{}^{\frac{e}{e\,'}}}\) の位数 \(=\dfrac{e}{\mr{gcd}\left(\dfrac{e}{e\,'},e\right)}=e\,'\)
である。\(\mr{gcd}(d\,',e\,')=1\) だから、
\(c=a^{{}^{\frac{d}{d\,'}}}\cdot b^{{}^{\frac{e}{e\,'}}}\)
とおくと、\(\bs{(1)}\) を使って、
となるが、\(e\) は \(d\) の約数ではないため、
\(\mr{lcm}(d,e) > d\)
である。つまり、\(c\) は位数が \(d\) より大きい元である。[証明終]
生成元の存在2
以降で \((\bs{Z}/p^n\bs{Z})^{*}\) にも生成元が存在することを証明します(ただし、\(p\neq2\))。まず、その証明に使う[補題8]を証明します。整数についての定理です。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
[証明]
表記を分かりやすくするため、まず \(m=1\) のときに成り立つことを証明する。\(m=1\) のときに[補題8]は、
[補題8]\(\bs{m=1}\)
\(p\) を奇素数とし、\(k\) を \(p\) と素な数( \(\mr{gcd}(k,p)=1\) )とする。このとき、
\((1+kp)^p=1+k\,'p^2\)
と表すことができて、\(k\,'\) は \(p\) と素である。
となる。\((1+kp)^p\) を2項定理で展開すると、
\((1+kp)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp+{}_{p}\mr{C}_{2}(kp)^2+{}_{p}\mr{C}_{3}(kp)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp)^{p-1}+(kp)^p\\
&&\:\: =&1+p^2(k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2})\\
&&\:\: =&1+k\,'p^2\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2}\\
\end{eqnarray}\)
となる。\(k\,'\) の第3項(\({}_{p}\mr{C}_{3}k^3p\))以降は \(p\) の指数が \(1\) 以上だから \(p\) で割り切れる。第2項の \(p\) に関係した式は、
\({}_{p}\mr{C}_{2}=\dfrac{p(p-1)}{2}\)
であるが、\(\bs{p}\) が奇素数(\(\bs{p\neq2}\))であるため、この第2項も \(p\) で割り切れる(\(p\) が奇数だと \(p\) で割り切れる)。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。
次に \(m\geq2\) のときであるが、\(m=1\) のときの上の証明において \(p\) を \(p^m\) に置き換えれば、同様の計算で証明できる。\((1+kp^m)^p\) を2項定理で展開すると、
\((1+kp^m)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp^m+{}_{p}\mr{C}_{2}(kp^m)^2+{}_{p}\mr{C}_{3}(kp^m)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp^m)^{p-1}+(kp^m)^p\\
&&\:\: =&1+p^{m+1}(k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1})\\
&&\:\: =&1+k\,'p^{m+1}\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1}\\
\end{eqnarray}\)
\(k\,'\) の第2項以降は \(m\geq2\) なので \(p\) の指数は \(1\) 以上であり、\(p\) で割り切れる。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は、第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。以上の結論として、題意が成り立つ。[証明終]
生成元の存在1の定理(25D)と[補題8]を用いて、\((\bs{Z}/p^n\bs{Z})^{*}\) に生成元が存在することを証明します。
\(p\) を \(p\neq2\) の素数(=奇素数)とする。また、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
[証明]
フェルマの小定理(25B)により、\((\bs{Z}/p\bs{Z})^{*}\) の任意の元は \((p-1)\) 乗すると \(1\) になる。従って、整数の記法で、
\(g^{p-1}=1+kp\)
と書ける。以降、
・\(k\) の素因数に \(p\) を含まないとき
・\(k\) の素因数に \(p\) を含むとき
の2つに分けて証明する。
\(k\) の素因数に \(p\) を含まないとき
この場合は以下が成り立つ。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
[証明(その1)]
\(g\) は \(p\) と互いに素なので \((\bs{Z}/p^n\bs{Z})^{*}\) の元でもある。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は、既約剰余類群の定義によって \(\varphi(p^n)\) である。\(p^n\) 以下で \(p\) で割り切れる数は、\(p^n\) を含んで \(\dfrac{p^n}{p}=p^{n-1}\) 個あるから、
\(\begin{eqnarray}
&&\:\:\varphi(p^n)&=p^n-p^{n-1}\\
&&&=p^{n-1}(p-1)\\
\end{eqnarray}\)
である。従って、オイラーの定理(25B)より、
\(g^{p^{n-1}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
が成り立つ。記述の簡素化のために、
\(h=g^{p-1}\)
とおく。
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
である。
仮定によって \(h\) は、
\(h=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表される。この \(h\) に対して "\(p\)乗する" 操作を \((n-1)\) 回繰り返すと、[補題8]を次々に使って、次のように計算できる。
この結果から、
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
であることがわかる。この式は \(n\geq1\) のすべての \(n\) で成り立つ。
従って、\(h^x\equiv1\:\:(\mr{mod}\:p^n)\) となる最小の \(x\) は \(p^{n-1}\) の約数であり、\((n-1)\) 個の \(p^i\:\:(1\leq i\leq n-1)\) のどれかである。
しかし、上の計算過程を見ると、
であって、\(1\leq i\leq n-2\) であれば右辺の \(k_i\cdot p^{i+1}\) は \(p^n\) で割り切れない。つまり、
\(h^{p^i}\not\equiv1\:\:(\mr{mod}\:p^n)\:\:(1\leq i\leq n-2)\)
である。従って、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
\(h\) は \(g^{p-1}\) であった。ゆえに、\(g\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その1)終]
\(k\) の素因数に \(p\) を含むとき
\(g^{p-1}=1+kp\) と表したときの \(k\) の素因数に \(p\) を含む場合、ある数 \(k\,''\) があって、
\(g^{p-1}=1+k\,''\cdot p^m\:\:(m\geq2)\)
\(\mr{gcd}(k\,'',p)=1\)
と表すことができる。ここで \(k\,''\) を改めて \(k\) と書くと、次が成り立つ。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
[証明(その2)]
\((g+p)^{p-1}\) を2項定理で展開する。
\((g+p)^{p-1}\)
\(=1+p(kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2})\)
\(=1+k\,'p\)
\(k\,'=kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2}\)
\(m\geq2\) なので、\(k\,'\) の第2項以外はすべて \(p\) で割り切れる。第2項は \((p-1)g^{p-2}\) だが、\((p-1)\) も \(g^{p-2}\) も \(p\) で割り切れない。つまり \(k\,'\) は第2項だけが唯一、\(p\) で割り切れないから、
\(\mr{gcd}(k\,',p)=1\)
である。まとめると、
\((g+p)^{p-1}=1+k\,'p\)
\(\mr{gcd}(k\,',p)=1\)
と表すことができる。ここで、
\(h=1+k\,'p\)
と書くと、[補題8]を次々と使うことで、次の計算が成り立つ。
この計算は「\(\bs{k}\) の素因数に \(\bs{p}\) を含まないとき」と全く同じである。従って、そのときの結論を踏襲できて、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
その \(h\) は、
\(h=1+k\,'p=(g+p)^{p-1}\)
であった。\(h\) が \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になるのだから、\(g+p\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その2)終]
以上により、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とすると、\(g\) か \(g+p\) のどちらかは \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。従って \((\bs{Z}/p^n\bs{Z})^{*}\) には生成元があり、群位数 \(p^{n-1}(p-1)\) の巡回群である。[証明終]
ちなみに、\(h=g^{p-1}\) とし、
\(h=1+kp^2\)
\(\mr{gcd}(k,p)=1\)
と表されているときは \(g+p\) が生成元ですが、\(\bs{g}\) は生成元ではありません。なぜなら[補題8]を次々と使うと、
となり、\(h\) を \(p^{n-1}\) 乗する前の \(h^{p^{n-2}}\) の段階で、
\(h^{p^{n-2}}\equiv1\:\:(\mr{mod}\:p^n)\)
\(\longrightarrow\:g^{p^{n-2}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
となってしまいます。つまり \(g\) は生成元ではないのです。\(g^{p-1}=1+kp^m\:\:(m > 2)\) と表されるときも同じです。
実は、\((\bs{Z}/p\bs{Z})^{*}\) の生成元を \(g\) とすると、ほとんどの場合で \(g\) は \((\bs{Z}/p^2\bs{Z})^{*}\) の(従って \((\bs{Z}/p^n\bs{Z})^{*}\) の)生成元になります。生成元の存在1であげた、\(100\) 以下の素数 \(p\) の最小原始根の表ですが、そのすべては \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です。それどころか「\(100\) 以下の素数 \(p\) の原始根が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならない」というケースは、計算してみると次の4つしかありません。
\(p=29,\:g=14\)
\(p=37,\:g=18\)
\(p=43,\:g=19\)
\(p=71,\:g=11\)
たとえば \(p=29\) の場合、\(\varphi(28)=12\) なので原始根 \(g\) は \(12\)個あります。リストすると、
\(g=2,\:3,\:8,\:10,\:11,\:14,\:15,\:18,\:19,\:21,\:26,\:27\)
の \(12\)個です。\(p^2=841\) であり、\((\bs{Z}/p^2\bs{Z})^{*}\) は \((\bs{Z}/841\bs{Z})^{*}\) のことです。その \((\bs{Z}/841\bs{Z})^{*}\) の群位数は、
\(\varphi(p^2)=p(p-1)=29\cdot28=812\)
です。
\(g\) のうち、\(14\) を除く \(11\)個の位数は \(812\) です。ところが \(14\) だけは違って、
\(14^{28}\equiv1\:\:(\mr{mod}\:841)\)
となり、位数は \(28\) です。もちろんこの場合でも、生成元の存在2(25E)の証明プロセスにあるように、
\(g+p=14+29=43\)
の位数は \(812\) で、\((\bs{Z}/841\bs{Z})^{*}\) の生成元です。以上をまとめると、
となります。
生成元の存在2(25E)の証明は、[補題8]の証明での \(\bs{{}_{p}\mr{C}_{2}}\) が \(\bs{p}\) で割り切れることがポイントになっていて、\(p\neq2\) である素数(奇素数)のときには成り立ちますが、\(p=2\) のときには成り立ちません。\(p=2\) では生成元が存在しないのです。
しかし \(p=2\) のとき、つまり \((\bs{Z}/2^n\bs{Z})^{*}\) は、生成元をもつ2つの巡回群の直積と同型であることが証明できます。
2のべき乗の既約剰余類群
2のべき乗の既約剰余類群は、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[証明]
まず \(n=5\) の場合である \((\bs{Z}/32\bs{Z})^{*}\) で考察する。
\((\bs{Z}/32\bs{Z})^{*}\) の元とは、\(1\) から \(31\) までの奇数の集合である。この奇数から「\(4\)で割ると \(1\) 余る奇数」を取り出して、集合 \(A\) とする。
\(A=\{1,\:5,\:9,\:13,\:17,\:21,\:25,\:29\}\)
である。集合 \(A\) の要素の数は、\(32/4=8\) である。ここで、
\(5\equiv1\:\:(\mr{mod}\:4)\)
であることに着目する。この両辺を \(k\) 乗(\(0\leq k\))すると、
\(5^k\equiv1\:\:(\mr{mod}\:4)\)
だから(21E)、\(5^k\) は「\(4\)で割ると \(1\) 余る奇数」である。ここで、\(5^k\) を \(32\) で割った余りを \(j\) とする。つまり、
\(5^k\equiv j\:\:(\mr{mod}\:32)\:\:(0\leq k,\:1\leq j\leq31)\)
である。すると \(j\) は「\(32\)未満の、\(4\)で割ると \(1\) 余る奇数」であり、\(A\) に含まれている。そこでもし、
\(5^x\equiv1\:\:(\mr{mod}\:32)\)
を満たす最小の \(x\)(つまり \(\mr{mod}\:32\) での \(5\) の位数)が \(8\) であれば、位数の定理(25A)の[補題2]によって「\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) はすべて異なる」から、それらは \(A\) そのものである。実際に計算してみると、
となって、\(\mr{mod}\:32\) での \(5\) の位数は \(8\) であり、\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) には \(A\) の元がすべて現れる。これは \(A\) が巡回群と同型であることを示している。
一方、\((\bs{Z}/32\bs{Z})^{*}\) の元から「\(4\)で割ると \(3\) 余る奇数」を取り出し、それを集合 \(B\) とすると、
\(B=\{3,\:7,\:11,\:15,\:19,\:23,\:27,\:31\}\)
である。ここで、\(A=\{4k+1\:|\:0\leq k\leq7\}\) と記述し、\(i=7-k\:\:(k=7-i)\) と定義すると、
\(\begin{eqnarray}
&&\:\:(-1)\cdot A&=\{-4k-1 &|\:0\leq k\leq7\}\\
&&&=\{-4(7-i)-1 &|\:0\leq i\leq7\}\\
&&&=\{4i+3-32 &|\:0\leq i\leq7\}\\
\end{eqnarray}\)
だから、\(\mr{mod}\:32\) でみると、
\(B\equiv(-1)\cdot A\)
である。\((-1)\cdot A\) は、集合 \(A\) の要素すべてに \(-1\) を掛けた集合の意味である。
\((\bs{Z}/32\bs{Z})^{*}\) の元は \(A\) と \(B\) の和であり、\(A\) と \(B\) に重複はない。従って、\((\bs{Z}/32\bs{Z})^{*}\) の元は、\(\mr{mod}\:32\) でみて、
\((-1)^j\cdot5^k\:\:(j=0,1)\) \((0\leq k\leq7)\)
の形に一意に表現できる。\(j=0\) の場合は \(A\) を、\(j=1\) なら \(B\) を表している。
\(\mr{mod}\:32\) でみて、\(5^k\) は群位数 \(8\) の巡回群であり、\((-1)^j\) は群位数 \(2\) の巡回群である。従って、\((\bs{Z}/32\bs{Z})^{*}\) は2つの巡回群の直積で表現できることになる。このことが成り立つキーポイントは、
\(\mr{mod}\:32\) でみた \(5\) の位数が \(\dfrac{32}{4}=8\)
ということである。もしこれが \(2^5=32\) だけでなく \(2^n\:\:(2\leq n)\) で成り立てば、一般論に拡張できる。その、\(2^n\) で成り立つことは、次のように、[補題9]として証明できる。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
[証明]
数学的帰納法で証明する。題意は \(n=2\) のときに成り立つので( \(5\equiv1\:\:(\mr{mod}\:4)\) )、\(n\) で成り立つと仮定し、\(n+1\) でも成り立つことを証明する。\(\mr{mod}\:2^{n+1}\) での \(5\) の位数を調べるため、
一般に \(a\equiv b\:\:(\mr{mod}\:p^n)\) なら、\(1\leq i < n\) とするとき \(a\equiv b\:\:(\mr{mod}\:p^i)\) である。従って \((\br{A})\) 式が成り立つとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^n)\)
も成り立つ。帰納法の仮定により \(\mr{mod}\:2^n\) での \(5\) の位数は \(2^{n-2}\) だから、位数の定理(25A)の[補題4]により \(x\) は \(2^{n-2}\) の倍数である。
従って \(x\) の最小値は \(2^{n-2}\) だが、\(x\) を \(2^{n-2}\) とすると \((\br{A})\) 式が成り立たない。なぜなら、
\((\br{A})\) 式の \(x\) は \(2^{n-2}\) の倍数であるが、\(x=2^{n-2}\) では \((\br{A})\) 式が成り立たないことが分かった。その次に小さな \(x\) の倍数は \(x=2\cdot2^{n-2}=2^{n-1}\) であり、これを \((\br{A})\) 式に入れると、
左辺\(=5^{2^{n-1}}\)
である。一方、\((\br{B})\) 式の両辺を2乗すると、
\(\begin{eqnarray}
&&\:\:5^{2^{n-1}}&\equiv(1+2^n)^2\:\:(\mr{mod}\:2^{n+1})\\
&&&=1+2^{n+1}+2^{2n}\\
&&&\equiv1\:\:(\mr{mod}\:2^{n+1})\\
\end{eqnarray}\)
であるから、\(x=2^{n-1}\) のとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
が成り立つ。つまり \((\br{A})\) 式が成り立つ \(x\) の最小値は \(2^{n-1}\) であり、\(5\) の \(\mr{mod}\:2^{n+1}\) での位数は \(2^{n-1}\) である。これで、帰納法によって[補題9]が正しいことが証明できた。[補題9の証明終]
[補題9]が正しいので、\(n=5\) の例で展開した論理により、\((\bs{Z}/2^n\bs{Z})^{*}\) の元は、\(\mr{mod}\:2^n\) でみて、
\((-1)^j5^k\:\:(j=0,1,\:\:0\leq k\leq2^{n-2}-1)\)
の形に一意に表現できることが分かった。
ここで、\((\bs{Z}/2^n\bs{Z})^{*}\) から \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) への写像 \(f\) を、
で定める。\((\bs{Z}/2^n\bs{Z})^{*}\) の群演算は乗算であり、\((\bs{Z}/2\bs{Z})\) と \((\bs{Z}/2^{n-2}\bs{Z})\) の群演算は加算であることに注意すると、\((\bs{Z}/2^n\bs{Z})^{*}\) の2つの元 \((-1)^j5^k\)、\((-1)^l5^m\) について、
\(\begin{eqnarray}
&&\:\:f((-1)^j5^k\cdot(-1)^l5^m)&=f((-1)^{j+l}5^{k+m})\\
&&&=(j+l,\:k+m)\\
&&\:\:f((-1)^j5^k)+f((-1)^l5^m)&=(j,k)+(l,m)\\
&&&=(j+l,\:k+m)\\
\end{eqnarray}\)
\(f((-1)^j5^k\cdot(-1)^l5^m)=f((-1)^j5^k)+f((-1)^l5^m)\)
となり、\(f\) は同型写像の要件を満たしている。従って、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
であり、\((\bs{Z}/2^n\bs{Z})^{*}\) は、群位数 \(2\) と群位数 \(2^{n-2}\) の2つの巡回群の直積に同型である。[証明終]
既約剰余類群の構造
ここまでの準備を行うと、既約剰余類群の構造を明らかにできます。これが第2章のゴールです。
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である。
[証明]
以下の記述では、
・\(a_j\) は \(a\) を \(j\) で割った余り
・\((a+b)_j\) は \((a+b)\) を \(j\) で割った余り
を表す。
\(j\) と \(k\) を 互いに素な整数 \((2\leq j,k)\) とする。\(a\) を \(\bs{Z}/(jk)\bs{Z}\) の元とし \((0\leq a\leq jk-1)\)、\(\bs{Z}/(jk)\bs{Z}\) から \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) への写像、\(f\) を次のように定義する。
\(j\) と \(k\) が 互いに素なので、中国剰余定理(21F)により、任意に選んだ \(a_j\) と \(a_k\) から \(a\) が一意に決まる。つまり、\(f\) は1対1写像(数学用語で "全単射")である。また、\(a\) とは別の \(\bs{Z}/(jk)\bs{Z}\) の元を \(b\) とすると、
\(\begin{eqnarray}
&&\:\:f(a+b)&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a)+f(b)&=(a_j,\:a_k)+(b_j,\:b_k)\\
&&&=(a_j+b_j,\:a_k+b_k)\\
&&&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a+b)&=f(a)+f(b)\\
\end{eqnarray}\)
となり、\(f\) は同型写像である。
いま、\(\mr{gcd}(a,jk)=1\)(\(a\) が \(jk\) と素)だとすると、既約剰余類群の定義により、\(a\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) の元である。
ここで一般的に、
\(\mr{gcd}(a,jk)=1\) なら
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\)
である。また \(\mr{gcd}(a,j)=1\) なら \(\mr{gcd}(j,a_j)=1\) である。なぜなら互除法の原理(21A)によって、\(a\) と \(j\) の公約数は \(j\) と \(a_j\) の公約数だからである。
従って、
\(\mr{gcd}(j,a_j)=1\) かつ \(\mr{gcd}(k,a_k)=1\)
になる。つまり、\(a_j\) は \((\bs{Z}/j\bs{Z})^{*}\) の元であり、\(a_k\) は \((\bs{Z}/k\bs{Z})^{*}\) の元である。また、
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\) なら
\(\mr{gcd}(a,jk)=1\)
も成り立つので、任意の \((\bs{Z}/j\bs{Z})^{*}\) の元と \((\bs{Z}/k\bs{Z})^{*}\) の元を決めれば、\((\bs{Z}/(jk)\bs{Z})^{*}\) の元が定まる。
さらに、既約剰余類群の群演算は乗算であるが、
\(\begin{eqnarray}
&&\:\:a_j\cdot b_j&=(a\cdot b)_j\\
&&\:\:a_k\cdot b_k&=(a\cdot b)_k\\
\end{eqnarray}\)
が成り立つので、
\(f(ab)=f(a)f(b)\)
であり、\(f\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) から \((\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\) への同型写像でもある。従って、\(j\) と \(k\) が互いに素という条件のもとで、
いま、\(p,\:q\) を2つの素数とし、\(n\) の素因数分解が、
\(n=p^a\cdot q^b\)
だとする。このとき \((\br{C})\) 式で \(j=p^a,\:k=q^b\) とおくと、
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\)
となる。さらに、\(p,\:q,\:r\) を3つの素数とし、
\(n=p^a\cdot q^b\cdot r^c\)
と表せたとする。\((\br{C})\) 式で \(j=p^a\cdot q^b,\:k=r^c\) とおくと、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/n\bs{Z})^{*}&\cong(\bs{Z}/(p^aq^b)\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
&&&\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
\end{eqnarray}\)
となる。\(n\) の素因数の数が4以上に増えてもこの操作は繰り返せるから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \((\bs{Z}/p^a\bs{Z})^{*}\) の形の既約剰余類群の直積と同型である。
\((\bs{Z}/p^a\bs{Z})^{*}\) は、\(p=2\) のときは2のべき乗の既約剰余類群の定理(25F)により、2つの巡回群の直積と同型である。また、\(p\neq2\) の素数のときは生成元の存在2の定理(25E)により、それ自体が巡回群である。従って、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \(n\) の値にかかわらず、巡回群の直積と同型である。[証明終]
具体例として、たとえば \(n=360\) とすると、\(n=2^3\cdot3^2\cdot5\) なので、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/2^3\bs{Z})^{*}\times(\bs{Z}/3^2\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
となり、\((\bs{Z}/360\bs{Z})^{*}\) は4つの巡回群の直積と同型です。
「既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型」(25G)は、ガロア理論の証明で次のように使います。\(1\) の \(n\)乗根(\(x^n-1=0\) の解)のうち、\(n\)乗して初めて \(1\) になるものを「\(1\) の原始\(n\)乗根」といいます。それを \(\zeta\) とすると、
となり、④が証明できます。① と ③ は別途証明します。④ の「\(\bs{Q}(\zeta)\) のガロア群は可解群」が重要で、方程式の可解性の必要条件を証明するときの一つのポイントになります。
ガロア理論では方程式の解を含む「体」の特性を分析することで、方程式が代数的に解けるかどうかを調べます。第3章ではその「体」と、方程式の元になる「多項式」に関する重要な定義と定理を説明します。
3.1 多項式
ガロア理論で対象とする多項式は、1つの変数(未知数)をもつ、有理数係数の多項式です。それを、
で表します。\(\bs{f(x)}\) の「\(\bs{0}\) でない最高次の係数 \(\bs{n}\)」を、多項式の「次数」といい、\(\bs{\mr{deg}\:f(x)}\) で表します。通常、\(\mr{deg}\:f(x)\geq1\) ですが、便宜上、\(a_0\) 以外の係数が \(0\) の場合(=定数項のみの場合)も多項式と呼び「\(\bs{0}\) 次多項式」とします。また、全ての係数が \(0\) の場合を「\(\bs{0}\) 多項式(零多項式)」と呼びます。
多項式 \(a(x)\) を 多項式 \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とすると、
\(a(x)=p(x)b(x)+r(x)\)
\((\:\mr{deg}\:r(x) < \mr{deg}\:b(x)\:)\)
です。整数のときと同じように互除法(21A)を用い、次に \(b(x)\) を \(r(x)\) で割って余りを求める操作を繰り返すと、\(\mr{deg}\:r(x)\) が単調減少するので、いずれ \(b(x)\) が \(r(x)\) で割り切れるとき(=互除法の最終段階)がきます。\(r(x)\) が \(0\) 次多項式(=定数)なら、\(b(x)\) は \(r(x)\) で割り切れるので、最終段階は必ずあります。
\(b(x)\) が \(r(x)\) で割り切れるとき、\(r(x)\) が \(a(x)\) と \(b(x)\) の「最大公約数」です。実際は "数" ではなく多項式なので、「最大公約式」や「最大公約因子」といった言い方もありますが、一般的には「最大公約数」で通っています。
最大公約数が定数(\(0\) 次多項式)のとき、\(a(x)\) と \(b(x)\) は互いに素である、といいます。このとき、整数における不定方程式の解の存在定理(21C)と同様の、次の定理が成り立ちます。
不定方程式
\(a(x)\) と \(b(x)\) が互いに素な多項式のとき、
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
[証明]
\(a(x)\) と \(b(x)\) に互除法(21A)を適用して次数を下げ、同時に \(f(x),\:g(x)\) を変換して同等の方程式に変形していく。\(a(x)\) を \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とする。
\(a(x)=p(x)b(x)+r(x)\)
\(\mr{deg}\:r(x) < \mr{deg}\:b(x)\)
である。互除法の次のステップの \(a_1(x),\:b_1(x)\)、\(f_1(x),\:g_1(x)\) を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1(x)=b(x)&\\
&&b_1(x)=r(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f_1(x)=p(x)f(x)+g(x)&\\
&&g_1(x)=f(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(f(x),\:g(x)\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f(x)=g_1(x)&\\
&&g(x)=f_1(x)-p(x)g_1(x)&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(a_1(x)f_1(x)+b_1(x)g_1(x)\)
\(=b(x)(p(x)f(x)+g(x))+r(x)f(x)\)
\(=p(x)b(x)f(x)+b(x)g(x)+r(x)f(x)\)
\(=(p(x)b(x)+r(x))f(x)+b(x)g(x)\)
\(=a(x)f(x)+b(x)g(x)\)
と計算できるので、不定方程式は、
\(a_1(x)f_1(x)+b_1(x)g_1(x)=1\)
となり、係数多項式 \(a_1(x),\:b_1(x)\) の次数が元々の \(a(x),\:b(x)\) より小さな方程式に変形できる。この方程式の解である \(f_1(x),\:g_1(x)\) が求まれば、\(\br{③}\) を使って \(f(x),\:g(x)\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i(x)\) を \(b_i(x)\) で割った商と余りを、
\(a_i(x)=p_i(x)b_i(x)+r_i(x)\)
\((\:\mr{deg}\:r_i(x) < \mr{deg}\:b_i(x)\:)\)
のように求め、次のステップを、
\(a_{i+1}(x)=b_i(x)\)
\(b_{i+1}(x)=r_i(x)\)
\(f_{i+1}(x)=p_i(x)f_i(x)+g_i(x)\)
\(g_{i+1}(x)=f_i(x)\)
とすることで、互除法を続けていける。このように係数多項式 \(a(x),\:b(x)\) の剰余算を繰り返し、同時に変数多項式 \(f(x),\:g(x)\) を変換していくと、この過程で \(\mr{deg}\:r_i(x)\) は単調減少していく。そして互除法の最終段階で、
\(a_n(x)f_n(x)+b_n(x)g_n(x)=1\)
となったとする。元々の \(a(x)\) と \(b(x)\) は互いに素だったから、この段階の \(b_n(x)\) は \(0\) 次多項式=定数である。その定数を \(c\) とすると、
\(a_n(x)f_n(x)+cg_n(x)=1\)
となるが、この不定方程式の解は、
\(f_n(x)=0\)
\(g_n(x)=\dfrac{1}{c}\)
である。この解を起点として \(f_i(x),\:g_i(x)\:\:(1\leq i\leq n)\) の変換過程を逆にたどると \(f(x),\:g(x)\) が求まる。
次に、
\(\mr{deg}\:g(x) < \mr{deg}\:a(x)\)
であるように選べることを示す。\(g(x)\) を \(a(x)\) で割った商を \(q(x)\)、余りを \(s(x)\) とする。
\(g(x)=q(x)a(x)+s(x)\)
\(s(x)=g(x)-q(x)a(x)\)
である。ここで、
\(F(x)=f(x)+b(x)q(x)\)
\(G(x)=s(x)\)
とおくと、
\(a(x)F(x)+b(x)G(x)\)
\(\begin{eqnarray}
&&\:\: =&a(x)(f(x)+b(x)q(x))+b(x)s(x)\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)(g(x)-q(x)a(x))\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)g(x)-b(x)q(x)a(x)\\
&&\:\: =&a(x)f(x)+b(x)g(x)\\
\end{eqnarray}\)
となるので、
\(a(x)f(x)+b(x)g(x)=1\)
であれば、
\(a(x)F(x)+b(x)G(x)=1\)
である。つまり \(f(x),\:g(x)\) が不定方程式の解であれば、\(F(x),\:G(x)\)も解である。\(\mr{deg}\:G(x)=\mr{deg}\:s(x) < \mr{deg}\:a(x)\) なので、\(F(x),\:G(x)\) が題意を満たす解である。
\((\br{A})\) 式を満たす \(f(x),\:g(x)\) が求まったとする。\((\br{A})\) 式の両辺に \(h(x)\) を掛けると、
\(a(x)f(x)h(x)+b(x)g(x)h(x)=h(x)\)
となる。
\(F(x)=f(x)h(x)\)
\(G(x)=g(x)h(x)\)
とおくと、\(F(x),\:G(x)\) は不定方程式、
\(a(x)F(x)+b(x)G(x)=h(x)\)
の解である。\((\br{A})\) 式の解を \(\mr{deg}\:g(x) < \mr{deg}\:a(x)\) となるように選べることを上で証明したが、この過程において方程式の右辺は無関係であった。従って、全く同じプロセスをたどることで、
\(\mr{deg}\:G(x) < \mr{deg}\:a(x)\)
とすることができる。[証明終]
既約多項式
有理数係数の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解がべき根で表現できるために必要十分条件を述べるのがガロア理論です。
このとき、多項式が有理数の範囲で因数分解できるのであれば、\(f(x)=0\) は、たとえば \(g(x)h(x)=0\)、\(g(x)=0,\:h(x)=0\) となって、より次数の低い方程式の問題に還元されてしまいます。これでは、たとえば \(f(x)\) が5次多項式だとしても、5次方程式の問題ではなくなる。
従って、方程式の解の議論をするときには「因数分解できない多項式」の議論をすればよいことになります。それが既約多項式です。
有理数 \(\bs{Q}\) を係数とする多項式で、\(\bs{Q}\) の範囲ではそれ以上因数分解できない多項式を \(\bs{Q}\) 上で既約な多項式という。
たとえば多項式 \(x^2-2\) は \(\bs{Q}\) 上では因数分解できませんが、\(\bs{R}\) 上では \((x-\sqrt{2})(x+\sqrt{2})\) と因数分解できます。\(x^2+2\) は \(\bs{R}\) 上では因数分解できませんが、\(\bs{C}\) 上では \((x-\sqrt{2}i)(x+\sqrt{2}i)\) と因数分解できます。「代数学の基本定理」によると、\(n\)次方程式は 複素数の範囲で\(n\)個の解をもつので、\(\bs{C}\) 上の既約多項式は1次多項式しかないことになります。つまり、既約多項式を議論するときには「どの体での既約多項式か」を明確にする必要があります。
なお、以降の説明において、\(f(x)\) を既約多項式とするとき、方程式 \(f(x)=0\) を「既約方程式」と記述することがあります。
以下、既約多項式の性質を調べますが、その前に次の定理を証明します。
整数係数の多項式 \(f(x)\) が \(\bs{Q}\) 上で(=有理数係数の多項式で)因数分解できれば、整数係数でも因数分解できる。
この定理の対偶をとると、
となります。有理数係数の多項式は、各係数を整数の分数で表現可能で、その分母の最小公倍数を多項式全体に掛けると整数係数の多項式になります。従って、ある多項式が既約かどうかという議論は整数係数の範囲で考えればよいことになり、話が随分シンプルになります。
これを証明するために、まず次の補題を証明します。
[補題]
2つの整数係数の多項式、\(g(x),\:\:h(x)\) があり、ともに係数の最大公約数は \(1\) とする。このとき、
\(r(x)=g(x)h(x)\)
で定義される多項式 \(r(x)\) の係数の最大公約数も \(1\) である。
[証明]
背理法を使う。\(r(x)\) の係数の最大公約数が \(2\) 以上と仮定する。最大公約数を素因数分解したときに現れる素数の一つを \(\bs{p}\) とする。
\(r(x)=a_0+a_1x+a_2x^2+\cd+a_nx^n\)
とおくと、\(a_i\:\:(0\leq i\leq n)\) のすべては \(p\) で割り切れる。ここで、
\(g(x)=b_0+b_1x+b_2x^2+\cd+b_mx^m\)
\(h(x)=c_0+c_1x+c_2x^2+\cd+c_kx^k\)
とすると、\(g(x)\) の係数の最大公約数は \(1\) なので、係数のすべてが \(p\) で割り切れることはなく、少なくとも \(1\) つの係数は \(p\) で割り切れない。ここで、\(p\) で割り切れない \(g(x)\) の係数のうち \(x\) の次数が最小の係数を考える。以降の数式を見やすくするため、\(b_2\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。このとき \(b_0,\:b_1\) は \(p\) で割り切れる。
全く同様にして \(h(x)\) に関しては、\(c_3\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。つまり \(c_0,\:c_1,\:c_2\) は \(p\) で割り切れる。
ここで、\(r(x)=g(x)h(x)\) の等式の \(x^5\) の係数を比較する。左辺の \(x^5\) の項は \(a_5x^5\) であるが、背理法の仮定によって係数 \(a_5\) は \(p\) で割り切れる。
一方、右辺の \(g(x)h(x)\) の \(x^5\) の項は、
\((b_0c_5+b_1c_4+b_2c_3+b_3c_2+b_4c_1+b_5c_0)x^5\)
であるが、この係数のうち \(b_2c_3\) は 素数 \(p\) で割り切れない。なぜなら、\(b_2\) も \(c_3\) も素数 \(p\) で割り切れないので、\(b_2c_3\) を素因数分解しても \(p\) が現れないからである。一方、\(b_2c_3\) 以外の5つの項は、\(b_0,\:b_1,\:c_0,\:c_1,\:c_2\) のいずれかを因数にもつから、\(p\) で割り切れる。従って、唯一、 \(b_2c_3\) だけが \(p\) で割り切れないので、右辺全体としては \(p\) で割り切れない。
ということは、\(r(x)=g(x)h(x)\) の等式は \(x^5\) の項に関して右辺が \(p\) で割り切れ、左辺が \(p\) で割り切れないことになり、矛盾が生じる。
表記を見やすくするために、\(b_2\) と \(c_3\) が素数 \(p\) で割り切れない最小の次数の係数としたが、これを \(b_i\:\:(0\leq i\leq m)\) と \(c_j\:\:(0\leq j\leq k)\) としても全く同じであり、左辺の \(x^{i+j}\) の係数である \(a_{i+j}\) が \(p\) で割り切れる(=背理法の仮定)にもかかわらず、右辺の \(x^{i+j}\) の係数が \(p\) で割り切れないという矛盾が生じる。
従って背理法の仮定は間違っていて、\(r(x)\) の係数すべてを割り切る素数はなく、係数の最大公約数は \(1\) である。[補題の証明終]
この補題を用いて、整数係数多項式の既約性の定理(31C)を証明します。
[証明]
整数係数の多項式 \(f(x)\) が、2つの有理数係数の多項式 \(g(x)\) と \(h(x)\) に因数分解されたとする。
\(f(x)=df_r(x)\)
であり、\(f_r(x)\) の係数の最大公約数は \(1\) である。
\(g(x)\) の係数は有理数(=整数の分数)であるが、適当な整数 \(m_g\) をかけることによって整数係数の多項式 \(m_gg(x)\) にすることができる。この多項式 \(m_gg(x)\) の係数の最大公約数を \(d_g\) とし、\(m_gg(x)\) の各係数を \(d_g\) で割った多項式を \(g_r(x)\) とする。
\(m_gg(x)=d_gg_r(x)\)
であり、\(g_r(x)\) の係数の最大公約数は \(1\) である。
同様に、\(h(x)\) の係数は有理数であるが、適当な整数 \(m_h\) をかけることによって整数係数の多項式 \(m_hh(x)\) にすることができる。この \(m_hh(x)\) の係数の最大公約数を \(d_h\) とし、\(m_hh(x)\) の各係数を \(d_h\) で割った多項式を \(h_r(x)\) とする。
\(m_hh(x)=d_hh_r(x)\)
であり、\(h_r(x)\) の係数の最大公約数は \(1\) である。
以上にもとづいて \((\br{B})\) 式を書き換えると、
となる。ここで、
\((\br{D})\) 式を \((\br{C})\) 式に代入すると、
(整数)\(\times\)(係数の最大公約数が \(1\) の整数係数多項式)
と表現する方法は1種類しかない。従って \((\br{E})\) 式の両辺の係数と多項式は同じものであり、多項式の部分は、
\(\begin{eqnarray}
&&\:\:f_r(x)&=r(x)\\
&&&=g_r(x)\cdot h_r(x)\\
\end{eqnarray}\)
である。従って \(f(x)=df_r(x)\) を使って、
\(f(x)=(dg_r(x))\cdot h_r(x)\)
と表現できる。結局、\(f(x)\) は整数係数の2つの多項式に因数分解できることになり、題意が証明された。[証明終]
この定理があるため、有理数係数の既約多項式を議論するときには、整数係数の既約多項式 \(f(x)\) を議論し、\(f(x)=0\) の解を調べればよいことになります。これ以降の説明では整数係数の方程式の例だけが出てきますが、その理由は整数係数の例で十分だからです。
多項式の不定方程式の定理(31A)のように、多項式は整数とのアナロジーがあります。そのアナロジーで言うと、既約多項式は整数における素数に相当します。例えば次の定理が成り立ちます。
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
[証明]
\(f(x)\) が \(p(x)\) で割り切れないとする。\(f(x)\) と \(p(x)\) は互いに素なので、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x),\:b(x)\) が存在する。両辺に \(g(x)\) を掛けると、
\(g(x)f(x)a(x)+g(x)p(x)b(x)=g(x)\)
となる。\(g(x)f(x)\) は \(p(x)\) で割り切れるので、
\(g(x)f(x)=p(x)h(x)\)
と書ける。これを代入して、
\(p(x)h(x)a(x)+g(x)p(x)b(x)=g(x)\)
\(p(x)\cdot(h(x)a(x)+g(x)b(x))=g(x)\)
となり、\(g(x)\) は \(p(x)\) で割り切れる。従って \(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。[証明終]
この定理の \(f(x)\) を \(g(x)\) に置き換えると次が言えます。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
\(a\) を整数とし、\(a^2\) が \(3\) で割り切れれば、\(a\) は \(3\) で割り切れます。しかし \(a^2\) が \(4\) で割り切れたとしても \(a\) が \(4\) で割り切れるとは限らない。これと既約多項式のアナロジーが成り立っています。
以下、既約多項式がもつ重要な性質を3つあげます。最初の3つは方程式に関するものです。
既約多項式の性質
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
[証明]
\(f(x)\) は \(p(x)\) で割り切れないと仮定して背理法で証明する。\(f(x)\) が \(p(x)\) で割り切れないのなら、\(f(x)\) と \(p(x)\) は互いに素である。なぜなら、もし互いに素でないとすると、1次式以上の多項式 \(h(x)\) があって、
\(f(x)=f_1(x)h(x)\)
\(p(x)=p_1(x)h(x)\)
と表現できるが、\(p(x)\) は既約多項式なので \(p_1(x)=1\) であり、つまり \(h(x)=p(x)\) である。そうすると \(f(x)=f_1(x)p(x)\) となり、\(f(x)\) は \(p(x)\) で割り切れることになって矛盾するからである。つまり、\(f(x)\) が \(p(x)\) で割り切れないのなら \(f(x)\) と \(p(x)\) は互いに素である。
\(f(x)\) と \(p(x)\) が互いに素なら、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x)\)、\(b(x)\) が存在する。そこで、方程式 \(p(x)=0\) と \(f(x)=0\) の共通の解を \(\al\in\bs{C}\) とし、この式に代入すると、左辺\(=0\) となって矛盾する。
従って、\(f(x)\) は \(p(x)\) で割り切れないとの仮定は矛盾を導くから、仮定は誤りであり、\(f(x)\) は \(p(x)\) で割り切れる。[証明終]
この定理は重要なことを言っています。\(\bs{Q}\) 上の方程式の解になる数を代数的数といいます。\(f(x)\) を既約多項式とし、ある代数的数 \(\al\) が \(f(x)=0\) の解とします。
もし、既約多項式 \(f(x)\) 以外の多項式 \(g(x)\) があって、\(g(x)=0\) の解の一つが\(\al\) だとすると、上記の定理により \(g(x)\) は \(f(x)\) で割り切れます。\(g(x)\) の次数が \(f(x)\) の次数と同じとすると、\(g(x)\) は \(f(x)\) の定数倍の既約多項式です。\(g(x)\) の次数が \(f(x)\) の次数より大きいとすると、\(g(x)\) は既約多項式ではありません。
つまり、\(\al\) を方程式の解とするとき、\(\bs{f(\al)=0}\) である既約多項式 \(\bs{f(x)}\) は、定数倍を除いて一意に決まることがわかります。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
[証明]
既約多項式の定理1(31E)により、もし方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば \(f(x)\) は \(p(x)\) で割り切れるので、多項式 \(h(x)\)(定数の場合を含む)を用いて
\(f(x)=p(x)h(x)\)
と表現できる。従って、
\(f(x)\) の次数 \(\geq\:p(x)\)の次数
である。つまり、
この定理は、既約多項式の定理1(31E)と同じことを別の視点で述べたものです。「3.2 体」の「単拡大体の基底」で、既約多項式の定理2(31F)を使った証明を行います。
\(p(x)\) を \(\bs{Q}\) 上の既約多項式とすると、方程式 \(p(x)=0\) は(複素数の範囲で)重解を持たない。
[証明]
方程式 \(p(x)=0\) が重解 \(\al\) を持つとすると、
\(p(x)=(x-\al)^2q(x)\)
となる。これを微分すると、
\(p\,'(x)=2(x-\al)q(x)+(x-\al)^2q\,'(x)\)
となる。以上の2式に \(\al\) を代入すると、
となる。つまり、
・既約多項式 \(p(x)\) の次数は \(2\) 以上
・\(p\,'(x)\) の次数は \(2\) 未満
であるにもかかわらず共通の解 \(\al\) を持つことになり、既約多項式の定理2(31F)に反して矛盾が生じる。従って方程式 \(p(x)=0\) は重解を持たない。[証明終]
この定理も重要です。以降で行う証明の中には「\(n\)次既約方程式 \(f(x)=0\) の \(n\) 個の解を \(\al_1,\al_2,\cd,\al_n\) とする」といった、「\(n\)次方程式は \(\bs{n}\) 個の異なった解を持つのが当然」のような記述が出てきますが、\(\bs{f(x)}\) が既約多項式ならこの定理で保証されているからです。
最小多項式
\(\al\) を 方程式の解とする。\(\al\) を解としてもつ、体 \(\bs{Q}\) 上の方程式のうち、次数が最小の多項式を、\(\al\) の \(\bs{Q}\) 上の最小多項式と言う。
\(\bs{Q}\) 上の方程式、\(f(x)=0\) が \(\al\) を解としてもつとき、
の2つは同値である。
[② \(\bs{\Rightarrow}\) ① の証明]
最小多項式 \(f(x)\) が既約多項式でなければ、\(f(x)=g(x)h(x)\) となる \(\bs{Q}\) 係数の多項式 \(g(x)\)、\(h(x)\) が存在する。\(x\) に \(\al\) を代入すると、
\(f(\al)=g(\al)h(\al)=0\)
となり、少なくとも \(g(\al)=0\)、\(h(\al)=0\) のどちらかは成り立つ。従って、\(f(x)\) より次数の低い多項式で \(\al\) を解にもつものが存在することになり、\(f(x)\) が最小次数であるという、最小多項式の定義に反する。従って \(f(x)\) は既約多項式である。
[① \(\bs{\Rightarrow}\) ② の証明]
\(g(x)\) を \(\al\) の \(\bs{Q}\) 上の最小多項式とする。すると、\(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) を持つことになり、\(f(x)\) は既約多項式なので、既約多項式の定理1(31E)により \(g(x)\) は \(f(x)\) で割り切れる。従って \(g(x)\) は多項式 \(h(x)\) を用いて、
\(g(x)=h(x)f(x)\)
と表せる。② \(\Rightarrow\) ①の証明により、最小多項式は既約多項式なので、\(g(x)\) は既約多項式である。既約多項式が \(1\)次多項式以上の因数をもつことはない。従って \(h(x)\) は \(0\)次多項式=定数である。ということは、\(f(x)\) も \(\al\) の最小多項式である。[証明終]
方程式 \(f(x)=0\) の解が \(\al\) である( \(f(\al)=0\) )という場合、方程式がまずあって、その解を考えます。しかしその逆、つまり代数的数 \(\al\) があり、\(\al\) を解にもつような方程式は何かと考えるのが最小多項式です。これは、ガロア理論でしばしば出てきます。
3.2 体
「体」とは何かを「1.2 体」で説明しました。それを前提として、ガロア理論に必要な「体」についての定義\(\cdot\)定理を説明します。
最小分解体
体 \(\bs{Q}\) 上の多項式 \(f(x)\) を、
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
この最小分解体は、あとに出てくるガロア拡大体と直結している重要な概念です。
\(\bs{Q}\) 上の方程式の解が四則演算とべき根で表されるかどうか、と言った場合、既約多項式だけを考えれば十分です。しかし最小分解体は、既約でない多項式をも含んだ定義です。ガロア理論でしばしば出てくるのは \(1\) の \(n\)乗根を求める、
\(x^n-1=0\)
という方程式ですが、左辺は因数分解ができるので既約多項式ではありません。最小分解体の定義は、一般の多項式としておく方が都合が良いのです。
単拡大定理
\(\bs{Q}\) 上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大である。つまり \(\bs{K}\) の元 \(\theta\) があって、\(\bs{K}=\bs{Q}(\theta)\) となる。この \(\theta\) を原始元という。
[証明]
\(\bs{Q}\) 上の方程式の解を \(\al\)、\(\beta\) とし、
\(\theta=\al+c\beta\:\:(c\in\bs{Q})\)
とおく。すると、\(\al+c\beta\) と有理数の四則演算で作れる数は、\(\al,\:\beta,\) 有理数の四則演算で作れるから、
\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。次に、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
が成り立つような \(c\) が存在することを示す。
\(\al\) の \(\bs{Q}\) 上の最小多項式を \(f(x)\) とし、\(\beta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とする。そして、
\(f(x)=0\) の解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\)
\(g(x)=0\) の解を \(\beta_1=\beta,\:\beta_2,\:\cd\:,\beta_m\)
とする。ここで、
\(h(x)=f(\al+c\beta-cx)\)
とおくと、
\(h(\beta)=f(\al)=0\)
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\:\:(2\leq i\leq m)\)
となる。
\(c\) は有理数であり、無数に選べるので、\(\al+c\beta-c\beta_i\:\:(2\leq i\leq m)\) のどれもが \(\al_1,\:\al_2,\:\cd\:,\al_n\) と一致しないようにできる。具体的には、もし \(\al_j\:\:(1\leq j\leq n)\) と一致したとしたら、
\(\al_j=\al+c\beta-c\beta_i\)
\(c=-\dfrac{\al-\al_j}{\beta-\beta_i}\)
なので、\(i\) と \(j\) を \((2\leq i\leq m,\:\:1\leq j\leq n)\) の範囲で振って \(n(m-1)\) 個の \(c\) を計算し、これら以外の値を選べばよい。このように \(c\) を選んだとする。そうすると \(\al+c\beta-c\beta_i\) は方程式 \(f(x)=0\) の解にはなり得ないので、
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\neq0\:\:(2\leq i\leq m)\)
であり、\(g(x)=0\) と \(h(x)=0\) の共通解は \(\beta=\beta_1\) のみになる。
そうすると \(h(x)\) と \(g(x)\) は唯一の共通の因数 \((x-\beta)\) をもつので、\(h(x)\) と \(g(x)\) に互除法(21A)を適用すると、\(k\) をある有理数として最後は \(k(x-\beta)\) で割り切れる。
\(g(x)\) は \(\bs{Q}\) 上の多項式だから、すなわち \(\bs{Q}(\al+c\beta)\) 上の多項式である。また、\(h(x)\) は \(h(x)=f(\al+c\beta-cx)\) と定義されるが、\(f(x)\) が \(\bs{Q}\) 上の多項式なので、\(h(x)\) は \(\bs{Q}(\al+c\beta)\) 上の多項式である。つまり \(h(x)\) も \(g(x)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。
従って、互除法の最終結果である \(k(x-\beta)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。これは、
\(k,\:k\beta\:\in\:\bs{Q}(\al+c\beta)\)
であることを意味しており、従って、
\(\beta\:\in\:\bs{Q}(\al+c\beta)\)
となる。また \(\al\) も、
\(\al=(\al+c\beta)-c\beta\:\in\:\bs{Q}(\al+c\beta)\)
である。この結果、\(\al\)、\(\beta\) の両方が \((\al+c\beta)\) の四則演算で表現できることになり、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。従って、\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\theta)\) と合わせて、
\(\bs{Q}(\al,\beta)=\bs{Q}(\theta)\)
が結論づけられた。
以上を繰り返し適用すると、\(\bs{Q}\) に添加する方程式の解は \(\al,\:\beta,\:\gamma,\:\cd\) と増やしていける。従って、
ことが証明できた。[証明終]
「すべての代数拡大体は単拡大である」というのは、ちょっと驚くような定理です。方程式の解を複数添加した体は、このような性質をもっています。方程式の解の議論をするときに解を含む体の性質で議論することのメリットは、このような単拡大定理が使えることにも現れています。次の「単拡大の体」に関する定理も、単拡大定理があることで任意の代数拡大体につながっています。
なお、上の証明で本質的な役割を果たしているのはユークリッドの互除法が成り立つ原理(21A)です。互除法の "奥の深さ" がわかります。
単拡大の体
ある代数的数 \(\al\) の \(\bs{Q}\) 上の最小多項式が \(n\)次多項式 \(f(x)\) であるとする。このとき 体 \(\bs{K}\) を、
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
[証明]
\(\bs{K}\) が四則演算で閉じていて体であることを証明する。\(\bs{K}\) の元は「\(\bs{Q}\) 上の、\(\al\) の \(n-1\) 次以下の式」で表されるので、\(\bs{K}\) の任意の2つの元を、\(\bs{Q}\) 上の \(n-1\) 次以下の2つの多項式 \(g(x),\:h(x)\) を用いて、\(g(\al),\:h(\al)\) とする。
\(g(\al)+h(\al),\:g(\al)-h(\al)\) は \(\al\) の \(n-1\) 次以下の式なので、\(\bs{K}\) は加減について閉じている。
乗法で閉じていることを言うため、\(g(x)h(x)\) を \(f(x)\) で割った商を \(q(x)\)、余りを \(r(x)\) とする。つまり、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。\(x=\al\) を代入すると、\(f(\al)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
となる。\(r(x)\) は \(f(x)\) で割ったときの余りなので、次数は \(f(x)\) の次数 \(n\) よりも小さく、\(n-1\) 以下である。従って、\(g(\al)h(\al)\) は \(\al\) の \(n-1\) 次以下の式になり、\(\bs{K}\) は乗法で閉じている。
除法で閉じていることは、\(h(\al)\neq0\) のとき、\(\dfrac{g(\al)}{h(\al)}\) が \(\bs{Q}\) 上の「\(\al\) の \(n-1\) 次以下の多項式」で表されることを示せればよい。\(s(x),\:t(x)\) を未知の多項式とし、次の不定方程式を立てる。
\(f(x)s(x)+h(x)t(x)=g(x)\)
\(f(x)\) は最小多項式なので、最小多項式は既約多項式の定理(31I)により既約多項式である。また、\(h(x)\) は \(f(x)\) で割り切れない。なぜなら、もし \(h(x)\) が \(f(x)\) で割り切れるとすると、\(h(x)=u(x)f(x)\) と書けるが、これに \(\al\) を代入すると \(h(\al)=u(\al)f(\al)=0\) となり、\(h(\al)\neq0\) に矛盾するからである。
\(h(x)\) が、既約多項式である \(f(x)\) で割り切れないので、\(h(x)\) と \(f(x)\) は互いに素である。すると、多項式の不定方程式の定理(31A)により、上記の不定方程式を満たす \(s(x),\:t(x)\) が存在して、\(t(x)\) を \(n-1\) 次以下にとることができる。不定方程式に \(x=\al\) を代入すると、
\(h(\al)t(\al)=g(\al)\)
\(\dfrac{g(\al)}{h(\al)}=t(\al)\)
となり、除法でも閉じていることが分かった。つまり \(\bs{K}\) は体である。
\(\bs{Q}(\al)\) は「有理数と\(\al\)」の四則演算で生成される全ての数から成る体である。\(\bs{K}\) の元は有理数と \(\al\) の四則演算で表現され、それは元の間の四則演算で完全に閉じている。従って \(\bs{K}=\bs{Q}(\al)\) である。
表現の一意性は次のようにして証明できる。もし \(\bs{Q}(\al)\) の元について \(g(\al)\) と\(h(\al)\) の2通りの表し方があったとする。つまり、
\(g(\al)=h(\al)\)
\(g(\al)-h(\al)=0\)
とする。\(g(x)-h(x)\) が1次式以上だと仮定すると、\(n-1\)次以下の方程式 \(g(x)-h(x)=0\) が \(\al\) を解にもつことになる。つまり \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解 \(\al\) を持つ。一方、\(f(x)\) は \(n\)次既約多項式であり、\(g(x)-h(x)\) は \(n-1\) 次以下の多項式である。この場合、既約多項式の定理2(31F)によって、方程式 \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解を持たない。従って矛盾が生じる。つまり \(g(x)-h(x)\) は1次式以上ではありえない。\(g(x)-h(x)\) は \(0\)次多項式=定数である。
\(g(x)-h(x)\) が定数であれば、\(g(\al)-h(\al)=0\) なので、その定数は \(0\) しかない。つまり \(g(x)\) と \(h(x)\) の係数は全く一致する。従って表現は一意である。[証明終]
単拡大定理(32B)と、この単拡大の体の定理(32C)を合わせると、
ことになります。このことは、分子\(\cdot\)分母が \(\al\) の多項式である分数式があったとしても、分数を取り払った \(\al\) の多項式に変換できることを意味します。1.2 節の「方程式の解を含む体」で触れた "分母の有理化" が、どんなに複雑な分母であっても常に可能であることが分かります。
| 2.整数の群 |
「2.整数の群」「3.多項式と体」「4.一般の群」の3つの章は、第5章以下のガロア理論の核心に入るための準備です。
第2章の目的は2つあり、一つは整数を素材にして「群」と、それに関連した「剰余類」「剰余群」「既約剰余類」など、ガロア理論の理解に必要な概念を説明することです。
もう一つは、第2章の最後にある「既約剰余類群は巡回群の直積と同型である」という定理を証明することです。この定理はガロア理論の最終段階(6.可解性の必要条件)で必要なピースになります。
まず、"整数の群" に入る前に、整数論の基礎ともいえる「ユークリッドの互除法」「不定方程式」「法による演算」「中国剰余定理」から始めます。これらは後の定理の証明にしばしば使います。
2.1 整数
ユークリッドの互除法
| (互除法の原理:21A) |
自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,\:b)\) で表す。自然数 \(a\) を \(b\) で割った余りを \(r\) とすると、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。
[証明]
記述を簡略化するため、最大公約数を、
\(\mr{gcd}(a,\:b)=x\)
\(\mr{gcd}(b,\:r)=y\)
で表す。\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とすると、
\(a=pb+r\) \((0\leq r < b)\)
と書ける。\(a\) と \(pb\) は \(x\) で割り切れるから、\(r\) も \(x\) で割り切れる。つまり \(x\) は \(r\) の約数である。\(x\) は \(b\) の約数でもあるから、\(x\) は \(b\) と \(r\) の公約数である。公約数は \(b\) と \(r\) の最大公約数 \(y\) 以下だから、
\(x\leq y\)
である。
一方、\(pb\) と \(r\) は \(y\) で割り切れるから、\(y\) は \(a\) の約数である。\(y\) は \(b\) の約数でもあるから、\(y\) は \(a\) と \(b\) の公約数である。公約数は \(a\) と \(b\) の最大公約数以下だから、
\(y\leq x\)
である。\(x\leq y\) かつ \(y\leq x\) なので \(x=y\)、つまり、
\(\mr{gcd}(a,\:b)=\mr{gcd}(b,\:r)\)
である。[証明終]
この原理を利用して \(\mr{gcd}(a,\:b)\) を求めることができます。もし \(a\) が \(b\) で割り切れるなら \(\mr{gcd}(a,\:b)=b\) です。そうでないなら、\(a\) を \(b\) で割った余り \(r\) を求め、
新 \(a\:\longleftarrow\:b\)
新 \(b\:\longleftarrow\:r\)
と定義し直して、\(a\) が \(b\) で割り切れるかどうかを見ます。こうして次々と \(a\) と \(b\) のペアを作っていけば(=互除法)、\(b\) は単調減少していくので、いずれ \(a\) が \(b\) で割り切れるときがきます。なかなか割り切れなくても、\(b\) が \(1\) までくると絶対に割り切れる。つまり、
\(\mr{gcd}(a,\:b)=b\)
となるのが最終段階で、そのときの \(b\) が最大公約数です。\(b\) が \(1\) までになってしまったら、最大公約数は \(\bs{1}\)、つまり \(\bs{a}\) と \(\bs{b}\) は互いに素です。
ちなみに、ユークリッドの互除法で a と b の最大公約数を求める関数 EUCLID を Python で記述すると次のようになります。
def EUCLID(a, b): if a % b == 0: return b else: return EUCLID(b, a % b) |
% は Python の剰余演算子で、a % b は「a を b で割った余り」の意味です(定理の記述では \(r\))。つまり、このコードは、
gcd( a, b )=gcd( b, a % b )
という互除法の原理(21A)をストレートに書いたものです(a と b の大小に関係なく動作します)。こういったアルゴリズムはプログラミング言語で記述した方がシンプルでわかりやすくなります。
互除法は多項式の演算にも適用できます。多項式は整数と同じように割り算はできませんが余り算はできるからです。多項式の性質を理解するときに互除法は必須になります。
1次不定方程式
| (不定方程式の解の存在:21B) |
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
このことは1次不定方程式が3変数以上であっても成り立つ。つまり
\(a_1x_1+a_2x_2+\:\cd\:+a_nx_n=c\)
(\(a_i\) は \(0\) 以外の整数)
とし、
\(d=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_n)\)
とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
[証明]
1次不定方程式が整数解を持つとしたら、方程式の左辺は \(d\) で割り切れる、つまり \(d\) の倍数だから、右辺の \(c\) も \(d\) の倍数である。このことの対偶は「\(c\) が \(d\) の倍数でなければ方程式は整数解を持たない」なので、題意の「そうでなければ整数解を持たない」が証明されたことになる。従って以降は「\(c=kd\) (\(k\) は整数)と表せるなら方程式は整数解を持つ」ことを証明する。まず、変数が2つの場合である。
係数の \(a\) と \(b\) に互除法(21A)を適用し、それと同時に \(x,\:y\) の変数を変換して方程式を変形していく。まず、\(a\) を \(b\) で割った商を \(p\)、余りを \(r\) とする。
\(a=pb+r\)
である。互除法の次のステップの係数と変数を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1=b&\\
&&b_1=r&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x_1=px+y&\\
&&y_1=x&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(x,\:y\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&x=y_1&\\
&&y=x_1-py_1&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(\begin{eqnarray}
&&\:\:a_1x_1+b_1y_1&=b(px+y)+rx\\
&&&=pbx+by+rx\\
&&&=(pb+r)x+by\\
&&&=ax+by\\
\end{eqnarray}\)
と計算できるので、不定方程式は、
\(a_1x_1+b_1y_1=c\)
となり、係数の値がより小さい方程式に変形できる。互除法の原理(21A)により、\(a_1\) と \(b_1\) の最大公約数は \(d\) のままである。この方程式の \(x_1,\:y_1\) が求まれば、\(\br{③}\) を使って \(x,\:y\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i\) を \(b_i\) で割った商と余りを、
\(a_i=p_ib_i+r_i\)
のように求め、互除法の次のステップを、
\(a_{i+1}=b_i\)
\(b_{i+1}=r_i\)
\(x_{i+1}=p_ix_i+y_i\)
\(y_{i+1}=x_i\)
とすることで続けていける。このように、係数に互除法の適用を繰り返し、同時に変数を変換していく。そして互除法の最終段階で、
\(a_nx_n+b_ny_n=c\)
となったとする。この段階では \(a_n\) は \(b_n\) で割り切れ、そのときの \(b_n\) は最大公約数 \(d\) である。つまり。
\(a_nx_n+dy_n=c\)
である。もし \(c\) が \(d\) の倍数であれば、つまり \(c=kd\) (\(k\) は整数)なら、
\(x_n=0\)
\(y_n=k\)
という整数解を必ずもつ。従って、変数の変換過程を逆にたどって \(x,\:y\) が求まる。以上で2変数の場合に題意が正しいことが証明でき、同時に1次不定方程式の解を求めるアルゴリズムも明らかになった。
ちなみに、一次不定方程式の解の一つを求めるアルゴリズムを Python の関数で記述すると、次のようにシンプルです。
def LinearDiophantineEq(a, b, c): def extendedEUCLID(a, b): # gcd(a,b) と ax+by=gcd(a,b) の解を求める r = a % b # % は剰余演算 if r == 0: return {"x": 0, "y": 1, "gcd": b} else: x, y, gcd = extendedEUCLID(b, r).values() p = a // b # // は切捨て除算 return {"x": y, "y": x - p * y, "gcd": gcd} x, y, gcd = extendedEUCLID(a, b).values() k = c // gcd if( k != c / gcd ): return None # 解なし else: return [x * k, y * k] # x, y のペアを返す |
数学的帰納法を使って、3変数以上の場合を証明する。\(n=2\) の場合に成り立つことを示したので、\(n=k\) の場合に成り立つと仮定する。つまり、
\(k\) 変数の不定方程式を、 \(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_k\) (\(a_i\) は \(0\) 以外の整数) \(d_k=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\) とするとき、 \(c_k=md_k\) (\(m\) は整数) なら整数解がある。 |
と仮定する。\(n=k+1\) の場合の不定方程式を、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k+a_{k+1}x_{k+1}=c_{k+1}\)
\(\begin{eqnarray}
&&\:\: d_k&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k)\\
&&\:\: d_{k+1}&=\mr{gcd}(a_1,a_2,\:\cd\:,\:a_k,\:a_{k+1})\\
\end{eqnarray}\)
とし、この方程式が整数解をもつ条件を調べる。方程式を移項すると、
\(a_1x_1+a_2x_2+\:\cd\:+a_kx_k=c_{k+1}-a_{k+1}x_{k+1}\)
となるが、この不定方程式が整数解をもつのは、数学的帰納法の仮定によって、
左辺\(=d_k\) の整数倍
のときである。つまり、
\(c_{k+1}-a_{k+1}x_{k+1}=d_k\cdot y\)
という、2つの変数 \(x_{k+1},\:y\) の不定方程式が整数解をもつときである。式を移項すると、
\(a_{k+1}x_{k+1}+d_k\cdot y=c_{k+1}\)
であるが、これは証明済みの \(n=2\) のときの定理によって、
\(c_{k+1}=m\cdot\mr{gcd}(d_k,\:a_{k+1})\) (\(m\) は整数)
の場合に整数解をもつ。ここで、
\(\mr{gcd}(d_k,\:a_{k+1})=d_{k+1}\)
なので、
\(c_{k+1}=m\cdot d_{k+1}\) (\(m\) は整数)
の場合にのみ、\(n=k+1\) の不定方程式は整数解をもつことになる。
つまり、\(n=k\) のときに題意が成り立つと仮定すると、\(n=k+1\) のときにも成り立つ。\(n=2\) のときには成り立つから、\(n\geq3\) でも成り立つ。[証明終]
重要なのは、係数が互いに素な場合です。不定方程式の解の存在(21B)から、次の定理がすぐに出てきます。
| (不定方程式の解の存在:21C) |
\(0\) でない整数 \(a\) と \(b\) が互いに素とすると、1次不定方程式、
\(ax+by=1\)
は整数解をもつ。また、\(n\) を任意の整数とすると、
\(ax+by=n\)
は整数解をもつ。あるいは、任意の整数 \(n\) は、
\(n=ax+by\) \((x,\:y\) は整数)
の形で表現できる。
これは3変数以上であっても成り立つ。たとえば3変数の場合は、\(0\) でない整数 \(a,\:b,\:c\) の最大公約数が \(1\)、つまり、
\(\mr{gcd}(a,b,c)=1\)
であるとき、\(n\) を任意の整数として、1次不定方程式、
\(ax+by+cz=n\)
は整数解を持つ。
互除法と同じように、不定方程式の解の存在定理 (21B)と(21C)も、多項式の性質を理解する上で重要です。
法による演算
| (法による演算の定義:21D) |
\(a,\:b\) を整数、\(n\) を自然数とする。\(a\) を \(n\) で割った余りと、\(b\) を \(n\) で割った余りが等しいとき、
\(a\equiv b\:\:(\mr{mod}\:n)\)
と書き、\(a\) と \(b\) は「法 \(n\) で合同」という。あるいは「\(\mr{mod}\:n\) で合同」、「\(\mr{mod}\:n\) で(見て)等しい」とも記述する。
法による演算の規則は、さまざまありますが、主なものは次の通りです。このような演算を以降の説明で適時使います。
| (法による演算規則:21E) |
\(a,\:b,\:c,\:d\) を整数、\(n,r\) を自然数とし、
\(a\equiv b\:\:(\mr{mod}\:n)\)
\(c\equiv d\:\:(\mr{mod}\:n)\)
とする。このとき、
| \((1)\:a+c\) | \(\equiv b+d\) | \((\mr{mod}\:n)\) | |
| \((2)\:a-c\) | \(\equiv b-d\) | \((\mr{mod}\:n)\) | |
| \((3)\:ac\) | \(\equiv bd\) | \((\mr{mod}\:n)\) | |
| \((4)\:a^r\) | \(\equiv b^r\) | \((\mr{mod}\:n)\) |
中国剰余定理
| (中国剰余定理:21F) |
\(n_1\) と \(n_2\) を互いに素な自然数とする。\(a_1\) と \(a_2\) を、\(0\leq a_1 < n_1,\:0\leq a_2 < n_2\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
の連立方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\) でみて唯一である。つまり、\(0\leq x < n_1n_2\) の範囲に解が唯一存在する。
[証明]
もし \(x\) と \(y\:\:(y\leq x)\) が連立方程式を満たすとすると、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(y\equiv a_1\:\:(\mr{mod}\:n_1)\)
なので、
\(x-y\equiv0\:\:(\mr{mod}\:n_1)\)
であり、\(x-y\) は \(n_1\) で割り切れる。同様にして \(x-y\) は \(n_2\) でも割り切れる。\(n_1\) と \(n_2\) は互いに素なので、\(x-y\) は \(n_1n_2\) で割り切れる。従って \(x-y\) は \(n_1n_2\) の倍数であり、
| \(x-y\equiv0\) | \((\mr{mod}\:n_1n_2)\) | |
| \(x\equiv y\) | \((\mr{mod}\:n_1n_2)\) |
\(n_1,\:n_2\) は互いに素なので、不定方程式の解の存在定理(21C)により、
\(n_1m_1+n_2m_2=1\)
を満たす \(m_1,\:m_2\) が存在する。ここで、
\(x=a_2n_1m_1+a_1n_2m_2\)
とおくと、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2n_1m_1+a_1(1-n_1m_1)\\
&&&=a_1+n_1m_1(a_2-a_1)\\
&&&\equiv a_1\:\:(\mr{mod}\:n_1)\\
\end{eqnarray}\)
であり、
\(\begin{eqnarray}
&&\:\:x&=a_2n_1m_1+a_1n_2m_2\\
&&&=a_2(1-n_2m_2)+a_1n_2m_2\\
&&&=a_2+n_2m_2(a_1-a_2)\\
&&&\equiv a_2\:\:(\mr{mod}\:n_2)\\
\end{eqnarray}\)
なので、\(x\) は連立方程式の解である。この解は、上での証明のとおり \(\mr{mod}\:n_1n_2\) でみて唯一である。[証明終]
中国剰余定理は3数以上に拡張できて、次が成り立ちます。
| (中国剰余定理・多連立:21G) |
\(n_1,\:n_2,\:\cd\:,\:n_k\) を、どの2つをとっても互いに素な自然数とする。\(a_i\) を \(0\leq a_i < n_i\:\:(1\leq i\leq k)\) を満たす整数とする。このとき、
\(x\equiv a_1\:\:(\mr{mod}\:n_1)\)
\(x\equiv a_2\:\:(\mr{mod}\:n_2)\)
\(\vdots\)
\(x\equiv a_k\:\:(\mr{mod}\:n_k)\)
の連立合同方程式を満たす整数 \(x\) が存在する。この \(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。つまり、\(0\leq x < n_1n_2\cd n_k\) の範囲では唯一の解が存在する。
[証明]
自然数 \(N\) を
\(N=n_1n_2\cd n_k\)
と定義する。
\(\mr{gcd}\left(\dfrac{N}{n_i},n_i\right)=1\:\:\:(1\leq i\leq k)\)
なので、不定方程式の解の存在の定理(21C)により、
\(\dfrac{N}{n_i}s_i+n_it_i=1\:\:\:(1\leq i\leq k)\)
を満たす整数解、\(s_i,\:t_i\:\:(1\leq i\leq k)\) が存在する。
\(x=\displaystyle\sum_{i=1}^{k}a_i\dfrac{N}{n_i}s_i\)
と定義すると、\(j\neq i\) である \(j\) について、
\(\dfrac{N}{n_j}\equiv0\:\:(\mr{mod}\:n_i)\)
だから、\(\mr{mod}\:n_i\) でみると、\(x\) を定義する総和記号のなかは \(i\) の項だけが残る。つまり、
\(\begin{eqnarray}
&&\:\:x&\equiv a_i\dfrac{N}{n_i}s_i\:\:(\mr{mod}\:n_i)\\
&&&=a_i(1-n_it_i)\\
&&&\equiv a_i\:\:(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となって、\(x\) は連立合同方程式の解である。
連立合同方程式に2つの解、\(x,\:y\) があったとすると、
\(\begin{eqnarray}
&&\:\:x-y&\equiv a_i-a_i &(\mr{mod}\:n_i)\\
&&&=0 &(\mr{mod}\:n_i)\\
\end{eqnarray}\)
となり、\(x-y\) は \(n_i\) の倍数である。これは \(1\leq i\leq k\) のすべての \(i\) で成り立ち、また \(n_i\:\:(1\leq i\leq k)\) は、どの2つをとっても互いに素である(=共通な因数が全くない)から、\(x-y\) は \(N\) の倍数である。従って、
\(x\equiv y\:\:(\mr{mod}\:N)\)
であり、\(x\) は \(\mr{mod}\:n_1n_2\cd n_k\) でみて唯一である。[証明終]
2.2 群
これ以降、整数を素材に「群」と、それに関連した概念の説明をします。まず、群の定義からです。
群の定義
| (群の定義:22A) |
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群(group)であると言う。
| \(G\) の任意の元 \(x,\:y\) に対して演算(\(\cdot\)で表す)が定義されていて、\(x\cdot y\in G\) である。 | |
| 演算について結合法則が成り立つ。つまり、 \((x\cdot y)\cdot z=x\cdot(y\cdot z)\) | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot e=e\cdot x=x\) を満たす元 \(e\) が存在する。\(e\) を単位元という。 | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot y=y\cdot x=e\) となる元 \(y\) が存在する。\(y\) を \(x\) の逆元といい、\(x^{-1}\) と表す。 |
整数 \(\bs{Z}\)
整数の集合を \(\bs{Z}\) と書きます。\(\bs{Z}\) は「加法(足し算)を演算とする群」になります。単位元は \(0\) で、元 \(x\) の逆元は \(-x\) です。この群の元の数は無限なので「無限群」です。
整数の加法は、\(x+y=y+x\) と演算の順序を入れ替えることができます。このような群が可換群です。アーベル群とも言います。
なお、有理数は \(\bs{Q}\)、実数は \(\bs{R}\)、複素数は \(\bs{C}\) で表しますが、\(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) は、\(\bs{Z}\) を同じように加法に関して群です(=加法群)。と同時に \(\bs{Q}\)、\(\bs{R}\)、\(\bs{C}\) から加法の単位元 \(0\) を除くと、乗法に関しても群になります。その単位元は \(1\) です。
部分群 \(n\bs{Z}\)
群 \(G\) の部分集合 \(H\) が、\(G\) と同じ演算で群としての定義を満たすとき、\(H\) を部分群(subgroup)と言います。
\(G\) の単位元 \(e\) だけから成る部分集合 \(\{\:e\:\}\) は群としての定義を満たし、部分群です。また \(G\) そのものも "\(G\)の部分集合" であり、部分群です。これらを \(G\) の自明な部分群と言います。
\(\bs{Z}\) の元の一つを \(n\) とし(\(n\neq0\))、\(n\) の倍数の集合を \(n\bs{Z}\) と表記します。\(n\bs{Z}\) は加法を演算として群の定義を満たすので、\(\bs{Z}\) の部分群です。\(n\bs{Z}\) も無限群かつ可換群です。たとえば \(n=6\) とすると、
\(6\bs{Z}=\{\cd,\:-6,\:0,\:6,\:12,\:18,\:\cd\}\)
です。
剰余類と剰余群
部分群を用いて、元の数が有限個である有限群を作ることができます。一般に、群 \(G\) の部分群を \(H\) とするとき(演算を "\(\cdot\)" とします)、\(G\) の任意の元 \(g\) を取り出して、
\(g\cdot H\)
とした集合を剰余類(coset / residue class)と言います。これは「\(g\) と、集合 \(H\) のすべての元を演算した結果の集合」の意味です。
\(\bs{Z}\) と その部分群 \(6\bs{Z}\) を例にとると、\(\bs{Z}\) の任意の元を \(i\) として、
\(i+6\bs{Z}\)
が剰余類です。具体的にその集合を書くと、
\(\vdots\)
\(0+6\bs{Z}=\{\cd,\:-6,\:\:0,\:\phantom{1}6,\:12,\:18,\:\cd\}\)
\(1+6\bs{Z}=\{\cd,\:-5,\:\:1,\:\phantom{1}7,\:13,\:19,\:\cd\}\)
\(2+6\bs{Z}=\{\cd,\:-4,\:\:2,\:\phantom{1}8,\:14,\:20,\:\cd\}\)
\(3+6\bs{Z}=\{\cd,\:-3,\:\:3,\:\phantom{1}9,\:15,\:21,\:\cd\}\)
\(4+6\bs{Z}=\{\cd,\:-2,\:\:4,\:10,\:16,\:22,\:\cd\}\)
\(5+6\bs{Z}=\{\cd,\:-1,\:\:5,\:11,\:17,\:23,\:\cd\}\)
\(6+6\bs{Z}=\{\cd,\:\phantom{-}0,\:\:6,\:12,\:18,\:24,\:\cd\}\)
\(7+6\bs{Z}=\{\cd,\:\phantom{-}1,\:\:7,\:13,\:19,\:25,\:\cd\}\)
\(\vdots\)
などです。以降、剰余類 \(i+6\bs{Z}\) を \(\ol{\,i\,}\) と記述します。つまり、
\(\ol{\,i\,}=i+6\bs{Z}\)
です。上の表示を見ると分かるように、たとえば \(\ol{\,1\,}\) と \(\ol{\,7\,}\) は集合として同じものです。さらに、
\(\cd=\ol{-11}=\ol{-5}=\ol{\,1\,}=\ol{\,7\,}=\ol{13}=\cd\)
であり、これらは同じ集合です。これらの集合の中から一つの元を選んで「代表元」と呼ぶことにします。以降、分かりやすいように \(1\) を代表元とします。その他の剰余類についても同じようにすると、部分群 \(6\bs{Z}\) による剰余類は、
\(\ol{\,0\,},\:\ol{\,1\,},\:\ol{\,2\,},\:\ol{\,3\,},\:\ol{\,4\,},\:\ol{\,5\,}\)
の6つで表されることになります。これらの剰余類には重複がありません。また、全部の和集合をとると \(\bs{Z}\) になります。記号で書くと、\(\phi\) を空集合として、
\(\ol{\,i\,}\:\cap\:\ol{\,j\,}\:=\:\phi\:\:(0\leq i,\:j\leq6,\:i\neq j)\)
\(\bs{Z}=\ol{\,0\,}\:\cup\:\ol{\,1\,}\:\cup\:\ol{\,2\,}\:\cup\:\ol{\,3\,}\:\cup\:\ol{\,4\,}\:\cup\:\ol{\,5\,}\)
です。別の見方をすると、\(i,\:j\) を任意の整数するとき、
| \(\ol{\,i\,}\) と \(\ol{\,j\,}\) の元は「全く同じ」か「全く重複しない」のどちらかである | |
| \(\bs{Z}\) は剰余類で分類される |
と言えます。平たく言うと、\(n\)(上の例では \(6\))で割った余りが同じ整数を集めたものが剰余類です。"剰余" という用語はそこからきています。
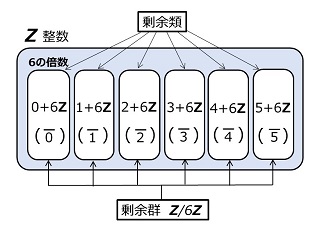
|
剰余類と剰余群 |
整数 \(\bs{Z}\) の部分集合 \(6\bs{Z}\)(\(6\)の倍数の集合)から、\(\ol{\,i\,}=i+6\bs{Z}\) \((0\leq i\leq5)\) の定義で6つの「剰余類」が作れる。これらに重複はなく、\(\bs{Z}\) はこの6つで "分類" される。 整数 \(i,\:j,\:k\) に \(i+j=k\) の関係があるとき、\(\ol{\,i\,}+\ol{\,j\,}=\ol{\,k\,}\) で剰余類の加算を定義すると、この定義で剰余類は群となる。この群を「剰余群」と呼び \(\bs{Z}/6\bs{Z}\) で表わす(単位元は \(\ol{\,0\,}\))。この群では \(\ol{\,3\,}+\ol{\,5\,}=\ol{\,2\,}\) などの演算になるが、これは整数の合同式 \(3+5\equiv2\) \((\mr{mod}\:6)\) と同一視できる。 |
剰余類のうち、\(\ol{\,0\,}\) は \(\bs{Z}\) の部分群ですが、\(\ol{\,i\,}\:(i\neq0)\) の集合は \(\bs{Z}\) の部分群ではありません。集合の元と元のたし算が集合を "はみ出す" からです。しかし、剰余類同士の演算(=集合と集合の演算)を定義することにより、剰余類を元とする群を構成できます。それが次です。
剰余類に加算を定義できます。つまり、\(\ol{\,i\,}+\ol{\,j\,}\) を、
\(\ol{\,i\,}+\ol{\,j\,}=\ol{(\:i+j\:)}\) (右辺の \(+\) は整数の加算)
と定義すると、この演算の定義で剰余類は群になり、
\(\bs{Z}/n\bs{Z}\)
と表します。この群の元は集合(=剰余類)です。この群を剰余群(あるいは商群。quotient group)と言います。元の数は有限なので有限群です。また演算が整数の加算なので可換であり、「有限可換群」です。
\(\bs{Z}/n\bs{Z}\) という記法では、\(\bs{Z}\) も \(n\bs{Z}\) も群(この場合は加法群)です。一般に「群\(/\)部分群」と書けば、剰余群(商群)の意味です。これに対して「拡大体\(/\)体」は "体の拡大" を意味します。 \(\bs{Q}(\al)/\bs{Q}\) などです。
一般に、有限群 \(G\) の元の数を群の位数(order)と呼び、
\(|G|\) あるいは \(\#G\)
で表します。剰余群では、
| \(|(\bs{Z}/n\bs{Z})|\) | \(=n\) | |
| \(\#(\bs{Z}/n\bs{Z})\) | \(=n\) |
生成元と巡回群
剰余群 \(\bs{Z}/n\bs{Z}\) は、元 \(\ol{\,1\,}\) だけをもとに群演算を繰り返すことによって、すべての元を作り出すことができます。\(\bs{Z}/6\bs{Z}\) を例にとると、
\(\ol{\,2\,}=\ol{\,1\,}+\ol{\,1\,}\)
\(\ol{\,3\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
などであり
\(\ol{\,0\,}=\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}+\ol{\,1\,}\)
です。群にこのような元がある場合、それを生成元(generator)と呼びます。\(\bs{Z}/6\bs{Z}\) の場合は \(\ol{\,1\,}\) のほかに \(\ol{\,5\,}\) も生成元です。\(\ol{\,i\,}\) を \(k\) 個加算することを、\(k\cdot\ol{\,i\,}\) と書くことにします。
\(k\cdot\ol{\,i\,}=\overbrace{\ol{\,i\,}+\ol{\,i\,}+\cd+\ol{\,i\,}}^{k\:個加算}\)
です。\(\ol{\,5\,}\) については、
\(1\cdot\ol{\,5\,}=\ol{\,5\,},\:\:2\cdot\ol{\,5\,}=\ol{\,4\,},\:\:3\cdot\ol{\,5\,}=\ol{\,3\,}\)
\(4\cdot\ol{\,5\,}=\ol{\,2\,},\:\:5\cdot\ol{\,5\,}=\ol{\,1\,},\:\:6\cdot\ol{\,5\,}=\ol{\,0\,}\)
のように、\(\ol{\,5\,}\) を起点として全部の元が生成され、\(\ol{\,5\,}\) が生成元であることがわかります。
剰余群 \(\bs{Z}/n\bs{Z}\) においては、\(1\leq g < n\) である整数 \(g\) が \(n\) と互いに素であるとき、\(\ol{\,g\,}\) は生成元になります。その理由ですが、
\(\ol{\,g\,},\:\:2\cdot\ol{\,g\,},\:\:3\cdot\ol{\,g\,},\:\cd\:,\:n\cdot\ol{\,g\,}\)
という \(n\) 個の剰余類の列を考えると、これらは全て違ったものだからです。なぜなら、もし \(1\leq i < j\leq n\) である \(i,\:j\) について、 \((\br{A})\)
\(i\cdot\ol{\,g\,}=j\cdot\ol{\,g\,}\)
だとすると、これは、法 \(n\) における整数の合同式で、
\(ig\equiv jg\:\:(\mr{mod}\:n)\)
を意味します。つまり、
\((j-i)g\equiv0\:\:(\mr{mod}\:n)\)
ですが、\(g\) が \(n\) と互いに素なため、\((j-i)\) は \(n\) で割り切れなければなりません。しかし \(1\leq(j-i)\leq(n-1)\) なので、矛盾します。従って、\(n\) 個の剰余類の列 \((\br{A})\) は、全て違ったものです。剰余群 \(\bs{Z}/n\bs{Z}\) の群位数は \(n\) なので、\((\br{A})\) は \(\bs{Z}/n\bs{Z}\) の全ての元であり、従って \(\ol{\,g\,}\) は生成元です。
\(n\) が素数 \(p\) の場合は、\(p\) 未満の自然数はすべて \(p\) と互いに素なので、単位元 \(\ol{\,0\,}\) を除く \(\bs{Z}/p\bs{Z}\) の元が生成元になります。
\(k\) 個の \(\ol{\,i\,}\) の群演算をして初めて、結果が単位元 \(\ol{\,0\,}\) になるときの \(k\) を、\(\ol{\,i\,}\) の位数(order)といいます。群の位数と紛らわしいですが、これは群の「元の位数」です。\(\bs{Z}/6\bs{Z}\) の場合、「元 \(\rightarrow\) 位数」の対応は、
\(\ol{\,0\,}\:\rightarrow\:1,\:\:\ol{\,1\,}\:\rightarrow\:6,\:\:\ol{\,2\,}\:\rightarrow\:3\)
\(\ol{\,3\,}\:\rightarrow\:2,\:\:\ol{\,4\,}\:\rightarrow\:3,\:\:\ol{\,5\,}\:\rightarrow\:6\)
です。位数という用語を使うと、生成元とは「位数が群位数に等しい元」のことです。
群 \(G\) が一つの生成元から生成されるとき、\(G\) を巡回群(cyclic group)と言います。\(\bs{Z}/10\bs{Z}\) の例をとると、\(10\) と互いに素な数を考えて、生成元は \(\ol{\,1\,},\:\ol{\,3\,},\:\ol{\,7\,},\:\ol{\,9\,}\) の4つです。従って、たとえば \(\ol{\,7\,}\) 同士の加算を繰り返すと、
| \(\ol{\,7\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,1\,}\:\rightarrow\)\( \:\ol{\,8\,}\:\rightarrow\)\( \:\ol{\,5\,}\:\rightarrow\)\( \:\ol{\,2\,}\:\rightarrow\)\( \:\ol{\,9\,}\:\rightarrow\)\( \:\ol{\,6\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,0\,}\:\rightarrow\)\( \:\ol{\,7\,}\:\rightarrow\)\( \:\ol{\,4\,}\:\rightarrow\)\( \:\ol{\,1\,}\:\rightarrow\)\( \:\ol{\,8\,}\:\rightarrow\)\( \:\cd\) |
群の直積
\(G,\:H\) を群とします。\(G\) の任意の元 \(g\) と \(H\) の任意の元 \(h\) のペア \((g,\:h)\) 作り、このペアを元とする集合を考えます。以降、群の演算を表す "\(\cdot\)" を省略します。
集合の任意2つの元を、
\(a=(g_a,\:h_a)\)
\(b=(g_b,\:h_b)\)
とし、\(a\) と \(b\) の演算を、
\(ab=(g_ag_b,\:h_ah_b)\)
| \(g_ag_b\) | は \(G\) での群演算 | |
| \(h_ah_b\) | は \(H\) での群演算 |
\(G\times H\)
で表します。有限群の場合、群の位数は、
\(|G\times H|=|G|\cdot|H|\) (\(\cdot\) は整数のかけ算)
です。以上は2つの群の直積ですが、同様に3つ以上の群の直積も定義できます。
群の同型
\(G\) と \(H\) を群とします。\(G\) から \(H\) への1対1の写像 \(f\) で、\(G\) の任意の2つの元 \(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
| \(xy\) は群 \(G\) の演算、\(f(x)f(y)\) は群 \(H\) の演算) |
\(G\cong H\)
と表します。同型であるということは、2つの群の元が1対1対応するのみならず、元の演算前、演算後も1対1対応していることを意味します。従って同型である群は「同じもの」と見なせます。
以降、剰余類を表す \(\bs{\ol{\,i\,}}\) のバーを省略して \(\bs{i}\) と書きます。従って \(i\) は整数か剰余類のどちらかを示しますが、2つは同一視できます。 |
\(\bs{Z}/15\bs{Z}\) で群の同型の例を示します。ここでは、整数 \(i\) を 整数 \(a\) で割った余りを \(i_a\) と書きます。\(\bs{Z}/15\bs{Z}\) の任意の元 \(i\:\:(0\leq i\leq14)\) について、写像 \(f\) を、
\(f\::\:i\:\longmapsto\:(i_3,\:i_5)\)
で定めると、\(f\) は \(\bs{Z}/15\bs{Z}\) から \((\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\) への同型写像になります。
そのことを確かめると、まず \(i\) を決めれば \(i_3,\:i_5\) は一意に決まります。また\(i_3,\:i_5\) を決めると、\(3\) と \(5\) は互いに素なので、中国剰余定理(21F)により、\(0\leq i\leq14\) の範囲で \(i\) が一意に決まります。つまり \(f\) は1対1写像(数学用語で "全単射")です。また、2つの元 \(i,\:j\) について
\(\begin{eqnarray}
&&\:\:f(i+j)&=(\:(i+j)_3,\:(i+j)_5\:)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i)+f(j)&=(i_3,\:i_5)+(j_3,\:j_5)\\
&&&=(i_3+j_3,\:i_5+j_5)\\
&&\:\:f(i+j)&=f(i)+f(j)\\
\end{eqnarray}\)
が成り立つので、\(f\) は同型写像の要件を満たします。従って、
\(\bs{Z}/15\bs{Z}\cong(\bs{Z}/3\bs{Z})\times(\bs{Z}/5\bs{Z})\)
です。一般に、\(a\) と \(b\) を互いに素な自然数とすると、
\(\bs{Z}/(ab)\bs{Z}\cong(\bs{Z}/a\bs{Z})\times(\bs{Z}/b\bs{Z})\)
です。これは2つの数だけでなく、\(n\) が \(k\)個の数 \(a_1,\:a_2,\:\cd\:a_k\) の積で表され、かつ、\(a_1,\:a_2,\:\cd\:a_k\) のどの2つをとっても互いに素なときには、中国剰余定理・多連立(21G)によって、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/a_1\bs{Z})\times(\bs{Z}/a_2\bs{Z})\times\cd\times(\bs{Z}/a_k\bs{Z})\)
が成り立ちます。一般に 自然数 \(n\) は \(p_i\) を素数として、
\(n=p_1^{n_1}p_2^{n_2}\cd p_k^{n_k}\)
と素因数分解され、\(p_i^{n_i}\:\:(1\leq i\leq k)\) はどの2つをとっても互いに素なので、
\(\bs{Z}/n\bs{Z}\cong(\bs{Z}/p_1^{n_1}\bs{Z})\times(\bs{Z}/p_2^{n_2}\bs{Z})\times\cd\times(\bs{Z}/p_k^{n_k}\bs{Z})\)
成り立ちます。
2.3 既約剰余類群
2.2 節の剰余群は、整数の加算を演算の定義とする群でした。これに対して、整数の乗算を演算の定義とする群が構成できます。それが既約剰余類群です。
| (既約剰余類群:23A) |
剰余群 \(\bs{Z}/n\bs{Z}\) から、代表元が \(n\) と互いに素なものだけを選び出したものを既約剰余類という。
「既約剰余類」は、乗算に関して群になる。これを「既約剰余類群」といい、\((\bs{Z}/n\bs{Z})^{*}\) で表す。
定義により、\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) である。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。\(n\) が素数 \(p\) の場合の群位数は \(\varphi(p)=p-1\) である。
[証明]
「既約剰余類」は、乗算に関して群になることを証明する。まず例をあげると、\((\bs{Z}/10\bs{Z})^{*}\) の元は \(10\) と互いに素な代表元をもつ \(1,\:3,\:7,\:9\) である。この元の乗算による演算表を作ると、
\(\begin{array}{r|rrrr}
&1&3&7&9\\ \hline
1&1&3&7&9\\
3&3&9&1&7\\
7&7&1&9&3\\
9&9&7&3&1\\
\end{array}\)
となって、演算は閉じていて、単元 \(1\) があり、逆元があることがわかる( \(3^{-1}=7,\:7^{-1}=3,\:9^{-1}=9\) である\()\)。つまり群として成り立っている。
一般に、\(a,\:b\) が \(n\) と素だとすると、\(ab\) も \(n\) と素なので、\((\bs{Z}/n\bs{Z})^{*}\) は乗算で閉じている。また、不定方程式の解の存在定理(21C)により、
\(ax+ny=1\)
を満たす \(x,\:y\) が存在する。この式の両辺を \(\mr{mod}\:n\) でみると、
\(ax\equiv1\:\:(\mr{mod}\:n)\)
となる。この方程式の解の一つ(=特殊解)を \(x_0\) とし、\(k\) を整数として、\(x=x_0+kn\) とおくと\(,\)
\(\begin{eqnarray}
&&\:\:ax&=a(x_0+kn)\\
&&&=ax_0+akn\\
&&&\equiv1\:\:(\mr{mod}\:n)\\
\end{eqnarray}\)
なので、\(x\) も解である。従って解を \(1\leq x < n\) の範囲で選ぶことができる。つまり、\((\bs{Z}/n\bs{Z})^{*}\) の元 \(a\) に対して逆元が定義できることになり、\((\bs{Z}/n\bs{Z})^{*}\) は群である。[証明終]
2.4 有限体 \(\bs{F}_p\)
\(\bs{Z}/p\bs{Z}\) は体
剰余群 \(\bs{Z}/n\bs{Z}\) において \(n\) が素数 \(p\) である \(\bs{Z}/p\bs{Z}\) を考えます。\(p\) 未満の自然数は \(p\) と互いに素なので、既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) は、\(\bs{Z}/p\bs{Z}\) から 加法の単位元 \(0\) を除いたものになります。つまり \(\bs{Z}/p\bs{Z}\) は加法について群であり、\(\bs{Z}/p\bs{Z}\:-\:\{\:0\:\}\) が乗法について群になっている。このような集合を体(field)と言います。
体とは加減乗除ができて、加法と乗法を結びつける分配則、
\(a(b+c)=ab+ac\)
が成り立つ集合です。\(\bs{Z}/p\bs{Z}\) は整数の演算をもとに定義されているので分配則が成り立ちます。
\(\bs{\bs{Z}/p\bs{Z}}\) を体としてみるとき、\(\bs{\bs{F}_p}\) と表記します。有理数 \(\bs{Q}\)、実数 \(\bs{R}\)、複素数 \(\bs{C}\) は体ですが、これらは無限集合です。一方、\(\bs{F}_p\) は有限集合なので有限体です。
有限体 \(\bs{F}_p\) における定数、変数、多項式、方程式の計算は、有理数/実数/複素数と同じようにできます。以下、今後の証明に使うので、\(\bs{F}_p\) 上の多項式と方程式を説明します。つまり、係数が \(\bs{F}_p\) の数である多項式や方程式です。
有限体の多項式と方程式
\(\bs{F}_p\) 上の多項式は、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:\:(a_i\in\bs{F}_p)\)
です。見た目は整数係数の多項式ですが、係数は \(\bs{F}_p\) の元です。\(\bs{F}_p\) は体なので、\(\bs{F}_p\) 上の多項式は加減算\(\cdot\)乗算\(\cdot\)余りをともなう除算(=剰余算、余り算)が、\(\bs{Q}\) 上の多項式と同じようにできます。従ってこれらの演算にもとづいた概念、定理は、\(\bs{Q}\) 上の多項式の場合と同じです。つまり、
| 因数分解 | |
| 割り切れる、割り切れないの概念 | |
| 最大公約数(共通に割り切る最大次数の多項式) | |
| 互除法による最大公約数の計算 | |
| 互いに素の概念(最大公約数が定数) | |
| 多項式の不定方程式(31A) | |
| 既約多項式(31B) | |
| 既約多項式と素数の類似性(31D) |
などです(なお、多項式\(\cdot\)方程式についてのこれらの概念や定理は「3.1 多項式」で説明します)。
たとえば、\(\bs{F}_5\) における多項式、\(x^2+1\) は、
\(x^2+1=(x-2)(x-3)\) [\(\bs{F}_5\)]
と、2つの1次多項式に因数分解できます。
\(\begin{eqnarray}
&&\:\:(x-2)(x-3)&=x^2-5x+6\\
&&&=x^2+1\\
\end{eqnarray}\)
が成り立つからです。従って、方程式、
\(x^2+1=0\) [\(\bs{F}_5\)]
の解は、\(x=2,\:3\) です。
一方、\(\bs{F}_7\) において \(x^2+1\) はこれ以上因数分解できない多項式です。なぜなら、
\(f(x)=x^2+1\) [\(\bs{F}_7\)]
とおくと、
\(f(k)\neq0\:\:(0\leq k\leq6)\) [\(\bs{F}_7\)]
だからです。もちろん剰余算(余り算)はできて、\(x^2+1\) を \(x-2\) で割ると、
\(x^2+1=(x-2)(x+2)+5\) [\(\bs{F}_7\)]
と計算できます。これは \(f(2)=5\)、つまり \(f(x)\) を \(x-2\) で割った余りは \(5\)、を意味します。
以上を踏まえて、\(\bs{F}_p\) 上の多項式\(\cdot\)方程式に関する次の定理を証明します(次節の定理の証明に使います)。方程式の "解" は "\(\bs{F}_p\) における解" の意味です。
| (有限体上の方程式1:24A) |
\(\bs{F}_p\) 上の1次方程式、
\(ax+b=c\)
は1個の解をもつ。
[証明]
両辺に \(b\) の加法の逆元 \(-b\) を加えると、
\(ax=c+(-b)\)
となり、この両辺に 乗法の逆元 \(a^{-1}\) を掛けると、
\(x=a^{-1}(c+(-b))\)
となり、唯一の解が求まる。[証明終]
| (有限体上の方程式2:24B) |
\(\bs{F}_p\) 上の多項式を \(f(x)\) とする。
\(f(a)=0\) なら、\(f(x)\) は \(x-a\) で割り切れる。
[証明]
\(f(x)\) を \(x-a\) で割った商を \(g(x)\)、余りを \(b\) とする。
\(f(x)=(x-a)g(x)+b\)
であるが、\(f(a)=0\) なので \(b=0\) である。従って、
\(f(x)=(x-a)g(x)\)
と表され、\(f(x)\) は \(x-a\) で割り切れる。[証明終]
| (有限体上の方程式3:24C) |
\(\bs{F}_p\) 上の \(n\)次多項式を \(f_n(x)\) とする。方程式、
\(f_n(x)=0\)
の解は、高々 \(n\) 個である。
[証明]
\(n\) に関する数学的帰納法を使う。\(\bs{F}_p\) 上 の1次方程式の解は1個だから(24A)、題意は成り立つ。\(n\) 以下で題意が成り立つと仮定する。
\(\bs{F}_p\) 上の \(n+1\) 次方程式 \(f_{n+1}(x)=0\) の解がなければ、\(n+1\) でも題意は成り立っている。もし1個の解 \(a\) があるとすると\(f_{n+1}(a)=0\) なので、\(f_{n+1}(x)\) は \(x-a\) で割り切れる(24B)。つまり、
\(f_{n+1}(x)=(x-a)g(x)\)
となるが、\(g(x)\) は \(n\)次多項式だから、方程式、
\(g(x)=0\)
の解は高々 \(n\) 個である。従って、\(f_{n+1}(x)=0\) の解は高々 \(n+1\) 個である。ゆえに帰納法により題意は正しい。[証明終]
2.5 既約剰余類群は巡回群
2.5 節の目的は、2章の最終目的である、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である
という定理を証明することです。証明には少々長いステップが必要ですが、この定理はガロア理論の最終段階で必要になります。まず、群の「元の位数」の性質から始めます。
位数
| (位数の定理:25A) |
\((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とする。以下が成り立つ。
[補題1]
\(a^x=1\) となる \(x\:\:(1\leq x)\) が必ず存在する。\(x\) のうち最小のものを \(d\) とすると、\(d\) を \(a\) の位数(order)と呼ぶ。
[補題2]
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。ないしは、
\(a^0=1,\:a,\:a^2,\:\cd\:,a^{d-1}\) は 全て異なる。
[補題3]
\(n=p\)(素数)とする。\(d\) 乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d\) がそのすべてである。
[補題4]
\(a^x=1\) となる \(x\) は \(d\) の倍数である。
[補題5]
\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
[証明]
[補題1]
\((\bs{Z}/n\bs{Z})^{*}\) は有限群だから、\(a^j=a^i\:\:(i < j)\) となる \(i,\:j\) は必ず存在する。\(a^{-i}\) を両辺に掛けると \(a^{j-i}=1\) となり\(a^x=1\) となる \(x\) が必ず存在する。従って \(a\) の位数が定義できる。
[補題2]
\(a^j=a^i\:\:(1\leq i < j\leq d)\) となる \(i,\:j\) があったとすると、両辺に \(a^{-1}\) を掛けて \(a^{j-i}=1\) となるが、\(j-i < d\) だから、\(a^x=1\) となる最小の \(x\) が \(d\) ということと矛盾する。従って、\(a,\:a^2,\:a^3,\:\cd\:,\:a^d=1\) は 全て異なる。
[補題3]
\(a^i\:\:(1\leq i\leq d)\) を \(d\) 乗すると、
\((a^i)^d=(a^d)^i=1\)
であり、これら \(d\) 個の元はすべて \(d\) 乗すると \(1\) になる。
一方、\(d\) 乗すると \(1\) になる 元は 有限体 \(\bs{F}_p\) 上の \(d\) 次方程式 \(x^d-1=0\) の解であるが、有限体上の方程式3の定理(24C)により、\(d\) 次方程式の解の数は高々 \(d\) 個である。従って、\(a^i\:\:(1\leq i\leq d)\) の \(d\) 個の元は、\(d\) 乗すると \(1\) になる 元のすべてである。
[補題4]
\(x\) を \(d\) で割った商を \(q\:\:(1\leq q)\)、余りを \(r\:\:(0\leq r < d)\)とすると、
\(\begin{eqnarray}
&&\:\:a^{qd+r}&=1\\
&&\:\:(a^d)^q\cdot a^r&=1\\
&&\:\:a^r=1&\\
\end{eqnarray}\)
となるが、もし \(r\neq0\) なら、\(d\) より小さい数 \(r\) で \(a^r=1\) となり、これは \(a\) の位数が \(d\) であることと矛盾する。従って \(r=0\) であり、\(x\) は \(d\) の倍数である。
[補題5]
\((\bs{Z}/n\bs{Z})^{*}\) を \(G\) と書く。集合 \(A\) を、
\(A=\{a,\:a^2,\:\cd\:,\:a^d=1\}\)
とする。もし \(|G|=d\) なら、題意は満たされている。
\(d < |G|\) の場合、\(A\) に含まれない \(G\) の元の一つを \(b_1\) とし、
\(A_1=\{b_1a,\:b_1a^2,\:\cd\:,\:b_1a^d\}\)
とする。この \(A_1\) に \(A\) と共通な元はない。なぜならもし、
\(a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-j}\) をかけて、
\(a^{i-j}=b_1\)
となるが、左辺は \(A\) の元であり、右辺の \(b_1\) が \(A\) の元となって矛盾するからである。もし \(A\) と \(A_1\) で \(G\) の元を尽くしているなら、\(|G|=2d\) であり、題意は満たされている。
そうでない場合、\(A\) と \(A_1\) に含まれない \(G\) の元の一つを \(b_2\) とし、
\(A_2=\{b_2a,\:b_2a^2,\:\cd\:,\:b_2a^d\}\)
とする。上の論理と同じで \(A_2\) と \(A\) に共通な元はない。のみならず、\(A_2\) と \(A_1\) に共通な元もない。なぜなら、もし、
\(b_2a^i=b_1a^j\:\:(1\leq i,j\leq d)\)
だとすると、両辺に \(a^{-i}\) をかけて、
\(b_2=b_1a^{j-i}\)
となるが、\(a^{j-i}\) は \(A\) の元だから、\(b_1a^{j-i}\) は \(A_1\) の元であり、\(b_2\) が \(A_1\) の元ということになって矛盾するからである。もし \(A,\:A_1,\:A_2\) で \(G\) の元を尽くしているなら、\(|G|=3d\) であり、題意は満たされている。
そうでない場合、この操作を続けていくと、\(G\) は有限群だから、ちょうど \(G\) の元が尽くされたところで、操作は止まる。最後に作った部分集合が \(A_n\) だったとすると \(|G|=(1+n)d\) であり、\(a\) の位数 \(d\) は群位数の約数である。
\((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\) なので(23A)、位数の定理(25A)の[補題5]から、次のフェルマの小定理とオイラーの定理が成り立つことがわかります。
| (オイラーの定理:25B) |
自然数 \(n\) と素な自然数 \(a\) について、
\(a^{\varphi(n)}=1\:\:(\mr{mod}\:n)\)
が成り立つ(オイラーの定理)。\(\varphi\) はオイラー関数で、\(\varphi(n)\) は \(n\) 以下で \(n\) と互いに素な自然数の数を表す。
\(n=p\)(素数)の場合は、\(p\) と素な数 \(a\) について、
\(a^{p-1}=1\:\:(\mr{mod}\:p)\)
となる(フェルマの小定理)。
生成元の存在1
\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在し、従って巡回群であることを証明します。まず、特定の位数 \(d\) をもつ元の数に関する定理からです。
| (位数 \(d\) の元の数:25C) |
\(p\) を素数とする。\((\bs{Z}/p\bs{Z})^{*}\) において、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。
[証明]
[補題1]により、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元に位数が定義できる。その位数は[補題5]により、群位数 \((p-1)\) の約数である。
\((p-1)\) の任意の約数を \(d\) とし、位数 \(d\) の元 \(a\) があったとする。[補題3]により、\(d\)乗すると \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は、
\(a,\:a^2,\:a^3,\:\cd\:,\:a^d(=1)\)
の「\(a\) 系列」がそのすべてである。\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元は、\(d\)乗すると \(1\) になるから、\(a\) 以外の位数 \(d\) の元も「\(a\) 系列」の中に含まれている。
ここで、\(\mr{gcd}(j,d)\neq1\) である \(j\:\:(1 < j\leq d)\) をとると、\(a^j\) の位数は \(d\) より小さくなる。なぜなら、\(\mr{gcd}(j,d)=c\:( > 1)\) とすると、2つの数 \(s,\:t\) を選んで、
\(j=c\cdot s\:\:(s < j)\)
\(d=c\cdot t\:\:(t < d)\)
と表されるが、そうすると、
\((a^j)t=a^{cst}=(a^d)^s=1\)
で、\(a^j\) の位数は \(t\) 以下だが、\(t < d\) なので \(a^j\) の位数は \(d\) より小さくなるからである。
一方、\(\mr{gcd}(j,d)\neq1\) である(=\(d\) と素な)\(j\:\:(1\leq j < d)\) をとると、\(a^j\) の位数は \(d\) になる。その理由は以下である。
\((a^j)^x\:\:(1\leq x\leq d)\) が \(x\) の値によってどう変わるかを調べると、まず、\(x=d\) のときは、
\((a^j)^x=(a^j)^d=(a^d)^j=1\)
である。
次に \(1\leq x < d\) のときは \(jx\) は \(d\) の倍数でない。なぜなら、\(j\) は \(d\) と素なため、もし \(jx\) が \(d\) の倍数だとすると、\(x\) が \(d\) の倍数ということになり、\(1\leq x < d\) に反するからである。従って、ある数 \(s,\:t\) を選んで、
\(jx=t\cdot d+s\:\:(0 < s < d)\)
と表せる。そうすると、
\((a^j)^x=a^{td+s}=(a^d)^t\cdot a^s=a^s\)
となるが、\(a\) の位数は \(d\) だから、\(d\) 未満の数 \(s\) で \(a^s\) が \(1\) になることはない。従って \(a^s\neq1\) であり、
\((a^j)^x\neq1\:\:(1\leq x < d)\)
である。
以上により
| \((a^j)^x\neq1\) | \((1\leq x < d)\) | |
| \((a^j)^x=1\) | \((x=d)\) |
まとめると、\((p-1)\) の任意の約数を \(d\) とし、\((\bs{Z}/p\bs{Z})^{*}\) の位数 \(d\) の元の数を \(\#\mr{ord}(d)\) と表記すると、
\(\#\mr{ord}(d)=\left\{
\begin{array}{l}
\begin{eqnarray}
&&\varphi(d)&\\
&&0&\\
\end{eqnarray}
\end{array}\right.\)
のどちらかである。また、\((\bs{Z}/p\bs{Z})^{*}\) のすべての元には位数が定義でき、\((\bs{Z}/p\bs{Z})^{*}\) の \((p-1)\) 個の元は位数で分類できるから、\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
が成り立つ。ここで \(d|(p-1)\) は、\((p-1)\) のすべての約数 \(d\) についての和をとる意味である。
次に、オイラー関数についてオイラー関数の総和の定理が成り立つことを証明する。
(オイラー関数の総和)
\(n\) を任意の自然数とするとき、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。\(d|n\) は、\(n\) のすべての約数 \(d\) についての和をとる。
[証明]
まず、次の2点に注意する。2つの自然数 \(a\) と \(b\) の最大公約数を \(\mr{gcd}(a,b)\) とすると、
\(\dfrac{a}{\mr{gcd}(a,b)}\) と \(\dfrac{b}{\mr{gcd}(a,b)}\) は互いに素
である。これは最大公約数の定義そのものである。
次に、\(n\) の約数の一つを \(a\) とし、\(n=a\cdot b\) と表すと、\(b\) もまた \(n\) の約数の一つである。\(n\) に \(r\) 個の約数、\(a_i\:\:(1\leq i\leq r)\) があるとき、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、\(b_i\:\:(1\leq i\leq r)\) もまた \(n\) の \(r\) 個の約数である。つまり、\(b_i\) は \(a_i\) を並び替えたものである。
以上の2点を前提に、まず \(n=12\) の場合で考察する。いま、\(1\) から \(12\) までの \(12\) 個の整数を「\(12\) との最大公約数で分類する」ことを考える。\(12\) の約数 \(d\) は、\(1,\:2,\:3,\:4,\:6,\:12\) の6つである。\(12\) との最大公約数が \(d\) である集合を \(S_d\) とすると、
| \(S_1\) | \(=\{\:1,\:5\:,7\:,11\:\}\) | |
| \(S_2\) | \(=\{\:2,\:10\:\}\) | |
| \(S_3\) | \(=\{\:3,\:9\:\}\) | |
| \(S_4\) | \(=\{\:4,\:8\:\}\) | |
| \(S_6\) | \(=\{\:6\:\}\) | |
| \(S_{12}\) | \(=\{\:12\:\}\) |
となる。各集合に含まれる整数の個数を \(\#S_d\) として順に見ていくと、まず、オイラー関数の定義より、
\(\#S_1=\varphi(12)\)
である。
次に、\(12\) との最大公約数が \(2\) の集合、\(S_2=\{\:2,\:10\:\}\) を考える。\(\{\:2,\:10\:\}\) を \(2\) で割り算した \(\{\:1,\:5\:\}\) のそれぞれは、最大公約数の定義により、\(12\) を \(2\) で割り算した \(6\) と互いに素である。従って、
\(\#S_2=\varphi(6)\)
である。同様に他の集合についても、
| \(\#S_2\) | \(=\varphi(4)\) | |
| \(\#S_4\) | \(=\varphi(3)\) | |
| \(\#S_6\) | \(=\varphi(2)\) | |
| \(\#S_{12}\) | \(=\varphi(1)\) |
| \(\varphi(12)+\varphi(6)+\varphi(4)+\varphi(3)+\varphi(2)+\varphi(1)=12\) |
\(\displaystyle\sum_{d|12}^{}\varphi(d)=12\)
である。
以上の考察は \(n=12\) の場合であるが、\(12\) に特別な意味はない。従って一般の \(n\) の場合も同様となる。
\(n\) が \(r\) 個の約数をもつとし、それらを \(a_i\:\:(1\leq i\leq r)\) とする。集合 \(S\) を \(1\) から \(n\) の \(n\) 個の整数の集合とし、その部分集合 \(S_i\) を、
\(S_i\):\(n\) との最大公約数が \(a_i\) である \(S\) の元の集合
とする。このとき、\(S_i\) の任意の元を \(x\) とすると、
\(\dfrac{x}{a_i}\) と \(\dfrac{n}{a_i}\) は互いに素
である。そもそも、そうなる \(x\) を集めたのが \(S_i\) であった。このことから、
\(S_i\) の元の個数は \(\dfrac{n}{a_i}\) と素である \(S\) の元の個数
ということになる。\(S_i\) の元の個数を \(\#S_i\) と書くと、
\(\#S_i=\varphi\left(\dfrac{n}{a_i}\right)\)
である。ここで \(b_i\) を、
\(b_i=\dfrac{n}{a_i}\:\:(1\leq i\leq r)\)
と定義すると、
\(\#S_i=\varphi(b_i)\)
となるが、この \(b_i\:\:(1\leq i\leq r)\) は \(n\) の約数のすべてであり、\(a_i\) を並び替えたものである。式の両辺の \((1\leq i\leq r)\) の総和をとると、\(\#S_i\) の総和は \(S\) の元の数なので、
左辺\(=\displaystyle\sum_{i=1}^{r}\#S_i=n\)
である。一方、右辺の総和は、
\(\begin{eqnarray}
&&\:\:右辺&=\displaystyle\sum_{i=1}^{r}\varphi(b_i)=\displaystyle\sum_{i=1}^{r}\varphi(a_i)\\
&&&=\displaystyle\sum_{d|n}^{}\varphi(d)\\
\end{eqnarray}\)
となって、
\(\displaystyle\sum_{d|n}^{}\varphi(d)=n\)
が成り立つ。
\((p-1)\) の約数に戻ると、オイラー関数の総和の定理より、
\(\displaystyle\sum_{d|(p-1)}^{}\varphi(d)=p-1\)
である。一方、位数 \(d\) の元の総和は、
\(\displaystyle\sum_{d|(p-1)}^{}\#\mr{ord}(d)=p-1\)
であった。この2点から、
\(\#\mr{ord}(d)=\varphi(d)\)
が結論づけられる。\(\#\mr{ord}(d)=0\) となる \((p-1)\) の約数 \(d\) は無い。もしあるとすると矛盾が生じる。
従って \((\bs{Z}/p\bs{Z})^{*}\) においては、群位数 \((p-1)\) の約数 \(d\) のすべてについて、位数 \(d\) の元が \(\varphi(d)\) 個存在する。[証明終]
この位数 \(\bs{d}\) の元の数の定理(25C)により、次の生成元の存在1が成り立つことが分かります。
| (生成元の存在1:25D) |
\(p\) を素数とするとき、\((\bs{Z}/p\bs{Z})^{*}\) には生成元が存在する。生成元とは、その位数が \((\bs{Z}/p\bs{Z})^{*}\) の群位数、\(p-1\) の元である。
なお、素数 \(p\) に対して、
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の原始根(primitive root)という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
\(a^x\equiv1\:\:(\mr{mod}\:p)\)
となる \(x\) の最小値が \(p-1\) であるような \(a\) を、\(p\) の原始根(primitive root)という。既約剰余類群 \((\bs{Z}/p\bs{Z})^{*}\) の生成元=原始根である。
ちなみに、\(100\)以下の素数 \(p\)(\(2\) を除く \(24\)個)について、原始根の数 = \(\varphi(p-1)\) と最小の原始根をパソコンで計算すると、次のようになります。
|
|
この表を見ると、\(2\) が最小原始根になることが多いのがわかります。全体の半分(\(12\)個の素数)でそうです。そうでなれければ素数が多い。ただし、\(p=41\) のときの \(6\) のように、合成数が最小原始根になる場合もあります。
\((\bs{Z}/p\bs{Z})^{*}\) の生成元を求める計算式はありません。しかし生成元を求めるアルゴリズムはあって、それが次です。これは、少なくとも一つの生成元が存在する証明になっています。
| (生成元の探索アルゴリズム:25D’) |
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
この証明のために2つの補題を証明する。以下において、
・\(a\) は \(b\) を割り切る
・\(a\) は \(b\) の約数である
・\(b\) は \(a\) で割り切れる
・\(b\) は \(a\) の倍数である
ことを、
\(a|b\)
と記述する。また \(a\) と \(b\) の最大値を、
\(\mr{max}(a,\:b)\)
と表す。
[補題6]
\(a,\:b\) を自然数とすると、2つの数、\(a\,',\:b\,'\) をとって、
\(a\,'|a\)
\(b\,'|b\)
\(\mr{gcd}(a\,',b\,')=1\)
\(\mr{lcm}(a,b)=a\,'b\,'\)
となるようにできる。
[証明]
\(a\) と \(b\) を素因数分解したときに現れるすべての素数を小さい方から順に並べて、
\(p_1,\:p_2,\:\cd\:,\:p_n\)
とする。この素数の列を用いて、\(a\) と \(b\) を、
\(a=p_1^{a_1}\cdot p_2^{a_2}\cdot\cd\cdot p_n^{a_n}\)
\(b=p_1^{b_1}\cdot p_2^{b_2}\cdot\cd\cdot p_n^{b_n}\)
と素因数分解する。もちろんこの表現では \(a_i=0\) や \(b_i=0\) もありうる。ここで、
\(c_i=\mr{max}(a_i,\:b_i)\:\:\:(1\leq i\leq n)\)
と定義すると、\(a,\:b\) の最小公倍数は、
\(\mr{lcm}(a,b)=p_1^{c_1}\cdot p_2^{c_2}\cdot\cd\cdot p_n^{c_n}\)
である。また、
\(\al_i=\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_i\:\:\:(a_i\geq b_i)&\\
&&0\:\:\:\:(a_i < b_i)&\\
\end{eqnarray}
\end{array}\right.\)
\(\beta_i=\left\{
\begin{array}{l}
\begin{eqnarray}
&&0\:\:\:\:(a_i\geq b_i)&\\
&&b_i\:\:\:(a_i < b_i)&\\
\end{eqnarray}
\end{array}\right.\)
と定義して(\(1\leq i\leq n\))、
\(a\,'=p_1^{\al_1}\cdot p_2^{\al_2}\cd\cd p_n^{\al_n}\)
とおくと、
\(a\,'|a\)
である。同様に、
\(b\,'=p_1^{\beta_1}\cdot p_2^{\beta_2}\cdot\cd\cdot p_n^{\beta_n}\)
とおくと、
\(b\,'|b\)
である。このように \(a\,'\) と \(b\,'\) を決めると、
\(a\,'b\,'=\mr{lcm}(a,b)\)
となり、\(a\,'\) と \(b\,'\) に共通の素因数はないから、
\(\mr{gcd}(a\,',b\,')=1\)
である。[補題6の証明終]
[補題7]
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(a^k\:\:(1\leq k\leq p-1)\) の位数を \(e\) とすると、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。
[証明]
\(\mr{gcd}(k,d)\) を \(g\) と書き、
\(k\,'=\dfrac{k}{g}\)
\(d\,'=\dfrac{d}{g}\)
とすると、
\(k=k\,'\cdot g\)
\(d=d\,'\cdot g\)
\(\mr{gcd}(k\,',d\,')=1\)
と表せる。\(a^k\) の位数を調べるため、
\((a^k)^x=1\)
とおくと、
\(a^{kx}=1\)
なので、[補題4](25A)により、
\(d|(kx)\)
である。つまり、
\((d\,'g)|(k\,'gx)\)
\(d\,'|k\,'x\)
となる。すると、\(\mr{gcd}(k\,',d\,')=1\) なので、
\(d\,'|x\)
が成り立つ。\(d\,'|x\) が成り立つ \(x\) の最小値は \(d\,'\) であり、\(x\) の最小値はすなわち \(a^k\) の位数 \(e\) だから、\(e=d\,'\) である。つまり、
\(e=\dfrac{d}{\mr{gcd}(k,d)}\)
である。[補題7の証明終]
[補題6]と[補題7]を用いて、生成元の探索アルゴリズム(25D’)を証明します。
\(p\) を素数とし、\((\bs{Z}/p\bs{Z})^{*}\) の元の一つを \(a\) とする。\(a\) の位数を \(d\) とし、\(d < p-1\) とする。このとき、\(d < e\) である位数 \(e\) をもつ \((\bs{Z}/p\bs{Z})^{*}\) の元が存在する。
[証明]
\(a\) の累乗の列、
\(a,\:a^2,\:a^3,\:\cd,\:a^d=1\)
は \(d\)個の異なる元である。\(d < p-1\)(群位数)なので、この列に含まれない任意の元を \(b\) とし、\(b\) の位数を \(e\) とする。[補題3](25A)により、\(d\) 乗して \(1\) になる \((\bs{Z}/p\bs{Z})^{*}\) の元は \(a\) の累乗の列で尽されているから、\(b^d\neq1\) である。従って \(b\) の位数 \(e\) は \(d\) の約数ではない。もちろん \(e > 1\) である。以降、証明を2つのケースに分ける。
\(\bs{(1)\:\:\mr{gcd}(d,e)=1}\) のとき
このとき、\(ab\) の位数が \(d\) より大きいことを以下で証明する。\(ab\) の位数を調べるために、
\((ab)^x=1\)
とおく。両辺を \(d\)乗すると、
\((ab)^{dx}=1\)
であり、また \(a^d=1\) から \((a^d)^x=1\) だから、
\(b^{dx}=(a^d)^xb^{dx}=(ab)^{dx}=1\)
となり、[補題4](25A)により \(dx\) は \(b\) の位数 \(e\) の倍数である。つまり、
\(e|dx\)
である。すると、\(\mr{gcd}(d,e)=1\) により、
\(e|x\)
となる。同様に、
\((ab)^{ex}=1\)
\(b^e=1\)
だから、
\(a^{ex}=a^{ex}(b^e)^x=(ab)^{ex}=1\)
となり、\(ex\) は \(a\) の位数 \(d\) の倍数である。つまり、
\(d|ex\)
である。すると \(\mr{gcd}(d,e)=1\) により、
\(d|x\)
である。以上の結果、\(e|x\) かつ \(d|x\) であり、
\((de)|x\)
が成り立つ。つまり \(x\) の最小値は \(de\) である。\((ab)^x=1\) となる \(x\) の最小値が \(ab\) の位数だから、
\(ab\) の位数\(=de\)
となる。\(e > 1\) なので、\(ab\) は位数が \(d\) より大きい元である。
\(\bs{(2)\:\:\mr{gcd}(d,e)\neq1}\) のとき
[補題6]により、2つの数、\(d\,',\:e\,'\) をとって、
\(d\,'|d\)
\(e\,'|e\)
\(\mr{gcd}(d\,',e\,')=1\)
\(\mr{lcm}(d,e)=d\,'e\,'\)
となるようにできる。
\(\mr{gcd}\left(\dfrac{d}{d\,'},d\right)=\dfrac{d}{d\,'}\)
だから、[補題7]を使って、
\(a^{{}^{\frac{d}{d\,'}}}\) の位数 \(=\dfrac{d}{\mr{gcd}\left(\dfrac{d}{d\,'},d\right)}=d\,'\)
であり、同様に、
\(b^{{}^{\frac{e}{e\,'}}}\) の位数 \(=\dfrac{e}{\mr{gcd}\left(\dfrac{e}{e\,'},e\right)}=e\,'\)
である。\(\mr{gcd}(d\,',e\,')=1\) だから、
\(c=a^{{}^{\frac{d}{d\,'}}}\cdot b^{{}^{\frac{e}{e\,'}}}\)
とおくと、\(\bs{(1)}\) を使って、
| \(c\) の位数 | \(=d\,'e\,'\) | |
| \(=\mr{lcm}(d,e)\) |
\(\mr{lcm}(d,e) > d\)
である。つまり、\(c\) は位数が \(d\) より大きい元である。[証明終]
生成元の存在2
以降で \((\bs{Z}/p^n\bs{Z})^{*}\) にも生成元が存在することを証明します(ただし、\(p\neq2\))。まず、その証明に使う[補題8]を証明します。整数についての定理です。
[補題8]
\(p\) を奇素数とし、\(k\) を \(p\) と素な数とする(\(\mr{gcd}(k,p)=1\))。また、整数 \(m\) を \(m\geq1\) とする。
このとき、
\((1+kp^m)^p=1+k\,'p^{m+1}\)
と表すことができて、\(k\,'\) は \(p\) と素である。
[証明]
表記を分かりやすくするため、まず \(m=1\) のときに成り立つことを証明する。\(m=1\) のときに[補題8]は、
[補題8]\(\bs{m=1}\)
\(p\) を奇素数とし、\(k\) を \(p\) と素な数( \(\mr{gcd}(k,p)=1\) )とする。このとき、
\((1+kp)^p=1+k\,'p^2\)
と表すことができて、\(k\,'\) は \(p\) と素である。
となる。\((1+kp)^p\) を2項定理で展開すると、
\((1+kp)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp+{}_{p}\mr{C}_{2}(kp)^2+{}_{p}\mr{C}_{3}(kp)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp)^{p-1}+(kp)^p\\
&&\:\: =&1+p^2(k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2})\\
&&\:\: =&1+k\,'p^2\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2+{}_{p}\mr{C}_{3}k^3p+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{p-3}+k^pp^{p-2}\\
\end{eqnarray}\)
となる。\(k\,'\) の第3項(\({}_{p}\mr{C}_{3}k^3p\))以降は \(p\) の指数が \(1\) 以上だから \(p\) で割り切れる。第2項の \(p\) に関係した式は、
\({}_{p}\mr{C}_{2}=\dfrac{p(p-1)}{2}\)
であるが、\(\bs{p}\) が奇素数(\(\bs{p\neq2}\))であるため、この第2項も \(p\) で割り切れる(\(p\) が奇数だと \(p\) で割り切れる)。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。
次に \(m\geq2\) のときであるが、\(m=1\) のときの上の証明において \(p\) を \(p^m\) に置き換えれば、同様の計算で証明できる。\((1+kp^m)^p\) を2項定理で展開すると、
\((1+kp^m)^p\)
\(\begin{eqnarray}
&&\:\: =&1+{}_{p}\mr{C}_{1}kp^m+{}_{p}\mr{C}_{2}(kp^m)^2+{}_{p}\mr{C}_{3}(kp^m)^3+\:\cd\:+\\
&&&{}_{p}\mr{C}_{p-1}(kp^m)^{p-1}+(kp^m)^p\\
&&\:\: =&1+p^{m+1}(k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1})\\
&&\:\: =&1+k\,'p^{m+1}\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\: k\,'=&k+{}_{p}\mr{C}_{2}k^2p^{m-1}+{}_{p}\mr{C}_{3}k^3p^{2m-1}+\:\cd\:+\\
&&& {}_{p}\mr{C}_{p-1}k^{p-1}p^{m(p-2)-1}+k^pp^{m(p-1)-1}\\
\end{eqnarray}\)
\(k\,'\) の第2項以降は \(m\geq2\) なので \(p\) の指数は \(1\) 以上であり、\(p\) で割り切れる。第1項の \(k\) は、定理の前提によって \(p\) で割り切れない。つまり \(k\,'\) は、第1項だけが唯一、\(p\) で割り切れず、他の項はすべて \(p\) で割り切れる。従って、
\(\mr{gcd}(k\,',p)=1\)
である。以上の結論として、題意が成り立つ。[証明終]
生成元の存在1の定理(25D)と[補題8]を用いて、\((\bs{Z}/p^n\bs{Z})^{*}\) に生成元が存在することを証明します。
| (生成元の存在2:25E) |
\(p\) を \(p\neq2\) の素数(=奇素数)とする。また、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。
このとき \(g\) または \(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。つまり、\((\bs{Z}/p^n\bs{Z})^{*}\) には生成元が存在する。
[証明]
フェルマの小定理(25B)により、\((\bs{Z}/p\bs{Z})^{*}\) の任意の元は \((p-1)\) 乗すると \(1\) になる。従って、整数の記法で、
\(g^{p-1}=1+kp\)
と書ける。以降、
・\(k\) の素因数に \(p\) を含まないとき
・\(k\) の素因数に \(p\) を含むとき
の2つに分けて証明する。
\(k\) の素因数に \(p\) を含まないとき
この場合は以下が成り立つ。
生成元の存在2(その1)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件で、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元でもある。
[証明(その1)]
\(g\) は \(p\) と互いに素なので \((\bs{Z}/p^n\bs{Z})^{*}\) の元でもある。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は、既約剰余類群の定義によって \(\varphi(p^n)\) である。\(p^n\) 以下で \(p\) で割り切れる数は、\(p^n\) を含んで \(\dfrac{p^n}{p}=p^{n-1}\) 個あるから、
\(\begin{eqnarray}
&&\:\:\varphi(p^n)&=p^n-p^{n-1}\\
&&&=p^{n-1}(p-1)\\
\end{eqnarray}\)
である。従って、オイラーの定理(25B)より、
\(g^{p^{n-1}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
が成り立つ。記述の簡素化のために、
\(h=g^{p-1}\)
とおく。
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
である。
仮定によって \(h\) は、
\(h=1+kp\)
\(\mr{gcd}(k,p)=1\)
と表される。この \(h\) に対して "\(p\)乗する" 操作を \((n-1)\) 回繰り返すと、[補題8]を次々に使って、次のように計算できる。
| \(h^p\) | \(=1+k_1p^2\) | \(\mr{gcd}(k_1,p)=1\) | ||
| \(h^{p^2}\) | \(=(1+k_1p^2)^p\) | \(=1+k_2p^3\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^3)^p\) | \(=1+k_3p^4\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-2})^p\) | \(=1+k_{n-2}p^{n-1}\) | \(\mr{gcd}(k_{n-2},p)=1\) | |
| \(h^{p^{n-1}}\) | \(=(1+k_{n-2}p^{n-1})^p\) | \(=1+k_{n-1}p^n\) | \(\mr{gcd}(k_{n-1},p)=1\) |
この結果から、
\(h^{p^{n-1}}\equiv1\:\:(\mr{mod}\:p^n)\)
であることがわかる。この式は \(n\geq1\) のすべての \(n\) で成り立つ。
従って、\(h^x\equiv1\:\:(\mr{mod}\:p^n)\) となる最小の \(x\) は \(p^{n-1}\) の約数であり、\((n-1)\) 個の \(p^i\:\:(1\leq i\leq n-1)\) のどれかである。
しかし、上の計算過程を見ると、
| \(h^{p^i}-1=k_i\cdot p^{i+1}\) | \((\mr{gcd}(k_i,p)=1)\) | |
| \((1\leq i\leq n-1)\) |
\(h^{p^i}\not\equiv1\:\:(\mr{mod}\:p^n)\:\:(1\leq i\leq n-2)\)
である。従って、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
\(h\) は \(g^{p-1}\) であった。ゆえに、\(g\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その1)終]
\(k\) の素因数に \(p\) を含むとき
\(g^{p-1}=1+kp\) と表したときの \(k\) の素因数に \(p\) を含む場合、ある数 \(k\,''\) があって、
\(g^{p-1}=1+k\,''\cdot p^m\:\:(m\geq2)\)
\(\mr{gcd}(k\,'',p)=1\)
と表すことができる。ここで \(k\,''\) を改めて \(k\) と書くと、次が成り立つ。
生成元の存在2(その2)
\(p\) を奇素数とし、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とする。また、\(g\) は、
\(g^{p-1}=1+kp^m\:\:(m\geq2)\)
\(\mr{gcd}(k,p)=1\)
と表されているとする。
この条件では、\(g+p\) が \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。
[証明(その2)]
\((g+p)^{p-1}\) を2項定理で展開する。
\((g+p)^{p-1}\)
| \(=g^{p-1}\) | \(+{}_{p-1}\mr{C}_{1}g^{p-2}p+{}_{p-1}\mr{C}_{2}g^{p-3}p^2+\:\cd\:+p^{p-1}\) | |
| \(=1+kp^m\) | \(+{}_{p-1}\mr{C}_{1}g^{p-2}p+{}_{p-1}\mr{C}_{2}g^{p-3}p^2+\:\cd\:+p^{p-1}\) |
\(=1+k\,'p\)
\(k\,'=kp^{m-1}+{}_{p-1}\mr{C}_{1}g^{p-2}+{}_{p-1}\mr{C}_{2}\cdot g^{p-3}p+\:\cd+p^{p-2}\)
\(m\geq2\) なので、\(k\,'\) の第2項以外はすべて \(p\) で割り切れる。第2項は \((p-1)g^{p-2}\) だが、\((p-1)\) も \(g^{p-2}\) も \(p\) で割り切れない。つまり \(k\,'\) は第2項だけが唯一、\(p\) で割り切れないから、
\(\mr{gcd}(k\,',p)=1\)
である。まとめると、
\((g+p)^{p-1}=1+k\,'p\)
\(\mr{gcd}(k\,',p)=1\)
と表すことができる。ここで、
\(h=1+k\,'p\)
と書くと、[補題8]を次々と使うことで、次の計算が成り立つ。
| \(h^p\) | \(=1+k_1p^2\) | \(\mr{gcd}(k_1,p)=1\) | ||
| \(h^{p^2}\) | \(=(1+k_1p^2)^p\) | \(=1+k_2p^3\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^3)^p\) | \(=1+k_3p^4\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-2})^p\) | \(=1+k_{n-2}p^{n-1}\) | \(\mr{gcd}(k_{n-2},p)=1\) | |
| \(h^{p^{n-1}}\) | \(=(1+k_{n-2}p^{n-1})^p\) | \(=1+k_{n-1}p^n\) | \(\mr{gcd}(k_{n-1},p)=1\) |
この計算は「\(\bs{k}\) の素因数に \(\bs{p}\) を含まないとき」と全く同じである。従って、そのときの結論を踏襲できて、\(h\) は \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。
その \(h\) は、
\(h=1+k\,'p=(g+p)^{p-1}\)
であった。\(h\) が \(p^{n-1}\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になるのだから、\(g+p\) は \(p^{n-1}(p-1)\) 乗して初めて \(1\:\:(\mr{mod}\:p^n)\) になる。\((\bs{Z}/p^n\bs{Z})^{*}\) の群位数は \(p^{n-1}(p-1)\) だから、\(g+p\) は \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。[証明(その2)終]
以上により、\(g\) を \((\bs{Z}/p\bs{Z})^{*}\) の生成元とすると、\(g\) か \(g+p\) のどちらかは \((\bs{Z}/p^n\bs{Z})^{*}\) の生成元である。従って \((\bs{Z}/p^n\bs{Z})^{*}\) には生成元があり、群位数 \(p^{n-1}(p-1)\) の巡回群である。[証明終]
ちなみに、\(h=g^{p-1}\) とし、
\(h=1+kp^2\)
\(\mr{gcd}(k,p)=1\)
と表されているときは \(g+p\) が生成元ですが、\(\bs{g}\) は生成元ではありません。なぜなら[補題8]を次々と使うと、
| \(h^p\) | \(=(1+kp^2)^p\) | \(=1+k_1p^3\) | \(\mr{gcd}(k_1,p)=1\) | |
| \(h^{p^2}\) | \(=(1+k_1p^3)^p\) | \(=1+k_2p^4\) | \(\mr{gcd}(k_2,p)=1\) | |
| \(h^{p^3}\) | \(=(1+k_2p^4)^p\) | \(=1+k_3p^5\) | \(\mr{gcd}(k_3,p)=1\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(h^{p^{n-2}}\) | \(=(1+k_{n-3}p^{n-1})^p\) | \(=1+k_{n-2}p^n\) | \(\mr{gcd}(k_{n-2},p)=1\) |
となり、\(h\) を \(p^{n-1}\) 乗する前の \(h^{p^{n-2}}\) の段階で、
\(h^{p^{n-2}}\equiv1\:\:(\mr{mod}\:p^n)\)
\(\longrightarrow\:g^{p^{n-2}(p-1)}\equiv1\:\:(\mr{mod}\:p^n)\)
となってしまいます。つまり \(g\) は生成元ではないのです。\(g^{p-1}=1+kp^m\:\:(m > 2)\) と表されるときも同じです。
実は、\((\bs{Z}/p\bs{Z})^{*}\) の生成元を \(g\) とすると、ほとんどの場合で \(g\) は \((\bs{Z}/p^2\bs{Z})^{*}\) の(従って \((\bs{Z}/p^n\bs{Z})^{*}\) の)生成元になります。生成元の存在1であげた、\(100\) 以下の素数 \(p\) の最小原始根の表ですが、そのすべては \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元です。それどころか「\(100\) 以下の素数 \(p\) の原始根が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならない」というケースは、計算してみると次の4つしかありません。
\(p=29,\:g=14\)
\(p=37,\:g=18\)
\(p=43,\:g=19\)
\(p=71,\:g=11\)
たとえば \(p=29\) の場合、\(\varphi(28)=12\) なので原始根 \(g\) は \(12\)個あります。リストすると、
\(g=2,\:3,\:8,\:10,\:11,\:14,\:15,\:18,\:19,\:21,\:26,\:27\)
の \(12\)個です。\(p^2=841\) であり、\((\bs{Z}/p^2\bs{Z})^{*}\) は \((\bs{Z}/841\bs{Z})^{*}\) のことです。その \((\bs{Z}/841\bs{Z})^{*}\) の群位数は、
\(\varphi(p^2)=p(p-1)=29\cdot28=812\)
です。
\(g\) のうち、\(14\) を除く \(11\)個の位数は \(812\) です。ところが \(14\) だけは違って、
\(14^{28}\equiv1\:\:(\mr{mod}\:841)\)
となり、位数は \(28\) です。もちろんこの場合でも、生成元の存在2(25E)の証明プロセスにあるように、
\(g+p=14+29=43\)
の位数は \(812\) で、\((\bs{Z}/841\bs{Z})^{*}\) の生成元です。以上をまとめると、
\(100\) 以下の素数を \(p\) とするとき、\((\bs{Z}/p\bs{Z})^{*}\) の生成元 \(g\) は、\(p=29,\:37,\:43,\:71\) のときを除いて、すべてが \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元であり、\(p=29,\:37,\:43,\:71\) の場合でも \(g\) が \((\bs{Z}/p^2\bs{Z})^{*}\) の生成元にならないケースは、それぞれについて1つしかない
となります。
生成元の存在2(25E)の証明は、[補題8]の証明での \(\bs{{}_{p}\mr{C}_{2}}\) が \(\bs{p}\) で割り切れることがポイントになっていて、\(p\neq2\) である素数(奇素数)のときには成り立ちますが、\(p=2\) のときには成り立ちません。\(p=2\) では生成元が存在しないのです。
しかし \(p=2\) のとき、つまり \((\bs{Z}/2^n\bs{Z})^{*}\) は、生成元をもつ2つの巡回群の直積と同型であることが証明できます。
以降、整数 \(a\) について、 \(a^x\equiv1\:\:(\mr{mod}\:n)\) となる最小の \(x\:(\geq1)\) が存在するとき、\(x\) を「\(\bs{\mr{mod}\:n}\) での \(\bs{a}\) の位数」あるいは「\(a\) の位数 \((\mr{mod}\:n)\)」と呼びます。 |
2のべき乗の既約剰余類群
| (2のべき乗の既約剰余類群:25F) |
2のべき乗の既約剰余類群は、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
である。つまり2つの巡回群の直積に同型である。
[証明]
まず \(n=5\) の場合である \((\bs{Z}/32\bs{Z})^{*}\) で考察する。
\((\bs{Z}/32\bs{Z})^{*}\) の元とは、\(1\) から \(31\) までの奇数の集合である。この奇数から「\(4\)で割ると \(1\) 余る奇数」を取り出して、集合 \(A\) とする。
\(A=\{1,\:5,\:9,\:13,\:17,\:21,\:25,\:29\}\)
である。集合 \(A\) の要素の数は、\(32/4=8\) である。ここで、
\(5\equiv1\:\:(\mr{mod}\:4)\)
であることに着目する。この両辺を \(k\) 乗(\(0\leq k\))すると、
\(5^k\equiv1\:\:(\mr{mod}\:4)\)
だから(21E)、\(5^k\) は「\(4\)で割ると \(1\) 余る奇数」である。ここで、\(5^k\) を \(32\) で割った余りを \(j\) とする。つまり、
\(5^k\equiv j\:\:(\mr{mod}\:32)\:\:(0\leq k,\:1\leq j\leq31)\)
である。すると \(j\) は「\(32\)未満の、\(4\)で割ると \(1\) 余る奇数」であり、\(A\) に含まれている。そこでもし、
\(5^x\equiv1\:\:(\mr{mod}\:32)\)
を満たす最小の \(x\)(つまり \(\mr{mod}\:32\) での \(5\) の位数)が \(8\) であれば、位数の定理(25A)の[補題2]によって「\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) はすべて異なる」から、それらは \(A\) そのものである。実際に計算してみると、
| \(5^0\equiv\:1\) | \((\mr{mod}\:32)\) | |
| \(5^1\equiv\:5\) | \((\mr{mod}\:32)\) | |
| \(5^2\equiv25\) | \((\mr{mod}\:32)\) | |
| \(5^3\equiv29\) | \((\mr{mod}\:32)\) | |
| \(5^4\equiv17\) | \((\mr{mod}\:32)\) | |
| \(5^5\equiv21\) | \((\mr{mod}\:32)\) | |
| \(5^6\equiv\:9\) | \((\mr{mod}\:32)\) | |
| \(5^7\equiv13\) | \((\mr{mod}\:32)\) | |
| \(5^8\equiv\:1\) | \((\mr{mod}\:32)\) |
となって、\(\mr{mod}\:32\) での \(5\) の位数は \(8\) であり、\(\mr{mod}\:32\) でみた \(5^k\:\:(0\leq k\leq7)\) には \(A\) の元がすべて現れる。これは \(A\) が巡回群と同型であることを示している。
一方、\((\bs{Z}/32\bs{Z})^{*}\) の元から「\(4\)で割ると \(3\) 余る奇数」を取り出し、それを集合 \(B\) とすると、
\(B=\{3,\:7,\:11,\:15,\:19,\:23,\:27,\:31\}\)
である。ここで、\(A=\{4k+1\:|\:0\leq k\leq7\}\) と記述し、\(i=7-k\:\:(k=7-i)\) と定義すると、
\(\begin{eqnarray}
&&\:\:(-1)\cdot A&=\{-4k-1 &|\:0\leq k\leq7\}\\
&&&=\{-4(7-i)-1 &|\:0\leq i\leq7\}\\
&&&=\{4i+3-32 &|\:0\leq i\leq7\}\\
\end{eqnarray}\)
だから、\(\mr{mod}\:32\) でみると、
\(B\equiv(-1)\cdot A\)
である。\((-1)\cdot A\) は、集合 \(A\) の要素すべてに \(-1\) を掛けた集合の意味である。
\((\bs{Z}/32\bs{Z})^{*}\) の元は \(A\) と \(B\) の和であり、\(A\) と \(B\) に重複はない。従って、\((\bs{Z}/32\bs{Z})^{*}\) の元は、\(\mr{mod}\:32\) でみて、
\((-1)^j\cdot5^k\:\:(j=0,1)\) \((0\leq k\leq7)\)
の形に一意に表現できる。\(j=0\) の場合は \(A\) を、\(j=1\) なら \(B\) を表している。
\(\mr{mod}\:32\) でみて、\(5^k\) は群位数 \(8\) の巡回群であり、\((-1)^j\) は群位数 \(2\) の巡回群である。従って、\((\bs{Z}/32\bs{Z})^{*}\) は2つの巡回群の直積で表現できることになる。このことが成り立つキーポイントは、
\(\mr{mod}\:32\) でみた \(5\) の位数が \(\dfrac{32}{4}=8\)
ということである。もしこれが \(2^5=32\) だけでなく \(2^n\:\:(2\leq n)\) で成り立てば、一般論に拡張できる。その、\(2^n\) で成り立つことは、次のように、[補題9]として証明できる。
[補題9]
\(n\geq2\) のとき、\(5\) の \(\mr{mod}\:2^n\) での位数は \(2^{n-2}\) である。
[証明]
数学的帰納法で証明する。題意は \(n=2\) のときに成り立つので( \(5\equiv1\:\:(\mr{mod}\:4)\) )、\(n\) で成り立つと仮定し、\(n+1\) でも成り立つことを証明する。\(\mr{mod}\:2^{n+1}\) での \(5\) の位数を調べるため、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
を満たす \(x\) について考察する。\(x\) の最小値が \(2^{n-1}\) であれば、[補題9]が証明されたことになる。 \((\br{A})\)
一般に \(a\equiv b\:\:(\mr{mod}\:p^n)\) なら、\(1\leq i < n\) とするとき \(a\equiv b\:\:(\mr{mod}\:p^i)\) である。従って \((\br{A})\) 式が成り立つとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^n)\)
も成り立つ。帰納法の仮定により \(\mr{mod}\:2^n\) での \(5\) の位数は \(2^{n-2}\) だから、位数の定理(25A)の[補題4]により \(x\) は \(2^{n-2}\) の倍数である。
従って \(x\) の最小値は \(2^{n-2}\) だが、\(x\) を \(2^{n-2}\) とすると \((\br{A})\) 式が成り立たない。なぜなら、
\(5^{2^{n-2}}\equiv1+2^n\:\:(\mr{mod}\:2^{n+1})\)
が言えるからである。 \((\br{B})\)
\((\br{B})\) 式が正しい理由を数学的帰納法で説明すると、\(n=2\) のとき \((\br{B})\) 式は \(5\equiv5\:\:(\mr{mod}\:8)\) だから成り立っている。そこで、ある整数 \(k\) を用いて \((\br{B})\) 式を等式化すると、
\(5^{2^{n-2}}+k2^{n+1}=1+2^n\)
となる。記述を見やすくするため \(5^{2^{n-2}}=\al\) とおくと、
\(\al+k2^{n+1}=1+2^n\)
である。この両辺を2乗すると、
\((\al+k2^{n+1})^2=(1+2^n)^2\)
\(\al^2+\al k2^{n+2}+k^22^{2n+2}=1+2^{n+1}+2^{2n}\)
となる。\(2\leq n\) のときは \(n+2\leq2n\) なので、両辺を \(\mr{mod}\:2^{n+2}\) でみると、左辺の第2項、第3項、右辺の第3項は \(0\) である。従って、
\(\al^2\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
\(5^{2^{n-1}}\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
となり、\((\br{B})\) 式は \(n\) を \(n+1\) に置き換えても成り立つ。従って \((\br{B})\) 式は正しい。
\(5^{2^{n-2}}+k2^{n+1}=1+2^n\)
となる。記述を見やすくするため \(5^{2^{n-2}}=\al\) とおくと、
\(\al+k2^{n+1}=1+2^n\)
である。この両辺を2乗すると、
\((\al+k2^{n+1})^2=(1+2^n)^2\)
\(\al^2+\al k2^{n+2}+k^22^{2n+2}=1+2^{n+1}+2^{2n}\)
となる。\(2\leq n\) のときは \(n+2\leq2n\) なので、両辺を \(\mr{mod}\:2^{n+2}\) でみると、左辺の第2項、第3項、右辺の第3項は \(0\) である。従って、
\(\al^2\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
\(5^{2^{n-1}}\equiv1+2^{n+1}\:\:(\mr{mod}\:2^{n+2})\)
となり、\((\br{B})\) 式は \(n\) を \(n+1\) に置き換えても成り立つ。従って \((\br{B})\) 式は正しい。
\((\br{A})\) 式の \(x\) は \(2^{n-2}\) の倍数であるが、\(x=2^{n-2}\) では \((\br{A})\) 式が成り立たないことが分かった。その次に小さな \(x\) の倍数は \(x=2\cdot2^{n-2}=2^{n-1}\) であり、これを \((\br{A})\) 式に入れると、
左辺\(=5^{2^{n-1}}\)
である。一方、\((\br{B})\) 式の両辺を2乗すると、
\(\begin{eqnarray}
&&\:\:5^{2^{n-1}}&\equiv(1+2^n)^2\:\:(\mr{mod}\:2^{n+1})\\
&&&=1+2^{n+1}+2^{2n}\\
&&&\equiv1\:\:(\mr{mod}\:2^{n+1})\\
\end{eqnarray}\)
であるから、\(x=2^{n-1}\) のとき、
\(5^x\equiv1\:\:(\mr{mod}\:2^{n+1})\)
が成り立つ。つまり \((\br{A})\) 式が成り立つ \(x\) の最小値は \(2^{n-1}\) であり、\(5\) の \(\mr{mod}\:2^{n+1}\) での位数は \(2^{n-1}\) である。これで、帰納法によって[補題9]が正しいことが証明できた。[補題9の証明終]
[補題9]が正しいので、\(n=5\) の例で展開した論理により、\((\bs{Z}/2^n\bs{Z})^{*}\) の元は、\(\mr{mod}\:2^n\) でみて、
\((-1)^j5^k\:\:(j=0,1,\:\:0\leq k\leq2^{n-2}-1)\)
の形に一意に表現できることが分かった。
ここで、\((\bs{Z}/2^n\bs{Z})^{*}\) から \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) への写像 \(f\) を、
| \(f\::\) | \((\bs{Z}/2^n\bs{Z})^{*}\) | \(\longrightarrow\) | \((\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\) | |
| \((-1)^j5^k\) | \(\longmapsto\) | \((j,\:k)\) |
\(\begin{eqnarray}
&&\:\:f((-1)^j5^k\cdot(-1)^l5^m)&=f((-1)^{j+l}5^{k+m})\\
&&&=(j+l,\:k+m)\\
&&\:\:f((-1)^j5^k)+f((-1)^l5^m)&=(j,k)+(l,m)\\
&&&=(j+l,\:k+m)\\
\end{eqnarray}\)
\(f((-1)^j5^k\cdot(-1)^l5^m)=f((-1)^j5^k)+f((-1)^l5^m)\)
となり、\(f\) は同型写像の要件を満たしている。従って、
\((\bs{Z}/2^n\bs{Z})^{*}\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2^{n-2}\bs{Z})\)
であり、\((\bs{Z}/2^n\bs{Z})^{*}\) は、群位数 \(2\) と群位数 \(2^{n-2}\) の2つの巡回群の直積に同型である。[証明終]
既約剰余類群の構造
ここまでの準備を行うと、既約剰余類群の構造を明らかにできます。これが第2章のゴールです。
| (既約剰余類群の構造:25G) |
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積に同型である。
[証明]
以下の記述では、
・\(a_j\) は \(a\) を \(j\) で割った余り
・\((a+b)_j\) は \((a+b)\) を \(j\) で割った余り
を表す。
\(j\) と \(k\) を 互いに素な整数 \((2\leq j,k)\) とする。\(a\) を \(\bs{Z}/(jk)\bs{Z}\) の元とし \((0\leq a\leq jk-1)\)、\(\bs{Z}/(jk)\bs{Z}\) から \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) への写像、\(f\) を次のように定義する。
| \(f\::\) | \(\bs{Z}/(jk)\bs{Z}\) | \(\longrightarrow\) | \((\bs{Z}/j\bs{Z})\times(\bs{Z}/k\bs{Z})\) | |
| \(a\) | \(\longmapsto\) | \((a_j,\:a_k)\) |
\(j\) と \(k\) が 互いに素なので、中国剰余定理(21F)により、任意に選んだ \(a_j\) と \(a_k\) から \(a\) が一意に決まる。つまり、\(f\) は1対1写像(数学用語で "全単射")である。また、\(a\) とは別の \(\bs{Z}/(jk)\bs{Z}\) の元を \(b\) とすると、
\(\begin{eqnarray}
&&\:\:f(a+b)&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a)+f(b)&=(a_j,\:a_k)+(b_j,\:b_k)\\
&&&=(a_j+b_j,\:a_k+b_k)\\
&&&=((a+b)_j,\:(a+b)_k)\\
&&\:\:f(a+b)&=f(a)+f(b)\\
\end{eqnarray}\)
となり、\(f\) は同型写像である。
いま、\(\mr{gcd}(a,jk)=1\)(\(a\) が \(jk\) と素)だとすると、既約剰余類群の定義により、\(a\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) の元である。
ここで一般的に、
\(\mr{gcd}(a,jk)=1\) なら
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\)
である。また \(\mr{gcd}(a,j)=1\) なら \(\mr{gcd}(j,a_j)=1\) である。なぜなら互除法の原理(21A)によって、\(a\) と \(j\) の公約数は \(j\) と \(a_j\) の公約数だからである。
従って、
\(\mr{gcd}(j,a_j)=1\) かつ \(\mr{gcd}(k,a_k)=1\)
になる。つまり、\(a_j\) は \((\bs{Z}/j\bs{Z})^{*}\) の元であり、\(a_k\) は \((\bs{Z}/k\bs{Z})^{*}\) の元である。また、
\(\mr{gcd}(a,j)=1\) かつ \(\mr{gcd}(a,k)=1\) なら
\(\mr{gcd}(a,jk)=1\)
も成り立つので、任意の \((\bs{Z}/j\bs{Z})^{*}\) の元と \((\bs{Z}/k\bs{Z})^{*}\) の元を決めれば、\((\bs{Z}/(jk)\bs{Z})^{*}\) の元が定まる。
さらに、既約剰余類群の群演算は乗算であるが、
\(\begin{eqnarray}
&&\:\:a_j\cdot b_j&=(a\cdot b)_j\\
&&\:\:a_k\cdot b_k&=(a\cdot b)_k\\
\end{eqnarray}\)
が成り立つので、
\(f(ab)=f(a)f(b)\)
であり、\(f\) は \((\bs{Z}/(jk)\bs{Z})^{*}\) から \((\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\) への同型写像でもある。従って、\(j\) と \(k\) が互いに素という条件のもとで、
\((\bs{Z}/(jk)\bs{Z})^{*}\cong(\bs{Z}/j\bs{Z})^{*}\times(\bs{Z}/k\bs{Z})^{*}\)
である。 \((\br{C})\)
いま、\(p,\:q\) を2つの素数とし、\(n\) の素因数分解が、
\(n=p^a\cdot q^b\)
だとする。このとき \((\br{C})\) 式で \(j=p^a,\:k=q^b\) とおくと、
\((\bs{Z}/n\bs{Z})^{*}\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\)
となる。さらに、\(p,\:q,\:r\) を3つの素数とし、
\(n=p^a\cdot q^b\cdot r^c\)
と表せたとする。\((\br{C})\) 式で \(j=p^a\cdot q^b,\:k=r^c\) とおくと、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/n\bs{Z})^{*}&\cong(\bs{Z}/(p^aq^b)\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
&&&\cong(\bs{Z}/p^a\bs{Z})^{*}\times(\bs{Z}/q^b\bs{Z})^{*}\times(\bs{Z}/r^c\bs{Z})^{*}\\
\end{eqnarray}\)
となる。\(n\) の素因数の数が4以上に増えてもこの操作は繰り返せるから、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \((\bs{Z}/p^a\bs{Z})^{*}\) の形の既約剰余類群の直積と同型である。
\((\bs{Z}/p^a\bs{Z})^{*}\) は、\(p=2\) のときは2のべき乗の既約剰余類群の定理(25F)により、2つの巡回群の直積と同型である。また、\(p\neq2\) の素数のときは生成元の存在2の定理(25E)により、それ自体が巡回群である。従って、既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は \(n\) の値にかかわらず、巡回群の直積と同型である。[証明終]
具体例として、たとえば \(n=360\) とすると、\(n=2^3\cdot3^2\cdot5\) なので、
\(\begin{eqnarray}
&&\:\:(\bs{Z}/360\bs{Z})^{*}&\cong(\bs{Z}/2^3\bs{Z})^{*}\times(\bs{Z}/3^2\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
&&&\cong(\bs{Z}/2\bs{Z})\times(\bs{Z}/2\bs{Z})\times(\bs{Z}/9\bs{Z})^{*}\times(\bs{Z}/5\bs{Z})^{*}\\
\end{eqnarray}\)
となり、\((\bs{Z}/360\bs{Z})^{*}\) は4つの巡回群の直積と同型です。
「既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型」(25G)は、ガロア理論の証明で次のように使います。\(1\) の \(n\)乗根(\(x^n-1=0\) の解)のうち、\(n\)乗して初めて \(1\) になるものを「\(1\) の原始\(n\)乗根」といいます。それを \(\zeta\) とすると、
| \(\bs{Q}(\zeta)\) のガロア群は \((\bs{Z}/n\bs{Z})^{*}\) と同型である。 | |
| \((\bs{Z}/n\bs{Z})^{*}\) は巡回群の直積と同型である(25G)。 | |
| 巡回群の直積は可解群である。 | |
| \(\bs{Q}(\zeta)\) のガロア群は可解群である。 |
となり、④が証明できます。① と ③ は別途証明します。④ の「\(\bs{Q}(\zeta)\) のガロア群は可解群」が重要で、方程式の可解性の必要条件を証明するときの一つのポイントになります。
| 3.多項式と体 |
ガロア理論では方程式の解を含む「体」の特性を分析することで、方程式が代数的に解けるかどうかを調べます。第3章ではその「体」と、方程式の元になる「多項式」に関する重要な定義と定理を説明します。
3.1 多項式
ガロア理論で対象とする多項式は、1つの変数(未知数)をもつ、有理数係数の多項式です。それを、
| \(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\:\:(a_i\in\bs{Q})\) |
で表します。\(\bs{f(x)}\) の「\(\bs{0}\) でない最高次の係数 \(\bs{n}\)」を、多項式の「次数」といい、\(\bs{\mr{deg}\:f(x)}\) で表します。通常、\(\mr{deg}\:f(x)\geq1\) ですが、便宜上、\(a_0\) 以外の係数が \(0\) の場合(=定数項のみの場合)も多項式と呼び「\(\bs{0}\) 次多項式」とします。また、全ての係数が \(0\) の場合を「\(\bs{0}\) 多項式(零多項式)」と呼びます。
多項式 \(a(x)\) を 多項式 \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とすると、
\(a(x)=p(x)b(x)+r(x)\)
\((\:\mr{deg}\:r(x) < \mr{deg}\:b(x)\:)\)
です。整数のときと同じように互除法(21A)を用い、次に \(b(x)\) を \(r(x)\) で割って余りを求める操作を繰り返すと、\(\mr{deg}\:r(x)\) が単調減少するので、いずれ \(b(x)\) が \(r(x)\) で割り切れるとき(=互除法の最終段階)がきます。\(r(x)\) が \(0\) 次多項式(=定数)なら、\(b(x)\) は \(r(x)\) で割り切れるので、最終段階は必ずあります。
\(b(x)\) が \(r(x)\) で割り切れるとき、\(r(x)\) が \(a(x)\) と \(b(x)\) の「最大公約数」です。実際は "数" ではなく多項式なので、「最大公約式」や「最大公約因子」といった言い方もありますが、一般的には「最大公約数」で通っています。
最大公約数が定数(\(0\) 次多項式)のとき、\(a(x)\) と \(b(x)\) は互いに素である、といいます。このとき、整数における不定方程式の解の存在定理(21C)と同様の、次の定理が成り立ちます。
不定方程式
| (多項式の不定方程式:31A) |
\(a(x)\) と \(b(x)\) が互いに素な多項式のとき、
\(a(x)f(x)+b(x)g(x)=1\)
を満たす多項式 \(f(x)\)、\(g(x)\)で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
また、\(a(x)\) と \(b(x)\) が互いに素な多項式で、\(h(x)\) が任意の多項式のとき、
\(a(x)f(x)+b(x)g(x)=h(x)\)
を満たす多項式 \(f(x)\)、\(g(x)\) で、
\(\mr{deg}\:g(x)\: < \:\mr{deg}\:a(x)\)
のものが存在する。
[証明]
\(a(x)\) と \(b(x)\) に互除法(21A)を適用して次数を下げ、同時に \(f(x),\:g(x)\) を変換して同等の方程式に変形していく。\(a(x)\) を \(b(x)\) で割った商を \(p(x)\)、余りを \(r(x)\) とする。
\(a(x)=p(x)b(x)+r(x)\)
\(\mr{deg}\:r(x) < \mr{deg}\:b(x)\)
である。互除法の次のステップの \(a_1(x),\:b_1(x)\)、\(f_1(x),\:g_1(x)\) を次のように決める。
\(\:\:\:\:\br{①}\left\{
\begin{array}{l}
\begin{eqnarray}
&&a_1(x)=b(x)&\\
&&b_1(x)=r(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\:\:\:\:\br{②}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f_1(x)=p(x)f(x)+g(x)&\\
&&g_1(x)=f(x)&\\
\end{eqnarray}
\end{array}\right.\)
\(\br{②}\) を \(f(x),\:g(x)\) について解くと、
\(\:\:\:\:\br{③}\left\{
\begin{array}{l}
\begin{eqnarray}
&&f(x)=g_1(x)&\\
&&g(x)=f_1(x)-p(x)g_1(x)&\\
\end{eqnarray}
\end{array}\right.\)
である。このよう定義すると、\(\br{①}\)、\(\br{②}\) を使って、
\(a_1(x)f_1(x)+b_1(x)g_1(x)\)
\(=b(x)(p(x)f(x)+g(x))+r(x)f(x)\)
\(=p(x)b(x)f(x)+b(x)g(x)+r(x)f(x)\)
\(=(p(x)b(x)+r(x))f(x)+b(x)g(x)\)
\(=a(x)f(x)+b(x)g(x)\)
と計算できるので、不定方程式は、
\(a_1(x)f_1(x)+b_1(x)g_1(x)=1\)
となり、係数多項式 \(a_1(x),\:b_1(x)\) の次数が元々の \(a(x),\:b(x)\) より小さな方程式に変形できる。この方程式の解である \(f_1(x),\:g_1(x)\) が求まれば、\(\br{③}\) を使って \(f(x),\:g(x)\) が求まる。
以上の式の変形は、\(1\leq i\) として、\(a_i(x)\) を \(b_i(x)\) で割った商と余りを、
\(a_i(x)=p_i(x)b_i(x)+r_i(x)\)
\((\:\mr{deg}\:r_i(x) < \mr{deg}\:b_i(x)\:)\)
のように求め、次のステップを、
\(a_{i+1}(x)=b_i(x)\)
\(b_{i+1}(x)=r_i(x)\)
\(f_{i+1}(x)=p_i(x)f_i(x)+g_i(x)\)
\(g_{i+1}(x)=f_i(x)\)
とすることで、互除法を続けていける。このように係数多項式 \(a(x),\:b(x)\) の剰余算を繰り返し、同時に変数多項式 \(f(x),\:g(x)\) を変換していくと、この過程で \(\mr{deg}\:r_i(x)\) は単調減少していく。そして互除法の最終段階で、
\(a_n(x)f_n(x)+b_n(x)g_n(x)=1\)
となったとする。元々の \(a(x)\) と \(b(x)\) は互いに素だったから、この段階の \(b_n(x)\) は \(0\) 次多項式=定数である。その定数を \(c\) とすると、
\(a_n(x)f_n(x)+cg_n(x)=1\)
となるが、この不定方程式の解は、
\(f_n(x)=0\)
\(g_n(x)=\dfrac{1}{c}\)
である。この解を起点として \(f_i(x),\:g_i(x)\:\:(1\leq i\leq n)\) の変換過程を逆にたどると \(f(x),\:g(x)\) が求まる。
次に、
\(a(x)f(x)+b(x)g(x)=1\)
の解が、 \((\br{A})\)
\(\mr{deg}\:g(x) < \mr{deg}\:a(x)\)
であるように選べることを示す。\(g(x)\) を \(a(x)\) で割った商を \(q(x)\)、余りを \(s(x)\) とする。
\(g(x)=q(x)a(x)+s(x)\)
\(s(x)=g(x)-q(x)a(x)\)
である。ここで、
\(F(x)=f(x)+b(x)q(x)\)
\(G(x)=s(x)\)
とおくと、
\(a(x)F(x)+b(x)G(x)\)
\(\begin{eqnarray}
&&\:\: =&a(x)(f(x)+b(x)q(x))+b(x)s(x)\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)(g(x)-q(x)a(x))\\
&&\:\: =&a(x)f(x)+a(x)b(x)q(x)+\\
&&&b(x)g(x)-b(x)q(x)a(x)\\
&&\:\: =&a(x)f(x)+b(x)g(x)\\
\end{eqnarray}\)
となるので、
\(a(x)f(x)+b(x)g(x)=1\)
であれば、
\(a(x)F(x)+b(x)G(x)=1\)
である。つまり \(f(x),\:g(x)\) が不定方程式の解であれば、\(F(x),\:G(x)\)も解である。\(\mr{deg}\:G(x)=\mr{deg}\:s(x) < \mr{deg}\:a(x)\) なので、\(F(x),\:G(x)\) が題意を満たす解である。
\((\br{A})\) 式を満たす \(f(x),\:g(x)\) が求まったとする。\((\br{A})\) 式の両辺に \(h(x)\) を掛けると、
\(a(x)f(x)h(x)+b(x)g(x)h(x)=h(x)\)
となる。
\(F(x)=f(x)h(x)\)
\(G(x)=g(x)h(x)\)
とおくと、\(F(x),\:G(x)\) は不定方程式、
\(a(x)F(x)+b(x)G(x)=h(x)\)
の解である。\((\br{A})\) 式の解を \(\mr{deg}\:g(x) < \mr{deg}\:a(x)\) となるように選べることを上で証明したが、この過程において方程式の右辺は無関係であった。従って、全く同じプロセスをたどることで、
\(\mr{deg}\:G(x) < \mr{deg}\:a(x)\)
とすることができる。[証明終]
既約多項式
有理数係数の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解がべき根で表現できるために必要十分条件を述べるのがガロア理論です。
このとき、多項式が有理数の範囲で因数分解できるのであれば、\(f(x)=0\) は、たとえば \(g(x)h(x)=0\)、\(g(x)=0,\:h(x)=0\) となって、より次数の低い方程式の問題に還元されてしまいます。これでは、たとえば \(f(x)\) が5次多項式だとしても、5次方程式の問題ではなくなる。
従って、方程式の解の議論をするときには「因数分解できない多項式」の議論をすればよいことになります。それが既約多項式です。
| (既約多項式の定義:31B) |
有理数 \(\bs{Q}\) を係数とする多項式で、\(\bs{Q}\) の範囲ではそれ以上因数分解できない多項式を \(\bs{Q}\) 上で既約な多項式という。
たとえば多項式 \(x^2-2\) は \(\bs{Q}\) 上では因数分解できませんが、\(\bs{R}\) 上では \((x-\sqrt{2})(x+\sqrt{2})\) と因数分解できます。\(x^2+2\) は \(\bs{R}\) 上では因数分解できませんが、\(\bs{C}\) 上では \((x-\sqrt{2}i)(x+\sqrt{2}i)\) と因数分解できます。「代数学の基本定理」によると、\(n\)次方程式は 複素数の範囲で\(n\)個の解をもつので、\(\bs{C}\) 上の既約多項式は1次多項式しかないことになります。つまり、既約多項式を議論するときには「どの体での既約多項式か」を明確にする必要があります。
なお、以降の説明において、\(f(x)\) を既約多項式とするとき、方程式 \(f(x)=0\) を「既約方程式」と記述することがあります。
以下、既約多項式の性質を調べますが、その前に次の定理を証明します。
| (整数係数多項式の既約性:31C) |
整数係数の多項式 \(f(x)\) が \(\bs{Q}\) 上で(=有理数係数の多項式で)因数分解できれば、整数係数でも因数分解できる。
この定理の対偶をとると、
整数係数の多項式 \(f(x)\) が整数係数で因数分解できなければ、有理数係数でも因数分解できず、つまり \(f(x)\) は既約多項式である
となります。有理数係数の多項式は、各係数を整数の分数で表現可能で、その分母の最小公倍数を多項式全体に掛けると整数係数の多項式になります。従って、ある多項式が既約かどうかという議論は整数係数の範囲で考えればよいことになり、話が随分シンプルになります。
これを証明するために、まず次の補題を証明します。
[補題]
2つの整数係数の多項式、\(g(x),\:\:h(x)\) があり、ともに係数の最大公約数は \(1\) とする。このとき、
\(r(x)=g(x)h(x)\)
で定義される多項式 \(r(x)\) の係数の最大公約数も \(1\) である。
[証明]
背理法を使う。\(r(x)\) の係数の最大公約数が \(2\) 以上と仮定する。最大公約数を素因数分解したときに現れる素数の一つを \(\bs{p}\) とする。
\(r(x)=a_0+a_1x+a_2x^2+\cd+a_nx^n\)
とおくと、\(a_i\:\:(0\leq i\leq n)\) のすべては \(p\) で割り切れる。ここで、
\(g(x)=b_0+b_1x+b_2x^2+\cd+b_mx^m\)
\(h(x)=c_0+c_1x+c_2x^2+\cd+c_kx^k\)
とすると、\(g(x)\) の係数の最大公約数は \(1\) なので、係数のすべてが \(p\) で割り切れることはなく、少なくとも \(1\) つの係数は \(p\) で割り切れない。ここで、\(p\) で割り切れない \(g(x)\) の係数のうち \(x\) の次数が最小の係数を考える。以降の数式を見やすくするため、\(b_2\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。このとき \(b_0,\:b_1\) は \(p\) で割り切れる。
全く同様にして \(h(x)\) に関しては、\(c_3\) が「\(p\) で割り切れない、\(x\) の次数が最小の係数」とする。つまり \(c_0,\:c_1,\:c_2\) は \(p\) で割り切れる。
ここで、\(r(x)=g(x)h(x)\) の等式の \(x^5\) の係数を比較する。左辺の \(x^5\) の項は \(a_5x^5\) であるが、背理法の仮定によって係数 \(a_5\) は \(p\) で割り切れる。
一方、右辺の \(g(x)h(x)\) の \(x^5\) の項は、
\((b_0c_5+b_1c_4+b_2c_3+b_3c_2+b_4c_1+b_5c_0)x^5\)
であるが、この係数のうち \(b_2c_3\) は 素数 \(p\) で割り切れない。なぜなら、\(b_2\) も \(c_3\) も素数 \(p\) で割り切れないので、\(b_2c_3\) を素因数分解しても \(p\) が現れないからである。一方、\(b_2c_3\) 以外の5つの項は、\(b_0,\:b_1,\:c_0,\:c_1,\:c_2\) のいずれかを因数にもつから、\(p\) で割り切れる。従って、唯一、 \(b_2c_3\) だけが \(p\) で割り切れないので、右辺全体としては \(p\) で割り切れない。
ということは、\(r(x)=g(x)h(x)\) の等式は \(x^5\) の項に関して右辺が \(p\) で割り切れ、左辺が \(p\) で割り切れないことになり、矛盾が生じる。
表記を見やすくするために、\(b_2\) と \(c_3\) が素数 \(p\) で割り切れない最小の次数の係数としたが、これを \(b_i\:\:(0\leq i\leq m)\) と \(c_j\:\:(0\leq j\leq k)\) としても全く同じであり、左辺の \(x^{i+j}\) の係数である \(a_{i+j}\) が \(p\) で割り切れる(=背理法の仮定)にもかかわらず、右辺の \(x^{i+j}\) の係数が \(p\) で割り切れないという矛盾が生じる。
従って背理法の仮定は間違っていて、\(r(x)\) の係数すべてを割り切る素数はなく、係数の最大公約数は \(1\) である。[補題の証明終]
この補題を用いて、整数係数多項式の既約性の定理(31C)を証明します。
[証明]
整数係数の多項式 \(f(x)\) が、2つの有理数係数の多項式 \(g(x)\) と \(h(x)\) に因数分解されたとする。
\(f(x)=g(x)h(x)\)
\(f(x)\) の係数の最大公約数を \(d\) とし、全部の係数を \(d\) で割って作った多項式を \(f_r(x)\) とする。つまり、 \((\br{B})\)
\(f(x)=df_r(x)\)
であり、\(f_r(x)\) の係数の最大公約数は \(1\) である。
\(g(x)\) の係数は有理数(=整数の分数)であるが、適当な整数 \(m_g\) をかけることによって整数係数の多項式 \(m_gg(x)\) にすることができる。この多項式 \(m_gg(x)\) の係数の最大公約数を \(d_g\) とし、\(m_gg(x)\) の各係数を \(d_g\) で割った多項式を \(g_r(x)\) とする。
\(m_gg(x)=d_gg_r(x)\)
であり、\(g_r(x)\) の係数の最大公約数は \(1\) である。
同様に、\(h(x)\) の係数は有理数であるが、適当な整数 \(m_h\) をかけることによって整数係数の多項式 \(m_hh(x)\) にすることができる。この \(m_hh(x)\) の係数の最大公約数を \(d_h\) とし、\(m_hh(x)\) の各係数を \(d_h\) で割った多項式を \(h_r(x)\) とする。
\(m_hh(x)=d_hh_r(x)\)
であり、\(h_r(x)\) の係数の最大公約数は \(1\) である。
以上にもとづいて \((\br{B})\) 式を書き換えると、
| \(df_r(x)\) | \(=\dfrac{d_g}{m_g}g_r(x)\cdot\dfrac{d_h}{m_h}h_r(x)\) | ||
| \(=\dfrac{d_gd_h}{m_gm_h}g_r(x)\cdot h_r(x)\) | \((\br{C})\) |
\(g_r(x)\cdot h_r(x)=r(x)\)
と定義すると、[補題]により、多項式 \(r(x)\) の係数の最大公約数は \(1\) である。 \((\br{D})\)
\((\br{D})\) 式を \((\br{C})\) 式に代入すると、
\(df_r(x)=\dfrac{d_gd_h}{m_gm_h}r(x)\)
となる。この式で \(f_r(x)\) と \(r(x)\) はともに係数の最大公約数が \(1\) であるが、整数係数の多項式を、 \((\br{E})\)
(整数)\(\times\)(係数の最大公約数が \(1\) の整数係数多項式)
と表現する方法は1種類しかない。従って \((\br{E})\) 式の両辺の係数と多項式は同じものであり、多項式の部分は、
\(\begin{eqnarray}
&&\:\:f_r(x)&=r(x)\\
&&&=g_r(x)\cdot h_r(x)\\
\end{eqnarray}\)
である。従って \(f(x)=df_r(x)\) を使って、
\(f(x)=(dg_r(x))\cdot h_r(x)\)
と表現できる。結局、\(f(x)\) は整数係数の2つの多項式に因数分解できることになり、題意が証明された。[証明終]
この定理があるため、有理数係数の既約多項式を議論するときには、整数係数の既約多項式 \(f(x)\) を議論し、\(f(x)=0\) の解を調べればよいことになります。これ以降の説明では整数係数の方程式の例だけが出てきますが、その理由は整数係数の例で十分だからです。
多項式の不定方程式の定理(31A)のように、多項式は整数とのアナロジーがあります。そのアナロジーで言うと、既約多項式は整数における素数に相当します。例えば次の定理が成り立ちます。
| (既約多項式と素数の類似性:31D) |
\(p(x)\) を既約多項式とし、\(f(x),\:g(x)\) を多項式とする。\(f(x)g(x)\) が \(p(x)\) で割り切れるなら、\(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。
[証明]
\(f(x)\) が \(p(x)\) で割り切れないとする。\(f(x)\) と \(p(x)\) は互いに素なので、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x),\:b(x)\) が存在する。両辺に \(g(x)\) を掛けると、
\(g(x)f(x)a(x)+g(x)p(x)b(x)=g(x)\)
となる。\(g(x)f(x)\) は \(p(x)\) で割り切れるので、
\(g(x)f(x)=p(x)h(x)\)
と書ける。これを代入して、
\(p(x)h(x)a(x)+g(x)p(x)b(x)=g(x)\)
\(p(x)\cdot(h(x)a(x)+g(x)b(x))=g(x)\)
となり、\(g(x)\) は \(p(x)\) で割り切れる。従って \(f(x),\:g(x)\) の少なくとも1つは \(p(x)\) で割り切れる。[証明終]
この定理の \(f(x)\) を \(g(x)\) に置き換えると次が言えます。
\(p(x)\) を既約多項式とし、\(g(x)\) を多項式とする。\((g(x))^2\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。また、\((g(x))^k\:\:(2\leq k)\) が \(p(x)\) で割り切れるなら、\(g(x)\) は \(p(x)\) で割り切れる。
\(a\) を整数とし、\(a^2\) が \(3\) で割り切れれば、\(a\) は \(3\) で割り切れます。しかし \(a^2\) が \(4\) で割り切れたとしても \(a\) が \(4\) で割り切れるとは限らない。これと既約多項式のアナロジーが成り立っています。
以下、既約多項式がもつ重要な性質を3つあげます。最初の3つは方程式に関するものです。
既約多項式の性質
| (既約多項式の定理1:31E) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
方程式 \(p(x)=0\) と \(f(x)=0\) が(複素数の範囲で)共通の解を1つでも持てば、\(f(x)\) は \(p(x)\) で割り切れる。
[証明]
\(f(x)\) は \(p(x)\) で割り切れないと仮定して背理法で証明する。\(f(x)\) が \(p(x)\) で割り切れないのなら、\(f(x)\) と \(p(x)\) は互いに素である。なぜなら、もし互いに素でないとすると、1次式以上の多項式 \(h(x)\) があって、
\(f(x)=f_1(x)h(x)\)
\(p(x)=p_1(x)h(x)\)
と表現できるが、\(p(x)\) は既約多項式なので \(p_1(x)=1\) であり、つまり \(h(x)=p(x)\) である。そうすると \(f(x)=f_1(x)p(x)\) となり、\(f(x)\) は \(p(x)\) で割り切れることになって矛盾するからである。つまり、\(f(x)\) が \(p(x)\) で割り切れないのなら \(f(x)\) と \(p(x)\) は互いに素である。
\(f(x)\) と \(p(x)\) が互いに素なら、多項式の不定方程式の定理(31A)によって、
\(f(x)a(x)+p(x)b(x)=1\)
を満たす \(a(x)\)、\(b(x)\) が存在する。そこで、方程式 \(p(x)=0\) と \(f(x)=0\) の共通の解を \(\al\in\bs{C}\) とし、この式に代入すると、左辺\(=0\) となって矛盾する。
従って、\(f(x)\) は \(p(x)\) で割り切れないとの仮定は矛盾を導くから、仮定は誤りであり、\(f(x)\) は \(p(x)\) で割り切れる。[証明終]
この定理は重要なことを言っています。\(\bs{Q}\) 上の方程式の解になる数を代数的数といいます。\(f(x)\) を既約多項式とし、ある代数的数 \(\al\) が \(f(x)=0\) の解とします。
もし、既約多項式 \(f(x)\) 以外の多項式 \(g(x)\) があって、\(g(x)=0\) の解の一つが\(\al\) だとすると、上記の定理により \(g(x)\) は \(f(x)\) で割り切れます。\(g(x)\) の次数が \(f(x)\) の次数と同じとすると、\(g(x)\) は \(f(x)\) の定数倍の既約多項式です。\(g(x)\) の次数が \(f(x)\) の次数より大きいとすると、\(g(x)\) は既約多項式ではありません。
つまり、\(\al\) を方程式の解とするとき、\(\bs{f(\al)=0}\) である既約多項式 \(\bs{f(x)}\) は、定数倍を除いて一意に決まることがわかります。
| (既約多項式の定理2:31F) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式、\(f(x)\) を \(\bs{Q}\) 上の多項式とする。
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は(複素数の範囲で)共通の解を持たない。
[証明]
既約多項式の定理1(31E)により、もし方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば \(f(x)\) は \(p(x)\) で割り切れるので、多項式 \(h(x)\)(定数の場合を含む)を用いて
\(f(x)=p(x)h(x)\)
と表現できる。従って、
\(f(x)\) の次数 \(\geq\:p(x)\)の次数
である。つまり、
方程式 \(p(x)=0\) と \(f(x)=0\) が共通の解を1つでも持てば、\(f(x)\) の次数 \(\geq\:p(x)\)の次数である
と言えるが、この対偶をとると、
\(f(x)\) の次数が1次以上で \(p(x)\) の次数未満のとき、方程式 \(p(x)=0\) と \(f(x)=0\) は共通の解を持たない
となる。[証明終]この定理は、既約多項式の定理1(31E)と同じことを別の視点で述べたものです。「3.2 体」の「単拡大体の基底」で、既約多項式の定理2(31F)を使った証明を行います。
| (既約多項式の定理3:31G) |
\(p(x)\) を \(\bs{Q}\) 上の既約多項式とすると、方程式 \(p(x)=0\) は(複素数の範囲で)重解を持たない。
[証明]
方程式 \(p(x)=0\) が重解 \(\al\) を持つとすると、
\(p(x)=(x-\al)^2q(x)\)
となる。これを微分すると、
\(p\,'(x)=2(x-\al)q(x)+(x-\al)^2q\,'(x)\)
となる。以上の2式に \(\al\) を代入すると、
| \(p(\al)\) | \(=0\) | |
| \(p\,'(\al)\) | \(=0\) |
・既約多項式 \(p(x)\) の次数は \(2\) 以上
・\(p\,'(x)\) の次数は \(2\) 未満
であるにもかかわらず共通の解 \(\al\) を持つことになり、既約多項式の定理2(31F)に反して矛盾が生じる。従って方程式 \(p(x)=0\) は重解を持たない。[証明終]
この定理も重要です。以降で行う証明の中には「\(n\)次既約方程式 \(f(x)=0\) の \(n\) 個の解を \(\al_1,\al_2,\cd,\al_n\) とする」といった、「\(n\)次方程式は \(\bs{n}\) 個の異なった解を持つのが当然」のような記述が出てきますが、\(\bs{f(x)}\) が既約多項式ならこの定理で保証されているからです。
最小多項式
| (最小多項式の定義:31H) |
\(\al\) を 方程式の解とする。\(\al\) を解としてもつ、体 \(\bs{Q}\) 上の方程式のうち、次数が最小の多項式を、\(\al\) の \(\bs{Q}\) 上の最小多項式と言う。
| (最小多項式は既約多項式:31I) |
\(\bs{Q}\) 上の方程式、\(f(x)=0\) が \(\al\) を解としてもつとき、
| \(f(x)\) が 体 \(\bs{Q}\) 上の既約多項式である | |
| \(f(x)\) が \(\al\) の \(\bs{Q}\) 上の最小多項式である |
の2つは同値である。
[② \(\bs{\Rightarrow}\) ① の証明]
最小多項式 \(f(x)\) が既約多項式でなければ、\(f(x)=g(x)h(x)\) となる \(\bs{Q}\) 係数の多項式 \(g(x)\)、\(h(x)\) が存在する。\(x\) に \(\al\) を代入すると、
\(f(\al)=g(\al)h(\al)=0\)
となり、少なくとも \(g(\al)=0\)、\(h(\al)=0\) のどちらかは成り立つ。従って、\(f(x)\) より次数の低い多項式で \(\al\) を解にもつものが存在することになり、\(f(x)\) が最小次数であるという、最小多項式の定義に反する。従って \(f(x)\) は既約多項式である。
[① \(\bs{\Rightarrow}\) ② の証明]
\(g(x)\) を \(\al\) の \(\bs{Q}\) 上の最小多項式とする。すると、\(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) を持つことになり、\(f(x)\) は既約多項式なので、既約多項式の定理1(31E)により \(g(x)\) は \(f(x)\) で割り切れる。従って \(g(x)\) は多項式 \(h(x)\) を用いて、
\(g(x)=h(x)f(x)\)
と表せる。② \(\Rightarrow\) ①の証明により、最小多項式は既約多項式なので、\(g(x)\) は既約多項式である。既約多項式が \(1\)次多項式以上の因数をもつことはない。従って \(h(x)\) は \(0\)次多項式=定数である。ということは、\(f(x)\) も \(\al\) の最小多項式である。[証明終]
方程式 \(f(x)=0\) の解が \(\al\) である( \(f(\al)=0\) )という場合、方程式がまずあって、その解を考えます。しかしその逆、つまり代数的数 \(\al\) があり、\(\al\) を解にもつような方程式は何かと考えるのが最小多項式です。これは、ガロア理論でしばしば出てきます。
3.2 体
「体」とは何かを「1.2 体」で説明しました。それを前提として、ガロア理論に必要な「体」についての定義\(\cdot\)定理を説明します。
最小分解体
| (最小分解体の定義:32A) |
体 \(\bs{Q}\) 上の多項式 \(f(x)\) を、
\(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\)
と、1次多項式で因数分解したとき、
\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\)
を \(f(x)\) の最小分解体と言う。\(f(x)\) は既約多項式でなくてもよい。
この最小分解体は、あとに出てくるガロア拡大体と直結している重要な概念です。
\(\bs{Q}\) 上の方程式の解が四則演算とべき根で表されるかどうか、と言った場合、既約多項式だけを考えれば十分です。しかし最小分解体は、既約でない多項式をも含んだ定義です。ガロア理論でしばしば出てくるのは \(1\) の \(n\)乗根を求める、
\(x^n-1=0\)
という方程式ですが、左辺は因数分解ができるので既約多項式ではありません。最小分解体の定義は、一般の多項式としておく方が都合が良いのです。
単拡大定理
| (単拡大定理:32B) |
\(\bs{Q}\) 上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大である。つまり \(\bs{K}\) の元 \(\theta\) があって、\(\bs{K}=\bs{Q}(\theta)\) となる。この \(\theta\) を原始元という。
[証明]
\(\bs{Q}\) 上の方程式の解を \(\al\)、\(\beta\) とし、
\(\theta=\al+c\beta\:\:(c\in\bs{Q})\)
とおく。すると、\(\al+c\beta\) と有理数の四則演算で作れる数は、\(\al,\:\beta,\) 有理数の四則演算で作れるから、
\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。次に、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
が成り立つような \(c\) が存在することを示す。
\(\al\) の \(\bs{Q}\) 上の最小多項式を \(f(x)\) とし、\(\beta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とする。そして、
\(f(x)=0\) の解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\)
\(g(x)=0\) の解を \(\beta_1=\beta,\:\beta_2,\:\cd\:,\beta_m\)
とする。ここで、
\(h(x)=f(\al+c\beta-cx)\)
とおくと、
\(h(\beta)=f(\al)=0\)
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\:\:(2\leq i\leq m)\)
となる。
\(c\) は有理数であり、無数に選べるので、\(\al+c\beta-c\beta_i\:\:(2\leq i\leq m)\) のどれもが \(\al_1,\:\al_2,\:\cd\:,\al_n\) と一致しないようにできる。具体的には、もし \(\al_j\:\:(1\leq j\leq n)\) と一致したとしたら、
\(\al_j=\al+c\beta-c\beta_i\)
\(c=-\dfrac{\al-\al_j}{\beta-\beta_i}\)
なので、\(i\) と \(j\) を \((2\leq i\leq m,\:\:1\leq j\leq n)\) の範囲で振って \(n(m-1)\) 個の \(c\) を計算し、これら以外の値を選べばよい。このように \(c\) を選んだとする。そうすると \(\al+c\beta-c\beta_i\) は方程式 \(f(x)=0\) の解にはなり得ないので、
\(h(\beta_i)=f(\al+c\beta-c\beta_i)\neq0\:\:(2\leq i\leq m)\)
であり、\(g(x)=0\) と \(h(x)=0\) の共通解は \(\beta=\beta_1\) のみになる。
そうすると \(h(x)\) と \(g(x)\) は唯一の共通の因数 \((x-\beta)\) をもつので、\(h(x)\) と \(g(x)\) に互除法(21A)を適用すると、\(k\) をある有理数として最後は \(k(x-\beta)\) で割り切れる。
\(g(x)\) は \(\bs{Q}\) 上の多項式だから、すなわち \(\bs{Q}(\al+c\beta)\) 上の多項式である。また、\(h(x)\) は \(h(x)=f(\al+c\beta-cx)\) と定義されるが、\(f(x)\) が \(\bs{Q}\) 上の多項式なので、\(h(x)\) は \(\bs{Q}(\al+c\beta)\) 上の多項式である。つまり \(h(x)\) も \(g(x)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。
従って、互除法の最終結果である \(k(x-\beta)\) も \(\bs{Q}(\al+c\beta)\) 上の多項式である。これは、
\(k,\:k\beta\:\in\:\bs{Q}(\al+c\beta)\)
であることを意味しており、従って、
\(\beta\:\in\:\bs{Q}(\al+c\beta)\)
となる。また \(\al\) も、
\(\al=(\al+c\beta)-c\beta\:\in\:\bs{Q}(\al+c\beta)\)
である。この結果、\(\al\)、\(\beta\) の両方が \((\al+c\beta)\) の四則演算で表現できることになり、
\(\bs{Q}(\al,\beta)\:\subset\:\bs{Q}(\al+c\beta)=\bs{Q}(\theta)\)
である。従って、\(\bs{Q}(\al,\beta)\:\sp\:\bs{Q}(\theta)\) と合わせて、
\(\bs{Q}(\al,\beta)=\bs{Q}(\theta)\)
が結論づけられた。
以上を繰り返し適用すると、\(\bs{Q}\) に添加する方程式の解は \(\al,\:\beta,\:\gamma,\:\cd\) と増やしていける。従って、
\(\bs{Q}\)上の方程式の解をいくつか添加した代数拡大体 \(\bs{K}\) は単拡大であり、ある \(\bs{K}\) の元 \(\theta\) を使って \(\bs{K}=\bs{Q}(\theta)\) と表せる
ことが証明できた。[証明終]
「すべての代数拡大体は単拡大である」というのは、ちょっと驚くような定理です。方程式の解を複数添加した体は、このような性質をもっています。方程式の解の議論をするときに解を含む体の性質で議論することのメリットは、このような単拡大定理が使えることにも現れています。次の「単拡大の体」に関する定理も、単拡大定理があることで任意の代数拡大体につながっています。
なお、上の証明で本質的な役割を果たしているのはユークリッドの互除法が成り立つ原理(21A)です。互除法の "奥の深さ" がわかります。
単拡大の体
| (単拡大の体:32C) |
ある代数的数 \(\al\) の \(\bs{Q}\) 上の最小多項式が \(n\)次多項式 \(f(x)\) であるとする。このとき 体 \(\bs{K}\) を、
| \(\bs{K}\) | \(\overset{\text{ }}{=}\) | \(\{a_{n-1}\al^{n-1}+\)\(\:\cd\:+\)\(a_2\al^2+\)\(a_1\al+\)\(a_0\:|\:a_i\in\bs{Q}\:\}\) | |
| \((0\leq i\leq n-1)\) |
と定義すると、\(\bs{K}\) は体になり、\(\bs{K}=\bs{Q}(\al)\) である。その元の表し方は一意である。
[証明]
\(\bs{K}\) が四則演算で閉じていて体であることを証明する。\(\bs{K}\) の元は「\(\bs{Q}\) 上の、\(\al\) の \(n-1\) 次以下の式」で表されるので、\(\bs{K}\) の任意の2つの元を、\(\bs{Q}\) 上の \(n-1\) 次以下の2つの多項式 \(g(x),\:h(x)\) を用いて、\(g(\al),\:h(\al)\) とする。
\(g(\al)+h(\al),\:g(\al)-h(\al)\) は \(\al\) の \(n-1\) 次以下の式なので、\(\bs{K}\) は加減について閉じている。
乗法で閉じていることを言うため、\(g(x)h(x)\) を \(f(x)\) で割った商を \(q(x)\)、余りを \(r(x)\) とする。つまり、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。\(x=\al\) を代入すると、\(f(\al)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
となる。\(r(x)\) は \(f(x)\) で割ったときの余りなので、次数は \(f(x)\) の次数 \(n\) よりも小さく、\(n-1\) 以下である。従って、\(g(\al)h(\al)\) は \(\al\) の \(n-1\) 次以下の式になり、\(\bs{K}\) は乗法で閉じている。
除法で閉じていることは、\(h(\al)\neq0\) のとき、\(\dfrac{g(\al)}{h(\al)}\) が \(\bs{Q}\) 上の「\(\al\) の \(n-1\) 次以下の多項式」で表されることを示せればよい。\(s(x),\:t(x)\) を未知の多項式とし、次の不定方程式を立てる。
\(f(x)s(x)+h(x)t(x)=g(x)\)
\(f(x)\) は最小多項式なので、最小多項式は既約多項式の定理(31I)により既約多項式である。また、\(h(x)\) は \(f(x)\) で割り切れない。なぜなら、もし \(h(x)\) が \(f(x)\) で割り切れるとすると、\(h(x)=u(x)f(x)\) と書けるが、これに \(\al\) を代入すると \(h(\al)=u(\al)f(\al)=0\) となり、\(h(\al)\neq0\) に矛盾するからである。
\(h(x)\) が、既約多項式である \(f(x)\) で割り切れないので、\(h(x)\) と \(f(x)\) は互いに素である。すると、多項式の不定方程式の定理(31A)により、上記の不定方程式を満たす \(s(x),\:t(x)\) が存在して、\(t(x)\) を \(n-1\) 次以下にとることができる。不定方程式に \(x=\al\) を代入すると、
\(h(\al)t(\al)=g(\al)\)
\(\dfrac{g(\al)}{h(\al)}=t(\al)\)
となり、除法でも閉じていることが分かった。つまり \(\bs{K}\) は体である。
\(\bs{Q}(\al)\) は「有理数と\(\al\)」の四則演算で生成される全ての数から成る体である。\(\bs{K}\) の元は有理数と \(\al\) の四則演算で表現され、それは元の間の四則演算で完全に閉じている。従って \(\bs{K}=\bs{Q}(\al)\) である。
表現の一意性は次のようにして証明できる。もし \(\bs{Q}(\al)\) の元について \(g(\al)\) と\(h(\al)\) の2通りの表し方があったとする。つまり、
\(g(\al)=h(\al)\)
\(g(\al)-h(\al)=0\)
とする。\(g(x)-h(x)\) が1次式以上だと仮定すると、\(n-1\)次以下の方程式 \(g(x)-h(x)=0\) が \(\al\) を解にもつことになる。つまり \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解 \(\al\) を持つ。一方、\(f(x)\) は \(n\)次既約多項式であり、\(g(x)-h(x)\) は \(n-1\) 次以下の多項式である。この場合、既約多項式の定理2(31F)によって、方程式 \(f(x)=0\) と \(g(x)-h(x)=0\) は共通の解を持たない。従って矛盾が生じる。つまり \(g(x)-h(x)\) は1次式以上ではありえない。\(g(x)-h(x)\) は \(0\)次多項式=定数である。
\(g(x)-h(x)\) が定数であれば、\(g(\al)-h(\al)=0\) なので、その定数は \(0\) しかない。つまり \(g(x)\) と \(h(x)\) の係数は全く一致する。従って表現は一意である。[証明終]
単拡大定理(32B)と、この単拡大の体の定理(32C)を合わせると、
代数拡大体のすべて元は、ある代数的数 \(\al\) の多項式で一意に表せる
ことになります。このことは、分子\(\cdot\)分母が \(\al\) の多項式である分数式があったとしても、分数を取り払った \(\al\) の多項式に変換できることを意味します。1.2 節の「方程式の解を含む体」で触れた "分母の有理化" が、どんなに複雑な分母であっても常に可能であることが分かります。
「3.2 体」終わり
(「3.多項式と体」は次回に続く)
(「3.多項式と体」は次回に続く)
2023-03-18 08:22
nice!(0)
No.354 - 高校数学で理解するガロア理論(1) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
今までに「高校数学で理解する ・・・・・・」と題した記事を何回か書きました。
の7つの記事です。「高校数学で理解する」という言葉の意味は、「高校までで習う数学の知識をベースに説明する」ということです。今回はそのシリーズの続編で、ガロア理論をテーマにします。その第1回目です。
ここで言う「ガロア理論」とは、
とし、その範囲に限定します。これが、そもそもの理論の発端であり、19世紀に夭折したフランスの数学者、ガロアが数学史に残した功績でした。
例によって、前提知識は高校までで習う数学に限定し、そこに含まれない定理は全部証明することにします。ただし、複素数と複素平面の知識は前提とします。また集合論の記号(\(\in\:\:\subset\:\:\sp\:\:\cup\:\:\cap\) など)を適時使います。さらに「すべての方程式は複素数の範囲に解をもつ」という "代数学の基本定理" は、証明はしませんが前提です。
以降の記述では、次の3つの本を特に参考にしました。
全体の内容は以下です。「高校の数学に含まれない定理は全部証明する」方針なので、証明の完結までにはかなりの論証が必要です。そのため、全体は少々長くなります。第1章は、その全体像を俯瞰したもので、第2章からが本論です。
方程式が解けるための必要十分条件の導出は、そこに至るためにかなり長いステップの証明が必要で、論理に論理を積み重ねる必要があります。そこでまず第1章で、証明の枠組みがどうなっているか、全体のアウトラインを説明します。
これは証明そのものではないし、数学的に曖昧なところもあります。しかし、ガロア理論の理解の道筋を示す意味で、2章からの本論の理解の助けになると思います。
1.1 方程式とその可解性
方程式
\(f(x)\) を、有理数を係数にもつ1変数の \(n\)次多項式とします。有理数の集合を \(\bs{Q}\) で表すので、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\)
\((\:a_n\neq0,\:a_i\in\bs{Q}\:)\)
と定義できます。以降のガロア理論で問題にする \(n\)次方程式とは、
\(f(x)=0\)
で表されるものです。これを \(\bs{\bs{Q}}\) 上の(=係数が有理数の)\(n\)次方程式といいます。
代数学の基本定理によると、複素数係数の方程式は複素数の集合 \(\bs{C}\) の中に必ず解をもちます。もちろん、有理数係数の方程式も複素数の集合 \(\bs{C}\) の中に解を持ちます。
有理数係数の方程式の解となる数を代数的数と呼びます。実数や複素数には代数的数でない数があり、たとえば円周率 \(\pi\) や、自然対数の底 \(e\) が有名です。
方程式の可解性
方程式の解が四則演算とべき根(\(\sqrt[n]{a}\))の組み合わせで記述できるとき、その方程式は、
・代数的に解ける
・代数的解法がある
・可解である
と言います(同じ意味です)。べき根(冪根)は累乗根ともいいます。
まず大切なところですが、べき根の定義を明確にしておきます。
\(\sqrt[n]{a}\:\:(\:a\in\bs{C}\:)\)
とは \(n\) 乗して \(a\) になる数の意味ですが、\(a\) が正の実数の場合、「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちの正の実数を表わす」とします。
そして \(a\) が正の実数以外の、負の実数や複素数の場合は「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちのどれかを表わす」とします。"どれか" とするのは、\(n\) 乗して \(a\) になる複数の数を区別する方法がないからです。たとえば \(\sqrt{-1}\) は「2乗して \(-1\) になる2つの数のどちらか」であり、その一方を \(i\) と書くと、もう一方が \(-i\) です。2つの数のどちらが \(i\) かを決めることはできません。複素平面で上の方が \(i\) のように見えますが、それは話が逆で、\(i\) とした方を上に書くのが複素平面です。
従って、方程式の解をべき根で書くときには注意が必要です。たとえば仮想的な例ですが、
\(\sqrt[3]{p}\:+\:\sqrt[3]{q}\)
という記述があったとき、3乗すると \(p,\:q\) になる数のどれでもよい場合もあります。3乗して特定の数になる数は基本的に3つあるので、3\(\times\)3=9種 のどれでもよい場合もあります。しかし、たとえば、
\(\sqrt[3]{p}\cdot\sqrt[3]{q}=r\) であること
といった付帯条件が付いている(付ける必要がある)場合もある。そうすると \(p,\:q\) の選び方には制約が出てきます。べき根が複数の中の何を指すのか、その選択には注意が必要です。
方程式の可解性に戻りますと、
ですが(2次方程式はもちろん可解です)、
のです。従って、2次・3次・4次方程式では解の公式、つまり任意の(=係数が変数の)方程式の解を示す公式がありますが、5次以上の方程式には解の公式がありません。
もちろん、可解でない方程式の解が求まらないわけではありません。現代では数値計算ソフトウェアを使って、いくらでも詳しい精度で解を求めることができます。ただ、その解が四則演算とべき根では表せないと言っているのです。
べき根 \(\sqrt[n]{a}\) は \(n\)乗の逆関数です。方程式が \(\bs{n}\)乗の組み合わせでできているのに、解が \(\bs{n}\)乗の逆関数で表現できない(場合がある)というのは少々不思議ですが、数の世界はそうなっているのです。
それでは、方程式がどういう条件だったら可解で、どういう条件だったら可解でないのか、その必要十分条件は何かが問題になってきます。その必要十分条件を示したのがガロア理論です。
1.2 体
体とは
ガロア理論の出発点は、方程式の解の特性を考えるときに「方程式の解を含む体」を考えて、体の性質でもって解の特性を語ることにあります。
体(field)とは、加減乗除の四則演算が成り立ち、加法と乗法を結びつける分配則が成り立つ集合です。分配則とは \(a(b+c)=ab+ac\) となることです。
は体で、これらは \(\bs{Q}\:\subset\:\bs{R}\:\subset\:\bs{C}\) の関係にあります。\(\bs{Z}\) で表す整数の集合は体ではありません。除算の結果が有理数になって、整数にはならないからです。一般に、集合の要素同士の演算結果がその集合の要素になるとき、集合はその演算に関して「閉じている」と言います。整数は加減乗算で閉じていますが、除算では閉じていません。
\(\bs{Q},\:\bs{R},\:\bs{C}\) はいずれも複素数の集合 \(\bs{C}\) の部分集合であり、これらを数体と呼びます。\(\bs{C}\) は四則演算と分配則が成り立つので、その部分集合は四則演算ができて分配則が成り立ちます。従って、部分集合が体(=数体)である条件は、四則演算で閉じていることです。
数体はこの3つだけではありません。ガロア理論で問題にするのは、方程式の解を含む体です。
方程式の解を含む体
有理数係数の \(n\)次方程式 \(f(x)=0\) の一つの解を\(\al\:(\al\notin\bs{Q})\) とするとき、\(\bs{Q}\) と \(\al\)を含む最小の集合で体の定義を満たすものを \(\bs{Q}(\al)\) と書きます。これは、有理数と \(\bs{\al}\) の四則演算で作り出せるすべの数の集合です。四則演算は何回繰り返してもかまいません。
\(\bs{Q}\) をもとにして \(\bs{Q}(\al)\) を作るのが体の拡大(extension)で、\(\bs{Q}(\al)\) を \(\bs{Q}\) の拡大体といい、「\(\bs{Q}\) に \(\al\) を添加した(ないしは付加した)体」ということもあります。\(\al\) は代数的数なので、\(\bs{Q}\) の代数拡大体ともいいます。集合の包括関係は \(\bs{Q}\:\subset\:\bs{Q}(\al)\) です。この拡大のことを \(\bs{Q}(\al)/\bs{Q}\) と書きます。「拡大体\(/\)元の体」の形です。
当然、\(\bs{Q}\) に複数の代数的数を付加した体も考えられて、
\(\bs{Q}(\al,\:\beta,\:\gamma,\:\cd)\)
というように書きます。\(\al,\:\beta,\:\gamma,\:\cd\) が違った方程式の解であってもかまいません。
例として \(x^2-2=0\) の解での一つである \(\sqrt{2}\) を付加した \(\bs{Q}(\sqrt{2})\) を考えます。この体の任意の数 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
で表されます。この表現は四則演算で閉じています。加算・減算・乗算で閉じているのはすぐにわかります。また除算でも閉じています。というのも、分母の有理化のテクニックを使うと、
\(\dfrac{1}{a+b\sqrt{2}}=\dfrac{a}{a^2-2b^2}-\dfrac{b}{a^2-2b^2}\sqrt{2}\)
となって、\(a+b\sqrt{2}\) の形になるからです(\(a,b\in\bs{Q}\) なので \(a^2\neq2b^2\) です)。従って、乗算で閉じているので除算でも閉じていることになります。上の有理化は方程式の解を一つだけ添加した体の場合ですが、複数の解を添加した体でも有理化は常に可能です。このことは別途きっちりと証明します。
べき根拡大
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) という体の拡大を一般化します。\(\bs{Q}\) 上の \(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{Q})\)
の解の一つで、\(\bs{Q}\) に属さないものを \(\al\) としたとき、
\(\bs{Q}(\al)\)
を \(\bs{Q}\) のべき根拡大体といい、\(\bs{Q}\) から \(\bs{Q}(\al)\) を作ることをべき根拡大(radical extension)といいます。さらにもっと一般化して、体 \(\bs{F}\) があったとき、\(\bs{F}\) 上の(=\(\bs{F}\) 係数の)\(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{F})\)
の解の一つで、\(\bs{F}\) に属さないものを \(\al\) としたとき、
\(\bs{F}(\al)\)
が \(\bs{F}\) のべき根拡大体です。
ここで、ある代数的数 \(\al\) を、
\(\al=\sqrt{3+\sqrt{2}}\)
とします。これは四則演算とべき根で表現された代数的数です。これを変形すると、
\(\al^2-3=\sqrt{2}\)
\(\al^4-6\al^2+7=0\)
となるので、\(\al\) は方程式
\(x^4-6x^2+7=0\)
という4次方程式の解の一つです。そこで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{3+\sqrt{2}})\)
という体の拡大を考えたとき、この拡大は、
の、2ステップの拡大と考えることができます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\:\sqrt{3+\sqrt{2}})\)
という体の拡大です。そうすると各ステップが、\(x^n-a=0\) というタイプの方程式の解による体の拡大=べき根拡大になります。つまり「べき根拡大の系列」ができます。このことを一般化していうと、
方程式 \(f(x)=0\) の解の一つを \(\al\) とするとき、\(\al\) が四則演算とべき根で書けるなら、\(\bs{Q}\) から始まって \(\bs{Q}(\al\))に到達する「べき根拡大の系列」が存在する
となります。ガロア理論では、\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体を考えます。それを \(\bs{Q}\) のガロア拡大体といいます。つまり、\(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\al_n)\) です。この記法を使うと、
\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}\) から始まって \(\bs{Q}(\al_1,\:\cd\:,\al_n)\) に到達する「べき根拡大の系列」が存在するなら、\(f(x)=0\) は可解である
と言えるわけです。式で書くと、
\(\bs{F}_0=\bs{Q},\:\:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\)
として、
であり、かつ、
1.3 ガロア群
そのガロア群を説明するために、まず群(group)とは何か、その定義を明確にしておきます。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群であると言う。
たとえば、有理数の集合 \(\bs{Q}\) は、加法という演算に関して群になります。単位元は \(0\) で、\(a\) の逆元は \(-a\) です。また、有理数の集合から \(0\) を除いた集合は、乗法という演算で群になります。単位元は \(1\) で、\(a\) の逆元は \(a^{-1}\) です。これらは無限個の元をもつ無限群であり、また \(ab=ba\) が成り立つ可換群(アーベル群とも言う)です。
元の数が有限個の有限群もあります。たとえば、裏表のある正3角形を、もとの形と重なるように回転移動する、ないしは対称軸で折り返すという "操作" は群になります。頂点に番号を付け、時計回りに \(1,\:2,\:3\) とします。この操作は6個あって、それに \(e\)、\(\sg\)(シグマ)、\(\tau\)(タウ)の記号をつけて列挙すると、
となります。「時計回りに \(120^\circ\)回転する」のは「反時計回りに \(240^\circ\)回転する」のと頂点番号が同じになるので \(\sg_2\) と同じものとします。「時計回りに \(240^\circ\)回転する」も同様です。
そこで、集合 \(G\) を、
\(G=\{e,\:\sg_1,\:\sg_2,\:\tau_1,\:\tau_2,\:\tau_3\:\}\)
とすると、この集合は「操作を続けてやるという演算」で群になります。なぜなら、
が成り立つからです。\(G\) は有限群です。有限群に含まれる元の数を、群の位数と呼び、\(|G|\) または \(\#G\) で表します。
この \(G\) は可換群ではありません。\(\tau_i\) がからむ演算を実際にやってみると、
\(\tau_1\sg_1=\tau_2,\:\:\sg_1\tau_1=\tau_3\)
\(\tau_2\tau_1=\sg_2,\:\:\tau_1\tau_2=\sg_1\)
などとなり、演算順序を変えると結果が違ってきます(演算は右を先に行う)。この群では \(\sg_1\) と \(\sg_2\) の演算だけが可換です。
正3角形を対称移動する操作の群は、結局、\(1,\:2,\:3\) という3つの文字を置き換える(=置換する)操作と同じです。この置換の数は3文字の順列なので \(3\:!\) 個です。従って、
という対応関係がつきます。\(G\) をこのような文字の置き換えととらえるとき、置換群といいます。一方、正3角形の対称移動ととらえたときは(3次の)2面体群です。"2面体" というのは、裏表がある、裏返せるという意味です。
体の自己同型写像
ガロア群とは「体の自己同型写像がつくる群」です。まず、自己同型写像(automorphism)の定義をします。次において、体 \(\bs{F}\) は \(\bs{Q}\) の代数拡大体とします。
体 \(\bs{F}\) から 体 \(\bs{F}\) への写像(=自分自身への写像)\(f\) が1対1写像であり、\(\bs{F}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(x-y)&=f(x)-f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
&&\:\:f\left(\dfrac{x}{y}\right)&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体 \(\bs{F}\) の自己同型写像という。
体 \(\bs{F}\) の部分集合である有理数体 \(\bs{Q}\) の元、\(a\) に対しては、
\(f(a)=a\)
である。つまり、有理数は自己同型写像で不変である。
この定義でわかるように、自己同型写像とは、四則演算してから写像しても、写像してから四則演算しても同じになる写像です。このことを簡潔に、四則演算を保存する写像と表現します。なお、定義にある「1対1写像」とは、
の2条件を満たす写像です。この定義の「有理数は自己同型写像で不変」のところは次のように証明できます。
\(f(x+y)=f(x)+f(y)\) において \(x=0,\:y=0\) とすると、
\(f(0+0)=f(0)+f(0)\)
\(f(0)=f(0)+f(0)\)
なので、
\(f(0)=0\)
です。また、\(f(xy)=f(x)f(y)\) において \(x=1,\:y=1\) とすると、
\(f(1\cdot1)=f(1)f(1)\)
\(f(1)=f(1)f(1)\)
となり、\(f(1)=0\) か \(f(1)=1\) です。しかし \(f(1)=0\) とすると \(f(0)=0\) かつ \(f(1)=0\) となってしまい、\(f\) が「1対1写像である」という定義に反します。従って、
\(f(1)=1\)
です。次に、\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn 個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)=n\\
\end{eqnarray}\)
なので、
\(f(n)=n\)
です。任意の有理数 \(a\) は、2つの整数 \(n(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるので、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は自己同型写像で不変である(=自己同型写像は有理数を固定する)ことがわかります。
どんな体においても恒等写像 \(e\) は常に自己同型写像です。従って「すべての自己同型写像が有理数に対しては恒等写像として働く」ということは、「有理数体 \(\bs{Q}\) の自己同型写像は恒等写像 \(e\) しかない」ことになります。
しかし、\(\bs{Q}\) の代数拡大体 \(\bs{F}\) については、\(e\) を含む複数個の自己同型写像があります。そして、この複数個の自己同型写像の集合は群になり、それがガロア群です。具体的な例で説明します。
ガロア群の例
\(x^2-2=0\)
上で説明したように、この方程式に対応したガロア拡大体は \(\bs{Q}(\sqrt{2})\) であり、 \(\bs{Q}(\sqrt{2})\) の任意の元 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
と表せます。ここで写像 \(\sg\) を「\(\sqrt{2}\) を \(-\sqrt{2}\) に置き換える写像」つまり、
\(\sg\::\:\sqrt{2}\:\longmapsto\:-\sqrt{2}\)
と定義します。これを、
\(\sg(\sqrt{2})=-\sqrt{2}\)
と表記します。この定義によって \(\sg\) は \(\bs{Q}(\sqrt{2})\) の自己同型写像になります。
そのことを確認しますが、記述を見やすくするため \(a,\:b\) を変数ではなく具体的な数値で書きます。もちろん、一般性を失わないようにする前提です。
\(\begin{eqnarray}
&&\:\:x&=2+3\sqrt{2}\\
&&\:\:y&=5-4\sqrt{2}\\
\end{eqnarray}\)
とすると、
\(\begin{eqnarray}
&&\:\:\sg(x+y)&=\sg(7-\sqrt{2})=7+\sqrt{2}\\
&&\:\:\sg(x)+\sg(y)&=(2-3\sqrt{2})+(5+4\sqrt{2})\\
&&&=7+\sqrt{2}\\
\end{eqnarray}\)
なので、\(\sg\)は加算を保存しています。減算についても同じです。また、
\(\sg(xy)\)
\(=\sg(2\cdot5-3\cdot4\cdot2+3\cdot5\sqrt{2}-2\cdot4\sqrt{2})\)
\(=\sg(-14+7\sqrt{2})\)
\(=-14-7\sqrt{2}\)
\(\sg(x)\sg(y)\)
\(=(2-3\sqrt{2})(5+4\sqrt{2})\)
\(=2\cdot5-3\cdot4\cdot2-3\cdot5\sqrt{2}+2\cdot4\sqrt{2}\)
\(=-14-7\sqrt{2}\)
なので、\(\sg\) は乗算を保存します。さらに、
\(\begin{eqnarray}
&&\:\:\dfrac{x}{y}&=\dfrac{2+3\sqrt{2}}{5-4\sqrt{2}}\\
&&&=\dfrac{(2+3\sqrt{2})(5+4\sqrt{2})}{(5-4\sqrt{2})(5+4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}-\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
なので、
\(\sg\left(\dfrac{x}{y}\right)=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\)
です。一方、
\(\begin{eqnarray}
&&\:\:\dfrac{\sg(x)}{\sg(y)}&=\dfrac{2-3\sqrt{2}}{5+4\sqrt{2}}\\
&&&=\dfrac{(2-3\sqrt{2})(5-4\sqrt{2})}{(5+4\sqrt{2})(5-4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
です。従って、
\(\sg\left(\dfrac{x}{y}\right)=\dfrac{\sg(x)}{\sg(y)}\)
となって、除算も保存しています。以上は具体的数値での計算ですが、\(a,\:b\) を変数としても成り立つことは、上の計算プロセスを追ってみると分かります。
このようになる理由は、\(\bs{\sg}\) が 方程式の解を、解のどれかに置き換える写像だからです。つまり、\(x^2-2=0\) の解は \(\sqrt{2}\) と \(-\sqrt{2}\) ですが、
\(\sg(\phantom{-}\sqrt{2})=-\sqrt{2}\)
\(\sg(-\sqrt{2})=\phantom{-}\sqrt{2}\)
となります。ここで「解を、解のどれかに置き換える」という表現は「解を自分自身に置き換える」ことも含みます。
このことは、\(x^2-2=0\) という "特別な" 方程式だけでなく、一般の2次方程で成り立ちます。2次方程式、
\(x^2+px+q=0\)
の解を \(\al,\:\beta\) とし、共に有理数ではないとします(\(\al,\:\beta\notin\bs{Q}\))。\(\bs{Q}\) の代数拡大体、\(\bs{Q}(\al,\beta)\) の自己同型写像を \(\sg\) とします。\(\al\) は、
\(\al^2+p\al+q=0\)
を満たしますが、この式の両辺に対して \(\sg\) による写像を行うと、
\(\sg(\al^2+p\al+q)=\sg(0)\)
\(\sg(\al)^2+p\sg(\al)+q=0\)
となります。\(\sg\) は四則演算を保存し、また \(\sg(0)=0\) だからこうなります。ということは、\(\sg(\al)\) は元の2次方程式の解です。従って、
\(\sg(\al)=\al\)
\(\sg(\al)=\beta\)
のどちらかです。\(\beta\) についても全く同じことが言えて、
\(\sg(\beta)=\beta\)
\(\sg(\beta)=\al\)
のどちらかです。従って \(\bs{Q}(\al,\beta)\) の自己同型写像 は、
\(e\)(恒等写像)
\(\sg(\al)=\beta\) となる写像
の2種類です。ここで、\(\sg\) を \(\sg(\al)=\beta\) となる写像と規定すると、必然的に \(\sg(\beta)=\al\) になります。なぜなら、もし \(\sg(\beta)=\beta\) だとすると、\(\sg(\al)=\beta\) かつ \(\sg(\beta)=\beta\) になり、\(\sg\) が1対1写像であるという、そもそもの自己同型写像の定義に反するからです。2次方程式の解による代数拡大体の自己同型写像は、恒等写像と「2つの解を入れ替える写像」の2つです。
ここで、自己同型写像 \(e,\:\sg\) の集合を \(G\) とします。つまり、
\(G=\{e,\:\sg\}\)
です。そうすると、\(G\) は群になります。\(e\) という恒等写像があり、
\(\sg^2(\al)=\sg(\sg(\al))=\sg(\beta)=\al\)
なので、
\(\sg^2=e\)
\(\sg^{-1}=\sg\)
となって、逆元があるからです。この \(G\) が \(\bs{Q}(\al,\beta)\) のガロア群です。しかもこのガロア群は、\(\sg\) の(群の要素としての)累乗をとっていくと、
\(\sg,\:\sg^2=e,\:\sg^3=\sg,\:\sg^4=e,\:\cd\)
というように1つの元を出発点として巡回します。このような群を巡回群(cyclic group)といいます。この場合、\(G\) は位数 \(2\) の巡回群です。位数 \(2\) の巡回群を \(C_2\) と表現します。
\(C_2\) は \(\sg,\:e,\:\sg,\:e,\:\cd\) と、2つの元が交互に現れるだけなので、"巡回感" が薄いかもしれませんが、位数 \(3\) の巡回群(\(C_3\))になると "巡回してる感" が出てきます。それが次の方程式の例です。
\(x^3-3x+1=0\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-3x+1\)
とします。
と計算できるので、方程式 \(f(x)=0\) は、\(2\) と \(1\) の間、\(1\) と \(0\) の間、\(-1\) と \(-2\) の間に3つの実数解があります。それを大きい順に \(\al,\:\beta,\:\gamma\) とします。
です。この \(\al,\:\beta,\:\gamma\) を実際に求めてみます。いずれの解も絶対値が \(2\) より小さいので、\(\theta\) を角度を表す変数として、
\(x=2\mr{cos}\theta\:\:(0\leq\theta\leq\pi)\)
とおいて \(x\) から \(\theta\) へ変数を変換すると、
\(f(x)=8\mr{cos}^3\theta-6\mr{cos}\theta+1\)
となります。ここで3倍角の公式、
\(\mr{cos}3\theta=4\mr{cos}^3\theta-3\mr{cos}\theta\)
を使うと、
\(f(x)=2\mr{cos}3\theta+1\)
となります。このことから \(f(x)=0\) の解は、
\(2\mr{cos}3\theta+1=0\)
\(\mr{cos}3\theta=-\dfrac{1}{2}\:\:(0\leq3\theta\leq3\pi)\)
を満たします。従って、
です。ここから、\(\theta_0=\dfrac{2\pi}{9}\) として、
\(\al=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}\theta_0\)
\(\beta=2\mr{cos}\dfrac{4\pi}{9}=2\mr{cos}2\theta_0\)
\(\gamma=2\mr{cos}\dfrac{8\pi}{9}=2\mr{cos}4\theta_0\)
\((\theta_0=\dfrac{2\pi}{9})\)
が求まります。なお、
\(\begin{eqnarray}
&&\:\:\al&=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}(2\pi-\dfrac{2\pi}{9})\\
&&&=2\mr{cos}\dfrac{16\pi}{9}=2\mr{cos}8\theta_0\\
\end{eqnarray}\)
です。ここで倍角の公式、
\(\mr{cos}2\theta=2\mr{cos}^2\theta-1\)
を使うと、
\(\begin{eqnarray}
&&\:\:\beta&=2\mr{cos}2\theta_0=2(2\mr{cos}^2\theta_0-1)\\
&&&=4\mr{cos}^2\theta_0-2=\al^2-2\\
\end{eqnarray}\)
となります。同様にして、
\(\begin{eqnarray}
&&\:\:\gamma&=2\mr{cos}4\theta_0=\beta^2-2\\
&&&=(\al^2-2)^2-2\\
&&\:\:\al&=2\mr{cos}8\theta_0=\gamma^2-2\\
&&&=(\beta^2-2)^2-2\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:\beta&=\al^2-2\\
&&&=(\gamma^2-2)^2-2\\
\end{eqnarray}\)
であることも分かります。従って、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
となり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できることになります。方程式 \(x^3-3x+1=0\) は、3つの解の間に "特別な関係" があります。
ここまで、\(\al,\:\beta,\:\gamma\) を求めると言っても三角関数で表示しただけであり、四則演算とべき根で表したわけではありません。しかし、\(\al,\:\beta,\:\gamma\) の "特別な関係" を使ってガロア群を求めることができます。それが次です。
\(\bs{Q}\) に \(x^3-3x+1=0\) の3つの解、\(\al,\:\beta,\:\gamma\) を添加した代数拡大体 \(\bs{Q}(\al,\beta,\gamma)\) を調べます。\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できるので、
\(\bs{Q}(\al,\:\beta,\:\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。以下、\(\bs{Q}(\al)\) で語ることにすると、\(\bs{Q}(\al)\) の任意の元 \(x\) は、
\(x=a\al^2+b\al+c\:\:(a,b,c\in\bs{Q})\)
という "標準形" で表されます。なぜなら、\(\al^3-3\al+1=0\)、つまり\(\al^3=3\al-1\) という関係があるので、四則演算の結果で現れる \(\al^3\) 以上の項は \(\al^2\) 以下に「次数下げ」ができるからです。
"標準形" で表現できる数が、加算、減算、乗算で閉じていることは明白でしょう。乗算の結果も「次数下げ」で "標準形" になります。除算が問題ですが、例えば、\(x=\al^2+\al+1\) の場合、
\(\begin{eqnarray}
&&\:\:\dfrac{1}{x}&=\dfrac{1}{\al^2+\al+1}\\
&&&=-\dfrac{3}{19}\al^2-\dfrac{2}{19}\al+\dfrac{14}{19}\\
\end{eqnarray}\)
というように "分母の有理化" ができるので、除算でも閉じています。この有理化の例を検算してみると、
(\(\al^2+\al+1)(-3\al^2-2\al+14)\)
\(\begin{eqnarray}
&&\:\: &=&-3\al^4-2\al^3+14\al^2-3\al^3-2\al^2+14\al\\
&&&& -3\al^2-2\al+14\\
&&&=&-3\al^4-5\al^3+9\al^2+12\al+14\\
&&&=&-3\al(\al^3-3\al+1)-5\al^3+15\al+14\\
&&&=&-5(\al^3-3\al+1)+19\\
&&&=&19\\
\end{eqnarray}\)
となって、正しい結果です。この検算で分かるように、分母の有理化は \(\al\) が方程式の解であること、つまり \(\al^3-3\al+1=0\) という関係だけをもとにしています。もちろん、\(x=a\al^2+b\al+c\) という任意の数で分母の有理化が可能です(ややこしい式になりますが)。このように、\(\bs{Q}(\al)=\bs{Q}(\al,\:\beta,\:\gamma)\) は体の定義を満たすことが確認できました。
次に \(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\) の自己同型写像を調べます。自己同型写像は、方程式の解を、解のどれかに移します。そこで \(\al\) に作用する自己同型写像を考えると、これには3つあります。
\(\sg_0(\al)=\al\)
\(\sg_1(\al)=\beta\)
\(\sg_2(\al)=\gamma\)
の \(\sg_0,\:\sg_1,\:\sg_2\) です。\(\sg_1\) は、\(\beta=\al^2-2\) なので、
\(\sg_1(\al)=\al^2-2\)
であり、\(\al\) を \(\al^2-2\) に置き換える写像です。
ここで \(\al\) に \(\sg_1\) を2回作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1^{\:2}(\al)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1(\al^2-2)\\
&&&=\sg_1(\al)^2-\sg_1(2)\\
&&&=\beta^2-2=\gamma\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:\sg_2(\al)&=\gamma\\
&&\:\:\sg_1^{\:2}(\al)&=\gamma\\
\end{eqnarray}\)
なので、
\(\sg_1^{\:2}=\sg_2\)
であることが分かります。
次に、\(\sg_1\) を \(\beta\) に作用させてみると、
\(\begin{eqnarray}
&&\:\:\sg_1(\beta)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1^{\:2}(\al)\\
&&&=\sg_2(\al)=\gamma\\
\end{eqnarray}\)
となります。また \(\sg_1\) を \(\gamma\) に作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1(\gamma)&=\sg_1(\beta^2-2)\\
&&&=\sg_1(\beta)^2-\sg_1(2)\\
&&&=\gamma^2-2=\al\\
\end{eqnarray}\)
となります。
\(\sg_2\) についても同様の計算をしてみると、
\(\begin{eqnarray}
&&\:\:\sg_2(\beta)&=\sg_1^{\:2}(\beta)\\
&&&=\sg_1(\sg_1(\beta))\\
&&&=\sg_1(\gamma)=\al\\
&&\:\:\sg_2(\gamma)&=\sg_1^{\:2}(\gamma)\\
&&&=\sg_1(\sg_1(\gamma))\\
&&&=\sg_1(\al)=\beta\\
\end{eqnarray}\)
です。
さらに、\(\sg_0(\al)=\al\) である \(\sg_0\) については、\(\beta\) と \(\gamma\) が \(\al\) の式で表されているので \(\sg_0(\beta)=\beta\)、\(\sg_0(\gamma)=\gamma\) であり、また、自己同型写像は有理数を固定するので、\(\sg_0\) は \(\bs{Q}(\al,\beta,\gamma)\) のすべての元を固定する恒等写像 \(e\) です。
まとめると、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つになります。この3つは、
\(e\::\) 恒等写像
\(\sg_1(\al)=\beta\)、\(\sg_1(\beta)=\gamma\)、\(\sg_1(\gamma)=\al\)
\(\sg_2(\al)=\gamma\)、\(\sg_2(\beta)=\al\)、\(\sg_2(\gamma)=\beta\)
というように、\(x^3-3x+1=0\) の3つの解を入れ替えます。また、
\(\sg_1\sg_2=\sg_2\sg_1=e\)
\(\sg_1^{-1}=\sg_2,\:\:\sg_2^{-1}=\sg_1\)
であることも分かりました。
解の入れ替えは他に3種が考えられます。つまり一つの解を固定し他の2つを入れ替える写像\(\cdot\)3種ですが、一つの解で他の2つの解が表されているので、一つの解を固定する写像は全部の解を固定します。「一つの解を固定し、他の2つを入れ替える写像」は、この方程式の場合は存在しません。従って、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つがすべてです。
\(G=\{e,\:\sg_1,\:\sg_2\}\) とすると、\(G\) は \(\bs{Q}(\al,\beta,\gamma)\) のガロア群になります。しかも \(\sg_2=\sg_1^{\:2}\)、\(\sg_2\sg_1=\sg_1^{\:3}=e\) の関係があります。ここで \(\sg_1\) をあらためて \(\sg\) と書くと、
が \(\bs{Q}(\al,\beta,\gamma)\) のガロア群です。\(\sg\) は、
で定義される自己同型写像です。
この \(G\) は位数 \(3\) の巡回群(\(C_3\) で表される)です。そして、ガロア群が巡回群であるというのが、方程式が可解であるための条件の一つなのです。
ちなみに、数式処理ソフトウェアを使って \(x^3-3x+1=0\) の解のうちの最大である \(\al\) を計算してみると、
\(\al=1.53208888623796\) ・・・
です。一方、3次方程式の根の公式を使って \(\al\) の厳密解を求めると、
\(\al=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{-3}}{2}}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{-3}}{2}}\)
となります。\(\sqrt{3}\:i\) と書かずにあえて \(\sqrt{-3}\) としました。この式はこれ以上簡略化できないし、また根号の中のマイナスを無くした表現にもできません。
つまり \(\al\) は、正真正銘の正の実数であるにもかかわらず、代数的に(=四則演算とべき根で)表そうとすると虚数を登場させざるを得ないわけです。
数学史をみると、そもそも虚数の必要性が認識されたのは3次方程式の解の表現からでした。そして、ガロア理論によると \(\bs{\sqrt{-3}=\sqrt{3}\:i}\) が現れるのは必然なのです。その理由はガロア理論の全体を理解することでわかります。
自己同型写像は方程式の解を入れ替えます("入れ替えない" を含む)。一般の3次方程式の場合、この入れ替えは \(3\:!\:=\:6\) 通りあります。解を \(1\:2\:3\) の文字で表すと、
の6通りです。入れ替えない、全部入れ替える(2個)、2つだけを入れ替える(3個)の6通りです。この6つの自己同型写像をもつ方程式の例が次です。
\(x^3-2=0\)
この方程式を解くため「\(1\) の原始 \(3\)乗根」を定義します(一般には、\(\bs{1}\) の原始\(\bs{n}\)乗根)。「\(1\) の原始 \(3\)乗根」とは、3乗して初めて \(1\) になる数です。これは \(x^3-1=0\) の根ですが、
\(x^3-1=(x-1)(x^2+x+1)\)
と因数分解できるので、\(1\) の原始 \(3\)乗根は2次方程式、
\(x^2+x+1=0\)
の、2つある解の両方です。そのどちらか一方を \(\omega\) とすると \(\omega^2\) も2次方程式を満たす原始 \(3\)乗根です。\(\omega,\:\omega^2\) を具体的に書くと、
です。逆でもかまいません。\(x^3-1=0\) の根は、
\(1,\:\:\omega,\:\:\omega^2\)
です。
これを使って方程式 \(x^3-2=0\) を解くと、
\(x^3-2=0\)
\(\left(\dfrac{x}{\sqrt[3]{2}}\right)^3=1\)
\(\dfrac{x}{\sqrt[3]{2}}=1,\:\:\omega,\:\:\omega^2\)
\(x=\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
と求まります。以降、\(\al=\sqrt[3]{2}\) とします。方程式 \(x^3-2=0\) の3つの解は、
\(\al,\:\:\al\omega,\:\:\al\omega^2\)
であり、これらを含む \(\bs{Q}\) の代数拡大体は、
\(\bs{Q}(\al,\:\al\omega,\:\al\omega^2)=\bs{Q}(\omega,\:\al)\)
です。この体のガロア群を調べます。
まず、写像 \(\tau\) を、
\(\tau(\omega)=\omega^2,\:\:\tau(\al)=\al\)
で定義される写像とします。この \(\tau\) は、
\(\tau(\al\omega)=\al\tau(\omega)=\al\omega^2\)
\(\tau(\al\omega^2)=\al\tau(\omega^2)=\al\omega^4=\al\omega\)
と、\(\al\omega\) と \(\al\omega^2\) を入れ替える自己同型写像です。\(\tau^2=e\) なので、
\(\{e,\:\tau\}\)
は位数 \(2\) の巡回群(\(C_2\))です。
次に、写像 \(\sg\) を、
\(\sg_i(\al)=\al\omega^i\:\:(i=0,1,2)\)
\(\sg_i(\omega)=\omega\)
と定義します。すると、
となって、\(\sg_i\) は解を、3つの解のどれかに移す写像です。また、
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_0\)
であることもわかります。\(\sg_0\) は恒等写像です。改めて、
\(\sg_0=e\)
\(\sg_1=\sg\)
と書くと、
\(\sg_i=\{e,\:\sg,\:\sg^2\}\)
であり、これは位数 \(3\) の巡回群(\(C_3\))です。
次に \(\{e,\:\tau\}\) の上に \(\{e,\:\sg,\:\sg^2\}\) を組み合わせた集合、\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\{\:\{e,\:\sg,\:\sg^2\}e,\:\{e,\:\sg,\:\sg^2\}\tau\}\\
&&&=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\\
\end{eqnarray}\)
と定義します。\(\sg\)、\(\tau\) の演算は右から順に行います。この \(G\) には恒等写像=単位元 \(e\) があり、次のように群の条件を満たします。
演算で閉じている
\(G\) は「写像を続けて行う」という演算に関して閉じています。なぜなら、\(\sg\) も \(\tau\) も3つの解を入れ替える写像であり、いくら続けてやっても3つの解を入れ替えることに変わりないからです。また3つの解を入れ替える写像は最大6つですが、\(G\) の位数は \(6\) であり、要素同士を演算すると \(G\) のどれかになります。
逆元がある
\(\sg\) と \(\tau\) の定義から
は明確ですが、\(\sg\tau,\:\sg^2\tau\) はどうかという問題です。ここで、\(\tau\sg\) を計算してみると、
となります。実はこれは \(\sg^2\tau\) と全く同じ写像です。確かめると、
となって、全く同じ写像だとわかります。
\(\sg\) と \(\tau\) は可換ではなく、
\(\tau\sg\neq\sg\tau\)
です。しかし、上の計算で分かるように、
\(\tau\sg=\sg^2\tau\)
という関係が成り立っています。いわば "弱い可換性" です。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。この弱可換性を使って計算すると、
\(\begin{eqnarray}
&&\:\:(\sg\tau)(\sg\tau)&=\sg(\tau\sg)\tau=\sg(\sg^2\tau)\tau\\
&&&=\sg^3\tau^2=e\\
&&\:\:(\sg^2\tau)(\sg^2\tau)&=\sg^2(\tau\sg)(\sg\tau)\\
&&&=\sg^2(\sg^2\tau)(\sg\tau)\\
&&&=\sg^4(\tau\sg)\tau=\sg^4(\sg^2\tau)\tau\\
&&&=\sg^6\tau^2=e\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:(\sg\tau)^{-1}&=\sg\tau\\
&&\:\:(\sg^2\tau)^{-1}&=\sg^2\tau\\
\end{eqnarray}\)
となって、すべての元の逆元が存在することが分かりました。以上により \(G\) は群であり、方程式 \(x^3-2=0\) の3つの解を含む代数拡大体、\(\bs{Q}(\omega,\al)\:\:(\al=\sqrt[3]{2})\) のガロア群は \(G\) です。
\(G\) の元が3つの解をどのように入れ替えるかをまとめます。3つの文字 \(1\:2\:3\) を使って、
とすると、
となり、これは正3角形の対称移動の群(3次の2面体群)と同じものです。
しかし重要なことは、\(G\) が \(\{e,\:\tau\}\) と \(\{e,\:\sg,\:\sg^2\}\) という2つの巡回群の "2階建て構造" になっていることです。"2階建て構造" というのはここだけの言葉で、数学用語ではありません。数学的にきっちりとした定義は別途行います。
実は、方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のときも、方程式は可解になります。このことをより正確に言うと以下のようになります。
可解群
方程式 \(x^3-2=0\) のガロア群、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
の性質をさらに調べます。この中の、\(\{e,\:\sg,\:\sg^2\}\) は、それだけで群を構成しています。つまり \(G\) の部分群(subgroup)です。これに \(H\) という名前をつけて、
\(H=\{e,\:\sg,\:\sg^2\}\)
とします。この \(H\) に左から \(\tau\) をかけて \(\tau H\) を作ります。\(\tau H\) とは、\(H\) のすべての元に左から \(\tau\) をかけた集合の意味です。弱可換性である \(\tau\sg=\sg^2\tau\) に注意して \(\tau H\) を計算してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
です。同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、
任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つ
わけです。このような性質をもつ部分群 \(H\) を、\(G\) の正規部分群(normal subgroup)と言います。ちなみに \(\{e,\:\tau\}\) も \(G\) の部分群(=巡回群)ですが、\(\sg\tau\neq\tau\sg\) なので、これは \(G\) の正規部分群ではありません。
上の例の場合、\(H\) は巡回群でしたが、\(\{e,\:\tau\}\) がそうであるように、巡回群だからといって正規部分群になるわけではありません。正規部分群はあくまで \(G\)(全体)と \(H\)(部分)の関係性に依存します。正規部分群が巡回群のこともある、というのが正しい認識です。
正規部分群 \(H\) の任意の元 \(h\) は、\(G\) の任意の元 \(x\) と可換ではありません。しかし、\(H\) の別の元 \(h\,'\) との間で \(xh=h\,'x\) が成り立ちます。つまり \(H\) は、\(G\) の任意の元とグループとして可換なのです。\(H\) の元は \(G\) の任意の元と弱い可換性がある、ともいえるでしょう。
そこで、方程式の可解性と正規部分群の関係です。\(x^3-2=0\) のガロア群のところで、
としました。しかしこれは少々曖昧な表現で、正確には、
です。そして、上の言い方の最後、「ただしその正規部分群が巡回群であること」の部分は、必ずしも巡回群でなくてもよいのです。つまり、ガロア群が "巡回群と正規部分群Aの2階建て構造" であり、その "正規部分群Aが、巡回群と正規部分群B(=巡回群)の2階建て構造" でもよいのです。いわば、正規部分群を介した巡回群の入れ子構造です。この入れ子の "深さ" は何段階でもかまいません。"正規部分群を介する" のは多段階でもよい。まとめると、
わけです。この正規部分群という概念が、ガロア理論の最大のキモです。先ほどの例の正規部分群 \(H=\{e,\:\sg,\:\sg^2\}\) は巡回群でしたが、一般に正規部分群は巡回群ではありません。そのため、"正規部分群を介した巡回群の入れ子構造" が重要な意味をもつのです。
方程式 \(x^3-3x+1=0\) のところで書いたように、ガロア群が巡回群であれば方程式は可解でした。ここまでのことを踏まえて可解群の定義をすると、
となります。可解群とは "ほぼ巡回群" であり、"広義の巡回群" だとも言えるでしょう。巡回群は、一つの元の演算だけで群のすべての元が作り出せるという "最もシンプルな" 群です。可解群は巡回群より広い概念ですが、"かなりシンプルな" 群です。このかなりのシンプルさが方程式の可解性と関わっているのです。
可解群という概念は、ガロア群とは関係なく純粋に群の特性として定義することが可能です。もちろん可解というネーミングでわかるように、方程式の可解性と直結しています。なお、可解群の数学的に厳密な定義は別途きちっとやります(第6章)。
1.4 可解性の必要十分条件
ガロア理論は、
というものでした。そこに、正規部分群の概念を利用した可解群という概念を持ち込むと、方程式の可解性の必要十分条件が導けます。
可解性の必要条件
\(n\)次方程式 \(f(x)\) の解を\(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
があるとしたら、\(\bs{L}\) のガロア群は可解群である。
なぜそう言えるのかの証明は、かなりのステップが必要です。それは別途やりますが、ここで重要なのは上の定理の対偶です。上の定理の対偶は、
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{L}\) のガロア群が可解群でなければ、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
は存在しない。
となります。\(\bs{\bs{Q}}\) から始まるべき根拡大の連続で \(\bs{\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)}\) に到達できないということは、すなわち \(\bs{\al_1,\al_2,\:\cd\:,\al_n}\) が四則演算とべき根では表現できないということに他なりません。ガロア群が可解群ということが、方程式が "代数的に解ける" ための必要条件なのです。
2・3・4次方程式のガロア群はすべて可解群ですが、5次方程式のガロア群は可解群であるものとそうでないものがあります。だから5次方程式の解の公式(=あらゆる5次方程式に通用する公式)はないのです。
ここで定義を振り返ってみると、可解群は、巡回群か、正規部分群を介した巡回群の入れ子構造の群でした。方程式の "解ける解けない" が問題になるのは5次方程式です。実は、可解な5次方程式のガロア群は、巡回群か "巡回群と正規部分群(=巡回群)の2階建て" です(そのような5次方程式もかなりのレア・ケースですが)。可解な5次方程式を考える限り、"正規部分群を介した巡回群の入れ子構造" の "入れ子" は、1段階の非常にシンプルなものに過ぎないのです。
しかし、ある5次方程式が可解でないことを証明するには正規部分群が威力を発揮します。つまり、その5次方程式のガロア群に "正規部分群を介した巡回群の入れ子構造"がないことを言えばよいのですが、そもそも正規部分群がないことを証明してしまえば、その5次方程式は可解ではなくなるからです。そして実際に、ある特定の5次方程式が可解でないことの証明に使われるのは、その5次方程式のガロア群に正規部分群がないということなのです。先ほど「正規部分群という概念がガロア理論の最大のキモ」としたのは、そういう意味を含みます。
可解性の十分条件
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。また、\(1\) の原始\(n\)乗根を \(\zeta\) とする。
\(\bs{L}\) のガロア群が可解群であれば、\(\bs{Q}(\zeta)\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}(\zeta)=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
が存在する。
なぜそう言えるのか、また、なぜここに突然 \(1\) の原始\(n\)乗根が登場するのかは、別途厳密に証明します。この定理で言えることは、「ガロア群が可解群であれば、\(n\)次方程式の解は、有理数と \(\zeta\) の四則演算・べき根の組み合わせで表現できる」ということです。
ここで \(1\) の原始 \(n\)乗根である \(\zeta\) が問題になります。実は、\(1\) の原始 \(n\)乗根は有理数の四則演算とべき根で表現できることがガロア理論とは無関係に証明できます(その証明も別途やります。ガロア理論で証明することもできます)。従って、方程式は可解なのです。
方程式が代数的に解けるキーワードは可解群です。巡回群は代表的な可解群であり、ガロア群が巡回群だと方程式をべき根で解く手法が存在します。ガロア群が巡回群の入れ子構造でも、その手法を多段階に使うことによって、\(\bs{Q}\) から始まるべき根拡大の系列で方程式の解を含む代数拡大体に到達できます。可解性の十分条件の証明は、そのような組み立てになっています。
以上の必要条件と十分条件を組み合わせると、以下が言えます。
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
\(n\)次方程式 \(f(x)=0\) が可解である、つまり四則演算とべき根で解が表現できるための必要十分条件は、\(\bs{L}\) のガロア群(= 自己同型写像が作る群)が可解群であることである。
ガロア理論は、方程式が解けるための必要十分条件を示すものです。従って、ある方程式が可解であることの証明、あるいは逆に、可解でないことの証明はできます。しかし、可解である方程式の解を、具体的に四則演算とべき根で求めるための実用的なアルゴリズムを示しているわけではありません。そこが注意点です。
ここまで、方程式の可解性の必要十分条件を解き明かすガロア理論の全体構造、アウトラインを説明しました。以降ではこれを精密化し、数学的に正しい、首尾一貫した証明にしていきます。目次にあるように、全体は次の8章から成ります。
1.証明の枠組み
2.整数の群
3.多項式と体
4.一般の群
5.ガロア群とガロア対応
6.可解性の必要条件
7.可解性の十分条件
8.結論
第5章から第7章までが、ガロア理論の核心の部分です。第2章から第4章までは、核心部分の証明に使う各種の定義や定理の説明です。この部分がかなり長いのは、高校までで習う数学(いわゆる "受験数学" ではない、教科書ベースの数学)だけを前提知識とし、そうでないものは全部証明するという方針によります。
今までに「高校数学で理解する ・・・・・・」と題した記事を何回か書きました。
No.310 - 高校数学で理解するRSA暗号の数理(1)
No.311 - 高校数学で理解するRSA暗号の数理(2)
No.313 - 高校数学で理解する公開鍵暗号の数理
No.315 - 高校数学で理解する楕円曲線暗号の数理(1)
No.316 - 高校数学で理解する楕円曲線暗号の数理(2)
No.325 - 高校数学で理解する誕生日のパラドックス
No.329 - 高校数学で理解するレジ行列の数理
No.311 - 高校数学で理解するRSA暗号の数理(2)
No.313 - 高校数学で理解する公開鍵暗号の数理
No.315 - 高校数学で理解する楕円曲線暗号の数理(1)
No.316 - 高校数学で理解する楕円曲線暗号の数理(2)
No.325 - 高校数学で理解する誕生日のパラドックス
No.329 - 高校数学で理解するレジ行列の数理
の7つの記事です。「高校数学で理解する」という言葉の意味は、「高校までで習う数学の知識をベースに説明する」ということです。今回はそのシリーズの続編で、ガロア理論をテーマにします。その第1回目です。
ここで言う「ガロア理論」とは、
方程式の解が四則演算記号と \(n\)乗根の記号(\(\sqrt[n]{a}\))で表現できる(=方程式が "解ける")ための必要十分条件を示す理論
とし、その範囲に限定します。これが、そもそもの理論の発端であり、19世紀に夭折したフランスの数学者、ガロアが数学史に残した功績でした。
例によって、前提知識は高校までで習う数学に限定し、そこに含まれない定理は全部証明することにします。ただし、複素数と複素平面の知識は前提とします。また集合論の記号(\(\in\:\:\subset\:\:\sp\:\:\cup\:\:\cap\) など)を適時使います。さらに「すべての方程式は複素数の範囲に解をもつ」という "代数学の基本定理" は、証明はしませんが前提です。
以降の記述では、次の3つの本を特に参考にしました。
草場 公邦 『ガロワと方程式』(朝倉書店 1989)
石井 俊全 『ガロア理論の頂を踏む』(ベレ出版 2013)
加藤 文元 『ガロア理論 12講』(KADOKAWA 2022)
石井 俊全 『ガロア理論の頂を踏む』(ベレ出版 2013)
加藤 文元 『ガロア理論 12講』(KADOKAWA 2022)
全体の内容は以下です。「高校の数学に含まれない定理は全部証明する」方針なので、証明の完結までにはかなりの論証が必要です。そのため、全体は少々長くなります。第1章は、その全体像を俯瞰したもので、第2章からが本論です。
|
| 1.証明の枠組み |
方程式が解けるための必要十分条件の導出は、そこに至るためにかなり長いステップの証明が必要で、論理に論理を積み重ねる必要があります。そこでまず第1章で、証明の枠組みがどうなっているか、全体のアウトラインを説明します。
これは証明そのものではないし、数学的に曖昧なところもあります。しかし、ガロア理論の理解の道筋を示す意味で、2章からの本論の理解の助けになると思います。
1.1 方程式とその可解性
方程式
\(f(x)\) を、有理数を係数にもつ1変数の \(n\)次多項式とします。有理数の集合を \(\bs{Q}\) で表すので、
\(f(x)=a_nx^n+a_{n-1}x^{n-1}+\:\cd\:+a_1x+a_0\)
\((\:a_n\neq0,\:a_i\in\bs{Q}\:)\)
と定義できます。以降のガロア理論で問題にする \(n\)次方程式とは、
\(f(x)=0\)
で表されるものです。これを \(\bs{\bs{Q}}\) 上の(=係数が有理数の)\(n\)次方程式といいます。
代数学の基本定理によると、複素数係数の方程式は複素数の集合 \(\bs{C}\) の中に必ず解をもちます。もちろん、有理数係数の方程式も複素数の集合 \(\bs{C}\) の中に解を持ちます。
有理数係数の方程式の解となる数を代数的数と呼びます。実数や複素数には代数的数でない数があり、たとえば円周率 \(\pi\) や、自然対数の底 \(e\) が有名です。
方程式の可解性
方程式の解が四則演算とべき根(\(\sqrt[n]{a}\))の組み合わせで記述できるとき、その方程式は、
・代数的に解ける
・代数的解法がある
・可解である
と言います(同じ意味です)。べき根(冪根)は累乗根ともいいます。
まず大切なところですが、べき根の定義を明確にしておきます。
\(\sqrt[n]{a}\:\:(\:a\in\bs{C}\:)\)
とは \(n\) 乗して \(a\) になる数の意味ですが、\(a\) が正の実数の場合、「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちの正の実数を表わす」とします。
そして \(a\) が正の実数以外の、負の実数や複素数の場合は「\(\sqrt[n]{a}\) は \(n\) 乗して \(a\) になる数のうちのどれかを表わす」とします。"どれか" とするのは、\(n\) 乗して \(a\) になる複数の数を区別する方法がないからです。たとえば \(\sqrt{-1}\) は「2乗して \(-1\) になる2つの数のどちらか」であり、その一方を \(i\) と書くと、もう一方が \(-i\) です。2つの数のどちらが \(i\) かを決めることはできません。複素平面で上の方が \(i\) のように見えますが、それは話が逆で、\(i\) とした方を上に書くのが複素平面です。
従って、方程式の解をべき根で書くときには注意が必要です。たとえば仮想的な例ですが、
\(\sqrt[3]{p}\:+\:\sqrt[3]{q}\)
という記述があったとき、3乗すると \(p,\:q\) になる数のどれでもよい場合もあります。3乗して特定の数になる数は基本的に3つあるので、3\(\times\)3=9種 のどれでもよい場合もあります。しかし、たとえば、
\(\sqrt[3]{p}\cdot\sqrt[3]{q}=r\) であること
といった付帯条件が付いている(付ける必要がある)場合もある。そうすると \(p,\:q\) の選び方には制約が出てきます。べき根が複数の中の何を指すのか、その選択には注意が必要です。
方程式の可解性に戻りますと、
| すべての3次方程式は可解 | |
| すべての4次方程式は可解 |
| 5次方程式には(ないしは5次以上の方程式には)可解であるものと可解でないものがある |
もちろん、可解でない方程式の解が求まらないわけではありません。現代では数値計算ソフトウェアを使って、いくらでも詳しい精度で解を求めることができます。ただ、その解が四則演算とべき根では表せないと言っているのです。
べき根 \(\sqrt[n]{a}\) は \(n\)乗の逆関数です。方程式が \(\bs{n}\)乗の組み合わせでできているのに、解が \(\bs{n}\)乗の逆関数で表現できない(場合がある)というのは少々不思議ですが、数の世界はそうなっているのです。
それでは、方程式がどういう条件だったら可解で、どういう条件だったら可解でないのか、その必要十分条件は何かが問題になってきます。その必要十分条件を示したのがガロア理論です。
1.2 体
体とは
ガロア理論の出発点は、方程式の解の特性を考えるときに「方程式の解を含む体」を考えて、体の性質でもって解の特性を語ることにあります。
体(field)とは、加減乗除の四則演算が成り立ち、加法と乗法を結びつける分配則が成り立つ集合です。分配則とは \(a(b+c)=ab+ac\) となることです。
| ・有理数 | (\(\bs{Q}\) で表す) | |
| ・実数 | (\(\bs{R}\) で表す) | |
| ・複素数 | (\(\bs{C}\) で表す) |
\(\bs{Q},\:\bs{R},\:\bs{C}\) はいずれも複素数の集合 \(\bs{C}\) の部分集合であり、これらを数体と呼びます。\(\bs{C}\) は四則演算と分配則が成り立つので、その部分集合は四則演算ができて分配則が成り立ちます。従って、部分集合が体(=数体)である条件は、四則演算で閉じていることです。
数体はこの3つだけではありません。ガロア理論で問題にするのは、方程式の解を含む体です。
方程式の解を含む体
有理数係数の \(n\)次方程式 \(f(x)=0\) の一つの解を\(\al\:(\al\notin\bs{Q})\) とするとき、\(\bs{Q}\) と \(\al\)を含む最小の集合で体の定義を満たすものを \(\bs{Q}(\al)\) と書きます。これは、有理数と \(\bs{\al}\) の四則演算で作り出せるすべの数の集合です。四則演算は何回繰り返してもかまいません。
\(\bs{Q}\) をもとにして \(\bs{Q}(\al)\) を作るのが体の拡大(extension)で、\(\bs{Q}(\al)\) を \(\bs{Q}\) の拡大体といい、「\(\bs{Q}\) に \(\al\) を添加した(ないしは付加した)体」ということもあります。\(\al\) は代数的数なので、\(\bs{Q}\) の代数拡大体ともいいます。集合の包括関係は \(\bs{Q}\:\subset\:\bs{Q}(\al)\) です。この拡大のことを \(\bs{Q}(\al)/\bs{Q}\) と書きます。「拡大体\(/\)元の体」の形です。
当然、\(\bs{Q}\) に複数の代数的数を付加した体も考えられて、
\(\bs{Q}(\al,\:\beta,\:\gamma,\:\cd)\)
というように書きます。\(\al,\:\beta,\:\gamma,\:\cd\) が違った方程式の解であってもかまいません。
例として \(x^2-2=0\) の解での一つである \(\sqrt{2}\) を付加した \(\bs{Q}(\sqrt{2})\) を考えます。この体の任意の数 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
で表されます。この表現は四則演算で閉じています。加算・減算・乗算で閉じているのはすぐにわかります。また除算でも閉じています。というのも、分母の有理化のテクニックを使うと、
\(\dfrac{1}{a+b\sqrt{2}}=\dfrac{a}{a^2-2b^2}-\dfrac{b}{a^2-2b^2}\sqrt{2}\)
となって、\(a+b\sqrt{2}\) の形になるからです(\(a,b\in\bs{Q}\) なので \(a^2\neq2b^2\) です)。従って、乗算で閉じているので除算でも閉じていることになります。上の有理化は方程式の解を一つだけ添加した体の場合ですが、複数の解を添加した体でも有理化は常に可能です。このことは別途きっちりと証明します。
べき根拡大
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) という体の拡大を一般化します。\(\bs{Q}\) 上の \(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{Q})\)
の解の一つで、\(\bs{Q}\) に属さないものを \(\al\) としたとき、
\(\bs{Q}(\al)\)
を \(\bs{Q}\) のべき根拡大体といい、\(\bs{Q}\) から \(\bs{Q}(\al)\) を作ることをべき根拡大(radical extension)といいます。さらにもっと一般化して、体 \(\bs{F}\) があったとき、\(\bs{F}\) 上の(=\(\bs{F}\) 係数の)\(n\)次方程式、
\(x^n-a=0\:\:(a\in\bs{F})\)
の解の一つで、\(\bs{F}\) に属さないものを \(\al\) としたとき、
\(\bs{F}(\al)\)
が \(\bs{F}\) のべき根拡大体です。
ここで、ある代数的数 \(\al\) を、
\(\al=\sqrt{3+\sqrt{2}}\)
とします。これは四則演算とべき根で表現された代数的数です。これを変形すると、
\(\al^2-3=\sqrt{2}\)
\(\al^4-6\al^2+7=0\)
となるので、\(\al\) は方程式
\(x^4-6x^2+7=0\)
という4次方程式の解の一つです。そこで、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{3+\sqrt{2}})\)
という体の拡大を考えたとき、この拡大は、
| \(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) を \(\bs{Q}\) に付加して体を拡大 | |
| 次に、\(\bs{\bs{Q}(\sqrt{2})}\) 上の方程式 \(\bs{x^2-(3+\sqrt{2})=0}\) の解 \(\sqrt{3+\sqrt{2}}\) を \(\bs{Q}(\sqrt{2})\) に付加して体を拡大 |
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\:\sqrt{3+\sqrt{2}})\)
という体の拡大です。そうすると各ステップが、\(x^n-a=0\) というタイプの方程式の解による体の拡大=べき根拡大になります。つまり「べき根拡大の系列」ができます。このことを一般化していうと、
方程式 \(f(x)=0\) の解の一つを \(\al\) とするとき、\(\al\) が四則演算とべき根で書けるなら、\(\bs{Q}\) から始まって \(\bs{Q}(\al\))に到達する「べき根拡大の系列」が存在する
となります。ガロア理論では、\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体を考えます。それを \(\bs{Q}\) のガロア拡大体といいます。つまり、\(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\al_n)\) です。この記法を使うと、
\(\bs{Q}\) 上の \(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とするとき、\(\bs{Q}\) から始まって \(\bs{Q}(\al_1,\:\cd\:,\al_n)\) に到達する「べき根拡大の系列」が存在するなら、\(f(x)=0\) は可解である
と言えるわけです。式で書くと、
\(\bs{F}_0=\bs{Q},\:\:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\)
として、
| \(\bs{Q}=\bs{F}_0\:\subset\)\( \:\bs{F}_1\:\subset\)\( \:\bs{F}_2\:\subset\)\( \:\cd\:\subset\)\( \:\bs{F}_k=\bs{Q}(\al_1,\:\cd\:,\al_n)\) |
各ステップの拡大 \(\bs{F}_{i+1}/\bs{F}_i\) が全部べき根拡大
の条件が成立するとき、\(f(x)=0\) は可解です。これが成り立つのはどういう場合なのか、その条件を、\(\bs{Q}(\al_1,\:\cd\:,\al_n)\) というガロア拡大体に "背後霊" のように付帯している "群"(=ガロア群)の性質で説明するのがガロア理論です。1.3 ガロア群
そのガロア群を説明するために、まず群(group)とは何か、その定義を明確にしておきます。
群の定義
集合 \(G\) が次の ① ~ ④ を満たすとき、\(G\) は群であると言う。
| \(G\) の任意の元 \(x,\:y\) に対して演算(\(\cdot\)で表す)が定義されていて、\(x\cdot y\in G\) である。 | |
| 演算について結合法則が成り立つ。つまり、 \((x\cdot y)\cdot z=x\cdot(y\cdot z)\) | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot e=e\cdot x=x\) を満たす元 \(e\) が存在する。\(e\) を単位元という。 | |
| \(G\) の任意の元 \(x\) に対して \(x\cdot y=y\cdot x=e\) となる元 \(y\) が存在する。\(y\) を \(x\) の逆元といい、\(x^{-1}\) と表す。 |
たとえば、有理数の集合 \(\bs{Q}\) は、加法という演算に関して群になります。単位元は \(0\) で、\(a\) の逆元は \(-a\) です。また、有理数の集合から \(0\) を除いた集合は、乗法という演算で群になります。単位元は \(1\) で、\(a\) の逆元は \(a^{-1}\) です。これらは無限個の元をもつ無限群であり、また \(ab=ba\) が成り立つ可換群(アーベル群とも言う)です。
元の数が有限個の有限群もあります。たとえば、裏表のある正3角形を、もとの形と重なるように回転移動する、ないしは対称軸で折り返すという "操作" は群になります。頂点に番号を付け、時計回りに \(1,\:2,\:3\) とします。この操作は6個あって、それに \(e\)、\(\sg\)(シグマ)、\(\tau\)(タウ)の記号をつけて列挙すると、
| ① 何もしない | \(=\:e\) | |
| ② 反時計回りに \(120^\circ\)回転する | \(=\:\sg_1\) | |
| ③ 反時計回りに \(240^\circ\)回転する | \(=\:\sg_2\) | |
| ④ 頂点 \(1\) を通る対称軸で折り返す | \(=\:\tau_1\) | |
| ⑤ 頂点 \(2\) を通る対称軸で折り返す | \(=\:\tau_2\) | |
| ⑥ 頂点 \(3\) を通る対称軸で折り返す | \(=\:\tau_3\) |
|
そこで、集合 \(G\) を、
\(G=\{e,\:\sg_1,\:\sg_2,\:\tau_1,\:\tau_2,\:\tau_3\:\}\)
とすると、この集合は「操作を続けてやるという演算」で群になります。なぜなら、
| 操作を続けてやっても元の配置と重なるのは間違いないので、演算で閉じている。 | |
| 単位元 \(e\) がある。 | |
| 逆元がある。つまり、 \(\sg_2\sg_1=\sg_1\sg_2=e\) : \(360^\circ\)回転すると元に戻る \(\tau_1\tau_1=e,\:\tau_2\tau_2=e,\:\tau_3\tau_3=e\) : 2回折り返すと元に戻る |
この \(G\) は可換群ではありません。\(\tau_i\) がからむ演算を実際にやってみると、
\(\tau_1\sg_1=\tau_2,\:\:\sg_1\tau_1=\tau_3\)
\(\tau_2\tau_1=\sg_2,\:\:\tau_1\tau_2=\sg_1\)
などとなり、演算順序を変えると結果が違ってきます(演算は右を先に行う)。この群では \(\sg_1\) と \(\sg_2\) の演算だけが可換です。
正3角形を対称移動する操作の群は、結局、\(1,\:2,\:3\) という3つの文字を置き換える(=置換する)操作と同じです。この置換の数は3文字の順列なので \(3\:!\) 個です。従って、
| \(e\) | \(:\:1\:2\:3\:\longmapsto\:1\:2\:3\) | |
| \(\sg_1\) | \(:\:1\:2\:3\:\longmapsto\:2\:3\:1\) | |
| \(\sg_2\) | \(:\:1\:2\:3\:\longmapsto\:3\:1\:2\) | |
| \(\tau_1\) | \(:\:1\:2\:3\:\longmapsto\:1\:3\:2\) | |
| \(\tau_2\) | \(:\:1\:2\:3\:\longmapsto\:3\:2\:1\) | |
| \(\tau_3\) | \(:\:1\:2\:3\:\longmapsto\:2\:1\:3\) |
体の自己同型写像
ガロア群とは「体の自己同型写像がつくる群」です。まず、自己同型写像(automorphism)の定義をします。次において、体 \(\bs{F}\) は \(\bs{Q}\) の代数拡大体とします。
体 \(\bs{F}\) から 体 \(\bs{F}\) への写像(=自分自身への写像)\(f\) が1対1写像であり、\(\bs{F}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(x-y)&=f(x)-f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
&&\:\:f\left(\dfrac{x}{y}\right)&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体 \(\bs{F}\) の自己同型写像という。
体 \(\bs{F}\) の部分集合である有理数体 \(\bs{Q}\) の元、\(a\) に対しては、
\(f(a)=a\)
である。つまり、有理数は自己同型写像で不変である。
この定義でわかるように、自己同型写像とは、四則演算してから写像しても、写像してから四則演算しても同じになる写像です。このことを簡潔に、四則演算を保存する写像と表現します。なお、定義にある「1対1写像」とは、
| \(x\neq y\) なら \(f(x)\neq f(y)\) | |
| 任意の \(y\) について \(f(x)=y\) となる \(x\) がある |
\(f(x+y)=f(x)+f(y)\) において \(x=0,\:y=0\) とすると、
\(f(0+0)=f(0)+f(0)\)
\(f(0)=f(0)+f(0)\)
なので、
\(f(0)=0\)
です。また、\(f(xy)=f(x)f(y)\) において \(x=1,\:y=1\) とすると、
\(f(1\cdot1)=f(1)f(1)\)
\(f(1)=f(1)f(1)\)
となり、\(f(1)=0\) か \(f(1)=1\) です。しかし \(f(1)=0\) とすると \(f(0)=0\) かつ \(f(1)=0\) となってしまい、\(f\) が「1対1写像である」という定義に反します。従って、
\(f(1)=1\)
です。次に、\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn 個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)=n\\
\end{eqnarray}\)
なので、
\(f(n)=n\)
です。任意の有理数 \(a\) は、2つの整数 \(n(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるので、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は自己同型写像で不変である(=自己同型写像は有理数を固定する)ことがわかります。
どんな体においても恒等写像 \(e\) は常に自己同型写像です。従って「すべての自己同型写像が有理数に対しては恒等写像として働く」ということは、「有理数体 \(\bs{Q}\) の自己同型写像は恒等写像 \(e\) しかない」ことになります。
しかし、\(\bs{Q}\) の代数拡大体 \(\bs{F}\) については、\(e\) を含む複数個の自己同型写像があります。そして、この複数個の自己同型写像の集合は群になり、それがガロア群です。具体的な例で説明します。
ガロア群の例
\(x^2-2=0\)
上で説明したように、この方程式に対応したガロア拡大体は \(\bs{Q}(\sqrt{2})\) であり、 \(\bs{Q}(\sqrt{2})\) の任意の元 \(x\) は、
\(x=a+b\sqrt{2}\:\:(a,b\in\bs{Q})\)
と表せます。ここで写像 \(\sg\) を「\(\sqrt{2}\) を \(-\sqrt{2}\) に置き換える写像」つまり、
\(\sg\::\:\sqrt{2}\:\longmapsto\:-\sqrt{2}\)
と定義します。これを、
\(\sg(\sqrt{2})=-\sqrt{2}\)
と表記します。この定義によって \(\sg\) は \(\bs{Q}(\sqrt{2})\) の自己同型写像になります。
そのことを確認しますが、記述を見やすくするため \(a,\:b\) を変数ではなく具体的な数値で書きます。もちろん、一般性を失わないようにする前提です。
\(\begin{eqnarray}
&&\:\:x&=2+3\sqrt{2}\\
&&\:\:y&=5-4\sqrt{2}\\
\end{eqnarray}\)
とすると、
\(\begin{eqnarray}
&&\:\:\sg(x+y)&=\sg(7-\sqrt{2})=7+\sqrt{2}\\
&&\:\:\sg(x)+\sg(y)&=(2-3\sqrt{2})+(5+4\sqrt{2})\\
&&&=7+\sqrt{2}\\
\end{eqnarray}\)
なので、\(\sg\)は加算を保存しています。減算についても同じです。また、
\(\sg(xy)\)
\(=\sg(2\cdot5-3\cdot4\cdot2+3\cdot5\sqrt{2}-2\cdot4\sqrt{2})\)
\(=\sg(-14+7\sqrt{2})\)
\(=-14-7\sqrt{2}\)
\(\sg(x)\sg(y)\)
\(=(2-3\sqrt{2})(5+4\sqrt{2})\)
\(=2\cdot5-3\cdot4\cdot2-3\cdot5\sqrt{2}+2\cdot4\sqrt{2}\)
\(=-14-7\sqrt{2}\)
なので、\(\sg\) は乗算を保存します。さらに、
\(\begin{eqnarray}
&&\:\:\dfrac{x}{y}&=\dfrac{2+3\sqrt{2}}{5-4\sqrt{2}}\\
&&&=\dfrac{(2+3\sqrt{2})(5+4\sqrt{2})}{(5-4\sqrt{2})(5+4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}-\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
なので、
\(\sg\left(\dfrac{x}{y}\right)=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\)
です。一方、
\(\begin{eqnarray}
&&\:\:\dfrac{\sg(x)}{\sg(y)}&=\dfrac{2-3\sqrt{2}}{5+4\sqrt{2}}\\
&&&=\dfrac{(2-3\sqrt{2})(5-4\sqrt{2})}{(5+4\sqrt{2})(5-4\sqrt{2})}\\
&&&=\dfrac{10+24+(8+15)\sqrt{2}}{25-32}\\
&&&=-\dfrac{34}{7}+\dfrac{23}{7}\sqrt{2}\\
\end{eqnarray}\)
です。従って、
\(\sg\left(\dfrac{x}{y}\right)=\dfrac{\sg(x)}{\sg(y)}\)
となって、除算も保存しています。以上は具体的数値での計算ですが、\(a,\:b\) を変数としても成り立つことは、上の計算プロセスを追ってみると分かります。
このようになる理由は、\(\bs{\sg}\) が 方程式の解を、解のどれかに置き換える写像だからです。つまり、\(x^2-2=0\) の解は \(\sqrt{2}\) と \(-\sqrt{2}\) ですが、
\(\sg(\phantom{-}\sqrt{2})=-\sqrt{2}\)
\(\sg(-\sqrt{2})=\phantom{-}\sqrt{2}\)
となります。ここで「解を、解のどれかに置き換える」という表現は「解を自分自身に置き換える」ことも含みます。
このことは、\(x^2-2=0\) という "特別な" 方程式だけでなく、一般の2次方程で成り立ちます。2次方程式、
\(x^2+px+q=0\)
の解を \(\al,\:\beta\) とし、共に有理数ではないとします(\(\al,\:\beta\notin\bs{Q}\))。\(\bs{Q}\) の代数拡大体、\(\bs{Q}(\al,\beta)\) の自己同型写像を \(\sg\) とします。\(\al\) は、
\(\al^2+p\al+q=0\)
を満たしますが、この式の両辺に対して \(\sg\) による写像を行うと、
\(\sg(\al^2+p\al+q)=\sg(0)\)
\(\sg(\al)^2+p\sg(\al)+q=0\)
となります。\(\sg\) は四則演算を保存し、また \(\sg(0)=0\) だからこうなります。ということは、\(\sg(\al)\) は元の2次方程式の解です。従って、
\(\sg(\al)=\al\)
\(\sg(\al)=\beta\)
のどちらかです。\(\beta\) についても全く同じことが言えて、
\(\sg(\beta)=\beta\)
\(\sg(\beta)=\al\)
のどちらかです。従って \(\bs{Q}(\al,\beta)\) の自己同型写像 は、
\(e\)(恒等写像)
\(\sg(\al)=\beta\) となる写像
の2種類です。ここで、\(\sg\) を \(\sg(\al)=\beta\) となる写像と規定すると、必然的に \(\sg(\beta)=\al\) になります。なぜなら、もし \(\sg(\beta)=\beta\) だとすると、\(\sg(\al)=\beta\) かつ \(\sg(\beta)=\beta\) になり、\(\sg\) が1対1写像であるという、そもそもの自己同型写像の定義に反するからです。2次方程式の解による代数拡大体の自己同型写像は、恒等写像と「2つの解を入れ替える写像」の2つです。
ここで、自己同型写像 \(e,\:\sg\) の集合を \(G\) とします。つまり、
\(G=\{e,\:\sg\}\)
です。そうすると、\(G\) は群になります。\(e\) という恒等写像があり、
\(\sg^2(\al)=\sg(\sg(\al))=\sg(\beta)=\al\)
なので、
\(\sg^2=e\)
\(\sg^{-1}=\sg\)
となって、逆元があるからです。この \(G\) が \(\bs{Q}(\al,\beta)\) のガロア群です。しかもこのガロア群は、\(\sg\) の(群の要素としての)累乗をとっていくと、
\(\sg,\:\sg^2=e,\:\sg^3=\sg,\:\sg^4=e,\:\cd\)
というように1つの元を出発点として巡回します。このような群を巡回群(cyclic group)といいます。この場合、\(G\) は位数 \(2\) の巡回群です。位数 \(2\) の巡回群を \(C_2\) と表現します。
\(C_2\) は \(\sg,\:e,\:\sg,\:e,\:\cd\) と、2つの元が交互に現れるだけなので、"巡回感" が薄いかもしれませんが、位数 \(3\) の巡回群(\(C_3\))になると "巡回してる感" が出てきます。それが次の方程式の例です。
\(x^3-3x+1=0\)
|
\(f(x)=x^3-3x+1\)
とします。
| \(f(\phantom{-}2)\) | \(=\phantom{-}3\) | |
| \(f(\phantom{-}1)\) | \(=-1\) | |
| \(f(\phantom{-}0)\) | \(=\phantom{-}1\) | |
| \(f(-1)\) | \(=\phantom{-}3\) | |
| \(f(-2)\) | \(=-1\) |
| \(\phantom{-}1\) | \( < \al< \phantom{-}2\) | |
| \(\phantom{-}0\) | \( < \beta< \phantom{-}1\) | |
| \(-2\) | \( < \gamma< -1\) |
\(x=2\mr{cos}\theta\:\:(0\leq\theta\leq\pi)\)
とおいて \(x\) から \(\theta\) へ変数を変換すると、
\(f(x)=8\mr{cos}^3\theta-6\mr{cos}\theta+1\)
となります。ここで3倍角の公式、
\(\mr{cos}3\theta=4\mr{cos}^3\theta-3\mr{cos}\theta\)
を使うと、
\(f(x)=2\mr{cos}3\theta+1\)
となります。このことから \(f(x)=0\) の解は、
\(2\mr{cos}3\theta+1=0\)
\(\mr{cos}3\theta=-\dfrac{1}{2}\:\:(0\leq3\theta\leq3\pi)\)
を満たします。従って、
| \(3\theta\) | \(=\dfrac{2\pi}{3},\:\dfrac{4\pi}{3},\:\dfrac{8\pi}{3}\) | |
| \(\theta\) | \(=\dfrac{2\pi}{9},\:\dfrac{4\pi}{9},\:\dfrac{8\pi}{9}\) |
\(\al=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}\theta_0\)
\(\beta=2\mr{cos}\dfrac{4\pi}{9}=2\mr{cos}2\theta_0\)
\(\gamma=2\mr{cos}\dfrac{8\pi}{9}=2\mr{cos}4\theta_0\)
\((\theta_0=\dfrac{2\pi}{9})\)
が求まります。なお、
\(\begin{eqnarray}
&&\:\:\al&=2\mr{cos}\dfrac{2\pi}{9}=2\mr{cos}(2\pi-\dfrac{2\pi}{9})\\
&&&=2\mr{cos}\dfrac{16\pi}{9}=2\mr{cos}8\theta_0\\
\end{eqnarray}\)
です。ここで倍角の公式、
\(\mr{cos}2\theta=2\mr{cos}^2\theta-1\)
を使うと、
\(\begin{eqnarray}
&&\:\:\beta&=2\mr{cos}2\theta_0=2(2\mr{cos}^2\theta_0-1)\\
&&&=4\mr{cos}^2\theta_0-2=\al^2-2\\
\end{eqnarray}\)
となります。同様にして、
\(\begin{eqnarray}
&&\:\:\gamma&=2\mr{cos}4\theta_0=\beta^2-2\\
&&&=(\al^2-2)^2-2\\
&&\:\:\al&=2\mr{cos}8\theta_0=\gamma^2-2\\
&&&=(\beta^2-2)^2-2\\
\end{eqnarray}\)
です。また、
\(\begin{eqnarray}
&&\:\:\beta&=\al^2-2\\
&&&=(\gamma^2-2)^2-2\\
\end{eqnarray}\)
であることも分かります。従って、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
となり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できることになります。方程式 \(x^3-3x+1=0\) は、3つの解の間に "特別な関係" があります。
ここまで、\(\al,\:\beta,\:\gamma\) を求めると言っても三角関数で表示しただけであり、四則演算とべき根で表したわけではありません。しかし、\(\al,\:\beta,\:\gamma\) の "特別な関係" を使ってガロア群を求めることができます。それが次です。
\(\bs{Q}\) に \(x^3-3x+1=0\) の3つの解、\(\al,\:\beta,\:\gamma\) を添加した代数拡大体 \(\bs{Q}(\al,\beta,\gamma)\) を調べます。\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できるので、
\(\bs{Q}(\al,\:\beta,\:\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。以下、\(\bs{Q}(\al)\) で語ることにすると、\(\bs{Q}(\al)\) の任意の元 \(x\) は、
\(x=a\al^2+b\al+c\:\:(a,b,c\in\bs{Q})\)
という "標準形" で表されます。なぜなら、\(\al^3-3\al+1=0\)、つまり\(\al^3=3\al-1\) という関係があるので、四則演算の結果で現れる \(\al^3\) 以上の項は \(\al^2\) 以下に「次数下げ」ができるからです。
"標準形" で表現できる数が、加算、減算、乗算で閉じていることは明白でしょう。乗算の結果も「次数下げ」で "標準形" になります。除算が問題ですが、例えば、\(x=\al^2+\al+1\) の場合、
\(\begin{eqnarray}
&&\:\:\dfrac{1}{x}&=\dfrac{1}{\al^2+\al+1}\\
&&&=-\dfrac{3}{19}\al^2-\dfrac{2}{19}\al+\dfrac{14}{19}\\
\end{eqnarray}\)
というように "分母の有理化" ができるので、除算でも閉じています。この有理化の例を検算してみると、
(\(\al^2+\al+1)(-3\al^2-2\al+14)\)
\(\begin{eqnarray}
&&\:\: &=&-3\al^4-2\al^3+14\al^2-3\al^3-2\al^2+14\al\\
&&&& -3\al^2-2\al+14\\
&&&=&-3\al^4-5\al^3+9\al^2+12\al+14\\
&&&=&-3\al(\al^3-3\al+1)-5\al^3+15\al+14\\
&&&=&-5(\al^3-3\al+1)+19\\
&&&=&19\\
\end{eqnarray}\)
となって、正しい結果です。この検算で分かるように、分母の有理化は \(\al\) が方程式の解であること、つまり \(\al^3-3\al+1=0\) という関係だけをもとにしています。もちろん、\(x=a\al^2+b\al+c\) という任意の数で分母の有理化が可能です(ややこしい式になりますが)。このように、\(\bs{Q}(\al)=\bs{Q}(\al,\:\beta,\:\gamma)\) は体の定義を満たすことが確認できました。
次に \(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\) の自己同型写像を調べます。自己同型写像は、方程式の解を、解のどれかに移します。そこで \(\al\) に作用する自己同型写像を考えると、これには3つあります。
\(\sg_0(\al)=\al\)
\(\sg_1(\al)=\beta\)
\(\sg_2(\al)=\gamma\)
の \(\sg_0,\:\sg_1,\:\sg_2\) です。\(\sg_1\) は、\(\beta=\al^2-2\) なので、
\(\sg_1(\al)=\al^2-2\)
であり、\(\al\) を \(\al^2-2\) に置き換える写像です。
ここで \(\al\) に \(\sg_1\) を2回作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1^{\:2}(\al)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1(\al^2-2)\\
&&&=\sg_1(\al)^2-\sg_1(2)\\
&&&=\beta^2-2=\gamma\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:\sg_2(\al)&=\gamma\\
&&\:\:\sg_1^{\:2}(\al)&=\gamma\\
\end{eqnarray}\)
なので、
\(\sg_1^{\:2}=\sg_2\)
であることが分かります。
次に、\(\sg_1\) を \(\beta\) に作用させてみると、
\(\begin{eqnarray}
&&\:\:\sg_1(\beta)&=\sg_1(\sg_1(\al))\\
&&&=\sg_1^{\:2}(\al)\\
&&&=\sg_2(\al)=\gamma\\
\end{eqnarray}\)
となります。また \(\sg_1\) を \(\gamma\) に作用させると、
\(\begin{eqnarray}
&&\:\:\sg_1(\gamma)&=\sg_1(\beta^2-2)\\
&&&=\sg_1(\beta)^2-\sg_1(2)\\
&&&=\gamma^2-2=\al\\
\end{eqnarray}\)
となります。
\(\sg_2\) についても同様の計算をしてみると、
\(\begin{eqnarray}
&&\:\:\sg_2(\beta)&=\sg_1^{\:2}(\beta)\\
&&&=\sg_1(\sg_1(\beta))\\
&&&=\sg_1(\gamma)=\al\\
&&\:\:\sg_2(\gamma)&=\sg_1^{\:2}(\gamma)\\
&&&=\sg_1(\sg_1(\gamma))\\
&&&=\sg_1(\al)=\beta\\
\end{eqnarray}\)
です。
さらに、\(\sg_0(\al)=\al\) である \(\sg_0\) については、\(\beta\) と \(\gamma\) が \(\al\) の式で表されているので \(\sg_0(\beta)=\beta\)、\(\sg_0(\gamma)=\gamma\) であり、また、自己同型写像は有理数を固定するので、\(\sg_0\) は \(\bs{Q}(\al,\beta,\gamma)\) のすべての元を固定する恒等写像 \(e\) です。
まとめると、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つになります。この3つは、
\(e\::\) 恒等写像
\(\sg_1(\al)=\beta\)、\(\sg_1(\beta)=\gamma\)、\(\sg_1(\gamma)=\al\)
\(\sg_2(\al)=\gamma\)、\(\sg_2(\beta)=\al\)、\(\sg_2(\gamma)=\beta\)
というように、\(x^3-3x+1=0\) の3つの解を入れ替えます。また、
\(\sg_1\sg_2=\sg_2\sg_1=e\)
\(\sg_1^{-1}=\sg_2,\:\:\sg_2^{-1}=\sg_1\)
であることも分かりました。
解の入れ替えは他に3種が考えられます。つまり一つの解を固定し他の2つを入れ替える写像\(\cdot\)3種ですが、一つの解で他の2つの解が表されているので、一つの解を固定する写像は全部の解を固定します。「一つの解を固定し、他の2つを入れ替える写像」は、この方程式の場合は存在しません。従って、\(\bs{Q}(\al,\beta,\gamma)\) の自己同型写像は、\(e,\:\sg_1,\:\sg_2\) の3つがすべてです。
\(G=\{e,\:\sg_1,\:\sg_2\}\) とすると、\(G\) は \(\bs{Q}(\al,\beta,\gamma)\) のガロア群になります。しかも \(\sg_2=\sg_1^{\:2}\)、\(\sg_2\sg_1=\sg_1^{\:3}=e\) の関係があります。ここで \(\sg_1\) をあらためて \(\sg\) と書くと、
\(G=\{e,\:\sg,\:\sg^2\}\) |
が \(\bs{Q}(\al,\beta,\gamma)\) のガロア群です。\(\sg\) は、
\(\begin{eqnarray}
&&\sg\:: &\al\longmapsto\beta\\
&&&\beta\longmapsto\gamma\\
&&&\gamma\longmapsto\al\\
\end{eqnarray}\) |
で定義される自己同型写像です。
この \(G\) は位数 \(3\) の巡回群(\(C_3\) で表される)です。そして、ガロア群が巡回群であるというのが、方程式が可解であるための条件の一つなのです。
ちなみに、数式処理ソフトウェアを使って \(x^3-3x+1=0\) の解のうちの最大である \(\al\) を計算してみると、
\(\al=1.53208888623796\) ・・・
です。一方、3次方程式の根の公式を使って \(\al\) の厳密解を求めると、
\(\al=\sqrt[3]{-\dfrac{1}{2}+\dfrac{\sqrt{-3}}{2}}+\sqrt[3]{-\dfrac{1}{2}-\dfrac{\sqrt{-3}}{2}}\)
となります。\(\sqrt{3}\:i\) と書かずにあえて \(\sqrt{-3}\) としました。この式はこれ以上簡略化できないし、また根号の中のマイナスを無くした表現にもできません。
つまり \(\al\) は、正真正銘の正の実数であるにもかかわらず、代数的に(=四則演算とべき根で)表そうとすると虚数を登場させざるを得ないわけです。
ただし、3次方程式の実数解のすべてに虚数 \(i\) が登場するわけではありません。3次方程式の実数解は、\(i\) なしで表わされるものと、\(i\) が必須の場合があります。このことは、任意の3次方程式の解を表わす公式には必ず \(\bs{i}\) が含まれることを意味します。
数学史をみると、そもそも虚数の必要性が認識されたのは3次方程式の解の表現からでした。そして、ガロア理論によると \(\bs{\sqrt{-3}=\sqrt{3}\:i}\) が現れるのは必然なのです。その理由はガロア理論の全体を理解することでわかります。
自己同型写像は方程式の解を入れ替えます("入れ替えない" を含む)。一般の3次方程式の場合、この入れ替えは \(3\:!\:=\:6\) 通りあります。解を \(1\:2\:3\) の文字で表すと、
| \(1\:2\:3\) | \(\longmapsto\:1\:2\:3\) | |
| \(\longmapsto\:2\:3\:1,\:\:3\:1\:2\) | ||
| \(\longmapsto\:1\:3\:2,\:\:3\:2\:1,\:\:2\:1\:3\) |
\(x^3-2=0\)
この方程式を解くため「\(1\) の原始 \(3\)乗根」を定義します(一般には、\(\bs{1}\) の原始\(\bs{n}\)乗根)。「\(1\) の原始 \(3\)乗根」とは、3乗して初めて \(1\) になる数です。これは \(x^3-1=0\) の根ですが、
\(x^3-1=(x-1)(x^2+x+1)\)
と因数分解できるので、\(1\) の原始 \(3\)乗根は2次方程式、
\(x^2+x+1=0\)
の、2つある解の両方です。そのどちらか一方を \(\omega\) とすると \(\omega^2\) も2次方程式を満たす原始 \(3\)乗根です。\(\omega,\:\omega^2\) を具体的に書くと、
| \(\omega\) | \(=\dfrac{-1+\sqrt{3}i}{2}\) | |
| \(\omega^2\) | \(=\dfrac{-1-\sqrt{3}i}{2}\) |
\(1,\:\:\omega,\:\:\omega^2\)
です。
|
\(x^3-2=0\)
\(\left(\dfrac{x}{\sqrt[3]{2}}\right)^3=1\)
\(\dfrac{x}{\sqrt[3]{2}}=1,\:\:\omega,\:\:\omega^2\)
\(x=\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
と求まります。以降、\(\al=\sqrt[3]{2}\) とします。方程式 \(x^3-2=0\) の3つの解は、
\(\al,\:\:\al\omega,\:\:\al\omega^2\)
であり、これらを含む \(\bs{Q}\) の代数拡大体は、
\(\bs{Q}(\al,\:\al\omega,\:\al\omega^2)=\bs{Q}(\omega,\:\al)\)
です。この体のガロア群を調べます。
まず、写像 \(\tau\) を、
\(\tau(\omega)=\omega^2,\:\:\tau(\al)=\al\)
で定義される写像とします。この \(\tau\) は、
\(\tau(\al\omega)=\al\tau(\omega)=\al\omega^2\)
\(\tau(\al\omega^2)=\al\tau(\omega^2)=\al\omega^4=\al\omega\)
と、\(\al\omega\) と \(\al\omega^2\) を入れ替える自己同型写像です。\(\tau^2=e\) なので、
\(\{e,\:\tau\}\)
は位数 \(2\) の巡回群(\(C_2\))です。
次に、写像 \(\sg\) を、
\(\sg_i(\al)=\al\omega^i\:\:(i=0,1,2)\)
\(\sg_i(\omega)=\omega\)
と定義します。すると、
| \(\sg_0(\al)\) | \(=\al\) | |
| \(\sg_0(\al\omega)\) | \(=\al\omega\) | |
| \(\sg_0(\al\omega^2)\) | \(=\al\omega^2\) | |
| \(\sg_1(\al)\) | \(=\al\omega\) | |
| \(\sg_1(\al\omega)\) | \(=\al\omega^2\) | |
| \(\sg_1(\al\omega^2)\) | \(=\al\omega^3=\al\) | |
| \(\sg_2(\al)\) | \(=\al\omega^2\) | |
| \(\sg_2(\al\omega)\) | \(=\al\omega^3=\al\) | |
| \(\sg_2(\al\omega^2)\) | \(=\al\omega^4=\al\omega\) |
\(\sg_1^{\:2}=\sg_2\)
\(\sg_1^{\:3}=\sg_0\)
であることもわかります。\(\sg_0\) は恒等写像です。改めて、
\(\sg_0=e\)
\(\sg_1=\sg\)
と書くと、
\(\sg_i=\{e,\:\sg,\:\sg^2\}\)
であり、これは位数 \(3\) の巡回群(\(C_3\))です。
次に \(\{e,\:\tau\}\) の上に \(\{e,\:\sg,\:\sg^2\}\) を組み合わせた集合、\(G\) を、
\(\begin{eqnarray}
&&\:\:G&=\{\:\{e,\:\sg,\:\sg^2\}e,\:\{e,\:\sg,\:\sg^2\}\tau\}\\
&&&=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\\
\end{eqnarray}\)
と定義します。\(\sg\)、\(\tau\) の演算は右から順に行います。この \(G\) には恒等写像=単位元 \(e\) があり、次のように群の条件を満たします。
演算で閉じている
\(G\) は「写像を続けて行う」という演算に関して閉じています。なぜなら、\(\sg\) も \(\tau\) も3つの解を入れ替える写像であり、いくら続けてやっても3つの解を入れ替えることに変わりないからです。また3つの解を入れ替える写像は最大6つですが、\(G\) の位数は \(6\) であり、要素同士を演算すると \(G\) のどれかになります。
逆元がある
\(\sg\) と \(\tau\) の定義から
| \(\sg^{-1}\) | \(=\sg^2\) | |
| \((\sg^2)^{-1}\) | \(=\sg\) | |
| \(\tau^{-1}\) | \(=\tau\) |
| \(\tau\sg(\al)\) | \(=\tau(\al\omega)\) | \(=\al\omega^2\) | |
| \(\tau\sg(\al\omega)\) | \(=\tau(\al\omega^2)\) | \(=\al\omega^4=\al\omega\) | |
| \(\tau\sg(\al\omega^2)\) | \(=\tau(\al\omega^3)\) | \(=\tau(\al)=\al\) |
| \(\sg^2\tau(\al)\) | \(=\sg^2(\al)=\sg(\sg(\al))\) | |
| \(=\sg(\al\omega)=\al\omega^2\) | ||
| \(\sg^2\tau(\al\omega)\) | \(=\sg^2(\al\omega^2)=\sg(\sg(\al\omega^2))\) | |
| \(=\sg(\al\omega^3)=\sg(\al)=\al\omega\) | ||
| \(\sg^2\tau(\al\omega^2)\) | \(=\sg^2(\al\omega^4)=\sg^2(\al\omega)\) | |
| \(=\sg(\sg(\al\omega))=\sg(\al\omega^2)\) | ||
| \(=\al\omega^3=\al\) |
\(\sg\) と \(\tau\) は可換ではなく、
\(\tau\sg\neq\sg\tau\)
です。しかし、上の計算で分かるように、
\(\tau\sg=\sg^2\tau\)
という関係が成り立っています。いわば "弱い可換性" です。これを "弱可換性" と呼ぶことにします(ここだけの用語です)。この弱可換性を使って計算すると、
\(\begin{eqnarray}
&&\:\:(\sg\tau)(\sg\tau)&=\sg(\tau\sg)\tau=\sg(\sg^2\tau)\tau\\
&&&=\sg^3\tau^2=e\\
&&\:\:(\sg^2\tau)(\sg^2\tau)&=\sg^2(\tau\sg)(\sg\tau)\\
&&&=\sg^2(\sg^2\tau)(\sg\tau)\\
&&&=\sg^4(\tau\sg)\tau=\sg^4(\sg^2\tau)\tau\\
&&&=\sg^6\tau^2=e\\
\end{eqnarray}\)
となります。つまり、
\(\begin{eqnarray}
&&\:\:(\sg\tau)^{-1}&=\sg\tau\\
&&\:\:(\sg^2\tau)^{-1}&=\sg^2\tau\\
\end{eqnarray}\)
となって、すべての元の逆元が存在することが分かりました。以上により \(G\) は群であり、方程式 \(x^3-2=0\) の3つの解を含む代数拡大体、\(\bs{Q}(\omega,\al)\:\:(\al=\sqrt[3]{2})\) のガロア群は \(G\) です。
\(G\) の元が3つの解をどのように入れ替えるかをまとめます。3つの文字 \(1\:2\:3\) を使って、
\(1\::\:\al\)、 \(2\::\:\al\omega\)、 \(3\::\:\al\omega^2\) |
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\) \(\begin{eqnarray} &&e &:\:1\:2\:3\:\longmapsto\:1\:2\:3\\ &&\sg&:\:1\:2\:3\:\longmapsto\:2\:3\:1\\ &&\sg^2 &:\:1\:2\:3\:\longmapsto\:3\:1\:2\\ &&\tau&:\:1\:2\:3\:\longmapsto\:1\:3\:2\\ &&\sg\tau&:\:1\:2\:3\:\longmapsto\:2\:1\:3\\ &&\sg^2\tau&:\:1\:2\:3\:\longmapsto\:3\:2\:1\\ \end{eqnarray}\) |
となり、これは正3角形の対称移動の群(3次の2面体群)と同じものです。
しかし重要なことは、\(G\) が \(\{e,\:\tau\}\) と \(\{e,\:\sg,\:\sg^2\}\) という2つの巡回群の "2階建て構造" になっていることです。"2階建て構造" というのはここだけの言葉で、数学用語ではありません。数学的にきっちりとした定義は別途行います。
実は、方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のときも、方程式は可解になります。このことをより正確に言うと以下のようになります。
可解群
方程式 \(x^3-2=0\) のガロア群、
\(G=\{e,\:\sg,\:\sg^2,\:\tau,\:\sg\tau,\:\sg^2\tau\}\)
の性質をさらに調べます。この中の、\(\{e,\:\sg,\:\sg^2\}\) は、それだけで群を構成しています。つまり \(G\) の部分群(subgroup)です。これに \(H\) という名前をつけて、
\(H=\{e,\:\sg,\:\sg^2\}\)
とします。この \(H\) に左から \(\tau\) をかけて \(\tau H\) を作ります。\(\tau H\) とは、\(H\) のすべての元に左から \(\tau\) をかけた集合の意味です。弱可換性である \(\tau\sg=\sg^2\tau\) に注意して \(\tau H\) を計算してみると、
\(\begin{eqnarray}
&&\:\:\tau H&=\{\tau,\:\tau\sg,\:\tau\sg^2\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^2\tau\sg\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg^4\tau\}\\
&&&=\{\tau,\:\sg^2\tau,\:\sg\tau\}\\
&&&=\{\tau,\:\sg\tau,\:\sg^2\tau\}\\
&&&=H\tau\\
\end{eqnarray}\)
となります。つまり、
\(\tau H=H\tau\)
です。さらに、この式に左から \(\sg\) をかけると、
\(\sg\tau H=\sg H\tau\)
ですが、\(H\) のすべての元は \(\sg\) で表現できるので、\(\sg H=H\sg\) です。従って、
\(\sg\tau H=H\sg\tau\)
です。同様にして、
\(\sg^2\tau H=H\sg^2\tau\)
も分かります。つまり、
任意の \(\bs{G}\) の元 \(\bs{x\in G}\) について、\(\bs{xH=Hx}\) が成り立つ
わけです。このような性質をもつ部分群 \(H\) を、\(G\) の正規部分群(normal subgroup)と言います。ちなみに \(\{e,\:\tau\}\) も \(G\) の部分群(=巡回群)ですが、\(\sg\tau\neq\tau\sg\) なので、これは \(G\) の正規部分群ではありません。
上の例の場合、\(H\) は巡回群でしたが、\(\{e,\:\tau\}\) がそうであるように、巡回群だからといって正規部分群になるわけではありません。正規部分群はあくまで \(G\)(全体)と \(H\)(部分)の関係性に依存します。正規部分群が巡回群のこともある、というのが正しい認識です。
正規部分群 \(H\) の任意の元 \(h\) は、\(G\) の任意の元 \(x\) と可換ではありません。しかし、\(H\) の別の元 \(h\,'\) との間で \(xh=h\,'x\) が成り立ちます。つまり \(H\) は、\(G\) の任意の元とグループとして可換なのです。\(H\) の元は \(G\) の任意の元と弱い可換性がある、ともいえるでしょう。
そこで、方程式の可解性と正規部分群の関係です。\(x^3-2=0\) のガロア群のところで、
方程式の解を含む代数拡大体のガロア群が "巡回群の2階建て構造" のとき、方程式は可解になる
としました。しかしこれは少々曖昧な表現で、正確には、
方程式の解を含む代数拡大体のガロア群が "巡回群と正規部分群の2階建て構造" のときに方程式は可解になる。ただしその正規部分群が巡回群であること
です。そして、上の言い方の最後、「ただしその正規部分群が巡回群であること」の部分は、必ずしも巡回群でなくてもよいのです。つまり、ガロア群が "巡回群と正規部分群Aの2階建て構造" であり、その "正規部分群Aが、巡回群と正規部分群B(=巡回群)の2階建て構造" でもよいのです。いわば、正規部分群を介した巡回群の入れ子構造です。この入れ子の "深さ" は何段階でもかまいません。"正規部分群を介する" のは多段階でもよい。まとめると、
方程式の解を含む代数拡大体のガロア群が、正規部分群を介した "巡回群の入れ子構造" になっているとき、方程式は可解である
わけです。この正規部分群という概念が、ガロア理論の最大のキモです。先ほどの例の正規部分群 \(H=\{e,\:\sg,\:\sg^2\}\) は巡回群でしたが、一般に正規部分群は巡回群ではありません。そのため、"正規部分群を介した巡回群の入れ子構造" が重要な意味をもつのです。
方程式 \(x^3-3x+1=0\) のところで書いたように、ガロア群が巡回群であれば方程式は可解でした。ここまでのことを踏まえて可解群の定義をすると、
ガロア群が、巡回群か、正規部分群を介した巡回群の入れ子構造のとき、その群を可解群という
となります。可解群とは "ほぼ巡回群" であり、"広義の巡回群" だとも言えるでしょう。巡回群は、一つの元の演算だけで群のすべての元が作り出せるという "最もシンプルな" 群です。可解群は巡回群より広い概念ですが、"かなりシンプルな" 群です。このかなりのシンプルさが方程式の可解性と関わっているのです。
|
正規部分群を介した巡回群の入れ子構造 |
可解群の「正規部分群を介した巡回群の入れ子構造」のイメージを図にしたものである。入れ子の深さは何段階でもよく、最後は正規部分群=巡回群で終わる。数学的には、巡回群 \(C_1\) は、\(C_1=G/H_1\) で定義される剰余群(商群)であり、また \(C_2=H_1/H_2\)、\(C_3=H_2/H_3\) である。各段階で剰余群が巡回群になるのが「入れ子構造」の条件である。 可解群は、方程式とは関係なく、純粋に群の構造として定義できる。ガロア理論では「方程式の解が四則演算とべき根で記述できるか」という問題が、群の構造の議論に置き換えられている。なお、この図はあくまでイメージであり、可解群の正確な定義は別途行う(第6章)。 |
可解群という概念は、ガロア群とは関係なく純粋に群の特性として定義することが可能です。もちろん可解というネーミングでわかるように、方程式の可解性と直結しています。なお、可解群の数学的に厳密な定義は別途きちっとやります(第6章)。
1.4 可解性の必要十分条件
ガロア理論は、
| 方程式の解の特性を「方程式の解を含む体の性質」で語る | |
| 「方程式の解を含む体の性質」を「体に付随した群=ガロア群の性質」で語る |
可解性の必要条件
\(n\)次方程式 \(f(x)\) の解を\(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
があるとしたら、\(\bs{L}\) のガロア群は可解群である。
なぜそう言えるのかの証明は、かなりのステップが必要です。それは別途やりますが、ここで重要なのは上の定理の対偶です。上の定理の対偶は、
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
もし、\(\bs{L}\) のガロア群が可解群でなければ、\(\bs{Q}\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
は存在しない。
となります。\(\bs{\bs{Q}}\) から始まるべき根拡大の連続で \(\bs{\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)}\) に到達できないということは、すなわち \(\bs{\al_1,\al_2,\:\cd\:,\al_n}\) が四則演算とべき根では表現できないということに他なりません。ガロア群が可解群ということが、方程式が "代数的に解ける" ための必要条件なのです。
2・3・4次方程式のガロア群はすべて可解群ですが、5次方程式のガロア群は可解群であるものとそうでないものがあります。だから5次方程式の解の公式(=あらゆる5次方程式に通用する公式)はないのです。
ここで定義を振り返ってみると、可解群は、巡回群か、正規部分群を介した巡回群の入れ子構造の群でした。方程式の "解ける解けない" が問題になるのは5次方程式です。実は、可解な5次方程式のガロア群は、巡回群か "巡回群と正規部分群(=巡回群)の2階建て" です(そのような5次方程式もかなりのレア・ケースですが)。可解な5次方程式を考える限り、"正規部分群を介した巡回群の入れ子構造" の "入れ子" は、1段階の非常にシンプルなものに過ぎないのです。
しかし、ある5次方程式が可解でないことを証明するには正規部分群が威力を発揮します。つまり、その5次方程式のガロア群に "正規部分群を介した巡回群の入れ子構造"がないことを言えばよいのですが、そもそも正規部分群がないことを証明してしまえば、その5次方程式は可解ではなくなるからです。そして実際に、ある特定の5次方程式が可解でないことの証明に使われるのは、その5次方程式のガロア群に正規部分群がないということなのです。先ほど「正規部分群という概念がガロア理論の最大のキモ」としたのは、そういう意味を含みます。
可解性の十分条件
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。また、\(1\) の原始\(n\)乗根を \(\zeta\) とする。
\(\bs{L}\) のガロア群が可解群であれば、\(\bs{Q}(\zeta)\) から始まって \(\bs{L}\) に至る "べき根拡大体" の列、
\(\bs{Q}(\zeta)=\bs{F}_0\subset\bs{F}_1\subset\bs{F}_2\subset\cd\subset\bs{F}_m=\bs{L}\)
が存在する。
なぜそう言えるのか、また、なぜここに突然 \(1\) の原始\(n\)乗根が登場するのかは、別途厳密に証明します。この定理で言えることは、「ガロア群が可解群であれば、\(n\)次方程式の解は、有理数と \(\zeta\) の四則演算・べき根の組み合わせで表現できる」ということです。
ここで \(1\) の原始 \(n\)乗根である \(\zeta\) が問題になります。実は、\(1\) の原始 \(n\)乗根は有理数の四則演算とべき根で表現できることがガロア理論とは無関係に証明できます(その証明も別途やります。ガロア理論で証明することもできます)。従って、方程式は可解なのです。
方程式が代数的に解けるキーワードは可解群です。巡回群は代表的な可解群であり、ガロア群が巡回群だと方程式をべき根で解く手法が存在します。ガロア群が巡回群の入れ子構造でも、その手法を多段階に使うことによって、\(\bs{Q}\) から始まるべき根拡大の系列で方程式の解を含む代数拡大体に到達できます。可解性の十分条件の証明は、そのような組み立てになっています。
以上の必要条件と十分条件を組み合わせると、以下が言えます。
\(n\)次方程式 \(f(x)=0\) の解を \(\al_1,\:\al_2,\:\cd\:,\al_n\) とし、これらの解を含む \(\bs{Q}\) の代数拡大体を \(\bs{L}=\bs{Q}(\al_1,\al_2,\:\cd\:,\al_n)\) とする。
\(n\)次方程式 \(f(x)=0\) が可解である、つまり四則演算とべき根で解が表現できるための必要十分条件は、\(\bs{L}\) のガロア群(= 自己同型写像が作る群)が可解群であることである。
ガロア理論は、方程式が解けるための必要十分条件を示すものです。従って、ある方程式が可解であることの証明、あるいは逆に、可解でないことの証明はできます。しかし、可解である方程式の解を、具体的に四則演算とべき根で求めるための実用的なアルゴリズムを示しているわけではありません。そこが注意点です。
ここまで、方程式の可解性の必要十分条件を解き明かすガロア理論の全体構造、アウトラインを説明しました。以降ではこれを精密化し、数学的に正しい、首尾一貫した証明にしていきます。目次にあるように、全体は次の8章から成ります。
1.証明の枠組み
2.整数の群
3.多項式と体
4.一般の群
5.ガロア群とガロア対応
6.可解性の必要条件
7.可解性の十分条件
8.結論
第5章から第7章までが、ガロア理論の核心の部分です。第2章から第4章までは、核心部分の証明に使う各種の定義や定理の説明です。この部分がかなり長いのは、高校までで習う数学(いわゆる "受験数学" ではない、教科書ベースの数学)だけを前提知識とし、そうでないものは全部証明するという方針によります。
「1.証明の枠組み」 終わり
(次回に続く)
(次回に続く)
2023-03-04 11:47
nice!(0)