No.329 - 高校数学で理解するレジ行列の数理 [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots}\)
No.149「我々は直感に裏切られる」で、数字に関して我々の直感が事実に反する例や、正しい直感が働かない例を書きました。その中の "誕生日のパラドックス"(= 23人のクラスで誕生日が同じ人がいる確率は 50% を超える)については、No.325「高校数学で理解する誕生日のパラドックス」でその数学的背景を書きました。今回もそういった直感が外れる例で、スーパーのレジや各種窓口の「待ち行列」を取り上げます。
No.325 以外にも「高校数学で理解する」とのタイトルの記事がいくつかあります。
です。これらの記事は、高等学校までの数学だけを予備知識として、現代の IT 社会の重要なインフラとなっている公開鍵暗号を解説したものでした。高校までに習わない公式や用語を使うときには、その公式の証明(ないしは用語の説明)を記しています。今回もその方針でやります。
レジ行列の観察
ある比較的小規模のスーパー・マーケットを例にとります(仮想の例です)。この店の店長は店舗運営の改善に熱心です。店長は「ある曜日のある時間帯」のレジを何回も観察して、次のような結果を得ました。
レジ係一人当たり、1時間で平均24人の客がきます。一方、レジ係りは1時間で平均60人の客をこなせる。レジ係りには余裕があり、過半はアキ時間(客を待っている時間)です。そこで店長は次のように考えました。
はたしてこの店長の考えは正しいのでしょうか。これを数学で解析するのが今回の目的です。問題として明示されている観察量は、24 と 60 ぐらいしかなく、あとは "ランダム" という言葉ですが、数学を使ってこれだけの情報から店長の判断の妥当性を検証します。
ランダムな事象\(\cdot\)連続量
1つのレジについて1時間当たり24人の客が "ランダムに" 到着します。またレジでの会計時間もランダムに決まる。ランダム、ないしは偶然に発生する事象(イベント)が主題であり、これは確率の問題です。まず、以降に出てくる「確率変数」と「確率(確率測度)」を、サイコロの例で説明します。確率変数 \(X\) とは、
で、値はふつう整数や実数です。確率変数は大文字で書きます。\(X\) がサイコロの目の数を表す確率変数の場合、
の6つの整数値をとる変数です。また、\(X\) に特定の条件をつけた事象が起こる確率(数学的には "確率測度"、Probability Measure)を
で表します。一般的には \(P(\)事象\()\) で、その事象が起こる確率を表します。確率なので \(0\leq P\leq1\) であり
です。\(X\)がサイコロの目の確率変数の場合、
です。サイコロの目の数は飛び飛びの値をとるので「離散型の確率」です。高校数学に出てくる確率は主に離散型の確率です。
一方、レジ行列の場合、到着時刻や到着間隔(= 1人の客が到着してから次の客が到着するまでの時間)、会計に要する時間は無限の可能性のある連続値です。つまり「連続型の確率」であり、これをどう扱うかが以下の主要なテーマです。
レジ行列のモデル
レジ行列を次のようにモデル化します。レジに数人の客が並んでいて、先頭の客は会計(バーコードののスキャン、代金の支払い\(\cdot\)精算)の最中とします。会計を待って並んでいる客と会計中の客を含めて「行列」と呼びます。
この行列には2種類の「イベント」が発生します。新しい客が最後尾に並ぶ「到着」と、会計が終了して客が行列から離れる「退出」です。
行列には単位時間(たとえば1時間)当たり平均で \(\lambda\)(ラムダ)人が到着します。ただし、到着はランダムです。また、レジ係は単位時間あたり平均で \(\mu\)(ミュー)人分の会計をこなします。つまり単位時間あたり \(\mu\)人が列から退出します。ただし、会計にかかる時間もまたランダムです。まとめると、
です。ここで \(\lambda\) が \(\mu\) より大きければ、レジ行列は長くなるばかりで、スーパーは機能しません。従って以降は、
とします。
客の到着確率
まず、微少時間 \(\Delta t\) の間に客が1人到着する確率を検討します。\(1\)時間に平均\(5\)人の客が到着する場合で考えます(\(\lambda=5\) の場合)。また、\(1\)時間を\(9\)秒で区切った\(400\)の微少時間 \(\Delta t=0.0025(h)\) を考えます。そうすると平均的に、
と言えるでしょう。つまり、
です。ただし、これでは考えに抜けがあります。\(9\)秒間に客が\(2\)人以上到着するかもしれないからで、それは大いにありうることです。しかしこれは微少時間 \(\Delta t\) を \(9\)秒としたからです。そこで、微少時間をどんどん小さくし「高々、客が1人到着するか、1人退出するかであるような微少時間」を考えます。つまり \(\Delta t\) の定義を、
とします。そうすると、
となります。これが「単位時間に \(\lambda\)人の客がランダムに到着する」ということの数学的表現です。\(\lambda\) を \(\mu\) に変えると、レジでの会計が終わって客がレジ列から退出する確率も全く同様になります。そこで、この表現を使って客の到着間隔の確率を求めます。
到着間隔の確率密度関数
\(1\)人の客が到着してから次の客が到着するまでの時間が「到着間隔」です。この到着間隔を表す確率変数 \(X\) とします。到着間隔は \(0\) 以上なので、以下では \(X > 0\) とします(一般的には確率変数は \(-\infty< X < \infty\) です)。単位時間に \(\lambda\)人の客がランダムに行列に到着するとき、到着間隔の確率 \(P\) はどう表現できるでしょうか。
サイコロと違って \(X\) は連続変数です。従って、たとえば \(P(X=0.2)\) 、つまり到着間隔が(ぴったり)\(12\)分である確率は定義できません。到着間隔には無限の可能性があるからです。しいて言うなら \(P(X=0.2)=0\) とするしかありません。連続型の確率の特徴です。
しかし、\(X\) が一定の範囲である確率は求まります。たとえば到着間隔が\(12\)分から\(15\)分の間である確率、\(P(0.2\leq X\leq0.25\:)\) は計算することができる。一般に、\(a < b\) とし、
であるような関数 \(f(x)\) があるとき、その関数を「確率密度関数」と言います。\(X\) が全ての値をとるときの確率は \(1\) なので、確率密度関数 \(f(x)\) は、
を満たします(\(X\geq0\) で考えています)。そこで、レジ行列の到着間隔の確率密度関数 \(f(x)\) がどうなるかです。到着間隔が \(t\) ~ \(t+\Delta t\) である確率は、確率密度関数の定義により、
です。\(\Delta t\) は微少時間なので、右辺は積分を掛け算で置き換えました。一方、別の視点で考えると、到着間隔が \(t\) ~ \(t+\Delta t\) である確率は、
です。"間隔" という言葉を使わずに "到着" だけで表現するとそうなります。\(0\) ~ \(t\) の間に到着が起こる確率(= 到着間隔が \(0\) ~ \(t\) である確率)は、確率密度関数の定義により、
なので、\(0\) ~ \(t\) の間に到着が起こらない確率は、
です。また、微少時間 \(\Delta t\) の間に到着が起こる確率は先ほどの考察から、
です。従って \(0\) ~ \(t\) の間に到着が起こらず、かつ \(t\) ~ \(t+dt\) の間に到着が起こる確率は、
と書けます。(\(\bs{\mr{A}}\)式)と(\(\bs{\mr{B}}\)式)は等しいはずなので次の等式が成立します。
この両辺を \(t\) で微分すると、
となります。この微分方程式の解は、\(C\) を定数として、
ですが、確率密度関数には、
条件があるので、この条件で \(C\) を決めると \(C\:=\:\lambda\) となります。最終的に、
が「到着間隔の確率密度関数」です。会計が終わって列から離れる間隔(= 退出間隔)も、\(\lambda\) を \(\mu\) に変えるだけで全く同じように求まります。以上をまとめると、
となります。これは「指数分布」と呼ばれている確率分布です。
この指数分布の平均値(確率の言葉では期待値)を実際に求めてみると、
となって、1時間に \(\lambda\)人の客が到着するときの到着間隔の平均は、確かに \(\dfrac{1}{\lambda}\) となっていることが分かります。\(\lambda=\:24\)(\(1\)時間に平均\(24\)人の客が到着)の場合は、到着間隔の平均は \(2\)分\(30\)秒 ということです。なお上の計算では部分積分と、\(xe^{-x}\rightarrow0\:(x\rightarrow\infty)\) を使いました。
到着間隔の確率密度関数は、ある時間について到着間隔がその時間付近である "確からしさ" を表しています。従って上のグラフから、
などが読み取れます。これは直感的に我々が経験していることと合致します。レジの運営としては、客がなるべく均等な到着間隔で来てくれた方が効率的ですが、しかしそうはならない。それが "ランダム" ということです。
到着間隔の累積分布関数
確率変数を \(X\)、確率密度関数 \(f(x)\) とします。問題にしている到着間隔は \(0\) 以上なので、\(X\geq0\) とします(一般的には \(-\infty< X < \infty\) です)。累積分布関数 \(F(x)\) とは
で定義される「確率密度を累積した値」です。確率密度は正の値で、\(\infty\)まで積分すると \(1\) になるので、累積分布関数は \(0 < F(x) < 1\) の単調増加関数です。\(X\) を到着間隔を表す確率変数とすると確率密度関数は指数分布になりますが、この累積分布関数を求めると、
となります。\(\lambda=24\) の場合(平均到着間隔が 2分30秒の場合)に \(F(t)\) が \(0.5\) となる時間 \(T_5\) を計算してみると、
となります。\(0.029(h)\) は1分43秒です。これは、
ことを意味します。しかも指数分布の形に見るように到着間隔が短い方が確率が高い。これがランダムに到着する場合の姿です。
シミュレーション
到着間隔と退出間隔の確率密度関数が求まったので、これを用いてパソコンでシミュレーションをしてみます。そのためには「確率密度関数に従う乱数」を発生させなければなりません。
パソコンのプログラミング言語には「一様分布の乱数」を発生させる関数があるので(random / rand などの名称)、これを「到着間隔や退出間隔の確率密度をもつ乱数」に変換することを考えます。
まず「一様分布」ですが、確率変数 \(U\:(0\leq U\leq1)\) が一様分布とは、確率密度が一定値のものです。つまり、
となる分布です(下図)。
今、分析したい確率変数 \(X\) の確率密度関数を \(f(x)\)、その累積分布関数を \(F(x)\:(0\leq F(x)\leq1)\) とします。そして \(F(x)\) の逆関数 \(F^{-1}(x)\) を作り、
とおくと、この \(Y\) は「確率密度関数 \(f(x)\) をもつ確率変数」となります。その理由は以下の通りです。\(Y\) の累積分布関数、\(P(Y\leq x)\) は、
と書けますが、\(F\) は単調増加関数なので、右辺の \(F^{-1}(U)\leq x\) の条件は、
としても同じことです。すなわち、
と表せます。従って、
となりますが、\(U\) は一様分布の確率変数なので、上式の右辺は、
であり(上の一様分布の説明参照)、この結果、
が得られます。この式は「確率変数 \(Y\) の累積分布関数は \(F(x)\)」という意味であり、従って \(Y\) の確率密度関数が \(f(x)\) であることが分かりました。この方法で特定の確率密度をもつ乱数を発生させる手法を「逆関数法」と呼びます。
到着間隔の累積分布関数は、
でした。この式を \(t\) について解くと、
です。従って \(F(t)\) の逆関数、\(F^{-1}(t)\) は
です。このことから \(u\) を一様分布の乱数として、
と計算できます。同様に、
です。この2式を使ってシミュレーションを実行できます。
シミュレーション:例1(1時間)
パソコンを使って、客がいない状態から1時間のシミュレーションしてみます。\(\lambda=24\)、\(\mu=60\) とします。その結果の一例が次の表です。これは、
を表にしたものです。このシミュレーションは開始から1時間が経過した直後のイベント(="到着"。時刻 61分02秒)で止めてあります。この間に22人の到着があり、21人が退出しました。22人目が到着する直前の行列の人数は 0 です。行列の最大人数は 4人(37′19″からの 45″間)になりました。
この表の「イベント後の行列人数」と「次のイベントまでの時間」から「行列が \(n\)人(\(n\geq0\))の時間合計」を求められます。それを計算したのが次の表です。
さらに、
と定義し、上の表のそれぞれの時間合計を全体のシミュレーション時間( 61′02″)で割ると、次の表が得られます。
このテーブルから「行列の平均人数 \(=\:L(t)\::\:t=1\) のとき 」を求めてみると、
となりました。これはあくまで1時間分のシミュレーションに過ぎません。使用した乱数も、到着と退出のイベントでそれぞれ20数個程度であり、発生させた乱数は指数分布の極めて荒い近似だと推測されます。
しかし、\(p_n(t)\) の \(t\) を増やしていき、それにもとづいて \(L(t)\) を計算していくと、近似は次第に正確になっていくはずです。それが次のシミュレーションです。
シミュレーション:例2(長時間)
シミュレーションの時間を増やして \(200\) 時間分の計算を実行し、行列の平均長がどうなるかを、途中経過とともに観察します。シミュレーション時間、\(t\) を増やしたときの行列の最大人数を \(m\) とすると、行列の平均長、\(L(t)\) は、
で計算できます。このシミュレーションを実行して \(L(t)\) をプロットしたのが次のグラフ(\(0\leq t\leq200\))です。もちろん、あくまで一例です。
グラフから分かるように、行列の平均長は一定値(\(0.6\)~\(0.7\) 程度)に近づいていきます。これはパソコンで発生させた乱数が一様分布乱数に近づき、従って逆関数法で作った関数が指数分布に近づくからです。また初期状態(シミュレーションでは行列の人数はゼロとした)の影響がなくなることもあるでしょう。
このように時間に依存しない状態が「定常状態」であり、これが行列の平均的な姿です。
シミュレーション:例3(同一シミュレーションの平均)
乱数を使ったシミュレーションでは、1回だけの計算では値がふらつき、必ずしも正確な姿が分かりません。こういう場合は、同一のシミュレーションを多数繰り返し、その平均をとるのが一般的です。
次図に、2.5 時間分のシミュレーションを 1000 回繰り返して平均をとった例をあげます。行列の平均長が 0.66~0.68 程度に収束していく様子が見て取れます。
レジ行列の微分方程式
今まではパソコンによるシミュレーションでしたが、これを数学的に厳密に解くことができます。
\(p_n(t)\) を「時刻 \(t\) において行列が \(n\)人である確率」とします。そして、時刻 \(t+\Delta t\) に \(p_n\:(t)\) がどう変化するかを考えます。まず \(p_0(t+\Delta t)\) ですが、起こり得るケースは、
\(p_0(t+\Delta t)\):
の2つのケースです。ここで、
なので、次の式が成り立ちます。
\(\Delta t\rightarrow0\) の極限をとると、次の微分方程式が得られます。
次に \(p_1(t+\Delta t)\) ですが、これには3つのケースがあります。つまり、
\(p_1(t+\Delta t)\):
の3つです。微少時間 \(\Delta t\) の間に起こるイベントは、起こったとしても一つだけであり、到着と退出が同時に起こることはないというのがそもそもの仮定でした。つまり \(\Delta t\) の時間内に起こる事象は、
のどれかであり、この3つは排他的です。従って \(\Delta t\) の間に
となります。排他的だから単純加算でよいわけです。従って、
です。以上の考察から \(p_1(t+\Delta t)\) は次のように表現できます。
従って、一般の \(p_n(t)\:(n\geq2)\) では、
と表現できます。以上をまとめると、
の2つの微分方程式によって、レジ行列の挙動が決まることが分かりました。
ここで、シミュレーションで確認したような "定常状態" での確率を求めます。定常状態では確率は時間的に変化しないので、上の2つの微分方程式の左辺はゼロになります。\((t)\) をなくして式を整理すると、
ですが、ここで、
と定義します。\(\rho\) は「稼働率」を呼ばれる数値です。レジ行列のモデルで仮定したように \(\lambda< \mu\) なので、
です。この \(\rho\) を使って式を書き直すと、
となります。ここで(2式)を次のように変形します。
これは数列 \((p_n-p_{n-1})\) が、初項 \((p_1-p_0\:)\) 、公比 \(\rho\) の等比数列であることを示しています。(1式)より \(p_1=\rho p_0\) なので、初項 \((p_1-p_0\:)\) は \(p_0(\rho-1)\) と表現できます。従ってこの等比数列の一般項は、
です。この式から \(p_n\) の形を求めます。以降の計算では高校数学で習う「等比数列の和の公式」を使います。つまり、
という公式です。(3式)の両辺の \(n=1\cd n\) の和をとると、
が得られます。ここで \(p_n\) は確率なので、その総和をとると \(1\) になるはずです。(4式)の両辺の \(n=1\cd n\) の和をとると、
となります。ここで \(n\rightarrow\infty\) とすると、\(\rho< 1\) なので、
となります。(5式)を(4式)に代入すると、
が得られました。(6式)が定常状態で列に \(n\)人が並ぶ確率です。ちなみに(5式)において \(p_0\) は、定常状態で「列に \(0\)人が並ぶ確率」であり、つまり、
ということに他なりません。\(\rho\) が(レジ係の)稼働率であるゆえんです。
行列の平均長
(6式)で行列の人数ごとの確率が求まったので、行列の平均長を計算することができます。つまり、
の総合計が行列の平均長(\(=L\))です。
ここで \(S_n\) を、
と定義すると、
です。従って、
と計算できます。ゆえに、行列の平均長 \(L\) は、
となります。
平均待ち時間
次に、客が行列に到着してから会計が始まるまでの時間、「平均待ち時間(=\(W\))」を計算してみます。これは、
平均待ち時間 =
であり、ということは、
平均待ち時間 =
です。平均会計時間は \(\dfrac{1}{\mu}\) なので、
となります。以上でレジ行列の数学的な解析ができました。
スーパーのレジ行列の分析
今までの数学的分析をまとめると、
のとき、レジ行列の平均長 \(L\) と平均待ち時間 \(W\) は、
で求めることができます。
最初に提示したスーパーのレジ係りの人数に戻ります。レジ係り一人あたり1時間あたりの平均の会計処理数は、\(\mu=60\) です(1人の客につき1分で処理)。現状(変更前)はレジ係り2人でそれぞれ24人の客を1時間あたりこなしているが、レジ係を1人にしたらどうなるかが問題でした。それを計算すると次のようになります。
変更前(レジ係2人)
変更後(レジ係1人)
つまりレジ係を半分に変更すると、変更前と比べて平均の行列長さ(\(L\))も平均待ち時間(\(W\))も6倍になります。店長の "せいぜい2倍程度だろう" という直感は、全くの "外れ" であることが分かります。
ちなみに、変更前(レジ係2人)の行列の平均長、\(L=0.67\) は、シミュレーション(例3)と一致しています。また、変更後(レジ係1人)の場合の平均長は理論上、\(L=4.0\) ですが、シミュレーションをしてみると次図ようになり、理論と一致します。
\(L\) も \(W\) も、稼働率 \(\rho\) が \(1\) に近づくと急激に上昇します。その様子をグラフにしたのが次です。
現象の本質が "ランダム" である場合、往々にして我々の直感がはずれます。上の例で変更後の稼働率が \(0.8\) ということは、レジ係りの時間の \(20\:\%\) は客待ち時間だというとです。それでも、客の視点からすると会計待ちの時間が大幅に延びる。このような問題では平均で考えると落とし穴にはまります。
以上のスーパーのレジの分析は「待ち行列理論」の初歩のそのまた第1歩です。世の中には「窓口」がいろいろあって、そこに並んで何らかの「サービス」を受けることが多々あります。「窓口」は、人が対応しない自販機でも ATM でも同じです。もっと一般化すると、サービス提供主体があり、サービスを受けようとする主体が複数あると "待ち行列" の問題が発生します。コールセンターに電話すると「ただいま込み合っております。そのまましばらくお待ちください」という自動応答が返ってくることがありますが、同じことです。
またコンピュータシステムにおいては、多数の処理要求に対して複数のサーバーが対応するケースが多々あります。Webによるチケットの予約システムなどはその典型でしょう。もっと広く考えると、現代のインターネットは世界中に何10億というサーバー資源(アプリケーション・サーバ、ファイル・サーバ、ルーター、・・・・・・)があり、そのサービスを受けようとする何億人かの "客" で構成されている巨大ネットワーク・システムだと言えるでしょう。その各所で、実は微少な「待ち行列」が発生しています。
そういった、世の中に多数ある "システム"(人間系・コンピュータ系)を設計する根幹のところに「待ち行列理論」があるのでした。
No.149「我々は直感に裏切られる」で、数字に関して我々の直感が事実に反する例や、正しい直感が働かない例を書きました。その中の "誕生日のパラドックス"(= 23人のクラスで誕生日が同じ人がいる確率は 50% を超える)については、No.325「高校数学で理解する誕生日のパラドックス」でその数学的背景を書きました。今回もそういった直感が外れる例で、スーパーのレジや各種窓口の「待ち行列」を取り上げます。
No.325 以外にも「高校数学で理解する」とのタイトルの記事がいくつかあります。
です。これらの記事は、高等学校までの数学だけを予備知識として、現代の IT 社会の重要なインフラとなっている公開鍵暗号を解説したものでした。高校までに習わない公式や用語を使うときには、その公式の証明(ないしは用語の説明)を記しています。今回もその方針でやります。
レジ行列の観察
ある比較的小規模のスーパー・マーケットを例にとります(仮想の例です)。この店の店長は店舗運営の改善に熱心です。店長は「ある曜日のある時間帯」のレジを何回も観察して、次のような結果を得ました。
|
レジ係一人当たり、1時間で平均24人の客がきます。一方、レジ係りは1時間で平均60人の客をこなせる。レジ係りには余裕があり、過半はアキ時間(客を待っている時間)です。そこで店長は次のように考えました。
|
はたしてこの店長の考えは正しいのでしょうか。これを数学で解析するのが今回の目的です。問題として明示されている観察量は、24 と 60 ぐらいしかなく、あとは "ランダム" という言葉ですが、数学を使ってこれだけの情報から店長の判断の妥当性を検証します。
ランダムな事象\(\cdot\)連続量
1つのレジについて1時間当たり24人の客が "ランダムに" 到着します。またレジでの会計時間もランダムに決まる。ランダム、ないしは偶然に発生する事象(イベント)が主題であり、これは確率の問題です。まず、以降に出てくる「確率変数」と「確率(確率測度)」を、サイコロの例で説明します。確率変数 \(X\) とは、
起こりうる事象に値を割り当てるとき、その値をとる変数
で、値はふつう整数や実数です。確率変数は大文字で書きます。\(X\) がサイコロの目の数を表す確率変数の場合、
\(X\:=\:1,\:2,\:3,\:4,\:5,\:6\)
の6つの整数値をとる変数です。また、\(X\) に特定の条件をつけた事象が起こる確率(数学的には "確率測度"、Probability Measure)を
\(P\:(X\) の条件\()\)
で表します。一般的には \(P(\)事象\()\) で、その事象が起こる確率を表します。確率なので \(0\leq P\leq1\) であり
| \(P(\)必ず起こる事象\()\) | \(=\:1\) | |
| \(P(\)決して起こらない事象\()\) | \(=\:0\) |
です。\(X\)がサイコロの目の確率変数の場合、
| \(P(1\leq X\leq6)\) | \(=1\) | |
| \(P(X=1)\) | \(=\dfrac{1}{6}\) | |
| \(P(X\leq3)\) | \(=\dfrac{1}{2}\) | |
| \(P(X=7)\) | \(=0\) |
です。サイコロの目の数は飛び飛びの値をとるので「離散型の確率」です。高校数学に出てくる確率は主に離散型の確率です。
一方、レジ行列の場合、到着時刻や到着間隔(= 1人の客が到着してから次の客が到着するまでの時間)、会計に要する時間は無限の可能性のある連続値です。つまり「連続型の確率」であり、これをどう扱うかが以下の主要なテーマです。
レジ行列のモデル
レジ行列を次のようにモデル化します。レジに数人の客が並んでいて、先頭の客は会計(バーコードののスキャン、代金の支払い\(\cdot\)精算)の最中とします。会計を待って並んでいる客と会計中の客を含めて「行列」と呼びます。
この行列には2種類の「イベント」が発生します。新しい客が最後尾に並ぶ「到着」と、会計が終了して客が行列から離れる「退出」です。
行列には単位時間(たとえば1時間)当たり平均で \(\lambda\)(ラムダ)人が到着します。ただし、到着はランダムです。また、レジ係は単位時間あたり平均で \(\mu\)(ミュー)人分の会計をこなします。つまり単位時間あたり \(\mu\)人が列から退出します。ただし、会計にかかる時間もまたランダムです。まとめると、
到着:\(\lambda\)人(単位時間あたり)
退出:\(\mu\)人(単位時間あたり)
退出:\(\mu\)人(単位時間あたり)
です。ここで \(\lambda\) が \(\mu\) より大きければ、レジ行列は長くなるばかりで、スーパーは機能しません。従って以降は、
\(\lambda< \mu\)
とします。
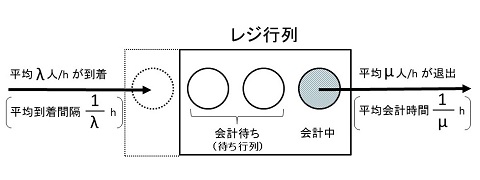
|
レジ行列のモデル |
客の到着確率
まず、微少時間 \(\Delta t\) の間に客が1人到着する確率を検討します。\(1\)時間に平均\(5\)人の客が到着する場合で考えます(\(\lambda=5\) の場合)。また、\(1\)時間を\(9\)秒で区切った\(400\)の微少時間 \(\Delta t=0.0025(h)\) を考えます。そうすると平均的に、
| \(400\) のうちの \(5\) つの微少時間では客が到着 | |
| \(400\) のうちの \(395\) の微少時間では客が到着しない |
と言えるでしょう。つまり、
| 微少時間に客が到着する確率は \(5/400\:=\:\lambda\Delta t\) | |
| 微少時間に客が到着しない確率は \((1\:-\:\lambda\Delta t)\) |
です。ただし、これでは考えに抜けがあります。\(9\)秒間に客が\(2\)人以上到着するかもしれないからで、それは大いにありうることです。しかしこれは微少時間 \(\Delta t\) を \(9\)秒としたからです。そこで、微少時間をどんどん小さくし「高々、客が1人到着するか、1人退出するかであるような微少時間」を考えます。つまり \(\Delta t\) の定義を、
微少時間 \(\Delta t\) では、イベント(到着か退出)が1つだけ起こるか、ないしはイベントが起こらないのどちらかである
とします。そうすると、
| 微少時間に1人の客が到着する確率は \(\lambda\Delta t\) | |
| 従って、微少時間に客が到着しない確率は \((1\:-\:\lambda\Delta t)\) | |
| 全ての微少時間は同等であり、同じ確率で到着が起こる(=ランダム) |
となります。これが「単位時間に \(\lambda\)人の客がランダムに到着する」ということの数学的表現です。\(\lambda\) を \(\mu\) に変えると、レジでの会計が終わって客がレジ列から退出する確率も全く同様になります。そこで、この表現を使って客の到着間隔の確率を求めます。
到着間隔の確率密度関数
\(1\)人の客が到着してから次の客が到着するまでの時間が「到着間隔」です。この到着間隔を表す確率変数 \(X\) とします。到着間隔は \(0\) 以上なので、以下では \(X > 0\) とします(一般的には確率変数は \(-\infty< X < \infty\) です)。単位時間に \(\lambda\)人の客がランダムに行列に到着するとき、到着間隔の確率 \(P\) はどう表現できるでしょうか。
サイコロと違って \(X\) は連続変数です。従って、たとえば \(P(X=0.2)\) 、つまり到着間隔が(ぴったり)\(12\)分である確率は定義できません。到着間隔には無限の可能性があるからです。しいて言うなら \(P(X=0.2)=0\) とするしかありません。連続型の確率の特徴です。
しかし、\(X\) が一定の範囲である確率は求まります。たとえば到着間隔が\(12\)分から\(15\)分の間である確率、\(P(0.2\leq X\leq0.25\:)\) は計算することができる。一般に、\(a < b\) とし、
\(P(a\leq X\leq b)=\displaystyle\int_{a}^{b}f(x)dx\)
であるような関数 \(f(x)\) があるとき、その関数を「確率密度関数」と言います。\(X\) が全ての値をとるときの確率は \(1\) なので、確率密度関数 \(f(x)\) は、
\(\displaystyle\int_{0}^{\infty}f(x)=1\)
を満たします(\(X\geq0\) で考えています)。そこで、レジ行列の到着間隔の確率密度関数 \(f(x)\) がどうなるかです。到着間隔が \(t\) ~ \(t+\Delta t\) である確率は、確率密度関数の定義により、
\(\displaystyle\int_{t}^{t+\Delta t}f(x)dx=f(t)\Delta t\) (\(\bs{\mr{A}}\)式)
です。\(\Delta t\) は微少時間なので、右辺は積分を掛け算で置き換えました。一方、別の視点で考えると、到着間隔が \(t\) ~ \(t+\Delta t\) である確率は、
\(0\) ~ \(t\) の間に到着が起こらず、かつ \(t\) ~ \(t+\Delta t\) の間に到着が起こる確率
です。"間隔" という言葉を使わずに "到着" だけで表現するとそうなります。\(0\) ~ \(t\) の間に到着が起こる確率(= 到着間隔が \(0\) ~ \(t\) である確率)は、確率密度関数の定義により、
\(\displaystyle\int_{0}^{t}f(x)dx\)
なので、\(0\) ~ \(t\) の間に到着が起こらない確率は、
\(1\:-\:\displaystyle\int_{0}^{t}f(x)dx\)
です。また、微少時間 \(\Delta t\) の間に到着が起こる確率は先ほどの考察から、
\(\lambda\Delta t\)
です。従って \(0\) ~ \(t\) の間に到着が起こらず、かつ \(t\) ~ \(t+dt\) の間に到着が起こる確率は、
\(\left(1-\displaystyle\int_{0}^{t}f(x)dx\right)\lambda\Delta t\) (\(\bs{\mr{B}}\)式)
と書けます。(\(\bs{\mr{A}}\)式)と(\(\bs{\mr{B}}\)式)は等しいはずなので次の等式が成立します。
| \(f(t)\Delta t\) | \(=\left(1-\displaystyle\int_{0}^{t}f(x)dx\right)\lambda\Delta t\) | |
| \(f(t)\) | \(=\left(1-\displaystyle\int_{0}^{t}f(x)dx\right)\lambda\) |
この両辺を \(t\) で微分すると、
\(f\,'(t)=-\lambda f(t)\)
となります。この微分方程式の解は、\(C\) を定数として、
\(f(t)=Ce^{-\lambda t}\)
ですが、確率密度関数には、
\(\displaystyle\int_{0}^{\infty}f(t)dt=1\)
条件があるので、この条件で \(C\) を決めると \(C\:=\:\lambda\) となります。最終的に、
\(f(t)=\lambda e^{-\lambda t}\)
が「到着間隔の確率密度関数」です。会計が終わって列から離れる間隔(= 退出間隔)も、\(\lambda\) を \(\mu\) に変えるだけで全く同じように求まります。以上をまとめると、
| 到着間隔の確率密度関数 \(f(t)=\lambda e^{-\lambda t}\) | |
| 退出間隔の確率密度関数 \(f(t)=\mu e^{-\mu t}\) |
となります。これは「指数分布」と呼ばれている確率分布です。
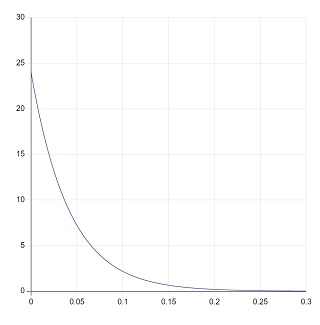
|
到着間隔の確率密度関数 |
\(\lambda=\:24(/h)\)。 横軸の単位は時間\((h)\)。\(0.05\) が\(3\)分。 |
この指数分布の平均値(確率の言葉では期待値)を実際に求めてみると、
\(\displaystyle\int_{0}^{\infty}tf(t)dt\)
\(=\displaystyle\int_{0}^{\infty}\lambda te^{-\lambda t}dt\)
\(=\left[-te^{-\lambda t}\right]_0^{\infty}+\displaystyle\int_{0}^{\infty}e^{-\lambda t}dt\)
\(=0+\left[-\dfrac{1}{\lambda}e^{-\lambda t}\right]_0^{\infty}\)
\(=\dfrac{1}{\lambda}\)
\(=\displaystyle\int_{0}^{\infty}\lambda te^{-\lambda t}dt\)
\(=\left[-te^{-\lambda t}\right]_0^{\infty}+\displaystyle\int_{0}^{\infty}e^{-\lambda t}dt\)
\(=0+\left[-\dfrac{1}{\lambda}e^{-\lambda t}\right]_0^{\infty}\)
\(=\dfrac{1}{\lambda}\)
となって、1時間に \(\lambda\)人の客が到着するときの到着間隔の平均は、確かに \(\dfrac{1}{\lambda}\) となっていることが分かります。\(\lambda=\:24\)(\(1\)時間に平均\(24\)人の客が到着)の場合は、到着間隔の平均は \(2\)分\(30\)秒 ということです。なお上の計算では部分積分と、\(xe^{-x}\rightarrow0\:(x\rightarrow\infty)\) を使いました。
到着間隔の確率密度関数は、ある時間について到着間隔がその時間付近である "確からしさ" を表しています。従って上のグラフから、
| 客が来るときには、たて続けに来る | |
| しかし間隔が長くあくこともある | |
| その平均として単位時間に \(\lambda\) 人の客が来る |
などが読み取れます。これは直感的に我々が経験していることと合致します。レジの運営としては、客がなるべく均等な到着間隔で来てくれた方が効率的ですが、しかしそうはならない。それが "ランダム" ということです。
到着間隔の累積分布関数
確率変数を \(X\)、確率密度関数 \(f(x)\) とします。問題にしている到着間隔は \(0\) 以上なので、\(X\geq0\) とします(一般的には \(-\infty< X < \infty\) です)。累積分布関数 \(F(x)\) とは
\(\begin{eqnarray}
&&F(x)&=P(0\leq X\leq x)\\
&&&=\displaystyle\int_{0}^{x}f(t)dt\\
\end{eqnarray}\)
で定義される「確率密度を累積した値」です。確率密度は正の値で、\(\infty\)まで積分すると \(1\) になるので、累積分布関数は \(0 < F(x) < 1\) の単調増加関数です。\(X\) を到着間隔を表す確率変数とすると確率密度関数は指数分布になりますが、この累積分布関数を求めると、
\(\begin{eqnarray}
&&F(t)&=P(X\leq t)\\
&&&=\displaystyle\int_{0}^{t}\lambda e^{-\lambda x}dx\\
&&&=1-e^{-\lambda t}\\
\end{eqnarray}\)
となります。\(\lambda=24\) の場合(平均到着間隔が 2分30秒の場合)に \(F(t)\) が \(0.5\) となる時間 \(T_5\) を計算してみると、
\(T_5=0.029\)
となります。\(0.029(h)\) は1分43秒です。これは、
到着間隔の平均は2分30秒だが、1分43秒以内に \(0.5\) の確率で次の客が到着する
ことを意味します。しかも指数分布の形に見るように到着間隔が短い方が確率が高い。これがランダムに到着する場合の姿です。
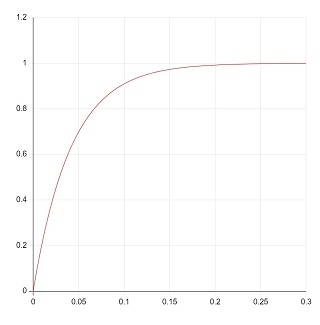
|
到着間隔の累積分布関数 |
\(\lambda=\:24(/h)\)。 横軸の単位は時間\((h)\)。\(0.05\) が\(3\)分。縦軸が \(F(t)\) の値である。到着間隔の平均(\(2\)分\(30\)秒)は \(0.05\) のすぐ左のところだが、そこでの \(F(t)\) の値は \(0.63\) 程度になる。 |
シミュレーション
到着間隔と退出間隔の確率密度関数が求まったので、これを用いてパソコンでシミュレーションをしてみます。そのためには「確率密度関数に従う乱数」を発生させなければなりません。
パソコンのプログラミング言語には「一様分布の乱数」を発生させる関数があるので(random / rand などの名称)、これを「到着間隔や退出間隔の確率密度をもつ乱数」に変換することを考えます。
まず「一様分布」ですが、確率変数 \(U\:(0\leq U\leq1)\) が一様分布とは、確率密度が一定値のものです。つまり、
| 確率密度関数 \(f(x)=1\) | |
| 累積分布関数 \(F(x)=\:P(U\leq x)=x\) |
となる分布です(下図)。
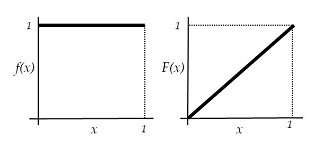
|
一様分布 |
確率密度関数(左)と累積分布関数(右) |
今、分析したい確率変数 \(X\) の確率密度関数を \(f(x)\)、その累積分布関数を \(F(x)\:(0\leq F(x)\leq1)\) とします。そして \(F(x)\) の逆関数 \(F^{-1}(x)\) を作り、
\(Y=F^{-1}(U)\)
とおくと、この \(Y\) は「確率密度関数 \(f(x)\) をもつ確率変数」となります。その理由は以下の通りです。\(Y\) の累積分布関数、\(P(Y\leq x)\) は、
\(P(Y\leq x)=P(F^{-1}(U)\leq x)\)
と書けますが、\(F\) は単調増加関数なので、右辺の \(F^{-1}(U)\leq x\) の条件は、
\(F(F^{-1}(U))\leq F(x)\)
としても同じことです。すなわち、
\(U\leq F(x)\)
と表せます。従って、
\(P(Y\leq x)=P(U\leq F(x))\)
となりますが、\(U\) は一様分布の確率変数なので、上式の右辺は、
\(P(U\leq F(x))=F(x)\)
であり(上の一様分布の説明参照)、この結果、
\(P(Y\leq x)=F(x)\)
が得られます。この式は「確率変数 \(Y\) の累積分布関数は \(F(x)\)」という意味であり、従って \(Y\) の確率密度関数が \(f(x)\) であることが分かりました。この方法で特定の確率密度をもつ乱数を発生させる手法を「逆関数法」と呼びます。
到着間隔の累積分布関数は、
\(F(t)=1-e^{-\lambda t}\)
でした。この式を \(t\) について解くと、
\(t=-\dfrac{1}{\lambda}\mr{log}(1-F(t))\)
です。従って \(F(t)\) の逆関数、\(F^{-1}(t)\) は
\(F^{-1}(t)=-\dfrac{1}{\lambda}\mr{log}(1-t)\)
です。このことから \(u\) を一様分布の乱数として、
到着間隔の確率密度を持つ乱数 =
\(-\dfrac{1}{\lambda}\mr{log}(1-u)\)
\(-\dfrac{1}{\lambda}\mr{log}(1-u)\)
と計算できます。同様に、
退出間隔の確率密度を持つ乱数 =
\(-\dfrac{1}{\mu}\mr{log}(1-u)\)
\(-\dfrac{1}{\mu}\mr{log}(1-u)\)
です。この2式を使ってシミュレーションを実行できます。
シミュレーション:例1(1時間)
パソコンを使って、客がいない状態から1時間のシミュレーションしてみます。\(\lambda=24\)、\(\mu=60\) とします。その結果の一例が次の表です。これは、
| 時刻(開始からの経過時間) | |
| 発生イベント(到着が退出か) | |
| イベント後の行列人数 | |
| 次のイベントまでの時間 |
を表にしたものです。このシミュレーションは開始から1時間が経過した直後のイベント(="到着"。時刻 61分02秒)で止めてあります。この間に22人の到着があり、21人が退出しました。22人目が到着する直前の行列の人数は 0 です。行列の最大人数は 4人(37′19″からの 45″間)になりました。
| 時刻 | イベント | 列 | 時間 |
| 0′00″ | --- | 0 | 5′40″ |
| 5′40″ | 到着 | 1 | 0′11″ |
| 5′51″ | 退出 | 0 | 2′11″ |
| 8′02″ | 到着 | 1 | 1′03″ |
| 9′05″ | 退出 | 0 | 7′29″ |
| 16′35″ | 到着 | 1 | 0′44″ |
| 17′18″ | 退出 | 0 | 0′33″ |
| 17′51″ | 到着 | 1 | 3′00″ |
| 20′51″ | 退出 | 0 | 1′54″ |
| 22′45″ | 到着 | 1 | 0′02″ |
| 22′48″ | 到着 | 2 | 0′13″ |
| 23′01″ | 退出 | 1 | 0′30″ |
| 23′31″ | 退出 | 0 | 5′32″ |
| 29′03″ | 到着 | 1 | 2′27″ |
| 31′30″ | 退出 | 0 | 0′13″ |
| 31′42″ | 到着 | 1 | 0′33″ |
| 32′16″ | 退出 | 0 | 3′18″ |
| 35′34″ | 到着 | 1 | 1′03″ |
| 36′37″ | 到着 | 2 | 0′19″ |
| 36′55″ | 到着 | 3 | 0′24″ |
| 37′19″ | 到着 | 4 | 0′45″ |
| 38′04″ | 退出 | 3 | 0′02″ |
| 38′06″ | 退出 | 2 | 0′38″ |
| 38′45″ | 退出 | 1 | 1′00″ |
| 39′45″ | 到着 | 2 | 0′46″ |
| 40′31″ | 退出 | 1 | 0′02″ |
| 40′34″ | 退出 | 0 | 0′10″ |
| 40′44″ | 到着 | 1 | 0′32″ |
| 41′15″ | 退出 | 0 | 0′39″ |
| 41′55″ | 到着 | 1 | 0′04″ |
| 41′58″ | 退出 | 0 | 4′28″ |
| 46′26″ | 到着 | 1 | 0′43″ |
| 47′10″ | 到着 | 2 | 0′08″ |
| 47′18″ | 退出 | 1 | 1′14″ |
| 48′31″ | 到着 | 2 | 0′29″ |
| 49′00″ | 到着 | 3 | 0′53″ |
| 49′53″ | 退出 | 2 | 1′32″ |
| 51′25″ | 退出 | 1 | 0′16″ |
| 51′41″ | 退出 | 0 | 2′57″ |
| 54′38″ | 到着 | 1 | 0′10″ |
| 54′48″ | 到着 | 2 | 0′53″ |
| 55′41″ | 退出 | 1 | 0′14″ |
| 55′54″ | 退出 | 0 | 5′08″ |
| 61′02″ | 到着 | 1 | --- |
この表の「イベント後の行列人数」と「次のイベントまでの時間」から「行列が \(n\)人(\(n\geq0\))の時間合計」を求められます。それを計算したのが次の表です。
| 行列が0人の時間合計 | 40′11″ |
| 行列が1人の時間合計 | 13′49″ |
| 行列が2人の時間合計 | 4′58″ |
| 行列が3人の時間合計 | 1′19″ |
| 行列が4人の時間合計 | 0′45″ |
| 合計 | 61′02″ |
さらに、
\(p_n(t)\) : \(t\) 時間のシミュレーションを行ったとき、行列人数が \(n\)人である時間の割合
と定義し、上の表のそれぞれの時間合計を全体のシミュレーション時間( 61′02″)で割ると、次の表が得られます。
| \(p_0(1)\):行列が0人の時間割合 | 0.658 |
| \(p_1(1)\):行列が1人の時間割合 | 0.226 |
| \(p_2(1)\):行列が2人の時間割合 | 0.082 |
| \(p_3(1)\):行列が3人の時間割合 | 0.022 |
| \(p_4(1)\):行列が4人の時間割合 | 0.012 |
このテーブルから「行列の平均人数 \(=\:L(t)\::\:t=1\) のとき 」を求めてみると、
\(L(1)=\displaystyle\sum_{n=0}^{4}np_n(1)=0.503\)
となりました。これはあくまで1時間分のシミュレーションに過ぎません。使用した乱数も、到着と退出のイベントでそれぞれ20数個程度であり、発生させた乱数は指数分布の極めて荒い近似だと推測されます。
しかし、\(p_n(t)\) の \(t\) を増やしていき、それにもとづいて \(L(t)\) を計算していくと、近似は次第に正確になっていくはずです。それが次のシミュレーションです。
シミュレーション:例2(長時間)
シミュレーションの時間を増やして \(200\) 時間分の計算を実行し、行列の平均長がどうなるかを、途中経過とともに観察します。シミュレーション時間、\(t\) を増やしたときの行列の最大人数を \(m\) とすると、行列の平均長、\(L(t)\) は、
\(L(t)=\displaystyle\sum_{n=0}^{m}np_n(t)\)
で計算できます。このシミュレーションを実行して \(L(t)\) をプロットしたのが次のグラフ(\(0\leq t\leq200\))です。もちろん、あくまで一例です。
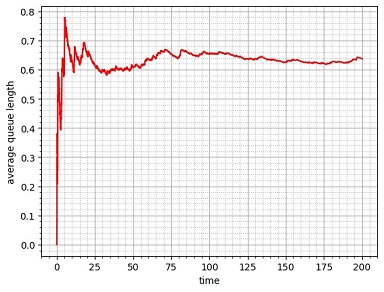
|
シミュレーション例(行列の平均長) |
\(200\)時間分のシミュレーションを行い、行列の平均長の途中経過をプロットした例。このシミュレーションでは最初の\(5\)時間までに行列が伸びる要因が重なった。グラフの形はシミュレーションのたびに変化するが、どれも \(0.6\)~\(0.7\) 付近の値に落ち着いて行く。 |
グラフから分かるように、行列の平均長は一定値(\(0.6\)~\(0.7\) 程度)に近づいていきます。これはパソコンで発生させた乱数が一様分布乱数に近づき、従って逆関数法で作った関数が指数分布に近づくからです。また初期状態(シミュレーションでは行列の人数はゼロとした)の影響がなくなることもあるでしょう。
このように時間に依存しない状態が「定常状態」であり、これが行列の平均的な姿です。
シミュレーション:例3(同一シミュレーションの平均)
乱数を使ったシミュレーションでは、1回だけの計算では値がふらつき、必ずしも正確な姿が分かりません。こういう場合は、同一のシミュレーションを多数繰り返し、その平均をとるのが一般的です。
次図に、2.5 時間分のシミュレーションを 1000 回繰り返して平均をとった例をあげます。行列の平均長が 0.66~0.68 程度に収束していく様子が見て取れます。
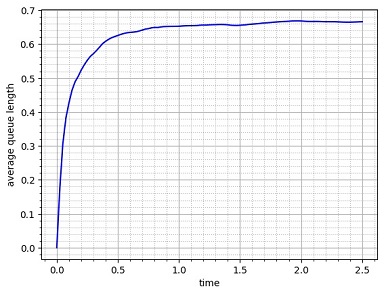
|
\(\bs{1000}\) 回のシミュレーションの平均 |
\(2.5\) 時間分のシミュレーションを \(1000\) 回繰り返して、その平均をとったグラフ。\(0.5\) 時間から1時間程度で収束値に近づく。ちなみに、このケースで最長の行列は \(9\)人であった。 |
レジ行列の微分方程式
今まではパソコンによるシミュレーションでしたが、これを数学的に厳密に解くことができます。
\(p_n(t)\) を「時刻 \(t\) において行列が \(n\)人である確率」とします。そして、時刻 \(t+\Delta t\) に \(p_n\:(t)\) がどう変化するかを考えます。まず \(p_0(t+\Delta t)\) ですが、起こり得るケースは、
\(p_0(t+\Delta t)\):
| \(p_0(t)\) から到着が起こらず \(p_0(t+\Delta t)\) になる | |
| \(p_1(t)\) から退出が起こって \(p_0(t+\Delta t)\) になる |
の2つのケースです。ここで、
\(\Delta t\) の時間で到着が起こる確率は \(\lambda\Delta t\)
\(\Delta t\) の時間で退出が起こる確率は \(\mu\Delta t\)
\(\Delta t\) の時間で退出が起こる確率は \(\mu\Delta t\)
なので、次の式が成り立ちます。
\(p_0(t+\Delta t)=p_0(t)(1-\lambda\Delta t)+p_1(t)\mu\Delta t\)
\(\dfrac{p_0(t+\Delta t)-p_0(t)}{\Delta t}=\mu p_1(t)-\lambda p_0(t)\)
\(\dfrac{p_0(t+\Delta t)-p_0(t)}{\Delta t}=\mu p_1(t)-\lambda p_0(t)\)
\(\Delta t\rightarrow0\) の極限をとると、次の微分方程式が得られます。
\(\dfrac{dp_0(t)}{dt}=\mu p_1(t)-\lambda p_0(t)\)
次に \(p_1(t+\Delta t)\) ですが、これには3つのケースがあります。つまり、
\(p_1(t+\Delta t)\):
| \(p_0(t)\) から到着が起こって \(p_1(t+\Delta t)\) になる | |
| \(p_2(t)\) から退出が起こって \(p_1(t+\Delta t)\) になる | |
| \(p_1(t)\) から到着も退出も起こらずに \(p_1(t+\Delta t)\) になる |
の3つです。微少時間 \(\Delta t\) の間に起こるイベントは、起こったとしても一つだけであり、到着と退出が同時に起こることはないというのがそもそもの仮定でした。つまり \(\Delta t\) の時間内に起こる事象は、
| 到着が起こる | |
| 退出が起こる | |
| 到着も退出も起こらない |
のどれかであり、この3つは排他的です。従って \(\Delta t\) の間に
到着または退出が起こる確率
\(=\lambda\Delta t+\mu\Delta t\)
\(=\lambda\Delta t+\mu\Delta t\)
となります。排他的だから単純加算でよいわけです。従って、
到着も退出も起こらない確率
\(=1-\lambda\Delta t-\mu\Delta t\)
\(=1-\lambda\Delta t-\mu\Delta t\)
です。以上の考察から \(p_1(t+\Delta t)\) は次のように表現できます。
\(p_1(t+\Delta t)=\)
\(p_0(t)\lambda\Delta t+p_2(t)\mu\Delta t+p_1(t)(1-\lambda\Delta t-\mu\Delta t)\)
\(p_0(t)\lambda\Delta t+p_2(t)\mu\Delta t+p_1(t)(1-\lambda\Delta t-\mu\Delta t)\)
\(\dfrac{p_1(t+\Delta t)-p_1(t)}{\Delta t}=\)
\(\lambda p_0(t)+\mu p_2(t)-(\lambda+\mu)p_1(t)\)
\(\lambda p_0(t)+\mu p_2(t)-(\lambda+\mu)p_1(t)\)
\(\dfrac{dp_1(t)}{dt}=\lambda p_0(t)+\mu p_2(t)-(\lambda+\mu)p_1(t)\)
従って、一般の \(p_n(t)\:(n\geq2)\) では、
\(\dfrac{dp_{n-1}(t)}{dt}=\lambda p_{n-2}(t)+\mu p_n(t)-(\lambda+\mu)p_{n-1}(t)\)
と表現できます。以上をまとめると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\dfrac{dp_0(t)}{d}=\mu p_1(t)-\lambda p_0(t)&\\
&&\dfrac{dp_{n-1}(t)}{dt}=\lambda p_{n-2}(t)+\mu p_n(t)-(\lambda+\mu)p_{n-1}(t)&\\
\end{eqnarray}
\end{array}\right.\)
の2つの微分方程式によって、レジ行列の挙動が決まることが分かりました。
ここで、シミュレーションで確認したような "定常状態" での確率を求めます。定常状態では確率は時間的に変化しないので、上の2つの微分方程式の左辺はゼロになります。\((t)\) をなくして式を整理すると、
\(\left\{
\begin{array}{l}
\begin{eqnarray}
&&\mu p_1=\lambda p_0&\\
&&\mu p_n=(\lambda+\mu)p_{n-1}-\lambda p_{n-2}&\\
\end{eqnarray}
\end{array}\right.\)
ですが、ここで、
\(\rho=\dfrac{\lambda}{\mu}\)
と定義します。\(\rho\) は「稼働率」を呼ばれる数値です。レジ行列のモデルで仮定したように \(\lambda< \mu\) なので、
\(\rho< 1\)
です。この \(\rho\) を使って式を書き直すと、
| \(p_1=\rho p_0\) | (1式) | |
| \(p_n=(1+\rho)p_{n-1}-\rho p_{n-2}\) | (2式) |
となります。ここで(2式)を次のように変形します。
\(p_n-p_{n-1}=\rho(p_{n-1}-p_{n-2})\)
これは数列 \((p_n-p_{n-1})\) が、初項 \((p_1-p_0\:)\) 、公比 \(\rho\) の等比数列であることを示しています。(1式)より \(p_1=\rho p_0\) なので、初項 \((p_1-p_0\:)\) は \(p_0(\rho-1)\) と表現できます。従ってこの等比数列の一般項は、
\(p_n-p_{n-1}=p_0(\rho-1)\rho^{n-1}\) (3式)
です。この式から \(p_n\) の形を求めます。以降の計算では高校数学で習う「等比数列の和の公式」を使います。つまり、
初項 \(a\)、公比 \(r\) の等比数列の第 \(1\)項から第 \(n\)項までの和は \(a\cdot\dfrac{1-r^n}{1-r}\) |
という公式です。(3式)の両辺の \(n=1\cd n\) の和をとると、
| \(p_n-p_0\) | \(=p_0(\rho-1)\dfrac{1-\rho^n}{1-\rho}\) | |
| \(=\:p_0\rho^n-p_0\) |
\(p_n=\:p_0\rho^n\) (4式)
が得られます。ここで \(p_n\) は確率なので、その総和をとると \(1\) になるはずです。(4式)の両辺の \(n=1\cd n\) の和をとると、
\(\displaystyle\sum_{k=0}^{n}p_k=p_0\displaystyle\sum_{k=0}^{n}\rho^k=p_0\dfrac{1-\rho^{n+1}}{1-\rho}\)
となります。ここで \(n\rightarrow\infty\) とすると、\(\rho< 1\) なので、
\(1=\dfrac{p_0}{1-\rho}\)
\(p_0=1-\rho\) (5式)
\(p_0=1-\rho\) (5式)
となります。(5式)を(4式)に代入すると、
\(p_n=(1-\rho)\rho^n\) (6式)
が得られました。(6式)が定常状態で列に \(n\)人が並ぶ確率です。ちなみに(5式)において \(p_0\) は、定常状態で「列に \(0\)人が並ぶ確率」であり、つまり、
レジ係りが客待ちの状態である確率は \(1-\rho\)
ということに他なりません。\(\rho\) が(レジ係の)稼働率であるゆえんです。
行列の平均長
(6式)で行列の人数ごとの確率が求まったので、行列の平均長を計算することができます。つまり、
\(np_n\:(0\leq n)\)
の総合計が行列の平均長(\(=L\))です。
\(L=\displaystyle\sum_{n=0}^{\infty}np_n=\displaystyle\sum_{n=0}^{\infty}n(1-\rho)\rho^n\)
ここで \(S_n\) を、
\(S_n=\displaystyle\sum_{k=0}^{n}kp_k=(1-\rho)\displaystyle\sum_{k=0}^{n}k\rho^k\)
と定義すると、
\(\rho S_n=(1-\rho)\displaystyle\sum_{k=0}^{n}k\rho^{k+1}\)
です。従って、
\(S_n-\rho S_n\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=0}^{n}k\rho^k-\displaystyle\sum_{k=0}^{n}k\rho^{k+1}\right)\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=1}^{n}k\rho^k-\displaystyle\sum_{k=1}^{n+1}(k-1)\rho^k\right)\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=1}^{n}\rho^k-n\rho^{n+1}\right)\)
\((1-\rho)S_n\)
\(=(1-\rho)\left(\rho\dfrac{1-\rho^n}{1-\rho}-n\rho^{n+1}\right)\)
\(S_n=\rho\dfrac{1-\rho^n}{1-\rho}-n\rho^{n+1}\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=0}^{n}k\rho^k-\displaystyle\sum_{k=0}^{n}k\rho^{k+1}\right)\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=1}^{n}k\rho^k-\displaystyle\sum_{k=1}^{n+1}(k-1)\rho^k\right)\)
\(=\:(1-\rho)\left(\displaystyle\sum_{k=1}^{n}\rho^k-n\rho^{n+1}\right)\)
\((1-\rho)S_n\)
\(=(1-\rho)\left(\rho\dfrac{1-\rho^n}{1-\rho}-n\rho^{n+1}\right)\)
\(S_n=\rho\dfrac{1-\rho^n}{1-\rho}-n\rho^{n+1}\)
と計算できます。ゆえに、行列の平均長 \(L\) は、
\(L=\displaystyle\lim_{n\rightarrow\infty}S_n=\dfrac{\rho}{1-\rho}\)
となります。
平均待ち時間
次に、客が行列に到着してから会計が始まるまでの時間、「平均待ち時間(=\(W\))」を計算してみます。これは、
平均待ち時間 =
列に到着したときに、既に列に並んでいる人全員の会計が終る平均時間
であり、ということは、
平均待ち時間 =
| レジ行列の平均長さ)\(\times\)(1人の平均会計時間) |
です。平均会計時間は \(\dfrac{1}{\mu}\) なので、
\(W=\dfrac{1}{\mu}\cdot\dfrac{\rho}{1-\rho}\)
となります。以上でレジ行列の数学的な解析ができました。
スーパーのレジ行列の分析
今までの数学的分析をまとめると、
| 客の平均到着数 \(\lambda\) (単位時間当たり) | |
| レジ係の平均会計数 \(\mu\) (単位時間当たり) | |
| 稼働率 \(\rho=\dfrac{\lambda}{\mu}\) |
のとき、レジ行列の平均長 \(L\) と平均待ち時間 \(W\) は、
| \(L=\dfrac{\rho}{1-\rho}\) | |
| \(W=\dfrac{1}{\mu}\cdot\dfrac{\rho}{1-\rho}\) |
で求めることができます。
最初に提示したスーパーのレジ係りの人数に戻ります。レジ係り一人あたり1時間あたりの平均の会計処理数は、\(\mu=60\) です(1人の客につき1分で処理)。現状(変更前)はレジ係り2人でそれぞれ24人の客を1時間あたりこなしているが、レジ係を1人にしたらどうなるかが問題でした。それを計算すると次のようになります。
変更前(レジ係2人)
| \(\mu\) | \(=60\) | |
| \(\lambda\) | \(=24\) | |
| \(\rho\) | \(=0.4\) | |
| \(L\) | \(=0.67\) | |
| \(W\) | \(=40\) 秒 |
変更後(レジ係1人)
| \(\mu\) | \(=60\) | |
| \(\lambda\) | \(=48\) | |
| \(\rho\) | \(=0.8\) | |
| \(L\) | \(=4.0\) | |
| \(W\) | \(=4\) 分 |
つまりレジ係を半分に変更すると、変更前と比べて平均の行列長さ(\(L\))も平均待ち時間(\(W\))も6倍になります。店長の "せいぜい2倍程度だろう" という直感は、全くの "外れ" であることが分かります。
ちなみに、変更前(レジ係2人)の行列の平均長、\(L=0.67\) は、シミュレーション(例3)と一致しています。また、変更後(レジ係1人)の場合の平均長は理論上、\(L=4.0\) ですが、シミュレーションをしてみると次図ようになり、理論と一致します。
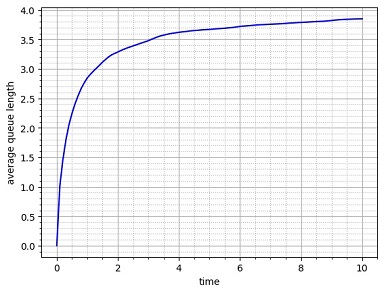
|
変更後の行列平均長(\(\bs{1000}\) 回の平均) |
\(10\) 時間分のシミュレーションを \(1000\) 回繰り返し、その平均をとったグラフ。\(4\)時間程度で収束値に近づく。ちなみに、このケースで最長の行列は \(50\)人であった。\(1000\) 回も繰り返すと、中には "長蛇の列" が発生する。 |
\(L\) も \(W\) も、稼働率 \(\rho\) が \(1\) に近づくと急激に上昇します。その様子をグラフにしたのが次です。
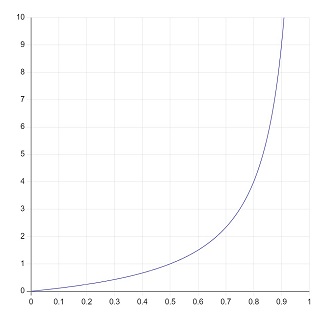
|
稼働率と行列の平均長の関係 |
稼働率 \(\rho\)(横軸)が \(1\) に近づくと、行列の平均長 \(L\)(縦軸)は急激に増える。 |
現象の本質が "ランダム" である場合、往々にして我々の直感がはずれます。上の例で変更後の稼働率が \(0.8\) ということは、レジ係りの時間の \(20\:\%\) は客待ち時間だというとです。それでも、客の視点からすると会計待ちの時間が大幅に延びる。このような問題では平均で考えると落とし穴にはまります。
以上のスーパーのレジの分析は「待ち行列理論」の初歩のそのまた第1歩です。世の中には「窓口」がいろいろあって、そこに並んで何らかの「サービス」を受けることが多々あります。「窓口」は、人が対応しない自販機でも ATM でも同じです。もっと一般化すると、サービス提供主体があり、サービスを受けようとする主体が複数あると "待ち行列" の問題が発生します。コールセンターに電話すると「ただいま込み合っております。そのまましばらくお待ちください」という自動応答が返ってくることがありますが、同じことです。
またコンピュータシステムにおいては、多数の処理要求に対して複数のサーバーが対応するケースが多々あります。Webによるチケットの予約システムなどはその典型でしょう。もっと広く考えると、現代のインターネットは世界中に何10億というサーバー資源(アプリケーション・サーバ、ファイル・サーバ、ルーター、・・・・・・)があり、そのサービスを受けようとする何億人かの "客" で構成されている巨大ネットワーク・システムだと言えるでしょう。その各所で、実は微少な「待ち行列」が発生しています。
そういった、世の中に多数ある "システム"(人間系・コンピュータ系)を設計する根幹のところに「待ち行列理論」があるのでした。
2022-01-22 09:50
nice!(0)



