No.344 - 算数文章題が解けない子どもたち [社会]
No.234「教科書が読めない子どもたち」は、国立情報学研究所の新井紀子教授が中心になって実施した「全国読解力調査」(対象は中学・高校生)を紹介したものでした。
この調査の経緯ですが、新井教授は日本数学会の教育委員長として、大学1年生を対象に「大学生数学基本調査」を実施しました。というのも、大学に勤める数学系の教員の多くが、入学してくる学生の学力低下を肌で感じていたからです。この数学基本調査で浮かび上がったのは、そもそも「誤答する学生の多くは問題文の意味を理解できていないのでは」という疑問だったのです。
そこで本格的に子どもたちの読解力を調べたのが「全国読解力調査」でした。その結果は No.234 に概要を紹介した通りです。
ところで最近、小学生の学力の実態を詳細に調べた本が出版されました。慶応義塾大学 環境情報学部教授の今井むつみ氏(他6名)の「算数文章題が解けない子どもたち ── ことば・思考の力と学力不振」(岩波書店 2022年6月)です(以下「本書」と記述)。新井教授の本とよく似た(文法構造が全く同じの)題名ですが、触発されたのかもしれません。
新井教授は数学者ですが、本書の今井教授は心理学者であり、認知科学(特に言語の発達)や教育心理学が専門です。いわば、読解力を含む「学力」とは何かを研究するプロフェッショナルです。そのテーマは「算数文章題」で、対象は小学3年生・4年生・5年生です。
私は教育関係者ではないし、小学生ないしは就学前の子どもがあるわけでもありません。しかしこの本を大変に興味深く読みました。その理由は、
と感じたからです。著者にそこまでの意図はなかったと思いますが、そういう風にも読める。ということは、要するに "良い本" だということです。そこで是非とも、本書の "さわり" を紹介したいと思います。以下の引用では、原文にはない下線や段落を追加したところがあります。また引用した問題文の漢字には、本書ではルビがふってありますが、省略しました。
問題意識
まず、本書の冒頭に次のように書いてあります。
著者(たち)は広島県教育委員会から「小学生の学力のベースとなる能力を測定し、学力不振の原因を明らかにすることができるアセスメントテストの作成」を依頼されました。県教委からは次のようにあったそうです(この引用の太字と下線は原文通りです)。
その「つまずいている子どもが なぜつまずいているのか」を知る目的で、著者は認知科学と教育心理学の長年の研究成果をもとに、2種類の「たつじんテスト」を開発しました。
の2つです。そして
の成績と「たつじんテスト」の成績の相関関係を統計的に明らかにしました。また、相関関係をみるだけでなく、子どもたちの誤答を詳細に分析し「なぜつまずいているのか」を明らかにしました。この詳細分析が最も重要な点だと言えるでしょう。
本書には「算数文章題テスト」と、2つの「たつじんテスト」の内容、誤答の分析、「算数文章題テスト」と「たつじんテスト」の相関関係、学力を育てる家庭環境とは何かなどが書かれています。それを順に紹介します。
算数文章題テスト
算数文章題テストは、広島県福山市の3つの小学校の3・4・5年生を対象に行われました。調査参加人数は、3年生:167人、4年生:148人、5年生:173人でした。問題は3・4年生用と5年生用に分かれています。
3・4年生用の算数文章題は8問です。いずれも教科書からとられたもので、
です。具体的な問題は次の通りでした。
これらの問題の正答率は次の通りでした。
本書では、このような全体の成績だけでなく、誤答を個別に分析し、誤答を導いた要因(= 子どもの認知のあり方)を推測しています。その例を2つ紹介します。
問題1(列の並び順)
問題1は小学1年の教科書から採られた問題ですが、正答率が衝撃的に低くなりました。3年生の正答率は30%を切り、4年生でも半分程度しか正解できていません
ちなみに、同じ問題を5年生もやりましたが、正答率は72.3% でした。つまり5年生になっても3割の子どもが間違えたわけで、これも衝撃的です。3・4年生の代表的な誤答を調べると次のようになります。まず、
という回答をした子がいます。2桁と1桁の掛け算は正確にできていますが、このタイプの子どもは「文の意味を深く考えず、問題文にある数字を全部使って式を立て、計算をして、何でもよいから答えを出そうという文章題解決に対する考え方を子どもがもっている可能性が高い」(本書)わけです。
そもそも「問題文の状況のイメージを式にできない」子どもがいることも分かりました。問題文のイメージをつかむために、回答用紙に図を描いた子どもはたくさんいます。つまり、14人の列の一人一人を ○ で描いた子どもです。しかしそれをやっても、問題文を正しく絵に出来ない子どもがいる。文章に書かれていることの意味を読み取れないのです。さらに、誤答の中に、
というのがありました。問題文に現れる人数を表す数字は 14 と 7 の2つだけです。従って上のような式になった。この子は「文章に現れる数字(だけ)を使って回答しなければならないという誤ったスキーマ」を持っていると考えられます。
ここで言うスキーマとは認知心理学の用語で「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。言うまでもなく正しい式は、
ですが、式には人数として 1 という、文章には現れない数字が必要であり、それを文章から読み取る必要があるわけです。
また、14 - 7 = 7 (答)7人 という回答をした子どもの中には、正しい図を描いた子もいました。このような誤答は「メタ認知能力」が働いていないと考えられます。
メタ認知能力とは「自分をちょっと離れたところから俯瞰的に眺め、自分の知識の状態や行動を客観的に認知する能力」のことです。批判的思考ができる能力と言ってもよいでしょう。7人が正しい答えかどうか、正しい図を書いているのだから「振り返ってみれば」分かるはずなのです。
問題2(必要ケーキ数)
この問題で多かった誤答の例を2つあげると次のようです。まず、
という答です。この回答は、問題文にある最初の2つの数字だけをみて、しかも問題文を勝手に読み替えています。つまり「ケーキを 4つ入れた箱から 2つを配ると何個残りますか」というような問題に読み替えている。問題文の読み取りが全くできていません。
という答もありました。もちろん問題2の正答は、
ですが、4 × 2 = 8、8 × 3 = 24 という2段階の思考が必要です。このような「マルチステップの認知処理上の負荷を回避する」傾向が誤答を招いた例がよくありした。
本書に「作業記憶と実行機能をうまく働かせられていない」と書いてあります。この問題に正答するためには、4 × 2 = 8 の「8こ」をいったん「作業記憶」にいれ、次には作業記憶の 8 と問題文の 3 だけに着目して(4 と 2 は忘れて)掛け算をする必要があります。心理学で言う「実行機能」の重要な側面は「必要な情報だけに集中し、余計な情報を無視できる認知機能」です。誤答する子どもはこれができないと考えられます。
5年生用の算数文章題は8問です。このうち問題1、4、5、6は3・4年生用の問題と共通です。まとめると次の通りです。
正答率は次の通りでした。
問題12:お菓子の量の問題
誤答の分析から1つだけを紹介します。問題12「お菓子の量の問題」に次のような回答がありました。以下の(図)は、回答用紙の(図)欄に子どもが書いたコメントです。
この回答を書いた子どもは増量の意味が分かっています。30% が 0.3 だということも分かっている。「答は増えるはずだ」という「メタ認知」もちゃんと働いています。しかも、小数での割り算(250 ÷ 0.3)もできて、おおよそですが合っています。何と、本当は掛け算にすべきだということまで分かっている!! そこまで分かっているにも関わらず、正しい立式ができていません。言うまでもなく正しい式は、
ですが、この問題の文章に 1.3 という数字はありません。この子は 30% 増量が 1.3 倍だということが思いつかなかったのです。ないしは2番目の立式のような「マルチステップの思考」ができなかったのです。
この例のように、算数文章題が苦手な子どもは「文章に書かれていない数字を常識で補って推論する」ことがとても苦手です。読解力で大切なのは「文章で使われている言葉の意味をきちんと理解し、常識を含む自分の知識で "行間を補う"」ことなのですが、誤答した多くの子どもはそれができないのです。
算数文章題の誤答分析
以上は3つの誤答の例ですが、3・4・5年生の誤答の全体を分析すると次のようになります。
まず、典型的な誤答では、小数や分数などの数の概念が理解できていないことが顕著でした。小数や分数を理解するためには、整数・分数・小数という演算間の関係性の理解、つまり「数」という "システム" の理解が必要ですが、それが全くできていないのです。つまり「数」の知識が「システム化された数の知識」になっていない。
また時間の計算においては「秒・分・時間・日」の単位変換が苦手なことが顕著でした(3・4・5年生の問題4の正解率参照)。これも「秒・分・時間・日」の概念をバラバラに覚えているだけで「システム化された知識」になっていないのが原因と考えられます。
また、しばしばある誤答の理由は、文章の読みとり(=読解)ができず、従って文章に描かれている状況がイメージできないという点です。その「読解ができない」ことの最大の要因は、推論能力が足りないことです。文章に書かれていないことを、自分のスキーマに従って補って推論する力が足りないのです。
さらに、多くの子供たちが「足し算とかけ算は数を大きくする、引き算と割り算は数を小さくするという誤ったスキーマ」をもっていることが見て取れました。
「誤ったスキーマ」の最たるものが「数はモノを数えるためにある」というスキーマです。数学用語を使うと「すべての数は自然数である」というスキーマです。このスキーマをもっていると、分数・小数の理解が阻害され、その結果として誤答を生み出す。
以上のような要因に加え、作業記憶が必要なマルチステップの問題や、実行機能(ある部分だけを注視して他を無視するなど)が必要な問題では、それによる「認知的負荷」が複合的に加わって、それが誤答を生み出しています。認知的負荷が高いと誤ったスキーマが顔を出す傾向も顕著でした。
ことばのたつじん
「ことばのたつじん」は、算数文章題に答えるための "基礎的な学力" と想定できる「言語力」の測定をするものです。これには、
の3つがあります。
これは "一般的な語彙力" をみるテストで、
の3種があります。「ことばの意味」は30問からなり、そのうちの25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。その例をあげます。
標準問題の例
チャレンジ問題の例
「にていることば」も30問からなり、25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。
標準問題の例
チャレンジ問題の例
「あてはまることば」は、慣用句や慣習的な比喩表現、一つの語から連想される "共起語" の知識をみるものです。29問の「標準問題」(3つの選択肢から1つの正解を選ぶ)と、5問の「チャレンジ問題」(4つの選択肢から2つの正解を選ぶ)から成ります。その例をあげます。
標準問題の例
チャレンジ問題の例
特に成績が悪かった問題の一つは、「ことばのいみ」の中の「期間」を正解とする、次の標準問題でした。
3年生の正答率は「きかん(=正解)」が64%、「きげん」が26%、4年生では「きかん(=正解)」が75%、「きげん」が23% でした。「きかん」と「きげん」と誤答するのは、
といった要因が複合していると推測されます。これらの要因があると正答率が下がるのは「にていることば」でも同様でした。本書に次のような記述があります。
①「語彙の深さと広さ」は一般的な語彙の知識のテストでしたが、②「空間・時間のことば」は、"空間ことば"(前後左右など)と "時間ことば"(2日前、5日後、1週間先など)に絞って、それらを状況に応じて柔軟かつ的確に運用できるかをみるテストです。その例を引用します。
宝物さがし問題(自分と同じ視点)
宝物さがし問題(自分と逆の視点)
この2つの問題の正答率は
でした。全般的に「空間ことば」の問題では、単純な質問では正しく答えられる子どもが多いのですが、上に引用した「宝探し問題」、特に「自分と逆の視点」では正答率が下がります。
「自分と逆の視点」に正解するためには、「視点変更能力」(= 自分以外の視点でものごとを見る力)や、「作業記憶」を使う認知能力、自分の視点を抑制する「実行機能」が必要です。つまり問題解決に必要な情報全体に目配りをしつつ部分を統合する必要があり、それが、部分部分の知識を「生きた知識」として活用できることなのです。
「生きた知識」を持っているかどうかは、他の情報との統合を必要とする "認知の負荷が高い状況" で、個々のことばの知識を本当に使えるのかを評価する必要があることがわかります。
カレンダー問題
上の例では「ちょうど一週間後」を聞いていますが、問題の全体では「あした・ちょうど一週間後・きのう・2日前・5日後・来週の月曜日・ちょうど1週間前・先週の月曜日・5日先・2日後・1週間先・2日先・5日前」の13種の日が、カレンダーでどの日に当たるかを質問しました。
著者は「この問題の正答率の低さに驚いた」と書いています。正答率の低い原因は、時間の関係を表す「前」「後」「先」が "分かりにくい" からです。その理由を著者は次のように書いています。
「先」ということばも曲者です。「さっき言ったでしょう」の「先」は過去ですが、「1週間さき」の「先」は未来です。また、同じ漢字を使う「先週」は過去です。耳からの言葉で覚えた子どもが「さっき」と「さき」を混同するのは分かるし、同じ「先」を使う「先週」を未来だと誤認するのも分かるのです。ちなみに、日本語を母語としない外国人にとって「先」にはとても苦労するそうです。
時間は目に見えない抽象概念であり、もともと子どもには理解しづらいものです。それに加え、日本語では「未来 → 過去」と「過去 → 未来」という2種のモデルが存在し、大人はそれを混在して使っています。子どもが "時間ことば" の理解や使用に苦労するのは当然なのです。
日常的な動作を表す動詞について、システム化された「生きた知識」をもっているかをテストするものです。たとえば、
というような、( )を埋める問題です。このタイプの問題に正答するためには、類似概念を日本語がどのように分割しているかを知っていなければなりません。たとえば身につける動作は、帽子なら「かぶる」、上着なら「きる」、パンツや靴なら「はく」です。かつ、動詞の活用の形(=文法)と統合して答える必要があります。システム化された「生きた知識」があってこそ正答できるのです。
「動作のことば」の回答を分析すると、問題ごとに正解率が大きく違うことがわかります。そして正解率が低いのは「チーズを縦に(裂いて)います」「草を鎌で(刈って)います」などの問題です。これらの動作は、小学生が日常生活で見たり、自分で行ったりすることが少ない動詞です。だから正答率が低い。
逆に、これらの動作の動詞を知っていて的確に使える子どもは、日常会話だけでなく、本などから語彙を学んでいると考えられるのです。
「ことばのたつじん」と学力の関係
「ことばのたつじん」と「算数文章題」の得点の相関係数は次のとおりでした。
この相関係数はすべて 0.1% の水準で統計的に有意(その値が偶然によってもたらされる確率が0.1% 以下)でした。
この表を見ると「ことばのたつじん」と学力(この場合は算数文章題)とが、極めて強い相関関係にあることがわかります。特に「空間・時間のことば」です。この傾向は標準学力テスト(国語・算数)との相関係数と同様でした。
かんがえるたつじん
「かず・かたち・かんがえるたつじん」(略称:かんがえるたつじん)は、子どもの思考力のアセスメントです。
の3部から構成されています。
大問1:整数の数直線上の相対位置
0 から 100 までの数直線の上に、与えられた数のだいたいの位置の目印を書き込む問題です。たとえば 18 と提示されたら、それは 20 に近いので、数直線をだいたい 5 分割して、それよりちょっと 0 に近いところに目印をつける、といった感じです。4つの小問(提示数:18, 71, 4, 23)があります。
これは「整数は相対的な大きさを示す」というスキーマを子どもたちが持っているかどうかを見るものです。このスキーマを理解していない子どもは、18 と提示されると定規を取り出して 18mm のところに目印をつけたりします。誤答をする少なからぬ子どもがそうしていました。
大問2:小数・分数の大小関係
どちらが大きいかを問う問題です。12の小問があります。5年生の平均正答率とともに引用します。
小問10、小問11、小問12 は「ケーキの12こ分と13こ分ではどちらがたくさん食べることができますか」のような "文章題" になっています。
特に正答率が悪いのは、小問2, 7, 8 です。小問2 と「同程度に難しいはず」の小問3 の正答率が高いのは(小問2 の正答率より 35% も跳ね上がっている)、小問3では「たまたま分母の数も分子の数も大きい方が大きい」からだと考えられます。
このデータは、少なからぬ子どもが分数や小数の概念的理解ができていないことを示しています。また分数や小数が、いかに直感的にとらえどころがないものかも示しています。
大問3:心的数直線上での小数・分数の相対位置
0 から 1 までの数直線があり、10分割した目盛りがついています。与えられた小数や分数が数直線上のどの位置にあるかの目印をつける問題です。6つの小問があります。
特に成績の悪かったのは、12と25でした。5年生の平均正答率では、12が 46.0%、25が 31.3% でした。
12は日常生活で頻繁に使われます。しかし正答できない子どもは、「ケーキ」のような具体的なモノが与えられずに、「1を基準にしたときにそれに対してどの割合の量なのか」という純粋な「数」としての理解ができていないのです。
25の正答率が異様に低いのは、0 から 1 の数直線に10分割した目盛りが振ってあるからです。つまり正答するためには「2目盛りを1単位としてそれが2つ」という心的操作をしなければならない。これが問題を特に難しくしています。
「1」には、モノを数えるときに「1個ある」という意味と、任意のモノを「1」として、それを分割したり比較のしたりするときの基準の意味があります。「数はモノを数えるもの」という誤ったスキーマを持っていると「基準としての1」が理解できません。この理解なしに分数や小数の意味は理解できないのです。
また大問2・大問3の誤答分析からは、誤答する子どもたちが整数・分数・小数をバラバラに理解していて、それらの関連付けがされていないことがわかります。分数の単元で分数だけ、小数の単元で小数だけという現在の小学校の教え方では「システム化」された知識の習得は難しいのです。
図形の問題です。図形を折る、隠す、回転させるという操作を心の中でできるかどうかです。具体的な問題の例をあげます。
大問4:図形を折ったときのイメージ
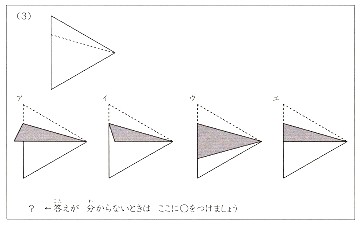
大問5:図形の隠れた部分のイメージ

大問6:図形を回転させたときのイメージ
これらの問題に正解するためには「複数のことを同時に処理しなければない」わけです。誤答を分析すると、一つの状況なら楽にできる心的操作が、複数のことを同時に処理しなければらない状況では破綻してしまい、その結果、問題解決に失敗する傾向が見て取れました。
また大問6に顕著ですが、正答する子どもは図形に補助線を引き、補助線が回転後にどうなるかを考えて答を出しています。つまり、図形の回転は認知的負荷が高いのを直感し、負荷を軽減する方略を自分で考えられたので正解できたのです。問題解決のための方略を自分で考えられるのが "できる" 子どもの特徴だと言えます。
「推論」が学力と関係しているという分析は本書のこれまでにもにありましたが、ここでは推論だけを純粋にとりあげます。問題の例を以下にあげます。
大問7:推移的推論
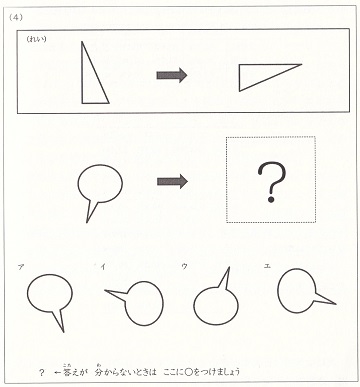
大問8:複数次元の変化を伴う類推
大問9:実行機能を伴う拡張的類推

大問9の例に関してですが、この場合の実行機能とは、注意点を取捨選択し、不要な注意点を抑制し、必要に応じて注意点を切り替えられる機能です。またこの例では見本のペアとその向きを常に短期記憶におきつつ、図の中から同じ関係のペアを見いだす必要があります。
絵の中には関係するものが複数あります。たとえば、木は葉っぱや鳥や鋸と関係がある。また糸だと、関係するのはハサミと針です。つまり「見本のペアの関係ではない関係への注意」を抑制する必要がある。これができて正解することができます。
以上の「かんがえるたつじん」と「算数文章題」の得点の相関係数は、0.37~0.48 で、高いものでした。最も高かったのが大問8(複数次元の変化を伴う類推)で、その次が 大問2(小数・分数の大小関係)でした。
算数文章題と「たつじん」テストの相関
本書には、次の6つの「たつじんテスト」、
「ことばのたつじん」
「かず・かたち・かんがえるたつじん」
の成績と、算数文章題の成績の相関係数を計算した表が本書にあります。それをみると、3・4年生では6つのテスト中5つが0.5を超え(「動作のことば」だけが0.38)、5年生では5つが 0.39~0.47の範囲になっています(「動作のことば」だけが0.3)。またすべてにおいて、0.1% 水準で有意(=全く偶然にその相関係数になるのは 0.1% 以下の確率)になっています。
ただ、6つの「たつじんテスト」は相互に相関関係があるはずなので、1つのテストが算数文章題と相関をもつと、それにつられて関係のある他のテストも算数文章題と相関します。つまり、どの「たつじんテスト」が算数文章題の成績に "利いて" いるのかは、相関係数だけでは分かりません。
そこで本書には、重回帰分析(説明変数=「たつじんテスト」の成績6種、被説明変数=算数文章題の成績)の結果が載っています。それによると、算数文章題の成績に最も寄与しているのが「空間・時間のことば」でした。これは国語と算数の標準学力テストでも同じでした。
従来からの心理学の研究で、言語能力が学力と深い関わりを持っていることが分かっていて、このことは広く受け入れられています。しかし想定されている「言語能力」とは「語彙のサイズ」(=どれだけ多くの言葉を知っているか)でした。
しかし今回の研究から、「語彙の広さと深さ」よりも「空間・時間のことばの運用」の方が頑健に「学力」を説明することがわかりました。このことは、教育現場で当たり前のようにして使われいている「言語能力」の考え方を見直す必要があることを示しています。
重回帰分析の結果から、「空間・時間のことば」の次には「推論の力」が算数文章題の成績に寄与していることも分かりました。その次が「整数・分数・小数の概念」です。
つまづきの原因
本書では全体の「まとめ」として「第6章:学習のつまずきの原因」と題した章があり、各種のテストでの誤答を分析した結果を総括し、これをもとに教育関係者への提言がされています。この中から「つまずきの原因」の何点かを紹介します。まず、
ことです。これは「たし算・引き算・かけ算・割り算」の関係性が理解できず、それぞれの計算手続きは分かるものの、問題解決に有効に使える知識になってないという意味です。それぞれの単元での学習結果が断片的な知識となっていて「数の世界の、計算というシステム」としての理解になっていない。また、
のもつまずきの原因です。算数文章題の場合、誤ったスキーマの根は一つです。それは「数はモノを数えるためのもの」というスキーマです。このスキーマをもっていると「1」が「全体を表すもの」あるいは「単位を表すもの」という概念が受け入れられません。
「足し算とかけ算は数を増やす計算」と「引き算と割り算は数を減らす計算」という誤ったスキーマもよく見られたものです。これは、まず「増やす計算」と「減らす計算」でそれぞれを教えるからだと考えれます。子どもたちは誤ったスキーマを自分で作り出してしまうのです。
似ているのが「割り算は必ず割り切れる」というスキーマです。これも 12÷4 のような割り切れる数の計算が最初に導入されるからです。誤ったスキーマをもってしまうと、答えが整数にならない割り算を教えられても、なかなか受け入れることができません。本書には「永遠の後出しじゃんけん」という表現を使って次のように書いてあります。
さらに、
のも、つまづきの要因です。「たつじんテスト」で最も強く学力を予測していたのは「空間・時間ことば」でしたが、前・後・左・右はまさに相対的であり、誰を基準にするか、どの点を基準にするかで変わってきます。
また、数直線上に与えられた数の位置を示すには、0~100 あるいは 0~1 というスケールの中で相対的に考える必要がありますが、これができない子どもが多数いました。著者は「驚くほど多かったのはショックだった」と書いています。これは「数」という概念の核である「数の相対性」が理解できていないことを端的に示しています。
「相対的にものごとを見る」ことは「視点を柔軟に変更・変換できる」ことと深い関係があります。そして視点変更の柔軟性は、ことばの多義性の理解につながります。「1」はモノが1個のことであるというスキーマをもった子どもが、「1」は「子ども 140人」でも「水 50リットル」でもよい、「全体」ないしは「単位」を表すものだという認識に進むためには、過去のスキーマの抜本的な修正が必要です。「相対的にものごとを見る能力」=「視点変更の柔軟性」は、誤ったスキーマを修正できる力に関わっています。そして誤ったスキーマを自ら修正できる力は、知識を発展させるための最重要の能力なのです。
その他、本書では
などが総括としてまとめられています。
ほんものの学力を生む家庭環境
本書では付録として、テストをうけた児童の保護者に44項目のアンケート調査をし、その結果と子どもの学力(たつじんテストと、国語・算数の標準学力テスト)の相関を示した大変に興味深い表が載っています。44項目の質問は、子どもの基本的生活習慣、家庭学習、しつけの考え方、読書習慣、小学校に入る前のひらがな・数字への関心、小学校に入る前の時間・ひらがな・数字の家庭教育など、多岐にわたります。
これらの中で、最も学力との相関が強かったのは「読書習慣・読み聞かせ」に関する3項目と、「家庭内の本の冊数」に関する2項目でした。その次に相関が強かったのは小学校入学前の「ひらがな・数字への興味・関心」の2項目と「時間・ひらがな・数字の教育」3項目でした。この結果から著者は次のように記しています。
本書の感想
最初に書いたように、本書は、
と思いました。つまり我々大人が社会で生きていく際に必要な思考力の重要な要素を示しているように感じたのです。
たとえばその一つは、「ある目的や機能を遂行する何か」を「システムとしてみる力」です。「システム」として捉えるということは、「何か」が複数のサブシステムからなり、それぞれのサブシステムは固有の目的や機能を持っている。それが有機的かつ相互依存的に結合してシステムとしての目的や機能を果たす。そのサブシステムは、さらに下位の要素からなる、という見方です。これは社会におけるさまざまな組織、自治体、ハードウェア、サービスの仕組み、プロジェクト、学問体系 ・・・・・ などなどを理解し、それらを構築・運用・発展させていく上で必須でしょう。
「相対的に考える」のも重要です。他者からみてどう見えるか、第3者の視点ではどうか、全体を俯瞰するとどうなるのか、対立項が何なのか、全体との対比で部分をみるとどうなるのか、という視点です。
そして、相対的に考える思考力は「スキーマを修正する力」につながります。本書のキーワードの一つである "スキーマ" とは「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。人は必ず何らかのスキーマに基づいて判断します。そして社会において個人が持つ「誤ったスキーマ」の典型は「自らの成功体験からくるスキーマ」です。社会環境が変化すると、そのスキーマには捨てなければならない部分や付け加えなければならないものが出てくる。本書に「スキーマを自ら修正できる力は、知識を発展させるための最重要の能力」とありますが、全くその通りです。
さらに「抽象的に考える」ことの重要性です。"良く練られた" 抽象的考えは、より一般性があり、より普遍的で、従ってよりパワーを発揮します。「抽象的でよく分からない、具体的にはどういうことか」というリクエストに答えて具体例を提示することは重要ですが、それは抽象的考えを理解する手だてとして重要なのです。
子どもは小学校から(公式に)抽象の世界に踏み出します。「言葉・語彙」がそうだし「数」がそうです。本書からの引用を再掲しますと、
とありました。抽象性の大きな壁である「9歳の壁」を乗り越えた子どもは、その次の段階へと行けます。これは中学校・高校・大学と「学び」を続ける限り、抽象性の壁を乗り越えることが繰り返されるはずです。だとすると、社会に出てからも繰り返されるはずだし、学校での「学び」はその訓練とも考えられます。
ともかく、10歳前後の小学生の誤答分析から明らかになった「学力」や「思考力」の源泉は、大人の社会に直結していると思いました。
分数は直感的に理解しづらい
最後に一つ、「分数は直感的に理解しづらい」ということの実例を書いておきます。
本書の「かんがえるたつじん ① 整数・分数・小数の概念」の「大問2:小数・分数の大小関係」のところで、テストの結果データの分析として「多くの子どもたちが、分数や小数の概念的な理解ができていない」と書かれていました。そして「これは、正答できない子どもたちの努力が足りないと片づけてよい問題ではない。分数・小数がいかに直感的に捉えどころがないものかを示すデータなのである」とも書いてありました。
分数で言うと、12や13は「任意の」モノを「1」としたとき、それを「均等に」2分割、あるいは3分割した数です。この「任意の」と「均等に」が非常に抽象的で、捉えどころがないのです。
我々大人は分数を理解していると思っているし、それを使えると思っています。大小関係も分かると自信を持っている。しかし本来「分数は直感的に捉えどころがない」のなら、それは大人にとってもそうであり、ほとんどの場合は正しく使えたとしても、何かの拍子に「捉えどころのなさ」が顔を出すはずです。
そのことを実例で示したような記述が本書にありました。「かんがえるたつじん ① 整数・分数・小数の概念」の「大問1:整数の数直線上の相対的位置」の説明のところです。どのような問題かを著者が説明した文章です。
えっ! と思いましたが、何度読み直しても、これでは 23 あたりに目印をつけることになります。本書に書いてある採点方法だと、5点満点の 3点(ないしは4点)です。
本書の著者は大学教授の方々、計7名で、原稿は著者の間で何回もレビューし、見直し、確認したはずです。岩波書店に渡った後も、原稿や校正刷りの各段階での何回ものチェックがされたはずです。それでも「100を4分割すると20」になってしまう。どの段階でこうなったかは不明ですが ・・・・・・。
これは単にケアレスミスというより、そもそも「14が分かりにくいから、ないしは15や20100が分かりにくいから」、つまり「分数は抽象的で理解しづらい概念」ということを示していると思います。子どもが算数文章題につまずく理由、その理由の一端を本書が "身をもって" 示しているのでした。
この調査の経緯ですが、新井教授は日本数学会の教育委員長として、大学1年生を対象に「大学生数学基本調査」を実施しました。というのも、大学に勤める数学系の教員の多くが、入学してくる学生の学力低下を肌で感じていたからです。この数学基本調査で浮かび上がったのは、そもそも「誤答する学生の多くは問題文の意味を理解できていないのでは」という疑問だったのです。
そこで本格的に子どもたちの読解力を調べたのが「全国読解力調査」でした。その結果は No.234 に概要を紹介した通りです。
ところで最近、小学生の学力の実態を詳細に調べた本が出版されました。慶応義塾大学 環境情報学部教授の今井むつみ氏(他6名)の「算数文章題が解けない子どもたち ── ことば・思考の力と学力不振」(岩波書店 2022年6月)です(以下「本書」と記述)。新井教授の本とよく似た(文法構造が全く同じの)題名ですが、触発されたのかもしれません。

|
新井教授は数学者ですが、本書の今井教授は心理学者であり、認知科学(特に言語の発達)や教育心理学が専門です。いわば、読解力を含む「学力」とは何かを研究するプロフェッショナルです。そのテーマは「算数文章題」で、対象は小学3年生・4年生・5年生です。
私は教育関係者ではないし、小学生ないしは就学前の子どもがあるわけでもありません。しかしこの本を大変に興味深く読みました。その理由は、
小学生の「算数文章題における学力とは何か」の探求を通して、「人間の思考力とは何か」や「考える力の本質は何か」という問題に迫っている
と感じたからです。著者にそこまでの意図はなかったと思いますが、そういう風にも読める。ということは、要するに "良い本" だということです。そこで是非とも、本書の "さわり" を紹介したいと思います。以下の引用では、原文にはない下線や段落を追加したところがあります。また引用した問題文の漢字には、本書ではルビがふってありますが、省略しました。
問題意識
まず、本書の冒頭に次のように書いてあります。
|
著者(たち)は広島県教育委員会から「小学生の学力のベースとなる能力を測定し、学力不振の原因を明らかにすることができるアセスメントテストの作成」を依頼されました。県教委からは次のようにあったそうです(この引用の太字と下線は原文通りです)。
|
その「つまずいている子どもが なぜつまずいているのか」を知る目的で、著者は認知科学と教育心理学の長年の研究成果をもとに、2種類の「たつじんテスト」を開発しました。
| ことばのたつじん」
→ ことばに関する知識を測る
| |
| かず・かたち・かんがえるたつじん」 | |
| 略称「かんがえるたつじん」)
→ 数と図形に関する知識と推論能力を測る
|
の2つです。そして
| 算数文章題テスト | |
| 主として教科書にある算数文章題) | |
| 国語・算数の標準学力テスト |
の成績と「たつじんテスト」の成績の相関関係を統計的に明らかにしました。また、相関関係をみるだけでなく、子どもたちの誤答を詳細に分析し「なぜつまずいているのか」を明らかにしました。この詳細分析が最も重要な点だと言えるでしょう。
本書には「算数文章題テスト」と、2つの「たつじんテスト」の内容、誤答の分析、「算数文章題テスト」と「たつじんテスト」の相関関係、学力を育てる家庭環境とは何かなどが書かれています。それを順に紹介します。
算数文章題テスト
算数文章題テストは、広島県福山市の3つの小学校の3・4・5年生を対象に行われました。調査参加人数は、3年生:167人、4年生:148人、5年生:173人でした。問題は3・4年生用と5年生用に分かれています。
| 3・4年生:問題とテスト結果 |
3・4年生用の算数文章題は8問です。いずれも教科書からとられたもので、
| :1年生の教科書 | |
| :3年生の教科書 |
です。具体的な問題は次の通りでした。
|
問題1 (順番) | 子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
|
問題2 (かけ算) | ケーキを4こずつ入れたはこを、1人に2はこずつ3人にくばります。ケーキは、全部で何こいりますか。 |
|
問題3 (時間の引き算1) | けんさんは、午前9時 20 分に家を出て、午前10時40分に遊園地へ着きました。家から遊園地まで、何時間何分かかりましたか。 |
|
問題4 (時間の引き算2) | えりさんは、山道を5時間10分歩きました。山をのぼるのに歩いた時間は、2時間 50 分です。山をくだるのに歩いた時間は、何時間何分ですか。 |
|
問題5 (割り算) | 1まいの画用紙から、カードが8まい作れます。45まいのカードを作るには、画用紙は何まいいりますか。 |
|
問題6 (分数) | りんさんが、ジュースを37L(リットル)のんだので、残りは27L(リットル)になりました。 はじめにジュースは、何 L(リットル)ありましたか。 |
|
問題7 (小数) | リボンが4m ありました。けんたさんが、何m か切り取ったので、リボンは1.7m になりました。けんたさんは、何m 切り取りましたか。 |
|
問題8 (倍率) | なおきさんのテープの長さは、えりさんのテープの長さの4 倍で、48 cm です。えりさんのテープの長さは何cm ですか。 |
これらの問題の正答率は次の通りでした。
| 3年生 | 4年生 | |
| 問題1 順番 | 28.1% | 53.4% |
| 問題2 かけ算 | 57.5% | 72.5% |
| 問題3 時間の引き算1 | 56.0% | 63.4% |
| 問題4 時間の引き算2 | 17.7% | 26.0% |
| 問題5 割り算 | 41.1% | 48.9% |
| 問題6 分数 | 84.4% | 87.0% |
| 問題7 小数 | 48.2% | 63.4% |
| 問題8 倍率 | 45.0% | 62.6% |
本書では、このような全体の成績だけでなく、誤答を個別に分析し、誤答を導いた要因(= 子どもの認知のあり方)を推測しています。その例を2つ紹介します。
問題1(列の並び順)
子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
問題1は小学1年の教科書から採られた問題ですが、正答率が衝撃的に低くなりました。3年生の正答率は30%を切り、4年生でも半分程度しか正解できていません
ちなみに、同じ問題を5年生もやりましたが、正答率は72.3% でした。つまり5年生になっても3割の子どもが間違えたわけで、これも衝撃的です。3・4年生の代表的な誤答を調べると次のようになります。まず、
(式)14 × 7 = 98 (答)98人 |
という回答をした子がいます。2桁と1桁の掛け算は正確にできていますが、このタイプの子どもは「文の意味を深く考えず、問題文にある数字を全部使って式を立て、計算をして、何でもよいから答えを出そうという文章題解決に対する考え方を子どもがもっている可能性が高い」(本書)わけです。
そもそも「問題文の状況のイメージを式にできない」子どもがいることも分かりました。問題文のイメージをつかむために、回答用紙に図を描いた子どもはたくさんいます。つまり、14人の列の一人一人を ○ で描いた子どもです。しかしそれをやっても、問題文を正しく絵に出来ない子どもがいる。文章に書かれていることの意味を読み取れないのです。さらに、誤答の中に、
(式)14 - 7 = 7 (答)7人 |
というのがありました。問題文に現れる人数を表す数字は 14 と 7 の2つだけです。従って上のような式になった。この子は「文章に現れる数字(だけ)を使って回答しなければならないという誤ったスキーマ」を持っていると考えられます。
ここで言うスキーマとは認知心理学の用語で「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。言うまでもなく正しい式は、
14 - 7 - 1 = 6 |
ですが、式には人数として 1 という、文章には現れない数字が必要であり、それを文章から読み取る必要があるわけです。
また、14 - 7 = 7 (答)7人 という回答をした子どもの中には、正しい図を描いた子もいました。このような誤答は「メタ認知能力」が働いていないと考えられます。
メタ認知能力とは「自分をちょっと離れたところから俯瞰的に眺め、自分の知識の状態や行動を客観的に認知する能力」のことです。批判的思考ができる能力と言ってもよいでしょう。7人が正しい答えかどうか、正しい図を書いているのだから「振り返ってみれば」分かるはずなのです。
問題2(必要ケーキ数)
ケーキを4こずつ入れたはこを、1人に2はこずつ3人にくばります。ケーキは、全部で何こいりますか。 |
この問題で多かった誤答の例を2つあげると次のようです。まず、
(式)4 - 2 = 2 (答)2こ |
という答です。この回答は、問題文にある最初の2つの数字だけをみて、しかも問題文を勝手に読み替えています。つまり「ケーキを 4つ入れた箱から 2つを配ると何個残りますか」というような問題に読み替えている。問題文の読み取りが全くできていません。
(式)4 × 3 = 12 (答)12こ |
という答もありました。もちろん問題2の正答は、
(式)4 × 2 × 3 = 24 (答)24こ |
ですが、4 × 2 = 8、8 × 3 = 24 という2段階の思考が必要です。このような「マルチステップの認知処理上の負荷を回避する」傾向が誤答を招いた例がよくありした。
本書に「作業記憶と実行機能をうまく働かせられていない」と書いてあります。この問題に正答するためには、4 × 2 = 8 の「8こ」をいったん「作業記憶」にいれ、次には作業記憶の 8 と問題文の 3 だけに着目して(4 と 2 は忘れて)掛け算をする必要があります。心理学で言う「実行機能」の重要な側面は「必要な情報だけに集中し、余計な情報を無視できる認知機能」です。誤答する子どもはこれができないと考えられます。
| 5年生:問題とテスト結果 |
5年生用の算数文章題は8問です。このうち問題1、4、5、6は3・4年生用の問題と共通です。まとめると次の通りです。
| :1年生の教科書 | |
| :3年生の教科書 | |
| :5年生の教科書、および作問したもの |
|
問題1 (順番) | 子どもが 14 人、1れつにならんでいます。ことねさんの前に7人います。ことねさんの後ろには、何人いますか。 |
|
問題4 (時間の引き算2) | えりさんは、山道を5時間10分歩きました。山をのぼるのに歩いた時間は、2時間 50 分です。山をくだるのに歩いた時間は、何時間何分ですか。 |
|
問題5 (割り算) | 1まいの画用紙から、カードが8まい作れます。45まいのカードを作るには、画用紙は何まいいりますか。 |
|
問題6 (分数) | りんさんが、ジュースを37 L(リットル)のんだので、残りは27L(リットル)になりました。 はじめにジュースは、何 L(リットル)ありましたか。 |
|
問題9 (距離の計算) | えみさんの家から学校までの距離は 3.6km で、あきらさんの家から学校までの距離より35km 遠いそうです。あきらさんの家から学校までは、何km ですか。 |
|
問題10 | こうたさんの学校の今年の児童数は 476人で、10年前の 200% に当たります。10年前の児童数は何人ですか。 |
|
問題11 | 2時間で108km 走る電車があります。この電車は、3時間で何km 進みますか。 |
|
問題12 (倍率・増量) | 250g入りのお菓子が、30%増量して売られるそうです。お菓子の量は、何gになりますか。 |
正答率は次の通りでした。
| 5年生 | |
| 問題1 順番 | 72.3% |
| 問題4 時間の引き算2 | 53.9% |
| 問題5 割り算 | 59.6% |
| 問題6 分数 | 87.2% |
| 問題9 距離の計算 | 17.7% |
| 問題10 倍率・割り戻し | 55.3% |
| 問題11 速さと距離の計算 | 66.7% |
| 問題12 倍率・増量 | 37.6% |
問題12:お菓子の量の問題
250g入りのお菓子が、30%増量して売られるそうです。お菓子の量は、何gになりますか。 |
誤答の分析から1つだけを紹介します。問題12「お菓子の量の問題」に次のような回答がありました。以下の(図)は、回答用紙の(図)欄に子どもが書いたコメントです。
(式)250 ÷ 0.3 = 800 (答え)800g (図)
ふつうならかけだけど かけにしてしまうと逆に減ってしまうので(0.3だから)÷ にしてふやす
|
この回答を書いた子どもは増量の意味が分かっています。30% が 0.3 だということも分かっている。「答は増えるはずだ」という「メタ認知」もちゃんと働いています。しかも、小数での割り算(250 ÷ 0.3)もできて、おおよそですが合っています。何と、本当は掛け算にすべきだということまで分かっている!! そこまで分かっているにも関わらず、正しい立式ができていません。言うまでもなく正しい式は、
250 × 1.3 = 325 ないしは、 250 × 0.3 = 75 250 + 75 = 325 |
ですが、この問題の文章に 1.3 という数字はありません。この子は 30% 増量が 1.3 倍だということが思いつかなかったのです。ないしは2番目の立式のような「マルチステップの思考」ができなかったのです。
この例のように、算数文章題が苦手な子どもは「文章に書かれていない数字を常識で補って推論する」ことがとても苦手です。読解力で大切なのは「文章で使われている言葉の意味をきちんと理解し、常識を含む自分の知識で "行間を補う"」ことなのですが、誤答した多くの子どもはそれができないのです。
算数文章題の誤答分析
以上は3つの誤答の例ですが、3・4・5年生の誤答の全体を分析すると次のようになります。
まず、典型的な誤答では、小数や分数などの数の概念が理解できていないことが顕著でした。小数や分数を理解するためには、整数・分数・小数という演算間の関係性の理解、つまり「数」という "システム" の理解が必要ですが、それが全くできていないのです。つまり「数」の知識が「システム化された数の知識」になっていない。
また時間の計算においては「秒・分・時間・日」の単位変換が苦手なことが顕著でした(3・4・5年生の問題4の正解率参照)。これも「秒・分・時間・日」の概念をバラバラに覚えているだけで「システム化された知識」になっていないのが原因と考えられます。
また、しばしばある誤答の理由は、文章の読みとり(=読解)ができず、従って文章に描かれている状況がイメージできないという点です。その「読解ができない」ことの最大の要因は、推論能力が足りないことです。文章に書かれていないことを、自分のスキーマに従って補って推論する力が足りないのです。
さらに、多くの子供たちが「足し算とかけ算は数を大きくする、引き算と割り算は数を小さくするという誤ったスキーマ」をもっていることが見て取れました。
「誤ったスキーマ」の最たるものが「数はモノを数えるためにある」というスキーマです。数学用語を使うと「すべての数は自然数である」というスキーマです。このスキーマをもっていると、分数・小数の理解が阻害され、その結果として誤答を生み出す。
以上のような要因に加え、作業記憶が必要なマルチステップの問題や、実行機能(ある部分だけを注視して他を無視するなど)が必要な問題では、それによる「認知的負荷」が複合的に加わって、それが誤答を生み出しています。認知的負荷が高いと誤ったスキーマが顔を出す傾向も顕著でした。
ことばのたつじん
「ことばのたつじん」は、算数文章題に答えるための "基礎的な学力" と想定できる「言語力」の測定をするものです。これには、
| 「語彙の深さと広さ」 | |
| 「空間・時間のことば」 | |
| 「動作のことば」 |
の3つがあります。
| ①「語彙の深さと広さ」 |
これは "一般的な語彙力" をみるテストで、
| ことばのいみ」 | |
| にていることば」 | |
| あてはまることば」 |
の3種があります。「ことばの意味」は30問からなり、そのうちの25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。その例をあげます。
標準問題の例
ねんどなどを 力を 入れて よく まぜること 1. まぶす 2. たたく 3. こねる |
チャレンジ問題の例
おゆが じゅうぶんに あつくなること 1. ほてる 2. ふっとうする 3. わく 4. こみあげる |
「にていることば」も30問からなり、25問は3つの選択肢から1つの正解を選ぶ「標準問題」、5問は4つの選択肢から2つの正解を選ぶ「チャレンジ問題」です。
標準問題の例
ひかくする : もちものを ひかくします。 1. ならべます 2. くらべます 3. しらべます |
チャレンジ問題の例
まず : まず 手を あらいましょう 1. 後で 2. 先に 3. はじめに 4. いちどに |
「あてはまることば」は、慣用句や慣習的な比喩表現、一つの語から連想される "共起語" の知識をみるものです。29問の「標準問題」(3つの選択肢から1つの正解を選ぶ)と、5問の「チャレンジ問題」(4つの選択肢から2つの正解を選ぶ)から成ります。その例をあげます。
標準問題の例
あつい( )を よせています。 1. しんらい 2. 親切 3. しんじつ |
チャレンジ問題の例
( )が 広いです。 1. 顔 2. かかと 3. きもち 4. 心 |
特に成績が悪かった問題の一つは、「ことばのいみ」の中の「期間」を正解とする、次の標準問題でした。
ある日から そのあとの ある日まで 何かが つづくこと 1. きげん 2. きかん 3. しゅるい |
3年生の正答率は「きかん(=正解)」が64%、「きげん」が26%、4年生では「きかん(=正解)」が75%、「きげん」が23% でした。「きかん」と「きげん」と誤答するのは、
| 発音の類似 | |
| 意味の類似 | |
| 漢語である | |
| 抽象名詞である | |
| そもそも時間の概念が抽象概念である |
といった要因が複合していると推測されます。これらの要因があると正答率が下がるのは「にていることば」でも同様でした。本書に次のような記述があります。
|
| ②「空間・時間のことば」 |
①「語彙の深さと広さ」は一般的な語彙の知識のテストでしたが、②「空間・時間のことば」は、"空間ことば"(前後左右など)と "時間ことば"(2日前、5日後、1週間先など)に絞って、それらを状況に応じて柔軟かつ的確に運用できるかをみるテストです。その例を引用します。
宝物さがし問題(自分と同じ視点)
あなたは 友だちと いっしょに 町に 来ました 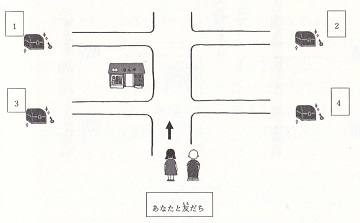 あなたが ほんやの 手前の 道を 右に まがると たからものがあります。 たからものは どこですか。 1ばん 2ばん 3ばん 4ばん |
宝物さがし問題(自分と逆の視点)
あなたは 友だちと いっしょに 町に 来ました 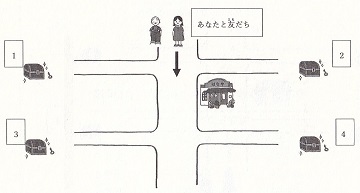 あなたが さいしょの こうさてんで 右に まがると たからものがあります。 たからものは どこですか。 1ばん 2ばん 3ばん 4ばん |
この2つの問題の正答率は
| 同じ視点 | 逆の視点 | |
| 3年生 | 59.1% | 42.7% |
| 4年生 | 72.8% | 55.0% |
でした。全般的に「空間ことば」の問題では、単純な質問では正しく答えられる子どもが多いのですが、上に引用した「宝探し問題」、特に「自分と逆の視点」では正答率が下がります。
「自分と逆の視点」に正解するためには、「視点変更能力」(= 自分以外の視点でものごとを見る力)や、「作業記憶」を使う認知能力、自分の視点を抑制する「実行機能」が必要です。つまり問題解決に必要な情報全体に目配りをしつつ部分を統合する必要があり、それが、部分部分の知識を「生きた知識」として活用できることなのです。
「生きた知識」を持っているかどうかは、他の情報との統合を必要とする "認知の負荷が高い状況" で、個々のことばの知識を本当に使えるのかを評価する必要があることがわかります。
カレンダー問題
りんちゃんの たん生日は 3月14日です。たん生日の ちょうど 一週間後は おわかれ会です。カレンダーの 中から おわかれ会の日を 一つ えらび ○をしましょう。  |
上の例では「ちょうど一週間後」を聞いていますが、問題の全体では「あした・ちょうど一週間後・きのう・2日前・5日後・来週の月曜日・ちょうど1週間前・先週の月曜日・5日先・2日後・1週間先・2日先・5日前」の13種の日が、カレンダーでどの日に当たるかを質問しました。
著者は「この問題の正答率の低さに驚いた」と書いています。正答率の低い原因は、時間の関係を表す「前」「後」「先」が "分かりにくい" からです。その理由を著者は次のように書いています。
|
|
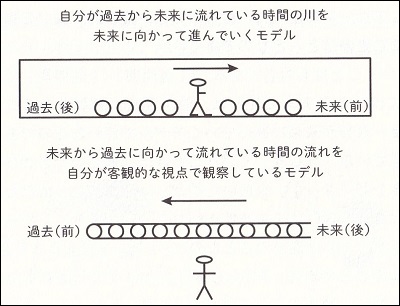
2つの時間モデル |
上のモデルでは、過去から未来への時の流れに乗って、自分が未来に向かって進んでいく。下のモデルは、未来から過去に流れる時の流れを、自分が客観的視点から観察している。この2つのモデルで「前」の意味は逆転する。日本語では2つのモデルを混在して使う。 |
「先」ということばも曲者です。「さっき言ったでしょう」の「先」は過去ですが、「1週間さき」の「先」は未来です。また、同じ漢字を使う「先週」は過去です。耳からの言葉で覚えた子どもが「さっき」と「さき」を混同するのは分かるし、同じ「先」を使う「先週」を未来だと誤認するのも分かるのです。ちなみに、日本語を母語としない外国人にとって「先」にはとても苦労するそうです。
時間は目に見えない抽象概念であり、もともと子どもには理解しづらいものです。それに加え、日本語では「未来 → 過去」と「過去 → 未来」という2種のモデルが存在し、大人はそれを混在して使っています。子どもが "時間ことば" の理解や使用に苦労するのは当然なのです。
| ③「動作のことば」 |
日常的な動作を表す動詞について、システム化された「生きた知識」をもっているかをテストするものです。たとえば、
何をしていますか。 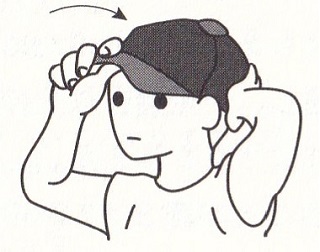 ぼうしを 頭に( )います。 |
というような、( )を埋める問題です。このタイプの問題に正答するためには、類似概念を日本語がどのように分割しているかを知っていなければなりません。たとえば身につける動作は、帽子なら「かぶる」、上着なら「きる」、パンツや靴なら「はく」です。かつ、動詞の活用の形(=文法)と統合して答える必要があります。システム化された「生きた知識」があってこそ正答できるのです。
「動作のことば」の回答を分析すると、問題ごとに正解率が大きく違うことがわかります。そして正解率が低いのは「チーズを縦に(裂いて)います」「草を鎌で(刈って)います」などの問題です。これらの動作は、小学生が日常生活で見たり、自分で行ったりすることが少ない動詞です。だから正答率が低い。
逆に、これらの動作の動詞を知っていて的確に使える子どもは、日常会話だけでなく、本などから語彙を学んでいると考えられるのです。
「ことばのたつじん」と学力の関係
「ことばのたつじん」と「算数文章題」の得点の相関係数は次のとおりでした。
| 3年生 | 4年生 | 5年生 | |
| ①語彙の深さと広さ | 0.49 | 0.58 | 0.44 |
| ②空間・時間のことば | 0.58 | 0.67 | 0.47 |
| ③動作のことば | 0.34 | 0.35 | 0.30 |
この相関係数はすべて 0.1% の水準で統計的に有意(その値が偶然によってもたらされる確率が0.1% 以下)でした。
この表を見ると「ことばのたつじん」と学力(この場合は算数文章題)とが、極めて強い相関関係にあることがわかります。特に「空間・時間のことば」です。この傾向は標準学力テスト(国語・算数)との相関係数と同様でした。
|
かんがえるたつじん
「かず・かたち・かんがえるたつじん」(略称:かんがえるたつじん)は、子どもの思考力のアセスメントです。
| 整数・分数・小数の概念 | |
| 図形イメージの心的操作 | |
| 推論の力 |
の3部から構成されています。
| ①整数・分数・小数の概念 |
大問1:整数の数直線上の相対位置
0 から 100 までの数直線の上に、与えられた数のだいたいの位置の目印を書き込む問題です。たとえば 18 と提示されたら、それは 20 に近いので、数直線をだいたい 5 分割して、それよりちょっと 0 に近いところに目印をつける、といった感じです。4つの小問(提示数:18, 71, 4, 23)があります。
これは「整数は相対的な大きさを示す」というスキーマを子どもたちが持っているかどうかを見るものです。このスキーマを理解していない子どもは、18 と提示されると定規を取り出して 18mm のところに目印をつけたりします。誤答をする少なからぬ子どもがそうしていました。
大問2:小数・分数の大小関係
どちらが大きいかを問う問題です。12の小問があります。5年生の平均正答率とともに引用します。
| 小問1 | 13と23 | 94.0% |
| 小問2 | 12と13 | 49.7% |
| 小問3 | 23と12 | 85.9% |
| 小問4 | 0.3 と 0.1 | 96.6% |
| 小問5 | 1 と 0.9 | 98.7% |
| 小問6 | 1.5 と 2 | 99.3% |
| 小問7 | 0.5 と13 | 42.3% |
| 小問8 | 12と 0.7 | 54.4% |
| 小問9 | 0.2 と12 | 82.6% |
| 小問10 | 12と13 | 78.5% |
| 小問11 | 13と23 | 71.8% |
| 小問12 | 13と14 | 69.1% |
小問10、小問11、小問12 は「ケーキの12こ分と13こ分ではどちらがたくさん食べることができますか」のような "文章題" になっています。
特に正答率が悪いのは、小問2, 7, 8 です。小問2 と「同程度に難しいはず」の小問3 の正答率が高いのは(小問2 の正答率より 35% も跳ね上がっている)、小問3では「たまたま分母の数も分子の数も大きい方が大きい」からだと考えられます。
このデータは、少なからぬ子どもが分数や小数の概念的理解ができていないことを示しています。また分数や小数が、いかに直感的にとらえどころがないものかも示しています。
大問3:心的数直線上での小数・分数の相対位置
0 から 1 までの数直線があり、10分割した目盛りがついています。与えられた小数や分数が数直線上のどの位置にあるかの目印をつける問題です。6つの小問があります。
特に成績の悪かったのは、12と25でした。5年生の平均正答率では、12が 46.0%、25が 31.3% でした。
12は日常生活で頻繁に使われます。しかし正答できない子どもは、「ケーキ」のような具体的なモノが与えられずに、「1を基準にしたときにそれに対してどの割合の量なのか」という純粋な「数」としての理解ができていないのです。
25の正答率が異様に低いのは、0 から 1 の数直線に10分割した目盛りが振ってあるからです。つまり正答するためには「2目盛りを1単位としてそれが2つ」という心的操作をしなければならない。これが問題を特に難しくしています。
「1」には、モノを数えるときに「1個ある」という意味と、任意のモノを「1」として、それを分割したり比較のしたりするときの基準の意味があります。「数はモノを数えるもの」という誤ったスキーマを持っていると「基準としての1」が理解できません。この理解なしに分数や小数の意味は理解できないのです。
また大問2・大問3の誤答分析からは、誤答する子どもたちが整数・分数・小数をバラバラに理解していて、それらの関連付けがされていないことがわかります。分数の単元で分数だけ、小数の単元で小数だけという現在の小学校の教え方では「システム化」された知識の習得は難しいのです。
| ②図形イメージの心的操作 |
図形の問題です。図形を折る、隠す、回転させるという操作を心の中でできるかどうかです。具体的な問題の例をあげます。
大問4:図形を折ったときのイメージ

大問5:図形の隠れた部分のイメージ

大問6:図形を回転させたときのイメージ

これらの問題に正解するためには「複数のことを同時に処理しなければない」わけです。誤答を分析すると、一つの状況なら楽にできる心的操作が、複数のことを同時に処理しなければらない状況では破綻してしまい、その結果、問題解決に失敗する傾向が見て取れました。
また大問6に顕著ですが、正答する子どもは図形に補助線を引き、補助線が回転後にどうなるかを考えて答を出しています。つまり、図形の回転は認知的負荷が高いのを直感し、負荷を軽減する方略を自分で考えられたので正解できたのです。問題解決のための方略を自分で考えられるのが "できる" 子どもの特徴だと言えます。
| ③推論の力 |
「推論」が学力と関係しているという分析は本書のこれまでにもにありましたが、ここでは推論だけを純粋にとりあげます。問題の例を以下にあげます。
大問7:推移的推論

大問8:複数次元の変化を伴う類推

大問9:実行機能を伴う拡張的類推

大問9の例に関してですが、この場合の実行機能とは、注意点を取捨選択し、不要な注意点を抑制し、必要に応じて注意点を切り替えられる機能です。またこの例では見本のペアとその向きを常に短期記憶におきつつ、図の中から同じ関係のペアを見いだす必要があります。
絵の中には関係するものが複数あります。たとえば、木は葉っぱや鳥や鋸と関係がある。また糸だと、関係するのはハサミと針です。つまり「見本のペアの関係ではない関係への注意」を抑制する必要がある。これができて正解することができます。
以上の「かんがえるたつじん」と「算数文章題」の得点の相関係数は、0.37~0.48 で、高いものでした。最も高かったのが大問8(複数次元の変化を伴う類推)で、その次が 大問2(小数・分数の大小関係)でした。
算数文章題と「たつじん」テストの相関
本書には、次の6つの「たつじんテスト」、
「ことばのたつじん」
| 語彙の深さと広さ | |
| 空間・時間のことば | |
| 動作のことば |
| 整数・分数・小数の概念 | |
| 図形イメージの心的操作 | |
| 推論の力 |
の成績と、算数文章題の成績の相関係数を計算した表が本書にあります。それをみると、3・4年生では6つのテスト中5つが0.5を超え(「動作のことば」だけが0.38)、5年生では5つが 0.39~0.47の範囲になっています(「動作のことば」だけが0.3)。またすべてにおいて、0.1% 水準で有意(=全く偶然にその相関係数になるのは 0.1% 以下の確率)になっています。
ただ、6つの「たつじんテスト」は相互に相関関係があるはずなので、1つのテストが算数文章題と相関をもつと、それにつられて関係のある他のテストも算数文章題と相関します。つまり、どの「たつじんテスト」が算数文章題の成績に "利いて" いるのかは、相関係数だけでは分かりません。
そこで本書には、重回帰分析(説明変数=「たつじんテスト」の成績6種、被説明変数=算数文章題の成績)の結果が載っています。それによると、算数文章題の成績に最も寄与しているのが「空間・時間のことば」でした。これは国語と算数の標準学力テストでも同じでした。
従来からの心理学の研究で、言語能力が学力と深い関わりを持っていることが分かっていて、このことは広く受け入れられています。しかし想定されている「言語能力」とは「語彙のサイズ」(=どれだけ多くの言葉を知っているか)でした。
しかし今回の研究から、「語彙の広さと深さ」よりも「空間・時間のことばの運用」の方が頑健に「学力」を説明することがわかりました。このことは、教育現場で当たり前のようにして使われいている「言語能力」の考え方を見直す必要があることを示しています。
重回帰分析の結果から、「空間・時間のことば」の次には「推論の力」が算数文章題の成績に寄与していることも分かりました。その次が「整数・分数・小数の概念」です。
つまづきの原因
本書では全体の「まとめ」として「第6章:学習のつまずきの原因」と題した章があり、各種のテストでの誤答を分析した結果を総括し、これをもとに教育関係者への提言がされています。この中から「つまずきの原因」の何点かを紹介します。まず、
知識が断片的でシステムの一部になっていない
ことです。これは「たし算・引き算・かけ算・割り算」の関係性が理解できず、それぞれの計算手続きは分かるものの、問題解決に有効に使える知識になってないという意味です。それぞれの単元での学習結果が断片的な知識となっていて「数の世界の、計算というシステム」としての理解になっていない。また、
誤ったスキーマをもっている
のもつまずきの原因です。算数文章題の場合、誤ったスキーマの根は一つです。それは「数はモノを数えるためのもの」というスキーマです。このスキーマをもっていると「1」が「全体を表すもの」あるいは「単位を表すもの」という概念が受け入れられません。
「足し算とかけ算は数を増やす計算」と「引き算と割り算は数を減らす計算」という誤ったスキーマもよく見られたものです。これは、まず「増やす計算」と「減らす計算」でそれぞれを教えるからだと考えれます。子どもたちは誤ったスキーマを自分で作り出してしまうのです。
似ているのが「割り算は必ず割り切れる」というスキーマです。これも 12÷4 のような割り切れる数の計算が最初に導入されるからです。誤ったスキーマをもってしまうと、答えが整数にならない割り算を教えられても、なかなか受け入れることができません。本書には「永遠の後出しじゃんけん」という表現を使って次のように書いてあります。
|
さらに、
相対的にものごとを見ることができない
のも、つまづきの要因です。「たつじんテスト」で最も強く学力を予測していたのは「空間・時間ことば」でしたが、前・後・左・右はまさに相対的であり、誰を基準にするか、どの点を基準にするかで変わってきます。
また、数直線上に与えられた数の位置を示すには、0~100 あるいは 0~1 というスケールの中で相対的に考える必要がありますが、これができない子どもが多数いました。著者は「驚くほど多かったのはショックだった」と書いています。これは「数」という概念の核である「数の相対性」が理解できていないことを端的に示しています。
「相対的にものごとを見る」ことは「視点を柔軟に変更・変換できる」ことと深い関係があります。そして視点変更の柔軟性は、ことばの多義性の理解につながります。「1」はモノが1個のことであるというスキーマをもった子どもが、「1」は「子ども 140人」でも「水 50リットル」でもよい、「全体」ないしは「単位」を表すものだという認識に進むためには、過去のスキーマの抜本的な修正が必要です。「相対的にものごとを見る能力」=「視点変更の柔軟性」は、誤ったスキーマを修正できる力に関わっています。そして誤ったスキーマを自ら修正できる力は、知識を発展させるための最重要の能力なのです。
その他、本書では
| 認知処理能力をコントロールしながら推論する力が弱い、また推論で行間を埋められない | |
| メタ知識が働かず、答えのモニタリングができない | |
| 学習無力感をもっている。何のために算数を学ぶのか分からず、算数の意味を感じ取れていない |
などが総括としてまとめられています。
ほんものの学力を生む家庭環境
本書では付録として、テストをうけた児童の保護者に44項目のアンケート調査をし、その結果と子どもの学力(たつじんテストと、国語・算数の標準学力テスト)の相関を示した大変に興味深い表が載っています。44項目の質問は、子どもの基本的生活習慣、家庭学習、しつけの考え方、読書習慣、小学校に入る前のひらがな・数字への関心、小学校に入る前の時間・ひらがな・数字の家庭教育など、多岐にわたります。
これらの中で、最も学力との相関が強かったのは「読書習慣・読み聞かせ」に関する3項目と、「家庭内の本の冊数」に関する2項目でした。その次に相関が強かったのは小学校入学前の「ひらがな・数字への興味・関心」の2項目と「時間・ひらがな・数字の教育」3項目でした。この結果から著者は次のように記しています。
|
本書の感想
最初に書いたように、本書は、
小学生の「算数文章題における学力とは何か」の探求を通して、「人間の思考力とは何か」や「考える力の本質は何か」という問題に迫っている
と思いました。つまり我々大人が社会で生きていく際に必要な思考力の重要な要素を示しているように感じたのです。
たとえばその一つは、「ある目的や機能を遂行する何か」を「システムとしてみる力」です。「システム」として捉えるということは、「何か」が複数のサブシステムからなり、それぞれのサブシステムは固有の目的や機能を持っている。それが有機的かつ相互依存的に結合してシステムとしての目的や機能を果たす。そのサブシステムは、さらに下位の要素からなる、という見方です。これは社会におけるさまざまな組織、自治体、ハードウェア、サービスの仕組み、プロジェクト、学問体系 ・・・・・ などなどを理解し、それらを構築・運用・発展させていく上で必須でしょう。
「相対的に考える」のも重要です。他者からみてどう見えるか、第3者の視点ではどうか、全体を俯瞰するとどうなるのか、対立項が何なのか、全体との対比で部分をみるとどうなるのか、という視点です。
そして、相対的に考える思考力は「スキーマを修正する力」につながります。本書のキーワードの一つである "スキーマ" とは「人が経験から一般化、抽象化した、無意識に働く思考の枠組み」のことです。人は必ず何らかのスキーマに基づいて判断します。そして社会において個人が持つ「誤ったスキーマ」の典型は「自らの成功体験からくるスキーマ」です。社会環境が変化すると、そのスキーマには捨てなければならない部分や付け加えなければならないものが出てくる。本書に「スキーマを自ら修正できる力は、知識を発展させるための最重要の能力」とありますが、全くその通りです。
さらに「抽象的に考える」ことの重要性です。"良く練られた" 抽象的考えは、より一般性があり、より普遍的で、従ってよりパワーを発揮します。「抽象的でよく分からない、具体的にはどういうことか」というリクエストに答えて具体例を提示することは重要ですが、それは抽象的考えを理解する手だてとして重要なのです。
子どもは小学校から(公式に)抽象の世界に踏み出します。「言葉・語彙」がそうだし「数」がそうです。本書からの引用を再掲しますと、
|
とありました。抽象性の大きな壁である「9歳の壁」を乗り越えた子どもは、その次の段階へと行けます。これは中学校・高校・大学と「学び」を続ける限り、抽象性の壁を乗り越えることが繰り返されるはずです。だとすると、社会に出てからも繰り返されるはずだし、学校での「学び」はその訓練とも考えられます。
ともかく、10歳前後の小学生の誤答分析から明らかになった「学力」や「思考力」の源泉は、大人の社会に直結していると思いました。
分数は直感的に理解しづらい
最後に一つ、「分数は直感的に理解しづらい」ということの実例を書いておきます。
本書の「かんがえるたつじん ① 整数・分数・小数の概念」の「大問2:小数・分数の大小関係」のところで、テストの結果データの分析として「多くの子どもたちが、分数や小数の概念的な理解ができていない」と書かれていました。そして「これは、正答できない子どもたちの努力が足りないと片づけてよい問題ではない。分数・小数がいかに直感的に捉えどころがないものかを示すデータなのである」とも書いてありました。
分数で言うと、12や13は「任意の」モノを「1」としたとき、それを「均等に」2分割、あるいは3分割した数です。この「任意の」と「均等に」が非常に抽象的で、捉えどころがないのです。
我々大人は分数を理解していると思っているし、それを使えると思っています。大小関係も分かると自信を持っている。しかし本来「分数は直感的に捉えどころがない」のなら、それは大人にとってもそうであり、ほとんどの場合は正しく使えたとしても、何かの拍子に「捉えどころのなさ」が顔を出すはずです。
そのことを実例で示したような記述が本書にありました。「かんがえるたつじん ① 整数・分数・小数の概念」の「大問1:整数の数直線上の相対的位置」の説明のところです。どのような問題かを著者が説明した文章です。
|
えっ! と思いましたが、何度読み直しても、これでは 23 あたりに目印をつけることになります。本書に書いてある採点方法だと、5点満点の 3点(ないしは4点)です。
本書の著者は大学教授の方々、計7名で、原稿は著者の間で何回もレビューし、見直し、確認したはずです。岩波書店に渡った後も、原稿や校正刷りの各段階での何回ものチェックがされたはずです。それでも「100を4分割すると20」になってしまう。どの段階でこうなったかは不明ですが ・・・・・・。
これは単にケアレスミスというより、そもそも「14が分かりにくいから、ないしは15や20100が分かりにくいから」、つまり「分数は抽象的で理解しづらい概念」ということを示していると思います。子どもが算数文章題につまずく理由、その理由の一端を本書が "身をもって" 示しているのでした。
2022-08-31 18:25
nice!(0)



