No.347 - 少なくともひとりは火曜日生まれの女の子 [科学]
No.149「我々は直感に裏切られる」と No.325「高校数学で理解する誕生日のパラドックス」でとりあげた「誕生日のパラドックス」から話を始めます。
有名な「誕生日のパラドックス」は「バースデー・パラドックス」とも言われ、
というものです。これは正確に言うとパラドックスではなく "疑似パラドックス" です。パラドックスとは「一見すると妥当そうに思える推論から、受け入れがたい結論が導かれること」ですが、疑似パラドックスは「数学的には全く正しいが、人間の直感に反するように感じられる結論」です。
この "疑似パラドックス" が成り立つ理由を一般化して言うと、「確率が直感に反することが多々ある」でしょう。さらにもっと一般化すると「確率は難しい」ということだと思います。裏から言うと「誤った確率の使い方は人を誤解に導く」ともなるでしょう。誤っていることが往々にして分からないからです。
我々は「コインを投げたとき、表が出る確率は 1/2」とか「サイコロを振ったとき 1の目が出る確率は 1/6」のように、"確率を理解している" と思っているかもしれません。「2つのサイコロを振ったとき、2つとも 1 の目が出る確率は 1/36」もよいでしょう。しかし、我々が常識の範囲で理解できるのは、せいぜいこのあたりまでで、ちょっと込み入ってくると手に負えなくなってしまうようなのです。
イアン・スチュアート著「不確実性を飼いならす ── 予測不能な世界を読み解く科学」(徳田 功訳。白揚社 2021)を読んでいたら、確率に関することがいろいろ出ていました。イアン・スチュアートは世界的に著名なイギリスの数学者です。その本の文章をちょっと紹介します。
イアン・スチュアートは「確率に対する人間の直感は絶望的」の典型例として、まず、モンティ・ホール問題をあげています。
モンティ・ホール問題
モンティ・ホール問題は確率に関する有名な問題です。モンティ・ホールとは、かつてのアメリカのテレビのゲーム・ショー番組「取引しよう」の初代司会者の名前です。
そのテレビ番組で行われたのは次のようなゲームです。3つの独立した部屋があり、前面にドアがあって閉じられています。3つの部屋のうちの1つには特別賞のクルマが、残りの2つには残念賞のヤギが隠されています。
クルマを当てたい回答者が一つのドアを選びます。ドアが開けられた時点で、そこにあるものはクルマであれヤギであれ、回答者のものになります。
そのとき司会者は、回答者が選ばなかった2つのドアのうち、ヤギがいる一つのドアを開けてヤギを見せます。そして回答者に「選ぶドアを変更してもよい」と言って、選び直しの機会を与えます。
クルマが欲しい回答者はどうすべきでしょうか。これが問題です。
クルマがあるのは、最初に回答者が選んだドアか、まだ開けられていないもう一つのドアか、そのどちらかです。従って「選び直しても、選び直さなかったとしても、クルマが当たる確率は同じ」と考えてしまいそうです。実際に回答者になって現場にいたとしたら、直感はそうでしょう。
さらに回答者としては「心理的な」直感も働く可能性が高い。つまり、司会者がわざわざ一つのドアをあけて「選び直してもよい」と言ったということは、選び直すように誘導しているに違いないと思う直感です。この2つの直感によって、回答者は選び直さない可能性の方が大きいと考えられます。
しかし真実は全く違います。クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高いのが正解です。
これは次のように考えると分かります。ドアを A、B、C の3つとし、最初に回答者が A を選んだとします。クルマがあるのは A、B、C のどれかであり、この3つのケースの確率は全く同じです。
クルマが A にある確率は 1/3 です。この場合は「選び直さない方がよい」わけです。司会者が B か C のドアをあけてヤギを見せたとしても「選び直さない方がよい」のは変わらない。司会者がドアをあけたことでクルマは移動しないからです。
クルマが B にある確率は 1/3 であり、この場合は「選び直した方がよい」わけです。司会者が C のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらない。選び直すとしたら B しかありません。つまり、この場合は選び直すと必ずクルマをゲットできることになります。
クルマが C にある確率も 1/3 で、この場合も「選び直した方がよい」わけです。司会者が B のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらないし、選び直すと必ずクルマをゲットできます。司会者が、わざわざ選び直しの対象としての B を除外してくれたのだから ・・・・・・。
以上で「選び直さない方がよい」ケースは3回に1回起こり、「選び直した方がよい」ケースは3回に2回起こります。この状況は、最初に回答者が選んだドアが B でも C でも全く同じです。
従って、クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高い、となります。
納得できたでしょうか。
NHK総合の「笑わない数学」の「確率論」(2022年9月21日放送)では、この問題を実際に実験していました。3つの箱の一つに景品を隠す実験です。回答者役と司会者役を2組用意し、一方の回答者は「必ず選び直す」、もう一方の回答者は「必ず選び直さない」とします。それぞれ100回の試行した結果、景品をゲットできた数は、
でした。選び直した方が2倍有利という確率論の結果が(実験であるがゆえの誤差を含みつつ)実証されたわけです。実験は大切です。
それでも、なぜそうなるのか納得できないという人もいるのではないでしょうか。
ドアが10個だとしたら
イアン・スチュアートの本では、それでも納得できないという人のために、ある仮想実験による説明をしています。トランプの52枚のカードを使ったものですが、同じことなので「10個のドア」に焼き直して紹介します。もちろん、実際にはあり得ない仮想実験です。
モンティ・ホール問題と基本的に同じです。ただしドアは10個あります。そのうちの一つにクルマが隠されていて、残りの9個には何もありません(ヤギを9匹用意するのは大変なので)。
あなたは司会者から1つのドアを選ぶように言われます。もしそこにクルマがあったとしたら、あなたのものになります。何もなければ、賞品は無しです。
1つのドアを選んだあなたはどう考えるでしょうか。「クルマが隠されているドアを選ぶ確率は 1/10 である。これは、まず当たらないな」と考えるのが普通でしょう。10回チャレンジしてようやく1回当たるかどうかという確率です。ほとんど無理と思うでしょう。
ところがです。司会者はあなたが選ばなかった9個ドアから8個を選び、それを次々と空けて、そこには何もないことを示したのです。そしてこう宣告します。「あなたが選んだドアのほかに、まだ閉じらているドアが1つあります。今からドアの選択を変えるチャンスをあげましょう。変えても、変えなくてもどちらでもよい。どうしますか?」
・・・・・・ という状況だったら、あなたは間違いなくドアの選択を変えるはずです。だってそうでしょう。最初に選択したドアにクルマがある確率は 1/10 で、ほぼハズレです。選択しなかった9個のドアのどれかにクルマがある確率は 9/10 です。ほどんどの場合、その9個のうちのどれかにクルマがあると、誰にでもわかる。
しかし、その9個のドアのうちの8個にはクルマがないことが分かってしまった。わざわざ司会者がそう示してくれたのです。とすると、残りの1個に高い確率でクルマがあるに違いない。確率的には、選択を変えた方が変えないよりも9倍、クルマをゲットできる可能性が高いことになります。
この「10枚のドア」の状況は、モンティ・ホール問題の「3枚のドア」と全く同じ構造をしています。「10枚のドア」ではなく「100枚のドア」でも問題の構造は同じです。100枚のドアだと、ドアの選択を変えると 99% の確率でクルマがゲットできる。つまり、ほぼ確実にクルマがもらえることになります。
2人とも女の子の確率
イアン・スチュアートの本ではさらに「確率と人間の直感」を考える問題として、
という問題と、その変形問題が示されています。まず前提として、子どもがいたとき、それが「男の子」か「女の子」かはどちらかに決まっているとします。常識的にはあたりまえなのですが、生物学的には男女の区別が曖昧というケースもあって、必ずしも正しくはない。しかしこういった生物学的な議論は無しにして、男か女のどちらであるとします。
さらに一番重要なのは、男の子が生まれる確率と女の子が生まれる確率は全く同じ、という前提です。これも生物学的にはそうではなく、人間においても男が生まれる確率がわずかに大きいことが知られています。また「男女の産み分け」も行われていて、そうなると半々だとはますます言えなくなります。しかしそういったことは一切抜きにして「男の子が生まれる確率と女の子が生まれる確率は全く同じ」が前提です。
さらに以下の説明で使うのでコメントしますが、2人の子どもを「第1子」と「第2子」と表現します。同時に生まれた双子だったとしても、兄・姉/弟・妹の区別をするので、兄・姉と呼ばれている子を「第1子」とします。
以上の前提のもと「スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか」という質問に対する答えは 1/4 が正解です。これは多くの人が納得でしょう。
高校などで、確率を習い始めの生徒がよくやる間違いは、子どもの組み合わせは「2人とも男」「男女一人ずつ」「2人とも女」の3つだから、答えは 1/3 とする間違いです。
この手の間違いを防止するために、ちょっと数学的になりますが、イアン・スチュアートの本にある「標本空間」と「標的事象」で考えてみます。
「標本空間」とは「起こりうる全ての事象をもれなく集めた集合」であり、「標的事象」とは、いま確率を問題にしている事象のことです。スミス夫妻の問題の場合の「標本空間」と「標的事象」を図で表すと、次のようになります。左側の青が「標本空間」、右側の赤が「標的事象」です。
図で分かるように、標本空間には4つの事象があり、その確率は同じです。標的事象(2人とも女の子)は1つですから、答えは 1/4 です。
少なくともひとりは女の子
問題を少し変えます。
この問題では、標的事象(2人とも女の子)は前の問題と同じですが「少なくともひとりは女の子」という情報が追加されたため、標本空間が変化します。標本空間は3つ、標的事象は1つですから、答えは 1/3 です。
ここまでは納得の範囲ではないでしょうか。少なくともひとりは女の子という情報が追加されたために、2人とも女の子の確率が上がった。最初の問題では 1/4 だった確率が 1/3 になる。直感とも合っているはずです。しかし問題になるのはこの次です。
少なくともひとりは火曜日生まれの女の子
さらに問題を少し変えます。
前提として「子どもが生まれる曜日はどの曜日も同じ確率」とします。この前提は現実社会では必ずしも正しくなく、「どの曜日もほぼ同じ確率」が正しいのですが、問題としては「同じ」とします。
この問題の答えは 13/27 です。えっ! と思うでしょう。"火曜日生まれの" という "些細な" 情報が追加されただけで、確率は劇的に変わってしまった。13/27 というと、ほぼ 1/2 の値です。1/4 が 1/3 になったよりも変化が大きい。全く直感に反しています。
そして、全く直感に反しているため、これは理にかなっていない、間違っている、と感じるのではないでしょうか。生まれた曜日など確率に関係ないと考える方が理にかなっている ・・・・・・。
しかし 13/27 は正しいのです。それは標本空間と標的事象を作ってみればわかります。この問題の標本空間を作るため、男女のそれぞれを曜日で7分割した図を用意します。
この図には 14 × 14 = 196 のマス目があります。もし単に「2人の子どもがいます」なら、この196の事象が起きる確率は全く同じです。
この図に「少なくともひとりは火曜日生まれの女の子」という条件を加味した標本空間を青く塗ってみると次の通りとなります。
さらに、この標本空間の中に含まれる標的事象(=2人も女の子)を赤で塗ると、次の図になります。
標本空間のマス目の数は 27、標本空間の中の標的事象のマス目の数は 13 なので、問題の解答は 13/27 です。問題には「火曜日」としましたが、これが何曜日であっても答は同じです。
これは、いわゆる「条件付き確率」です。
の条件では、女の子は「ひとりの可能性」と「2人の可能性」があって、2人の可能性は 1/3 です。この場合、2人の女の子を区別できる情報はありません。
これに「女の子が2人だった場合に、その2人を区別できる可能性を高める情報」が付け加えられると、その区別可能性が高いほど2人である確率は高まります。たとえば、"火曜日に生まれた" より区別可能性が高い情報を付け加えた例ですが、
という問題にすると、第1子はひとりしかいないので、答えは 1/2 となります。"火曜日生まれ" だと、2人とも火曜日生まれの可能性があって、必ずしも2人を区別できない。"第1子" は2人の女の子を区別するのに絶対に確実な情報です。
少なくともひとりは女の子だけれど、それが第1子か第2子かという情報(やその他の情報)が全くない状況では、確率が 1/3 に減ってしまうのです。
"火曜日に生まれた" より区別可能性が低い情報を付け加えた例を作ってみます(これはイアン・ステュアートの本にはありません)。男女とも血液型が A 型である確率を統計的に 50% とすると、
の答えは、3/7 になり、13/27 と 1/3 の間の数になります。
確率は直感に反する
最初の「モンティ・ホール問題」は直感に反するように思えます。ただ、3つのドアではなく「10個のドア」とか「100個のドア」で説明されると、なるほどそうかという気にもなる。
しかし「少なくともひとりは火曜日生まれの女の子」問題は、いくら理論的に説明されても直感的には納得できません。
この話の教訓は「"正しい確率" は理解が難しい」ということであり、「"正しい確率" が直感に反するのは、むしろ当然」ぐらいに思った方がよいということだと思います。
このことを全く逆から言うと、「確率を持ち出して、そこからいかにも直感に合致する結論を主張する言説」があったとしたら、サイコロの目とかコインの裏表のように誰がみても明らかなものを除いて、そもそもその持ち出された "確率" なるものが怪しいのでは、と疑ってみた方がよいと言えるでしょう。
なぜなら、イアン・ステュアートが言っているように「確率に対する人間の直感は絶望的」であり、平たく言うと "正しい確率は直感と合致しない" のだから ・・・・・・。
有名な「誕生日のパラドックス」は「バースデー・パラドックス」とも言われ、
23人のクラスで同じ誕生日のペアがいる確率は 0.5 を超える
というものです。これは正確に言うとパラドックスではなく "疑似パラドックス" です。パラドックスとは「一見すると妥当そうに思える推論から、受け入れがたい結論が導かれること」ですが、疑似パラドックスは「数学的には全く正しいが、人間の直感に反するように感じられる結論」です。
この "疑似パラドックス" が成り立つ理由を一般化して言うと、「確率が直感に反することが多々ある」でしょう。さらにもっと一般化すると「確率は難しい」ということだと思います。裏から言うと「誤った確率の使い方は人を誤解に導く」ともなるでしょう。誤っていることが往々にして分からないからです。
イアン・スチュアート著「不確実性を飼いならす ── 予測不能な世界を読み解く科学」(徳田 功訳。白揚社 2021)を読んでいたら、確率に関することがいろいろ出ていました。イアン・スチュアートは世界的に著名なイギリスの数学者です。その本の文章をちょっと紹介します。
|
イアン・スチュアートは「確率に対する人間の直感は絶望的」の典型例として、まず、モンティ・ホール問題をあげています。
モンティ・ホール問題
モンティ・ホール問題は確率に関する有名な問題です。モンティ・ホールとは、かつてのアメリカのテレビのゲーム・ショー番組「取引しよう」の初代司会者の名前です。
そのテレビ番組で行われたのは次のようなゲームです。3つの独立した部屋があり、前面にドアがあって閉じられています。3つの部屋のうちの1つには特別賞のクルマが、残りの2つには残念賞のヤギが隠されています。
クルマを当てたい回答者が一つのドアを選びます。ドアが開けられた時点で、そこにあるものはクルマであれヤギであれ、回答者のものになります。
そのとき司会者は、回答者が選ばなかった2つのドアのうち、ヤギがいる一つのドアを開けてヤギを見せます。そして回答者に「選ぶドアを変更してもよい」と言って、選び直しの機会を与えます。
クルマが欲しい回答者はどうすべきでしょうか。これが問題です。
クルマがあるのは、最初に回答者が選んだドアか、まだ開けられていないもう一つのドアか、そのどちらかです。従って「選び直しても、選び直さなかったとしても、クルマが当たる確率は同じ」と考えてしまいそうです。実際に回答者になって現場にいたとしたら、直感はそうでしょう。
さらに回答者としては「心理的な」直感も働く可能性が高い。つまり、司会者がわざわざ一つのドアをあけて「選び直してもよい」と言ったということは、選び直すように誘導しているに違いないと思う直感です。この2つの直感によって、回答者は選び直さない可能性の方が大きいと考えられます。
しかし真実は全く違います。クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高いのが正解です。
これは次のように考えると分かります。ドアを A、B、C の3つとし、最初に回答者が A を選んだとします。クルマがあるのは A、B、C のどれかであり、この3つのケースの確率は全く同じです。
クルマが A にある確率は 1/3 です。この場合は「選び直さない方がよい」わけです。司会者が B か C のドアをあけてヤギを見せたとしても「選び直さない方がよい」のは変わらない。司会者がドアをあけたことでクルマは移動しないからです。
クルマが B にある確率は 1/3 であり、この場合は「選び直した方がよい」わけです。司会者が C のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらない。選び直すとしたら B しかありません。つまり、この場合は選び直すと必ずクルマをゲットできることになります。
クルマが C にある確率も 1/3 で、この場合も「選び直した方がよい」わけです。司会者が B のドアをあけてヤギを見せたとしても「選び直した方がよい」のは変わらないし、選び直すと必ずクルマをゲットできます。司会者が、わざわざ選び直しの対象としての B を除外してくれたのだから ・・・・・・。
以上で「選び直さない方がよい」ケースは3回に1回起こり、「選び直した方がよい」ケースは3回に2回起こります。この状況は、最初に回答者が選んだドアが B でも C でも全く同じです。
従って、クルマが当たる確率は、選び直した方が、選び直さないよりが2倍高い、となります。
納得できたでしょうか。
NHK総合の「笑わない数学」の「確率論」(2022年9月21日放送)では、この問題を実際に実験していました。3つの箱の一つに景品を隠す実験です。回答者役と司会者役を2組用意し、一方の回答者は「必ず選び直す」、もう一方の回答者は「必ず選び直さない」とします。それぞれ100回の試行した結果、景品をゲットできた数は、
| : 70回 | |
| : 33回 |
でした。選び直した方が2倍有利という確率論の結果が(実験であるがゆえの誤差を含みつつ)実証されたわけです。実験は大切です。
それでも、なぜそうなるのか納得できないという人もいるのではないでしょうか。
ドアが10個だとしたら
イアン・スチュアートの本では、それでも納得できないという人のために、ある仮想実験による説明をしています。トランプの52枚のカードを使ったものですが、同じことなので「10個のドア」に焼き直して紹介します。もちろん、実際にはあり得ない仮想実験です。
モンティ・ホール問題と基本的に同じです。ただしドアは10個あります。そのうちの一つにクルマが隠されていて、残りの9個には何もありません(ヤギを9匹用意するのは大変なので)。
あなたは司会者から1つのドアを選ぶように言われます。もしそこにクルマがあったとしたら、あなたのものになります。何もなければ、賞品は無しです。
1つのドアを選んだあなたはどう考えるでしょうか。「クルマが隠されているドアを選ぶ確率は 1/10 である。これは、まず当たらないな」と考えるのが普通でしょう。10回チャレンジしてようやく1回当たるかどうかという確率です。ほとんど無理と思うでしょう。
ところがです。司会者はあなたが選ばなかった9個ドアから8個を選び、それを次々と空けて、そこには何もないことを示したのです。そしてこう宣告します。「あなたが選んだドアのほかに、まだ閉じらているドアが1つあります。今からドアの選択を変えるチャンスをあげましょう。変えても、変えなくてもどちらでもよい。どうしますか?」
・・・・・・ という状況だったら、あなたは間違いなくドアの選択を変えるはずです。だってそうでしょう。最初に選択したドアにクルマがある確率は 1/10 で、ほぼハズレです。選択しなかった9個のドアのどれかにクルマがある確率は 9/10 です。ほどんどの場合、その9個のうちのどれかにクルマがあると、誰にでもわかる。
しかし、その9個のドアのうちの8個にはクルマがないことが分かってしまった。わざわざ司会者がそう示してくれたのです。とすると、残りの1個に高い確率でクルマがあるに違いない。確率的には、選択を変えた方が変えないよりも9倍、クルマをゲットできる可能性が高いことになります。
この「10枚のドア」の状況は、モンティ・ホール問題の「3枚のドア」と全く同じ構造をしています。「10枚のドア」ではなく「100枚のドア」でも問題の構造は同じです。100枚のドアだと、ドアの選択を変えると 99% の確率でクルマがゲットできる。つまり、ほぼ確実にクルマがもらえることになります。
2人とも女の子の確率
イアン・スチュアートの本ではさらに「確率と人間の直感」を考える問題として、
スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか。 |
という問題と、その変形問題が示されています。まず前提として、子どもがいたとき、それが「男の子」か「女の子」かはどちらかに決まっているとします。常識的にはあたりまえなのですが、生物学的には男女の区別が曖昧というケースもあって、必ずしも正しくはない。しかしこういった生物学的な議論は無しにして、男か女のどちらであるとします。
さらに一番重要なのは、男の子が生まれる確率と女の子が生まれる確率は全く同じ、という前提です。これも生物学的にはそうではなく、人間においても男が生まれる確率がわずかに大きいことが知られています。また「男女の産み分け」も行われていて、そうなると半々だとはますます言えなくなります。しかしそういったことは一切抜きにして「男の子が生まれる確率と女の子が生まれる確率は全く同じ」が前提です。
さらに以下の説明で使うのでコメントしますが、2人の子どもを「第1子」と「第2子」と表現します。同時に生まれた双子だったとしても、兄・姉/弟・妹の区別をするので、兄・姉と呼ばれている子を「第1子」とします。
以上の前提のもと「スミス夫妻には2人の子どもがいます。2人とも女の子である確率はどれだけですか」という質問に対する答えは 1/4 が正解です。これは多くの人が納得でしょう。
高校などで、確率を習い始めの生徒がよくやる間違いは、子どもの組み合わせは「2人とも男」「男女一人ずつ」「2人とも女」の3つだから、答えは 1/3 とする間違いです。
この手の間違いを防止するために、ちょっと数学的になりますが、イアン・スチュアートの本にある「標本空間」と「標的事象」で考えてみます。
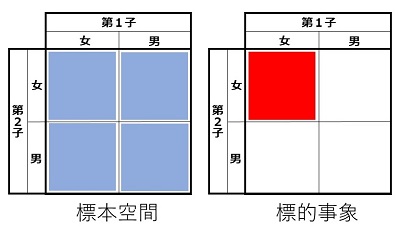
「標本空間」とは「起こりうる全ての事象をもれなく集めた集合」であり、「標的事象」とは、いま確率を問題にしている事象のことです。スミス夫妻の問題の場合の「標本空間」と「標的事象」を図で表すと、次のようになります。左側の青が「標本空間」、右側の赤が「標的事象」です。
|
「2人の子どもがいます」の標本空間(左、青)と「2人とも女の子」に相当する標的事象(右、赤) |
図で分かるように、標本空間には4つの事象があり、その確率は同じです。標的事象(2人とも女の子)は1つですから、答えは 1/4 です。
少なくともひとりは女の子
問題を少し変えます。
スミス夫妻には2人の子どもがいて、少なくともひとりは女の子です。2人とも女の子である確率はどれだけですか。 |
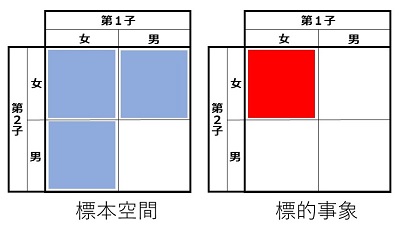
この問題では、標的事象(2人とも女の子)は前の問題と同じですが「少なくともひとりは女の子」という情報が追加されたため、標本空間が変化します。標本空間は3つ、標的事象は1つですから、答えは 1/3 です。
|
「2人の子どもがいて、少なくともひとりは女の子」の標本空間(左、青)と「2人とも女の子」に相当する標的事象(右、赤) |
ここまでは納得の範囲ではないでしょうか。少なくともひとりは女の子という情報が追加されたために、2人とも女の子の確率が上がった。最初の問題では 1/4 だった確率が 1/3 になる。直感とも合っているはずです。しかし問題になるのはこの次です。
少なくともひとりは火曜日生まれの女の子
さらに問題を少し変えます。
スミス夫妻には2人の子どもがいて、少なくともひとりは火曜日生まれの女の子です。2人とも女の子である確率はどれだけですか。 |
前提として「子どもが生まれる曜日はどの曜日も同じ確率」とします。この前提は現実社会では必ずしも正しくなく、「どの曜日もほぼ同じ確率」が正しいのですが、問題としては「同じ」とします。
この問題の答えは 13/27 です。えっ! と思うでしょう。"火曜日生まれの" という "些細な" 情報が追加されただけで、確率は劇的に変わってしまった。13/27 というと、ほぼ 1/2 の値です。1/4 が 1/3 になったよりも変化が大きい。全く直感に反しています。
そして、全く直感に反しているため、これは理にかなっていない、間違っている、と感じるのではないでしょうか。生まれた曜日など確率に関係ないと考える方が理にかなっている ・・・・・・。
しかし 13/27 は正しいのです。それは標本空間と標的事象を作ってみればわかります。この問題の標本空間を作るため、男女のそれぞれを曜日で7分割した図を用意します。
|
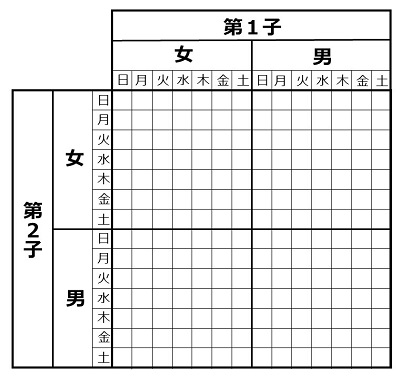
男女のそれぞれを曜日で7分割した図。これは「2人の子どもがいます」という条件だけなら、この 14 × 14 = 196 のマス目の確率は全く同じである。 |
この図には 14 × 14 = 196 のマス目があります。もし単に「2人の子どもがいます」なら、この196の事象が起きる確率は全く同じです。
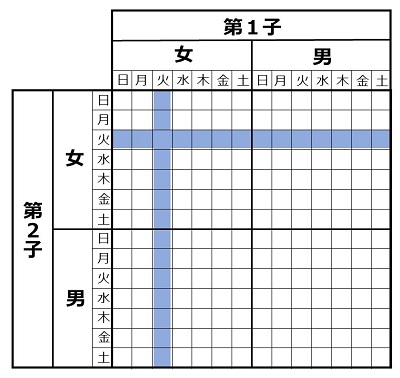
この図に「少なくともひとりは火曜日生まれの女の子」という条件を加味した標本空間を青く塗ってみると次の通りとなります。
|
「2人の子どもがいます。少なくとも一人は火曜日生まれの女の子」の標本空間。マス目は 27 になる。 |
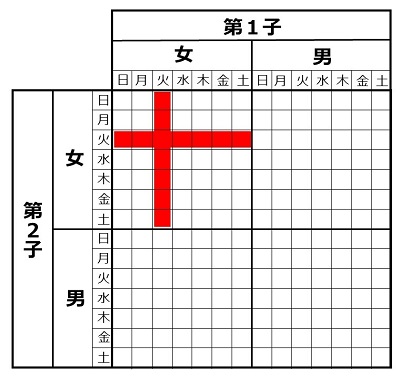
さらに、この標本空間の中に含まれる標的事象(=2人も女の子)を赤で塗ると、次の図になります。
|
標本空間の中で「2人とも女の子」に相当する標的事象。マス目は 13 である。 |
標本空間のマス目の数は 27、標本空間の中の標的事象のマス目の数は 13 なので、問題の解答は 13/27 です。問題には「火曜日」としましたが、これが何曜日であっても答は同じです。
これは、いわゆる「条件付き確率」です。
少なくとも一人は女の子
の条件では、女の子は「ひとりの可能性」と「2人の可能性」があって、2人の可能性は 1/3 です。この場合、2人の女の子を区別できる情報はありません。
これに「女の子が2人だった場合に、その2人を区別できる可能性を高める情報」が付け加えられると、その区別可能性が高いほど2人である確率は高まります。たとえば、"火曜日に生まれた" より区別可能性が高い情報を付け加えた例ですが、
スミス夫妻には2人の子どもがいて、少なくとも一人は第1子の女の子です。2人とも女の子である確率はどれだけですか。 |
という問題にすると、第1子はひとりしかいないので、答えは 1/2 となります。"火曜日生まれ" だと、2人とも火曜日生まれの可能性があって、必ずしも2人を区別できない。"第1子" は2人の女の子を区別するのに絶対に確実な情報です。
少なくともひとりは女の子だけれど、それが第1子か第2子かという情報(やその他の情報)が全くない状況では、確率が 1/3 に減ってしまうのです。
"火曜日に生まれた" より区別可能性が低い情報を付け加えた例を作ってみます(これはイアン・ステュアートの本にはありません)。男女とも血液型が A 型である確率を統計的に 50% とすると、
スミス夫妻には2人の子どもがいて、少なくとも一人は血液型がA型の女の子です。2人とも女の子である確率はどれだけですか。 |
の答えは、3/7 になり、13/27 と 1/3 の間の数になります。
確率は直感に反する
最初の「モンティ・ホール問題」は直感に反するように思えます。ただ、3つのドアではなく「10個のドア」とか「100個のドア」で説明されると、なるほどそうかという気にもなる。
しかし「少なくともひとりは火曜日生まれの女の子」問題は、いくら理論的に説明されても直感的には納得できません。
この話の教訓は「"正しい確率" は理解が難しい」ということであり、「"正しい確率" が直感に反するのは、むしろ当然」ぐらいに思った方がよいということだと思います。
このことを全く逆から言うと、「確率を持ち出して、そこからいかにも直感に合致する結論を主張する言説」があったとしたら、サイコロの目とかコインの裏表のように誰がみても明らかなものを除いて、そもそもその持ち出された "確率" なるものが怪しいのでは、と疑ってみた方がよいと言えるでしょう。
なぜなら、イアン・ステュアートが言っているように「確率に対する人間の直感は絶望的」であり、平たく言うと "正しい確率は直感と合致しない" のだから ・・・・・・。
2022-10-09 09:31
nice!(0)




