No.294 - 鳥が恐竜の子孫という直感 [科学]
No.210「鳥は "奇妙な恐竜"」で、鳥が恐竜の子孫であることが定説となった経緯を日経サイエンスの論文から紹介しました。特に、1990年代以降に発見された「羽毛恐竜」の化石が決定打になったという話でした。
その「鳥は恐竜の子孫」に関係した話を、歌人で情報科学者(東京大学教授)の坂井修一氏が日本経済新聞に連載中のコラム、"うたごころは科学する" に書かれていました。坂井氏の奥様のことなのですが、興味深い内容だったのでそのコラムを引用して感想を書きたいと思います。
見ればわかる
40年前に「鳥は恐竜の子孫」と直感した坂井氏の奥様は、歌人の米川千嘉子さんです。コラムには名前が書いていないので、以下「彼女」と記述します。
40年前というと1980年です。坂井氏は1958年生まれで、彼女は1歳年下ということなので、二人とも20~22歳頃の話です。ということは、2人は東京の大学の大学生です。2人の学生が東京で知り合い、井の頭公園にデートに行く。いかにもありそうな情景です。井の頭公園は現在でも定番のデート・スポットなので、おそらく40年前もそうだったのでしょう。
よくありそうな情景には違いないが、そのデートの場で彼女が「池で泳いでいる鴨を見て、鳥は恐竜の直系の子孫であると強く主張」したのは、確かにちょっと変わっています。デートの場でどんな会話をしようと全くかまわないのですが、「鳥は恐竜の直系の子孫」という話題は、井の頭公園での男女の語らいとしては大変に斬新です。デート相手の女性にそんな主張を強くされたとしたら、男性としては一瞬、たじろぐでしょう。
しかも、その理由は「見ればわかる」ということのようなのです。これは一般的な意味での "理由" になっていません。男性としては一層不安になる。まして坂井氏は科学者(をめざす学生)です。帰納と演繹を繰り返して確認してからでないと不安、とコラムにある通りです。「見ればわかる」というのでは "帰納" の部分がゼロです。
そこで、今となっては科学的に全く正しい「鳥は恐竜の直系の子孫」という説を、1980年の時点でなぜ彼女が強く主張できたのか、その理由を何点か推測してみたいと思います。
鳥が恐竜の子孫という直感の理由
推測の1番目は歴史的経緯です。No.210「鳥は "奇妙な恐竜"」に書いたように、"鳥は恐竜の子孫ではないか" という考えは、実は19世紀半ばからありました。その契機になったのは1860年代にドイツで発見された、いわゆる「始祖鳥」の化石です。イギリスの高名な生物学者ハクスリーはこの化石が小型肉食恐竜に似ていることに気づき、鳥は恐竜の子孫という説を発表しました。当時、この説を支持する学者もいたようですが、多くの学者は反対しました。その後、議論は行ったり来たりの状態でした。
この説に決着がついたのは、1960年代以降に鳥類と酷似した恐竜化石が発見されたことであり、特に決定的だったのが1990年代以降の "羽毛付き恐竜化石" の発見でした。羽毛の化石は普通は残らないのですが、奇跡的な条件で化石になったものが中国で発見されたのです。
この経緯からすると「始祖鳥」の化石発見から100数十年の間、「鳥は恐竜の子孫説」が潜在していたことになります。つまり、これは大変に由緒ある説なのです。従って本などに書かれていた可能性が高い。ひょっとして「始祖鳥」の復元図とともに「鳥は恐竜の子孫説」を紹介した文章があったかもしれません。
井の頭公園で「鳥は恐竜の子孫」と主張した彼女も、そういった記述にどこかで触れ、それに惹かれ、そのことが潜在意識として残り、その潜在意識がデートの場で鴨を見てひょっと浮かび上がった。そういう可能性があると思うのです。これが第1の推測です。
第2の推測は鳥の骨格です。坂井氏は「駝鳥や海鵜を見ると、まあそれもありかなと思うが、彼女は公園の鴨や鳩を見てもそう感じるのだそうだ」と書いています。「鴨や鳩を見ても恐竜の子孫だと感じる」のがポイントですが、その理由は骨格ではないでしょうか。
まず、恐竜の骨格標本は子供の時代に多くの人が見たことがあると思います。恐竜の実物の(ないしは実物大レプリカの)骨格標本は、全国の博物館の超人気アイテムです。小学校高学年以上の子供であれば、その恐竜の姿に心を踊らせるのは当然でしょう。たとえ実物やレプリカを見たことがなくても、恐竜の骨格の写真は雑誌を始めとする各種メディアにあるので、それを見たことが無いという人はまずいないと思います。
一方、鴨や鳩の骨格標本を見る機会はあまりないと思いますが、博物館にはあります。彼女は、鴨か鳩の骨格標本をどこかで見たのではないでしょうか。実物を見たことがないにしても、写真とかイラストで見たのではと思います。ごく一般的な鳩の写真と、鳥の解剖学的イラストを掲げます。イラストは No.210「鳥は "奇妙な恐竜"」の図を再掲したものです。
解剖学的イラストを見て気づくのは、鳥の首の骨が異様に長いことです。羽とか胸のあたりとか足とか、そういう骨は想像どおりだが、首の骨は鳩の外見からは想像しにくい。鳥の頸椎(首の骨)は、11~25個もあります(種類によって違う)。人間を含む哺乳類は、普通は7個です。キリンでも7個です。それに対して鳥は多い。
フクロウは首を270度回転することができますが(1回転できるというのは誤解)、こんなことは哺乳類では絶対に無理です。なぜフクロウが可能かというと、頸椎が多いからです(14個)。従って少しづつ回転させると270度になる。フクロウは外見上は首長に見えないのですが、骨格からみるとそうなのです。上の画像の鳩もそうです。外形からは首が長いように見えないが、頸椎は13個あって、首の骨格はひょろっと長い。
外見上、明らかに首長だと見える鶴とか鵜、鷺、ダチョウの頸椎が長いのは当然ですが、一見そうは見えない鳩などの鳥も意外に長いのです。もちろん、井の頭公園で泳いでいる鴨の頸椎も長い。そしてこの鳥の骨格(頸椎)の姿は暗黙に、恐竜の中で首の長い種類(草食の4つ足の恐竜。専門的には竜脚類)の骨格を連想させないでしょうか。
どこかで見た鳥の骨格標本(ないしは骨格のイラスト図)が、子供のころに親しんだ竜脚類の骨格と無意識下で結びつき、それが井の頭公園でのデートで鴨を見たときにフッと浮かび上がった。これが第2の推測です。
第3の推測は人間の潜在意識です。往年の名監督、アルフレッド・ヒッチコック(1899-1980)の映画に『鳥』(1963)がありました。あらゆる種類の鳥が人間を襲い出すというパニック映画(かつホラー映画)です。大挙して部屋に進入してきた鳥に襲われて人が血まみれになるなど、衝撃的なシーンがいろいろありました。
これはイギリスの作家、ダフネ・デュ・モーリア(1907-1989。原音に近く "ダフニ・デュ・モーリエ" とも書かれる)の短編小説、"The Birds"(1952)が原作です。ダフネ・デュ・モーリアは畑で農夫がカモメに襲われるのを見て小説のインスピレーションを得たそうですが(Wikipedia による)、なぜそのことが小説を書く契機になったのでしょうか。また、ヒッチコックはなぜ映画化しようと考えたのでしょうか。なぜ、鳥が人間を襲うという小説や映画が "ホラー" として成立するのでしょうか。
ある説を読んだことがあります。いつだったか、誰の説だったか全く忘れましたが、哺乳類と恐竜の関係です。哺乳類の起源は恐竜と同程度に古いことが知られています。そして地球上で恐竜が全盛期のとき、哺乳類は体も小さく、恐竜から隠れるように "ひっそりと" 暮らしていた。肉食恐竜などはまさに哺乳類の恐れの対象だった。そして6500万年前に非鳥型恐竜が滅びた後も鳥型恐竜(=鳥)は生き残り、その飛行能力で世界中に広がった。そして哺乳類に刷り込まれていた "恐竜への恐れ" は、その恐れの対象が鳥へと引き継がれた。哺乳類の一種であるヒトも、無意識下でその遙か昔の感情がある。だから映画『鳥』がホラーとして成り立つ ───。
この説がまじめなものなのか、ジョークなのか、あるいは鳥が恐竜の子孫という最新の知識をひけらかしただけのものなのか、それは分かりません。科学的には大いにクエスチョンがつく説でしょう。しかし鳩やカラスが "本能的に" 猛禽類(鷹など)を恐れるということもあるので、これはこれで興味深い。そして人間の隠された潜在意識として鳥への恐れがあるのなら、鳥と恐竜を同一視する潜在意識もまたあると思うのです。それが、ある時、あるタイミングで、ある人の意識上にフッと浮上する。これが井の頭公園で池を泳ぐ鴨を見たときの彼女だった ───。これが第3の推測です。
何らかの類似性を直感できる能力
以上の歴史的経緯、骨格、潜在意識の3つは、科学的知識なしに「鳥が恐竜の子孫」と直感できた理由を推測したものです。もちろん当たっているかどうかは分かりません。ただ思うのですが、このような説明より、彼女は「歴史的経緯・骨格・潜在意識」などとは全く関係なく、
と考えた方が、より本質に迫っているのかもしれません。坂井氏は彼女が、
と強調することで彼女の意外な直感力に感心していますが、文系人間どうのこうのは全く関係ないと思います。それは理系人間的な偏見です。つまり、
だと思うのです。いわゆる "ひらめき" や "フッと浮かぶアイデア" です。あるいは、"突然思い付いた着想" や "発想の不連続的な飛躍" です。
文学の世界(小説、戯曲、詩、短歌など)で多用される "比喩" もその一つでしょう。一見、何の関係もなさそうなモノを本体を表す比喩表現として使う。それは作者が論理的に考えたものでないはずです。論理的に考えたものがあるかもしれないが、そういう比喩はおもしろくない。やはり直感で出てきたものにこそ意外性があって、価値がある。読者としても読んだときにはエッと思うが、よくよく考えてみると "当たっている" と思えるし、あるいは最後までその比喩表現の理由は不明だとしても(変な喩えだな!)そこに作者の感性を感じる。論理的な説明はできないけれど、文章に作者独特のムードが漂い、読者としてはそれに浸る。そういうことって、文学作品にはあると思うのです。
サイエンスに目を向けると「ニュートンがリンゴが木から落ちるのを見て万有引力を発見した」という有名な話があります。後世の作り話だと思いますが、作り話だとしてもよくできています。ニュートンの時代、重力はすでに知られていました。しかし「リンゴが地表に落ちる」ことと「惑星が太陽に引かれる」(ないしは月が地球に引かれる)ことという、全く関係がなさそうな事象が相似形だと気づいたとき、重力を越えた「万有引力」に発想が至るわけです。科学におけるインスピレーションの典型例を一つの寓話に仕立てたものだと思います。
要するに、何らかの抽象化をすれば2つのモノや概念が「同一の構造をしている」とか「そのモノや概念を成り立たせている基本のところが同型である、同一のフォルムである」というのは、文系・理系を問わず発想や創造の源泉の一つだと思います。
こういった発想や "ひらめき" は、根を詰めて解決策を探っている真っ最中には浮かびません。文章表現を絞り出しながらモノを書いているときにも出てこない。出てきたとしても斬新さがなく、面白味のないものになってしまうでしょう。なぜなら考えているフレームが決まっていて、フレームを越えた飛躍ができないからです。こうだからこうなるという論理的な文章や推論ならそれでよいが、それは "ひらめき" ではない。
発想や "ひらめき" は、解決策を探っている中でいったん頭を休め、ボーッとしている時に現れるとよく言われます。中国の古典に「三上」という言葉があります。文章を練るのに適した場所が、馬に乗っているとき(馬上)、寝床に入っているとき(枕上)、厠(便所)にいるとき(厠上)とするものですが、これは文章だけのことではないでしょう。散歩やそぞろ歩きの時に科学的発見のアイデアが浮かんだという話もよく聞きます。
最新の脳科学によると、人間はボーッとしているときにも脳が活発に活動していて、さまざまな記憶の断片をつなぎ合わせています。例えば、解決策を模索している問題に、あるとき(意外な時に)フッとアイデアがひらめくのは、脳が同一構造の過去の問題とその解決策をもとに、無意識下にアイデアを提示したのではと思います。ボーッとしているときに脳は「異質なモノ」や「かけ離れた記憶」の間にリンクをつけ、そのリンクがアイデアや直感やひらめきになるのでしょう。
本題に戻ります。ボーッとしているときに脳は「異質なモノ」の間にリンクをつけるのだとすると、井の頭公園の池で泳ぐ鴨を見て「鳥は恐竜の直系の子孫である」と直感した彼女は、その直感を別の機会に得たはずです。デートの時に "ボーッとしている" とは考えにくいからです。坂井氏のコラムから推測すると、彼女が1人で公園で鴨か鳩を "ボーッと" 眺めているときに突然ひらめいた。以降、公園で鴨や鳩を見るたびにそれを思い出す。井の頭公園でのデートで鴨を見たときもそうだった、ということでしょう。
理由は分からないが「鳥が恐竜の子孫」と直感し、確信できるのは人間の素晴らしいところだと思います。彼女の場合は "たまたま" 科学的に正しいことだったが、"科学的には間違っている" ことでもかまいません。その人にとっての直感はそうなのだし、小説家であればダフネ・デュ・モーリアのように、鳥が人間を襲い始めるというホラー小説を書けるかもしれません。
井の頭公園でのデートの最中に「鳥が恐竜の子孫だと、見ればわかった」坂井氏の奥様は、現在の人工知能(AI)の枠組みでは及ばない人間の価値を具現化していた、そのように思えました。
その「鳥は恐竜の子孫」に関係した話を、歌人で情報科学者(東京大学教授)の坂井修一氏が日本経済新聞に連載中のコラム、"うたごころは科学する" に書かれていました。坂井氏の奥様のことなのですが、興味深い内容だったのでそのコラムを引用して感想を書きたいと思います。
見ればわかる
|
40年前に「鳥は恐竜の子孫」と直感した坂井氏の奥様は、歌人の米川千嘉子さんです。コラムには名前が書いていないので、以下「彼女」と記述します。
40年前というと1980年です。坂井氏は1958年生まれで、彼女は1歳年下ということなので、二人とも20~22歳頃の話です。ということは、2人は東京の大学の大学生です。2人の学生が東京で知り合い、井の頭公園にデートに行く。いかにもありそうな情景です。井の頭公園は現在でも定番のデート・スポットなので、おそらく40年前もそうだったのでしょう。
よくありそうな情景には違いないが、そのデートの場で彼女が「池で泳いでいる鴨を見て、鳥は恐竜の直系の子孫であると強く主張」したのは、確かにちょっと変わっています。デートの場でどんな会話をしようと全くかまわないのですが、「鳥は恐竜の直系の子孫」という話題は、井の頭公園での男女の語らいとしては大変に斬新です。デート相手の女性にそんな主張を強くされたとしたら、男性としては一瞬、たじろぐでしょう。
しかも、その理由は「見ればわかる」ということのようなのです。これは一般的な意味での "理由" になっていません。男性としては一層不安になる。まして坂井氏は科学者(をめざす学生)です。帰納と演繹を繰り返して確認してからでないと不安、とコラムにある通りです。「見ればわかる」というのでは "帰納" の部分がゼロです。
そこで、今となっては科学的に全く正しい「鳥は恐竜の直系の子孫」という説を、1980年の時点でなぜ彼女が強く主張できたのか、その理由を何点か推測してみたいと思います。
鳥が恐竜の子孫という直感の理由
推測の1番目は歴史的経緯です。No.210「鳥は "奇妙な恐竜"」に書いたように、"鳥は恐竜の子孫ではないか" という考えは、実は19世紀半ばからありました。その契機になったのは1860年代にドイツで発見された、いわゆる「始祖鳥」の化石です。イギリスの高名な生物学者ハクスリーはこの化石が小型肉食恐竜に似ていることに気づき、鳥は恐竜の子孫という説を発表しました。当時、この説を支持する学者もいたようですが、多くの学者は反対しました。その後、議論は行ったり来たりの状態でした。
この説に決着がついたのは、1960年代以降に鳥類と酷似した恐竜化石が発見されたことであり、特に決定的だったのが1990年代以降の "羽毛付き恐竜化石" の発見でした。羽毛の化石は普通は残らないのですが、奇跡的な条件で化石になったものが中国で発見されたのです。
この経緯からすると「始祖鳥」の化石発見から100数十年の間、「鳥は恐竜の子孫説」が潜在していたことになります。つまり、これは大変に由緒ある説なのです。従って本などに書かれていた可能性が高い。ひょっとして「始祖鳥」の復元図とともに「鳥は恐竜の子孫説」を紹介した文章があったかもしれません。
井の頭公園で「鳥は恐竜の子孫」と主張した彼女も、そういった記述にどこかで触れ、それに惹かれ、そのことが潜在意識として残り、その潜在意識がデートの場で鴨を見てひょっと浮かび上がった。そういう可能性があると思うのです。これが第1の推測です。
第2の推測は鳥の骨格です。坂井氏は「駝鳥や海鵜を見ると、まあそれもありかなと思うが、彼女は公園の鴨や鳩を見てもそう感じるのだそうだ」と書いています。「鴨や鳩を見ても恐竜の子孫だと感じる」のがポイントですが、その理由は骨格ではないでしょうか。
まず、恐竜の骨格標本は子供の時代に多くの人が見たことがあると思います。恐竜の実物の(ないしは実物大レプリカの)骨格標本は、全国の博物館の超人気アイテムです。小学校高学年以上の子供であれば、その恐竜の姿に心を踊らせるのは当然でしょう。たとえ実物やレプリカを見たことがなくても、恐竜の骨格の写真は雑誌を始めとする各種メディアにあるので、それを見たことが無いという人はまずいないと思います。
一方、鴨や鳩の骨格標本を見る機会はあまりないと思いますが、博物館にはあります。彼女は、鴨か鳩の骨格標本をどこかで見たのではないでしょうか。実物を見たことがないにしても、写真とかイラストで見たのではと思います。ごく一般的な鳩の写真と、鳥の解剖学的イラストを掲げます。イラストは No.210「鳥は "奇妙な恐竜"」の図を再掲したものです。

|
飛行中の鳩 |
(Wikimedia Commoms) |

| ||
|
鳥類の解剖学的特徴
翼、長い前肢、短い尾骨、竜骨、貫流式の肺、叉骨(さこつ)、大きな脳など、鳥類は他の現世動物にはない特徴がある。これら特徴のおかげで鳥類は飛行できる。
(日経サイエンス 2017年6月号より)
| ||
解剖学的イラストを見て気づくのは、鳥の首の骨が異様に長いことです。羽とか胸のあたりとか足とか、そういう骨は想像どおりだが、首の骨は鳩の外見からは想像しにくい。鳥の頸椎(首の骨)は、11~25個もあります(種類によって違う)。人間を含む哺乳類は、普通は7個です。キリンでも7個です。それに対して鳥は多い。
フクロウは首を270度回転することができますが(1回転できるというのは誤解)、こんなことは哺乳類では絶対に無理です。なぜフクロウが可能かというと、頸椎が多いからです(14個)。従って少しづつ回転させると270度になる。フクロウは外見上は首長に見えないのですが、骨格からみるとそうなのです。上の画像の鳩もそうです。外形からは首が長いように見えないが、頸椎は13個あって、首の骨格はひょろっと長い。
外見上、明らかに首長だと見える鶴とか鵜、鷺、ダチョウの頸椎が長いのは当然ですが、一見そうは見えない鳩などの鳥も意外に長いのです。もちろん、井の頭公園で泳いでいる鴨の頸椎も長い。そしてこの鳥の骨格(頸椎)の姿は暗黙に、恐竜の中で首の長い種類(草食の4つ足の恐竜。専門的には竜脚類)の骨格を連想させないでしょうか。
どこかで見た鳥の骨格標本(ないしは骨格のイラスト図)が、子供のころに親しんだ竜脚類の骨格と無意識下で結びつき、それが井の頭公園でのデートで鴨を見たときにフッと浮かび上がった。これが第2の推測です。
第3の推測は人間の潜在意識です。往年の名監督、アルフレッド・ヒッチコック(1899-1980)の映画に『鳥』(1963)がありました。あらゆる種類の鳥が人間を襲い出すというパニック映画(かつホラー映画)です。大挙して部屋に進入してきた鳥に襲われて人が血まみれになるなど、衝撃的なシーンがいろいろありました。

|
ヒッチコック「鳥」(1963) |
主人公(ティッピ・ヘドレン)は大量の鳥が小学校の周りに集まっているのを見て子供たちを避難させるが、その途中で鳥の大群に襲われる。 |
これはイギリスの作家、ダフネ・デュ・モーリア(1907-1989。原音に近く "ダフニ・デュ・モーリエ" とも書かれる)の短編小説、"The Birds"(1952)が原作です。ダフネ・デュ・モーリアは畑で農夫がカモメに襲われるのを見て小説のインスピレーションを得たそうですが(Wikipedia による)、なぜそのことが小説を書く契機になったのでしょうか。また、ヒッチコックはなぜ映画化しようと考えたのでしょうか。なぜ、鳥が人間を襲うという小説や映画が "ホラー" として成立するのでしょうか。
ある説を読んだことがあります。いつだったか、誰の説だったか全く忘れましたが、哺乳類と恐竜の関係です。哺乳類の起源は恐竜と同程度に古いことが知られています。そして地球上で恐竜が全盛期のとき、哺乳類は体も小さく、恐竜から隠れるように "ひっそりと" 暮らしていた。肉食恐竜などはまさに哺乳類の恐れの対象だった。そして6500万年前に非鳥型恐竜が滅びた後も鳥型恐竜(=鳥)は生き残り、その飛行能力で世界中に広がった。そして哺乳類に刷り込まれていた "恐竜への恐れ" は、その恐れの対象が鳥へと引き継がれた。哺乳類の一種であるヒトも、無意識下でその遙か昔の感情がある。だから映画『鳥』がホラーとして成り立つ ───。
この説がまじめなものなのか、ジョークなのか、あるいは鳥が恐竜の子孫という最新の知識をひけらかしただけのものなのか、それは分かりません。科学的には大いにクエスチョンがつく説でしょう。しかし鳩やカラスが "本能的に" 猛禽類(鷹など)を恐れるということもあるので、これはこれで興味深い。そして人間の隠された潜在意識として鳥への恐れがあるのなら、鳥と恐竜を同一視する潜在意識もまたあると思うのです。それが、ある時、あるタイミングで、ある人の意識上にフッと浮上する。これが井の頭公園で池を泳ぐ鴨を見たときの彼女だった ───。これが第3の推測です。
何らかの類似性を直感できる能力
以上の歴史的経緯、骨格、潜在意識の3つは、科学的知識なしに「鳥が恐竜の子孫」と直感できた理由を推測したものです。もちろん当たっているかどうかは分かりません。ただ思うのですが、このような説明より、彼女は「歴史的経緯・骨格・潜在意識」などとは全く関係なく、
恐竜と井の頭公園の鴨との間に何らかの意味での類似性を感じ取り、鳥が恐竜の子孫と直感して、確信した
と考えた方が、より本質に迫っているのかもしれません。坂井氏は彼女が、
| いわゆる文系人間であり | |
| リモコンが使いこなせず | |
| パソコンやスマホでのSNSも得意ではない |
と強調することで彼女の意外な直感力に感心していますが、文系人間どうのこうのは全く関係ないと思います。それは理系人間的な偏見です。つまり、
まったく違うと思える2つのモノや概念の間に何らかの意味での類似性を直感したり、相互に連想を働かせることは、文学や芸術における創造、サイエンスや工学分野での発見・発明、ビジネスにおける問題解決プロセスの導出などにおいて、とても重要なこと
だと思うのです。いわゆる "ひらめき" や "フッと浮かぶアイデア" です。あるいは、"突然思い付いた着想" や "発想の不連続的な飛躍" です。
文学の世界(小説、戯曲、詩、短歌など)で多用される "比喩" もその一つでしょう。一見、何の関係もなさそうなモノを本体を表す比喩表現として使う。それは作者が論理的に考えたものでないはずです。論理的に考えたものがあるかもしれないが、そういう比喩はおもしろくない。やはり直感で出てきたものにこそ意外性があって、価値がある。読者としても読んだときにはエッと思うが、よくよく考えてみると "当たっている" と思えるし、あるいは最後までその比喩表現の理由は不明だとしても(変な喩えだな!)そこに作者の感性を感じる。論理的な説明はできないけれど、文章に作者独特のムードが漂い、読者としてはそれに浸る。そういうことって、文学作品にはあると思うのです。
サイエンスに目を向けると「ニュートンがリンゴが木から落ちるのを見て万有引力を発見した」という有名な話があります。後世の作り話だと思いますが、作り話だとしてもよくできています。ニュートンの時代、重力はすでに知られていました。しかし「リンゴが地表に落ちる」ことと「惑星が太陽に引かれる」(ないしは月が地球に引かれる)ことという、全く関係がなさそうな事象が相似形だと気づいたとき、重力を越えた「万有引力」に発想が至るわけです。科学におけるインスピレーションの典型例を一つの寓話に仕立てたものだと思います。
要するに、何らかの抽象化をすれば2つのモノや概念が「同一の構造をしている」とか「そのモノや概念を成り立たせている基本のところが同型である、同一のフォルムである」というのは、文系・理系を問わず発想や創造の源泉の一つだと思います。
こういった発想や "ひらめき" は、根を詰めて解決策を探っている真っ最中には浮かびません。文章表現を絞り出しながらモノを書いているときにも出てこない。出てきたとしても斬新さがなく、面白味のないものになってしまうでしょう。なぜなら考えているフレームが決まっていて、フレームを越えた飛躍ができないからです。こうだからこうなるという論理的な文章や推論ならそれでよいが、それは "ひらめき" ではない。
発想や "ひらめき" は、解決策を探っている中でいったん頭を休め、ボーッとしている時に現れるとよく言われます。中国の古典に「三上」という言葉があります。文章を練るのに適した場所が、馬に乗っているとき(馬上)、寝床に入っているとき(枕上)、厠(便所)にいるとき(厠上)とするものですが、これは文章だけのことではないでしょう。散歩やそぞろ歩きの時に科学的発見のアイデアが浮かんだという話もよく聞きます。
最新の脳科学によると、人間はボーッとしているときにも脳が活発に活動していて、さまざまな記憶の断片をつなぎ合わせています。例えば、解決策を模索している問題に、あるとき(意外な時に)フッとアイデアがひらめくのは、脳が同一構造の過去の問題とその解決策をもとに、無意識下にアイデアを提示したのではと思います。ボーッとしているときに脳は「異質なモノ」や「かけ離れた記憶」の間にリンクをつけ、そのリンクがアイデアや直感やひらめきになるのでしょう。
ちょっと脱線しますが、こういった脳の働きに関連して「デジャヴュ」(=デジャヴ、既視感)を思いだしました。デジャヴュは「一度も体験したことがないのに、すでにどこかで体験したように感じる現象」のことです。視覚だけでなく聴覚、触覚などについても言うので「既知感」と言うことあります。
個人的には視覚のデジャヴュ経験は記憶にないのですが、聴覚(=音楽)なら時々あります。その一つの例ですが、No.262「ヴュイユマンのカンティレーヌ」で、ヴュイユマン作曲の「カンティレーヌ」というピアノ曲を初めて聴いたとき、これはシューマンの曲に違いないと思ったが、しかしそれはシューマン作曲「謝肉祭」への連想だったという自己分析を書きました。「カンティレーヌ」と「謝肉祭」はかなり違った雰囲気の曲(そもそも拍子が違う)ですが、無意識に2つの曲の間に何らかのリンクがついたのだと思います。
個人的には視覚のデジャヴュ経験は記憶にないのですが、聴覚(=音楽)なら時々あります。その一つの例ですが、No.262「ヴュイユマンのカンティレーヌ」で、ヴュイユマン作曲の「カンティレーヌ」というピアノ曲を初めて聴いたとき、これはシューマンの曲に違いないと思ったが、しかしそれはシューマン作曲「謝肉祭」への連想だったという自己分析を書きました。「カンティレーヌ」と「謝肉祭」はかなり違った雰囲気の曲(そもそも拍子が違う)ですが、無意識に2つの曲の間に何らかのリンクがついたのだと思います。
本題に戻ります。ボーッとしているときに脳は「異質なモノ」の間にリンクをつけるのだとすると、井の頭公園の池で泳ぐ鴨を見て「鳥は恐竜の直系の子孫である」と直感した彼女は、その直感を別の機会に得たはずです。デートの時に "ボーッとしている" とは考えにくいからです。坂井氏のコラムから推測すると、彼女が1人で公園で鴨か鳩を "ボーッと" 眺めているときに突然ひらめいた。以降、公園で鴨や鳩を見るたびにそれを思い出す。井の頭公園でのデートで鴨を見たときもそうだった、ということでしょう。
理由は分からないが「鳥が恐竜の子孫」と直感し、確信できるのは人間の素晴らしいところだと思います。彼女の場合は "たまたま" 科学的に正しいことだったが、"科学的には間違っている" ことでもかまいません。その人にとっての直感はそうなのだし、小説家であればダフネ・デュ・モーリアのように、鳥が人間を襲い始めるというホラー小説を書けるかもしれません。
井の頭公園でのデートの最中に「鳥が恐竜の子孫だと、見ればわかった」坂井氏の奥様は、現在の人工知能(AI)の枠組みでは及ばない人間の価値を具現化していた、そのように思えました。
2020-09-19 11:52
nice!(0)
No.293 - "自由で機会均等" が格差を生む [科学]
今回は、日経サイエンス 2020年9月号に掲載された論文「数理が語る格差拡大のメカニズム」の内容を紹介するのが目的です。この論文は、自由主義経済においては公平でフェアな取引きを繰り返すと必然的に格差が拡大することを数理モデルで論証したものです。
なぜこの論文を取り上げるかというと、No.165「データの見えざる手(1)」で紹介した "玉の移動シミュレーション" と本質的に同じことを言っているからです。そこでまず、No.165のシミュレーションを復習してから本題に入りたいと思います。
コインの移動シミュレーション
No.165は、矢野和男・著「データのみえざる手」(草思社 2014)の内容の一部を紹介したものでした。この中に出てきたシミュレーションをここで再掲します。ただし本質をより明確にするため、シミュレーションの初期設定を変え、またシミュレーションの実行は繰り返し回数を変えて3種類にします。No.165では「玉」と書きましたが、本題につなげるために「コイン」とします(同じことです)。
まず 30 × 30 = 900 のセルを用意し、これらのセルに初期状態としてコインをそれぞれ 80 割り当てます。従って割り当てるコインの総数は、
80 × 900 = 72,000
です。900 とか 80 という数字は、No.165「データの見えざる手(1)」に合わせるためにそうしただけで、他意はありません。今回は別の数でもかまわないのですが、シミュレーション・プログラムをそのまま再利用するために、この値とします(ただし「データの見えざる手」ではこの値が実世界上の意味を持っていました。No.165 参照)。
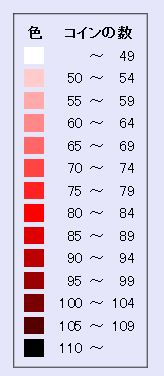
以下、シミュレーションの各段階のセルの状態を図示するため、セルが保有するコインの数に応じてセルを色分け表示します。色分けのルールは、コインが初期値の80のセルを赤(ピュアな赤)とし、コインが少なくなるにつれて白っぽい赤になり、コインの数が50未満だと真っ白とします。逆にコインの数が80より増えるとセルの色は黒っぽくなり、コインの数が110以上になる真っ黒とします。色分けの凡例を示したのが左の「セルの色分け」図です。
シミュレーションの進展によってセルのコインの数は変化しますが、この色の塗り方では、平均値 = 80 の ±30 の範囲が赤のグラディエーションで、それ以下では白、それ以上は黒になります。この色塗りの閾値はNo.165での説明の都合上で決めた値で、他の値でもかまいません。
初期状態では各セルに均等に 80 のコインを割り当てるので、それを図示すると全部のセルが同じ色(ピュアな赤)で表示されます。
シミュレーションは以下のように進めます。
以上の ① ② ③ を多数繰り返します。今回の繰り返し回数は10万回、100万回、1000万回の3種とします。コインは単に移動するだけなので、セルがもつコインの平均値は初期値である80のままで変わりません。
この「移動の繰り返しシミュレーション」で各セルのコインの数はどのように変化するでしょうか。おそらくほとんどの人は次のようの推論するのではないでしょうか。
これはいかにも理性的というか、真っ当な推論であり、妥当な予想だと思います。しかし実際に移動シミュレーションを行ってみるとこの予想は大きくはずれ、全く違った様相になります。それが次です。
移動シミュレーションを10万回行う試行をして、その結果を凡例に従って色分け表示したのが次の図です。この結果では、全体のおよそ95%のセル(859のセル)のコイン数が50~109の範囲に収まっています。従ってほとんどが赤のグラディエーションで塗られています。一方、白のセル(コイン数が50未満)は17個、黒のセル(コイン数が110以上)は24個です。最も少ないセルのコイン数は40で、最も多いセルのコイン数は130です。
この10万回の移動シミュレーションの結果は、ほぼ予想どおりと言っていいでしょう。
もちろん乱数を使ってシミュレーションをしているので、毎回まったく同じ結果になるわけではありません。しかし10万回のシミュレーションを何度繰り返しても、ほぼ類似の結果になります。
シミュレーションを 100万回繰り返すと様相がかなり違ってきます(次図)。
このシミュレーションでは
です。10万回のシミュレーションではコイン数:50~109のセルがほどんどでしたが、100万回になるとそれは全体(900)の約半分になります。それ以上とそれ以下がほぼ同数あり、「格差」が広がっていることがわかります。また最多のコインを持っているセルのコインの数は平均(=80)の約3倍です。さらに、コインが無くなるセルが出現しました(4つのセル)。
移動の繰り返しが1000万回になると「格差」はもっと激しくなります(次図)。
このシミュレーションでは
でした。コイン数が110以上のセル(裕福なセル)の数(247)は 100万回のシミュレーションの場合(231)より増えますが、大して変わりません。しかし最大コイン数が 382であるように、コインは裕福なセルに集中してきます。これと相対応して、コイン数49以下のセル(貧しいセル)が増えていきます。結果の色分け表示を見ても全体が白っぽく表示されるようになります。
900のセルが「裕福」「中間」「貧困」に分かれましたが、どのセルがどの層にいくかはシミュレーションをするたびに異なります。あくまで偶然にそうなった、ないしは、たまたまそうなったということなのです。
ローレンツ曲線とジニ係数
以下、移動回数が1000万回の場合で考えます。各セルを「人」、コインを「その人が保有している資産」と考えると、
と見なせるわけです。ここで、この集団の格差の状況を1つの数値で表すことを考えます。このために昔から使われるのがローレンツ曲線とジニ係数です。ローレンツ曲線は、
の2次元 x-y平面に描かれます。まず900のセル(人)を、保有するコイン(資産)の数で小さい人から大きい人まで昇順に並べます。
ローレンツ曲線の x 軸は「累積人数比率(総人数を母数とする割合)」です。つまり x = 0.5 とは、資産の少ない方から数えて全体(900)の半分(450)までの人々を表します。
ローレンツ曲線の y 軸とは「累積資産比率」で、累積人数比率の人々が持つ資産総計の、全体(72,000)を母数とする割合です。
初期状態は各人は平等(資産は全員80)なので、この時のローレンツ曲線は (0, 0) と (1, 1) を結ぶ45°の直線になります。しかし格差が広がるにつれて、ローレンツ曲線は (0, 0) から始まってわずかずつ上昇し、最後は尻上がりに (1, 1) に至る曲線となります。上の 1000万回の移動シミュレーションの結果のローレンツ曲線を描いたのが次の図です。この図には初期状態の斜め45°の直線(点線)も描いてあります。
この図で「斜め45°の直線」と「ローレンツ曲線」で囲まれた半月状の形の面積を考えてみると、格差がない状態では面積=0、資産を一人が独占している状態では面積=0.5 となります。この面積の2倍が「ジニ係数」で、格差が全くない場合は 0、一人が資産を独占している場合は 1 です。上の例の1000万回の移動シミュレーションの場合、
ジニ係数=0.49
となりました。シミュレーションは乱数(正確に言うとパソコンで作り出す疑似乱数)をもとに計算しているので、1000万回の試行を何回かやるとジニ係数も変化します。しかし必ず 0.5付近の値になります。ちなみに10万回と100万回も含めてジニ係数をリストすると、
となりました。シミュレーションの回数が増えるに従って格差が拡大します。
以上のシミュレーションは何らかの意味があるのでしょうか。それとも単なるコンピュータを使った "遊び" でしょうか。
「データの見えざる手」において著者の矢野和男氏は次のように書いています。
セルを人、コインを資産とすると、このシミュレーションは2人の間で経済取引をするときの最も素朴なモデルになっています。経済取引とはモノやサービスの売買です。商品の販売や購入がそうだし、労働サービスを提供してその対価としての給料を得るのも経済取引です。株券の売買や、先物取引のような「売買する権利の売買」も経済取引です。
今の自由主義経済では、経済取引は自由に行ってよいわけです。もちろん独占禁止法とか最低賃金法があって「不当な利益」はあげられないようになっている。その各種の規制やルールの範囲内で、どんなモノやサービスをどんな価格で売買するかは自由です。
しかしモノやサービスの売買では、損をする人と得をする人が発生します。つまりモノやサービスがその時にもっている "真の価値" 以上の値段で買うと損になり、真の価値以下の価格で買うと得になります。損か得かは売買をする2人で逆転します。この「損得の発生」は「資産が2人の間で移動した」と考えられるわけです。ここでの「資産」は「保有しているモノとお金の価値合計」ぐらいに考えておきます。Aさんが100円の価値のものを110円でBさんに打ったとすると、10円の資産がBさんからAさんに移動したと考えるわけです。
大切なところは、AさんとBさんのどちらが損をするか得をするかは分からないいことです。特に取引の前に損得は分からない。なぜなら、モノやサービスの "真の価値" を知り得ないからです。従って損得はランダムに(確率的に)決まる。これは上のシミュレーションにおいてコインの移動方向をランダムに(確率的に)決めたことに相当します。
以上が、このシミュレーションが「自由な経済取引の素朴なモデル」になっている理由です。このモデルでは取引を重ねるほど格差が増大します。矢野氏の著書の名前である「データの見えざる手」は、もちろんアダム・スミスの「神の見えざる手」の "もじり" ですが、これは言い得て妙という感じがします。「見えざる手」論は、自由な市場が価格変動を調節して資源の最適配分に導くという主張ですが、実はこの「神の手」は取引の繰り返しによって格差を生み出すことに役だっているようなのです。
公正で機会均等な取引が格差を生む ────。このことを経済学の論文として明らかにした雑誌記事を次に紹介します。前置きが長くなりましたが、ここからが本題です。
数理が語る格差拡大のメカニズム
これ以降、日経サイエンス 2020年9月号に掲載された論文「数理が語る格差拡大のメカニズム」の内容を紹介します。この論文は、タフツ大学(米国・マサチューセッツ州)のブルース・ボゴシアン教授が執筆したものです。ボゴシアン教授は数学者で、論文の内容を一言で要約すると、
ことを数理モデルで論証したものです。論文ではまず、世界の様々な国で富の不平等が拡大していることが語られます。
このような富(資産)の集中がどうして起こるのか、それを数理モデルで解析しようするのがボゴシアン教授の目的です。
資産の分布とエージェントモデル
まず前提として資産とは何かですが、論文ではその定義が書いてありません(自明のこととしてあります)。従って一般的な理解で言いますと、これは個人が保有している資産(家計資産)のことです(法人や企業の資産ではない)。またその資産の内容は、金融資産(現金や株券・債権など)に非金融資産(不動産や貴金属などで換金可能なもの)を加え、そこから負債(借金)を引いたものです。従って資産はマイナスになり得ることに注意しましょう。ボゴシアン教授の数理モデルにもそれが出てきます。
資産の分布をモデル化する出発点は「エージェントベースの資産分布モデル」です。エージェントとは商取引を行う「主体」のことで、2人のエージェントが行う商取引がモデルのベースです。つまり2人のエージェントが自由意志で、互いに納得した価格で財貨を交換する。たとえば「商品を買う」「労働の対価として賃金を得る」などです。このエージェント同士が行う商取引を膨大に積み重ねた結果として社会全体の資産分布が決まるというのが、今回の数理モデルです。
この「自由意志で、互いに納得した価格で財貨を交換」するモデルは、現代社会において公正でフェアだと考えられています。また上に引用した「神の見えざる手」論のように、需要と供給をバランスを調整して安定した経済体系を作るとされていて、いかにも "自然な" モデルです。しかし、実はそこに格差を生み出すメカニズムが潜んでいるというのが、以下の論です。
ヤードセールモデル
2002年、インドのサハ核物理学研究所のチャクラボルティ(Aanirban Chakraborti)は、上記のエージェントモデルの一種である「ヤードセールモデル」を導入しました。ボゴシアン教授はこのモデルを出発点にしています。
「ヤードセール」とは、家の庭(yard)で行う不要品販売セールのことです。このモデルは「不要品販売セールにみられる1対1取引きの特徴」があるのでこの名前がつきました。次のようなモデルです。
このモデルはいかにも妥当に思えます。つまり「売り手・買い手のどちらに資産が移動するかはランダムにきまる。かつ資産の移動量(Δw)は貧しい方の人の資産の一部」というところは、実際の経済生活を通じてほとんどの人が経験してきたことであり、また自分に課している制限だと考えられるからです。
このヤードセールモデルによる取引を、例えば1000人の集団で行います。各人が最初に持っている資産は完全に同額です。ここからランダムに選ばれた2人が取引をします。これを何100万回、何億回と繰り返すシミュレーションをしたらどうなるか。
ここで、Δwを「貧しい方の人が保有している資産の20%」とする必然性はありません(明らかに20%は過大です)。数字は問題ではなく、2%でも何%でもよい。数字が少なくなるとシミュレーションの収束に時間がかかるだけで結果は同じだからです。それどころか、次のような「ヤードセールモデルの変種」でもよい。つまり、
とするわけです。つまり貧しい人が相対的に少し有利になる設定です。しかしこの設定でも結果は変わりません。論文から引用します。
論文にはありませんが、このシミュレーションを実際にやってみました。基礎数値は「データの見えざる手」のものを採用します。
このシミュレーションのローレンツ曲線とジニ係数が次の図です。きわめて極端な格差が生まれていることが分かります。
このシミュレーションを1000万回ではなくもっと多数繰り返していくと、資産が一人に集中する「寡頭支配」になります。論文に「他の999人にはほとんと何も残らない」と書いてあるのは、このシミュレーションではどの人も資産がゼロになることはないからです。しかし999人はゼロに極めて近い値になる。つまり「ほとんと何も残らない」のです。
ちなみに上のシミュレーションを1000万回で止めたのは、あまりやると極端な独占が進み、ローレンツ曲線が曲線らしくなくなるからでした。
論文に戻って、ボゴシアン教授の論を続けます。
"この種の現象を物理学者は「対称性の破れ」と呼んでいる" とありますが、日経サイエンスでは「対称性の破れ」を "相転移" の例で解説しています。たとえば磁石ですが、なぜ磁力が発生するかというと磁石の中の分子が極小の磁石となっていて、その磁力の向き(N極とS極)が揃っているからです。
ところが温度を上げて特定の温度(=キュリー温度)に達すると、突然、磁力がなくなります。キュリー温度以上では極小磁石の向きがバラバラになるからです。このバラバラになった状態では、どの方向から観察しても性質が同じなので「対称性がある」と表現されます。
逆に、キュリー温度以上から徐々に温度を下げると、キュリー温度のところで突如「対称性の破れ」が発生し、極小磁石は同じ向きに整列し、方向によって違う物理性質を示します。つまり磁石になります。
ボゴシアン教授の説明は続きます。
引用の最後のところにあるヤードセールモデルは、オリジナルのものです。つまり商取引で移動する資産は移動方向に関わらす同じ(例えば、貧しい主体の20%)というモデルです。一方、上のシミュレーション例は貧者が少しだけ有利な「ヤードセールモデルの変種」でした。もちろん「ヤードセールモデルの変種」よりも「ヤードセールモデル」の方が富の集中は急速に進みます。以下の議論は、オリジナルのヤードセールモデルに基づきます。
再分配パラメータの導入
ヤードセールモデルが社会の資産の偏在を表現しているというのではありません。このモデルではシミュレーションが進むにつれて資産が1人に独占されますが、現実社会はそうなっていないからです。
そこで「再分配パラメータ」を導入します。これは、各主体が取引を行うごとに、各主体の資産を社会全体の資産の平均値に少しだけ近づけるものです。これをコントールするパラメータを χ(カイ。ギリシャ文字)とし、
再分配 =
(資産の平均値 ー 取引主体の資産)× χ
だけの資産を各主体にプラスします。従って、平均値以下の主体の資産は増額され、平均値以上の主体の資産は減額されることになります。これは裕福な人に富裕税を課し、それを貧しい人に配分するということに相当します。
資産バイアス・パラメータの導入
ここまでの議論では、取引において資産が移動する方向は全くランダム(確率でいうと 0.5 / 0.5)としていました。しかし現実の社会では、富裕層が低金利融資や専門家による財産形成のアドバイスといった経済的恩恵を受けているのに対し、貧しい人々は高金利の借金をしたり最適価格の品を探す時間的余裕がないなど、経済的には不利な状況にあります。
そこでこの状況を模擬するために「資産バイアスパラメータ」の ζ(ゼータ。ギリシャ文字)を導入します。そして
資産バイアス =
(取引主体の資産差額 / 資産の平均額)× ζ
とし、資産バイアスの確率だけ裕福な者が有利になるようにします(取引主体の資産差額は絶対値)。論文には詳細が書いてありませんが、たとえば
裕福な者が得をする確率 =
0.5 + 資産バイアス / 2
貧しい者が得をする確率 =
0.5 - 資産バイアス / 2
とすれば、ちょうど資産バイアスだけの確率差がつくことになります。この定義の資産バイアスは1以上になる可能性があります。たとえば ζ を0.05 とすると、取引主体の資産差額が集団の資産の平均額の20倍あるとちょうど1になります。こうなると必ず裕福なものが得をすることになる。従って実際のシミュレーションでは資産バイアスが 1 以下になるような、何らかの調整が必要なはずです。
ともかく、再分配パラメータに加えて資産バイアスパラメータを考慮したモデルの解析結果が次です。
著者によると、ζ が χ を下回った場合は寡頭集中のない安定的な状態に落ち着くそうです。
ちなみに「米国と欧州諸国の資産分布の経験的データと誤差 x% で一致」という表現についてですが、χ や ζ といったパラメータを国ごとにどのように設定すれば資産分布の経験的データを最もよく表現できるかをサーベイし、その結果の最適値のときの誤差が x% という意味です。
マイナス資産の導入
さらにモデルの改良は続きます。これまでのモデルではシミュレーションをいくら繰り返しても資産がマイナスになることはありません。もちろん寡頭集中が起こったりすると多数の人の資産がゼロに近づくのですが、原理上マイナスにはなりません。
しかし実社会では資産がマイナスということが起こります。保有している現金や不動産などの額より負債額が多ければ資産はマイナスだからです。しかし資産がマイナスであっても商取引は可能であり、社会では実際に行われています。
この状況をモデル化するために、新たなパラメータ κ(カッパ。ギリシャ文字)を導入し、最大マイナス資産(=S)を次の式で計算します。
最大マイナス資産(S)=
資産の平均額 × κ
そして、拡張ヤードセールモデル(χ と ζ を入れたモデル)による取引をする前に、2つの取引主体の資産に S を加え、取引が終わったあとに2つの取引主体の資産から S を引くという操作をします。この操作によって、集団の中で最も資産が少ない人の資産額が -S となります。
いままで出てきた3つのパラメータ、χ と ζ と κ を導入したモデルが最終のもので、著者はこれを数学者らしく「アフィン型資産モデル(AWM)」と呼んでいます。
上に向かって流れる富
ボゴシアン教授の数理モデルは、欧米各国の資産分布モデルを極めて正確に再現できることがわかりました。これは今まで作られてきた各種モデルの中で現実に最もよく合致するものです。次が論文の結論部分です。
この論文の原題は「The Inescapable Casino」です。直訳すると「逃げ出せないカジノ」で、これは現代の自由主義経済の社会そのものを言っています。論文に出てきたヤードセールモデルは、カジノにおける客とディーラーの賭とそっくりです。客の資金は限られているがディーラー(=カジノの代表)の資金は客に比べると膨大です。賭を長く続ければ続けるほど客の資金は底をつく。カジノで損をしないためには一刻も早くカジノから出るしかありません。しかし現代の自由主義経済社会というカジノから逃げ出すことはできないのです。
この論文で展開されているのは「数理モデル」であって、現実の人間社会の経済活動ではありません。しかしこれだけ正確に各国の経済格差をモデル化できるということは、そこに何かしらの真実が含まれていると考えるべきでしょう。
公正でフェアで機会(チャンス)が均等な取引の積み重ねが富の格差を生み出す。しかも、社会に参加する時点で人が保有している富に差がついていると有利・不利が初めから決まってしまう。このことを警鐘として受け止めるべきだと思いました。
またこの論文は、我々にある種の思い込みがあることを明らかにしていると思います。それは "すべての結果には原因がある" という思い込みです。結果をもたらすに至った原因を追求することは社会活動の大原則です。なぜそうなったか、その根本原因を追求して対策を打つ。それで社会が成り立っています。
しかし、すべての結果に原因があるわけではないのです。裕福な者と貧しい者、その差は本人の能力や努力の結果であり、さらにはどういう家庭に生まれたかの差である。そう考えることは正しいが、そればかりではない。偶然に差がついたという要素もあるのです。
知らず知らずのあいだに我々の思考を束縛する "思い込み" は排除しなければならない。そう感じました。
さらに思ったことがあります。「公平で機会均等な取引の積み重ねが富の格差を生み出す」という結果はコンピュータがないとしたら絶対に発見できなかっただろう、ということです。手作業や紙と鉛筆だけでの思考では無理です。コンピュータがあるからこそ(私のように)家庭用パソコンでも簡単に検証できてしまう。その結果は、全く意外なものです。
ボゴシアン教授は論文で「ヤードセールモデルが富を貧者から富める者へと移動させることの数学的な証明を与えた」と説明していました。数学的な発見があって、結果がどうなるかを見い出したのではありません。コンピュータ・シミュレーションによる結果がまずあり、なぜそうなるのかという数学的証明を後から行ったわけです。この論文は、今さらながらですが、コンピュータの威力と可能性を示しているのでした。
本文で紹介したのは日経サイエンス 2020年9月号に掲載された「数理が語る経済格差のメカニズム」の内容でしたが、同じ日経サイエンスの2021年4月号に米国の経済格差の変遷が出ていました。1人あたりの GDP が増えるにつれて経済格差が増大してきたことを示すグラフです。ここでは経済格差の指標として「所得のジニ係数」を取り上げています。本文は「資産のジニ係数」の話だったので注意ください。
このグラフにつけられた説明には次のようにありました。この説明の中には「資産の経済格差」も出てきます。
なぜこの論文を取り上げるかというと、No.165「データの見えざる手(1)」で紹介した "玉の移動シミュレーション" と本質的に同じことを言っているからです。そこでまず、No.165のシミュレーションを復習してから本題に入りたいと思います。
コインの移動シミュレーション
No.165は、矢野和男・著「データのみえざる手」(草思社 2014)の内容の一部を紹介したものでした。この中に出てきたシミュレーションをここで再掲します。ただし本質をより明確にするため、シミュレーションの初期設定を変え、またシミュレーションの実行は繰り返し回数を変えて3種類にします。No.165では「玉」と書きましたが、本題につなげるために「コイン」とします(同じことです)。
まず 30 × 30 = 900 のセルを用意し、これらのセルに初期状態としてコインをそれぞれ 80 割り当てます。従って割り当てるコインの総数は、
80 × 900 = 72,000
|
以下、シミュレーションの各段階のセルの状態を図示するため、セルが保有するコインの数に応じてセルを色分け表示します。色分けのルールは、コインが初期値の80のセルを赤(ピュアな赤)とし、コインが少なくなるにつれて白っぽい赤になり、コインの数が50未満だと真っ白とします。逆にコインの数が80より増えるとセルの色は黒っぽくなり、コインの数が110以上になる真っ黒とします。色分けの凡例を示したのが左の「セルの色分け」図です。
シミュレーションの進展によってセルのコインの数は変化しますが、この色の塗り方では、平均値 = 80 の ±30 の範囲が赤のグラディエーションで、それ以下では白、それ以上は黒になります。この色塗りの閾値はNo.165での説明の都合上で決めた値で、他の値でもかまいません。
初期状態では各セルに均等に 80 のコインを割り当てるので、それを図示すると全部のセルが同じ色(ピュアな赤)で表示されます。
 |
初期状態 |
初期状態では30×30のセルにそれぞれ80のコインを割り当てる。 |
| シミュレーションの進め方 |
シミュレーションは以下のように進めます。
| 2つの異なるセルをランダムに選ぶ。 | |
| 選ばれた2つのセルについて、一方のセルからもう一方のセルにコインを1枚移す。つまり一方のセルのコインを1だけ増やし、他方を1だけ減らす。このとき、どちらからどちらへコインを移すかはランダムに決める。2つのセルのその時のコインの数は全く考慮しない。 | |
| ただし、移動元となったセルのコインの数がゼロだった場合は何もしない。 |
以上の ① ② ③ を多数繰り返します。今回の繰り返し回数は10万回、100万回、1000万回の3種とします。コインは単に移動するだけなので、セルがもつコインの平均値は初期値である80のままで変わりません。
この「移動の繰り返しシミュレーション」で各セルのコインの数はどのように変化するでしょうか。おそらくほとんどの人は次のようの推論するのではないでしょうか。
| 1回の移動で選ばれるセルの数は2で、全体の 1/450 である。従って、たとえば10万回繰り返すとすると、一つのセルに注目した場合、100,000 / 450 = 約220回、移動の対象なるに違いない。もちろんランダムに選択するので220回ということはなく、180回からもしれないし、250回かもしれない。しかし極端なこと(数回しか選ばれないとか、1万回選ばれるとか)は起こらないはずだ。 | |
| 選ばれた各回において、セルが移動元となるか(コインが - 1)、移動先となるか(コインが + 1)は全くランダムに決まる。その時のセルのコイン数は全く考慮されない。従ってこれを220回程度繰り返すと、初期値の80に近い値になるだろう。各セルのコイン数は、80を中心として、せいぜい 50 ~ 110 程度(例えば)に収まるのではないか。 | |
| この状況は、移動回数が100万回になっても、1000万回になっても変わらないはずだ。すべてはランダムに決まっているのだから。 |
これはいかにも理性的というか、真っ当な推論であり、妥当な予想だと思います。しかし実際に移動シミュレーションを行ってみるとこの予想は大きくはずれ、全く違った様相になります。それが次です。
| 移動回数:10万回 |
移動シミュレーションを10万回行う試行をして、その結果を凡例に従って色分け表示したのが次の図です。この結果では、全体のおよそ95%のセル(859のセル)のコイン数が50~109の範囲に収まっています。従ってほとんどが赤のグラディエーションで塗られています。一方、白のセル(コイン数が50未満)は17個、黒のセル(コイン数が110以上)は24個です。最も少ないセルのコイン数は40で、最も多いセルのコイン数は130です。
この10万回の移動シミュレーションの結果は、ほぼ予想どおりと言っていいでしょう。
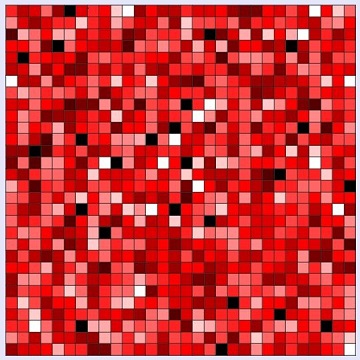 |
移動回数:10万回 |
およそ95%のセルのコイン数が50~109の範囲(赤のグラディエーションの範囲)に収まっている。それ以下のセル(白)は17、それ以上のセル(黒)は24である。 |
もちろん乱数を使ってシミュレーションをしているので、毎回まったく同じ結果になるわけではありません。しかし10万回のシミュレーションを何度繰り返しても、ほぼ類似の結果になります。
| 移動回数:100万回 |
シミュレーションを 100万回繰り返すと様相がかなり違ってきます(次図)。
 |
移動回数:100万回 |
コイン数が50~109のセルが全体の半分以下になった。それ以上とそれ以下がほぼ同数あり「格差」が広がることがわかる。最大のコイン数は平均の3倍以上で、コイン数ゼロのセルも現れた。 |
このシミュレーションでは
| 231 | |
| 423 | |
| 246 | |
| | |
| 249 | |
| 0(4セル) |
です。10万回のシミュレーションではコイン数:50~109のセルがほどんどでしたが、100万回になるとそれは全体(900)の約半分になります。それ以上とそれ以下がほぼ同数あり、「格差」が広がっていることがわかります。また最多のコインを持っているセルのコインの数は平均(=80)の約3倍です。さらに、コインが無くなるセルが出現しました(4つのセル)。
| 移動回数:1000万回 |
移動の繰り返しが1000万回になると「格差」はもっと激しくなります(次図)。
 |
移動回数:1000万回 |
格差がさらに広がる。白(コイン数49以下)のセルは400を越し、コインは「裕福な」セルに集中していく。 |
このシミュレーションでは
| 247 | |
| 247 | |
| 406 | |
| | |
| 382 | |
| 0(12セル) |
でした。コイン数が110以上のセル(裕福なセル)の数(247)は 100万回のシミュレーションの場合(231)より増えますが、大して変わりません。しかし最大コイン数が 382であるように、コインは裕福なセルに集中してきます。これと相対応して、コイン数49以下のセル(貧しいセル)が増えていきます。結果の色分け表示を見ても全体が白っぽく表示されるようになります。
900のセルが「裕福」「中間」「貧困」に分かれましたが、どのセルがどの層にいくかはシミュレーションをするたびに異なります。あくまで偶然にそうなった、ないしは、たまたまそうなったということなのです。
ローレンツ曲線とジニ係数
以下、移動回数が1000万回の場合で考えます。各セルを「人」、コインを「その人が保有している資産」と考えると、
| 初期状態では各人は平等だったが(資産は全員80) | |
| 資産の移動を1000万回繰り返すと、資産格差が生まれた(最も少ない人は 0、最も多い人は382) |
と見なせるわけです。ここで、この集団の格差の状況を1つの数値で表すことを考えます。このために昔から使われるのがローレンツ曲線とジニ係数です。ローレンツ曲線は、
0 ≦ x ≦ 1
0 ≦ y ≦ 1
0 ≦ y ≦ 1
の2次元 x-y平面に描かれます。まず900のセル(人)を、保有するコイン(資産)の数で小さい人から大きい人まで昇順に並べます。
ローレンツ曲線の x 軸は「累積人数比率(総人数を母数とする割合)」です。つまり x = 0.5 とは、資産の少ない方から数えて全体(900)の半分(450)までの人々を表します。
ローレンツ曲線の y 軸とは「累積資産比率」で、累積人数比率の人々が持つ資産総計の、全体(72,000)を母数とする割合です。
初期状態は各人は平等(資産は全員80)なので、この時のローレンツ曲線は (0, 0) と (1, 1) を結ぶ45°の直線になります。しかし格差が広がるにつれて、ローレンツ曲線は (0, 0) から始まってわずかずつ上昇し、最後は尻上がりに (1, 1) に至る曲線となります。上の 1000万回の移動シミュレーションの結果のローレンツ曲線を描いたのが次の図です。この図には初期状態の斜め45°の直線(点線)も描いてあります。
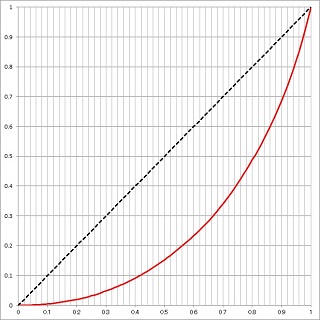 |
ローレンツ曲線 シミュレーション回数:10,000,000 ジニ係数=0.49 |
この図で「斜め45°の直線」と「ローレンツ曲線」で囲まれた半月状の形の面積を考えてみると、格差がない状態では面積=0、資産を一人が独占している状態では面積=0.5 となります。この面積の2倍が「ジニ係数」で、格差が全くない場合は 0、一人が資産を独占している場合は 1 です。上の例の1000万回の移動シミュレーションの場合、
ジニ係数=0.49
となりました。シミュレーションは乱数(正確に言うとパソコンで作り出す疑似乱数)をもとに計算しているので、1000万回の試行を何回かやるとジニ係数も変化します。しかし必ず 0.5付近の値になります。ちなみに10万回と100万回も含めてジニ係数をリストすると、
| 0.11 | |
| 0.31 | |
| 0.49 |
となりました。シミュレーションの回数が増えるに従って格差が拡大します。
以上のシミュレーションは何らかの意味があるのでしょうか。それとも単なるコンピュータを使った "遊び" でしょうか。
「データの見えざる手」において著者の矢野和男氏は次のように書いています。
|
セルを人、コインを資産とすると、このシミュレーションは2人の間で経済取引をするときの最も素朴なモデルになっています。経済取引とはモノやサービスの売買です。商品の販売や購入がそうだし、労働サービスを提供してその対価としての給料を得るのも経済取引です。株券の売買や、先物取引のような「売買する権利の売買」も経済取引です。
今の自由主義経済では、経済取引は自由に行ってよいわけです。もちろん独占禁止法とか最低賃金法があって「不当な利益」はあげられないようになっている。その各種の規制やルールの範囲内で、どんなモノやサービスをどんな価格で売買するかは自由です。
しかしモノやサービスの売買では、損をする人と得をする人が発生します。つまりモノやサービスがその時にもっている "真の価値" 以上の値段で買うと損になり、真の価値以下の価格で買うと得になります。損か得かは売買をする2人で逆転します。この「損得の発生」は「資産が2人の間で移動した」と考えられるわけです。ここでの「資産」は「保有しているモノとお金の価値合計」ぐらいに考えておきます。Aさんが100円の価値のものを110円でBさんに打ったとすると、10円の資産がBさんからAさんに移動したと考えるわけです。
大切なところは、AさんとBさんのどちらが損をするか得をするかは分からないいことです。特に取引の前に損得は分からない。なぜなら、モノやサービスの "真の価値" を知り得ないからです。従って損得はランダムに(確率的に)決まる。これは上のシミュレーションにおいてコインの移動方向をランダムに(確率的に)決めたことに相当します。
以上が、このシミュレーションが「自由な経済取引の素朴なモデル」になっている理由です。このモデルでは取引を重ねるほど格差が増大します。矢野氏の著書の名前である「データの見えざる手」は、もちろんアダム・スミスの「神の見えざる手」の "もじり" ですが、これは言い得て妙という感じがします。「見えざる手」論は、自由な市場が価格変動を調節して資源の最適配分に導くという主張ですが、実はこの「神の手」は取引の繰り返しによって格差を生み出すことに役だっているようなのです。
公正で機会均等な取引が格差を生む ────。このことを経済学の論文として明らかにした雑誌記事を次に紹介します。前置きが長くなりましたが、ここからが本題です。
数理が語る格差拡大のメカニズム
|
自由主義経済においては、公平でフェアな取引きを繰り返すと必然的に格差が拡大する
ことを数理モデルで論証したものです。論文ではまず、世界の様々な国で富の不平等が拡大していることが語られます。
以下の引用では段落を増やした(減らした)ところがあります。また下線は原文にはありません。
|
このような富(資産)の集中がどうして起こるのか、それを数理モデルで解析しようするのがボゴシアン教授の目的です。
資産の分布とエージェントモデル
まず前提として資産とは何かですが、論文ではその定義が書いてありません(自明のこととしてあります)。従って一般的な理解で言いますと、これは個人が保有している資産(家計資産)のことです(法人や企業の資産ではない)。またその資産の内容は、金融資産(現金や株券・債権など)に非金融資産(不動産や貴金属などで換金可能なもの)を加え、そこから負債(借金)を引いたものです。従って資産はマイナスになり得ることに注意しましょう。ボゴシアン教授の数理モデルにもそれが出てきます。
資産の分布をモデル化する出発点は「エージェントベースの資産分布モデル」です。エージェントとは商取引を行う「主体」のことで、2人のエージェントが行う商取引がモデルのベースです。つまり2人のエージェントが自由意志で、互いに納得した価格で財貨を交換する。たとえば「商品を買う」「労働の対価として賃金を得る」などです。このエージェント同士が行う商取引を膨大に積み重ねた結果として社会全体の資産分布が決まるというのが、今回の数理モデルです。
この「自由意志で、互いに納得した価格で財貨を交換」するモデルは、現代社会において公正でフェアだと考えられています。また上に引用した「神の見えざる手」論のように、需要と供給をバランスを調整して安定した経済体系を作るとされていて、いかにも "自然な" モデルです。しかし、実はそこに格差を生み出すメカニズムが潜んでいるというのが、以下の論です。
ヤードセールモデル
2002年、インドのサハ核物理学研究所のチャクラボルティ(Aanirban Chakraborti)は、上記のエージェントモデルの一種である「ヤードセールモデル」を導入しました。ボゴシアン教授はこのモデルを出発点にしています。
「ヤードセール」とは、家の庭(yard)で行う不要品販売セールのことです。このモデルは「不要品販売セールにみられる1対1取引きの特徴」があるのでこの名前がつきました。次のようなモデルです。
| 1対1取引を行う片方が "間違う" ことによって、資産が移動すると考える。 | |
| 取引した品物の価格が、その品物の価値と一致しているなら資産の移動は起こらない。 | |
| しかし買い手が払いすぎたり(=買い手が間違う)、売り手の受領額が品物の価値より少ない(=売り手が間違う)場合は、売り手と買い手の間で資産(Δw)の移動が起こる。 | |
| 資産の移動(Δw)がどの方向に発生するか(買い手が間違うか、売り手が間違うか)は、ランダムに(=コイン投げで表が出るか裏が出るか)決まる。 | |
| 破産したいと望む人はいない。従って、資産の移動(Δw)は貧しい方の人が保有している資産の一部にとどまるとする。たとえば、貧しい方の人が保有している資産の20%がΔwと仮定する。 |
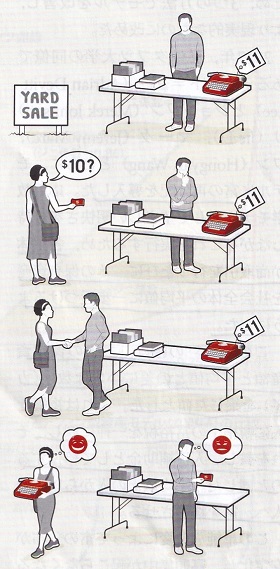 |
ヤードセールモデル |
売り手が庭で不要品を販売している。タイプライターに $11 の値がついているが、買い手は $10 でどうかと交渉した。両者の自由意志での合意の上で、$10 で取引が成立した。買い手は $1 得をしたと思い、売り手は $1 損をしたと思っているが、果たして本当にそうなのかは分からない。日経サイエンス 2020年9月号より。 |
このモデルはいかにも妥当に思えます。つまり「売り手・買い手のどちらに資産が移動するかはランダムにきまる。かつ資産の移動量(Δw)は貧しい方の人の資産の一部」というところは、実際の経済生活を通じてほとんどの人が経験してきたことであり、また自分に課している制限だと考えられるからです。
このヤードセールモデルによる取引を、例えば1000人の集団で行います。各人が最初に持っている資産は完全に同額です。ここからランダムに選ばれた2人が取引をします。これを何100万回、何億回と繰り返すシミュレーションをしたらどうなるか。
ここで、Δwを「貧しい方の人が保有している資産の20%」とする必然性はありません(明らかに20%は過大です)。数字は問題ではなく、2%でも何%でもよい。数字が少なくなるとシミュレーションの収束に時間がかかるだけで結果は同じだからです。それどころか、次のような「ヤードセールモデルの変種」でもよい。つまり、
| 貧しい人が損をする場合は自己資産の17%の損 | |
| 貧しい人が得をする場合は自己資産の20%の得 |
とするわけです。つまり貧しい人が相対的に少し有利になる設定です。しかしこの設定でも結果は変わりません。論文から引用します。
|
論文にはありませんが、このシミュレーションを実際にやってみました。基礎数値は「データの見えざる手」のものを採用します。
| 集団は900人とする。初期状態では各人が80の資産を持つ。 | |
| ランダムに選ばれた2人が商取引を行う。この結果として2人の間で資産が移動する。移動の方向はランダムに(確率0.5で)決まる。 | |
| 「貧しい人」から「金持ちの人」へと資産が移動する場合は「貧しい人の資産の17%」が移動する。逆に「金持ちの人」から「貧しい人」へと資産が移動する場合は「貧しい人の資産の20%」が移動する(=ヤードセールモデルの変種)。 | |
| この商取引を1000万回繰り返す。 |
このシミュレーションのローレンツ曲線とジニ係数が次の図です。きわめて極端な格差が生まれていることが分かります。
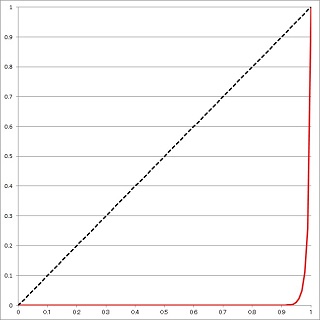 |
「ヤードセールモデルの変種」 シミュレーション回数:10,000,000 ジニ係数=0.984 |
このシミュレーションでは、人口の1%が全資産の74%を占め、人口の2%が全資産の89%を独占した。シミュレーション回数をさらに増やすと独占者が出現し、ジニ係数は 1 に近づく。オリジナルの「ヤードセールモデル」ではもっと急速に 1 に近づく。 |
このシミュレーションを1000万回ではなくもっと多数繰り返していくと、資産が一人に集中する「寡頭支配」になります。論文に「他の999人にはほとんと何も残らない」と書いてあるのは、このシミュレーションではどの人も資産がゼロになることはないからです。しかし999人はゼロに極めて近い値になる。つまり「ほとんと何も残らない」のです。
ちなみに上のシミュレーションを1000万回で止めたのは、あまりやると極端な独占が進み、ローレンツ曲線が曲線らしくなくなるからでした。
論文に戻って、ボゴシアン教授の論を続けます。
|
"この種の現象を物理学者は「対称性の破れ」と呼んでいる" とありますが、日経サイエンスでは「対称性の破れ」を "相転移" の例で解説しています。たとえば磁石ですが、なぜ磁力が発生するかというと磁石の中の分子が極小の磁石となっていて、その磁力の向き(N極とS極)が揃っているからです。
ところが温度を上げて特定の温度(=キュリー温度)に達すると、突然、磁力がなくなります。キュリー温度以上では極小磁石の向きがバラバラになるからです。このバラバラになった状態では、どの方向から観察しても性質が同じなので「対称性がある」と表現されます。
逆に、キュリー温度以上から徐々に温度を下げると、キュリー温度のところで突如「対称性の破れ」が発生し、極小磁石は同じ向きに整列し、方向によって違う物理性質を示します。つまり磁石になります。
ボゴシアン教授の説明は続きます。
|
引用の最後のところにあるヤードセールモデルは、オリジナルのものです。つまり商取引で移動する資産は移動方向に関わらす同じ(例えば、貧しい主体の20%)というモデルです。一方、上のシミュレーション例は貧者が少しだけ有利な「ヤードセールモデルの変種」でした。もちろん「ヤードセールモデルの変種」よりも「ヤードセールモデル」の方が富の集中は急速に進みます。以下の議論は、オリジナルのヤードセールモデルに基づきます。
再分配パラメータの導入
ヤードセールモデルが社会の資産の偏在を表現しているというのではありません。このモデルではシミュレーションが進むにつれて資産が1人に独占されますが、現実社会はそうなっていないからです。
そこで「再分配パラメータ」を導入します。これは、各主体が取引を行うごとに、各主体の資産を社会全体の資産の平均値に少しだけ近づけるものです。これをコントールするパラメータを χ(カイ。ギリシャ文字)とし、
再分配 =
(資産の平均値 ー 取引主体の資産)× χ
だけの資産を各主体にプラスします。従って、平均値以下の主体の資産は増額され、平均値以上の主体の資産は減額されることになります。これは裕福な人に富裕税を課し、それを貧しい人に配分するということに相当します。
|
資産バイアス・パラメータの導入
ここまでの議論では、取引において資産が移動する方向は全くランダム(確率でいうと 0.5 / 0.5)としていました。しかし現実の社会では、富裕層が低金利融資や専門家による財産形成のアドバイスといった経済的恩恵を受けているのに対し、貧しい人々は高金利の借金をしたり最適価格の品を探す時間的余裕がないなど、経済的には不利な状況にあります。
そこでこの状況を模擬するために「資産バイアスパラメータ」の ζ(ゼータ。ギリシャ文字)を導入します。そして
資産バイアス =
(取引主体の資産差額 / 資産の平均額)× ζ
とし、資産バイアスの確率だけ裕福な者が有利になるようにします(取引主体の資産差額は絶対値)。論文には詳細が書いてありませんが、たとえば
裕福な者が得をする確率 =
0.5 + 資産バイアス / 2
貧しい者が得をする確率 =
0.5 - 資産バイアス / 2
とすれば、ちょうど資産バイアスだけの確率差がつくことになります。この定義の資産バイアスは1以上になる可能性があります。たとえば ζ を0.05 とすると、取引主体の資産差額が集団の資産の平均額の20倍あるとちょうど1になります。こうなると必ず裕福なものが得をすることになる。従って実際のシミュレーションでは資産バイアスが 1 以下になるような、何らかの調整が必要なはずです。
ともかく、再分配パラメータに加えて資産バイアスパラメータを考慮したモデルの解析結果が次です。
|
著者によると、ζ が χ を下回った場合は寡頭集中のない安定的な状態に落ち着くそうです。
ちなみに「米国と欧州諸国の資産分布の経験的データと誤差 x% で一致」という表現についてですが、χ や ζ といったパラメータを国ごとにどのように設定すれば資産分布の経験的データを最もよく表現できるかをサーベイし、その結果の最適値のときの誤差が x% という意味です。
マイナス資産の導入
さらにモデルの改良は続きます。これまでのモデルではシミュレーションをいくら繰り返しても資産がマイナスになることはありません。もちろん寡頭集中が起こったりすると多数の人の資産がゼロに近づくのですが、原理上マイナスにはなりません。
しかし実社会では資産がマイナスということが起こります。保有している現金や不動産などの額より負債額が多ければ資産はマイナスだからです。しかし資産がマイナスであっても商取引は可能であり、社会では実際に行われています。
この状況をモデル化するために、新たなパラメータ κ(カッパ。ギリシャ文字)を導入し、最大マイナス資産(=S)を次の式で計算します。
最大マイナス資産(S)=
資産の平均額 × κ
そして、拡張ヤードセールモデル(χ と ζ を入れたモデル)による取引をする前に、2つの取引主体の資産に S を加え、取引が終わったあとに2つの取引主体の資産から S を引くという操作をします。この操作によって、集団の中で最も資産が少ない人の資産額が -S となります。
いままで出てきた3つのパラメータ、χ と ζ と κ を導入したモデルが最終のもので、著者はこれを数学者らしく「アフィン型資産モデル(AWM)」と呼んでいます。
この "アフィン" という用語ですが、「アフィン変換」が大学の数学で出てきます。これは、乗法(幾何イメージは拡大・縮小)と加法(幾何イメージは平行移動)の両方を含んだ変換を言います。著者のモデルは取引主体の保有資産から決まる量に(乗法的に)依存したやりとりと、集団の平均資産から決まる量に(加法的に)依存したやりとりの両方があります。それを "アフィン" という用語で表しています。
|
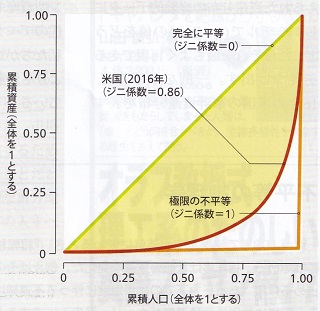 |
米国(2016年)の保有資産のローレンツ曲線 ジニ係数=0.86 (日経サイエンス 2020年9月号より) |
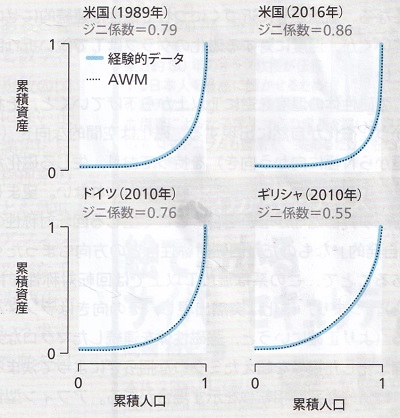 |
経験的データとアフィン型資産モデル(AWM)の比較 (日経サイエンス 2020年9月号より) |
上に向かって流れる富
ボゴシアン教授の数理モデルは、欧米各国の資産分布モデルを極めて正確に再現できることがわかりました。これは今まで作られてきた各種モデルの中で現実に最もよく合致するものです。次が論文の結論部分です。
|
この論文の原題は「The Inescapable Casino」です。直訳すると「逃げ出せないカジノ」で、これは現代の自由主義経済の社会そのものを言っています。論文に出てきたヤードセールモデルは、カジノにおける客とディーラーの賭とそっくりです。客の資金は限られているがディーラー(=カジノの代表)の資金は客に比べると膨大です。賭を長く続ければ続けるほど客の資金は底をつく。カジノで損をしないためには一刻も早くカジノから出るしかありません。しかし現代の自由主義経済社会というカジノから逃げ出すことはできないのです。
この論文で展開されているのは「数理モデル」であって、現実の人間社会の経済活動ではありません。しかしこれだけ正確に各国の経済格差をモデル化できるということは、そこに何かしらの真実が含まれていると考えるべきでしょう。
公正でフェアで機会(チャンス)が均等な取引の積み重ねが富の格差を生み出す。しかも、社会に参加する時点で人が保有している富に差がついていると有利・不利が初めから決まってしまう。このことを警鐘として受け止めるべきだと思いました。
またこの論文は、我々にある種の思い込みがあることを明らかにしていると思います。それは "すべての結果には原因がある" という思い込みです。結果をもたらすに至った原因を追求することは社会活動の大原則です。なぜそうなったか、その根本原因を追求して対策を打つ。それで社会が成り立っています。
しかし、すべての結果に原因があるわけではないのです。裕福な者と貧しい者、その差は本人の能力や努力の結果であり、さらにはどういう家庭に生まれたかの差である。そう考えることは正しいが、そればかりではない。偶然に差がついたという要素もあるのです。
知らず知らずのあいだに我々の思考を束縛する "思い込み" は排除しなければならない。そう感じました。
さらに思ったことがあります。「公平で機会均等な取引の積み重ねが富の格差を生み出す」という結果はコンピュータがないとしたら絶対に発見できなかっただろう、ということです。手作業や紙と鉛筆だけでの思考では無理です。コンピュータがあるからこそ(私のように)家庭用パソコンでも簡単に検証できてしまう。その結果は、全く意外なものです。
ボゴシアン教授は論文で「ヤードセールモデルが富を貧者から富める者へと移動させることの数学的な証明を与えた」と説明していました。数学的な発見があって、結果がどうなるかを見い出したのではありません。コンピュータ・シミュレーションによる結果がまずあり、なぜそうなるのかという数学的証明を後から行ったわけです。この論文は、今さらながらですが、コンピュータの威力と可能性を示しているのでした。
| 補記 |
本文で紹介したのは日経サイエンス 2020年9月号に掲載された「数理が語る経済格差のメカニズム」の内容でしたが、同じ日経サイエンスの2021年4月号に米国の経済格差の変遷が出ていました。1人あたりの GDP が増えるにつれて経済格差が増大してきたことを示すグラフです。ここでは経済格差の指標として「所得のジニ係数」を取り上げています。本文は「資産のジニ係数」の話だったので注意ください。
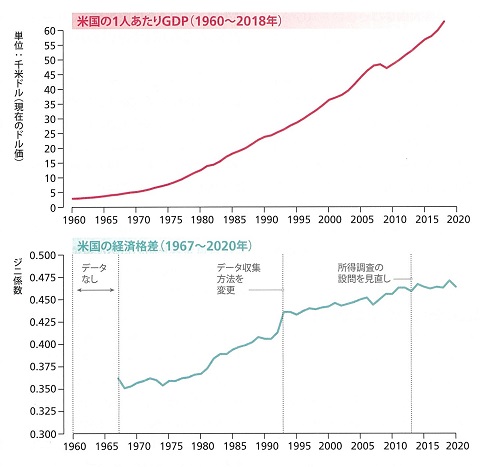
|
米国の「1人あたりのGDP」と「所得のジニ係数」変遷 (日経サイエンス 2021.4 より) |
このグラフにつけられた説明には次のようにありました。この説明の中には「資産の経済格差」も出てきます。
|
2020-09-05 11:43
nice!(0)