No.356 - 高校数学で理解するガロア理論(3) [科学]
\(\newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\mr}[1]{\mathrm{#1}} \newcommand{\br}[1]{\textbf{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\sb}{\subset} \newcommand{\sp}{\supset} \newcommand{\al}{\alpha} \newcommand{\sg}{\sigma}\newcommand{\cd}{\cdots} \newcommand{\fz}{0^{\tiny F}} \newcommand{\kz}{0^{\tiny K}} \newcommand{\fo}{1^{\tiny F}} \newcommand{\ko}{1^{\tiny K}}\)
3.3 線形空間
ガロア理論の一つの柱は、代数拡大体を線形空間(ベクトル空間)としてとらえることで、線形空間の「次元」や「基底」を使って理論が組み立てられています。線形空間には精緻な理論体系がありますが、ここではガロア理論に必要な事項の説明をします。
線形空間の定義
集合 \(V\) と 体 \(\bs{K}\) が次を満たすとき、\(V\) を \(\bs{\bs{K}}\) 上の線形空間(=ベクトル空間。linear space / vector space)と言う。
加算の定義
\(V\) の任意の元 \(\br{u},\:\br{v}\) に対して \((\br{u}+\br{v})\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
スカラー倍の定義
\(V\) の任意の元 \(\br{u}\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(k\br{u}\in V\) が定義されていて、加算との間に次の性質がある。\(\br{u},\:\br{v}\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(m\br{u})=(km)\br{u}\)
\((2)\:\:(k+m)\br{u}=k\br{u}+m\br{u}\)
\((3)\:\:k(\br{u}+\br{v})=k\br{u}+k\br{v}\)
\((4)\:\:1\br{v}=\br{v}\)
高校数学に出てくる "2次元ベクトル" とは、上記の定義の \(\bs{K}\) を \(\bs{R}\)(実数の体)とし、\(V\) を2つの実数のペアの集合 \(\{\:(x,y)\:|\:x,y\in\bs{R}\:\}\) とするベクトル空間(の要素)のことです。
上の定義の \(0\) は線形空間 \(V\) の元です。以下、\(V\) の単位元 \(0\)(= \(0\) ベクトル)と、体 \(\bs{K}\) の加法の単位元 \(0\) が混在しますが、文脈や式から明らかなので、同じ \(0\) で記述します。
1次独立と1次従属
1次独立
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次従属であるという。
基底
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、次の2つが満たされるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) を基底という。
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が基底だと、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) は基底ではありません。なぜなら、もし \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) が基底だとすると、
\(\br{v}_n=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}\)
と表せますが、これは、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}-\br{v}_n=0\)
ということであり、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が1次従属となってしまって、基底の要件を満たさなくなるからです。基底に、別の1つの元を加えるケースも同じことです。
\(\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) である。
[証明]
この定理の証明のために、まず次の補題を証明する。
[補題]
線形空間 \(V\) の任意の \(n\) 個の元を \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) とする(基底でなくてもよい)。線形空間 \(V\) の \(n+1\) 個の元 \(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) がすべて \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) の1次結合で表されるなら、\(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) は1次従属である。
数学的帰納法を使う。まず、\(n=1\) のとき、この定理は成り立つ。つまり、
\(\br{w}_1=k_1\br{u}_1\)
\(\br{w}_2=k_2\br{u}_1\)
と表されるなら、
\(k_2\br{w}_1-k_1\br{w}_2=0\)
であり、\(\br{w}_1\) と \(\br{w}_2\) は1次従属である。そこで、\(n\) が \(k\:\:(\geq1)\) のときに成り立つとし、\(n=k+1\) でも成り立つことを証明する。
以降、表記を見やすくするため、\(k=3\) の場合で記述する。ただし、一般性を失うことがないように記述する。\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) が、
\(\br{w}_1=a_{11}\br{u}_1+a_{12}\br{u}_2+a_{13}\br{u}_3\)
\(\br{w}_2=a_{21}\br{u}_1+a_{22}\br{u}_2+a_{23}\br{u}_3\)
\(\br{w}_3=a_{31}\br{u}_1+a_{32}\br{u}_2+a_{33}\br{u}_3\)
\(\br{w}_4=a_{41}\br{u}_1+a_{42}\br{u}_2+a_{43}\br{u}_3\)
と表せたとする。ここで \(\br{w}_4\) の係数に注目する。もし、
\(a_{41}=a_{42}=a_{43}=0\)
であれば、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属である。なぜなら、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3+b_4\br{w}_4=0\)
の式を満たす \(b_1,b_2,b_3,b_4\) は、
\(b_1=b_2=b_3=0\)
\(b_4\neq0\)
として実現でき、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属の定義を満たすからである。そこで、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つあるとする。それを \(a_{43}\) とし、
\(a_{43}\neq0\)
とする。この仮定で一般性を失うことはない。ここで、
\(\br{x}_i=\br{w}_i-\dfrac{a_{i3}}{a_{43}}\br{w}_4\:\:(i=1,2,3)\)
とおいて \(\br{u}_3\) の項を消去する。計算すると、
\(\begin{eqnarray}
&&\:\:\br{x}_1=&\left(a_{11}-\dfrac{a_{13}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{12}-\dfrac{a_{13}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_2=&\left(a_{21}-\dfrac{a_{23}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{22}-\dfrac{a_{23}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_3=&\left(a_{31}-\dfrac{a_{33}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{32}-\dfrac{a_{33}a_{42}}{a_{43}}\right)\br{u}_2\\
\end{eqnarray}\)
となる。そうすると、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は「線形空間 \(V\) の2つの元 \(\br{u}_1,\br{u}_2\) の1次結合で表された3つの元」である。従って、帰納法の仮定により、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は1次従属である。1次従属だから、
\(\br{x}_1=\br{w}_1-\dfrac{a_{13}}{a_{43}}\br{w}_4\)
\(\br{x}_2=\br{w}_2-\dfrac{a_{23}}{a_{43}}\br{w}_4\)
\(\br{x}_3=\br{w}_3-\dfrac{a_{33}}{a_{43}}\br{w}_4\)
だったから、これを \((\br{A})\) 式に代入すると、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3-\)
\(\dfrac{1}{a_{43}}(b_1a_{13}+b_2a_{23}+b_3a_{33})\br{w}_4=0\)
となる。この式における \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) の係数の少なくとも一つは \(0\) ではない。従って、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つある場合にも \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) は1次従属である。
以上で、線形空間 \(V\) の \(k=3\) 個の元(\(\br{u}_1,\br{u}_2,\br{u}_3\))の1次結合で、\(k+1=4\) 個の元(\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\))のすべてが表されば、その4個の元は1次従属であることが証明できた。\(k=3\) としたのは表記を見やすくするためであり、\(k=3\) であることの特殊性は使っていない。つまり、\(k\geq1\) のすべてで成り立つ。従って数学的帰納法により補題が正しいことが証明できた。[補題の証明終]
以上を踏まえて、\(A=\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(B=\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) となることを証明する。
もし仮に \(m < n\) だとすると、\(B\) の中から \((m+1)\) 個の元を選べる。それを \(B\:'=\{\br{v}_1,\br{v}_2,\cd,\br{v}_{m+1}\}\) とすると、\(A\) は 線形空間 \(V\) の基底だから、\(B\:'\) の元は \(A\) の元の1次結合で表現できる。つまり \(B\:'\) の \((m+1)\)個の元のすべては \(m\)個の元の1次結合で表されるから、[補題]によって \(B\:'\) は1次従属である。\(B\) は \(B\:'\) と同じものか、または \(B\:'\) に数個の元を付け加えたものだから、\(B\:'\) が1次従属なら \(B\) も1次従属である。しかし、\(B\) は線形空間 \(V\) の基底だから1次独立であり、矛盾が生じる。従って、\(m\geq n\) である。
もし仮に \(m > n\) だとしても、全く同様の考察により矛盾が生じる。従って、\(m\leq n\) である。この結果、\(m=n\) であることが証明できた。[証明終]
この基底の数の不変性の定理(33D)により、線形空間には次のように「次元」が定義できることになります。
次元
線形空間の基底に含まれる元の数が有限個のとき、その個数を線形空間の次元と言う。次元は基底の取り方によらない。
線形空間の次元や基底と、代数拡大体を結びつけるのが次の定理です。
単拡大体の基底
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。単拡大体である \(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間であり、\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) は \(\bs{Q}(\al)\) の基底である。
[証明]
\(\bs{Q}(\al)\) の基底であるための条件は、
の2つである。② は単拡大の体の定理(32C)で証明されているので、① を証明する。多項式 \(g(x)\) を、
\(g(x)=a_0+a_1x+a_2x^2+\cd+a_{n-1}x^{n-1}\)
とおく。\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立であることを言うには、
\(g(\al)=0\) であれば \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\)
を言えばよい。以降、背理法を使って証明する。\(g(\al)=0\) で、\(a_i\:\:(0\leq i\leq n-1)\) のうち、少なくとも1つはゼロでないと仮定する。
\(g(x)\) が定数(つまり \(a_0\) の項のみ)のときは、\(g(\al)=0\) なら \(a_0=0\) なので、「少なくとも1つはゼロでない」に反する。そこで \(g(x)\) は1次以上の多項式であるとする。
そうすると、2つの方程式 \(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) をもつことになる。しかし、\(f(x)\) は \(n\)次の既約多項式であり、\(g(x)\) は1次以上で \(n\)次未満の多項式である。既約多項式の定理2(31F)により、このような2つの方程式は共通の解を持たない。ゆえに矛盾が生じる。従って、\(g(\al)=0\) のとき \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\) であり、① が証明された。
基底の数が線形空間の次元であり、\(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間である。[証明終]
もし、\(f(x)\) が\(n\)次多項式だとしたら(既約多項式を含む)、\(\bs{Q}(\al)\) の次元は \(n\)以下になります。\(f(x)=0\) の解の一つ、\(\al\) の最小多項式(31H)を \(m\)次多項式である \(g(x)\) とすると、\(g(x)\) は既約多項式であり(31I)、\(\al\) は \(f(x)=0\) と \(g(x)=0\) の共通の解なので、既約多項式の定理1(31E)により \(f(x)\) は \(g(x)\) で割り切れます。つまり、
\(f(x)=h(x)g(x)\)
と書けるので、
\(\mr{deg}\:f(x)\:\geq\:\mr{deg}\:g(x)\)
\(n\:\geq\:m\)
ですが、単拡大体の基底の定理(33F)により \(\bs{Q}(\al)\) の次元は \(m\) なので、\(n\)以下です。
拡大次数とその連鎖律
方程式の解になる数が代数的数で、\(\bs{Q}\) に代数的数を添加した体が代数拡大体です。「3.2 体」の「単拡大の体」でとりあげた \(\bs{Q}(\al)\) は代数拡大体であり、次元は \(n\) でした(32C)。この次元を「体の拡大」の視点で考えてみます。
「体 \(\bs{K}\) 上の線形空間 \(V\)」の定義において、\(\bs{K}=\bs{Q}\) とし \(V=\bs{Q}\) とすると、「有理数体 \(\bs{Q}\) は、\(\bs{Q}\) 上の線形空間」であると言えます。\(\bs{Q}\) では加算もスカラー倍(=乗算)も定義されていて、可換だからです。線形空間の定義にある各種の演算は、体の演算の一部です。
線形空間 \(\bs{Q}\) の基底は、\(0\) ではない \(\bs{Q}\) の元 \(v\) です。\(0\) を含む \(\bs{Q}\) の任意の元を \(a\) とすると、
\(av=0\:\:\:(v\neq0)\)
が成り立つのは \(a=0\) しかないので \(v\) は1次独立であり、また \(av\) で全ての \(\bs{Q}\) の元が表されるからです。一方、\(0\) は、
\(a\cdot0=0\)
が \(0\) ではない \(a\) について成り立つので1次従属です。以上から、線形空間 \(\bs{Q}\) の基底として \(1\) を選ぶことにします。次元は \(1\) です。
\(\bs{Q}\) に \(\sqrt{2}\) を添加した \(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) の代数拡大体で、\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) です。\(\bs{Q}(\sqrt{2})\) は \(\bs{\bs{Q}}\) 上の線形空間です。\(\bs{Q}(\sqrt{2})\) の基底としては、まず \(1\) を選ぶことができます。\(1\) を \(\bs{Q}\) の元でスカラー倍すると、\(\bs{Q}(\sqrt{2})\) の部分集合である \(\bs{Q}\) の元の全てが表せます。
\(\bs{Q}(\sqrt{2})\) の元の全てを表現するためには、さらに基底に \(\sqrt{2}\) を追加します。\(\sqrt{2}\) は \(\bs{Q}\) の元の1次結合では表せないので、\(1\) と \(\sqrt{2}\) は 1次独立です。\(1,\:\sqrt{2}\) が \(\bs{Q}(\sqrt{2})\) の基底で、次元は \(2\) です。
さらに \(\bs{Q}(\sqrt{2})\) に \(\sqrt{3}\) を添加した代数拡大体 \(\bs{Q}(\sqrt{2},\sqrt{3})\) を考えてみると、\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間であり、基底は \(1,\:\sqrt{3}\) です。\(1\) と \(\sqrt{3}\) は 1次独立であり、\(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の全ての元は、\(\bs{\bs{Q}(\sqrt{2})}\) の元を係数とする \(\bs{1}\) と \(\bs{\sqrt{3}}\) の1次結合で表現できるからです。\(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間 \(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の次元は \(\bs{2}\) です。
ここで \(\bs{Q}(\sqrt{2},\sqrt{3})\) を \(\bs{\bs{Q}}\) 上の線形空間と考えると、その基底はまず、\(1,\:\sqrt{2},\:\sqrt{3}\) ですが、これだけでは不足で、\(\sqrt{6}\) を加える必要があります。\(\sqrt{6}\) は体としての演算(乗算)でできる数ですが、\(1,\:\sqrt{2},\:\sqrt{3}\) の1次結合では表現できないからです。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は \(1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\) であり、次元は \(4\) です。
ここまでの基底の表現はあくまで一例ですが、どういう基底を選ぼうと基底の数=次元は不変量であるというのが「次元の不変性」でした。以上の考察を踏まえて、拡大次数を定義し、拡大次数の連鎖律を証明します。
代数拡大体 \(\bs{F},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{K}\) であるとき、\(\bs{K}\) は \(\bs{F}\) 上の線形空間である。\(\bs{K}\) の次元を、\(\bs{K}\)の(\(\bs{F}\)からの)拡大次数といい、
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
代数拡大体 \(\bs{F},\:\bs{M},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{M}\:\subset\:\bs{K}\) であるとき、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
[証明]
\([\:\bs{M}\::\:\bs{F}\:]=m\)、\([\:\bs{K}\::\:\bs{M}\:]=n\) とする。以下、表記を見やすくするため、\(m=3,\:n=2\) の場合で記述する。もちろん一般性を失わないように記述する。
\(\bs{F}\) 上の線形空間 \(\bs{M}\) の基底を
\(u_1,\:u_2,\:u_3\)
とすると、\(\bs{M}\) の任意の元 \(b\) は、
\(b=a_1u_1+a_2u_2+a_3u_3\:\:(a_i\in\bs{F},\:u_i\in\bs{M},\:1\leq i\leq m)\)
と表せる。
\(\bs{M}\) 上の線形空間 \(\bs{K}\) の基底を
\(v_1,\:v_2\)
とすると、\(\bs{K}\) の任意の元 \(x\) は、
\(x=b_1v_1+b_2v_2\:\:(b_j\in\bs{M},\:v_j\in\bs{K},\:1\leq j\leq n)\)
と表せる。\(b_1,\:b_2\) を \(\bs{M}\) の基底 \(u_1,u_2,u_3\) で表すと、
\(b_1=a_{11}u_1+a_{21}u_2+a_{31}u_3\)
\(b_2=a_{12}u_1+a_{22}u_2+a_{32}u_3\)
\((\:a_{ij}\in\bs{F}\:)\)
となるが、これを用いて \(x\) を表すと、
\(\begin{eqnarray}
&&\:\:x=&a_{11}u_1v_1+a_{21}u_2v_1+a_{31}u_3v_1+\\
&&&a_{12}u_1v_2+a_{22}u_2v_2+a_{32}u_3v_2\\
\end{eqnarray}\)
となる。つまり、\(\bs{K}\) の任意の元は \(\bs{F}\) の元を係数とする、\(u_1v_1\)、\(u_2v_1\)、\(u_3v_1\)、\(u_1v_2\)、\(u_2v_2\)、\(u_3v_2\) の1次結合で表現できる。
ここで \(x=0\) とすると、
\((a_{11}u_1+a_{21}u_2+a_{31}u_3)v_1+\)
\((a_{12}u_1+a_{22}u_2+a_{32}u_3)v_2=0\)
であるが、\(v_1,v_2\) は \(\bs{K}\) の基底なので1次独立であり、従って、
\(a_{11}u_1+a_{21}u_2+a_{31}u_3=0\)
\(a_{12}u_1+a_{22}u_2+a_{32}u_3=0\)
である。すると、\(u_1,u_2,u_3\) は \(\bs{M}\) の基底なので1次独立であり、
\(a_{11}=a_{21}=a_{31}=a_{12}=a_{22}=a_{32}=0\)
である。従って、\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) は1次独立である。
\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) の \(mn\) 個の元は、
から、\(\bs{F}\) 上の線形空間 \(\bs{K}\) の基底であり、\(\bs{K}\) の次元は \(mn\) である。以上により、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
である。[証明終]
体の一致
2つの代数拡大体 \(\bs{F}\) と \(\bs{K}\) の次元が一致するとします。たとえば \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) の次元はいずれも \(2\) です。もちろん \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) は体として別物です。
それでは、\(\bs{F}\subset\bs{K}\) という関係があり、かつ \(\bs{F}\) と \(\bs{K}\) の次元が一致するとき、\(\bs{F}\) と \(\bs{K}\) は体として一致すると言えるのでしょうか。
これはイエスで、それを次に証明します。この定理は、ガロア理論の証明の過程において、2つの体が実は同じものであることを言うときに使われる論法です。証明の都合上、\(\bs{F}\) ではなく \(\bs{K}_0\) と書きます。
体 \(\bs{K}_0\) と 体 \(\bs{K}\) があり、\(\bs{K}_0\:\subset\:\bs{K}\) を満たしている。\(\bs{K}_0\) と \(\bs{K}\) が有限次元であり、その次元が同じであれば、\(\bs{K}_0=\bs{K}\) である。
[証明]
体 \(\bs{K}_0\) と \(\bs{K}\) を、\(\bs{Q}\) 上の線形空間と見なし、その次元を \(n\) とする。\(\bs{K}_0\) の基底を \(\{a_1,\:a_2,\:\cd\:,a_n\}\) とする。\(\bs{K}_0\) が \(\bs{K}\) の真部分集合である、つまり \(\bs{K}_0\:\subsetneq\:\bs{K}\) と仮定して、背理法で証明する。
\(\bs{K}_0\:\subsetneq\:\bs{K}\) だと、\(a_{n+1}\notin\bs{K}_0,\:a_{n+1}\in\bs{K}\) である元 \(a_{n+1}\) が存在する。この \(a_{n+1}\) は \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合では表せない。なぜなら、もし表せたとしたら、\(\bs{K}_0\) の全ての元は基底である \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されるので \(a_{n+1}\in\bs{K}_0\) になってしまうからである。
そこで、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) を考えると、この元の並びは1次独立である。なぜなら、もし1次従属だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n+a_{n+1}x_{n+1}=0\)
となる \(x_i\in\bs{Q}\:\:(1\leq i\leq n+1)\) があって、そのうち少なくとも一つは \(0\) ではない。もし \(x_{n+1}\neq0\) だとすると、\(a_{n+1}\) が \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されることになり、\(a_{n+1}\in\bs{K}_0\) となって矛盾が生じる。また \(x_{n+1}=0\) だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n=0\)
であるが、この場合は \(x_i\:\:(1\leq i\leq n)\) の中に少なくとも一つは \(0\) でないものがあることになり、\(\{a_1,\:a_2,\:\cd\:,a_n\}\) が基底である(=1次独立である)ことに矛盾する。従って \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は1次独立である。
\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表される全ての元の集合を \(\bs{K}_1\) とする。\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) はすべて \(\bs{K}\) の元であるから、\(\bs{K}_1\:\subset\:\bs{K}\) である。また \(\bs{K}_1\) の任意の元は1次独立である \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表されるから、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は \(\bs{K}_1\) の基底であり、すなわち \(\bs{K}_1\) の次元は \(n+1\) である。\(\bs{K}_1=\bs{K}\) なら \(\bs{K}\) の次元が \(n+1\) になって矛盾するから、\(\bs{K}_1\neq\bs{K}\) つまり \(\bs{K}_1\:\subsetneq\:\bs{K}\) である。
以上の論理を繰り返すと \(\bs{K}_2\:\subsetneq\:\bs{K}\) である \(n+2\) 次元の \(\bs{K}_2\) の存在を示せるが、この操作は無限に繰り返えせるから、\(\bs{K}\) は無限個の基底をもつ無限次元の体となる。これは \(\bs{K}\) の次元が有限次元の \(n\) であることに矛盾する。従って背理法の仮定は誤りであり、\(\bs{K}_0\:=\:\bs{K}\) である。[証明終]
代数拡大体の構造
多項式と代数拡大体の相互関係をまとめると次のようになります。
以下、例をいくつかあげます。
\(x^4-5x^2+6\)
\(f(x)\) を4次多項式、
\(f(x)=x^4-5x^2+6\)
とします。\(f(x)\) は、
\(f(x)=(x^2-2)(x^2-3)\)
と因数分解できるので既約多項式ではありません。また、
\(f(x)=(x-\sqrt{2})(x+\sqrt{2})(x-\sqrt{3})(x+\sqrt{3})\)
なので、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt{2},\sqrt{3})\)
です。\(\bs{Q}(\sqrt{2},\:\sqrt{3})\) は、\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) による拡大体を \(\bs{Q}(\sqrt{2})\) とし、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-3=0\) の解 \(\sqrt{3}\) による拡大体が \(\bs{Q}(\sqrt{2},\:\sqrt{3})\) であると見なせます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})\)
です。拡大次数は
\([\:\bs{Q}(\sqrt{2}):\bs{Q}\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}(\sqrt{2})\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}\:]=4\)
です。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は、
\(\begin{eqnarray}
&&\:\:B_1&=(\:1,\:\sqrt{2},\:1\cdot\sqrt{3},\:\sqrt{2}\cdot\sqrt{3}\:)\\
&&&=(\:1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\:)\\
\end{eqnarray}\)
とすることができます。
一方、
\(\theta=\sqrt{2}+\sqrt{3}\)
とおくと、
\(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\)
となります。なぜなら、
\(\sqrt{2}=\dfrac{1}{2}(\theta-\dfrac{1}{\theta})\)
\(\sqrt{3}=\dfrac{1}{2}(\theta+\dfrac{1}{\theta})\)
であり、\(\sqrt{2}\) と \(\sqrt{3}\) が \(\theta\) と有理数の加減乗除で表現できるからです。\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{Q}(\sqrt{2}+\sqrt{3})\) という単拡大体です。
\(\theta=\sqrt{2}+\sqrt{3}\) から根号を消去すると、
\(\theta^4-10\theta^2+1=0\)
となるので、\(\theta\)の最小多項式は、
\(g(x)=x^4-10x^2+1\)
であり、この \(g(x)\) は既約多項式です。\(y=x^2-5\) とおくと、
\(\begin{eqnarray}
&&\:\:g(x)&=y^2-24\\
&&&=(y-2\sqrt{6})(y+2\sqrt{6})\\
\end{eqnarray}\)
なので、
\(\begin{eqnarray}
&&\:\:g(x)&=&(x^2-5-2\sqrt{6})(x^2-5+2\sqrt{6})\\
&&&=&(x-\sqrt{2}-\sqrt{3})(x+\sqrt{2}-\sqrt{3})\cdot\\
&&&& (x-\sqrt{2}+\sqrt{3})(x+\sqrt{2}+\sqrt{3})\\
\end{eqnarray}\)
となり、\(g(x)=0\) の解は、\(\sqrt{2}+\sqrt{3}\)、\(-\sqrt{2}+\sqrt{3}\)、\(\sqrt{2}-\sqrt{3}\)、\(-\sqrt{2}-\sqrt{3}\) の4つです。その \(g(x)=0\) の解の一つが \(\theta=\sqrt{2}+\sqrt{3}\) なので、単拡大体の基底の定理(33F)を適用して、\(\bs{Q}(\theta)\) の基底を、
\(B_2=(\:1,\:\:\theta,\:\:\theta^2,\:\:\theta^3\:)\)
の4個に選ぶことができます。拡大次数は \([\:\bs{Q}(\theta):\bs{Q}\:]=4\) です。
\(B_1\) と \(B_2\) は、同じ体である \(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\) の基底なので、相互に1次結合で表現できます。\(B_2\) の1次結合で \(B_1\) を表現すると、
\(\sqrt{2}=\dfrac{1}{2}(\phantom{-}\theta^3-9\theta)\)
\(\sqrt{3}=\dfrac{1}{2}(-\theta^3+11\theta)\)
\(\sqrt{6}=\dfrac{1}{2}(\phantom{-}\theta^2-5)\)
となります。
\(x^3-2\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-2\)
とします。これは既約多項式です。
\(x^3-1=0\) 解で \(1\) でないもの一つを \(\omega\) とします(= \(1\) の原始\(3\)乗根)。
\(x^3-1=(x-1)(x^2+x+1)\)
なので \(\omega\) は、
\(\omega^2+\omega+1=0\)
を満たします。この2次方程式の解は2つありますが、
\(\omega=\dfrac{-1+\sqrt{3}\:i}{2}\)
とします。方程式 \(x^3-2=0\) の解は、
\(\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
の3つです、従って、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt[3]{2},\:\sqrt[3]{2}\omega,\:\sqrt[3]{2}\omega^2)=\bs{Q}(\sqrt[3]{2},\:\omega)\)
です。これは、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt[3]{2})\:\subset\:\bs{Q}(\sqrt[3]{2},\:\omega)\)
という構造をしています。基底は、単拡大体の基底の定理(33F)を順次適用して、
\(\bs{Q}(\sqrt[3]{2})\) の基底(\(\bs{Q}\) 上の線形空間)
\(1,\:\sqrt[3]{2},\:(\sqrt[3]{2})^2\)
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}(\sqrt[3]{2})\) 上の線形空間\()\)
\(1,\:\omega\)
です。これらを総合すると、
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}\) 上の線形空間\()\)
です。拡大次数は
\([\:\bs{Q}(\sqrt[3]{2}):\bs{Q}\:]=3\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}(\sqrt[3]{2})\:]=2\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}\:]=6\)
となります。
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の原始元 \(\theta\) を、
\(\theta=\sqrt[3]{2}+\omega\)
と選ぶことができます。なぜなら、計算は省きますが、
と表せるので、\(\bs{Q}\) に \(\sqrt[3]{2},\:\omega\) を添加した拡大体は \(\theta\) を添加した拡大体と同じものでからです。さらに、
\(\theta=\sqrt[3]{2}+\dfrac{-1+\sqrt{3}\:i}{2}\)
の式を2乗や3乗して \(i\) と根号を消去すると、計算過程は省きますが、
\(\theta^6+3\theta^5+6\theta^4+3\theta^3+9\theta+9=0\)
となります。従って、\(\theta\) の最小多項式を \(g(x)\) とすると、
\(g(x)=x^6+3x^5+6x^4+3x^3+9x+9\)
という6次多項式です。\(\bs{Q}(\sqrt[3]{2},\:\omega)\) は 6次方程式 \(g(x)=0\) の根の一つである \(\theta\) を使って、
\(\bs{Q}(\sqrt[3]{2},\:\omega)=\bs{Q}(\theta)\)
という単拡大体(次元は \(6\))と表現できます。
\(x^3-3x+1\)
「1.3 ガロア群」の「ガロア群の例」で書いたように、\(x^3-3x+1=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
の関係があり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できます。これにより、\(f(x)=x^3-3x+1\) の最小分解体は、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。基底は、たとえば \(1,\:\al,\:\al^2\) であり、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]=3\)
です。\(\al\) の最小多項式は、3次多項式である \(f(x)=x^3-3x+1\) です。
ちなみに、3次多項式の最小分解体の次元が \(3\) になる条件を書いておきます。まず、2次方程式の例ですが、
\(x^2+ax+b=0\)
の方程式の解を \(\al,\:\beta\) とすると、
\(x^2+ax+b=(x-\al)(x-\beta)\)
です。そうすると、根と係数の関係から、
\(a=-(\al+\beta)\)
\(b=\al\beta\)
です。ここで、判別式 \(\bs{D}\) を、
\(D=(\al-\beta)^2\)
と定義すると、
\(\begin{eqnarray}
&&\:\:D=&\al^2-2\al\beta+\beta^2\\
&&&=(\al+\beta)^2-4\al\beta\\
&&&=a^2-4b\\
\end{eqnarray}\)
となります。この判別式を使って解の状況がわかります。つまり、
以上を3次方程式に拡張できます。2乗の項がない既約な3次方程式を、
\(x^3+ax+b=0\)
とし、3つの根を \(\al,\:\beta,\:\gamma\) とすると、
\(\al\beta\gamma=-b\)
となります。3次方程式の判別式 \(D\) は、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
で定義されます。計算すると、
\(D=-4a^3-27b^2\)
となります。
ここで、\(D\) が、ある有理数 \(q\) の2乗の場合を考えます。つまり、
\(D=q^2\)
です。そうすると、
\((\br{A})\) 式の両辺を \(x\) で微分して \(x=\al\) を代入すると、
\(\beta=\dfrac{2a\al+3b-q}{2(3\al^2+a)}\)
\(\gamma=\dfrac{2a\al+3b+q}{2(3\al^2+a)}\)
です。式の形はともかく、要するに、
\(\beta\) と \(\gamma\) が \(\al\) の加減乗除で表現できる
わけです。このことは、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
であることを意味します。\(\bs{Q}(\al,\beta,\gamma)\) は、既約な3次方程式の根の一つである \(\al\) の単拡大体なので、その次元は \(3\) です。
まとめると、判別式 \(D\) が有理数の2乗であるとき、既約 \(3\)次多項式の最小分解体の次元が \(3\) になります。\(x^3-3x+1\) の場合、\(a=-3,\:b=1\) なので、
\(D=-4a^3-27b^2=81=9^2\)
となり、次元が \(3\) です。
既約多項式ではない3次多項式の拡大次数はもっと小さくなります。たとえば \((x-1)(x^2+2)\) の最小分解体は \(\bs{Q}(\sqrt{2}\:i)\) であり、拡大次数は \(2\) です。また \((x-2)^3\) の最小分解体は \(\bs{Q}\) そのもので、拡大次数は \(1\) です。
まとめると、3次多項式 \(f(x)\) の最小分解体の拡大次数は、\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]\:=\:6,\:3,\:2,\:1\)
の4種あることになります(この4種しかないことの理由は後の章にあります)。
ガロア理論の核心(第5章以降)に入る前の最後として、群についての各種の定義や定理を説明します。これらはいずれも第5章以降で必要になります。
4.1 部分群\(\cdot\)正規部分群、剰余類\(\cdot\)剰余群
部分集合の演算
以降の証明では集合の演算が多々出てきます。その定義は次の通りでです。これはあくまで群の "部分集合" に関するもので、それが部分群かどうかは別問題です。
群 \(G\) の2つの部分集合を \(H,\:N\) とする。\(H\) と \(N\) の演算結果である \(G\) の部分集合、\(HN\) を次の式で定義する。
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
部分群の定理
部分群に関する定理をいくつかあげます。これらはいずれも後の定理の証明の過程で使います。
部分群の十分条件
群 \(G\) の部分集合を \(N\) とし、\(N\) の任意の2つの元を \(x,\:y\) とする。
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
[証明]
\(N\) の元 \(x,\:y\) は \(G\) の元でもあるので、\(xy,\:x^{-1},\:y^{-1}\) は \(G\) の演算として定義されている。
\(y=x^{-1}\) とおくと \(xy=xx^{-1}=e\in N\) なので、\(N\) は単位元を含む。つまり、\(N\) は演算で閉じていて、単位元が存在し、逆元が \(N\) の元である。また結合則は \(G\) の元として成り立っている。従って \(N\) は \(G\) の部分群である。[証明終]
部分群の元の条件
群 \(G\) の部分群を \(N\) とし、\(G\) の 元を \(x\) とすると、次の2つは同値である。
① \(xN\:=\:N\)
② \(x\:\in\:N\)
[証明]
[① \(\bs{\Rightarrow}\) ②]
\(N\) には \(G\) の単位元 \(e\) が含まれるから、\(xe\) は \(xN\) に含まれる。
\(x=xe\in xN=N\) \(\Rightarrow\) \(x\in N\)
である。
[② \(\bs{\Rightarrow}\) ①]
\(x\in N\) とし、\(N\) の任意の元を \(a\) とすると、\(N\) は群だから \(xa\in\:N\) である。\(N\) の異なる2つの元を \(a,\:b\:\:(a\neq b)\) とすると、\(xa\neq xb\) である。なぜなら、もし \(xa=xb\) だとすると、\(x\) の逆元 \(x^{-1}\) を左からかけて \(a=b\) となり、矛盾するからである。以上により、\(xH\) は \(H\) の全ての元を含むから \(xH=H\) である。[証明終]
部分群の共通部分
\(G\) の部分群を \(H,\:N\) とすると、\(H\cap N\) は部分群である。
[証明]
\(G\) の部分群を \(H,\:N\) とし、\(H\cap N\) の任意の2つの元を \(x,\:y\) とすると、\(x,\:y\in H,\:\:x,\:y\in N\) なので、
\(xy\in H,\:x^{-1}\in H\)
\(xy\in N,\:x^{-1}\in N\)
であり、
\(xy\in H\cap N,\:x^{-1}\in H\cap N\)
となって、部分群の十分条件の定理(41B)により \(H\cap N\) は部分群である。[証明終]
剰余類
有限群 \(G\) の位数を \(n\) とし( \(|G|=n\) )、\(H\) を \(G\) の部分群とする。\(H\) に左から \(G\) のすべての元、\(g_1,\:g_2,\:\cd\:,\:g_n\) かけて、集合、
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
[証明]
\(|G|=[\:G\::\:H\:]\cdot|H|\) であることを証明する。2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとする。その共通な元が、\(x_1H\) では \(x_1h_i\)、\(x_2H\) では \(x_2h_j\) と表されているものとする。
\(x_1h_i=x_2h_j\)
左から \(x_2^{-1}\)、右から \(h_i^{-1}\) をかけると、
\(x_2^{-1}x_1h_ih_i^{-1}=x_2^{-1}x_2h_jh_i^{-1}\)
\(x_2^{-1}x_1=h_jh_i^{-1}\)
\(h_jh_i^{-1}\in H\) だから、
\(x_2^{-1}x_1\in H\)
を得る。部分群の元の条件の定理(41C)により、\(xH=H\) と \(x\in H\) は同値だから、
\(x_2^{-1}x_1H=H\)
となる。左から \(x_2\) をかけると、
\(x_1H=x_2H\)
を得る。これは、「2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとすると、2つの剰余類は一致する」ことを示している。従って、
である。\(H\) は 単位元 \(e\) を含むから、
\(g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
という和集合を作ると、そこには \(G\) のすべての元が含まれる。従って、
\(G=g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
である。剰余類 \(x_1H,\:x_2H,\:\cd\:x_dH\) は、\(g_1H,\:g_2H,\:\cd\:,g_nH\) を整理・分類したものだから、
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。この式の右辺の剰余類は共通の元がなく、それぞれの剰余類の元の数はすべて \(|H|\) だから、
\(|G|=d\cdot|H|\)
である。従ってラグランジュの定理、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
が成り立つ。[証明終]
ラグランジュの定理から、
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
ことがわかります。なぜなら、
\(H=\{e,\:g,\:g^2,\:\cd\:,\:g^{n-1}\}\)
とおくと、\(H\) は \(G\) の部分群(巡回群)になり、ラグランジュの定理によって \(|H|=n\) が \(|G|\) の約数になるからです。これは、位数の定理(25A)の[補題5]、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とし、\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
の一般化になっています。 \((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\)(\(\varphi\)はオイラー関数)なので、ラグランジュの定理はオイラーの定理やフェルマの小定理(25B)の一般化であるとも言えます。さらに、
群位数が素数の群は巡回群である。
こともわかります。なぜなら、群 \(G\) の位数を \(p\)(素数)とすると、単位元ではない \(G\) の任意の元 \(g\:(\neq e)\) の位数は \(p\) であり、つまり \(G\) は \(g\) を生成元とする位数 \(p\) の巡回群(\(C_p\))だからです。
次の「正規部分群」はガロア理論のキモといえる概念です。これは純粋に群の属性として定義できるのでここにあげますが、ガロア理論の核心である第5章以降で展開される論証の多くは正規部分群に関係しています。
正規部分群
有限群 \(G\) の部分群を \(H\) とする。\(G\) の全ての元 \(g\) について、
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
正規部分群 \(H\) の定義は、\(G\) の任意の元 \(g\) に対して、
\(gHg^{-1}=H\)
となる \(H\)、としても同じです。また 任意の \(h\in H\) について、
\(ghg^{-1}\in H\)
となる \(H\)、としても同じです。
剰余群
有限群 \(G\) の正規部分群を \(H\) とする。\(G\) の \(H\) による剰余類
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
[証明]
\(H\) が正規部分群のとき、剰余類が群になることを証明する。\(x_iH\) は \(G\) の剰余類なので、
\(G=x_1H\cup x_2H\cup\cd\cup x_dH\)
\((i\neq j\:のとき\:x_iH\cap x_jH=\phi)\)
と表されている。2つの剰余類、\(x_iH,\:x_jH\) の演算を行うと、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_iHx_jH=x_i(Hx_j)H\\
&&&=x_i(x_jH)H=x_ix_jHH\\
&&&=x_ix_j(HH)=x_ix_jH\\
\end{eqnarray}\)
つまり、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_ix_jH\\
\end{eqnarray}\)
となる。\(H\) は正規部分群なので \(Hx_j=x_jH\) であることと、\(H\) は部分群なので \(HH=H\) であることを用いた。
\(x_ix_j\) は \(G\) の元だから、\(x_ix_jH\) は \(G\) の剰余類のうちの一つである。従って \((x_iH)(x_jH)\) の演算は \(G\) の剰余類の中で閉じている。また、
\((x_iH\cdot x_jH)\cdot x_kH=x_ix_jH\cdot x_kH=x_ix_jx_kH\)
\(x_iH\cdot(x_jH\cdot x_kH)=x_iH\cdot x_jx_kH=x_ix_jx_kH\)
\((x_iH\cdot x_jH)\cdot x_kH=x_iH\cdot(x_jH\cdot x_kH)\)
であるから、結合法則が成り立っている。さらに、
\(H\cdot xh=eH\cdot xH=(ex)H=xH\)
\(xH\cdot H=xH\cdot eH=(xe)H=xH\)
なので、剰余類 \(H\) が単位元になる。また、
\(xH\cdot x^{-1}H=(xx^{-1})H=eH=H\)
\(x^{-1}H\cdot xH=(x^{-1}x)H=eH=H\)
であり、\(xH\) に対する逆元は \(x^{-1}H\) である。従って剰余類 \(G/H\) は群である。[証明終]
群の位数、元の位数、ラグランジュの定理、巡回群は、いずれも有限群の概念や定理です。しかし、剰余類、正規部分群、剰余群は、元の数が無限であっても成り立つ概念です。たとえば、整数の加法群 \(\bs{Z}\) は可換群なので、すべての部分群は正規部分群です。従って、\(n\) の倍数から成る部分群を \(n\bs{Z}\) とすると、\(\bs{Z}/n\bs{Z}\) は剰余群です。\(\bs{Z}/n\bs{Z}\) という表記は \(n\bs{Z}\) が \(\bs{Z}\) の正規部分群であることが暗黙の前提なのでした。
巡回群の部分群による剰余群は巡回群である。
[証明]
群 \(G\) を、位数 \(n\)、生成元 \(g\) の巡回群とし、その元を、
\(G\:=\:\{g,\:g^2,\:g^3,\:\cd,\:g^n=e\:\}\)
とする。\(G\) の部分群を \(H\) とし、\(H\) の元のうち \(g\) の指数が一番小さいものを \(g^{d}\:\:(1\leq d\leq n)\) とする。\(d=1\) なら \(H=G\) であり、また \(d=n\) なら \(H=\{\:e\:\}\) である。
\(n\) を \(d\) で割った商を \(q\)、余りを \(r\) とする。つまり、
\(n=qd+r\:\:(1\leq q\leq n,\:0\leq r < d)\)
とする。\(g^d\) は \(H\) の元だから その \(q\) 乗も \(H\) の元であり、
\((g^d)^q=g^{dq}\in H\)
である。また \(g^{dq}\) の逆元も \(H\) に含まれるから
\((g^{dq})^{-1}\in H\)
である。仮にもし \(1\leq r < d\) なら
\(g^{dq}g^{r}=g^{qd+r}=g^n=e\)
となるので、この式に左から \((g^{dq})^{-1}\) をかけると、
\(g^r=(g^{dq})^{-1}\in H\)
となり、\(d\) 未満の数 \(r\) が指数の \(g^r\) が \(H\) の元ということになるが、これは \(d\) が最小の指数であるという仮定に反する。従って \(r=0\) であり、\(qd=n\) である。つまり \(d\) と \(q\) は \(n\) の約数である。そうすると \(g^d\) を \(q\) 乗すると \(g^{dq}=g^n=e\) となるので、\(H\) は \(g^d\) を生成元とする位数 \(q\) の巡回群、
次に、剰余類 \(g^kH\:\:(1\leq k\leq n)\) を考える。\(k\) を \(d\) で割った商を \(m\)、余りを \(i\) とする。\(qd=n\) なので \(m\) の最大値は \(q\) であり、
\(k=md+i\) \((0\leq m\leq q,\:0\leq i < d)\)
と表現できる。以下、\(m,\:i\) の値によって3つに分ける。
\(k=i\:\:(m=0,\:1\leq i < d)\) のときは、\(H\) が単位元を含んでいるので、
\(g^k=g^i\in g^iH\)
である。
\(m\neq0,\:1\leq i < d\) のときは、
\(g^k=g^{md+i}=g^ig^{md}\)
となるが、\((\br{A})\) 式により、
\(g^{md}\in H\:\:(1\leq m\leq q)\)
なので、
\(g^ig^{md}\in g^iH\)
\(g^k\in g^iH\:\:(1\leq i < d)\)
となる。
また、\(m\neq0,\:i=0\) のときは、
\(g^k=g^{md}\in H\)
である。
結局、\(G\) の元 \(g^k\) は、\(\{\:H,\:g^iH\:\:(1\leq i < d)\:\}\) のどれかに含まれる。ここで、形式上 \(g^0H\:=\:H\) と定義すると、\(H,\:g^iH\) は、
\(g^iH\:=\:\{\:g^{i+md}\:|\:0\leq i < d,\:\:0\leq m\leq q\:\}\)
と表記できる。\(0\leq i,j < d,\:\:0\leq m_i,m_j\leq q\) で、\(i\neq j\) なら、
\(i+m_id\neq j+m_jd\)
なので、\(g^iH\) と \(g^jH\) に共通の元はなく、
\(g^iH\:\cap\:g^jH=\phi\:\:(i\neq j)\)
である。
以上より、巡回群 \(G\) は剰余類によって、
\(G=H\:\cup\:gH\:\cup\:g^2H\:\cup\:\cd\:\cup\:g^{d-1}\)
\(g^iH\:\cap\:g^jH=\phi\) \((i\neq j)\)
と分解できる。
\(H\) は \(G\) の正規部分群であった。従って \(G\) の \(H\) による剰余類は剰余群になり、
\(G/H=\{\:H,\:gH,\:g^2H,\:\cd\:,g^{d-1}H\:\}\)
である。ここで \(gH\) の累乗を調べると、
\((gH)^2=gHgH=ggHH=g^2H\)
\((gH)^3=gHgHgH=g^2HgH=g^2gHH=g^3H\)
のように計算でき、
\((gH)^i=g^iH\) \((1\leq i\leq d-1)\)
である。また、同じ計算によって、
\((gH)^d=g^dH\)
となるが、\(g^d\in H\) なので部分群の元の条件の定理(41C)により \(g^dH=H\) であり、つまり、
\((gH)^d=H\)
である。
以上により 剰余群 \(G/H\) は、
\(G/H=\{gH,\:(gH)^2,\:\cd\:,(gH)^{d-1},\:(gH)^{d}=H\}\)
と表され、生成元が \(gH\)、単位元が \(H\)、位数が \(d\) の巡回群である。[証明終]
部分群と正規部分群
\(G\) の正規部分群を \(H\)、部分群を \(N\) とする。このとき、
が成り立つ。
(a) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(NH\) は部分群である。
\(NH\) の任意の2つの元を
\(nx\:\:(n\in N,\:x\in H),\:\:my\:\:(m\in N,\:y\in H)\)
とすると、
\(nx\in nH,\:my\in mH\)
である。\(H\) は正規部分群だから、\(mH=Hm\) であることを用いると、
\((nx)(my)\in(nH)(mH)=nHmH=nmHH=nmH\)
となる。\(n,m\in N\) なので \(nm\in N\) であり、従って \(nmH\subset NH\) である。結局、
\((nx)(my)\in NH\)
となって、\(NH\) の2つの元の演算は \(NH\) で閉じていることが分かる(=\(\:\br{①}\:\))。
また一般に、\((xy)^{-1}=y^{-1}x^{-1}\) である。なぜなら、
\(xy(y^{-1}x^{-1})=x(yy^{-1})x^{-1}=xex^{-1}=xx^{-1}=e\)
\((y^{-1}x^{-1})xy=y^{-1}(x^{-1}x)y=y^{-1}ey=y^{-1}y=e\)
が成り立つからである。
\(G\) の部分群 \(N\) と正規部分群 \(H\) において、\(n\in N,\:x\in H\) とすると、\(n^{-1}\in N,\:x^{-1}\in H\) なので、
\((nx)^{-1}=x^{-1}n^{-1}\in Hn^{-1}\)
となるが、\(H\) が正規部分群なので、\(Hn^{-1}=n^{-1}H\)である。さらに、\(n^{-1}H\subset NH\) なので、結局、
\((nx)^{-1}\subset NH\)
となり、\(NH\) の任意の元 \(nx\) について逆元 \((nx)^{-1}\) が \(NH\) に含まれる(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) が成り立つので、部分群の十分条件の定理(41B)によって \(NH\) は \(G\) の部分群である。[証明終]
(b) の証明
\(G\) の正規部分群を \(H\)、部分群を \(N\) とするとき、\(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。\(N\) は \(G\) の 部分集合だから、\(N\) の任意の元 \(y\) についても、
\(yH=Hy\)
が成り立つ。従って \(H\) は \(N\) の正規部分群である。[証明終]
(c) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(N\cap H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。この式に右から \(x^{-1}\) をかけると、
\(xHx^{-1}=H\)
となる。これは、\(H\) の任意の元 \(h\) を決めると、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
となることを意味する。これは \(H\) が正規部分群であることの定義と等価である。以降、この形で \(N\cap H\) が正規部分群であることを証明する。
部分群 \(N\) の任意の元を \(y\)、正規部分群 \(H\) の任意の元を \(h\)、\(N\cap H\) の任意の元を \(n\) とする。\(y,\:y^{-1},\:n\) は全て \(N\) の元だから、
\(yny^{-1}\in N\)
である(=\(\:\br{①}\:\))。また \(H\) は \(G\) の正規部分群であるから、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
が成り立つ。ここで、\(G\:\sp\:N\) なので \(x=y\) とおくことができ、また \(H\:\sp\:N\cap H\) なので \(h=n\) とおくこともできる。従って、
\(yny^{-1}\in H\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、\(N\cap H\) の任意の元 \(n\) を決めると、\(N\) の全ての元 \(y\) について、
\(yny^{-1}\in N\cap H\)
となる。つまり \(N\cap H\) は \(N\) の正規部分群である。[証明終]
4.2 準同型写像
この節の写像の説明には「全射」「単射」「全単射」などの用語ができてます。その用語の意味は次の図の通りです。
準同型写像と同型写像
群 \(G\) から群 \(G\,'\) への写像 \(f\) がある。\(G\) の任意の2つの元、\(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
準同型写像の像と核
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(G\) の元を \(f\) で移した元の集合を「\(f\) の像(image)」といい、\(\mr{Im}\:f\) と書く。\(\mr{Im}\:f\) を \(f(G)\) と書くこともある。
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
[証明]
\(\mr{Im}\:f\) と \(\mr{Ker}\:f\) が群であることを証明する。
\(\mr{Im}\:f\) は群
\(\mr{Im}\:f\) の任意の2つの元を \(f(x),f(y)\:\:(x,y\in G)\) とすると、
\(f(x)f(y)=f(xy)\:\in\mr{Im}\:f\)
である(=\(\:\br{①}\:\))。
\(\mr{Im}\:f\) の任意の元 \(f(x)\) について、
\(f(e)f(x)=f(ex)=f(x)\)
\(f(x)f(e)=f(xe)=f(x)\)
なので、
\(f(e)=e\,'\)
である。\(G\) は群なので、任意の元 \(x\) について逆元 \(x^{-1}\) が存在する。
\(f(x)f(x^{-1})=f(xx^{-1})=f(e)=e\,'\)
\(f(x^{-1})f(x)=f(x^{-1}x)=f(e)=e\,'\)
であるから、
\(f(x)^{-1}=f(x^{-1})\:\in\mr{Im}\:f\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、部分群の十分条件の定理(41B)によって \(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(\mr{Ker}\:f\) は群
\(\mr{Ker}\:f\) の任意の元を \(x,\:y\) とすると、
\(f(xy)=f(x)f(y)=e\,'e\,'=e\,'\)
なので、
\(xy\:\in\mr{Ker}\:f\)
である(\(\:\br{③}\:\))。
また \(x\) は \(G\) の元だから \(x^{-1}\) が定義されている。
\(\begin{eqnarray}
&&\:\:f(x^{-1})&=f(x^{-1})e\,'=f(x^{-1})f(x)\\
&&&=f(x^{-1}x)=f(e)\\
&&&=e\,'\\
\end{eqnarray}\)
となるので、
\(x^{-1}\:\in\mr{Ker}\:f\)
である(\(\:\br{④}\:\))。\(\br{③}\:\:\br{④}\) より、部分群の十分条件の定理(41B)によって \(\mr{Ker}\:f\) は \(G\) の部分群である。[証明終]
核が単位元なら単射
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。このとき
である。
[証明]
"\(f\) は全射" については、全射の定義そのものである。
\(\mr{Ker}\:f\:=\:\{e\}\) とし、\(G\) の任意の2つの元を \(x,\:y\) とする。ここで、
\(f(x)=f(y)\)
であったとする。\(\mr{Im}\:f\) は群だから \(f(y)^{-1}\in\:\mr{Im}\:f\) である。上の式に左から \(f(y)^{-1}\) をかけると、
\(f(y)^{-1}f(x)=f(y)^{-1}f(y)\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)\in\:\mr{Ker}\:f\)
\(y^{-1}x=e\)
\(x=y\)
となる。\(f(x)=f(y)\) であれば \(x=y\) なので、\(f\) は単射である。[証明終]
核は正規部分群
群 \(G\) から群 \(G\,'\) への準同型写像を \(f\) とする。このとき \(\mr{Ker}\:f\) は \(G\) の正規部分群である。
[証明]
\(\mr{Ker}\:f\) を \(H\) と記述する。\(G\) の 任意の元を \(x\) とし、\(H\) の任意の元を \(y\) とする。すると、
\(\begin{eqnarray}
&&\:\:f(xyx^{-1})&=f(x)f(y)f(x^{-1})\\
&&&=f(x)e\,'f(x^{-1})=f(x)f(x^{-1})\\
&&&=f(xx^{-1})=f(e)=e\,'\\
\end{eqnarray}\)
と計算できるから、
\(xyx^{-1}\in H\)
である。\(y\) は \(H\) の任意の元だから、
\(xHx^{-1}\subset H\)
である。\(x\) は任意にとることができるので、\(x\) を \(x^{-1}\) に置き換えると、
\(x^{-1}Hx\subset H\)
を得る。この式に左から \(x\)、右から \(x^{-1}\) をかけると、
\(H\subset xHx^{-1}\)
となる。つまり
\(H\subset xHx^{-1}\subset H\)
\(xHx^{-1}=H\)
である。さらに右から \(x\) をかけると、
\(xH=Hx\)
となり、\(x\) は任意の \(G\) の元だから、\(H\:\:(=\mr{Ker}\:f)\) は \(G\) の正規部分群である。[証明終]
4.3 同型定理
準同型定理=第1同型定理
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(H=\mr{Ker}\:f\) とすると、\(G\) の \(H\) による剰余群は、\(G\) の \(f\) による像と同型である。つまり、
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
[証明]
\(H\:=\:\mr{Ker}\:f\) は、核は正規部分群の定理(42D)により、\(G\) の正規部分群である。従って剰余群 \(G/H\) が定義できる。\(G/H\) から \(\mr{Im}\:f\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G/H &\longrightarrow&\mr{Im}\:f\\
&&&xH &\longmapsto&f(x)\\
\end{eqnarray}\)
と定義する。まず、この写像が剰余類 \(xN\) の代表元 \(x\) のとりかたに依存しないこと、つまり \(xH=yH\) なら \(f(x)=f(y)\) であることを示す。\(xH=yH\) を変形すると、
\(xH=yH\)
\(y^{-1}xH=y^{-1}yH\)
\(y^{-1}xH=H\)
ゆえに部分群の元の条件の定理(41C)から \(y^{-1}x\in H\) である。そうすると、\(H\) は \(\mr{Ker}\:f\) のことだから、\(f(y^{-1}x)=e\,'\) である。これを変形すると、
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
となる。最後の変形では、準同型写像の像と核の定理(42B)の「\(\mr{Im}\:f\) は群」の証明から、\(f(y^{-1})=f(y)^{-1}\) であることを用いた。ここから、
\(f(y)^{-1}f(x)=e\,'\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(x)=f(y)\)
となり、\(f(x)=f(y)\) が証明できた。
以上の変形は逆も辿れる。つまり、
\(f(x)=f(y)\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1}x)\in H\)
\(y^{-1}xH=H\)
\(xH=yH\)
となる。これは \(f(x)=f(y)\) なら \(xH=yH\) であることを示していて、すなわち \(\sg\) は単射である。と同時に、\(\sg\) による写像の先は \(\mr{Im}\:f\) に限定しているので \(\sg\) は全射である。つまり \(\sg\) は 全単射である(=\(\:\br{①}\:\))。
さらに、
\(\begin{eqnarray}
&&\:\:\sg((xH)(yH))&=\sg(x(Hy)H)=\sg(x(yH)H)\\
&&&=\sg(xyH)=f(xy)=f(x)f(y)\\
&&&=\sg(xH)\sg(yH)\\
\end{eqnarray}\)
であり、つまり \(\sg((xH)(yH))=\sg(xH)\sg(yH)\) が成り立っている(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) により \(\sg\) は同型写像である。\(G/H\) から \(\mr{Im}\:f\) への同型写像が存在するから、
\(G/H\:\cong\:\mr{Im}\:f\)
である。[証明終]
第2同型定理
群 \(G\) の正規部分群を \(H\)、部分群を \(N\) とすると、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
[証明]
まず、部分群と正規部分群の定理(41I)により、\(G\) の正規部分群が \(H\)、部分群が \(N\) の場合、
である。従って剰余群の定義(41G)により、\(N/(N\cap H)\) および \(NH/H\) は剰余群となる。
\(G\) の任意の元を \(x,\:y\) とし、\(G\) から \(G/H\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G &\longrightarrow&G/H\\
&&&x &\longmapsto&xH\\
\end{eqnarray}\)
と定義する。この写像は、
\(\begin{eqnarray}
&&\:\:\sg(xy)&=xyH=xyHH=xHyH=(xH)(yH)\\
&&&=\sg(x)\sg(y)\\
\end{eqnarray}\)
を満たすから準同型写像である(ちなみに \(G\) とその正規部分群 \(H\) があるとき、上記の定義による \(\sg\) を自然準同型と呼ぶ)。
\(\sg\) の定義域は \(G\) であるが、\(\sg\) の定義域を \(G\) の部分群である \(N\) に制限した写像 \(\tau\)(タウ) を考える。\(N\) の任意の元を \(z\) とすると、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
&&&z &\longmapsto&zH\\
\end{eqnarray}\)
である。この \(\tau\) の像 \(\mr{Im}\:\tau\) を考えてみると、\(z\) が \(N\) の元のすべてを動くとき、\(\tau(z)=zH\) として出てくる \(G\) の元は \(NH\) の元である。つまり \(\tau\) は、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
として定義したが、\(\tau(z)\) が \(G/H\) の全てを尽くすわけではなく、全射ではない。写像による移り先は、\(G\) の部分群 \(NH\) を \(H\) で分類した剰余群、\(NH/H\) である。つまり \(\tau(N)=NH/H\) であり、
\(\mr{Im}\:\tau=NH/H\)
である。
次に準同型写像の核を考える。\(G/H\) の単位元は、
\(xH\cdot H=xH\)
\(H\cdot xH=HxH=xHH=xH\)
なので、\(H\) である。
\(G\) の元 \(x\) が \(\mr{Ker}\:\sg\) の元とする。つまり、
\(x\in\mr{Ker}\:\sg\)
とする。これは \(\sg(x)\) が \(G/H\) の単位元になるということだから、
\(\sg(x)=H\)
であり、\(\sg(x)=xH\) なので、
\(xH=H\)
である。これは部分群の元の条件の定理(41C)によって、
\(x\in H\)
と同値である。従って、
\(x\in\mr{Ker}\:\sg\)
\(x\in H\)
の2つは同値であり、つまり、
\(\mr{Ker}\:\sg=H\)
である。
\(\tau\) は \(\sg\) の定義域を \(N\) に制限したものなので、\(\mr{Ker}\:\tau\) は「\(\mr{Ker}\:\sg=H\) のうちで \(N\) に含まれるもの」であり、すなわち、
\(\mr{Ker}\:\tau=(N\cap H)\)
である。
ここで、\(\tau\) の定義である、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
に準同型定理(43A)を適用すると、
\(\begin{eqnarray}
&&\:\:N/(\mr{Ker}\:\tau) &\cong\:\mr{Im}\:\tau\\
&&\:\:N/(N\cap H) &\cong\:NH/H\\
\end{eqnarray}\)
となって、題意が成り立つ。[証明終]
第2同型定理を整数の剰余群で確認してみます。上の定理における \(G,\:H,\:N\) を、
\(G=\bs{Z}\)
\(H=10\bs{Z}\) (\(10\) の倍数)
\(N=\phantom{1}6\bs{Z}\) (\(\phantom{1}6\) の倍数)
の群とします。この群の演算は加算であり、可換群なので、\(\bs{Z}\) の部分群はすべて正規部分群です。
\(N\cap H\) は「\(10\) の倍数、かつ \(6\) の倍数」の集合なので、
\(N\cap H=30\bs{Z}\)
です。また \(NH\) は、\(10\) の倍数と\(6\) の倍数の加算の結果の集合です。つまり、
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
ですが、これが何を意味するかは不定方程式の解の存在の定理(21B)から分かります。定理を再掲すると、
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
です。\(c=kd\) なら、式を満たす \(x,\:y\) が必ず存在します。また任意の \(x,\:y\) について \(ax+by\) を計算すると、その結果の \(c\) は必ず \(c=kd\) の形になります。そうでなければ、\(c\) が最大公約数の倍数でないにも関わらず不定方程式が解をもつことになって定理に矛盾します。従って、\(ax+by=c\) の \(x,\:y\) を任意の整数とすると、\(c\) は \(a,\:b\) の "最大公約数の整数倍のすべて" になります。
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
とした場合、\(10\) と \(6\) の最大公約数は \(2\) なので、
\(NH=2\bs{Z}\)
です。この結果、
\(N/(N\cap H)\)
\(=6\bs{Z}/30\bs{Z}\)
\(=\{30\bs{Z},\:6+30\bs{Z},\:12+30\bs{Z},\:18+30\bs{Z},\:24+30\bs{Z}\}\)
\(NH/H\)
\(=2\bs{Z}/10\bs{Z}\)
\(=\{10\bs{Z},\:2+10\bs{Z},\:4+10\bs{Z},\:6+10\bs{Z},\:4+10\bs{Z}\}\)
となります。この2つの剰余群は位数 \(5\) の巡回群( \(C_5\) )で、\(\bs{Z}/5\bs{Z}\) に同型です。つまり、
であり、
\(N/(N\cap H)\:\cong\:NH/H\)
となって、第2同型定理が確認できました。
第2同型定理を数式で書くと何だか難しそうな感じがしますが、図にするといかにも自明なことという気がします。数学におけるイメージ図の威力が実感できます。
第2同型定理は、後ほど「可解群の部分群は可解群」という定理の証明に使います。「可解群の部分群は可解群」の定理は、5次方程式に可解でないものがあることを証明する際に鍵となる定理です。その第2同型定理は準同型定理を使って証明される、という構造になっているのでした。
2章から4章までは、多項式、体、線形空間、剰余類、群、剰余群、既約剰余類群、正規部分群といった、ガロア理論の基礎となる概念の説明でした。この第5章から、理論の核心に入っていきます。
5.1 体の同型写像
同型写像の定義
体 \(\bs{K}\) から 体 \(\bs{F}\) への写像 \(f\) が全単射であり、\(\bs{K}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
[証明]
上の定義による同型写像が、減法と除法を保存することを証明する。\(\bs{K}\) と \(\bs{F}\) は体だから、加法と乗法について群になっている。\(\bs{K}\) の加法の単位元を \(\kz\)、\(\bs{F}\) の加法の単位元を \(\fz\) とする。また、乗法の単位元をそれぞれ \(\ko\) と \(\fo\) とする。まず、\(f(\ko)=\fo\) で \(f(\kz)=\fz\) であることを示す。
\(f(x+y)=f(x)+f(y)\) において \(x=\kz,\:y=\kz\) とすると、
\(f(\kz+\kz)=f(\kz)+f(\kz)\)
\(f(\kz)=f(\kz)+f(\kz)\)
両辺に \(\bs{F}\) における \(f(\kz)\) の逆元 \(-f(\kz)\) を加えると、
\(f(\kz)+(-f(\kz))=f(\kz)\)
\(\fz=f(\kz)\)
となり、\(f(\kz)=\fz\) である。
\(f(xy)=f(x)f(y)\) において \(x=\ko,\:y=\ko\) とすると、
\(f(\ko\times\ko)=f(\ko)f(\ko)\)
\(f(\ko)=f(\ko)f(\ko)\)
両辺に \(\bs{F}\) における \(f(\ko)\) の逆元 \(-f(\ko)\) を加えると、
\(f(\ko)+(-f(\ko))=f(\ko)f(\ko)+(-f(\ko))\)
\(\fz=f(\ko)f(\ko)+(-f(\ko))\)
この式に現れているのは全て \(\bs{F}\) の元だから、分配則を使って、
\(f(\ko)(f(\ko)-\fo)=\fz\)
ここで \(f(\ko)=\fz\) と仮定すると、\(f(\kz)=\fz\)かつ \(f(\ko)=\fz\) となってしまい \(f\) が単射であることと矛盾する。従って \(f(\ko)\neq\fz\) である。上式の両辺を \(f(\ko)\) で割ると、
\(f(\ko)-\fo=\fz\)
\(f(\ko)=\fo\)
となる。
以上を踏まえると、同型写像が減法を保存することは次のようにしてわかる。\(\bs{K}\) は加法について群なので任意の元 \(x\in\bs{K}\) について逆元 \(-x\) がある。また \(\bs{F}\) も加法についても群だから \(f(x)\) の逆元 \(-f(x)\) がある。
\(f(-x)+f(x)=f(-x+x)=f(\kz)=\fz\)
両辺に \(-f(x)\) を足すと、
\(f(-x)+f(x)+(-f(x))=\fz+(-f(x))\)
\(f(-x)+\fz=\fz+(-f(x))\)
\(f(-x)=-f(x)\)
である。\(\bs{K}\) の任意の元を \(x,\:y\) とすると、
\(\begin{eqnarray}
&&\:\:f(x-y)&=f(x+(-y))\\
&&&=f(x)+f(-y)\\
&&&=f(x)+(-f(y))\\
&&&=f(x)-f(y)\\
\end{eqnarray}\)
となって、減法は保存されている。
除法を保存することは次のようにしてわかる。\(\bs{K}\) は乗法について群なので、任意の元 \(x\:\:(\neq\kz)\) について逆元 \(x^{-1}\) がある。\(\bs{F}\) も乗法についての群だから、\(f(x)\) の逆元である \(f(x)^{-1}\) がある。\(x\neq\kz\) なら \(f(x)\neq\fz\) なので逆元が定義できる。すると、
\(f(x^{-1})f(x)=f(x^{-1}x)=f(\ko)=\fo\)
である。この式の両辺に \(f(x)^{-1}\) をかけると、
\(f(x^{-1})f(x)f(x)^{-1}=\fo\times f(x)^{-1}\)
\(f(x^{-1})\times\fo=\fo\times f(x)^{-1}\)
\(f(x^{-1})=f(x)^{-1}\)
となる。\(\bs{K}\) の任意の元を \(x,\:y\:\:(y\neq\kz)\) とすると、
\(\begin{eqnarray}
&&\:\:f\left(\dfrac{x}{y}\right)&=f(xy^{-1})\\
&&&=f(x)f(y^{-1})\\
&&&=f(x)f(y)^{-1}\\
&&&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
となり、除法が保存されていることが分かる。
有理数の同型写像を考える。\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn\:個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)\\
&&&=n\\
\end{eqnarray}\)
なので、\(f(n)=n\) である。任意の有理数 \(a\) は、2つの整数 \(n\:(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるから、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は同型写像で不変である。[証明終]
同型写像と有理式の順序交換
変数 \(x\) の多項式(係数は \(\bs{Q}\) の元)を分母・分子とする分数式を、\(\bs{Q}\) 上の有理式という。
\(\bs{Q}\) 上の多項式は、有理数と \(x\) の加・減・乗算で作られる式です。一方、\(\bs{Q}\) 上の有理式とは、有理数と \(x\) の除算を含む四則演算で作られる式です。
体 \(\bs{K}\) と 体 \(\bs{F}\) は \(\bs{Q}\) を含むものとする。\(\sg\) を \(\bs{K}\) から \(\bs{F}\) への同型写像とし、\(a\) を \(\bs{K}\) の元とする。\(f(x)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
[証明]
\(a\in\bs{K},\:b_i\in\bs{Q},\:c_i\in\bs{Q}\) とし、1変数 \((=a)\) の2次多項式の分数式の場合を例に書くと、
\(\sg\left(\dfrac{b_2a^2+b_1a+b_0}{c_2a^2+c_1a+c_0}\right)\)
\(=\dfrac{\sg(b_2a^2+b_1a+b_0)}{\sg(c_2a^2+c_1a+c_0)}\)
\(=\dfrac{b_2\sg(a^2)+b_1\sg(a)+b_0}{c_2\sg(a^2)+c_1\sg(a)+c_0}\)
\(=\dfrac{b_2\sg(a)^2+b_1\sg(a)+b_0}{c_2\sg(a)^2+c_1\sg(a)+c_0}\)
であるから、題意は成り立つ。これは \(n\)次多項式の場合でも同じである。[証明終]
「同型写像と有理式は順序交換可能」は、\(\bs{Q}\) の拡大体の上の有理式でも成り立ちます。つまり、次が成り立ちます。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
同型写像は解を共役な解に移す
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とする。\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つを \(\al\) とし、\(\al\) は \(\bs{K}\) の元とする。すると \(\sg(\al)\) も \(f(x)=0\) の解である。
[証明]
\(\al\) は \(f(x)=0\) の解なので \(f(\al)=0\) が成り立つ。すると、
\(f(\sg(\al))=\sg(f(\al))=\sg(0)=0\)
となり、\(\sg(\al)\) も \(f(x)=0\) の解である。[証明終]
同じ方程式の解同士を「共役な解」「共役である」と言います。この定理により、同型写像は解を共役な解に移すこと分かります。
同型写像は解を入れ替える
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とし、\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。方程式 \(f(x)=0\) の \(n\)個の解を \(\al_1,\al_2,\cd,\al_n\) とし、これらが全て \(\bs{K}\) に含まれるとする。
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
[証明]
\(f(x)\) は既約多項式なので、方程式 \(f(x)=0\) は \(n\)個の解をもち、それらは全て異なる(31G)。同型写像は解を共役な解に移す(51D)ので、\(\sg(\al_i)\) も \(f(x)=0\) の解である。\(\sg\) は同型写像なので全単射であり、\(i\neq j\) なら \(\sg(\al_i)\neq\sg(\al_j)\) である。従って \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。[証明終]
同型写像を定義してその性質を述べてきましたが、あたかも「同型写像はあるのが当然」のような話でした。しかし、同型写像があったとしたらこういう性質をもつというのが正しく、同型写像が必ずあるとは証明していません。
同型写像の存在を示すには、第1章でやったように、\(\bs{Q}(\sqrt{2})\)において
\(\sg(\sqrt{2})=-\sqrt{2}\)
という写像を定義すると、体のすべての元について \(\sg\) は同型写像の定義を満たす、というような証明が必要です。それが次です。
単拡大体の同型写像の存在
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(\al,\:\beta\) を方程式 \(f(x)=0\) の異なる解とする。
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
[証明]
\(\bs{Q}(\al)\) の任意の元を \(a\)、\(\bs{Q}(\beta)\) の任意の元を \(b\) とする。単拡大体の基底の定理(33F)により、\(a,\:b\) は、
\(\begin{eqnarray}
&&\:\:\sg\:: &a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\\
&&&\longmapsto\:a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
と定義する。\(a=\al\) の場合は、\(a_1=1,\:a_i=0\:\:(i=0,\:2\leq i\leq n-1)\) だから、\(\sg(\al)=\beta\) である。以下、この \(\sg\) が同型写像であることを証明する。定義により(51A)同型写像であることは加法と乗法を保存することを言えばよい。
\(\bs{Q}(\al)\) の任意の2つの元を \(s,\:t\) とし、
\(p(x)=g(x)+h(x)\) とおくと、
\(p(\al)=g(\al)+h(\al)=s+t\)
である。また \(\sg\)の定義により、
\(\sg(p(\al))=p(\beta)\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\sg(s+t)&=\sg(p(\al))\\
&&&=p(\beta)\\
&&&=g(\beta)+h(\beta)\\
&&&=\sg(s)+\sg(t)\\
\end{eqnarray}\)
となり、加法は保存される。
\(g(x)h(x)\) を \(f(x)\) で割ったときの商を \(q(x)\)、余りを \(r(x)\) とすると、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。この式に \(x=\al,\:x=\beta\) のそれぞれを代入すると、\(f(\al)=0,\:f(\beta)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
\(g(\beta)h(\beta)=r(\beta)\)
となる。すると、
\(\begin{eqnarray}
&&\:\:\sg(st)&=\sg(g(\al)h(\al))\\
&&&=\sg(r(\al))=r(\sg(\al))\\
&&&=r(\beta)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:\sg(s)\sg(t)&=\sg(g(\al))\sg(h(\al))\\
&&&=g(\sg(\al))h(\sg(\al))\\
&&&=g(\beta)h(\beta)\\
&&&=r(\beta)\\
\end{eqnarray}\)
であり、
\(\sg(st)=\sg(s)\sg(t)\)
となって乗法も保存されている。従って \(\sg\) は同型写像である。
逆に、\(\bs{Q}(\al)\) に作用する同型写像 \(\tau\) があったとする。同型写像は \(\al\) を共役な元に移すので、その移り先の元を \(\beta\)、つまり \(\tau(\al)=\beta\) とする。\(\bs{Q}(\al)\) の任意の元 \(a\) に \(\tau\) を作用させると、
\(\begin{eqnarray}
&&\:\:\tau(a)&=\tau(a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0)\\
&&&=a_{n-1}\tau(\al^{n-1})+\:\cd\:+a_2\tau(\al^2)+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\tau(\al)^{n-1}+\:\cd\:+a_2\tau(\al)^2+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
となるので、同型写像はこの式を満たさなければならない。従って、上で定義した \(\sg\) が \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) の唯一の同型写像である。[証明終]
同型写像の存在(51F)を一般化すると、次のことが言えます。
単拡大体の同型写像は \(n\) 個
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(f(x)=0\) の全ての解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\) とする。このとき \(\bs{Q}(\al)\) に作用する同型写像は \(n\)個あり、それらは、
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
同型写像を別の視点で考えます。\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{K}\) といった体の拡大列があったとき、\(\bs{F}\) の同型写像と \(\bs{K}\) の同型写像には密接な関係があります。それが次の同型写像の延長の定理です。単拡大定理(32B)により、\(\bs{F}=\bs{Q}(\al)\)、\(\bs{K}=\bs{Q}(\al,\beta)\) としてよいので、その形を使います。
同型写像の延長
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
[証明]
\(\bs{Q}(\al)\) 上の \(m\)次既約多項式 \(g(x)\) を、
\(g(x)=x^m+a_1x^{m-1}+\cd+a_m\:\:(a_j\in\bs{Q}(\al))\)
とする。\(\beta\) は \(g(x)=0\) の解だから
\(g(\beta)=\beta^m+a_1\beta^{m-1}+\cd+a_m=0\)
である。また、多項式 \(\tau(g(x))\) を、
\(\tau(g(x))=x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_{m-1})x+\tau(a_m)\)
と定義し、方程式
\(\tau(g(x))=0\)
の解を \(t_j\:\:(0\leq j < m)\)とする。つまり \(\tau(g(t_j))=0\) である。
\(\bs{Q}(\al,\beta)\) は \(\bs{Q}(\al)\) 上の線形空間であり、単拡大体の基底の定理(33F)により、その基底を \(\{1,\:\beta,\:\beta^2,\:\cd\:\beta^{m-1}\}\) にとれるから、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) は、
と表せる。そこで、\(\bs{Q}(\al,\beta)\) の元に作用する写像 \(\sg_j\) を
と定義する。この定義における \(\sg_j\) は \(\bs{Q}(\al,\beta)\) の同型写像になる。同型写像になることは体の加算と乗算で示せればよい(51A)。\(\bs{Q}(\al,\beta)\) の2つの元を、
\(p=c_0+c_1\beta+c_2\beta^2\:+\cd+\:c_{m-1}\beta^{m-1}\:\:(c_j\in\:\bs{Q}(\al)\:)\)
\(q=d_0+d_1\beta+d_2\beta^2\:+\cd+\:d_{m-1}\beta^{m-1}\:\:(d_j\in\:\bs{Q}(\al)\:)\)
とし、2つの多項式を、
\(p(x)=c_0+c_1x+c_2x^2\:+\cd+\:c_{m-1}x^{m-1}\)
\(q(x)=d_0+d_1x+d_2x^2\:+\cd+\:d_{m-1}x^{m-1}\)
と定義する。加算で同型写像になるのは明白なので、乗算で同型写像になることを示す。
\(p(x)q(x)\) を \(g(x)\) で割ったときの商を \(t(x)\)、余りを \(r(x)\) とすると、
すると \(g(\beta)=0\) だから、
である。そうすると、\(\sg_j(pq)\) は \(\sg_j\) の定義により、
となる。
\(\tau\) は \(\bs{Q}(\al)\) の同型写像だから、\(\bs{Q}(\al)\) の元の有理式である \(s_j(c_j,d_j)\) に作用させると、同型写像と有理式の順序交換の定理(51C)により、
\(\tau(s_j(c_j,d_j))=s_j(\tau(c_j),\tau(d_j))\)
となる。従って、
である。
\(p(x)\) の係数 \(c_j\) を \(\tau(c_j)\) で置き換え、\(q(x)\) の係数 \(d_j\) を \(\tau(d_j)\) で置き換えた2つの多項式を、
\(\tau(p(x))=\tau(c_0)+\tau(c_1)x+\tau(c_2)x^2+\cd+\tau(c_{m-1})x^{m-1}\)
\(\tau(q(x))=\tau(d_0)+\tau(d_1)x+\tau(d_2)x^2+\cd+\tau(d_{m-1})x^{m-1}\)
とする。
\(\tau(p(x))\tau(q(x))\)を\(\tau(g(x))\)で割ったときの商を\(\tau(t(x))\)、余りを\(\tau(r(x))\)とする。つまり、
\(\tau(p(x))\tau(q(x))=\tau(g(x))\tau(t(x))+\tau(r(x))\)
である。\(c_j\) と \(d_j\) の有理式、\(s_j(c_j,d_j)\) を使って \(\tau(r(x))\) を表すと、
となる。\(\sg_j\) の定義により、
である。従って、
また、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) を、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表したとき、\(k\) が \(\bs{Q}(\al)\) の元だとすると \(k=b_0\:\:(b_0\in\bs{Q}(\al))\)、\(b_j=0\:\:(1\leq j < m)\) なので、
\(\sg_j(k)=\tau(b_0)=\tau(k)\)
となり、\(\sg_j\) の \(\bs{Q}(\al)\) の元に対する作用は \(\tau\) と一致する。従って、
\(\sg_j\) の定義式、
一方、\(\al\) は \(\bs{Q}\) 上の \(n\)次既約多項式 \(f(x)\) の解の一つだから、\(\bs{Q}(\al)\) の同型写像 \(\tau\) は \(n\)個ある。これを \(\tau_i\:\:(0\leq i < n)\) と書くと、それぞれの \(\tau_i\) に対して同型写像の拡張 \(\sg_{ij}\:\:(0\leq i < n,\:0\leq j < m)\) がある。従って \(\bs{Q}(\al,\beta)\) の 同型写像 \(\sg_{ij}\) は \(nm\)個ある。[証明終]
5.2 ガロア拡大とガロア群
ガロア拡大
ガロア拡大は次のように定義される。この2つの定義は同値である。
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
[① \(\bs{\Rightarrow}\) ②の証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。その解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{F}\) の元を不変にする \(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。
一方、\(\bs{L}\) は \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{F}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式(係数は \(\bs{F}\) の元)で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は \(\bs{F}\) の元)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させる。\(\bs{F}\) 係数の有理式と \(\bs{F}\) を不変にする同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移す(51D)から、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。
[② \(\bs{\Rightarrow}\) ①の証明]
単拡大定理(32B)により、\(\bs{K}\) は、\(\bs{K}\) の元 \(\theta\) を用いて \(\bs{K}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(f(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(f(x)\) は既約多項式である。また既約多項式の定理3(31G)により、方程式 \(f(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。
\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、\(\bs{F}\) 上の方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する。\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像は自己同型写像なので、\(\sg_i(\theta)=\theta_i\) は全て \(\bs{K}\) の元である。従って \(\bs{K}\) は \(\bs{F}\) 上の既約多項式 \(f(x)\) の解 \(\theta_i\) を用いて、
\(\begin{eqnarray}
&&\:\:\bs{K}&=\bs{F}(\theta)\\
&&&=\bs{F}(\theta_1,\:\theta_2,\:\cd,\:\theta_m)\\
\end{eqnarray}\)
と表される。\(\bs{K}\) は \(\bs{F}\) 上の既約多項式の最小分解体である。[証明終]
① の定義は、方程式の解のありようを議論するガロア理論にとっては "ノーマルな" 定義のように見えます。しかし ② のように方程式という言葉を全く使わない定義もメリットがあります。たとえば「次数が違う2つの方程式の解によるガロア拡大が同じ」ということは、いくらでもありうるからです。
また、ガロア拡大は次のような定義もできます。
方程式という言葉は使っていますが、拡大体から始まる定義です。言い換えると、\(\bs{K}\) がガロア拡大体のとき \(\bs{K}\) の任意の元に共役な元は \(\bs{K}\) に含まれるということです。
このように、互いに同値である多種の定義ができることがガロア理論の分かりにくいところですが、逆に「それだけ豊かな数学的内容を含んだ理論」とも言えるでしょう。
最小分解体の次数=ガロア群の位数
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\)、ガロア群を \(G\) とするとき、\([\:\bs{L}\::\:\bs{Q}\:]=|G|\) である。
[証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{Q}(\theta)\) と表すことができる。\(\theta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。ここで、\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{Q}\) の元を不変にするから、\(\bs{L}=\bs{Q}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。単拡大体 \(\bs{Q}(\theta)\) に作用する同型写像は \(m\)個だから(51G)、これが同型写像のすべてである。
一方、\(\bs{L}\) は \(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{Q}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は有理数)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させると、有理式と同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移すから(51D)、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。以上により、
\(\mr{Gal}(\bs{L}/\bs{Q})=\{\sg_1,\:\sg_2,\:\cd,\:\sg_m\}\)
であり、\(|G|=m\) である。
\(\theta\) の \(\bs{Q}\) 上の最小多項式(=既約多項式)の次数が \(m\) だから、単拡大体の基底の定理(33F)によって、最小分解体 \(\bs{L}=\bs{Q}(\theta)\) は \(\bs{Q}\) の \(m\)次拡大体であり、
\([\:\bs{L}\::\:\bs{Q}\:]=|G|\)
である。[証明終]
この定理では \(\bs{Q}\) としましたが、任意の代数拡大体 \(\bs{F}\) としても成り立ちます。また、最小分解体はガロア拡大体です。従って、最も一般的に言うと次のようになります。
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
中間体
\(\bs{K}\) を \(\bs{F}\) のガロア拡大体とし、\(\bs{M}\) を \(\bs{F}\subset\bs{M}\subset\bs{K}\) である任意の体(=中間体)とするとき、\(\bs{K}\) は \(\bs{M}\) のガロア拡大体でもある。
[証明]
最小分解体定義による
\(\bs{K}\) が \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であるとする。この方程式の解を \(\al_1,\:\al_2,\:\cd\:\al_n\) とすると、\(\bs{K}=\bs{F}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(\bs{F}\subset\bs{M}\subset\bs{L}\) なので、
\(\bs{F}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{M}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{K}(\al_1,\:\cd\:\al_n)=\bs{K}\)
となるが、すなわち、
\(\bs{F}\:\subset\:\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\:\subset\:\bs{K}\)
であり、\(\bs{K}=\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(f(x)=0\) は \(\bs{M}\) 上の方程式でもあるので、\(\bs{K}\) は \(\bs{M}\) 上の方程式の最小分解体であり、\(\bs{M}\) のガロア拡大体である。
自己同型定義による
\(\bs{L}\) の同型写像のうち、\(\bs{M}\) の元を固定する任意の同型写像を \(\sg\) とする。そうすると \(\sg\) は \(\bs{M}\) の部分集合である \(\bs{F}\) の元も固定する。\(\bs{L}\) は \(\bs{F}\) のガロア拡大体なので、\(\bs{F}\) の元を固定する \(\bs{L}\) の同型写像は自己同型写像である。従って \(\sg\) も自己同型写像であり、\(\bs{L}\) は \(\bs{M}\) のガロア拡大体である。[証明終]
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列があったとき、\(\bs{F}\subset\bs{K}\) がガロア拡大だと上の定理(52C)によって \(\bs{M}\subset\bs{K}\) もガロア拡大です。しかし、\(\bs{F}\subset\bs{M}\) がガロア拡大になるとは限りません。\(\bs{F}\subset\bs{M}\) がガロア拡大になるためには条件が必要で、その条件が満たされば、\(\bs{F}\subset\bs{M}\subset\bs{K}\) は「ガロア拡大の連鎖」になり、そのことが方程式の可解性と結びつきます。それが次の節の大きな主題です。
5.3 ガロア対応
固定体と固定群
体 \(\bs{F}\) 上の方程式の最小分解体(=ガロア拡大体)を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる。これを \(\bs{K}\) における \(H\) の固定体といい、\(\bs{K}(H)\) で表す(または \(\bs{K}^H\))。
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
[証明]
固定体と固定群の定義において、
の2点を証明する。
① の証明
\(\bs{M}\) が体であることを証明するには、四則演算で閉じていることを言えばよい(1.2 体)。\(\bs{M}\) の任意の2つの元を \(x,\:y\) とし、\(H\) の任意の元を \(\sg\) とする。\(x,\:y\) は \(\bs{K}\) の元でもあるから、
\(x+y\in\bs{K}\)
である。\(H\) の元 \(\sg\) は \(G\) の元でもあるから \(\sg(x+y)\) が定義できる。\(x,\:y\) は \(\bs{M}\) の元だから、\(H\) の元である \(\sg\) を作用させても不変であり、
\(\sg(x)=x\)
\(\sg(y)=y\)
である。すると、
\(\sg(x+y)=\sg(x)+\sg(y)=x+y\)
となって、\(x+y\) は \(\sg\) によって不変であり、
\(x+y\in\bs{M}\)
である。以上のことが加減乗除のすべてで成り立つことは明白だから、\(\bs{M}\) は四則演算で閉じていて、体である。
② の証明
\(\bs{M}\) の任意の元を \(x\)、\(H\) の2つの元を \(\sg,\:\tau\) とする。
\(\sg(x)=x\)
\(\tau(x)=x\)
である。すると、
\(\sg\tau(x)=\sg(\tau(x))=\sg(x)=x\)
となり、\(\sg\tau\in H\) となって、\(H\) の元は群演算で閉じている。
また \(H\) の元はもともと \(G\) の元なので、結合法則も成り立つ。\(G\) の単位元を \(e\) とすると、\(e(x)=x\) なので \(e\in H\) である。
さらに \(\sg\) は \(G\) の元なので、\(G\) の中に \(\sg^{-1}\) が存在する。すると、\(\sg(x)=x\) の両辺に左から \(\sg^{-1}\) をかけると、
\(\sg^{-1}\sg(x)=\sg^{-1}(x)\)
\(x=\sg^{-1}(x)\)
となり、
\(\sg^{-1}\in H\)
である。\(H\) は演算で閉じていて、結合法則が成り立ち、単位元と逆元が存在するので、群の定義(22A)を満たしている。[証明終]
以上の固定体と固定群の概念を用いると、次のガロア対応の定理が成り立ちます。以降の論証の基礎となる定理です。
ガロア対応の定理
\(\bs{F}\) のガロア拡大体を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の任意の部分群を \(H\) とし、\(H\) による \(\bs{K}\) の固定体 \(\bs{K}(H)\) を \(\bs{M}\) とする(次式)。
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
[証明]
\(G\) の任意の部分群である \(H\) は \(\bs{K}\) の部分集合 \(\bs{M}\) を固定する。一方、\(G(\bs{M})\) は \(\bs{M}\) を固定する \(G\) のすべての元の集合で、それが部分群になっている。従って、\(G(\bs{M})\) は \(H\) を含む。つまり
\(H\:\subset\:G(\bs{M})\)
であり、群位数は、
\(\bs{K}/\bs{F}\) はガロア拡大であり、\(\bs{M}\) はその中間体だから、中間体からのガロア拡大の定理(52C)によって、\(\bs{K}/\bs{M}\) はガロア拡大である。また、すべての代数拡大体は単拡大体だから(32B)、\(\bs{K}\) の元 \(\theta\) があって \(\bs{K}=\bs{F}(\theta)\) と表せる。これは、\(\bs{K}=\bs{M}(\theta)\) ということでもある。
\(H\) の \(|H|\) 個の元を \(\sg_i\:\:(1\leq i\leq|H|)\) とし、多項式
\(f(x)=\displaystyle\prod_{i=1}^{|H|}(x-\sg_i(\theta))\)
を考える。この多項式の次数は \(|H|\) である。\(\sg_i(\theta)\) は \(\theta\) の共役な元のどれかである。
\(f(x)\) を展開すると、その係数は \(\sg_i(\theta)\:\:(1\leq i\leq|H|)\) の対称式になる。また、\(\sg_i(\theta)\) に \(H\) の任意の元 \(\sg_k\) を作用させても、\(\sg_i\) は部分群だから演算で閉じており、\(\sg_i(\theta)\) を入れ替えるだけである(51E)。従って \(\sg_i(\theta)\) の対称式に \(\sg_k\) を作用させても不変である。つまり、\(H\) の任意の元は \(f(x)\) の係数を固定する。ということは、\(\bs{M}\) の定義(= \(H\) による \(\bs{K}\) の固定体が \(\bs{M}\))によって、\(f(x)\) の係数は \(\bs{M}\) の元である。
\(\sg_i\) は群だから単位元を含む。従って、
\(f(\theta)=\displaystyle\prod_{i=1}^{|H|}(\theta-\sg_i(\theta))=0\)
となり、\(\bs{\theta}\) は \(\bs{\bs{M}}\) 上の \(\bs{|H|}\) 次方程式 \(\bs{f(x)=0}\) の解の一つである。ゆえに \(\bs{M}\) から単拡大体 \(\bs{K}=\bs{M}(\theta)\) への拡大次数は、\(f(x)\) が \(\bs{M}\) 上の既約多項式なら単拡大体の基底の定理(33F)により \(|H|\) であり、一般には \(|H|\) 以下である。つまり、
\([\:\bs{K}\::\:\bs{M}\:]\leq|H|\)
である。次数と位数の同一性(52B)によると、拡大次数 \([\:\bs{K}\::\:\bs{M}\:]\) は、ガロア群 \(\mr{Gal}(\bs{K}/\bs{M})\) の位数に等しい。従って、
\(|\mr{Gal}(\bs{K}/\bs{M})|\leq|H|\)
\(|G(\bs{M})|=|H|\)
であり、\(G(\bs{M})\:\subset\:H\) と合わせると、
\(G(\bs{M})=H\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
である。[証明終]
証明の中に対称式という言葉が出てきます。対称式とは、
変数の任意の入れ替えで不変な多項式
です。2変数 \(x,\:y\) だと、
\(x+y,\:xy\)(ここまでが基本対称式)、\(x^2+y^2,\:\:(x-y)^2\)
などです。3変数 \(x,\:y\:,z\) だと、
\(x+y+z,\:xy+yz+zx,\:xyz\)(基本対称式)、\(((x-y)(y-z)(z-x))^2\)
などです。
対称式でよく出てくるのは、方程式の根と係数の関係です。たとえば、\(\bs{Q}\) 上の既約な3次多項式を \(f(x)\) をとし、\(f(x)=0\) の解を \(\al,\beta,\gamma\) とします。
\(\begin{eqnarray}
&&\:\:f(x)&=x^3-ax^2+bx-c\\
&&&=(x-\al)(x-\beta)(x-\gamma)\\
\end{eqnarray}\)
と書くと、
\(a=\al+\beta+\gamma\)
\(b=\al\beta+\beta\gamma+\gamma\al\)
\(c=\al\beta\gamma\)
と、係数が解の基本対称式で表現されます。
また ガロア群 \(\mr{Gal}(\bs{Q}(\al,\beta,\gamma)/\bs{Q})\) の任意の元 を \(\sg\) とします。\(\al,\beta,\gamma\) の任意の対称式を \(S(\al,\beta,\gamma)\in\bs{Q}(\al,\beta,\gamma)\) とすると、
\(\sg(S(\al,\beta,\gamma))=S(\al,\beta,\gamma)\)
です。ガロア群の元は自己同型写像であり、方程式の解を解の一つに置き換えるので、これが成り立ちます。自己同型写像を作用させて不変なのは有理数です(51A)。従って、\(S(\al,\beta,\gamma)\) は有理数です。もちろん \(f(x)\) が \(n\)次多項式であっても成り立ちます。
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列で \(\bs{F}\subset\bs{K}\) がガロア拡大のとき、\(\bs{M}\subset\bs{K}\) は自動的にガロア拡大ですが(52C)、ある条件があれば \(\bs{F}\subset\bs{M}\) もガロア拡大になって、\(\bs{F}\subset\bs{M}\subset\bs{K}\) が「ガロア拡大の連鎖」になります。その条件は「ガロア対応」と「正規部分群」の概念を用いて示されます。それが次の正規性定理です。次では \(\bs{Q}\) から始まる体の拡大列で記述しています。
正規性定理
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とし、\(\mr{Gal}(\bs{K}/\bs{Q})=G\) とする。\(\bs{K}\) の中間体 \(\bs{M}\) と \(G\) の部分群 \(H\) がガロア対応になっているとする。このとき
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) の任意の元を \(g\) とし、\(\bs{M}\) の任意の元を \(m\) とする。
\(\bs{M}\) が \(\bs{Q}\) のガロア拡大なので、\(m\) の共役な元は \(\bs{M}\) に含まれる。\(g\) は同型写像だから、\(\bs{K}\) の元を共役な元に移す(51D)。つまり、\(g\) を \(m\) に作用させると \(m\) と共役な元に移すことになり、 \(g(m)\in\bs{M}\) である。また \(g^{-1}\) も \(G\) の元だから \(g^{-1}(m)\in\bs{M}\) である。
\(H\) の任意の元を \(h\) とする。\(H\) は \(\bs{M}\) とガロア対応をしているから、\(h\) は \(\bs{M}\) の元を不動にする。ゆえに、
\(hg^{-1}(m)=g^{-1}(m)\)
である。従って、
\(ghg^{-1}(m)=gg^{-1}(m)=m\)
となり、\(ghg^{-1}\) は \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(gHg^{-1}\:\subset\:H\)
また、\(g(m)\) も \(\bs{M}\) の元なので、
\(hg(m)=g(m)\)
である。従って、
\(g^{-1}hg(m)=g^{-1}g(m)=m\)
となり、\(g^{-1}hg\) も \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(g^{-1}Hg\:\subset\:H\)
\(gH=Hg\)
となって、左剰余類と右剰余類が一致するから、\(H\) は \(G\) の正規部分群である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{M}\) の任意の元を \(m\) とする。同型写像の延長の定理(51H)により、\(\bs{M}\) の同型写像 \(s\) は \(\bs{K}\) の同型写像 \(g\) に延長できる。つまり、\(g\) を \(\bs{M}\) の元に限定して作用させたとき \(g(m)=s(m)\) となる \(g\) がある。
\(H\) の任意の元を \(h\) とすると、\(h\) は正規部分群の元なので、
\(g^{-1}hg\:\in\:H\)
である。従って、
\(g^{-1}hg(m)=m\)
\(hg(m)=g(m)\)
となり、\(g(m)\) は \(H\) の任意の元で不動である。
ガロア対応の原理により \(\bs{K}(H)=\bs{M}\) なので、
\(g(m)\:\in\:\bs{M}\)
となり、\(g(m)\) は \(H\) の固定体 \(\bs{M}\) の元である。
\(\bs{M}\)の元に \(g\) を作用させるときは \(g(m)\) は \(s(m)\) そのものなので、
\(s(m)\:\in\:\bs{M}\)
となる。
以上により、\(\bs{M}\) の同型写像による \(m\) の移り先(= \(m\) と共役な元)は \(\bs{M}\) に含まれることになり、\(\bs{M}/\bs{Q}\) はガロア拡大である。[証明終]
[\(\bs{\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H}\) の証明]
同型写像の延長の定理(51H)の証明で示したように、\(\bs{M}\) の同型写像 \(s\) を \(\bs{K}\) の同型写像に延長する可能性は複数ある。\(g_1\) と \(g_2\) を \(s\) の2つの延長とし、\(\bs{M}\)の元を \(m\) とする。\(g_1,\:g_2\) は、\(\bs{M}\) に限定して適用すると \(s\) に等しいから、
\(g_1(m)=s(m)\)
\(g_2(m)=s(m)\)
が成り立つ。
\(g_1^{-1}g_2\) を \(m\) に作用させると
\(\begin{eqnarray}
&&\:\:g_1^{-1}g_2(m)&=g_1^{-1}(s(m))\\
&&&=g_1^{-1}(g_1(m))=m\\
\end{eqnarray}\)
となり、\(g_1^{-1}g_2\) は \(\bs{M}\) の元を不動にする。よって、
\(g_1^{-1}g_2\in\:H\)
\(g_2\in\:g_1H\)
である。
つまり、\(g_2\) は \(H\) の剰余類の一つの集合 \(g_1H\) に入る。以上で、\(\bs{M}\) の同型写像 \(s\) は、同型写像の延長を通して 剰余類 \(G/H\) の一つを定めることが分かる。
逆に \(g_1\) と \(g_2\) が 剰余類 \(G/H\) の同じ集合に属すると、
\(g_2\in\:g_1H\)
\(g_1^{-1}g_2\in\:H\)
\(g_1^{-1}g_2(m)=m\)
\(g_2(m)=g_1(m)\)
となり、\(g_1\) と \(g_2\) は \(\bs{M}\) 上で全く同じ作用をする。従って、\(\bs{M}\) 上で \(g_1,\:g_2\) と同じ作用をする \(\mr{Gal}(\bs{M}/\bs{Q})\) の元 \(s\) を定められる。つまり、剰余類 \(G/H\) の一つの集合が \(\mr{Gal}(\bs{M}/\bs{Q})\) の元を一つ定める。
従って、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
である。[証明終]
| 3.多項式と体(続き) |
3.3 線形空間
ガロア理論の一つの柱は、代数拡大体を線形空間(ベクトル空間)としてとらえることで、線形空間の「次元」や「基底」を使って理論が組み立てられています。線形空間には精緻な理論体系がありますが、ここではガロア理論に必要な事項の説明をします。
線形空間の定義
| (線形空間の定義:33A) |
集合 \(V\) と 体 \(\bs{K}\) が次を満たすとき、\(V\) を \(\bs{\bs{K}}\) 上の線形空間(=ベクトル空間。linear space / vector space)と言う。
加算の定義
\(V\) の任意の元 \(\br{u},\:\br{v}\) に対して \((\br{u}+\br{v})\in V\) が定義されていて、この加算(\(+)\) の定義に関して \(V\) は可換群である。すなわち、
\((1)\) 単位元の存在
\(\br{u}+\br{x}=\br{x}\) となる \(\br{x}\) が存在する。これを \(0\) と書く。
\((2)\) 逆元の存在
\(\br{u}+\br{x}=0\) となる \(\br{x}\) が存在する。これを \(-\br{u}\) と書く。
\((3)\) 結合則が成り立つ
任意の元 \(\br{u},\:\br{v}\:,\br{w}\) について、\((\br{u}+\br{v})+\br{w}=\br{u}+(\br{v}+\br{w})\)
\((4)\) 交換則が成り立つ
\(\br{u}+\br{v}=\br{v}+\br{u}\)
スカラー倍の定義
\(V\) の任意の元 \(\br{u}\) と \(\bs{K}\) の任意の元 \(k\) に対して、スカラー倍 \(k\br{u}\in V\) が定義されていて、加算との間に次の性質がある。\(\br{u},\:\br{v}\) を \(V\) の元、\(k,\:m\) を \(\bs{K}\) の元とし、\(\bs{K}\) の乗法の単位元を \(1\) とする。
\((1)\:\:k(m\br{u})=(km)\br{u}\)
\((2)\:\:(k+m)\br{u}=k\br{u}+m\br{u}\)
\((3)\:\:k(\br{u}+\br{v})=k\br{u}+k\br{v}\)
\((4)\:\:1\br{v}=\br{v}\)
高校数学に出てくる "2次元ベクトル" とは、上記の定義の \(\bs{K}\) を \(\bs{R}\)(実数の体)とし、\(V\) を2つの実数のペアの集合 \(\{\:(x,y)\:|\:x,y\in\bs{R}\:\}\) とするベクトル空間(の要素)のことです。
上の定義の \(0\) は線形空間 \(V\) の元です。以下、\(V\) の単位元 \(0\)(= \(0\) ベクトル)と、体 \(\bs{K}\) の加法の単位元 \(0\) が混在しますが、文脈や式から明らかなので、同じ \(0\) で記述します。
1次独立と1次従属
| (1次独立と1次従属:33B) |
1次独立
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) が、\(a_1=a_2=\cd=a_n=0\) しかないとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次独立であるという。
1次従属
1次独立でないときが1次従属である。つまり、線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n=0\)
を満たす、少なくとも一つは \(0\) でない \(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) があるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) は1次従属であるという。
基底
| (基底の定義:33C) |
線形空間 \(V\) の元の組、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) に対して、次の2つが満たされるとき、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) を基底という。
| \({\br{v}_1,\br{v}_2,\cd,\br{v}_n}\) は1次独立である。 | |
| \(V\) の任意の元 \(\br{v}\) は、\(\bs{K}\) の元 \(a_1,a_2,\cd,a_n\) を選んで、
\(\br{v}=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_n\br{v}_n\)
と表せる。 |
基底から1つの元を除外したものは基底ではなくなる。また基底に1つの元を加えたものも基底ではない。
\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が基底だと、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) は基底ではありません。なぜなら、もし \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_{n-1}\}\) が基底だとすると、
\(\br{v}_n=a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}\)
と表せますが、これは、
\(a_1\br{v}_1+a_2\br{v}_2+\)..\(+a_{n-1}\br{v}_{n-1}-\br{v}_n=0\)
ということであり、\(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) が1次従属となってしまって、基底の要件を満たさなくなるからです。基底に、別の1つの元を加えるケースも同じことです。
| (基底の数の不変性:33D) |
\(\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) である。
[証明]
この定理の証明のために、まず次の補題を証明する。
[補題]
線形空間 \(V\) の任意の \(n\) 個の元を \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) とする(基底でなくてもよい)。線形空間 \(V\) の \(n+1\) 個の元 \(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) がすべて \(\{\br{u}_1,\br{u}_2,\cd,\br{u}_n\}\) の1次結合で表されるなら、\(\{\br{w}_1,\br{w}_2,\cd,\br{w}_n,\br{w}_{n+1}\}\) は1次従属である。
数学的帰納法を使う。まず、\(n=1\) のとき、この定理は成り立つ。つまり、
\(\br{w}_1=k_1\br{u}_1\)
\(\br{w}_2=k_2\br{u}_1\)
と表されるなら、
\(k_2\br{w}_1-k_1\br{w}_2=0\)
であり、\(\br{w}_1\) と \(\br{w}_2\) は1次従属である。そこで、\(n\) が \(k\:\:(\geq1)\) のときに成り立つとし、\(n=k+1\) でも成り立つことを証明する。
以降、表記を見やすくするため、\(k=3\) の場合で記述する。ただし、一般性を失うことがないように記述する。\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) が、
\(\br{w}_1=a_{11}\br{u}_1+a_{12}\br{u}_2+a_{13}\br{u}_3\)
\(\br{w}_2=a_{21}\br{u}_1+a_{22}\br{u}_2+a_{23}\br{u}_3\)
\(\br{w}_3=a_{31}\br{u}_1+a_{32}\br{u}_2+a_{33}\br{u}_3\)
\(\br{w}_4=a_{41}\br{u}_1+a_{42}\br{u}_2+a_{43}\br{u}_3\)
と表せたとする。ここで \(\br{w}_4\) の係数に注目する。もし、
\(a_{41}=a_{42}=a_{43}=0\)
であれば、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属である。なぜなら、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3+b_4\br{w}_4=0\)
の式を満たす \(b_1,b_2,b_3,b_4\) は、
\(b_1=b_2=b_3=0\)
\(b_4\neq0\)
として実現でき、\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\) は1次従属の定義を満たすからである。そこで、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つあるとする。それを \(a_{43}\) とし、
\(a_{43}\neq0\)
とする。この仮定で一般性を失うことはない。ここで、
\(\br{x}_i=\br{w}_i-\dfrac{a_{i3}}{a_{43}}\br{w}_4\:\:(i=1,2,3)\)
とおいて \(\br{u}_3\) の項を消去する。計算すると、
\(\begin{eqnarray}
&&\:\:\br{x}_1=&\left(a_{11}-\dfrac{a_{13}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{12}-\dfrac{a_{13}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_2=&\left(a_{21}-\dfrac{a_{23}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{22}-\dfrac{a_{23}a_{42}}{a_{43}}\right)\br{u}_2\\
&&\:\:\br{x}_3=&\left(a_{31}-\dfrac{a_{33}a_{41}}{a_{43}}\right)\br{u}_1+\left(a_{32}-\dfrac{a_{33}a_{42}}{a_{43}}\right)\br{u}_2\\
\end{eqnarray}\)
となる。そうすると、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は「線形空間 \(V\) の2つの元 \(\br{u}_1,\br{u}_2\) の1次結合で表された3つの元」である。従って、帰納法の仮定により、\(\br{x}_1,\:\br{x}_2,\:\br{x}_3\) は1次従属である。1次従属だから、
\(b_1\br{x}_1+b_2\br{x}_2+b_3\br{x}_3=0\)
となる少なくとも一つは \(0\) ではない \(b_1,\:b_2,\:b_3\) がある。 \((\br{A})\)
\(\br{x}_1=\br{w}_1-\dfrac{a_{13}}{a_{43}}\br{w}_4\)
\(\br{x}_2=\br{w}_2-\dfrac{a_{23}}{a_{43}}\br{w}_4\)
\(\br{x}_3=\br{w}_3-\dfrac{a_{33}}{a_{43}}\br{w}_4\)
だったから、これを \((\br{A})\) 式に代入すると、
\(b_1\br{w}_1+b_2\br{w}_2+b_3\br{w}_3-\)
\(\dfrac{1}{a_{43}}(b_1a_{13}+b_2a_{23}+b_3a_{33})\br{w}_4=0\)
となる。この式における \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) の係数の少なくとも一つは \(0\) ではない。従って、\(a_{41},a_{42},a_{43}\) のうち \(0\) でないものが少なくとも一つある場合にも \(\br{w}_1,\:\br{w}_2,\:\br{w}_3,\:\br{w}_4\) は1次従属である。
以上で、線形空間 \(V\) の \(k=3\) 個の元(\(\br{u}_1,\br{u}_2,\br{u}_3\))の1次結合で、\(k+1=4\) 個の元(\(\br{w}_1,\br{w}_2,\br{w}_3,\br{w}_4\))のすべてが表されば、その4個の元は1次従属であることが証明できた。\(k=3\) としたのは表記を見やすくするためであり、\(k=3\) であることの特殊性は使っていない。つまり、\(k\geq1\) のすべてで成り立つ。従って数学的帰納法により補題が正しいことが証明できた。[補題の証明終]
以上を踏まえて、\(A=\{\br{u}_1,\br{u}_2,\cd,\br{u}_m\}\) と \(B=\{\br{v}_1,\br{v}_2,\cd,\br{v}_n\}\) がともに線形空間 \(V\) の基底であるとき、\(m=n\) となることを証明する。
もし仮に \(m < n\) だとすると、\(B\) の中から \((m+1)\) 個の元を選べる。それを \(B\:'=\{\br{v}_1,\br{v}_2,\cd,\br{v}_{m+1}\}\) とすると、\(A\) は 線形空間 \(V\) の基底だから、\(B\:'\) の元は \(A\) の元の1次結合で表現できる。つまり \(B\:'\) の \((m+1)\)個の元のすべては \(m\)個の元の1次結合で表されるから、[補題]によって \(B\:'\) は1次従属である。\(B\) は \(B\:'\) と同じものか、または \(B\:'\) に数個の元を付け加えたものだから、\(B\:'\) が1次従属なら \(B\) も1次従属である。しかし、\(B\) は線形空間 \(V\) の基底だから1次独立であり、矛盾が生じる。従って、\(m\geq n\) である。
もし仮に \(m > n\) だとしても、全く同様の考察により矛盾が生じる。従って、\(m\leq n\) である。この結果、\(m=n\) であることが証明できた。[証明終]
この基底の数の不変性の定理(33D)により、線形空間には次のように「次元」が定義できることになります。
次元
| (次元の不変性:33E) |
線形空間の基底に含まれる元の数が有限個のとき、その個数を線形空間の次元と言う。次元は基底の取り方によらない。
線形空間の次元や基底と、代数拡大体を結びつけるのが次の定理です。
単拡大体の基底
| (単拡大体の基底:33F) |
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。単拡大体である \(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間であり、\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) は \(\bs{Q}(\al)\) の基底である。
[証明]
\(\bs{Q}(\al)\) の基底であるための条件は、
| \(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立である | |
| \(\bs{Q}(\al)\) の任意の元が \(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) の1次結合で表される |
の2つである。② は単拡大の体の定理(32C)で証明されているので、① を証明する。多項式 \(g(x)\) を、
\(g(x)=a_0+a_1x+a_2x^2+\cd+a_{n-1}x^{n-1}\)
とおく。\(\{1,\:\al,\:\al^2,\:\cd\:,\al^{n-1}\}\) が1次独立であることを言うには、
\(g(\al)=0\) であれば \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\)
を言えばよい。以降、背理法を使って証明する。\(g(\al)=0\) で、\(a_i\:\:(0\leq i\leq n-1)\) のうち、少なくとも1つはゼロでないと仮定する。
\(g(x)\) が定数(つまり \(a_0\) の項のみ)のときは、\(g(\al)=0\) なら \(a_0=0\) なので、「少なくとも1つはゼロでない」に反する。そこで \(g(x)\) は1次以上の多項式であるとする。
そうすると、2つの方程式 \(f(x)=0\) と \(g(x)=0\) は共通の解 \(\al\) をもつことになる。しかし、\(f(x)\) は \(n\)次の既約多項式であり、\(g(x)\) は1次以上で \(n\)次未満の多項式である。既約多項式の定理2(31F)により、このような2つの方程式は共通の解を持たない。ゆえに矛盾が生じる。従って、\(g(\al)=0\) のとき \(a_i\:\:(0\leq i\leq n-1)\) は全て \(0\) であり、① が証明された。
基底の数が線形空間の次元であり、\(\bs{Q}(\al)\) は \(\bs{Q}\) 上の \(n\)次元線形空間である。[証明終]
もし、\(f(x)\) が\(n\)次多項式だとしたら(既約多項式を含む)、\(\bs{Q}(\al)\) の次元は \(n\)以下になります。\(f(x)=0\) の解の一つ、\(\al\) の最小多項式(31H)を \(m\)次多項式である \(g(x)\) とすると、\(g(x)\) は既約多項式であり(31I)、\(\al\) は \(f(x)=0\) と \(g(x)=0\) の共通の解なので、既約多項式の定理1(31E)により \(f(x)\) は \(g(x)\) で割り切れます。つまり、
\(f(x)=h(x)g(x)\)
と書けるので、
\(\mr{deg}\:f(x)\:\geq\:\mr{deg}\:g(x)\)
\(n\:\geq\:m\)
ですが、単拡大体の基底の定理(33F)により \(\bs{Q}(\al)\) の次元は \(m\) なので、\(n\)以下です。
拡大次数とその連鎖律
方程式の解になる数が代数的数で、\(\bs{Q}\) に代数的数を添加した体が代数拡大体です。「3.2 体」の「単拡大の体」でとりあげた \(\bs{Q}(\al)\) は代数拡大体であり、次元は \(n\) でした(32C)。この次元を「体の拡大」の視点で考えてみます。
「体 \(\bs{K}\) 上の線形空間 \(V\)」の定義において、\(\bs{K}=\bs{Q}\) とし \(V=\bs{Q}\) とすると、「有理数体 \(\bs{Q}\) は、\(\bs{Q}\) 上の線形空間」であると言えます。\(\bs{Q}\) では加算もスカラー倍(=乗算)も定義されていて、可換だからです。線形空間の定義にある各種の演算は、体の演算の一部です。
線形空間 \(\bs{Q}\) の基底は、\(0\) ではない \(\bs{Q}\) の元 \(v\) です。\(0\) を含む \(\bs{Q}\) の任意の元を \(a\) とすると、
\(av=0\:\:\:(v\neq0)\)
が成り立つのは \(a=0\) しかないので \(v\) は1次独立であり、また \(av\) で全ての \(\bs{Q}\) の元が表されるからです。一方、\(0\) は、
\(a\cdot0=0\)
が \(0\) ではない \(a\) について成り立つので1次従属です。以上から、線形空間 \(\bs{Q}\) の基底として \(1\) を選ぶことにします。次元は \(1\) です。
\(\bs{Q}\) に \(\sqrt{2}\) を添加した \(\bs{Q}(\sqrt{2})\) は \(\bs{Q}\) の代数拡大体で、\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\) です。\(\bs{Q}(\sqrt{2})\) は \(\bs{\bs{Q}}\) 上の線形空間です。\(\bs{Q}(\sqrt{2})\) の基底としては、まず \(1\) を選ぶことができます。\(1\) を \(\bs{Q}\) の元でスカラー倍すると、\(\bs{Q}(\sqrt{2})\) の部分集合である \(\bs{Q}\) の元の全てが表せます。
\(\bs{Q}(\sqrt{2})\) の元の全てを表現するためには、さらに基底に \(\sqrt{2}\) を追加します。\(\sqrt{2}\) は \(\bs{Q}\) の元の1次結合では表せないので、\(1\) と \(\sqrt{2}\) は 1次独立です。\(1,\:\sqrt{2}\) が \(\bs{Q}(\sqrt{2})\) の基底で、次元は \(2\) です。
さらに \(\bs{Q}(\sqrt{2})\) に \(\sqrt{3}\) を添加した代数拡大体 \(\bs{Q}(\sqrt{2},\sqrt{3})\) を考えてみると、\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間であり、基底は \(1,\:\sqrt{3}\) です。\(1\) と \(\sqrt{3}\) は 1次独立であり、\(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の全ての元は、\(\bs{\bs{Q}(\sqrt{2})}\) の元を係数とする \(\bs{1}\) と \(\bs{\sqrt{3}}\) の1次結合で表現できるからです。\(\bs{\bs{Q}(\sqrt{2})}\) 上の線形空間 \(\bs{\bs{Q}(\sqrt{2},\sqrt{3})}\) の次元は \(\bs{2}\) です。
ここで \(\bs{Q}(\sqrt{2},\sqrt{3})\) を \(\bs{\bs{Q}}\) 上の線形空間と考えると、その基底はまず、\(1,\:\sqrt{2},\:\sqrt{3}\) ですが、これだけでは不足で、\(\sqrt{6}\) を加える必要があります。\(\sqrt{6}\) は体としての演算(乗算)でできる数ですが、\(1,\:\sqrt{2},\:\sqrt{3}\) の1次結合では表現できないからです。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は \(1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\) であり、次元は \(4\) です。
ここまでの基底の表現はあくまで一例ですが、どういう基底を選ぼうと基底の数=次元は不変量であるというのが「次元の不変性」でした。以上の考察を踏まえて、拡大次数を定義し、拡大次数の連鎖律を証明します。
| (拡大次数の定義:33G) |
代数拡大体 \(\bs{F},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{K}\) であるとき、\(\bs{K}\) は \(\bs{F}\) 上の線形空間である。\(\bs{K}\) の次元を、\(\bs{K}\)の(\(\bs{F}\)からの)拡大次数といい、
\([\:\bs{K}\::\:\bs{F}\:]\)
で表す。
| (拡大次数の連鎖律:33H) |
代数拡大体 \(\bs{F},\:\bs{M},\:\bs{K}\) が \(\bs{F}\:\subset\:\bs{M}\:\subset\:\bs{K}\) であるとき、
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
が成り立つ。
[証明]
\([\:\bs{M}\::\:\bs{F}\:]=m\)、\([\:\bs{K}\::\:\bs{M}\:]=n\) とする。以下、表記を見やすくするため、\(m=3,\:n=2\) の場合で記述する。もちろん一般性を失わないように記述する。
\(\bs{F}\) 上の線形空間 \(\bs{M}\) の基底を
\(u_1,\:u_2,\:u_3\)
とすると、\(\bs{M}\) の任意の元 \(b\) は、
\(b=a_1u_1+a_2u_2+a_3u_3\:\:(a_i\in\bs{F},\:u_i\in\bs{M},\:1\leq i\leq m)\)
と表せる。
\(\bs{M}\) 上の線形空間 \(\bs{K}\) の基底を
\(v_1,\:v_2\)
とすると、\(\bs{K}\) の任意の元 \(x\) は、
\(x=b_1v_1+b_2v_2\:\:(b_j\in\bs{M},\:v_j\in\bs{K},\:1\leq j\leq n)\)
と表せる。\(b_1,\:b_2\) を \(\bs{M}\) の基底 \(u_1,u_2,u_3\) で表すと、
\(b_1=a_{11}u_1+a_{21}u_2+a_{31}u_3\)
\(b_2=a_{12}u_1+a_{22}u_2+a_{32}u_3\)
\((\:a_{ij}\in\bs{F}\:)\)
となるが、これを用いて \(x\) を表すと、
\(\begin{eqnarray}
&&\:\:x=&a_{11}u_1v_1+a_{21}u_2v_1+a_{31}u_3v_1+\\
&&&a_{12}u_1v_2+a_{22}u_2v_2+a_{32}u_3v_2\\
\end{eqnarray}\)
となる。つまり、\(\bs{K}\) の任意の元は \(\bs{F}\) の元を係数とする、\(u_1v_1\)、\(u_2v_1\)、\(u_3v_1\)、\(u_1v_2\)、\(u_2v_2\)、\(u_3v_2\) の1次結合で表現できる。
ここで \(x=0\) とすると、
\((a_{11}u_1+a_{21}u_2+a_{31}u_3)v_1+\)
\((a_{12}u_1+a_{22}u_2+a_{32}u_3)v_2=0\)
であるが、\(v_1,v_2\) は \(\bs{K}\) の基底なので1次独立であり、従って、
\(a_{11}u_1+a_{21}u_2+a_{31}u_3=0\)
\(a_{12}u_1+a_{22}u_2+a_{32}u_3=0\)
である。すると、\(u_1,u_2,u_3\) は \(\bs{M}\) の基底なので1次独立であり、
\(a_{11}=a_{21}=a_{31}=a_{12}=a_{22}=a_{32}=0\)
である。従って、\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) は1次独立である。
\(u_iv_j\:\:(1\leq i\leq m,\:1\leq j\leq n)\) の \(mn\) 個の元は、
| 1次独立 | |
| \(\bs{F}\) の元を係数とする1次結合で \(\bs{K}\) の元のすべてを表せる |
\([\:\bs{K}\::\:\bs{F}\:]=[\:\bs{K}\::\:\bs{M}\:][\:\bs{M}\::\:\bs{F}\:]\)
である。[証明終]
体の一致
2つの代数拡大体 \(\bs{F}\) と \(\bs{K}\) の次元が一致するとします。たとえば \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) の次元はいずれも \(2\) です。もちろん \(\bs{Q}(\sqrt{2})\) と \(\bs{Q}(\sqrt{3})\) は体として別物です。
それでは、\(\bs{F}\subset\bs{K}\) という関係があり、かつ \(\bs{F}\) と \(\bs{K}\) の次元が一致するとき、\(\bs{F}\) と \(\bs{K}\) は体として一致すると言えるのでしょうか。
これはイエスで、それを次に証明します。この定理は、ガロア理論の証明の過程において、2つの体が実は同じものであることを言うときに使われる論法です。証明の都合上、\(\bs{F}\) ではなく \(\bs{K}_0\) と書きます。
| (体の一致:33I) |
体 \(\bs{K}_0\) と 体 \(\bs{K}\) があり、\(\bs{K}_0\:\subset\:\bs{K}\) を満たしている。\(\bs{K}_0\) と \(\bs{K}\) が有限次元であり、その次元が同じであれば、\(\bs{K}_0=\bs{K}\) である。
[証明]
体 \(\bs{K}_0\) と \(\bs{K}\) を、\(\bs{Q}\) 上の線形空間と見なし、その次元を \(n\) とする。\(\bs{K}_0\) の基底を \(\{a_1,\:a_2,\:\cd\:,a_n\}\) とする。\(\bs{K}_0\) が \(\bs{K}\) の真部分集合である、つまり \(\bs{K}_0\:\subsetneq\:\bs{K}\) と仮定して、背理法で証明する。
\(\bs{K}_0\:\subsetneq\:\bs{K}\) だと、\(a_{n+1}\notin\bs{K}_0,\:a_{n+1}\in\bs{K}\) である元 \(a_{n+1}\) が存在する。この \(a_{n+1}\) は \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合では表せない。なぜなら、もし表せたとしたら、\(\bs{K}_0\) の全ての元は基底である \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されるので \(a_{n+1}\in\bs{K}_0\) になってしまうからである。
そこで、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) を考えると、この元の並びは1次独立である。なぜなら、もし1次従属だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n+a_{n+1}x_{n+1}=0\)
となる \(x_i\in\bs{Q}\:\:(1\leq i\leq n+1)\) があって、そのうち少なくとも一つは \(0\) ではない。もし \(x_{n+1}\neq0\) だとすると、\(a_{n+1}\) が \(\{a_1,\:a_2,\:\cd\:,a_n\}\) の1次結合で表されることになり、\(a_{n+1}\in\bs{K}_0\) となって矛盾が生じる。また \(x_{n+1}=0\) だとすると、
\(a_1x_1+a_2x_2+\cd+a_nx_n=0\)
であるが、この場合は \(x_i\:\:(1\leq i\leq n)\) の中に少なくとも一つは \(0\) でないものがあることになり、\(\{a_1,\:a_2,\:\cd\:,a_n\}\) が基底である(=1次独立である)ことに矛盾する。従って \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は1次独立である。
\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表される全ての元の集合を \(\bs{K}_1\) とする。\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) はすべて \(\bs{K}\) の元であるから、\(\bs{K}_1\:\subset\:\bs{K}\) である。また \(\bs{K}_1\) の任意の元は1次独立である \(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) の1次結合で表されるから、\(\{a_1,\:a_2,\:\cd\:,a_n,\:a_{n+1}\}\) は \(\bs{K}_1\) の基底であり、すなわち \(\bs{K}_1\) の次元は \(n+1\) である。\(\bs{K}_1=\bs{K}\) なら \(\bs{K}\) の次元が \(n+1\) になって矛盾するから、\(\bs{K}_1\neq\bs{K}\) つまり \(\bs{K}_1\:\subsetneq\:\bs{K}\) である。
以上の論理を繰り返すと \(\bs{K}_2\:\subsetneq\:\bs{K}\) である \(n+2\) 次元の \(\bs{K}_2\) の存在を示せるが、この操作は無限に繰り返えせるから、\(\bs{K}\) は無限個の基底をもつ無限次元の体となる。これは \(\bs{K}\) の次元が有限次元の \(n\) であることに矛盾する。従って背理法の仮定は誤りであり、\(\bs{K}_0\:=\:\bs{K}\) である。[証明終]
代数拡大体の構造
多項式と代数拡大体の相互関係をまとめると次のようになります。
| 体 \(\bs{Q}\) 上の\(\bs{n}\)次多項式 \(f(x)\) が(複素数の範囲で) \(f(x)=(x-\al_1)(x-\al_2)\cd(x-\al_n)\) と因数分解できるとき、 \(\bs{Q}(\al_1,\:\:\al_2,\:\:\cd\:\:,\:\:\al_n)\) を \(f(x)\) の最小分解体と言う(32A)。つまり、\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解のすべてを \(\bs{Q}\) に添加した体が最小分解体である。 | |
| すべての代数拡大体は単拡大体である(32B)。従って最小分解体も単拡大体である。つまり原始元 \(\theta\) があって、\(\bs{Q}(\theta)\) と表せる。 | |
| \(\theta\) の最小多項式を \(\bs{m}\)次多項式の \(g(x)\) とすると、\(g(x)\) は既約多項式である(31I)。 | |
| 方程式 \(g(x)=0\) の解の一つが \(\theta\) であるから、 \(1,\:\:\theta,\:\:\theta^2,\:\:\cd,\:\:\theta^{m-1}\) の \(m\)個の元は \(\bs{Q}(\theta)\) の基底である(33F)。つまり \(\bs{Q}(\theta)\) は \(m\)次元である。従って、\(\bs{Q}(\al_1,\:\al_2,\:\cd\:,\:\al_n)\) も \(m\)次元である。 |
以下、例をいくつかあげます。
\(x^4-5x^2+6\)
\(f(x)\) を4次多項式、
\(f(x)=x^4-5x^2+6\)
とします。\(f(x)\) は、
\(f(x)=(x^2-2)(x^2-3)\)
と因数分解できるので既約多項式ではありません。また、
\(f(x)=(x-\sqrt{2})(x+\sqrt{2})(x-\sqrt{3})(x+\sqrt{3})\)
なので、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt{2},\sqrt{3})\)
です。\(\bs{Q}(\sqrt{2},\:\sqrt{3})\) は、\(\bs{Q}\) 上の方程式 \(x^2-2=0\) の解 \(\sqrt{2}\) による拡大体を \(\bs{Q}(\sqrt{2})\) とし、\(\bs{Q}(\sqrt{2})\) 上の方程式 \(x^2-3=0\) の解 \(\sqrt{3}\) による拡大体が \(\bs{Q}(\sqrt{2},\:\sqrt{3})\) であると見なせます。つまり、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt{2})\:\subset\:\bs{Q}(\sqrt{2},\sqrt{3})\)
です。拡大次数は
\([\:\bs{Q}(\sqrt{2}):\bs{Q}\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}(\sqrt{2})\:]=2\)
\([\:\bs{Q}(\sqrt{2},\sqrt{3}):\bs{Q}\:]=4\)
です。\(\bs{Q}\) 上の線形空間 \(\bs{Q}(\sqrt{2},\sqrt{3})\) の基底は、
\(\begin{eqnarray}
&&\:\:B_1&=(\:1,\:\sqrt{2},\:1\cdot\sqrt{3},\:\sqrt{2}\cdot\sqrt{3}\:)\\
&&&=(\:1,\:\sqrt{2},\:\sqrt{3},\:\sqrt{6}\:)\\
\end{eqnarray}\)
とすることができます。
一方、
\(\theta=\sqrt{2}+\sqrt{3}\)
とおくと、
\(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\)
となります。なぜなら、
\(\sqrt{2}=\dfrac{1}{2}(\theta-\dfrac{1}{\theta})\)
\(\sqrt{3}=\dfrac{1}{2}(\theta+\dfrac{1}{\theta})\)
であり、\(\sqrt{2}\) と \(\sqrt{3}\) が \(\theta\) と有理数の加減乗除で表現できるからです。\(\bs{Q}(\sqrt{2},\sqrt{3})\) は \(\bs{Q}(\sqrt{2}+\sqrt{3})\) という単拡大体です。
\(\theta=\sqrt{2}+\sqrt{3}\) から根号を消去すると、
\(\theta^4-10\theta^2+1=0\)
となるので、\(\theta\)の最小多項式は、
\(g(x)=x^4-10x^2+1\)
であり、この \(g(x)\) は既約多項式です。\(y=x^2-5\) とおくと、
\(\begin{eqnarray}
&&\:\:g(x)&=y^2-24\\
&&&=(y-2\sqrt{6})(y+2\sqrt{6})\\
\end{eqnarray}\)
なので、
\(\begin{eqnarray}
&&\:\:g(x)&=&(x^2-5-2\sqrt{6})(x^2-5+2\sqrt{6})\\
&&&=&(x-\sqrt{2}-\sqrt{3})(x+\sqrt{2}-\sqrt{3})\cdot\\
&&&& (x-\sqrt{2}+\sqrt{3})(x+\sqrt{2}+\sqrt{3})\\
\end{eqnarray}\)
となり、\(g(x)=0\) の解は、\(\sqrt{2}+\sqrt{3}\)、\(-\sqrt{2}+\sqrt{3}\)、\(\sqrt{2}-\sqrt{3}\)、\(-\sqrt{2}-\sqrt{3}\) の4つです。その \(g(x)=0\) の解の一つが \(\theta=\sqrt{2}+\sqrt{3}\) なので、単拡大体の基底の定理(33F)を適用して、\(\bs{Q}(\theta)\) の基底を、
\(B_2=(\:1,\:\:\theta,\:\:\theta^2,\:\:\theta^3\:)\)
の4個に選ぶことができます。拡大次数は \([\:\bs{Q}(\theta):\bs{Q}\:]=4\) です。
\(B_1\) と \(B_2\) は、同じ体である \(\bs{Q}(\theta)=\bs{Q}(\sqrt{2},\sqrt{3})\) の基底なので、相互に1次結合で表現できます。\(B_2\) の1次結合で \(B_1\) を表現すると、
\(\sqrt{2}=\dfrac{1}{2}(\phantom{-}\theta^3-9\theta)\)
\(\sqrt{3}=\dfrac{1}{2}(-\theta^3+11\theta)\)
\(\sqrt{6}=\dfrac{1}{2}(\phantom{-}\theta^2-5)\)
となります。
\(x^3-2\)
\(f(x)\) を3次多項式、
\(f(x)=x^3-2\)
とします。これは既約多項式です。
\(x^3-1=0\) 解で \(1\) でないもの一つを \(\omega\) とします(= \(1\) の原始\(3\)乗根)。
\(x^3-1=(x-1)(x^2+x+1)\)
なので \(\omega\) は、
\(\omega^2+\omega+1=0\)
を満たします。この2次方程式の解は2つありますが、
\(\omega=\dfrac{-1+\sqrt{3}\:i}{2}\)
とします。方程式 \(x^3-2=0\) の解は、
\(\sqrt[3]{2},\:\:\sqrt[3]{2}\omega,\:\:\sqrt[3]{2}\omega^2\)
の3つです、従って、\(f(x)\) の最小分解体は、
\(\bs{Q}(\sqrt[3]{2},\:\sqrt[3]{2}\omega,\:\sqrt[3]{2}\omega^2)=\bs{Q}(\sqrt[3]{2},\:\omega)\)
です。これは、
\(\bs{Q}\:\subset\:\bs{Q}(\sqrt[3]{2})\:\subset\:\bs{Q}(\sqrt[3]{2},\:\omega)\)
という構造をしています。基底は、単拡大体の基底の定理(33F)を順次適用して、
\(\bs{Q}(\sqrt[3]{2})\) の基底(\(\bs{Q}\) 上の線形空間)
\(1,\:\sqrt[3]{2},\:(\sqrt[3]{2})^2\)
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}(\sqrt[3]{2})\) 上の線形空間\()\)
\(1,\:\omega\)
です。これらを総合すると、
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の基底(\(\bs{Q}\) 上の線形空間\()\)
| \(1,\) | \(\sqrt[3]{2},\) | \((\sqrt[3]{2})^2,\) | |
| \(\omega,\) | \(\sqrt[3]{2}\omega,\) | \((\sqrt[3]{2})^2\omega\) |
\([\:\bs{Q}(\sqrt[3]{2}):\bs{Q}\:]=3\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}(\sqrt[3]{2})\:]=2\)
\([\:\bs{Q}(\sqrt[3]{2},\:\omega):\bs{Q}\:]=6\)
となります。
\(\bs{Q}(\sqrt[3]{2},\:\omega)\) の原始元 \(\theta\) を、
\(\theta=\sqrt[3]{2}+\omega\)
と選ぶことができます。なぜなら、計算は省きますが、
| \(\sqrt[3]{2}\) | \(=\dfrac{1}{9}(\) | \(2\theta^5+3\theta^4+6\theta^3-6\theta^2+9\theta\) | \(+18)\) | |
| \(\omega\) | \(=\dfrac{1}{9}(-\) | \(2\theta^5-3\theta^4-6\theta^3+6\theta^2\) | \(-18)\) |
\(\theta=\sqrt[3]{2}+\dfrac{-1+\sqrt{3}\:i}{2}\)
の式を2乗や3乗して \(i\) と根号を消去すると、計算過程は省きますが、
\(\theta^6+3\theta^5+6\theta^4+3\theta^3+9\theta+9=0\)
となります。従って、\(\theta\) の最小多項式を \(g(x)\) とすると、
\(g(x)=x^6+3x^5+6x^4+3x^3+9x+9\)
という6次多項式です。\(\bs{Q}(\sqrt[3]{2},\:\omega)\) は 6次方程式 \(g(x)=0\) の根の一つである \(\theta\) を使って、
\(\bs{Q}(\sqrt[3]{2},\:\omega)=\bs{Q}(\theta)\)
という単拡大体(次元は \(6\))と表現できます。
\(x^3-3x+1\)
「1.3 ガロア群」の「ガロア群の例」で書いたように、\(x^3-3x+1=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\(\beta=\al^2-2\)
\(\gamma=\beta^2-2\)
\(\al=\gamma^2-2\)
の関係があり、\(\al,\:\beta,\:\gamma\) のどれか一つの加減乗除で他の2つが表現できます。これにより、\(f(x)=x^3-3x+1\) の最小分解体は、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)=\bs{Q}(\beta)=\bs{Q}(\gamma)\)
です。基底は、たとえば \(1,\:\al,\:\al^2\) であり、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]=3\)
です。\(\al\) の最小多項式は、3次多項式である \(f(x)=x^3-3x+1\) です。
ちなみに、3次多項式の最小分解体の次元が \(3\) になる条件を書いておきます。まず、2次方程式の例ですが、
\(x^2+ax+b=0\)
の方程式の解を \(\al,\:\beta\) とすると、
\(x^2+ax+b=(x-\al)(x-\beta)\)
です。そうすると、根と係数の関係から、
\(a=-(\al+\beta)\)
\(b=\al\beta\)
です。ここで、判別式 \(\bs{D}\) を、
\(D=(\al-\beta)^2\)
と定義すると、
\(\begin{eqnarray}
&&\:\:D=&\al^2-2\al\beta+\beta^2\\
&&&=(\al+\beta)^2-4\al\beta\\
&&&=a^2-4b\\
\end{eqnarray}\)
となります。この判別式を使って解の状況がわかります。つまり、
\(\cdot D\:\geq\:0\) なら2つの実数解(重根は2と数える)
\(\cdot D\:\geq\:0\) で \(\sqrt{D}\) が有理数なら、2つの有理数解
をもちます。\(\cdot D\:\geq\:0\) で \(\sqrt{D}\) が有理数なら、2つの有理数解
以上を3次方程式に拡張できます。2乗の項がない既約な3次方程式を、
\(x^3+ax+b=0\)
とし、3つの根を \(\al,\:\beta,\:\gamma\) とすると、
\(x^3+ax+b=(x-\al)(x-\beta)(x-\gamma)\)
\((\br{A})\)
\(\al+\beta+\gamma=0\)
\(\al\beta+\beta\gamma+\gamma\al=a\) \((\br{B})\)
\(\al\beta\gamma=-b\)
となります。3次方程式の判別式 \(D\) は、
\(D=(\al-\beta)^2(\beta-\gamma)^2(\gamma-\al)^2\)
で定義されます。計算すると、
\(D=-4a^3-27b^2\)
となります。
ここで、\(D\) が、ある有理数 \(q\) の2乗の場合を考えます。つまり、
\(D=q^2\)
です。そうすると、
\(q=(\al-\beta)(\beta-\gamma)(\gamma-\al)\)
です(\(-q\) でも成り立ちますが割愛します)。 \((\br{C})\)
\((\br{A})\) 式の両辺を \(x\) で微分して \(x=\al\) を代入すると、
\(3\al^2+a=(\al-\beta)(\al-\gamma)\)
が得られます。\((\br{C})\) 式と \((\br{D})\) 式の両辺同士を割り算すると、 \((\br{D})\)
\(\dfrac{q}{3\al^2+a}=-(\beta-\gamma)\)
となります。そうすると、\((\br{B})\) 式と \((\br{E})\) 式を用いて、\(\beta\) と \(\gamma\) を \(\al\) の式として表現できます。その結果は、 \((\br{E})\)
\(\beta=\dfrac{2a\al+3b-q}{2(3\al^2+a)}\)
\(\gamma=\dfrac{2a\al+3b+q}{2(3\al^2+a)}\)
です。式の形はともかく、要するに、
\(\beta\) と \(\gamma\) が \(\al\) の加減乗除で表現できる
わけです。このことは、
\(\bs{Q}(\al,\beta,\gamma)=\bs{Q}(\al)\)
であることを意味します。\(\bs{Q}(\al,\beta,\gamma)\) は、既約な3次方程式の根の一つである \(\al\) の単拡大体なので、その次元は \(3\) です。
まとめると、判別式 \(D\) が有理数の2乗であるとき、既約 \(3\)次多項式の最小分解体の次元が \(3\) になります。\(x^3-3x+1\) の場合、\(a=-3,\:b=1\) なので、
\(D=-4a^3-27b^2=81=9^2\)
となり、次元が \(3\) です。
既約多項式ではない3次多項式の拡大次数はもっと小さくなります。たとえば \((x-1)(x^2+2)\) の最小分解体は \(\bs{Q}(\sqrt{2}\:i)\) であり、拡大次数は \(2\) です。また \((x-2)^3\) の最小分解体は \(\bs{Q}\) そのもので、拡大次数は \(1\) です。
まとめると、3次多項式 \(f(x)\) の最小分解体の拡大次数は、\(f(x)=0\) の解を \(\al,\:\beta,\:\gamma\) とすると、
\([\:\bs{Q}(\al,\beta,\gamma):\bs{Q}\:]\:=\:6,\:3,\:2,\:1\)
の4種あることになります(この4種しかないことの理由は後の章にあります)。
| 4.一般の群 |
ガロア理論の核心(第5章以降)に入る前の最後として、群についての各種の定義や定理を説明します。これらはいずれも第5章以降で必要になります。
4.1 部分群\(\cdot\)正規部分群、剰余類\(\cdot\)剰余群
部分集合の演算
以降の証明では集合の演算が多々出てきます。その定義は次の通りでです。これはあくまで群の "部分集合" に関するもので、それが部分群かどうかは別問題です。
| (部分集合の演算:41A) |
群 \(G\) の2つの部分集合を \(H,\:N\) とする。\(H\) と \(N\) の演算結果である \(G\) の部分集合、\(HN\) を次の式で定義する。
\(HN\:=\:\{\:hn\:|\:h\in H,\:n\in N,\:hn\) は群の演算定義による \(\}\)
群 \(G\) の元の演算では結合則が成り立つから、部分集合の演算でも結合則が成り立つ。つまり \(H_1,\:H_2,\:H_3\) をを3つの部分群とすると、
\((H_1H_2)H_3=H_1(H_2H_3)\)
である。部分集合の元は \(1\)つでもよいから、\(x\) が \(G\) の元で \(x\) だけの部分集合を \(\{x\}\) とすると、
\(H_1(\{x\}H_2)=(H_1\{x\})H_2\)
である。これを、
\(H_1(xH_2)=(H_1x)H_2\)
と記述する。
部分群の定理
部分群に関する定理をいくつかあげます。これらはいずれも後の定理の証明の過程で使います。
部分群の十分条件
| (部分群の十分条件:41B) |
群 \(G\) の部分集合を \(N\) とし、\(N\) の任意の2つの元を \(x,\:y\) とする。
\(xy\in N,\:x^{-1}\in N\)
なら、\(N\) は \(G\) の部分群である。
[証明]
\(N\) の元 \(x,\:y\) は \(G\) の元でもあるので、\(xy,\:x^{-1},\:y^{-1}\) は \(G\) の演算として定義されている。
\(y=x^{-1}\) とおくと \(xy=xx^{-1}=e\in N\) なので、\(N\) は単位元を含む。つまり、\(N\) は演算で閉じていて、単位元が存在し、逆元が \(N\) の元である。また結合則は \(G\) の元として成り立っている。従って \(N\) は \(G\) の部分群である。[証明終]
部分群の元の条件
| (部分群の元の条件:41C) |
群 \(G\) の部分群を \(N\) とし、\(G\) の 元を \(x\) とすると、次の2つは同値である。
① \(xN\:=\:N\)
② \(x\:\in\:N\)
[証明]
[① \(\bs{\Rightarrow}\) ②]
\(N\) には \(G\) の単位元 \(e\) が含まれるから、\(xe\) は \(xN\) に含まれる。
\(x=xe\in xN=N\) \(\Rightarrow\) \(x\in N\)
である。
[② \(\bs{\Rightarrow}\) ①]
\(x\in N\) とし、\(N\) の任意の元を \(a\) とすると、\(N\) は群だから \(xa\in\:N\) である。\(N\) の異なる2つの元を \(a,\:b\:\:(a\neq b)\) とすると、\(xa\neq xb\) である。なぜなら、もし \(xa=xb\) だとすると、\(x\) の逆元 \(x^{-1}\) を左からかけて \(a=b\) となり、矛盾するからである。以上により、\(xH\) は \(H\) の全ての元を含むから \(xH=H\) である。[証明終]
部分群の共通部分
| (部分群の共通部分は部分群:41D) |
\(G\) の部分群を \(H,\:N\) とすると、\(H\cap N\) は部分群である。
[証明]
\(G\) の部分群を \(H,\:N\) とし、\(H\cap N\) の任意の2つの元を \(x,\:y\) とすると、\(x,\:y\in H,\:\:x,\:y\in N\) なので、
\(xy\in H,\:x^{-1}\in H\)
\(xy\in N,\:x^{-1}\in N\)
であり、
\(xy\in H\cap N,\:x^{-1}\in H\cap N\)
となって、部分群の十分条件の定理(41B)により \(H\cap N\) は部分群である。[証明終]
剰余類
| (剰余類の定義:41E) |
有限群 \(G\) の位数を \(n\) とし( \(|G|=n\) )、\(H\) を \(G\) の部分群とする。\(H\) に左から \(G\) のすべての元、\(g_1,\:g_2,\:\cd\:,\:g_n\) かけて、集合、
\(g_1H,\:g_2H,\:\cd\:,g_nH\)
を作る。
\(g_1H,\:g_2H,\:\cd\:,g_nH\) から、同じになる集合を集めたものを剰余類と呼ぶ。その同じになる集合から代表的なものを一つ取り出し、
\(xH\:\:(x\in G)\)
の形で剰余類を表す。\(g_1H,\:g_2H,\:\cd\:,g_nH\) から剰余類が \(d\) 個できたとし、それらを、
\(x_1H,\:x_2H,\:\cd\:,x_dH\)
とすると、
\(i\neq j\) のとき \(x_iH\:\cap\:x_jH=\phi\)
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。剰余類は、群 \(G\) の元を部分群 \(H\) によって分類したものといえる。
\(x_1H,\:x_2H,\:\cd\:,x_dH\) を「左剰余類」という。同じことが \(G\) の元を右からかけたときにも成り立ち、\(Hx_1{}^{\prime},\:Hx_2{}^{\prime},\:\cd\:,Hx_d\,'\) を「右剰余類」という。
群 \(G\) の 部分群 \(H\) による剰余類の個数 \(d\) について、\(d\cdot|H|=|G|\) が成り立つ。この \(d\) を「\(G\) の \(H\) による指数」といい、\([\:G\::\:H\:]\) で表す。つまり、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
である(ラグランジュの定理)。
[証明]
\(|G|=[\:G\::\:H\:]\cdot|H|\) であることを証明する。2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとする。その共通な元が、\(x_1H\) では \(x_1h_i\)、\(x_2H\) では \(x_2h_j\) と表されているものとする。
\(x_1h_i=x_2h_j\)
左から \(x_2^{-1}\)、右から \(h_i^{-1}\) をかけると、
\(x_2^{-1}x_1h_ih_i^{-1}=x_2^{-1}x_2h_jh_i^{-1}\)
\(x_2^{-1}x_1=h_jh_i^{-1}\)
\(h_jh_i^{-1}\in H\) だから、
\(x_2^{-1}x_1\in H\)
を得る。部分群の元の条件の定理(41C)により、\(xH=H\) と \(x\in H\) は同値だから、
\(x_2^{-1}x_1H=H\)
となる。左から \(x_2\) をかけると、
\(x_1H=x_2H\)
を得る。これは、「2つの剰余類 \(x_1H\) と \(x_2H\) が共通の元をもつとすると、2つの剰余類は一致する」ことを示している。従って、
2つの剰余類 \(x_1H\) と \(x_2H\) は、\(x_1H=x_2H\) か \(x_1H\cap x_2H=\phi\) のどちらか
である。\(H\) は 単位元 \(e\) を含むから、
\(g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
という和集合を作ると、そこには \(G\) のすべての元が含まれる。従って、
\(G=g_1H\:\cup\:g_2H\:\cup\:\cd\:\cup\:g_nH\)
である。剰余類 \(x_1H,\:x_2H,\:\cd\:x_dH\) は、\(g_1H,\:g_2H,\:\cd\:,g_nH\) を整理・分類したものだから、
\(G=x_1H\:\cup\:x_2H\:\cup\:\cd\:\cup\:x_dH\)
である。この式の右辺の剰余類は共通の元がなく、それぞれの剰余類の元の数はすべて \(|H|\) だから、
\(|G|=d\cdot|H|\)
である。従ってラグランジュの定理、
\(|G|=[\:G\::\:H\:]\cdot|H|\)
が成り立つ。[証明終]
ラグランジュの定理から、
群 \(G\) の元 \(g\) の位数(\(g^x=e\) となる最小の \(x\))を \(n\) とすると、\(n\) は群位数 \(|G|\) の約数である。
ことがわかります。なぜなら、
\(H=\{e,\:g,\:g^2,\:\cd\:,\:g^{n-1}\}\)
とおくと、\(H\) は \(G\) の部分群(巡回群)になり、ラグランジュの定理によって \(|H|=n\) が \(|G|\) の約数になるからです。これは、位数の定理(25A)の[補題5]、
既約剰余類群 \((\bs{Z}/n\bs{Z})^{*}\) の元を \(a\) とし、\(a\) の位数を \(d\) とすると、\(d\) は 群位数 の約数である。
の一般化になっています。 \((\bs{Z}/n\bs{Z})^{*}\) の群位数は \(\varphi(n)\)(\(\varphi\)はオイラー関数)なので、ラグランジュの定理はオイラーの定理やフェルマの小定理(25B)の一般化であるとも言えます。さらに、
群位数が素数の群は巡回群である。
こともわかります。なぜなら、群 \(G\) の位数を \(p\)(素数)とすると、単位元ではない \(G\) の任意の元 \(g\:(\neq e)\) の位数は \(p\) であり、つまり \(G\) は \(g\) を生成元とする位数 \(p\) の巡回群(\(C_p\))だからです。
次の「正規部分群」はガロア理論のキモといえる概念です。これは純粋に群の属性として定義できるのでここにあげますが、ガロア理論の核心である第5章以降で展開される論証の多くは正規部分群に関係しています。
正規部分群
| (正規部分群の定義:41F) |
有限群 \(G\) の部分群を \(H\) とする。\(G\) の全ての元 \(g\) について、
\(gH=Hg\)
が成り立つとき、\(H\) を \(G\) の正規部分群(normal subgroup)という。正規部分群では左剰余類と右剰余類が一致する。
定義により、\(G\) および \(\{e\}\) は \(G\) の正規部分群である。また \(G\) が可換群であると、その部分群は正規部分群である。巡回群は可換群だから、巡回群の部分群は正規部分群である。
正規部分群 \(H\) の定義は、\(G\) の任意の元 \(g\) に対して、
\(gHg^{-1}=H\)
となる \(H\)、としても同じです。また 任意の \(h\in H\) について、
\(ghg^{-1}\in H\)
となる \(H\)、としても同じです。
剰余群
| (剰余群の定義:41G) |
有限群 \(G\) の正規部分群を \(H\) とする。\(G\) の \(H\) による剰余類
\(x_1H,\:x_2H,\:\cd\:,x_dH\:\:(\:x_i\in G,\:d=[\:G\::\:H\:]\:)\)
は部分集合の演算の定義(41A)で群になる。この群を \(G\) の \(H\) による剰余群(quotient group)といい、\(G/H\) で表す。剰余群は商群とも言う。
[証明]
\(H\) が正規部分群のとき、剰余類が群になることを証明する。\(x_iH\) は \(G\) の剰余類なので、
\(G=x_1H\cup x_2H\cup\cd\cup x_dH\)
\((i\neq j\:のとき\:x_iH\cap x_jH=\phi)\)
と表されている。2つの剰余類、\(x_iH,\:x_jH\) の演算を行うと、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_iHx_jH=x_i(Hx_j)H\\
&&&=x_i(x_jH)H=x_ix_jHH\\
&&&=x_ix_j(HH)=x_ix_jH\\
\end{eqnarray}\)
つまり、
\(\begin{eqnarray}
&&\:\:(x_iH)(x_jH)&=x_ix_jH\\
\end{eqnarray}\)
となる。\(H\) は正規部分群なので \(Hx_j=x_jH\) であることと、\(H\) は部分群なので \(HH=H\) であることを用いた。
\(x_ix_j\) は \(G\) の元だから、\(x_ix_jH\) は \(G\) の剰余類のうちの一つである。従って \((x_iH)(x_jH)\) の演算は \(G\) の剰余類の中で閉じている。また、
\((x_iH\cdot x_jH)\cdot x_kH=x_ix_jH\cdot x_kH=x_ix_jx_kH\)
\(x_iH\cdot(x_jH\cdot x_kH)=x_iH\cdot x_jx_kH=x_ix_jx_kH\)
\((x_iH\cdot x_jH)\cdot x_kH=x_iH\cdot(x_jH\cdot x_kH)\)
であるから、結合法則が成り立っている。さらに、
\(H\cdot xh=eH\cdot xH=(ex)H=xH\)
\(xH\cdot H=xH\cdot eH=(xe)H=xH\)
なので、剰余類 \(H\) が単位元になる。また、
\(xH\cdot x^{-1}H=(xx^{-1})H=eH=H\)
\(x^{-1}H\cdot xH=(x^{-1}x)H=eH=H\)
であり、\(xH\) に対する逆元は \(x^{-1}H\) である。従って剰余類 \(G/H\) は群である。[証明終]
群の位数、元の位数、ラグランジュの定理、巡回群は、いずれも有限群の概念や定理です。しかし、剰余類、正規部分群、剰余群は、元の数が無限であっても成り立つ概念です。たとえば、整数の加法群 \(\bs{Z}\) は可換群なので、すべての部分群は正規部分群です。従って、\(n\) の倍数から成る部分群を \(n\bs{Z}\) とすると、\(\bs{Z}/n\bs{Z}\) は剰余群です。\(\bs{Z}/n\bs{Z}\) という表記は \(n\bs{Z}\) が \(\bs{Z}\) の正規部分群であることが暗黙の前提なのでした。
| (巡回群の剰余群は巡回群:41H) |
巡回群の部分群による剰余群は巡回群である。
[証明]
群 \(G\) を、位数 \(n\)、生成元 \(g\) の巡回群とし、その元を、
\(G\:=\:\{g,\:g^2,\:g^3,\:\cd,\:g^n=e\:\}\)
とする。\(G\) の部分群を \(H\) とし、\(H\) の元のうち \(g\) の指数が一番小さいものを \(g^{d}\:\:(1\leq d\leq n)\) とする。\(d=1\) なら \(H=G\) であり、また \(d=n\) なら \(H=\{\:e\:\}\) である。
\(n\) を \(d\) で割った商を \(q\)、余りを \(r\) とする。つまり、
\(n=qd+r\:\:(1\leq q\leq n,\:0\leq r < d)\)
とする。\(g^d\) は \(H\) の元だから その \(q\) 乗も \(H\) の元であり、
\((g^d)^q=g^{dq}\in H\)
である。また \(g^{dq}\) の逆元も \(H\) に含まれるから
\((g^{dq})^{-1}\in H\)
である。仮にもし \(1\leq r < d\) なら
\(g^{dq}g^{r}=g^{qd+r}=g^n=e\)
となるので、この式に左から \((g^{dq})^{-1}\) をかけると、
\(g^r=(g^{dq})^{-1}\in H\)
となり、\(d\) 未満の数 \(r\) が指数の \(g^r\) が \(H\) の元ということになるが、これは \(d\) が最小の指数であるという仮定に反する。従って \(r=0\) であり、\(qd=n\) である。つまり \(d\) と \(q\) は \(n\) の約数である。そうすると \(g^d\) を \(q\) 乗すると \(g^{dq}=g^n=e\) となるので、\(H\) は \(g^d\) を生成元とする位数 \(q\) の巡回群、
\(H=\{\:g^{d},\:g^{2d},\:\cd,\:g^{qd}=g^n=e\:\}\)
である。また、\(G\) は巡回群、つまり可換群だから、その部分群である \(H\) は \(G\) の正規部分群である。 \((\br{A})\)
次に、剰余類 \(g^kH\:\:(1\leq k\leq n)\) を考える。\(k\) を \(d\) で割った商を \(m\)、余りを \(i\) とする。\(qd=n\) なので \(m\) の最大値は \(q\) であり、
\(k=md+i\) \((0\leq m\leq q,\:0\leq i < d)\)
と表現できる。以下、\(m,\:i\) の値によって3つに分ける。
\(k=i\:\:(m=0,\:1\leq i < d)\) のときは、\(H\) が単位元を含んでいるので、
\(g^k=g^i\in g^iH\)
である。
\(m\neq0,\:1\leq i < d\) のときは、
\(g^k=g^{md+i}=g^ig^{md}\)
となるが、\((\br{A})\) 式により、
\(g^{md}\in H\:\:(1\leq m\leq q)\)
なので、
\(g^ig^{md}\in g^iH\)
\(g^k\in g^iH\:\:(1\leq i < d)\)
となる。
また、\(m\neq0,\:i=0\) のときは、
\(g^k=g^{md}\in H\)
である。
結局、\(G\) の元 \(g^k\) は、\(\{\:H,\:g^iH\:\:(1\leq i < d)\:\}\) のどれかに含まれる。ここで、形式上 \(g^0H\:=\:H\) と定義すると、\(H,\:g^iH\) は、
\(g^iH\:=\:\{\:g^{i+md}\:|\:0\leq i < d,\:\:0\leq m\leq q\:\}\)
と表記できる。\(0\leq i,j < d,\:\:0\leq m_i,m_j\leq q\) で、\(i\neq j\) なら、
\(i+m_id\neq j+m_jd\)
なので、\(g^iH\) と \(g^jH\) に共通の元はなく、
\(g^iH\:\cap\:g^jH=\phi\:\:(i\neq j)\)
である。
以上より、巡回群 \(G\) は剰余類によって、
\(G=H\:\cup\:gH\:\cup\:g^2H\:\cup\:\cd\:\cup\:g^{d-1}\)
\(g^iH\:\cap\:g^jH=\phi\) \((i\neq j)\)
と分解できる。
\(H\) は \(G\) の正規部分群であった。従って \(G\) の \(H\) による剰余類は剰余群になり、
\(G/H=\{\:H,\:gH,\:g^2H,\:\cd\:,g^{d-1}H\:\}\)
である。ここで \(gH\) の累乗を調べると、
\((gH)^2=gHgH=ggHH=g^2H\)
\((gH)^3=gHgHgH=g^2HgH=g^2gHH=g^3H\)
のように計算でき、
\((gH)^i=g^iH\) \((1\leq i\leq d-1)\)
である。また、同じ計算によって、
\((gH)^d=g^dH\)
となるが、\(g^d\in H\) なので部分群の元の条件の定理(41C)により \(g^dH=H\) であり、つまり、
\((gH)^d=H\)
である。
以上により 剰余群 \(G/H\) は、
\(G/H=\{gH,\:(gH)^2,\:\cd\:,(gH)^{d-1},\:(gH)^{d}=H\}\)
と表され、生成元が \(gH\)、単位元が \(H\)、位数が \(d\) の巡回群である。[証明終]
部分群と正規部分群
| (部分群と正規部分群:41I) |
\(G\) の正規部分群を \(H\)、部分群を \(N\) とする。このとき、
(a) \(NH\) は \(G\) の部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
(b) \(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
(c) \(N\cap H\) は \(N\) の正規部分群である。
が成り立つ。
(a) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(NH\) は部分群である。
\(NH\) の任意の2つの元を
\(nx\:\:(n\in N,\:x\in H),\:\:my\:\:(m\in N,\:y\in H)\)
とすると、
\(nx\in nH,\:my\in mH\)
である。\(H\) は正規部分群だから、\(mH=Hm\) であることを用いると、
\((nx)(my)\in(nH)(mH)=nHmH=nmHH=nmH\)
となる。\(n,m\in N\) なので \(nm\in N\) であり、従って \(nmH\subset NH\) である。結局、
\((nx)(my)\in NH\)
となって、\(NH\) の2つの元の演算は \(NH\) で閉じていることが分かる(=\(\:\br{①}\:\))。
また一般に、\((xy)^{-1}=y^{-1}x^{-1}\) である。なぜなら、
\(xy(y^{-1}x^{-1})=x(yy^{-1})x^{-1}=xex^{-1}=xx^{-1}=e\)
\((y^{-1}x^{-1})xy=y^{-1}(x^{-1}x)y=y^{-1}ey=y^{-1}y=e\)
が成り立つからである。
\(G\) の部分群 \(N\) と正規部分群 \(H\) において、\(n\in N,\:x\in H\) とすると、\(n^{-1}\in N,\:x^{-1}\in H\) なので、
\((nx)^{-1}=x^{-1}n^{-1}\in Hn^{-1}\)
となるが、\(H\) が正規部分群なので、\(Hn^{-1}=n^{-1}H\)である。さらに、\(n^{-1}H\subset NH\) なので、結局、
\((nx)^{-1}\subset NH\)
となり、\(NH\) の任意の元 \(nx\) について逆元 \((nx)^{-1}\) が \(NH\) に含まれる(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) が成り立つので、部分群の十分条件の定理(41B)によって \(NH\) は \(G\) の部分群である。[証明終]
(b) の証明
\(G\) の正規部分群を \(H\)、部分群を \(N\) とするとき、\(G\:\sp\:N\:\sp\:H\) なら、\(H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。\(N\) は \(G\) の 部分集合だから、\(N\) の任意の元 \(y\) についても、
\(yH=Hy\)
が成り立つ。従って \(H\) は \(N\) の正規部分群である。[証明終]
(c) の証明
\(G\) の正規部分群を \(H\)、 部分群を \(N\) とするとき、\(N\cap H\) は \(N\) の正規部分群である。
\(H\) は \(G\) の正規部分群だから、\(G\) の任意の元 \(x\) について
\(xH=Hx\)
が成り立つ。この式に右から \(x^{-1}\) をかけると、
\(xHx^{-1}=H\)
となる。これは、\(H\) の任意の元 \(h\) を決めると、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
となることを意味する。これは \(H\) が正規部分群であることの定義と等価である。以降、この形で \(N\cap H\) が正規部分群であることを証明する。
部分群 \(N\) の任意の元を \(y\)、正規部分群 \(H\) の任意の元を \(h\)、\(N\cap H\) の任意の元を \(n\) とする。\(y,\:y^{-1},\:n\) は全て \(N\) の元だから、
\(yny^{-1}\in N\)
である(=\(\:\br{①}\:\))。また \(H\) は \(G\) の正規部分群であるから、\(G\) の任意の元 \(x\) について、
\(xhx^{-1}\in H\)
が成り立つ。ここで、\(G\:\sp\:N\) なので \(x=y\) とおくことができ、また \(H\:\sp\:N\cap H\) なので \(h=n\) とおくこともできる。従って、
\(yny^{-1}\in H\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、\(N\cap H\) の任意の元 \(n\) を決めると、\(N\) の全ての元 \(y\) について、
\(yny^{-1}\in N\cap H\)
となる。つまり \(N\cap H\) は \(N\) の正規部分群である。[証明終]
4.2 準同型写像
この節の写像の説明には「全射」「単射」「全単射」などの用語ができてます。その用語の意味は次の図の通りです。
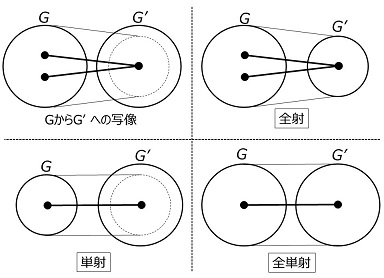
|
全射:\(G\,'\)の任意の元 \(y\) について \(f(x)=y\) となる \(x\in G\) がある。 単射:\(x\neq y\:(x,y\in G)\) なら \(f(x)\neq f(y)\)。 全単射:全射かつ単射。 |
準同型写像と同型写像
| (準同型写像と同型写像:42A) |
群 \(G\) から群 \(G\,'\) への写像 \(f\) がある。\(G\) の任意の2つの元、\(x,\:y\) について、
\(f(xy)=f(x)f(y)\)
が成り立つとき、\(f\) を \(G\) から \(G\,'\) への準同型写像(homomorphism)という。右辺は群 \(G\,'\) の演算定義に従う。
また、\(f\) が全単射写像のとき、\(f\) を同型写像(isomorphism)という。群 \(G\) から \(G\,'\) への同型写像が存在するとき、\(G\) と \(G\,'\) は同型であるといい、
\(G\:\cong\:G\,'\)
で表す。
準同型写像の像と核
| (準同型写像の像と核:42B) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(G\) の元を \(f\) で移した元の集合を「\(f\) の像(image)」といい、\(\mr{Im}\:f\) と書く。\(\mr{Im}\:f\) を \(f(G)\) と書くこともある。
\(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(G\) の単位元を \(e\)、\(G\,'\) の単位元を \(e\,'\) とする。準同型写像 \(f\) によって \(e\,'\) に移る \(G\) の元の集合を「\(f\) の核(kernel)」といい、\(\mr{Ker}\:f\) と書く。
\(\mr{Ker}\:f\) は \(G\) の部分群である。
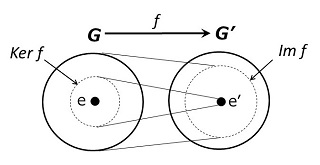
|
[証明]
\(\mr{Im}\:f\) と \(\mr{Ker}\:f\) が群であることを証明する。
\(\mr{Im}\:f\) は群
\(\mr{Im}\:f\) の任意の2つの元を \(f(x),f(y)\:\:(x,y\in G)\) とすると、
\(f(x)f(y)=f(xy)\:\in\mr{Im}\:f\)
である(=\(\:\br{①}\:\))。
\(\mr{Im}\:f\) の任意の元 \(f(x)\) について、
\(f(e)f(x)=f(ex)=f(x)\)
\(f(x)f(e)=f(xe)=f(x)\)
なので、
\(f(e)=e\,'\)
である。\(G\) は群なので、任意の元 \(x\) について逆元 \(x^{-1}\) が存在する。
\(f(x)f(x^{-1})=f(xx^{-1})=f(e)=e\,'\)
\(f(x^{-1})f(x)=f(x^{-1}x)=f(e)=e\,'\)
であるから、
\(f(x)^{-1}=f(x^{-1})\:\in\mr{Im}\:f\)
である(=\(\:\br{②}\:\))。\(\br{①}\:\:\br{②}\) より、部分群の十分条件の定理(41B)によって \(\mr{Im}\:f\) は \(G\,'\) の部分群である。
\(\mr{Ker}\:f\) は群
\(\mr{Ker}\:f\) の任意の元を \(x,\:y\) とすると、
\(f(xy)=f(x)f(y)=e\,'e\,'=e\,'\)
なので、
\(xy\:\in\mr{Ker}\:f\)
である(\(\:\br{③}\:\))。
また \(x\) は \(G\) の元だから \(x^{-1}\) が定義されている。
\(\begin{eqnarray}
&&\:\:f(x^{-1})&=f(x^{-1})e\,'=f(x^{-1})f(x)\\
&&&=f(x^{-1}x)=f(e)\\
&&&=e\,'\\
\end{eqnarray}\)
となるので、
\(x^{-1}\:\in\mr{Ker}\:f\)
である(\(\:\br{④}\:\))。\(\br{③}\:\:\br{④}\) より、部分群の十分条件の定理(41B)によって \(\mr{Ker}\:f\) は \(G\) の部分群である。[証明終]
核が単位元なら単射
| (核が単位元なら単射:42C) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。このとき
| \(\mr{Im}\:f\) | \(=\:G\,'\) | なら \(f\) は全射 | |
| \(\mr{Ker}\:f\) | \(=\:\{e\}\) | なら \(f\) は単射 |
である。
[証明]
"\(f\) は全射" については、全射の定義そのものである。
\(\mr{Ker}\:f\:=\:\{e\}\) とし、\(G\) の任意の2つの元を \(x,\:y\) とする。ここで、
\(f(x)=f(y)\)
であったとする。\(\mr{Im}\:f\) は群だから \(f(y)^{-1}\in\:\mr{Im}\:f\) である。上の式に左から \(f(y)^{-1}\) をかけると、
\(f(y)^{-1}f(x)=f(y)^{-1}f(y)\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)\in\:\mr{Ker}\:f\)
\(y^{-1}x=e\)
\(x=y\)
となる。\(f(x)=f(y)\) であれば \(x=y\) なので、\(f\) は単射である。[証明終]
核は正規部分群
| (核は正規部分群:42D) |
群 \(G\) から群 \(G\,'\) への準同型写像を \(f\) とする。このとき \(\mr{Ker}\:f\) は \(G\) の正規部分群である。
[証明]
\(\mr{Ker}\:f\) を \(H\) と記述する。\(G\) の 任意の元を \(x\) とし、\(H\) の任意の元を \(y\) とする。すると、
\(\begin{eqnarray}
&&\:\:f(xyx^{-1})&=f(x)f(y)f(x^{-1})\\
&&&=f(x)e\,'f(x^{-1})=f(x)f(x^{-1})\\
&&&=f(xx^{-1})=f(e)=e\,'\\
\end{eqnarray}\)
と計算できるから、
\(xyx^{-1}\in H\)
である。\(y\) は \(H\) の任意の元だから、
\(xHx^{-1}\subset H\)
である。\(x\) は任意にとることができるので、\(x\) を \(x^{-1}\) に置き換えると、
\(x^{-1}Hx\subset H\)
を得る。この式に左から \(x\)、右から \(x^{-1}\) をかけると、
\(H\subset xHx^{-1}\)
となる。つまり
\(H\subset xHx^{-1}\subset H\)
\(xHx^{-1}=H\)
である。さらに右から \(x\) をかけると、
\(xH=Hx\)
となり、\(x\) は任意の \(G\) の元だから、\(H\:\:(=\mr{Ker}\:f)\) は \(G\) の正規部分群である。[証明終]
4.3 同型定理
準同型定理=第1同型定理
| (準同型定理:43A) |
群 \(G\) から群 \(G\,'\) への準同型写像 \(f\) がある。\(H=\mr{Ker}\:f\) とすると、\(G\) の \(H\) による剰余群は、\(G\) の \(f\) による像と同型である。つまり、
\(G/H\:\cong\:\mr{Im}\:f\)
が成り立つ。
[証明]
\(H\:=\:\mr{Ker}\:f\) は、核は正規部分群の定理(42D)により、\(G\) の正規部分群である。従って剰余群 \(G/H\) が定義できる。\(G/H\) から \(\mr{Im}\:f\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G/H &\longrightarrow&\mr{Im}\:f\\
&&&xH &\longmapsto&f(x)\\
\end{eqnarray}\)
と定義する。まず、この写像が剰余類 \(xN\) の代表元 \(x\) のとりかたに依存しないこと、つまり \(xH=yH\) なら \(f(x)=f(y)\) であることを示す。\(xH=yH\) を変形すると、
\(xH=yH\)
\(y^{-1}xH=y^{-1}yH\)
\(y^{-1}xH=H\)
ゆえに部分群の元の条件の定理(41C)から \(y^{-1}x\in H\) である。そうすると、\(H\) は \(\mr{Ker}\:f\) のことだから、\(f(y^{-1}x)=e\,'\) である。これを変形すると、
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
となる。最後の変形では、準同型写像の像と核の定理(42B)の「\(\mr{Im}\:f\) は群」の証明から、\(f(y^{-1})=f(y)^{-1}\) であることを用いた。ここから、
\(f(y)^{-1}f(x)=e\,'\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(x)=f(y)\)
となり、\(f(x)=f(y)\) が証明できた。
以上の変形は逆も辿れる。つまり、
\(f(x)=f(y)\)
\(f(y)f(y)^{-1}f(x)=f(y)e\,'\)
\(f(y)^{-1}f(x)=e\,'\)
\(f(y^{-1})f(x)=e\,'\)
\(f(y^{-1}x)=e\,'\)
\(f(y^{-1}x)\in H\)
\(y^{-1}xH=H\)
\(xH=yH\)
となる。これは \(f(x)=f(y)\) なら \(xH=yH\) であることを示していて、すなわち \(\sg\) は単射である。と同時に、\(\sg\) による写像の先は \(\mr{Im}\:f\) に限定しているので \(\sg\) は全射である。つまり \(\sg\) は 全単射である(=\(\:\br{①}\:\))。
さらに、
\(\begin{eqnarray}
&&\:\:\sg((xH)(yH))&=\sg(x(Hy)H)=\sg(x(yH)H)\\
&&&=\sg(xyH)=f(xy)=f(x)f(y)\\
&&&=\sg(xH)\sg(yH)\\
\end{eqnarray}\)
であり、つまり \(\sg((xH)(yH))=\sg(xH)\sg(yH)\) が成り立っている(=\(\:\br{②}\:\))。
\(\br{①}\:\:\br{②}\) により \(\sg\) は同型写像である。\(G/H\) から \(\mr{Im}\:f\) への同型写像が存在するから、
\(G/H\:\cong\:\mr{Im}\:f\)
である。[証明終]
第2同型定理
| (第2同型定理:43B) |
群 \(G\) の正規部分群を \(H\)、部分群を \(N\) とすると、
\(N/(N\cap H)\:\cong\:NH/H\)
が成り立つ。
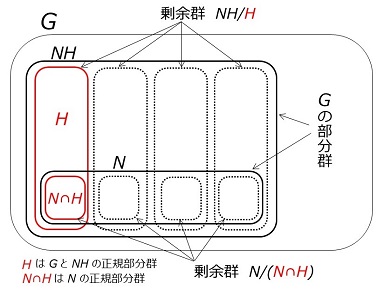
|
[証明]
まず、部分群と正規部分群の定理(41I)により、\(G\) の正規部分群が \(H\)、部分群が \(N\) の場合、
| \(N\cap H\) は \(N\) の正規部分群 | |
| \(NH\) は \(G\) の部分群 | |
| \(G\:\sp\:NH\:\sp\:H\) なので、\(H\) は \(NH\) の正規部分群 |
\(G\) の任意の元を \(x,\:y\) とし、\(G\) から \(G/H\) への写像 \(\sg\) を、
\(\begin{eqnarray}
&&\:\:\sg\:: &G &\longrightarrow&G/H\\
&&&x &\longmapsto&xH\\
\end{eqnarray}\)
と定義する。この写像は、
\(\begin{eqnarray}
&&\:\:\sg(xy)&=xyH=xyHH=xHyH=(xH)(yH)\\
&&&=\sg(x)\sg(y)\\
\end{eqnarray}\)
を満たすから準同型写像である(ちなみに \(G\) とその正規部分群 \(H\) があるとき、上記の定義による \(\sg\) を自然準同型と呼ぶ)。
\(\sg\) の定義域は \(G\) であるが、\(\sg\) の定義域を \(G\) の部分群である \(N\) に制限した写像 \(\tau\)(タウ) を考える。\(N\) の任意の元を \(z\) とすると、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
&&&z &\longmapsto&zH\\
\end{eqnarray}\)
である。この \(\tau\) の像 \(\mr{Im}\:\tau\) を考えてみると、\(z\) が \(N\) の元のすべてを動くとき、\(\tau(z)=zH\) として出てくる \(G\) の元は \(NH\) の元である。つまり \(\tau\) は、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
として定義したが、\(\tau(z)\) が \(G/H\) の全てを尽くすわけではなく、全射ではない。写像による移り先は、\(G\) の部分群 \(NH\) を \(H\) で分類した剰余群、\(NH/H\) である。つまり \(\tau(N)=NH/H\) であり、
\(\mr{Im}\:\tau=NH/H\)
である。
次に準同型写像の核を考える。\(G/H\) の単位元は、
\(xH\cdot H=xH\)
\(H\cdot xH=HxH=xHH=xH\)
なので、\(H\) である。
\(G\) の元 \(x\) が \(\mr{Ker}\:\sg\) の元とする。つまり、
\(x\in\mr{Ker}\:\sg\)
とする。これは \(\sg(x)\) が \(G/H\) の単位元になるということだから、
\(\sg(x)=H\)
であり、\(\sg(x)=xH\) なので、
\(xH=H\)
である。これは部分群の元の条件の定理(41C)によって、
\(x\in H\)
と同値である。従って、
\(x\in\mr{Ker}\:\sg\)
\(x\in H\)
の2つは同値であり、つまり、
\(\mr{Ker}\:\sg=H\)
である。
\(\tau\) は \(\sg\) の定義域を \(N\) に制限したものなので、\(\mr{Ker}\:\tau\) は「\(\mr{Ker}\:\sg=H\) のうちで \(N\) に含まれるもの」であり、すなわち、
\(\mr{Ker}\:\tau=(N\cap H)\)
である。
ここで、\(\tau\) の定義である、
\(\begin{eqnarray}
&&\:\:\tau\:: &N &\longrightarrow&G/H\\
\end{eqnarray}\)
に準同型定理(43A)を適用すると、
\(\begin{eqnarray}
&&\:\:N/(\mr{Ker}\:\tau) &\cong\:\mr{Im}\:\tau\\
&&\:\:N/(N\cap H) &\cong\:NH/H\\
\end{eqnarray}\)
となって、題意が成り立つ。[証明終]
第2同型定理を整数の剰余群で確認してみます。上の定理における \(G,\:H,\:N\) を、
\(G=\bs{Z}\)
\(H=10\bs{Z}\) (\(10\) の倍数)
\(N=\phantom{1}6\bs{Z}\) (\(\phantom{1}6\) の倍数)
の群とします。この群の演算は加算であり、可換群なので、\(\bs{Z}\) の部分群はすべて正規部分群です。
\(N\cap H\) は「\(10\) の倍数、かつ \(6\) の倍数」の集合なので、
\(N\cap H=30\bs{Z}\)
です。また \(NH\) は、\(10\) の倍数と\(6\) の倍数の加算の結果の集合です。つまり、
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
ですが、これが何を意味するかは不定方程式の解の存在の定理(21B)から分かります。定理を再掲すると、
2変数 \(x,\:y\) の1次不定方程式を、
\(ax+by=c\)
(\(a,\:b,\:c\) は整数。\(a\neq0,\:b\neq0\))
とし、\(a\) と \(b\) の最大公約数を \(d\) とする。このとき、
\(c=kd\) (\(k\) は整数)
なら方程式は整数解を持ち、そうでなければ整数解を持たない。
です。\(c=kd\) なら、式を満たす \(x,\:y\) が必ず存在します。また任意の \(x,\:y\) について \(ax+by\) を計算すると、その結果の \(c\) は必ず \(c=kd\) の形になります。そうでなければ、\(c\) が最大公約数の倍数でないにも関わらず不定方程式が解をもつことになって定理に矛盾します。従って、\(ax+by=c\) の \(x,\:y\) を任意の整数とすると、\(c\) は \(a,\:b\) の "最大公約数の整数倍のすべて" になります。
\(NH=\{\:10x+6y\:|\:x,y\in\bs{Z}\:\}\)
とした場合、\(10\) と \(6\) の最大公約数は \(2\) なので、
\(NH=2\bs{Z}\)
です。この結果、
\(N/(N\cap H)\)
\(=6\bs{Z}/30\bs{Z}\)
\(=\{30\bs{Z},\:6+30\bs{Z},\:12+30\bs{Z},\:18+30\bs{Z},\:24+30\bs{Z}\}\)
\(NH/H\)
\(=2\bs{Z}/10\bs{Z}\)
\(=\{10\bs{Z},\:2+10\bs{Z},\:4+10\bs{Z},\:6+10\bs{Z},\:4+10\bs{Z}\}\)
となります。この2つの剰余群は位数 \(5\) の巡回群( \(C_5\) )で、\(\bs{Z}/5\bs{Z}\) に同型です。つまり、
| \(N/(N\cap H)\) | \(\cong\:\bs{Z}/5\bs{Z}\) | |
| \(NH/H\) | \(\cong\:\bs{Z}/5\bs{Z}\) |
\(N/(N\cap H)\:\cong\:NH/H\)
となって、第2同型定理が確認できました。
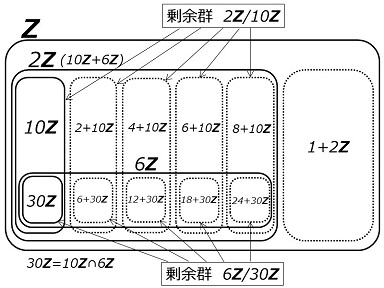
|
第2同型定理 : \(\bs{6\bs{Z}/30\bs{Z}\:\cong\:2\bs{Z}/10\bs{Z}}\) |
この図をみると、\(NH/H=2\bs{Z}/10\bs{Z}\) と \(N/(N\cap H)=6\bs{Z}/30\bs{Z}\) が同型であることがヴィジュアルにイメージできる。両方とも位数 \(5\) の巡回群である。 |
第2同型定理を数式で書くと何だか難しそうな感じがしますが、図にするといかにも自明なことという気がします。数学におけるイメージ図の威力が実感できます。
第2同型定理は、後ほど「可解群の部分群は可解群」という定理の証明に使います。「可解群の部分群は可解群」の定理は、5次方程式に可解でないものがあることを証明する際に鍵となる定理です。その第2同型定理は準同型定理を使って証明される、という構造になっているのでした。
| 5.ガロア群とガロア対応 |
2章から4章までは、多項式、体、線形空間、剰余類、群、剰余群、既約剰余類群、正規部分群といった、ガロア理論の基礎となる概念の説明でした。この第5章から、理論の核心に入っていきます。
5.1 体の同型写像
同型写像の定義
| (体の同型写像:51A) |
体 \(\bs{K}\) から 体 \(\bs{F}\) への写像 \(f\) が全単射であり、\(\bs{K}\) の任意の元、\(x,\:y\) に対して、
\(\begin{eqnarray}
&&\:\:f(x+y)&=f(x)+f(y)\\
&&\:\:f(xy)&=f(x)f(y)\\
\end{eqnarray}\)
が成り立つとき、\(f\) を体の同型写像という。この定義による同型写像は、加法と乗法のみならず、四則演算を保存する。
特に、\(\bs{K}\) から \(\bs{K}\) への同型写像を自己同型写像という。
\(\bs{K}\) から \(\bs{F}\) への同型写像が存在するとき、体 \(\bs{K}\) と 体 \(\bs{F}\) は同型であるといい、\(\bs{K}\:\cong\:\bs{F}\) で表す。
体 \(\bs{K}\) と \(\bs{F}\) がともに \(\bs{Q}\) を含むとき、\(a\in\bs{Q}\) に対して、
\(f(a)=a\)
である。つまり有理数は同型写像で不変である。
[証明]
上の定義による同型写像が、減法と除法を保存することを証明する。\(\bs{K}\) と \(\bs{F}\) は体だから、加法と乗法について群になっている。\(\bs{K}\) の加法の単位元を \(\kz\)、\(\bs{F}\) の加法の単位元を \(\fz\) とする。また、乗法の単位元をそれぞれ \(\ko\) と \(\fo\) とする。まず、\(f(\ko)=\fo\) で \(f(\kz)=\fz\) であることを示す。
\(f(x+y)=f(x)+f(y)\) において \(x=\kz,\:y=\kz\) とすると、
\(f(\kz+\kz)=f(\kz)+f(\kz)\)
\(f(\kz)=f(\kz)+f(\kz)\)
両辺に \(\bs{F}\) における \(f(\kz)\) の逆元 \(-f(\kz)\) を加えると、
\(f(\kz)+(-f(\kz))=f(\kz)\)
\(\fz=f(\kz)\)
となり、\(f(\kz)=\fz\) である。
\(f(xy)=f(x)f(y)\) において \(x=\ko,\:y=\ko\) とすると、
\(f(\ko\times\ko)=f(\ko)f(\ko)\)
\(f(\ko)=f(\ko)f(\ko)\)
両辺に \(\bs{F}\) における \(f(\ko)\) の逆元 \(-f(\ko)\) を加えると、
\(f(\ko)+(-f(\ko))=f(\ko)f(\ko)+(-f(\ko))\)
\(\fz=f(\ko)f(\ko)+(-f(\ko))\)
この式に現れているのは全て \(\bs{F}\) の元だから、分配則を使って、
\(f(\ko)(f(\ko)-\fo)=\fz\)
ここで \(f(\ko)=\fz\) と仮定すると、\(f(\kz)=\fz\)かつ \(f(\ko)=\fz\) となってしまい \(f\) が単射であることと矛盾する。従って \(f(\ko)\neq\fz\) である。上式の両辺を \(f(\ko)\) で割ると、
\(f(\ko)-\fo=\fz\)
\(f(\ko)=\fo\)
となる。
以上を踏まえると、同型写像が減法を保存することは次のようにしてわかる。\(\bs{K}\) は加法について群なので任意の元 \(x\in\bs{K}\) について逆元 \(-x\) がある。また \(\bs{F}\) も加法についても群だから \(f(x)\) の逆元 \(-f(x)\) がある。
\(f(-x)+f(x)=f(-x+x)=f(\kz)=\fz\)
両辺に \(-f(x)\) を足すと、
\(f(-x)+f(x)+(-f(x))=\fz+(-f(x))\)
\(f(-x)+\fz=\fz+(-f(x))\)
\(f(-x)=-f(x)\)
である。\(\bs{K}\) の任意の元を \(x,\:y\) とすると、
\(\begin{eqnarray}
&&\:\:f(x-y)&=f(x+(-y))\\
&&&=f(x)+f(-y)\\
&&&=f(x)+(-f(y))\\
&&&=f(x)-f(y)\\
\end{eqnarray}\)
となって、減法は保存されている。
除法を保存することは次のようにしてわかる。\(\bs{K}\) は乗法について群なので、任意の元 \(x\:\:(\neq\kz)\) について逆元 \(x^{-1}\) がある。\(\bs{F}\) も乗法についての群だから、\(f(x)\) の逆元である \(f(x)^{-1}\) がある。\(x\neq\kz\) なら \(f(x)\neq\fz\) なので逆元が定義できる。すると、
\(f(x^{-1})f(x)=f(x^{-1}x)=f(\ko)=\fo\)
である。この式の両辺に \(f(x)^{-1}\) をかけると、
\(f(x^{-1})f(x)f(x)^{-1}=\fo\times f(x)^{-1}\)
\(f(x^{-1})\times\fo=\fo\times f(x)^{-1}\)
\(f(x^{-1})=f(x)^{-1}\)
となる。\(\bs{K}\) の任意の元を \(x,\:y\:\:(y\neq\kz)\) とすると、
\(\begin{eqnarray}
&&\:\:f\left(\dfrac{x}{y}\right)&=f(xy^{-1})\\
&&&=f(x)f(y^{-1})\\
&&&=f(x)f(y)^{-1}\\
&&&=\dfrac{f(x)}{f(y)}\\
\end{eqnarray}\)
となり、除法が保存されていることが分かる。
有理数の同型写像を考える。\(n\) を整数とすると、
\(\begin{eqnarray}
&&\:\:f(n)&=f(\:\overbrace{1+1+\cd+1}^{1をn\:個加算}\:)\\
&&&=f(1)+f(1)+\cd+f(1)\\
&&&=nf(1)\\
&&&=n\\
\end{eqnarray}\)
なので、\(f(n)=n\) である。任意の有理数 \(a\) は、2つの整数 \(n\:(\neq0),\:m\) を用いて、
\(a=\dfrac{m}{n}\)
と表されるから、
\(\begin{eqnarray}
&&\:\:f(a)&=f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{f(n)}=\dfrac{m}{n}\\
&&&=a\\
\end{eqnarray}\)
となり、有理数は同型写像で不変である。[証明終]
同型写像と有理式の順序交換
| (有理式の定義:51B) |
変数 \(x\) の多項式(係数は \(\bs{Q}\) の元)を分母・分子とする分数式を、\(\bs{Q}\) 上の有理式という。
\(\bs{Q}\) 上の多項式は、有理数と \(x\) の加・減・乗算で作られる式です。一方、\(\bs{Q}\) 上の有理式とは、有理数と \(x\) の除算を含む四則演算で作られる式です。
| (同型写像と有理式の順序交換:51C) |
体 \(\bs{K}\) と 体 \(\bs{F}\) は \(\bs{Q}\) を含むものとする。\(\sg\) を \(\bs{K}\) から \(\bs{F}\) への同型写像とし、\(a\) を \(\bs{K}\) の元とする。\(f(x)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。これは多変数の有理式でも成り立つ。\(a_1,a_2,\cd,a_n\) を \(\bs{K}\) の元、\(f(x_1,x_2,\cd,x_n)\) を \(\bs{Q}\) 上の有理式とすると、
\(\sg(f(a_1,a_2,\cd,a_n))=f(\sg(a_1),\sg(a_1),\cd,\sg(a_n))\)
である。
[証明]
\(a\in\bs{K},\:b_i\in\bs{Q},\:c_i\in\bs{Q}\) とし、1変数 \((=a)\) の2次多項式の分数式の場合を例に書くと、
\(\sg\left(\dfrac{b_2a^2+b_1a+b_0}{c_2a^2+c_1a+c_0}\right)\)
\(=\dfrac{\sg(b_2a^2+b_1a+b_0)}{\sg(c_2a^2+c_1a+c_0)}\)
\(=\dfrac{b_2\sg(a^2)+b_1\sg(a)+b_0}{c_2\sg(a^2)+c_1\sg(a)+c_0}\)
\(=\dfrac{b_2\sg(a)^2+b_1\sg(a)+b_0}{c_2\sg(a)^2+c_1\sg(a)+c_0}\)
であるから、題意は成り立つ。これは \(n\)次多項式の場合でも同じである。[証明終]
「同型写像と有理式は順序交換可能」は、\(\bs{Q}\) の拡大体の上の有理式でも成り立ちます。つまり、次が成り立ちます。
\(\bs{Q}\) を含む体を \(\bs{K}\) とし、\(\bs{K}\)の拡大体を \(\bs{F}\:,\bs{F}'\) とする。\(\sg\) を \(\bs{K}\) を不変にする \(\bs{F}\) から \(\bs{F}'\) への同型写像とし、\(a\) を \(\bs{F}\) の元とする。\(f(x)\) を \(\bs{K}\) 上の有理式とすると、
\(\sg(f(a))=f(\sg(a))\)
である。
同型写像は解を共役な解に移す
| (同型写像での移り先:51D) |
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とする。\(\bs{Q}\) 上の方程式 \(f(x)=0\) の解の一つを \(\al\) とし、\(\al\) は \(\bs{K}\) の元とする。すると \(\sg(\al)\) も \(f(x)=0\) の解である。
[証明]
\(\al\) は \(f(x)=0\) の解なので \(f(\al)=0\) が成り立つ。すると、
\(f(\sg(\al))=\sg(f(\al))=\sg(0)=0\)
となり、\(\sg(\al)\) も \(f(x)=0\) の解である。[証明終]
同じ方程式の解同士を「共役な解」「共役である」と言います。この定理により、同型写像は解を共役な解に移すこと分かります。
同型写像は解を入れ替える
| (同型写像による解の置換:51E) |
\(\sg\) を体 \(\bs{K}\) から 体 \(\bs{F}\) への同型写像とし、\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。方程式 \(f(x)=0\) の \(n\)個の解を \(\al_1,\al_2,\cd,\al_n\) とし、これらが全て \(\bs{K}\) に含まれるとする。
すると \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。
[証明]
\(f(x)\) は既約多項式なので、方程式 \(f(x)=0\) は \(n\)個の解をもち、それらは全て異なる(31G)。同型写像は解を共役な解に移す(51D)ので、\(\sg(\al_i)\) も \(f(x)=0\) の解である。\(\sg\) は同型写像なので全単射であり、\(i\neq j\) なら \(\sg(\al_i)\neq\sg(\al_j)\) である。従って \(\sg(\al_1),\sg(\al_2),\cd,\sg(\al_n)\) は、\(\al_1,\al_2,\cd,\al_n\) を入れ替えたものである。[証明終]
同型写像を定義してその性質を述べてきましたが、あたかも「同型写像はあるのが当然」のような話でした。しかし、同型写像があったとしたらこういう性質をもつというのが正しく、同型写像が必ずあるとは証明していません。
同型写像の存在を示すには、第1章でやったように、\(\bs{Q}(\sqrt{2})\)において
\(\sg(\sqrt{2})=-\sqrt{2}\)
という写像を定義すると、体のすべての元について \(\sg\) は同型写像の定義を満たす、というような証明が必要です。それが次です。
単拡大体の同型写像の存在
| (同型写像の存在:51F) |
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(\al,\:\beta\) を方程式 \(f(x)=0\) の異なる解とする。
すると \(\sg(\al)=\beta\) を満たす \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への唯一の同型写像 \(\sg\) が存在する。
[証明]
\(\bs{Q}(\al)\) の任意の元を \(a\)、\(\bs{Q}(\beta)\) の任意の元を \(b\) とする。単拡大体の基底の定理(33F)により、\(a,\:b\) は、
\(a=a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\:\:(a_i\in\bs{Q})\)
\(b=b_{n-1}\beta^{n-1}+\:\cd\:+b_2\beta^2+b_1\beta+b_0\:\:(b_i\in\bs{Q})\)
の形に一意に表される。ここで \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) への同型写像 \(\sg\) を、\(b=b_{n-1}\beta^{n-1}+\:\cd\:+b_2\beta^2+b_1\beta+b_0\:\:(b_i\in\bs{Q})\)
\(\begin{eqnarray}
&&\:\:\sg\:: &a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0\\
&&&\longmapsto\:a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
と定義する。\(a=\al\) の場合は、\(a_1=1,\:a_i=0\:\:(i=0,\:2\leq i\leq n-1)\) だから、\(\sg(\al)=\beta\) である。以下、この \(\sg\) が同型写像であることを証明する。定義により(51A)同型写像であることは加法と乗法を保存することを言えばよい。
\(\bs{Q}(\al)\) の任意の2つの元を \(s,\:t\) とし、
\(s=s_{n-1}\al^{n-1}+\:\cd\:+s_2\al^2+s_1\al+s_0\)
\(t=t_{n-1}\al^{n-1}+\:\cd\:+t_2\al^2+t_1\al+t_0\)
とする。また多項式 \(g(x)\) と \(h(x)\) を、\(t=t_{n-1}\al^{n-1}+\:\cd\:+t_2\al^2+t_1\al+t_0\)
\(g(x)=s_{n-1}x^{n-1}+\:\cd\:+s_2x^2+s_1x+s_0\)
\(h(x)=t_{n-1}x^{n-1}+\:\cd\:+t_2x^2+t_1x+t_0\)
と定義する。\(s_i,t_i\in\bs{Q}\) であり、\(s=g(\al),\:t=h(\al)\) である。また \(\sg\) の定義により \(\sg(s)=g(\beta),\:\sg(t)=h(\beta)\) である。\(h(x)=t_{n-1}x^{n-1}+\:\cd\:+t_2x^2+t_1x+t_0\)
\(p(x)=g(x)+h(x)\) とおくと、
\(p(\al)=g(\al)+h(\al)=s+t\)
である。また \(\sg\)の定義により、
\(\sg(p(\al))=p(\beta)\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\sg(s+t)&=\sg(p(\al))\\
&&&=p(\beta)\\
&&&=g(\beta)+h(\beta)\\
&&&=\sg(s)+\sg(t)\\
\end{eqnarray}\)
となり、加法は保存される。
\(g(x)h(x)\) を \(f(x)\) で割ったときの商を \(q(x)\)、余りを \(r(x)\) とすると、
\(g(x)h(x)=q(x)f(x)+r(x)\)
である。この式に \(x=\al,\:x=\beta\) のそれぞれを代入すると、\(f(\al)=0,\:f(\beta)=0\) なので、
\(g(\al)h(\al)=r(\al)\)
\(g(\beta)h(\beta)=r(\beta)\)
となる。すると、
\(\begin{eqnarray}
&&\:\:\sg(st)&=\sg(g(\al)h(\al))\\
&&&=\sg(r(\al))=r(\sg(\al))\\
&&&=r(\beta)\\
\end{eqnarray}\)
\(\begin{eqnarray}
&&\:\:\sg(s)\sg(t)&=\sg(g(\al))\sg(h(\al))\\
&&&=g(\sg(\al))h(\sg(\al))\\
&&&=g(\beta)h(\beta)\\
&&&=r(\beta)\\
\end{eqnarray}\)
であり、
\(\sg(st)=\sg(s)\sg(t)\)
となって乗法も保存されている。従って \(\sg\) は同型写像である。
逆に、\(\bs{Q}(\al)\) に作用する同型写像 \(\tau\) があったとする。同型写像は \(\al\) を共役な元に移すので、その移り先の元を \(\beta\)、つまり \(\tau(\al)=\beta\) とする。\(\bs{Q}(\al)\) の任意の元 \(a\) に \(\tau\) を作用させると、
\(\begin{eqnarray}
&&\:\:\tau(a)&=\tau(a_{n-1}\al^{n-1}+\:\cd\:+a_2\al^2+a_1\al+a_0)\\
&&&=a_{n-1}\tau(\al^{n-1})+\:\cd\:+a_2\tau(\al^2)+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\tau(\al)^{n-1}+\:\cd\:+a_2\tau(\al)^2+a_1\tau(\al)+a_0\\
&&&=a_{n-1}\beta^{n-1}+\:\cd\:+a_2\beta^2+a_1\beta+a_0\\
\end{eqnarray}\)
となるので、同型写像はこの式を満たさなければならない。従って、上で定義した \(\sg\) が \(\bs{Q}(\al)\) から \(\bs{Q}(\beta)\) の唯一の同型写像である。[証明終]
同型写像の存在(51F)を一般化すると、次のことが言えます。
単拡大体の同型写像は \(n\) 個
| (単拡大体の同型写像:51G) |
\(f(x)\) を \(\bs{Q}\) 上の \(n\)次既約多項式とする。\(f(x)=0\) の全ての解を \(\al_1=\al,\:\al_2,\:\cd\:,\al_n\) とする。このとき \(\bs{Q}(\al)\) に作用する同型写像は \(n\)個あり、それらは、
\(\sg_i(\al)=\al_i\) \((1\leq i\leq n)\)
で定められ、\(\sg_i\) は \(\bs{Q}(\al)\) から \(\bs{Q}(\al_i)\) への同型写像となる。
同型写像を別の視点で考えます。\(\bs{Q}\:\subset\:\bs{F}\:\subset\:\bs{K}\) といった体の拡大列があったとき、\(\bs{F}\) の同型写像と \(\bs{K}\) の同型写像には密接な関係があります。それが次の同型写像の延長の定理です。単拡大定理(32B)により、\(\bs{F}=\bs{Q}(\al)\)、\(\bs{K}=\bs{Q}(\al,\beta)\) としてよいので、その形を使います。
同型写像の延長
| (同型写像の延長:51H) |
\(\bs{Q}\) 上の \(n\)次既約多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の解の一つを \(\al\) とする。
\(\bs{\bs{Q}(\al)}\) 上の \(m\)次既約多項式を \(g(x)\) とし、方程式 \(g(x)=0\) の解の一つを \(\beta\) とする。また、\(\bs{Q}(\al)\) の同型写像の一つを \(\tau\) とする。
このとき、\(\tau\) は \(\bs{Q}(\al,\beta)\) の同型写像 \(\sg_j\) に延長できる。延長とは、\(\sg_j\) の作用を \(\bs{Q}(\al)\) に限定した写像の作用が \(\tau\) と一致することを言う。\(\tau\) を延長した同型写像 \(\sg_j\) は \(m\)個ある(\(0\leq j < m\))。
[証明]
\(\bs{Q}(\al)\) 上の \(m\)次既約多項式 \(g(x)\) を、
\(g(x)=x^m+a_1x^{m-1}+\cd+a_m\:\:(a_j\in\bs{Q}(\al))\)
とする。\(\beta\) は \(g(x)=0\) の解だから
\(g(\beta)=\beta^m+a_1\beta^{m-1}+\cd+a_m=0\)
である。また、多項式 \(\tau(g(x))\) を、
\(\tau(g(x))=x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_{m-1})x+\tau(a_m)\)
と定義し、方程式
\(\tau(g(x))=0\)
の解を \(t_j\:\:(0\leq j < m)\)とする。つまり \(\tau(g(t_j))=0\) である。
\(\bs{Q}(\al,\beta)\) は \(\bs{Q}(\al)\) 上の線形空間であり、単拡大体の基底の定理(33F)により、その基底を \(\{1,\:\beta,\:\beta^2,\:\cd\:\beta^{m-1}\}\) にとれるから、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) は、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表せる。そこで、\(\bs{Q}(\al,\beta)\) の元に作用する写像 \(\sg_j\) を
\(\sg_j(k)=\tau(b_0)+\tau(b_1)t_j+\tau(b_2)t_j^2+\cd+\tau(b_{m-1})t_j^{m-1}\)
と定義する。この定義における \(\sg_j\) は \(\bs{Q}(\al,\beta)\) の同型写像になる。同型写像になることは体の加算と乗算で示せればよい(51A)。\(\bs{Q}(\al,\beta)\) の2つの元を、
\(p=c_0+c_1\beta+c_2\beta^2\:+\cd+\:c_{m-1}\beta^{m-1}\:\:(c_j\in\:\bs{Q}(\al)\:)\)
\(q=d_0+d_1\beta+d_2\beta^2\:+\cd+\:d_{m-1}\beta^{m-1}\:\:(d_j\in\:\bs{Q}(\al)\:)\)
とし、2つの多項式を、
\(p(x)=c_0+c_1x+c_2x^2\:+\cd+\:c_{m-1}x^{m-1}\)
\(q(x)=d_0+d_1x+d_2x^2\:+\cd+\:d_{m-1}x^{m-1}\)
と定義する。加算で同型写像になるのは明白なので、乗算で同型写像になることを示す。
\(p(x)q(x)\) を \(g(x)\) で割ったときの商を \(t(x)\)、余りを \(r(x)\) とすると、
\(p(x)q(x)=t(x)g(x)+r(x)\)
と書ける。ここで \(s_j()\) は \(c_j,\:d_j\:\:(0\leq j\leq m-1)\)の有理式である。\(()\) の中を全部書くと \(s_j(c_0,c_1,\cd,c_{m-1},d_0,d_1,\cd,d_{m-1})\) という \(2m\)個の \(\bs{Q}(\al)\) の元の有理式を表わしていて、それを簡略表記している。| \(r(x)\) | \(\overset{\text{ }}{=}\) | \(s_0(c_j,d_j)+s_1(c_j,d_j)x+s_2(c_j,d_j)x^2+\cd+s_{m-1}(c_j,d_j)x^{m-1}\) |
すると \(g(\beta)=0\) だから、
| \(pq\) | \(\overset{\text{ }}{=}\) | \(p(\beta)q(\beta)\) | |
| \(\overset{\text{ }}{=}\) | \(r(\beta)\) | ||
| \(\overset{\text{ }}{=}\) | \(s_0(c_j,d_j)+\)\(s_1(c_j,d_j)\beta+\)\(s_2(c_j,d_j)\beta^2\:+\)\(\cd+\)\(s_{m-1}(c_j,d_j)\beta^{m-1}\) |
| \(\sg_j(pq)\) | \(\overset{\text{ }}{=}\) | \(\tau(s_0(c_j,d_j))+\)\(\tau(s_1(c_j,d_j))t_j+\)\(\tau(s_2(c_j,d_j))t_j^2+\)\(\cd+\)\(\tau(s_{m-1}(c_j,d_j))t_j^{m-1}\) |
\(\tau\) は \(\bs{Q}(\al)\) の同型写像だから、\(\bs{Q}(\al)\) の元の有理式である \(s_j(c_j,d_j)\) に作用させると、同型写像と有理式の順序交換の定理(51C)により、
\(\tau(s_j(c_j,d_j))=s_j(\tau(c_j),\tau(d_j))\)
となる。従って、
| \(\sg_j(pq)\) | \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))t_j\:+\)\(s_2(\tau(c_j),\tau(d_j))t_j^2+\)\(\cd+\)\(s_{m-1}(\tau(c_j),\tau(d_j))t_j^{m-1}\) |
\(p(x)\) の係数 \(c_j\) を \(\tau(c_j)\) で置き換え、\(q(x)\) の係数 \(d_j\) を \(\tau(d_j)\) で置き換えた2つの多項式を、
\(\tau(p(x))=\tau(c_0)+\tau(c_1)x+\tau(c_2)x^2+\cd+\tau(c_{m-1})x^{m-1}\)
\(\tau(q(x))=\tau(d_0)+\tau(d_1)x+\tau(d_2)x^2+\cd+\tau(d_{m-1})x^{m-1}\)
とする。
\(\tau(p(x))\tau(q(x))\)を\(\tau(g(x))\)で割ったときの商を\(\tau(t(x))\)、余りを\(\tau(r(x))\)とする。つまり、
\(\tau(p(x))\tau(q(x))=\tau(g(x))\tau(t(x))+\tau(r(x))\)
である。\(c_j\) と \(d_j\) の有理式、\(s_j(c_j,d_j)\) を使って \(\tau(r(x))\) を表すと、
| \(\tau(r(x))\) | \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))x+\)\(s_2(\tau(c_j),\tau(d_j))x^2\:+\)\(\cd+\)\(s_{m-1}(\tau(c_j),\tau(d_j))x^{m-1}\) |
| \(\sg_j(p)\) | \(\overset{\text{ }}{=}\) | \(\tau(c_0)+\)\(\tau(c_1)t_j+\)\(\tau(c_2)t_j^2+\)\(\cd+\)\(\tau(c_{m-1})t_j^{m-1}\) | |
| \(\overset{\text{ }}{=}\) | \(\tau(p(t_j))\) | ||
| \(\sg_j(q)\) | \(\overset{\text{ }}{=}\) | \(\tau(d_0)+\)\(\tau(d_1)t_j+\)\(\tau(d_2)t_j^2+\)\(\cd+\)\(\tau(d_{m-1})t_j^{m-1}\) | |
| \(\overset{\text{ }}{=}\) | \(\tau(q(t_j))\) |
\(\sg_j(p)\sg_j(q)\)
となり、\(\sg_j\) は同型写像の定義を満たしている。| \(\overset{\text{ }}{=}\) | \(\tau(p(t_j))\tau(q(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(\tau(f(t_j))\tau(t(t_j))+\tau(r(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(\tau(r(t_j))\) | ||
| \(\overset{\text{ }}{=}\) | \(s_0(\tau(c_j),\tau(d_j))+\)\(s_1(\tau(c_j),\tau(d_j))t_j+\)\(s_2(\tau(c_j),\tau(d_j))t_j^2+\)\(\cd+\)\(s_{n-1}(\tau(c_j),\tau(d_j))t_j^{m-1}\) | ||
| \(\overset{\text{ }}{=}\) | \(\sg_j(pq)\) |
また、\(\bs{Q}(\al,\beta)\) の任意の元 \(k\) を、
\(k=b_0+b_1\beta+b_2\beta^2\:+\cd+\:b_{n-1}\beta^{m-1}\:\:(b_j\in\bs{Q}(\al))\)
と表したとき、\(k\) が \(\bs{Q}(\al)\) の元だとすると \(k=b_0\:\:(b_0\in\bs{Q}(\al))\)、\(b_j=0\:\:(1\leq j < m)\) なので、
\(\sg_j(k)=\tau(b_0)=\tau(k)\)
となり、\(\sg_j\) の \(\bs{Q}(\al)\) の元に対する作用は \(\tau\) と一致する。従って、
\(\sg_j\)は、その作用を \(\bs{Q}(\al)\) に限定したとき \(\tau\) と一致する \(\bs{Q}(\al,\beta)\) の同型写像
であり、\(\bs{Q}(\al)\) の同型写像 \(\tau\) の延長である。\(\sg_j\) の定義式、
\(\sg_j(k)=\tau(b_0)+\tau(b_1)t_j+\tau(b_2)t_j^2+\cd+\tau(b_{m-1})t_j^{m-1}\)
における \(t_j\) は、 \(\bs{Q}(\al)\) 上の \(m\)次方程式、
\(x^m+\tau(a_1)x^{m-1}+\cd+\tau(a_m)=0\)
の解であった。従って \(t_j\) の選択肢は \(m\) 個あり、\(\bs{Q}(\al)\) の同型写像 \(\tau\) の延長は \(m\) 個ある。一方、\(\al\) は \(\bs{Q}\) 上の \(n\)次既約多項式 \(f(x)\) の解の一つだから、\(\bs{Q}(\al)\) の同型写像 \(\tau\) は \(n\)個ある。これを \(\tau_i\:\:(0\leq i < n)\) と書くと、それぞれの \(\tau_i\) に対して同型写像の拡張 \(\sg_{ij}\:\:(0\leq i < n,\:0\leq j < m)\) がある。従って \(\bs{Q}(\al,\beta)\) の 同型写像 \(\sg_{ij}\) は \(nm\)個ある。[証明終]
5.2 ガロア拡大とガロア群
ガロア拡大
| (ガロア拡大:52A) |
ガロア拡大は次のように定義される。この2つの定義は同値である。
| (最小分解体定義)体 \(\bs{F}\) 上の多項式を \(f(x)\) とし、方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\) とするとき、\(\bs{L}/\bs{F}\) をガロア拡大という。 | |
| (自己同型定義)体 \(\bs{F}\) の代数拡大体 \(\bs{K}\) があったとき、\(\bs{F}\) の元を不動にする \(\bs{K}\) の同型写像がすべて自己同型写像になるとき、\(\bs{K}/\bs{F}\) をガロア拡大という。 |
\(\bs{K}/\bs{F}\) がガロア拡大のとき、\(\bs{\bs{F}}\) を不変にする \(\bs{K}\) の自己同型写像の集合は群になる。これをガロア群といい、\(\mr{Gal}(\bs{K}/\bs{F})\) で表す。
[① \(\bs{\Rightarrow}\) ②の証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。その解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{F}\) の元を不変にする \(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。
一方、\(\bs{L}\) は \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{F}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式(係数は \(\bs{F}\) の元)で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は \(\bs{F}\) の元)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させる。\(\bs{F}\) 係数の有理式と \(\bs{F}\) を不変にする同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移す(51D)から、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。
[② \(\bs{\Rightarrow}\) ①の証明]
単拡大定理(32B)により、\(\bs{K}\) は、\(\bs{K}\) の元 \(\theta\) を用いて \(\bs{K}=\bs{F}(\theta)\) と表すことができる。\(\theta\) の \(\bs{F}\) 上の最小多項式を \(f(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(f(x)\) は既約多項式である。また既約多項式の定理3(31G)により、方程式 \(f(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。
\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{F}\) の元を不変にするから、\(\bs{L}=\bs{F}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、\(\bs{F}\) 上の方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する。\(\bs{F}\) の元を不変にする \(\bs{K}\) 上の同型写像は自己同型写像なので、\(\sg_i(\theta)=\theta_i\) は全て \(\bs{K}\) の元である。従って \(\bs{K}\) は \(\bs{F}\) 上の既約多項式 \(f(x)\) の解 \(\theta_i\) を用いて、
\(\begin{eqnarray}
&&\:\:\bs{K}&=\bs{F}(\theta)\\
&&&=\bs{F}(\theta_1,\:\theta_2,\:\cd,\:\theta_m)\\
\end{eqnarray}\)
と表される。\(\bs{K}\) は \(\bs{F}\) 上の既約多項式の最小分解体である。[証明終]
① の定義は、方程式の解のありようを議論するガロア理論にとっては "ノーマルな" 定義のように見えます。しかし ② のように方程式という言葉を全く使わない定義もメリットがあります。たとえば「次数が違う2つの方程式の解によるガロア拡大が同じ」ということは、いくらでもありうるからです。
また、ガロア拡大は次のような定義もできます。
| (正規拡大定義)体 \(\bs{F}\) の代数拡大体 \(\bs{K}\) があったとき、\(\bs{K}\) の任意の元の \(\bs{F}\) 上の最小多項式を \(f(x)\) とする。\(f(x)=0\) のすべての解が \(\bs{K}\) の元のとき、\(\bs{K}\) を \(\bs{F}\) の正規拡大と言う。ガロア拡大とは正規拡大のことである。 |
方程式という言葉は使っていますが、拡大体から始まる定義です。言い換えると、\(\bs{K}\) がガロア拡大体のとき \(\bs{K}\) の任意の元に共役な元は \(\bs{K}\) に含まれるということです。
このように、互いに同値である多種の定義ができることがガロア理論の分かりにくいところですが、逆に「それだけ豊かな数学的内容を含んだ理論」とも言えるでしょう。
最小分解体の次数=ガロア群の位数
| (次数と位数の同一性:52B) |
\(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体を \(\bs{L}\)、ガロア群を \(G\) とするとき、\([\:\bs{L}\::\:\bs{Q}\:]=|G|\) である。
[証明]
単拡大定理(32B)により、\(\bs{L}\) は、\(\bs{L}\) の元 \(\theta\) を用いて \(\bs{L}=\bs{Q}(\theta)\) と表すことができる。\(\theta\) の \(\bs{Q}\) 上の最小多項式を \(g(x)\) とし、その次数を \(m\) とする。最小多項式は既約多項式の定理(31I)により、\(g(x)\) は既約多項式である。また、既約多項式の定理3(31G)により、方程式 \(g(x)=0\) の \(m\)個の解は全て異なっている。解の一つは \(\theta\) なので、\(m\)個の解を、
\(\theta=\theta_1,\:\theta_2,\:\cd,\:\theta_m\)
とする。ここで、\(\theta_i\:\:(2\leq i\leq m)\) が \(\bs{L}\) の元かどうかは(この段階では)分からない。
\(\bs{L}\) 上の同型写像の一つを \(\sg\) とする。\(\sg\) は \(\bs{Q}\) の元を不変にするから、\(\bs{L}=\bs{Q}(\theta)\) においては \(\sg(\theta)\) を決めることによって \(\sg\) が定義される。その同型写像は、方程式の解を共役な解に移す(51D)。そこで、\(m\)個の同型写像を、
\(\sg_i(\theta)=\theta_i\)
と定義する(\(\sg_1=e\))。単拡大体 \(\bs{Q}(\theta)\) に作用する同型写像は \(m\)個だから(51G)、これが同型写像のすべてである。
一方、\(\bs{L}\) は \(\bs{Q}\) 上の方程式 \(f(x)=0\) の最小分解体であった。\(f(x)=0\) の解を、
\(\al_1,\:\al_2,\:\cd,\:\al_n\)
の \(n\)個とする。そうすると、
\(\bs{L}=\bs{Q}(\al_1,\:\al_2,\:\cd,\:\al_n)\)
である。\(\bs{L}\) の任意の元 は、\(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表せる。\(\theta\) を有理式で表す式を、\(n\)変数の有理式 \(h(x_1,x_2,\cd,x_n)\) を使って、
\(\theta=h(\al_1,\:\al_2,\:\cd,\:\al_n)\)
と表したとする。\(h(x_i)\)は、\(n\)変数の多項式(係数は有理数)を \(s(x_i)\) と \(t(x_i)\) として、
\(h(\al_1,\:\al_2,\:\cd,\:\al_n)=\dfrac{s(\al_1,\:\al_2,\:\cd,\:\al_n)}{t(\al_1,\:\al_2,\:\cd,\:\al_n)}\)
である。
\(\theta\) に同型写像 \(\sg_i\) を作用させると、有理式と同型写像の演算順序は交換可能(51C)だから、
\(\begin{eqnarray}
&&\:\:\sg_i(\theta)&=\sg_i(h(\al_1,\:\al_2,\:\cd,\:\al_n))\\
&&&=h(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n))\\
\end{eqnarray}\)
となる。同型写像は方程式の解を共役な解に移すから(51D)、\(\sg_i(\al_1),\:\sg_i(\al_2),\:\cd,\:\sg_i(\al_n)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) を入れ替えたものである(51E)。つまり \(\sg_i(\theta)\) は \(\al_1,\:\al_2,\:\cd,\:\al_n\) の有理式で表現される。従って、
\(\sg_i(\theta)\:\in\:\bs{L}\)
である。\(\sg_i(\theta)=\theta_i\) と定義したので、
\(\theta_i\:\in\:\bs{L}\)
である。つまり \(m\)個の同型写像 \(\sg_i\:\:(1\leq i\leq m)\) は全て \(\bs{L}\) の自己同型写像である。以上により、
\(\mr{Gal}(\bs{L}/\bs{Q})=\{\sg_1,\:\sg_2,\:\cd,\:\sg_m\}\)
であり、\(|G|=m\) である。
\(\theta\) の \(\bs{Q}\) 上の最小多項式(=既約多項式)の次数が \(m\) だから、単拡大体の基底の定理(33F)によって、最小分解体 \(\bs{L}=\bs{Q}(\theta)\) は \(\bs{Q}\) の \(m\)次拡大体であり、
\([\:\bs{L}\::\:\bs{Q}\:]=|G|\)
である。[証明終]
この定理では \(\bs{Q}\) としましたが、任意の代数拡大体 \(\bs{F}\) としても成り立ちます。また、最小分解体はガロア拡大体です。従って、最も一般的に言うと次のようになります。
\(\bs{F}\) を代数拡大体とし、\(\bs{F}\) のガロア拡大を \(\bs{L}\) とする。\(\bs{L}\) のガロア群の位数は \(\bs{F}\) から \(\bs{L}\) への拡大次数に等しい。つまり、
\([\:\bs{L}\::\:\bs{F}\:]=|\mr{Gal}(\bs{L}/\bs{F})|\)
である。
中間体
| (中間体からのガロア拡大:52C) |
\(\bs{K}\) を \(\bs{F}\) のガロア拡大体とし、\(\bs{M}\) を \(\bs{F}\subset\bs{M}\subset\bs{K}\) である任意の体(=中間体)とするとき、\(\bs{K}\) は \(\bs{M}\) のガロア拡大体でもある。
[証明]
最小分解体定義による
\(\bs{K}\) が \(\bs{F}\) 上の方程式 \(f(x)=0\) の最小分解体であるとする。この方程式の解を \(\al_1,\:\al_2,\:\cd\:\al_n\) とすると、\(\bs{K}=\bs{F}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(\bs{F}\subset\bs{M}\subset\bs{L}\) なので、
\(\bs{F}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{M}(\al_1,\:\cd\:\al_n)\:\subset\:\bs{K}(\al_1,\:\cd\:\al_n)=\bs{K}\)
となるが、すなわち、
\(\bs{F}\:\subset\:\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\:\subset\:\bs{K}\)
であり、\(\bs{K}=\bs{M}(\al_1,\:\al_2,\:\cd\:\al_n)\) である。\(f(x)=0\) は \(\bs{M}\) 上の方程式でもあるので、\(\bs{K}\) は \(\bs{M}\) 上の方程式の最小分解体であり、\(\bs{M}\) のガロア拡大体である。
自己同型定義による
\(\bs{L}\) の同型写像のうち、\(\bs{M}\) の元を固定する任意の同型写像を \(\sg\) とする。そうすると \(\sg\) は \(\bs{M}\) の部分集合である \(\bs{F}\) の元も固定する。\(\bs{L}\) は \(\bs{F}\) のガロア拡大体なので、\(\bs{F}\) の元を固定する \(\bs{L}\) の同型写像は自己同型写像である。従って \(\sg\) も自己同型写像であり、\(\bs{L}\) は \(\bs{M}\) のガロア拡大体である。[証明終]
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列があったとき、\(\bs{F}\subset\bs{K}\) がガロア拡大だと上の定理(52C)によって \(\bs{M}\subset\bs{K}\) もガロア拡大です。しかし、\(\bs{F}\subset\bs{M}\) がガロア拡大になるとは限りません。\(\bs{F}\subset\bs{M}\) がガロア拡大になるためには条件が必要で、その条件が満たされば、\(\bs{F}\subset\bs{M}\subset\bs{K}\) は「ガロア拡大の連鎖」になり、そのことが方程式の可解性と結びつきます。それが次の節の大きな主題です。
5.3 ガロア対応
固定体と固定群
| (固定体と固定群:53A) |
体 \(\bs{F}\) 上の方程式の最小分解体(=ガロア拡大体)を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる。これを \(\bs{K}\) における \(H\) の固定体といい、\(\bs{K}(H)\) で表す(または \(\bs{K}^H\))。
また \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる。これを \(G\) における \(\bs{M}\) の固定群と呼び、\(G(\bs{M})\) で表す(または \(G^M\))。
[証明]
固定体と固定群の定義において、
| \(G\) の部分群 \(H\) によって不変な \(\bs{K}\) の元の集合 \(\bs{M}\) は体になる | |
| \(\bs{K}\) の中間体 \(\bs{M}\) のすべての元を不変にする \(G\) の部分集合 \(H\) は群になる |
の2点を証明する。
① の証明
\(\bs{M}\) が体であることを証明するには、四則演算で閉じていることを言えばよい(1.2 体)。\(\bs{M}\) の任意の2つの元を \(x,\:y\) とし、\(H\) の任意の元を \(\sg\) とする。\(x,\:y\) は \(\bs{K}\) の元でもあるから、
\(x+y\in\bs{K}\)
である。\(H\) の元 \(\sg\) は \(G\) の元でもあるから \(\sg(x+y)\) が定義できる。\(x,\:y\) は \(\bs{M}\) の元だから、\(H\) の元である \(\sg\) を作用させても不変であり、
\(\sg(x)=x\)
\(\sg(y)=y\)
である。すると、
\(\sg(x+y)=\sg(x)+\sg(y)=x+y\)
となって、\(x+y\) は \(\sg\) によって不変であり、
\(x+y\in\bs{M}\)
である。以上のことが加減乗除のすべてで成り立つことは明白だから、\(\bs{M}\) は四則演算で閉じていて、体である。
② の証明
\(\bs{M}\) の任意の元を \(x\)、\(H\) の2つの元を \(\sg,\:\tau\) とする。
\(\sg(x)=x\)
\(\tau(x)=x\)
である。すると、
\(\sg\tau(x)=\sg(\tau(x))=\sg(x)=x\)
となり、\(\sg\tau\in H\) となって、\(H\) の元は群演算で閉じている。
また \(H\) の元はもともと \(G\) の元なので、結合法則も成り立つ。\(G\) の単位元を \(e\) とすると、\(e(x)=x\) なので \(e\in H\) である。
さらに \(\sg\) は \(G\) の元なので、\(G\) の中に \(\sg^{-1}\) が存在する。すると、\(\sg(x)=x\) の両辺に左から \(\sg^{-1}\) をかけると、
\(\sg^{-1}\sg(x)=\sg^{-1}(x)\)
\(x=\sg^{-1}(x)\)
となり、
\(\sg^{-1}\in H\)
である。\(H\) は演算で閉じていて、結合法則が成り立ち、単位元と逆元が存在するので、群の定義(22A)を満たしている。[証明終]
以上の固定体と固定群の概念を用いると、次のガロア対応の定理が成り立ちます。以降の論証の基礎となる定理です。
ガロア対応の定理
| (ガロア対応:53B) |
\(\bs{F}\) のガロア拡大体を \(\bs{K}\) とし、ガロア群を \(G\) とする。\(G\) の任意の部分群を \(H\) とし、\(H\) による \(\bs{K}\) の固定体 \(\bs{K}(H)\) を \(\bs{M}\) とする(次式)。
\(\begin{eqnarray}
&&G\:\sp\:H &\sp\:\{e\}\\
&&\bs{F}\:\subset\:\bs{K}(H)=\bs{M} &\subset\:\bs{K}\\
\end{eqnarray}\)
\(\bs{M}\)の固定群を \(G(\bs{M})\) とする(次式)。ガロア群の定義により \(G(\bs{M})=\mr{Gal}(\bs{K}/\bs{M})\) である。
\(\begin{eqnarray}
&&\bs{F}\:\subset\:\bs{M} &\subset\:\bs{K}\\
&&G\:\sp\:G(\bs{M}) &\sp\:\{e\}\\
\end{eqnarray}\)
このとき、
\(G(\bs{M})=H\)
つまり、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
が成り立つ。
[証明]
\(G\) の任意の部分群である \(H\) は \(\bs{K}\) の部分集合 \(\bs{M}\) を固定する。一方、\(G(\bs{M})\) は \(\bs{M}\) を固定する \(G\) のすべての元の集合で、それが部分群になっている。従って、\(G(\bs{M})\) は \(H\) を含む。つまり
\(H\:\subset\:G(\bs{M})\)
であり、群位数は、
\(|H|\:\leq\:|G(\bs{M})|\)
である。 \((\br{A})\)
\(\bs{K}/\bs{F}\) はガロア拡大であり、\(\bs{M}\) はその中間体だから、中間体からのガロア拡大の定理(52C)によって、\(\bs{K}/\bs{M}\) はガロア拡大である。また、すべての代数拡大体は単拡大体だから(32B)、\(\bs{K}\) の元 \(\theta\) があって \(\bs{K}=\bs{F}(\theta)\) と表せる。これは、\(\bs{K}=\bs{M}(\theta)\) ということでもある。
\(H\) の \(|H|\) 個の元を \(\sg_i\:\:(1\leq i\leq|H|)\) とし、多項式
\(f(x)=\displaystyle\prod_{i=1}^{|H|}(x-\sg_i(\theta))\)
を考える。この多項式の次数は \(|H|\) である。\(\sg_i(\theta)\) は \(\theta\) の共役な元のどれかである。
\(f(x)\) を展開すると、その係数は \(\sg_i(\theta)\:\:(1\leq i\leq|H|)\) の対称式になる。また、\(\sg_i(\theta)\) に \(H\) の任意の元 \(\sg_k\) を作用させても、\(\sg_i\) は部分群だから演算で閉じており、\(\sg_i(\theta)\) を入れ替えるだけである(51E)。従って \(\sg_i(\theta)\) の対称式に \(\sg_k\) を作用させても不変である。つまり、\(H\) の任意の元は \(f(x)\) の係数を固定する。ということは、\(\bs{M}\) の定義(= \(H\) による \(\bs{K}\) の固定体が \(\bs{M}\))によって、\(f(x)\) の係数は \(\bs{M}\) の元である。
\(\sg_i\) は群だから単位元を含む。従って、
\(f(\theta)=\displaystyle\prod_{i=1}^{|H|}(\theta-\sg_i(\theta))=0\)
となり、\(\bs{\theta}\) は \(\bs{\bs{M}}\) 上の \(\bs{|H|}\) 次方程式 \(\bs{f(x)=0}\) の解の一つである。ゆえに \(\bs{M}\) から単拡大体 \(\bs{K}=\bs{M}(\theta)\) への拡大次数は、\(f(x)\) が \(\bs{M}\) 上の既約多項式なら単拡大体の基底の定理(33F)により \(|H|\) であり、一般には \(|H|\) 以下である。つまり、
\([\:\bs{K}\::\:\bs{M}\:]\leq|H|\)
である。次数と位数の同一性(52B)によると、拡大次数 \([\:\bs{K}\::\:\bs{M}\:]\) は、ガロア群 \(\mr{Gal}(\bs{K}/\bs{M})\) の位数に等しい。従って、
\(|\mr{Gal}(\bs{K}/\bs{M})|\leq|H|\)
\(|G(\bs{M})|\leq|H|\)
となる。\((\br{A})\) と \((\br{B})\) により、 \((\br{B})\)
\(|G(\bs{M})|=|H|\)
であり、\(G(\bs{M})\:\subset\:H\) と合わせると、
\(G(\bs{M})=H\)
となる。従って、
\(\begin{eqnarray}
&&\:\:\mr{Gal}(\bs{K}/\bs{M})&=H \\
&&\:\:\bs{K}(G(\bs{M}))&=\bs{M}\\
\end{eqnarray}\)
である。[証明終]
証明の中に対称式という言葉が出てきます。対称式とは、
変数の任意の入れ替えで不変な多項式
です。2変数 \(x,\:y\) だと、
\(x+y,\:xy\)(ここまでが基本対称式)、\(x^2+y^2,\:\:(x-y)^2\)
などです。3変数 \(x,\:y\:,z\) だと、
\(x+y+z,\:xy+yz+zx,\:xyz\)(基本対称式)、\(((x-y)(y-z)(z-x))^2\)
などです。
対称式でよく出てくるのは、方程式の根と係数の関係です。たとえば、\(\bs{Q}\) 上の既約な3次多項式を \(f(x)\) をとし、\(f(x)=0\) の解を \(\al,\beta,\gamma\) とします。
\(\begin{eqnarray}
&&\:\:f(x)&=x^3-ax^2+bx-c\\
&&&=(x-\al)(x-\beta)(x-\gamma)\\
\end{eqnarray}\)
と書くと、
\(a=\al+\beta+\gamma\)
\(b=\al\beta+\beta\gamma+\gamma\al\)
\(c=\al\beta\gamma\)
と、係数が解の基本対称式で表現されます。
また ガロア群 \(\mr{Gal}(\bs{Q}(\al,\beta,\gamma)/\bs{Q})\) の任意の元 を \(\sg\) とします。\(\al,\beta,\gamma\) の任意の対称式を \(S(\al,\beta,\gamma)\in\bs{Q}(\al,\beta,\gamma)\) とすると、
\(\sg(S(\al,\beta,\gamma))=S(\al,\beta,\gamma)\)
です。ガロア群の元は自己同型写像であり、方程式の解を解の一つに置き換えるので、これが成り立ちます。自己同型写像を作用させて不変なのは有理数です(51A)。従って、\(S(\al,\beta,\gamma)\) は有理数です。もちろん \(f(x)\) が \(n\)次多項式であっても成り立ちます。
\(\bs{F}\subset\bs{M}\subset\bs{K}\) という体の拡大列で \(\bs{F}\subset\bs{K}\) がガロア拡大のとき、\(\bs{M}\subset\bs{K}\) は自動的にガロア拡大ですが(52C)、ある条件があれば \(\bs{F}\subset\bs{M}\) もガロア拡大になって、\(\bs{F}\subset\bs{M}\subset\bs{K}\) が「ガロア拡大の連鎖」になります。その条件は「ガロア対応」と「正規部分群」の概念を用いて示されます。それが次の正規性定理です。次では \(\bs{Q}\) から始まる体の拡大列で記述しています。
正規性定理
| (正規性定理:53C) |
\(\bs{Q}\) のガロア拡大を \(\bs{K}\) とし、\(\mr{Gal}(\bs{K}/\bs{Q})=G\) とする。\(\bs{K}\) の中間体 \(\bs{M}\) と \(G\) の部分群 \(H\) がガロア対応になっているとする。このとき
| \(\bs{M}/\bs{Q}\) がガロア拡大である | |
| \(H\)が\(G\)の正規部分群である |
の2つは同値である。また、これが成り立つとき、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
という群の同型が成り立つ。
[① \(\bs{\Rightarrow}\) ②の証明]
\(G\) の任意の元を \(g\) とし、\(\bs{M}\) の任意の元を \(m\) とする。
\(\bs{M}\) が \(\bs{Q}\) のガロア拡大なので、\(m\) の共役な元は \(\bs{M}\) に含まれる。\(g\) は同型写像だから、\(\bs{K}\) の元を共役な元に移す(51D)。つまり、\(g\) を \(m\) に作用させると \(m\) と共役な元に移すことになり、 \(g(m)\in\bs{M}\) である。また \(g^{-1}\) も \(G\) の元だから \(g^{-1}(m)\in\bs{M}\) である。
\(H\) の任意の元を \(h\) とする。\(H\) は \(\bs{M}\) とガロア対応をしているから、\(h\) は \(\bs{M}\) の元を不動にする。ゆえに、
\(hg^{-1}(m)=g^{-1}(m)\)
である。従って、
\(ghg^{-1}(m)=gg^{-1}(m)=m\)
となり、\(ghg^{-1}\) は \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(gHg^{-1}\:\subset\:H\)
\(gH\:\subset\:Hg\)
が成り立つ。 \((\br{C})\)
また、\(g(m)\) も \(\bs{M}\) の元なので、
\(hg(m)=g(m)\)
である。従って、
\(g^{-1}hg(m)=g^{-1}g(m)=m\)
となり、\(g^{-1}hg\) も \(\bs{M}\) の元を不動にするから \(H\) の元である。そうすると、
\(g^{-1}Hg\:\subset\:H\)
\(Hg\:\subset\:gH\)
が成り立つ。\((\br{C})\) と \((\br{D})\) により、 \((\br{D})\)
\(gH=Hg\)
となって、左剰余類と右剰余類が一致するから、\(H\) は \(G\) の正規部分群である。
[② \(\bs{\Rightarrow}\) ①の証明]
\(\bs{M}\) の任意の元を \(m\) とする。同型写像の延長の定理(51H)により、\(\bs{M}\) の同型写像 \(s\) は \(\bs{K}\) の同型写像 \(g\) に延長できる。つまり、\(g\) を \(\bs{M}\) の元に限定して作用させたとき \(g(m)=s(m)\) となる \(g\) がある。
\(H\) の任意の元を \(h\) とすると、\(h\) は正規部分群の元なので、
\(g^{-1}hg\:\in\:H\)
である。従って、
\(g^{-1}hg(m)=m\)
\(hg(m)=g(m)\)
となり、\(g(m)\) は \(H\) の任意の元で不動である。
ガロア対応の原理により \(\bs{K}(H)=\bs{M}\) なので、
\(g(m)\:\in\:\bs{M}\)
となり、\(g(m)\) は \(H\) の固定体 \(\bs{M}\) の元である。
\(\bs{M}\)の元に \(g\) を作用させるときは \(g(m)\) は \(s(m)\) そのものなので、
\(s(m)\:\in\:\bs{M}\)
となる。
以上により、\(\bs{M}\) の同型写像による \(m\) の移り先(= \(m\) と共役な元)は \(\bs{M}\) に含まれることになり、\(\bs{M}/\bs{Q}\) はガロア拡大である。[証明終]
[\(\bs{\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H}\) の証明]
同型写像の延長の定理(51H)の証明で示したように、\(\bs{M}\) の同型写像 \(s\) を \(\bs{K}\) の同型写像に延長する可能性は複数ある。\(g_1\) と \(g_2\) を \(s\) の2つの延長とし、\(\bs{M}\)の元を \(m\) とする。\(g_1,\:g_2\) は、\(\bs{M}\) に限定して適用すると \(s\) に等しいから、
\(g_1(m)=s(m)\)
\(g_2(m)=s(m)\)
が成り立つ。
\(g_1^{-1}g_2\) を \(m\) に作用させると
\(\begin{eqnarray}
&&\:\:g_1^{-1}g_2(m)&=g_1^{-1}(s(m))\\
&&&=g_1^{-1}(g_1(m))=m\\
\end{eqnarray}\)
となり、\(g_1^{-1}g_2\) は \(\bs{M}\) の元を不動にする。よって、
\(g_1^{-1}g_2\in\:H\)
\(g_2\in\:g_1H\)
である。
つまり、\(g_2\) は \(H\) の剰余類の一つの集合 \(g_1H\) に入る。以上で、\(\bs{M}\) の同型写像 \(s\) は、同型写像の延長を通して 剰余類 \(G/H\) の一つを定めることが分かる。
逆に \(g_1\) と \(g_2\) が 剰余類 \(G/H\) の同じ集合に属すると、
\(g_2\in\:g_1H\)
\(g_1^{-1}g_2\in\:H\)
\(g_1^{-1}g_2(m)=m\)
\(g_2(m)=g_1(m)\)
となり、\(g_1\) と \(g_2\) は \(\bs{M}\) 上で全く同じ作用をする。従って、\(\bs{M}\) 上で \(g_1,\:g_2\) と同じ作用をする \(\mr{Gal}(\bs{M}/\bs{Q})\) の元 \(s\) を定められる。つまり、剰余類 \(G/H\) の一つの集合が \(\mr{Gal}(\bs{M}/\bs{Q})\) の元を一つ定める。
従って、
\(\mr{Gal}(\bs{M}/\bs{Q})\:\cong\:G/H\)
である。[証明終]
「5.ガロア群とガロア対応」終わり
(次回に続く)
(次回に続く)
2023-04-01 08:44
nice!(0)



