No.244 - ポロック作品に潜むフラクタル

No.243「視覚心理学が明かす名画の秘密」で、三浦佳世氏の同名の著書の "さわり" を紹介したのですが、その中で、ジャクソン・ポロックのいわゆる "アクション・ペインティング"（ = ドリップ・ペインティング）がフラクタル構造を持っているとありました。

		日経サイエンス （2003年3月号）

実はこのことは 2002年の「Scientific American」誌で論文が発表されていて、その日本語訳が「日経サイエンス 2003年3月号」に掲載されました。おそらく三浦氏もこの論文を参照して「視覚心理学が明かす名画の秘密」のポロックの章を書いたのだと思います。

今回はその論文を紹介したいと思います。リチャード P. テイラー「ポロックの抽象画にひそむフラクタル」です。筆者は米・オレゴン大学の物理学の教授で、オーストラリアのニューサウスウェールズ大学の物性物理学科長だった時に、ポロックの抽象画に潜むフラクタルに気づいて謎解きを始めました。

---

アートかデタラメか

---

テイラー教授の論文はまず、ジャクソン・ポロックの代表作である『Blue Poles : No.11, 1952』の話から始まります。

ジャクソン・ポロック（Jackson Pollock, 1912 ～ 1956）は米国の美術史を代表する抽象表現主義の画家だ。彼が傑作『Blue Poles : No.11, 1952』の制作に取りかかったのは、ある３月の嵐の夜だった。すきま風が吹き込む納屋のようなアトリエで、酒によってやけになっていた彼は床に大きなカンバスを広げた。木の棒を使い、古ぼけた缶に入った家庭用ペンキをカンバスにたらした。 もっとも、絵の具をたらす「ドリップペインティング」の試みは、この時が最初というわけではなかった。水平に置いたカンバスにペイントを連続的に注ぐという斬新な手法をポロックは開発した。これにより、絵筆で描いた途切れ途切れの線とは異なり、独特の連続した軌跡がカンバスに残る。 一見すると単純このうえないこの画法について、美術界の評価は真っぷたつに割れた。この素朴な画法は非凡な才能の発露だったのか、それともポロックは美術界の伝統をあざ笑うただの酔っぱらいにすぎなかったのか？ リチャード P. テイラー（オレゴン大学） 『ポロックの抽象画にひそむフラクタル』 （日経サイエンス 2003年3月号）

	Jackson Pollock（1912 - 1956） 「Blue Poles : No.11, 1952」 （オーストラリア国立美術館） ポロックの代表作で、210cm×486.8cmの作品。絵の具を何度も重ねて垂らし、複雑なパターンを描き出している。この作品の制作期間は６ヶ月に及んだ。

---

テイラー教授の発見

---

物理学者であるテイラー教授は、趣味で抽象画を描いていました。そして何と、英国のマンチェスター美術学校に入学して絵の勉強を始め、そこで偶然にもポロックの作品がもつ "ある種の規則性" に気づきました。この論文の一番おもしろいところは、この "気づき" の経緯かも知れません。

私は以前からポロック作品に興味を持ち続けていた。私自身、物理学者としての生活の傍ら、抽象画を描いていたからだ。そんなわけで、1994年に私は科学者としての仕事をひとまずやめ、絵描きに専念する決心をした。ニューサウスウェールズ大学物理学科を辞し、英国のマンチェスター美術学校に進んだ。画家になるべく、いちかばちかの挑戦に出たわけだ。 寒さの厳しい2月、美術学校は私たち学生を英国北部ヨークシャー地方の荒野に追い出し、底で見たものを１週間の滞在中に風景画に仕上げるという課題を与えた。しかし、猛烈な吹雪のために写生は不可能になり、一行は宿に足止めを食らった。そこで私たちは、自分たちに代わって自然そのものに絵を描かせようというアイデアを思いついた。 このアイデアを実行に移すため、私たちは強風で折れた木の枝を集め、巨大な構造物をこしらえた。その一部は大きな帆のような役割を果たし、周囲は渦巻く風を受けて動く。この動きが構造物の他の部分へと伝わり、そこに固定してある絵の具入りの容器を動かす。地面に広げたカンバスに絵の具がしたたり落ち、風に応じたパターンを描き出す仕組みだ。 再び嵐が近づいてきたので私たちは室内に退却し、一晩でどんな絵が出来上がるかを待つことにした。翌朝、嵐が過ぎ去り、１枚の絵が残された。驚いたことに、それがポロック作品に実によく似ていたのだ。 「同上」

---

カオスとフラクタル

---

物理学者（物性物理）であるテイラー教授は、風の力で木の枝が描き出したパターンが全くのデタラメではないことを知っていました。その背景にあるのが1960年代から発達した「カオス理論」であり、そこから派生した「フラクタル」です。

1960年代、天候などの自然現象が時とともにどう変化するかについて科学的な考察が進んだ。その結果、こうした自然現象は決してデタラメではないことがわかった。非常に微妙な秩序が背景に潜んでいるのだ。こうした性質は「カオス」と名づけられ、カオス理論という新しい科学が生まれた。 一方、1970年代になると、こうしたカオス的過程から生まれる図形に関して、新しい幾何学が生まれた。発見者のマンデルブロ（Benoit Mandelbrot）が「フラクタル」と名づけたこの図形は、普通のユークリッド図形とはまったく違う。人工的に引いた直線はギザギザのない滑らかな線だが、フラクタルな図形は細部を拡大すると似たようなパターンが繰り返し出現する。非常に複雑なパターンが集まって、図形全体を作り出しているのだ。 木の枝で作った装置が描き出した絵を見て、私はピンときた。一見すると不規則に見えるポロック作品にも微妙な秩序が隠されており、フラクタルになっているのではないか？ 「同上」

フラクタル図形を特徴づけるのは "自己相似性" です。部分を拡大すると全体とよく似た図形、ないしは全体と相似形の図形が現れる。この "自己相似性" には「厳密な自己相似性」と「統計的な自己相似性」があります。

下の左の図はコンピュータで描いた木ですが、細部を拡大すると厳密に全体と相似形の図が現れます。一方、右の図は実際の木で、厳密な自己相似性ではなく、同じ統計的性質をもつパターンが繰り返し現れます。

	厳密な自己相似性を示す人工的に作った木（左）と、統計的な自己相似性がある実際の木（右） （日経サイエンス 2003.3）

自己相似性をもつ図形は、厳密か統計的かにかかわらず、フラクタル次元（= D）を定義することができます。No.243「視覚心理学が明かす名画の秘密」にも書いたのですが、フラクタル次元 D の計算方法は次のようです（計算方法はテイラー教授の論文には書いてありません）。

前提として、長方形ないしは正方形の２次元の２値画像としてます。つまり真っ白の画面に黒でパターンが描かれているものとします。このような２次元・２値画像のフラクタル次元は "ボックス・カウンティング法" で計測できます。

長方形ないしは正方形の２次元・２値画像を１×１の正方形領域にマッピングしたとします。正方形の縦横をそれぞれ N 分割し、N×N 個の小領域（ボックス）に分けます。そしてパターンの黒がある小領域の数をカウントして、その数を P(N) とします。するとフラクタル次元 D は、N が適度に大きいとして、次のように定義できます。

　　D = log P(N) / log N

もし、画像に直線が横１線に描かれているだけとしたら、P(N) = N なので、N の値にかかわらず D = 1 となります（＝１次元）。直線は１次元の自己相似形です。もし画像が黒で埋め尽くされているのなら、P(N) = N * N なので D = 2（＝２次元）となります。真っ黒の画像も自己相似形です。数学的には平面を埋め尽くすような曲線が定義できるのですが（＝空間充填曲線。ペアノ曲線など）、そのような曲線のフラクタル次元 D は 2（＝２次元平面と同じ）になります。

一般の画像では、Nの値を変えてP(N)を計測します。そして両対数グラフに [ N, P(N) ] の点をプロットすると、自己相似性がある場合は点が直線の近傍に並びます。その直線の傾きがフラクタル次元 D で、Nが適度に大きい範囲で「１以上、２未満」で定まります。自己相似性がないとプロットした点は直線の近傍に集まらず、一定の D が定まりません。

ちなみに N=2 だと、2×2の合計4つの小領域（ボックス）には全てパターンがあると（普通の画像では）考えられるので、

　　P(2) = 4　（N = 2 のとき）

となり、D = 2 です。N が増えるとパターンが全く無い真っ白な小領域が出てきて、D の値は小さくなっていきます。N が極めて大きいとすると、小領域は「真っ黒」か「真っ白」の２種類で大部分を占めることになります。従って、画像の黒の部分の面積割合を α （0 < α < 1）とすると、

　　P(N) = N × N × α　（Nが極めて大きいとき）

となり、logα < log N なので、定義から D は "2に近い値" になります。つまり、N が大きくなるにつれて D = 2 に近づきます。

以上のように「D は 2 に始まり（N = 2）、N の増大に従って小さくなり、再び大きくなって 2 に近づく」という過程をたどります。画像がフラクタルであるということは、この過程において D の値が一定である N の区域がある（＝それなりの大きさの N 範囲で D がほぼ一定）ということです。

フラクタル次元 D は、自己相似性をもつ図形の "複雑さ" の度合いです。D の値が小さいと繰り返し構造は目立たず、隙間の多い図形になります。D の値が 2 に近づくにつれ、自己相似の繰り返しが密になり、細部まで複雑に入り組んだ図形になります。

---

テイラー教授によるポロック作品の分析

---

ヨークシャー地方の荒野での発見のあと、テイラー教授はニューサウスウェールズ大学の研究室に戻り、ポロック作品の分析を始めました。

ポロックの作品はフラクタル次元の考え方で分析できるのだろうか。また、できるとしたらどんな方法で ？ それを明らかにしようと、私はニューサウスウェールズの研究室に戻り、カンバスに描かれたパターンをコンピューターを使って定量化することにした。コンピューターの正確さと計算能力なしでは、この種の分析は不可能だ。 そこでコンピューターの専門家に協力を求めた。半導体素子の分野で博士号を取るためにフラクタル解析を研究していたミコリッチ（Adam Micolich）と、画像処理に通じたジョーナス（Davis Jonas）の２人だ。 私たちはまずポロックの絵をスキャンしてコンピューターに取り込むことから始めた。次に、同じ大きさのマス目からなるメッシュをコンピューター上で合成し、画像にかぶせる。マス目が絵のパターンを含んでるかどうかをマス目ごとにチェックして分析すると、絵の特徴を統計的に算出できる。 マス目のサイズを小さくすれば、拡大して見るのと同様の効果が生じ、細部にわたる分析が可能だ。一滴の絵の具が残した小さな点から約1m 四方の領域まで、私たちは拡大率をさまざまに変えて調べた。 驚いたことに、ポロックの絵はフラクタルだった。しかも、大から小まであらゆる拡大率でフラクタルだ。大小のパターンでは大きさに1000倍もの開きがあるのに、すべてフラクタルだ。 自然界のフラクタル構造が発見される25年前に、ポロックはすでにそれをカンバスに描いていたのだ。 「同上」

画家になるという "いちかばちか" の挑戦のためにマンチェスター美術学校に進んだテイラー教授ですが、ニューサウスウェールズ大学の研究室に戻ったのは「自分には画家になるだけの才能がない」と自覚したからと想像します。いやそれとも、美術学校でポロック作品はフラクタルではないかと思い当たって、それがテイラー教授の学者魂に再び火を付けたのかもしれません。

ともかく、テイラー教授は 20点のポロック作品を分析しましたが、それらすべてがフラクタルでした。

	Jackson Pollock 「Autumn Rhythm」（1950） 266.7cm×525.8cm （メトロポリタン美術館）

	「Autumn Rhythm」のうち、黒色で描かれたパターンの一部を拡大した画像。フラクタル解析は、絵のパターンを色別に分けて行う。 （日経サイエンス 2003.3）

	ボックス・カウンティング法により、パターンを含むマス目（薄い青）と含まないマス目（白）コンピューターでカウントする。マス目の大きさを変えながらデータを取り、これをもとにフラクタル次元を算出する。 （日経サイエンス 2003.3）

---

"ポロックもどき" のドリップ・ペインティングでは ･･････

---

テイラー教授の論文には、ポロック作品ではないドリップ・ペインティングを分析した結果がのっています。それによると「非ポロック作品」はフラクタルではなく、一定の D の値は見い出せませんでした。ポロックの作品では、特にボックスの大きさが 1mm～10mm の範囲で D が一定になる傾向が強く、それに対して非ポロック作品ではこのような傾向がありません。

	右の列の３枚はポロックの「Number 32, 1950」を、下から上に順次拡大していったもの。拡大しても類似のパターンが現れる。左の列は非ポロック作品の例。拡大すると "まばらな" 部分が現れて全体とは違って見える。 （日経サイエンス 2003.3）

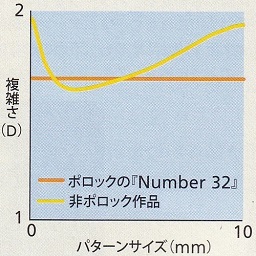
	横軸はパターンサイズ（＝ボックスの大きさ）で、縦軸が D の値。ポロック作品ではボックスの大きさが 1mm～10mm の範囲で D が一定だが、非ポロック作品には一定の値をとる傾向が見られない。なお、横軸の左端は 0 になっているが、実際のボックスの大きさはゼロより大である。 （日経サイエンス 2003.3）

この事実を利用して、ポロックのドリップ・ペインティング作品の鑑定ができると、テイラー教授は書いています。教授はある絵画コレクターが持つ5点のドリップ・ペインティングを分析しました。コレクターはこれら5点はポロック作品だと思っていましたが、分析の結果フラクタルではないことがわかり、教授は「ポロック作品ではない」と推定しました。つまりフラクタル解析はポロック作品の "真贋判定" に使えるわけです。

---

年代とともに上昇するフラクタル次元

---

テイラー教授が 20点のポロック作品を分析して発見したもう一つの事実は、フラクタル次元 D が制作年代とともに上昇することです。

面白いことに、彼がドリップペインティングで描いていた10年あまりの期間を通じて、D の値はずっと上昇を続けた。1945年の作品では 1.12 だったものが、1952年では 1.7 になっている。さらに D が 1.9 に達した特異な例もあるが、この作品はポロック自身によって後に破棄された。 「同上」

論文によると、ポロック作品に多いのは D = 1.4～1.7 程度です。一方、人間が最も心地よいと感じるパターンは D = 1.3～1.5 程度だそうです（たとえば、雲のフラクタル次元は 1.3）。D が大きくなるにつれて、パターンはより複雑になり、稠密になります。ポロックはアーティストとしての感覚から、人間にとって心地よいパターンより少し複雑・稠密なものがアートとして最良と考えたのではないかと、テイラー教授は推測しています。D が 1.9 にまでなると複雑すぎる、だからその作品を破棄したというわけです。

---

ポロックの制作方法

---

なぜポロックはフタクタルのドリップ・ペインティングを描けたのか。それは彼の制作方法によるとテイラー教授は言っています。

ポロックの絵画は考え抜かれた技法によって計画的に描かれたことがはっきりわかる。ポロックはまず、カンバスのところどころに「島」のようなパターンを描くことから始めた。自然に見られるパターンにも、最初は小さな核のようなものから始まり、それが広がって合体していく例がある。ポロックの作画法にこれに通じた面があるのは興味深い。 彼は次に、より長い軌跡を描いてこれらの「島」を結びつけ、次第に「島」を覆い隠すようにして、クモの巣状の稠密なフラクタル図形を創出した。こうして「基礎層」ができた後は、これに従って作画を続けた。「島」を結びつける過程で、絵の複雑さ（D の値）は一筆ごとに上昇した。こうして素早く集中的な仕事をした後、ポロックは一息入れるのが常だった。 再びカンバスに向かうと、黒で描いた基礎層の上にさまざまな色の絵の具を重ね、２日から６ヶ月をかけて作品を仕上げていった。基礎層によって確立した複雑さを微調整していたのだろう。さらに、作画が完了した後にカンバスの周辺部をカットした。周辺部はフラクタル特性が低下しているので、これを除いて最適化したのだ。 「同上」

	ポロックの制作風景 「One」を制作中のポロック（1950年）。椅子で見守るのは妻のリー・クラスナーで、彼女も抽象主義の画家である。 （日経サイエンス 2003.3）

ポロックは「私の関心は自然のリズムにある」と語っていたそうです。テイラー教授が英国北部ヨークシャー地方で嵐の力を借りて "制作" した"作品" が "ポロック風" だったのは、当然そうなるところだったのでしょう。

	上から順に、水に揺らぐ海藻、ポロックの「Full Fantom Five」（1947年）、テイラー教授が嵐の力を借りて偶然に創作したポロック風の作品。 （日経サイエンス 2003.3）

---

ポロック作品はデタラメでは決してなく、そこには微妙な秩序が隠されている。その秩序とは自然界にしばしば見られる "フラクタル構造" で、ポロックにしか創り出せなかった ･･････。このことを知るだけでも作品の見方が変わると思いました。

---

墨流し

---

ここからは余談です。ジャクソン・ポロックの作品の作り方で連想するのが、日本の古来の「墨流し」の技法です。水槽に水を張り、墨を垂らして慎重にかき混ぜ、流水模様を作る。その上に和紙を置いて模様を転写する技法です。これは布でもできるし、色の顔料を使ってカラー化も可能です。色を使うものは「色流し」という言い方もあるようです。掲載した画像は、京都友禅共同組合のページに掲載されている墨流し（色流し）による染色です。英語ではこの技法をマーブリングと言います。マーブル（marble）とは大理石のことで、流水模様が大理石に似ていることによります。フィレンツェの伝統工芸である「マーブル紙」は、まさにマーブリングで作られています。

京都友禅共同組合のサイトにある「色流し」の例。

この墨流し（ないしはマーブリング）はアクション・ペンティングと似ているところがあります。職人が墨を垂らして人為的に模様を作りますが、そのコントロールには限界がある。ポロックは「私の関心は自然のリズムにある」と語ったそうですが、墨流しにも "自然のリズム" が含まれています。水面を微妙にかき回すことによる表面水流や、墨・顔料の分子同士や水分子との相互作用、そういうものが加味されて流水模様か形作られていく。当然、偶然の要素が入り込みます。人と自然の共同作業と言えるでしょう。

ひょっとしたら、ポロック作品と同じように、墨流しの達人が作った模様はフラクタル構造になっているのかもしれません。模様の作成は素人にもできます（紙・生地への転写は難しそうだけれど）。しかし人が見て "心地よい" と感じる流水模様は、ポロック作品がそうであるように誰にでもできるものではなく、技法に長たけた人でないと無理ではないか ･･････。ポロック作品のフラクタル構造の記事を読んで、そんな連想をしました。

---

---

タグ：マーブリング 墨流し 色流し 京都友禅共同組合 ジャクソン・ポロック アクション・ペインティング ドリップ・ペインティング フラクタル カオス リチャード・テイラー 日経サイエンス